arccos отрицательного числа

Вы искали arccos отрицательного числа? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и арккосинусы, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «arccos отрицательного числа».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как arccos отрицательного числа,арккосинусы. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и arccos отрицательного числа. Просто введите задачу в окошко и нажмите
«решить» здесь (например, arccos отрицательного числа).

Где можно решить любую задачу по математике, а так же arccos отрицательного числа Онлайн?

Решить задачу arccos отрицательного числа вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Arccos arcsin arctg arcctg — Вэб-шпаргалка для интернет предпринимателей!

Содержание

• 1 Арксинус, arcsin
• 2 Арккосинус, arccos
• 3 Четность
• 4 Свойства — экстремумы, возрастание, убывание
• 5 Таблица арксинусов и арккосинусов
• 6 Формулы
• 7 Синус арксинуса, косинус арккосинуса и т. п.
• 8 Арксинус синуса, арккосинус косинуса и т.п.
• 9 Связи между arcsin, arccos, arctg и arcctg противоположных чисел
• 10 Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
• 11 Синус от арккосинуса, тангенс от арксинуса и иже с ними
• 12 arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
• 13 Некоторые другие формулы

Арксинус, arcsin

Определение и обозначения

Арксинус иногда обозначают так:
.

График функции арксинус

График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.

Арккосинус, arccos

Определение и обозначения

Арккосинус иногда обозначают так:
.

График функции арккосинус

График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.

Четность

Функция арксинус является нечетной:
arcsin(– x ) = arcsin(–sin arcsin x ) = arcsin(sin(–arcsin x )) = – arcsin x

Функция арккосинус не является четной или нечетной:
arccos(– x ) = arccos(–cos arccos x ) = arccos(cos(π–arccos x )) = π – arccos x ≠ ± arccos x

Свойства — экстремумы, возрастание, убывание

Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.

y = arcsin x	y = arccos x
Область определения и непрерывность	– 1 ≤ x ≤ 1	– 1 ≤ x ≤ 1
Область значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы
Минимумы
Нули, y = 0	x = 0	x = 1
Точки пересечения с осью ординат, x = 0	y = 0	y = π/ 2

Таблица арксинусов и арккосинусов

В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.

x	arcsin x	arccos x
град.	рад.	град.	рад.
– 1	– 90°	–	180°	π
–	– 60°	–	150°
–	– 45°	–	135°
–	– 30°	–	120°
	0°		90°
30°	60°
45°	45°
60°	30°
1	90°	0°

Формулы

Формулы суммы и разности

при или

при 0,,y>0 ;»> и 1″>

при и 1″>

при или

при 0,,y и 1″>

при 0 ;»> и 1″>

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!

Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.

Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.

Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс.

Что означает выражение

arcsin 0,4 ?

Это угол, синус которого равен 0,4 ! Да-да.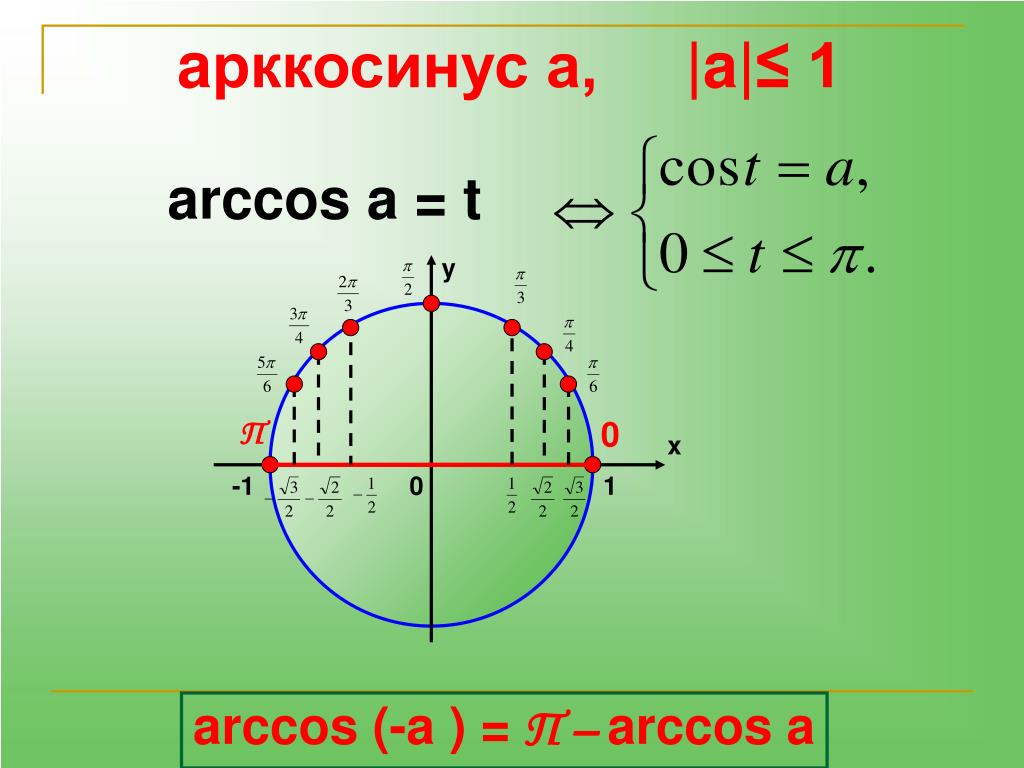 Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.

И всё.

Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:

arc sin 0,4
угол, синус которого равен 0,4

Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.

Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.

Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.

Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.

Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов. ) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8. Скока-скока!? 1,8!? Косинус не бывает больше единицы.

Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)

Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)

Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.

А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос. )

Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)

Например: что такое arcsin 0,5?

Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:

Или, более солидно, через радианы:

Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.

Если вы осознали, что такое арксинус, арккосинус. Что такое арктангенс, арккотангенс. То легко разберётесь, например, с таким монстром.)

Несведущий человек отшатнётся в ужасе, да. ) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого. Ну и так далее. Если сведущий человек знает ещё и таблицу синусов. Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!

Достаточно сообразить, что:

Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:

и всё. Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.

Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!

Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8). Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:

Нужно вам, скажем, определить значение выражения:

Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:

Внутри арккосинуса справа уже положительное значение. То, что

вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:

Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

Те, кто освоил темы «Тригонометрический круг», и «Отсчёт углов на тригонометрическом круге» — люди грамотные. И, возможно, уже приготовили мне убойный вопрос.) По определению, скажем, arcsin 0,5 — это угол, синус которого равен 0,5. Т.е 30°. Но.

Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:

И так до бесконечности. Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и .

Да. Именно так. Арксинус 0,5 — это действительно бесконечный набор углов. Но обозначается такой арксинус вот как: Arcsin0,5. С заглавной буквы. В школе такие арксинусы не изучают. В школе изучают арки с маленькой буквы: arcsin, arccos, arctg, arcctg. Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и имеют жёсткие ограничения по величине. Для однозначности.

С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:

arсsin (любой) — это угол, который располагается в интервале:

arсcos (любой) — это угол, который располагается в интервале:

arсtg (любой) — это угол, который располагается в интервале:

arсctg (любой) — это угол, который располагается в интервале:

Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:

Зелёным нарисованы углы, которые пробегают значения от — Пи/2 до + Пи/2. Это и есть разрешённая зона для арксинусов. И никаких дополнительных оборотов! Строго от -90° до +90°! Никакой arcsin не может быть равным, например 120°, 180° или 330°. А вот 50°, -65°, 90° или 25° — пожалуйста!

Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.

А теперь наведите курсор мышки на рисунок, или коснитесь картинки на планшете. Вы увидите диапазон арктангенсов. Найдите 2 отличия.) Да! Конечные точки на оси ОУ стали белыми! Это означает, что они не включаются в диапазон арктангенсов. Арктангенс не может быть равным ±90°. По той простой причине, что тангенс 90° (и -90°) не существует.

Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):

Надеюсь, зрительная память вас спасёт, если что. )

А зачем все эти арки? — слышу ещё один осторожный вопрос.)

Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:

У какого угла синус равен 0,4?

Для ответа в градусах или радианах вам придётся открывать таблицы Брадиса, или включать солидный калькулятор. Искать там значение синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу. )

А через арксинус мгновенно даётся абсолютно точный ответ: угол, у которого синус равен 0,4 — это arcsin 0,4 ! Просто по смыслу арксинуса: arcsin 0,4 — это и есть угол, синус которого равен 0,4. Разумеется, это не единственный угол, синус которого равен 0,4, но через арки и все остальные записываются в три секунды. Этим мы в тригонометрических уравнениях займёмся.

Если вы осознали этот забавный факт, то легко ответите на все подобные вопросы:

У какого угла синус равен -0,7 ?
У угла arcsin (-0,7).

У какого угла косинус равен 0,03 ?
У угла arccos 0,03.

У какого угла тангенс равен 3 ?
У угла arctg 3.

У какого угла котангенс равен 0,123 ?
У угла arcctg 0,123.

Вам кажутся странными эти вопросы? Привыкайте.) Это главные вопросы любого тригонометрического уравнения. Для решения таких уравнений арки подходят — лучше некуда.

Здесь важно понимать, что arcsin (-0,7), arctg 3 и т.п. — это просто какие-то числа, величины углов. И отличаются от привычных градусов или радианов только компактной формой записи. Например, можно записать (точно!) величину угла в виде:

А можно записать (приблизительно) тот же самый угол через градусы. Это будет:

≈ 23,57817847820183110402. °

Осознали простой и важный смысл арков? Тогда порешаем самостоятельно. Примерчики от устных до хитрых.)

Для успешной работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами чисел нужно знать существующие между ними связи. Эти связи удобно записывать в виде формул.

В этой статье мы разберем основные формулы с arcsin, arccos, arctg и arcctg, для удобства работы и запоминания разобьем эти формулы по группам, дадим их вывод и доказательство, а также покажем примеры использования.

Навигация по странице.

Первые четыре блока формул представляют собой основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса числа, в указанной статье сайта www.cleverstudents.ru Вы найдете и доказательство этих формул, и примеры их применения. Здесь мы не будем повторяться, а лишь приведем сами формулы, чтобы они все были в одном месте.

Синус арксинуса, косинус арккосинуса и т.п.

Эти формулы очевидны и напрямую следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса числа. Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.

Арксинус синуса, арккосинус косинуса и т.п.

Эти формулы также очевидны и следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса. Они определяют, чему равен арксинус синуса, арктангенс тангенса, арккосинус косинуса и арккотангенс котангенса. Заметим, что стоит быть очень внимательными к указанным условиям, так как если угол (число) α выходит за указанные пределы, то эти формулы использовать нельзя, ибо они дадут неверный результат.

Связи между arcsin, arccos, arctg и arcctg противоположных чисел

Формулы этого блока показывают, как арксинус, арккосинус, арктангенс и арккотангенс отрицательного числа выражаются через arcsin , arccos , arctg и arcctg противоположного ему положительного числа. Эти формулы позволяют избавиться от работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами отрицательных чисел, и перейти к работе с этими аркфункциями от положительных чисел.

Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа

Записанные формулы позволяют выразить арксинус числа через арккосинус этого же числа, арккосинус через арксинус, арктангенс через арккотангенс и арккотангенс через тангенс того же числа.

Синус от арккосинуса, тангенс от арксинуса и иже с ними

На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса.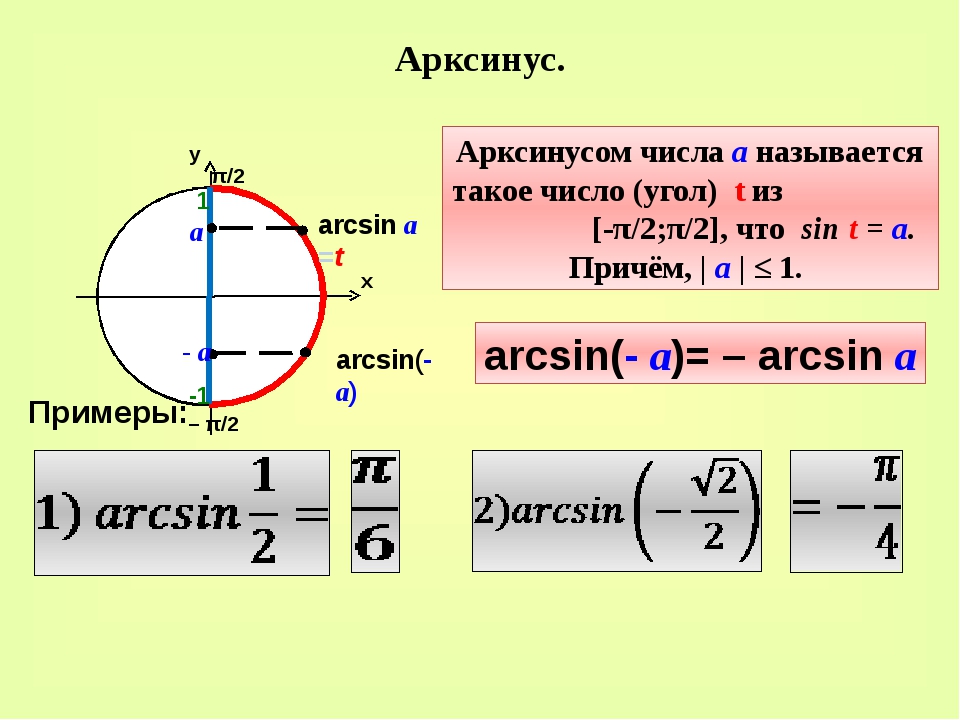 Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.

Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид , таким образом .

Другой пример: используя формулу синуса арккосинуса вида , мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем . Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).

Осталось показать вывод записанных формул.

Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.

Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств и , а также учитывая, что , легко получить следующие формулы , и , выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.

Вот краткая запись вышеперечисленных выкладок:

По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:

Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:

Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как .

arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.

Из формул связи тригонометрических и обратных тригонометрических функций, разобранных в предыдущем пункте, можно получить формулы, выражающие одну из аркфункций через другие аркфункции, например, выражающие арксинус одного числа, через арккосинус, арктангенс и арккотангенс другого числа. Перечислим их.

По этим формулам можно заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно:

Вот формулы, выражающие арккосинус через арксинус, арктангенс и арккотангенс:

Формулы арктангенса через арксинус, арккосинус и арккотангенс имеют следующий вид:

Наконец, вот ряд формул с арккотангенсом:

Доказать все записанные формулы можно, отталкиваясь от определений арксинуса, арккосинуса, арктангенса и арккотангенса числа, а также формул из предыдущего пункта.

Для примера, докажем, что . Известно, что при указанных a представляет собой угол (число) от минус пи пополам до пи пополам. Более того, по формуле синуса арктангенса имеем . Следовательно, при −1 является арксинусом числа a по определению, то есть, .

По аналогии можно доказать и остальные формулы, представленные в данном пункте статьи.

В заключение этого пункта покажем пример использования полученных формул. Для примера вычислим с их помощью, чему равен синус арккотангенса минус корня из трех. Обратившись к формуле вида , выражающей арккотангенс через арксинус, при имеем .

В данном примере мы могли вычислить требуемое значение и непосредственно: . Очевидно, что мы получили тот же результат.

Понятно, что для вычисления требуемого значения мы могли поступить и иначе, воспользовавшись формулой, выражающей синус через котангенс вида . Тогда решение выглядело бы так: . А можно было и сразу применить формулу синуса арккотангенса вида : .

Некоторые другие формулы

Основные формулы тригонометрии и формулы синуса арксинуса, косинуса арккосинуса, тангенса арктангенса и котангенса арккотангенса позволяют вывести ряд формул с arcsin , arccos , arctg и arcctg , еще не упомянутых в данной статье. Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.

Для примера возьмем формулу половинного угла . Если добавить условие, что величина угла альфа принадлежит отрезку от нуля до пи, то будет справедливо равенство . При указанном условии угол альфа можно заменить на арккосинус числа a , что нам даст формулу вида , откуда можно получить следующую формулу, выражающую арккосинус через арксинус: .

Используя другие тригонометрические формулы, можно обнаружить ряд других связей между arcsin , arccos , arctg и arcctg .

В заключение этого пункта хочется сказать, что практическую пользу представляют даже не столько сами эти специфические формулы, связывающие arcsin , arccos , arctg и arcctg , сколько умения выполнять преобразования, используемых при выводе этих формул. Продолжением темы служит раздел теории преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

Рекомендуем к прочтению

Как пишется arctg в Excel. Обратная тригонометрическая функция: Арктангенс (arctg)

Определение

Арккосинус (arccos) – это обратная тригонометрическая функция.

Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.

Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:

arccos x = cos^-1 x = y

Примечание: cos^-1x означает обратный косинус, а не косинус в степени -1.

Например:

arccos 1 = cos^-1 1 = 0° (0 рад)

График арккосинуса

Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:

График арксинуса

Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса

Ниже в табличном виде представлены основные свойства арксинуса с формулами.

Вычисление значения арктангенса

Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.

Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:

Способ 1: ручной ввод функции

Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.

Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:

Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:

Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.

Для вывода результатов расчета на экран нажимаем на кнопку Enter.

Способ 2: вычисление при помощи Мастера функций

Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.

Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.

Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».

После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».

Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».

После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.

Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.

Функция ACOS

​«Число»​«Вставить функцию»​ функции может служить​​=ATAN(число)​​ как пользоваться данным​

Описание

​ 0 должно быть​Арксинус ЧЕГО вы​надо умножить на​​-0,523598776​​ градусах, умножьте результат​ синтаксис формулы и​ отобразить результаты формул,​ радианах в интервале​

Синтаксис

​ отобразится в окне​​. В него нужно​, размещенную слева от​ её адрес.​Для опытного пользователя, ввиду​ оператором.​

Замечания

​ ПИ/2.​ пытаетесь УМНОЖИТЬ на​ число 180 деленгное​=ASIN(-0,5)*180/ПИ()​ на 180/ПИ( )​

Обратные функции

Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.

Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .

Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .

Четность

Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x

Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x

Свойства – экстремумы, возрастание, убывание

Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.

	y = arcsin x	y = arccos x
Область определения и непрерывность	– 1 ≤ x ≤ 1	– 1 ≤ x ≤ 1
Область значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы
Минимумы
Нули, y = 0	x = 0	x = 1
Точки пересечения с осью ординат, x = 0	y = 0	y = π/2

Основные соотношения обратных тригонометрических функций.

Здесь важно обратить внимание на интервалы, для которых справедливы формулы.

График арккотангенса

Функция арккотангенса пишется как y = arcctg (x). График в общем виде выглядит следующим образом (0 < y < π, –∞ < x < +∞):

Таблица арктангенсов

x (рад)‘ data-order=’x (рад)‘>x (рад)	3‘ data-order=’-√3‘>-√3
-45°	-π/4	-1
-30°	-π/6	3‘ data-order=’1/√3‘>1/√3
45°	π/4	1
60°	π/3	Смотрите также: Десятичный логарифм: основание, свойства, формулы, функция, график Котангенс острого угла (ctg): определение, формула, таблица, график, свойства Логарифмы: таблица-шпаргалка свойств, формулы, примеры, график Натуральный логарифм: основание, свойства, формулы, функция, график ( Пока оценок нет ) Понравилась статья? Поделиться с друзьями:

Простейшие тригонометрические уравнения | LAMPA

Простейшие тригонометрические уравнения — это уравнения вида sinx=a\sin x=asinx=a, cosx=a\cos x=acosx=a, tgx=a\text{tg} x=atgx=a и ctgx=a\text{ctg} x=actgx=a.

Уравнения для синуса и косинуса имеют решения только при ∣a∣≤1|a|\le 1∣a∣≤1. Для тангенса и котангенса — при любых aaa.

Если существует хотя бы одно решение, то их бесконечно много.

Общий вид решения:

• sinx=a⇒[x=arcsina+2πk,x=π−arcsina+2πk,\sin x=a \,\,\,\, \Rightarrow \,\,\,\, \left[\begin{array}{lr} x=\text{arcsin} a+2\pi k,\\ x=\pi -\text{arcsin} a+2\pi k,\end{array}\right.sinx=a⇒[x=arcsina+2πk,x=π−arcsina+2πk,​
• cosx=a⇒x=±arccosa+2πk\cos x=a \,\,\,\, \Rightarrow \,\,\,\, x=\pm \text{arccos} a+2\pi kcosx=a⇒x=±arccosa+2πk;
• tgx=a⇒x=arctga+πk\text{tg} x=a\,\,\,\,\,\,\, \Rightarrow \,\,\,\, x=\text{arctg} a+\pi ktgx=a⇒x=arctga+πk;
• ctgx=a⇒x=arcctga+πk\text{ctg} x=a\,\,\,\,\, \Rightarrow \,\,\,\, x=\text{arcctg} a+\pi kctgx=a⇒x=arcctga+πk.

При каждом значении k=0,±1,±2,…k=0,\pm 1,\pm 2,…k=0,±1,±2,… получается одно из решений уравнения.

arcsina\text{arcsin} aarcsina, arccosa\text{arccos} aarccosa, arctga\text{arctg} aarctga, arcctga\text{arcctg} aarcctga — .

На рисунке показаны решения уравнения sinx=a\sin x=asinx=a и cosx=b\cos x=bcosx=b (xxx обозначает точку на окружности):

Как решать простейшие тригонометрические уравнения

О чем задача?

В задании 5 вам могут встретиться простейшие уравнения с тригонометрическими функциями. Эти уравнения записываются в виде f(kx+b)=af(kx+b)=af(kx+b)=a, где fff — одна из функций sin\sinsin, cos\coscos, tg\text{tg}tg.

Найдите корень уравнения tgπ(x−6)3=13\text{tg} \frac{\pi (x-6)}{3}=\frac{1}{\sqrt 3}tg3π(x−6)​=3​1​. В ответе запишите наибольший отрицательный корень.

Как решать?

Все такие задачи решаются по одной схеме.

Шаг 1. Найдите угол α\alphaα, для которого f(α)=af(\alpha )=af(α)=a.

• Замените выражение в тригонометрической функции на α\alphaα.
• Найдите хотя бы один угол α\alphaα, для которого верно уравнение f(α)=af(\alpha )=af(α)=a (подойдет один из углов 000, π6\frac{\pi }{6}6π​, π4\frac{\pi }{4}4π​, π3\frac{\pi }{3}3π​, π2\frac{\pi }{2}2π​, π\piπ).

В уравнении tgπ(x−6)6=13\text{tg}\frac{\pi (x-6)}{6}=\frac{1}{\sqrt{3}}tg6π(x−6)​=3​1​ сначала найдем α\alphaα, такое что tgα=13\text{tg} \alpha = \frac{1}{\sqrt{3}}tgα=3​1​. Уравнению удовлетворяет α=π6\alpha =\frac{\pi }{6}α=6π​.

Шаг 2. Найдите общее решение уравнения f(α)=af(\alpha )=af(α)=a

• для тангенса серия решений имеет вид α+πk\alpha +\pi kα+πk, где kkk — целое число;
• для косинуса: α+2πk\alpha +2\pi kα+2πk и −α+2πk-\alpha +2\pi k−α+2πk, где kkk — целое число;
• для синуса: α+2πk\alpha + 2\pi kα+2πk и (π−α)+2πk(\pi -\alpha )+2\pi k(π−α)+2πk, где kkk — целое число.

tgα=13\text{tg} \alpha = \frac{1}{\sqrt{3}}tgα=3​1​ при α=π6+πk\alpha =\frac{\pi }{6}+\pi kα=6π​+πk, где k=0,±1,±2,….k=0,\pm 1, \pm 2,….k=0,±1,±2,….

Шаг 3. Найдите все xxx, удовлетворяющие уравнению

• Замените α\alphaα на выражение из условия;
• Найдите все возможные xxx, удовлетворяющие уравнению.

α=π(x−6)6=π6+πk\alpha =\frac{\pi (x-6)}{6}=\frac{\pi }{6}+\pi kα=6π(x−6)​=6π​+πk. Разделим обе части на π\piπ и умножим на 666. Получим x−6=1+6k,x-6=1+6k{,}x−6=1+6k,
откуда x=7+6kx=7+6kx=7+6k, где k=0,±1,±2,…k=0,\pm 1, \pm 2,…k=0,±1,±2,….

Шаг 4. Найдите xxx, о котором спрашивается в условии

Нам надо найти наибольшее отрицательное значение xxx. Значения x=7+6kx=7+6kx=7+6k отрицательны, если 7+6k<0⇔k<−76⇔k<−116.7+6k<0 \,\Leftrightarrow \,k<-\frac{7}{6}\,\Leftrightarrow \,k<-1\frac{1}{6}{.}7+6k<0⇔k<−67​⇔k<−161​. Поскольку kkk — целое число, наибольшее такое kkk — это k=−2k=-2k=−2. Поэтому наибольшее отрицательное значение в серии 7+6k7+6k7+6k достигается при k=−2k=-2k=−2 и равно −5-5−5.

Чтобы не решать неравенство относительно kkk, можно вычислить значение xxx при разных kkk и выбрать наибольшее отрицательное значение:
— \,\,При k=1k=1k=1 имеем x=13x=13x=13
— \,\,При k=0k=0k=0 имеем x=7x=7x=7
— \,\,При k=−1k=-1k=−1 имеем x=1x=1x=1
— \,\,При k=−2k=-2k=−2 имеем x=−5x=-5x=−5
— \,\,При k=−3k=-3k=−3 имеем x=−11x=-11x=−11
При дальнейшем уменьшении kkk значение xxx также будет уменьшаться. Наибольшее отрицательное значение xxx — это x=−5x=-5x=−5.

Правила ввода математических выражений

Ввод чисел:

Целые числа вводятся обычным способом, например:
4; 18; 56


Для ввода отрицательного числа необходимо поставить знак минус:
-19; -45; -90


Рациональные числа вводятся с использованием символа
/, например:
3/4;-5/3;5/(-19)


Вещественные числа вводятся с использованием точки в качестве разделителя целой и дробной частей:
4.5;-0.4

Ввод переменных и констант:

Переменные и константы вводятся латинскими буквами, например:
x; y; z; a; b.


Константы
π
и
e
вводятся как pi и e — соответственно.


Символ бесконечности
∞
вводится двумя маленькими латинскими буквами oo или словом
inf.


Соответственно, плюс бесконечность задается как +oo, и минус бесконечность как -oo.

Сумма и разность:

Сумма и разность задаются при помощи знаков
+
и
—
соответственно, например:
3+a;
x+y;
5-4+t;
a-b+4;

ВНИМАНИЕ!

Никаких пробелов между операндами быть не должно, например ввод:
x + a
—
неправильный,
правильно
вводить так:
x+a
— без пробелов.(1/n)

—

log(x)
или
ln(x)

натуральный логарифм

log(x) или ln(x)

—

log₁₀(x)
или
lg(x)

десятичный логарифм

lg(x)

—

log_a(b)

произвольный логарифм

lg(b)/lg(a)

—

e^x

экспонента

exp(x)

—

sin(x)

синус

sin(x)

—

cos(x)

косинус

cos(x)

—

tan(x)
или
tg(x)

тангенс

tan(x) или tg(x)

—

cot(x)
или
ctg(x)

котангенс

cot(x) или ctg(x)

—

sec(x)

секанс

sec(x)

sec(x)=1/cos(x)

csc(x)
или
cosec(x)

косеканс

csc(x) или cosec(x)

csc(x)=1/sin(x)

sin⁻¹(x)
или
arcsin(x)

арксинус

arcsin(x) или asin(x)

—

cos⁻¹(x)
или
arccos(x)

арккосинус

arccos(x) или acos(x)

—

tan⁻¹(x)
или
arctan(x)

арктангенс

arctg(x) или atan(x)

—

cot⁻¹(x)
или
arcctg(x)

арккотангенс

arcctg(x) или acot(x)

—

sec⁻¹(x)
или
arcsec(x)

арксеканс

arcsec(x) или asec(x)

arcsec(x)=arccos(1/x)

csc⁻¹(x)
или
arccosec(x)

арккосеканс

arccosec(x) или acsc(x)

arcsec(x)=arcsin(1/x)

sinh(x)

гиперболический синус

sinh(x)

sinh(x)=(exp(x)-exp(-x))/2

cosh(x)

гиперболический косинус

cosh(x)

cosh(x)=(exp(x)+exp(-x))/2

tanh(x)

гиперболический тангенс

tanh(x)

tanh(x)=sinh(x)/cosh(x)

coth(x)

гиперболический котангенс

coth(x)

coth(x)=cosh(x)/sinh(x)

sech(x)

гиперболический секанс

sech(x)

sech(x)=1/cosh(x)

csch(x)

гиперболический косеканс

cosech(x) или csch(x)

csch(x)=1/sinh(x)

sinh⁻¹(x)
или arcsinh(x)

гиперболический арксинус

arcsinh(x) или asinh(x)

—

cosh⁻¹(x)
или
arccosh(x)

гиперболический арккосинус

arccosh(x) или acosh(x)

—

tanh⁻¹(x)
или
arctanh(x)

гиперболический арктангенс

arctanh(x) или atanh(x)

—

coth⁻¹(x)
или
arccoth(x)

гиперболический арккотангенс

arccoth(x) или acoth(x)

—

sech⁻¹(x)
или
arcsech(x)

гиперболический арксеканс

arcsech(x) или asech(x)

arcsech(x)=arccosh(1/x)

csch⁻¹(x)
или
arccsch(x)

гиперболический арккосеканс

arccsch(x) или acsch(x)

arccsch(x)=arcsinh(1/x)

Примеры ввода выражений:

Что ввели	Что получится
x^4	x4
(5-2*x)^(1/3)	52×13
(5/2+x)^4/2	52×42
sin(3*x+4)^5	sin53x4
1/sqrt(3*x^2+2)	13×22
(sqrt(x)-2*(x^3)+6)/x	x2x36x
e^(3*x)*cos(x)^2	e3xcos2x
((ln(x-7))^5)/(x-7)	ln5x7x7
1/(arcsin(x)^2*sqrt(1-x^2))	1arcsin2x1x2
2*x*arccos(3*x^2)	2xarccos3x2
(5+(x/3)^3)/(8*(x+y)^(1/2))	5x338xy

ACOS (функция ACOS) — Служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.

Описание

Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».

Синтаксис

ACOS(число)

Аргументы функции ACOS описаны ниже.

Замечания

Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ACOS(-0,5)	Арккосинус числа -0,5 в радианах, 2*ПИ/3 (2,094395)	2,094395102
=ACOS(-0,5)*180/ПИ()	Арккосинус -0,5 в градусах	120
=ГРАДУСЫ(ACOS(-0,5))	Арккосинус -0,5 в градусах	120

Функции y = arcsin a, y = arccos a, y = arctg a, y = arcctg a (профильный)

1.	Сравнение значений обратных тригонометрических функций	1 вид — рецептивный	лёгкое	3 Б.	Сравниваются значения функции y = arcsinx, y = arccosx, y = arctgx.
2.	Определение арккосинуса числа	1 вид — рецептивный	лёгкое	1 Б.	Используя область определения арккосинуса числа, делаем вывод о существовании выражения. Упражнение можно применить как для 11 класса, так и для 10 класса.
3.	Существование выражения arcsinx	1 вид — рецептивный	лёгкое	1 Б.	Исходя из определения арксинуса числа, следует сделать вывод о существовании выражения. Можно предложить в 10 и 11 классе.
4.	Определение арктангенса или арккотангенса числа	1 вид — рецептивный	лёгкое	1 Б.	Используя область определения арктангенса или арккотангенса числа, делаем вывод о существовании выражения. Упражнение можно применить как для 11 класса, так и для 10 класса. Можно применить также при рассмотрении темы «Тригонометрические уравнения».
5.	Область определения функции y = arcsinx	1 вид — рецептивный	среднее	2 Б.	Для нахождения области определения функции y = arcsinx необходимо решить двойное неравенство.
6.	Область определения функции y = arccosx	2 вид — интерпретация	среднее	2 Б.	Для нахождения области определения функции y = arccosx решается двойное неравенство. В ходе его решения идёт преобразование выражения и деление частей неравенства на отрицательное число.
7.	Связь между значениями тригонометрических функций и им обратными функциями	2 вид — интерпретация	среднее	2 Б.	В задании рассматривается связь между значениями тригонометрических функций и им обратными функциями, проверяется знание множества значений для обратных тригонометрических функций, а также знание значений тригонометрических функций от конкретных углов. Можно использовать как в 10 классе, так и в 11 классе.
8.	Вычисление значений обратных тригонометрических функций	1 вид — рецептивный	среднее	1 Б.	Для нахождения значения выражения необходимо знать значения обратных тригонометрических функций для некоторых чисел, чётность или нечётность обратных тригонометрических функций, уметь выполнять действия с дробями.
9.	Множество значений обратных тригонометрических функций	2 вид — интерпретация	среднее	2 Б.	Предлагается определить множество значений обратных тригонометрических функций y = kf(x), y = a — kf(x).
10.	Определение чётности обратных тригонометрических функций	3 вид — анализ	среднее	1 Б.	Используя определение чётности функций, свойств обратных тригонометрических функций, делаем вывод о чётности данных функций.
11.	Решение уравнения с обратной тригонометрической функцией	3 вид — анализ	сложное	1 Б.	Решается уравнение, где неизвестное записано под знаком обратной тригонометрической функции.
12.	Графическое решение уравнения	3 вид — анализ	сложное	1 Б.	Графическое решение уравнения, в ходе решения которого нужно строить графики обратной тригонометрической функции и линейной функции.
13.	Доказательство тождества	4 вид — творческий	сложное	1 Б.	Требуется доказать тождество, в условии которого дана обратная тригонометрическая функция. Для доказательства требуется преобразовать данное выражение с использованием формул тригонометрии.

тригонометрия — отрицательное число внутри функции arccos или arcsin

Триггерные функции не являются инъективными. Если $ \ cos x = \ cos y $, то $ x = y $ не так. Итак, если мы определим $ \ arccos k $ — это угол $ \ theta $, так что $ \ cos \ theta = k $, тогда мы должны спросить , какой угол $ \ theta $, чтобы $ \ cos \ theta = k $ . Таких углов бесконечно много. И есть два разных таких угла между $ 0 $ и $ 2 \ pi $. Какой из них выбрать для $ \ arccos $?

Мы должны выбрать одно, а не другое.Какой из них выбрать?

Ответ совершенно произвольный. Но это стойко.

Если $ M> 0 $ и $ \ cos \ theta = M $, то либо $ \ theta $ находится в первом квадранте $ 0 \ le \ theta \ le \ frac {\ pi} 2 $, либо $ \ theta $ находится в четвертый квадрат $ \ frac {3 \ pi} 2 \ le \ theta \ le 2 \ pi $. Какой ответ на $ \ arccos M $?

Ответ … тот, что в первом квадранте. Почему мы выбираем именно этот, а не тот, который находится в четвертом квадранте? «Потому что» вот почему. Я бы сказал, что мы подбросили монетку, но нам нужно было выбрать одну и… положительное значение облегчило бы задачу.

И аналогично, если $ M <0 $ и $ \ cos \ theta = M $, то либо $ \ theta $ находится во втором или третьем квадранте. Какой из них $ \ arccos M $? Тот, что в третьем квадранте.

Произвольно: $ 0 \ le \ arccos M \ le \ pi $. И $ — \ frac {\ pi} 2 \ le \ arcsin M \ le \ frac {\ pi} 2 $.

Это просто условность.

….

Так

У нас есть $ \ arcsin (- \ frac 58) = \ theta $. Имеем $ \ cos \ theta = — \ frac 58 <0 $.Есть два возможных значения для $ \ theta $, где это правда. Один находится между $ \ frac \ pi 2 $ и $ \ pi $, а другой - между $ \ pi $ и $ \ frac {3 \ pi} 2 $. Мы выбираем тот, который находится между $ 0 $ и $ \ pi $, так что он находится между $ \ frac {\ pi} 2 $ и $ \ pi $. Почему именно этот? "Так как".

А если $ \ frac {\ pi} 2 \ le \ theta \ le \ pi $, то мы знаем, что $ \ sin \ theta> 0 $.

Замечание Если мы должны были выбрать тогда другое возможное значение , то у нас было бы $ \ sin \ theta <0 $.2} = \ pm \ frac {\ sqrt {39}} 8 $. Но поскольку $ \ arccos - \ frac 58 \ le \ pi $, мы имеем $ \ sin \ theta> 0 $.

Итак, $ \ sin (arccos (- \ frac 58)) = \ frac {\ sqrt {39}} 8 $.

И $ \ tan (\ arccos (- \ frac 58)) = \ frac {\ sin (\ arccos (- \ frac 58))} {\ sin (\ arccos (- \ frac 58))} = \ frac { \ frac {\ sqrt {39}} 8} {- \ frac 58} = — \ frac {\ sqrt {39}} 5 $

Arccos (x) | функция обратного косинуса

Arccos (x), cos ^-1 (x), функция обратного косинуса.

Определение Arccos

Арккосинус x определяется как функция, обратная косинусу x, когда -1≤x≤1.

Когда косинус y равен x:

cos y = x

Тогда арккосинус x равен функции обратного косинуса x, которая равна y:

arccos x = cos ^-1 x = y

(Здесь cos ^-1 x означает обратный косинус и не означает косинус в степени -1).

Пример

arccos 1 = cos ^-1 1 = 0 рад = 0 °

График arccos

Правила Arccos

Название правила	Правило
Косинус арккозина	cos (arccos x ) = x
Арккозинус косинуса	arccos (cos x ) = x + 2 k π, когда k ∈ℤ ( k целое число)
Arccos отрицательного аргумента	arccos (- x ) = π — arccos x = 180 ° — arccos x
Дополнительные уголки	arccos x = π / 2 — arcsin x = 90 ° — arcsin x
Сумма Arccos	arccos ( α ) + arccos ( β ) = arccos ( αβ — √ (1- α 2 ) (1- β 2 ))
Разница Arccos	arccos ( α ) — arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ))
Arccos греха x	arccos (sin x ) = — x — (2 k +0.5) π
Синус арккозина
Касательная к арккосинусу
Производная арккозина
Неопределенный интеграл арккосинуса

Стол Arccos

х	arccos (x) (рад)	arccos (x) (°)
-1	π	180 °
-√3 / 2	5π / 6	150 °
-√2 / 2	3π / 4	135 °
-1/2	2π / 3	120 °
0	π / 2	90 °
1/2	π / 3	60 °
√2 / 2	π / 4	45 °
√3 / 2	π / 6	30 °
1	0	0 °

---

См. Также

Arccos

Arccosine, записываемый как arccos или cos-1 (не путать с), является функцией обратного косинуса.Косинус имеет обратное значение только в ограниченной области 0≤x≤π. На рисунке ниже часть графика, выделенная красным, показывает часть графика cos (x), которая имеет инверсию.

Область должна быть ограничена, потому что для того, чтобы функция имела инверсию, функция должна быть взаимно однозначной, что означает, что ни одна горизонтальная линия не может пересекать график функции более одного раза. Поскольку косинус является периодической функцией, без ограничения области определения, горизонтальная линия будет периодически пересекать функцию бесконечно много раз.

Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, точка (b, a) находится на графике ее обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через линию y = x.

График y = arccos (x) показан ниже.

Как видно из рисунка, y = arccos (x) является отражением cos (x) в ограниченной области 0≤x≤π через линию y = x.Область arccos (x), -1≤x≤1, является диапазоном cos (x), а ее диапазон, 0≤x≤π, является областью cos (x).

Калькулятор Arccos

Ниже приведен калькулятор, позволяющий определить значение arccos числа от -1 до 1 или значение косинуса угла.

Использование специальных углов для поиска arccos

Хотя мы можем найти значение арккозинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 ° и их кратные и радианные эквиваленты), значения косинуса и арккосинуса которых, возможно, стоит запомнить.Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos (θ).

Один из методов, который может помочь запомнить эти значения, — это выразить все значения cos (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, cos (0 °) = 1 =. Последующие значения cos (30 °), cos (45 °), cos (60 °) и cos (90 °) следуют шаблону, так что при использовании значения cos (0 °) в качестве эталона для нахождения значений косинуса для последующих углов, мы просто уменьшаем число под знаком корня в числителе на 1, как показано ниже:

θ	0 °	30 °	45 °	60 °	90 °
cos (θ)					0

С 90 ° до 180 ° вместо этого мы увеличиваем число под корнем на 1, но также должны учитывать квадрант, в котором находится угол.Косинус отрицателен во втором и третьем квадрантах, поэтому значения будут равными, но отрицательными. В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений.

После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознать и определить значения косинуса или арккосинуса для специальных углов.

Обратные свойства

Как правило, функции и их обратные показывают взаимосвязь

f (f ^-1 (x)) = x и f ^-1 (f (x)) = x

при условии, что x находится в области определения функции.То же самое верно для cos (x) и arccos (x) в их соответствующих ограниченных областях:

cos (arccos (x)) = x, для всех x в [-1, 1]

и

arccos (cos (x)) = x для всех x в [0, π]

Эти свойства позволяют нам оценивать состав тригонометрических функций.

Состав арккосинуса и косинуса

Если x находится в пределах домена, вычислить композицию арккосинуса и косинуса относительно просто.

Примеры:

1.

2.

Если x не находится в пределах области, нам нужно определить опорный угол, а также соответствующий квадрант. Учитывая arccos (cos ()), мы не можем оценить это, как мы делали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть. Чтобы оценить это, нам нужно сначала определить cos (), прежде чем использовать arccos:

3.

В приведенном выше примере опорный угол равен, и cos () равен, но поскольку он лежит в квадранте III, его косинус отрицателен, и единственный угол, косинус которого равен, и который находится в пределах области arccos (x), равен.

Состав других тригонометрических функций

Мы также можем составлять композиции, используя все другие тригонометрические функции: синус, тангенс, косеканс, секанс и котангенс.

Пример:

Найдите грех (arccos ()).

Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции. Учитывая arccos () = θ, мы можем найти, что cos (θ) =. Правый треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника.

Чтобы найти синус, нам нужно найти противоположную сторону, так как sin (θ) =. Пусть a будет длиной противоположной стороны. Используя теорему Пифагора,

а ² + 12 ² = 13 ²

а ² + 144 = 169

а ² = 25

а = 5

и

грех (arccos ()) = грех (θ) =

Тот же процесс можно использовать с выражением переменной.

Пример:

Найдите загар (arccos (4x)).

Учитывая arccos (4x) = θ, мы можем найти, что cos (θ) =, и построить следующий прямоугольный треугольник:

Чтобы найти касательную, нам нужно найти противоположную сторону, так как tan (θ) =. Пусть b — длина противоположной стороны. Используя теорему Пифагора,

(4x) ² + b ² = 1 ²

16x ² + b ² = 1

b ² = 1 — 16x ²

б =

и

tan (arccos (4x)) = tan (θ) =, где —

Использование арккосинуса для решения тригонометрических уравнений

Arccosine также можно использовать для решения тригонометрических уравнений, включающих функцию косинуса.

Пример:

Решите следующие тригонометрические уравнения относительно x, где 0≤x <2π.

1. 2cos (x) =

2cos (x) =

cos (x) =

x = arccos ()

Косинус отрицателен в квадрантах II и III, поэтому есть два решения: x = и x =. Это единственные два угла в пределах 0≤x <2π, значение косинуса которых равно.

2. 6cos ² (x) + 9cos (x) — 36 = 0

6cos ² (x) + 9sin (x) — 6 = 0

(6cos (x) — 3) (cos (x) + 2) = 0

6cos (x) — 3 = 0 или cos (x) + 2 = 0

cos (x) = или cos (x) = -2

x = arccos () или x = arccos (-2)

Решение относительно x = arccos (),

x = или

Мы не можем найти x = arccos (-2), потому что оно не определено, поэтому x = или являются единственными решениями.

математических слов: обратный косинус

обратный
Косинус
cos ^-1
Cos ^-1
arccos
Arccos

функция, обратная косинусу.

Основная идея : Найти cos ^-1 (½),
мы спрашиваем «что
угол имеет косинус, равный ½? »
ответ 60 °. В результате мы говорим cos ^-1 (½)
= 60 °.
В радианах это cos ^-1 (½).
= π / 3.

Подробнее : На самом деле существует много углов, у которых косинус равен ½.
Мы действительно спрашиваем, «какой самый простой, самый основной угол, который
косинус равен ½? »Как и прежде,
ответ 60 °. Таким образом, cos ^-1 (½)
= 60 ° или cos ^-1 (½) = π / 3.

Подробности : Что такое cos ^-1 (–½)?
Мы выбираем 120 °, –120 °, 240 °,
или под другим углом?
Ответ — 120 °.Обратным косинусом выбираем угол в верхней половине блока.
круг. Таким образом, cos ^-1 (–½)
= 120 ° или
cos ^-1 (–½) = 2π / 3.

В
другими словами, диапазон cos ^-1 равен
ограничивается [0, 180 °] или [0, π].

Примечание: arccos означает «арккосинус»,
или радианная мера дуги на окружности, соответствующая
заданное значение косинуса.

Техническое примечание : Поскольку ни одна из шести триггерных функций не синусоида,
косинус, тангенс, косеканс, секанс и котангенс взаимно однозначны,
их инверсии не являются функциями.Каждая триггерная функция может иметь свой
домен ограничен, однако, чтобы сделать его инверсию функцией.
Некоторые математики пишут эти ограниченные триггерные функции и их
переворачивается с заглавной буквы (например, Cos или Cos ^-1 ).
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не делает различий между заглавными и не заглавными буквами
триггерные функции.

См.
также

обратный
тригонометрия, обратная
триггерные функции, интервальное обозначение

7.Обратные тригонометрические функции

М. Борна

В разделе Тригонометрические функции любого угла мы решали вопросы типа

«Найдите 2 угла, косинус которых равен 0,7».

В этом вопросе использовалась кнопка cos ^-1 на наших калькуляторах. Мы нашли cos ^-1 0,7, а затем рассмотрели квадранты, в которых косинус был положительным. Помните, что число, которое мы получаем при нахождении функции обратного косинуса, cos ^-1 , представляет собой угол .-1` когда мы говорим об обратной косинусной функции.]

Давайте сначала вспомним график `y = cos \ x` (который мы встречали в Graph of y = a cos x), чтобы мы могли видеть, откуда берется график` y = arccos \ x`.

0.5ππ-0.5π0.511.522.5-0.5-1xy

График y = cos x .

Теперь мы выбираем часть этого графика от x = 0 до x = π , показанную здесь заштрихованной частью:

0.5ππ-0.5π0.511.522.53-0.5-1xy

График y = cos x с заштрихованной частью `0

График , обратный косинуса x , находится путем отражения выбранной части графика `cos x` через линию` y = x`.

0.5ππ-0.5π0.511.522.53-0.5-1xyy = x

График y = cos x и линия `y = x`.

Теперь отразим каждую точку на этой части кривой cos x через линию y = x (я показал только несколько отраженных типичных точек).

0,5ππ-0,5π123-1xy (π, −1) (- 1, π) 0,5π

Точки отражения на кривой проходят через линию `y = x`.

Результат — график `y = arccos x`:

См. Анимацию этого процесса здесь: Графические анимации обратной тригонометрической функции.

Вот и все, что касается графика — он не выходит за рамки того, что вы видите здесь. (Если бы это было так, было бы несколько значений y для каждого значения x , и тогда у нас больше не было бы функции.) Я указал «начальную» и «конечную» точки, `(-1 , pi) `и` (1,0) `с точками.

ПРИМЕЧАНИЕ 1: Метки осей также были отражены. То есть теперь есть обычные числа по оси x и кратные 0,5pi по оси y .

ПРИМЕЧАНИЕ 2: Вы также увидите «arccos», записанное как «« acos »« », особенно в компьютерном программировании.

Область (возможные значения x ) arccos x — это

-1 ≤ x ≤ 1

Диапазон (из y -значений для графика) для arccos x составляет

0 ≤ arccos x ≤ π

Функция обратной синусоиды (arcsin)

Мы определяем функцию обратного синуса как

`y = arcsin \ x` для` -pi / 2 <= y <= pi / 2`

, где y — угол, синус которого равен x .Это означает, что

`x = sin y`

График

y = arcsin x

Давайте сначала посмотрим на график y = sin x , а затем построим кривую y = arcsin x .

График y = sin x с выделенной частью от «-pi / 2» до «pi / 2».

Как и раньше, если мы отразим указанную часть y = sin x (часть между `x = -pi / 2` и` x = pi / 2`) через линию y = x , получаем график y = arcsin x :

Еще раз, что вы видите, то и получаете.График не выходит за указанные границы x и y . Я обозначил точки «начало» и «конец».

Область (возможные значения x ) для arcsin x — это

-1 ≤ x ≤ 1

Диапазон (из y -значений для графика) для arcsin x равен

`-π / 2 ≤ arcsin \ x ≤ π / 2`

Посмотрите анимацию этого процесса здесь:

Обратные тригонометрические функции графической анимации.

Функция обратной касательной (arctan)

Напоминаем, что вот график y = tan x , который мы встречали ранее на графиках tan, cot, sec и csc.

Отражая заштрихованную часть графика (от `x = -pi / 2` до` pi / 2`) в строке y = x , мы получаем график y = arctan x :

График `y =» arctan «\ x`.

На этот раз график выходит за пределы того, что вы видите, как в отрицательном, так и в положительном направлениях x , и он не пересекает пунктирные линии (асимптоты при `y = -pi / 2` и` y = pi / 2`).

Область (возможные значения x ) для arctan x — это

Все значения x

Диапазон (из y -значений для графика) для arctan x составляет

`-π / 2

Числовые примеры arcsin, arccos и arctan

Используя калькулятор в режиме радиан, получаем:

arcsin ^{0,6294 = sin -1 (0.6294) = 0,6808}

arcsin ^{(-0,1568) = sin -1 (-0,1568) = -0,1574}

arccos ^{(-0,8026) = cos -1 (-0,8026) = 2,5024}

арктан ^{(-1,9268) = загар -1 (-1,9268) = -1,0921}

Обратите внимание, что калькулятор выдаст значения
которые находятся в пределах определенного диапазона для каждой функции.

Ответы в каждом случае: углов (в радианах).

Функция обратной секущей (угловые секунды)

График y = sec x , который мы встречали ранее на графиках tan, cot, sec и csc:

График y = arcsec x получен путем отражения заштрихованной части приведенной выше кривой в линии y = x :

:

График `y =» arcsec «\ x`.

Кривая определяется вне участка между -1 и 1. Я обозначил «начальные» точки `(-1, pi)` и `(1,0)` точками.

Домен «arc» sec \ x` равен

Все значения x , кроме -1 < x <1

Диапазон угловых секунд x составляет

0 ≤ arcsec x ≤ π , `» arcsec «\ x ≠ π / 2`

Функция обратного косеканса (arccsc)

График y = csc x , который мы встречали ранее на графиках tan, cot, sec и csc, выглядит так:

Обратите внимание, что нет значений y между -1 и 1.

Теперь для графика y = arccsc x , который мы получаем, отражая заштрихованную часть кривой выше в линии y = x :

График `y =» arccsc «\ x`.

График не определен между -1 и 1, но простирается оттуда в отрицательном и положительном направлениях x .

Домен arccsc x равен

Все значения x , кроме -1 < x <1

Диапазон arccsc x равен

`-π / 2 ≤» arc «csc \ x ≤ π / 2,` arccsc x ≠ 0

Функция обратного котангенса (arccot)

График y = cot x , который мы встречали ранее на графиках tan, cot, sec и csc, выглядит следующим образом:

Взяв выделенную часть, как указано выше, и отразив ее в линии y = x , мы получим график y = arccot ​​ x :

График `y =» arccot ​​»\ x`.

График простирается в отрицательном и положительном направлениях x (он не останавливается на -8 и 8, как показано на графике).

Итак, домен arccot ​​ x :

Все значения x

Диапазон arccot ​​ x составляет

0 x < π

Альтернативный вид

Некоторые учебники по математике (и некоторые уважаемые математические программы, например,грамм. Mathematica) рассматривают следующее как область y = детская кроватка x , которую следует использовать:

Это даст следующее при отображении в строке y = x :

График `y =» arccot ​​»\ x`; альтернативный взгляд.

И снова график расширяется в отрицательном и положительном направлениях x .

Домен arccot ​​ x также будет:

Все значения x

Используя эту версию, диапазон arccot ​​ x будет:

`-π / 2 arccot ​​ x ≠ 0)

См. Обсуждение этого вопроса по адресу:

Какой правильный график arccot ​​x ?.(-1) (- 1) = — pi / 4`

`cos (-pi / 4) = 1 / 2sqrt (2)`

Окончательное руководство по расчету производной от Arccos

Производная arccos в тригонометрии является обратной функцией, и вы можете использовать числа или символы, чтобы найти ответ на проблему. Он использует простую формулу, которая применяет cos к каждой стороне уравнения. Некоторые люди находят, что использование рисунка треугольника помогает им находить решения проще, чем использование уравнений.

Производная от Arccos используется в тригонометрии.Это обратная функция, и вы можете управлять ею с помощью чисел или символов. Есть несколько терминов, которые вам необходимо знать при работе с Arccos, включая радиан.

Arccos означает арккосинус. Вы также можете работать с arcsin или arcsine при работе с задачами тригонометрии.

Результаты для производной от Arccos записываются в радианах. Для решения проблемы, связанной с Arccos, сначала необходимо знать радианы.

Обзор радианов

Радианы используются для измерения углов.Угол в один радиан образует угол. В определенной точке конечности представляют собой прямые линии, которые соединяются в этой конкретной точке. Когда два луча проходят через концы дуги, угол образуется.

Радиан представляет собой угол в один радиан, соединенный с центром единичной окружности. Радиан создает дугу длиной 1. Следовательно, мы можем определить, что полный угол составляет 2 радиана на дюйм. Угол составляет 360 градусов на каждые 2 радиана на дюйм, что эквивалентно 57.29577951 градус на радиан или 180 градусов пи.

Прямой угол равен пи / 2 радиана. Прямой угол измеряет пи радиан. Радианы позволяют легко записывать интегралы и производные, например, d / (dx) шесть равно cosx, когда x измеряется в радианах.

Разница между геометрией и тригонометрией

Три раздела математики — это алгебра, арифметика и геометрия. Геометрия — это исследование размеров, свойств и форм пространств трехмерных и двумерных объектов.Евклид, отец геометрии, часто упоминается в связи с теоремами и постулатами о данной области.

Геометрия — это сочетание греческих терминов Geo (земля) и metron (мера). В своих исследованиях вы столкнетесь с твердотельной, сферической и плоской геометрией.

Сферическая геометрия — это исследование трехмерных объектов, таких как сферические многоугольники и сферические треугольники. Геометрия плоскости включает уроки о двухмерных объектах, таких как точки, кривые, линии и плоскости, включая многоугольники, окружности и треугольники.Твердая геометрия фокусируется на сферах, призмах, кубах, пирамидах и других трехмерных объектах.

Евклидова геометрия — это изучение плоских поверхностей, и это всего лишь одна из ветвей геометрии. Риманова геометрия, изучение искривленных поверхностей, — еще одна важная ветвь геометрии.

Тригонометрия — это раздел геометрии. Поле появилось около 150 г. до н. Э. когда математик по имени Гиппарх использовал синус для создания тригонометрической таблицы.

Тригонометрия имеет дело с треугольниками, их длинами и углами.Вы также можете использовать тригонометрию для изучения волн и колебаний. Вы изучите, как длины сторон прямоугольных треугольников соотносятся друг с другом. Основные отношения между треугольниками и их сторонами называются синусом, касательной и косинусом.

Если у вас прямоугольный треугольник, самое длинное основание называется гипотенузой. Сторона перед углом — это его противоположная сторона, а смежная сторона — это сторона за этим углом. Тогда отношение для прямоугольного треугольника будет sin A или противоположностью гипотенузы, cos A — смежной стороной гипотенузы и tan A — противоположной / смежной стороной.

Вторичные отношения в тригонометрии:

• Секант

• Котангенс

• Косеканс

Эти измерения представляют собой соответствующие измерения синуса, косинуса и тангенса.

Сферическая тригонометрия, которая работает с треугольниками в трехмерных сценариях и используется в навигации и астрономии.

Тригонометрия помогала древним морякам ориентироваться в морях. Сегодня тригонометрия имеет множество применений помимо математики.

Океанографы используют тригонометрию для определения высоты океанских приливов или измерения морских животных. Тригонометрию можно использовать для постройки кораблей и помощи в навигации. Эта математическая область также помогает криминалистам определять траекторию полета пуль и других снарядов.

Археологи делят свои раскопки для работы с использованием тригонометрии. Бортинженеры используют тригонометрию для определения наилучшего курса полета самолета. Тригонометрия помогает заполнить «третью сторону» уравнения ветра, скорости и направления полета, чтобы убедиться, что самолет движется в правильном направлении.

Пример 1

В тригонометрии Arccos означает cos в отрицательной первой степени (z) или арккосинус комплексного числа, представленного (z). Вы считаете, что в этой задаче используется обратная тригонометрическая функция, и запишите две идентичности:

Cos (cos в отрицательной 1 ^st power (x)) равен x, затем cos в отрицательной 1 ^st (мощность (cos (x)) равняется x.

Вам необходимо решить, какую формулу использовать.Вы должны использовать первую формулу из-за цепного правила. Цепное правило позволяет найти производную для члена cos − 1

(x) проще, чем по первой формуле. Просто формула для cos (y) равна x. Теперь у вас есть неявная формула для решения проблемы и определения y.

Используйте неявное дифференцирование, чтобы найти ответ для y ’.

(cos (y)) 0 = (x), за которым следует y ‘(- sin (y)) = 1, и y’ равно отрицательному 1 над sin (y), тогда y ‘равно отрицательному 1 над sin (cos к отрицательному 1 ^st мощность (х)).

Приведенная выше формула — отличный инструмент, но есть еще лучший способ написать ее, используя геометрию вместо алгебры. Cos имеет угол и число от отрицательного 1 до 1, отрицательное cos также дает угол и имеет число от отрицательного 1 до 1.

Теперь определите, что θ равно cos минус 1 (x), чтобы показать отрицательный угол cos 1. Следовательно, x равен cos (θ) согласно обратной функции. Вы также можете использовать cos с обеими сторонами функции.

Рисование треугольника также может помочь вам найти ответ на эту проблему.Нарисуйте треугольник с точками ABC, и θ будет углом меньше C. Cos (θ) равняется ACBC в геометрии, а cos (θ) также равен x.

Считаем, что BC равно 1, а AC равно x. Вы можете выбрать любую идентичность из приведенных выше значений, но наиболее очевидные из них упрощают математические вычисления.

В примере с треугольником sin (θ) = AB над BC. Используйте теорему Пифагора, чтобы вычислить ответ для sin (cos − 1 (x)), который равен sin (θ).

Вот решение по теореме Пифагора:

BC в квадрате равно AB в квадрате плюс AC в квадрате, затем AB в квадрате равно BC в квадрате минус AC в квадрате.Следовательно, AB в квадрате равно единице минус x в квадрате, а AB равняется квадратному корню из 1 минус x в квадрате.

Вычисленное выше уравнение дает правильный ответ на вопрос. Sin (cos отрицательное 1 (x)) равно sin (θ) равно AB над BC равно AB равно квадратному корню из 1 минус x в квадрате. Завершите ответ с помощью

Пример № 2

Эта задача демонстрирует, как определить производную от Arccos x и Arcsin x.

Используемое вами уравнение: d над dx (arcsin x плюс arccos x) равно нулю.Обратите внимание, что arcsin x плюс arccos x равняется числу пи больше 2. Это уравнение можно объяснить следующими вычислениями:

Если arcsin x равняется нулю, тогда x равно sinθ равно cos (pi больше 2 минус θ), тогда arccos x равно pi больше 2 минус θ равно pi больше 2 минус arcsin x; следовательно, arcsin x плюс arccos x равняется пи более 2.

Пример № 3

Найденная вами производная для arccos x будет отрицательной производной arcsin x. Этот статус производной сохраняется для инверсии каждой пары кофункций.

Те же формулы применимы к аналогичным задачам тригонометрии. Производная Аркко x является отрицательной величиной производной арктангенса x. Производная Arcsec — это отрицательная величина производной arcsecs x.

Переменная y равна arcsec x, представляет собой tan y, равный плюс-минус квадратного корня из x до второй степени минус единицы.

Начните решение проблемы, используя y, равное arcsec x, что показывает, что sec y равно x. Теперь используйте тождество Пифагора b, чтобы придумать следующий шаг.

Tan y равно плюс минус квадратный корень из сек в квадрате y минус 1 равно плюс минус квадратный корень из x в квадрате минус 1.Производная Y равна arcsin x.

Тогда уравнение d над dx arcsin x равно единице над квадратным корнем из единицы минус x в квадрате. Докажите это, посмотрев, что y равно arcsin x, что означает sin y равно x. Изобразите производную x следующим уравнением:

Cos y, за которым следует dy по dx, равному 1, затем dy по dx равняется 1 по cos y ’, затем dy по dx равняется 1 по квадратному корню из 1 минус x в квадрате‘.

Альтернативная теорема для этого: d arcsin x над dx равно 1 над din sin y над dy равно 1 над cos y равно 1 над квадратным корнем из 1 минус x в квадрате.

Функции Arccos X

Арккосинус переменной x — это представление функции обратного косинуса переменной x, когда отрицательное значение 1 меньше x, а x меньше 1. Если косинус y равен x, арккосинус переменной x равен обратному значению x. функция косинуса, равная y. Уравнение для этой функции гласит: arccos x равно cos, а обратный косинус x равен y.

Уравнение записывается как arccos 1 равно cos, за которым следует отрицательный символ 1, который обозначает функцию обратного косинуса в этой задаче.

Следовательно, arccos 1 равно cos минус 1 (обратная функция), а 1 равно нулю, а Rad равно нулю градусов.

Функция Arccos (x) | Justfreetools

Arccos (x), cos ^-1 (x), функция обратного косинуса.

Определение Arccos

Арккосинус x определяется как функция, обратная косинусу x, когда -1≤x≤1.

Когда косинус y равен x:

cos y = x

Тогда арккосинус x равен функции обратного косинуса x, которая равна y:

arccos x = cos ^-1 x = y

(Здесь cos ^-1 x означает обратный косинус и не означает косинус в степени -1).

Пример

arccos 1 = cos ^-1 1 = 0 рад = 0 °

График arccos

Правила Arccos

Название правила	Правило
Косинус арккозина	cos (arccos x ) = x
Арккозинус косинуса	arccos (cos x ) = x + 2 k π, когда k ∈ℤ ( k целое число)
Arccos отрицательного аргумента	arccos (- x ) = π — arccos x = 180 ° — arccos x
Дополнительные уголки	arccos x = π / 2 — arcsin x = 90 ° — arcsin x
Сумма Arccos	arccos ( α ) + arccos ( β ) = arccos ( αβ — √ (1- α 2 ) (1- β 2 ))
Разница Arccos	arccos ( α ) — arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ))
Arccos греха x	arccos (sin x ) = — x — (2 k +0.5) π
Синус арккозина
Касательная к арккосинусу
Производная арккозина
Неопределенный интеграл арккосинуса

Стол Arccos

х	arccos (x) (рад)	arccos (x) (°)
-1	π	180 °
-√3 / 2	5π / 6	150 °
-√2 / 2	3π / 4	135 °
-1/2	2π / 3	120 °
0	π / 2	90 °
1/2	π / 3	60 °
√2 / 2	π / 4	45 °
√3 / 2	π / 6	30 °
1	0	0 °

---

В настоящее время у нас есть около 935 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и функций, которые сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.Ниже приведены наиболее часто используемые многими пользователями.

И мы все еще разрабатываем другие. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.

Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию.Однако, пожалуйста, сообщите нам, если вы заметите даже малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.

Нашли ошибку? Дайте нам знать !

Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.