Arcsin sin 2: Mathway | Популярные задачи

alexxlab

Содержание

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень 3)
24Найти точное значениеcsc(60 град. )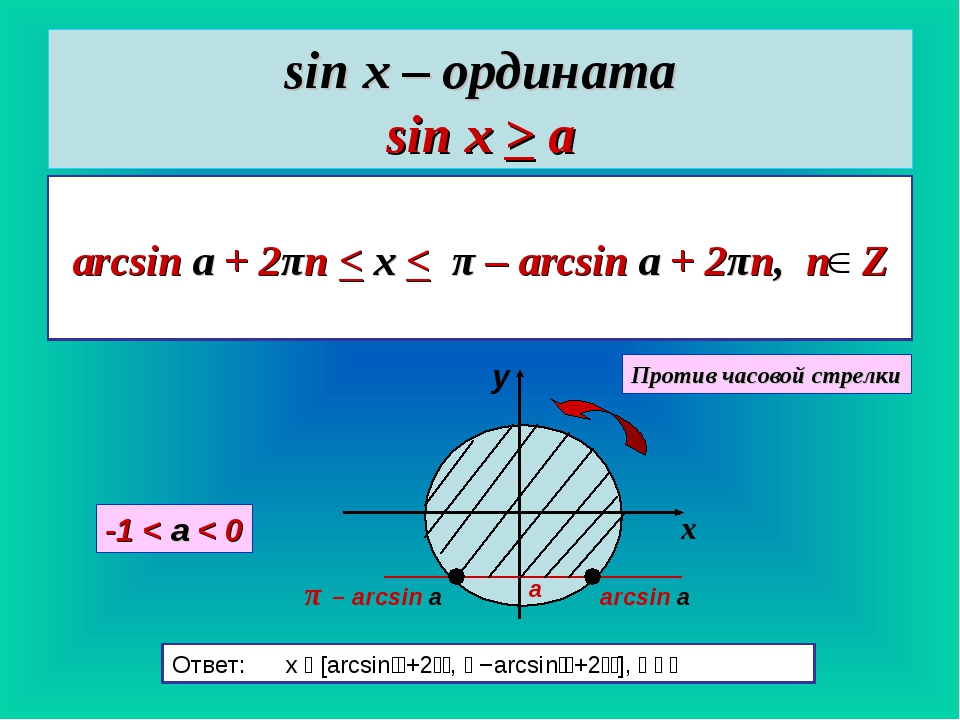
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )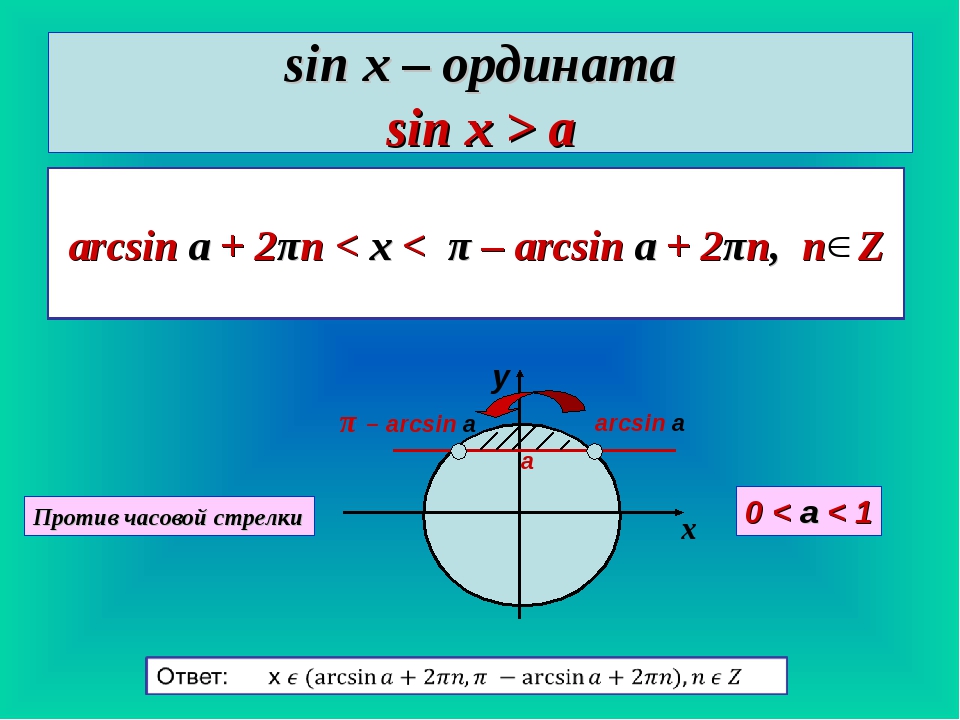
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )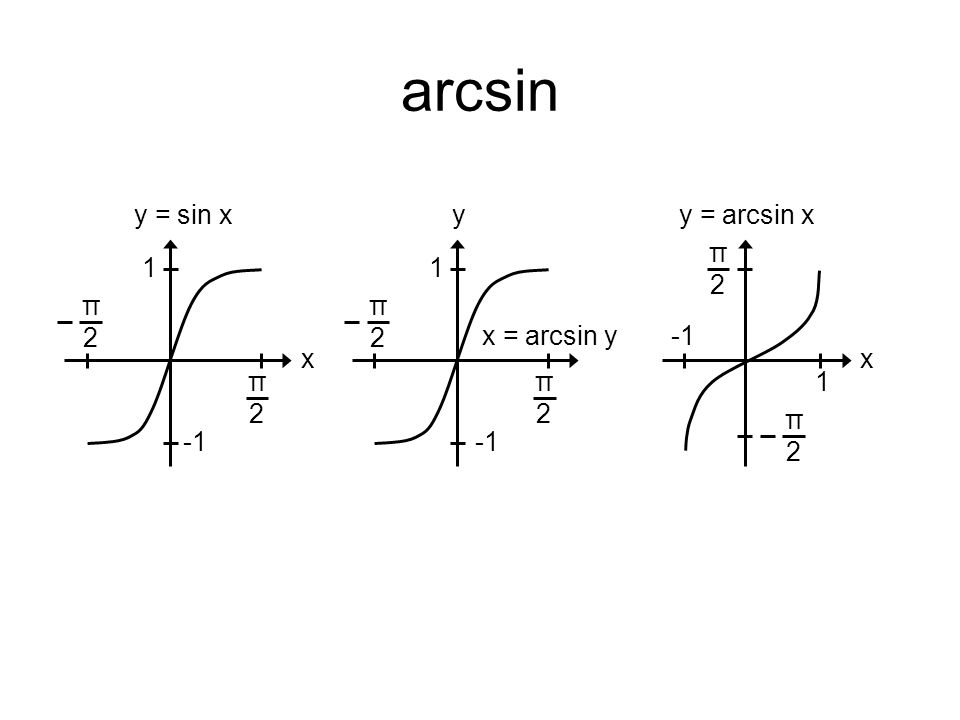
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень 2)/2)
100Преобразовать из градусов в радианы88 град.

определение, формула, таблица, график, свойства

Определение

Арксинус (arcsin) – это обратная тригонометрическая функция.

Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.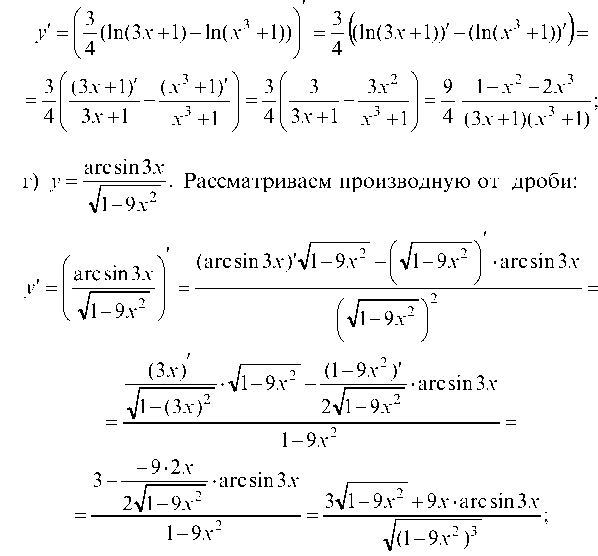

Если синус угла у равен х (sin y = x), значит арксинус x равняется y:

arcsin x = sin-1 x = y

Примечание: sin-1x означает обратный синус, а не синус в степени -1.

Например:

arcsin 1 = sin-1 1 = 90° (π/2 рад)

График арксинуса

Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса

Ниже в табличном виде представлены основные свойства арксинуса с формулами.

Таблица арксинусов

xarcsin x (рад)arcsin x (°)
-1-π/2-90°
-√3/2-π/3-60°
-√2/2-π/4-45°
-1/2-π/6-30°
000°
1/2π/630°
√2/2π/445°
√3/2π/360°
1π/290°

microexcel. ru

Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом

Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg

Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.

Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.

Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса

Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.

для α∈-1, 1  sin(arccis α)=α,   cos(arccos α)=α,для α∈(-∞, ∞)  tg(arctg α)=α, ctg(arcctg α)=α

Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.

Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса

для -π2≤α≤π2  arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α

Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.

Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел

В этом блоке мы сформулируем важное утверждение:

Определение 1

Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.

для α∈-1, 1  arccis (-α)=-arcsin α,   arccos (-α)=π-arccos α,для α∈(-∞, ∞)  arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α

Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.

Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс

Они выглядят следующим образом:

для α∈-1, 1  arccis α+arccos α=π2,для α∈(-∞, ∞)  arctg α+arcctg α=π2

Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.

Формулы связи между прямыми и обратными тригонометрическими функциями

Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.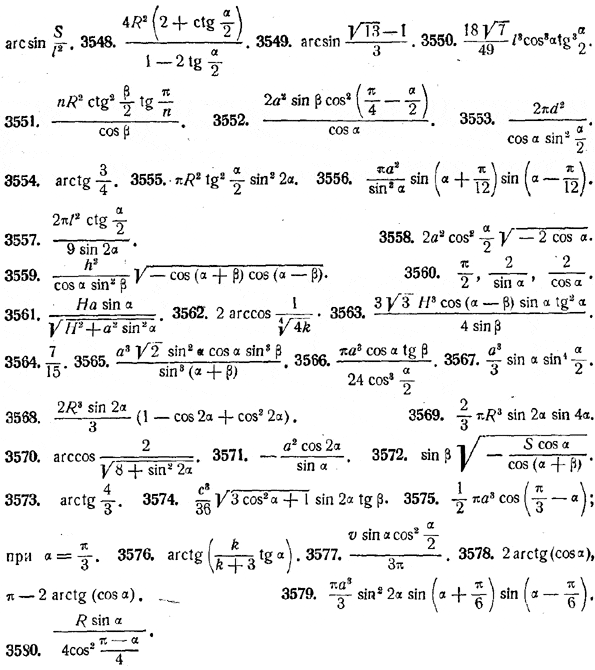

-1≤α≤1,sin (arcsin α)=α-1≤α≤1,sin (arccos α)=1-α2-∞≤α≤+∞,sin (arctg α)=α1+α2-∞≤α≤+∞, sin (arcctg α)=11+α2
-1≤α≤1,cos (arcsin α)=1-α2-1≤α≤1,cos (arccos α)=α-∞≤α≤+∞,cos (arctg α)=11+α2-∞≤α≤+∞, cos (arcctg α)=11+α2
-1<α<1,tg (arcsin α) =α1-α2α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α-∞≤α≤+∞,tg (arctg α)=αα≠0 ,tg (arcctg α)=1α
α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α-1<α<1,ctg (arccos α)=α1-α2α≠0,ctg (arctg α)=1α-∞≤α≤+∞, ctg (arcctg α)=α

Теперь разберем примеры, как они применяются в задачах.

Пример 1

Вычислите косинус арктангенса из 5.

Решение

У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2

Подставляем нужное значение: cos(arctg5)=11+(5)2=26

Пример 2

Вычислить синус арккосинуса 12.

Решение

Для этого нам понадобится формула: sin (arccos α)=1-a2

Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32

Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32

Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.

Доказательства формул синусов арккосинуса, арккотангенса и арктангенса

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:

sin2α+cos2α=11+ctg2α=1sin2α

Вспомним, что tgα·ctgα=1. Из этого можно получить:

sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π

У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.

Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.

Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.

Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.

Все наши расчеты можно сформулировать более емко:

  1. sinα=1-cos2α, 0≤α≤π

Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2

  1. sinα=tgα1+tgα, -π2<α<π2,

Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2

  1. sinα=11+ctg2α, 0<α<π

Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2

Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.

Их мы выведем по имеющемуся шаблону:

  1. Из cosα=1-sin2α, -π2≤α≤π2 следует, что

cos(arcsin α)=1-sin2(arcsin α)=1-a2

  1. Из cosα=11+tg2α, -π2<α<π2 следует, что
  2. Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2

следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2

Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса

  1. Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
  2. Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем

tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).

  1. Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.

Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:

ctgα=1tgα

Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.

Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее

Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.

Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:

arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0

А так мы выразим арккосинус через остальные обратные функции:

arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1

Формула выражения арктангенса:

arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0

Последняя часть – выражение арккотангенса через другие обратные функции:

arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0

Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.

Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.

Мы знаем, что arctgα1-α2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:

sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α

Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.

Вывод: arcsina=arctga1-a2, -1<a<1

Прочие формулы доказываются по аналогии.

В завершение разберем один пример применения формул на практике.

Пример 3

Условие Вычислить синус арккотангенса минус корня из 3.

Решение

Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0

Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π

В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12

Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2  sin(arcctg(-3))=11+(-3)2=12

Прочие формулы с обратными функциями

Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.

Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:

sin2α2=1-cosα2

Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:

sinα2=1-cosα2

Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:

sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2

Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:

arccosα2=arcsin1-α2

Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.

В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

Арксинус. Решение простейших уравнений с синусом. Часть 2

Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac{π}{2};\frac{π}{2}]\) синус которого равен \(a\) т.е.


\(\arcsin ⁡a=x\)     \(<=>\)     \(\sin ⁡x=a\)


Примеры:


\(\arcsin⁡{\frac{\sqrt{2}}{2}}=\frac{π}{4}\) потому что \(\sin ⁡\frac{π}{4}=\frac{\sqrt{2}}{2}\) и \(\frac{π}{4}∈[-\frac{π}{2}; \frac{π}{2}]\)

\(\arcsin ⁡1=\frac{π}{2}\) потому что \(\sin⁡\frac{π}{2}=1\) и \(\frac{π}{2}∈[-\frac{π}{2};\frac{π}{2}]\)

\(\arcsin ⁡0=0\) потому что \(\sin ⁡0=0\) и \(0∈[-\frac{π}{2};\frac{π}{2}] \)

\(\arcsin⁡\sqrt{3}\) – не определен, потому что \(\sqrt{3}>1\)


Проще говоря, арксинус обратен синусу.


На круге это выглядит так:


     

Как вычислить арксинус?

Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac{π}{2}\) до \(\frac{π}{2}\) ) равен аргументу арксинуса?


Например, вычислите значение арксинуса:


а) \(\arcsin⁡(-\frac{1}{2})\)

б) \(\arcsin⁡(\frac{\sqrt{3}}{2})\)

в) \(\arcsin(-1)\)


а) Синус какого числа равен \(-\frac{1}{2}\)? Или в более точной формулировке можно спросить так: если \(\sin ⁡x=-\frac{1}{2}\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac{π}{2}\) и \(\frac{π}{2}\). Ответ очевиден:


\(\arcsin⁡(-\frac{1}{2})=-\frac{π}{6}\)


б) Синус какого числа равен \(\frac{\sqrt{3}}{2}\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac{π}{3}\).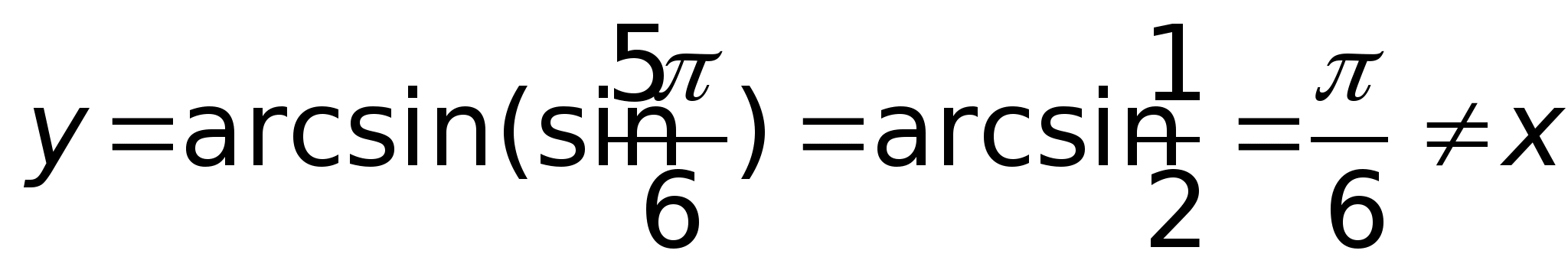


\(\arcsin⁡(-\frac{\sqrt{3}}{2})=-\frac{π}{3}\)


в) Синус от чего равен \(-1\)?

Иначе говоря, \(\sin ⁡x=-1\), \(x=\) ?


\(\arcsin⁡(-1)=-\frac{π}{2}\)


Тригонометрический круг со всеми стандартными арксинусами:


Зачем нужен арксинус? Решение уравнения \(\sin x=a\)


Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin ⁡x=\frac{1}{2}\).


Это не вызывает затруднений:


\( \left[ \begin{gathered}x=\frac{π}{6}+2πn, n∈Z\\ x=\frac{5π}{6}+2πl, l∈Z\end{gathered}\right.\)


Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.


А теперь решите уравнение: \(\sin ⁡x=\frac{1}{3}\).


Что тут будет ответом? Не \(\frac{π}{6}\), не \(\frac{π}{4}\), даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?


Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin⁡\frac{1}{3}\), потому что известно, что синус равен \(\frac{1}{3}\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin⁡\frac{1}{3}\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin⁡\frac{1}{3}\) от \(π\), то её значение составляет \(π- \arcsin⁡\frac{1}{3}\).


Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{3}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{3}+2πl, l∈Z\end{gathered}\right.\) Без арксинусов решить уравнение \(\sin ⁡x=\frac{1}{3}\) не получилось бы. Как и уравнение \(\sin ⁡x=0,125\), \(\sin ⁡x=-\frac{1}{9}\), \(\sin⁡ x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:



С арксинусом – бесконечное количество.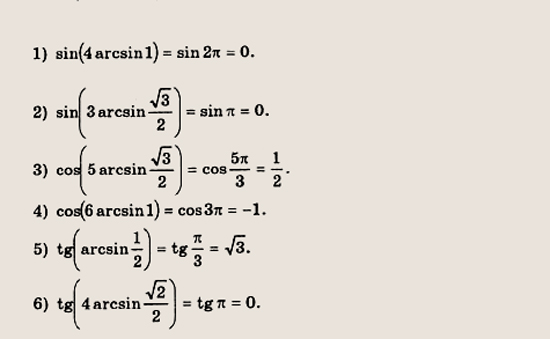


Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac{1}{\sqrt{3}}\).
Решение:



Ответ:   \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)


Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac{1}{\sqrt{2}}\).


Решение:

Кто поторопился написать ответ \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{2}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{2}}+2πl, l∈Z\end{gathered}\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin⁡ \frac{1}{\sqrt{2}}\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:


\(\arcsin⁡ \frac{1}{\sqrt{2}} = \arcsin \frac{\sqrt{2}}{2}=\frac{π}{4}\)


Значит в ответе вместо арксинусов нужно написать \(\frac{π}{4}\).


Ответ:   \( \left[ \begin{gathered}x=\frac{π}{4}+2πn, n∈Z\\ x=\frac{3π}{4}+2πl, l∈Z\end{gathered}\right.\)


Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac{7}{6}\).


Решение:

И вновь тот, кто поторопился написать \( \left[ \begin{gathered}x= \arcsin \frac{7}{6}+2πn, n∈Z\\ x=π- \arcsin\frac{7}{6}+2πl, l∈Z\end{gathered}\right.\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin⁡\frac{7}{6}\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.



Ответ:   решений нет.


Думаю, вы уловили закономерность.

Если \(\sin ⁡x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \begin{gathered}x= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end{gathered}\right.\)

Арксинус отрицательного числа


Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:



\(\arcsin⁡({-a})=-\arcsin ⁡a\)


Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:


Примеры:


\(\arcsin⁡(-0,7)=-\arcsin⁡ 0,7\)

\(\arcsin⁡(-\frac{\sqrt{3}}{2})=-\arcsin⁡\frac{\sqrt{3}}{2}=-\frac{π}{6}\)

\(\arcsin⁡(-\frac{\sqrt{7}}{2}) \neq -\arcsin⁡\frac{\sqrt{7}}{2}\)


Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin⁡(-\frac{\sqrt{7}}{2})\) в принципе неверна, ведь \(-\frac{\sqrt{7}}{2}<-1\), а значит арксинус от \(-\frac{\sqrt{7}}{2}\) взять нельзя – он не вычислим, не существует, точно также как \(\sqrt{-5}\) или \(\frac{3}{0}\).


Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=-\frac{1}{\sqrt{3}}\).


Решение:

Можно воспользоваться готовой формулой и написать:


\( \left[ \begin{gathered}x=\arcsin (-\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π-\arcsin (-\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)


\( \left[ \begin{gathered}x=-\arcsin (\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π+\arcsin (\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)


Но я фанатка круга, поэтому:



Ответ:   \( \left[ \begin{gathered}x=-\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π+\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)


На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.


Смотрите также:
Синус
Тригонометрические уравнения

Практическая тетрадь по теме «Тригонометрия»

ПРАКТИЧЕСКАЯ ТЕТРАДЬ

по теме «Тригонометрия»

Пояснительная записка:

Практическая тетрадь «Тригонометрия» предназначена в первую очередь для самоконтроля учащихся усвоения ЗУН по вышеуказанной теме. Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.

Тема: ТРИГОНОМЕТРИЯ

СПРАВОЧНЫЙ МАТЕРИАЛ

1)Значение тригонометрических функций

Угол

Функция

00

0

300

450

600

900

1800

2700

3600

sinα

1

0

-1

0

cosα

1

0

-1

0

1

tgα

0

1

—

0

—

0

ctgα

 

1

0

—

0

—

2)Знаки синуса, косинуса, тангенса, котангенса в каждой из координатных четвертей.

Знаки синуса Знаки косинуса Знаки тангенса и

котангенса

 

+ + — + — +

 

— — — + + —

3) sin(-α) = -sinα нечетная функции

tg (-α) = -tgα нечетная функции

ctg (-α) = -ctgα нечетная функции

cos (-α) = cosα} – четная функция

Формулы тригонометрии

Основные тригонометрические тождества

Формулы двойного угла

sin2α +cos2α =1

tgα ∙ctgα =1

sin2α = 2sinα ∙ cosα

cos2α = cos2α – sin2α

cos2α = 1-sin2α

cos2α =2cos2α -1

 

Формулы половинного угла

Формулы сложения

sin (α+β) =sinα cosβ +cosα sinβ

sin (α-β) =sinα cosβ-cosα sinβ

cos (α+β) = cosα cosβ -sinα sinβ

cos (α-β) = cosα cosβ +sinα sinβ

Формулы суммы и разност

Тема: ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

СПРАВОЧНЫЙ МАТЕРИАЛ

Решите уравнение:

1. arcsin(-a) = -arcsin a arcsin = ; arcsin(- ) = —

2. arccos(-a) = π – arccos a arccos = ; arccos(- ) = π — = π

3. arctg(-a) = -arctg a arctg1 = ; arctg(-1) = —

4. arcctg(-a) = π – arcctg a arcctg1 = ; arcctg(-1) = π — = π

5. sin (arcsin a) = a

cos (arccos a) = a

6. arcsin (sin х) = х

arccos (cos х) = х

7 .tg (arctg a) = a

arctg (tg х) = х, если х€

 

Найдите значение выражения:

a) arcsin 1 г) arctg 0 ж) arccos (-)

б) arcsin (- ) д) arctg (-) з) arcctg (-)

в) arccos е) arcctg ()

Тема: ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ

СПРАВОЧНЫЙ МАТЕРИАЛ

Уравнения вида sin x = a, cos x = a, tg x = a, ctg x =a называются простейшими тригонометрическими уравнениями. Любое другое тригонометрическое уравнение с помощью преобразований можно привести к простейшим.

 

1) sin x = a, -1 ≤ a ≤ 1

х = (-1)k arcsin a + πk, k€z

Частные случаи

sinx = 0; x = πk, k€z

sinx = 1; x = + 2πk, k€z

sinx = -1; x = — + 2πk, k€z

sin2x = a; x = ±arcsin + πn

2) cos x = a, -1 ≤ a ≤ 1

х = ±arccos a + 2πk, k€z

Частные случаи

cosx = 0; x = — + πk, k€z

cosx = 1; х=2πk, k€z

cosx = -1; х= π + 2πk, k€z

cos2x = ±arccos + πn, n€z

 

3) tg x = a

х = arctg a + πk, k€z

УПРАЖНЕНИЯ С РЕШЕНИЯМИ

 

Пример 1. Решить уравнение:

sinx = —

x = (-1)k arcsin (- ) + πk, k€z

x = (-1)k+1 + πk, k€z

Ответ: x = (-1)k+1 + πk, k€z

Пример 3. Решить уравнение:

sin2x =

2x = (-1)k arcsin + πk, k€z

2x = (-1)k + πk, k€z

х = (-1)k + k, k€z

Ответ: х = (-1)k + k, k€z

 

Пример 2. Решить уравнение:

2 cosx + 1 = 0

2cosx = -1

cosx = —

x = ±arccos(- ) + 2πk, k€z

x = ±() + 2πk, k€z

Ответ: x = ±() + 2πk, k€z

Пример 4. Решить уравнение:

3tgx -1 = 0

tgx =

x = arctg + πk, k€z

Ответ: x = arctg + πk, k€z

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

Решите уравнения:

1. cos x = 7. sin x = -0,6

2. cos x = -1 8. cos (-4x )= 0

3. sin(- x) = 0,5 9. cos = —

4. 2 sin x = 0 10. tg( x+π/4) =

5. ctg х + 1 = 0 11. 2 sin x + = 0

6. sin 3x = 12. cos x = 3

Тема: РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Уравнения, сводящиеся к квадратным

    (Виды уравнений: а sin2x + b sinx + c= 0, а cos2x + b sinx + c = 0)

     

    Алгоритм решения:

    а) Выполнить преобразования, приводящие к уравнению с одной функцией

    б) Решить квадратное уравнение относительно данной функции

    в) Решить простейшие тригонометрические уравнения

    Пример: 2 sin2 x + 5 sin x – 3 = 0

    Замена: sinx = t , |t| ≤ 1

    2 t2 + 5 t – 3 = 0 , t = -3

    t = Обратная замена: sin x=-3 нет решения,

    sinx = (простейшее уравнение)

    (см. таблицу)

     

    2) Уравнения вида a sinx + b cosx = 0 (однородное уравнение первого порядка)

    Решается делением на sin x ≠ 0 или cos х ≠ 0

    Например: поделим на cos x, получим уравнение а tgx + b = 0

    tgx = — (простое тригонометрическое уравнение)

    Уравнения, решаемые разложением левой части на множители, если справа 0

      (левую часть уравнения раскладываем на множители, затем каждый из сомножителей приравниваем к нулю)

      а sin2x + b sinxcosx = 0 (вынесем за скобки sin х)

      sinx (a sinx + b cosx) = 0 (данное уравнение распадается на 2 уравнения:

      1) sinx = 0 (прост. триг. уравнение) . 2) а sinx + b cosx = 0 (однородное триг. уравнение 1-го порядка, смотри пункт 2)

      4) Однородные тригонометрические уравнения 2-го порядка

      а sin2 x + b sinx cosx + c cos2x = 0 Примечание: если уравнение имеет вид

      а sin2 x + bsinx cosx + c cos2x = d, то правую часть

      уравнения умножаем на 1, т.е.

      Решается делением на сos2 х≠ 0

      a tg2x + b tgx + c = 0 (смотри пункт 1)

      замена: tgx = t

      at2 + bt + c =0 …

      ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

      Решите уравнение

      1.2 cos2x + 9 sinx + 3 = 0, (указание: заменить на 1-sin2x) 2. sinx + cosx = 0

       

      Ответ: — + πn, n€z Ответ: (-1)n+1 + πn, n€z

      3. 2sin cosx – sinx = 0 4. 3 sin2x + sinxcosx = 2cos2x

       

      Ответ: x = — + πn, x = arctg + πn, n€z Ответ: x = ± + 2πn, n€z, x = πn, n€z

       

      ТЕСТ № 1

      1. Решите уравнение: sinx =

      А) (-1)k + πk, k€z B) ± + 2πk C) (-1)k + πk D) (-1)k + 2πk

      2. Решите уравнение: 2 cos2x =

      A) + 2πk B) ± + πk C) + πk D) ± + 2πk

      3. Решите уравнение: 3tg3x = 3

      A) + k B) — + πk C)k D) +

      4. Решите уравнение: 2cos2x – 5cosx = -3

      A) 2πn, n€z B) нет решения C) πn, n€z D) π + 2πn, n€z

       

      5. Решите уравнение: sin2x – 2sinx = 0

      A) πn, n€z B) (-1)k + πк C) ± + 2πn D) π + 2πn, n€z

      6. Решите уравнение:

      A) нет решения B) C) D) ± + 2πn, n€z

       

      7. Решите уравнение: 2sin + = 0

      A) (-1)k + 2πk B) (-1)k + 1 + 2πk C) (-1)k + πk D) (-1)k + 1 + πk

      8. Решите уравнение: sinx – cosx = 0

      A) + πn B) + πn C) ± +2 πn D) ± + πn

      9. Решите уравнение: sin2 + sin cos = 0

      A) — + 2 πn, n€z, 2πn, n€z B) + 2 πn, n€z C) + πn, n€z D) — + πn, n€z, πn, n€z

      10. Решите уравнение: 3tg6x + = 0

      A) + πn, n€z B) + 6 πn, n€z C) + 3 πn, n€z D) — n, n€z

       

      ТЕСТ №2

      1. Решите уравнение:

      А) В) С)D)

      2. Решите уравнение если

      А) В) С) D)

      3. Решите уравнение:

      А); В);

      С); D).

      4. Решите уравнение: .

      А); В); С); D).

      5. Найдите корень уравнение принадлежащий []

      А)300; В)450; С)200; D)150.

      6. Решите уравнение: .

      А) В) С)D)

      7. Решите уравнение:

      А) В) С) D)

      8. Решите уравнение: .

      А); В); С) ; D).

      9. Решите уравнение: .

      А); В);

      С) ; D).

      10. Решите уравнение:

      А) ; В) ;

      С) ; D) .

      Оценка

      : arcsin (sin 2) — школьные Знания

      h e y h e r с y o u r e r

      Диапазон arcsin — π 2 ≤ θ ≤ π 2.2 π 2, поэтому он лежит вне диапазона.

      Диапазон arcsin равен — π 2 ≤ θ ≤ π 2. 2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ

      Диапазон arcsin — π 2 ≤ θ ≤ π 2. 2 π 2, чтобы он лежал за пределами диапазона. Используйте sin (π — θ) = sin θ

      Диапазон arcsin — π 2 ≤ θ ≤ π 2. 2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ Тогда sin 2 = sin (π — 2)

      Диапазон arcsin составляет — π 2 ≤ θ ≤ π 2.2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ Тогда sin 2 = sin (π — 2)

      Диапазон arcsin составляет — π 2 ≤ θ ≤ π 2. 2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ Тогда sin 2 = sin (π — 2) π — 2 ≅ 1,14

      Диапазон arcsin составляет — π 2 ≤ θ ≤ π 2. 2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ Тогда sin 2 = sin (π — 2) π — 2 ≅ 1,14, поэтому 0 <π - 2 <π 2

      Диапазон arcsin равен — π 2 ≤ θ ≤ π 2.2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ Тогда sin 2 = sin (π — 2) π — 2 ≅ 1,14, поэтому 0 <π - 2 <π 2

      Диапазон arcsin равен — π 2 ≤ θ ≤ π 2. 2 π 2, поэтому он лежит за пределами диапазона. Используйте sin (π — θ) = sin θ Тогда sin 2 = sin (π — 2) π — 2 ≅ 1.14, поэтому 0 <π - 2 <π 2 Итак, arcsin (sin (2 )) = π - 2

      убедитесь, что это разумно, пожалуйста,

      тригонометрии — Как можно вычислить $ \ sin (2 * \ arcsin (3/5)) $ вручную?

      тригонометрия — Как можно вычислить $ \ sin (2 * \ arcsin (3/5)) $ вручную? — Обмен математическим стеком

      Сеть обмена стеков

      Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

      Посетить Stack Exchange

      2. 0

      3. +0

      6. Авторизоваться
        Зарегистрироваться

      Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

      Зарегистрируйтесь, чтобы присоединиться к этому сообществу

      Кто угодно может задать вопрос

      Кто угодно может ответить

      Лучшие ответы голосуются и поднимаются наверх

      Спросил

      Просмотрено
      1к раз

      $ \ begingroup $

      Хотя достаточно просто пойти на Wolfram Alpha и увидеть, что ответ — 24/25, я хотел бы узнать, как доказать это вручную, если это возможно.К сожалению, arcsin (3/5) — трансцендентное число, и кажется, что оно состоит из бесконечных цифр.

      Есть ли способ оценить sin (2 * arcsin (3/5)) как 24/25 без перехода в компьютерные функции?

      S.C.B.

      22.5k33 золотых знака3232 серебряных знака5656 бронзовых знаков

      Создан 23 янв.

      ГаленГален

      55333 серебряных знака1717 бронзовых знаков

      $ \ endgroup $

      4

      $ \ begingroup $

      Давайте воспользуемся прямоугольным треугольником.2 \ theta = \ frac {16} {25}. $ Обратите внимание, что это не делает $ \ cos \ theta = — \ frac {4} {5} $ благодаря определению arcsin. 2 \ тета = 1
      $$
      вы можете вычислить $ \ cos \ theta $, чтобы закончить? (как вы интерпретируете тот факт, что существует два возможных значения $ \ cos \ theta $?)

      Создан 23 янв.

      Дэвид ХолденДэвид Холден

      17.2,112 золотых знаков1414 серебряных знаков3030 бронзовых знаков

      $ \ endgroup $

      Mathematics Stack Exchange лучше всего работает с включенным JavaScript

      Ваша конфиденциальность

      Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

      Принимать все файлы cookie

      Настроить параметры

      Упростите обратные тригонометрические функции

      Бесплатная практика для тестов SAT, ACT
      и Compass Maths

      Как упростить выражения, включая обратные тригонометрические функции, для математики в 12 классе.Также включены вопросы с подробными решениями.

        Вопрос 1

        Упростите выражения:

        a) sin (arcsin (x)) и arcsin (sin (x))

        b) cos (arccos (x)) и arccos (cos (x))

        c) загар (арктан (x)) и арктан (загар (x))

        Решение

        a) sin и arcsin противоположны друг другу, и поэтому свойства обратных функций могут использоваться для записи

        sin (arcsin (x)) = x, для -1 ≤ x ≤ 1

        arcsin (sin (x)) = x, для x ∈ [-π / 2, π / 2]

        ПРИМЕЧАНИЕ: Если x в arcsin (sin (x)) не находится в интервале [-π / 2, π / 2], найдите θ в интервале [-π / 2, π / 2] так, чтобы sin (x) = sin (θ), а затем упростим arcsin (sin (x)) = θ

        b) cos и arccos являются обратными друг другу, и поэтому свойства обратных функций могут использоваться для записи

        cos (arccos (x)) = x, для -1 ≤ x ≤ 1

        arccos (cos (x)) = x, для x ∈ [0, π]

        ПРИМЕЧАНИЕ: Если x в arccos (cos (x)) не находится в интервале [0/2, π], найдите θ в интервале [0, π] так, чтобы cos (x) = cos (θ), а затем упростите arccos (cos (x)) = θ

        c) tan и arctan противоположны друг другу, и поэтому свойства обратных функций могут использоваться для записи

        загар (arctan (x)) = x

        arctan (tan (x)) = x для x ∈ (-π / 2, π / 2)

        ПРИМЕЧАНИЕ: Если x в arctan (tan (x)) не находится в интервале (-π / 2, π / 2), найдите θ в интервале (-π / 2, π / 2) так, чтобы tan (x) = tan (θ), а затем упростить arctan (tan (x)) = θ

        Вопрос 2

        Выразите следующее в виде алгебраических выражений:

        грех (arccos (x)) и загар (arccos (x))

        Решение

        Пусть A = arccos (x).Следовательно

        cos (A) = cos (arccos (x)) = x

        Используйте прямоугольный треугольник с углом A таким образом, что cos (A) = x (или x / 1), найдите вторую ногу и вычислите sin (A) и tan (A)

        .

        sin (arccos (x)) = sin (A) = √ (1 — x 2 ) / 1 = √ (1 — x 2 ) для x ∈ [-1, 1]

        tan (arccos (x)) = tan (A) = √ (1 — x 2 ) / x для x ∈ [-1, 0) ∪ (0, 1]

        Вопрос 3

        Выразите следующее в виде алгебраических выражений:

        cos (arcsin (x)) и tan (arcsin (x))

        Решение

        Пусть A = arcsin (x).Следовательно

        sin (A) = sin (arcsin (x)) = x

        Используйте прямоугольный треугольник с углом A таким образом, что sin (A) = x (или x / 1), найдите вторую ногу и вычислите cos (A) и tan (A)

        .

        cos (arcsin (x)) = cos (A) = √ (1 — x 2 ) / 1 = √ (1 — x 2 ) для x ∈ [-1, 1]

        tan (arcsin (x)) = tan (A) = x / √ (1 — x 2 ) для x ∈ (-1, 1)

        Вопрос 4

        Выразите следующее в виде алгебраических выражений:

        sin (arctan (x)) и cos (arctan (x))

        Решение

        Пусть A = arctan (x).Следовательно

        загар (A) = загар (arctan (x)) = x

        Используйте прямоугольный треугольник с углом A таким образом, что tan (A) = x (или x / 1), найдите гипотенузу и вычислите sin (A) и cos (A)

        .

        sin (arctan (x)) = sin (A) = x / √ (1 + x 2 )

        cos (arctan (x)) = cos (A) = 1 / √ (1 + x 2 )

        Вопрос 5

        Упростите следующие выражения:

        а) arccos (0), arcsin (-1), arctan (-1)

        b) sin (arcsin (-1/2)), arccos (cos (π / 2)), arccos (cos (-π / 2))

        c) cos (arcsin (-1/2)), arcsin (sin (π / 3)), arcsin (tan (3π / 4))

        d) arccos (tan (7π / 4)), arcsin (sin (13π / 3)), arctan (tan (-17π / 4)), arcsin (sin (9π / 5))

        Решение

        а) Используйте определение.
        arccos (0) = π / 2, потому что cos (π / 2) = 0 и π / 2 находится в пределах диапазона arccos, который равен [0, π]

        arcsin (-1) = -π / 2, потому что sin (-π / 2) = -1 и -π / 2 находится в пределах диапазона arcsin, который равен [-π / 2, π / 2]

        arctan (-1) = -π / 4, потому что tan (-π / 4) = -1 и -π / 4 находится в пределах диапазона arctan, который равен (-π / 2, π / 2)

        б) Упростите внутренние функции, а затем внешние функции, используя определения.

        грех (arcsin (-1/2)) = sin (-π / 6) = -1/2

        arccos (cos (π / 2)) = arccos (0) = π / 2

        arccos (cos (-π / 2)) = arccos (0) = π / 2

        c) Упростите внутренние функции, а затем внешние функции, используя определения.
        cos (arcsin (-1/2)) = cos (-π / 6) = √3 / 2

        arcsin (sin (π / 3)) = arcsin (√3 / 2) = π / 3

        arcsin (tan (3π / 4)) = arcsin (-1) = -π / 2

        d) Упростите внутренние функции, а затем внешние функции, используя определения.

        arccos (tan (7π / 4)) = arccos (-1) = π

        arcsin (sin (13π / 3)) = arcsin (sin (4π + π / 3)) = arcsin (sin (π / 3)) = π / 3

        arctan (тангенс (- 17π / 4)) = arctan (тангенс (- 4π-π / 4)) = arctan (тангенс (- π / 4)) = — π / 4

        arcsin (sin (9π / 5)) = arcsin (sin (2π — π / 5)) = arcsin (sin (- π / 5)) = — π / 5

        Вопрос 6

        Пусть A = arcsin (2/3) и B = arccos (-1/2).Найдите точное значение sin (A + B).

        Решение

        Используйте отступ sin (A + B) = sin (A) cos (B) + cos (A) sin (B), чтобы расширить данное выражение.

        sin (A + B) = sin (arcsin (2/3)) cos (arccos (-1/2)) + cos (arcsin (2/3)) sin (arccos (-1/2))

        Используйте указанные выше отступы, чтобы упростить каждый термин в приведенном выше выражении.

        sin (arcsin (2/3)) = 2/3
        (мы использовали sin (arcsin (x)) = x))

        cos (arccos (-1/2)) = -1/2
        (мы использовали cos (arccos (x)) = x))

        cos (arcsin (2/3)) = √ (1 — (2/3) 2 ) = √5 / 3
        (мы использовали cos (arcsin (x)) = √ (1 — x 2 ))

        sin (arccos (-1/2)) = √ (1 — (- 1/2) 2 ) = √3 / 2
        (мы использовали sin (arccos (x)) = √ (1 — x 2 ))
        Подставим и посчитаем.
        sin (A + B) = (2/3) (- 1/2) + (√5 / 3) (√3 / 2) = -1/3 + √ (15) / 6

        Вопрос 7

        Запишите Y = sin (2 arcsin (x)) как алгебраическое выражение.

        Решение

        Пусть A = arcsin (x). Следовательно, Y можно записать как

        Y = sin (2 А)

        Используйте тождество sin (2 A) = 2 sin (A) cos (A), чтобы переписать Y следующим образом:

        Y = 2 sin (A) cos (A) = 2 sin (arcsin (x)) cos (arcsin (x))

        Используйте тождества sin (arcsin (x)) = x и cos (arcsin (x)) = √ (1-x 2 ), чтобы переписать Y следующим образом:

        Y = 2 x √ (1 — x 2 )

        Вопрос 8

        Найдите точное значение Y = sin (2 arctan (3/4)).
        Решение

        Пусть A = arctan (3/4). Следовательно, Y можно записать как

        Y = sin (2 A) = 2 sin (A) cos (A)

        sin (A) = sin (arctan (3/4)) = (3/4) / √ (1 + (3/4) 2 ) = 3/5

        cos (A) = cos (arctan (3/4)) = 1 / √ (1 + (3/4) 2 ) = 4/5

        Y = 2 (3/5) (4/5) = 24/25

      Дополнительные ссылки и ссылки

      Обратные тригонометрические функции
      Решение вопросов по обратным тригонометрическим функциям
      Математика для средней школы (10, 11 и 12 классы) — бесплатные вопросы и задачи с ответами
      Математика в средней школе (6, 7, 8, 9 классы ) — Бесплатные вопросы и проблемы с ответами

      Arcsin Calculator.Нахождение обратной функции синуса.

      С помощью этого калькулятора арксинуса (или калькулятора обратного синуса) у вас не будет проблем с поиском арксинуса в вашей задаче. Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно запомнить, это ограниченная область арксинуса (−1 ≤ sine ≤ 1). Если вам интересно, , что такое арксинус или , как выглядит график arcsin x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинусов, таких как отношения между интегралом арксинуса и производной.И так, чего же ты ждешь?

      Что такое арксинус?

      Арксинус — это функция, обратная синусоиде. Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале.

      Синус — периодическая функция, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0, sin (-π) = 0 и sin (-326π) = 0.Следовательно, если кто-то хочет вычислить arcsin (0), ответ может быть 0, 2π (360 °) или -π (-180 °), чтобы назвать несколько вариантов! Все они верны, но обычно мы даем только одно число, называемое основным значением .

      Сокращение Определение Домен arcsin x
      для реального результата      		 Диапазон обычных
      основных значений
      arcsin (x)
      sin -1 x,
      asin       		х = грех (у) -1 ≤ х ≤ 1 -π / 2 ≤ y ≤ π / 2
      -90 ° ≤ y ≤ 90 °

      Arcsin (x) — наиболее распространенное обозначение, поскольку sin -1 x может привести к путанице (потому что sin -1 x ≠ 1 / sin (x)).Аббревиатура asin обычно используется в языках программирования.

      График arcsin x

      Поскольку синус основной функции не является взаимно однозначным, ее область должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π / 2 ≤ y ≤ π / 2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции arcsin равен [−π / 2, π / 2], а область arcsine находится между [−1,1]. Ниже вы можете найти график arcsin (x), а также некоторые часто используемые значения арксинуса:

      x арксин (х) График
      ° рад
      -1 -90 ° -π / 2 Компьютерщик 3, CC BY-SA 4.0 через Wikimedia Commons
      -√3 / 2 -60 ° -π / 3
      -√2 / 2 -45 ° -π / 4
      -1/2 -30 ° -π / 6
      0 0 ° 0
      1/2 30 ° π / 6
      √2 / 2 45 ° π / 4
      √3 / 2 60 ° π / 3
      1 90 ° π / 2

      Хотите знать, откуда взялся этот график arcsin x? Его можно найти, отразив график sin (x) в диапазоне [-π / 2 π / 2] через линию y = x:

      Jaro.p CC BY-SA 3.0, через Wikimedia Commons

      Обратный синус, тригонометрические функции и другие отношения

      Связь между тригонометрическими функциями и арксинусом может помочь вам еще лучше понять тему. Прямоугольный треугольник с гипотенузой длины 1 — хорошая отправная точка.

      Просто быстрое напоминание: для прямоугольного треугольника функция синуса принимает угол θ и возвращает отношение противоположности / гипотенузы, которое равно x в нашем примерном треугольнике.Функция обратного синуса, арксинус, принимает отношение противоположности / гипотенузы (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin (x) = θ, мы также можем записать, что:

      • Синус: sin (arcsin (x)) = x
      • Косинус: cos (arcsin (x)) = √ (1-x²)
      • Касательная: tan (arcsin (x)) = x / √ (1-x²)

      Другие полезные отношения с арксинусом:

      • arcsin (x) = π / 2 - arccos (x)
      • arcsin (-x) = -arcsin (x)

      Иногда также нужны интеграл и производная от arcsin:

      • интеграл от arcsin: arcsin (x) dx = x arcsin (x) + √ (1 - x²) + C

      • производная от arcsin: d / dx arcsin (x) = 1 / √ (1 - x²) где x ≠ -1, 1

      Пример использования калькулятора arcsin

      Арксинус — полезная функция e.грамм. в нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, хорошо известная теорема Пифагора не будет столь полезной. Чтобы найти углы прямоугольного треугольника, нужно применить арксинус:

      • для α: sin (α) = a / c, поэтому α = arcsin (a / c)
      • для β: sin (β) = b / c, поэтому β = arcsin (b / c)

      Итак, предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α:

      1. Введите значение, по которому вы хотите найти арксинус .В нашем случае это 6/10. Таким образом, вы можете ввести значение 0,6, но форма 6/10 также будет работать. Просто помните, что значение должно быть между -1 и 1.
      2. И … все! Калькулятор arcsin выполнил свою работу, и вы нашли арксинус своего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 °

      Отлично! Теперь, когда вы понимаете, что такое арксинус, может быть, вы захотите познакомиться с более продвинутыми приложениями тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач треугольника.

      arcsin (x) | функция обратного синуса

      arcsin (x), sin -1 (x), функция обратного синуса.

      Определение Arcsin

      Арксинус x определяется как функция, обратная синусу x, когда -1≤x≤1.

      Когда синус y равен x:

      грех y = x

      Тогда арксинус x равен функции обратного синуса x, которая равна y:

      arcsin x = sin -1 x = y

      Пример

      arcsin 1 = sin -1 1 = π / 2 рад = 90 °

      График arcsin

      Правила Arcsin

      Название правила Правило
      Синус арксинуса sin (arcsin x ) = x
      Арксинус синуса arcsin (sin x ) = x +2 k π,
      когда k ∈ℤ ( k
      целое число)
      Арксин отрицательного аргумента arcsin (- x ) = — arcsin x
      Дополнительные уголки arcsin x = π / 2 — arccos x = 90 °
      — arccos x
      Сумма арксина arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 )
      + β√ (1- α 2 ))
      Разница по арксину arcsin α — arcsin ( β ) = arcsin ( α√ (1- β 2 )
      — β√ (1- α 2 ))
      Косинус арксинуса
      Касательная к арксинусу
      Производная арксинуса
      Неопределенный интеграл от арксинуса

      Стол Arcsin

      x arcsin (x)

      (рад)

      		 arcsin (x)

      (°)

      -1 -π / 2 -90 °
      -√3 / 2 -π / 3 -60 °
      -√2 / 2 -π / 4 -45 °
      -1/2 -π / 6 -30 °
      0 0 0 °
      1/2 π / 6 30 °
      √2 / 2 π / 4 45 °
      √3 / 2 π / 3 60 °
      1 π / 2 90 °

      См. Также

      Калькулятор

      — arcsin (sin (2)) — Solumaths

      Описание:

      Функция arcsin позволяет вычислять арксинус числа.Функция арксинуса является обратной функцией функции синуса.

      arcsin онлайн

      Описание:

      Функция arcsine является обратной функцией
      синусоидальная функция,
      это позволяет вычислить арксинус из числа онлайн .

      Число, к которому вы хотите применить функцию арксинуса, должно принадлежать диапазону [-1,1].

      1. Расчет арксинуса

        2. Чтобы вычислить арксинус числа, просто введите число и примените
        функция arcsin .2) `.

      Функция arcsin позволяет вычислять арксинус числа.
      Функция арксинуса является обратной функцией функции синуса.

      Синтаксис:

      arcsin (x), где x — число. 2)`

      Первоначальный арксинус:

      Калькулятор первообразной функции арксинуса.2) `

      Предельный арксинус:

      Калькулятор пределов позволяет вычислить пределы функции арксинуса.

      Предел для arcsin (x) — limit_calculator (`» arcsin «(x)`)

      Арксинус обратной функции:

      Функция, обратная арксинусу , является синусоидальной функцией, отмеченной как sin.

      Графическая арксинус:

      Графический калькулятор может строить функцию арксинуса в интервале ее определения.

      Свойство функции arcsine:

      Функция арксинуса — нечетная функция.

      Расчет онлайн с помощью arcsin (арксинус)

      Функция тригонометрии arcsin () — обратный синус — определение математического слова

      Функция тригонометрии arcsin () — обратный синус — определение математического слова — Math Open Reference

      Функция arcsin — это функция, обратная синусоиде.
      Возвращает угол, синус которого является заданным числом.

      Попробуй это
      Перетащите любой
      вершине треугольника и посмотрите, как вычисляется угол C с помощью функции arcsin ().

      Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.
      Эти обратные функции имеют то же имя, но с дугой впереди.
      (На некоторых калькуляторах кнопка arcsin может быть помечена как asin, а иногда
      грех -1 .)
      Итак, обратное к греху — это arcsin и т. Д. Когда мы видим «arcsin A», мы понимаем его как «угол, грех которого равен A».

      sin30 = 0.5 Означает: синус 30 градусов равен 0,5
      arcsin 0,5 = 30 Означает: Угол, грех которого равен 0,5, равен 30 градусам.

      Используйте arcsin, если вы знаете синус угла и хотите узнать фактический угол.
      См. Также Обратные функции — тригонометрия

      Пример — использование arcsin для нахождения угла

      На рисунке выше нажмите «Сброс».
      Нам известны длины сторон, но нам нужно найти величину угла C.

      Мы знаем, что

      поэтому нам нужно знать угол, грех которого равен 0.5, или формально:

      Используя калькулятор, чтобы найти arcsin 0,5, мы находим, что это 30 °.

      Большие и отрицательные углы

      Напомним, что мы можем применить
      триггерные функции на любой угол, включая большие и отрицательные углы. Но когда мы
      Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же синус.
      Например, 45 ° и 360 + 45 ° будут иметь одинаковый синус. Подробнее об этом см.
      Обратные тригонометрические функции.

      Чтобы решить эту проблему,
      диапазон
      обратных триггерных функций ограничены
      таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.

      Диапазон и домен arcsin

      Напомним, что область определения функции — это набор допустимых входных данных для нее. Диапазон — это набор возможных выходов.

      Для y = arcsin x:

      По соглашению диапазон arcsin ограничен от -90 ° до + 90 °.
      Итак, если вы используете калькулятор для решения, скажем, arcsin 0,55, из бесконечного числа возможностей он вернет 33,36 °,
      тот, который находится в диапазоне функции.

      Что попробовать

      1. На рисунке выше нажмите «сбросить» и «скрыть детали».
      2. Отрегулируйте треугольник до нового размера
      3. Используя функцию arcsin, вычислите значение угла C из длин сторон
      4. Щелкните «Показать подробности», чтобы проверить ответ.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *