Что делать если не извлекается дискриминант: Что делать когда дискриминант не извлекается из под корня? Пример такой: Х= 7+/- (21 под — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Что делать, если из дискриминанта корень не извлекается? Я обычно грущу

Мужчины различные бродят по свету.Буквально слов двести — на тему на эту.Во-первых, мужчины есть настоящие.Есть очень красивые, просто блестящие.Есть ноги-как-спички. Есть тяжеловесы.Есть очень серьезные. И просто повесы.Мужчины-задиры, мужчины-зануды,Мужчины-трактиры. мужчины-приблуды.Есть супермужчины. Есть ежики в шортах.Есть странные дяди и мастера спорта.Есть маразматики. Есть академикиМужчины-прагматики, мужчины-полемики.Есть с большой буквы. Есть с большой цифры.Есть абсолютно не ждущие рифмыМужчина-женюсь и мужик ни-за-что!,Мужчина, всегда подающий пальто.Есть одноклассники, есть одногруппники,Мужчины — спасители, мужчины — заступникиМанящие вечно и спящие рядомМужчина, способный увлечь одним взглядом.И просто конец всему — мальчик-отличник,Мужчинка-бухгалтер, Васек-пограничник.Но двух одинаковых нету на свете.Мы кое-что поняли в этом предмете.Мягки и наивны мужчины-подушки,Несет Казанова вам ересь на ушко,Весьма предсказуем мужчина семейныйИ в семьдесят мужествен будет идейный. Мужчина-ревнивец достанет вас просто,Никак не отстанет мужчина-коростаВсе время колеблется мужчина-синус.И нет своих плюсов у мужика-минус.У идеала — огромное сердце.Душа на защелке — у старого перцаУжасны мужчины-туманные-очиПрекрасны мужчины-бессонные ночи.У мужика-деда — простая натура.А у атлета — большая фигура.В глазах полстраны у мальчишки-студента.Желанье все бросить — у суперагента.В беседках беседы — с мальчиком-ямб.Но сладость победы — с мужчиною-штампВедут мужики себя неодинаково.Уж мы-то от них навидалися всякого.С рассветом поднимет мужчина-будильник,А ночью обжора залез в холодильник.От снега, от ливня, от града укроетПротивный, но нужный мужик-рубероид.Лишит вас рассудка мужик-ловелас.На место поставит мужик-выкрутас.Заставит покаяться мальчик-безбожник,Утащит в тайгу вас мужик-внедорожник.Мужчина-окурок сгорает от страсти.Из памяти стерся мужчина-ластик.Вот Дон-Жуан наш куда-то слинял.Мужчина-на-раз нас зачем поменял?Что нужно мужчине, который не знаетКуда и зачем он сейчас уезжает?Доколь подстрекать будут нас на поступкиМужчины, идущие нам на уступки?Застряв, словно в джунглях, в словах непролазных,Мы ищем в вас нежных, зовущих и страстныхМужчину-героя и способ от скуки,Юношу-праздник и сильные-рукиПобольше мужчин нам — хороших и разных!Поменьше болтливых, глупых и праздных!Заметим от имени женщин Земли:Мы для вас сделали все, что смогли!Мы мамы, любовницы, сестры, подруги,Лекарства и дети, мечты и супруги.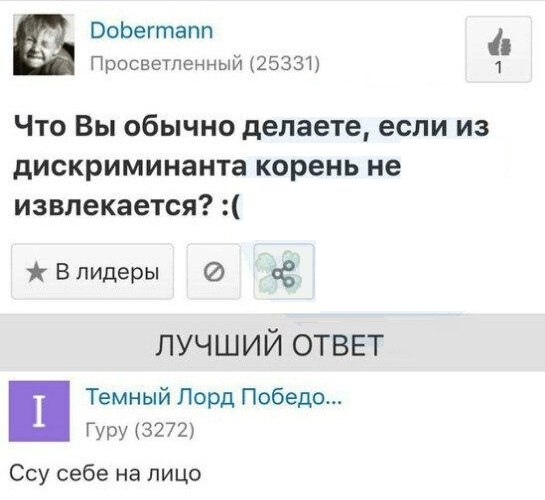 2 + j * w + k равный 0, где «i» и «j» — первый и второй коэффициент соответственно, «k» — константа, которую иногда именуют «свободным членом», а «w» — переменная. Его корнями окажутся все значения переменной, при которых оно превращается в тождество. Такое равенство допустимо переписать, как произведение i, (w — w1) и (w — w2) равное 0. В этом случае очевидно, что если коэффициент «i» не обращается в ноль, то функция в левой части станет нулевой только в случае, если x принимает значение w1 или w2. Эти значения являются результатом приравнивания многочлена к нулю.

Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?

Она говорит, имеются ли действительные результаты.
Она помогает их высчитать.

Как это значение показывает наличие вещественных корней:

Если оно положительное, то можно найти два корня в области действительных чисел. (1/2).
Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
Подстановка полученного результата в исходное равенство для проверки.

Некоторые частные случаи

В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:

многочлен раскладывается в разность квадратов при отрицательном свободном члене;
при положительной константе действительных решений найти нельзя.

Если свободный член нулевой, то корни будут {0; -j}

Но есть и другие частные случаи, упрощающие нахождение решения.

Приведенное уравнение второй степени

Приведенным именуют
такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k». 2 + 18 * i * j * k * m.

Допустим, дискриминант превосходит ноль
. Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D

Видео

Наше видео подробно расскажет о вычислении дискриминанта.

Не получили ответ на свой вопрос? Предложите авторам тему.

Поработаем с квадратными уравнениями
. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:

Например:

Здесь а
=1; b
= 3; c
= -4

Здесь а
=2; b
= -0,5; c
= 2,2

Здесь а
=-3; b
= 6; c
= -18

Ну, вы поняли…

Как решать квадратные уравнения?
Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант

. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант
. Как видим, для нахождения икса, мы используем только a, b и с
. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с
в это формулу и считаем. Подставляем со своими знаками!

Например, для первого уравнения а
=1; b
= 3; c
= -4. Вот и записываем:

Пример практически решён:

Вот и всё.

Какие случаи возможны при использовании этой формулы? Всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых
. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с
. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте
!

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится
. Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Итак, как решать квадратные уравнения
через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с
. Умеете внимательно
подставлять их в формулу корней и внимательно
считать результат. Вы поняли, что ключевое слово здесь – внимательно?

Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:

Это неполные квадратные уравнения

. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с
.

Сообразили? В первом примере a = 1; b = -4;
а c
? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0

! Вот и всё. Подставляем в формулу ноль вместо c,
и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с
, а b
!

Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0
, или х = 4

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х = +3 и х = -3
.

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый
. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с.
Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй.
Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее
уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1
, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком

. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b
с противоположным

знаком. В нашем случае -1+2 = +1. А коэффициент b
, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1.
Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий
. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно
.

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Дробные уравнения. ОДЗ.

Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения
. Или их ещё называют гораздо солиднее – дробные рациональные уравнения
. Это одно и то же.

Дробные уравнения.

Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе
. Хотя бы в одном. Например:

Напомню, если в знаменателях только числа
, это линейные уравнения.

Как решать дробные уравнения
? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.

Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.

Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:

Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?

В левой части для сокращения знаменателя требуется умножение на х+2
. А в правой требуется умножение на 2.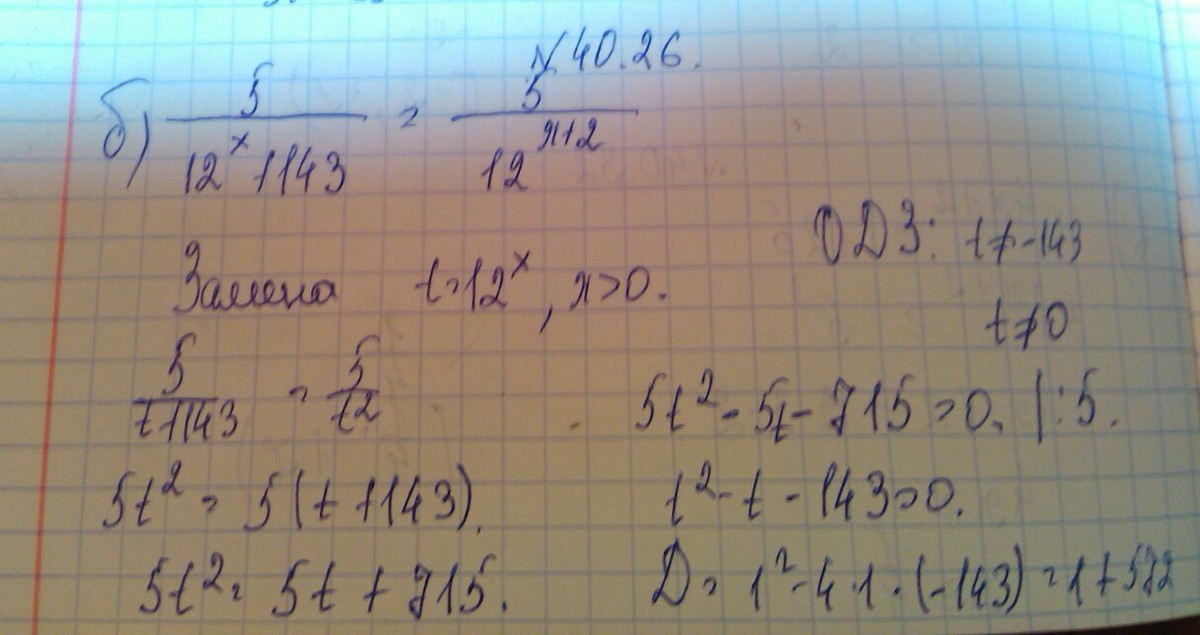 Значит, уравнение надо умножать на 2(х+2)
. Умножаем:

Это обычное умножение дробей, но распишу подробно:

Обратите внимание, я пока не раскрываю скобку (х + 2)
! Так, целиком, её и пишу:

В левой части сокращается целиком (х+2)
, а в правой 2. Что и требовалось! После сокращения получаем линейное
уравнение:

А это уравнение уже решит всякий! х = 2
.

Решим ещё один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2х = 2х/
1, можно записать:

И опять избавляемся от того, что нам не очень нравится – от дробей.

Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2)
. А единицы нам не помеха. Ну и умножаем. Всю
левую часть и всю
правую часть:

Опять скобки (х – 2)
я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.

С чувством глубокого удовлетворения сокращаем (х – 2)
и получаем уравнение безо всяких дробей, в линеечку!

А вот теперь уже раскрываем скобки:

Приводим подобные, переносим всё в левую часть и получаем:

Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:

Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3
. Два корня.

Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым
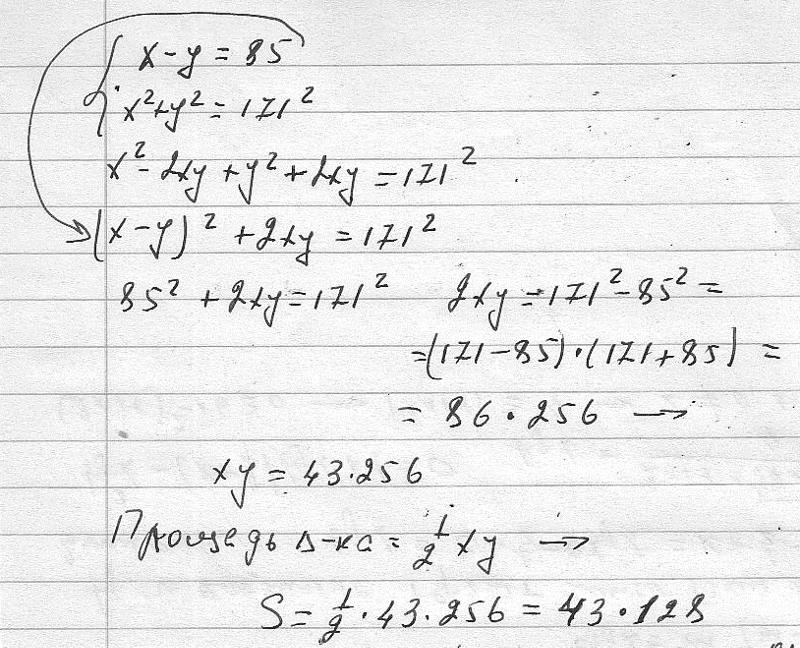. Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет
! При любом иксе получается неправда.

Осознали главный способ решения дробных уравнений
? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда
будем от всего этого избавляться.

Однако менять исходное выражение в нужную нам сторону надо по правилам
, да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.

Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ
! Но для начала посмотрим, попадаете вы в неё, или нет?

Разберём простой пример:

Дело уже знакомое, умножаем обе части на (х – 2)
, получаем:

Напоминаю, со скобками (х – 2)
работаем как с одним, цельным выражением!

Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2
ничего нет, можно и не рисовать. Сокращаем:

Раскрываем скобки, переносим всё влево, приводим подобные:

Решаем, проверяем, получаем два корня. х = 2
и х = 3
. Отлично.

Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?

Если решите, что ответ 5, – вы попали в засаду
. И задание вам не засчитают. Зря трудились… Правильный ответ 3.

В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный
пример. И если при х = 3
у нас всё чудненько срастётся, получим 9 = 9, то при х = 2
получится деление на ноль! Чего делать нельзя категорически. Значит х = 2
решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3
.

Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!

Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля
. А х – 2
при х = 2
равно нулю! Так что всё честно.

И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!

Спокойно! Без паники!

В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ

. Область Допустимых Значений.

Важно! В корнях четной кратности функция знак не меняет.

Обратите внимание! Любое нелинейное неравенство школьного курса алгебры нужно решать с помощью метода интервалов.

Предлагаю вам подробный алгоритм решения неравенств методом интервалов
, следуя которому вы сможете избежать ошибок прирешении нелинейных неравенств
.

Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i
2 = — 1.

Вместе с тем

(- i

) 2 = (- 1 i

) 2 = (- 1) 2 i

2 = -1.

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i

и — i

. Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi

равен — 1. Тогда

(а + bi

) 2 = — 1,

а
2 + 2аbi

— b

2 = — 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

{	а 2 — b 2 = — 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а

и b

должно равняться нулю. Если b

= 0, то из первого уравнения получается а

2 = — 1. Число а

действительное, и поэтому а

2 >
0. Неотрицательное число а

2 не может равняться отрицательному числу — 1. Поэтому равенство b

= 0 в данном случае невозможно. Остается признать, что а

= 0, но тогда из первого уравнения системы получаем: —b

2 = — 1, b

= ± 1.

Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i

и —i

, Условно это записывается в виде:

√-1 = ± i

.

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а

. Такими числами являются √ai

и -√ai

. Условно это записывается так:

√— а

= ± √ai

.

Под √a

здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому

√-4 = + 2i

, √-9= ± 3i

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x

2 + 2х

+ 5 = 0; тогда

х
1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i

.

Итак, данное уравнение имеет два корня: х

1 = — 1 +2i

, х

2 = — 1 — 2i

. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

Понятие комплексного числа

Комплексным числом называется выражение вида a + ib , где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
a = b и c = d .
Суммой двух комплексных чисел a + ib и c + id называется комплексное число
a + c + i (b + d).
Произведением двух комплексных чисел a + ib и c + id называется комплексное число
ac – bd + i (ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib . Действительное число a называется действительной частью комплексного числа z , действительная часть обозначается a = Re z . Действительное число b называется мнимой частью комплексного числа z , мнимая часть обозначается b = Im z . Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi , например, 0 + i 3 = 3 i . Чисто мнимое число i1 = 1 i = i обладает удивительным свойством:
Таким образом,

№ 4 .1.
В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множествавещественных чисел или множества комплексных чисел .

График функции

Фрагмент графика функции

Способы задания функции

[править]Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.

[править]Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

[править]Графический способ

Осциллограмма задаёт значение некоторой функции графически.

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

[править]Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

факториал;
числа Фибоначчи;
функция Аккермана.

[править]Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

функция, возвращающая цифру в записи числа пи по её номеру;
функция, возвращающая число атомов во вселенной в определённый момент времени;
функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождени

В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители

Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.

Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax 2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax 2 , оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.

Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax 2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.

Пример

x=0 или 8х — 3 = 0

В результате получаем два корня уравнения: 0 и 0,375.

Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v 0 t + gt 2 /2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители

Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.

X 2 — 33x + 200 = 0

Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.

Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.

Например: 2x 3 + 2x 2 — 18x — 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).

В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.

Извлечение квадратного корня

Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax 2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.

В данном случае корнями уравнения окажутся числа -4 и 4.

Вычисление пощади земельного участка

Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.

Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м 2 .

Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.

Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.

Дискриминант

Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x 2 + 16x — 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.

Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b 2 — 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D

О корнях и их формуле

В нашем случае дискриминант равен: 256 — 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.

Это значит, что в представленном случае: x 1 =18, x 2 =-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м 2).

Примеры и задачи

Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.

1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1

Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.

15x 2 + 20x + 5 — 12x 2 — 27x — 1 = 0

Сложив подобные, определим дискриминант: D = 49 — 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.

2) Теперь раскроем загадки другого рода.

Выясним, есть ли вообще здесь корни x 2 — 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 — 20 = -4, а значит, корней действительно нет.

Теорема Виета

Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.

Теперь рассмотрим конкретные задачи.

3x 2 + 21x — 54 = 0

Для простоты преобразуем выражение:

x 2 + 7x — 18 = 0

Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.

График и уравнение параболы

Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a

Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x 0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y 0 , то есть вторую координату вершины параболы, принадлежащую оси ординат.

Пересечение ветвей параболы с осью абсцисс

Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у 0 принимает отрицательные значения. А для a0. В противном случае D

По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

Из истории

С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. 2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.

Геометрический смысл квадратного уравнения

Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х)
. Из этого следует, что есть три возможных случая:
1)
парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).

2)
парабола имеет одну точку пересечения с осью Ох
. Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).

3)
Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2
и осуществим преобразование

Отсюда находим

Формула дискриминанта и корней квадратного уравнения

Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0
При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле

Теорема Виета

Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p
, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q
. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а
отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0
.

Решение:
В случаях когда есть малые коэффициенты при х
целесообразно применять теорему Виета. По ее условию получаем два уравнения

С второго условия получаем, что произведение должно быть равно -6
. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}
. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны

Задача 5.
Найти длины сторон прямоугольника, если его периметр 18
см, а площадь 77
см 2 .

Решение:
Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х
– большую сторону, тогда 18-x
меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;

или
х 2 -18х+77=0.

Найдем дискриминант уравнения

Вычисляем корни уравнения

Если х=11
,
то 18-х=7
,
наоборот тоже справедливо (если х=7
, то 21-х=9
).

Задача 6.
Разложить квадратное 10x 2 -11x+3=0
уравнения на множители.

Решение:
Вычислим корни уравнения, для этого находим дискриминант

Подставляем найденное значение в формулу корней и вычисляем

Применяем формулу разложения квадратного уравнения по корнями

Раскрыв скобки получим тождество. 2+(2а+6)х-3а-9=0
имеет более одного корня?

Решение:
Рассмотрим сначала особые точки, ими будут значения а=0
и а=-3
. При а=0
уравнение упростится до вида 6х-9=0; х=3/2
и будет один корень. При а= -3
получим тождество 0=0
.
Вычислим дискриминант

и найдем значения а
при котором оно положительно

С первого условия получим а>3
. Для второго находим дискриминант и корни уравнения

Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0
получим 3>0
.
Итак, за пределами промежутка (-3;1/3)
функция отрицательная. Не стоит забывать о точке а=0
,
которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи

Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.

– Что Вы делаете, если из дискриминанта корень не

АНЕКДОТ

Препод студенту:
– Что Вы делаете, если из дискриминанта корень не извлекается?
– Я обычно грущу.

3 года назад

+17

лучшие за день |
топ недели |
лучшие за месяц |
случайный анекдот

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение
ключевым словом является «квадратное».
Оно означает, что в уравнении обязательно
должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член).
И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с
– какие-то числа. b и c
– совсем любые, а а
– любое, кроме нуля. Например:

Здесь а
=1; b
= 3; c
= -4

Здесь а
=2; b
= -0,5; c
= 2,2

Здесь а
=-3; b
= 6; c
= -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор
членов. Икс в квадрате с коэффициентом а,
икс в первой степени с коэффициентом b
и свободный член с.

Такие квадратные уравнения называются полными.

А если b
= 0, что у нас получится? У нас пропадёт икс в первой степени.
От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b
и c
равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями.
Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а
не может быть равно нулю? А вы подставьте вместо а
нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а
, b
и c
.

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант
. Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с
.
Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с
в эту формулу и считаем. Подставляем со своими знаками!

Например, в уравнении:

а
=1; b
= 3; c
= -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с
. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте
!

Предположим, надо вот такой примерчик решить:

Здесь a
= -6;
b
= -5;
c
= -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения
.

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с
.

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1
— то, что меньше, а х 2
— то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня.
х 1 = -3
, х 2 = 3
.

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант

! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых
квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D
. Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта?
Ведь -b,
или 2a
в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный.
Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю.
Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых
. Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный.
Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта
не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения
через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с
. Умеете внимательно
подставлять их в формулу корней и внимательно
считать результат. Вы поняли, что ключевое слово здесь – внимательно?

Приём первый

. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1.

Приём второй.

Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее
уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1
, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком

. Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b
с противоположным

знаком. В нашем случае -1+2 = +1. А коэффициент b
, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1.
Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий

. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно
.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0

х 2 = 5

х 1,2 =
2

х 1 = 2

х 2 = -0,5

х — любое число

х 1 = -3

х 2 = 3

решений нет

х 1 = 0,25

х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные
ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант
.

Дискриминант

Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D
= 0, есть ровно один корень;
Если D
> 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:
x
2 − 8x
+ 12 = 0;
5x
2 + 3x
+ 7 = 0;
x
2 − 6x
+ 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

x
2 − 2x
− 3 = 0;
15 − 2x
− x
2 = 0;
x
2 + 12x
+ 36 = 0.

Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.

D
> 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.

D
> 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x
2 + 9x
= 0;
x
2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b
= c
= 0. В этом случае уравнение принимает вид ax
2 = 0. Очевидно, такое уравнение имеет единственный корень: x
= 0.

Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:

Если в неполном квадратном уравнении вида ax
2 + c
= 0 выполнено неравенство (−c
/a
) ≥ 0, корней будет два. Формула дана выше;
Если же (−c
/a
)

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax
2 + bx
= 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:
x
2 − 7x
= 0;
5x
2 + 30 = 0;
4x
2 − 9 = 0.

x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.

5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5.

Нахождение дискриминанта, формула, сравнение с нулём

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

с помощью факторизации;
используя формулу для полного квадрата;
применяя график соответствующей квадратичной функции;
используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
D=0: у уравнения всего один корень, и он является действительным числом.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.

Виды квадратных уравнений

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с
– какие-то числа. b и c
– совсем любые, а а
– любое, кроме нуля. Например:

Здесь а
=1; b
= 3; c
= -4

Здесь а
=2; b
= -0,5; c
= 2,2

Здесь а
=-3; b
= 6; c
= -18

Ну, вы поняли…

Такие квадратные уравнения называются полными.

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b
и c
равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Формула для нахождения корней квадратного уравнения выглядит так:

а
=1; b
= 3; c
= -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Предположим, надо вот такой примерчик решить:

Здесь a
= -6;
b
= -5;
c
= -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения
.

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с
.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня.
х 1 = -3
, х 2 = 3
.

Дискриминант. Формула дискриминанта.

D = b 2 — 4ac

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1.

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно
.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0

х 2 = 5

х 1,2 =
2

х 1 = 2

х 2 = -0,5

х — любое число

х 1 = -3

х 2 = 3

решений нет

х 1 = 0,25

х 2 = 0,5

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

можно познакомиться с функциями и производными.

Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0.

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

Дискриминант

Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
.

Если D
Если D
= 0, есть ровно один корень;
Если D
> 0, корней будет два.

Задача. Сколько корней имеют квадратные уравнения:
x
2 − 8x
+ 12 = 0;
5x
2 + 3x
+ 7 = 0;
x
2 − 6x
+ 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

x
2 − 2x
− 3 = 0;
15 − 2x
− x
2 = 0;
x
2 + 12x
+ 36 = 0.

Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.

D
> 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.

D
> 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

x
2 + 9x
= 0;
x
2 − 16 = 0.

Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю.

Если в неполном квадратном уравнении вида ax
2 + c
= 0 выполнено неравенство (−c
/a
) ≥ 0, корней будет два. Формула дана выше;
Если же (−c
/a
)

Вынесение общего множителя за скобку

Задача. Решить квадратные уравнения:
x
2 − 7x
= 0;
5x
2 + 30 = 0;
4x
2 − 9 = 0.

x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.

5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2
– 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2

+ х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет
.

Решить уравнение 2х 2

+ 5х – 7 = 0
.

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1
.

Итак представим решение полных квадратных уравнений схемой на рисунке1.

ах 2

+ bx + c,
иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Пример. Решить уравнение

3х 2

+ 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Найдем корни уравнения по формулам \(x_1=\frac{-b + \sqrt{D}}{2a}\) и \(x_1=\frac{-b — \sqrt{D}}{2a}\).

\(x_1=\frac{-1 + \sqrt{-23}}{2·3}\)

\(x_2=\frac{-1- \sqrt{-23}}{2·3}\)

Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Ответ: нет корней.

Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут).

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета. Это быстрее, но требует определенного навыка.2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут \(6\), а в сумме \(7\). Простым подбором получаем, что эти числа: \(1\) и \(6\). Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: \(x_1=1\), \(x_2=6\).

Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты \(b\) и \(c\).

Примеры решения полных, неполных и приведенных квадратных уравнений

Смотрите также:
Квадратные уравнения (шпаргалка)

Скачать статью

Как решить уравнение корней квадратного уравнения. Квадратные уравнения

Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение
, и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.

Навигация по странице.

Что такое уравнение?

Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения
:

Определение.

Уравнение
– это равенство, содержащее неизвестное число, которое надо найти.

Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p
, t
, u
и т.п., но наиболее часто используются буквы x
, y
и z
.

Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.

Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
, y=3
и т.п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.

Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18
и x+3·(x+2·(x−2))=3
. Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9
, также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8
, 7−3=z+1
или 3·x−4=2·(x+12)
.

Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений
, изучающиеся в школе.

В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:

Определение.

Уравнением
называют равенство, содержащее переменную, значение которой нужно найти.

Например, уравнение x+3=6·x+7
– уравнение с переменной x
, а 3·z−1+z=0
– уравнение с переменной z
.

На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.

Определение.

Уравнения с одной, двумя, тремя и т.д. переменными
– это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.

Например, уравнение 3,2·x+0,5=1
– это уравнение с одной переменной x
, в свою очередь уравнение вида x−y=3
– это уравнение с двумя переменными x
и y
. И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27
. Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.

Что такое корень уравнения?

С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.

Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a
в уравнение a+1=5
подставить число 2
, то получится неверное числовое равенство 2+1=5
. Если же мы в это уравнение подставим вместо a
число 4
, то получится верное равенство 4+1=5
.

На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.

Определение.

Корень уравнения
– это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.

Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.

Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5
. Согласно озвученному определению корня уравнения, число 4
есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5
, а число 2
не является его корнем, так как ему отвечает неверное равенство вида 2+1=5
.

На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.

Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5
имеет корень 4
, а уравнение 0·x=5
не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x
, мы получим неверное равенство 0=5
.

Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4
имеет единственный корень 6
, корнями уравнения x 2 =9
являются два числа −3
и 3
, уравнение x·(x−1)·(x−2)=0
имеет три корня 0
, 1
и 2
, а решением уравнения x=x
является любое число, то есть, оно имеет бесконечное множество корней.

Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества
в фигурных скобках. Например, если корнями уравнения являются числа −1
, 2
и 4
, то пишут −1
, 2
, 4
или {−1, 2, 4}
. Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
, и корнями этого уравнения являются числа 3
и 5
, то можно записать x=3
, x=5
, также переменной часто добавляют нижние индексы x 1 =3
, x 2 =5
, как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .

Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.

Определение.

Решением уравнения с двумя, тремя и т.д. переменными
называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.

Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
. Подставим в него вместо x
число 1
, а вместо y
число 2
, при этом имеем равенство 1+2=7
. Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.

Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.

Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7
. Решение этого уравнения x=4
, y=3
кратко можно записать как (4, 3)
.

Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений
.

Список литературы.

Математика
. 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
Алгебра:
учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
Алгебра:
9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.

Виды квадратных уравнений

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с
– какие-то числа. b и c
– совсем любые, а а
– любое, кроме нуля. Например:

Здесь а
=1; b
= 3; c
= -4

Здесь а
=2; b
= -0,5; c
= 2,2

Здесь а
=-3; b
= 6; c
= -18

Ну, вы поняли…

Такие квадратные уравнения называются полными.

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b
и c
равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Формула для нахождения корней квадратного уравнения выглядит так:

а
=1; b
= 3; c
= -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Предположим, надо вот такой примерчик решить:

Здесь a
= -6;
b
= -5;
c
= -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно?
Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения
.

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с
.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня.
х 1 = -3
, х 2 = 3
.

Дискриминант. Формула дискриминанта.

D = b 2 — 4ac

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1.

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно
.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0

х 2 = 5

х 1,2 =
2

х 1 = 2

х 2 = -0,5

х — любое число

х 1 = -3

х 2 = 3

решений нет

х 1 = 0,25

х 2 = 0,5

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

можно познакомиться с функциями и производными.

Уравнение вида

Выражение D
= b
2
— 4 ac
называют дискриминантом
квадратного уравнения. Если
D
= 0, то уравнение имеет один действительный корень; если D
> 0, то уравнение имеет два действительных корня.

В случае, когда D
= 0
, иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Используя обозначение D
= b
2
— 4 ac
, можно переписать формулу (2) в виде

Если b
= 2 k
, то формула (2) принимает вид:

где k
= b
/ 2
.
Последняя формула особенно удобна в тех случаях, когда b
/ 2
— целое число, т.е. коэффициент b
— четное число.
Пример 1:
Решить уравнение 2
x
2
—
5 x
+
2
=
0
. Здесь a = 2, b = -5, c = 2
. Имеем D
= b
2
—
4 ac
=
(-5) 2-
4*2*2
=
9
. Так как D
>
0
, то уравнение имеет два корня. Найдем их по формуле (2)

Итак x
1
=(5 + 3) / 4 = 2, x
2
=(5 — 3) / 4 = 1 / 2
,
то есть x
1
=
2
и x
2
=
1
/
2
— корни заданного уравнения.
Пример 2:
Решить уравнение 2
x
2
— 3 x
+ 5 = 0
. Здесь a = 2, b = -3, c = 5
. Находим дискриминант D
= b
2
—
4 ac
=
(-3) 2- 4*2*5 = -31
. Так как D
0
, то уравнение не имеет действительных корней.

Неполные квадратные уравнения.

Если в квадратном уравнении ax
2
+ bx
+ c
=0
второй коэффициент b
или свободный член c
равен нулю, то квадратное уравнение называется неполным
. Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Пример 1:
решить уравнение 2
x
2
— 5 x
= 0
.
Имеем x
(2 x
— 5) = 0
. Значит либо x
= 0
, либо 2
x
— 5 = 0
, то есть x
=
2.5
. Итак, уравнение имеет два корня: 0
и 2.5

Пример 2:
решить уравнение 3
x
2
— 27 = 0
.
Имеем 3
x
2
= 27
. Следовательно корни данного уравнения — 3
и -3
.

Теорема Виета.

Если приведенное квадратное уравнение x
2
+ px
+ q
=0
имеет действительные корни, то их сумма равна —
p
, а произведение равно q
, то есть

x 1 + x 2 = -p ,
x 1 x 2 = q

(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).

Квадратное уравнение – решается просто! *Далее в тексте «КУ».
Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим!
Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a,
b
и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1:
Решить 2x
2
+8
x
–192=0

а=2 b=8 c= –192

D = b
2
–4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2:
Решить

x 2
–22
x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3:
Решить

x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi

– это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а
x
2
+
bx
+
c
=0
выполняется равенство

a
+
b
+ с = 0,
то

— если для коэффициентов уравнения а
x
2
+
bx
+
c
=0
выполняется равенство

a
+ с =
b
,
то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001
x
2
–4995
x
– 6=0

Сумма коэффициентов равна 5001+(–
4995)+(–
6) = 0, значит

Пример 2: 2501
x
2
+2507
x
+6=0

Выполняется равенство a
+ с =
b
,
значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении
ax 2
+ bx
–
c = 0
коэффициент «b»

равен (a 2

– 1), а коэффициент «c»

численно равен коэффициенту «a»
,
то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а
± b+c
≠ 0, то используется прием переброски, например:

2х
2 – 11х+
5 = 0 (1) => х
2 – 11х+
10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1
= 5 х 2
=
0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

1. Линейное уравнение

Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х 1,2 = (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а

Также можно определить визуально количество корней, не вычисляя дискриминант. Для этого нужно найти вершину параболы и определить в какую сторону направлены ветви. Определить координату x вершины можно по формуле: х 0 = -b / 2a. В этом случае координата y вершины находится простой подстановкой значения х 0 в изначальное уравнение.

Квадратное уравнение x 2 — 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (-8) 2 — 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

3. Тригонометрические уравнения

Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

в линейном уравнении mx = n значение m = 0 и n = 0;
в квадратном уравнении, если дискриминант меньше нуля;
в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Квадратичная формула — объяснение и примеры

К настоящему времени вы знаете, как решать квадратные уравнения с помощью таких методов, как завершение квадрата, разность квадрата и формула трехчлена полного квадрата.

В этой статье мы узнаем, как решать квадратные уравнения, используя два метода, а именно квадратную формулу и графический метод . Прежде чем мы углубимся в эту тему, давайте вспомним, что такое квадратное уравнение.

Что такое квадратное уравнение?

Квадратное уравнение в математике определяется как многочлен второй степени, стандартная форма которого — ax ² + bx + c = 0, где a, b и c — числовые коэффициенты, а a 0.

Термин второй степени означает, что хотя бы один член в уравнении возведен в степень двойки. В квадратном уравнении переменная x является неизвестным значением, для которого нам нужно найти решение.

Примеры квадратных уравнений: 6x² + 11x — 35 = 0, 2x² — 4x — 2 = 0, 2x² — 64 = 0, x² — 16 = 0, x² — 7x = 0, 2x² + 8x = 0 и т. Д.Из этих примеров вы можете заметить, что в некоторых квадратных уравнениях отсутствуют члены «c» и «bx».

Как пользоваться формулой корней квадратного уравнения?

Предположим, что ax ² + bx + c = 0 — наше стандартное квадратное уравнение. Мы можем вывести квадратную формулу, заполнив квадрат, как показано ниже.

Выделите член c в правой части уравнения

ax ² + bx = -c

Разделите каждый член на a.

x ² + bx / a = -c / a

Выразить как полный квадрат
x ² + b x / a + (b / 2a) ² = — c / a + (b / 2a) ²

(x + b / 2a) ² = (-4ac + b ²) / 4a ²

(x + b / 2a) = ± √ (-4ac + b ²) / 2a

x = — b / 2a ± √ (b ² — 4ac) / 2a

x = [- b ± √ (b ² — 4ac)] / 2a …… ….(Это квадратная формула)

Наличие плюса (+) и минуса (-) в квадратной формуле означает, что существует два решения, например:

x ₁ = (-b + √b2 — 4ac) / 2a

AND,

x ₂ = (-b — √b2 — 4ac) / 2a

Два вышеуказанных значения x известны как корни квадратного уравнения. Корни квадратного уравнения зависят от природы дискриминанта. Дискриминант является частью формулы корней квадратного уравнения в виде b ² — 4 ac.Квадратное уравнение имеет два разных действительных корня дискриминанта.

Когда значение дискриминанта равно нулю, уравнение будет иметь только один корень или решение. А если дискриминант отрицательный, то квадратное уравнение не имеет действительного корня.

Как решать квадратные уравнения?

Давайте решим несколько примеров задач, используя формулу корней квадратного уравнения.

Пример 1

Используйте формулу корней квадратного уравнения, чтобы найти корни x ² -5x + 6 = 0.

Решение

Сравнение уравнения с общей формой ax ² + bx + c = 0 дает

a = 1, b = -5 и c = 6

b ² — 4ac = ( -5) 2-4 × 1 × 6 = 1

Подставляем значения в формулу корней квадратного уравнения

x ₁ = (-b + √b2-4ac) / 2a

⇒ (5 + 1) / 2

= 3

x ₂ = (-b — √b2-4ac) / 2a

⇒ (5-1) / 2

= 2

Пример 2

Решите квадратное уравнение ниже используя квадратную формулу:

3x ² + 6x + 2 = 0

Решение

Сравнение задачи с общей формой квадратного уравнения ax ² + bx + c = 0 дает,

a = 3 , b = 6 и c = 2

x = [- b ± √ (b ² — 4ac)] / 2a

⇒ [- 6 ± √ (6 ² — 4 * 3 * 2)] / 2 * 3

⇒ [- 6 ± √ (36-24)] / 6

⇒ [- 6 ± √ (1 2)] / 6

x ₁ = (-6 + 2√3) / 6

⇒ — (2/3) √3

x ₂ = (-6– 2√3) / 6

⇒ — (4/3) √3

Пример 3

Решить 5x ² + 6x + 1 = 0

Решение

Сравнивая с квадратным уравнением, получаем

a = 5, b = 6, c = 1

Теперь примените квадратную формулу:

x = −b ± √ (b ² — 4ac) 2a

Подставьте значения a, b и c

⇒ x = −6 ± √ (6 ² — 4 × 5 × 1) 2 × 5

⇒ x = −6 ± √ (36-20) 10

⇒ x = −6 ± √ (16) 10

⇒ x = −6 ± 410

⇒ x = — 0.2, −1

Пример 4

Решить 5x ² + 2x + 1 = 0

Решение

Коэффициенты:

a = 5, b = 2, c = 1

В этом случае дискриминант отрицательный:

b ² — 4ac = 2 ² — 4 × 5 × 1

= −16

Теперь примените формулу корней квадратного уравнения;

x = (−2 ± √ −16) / 10

⇒√ (−16) = 4

Где i — мнимое число √ − 1

⇒x = (−2 ± 4i) / 10

Следовательно, x = −0.2 ± 0,4i

Пример 5

Решить x ² — 4x + 6,25 = 0

Решение

Согласно стандартной форме квадратного уравнения ax ² + bx + c = 0, мы можем это наблюдать;

a = 1, b = −4, c = 6,25

Определите дискриминанты.

b ² — 4ac = (−4) ² — 4 × 1 × 6,25

= −9 ………………. (отрицательный дискриминант)

⇒ x = — (- 4) ± √ (−9) / 2

⇒ √ (−9) = 3i; где i — мнимое число √ − 1

⇒ x = (4 ± 3i) / 2

Следовательно, x = 2 ± 1.5i

Как построить квадратное уравнение?

Чтобы построить квадратное уравнение, выполните следующие действия:

Для квадратного уравнения перепишите уравнение, приравняв его к y или f (x)
Выберите произвольные значения x и y для построения кривой
Теперь изобразите функцию.
Считайте корни там, где кривая пересекает или касается оси x.

Решение квадратных уравнений с помощью построения графиков

Построение графиков — это еще один метод решения квадратных уравнений.Решение уравнения получается путем считывания отрезков x на графике.

Есть три возможности при решении квадратных уравнений графическим методом:

Уравнение имеет один корень или решение, если точка пересечения по оси x графика равна 1.
Уравнение с двумя корнями имеет 2 точки пересечения x
Если нет x-точек пересечения, то уравнение не имеет реальных решений.

Давайте изобразим несколько примеров квадратных уравнений.В этих примерах мы нарисовали наши графики с помощью графического программного обеспечения, но чтобы вы хорошо поняли этот урок, нарисуйте свои графики вручную.

Пример 1

Решите уравнение x ² + x — 3 = 0 графическим методом

Решение

Наши произвольные значения показаны в таблице ниже:

x- точки пересечения: x = 1,3 и x = –2,3. Следовательно, корни квадратного уравнения равны x = 1.3 и x = –2,3

Пример 2

Решите уравнение 6x — 9 — x ² = 0.

Решение

Выберите произвольные значения x.

Кривая касается оси x в точке x = 3. Следовательно, 6 x — 9 — x ² = 0 имеет одно решение (x = 3).

Пример 3

Решите уравнение x ² + 4x + 8 = 0 графическим методом.

Решение

Выберите произвольные значения x.

В этом примере кривая не касается и не пересекает ось x. Следовательно, квадратное уравнение x ² + 4x + 8 = 0 не имеет действительных корней.

Практические вопросы

Решите следующие квадратные уравнения, используя как квадратную формулу, так и графический метод:

x ² — 3x −10 = 0
x ² + 3x + 4 = 0
x ² −7x + 12 = 0
x ² + 14x + 45 = 0
9 + 7x = 7x ²
x ² + 4x + 4 = 0
x ² — 9x + 14 = 0
2x ² — 3x = 0
4𝑥 ² — 4𝑥 + 5 = 0
4𝑥 ² — 8𝑥 + 1 = 0
x ² + 4x — 12 = 0
10x ² + 7x — 12 = 0
10 + 6x — x ² = 0
2x ² + 8x — 25 = 0
x ² + 5x — 6 = 0
3x ² — 27x + 9
15 — 10x — x ²
5x ² + 10x + 15
24 + 12x — 2x ²
x ² −1 2x + 35 = 0

Предыдущий урок | Главная страница | Следующий урок

6. {2} + b x + c = 0 \)

как уравнение вида

Этот процесс называется , завершение квадрата ⁴.{2} = \ color {Cerulean} {1} \)

Чтобы завершить квадрат, добавьте \ (1 \) к обеим сторонам, завершите квадрат и затем решите, извлекая корни.

На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно.

Ответ :

Решения: \ (- 8 \) и \ (6 \).

Примечание

В предыдущем примере решения — целые числа. Если это так, то будет учитываться исходное уравнение.

Если уравнение множится, мы можем решить его путем факторизации.{2} — 10 х + 26 = 0 \).

Решение

Начните с вычитания \ (26 \) из обеих частей уравнения.

Здесь \ (b = -10 \), и мы определяем значение, завершающее квадрат, следующим образом:

Чтобы получить квадрат, добавьте \ (25 \) к обеим сторонам уравнения. {2} + 18 \), где \ (t \) представляет время через секунды после падения объекта.{2} + 50 \), где \ (t \) представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю? (Округлите до ближайшей сотой доли секунды.)

Какова высота лестницы длиной \ (22 \) футов, если ее основание находится в \ (6 \) футах от здания, на которое она опирается? Округлите до ближайшей десятой доли фута.
Высота треугольника равна \ (\ frac {1} {2} \) длине его основания. Если площадь треугольника составляет \ (72 \) квадратных метров, найдите точную длину основания треугольника.

Ответ

1. \ (\ pm 9 \)

3. \ (\ pm \ frac {1} {3} \)

5. \ (\ pm 2 \ sqrt {3} \)

7. \ (\ pm \ frac {3} {4} \)

9. \ (\ pm \ frac {\ sqrt {2}} {2} \)

11. \ (\ pm 2 \ sqrt {10} \)

13. \ (\ pm i \)

15. \ (\ pm \ frac {\ sqrt {5}} {5} \)

17. \ (\ pm \ frac {\ sqrt {2}} {4} i \)

19.\ (\ pm 2 i \)

21. \ (\ pm \ frac {2} {3} \)

23. \ (\ pm 2 \ sqrt {2} \)

25. \ (\ pm 2 i \ sqrt {2} \)

27. \ (\ pm \ frac {\ sqrt {10}} {5} \)

29. \ (- 9, -5 \)

31. \ (5 \ pm 2 \ sqrt {5} \)

33. \ (- \ frac {2} {3} \ pm \ frac {\ sqrt {6}} {3} i \)

35. \ (\ frac {- 2 \ pm 3 \ sqrt {3}} {6} \)

37. \ (\ frac {1} {3} \ pm \ frac {\ sqrt {6}} {6} i \)

39.{2} = 3 (3 т + 1) \)

\ ((3 t + 2) (t-4) — (t-8) = 1-10 t \)

Ответ

1. \ (- 15 \ pm \ sqrt {10} \)

3. 1 \ (\ pm 2 \ sqrt {2} \)

5. 1 \ (\ pm i \ sqrt {3} \)

7. \ (- 15,5 \)

9. \ (- \ frac {1} {3}, 1 \)

11. \ (\ frac {-1 \ pm \ sqrt {5}} {2} \)

13. \ (\ frac {-3 \ pm \ sqrt {17}} {2} \)

15. \ (- \ frac {3} {2} \ pm \ frac {\ sqrt {11}} {2} i \)

17.\ (\ frac {7 \ pm 3 \ sqrt {3}} {2} \)

19. \ (\ frac {1 \ pm \ sqrt {17}} {4} \)

21. \ (\ frac {2 \ pm \ sqrt {5}} {2} \)

23. \ (\ frac {-3 \ pm \ sqrt {6}} {3} \)

25. \ (\ frac {-1 \ pm \ sqrt {10}} {3} \)

27. \ (\ frac {3 \ pm 2 \ sqrt {6}} {2} \)

29. 1 \ (\ pm 2 i \)

31. \ (\ frac {1 \ pm \ sqrt {17}} {4} \)

33. \ (\ frac {-1 \ pm \ sqrt {7}} {3} \)

35. 2 \ (\ pm 2 \ sqrt {5} \)

37.{2} -6 (6 x + 1) = 0 \)

Ответ

1. \ (0.19,1.31 \)

3. \ (- 0,45,1,12 \)

5. \ (0,33,0,67 \)

Упражнение \ (\ PageIndex {11} \)

Создайте собственное уравнение, которое можно решить, извлекая корни. Поделитесь им вместе с решением на доске обсуждений.
Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.{2} = q \).
Извлечение квадратного корня
Извлечение квадратного корня
Напомним, что квадратное уравнение имеет стандартную форму Любое квадратное уравнение в форме ax2 + bx + c = 0, где a , b и c — действительные числа и a 0. если он равен 0:
, где a , b и c — действительные числа и a 0. Решение такого уравнения называется корневым решением квадратного уравнения в стандартной форме.. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Если квадратное выражение слева множители, то мы можем решить его путем факторизации. Обзор шагов, используемых для решения с помощью факторинга, следующий:
Шаг 1: Выразите квадратное уравнение в стандартной форме.
Шаг 2: Разложите квадратное выражение на множители.
Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным 0.
Шаг 4: Решите полученные линейные уравнения.
Например, мы можем решить x2−4 = 0, разложив на множители следующим образом:
Двумя решениями являются −2 и 2. Цель этого раздела — разработать альтернативный метод, который можно использовать для простого решения уравнений, где b = 0, что дает форму
Уравнение x2−4 = 0 находится в этой форме и может быть решено путем выделения x2 вначале.
Если извлечь квадратный корень из обеих частей этого уравнения, мы получим следующее:
Здесь мы видим, что x = −2 и x = 2 являются решениями полученного уравнения. В общем, это описывает свойство квадратного корня для любого действительного числа k , если x2 = k, то x = ± k .; для любого действительного числа k ,
Обозначение «±» читается как «плюс или минус» и используется как компактное обозначение, обозначающее два решения.Следовательно, утверждение x = ± k указывает, что x = −k или x = k. Применение свойства квадратного корня как средства решения квадратного уравнения называется извлечением корней Применение свойства квадратного корня как средства решения квадратного уравнения.
Пример 1: Решить: x2−25 = 0.
Решение: Начните с выделения квадрата.
Затем примените свойство квадратного корня.
Ответ: Решения — 5 и 5.Чек предоставляется читателю.
Конечно, предыдущий пример можно было бы так же легко решить с помощью факторинга. Тем не менее, он демонстрирует метод, который можно использовать для решения уравнений в этой форме, которые не учитывают факторы.
Пример 2: Решить: x2−5 = 0.
Решение: Обратите внимание, что квадратное выражение слева не множится. Мы можем извлечь корни, если сначала выделим главный член x2.
Примените свойство квадратного корня.
Для полноты проверьте, что эти два действительных решения решают исходное квадратное уравнение. Как правило, проверка не является обязательной.
Ответ: Решения — 5 и 5.
Пример 3: Решить: 4×2-45 = 0.
Решение: Начните с изоляции x2.
Примените свойство квадратного корня, а затем упростите.
Ответ: Решения — 352 и 352.
Иногда квадратные уравнения не имеют реального решения.
Пример 4: Решить: x2 + 9 = 0.
Решение: Начните с изоляции x2.
После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, у этого уравнения нет реального решения.
Ответ: Реального решения нет
Обратитесь к этому процессу, чтобы найти уравнения с заданными решениями вида ± k .
Пример 5: Найдите уравнение с решениями −23 и 23.
Решение: Начните с возведения в квадрат обеих частей следующего уравнения:
Наконец, вычтите 12 из обеих частей и представьте уравнение в стандартной форме.
Ответ: x2−12 = 0
Попробуй! Решить: 9×2−8 = 0.
Ответ: x = −223 или x = 223
Рассмотрите возможность решения следующего уравнения:
Чтобы решить это уравнение путем факторизации, сначала возведите в квадрат x + 2, а затем представьте его в стандартной форме, равной нулю, путем вычитания 25 из обеих частей.
Коэффициент
, а затем применить свойство нулевого произведения.
Два решения: −7 и 3.
Когда уравнение имеет такую форму, мы можем получить решения за меньшее количество шагов, извлекая корни.
Пример 6: Решите: (x + 2) 2 = 25.
Решение: Решите, извлекая корни.
На этом этапе разделите «плюс или минус» на два уравнения и упростите каждое по отдельности.
Ответ: Решения −7 и 3.
В дополнение к меньшему количеству шагов этот метод позволяет нам решать уравнения, которые не учитывают множители.
Пример 7: Решите: (3x + 3) 2−27 = 0.
Решение: Начните с выделения квадрата.
Затем извлеките корни и упростите.
Решите для x .
Ответ: Решения: −1−3 и −1 + 3.
Пример 8: Решить: 9 (2x − 1) 2−8 = 0.
Решение: Начните с выделения квадратного множителя.
Примените свойство квадратного корня и решите.
Ответ: Решения 3−226 и 3 + 226.
Попробуй! Решите: 3 (x − 5) 2−2 = 0.
Ответ: 15 ± 63
Пример 9: Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.
Решение:
Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы:
Решить.
Здесь мы получаем два решения, w = −25 и w = 25. Поскольку в задаче требовалась длина прямоугольника, мы игнорируем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе.
Обратно подставить, чтобы найти длину.
Ответ: Длина прямоугольника составляет 455 футов, а ширина — 255 футов.
Основные выводы
Решите уравнения вида ax2 + c = 0, извлекая корни.
Извлечение корней включает выделение квадрата и последующее применение свойства квадратного корня. После применения свойства квадратного корня у вас есть два линейных уравнения, каждое из которых можно решить. Обязательно упростите все радикальные выражения и при необходимости рационализируйте знаменатель.
Тематические упражнения
Часть A: извлечение квадратного корня
Решите с помощью факторизации, а затем извлеките корни.Проверить ответы.
1. x2−36 = 0
2. x2−81 = 0
3. 4y2−9 = 0
4. 9y2−25 = 0
5. (x − 2) 2−1 = 0
6. (x + 1) 2−4 = 0
7. 4 (y − 2) 2−9 = 0
8. 9 (y + 1) 2−4 = 0
9. −3 (t − 1) 2 + 12 = 0
10. −2 (t + 1) 2 + 8 = 0
11. (x − 5) 2−25 = 0
12. (x + 2) 2−4 = 0
Решите, извлекая корни.
13. x2 = 16
14. x2 = 1
15. y2 = 9
16. y2 = 64
17. x2 = 14
18. x2 = 19
19. y2 = 0,25
20. y2 = 0,04
21. x2 = 12
22. x2 = 18
23. 16×2 = 9
24. 4×2 = 25
25. 2t2 = 1
26.3t2 = 2
27. x2−100 = 0
28. x2−121 = 0
29. y2 + 4 = 0
30. y2 + 1 = 0
31. x2−49 = 0
32. x2−925 = 0
33. y2−0.09 = 0
34. y2−0,81 = 0
35. x2−7 = 0
36. x2−2 = 0
37. x2−8 = 0
38. t2−18 = 0
39. x2 + 8 = 0
40.х2 + 125 = 0
41. 16×2−27 = 0
42. 9×2-8 = 0
43. 2y2−3 = 0
44. 5y2−2 = 0
45. 3×2−1 = 0
46. 6×2−3 = 0
47. (x + 7) 2−4 = 0
48. (x + 9) 2−36 = 0
49. (2y − 3) 2−81 = 0
50. (2у + 1) 2−25 = 0
51. (x − 5) 2−20 = 0
52. (x + 1) 2−28 = 0
53.(3t + 2) 2−6 = 0
54. (3т − 5) 2−10 = 0
55,4 (y + 2) 2−3 = 0
56. 9 (y − 7) 2−5 = 0
57,4 (3x + 1) 2−27 = 0
58. 9 (2x − 3) 2−8 = 0
59. 2 (3x − 1) 2 + 3 = 0
60,5 (2x − 1) 2−3 = 0
61,3 (y − 23) 2−32 = 0
62. 2 (3y − 13) 2−52 = 0
Найдите квадратное уравнение стандартной формы со следующими решениями.
63. ± 7
64. ± 13
65. ± 7
66. ± 3
67. ± 35
68. ± 52
69. 1 ± 2
70,2 ± 3
Решите и округлите решения до сотых.
71. 9x (x + 2) = 18x + 1
72. x2 = 10 (x2−2) −5
73. (x + 3) (x − 7) = 11−4x
74.(x − 4) (x − 3) = 66−7x
75. (x − 2) 2 = 67−4x
76. (x + 3) 2 = 6x + 59
77. (2x + 1) (x + 3) — (x + 7) = (x + 3) 2
78. (3x − 1) (x + 4) = 2x (x + 6) — (x − 3)
Составьте алгебраическое уравнение и используйте его для решения следующих задач.
79. Если 9 вычесть из четырех квадратов числа, то результат будет 3. Найдите число.
80. Если из квадрата числа вычесть 20, то получится 4.Найдите номер.
81. Если 1 прибавить к троекратному квадрату числа, то получится 2. Найдите число.
82. Если 3 прибавить к двукратному квадрату числа, получится 12. Найдите число.
83. Если квадрат имеет площадь 8 квадратных сантиметров, найдите длину каждой стороны.
84. Если круг имеет площадь 32π квадратных сантиметра, найдите длину радиуса.
85.Объем правого кругового конуса составляет 36π кубических сантиметров при высоте 6 сантиметров. Найдите радиус конуса. (Объем правого кругового конуса равен V = 13πr2h.)
86. Площадь поверхности сферы составляет 75π квадратных сантиметров. Найдите радиус сферы. (Площадь поверхности сферы определяется как SA = 4πr2.)
87. Длина прямоугольника в 6 раз больше его ширины. Если площадь составляет 96 квадратных дюймов, найдите размеры прямоугольника.
88. Основание треугольника вдвое больше его высоты. Если площадь составляет 16 квадратных сантиметров, то найдите длину его основания.
89. Квадрат имеет площадь 36 квадратных единиц. На какую равную величину необходимо увеличить стороны, чтобы получить квадрат с удвоенной заданной площадью?
90. Круг имеет площадь 25π квадратных единиц. На какую величину нужно увеличить радиус, чтобы создать круг с удвоенной заданной площадью?
91.Если стороны квадрата равны 1 единице, то найдите длину диагонали.
92. Если стороны квадрата равны 2 единицам, найдите длину диагонали.
93. Диагональ квадрата составляет 5 дюймов. Найдите длину каждой стороны.
94. Диагональ квадрата составляет 3 дюйма. Найдите длину каждой стороны.
95. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 10 футов, найдите размеры прямоугольника.
96. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 8 футов, найдите размеры прямоугольника.
97. Длина прямоугольника в 3 раза больше его ширины. Если диагональ 5 метров, то найдите размеры прямоугольника.
98. Длина прямоугольника в 3 раза больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.
99. Высота в футах объекта, падающего с 9-футовой лестницы, определяется выражением h (t) = — 16t2 + 9, где t представляет время в секундах после падения объекта.Сколько времени нужно, чтобы объект упал на землю? (Подсказка: когда объект ударяется о землю, высота равна 0.)
100. Высота в футах объекта, падающего с 20-футовой платформы, определяется выражением h (t) = — 16t2 + 20, где t представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю?
101. Высота в футах объекта, падающего с вершины 144-футового здания, определяется выражением h (t) = — 16t2 + 144, где t измеряется в секундах.
а. Сколько времени потребуется, чтобы достичь половины расстояния до земли, 72 фута?
г. Сколько времени потребуется, чтобы добраться до земли?
Округлите до сотых долей секунды.
102. Высота в футах объекта, сброшенного с самолета на высоте 1600 футов, определяется выражением h (t) = — 16t2 + 1,600, где t — секунды.
а. Сколько времени потребуется, чтобы добраться до земли на половину расстояния?
г.Сколько времени потребуется, чтобы добраться до земли?
Округлить до сотых долей секунды .
Часть B: Обсуждение
103. Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им вместе с решением на доске обсуждений.
104. Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.
105. Объясните своими словами, как решить, извлекая корни.
106. Выведите формулу диагонали квадрата через его стороны.
Ответы
1: −6, 6
3: −3/2, 3/2
5: 1, 3
7: 1/2, 7/2
9: -1, 3
11: 0, 10
13: ± 4
15: ± 3
17: ± 1/2
19: ± 0.5
21: ± 23
23: ± 3/4
25: ± 22
27: ± 10
29: Реального решения нет
31: ± 2/3
33: ± 0,3
35: ± 7
37: ± 22
39: Реального решения нет
41: ± 334
43: ± 62
45: ± 33
47: −9, −5
49: −3, 6
51: 5 ± 25
53: −2 ± 63
55: −4 ± 32
57: −2 ± 336
59: Реального решения нет
61: 4 ± 326
63: x2−49 = 0
65: x2−7 = 0
67: x2-45 = 0
69: x2−2x − 1 = 0
71: ± 0.33
73: ± 5,66
75: ± 7,94
77: ± 3.61
79: −3 или 3
81: −33 или 33
83:22 сантиметра
85:32 сантиметра
87: Длина: 24 дюйма; ширина: 4 дюйма
89: −6 + 62≈2,49 ед.
91: 2 шт.
93: 522 дюйма
95: Длина: 45 футов; ширина: 25 футов
97: Длина: 3102 метра; ширина: 102 метра
99: 3/4 секунды
101: а.2,12 секунды; б. 0,88 секунды
.

Что делать, если из дискриминанта корень не извлекается? Я обычно грущу

Некоторые частные случаи

Приведенное уравнение второй степени

Видео

Разобьём выражение на составляющие множители

Пример

Разложение выражения на множители

Извлечение квадратного корня

Вычисление пощади земельного участка

Дискриминант

О корнях и их формуле

Примеры и задачи

Теорема Виета

График и уравнение параболы

Пересечение ветвей параболы с осью абсцисс

Из истории

Геометрический смысл квадратного уравнения

Формула дискриминанта и корней квадратного уравнения

Теорема Виета

– Что Вы делаете, если из дискриминанта корень не

АНЕКДОТ

Похожие:

Виды квадратных уравнений

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Решение неполных квадратных уравнений.

Дискриминант. Формула дискриминанта.

Дискриминант

Корни квадратного уравнения

Неполные квадратные уравнения

Нахождение дискриминанта, формула, сравнение с нулём

О каких уравнениях пойдет речь?

Способы решения уравнений второго порядка

Формула для получения корней уравнения

Понятие о дискриминанте

Задача на определение дискриминанта

Пример неравенства через дискриминант

Пример решения уравнения

Геометрическая задача

Виды квадратных уравнений

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Решение неполных квадратных уравнений.

Дискриминант. Формула дискриминанта.

Дискриминант

Корни квадратного уравнения

Неполные квадратные уравнения

Примеры решения полных, неполных и приведенных квадратных уравнений

Как решить уравнение корней квадратного уравнения. Квадратные уравнения

Что такое уравнение?

Что такое корень уравнения?

Виды квадратных уравнений

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Решение неполных квадратных уравнений.

Дискриминант. Формула дискриминанта.

Какое уравнение не имеет корней?

1. Линейное уравнение

2. Квадратное уравнение

3. Тригонометрические уравнения

4. Системы уравнений

Рекомендации по решению квадратных уравнений и приложений

Тематические упражнения

Ответы

Квадратичная формула — объяснение и примеры

Что такое квадратное уравнение?

Как пользоваться формулой корней квадратного уравнения?

Как решать квадратные уравнения?

Как построить квадратное уравнение?

Решение квадратных уравнений с помощью построения графиков

6. {2} + b x + c = 0 \)

Извлечение квадратного корня

Извлечение квадратного корня

Основные выводы

Тематические упражнения

Ответы

Добавить комментарий Отменить ответ