Дискриминант деленный на 4: Дискриминант деленный на 4 примеры. Решение квадратных уравнений

alexxlab

Содержание

★ Формула дискриминанта | Информация

Пользователи также искали:



алгебра 9 класс,

дискриминант 0,

дискриминант 1,

дискриминант меньше нуля,

дискриминант равен 0,

дискриминант решение,

дискриминант,

формула дискриминанта и корней,

формула дискриминанта квадратного уравнения,

формула дискриминанта на 4,

формула дискриминанта пример,

Формула Кардано,

формула корней дискриминанта,

формула нахождения дискриминанта,

формула сокращенного дискриминанта,

формулы дискриминанта,

гдз по алгебре 9 класс макарычев,

корни дискриминанта формула,

решение квадратных уравнений,

теорема виета,

                                     



Решение корни квадратного уравнения. Квадратные. Алгоритмы решения уравнения неравенства. Формулы дискриминанта и корней квадратного. .. Решение квадратных уравнений. Дискриминант. Формула. Решить квадратное уравнение можно через дискриминант и с помощью Формула для вычисления дискриминанта достаточно проста, поэтому. .. Дискриминант Онлайн калькулятор. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения. Вернемся к нашей формуле для нахожденя. .. Дискриминант 0. Формула №1: b ± √ x, где b2 – 4ac. 2a. Латинской буквой D обозначают. Дискриминант это выражение, от которого. .. Дискриминант. Формула дискриминанта.. 5 фев 2014 Об отдельных случаях вычисления дискриминанта Прежде чем разбирать примеры, вспомним все же формулу дикриминанта D. .. Формулы корней квадратного уравнения. Дискриминант. 18 май 2010 решать полные неполные квадратные уравнения? Формула и смысл дискриминанта. Как резко снизить количество ошибок?. .. Квадратные уравнения. Решение квадратных уравнений. 27 июн 2016 Решение квадратного уравнения, нахождение корней через дискриминант. Поддержать Проект:. .. Дискриминант квадратного уравнения. Формулы дискриминанта. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Дискриминат 4 и на 1. Теорема Виета. 3 способа. от. .. Дискриминант, формула дискриминанта многочлена. Вычисление квадратного многочлена и многочленов более высоких Из школьного курса хорошо известна формула дискриминанта. .. Дискриминант, делённый на 4 ВКонтакте. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Дискриминат 4 и на 1. Теорема Виета. 3 способа..
Квадратные уравнения и неравенства. Алгоритмы решения. Дискриминант, формула дискриминанта, гурвициан многочлена, критерий Гурвица.. .. Квадратные уравнения. Дискриминант. Решение, примеры.. Рассмотрено что такое дискриминант в формулах нахождения корней уравнений, формулы дискриминантов. Решение квадратных. .. макsим on Twitter формула дискриминанта мозг: хз я: а че там. 28 ноя 2018: формула дискриминанта: хз: а че там за песня была заставке букиных мозг: хочешь я взгляну в твои глаза и слова. .. § Дискриминант. Решение квадратных уравнений через. Эта подсказка поможет легко запомнить формулу корней квадратного уравнения, если дискриминант равен 0.. .. Решение квадратных уравнений. 6 июл 2011 Эту формулу надо знать наизусть. Откуда она берется сейчас неважно. Важно другое: по знаку дискриминанта можно определить,. .. Дискриминант квадратного уравнения с большими. 26 сен 2018 Формула дискриминанта, деленного на 4: Как и для случая с обычным дискриминантом, количество корней квадратного уравнения. .. Квадратное уравнение. Решение квадратных уравнений. Квадратное уравнение. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Дискриминат 4 и на 1. Теорема Виета. 3. .. Дискриминант. Теорема Виета. Дискриминант. Квадратичная функция имеет вид: ax2 bx c 0. Формула дискриминанта: D b2 4ac. Онлайн калькулятор предназначен для нахождения. .. Квадратное уравнение, дискриминант, формула корней YouTube. . Сам термин образован от лат. discriminar, что в переводе разбирать, различать. Формула дискриминанта. Дискриминант D. .. Дискриминант онлайн. Как решить квадратное уравнение, то есть найти его корни теория и примеры, формула дискриминанта, применение корней квадратного уравнения в.

«Повторение: Решение линейных, квадратных, рациональных уравнений»

Тема урока «Повторение:

 Решение линейных, квадратных, рациональных уравнений»

Цели урока:

  1. обучающие: актуализировать умение решать уравнения как аналитически, так и графически,

  2. развивающие: развивать умение учащихся систематизировать учебный материал, развивать коммуникативную культуру,

  3. воспитывающие:  формировать у учащихся интерес к предмету.

Тип урока: урок обобщения изученного материала

План урока

  1. организационный момент,

  2. актуализация теоретических знаний по теме,

  3. постановка цели занятия перед учащимися, объявление темы урока,

  4. практическая работа на построение графиков изученных функций и применение их для решения уравнений,

  5. повторение алгоритма аналитического способа решения уравнений (памятка для учащихся, имеющих трудности в обучении),

  6. диагностика усвоения материала по теме (разноуровневая самостоятельная работа),

  7. запись домашнего задания (пояснения),

  8. подведение итогов урока.

  9. Оборудование

Мультимедийные средства обучения, раздаточные материалы.

                                                          Ход урока

  1. Организационный момент, характеризующийся внешней и внутренней (психологической) готовностью к уроку.

(Перед уроком приготовить раздаточный материал, предусмотреть наличие линеек, карандашей).

  1. Актуализация теоретических знаний по теме «Решение уравнений»Учащимся предлагается тест-разминка «Проверь себя» — продолжительностью 5-6 минут (приложение 1). Проверка правильности выполнения осуществляется непосредственно самими учащимися через показ ответов на слайде. Учащиеся имеют возможность оценить свою подготовку к уроку (Критерии оценки прилагаются).

№п/п

Задание

Ответ

1

Равенство с переменной называется…

 уравнением

2

Значение переменной, подстановка которого в уравнение превращает его в верное равенство, называется…

Корнем уравнения

3

Найдите корни уравнения 3х + 9 = 9

0

4

Найдите корни уравнения 0х = 0

0

5

Найдите корни уравнения х2 – 16 = 0

-4; 4

6

Найдите корни уравнения х2 – 4х + 4 = 0

2

7

Как называется выражение D = b2 – 4ac

дискриминантом

8

Назовите условие, при котором в квадратном уравнении 2 корня,

один корень,

нет корней

D>0

D=0

D<0

9

В каком случае корни квадратного уравнения будут иррациональными числами

Если  — иррациональное число

10

Верно ли записана формула корней квадратного уравнения х =

Неверно, правильный ответ х =

11

Когда квадратное уравнение считают полным

Если в нем a,b,c ≠0

12

Заполните пропуски в стихотворении:

О свойстве корней теорема …

Что лучше, скажи, постоянства такого?

Умножишь ты корни, и дробь уж готова:

В числителе …, в знаменателе – «a».

И сумма корней тоже дроби равна.

Хоть с минусом дробь эта, что за беда.

В числителе …, в знаменателе — …

Виета

c

-b;   a

13

Угадайте корни уравнения с помощью данной теоремы:

х2 – х – 6 = 0

х2 + 5х – 6 = 0

х2 + 2004х – 2005 = 0

-х2 + 8х – 12 = 0

-2; 3

-6; 1

-2005; 1

2; 6

14

Перечислите способы решения уравнений

Графический и аналитический

15

Функция вида y = ax + b называется…, ее графиком является…

Линейной, прямая

16

Функция вида y = ax2 + bx + c, a≠ 0,  называется…, ее графиком является…

Квадратичной, парабола

17

Функция видаy k/x, x≠ 0, называется…, ее графиком является…

Обратной пропорциональностью, гипербола

II вариант

№п/п

Задание

Ответ

1

Что значит решить уравнение

 Найти корни уравнения или доказать, что в уравнении корней нет

2

Найдите корни уравнения 0х = 15,3

Корней нет

3

Найдите корни уравнения 3х + 9 = 0

-3

4

Найдите корни уравнения х2 – 4х = 0

0; 4

5

Найдите корни уравнения х2 + 16 = 0

Корней нет

6

Найдите корни уравнения х2 + 4х + 4 = 0

-2

7

Для чего нужен дискриминант

Для решения полных квадратных уравнений

8

Назовите условие, при котором в квадратном уравнении 2 корня,

один корень,

нет корней

D>0

D=0

D<0

9

В каком случае корни квадратного уравнения будут иррациональными числами

Если  — иррациональное число

10

Верно ли записана формула корней квадратного уравнения х =

Неверно, правильный ответ х =

11

Когда квадратное уравнение считают приведенным

Если в нем a=1

12

Заполните пропуски в стихотворении:

О свойстве корней теорема …

Что лучше, скажи, постоянства такого?

Умножишь ты корни, и дробь уж готова:

В числителе …, в знаменателе – «a».

И сумма корней тоже дроби равна.

Хоть с минусом дробь эта, что за беда.

В числителе …, в знаменателе — …

Виета

c

-b;   a

13

Угадайте корни уравнения с помощью данной теоремы:

х2 – х – 6 = 0

х2 + 5х – 6 = 0

х2 + 2004х – 2005 = 00

-х2 + 8х – 12 = 0

-2; 3

-6; 1

-2005; 1

2; 6

14

Перечислите способы решения уравнений

Графический и аналитический

15

Функция вида y = ax + b называется…, ее графиком является…

Линейной, прямая

16

Функция вида y = ax2 + bx + c, a≠ 0,  называется…, ее графиком является…

Квадратичной, парабола

17

Функция видаy k/x, x≠ 0, называется…, ее графиком является…

Обратной пропорциональностью, гипербола

  1. Постановка цели занятия перед учащимися, объявление темы урока.

(Показ слайда, учащиеся отражают тему урока в тетрадях)

  1.  Практическая работа на построение графиков изученных функций и применение их для решения уравнений, систем уравнений. На стенде к уроку висят справочные таблицы с порядком построения графиков отдельных функций, однако на них учитель не указывает. Слабоуспевающие дети, как правило, используют их в работе на уроке.(Данные таблицы приведены в конце)  

  1. Построение графика линейной функции вида y = kx + b;

  2. Построение графика квадратичной функции y = ax2 + bx + c, a ≠ 0;

  3. Построение графика обратной пропорциональности y = k / x, x ≠ 0;

  4. Решение конкретных уравнений графическим способом (Приложение 2).

  1. Построение графика линейной функции вида y = kx + b

График линейной функции – прямая, прямую строят по 2-м точкам (см. аксиому геометрии)

Например, y = -2x + 3

x

0

2

y

Постройте данную прямую на координатной плоскости в рабочих тетрадях.

  1. Построение графика квадратичной функции y = ax2 + bx + c, a ≠ 0

График квадратичной функции — …, кривая, поэтому надо иметь для построения много точек, более трех.

  1. Например, y = (x – 2)2 + 1. Используем обычную параболу y = x2     Сдвинем ее на 2 единицы вправо, затем на единицу вверх.

Постройте данную параболу в рабочих тетрадях.

  1. Например, y = x2 — 6x + 8.

  2. = …,  а < 0 или а > 0, ветви параболы направлены …

Вершина параболы

  1. в =  , т.е. xв = …, yв = …

Дополнительные точки

x

  1. в – 2

  1. в – 1

  1. в

  1. в + 1

  1. в + 2

y

  1. в

Заполните таблицу, постройте данную параболу в рабочих тетрадях

  1. Построение графика обратной пропорциональности y = k / x, x ≠ 0

График данной функции — …, кривая, поэтому надо иметь для построения много точек (более 5).

  1. Например, y = 4 / x.

  2. ≠ …

x

  1.  

  1.  

  1.  

  1.  

  1.  

  1.  

y

Заполните таблицу, постройте данную гиперболу в рабочих тетрадях в той же системе координат, что и параболу.

Дополнительно: Как изменился бы график, если бы он был задан формулами

  1. = 4 / (x + 3) – 2,  y = 4 / (x — 4) + 3?

Пересекаются ли парабола и гипербола? Можно ли утверждать, что абсцисса точки пересечения есть корень уравнения

  1. 2 — 6x + 8 = 4 / x ?      x ≈ …

Дополнительно: В чем недостаток графического способа решения уравнений? – (громоздкость, неточность).

  1. Повторение алгоритма аналитического способа решения уравнений (памятка для учащихся, имеющих трудности в обучении).

Памятка для решения квадратных уравнений (любых)

  1. Выписать a, b, c

  2. Найти по формуле дискриминант

  3. Найти корни уравнения по формуле корней

Памятка для решения квадратных уравнений (с четным b)

  1. Выписать a, b, c

  2. Найти по формуле дискриминант, деленный на 4 (D1)

  3. Найти корни уравнения по частной формуле корней через D1

Памятка для решения приведенных квадратных уравнений способом подбора по теореме, обратной теореме Виета

  1. Записать сумму корней и их произведение на основе теоремы                   x1 + x2 = ;  x1 ? x2 =

  2. Угадать корни квадратного уравнения, обладающие выше перечисленными свойствами

Памятка для решения рациональных уравнений

Биквадратных

  1. Ввести новую переменную (y = x2)

  2. Решить как обычное квадратное уравнение с переменной y

  3. Вернуться к исходной переменной, решив уравнения y = x2

Рациональных

  1. Разложить все знаменатели дробей на множители

  2. Избавиться от деления умножением на общий знаменатель всех дробей, при этом учесть ОДЗ

  3. Решить целое уравнение и проверить корни с учетом ОДЗ

Распечатанные памятки можно предложить учащимся, которые претендуют на «3»

  1. Разноуровневая самостоятельная работа

Решить квадратные уравнения аналитически:

а) желательно с помощью теоремы, обратной теореме Виета х2 – 2х — 63 = 0

б) с помощью дискриминанта

3х2 – 8х – 3 = 0

в) наиболее рациональным способом

3х2 + х = 0   и  5х2 – 10 = 0

Решить квадратные уравнения аналитически:

а) желательно с помощью теоремы, обратной теореме Виета   х2 – 11х + 6 = 0

б) с помощью дискриминанта

4х2 + 3х – 1 = 0   и  5х2 + 12х + 4 = 0

в) наиболее рациональным способом

 (2х – 5)(2 + х) = 0  и    х2 – 2х = 0

Решить рациональное уравнение методом введения новой переменной

х4 – 10х2 + 21 = 0

Решить рациональное уравнение

3х4 – 8х2 — 3 = 0 и           +  =

Решить уравнение  =

Прочитайте задачу

Лодка проплыла от одного причала до другого, расстояние между которыми 25 км, и вернулась обратно. На путь по течению лодка затратила на 1 час меньше, чем на путь против течения. Найдите скорость течения реки, если собственная скорость лодки 8 км/ч.

Обозначьте буквой х скорость течения реки ( км/ч) и составьте уравнение по условию задачи

  1. Домашнее задание (разноуровневое) – с учетом выбора учащимися. Подведение итогов урока

Выводы о проделанной работе, самооценка эффективности учебной деятельности учащимися на уроке как среднее арифметическое за 3 вида самостоятельно выполненных заданий.

Спасибо за урок, за вашу работу на уроке.


Просмотр содержимого документа

««Повторение: Решение линейных, квадратных, рациональных уравнений»»

Тема урока «Повторение:

Решение линейных, квадратных, рациональных уравнений»

Цели урока:

  1. обучающие: актуализировать умение решать уравнения как аналитически, так и графически,

  2. развивающие: развивать умение учащихся систематизировать учебный материал, развивать коммуникативную культуру,

  3. воспитывающие: формировать у учащихся интерес к предмету.

Тип урока: урок обобщения изученного материала

План урока

  1. организационный момент,

  2. актуализация теоретических знаний по теме,

  3. постановка цели занятия перед учащимися, объявление темы урока,

  4. практическая работа на построение графиков изученных функций и применение их для решения уравнений,

  5. повторение алгоритма аналитического способа решения уравнений (памятка для учащихся, имеющих трудности в обучении),

  6. диагностика усвоения материала по теме (разноуровневая самостоятельная работа),

  7. запись домашнего задания (пояснения),

  8. подведение итогов урока.

  9. Оборудование

Мультимедийные средства обучения, раздаточные материалы.

Ход урока

  1. Организационный момент, характеризующийся внешней и внутренней (психологической) готовностью к уроку.

(Перед уроком приготовить раздаточный материал, предусмотреть наличие линеек, карандашей).

  1. Актуализация теоретических знаний по теме «Решение уравнений»Учащимся предлагается тест-разминка «Проверь себя» — продолжительностью 5-6 минут (приложение 1). Проверка правильности выполнения осуществляется непосредственно самими учащимися через показ ответов на слайде. Учащиеся имеют возможность оценить свою подготовку к уроку (Критерии оценки прилагаются).

№п/п

Задание

Ответ

1

Равенство с переменной называется…

уравнением

2

Значение переменной, подстановка которого в уравнение превращает его в верное равенство , называется…

Корнем уравнения

3

Найдите корни уравнения 3х + 9 = 9

0

4

Найдите корни уравнения 0х = 0

0

5

Найдите корни уравнения х2 – 16 = 0

-4; 4

6

Найдите корни уравнения х2 – 4х + 4 = 0

2

7

Как называется выражение D = b2 – 4ac

дискриминантом

8

Назовите условие, при котором в квадратном уравнении 2 корня,

один корень,

нет корней

D0

D=0

D

9

В каком случае корни квадратного уравнения будут иррациональными числами

Если — иррациональное число

10

Верно ли записана формула корней квадратного уравнения х =

Неверно, правильный ответ х =

11

Когда квадратное уравнение считают полным

Если в нем a,b,c ≠0

12

Заполните пропуски в стихотворении:

О свойстве корней теорема …

Что лучше, скажи, постоянства такого?

Умножишь ты корни, и дробь уж готова:

В числителе …, в знаменателе – «a».

И сумма корней тоже дроби равна.

Хоть с минусом дробь эта, что за беда.

В числителе …, в знаменателе — …

Виета

c

-b; a

13

Угадайте корни уравнения с помощью данной теоремы:

х2 – х – 6 = 0

х2 + 5х – 6 = 0

х2 + 2004х – 2005 = 0

-х2 + 8х – 12 = 0

-2; 3

-6; 1

-2005; 1

2; 6

14

Перечислите способы решения уравнений

Графический и аналитический

15

Функция вида y = ax + b называется…, ее графиком является…

Линейной, прямая

16

Функция вида y = ax2 + bx + c, a≠ 0, называется…, ее графиком является…

Квадратичной, парабола

17

Функция видаy k/x, x≠ 0, называется…, ее графиком является…

Обратной пропорциональностью, гипербола

II вариант

№п/п

Задание

Ответ

1

Что значит решить уравнение

Найти корни уравнения или доказать, что в уравнении корней нет

2

Найдите корни уравнения 0х = 15,3

Корней нет

3

Найдите корни уравнения 3х + 9 = 0

-3

4

Найдите корни уравнения х2 – 4х = 0

0; 4

5

Найдите корни уравнения х2 + 16 = 0

Корней нет

6

Найдите корни уравнения х2 + 4х + 4 = 0

-2

7

Для чего нужен дискриминант

Для решения полных квадратных уравнений

8

Назовите условие, при котором в квадратном уравнении 2 корня,

один корень,

нет корней

D0

D=0

D

9

В каком случае корни квадратного уравнения будут иррациональными числами

Если — иррациональное число

10

Верно ли записана формула корней квадратного уравнения х =

Неверно, правильный ответ х =

11

Когда квадратное уравнение считают приведенным

Если в нем a=1

12

Заполните пропуски в стихотворении:

О свойстве корней теорема …

Что лучше, скажи, постоянства такого?

Умножишь ты корни, и дробь уж готова:

В числителе …, в знаменателе – «a».

И сумма корней тоже дроби равна.

Хоть с минусом дробь эта, что за беда.

В числителе …, в знаменателе — …

Виета

c

-b; a

13

Угадайте корни уравнения с помощью данной теоремы:

х2 – х – 6 = 0

х2 + 5х – 6 = 0

х2 + 2004х – 2005 = 00

-х2 + 8х – 12 = 0

-2; 3

-6; 1

-2005; 1

2; 6

14

Перечислите способы решения уравнений

Графический и аналитический

15

Функция вида y = ax + b называется…, ее графиком является…

Линейной, прямая

16

Функция вида y = ax2 + bx + c, a≠ 0, называется…, ее графиком является…

Квадратичной, парабола

17

Функция видаy k/x, x≠ 0, называется…, ее графиком является…

Обратной пропорциональностью, гипербола

  1. Постановка цели занятия перед учащимися, объявление темы урока.

(Показ слайда, учащиеся отражают тему урока в тетрадях)

  1. Практическая работа на построение графиков изученных функций и применение их для решения уравнений, систем уравнений. На стенде к уроку висят справочные таблицы с порядком построения графиков отдельных функций, однако на них учитель не указывает. Слабоуспевающие дети, как правило, используют их в работе на уроке.(Данные таблицы приведены в конце)

  1. Построение графика линейной функции вида y = kx + b;

  2. Построение графика квадратичной функции y = ax2 + bx + c, a ≠ 0;

  3. Построение графика обратной пропорциональности y = k / x, x ≠ 0;

  4. Решение конкретных уравнений графическим способом (Приложение 2).

  1. Построение графика линейной функции вида y = kx + b

График линейной функции – прямая, прямую строят по 2-м точкам (см. аксиому геометрии)

Например, y = -2x + 3

Постройте данную прямую на координатной плоскости в рабочих тетрадях.

  1. Построение графика квадратичной функции y = ax2 + bx + c, a ≠ 0

График квадратичной функции — …, кривая, поэтому надо иметь для построения много точек, более трех.

  1. Например, y = (x – 2)2 + 1. Используем обычную параболу y = x2 Сдвинем ее на 2 единицы вправо, затем на единицу вверх.

Постройте данную параболу в рабочих тетрадях.

  1. Например, y = x2 — 6x + 8.

a = …, а 0, ветви параболы направлены …

Вершина параболы

xв = , т.е. xв = …, yв = …

Дополнительные точки

x

xв – 2

xв – 1

xв

xв + 1

xв + 2

y

yв

Заполните таблицу, постройте данную параболу в рабочих тетрадях

  1. Построение графика обратной пропорциональности y = k / x, x ≠ 0

График данной функции — …, кривая, поэтому надо иметь для построения много точек (более 5).

  1. Например, y = 4 / x.

x ≠ …

Заполните таблицу, постройте данную гиперболу в рабочих тетрадях в той же системе координат, что и параболу.

Дополнительно: Как изменился бы график, если бы он был задан формулами

y = 4 / (x + 3) – 2, y = 4 / (x — 4) + 3?

Пересекаются ли парабола и гипербола? Можно ли утверждать, что абсцисса точки пересечения есть корень уравнения

x2 — 6x + 8 = 4 / x ? x ≈ …

Дополнительно: В чем недостаток графического способа решения уравнений? – (громоздкость, неточность).

  1. Повторение алгоритма аналитического способа решения уравнений (памятка для учащихся, имеющих трудности в обучении).

Памятка для решения квадратных уравнений (любых)

  1. Выписать a, b, c

  2. Найти по формуле дискриминант

  3. Найти корни уравнения по формуле корней

Памятка для решения квадратных уравнений (с четным b)

  1. Выписать a, b, c

  2. Найти по формуле дискриминант, деленный на 4 (D1)

  3. Найти корни уравнения по частной формуле корней через D1

Памятка для решения приведенных квадратных уравнений способом подбора по теореме, обратной теореме Виета

  1. Записать сумму корней и их произведение на основе теоремы x1 + x2 = ; x1 ∙ x2 =

  2. Угадать корни квадратного уравнения, обладающие выше перечисленными свойствами

Памятка для решения рациональных уравнений

Биквадратных

  1. Ввести новую переменную (y = x2)

  2. Решить как обычное квадратное уравнение с переменной y

  3. Вернуться к исходной переменной, решив уравнения y = x2

Рациональных

  1. Разложить все знаменатели дробей на множители

  2. Избавиться от деления умножением на общий знаменатель всех дробей, при этом учесть ОДЗ

  3. Решить целое уравнение и проверить корни с учетом ОДЗ

Распечатанные памятки можно предложить учащимся, которые претендуют на «3»

  1. Разноуровневая самостоятельная работа

Решить квадратные уравнения аналитически:

а) желательно с помощью теоремы, обратной теореме Виета х2 – 2х — 63 = 0

б) с помощью дискриминанта

3х2 – 8х – 3 = 0

в) наиболее рациональным способом

3х2 + х = 0 и 5х2 – 10 = 0

Решить квадратные уравнения аналитически:

а) желательно с помощью теоремы, обратной теореме Виета х2 – 11х + 6 = 0

б) с помощью дискриминанта

4х2 + 3х – 1 = 0 и 5х2 + 12х + 4 = 0

в) наиболее рациональным способом

(2х – 5)(2 + х) = 0 и х2 – 2х = 0

Решить рациональное уравнение методом введения новой переменной

х4 – 10х2 + 21 = 0

Решить рациональное уравнение

3х4 – 8х2 — 3 = 0 и + =

Решить уравнение =

Прочитайте задачу

Лодка проплыла от одного причала до другого, расстояние между которыми 25 км, и вернулась обратно. На путь по течению лодка затратила на 1 час меньше, чем на путь против течения. Найдите скорость течения реки, если собственная скорость лодки 8 км/ч.

Обозначьте буквой х скорость течения реки ( км/ч) и составьте уравнение по условию задачи

  1. Домашнее задание (разноуровневое) – с учетом выбора учащимися. Подведение итогов урока

Выводы о проделанной работе, самооценка эффективности учебной деятельности учащимися на уроке как среднее арифметическое за 3 вида самостоятельно выполненных заданий.

Спасибо за урок, за вашу работу на уроке.

Как найти дискрименант

В школьной программе часто приходитсясталкиваться с решением квадратного уравнения типа: ax² + bx + c = 0, где а, b — первый и второй коэффициенты квадратного уравнения, с — свободный член. С помощью значения дискриминанта можно понять, есть ли у уравнения решения или нет, а если есть, то сколько. 2 — 4*4*25 = 400-400 = 0. Квадратный трехчлен имеет два равных корня, найдем их по формулеx = -b/2a = — (-20)/2*4 = 20/8 = 2,5. Если дискриминант равен нулю, значит существует один вещественный корень, график функции пересекает ось OX в одном месте. При этом, если а > 0, график располагается выше оси OX, а если a < 0, ниже этой оси.

При D < 0 вещественных корней не существует. Если дискриминант меньше нуля, значит не существует вещественных корней, а только комплексные корни, график функции не пересекает ось ОX. Комплексные числа — расширение множества вещественных чисел. Комплексное число можно представить как формальную сумму x + iy, где x и y — вещественные числа, i — мнимая единица.

При каких натуральных n существует рациональное число x, удовлетворяющее равенству

 {module Адаптивный блок Адсенс в начале статьи}

  При каких натуральных n существует рациональное число x, удовлетворяющее равенству

n2 + 2 = (2n − 1)x ?

 

  Решение:

  Так как при всех натуральных n верно неравенство

(n2 + 2) > (2n − 1),

  то искомое число x = k/m больше единицы, откуда k > m.

  Для чисел, удовлетворяющих условию задачи, равенство

(n2 + 2)m = (2n − 1)k

  определяет натуральное число, единственным образом разлагаемое на простые множители. Это значит, что в разложении на простые множители числа (2n − 1) присутствуют все простые множители числа (n2 + 2), но в меньших степенях. Это значит, что (n2 + 2) делится на (2n − 1).

  Следовательно,

n2 + 2 = d(2n − 1),

  где d — натуральное число.

  Рассмотрим квадратное уравнение относительно n:

n2 − 2dn + (d + 2) = 0.

  Его дискриминант, делённый на 4, должен быть квадратом натурального числа, которое обозначим j (убеждаемся, конечно, что при равном нулю дискриминанте чисел, удовлетворяющих исходному равенству, нет):

d2 − d − 2 = j2.

  Тогда (d − j)(d + j) = d + 2. Но j = 1 не дает нам натурального d и, следовательно, натурального n. При j = 2 имеем d = 3, откуда находим, что n = 5, x = 1,5 (при n = 1, втором корне квадратного уравнения, исходное уравнение не имеет решений).

  Если j > 2, то левая часть равенства

(d − j)(d + j) = d + 2

  больше правой, так как

d + j > d + 2,

  да ещё умножается на натуральное число (d − j). То есть для j > 2 равенство

(d − j)(d + j) = d + 2

  невозможно.

  Итак, лишь при n = 5 исходное уравнение имеет рациональный корень.

  Ответ: При n = 5.

 {module Адаптивный блок Адсенс в конце статьи}

Формулы корней квадратных уравнений

здравствуйте тема этого урока формула корней квадратного уравнения мы уже с вами знаем что уравнение вида x квадрат плюс bx плюс c равна нулю называется полным квадратным уравнением а этот урок вам поможет узнать как решать такие уравнения что такое дискриминант и как с помощью значения дискриминанта определить количество корней как использовать формулы для решения квадрату полных квадратных уравнений начнем с первого понятия что такое дискриминант дискриминант квадратного уравнения называется выражение в квадрат минус 4 акция и реакция где b a и c это коэффициенты квадратного уравнения обозначается дискриминант большой латинской буквой д а вычисляется формулой d равна b квадрат минус 4 от c при решении дискриминанта возможны три случая дискриминант может быть больше 0 может оказаться значение равное нулю и может быть значение меньше 0 давайте рассмотрим случай если дискриминант больше нуля в этом случае уравнение имеет два действительных корни которые вычисляются по следующей формуле минус b плюс минус корень квадратный из дискриминанта разделить на 2а где b это коэффициент квадратного уравнения минус bms коэффициент минус b мы используем для ночь и счисления корней квадратного уравнения а значит коэффициент бы сюда мы должны поставлять противоположным знаком и коэффициент а мы используем для того чтобы вычислить корни квадратного уравнения если дискриминант меньше нуля то уравнение корней не имеет и действительно нам необходимо будет вычислять арифметический квадратный корень из дискриминанта а мы уже знаем по свой что по свойству что арифметический квадратный корень из отрицательного числа не существует поэтому атлетам такое уравнение всегда будет решений нет если дискриминант равен нулю в этом случае уравнение имеет один действительный корень и действительно проверим если мы формулу корней минус b плюс минус корень квадратный из 0 разделить на над на 2-ом проведем вычисления то получаем что корень квадратный корень данного квадратного уравнения можно вычислить минус b разделить на 2а это будет единственный корень уравнения рассмотрим пример решим такое вот простое уравнение 2x квадрат минус 5 x плюс 2 равна нулю решаются не очень просто и легко главное запомнить три главных шага первое определяем официанты вспоминаем что коэффициентами уравнения квадратного являются значение стоящие для коэффициента а это значение стоящая перед x квадрат знать о коэффициент б это значение стоящие перед x с его знаком и коэффициент ция это свободный член уравнения итак нашем уравнении коэффициента равны и равен двум b равно минус 5 и c равно 2 следующий шаг мы находим дискриминант для этого используем формулу квадратных корней формула дискриминанта d равно b квадрат минус 4 отце где b a и c это те значения которые мы определились этого уравнения коэффициенты этого уравнения подставляя коэффициенты полученные выше мы получаем результат в данной ситуации дискриминант равен 9 а мы уже говорили выше так как дискриминант больше нуля то уравнение имеет два действительных корни находим корни по формуле x равно минус b плюс-минус арифметический квадратный корень из дискриминанта разделить на два соответственно подставляем x 1 находим у нас коэффициент b равен был -5 формулу корней мы подставляем положительное число 5 корень квадратный из дискриминанта равен 3 помним что дискриминант у нас данной ситуации был равен 9 знаменателе 2 умножить на коэффициент а который был равен двум выполнив это вычисление мы получаем корень 1 2 же нахождение 2 корня единственно что изменяется это знак 5 плюс 3 и деленное на те же множитель едва-едва в результате вычислений мы получаем второй корень и тогда в ответ этого уравнения мы записываем x первое равное 2 и 2 равна целых пять десятых рассмотрим следующее уравнение 2x квадрат минус 3 x плюс пять равно нулю действую тем же самым способом первое находим коэффициенты в этом уравнении коэффициентами будет а равное 2 b равна -3 и c равная 5 находим дискриминант подставляем формула дискриминанта b квадрат минус 4 акция соответствующие коэффициенты то есть вместо b подставляем минус 3 и возводим в квадрат вместо а подставляем 2 вместо c подставляем множитель 5 в результате вычисления мы получаем минус 31 из вышесказанного мы знаем так как дискриминант меньше нуля то уравнения не имеют действительных корней а значит в ответ уравнения мы напишем решений нет есть уравнение решения не имеет решим еще одно уравнение x квадрат минус 2 x плюс 1 равная действием точно также первый шаг всегда находим коэффициенты определяем в этом уравнении а равную 1 b равно минус 2 и c равно единице следующий шаг находим дискриминант формула тоже самое b квадрат минус 4ac и подставляя формулу коэффициенты которые мы получили из этого уравнения мы получаем значение дискриминанта и в данном уравнении дискриминант равен нулю мы уже знаем что равенстве дискриминанта нулю уравнение имеет один корень а значит подставляя формулу x равна минус b разделить на 2 мы сможем найти этот корень уравнения подставляем в значение вместо b значения минус 2 вместо а значение 1 вычисление нам дает икс равное единице и в ответ мы записываем что решением уравнения является корень x равна 1 решение квадратных уравнений уравнений с использованием формул квадратных корней очень легкий способ главное запомнить и правильно определить первое во значит определить коэффициенты данного уравнения напоминаю что коэффициентами являются значения стоящей коэффициент а это значение перед x квадрат с его знаком значит коэффициент б это значение стоящие перед x с его знаком и коэффициент ция это свободный член уравнения с его знаком следующий шаг мы находим дискриминант подставляя формулу b квадрат минус 4 акции значение b и c соответственно выбор взятые в данном уравнении и уже по значению которое мы получаем дискриминанта мы можем дать ответ если дискриминант равен нулю соответственно мы выбираем форму x равно минус b разделить на 2а если дискриминант меньше нуля то уравнение решения и если дискриминант больше нуля то мы вычисляем корни данного уравнения по формуле минус b плюс минус корень квадратный из дискриминанта разделить на 2а если вы будете следовать этому алгоритму у вас все получится желаю успехов до новых уроков

Ю.

О. Пукас. Решение задачи С18 из диагностической работы (12.2008) МИОО | Шевкин.Ru

Пукас Ю. О., гимназия г. Троицка

С18. При каких натуральных n существует рациональное число x, удовлетворяющее равенству

                              n2 + 2 = (2n – 1)x?                                                                (1)

Решение. 1. Из того, что при всех n: (n2 + 2) > (2n – 1), следует, что искомое число x = k/m больше единицы: k > m.

  1. Для чисел, удовлетворяющих условию задачи, равенство (n2 + 2)m = (2n – 1)kопределяет натуральное число, единственным образом разлагаемое на простые множители. Это значит, что в разложении на простые множители числа (2n – 1) присутствуют все простые множители числа (n2 + 2), но в меньших степенях. Это значит, что (n2 + 2) делится на (2n – 1).

  2. Следовательно, n2 + 2 = d(2n – 1), где d — натуральное число. Рассмотрим квадратное уравнение относительно n:

                                 n2 – 2dn + (d + 2) = 0.                                                                (2)

Его дискриминант, деленный на 4, должен быть квадратом натурального числа, которое обозначим j. То есть j2 = d2 – d – 2 = (d – 2)(d + 1). Так как j = 0 лишь при d = 2 (d — натуральное число), то уравнение (2) имеет единственный корень n = 2, для которого исходное уравнение (1) не имеет рационального корня.

Тогда (d – j)(d + j) = d + 2. Но j = 1 не дает нам натурального d и, следовательно, натурального n. При j = 2 имеем d = 3, откуда находим, что n = 5, x = 3/2 (при n = 1 исходное уравнение не имеет корней).

Если j > 2, то левая часть равенства (d – j)(d + j) = d + 2 больше правой, так как
d + j > d + 2, и не забудем, что d – j должно быть натуральным числом. То есть для
j > 2 равенство (d – j)(d + j) = d + 2 невозможно.

Итак, лишь при n = 5 исходное уравнение имеет рациональный корень.

Ответ. При n = 5.

Решение итоговой работы по математике 2015 8 класс

Решение итоговой работы по математике

8 класс, 2015 г

Условия задач здесь

1.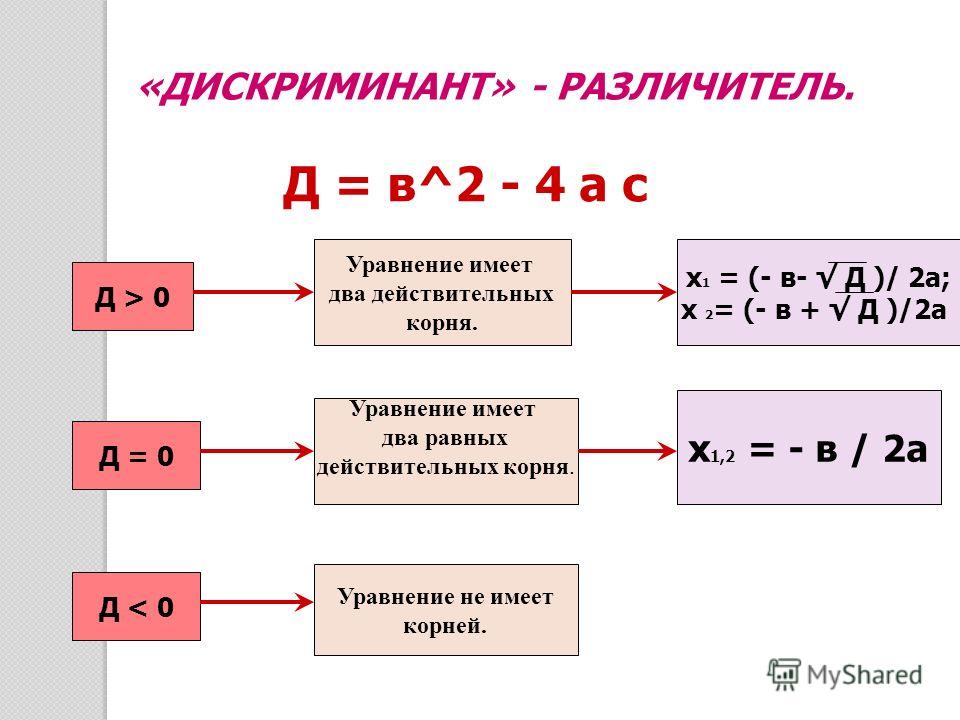 Применим свойства и . Тогда . После подстановки получаем, что . Типичная ошибка: вместо записать , что оказывается равным , так как в квадрат возводится только число . Это материал сайта www.itmathrepetitor.ru

2. Так как при условии, что все подкоренные выражения неотрицательны, то . Далее заметим, что (не !) и , и в результате получим, что .

3.1. Это материал сайта www.itmathrepetitor.ru. Можно добросовестно решить данное квадратное уравнение с помощью формул для корней через дискриминант. Подробности смотрите здесь. Но лучше применить теорему Виета, согласно которой сумма корней уравнения равна , то есть коэффициенту при с противоположным знаком, деленному на коэффициент при , равный 1. Строго говоря, в таком решение кроется коварная ошибка: теорему Виета можно применять только если корни существуют. Поэтому сначала необходимо убедиться, что дискриминант уравнения неотрицателен. Мы же этот этап пропустили (будем считать, что проверили устно).

3.2 Так как правая часть уравнения равна нулю, то разложим левую часть уравнения на множители . Так как произведение равно нулю, то хотя бы один из множителей равен нулю и уравнение распадается на две более простых случая: или , или . Во втором уравнении дискриминант и , откуда или . Исходное уравнение имеет три корня , и . Наибольший из них равен . Заметим, что часть работы можно было сократить, если в процессе решения помнить, что нужен только наибольший корень. Например, при поиске корней квадратного уравнения стоит искать только один корень по формуле , так как второй корень заведомо будет меньше этого первого.

4. Это материал сайта www.itmathrepetitor.ru. По теореме Пифагора для треугольника ABC катет АС равен . Так как средняя линия равна половине параллельной стороны (следует из подобия треугольников), то MN равно .

5. 1) Нет, так как один из углов при основании равен , а если и второй угол при основании будет равен , то данная фигура окажется прямоугольником, а не трапецией. Напомню, что по определению в трапеции не может быть двух пар параллельных сторон. Поэтому говорить, что прямоугольник — это частный случай трапеции, ошибочно.

2) Да, так как диагональ делит квадрат на два равнобедренных прямоугольных треугольника. То есть у этих треугольников углы при гипотенузе равны.

3) Да, так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Если диагонали равны, то они делят ромб на четыре прямоугольных равнобедренных треугольника, острые углы которых равны 45о. Осталось вспомнить, что диагонали являются биссектрисами углов ромба. Это материал сайта www.itmathrepetitor.ru.

4) Нет. Например, треугольник с углами 120о, 30о, 30о, в котором 30o+30o<120o. Конечно, осталось доказать, что такой треугольник существует (это необходимости для строгости, но излишне для решения данной итоговой работы). И небольшое замечание по условию: «В любом треугольнике сумма двух углов больше третьего». Здесь не совсем понятно: сумма любых двух углов или сумма каких-то двух углов. Строго говоря, без этих слов условие задачи некорректно, то есть не является математическим утверждением.

6.1 Это материал сайта www.itmathrepetitor.ru. Количество способов выбрать произвольный билет равно 30. Количество способов выбрать билет по теме «Динамика» равно 30-12=18. Тогда искомая вероятность равна . Теорию и задачи с решениями по классической вероятности можно посмотреть здесь.

6.2  Это материал сайта www.itmathrepetitor.ru. Найдем вероятность того, что ни один из лифтов не находится на первом этаже. То есть рассмотрим противоположное событие для события «Хотя бы один лифт находится на первом этаже». Тогда искомая вероятность будет равна , так как противоположные события образуют полную группу событий и сумма их вероятностей равна 1. По правилу произведения вероятность события «Ни один из лифтов не находится на первом этаже» равна , так как вероятность того, что данный лифт не окажется на первом этаже, равна . Тогда искомая вероятность равна . Теорию и задачи с решениями по классической вероятности можно посмотреть здесь.

10. Если 15% школьников ответили, что они из многодетных семей, то 100 — 15 = 85% школьников ответили, что они не из многодетных семей. То есть 510 учеников составляют 85 % от общего количества детей в школе. Тогда 100% составляют учеников. Хотя по условию не сказано, но мы считали, что ответы школьников были только двух видов.  Задачи с решениями на проценты можно разобрать здесь.

11. Если дано четыре числа , то возможны сравнения   и , и и так далее (всего 6 пар). Чтобы не оформлять каждое сравнение, стоит сначала на черновике выяснить ответ и затем привести доказательство лишь трех неравенств. Например, если ответ , то достаточно сравнить  и , и , и .
Приступим к решению данной задачи. Докажем, что .
Еще раз повторю: ответ был найден сначала на черновике, а при оформлении все тупиковые и лишние фрагменты черновика не упоминаются, из-за чего решение получается с оттенком волшебства. 2-32 $ $ y = 2 (x-3) (x + 5)

$
y-перехват на
$ (0, -30)

$

вершина при
$ (- 1, -32)

$

x-перехватов на
$ (3, 0) $ и $ (- 5, 0) $
Парабола

График квадратного уравнения называется параболой .
Если a> 0, то его вершина указывает вниз:

Если a <0, то его вершина указывает вверх: Если a = 0, график не парабола, а прямая линия.

Вершина параболы равна $ x = — \ frac {b} {2a} $.

Формулы Виета

Если x 1 и x 2 являются корнями квадратного уравнения ax 2 + bx + c = 0
затем:
$ x_1 + x_2 = — \ frac {b} {a} $
$ x_1x_2 = \ frac {c} {a} $
Эти формулы называются формулами Виета .
Мы можем найти корни x 1 и x 2 квадратного уравнения, решив совместные уравнения.

Задачи на квадратные уравнения

Задача 1. Решите уравнение:
x 2 — 4 = 0
Решение: x 2 — 4 = (x — 2) (x + 2)
(x — 2) (x + 2 ) = 0
x — 2 = 0 или x + 2 = 0
Корни равны x = 2 или x = -2

Решение 2:
a = 1, b = 0, c = -4
D = 0 2 — 4 ⋅ 1 ⋅ (-4) = 16
$ x_1 = \ frac {-b — \ sqrt {D}} {2a} = \ frac {- 0 — \ sqrt {16}} {2 \ cdot 1} = \ frac {-4} {2} = -2 $
$ x_2 = \ frac {-b + \ sqrt {D}} {2a } = \ frac {- 0 + \ sqrt {16}} {2 \ cdot 1} = \ frac {4} {2} = 2 $

Задача 2. Решите уравнение:
3x 2 + 4x + 5 = 0
Решение: дискриминант D = 4 2 — 4⋅3⋅5 = 16-60 = -44
Итак, квадратное уравнение не имеет реальных корней.

Задача 3. Решите уравнение:
x 2 + 4x — 5 = 0; х =?
Решение: Дискриминант 4 2 — (-4⋅1⋅5) = 16 + 20 = 36> 0
Уравнение имеет 2 действительных корня: $ \ frac {-4 \ pm \ sqrt {36} } {2}
долларов США x = 1 или x = -5

Задача 4. Решите уравнение:
x 2 + 4x + 4 = 0; х =?
Решение: Дискриминант 4 2 — (4⋅1⋅4) = 16-16 = 0
Итак, есть одно реальное решение: $ x = \ frac {-4} {2} $
x = -2

Задача 5. Решите уравнение:
x 2 — 13x + 12 = 0
Корни: 1, 12

Задача 6. Решите уравнение:
8x 2 — 30x + 7 = 0
Корни: 3.2 $, это означает, что $ \ sqrt {\ Delta} $ равно (плюс или минус) $ \ alpha — \ beta $. Итак, $ \ alpha $ и $ \ beta $ — это два числа, из которых у нас есть сумма ($ -b $) и разность ($ \ sqrt {\ Delta} $). Мы можем извлечь сами $ \ alpha, \ beta $, решив линейную систему:

$$ \ alpha + \ beta = -b $$
$$ \ alpha — \ beta = \ sqrt {\ Delta} $$

Сложив два уравнения вместе, мы получим $ 2 \ alpha = -b + \ sqrt {\ Delta} $, другими словами, $ \ alpha = \ frac {-b + \ sqrt {\ Delta}} {2} $. Вычитая их, получаем $ 2 \ beta = -b- \ sqrt {\ Delta} $, т.е.е. $ \ beta = \ frac {-b- \ sqrt {\ Delta}} {2} $.

Математическая задача: Дискриминант — математическая задача (711), алгебра, квадратное уравнение

Определите дискриминант уравнения:

7×2 − x + 7 = 17×2 − x + 7 = 1

Правильный ответ:

Чтобы решить эту математическую задачу со словами, вам необходимо знать следующие знания:

Сопутствующие математические задачи и вопросы:

  • Квадратное уравнение
    Определите числа b, c, что числа x 1 = -1 и x 2 = 3 были корнями квадратного уравнения:?
  • Корни
    Определите абсолютный коэффициент q квадратного уравнения, что уравнение имеет действительный двойной корень и корень x вычислите:?
  • Чистое квадратное уравнение
    Решить чистое квадратное уравнение?.
  • Квадратное уравнение
    Найдите корни квадратного уравнения: 3x 2 -4x + (-4) = 0.
  • EQ2
    Решите квадратное уравнение:?
  • Квадратичная функция
    Дана квадратичная функция y = -4x 2 + 5x + c с неизвестным коэффициентом c. Определите наименьшее целое число c, для которого график f пересекает ось x в двух разных точках.
  • Квадратное уравнение
    Квадратное уравнение 7x 2 + bx + c = 0 имеет корни x 1 = 67 и x 2 = -84.Рассчитайте коэффициенты b и c.
  • Квадратное уравнение
    Решите квадратное уравнение: 2x 2 + 28x-550 = 0
  • Уравнение
    Уравнение -2x 2 + bx -82 = 0 имеет один корень x 1 = -8. Определите коэффициент b и второй корень x 2 .
  • Завершение квадрата
    Решите квадратное уравнение: m 2 = 4m + 20, используя метод квадратов
  • Квадратичная функция
    Напишите уравнение квадратичной функции, которое включает точки A (-1, 10), B (2 , 19), C (1,4)
  • Квадратичное неравенство
    Если 5x + x²> 100, то x не равно
  • Квадрат
    Предположим, что длина сторон квадрата уменьшается на 25% в области содержимого на 28 см 2 . 2 + bx-9 = 0 — это один корень x1 = -3/2. Определите второй корень и коэффициент b.
  • Метод замены
    Решите гониометрическое уравнение: sin 4 θ — 1 / cos 2 θ = cos 2 θ — 2
  • Right
    Определите углы прямоугольного треугольника с гипотенузой c и катетами a, b, если: ?
  • Уравнение со значением абс.
    Сколько решений имеет уравнение? в реальных числах?

Дискриминант | Блог Шеннон

На прошлой неделе мы научились определять количество решений квадратного уравнения, не решая его.Чтобы это сделать, мы смотрим на дискриминант!

Дискриминант — подкоренное выражение формулы корней квадратного уравнения:

Вот как по дискриминанту определять количество решений.

  • Два действительных корня при> 0

Если дискриминант положительный (т.е. больше 0), у него есть два решения. (Он дважды касается оси x)

  • Ровно один действительный корень при = 0

Если дискриминант равен нулю, это означает, что существует ровно одно решение (просто касается оси x один раз)

  • Нет реальных корней, если <0

Если дискриминант является отрицательным числом (меньше 0), он не имеет решений (не касается оси x)

Теперь, когда мы понимаем, как использовать дискриминант для определения количества решений, давайте применим их к некоторым уравнениям.

Первый пример: вычислить значение дискриминанта и определить, сколько решений.

Помните квадратное уравнение:

Следовательно: a = 4, b = 2, c = 3

Подставьте числа, чтобы определить дискриминант.

4-16 (3)

4-48

-44

Поскольку дискриминант отрицательный, у него нет решений; настоящих корней нет.

Теперь давайте посмотрим на другой пример, в котором нам нужно создать уравнение с заданным числом корней.

Определите значения y уравнения, имеющего два действительных корня.

Чтобы иметь два действительных корня, значение его дискриминанта должно быть больше 0.

Итак, мы используем:> 0

Заменитель: a = 5, b = 3 и c = y

> 0

Упростить.

9–20 лет> 0

Переместите 9 на другую сторону, чтобы изолировать переменную.

-20лет> -9

Разделите обе стороны на -20.

г>

Поскольку мы разделили обе стороны отрицательным числом, мы должны поменять местами символ неравенства.

г <

Факторинг над комплексными числами

Факторинг над комплексными числами

Теперь вы увидите, как работают математики: упрощая простые вещи, делать их труднее!

Дедушка всех примеров.

Рассмотрим многочлен. Его нельзя разложить на реальные числа, так как на его графике нет интерцептов x . (График представляет собой стандартную параболу, сдвинутую на одну единицу вверх!)

Как мы можем сказать, что многочлен неприводим, когда мы выполняем пополнение квадратов или используем квадратную формулу?
Попробуем дополнить квадрат:
Здесь не так много работы, перенос постоянного члена — это все, что нам нужно сделать, чтобы понять, в чем проблема:

Сейчас мы не можем извлекать квадратные корни, поскольку квадрат каждого действительного числа неотрицателен!

Вот тут-то и вмешивается математик: она (или он) представляет , что есть корни из -1 (хотя и не вещественные числа), и называет их i и — i .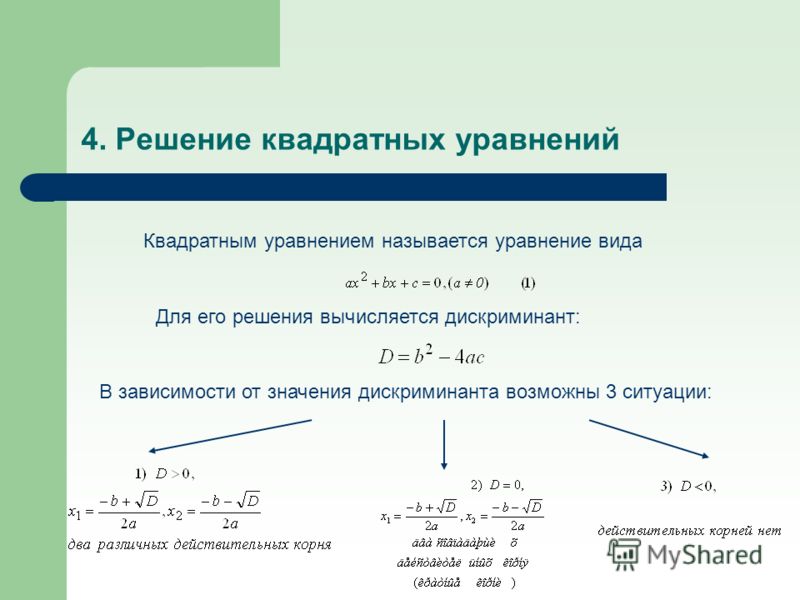 Итак, определяющим свойством этого воображаемого числа и является то, что

Теперь многочлен внезапно стал приводимым , мы можем написать

Комплексные числа.

Давайте разберемся: число в форме, где a и b — действительные числа, называется комплексным числом . Вот некоторые примеры:

Число a называется действительной частью числа a + bi , число b называется мнимой частью числа a + bi .

К счастью, алгебра с комплексными числами работает очень предсказуемо, вот несколько примеров:

В общем, умножение работает с методом FOIL:

Два комплексных числа a + bi и a — bi называются комплексно-сопряженной парой . Хорошим свойством комплексно сопряженной пары является то, что их произведение всегда является неотрицательным действительным числом:

Используя это свойство, мы можем увидеть, как разделить два комплексных числа. Давайте посмотрим на пример

Магический трюк состоит в том, чтобы умножить числитель и знаменатель на комплексно-сопряженный спутник знаменателя, в нашем примере мы умножаем на 1+ i :

Поскольку (1+ i ) (1- i ) = 2 и (2 + 3 i ) (1+ i ) = — 1 + 5 i , получаем

и готово!

Вы можете найти дополнительную информацию в нашем разделе «Комплексные числа».

Квадратичные многочлены с комплексными корнями.

Рассмотрим многочлен

Используя формулу корней квадратного уравнения, корни вычисляются как

Из формы квадратичной формулы нетрудно увидеть, что если квадратный многочлен имеет комплексные корни, то всегда будет комплексно сопряженной парой !

Другой пример. Рассмотрим многочлен

Его корни даны

Дискриминант.

Мы можем видеть из графика многочлена, имеет ли он действительные корни или неприводим над действительными числами. Как мы можем алгебраически определить , имеет ли квадратный многочлен действительный или комплексный корень?
Символ i появляется на картинке именно тогда, когда член под квадратным корнем в формуле корней квадратного уравнения равен отрицательным.
Этот термин

называется дискриминантом .

Рассмотрим дискриминант квадратичного многочлена.

  • Если дискриминант положительный, многочлен имеет 2 различных действительных корня.
  • Если дискриминант отрицательный, многочлен имеет 2 комплексных корня, которые образуют комплексно сопряженную пару.
  • Если дискриминант равен нулю, многочлен имеет один действительный корень кратности 2.
Основная теорема алгебры, дубль два.

Мы уже знаем, что каждый многочлен можно разложить по действительным числам на произведение линейных множителей и неприводимых квадратичных многочленов. Но теперь мы также заметили, что каждый квадратный многочлен можно разложить на 2 линейных фактора, если мы допустим комплексные числа. Следовательно, сложная версия Фундаментальной теоремы
алгебры выглядит следующим образом:

По комплексным числам каждый многочлен (с действительными коэффициентами) может быть разложен на линейные множители.

Мы можем заявить это также на корневом языке:

По комплексным числам каждый многочлен степени n (с действительными коэффициентами) имеет n корня, подсчитанных в соответствии с их кратностью.

Использование комплексных чисел делает утверждения проще и «красивее»!

Упражнение 1.

Найдите все (действительные или комплексные) корни многочлена.

Ответ.
Упражнение 2.

Полностью разложите полином на множители (a) над действительными числами, (b) над комплексными числами.

Ответ.
Упражнение 3.

Для каких значений c многочлен имеет два комплексно сопряженных корня?

Ответ.

Упражнение 4.

При каких значениях и многочлен имеет два различных действительных корня?

Ответ.
Упражнение 5.

Каждый квадратичный многочлен имеет либо 2 различных действительных корня, либо один действительный корень кратности 2, либо 2 комплексных корня.Какие случаи могут иметь место для многочлена степени 3? Приведите пример для каждого из этих случаев.

Ответ.
Упражнение 6.

(a) Покажите, что каждый многочлен степени 3 имеет по крайней мере один интервал x .

(b) Приведите пример полинома степени 4 без каких-либо перехватов x .

Ответ.
Упражнение 7.

Приведите пример полинома степени 5, единственные действительные корни которого равны x = 2 с кратностью 2 и x = -1 с кратностью 1.

Ответ.

[Назад]
[Следующий]

[Алгебра]
[Тригонометрия]
[Комплексные переменные]
[Исчисление]
[Дифференциальные уравнения]
[Матричная алгебра] Домашняя страница S. 2» .

Пошаговое решение:

Шаг 1:

Попытка разложить на множители путем разделения среднего члена

1,1 Факторинг m 2 -5m + 4

Первый член равен, m 2 , его коэффициент равен 1.
Средний член, -5m, его коэффициент -5.
Последний член, «константа», равен +4

Шаг-1: Умножьте коэффициент первого члена на константу 1 • 4 = 4

Шаг-2: Найдите два множителя 4, сумма которых равна коэффициенту среднего члена, который равен -5.

-4 +-1 =-5 Вот и все

Шаг 3: Перепишите полиномиальное разбиение среднего члена, используя два найденных фактора на шаге 2 выше, -4 и -1
м 2 — 4 м — 1 м — 4

Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
м • (м-4)
Сложите последние 2 члена, извлекая общие множители:
1 • (m-4)
Шаг 5: сложите четыре члена шага 4:
(m-1) • (m-4)
Какая желаемая факторизация

Уравнение в конце шага 1: 
 (м - 1) • (м - 4) = 0

Шаг 2:

Теория — Корни продукта:

2. 1 Произведение нескольких членов равно нулю.

Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.

Теперь мы решим каждый член = 0 отдельно

Другими словами, мы собираемся решить столько уравнений, сколько членов есть в произведении

Любое решение для члена = 0 также решает продукт = 0.

 
 Решение уравнения с одной переменной: 
 
 2.2 Решите: m-1 = 0 
 
 Добавьте 1 к обеим сторонам уравнения: 
 m = 1 
 
 
 
 Решение уравнения с одной переменной: 
 
 2.3 Решите: m-4 = 0 
 
 Добавьте 4 к обеим сторонам уравнения: 
 m = 4 
 
 
 
 Дополнение: Решение квадратного уравнения напрямую 
 
 Решение m  2  -5m + 4 = 0 напрямую 
 Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
 
 Парабола, найдя вершину: 
 3. 1 Найдите вершину y = m  2  -5m + 4
 Параболы имеют наибольшее или самая низкая точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
 Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
 Для любой параболы Am  2  + Bm + C m -координата вершины задается как -B / (2A). В нашем случае координата m равна 2.5000
 Подставляя в формулу параболы 2,5000 для m, мы можем вычислить координату y: 
 y = 1,0 * 2,50 * 2,50 — 5,0 * 2,50 + 4,0 
 или y = -2,250
 Парабола, графическая вершина и пересечения по оси X: 
 Корневой график для: y = m  2  -5m + 4 
 Ось симметрии (пунктирная линия) {m} = {2.50} 
 Вершина в {m, y} = {2.50, -2.25} 
 м -Переходы ( Roots): 
 Корень 1 в {m, y} = {1.00, 0.00} 
 Корень 2 в {m, y} = {4.00, 0.00}
 Решите квадратное уравнение, заполнив квадрат 
 3.2 Решение m  2  -5m + 4 = 0, заполнив квадрат.
 Вычтем 4 из обеих частей уравнения: 
 m  2  -5m = -4
 Теперь умный бит: возьмите коэффициент m, равный 5, разделите на два, получим 5/2 и, наконец, возведем в квадрат. это дает 25/4
 Добавьте 25/4 к обеим частям уравнения: 
 В правой части мы имеем: 
-4 + 25/4 или, (-4/1) + (25/4) 
. общий знаменатель этих двух дробей равен 4. Сложение (-16/4) + (25/4) дает 9/4 
 Таким образом, сложив обе стороны, мы, наконец, получаем: 
 m  2  -5m + (25/4) = 9 / 4
 Добавление 25/4 завершило левую часть в полный квадрат: 
 m  2  -5m + (25/4) = 
 (m- (5/2)) • (m- (5/2) ) = 
 (m- (5/2))  2  
 Вещи, которые равны одному и тому же, также равны друг другу.Так как 
 м  2 -5 м + (25/4) = 9/4 и 
 м  2 -5 м + (25/4) = (м- (5/2))  2  
 то по закону транзитивности, 
 (m- (5/2))  2  = 9/4
 Мы будем называть это уравнение уравнением. # 3.2.1
 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
 Обратите внимание, что квадратный корень из 
 (m- (5/2))  2  равен 
 (m- (5/2))  2/2  = 
 (m- (5/2))  1  = 
 м- (5/2)
 Теперь, применяя принцип квадратного корня к уравнению. # 3.2.1 получаем: 
 m- (5/2) = √ 9/4
 Добавьте 5/2 к обеим сторонам, чтобы получить: 
 m = 5/2 + √ 9/4
 Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 
 m  2  — 5m + 4 = 0 
 имеет два решения: 
 m = 5/2 + √ 9/4 
 или 
 m = 5/2 — √ 9/4
 Обратите внимание, что √ 9/4 можно записать как 
 √ 9 / √ 4, что равно 3/2
 Решите квадратное уравнение с помощью квадратичной формулы 
 3.3 Решение m  2  -5m + 4 = 0 по квадратичной формуле.
 Согласно квадратичной формуле, m, решение для Am  2  + Bm + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: 
   
 — B ± √ B  2  -4AC 
 m = ———————— 
 2A
 В нашем случае A = 1 
 B = -5 
 C = 4
 Соответственно B  2  — 4AC = 
 25 — 16 = 
 9
 Применение формулы квадратного уравнения:
 5 ± √ 9 
 m = ———— 
 2
 Можно ли упростить √ 9?
 Да! Разложение 9 на простые множители равно 
 3 • 3 
 Чтобы можно было удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i. е. второй корень).
 √ 9 = √ 3 • 3 = 
 ± 3 • √ 1 = 
 ± 3
 Итак, теперь мы смотрим на: 
 m = (5 ± 3) / 2
 Два реальных решения:
 m = ( 5 + √9) / 2 = (5 + 3) / 2 = 4.000
 или:
 m = (5-√9) / 2 = (5-3) / 2 = 1.000
 Были найдены два решения: 
  1.  m = 4
  2.  m = 1
 Запишите дискриминант следующих квадратных уравнений:
 (i) 2x² — 5x + 3 = 0
 (ii) x² + 2x + 4 = 
2x² — 5x + 3 = 0
 При сравнении данного уравнения с ax² + bx + c = 0
 Здесь a = 2, b = -5 и c = 3
 D (дискриминант) = b² — 4ac
 D = (-5) ² — 4 x 2 x 3
 D = 25 — 24 = 1
 D = 1
 Следовательно, дискриминант квадратного уравнения 2x² — 5x + 3 = 0 равен 1.
 2) Дано: x² + 2x + 4 = 0
 При сравнении данного уравнения с ax² + bx + c = 0
 Здесь a = 1, b = 2 и c = 4
 D (дискриминант) = b² — 4ac
 D = (2) ² — 4 x 1 x 4
 D = 4 — 16 = — 12
 D = -12
 Следовательно, дискриминант квадратного уравнения x² + 2x + 4 = 0 равно — 12.
 3) Дано: (x -1) (2x -1) = 0
 (x -1) (2x -1) = 0
 2x² — x — 2x + 1 = 0
 2x² — 3x + 1 = 0
 При сравнении данного уравнения с ax² + bx + c = 0
 Здесь a = 2, b = -3, c = 1
 D (дискриминант) = b² — 4ac
 D = (-3) ² — 4 x 2 x 1
 D = 9 — 8 = 1
 D = 1
 Следовательно, дискриминант квадратного уравнения (x -1) (2x -1) = 0 равен = 1
 4) Дано: x² — 2x + k = 0
 При сравнении данного уравнения с ax² + bx + c = 0
 Здесь a = 1, b = -2 и c = k
 D (дис criminant) = b² — 4ac
 D = (-2) ² — 4 (1) (k)
 D = 4 — 4k
 Следовательно, дискриминант квадратного уравнения x² — 2x + k = 0 равен (4 — 4k)
 5) Дано: 3√x² + 2√2x – 2√3 = 0
 При сравнении данного уравнения с ax² + bx + c = 0
 Здесь a = √3, b = 2√2 и c = −2√3
 D (дискриминант) = b² — 4ac
 D = (2√2) ² — (4 × √3 × -2√3)
 D = 8 + 24 = 32
 D = 32
 Следовательно, дискриминант квадратного уравнения 3√x² + 2√2x – 2√3 = 0 равен 32.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *