Содержание
Геометрическая прогрессия | umath.ru
Определение геометрической прогрессии
Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.
То есть геометрическая прогрессия определяется рекуррентным соотношением
Итак, для n-го члена геометрической прогрессии справедлива формула
Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Доказательство. Из определения геометрической прогрессии
Следовательно,
откуда
Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.
Сумма первых n членов геометрической прогрессии
Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :
(1)
Умножим это равенство на :
или
(2)
Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как имеем
или
(3)
Так как то формулу (3) можно переписать в виде
(4)
Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.
Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии
По формуле (3) получаем
Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.
Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогресcии выражается формулой
(5)
формула, как найти q, сумма первых n чисел
Что такое геометрическая прогрессия
Геометрическая прогрессия являет собой последовательность чисел. Когда каждому натуральному числу n поставлено в соответствие число \(Xn\), то говорят, что представлена числовая последовательность. Она имеет вид: \(X_1, X_2\)
,…,\(X_n\), или \({[X_n]}\). Для задания последовательности необходимо знать закон, по которому каждому натуральному числу n соответственно поставлено общее число последовательности \(f(n)=X_n.\)
Геометрическая прогрессия — последовательность с заданным первым членом \(b_1\), в которой каждый следующий, начиная со второго, получается умножением предыдущего на одно и то же число \(q\).
Числа \( b_1\) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:
\(b_n=b_{n-1}\cdot q,\)
Где \(b_n\) — \(n-й\) член прогрессии, \(q\) — знаменатель прогрессии.
Геометрическая прогрессия может быть задана рекуррентным соотношением:
\(b_1=b,\) \(b_{n+1}=b_n\cdot q,\) \(n\in N,\) \(b\neq0\), \(q\neq0.\)
Примечание
Рекуррентное соотношение задается формулой, выражающей \(Xn\) через предшествующие ему члены последовательности.
Примеры геометрических прогрессий:
- 1, 2, 4, 8, 16, 32 …; \(b_1 = 1\), \(q = 2;\)
- 1, 3, 9, 27, 81…; \(b_1 = 1\), \(q = 3;\)
- 2, -8, 32, -128, 512…:\(b_1 = 2\), \(q = -4.\)
Каждый член геометрической прогрессии, начиная со второго, рассчитывается как модуль среднего геометрического соседних членов:
\(\left|b_n\right|=\sqrt{b_{n-1}\cdot b_{n+1}},\) \(n\geq2, \)
или
\(b_n^2=b_{n-1}\cdot b_{n+1}. \)
\)
Если \(b_1 > 0\) и \(q > 1\) или \(b_1 < 0\) и \(0 < q < 1\), то для геометрической последовательности характерно возрастание.
Если \(b_1 > 0\) и 0 < \(q < 1\) или \(b_1 < 0\) и \(q > 1\), то для нее характерно убывание.
Примеры геометрических прогрессий в жизни:
- Размножение бактерий крайне велико и осуществляется по геометрической прогрессии: каждая клетка делится на две, новые — делятся еще на две и т.д. Знание принципов размножения бактерий находит свое применение в биотехнологии, пищевой промышленности, медицине и т.д.
- Зная формулу суммы геометрической прогрессии, можно находить площади и объемы геометрических фигур. Еще Архимед заметил связь между прогрессиями и вывел формулу для нахождения площади сегмента параболы через сумму бесконечно убывающей геометрической прогрессии.
- Возрастание скорости химических реакций происходит в геометрической прогрессии при увеличении температуры по арифметической прогрессии.
 2}\Rightarrow1+q=3\Rightarrow q=2.\)
2}\Rightarrow1+q=3\Rightarrow q=2.\)Ответ: \(q=2. \)
Сумма геометрической прогрессии | Онлайн калькулятор
Сумма геометрической прогрессии имеет несколько различных представлений, которые зависят от знаменателя прогрессии. Для возрастающей положительной, отрицательной или знакочередующейся прогрессии имеет место исключительно сумма нескольких первых членов геометрической прогрессии, количество которых должно быть ограничено, так как сама последовательность будет бесконечной.
Для прогрессии, знаменатель которой заключен между нулем и единицей, то есть является правильной дробью (0, сумма всей последовательности будет вполне однозначным конкретным числом, так как весь числовой ряд будет убывающим. Сумма бесконечно убывающей геометрической прогрессии имеет свою отдельную формулу, которую можно найти в соответствующем разделе, вместе с калькулятором.
Чтобы найти сумму первых членов геометрической прогрессии, необходимо знать первый член и знаменатель прогрессии.
 Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.
Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.Формула суммы первых трех, четырех или n членов геометрической прогрессии выводится с использованием среднего геометрического, как основного свойства данной прогрессии. Любое из чисел, стоящих в ряду, будет равно среднему геометрическому его соседей:
Если объединить это свойство с отношением двух последовательных членов прогрессии, которые неизменно равно одному и тому же числу — знаменателю, то путем нехитрых сокращений, сумма первых нескольких членов геометрической прогрессии приводится к такому виду:
В некоторых источниках встречается похожий вариант, но с другими знаками в скобках — по сути окончательного значения это не меняет, и для ручного расчета, когда даны первые несколько членов, уместно использовать более удобную на момент формулу.

Геометрическая прогрессия (ЕГЭ — 2021)
Многие знают, что шахматная игра была придумана в Индии. Когда индусский царь познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его подданных, царь решил лично наградить его. Он вызвал изобретателя к себе и приказал просить у него все, что он пожелает, пообещав исполнить даже самое искусное желание.
Сета попросил время на размышления, а когда на другой день Сета явился к царю, он удивил царя беспримерной скромностью своей просьбы. Он попросил выдать за первую клетку шахматной доски \( \displaystyle 1\) пшеничное зерно, за вторую \( \displaystyle 2\) пшеничных зерна, за третью \( \displaystyle -4\), за четвертую \( \displaystyle -8\) и т.д.
Царь разгневался, и прогнал Сета, сказав, что просьба слуги недостойна царской щедрости, но пообещал, что слуга получит свои зерна за все \( \displaystyle 64\) клетки доски.
А теперь вопрос: используя формулу суммы членов геометрической прогрессии, посчитай, сколько зерен должен получить Сета?
Начнем рассуждать.
 {64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)
{64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)Конечно, если ты хочешь, то можешь взять калькулятор и посчитать, что за число в итоге у тебя получится, а если нет, придется поверить мне на слово: итоговым значением выражения будет \( \displaystyle 18~\ 446~\ 744~\ 073~\ 709~\ 551~\ 615\).
То есть:
\( \displaystyle 18\) квинтильонов \( \displaystyle 446\) квадрильонов \( \displaystyle 744\) триллиона \( \displaystyle 73\) миллиарда \( \displaystyle 709\) миллионов \( \displaystyle 551\) тысяч \( \displaystyle 615\).
Фух) Если желаете представить себе огромность этого числа, то прикиньте, какой величины амбар потребовался бы для вмещения всего количества зерна.
При высоте амбара \( \displaystyle 4\) м и ширине \( \displaystyle 10\) м длина его должна была бы простираться на \( \displaystyle 300\text{ }000\text{ }000\) км, — т.е. вдвое дальше, чем от Земли до Солнца.
Если бы царь был бы силен в математике, то он мог бы предложить самому ученому отсчитывать зерна, ведь чтобы отсчитать миллион зерен, ему бы понадобилось не менее \( \displaystyle 10\) суток неустанного счета, а учитывая, что необходимо отсчитать \( \displaystyle 18\) квинтильонов, зерна пришлось бы отсчитывать всю жизнь.

А теперь решим простую задачку на сумму членов геометрической прогрессии.
Сумма бесконечно убывающей геометрической прогрессии
Дата:24.12.2012 Алгебра 9 рус
Тема урока: Сумма бесконечно убывающей геометрической прогрессии
Цели и задачи урока: Научить приёмам комбинирования формул, определений, свойств арифметической и геометрической прогрессий. Научить приёму оформления задач через таблицу.
Развить навыки применения формул, составления уравнений, систем уравнений и методов их решений. Развить математический кругозор, мышление, математическую речь;
Воспитать активную работу на уроке, сознательное отношение к учёбе, интерес к изучению математики, воспитывать стремление к непрерывному совершенствованию.
План урока.
Организационный момент.
Немного истории.
Теоретический опрос.
Решение задач.
Рефлексия. Ответьте на вопросы сами себе.
Домашнее задание.
Ход урока.

Организационный момент.
Немного истории.
В клинописных табличках вавилонян, в египетских папирусах, относящихся ко 2 тысячелетию до нашей эры, встречаются примеры арифметических и геометрических прогрессий. Первые теоретические сведения, связанные с прогрессиями, дошли до нас в документах Древней Греции. Некоторые формулы, относящиеся к прогрессиям, были известны и индийским учёным. Правило для нахождения суммы членов произвольной арифметической прогрессии даётся в «Книге абака» (1202г.) Леонардо Фибоначчи. А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Н. Шюке «Наука о числах», в 1484 году.
Теоретический опрос.
Задание. Записать номер формулы.
Определение арифметической прогрессии.
Формулу суммы n-первых членов арифметической прогрессии через первый член и последний.
Формулу суммы членов бесконечно убывающей геометрической прогрессии.

Формулу суммы n-первых членов геометрической прогрессии.
Общую формулу для вычисления разности арифметической прогрессии.
Формулу свойства членов геометрической прогрессии.
Формулу суммы n-первых членов арифм-кой прогрессии через первый член и разность.
Общую формулу для вычисления знаменателя геометрической прогрессии.
Определение геометрической прогрессии.
Формулуn-го члена геометрическую прогрессии.
Формулу свойства членов арифметической прогрессии.
Формулуn-го члена арифметической прогрессии.
an+1 = an + d 7)
8)
an= a1+ (n – 1)d 9)
0)
6) 11)
12)
Проверить код ответов ( 1, 6, 12, 11, 2,0.
Расшифровать полученные числа, как день16.
 12.11. 20-летия Независимости Казахстана.
12.11. 20-летия Независимости Казахстана.Решение комбинированных задач.
Даны 4 числа. Первые 3 из них составляют геометрическую
прогрессию со знаменателем 2, а последние 3 — арифметическую прогрессию с
разностью 6. Найти данные числа.
Дано: а, в, с, е – искомые числа. Из них геометр. прогрессия{ а, в, с} и q = 2,
арифмет.прогрессия{ в, с, е} и d = 6.
Найти: а, в, с, е.
Решение:
а
в
с
е
Геометр.
прогрессия
а
аq = 2а
аq2= 4а
—
Арифмет.
прогрессия
—
в
в + d = в + 6
в + 2d = в + 12
По данным составим таблицу.
По таблице видно, что 2а = в и 4а = в + 6.
Имеем 4а = 2а + 6, 2а = 6, а = 3. Тогда в = 2
Ответ: 3, 6, 12, 18.

Сумма трёх чисел, образующих арифмет. прогрессию, равна 27.
Если от этих чисел отнять соответственно 1; 3; 2, то полученные числа будут
образовывать геометрическую прогрессию. Найти исходные три числа.
Дано: а, в, с – искомые числа, арифмет. прогрессия { а, в, с},
геометр. прогрессия {а – 1, в – 3, с – 1}.
Найти: а, в, с.
Искомые числа
а
в
с
Арифмет.
прогрессия
а
в = а+d
с = а + 2d
Геометр.
прогрессия
а — 1
(а + d) – 3
а + 2d – 2
Решение:
По данным составим таблицу.
По условию сумма трёх чисел, образующих арифметическую прогрессию, равна 27, тогда можно записать: а + а + d + а + 2d = 27, 3а + 3d = 27, а + d = 9 (1).
По данным таблицы получили при решении в = 9, так как в = а + d.

Используем свойство членов геометрической прогрессии. Получим уравнение:
(а + d – 3)2 = (а – 1)(а + 2d – 2), (9 – 3)2= (а – 1)( а + d + d – 2), 62 = (а – 1)(7 + d)(2)
Составим систему уравнений из уравнений (1) и (2) решим её.
d2 – d – 20 = 0
По теореме Виета и ей обратной найдём корни полученного уравнения:
Найдём искомые числа: 1) а = 9 – (– 4) = 13, в = 9, с = 9 – 4 = 5.2) а = 9 – 5 = 4, в = 9, с = 9 + 5 = 14.
Ответ: 13, 9, 4 или 4, 9, 14.
Даны 4 числа, составляющих геометрическую прогрессию. Если от
этих чисел отнять соответственно 10; 11; 9; 1, то полученные числа будут
образовывать арифметическую прогрессию. Найти данные числа.
Дано: а, в, с, е – искомые числа. Из них геометр. прогрессия { а, в, с, е},
арифмет. прогрессия { а – 10, в – 11, с – 9, е – 1}.
Найти: а, в, с, е.
 Решение:По данным составим таблицу.
Решение:По данным составим таблицу.Числа
а
в
с
е
Геометр.
прогрессия
а
аq
аq2
аq3
Арифмет.
прогрессия
а – 10
в – 11 = аq – 11
с – 9 = аq2 – 9
е – 1 = аq3 – 1
По таблице используем данные и применим свойство арифметической прогрессии 1) , 2аq – 22 = a + аq2 – 19, аq2 — 2аq + a = – 3,
a(q2 — 2q + 1) = – 3, a(q – 1)2 = – 3 (1).
2) , 2аq2 – 18 = aq + аq3 – 12, аq3 — 2аq2 + aq = – 6,
aq(q2 — 2q + 1) = – 6, aq(q – 1)2 = – 6 (2).
Почленно разделим равенство (2) на равенство (1) = ,
После сокращения дробей получим q = 2.

Найдём значение а из равенства (1) а = – 3.
Вычислим остальные числа: в = – 3 · 2 = – 6, с = – 6 ·2 = – 12, е = – 12 · 2 = –24.
Ответ: – 3, – 6, – 12, – 24.
Даны 3 различных числа, составляющих геометрическую
прогрессию. Необходимо между вторым и третьим членом этой
последовательности вставить число, чтобы получившаяся последовательность
была арифметической прогрессией. Найти знаменатель заданной
геометрической прогрессии.
Дано: а, в, с – искомые числа, геометрическая прогрессия { а, в, с},
арифметическая прогрессия { а, в, х, с}.
Найти:q
Решение: Так как по условию 3 различных числа, составляющих геометрическую прогрессию, то q для арифметической прогрессии d
а
в
х
с
Геометр.
прогрессия
а
аq
—
аq2
Арифмет.

прогрессия
а
а + d
а + 2d
а + 3d
По данным составим таблицу.
По таблице видно, что 1) аq = а + d, d = аq – а, d = а(q – 1) (1)
2 ) аq2 = а + 3d, 3d = аq2 – а , 3d = а(q2 – 1) (2)
Подставим равенство (1) в равенство (2) 3а(q – 1) = а(q2 – 1).
Разделим полученное равенство на а(q – 1) , получим 3 = q + 1, q = 2. Ответ: 2.
Решить неравенство (3х + 7 + 3 – 1 – …)(2 + 4 + 8 + …+ х) 0, где в скобках по 6 числовых слагаемых.
Решение. 1) Рассмотрим числовые слагаемые первой скобки: 7; 3; — 1;…
Заметим, что 3 – 7 = – 4, – 1 – 3 = – 4 раз другие слагаемые не предлагаются, значит эта закономерность сохраняется и эти 6 слагаемых и они образуют арифметическую прогрессию с d = – 4 и а1= 7.
По формуле суммы n-первых членов арифметической прогрессии найдём сумму 6 членов:
Рассмотрим числовые слагаемые второй скобки: 2; 4; 8;…
Заметим, что 4 : 2 = 8: 4 = 2 раз не другие слагаемые не предлагаются, значит эта закономерность сохраняется и все 6 слагаемых образуют геометрическую прогрессию с
q = 2 и в1 = 2.

По формуле суммы n-первых членов геометрической прогрессии найдём сумму 6 членов:
Полученные данные подставим в заданное неравенство (3х – 18)(126 + х) 0 и решим его методом интервалов.
П остроим чертёж + –– +
– 126 6
Ответ: (-
Решить уравнение х2 – 6│х│ – 21 – 15 – 9 — … = 3 + 2 + 1 + 0,5 + ….. где в левой части уравнения 8 числовых слагаемых.
Решение.
Рассмотрим числовые слагаемые левой части уравнения: — 21; — 15; — 9;…
Заметим, что – 21 – (– 15) = – 15 – (– 9) = 6, раз другие слагаемые не предлагаются, значит эта закономерность сохраняется и эти 8 слагаемых образуют арифметическую прогрессию с d = 6 и а1= – 21.
По формуле суммы n-первых членов арифмет. прогрессии найдём сумму 8 членов:
Рассмотрим числовые слагаемые правой части уравнения без числа 3: 2; 1; 0,5;…
Заметим, что 1 : 2 = 0,5: 1 = 0,5 раз не другие слагаемые из этой последовательности не предлагаются, значит эта закономерность сохраняется и все слагаемые образуют бесконечно убывающую геометрическую прогрессию с q = 0,5 и в1 = 2.

По формуле суммы членов бесконечно убывающей геометрической прогрессии найдём сумму всех членов:
Подставим полученные результаты в уравнение х2 – 6│х│+ 0 = 3 + 4 и решим его.
х2 – 6│х│ = 7, х2 – 6│х│ – 7 = 0. Раскроем модуль по определению.
Если хто уравнение примет вид х2 – 6х – 7 = 0. Найдём его корни по второму свойству коэффициентов квадратного уравнения
Если хто уравнение примет вид х2 + 6х – 7 = 0. Найдём его корни по первому свойству коэффициентов квадратного уравнения
Ответ:
Рефлексия. Ответьте на вопросы сами себе.
Домашнее задание.
Три числа составляют арифметическую прогрессию с разностью равной 4. Если к третье число увеличить на 8, эти три числа будут образовывать геометрическую прогрессию. Найти данные числа. (2, 6, 10)
Даны три числа образующих геометрическую прогрессию, первое из которых равно 8. Если второе число увеличить на 1, то эта последовательность станет арифметической прогрессией.
 Найти знаменатель геометрической прогрессии.(1,5 или 0,5)
Найти знаменатель геометрической прогрессии.(1,5 или 0,5)Даны четыре числа. Первые три образуют геометрическую прогрессию, а последние три — арифметическую прогрессию. Сумма первого и последнего чисел равна 32, а сумма средних чисел – 24. Найти данные числа.(32, 16, 8, 0 или 2, 6, 18, 30)
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/48200-summa-beskonechno-ubyvajuschej-geometrichesko
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Определение 1. Числовую последовательность
b1 , b2 , … bk , …
все члены которой отличны от нуля, называют геометрической прогрессией, если справедливы равенства
Определение 2. Если последовательность чисел
b1 , b2 , … bk , …
является геометрической прогрессией, то число q , определенное формулой
называют знаменателем этой геометрической прогрессии.

Из определений 1 и 2 следует, что для того, чтобы задать геометрическую прогрессию, нужно знать два числа, например, первый член геометрической прогрессии b1 и знаменатель геометрической прогрессии q . Если числа b1 и q известны, то все остальные члены прогрессии можно найти по формулам:
b2 = b1q , b3 = b2q , … bk = bk – 1q … (1) По этой причине многие задачи на геометрическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел b1 и q.
Из формул (1) вытекает общая формула
bk = b1qk – 1,
k = 1, 2, 3, …(2) позволяющая по любому номеру k вычислить член bk геометрической прогрессии, зная первый член и знаменатель прогрессии.
 Эта формула носит название формулы общего члена геометрической прогрессии.
Эта формула носит название формулы общего члена геометрической прогрессии.Из формулы (2) вытекает утверждение, называемое характеристическим свойством геометрической прогрессии. Это свойство формулируется так: — «Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению своих соседних членов». Таким образом, характеристическое свойство геометрической прогрессии утверждает, что при справедливо равенство
(3) В случае, когда
b1 > 0 и q > 0
все члены геометрической прогрессии будут положительными, и формулу (3) можно переписать в другом виде:
(4) Равенство (4) означает, что каждый член такой геометрической прогрессии, начиная со второго, равен среднему геометрическому своих соседних членов.

Если для суммы первых k членов геометрической прогрессии ввести обозначение
Sk = b1 + b2 + … + bk ,
k = 1, 2, 3, …то, воспользовавшись равенствами (1), получаем
q Sk =
= b1q + b2q + … + bk q =
= b2 + b3 + … + bk +1 .Следовательно,
Sk – q Sk = b1 – bk +1 .
Таким образом , при будет справедливо равенство
которое называется формулой для суммы первых k членов геометрической прогрессии.
В случае, когда q = 1, все члены геометрической прогрессии равны, что не представляет особого интереса.

Бесконечно убывающая геометрическая прогрессия
Определение 3. Геометрическую прогрессию называют бесконечно убывающей, если её знаменатель удовлетворяет неравенству
| q | < 1 .
В этом случае выполнено равенство
а величину S называют суммой бесконечно убывающей геометрической прогрессии.
Более подробно с понятием предела числовой последовательности можно ознакомиться в в разделе «Пределы числовых последовательностей» нашего справочника.
С примерами решений различных задач по теме «Геометрическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Бесконечно убывающая геометрическая прогрессия
Напомним,
что геометрическая прогрессия – это числовая
последовательность,
,
,
…, ,
…, где,
что для всех натуральных выполняется
равенство,
где .
Число называется
знаменателем геометрической последовательности, число –первым
её членом, а число –
общим её членом.,
,
,
,
…, ,
…,, , , , …, , …,
Также
напомним, что —ый
член геометрической прогрессии можно вычислить по формулеА
сумму первых членов
геометрической прогрессии можно вычислить по формуле , если ;, если .
Однако
среди геометрических прогрессий особый интерес вызывают так
называемые бесконечно убывающие геометрические прогрессии.
Давайте познакомимся с такими прогрессиями.Начнём
с примера. Итак, перед вами изображены квадраты.Сторона
первого, самого большого квадрата равна ,
сторона второго равна ,
сторона третьего квадрата – ,
сторона четвёртого квадрата – ,
сторона пятого квадрата – и
так далее.Обратите
внимание! Стороны наших квадратов образуют геометрическую прогрессию:
, , , , , …Перепишем
эту геометрическую прогрессию в таком виде: , , , , , …, , …Знаменатель
этой геометрической прогрессии равен .Заметим,
что и площади этих квадратов также образуют геометрическую прогрессию:,
,
,
,
,
…,
,
,
,
,
…, ,
…Хотелось
бы отметить, что стороны квадратов и их площади с возрастанием номера становятся
всё меньше и всё больше приближаются к.
Так вот, каждую из прогрессий, что мы с вами записали, называют бесконечно
убывающей геометрической прогрессией.А
теперь давайте рассмотрим следующую геометрическую прогрессию:, , , , …, , …
Здесь, , , , … , знаменатель нашей
геометрической прогрессии .Видим,
что с возрастанием номера члены
этой прогрессии приближаются к.
Значит, эта прогрессия является бесконечно убывающей геометрической
прогрессией. Обратите внимание! .Запомните:
геометрическая прогрессия называется бесконечно убывающей,
если модуль её знаменателя меньше единицы.А
теперь давайте перейдём к выводу формулы суммы бесконечно убывающей
геометрической прогрессии.Итак,
на экране вы видите квадрат со стороной равной единице. Разделим этот квадрат
пополам. Заштрихуем обе части нашего квадрата, как показано на экране. Продолжим
Продолжим
делить пополам наши квадраты и штриховать их. Заметим, что площади
заштрихованных прямоугольников образуют бесконечно убывающую
геометрическую прогрессию: , , , , , …Если
мы заштрихуем все получающиеся таким образом прямоугольники, то понятно, что
весь квадрат покроется штриховкой. Разумеется, сумма площадей всех
заштрихованных прямоугольников будет равна единице. То есть …Обратите
внимание: в левой части нашего равенства стоит сумма бесконечного
числа слагаемых.Давайте
рассмотрим сумму первых слагаемых.
Применяя формулу суммы членов
геометрической прогрессии, имеем ….
Получим, что .Заметим,
что если неограниченно
возрастает, то будет
как угодно близко приближаться к 0. Это выражение записывают следующим образом:
при
,
а читают так: «единица делённая на два в степени эн стремится к нулю при эн
стремящемся к бесконечности, или предел единицы делённой на два в степени эн
при эн стремящемся к бесконечности равен нулю».
Так
как при
,
то при
,
то есть или
.
Поэтому бесконечную сумму ….В
этом случае говорят, что сумма бесконечно убывающей геометрической прогрессии
есть предел последовательности , , , …, , …Например,
если мы возьмём бесконечно убывающую геометрическую прогрессию , , , , …, , …Где
,.,
,
,
…,,
…Так
как ,
то .А
теперь выведем формулу суммы бесконечно убывающей геометрической
прогрессии.Мы
помним, что сумму первых членов
геометрической прогрессии можно вычислить по формуле .Перепишем
эту формулу таким образом: .Так
как ,
то ,.Следовательно,
.Таким
образом, сумму бесконечно
убывающей геометрической прогрессии можно вычислить по формуле: .Из
этой формулы при имеем
.
Это
равенство обычно записывают следующим образом:… … .
Обратите
внимание: это равенство справедливо при ,
в частности при .Задание
1.Докажите,
что геометрическая прогрессия:…
, является бесконечно убывающей.Решение.
, .
Следовательно,
данная геометрическая прогрессия является бесконечно убывающей.Задание
2.Найдите
сумму бесконечно убывающей геометрической прогрессии …Решение.
,
.Задание
3.Найдите
сумму бесконечно убывающей геометрической прогрессии, если , .Решение.
По условию нам даны и
прогрессии.,
.Сумма первых n членов геометрической последовательности
Если последовательность геометрическая, есть способы найти сумму первых n элементов.

термины, обозначенные Sn, без фактического добавления всех терминов.Чтобы найти сумму первых Sn
члены геометрической последовательности используют формулу
Sn = a1 (1 − rn) 1 − r, r ≠ 1,
, где n
— количество слагаемых, a1
— первый член, а r
это обычное отношение.Сумма первых n
термины геометрической последовательности называется геометрической серией.Пример 1:
Найдите сумму первых 8 членов геометрического ряда, если a1 = 1
и r = 2.S8 = 1 (1-28) 1-2 = 255
Пример 2:
Найдите S10
геометрической последовательности 24,12,6, ⋯.Сначала найдите r.
r = r2r1 = 1224 = 12
Теперь найдите сумму:
S10 = 24 (1− (12) 10) 1−12 = 306964
Пример 3:
Вычислить.
∑n = 1103 (−2) n − 1
(Вы находите S10
для ряда 3−6 + 12−24 + ⋯, значащий коэффициент которого равен −2.)Sn = a1 (1 − rn) 1 − rS10 = 3 [1 — (- 2) 10] 1 — (- 2) = 3 (1−1024) 3 = −1023
Для того, чтобы бесконечный геометрический ряд имел сумму, должно быть стандартное отношение r
должно быть между -1
и 1. Тогда при n
Тогда при n
увеличивается, рН
становится все ближе и ближе к 0. Чтобы найти сумму бесконечного геометрического ряда, имеющего отношения с абсолютным значением меньше единицы, используйте формулу S = a11 − r, где a1
— первый член, а r
это обычное отношение.Пример 4:
Найдите сумму бесконечной геометрической последовательности
27,18,12,8, ⋯.Сначала найдите r:
r = a2a1 = 1827 = 23
Затем найдите сумму:
S = a11 − r
S = 271−23 = 81
Пример 5:
Найдите сумму бесконечной геометрической последовательности
8,12,18,27, ⋯
если он существует.Сначала найдите r:
r = a2a1 = 128 = 32
Так как r = 32
не меньше единицы. Серия не имеет суммы.
Существует формула для вычисления n th члена геометрического ряда, то есть суммы первых n
члены геометрической последовательности.См. Также: сигма-обозначение ряда
и сумма первых n
члены арифметической последовательностиГеометрическая серия
А
геометрическая серия
эторяд
чьи родственные
последовательность
геометрический.
 Это результат добавления
Это результат добавлениятермины
из
геометрическая последовательность
.
Пример 1:
Конечная геометрическая последовательность:
1
2
,
1
4
,
1
8
,
1
16
,
…
,
1
32768
Связанные конечные геометрические ряды:
1
2
+
1
4
+
1
8
+
1
16
+
…
+
1
32768
Написано в сигма-нотации:
∑
k
знак равно
1
15
1
2
k
Пример 2:
Бесконечная геометрическая последовательность:
2
,
6
,
18
,
54
,
.
 ..
..Связанные бесконечные геометрические серии:
2
+
6
+
18
+
54
+
…
Написано в сигма-нотации:
∑
п
знак равно
1
∞
(
2
⋅
3
п
—
1
)
Конечный геометрический ряд
Чтобы найти сумму конечного геометрического ряда, используйте формулу
Sп
знак равно
а
1
(
1
—
р
п
)
1
—
р
,
р
≠
1
,
гдеп
это количество терминов,
а
1
это первый член и
р
это
обычное отношение
.

Пример 3:
Найдите сумму первых
8
члены геометрического ряда, если
а
1
знак равно
1
а также
р
знак равно
2
.
S
8
знак равно
1
(
1
—
2
8
)
1
—
2
знак равно
255
Пример 4:
Находить
S
10
, десятая частичная сумма бесконечного геометрического ряда
24
+
12
+
6
+
…
.
Сначала найдите
р
.
р
знак равно
а
2
а
1
знак равно
12
24
знак равно
1
2
Теперь найдите сумму:
S
10
знак равно
24
(
1
—
(
1
2
)
10
)
1
—
1
2
знак равно
3069
64
Пример 5:
Оценивать.

∑
п
знак равно
1
10
3
⋅
(
—
2
)
п
—
1
(Вы находите
S
10
для сериала
3
—
6
+
12
—
24
+
…
, обыкновенное отношение которого
—
2
.)
S
п
знак равно
а
1
(
1
—
р
п
)
1
—
р
S
10
знак равно
3
[
1
—
(
—
2
)
10
]
1
—
(
—
2
)
знак равно
3
(
1
—
1024
)
3
знак равно
—
1023
Бесконечная геометрическая серия
Чтобы найти сумму бесконечного геометрического ряда, имеющего отношения с
абсолютная величина
меньше единицы, используйте формулу,
S
знак равно
а
1
1
—
р
,
гдеа
1
это первый член и
р
это обычное отношение.

Пример 6:
Найдите сумму бесконечного геометрического ряда
27+
18
+
12
+
8
+
…
.
Первая находка
р
:
р
знак равно
а
2
а
1
знак равно
18
27
знак равно
2
3
Затем найдите сумму:
S
знак равно
а
1
1
—
р
S
знак равно
27
1
—
2
3
знак равно
81 год
Пример 7:
Найдите сумму бесконечного геометрического ряда
8+
12
+
18
+
27
+
.
 ..
..если он существует.
Первая находка
р
:
р
знак равно
а
2
а
1
знак равно
12
8
знак равно
3
2
С
р
знак равно
3
2
не меньше единицы, ряды не сходятся.То есть в нем нет суммы.
геометрических последовательностей и серий | Безграничная алгебра
Геометрические последовательности
Геометрическая последовательность — это упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на константу, называемую [латекс] r [/ латекс], обычное отношение.
Цели обучения
Вычислить [латекс] n [/ латекс] -й член геометрической последовательности с учетом начального значения [латекс] a [/ латекс] и общего отношения [латекс] r [/ латекс]
Основные выводы
Ключевые моменты
- Общая форма геометрической последовательности: [латекс] a, ar, ar ^ 2, ar ^ 3, ar ^ 4, \ cdots [/ latex]
- [латекс] n [/ латекс] -й член геометрической последовательности с начальным значением [латекс] n [/ латекс] и общим соотношением [латекс] r [/ латекс] задается следующим образом: [латекс] {a} _ { n} = a {r} ^ {n-1} [/ латекс].

Ключевые термины
- геометрическая последовательность : упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением. Также известна как геометрическая прогрессия.
Определение геометрических последовательностей
Геометрическая прогрессия, также известная как геометрическая последовательность, представляет собой упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое обычным соотношением [латекс] r [/ latex ].{n-1} [/ latex]
Такая геометрическая последовательность также следует рекурсивному соотношению:
[латекс] a_n = ra_ {n-1} [/ латекс]
для каждого целого числа [латекс] n \ ge 1. [/ Latex]
Поведение геометрических последовательностей
Обычно, чтобы проверить, является ли данная последовательность геометрической, просто проверяют, все ли последовательные записи в последовательности имеют одинаковое соотношение.
 Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].Поведение геометрической последовательности зависит от значения общего отношения. Если общее отношение:
- Положительно, все термины будут того же знака, что и исходный термин
- Отрицательный, члены будут чередоваться между положительным и отрицательным
- Больше, чем [latex] 1 [/ latex], будет экспоненциальный рост в сторону положительной бесконечности ([latex] + \ infty [/ latex])
- [latex] 1 [/ latex], прогрессия будет постоянной
- Между [латексом] -1 [/ латексом] и [латексом] 1 [/ латексом], но не [латексом] 0 [/ латексом] будет экспоненциальный спад в сторону [латекса] 0 [/ латекса]
- [latex] -1 [/ latex], прогрессия — чередующаяся последовательность (см.
 Чередующиеся серии)
Чередующиеся серии) - Меньше [latex] -1 [/ latex], для абсолютных значений наблюдается экспоненциальный рост в сторону положительной и отрицательной бесконечности (из-за чередования знаков)
Геометрические последовательности (с общим соотношением, не равным [латекс] -1 [/ латекс], [латекс] 1 [/ латекс] или [латекс] 0 [/ латекс]) показывают экспоненциальный рост или экспоненциальное затухание, в отличие от линейный рост (или снижение) арифметической прогрессии, такой как [латекс] 4, 15, 26, 37, 48, \ cdots [/ латекс] (с общим отличием [латекс] 11 [/ латекс]).Этот результат был получен T.R. Мальтуса в качестве математической основы его принципа народонаселения. Обратите внимание, что два вида прогрессии связаны между собой: возведение в степень каждого члена арифметической прогрессии дает геометрическую прогрессию, а логарифм каждого члена в геометрической прогрессии с положительным общим отношением дает арифметическую прогрессию.
Интересным результатом определения геометрической прогрессии является то, что для любого значения общего отношения любые три последовательных термина [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс] удовлетворяет следующему уравнению:
[латекс] {b} ^ {2} = ac [/ latex]
Суммирование первых n членов геометрической последовательности
Используя обычное отношение и первый член геометрической последовательности, мы можем суммировать его члены.
 {n}} {1-r}} [/ латекс].
{n}} {1-r}} [/ латекс]. - геометрическая серия : Бесконечная последовательность добавляемых чисел, члены которой находятся путем умножения предыдущего члена на фиксированное ненулевое число, называемое обычным отношением.
- геометрическая прогрессия : серия чисел, в которой каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением.
- [латекс] 4 + 40 + 400 + 4000 + \ точки [/ латекс] имеет общее соотношение [латекс] 10 [/ латекс]
- [латекс] \ displaystyle {9 + 3 + 1 + \ frac {1} {3} + \ frac {1} {9} + \ dots} [/ latex] имеет общее соотношение [латекс] {\ frac {1 } {3}} [/ латекс]
- [латекс] 3 + 3 + 3 + 3 + \ точки [/ латекс] имеет общее соотношение [латекс] 1 [/ латекс]
- [латекс] \ displaystyle {1- \ frac {1} {2} + \ frac {1} {4} — \ frac {1} {8} + \ dots} [/ latex] имеет общее соотношение [латекс] — \ frac {1} {2} [/ latex]
- [латекс] 3-3 + 3-3 + \ точки [/ латекс] имеет общее соотношение [латекс] -1 [/ латекс]
- Если [латекс] r [/ латекс] находится между [латекс] -1 [/ латекс] и [латекс] +1 [/ латекс], члены ряда становятся все меньше и меньше, приближаясь к нулю в пределе, и ряд сходится к сумме.
 Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице.
Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице. - Если [латекс] r [/ латекс] больше [латекс] 1 [/ латекс] или меньше [латекс] -1 [/ латекс], члены ряда становятся все больше и больше по величине. Сумма членов также становится все больше и больше, и в серии нет суммы. Сериал расходится.
- Если [latex] r [/ latex] равно [latex] 1 [/ latex], все члены серии совпадают.Сериал расходится.
- Если [latex] r [/ latex] равно [latex] -1 [/ latex], термины принимают поочередно два значения [latex] \ left (\ text {eg}, 2, -2,2, -2,2 , -2, \ cdots \ right) [/ латекс]. Сумма членов колеблется между двумя значениями [latex] \ left (\ text {eg.}, 2,0,2,0,2,0, \ cdots \ right) [/ latex]. Это другой тип дивергенции, и снова у ряда нет суммы.
- Сумма геометрического ряда конечна, пока члены стремятся к нулю; поскольку числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
- Для бесконечного геометрического ряда, который сходится, его сумму можно вычислить по формуле [latex] \ displaystyle {s = \ frac {a} {1-r}} [/ latex].
- сходиться : приблизиться к конечной сумме.
- геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно меняются с общим соотношением.

- Повторяющаяся десятичная дробь может рассматриваться как геометрическая последовательность, общее отношение которой равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].
- Архимед использовал сумму геометрического ряда для вычисления площади, заключенной между параболой и прямой линией.
- Внутренняя часть снежинки Коха представляет собой объединение бесконечного множества треугольников.При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры.
- Знание бесконечных рядов позволяет нам решать древние проблемы, такие как парадоксы Зенона.
- геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно изменяются с общим соотношением.
- фрактал : природное явление или математический набор, который демонстрирует повторяющийся узор, который можно увидеть в любом масштабе.
- Если \ (\ mid r \ mid <1 \) , то ряд сходится и у ряда есть сумма.
- Если \ (\ mid r \ mid> 1 \) , то ряд не сходится и у него нет суммы. Это расходится.
- Для \ (r = 1 \) сумма GP \ (= na \).
- Сумма бесконечных GP равна \ (S_ \ infty = \ dfrac {a} {1-r} \)
- Если сумма трех действительных чисел в GP равна 26, а сумма их квадратов равна 364, найдите наибольшее число.
- Найдите сумму бесконечного GP 0.3+ 0,33+ 0,333 + …. [подсказка: \ (0,3 = \ dfrac {3} {10} \)]
Оценить S
10 для 250, 100, 40, 16 ,….
Найдите
a n , если S 4 = 26/27 и r = 1/3.
Покажите с помощью геометрического ряда, что 0.3333 … равно 1/3.
Преобразуйте 1,363636 … в дробную форму с помощью геометрического ряда.
- Отрицательный, результаты будут чередоваться между положительными и отрицательными .
Пример:
1, -2, 4, -8, 16, -32 … — обычное отношение равно -2, а первый член равен 1. - Больше чем 1, будет экспоненциальный рост к бесконечности (положительный) .
Пример :
1, 5, 25, 125, 625 … — обычное отношение равно 5. - Менее -1, будет экспоненциальный рост к бесконечности (положительный и отрицательный) .
Пример :
1, -5, 25, -125, 625, -3125, 15625, -78125, 3, -1953125 … — обычное отношение -5.
- Между 1 и -1, будет экспоненциальный спад к нулю .
Пример :
4, 2, 1, 0,5, 0,25, 0,125, 0,0625 … — обычное отношение $ \ frac {1} {2} $
4, -2, 1, -0,5, 0,25, -0,125, 0,0625 … — обычное отношение $ — \ frac {1} {2} $. - Ноль, результаты останутся на нуле .
Пример :
4, 0, 0, 0, 0 … — обычное отношение равно 0, а первый член равен 4.
Ключевые термины
Геометрические ряды являются примерами бесконечных рядов с конечными суммами, хотя не все из них обладают этим свойством.Исторически геометрические ряды играли важную роль в раннем развитии исчисления, и они по-прежнему занимают центральное место в изучении сходимости рядов. Геометрические ряды используются в математике и имеют важные приложения в физике, инженерии, биологии, экономике, информатике, теории очередей и финансах.
Члены геометрического ряда образуют геометрическую прогрессию, что означает, что соотношение следующих друг за другом членов в ряду постоянно. {n}}}} [/ латекс]
{n}}}} [/ латекс]
является геометрическим, потому что каждый последующий член может быть получен умножением предыдущего члена на [latex] \ displaystyle {\ frac {1} {2}} [/ latex].{n}}} [/ латекс]
Эту концепцию можно визуализировать с помощью диаграммы:
Бесконечная геометрическая серия: Каждый из фиолетовых квадратов получается путем умножения площади следующего большего квадрата на [latex] \ displaystyle {\ frac {1} {4}} [/ latex]. Площадь первого квадрата составляет [латекс] \ displaystyle {\ frac {1} {2} \ cdot \ frac {1} {2} = \ frac {1} {4}} [/ latex], а площадь второй квадрат — [латекс] \ displaystyle {\ frac {1} {4} \ cdot \ frac {1} {4} = \ frac {1} {16}} [/ latex].
Ниже приведены несколько геометрических рядов с разными общими отношениями.Поведение терминов зависит от общего соотношения [латекс] г [/ латекс]:
Значение [latex] r [/ latex] предоставляет информацию о характере серии:
Мы можем использовать формулу, чтобы найти сумму конечного числа членов в последовательности. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
{5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
Бесконечная геометрическая серия
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Вычислить сумму бесконечного геометрического ряда и определить, когда геометрический ряд будет сходиться
Основные выводы
Ключевые моменты
Ключевые термины
Геометрический ряд — это бесконечный ряд, члены которого находятся в геометрической прогрессии или чьи последовательные члены имеют общее отношение. Если члены геометрического ряда стремятся к нулю, сумма его членов будет конечной. Когда числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
Говорят, что геометрический ряд с конечной суммой сходится. Ряд сходится тогда и только тогда, когда абсолютное значение общего отношения меньше единицы:
.
[латекс] \ левый | г \ право | <1 [/ латекс]
Что следует на примере бесконечного ряда с конечной суммой. Подсчитаем сумму [latex] s [/ latex] следующей серии:
[латекс] \ displaystyle {s = 1+ \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ cdots} [/ latex]
Эта серия имеет общее соотношение [латекс] \ displaystyle {\ frac {2} {3}} [/ latex].Если мы умножим на это обычное соотношение, то начальный член [латекс] 1 [/ latex] станет [latex] \ displaystyle {\ frac {2} {3}} [/ latex], [latex] \ displaystyle {\ frac {2} {3}} [/ latex] становится [latex] \ displaystyle {\ frac {4} {9}} [/ latex] и так далее:
[латекс] \ displaystyle {\ frac {2} {3} s = \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ frac {16} { 81} + \ cdots} [/ латекс]
Эта новая серия такая же, как и исходная, за исключением того, что отсутствует первый член. Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
[латекс] \ displaystyle {\ begin {align} s- \ frac {2} {3} s & = 1 \\ \ поэтому s & = 3 \ end {align}} [/ latex]
Подобный метод можно использовать для вычисления любого самоподобного выражения.n \ rightarrow 0 \\ & = \ frac {a} {1-r} \ end {align}} [/ latex]
Следовательно, для [latex] | r | <1 [/ latex] мы можем записать бесконечную сумму как:
[латекс] \ displaystyle {s = \ frac {a} {1-r}} [/ латекс]
Пример
Найдите сумму бесконечного геометрического ряда [латекс] 64+ 32 + 16 + 8 + \ cdots [/ latex]
Сначала найдите [latex] r [/ latex], или постоянное соотношение между каждым членом и тем, что ему предшествует:
[латекс] \ displaystyle {\ begin {align} r & = \ frac {32} {64} \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Подставьте [латекс] a = 64 [/ latex] и [latex] \ displaystyle r = \ frac {1} {2} [/ latex] в формулу суммы бесконечного геометрического ряда:
[латекс] \ displaystyle {\ begin {align} s & = \ frac {64} {1- \ frac {1} {2}} \\ & = \ frac {64} {\ frac {1} {2} } \\ & = 128 \ end {align}} [/ latex]
Применения геометрической серии
Геометрические ряды применяются в математике и естественных науках и являются одним из простейших примеров бесконечных рядов с конечными суммами.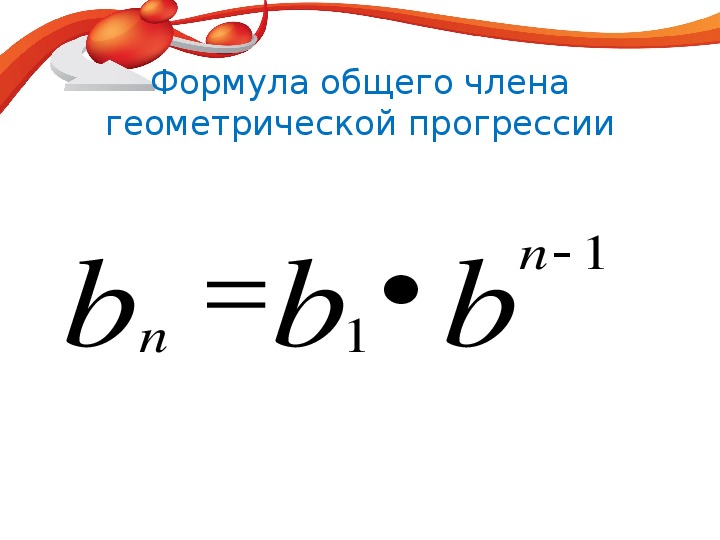
Цели обучения
Применение геометрических последовательностей и рядов к различным физическим и математическим темам
Основные выводы
Ключевые моменты
Ключевые термины
Геометрические ряды сыграли важную роль в раннем развитии исчисления и продолжают оставаться центральной частью изучения сходимости рядов. Геометрические ряды используются во всей математике. У них есть важные приложения в физике, инженерии, биологии, экономике, информатике, теории массового обслуживания и финансах.
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами, хотя не все они обладают этим свойством.
Повторяющаяся десятичная дробь
Повторяющееся десятичное число можно рассматривать как геометрический ряд, общее отношение которого равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].Например:
[латекс] \ displaystyle {0,7777 \ cdots = \ frac {7} {10} + \ frac {7} {100} + \ frac {7} {1000} + \ frac {7} {10000} + \ cdots} [/ латекс]
Формула суммы геометрического ряда может использоваться для преобразования десятичной дроби в дробь:
[латекс] \ displaystyle {\ begin {align} 0,7777 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {7} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {7} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {7} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {7} {9} \ end {align}} [/ latex]
Формула работает для любого повторяющегося термина.Еще несколько примеров:
[латекс] \ displaystyle {\ begin {align} 0.123412341234 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1234} {10000}} {1- \ frac {1 } {10000}} \\ & = \ frac {\ left (\ frac {1234} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left ( \ frac {1234} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1234} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,0
0909 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {100}} {1- \ frac {1 } {100}} \\ & = \ frac {\ left (\ frac {9} {100} \ right)} {\ left (\ frac {99} {100} \ right)} \\ & = \ left ( \ frac {9} {100} \ right) \ left (\ frac {100} {99} \ right) \\ & = \ frac {9} {99} \\ & = \ frac {1} {11} \ конец {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0.143814381438 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1438} {10000}} {1- \ frac {1} {10000}} \\ & = \ frac { \ left (\ frac {1438} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left (\ frac {1438} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1438} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,9999 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {9} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {9} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {9} {9} \\ & = 1 \ end {align}} [/ латекс]
То есть повторяющаяся десятичная дробь с повторяющейся частью длины [латекс] n [/ latex] равна частному повторяющейся части (как целое число) и [латекс] 10 ^ n — 1 [/ latex].
Квадратура Параболы Архимеда
Архимед использовал сумму геометрического ряда для вычисления площади, заключенной между параболой и прямой линией. Его метод заключался в том, чтобы разрезать область на бесконечное количество треугольников.
Теорема Архимеда: Разбиение Архимеда параболического сегмента на бесконечное множество треугольников.
Теорема Архимеда утверждает, что общая площадь под параболой равна [latex] \ displaystyle {\ frac {4} {3}} [/ latex] площади синего треугольника.{3} + \ cdots} [/ latex]
Первый член представляет площадь синего треугольника, второй член — площади двух зеленых треугольников, третий член — площади четырех желтых треугольников и так далее. Упрощение дробей дает:
[латекс] \ displaystyle {1+ \ frac {1} {4} + \ frac {1} {16} + \ frac {1} {64} + \ cdots} [/ latex]
Это геометрическая серия с общим соотношением [латекс] \ displaystyle {\ frac {1} {4}} [/ latex], а дробная часть равна [latex] \ displaystyle {\ frac {1} {3} }[/латекс].
Фрактальная геометрия
Снежинка Коха: Внутренняя часть снежинки Коха состоит из бесконечного количества треугольников.
Снежинка Коха — это фрактальная форма, внутренность которой состоит из бесконечного количества треугольников. При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры. В случае снежинки Коха ее площадь можно описать геометрическим рядом.
Построение снежинки Коха: первые четыре итерации: каждая итерация добавляет набор треугольников снаружи формы.
Область внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников. На диаграмме выше треугольники, добавленные во второй итерации, имеют размер [latex] \ displaystyle {\ frac {1} {3}} [/ latex], равный размеру стороны наибольшего треугольника, поэтому они имеют ровно [latex ] \ displaystyle {\ frac {1} {9}} [/ latex] область. Точно так же каждый треугольник, добавленный во второй итерации, имеет [latex] \ displaystyle {\ frac {1} {9}} [/ latex] площадь треугольников, добавленных в предыдущей итерации, и так далее.{3} + \ cdots} [/ latex]
Первый член этого ряда представляет площадь первого треугольника, второй член — общую площадь трех треугольников, добавленных во второй итерации, третий член — общую площадь двенадцати треугольников, добавленных в третьей итерации, и т. Д. . За исключением начального члена [латекс] 1 [/ латекс], этот ряд является геометрическим с постоянным соотношением [латекс] \ displaystyle {r = \ frac {4} {9}} [/ latex]. Первый член геометрического ряда — [латекс] \ displaystyle {a = 3 \ frac {1} {9} = \ frac {1} {3}} [/ latex], поэтому сумма составляет:
[латекс] \ displaystyle {\ begin {align} 1+ \ frac {a} {1-r} & = 1 + \ frac {\ frac {1} {3}} {1- \ frac {4} {9 }} \\ & = \ frac {8} {5} \ end {align}} [/ latex]
Таким образом, снежинка Коха имеет [latex] \ displaystyle {\ frac {8} {5}} [/ latex] площади основного треугольника.
Парадоксы Зенона
Парадоксы Зенона — это набор философских проблем, изобретенных древнегреческим философом для поддержки учения о том, что истина противоречит нашим чувствам. Проще говоря, один из парадоксов Зенона гласит: существует точка A, которая хочет переместиться в другую точку B. Если A перемещается только на половину расстояния между ней и точкой B за один раз, она никогда не доберется туда, потому что вы можете продолжать делить оставшееся пространство пополам навсегда. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной.Теперь мы знаем, что его парадокс не соответствует действительности, о чем свидетельствует сходимость геометрического ряда с [латексом] \ displaystyle {r = \ frac {1} {2}} [/ latex]. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда, чтобы найти сумму пройденных расстояний.
Сумма GP | Геометрическая прогрессия | Решенные примеры
В этом мини-уроке мы нацелены на определение суммы GP. Давайте научимся находить сумму n членов GP, сумму бесконечных GP, сумму формулы GP, сумму членов в GP, сумму конечных GP, сумму бесконечных членов в GP, сумму геометрических прогрессия
Клара определенным образом экономит несколько долларов каждую неделю.На 1-й неделе она вносит 2 доллара. На 2 неделе — 4 доллара, на 3 неделе — 8 долларов, на 4 неделе — 16 долларов и т. Д. Сколько у нее останется в копилке по истечении 6 недель?
Ряд чисел, полученный путем умножения или деления каждого предыдущего члена, так что существует общее отношение между членами (которое не равно 0), представляет собой геометрическую прогрессию, а сумма всех этих членов образуется так, что является суммой геометрическая прогрессия.
Здесь сумма, накапливаемая каждую неделю, имеет постоянный коэффициент 2 доллара, а начальное значение — 2 доллара.
Каждую неделю вносится сумма: 2, 4, 8, 16, 32, 64 доллара.
Итак, через 6 недель в ее копилке накопится 2 + 4 + 8 + 16 + 32 + 64 + 126 долларов.
Мы можем найти то же самое, используя формулу суммы GP «n» членов. Научимся его рассчитывать сейчас.
План урока
Что такое сумма геометрической прогрессии?
Давайте обсудим, как суммировать произвольный GP. Рассмотрим сумму первых n членов GP с первым членом \ (a \) и общим отношением \ (r \).n)} {1 — r}, r \ neq 1 \)
Если \ (r = 1 \),
Учитывая указанную выше проблему копилки, сумма ЗП находится следующим образом.
Сумма GP
Обратите внимание на то, что мяч падает с высоты на приведенной ниже анимации.
Отрегулируйте его высоту (a) и время (r) с помощью ползунков, показанных вверху.
Мяч теряет энергию, и последовательность максимальных высот приблизительно геометрическая.6)} {1- \ dfrac {1} {3}} \\\\ & = \ dfrac {1} {2} \ dfrac {(1- \ dfrac {1} {729})} {(\ dfrac { 2} {3})} \\\\ & = \ dfrac {182} {243} \\\\ & = 0,76 \ end {align} \]
Как рассчитать сумму n условий терапевта?
Сумма конечных GP
Определите геометрическую прогрессию и определите общее отношение «r» и первый член «a».
Найдите количество элементов «n», для которых должна быть вычислена сумма. n-1)} {r — 1} \) и вычисляем сумму всех членов GP.
Сумма бесконечных GP
Чтобы найти сумму бесконечной геометрической прогрессии, у нас есть первый член и постоянное соотношение между членами. Мы бы не узнали последний срок. Тогда \ (s_n = \ dfrac {a_1} {1-r} \)
Например, Квадрат нарисован путем соединения середин сторон исходного квадрата.2 \ end {align} \]
| \ (s_n = \ dfrac {a_1} {1-r} \) |
Калькулятор суммы бесконечных GP
Найдите симуляцию ниже. Введите первый член и общее отношение и проверьте, как сумма бесконечного GP сходится к меньшему значению.
Например: Рассмотрим бесконечную серию суммы, обратной простым числам,
\ [- \ dfrac {5} {10} + \ dfrac {15} {10} — \ dfrac {45} {10} + \ dfrac {135} {10} +.п -1)} {г -1} \).
Решенные примеры
В GP сумма первых трех членов равна 16, а сумма следующих трех членов равна 128. Найдите сумму первых n членов GP.
Решение
Пусть a и r будет первым членом и общим отношением GP.п-1)} {7} \)
Сара поделилась сообщением с 5 уникальными людьми в час ночи. В 2 часа ночи каждая из ее подруг поделилась им с 5 уникальными людьми. Затем в 15:00 каждый из их друзей поделился с 5 уникальными людьми. Сколько уникальных людей получили бы сообщение в этой последовательности к 8 часам утра?
Решение
Очевидно, мы находим, что это геометрическая прогрессия, поскольку первый член равен 5
Общий коэффициент \ (= \ dfrac {25} {5} = \ dfrac {125} {25} = 5 \)
\ [\ begin {align} S_8 & = \ dfrac {5 (5 ^ 8-1)} {5-1} \\\\ & = \ dfrac {5 (3
)} {4} \\\\ & = 5 \ times 97656 \\\\ & = 488,280 \ text {people} \ end {align} \]
| \ (\ следовательно \) 488 820 человек получили бы сообщение к 8 утра. |
Расстояние, пройденное мячом, сброшенным с высоты (в дюймах): \ (\ dfrac {128} {9}, \ dfrac {32} {3} \), 8, 6 … Какое может быть пройденное расстояние? мячом перед отдыхом?
Решение
Расстояние, пройденное мячом \ (= \ dfrac {128} {9}, \ dfrac {32} {3}, 8, 6 … \)
Здесь начальный член \ (a = \ dfrac {128} {9} \) и обычное отношение:
\ [\ begin {align} r & = \ dfrac {(\ dfrac {32} {3})} {(\ dfrac {128} {9})} \\\\ & = \ dfrac {32} {3} \ times \ dfrac {9} {128} \\\\ & = \ dfrac {3} {4} \ end {align} \]
Общее расстояние, пройденное мячом, будет суммой этого бесконечного GP.
Сумма бесконечных GP: \ [\ begin {align} & = \ dfrac {a} {1-r} \\\\ & = \ dfrac {\ dfrac {128} {9}} {1 — \ dfrac {3} {4}} \\\\ & = \ dfrac {128} {9} \ times 4 \\\\ & = \ dfrac {512} {9} \ text {in} \\\\ & = 56,88 \ text {in} \ end {align} \]
| \ (\ следовательно \) Общее расстояние = 56,88 дюйма |
Интерактивные вопросы
Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции суммы GP.Математическое путешествие вокруг суммы GP началось с того, что студент уже знал, и продолжилось творчески, создавая новую концепцию в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Что такое полная форма GP?
Полная форма GP — это геометрическая прогрессия.
2. Что такое GP по математике?
Последовательность в математике, полученная, в которой последовательные члены находятся в постоянном соотношении, называется геометрической прогрессией.{n-1} \]
геометрическая серия | Purplemath
Purplemath
Можно взять сумму конечного числа членов геометрической последовательности. И по причинам, которые вы будете изучать в области математического анализа, вы можете взять сумму бесконечной геометрической последовательности , но только в особых обстоятельствах, когда общее отношение r находится между –1 и 1; то есть у вас должно быть | r | <1.
Для геометрической последовательности с первым членом a 1 = a и обыкновенным отношением r сумма первых n членов определяется по формуле:
MathHelp.com
Примечание. В вашей книге может быть немного другая форма приведенной выше формулы частичной суммы. Например, « a » можно умножить через числитель, множители дроби можно поменять местами, или суммирование может начаться с i = 0 и иметь степень n + 1 в числителе.Все эти формы эквивалентны, и приведенная выше формулировка может быть получена из полиномиального деления в столбик.
В частном случае, | r | <1, бесконечная сумма существует и имеет следующее значение:
Первые несколько членов: –6, 12, –24:
.
a 1 = 3 (–2) 1 = (3) (- 2) = –6
a 2 = 3 (–2) 2 = (3) (4) = 12
a 3 = 3 (–2) 3 = (3) (- 8) = –24
Итак, это геометрический ряд с знаменателем r = –2.(Я также могу сказать, что это должен быть геометрический ряд из-за формы, данной каждому члену: по мере увеличения индекса каждый член будет умножаться на дополнительный коэффициент –2.)
Первый член последовательности — a = –6. Подставляя в формулу суммирования, получаем:
Итак, сумма суммирования равна:
.
Обозначение «S10» означает, что мне нужно найти сумму первых десяти членов. Первый член — a = 250. Разделив пары терминов, я получу:
100 ÷ 250 = 2/5
40 ÷ 100 = 2/5
… и так далее, поэтому добавляемые члены образуют геометрическую последовательность с общим отношением
r = 2/5.
В отличие от формулы для n -й частичной суммы арифметического ряда, мне не нужно значение последнего члена при нахождении n -й частичной суммы геометрического ряда. Итак, у меня есть все, что нужно для продолжения. Когда я вставляю значения первого члена и общего отношения, формула суммирования дает мне:
Я не буду «упрощать» это, чтобы получить десятичную форму, потому что это почти наверняка будет считаться «неправильным» ответом.Вместо этого мой ответ:
Примечание. Если вы попытаетесь выполнить указанные выше вычисления на своем калькуляторе, он вполне может вернуть десятичное приближение 416,62297 … вместо дробного (и точного) ответа.
Как вы можете видеть на снимке экрана выше, ввод значений в дробной форме и использование команды «преобразовать в дробь» по-прежнему приводит только к десятичной аппроксимации ответа.Но (на самом деле!) Десятичное приближение почти наверняка будет расценено как «неправильный» ответ. Найдите время, чтобы найти дробную форму.
Они дали мне сумму первых четырех членов, S 4 , и значение общего отношения r .Поскольку существует общее соотношение, я знаю, что это должен быть геометрический ряд. Вставив в формулу геометрического ряда-суммы, я получу:
Умножая обе стороны на
27/40, чтобы найти первый член a = a 1 , я получаю:
Затем, подставляя формулу для n -го члена геометрической последовательности, я получаю:
В этом есть одна хитрость. Сначала мне нужно разбить повторяющуюся десятичную дробь на отдельные части; то есть «0,3333 …» становится:
0,3 + 0,03 + 0,003 + 0,0003 + …
Разделение десятичной формы таким образом явно подчеркивает повторяющуюся модель непрерывной (то есть бесконечной) десятичной дроби: для каждого члена у меня есть десятичная точка, за которой следует постоянно увеличивающееся количество нулей, а затем заканчивая цифрой «3».Эта расширенная десятичная форма может быть записана в дробной форме, а затем преобразована в форму геометрической последовательности:
Это доказывает, что 0,333 … является (или, по крайней мере, может быть выражено как) бесконечный геометрический ряд с
a = 3/10 и r = 1/10. Поскольку | r | <1, я могу использовать формулу для суммирования бесконечных геометрических рядов:
Для приведенного выше доказательства, используя формулу суммирования, чтобы показать, что геометрический ряд «разложен» 0.333 … имеет значение одной трети. — — это «показатель», о котором просило упражнение (поэтому очень важно выполнять свою работу аккуратно и логично). И вы можете использовать этот метод для преобразования любого повторяющегося десятичного числа в его дробную форму.
Сначала я разобью это на составные части, чтобы найти узор:
1.363636 .. = 1 + 0,36 + 0,0036 + 0,000036 + …
Две цифры повторяются, поэтому дроби немного отличаются. Но это все же геометрический ряд:
Это показывает, что исходная десятичная дробь может быть выражена как ведущая «1», добавленная к геометрическому ряду, имеющему
a = 9/25 и r = 1/100. Поскольку значение общего отношения достаточно мало, я могу применить формулу для бесконечных геометрических рядов.Тогда сумма оценивается как:
Таким образом, эквивалентная дробь в форме неправильных дробей и смешанных чисел:
Кстати, с помощью этой техники можно доказать, что 0,999 … = 1.
URL: https://www.purplemath.com/modules/series5.htm
Формулы геометрической прогрессии, геометрические ряды, бесконечные геометрические ряды
В математике геометрическая прогрессия (последовательность) (также неточно известная как геометрическая последовательность ) представляет собой последовательность
чисел, так что частное любых двух последовательных членов последовательности является константой, называемой
обычное отношение последовательности.
Геометрическую прогрессию можно записать как:
ar 0 = a, ar 1 = ar, ar 2 , ar 3 , …
где r ≠ 0, r — обычное отношение, а a — коэффициент масштабирования (также первый член) .
Примеры
Геометрическая прогрессия с общим соотношением 2 и масштабным коэффициентом 1 равна
1, 2, 4, 8, 16, 32 …
Геометрическая последовательность с общим соотношением 3 и масштабным коэффициентом 4 равна
4, 12, 36, 108, 324 …
Геометрическая прогрессия с обычным соотношением -1 и масштабным коэффициентом 5 равна
5, -5, 5, -5, 5, -5 ,…
Формулы
Формулу для n-го члена можно определить как:
a n = a n-1 r
a n = a 1 ⋅r n-1
Формула обыкновенного отношения:
Если общее соотношение:
Свойства геометрической прогрессии
a 2 k = a k-1 ⋅a k + 1
a 1 ⋅a n = a 2 ⋅a n-1 =… = a k ⋅a n-k + 1
Формула суммы первых n чисел геометрического ряда
| S n = | a 1 — a n r 1 — г | = 1 . | 1 — р н 1 — г |
Бесконечный геометрический ряд, где | r |
<1
Если | r | <1, тогда a n -> 0,
когда n -> ∞.
Сумма S такого бесконечного геометрического ряда определяется формулой:
что справедливо только при | r | <1.
1 — первый член.
Калькулятор геометрической прогрессии
Задачи геометрической прогрессии
Задача 1.
Последовательность 2, 4, 6, 8 … геометрическая прогрессия?
Решение: Нет, это не так. (2, 4, 8 — геометрическая прогрессия)
Задача 2
Если 2, 4, 8 … образуют геометрическую прогрессию. Какой 10-й срок?
Решение: Мы можем использовать формулу a n = a 1 ⋅ r n-1
a 10 = 2 ⋅ 2 10-1 = 2 ⋅ 512 = 1024
Задача 3
Найдите масштабный коэффициент и командное отношение геометрической прогрессии, если
a 5 — a 1 = 15
a 4 — a 2 = 6
Решение: есть две геометрические прогрессии.У первого есть
масштабный коэффициент 1 и общее отношение = 2
, второе решение -16, 1/2
Дополнительные задачи:
Геометрическая прогрессия — задачи
Задачи с прогрессиями
Геометрические прогрессии на математическом форуме
Присоединяйтесь к нашему математическому форуму (регистрация не требуется!)
Форумы с прогрессиями
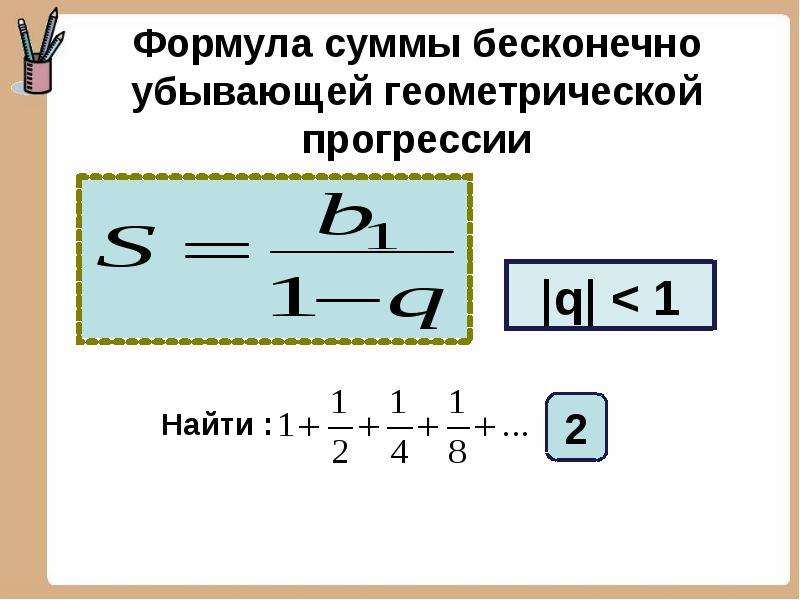
| Последовательности. Числовые последовательности.Общий член числовой последовательности. Арифметическая прогрессия. Геометрическая прогрессия. Бесконечно убывающая геометрической прогрессии. Преобразование повторяющейся десятичной дроби в обычную дробь. Последовательности. Рассмотрим ряд натуральных чисел: 1, 2, 3,, n 1, n ,. u 1 , u 2 , u 3 ,, u n — 1 , u n « называется числовой последовательностью .Число u n называется общим термином числовой последовательности. 2, 4, 6, 8, 10,, 2 n ,; 1, 4, 9, 16, 25,, n ²,; 1, 1/2, 1/3, 1/4, 1/5« 1/ n ,. Арифметическая прогрессия. Числовая последовательность, в которой каждый следующий член, начиная со второго, равен предыдущему члену, добавленному с константой для этого порядкового номера d , называется арифметической прогрессией .Число d называется общей разницей . Любой член арифметической прогрессии рассчитывается по формуле: a n = a 1 + d (n 1 ) . Сумма n первых членов арифметической прогрессии рассчитывается как: E x a m p l e. Найдите сумму первых 100 нечетных чисел. 1 = 1, d = 2 . Итак, имеем: Геометрическая прогрессия. Числовая последовательность, в которой каждый следующий член, начинающийся со второго, равен предыдущему члену, умноженному на константу для этого порядкового номера q , называется геометрической прогрессией . Число q называется обыкновенным отношением . Любой член геометрической прогрессии рассчитывается по формуле: b n = b 1 q n - 1 . Сумма n первых членов геометрической прогрессии рассчитывается как: Бесконечно убывающая геометрическая прогрессия. Это геометрическая прогрессия с E x a m p l e. Найдите сумму в бесконечно убывающей геометрической прогрессии: S o l u t i o n. Воспользуйтесь последней формулой. Здесь b 1 = 1, q = 1/2. |

 2}\Rightarrow1+q=3\Rightarrow q=2.\)
2}\Rightarrow1+q=3\Rightarrow q=2.\) Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.
Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.
 {64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)
{64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)


 12.11. 20-летия Независимости Казахстана.
12.11. 20-летия Независимости Казахстана.

 Решение:По данным составим таблицу.
Решение:По данным составим таблицу.
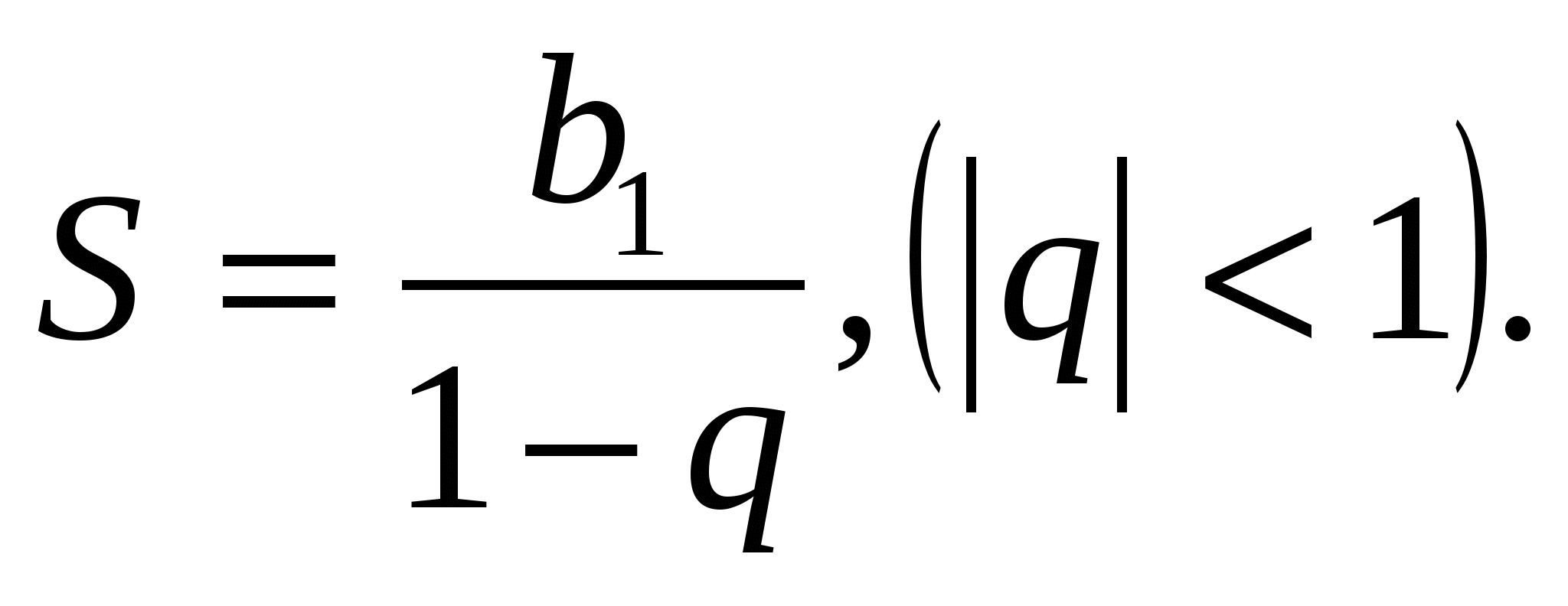


 Найти знаменатель геометрической прогрессии.(1,5 или 0,5)
Найти знаменатель геометрической прогрессии.(1,5 или 0,5)
 Эта формула носит название формулы общего члена геометрической прогрессии.
Эта формула носит название формулы общего члена геометрической прогрессии.




 Продолжим
Продолжим



 Тогда при n
Тогда при n Это результат добавления
Это результат добавления ..
..


 ..
..
 Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс]. Чередующиеся серии)
Чередующиеся серии) {n}} {1-r}} [/ латекс].
{n}} {1-r}} [/ латекс]. Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице.
Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице.