Содержание
Физика боюнча формулалар
Просмотр содержимого документа
«Физика боюнча формулалар»
Ылдамдык
ϴтулгөн жол
Сызыктуу ылдамдык
Ʋ= |
Борборго умтулуучу ылдамдануу
а = |
Ньютондун 2-закону
Ньютондун 3-закону
Импульс
Бүткүл дүйнөлүк тартылуу закону
F= |
Салмак
Сүрүлүү күчү
Механикалык жумуш
Кубаттуулук
𝐍= |
Кинетикалык энергия
Потенциалдык энергия
Чыналыш
σ= |
Гук закону
Басым
P= |
Архимед күчү
Маятниктин термелүү мезгили
Т=2п |
Толкундун таралуу ылдамдыгы
Ʋ= |
Заттын саны
ν= |
Термодинамикадагы жумуш
Беттик тартылуу коэффициенти
σ= |
Беттик тартылуу күчү
σι |
Буулануу же конденсация жылуулугу
Эруунун же кристаллдашуунун салыштырмалуу жылуулук сыйымдуулугу
Кулондун закону
F=k |
Заряддын беттик тыгыздыгы
σ= |
Электр талаасынын чыналышы
E= |
Чыналуу
U= |
Сыйыдуулук
с= |
Ток күчү
I= |
Чынжырдын бөлүгү үчүн Омдун закону
I= |
Өткөргүчтүн каршылыгы
R=ρ |
Салыштырма каршылык
ρ = |
Толук чынжыр үчүн
Омдун закону
𝐈= |
Масса
Борборго умтулуучу күч
F= |
Бурчтук ылдамдык
ω |
Фарадейдин закону
Фотондун энергиясы
Ампер күчү
F=BIL |
Магниттик агым
Лоренц күчү
Индукциянын электр кыймылдаткыч күчү
ε= |
Фотондун импульсу
𝐏= |
Жарык күчү
J= |
Жарыктаныш
E= |
| Формула расчета силы Ампера | FA = B I L sinα | Закон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником. | FA – сила Ампера, [Н] В – магнитная индукция, [Тл] I – сила тока, [А] L – длина проводника, [м] |
| Формула расчета силы Лоренца | Fл= q B υ sinα | Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы. | Fл – сила Лоренца, [Н] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] |
| Формула радиуса движения частицы в магнитном поле | r= mυ/qB | r – радиус окружности, по которой движется частица в магнитном поле, [м] m – масса частицы, [кг] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] | |
| Формула для вычисления магнитного потока | Ф = B S cosα | Ф – магнитный поток, [Вб] В – магнитная индукция, [Тл] S – площадь контура, [м2] | |
| Формула для вычисления величины заряда | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Закон Ома для участка цепи | I = U/R | Закон Ома — сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления удельного сопротивления проводника | R = ρ L/S ρ = R S/L | Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник. | ρ – удельное сопротивление вещества, [Ом·мм2/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [ммБ2] L – длина проводника, [м] |
| Законы последовательного соединения проводников | I = I1 = I2 U = U1 + U2 Rобщ = R1 + R2 | Последовательным соединением называется соединение, когда элементы идут друг за другом. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Законы параллельного соединения проводников | U = U1 = U2 I = I1 + I2 1/Rобщ =1/R1 +1/R2 | Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления величины заряда. | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула для нахождения работы электрического тока. | A = Uq A = UIt | Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д. д.Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. | A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула электрической мощности | P = A/t P = UI P = U2/R | Мощность – работа, выполненная в единицу времени. | P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом] |
| Формула закона Джоуля-Ленца | Q=I2Rt | Закон Джоуля-Ленца при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.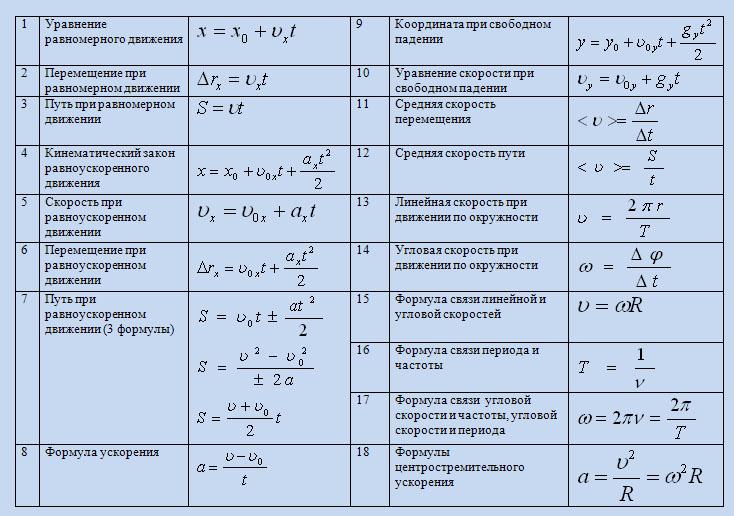 | Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом]. |
| ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ | |||
| Закон отражения света | Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча. | ||
| Закон преломления | sinα/sinγ = n2/n1 | При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого. | n – показатель преломления одного вещества относительно другого |
| Формула вычисления абсолютного показателя преломления вещества | n = c/v | Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде. | n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с] |
| Закон Снеллиуса | sinα/sinγ = v1/v2=n | Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная.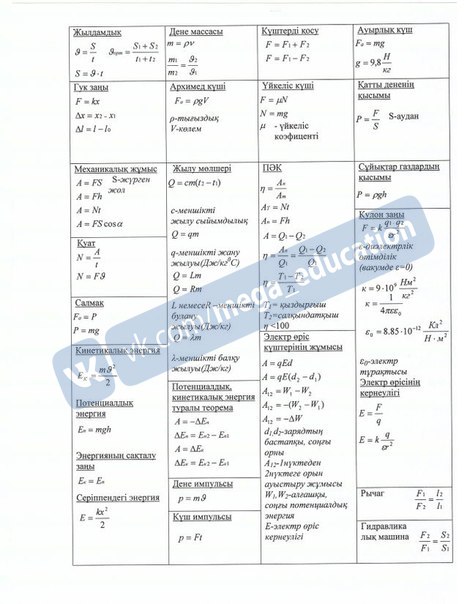 | |
| Показатель преломления среды | sinα/sinγ = n | Отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления среды |
| Преломляющий угол призмы | δ = α(n – 1) | δ – угол отклонения α – угол падения n – показатель преломления среды | |
| Линейное увеличение оптической системы | Г = H/h | Г – линейное увеличение оптической системы H – размер изображения, [м] h – размер предмета, [м] | |
| Формула оптической силы линзы | D = 1/F | Оптическая сила линзы – способность линзы преломлять лучи. | D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м] |
| Формула тонкой линзы | 1/F = 1/d+1/f | F – фокусное расстояние линзы, [м] d – расстояние от предмета до линзы, [м] f – расстояние от линзы до изображения, [м] | |
| Максимальная результирующая интенсивность | Δt = mT | Δt – максимальная результирующая интенсивность Т – период колебании, [с] | |
| Минимальная результирующая интенсивность | Δt = (2m + 1)T/2 | Δt – минимальная результирующая интенсивность Т – период колебании, [с] | |
| Геометрическая разность хода интерферирующих волн | Δ = mλ | Δ – геометрическая разность хода интерферирующих волн λ – длина волны, [м] | |
| Условие интерференционного минимума | Δ = (2m + 1)λ/2 | λ – длина волны, [м] | |
| Условие дифракционного минимума на щели | Asinα = m λ | A – ширина щели, [м] λ – длина волны, [м] | |
| Условие главных максимумов при дифракции | dsinα = m λ | d – период решетки λ – длина волны, [м] | |
| Энергия кванта излучения | E = hϑ | Е – энергия кванта излучения, [Дж] ϑ – частота излучения h – постоянная Планка | |
| Закон смещения Вина | λT = b | b – постоянная Вина λ – длина волны, [м] Т – температура черного тела | |
| Закон Стефана-Больцмана | R = ϭT4 | ϭ – постоянная Стефана-Больцмана Т – абсолютная температура черного тела R – интегральная светимость абсолютно черного тела | |
| Уравнение Эйнштейна для фотоэффекта | А – работа выхода, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с] ϑ – частота излучения h – постоянная Планка | ||
| ФИЗИКА ВЫСОКИХ ЭНЕРГИИ | |||
| Массовое число | M = Z + N | M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов | |
| Формула массы ядра | МЯ = МА – Z me | MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг] | |
| Формула дефекта масс | ∆m = Zmp+ Nmn – MЯ | Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.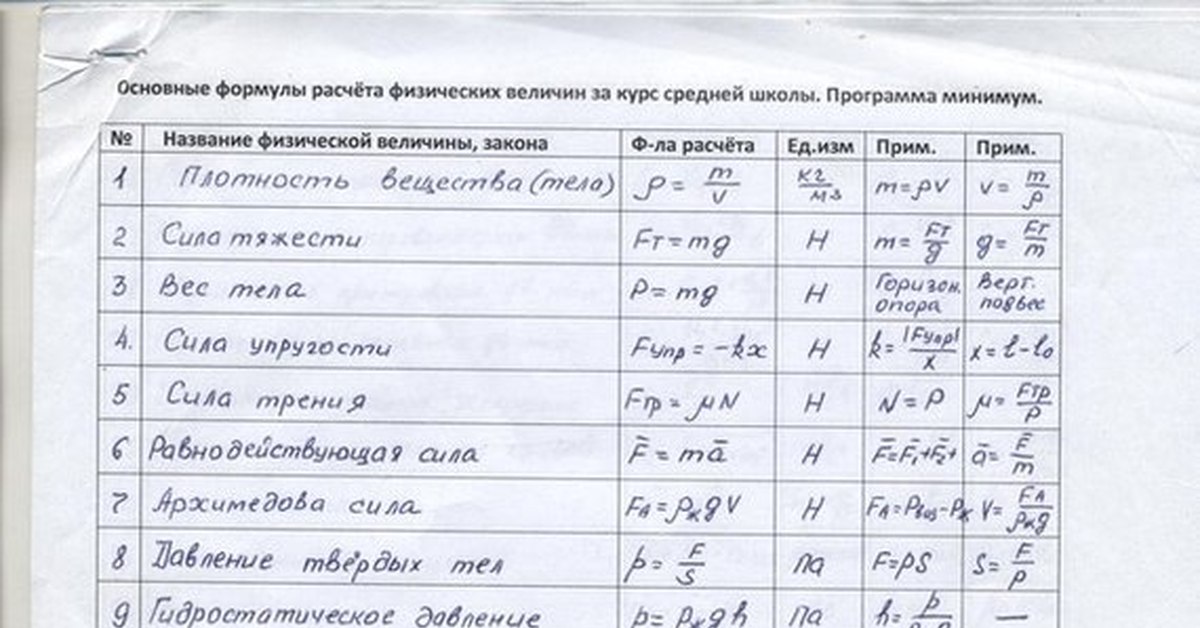 | ∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг] |
| Формула энергии связи | Есвязи = ∆m c2 | Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). | Есвязи – энергия связи, [Дж] m – масса, [кг] с = 3·108м/с – скорость света |
| Закон радиоактивного распада | N = N02 –t/T1/2 | N0 – первоначальное количество ядер N – конечное количество ядер T – период полураспада, [c] t – время, [c] | |
| Доза поглощенного излучения | D = E/m | D – доза поглощенного излучения, [Гр] E – энергия излучения, [Дж] m – масса тела, [кг] | |
| Эквивалентная доза поглощенного излучения | H = Dk | H – эквивалентная доза поглощенного излучения, [Зв] D – доза поглощенного излучения, [Гр] k – коэффициент качества | |
Оптика — Основные формулы
1.
 Фотометрия и светотехника
Фотометрия и светотехника
1.1 Поток излучения
Φ — поток излучения,
W — энергия излучения,
t — время прохождения энергии излучения.
1.2 Сила света
I — сила света,
Φ — поток излучения,
Ω — телесный угол, через который проходит поток излучения.
1.3 Освещенность
E — освещенность,
Φ — поток излучения,
σ — площадь, через которую проходит поток излучения.
1.4 Яркость источника света
L — яркость источника света,
I — сила света,
σ — площадь видимой светящейся поверхности.
1.5 Коэффициент поглощения
α — коэффициент поглощения,
Φα — световой поток, поглощенный телом,
Φi — световой поток, падающий на тело.
1.6 Коэффициент отражения
ρ — коэффициент отражения,
Φρ — световой поток, отраженный телом,
Φi — световой поток, падающий на тело.
1.7 Коэффициент пропускания
τ — коэффициент пропускания,
Φτ — световой поток, пропущенный телом,
Φi — световой поток, падающий на тело.
2. Геометрическая оптика
2.1 Относительный показатель преломления
n — относительный показатель преломления для граничащих сред
n2 — абсолютный показатель преломления для второй среды,
n1 — абсолютный показатель преломления для первой среды.
2.2 Закон преломления света
i — угол отражения,
r — угол преломления,
n — относительный показатель преломления для граничащих сред.
2.3 Предельный угол полного внутреннего отражения
iпр — предельный угол полного внутреннего отражения,
n — относительный показатель преломления для граничащих сред.
2.4 Основная формула тонкой линзы
a — расстояние от источника света до линзы,
a’ — расстояние от линзы до изображения источника света,
f — фокусное расстояние линзы.
2.5 Основная формула сферического зеркала
a — расстояние от источника света до зеркала,
a’ — расстояние от зеркала до изображения источника света,
R — радиус кривизны зеркала,
f — фокусное расстояние зеркала.
2.6 Линейное увеличение
β — линейное увеличение линзы или зеркала,
h — высота источника света,
h’ — высота изображения источника света,
a — расстояние от источника света до линзы или зеркала,
a’ — расстояние от линзы или зеркала до изображения источника света.
2.7 Угловое увеличение
γ — угловое увеличение линзы или зеркала,
β — линейное увеличение линзы или зеркала.
2.8 Оптическая сила линзы
D — оптическая сила линзы,
f — фокусное расстояние.
2.9 Светосила линзы
E — светосила линзы,
d — диаметр линзы или диафрагмы, закрывающей линзу,
f — фокусное расстояние.
3. Оптические приборы
3.1 Увеличение лупы
N — увеличение лупы,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние лупы.
3.2 Увеличение микроскопа
N — увеличение микроскопа,
N1 — увеличение окуляра микроскопа,
N2 — увеличение объектива микроскопа,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние системы линз микроскопа: окуляра и объектива.
3.3 Увеличение зрительной (подзорной) трубы
N — увеличение зрительной (подзорной) трубы,
f1 — фокусное расстояние объектива,
f2 — фокусное расстояние окуляра.
Формулы молекул | Русская Физика
18.
 Формулы молекул
Формулы молекул
Формулы молекул бывают разные; одну и ту же молекулу можно изобразить по-разному. Одно у них общее – атомы отображаются латинскими буквами.
Самая простая формула отражает атомарный состав молекулы и количество входящих в неё атомов. Количество указывается в виде индексов. Если атом – один, то индекс не указывается.
Молекулу воды можно изобразить как H2O; читается – аш-два-о. Из формулы видно, что молекула воды состоит из двух атомов водорода и одного атома кислорода. Ни соразмерности атомов, ни их построение в данной формуле не отражены.
Ту же молекулу можно изобразить как (H2)O, подчёркивая тем самым молекулярное строение атомов водорода; читается – аш молекулярный-о. Молекулярный водород обозначается как Hm; с учётом этого формула молекулы воды примет вид HmO.
Если учитывать соразмерности атомов, то формулу молекулы воды следует изображать как OHm — к крупному атому кислорода прикреплена мелкая молекула водорода.
Молекула метана (болотного газа) состоит из одного атома углерода и четырёх атомов водорода. Формула состава этой молекулы выглядит как CH4.
Два атома водорода здесь объединены в молекулу; поэтому формулу можно уточнить – CHmH2. Атом углерода C в этом соединении внешне похож на латинскую букву U. Молекула водорода Hm укладывается во впадину, а два отдельных атома водорода H и H присоединяются к вершинам. Представим это соединение лежащим на боку; ему больше будет соответствовать формула C(Hm)H2.
Сложные молекулы, как правило, собираются из более простых молекул с последовательным многоступенчатым присоединением каждой из них. Общая формула может отражать и состав исходных молекул и порядок их соединения.
Покажем это на примере молекулы серной кислоты; формула её молекулы состава – H2SO4.
Эта молекула состоит из двух отдельных молекул: серного ангидрида – SO3 и воды – OHm. Их наличие можно отразить в формуле с помощью скобок: H2SO4 = (SO3)(OHm).
В свою очередь, молекула воды включает в себя молекулу водорода Hm: OHm = (O(H2)). А молекулу серного ангидрида можно даже разложить на две ступени: состоящей из молекулы сернистого газа SO2: SO3 = ((SO2)O), а та включает молекулу кислорода O2: SO2 = (S(O2)).
В общей сложности формула молекулы серной кислоты примет вид:
H2SO4 = ((S(O2))O)(O(H2)
В таком изображении формул виден не только порядок формирования крупных молекул, но и то, в какой последовательности они разрушаются. При нагреве молекула серной кислоты в первую очередь распадается на молекулу серного ангидрида и молекулу воды.
Если воду нагревать дальше, то её молекулы будут распадаться на атомы кислорода и молекулы водорода. И уж при очень сильном нагреве молекулы водорода распадутся на атомы. Такое состояние вещества называется плазмой.
Подобное будет происходить и с молекулами серного ангидрида при его дальнейшем нагреве. При достаточно высокой температуре он распадается на сернистый газ и атомарный кислород. Если температуру нагрева повышать и дальше, сернистый газ начнёт распадаться на молекулярный кислород и серу. Дальнейший нагрев породит плазму – только атомарное состояние вещества.
При достаточно высокой температуре он распадается на сернистый газ и атомарный кислород. Если температуру нагрева повышать и дальше, сернистый газ начнёт распадаться на молекулярный кислород и серу. Дальнейший нагрев породит плазму – только атомарное состояние вещества.
Если требуется отобразить в формуле порядок жёлобового слипания, то молекулу серной кислоты можно представить как
H2SO4 = S(_(O2(_(O(_(O_(Hm = S((O2((O((O((Hm
Скобки в этой формуле являются символами жёлобов.
Количество скобок в формуле можно сократить:
H2SO4 = S(O2(O(O(Hm
Рассмотренные изображения молекул вписываются в строку; поэтому их можно назвать строчными.
Кроме строчного одномерного представления формул молекул, используются и другие – плоские, двумерные (как сложный рисунок на листе бумаги) и даже объёмные, трёхмерные (на экране компьютера). Компьютерные, трёхмерные формулы особенно необходимы для изображения крупных молекул органических веществ и для отображения хода химических процессов.
В общем нет никаких запретов на иное представление молекул; главное в этих представлениях – наглядность и простота понимания.
Формулалар жинағы 11 сынып
11-сынып формула
Тербеліс периоды
Циклдік жиілік
T=; =3,14* рад/с
Жиілік
v=
Конденсатордың сыйымдылығы
; C=
Тербеліс фазасы
Гармоникалық тербелістерінің теңдеуі
q = cos
Квазистанционар ток үшін Ом заңы
=
Индукциялық ЭКҚ-і
Тізбектің толық кедергісі
Z=
Айнымалы ток тізбегіндегі қуат
P=IUcos
Айнымалы ток күшінің әсерлік
I=
Анымалы кернеудің әсерлік формуласы
U=
Конденсаторға түсетін кернеу
u=C cos
Ток күші тербелістердің теңдеуі
i=
Сыйымдылық кедергісі үшін
=
Катушкадағы ток күшінің амплитудасы
Индуктивті кедергі
=
Айнымалы ток ұшін Ом заңы
Генератор өндіретін айнымалы ток жиілігі
v=nf
Электромагниттік толқын ұзындығы
λ =cT=
Электромагниттік толқын шығару ағынының тығыздығы
I= ; I=
Шағын көлем ішіндегі энергия
Көлемдегі электромагниттік өрістің энергиясы
W== I=
Толқындардың жол айырымы
Толқын энергиясының тығыздығы
Энергия тығыздығы
W= немесе W=
W=
Электромагниттік индукция заңына сәйкес ЭҚК-і
Дифракциялық тор үшін
d sin
Жарықтың сынуы
=n
Сфералық айнаның формуласы
+=
Дөңес сфералық айнаның формуласы
-=
Айнаның ұлғайтуы
Г=
Линзаның оптикалық күші
D=
Лоренц күші
F=ϑB sinα
Магнит өрісінің индукциясы
B=
Максвелл теңдеуінің вакуумдегі жарық жылдамдығы
c= ;
Массаның жылдамдыққа тәуелділігі
m =
Ұзындықтың жылдамдыққа тәелділігі
l =
Дененің релятивтік импульсі
P=
Тыныштық энергия
E=m E=
Спектрлік тығыздық немесе дененің сәулелену қабілеті
r =
Стефан-Больцман заңы
R=
Абсолют қара дененің сәулелену қабілеті
Винн заңы
Фотонның энергиясы,импульсі
Е=hv; p=nk
Эйнштейн теңдеуі
hv=+
Бальмер сериясы
v=R()
Элементар электр заряды
q = Z*e
Атом ядросының пішіні мен өлшемі
R=
Ядродағы нуклондардың жалпы саны
А=Z+N
Меншікті байланыс энергиясы
Массалар ақауы
Де Бройль толқын
Радиоактивті ыдырау заңының формуласы
N= N=
Атомдардың санын анықтау
=*
Радиоактивті заттың активтілігі
A=
Шығарылған сәуленің жұтылған доза
D= =k*D
Кометаның жарық ағыны
Ф=
Галактиканың алыстау жылдамдығы
Законы электролиза Фарадея | Физика.
 Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
В 1833 г. М. Фарадей установил:
Масса вещества, которое выделяется при прохождении электрического тока в электролитах на аноде или катоде, прямо пропорциональна заряду, который при этом переносится ионами через электролит:
m = kq,
где m — масса вещества, кг; q — заряд, Кл.
Коэффициент пропорциональности k = m / q называется электрохимическим эквивалентом данного вещества.
Электрохимический эквивалент вещества показывает, какая масса вещества в килограммах выделяется на электроде при прохождении тока, переносящего заряд, равный одному кулону:
k = m / q
Если иметь в виду, что при постоянном токе в цепи q = IΔt, где I — сила тока (ампер), а Δt — время прохождения тока (секунд), то закон Фарадея можно записать в виде
m = kIΔt.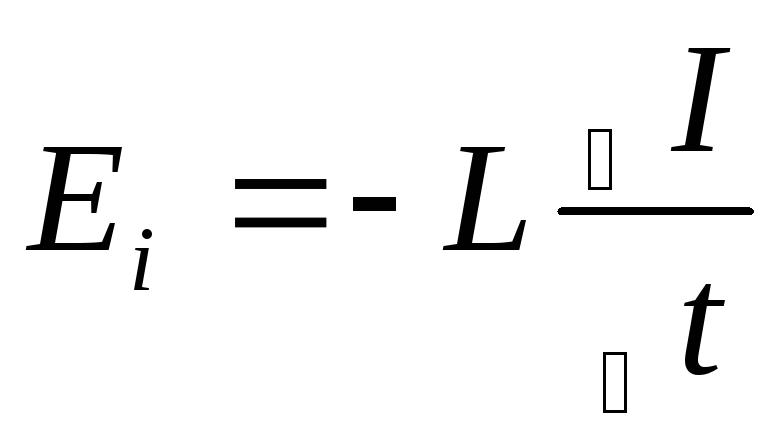
Исходя из современных представлений, закон для электролиза можно установить теоретически. Пусть за время Δt через электролит переносится заряд q. Заряд одного иона q0i = ne, где n — валентность иона, а e — значение элементарного электрического заряда. Следовательно, q = neNi, где Ni — количество ионов, которые достигли электрода.
С другой стороны, масса вещества, выделяющегося на электроде m = m0iNi, где m0i — масса иона, которая может быть определена по молярной массе вещества M и постоянной Авогадро NA:
m0i = M / NA; m = (M / NA) • Ni.
Из уравнения для заряда q = neNi можно определить Ni: Ni = q / ne. Подставив значения Niв выражение для массы, получаем:
Подставив значения Niв выражение для массы, получаем:
m = (M / neNA) • q,
что также является законом Фарадея для электролиза. Итак, электрохимический эквивалент вещества
k = M / neNA,
где все величины для данного вещества являются постоянными.
В последней формуле значение элементарного заряда e и постоянная Авогадро одинаковы для всех веществ. Их произведение назвали постоянной Фарадея:
F = eNA.
Значение постоянной Фарадея:
F = 1,6 • 10-19 Кл • 6,023 • 1023 моль-1 = -9,65 • 104 Кл/моль.
Теперь для электрохимического эквивалента вещества имеем Материал с сайта http://worldofschool. ru
ru
k = (1 / F) • (M / n),
что и является вторым законом для электролиза.
Второй закон электролиза. Электрохимические эквиваленты веществ прямо пропорциональны массам их молей и обратно пропорциональны их валентностям.
Чтобы удобно было решать многие задачи, оба закона можно объединить в одном выражении (объединенный закон электролиза):
m = (1 / F) • (M / n) • q,
или
m = (1 / F) • (M / n) • IΔt.
На этой странице материал по темам:
Все формулы по закону фпрадея
Закон и формула фарадея
Законы фарадея формулы
Закон фарадея формула видео
Закон электролиза фарадея задачи
Вопросы по этому материалу:
Сформулируйте закон Фарадея для электролиза, запишите его формулу.

Запишите формулы объединенного закона электролиза.
Что такое постоянная Фарадея?
Физика пәнінен формулалар жинағы
«Қ.Игенбайұлы атындағы
орта мектеп-бақшасы» КММ
ФИЗИКА ПӘНІНЕН
ФОРМУЛАЛАР ЖИНАҒЫ
Оразканова
М.Ф.
7-сынып
диаметр
(мм)
жылдамдық (м/с)
орын
ауыстыру (м)
уақыт
(м)
орташа
дылдамдық
орын
ауыстыру (м)
уақыт
(м)
тығыздық
(кг/м3)
масса
(кг)
көлем
(м3)
Гук заңы
(Н)
Ауырлық
күші (Н)
салмақ
(кг)
үйкеліс
күші (Н)
қысым
(Па)
қысым
күші (Н)
күш
түсетін дененің ауданы (м2)
сұйық
бағанының ыдыстың табанына түсіретін қысымы
Қатынас
ыдыстар
Архимед
заңы
Механикалық жұмыс (Дж)
қуат
(Вт)
жұмыс
(Дж)
потенциалдық энергия (Дж)
кинетикалық энергия (Дж)
механикалық энергия
Күш
моменті (
)
Механизмнің немесе машинаның пайдалы әсер коэффициенті
(ПӘК)
8-сынып
Температура
жылу мөлшері
(Дж)
Заттың
меншікті жылу сыйымдылығы
Отынның
меншікті жану жылуы
Меншікті
балқу жылуы
Ауаның
салыстырмалы ылғалдылығы
Меншікті
булану жылуы
Термодинамиканың І-заңы
Газдың
атқарған жұмысы
Жылу
машиналарының ПӘК-і
Кулон
заңы
Электр
өрісінің кернеулігі
SI
жүйесіндегі кернеулік
Өріс
потенциалы
Электр
өрісі күштерінің атқаратын жұмысы (Дж)
Потенциалдар айырымы немесе кернеу (В)
Конденсатордың электрсыйымдылығы (Ф- фарад)
Жазық
конденсатордың сыйымдылығы
Электр
қозғаушы күші (1 Вольт)
Ток күші (1
Ампер)
Заряд
Кернеу (1
Вольт)
Ом заңы (1
Ампер)
Меншікті
кедергі
Өткізгіштерді тізбектей жалғау
Өткізгіштерді параллель жалғау
Электр
тогының жұмысы (Джоуль)
Электр
тогының қуаты ( Ватт)
Джоуль-Ленц
заңы
Фарадей
заңы
Жарықтың
сынуының екінші заңы (Снеллиус заңы)
Линзаның
оптикалық күші
Жұқа
линзаның формуласы
Сызықтық
үлкейту
9
сынып
Векторларды
қосу
Векторларды
азайту
Векторларды
скалярға көбейту (бөлу)
немесе
Үдеу
(м/с2)
Үдеудің
формуласынан табылған жылдамдық (м/с)
Теңбаяулайтын қозғалыс (м)
Теңүдемелі
қозғалыс (м)
Қозғалыс
заңы (м)
Түсу уақыты
(с)
Жерге түскен
кездегі жылдамдық (м/с)
Айналу
жиілігі (1 с-1)
Айналу
периоды (с)
немесе
Бұрыштық жылдамдық
( )
Центрге
тартқыш үдеу (м/с2)
Ауырлық
күші
Үйкеліс
күші
Ньютонның ІІ
заңы
Динамиканың
негізгі теңдеуі (Теңәрекетті күш) (1Н)
Ньютонның
ІІІ заңы
Бүкіләлемдік
тартылыс заңы
Бірінші
ғарыштық жылдамдық
Күш импульсі
( )
Импульстің
сақталу заңы
потенциалдық энергия (Дж)
кинетикалық энергия (Дж)
Толық
механикалық энергия
Гук
заңы
Маятниктің
тербеліс периоды
Серіппелі
маятниктің тербеліс периоды
Томсон
формуласы
Толқын
жылдамдығы
Әртүрлі
заттарда электомагниттік толқынның таралу жылдамдығы
Электомагниттік толқынның вакуумдегі толқындық
ұзындығы
Электомагниттік толқынның әртүрлі заттардағы толқындық
ұзындығы
Планк
формуласы
Энштейн
формуласы
Атом
ядроларының заряды
Энштейн
қатынасы (Дж)
Байланыс энергия
Меншікті
байланысты энергия
Ядролық
энергия
Сәуленің
жұтылған дозасы (Грей (Гр))
Альфа және
бета ыдыраулардың формулалары
Ядролардың
радиоактивті ыдырау заңы Резерфорд пен Содди формуласы арқылы
өрнектеледі
Бета-ыдыраудағы нейтронның протон мен электронға түрлену
формуласы
нейтрон
(Уран-235 изотопы ядросының бөліну формуласы)
Сутегі
изотоптары ядроларының бірігу формуласы
Алюминийді α-бөлшекпен, фосфор радио-изотобын алу формуласы
нейтрондармен кольбат-59 изотобын атқылап кольбат-60
радиоизотобын алу формуласы
10-сынып
Орташа
жылдамдық
Лездік
жылдамдық
немесе
Үдеу
(м/с2)
Сызықтық
жылдамдық
Бұрыштық
жылдамдық ( )
Айналу
периоды (1 с)
Айналу
жиілігі (1 с-1)
Жылдамдықты
қосудың классикалық заңы
Ньютонның І
заңы
Ньютонның ІІ
заңы
Ньютонның
ІІІ заңы
Бүкіләлемдік
тартылыс заңы
Ауырлық
күші
Еркін түсу
үдеуі
Маятник
тербелісінің периоды
Бірінші
ғарыштық жылдамдық
Гук
заңы
үйкеліс
күші (Н)
Күш импульсі
( )
Импульстің
сақталу заңы
Реактивті
күш
Механикалық
жұмыс (Дж)
Қуат
(Вт)
Кинетикалық
энергия туралы теорема (Дж)
Потенциалдық энергия туралы теорема (Дж)
Серіппенің
жинақталған потенциалдық энергиясы
Энергияның
сақталу заңы
Cсұйықтың
үздіксіз теңдеуі
Бернулли
заңы
Молекула
диаметрі
Заттың
салыстырмалы массасы
Зат
мөлшері
Молярлық
масса
Молекула
саны
Газ
молекулаларының концентрациясы
Газдардың
молекулалы-кинетикалық теориясының негізгі теңдеуі (Клаузиус
теңдеуі)
Термодинамикалық температура
Больцман
тұрақтысы
Газ
кысымы
Бойль-Мариотт заңы
Гей-Люссак
заңы
Шарль
заны
Идеал газ
күйінің теңдеуі
Менделеев –
Клапейрон теңдеуі
Идеал газдың
ішкі энергиясы
Идеал
газдың ішкі энергиясының өзгерісі
Макроскопиялық денелердің ішкі энергиясы
Жылу
алмасу
Термодинамиканың І заңы
Изотермиялық
процесс (Т=const)
Изохоралық
процесс (V=const)
Изобаралық
процесс (p=const)
Изобаралық
ұлғаюдағы жұмысы
ПӘК
Жылу
қозғалтқышының максимал ПӘК-і
Кез-келген
жылу қозғалтқышының ПӘК-і
11-СЫНЫП
Электр
заряды
Химиялық
элементтердің атом ядроларының заряды
Электр
зарядының сақталу заңы
Кулон
заңы
Электр
өрісінің кернеулігі
Нүктелік
заряд
Суперпозиция принципі
Потенциалдар
айырымы
Зарядтың
электр өрісіндегі орын ауыстыру жұмысы
Электр
өрісінің кернеулігі мен потенциалдар айырымы
Конденсаторлардың электрсыйымдылығы
Жазық
конденсатордың сыйымдылығы
Зарядталған
конденсатордың энергиясы
Ток күші
(А)
Кернеудің
түсуі
ЭҚК-і
Потенциалдар
айырымы
Кернеу
Тізбек
бөлігі үшін Ом заңы
Толық
(тұйық) тізбек үшін Ом заңы
Тізбек
бөлігіндегі токтың жұмысы
Джоуль-Ленц
заңы
Магнит
индукциясының векторы
Ампер
күші
Лоренц
күші
Ортаның
салыстырмалы магнит өтімділігі
ЭҚК-і
Өшпейтін
тербелістер периоды түрде өзгеретін индукциялық ЭҚК-і
Индукциялық
ЭҚК-інің әсерінен тұйық өткізгіштегі индукциялық ток
Электрмагниттік толқындардың кез-келген ортадағы
жылдамдықтары
Жарық
жылдамдығының тұрақтылық принципі
Жылдамдықтарды қосудың релятивтік заңы
Энштейннің
масса мен энергияның өзара байланысы туралы заңы
Тұрақты
шамалар:
Солтүстік
полюсте
Экваторда
Географиялық ендікте
Теңіз
деңгейінде
Хан
тәңірі шыңында
Электрон заряды
Электрон массасы
Пропорционалдық коэффициент
Электр
тұрақтысы
Вакуумдегі
жарық жылдамдығы
Гравитациялық тұрақты
Бірінші
ғарыштық жылдамдық
Планк
тұрақтысы
1
м. а.б.=1.6605406·10-27кг=931
а.б.=1.6605406·10-27кг=931
МэВ=1,49·10-10Дж Массаның атомдық
бірлігі
Ондық еселіктер
Атауы
Белгіленуі
Көбейткіш
Милли
микро
нано
пико
тера
гига
мега
кило
м
мк
н
п
Т
Г
М
К
10-3
10-6
10-9
10-12
1012
109
106
103
Тіркес сөздердің
белгіленуі, сан мәндері мен жазылуы
Тіркес сөздер атауы | Белгі- ленуі | Сан мәндері | Қысқа ша жазы луы |
Мега Кило Гекто (еселеу) Дека | М к г да | 1 000 000 1 000 100 10 | 106 103 102 101=10 |
Деци Санти Милли Микро | д с м мк | 0,1 0,01 0,001 0,000 | 10-1 10-2 10-3 10-6 |
Есептеулерге қажет
өлшем бірліктер
1
км=1000м=103м
1
дм=0,1м=10-1м
1
см=0,01м=10-2м
1
мм= 0,001м=10-3м
1
га=10 000м2=104м2
1 л=
1 дм3=0,001м3=10-3м3
1
мл=0,001л=1 см3
1
кН=1000 Н=103Н
1 т=
1000 кг= 103кг
1
г=0,001 кг=10-3кг
1
мг= 0,000001 кг=10-6кг
1кПа=1000 Па= 103Па
1гПа=100 Па=102Па
1мм
сын. Бағ.=133 Па
Бағ.=133 Па
1
кДж=1000 Дж=103Дж
1
кВт=1000 Вт=103Вт
| символ | количество | символ | шт. |
|---|---|---|---|
| r , r | положение, разделение, радиус, радиус кривизны | кв.м | метр |
| с , с | перемещение, расстояние | кв.м | метр |
| θ , φ , | угол, угловое перемещение, угловое разделение, угол поворота | рад | радиан |
| x , y , z | декартовы координаты | кв. м м | метр |
| до , ĵ , k̂ | декартовых единичных векторов | безразмерный | |
| r , θ, φ | сферические координаты | м, | метр, радиан |
| r̂, θ̂, φ̂ | сферические единичные векторы | безразмерный | |
| ρ, φ, z | цилиндрические координаты | м, | метр, радиан |
| ρ̂, φ̂, ẑ | цилиндрические единичные векторы | безразмерный | |
| № | нормальный единичный вектор | безразмерный | |
| т | тангенциальный единичный вектор | безразмерный | |
| ч | высота, глубина | кв. м м | метр |
| ℓ, л | длина | кв.м | метр |
| г | расстояние, отрыв, толщина | кв.м | метр |
| т | толщина | кв.м | метр |
| Д | диаметр | кв.м | метр |
| К | окружность | кв.м | метр |
| А , А | площадь, площадь поперечного сечения, площадь проекции, площадь поверхности | м 2 | квадратных метров |
| В | том | м 3 | м куб |
| т | раз, продолжительность | с | второй |
| т | , периодическое время | с | второй |
| τ | постоянная времени | с | второй |
| f | частота | Гц | герц |
| ω | угловая частота | рад / с | радиан в секунду |
| символ | количество | символ | шт. |
| в , в | скорость, скорость | м / с | метр в секунду |
| а , а | разгон | м / с 2 | метр в секунду в квадрате |
| a c , a c | центростремительное ускорение, центробежное ускорение | м / с 2 | метр в секунду в квадрате |
| г , г | гравитационное поле, ускорение свободного падения | м / с 2 | метр в секунду в квадрате |
| м | масса | кг | килограмм |
| F , F | сила | N | ньютон |
| F г , | сила тяжести, вес | N | ньютон |
| F n , | нормальная сила, нормальная | N | ньютон |
| F f , | Сила трения (статическая, кинетическая) | N | ньютон |
| μ с , μ k | коэффициент трения (статический, кинетический) | безразмерный | |
| p , p | импульс | кг м / с | килограмм-метр в секунду |
| Дж , Дж | импульс | Н с | ньютон секунда |
| Вт | работа | Дж | джоуль |
| E | энергия, общая энергия | Дж | джоуль |
| K , | кинетическая энергия (поступательная, вращательная) | Дж | джоуль |
| U , | потенциальная энергия (гравитационная, пружинная) | Дж | джоуль |
| V г | гравитационный потенциал | Дж / кг | джоуль на килограмм |
| η | КПД | безразмерный | |
п. | мощность | Вт | ватт |
| ω , ω | скорость вращения, частота вращения | рад / с | радиан в секунду |
| α , α | ускорение вращения | рад / с 2 | радиан на секунду в квадрате |
| τ , τ | крутящий момент | Н м | Ньютон-метр |
| I | момент инерции | кг м 2 | килограмм метр в квадрате |
| л , л | Угловой момент | кг · м 2 / с | килограмм-метр в секунду |
| H , H | угловой импульс | Н м | ньютон-метр секунда |
| к | жесткость пружины | Н / м | ньютон на метр |
п. | давление | Па | паскаль |
| σ | нормальное напряжение | Па | паскаль |
| τ | напряжение сдвига | Па | паскаль |
| ρ | плотность, объемно-массовая плотность | кг / м 3 | килограмм на кубический метр |
| σ | удельная масса поверхности, поверхностная плотность массы | кг / м 2 | килограмм на квадратный метр |
| λ | линейная массовая плотность | кг / м | килограмм на метр |
| F B , | Плавучесть, подъемная сила | N | ньютон |
| q м | массовый расход | кг / с | килограмм в секунду |
| q V | объемный расход | м 3 / с | кубометров в секунду |
| F D , | сопротивление, аэродинамическое сопротивление, сопротивление воздуха | N | ньютон |
| C , C D | Коэффициент аэродинамического сопротивления, коэффициент аэродинамического сопротивления | безразмерный | |
| η | , динамическая вязкость | Па · с | паскаль секунды |
| ν | кинематическая вязкость | м 2 / с | квадратных метров в секунду |
| млн лет | Машинный номер | безразмерный | |
| Re | число Рейнольдса | безразмерный | |
| Fr | номер марки | безразмерный | |
| E | Модуль Юнга, модуль упругости | Па | паскаль |
| G | Модуль сдвига, модуль жесткости | Па | паскаль |
| К | Модуль объемной упругости, модуль сжатия | Па | паскаль |
| ε | линейная деформация | безразмерный | |
| γ | деформация сдвига | безразмерный | |
| θ | объемная деформация | безразмерный | |
| γ | поверхностное натяжение | Н / м | ньютон на метр |
| символ | количество | символ | шт. |
| т | температура | К | кельвин |
| α | линейное расширение, коэффициент линейного теплового расширения | К -1 | обратный кельвин |
| β | объемное расширение, коэффициент объемного теплового расширения | К -1 | обратный кельвин |
| Q | тепло | Дж | джоуль |
| c | удельная теплоемкость, удельная теплоемкость | Дж / кг K | джоуль на килограмм кельвина |
| л | скрытая теплота, удельная скрытая теплота | Дж / кг | джоуль на килограмм |
| n | количество вещества | моль | |
| N | количество частиц | безразмерный | |
п. | тепловой поток | Вт | ватт |
| к | теплопроводность | Вт / м K | ватт на метр кельвина |
| ε | излучательная способность | безразмерный | |
| U | внутренняя энергия | Дж | джоуль |
| S | энтропия | Дж / К | джоуль на кельвин |
| w | путей, количество одинаковых микросостояний | безразмерный | |
| COP | коэффициент полезного действия | безразмерный | |
| символ | количество | символ | шт. |
| q , Q | заряд, электрический заряд | С | кулон |
| ρ | , объемная плотность заряда | С / м 3 | кулонов на кубический метр |
| σ | поверхностная плотность заряда, поверхностная плотность заряда | С / м 2 | кулонов на квадратный метр |
| λ | линейная плотность заряда | С / м | кулонов на метр |
| F E , F E | электрическая сила, электростатическая сила | N | ньютон |
| E , E | электрическое поле | Н / К, В / м | ньютон на кулон, вольт на метр |
| Φ E | электрический поток | Н · м 2 / C, В · м | Ньютон-метр в квадрате на кулон, вольтметр |
| U , U E | потенциальная энергия, электрическая потенциальная энергия | Дж | джоуль |
| В, В E | напряжение, потенциал, электрический потенциал | В | вольт |
| ℰ | Электродвижущая сила, ЭДС | В | вольт |
| К | емкость | F | фарад |
| κ | диэлектрическая проницаемость | безразмерный | |
| I | ток, электрический ток | А | ампер |
| R , R | сопротивление, электрическое сопротивление, внутреннее сопротивление | Ом | Ом |
| ρ | удельное сопротивление | Ом · м | омметр |
| G | проводимость | S | сименс |
| σ | проводимость | См / м | сименс на метр |
| F B , F B | магнитная сила | N | ньютон |
| B , B | магнитное поле | т | тесла |
| Φ B | магнитный поток | Вт | Вебер |
| N | количество витков | безразмерный | |
| n | витков на единицу длины, плотность витков | м −1 | обратный счетчик |
| η | плотность энергии | Дж / м 3 | джоуль на кубический метр |
| S , S | вектор пойнтинга, интенсивность | Вт / м 2 | ватт на квадратный метр |
| символ | описание | ||
| + | плюс, сложение, плюс | ||
| – | минус, вычесть, минус | ||
| ± | неопределенность, погрешность, плюс-минус | ||
| · | умножение, точка, скалярное произведение, скалярное произведение | ||
| × | умножение, крест, векторное произведение, векторное произведение | ||
| ÷, / | делить | ||
| x 2 | квадрат | ||
| x 3 | куб | ||
| √ | корень квадратный, корень, корень | ||
| ∛ | кубический корень | ||
| 1 x , x −1 | обратное, обратное | ||
| = | равно, равенство | ||
| ≈ | примерно равно | ||
| ∝ | пропорционально | ||
| ≠ | не равно, неравенство | ||
| ~ | на заказ, тильда | ||
| < | менее | ||
| > | больше | ||
| ≤ | меньше или равно | ||
| ≥ | больше или равно | ||
| ⇒, | логическое следствие | ||
| ⇔ | логическая эквивалентность | ||
| … | и так далее, многоточие | ||
| ∴ | следовательно | ||
| f ( x ) | (функция | ||
| грех | синус | ||
| cos | косинус | ||
| желто-коричневый | касательная | ||
| синх | гиперболический синус | ||
| cosh | гиперболический косинус | ||
| танх | гиперболический тангенс | ||
| x̂ | единичный вектор, шляпа, циркумфлекс | ||
| ∥ | параллельно | ||
| ⟂ | перпендикуляр | ||
| x | среднее, среднее, античастица, черта, черта | ||
| x | медиана, суперсиметрическая частица, тильда | ||
| ⟨⟩ | среднее по времени, среднее по ансамблю, скобка | ||
| p ( x ) | Распределение вероятностей, функция плотности вероятности | ||
| ∆ | приращение, изменение, дельта | ||
| г | дифференциал, d | ||
| ∂ | частичный дифференциал, d частичный | ||
| ∇ | градиент, дель | ||
| · | расхождение, деление, точка | ||
| ∇ × | локон, дель-крест | ||
| ∇ 2 | лапласиан, дель-квадрат | ||
| ∑ | суммирование, сигма | ||
| ∫ | интегральный | ||
| ∬ | двойной интеграл | ||
| ∭ | тройной интеграл | ||
| ∮ | контур интегральный | ||
| ∯ | поверхность интегральная | ||
| ∰ | интегральный объем | ||
| ∞ | бесконечность | ||
| ℵ 0 | , алеф ноль |
Физические формулы
Это
На странице есть все необходимые вам формулы физики. В первом разделе у нас есть СИ
В первом разделе у нас есть СИ
единицы измерения. В следующем разделе мы рассмотрим уравнения механики и уравнения электричества.
Эти
Уравнения физики описывают взаимосвязь между скоростью, ускорением,
силы и т. д. Как только мы поймем основную физику, уравнения могут служить в качестве мысленных
структуры, которые мы можем использовать, чтобы понять и предсказать исход физического явления.
Конечно, эти уравнения также будут неоценимы, когда дело доходит до расчета
неизвестные значения из известных.
Физика
это наука, которая в значительной степени полагается на математические навыки. Основной из них является алгебра, поскольку вам нужно иметь возможность заменять и переставлять уравнение
, если это необходимо. Помните, что мы всегда можем изменить формулу в соответствии с конкретным приложением.
Примечание: Все эти физические формулы требуют использования единиц СИ
(Международная система единиц)
единиц СИ
| Кол-во | Количество символ | Блок | символ |
| Масса | м | килограммы | кг |
| Усилие | F | Ньютон | N |
| расстояние | д | метра | м |
| скорость | v | Скорость | v |
| Давление | п. | Паскаль | Па |
| Работа | Вт | Джоулей | Дж |
| Энергия | E | Джоулей | Дж |
| Время | т | секунды | с |
https: // www.easy-science-experiments.com/#show-hide
Наши лучшие подарки для молодых ученых
https://www.easy-science-experiments.com/#show-hide
Уравнения механики
$$ v = \ frac {\ Delta d} {\ Delta t} $$
$$ velocity = \ frac {\ text {изменение смещения}} {\ text {изменение во времени}} $$
$$ a = \ frac {\ Delta v} {\ Delta t} $$
$$ ускорение = \ frac {\ text {изменение скорости}} {\ text {изменение во времени}} $$
$$ Сила = масса \ раз ускорение $$
$$ Работа = Сила \ умноженное на расстояние $$
$$ Мощность = \ frac {Работа} {время} $$
$$ крутящий момент = Сила \ умноженное на расстояние $$
$$ Force = — \ text {постоянная эластичности} \ times extension $$
Уравнения кругового движения
$$ a_c = \ frac {v ^ 2} {r} $$ | $$ \ text {центростремительное ускорение} = \ frac {скорость ^ 2} {радиус} $$ |
$$ F_c = \ frac {mv ^ 2} {r} $$ | $$ \ text {центростремительная сила} = \ frac {масса \ умноженная на скорость ^ 2} {радиус} $$ |
$$ C = 2 \ pi r $$ | $$ Окружность = 2 \ пи \ умножить на радиус $$ |
Импульс
$$ импульс = масса \ умноженная на скорость $$
$$ \ Delta p = F \ Delta t $$
$$ \ text {изменение импульса} = Сила \ раз \ text {изменение во времени} $$
Уравнения энергии
$$ E_p = \ frac {1} {2} kx ^ 2 $$
$$ \ text {Упругая потенциальная энергия} = \ frac {1} {2} \ text {постоянная упругости} \ times extension ^ 2 $$
$$ E_k = \ frac {1} {2} mv ^ 2 $$
$$ \ text {Кинетическая энергия} = \ frac {1} {2} масса \ умноженная на скорость ^ 2 $$
$$ \ Delta E_p = мг \ Delta ч $$
$$ \ text {потенциальная энергия гравитации} = масса \ times \ text {ускорение свободного падения} \ times \ text {изменение высоты} $$
Ep означает энергетический потенциал, который представляет собой запасенную энергию. 2 + 2ad $$
2 + 2ad $$
$$ d = (\ frac {v_f + v_f} {2}) t $$
Уравнения электричества
$$ Напряжение = ток \ умноженное на сопротивление $$
$$ P = I V $$
$$ P = \ frac {\ Delta E} {t} $$
$$ Мощность = Ток \ раз Напряжение $$
$$ Мощность = \ frac {Изменение энергии} {время} $$
$$ R_T = R_1 + R_2 + R_3 + … $$
Полное сопротивление резистора, включенного параллельно, равно сумме обратных сопротивлений резисторов.
$$ \ frac {1} {R_T} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +… $$
Суммарное сопротивление последовательно включенных резисторов — сумма всех последовательно включенных резисторов.
$$ \ text {Напряженность электрического поля} = \ frac {\ text {Разница потенциалов (напряжение)}} {расстояние} $$
$$ \ text {Электрическая сила} = \ text {Напряженность электрического поля} \ times charge $$
$$ Current = \ frac {charge} {timt} $$
$$ V = \ frac {\ Delta E} {Q} $$
$$ V = \ frac {изменение энергии} {Charge} $$
$$ \ Delta E = qEd $$
$$ \ text {Изменение энергии} = заряд \ раз \ text {напряженность электрического поля} \ раз расстояние $$
https: // www. easy-science-experiments.com/#show-hide
easy-science-experiments.com/#show-hide
Перестановка физических формул
Помните: Мы можем переставить физические формулы, применяя простую алгебру, чтобы гарантировать, что все символы в правой части уравнения известны.
Например, если мы знаем силу, действующую на объект, и массу объекта, как рассчитать ускорение, испытываемое объектом, с помощью уравнения:
$$ F = ma $$
Нам нужно переставить уравнение так, чтобы a было слева, а F — справа.
$$ a = \ frac {m} {F} $$
Теперь мы можем вставить m и F, чтобы получить a. Пока есть только одно неизвестное, мы можем легко изменить уравнения, чтобы дать нам ответ.
Вернитесь из «Физических формул» на ГЛАВНУЮ.
https://www.easy-science-experiments.com/#show-hide
Мягкий вопрос — Как вычислить формулы?
Формулы вычисляются посредством процесса, который трудно описать, потому что это происходит только один раз для каждой формулы, и он отличается, когда формула может быть выведена каким-либо образом, и когда это чисто новое отношение между количества, которые ранее не были связаны. 2 $ правильно?
2 $ правильно?
Самым важным инструментом, которым обладают физики, являются принципы симметрии, их можно использовать для вывода многих классических соотношений. Но этого недостаточно, и нет общего способа описать, как рассуждать о физике, чтобы вывести новые законы — это нужно изучать на примерах. Есть много ярких примеров, но, пожалуй, лучшим из них является вывод квантовой механики Гейзенбергом 1925 года. Я считаю это самым странным, самым проницательным и требующим величайшего воображения.Это описано на странице Википедии, посвященной механике матриц.
Приведенное вами уравнение — не лучший пример, потому что вы всегда можете сказать, что это определение силы. Это неверно, поскольку неявно предполагается, что сила является физическим свойством конфигурации частиц, а не конкретной траектории частицы, но чтобы полностью избавиться от округлости, предположим, что вы знакомы со статикой, так что у вас есть архимедовское определение силы.
Архимед демонстрирует, что вы можете думать о гравитации как о создании силы на рычаге, пропорциональной массе. Затем вы знаете из экспериментов Галилея, что ускорение свободного падения постоянно, и из аргументов Галилея вы знаете, что существует принцип относительности Галилея. Вы делаете вывод, что сила должна быть пропорциональна ускорению, которое инвариантно относительно галилеевых надстроек, и, поскольку все ускорения имеют одинаковую скорость, архимедовское понятие гравитационной массы также является понятием инертной массы в F = ma. Что-то вроде этого, вероятно, происходило в головах физиков 17 века.Трудно сказать, потому что F = ma ценили все во времена Ньютона, а не только Ньютон.
Затем вы знаете из экспериментов Галилея, что ускорение свободного падения постоянно, и из аргументов Галилея вы знаете, что существует принцип относительности Галилея. Вы делаете вывод, что сила должна быть пропорциональна ускорению, которое инвариантно относительно галилеевых надстроек, и, поскольку все ускорения имеют одинаковую скорость, архимедовское понятие гравитационной массы также является понятием инертной массы в F = ma. Что-то вроде этого, вероятно, происходило в головах физиков 17 века.Трудно сказать, потому что F = ma ценили все во времена Ньютона, а не только Ньютон.
Physics Formula Sheet.indd
% PDF-1.6
%
348 0 объект
>
эндобдж
345 0 объект
>
эндобдж
347 0 объект
> поток
application / pdf
2019-02-05T12: 58: 51 + 10: 30Adobe InDesign CC 13.0 (Windows) 2019-02-05T12: 58: 51 + 10: 30Acrobat Distiller 18.0 (Windows) uuid: d5c2d030-6bc8-42bf-a66b-13e60d1ba032uuid: a44ce26e -9da5-439f-be07-d3cac1875b43
конечный поток
эндобдж
335 0 объект
>
эндобдж
332 0 объект
>
эндобдж
65 0 объект
>
эндобдж
1 0 obj
>
эндобдж
68 0 объект
>
эндобдж
69 0 объект
> поток
h [YǑ ~ _я =
Калькулятор ускорения | Определение | Формула
Калькулятор ускорения — это инструмент, который поможет вам узнать, как быстро изменяется скорость объекта . Он работает тремя разными способами, в зависимости от:
Он работает тремя разными способами, в зависимости от:
- разница между скоростями в два разных момента времени,
- расстояние, пройденное при разгоне,
- масса ускоряющегося объекта и сила, действующая на него.
Если вы спрашиваете себя, что такое ускорение, какова формула ускорения или каковы единицы ускорения, продолжайте читать, и вы узнаете, как найти ускорение. Ускорение строго связано с движением объекта, и каждый движущийся объект обладает определенной энергией.Если вам нужно это оценить, посетите другие наши калькуляторы, где вы можете найти формулу кинетической энергии и ее угловую версию — формулу кинетической энергии вращения.
Чтобы все было понятно, мы также подготовили несколько примеров ускорения, которые распространены в физике. Вы можете найти там:
- центростремительное ускорение и тангенциальное ускорение,
- угловое ускорение,
- ускорение свободного падения,
- ускоритель частиц.

Ускорение всегда происходит, когда на объект действует ненулевая чистая сила.Вы можете почувствовать это в лифте, когда вы станете немного тяжелее (ускорение) или легче (замедление), или когда вы едете по крутому склону на санях по снегу. Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже ускоряется! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что каждый масштаб в мире тоже расширяется.
Что такое ускорение? — определение ускорения
Ускорение — скорость изменения скорости объекта; другими словами, насколько быстро меняется скорость. Согласно второму закону Ньютона, ускорение прямо пропорционально сумме всех сил, действующих на объект, и обратно пропорционально его массе. Это все здравый смысл — если несколько разных сил толкают объект, вам нужно выяснить, к чему они складываются (они могут действовать в разных направлениях), а затем разделить результирующую чистую силу на массу вашего объекта.
Это определение ускорения говорит, что ускорение и сила, по сути, одно и то же. При изменении силы изменяется и ускорение, но величина его изменения зависит от массы объекта. Это неверно в ситуации, когда масса также изменяется, например, при ракетной тяге, когда сгоревшее топливо выходит из сопла ракеты. Если вы когда-нибудь задумывались, какова физика космических путешествий, взгляните на это уравнение ракеты Циолковского.
Мы можем измерить ускорение объекта напрямую с помощью акселерометра .Если повесить объект на акселерометр, он покажет ненулевое значение. Это почему? Ну, это из-за гравитационных сил, которые действуют на каждую частицу, имеющую массу. А где чистая сила, там и ускорение. Таким образом, акселерометр в состоянии покоя измеряет ускорение свободного падения, которое на поверхности Земли составляет около 31,17405 фут / с² (9,80665 м / с²) . Другими словами, это ускорение свободного падения, которое любой объект получает при свободном падении в вакууме.
Кстати о пылесосах, вы когда-нибудь смотрели «Звездные войны» или другой фильм, действие которого происходит в космосе? Эпические сражения космических кораблей, звуки бластеров, двигателей и взрывов.Что ж, это ложь. Космос — это вакуум, и в нем нельзя услышать звук (для распространения звуковых волн требуется материя). Эти битвы должны быть беззвучными! В космосе никто не услышит твой крик. Чтобы проверить скорость звука в воздухе или воде, воспользуйтесь нашим калькулятором скорости звука. Учитывается даже температура!
Как найти ускорение? — счетчик ускорения
Калькулятор ускорения на этом сайте учитывает только ситуацию, в которой объект имеет равномерное (постоянное) ускорение.В этом случае уравнение ускорения по определению представляет собой отношение изменения скорости за определенный период времени. Однако здесь вы можете узнать, как найти ускорение еще двумя способами. Давайте посмотрим, как пользоваться нашим калькулятором (уравнения ускорения вы можете найти в разделе после):
- В зависимости от имеющихся данных вы можете рассчитать ускорение тремя разными способами.
 Сначала выберите соответствующее окно (# 1, # 2 или # 3),
Сначала выберите соответствующее окно (# 1, # 2 или # 3), - [если вы выбрали # 1] — Введите начальную
v_iи конечнуюv_fскорости объекта, а также сколько времениΔtпотребовалось для изменения скорости. - [при выборе # 2] — Введите начальную скорость
v_i, пройденное расстояниеΔdи времяΔt, пройденное во время ускорения. Здесь вам не нужно знать конечную скорость. - [при выборе # 3] — Введите массу
мобъекта и чистую силуF, действующую на этот объект. Это совершенно другой набор переменных, который возникает из второго закона движения Ньютона (другое определение ускорения). - Считайте результирующее ускорение из последнего поля. Вы также можете выполнить вычисления другим способом, если знаете, что такое ускорение, например, чтобы оценить расстояние
Δd. Просто укажите остальные параметры в этом окне.
Просто укажите остальные параметры в этом окне.
Знание того, что такое ускорение, необходимо для анализа движения объектов. Например, вы можете определить изменение импульса за определенный период времени с помощью этой формулы для импульса. Это одна из физических величин, которые мы используем в нашем калькуляторе автокатастроф, где мы объясняем и визуализируем важность ремней безопасности с помощью чисел и определяем, с какой скоростью вы можете погибнуть в автокатастрофе.Повышение скорости и содержание алкоголя в крови — главные причины автомобильных аварий. Пожалуйста, водите осторожно!
Формула ускорения — три уравнения ускорения
В 17 веке сэр Исаак Ньютон , один из самых влиятельных ученых всех времен, опубликовал свою знаменитую книгу Начала . В нем он сформулировал закон всемирного тяготения, согласно которому любые два объекта с массой будут притягиваться друг к другу с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния). Чем тяжелее объекты, тем больше сила тяжести. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
Чем тяжелее объекты, тем больше сила тяжести. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
В Principia Ньютон также включает три закона движения, которые являются центральными для понимания физики нашего мира. Калькулятор ускорения основан на трех различных уравнениях ускорения, третье из которых получено из работы Ньютона:
-
а = (v_f - v_i) / Δt, -
a = 2 * (Δd - v_i * Δt) / Δt², -
a = Ф / м,
где:
-
a— ускорение, -
v_iиv_f— соответственно начальная и конечная скорости, -
Δt— время разгона, -
Δd— расстояние, пройденное при ускорении, -
F— чистая сила, действующая на объект, который ускоряется, -
м— масса этого объекта.
Теперь вы знаете, как рассчитать ускорение! В следующем абзаце мы обсудим единицы ускорения (СИ и британские). Вы уже видели наши калькуляторы конвертации? Они могут сэкономить вам много времени при работе с различными юнитами. В случае расстояния вас может заинтересовать конвертер длины, который включает в себя таблицу преобразования длины. Если вы хотите переключаться между разными единицами массы, вот наш конвертер веса. Оба калькулятора позволяют быстро выполнять вычисления с любым набором единиц измерения.Попробуйте!
Блоки ускорения
Если вы уже умеете рассчитывать ускорение, давайте сосредоточимся на единицах ускорения. Вы можете вывести их из приведенных выше уравнений. Все, что вам нужно знать, это то, что скорость выражается в футах в секунду (британская / американская система) или в метрах в секунду (система СИ), а время — в секундах. Следовательно, если вы разделите скорость на время (как мы делаем в первой формуле ускорения), вы получите единицу ускорения фут / с² или м / с² в зависимости от того, какую систему вы используете.
В качестве альтернативы можно использовать третье уравнение. В этом случае вам нужно разделить силу (фунты в США и ньютоны в СИ) на массу (фунты в США и килограммы в СИ), получив фунтов / фунт или Н / кг . Они оба представляют одно и то же, поскольку фунт составляет фунт-сила-дюйм = фунт * фут / с² , а ньютон составляет Н = кг * м / с² . Когда вы замените его и уменьшите единицы, вы получите (фунт * фут / с²) / фунт = фут / с² или (кг * м / с²) / кг = м / с² .
Существует также третий вариант, который фактически широко используется.Вы можете выразить ускорение с помощью стандартного ускорения , обусловленного силой тяжести у поверхности Земли, которое определяется как g = 31,17405 фут / с² = 9,80665 м / с² . Например, если вы говорите, что лифт движется вверх с ускорением 0,2 g , это означает, что он ускоряется примерно со скоростью 6,2 фут / с² или 2 м / с² (т. Е. 0,2 * g ) . Мы округлили приведенные выше выражения до двух значащих цифр с помощью правил значащих цифр, которые вы можете найти в нашей математической категории.
Примеры разгона
Центростремительное ускорение и тангенциальное ускорение
Ускорение — это обычно вектор, поэтому его всегда можно разложить на компоненты. Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму дорожки, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения.Он изменяет только значение скорости , но не ее направление.
В круговом движении (крайний левый рисунок ниже), когда объект движется по окружности круга, присутствует только центростремительная составляющая. Объект будет поддерживать постоянную скорость; подумайте о Земле, которая имеет центростремительное ускорение из-за силы тяжести Солнца (на самом деле ее скорость немного меняется в течение года — см. калькулятор орбитальной скорости и калькулятор орбитального периода для получения дополнительной информации).
Когда присутствуют оба компонента, траектория объекта выглядит как на правом изображении. Что будет, если есть только тангенциальное ускорение? Затем происходит линейное движение. Это похоже на нажатие педали газа в автомобиле на прямом участке автострады. А если вы водитель, наш счетчик бензина может вас заинтересовать; оценивает стоимость проезда на автомобиле. Вы указываете экономию топлива, расстояние и цену на бензин, и вы быстро получаете стоимость поездки. Есть даже возможность разделить его на несколько человек, ведь вместе путешествовать весело и выгодно! Группа разговорчивых друзей в вашей машине будет: e.g., не дать вам заснуть.
Угловое ускорение
Угловое ускорение играет важную роль в описании вращательного движения. Однако не путайте это с ранее упомянутыми центростремительными или тангенциальными ускорениями. Эта физическая величина соответствует скорости изменения угловой скорости. Другими словами, он сообщает вам, насколько быстро ускоряется вращение объекта — объект вращается все быстрее и быстрее (или все медленнее и медленнее, если угловое ускорение меньше нуля).
Знаете ли вы, что мы можем найти аналогию между этим и законом динамики Ньютона во вращательном движении? Согласно его второму закону, если вы можете переключить ускорение на угловое ускорение, силу на крутящий момент и массу на момент инерции, вы получите уравнение углового ускорения. Вы могли заметить, что некоторые физические законы, подобные этому, универсальны, что делает их действительно важными для физики.
Ускорение свободного падения
Мы несколько раз упоминали ускорение свободного падения.Он возникает из-за гравитационной силы, которая существует между каждыми двумя объектами, имеющими массу (обратите внимание, что уравнение гравитации не зависит от объема объекта — здесь важна только масса). Сначала это может показаться странным, но согласно третьему закону движения Ньютона вы действуете на Землю с той же силой, что и Земля на вас . Однако масса Земли намного больше, чем масса человека (в ~ 10 ² раз больше), поэтому наше воздействие на Землю практически равно нулю. Это аналогично всем бактериям (в ~ 10¹⁸ раз легче человека), живущим на вашей руке; вы их даже не заметите! С другой стороны, мы чувствуем влияние нашей планеты, и это ускорение силы тяжести.
Стандартная сила тяжести по определению составляет 31,17405 фут / с² (9,80665 м / с²), поэтому, если человек весит 220 фунтов (около 100 кг), на него действует сила тяжести около 7000 фунтов на квадратный дюйм (1000 Н). Давайте введем это значение в окно №3 нашего калькулятора вместе с массой Земли (1,317 × 10²⁵ фунта или 5,972 × 10²⁴ кг в экспоненциальном представлении). Что такое расчетное ускорение? Это настолько маленькое , что наш калькулятор считает, что это ноль . Мы ничего не значим по сравнению с планетой!
Ускоритель частиц
Поговорив об огромных объектах в космосе, перейдем к микроскопическому миру частиц.Хотя мы не можем видеть их глазами, мы использовали частицы высоких энергий, такие как электроны и протоны, и регулярно используем их в ускорителях частиц; распространены в физике, химии и медицине. Мы используем их для уничтожения раковых клеток, сохраняя при этом окружающую здоровую ткань, или исследуем структуру материала в атомном масштабе. В последнее время рак — одна из болезней достатка, которая, вероятно, является следствием роста благосостояния в обществе. Даже неправильное питание может увеличить риск рака! С помощью этого ежедневного калькулятора протеина вы можете проверить, сколько протеина вам нужно в день, и, если вы также хотите улучшить свою физическую форму, наш макро-калькулятор здесь, чтобы помочь вам.
Вы, наверное, знаете о Большом адронном коллайдере (ЦЕРН), самом мощном ускорителе элементарных частиц в мире. Это позволяет нам сделать шаг вперед, чтобы понять, как устроена Вселенная, и разработать технологии, которые могут найти множество важных приложений в будущем. Однако, чтобы достичь таких высоких энергий, мы должны разогнать частицы до скоростей, близких к скорости света. Вкратце, мы можем сделать это с помощью магнитных или электрических полей. Чтобы увидеть, насколько быстро частицы ускоряются по сравнению со стандартной силой тяжести, посмотрите наше ускорение в калькуляторе электрического поля, где мы объяснили, как рассчитать ускорение заряженных частиц.
Мир микроскопических частиц управляется статистической физикой, которая уделяет особое внимание концепции вероятности. У нас есть много калькуляторов, связанных с этой темой. Взгляните на калькулятор вероятностей, чтобы узнать, как найти вероятность, или попробуйте калькулятор перестановок, чтобы определить количество способов, которыми вы можете упорядочить определенное количество элементов. Физики используют перестановку для предсказания теоретических свойств материала, которые затем можно наблюдать в повседневной жизни. Например, вы можете узнать, какова средняя скорость частиц газа.
FAQ
Является ли ускорение вектором?
Да , ускорение является вектором, так как имеет как величину, так и направление . Величина — это скорость ускорения объекта, а направление — это ускорение в том направлении, в котором движется объект, или против него. Это соответственно ускорение и замедление.
Как масса влияет на ускорение?
Если сила, с которой объект толкает, остается неизменной, ускорение будет уменьшаться по мере увеличения массы .Это потому, что F / m = a, поэтому с увеличением массы фракция становится все меньше и меньше.
Может ли ускорение быть отрицательным?
Да , ускорение может быть отрицательным, , которое известно как замедление . Два объекта с равным, но противоположным ускорением будут ускоряться на одинаковую величину, только в двух противоположных направлениях.
Как найти среднее ускорение?
- Определите изменение скорости за заданное время.
- Рассчитайте изменение времени за рассматриваемый период.
- Разделите изменение скорости на изменение во времени.
- Результат — среднее ускорение за этот период.
Как узнать величину ускорения?
- Преобразуйте величину силы в Ньютоны.
- Измените Масса объекта на килограммы.
- Умножьте оба значения на вместе, чтобы найти ускорение в м / с 2 .
В чем разница между ускорением и скоростью?
Скорость — это скорость, с которой объект движется в определенном направлении, а ускорение — это то, как скорость этого объекта изменяется со временем. Оба имеют величину и направление, но их единицы измерения — м / с и м / с 2 соответственно.
Как найти угловое ускорение?
- Используйте уравнения углового ускорения:
a = Δv / Δt. - Найдите начальную и конечную угловую скорость в радианах / с.
- Вычтите начальную угловую скорость из конечной угловой скорости, чтобы получить изменение угловой скорости .
- Найдите начальное и конечное время для рассматриваемого периода.
- Вычтите начальное время из последнего, чтобы получить изменение времени .
- Разделите изменение угловой скорости на изменение во времени, чтобы получить угловое ускорение в радианах / с 2 .
| Формула | Определение и объяснения |
|---|---|
s_ {av} = \ dfrac {d} {\ Delta t} | s av — средняя скорость (скалярная ) d — расстояние Δ t — прошедшее время |
v_ {av} = \ dfrac {x_f — x_i} {t_f — t_i} = \ dfrac {\ Delta x} {\ Delta t} | v av — средняя скорость (вектор) Δ x — смещение (вектор) Δ t — прошедшее время |
a_ {av} = \ dfrac {v_f — v_i} {t_f — t_i} = \ dfrac {\ Delta v} {\ Delta t} | a av — среднее ускорение (вектор) Δ v — изменение скорости ( вектор) Δ t — истекшее время |
v_ {av} = \ dfrac {v_i + v_f} {2} | v av — средняя скорость (вектор) v i — начальная скорость (вектор) v f — конечная скорость (вектор) |
v_ {f } = v_ {i} + a \ Delta t | v f — конечная скорость (вектор) v i — начальная скорость (вектор) a — ускорение (вектор ) |
\ Delta x = v_i \ Delta t + \ dfrac {1} {2} a (\ Delta t) ^ 2 | Δ x — смещение (вектор) v i — начальная скорость (вектор) a — ускорение (вектор) |
\ Delta x = v_f \ Delta t — \ dfrac {1} {2} a (\ Delta t) ^ 2 | Δ x — смещение (вектор) v f — конечная скорость (вектор) a is th e ускорение (вектор) |
\ Delta x = \ dfrac {v_f + v_i} {2} \ Delta t | Δ x — это смещение (вектор) v f — это конечная скорость (вектор) v i — начальная скорость (вектор) |
v ^ 2_f = v ^ 2_i + 2 a \ cdot \ Delta x | v f is конечная скорость (вектор) v i — начальная скорость (вектор) Δ x — смещение (вектор) a — ускорение (вектор) |
Формулы или код? Когда дело доходит до физики, все числа
Все уже используют компьютеры в физике.По крайней мере, студенты используют карманные калькуляторы (я сомневаюсь, что кто-то до сих пор пользуется калькулятором на основе логарифмической линейки). Кроме того, все чаще ученики решают физические задачи, создавая и кодируя свои собственные программы — и я думаю, что это хорошо. Если вы не знакомы с этими численными расчетами (другое название вычислительной физики), основная идея состоит в том, чтобы разбить проблему на множество более мелких и простых задач. Эти более мелкие задачи легче решить, но вы получаете так много вычислений, что вам в основном приходится писать компьютерную программу для их выполнения (но вам технически не нужно использовать компьютер).
Но поскольку численные методы становятся все более распространенными, мы также должны обсудить роль этих методов с точки зрения природы науки. Я часто вижу такие цитаты: «Вычислительные методы расширяют наш набор инструментов в физике. Теперь у нас есть три части науки: эксперимент, теория и вычисления».
Однако это неправда. Нельзя разделить науку на три разные части. Вычислительные методы и теория — это на самом деле всего лишь две версии вычислений, и на самом деле они не так уж сильно отличаются.Я собираюсь показать вам, как это одно и то же, но сначала позвольте мне прояснить природу науки. Наука — это построение и тестирование моделей. Мы создаем модели того, как устроена Вселенная, а затем проверяем эти модели экспериментальными данными. Эти модели могут быть реальной физической моделью (например, глобус), концептуальной моделью, уравнением или даже компьютерной программой. Итак, и «теория», и «вычисления» являются моделями.
Начнем с массы, соединенной с пружиной.Честно говоря, мы, физики, ЛЮБИМ эту ситуацию. Это достаточно легко решить, но достаточно сложно, чтобы мы могли аппроксимировать многие другие вещи как просто массу на пружине. Например, когда блок находится на столе, сила контакта может быть смоделирована как пружина. Даже взаимодействие между атомами в твердом теле можно представить как силу пружины. Действительно, эта проблема есть везде. Но здесь он в самом простом виде.
Видео: Rhett Allain
Я собираюсь решить эту проблему двумя способами. Во-первых, я решу ее численно, разбив ее на мелкие части (и используя некоторый код Python).После этого я найду аналитическое решение — решение, которое представляет собой функцию замкнутой формы (например, в терминах косинуса), так что вы можете ввести любые числа и параметры, которые хотите, чтобы получить набор решений. Но в конце я покажу вам, что эти два метода на самом деле не так уж сильно отличаются.
Численное решение
Чтобы построить численную модель для массы, связанной с пружиной, нам нужно выражение для силы, оказываемой пружиной. Если вы возьмете пружину и потянете ее, она потянет назад с некоторой силой.Чем больше вы его растягиваете, тем сильнее он тянет. Предположим, что положение груза задается переменной x, так что это также растяжение пружины. В этом случае сила пружины (в одном измерении) будет:
.
