алгебра все о функциях

Вы искали алгебра все о функциях? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра все функции, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «алгебра все о функциях».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгебра все о функциях,алгебра все функции,алгебра график,алгебра графики,алгебра графики функций,алгебра функции,алгебра функции виды,алгебра функции все,алгебра функции их свойства и графики,алгебра функция,алгебра функция это,алгебра что такое функция,в алгебре функция,вид функции,виды графики функций,виды графиков все,виды графиков функции,виды графиков функций,виды графиков функций и их формулы,виды парабол и их графики,виды функции алгебра,виды функции графиков,виды функций,виды функций в математике,виды функций графики,виды функций и их графики,виды функция,все виды графиков,все виды графиков функции и их формулы,все виды функций и их графики,все графики и их функции,все графики функции,все графики функции и их формулы,все графики функций,все графики функций и их формулы,все графики функций и их формулы таблица,все о функциях алгебра,все о функциях и графиках,все функции,все функции алгебра,все функции в алгебре,все функции графики,все функции и их графики,все функции и их графики и свойства,все функции и их графики и свойства таблица,все функции и их графики и свойства таблица 9 класс,все функции и их свойства и графики,высшая математика графики функций,геометрические функции,график алгебра,график и их функции,график общего вида функции,график функции как находить,график функции как решать,график функции как читать,график функции общего вида,график функции определение,график функции примеры,график функции тема,график функции функция,график функции четверти,график функции что это,график функции это,график функции это определение,график функции это что,график функций как решать,графика простая,графика функция,графики алгебра,графики в математике,графики всех функций,графики и их названия,графики и их свойства,графики и их формулы,графики и их функции,графики и их функции и формулы,графики и их функция,графики и формулы,графики и формулы функции,графики и функции,графики и функции все,графики и функции формулы,графики как понять как,графики какие бывают,графики математика,графики математические,графики математических функций,графики основных и обратных функций,графики основных функций,графики по алгебре,графики по математике,графики пример,графики примеры,графики произвольных функций,графики простейших функций,графики простых функций,графики различных функций,графики формулы,графики функции все,графики функции и их графики таблица,графики функции и их свойства,графики функции и их формулы,графики функции и их формулы 9 класс шпаргалка,графики функции и их формулы все,графики функции и формулы,графики функции как строить,графики функции какие бывают,графики функции примеры,графики функций 9 класс и их формулы,графики функций алгебра,графики функций виды,графики функций виды функций,графики функций все,графики функций всех,графики функций высшая математика,графики функций и их,графики функций и их название,графики функций и их названия,графики функций и их свойства,графики функций и их уравнения,графики функций и их формулы,графики функций и их формулы 8 класс алгебра,графики функций и их формулы 9 класс,графики функций и их формулы все,графики функций и их формулы шпаргалка,графики функций и их формулы шпаргалка 9,графики функций и их формулы шпаргалка 9 класс,графики функций и формулы,графики функций как понять,графики функций как строить и решать,графики функций какие бывают,графики функций картинки,графики функций математика,графики функций примеры,графики функций различных,графики функций таблица,графики функций формулы,графиков примеры,графиков функций примеры,графические функции,графіки функції,графіки функцій,для функции y,как изобразить график функции,как называется функция,как найти график функции,как определить график функции по формуле,как определить по формуле график функции,как по формуле определить график функции,как понять графики функций,как решать функции,как решать функции по алгебре,как строить графики функций,как чертить графики функций,как читать график функции,как читать графики функций,как читать функцию,какая функция,какие бывают графики,какие бывают графики функции,какие бывают графики функций,какие бывают функции,какие бывают функции в алгебре,какие бывают функции в алгебре и их графики,какие графики бывают,какие графики функции бывают,какие графики функций бывают,какие есть функции,какие функции,какие функции бывают,какие функции бывают в алгебре,какие функции в,какие функции есть,какой график,какую функцию,картинки графики функций,математика высшая функции,математика графики,математика графики функций,математика функции,математика функции их свойства и графики,математика функция,математика функция это,математика что такое функция,математическая функция,математические графики,математические основные функции,математические функции,название графиков,название графиков функций,название функций,названия графиков,названия графиков функций,названия функций,названия функций графиков,названия функций и их графики,называется графиком функции,описание функций графиков,определение график функции,определение графика функции,определение по графику функции,определение функции,определение функции в алгебре,определение функции график,определение функции графика,определение функции по графику,определение что такое функция в алгебре,определения функция,основные графики и их функции,основные графики функций,основные функции и их графики,основные функции математические,парабола гипербола и другие графики,парабола гипербола и другие графики формулы,понятие графика функции,понятие функции графика функции,построить график функции что значит,приведите пример функции удовлетворяющей следующим условиям графиком является парабола,пример график,пример графика,пример функции,примеры график функции,примеры графики функции,примеры графики функций,примеры графиков,примеры графиков функций,примеры функции,примеры функций,примеры функций графиков,простая графика,простейшие графики и их функции,простейшие функции и их графики,простейшие функции их графики и свойства,простейшие функции их свойства и графики,таблица графики функций,таблица графиков функций и их формулы,таблица функций,тема график функции,типы графиков функций,укажите график функции,уравнения графиков функций,уравнения функций и их графики,формула графика прямой,формула графика функции,формула параболы на графике функции,формула прямой на графике функции,формула функции,формула функции y x,формула функции графика,формулы графики,формулы графики функций,формулы графиков функций,формулы графиков функций 9 класс,формулы и графики,формулы и графики функции,формулы и графики функций,формулы и их графики,формулы и их функции,формулы и функции графики,формулы функции,формулы функции и графики,формулы функций,формулы функций графиков,формулы функций графиков 9 класс,формулы функция,фукция,функ,функции,функции алгебра,функции алгебра все,функции в алгебре,функции в алгебре и их графики,функции в алгебре определение,функции в математике,функции в математике виды и их графики,функции виды,функции виды графиков,функции виды математика,функции все,функции все алгебра,функции геометрические,функции график формулы,функции графика,функции графики,функции графики и формулы,функции графики примеры,функции графиков и их формулы,функции графические,функции и графики,функции и графики формулы,функции и графики шпаргалка,функции и их график,функции и их графики,функции и их графики и свойства,функции и их графики и свойства таблица,функции и их свойства и графики,функции и их формулы,функции и их формулы и графики,функции и формулы,функции и формулы графики,функции их свойства и графики,функции какие есть,функции математика,функции математики,функции математические,функции название,функции определения,функции по алгебре,функции пример,функции примеры,функции таблица,функции формула,функции формулы,функции формулы и графики,функций виды в алгебре,функций их названия и графики,функция алгебра,функция алгебра это,функция в алгебре,функция в алгебре это,функция в математике,функция в математике это,функция виды,функция график функции,функция графика,функция и ее график,функция и их свойства и графики,функция и не функция картинки,функция математика,функция математика что такое,функция математика это,функция математическая,функция формулы,функция это алгебра,функция это в алгебре,функция это в математике,функция это математика,четверти график функции,четверти графика,четверти графика функции,что называется графиком функции,что называют графиком функции,что такое график функции,что такое график функции в алгебре,что такое график функций,что такое значение функции в алгебре,что такое функция в алгебре,что такое функция в алгебре определение,что такое функция в математике,что такое функция определение в алгебре,что является графиком функции. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и алгебра все о функциях. Просто введите задачу в окошко и нажмите
«решить» здесь (например, алгебра график).

Где можно решить любую задачу по математике, а так же алгебра все о функциях Онлайн?

Решить задачу алгебра все о функциях вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Что такое функция — материалы для подготовки к ЕГЭ по Математике

 

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины по определенному закону, или правилу, обозначаемому .

Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .

Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .

В технической литературе встречается определение функции как устройства, на вход которого подается – а на выходе получается .

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .

 

Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется областью определения функции. Множество – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества: и .

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример.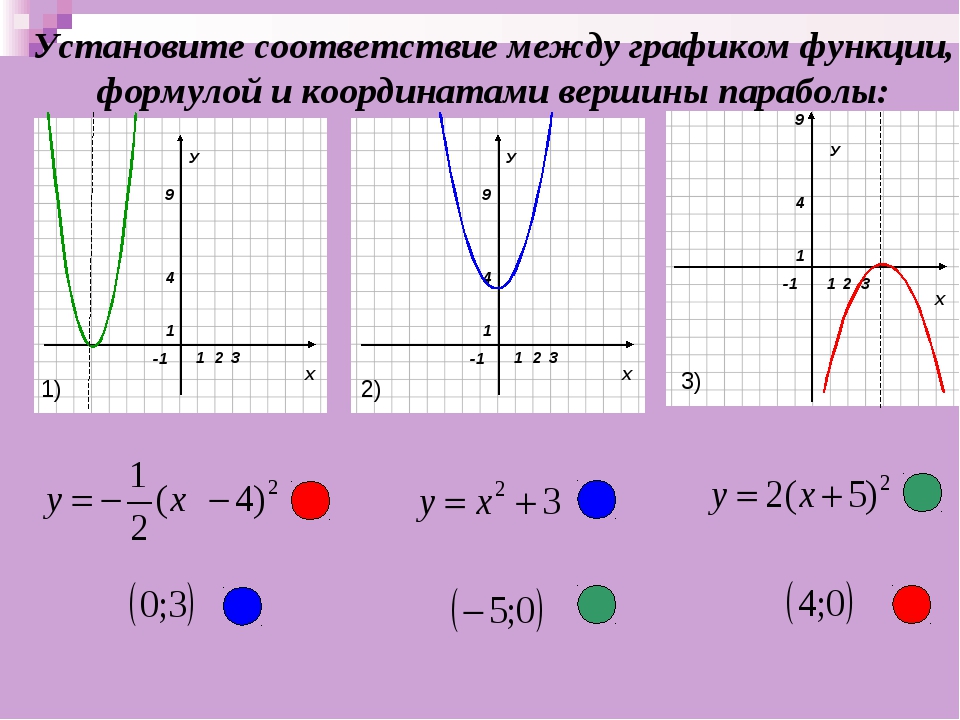 На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .

Ты нашел то, что искал? Поделись с друзьями!

Перечислим способы задания функции.

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

,

,

,

.

Это примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3.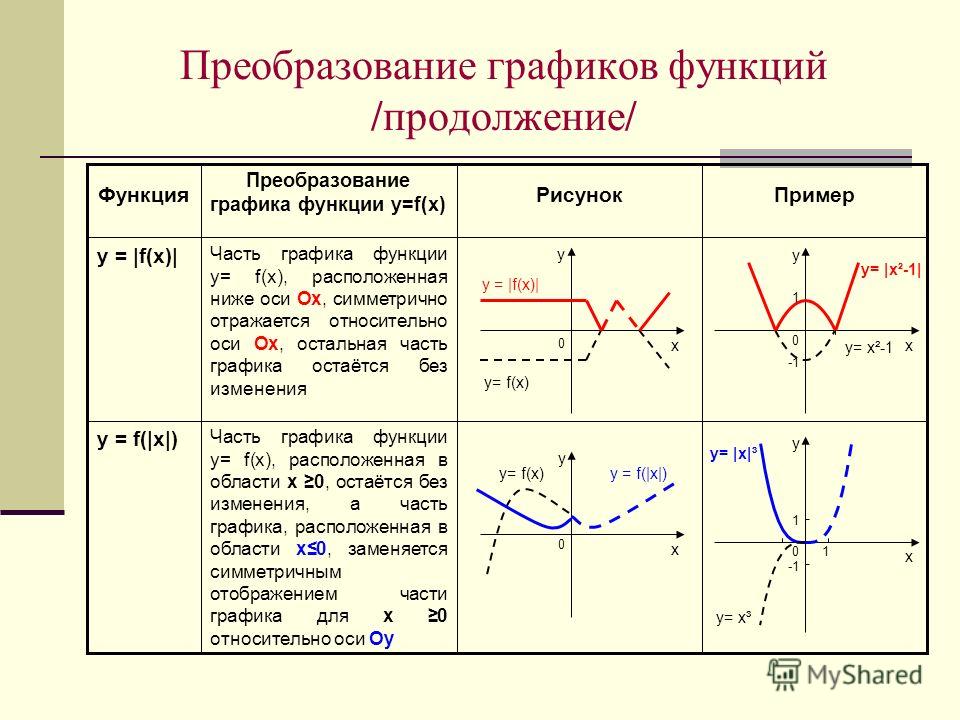 С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:

Читайте также: Чтение графика функции

Построение в Excel графиков математических и тригонометрических функций — Трюки и приемы в Microsoft Excel

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений.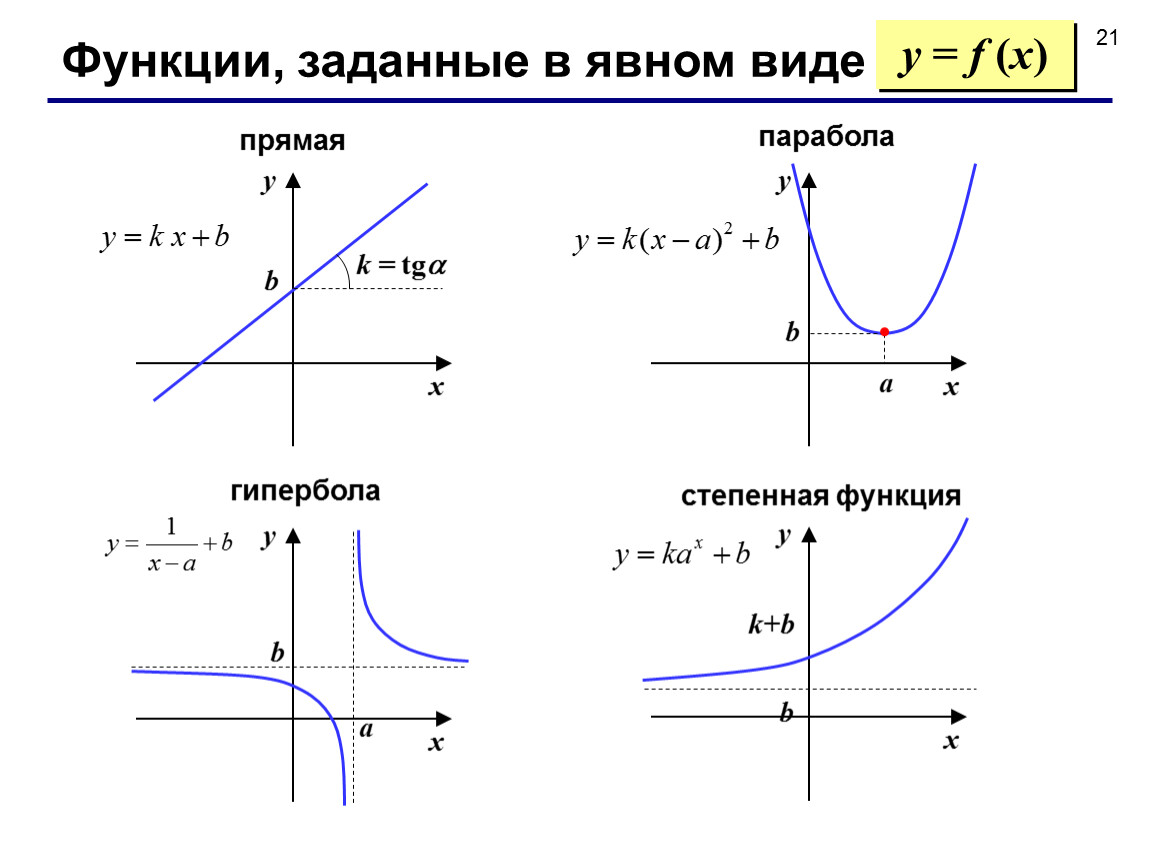 Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x).

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).

Чтобы создать эту диаграмму, выполните следующие действия.

1. Выделите диапазон А1:В22.
2. Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. 2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.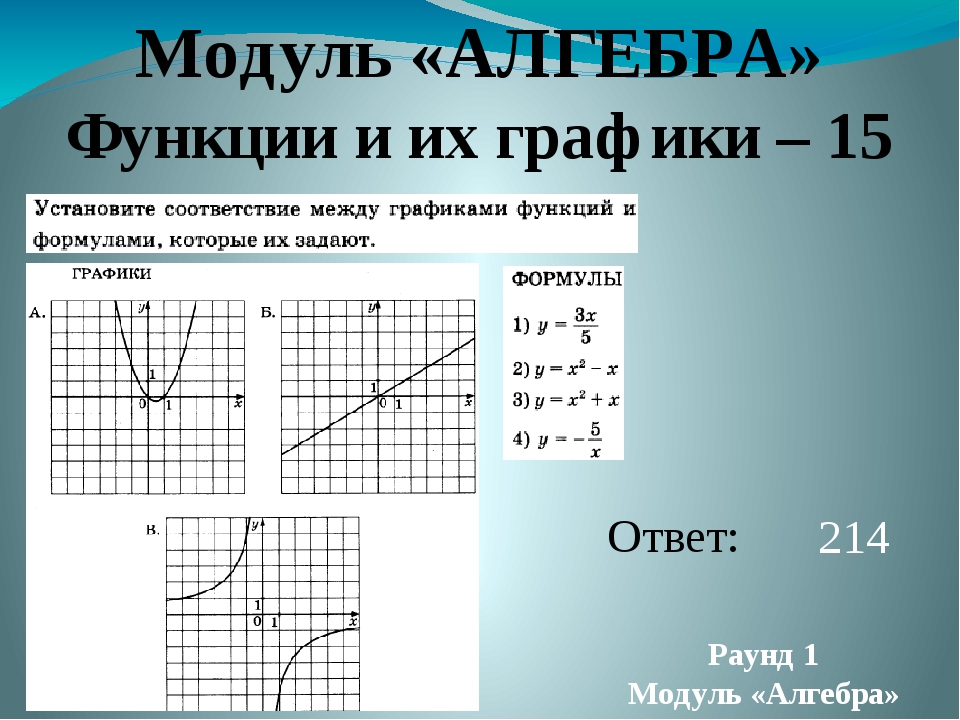

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).

Чтобы создать диаграмму, выполните приведенные ниже действия.

1. Выделите диапазон A1:V22.
2. Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)

График функции.

Формула функции — презентация онлайн

Поработаем в парах в тпо!
Вам надо выбрать ответ и
занести его в лист ответов!
Вопрос 1
у ах b
Дан график функции
Какая формула задаёт эту функцию?
1
1) у х 1
2
у
1
2) у 2 х 1
3) у 2 х 1
1
4) у х 1
2
1
2
0
х
Вопрос 2
у 1,5 х 5
Для функции найдите значение х ,
при котором значение у = 1
1)2,5
2)-2
3)-1,5 4)-4
у 2 х 3
Вопрос 3
Какой из приведённых графиков является
графиком функции?
у
3
у
3)
1)
4)
х
1,5
0
у
3
3
у
х
-1,5
0
1,5
х
2)
3
0
х
-2
0
Вопрос 4
Для линейной функции назовите
коэффициент k и ординату точки
пересечения графика функции с осью Оу:
х
у 1
3
k = -1
k=
y=1
1
3
1
k=
3
1
k= 3
y = -1
1
y=
3
y = -1
Вопрос 5
Задайте формулой линейную функцию,
если известен её угловой коэффициент и
точка пересечения с осью Оу:
k = -2; A (0; 3)
1) у 2 х 3
2) у 2 х 3
3) у 2 х 3
4) у 2 х 3
Поменяетесь тетрадями тпо
для взаимопроверки в
учениками за другой партой!
Проверяем!
Вопрос 1
у ах b
Дан график функции
Какая формула задаёт эту функцию?
у
3)к 0, у 2 1 1 1
1
1
2
0
х
Вопрос 2
у 1,5 х 5
Для функции найдите значение х ,
при котором значение у = 1
1 1,5 х 5
1,5 х 5 1
1,5 х 6
х 4
4)-4
Вопрос 3
у 2 х 3
Какой из приведённых графиков является
графиком функции?
у
3
к
1)
1,5
0
х
у 2 1,5 3 3 3 0
у 2 3 3 3
Вопрос 4
Для линейной функции назовите
коэффициент k и ординату точки
пересечения графика функции с осью Оу:
х
у 1
3
1
k= 3
y = -1
Вопрос 5
Задайте формулой линейную функцию,
если известен её угловой коэффициент и
точка пересечения с осью Оу:
k = -2; A (0; 3)
4) у 2 х 3
3 2 0 3
Подведём итоги работы в парах? Какие
критерии вы можете предложить?
У кого
«5»?
В лист
самооценки
выставите
свою
отметку!

Открытая Математика.

Функции и Графики. Гиперболические функции

Функция

shx=ex-e-x2

называется гиперболическим синусом. Функция

chx=ex+e-x2н азывается гиперболическим косинусом.

Подобно тому, как тригонометрические синус и косинус являются координатами точки на координатной окружности, гиперболические синус и косинус являются координатами точки на гиперболе.

Эти функции определены и непрерывны на всей числовой оси. Гиперболический синус является нечетной функцией, возрастающей на всей числовой оси. Гиперболический косинус является четной функцией, убывающей на промежутке (–∞; 0) и возрастающей на промежутке (0; +∞). Точка (0; 1) является минимумом этой функции.

Графики функций y = sh x и y = ch x

По аналогии с тригонометрическими функциями определены гиперболические тангенс и котангенс:

thx=shxchx, 
cthx=chxshx.

Тангенс определён на всей числовой оси, котангенс – при всех x ≠ 0


(limx→±0cthx=±∞).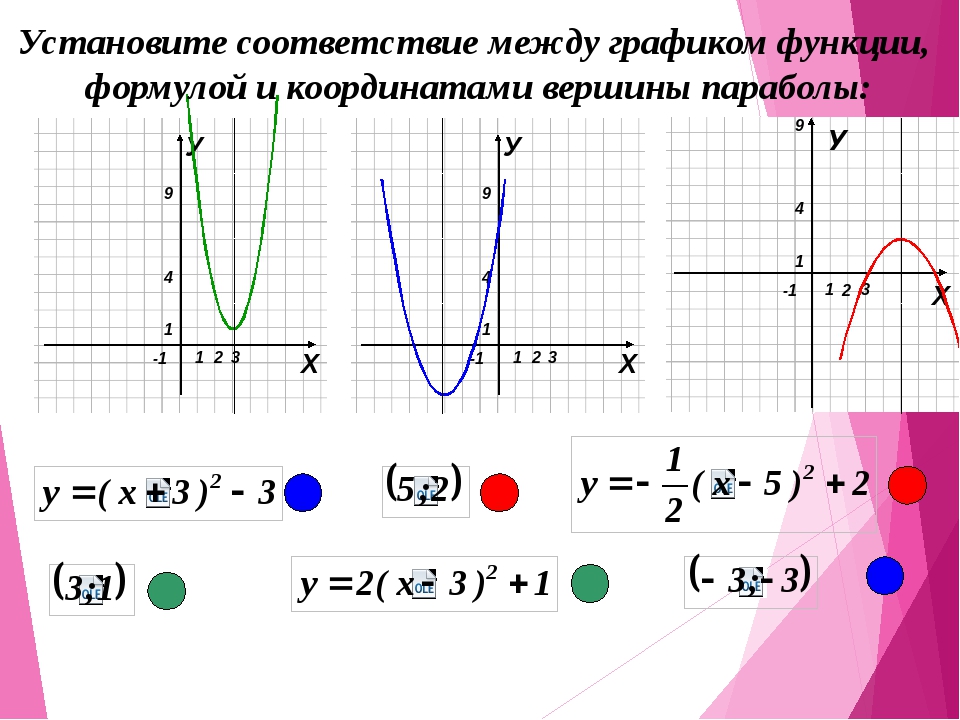


Обе функции непрерывны на всей области определения, нечетны и имеют горизонтальные асимптоты y = –1 (при x → –∞) и y = 1 (при x → +∞).

Графики функций y = th x и y = сth x

Приведём некоторые формулы, связанные с гиперболическими функциями.

sh x + ch x = e^x
ch² x – sh² x = 1
ch 2x = ch² x + sh² x

sh 2x = 2 sh x ch x
sh (x + y) = sh x ch y + ch x sh y
ch (x + y) = ch x ch y + sh x sh y

Функции, обратные гиперболическим синусу и тангенсу, определены и непрерывны на всей числовой оси. Они обозначаются соответственно arsh x и arth x. У гиперболического косинуса определены сразу две обратные функции: arch_– x при x ≤ 0 и arch₊ x при x ≥ 0.

Графики функций y = arsh x и y = arth x.

Графики функции y = arch_– x и y = arch₊ x.

В заключение приведём формулы для обратных гиперболических функций:

arshx=lnx+1+x2, 
x∈ℝarthx=12ln1+x1-x, |x| < 1,
arch-x=lnx-x2-1, x ≥ 1,
arch+x=lnx+x2-1, x ≥ 1.

Онлайн калькулятор: Аппроксимация функции одной переменной

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной

83 71 64 69 69 64 68 59 81 91 57 65 58 62

Значения x, через пробел

183 168 171 178 176 172 165 158 183 182 163 175 164 175

Значения y, через пробел

Линейная аппроксимация Квадратичная аппроксимация Кубическая аппроксимация Аппроксимация степенной функцией Показательная аппроксимация Логарифмическая аппроксимация Гиперболическая аппроксимация Экспоненциальная аппроксимацияТочность вычисления

Знаков после запятой: 4

Линейная регрессия

 

Коэффициент линейной парной корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Квадратичная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Кубическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Степенная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Показательная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Логарифмическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Гиперболическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Экспоненциальная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить
close

content_copy Ссылка save Сохранить extension Виджет

Линейная регрессия

Уравнение регрессии:

Коэффициент a:

Коэффициент b:

Коэффициент линейной парной корреляции:

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Квадратичная регрессия

Уравнение регрессии:

Система уравнений для нахождения коэффициентов a, b и c:

Коэффициент корреляции:
,
где

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Кубическая регрессия

Уравнение регрессии:

Система уравнений для нахождения коэффициентов a, b, c и d:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Показательная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Гиперболическая регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Логарифмическая регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Экспоненциальная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:

Для функции вида частные производные равны:
,

Подставив производные, получим:

Далее:

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

функций и их графиков

Функции: \ (f \), \ (g \), \ (y \), \ (u \)
Аргумент (независимая переменная): \ (x \)
Набор натуральных чисел: \ (\ mathbb {N} \)
Набор действительных чисел: \ (\ mathbb {R} \)
Основание натурального логарифма: \ (e \)

Натуральные числа: \ (n \)
Целые числа: \ (k \)
Действительные числа: \ (a \), \ (b \), \ (c \), \ (d \)
Угол: \ (\ alpha \)
Период функции: \ (T \)

1. Понятие функции — одно из важнейших в математике. Это определяется следующим образом. Пусть даны два множества \ (X \) и \ (Y \). Если для каждого элемента \ (x \) в множестве \ (X \) есть ровно один элемент (изображение) \ (y = f \ left (x \ right) \) в множестве \ (Y \), то говорят, что функция \ (f \) определена на множестве \ (X \). Элемент \ (x \) называется независимой переменной, и, соответственно, выход \ (y \) функции называется зависимой переменной. Если мы рассмотрим наборы чисел \ (X \ subset \ mathbb {R} \), \ (Y \ subset \ mathbb {R} \) (где \ (\ mathbb {R} \) — множество действительных чисел), тогда функция \ (y = f \ left (x \ right) \) может быть представлена ​​в виде графика в декартовой системе координат \ (Oxy \).
2. Четная функция
   \ (f \ left ({- x} \ right) = f \ left (x \ right) \)
3. Нечетная функция
   \ (f \ left ({- x} \ right) = -f \ left (x \ right) \)
4. Периодическая функция
   \ (f \ left ({x + kT} \ right) = f \ left (x \ right), \)
   где \ (k \) — целое число, \ (T \) — период функция.
5. Обратная функция
   Дана функция \ (y = f \ left (x \ right) \). Чтобы найти обратную ему функцию, необходимо решить уравнение \ (y = f \ left (x \ right) \) для \ (x \), а затем поменять местами переменные \ (x \) и \ (y \) .{- 1}} \ left (x \ right) \). Графики исходной и обратной функций симметричны относительно прямой \ (y = x \).
6. Составная функция
   Предположим, что функция \ (y = f \ left (u \ right) \) зависит от промежуточной переменной \ (u \), которая, в свою очередь, является функцией независимой переменной \ (x \): \ (и = г \ влево (х \ вправо) \). В этом случае связь между \ (y \) и \ (x \) представляет собой «функцию функции» или составную функцию, которую можно записать как \ (y = f \ left ({g \ left (x \верно-верно)\).Двухслойные составные функции можно легко обобщить на произвольное количество «слоев».
7. Линейная функция
   \ (y = ax + b, \) \ (x \ in \ mathbb {R} \).
   Здесь число \ (a \) называется наклоном прямой. Он равен тангенсу угла между прямой и положительным направлением оси \ (x \): \ (a = \ tan \ alpha \).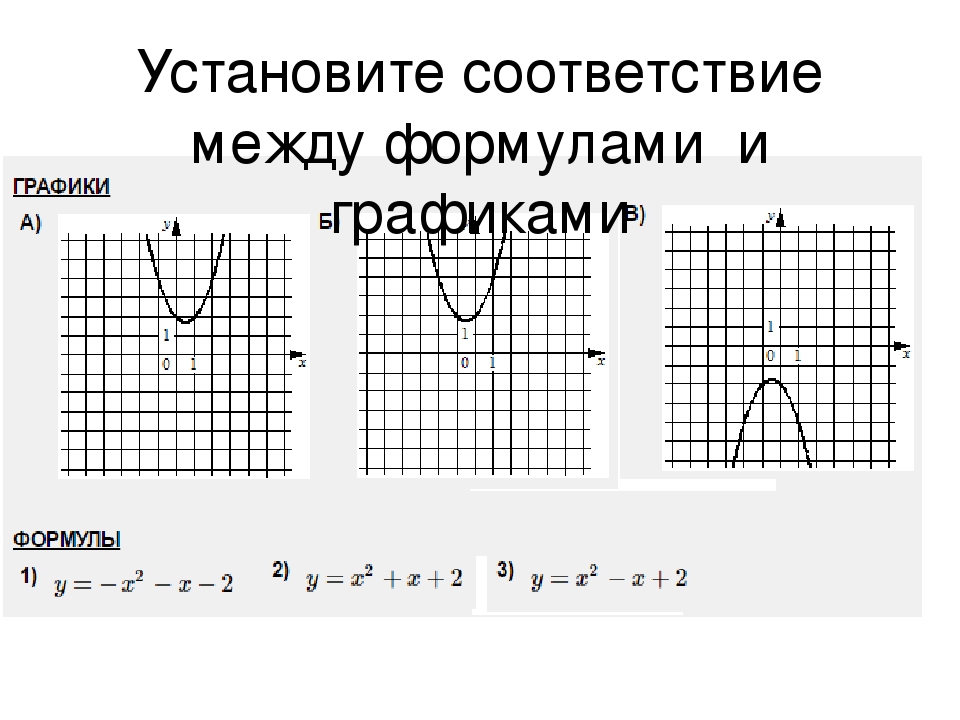 {- x}}}}} {2} \ normalsize}, \) \ (х \ в \ mathbb {R}.{- x}}}} \ normalsize}, \) \ (x \ in \ mathbb {R}, \) \ (x \ ne 0. \)
8. Функция обратного гиперболического синуса
   \ (y = {\ mathop {\ rm arcsinh} \ nolimits} \, x, \) \ (x \ in \ mathbb {R}. \)
9. Функция обратного гиперболического косинуса
   \ (y = {\ mathop {\ rm arccosh} \ nolimits} \, x, \) \ (x \ in \ left [{1, \ infty} \ right). \)
10. Функция обратной гиперболической касательной
    \ (y = {\ mathop {\ rm arctanh} \ nolimits} \, x, \) \ (x \ in \ left ({-1,1} \ right). \)
11. Функция обратного гиперболического котангенса
    \ (y = {\ mathop {\ rm arccoth} \ nolimits} \, x, \) \ (x \ in \ left ({- \ infty, — 1} \ right) \ cup \ left ({1, \ infty} \ right).\)
12. Обратная гиперболическая секущая функция
    \ (y = {\ mathop {\ rm arcsech} \ nolimits} \, x, \) \ (x \ in \ left ({0,1} \ right]. \)
13. Обратная гиперболическая функция косеканса
    \ (y = {\ mathop {\ rm arccsch} \ nolimits} \, x, \) \ (x \ in \ mathbb {R}, \; x \ ne 0. \)

% PDF-1.3
%
929 0 объект
>
эндобдж
xref
929 57
0000000016 00000 н.
0000001491 00000 н.
0000001714 00000 н.
0000001834 00000 н.
0000001894 00000 н.
0000001954 00000 н.
0000002014 00000 н.
0000002072 00000 н.
0000002131 00000 п.
0000002479 00000 н.
0000002538 00000 н.
0000002597 00000 н.
0000002657 00000 н.
0000002715 00000 н.
0000002839 00000 н.
0000002950 00000 н.
0000003754 00000 н.
0000004030 00000 н.
0000004125 00000 н.
0000004222 00000 п.
0000004319 00000 н.
0000004416 00000 н.
0000004594 00000 н.
0000005172 00000 п.
0000005638 00000 п.
0000005874 00000 н.
0000006104 00000 п.
0000006145 00000 п.
0000006167 00000 н.
0000006811 00000 н.
0000007047 00000 н.
0000007444 00000 н.
0000007466 00000 н.
0000007993 00000 н.
0000008015 00000 н.
0000008445 00000 н.
0000008859 00000 н.
0000009015 00000 н.
0000009037 00000 н.
0000009600 00000 н.
0000009622 00000 н.
0000010168 00000 п.
0000010190 00000 п.
0000010725 00000 п.
0000010747 00000 п.
0000011260 00000 п.
0000011282 00000 п.
0000011821 00000 п.
0000014499 00000 п.
0000014578 00000 п.
0000053486 00000 п.
0000077515 00000 п.
0000077912 00000 п.
0000088692 00000 п.
0000097865 00000 п.
0000003057 00000 н.
0000003732 00000 н.
трейлер
]
>>
startxref
0
%% EOF

930 0 объект
>
эндобдж
931 0 объект
[
932 0 R 933 0 R 934 0 R 935 0 R 936 0 R 937 0 R 938 0 R 939 0 R 940 0 R
941 0 руб. 942 0 руб. 943 0 руб.
]
эндобдж
932 0 объект
>
/ Ж 946 0 Р
>>
эндобдж
933 0 объект
>
/ Ж 947 0 Р
>>
эндобдж
934 0 объект
>
/ Ж 948 0 Р
>>
эндобдж
935 0 объект
>
/ F 5 0 R
>>
эндобдж
936 0 объект
>
/ Ж 10 0 Р
>>
эндобдж
937 0 объект
>
/ Ж 14 0 Р
>>
эндобдж
938 0 объект
>
/ Ж 21 0 Р
>>
эндобдж
939 0 объект
>
/ Ж 22 0 Р
>>
эндобдж
940 0 объект
>
/ Ж 949 0 Р
>>
эндобдж
941 0 объект
>
/ Ж 6 0 Р
>>
эндобдж
942 0 объект
>
/ Ж 45 0 Р
>>
эндобдж
943 0 объект
>
/ Ж 35 0 Р
>>
эндобдж
944 0 объект
>
эндобдж
984 0 объект
>
поток
Hb«`f`AXX8 & 040400800lql | y`mC, JL / ‘: e] H0> d +
T2Kp (Rr ~ 9iBewa_ «T}, 9z: 69qiIʇ: xTf
, 1NG & kx-kd ؅ «ШKu2I-W9l% a ֧ Ec
; s = Lr8aFN @. iVb3k) g0a? Cc / C3ho20.g’a6 [yN13H 3 (

Экспоненциальные функции и их графики

4.1 — Экспоненциальные функции и их графики

Экспоненциальные функции

До сих пор мы имели дело с алгебраическими функциями. Алгебраические функции — это функции, которые
могут быть выражены с помощью арифметических операций и значения которых либо рациональны, либо являются корнем
Рациональное число. Теперь мы будем иметь дело с трансцендентными функциями. Трансцендентный
функции возвращают значения, которые не могут быть выражены как рациональные числа или корни рациональных
числа.

Алгебраические уравнения в большинстве случаев можно решить вручную. Трансцендентные функции часто могут
можно решить вручную с помощью калькулятора, необходимого, если вы хотите десятичное приближение. тем не мение
когда трансцендентные и алгебраические функции смешиваются в уравнении, графическом или числовом
методы иногда являются единственным способом найти решение.

Простейшая экспоненциальная функция: f (x) = a ^x , a> 0,
а ≠ 1

Причины ограничений просты. Если a≤0, то когда вы возведете его в рациональную степень,
вы можете не получить реальный номер. Пример: если a = -2, то (-2) ^0,5 = sqrt (-2), что нереально. Если a = 1,
тогда независимо от того, что такое x, значение f (x) равно 1. Это довольно скучная функция, и это, безусловно,
не один на один.

Напомним, что у однозначных функций есть несколько свойств, которые делают их желательными. Они имеют
инверсии, которые также являются функциями. Их можно применять к обеим сторонам уравнения.

Графики экспоненциальных функций

График y = 2 ^x показан справа.Вот некоторые
свойства экспоненциальной функции, когда основание
больше 1.

• График проходит через точку (0,1)
• Домен — это все вещественные числа
• Диапазон: y> 0.
• График увеличивается
• График асимптотичен по оси x, когда x приближается к
  отрицательная бесконечность
• График неограниченно увеличивается по мере приближения x
  положительная бесконечность
• График непрерывный
• График плавный

Каким будет перевод, если вы замените каждый x на
-Икс? Это было бы отражение относительно оси y.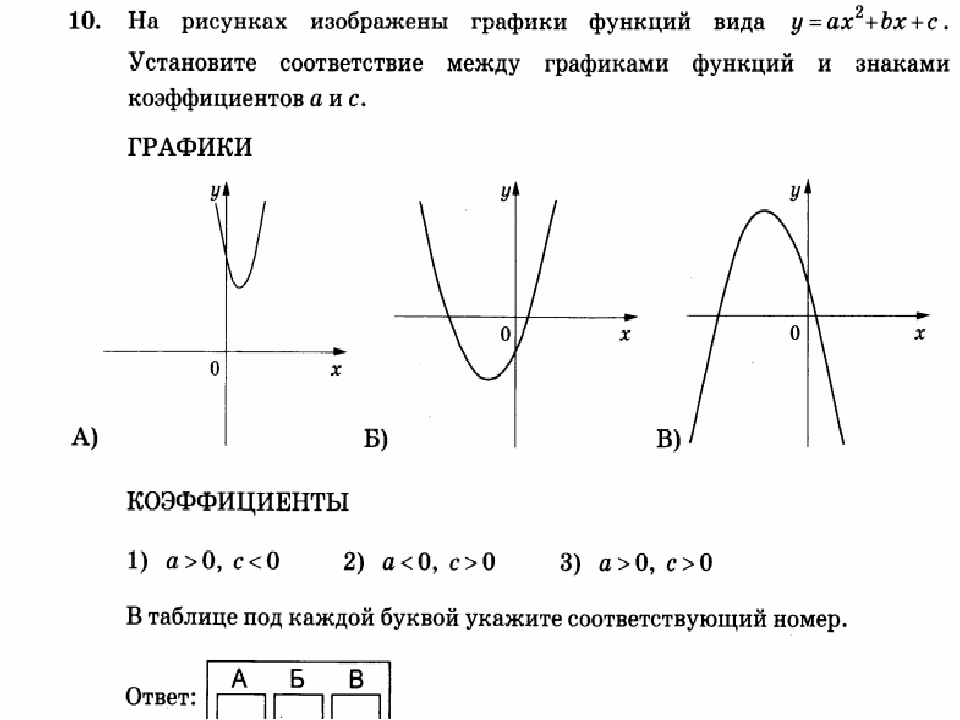 Мы также
знайте, что когда мы поднимаем базу до отрицательной силы,
один результат состоит в том, что берется обратное число. Так,
если бы мы построили график y = 2 ^-x , график был бы
отражение относительно оси y y = 2 ^x , и функция будет
быть эквивалентным y = (1/2) ^x .

График y = 2 ^-x показан справа. Свойства
экспоненциальная функция и ее график при базисе
дано от 0 до 1.

• График проходит через точку (0,1)
• Домен — это все вещественные числа
• Диапазон: y> 0.
• График убывает
• График асимптотичен по оси x, когда x стремится к положительной бесконечности
• График неограниченно увеличивается по мере приближения x к отрицательной бесконечности
• График непрерывный
• График плавный

Обратите внимание, единственная разница в том, увеличивается или уменьшается функция, и
поведение на левом и правом концах.

Переводы экспоненциальных графиков

Вы можете применить то, что знаете о переводах (из раздела 1. 5) чтобы помочь вам нарисовать график
экспоненциальных функций.

Горизонтальный сдвиг может повлиять на увеличение / уменьшение (если умножается на отрицательное),
левостороннее / правостороннее поведение графика и точка пересечения по оси Y, но это не изменит местоположение
горизонтальной асимптоты.

Вертикальное перемещение может влиять на увеличение / уменьшение (если умножается на отрицательное), точку пересечения по оси Y и положение горизонтальной асимптоты. Не изменится ли график
без границ или является асимптотическим (хотя он может меняться там, где он является асимптотическим) влево или
верно.Икс
приблизится к трансцендентному числу e .

Показанные предельные обозначения взяты из расчетов. Обозначение предела — это способ спросить, что
происходит с выражением, когда x приближается к показанному значению. Предел — это разделительная линия
между исчислением и алгеброй. Исчисление — это алгебра с понятием предела. Люди всегда
я не могу понять этого страха перед расчетом. Само исчисление простое. Причина
люди не преуспевают в исчислении не из-за исчисления, а из-за того, что они плохие
по алгебре.

Значение для e составляет приблизительно 2,718281828. Вот чуть более точный, но не более
полезное, приближение.

2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772
40766 30353 54759 45716 82178 52516 64274 27466 39193 20030 59921 81741 35966
29043 57290 03342 95260 59563 07381 32328 62794 34907 63233 82988 07531 95251
01901 15738 34187 93070 21540 89149 93488 41675 09244 76146 06680 82264 80016
84774 11853 74234 54424 37107 53907 77449 ​​92069 55170 27618 38606 26133

Когда используется основание e , экспоненциальная функция принимает вид f (x) = e ^x .Икс. На калькуляторах TI-8x он находится слева как
a [2 ^nd ] [Ln]. В
экспоненциальная функция с основанием e иногда сокращается как exp (). Одно общее место это
аббревиатура появляется при написании компьютерных программ. Я упоминаю об этом, поэтому, когда я пишу exp (x),
ты знаешь о чем я говорю.

Сложные проценты

Сумма на вашем сберегательном счете может быть вычислена с экспоненциальной функцией. Каждый период (я
предположим, ежемесячно), вы получаете 1/12 годовой процентной ставки (r), применяемой к вашему счету.Новый
сумма на счете составляет 100% от того, с чего вы начали, плюс r% / 12 от того, с чего вы начали.
Это означает, что теперь у вас есть (100% + r% / 12) того, с чего вы начали. В следующем месяце вы
будет то же самое, за исключением того, что он будет основан на том, что у вас было в конце первого месяца.

Непонятно, знаю. На странице 304 текста есть объяснение, но
полученная формула для
Сложный процент равен A = P (1 + i) ⁿ .

A — это сумма на счете.P — это принципал, с которого вы начали. я
— периодическая ставка, которая представляет собой годовой процент (записанный в виде десятичной дроби) r,
разделенный
по количеству периодов в году, м. n — количество периодов начисления сложных процентов,
что равно
количество периодов в году, м, умноженное на время в годах, т. Формула
Я показал выше немного отличается от формулы в книге, но согласен
с формулой, которую вы будете использовать, если пойдете
по конечной математике (Math 160). В конечной математике есть
целая глава о финансах и соответствующих формулах.

Непрерывное смешивание и рост / распад

Раньше было постоянное начисление процентов. Ты не
найти его больше, потому что он дает максимальную отдачу от инвестиций,
и банки в бизнесе, чтобы сделать
деньги, как и любое другое коммерческое учреждение.

Модель для непрерывного
компаундирование: A = P e ^rt .

A — сумма, P — основная сумма, r — годовая процентная ставка (написано
в виде десятичной дроби), а t — время в годах. e — основание для натурального логарифма.

Однако непрерывная модель имеет смысл для роста населения и радиоактивного распада.
Радиоактивность изотопа не меняется раз в месяц в конце месяца, а не меняется.
постоянно меняется.

Экспоненциальная модель: y = A e ^kt ,

, где y — количество, присутствующее в момент времени t. А — начальное количество,
и k — скорость роста (если положительна) или скорость распада
(если отрицательный).{d (x-c)} + ky = abd (x − c) + k

Приведенная выше формула немного сложнее, чем предыдущие функции, с которыми вы, вероятно, работали, поэтому давайте определим все переменные.

y — значение по оси y

a — коэффициент вертикального растяжения или сжатия

б — базовое значение

x — значение по оси x

c — коэффициент горизонтального перевода

d — коэффициент горизонтального растяжения или сжатия

k — коэффициент вертикального перевода

В этом уроке мы рассмотрим только самые простые экспоненциальные функции, поэтому вам не нужно беспокоиться о некоторых из перечисленных выше переменных. (x-2)

Сделав это преобразование, мы сдвинули весь график вправо на две единицы.x + 2y = 2x + 2, k = 2, и поэтому горизонтальная асимптота равна 2. Нет значения для x, которое мы могли бы использовать, чтобы сделать y = 2.

И это все переменные! Опять же, некоторые из них сложнее других, поэтому потребуется время, чтобы привыкнуть работать со всеми ними и научиться их находить. Чтобы лучше изучить экспоненциальные функции и ознакомиться с приведенным выше общим уравнением, посетите этот превосходный веб-сайт графического калькулятора здесь. Не торопитесь, чтобы поиграть с переменными и лучше почувствовать, как изменение каждой из переменных влияет на характер функции.

А теперь приступим к делу. Учитывая график экспоненциальной функции, как мы можем найти экспоненциальное уравнение?

Как найти экспоненциальные функции

Нахождение уравнения экспоненциальных функций часто представляет собой многоэтапный процесс, и каждая задача различается в зависимости от информации и типа графа, который нам дан. Учитывая график экспоненциальных функций, нам нужно иметь возможность брать некоторую информацию из самого графика, а затем решать то, что мы не можем взять непосредственно из графика.Ниже приведен список всех переменных, которые нам, возможно, придется искать, и того, как их обычно находить:

a — решите его по алгебре, иначе дадут

b — решите его по алгебре, иначе дадут

c — пусть x = 0 и представьте, что «c» там нет, значение y будет равно пересечению по оси y; теперь посчитайте, на сколько единиц значение y для точки пересечения y от оси y, и это будет равно «c»

.

d — решите это с помощью алгебры

k — равно значению горизонтальной асимптоты

Конечно, это лишь общие шаги, которые необходимо предпринять, чтобы найти уравнение экспоненциальной функции.xy = abx данного графа.

Нахождение экспоненциальной функции по ее графику

Чтобы решить эту проблему, нам нужно найти переменные «a» и «b». Кроме того, нам придется решить оба эти вопроса алгебраически, поскольку мы не можем определить их из самого графика экспоненциальной функции.

Шаг 1. Решите относительно «a»

Чтобы найти «a», мы должны выбрать точку на графике, где мы можем исключить bx, потому что мы еще не знаем «b», и поэтому мы должны выбрать y-точку пересечения (0,3).{dx} + ky = a2dx + k данного графа.

Нахождение экспоненциальной функции по ее графику

Чтобы решить эту проблему, нам нужно найти переменные «a», «d» и «k». Помните, что мы можем найти «k» на графике, поскольку это горизонтальная асимптота. Однако для «a» и «d» нам придется решать их алгебраически, поскольку мы не можем определить их из самого графика экспоненциальной функции.

Шаг 1. Найдите «k» на графике

Чтобы найти «k», все, что нам нужно сделать, это найти горизонтальную асимптоту, которая явно равна y = 6.(bx) + k

И это все, что касается экспоненциальных функций! Опять же, эти функции немного сложнее, чем уравнения для линий или парабол, поэтому обязательно выполните много практических задач, чтобы освоить новые переменные и методы. По мере практики, скоро экспоненциальные уравнения и графики экспоненциальных функций не будут проблемой!

Написать уравнение полиномиальной функции на основе ее графика

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Рисование графиков математических функций с помощью Math Assistant в OneNote

Сначала создайте уравнение, используя рукописный ввод или текст.

На вкладке Draw напишите или введите свое уравнение. Используйте инструмент Lasso Select , чтобы нарисовать круг вокруг уравнения. Затем выберите Math . Это откроет панель Math Assistant.

Из Выберите действие в раскрывающемся меню на панели Math выберите График в 2D или График с обеих сторон в 2D .

Чтобы настроить график, созданный Math Assistant, выполните одно из следующих действий (если возможно):

• Выберите (или нажмите и удерживайте), а затем перетащите график в любом направлении, чтобы переместить его положение.

• Щелкайте или касайтесь кнопок лупы + и — столько раз, сколько необходимо, чтобы изменить значения параметров в вашем уравнении, увеличивая или уменьшая масштаб.

Примечание. Если вы используете OneNote на устройстве с сенсорным экраном, вы также можете настроить график пальцами. Используйте один палец, чтобы изменить положение графика, или увеличьте масштаб двумя пальцами, чтобы изменить уровень увеличения.В OneNote в Интернете вы можете использовать стрелки по бокам графика, чтобы изменить его положение.

• Щелкните или коснитесь значка с двойной стрелкой Сбросить , чтобы вернуть график в исходное состояние.

• Когда график будет выглядеть так, как вы хотите, щелкните или коснитесь Вставить на странице , чтобы разместить его как снимок экрана на текущей странице.

Примечание: Чтобы изменить способ отображения графика (градусы, радианы, градианы), щелкните или коснитесь Настройки , когда панель «Математика» открыта.

Расширенные возможности построения графиков

Другие функции могут быть доступны в зависимости от типа вашего графика.

• Считывание значений x-y: Наведите указатель мыши на точку на линии графика, чтобы увидеть значения x и y в OneNote для Windows 10. В OneNote в Интернете щелкните строку, чтобы просмотреть значения.

• Управление параметрами: Если у вас есть уравнение с параметрами, например ax + b, используйте знаки плюс + и минус — под графиком, чтобы изменить значения a и b.

• Ключевые особенности графика: Math Assistant вычисляет интересную информацию о графике, такую ​​как нули, точки пересечения, минимумы, максимумы и многое другое. Используйте флажки, чтобы выбрать, какие функции вы хотите отобразить на графике.

Создавайте математические уравнения с помощью рукописного ввода или текста с помощью Math Assistant в OneNote

Решайте математические уравнения с помощью Math Assistant в OneNote

Типы задач, поддерживаемые Math Assistant

Создайте практическую викторину по математике

Типы задач, поддерживаемые Math Assistant

Когда вы используете Math Assistant в OneNote, вы заметите, что раскрывающийся список Выберите действие под уравнением изменяется в зависимости от выбранного вами уравнения.Вот некоторые из типов задач, которые поддерживаются в зависимости от уравнения, которое вы пытаетесь решить.

Массивы	Для списка действительных чисел поддерживаются все перечисленные ниже.
Выражения	Для любого выражения доступны следующие действия: Оценить Проверить Развернуть (если применимо) Коэффициент (если применимо) График в 2D (доступен только при наличии переменной) Дифференцировать (доступно только при наличии переменной) Интегрировать (доступно только при наличии переменной)
Уравнения и неравенства	Для уравнений и неравенств доступны следующие действия: Решите для {вашей переменной} Обе стороны графика в 2D — Каждая из сторон равенства или неравенства изображена на графике как отдельная функция. График в 2D — график решений уравнения или неравенства Graph Inequality — отмечает область решения на графике
Системы	Важно иметь равное количество уравнений и переменных, чтобы обеспечить доступность правильных функций.Системы можно записать двумя способами: Один под другим, с большой распоркой перед ними или без нее Через запятую
Производные и интегралы	Производные могут быть записаны либо с d / dx перед функцией, либо со штрихом. Действия, доступные для производных и интегралов:
Матрицы	Матрицы можно записывать в квадратных или круглых скобках. Для матриц поддерживаются следующие действия: Оценить Вычислить определитель Инвертировать матрицу Вычислить трассировку Матрица транспонирования Размер матрицы Уменьшить матрицу Матричные уравнения в настоящее время не поддерживаются.
Построение графика в полярных координатах	Чтобы построить график функции в полярных координатах, необходимо выразить r как функцию от тета.
Комплексный режим	Примечание: Выберите Настройки , чтобы переключаться между действительными и комплексными числами. Для сложных выражений и чисел, содержащих мнимую единицу i, , доступны следующие действия.

Узнать больше

Создайте математический тест в Microsoft Forms

Создайте практическую викторину по математике с помощью Math Assistant в OneNote

Решайте математические уравнения с помощью Math Assistant в OneNote

Как построить график функции в Excel | Small Business

Математическая функция — это формула, которая принимает входные данные x, применяет к ним набор вычислений и производит выходные данные с именем y.Вычисляя функцию с большим количеством заданных интервалов, можно создать диаграмму рассеяния функции. В бизнесе это имеет множество применений. Например, вы можете построить график прибыли за вычетом затрат на различных уровнях продаж, или общие затраты можно оценить, нанеся на график постоянные затраты с разными приращениями переменных затрат.

Создайте заголовки для таблицы данных. Введите входную переменную в ячейку A1 и выходную переменную в ячейку B1. Если хотите, вы можете использовать математические стандарты «x» и «y» или использовать что-то более наглядное, например «продажи» и «прибыль».«

Введите первый и второй интервалы входной переменной (например,« x »или« продажи »), которые вы будете использовать для построения графика функции. Например, если ваши интервалы представляют собой целые числа, вы можете начать с введите «1» в ячейку A2 и «2» в ячейку A3. Выберите обе эти ячейки, а затем щелкните и перетащите маленький черный квадрат в правом нижнем углу области выбора вниз, пока не получите столько значений, сколько хотите. plot

Введите знак равенства «=» в ячейку B2, а затем введите формулу сразу после него, не оставляя пробелов.Например, чтобы определить количество продаж определенного продукта для покрытия расходов, вы можете использовать:

= (A2 * 50) -3500

Замените «50» продажной ценой, а «3500» — ваши расходы.

Выберите ячейку B2, а затем перетащите, чтобы скопировать формулу вниз по столбцу тем же методом, который вы использовали на шаге 2. Убедитесь, что каждое из ваших значений x имеет соответствующую функцию справа от него. При этом столбец автоматически заполнится решениями для каждой функции на основе значения x в столбце A.

Выберите все ячейки, в которые вы ввели данные, включая заголовок.

Щелкните вкладку «Вставка», щелкните «Разброс» в области графиков, а затем щелкните нужный тип графика. График появится на вашем листе.

Биография писателя

Уоррен Дэвис пишет с 2007 года, уделяя особое внимание индивидуальным проектам для онлайн-клиентов, таких как PsyT и Институт коучинга.