Формулы sinx a: Арксинус и уравнение sin x = a — урок. Алгебра, 10 класс.

alexxlab

Содержание

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия

      Простейшими тригонометрическими уравнениями называют уравнения вида:

sin x = a ,     cos x = a ,     
tg x = a ,     ctgx = a .

где a – произвольное число.

Решение уравнения   sin 

x = a

Обычная форма
записи решения
Более удобная форма
записи решения
Ограничения
на число a		В случае, когда ,
уравнение решений не имеет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

В случае, когда , уравнение решений не имеет.

      Графическое обоснование решения уравнения   sin x = a представлено на рисунке 1

Рис. 1

Частные случаи решения уравнений   sin x = a

Уравнение:

sin x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

>

Уравнение:

sin x = 0

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

sin x = 1

Решение:

Решение уравнения   cos 

x = a

Обычная форма
записи решения
Более удобная форма
записи решения
Ограничения
на число a		В случае, когда ,
уравнение решений не имеет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a

В случае, когда , уравнение решений не имеет.

      Графическое обоснование решения уравнения   cos x = a   представлено на рисунке 2

Рис. 2

Частные случаи решения уравнений   cos x = a

Уравнение:

cos x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

cos x = 0

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

cos x = 1

Решение:

Решение уравнения   tg 

x = a

Обычная форма
записи решения:
Более удобная форма
записи решения
Ограничения
на число a		Ограничений нет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

Ограничений нет.

      Графическое обоснование решения уравнения   tg x = a представлено на рисунке 3.

Рис. 3

Частные случаи решения уравнений   tg x = a

Уравнение:

Решение:

Уравнение:

tg x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

tg x = 0

Решение:

Уравнение:

Решение:

Уравнение:

tg x = 1

Решение:

Уравнение:

Решение:

Решение уравнения   ctg 

x = a

Обычная форма
записи решения
Более удобная форма
записи решения
Ограничения
на число a		Ограничений нет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

Ограничений нет.

    Графическое обоснование решения уравнения   ctg x = a представлено на рисунке 4.

Рис. 4

Частные случаи решения уравнений   ctg x = a

Уравнение:

Решение:

Уравнение:

ctg x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

ctg x = 0

Решение:

Решение:

Уравнение:

ctg x = 1

Решение:

Уравнение:

Решение:

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Урок 42. уравнение sin x = a — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №42. Уравнение sin x = a.

Перечень вопросов, рассматриваемых в теме:

1) Понятие арксинус числа;

2) Тождества, связанные с арксинусом;

3) Решение тригонометрических уравнений;

Глоссарий по теме

Арксинусом числа m называется такое число α, что: и .

Арксинус числа m обозначают: .

Заметим, что такой промежуток для α берется потому, что синус на отрезке принимает все свои значения ровно по одному разу.

Из определения следует, что для

С другой стороны, если и , то

Таким образом, получаем два простейших тождества для арксинуса.

  1. для любого m:
  2. для любого α: .

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 4-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, с. 310-314.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege. sdamgia.ru/

Теоретический материал для самостоятельного изучения

  1. Так как является абсциссой точки М(α) координатной окружности, то для решения уравнения нужно сначала найти на этой окружности точки, имеющие абсциссу m, то есть точки пересечения окружности с прямой x=m. Если , то таких точек нет, если , то такая точка одна, если , то таких точек две.

После отыскания этих точек нужно найти все такие числа α, которые соответствуют этим точкам. Множество таких чисел и будет решением уравнения .

Примеры и разбор решения заданий тренировочного модуля

Рассмотрим пример на вычисление арксинуса.

Пример.

Вычислить

Решение:

Так как и то

Ответ: .

Задание.

Вычислить .

Ответ: .

На рисунке показано, как связаны друг с другом числа m и

Из рисунка видно, что

Запишем теперь с помощью арксинуса решение уравнения

Одним из решений уравнения является число . Так как , то число также является решением данного уравнения.

Точка соответствует всем числам вида

Точка соответствует всем числам вида

Таким образом, решением уравнения sinα=m являются все числа вида

(*)

Пример.

Решим уравнение

Решение:

Так как , то по формуле (*) получаем:

.

Задание

Решите уравнение

Ответ: .

Рассмотрим решение более сложных уравнений с синусом.

  1. Рассмотрим решение уравнения .

Решение:

, поэтому

Отсюда , или

Тогда

Ответ: .

  1. Рассмотрим решение уравнения

Решение:

, поэтому .

Отсюда получаем:

Мы получили два квадратных уравнения с параметром k.

Запишем их решения.

Для того чтобы число х было действительным, дискриминант должен быть неотрицательным. То есть:

(1) и (2)

Неравенство (1) выполняется при , так как k – целое, то .

Неравенство (2) выполняется при , так как k – целое, то .

Таким образом, получаем, что при целых значениях исходное уравнение имеет две серии решений:

При уравнение имеет два решения:

Ответ: а) при ,

б) при ,

в) нет решений при .

  1. Рассмотрим решение уравнения

Решение:

Так как синусы равны, то их аргументы связаны соотношением:

Отсюда:

Первое уравнение имеет решение при или при .

Второе уравнение имеет решение при или при .

Таким образом:

Ответ:

а) при ,

б) , при при ,

в) нет решений при .

  1. Рассмотрим решение уравнения

Решение:

Уравнение равносильно совокупности уравнений:

или:

Решение первого уравнения: .

Решение второго уравнения: .

Ответ:

  1. Рассмотрим решение уравнения

Решение:

Выразим синус:

Имеем две серии решений:

.

Изобразим эти множества на тригонометрической окружности:

Можно записать эти две серии в виде одного равенства:

.

Ответ: .

Заметим, что для краткости решение тригонометрического уравнения sin x=m можно записать в виде:

Пример 1.

Рассмотрим решение уравнения .

Прямая пересекает тригонометрическую окружность в двух точках:

M(π/3) и N(2π/3).

Точка M(π/3) соответствует всем числа вида .

Точка N(2π/3) соответствует всем числа вида .

Таким образом, решение уравнения можно записать так:

.

Ответ: .

Пример 2.

Рассмотрим решение уравнения .

Прямая y=1 имеет с тригонометрической окружностью одну общую точку: .

Этой точке соответствуют все числа вида . Поэтому решение уравнения имеет вид .

Ответ: .

Пример 3.

Рассмотрим решение уравнения .

Прямая y=0 имеет с тригонометрической окружностью две общие точки: С() и К(π).

Поэтому решение уравнения можно записать так: .

Ответ: .

Задание.

Решите уравнение .

Ответ: .

2. Мы можем записать решение уравнение для любых табличных значений m. В тех случаях, когда мы не знаем значения аргумента, соответствующее значению m, чтобы уметь решать уравнение для произвольных значений m, введем понятие арксинуса.

Уравнение sinx=a

Напомним,
что уравнение, которое содержит переменную под знаком тригонометрических
функций, называется тригонометрическим уравнением. Уравнения вида
, ,  и , где  –
переменная, а число , называются простейшими
тригонометрическими уравнениями. На этом уроке мы с вами подробно
рассмотрим решение уравнений вида .

Вы
уже знаете, что синусом угла  называется ордината
точки , полученной
поворотом точки  вокруг начала
координат на угол .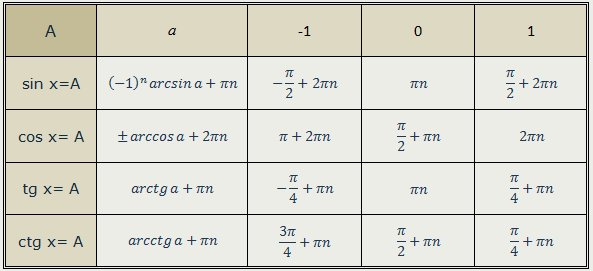 При этом не
забудем отметить, что так как координаты  и  точек единичной
окружности удовлетворяют неравенствам  и , то для  справедливо
неравенство . Из этого
следует, что уравнение  имеет корни
только при .

Так
как же решают такие уравнения? Давайте рассмотрим два уравнения:  и .

Чтобы
найти х в первом уравнении, нам нужно ответить на вопрос, чему равен
синус точки . Для этого нам
достаточно вспомнить таблицу значений синуса.

Тогда
. Давайте покажем
это на единичной окружности. Отметим точку . У этой точки,
как и у любой другой, есть свои координаты. Если мы опустим перпендикуляр из
точки  на ось ординат,
то попадём в .

А
теперь вернёмся ко второму уравнению . Чтобы найти х
в этом уравнении, нам нужно ответить на вопрос, синус каких точек равен .

Давайте
ненадолго отвлечёмся от тригонометрии. Начертим координатную плоскость. А
теперь найдём все те точки, у которых ордината равна . Несложно
догадаться, что таких точек будет бесконечное множество и все они будут лежать
на горизонтальной прямой, проходящей через точки с ординатой, равной .

А
теперь вернёмся к тригонометрии. Нас будут интересовать все точки, которые
лежат на единичной окружности и пересекаются горизонтальной прямой, проходящей
через точки, имеющие ординату, равную . Заметим, что
наша прямая пересекает единичную окружность в двух точках –  и . Исходя из
таблицы значений синуса, точка  получается из
начальной точки  поворотом на угол
, а точка  – поворотом на
угол . Тогда решением нашего
уравнения будут два корня  и . Но ведь в эти точки
мы можем попасть не по одному разу. Если мы сделаем полный оборот по единичной
окружности, то снова попадём в эти точки. Сделав ещё полный оборот, снова
попадём в эти точки и так далее. Тогда окончательным решением нашего уравнения
будет серия корней:

Второй корень мы можем переписать как . Как правило, эти
два корня совмещают и записывают как .

Заметим,
что если , то из последней
формулы получаем: , а если , то из последней
формулы получаем: .

Вообще,
при решении уравнений вида  возможны четыре
случая.

Первый
случай: . Раскрывая
модуль, имеем . В этом случае на
единичной окружности будут располагаться две точки –  и , ординаты которых
равны а. Эти точки получаются путём поворота начальной точки на угол  и  соответственно.
Тогда решения уравнения  можно записать в
виде: , и . Заметим, что эти
точки симметричны относительно оси ординат. Следовательно, . Чаще всего эти
серии решений объединяют в одну формулу: .

Например,
решим следующие уравнения  и . Ординату, равную
, имеют две точки
единичной окружности. Так как , то угол , а тогда угол . Следовательно,
все корни уравнения  можно найти по
формуле . При чётном n
получим первую серию решений, при нечётном – вторую.

Перейдём
ко второму уравнению . Ординату, равную
, имеют две точки
единичной окружности. Так как , то угол , а тогда угол . Следовательно,
все решения уравнения  можно найти по
формуле .

Обратите
внимание, каждое из уравнений  и  имеет бесконечное
множество корней. Однако на отрезке  каждое из этих
уравнений имеет только один корень. Так, , – это корень
уравнения , а , – это корень
уравнения . Число  называют
арксинусом числа . Записывают так: . Число  называют
арксинусом числа . Записывают так: .

Кстати,
«арксинус» в переводе с латинского означает «дуга» и «синус». Это обратная
функция.

Вообще,
уравнение , где , на отрезке  имеет только один
корень. Если , то этот корень
заключён в промежутке ;

если
же , то корень
располагается в промежутке .

Этот
корень называют арксинусом числа а и обозначают так .

Запомните! Арксинусом
числа а, , называется такое
число , синус которого
равен а.

, если  и

Например,
, так как , . , так как , .

Возвращаясь
к нашему уравнению , где , можно
утверждать, что все корни уравнения можно найти по формуле: .

Запомните!
Для любого  справедлива
формула . Эта формула
позволяет находить значения арксинусов отрицательных чисел через значения
арксинусов положительных чисел.

Например,
.

Второй
случай: . Раскрывая модуль,
имеем  и . Поскольку для  справедливо
неравенство , то понятно, что
в этом случае уравнение  не будет иметь
корней.

Например,
уравнения  и  не имеют корней.

Третий
случай (частный): . В этом случае
есть две точки тригонометрической окружности, которые имеют ординату, равную 0.
Точка  представляет
все числа вида , а точка  – все числа вида . Заметим, что две
записанные серии решений уравнения  можно выразить
одной формулой: . Так как при  получится первая
серия решений , а при  – .

И
последний, четвёртый случай (тоже частный): . Раскрывая
модуль, имеем , и . В этом случае горизонтальные
прямые, проходящие через точки, имеющие ординаты, равные –1 и 1, будут касаться
единичной окружности в точках с координатами (0;1) и (0;–1). Эти точки
получаются путём поворота начальной точки на угол  и . Тогда уравнение  имеет серию
решений: . А решением
уравнения  будет следующее: .

А
теперь давайте приступим к практической части нашего урока.

Задание. Решите
уравнение .

Решение. Для
начала преобразуем уравнение. Единицу перенесём в правую часть, затем разделим
обе части равенства на –2. Получим . По формуле
нахождения корней уравнения , имеем . . Отсюда . Перенесём
4 в правую часть равенства. Затем разделим обе части равенства на 3. Отсюда х
равен: .

Формулы для решения простейших тригонометрических уравнений

Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше. n arcsin a + \pi n, n \in Z`

Таблица арксинусов

2. Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| \leq 1` имеет бесконечное множество решений.

Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Таблица арккосинусов

Частные случаи для синуса и косинуса в графиках.

3. Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + \pi n, n \in Z`

Таблица арктангенсов

4. Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + \pi n, n \in Z`

Таблица арккотангенсов

Формулы корней тригонометрических уравнений в таблице

Для синуса:Для косинуса:Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

  • с помощью тригонометрических формул преобразовать его до простейшего;
  • решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы. 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.

    1. `sin x=0`, `x=\pi n`, `n \in Z`
    2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

    Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.

    Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

    Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!

    Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.

    Материалы по теме:

    Поделиться с друзьями:

    Загрузка. ..

    § 19. РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

    РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

    Простейшими тригонометрическими уравнениями называют уравнения

    cos x = a, sin x = a, tg x = a, ctg x = a.

    Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

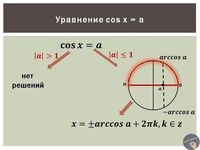
    19.1. Уравнение cos x = a

    Таблица 1

    Объяснение и обоснование

    1. Корни уравнения cos x = a.

    При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a < -1 не пересекает график функции y = cos x).

    Пусть | a | ≤ 1. Тогда прямая y = a пересекает график функции y = cos x (рис. из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).

    Косинус – четная функция, поэтому на промежутке [-π; 0] уравнение cos x = a также имеет только один корень – число, противоположное x1, то есть                x2 = — arccos a.

    Таким образом, на промежутке [-π; π] (длиной 2π) уравнение cos x = a при |a| ≤ 1 имеет только корни x = ±arccos a.

    Функция y = cos x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных на 2πn (n ∈  Z). Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1:

    x = ±arccos a + 2πn, n ∈  Z         (1)

    1. Частые случаи решения уравнения cos x = a.

    Полезно помнить специальные записи корней уравнения cos x = a при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность.

    Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка А или точка В (рис. из пункта 2 табл. 1). Тогда

    Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка С, следовательно, x = 2πk, k ∈  Z.

    Также cos x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, x = п + 2πk, k ∈  Z

    Примеры решения задач

    19. 2. Уравнение sin x = a

    Таблица 2

    Объяснение и обоснование

    1.Корни уравнения sin x = a.

    При |a| > 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a < -1 не пересекает график функции y = sin x).

    Рисунок 1

    Пусть |a| ≤ 1. Тогда прямая y = a пересекает график функции y = sin x (рис. 1). На промежутке  функция y = sin x возрастает от -1 до 1. Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень, который по определению арксинуса равен: x1 = arcsin a (и для этого корня sin x = a).

    На промежутке  функция y = sin x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень x2 = π — arcsin a (рис. 1). Для проверки правильности записи значения второго корня x2 заметим, что x2 = π — x1, тогда sin x2 = sin (π- x1) = sin x1 = a. То есть x2 – корень уравнения sin x = a.

    Таким образом на промежутке   (длиной 2π) уравнение sin x = a при |a| ≤ 1 имеет только корни x1 = arcsin a, x2 = π — arcsin a.

    Функция y = sin x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных 2πk (k ∈ Z). Получаем следующие формулы корней уравнения sin x = a при |a| ≤ 1:

    x=arcsin a + 2πk, k ∈  Z.            (1)

    x= π — arcsin a + 2πk, k ∈  Z.      (2)

    Все значения корней уравнения sin x = a при |a| ≤ 1, которые дают формулы (1) и (2), можно записать с помощью одной формулы

    x=(-1)n arcsin a + 2πn, n ∈  Z      (3)

    Действительно, из формулы (3) при четном n = 2k получаем x = arcsin a + 2πk – формулу (1), а при нечетном n = 2k +1 – формулу x= — arcsin a + π(2k+1)= π — arcsin a + 2πk, то есть формулу (2).

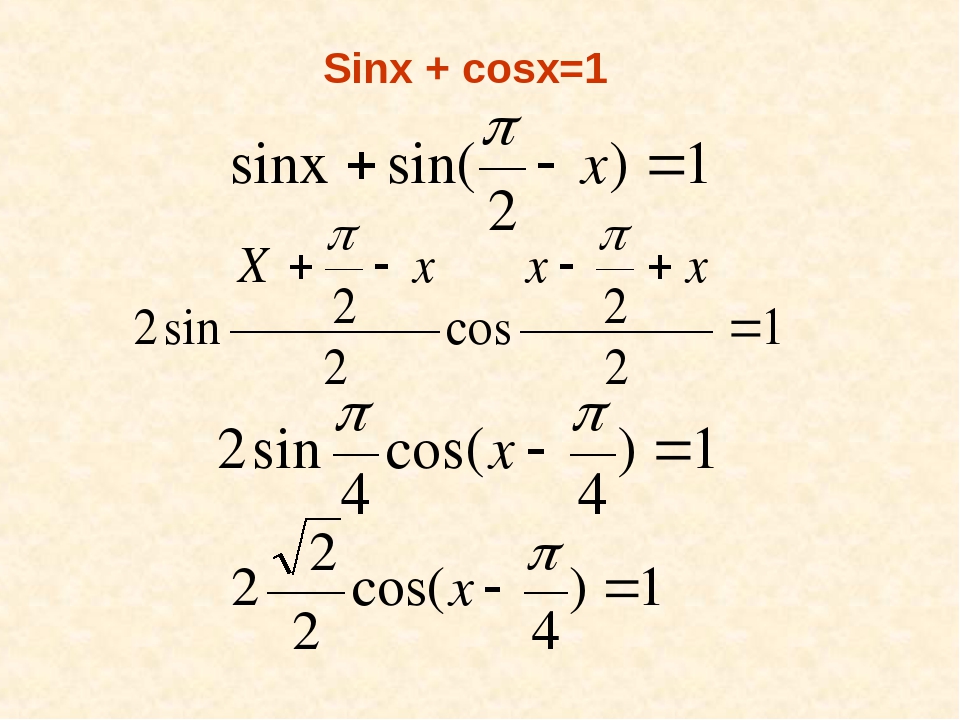
    2.Частые случаи решения уравнения sin x = a.

    Рисунок 2

    Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

    Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

    Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

    Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

    Примеры решения задач

    Замечание. Ответ к задаче 1 часто записывают в виде:

     

    19.3. Уравнения tg x = a и ctg x = a

    Объяснение и обоснование

    1.Корни уравнений tg x = a и ctg x = a

    Рассмотрим уравнение tg x = a. На промежутке  функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.

    Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈  Z). Получаем следующую формулу корней уравнения tg x = a:

    При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈  Z).

    Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). 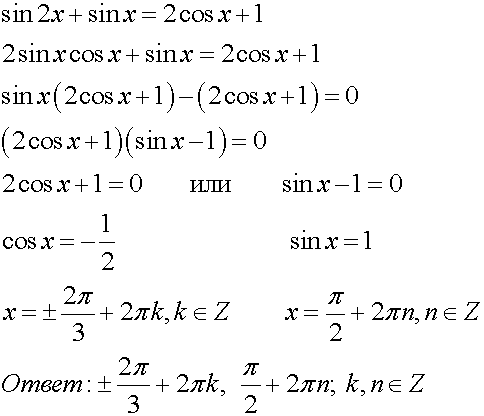Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.

    Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈  Z). Получаем следующую формулу корней уравнения ctg x = a:

    При a = 0

     

    таким образом, уравнение ctg x = 0 имеет корни

     

    Примеры решения задач

    Вопросы для контроля

    1. Какие уравнения называют простейшими тригонометрическими?

    2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?

    3. Выведите формулы решения простейших тригонометрических уравнений.

    4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

    Упражнения

    Решите уравнение (1-11)

    Найдите корни уравнения на заданном промежутке (12-13)

     

     

     

     

     

     

    Простейшие тригонометрические уравнения

    Простейшими тригонометрическими уравнениями называют уравнения

    Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a

    Уравнение cos (x) = a

    Объяснение и обоснование

     

    1. Корни уравнения cosx = а. При | a | > 1 уравнение не имеет корней, по­скольку | cosx | < 1 для любого x (прямая y = а при а > 1 или при а < -1 не пересекает график функцииy = cosx).

    Пусть | а | < 1. Тогда прямая у = а пересекает график функции

    у = cos х. 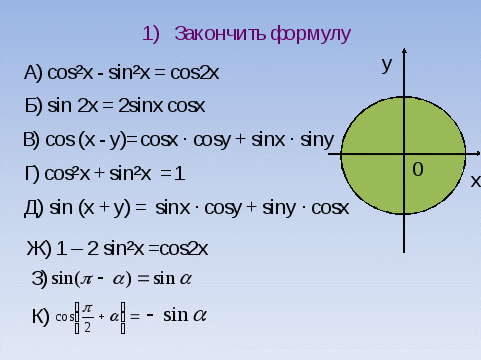На промежутке [0; п] функция y = cos x убы­вает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = а имеет на этом промежутке только один корень, который по опреде­лению арккосинуса равен: x1 = arccos а (и для этого корня cos x = а).

    Косинус — четная функция, поэтому на промежутке [-п; 0] уравнение cos x = а также имеет только один корень — число, противоположное x1, то есть

    x2 = -arccos а.

    Таким образом, на промежутке [-п; п] (длиной 2п) уравнение cos x = а при | а | < 1 имеет только корни x = ±arccos а.

    Функция y = cos x периодическая с периодом 2п, поэтому все остальные корни отличаются от найденных на 2пп (n € Z). Получаем следующую фор­мулу корней уравнения cos x = а при

    | а | < 1:

    x = ±arccos а + 2пп, n £ Z.

    1. Частные случаи решения уравнения cosx = а.

    Полезно помнить специальные записи корней уравнения cos x = а при

    а = 0, а = -1, а = 1, которые можно легко получить, используя как ори­ентир единичную окружность.

    Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответ­ствующей точкой единичной окружности является точка A или точка B.

    Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно,

    x = 2πп, k € Z.

    Также cos х = —1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, х = п + 2пn,

    k € Z.

    Примеры

    Уравнение sin (x) = a

    Объяснение и обоснование

    1. Корни уравнения sinx = а. При | а | > 1 уравнение не имеет корней, по­скольку | sinx | < 1 для любого x (прямая y = а на рисунке при а > 1 или при а < -1 не пересекает график функции y = sinx).

    Решение тригонометрических уравнений | Математика, которая мне нравится

    Простейшие тригонометрические уравнения

    Уравнение при решений не имеет,

    при имеет решения ,

    при  имеет решения ,

    при имеет решения ,

    при всех остальных имеет решения .

    Уравнение при решений не имеет,

    при имеет решения ,

    при  имеет решения >,

    при имеет решения ,

    при всех остальных имеет решения .

    Уравнение имеет решения .

    Уравнение имеет решения .

    Приемы решения тригонометрических уравнений

    1. Сведение к одной функции

    1. заменяем на , — на .

    Пример 1.

       

       

    Пример 2.

       

    2. заменяем на , — на , — на .

    Пример 1.

       

    1) 2) ,
    В первом случае решений нет, во втором .

    Пример 2.

       

       

    Пример 3.

       

    3. Однородные уравнения относительно .

       

    Если , то деля обе части уравнения на или на , получаем равносильные уравнения. Действительно, пусть — корень уравнения и . Подставляя в уравнение, получаем, что и , а это невозможно.

    Пример.

       

    4. Уравнения, приводящиеся к однородным

    а) Домножение на

    Пример.

       

    б) Переход к половинному аргументу

    Пример.

       

       

    5. Использование формулы

    Пример.

       

    6. Замена .
    Пример.

       

       

    Разложение на множители

    1. Формулы преобразования суммы в произведение

    2. Формулы

       

    Пример 1.

       

    Ответ. .

    Пример 2.

       

       

    ,  решений нет,

       

    Ответ. , .

    Понижение степени

    Использование формул

       

    Сравнение левой и правой части

    Пример 1.

       

    что невозможно.

    Ответ. .
    Пример 2.

       

    Ответ. .
    Пример 3.

       

    Пусть

       

    Подставляем во второе уравнение:

       

    Ответ. .

    Пример 4.

       

    или

       

    Если , то . Если , то .

       

    Ответ. .

    Тригонометрические тождества и формулы

    Ниже приведены некоторые из наиболее важных определений, тождеств и формул в тригонометрии.

    1. Тригонометрические функции острых углов

      грех X = opp / hyp = a / c, csc X = hyp / opp = c / a

      загар X = opp / adj = a / b, детская кроватка X = adj / opp = b / a

      cos X = adj / hyp = b / c, сек X = hyp / adj = c / b,

    2. Тригонометрические функции произвольных углов

      грех X = b / r, csc X = r / b

      tan X = b / a, детская кроватка X = a / b

      cos X = a / r, сек X = r / a

    3. Особые треугольники

      С помощью специальных треугольников можно найти тригонометрические функции специальных углов: 30, 45 и 60 градусов.

    4. Синус и косинус в треугольниках

      В любом треугольнике мы имеем:

      1 — Синус-закон

      грех A / a = грех B / b = грех C / c

      2 — Законы косинусов

      a 2 = b 2 + c 2 — 2 b c cos A

      b 2 = a 2 + c 2 — 2 a c cos B

      c 2 = a 2 + b 2 — 2 a b cos C

    5. Отношения между тригонометрическими функциями

      cscX = 1 / sinX

      sinX = 1 / cscX

      сек X = 1 / cos X

      cosX = 1 / секX

      tanX = 1 / cotX

      cotX = 1 / tanX

      tanX = sinX / cosX

      cotX = cosX / sinX

    6. Пифагорейские тождества

      sin 2 X + cos 2 X = 1

      1 + загар 2 X = сек 2 X

      1 + детская кроватка 2 X = csc 2 X

    7. Идентификаторы с отрицательным углом

      sin (-X) = — sinX, нечетная функция

      csc (-X) = — cscX, нечетная функция

      cos (-X) = cosX, четная функция

      сек (-X) = секX, четная функция

      tan (-X) = — tanX, нечетная функция

      cot (-X) = — cotX, нечетная функция

    8. Cofunctions Identities

      sin (π / 2 — X) = cosX

      cos (π / 2 — X) = sinX

      загар (π / 2 — X) = cotX

      детская кроватка (π / 2 — X) = tanX

      сек (π / 2 — X) = cscX

      csc (π / 2 — X) = secX

    9. Формулы сложения

      cos (X + Y) = cosX cosy — sinX sinY

      cos (X — Y) = cosX cosy + sinX sinY

      sin (X + Y) = sinX cosy + cosX sinY

      sin (X — Y) = sinX уютно — cosX sinY

      tan (X + Y) = [tanX + tanY] / [1 — tanX tanY]

      tan (X — Y) = [tanX — tanY] / [1 + tanX tanY]

      детская кроватка (X + Y) = [cotX cotY — 1] / [cotX + cotY]

      детская кроватка (X — Y) = [cotX cotY + 1] / [cotY — cotX]

    10. Формулы суммы к произведению

      cosX + cosy = 2cos [(X + Y) / 2] cos [(X — Y) / 2]

      sinX + sinY = 2sin [(X + Y) / 2] cos [(X — Y) / 2]

    11. Отличие от формул продукта

      cosX — cosy = — 2sin [(X + Y) / 2] sin [(X — Y) / 2]

      sinX — sinY = 2cos [(X + Y) / 2] sin [(X — Y) / 2]

    12. Формулы произведения суммы / разности

      cosX cosy = (1/2) [cos (X — Y) + cos (X + Y)]

      sinX cosy = (1/2) [sin (X + Y) + sin (X — Y)]

      cosX sinY = (1/2) [sin (X + Y) — sin [(X — Y)]

      sinX sinY = (1/2) [cos (X — Y) — cos (X + Y)]

    13. Формула разности квадратов

      sin 2 X — грех 2 Y = sin (X + Y) sin (X — Y)

      cos 2 X — cos 2 Y = — sin (X + Y) sin (X — Y)

      cos 2 X — sin 2 Y = cos (X + Y) cos (X — Y)

    14. Формулы двойных углов

      грех (2X) = 2 sinX cosX

      cos (2X) = 1-2sin 2 X = 2cos 2 X — 1

      загар (2X) = 2tanX / [1 — загар 2 X]

    15. Формулы множественных углов

      sin (3X) = 3sinX — 4sin 3 X

      cos (3X) = 4cos 3 X — 3cosX

      sin (4X) = 4sinXcosX — 8sin 3 XcosX

      cos (4X) = 8cos 4 X — 8cos 2 X + 1

    16. Формулы полууглов

      sin (X / 2) = + или — √ ((1 — cosX) / 2)

      cos (X / 2) = + или — √ ((1 + cosX) / 2)

      tan (X / 2) = + или — √ ((1 — cosX) / (1 + cosX))

      = sinX / (1 + cosX) = (1 — cosX) / sinX

    17. Формулы снижения мощности

      sin 2 X = 1/2 — (1/2) cos (2X))

      cos 2 X = 1/2 + (1/2) cos (2X))

      sin 3 X = (3/4) sinX — (1/4) sin (3X)

      cos 3 X = (3/4) cosX + (1/4) cos (3X)

      sin 4 X = (3/8) — (1/2) cos (2X) + (1/8) cos (4X)

      cos 4 X = (3/8) + (1/2) cos (2X) + (1/8) cos (4X)

      sin 5 X = (5/8) sinX — (5/16) sin (3X) + (1/16) sin (5X)

      cos 5 X = (5/8) cosX + (5/16) cos (3X) + (1/16) cos (5X)

      sin 6 X = 5/16 — (15/32) cos (2X) + (6/32) cos (4X) — (1/32) cos (6X)

      cos 6 X = 5/16 + (15/32) cos (2X) + (6/32) cos (4X) + (1/32) cos (6X)

    18. Периодичность тригонометрических функций

      sin (X + 2π) = sin X, период 2π

      cos (X + 2π) = cos X, период 2π

      сек (X + 2π) = сек X, период 2π

      csc (X + 2π) = csc X, период 2π

      tan (X + π) = tan X, период π

      детская кроватка (X + π) = детская кроватка X, период π

    19. Тригонометрические таблицы.
    20. Свойства шести тригонометрических функций. График, область, диапазон, асимптоты (если есть), симметрия, пересечения по осям x и y, а также точки максимума и минимума каждой из 6 тригонометрических функций.

    Дополнительные ссылки и ссылки по тригонометрии

    Тригонометрия.

    Решите задачи тригонометрии.

    Бесплатные вопросы по тригонометрии с ответами.
    пожаловаться на это объявление

    тригонометрических идентичностей | Purplemath

    Purplemath

    В математике «идентичность» — это всегда истинное уравнение.Они могут быть «тривиально» истинными, например « x = x », или полезными, например, « a 2 + b 2 = c 2 » теоремы Пифагора для прямоугольные треугольники. Существует множество тригонометрических отождествлений, но следующие из них вы, скорее всего, увидите и будете использовать.

    Базовый и пифагорейский, сумма углов и разность, двойной угол, полуугол, сумма, произведение

    MathHelp.com

    Нужен индивидуальный курс математики?
    K12 | Колледж | Подготовка к экзамену

    Основные и пифагорейские тождества

    Обратите внимание на то, что триггерное отношение «со- (чего-то)» всегда является обратной величиной некоторого «несоответствующего» отношения. Вы можете использовать этот факт, чтобы понять, что косеканс идет с синусом, а секанс — с косинусом.

    Следующие ниже тождества (в частности, первая из трех ниже) называются «пифагорейскими» идентичностями.

    sin 2 ( t ) + cos 2 ( t ) = 1

    желто-коричневый 2 ( т ) + 1 = сек 2 ( т )

    1 + детская кроватка 2 ( т ) = csc 2 ( т )

    Обратите внимание, что все три тождества включают в себя возведение в квадрат и число 1.Вы можете ясно увидеть отношение Пифагора-Тэома, если вы рассмотрите единичную окружность, где угол составляет t , «противоположная» сторона — sin ( t ) = y , «смежная» сторона — cos ( t ) = x , а гипотенуза равна 1.

    У нас есть дополнительные идентификаторы, связанные с функциональным статусом триггерных соотношений:

    sin ( –t ) = — sin ( t )

    cos ( –t ) = cos ( t )

    tan ( –t ) = — tan ( t )

    Обратите внимание, в частности, что синус и тангенс являются нечетными функциями, симметричными относительно начала координат, а косинус — четной функцией, симметричной относительно оси y . Тот факт, что вы можете вынести знак «минус» аргумента за пределы (для синуса и тангенса) или полностью исключить его (для косинуса), может быть полезным при работе со сложными выражениями.

    Тождества суммы углов и разности

    sin (α + β) = sin (α) cos (β) + cos (α) sin (β)

    sin (α — β) = sin (α) cos (β) — cos (α) sin (β)

    cos (α + β) = cos (α) cos (β) — sin (α) sin (β)

    cos (α — β) = cos (α) cos (β) + sin (α) sin (β)

    Кстати, в приведенных выше тождествах углы обозначаются греческими буквами.Буква типа «а» называется «альфа», что произносится как «аль-фу». Буква b-типа, «β», называется «бета», что произносится как «BAY-tuh».

    Двойные уголки

    sin (2 x ) = 2 sin ( x ) cos ( x )

    cos (2 x ) = cos 2 ( x ) — sin 2 ( x ) = 1-2 sin 2 ( x ) = 2 cos 2 ( x ) — 1

    Полуугловые идентичности

    Приведенные выше тождества можно переформулировать, возведя каждую сторону в квадрат и удвоив все угловые меры. Результаты следующие:

    sin 2 ( x ) = ½ [1 — cos (2 x )]

    cos 2 ( x ) = ½ [1 + cos (2 x )]

    Партнер

    Сумма идентификаторов

    Обозначения продукта

    Вы будете использовать все эти тождества или почти все эти тождества для доказательства других триггерных тождеств и для решения тригонометрических уравнений.Однако, если вы собираетесь изучать исчисление, обратите особое внимание на пересчитанные тождества синуса и косинуса половинного угла, потому что вы будете использовать их в интегральном исчислении с лотом и .

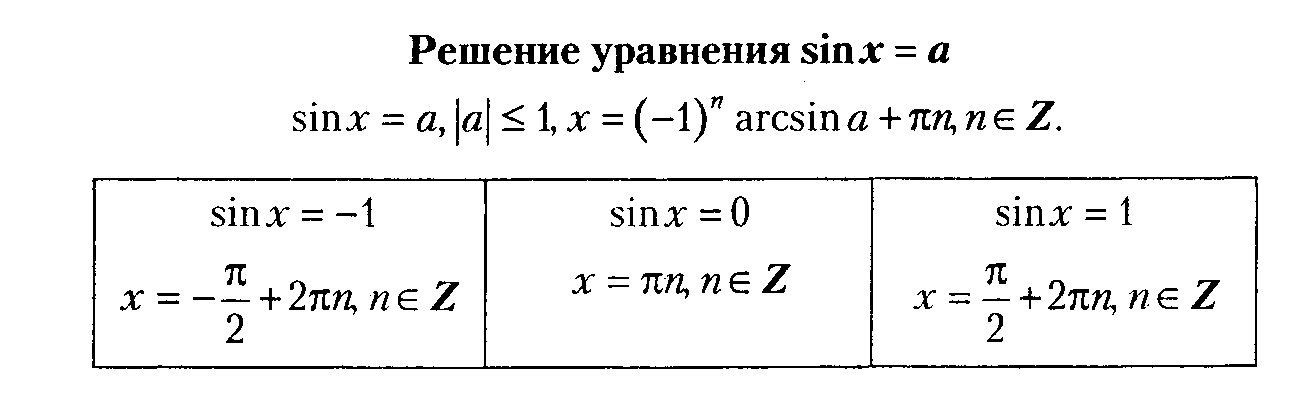
    URL: https://www.purplemath.com/modules/idents.htm

    Основные тригонометрические уравнения

    Углы (аргументы функций): \ (x, \) \ ({x_1}, \) \ ({x_2} \)
    Набор целых чисел: \ (\ mathbb {Z} \)
    Целое число: \ (n \)
    Вещественное число: \ (a \)

    Тригонометрические функции: \ (\ sin x, \) \ (\ cos x, \) \ (\ tan x, \) \ (\ cot x \)
    Обратные тригонометрические функции: \ (\ arcsin a, \) \ (\ arccos a, \) \ (\ arctan a, \) \ (\ text {arccot} a \)

    1. Уравнение, включающее тригонометрические функции неизвестного угла, называется тригонометрическим уравнением.n} \ arcsin a + \ pi n, \) \ (n \ in \ mathbb {Z}. \)
      Эта формула содержит две ветви решений:
      \ ({x_1} = \ arcsin a + 2 \ pi n \ ), \ ({X_2} = \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \).
    2. В простом случае \ (\ sin x = 1 \) решение имеет вид
      \ (x = \ pi / 2 + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \).
    3. Аналогично, решение уравнения \ (\ sin x = -1 \) дается выражением
      \ (x = — \ pi / 2 + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \ ).
    4. Случай \ (\ sin x = 0 \) (нули синуса)
      \ (x = \ pi n, \) \ (n \ in \ mathbb {Z} \).

      5. Уравнение \ (\ cos x = a \)

    5. Если \ (\ left | a \ right | \ gt 1, \), уравнение \ (\ cos x = a \) не имеет решений.
    6. Если \ (\ left | a \ right | \ le 1, \), общее решение уравнения \ (\ cos x = a \) имеет вид
      \ (x = \ pm \ arccos a + 2 \ pi n , \) \ (n \ in \ mathbb {Z}. \)
      Эта формула включает два набора решений:
      \ ({x_1} = \ arccos a + 2 \ pi n \), \ ({x_2} = — \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \).
    7. В случае \ (\ cos x = 1 \) решение записывается как
      \ (x = 2 \ pi n, \) \ (n \ in \ mathbb {Z} \).
    8. Случай \ (\ cos x = -1 \)
      \ (x = \ pi + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \).
    9. Случай \ (\ cos x = 0 \) (нули косинуса)
      \ (x = \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \).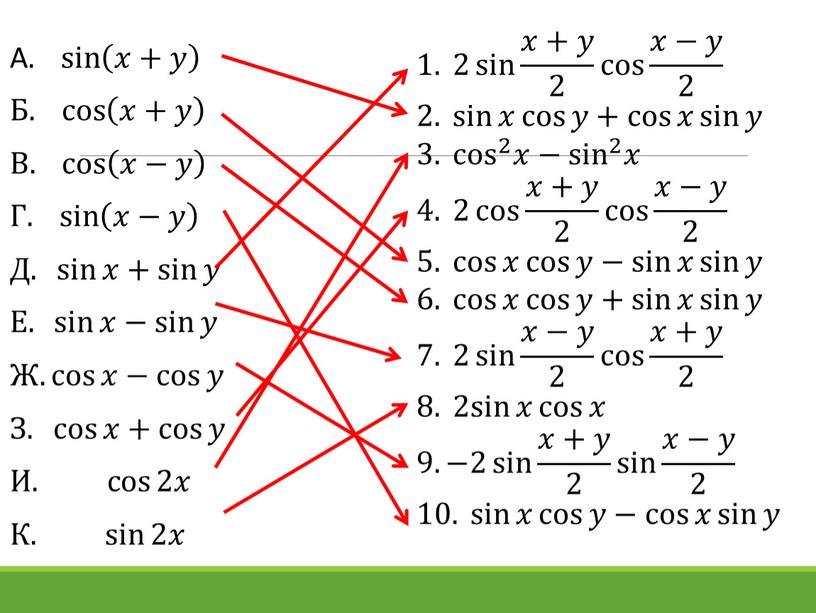

      10. Уравнение \ (\ tan x = a \)

    10. Для любого значения \ (a \) общее решение уравнения \ (\ tan x = a \) имеет вид
      \ (x = \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z}. \)
    11. Случай \ (\ tan x = 0 \) (нули касательной)
      \ (x = \ pi n, \) \ (n \ in \ mathbb {Z}. \)

      12. Уравнение \ (\ cot x = 0 \)

    12. Для любого значения \ (a \) общее решение тригонометрического уравнения \ (\ cot x = 0 \) записывается как
      \ (x = \ text {arccot} a + \ pi n, \) \ ( п \ в \ mathbb {Z}.\)
    13. Случай \ (\ cot x = 0 \) (нули котангенса)
      \ (x = \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z}. \)

    4. Формулы полуугловых

    М. Борн

    Мы разработаем формулы для синуса, косинуса и тангенса половинного угла.

    Формула полуугла — синус

    Начнем с формулы косинуса двойного угла, с которой мы познакомились в предыдущем разделе.

    cos 2 θ = 1− 2sin2 θ

    Сводка формул

    На этой странице мы выводим следующие формулы:

    `sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2`

    `cos (альфа / 2) = + — sqrt ((1 + cos alpha) / 2`

    `tan (альфа / 2) = (1-cos alpha) / (sin alpha`

    Теперь, если мы позволим

    `тета = альфа / 2`

    , затем 2 θ = α , и наша формула принимает следующий вид:

    `cos α = 1-2 \ sin ^ 2 (α / 2)`

    Теперь решаем

    `sin (альфа / 2)`

    (То есть мы получаем sin (alpha / 2) слева от уравнения, а все остальное справа):

    `2 \ sin ^ 2 (α / 2) = 1 — cos α`

    `sin ^ 2 (α / 2) = (1 — cos α) / 2`

    Решение дает нам следующий синус для тождества полуугла :

    `sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2`

    Знак (положительный или отрицательный) для `sin (alpha / 2)` зависит от квадранта
    в котором лежит `α / 2`. 2 (альфа / 2) = (1 + cos alpha) / 2`

    Решая относительно cos (α / 2), получаем:

    `cos (альфа / 2) = + — sqrt ((1 + cos alpha) / 2`

    Как и раньше, нужный нам знак зависит от квадранта.

    Если α / 2 находится в первом или четвертом квадранте , формула использует положительный случай:

    `cos (альфа / 2) = sqrt ((1 + cos alpha) / 2`

    Если α / 2 находится во втором или третьем квадранте , в формуле используется отрицательный регистр:

    `cos (альфа / 2) = — sqrt ((1 + cos alpha) / 2`

    Формула полуугла — касательная

    Тангенс половины угла определяется по формуле:

    `tan (alpha / 2) = (1-cos alpha) / (sin alpha)`

    Проба

    Сначала напомним `tan x = (sin x) / (cos x)`.2а)) `

    Затем находим квадратный корень:

    `= (1-cos a) / (sin a)`

    Конечно, нам нужно будет делать поправку на положительные и отрицательные знаки, в зависимости от рассматриваемого квадранта. @`, используя приведенное выше соотношение половинного угла синуса.(текст (o))) / 2) `

    `= + — sqrt (((1 + 0.866)) / 2)`

    `= 0,9659`

    Первый квадрант, значит, положительный.

    2. Найдите значение sin (alpha / 2), если cos alpha = 12/13, где 0 ° < α <90 °.

    Ответ

    `sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2)`

    `= sqrt ((1-12 / 13) / 2)`

    `= sqrt ((1/13) / 2)`

    `= sqrt (1/26)`

    `= 0,1961`

    Мы выбираем позитив, потому что находимся в первом квадранте.2сек \ theta`

    `= (1 + cos theta) sec \ theta`

    `= (1 + cos theta) 1 / (cos theta)`

    `= сек \ theta + 1`

    `=» RHS «`

    Дополнительные идентификаторы

    Фундаментальные (базовые) идентификаторы, рассмотренные в предыдущем разделе, включают только одну переменную. Следующие тождества, включающие две переменные, называются тождествами с тригонометрическим сложением .

    Эти четыре идентичности иногда называют идентичностью суммы для синуса , идентичностью разности для синуса , идентичностью суммы для косинуса и идентичностью разности для косинуса соответственно.Проверка этих четырех тождеств следует из основных тождеств и формулы расстояния между точками в прямоугольной системе координат. Пояснения к каждому шагу доказательства будут даны только для первых нескольких следующих примеров.

    Пример 1 : преобразовать sin 80 ° cos 130 ° + cos 80 ° sin 130 ° в тригонометрическую функцию в одной переменной (рисунок 1).

    Рисунок 1
    Рисунок для примера 1.

    Дополнительные тождества могут быть получены из тождеств суммы и разности для косинуса и синуса.

    Пример 2: Убедитесь, что cos (180 ° — x ) = — cos x

    Пример 3: Убедитесь, что cos (180 ° + x ) = — cos x

    Пример 4: Убедитесь, что cos (360 ° — x ) = cos x

    Предыдущие три примера проверяют три формулы, известные как формулы приведения для косинуса . Эти формулы сокращения полезны при переписывании косинусов углов, превышающих 90 °, как функций острых углов.

    Пример 5: Убедитесь, что sin (180 ° — x ) = sin x

    Пример 6: Убедитесь, что sin (180 ° + x ) = — sin x

    Пример 7: Убедитесь, что sin (360 ° — x ) = — sin x

    Предыдущие три примера проверяют три формулы, известные как формулы редукции для синуса .Эти формулы сокращения полезны при переписывании синусов углов, превышающих 90 °, в зависимости от острых углов.

    Напомним, что ниже приведены формулы сокращения (тождества) для синуса и косинуса. Они действительны как для градуса, так и для радиана.

    Пример 8: Убедитесь, что sin 2 x = 2 sin x cos x .

    Пример 9: Запишите cosβcos (α — β) — sinβsin (α — β) как функцию одной переменной.

    Пример 10: Запишите cos 303 ° в форме sinβ, где 0 <β <90 °.

    Пример 11: Запишите sin 234 ° в форме cos 0 <β <90 °.

    Пример 12: Найдите sin (α + β), если sin (α + β), если sin α =, а α и β — углы четвертого квадранта.

    Сначала найдите cos α и sin β. В четвертом квадранте синус отрицательный, а косинус положительный.

    Математическая сцена — Правила тригонометрии

    Математическая сцена — Правила тригонометрии — Урок 3

    2008 Rasmus ehf и Jhann sak

    Триггерные правила

    Урок
    3

    Уравнения
    типа a sin x + b cos x = c

    На схеме показан график f (x)
    = грех х + 2 соз х.

    Удивительно выглядит обыкновенная синусоида.
    который был переведен в одну сторону и с амплитудой больше, чем
    что основной волны. Мы видели раньше, что влияет на амплитуду
    и как амплитуду можно увеличить от значения 1 путем умножения на
    константа больше 1. (см. триггерные функции, урок 3). Мы также видели, что график основных
    Функция может быть переведена по горизонтали, добавив к углу константу.С участием
    это разум, мы должны иметь возможность переписать наше уравнение в форме m sin (x +
    v), что

    кв.м.
    грех (х + v) = грех х + 2 соз х

    Теперь посмотрим на график g (x) = sin x — 2.
    соз х.

    Это, очевидно, та же кривая, за исключением
    тот факт, что перевод теперь идет в направлении, противоположном предыдущему,
    сдвинут вправо на ту же длину, что и предыдущая кривая.
    Слева.В этом случае мы сможем составить эквивалентное уравнение.

    кв.м.
    грех (х — v) = грех х — 2 соз х

    Теперь перепишем эти выражения, используя
    формула сложения:

    грех
    (x + v) = sin x cos v + cos x sin v

    грех
    (x — v) = sin x cos v — cos x sin v

    Умножая на m, получаем:

    кв. м.
    грех (x + v) = m sin x cos v + m cos x sin v

    м грех
    (x — v) = m sin x cos v — m cos x sin v

    Сравните результат с исходным уравнением.

    кв.м.
    грех (х + v) = 1 грех х + 2 соз х

    = m cos v sin x + m sin v cos x

    кв.м.
    грех (х — v) = 1 грех х — 2 соз х

    = m cos v sin x — m sin v cos x

    Мы видим, что в обоих случаях должно быть
    правда:

    кв.м.
    cos v = 1

    м sin v = 2

    Если мы разделим нижнее уравнение на верхнее, мы
    получим следующее:

    загар
    v = 2 / 1

    Что дает угол v = tan −1 (2) ≈ 63.4 °.

    Если мы нарисуем прямоугольный треугольник с
    более короткие стороны 1 и 2, те же значения, что и в уравнении, тогда мы можем
    вычислите длину гипотенузы и увидите, что:

    cos v = 1 / и sin v = 2 /.

    Использование уравнений

    кв.м.
    cos v = 1

    м sin v = 2.

    Дает нам, что:

    м1 / = 1

    м =

    Другими словами, мы можем переписать уравнение как:

    Мы видим, что амплитуда волны в
    функции
    f (x) = sin x + 2 cos x и g (x) = sin x — 2 cos x равно.

    Обобщение и использование a и b для констант
    получаем следующее правило:

    Угол v можно найти как:

    tan v = b / a
    где a> 0, b> 0 и 0 °

    Пример 1

    Найдите амплитуду
    функция f (x) = 3 sin x + 4 cos x.

    Начнем с переписывания
    функция.

    Амплитуда 5.

    Пример 2

    График функции
    f (x) = 3 sin x + 4 cos x — преобразованная синусоида. Рассчитать по
    на сколько градусов и в каком направлении была перемещена волна.

    f (x) = 3 sin x + 4 cos x

    = 5 грехов (x + v)

    v = tan −1 ( 4 / 3 ) ≈ 53.1 °

    Волна переведена
    на 53,1 ° влево
    (f (x) ≈ 5 sin (x + 53,1 °).

    Пример 3

    Учитывая функцию f (x) = 5
    sin x + 12 cos x + 3. Найдите амплитуду, максимальную высоту и перевод
    волны.

    Записываем f (x).

    тангенс угла −1 (12/5) ≈ 67,4 °

    f (x) = 13 sin (x + 67,4 °)
    + 3

    Амплитуда 13, поэтому
    максимальная высота 13 + 3 = 16.Посмотрите на график.

    Пример 4

    Решите уравнение 3 sin x + 4 cos x = 5 на
    интервал
    0 ° x <360 °.

    3
    грех х + 4 соз х = 5

    = 5 грех (х + 53,1 °)

    грех (х + 53,1 °)
    = 5 / 5 = 1

    x + 53,1 ° = грех −1
    1 = 90 + к360 °

    х = -53.1
    + 90 + к360 °


     х = 36,9 °

    Это дает одно решение 36,9 ° в первом квадранте.

    Интересно посмотреть на график. Мы видим
    на требуемом интервале другого решения нет.


    Пример 5

    Найдите все решения
    уравнение sin x — 3 cos x = 1 .


    Мы видим, что tan v =
    3 и v = tan −1 (3) =
    / 3 (60 °).


    Так что грех (х —

    / 3 ) =

    (х —
    / 3 ) = sin −1 () =
    / 6 + к2


    / 6

    = 30

    х =

    / 3 +

    / 6 + к2


    знак равно

    / 2 + к2

    Или вторая возможность


    (х —

    / 3 ) =

    —

    / 6 + к2


    х =

    / 3 +

    —

    / 6 + к2

    х = 7 / 6 + к2

    7 / 6

    = 210

    Попробуйте пройти тест 1 по правилам тригонометрии.

    Не забудьте использовать контрольный список, чтобы отслеживать свою работу.

    Производная sin x — подход к исчислению

    12

    Производная sin x

    Производная cos x

    Производная от tan x

    Производная от детской кроватки x

    Производная sec x

    Производная от csc x

    ПРОИЗВОДНАЯ sin x — это cos x .Чтобы доказать это, мы будем использовать следующий идентификатор:

    sin A — sin B = 2 cos ½ ( A + B ) sin ½ ( A — B ).

    (Тема 20 Тригонометрии.)

    Проблема 1. Используйте это удостоверение, чтобы показать:

    sin ( x + h ) — sin x =

    Чтобы увидеть доказательство, наведите указатель мыши на цветную область.
    Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
    Сначала решите проблему сами!

    sin ( x + h ) — sin x = 2 cos ½ ( x + h + x ) sin ½ ( x + h — x )
    = 2 cos ½ (2 x + h ) sin ½ h
    =

    Однако, прежде чем перейти к производной sin x , мы должны доказать лемму; что является предварительной вспомогательной теоремой, необходимой для доказательства основной теоремы.Эта лемма требует следующего тождества:

    Задача 2. Докажите, что tan θ, разделенный на sin θ, равен.

    tan θ
    sin θ    		 = 1
    cos θ    		.

    (См. Раздел 20 Тригонометрии.)

    tan θ
    sin θ    		 = загар θ · 1
    sin θ    		 = sin θ
    cos θ    		 · 1
    sin θ    		 = 1
    cos θ

    Лемма, которую мы должны доказать, обсуждается в теме 14 Тригонометрии.(Взгляните на это.) Вот он:

    ЛЕММА.
    Когда θ измеряется в радианах, тогда

    Доказательство. Это невозможно доказать, применяя обычные теоремы о пределах (Урок 2). Мы должны перейти к геометрии и к значениям sin θ и радианной меры.

    Пусть O будет центром единичной окружности, то есть окружности радиуса 1;

    , и пусть θ будет центральным углом BOA первого квадранта, измеренным в радианах.

    Тогда, поскольку длина дуги с = r θ и r = 1, дуга BA равна θ. (Тема 14 Тригонометрии.)

    Угол натяжения B’OA равен углу θ, в результате дуга AB ‘ равна дуге BA ;

    начертите прямую BB ‘, разрезав AO на P ;

    и проведем прямые BC, B’C , касательные к окружности.

    Затем

    BB ‘ BAB’ BC + CB ‘.

    Теперь, в этом единичном круге, BP = PB ‘ = sin θ, (Тема 17 Тригонометрии),

    , так что BB ‘ = 2 sin θ;

    и BC = CB ‘ = tan θ. (Для tg θ = BC
    OB     		= BC
    1    		 = до н.э. .)

    Таким образом, продолжающееся неравенство, приведенное выше, становится:

    2 грех θ θ θ.

    При делении каждого члена на 2 sin θ:

    1 θ
    sin θ    		 1
    cos θ    		.

    (Задача 2.) И, взяв обратные, изменив тем самым смысл:

    1> sin θ
    θ    		> cos θ.

    (11-й урок алгебры, теорема 5.)

    При смене знаков снова меняется смысл:

    -1 sin θ
    θ    		 −cos θ,

    (Урок 11 алгебры, теорема 4),

    и если мы добавим 1 к каждому члену:

    0 1 — sin θ
    θ    		 1 — cos θ.

    Теперь, когда θ становится очень близким к 0 (θ 0), cos θ становится очень близким к 1; следовательно, 1 — cos θ становится очень близким к 0. Выражение в середине, будучи меньше , чем 1 — cos θ, становится еще ближе к 0 (а слева ограничено 0), поэтому выражение в середине точно приблизится к нулю. Это означает:

    Что мы и хотели доказать.

    Учащийся должен помнить, что для «приближения» переменной к нулю или любому пределу (определение 2.1), не означает, что переменная когда-либо равна этому пределу.

    Производная sin x

    d
    dx     		грех x = cos x

    Чтобы доказать это, мы применим определение производной (Урок 5). Сначала мы рассчитаем коэффициент разницы.

    =, проблема 1,
    =, при делении числителя
    и знаменателя на 2,
    =

    Теперь возьмем предел ч 0.Но предел продукта равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ / θ. Следовательно, согласно лемме при h 0 его предел равен 1. Следовательно,

    d
    dx     		грех x = cos x .

    Мы установили формулу.

    Производная cos x

    d
    dx     		cos x = −sin x

    Для этого мы будем использовать следующий идентификатор:

    cos x = sin ( π
    2    		 — х ).

    Функция любого угла равна совместной функции его дополнения.

    (Тема 3 тригонометрии).

    Следовательно, при применении цепного правила:

    Мы установили формулу.

    Производная от tan x

    Теперь загар x = sin x
    cos x     		. (Тема 20 тригонометрии.)

    Следовательно, согласно правилу частного:

    d
    dx     		коричневый x = d
    dx     		sin x
    cos x     		= cos x · cos x — sin x (−sin x )
    cos 2 x
    = cos 2 x + sin 2 x
    cos 2 x
    = 1
    cos 2 x
    = сек 2 x .

    Мы установили формулу.

    Задача 3. Производная от детской кроватки х . Доказательство:

    d
    dx     		детская кроватка x = −csc 2 x
    d
    dx     		детская кроватка x = d
    dx     		cos x
    sin x
    = sin x (−sin x ) — cos x · cos x
    sin 2 x
    = — (sin 2 x + cos 2 x )
    sin 2 x
    =– 1
    sin 2 x
    = −csc 2 x .

    Производная sec x

    d
    dx     		сек x = сек x желто-коричневый x
    Так как sec x = 1
    cos x     		= (cos x ) −1 ,

    , затем об использовании цепного правила и общего правила мощности:

    Мы установили формулу.

    Проблема 4. Производная от csc x . Доказательство:

    d
    dx     		csc x = −csc x детская кроватка x

    Пример. Вычислить производную sin ax 2 .

    Решение . При применении цепного правила,

    d
    dx     		грех топор 2 = cos ax 2 · d
    dx     		топор 2 = cos ax 2 · 2 топор = 2 ax cos ax 2 .

    Задача 5. Вычислить эти производные.

    а) d
    dx     		грех 5 x = 5 cos 5 x
    б) d
    dx     		½ sin 2 x = sin x cos x
    c) d
    dx     		2 cos 3 x = −6 sin 3 x
    г) d
    dx     		x cos x = cos x — x sin x
    e) d
    dx     		sin 2 x cos x = 2 cos 2 x cos x — sin 2 x sin x
    е) d
    dx     		желто-коричневый (3 x ) 2 = 18 x сек 2 (3 x ) 2
    г) d
    dx     		2 детская кроватка x
    2    		 = — csc 2 x
    2
    h) d
    dx     		сек 4 x = 4 секунды 4 x желто-коричневый 4 x
    i) d
    dx     		a csc bx = — ab csc bx детская кроватка bx
    j) =

    Проблема 6.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *