Урок алгебры по теме»Функция y=√x «

Донецкая общеобразовательная школа-интернат

І-ІІІ ступеней №3

Открытый урок по алгебре в 8 классе.

Тема:

«Функция у=, её свойства и график».

Разработала и провела

учитель I категории

Плахотник Н.С.

Цель урока:

1. Обучающая

— познакомить учащихся с функцией квадратного корня и ее графиком, научить использовать график функции квадратного корня при решении иррациональных уравнений.

2. Развивающие

— развивать логическое мышление, внимание, математическую речь учащихся, самосознание, самооценку

3. Воспитательная

— воспитывать личностные качества: ответственность, добросовестность, самостоятельность, умение слушать друг друга

Ход урока.

Добрый день, ребята! Я рада вас видеть.

«День прожит не зря, если вы узнали что-то новое» — так сказал ученый Дэвид Эддингс.

Вот и сегодня на уроке вы познакомитесь с новой функцией, функцией у=√х; научитесь изображать график этой функции, изучите её свойства. В конце урока мы проверим ваши знания с помощью теста.

Откройте тетради и запишите тему урока:

А сейчас повторим изученный вами ранее материал, который пригодиться вам при изучении новой темы

І. Актуализация опорных знаний.

1. Сформулируйте определение арифметического квадратного корня.

2. При каких значениях a выражение √a имеет смысл?
   √100, √81, √0, √-25

3. Имеет ли уравнение x² = a корни при а > 0, a = 0, a < 0, и если имеет, то сколько?

4. Решите уравнения: x² = 4, x² =5, x² =
   = 4, = 5, =

5. Сократите дробь: , , ,

6. Найдите площадь фигуры.

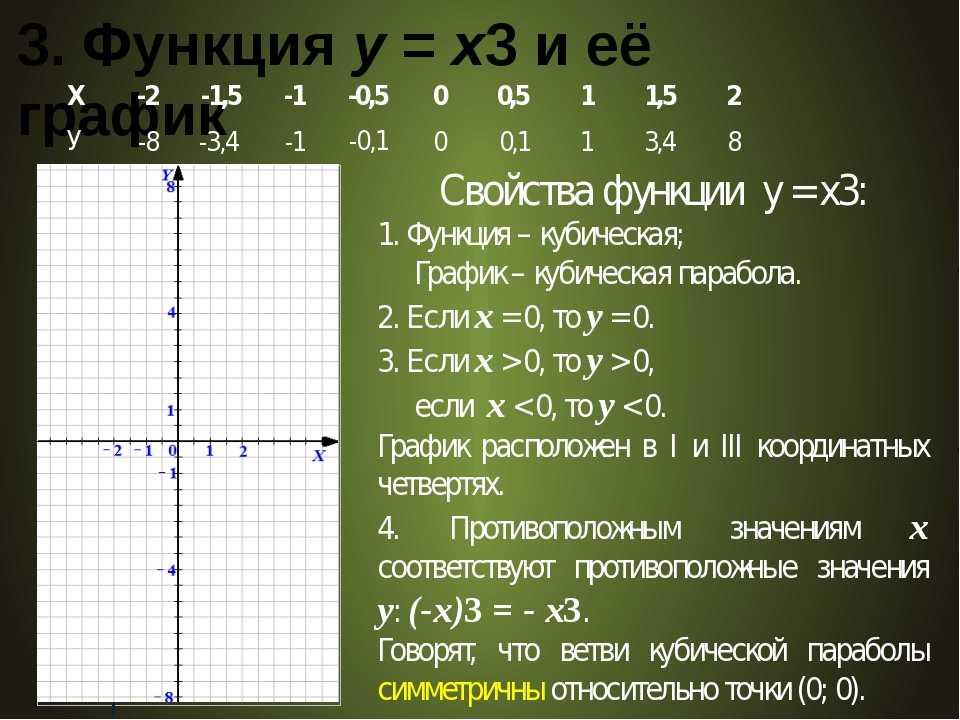
7. Задачи, приводящие к понятию функции y = √x.

а) сторона квадрата а = √S;

б) радиус круга r =

– Что особенного в этих заданиях? (Зависимость задана формулой y = с которой мы еще не встречались).

ІІ. Изложение новой темы.

Для построения графика функции у=√х, дадим как обычно, независимой переменной х несколько конкретных значений и вычислим соответствующие значения переменной у. Как вы думаете, могу ли я взять для вычислений, отрицательные значения х? (нет, так как квадратный корень из отрицательного числа не существует.)

Мы будем давать переменной х такие значения, для которых известно точное значение квадратного корня.

Итак: если х=0, то у= √0=0

Если х=1, то у= √1=1

Если х=4, то у= √4=2

Если х=6,25 то у= √6,25=2,5

Если х=9, то у= √9=3

Составим таблицу значений функций.

Запишите её.

Построим найденные точки на координатной плоскости. Они располагаются на некоторой линии, начертите её. Мы построили график функции у = √х.

1. Работа по графику функции:

2. -найдите значение у, если х = 1,5; 5,5; 7,2; 15.
   — найдите значение х, если у = 1,5; 1,8; 2,5.

3. Принадлежат ли графику функции точки: А(64; 8), B(100; 10), С(-81; 9), D(25; -5).

4. С помощью графика сравнить числа: √0,5 и √0,8; √4,2 и √5,7; √7 и √8.

Свойства функции:

1. область определения: луч [0;+∞) или х≥0;

2. если х=0, то у=0;

3. у>0 при х>0;

4. f(х) возрастает при х принадлежащем [0;+∞);

5. у наим.=0 (при х=0), у наиб. не существует.

ІІІ. Первичное закрепление. А сейчас вы будете работать с тестом. Задания выполняйте по порядку, выписывая те буквы, под которыми находятся правильные ответы. Если задания будут выполнены верно, то вы получите фамилию математика. (ДЕКАРТ).

Тест

1) Какой из графиков соответствует графику функции у=√х ? (чертежи подготовить учителю)

В) Г) Д) Б)

2) Какая из заданных точек принадлежит графику функции у=√х ?

К) (-1; 1) Л) (0; 5) М) (2; 4) Е) (4; 2).

3) Наименьшее значение функции у=√х равно :

А) 0,001 К) 0 В) 1 Г) не существует.

4) Область определения функции у= √х :

А) х ≥ 0 Н) х > 0 П) х < 0 О) х ≤ 0.

5) Корнем уравнения √х = 2-х является число, равное

П) 4; К) 0; С) 3; Р) 1.

6) Между какими целыми числами заключено число √27

В) 26 и 28; Т) 5 и 6; М) 13 и 14; К) 0 и 7

Что вы знаете об этом математике?

IV. Домашнее задание: §15 прочитать, выучить свойства функции,
решить № 355, 356, 363. Разгадать кроссворд.

V. Подведение итогов, выставление оценок.

VI. Рефлексия. Ребята, выберите смайлик, который больше всего подходит вашему настроению.

Функция х в степени n

Предмет. Математика. Класс. 10. Дата. 19,10,2016. № урока 21

Тема урока. Функция

Цели урока:

Цели урока:

• Развивающие: Развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы. Формировать умения чётко и ясно излагать свои мысли. Развивать пространственное воображение учащихся.

Оборудование, наглядность, раздаточный материал. Презентация PowerPoint. Набор графиков и формул функций для игры «Графическое лото»

Ход урока

1. Организационный момент

2. Целеполагание и мотивация

Сообщаем тему и цель урока: «Функция » и цель урока: обобщить и систематизировать знания и умения по теме «Степенные функции, их свойства и графики»

Задачи урока:

1.видеть график степенной функции по формуле;

2.определять по графику функцию;

3.уметь анализировать график;

4.уметь сравнивать числа, решать неравенства с помощью графиков и свойств степенной функции.

3. Актуализация опорных знаний (повторение):

1.Что называется функцией (Функция — это зависимость между двумя множествами, при котором каждому элементу из одного множества ставится в соответствии с некоторым правилом, законом единственный элемент из другого множества).

2.Что такое степенная функция? (Степенными функциями называются функции вида , где п – заданное рациональное число).

3.Что такое п ? (Это показатель степени)

4.А что зависит от показателя степени? (свойства и график функции)

5.Повторим свойства и графики функций

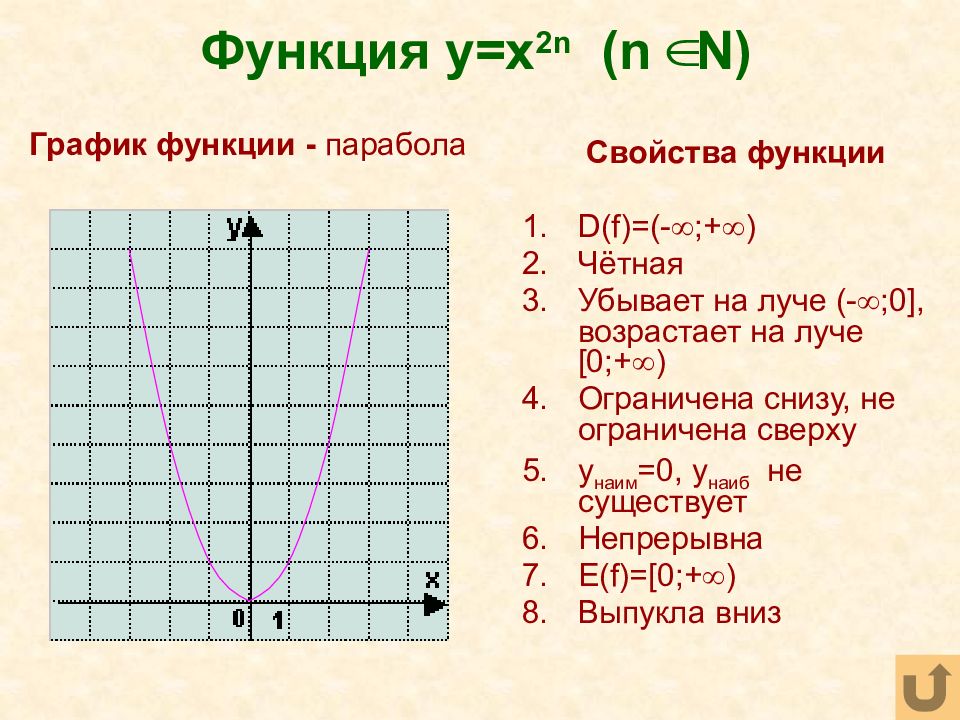
Рассмотрим степную функцию с четным натуральным показателем, графиком данной функции является?

Обратить внимание на то, что чем больше показатель степени, тем ближе оси параболы расположены к оси Оy.

Вспомним свойства этой функции

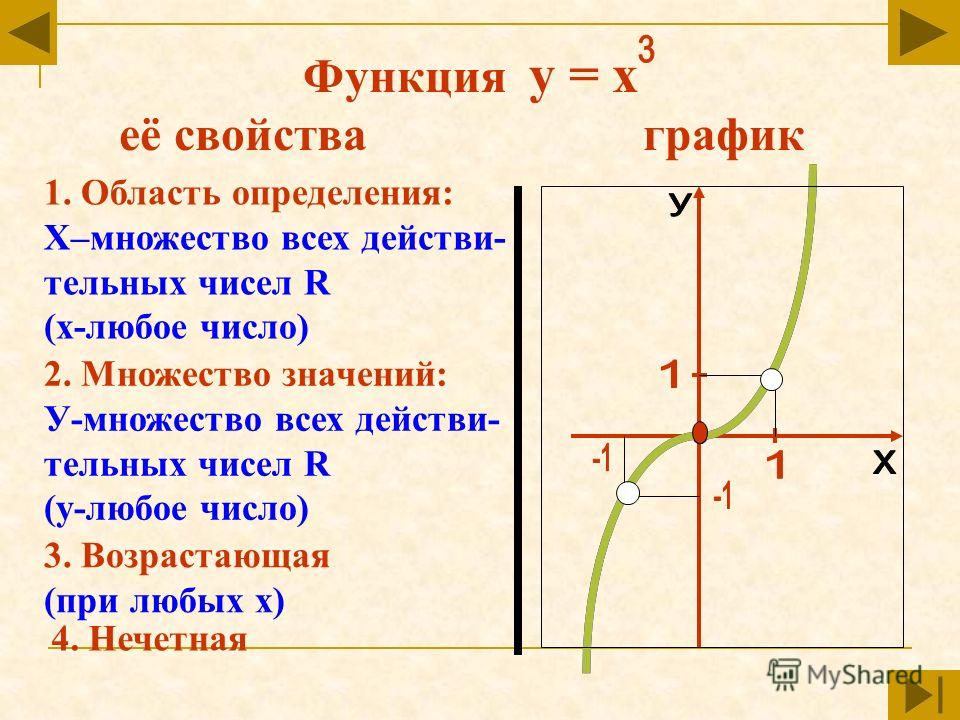
Рассмотрим степную функцию с нечетным натуральным показателем, графиком данной функции является? ( кубическая парабола)Вспомним свойства этой функции

Рассмотрим степную функцию с целым отрицательным нечётным показателем, графиком данной функции является? ( гипербола)

Вспомним свойства этой функции

Рассмотрим степную функцию с целым отрицательным чётным показателем, графиком данной функции является? ( гипербола)

Вспомним свойства этой функции

6.А вот если показатель степени равен 1, что это за функция и что является ее графиком? (линейная, а ее график прямая, которая является биссектрисой 1 и 3 координатной четверти)

7. А если показатель равен 0? (получаем функцию y = 1, где x не равен 0)

8.Через какую точку проходит график любой степенной функции? (через точку (1;1))

4. Применение знаний и умений

2.Напоминаю о том, что опираясь на свойства степенных функций можно решать уравнения и неравенства.

Т.е. мы с вами решаем неравенства, а при каких значениях x значения одной функции будут равны значениям другой (в точки где графики пересеклись) это уже уравнение

3.Напоминаю о простейших преобразованиях графиков функций (сдвиг по оси Ох и Оу).

4.Смещение по оси Оx.

На интерактивной доске обучающиеся сами преобразовывают график, а потом проверяем.

5.Смещение по оси Оy.

На интерактивной доске обучающиеся сами преобразовывают график, а потом проверяем.

6.Смещение по оси Оx и по оси Оy.

На интерактивной доске обучающиеся сами преобразовывают график, а потом проверяем.

7. 2)/730)))

или y равно 1 — (e power минус (x-square/730))

Как я представляю такие сложные функции в R? Я хочу нарисовать кривую (график), соединяющую все эти точки. Я также хочу отметить ось x от 0 до 370 с интервалом 10. Я знаю, как сохранить разрывы, но я не знаю, как я могу обозначить оси цифрами. Если где-то будет оказана помощь, пожалуйста, направьте меня по этой ссылке. Очень ценю.

r

Поделиться

Источник

Justin Carrey    

06 сентября 2012 в 02:06

1 ответ

• Функция (x, y), которая возвращает x количество@, разделенных y количеством пробелов

  В Python 3.3 Как я мог бы написать функцию, которая принимает два целочисленных параметра, x и y, и печатает строку из x чисел@, разделенных y числом пробелов? Например: функция (4,2) вернет строку @ @ @ @ а функция (2,4) вернет строку @ @ Спасибо за любую помощь и предложения!

• Интегральная функция (x,y) в python

  У меня есть такая функция, как: (np. 2/730),from=0,to=370,axes=FALSE)
  axis(side=2) ## add default lefthand axis
  axis(side=1,at=seq(0,370,by=10)) ## add custom bottom axis
  box(bty=»l») ## add a box
  

  Следует отметить, что R подавляет перекрывающиеся метки, поэтому, если у вас нет очень широкого графика, вы фактически не увидите каждую метку оси. Вы можете попробовать добавить cex.axis=0.5 (или даже меньше) к вашей оси side-1, Если хотите. Вы также можете проверить функцию staxlab из пакета plotrix или повернуть метки осей.
  (В вашем выражении было много лишних скобок; больше скобок на самом деле не повредит, но в долгосрочной перспективе вы можете сделать более чистый код (и потратить меньше времени на подсчет скобок), если вы изучите порядок операций.)

  Поделиться

  
  Ben Bolker    

  06 сентября 2012 в 02:25

  ---

  Похожие вопросы:

  Вычисление матрицы Якоби для x^2*y, 5*x+sin(y)

  Если у меня есть функция R^n —> R^m, как я могу создать ее якобиеву матрицу? Например: expression( x^2*y, 5*x+sin(y) ) # f : R^2 —> R^2 Я хотел бы иметь матрицу выражений типа:. ..

  Тот же масштаб по осям X и Y в Кривой R

  Когда я использую функцию R curve() , есть ли способ заставить ее использовать один и тот же масштаб на осях X и Y? Например, рассмотрим этот код R mean <- 5 variance <- 0.05 curve(exp((((x -…

  функция построения дендрограммы для координат x, y,z в R

  для следующего файла dental.csv item,x,y,z A1,66,89,122 A2,14,44,-9 A3,-17,199,11 A35,99,0,12 test,15,144,15 я написал следующий сценарий R mycoord<-read.csv(dental.csv) d<-dist(mycoord)…

  Функция (x, y), которая возвращает x количество@, разделенных y количеством пробелов

  В Python 3.3 Как я мог бы написать функцию, которая принимает два целочисленных параметра, x и y, и печатает строку из x чисел@, разделенных y числом пробелов? Например: функция (4,2) вернет строку…

  Интегральная функция (x,y) в python

  У меня есть такая функция, как: (np.sqrt((X)**2 + (Y)**2))/(np. sqrt((X)**2 + (Y)**2 + d**2)) Я написал программу для вычисления интеграла с помощью рядов: for i in range (num): # for X print i…

  r изображение (x, y, col=rgb,…) функция, дающая ошибку

  У меня есть следующий код в R: img = read.csv(file=img119.csv) img загружается вот так: X Y R G B 1 0 0 0.48046875 0.65234375 0.83593750 2 0 1 0.40234375 0.57031250 0.73828125 3 0 2 0.24609375…

  смоделируйте Y, если Y = log (X) и X ~ Gamma в R

  Этот вопрос очень тесно связан с постами здесь и здесь . Предположим, что случайная величина X = гамма(k, тета), и меня интересует моделирование Y, где Y = log (X). Не могли бы вы предложить…

  Эквивалентно выборке R(x, y, prob=) в Julia

  Julia-пользователи: существует ли эквивалент R sample(x,y,prob=) для выборки из заданного набора значений с взвешенными вероятностями? Функция rand() эквивалентна sample(x,y) , но, насколько мне…

  Создание рекурсивной функции для вычисления R = x-N * y с условиями

  Я хочу создать функцию для вычисления R = x-N * y, где x и y-поплавки, а N-наибольшее положительное целое число, так что x > N * y. 2x = 1$

  ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ

  sh(-x) = -sh x

  ch(-x) = ch x

  th(-x) = -th x

  csch(-x) = -csch x

  sech(-x) = sech x

  cth(-x) = -cth x

  ФОРМУЛЫ СЛОЖЕНИЯ

  sh (x ± y) = sh x ch y ± ch x sh y

  ch (x ± y) = ch x ch y ± sh x sh y

  th(x ± y) = (th x ± th y)/(1 ± th x.th y)

  cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)

  ФОРМУЛЫ ДВОЙНЫХ УГЛОВ

  sh 2x = 2 sh x ch x

  ch 2x = ch²x + sh²x = 2 ch²x — 1 = 1 + 2 sh²x

  th 2x = (2th x)/(1 + th²x)

  ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ

  $\text{sh} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{2}}$ [+ если x > 0, — если x

  $\text{ch} \frac{x}{2} = \sqrt{\frac{\text{ch} x + 1}{2}}$

  $\text{th} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{\text{ch} x + 1}}$ [+ если x > 0, — если x

  $= \frac{\text{sh} x}{\text{ch} x — 1} = \frac{\text{ch} x + 1}{\text{sh} x}$

  ФОРМУЛЫ КРАТНОСТИ УГЛОВ

  sh 3x = 3 sh x + 4 sh³ x

  ch 3x = 4 ch³ x — 3 ch x

  th 3x = (3 th x + th³ x)/(1 + 3 th²x)

  sh 4x = 8 sh³ x ch x + 4 sh x ch x

  ch 4x = 8 ch⁴ x — 8 ch² x + 1

  th 4x = (4 th x + 4 th³ x)/(1 + 6 th² x + th⁴ x)

  СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

  sh²x = ½ch 2x — ½

  ch² x = ½ch 2x + ½

  sh³x = ¼sh 3x — ¾sh x

  ch³ x = ¼ch 3x + ¾ch x

  sh⁴x = 3/8 — ½ch 2x + 1/8ch 4x

  ch⁴ x = 3/8 + ½ch 2x + 1/8ch 4x

  СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

  sh x + sh y = 2 sh ½(x + y) ch ½(x — y)

  sh x — sh y = 2 ch ½(x + y) sh ½(x — y)

  ch x + ch y = 2 ch ½(x + y) ch ½(x — y)

  ch x — ch y = 2 sh ½(x + y) sh ½(x — y)

  sh x sh y =    ½(ch (x + y) — ch (x — y))

  ch x ch y = ½(ch (x + y) + ch (x — y))

  sh x ch y = ½(sh (x + y) + sh (x — y))

  ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ

  В следующем мы принимаем, что x > 0. 2} + 1})$   $x \neq 0$

  ОТНОШЕНИЯ МЕЖДУ ОБРАТНЫМИ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ

  csch^-1 x = sh^-1 (1/x)

  sech^-1 x = ch^-1 (1/x)

  cth^-1 x = th^-1 (1/x)

  sh^-1(-x) = -sh^-1x

  th^-1(-x) = -th^-1x

  cth^-1 (-x) = -cth^-1x

  csch^-1 (-x) = -csch^-1x

  ГРАФИКИ ОБРАТНЫХ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

  y = sh^-1x
  y = ch^-1x

   

  y = th^-1x
  y = cth^-1x

   

  y = sech^-1x
  y = csch^-1x

  ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ и ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ

  sin(ix) = i sh x	cos(ix) = ch x	tan(ix) = i th x
  csc(ix) = -i csch x	sec(ix) = sech x	cot(ix) = -i cth x
  sh(ix) = i sin x	ch(ix) = cos x	th(ix) = i tan x
  csch(ix) = -i csc x	sech(ix) = sec x	cth(ix) = -i cot x

  ПЕРИОДИЧНОСТЬ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

  In the following k is any integer.

  sh (x + 2kπi) = sh x     csch (x + 2kπi) = csch x

  ch (x + 2kπi) = ch x     sech (x + 2kπi) = sech x

  th (x + kπi) = th x     cth (x + kπi) = cth x

  ОТНОШЕНИЕ МЕЖДУ ОБРАТНЫМИ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ОБРАТНЫМИ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ

  sin-1 (ix) = ish-1x	sh-1(ix) = i sin-1x
  cos-1 x = ±i ch-1 x	ch-1x = ±i cos-1x
  tan-1(ix) = i th-1x	th-1(ix) = i tan-1x
  cot-1(ix) = -i cth-1x	cth-1 (ix) = -i cot-1x
  sec-1 x = ±i sech-1x	sech-1 x = ±i sec-1x
  csc-1(ix) = -i csch-1x	csch-1(ix) = -i csc-1x

  Как найти икс нулевое

  В качестве «икс нулевое» обозначается координата вершины параболы по оси абсцисс. В этой точке функция принимает наибольшее или наименьшее значение, поэтому x0 − точка экстремума функции.

  Если имеется аналитическое задание функции, приведите ее к стандартному виду: A*x²+B*x+C=y(x), где A − старший коэффициент при x², B − средний коэффициент при x, C − свободный член. Обратите внимание, чтобы коэффициент при x² не равнялся нулю, иначе это будет уже не квадратичная функция.

  Координата вершины параболы x0 по оси абсцисс находится по формуле: x0=-B/2A. В случае приведенного квадратного уравнения, то есть, когда A=1, формула упрощается: x0=-B/2. Если в уравнении нет «икса» в первой степени, значит, коэффициент B=0, и тогда x0 тоже обращается в нуль.

  Чтобы найти координату вершины параболы по оси ординат, подставьте полученное значение для x0 в уравнение. Когда вы упростите выражение, с одной стороны у вас останется «игрек», с другой − некоторое число Q. Оно и показывает ординату вершины параболы: y0=Q.

  Итак, исследование аналитически заданной функции дало вам точку на графике с координатами (x0;y0). Если старший коэффициент A > 0, то ветви параболы направлены вверх, и в вершине промежуток убывания будет сменяться промежутком возрастания. Если же A Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.
  Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.

  Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.

  Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.

  Реестр иностранных средств массовой информации, выполняющих функции иностранного агента :: Министерство юстиции Российской Федерации

  Реестр иностранных средств массовой информации, выполняющих функции иностранного агента :: Министерство юстиции Российской Федерации

  Реестр иностранных средств массовой информации, выполняющих функции иностранного агента

  Реестр иностранных средств массовой информации, выполняющих функции иностранного агента

   

  Порядковый номер	Название иностранных средств массовой информации	Дата включения в реестр
  1.	«Голос Америки»	05.12.2017
  2.	«Idel.Реалии»	05.12.2017
  3.	Кавказ.Реалии	05.12.2017
  4.	Крым.Реалии	05.12.2017
  5.	Телеканал Настоящее Время	05.12.2017
  6.	Татаро-башкирская служба Радио Свобода (Azatliq Radiosi)	05.12.2017
  7.	Радио Свободная Европа/Радио Свобода (PCE/PC)	05. 12.2017
  8.	«Сибирь.Реалии»	05.12.2017
  9.	«Фактограф»	05.12.2017
  10.	«Север.Реалии»	15.11.2019
  11.	Общество с ограниченной ответственностью «Радио Свободная Европа/Радио Свобода»	11.02.2020
  12.	Чешское информационное агентство «MEDIUM-ORIENT»	21.12.2020
  13.	Пономарев Лев Александрович	28. 12.2020
  14.	Савицкая Людмила Алексеевна	28.12.2020
  15.	Маркелов Сергей Евгеньевич	28.12.2020
  16.	Камалягин Денис Николаевич	28.12.2020
  17.	Апахончич Дарья Александровна	28.12.2020
  18.	Юридическое лицо, зарегистрированное в Латвийской Республике, SIA «Medusa Project» (регистрационный номер 40103797863, дата регистрации 10.06.2014)	23.04.2021
  19.	Общество с ограниченной ответственностью «Первое антикоррупционное СМИ»	23. 04.2021
  20.	Юридическое лицо, зарегистрированное в Королевстве Нидерландов, Stichting 2 Oktober (регистрационный номер № 69126968), являющееся администратором доменного имени интернет-ресурса «VTimes.io»	14.05.2021

   

  Опубликовано на сайте:
  14 мая 2021

  Официальный интернет-ресурс Министерства юстиции Российской Федерации.

  Что такое функция пользователя(UDF)?

  Хитрости »
  1 Май 2011       Дмитрий       121606 просмотров

  ---

  Если потребовалось заиметь в Excel функцию, которой там еще нет, но она очень нужна или её применение значительно упростило бы жизнь при выполнение определенных задач, то самое время посмотреть в сторону функций пользователя.

  Функция пользователя(UDF) — или в дословном переводе Функция, Определенная Пользователем, т. к. в оригинале она звучит как: User Defined Function. Так же их называют пользовательские функции.
  Такие функции вызываются через Мастер функций -категория Определенные пользователем (User Defined):

  Так что же это за функции такие? Функция пользователя это функция, написанная при помощи языка Visual Basic for Application (VBA) и вызываемая как любая другая функция с листа. Но т.к. эти функции пишутся самостоятельно — можно создать любую функцию, которая будет делать то, что ни одна стандартная функция делать не умеет. Естественно, теперь возникает вопрос как написать такую функцию. Для написания UDF понадобятся хотя бы базовые знания языка VBA. Я в статье опишу лишь принципы создания таких функций и после прочтения вы сможете создать простейшую функцию. Но это никак не означает, что я научу создавать функции на все случаи жизни, ибо это сводится к обучению самому языку программирования. В статье же рассмотрим основные принципы создания, некоторые нюансы и как уже написанные функции использовать в своей книге.

   
  Основные ограничения функций пользователя
  Самое главное, что необходимо усвоить — это определенные ограничения, накладываемые на функцию пользователя(UDF), вызываемую с листа:

  1. UDF не может изменять значения других ячеек (с небольшими недокументированными исключениями)
  2. UDF не может изменять форматы ячеек либо присваивать форматы (с небольшими недокументированными исключениями)
  3. UDF не может изменять так называемые объекты окружения самого Excel. Например, сменить стиль ссылок или параметры вычислений формул, вид курсора и т.п.
  4. UDF будет некорректно работать с такими методами как FindNext, SpecialCells, CurrentRegion, CurrentArray, Select, ShowPrecedents и ShowDependents(выделение зависимостей ячеек), Application.GoTo и т.п. Хотя методы вроде Range. End(xlUp), Range.End(xlDown), обычный Find(без FindNext) проблем не вызывают.Подробнее про работу этих методов из UDF можно узнать из статьи: Глюк работы в UDF методов SpecialCells и FindNext
  5. UDFможет возвращать результат только в ту ячейку, в которой записана сама функция
  6. для работы функции пользователя(UDF) обязательно должны быть разрешены макросы

  ---

   
  Как создать функцию пользователя

  Предполагается, что Вы уже обладаете начальными навыками написания процедур в VBA и умеете создавать эти самые процедуры, хотя бы самые простые.
  Однако прежде чем читать дальше советую ознакомиться так же со статьей: Что такое модуль? Какие бывают модули?
  Основные моменты, которые следует помнить при создании функции пользователя:

  • в отличие от процедуры(Sub) функция всегда начинается именно со слова Function, а не Sub;
  • в теле функции всегда должно быть присвоение ей значения, иначе функция не вернет необходимый результат;
  • функция должна располагаться в стандартном модуле или в модуле книги, если Вы планируете вызывать её непосредственно с листа Excel
  • функции пользователя «привязаны» к той книге, в которой созданы и по умолчанию не будут работать в других (для этого надо будет всегда указывать имя книги с функцией). Чтобы созданные функции работали удобно и без проблем в любой книге необходимо книгу с функциями сохранить как надстройку: Как создать свою надстройку?

  Самая простая функция пользователя может выглядеть так:

  Function ТекущаяДата() 'присваиваем функции значение, чтобы она вернула его на лист(обязательно!) ТекущаяДата = Date 'ТекущаяДата - имя функции и именно ему необходимо передать результат End Function

  Function ТекущаяДата()
  ‘присваиваем функции значение, чтобы она вернула его на лист(обязательно!)
  ТекущаяДата = Date ‘ТекущаяДата — имя функции и именно ему необходимо передать результат
  End Function

  Эта функция делает одно — возвращает в ячейку, в которую записана, текущую дату. В ячейке эта функция будет выглядеть так:
  =ТекущаяДата()
  К записи пользовательских функций в ячейку предъявляются такие же требования, как и к встроенным функциям. Это касается так же и скобок на конце функции, у которой нет аргументов. И так же это означает, что в функцию могут быть переданы наши собственные аргументы

  ---

   
  Аргументы функции пользователя

  Function MySum(vArg1 As Double, vArg2 As Double) Dim dblSum as Double 'получаем сумму двух аргументов dblSum = vArg1 + vArg2 'присваиваем функции значение, чтобы она вернула его на лист(обязательно!) MySum = dblSum 'MySum имя функции и именно ему необходимо передать результат End Function

  Function MySum(vArg1 As Double, vArg2 As Double)
  Dim dblSum as Double
  ‘получаем сумму двух аргументов
  dblSum = vArg1 + vArg2
  ‘присваиваем функции значение, чтобы она вернула его на лист(обязательно!)
  MySum = dblSum ‘MySum имя функции и именно ему необходимо передать результат
  End Function

  В приведенном выше коде я упростил стандартную функцию СУММ(SUM) до двух аргументов. Записанная на лист функция будет иметь такой вид:
  =Mysum(A1;A2)
  где:
  A1 — первый аргумент(vArg1), ссылка на ячейку или число
  A2 — второй аргумент(vArg2), ссылка на ячейку или число
  Функция вернет #ЗНАЧ!(#VALUE!), если в качестве одного из аргументов передано не числовое значение.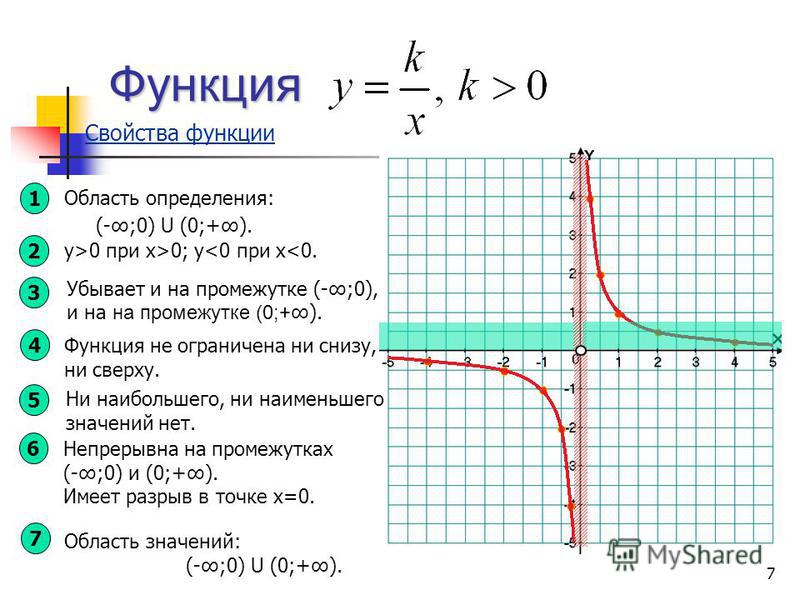

  ---

   
  Необязательные аргументы функции пользователя
  Однако иногда бывает неизвестно, сколько аргументов будет передано в функцию: 1, 2 или 10. Для этого можно использовать ключевой параметр Optional перед аргументом, который укажет функции, что этот аргумент является не обязательным, т.е. указывать его в функции при вызове этой функции не обязательно. На примере приведенной выше функции мы можем сделать обязательным только один параметр, а еще 4 необязательными:

  Function SumFiveArgs(arg1 As Double, Optional arg2 As Double, Optional arg3 As Double, Optional arg4 As Double, Optional arg5 As Double) Dim dblSum As Double dblSum = arg1 dblSum = dblSum + arg2 dblSum = dblSum + arg3 dblSum = dblSum + arg4 dblSum = dblSum + arg5 SumFiveArgs = dblSum End Function

  Function SumFiveArgs(arg1 As Double, Optional arg2 As Double, Optional arg3 As Double, Optional arg4 As Double, Optional arg5 As Double)
  Dim dblSum As Double
  dblSum = arg1
  dblSum = dblSum + arg2
  dblSum = dblSum + arg3
  dblSum = dblSum + arg4
  dblSum = dblSum + arg5
  SumFiveArgs = dblSum
  End Function

  Функция будет работать отлично, даже если передать одно или два числа. Но это только в том случае, если для аргументов у нас заданы строгие типы данных — в примере это Double. Если тип не задан — получим ошибку #ЗНАЧ! (#VALUE!):

  Function SumFiveArgs(arg1 As Double, Optional arg2, Optional arg3, Optional arg4, Optional arg5) Dim dblSum As Double dblSum = arg1 dblSum = dblSum + arg2 dblSum = dblSum + arg3 dblSum = dblSum + arg4 dblSum = dblSum + arg5 SumFiveArgs = dblSum End Function

  Function SumFiveArgs(arg1 As Double, Optional arg2, Optional arg3, Optional arg4, Optional arg5)
  Dim dblSum As Double
  dblSum = arg1
  dblSum = dblSum + arg2
  dblSum = dblSum + arg3
  dblSum = dblSum + arg4
  dblSum = dblSum + arg5
  SumFiveArgs = dblSum
  End Function

  Можно, конечно, всегда задавать тип данных, как в первом примере. Но стоит учитывать, что для числовых типов данных(Double, Integer, Long) значение по умолчанию будет всегда 0, даже если мы аргумент не передали в функцию(для типа String значение по умолчанию нулевая строка — «»). Это нам не мешает произвести операцию сложения и вычитания. Но операция внутри функции может быть умножением или делением и в этом случае мы получим ошибку или неверный результат:

  'функция деления аргументов между собой Function DivideFiveArgs(arg1 As Double, Optional arg2 As Double, Optional arg3 As Double, Optional arg4 As Double, Optional arg5 As Double) Dim dblSum As Double dblSum = arg1 dblSum = dblSum / arg2 dblSum = dblSum / arg3 'уже здесь получим ошибку "на ноль делить нельзя" dblSum = dblSum / arg4 dblSum = dblSum / arg5 DivideFiveArgs = dblSum End Function

  ‘функция деления аргументов между собой
  Function DivideFiveArgs(arg1 As Double, Optional arg2 As Double, Optional arg3 As Double, Optional arg4 As Double, Optional arg5 As Double)
  Dim dblSum As Double
  dblSum = arg1
  dblSum = dblSum / arg2
  dblSum = dblSum / arg3 ‘уже здесь получим ошибку «на ноль делить нельзя»
  dblSum = dblSum / arg4
  dblSum = dblSum / arg5
  DivideFiveArgs = dblSum
  End Function

  'функция перемножения аргументов между собой Function MultipleFiveArgs(arg1 As Double, Optional arg2 As Double, Optional arg3 As Double, Optional arg4 As Double, Optional arg5 As Double) Dim dblSum As Double dblSum = arg1 dblSum = dblSum * arg2 dblSum = dblSum * arg3 'здесь arg3 равен нулю, значит далее сумма будет тоже равна нулю dblSum = dblSum * arg4 dblSum = dblSum * arg5 MultipleFiveArgs = dblSum End Function

  ‘функция перемножения аргументов между собой
  Function MultipleFiveArgs(arg1 As Double, Optional arg2 As Double, Optional arg3 As Double, Optional arg4 As Double, Optional arg5 As Double)
  Dim dblSum As Double
  dblSum = arg1
  dblSum = dblSum * arg2
  dblSum = dblSum * arg3 ‘здесь arg3 равен нулю, значит далее сумма будет тоже равна нулю
  dblSum = dblSum * arg4
  dblSum = dblSum * arg5
  MultipleFiveArgs = dblSum
  End Function

  Передав меньше аргументов в функцию =DivideFiveArgs(A1;A4) мы получим ошибку #ЗНАЧ!(#VALUE!), которую вызовет деление на ноль внутри кода на третьем аргументе.
  А передав меньше аргументов в функцию умножения =MultipleFiveArgs(A1;A4)) — получим в качестве результата 0, т.к. на третьем аргументе умножим общую сумму на аргумент, который равен 0.

  Проверять каждый аргумент на равенство нулю(If arg2 = 0 Then) тоже будет неверно — вдруг какой-либо реально переданный аргумент будет действительно равен 0? Будет неверный результат функции. Поэтому, чтобы функции выше заработали правильно — нужна проверка на отсутствие в аргументе значения.
  Тут надо знать, что если тип аргумента не указан и сам аргумент в функцию не был передан — то ему назначается особый тип — Missing. Который и дает понять, что аргумент просто не передавался в функцию(Missing в переводе можно представить как «пропущен»). И в VBA для таких случаев есть специальная функция — IsMissing. Тогда можно более гибко манипулировать аргументами(на примере функции с умножением):

  Function MultipleFiveArgs(arg1 As Double, Optional arg2, Optional arg3, Optional arg4, Optional arg5) Dim dblSum As Double dblSum = arg1 'проверяем, что аргумент передан(NOT IsMISSING) If Not IsMissing(arg2) Then dblSum = dblSum * arg2 End If If Not IsMissing(arg3) Then dblSum = dblSum * arg3 End If If Not IsMissing(arg4) Then dblSum = dblSum * arg4 End If If Not IsMissing(arg5) Then dblSum = dblSum * arg5 End If MultipleFiveArgs = dblSum End Function

  Function MultipleFiveArgs(arg1 As Double, Optional arg2, Optional arg3, Optional arg4, Optional arg5)
  Dim dblSum As Double
  dblSum = arg1
  ‘проверяем, что аргумент передан(NOT IsMISSING)
  If Not IsMissing(arg2) Then
  dblSum = dblSum * arg2
  End If
  If Not IsMissing(arg3) Then
  dblSum = dblSum * arg3
  End If
  If Not IsMissing(arg4) Then
  dblSum = dblSum * arg4
  End If
  If Not IsMissing(arg5) Then
  dblSum = dblSum * arg5
  End If
  MultipleFiveArgs = dblSum
  End Function

  Как видно — теперь Optional можно использовать вполне эффективно. Но надо помнить одно правило: аргументы, заданные в функции с ключевым Optional должны быть заданы самими последними. Т.е. после них не может идти никаких других обязательных аргументов(без ключевого Optional). Впрочем, в этом случае VBA сообщит нам об этом ошибкой «Expected: Optional», что означает: Ожидался не обязательный аргумент.

  ---

   
  Динамическое количество аргументов в функции пользователя(ParamArray)
  Сразу после некоторого использования Optional напрашивается вопрос: а если заранее неизвестно сколько аргументов будет передано? Может их будет передано 50? Или 70? Что, все перечислять? В принципе, можно сделать и так. Но можно и иначе. В VBA предусмотрен очень интересный тип данных — ParamArray. Он представляет собой динамический массив, размер которого зависит от количества переданных аргументов. На примере суммирования данных функция будет выглядеть следующим образом:

  Function SumMultiple(ParamArray args()) Dim dblSum As Double, arg On Error Resume Next For Each arg In args dblSum = dblSum + arg Next SumMultiple = dblSum End Function

  Function SumMultiple(ParamArray args())
  Dim dblSum As Double, arg
  On Error Resume Next
  For Each arg In args
  dblSum = dblSum + arg
  Next
  SumMultiple = dblSum
  End Function

  Но такая функция может выдать ошибку, если в качестве любого аргумента будет передана не одна единственная ячейка или значение — а диапазон ячеек(A1:A4) или массив({10;20;30}). В этом случае внутри функции обязательно придется определять тип данных внутри ParamArray. Сделать это можно следующим образом:

  Function SumMultiple_DiffTypes(ParamArray args()) Dim dblSum As Double, arg, rc As Range, x On Error Resume Next For Each arg In args Select Case TypeName(arg) Case "Range" 'это диапазон 'цикл по всем ячейкам For Each rc In arg.Cells 'проверяем, что в ячейке числовой тип данных If IsNumeric(rc.Value) Then dblSum = dblSum + rc.Value End If Next Case "Variant()" 'это произвольный массив({10;20;30}) 'цикл по всем ячейкам For Each x In arg 'проверяем, что это числовой тип данных If IsNumeric(x) Then dblSum = dblSum + x End If Next Case "Double", "Long", "Integer" 'это любой числовой тип 'суммируем dblSum = dblSum + arg 'все остальные типы игнорируем End Select Next SumMultiple_DiffTypes = dblSum End Function

  Function SumMultiple_DiffTypes(ParamArray args())
  Dim dblSum As Double, arg, rc As Range, x
  On Error Resume Next
  For Each arg In args
  Select Case TypeName(arg)
  Case «Range» ‘это диапазон
  ‘цикл по всем ячейкам
  For Each rc In arg.Cells
  ‘проверяем, что в ячейке числовой тип данных
  If IsNumeric(rc.Value) Then
  dblSum = dblSum + rc.Value
  End If
  Next
  Case «Variant()» ‘это произвольный массив({10;20;30})
  ‘цикл по всем ячейкам
  For Each x In arg
  ‘проверяем, что это числовой тип данных
  If IsNumeric(x) Then
  dblSum = dblSum + x
  End If
  Next
  Case «Double», «Long», «Integer» ‘это любой числовой тип
  ‘суммируем
  dblSum = dblSum + arg
  ‘все остальные типы игнорируем
  End Select
  Next
  SumMultiple_DiffTypes = dblSum
  End Function

  И в такую функцию может быть передан любой из наиболее распространенных типов данных:
  =SumMultiple_DiffTypes({10;20;30};A1:A4;10;C1)
  Но и у ParamArray есть недостаток: он не может использоваться одновременно с необязательными аргументами(Optional). Вместе с ParamArray могут быть использованы только обязательные аргументы и они должны обязательно идти ДО ParamArray. Если хоть один будет указан после, то получим ошибку компилятора: «Expected: )». Т.е. ожидалась завершающая скобка функции.

  ---

   
  И для большего кругозора еще одна простая функция, но которая работает уже с текстом и вернет строку до первого пробела:

  Function ТекстДоПервогоПробела(Текст As String) As String Dim i As Long Dim Result As String 'переменная для результата i = InStr(1, Текст, " ", 1) 'ищем позицию первого пробела в переданном тексте 'если пробел есть и он не первый символ в строке If i > 1 Then Result = Mid(Текст, 1, i - 1) 'получаем текст до первого пробела Else 'если пробела нет - возвращаем всю строку Result = Текст End If 'присваиваем результат функции для возврата его на лист ТекстДоПервогоПробела = Result End Function

  Function ТекстДоПервогоПробела(Текст As String) As String
  Dim i As Long
  Dim Result As String ‘переменная для результата
  i = InStr(1, Текст, » «, 1) ‘ищем позицию первого пробела в переданном тексте
  ‘если пробел есть и он не первый символ в строке
  If i > 1 Then
  Result = Mid(Текст, 1, i — 1) ‘получаем текст до первого пробела
  Else
  ‘если пробела нет — возвращаем всю строку
  Result = Текст
  End If
  ‘присваиваем результат функции для возврата его на лист
  ТекстДоПервогоПробела = Result
  End Function

  Text — ссылка на ячейку или непосредственно текст, первое слово из которого надо извлечь. Если переданный текст не будет содержать пробелов или это будет число — функция вернет весь текст. Если ячейка будет пустая — функция вернет пусто и не выдаст ошибки.
  Эту функцию можно записать и намного короче:

  Function ТекстДоПервогоПробела(Текст As String) As String ТекстДоПервогоПробела = Split(Текст, " ")(0) End Function

  Function ТекстДоПервогоПробела(Текст As String) As String
  ТекстДоПервогоПробела = Split(Текст, » «)(0)
  End Function

  Но в таком виде функция вернет значение ошибки #ЗНАЧ!(#VALUE!), если ячейка с текстом будет пустой. Вдаваться в подробности не буду. Могу лишь написать, что функция VBA Split разбивает указанный текст на отдельные части, используя для разбиения указанный разделитель. И создает из разбитых частей одномерный массив с нижней границей, равной нулю. А функция выше просто возвращает первый элемент этого массива.
  Обе функции можно дополнить не обязательным аргументом — разделитель слов. И сделать его по умолчанию пробелом. Значение по умолчанию в данном случае задается сразу при объявлении аргумента. Выглядеть это будет так:

  Function ТекстДоУказанногоСимвола(Текст As String, Optional Разделитель As String = " ") As String ТекстДоУказанногоСимвола = Split(Текст, Разделитель)(0) End Function

  Function ТекстДоУказанногоСимвола(Текст As String, Optional Разделитель As String = » «) As String
  ТекстДоУказанногоСимвола = Split(Текст, Разделитель)(0)
  End Function

  В данном примере если вызвать функцию так:
  =ТекстДоУказанногоСимвола(A1)
  то функция будет использовать в качестве разделителя пробел(Optional Разделитель As String = » «). Или можно задать символ разделения напрямую в функции и это может быть как пробел, так и любой другой символ:
  =ТекстДоУказанногоСимвола(A1;»;»)
  Так же можно применить ParamArray, чтобы указывать «неограниченное» количество аргументов для сцепления значений из ячеек в одну строку с указанным разделителем:

  Function ОбъединитьВсеСРазделителем(Разделитель As String, ParamArray Значения()) As String Dim result As String, arg, x, rc As Range For Each arg In Значения Select Case TypeName(arg) Case "Range" 'это диапазон 'цикл по всем ячейкам For Each rc In arg.Cells If result = "" Then result = rc.Value Else result = result & Разделитель & rc.Value End If Next Case "Variant()" 'это произвольный массив({"а";"б";"в"}) 'цикл по всем ячейкам For Each x In arg If result = "" Then result = x Else result = result & Разделитель & x End If Next Case Else 'это любой другой тип 'суммируем If result = "" Then result = arg Else result = result & Разделитель & arg End If End Select Next ОбъединитьВсеСРазделителем = result End Function

  Function ОбъединитьВсеСРазделителем(Разделитель As String, ParamArray Значения()) As String
  Dim result As String, arg, x, rc As Range
  For Each arg In Значения
  Select Case TypeName(arg)
  Case «Range» ‘это диапазон
  ‘цикл по всем ячейкам
  For Each rc In arg.Cells
  If result = «» Then
  result = rc.Value
  Else
  result = result & Разделитель & rc.Value
  End If
  Next
  Case «Variant()» ‘это произвольный массив({«а»;»б»;»в»})
  ‘цикл по всем ячейкам
  For Each x In arg
  If result = «» Then
  result = x
  Else
  result = result & Разделитель & x
  End If
  Next
  Case Else ‘это любой другой тип
  ‘суммируем
  If result = «» Then
  result = arg
  Else
  result = result & Разделитель & arg
  End If
  End Select
  Next
  ОбъединитьВсеСРазделителем = result
  End Function

  Пример вызова такой функции с листа(первым обязательно передается разделитель, а далее уже что объединять — любой тип данных):
  =ОбъединитьВсеСРазделителем(«; «;A1:A4;C1;»Привет»;{«а»;»б»;»в»})

  ---

   
  Как добавить уже созданную функцию в свою книгу

  Для начала необходимо создать стандартный модуль(Insert —Module). Затем в этот модуль вставить весь текст функции(код). Все, теперь функция доступна из диспетчера функций в категории Определенные пользователем(User defined), так же можно будет вводить эту функцию напрямую в ячейки той книги, в которой содержится код функции. Чтобы функция заработала очень важно разрешить макросы. Иначе результатом будет ошибка #ИМЯ!(#NAME!)
  GIF-ка с инструкцией, как вставить функцию к себе в книгу на примере функции ТекстДоПервогоПробела из этой статьи:

  Если Вы используете версию Excel 2007 и выше, то книгу необходимо будет сохранить с поддержкой макросов: Меню -Сохранить как -Книга Excel с поддержкой макросов.

   
  Обновление расчетов функции пользователя UDF(автопересчет)
  По умолчанию функции пользователя не пересчитываются вместе с пересчетом листа или по нажатию F9(Shift+F9). Чтобы функция пользователя пересчиталась, как правило необходимо либо изменить значение любого аргумента функции(например, изменить значение участвующей в расчетах ячейки) или имитировать редактирование самой функции последовательным нажатием клавиш F2-Enter. Это не всегда удобно и часто возникает вопрос: как заставить функцию пересчитываться при любом изменении листа и при пересчете листа/книги клавишами(F9 или Shift+F9). Между тем делается это довольно просто и при этом сделать можно для каждой отдельной функции. На примере простой функции записи даты-времени в ячейку:

  Function ТекущаяДатаВремя() ТекущаяДатаВремя = Now 'Now - возвращает текущие дату и время End Function

  Function ТекущаяДатаВремя()
  ТекущаяДатаВремя = Now ‘Now — возвращает текущие дату и время
  End Function

  Если записать её в таком виде, то после записи в ячейку:
  =ТекущаяДатаВремя()
  при первой записи будут показаны текущие дата и время. Чтобы эксперимент был более наглядным, лучше перейти в Формат ячеек и выставить для ячейки с функцией формат «ДД.ММ.ГГ ч:мм:сс;@». С небольшим интервалом времени понажимайте клавишу F9, чтобы вызвать пересчет книги. Тогда наглядно будет видно, что при пересчете значение функции не изменяется — секунды «застынут» на том месте, где были при начальном вводе функции. Выделите ячейку с функцией — нажмите F2-Enter. Только тогда значение будет пересчитано. А теперь чуть изменим функцию — добавим ключевой параметр пересчета — Application.Volatile:

  Function ТекущаяДатаВремя() Application.Volatile True ТекущаяДатаВремя = Now 'Now - возвращает текущие дату и время End Function

  Function ТекущаяДатаВремя()
  Application.Volatile True
  ТекущаяДатаВремя = Now ‘Now — возвращает текущие дату и время
  End Function

  Теперь при каждом пересчете листа и при любом изменении на листе функция будет пересчитываться. В некоторых случаях это делать просто необходимо(например, если применяется функция получения имени листа или книги).
  Но стоит всегда учитывать тот факт, что не всегда такой автопересчет полезен. Если функция пользователя использует «тяжелые» расчеты и выполняется долго — добавление автопересчета может значительно затормозить работу с файлом. Поэтому применять параметр следует с осторожностью.
  Если надо, чтобы функция пересчитывалась только при изменениях в конкретном диапазоне/ячейках, можно просто сделать необязательные параметры:

  Function ТекущаяДатаВремя(Optional ДиапазонОбновления As Range = Nothing) ТекущаяДатаВремя = Now End Function

  Function ТекущаяДатаВремя(Optional ДиапазонОбновления As Range = Nothing)
  ТекущаяДатаВремя = Now
  End Function

  тогда при любом изменении в ячейках аргумента ДиапазонОбновления функция будет пересчитана. При этом использовать хоть как-то сам этот аргумент внутри функции совершенно необязательно. Выглядеть запись такой функции будет так:
  =ТекущаяДатаВремя(E:E)
  при любом изменении в столбце E функция будет пересчитана.

  ---

  Некоторые примеры функций пользователя можно увидеть здесь на сайте:

  ---

  Чтобы использовать функции пользователя более удобно, их лучше размещать в специальных файлах — надстройках: Как создать свою надстройку?

  ---

  Статья помогла? Поделись ссылкой с друзьями!

      Видеоуроки

  ---

  Поиск по меткам

  Access
  apple watch
  Multex
  Power Query и Power BI
  VBA управление кодами
  Бесплатные надстройки
  Дата и время
  Записки
  ИП
  Надстройки
  Печать
  Политика Конфиденциальности
  Почта
  Программы
  Работа с приложениями
  Разработка приложений
  Росстат
  Тренинги и вебинары
  Финансовые
  Форматирование
  Функции Excel
  акции MulTEx
  ссылки
  статистика

  14.1: Функции нескольких переменных

  Нашим первым шагом является объяснение того, что такое функция нескольких переменных, начиная с функций двух независимых переменных. Этот шаг включает в себя определение области и диапазона таких функций и обучение их построению в виде графиков. Мы также исследуем способы связать графики функций в трех измерениях с графиками более знакомых плоских функций.

  Функции двух переменных

  Определение функции двух переменных очень похоже на определение функции одной переменной.2 \) на уникальное действительное число z . Множество \ (D \) называется областью определения функции. Диапазон \ (f \) — это набор всех действительных чисел z , который имеет хотя бы одну упорядоченную пару \ ((x, y) ∈D \) такую, что \ (f (x, y) = z \) как показано на рисунке \ (\ PageIndex {1} \).

  Рисунок \ (\ PageIndex {1} \): Область определения функции двух переменных состоит из упорядоченных пар \ ((x, y) \).

  Определение области определения функции двух переменных включает в себя учет любых ограничений области, которые могут существовать.2 \). Чтобы определить диапазон, сначала выберите значение z . Нам нужно найти решение уравнения \ (f (x, y) = z, \) или \ (3x − 5y + 2 = z. \). Одно такое решение можно получить, сначала положив \ (y = 0 \ ), что дает уравнение \ (3x + 2 = z \). Решением этого уравнения является \ (x = \ dfrac {z − 2} {3} \), что дает упорядоченную пару \ (\ left (\ dfrac {z − 2} {3}, 0 \ right) \) как решение уравнения \ (f (x, y) = z \) для любого значения \ (z \). Следовательно, диапазон функции — это все действительные числа или \ (R \).

  г.2≤4 \), граница которого имеет окружность радиуса \ (2 \). Диапазон равен \ ([0,6]. \)

  .

  Графические функции двух переменных

  Предположим, мы хотим построить график функции \ (z = (x, y). \) Эта функция имеет две независимые переменные (\ (x \) и \ (y \)) и одну зависимую переменную \ ((z) \) . При построении графика функции \ (y = f (x) \) одной переменной мы используем декартову плоскость. Мы можем построить график любой упорядоченной пары \ ((x, y) \) на плоскости, и каждая точка на плоскости имеет связанную с ней упорядоченную пару \ ((x, y) \).С функцией двух переменных каждая упорядоченная пара \ ((x, y) \) в области определения функции отображается в действительное число \ (z \). Следовательно, график функции \ (f \) состоит из упорядоченных троек \ ((x, y, z) \). График функции \ (z = (x, y) \) двух переменных называется поверхностью.

  Чтобы более полно понять концепцию построения набора упорядоченных троек для получения поверхности в трехмерном пространстве, представьте плоскую систему координат \ ((x, y) \). Тогда каждая точка в области определения функции f имеет уникальное значение z , связанное с ней.2, \ nonumber \]

  , где \ (x \) — количество гаек, проданных в месяц (в тысячах), а \ (y \) — количество болтов, проданных за месяц (в тысячах). Прибыль измеряется тысячами долларов. Нарисуйте график этой функции.

  Решение

  Эта функция является полиномиальной функцией от двух переменных. 2 = 16 -Z.\ end {align *} \]

  Поскольку \ (z <16, \), мы знаем, что \ (16 − z> 0, \), поэтому предыдущее уравнение описывает круг с радиусом \ (\ sqrt {16 − z} \) с центром в точке \ (( 3,2) \). Следовательно. диапазон \ (f (x, y) \) равен \ (\ {z∈ \ mathbb {R} | z≤16 \}. \) График \ (f (x, y) \) также является параболоид, и этот параболоид указывает вниз, как показано.

  Рисунок \ (\ PageIndex {5} \): График данной функции двух переменных также является параболоидом.

  Кривые уровня

  Если туристы идут по пересеченным тропам, они могут использовать топографическую карту, показывающую, насколько круто меняются маршруты.Топографическая карта содержит изогнутые линии, называемые контурными линиями. Каждая горизонтальная линия соответствует точкам на карте, которые имеют одинаковую высоту (Рисунок \ (\ PageIndex {6} \)). Линия уровня функции двух переменных \ (f (x, y) \) полностью аналогична контурной линии на топографической карте.

  Рисунок \ (\ PageIndex {6} \): (а) Топографическая карта Башни Дьявола, Вайоминг. Линии, расположенные близко друг к другу, указывают на очень крутой рельеф. (б) Перспективное фото Башни Дьявола показывает, насколько круты ее стены.2 = 5. \]

  Это уравнение описывает круг с центром в начале координат и радиусом \ (\ sqrt {5} \). Использование значений c между \ (0 \) и \ (3 \) дает другие круги, также с центром в начале координат. Если \ (c = 3 \), то круг имеет радиус \ (0 \), поэтому он состоит исключительно из начала координат. На рисунке \ (\ PageIndex {7} \) показан график линий уровня этой функции, соответствующих \ (c = 0,1,2, \) и \ (3 \). Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя обе части в квадрат.2 = 25, \), который представляет собой окружность радиуса \ (5 \) с центром в точке \ ((3, −1). \)

  Другой полезный инструмент для понимания графика функции двух переменных называется вертикальной кривой. Кривые уровня всегда отображаются в плоскости \ (xy-plane \), но, как следует из их названия, вертикальные кривые отображаются в плоскостях \ (xz- \) или \ (yz- \). 2 \).Вертикальный след функции может быть либо набором точек, который решает уравнение \ (f (a, y) = z \) для данной константы \ (x = a \), либо \ (f (x, b ) = z \) для данной константы \ (y = b. \)

  Пример \ (\ PageIndex {5} \): поиск вертикальных следов

  Найдите вертикальные следы для функции \ (f (x, y) = \ sin x \ cos y \), соответствующей \ (x = — \ dfrac {π} {4}, 0, \) и \ (\ dfrac { π} {4} \) и \ (y = — \ dfrac {π} {4}, 0 \) и \ (\ dfrac {π} {4} \).

  Решение

  Сначала задайте \ (x = — \ dfrac {π} {4} \) в уравнении \ (z = \ sin x \ cos y: \)

  \ (z = \ sin (- \ dfrac {π} {4}) \ cos y = — \ dfrac {\ sqrt {2} \ cos y} {2} ≈ −0.7071 \ cos y. \)

  Это описывает косинусный граф на плоскости \ (x = — \ dfrac {π} {4} \). Остальные значения z показаны в следующей таблице.

  Вертикальные трассы, параллельные \ (xz-Plane \) для функции \ (f (x, y) = \ sin x \ cos y \)

  \ (с \)	Вертикальный след для \ (x = c \)
  \ (- \ dfrac {π} {4} \)	\ (z = — \ dfrac {\ sqrt {2} \ cos y} {2} \)
  0	\ (г = 0 \)
  \ (\ dfrac {π} {4} \)	\ (z = \ dfrac {\ sqrt {2} \ cos y} {2} \)

  Аналогичным образом мы можем подставить \ (значения y \) в уравнение \ (f (x, y) \), чтобы получить следы в \ (yz-plane, \), как указано в следующая таблица.

  Вертикальные трассы, параллельные \ (yz-Plane \) для функции \ (f (x, y) = \ sin x \ cos y \)

  \ (г \)	Вертикальный след для \ (y = d \)
  \ (\ dfrac {π} {4} \)	\ (z = \ dfrac {\ sqrt {2} \ sin x} {2} \)
  0	\ (г = \ грех х \)
  \ (- \ dfrac {π} {4} \)	\ (z = \ dfrac {\ sqrt {2} \ sin x} {2} \)

  Три следа в \ (xz-плоскости \) являются косинусоидальными функциями; три следа в \ (yz-плоскости \) являются синусоидальными функциями.2 \). Эта функция описывает параболу, раскрывающуюся вниз в плоскости \ (y = 3 \).

  Функции двух переменных могут создавать поразительные поверхности. На рисунке \ (\ PageIndex {11} \) показаны два примера.

  Рисунок \ (\ PageIndex {11} \): Примеры поверхностей, представляющих функции двух переменных: (а) комбинация степенной функции и синусоидальной функции и (б) комбинация тригонометрических, экспоненциальных и логарифмических функций.

  Функции более двух переменных

  До сих пор мы рассматривали только функции двух переменных.2) \ sin t− (3x + 5y) \ cos t. \]

  В первой функции \ ((x, y, z) \) представляет точку в пространстве, а функция \ (f \) сопоставляет каждую точку в пространстве с четвертой величиной, такой как температура или скорость ветра. Во второй функции \ ((x, y) \) может представлять точку на плоскости, а \ (t \) может представлять время. Функция может сопоставлять точку на плоскости с третьей величиной (например, давлением) в данный момент времени \ (t \). Метод поиска области определения функции более двух переменных аналогичен методу для функций одной или двух переменных.2−4 \} \ nonumber \]

  Функции двух переменных имеют кривые уровня, которые показаны как кривые на \ (xy-плоскости. \). Однако, когда функция имеет три переменных, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.

  Определение: ровная поверхность функции трех переменных

  Для функции \ (f (x, y, z) \) и числа \ (c \) в диапазоне \ (f \) поверхность уровня функции трех переменных определяется как множество точек, удовлетворяющих уравнению \ (f (x, y, z) = c.2 = 16 \) описывает сферу радиуса \ (4 \) с центром в точке \ ((1, −2,3). \)

  функций

  Что такое функция?
  

  А
  
  функция
  
  способ справиться с
  
  «Вход»
  
  , применяя некоторые
  
  «правило»
  
  (функция), а затем получив
  
  «выход»
  
  .

  А
  
  функция
  
  это набор

  заказанные пары

  в котором никакие две разные упорядоченные пары не имеют одинаковых

  Икс

  -координат.Уравнение, которое создает такой набор упорядоченных пар, определяет функцию.

  В чем подвох? Для каждого входа может быть не более одного выхода. Входные данные, которые имеют «смысл», образуют

  домен

  функции, а ответы или выходы образуют

  диапазон

  .

  Обозначение функций
  

  Мы можем назвать ввод
  

  Икс
  
  , правило

  ж

  , а затем на выходе

  ж

  (

  Икс

  )

  , читать »

  ж

  из

  Икс

  «.

  Это НЕ означает »

  ж

  раз

  Икс

  «, это просто устройство записи для записи ввода и вывода.

  Например, найдите вывод функции

  ж

  (

  Икс

  )

  знак равно

  Икс

  2

  когда вход,

  Икс

  знак равно

  3

  .

  Чтобы найти выходное значение, когда

  Икс

  знак равно

  3

  , заменять

  3

  для

  Икс

  в функции.

  ж

  (

  3

  )

  знак равно

  3

  2

  3

  2

  средства

  3

  раз

  3

  .

  ж

  (

  3

  )

  знак равно

  3

  ×

  3

  знак равно

  9

  (Примечание:

  ж

  (

  3

  )

  не является

  ж

  раз

  3

  )

  Думать о

  ж

  (

  Икс

  )

  знак равно

  Икс

  2

  в виде

  ж

  (

  )

  знак равно

  (

  )

  2

  ; таким образом вы можете безопасно вставлять отрицательные числа или даже другие выражения:

  ж

  (

  —

  5

  )

  знак равно

  (

  —

  5

  )

  2

  знак равно

  25

  ж

  (

  Икс

  +

  час

  )

  знак равно

  (

  Икс

  +

  час

  )

  2

  Функции и отношения
  

  Функция — это особый тип

  связь

  .Отношение — это просто набор упорядоченных пар

  (

  Икс

  ,

  y

  )

  . На формальном математическом языке функция — это отношение, для которого:

  если

  (

  Икс

  1

  ,

  y

  )

  а также

  (

  Икс

  2

  ,

  y

  )

  оба находятся в соотношении, то

  Икс

  1

  знак равно

  Икс

  2

  .

  Это просто говорит о том, что в функции нельзя иметь две упорядоченные пары с одинаковыми

  Икс

  -значение, но другое

  y

  -значения.

  Если у вас есть график отношения, вы можете использовать

  тест вертикальной линии

  чтобы узнать, является ли отношение функцией.

  Функция

  xy.coords — RDocumentation

  Описание

  xy.coords используется многими функциями для получения
  Координаты x и y для построения графика. Использование этого общего механизма
  во всех соответствующих функциях R обеспечивает некоторую согласованность.

  Использование

   xy.coords (x, y = NULL, xlab = NULL, ylab = NULL, log = NULL,
            recycle = FALSE, setLab = TRUE) 

  Аргументы

  x, y

  координаты x и y набора точек.В качестве альтернативы можно указать один аргумент x .

  xlab, ylab

  имена извлекаемых переменных x и y.

  журнал

  символа, "x" , "y" или оба, как для
  участок . Устанавливает отрицательные значения на NA и
  дает предупреждение.

  перезапуск

  логический; если ИСТИНА , переработать ( реп. )
  более короткий из x или y , если их длина различается.

  setLab

  логическое указание, если результирующие xlab и
  ylab должен быть построен из «вида» (x, y) ;
  в противном случае используются аргументы xlab и ylab .

  Значение

  Список с компонентами

  x

  числовой (т.е. "двойной" ) вектор значений абсцисс.

  y

  числовой вектор той же длины, что и x .

  xlab

  символ (1) или NULL , «метка»
  х .

  ylab

  символ (1) или NULL , «метка»
  y .

  Детали

  Сделана попытка интерпретировать аргументы x и y в
  способ, подходящий для двумерного построения (или других двумерных процедур).

  Если y равно NULL и x является формулой

  :

  в форме yvar ~ xvar . xvar и
  yvar используются как переменные x и y.

  список:

  , содержащий компоненты x и y , это
  используется для определения координат черчения.

  временной ряд:

  значения x принимаются равными
  time (x) и значения y должны быть временными рядами.

  матрица или data.frame с двумя или более
  столбцы:

  предполагается, что первый содержит значения x и
  во-вторых, значения y. Примечание , что также верно, если x
  имеет столбцы с именами "x" и "y" ; эти имена будут
  здесь неактуально.

  В любом другом случае аргумент x приводится к вектору и
  возвращается как компонент y , где результирующий x просто
  индексный вектор 1: n . В данном случае получается xlab
  компонент установлен на «Индекс» (если setLab истинно по умолчанию).

  Если x (после преобразования, как указано выше) наследуется от класса
  "POSIXt" приведен к классу "POSIXct" .

  См. Также

  plot.default , строк , точек
  и lowess являются примерами функций, которые используют этот механизм.

  Примеры

   # NOT RUN {
  ff <- stats :: fft (1: 9)
  xy.coords (ff)
  xy.coords (ff, xlab = "fft") # метки "Re (fft)", "Im (fft)"
  #}
  # НЕ РАБОТАТЬ {
  
  #}
  # НЕ РАБОТАТЬ {
  с (автомобили, ху.coords (dist ~ speed, NULL) $ xlab) # = "скорость"
  
  xy.coords (1: 3, 1: 2, recycle = TRUE) # иначе ошибка "длины отличаются"
  xy.coords (-2: 10, log = "y")
  ##> xlab: "Index" \\ предупреждение: 3 значения y <= 0 опущены ..
  #}
   

  plot.xy: Базовая функция внутреннего графика

  Описание

  Применение

  Аргументы

  Подробности

  Смотрите также

  Примеры

  Описание

  Это внутренняя функция , которая выполняет базовое построение графика
  точки и линии.Обычно лучше использовать более высокий уровень
  функции вместо этого и обратитесь к их страницам справки для объяснения
  аргументы.

  Использование

  Аргументы

  xy	Список из четырех элементов, полученный в результате xy.coords .
  тип	1 символьный код: см. График . по умолчанию . NULL принимается как синоним «p» .
  шт	символьный или целочисленный код для обозначения вида точек, см. баллов.по умолчанию .
  лты	Код типа линии , см. строки .
  столбик	код цвета или название, см. цветов , палитра . Здесь NULL означает цвет 0.
  bg	цвет фона (заливки) для символов открытого графика 21:25: см. баллов. по умолчанию .
  cex	Расширение на символов.
  lwd	Ширина линии , также используется для (незакрашенных) графических символов, см. строк и точек .
  ...	дополнительные графические параметры, такие как xpd , lend , ljoin и lmitre .

  Детали

  Аргументы пч , col , bg , cex ,
  lwd могут быть векторами и могут быть переработаны, в зависимости от
  тип : см. точки и строки для
  специфика.В частности, обратите внимание, что lwd рассматривается как вектор
  для точек и как одно (первое) значение для линий.

  cex - это числовой коэффициент в дополнение к par ("cex") , который
  влияет на символы и символы, нарисованные по типу "p" ,
  "o" , "b" и "c" .

  См. Также

  участок , г.
  plot.default ,
  баллов ,
  строк .

  Примеры

  Исчисление III - Функции нескольких переменных

  Показать общее уведомление

  Показать мобильное уведомление

  Показать все заметки Скрыть все заметки

  Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

  Пол
  6 мая 2021 г.

  Похоже, вы используете устройство с "узкой" шириной экрана (, то есть , вероятно, вы используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

  Раздел 1-5: Функции нескольких переменных

  В этом разделе мы хотим рассмотреть некоторые основные идеи о функциях более чем одной переменной.

  Во-первых, помните, что графики функций двух переменных, \ (z = f \ left ({x, y} \ right) \) - это поверхности в трехмерном пространстве.2} - 4 \).

  Это эллиптический параболоид, являющийся примером квадратичной поверхности. Мы видели несколько из них в предыдущем разделе. В дальнейшем в исчислении III мы будем довольно часто видеть квадратичные поверхности.

  Другой распространенный график, который мы будем часто видеть в этом курсе, - это график плоскости. У нас есть соглашение для построения графиков плоскостей, которое упростит их построение и, надеюсь, визуализацию.

  Напомним, что уравнение плоскости задается формулой

  .

  \ [ax + by + cz = d \]

  , или если мы решим это для \ (z \), мы можем записать его в терминах обозначения функций.Это дает,

  \ [f \ left ({x, y} \ right) = Ax + By + D \]

  Для построения графика плоскости мы обычно находим точки пересечения с тремя осями, а затем строим треугольник, соединяющий эти три точки. Этот треугольник будет частью плоскости и даст нам довольно хорошее представление о том, как должна выглядеть сама плоскость. Например, давайте изобразим плоскость в виде

  .

  \ [f \ left ({x, y} \ right) = 12 - 3x - 4y \]

  Для построения графика, вероятно, было бы проще записать это как,

  \ [z = 12 - 3x - 4y \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} \, \, \, \, \, 3x + 4y + z = 12 \]

  Теперь каждая из точек пересечения с тремя главными осями координат определяется тем фактом, что две из координат равны нулю. Например, пересечение с осью \ (z \) - определяется как \ (x = y = 0 \). Итак, три точки пересечения:

  \ [\ begin {align *} & x - {\ mbox {axis:}} \ left ({4,0,0} \ right) \\ & y - {\ mbox {axis:}} \ left ({0 , 3,0} \ right) \\ & z - {\ mbox {axis:}} \ left ({0,0,12} \ right) \ hspace {0.25 дюймов} \ end {align *} \]

  Вот график самолета.

  Теперь, если продолжить, графики функций вида \ (w = f \ left ({x, y, z} \ right) \) будут четырехмерными поверхностями. Конечно, мы не можем нанести их на график, но не помешает указать на это.

  Далее мы хотим поговорить об областях функций более чем одной переменной. Напомним, что домены функций одной переменной \ (y = f \ left (x \ right) \) состояли из всех значений \ (x \), которые мы могли подключить к функции и получить обратно действительное число.Теперь, если мы подумаем об этом, это означает, что область определения функции одной переменной - это интервал (или интервалы) значений из числовой прямой или одномерного пространства.

  Область функций двух переменных, \ (z = f \ left ({x, y} \ right) \), является областями из двухмерного пространства и состоит из всех пар координат, \ (\ left ({x, y} \ right) \), чтобы мы могли подключиться к функции и получить действительное число.

  Пример 1 Определите домен каждого из следующих.2}} \ справа) \)

Показать все решения Скрыть все решения

a \ (f \ left ({x, y} \ right) = \ sqrt {x + y} \) Показать решение

В этом случае мы знаем, что не можем извлечь квадратный корень из отрицательного числа, поэтому это означает, что мы должны требовать,

\ [х + у \ ge 0 \]

Вот набросок графика этого региона.

b \ (f \ left ({x, y} \ right) = \ sqrt x + \ sqrt y \) Показать решение

Эта функция отличается от функции в предыдущей части.2}> 16 \]

Итак, область определения этой функции - это набор точек, полностью лежащих вне сферы радиуса 4 с центром в начале координат.

Следующая тема, на которую мы должны обратить внимание, - это кривые уровня или контурные кривые . Кривые уровня функции \ (z = f \ left ({x, y} \ right) \) - это двумерные кривые, которые мы получаем, полагая \ (z = k \), где \ (k \) - любое число. Итак, уравнения линий уровня: \ (f \ left ({x, y} \ right) = k \).Обратите внимание, что иногда уравнение будет иметь вид \ (f \ left ({x, y, z} \ right) = 0 \), и в этих случаях уравнения кривых уровня имеют вид \ (f \ left ({x, y, k} \ right) = 0 \).

Вы, наверное, уже видели кривые уровня (или контурные кривые, как бы вы их ни называли) раньше. Если вы когда-нибудь видели карту высот для участка земли, это не что иное, как контурные кривые для функции, которая дает высоту земли в этой области. Конечно, у нас, вероятно, нет функции, которая дает высоту, но мы можем, по крайней мере, изобразить контурные кривые.2}} \]

Вспомните из раздела «Квадрические поверхности», что это верхняя часть «конуса» (или поверхности в форме песочных часов).

Обратите внимание, что этого не требовалось для решения данной проблемы. Это было сделано для практики распознавания поверхности, и это может пригодиться в будущем.

А теперь перейдем к реальной проблеме. Кривые уровня (или контурные кривые) для этой поверхности задаются уравнением, которое находится путем замены \ (z = k \).2} \]

, где \ (k \) - любое число. Итак, в этом случае кривые уровня представляют собой окружности радиуса \ (k \) с центром в начале координат.

Мы можем построить график одним из двух способов. Мы можем либо изобразить их на самой поверхности, либо изобразить в двухмерной системе осей. Вот каждый график для некоторых значений \ (k \).

Обратите внимание, что мы можем думать о контурах в терминах пересечения поверхности, которая задается \ (z = f \ left ({x, y} \ right) \) и плоскостью \ (z = k \).Контур будет представлять собой пересечение поверхности и плоскости.

Для функций вида \ (f \ left ({x, y, z} \ right) \) мы время от времени будем смотреть на поверхности уровня . Уравнения поверхностей уровня задаются формулой \ (f \ left ({x, y, z} \ right) = k \), где \ (k \) - любое число.

Последняя тема в этом разделе - трассировка . В чем-то они похожи на контуры. Как отмечалось выше, мы можем думать о контурах как о пересечении поверхности, задаваемой \ (z = f \ left ({x, y} \ right) \), и плоскости \ (z = k \).2} \]

, и это будет отображено в плоскости, заданной как \ (x = 1 \).

Ниже представлены два графика. 2} \ hspace {0.2} \]

, а вот и эскизы кейса.

Быстрые функции | Программное обеспечение для многоканальных измерений | Галстук

Введение

Эта страница покажет вам, как использовать быстрые функции, чтобы легко использовать вашу технологию TiePie.
измерительный прибор как различные виртуальные инструменты: осциллограф, анализатор спектра,
регистратор данных или вольтметр.

Доступ к быстрым функциям можно получить через главное меню и панель инструментов быстрых функций.

Доступные функции

Самый простой способ использовать быстрые функции - использовать кнопки быстрых функций.
панель инструментов, но к ним также можно получить доступ через главное меню.

Доступные быстрые функции перечислены в следующей таблице.

Быстрые функции действуют на активный инструмент, в настройках программы
можно определить, на каких каналах действуют быстрые функции.

Пример каждой функции приведен в следующих разделах.Используется Handyscope HS3, но можно использовать и другие инструменты, поддерживаемые программным обеспечением многоканального осциллографа.
использовал.

Новый график

Чтобы создать новый пустой график, щелкните значок
Добавить график
на панели инструментов быстрой функции.
Это создаст новый график в области самого большого доступного графика, разделив эту область на две части.
Когда ширина области больше, чем √2 ее высоты, новый график будет
создается рядом с существующим графиком.В противном случае он будет создан под ним.
Новый график станет активным.

Осциллограф

Осциллограф можно использовать для отображения измерений в зависимости от времени ( Yt mode ) или
для отображения одного канала на другой ( режим XY ). Вы можете вручную установить график на
либо режим Yt, либо XY, и перетащите нужные каналы на график, либо вы можете использовать
Yt или XY быстрые функции.

Информацию об использовании графиков можно найти в
раздел графика.Чтобы узнать больше об основных измерениях, прочтите
страница сбора цифровых данных и
запускающая страница.

Yt режим

Чтобы использовать активный измерительный прибор в качестве осциллографа в режиме Yt, щелкните значок
Yt mode
на панели инструментов быстрой функции.

Каналы активного инструмента будут показаны на пустом графике.
Если нет пустого графика, будет создан новый график.
Новый график станет активным.

Режим XY

Чтобы использовать активный измерительный прибор в качестве осциллографа в режиме XY, щелкните значок
Режим XY
на панели инструментов быстрой функции.

Каналы 1 и 2 активного инструмента будут показаны на пустом графике.
Если нет пустого графика, будет создан новый график.
Новый график станет активным.

Эта функция отключена, если у активного инструмента меньше двух каналов.

Анализатор спектра

Чтобы использовать активный измерительный прибор в качестве анализатора спектра, щелкните значок
Анализатор спектра кнопка на панели быстрых функций.

Будет создан объект БПФ, который будет подключен к каждому каналу активного инструмента.
Объекты БПФ преобразуют измеренные сигналы временной развертки в спектр с помощью быстрого преобразования Фурье .
Его оконная функция установлена ​​на Flat top .
Выходы вновь созданных объектов БПФ будут показаны на пустом графике.
Если нет пустого графика, будет создан новый график.
Новый график станет активным.

Регистратор данных

Чтобы использовать активный измерительный прибор в качестве регистратора данных, щелкните значок
Регистратор данных кнопка на панели быстрых функций.

Активный инструмент будет установлен в режим потоковой передачи, а сборщик данных
объект будет создан и подключен к каждому каналу активного инструмента.
Выходные данные вновь созданных объектов сборщика данных будут показаны на пустом графике.
Если нет пустого графика, будет создан новый график.
Новый график станет активным.

Регистратор данных обычно используется для относительно медленных сигналов.
Инструмент установлен в потоковый режим.
Преимущества перед обычным режимом работы осциллографа:

• Дисплей измерений постоянно обновляется во время измерения.Вам не нужно ждать завершения всего измерения, чтобы увидеть результат.
• Возможны более длительные измерения, чем уместилось бы в памяти прибора при нормальной работе осциллографа.

Узнайте больше о различиях между режимом осциллографа и режимом потоковой передачи на
страница потоковых измерений.

Вольтметр

Чтобы использовать активный измерительный прибор в качестве вольтметра, щелкните значок
Измеритель кнопка на панели быстрых функций.

Каналы активного инструмента будут показаны во вновь созданном объекте измерителя.

По умолчанию измерения «Среднее» и «Среднеквадратичное значение» включены.
Для каждого канала можно добавить другие измерения.
Примеры: минимум, максимум, верх-низ, дисперсия, стандартное отклонение, частота и для
частотные данные: полное гармоническое искажение.

CAN декодер

Чтобы использовать активный измерительный прибор в качестве CAN декодера , щелкните значок
CAN декодер кнопка на панели быстрых функций.Будет создан новый ввод-вывод CAN-декодера, который будет подключен к
вновь созданный приемник таблицы для отображения декодированных данных CAN.

Если активный инструмент имеет два или более каналов, пользователя спрашивают, следует ли использовать один или два канала.
При использовании двух каналов необходимо измерять сигнал CAN high и CAN low .
Разностный сигнал H-L вычисляется с помощью ввода / вывода сложения / вычитания и подается в
анализатор.
Если используется только один канал, это может измерять CAN high или дифференциальный сигнал CAN H-L .Последнее возможно только с дифференциальным входом.

Измерение на шине CAN с декодированными данными CAN.

I

² C декодер

Чтобы использовать активный измерительный прибор в качестве декодера I ² C , щелкните значок
I ² C декодер кнопка на панели быстрых функций.
Новый I ² C декодер ввода / вывода будет создан и подключен к
первые два канала активного инструмента и подключены к
вновь созданный приемник таблицы для отображения декодированных данных I ² C.Декодер I2C можно использовать только с инструментами с двумя или более каналами.
Первый канал будет использоваться как I ² C SCL (часы), а второй как I ² C SDA (данные).

Расшифрованные данные I ² C.

UART / Последовательный декодер

Чтобы использовать активный измерительный прибор в качестве последовательного декодера , щелкните значок
UART / Последовательный декодер кнопка на панели быстрых функций.
Будет создан новый ввод / вывод UART / последовательного декодера, который будет подключен к
первый активный канал активного инструмента и подключен к
вновь созданный приемник таблицы для отображения декодированных данных UART / Serial.Его можно использовать для анализа RS232, RS485, MIDI, DMX или других совместимых последовательных шин.

Декодированные последовательные данные.

Локальное поведение полиномиальных функций

Результаты обучения

• Определите точки поворота полиномиальной функции по ее графику.
• Определите количество точек поворота и точек пересечения полиномиальной функции от ее степени.
• Определите пересечения по осям x и y полиномиальной функции с учетом ее уравнения в факторизованной форме.

Определение локального поведения полиномиальных функций

Помимо конечного поведения полиномиальных функций, нас также интересует, что происходит в «середине» функции. В частности, нас интересуют места, где меняется поведение графа. Точка поворота - это точка, в которой значения функции изменяются от увеличения к уменьшению или от уменьшения к увеличению.

Нас также интересуют перехваты. Как и во всех функциях, точка пересечения y- - это точка, в которой график пересекает вертикальную ось.Точка соответствует паре координат, в которой входное значение равно нулю. Поскольку многочлен - это функция, каждому входному значению соответствует только одно выходное значение, поэтому может быть только один перехват y- [latex] \ left (0, {a} _ {0} \ right) [/ latex]. Перехваты x- происходят при входных значениях, которые соответствуют нулевому выходному значению. Возможно иметь более одной точки пересечения x-.

Общее примечание: точки пересечения и поворотные точки полиномиальных функций

• Точка поворота графика - это точка, в которой график изменяется от увеличения к уменьшению или от уменьшения к увеличению.
• Перехват y- - это точка, в которой функция имеет нулевое входное значение.
• -перехваты x - это точки, в которых выходное значение равно нулю.
• Многочлен степени n будет иметь самое большее n x -перехватывание и n - 1 точек поворота.

Определение количества поворотных точек и пересечений по степени полинома

Непрерывная функция не имеет разрывов в графике: график можно нарисовать, не отрывая ручку от бумаги.Плавная кривая - это график без острых углов. Поворотные точки гладкого графика всегда должны приходиться на закругленные кривые. Графики полиномиальных функций бывают как непрерывными, так и гладкими.

Степень полиномиальной функции помогает нам определить количество точек пересечения x и количество точек поворота. Полиномиальная функция n -й степени является произведением факторов n , поэтому она будет иметь не более n корней или нулей, или x -перехваты. {3} [/ latex]

Показать решение

Существует не более 12 точек пересечения x и не более 11 точек поворота.

Как: для заданной полиномиальной функции определить точки пересечения

1. Определите точку пересечения y- , установив [latex] x = 0 [/ latex] и найдя соответствующее выходное значение.
2. Определите перехват x , установив функцию равной нулю и вычислив входные значения.

Использование принципа нулевого произведения для нахождения корней многочлена в факторизованной форме

Принцип нулевого произведения гласит, что если произведение n чисел равно 0, то хотя бы один из множителей равен 0.2 (x + 1) (x-7) [/ латекс]

- это факторизованная форма. В следующих примерах мы покажем процесс факторизации многочлена и вычисления его пересечений по осям x и y.

Пример: определение точек пересечения полиномиальной функции

Дана полиномиальная функция [латекс] f \ left (x \ right) = \ left (x - 2 \ right) \ left (x + 1 \ right) \ left (x - 4 \ right) [/ latex], записывается в факторизованной форме для вашего удобства определите интервалы перехвата y и x .

Показать решение

Перехват y- происходит, когда входной сигнал равен нулю, поэтому замените 0 на x .

[латекс] \ begin {array} {l} f \ left (0 \ right) = \ left (0-2 \ right) \ left (0 + 1 \ right) \ left (0-4 \ right) \ hfill \\ \ text {} f \ left (0 \ right) = \ left (-2 \ right) \ left (1 \ right) \ left (-4 \ right) \ hfill \\ \ text {} f \ left ( 0 \ right) = 8 \ hfill \ end {array} [/ latex]

Перехват y- равен (0, 8).

-Перехват x происходит, когда выход [latex] f (x) [/ latex] равен нулю.

[латекс] 0 = \ left (x - 2 \ right) \ left (x + 1 \ right) \ left (x - 4 \ right) [/ латекс]

[латекс] \ begin {array} {llllllllllll} x - 2 = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x + 1 = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x - 4 = 0 \ hfill \\ \ text {} x = 2 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & \ text {} x = -1 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x = 4 \ end {array} [/ latex]

Преобразования x : [латекс] \ left (2,0 \ right), \ left (-1,0 \ right) [/ latex] и [latex] \ left (4,0 \ right) [ /латекс]. {2} -20x [/ latex], определите y и x- перехватывает.

Показать решение

y - перехват [латекс] \ влево (0,0 \ вправо) [/ латекс]; x -перехват [латекс] \ влево (0,0 \ вправо), \ влево (-2,0 \ вправо) [/ латекс] и [латекс] \ влево (5,0 \ вправо) [/ латекс]

Изображение целиком

Теперь мы можем объединить две концепции точек поворота и точек пересечения, чтобы получить общую картину поведения полиномиальных функций. Эти типы анализа полиномов были разработаны до появления массовых вычислений как способ быстро понять общее поведение полиномиальной функции.Теперь у нас есть быстрый способ с помощью компьютеров графически отображать и вычислять важные характеристики многочленов, которые когда-то требовали много алгебры.

В первом примере мы определим наименьшую степень полинома на основе количества точек поворота и пересечений.

Пример: построение выводов о полиномиальной функции из ее графика

Учитывая график полиномиальной функции ниже, определите наименьшую возможную степень полинома и его четность или нечетность.Используйте конечное поведение, количество перехватов и количество поворотных точек, чтобы помочь вам.

Показать решение

Конечное поведение графа говорит нам, что это граф полинома четной степени.

График имеет 2 точки пересечения x , что соответствует степени 2 или больше, и 3 точки поворота, что соответствует степени 4 или больше. Исходя из этого, было бы разумно сделать вывод, что степень ровная и не менее 4.

Теперь вы пытаетесь определить наименьшую возможную степень многочлена по его графику.

Попробуй

Учитывая график полиномиальной функции ниже, определите наименьшую возможную степень полинома и его четность или нечетность. Используйте конечное поведение, количество перехватов и количество поворотных точек, чтобы помочь вам.

Показать решение

Конечное поведение указывает на полиномиальную функцию нечетной степени; имеется 3 перехвата x и 2 точки поворота, поэтому степень нечетная и не менее 3. Из-за конечного поведения мы знаем, что ведущий коэффициент должен быть отрицательным.

Теперь мы покажем, что вы также можете определить наименьшую возможную степень и количество точек поворота полиномиальной функции, заданной в факторизованной форме.

Пример: построение выводов о полиномиальной функции из факторов ЕГО

Учитывая функцию [латекс] f \ left (x \ right) = - 4x \ left (x + 3 \ right) \ left (x - 4 \ right) [/ latex], определите локальное поведение.

Показать решение

Перехват y находится путем вычисления [latex] f \ left (0 \ right) [/ latex].

[латекс] \ begin {array} {c} f \ left (0 \ right) = - 4 \ left (0 \ right) \ left (0 + 3 \ right) \ left (0 - 4 \ right) \ hfill \ hfill \\ \ text {} f \ left (0 \ right) = 0 \ hfill \ end {array} [/ latex]

Перехват y - [латекс] \ left (0,0 \ right) [/ latex].

Перехваты x находятся путем установки функции равной 0.

[латекс] 0 = -4x \ влево (x + 3 \ вправо) \ влево (x - 4 \ вправо) [/ латекс]

[латекс] \ begin {array} {lllllllllllllll} -4x = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x + 3 = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & x - 4 = 0 \ hfill \\ x = 0 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & \ text {} x = -3 \ hfill & \ hfill & \ text {или} \ hfill & \ hfill & \ text {} x = 4 \ end {array} [/ latex]

Преобразование x : [латекс] \ left (0,0 \ right), \ left (-3,0 \ right) [/ latex] и [латекс] \ left (4,0 \ right) [ /латекс].