Содержание
Функция. Функция графигі — алгебра, уроки
Оқушыларға «Функция» терминін математикаға тұңғыш енгізген ғалым туралы қысқаша тарихи мағұлмат беру (немесе – өздерінің іздеп табуларына жағдай жасау).
Готфрид Вильгельм Лейбниц (немісше Gottfried Wilhelm Leibniz (1646-1716)) – неміс философы және ғалымы,математигі, физигі әрі өнертапқыш тарихшысы.
Топтық жұмыс
Оқушыларға карточкада жазылған терминологияларды таратып беріп, оларды сәйкестендіру арқылы топтарға бөлу. (қазақша сөздер тобы «1-топ», орысша сөздер тобы «2-топ», ағылшынша сөздер тобы «3-топ»)
Топтарға төмендегідей тапсырмалар беріліді. Тапсырмалар орындалып болған соң тапсырманың дұрыс орындалуы сыныпта талданып, талқыланады.
Қазақ тілінде | Орыс тілінде | Ағылшын тілінде | |
1-топ | функцияаргументі | aргумент функции | argumentof a function |
2-топ | тәуелсіз айнымалы | независимая переменная | independentvariable |
3-топ | абсцисса | абсцисса | abscissa |
4-топ | ордината | ордината | ordinate |
1-топ
Тапсырма
Квадраттың қабырғасы a см. Оның периметрін (Р) табыңыздар. Мұндағы а=2; 3; 4.
Оның периметрін (Р) табыңыздар. Мұндағы а=2; 3; 4.
2-топ
Тапсырма
Машина 70 км/сағ жылдамдықпен қозғалып келеді.Машинаның t сағатта қанша жол жүретінін табыңыздар. Мұндағы t = 1; 1,5; 3.
3-топ
Тапсырма
Берілген гарафик бойынша ауа температурасының тәуліктік уақытқа тәуелділігін көрсетіңіздер.
4-топ
Тәуелді айнымалы(y) тәуелсіз айнымалының(x-тің) квадратына тең – деген сөйлемді математикалықтеңдеу түрінде қалай жазуға болады?
Тапсырмаларды орындап болған соң топтар тақтадағы жауаптармен өз жауаптарын тексере отырып, тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының тек бір мәні сәйкес келетінін тұжырымдаулары керек.
Анықтама
Тәуелсіз айнымалының әрбір мәніне тәуелі айнымалының тек бір ғана мәні сәйкес келетін тәуелділікті функционалдық тәуелділік немесе функция деп атайды.
Графикті пайдаланып, аргументтің берілген мәніндегі функцияның мәнін табуға болады.
f: A → R , мұндағы А R-дың ішкі жиыны болсын. А-дағы х – тың әрбір мәні f(x) -тың нақты бір мәнімен байланысты. Бұл байланыс, координата жазықтығының бір ғана нүктесінде (х, f (x)) бейнеленеді.
Топтарға бастапқыда берілген тапсырмаларға сүйене отырып,функционалдық тәуелділіктің берілу тәсілдерін өздері айта алуларына мүмкіндік беру.Топта талдап, жауап беру.
Функционалдық тәуелділіктің берілу тәсілдері
Функцияның формуламен (аналитикалық түрде) берілуі
Графикпен берілуі
Кестемен берілуі
Сөзбен, шартпен берілуі
Тәуелсіз айнымалының қабылдайтын мәндерінің жиыны функцияның анықталу аймағы деп аталады. Мысалдар келтіру.
Функцияның мәндерінің жиыны функцияның мәндерінің аймағы деп аталады. Мысалдар келтіру.
Ауызша тапсырма (презентация)
Жұптық жұмыс
Қисықтардың қайсысы функция графигі бола алады?
f (x ) = 3x + 5 функциясы үшін: f (2), f (-4) мәндерін табыңыз.
Берілген функциялардың анықталу аймақтарын табыңыз:
а) у = 15 – 4х ; b) у =
4. Егер у(х)=2х + 4 функцияның мәні 5,4-ке тең болса, онда функцияның берілген мәні бойынша аргументтің сәйкес мәнін табыңыз.
Жеке тапсырма
№1. Қисықтардың қайсысы функция графигі бола алады? Жауаптарыңызды негіздеңіздер.
Жауабы: ____________________________________
№2.функциясы берілген.
мәндерін табыңыз;
болса, х-ті табыңыз;
берілген функцияның анықталу аймағын тауып, сан аралығында жазып көрсетіңіз.
№3. Функцияны формуламен жазыңыз:
Функцияның мәні аргументке қарама-қарсы;
Функцияның мәні аргументтен 2 есе көп;
Функцияның мәні аргументтің 2 еселенген мәнінен 3 есе кем;
Функция мәні аргумент мәніне тең;
Функция мәні аргументтің екі еселенген мәнінен 1-ге артық.
№4.Берілген функциялардың графигін салып, оның анықталу облысы мен мәндер облысын анықтаңыз:
а) y;
b) ;
c) , мұндағы x ≤ 3;
d).
Деңгейлік тапсырмалар
№1.Егер функцияның анықталу облысы берілсе, онда функциясын жазыңыз.
№2.сызықтық функциясының графигін салып, оның көмегімен
графиктің координата осьтерімен қиылысу нүктелерінің координаталарын;
теңсіздігі орындалатындай аргументтің барлық мәндерін;
теңсіздігі орындалатындайх осінің кесіндісін;
сызықтық функцияның кесіндісіндегі ең үлкен және ең кіші мәндерін анықтаңыз.
Қалыптастырушы бағалау жұмысы (бірін-бірі бағалау) Тапсырманы алғашқы болып орындаған оқушылар мұғалімнің көмегімен, келесі оқушылардың орындаған тапсырмаларын тексеріп, жетістік критерийлеріне сүйене отырып, оқушы бүгінгі сабақ барысында оқу мақсаттарына қаншалықты жеткендіктеріне баға береді.
Барлық берілген тапсырманы орындаған оқушыларға қосымша тапсырма ретінде http://bilimland.kz ресурсынан №1-№14-ші жаттығуларды орындау ұсынылады.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция у = cos x и её график
Сегодня на уроке мы с вами поговорим о функции . Рассмотрим график функции , а также основные свойства этой функции.
Рассмотрим график функции , а также основные свойства этой функции.
Прежде чем приступить к рассмотрению новой темы, давайте напомним,
что функция определена на всей числовой прямой, а множеством её значений
является отрезок . Функция ограничена и её график расположен в полосе между прямыми и .
Также мы знаем, что функция периодическая с периодом , а значит, достаточно построить её график на промежутке длиной . Например, на отрезке .
На предыдущем уроке мы с вами выяснили, что функция является чётной. Известно, что график чётной функции симметричен
относительно оси ординат.
Тогда для построения графика на отрезке нам достаточно построить его на отрезке , а затем симметрично отразить относительно оси Oy.
Прежде чем мы перейдём к построению графика, покажем, что функция убывает на отрезке .
Давайте на единичной окружности с центром в начале координат
отметим точку . Тогда при повороте точки вокруг начала координат против часовой стрелки на угол получим точку .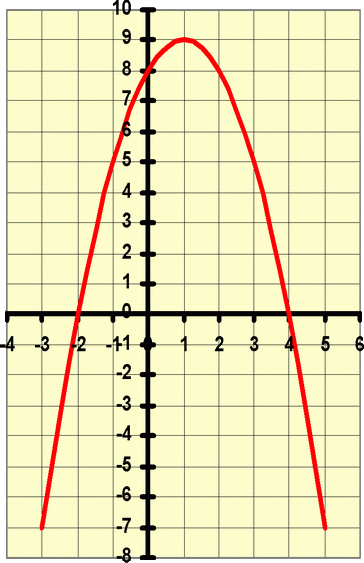 Абсцисса этой точки – .
Абсцисса этой точки – .
При повороте точки вокруг начала координат против часовой стрелки на угол получим точку . Абсцисса этой точки – .
Обратите внимание, что при повороте точки вокруг начала координат против часовой стрелки на угол от до абсцисса точки, то есть , уменьшается от до . Поэтому если , то . Это значит, что функция убывает на отрезке .
Теперь давайте найдём координаты некоторых точек графика функции и заполним таблицу значений функции.
Используя свойство убывания функции и отметив полученные точки на координатной плоскости, построим
график функции на отрезке .
Так как функция игрек равно косинус икс является чётной, то мы
можем отразить построенный на отрезке график симметрично относительно оси Oy. В результате получим график
этой функции на отрезке .
Длина этого отрезка равна , то есть равна периоду функции. А значит, мы можем распространить
график по всей числовой прямой с помощью сдвигов на , и так далее вправо и на , и так далее влево, то есть на , .
Получается, что мы геометрически построили график функции на всей числовой прямой, начав с построения его части на отрезке .
Тогда свойства рассматриваемой функции можно получить, опираясь на
её свойства на отрезке .
Так, например, мы выяснили, что функция убывает на отрезке и является чётной, а значит, на отрезке она возрастает.
А сейчас давайте поговорим об основных свойствах функции .
Вы уже знаете, что область определения функции – множество всех действительных чисел.
Множество значений – отрезок .
Функция является чётной, то есть .
График функции симметричен относительно оси ординат.
Функция периодическая с периодом .
Функция принимает значение, равное , при , .
Наибольшее значение функция принимает при .
Наименьшее значение функция принимает при ,.
при , .
при , .
Возрастает функция на отрезках , .
Убывает функция на отрезках , .
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите все корни уравнения
, принадлежащие отрезку .
Решение.
Задание второе. Найдите все решения
неравенства , принадлежащие отрезку .
Решение.
Оператор | Описание |
Простейшие математические операции | |
+ — * / () | Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 | Десятичные дроби записываются через точку:
|
ln(x) | Натуральный логарифм (логарифм c основанием e): log(x) |
logax | Логарифм от x по основанию a: log(x)/log(a) |
lg(x) | Десятичный логарифм (логарифм по основанию 10): log(x)/log(10) |
ex | Экспоненциальная функция: exp(x) |
Тригонометрические функции | |
sin(x) | Синус от x: sin(x) |
cos(x) | Косинус от x: cos(x) |
tg(x) | Тангенс от x: tan(x) |
ctg(x) | Котангенс от x: 1/tan(x) |
arcsin(x) | Арксинус от x: arcsin(x) |
arccos(x) | Арккосинус от x: arccos(x) |
arctan(x) | Арктангенс от x: arctan(x) |
arcctg(x) | Арккотангенс от x: \pi/2 — arctan(x) |
Некоторые константы | |
e | Число Эйлера e: \e |
π | Число π: \pi |
Сызықтық функция және оның графигі
у = kx + l (мұндағы x – тәуелсіз айнымалы, k және l – қандай бір сандар) формуласымен берілген функция сызықтық деп аталады.
Мысалы, \(y=2x-3, \,y=-5x+1,2,\,\) т.с.с.
Сызықтық функцияның графигі түзу сызық болады.
Сызықтық функцияның графигі түзу болғандықтан, екі нүктенің координатасын тауып, түзу салу керек.
Ол нүктенің бірі ретінде абсциссасы 0-ге тең нүктені алған тиімді.
Мысалы, \(y={2\over3}x-y\) функциясының графигін салайық. Ол үшін х = 0, у = –4, А(0; –4) және х = 3, y = –2, В (3; –2) нүктелерді координаталық жазықтықта белгілеп, осы нүктелер арқылы түзу сызу жеткілікті.
Берілген нүктенің түзуге тиісті немесе тиісті болмауын анықтау үшін нүктенің координаталары х пен у-тың орнына қойып, дұрыс теңсіздік шығатынын тексеру керек.
Мысалы, у = 2х + 3 функциясының графигіне А(–1; 1) және В(2; 5) нүктелерінің тиісті болатынын не болмайтынын анықтайық. Ол үшін:
А нүктесі: 1 = 2 · (–1) + 3; 1 = 1 ⇒ тиісті;
В нүктесі: 5 = 2 · 2 + 3; 5\(\neq\)7 ⇒ тиісті емес.
\(y=kx+l\) функциясының графигі k > 0 болса, І және ІІІ ширекте, k < 0 болса, ІІ және ІV ширекте орналасады.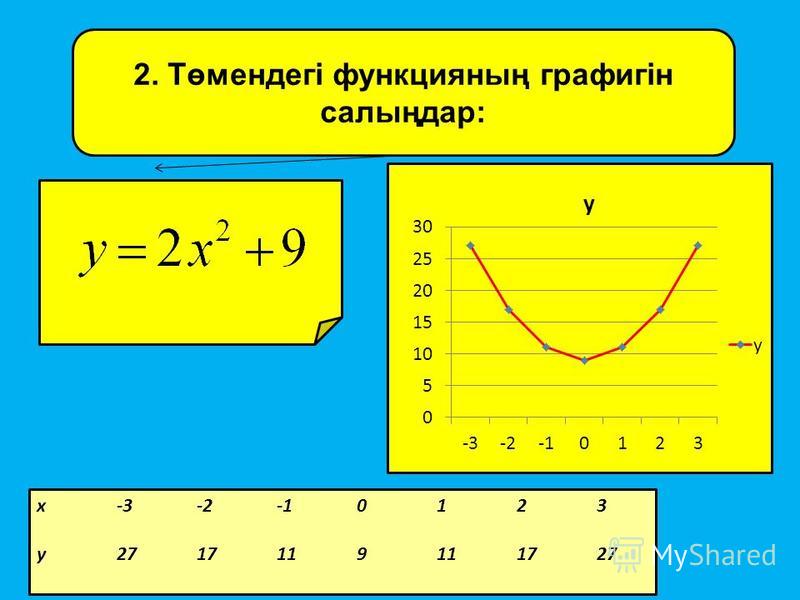
Cызықтық функцияның дербес жағдайлары
\(y=kx+l\) функциясында l = 0 болса, онда \(y=kx\) түрінде болады.
\(y=kx\) формуласымен берілген функцияны тура пропорционалдық деп аталады.
Мысалы, у = 2x; \(y={3\over2}x; \, y=-1,2x; \, y=-{5\over8}x;\) у = kx тура пропорционалдығының графигі – координаталар басы арқылы өтетін түзу болса, І, ІІІ ширекте, k > 0 болса, ІІ, ІV ширекте жатады.
k = 0 болса, онда у = l тұрақты функция болады, оның графигі ОХ осіне параллель түзулер.
Егер k мәндері тең болса, у = kx және у = kx + l түзулері өзара параллель болып орналасады.
Сызықтық функциялар графиктерінің орналасуы
Бір координаталық жазықтықта орналасқан екі сызықтық функциялардың графиктері қиылысу үшін бұрыштық коэффициенттері (х-тың алдындағы коэффициент) тең болмауы керек.
Мысалы, y = 3x + 2 мен y = 2x – 3 болса, онда бұл графиктер бір нүктеде қиылысады.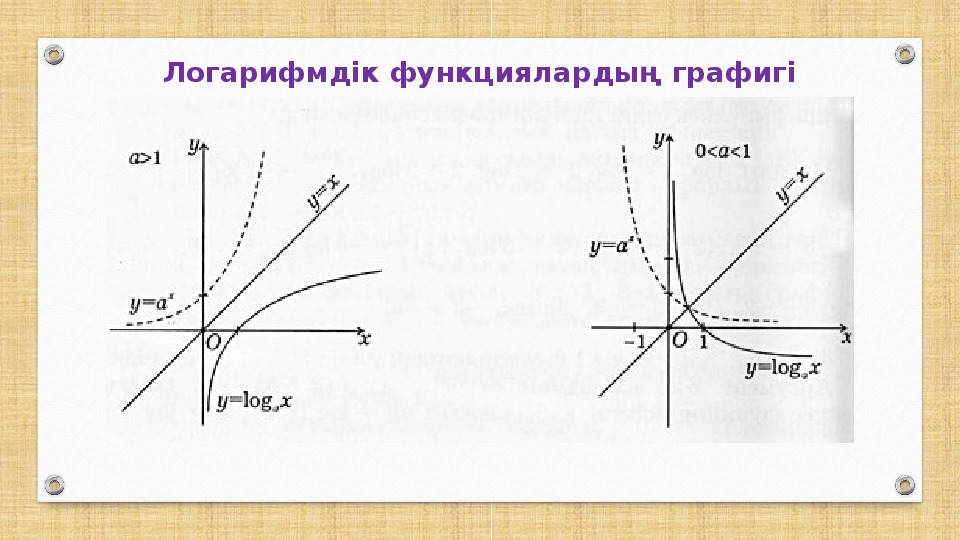 Оны табу үшін: 3x + 2 = 2x – 3, x = –5, y = 3 · (–5) + 2 = –15 + 2 = –13. Ендеше (–5; –13) нүктесінде қиылысады.
Оны табу үшін: 3x + 2 = 2x – 3, x = –5, y = 3 · (–5) + 2 = –15 + 2 = –13. Ендеше (–5; –13) нүктесінде қиылысады.
Егер сызықтық функциялардың бұрыштық коэффициенттері тең болса, онда олардың графиктері параллель болатын түзулер болады.
Мысалы, \(y={2\over3}x-5\) және \(y={2\over3}x+3\) функциялардың бұрыштық коэффициенттері тең \(k={2\over3}\), олар параллель болады.
График функции с модулем | Алгебра
Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.
Рассмотрим примеры таких заданий.
1) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
x-2=0, x=2.
Найдём значение функции при x=2.
y(2)=5·0-2²+5∙2-3∙0-6=0.
Получили точку (2;0).
2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.
Если x-2>0, то есть при x>2, |х-2|=x-2,
y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.
y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
Координаты вершины параболы
то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).
3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.
Если x-2<0, то есть при x<2, |х-2|=-(x-2),
y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.
y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.
Координаты вершины параболы
то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².
Прямая x=2 разбивает координатную плоскость на две полуплоскости.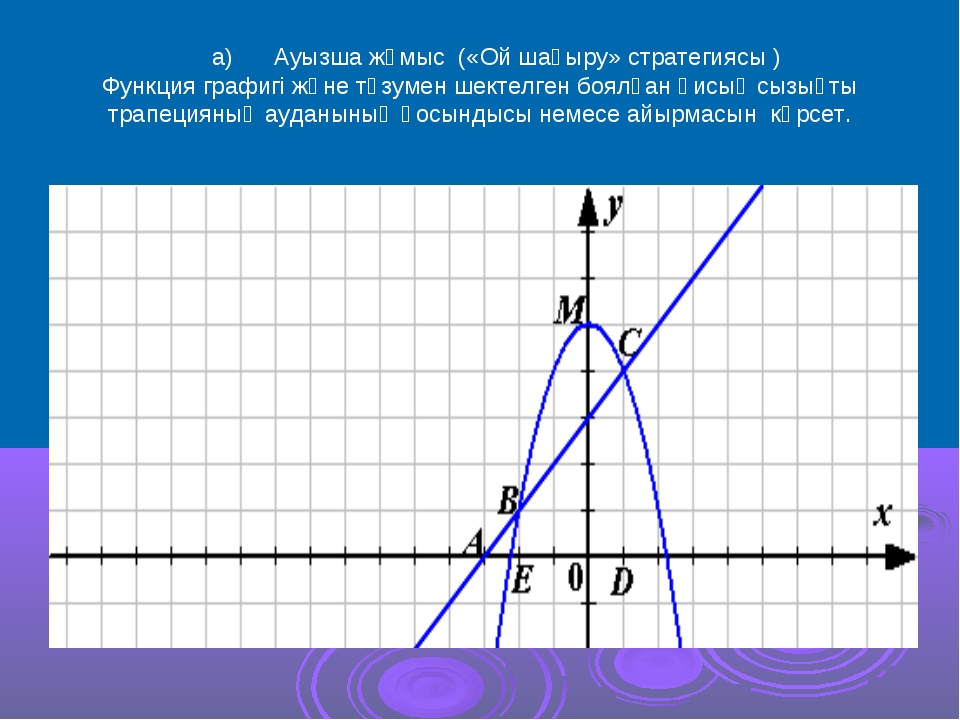 Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:
Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:
График функции с модулем можно рассматривать и как график кусочной функции:
Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:
Ответ: 0; 4.
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.
y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).
Координаты вершины параболы
Так как a=1, от вершины (3;-10) строим график y=x².
|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.
y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.
График — парабола ветвями вверх.
Координаты вершины параболы
от вершины (-3;-8) строим график y=x².
Или:
Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:
Ответ: -8; 1/36.
3) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x=0, y=|0|·0+3·|0|-5·0=0.
2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.
y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).
Координаты вершины параболы
От вершины (1;-1) строим параболу y=x² (так как a=1).
3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.
y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).
Координаты вершины параболы
От вершины (-4;16) строим параболу y=-x² (так как a=-1).
Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:
Альтернативный вариант:
Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:
Ответ: -1; 16.
4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
Область определения функции D(y): x∈R.
Построим график функции y=x²+2x-3.
Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.
Координаты вершины параболы
, то есть вершина параболы — точка (-1;-4).
От вершины строим график функции y=x²:
График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.
Или y=|x²+2x-3|
Вершина параболы (-1;-4) при этом переходит в точку (-1;4):
Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).
Ответ: 4.
Сызықтық функция және оның графигі • Martebe.kz білім сайты
ІІ. Ынталандыру жұмысы. Үштілділікті жүзеге асыру үшін орындалады. Оқушыларға жеке үлестірме қағаздары тарқатылады. Әрбір оқушы тапсырманы жеке орындайды. Мұғалім дұрыс жауабын айтады, оқушылар өзін-өзі тексереді.
| English | Русский | Қазақ |
| Linear function | Линейная функция | Сызықтық функция |
Алдыңғы білімді жаңғырту: Жеке жұмыс
Cіз Оралдан Ақтөбе қаласына шықтыңыз және сіз мотоциклмен, жаяу және вертолетпен әр түрлі тәсілдермен жүрдіңіз.
1) Сіз 2 сағ. кейін жол басынан бастап қандай қашықтықта болдыңыз?
2) Қашан және қанша сағат сіз демалып тұрдыңыз?
3) Сонда сізге барлық жолға неше уақыт кетті?
Жаңа білімді меңгерту.
Жалпы сұрақ:
Жылдамдығы тұрақты 60км/сағ болатын машинаны қарастырайық. Яғни машина 1 сағатта 60 км жол жүреді. Өздеріңізге сұрақ қойыңыз: машина 2 сағатта қанша жол жүреді? Машинаның 2 сағаттағы жолын табу үшін 60км жолды 2 сағатта көбейтетінімізді білеміз. Бұдан біз 60*2, яғни 120 км екенін табамыз.
Әртүрлі уақытта машина қандай жол жүретінін кестеден таба аламыз. Кестеден машинаның жолды жүріп өткен уақыт пен жолдың арасында тәуелділік барын көреміз. У (жол)тәуелді х-тен(уақыт) деп алайық. у=60*x деп аламыз.
Оқушылар өз жауаптарын А3 қағазына жазып көрсетеді. Дұрыс жауабын бірге талдайды.
Мұғалім презентация арқылы сызықтық функцияның анықтамасын айтады.
Анықтама. ( мұндағы х-тәуелсіз айнымалы, k және b-қандай да бір сандар) формуласымен берілген функция сызықтық функция деп аталады.
Мыс:
Жоғарды берілген функциялардың к-бұрыштық коэффициенттері мен b табайық.
сызықтық функциясының графигін салып үйренейік.
Есте сақтаңыз! Сызықтық функцияның графигі түзу сызық болады.
Функцияның графигін салу үшін кесте құрып, аргумент х-ке 2 мән беріп у функцияның мәнін тапсақ жеткілікті.
Мыс.y=-2x+1 функциясының графигін салайық. Х-тің мәніне 1 және 0 сандарын алған жеңіл, өйткені есептеуге оңай.Мәндерін беріп, координаталық жүйеге нүктелерді салып, екеуін қосып, түзу сызық саламыз.
1)Сызықтық функциялардың графиктерін салу дағдыларын дамыту үшін оқушыларға жұптық жұмысты ұсынамыз. Оқушылар жұпқа бөлініп, тапсырма орындайды. Жұптар бірін –бірі бағалайды.
1- тапсырма
а) Берілген функциялардың графиктерін салыңдар
2- тапсырма
Берілген графиктер арасынан сызықтық функция графиктерін айқындаңдар
a)
b)
с)
d)
| № | Дискрипторлар | |
|
1
| y = kx+l функциясының анықтамасын біледі | 1 |
| функциясының графигін дұрыс салады
| 1 | |
| функциясының графигі дұрыс салады
| 1 | |
| 2 | берілген графиктер арасынан сызықтық функция графиктерін айқындайды | 1 |
2) Топтық жұмыс.
Топтық жұмыстың мақсаты: Сызықтық функциялардың орналасуын түсіну.
Құндылықтарды дарыту: топта бір-бірінін пікірін тындай білу;
Оқушылар кестеде көрсетілген таңбаларға сәйкес келетін коэффициенттері кез келген сызықтық функцияларды жазып және олардың графиктерін салу керек. Содан соң оқушылар өздері салған графиктерді көрсетеді және басқа оқушылардың графиктерімен салыстырады. Оқушылар салыстыру нәтижелерін талдайды.
Мұғалім топтардың жұмысын бағалап, сыни сұрақтар қойып, оқушылардың зерттеушілік қабілетін оятады. Сонында оқушылар ұстаздарымен бірге қорытынды жасайды.
3) Оқушылармен координаталық осьтерінде орналасқан нүктелердің координаталары туралы талқылаймыз. (Ох осінде, (а; 0), Оу осінде (0; а)). Оқушыларға графиктің осімен қиылысу нүктелері графикке де, оське де тиісті екенін түсіндіру керек, яғни оның координаталары (0; а) немесе (а; 0) нүктесінің координаталарымен сәйкес келеді, бұдан функционалдық тәуелділік теңдігін дұрыс сандық тепе-теңдікке айналдырады. Осылайша оқушыларға сызықтық функция графиктерінің координаталық осьтерімен қиылысу нүктелерінің координаталарын табу алгоритмін жазуды ұсынамыз.
Жұптық жұмыс. Бір оқушы берілген функция графигінің Оу осімен, екіншісі Ох осімен қиылысу нүктесін табады. Оқушылар бір-біріне өз шешімдерін түсіндіреді.
в) Берілген фунциялардың графиктерін салмай олардың Ох осімен және Оу осімен қиылысу нүктесін табыңдар.
| № | Дискрипторлар | |
| а) | Сызықтық функцияның Ох осімен қиылысу нүктесінің координатасын дұрыс таба біледі | 1 |
| Сызықтық функцияның Оу осімен қиылысу нүктесінің координатасын дұрыс таба біледі | 1 | |
| b) | Сызықтық функцияның Ох осімен қиылысу нүктесінің координатасын дұрыс таба біледі | 1 |
| Сызықтық функцияның Оу осімен қиылысу нүктесінің координатасын дұрыс таба біледі | 1 |
Жоғары деңгейлі оқушылар үшін:
Суреттегі түзулер графигі болатын сызықтық функцияларды формуламен жазыңдар.
Бағалау критерийлері.
| № | Дескрипторлар | |
| 1 | Графигі (m) бойынша функцияның графигін дұрыс анықтайды. | 1 |
| Графигі (n) бойынша функцияның графигін дұрыс анықтайды. | 1 | |
| Графигі (l) бойынша функцияның графигін дұрыс анықтайды. | 1 |
График функций и калькулятор
Описание :: Все функции
Описание
Function Grapher — это полнофункциональная графическая утилита, которая поддерживает одновременное построение графиков до 5 функций.
Вы также можете сохранить свою работу как URL (ссылка на веб-сайт).
Использование
Чтобы построить функцию, просто введите ее в поле функции.
Используйте «x» в качестве переменной, например:
Примеры:
- грех (x)
- 2x − 3
- соз (х ^ 2)
- (х − 3) (х + 3)
Масштабирование и повторное центрирование
Для увеличения используйте ползунок масштабирования.
Функции
| кв. | Квадратный корень значения или выражения. | |
|---|---|---|
| грех | синус значения или выражения | |
| cos | Косинус значения или выражения | |
| желто-коричневый | тангенс значения или выражения | |
| asin | обратный синус (арксинус) значения или выражения | |
| acos | обратный косинус (arccos) значения или выражения | |
| атан | Арктангенс (арктангенс) значения или выражения | |
| шин | Гиперболический синус (sinh) значения или выражения | |
| кош | Гиперболический косинус (cosh) значения или выражения | |
| танх | Гиперболический тангенс (tanh) значения или выражения | |
| эксп. | e (константа Эйлера) в степени значения или выражения | |
| пер. | Натуральный логарифм значения или выражения | |
| журнал | Логарифм по основанию 10 значения или выражения | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. | |
| потолок | Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу. | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| знак | Знак (+1 или -1) значения или выражения | |
| факт | факториальная функция |
Константы
| пи | Константа π (3.141592654 …) | |
|---|---|---|
| e | Число Эйлера (2,71828 …), основание натурального логарифма |
Описание графика функции
Иногда вам нужно описать график функции несимвольным образом. Например, вас могут спросить
- увеличивается или уменьшается функция;
- имеет ли он одно минимальное значение или максимальное значение, или несколько таких значений
- линейно это или нет
- будь то
скорость изменения
постоянно, увеличивается или уменьшается
- имеет ли он верхнюю или нижнюю границу.
Пример 1:
Опишите две функции
ж
(
Икс
)
а также
грамм
(
Икс
)
, используя термины «возрастание», «убывание», «максимум» и «минимум».
График
ж
(
Икс
)
периодический. Он уменьшается для
—
3
< Икс < - 1 , то увеличивается при - 1 < Икс < 1 , затем снова уменьшается при 1 < Икс < 3 , так далее.
Имеет максимальное значение
1
и минимальное значение
—
1
, и он многократно достигает этих максимумов и минимумов. Верхняя граница функции равна
1
и нижняя граница
—
1
.
График
грамм
(
Икс
)
увеличивается для
—
∞
< Икс < - 1 и уменьшается для - 1 < Икс < ∞ .График принимает максимальное значение 3 в Икс знак равно - 1 . У него нет минимума.
Пример 2:
Какой график имеет более высокую скорость изменения?
Оба графика начинаются вместе в
(
0
,
0
)
. Сначала линейная функция,
грамм
(
Икс
)
, имеет более высокую скорость изменения.
Но
ж
(
Икс
)
скоро догоняет и превосходит
грамм
(
Икс
)
в
(
8
,
16
)
, и продолжает увеличиваться более быстрыми темпами.
Как построить график функций кривых
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Функции и графики
Автор M Bourne
В реальном мире очень часто одна величина зависит от другой величины.
Например, если вы работаете в заведении быстрого питания, ваш пакет заработной платы зависит от количества часов, которые вы работаете. Или количество бетона, которое вам нужно заказать при строительстве здания, будет зависеть от высоты здания.
1234-1-212345-1xy Открыть изображение на новой странице
Декартова плоскость
В этой главе рассказывается о функциях (так мы выражаем отношения между величинами) и их графиках .
График функции действительно полезен, если мы пытаемся смоделировать как реальную проблему.(«Моделирование» — это процесс нахождения взаимосвязей между величинами.)
Иногда мы можем не знать выражения для функции, но знаем некоторые значения (возможно, из эксперимента). График может дать нам хорошее представление о том, какую функцию можно применить к ситуации для решения проблемы.
В этой главе
Обзор функций
1. Введение в функции — определение функции, обозначение функций и примеры
2. Функции из словесных заявлений — превращение словесных задач в функции
Графики функций
3.Прямоугольные координаты — система, которую мы используем для построения графиков наших функций
4. График функции — примеры и приложение
Домен и диапазон функции — значения x и y, которые может принимать функция
5. Построение графиков с помощью системы компьютерной алгебры — некоторые мысли об использовании компьютеров для построения графиков функций
6. Графики функций, определяемых таблицами данных — часто у нас нет алгебраического выражения для функции, только таблицы
7. Непрерывные и разрывные функции — разница становится важной в более поздней математике
8.Функции разделения — они имеют разные выражения для разных значений независимой переменной
.
9. Четные и нечетные функции — полезны в более сложной математике.
Давайте теперь узнаем об определении функции и обозначении функции.
Как построить график функции
Обновлено 4 декабря 2020 г.
Автор: Джон Папевски
Построить график математических функций не так уж сложно, если вы знакомы с функцией, которую строите на графике.Каждый тип функции, будь то линейная, полиномиальная, тригонометрическая или какая-либо другая математическая операция, имеет свои особенности и особенности. Подробная информация об основных классах функций дает отправные точки, подсказки и общие рекомендации по их построению в виде графиков.
TL; DR (слишком долго; не читал)
Чтобы построить график функции, вычислите набор значений оси y на основе тщательно выбранных значений оси x , а затем постройте график полученные результаты.
Построение графиков линейных функций
Линейные функции являются одними из самых простых для построения графиков; каждый — просто прямая линия.Чтобы построить линейную функцию, вычислите и отметьте две точки на графике, а затем проведите прямую линию, проходящую через обе из них. Формы point-slope и y -intercept сразу дают вам одно очко; линейное уравнение с перехватом y имеет точку (0, y ), а наклон точки имеет произвольную точку ( x , y ). Чтобы найти еще одну точку, вы можете, например, установить y = 0 и найти x . Например, для построения графика функции:
y = 11x + 3
3 — пересечение y , поэтому одна точка равна (0, 3).
Установка y на ноль дает следующее уравнение:
0 = 11x + 3
Вычтем 3 с обеих сторон:
0 — 3 = 11x + 3 — 3
-3 = 11x
\ frac {-3} {11} = \ frac {11x} {11}
\ frac {-3} {11} = x
Итак, ваша вторая точка (−0,273, 0)
При использовании В общем виде вы устанавливаете y = 0 и решаете для x , а затем устанавливаете x = 0 и решаете для y , чтобы получить две точки.Чтобы построить график функции, x — y = 5, например, установка x = 0 дает y из -5, а установка y = 0 дает x из 5. Две точки — (0, −5) и (5, 0).
Графические триггерные функции
Тригонометрические функции, такие как синус, косинус и тангенс, являются циклическими, а график, построенный с помощью триггерных функций, имеет регулярно повторяющийся волнообразный узор. Например, функция
y = \ sin (x)
начинается с y = 0, когда x = 0 градусов, затем плавно увеличивается до значения 1, когда x = 90, уменьшается до 0, когда x = 180, уменьшается до -1, когда x = 270, и возвращается к 0, когда x = 360.Шаблон повторяется бесконечно. Для простых функций sin ( x ) и cos ( x ) y никогда не выходит за пределы диапазона от -1 до 1, и функции всегда повторяются каждые 360 градусов. Функции касательной, косеканса и секанса немного сложнее, хотя они тоже следуют строго повторяющимся образцам.
Более общие триггерные функции, такие как
y = A × \ sin (Bx + C)
, предлагают свои собственные сложности, хотя с изучением и практикой вы можете определить, как эти новые термины влияют на функцию.Например, константа A, изменяет максимальное и минимальное значения, поэтому она становится A и отрицательной A вместо 1 и -1. Постоянное значение B увеличивает или уменьшает частоту повторения, а постоянное значение C сдвигает начальную точку волны влево или вправо.
Построение графиков с помощью программного обеспечения
Помимо построения графиков вручную на бумаге, вы можете автоматически создавать графики функций с помощью компьютерного программного обеспечения.Например, многие программы для работы с электронными таблицами имеют встроенные возможности построения графиков. Чтобы построить график функции в электронной таблице, вы создаете один столбец со значениями x , а другой, представляющий ось y , как вычисленную функцию столбца значений x . Когда вы заполнили оба столбца, выберите их и выберите функцию точечной диаграммы программного обеспечения. 2} + 4 \ hspace {0.25 дюймов} & {\ mbox {on}} \ hspace {0,25 дюйма} x
Нам нужно быть немного осторожнее с тем, что происходит прямо в \ (x = 1 \), поскольку технически это будет справедливо только для нижняя функция. Однако мы разберемся с этим в самом конце, когда фактически построим график. На данный момент мы будем использовать \ (x = 1 \) в обеих функциях.
Первое, что нужно сделать здесь, это получить таблицу значений для каждой функции в указанном диапазоне, и снова мы будем использовать \ (x = 1 \) в обоих, хотя технически это должно использоваться только с нижней функцией.2} + 4 \)
| \ (х \) | \ (2x — 1 \) | \ (\ влево ({х, у} \ вправо) \) |
|---|---|---|
| 1 | 1 | \ (\ слева ({1,1} \ справа) \) |
| 2 | 3 | \ (\ влево ({2,3} \ вправо) \) |
| 3 | 5 | \ (\ влево ({3,5} \ вправо) \) |
Вот набросок графика и обратите внимание, как мы обозначили точки в \ (x = 1 \).Для верхней функции мы использовали открытую точку для точки в \ (x = 1 \), а для нижней функции мы использовали закрытую точку в \ (x = 1 \). Таким образом мы проясняем на графике, что только нижняя функция действительно имеет точку в \ (x = 1 \).
Обратите внимание, что, поскольку два графика не пересекаются в точке \ (x = 1 \), мы оставили пустое место в графике. НЕ соединяйте эти две точки линией. Там действительно должен быть перерыв, чтобы показать, что две части не пересекаются в точке \ (x = 1 \).
Иногда две части встречаются в этих точках, а иногда нет. Мы никогда не должны ожидать, что они встретятся или не встретятся, пока мы на самом деле не набросаем график.
Мобильная версия | Выходные данные и конфиденциальность | Математика / Анализ — Плоттер — Калькулятор 4.0
+ C: ConnectDottedDashed –Dashed –Заполнить заполнитьЗаполнить
+ C: ConnectDottedDashed –Dashed –Заполнить заполнитьЗаполнить
+ C: ConnectDottedDashed –Dashed –Заполнить заполнитьЗаполнить
| |||||

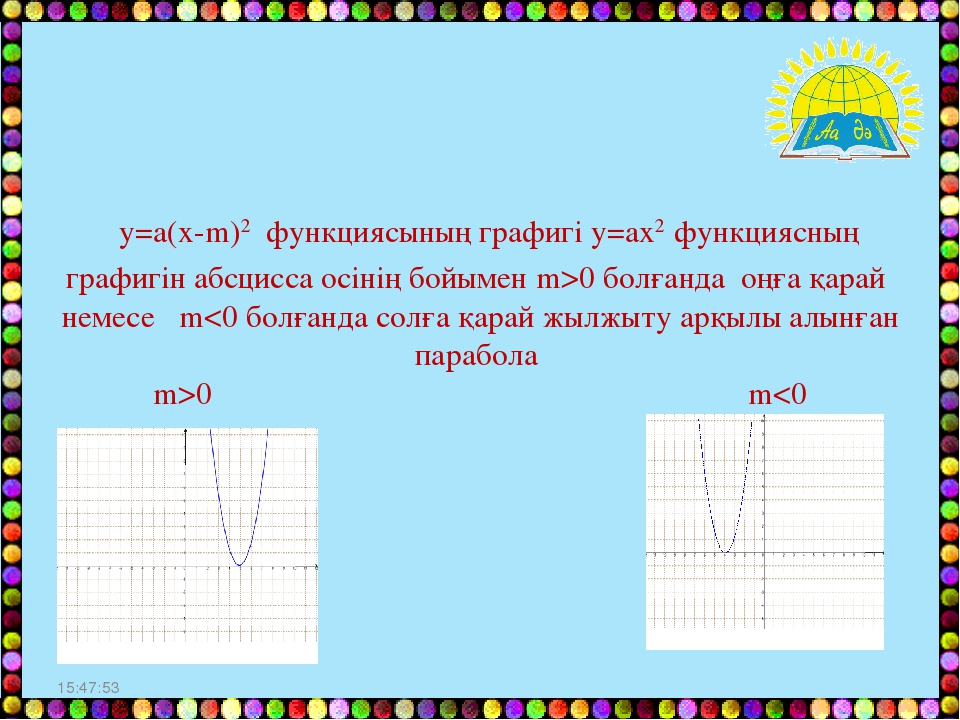 Л.Галицкий. Сборник задач по алгебре, №8.159)
Л.Галицкий. Сборник задач по алгебре, №8.159)
 Н.Шыныбеков. Алгебра, учебник 8 кл, №3.45)
Н.Шыныбеков. Алгебра, учебник 8 кл, №3.45)
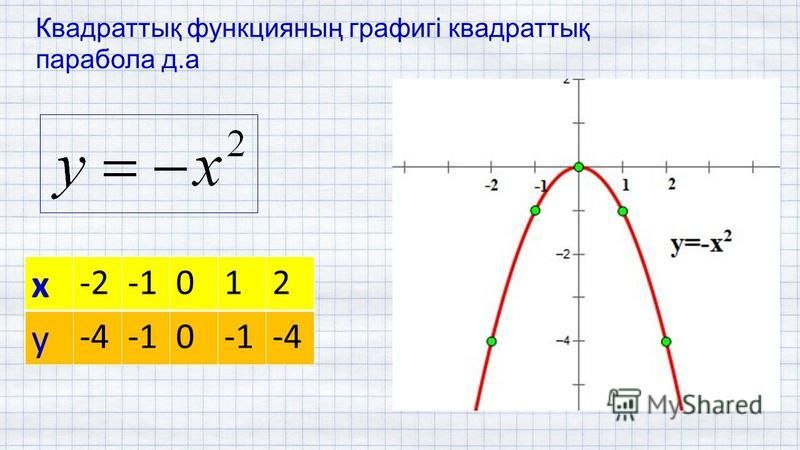 И. Шабунин. Методическое пособие математика, стр.175)
И. Шабунин. Методическое пособие математика, стр.175)
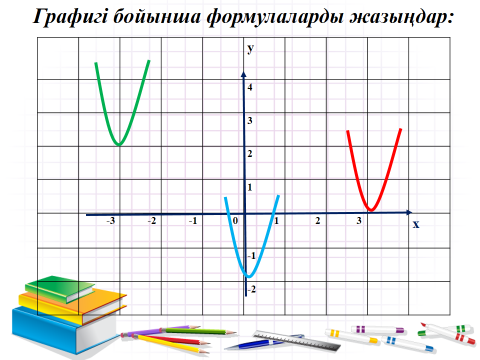 Л.Галицкий. Сборник задач по алгебре, №8.98)
Л.Галицкий. Сборник задач по алгебре, №8.98)
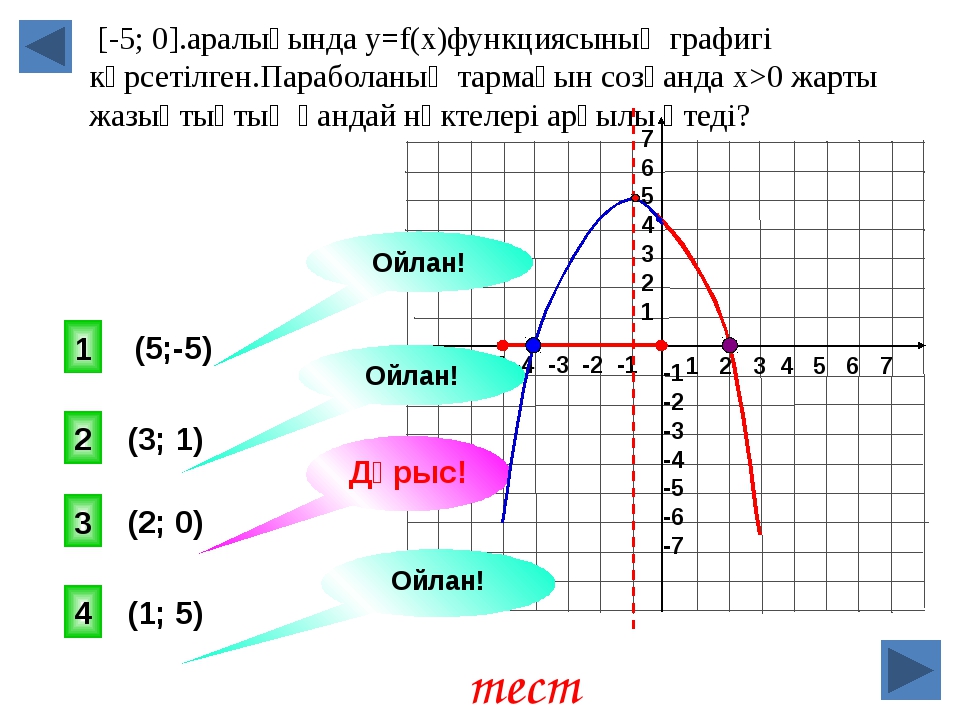 П. Иванов. Сборник задач по математике стр. 61, №65)
П. Иванов. Сборник задач по математике стр. 61, №65)
 А. Бачурин. Задачи по элементарной математике стр. 415, №17)
А. Бачурин. Задачи по элементарной математике стр. 415, №17)
 Л.Галицкий. Сборник задач по алгебре, №8.159)
Л.Галицкий. Сборник задач по алгебре, №8.159)
 Н.Шыныбеков. Алгебра,учебник 8 кл., №3.45)
Н.Шыныбеков. Алгебра,учебник 8 кл., №3.45)
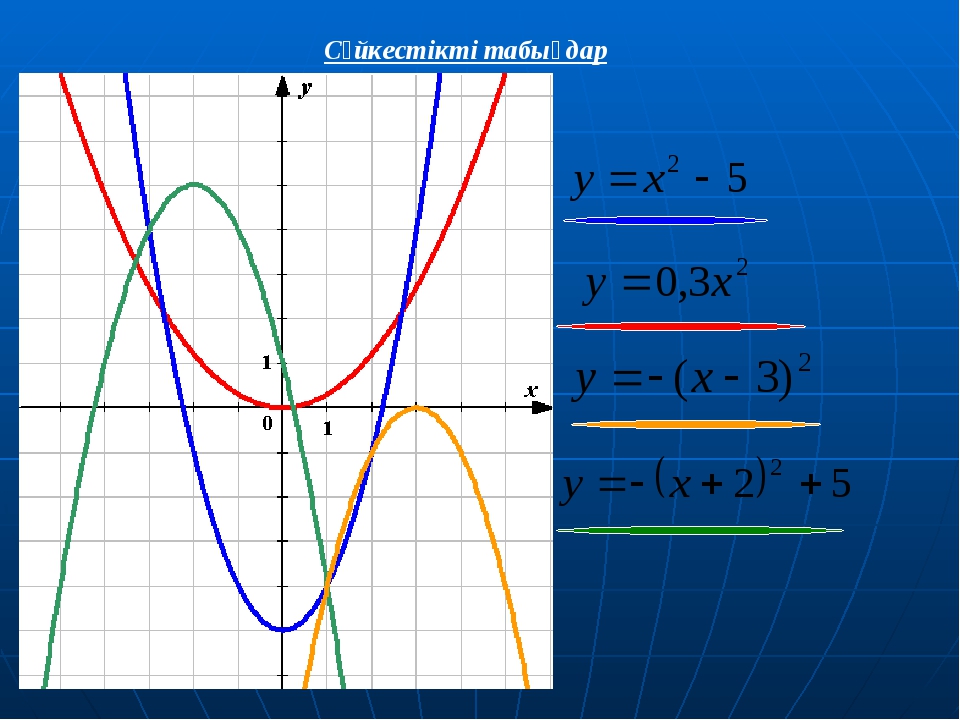 И. Шабунин. Методическое пособие математика, стр.175)
И. Шабунин. Методическое пособие математика, стр.175)
 Л.Галицкий. Сборник задач по алгебре, №8.98)
Л.Галицкий. Сборник задач по алгебре, №8.98)
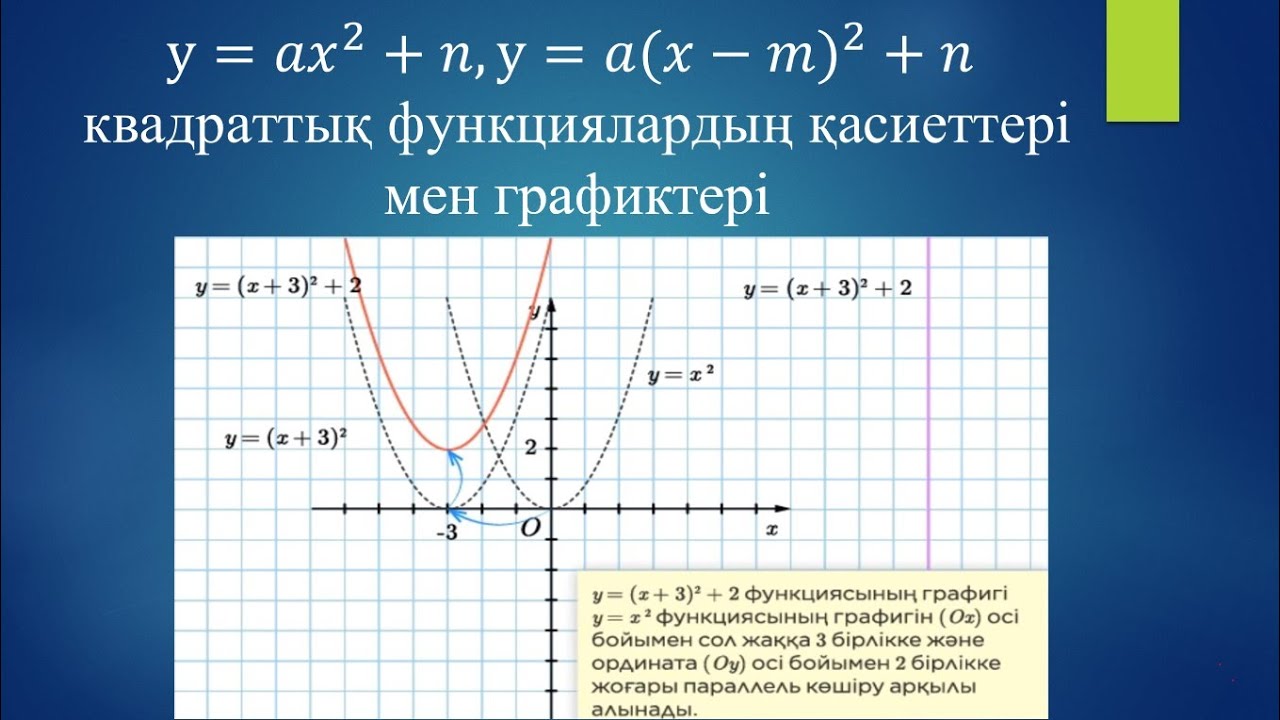 П. Иванов. Сборник задач по математике стр. 61, №65)
П. Иванов. Сборник задач по математике стр. 61, №65)
 А. Бачурин. Задачи по элементарной математике стр. 415, №17)
А. Бачурин. Задачи по элементарной математике стр. 415, №17)
 (1/n)
(1/n)