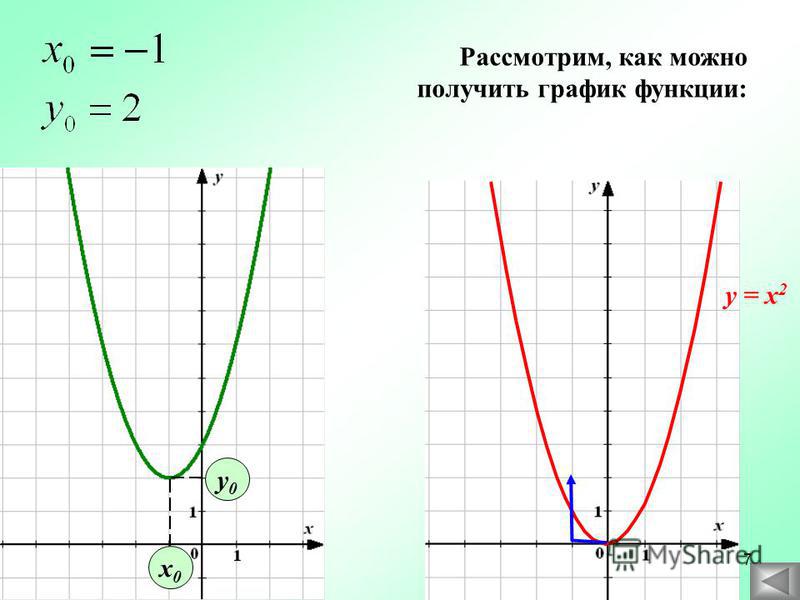
Содержание
Функция у=х2 и её график
1. Функция y = x2 и её график
Функция y =
и её график
2
x
Урок алгебры в 7 классе.
2. «Величие человека в его способности мыслить»
Блез Паскаль
3. Фалес:
— Что есть больше всего на свете?
— Пространство.
— Что быстрее всего?
— Ум.
—
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого результата.
(2;-2)
(- 2;2)
(1;2)
(-2; 2)
(-1;1)
(1;-1)
(2;2)
Ф
У
Н
К
Ц
И
Я
Объясните термины
Функция
График функции
Область
определения
Аргумент
Линейная функция
Укажите
область определения функции:
y = 16 – 5x
10
y
х
х – любое
число
х≠0
1
y
х 7
х≠7
7. Зависимость площади квадрата от длины его стороны
S a
Зависимая
переменная
а
а
2
Независимая
переменная
2
y
y = xx
квадратичная функция
8.
 Функция y = x2 и её график
Функция y = x2 и её график
Функция y =
и её график
2
x
9. Цели урока:
• рассмотреть график и свойства
функции у = х2 ;
• научиться строить и «читать» график
данной функции.
Оноре де Бальзак
Ключом ко всякой науке
является вопросительный
знак?
Математическое
исследование
Функция y =
2
x
Заполните таблицу значений функции y = x2:
х
y
— 3 — 2,5
9
6,25
4
2,25
1
0,25
0
х
y
0
0,5
1
1,5
2
2,5
3
0
0,25
1
2,25
4
6,25
9
— 2 — 1,5
— 1 — 0,5
0
Постройте
график
функции y
= x2
Историческая справка
Древнегреческий математик
Аполлоний Пергский
( Перге, 262 до н.э. — 190 до н.э.)
разрезав конус, линию среза назвал
параболой, что в переводе с греческого
означает «приложение» или «притча»,
о чём математик и написал в
восьмитомнике «Конические сечения».
И долгое время параболой называли
лишь линию среза конуса, пока не
появилась квадратичная функция.
Знаете ли вы?
Траектория камня,
брошенного под углом к
горизонту
Невероятно,
но факт!
Перевал Парабола
17. Свойства функции y = x2
Свойства функции
y=
2
x
• Область
определения
функции :
х – любое число.
• Область значений
функции:
все значения у ≥ 0.
• Если х = 0, то у = 0.
График функции
проходит через
начало координат.
II
I
• Если х ≠ 0,
то у > 0.
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
• Противоположным
значениям х
соответствует одно
и то же значение у.
График функции
симметричен
относительно оси
ординат.
(- х)2 = х2 при любом х
Геометрические
свойства параболы
• Обладает симметрией
• Ось разрезает параболу
на две части: ветви
параболы
• Точка (0; 0) – вершина
параболы
• Парабола касается оси
абсцисс
Ось
симметрии
Найдите у, если:
«Знание – орудие,
а не цель»
х = 1,4 — 1,4
у ≈ 1,9
х = — 2,6
у ≈ 6,7
х = 3,1 — 3,1
у ≈ 9,6
Найдите х, если:
Л. Н. Толстой
Н. Толстой
у=6
у=4
х ≈ 2,5 х ≈ -2,5
х=2
х=-2
Найдите
несколько значений
х, при которых
значения функции :
меньше 4
больше 4
• Принадлежит ли графику функции у = х2 точка:
P(-18; 324)
R(-99; -9081)
принадлежит
не принадлежит
S(17; 279)
не принадлежит
• Не выполняя вычислений, определите, какие из
точек не принадлежат графику функции у = х2:
(-1; 1)
(-2; 4)
(0; 8)
(3; -9)
(1,8; 3,24)
(16; 0)
• При каких значениях а точка Р(а; 64) принадлежит
графику функции у = х2.
а = 8; а = — 8
Решите графически
уравнение:
х2 = 5
y=х
х ≈ y- 2,2;
= 5 х ≈ 2,2
х2 = — 1
нетy решений
=-1
x2 = х +1
х ≈ y- 0,6;
= x +х1≈ 1,6
2
27. Цели урока:
• рассмотреть график и свойства
функции у = х2 ;
• научиться строить и «читать» график
данной функции.
Я узнал …
Я почувствовал ….
Я увидел….
Я сначала испугался, а потом ….
Я заметил, что ….
Я сейчас слушаю и думаю …..
Мне интересно следить за ….
Параграф 6
§ 6. ГРАФИКИ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ
Таблица 12
1. Построение графиков функции вида y = f (x) + g (x)
Если нам известны графики функций y = f (x) и y = g (x), то эскиз графика функции y = f (x) + g (x) можно построить так: изобразить в одной системе координат графики функций f (x) и g (x), а потом построить искомый график по точкам, выполняя для каждого значения х (из области определения функции f (x) + g (x)) необходимые операции с отрезками, изображающими соответствующие ординаты f (x) и g (x).
Аналогично можно построить и схематические графики функций
y = f (x)-g (x) и y = -1-.
f (x)
86 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
Продолж. табл. 12
Пример
Комментарий
Постройте график функции
2 1
у = х2 + -.
X
Построим в одной системе коор-динат графики функций-слагаемых: у = х2 и у = — (на рисунке они
X
показаны штриховыми линиями). Для каждого значения х (кроме х = 0, которое не принадлежит области определения заданной функции) справа от оси Оу прибавляем соответствующие отрезки — значения функций f (х) и g (х) (обе функции имеют одинаковые знаки), слева от оси Оу — вычитаем (функции имеют противоположные знаки). На рисунке синей линией изобра-
2 —
жен график функции у = х +—.
2. Графики уравнений и неравенств с двумя переменными
Определение. Графиком уравнения (неравенства) с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х; у), где пара чисел (х; у) является решением соответствующего уравнения (неравенства).
Графики некоторых уравнений и неравенств
У1 y>f(x) К&/ л/ y<f(x) У1 3 II * х>а У’ х<а в II н
0 X 0 а X 0 а х
у’ х2 + у2 > R2 \
1
1
\
\
\
\ о ; х t t *
-Д. ‘
‘
х2 + у2 < R2
\R
§ 6. Графики уравнений и неравенств с двумя переменными 87
Продолж. табл. 12
3. Геометрические преобразования графика уравнения F (x; у) = 0
Преобразование
Пример
F (я — a; у — Ъ) = 0
Параллельный перенос графика уравнения F (x; у) = 0 на вектор n (a; b).
F (| я |; у) = 0
Часть графика уравнения F (х; у) = 0 справа от оси Оу (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Оу.
F (я; | у |) = 0
Часть графика уравнения F (х; у) = 0 выше оси Ох (и на самой оси) остается без из-менений, и эта же часть гра-фика отображается симме-трично относительно оси Оx.
Объяснение и обоснование
1. Построение графиков функций вида у = f (я) + g (я). Если известны графики функций y = f (x) и y = g (x), то можно построить ориентировочный вид
графика функции y = f (x) + g (x), или y = f (x) • g (x), или y = —^.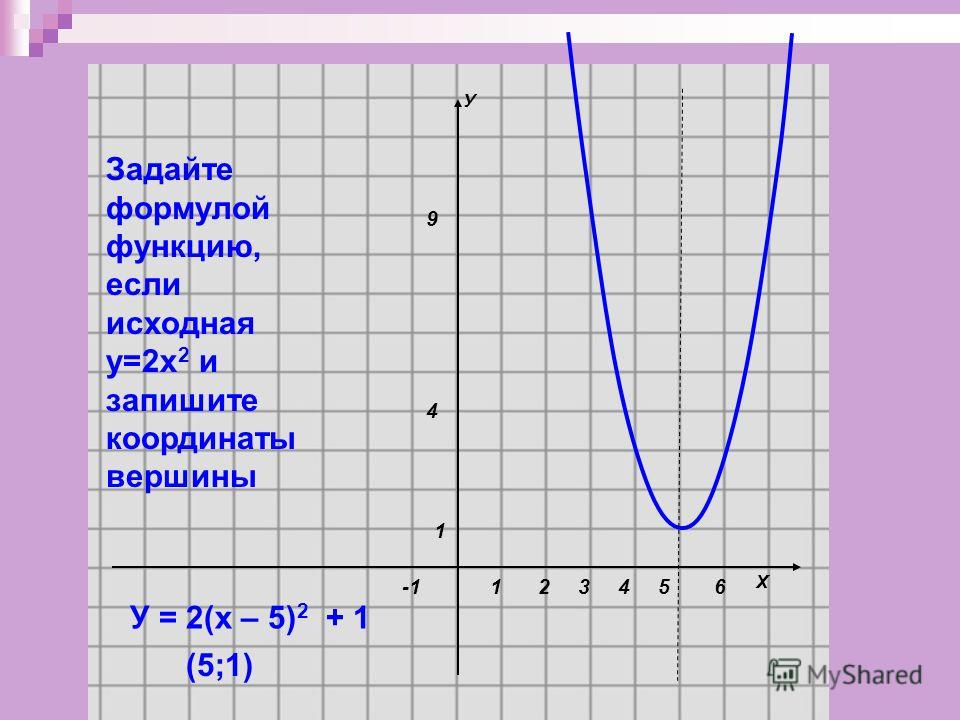 — на с. 92 (в последнем случае
— на с. 92 (в последнем случае
f (x)
удобно строить графики функций y = f (x) и у = не в одной системе
f (x)
координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).
Заметим, что такой способ построения графика функции не всегда дает возможность определить все характерные особенности поведения графика (часто это можно сделать только в результате специального исследования функции, которое будет рассмотрено в учебнике для 11 класса), но во многих случаях приведенный способ позволяет получить определенное представление о виде графика заданной функции.
2. Графики уравнений и неравенств с двумя переменными. С понятием графика уравнения с двумя переменными вы ознакомились в курсе алгебры. Аналогично вводится и понятие графика неравенства с двумя переменными. Поэтому можно дать общее определение этих графиков:
Графиком уравнения (неравенства) с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х; у), где пара чисел (х; у) является решением соответствующего уравнения (неравенства).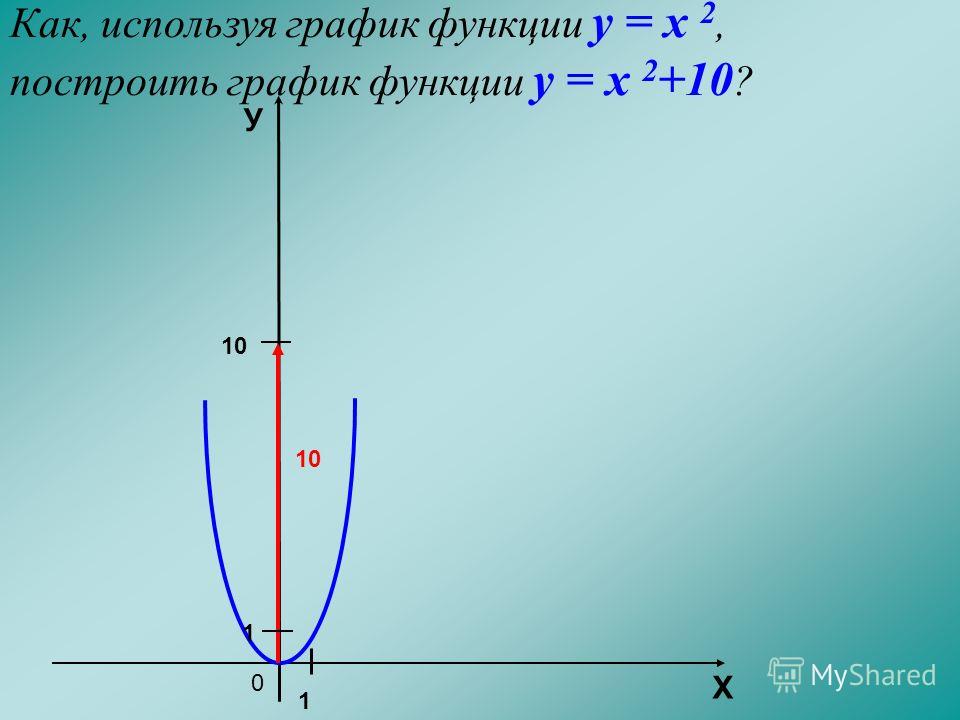
9 Для построения графика неравенства y > f (x) (или y < f (x)) достаточно иметь график функции y = f (x). Действительно, по определению график функции y = f (x) состоит из всех точек M координатной плоскости с координатами (x; y) = (x; f (x)). Тогда для каждого значения x точки, координаты которых удовлетворяют неравенству y > f (x), будут находиться выше точки M (рис. 42, а), а точки, координаты которых удовлетворяют неравенству y < f (x), будут находиться ниже точки M (рис. 42, б). Таким образом,
график неравенства y > f (x) состоит из всех точек координатной плоскости, находящихся выше графика функции y = f (я), а график неравенства y < f (я) состоит из всех точек координатной плоскости, находящихся ниже графика функции y = f (я). О
Например, на рисунке 43 изображен график неравенства y > x2, а на рисунке 44 — график неравенства y < x2. Поскольку точки графика y = x2 не принадлежат графику неравенства y > x2, то на первом графике парабола y = x2 изображена штриховой линией; а так как точки графика y = x2 принадлежат графику неравенства y < x2, то на втором графике парабола y = x2 изображена сплошной линией.
Аналогично, если на координатной плоскости есть прямая x = а, то графиком неравенства x > а будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства x < а будут все точки координатной плоскости, находящиеся слева от этой прямой.
§ 6. Графики уравнений и неравенств с двумя переменными 89
у\ 1
/(*)
*
*
* V>f(x) , А?’
1 0 х х
У f(x) У $ М%» y<f{x)
/
/
# 0 X
У1
1
1
1
1
t
1
1
V
V \
1
\
\
\ У > х21 1 1 1 1 1 1 1 / i / /
0 ж
Рис. 42
Рис. 43
Рис. 45
Например, на рисунке 45 изображен график неравенства x> 2, а на рисунке 46 — график неравенства x < —1.
Отметим, что в том случае, когда на координатной плоскости есть изо-бражение окружности x2 + y2 = R2, то
графиком неравенства x2 + y2 < R2 будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства x2 + y2 > R2 будут все точки координатной плоскости, находящиеся вне окружности.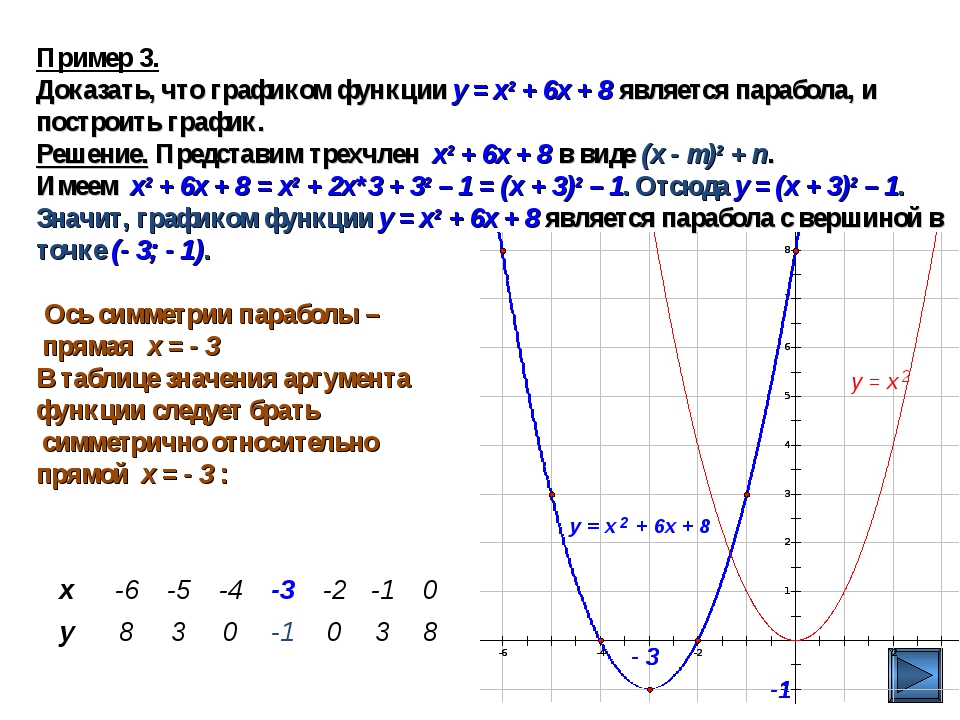
0 Действительно, если на координатной плоскости рассмотреть точку M (x, y), то OM2 = x2 + y2 (O — начало координат). Если x2 + y2 = R2 (где R > 0), то OM2 = R2, таким образом, OM = R — точка M лежит на окружности радиуса R с центром в начале координат (рис. 47, а).
Если x2 + y2 < R2, то OM2 < R2, таким образом, OM< R. То есть неравенству x2 + y2 < R2 удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса R с центром в начале координат (рис. 47, б).
Если x2 + y2 > R2, то OM2 >R2, таким образом, OM> R. То есть неравенству x2 + y2 > R2 удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса R (рис. 47, в).
Аналогично, если на плоскости есть изображение окружности (x — а)2 + + (y — b)2 = R2, то графиком неравенства (x — а)2 + (y — b)2 < R2 будут все точ
б
а
90 Раздел 1. !Я 1 t * / ✓ и
!Я 1 t * / ✓ и
Рис. 47
У’ * * / / / 1 1 х2 + у2>9 ч ч ч \ \ 1 1
1
1
\
\
\
ч
ч о з: х t / / / г *
Рис. 48
3. Геометрические преобразования графика уравнения F (я; у) = 0.
О По определению график уравнения
F (х; у) = 0 (1)
состоит из всех точек М (х0; у0) координатной плоскости, координаты (х0; у0) которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел (х0; у0) в данное уравнение оно обращается в верное числовое равенство, таким образом, F (х0; у0) = 0 — верное равенство.
Рассмотрим точку М1 (х0 + а; у0 + b). Если координаты этой точки подставить в уравнение
F (х — а; у — b) = 0, (2)
то получим верное равенство F (х0; у0) = 0. Поэтому координаты точки М1 являются решениями уравнения (2), значит, точка M1 принадлежит графику уравнения F (х — а; у — b) = 0.
Точку М1 (х0 + а; у0 + b) можно получить из точки М (х0; у0) параллельным переносом ее на вектор n (a; b). Поскольку каждая точка М1 графика
Поскольку каждая точка М1 графика
уравнения F (х — а; у — b) = 0 получается из точки М графика уравнения F (х; у) = 0 параллельным переносом ее на вектор n (a; b) (рис. 50), то и весь
I
график уравнения F (я — a; у — b) = 0 можно получить из графика уравнения F (х; у) = 0 параллельным переносом его на вектор
n (a; b). О
• Для обоснования связи между графиками F (х; у) = 0 и F (| х |; у) = 0 до-статочно заметить, что при х 1 0 уравнение F (| х |; у) = 0 совпадает с урав-нением F (х; у) = 0, таким образом, совпадают и их графики справа от оси Оу и на самой оси. Пусть точка M (х0; у0) (где х0 1 0) — одна из общих точек этих графиков. Тогда F (х0; у0) = 0 — верное равенство.
Рассмотрим точку М1 (-х0; у0 ). Если координаты этой точки подставить в уравнение F (| х |; у) = 0 и учесть, что х0 1 0, то получим равенство F (х0; у0) = 0. Поэтому координаты точки М1 являются решениями уравнения F (| х |; у) = 0, значит, точка M1 принадлежит графику этого уравнения.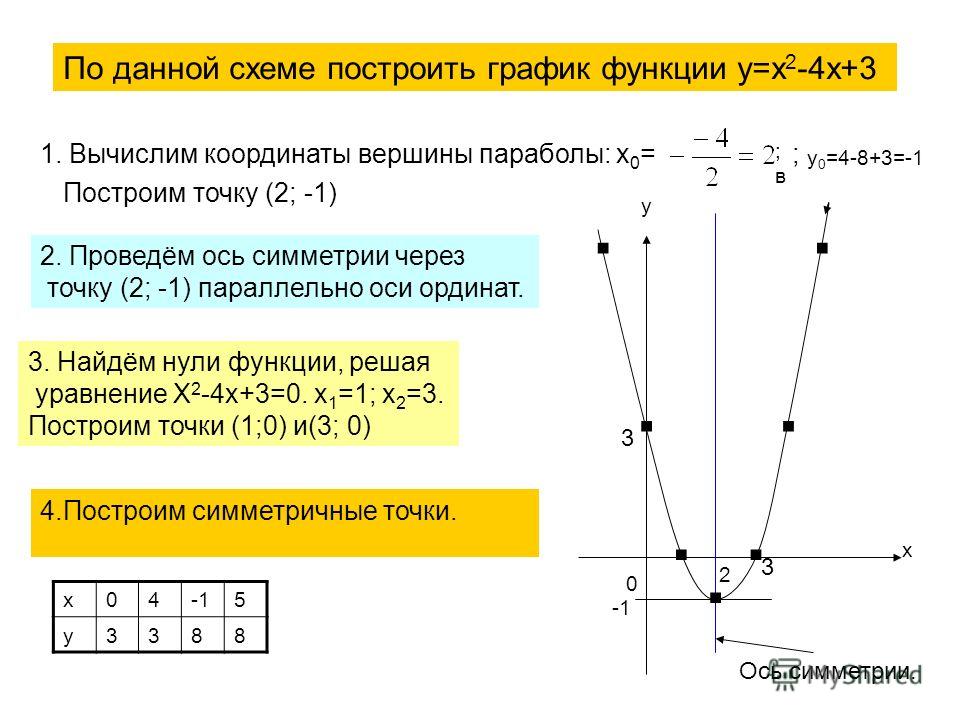 Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем:
Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем:
I
график уравнения F (| х |; у) = 0 можно получить из графика урав-нения F (х; у) = 0 следующим образом: часть графика уравнения F (х; у) = 0 справа от оси Оу (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Оу. О
Аналогично обосновывается, что
1
для построения графика уравнения F (х; | у |) = 0 часть графика уравнения F (х; у) = 0 выше оси Ох (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Ох.
В таблице 12 приведены простейшие примеры использования геометрических преобразований графиков уравнений. Указанные соотношения приходится применять в заданиях типа: построить график уравнения или неравенства или изобразить на координатной плоскости множество точек, координаты которых удовлетворяют заданному уравнению (неравенству).
92 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
Задача 1*
Примеры решения задач
—
Постройте график функции у =
2
х — 9
Решение
► х2 — 9 = 0 при х = ±3. = ~2——. Поэтому
= ~2——. Поэтому
проведем через эти точки вертикаль- ные прямые, которые не пересекают
—
график функции у =
f (х)
Затем для
каждого значения х разделим 1 на соответствующее значение ординаты f (х) (используя то, что ординаты f (х) отмечены на верхнем графике). На рисунке синей линией изображен результат — график функции
у = ~2——. (Для построения этого гра-
х2 — 9
фика масштаб по осям Ох и Оу выбран разный.)
Задача 2
Покажите штриховкой на координатной плоскости множество
х2 + у m о, х — у < 2.
Комментарий
точек, координаты которых удовлетворяют системе
Решение ► Заданная система равносильна си-
\у m -х2,
стеме
у > х — 2.
Перепишем заданную систему так, чтобы было удобно изображать графики данных неравенств (то есть запишем неравенства в виде у > f (х)
§ 6. Графики уравнений и неравенств с двумя переменными 93
Изобразим штриховкой графики неравенств системы (первого — вер-тикальной штриховкой, второго — горизонтальной):
наты которых удовлетворяют системе, будет таким:
Задача 3*
или у < f (х)).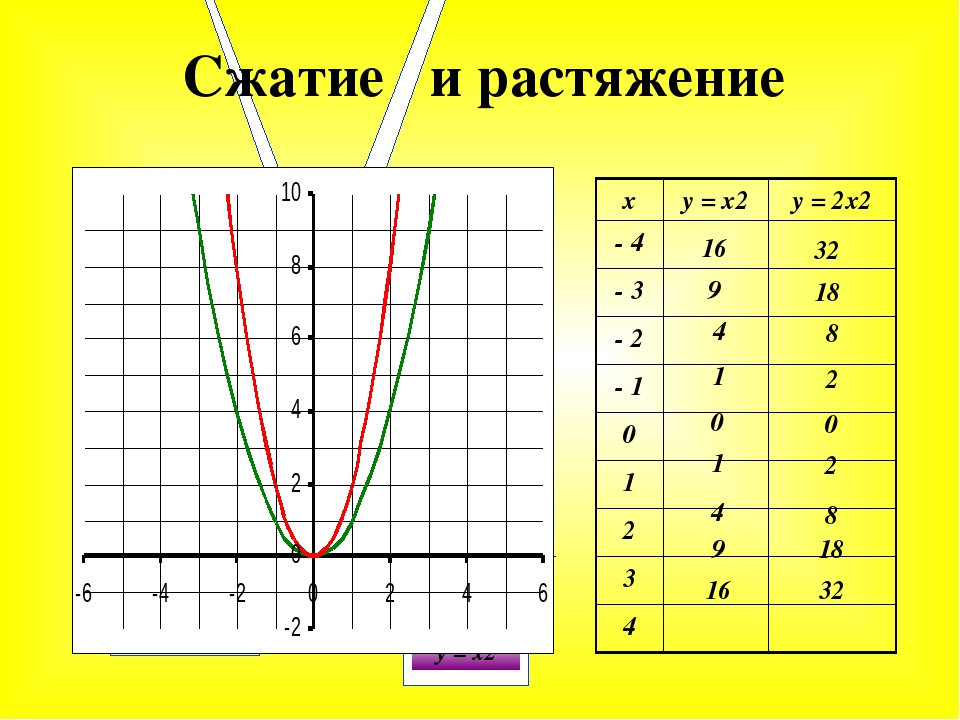 Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой).
Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой).
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, заданных каждым из неравенств данной системы (на рисунке пересечению множеств соответствует та область, где штриховки наложились друг на друга).
Заметим, что в подобных заданиях можно не выполнять промежуточных рисунков, а сразу штриховать искомое множество точек координатной плоскости (выше прямой у = х — 2 и ниже параболы у = -х2 вместе с той частью параболы, которая лежит выше прямой).
Постройте график уравнения | х — у | + 2 | х+у | = х + 6. Ориентир
Ориентир
Для упрощения выражения с несколькими модулями с двумя переменными можно найти нули подмодульных выражений (то есть приравнять их к нулю) и разбить область определения рассматриваемого выражения на несколько частей, в каждой из которых знак каждого модуля раскрывается однозначно.
Используя этот ориентир, получаем план решения примера.
Приравняем к нулю подмодульные выражения х — у = 0 (отсюда у = х) и х + у = 0 (отсюда у = -х). Прямые у = х и у = -х разбивают координатную плоскость на четыре области. В каждой из этих областей знак каж
94 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА
дого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.
Решение
► 1. Область определения: х — любое действительное число, у — любое действительное число.
2. х — у = 0 при у = х; х + у = 0 при у = -х.
3. Прямые у = х и у = -х разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго под- модульных выражений (рис.
Вопросы для контроля
1. Объясните на примерах, как можно, имея графики функций y = f (х) и y = g (х), построить эскиз графика функции y = f (х) + g (х) и функции
_ 1 у _ f (х).
2. Что называется графиком уравнения с двумя переменными? Что называ-ется графиком неравенства с двумя переменными? Приведите примеры.
3. Как, зная график функции y = f (х), построить график неравенства y > f (х) и неравенства y < f (х)? Приведите примеры.
4. Как, зная график уравнения F (х; y) = 0, можно построить график урав-нения F (х — a; y — b) = 0 и уравнений F (| х| ; y) = 0 и F (х; | y |) = 0? При-ведите примеры.
5*. Обоснуйте правила геометрических преобразований графика уравнения F (х; y) = 0 для получения графиков уравнений F (х — a; y — b) = 0, F (| х |; y) = 0, F (х; | y |) = 0.
6. Объясните на примере, как можно найти на координатной плоскости мно-жество точек, координаты которых удовлетворяют системе неравенств с двумя переменными.
Упражнения
1. Постройте эскиз графика функции:
Постройте эскиз графика функции:
1) у _ х + —; 2) у _ х — —; 3*) у _ х3 + —; 4*) у _ х2 — —.
х х х х
2. Постройте график уравнения:
1) | y | = х — 2; 2) | y | = х2- х; 3) | х | = -y2;
4) | х | +| y | = 2; 5) | х | — | y | = 2.
3. Постройте график неравенства:
1) y > х2 — 3; 2) у < —; 3) х2 + y2 m 25;
х
4) (х — 2)2 + (y + 3 )2 > 4.
4. Покажите штриховкой на координатной плоскости множество точек, ко-ординаты которых удовлетворяют системе:
у m 5 — х,
у 1 х,
у m 2х + 4.
5*. Постройте график уравнения:
1) | х — у | — | х + у | = y + 3; 2) | х — 2у | + | 2х — у | = 2 — y;
3) | 3х + у | + | х — у | = 4.
Постройте график функции y х2 3х 2. Квадратичная и кубическая функции
Разделы:
Математика
Тема:
“Построение графика квадратной
функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)
Цель.
- Исследовать расположение графика функции на
координатной плоскости в зависимости от модуля.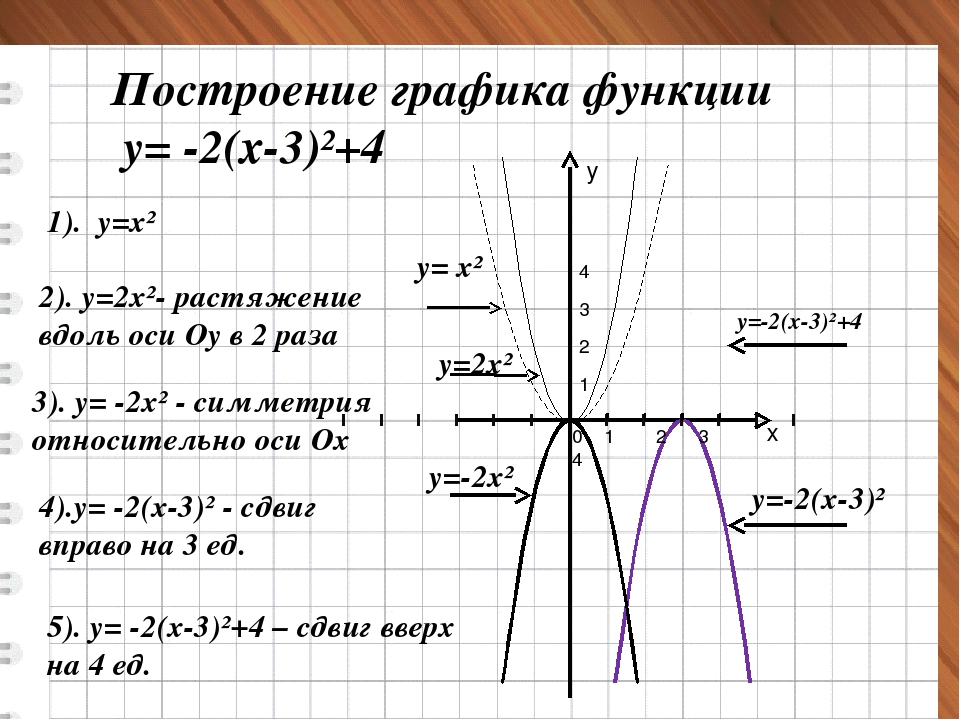
- Развить навыки построения графика функции,
содержащей модуль.
Ход урока.
1. Этап актуализации знаний.
а) Проверка домашнего задания.
Пример 1.
Построить график
функции у = х 2 — 6х + 3. Найти нули функции.
Решение.
2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3,
у(3) = 9 – 18 + 3 = — 6, А(3; -6).
4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 =
36 – 12 = 24, D>0,
x 1,2 = (6 ± )/2
= 3 ± ; В(3 — ;0), С(3 + ;0).
График на рис.1.
Алгоритм построения графика квадратной
функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных
функций, содержащих модуль:
1. у = |х|. График функции на рисунке 2.
2.у = |х| + 1. График функции на рисунке 3.
3. у = |х + 1|. График функции рисунке 4.
Вывод.
1. График функции у = |х| + 1 получается из графика
функции у = |х| параллельным переносом на вектор
{0;1}.
2. График функции у = |х + 1| получается из графика
функции у = |х| параллельным переносом на вектор
{-1;0}.
2.Опирационно-исполнительная часть.
Этап исследовательской работы. Работа в
группах.
Группа 1. Построить графики функций:
а) у = х 2 — 6|x| + 3,
б) у = |х 2 — 6х + 3|.
Решение.
1.Построить график функции у = х 2 -6х+3.
2. Отобразить его симметрично относительно оси
Оу.
График на рисунке 5.
б) 1. Построить график функции у = х 2 — 6х + 3.
2. Отобразить его симметрично относительно оси
Ох.
График функции на рисунке 6.
Вывод.
1. График функции у = f(|x|) получается из графика
функции у = f(x), отображением относительно оси Оу.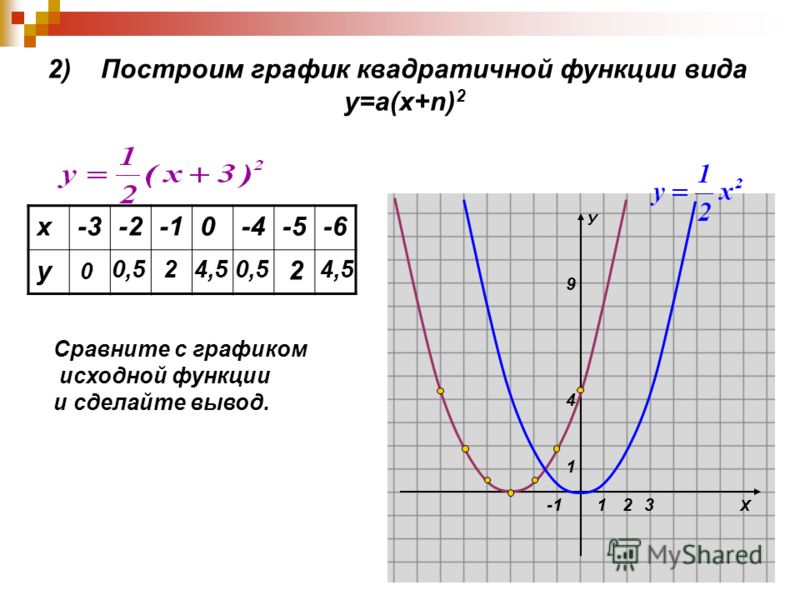
2. График функции у = |f(x)| получается из графика
функции у = f(x), отображением относительно оси Ох.
Группа 2.Построить графики функций:
а) у = |x 2 — 6|x| + 3|;
б) y = |x 2 — 6x + 3| — 3.
Решение.
1. График функции у = х 2 + 6x + 3 отображаем
относительно оси Оу, получается график функции у
= х 2 — 6|x| + 3.
2. Полученный график отображаем симметрично
относительно оси Ох.
График функции на рисунке 7.
Вывод.
График функции y = |f (|x|)| получается из графика
функции у = f(х), последовательным отображением
относительно осей координат.
1. График функции у = х 2 — 6х + 3 отображаем
относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
Вывод.
График функции у = |f(x)| + a
получается из графика функции у = |f(x)|
параллельным переносом на вектор {0,a}.
Группа 3.Построить график функции:
а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.
Решение.
а) у = |x| (x — 6) + 3, имеем совокупность систем:
Строим график функции у = -х 2 + 6x + 3 при х
График функции на рисунке 9.
б) у = х |х — 6| + 3, имеем совокупность систем:
Строим график функции у = — х 2 + 6х + 3 при х 6.
2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2,
А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Строим график функции у = х 2 — 6х + 3 при х = 7
у(7) = 10.
График на рис.10.
Вывод.
При решении данной группы
уравнений необходимо рассматривать нули
модулей, содержащихся в каждом из уравнений.
Затем строить график функции на каждом из
полученных промежутков.
(При построении графиков данных функций каждая
группа исследовала влияние модуля на вид графика
функции и сделала соответствующие заключения. )
)
Получили сводную таблицу для графиков функций,
содержащих модуль.
Таблица построения графиков
функций, содержащих модуль.
Группа 4.
Построить график функции:
а) у = х 2 — 5x + |x — 3|;
б) у = |x 2 — 5x| + x — 3.
Решение.
а) у = х 2 — 5х + |х — 3|, переходим к
совокупности систем:
Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по
точкам у(4) = -3, у(5) = 2, у(6) = 9.
График функции на рисунке 11.
б) у = |х 2 — 5х| + х — 3, переходим к
совокупности систем:
Строим каждый график на соответствующем
интервале.
График функции на рисунке 12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на
вид графика.
Самостоятельная работа.
Построить график функции:
а) у = |х 2 — 5х + |x — 3||,
б) у= ||x 2 — 5x| + х — 3|.
Решение.
Предыдущие графики отображаем относительно
оси Ох.
Группа.5
Построить график функции: у =| х — 2| (|x| — 3) — 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0.
Получим интервалы постоянного знака.
Имеем совокупность систем уравнений:
Строим график на каждом из интервалов.
График на рисунке 15.
Вывод.
Два модуля в предложенных
уравнениях существенно усложнили построение
общего графика, состоящего из трех отдельных
графиков.
Учащиеся записывали выступления каждой из
групп, записывали выводы, участвовали в
самостоятельной работе.
3. Задание на дом.
Построить графики функций с различным
расположением модуля:
1. у = х 2 + 4х + 2;
2. у = — х 2 + 6х — 4.
4. Рефлексивно – оценочный этап.
1.Оценки за урок складываются из отметок:
а) за работу в группе;
б) за самостоятельную работу.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Функции у = х2 и у = х3 и их графики. Алгебра 7 класс.
Конспект урока алгебры в 7 классе.
/Учебник «Алгебра 7 класс». Авторы: Ю.Н. Макарычев, Н.Г. Миндюк и др./
Тема урока: Функции у = х2 и у = х3 и их графики.
Тип урока по дидактическим целям: урок получения новых знаний
Цели урока:
образовательная – формирование знаний учащихся функций у = х2 и у = х3,
их графиков, свойств и умений использовать знания при
решении упражнений;
развивающая – развитие устной и письменной математической речи,
логического мышления, памяти учащихся;
воспитательная — воспитание дисциплины, трудолюбия и организованности.
Задачи урока :
1. Уметь построить графики рассматриваемых функций на базе ранее
полученных знаний по построению графиков;
2. Совместно с учителем определить свойства рассматриваемых функций и
записать их;
3. Закрепить полученные знания решением упражнений.
4. В работе задействовать как можно больше детей.
К ведению урока:
1. Организация начала урока
Тема урока, цель урока
2. Проверка домашней работы ( № 477, № 480 )
Правильность выполнения домашней работы проверяем фронтальным опросом
учащихся. Неверно выполненные задания рассмотреть на доске.
3. Актуализация знаний по теме
1) Какая функция называется линейной?
2) Что является графиком линейной функции и сколько точек достаточно для
ее построения?
3) Какая функция называется прямой пропорциональностью?
4) Что является графиком прямой пропорциональности и сколько точек
достаточно для ее построения?
5) Как определить принадлежит ли точка М (-2; 6) графику функции у = 4х – 2?
6) Это были вопросы, ответы на которые мы знаем. А что делать, если мне
нужно построить график функции, ранее мне не встречавшейся.
4. Изложение нового материала
1) Рассмотрим зависимость площади квадрата от его стороны: S = a2.
Как будет выглядеть соответствующая этой формуле функция? у = х2.
2) Рассмотрим зависимость объема куба от его ребра: V = a3.
Как будет выглядеть соответствующая этой формуле функция? у = х3.
3) Построим теперь графики данных функций и запишем их свойства.
(Для построения страницу тетради разделим на две равные части. Слева построим график у = х2, а справа у = х3 )
у = х2
у = х3
Предложить детям заполнить таблицу от -3 до 3 с шагом 1 / необходим контроль со стороны учителя /
По точкам учащиеся самостоятельно строят график.
Для построения второго графика ученикам предлагается самостоятельно подобрать значения независимой переменной для заполнения таблицы / контроль со стороны учителя /
По точкам учащиеся самостоятельно строят график.
Квадратичная функция. Графиком является парабола.
Кубическая функция. Графиком является кубическая парабола.
Свойства функции у = х2:
1. Если х = 0, то у = ?
2. Если х 0, то у — ?
3. Противоположным значениям аргумента соответствуют равные значения функции.
Свойства функции у = х3:
1. Если х = 0, то у = ?
2. Если х 0, то у — ?
3. Если х 0, то у — ?
4. Противоположным значениям аргумента соответствуют противоположные значения функции.
5. Первичное закрепление знаний учащихся по теме
№ 484, № 488 (из учебника)
6. Задание на дом: № 485, № 489, № 490 (б).
Квадратичная и кубическая функции и их графики 7 класс онлайн-подготовка на Ростелеком Лицей
84. Функции у = х2 и у = х3 и их графики
Начнем с функции у = х2. Самый простой пример зависимости, которую может выражать эта функция – это зависимость площади квадрата от его стороны.
Построим график этой функции по точкам.
х
-3
-2
-1
0
1
2
3
у
9
4
1
0
1
4
9
Отметим точки на координатной плоскости и соединим их плавной кривой.
Получился график, который называется квадратичная парабола. Исследуем его.
Область определения D(y) = (- ∞;∞).
Область значений Е(у) = [0;∞).
Точки пересечения с осями координат х = 0, у =02 =0. Единственная точка пересечения с осями – (0;0).
Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).
График функции у=х2 симметричен относительно оси у.
Рассмотрим функцию y=x3 Приведите пример зависимости, которую может выражать эта функция. Простой пример такой зависимости – зависимость объема куба от длины ребра.
Построим график функции по точкам.
х
-3
-2
-1
0
1
2
3
у
-27
-8
-1
0
1
8
27
График этой функции тоже называется параболой. Это кубическая парабола.
Исследуем его
Область определения. D(y) = (- ∞;∞).
Область значений Е(у) = (- ∞;∞).
Точка пересечения с осями координат, как и в случае с графиком у=х2, одна – (0;0).
График функции возрастает на всей области определения.
При х0 y>0.
График функции симметричен относительно начала координат.
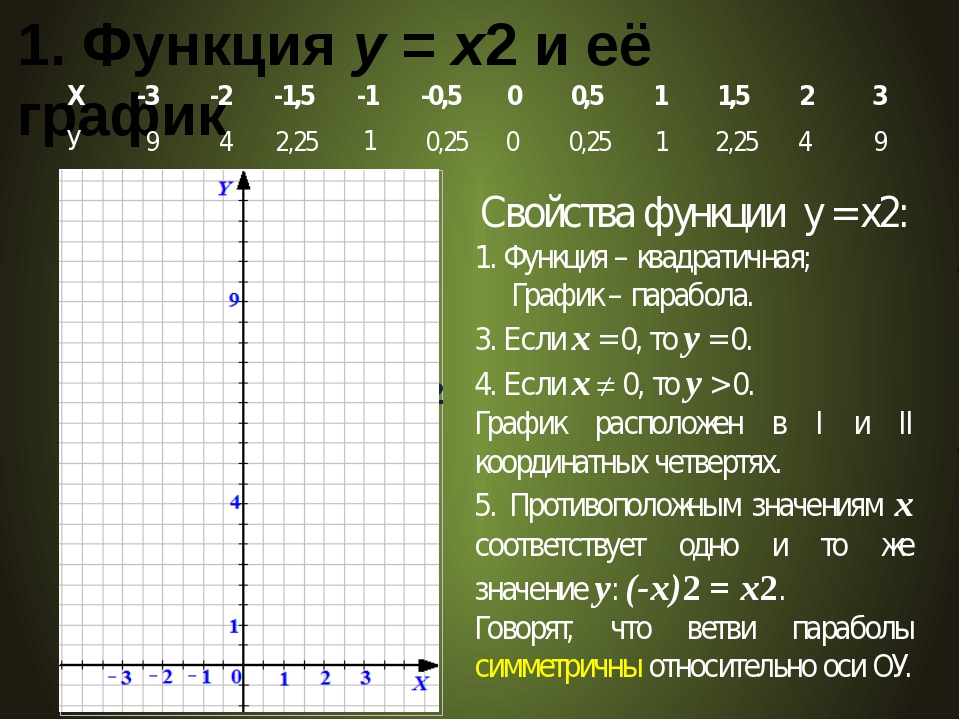
Квадратичная функция: Функция у=х2
Разработка состоит из технологической карты урока и презентации.
Цель урока: продолжить работу по формированию навыка использования свойств графика функции при решении задач.
Предметные результаты: знают свойства функции у = х2; умеют применять их при решении учебных и познавательных задач.
Метапредметные результаты:
регулятивные: умеют определять и формулировать цель на уроке с помощью учителя; проговаривают последовательность действий на уроке; работают по коллективно составленному плану; планируют своё действие в соответствии с поставленной целью; вносят необходимые коррективы в действие после его завершения на основе оценки и учёта характера сделанных ошибок; высказывают своё предположение;
коммуникативные: умеют оформлять свои мысли в устной и письменной форме; слушают и понимают речь других; совместно договариваются о правилах поведения и общения; учитывают разные мнения и стремиться к координации различных позиций в сотрудничестве; выражают свои мысли с достаточной полнотой и точностью в соответствии с задачами коммуникации; формулируют и аргументируют своё мнение, допускают возможность существования у людей различных точек зрения; используют речь для регуляции своего действия;
познавательные: умеют строить логические цепочки рассуждений, осознанно и произвольно строить речевое высказывание; проводить сравнение по заданным критериям, осуществлять анализ объектов; преобразовывать информацию из одной формы в другую.
Личностные результаты: умеют ясно, точно, грамотно излагать свои мысли; способность к самооценке на основе критерия успешности учебной деятельности; проявление положительного отношения к урокам математики, доброжелательного отношения к сверстникам; ориентация на понимание причин успеха в учебной деятельности.
Оборудование: ПК, проектор и экран; раздаточный материал.
Тип урока: урок комплексного применения знаний и умений (в рамках деятельностного подхода)
Форма урока: комбинированный урок
Технология: урок в системно-деятельностном подходе
Обучающиеся знакомы с понятиями: квадратичная функция; умеют находить значение функции по значению аргумента, находить значение аргумента по значению функции, строить график функции у = х2. На этом уроке продолжат работать с графиком функции у= х2, определять координаты точек пересечения графика функции у = х2 и графика линейной функции.
Bоронцова Елена Васильевна-70%
Курсы повышения квалификации
Продолжительность 36 часов
Документ: Удостоверение о повышении квалификации
Похожие файлы
Презентация » Квадратичная функция» .
библиотека
материаловСодержание слайдов
Номер слайда 1
Определение: Функция вида y = kx +b, где k и b числа, а x и y переменные, называется линейной функцией. x – независимая переменная (аргумент) y – зависимая переменная (функция) Ефимцева И.В.
Номер слайда 2
Построим график функции: х у у = 2х–5 0 3 -5 1
Номер слайда 3
Функция и ее график 7 класс.
Номер слайда 4
Примеры, приводящие к понятию функции 1. 2. Зависимая переменная Независимая переменная
Номер слайда 5
График функции Построим график функции по точкам:
Номер слайда 6
парабола
Номер слайда 7
Номер слайда 8
Свойства функции:
Номер слайда 9
Свойства функции 5)Если х=0, то у=0. У наим.=0 ; У наиб- не существует Если , то у>0. 6) Противоположным значениям х соответствует одно и то же значение у (график симметричен относительно оси у). 7) у = х2 — непрерывная функция.
Номер слайда 10
Постройте график функции: 4.
Номер слайда 11
1. Сравните числа:
Номер слайда 12
Построить в одной системе координат графики функций х -3 -2 -1 0 1 2 3 у -9 -4 -1 0 -1 -4 -9 а = 1 а > 0 х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9 а = — 1 а
Номер слайда 13
Решите уравнение: -х2 – 2х + 3 =0 -х2 = 2х — 3 Квадратичная функция Линейная функция
Номер слайда 14
х 1 -1 у -1 -5 х -2 -1 0 1 у -4 -1 0 -1 у = -х2 –квадратичная функция, графиком является парабола, ветви которой направлены вниз у = 2х – 3 – линейная функция, графиком является прямая Ответ: х = -3; х = 1 Х У 1 1 -2 2 3 -1 -3
Номер слайда 15
Постройте график функции: 2.
Номер слайда 16
Номер слайда 17
Укажите номер рисунка, соответствующий графику функции: 3. 1. 2. 3. Не верно Молодец! Подумай!
Номер слайда 18
Постройте график функции: 4.
Номер слайда 19
Номер слайда 20
«Знание – орудие, а не цель» Л. Н. Толстой Найдите у, если: х ≈ -2,5 х = — 2 у ≈ 1,9 у ≈ 6,7 у ≈ 9,6 х = 1,4 х = — 2,6 х = 3,1 у = 6 у = 4 Найдите х, если: - 1,4 - 3,1 х ≈ 2,5 х = 2
Номер слайда 21
Найдите несколько значений х, при которых значения функции : меньше 4 больше 4
Номер слайда 22
Решите графически уравнение: х2 = х2 = — x2 = х 5 +1 y = — 1 y = x + 1 y = х2 y = 5 нет решений х ≈ — 2,2; х ≈ 2,2 х ≈ — 0,6; х ≈ 1,6 1
Номер слайда 23
При каких значениях а точка Р(а; 64) принадлежит графику функции у = х2. Принадлежит ли графику функции у = х2 точка: Не выполняя вычислений, определите, какие из точек не принадлежат графику функции у = х2: P(-18; 324) R(-99; -9081) S(17; 279) (-1; 1) (0; 8) (-2; 4) (3; -9) (1,8; 3,24) (16; 0) а = 8; а = — 8 принадлежит не принадлежит не принадлежит
Номер слайда 24
Укажите номер рисунка, соответствующий графику функции: 5. 1. 2. 3. Не верно Подумай! Молодец!
Номер слайда 25
Номер слайда 26
Определите график функции: 6. 1. 2. 3. Не верно Подумай! Молодец!
Номер слайда 27
Постройте график функции: 4.
Номер слайда 28
Постройте график функции, используя правила перемещения: 7.
Номер слайда 29
Определите соответствие, между графиком функции и формулой: 8.
Номер слайда 30
Определите соответствие, между графиком функции и формулой: 8.
Номер слайда 31
Определите соответствие, между графиком функции и формулой: 8.
Номер слайда 32
Определите соответствие, между графиком функции и формулой: 8.
Номер слайда 33
Определите соответствие, между графиком функции и формулой: 8. Самостоятельно построить график функции. График какой функции отсутствовал в задании?.
Номер слайда 34
Графики функций y = x2, y = 2×2 и y = -2×2 фиолетовым, красным и
синий соответственноИсследование парабол
По Туи Нгуен
В этом исследовании мы хотим увидеть
что происходит, когда мы строим графики для параболы y = ax 2 +
bx + c с разными значениями a, b и c. Начнем сначала с построения графиков для y = ax 2
с разными значениями a.В
Ниже приведены графики для a = -2, 1, 2 синим, фиолетовым и красным цветом соответственно:Сначала отметим, что когда a — отрицательное значение, график
отражается поперек оси x, и вершина становится точкой максимума. Далее отметим, что поскольку значение a
увеличивается, парабола сужается по отношению к оси абсцисс.Сейчас
мы хотим исправить a (пусть a = 1) и исследуем уравнение y = x 2 + bx.Пусть b = -2, 1, 3 красным, синим и
фиолетовый соответственно на следующем графике:Мы видим, что значения b влияют на то, где
парабола пересекает ось абсцисс.
Теперь давайте посмотрим, что произойдет, если мы изменим оба значения a = 2, 4, 6
и b = -2, 1, 3:Ага! Итак
парабола имеет две точки пересечения:
(0,0) и (- (b / a), 0).Наконец,
мы хотим изучить, как значения c могут повлиять на параболу.Зафиксируем a = 1, b = 0 и изменим c
= -2, ½, 2 соответственно красным, синим, фиолетовым:Мы сразу видим, что c определяет пересечение
парабола на оси ординат. Это,
парабола y = ax 2 + bx + c пересекает ось y в точке y = c. Давайте посмотрим, что произойдет, когда мы изменим
значения a:y = 10 x 2 + x + 2, фиолетовый
y = -10 x 2 + x + 2, синий
y = 2 x 2 + x + 2, зеленый
y = 1/2 x 2 + x + 2, бирюзовый
y = 1/20 x 2 + x + 2, темно-серый
y = 1/100 x 2 + x + 2, красный
Отметим здесь, что когда c вводится в уравнение y =
ax 2 + bx + c, то, что парабола пересекает
Ось x при x = 0 и x = — (b / a).
Но мы можем связать b с графом, когда введем c: вершина параболы равна (b / 2a, b 2 / 4a
— б 2 / 2а + в).
Координату x в вершине получаем при просмотре графов и при x =
-b / 2a, тогда y = a (bb / 4aa) + -bb / 2a + c = bb / 4a — bb / 2a + c = b 2 / 4a
— б 2 / 2a + c. Давай сделаем
пример! Пусть a = 2, b = 3, c =
2. Тогда у нас должно получитьсявершина = (-b / 2a, b 2 / 4a — b 2 / 2a + c)
=
(-3/4, 9/8 — 9/4 + 2)=
(-0.75, 0,875)Графический калькулятор
согласен с нашим ответом:
Возврат
Парабола (дни 4 и 5)
Учебный блок: Парабола (дни 4 и 5)
Учебное пособие
Парабола: графический подход
День 4 и 5Учебные заметки:
На этом уроке учащиеся изучают график параболы.Студенты, вероятно, больше всего знакомы с
глядя на параболу таким образом. В этом уроке обсуждаются изменения параметров эталона параболы.
полиномиальная форма: y = ax 2 + bx + c. Программное обеспечение Graphing Calculator будет использоваться, чтобы помочь студентам
визуализировать изменения параметров. Очень полезным аспектом графического калькулятора является «n-анимация».
характерная черта. Подставив «n» для одного из параметров, который нужно изменить, а затем выберите диапазон
значения для него, студенты могут очень легко увидеть эффект от изменения переменной.Студенты должны изобразить каждый
данных уравнений вместе с y = x 2 и определить влияние каждого из параметров на
график параболы.Введение:
Мы начнем с построения графика y = x 2 в качестве ориентира. Во всех будущих графиках этот график будет представлен
в сером.График: y = x 2
Замена «а»:
Теперь изменим параметр «а».Посмотрим на графики y = ax 2 .
График: y = 2x 2 и y = x 2
График: y = 5x 2 и y = x 2
Увеличение значения «a» больше 1, похоже, сужает график.
График: y = (1/2) x 2 и y = x 2
График: y = (1/5) x 2 и y = x 2
Уменьшение значения «a» меньше 1, но больше нуля, кажется, расширяет график.
График: y = -x 2 и y = x 2
График: y = — (1/5) x 2 и y = x 2
График: y = -2x 2 и y = x 2
Отрицательные значения «a» ведут себя таким же образом, но отражаются поперек оси x.
Резюме:
В общем, отрицание значения «а» отразит существующий график по оси x.В виде
«a» увеличивается (положительные значения) или уменьшается (отрицательные значения) от нуля, парабола будет
узкий.Замена «b»:
Теперь изменим параметр «b». Посмотрим на графики y = x 2 + bx.
Дополнительные примечания для учителей:
Студентам часто трудно увидеть эффект параметра «b». В этом случае Graphing
Функция n-анимации калькулятора будет очень полезна.Студенты должны составить уравнение
y = x 2 + nx, а затем установите диапазон для n, используя достаточное количество шагов. Две анимации
приведены здесь в качестве примера. Акцент на этих анимациях — путь, по которому вершина
следует анимированная парабола.График: y = x 2 + nx (красный / n изменяется от 0 до -10) и y = -x 2 (фиолетовый) и y = x 2
График: y = x 2 + nx (красный / n изменяется от 0 до 10) и y = -x 2 (фиолетовый) и y = x 2
Резюме:
Как правило, изменение значения «b» вызывает перемещение по параболической траектории.Вершина
переводится по параболическому пути, который является отражением исходного графика поперек оси x.Дополнительные примечания для учителей:
Учащимся может быть трудно представить себе «параболический путь», по которому движется парабола. Большинство
студенты, вероятно, скажут, что он переводится по диагонали. Может потребоваться некоторая помощь учителя, чтобы
студенты, чтобы найти правильный путь.Замена «c»:
Теперь изменим параметр «c».Посмотрим на графики y = x 2 + c.
График: y = x 2 + 3 и y = x 2
График: y = x 2 — 4 и y = x 2
Резюме:
Как правило, изменение значения «c» вызывает вертикальный сдвиг. По мере увеличения «c»
парабола переводится вверх. По мере уменьшения «c» парабола перемещается вниз.Взаимодействие параметров:
Конечно, все эти параметры могут изменяться одновременно, что приводит к сужению, расширению и множеству
переводы. Студенты должны изобразить несколько парабол, которые имеют разные значения для a, b и c. потом
они должны попытаться визуализировать каждое из изменений параметров, последствия которых им теперь известны.Домашние задания:
Изобразите следующие параболы:
- y = x 2 (раствор серого цвета)
- y = -x 2 + 4 (решение красным)
- y = — (1/2) x 2 + 2x (решение фиолетового цвета)
- y = 4x 2 + x — 3 (решение синего цвета)
- y = (1/3) x 2 + 4x + 2 (решение зеленого цвета)
Решения для домашних заданий:
Вернуться на главную страницу
квадратичных функций
квадратичных функций
Содержание : Эта страница соответствует § 3.1 (стр.
244) текста.Предлагаемые задачи из текста:
с. 251 # 1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
Графики
Стандартная форма
Приложения
Графики
Квадратичная функция является одной из форм f (x) = ax 2 + bx + c , где a ,
b и c — числа, где a не равны нулю.График квадратичной функции — это кривая, называемая параболой . Параболы могут открываться вверх или вниз
и различаются по «ширине» или «крутизне», но все они имеют одинаковую базовую U-образную форму. В
На рисунке ниже показаны три графика, и все они являются параболами.Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекает
его ось симметрии находится в точке, называемой вершиной параболы.Вы знаете, что две точки определяют линию. Это означает, что если вам даны любые две точки на плоскости, то
есть одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать о точках и квадратичных
функции.Учитывая три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой, существует ровно
одна квадратичная функция f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт.График
содержит три точки и параболу, проходящую через все три. Соответствующая функция показана в тексте
поле под графиком. Если вы перетащите любую из точек, функция и парабола обновятся.Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения / сжатия и сдвига.
(перевод) парабола y = x 2 . (См. Раздел о работе с
графики.)Пример 1 .
Нарисуйте график y = x 2 /2. Начиная с графика y = x 2 , мы сокращаемся в раз
половины. 2-5.Начнем с графика y = x 2 , сдвинем на 4 единицы вправо, затем
5 единиц вниз.Упражнение 1 :
(a) Нарисуйте график y = (x + 2) 2 — 3. Ответ
(b) Нарисуйте график y = — (x — 5) 2 + 3. Ответ
Вернуться к содержанию
Стандартная форма
Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме .Когда квадратичная функция имеет стандартную форму, ее график легко построить, отражая, сдвигая и
растяжение / сжатие параболы y = x 2 .Квадратичная функция f (x) = a (x — h) 2 + k, не равная нулю, считается в стандартной форме .
Если а положительно, график открывается вверх, а если отрицательно, то открывается вниз. Линия симметрии
— это вертикальная линия x = h, а вершина — это точка (h, k).Любую квадратичную функцию можно переписать в стандартной форме, добавив , завершив квадрат . (См. Раздел о
решая уравнения алгебраически, чтобы просмотреть завершение квадрата.)
Шаги, которые мы используем в этом разделе для завершения квадрата, будут выглядеть немного иначе, потому что наш главный
цель здесь не в решении уравнения.Обратите внимание, что когда квадратичная функция имеет стандартную форму, ее нули также легко найти с помощью квадратного корня.
принцип.Пример 3 .
Запишите функцию f (x) = x 2 — 6x + 7 в стандартном виде. Нарисуйте график функции f и найдите его нули
и вершина.f (x) = x 2 — 6x + 7.
= (x 2 — 6x) + 7. Сгруппируйте члены x 2 и x и
затем заполните квадрат на этих условиях.= (x 2 — 6x + 9 — 9) + 7.
Нам нужно добавить 9, потому что это квадрат половины коэффициента при x, (-6/2) 2 = 9. Когда мы
решая уравнение, мы просто добавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9
так что мы не меняем функцию.= (x 2 — 6x + 9) — 9 + 7. Мы видим, что x 2 — 6x + 9 — это полный квадрат, а именно (x — 3) 2 .
f (x) = (x — 3) 2 — 2.Это стандартная форма .
Из этого результата легко найти, что вершина графа f равна (3, -2).
Чтобы найти нули f, мы устанавливаем f равным 0 и решаем относительно x.
(x — 3) 2 — 2 = 0.
(x — 3) 2 = 2.
(x — 3) = ± sqrt (2).
х = 3 ± sqrt (2).
Чтобы нарисовать график f, сдвинем график y = x 2 на три единицы вправо и на две единицы вниз.
Если коэффициент при x 2 не равен 1, то мы должны вынести этот коэффициент из x 2 и
x, прежде чем продолжить.Пример 4 .
Запишите f (x) = -2x 2 + 2x + 3 в стандартной форме и найдите вершину графика f.
f (x) = -2x 2 + 2x + 3.
= (-2x 2 + 2x) + 3.
= -2 (x 2 — x) + 3.
= -2 (x 2 — x + 1/4 — 1/4) + 3.
Мы складываем и вычитаем 1/4, потому что (-1/2) 2 = 1/4, а -1 — коэффициент при x.
= -2 (x 2 — x + 1/4) -2 (-1/4) + 3.
Обратите внимание, что все в круглых скобках умножается на -2, поэтому, когда мы убираем -1/4 из круглых скобок, мы
необходимо умножить на -2.= -2 (x — 1/2) 2 + 1/2 + 3.
= -2 (х — 1/2) 2 + 7/2.
Вершина — это точка (1/2, 7/2). Поскольку граф открывается вниз (-2 <0), вершина является высшей точкой на графике.
Упражнение 2 :
Запишите f (x) = 3x 2 + 12x + 8 в стандартной форме.Нарисуйте график функции f, найдите его вершину и найдите
нули f. ОтветАльтернативный метод поиска вершины
В некоторых случаях завершение квадрата — не самый простой способ найти вершину параболы. Если график
квадратичная функция имеет два пересечения по оси x, тогда линия симметрии — это вертикальная линия, проходящая через среднюю точку
х-перехватчиков.Х-точки пересечения графика выше находятся в точках -5 и 3.Линия симметрии проходит через -1, что является средним
-5 и 3. (-5 + 3) / 2 = -2/2 = -1. Как только мы узнаем, что линия симметрии x = -1, мы узнаем первую координату
вершины -1. Вторую координату вершины можно найти, вычислив функцию при x = -1.Пример 5 .
Найдите вершину графика функции f (x) = (x + 9) (x — 5).
Поскольку формула для f разложена на множители, легко найти нули: -9 и 5.
Среднее значение нулей (-9 + 5) / 2 = -4/2 = -2. Итак, линия симметрии x = -2 и первая координата
вершины -2.Вторая координата вершины: f (-2) = (-2 + 9) (- 2 — 5) = 7 * (- 7) = -49.
Следовательно, вершина графика f равна (-2, -49).
Вернуться к содержанию
Приложения
Пример 6 .
У владельца ранчо есть 600 метров забора, чтобы ограждать прямоугольный загон с другим забором, разделяющим его посередине.
как на схеме ниже.Как показано на схеме, каждая из четырех горизонтальных секций забора будет иметь длину х метров, а три
каждая вертикальная секция будет иметь длину y метров.Цель владельца ранчо — использовать весь забор, а оградить как можно большую площадь .
Каждый из двух прямоугольников имеет площадь xy, поэтому мы имеем
Общая площадь: A = 2xy.
Мы мало что можем сделать с величиной A, если она выражается как произведение двух переменных. Тем не мение,
Тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому должны удовлетворять x и y.3г + 4х = 1200.
3y = 1200 — 4x.
y = 400 — 4x / 3.
Теперь у нас есть y, выраженный как функция от x, и мы можем подставить это выражение для y в формулу для общего
площадь А.A = 2xy = 2x (400 -4x / 3).
Нам нужно найти значение x, которое делает A как можно большим. A — квадратичная функция от x, а график
открывается вниз, поэтому наивысшая точка на графике A — вершина. Поскольку A разложено на множители, самый простой способ найти
вершина — найти пересечения по оси x и усреднить.2x (400 -4x / 3) = 0,
2x = 0 или 400 -4x / 3 = 0.
x = 0 или 400 = 4x / 3.
x = 0 или 1200 = 4x.
х = 0 или 300 = х.
Следовательно, линия симметрии графика A равна x = 150, среднему от 0 до 300. {2} + k [/ latex]
где [latex] \ left (h, \ text {} k \ right) [/ latex] — вершина.2 [/ латекс]
Величина [латекс] а [/ латекс] указывает на растяжение графика. Если [latex] | a |> 1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается дальше от оси [latex] x [/ latex] –, поэтому график кажется, становится уже, и появляется вертикальная растяжка. Но если [latex] | a | <1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается ближе к оси [latex] x [/ latex] –, поэтому график кажется шире, но на самом деле есть вертикальное сжатие.{2}} {4a} \ end {align} [/ latex]
На практике, однако, обычно легче запомнить, что [latex] h [/ latex] является выходным значением функции, когда входом является [latex] h [/ latex], поэтому [latex] f \ left (h \ right) = f \ left (- \ dfrac {b} {2a} \ right) = k [/ latex].
Попробуй
Координатная сетка наложена на квадратную траекторию баскетбольного мяча на рисунке ниже. {2} +7 [/ латекс].Чтобы сделать снимок, [latex] h \ left (-7,5 \ right) [/ latex] должно быть около 4, но [latex] h \ left (-7,5 \ right) \ приблизительно 1,64 [/ latex]; он не выживает.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи: a) Представьте функцию в форме y = a (x
РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5, выполнять следующие задачи:
а) Представьте функцию в виде y = a (x — h) 2 + k.Отвечать:Показать работы в этой области
б) Что такое т
Алгебра ->
Квадратичные уравнения и параболы
-> РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи:
а) Представьте функцию в виде y = a (x — h) 2 + k.
Отвечать:Показать работы в этой области
б) Что такое т
Войти в систему
Вопрос 71677: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи:
a) Представьте функцию в форме y = a (x — h) 2 + k. 2
(x-2) перемещает все точки 2 вправо.
Когда x = 2, y = -9; -9 перемещает все точки на 9 вниз.
========
Ура,
Стэн Х.Ответ по общей химии для айлола # 149193
y = x² для получения y = -2 (x + 5) ²- 3
y = ( x — 6) ( x — 4)
Когда x = 0, y = 24,
, поэтому интервал y равен 24.
Когда y = 0, x = 4 или x = 6,
, поэтому значения интерцепции x равны 4 и 6.
Принимая среднее значение интерцептов x , получаем
x = 5 — ось симметрии.
Когда x = 5, y = (5-6) (5-4) = -1,
, поэтому вершина равна (5, -1).
b
y = — x 2 + x + 6
Это перевернутая парабола.
Когда x = 0, y = 6, то это интервал y .
y = — x 2 + x + 6 = — ( x 2- x -6) = — ( x -3) ( x + 2)
Итак x -перехваты — это 3 и −2.
Принимая их среднее значение, ось симметра y равна x =.
Когда x =, y = — + + 6 = 6, то вершина равна, 6.
c
y = 5 x 2-20 x + 15
Если x = 0, тогда y = 15.
y = 5 x 2-20 x + 15 = 5 ( x 2-4 x + 3) = 5 ( x -3) ( x -1)
Таким образом, два интерцепта x равны x = 1 и x = 3.
Следовательно, ось симметра y равна x = 2, а вершина равна (2, −5).
y = ( x — 6) ( x — 4)
Когда x = 0, y = 24,
, поэтому интервал интервала y равен 24.
Когда y = 0, x = 4 или x = 6,
, таким образом, x -преятия равны 4 и 6.
Взяв среднее значение x -перехваченных,
x = 5 — ось симметрии.
Когда x = 5, y = (5-6) (5-4) = -1,
, поэтому вершина равна (5, -1).
b
y = — x 2 + x + 6
Это перевернутая парабола.
Когда x = 0, y = 6, то это интервал y .
y = — x 2 + x + 6 = — ( x 2- x -6) = — ( x -3) ( x + 2)
Итак x -перехваты — это 3 и −2.
Принимая их среднее значение, ось симметра y равна x =.
Когда x =, y = — + + 6 = 6, поэтому вершина равна, 6.
c
y = 5 x 2-20 x + 15
Когда x = 0, тогда y = 15.
y = 5 x 2-20 x + 15 = 5 ( x 2-4 x + 3) = 5 ( x — 3) ( x — 1)
Таким образом, два интерцепта x равны x = 1 и x = 3.
Следовательно, ось симметра y равна x = 2, а вершина равна (2, −5).
Функции мощности На рисунках показаны части графиков y = x 2, y = x 3, y = x 4, y = x 5 и y = x 6. Определите, какая функция принадлежит каждому графику.
Показаны графики двух функций с указанием площадей областей между кривыми. (а) Что такое …
Исчисление одной переменной: ранние трансцендентальные методы, том I
Упростите выражения в упражнениях 97106.21/32122/321/3
Прикладное исчисление
В упражнениях 3148 (а) множите данное выражение и (б) устанавливайте выражение равным нулю и решайте для …
Конечная математика и прикладное исчисление ( Список курсов MindTap)
Упрощение выражения В упражнениях 113 и 114 запишите выражение в алгебраической форме. cos (arccscx4)
Исчисление: ранние трансцендентные функции
Найдите вектор, не используя детерминанты, а используя свойства перекрестных произведений.10. k (i 2j)
Многопараметрическое исчисление
Производитель смоделировал свою годовую производственную функцию P (стоимость всей своей продукции, в миллионах …
Исчисление: ранние трансцендентальные методы
Аппроксимация наклона графика В упражнениях 712 приблизительно определите наклон графика в точке (x, y). (E …
Исчисление: прикладной подход (список курсов MindTap)
Найдите медиану для следующего набора баллов: 1, 9, 3, 6, 4, 3, 11, 10
Основы статистики для поведенческих наук (список курсов MindTap)
SOC / SW Исследователь составил файл информации о случайной выборке из 317 семей, страдающих хроническими заболеваниями. , вот…
Основы статистики
Нарисуйте область, ограниченную данными кривыми, и найдите ее площадь. y = cos2xsinx, y = sinx, 0x
Исчисление (список курсов MindTap)
Исследователи отметили снижение когнитивных функций с возрастом людей (Bartus, 1990). Тем не менее, результаты …
Статистика для поведенческих наук (список курсов MindTap)
Исследователи измерили концентрацию алкоголя в крови (BAC) восьми взрослых мужчин после быстрого потребления…
Исчисление с одной переменной
(exex2) 1/2
Прикладное исчисление для управленческих, жизненных и социальных наук: краткий подход
Решите уравнения из упражнений 126. (x2 + 1) x + 1 ( x + 1) 3 = 0
Конечная математика
Интерпретация Вау! В задачах 5-13 вы собрали много информации о pH земли в западном Техасе …
Понимание базовой статистики
Предположим, что транспортные средства, выезжающие на конкретный выезд с автострады, могут повернуть направо (R), повернуть налево (L) или идите прямо (S).C …
Вероятность и статистика для инженерии и науки
Для задач 55-94 упростите каждое числовое выражение. Задачи 7 69 + 1187 + 14
Промежуточная алгебра
В упражнениях с 23 по 26 используйте отрезки линий длиной a и c, как показано. Постройте равнобедренный треугольник с вершиной …
Элементарная геометрия для студентов колледжа, 7e
В задачах 5-8 найдите производную, но не упрощайте свой ответ.
7.Математические приложения для управления, жизни и социальных наук
Решите каждое уравнение и проверьте: 2y + 8 = 5y1
Элементарная техническая математика
В упражнениях с 53 по 62 используйте обозначение набора для описания заштрихованной области.Вы можете использовать любой из следующих символов …
Математические экскурсии (список курсов MindTap)
Рассчитайте приведенную стоимость (основную сумму) и сложные проценты для следующих инвестиций. Используйте Таблицу 11-2 …
Современная математика для бизнеса и потребителей
Интервалы, на которых функция увеличивается или уменьшается в упражнениях 11-22, найдите открытые интервалы, на которых …
Исчисление: ранние трансцендентные функции ( Список курсов MindTap)
Урожайность древесины Урожайность V (в миллионах кубических футов на акр) для древостоя в возрасте t составляет V = 6.7e48.1 / t, w …
Вычисление одной переменной
Напишите выражение для наклона касательной к кривой y = f (x) в точке (a, f (a)).
Исчисление с одной переменной: ранние трансцендентальные методы
31. Докажите, что если положительное и отрицательное значение, то отрицательное.
Элементы современной алгебры
Спасательные Вертолет совершает вынужденную посадку в море. Последний радиосигнал, полученный на станции C, дает представление о …
Тригонометрия (Список курсов MindTap)
Для y = x sin x, y = _____.a) x cos x b) x cos x + 1 c) cos x d) x cos x + sin x
Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные числа, 8-я
Гармонический ряд:
1 + 2 + 3 + 4 +…Учебное пособие по многомерному исчислению Стюарта, 8-е
Рассмотрим следующую популяцию: {1, 2, 3, 4}. Для этой генеральной совокупности среднее значение равно = 1 + 2 + 3 + 44 = 2,5. Предположим, что a r …
Введение в статистику и анализ данных
Покажите, что уравнение прямой, проходящей через точки (a, 0) и ( 0, б) с a0 и b0 можно записать в виде xa…
Конечная математика для управленческих, жизненных и социальных наук
Одна сторона прямоугольника на 2 см длиннее второй. Если площадь 35 см2, найдите размеры rec …
Элементарная геометрия для студентов колледжа
Нахождение проекции u на v В упражнениях 27 и 28, (a) найдите проекцию u на v, и ( b) найти th …
Многопараметрическое исчисление
Создание эскиза поверхности уровня В упражнениях 71-76 опишите и нарисуйте график поверхности уровня f (x, y, z) = c at…
Исчисление
Использование основных правил интеграции В Упражнении 18 используйте основные правила интеграции, чтобы найти или оценить интеграл …
Исчисление (список курсов MindTap)
Оценочные оценки курса для четырех преподавателей колледжа показаны в таблице следующая таблица. Используйте = .05 и проверьте …
Статистика для бизнеса и экономики, пересмотренная (список курсов MindTap)
Найдите 5A. A = [312825]
College Algebra (Список курсов MindTap)
J.D. Power and Associates опрашивает новых владельцев автомобилей, чтобы узнать о качестве недавно приобретенных автомобилей …
СТАТИСТИКА F / БИЗНЕС + ЭКОНОМИКА-ТЕКСТ
Найдите размер A с точностью до минуты.
Математика для машинной техники
Определите достоверность измерения и объясните, почему и как оно измеряется.
Методы исследования поведенческих наук (Список курсов MindTap)
Опишите три метода, используемые для количественной оценки поведенческих наблюдений, и три метода, используемые для выборки…
Методы исследования поведенческих наук (Список курсов MindTap)
Значение размера автопарка для доходов от аренды автомобилей. Компании на рынке аренды автомобилей в США сильно различаются по показателям …
Основы статистики для бизнеса и экономики
Тимо и Хенке пять раз играли в гольф во время отпуска. Их оценка представлена на рисунке 4.160. Тимо 103 99 …
Математика: Практическая одиссея
Напоминание Округлите все ответы до двух десятичных знаков, если не указано иное.Инвестиция Вы открываете счет …
Функции и изменения: моделирующий подход к университетской алгебре (список курсов MindTap)
Найдите контрпримеры, чтобы показать, что утверждения в 9-12 ложны. действительные числа x и y, x + y = x + y.
Дискретная математика с приложениями
Допустима ли замена u = 1×2 02x1x2dx? Если нет, то почему бы не в определенном интеграле
Calculus Volume 2
Random Selection В упражнениях 7-14 определите количество способов, которыми компьютер может случайным образом сгенерировать одно или несколько s…
College Algebra
В следующих упражнениях используйте прямую подстановку для оценки каждого предела. 88. limx2 (4×21)
Calculus Volume 1
Случайным образом был выбран последний год с 1985 года по настоящее время.