Содержание
Урок 21. показательная функция — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
— какая функция называется показательной;
— какие свойства имеет показательная функция в зависимости от ее основания;
— какой вид имеет график показательной функции в зависимости от ее основания;
— примеры реальных процессов, описываемых показательной функцией.
Глоссарий по теме
Функция вида , a>0, а≠1 называется показательной функцией с основанием а.
Функция называется монотонно возрастающей на промежутке <a; b>, если (чем больше аргумент, тем больше значение функции).
Функция называется монотонно убывающей на промежутке <a; b>, если (чем больше аргумент, тем меньше значение функции).
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
http://fcior.edu.ru/ — Федеральный центр информационно-образовательных ресурсов
http://school-collection.edu.ru/ — Единая коллекция цифровых образовательных ресурсов
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Определение:
Функция вида y=ах, a>0, а≠1 называется показательной функцией с основанием а.
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Для положительного основания значение степени ах можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.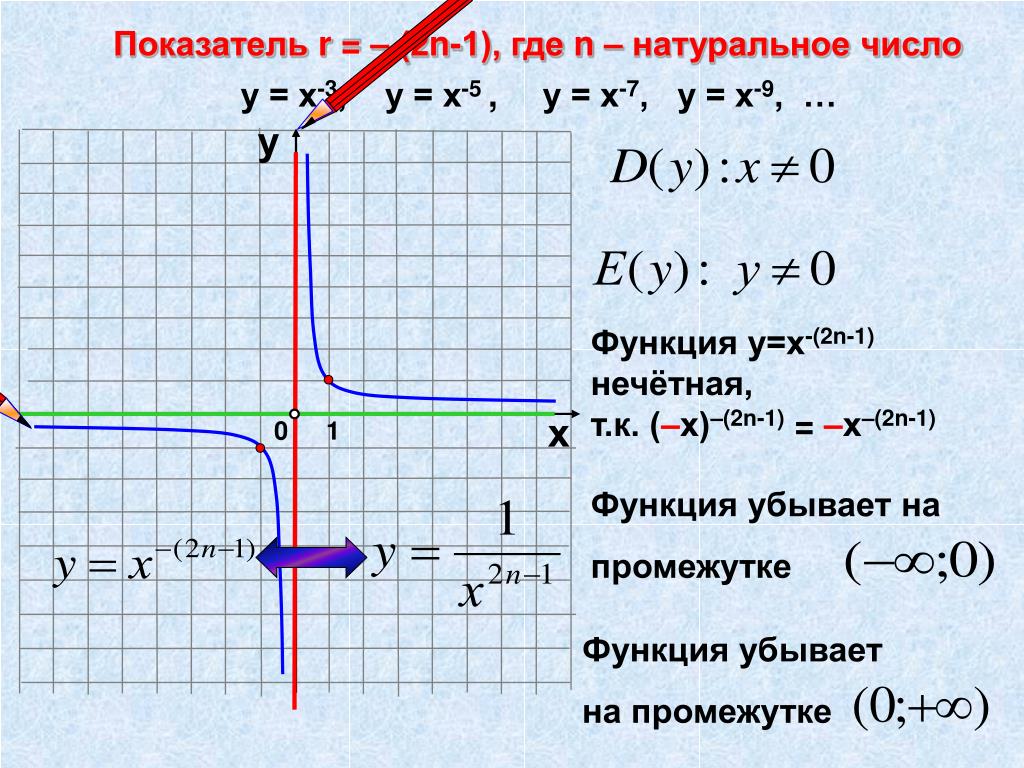
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень ах для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
Множество значений показательной функции Е(y)=R+, или Е(y)=(0; +∞).
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
4. Монотонность.
При a>1 функция монотонно возрастает.
При 0<a<1 функция монотонно убывает.
5. При любом значении а значение функции y (0) = а0 =1.
6. График функции.
При a>1
Рисунок 1 – График показательной функции при a>1
При 0<a<1
Рисунок 2 – График показательной функции при 0<a<1
Независимо от значения основания а график функции имеет горизонтальную асимптоту y=0.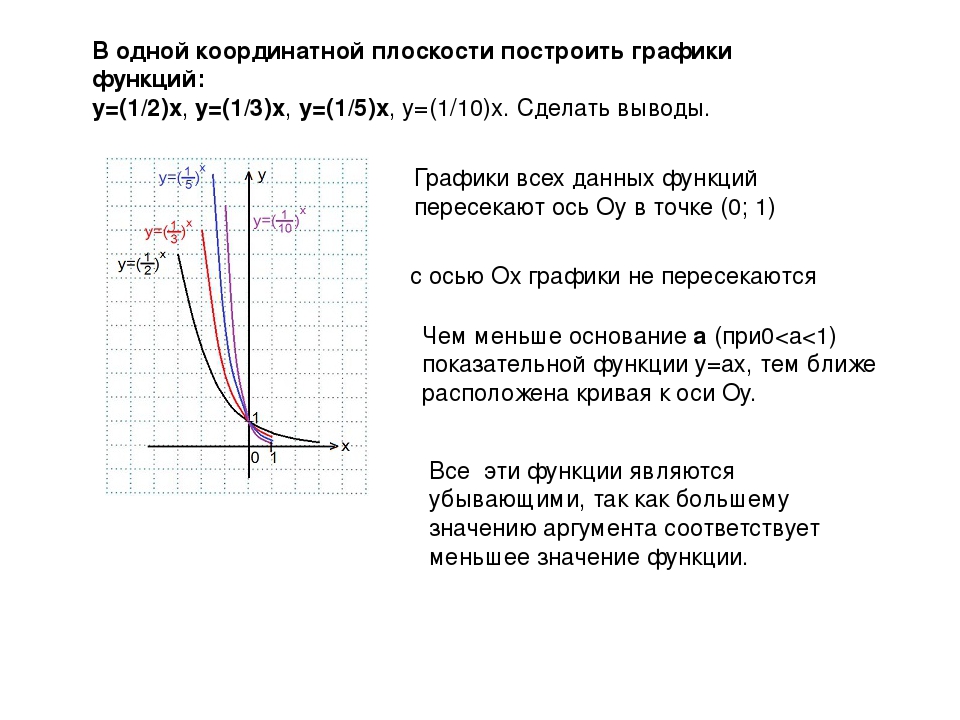 Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3х+1.
Решение:
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3х>0, то –3х<0, значит, –3х+1<1, то есть множество значений функции y=–3х+1 представляет собой промежуток (-∞; 1).
3) Так как функция y=3х монотонно возрастает, то функция y=–3х монотонно убывает. Значит, и функция y=–3х+1 также монотонно убывает.
4) Эта функция будет иметь корень: –3х+1=0, 3х=1, х=0.
5) График функции
Рисунок 3 – График функции y=–3х+1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
1) Рост различных микроорганизмов, бактерий, дрожжей и ферментов описывает формула: N= N0·akt, N– число организмов в момент времени t, t – время размножения, a и k – некоторые постоянные, которые зависят от температуры размножения, видов бактерий. Вообще это закон размножения при благоприятных условиях (отсутствие врагов, наличие необходимого количества питательных веществ и т.п.). Очевидно, что в реальности такого не происходит.
2) Давление воздуха изменяется по закону: P=P0·a-kh, P– давление на высоте h, P0 – давление на уровне моря, h – высота над уровнем моря, a и k – некоторые постоянные.
3) Закон роста древесины: D=D0·akt, D– изменение количества древесины во времени, D0 – начальное количество древесины, t – время, a и k – некоторые постоянные.
4) Процесс изменения температуры чайника при кипении описывается формулой: T=T0+(100– T0)e-kt.
5) Закон поглощения света средой: I=I0·e-ks, s– толщина слоя, k – коэффициент, который характеризует степень замутнения среды.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Если предположить, что поток информации изменялся по тому же закону до того года, который принят за начальный, то будем двигаться по оси абсцисс влево от начала координат и над значениями аргумента -10, -20 и т.д. будем наносить на график значения функции уже в порядке убывания — уменьшая каждый раз вдвое.
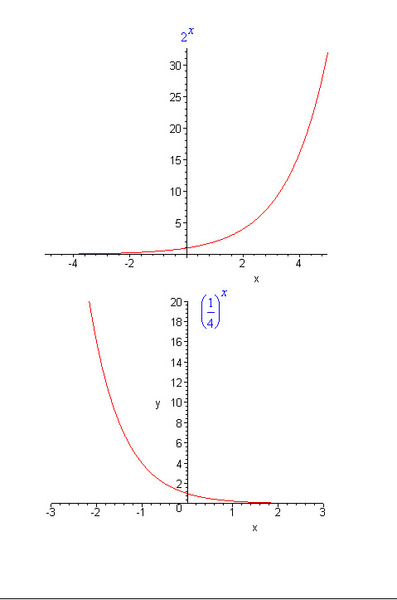
Рисунок 4 – График функции y=2х – изменение количества информации
Закон изменения количества информации описывается показательной функцией y=2х.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Выберите показательные функции, которые являются монотонно убывающими.
- y=3x-1
- y=(0,4)x+1
- y=(0,7)-х
- y=
- y=3-2х
- y=102x +1
Решение:
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:
2) 4) 5)
Пример 2.
Найдите множество значений функции y=3x+1– 3.
Решение:
Рассмотрим функцию.
Так как 3x+1>0, то 3x+1– 3>–3, то есть множество значений:
(– 3; +∞).
Пример 3.
Найдите множество значений функции y=|2x– 2|
Рассмотрим функцию. n$, тогда график нашей функции $y=\sqrt[n]{x}$ будет симметричен относительно прямой $y=x$. Не забываем, что мы рассматриваем случай неотрицательного значения аргумента, то есть $х≥0$.
n$, тогда график нашей функции $y=\sqrt[n]{x}$ будет симметричен относительно прямой $y=x$. Не забываем, что мы рассматриваем случай неотрицательного значения аргумента, то есть $х≥0$.
Свойства функции
Свойства функции $y=\sqrt[n]{x}$ при $x≥0$:
1. $D(f)=[0;+∞)$.
2. Функция не является ни четной, ни нечетной.
3. Возрастает на $[0;+∞)$.
4. Не ограничена сверху, ограничена снизу.
5. Наименьшее значение равно нулю, наибольшего значения нет.
6. Непрерывна.
7. $E(f)=[0;+∞)$.
8. Выпукла вверх на луче $[0;+∞)$.
9. Внимательно посмотрев на наш график функции мы можем сказать, что в любой точке к нему можно провести касательную (точку $х=0$ не рассматриваем). А это значит, что наша функция дифференцируема в любой точке. Производной в точке $х=0$ не существует, так как касательная в этой точке совпадает с осью ординат.
Примеры построения графиков функции и решения уравнений
Пример. Построить график функции $y=\sqrt[4]{(x+2)}-2$.
Решение.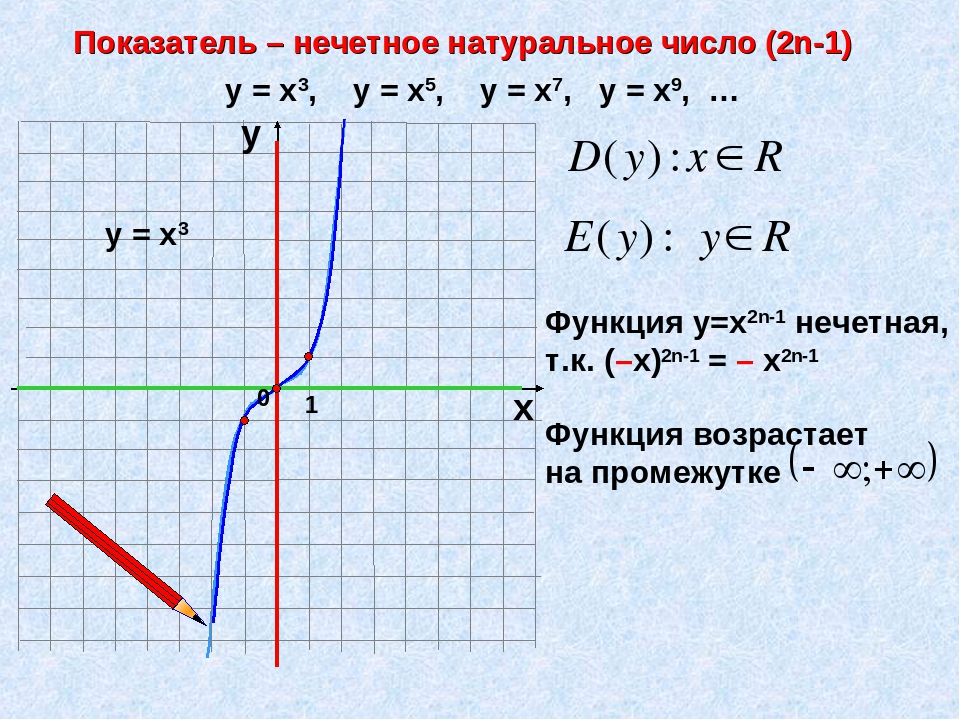 График нашей функции получается из графика $y=\sqrt[4]{x}$ смещением на две единицы влево и на две единицы вниз относительно начала координат.
График нашей функции получается из графика $y=\sqrt[4]{x}$ смещением на две единицы влево и на две единицы вниз относительно начала координат.
Пример. Решить уравнение $\sqrt[8]{x}=2x-1$.
Решение. Решим наше уравнение графическим способом. Построим два графика функции $\sqrt[8]{x}$ и $y=2x-1$. Найдем точку их пересечения.
Наши графики пересекаются в одной точке (1;1). Подставив $x=1$ в исходное уравнение, получаем верное тождество $1=1$, значит точка $х=1$ — решение нашего уравнения.
Теперь давайте рассмотрим исходную функцию для нечетного показателя корня. На прошлом уроке мы с вами узнали, что $\sqrt[n]{x}$, если n нечетное существует и при $х
$f(-x)=\sqrt[n]{(-x)}=-\sqrt[n]{x}=-f(x)$,где $n=3,5,7,9…$.
Вспомнив свойство графика нечетной функции – симметричность относительно начала координат, давайте построим график функции $y=\sqrt[n]{x}$ для $n=3,5,7,9…$.
Отразим график функции, которой мы получили вначале, относительно начала координат.
Заметим, что ось ординат является касательной к графику нашей функции в точке $х=0$.
Пример.
Построить и прочитать график функции $y=f(x)$, где $f(x)$:
$f(x)=\begin{cases}\sqrt[5]{x}, x≤1\\ \frac{1}{x}, x>1\end{cases}$.
Решение. Последовательно построим два графика функции на разных координатных плоскостях, после полученные графики объединим в один.
Построим график функции $y=\sqrt[5]{x}$, $x≤1$.
Таблица значений:
График функции $y=\frac{1}{x}$ нам хорошо известен, это гипербола, давайте построим график при $x>1$.
Объединим оба графика:
Ребята, давайте опишем свойства, которыми обладает наша функция:
1. $D(f)=(-∞;+∞)$.
2.Ни четная, ни нечетная.
3. Убывает на $[1; +∞)$ и возрастает на $(-∞;1]$.
4. Неограниченна снизу, ограничена сверху.
5. Наименьшего значения нет, наибольшее значение равно 1.
6. Непрерывна.
7. $E(f)=( -∞;1]$.
8. Функция дифференцируема всюду, кроме точек $х=0$ и $х=1$.
9. $\lim_{x \rightarrow +∞} f(x)=0$.
Пример. Найти область определения функций:
а) $y=\sqrt[6]{2x-10}$.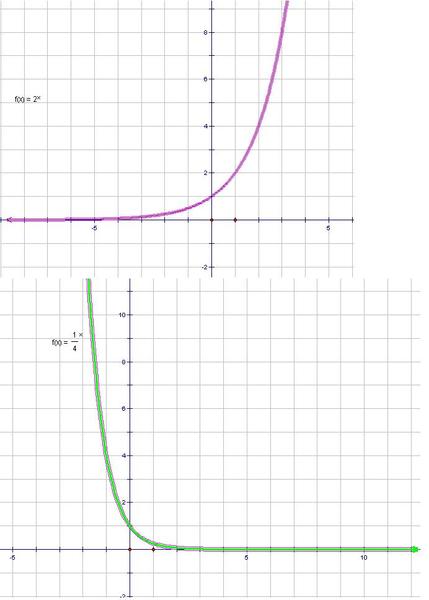 2}$.
2}$.
Функция корень n — степени из x, свойства и график
Вопросы
занятия:
·
рассмотреть
свойства функции корень n-ой степени из x;
·
рассмотреть
график функции корень n-ой степени из x;
·
рассмотреть
примеры на построение и нахождение свойств функций этого вида.
Материал
урока
Прежде чем перейти к изучению нового
материала, давайте повторим основные понятия, с которыми мы познакомились на
предыдущих уроках.
Корнем n-ой степени из
неотрицательного числа a
называют
такое неотрицательное число, при возведении которого в степень n
получается число а.
Корнем нечётной степени n-ой из
отрицательного числа а называют такое
отрицательное число, при возведении которого в степень n получается а.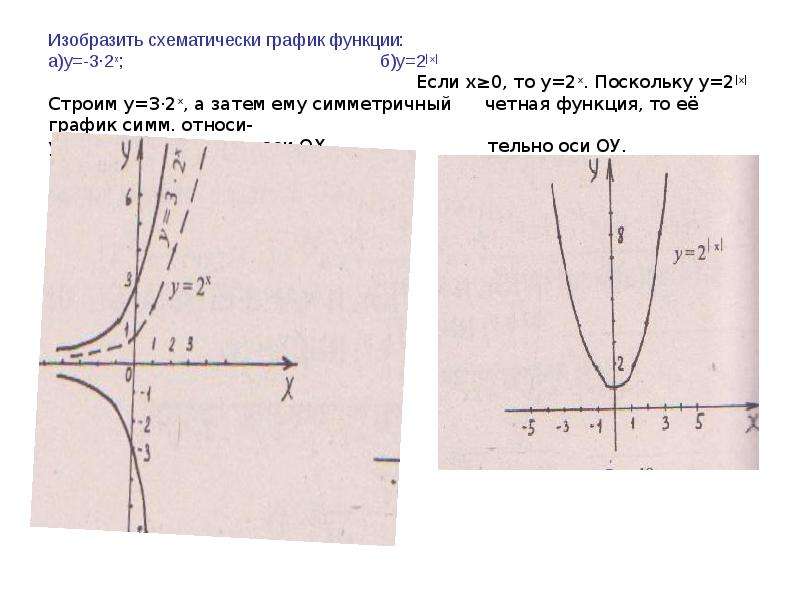
Обозначают:
Число а – это подкоренное
число, число n – показатель корня.
Обобщая
эти понятия, можно сказать, что из любого неотрицательного числа можно извлечь
корень любой степени (второй, третьей, четвертой и так далее), а из
отрицательного числа можно извлечь только корень нечётной степени.
То
есть на [0; +∞) каждому числу x
можно поставить в соответствие единственное число корень n-ой
степени из x при любом значении n.
Другими
словами, на множестве [0; +∞) можно говорить о функции:
Давайте
попробуем найти свойства этой функции и построить её график.
Основные
свойства:
Областью
определения будет являться промежуток [0;
+∞).
Поскольку
корнем n-ой степени из неотрицательного числа является неотрицательное
число, то областью значений функции будет промежуток [0; +∞).-(Stepennye-funkcii)-reshenie-38.1.jpg)
Поскольку
область определения функции не является симметричным множеством, то функция не
является ни чётной, ни нечётной.
Операцию
извлечения корня мы вводили как операцию обратную возведению в соответствующую
степень.
Тогда
можно сказать, что:
Зная
это, нетрудно построить график функции.
Используя построенный график, мы можем записать
оставшиеся свойства функции.
Функция возрастает на промежутке
[0; +∞).
Функция не ограничена сверху, но ограничена
снизу, например, прямой y = -0,5.
Наименьшим
значением функции будет 0, наибольшего значения функция не имеет.
Функция непрерывна на всей
области определения.
Функция выпукла вверх на всей
области определения.
При изучении темы дифференцирование
функций, мы говорили, что если функция дифференцируема в каждой точке
некоторого промежутка, то она непрерывна на данном промежутке. Из курса базовой
Из курса базовой
школы мы знаем:
Тогда:
Эта производная существует в любой точке
промежутка [0; +∞) за исключением точки 0.
Таким образом, функция имеет производную
в любой точке промежутка (0; +∞), то есть функция дифференцируема
на промежутке (0; +∞).
Рассмотрим несколько примеров.
Пример.
Пример.
Мы с вами говорили о функции y
равно корень n—ой
степени из x только для
неотрицательных значений аргумента.
Но если эн нечётное число, то выражение
корень n—ой
степени из x
имеет
смысл и для отрицательных x.
Значит, можно говорить о функции:
Теперь давайте запишем свойства этой
функции.
Областью определения
будет промежуток (– ∞; + ∞).
Областью значений
будет промежуток (– ∞; + ∞).
Поскольку область определения является
симметричным множеством, то можно исследовать данную функцию на чётность:
Получаем, что функция при нечётном n
будет нечётной.
Давайте построим график функции.
Воспользуемся свойством нечётности
функции и добавим к этой ветви ветвь, симметричную ей относительно начала
координат.
По графику легко записать оставшиеся
свойства функции.
Функция возрастает на всей
области определения.
Функция не ограничена ни сверху ни
снизу.
Функция не имеет ни наименьшего, ни
наибольшего значений.
Функция непрерывна на всей
области определения.
Функция выпукла вниз на
промежутке (– ∞; 0) и выпукла вверх на промежутке (0; +
∞).
Функция дифференцируема на всей
области определения за исключением точки 0.
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
Семинары и мероприятия
Для записи на обучение и уточнения информации обращайтесь в Отдел внебюджетных услуг, маркетинга и развития КК ИПК по адресу: г. Красноярск, ул. Матросова, 19, каб. 1-10.
8(391)236-00-07, 8 (391) 206-99-19, доб. 153
Обучающие вебинары по методике преподавания английского языка
Ключевые подходы к оцениванию экзаменационных работ ОГЭ по русскому языку (опыт работы предметной комиссии)
Правовые основы организации сетевой формы реализации образовательной программы в образовательной организации
Обобщение и оформление педагогического опыта для Регионального атласа образовательных практик
Финансовая математика на уроках в основной и старшей школе
Опыт работы в сенсорной комнате с разными категориями обучающихся
Как организовать внеурочную деятельность по индивидуальным программам?
Планирование образовательной деятельности в дошкольной образовательной организации
Шкала оценки качества образования в дошкольных образовательных организациях (ECERS)
Шкала оценки качества образовательной среды школы (SACERS)
Обучение работодателей и работников вопросам охраны труда
Проектирование рабочей программы в школе
Тренинг по финансовой математике в старшей школе. Учимся решать задание 17 ЕГЭ по математике профильного уровня
Учимся решать задание 17 ЕГЭ по математике профильного уровня
Компьютерный ЕГЭ по информатике: новые вызовы и новые задачи
Особенности организации развивающей предметно-пространственной среды для детей раннего и дошкольного возраста
Обновление деятельности школьной библиотеки: цифровая жизнь традиционных форм работы
Творческая мастерская
Проектирование муниципальной и школьной модели инклюзивного образования
Инклюзивные практики в общеобразовательных учреждениях
Актуальные направления современной психокоррекционной работы в образовательной организации
Содержание и организация педагогической супервизии для учителей, реализующих практику формирования функциональной грамотности школьников
Учимся решать задание 19 ЕГЭ по математике профильного уровня
Основные трудности младших школьников при выполнении итоговых работ по математике
Новая модель КИМ ОГЭ по математике 9 класса: как готовить?
Учимся решать задания повышенного уровня сложности ОГЭ и ЕГЭ по математике профильного уровня по планиметрии (модуль «Окружность»)
Организация платных услуг в образовательной организации
Новая модель КИМ ОГЭ по информатике 9 класса: как подготовить обучающихся
Разработка индивидуальных образовательных программ сопровождения интеллектуально одаренных обучающихся
Экспертиза моделей инклюзивного образования образовательной организации
Особенности организации развивающей предметно-пространственной среды для детей раннего и дошкольного возраста в соответствии с требованиями ФГОС ДО
Степенная функция ⋆ ДПА и ЗНО онлайн
Степенной функцией называется функция вида $$y=x^{\alpha}.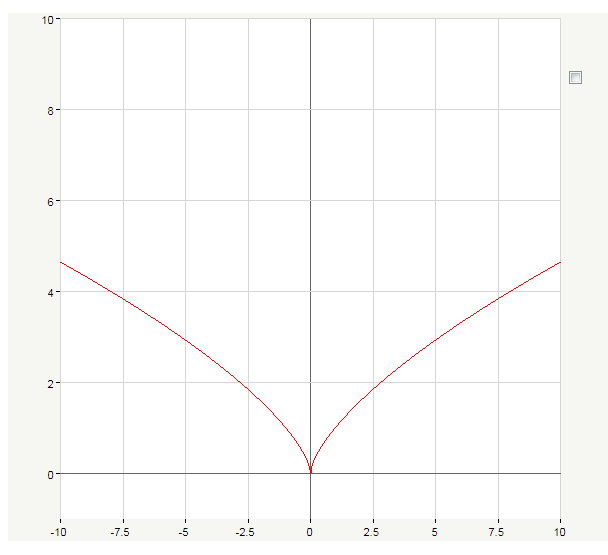 {-\frac{3}{2}}.$$
{-\frac{3}{2}}.$$
постройте график функции y=x в 5 степени является ли функция четной или нечетной?
Решение в приложении)
Ответ: 2
Предположим, что может.
b²-4ac=27; 4ac=b²-27; Выражение справа делится на 4, значит, должно делиться на 4 и выражение b²-24-3.
-24 делится на 4, осталось выяснить, делится ли в²-3 на 4
Очевидно, что b должно быть нечетным, т. е. иметь вид b=2n+1, т.к. если от четного отнять 3, то получим нечетное, а оно не делится на 4.
Подставим (4n²+4n+1)-3=4n²+4n-2 =(4n²+4n)-2
Последнее выражение не делится на 4. Значит, предположение — ложно. И ни при каких целых a, b, c дискриминант квадратного уравнения не может быть равным 27.
5²=x²*(x²-24)
x⁴ -24x²-25=0
y=x²
y²-24y-25=0
D=576+100=676
y₁=(24-26)/2=-1
y₂=(24+26)/2=25
При у=-1
x²= -1
нет решений.
При у=25
x²=25
x₁=5
x₂= -5 — не является натуральным
Ответ: х=5.
Корекнь 1369- 37 ккорень136900- 370 корень с 0.001369- 0.037
Степенная функция, ее свойства и график
Вы знакомы с функциями y=x, y=x2, y=x3, y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=xp, где p — заданное действительное число.
д. Все эти функции являются частными случаями степенной функции, т. е. функции y=xp, где p — заданное действительное число.
Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень xp. Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.
- Показатель p=2n -четное натуральное число.
В этом случае степенная функция y=x2n, где n — натуральное число, обладает следующими
свойствами:
- область определения — все действительные числа, т. е. множество R;
- множество значений — неотрицательные числа, т. е. y больше или равно 0;
- функция y=x2n четная, так как x2n=(-x)2n
- функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.
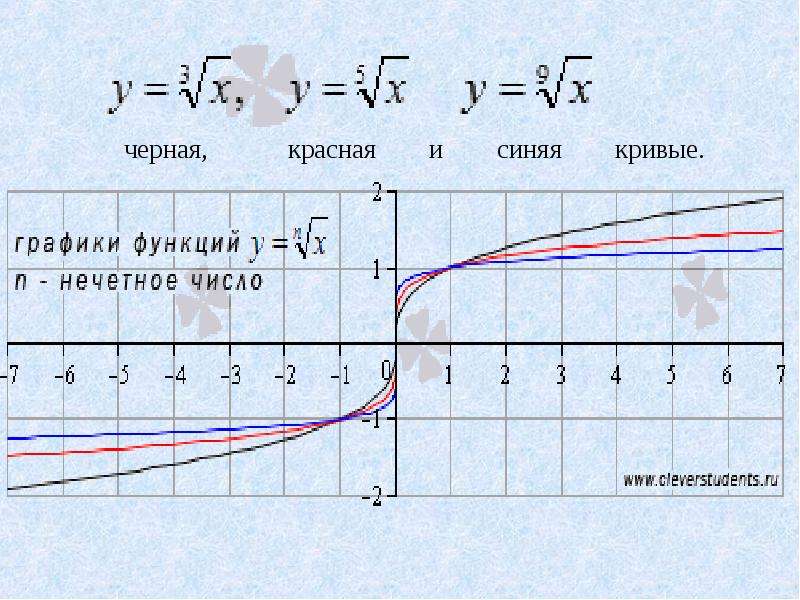
График функции y=x2n имеет такой же вид, как например график функции y=x4.
2. Показатель p=2n-1— нечетное натуральное число
В этом случае степенная функция y=x2n-1 , где натуральное число, обладает следующими свойствами:
- область определения — множество R;
- множество значений — множество R;
- функция y=x2n-1 нечетная, так как (-x)2n-1=x2n-1;
- функция является возрастающей на всей действительной оси.
График функции y=x2n-1 имеет такой же вид, как, например, график функции y=x3.
3.Показатель p=-2n, где n — натуральное число.
В этом случае степенная функция y=x-2n=1/x2nобладает следующими свойствами:
- область определения — множество R, кроме x=0;
- множество значений — положительные числа y>0;
- функция y=1/x2n четная, так как 1/(-x)2n=1/x2n;
- функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.
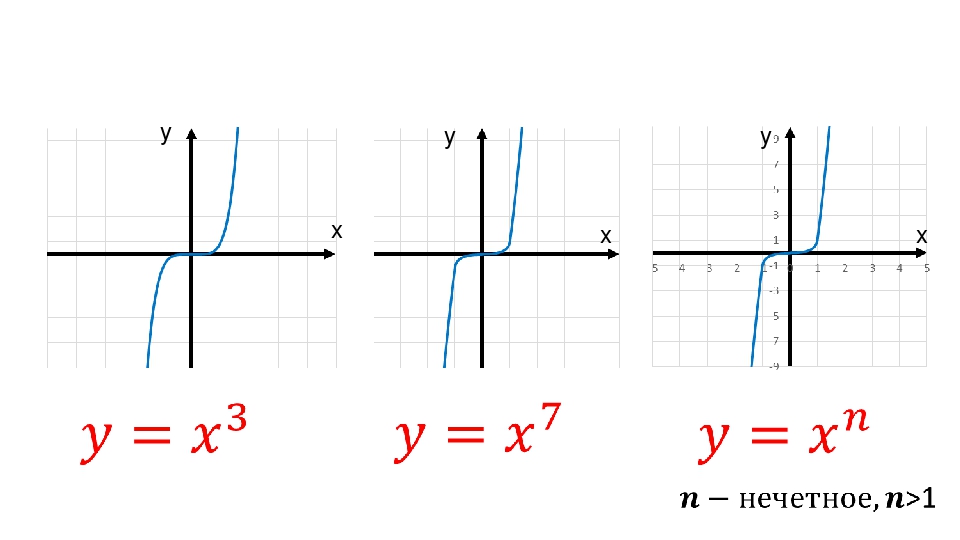
График функции y=1/x2n имеет такой же вид, как, например, график функции y=1/x2.
4.Показатель p=-(2n-1), где n — натуральное число.
В этом случае степенная функция y=x-(2n-1) обладает следующими свойствами:
- область определения — множество R, кроме x=0;
- множество значений — множество R, кроме y=0;
- функция y=x-(2n-1) нечетная, так как (-x)-(2n-1) =-x-(2n-1);
- функция является убывающей на промежутках x<0 и x>0.
График функции y=x-(2n-1) имеет такой же вид, как, например, график функции y=1/x3.
Графики Разделы: Вводные концепции, Пошаговые инструкции Графические экспоненциальные функции Помните, что основной
С левой стороны Так почему же это выглядит как
Но не стоит забывать
Это видно на Обычно вы не будете Верх
|
Функция, обратная квадратному корню
Чтобы найти обратную функцию квадратного корня, очень важно сначала набросать или изобразить данную проблему, чтобы четко определить, что такое область и диапазон.Я буду использовать область и диапазон исходной функции, чтобы описать область и диапазон обратной функции, меняя их местами. Если вам нужна дополнительная информация о том, что я имел в виду под «обменом доменов и диапазонов» между функцией и ее обратной, см. Мой предыдущий урок об этом.
Примеры того, как найти обратную функцию квадратного корня
Пример 1: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Укажите его домен и диапазон.
Каждый раз, когда я сталкиваюсь с функцией квадратного корня с линейным членом внутри радикального символа, я всегда думаю о ней как о «половине параболы», нарисованной в сторону.Поскольку это положительный случай функции квадратного корня, я уверен, что ее диапазон будет становиться все более положительным, проще говоря, стремительно увеличиваясь до положительной бесконечности.
Эта конкретная функция извлечения квадратного корня имеет этот график с указанием области и диапазона.
С этого момента мне придется решать обратную алгебру, следуя предложенным шагам. По сути, замените \ color {red} f \ left (x \ right) на \ color {red} y, поменяйте местами x и y в уравнении, решите для y, которое вскоре будет заменено соответствующей обратной записью, и, наконец, укажите домен и диапазон.
Не забудьте использовать приемы решения радикальных уравнений для решения обратной задачи. Возведение квадратного корня в квадрат или во вторую степень должно устранить радикал. Однако вы должны сделать это с обеими сторонами уравнения, чтобы сохранить баланс.
Однако вы должны сделать это с обеими сторонами уравнения, чтобы сохранить баланс.
Убедитесь, что вы проверили домен и диапазон обратной функции из исходной функции. Они должны быть «противоположны друг другу».
Размещение графиков исходной функции и обратной к ней по одной координатной оси.2} = 1. Его домен и диапазон будут замененной «версией» исходной функции.
Пример 3: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Это график исходной функции, показывающий ее домен и диапазон.
Определение дальности обычно является сложной задачей. Лучший способ найти это — использовать график данной функции с ее областью определения. Проанализируйте, как функция ведет себя по оси Y, учитывая значения x из области.
Вот шаги, чтобы решить или найти обратное значение данной функции квадратного корня.
Как видите, все очень просто. Убедитесь, что вы делаете это осторожно, чтобы избежать ненужных алгебраических ошибок.
Пример 4: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Эта функция составляет 1/4 (четверть) окружности с радиусом 3, расположенной в Квадранте II. С другой стороны, это половина полукруга, расположенная над горизонтальной осью.
Я знаю, что он пройдет проверку горизонтальной линии, потому что ни одна горизонтальная линия не пересечет ее более одного раза. Это хороший кандидат на обратную функцию.
Опять же, я могу легко описать диапазон, потому что потратил время, чтобы построить его график. Что ж, я надеюсь, что вы понимаете важность наличия наглядного пособия, которое поможет определить этот «неуловимый» диапазон.
Присутствие члена в квадрате внутри радикального символа говорит мне, что я буду применять операцию извлечения квадратного корня к обеим сторонам уравнения, чтобы найти обратное.Поступая так, у меня будет положительный или отрицательный результат. Это ситуация, когда я приму решение, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу позволить получить два ответа.
Это ситуация, когда я приму решение, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу позволить получить два ответа.
Как я решу, какой выбрать? Ключевым моментом является рассмотрение домена и диапазона исходной функции. Я поменяю их местами, чтобы получить домен и диапазон обратной функции. Используйте эту информацию, чтобы определить, какая из двух функций-кандидатов удовлетворяет требуемым условиям.
Хотя у них один и тот же домен, диапазон здесь — решающий фактор! Диапазон говорит нам, что обратная функция имеет минимальное значение y = -3 и максимальное значение y = 0.
Случай положительного квадратного корня не соответствует этому условию, поскольку он имеет минимум при y = 0 и максимум при y = 3. Отрицательный случай должен быть очевидным выбором, даже после дальнейшего анализа.
Пример 5: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.
Полезно увидеть график исходной функции, потому что мы можем легко определить ее домен и диапазон.
Отрицательный знак функции квадратного корня означает, что он находится ниже горизонтальной оси. Обратите внимание, что это похоже на Пример 4. Это также одна четверть круга, но с радиусом 5. Область вынуждает четверть круга оставаться в Квадранте IV.
Вот как мы алгебраически находим обратное.
Вы выбрали правильную обратную функцию из двух возможных? Ответ — случай с положительным знаком.
Практика с рабочими листами
Возможно, вас заинтересует:
Инверсия матрицы 2 × 2
Функция, обратная абсолютному значению
Функция, обратная постоянной
Функция, обратная экспоненте
Функция, обратная линейной
Обратная логарифмическая функция
Обратная квадратичная функция
Обращение рациональной функции
графиков Джеффри
графиков Джеффри
Джеффри, переходя в 5-е место
оценка, график x = y, x 2 = y, x 3
= y и x 4 = y от x = — 1
до 1 на 0. 1’s
1’s
Джеффри выяснил правило для шаттла
головоломка P (P + 2) = M, и Дон попросил его построить график этой функции как x (x + 2) = y. Он получил
парабола. Они посмотрели на узор в параболе — от (0,0) идет 1
вправо, 1 вверх, 1 вправо, затем 3 вверх, 1 вправо, затем 5 вверх, и продолжил движение вверх по
нечетные числа. Затем Дон попросил Джеффри построить график x = y, x 2 =
y, x 3 = y и x 4 = y от x = — 1
к 1 по 0,1 на той же миллиметровой бумаге. Он сделал это ниже:
Затем Дон попросил его написать о том, что он нашел на графиках.
«Когда x отрицательно, а y = x в нечетной степени, оба
x и y отрицательны, потому что если вы умножите — .9
по — ,9 по — ,9
вы должны получить отрицательное число, потому что отрицательное значение, умноженное на отрицательное, является
положительный, и отрицательный, умноженный на положительный, является отрицательным.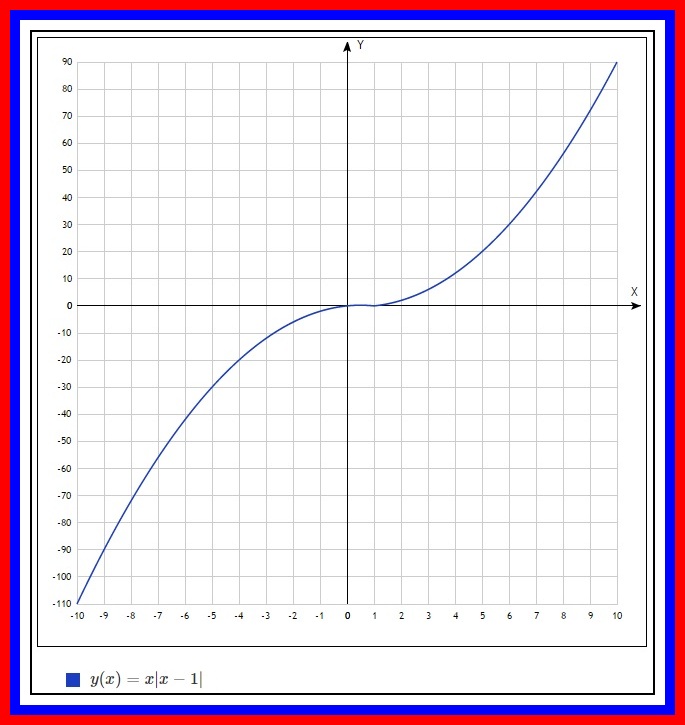
Когда x 4 = y на графике
больше похож на половину квадрата, потому что когда вы умножаете число от 0 до 1
и вы дойдете до четвертой степени, она станет намного меньше, потому что это своего рода
нравится делить, потому что.1 2 = 0,1 x 0,1 = 0,01 дюйма
Джеффри работал над перемещением
парабола y = x 2
до 2 единиц (он обнаружил, что это уравнение имеет вид y = x 2
+2) и правее 3 единицы (он обнаружил, что это уравнение имеет вид y = (x
— 3) 2 ).
Отличная работа
Джеффри!
Джеффри работал над
Тест SSAT снова и снова, готовимся к тесту в следующем году. Дон показал Джеффри
как умножить 12×13 в его голове, а в итоге умножить 22×23 в его голове.Дон также показал Джеффри, как возвести 2 числа в квадрат из 5, например 25×25.
знак равно Что ж, ответ имеет 25 справа _ 2 5. Возьми
другое число 2, прибавьте 1, чтобы получить 3, затем умножьте на 2 на 3, чтобы получить 6.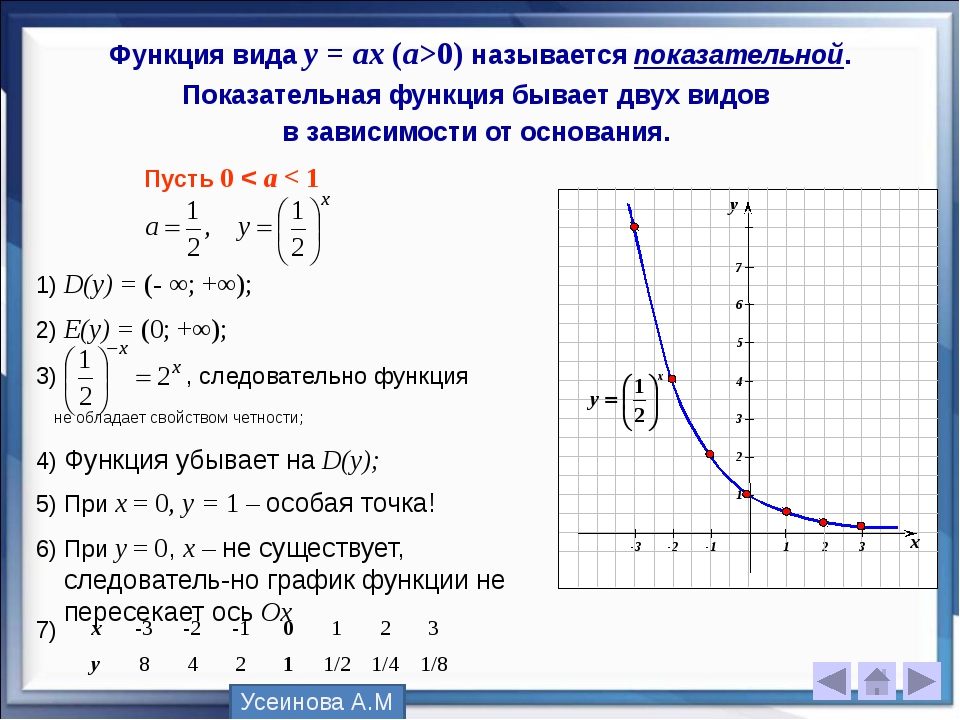 Ответ на
Ответ на
25×25 = 625. Делая что-то в школе, он говорил о 5 8
= 625 2 и он приступил к умножению 625×625 в своей голове!
Кому
Работа Джеффри о силах силы
Кому
Работа Джеффри над площадью под кривыми и интегралом
К
Работа Джеффри над бесконечной серией
To
Работа Джеффри над числами Фибоначчи
Кому
Работа Джеффри над шестью триггерами
Кому
другие открытия
На заказ
Материалы Дона
Mathman home
Тест опережающего коэффициента
График
полиномиальная функция
ж
(
Икс
)
знак равно
а
п
Икс
п
+
а
п
—
1
Икс
п
—
1
+
…
+
а
1
Икс
+
а
0
в конечном итоге повышается или понижается в зависимости от ведущего коэффициента
(
а
п
)
и
степень полинома
функция.
Дело
Конечное поведение графика
Когда п
это странно и
а
п
положительный
График падает влево и поднимается вправо Когда п
это странно и
а
п
отрицательный
График поднимается влево и опускается вправо Когда п
даже и
а
п
положительный
График поднимается влево и вправо Когда п
даже и
а
п
отрицательный
График падает влево и вправо
Пример:
Используйте тест опережающего коэффициента, чтобы определить конечное поведение графика полиномиальной функции.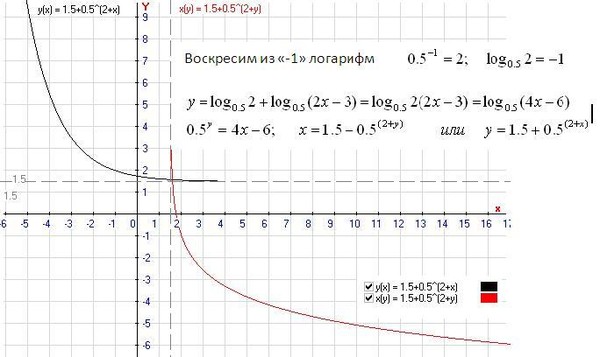
ж
(
Икс
)
знак равно
—
Икс
3
+
5
Икс
.x $ определяется где-то в строке действительных чисел, если $ x $ является отрицательным целым числом или рациональным числом с нечетным знаменателем при полном уменьшении. Любое другое значение $ x $ даст ответ, который не определен в строке действительных чисел.
Чтобы объяснить почему, позвольте мне перейти к делу и обойти некоторые технические математические вопросы, которые помогут вам визуализировать интуицию.
Для начала нам нужно взглянуть на набор комплексных чисел. Мы можем записать комплексные числа как $ x + yi $, но они также могут быть представлены в так называемой полярной форме, как угол и величина.{x \ ln {(- x)}} (\ cos {\ pi x} + i \ sin {\ pi x})
$
Теперь это четко определенное комплексное число!
Калькулятор проблемы?
Причина, по которой ваш калькулятор ломается, заключается в том, как он проверяет и выбирает значения.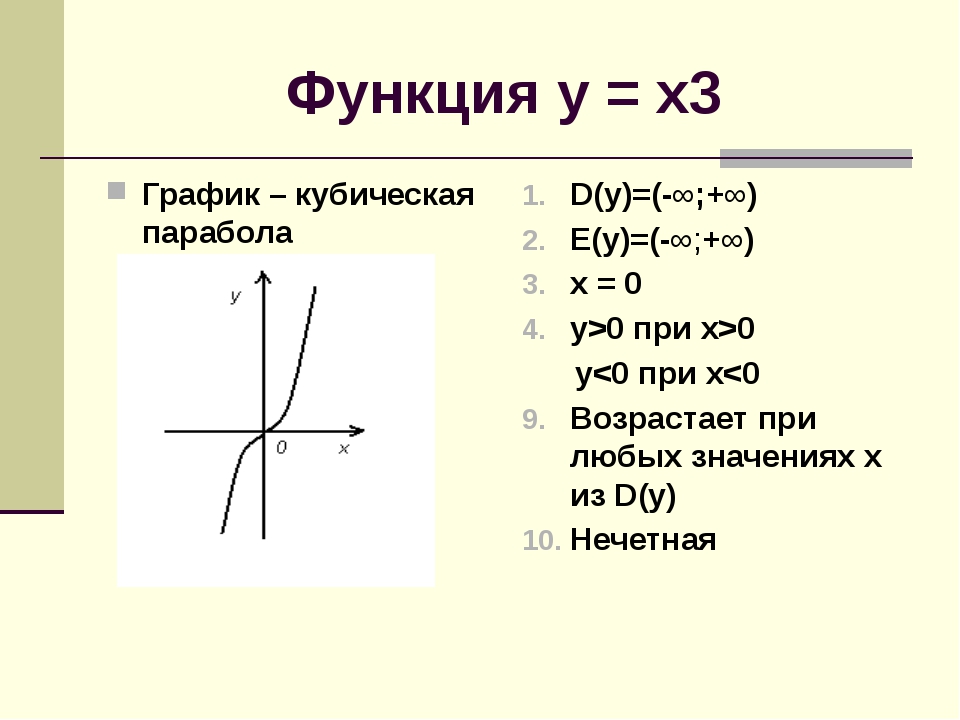 Если он выбирает десятичные значения, он никогда не сможет вычислить какие-либо из них в строке действительных чисел, за исключением отрицательных целочисленных значений. Если он каким-то образом может выполнять эти сложные операции и может проверять точные рациональные значения по формуле, которую я привел с использованием символьной оценки, то он даст вам некоторые значения для тех, которые он проверяет.Но в противном случае вам не повезет, поскольку большинство из этих значений дадут вам комплексные числа!
Если он выбирает десятичные значения, он никогда не сможет вычислить какие-либо из них в строке действительных чисел, за исключением отрицательных целочисленных значений. Если он каким-то образом может выполнять эти сложные операции и может проверять точные рациональные значения по формуле, которую я привел с использованием символьной оценки, то он даст вам некоторые значения для тех, которые он проверяет.Но в противном случае вам не повезет, поскольку большинство из этих значений дадут вам комплексные числа!
Обратные функции — Темы в предварительном исчислении
19
Определение обратных чисел
Извлечение аргумента
Запись обратного
Обозначение
График обратной функции
ИНВЕРСИЯ функции отменяет действие этой функции.Простейший пример — умножение и деление.
Скажем, мы начинаем с 5 — и умножаем ее на 3.
5 × 3 = 15.
Чтобы отменить это и вернуться к 5, мы должны разделить на 3.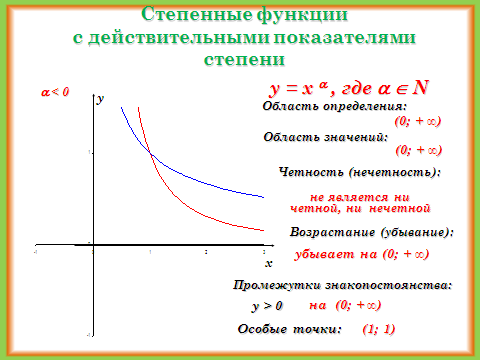
15 ÷ 3 = 5.
На языке функций, пусть f будет функцией, которая умножает свой аргумент на 3. Пусть g будет функцией, которая делит на 3.
Функция f действует на 5, производя f (5).Поскольку g является обратной величиной f , тогда g , действуя на f (5), вернет 5.
г ( ф (5)) = 5.
Фактически, g должен делать это для всех значений в домене f . И f должен делать это для всех значений в области g .
Как правило, если функция f воздействует на значение x , производя f ( x ),
, тогда, если g — обратное, то g , действующее на f ( x ) — g ( f ( x )) — вернет x .
Вот определение:
Функции f ( x ) и g ( x ) — это , инвертирующие друг друга, если:
f ( g ( x )) = x и g ( f ( x )) = x ,
для всех значений x в соответствующих доменах._ih_svojstva_i_grafik_11.2.jpg)
Задача 1. Пусть f ( x ) и g ( x ) — обратные.Тогда если
f (0) = 8,
сколько стоит г (8)?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
г (8) = 0.
Так, f , действуя на 0, дает 8. Таким образом, поскольку g является обратным, тогда, когда оно действует на 8, оно вернет 0.
г ( f ( x )) = x .
Пример 1. Сложение и вычитание — обратные. Вычитание определенного числа отменяет или отменяет результат добавления.
На языке функций пусть
f ( x ) = x + 2 и г ( x ) = x — 2.
f ( x ) добавляет 2 к своему аргументу. г ( x ) вычитает 2.
При применении определения:
f ( g ( x )) = f ( x — 2) = ( x — 2) + 2 = x ,
и
г ( f ( x )) = г ( x + 2) = ( x + 2) — 2 = x .
Тема 3
Определению удовлетворяет.Функции f и g являются обратными.
Задача 2. Пусть f ( x ) = x 2 и g ( x ) = x ½ . Покажите, что они противоположны друг другу. (Домен f должен быть ограничен x 0.)
Чтобы показать, что они инверсны, мы должны показать, что они удовлетворяют определению инверсии.
f ( г ( x )) = f ( x ½ ) = ( x ½ ) 2 = x ,
и
г ( f ( x )) = г ( x 2 ) = ( x 2 ) ½ = x .
Извлечение аргумента
Когда мы пишем
( х + 3) 4 ,
, тогда x + 3 — аргумент функции
f ( x ) = x 4 .
f — это функция, которая принимает 4-ю степень своего аргумента.
Обратный ему, g ( x ), будет иметь 4-й корень.
г ( x ) = x ¼ .
Пример 2. Решите для x :
( x + 3) 4 = 16.
Решение . Для этого мы должны освободить или извлечь аргумент x + 3. Следующая строка для записи —
.
х + 3 =. . .
Чтобы извлечь аргумент любой функции, просто возьмите его обратный.В этом примере мы извлекаем корень 4-й степени из обеих частей уравнения. Можем сразу написать
x + 3 = 16 ¼ = 2.
Следовательно,
х = 2-3 = -1.
Задача 3. Решите для x :
Обратное от корня 5-й степени принимает 5-ю степень. Следовательно, взяв 5-ю степень у обеих сторон и тем самым освободив аргумент:
x — 4 = 2 5 = 32.
х = 36.
Запись обратного
Инверсия любой функции должна быть немедленно очищена. Обратное x + 2 равно x -2. (Пример 1) Обратное x 2 равно x ½ . (Проблема 2.) В теме 21 мы увидим, что обратная логарифмическая функция, y = log b x , является экспоненциальной функцией y = b x .И в теме 19 тригонометрии мы видим, что обратное значение y = sin x равно y = arcsin x .
Предполагается, что в математике ученик знает эти обратные значения.
Иногда можно увидеть, что чтобы «найти» обратную функцию, необходимо найти x и поменять местами переменные.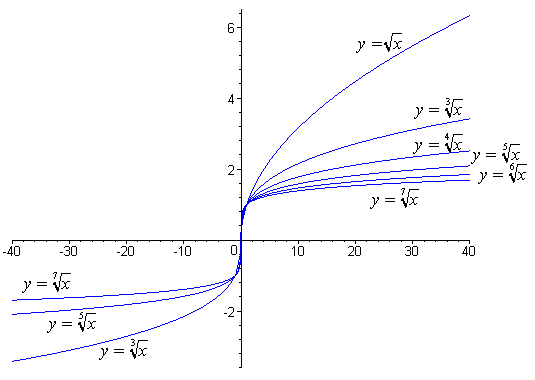 Фактически, это круговой метод, потому что для его применения вы должны уже знать обратное! Если y = x 2 , то на сторонах обмена: x = y 2 .Чтобы решить относительно и , вы должны знать, что величина, обратная квадрату, — это квадратный корень.
Фактически, это круговой метод, потому что для его применения вы должны уже знать обратное! Если y = x 2 , то на сторонах обмена: x = y 2 .Чтобы решить относительно и , вы должны знать, что величина, обратная квадрату, — это квадратный корень.
Сравнить Задачу 2.
Скажем, мы хотим написать обратную функцию этой функции:
f ( x ) = 3 x — 4.
Предположим, что x = 5. Какова будет последовательность операций?
Сначала умножим на 3, а затем вычтем 4. Мы получим 11.Следовательно, чтобы инвертировать это и вернуться к 5, мы должны добавить 4 и затем разделить на 3.
| г ( x ) | = | x + 4 3 | . |
Эта функция обратная. Студент должен это увидеть и понять.
Задача 4. а) Запишите обратное f ( x ) = −5 x .
| г ( x ) = | x −5 | = — | x 5 |
Деление на −5 является обратным умножению на −5.
б) Докажите, что они обратны.
| f ( g ( x )) = f (- | x 5 | ) = −5 · | x −5 | = х . |
и
| г ( f ( x )) = г (−5 x ) = | −5 x −5 | = х . |
f умножает свой аргумент на −5. г делит свой аргумент на −5.
Задача 5. а) Пусть f ( x ) = −½ x + 1.Можете ли вы сразу написать обратное, g ( x )?
г ( x ) = −2 x + 2.
В самом деле, f — это функция, которая умножает свой аргумент на −½ — эквивалентно делит на −2 — и затем прибавляет 1. Следовательно, ее обратная функция сначала вычитает 1:
х — 1
а затем умножить на −2:
−2 ( x — 1) = −2 x + 2.
b) Докажите, что f ( x ) и g ( x ) являются обратными.
f ( г ( x )) = −½ (−2 x + 2) + 1 = x — 1 + 1 = x .
и
г ( f ( x )) = −2 (−½ x + 1) + 2 = x — 2 + 2 = x .
Проблема 6.& nbsp Пусть f ( x ) = 2 x + 3. Запишите обратное.
| г ( x ) | = | x — 3 2 | . |
Обозначение
Функция I ( x ) = x называется функцией идентичности. Он всегда возвращает x .
Он всегда возвращает x .
В качестве обозначения обратной функции f мы иногда видим f -1 (« f обратная»). «-1» не показатель степени. Это обозначение используется потому, что на языке композиции функций мы можем написать:
f o
f −1 = I
Это аналогично форме умножению чисел: a · a −1 = 1.
Обратные тригонометрические функции см. В теме 19 «Тригонометрии».
График обратной функции
График обратной функции f ( x ) можно найти следующим образом:
Отразите график относительно оси x , затем поверните его на 90 ° против часовой стрелки
(Если мы возьмем график слева как правую ветвь y = x 2 , то график справа будет обратным, y =.)
Чтобы увидеть обратный график, пусть A будет любой точкой на
.
график f ( x ), пусть его координаты будут ( a , b ), пусть это будет расстояние d от начала координат C , и пусть AC образует угол θ с осью x ; треугольник ABC прямоугольный.
На рисунке слева показано отражение A относительно оси x до точки D .На рисунке справа показан поворот D на 90 ° против часовой стрелки до точки C ‘.
Мы увидим, что координаты C ‘ равны ( b , a ) — и это координаты на графике, обратном f ( x ). g ( x ), затем, согласно рисунку слева,
f ( a ) = b .
и g ( b ) — цифра справа — возвращает нас к a :
г ( b ) = a .
Определение обратного выполнено.
Чтобы увидеть, что координаты C ‘ равны ( b , a ), примите во внимание, что, поскольку угол C’A’D равен 90 °, тогда C’A’ составляет угол 90 ° — θ с осью x . То есть угол C’A’B ‘ является дополнением угла B’A’D , который является углом θ. Следовательно, в прямоугольном треугольнике A’B’C ‘ угол при C’ равен θ.
То есть угол C’A’B ‘ является дополнением угла B’A’D , который является углом θ. Следовательно, в прямоугольном треугольнике A’B’C ‘ угол при C’ равен θ.
Но угол при A является дополнением к θ. Следовательно, треугольники ABC, A’B’C ‘ конгруэнтны (угол-сторона-угол), и те стороны равны, что противоположны равным углам:
A’B ‘ равно AB — что составляет b , y — равен f ( x ).
B’C ‘ равно BC , что составляет a , x — эквивалент f ( x ).
Следовательно, координаты C ‘ равны ( b , a ).
Итак, когда каждая точка ( a , b ) на f ( x ) преобразуется в ( b , a ), то полученный график является обратным.
Каждая точка ( a , b ) также будет преобразована в ( b , a ), когда ( a , b ) отражается относительно линии y = x .
Поэтому мы говорим, что графики функции и обратной симметричны относительно прямой y = x .
Следующая тема: Логарифмы
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Калькулятор кубического корня | Определение
Наш калькулятор кубического корня — удобный инструмент, который поможет вам определить кубический корень, также называемый корнем 3 rd , любого положительного числа . Вы можете сразу воспользоваться нашим калькулятором; просто введите число, из которого вы хотите найти кубический корень, и готово! Более того, вы можете делать вычисления наоборот и использовать их для кубических чисел.Для этого просто введите число, которое вы хотите возвести в третью степень, в последнее поле! Это может быть чрезвычайно полезно при поиске так называемых идеальных кубов. Подробнее о них вы можете прочитать в следующей статье.
Подробнее о них вы можете прочитать в следующей статье.
Благодаря нашему калькулятору кубического корня, вы также можете вычислить корни из других степеней . Для этого вам нужно изменить число в градусах корневого поля . Если вы хотите узнать больше об определении корня куба, ознакомиться со свойствами функции корня куба и найти список префектных кубов, мы настоятельно рекомендуем вам продолжить чтение этого текста.Там вы также можете найти некоторые уловки, как найти кубический корень на калькуляторе или как вычислить его в уме.
Если вас интересует история символа корня, загляните в калькулятор квадратного корня, где мы ее обсудим. Кроме того, не забудьте попробовать другие наши математические калькуляторы, такие как калькулятор наибольшего общего множителя или калькулятор гиперболических функций.
Определение кубического корня
Предположим, вы хотите найти кубический корень числа x . Кубический корень y — это такое число, которое, если возвести его в третью степень, даст в результате x . (1/3)
(1/3)
Геометрический пример может помочь вам понять это. Лучший пример, который мы можем привести, — это куб. Итак, кубический корень объема куба — это длина его ребра. Так, например, если куб имеет объем 27 см³, то длина его граней равна кубическому корню из 27 см³, что составляет 3 см. Легкий?
Вы должны помнить, что в большинстве случаев кубический корень не будет рациональным числом . Эти числа могут быть выражены как частное двух натуральных чисел, т.е.е. фракция. Дроби могут вызвать определенные трудности, особенно когда дело касается их сложения. Если у вас возникли проблемы с нахождением общего знаменателя двух дробей, воспользуйтесь нашим калькулятором НОК, который вычисляет наименьшее общее кратное двух заданных чисел.
Что такое кубический корень из …?
С помощью нашего калькулятора кубического корня действительно легко найти кубический корень любого положительного числа! Просто введите любое число, чтобы найти его кубический корень. Например, кубический корень из 216 равен 6. Чтобы просмотреть список идеальных кубиков, перейдите к следующему разделу.
Например, кубический корень из 216 равен 6. Чтобы просмотреть список идеальных кубиков, перейдите к следующему разделу.
Обратите внимание, что можно найти кубический корень и из отрицательного числа, в конце концов, отрицательное число в третьей степени все еще отрицательно — например, (-6) ³ = -216 .
Однако вы должны помнить, что любое ненулевое число имеет три кубических корня: по крайней мере, один действительный и два мнимых. Этот калькулятор кубического корня работает только с действительными числами, но, если вам интересно, мы рекомендуем вам прочитать больше о мнимых числах!
Наиболее распространенные значения — список perfect cubes
Ниже приведены наиболее распространенные значения кубического корня.Эти числа также очень часто называют совершенных кубов , потому что их кубические корни являются целыми числами. Вот список из десяти первых идеальных кубиков:
- кубический корень из 1:
∛1 = 1, так как1 * 1 * 1 = 1; - кубический корень из 8:
∛8 = 2, так как2 * 2 * 2 = 8; - кубический корень из 27:
∛27 = 3, так как3 * 3 * 3 = 27; - кубический корень из 64:
∛64 = 4, так как4 * 4 * 4 = 64; - кубический корень из 125:
∛125 = 5, так как5 * 5 * 5 = 125; - кубический корень из 216:
∛216 = 6, так как6 * 6 * 6 = 216; - кубический корень из 343:
∛343 = 7, так как7 * 7 * 7 = 343; - кубический корень из 512:
∛512 = 8, так как8 * 8 * 8 = 512; - кубический корень из 729:
∛729 = 9, так как9 * 9 * 9 = 729; - кубический корень из 1000:
∛1000 = 10, так как10 * 10 * 10 = 1000;
Как видите, числа очень быстро становятся очень большими, но иногда вам придется иметь дело с еще большими числами, такими как факториалы.В этом случае мы рекомендуем использовать научную нотацию, которая является гораздо более удобным способом записывать действительно большие или очень маленькие числа.
С другой стороны, большинство других чисел не являются идеальными кубиками , но некоторые из них все еще используются часто. Вот список некоторых несовершенных кубов с округлением до сотых:
- кубический корень из 2:
∛2 ≈ 1,26; - кубический корень из 3:
∛3 ≈ 1,44; - кубический корень из 4:
∛4 ≈ 1.59; - кубический корень из 5:
∛5 ≈ 1,71; - кубический корень из 10:
∛10 ≈ 2,15;
Не сомневайтесь, воспользуйтесь нашим калькулятором кубического корня, если нужного вам числа нет в этом списке!
Функция кубического корня и график
Вы можете построить график функции y = ∛ (x) . В отличие от, например, логарифмическая функция, функция кубического корня является нечетной функцией — это означает, что она симметрична относительно начала координат и удовлетворяет условию - f (x) = f (-x) .Эта функция также проходит через ноль.
Благодаря этой функции вы можете построить график кубического корня, который показан ниже. Мы также рекомендуем вам воспользоваться калькулятором квадратичных формул, чтобы узнать о других функциональных формулах!
Как вычислить кубический корень в своей голове?
Как вы думаете, можно ли решить простые задачи с кубическими корнями без онлайн-калькулятора или даже карандаша или бумаги? Если вы думаете, что это невозможно или не можете сделать это, воспользуйтесь этим методом, это очень просто.Однако работает только для идеальных кубиков . Забудьте обо всех правилах из учебников по арифметике и рассмотрите на мгновение следующий метод, описанный Робертом Келли.
Прежде всего, необходимо запомнить кубики чисел от 1 до 10 и последнюю цифру их кубиков. Он представлен в таблице ниже.
| Номер | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Куб | 1 | 8 | 27 | 64 | 126 | 216 | 343 | 512 | 729 | 1000 |
| Последняя цифра | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 | 0 |
Если у вас есть число, которое вы хотите найти кубический корень, сначала посмотрите на тысячи (пропустите последние три цифры).Например, для числа 185 193 тысячи равны 185. Куб из 5 равен 125, а из 6 — 216. Следовательно, очевидно, что число, которое вы ищете, находится между 50 и 60. Следующий шаг — игнорировать все остальные цифры, кроме последней цифры. Мы видим, что это 3, так что проверьте свою память или в нашей таблице. Вы обнаружите, что число, которое вы ищете, — 7. Итак, ответ: 57 ! Легкий?
Давайте возьмем еще один пример и сделаем это шаг за шагом!
- Подумайте о числе, которое вы хотите узнать как кубический корень.Возьмем 17576 .
- Пропустить три последние цифры.
- Найдите два ближайших известных вам кубических корня. Кубический корень из 8 равен 2, а кубический корень из 27 равен 3. Таким образом, ваше число находится между 20 и 30.
- Посмотрите на последнюю цифру. Последняя цифра 17576 — 6.
- Проверьте свою память (или по нашей таблице) — последняя цифра 6 соответствует цифре 6. Это последняя цифра вашего числа.
- Объедините два: 26 . Это кубический корень из 17576!
Напоминаем, что этот алгоритм работает только для идеальных кубиков! А вероятность того, что случайное число является идеальным кубом, увы, очень мала.У вас есть только 0,0091% шанс найти человека между 1 000 и 1 000 000. Если вы не уверены в своем числе, просто забудьте об этом правиле и воспользуйтесь нашим калькулятором кубического корня 🙂
Как найти кубический корень на обычном калькуляторе?
- Сначала нужно набрать число, для которого нужно найти кубический корень
- Нажмите
√(корневой ключ) два раз - Пресс
x(множественный знак) - Нажмите
√(корневой ключ) четыре раз - Пресс
x(множественный знак) - Нажмите
√(корневой ключ) восемь раз - Пресс
x(множественный знак) - В последний раз нажмите
√(корневой ключ) два раз - А теперь можно нажать
=(знак равенства)! Вот тебе ответ!
Вы не верите? Проверьте это еще раз на другом примере!
Примеры вопросов о кубическом корне
Допустим, вам нужно сделать шар объемом 33.5 мл. Для его приготовления нужно знать его радиус. Как вы, наверное, знаете, уравнение для вычисления объема шара выглядит следующим образом:
В = (4/3) * π * r³
Итак, уравнение для радиуса выглядит так:
r = ∛ (3V / 4π)
Вы знаете, что объем 33,5 мл. Сначала вам нужно переключиться на другие единицы громкости. Самый простой перевод в см³: 33,5 мл = 33,5 см³. Теперь вы можете решить радиус:
r = ∛ (100.5 / 12,56)
r = ∛ (8)
г = 2
Чтобы шар имел объем 33,5 мл, его радиус должен составлять 2 сантиметра.
Калькулятор энного корня
С помощью нашего калькулятора корней вы также можете вычислить другие корни. Просто введите число в поле Degree of the root , и вы получите любой выбранный калькулятор корня n-й степени . Наш калькулятор автоматически сделает все необходимые расчеты, и вы можете свободно использовать его в своих расчетах!
Итак, давайте рассмотрим несколько примеров.Предположим, вам нужно вычислить корень четвертой степени из 1296 . Сначала вам нужно написать соответствующее число, которое вы хотите получить root — 1296. Затем измените степень корня на 4 . И вот результат! Корень четвертой степени из 1296 равен 6 .
Наш калькулятор корня n-й степени также позволяет вычислять корень иррациональных чисел. Попробуем вычислить π-го корня из . Символ π представляет собой отношение длины окружности к ее диаметру.Его значение постоянно для каждого круга и составляет примерно 3,14. Допустим, вы хотите вычислить корень π-степени из 450 . Сначала напишите 450 в поле числа . Затем изменим угол корня — округлим и напишем 3,14 вместо π. И теперь вы можете увидеть результат. Это почти 7 .
Три решения кубического корня
В конце этой статьи мы подготовили раздел продвинутой математики для самых настойчивых из вас.Вы, наверное, знаете, что положительные числа всегда имеют два квадратных корня: отрицательный и положительный. Например, √4 = -2 и √4 = 2 . Но знаете ли вы, что подобное правило применяется к кубическим корням? Все действительные числа (кроме нуля) имеют ровно три кубических корня : одно действительное число и пару комплексных. Комплексные числа были введены математиками давным-давно, чтобы объяснить проблемы, с которыми не могут справиться действительные числа. Обычно мы выражаем их в следующей форме:
х = а + б * я
, где x — комплексное число с действительной a и мнимой b частями (для действительных чисел b = 0 ).Загадочное воображаемое число i определяется как квадратный корень из -1 :
я = √ (-1)
Хорошо, но как это знание влияет на количество решений кубического корня? В качестве примера рассмотрим кубические корни из 8 , которые равны 2 , -1 + i√3 и -1 - i√3 .

 Однако по своей природе
Однако по своей природе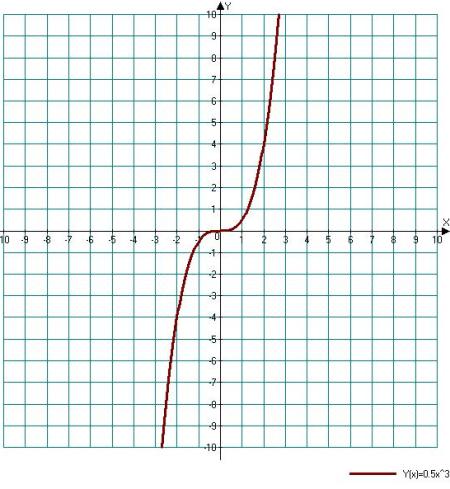
 Если
Если Как я
Как я
 «Графические экспоненциальные функции: Введение». Пурпурная математика .
«Графические экспоненциальные функции: Введение». Пурпурная математика .