Содержание
Исследование несобственного интеграла на сходимость
Примеры исследования несобственных интегралов на сходимость
Пример 1 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a 0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
, а интеграл сходится при m+n -1 и m+n -1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n -2 и m+n -1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается.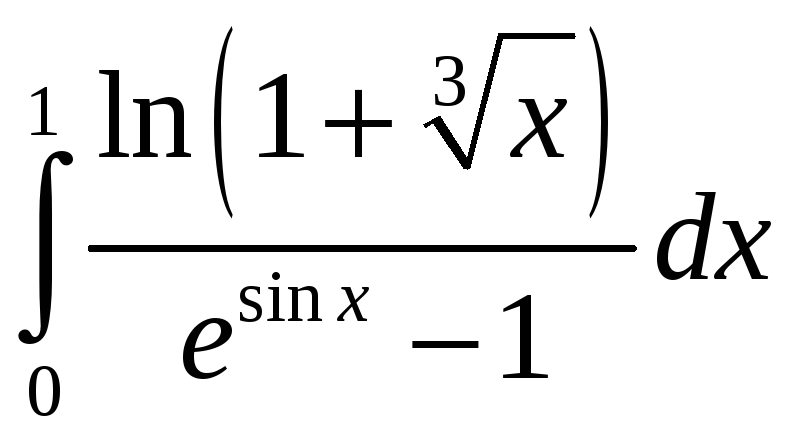 Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax -1.
Пример 6 Исследовать на сходимость .
Проведем замену переменной: t = lnx, и получим
.
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q 1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p 0, и, следовательно, начиная с некоторого А>1 выполнено T–QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
Тогда для интеграла I2 справедлива оценка
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q 1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость .
Разобьем исходный интеграл на два:
.
Сходимость. Интеграл I1 эквивалентен , т. е. сходится при p 0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
, при p>0.
Таким образом, интеграл сходится при 0
Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:
, т. е. интеграл сходится при p>1.
е. интеграл сходится при p>1.
Для доказательства расходимости при p£1 оценим интеграл снизу
.
Разобьем последний интеграл от разности функций на разность интегралов
.
Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится – то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.
расходится (пример 1) при p p>0 (см. Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится.
Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится.
Таким образом, исходный интеграл сходится абсолютно при 0
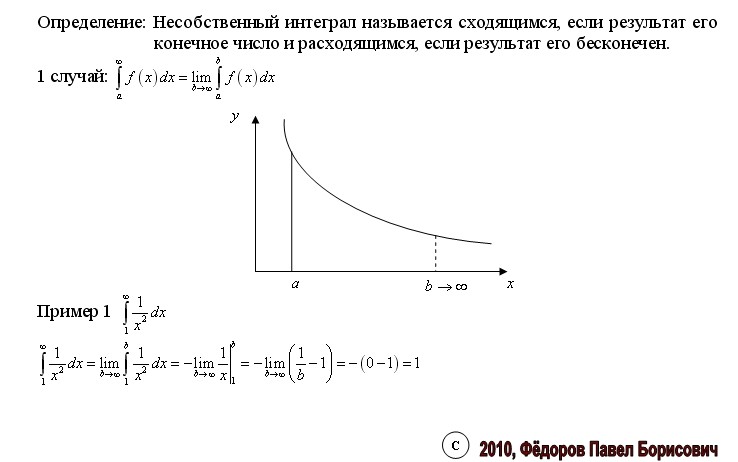
1. Несобственные интегралы с бесконечными пределами
Вспомним определение интеграла как предела интегральных сумм:
В определении предполагается, что интервал интегрирования конечен, а функция f (x) непрерывна в нем. Нарушение этих предположений приводит к несобственным интегралам.
Нарушение этих предположений приводит к несобственным интегралам.
Определение. Если интеграл стремится к конечному пределу при неограниченном возрастании “b”, то этот предел называют несобственным интегралом с бесконечной верхней границей от функции f (x) и обозначают символом
В этом случае говорят, что несобственный интеграл существует или сходится.
Если указанный предел не существует или существует, но бесконечен, то говорят, что интеграл не существует или расходится.
Аналогично определяется несобственный интеграл с бесконечной нижней границей:
Несобственный интеграл с двумя бесконечными границами определяется формулой:
где с – любая фиксированная точка на оси Ох.
Итак, несобственные интегралы могут быть с бесконечно нижней границей, с бесконечно верхней границей, а также с двумя бесконечными границами.
Признаки сходимости. Абсолютная и условная сходимость
Интеграл существует только тогда, когда существует каждый из интегралов: и .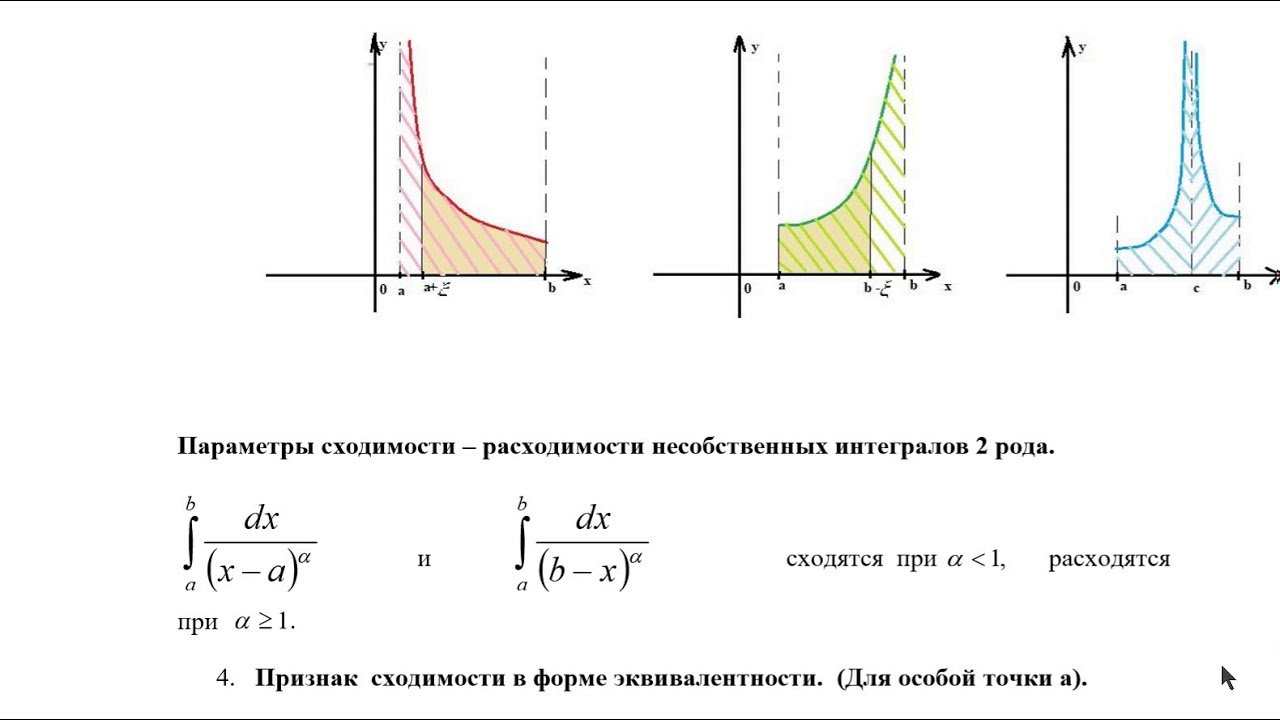
Пример. Исследовать на сходимость интеграл
Полагая с = 0, получим:
т.е. интеграл сходится.
Иногда нет необходимости вычислять несобственный интеграл, а достаточно лишь знать, сходится он или расходится, сравнив его с другим интегралом.
Теорема сравнения несобственных интегралов.
Пусть в интервале [a; +¥) функции f (x) и j (х) непрерывны и удовлетворяют неравенству 0 £ j (x) £ f (x). Тогда:
а) если интеграл сходится, то сходится
б) если интеграл расходится, то также расходится.
Пример.1. Исследовать, сходится ли интеграл:
Решение. Заметим, что при 1 £ x :
= 1
Следовательно, сходится и его значение, меньше 1.
Пример. 2. Исследовать, сходится ли интеграл
Замечаем, что
Но, .
Следовательно, расходится и данный интервал.
Теорема. Если интеграл сходится, то сходится и интеграл .
Если интеграл сходится, то сходится и интеграл .
В этом случае последний интеграл называется абсолютно сходящимся.
Если интеграл от расходится, то об интеграле от f (x) на одном этом основании ещё ничего сказать нельзя: он может расходиться, а может и сходиться. В последнем случае (т.е. когда сходится, расходится говорят, что сходится условно (не абсолютно).
Пример. Исследовать сходимость интеграла
Здесь подынтегральная функция – знакопеременная.
Замечаем, что
Но
Следовательно, интеграл сходится.
Отсюда следует, что сходится и данный интеграл.
Итак, для определения сходимости несобственного интеграла можно его сравнивать с другим интегралом, который заведомо сходится или расходится.
Несобственные интегралы от разрывных функций
Если на отрезке [a; b] функция f (x) имеет несколько (конечное число) точек разрыва первого рода, это “препятствие” легко устранить, разбив отрезок точками разрыва на несколько отрезков, вычислить определенные интегралы на каждом отдельном участке и результаты сложить.
Рассмотрим определенный интеграл от функции, неограниченной при приближении к одному из концов отрезка [a; b], например, .
(В таких случаях обычно говорят : ’’Функция имеет бесконечный разрыв на правом конце отрезка интегрирования’’.)
Ясно, что обычное определение интеграла здесь теряет свой смысл.
Определение. Несобственным интегралом от функции f(x), непрерывной при а £ х
Таким образом, данный интеграл расходится на всем отрезке [-1, 1]. Отметим, что если бы мы стали вычислять данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке x = 0, то получили бы неверный результат. Действительно,
, что невозможно.
Итак, для исследования несобственного интеграла от разрывной функции, необходимо «разбить» его на несколько интегралов и исследовать их.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: «Что-то тут концом пахнет». 8413 – | 8030 – или читать все.
8413 – | 8030 – или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Введите функцию, для которой необходимо вычислить несобственный интеграл
Найдём решение несобственного интеграла с заданными пределами интегрирования.
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Правила ввода выражений и функций
© Контрольная работа РУ – калькуляторы онлайн
Абсолютная и условная сходимость несобственных интегралов по бесконечному промежутку
§5. Абсолютная
Абсолютная
и условная сходимость несобственных
интегралов по бесконечному промежутку
До сих
пор рассматривались интегралы от
знакоположительных (знакопостоянных)
функций. Теперь пусть подынтегральная
функция таких ограничений не имеет, то
есть может быть и знакочередующейся
функцией.
Если
наряду с собственным интегралом по
бесконечному промежутку
сходится
и интеграл
по этому же промежутку, то первый интеграл
называется абсолютно сходящимся.
Если
интеграл
сходится,
а интеграл
расходится, то первый интеграл называется
условно сходящимся.
Пример
8. Исследовать на абсолютную сходимость
интеграл: .
Решение.
В начале исследуется данный интеграл
вообще на сходимость, для чего проведем
интегрированние по частям: пусть
тогда
,
далее
.
Так как последний интеграл сходится,
то по признаку сравнения сходится и
интеграл
,
причем абсолютно. Исходный интеграл
при этом является сходящимся (кстати,
сходимость этого можно определить
быстрее с помощью признака сходимости
Дирихле, который будет рассмотрен
позже). Чтобы исследовать исходный
Чтобы исследовать исходный
интеграл на абсолютную сходимость, надо
рассмотреть интеграл:
.
Так как
при
,
то имеем:
.
Интеграл
аналогично исходному интегралу
сходится, а интеграл
расходится; стало быть, и интеграл
является расходящимся. При этом исходный
интеграл является условно сходящимся.
Упражнение
8. Установить условную сходимость
интеграла:
.
Пример
9. Исследовать на абсолютную сходимость
интеграл:
.
Решение:
;
стало быть, интеграл сходится абсолютно.
Упражнение 9. Установить
абсолютную сходимость интеграла:
.
Установить
условную сходимость при отсутствии
абсолютной сходимости в ряде случаев
позволяет так называемый признак
сходимости Дирихле, в котором
исследуется структура подынтегральной
функции, если ее можно представить в
виде произведения двух функций, а именно:
,
где
интегрируема и ограничена, то есть:
(7) ;
а функция
при
непрерывно дифференцируема и монотонна,
причем:
(8) .
При
выполнении условий, налагаемых на
функции
и
интеграл
(9)
сходится.
С
помощью этого признака условную
сходимость интеграла в примере 8 при
отсутсвии абсолютной сходимости можно
определить следующим образом:
Имеем
интеграл
,
который не является абсолютно сходящимся.
Представим
подынтегральную функцию этого интеграла
в виде произведения двух функций, то
есть:
,
где
,
а
.
Функция
интегрируема и ограничена на бесконечном
промежутке, так как:
,
а
.
Поскольку все условия признака Дирихле
(Формулы (7) и (8)) выполнены, то
исследуемый интеграл
сходится условно, ибо абсолютная
сходимость этого интеграла места не
имеет, что было показано в примере 8.
Пример
10. Исследовать на абсолютную и условную
сходимость интеграл:
Решение. Сначала
сделаем в исследуемом интеграле замену
переменной:
пусть
,
тогда
;
если
;
если
;
итак, имеем:
где
является функцией интегрируемой и
ограниченной на бесконечном промежутке
(формула (7)), а
(выполняется формула (8)). Поскольку
Поскольку
все условия признака Дирихле (формулы
(7) и (8)) выполнены, то исследуемый
интеграл
сходится. Исследуем интеграл на абсолютную
сходимость, для чего рассмотрим интеграл
.
Т.к.
при
,
то
.
Интеграл
сходится по признаку Дирихле, а интеграл
расходящийся; стало быть, интеграл
тоже расходящийся, при этом исследуемый
интеграл
сходится условно.
Упражнение
10. Установить условную сходимость
интегралов Фронеля:
; .
Интеграл
типа (9) можно исследовать на условную
сходимость ещё и с помощью так называемого
признака сходимости Абеля, в котором
так же исследуется структура подынтегральной
функции, если её можно представить в
виде произведения двух функций
и
,
на которые теперь наклкдываются
следующие ограничения: интеграл от
функции
по бесконечному промежутку, то есть:
(10)
сходится,
а функция
при
непрерывно дифференциируема, монотонна
и непрерывна, а потому имеет конечный
предел, то есть:
(11) ,
.
При
выполнении указанных условий ((10) и
(11)) интеграл типа (9) сходится.
Пример 11. Установить сходимость
интеграла:
,
используя признак Абеля.
Решение. Исследуемый интеграл
представим следующим образом:
,
где
,
а
.
Так как интеграл от функции
по бесконечному промежутку сходится
(см. пример (8)), а
,
то все условия признака Абеля выполнены;
стало быть, исследуемый интеграл
сходящийся. Характер сходимости исходного
итеграла (сходится условно или абсолютно)
определится после исследования данного
интеграла на абсолютную сходимость,
для чего надо исследовать интеграл:
.
Так как
,
то
.
Интеграл
сходится по признаку Дирихле, так как
,
а
.
Интеграл
расходится, что можно установить по
предельному признаку сравнения:
при
;
тогда в кочестве сопоставляемой функции
имеем
,
а
,
что означает расходимость интеграла
.
Стало быть, интеграл
тоже расходящийся. Теперь ясен и характер
сходимости исходного интеграла
:
он сходится условно.
Упражнение
11. Исследовать характер сходимости
интеграла:
.
§6.
Признаки сравнения несобственных
интегралов
от
разрывных функций
Общий
и предельный признаки сравнения
несобственных интегралов от разрывных
функций аналогичны таким же признакам
для несобственных интегралов по
бесконечному промежутку (формулы (4) и
(6)). Пусть функции
и
,
неотрицательные на промежутке
и интегрируемы на каждом отрезке
,.
Тогда, если функции
и
удовлетворяют на промежутке
неравенству:
,
то имеем:
и из сходимости интеграла
следует сходимость интеграла
,
а из расходимости интеграласледует
расходимость интеграла
.
Возможные ситуации сопоставлений
интегралов исследуемого и известного
такие же, как это представлено в
соотношениях
.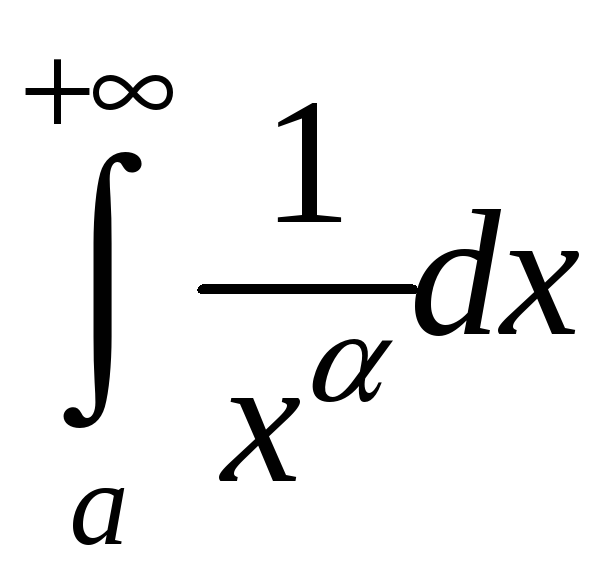
Далее, если существует, отличный от
нуля, конечный предел:
(12)
,
то
интегралы
и
ведут себя одинаково: то есть сходятся
или расходятся одновременно. В частности,
если функции
и
эквивалентны при
,
то эти функции одновременно либо
интегрируемы, либо неинтегрируемы на
промежутке
.
В
качестве частного признака сравнения
несобственных интегралов от разрывных
функций используется интеграл с
параметром
:
(13)
,
который
сходится при
и
расходится при
.
В самом деле,
,
откуда следует, что дробь, стоящая в
правой части равенства терпит бесконечный
разрыв при
и
;
если же
,
то дробь разрыва не имеет и интеграл
(13) сходящийся. В более общей форме
частный признак сравнения несобственных
интегралов от разрывных функций можно
представить так:
(13
а,б)
или
,
где,
как и раньше, интегралы сходятся при
и расходятся при
.
Пример
12. Исследовать несобственные
интегралы от разрывных функций на
сходимость:
а).
;
б).
;
в).
;
г).
.
Решения.
а). Так как на промежутке
имеет место неравенство:
,
то имеем сопоставление интегралов в
виде частного и общего признаков
сравнения:
.
Поскольку
интеграл в правой части неравенства
сходится (формула(13)),то исследуемый
интеграл тоже сходится согласно общему
признаку сравнения несобственных
интегралов.
б).
Пусть
,
а
;
тогда имеем сопоставление интегралов:
опорного (формула(13а))
и исследуемого в виде предельного
признака сравнения (формула (12)):
;
так как опорный интеграл расходится,
то расходится и исследуемый интеграл.
в).
Используем методику поиска опорного
интеграла, описанную для несобственных
интегралов первого рода:
1).,
что означает, что подынтегральная
функция
имеет
одну особенность в точке
,
где она терпит бесконечный разрыв (при
вычислении предела использовалась
эквивалентность функций при
,
а именно:
).
2). в
качестве сопоставляемой функции
используем
, которая эквивалентна функции
при
;
то есть:
,
а поскольку интеграл
сходящийся (формула(13)), то и исследуемый
интеграл тоже сходящийся.
г).
Подынтегральная функция
терпит
бесконечный разрыв в точке
,
так как
.
Исследуя разложение функции
в точке
,
будем иметь:
;
в качестве функции
возьмём
;
тогда предельный признак сравнения
даёт:
,
а поскольку
расходится, то расходится и исследуемый
интеграл.
Упражнения
12. Исследовать интегралы на
сходимость:
а)
; б);
в);
г).
§7. Абсолютная
и условная сходимость несобственных
интегралов от разрывных функций
Как и в
случае несобственных интегралов по
бесконечному промежутку, критерий Коши
(формула (3)) для несобственных интегралов
от разрывных функций в практических
целях мало пригоден (используется иногда
для установления расходимости). Тем не
Тем не
менее, определим этот критерий для
несобственных интегралов второго рода.
Итак, пусть функция f(x)
определена на промежутке [a,
b), интегрируема на
любом отрезке [a, c],
с<b, и неограниченна
в левой окрестности точки x=b.
Тогда для сходимости интеграла
необходимо и достаточно, чтобы для
любого числа
существовало такое число
,
чтобы при любых
и
,
принадлежащих интервалу
,
выполнялось соотношение:
(14) .
Абсолютная
и условная сходимость для несобственных
интегралов от разрывных функций
определяется аналогично тому, как это
было сделано для несобственных интегралов
по бесконечному промежутку ( см. §5) , а
именно: несобственный интеграл от
разрывной функций
называется абсолютно сходящимся, если
сходится интеграл
,
и условно сходящимся, если интеграл
сходится, а интеграл
расходится.
Пример
13. Установить абсолютную
сходимость интеграла:
Решение.
. Так как последний интеграл сходится,
то искомый интеграл J
сходится по общему признаку сравнения,
причём сходится абсолютно.
Упражнение
13. Установить абсолютную
сходимость интеграла:
.
Если абсолютная
сходимость несобственного интеграла
от разрывной функции места не имеет, то
исследовать исходный интеграл на
условную сходимость как и в случае с
несобственными интегралами по бесконечному
промежутку помогают достаточные признаки
сходимости Дирихле и Абеля (формулы
(7)(11)).
В случае несобственных интегралов
второго рода упомянутые признаки
сходимости определяются так:
15. Признак
Дирихле. Интеграл
сходится, если: 1).функция
непрерывна
и имеет ограниченную первообразную
на;
2).функция
непрерывно дифференцируема и монотонна
на
,
причём.
16. Признак
Абеля. Интеграл
сходится, если: 1).функция
непрерывна на
и интеграл
сходится; 2).функция
ограничена,
непрерывно дифференцируема и монотонна
на
,
то есть имеет конечный предел:.
Пример
14. Определить характер сходимости
интеграла:
.
Решение.
Сходимость интеграла устанавливаем с
помощью признака Абеля: пусть
, тогда
,
а
,
и сходимость интеграла:
(это несобственный интеграл первого
рода от знакопеременной подынтегральной
функции, который сходится по признаку
Дирихле (см. пример и упражнение №8)),
при этом исходный интеграл J
сходится по признаку Абеля.
Характер
сходимости исходного интеграла J
можно установить, исследовав его на
абсолютную сходимость, то есть изучив
интеграл:
.
Так как
,
то
расходится,
,где
;
пусть
,
,
;
если x=0+,
;
если x =1, t
= 2.
Этот интеграл
сходится по признаку Дирихле, а интеграл
расходится, так как расходится
;
итак, исходный интеграл
сходится условно.
Упражнение
14. Определить характер сходимости
интеграла:
Пример
15. Исследовать сходимость интеграла:
.
Решение.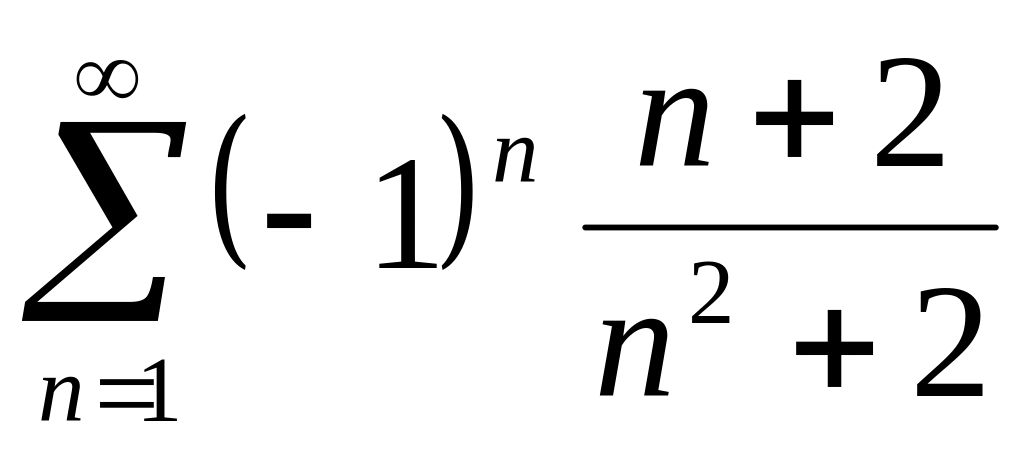
Исследуемый интеграл имеет одну
особенность в точке x=0.
Пусть:
,
,
;
если x = 0+, то
;
если
,
.
Тогда:
и интеграл исходный является расходящимся.
Упражнение
15. Исследовать интеграл на
сходимость:
.
Литература
Агеев О.Н.,
Шведова И.Г. Несобственные интегралы
и интегралы, зависящие от параметра.
Учебное пособие, М., МГТУ, 1993.
Зарубин В.С.
и др. Интегральное исчисление функций
одного переменного. М., МГТУ, 1999.
Ильин В.А.,
Поздняк Э.Г. Основы математического
анализа. Часть II. М., Наука,
1973.
Кудрявцев
и др. Сборник задач по математическому
анализу (интегралы, ряды). М., Наука,
1986.
Данко П.Е. и
др. Высшая математика в упражнениях и
задачах. Часть I. М., Высшая
школа, 1986.
Ляшко И.И. и
др. Справочное пособие по математическому
Справочное пособие по математическому
анализу (введение в анализ, производная,
интеграл). Киев, Высшая школа, 1984.
Ответы к упражнениям
Упр. 1). а).
;
б). расходится; в).
.
Упр. 2). а).
;
б). 1; в).
.
Упр. 3). а).
; б). –1; в). расходится.
Упр. 4). а).
;
б). расходится; в).
.
Упр. 5). а).
Расходится; б). сходится.
Упр. 6). а).
Сходится ; б). расходится.
Упр. 7). а).
Сходится; б). сходится; в). сходится; г).
расходится.
Упр. 11). Сходится
условно.
Упр. 12). а).
Сходится; б). сходится; в). сходится; г).
расходится.
Упр. 14). Сходится
условно.
Упр. 15).
Расходится.
Приложение
1. Главные значения расходящихся
несобственных интегралов
К несобственным интегралам
относятся так называемые интегралы в
смысле главного значения. Если
несобственный интеграл существует
(сходится), то существует и интеграл в
смысле главного значения и эти интегралы
совпадают. Из существования интеграла
Из существования интеграла
в смысле главного значения не следует
существование (сходность) соответствующего
несобственного интеграла. Рассмотрим
подробнее главные значения расходящихся
несобственных интегралов по бесконечному
промежутку и от разрывных функций.
Пусть функция f
(x) определена на всей
числовой оси и интегрируема на любом
отрезке этой оси. Если существует предел:
1.
,
то он
называется главным значением несобственного
интеграла по бесконечному промежутку
от функции f (x)
и обозначается символом:
,
где V и P
есть начальные буквы французских слов
«Valeur Principal»,
обозначающих «главное значение».
Итак, имеем по определению
2.
.
В случае неотрицательной функции
f (x) главное
значение несобственного интеграла по
бесконечному промежутку отождествляется
с площадью неограниченной области между
осью абсцисс и графиком этой функции.
Интеграл от нечетной функции fh
(x) (fh
(-x)= -fh
(x)) по любому симметричному
относительно начала координат отрезку
[-R; R] равен
нулю.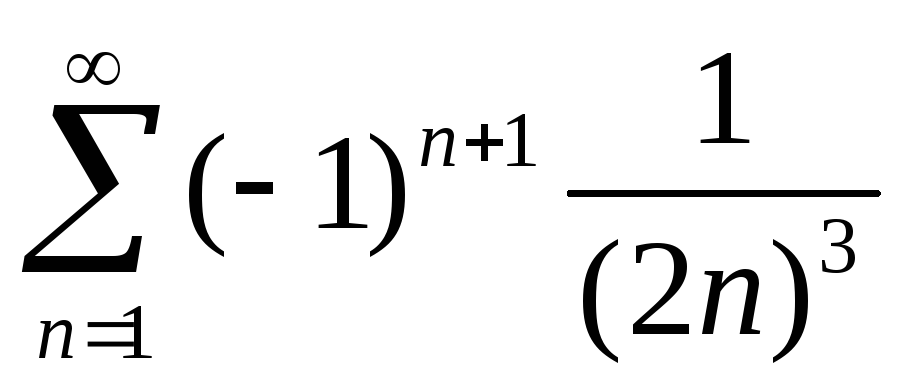 По этой причине и главное значение
По этой причине и главное значение
несобственного интеграла по бесконечному
промежутку от такой функции принимается
равным нулю, то есть:
3.
,
где fh
(x) есть функция нечетная.
Например,
,
в то время как несобственный интеграл
есть расходящийся; в самом деле:
,
то есть оба предела бесконечны; стало
быть и сам несобственный интеграл
расходится.
Аналогично равны нулю главные
значения следующих расходящихся
несобственных интегралов от нечетных
функций по бесконечному промежутку:
;
;
.
Интеграл от четной функции fr
(x) (fr
(x)= fr
(-x)) по любому симметричному
относительно начала координат отрезку
[-R; R] равен
удвоенному значению интеграла от этой
функции на отрезке [0; R].
Главное значение несобственного
интеграла по бесконечному промежутку
от четной функции fr
(x) существует, если
несобственный интеграл от этой функции
по промежутку [0; +)
сходится.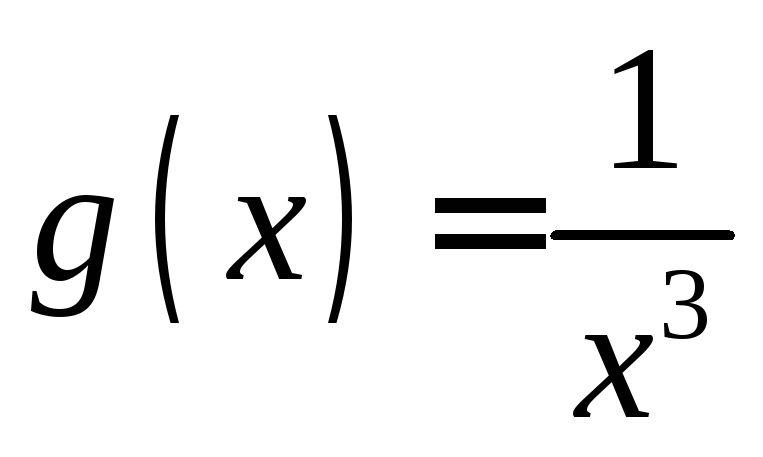 Таким образом, имеем:
Таким образом, имеем:
4.
,
где fr
(x) есть функция четная.
Например,
,
в то время как несобственный интеграл
расходится; в самом деле:
,
где интегралы j2 и
j4 есть расходящиеся,
а потому и исходный интеграл расходится.
Главные значения несобственных
интегралов по бесконечному промежутку
от следующих четных функций:
;
;
— не существуют, ибо расходятся
соответствующие несобственные интегралы
от этих функций; в самом деле:
;
;
,
;
xdx= =dv,
,
где безынтегральный член и предпоследний
интеграл расходятся; стало быть и
исходный интеграл расходится.
Упражнения: а)
;
б) .
Известно, что сумма, разность и
произведение четных функций есть функция
тоже четная; сумма и разность нечетных
функций есть функция нечетная, а
произведение четного числа нечетных
функций есть функция четная, в то время
как произведение нечетного числа
нечетных функций есть функция нечетная.
Области определений четной и нечетной
функций симметричны относительно начала
координат. Любую функцию общего вида
(ни четную, ни нечетную), определенную
на симметричном относительно начала
координат интервале, можно представить
в виде суммы двух функций: четной (fr
(x)) и нечетной (fh
(x)) c общей
для всех трех функций областью определения,
то есть:
5.
f (x)= fr
(x)+ fh
(x).
Это представление единственно,
что нетрудно показать: так как f
(-x)= fr
(-x)+ +fh
(-x)= fr
(x)- fh
(x), то с учетом соотношения
(5) имеем систему двух уравнений с двумя
неизвестными fr
(x) и fh
(x):
из которой выражения для функций: четной
fr (x)
и нечетной fh
(x),- определяется однозначно,
а именно:
6а.
,
6б.
.
Например, представим функцию
общего вида
в виде суммы функций четной fr
(x) и нечетной fh
(x): согласно формул (6а) и
(6б) имеем:
;
;
что верно, ибо:
.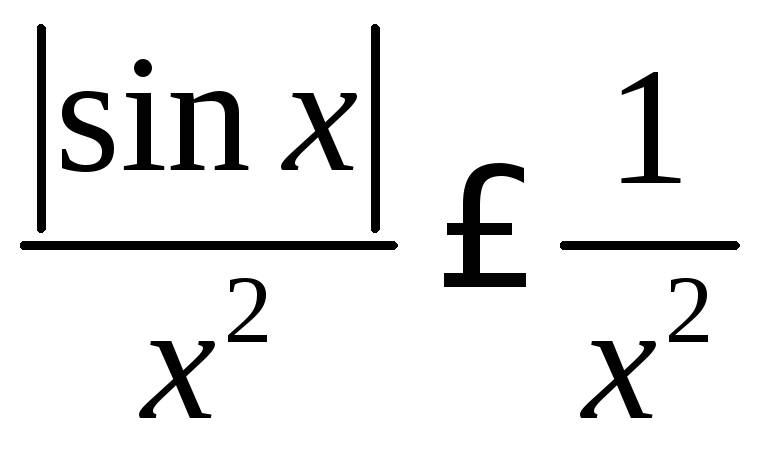
Понятие главного значения можно
применить и к несобственным интегралам
от разрывных функций, если особая точка,
в которой имеет место разрыв функции,
находится внутри отрезка интегрирования.
Пусть функция f (x)
интегрируема на промежутках: (a;
с-ε] и [с+ε; b),
ε> 0,- и неограниченна в окрестности
точки
;
тогда интегралом в смысле главного
значения несобственного интеграла от
разрывной функции называется предел:
7.
.
Этот
предел обозначается так:
.
Итак, имеем по определению:
8.
,
где f
(c)=
.
Если существует несобственный интеграл
от разрывной функции
,
то существует и интеграл в смысле
главного значения, и эти интегралы
равны. Из существования интеграла в
смысле главного значения не следует
существование соответствующего
несобственного интеграла от разрывной
функции.
Например,
,
в то время как несобственный интеграл
не существует; в самом деле:
,
где оба интеграла расходятся.
Упражнения: а)
;
б)
.
Пример:
.
Решение.
В исследуемом интеграле две особые
точки (x1= 1, x2=
2) и бесконечный промежуток интегрирования;
поэтому разбиваем исходный интеграл
на пять (!) интегралов, в каждом из которых
будет только по одной особенности:
.
Последний интеграл сходится, а потому
его величина равна главному значению
этого интеграла, то есть
.
Далее найдем величину этого интеграла:
.
Остальные интегралы расходящиеся, а
потому и исходный интеграл расходится.
Посчитаем теперь главное значение
расходящейся части интеграла, то есть:
.
Для этого разобьем интеграл на два
интеграла, в каждом из которых особая
точка будет находиться внутри
соответствующего отрезка интегрирования:
.
Далее
;
.
Итак, имеем:
.
Упражнения: а)
б)
.
Приложение 2 . Варианты контрольных
заданий: исследовать на
сходимость.
1 | сх. | 13 | сх. | 25 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 | сх.усл. | 14 | расх. | 26 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 | сх. | 15 | расх. | 27 | сх | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 | сх. | 16 | сх. | 28 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 | расх. | 17 | расх. | 29 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 | расх | 18 | сх.усл. | 30 | сх | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7 | расх. | 19 | сх. | 31 | сх | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8 | сх. усл. | 20 | сх. | 32 | сх. усл. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 | сх. | 21 | сх. абс. | 33 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10 | сх.усл | 22 | сх. | 34 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
11 | сх. | 23 | сх.аб. | 35 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
12 | расх. | 24 | сх. | 36 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
37 | расх. | 50 | сх. | 63 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
38 | сх. | 51 | расх. | 64 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
39 | расх. | 52 | сх.абс. | 65 | т сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
40 | расх. | 53 | сх.абс. | 66 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
41 | сх. | 54 | сх. | 67 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
42 | сх. | 55 | сх. | 68 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
43 | cх. | 56 | сх. | 69 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
44 | сх. | 57 | сх. | 70 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
45 | сх. | 58 | сх. | 71 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
46 | сх. абс. | 59 | сх. | 72 | сх. абс. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
47 | сх. | 60 | сх. | 73 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
48 | сх. абс. | 61 | сх. | 74 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
49 | расх. | 62 | сх. | 75 | сх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
76 | сх. | 78 | расх. | 80 | расх. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
77 | сх. [свернуть] К оглавлению Список литературыК оглавлению ТестЛимит времени: 0 ИнформацияРекомендую проверить насколько хорошо усвоен материал, пройдя следующий тест. Вы уже проходили тест ранее. Вы не можете запустить его снова. Тест загружается… Вы должны войти или зарегистрироваться для того, чтобы начать тест. Вы должны закончить следующие тесты, чтобы начать этот: Правильных ответов: 0 из 2 Ваше время: Время вышло Вы набрали 0 из 0 баллов (0)
Рубрики
Ваш результат был записан в таблицу лидеров
Таблица лучших: Несобственные интегралы, зависящие от параметра
Поделиться ссылкой:Похожее Calculus II — интегральный тестПоказать общее уведомление Показать мобильное уведомление Показать все заметки Скрыть все заметки Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST. Пол Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Раздел 4-6: Интегральное испытание Последней темой, которую мы обсуждали в предыдущем разделе, был гармонический ряд. , и поэтому мы назвали это интегральное расхождение (да, это тот же термин, который мы здесь используем для рядов…). Итак, как это помогает нам доказать, что гармонический ряд расходится? Что ж, вспомните, что мы всегда можем оценить площадь, разбив интервал на сегменты, а затем нарисовав прямоугольники и используя сумму площадей всех прямоугольников в качестве оценки фактической площади. Давайте сделаем то же самое для этой задачи и посмотрим, что у нас получится. Мы разделим интервал на подынтервалы шириной 1 и возьмем значение функции в левой конечной точке как высоту прямоугольника. На изображении ниже показаны первые несколько прямоугольников для этой области. Итак, площадь под кривой примерно равна . \ [\ begin {align *} A & \ приблизительно \ left ({\ frac {1} {1}} \ right) \ left (1 \ right) + \ left ({\ frac {1} {2}} \ справа) \ left (1 \ right) + \ left ({\ frac {1} {3}} \ right) \ left (1 \ right) + \ left ({\ frac {1} {4}} \ right) \ left (1 \ right) + \ left ({\ frac {1} {5}} \ right) \ left (1 \ right) + \ cdots \\ & = \ frac {1} {1} + \ frac { 1} {2} + \ frac {1} {3} + \ frac {1} {4} + \ frac {1} {5} + \ cdots \\ & = \ sum \ limits_ {n = 1} ^ \ infty {\ frac {1} {n}} \ end {align *} \] Теперь обратите внимание на несколько моментов, связанных с этим приближением. Поскольку все члены положительны, мы знаем, что частичные суммы должны быть возрастающей последовательностью.2}}}} , поэтому последовательность частичных сумм является ограниченной последовательностью. Во втором разделе, посвященном последовательностям, мы привели теорему, которая утверждает, что ограниченная и монотонная последовательность гарантированно сходится. Это означает, что последовательность частичных сумм является сходящейся последовательностью. Итак, кого это волнует? Напомним, это означает, что ряды также должны быть сходящимися! Итак, мы снова смогли связать ряд с несобственным интегралом (который мы могли вычислить), и ряд и интеграл имели одинаковую сходимость. Мы проделали изрядную работу в обоих этих примерах, чтобы определить сходимость двух рядов. К счастью для нас, нам не нужно делать всю эту работу каждый раз. Идеи этих двух примеров можно обобщить в следующем тесте. Интегральный тестПредположим, что \ (f \ left (x \ right) \) — непрерывная положительная убывающая функция на интервале \ (\ left [{k, \ infty} \ right) \) и что \ (f \ left ( n \ right) = {a_n} \) тогда
Формальное доказательство этого теста можно найти в конце этого раздела. Следует отметить несколько моментов по поводу интегрального теста. Во-первых, нижний предел неправильного интеграла должен быть тем же значением, с которого начинается ряд. Во-вторых, функция не обязательно должна быть убывающей и положительной везде в интервале. Все, что действительно требуется, — это чтобы в конечном итоге функция стала положительной и убывающей.\ infty {{a_n}} \] Итак, первая серия — это не что иное, как конечная сумма (независимо от того, насколько велика \ (N \)) конечных членов, и поэтому она будет конечной. Таким образом, исходный ряд будет сходящимся / расходящимся только в том случае, если второй бесконечный ряд справа сходится / расходится, и проверка может быть выполнена на втором ряду, поскольку он удовлетворяет условиям проверки. Аналогичное рассуждение можно сделать и с использованием несобственного интеграла. Требование теста, чтобы функция / серия была убывающей и положительной во всем диапазоне, требуется для доказательства.Однако на практике нам нужно только убедиться, что функция / ряд в конечном итоге является убывающей и положительной функцией / рядом. Также обратите внимание, что при вычислении интеграла в тесте нам фактически не нужно вырезать увеличивающуюся / отрицательную часть, поскольку наличие небольшого диапазона, в котором функция увеличивается / отрицательно, не изменит интеграл с сходящегося на расходящийся или с расходящиеся к сходящимся. Есть еще один очень важный момент, который необходимо сделать в связи с этим тестом.2}}}} Итак, мы получили верхнюю границу значения ряда, но не фактическое значение ряда. Фактически, с этого момента мы не будем спрашивать значение ряда, мы будем только спрашивать, сходится ли ряд или расходится. В следующем разделе мы рассмотрим оценку значений ряда, но даже в этом разделе мы не сможем получить значения ряда. {{\, t}} {{\ frac {1} {{x \ ln x}} \, dx}} \ hspace {0.2}} \ справа) \] Эта функция имеет две критические точки (которые сообщают нам, где производная меняет знак) в \ (x = \ pm \ frac {1} {{\ sqrt 2}} \). Поскольку мы начинаем с \ (n = 0 \), мы можем игнорировать отрицательную критическую точку. Выбрав пару контрольных точек, мы увидим, что функция возрастает на интервале \ (\ left [{0, \ frac {1} {{\ sqrt 2}}} \ right] \) и убывает на \ ( \ left [{\ frac {1} {{\ sqrt 2}}, \ infty} \ right) \). Следовательно, в конечном итоге функция будет уменьшаться, и это все, что нам нужно для использования интегрального теста.\ infty {\ frac {1} {{\ sqrt n}}} \) Показать решение Для этого ряда \ (p = \ frac {1} {2} \ le 1 \) и поэтому ряд расходится по факту. Последнее, что мы сделаем в этом разделе, — это быстрое доказательство выполнения интегрального теста. По сути, мы провели доказательство уже в начале раздела, когда вводили интегральный тест, но давайте рассмотрим его формально для общей функции. \ infty {{a_n}} \).Первоначальный тестовый оператор был для серии, которая начиналась с общего \ (n = k \), и хотя доказательство может быть выполнено для этого, будет проще, если мы предположим, что серия начинается с \ (n = 1 \). Другой способ справиться с \ (n = k \) — мы можем выполнить сдвиг индекса и начать серию с \ (n = 1 \), а затем выполнить интегральный тест. В любом случае будет достаточно доказательства теста для \ (n = 1 \). Также обратите внимание, что хотя мы позволили первым нескольким членам ряда увеличиваться и / или быть отрицательными в рабочих задачах, это доказательство действительно требует, чтобы все члены были убывающими и положительными. Давайте начнем и оценим площадь под кривой на интервале \ (\ left [{1, n} \ right] \), и мы недооценим площадь, взяв прямоугольники шириной один, высота которых является правой конечной точкой. Это дает следующий рисунок. Теперь обратите внимание, что, \ [f \ left (2 \ right) = {a_2} \ hspace {0,5 дюйма} f \ left (3 \ right) = {a_3} \ hspace {0,5 дюйма} \ cdots \ hspace {0,5 дюйма} f \ left (n \ right) = {a_n} \] Приблизительная площадь \ [A \ приблизительно \ left (1 \ right) f \ left (2 \ right) + \ left (1 \ right) f \ left (3 \ right) + \ cdots + \ left (1 \ right) f \ left (n \ right) = {a_2} + {a_3} + \ cdots {a_n} \] , и мы знаем, что это занижает фактическую площадь, поэтому \ [\ sum \ limits_ {i = 2} ^ n {{a_i}} = {a_2} + {a_3} + \ cdots {a_n} <\ int _ {{\, 1}} ^ {{\, n} } {{е \ влево (х \ вправо) \, dx}} \] Теперь предположим, что \ (\ int _ {{\, 1}} ^ {{\, \ infty}} {{f \ left (x \ right) \, dx}} \) сходится, и поэтому \ ( \ int _ {{\, 1}} ^ {{\, \ infty}} {{f \ left (x \ right) \, dx}} \) должно иметь конечное значение. {{\, \ infty}} {{f \ left (x \ right) \, dx}} \) расходится.\ infty {{a_n}} \) расходящийся ряд. Перед тем, как покинуть этот раздел, важно отметить, что для использования интегрального теста члены ряда ДОЛЖНЫ в конечном итоге быть убывающими и положительными. В противном случае тест не работает. Также помните, что тест определяет только сходимость ряда и НЕ дает значения ряда. Сходимость и расходимость несобственных интеграловСходимость и расходимость несобственных интегралов Сходимость и расходимость несобственных интегралов Рассмотрим функцию f ( x ), которая демонстрирует поведение типа I или типа II.
Если несобственный интеграл разбить на Пример. Рассмотрим функцию на [0,1]. У нас есть Следовательно, несобственный интеграл сходится тогда и только тогда, когда несобственные интегралы сходятся. Другими словами, если один из этих интегралов равен p-интегралы Рассмотрим функцию (где p > 0) для. Смотря на нам нужно изучить два несобственных интеграла У нас есть а также Для обоих пределов нам нужно вычислить неопределенный интеграл У нас есть два случая:
Чтобы принять решение о схождении или расхождении двух вышеупомянутых
p-Test: Независимо от значения числа p , всегда расходится.Кроме того, у нас есть
На следующих страницах мы увидим, как несколько простых тестов помогут в [Геометрия] [Исчисление] С.Домашняя страница O.S MATHematics Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard. Mohamed A. KhamsiВт 3 декабря 17:39:00 MST 1996 Авторские права 1999-2021 MathMedics, LLC. Все права защищены. 11.3 Тесты на сходимость неправильных интегралов
Возврат Существуют несобственные интегралы, которые нельзя вычислить Перейти к проблемам и решениям Вернуться к Проверки сходимости несобственных интегралов выполняются
Модель p — Интегралы Все 4 интеграла выше с показателем p в знаменателе называются p -интегралами .Различить их Обратите внимание, что at в имени интеграла используется для указания неправильного Теорема 2.1 p — Интегралы
Доказательство Следовательно, Пример 2.1 Для каждого из следующих интегралов определите, РешениеEOS Перейти к проблемам и решениям Вернуться к
Предположим, у нас есть функция f
Доказательство теоремы 3.1 ниже использует следующие Фундаментальный Теорема 3.1
Доказательство EOP Примечания 3.1 Пример 3.1 Установить совпадение или расхождение следующих Решениесходится. EOS Перейти к проблемам и решениям Вернуться к
SCT не всегда применяетсяСоотношение интегрантов Теорема 4.1
Доказательство EOP Когда мы не можем найти неподходящий интеграл для применения Пример 4.1 Определите, сходится ли следующий интеграл или Решение 1 Таким образом, по LCT данный интеграл сходится. EOS Решение 2 EOS Пример 4.2 Установить сходимость или расхождение этого интеграла. Раствор EOS Перейти к проблемам и решениям Вернуться к Сравнения Сравнение собственных интегралов происходит из Сравнения с p -интегралы Вернуться к началу страницы 1. Для каждого из следующих интегралов определите Раствор а. Единственный неправильный балл — 0. Нарушение: Вернуться к началу страницы 2. Установить схождение или расхождение каждого из Раствор Вернуться к началу страницы 3. Для каждого из следующих интегралов решите Раствор расходится. Вернуться к началу страницы Раствор г. У нас: Примечание В части b первое сравнение проводится между надлежащими Вернуться к началу страницы 5. Докажите, что: сходится, не пытаясь вычислить его значение. Раствор Вернуться к началу страницы Вернуться 5.3. Тесты на расхождение и интегральные характеристики — Calculus Volume 2Цели обучения
В предыдущем разделе мы определили сходимость или расходимость нескольких рядов, явно вычисляя предел последовательности частичных сумм {Sk}. {Sk}. На практике точное вычисление этого предела может быть затруднено или невозможно. К счастью, существует несколько тестов, которые позволяют нам определять сходимость или расхождение для многих типов рядов. В этом разделе мы обсудим два из этих тестов: тест дивергенции и интегральный тест.В оставшейся части этой главы мы рассмотрим несколько других тестов, а затем резюмируем, как и когда их использовать. Тест расходимостиЧтобы ряд ∑n = 1∞an∑n = 1∞an сходился, n-й член anan должен удовлетворять условию an → 0an → 0 при n → ∞.n → ∞. Следовательно, из алгебраических предельных свойств последовательностей limk → ∞ak = limk → ∞ (Sk − Sk − 1) = limk → ∞Sk − limk → ∞Sk − 1 = S − S = 0. limk → ∞ak = limk → ∞ (Sk − Sk − 1) = limk → ∞Sk − limk → ∞Sk − 1 = S − S = 0. Следовательно, если ∑n = 1∞an∑n = 1∞an сходится, n-й член an → 0an → 0 при n → ∞.п → ∞. Важным следствием этого факта является следующее заявление: Еслиan0asn → ∞, ∑n = 1∞ расходится. Еслиan↛0asn → ∞, n = 1∞ расходится. (5,8) Этот тест известен как тест дивергенции, потому что он дает способ доказать, что ряд расходится. Теорема 5.8 Тест расходимостиЕсли limn → ∞an = c ≠ 0limn → ∞an = c ≠ 0 или limn → ∞anlimn → ∞an не существует, то ряд ∑n = 1∞an∑n = 1 ∞an расходится. Важно отметить, что обратное утверждение этой теоремы неверно.То есть, если limn → ∞an = 0, limn → ∞an = 0, мы не можем сделать никаких выводов о сходимости ∑n = 1∞an.∑n = 1∞an. Например, limn → 0 (1 / n) = 0, limn → 0 (1 / n) = 0, но гармонический ряд ∑n = 1∞1 / n∑n = 1∞1 / n расходится. В этом разделе и в остальных разделах этой главы мы покажем еще много примеров из таких серий. Следовательно, хотя мы можем использовать тест расходимости, чтобы показать, что ряд расходится, мы не можем использовать его, чтобы доказать, что ряд сходится. В частности, если an → 0, an → 0, проверка дивергенции неубедительна. Пример 5.13Использование теста дивергенцииДля каждой из следующих серий примените тест дивергенции. Если тест на расхождение доказывает, что ряд расходится, укажите это. В противном случае укажите, что тест дивергенции безрезультатен.
Решение
КПП 5.12 Что тест расходимости говорит нам о ряду ∑n = 1∞cos (1 / n2)? ∑n = 1∞cos (1 / n2)? Интегральный тестВ предыдущем разделе мы доказали, что гармонический ряд расходится, рассматривая последовательность частичных сумм {Sk} {Sk} и показывая, что S2k> 1 + k / 2S2k> 1 + k / 2 для всех натуральных чисел k.k. В этом разделе мы используем другую технику, чтобы доказать расходимость гармонического ряда. Этот метод важен, потому что он используется для доказательства расходимости или сходимости многих других рядов. Этот тест, называемый интегральным тестом, сравнивает бесконечную сумму с неправильным интегралом. Важно отметить, что этот тест может применяться только тогда, когда мы рассматриваем ряд, все члены которого положительны. Чтобы проиллюстрировать, как работает интегральный тест, используйте в качестве примера гармонический ряд.На рисунке 5.12 мы изобразили гармонический ряд, нарисовав последовательность прямоугольников с областями 1,1 / 2,1 / 3,1 / 4,… 1,1 / 2,1 / 3,1 / 4,… вместе с функция f (x) = 1 / xf (x) = 1 / x. Из графика мы видим, что N = 1k1n = 1 + 12 + 13 + ⋯ + 1k> ∫1k + 11xdx. N = 1k1n = 1 + 12 + 13 + ⋯ + 1k> ∫1k + 11xdx. Следовательно, для каждого k, k k-я частичная сумма SkSk удовлетворяет Sk = ∑n = 1k1n> ∫1k + 11xdx = lnx | 1k + 1 = ln (k + 1) −ln (1) = ln (k + 1). Sk = ∑n = 1k1n> ∫1k + 11xdx = lnx | 1k + 1 = ln (k + 1) — ln (1) = ln (k + 1). Поскольку limk → ∞ln (k + 1) = ∞, limk → ∞ln (k + 1) = ∞, мы видим, что последовательность частичных сумм {Sk} {Sk} не ограничена.Следовательно, {Sk} {Sk} расходится, и, следовательно, расходится и ряд ∑n = 1∞1n∑n = 1∞1n. Рисунок 5.12 Сумма площадей прямоугольников больше площади между кривой f (x) = 1 / xf (x) = 1 / x и осью xx для x≥1.x≥1. Поскольку площадь, ограниченная кривой, бесконечна (как вычислено с помощью неправильного интеграла), сумма площадей прямоугольников также бесконечна. Теперь рассмотрим ряд ∑n = 1∞1 / n2.n = 1∞1 / n2. Мы покажем, как с помощью интеграла можно доказать сходимость этого ряда.На рис. 5.13 мы зарисовываем последовательность прямоугольников с областями 1,1 / 22,1 / 32,… 1,1 / 22,1 / 32,… вместе с функцией f (x) = 1 / x2.f (x ) = 1 / х2. Из графика видим, что N = 1k1n2 = 1 + 122 + 132 + ⋯ + 1k2 <1 + ∫1k1x2dx. N = 1k1n2 = 1 + 122 + 132 + ⋯ + 1k2 <1 + ∫1k1x2dx. Следовательно, для каждого k, k k-я частичная сумма SkSk удовлетворяет Sk = ∑n = 1k1n2 <1 + ∫1k1x2dx = 1−1x | 1k = 1−1k + 1 = 2−1k <2. Sk = ∑n = 1k1n2 <1 + ∫1k1x2dx = 1−1x | 1k = 1− 1к + 1 = 2−1к <2. Мы заключаем, что последовательность частичных сумм {Sk} {Sk} ограничена.Мы также видим, что {Sk} {Sk} — возрастающая последовательность: Sk = Sk − 1 + 1k2fork≥2. Sk = Sk − 1 + 1k2fork≥2. Поскольку {Sk} {Sk} возрастает и ограничено, по теореме о монотонной сходимости оно сходится. Следовательно, ряд ∑n = 1∞1 / n2∑n = 1∞1 / n2 сходится. Рисунок 5.13 Сумма площадей прямоугольников меньше суммы площади первого прямоугольника и площади между кривой f (x) = 1 / x2f (x) = 1 / x2 и осью xx для x. ≥1.x≥1. Поскольку площадь, ограниченная кривой, конечна, сумма площадей прямоугольников также конечна. Мы можем расширить эту идею, чтобы доказать сходимость или расхождение для многих различных рядов. Предположим, что ∑n = 1∞an∑n = 1∞an — это ряд с положительными членами anan такой, что существует непрерывная положительная убывающая функция ff, где f (n) = anf (n) = an для всех натуральных чисел. Тогда, как на рис. 5.14 (a), для любых целых k, k k-я частичная сумма SkSk удовлетворяет Sk = a1 + a2 + a3 + ⋯ + ak Sk = a1 + a2 + a3 + ⋯ + ak> ∫1k + 1f (x) dx. Sk = a1 + a2 + a3 + ⋯ + ak> ∫1k + 1f (x) dx. Если limk → ∞∫1k + 1f (x) dx = ∞, limk → ∞∫1k + 1f (x) dx = ∞, то {Sk} {Sk} является неограниченной последовательностью и поэтому расходится.В результате расходится и ряд ∑n = 1∞an∑n = 1∞an. Мы заключаем, что если ∫1∞f (x) dx∫1∞f (x) dx расходится, то n = 1∞an∑n = 1∞an расходится. Рисунок 5.14 (a) Если мы можем вписать прямоугольники внутри области, ограниченной кривой y = f (x) y = f (x) и осью xx, а площадь, ограниченная этими кривыми для x≥1x≥1, будет конечной , то сумма площадей прямоугольников также конечна. (b) Если набор прямоугольников описывает область, ограниченную y = f (x) y = f (x) и осью xx для x≥1x≥1, и область имеет бесконечную площадь, то сумма площадей прямоугольники тоже бесконечны. Теорема 5.9 Интегральный тестПредположим, что ∑n = 1∞an∑n = 1∞an — это ряд с положительными членами an.an. Предположим, что существуют функция ff и натуральное число NN такие, что выполняются следующие три условия:
Хотя сходимость N∞f (x) dx∫N∞f (x) dx влечет сходимость соответствующего ряда ∑n = 1∞an, ∑n = 1∞an, это не означает, что значение интеграла и серии такие же.Они могут быть разными, и часто бывают такими. Например, ∑n = 1∞ (1e) n = 1e + (1e) 2+ (1e) 3 + ⋯ ∑n = 1∞ (1e) n = 1e + (1e) 2+ (1e) 3 + ⋯ — геометрический ряд с начальным членом a = 1 / ea = 1 / e и отношением r = 1 / e, r = 1 / e, который сходится к 1 / e1− (1 / e) = 1 / e (e − 1) /e=1e−1.1/e1− (1 / e) = 1 / e (e − 1) / e = 1e − 1. Однако соответствующий интеграл ∫1∞ (1 / e) xdx∫1∞ (1 / e) xdx удовлетворяет условию ∫1∞ (1e) xdx = ∫1∞e − xdx = limb → ∞∫1be − xdx = limb → ∞ − e − x | 1b = limb → ∞ [−e − b + e − 1] = 1e.∫ 1∞ (1e) xdx = ∫1∞e − xdx = limb → ∞∫1be − xdx = limb → ∞ − e − x | 1b = limb → ∞ [−e − b + e − 1] = 1e. Пример 5.14Использование интегрального тестаДля каждого из следующих рядов используйте интегральный тест, чтобы определить, сходится ли ряд или расходится.
Решение
КПП 5.13 Используйте интегральный тест, чтобы определить, сходится или расходится ряд ∑n = 1∞n3n2 + 1∑n = 1∞n3n2 + 1. Модельp — серия Гармонический ряд ∑n = 1∞1 / n∑n = 1∞1 / n и ряд ∑n = 1∞1 / n2∑n = 1∞1 / n2 являются примерами типа ряда, называемого р -серия. ОпределениеДля любого действительного числа p, p ряд называется серией p . Мы знаем, что серия p сходится, если p = 2p = 2, и расходится, если p = 1.p = 1. А как насчет других значений p? P? В общем, трудно, если не невозможно, вычислить точное значение большинства pp-серий.Однако мы можем использовать представленные до сих пор тесты, чтобы доказать, сходится ли pp-ряд или расходится. Если p <0, p <0, то 1 / np → ∞, 1 / np → ∞, а если p = 0, p = 0, то 1 / np → 1.1 / np → 1. Следовательно, по тесту дивергенции ∑n = 1∞1 / np расходится, если p≤0. ∑n = 1∞1 / np расходится, еслиp≤0. Если p> 0, p> 0, то f (x) = 1 / xpf (x) = 1 / xp — положительная непрерывная убывающая функция. Поэтому при p> 0, p> 0 воспользуемся интегральным тестом, сравнивая N = 1∞1npand∫1∞1xpdx. N = 1∞1npand∫1∞1xpdx. Мы уже рассматривали случай, когда p = 1.р = 1. Здесь мы рассматриваем случай, когда p> 0, p ≠ 1. p> 0, p ≠ 1. В этом случае ∫1∞1xpdx = limb → ∞∫1b1xpdx = limb → ∞11 − px1 − p | 1b = limb → ∞11 − p [b1 − p − 1]. 1∞1xpdx = limb → ∞∫1b1xpdx = limb → ∞ 11 − px1 − p | 1b = конечность → ∞11 − p [b1 − p − 1]. Потому что b1 − p → 0ifp> 1 и b1 − p → ∞ifp <1, b1 − p → 0ifp> 1 и b1 − p → ∞ifp <1, заключаем, что ∫1∞1xpdx = {1p − 1ifp> 1∞ifp≤1.∫1∞1xpdx = {1p − 1ifp> 1∞ifp≤1. Следовательно, ∑n = 1∞1 / np∑n = 1∞1 / np сходится, если p> 1p> 1, и расходится, если 0 Таким образом, ∑n = 1∞1np {сходится, если p> 1, расходится, если p≤1.∑n = 1∞1np {сходится, если p> 1, расходится, если p≤1. (5,9) Пример 5.15Испытание на сходимостьp -серии Для каждого из следующих рядов определите, сходится он или расходится.
Решение
КПП 5.14 Сходится или расходится ряд ∑n = 1∞1n5 / 4∑n = 1∞1n5 / 4? Оценка стоимости серииПредположим, мы знаем, что ряд ∑n = 1∞an∑n = 1∞an сходится, и хотим оценить сумму этого ряда. Конечно, мы можем аппроксимировать эту сумму, используя любую конечную сумму ∑n = 1Nan∑n = 1Nan, где NN — любое положительное целое число. Вопрос, который мы здесь рассматриваем, заключается в следующем: для сходящегося ряда ∑n = 1∞an, ∑n = 1∞an, насколько хорошо приближение ∑n = 1Nan? ∑n = 1Nan? Более конкретно, если мы допустим RN = ∑n = 1∞an − ∑n = 1NanRN = ∑n = 1∞an − ∑n = 1Nan будет остатком, когда сумма бесконечного ряда аппроксимируется N-йN-й частичной суммой, насколько велико RN? RN? Для некоторых типов рядов мы можем использовать идеи интегрального теста для оценки RN.РН. Теорема 5.10 Оценка остатка из интегрального тестаПредположим, что ∑n = 1∞an∑n = 1∞an — сходящийся ряд с положительными членами. Предположим, что существует функция ff, удовлетворяющая следующим трем условиям:
Пусть SNSN будет N -й частичной суммой ∑n = 1∞an.∑n = 1∞an. Для всех натуральных чисел N, N, SN + ∫N + 1∞f (x) dx <∑n = 1∞an N + 1∞f (x) dx Это известно как оценка остатка. Мы проиллюстрировали оценку остатка от интегрального теста на рис. 5.15. В частности, представляя остаток RN = aN + 1 + aN + 2 + aN + 3 + ⋯ RN = aN + 1 + aN + 2 + aN + 3 + ⋯ как сумму площадей прямоугольников, мы видим, что площадь прямоугольников ограничено сверху N∞f (x) dx∫N∞f (x) dx и ограничено снизу N + 1∞f (x) dx.∫N + 1∞f (x) dx. Другими словами, RN = aN + 1 + aN + 2 + aN + 3 + ⋯> ∫N + 1∞f (x) dxRN = aN + 1 + aN + 2 + aN + 3 + ⋯> ∫N + 1∞f (x) dx и RN = aN + 1 + aN + 2 + aN + 3 + ⋯ <∫N∞f (x) dx. RN = aN + 1 + aN + 2 + aN + 3 + ⋯ <∫N∞f (x) dx. Мы заключаем, что N + 1∞f (x) dx N = 1∞an = SN + RN, ∑n = 1∞an = SN + RN, , где SNSN — N-я частичная сумма, заключаем, что SN + ∫N + 1∞f (x) dx <∑n = 1∞an Пример 5.16Оценка стоимости серииРассмотрим ряд ∑n = 1∞1 / n3.∑n = 1∞1 / n3.
Решение
КПП 5.15 Для ∑n = 1∞1n4, ∑n = 1∞1n4 вычислите S5S5 и оцените ошибку R5.R5. Раздел 5.3. УпражненияДля каждой из следующих серий, если применяется проверка дивергенции, либо укажите, что limn → ∞anlimn → ∞an не существует, либо найдите limn → ∞an.limn → ∞an. Если тест на расхождение неприменим, укажите, почему. 141. an = (2n + 1) (n — 1) (n + 1) 2an = (2n + 1) (n — 1) (n + 1) 2 142. an = (2n + 1) 2n (3n2 + 1) nan = (2n + 1) 2n (3n2 + 1) n 144. ан = 2n + 3n10n / 2an = 2n + 3n10n / 2 148. an = 1 − cos2 (1 / n) sin2 (2 / n) an = 1 − cos2 (1 / n) sin2 (2 / n) 149. ан = (1−1n) 2nan = (1−1n) 2n Укажите, сходится ли данный pp-ряд. 154. ∑n = 1∞1n23∑n = 1∞1n23 155. ∑n = 1∞1n43∑n = 1∞1n43 156. ∑n = 1∞nenπ∑n = 1∞nenπ 157. ∑n = 1∞nπn2e∑n = 1∞nπn2e Используйте интегральный тест, чтобы определить, сходятся ли следующие суммы. 158. ∑n = 1∞1n + 5∑n = 1∞1n + 5 159. ∑n = 1∞1n + 53∑n = 1∞1n + 53 160. ∑n = 2∞1nlnn∑n = 2∞1nlnn 161. ∑n = 1∞n1 + n2∑n = 1∞n1 + n2 162. ∑n = 1∞en1 + e2n∑n = 1∞en1 + e2n 163. ∑n = 1∞2n1 + n4∑n = 1∞2n1 + n4 164. ∑n = 2∞1nln2n∑n = 2∞1nln2n Выразите следующие суммы как pp-ряды и определите, сходится ли каждая из них. 165. ∑n = 1∞2 − lnn∑n = 1∞2 − lnn ( Подсказка: 2 − lnn = 1 / nln22 − lnn = 1 / nln2.) 166. ∑n = 1∞3 − lnn∑n = 1∞3 − lnn ( Подсказка: 3 − lnn = 1 / nln33 − lnn = 1 / nln3.) 167. ∑n = 1∞n2−2lnn∑n = 1∞n2−2lnn 168. ∑n = 1∞n3−2lnn∑n = 1∞n3−2lnn Используйте оценку RN≤∫N∞f (t) dtRN≤∫N∞f (t) dt, чтобы найти оценку остатка RN = ∑n = 1∞an − ∑n = 1NanRN = ∑n = 1∞an −n = 1Nan, где an = f (n) .an = f (n). 169. ∑n = 110001n2∑n = 110001n2 170. ∑n = 110001n3∑n = 110001n3 171. ∑n = 1100011 + n2∑n = 1100011 + n2 172. ∑n = 1100n / 2n∑n = 1100n / 2n [T] Найдите минимальное значение NN такое, что оценка остатка ∫N + 1∞f 173. an = 1n2, an = 1n2, ошибка <10-4 <10-4 174. an = 1n1.1, an = 1n1.1, ошибка <10-4 <10-4 175. an = 1n1.01, an = 1n1.01, погрешность <10-4 <10-4 176. an = 1nln2n, an = 1nln2n, ошибка <10-3 <10-3 177. an = 11 + n2, an = 11 + n2, ошибка <10-3 <10-3 В следующих упражнениях найдите такое значение NN, чтобы RNRN было меньше желаемой ошибки. Вычислите соответствующую сумму ∑n = 1Nan∑n = 1Nan и сравните ее с данной оценкой бесконечного ряда. 178. an = 1n11, an = 1n11, ошибка <10−4, <10−4, ∑n = 1∞1n11 = 1.000494… ∑n = 1∞1n11 = 1.000494… 179. an = 1en, an = 1en, ошибка <10−5, <10−5, ∑n = 1∞1en = 1e − 1 = 0.581976… ∑n = 1∞1en = 1e − 1 = 0,581976… 180. an = 1en2, an = 1en2, ошибка <10-5, <10-5, ∑n = 1∞n / en2 = 0,40488139857… ∑n = 1∞n / en2 = 0,40488139857… 181. an = 1 / n4, an = 1 / n4, ошибка <10−4, <10−4, ∑n = 1∞1 / n4 = π4 / 90 = 1.08232 ... ∑n = 1∞1 / n4 = π4 / 90 = 1,08232 ... 182. an = 1 / n6, an = 1 / n6, ошибка <10−6, <10−6, ∑n = 1∞1 / n4 = π6 / 945 = 1.01734306 ..., ∑n = 1∞1 / n4 = π6 / 945 = 1,01734306 ..., 183. Найдите предел при n → ∞n → ∞ для 1n + 1n + 1 + ⋯ + 12n. 1n + 1n + 1 + ⋯ + 12n. ( Подсказка: Сравните с ∫n2n1tdt.) ∫n2n1tdt.) 184. Найти предел при n → ∞n → ∞ для 1n + 1n + 1 + ⋯ + 13n1n + 1n + 1 + ⋯ + 13n Следующие несколько упражнений призваны дать представление о приложениях, в которых возникают частичные суммы гармонических рядов. 185. В некоторых приложениях вероятности, таких как так называемая оценка Уоттерсона для прогнозирования частоты мутаций в популяционной генетике, важно иметь точную оценку числа Hk = (1 + 12 + 13 + + 1k). Hk = (1 + 12 + 13 + ⋯ + 1к). Напомним, что Tk = Hk − lnk Tk = Hk − lnk убывает.Вычислите T = limk → ∞TkT = limk → ∞Tk с точностью до четырех знаков после запятой. ( Подсказка: 1k + 1 <∫kk + 11xdx1k + 1 <∫kk + 11xdx.) 186. [T] Полная выборка с заменой, иногда называемая проблемой сборщика купонов , формулируется следующим образом: Предположим, у вас есть NN уникальных элементов в корзине. На каждом этапе предмет выбирается случайным образом, идентифицируется и кладется обратно в корзину. Задача спрашивает, каково ожидаемое количество шагов E (N) E (N), которое требуется, чтобы нарисовать каждый уникальный элемент хотя бы один раз.Оказывается, E (N) = NE (N) = N. HN = N (1 + 12 + 13 + + 1N) HN = N (1 + 12 + 13 + ⋯ + 1N). Найдите E (N) E (N) для N = 10,20 и 50N = 10,20 и 50. 187. [T] Самый простой способ перетасовать карты — это взять верхнюю карту и вставить ее в случайное место в колоде, что называется случайной вставкой сверху, и затем повторить. Мы будем считать, что колода перемешивается случайным образом после того, как было сделано достаточно случайных верхних вставок, чтобы карта, изначально находившаяся внизу, достигла верха, а затем была вставлена случайным образом. Если в колоде nn карт, то вероятность того, что вставка будет ниже карты, изначально внизу (назовите эту карту B) B), равна 1 / n.1 / п. Таким образом, ожидаемое количество случайных вставок вверху, прежде чем BB перестанет быть внизу, равно n . Как только одна карта оказывается ниже B, B, есть два места ниже BB, и вероятность того, что случайно вставленная карта окажется ниже BB, равна 2 / n.2 / n. Ожидаемое количество верхних случайных вставок до того, как это произойдет, будет n / 2.n / 2. Две карты под BB теперь расположены в случайном порядке. Продолжая этот путь, найдите формулу для ожидаемого числа верхних случайных вставок, необходимых для того, чтобы колода была перемешана случайным образом. 188. Предположим, скутер может проехать 100100 км с полным баком топлива. Предполагая, что топливо может передаваться от одного скутера к другому, но может перевозиться только в баке, представьте процедуру, которая позволит одному из скутеров проехать 100HN100HN км, где HN = 1 + 1/2 + ⋯ + 1 / N. HN = 1 + 1/2 + ⋯ + 1 / N. 189. Покажите, что для применения оценки остатка на [N, ∞) [N, ∞) достаточно, чтобы f (x) f (x) убывала на [N, ∞), [N, ∞), но для ff требуется не убывает на [1, ∞). [1, ∞). 190. [T] Используйте оценку остатка и интегрирование по частям, чтобы аппроксимировать ∑n = 1∞n / en∑n = 1∞n / en с погрешностью меньше 0,0001.0,0001. 191. Сходится ли ∑n = 2∞1n (lnn) p∑n = 2∞1n (lnn) p, если pp достаточно велико? Если да, то для какого p? P? 192. [T] Предположим, что компьютер может суммировать один миллион членов в секунду расходящегося ряда ∑n = 1N1n.∑n = 1N1n. Используйте интегральный тест, чтобы приблизительно определить, сколько секунд потребуется, чтобы сложить достаточно членов, чтобы частичная сумма превысила 100.100. 193. [T] Быстрый компьютер может суммировать один миллион членов в секунду расходящегося ряда ∑n = 2N1nlnn.∑n = 2N1nlnn. Используйте интегральный тест, чтобы приблизительно определить, сколько секунд потребуется, чтобы сложить достаточно членов, чтобы частичная сумма превысила 100,100. Репетитор по математике — Интеграл — Теория — Неправильный интеграл Довольно часто нас не заботит точное значение интеграла, мы Сначала предположим, что задействованные функции положительны. Этот Теорема (Сравнительный тест). Если Если Идея этого теста должна быть ясна из рисунка: Если площадь под графиком г конечна, то и должна быть Изображение также дает понять, что сравнение может работать только в одном Пример: Этот интеграл может быть фактически вычислен с использованием дробных дробей, но он сходится (это мы помним, см. Мы только что увидели главное преимущество сравнительного теста: очень часто он очень Пример: Опять же, этот интеграл можно фактически вычислить с использованием дробных дробей, но сходится (как и раньше), но на этот раз неравенство сравнения идет не так Этот пример показывает, что недостаточно просто провести сравнение. Дано Сравнительный тест также можно рассматривать как обобщение Если f и g интегрируемы по Риману на [a, b] и По сути, сравнительный тест говорит, что то же самое верно и для С другой стороны, если «больший интеграл» конечен, то так и должно быть. В первом мы можем представить, что интегрируя неравенство Теперь кажется естественным, что данный интеграл сходится, мы даже получаем Во втором примере мы можем представить, что интегрируя неравенство В этом неравенстве данный интеграл может быть конечным числом, но Теперь также должно быть более ясно, почему мы требуем, чтобы функция f была Теорема (Сравнительный тест — версия абсолютного значения). Если сходится. Следующий тест — гораздо более сильный инструмент, чем тест сравнения. В Теорема (предельное сравнение). сходится тогда и только тогда, когда интеграл сходится. Этот тест работает несколько иначе.Учитывая функцию f , мы Таким образом, эти интегралы должны быть примерно одинаковыми, и вывод Проверка сравнения пределов также верна для функций, которые всегда Пример: Если x близко к бесконечности, то есть если это действительно большое число, то Предел существует и не равен нулю, поэтому данная функция и сходится, следует, что сходится и данный интеграл. Это была типичная задача теста сравнения предельных значений. Сначала мы нашли тест Следует отметить, что тест сравнения пределов не лучше (в смысле Все три указанных выше теста имеют сопутствующую версию, которая обрабатывает этот случай. Пример: Имеется проблема x = 2. Мы утверждаем, что если Мы видим, что наше предположение было правильным, поскольку предел дал ненулевое число. Этот интеграл расходится, так как это одна из степеней, которые мы исследовали в Хотя приведенное выше решение правильно соответствует тесту сравнения предельных значений, оно может Поскольку тестовый интеграл справа расходится и умножение на Теперь читатель, вероятно, задается вопросом, как мы пришли к тестовой функции. Назад к теории — несобственные интегралы Определение сходимости и расхождения в серии Неполная сумма ряда n th a n определяется как S n = a 1 + a 2 + 3 +… + а № . Если последовательность этих частичных sum {S n } сходится к L, тогда сумма ряда сходится к L. Если {S n } расходится, то сумма ряда расходится. Операции с конвергентными сериями Если n = A, а b n = B, то также сходятся, как указано: ca n = cA (a n + b n ) = A + B — b n ) = A — B Список тестов сходимости в алфавитном порядке Абсолютная сходимость Если серия | a n | сходится, то ряд n тоже сходится. Испытание чередующейся серии Если для всех n, значение n положительное, не возрастающее (т. Е. 0 n + 1 <= a n ) и приближается к нулю, то переменная серия a n и (-1) н-1 а н оба сходятся. Если чередующийся ряд сходится, то остаток R N = S — S N (где S — точная сумма бесконечного ряда и S N — сумма первых N членов ряда) ограничена по | R N | <= a N + 1 Удаление первых N условий Если N — натуральное число, то ряд a n и а н п = N + 1 оба сходятся или оба расходятся. Тест прямого сравнения Если 0 <= a n <= b n для всех n больше чем некоторое положительное целое число N, то применяются следующие правила: Если b n сходится, то n сходится. Если n расходится, то b n расходится. Сходимость геометрических серий Геометрический ряд равен a r n = a + a r + a r 2 + a r 3 + … Если | r | <1, то следующий геометрический ряд сходится к a / (1 - р). Если | r | > = 1, то указанный геометрический ряд расходится. Интегральный тест Если для всех n> = 1, f (n) = a n и f положительно, непрерывный, а затем убывающий либо оба сходятся, либо оба расходятся. Если указанный ряд сходится, то остаток R N = S — S N (где S — точная сумма бесконечного ряда, а S N является суммой первых N членов ряда) ограничено 0 <= R N <= (Н..) f (x) dx. Тест сравнения предельных значений Если lim (n ->) (a n / b n ) = L, где a n , b n > 0 и L конечно и положительно, затем сериал a n и b n либо сходятся, либо расходятся. n th -Term Test for Divergence Если последовательность {a n } не сходится к нулю, то ряд a n расходится. Конвергенция серии p Серия p определяется номером = 1/1 p + 1/2 p + 1/3 p + … где p> 0 по определению. Если p> 1, то ряд сходится. Если 0 Тест на соотношение Если для всех n, n 0, то применяются следующие правила: Пусть L = lim (n ->) | a n + 1 / a n |. Если L <1, то ряд n сходится. Если L> 1, то ряд a n расходится. Если L = 1, то проверка в безрезультатна . Корневой тест Пусть L = lim (n ->) | a n | 1 / п . Если L <1, то ряд n сходится. Если L> 1, то ряд a n расходится. Если L = 1, то проверка в безрезультатна . Конвергенция серии Тейлора Если f имеет производные всех порядков в интервале I с центром в точке c, то ряд Тейлора сходится, как показано: f (n) (c) (x — c) n = f (x) тогда и только тогда, когда lim (n ->) RN = 0 для всех x в I. Остаток R N = S — S N ряда Тейлора (где S — это точная сумма бесконечного ряда, а S N — сумма первых N членов ряда) равно (1 / (n + 1)!) f (n + 1) (z) (x — c) n + 1 , где z — некоторая константа между x и c. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

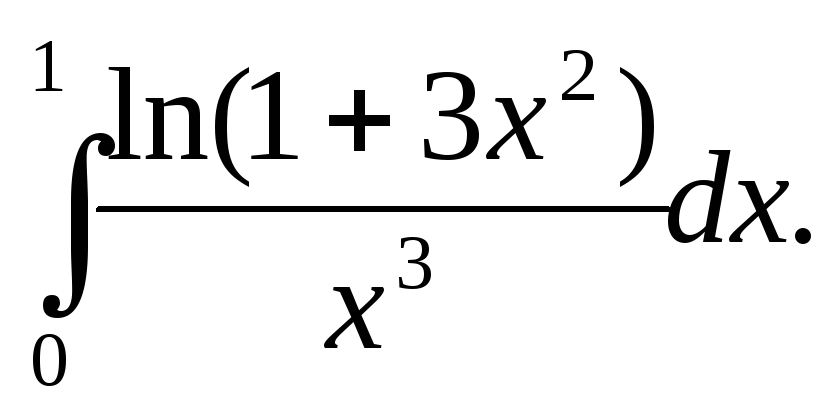 Справочное пособие по математическому
Справочное пособие по математическому

 абс.
абс.
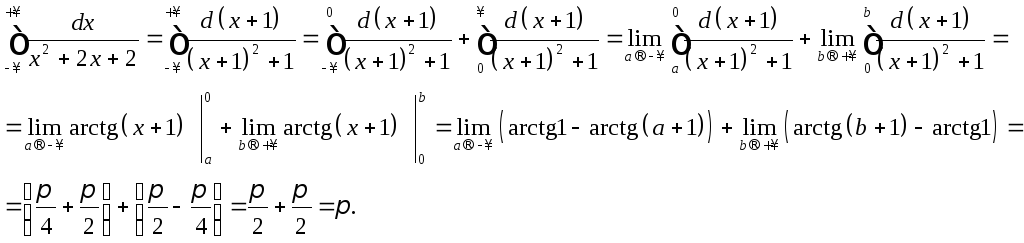

 {-1} = \varepsilon,$$ и поэтому исходный интеграл сходится неравномерно по параметру $y$ на множестве $Y = [0, +\infty)$.
{-1} = \varepsilon,$$ и поэтому исходный интеграл сходится неравномерно по параметру $y$ на множестве $Y = [0, +\infty)$.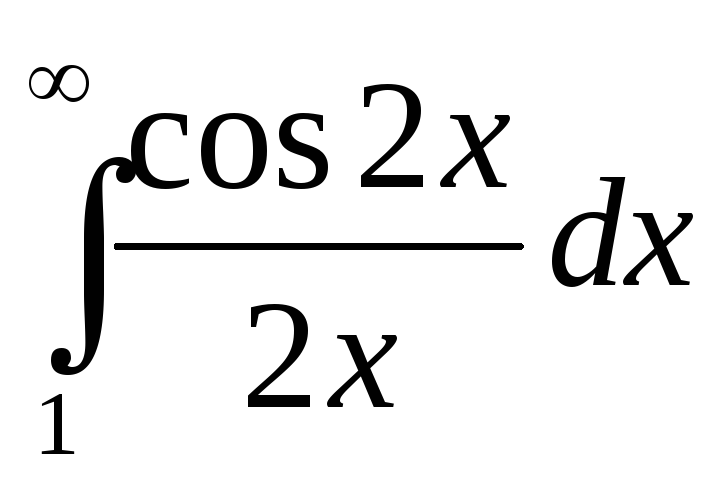 b f(x,y) \, dx < \varepsilon$
b f(x,y) \, dx < \varepsilon$ Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех. В этом обсуждении мы заявили, что гармонический ряд является расходящимся рядом.{{\, \ infty}} {{\ frac {1} {x} \, dx}} = \ infty \]
В этом обсуждении мы заявили, что гармонический ряд является расходящимся рядом.{{\, \ infty}} {{\ frac {1} {x} \, dx}} = \ infty \] 2}}}} \]
2}}}} \]