Содержание
Решение уравнений и неравенств содержащие модули
Управление образования
администрации г. Чебоксары
Муниципальное образовательное
учреждение
«Средняя общеобразовательная
школа №55»
Решение уравнений
и неравенств, содержащие модули.
Учитель математики
Морозова Галина Сергеевна.
.
Чебоксары
2010 г
Пояснительная записка.
Существенной характеристикой числа,
как в действительной, так и в комплексной
области является понятие его абсолютной
величины (модуля).
Это понятие имеет широкое распространение
в различных отделах физико-математических
наук. Так, в математическом анализе одно
из первых и фундаментальных понятий –
понятие предела – в своем определении
содержит понятие абсолютной величины
числа. В теории приближенных вычислений
первым, важнейшим понятием, является
понятие абсолютной погрешности
приближенного числа. В механике основным
В механике основным
первоначальным понятием является
понятие вектора, важнейшей характеристикой
которого служит его абсолютная величина
(модуль).
С понятием модуля (абсолютной величины)
действительного числа учащиеся знакомятся
еще в 6 классе. Однако в программах
общеобразовательных школ и соответствующих
учебниках в дальнейшем это понятие ни
в теоретических материалах, ни в задачах
и упражнениях почти не применяется.
Возможность решения уравнений и
неравенств, содержащих неизвестные под
знаком модуля, имеют учащиеся классов
или школ с углубленным изучением
математики и некоторых других
альтернативных школ, однако и в учебниках
для этих школ задач подобного рода до
обидного мало. В то же время на ЕГЭ задачи
с модулем предлагаются все чаще и чаще.
Несмотря на кажущуюся простоту определения
модуля числа, решение уравнений и
неравенств, содержащих неизвестные под
знаком модуля, вызывает у учащихся
определенные трудности. По-видимому,
они связаны с тем, что решение задач
подобного рода предполагает элементарные
навыки исследования, логического
мышления, заключающиеся в переборе
различных возможных случаев, так как в
подавляющем большинстве задач одно
уравнение или неравенство с модулем
равносильно совокупности или системе
нескольких уравнений и неравенств,
освобожденных от знака модуля.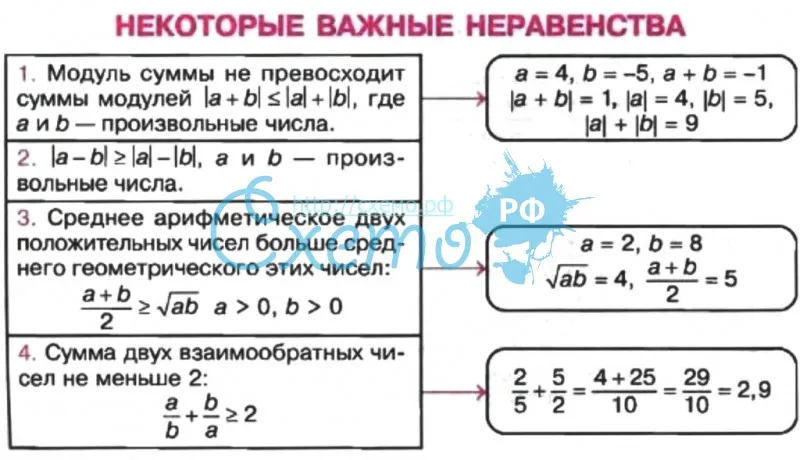
Цели курса:
классификации способов решений уравнений
и неравенств, содержащих неизвестную
под знаком модуля;систематизации и обобщении различной
информации о модуле и решении задач с
модулем, содержащихся в многочисленной
литературе;рассмотрение некоторых методов при
решении задач с модулем.
Задачами данной методической разработки
стали:
ввести
определение модуля и показать
геометрический смысл модуля; рассмотреть
свойства модуля;рассмотреть
решения основных видов уравнений,
содержащих переменную под знаком
модуля;показать
решения основных видов неравенств,
содержащих переменную под знаком
модуля;расширить
сферу математических знаний, общекультурный
кругозор у учащихся.
Методические
рекомендации.
Разработанный
курс может быть использован учителями
математики при подготовке к математическим
олимпиадам, ЕГЭ, централизованному
тестированию и вступительным экзаменам
в ВУЗ.
Для реализации
целей и задач этого курса предполагаются
следующие формы занятий: лекции учителя,
доклады учеников, самостоятельная
работа по разборке решенных уравнений
и неравенств.
Успешность
усвоения курса определяется преобладанием
самостоятельной творческой работы
ученика в содружестве с учителем.
Содержание
Введение
Определение
модуля. Свойства модуля.
Определение
модуля.Геометрический
смысл модуля.Формула
расстояния между двумя точками числовой
прямой.
Свойства
модуля.
Решение
уравнений с модулем.
Уравнения
вида |f(x)|=a.Уравнения
вида |f(x)|=|g(x)|Уравнения
вида |f(x)|=
g(x)Уравнения
вида .
Решение
неравенств с модулем.
Неравенства
вида |f(x)|aНеравенства
видаНеравенства
вида
и .Метод
интервалов.
План
урока по теме «Решение
уравнений, содержащих знак абсолютной
величины (модуля)»(8 класс)Примерные
тесты для подготовки к ЕГЭ.Заключение.
Литература
Урок
по теме:
«Решение уравнений,
содержащих знак абсолютной величины
(модуля)»
(9 класс)
Цель урока: Обобщение и
систематизация знаний учащихся , развитие
навыка решения уравнений и логического
мышления учащихся.
Оборудование урока: таблица
“Модуль”, плакаты с изображением
уравнений содержащих переменную под
знаком модуля и с графическим способом
решения уравнений.
План урока
Вступительное
слово учителя.Некоторые
способы решения уравнений, содержащих
переменную под знаком модуля. (Сообщения
учащихся).
а)Метод интервалов.
б)Графический метод.
в)Раскрытие модуля по определению
Решение
уравнения, в котором под знаком модуля
находится выражение, тоже содержащее
модуль. (Сообщение учителя).
Подведение
итогов урока.
Ход урока.
Вступительное слово учителя. Сообщается
план семинара и почему именно эта тема
выбрана.
Вступительное
слово учителя.
Математика за 2500 лет своего существования
накопила богатейший инструмент для
исследования окружающего нас мира.
Однако, как заметил один из ведущих
математиков, кораблестроителей академик
Крылов, человек обращается к математике
не затем, чтобы любоваться неисчислимыми
сокровищами, ему, прежде всего, необходимо
ознакомиться со столетними испытанными
инструментами, научится ими искусно
владеть.
Существенной характеристикой
действительного числа является абсолютная
величина. Это понятие имеет широкое
распространение в различных отделах
физико-математических и технических
наук. Так в математическом анализе одно
из первых и фундаментальных понятий –
понятие предела – в своем определении
содержит понятие абсолютной величины
числа. В теории приближенных вычислений
первым важнейшим понятием является
понятие абсолютной погрешности
приближенного числа. В механике основным
первоначальным понятием является
понятие вектора, важнейшей характеристикой
которого служит его абсолютная величина.
При решении уравнений, содержащих
переменную под знаком модуля, чаще всего
применяются следующих методы: 1) раскрытие
модуля по определению, 2) возведение
обоих частей в квадрат, 3) метод разбиения
на промежутки, 4) графический метод.
Сообщение
№1
«Некоторые
способы решения уравнений с модулями».
Напомним сначала определение числа x:
Приведем
также основные свойства модуля, часто
применяемых в решение задач:
|ab|=|a||b|;
|a|n=|an|;
|a|=0,
если a=0
Поговорим о некоторых способах решения
задач с модулем. Среди них один занимает
самое главное место, так как он является
самым общим, однако, иногда не самым
рациональным. Заключается он в следующем.
Метод
интервалов.
Предположим, что имеется уравнение или
неравенство, в которое входят один или
несколько модулей.
Первым делом нужно отделить критические
точки. Под этим мы понимаем все значения
переменной, при которых один из модулей
обращается в нуль.
Нанесите полученное множество значений
на ось данной переменной, например Ox.
Прямая разобьется на несколько конечных
и два бесконечных интервала. Каждый
интервал соответствует знакопостоянству
подмодульных выражений.Рассмотреть столько случаев решения,
сколько получилось интервалов. При
этом освобождаться от модулей нужно,
проверяя знак подмодульного выражения.
Т.е. изменять его на противоположный,
если выражение отрицательно и оставлять
его прежним в противном случае. Важно
не забыть, что частным
ответом в каждом из полученных случаев
является пересечение интервала и
найденного решения.Объединить полученные в каждом интервале
ответы в один.
Рассмотрим
подробнее этот метод на следующем
примере.
|x + 2| +
|x — 3| = 5
Нанесем
на числовую прямую значение x, при котором
x + 2 = 0 и значение x, при котором x – 3 = 0.
Числовая прямая разобьется на промежутки
(-;
-2), [-2; 3], (3; +).
Решим
уравнений на каждом из этих интервалов.
х | (-; | [-2;3] | (3; +) |
х+2 | — | + — + | + |
x-3 | — | — — | + |
Рассмотрим первый промежуток, чтобы
определить знак подмодульного выражения,
возьмем контрольную точку x = 3, подставим
ее в наше уравнение –3 + 2 < 0 и во второе
-3 – 3 < 0. Аналогично рассмотрим знаки
подмодульных выражений на втором и
третьем промежутках.
Решим
уравнение на каждом из этих промежутков,
т.е. решим равносильную уравнению
совокупность смешанных систем:
1) –х – х = Не может быть корнем. | 2) х + 2 3) х + 2 + х – 3 = 5, x = 3 , |
Вывод:
Решение второй системы является
объединением решений 3-х систем.
Ответ:
x принадлежит [-2;3] или все значения
сегмента [-2;3].
Сообщение
№2 Графический метод.
Этот способ уже не столь универсален,
но им нельзя пренебрегать, если он
применим. Часто уравнение или неравенства
с модулем содержит только линейные
выражения относительно переменной. В
этом случае существует очень простой
рецепт построения графиков с модулями,
что часто существенно облегчает решение
задачи. Он базируется на простом замечании
Он базируется на простом замечании
– графики таких выражений состоят из
кусков линий, т.е. являются ломаными.
Метод состоит в следующем:
Найти, как и раньше, все критические
точки и нанести их на ось абсцисс. Найти
непосредственно значения заданной
функции в этих точках (это удобно делать
с помощью отдельной таблицы) и нанести
их на координатную плоскость.В каждой из конечных интервалов,
получаемых после разбиения критическими
точками, график является прямой и может
быть простым соединением нанесенных
в предыдущем пункте точек на координатной
плоскости.Выбрать две удобные для вычисления
точки, расположенные в левом и правом
бесконечных интервалах и аналогично
п.1 найти значения функций в них.
Окончательно, соединяя построенный
участок графика с оставшимися двумя
точками, получим требуемый график.
Проиллюстрируем
это на примере построения графика
|x+2|+|x-3|=5.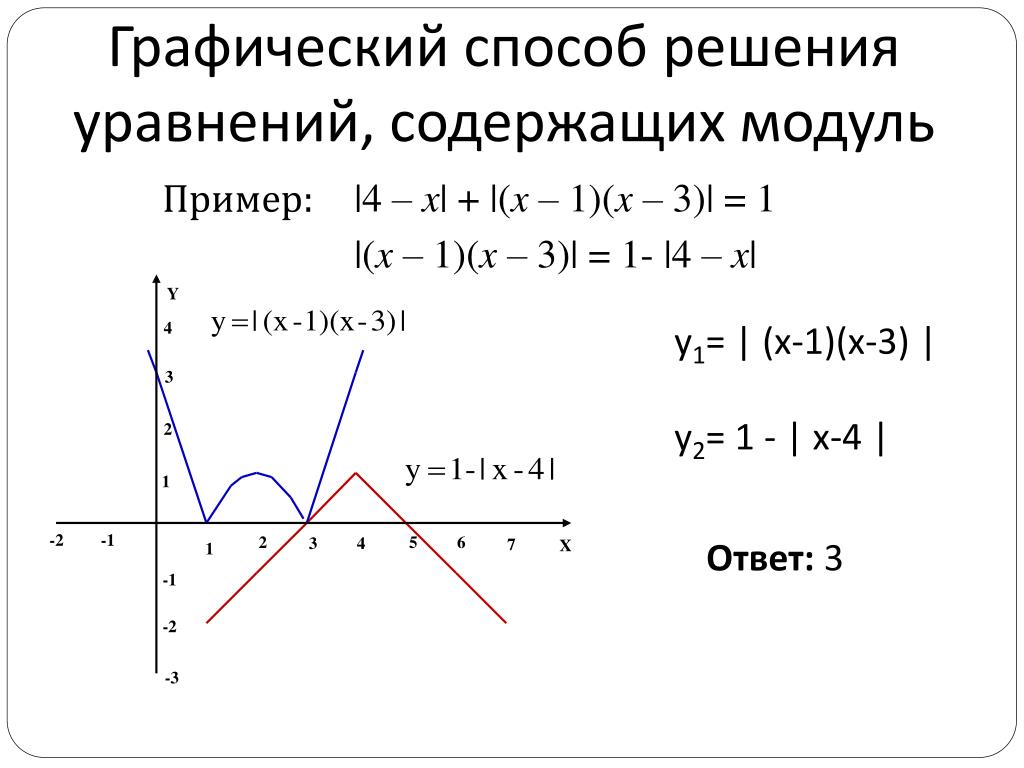 Построим график функции
Построим график функции
у = |x +
2| + |x – 3| и y = 5
х + 2 =
0, x –3 = 0
x1 =
–2 x2 = 3
Наносим на ось корни линейных функций
стоящих под знаком модуля. На каждом из
трех промежутков знаки этих линейных
функций постоянны и мы можем избавиться
от знака модуля.
если x
< – 2, то y =-(x + 2) – (x – 3) = –2x + 1
если –2
< x < 3, то y = +(x + 2) – (x – 3) = x + 2 – x + 3 =
5
если x > 3, то y = +(x + 2) + (x – 3) = 2x – 1
При построении графика провести
вертикальные прямые x = –2 и x = 3, которые
разобьют плоскость на три части. В левой
части надо провести прямую y=–2x + 1, в
центральной полосе y = 5 и в правой y = 2x –
1: (для контроля надо следить, чтобы
ломаная была непрерывной, т.е. чтобы
значения в разделяющих точках изломах,
вычисленные по соседним формулам
совпали). В нашем случае при x — 2 значение
функции y = –2x + 1 совпадает со значением
y = 5, точно так же при x=3 совпадают значения
функции y = 5 и y=2x – 1
Строим график 1) y = | 2) у = | 3) y = |
Графики и
y = 5 пересекаются на промежутке, если
.
Ответ
Сообщение
№3 Раскрытие модуля по определению .
Решить
уравнение
Решение.
.
Проверим
справедливость неравенства
для найденных значений х:
верное неравенство, значит 0 – корень
данного уравнения.неверное
неравенство, значит
— посторонний корень.верное
неравенство, значит
– корень данного уравнения
Ответ:
;
0.
Решение
уравнения, в котором под знаком модуля
находится выражение содержащее модуль.
Решить
уравнение
Решение.
.
Ответ:
.
Итоги урока.
Домашнее задание.
Всем
учащимся даются задания для самостоятельного
решения:
Записать в тетради решения
уравнений вида:
1.
|2x-3|=11
2.
|2x-5|=5-4x
3.
|4x-3|=4x-3
4.
|x+2|+|x-3|=5
5.
|x+1|-|x-2|+|3x+6|=5
6.
2u+v=7, |u-v|=2
7.
3|x+1|+2|y-2|=20, x+2y=4
8.
x+1|+|y+1|=8, 2x-|y+1|=5
9.
|x+1|-|x|+3|x-1|-2|x-2|=x+2
10.
Найти все значения, при которых система
уравнения ах+(а–1)y =
2+4а 3|x|+2у=а-5.
Имеет
единственное решение. Найти это решение.
Примерные тесты для подготовки к ЕГЭ.
Тест №1
Тест №2
Заключение.
В практике преподавания математики в
средней школе и других средних учебных
заведениях понятие абсолютной величины
числа (модуля числа) встречаются
неоднократно.
В VI классе, в курсе приближенных
вычислений, при уяснении понятия
абсолютной погрешности приближенного
числа формируется понятие абсолютной
величины числа. Во втором полугодии VI
класса вводится определение абсолютной
величины числа, с помощью этого понятия
формулируются правила действий над
рациональными числами.
В VIII классе при рассмотрении свойств
арифметического квадратного корня
находит свое новое приложение понятие
абсолютной величины числа.
В VIII классе при рассмотрении свойств
арифметического квадратного корня
находит свое новое приложение понятие
абсолютной величины числа. Например:
, и другие.
В IX классе в теме “Степень с рациональным
показателем” рассматриваются свойства
корней n – й степени, где также используется
понятие абсолютной величины числа; так,
например,
, если m – нечетное.
В X классе понятие абсолютной величины
числа встречается при изучении предела
функций, при исследование функций на
ограниченность и при изучение комплексных
чисел, где понятие абсолютной величины
получает свое дальнейшее развитие в
более общей числовой области.
Таким образом, во всех классах, в
соответствии с учебной программой,
следует включать и рассматривать
упражнения, содержащие знак абсолютной
величины числа.
В VI классе можно решать уравнения вида:k
· |x| + b = k1 · |x| + b1
и |k·x+b|=a.
В VII классе имеется возможность
рассматривать решения уравнений вида
|k·|x|+b|=c; |kx+b|=ax+c и т.п., систем уравнений
вида:|2x-y|=1, |x+2y|=2x-4, а так же построение
графиков функций вида: y=k·|x|+b; y=|k·x+b|;
y=|k·|x|+b|; y=1/|x| и др.
В VIII классе приложения понятия абсолютной
величины распространяются на квадратные
уравнения, график квадратного трехчлена
и др. Можно решать уравнения вида:
Можно решать уравнения вида:
ax2+b·|x|+c=0;
Можно рассмотреть построение графиков
функций:
y=ax2+b·|x|+c;
y=|ax2+bx+c|;
y=|ax2+b·|x|+c|;
;
;
y=||||x|-2|+1|-3| и др.
При построении графиков целесообразно
пользоваться методом преобразования
графиков (Параллельный перенос, симметрия
и др.).
В IX-X классе решение уравнений, систем
уравнений, неравенств и построение
графиков функций, аналитические выражения
которых содержат знак абсолютной
величины, рассматриваются для
трансцендентных функций и уравнений,
изучаемых в школе.
Таким образом, поставленные и решённые
задачи в данной методической разработке
имеют большое значение при составлении
промежуточного контроля и при подготовке
к ЕГЭ.
Литература
Гайдуков
И. И. Абсолютная величина. М., Просвещение,
И. Абсолютная величина. М., Просвещение,
1966.Гусев
В.А. и др. 300 задач. М., Просвещение, 1993.Литвиненко
В.Н, Мордкович А.Г. Практикум по решению
задач. Алгебра. Тригонометрия. М.,
Просвещение, 1991.Сидоров
Н.Н. Модуль числа. Уравнения и неравенства:
Учебное пособие. Чебоксары:1998.
Уравнения и неравенства с модулем
1. Уравнения и неравенства с модулем часть 2
2. Уравнение вида | f(x)| = g(x)
Чтобы решить уравнение с модулем
надо избавиться от модульных
скобок по определению модуля
|a|=
a,
условие1 a ≥ 0
-a,
условие2 a
3. Уравнение вида | f(x)| = g(x)
Условие 1 f(х)≥0 (решаем
полученное неравенство)
2. Раскрываем модульные скобки с
использование условия
f(x)=g(x)
3. Решаем полученное уравнение
4. Проверяем соответствие корней
условию
1.
4. Уравнение вида | f(x)| = g(x)
Условие 2 f(х)
полученное неравенство)
2. Раскрываем модульные скобки с
Раскрываем модульные скобки с
использование условия
-f(x)=g(x)
3. Решаем полученное уравнение
4. Проверяем соответствие корней
условию
1.
5. Решить уравнение |2x+5|=3x-1
1. Условие: 2x+5≥0
x≥-2,5
Раскрываем модульные скобки: по условию
выражение под модулем положительно,
то модульные скобки просто убираем
2x+5=3x-1
2х-3х=-1-5
-x=-6
X=6 – подходит по условию, следовательно
корень
6. Решить уравнение |2x+5|=3x-1
1. Условие: 2x+5
x
Раскрываем модульные скобки: по условию
выражение под модулем отрицательно, то
модульные скобки раскрываем со знаком
минус
-(2x+5)=3x-1
-2x-5=3x-1
-2х-3х=-1+5
-5x=4
X=-0,8 – не подходит по условию,
следовательно не корень
Ответ: 6
7. Неравенство вида | f(x)| ≥ g(x)
Решаем аналогично уравнению.
1.
Ставим условие 1 и решаем его
2.
Раскрываем модульные скобки в
соответствии с условием
3.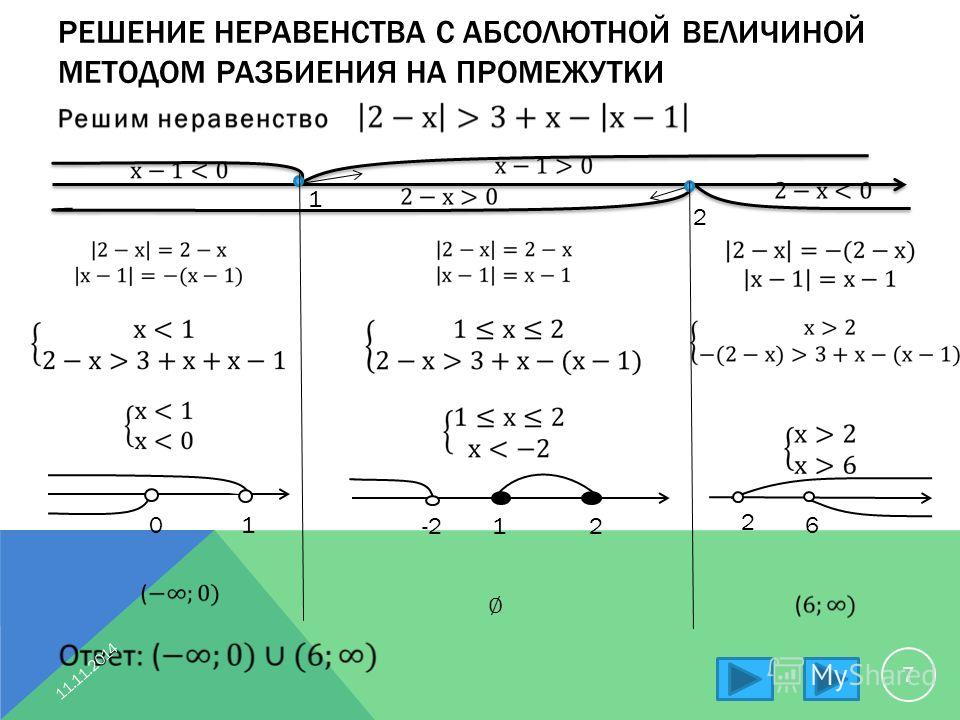
Решаем полученное неравенство
4.
Находим общее решение для условия и
решенного неравенства
5.
Ставим условие 2 и выполняем пункты
со 2 по 4
6.
Объединяем все полученные
промежутки
8. Решить уравнение |2x+5|>3x-1
Решить уравнение |2x+5|>3x-1
1. Условие: 2x+5≥0
x≥-2,5
Раскрываем модульные скобки: по условию
выражение под модулем положительно, то
модульные скобки просто убираем
2x+5>3x-1
2х-3х>-1-5
-x>-6
X
[-2,5;6)
-2,5
6
9. Решить уравнение |2x+5|>3x-1
Решить уравнение |2x+5|>3x-1
2. Условие: 2x+5
x
Раскрываем модульные скобки: по условию
выражение под модулем отрицательно, то
модульные скобки раскрываем с минусом
-(2x+5)>3x-1
-2х-5>3х-1
-2х-3х>-1+5
-5x>4
Х
-2,5
(-∞;-2,5)
-0,8
10. Решить уравнение |2x+5|>3x-1
Решить уравнение |2x+5|>3x-1
Объединим полученные интервалы
(-∞;-2,5)и [-2,5;6)
-2,5
Ответ: (-∞;6)
6
11.
 {2}}+2\) обе части неравенства и тем самым убрать этот множитель, чтоб глаза не мозолил.
{2}}+2\) обе части неравенства и тем самым убрать этот множитель, чтоб глаза не мозолил.
Имеем:
\( \frac{{x}-1}{{x}-4}\ge 0\)
Пришло время интервалы рисовать, для этого нужно определить те пограничные значения, при отступлении \( x\) от которых множители \( ({x}-1)\) и \( ({x}-4)\) будут больше и меньше нуля.
Но обрати внимание, что здесь знак \( \ge \), значит точку, в которой левая часть неравенства принимает нулевое значение, выкалывать не будем, она ведь входит в число решений, такая точка у нас одна, это точка, где икс равен одному.
А точку, где знаменатель равен нулю, закрасим? – Конечно, нет!
Знаменатель не должен быть равен нулю, поэтому интервал будет выглядеть так:
Общие сведения о неравенствах
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Предварительные навыки
Определения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, <, ≥, ≤ или ≠.
Пример: 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
Если 5 > 3, то 3 < 5. То есть левую и правую часть неравенства можно поменять местами, изменив знак неравенства на противоположный. В ситуации с весами: большой арбуз можно положить на правую чашу, а маленький арбуз на левую. Тогда правая чаша перевесит левую, и экран покажет знак <
Если в неравенстве 5 > 3, не трогая левую и правую часть, поменять знак на <, то получится неравенство 5 < 3. Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Рассмотрим некоторые важные свойства для неравенства 5 > 3.
В будущем эти свойства будут работать и для других неравенств.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Например, перенесём в неравенстве 5 > 3, член 5 из левой части в правую часть, изменив знак этого члена. После переноса члена 5 в правую часть, в левой части ничего не останется, поэтому запишем там 0
0 > 3 − 5
0 > −2
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь отрицательное число, скажем на число −2. Тогда получим:
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Например, чтобы ответить на вопрос является ли верным неравенство 7 > 3, нужно проверить выполняется ли условие «больше ли 7, чем 3». Мы знаем, что число 7 больше, чем число 3. То есть условие выполнено, а значит и неравенство 7 > 3 верно.
Неравенство 8 < 6 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Составим разность из членов 7 и 3. Тогда получим 7 − 3 = 4. Согласно правилу, число 7 будет больше числа 3, если разность 7 − 3 окажется положительной. У нас она равна 4, то есть разность положительна. А значит число 7 больше числа 3.
Проверим с помощью разности верно ли неравенство 3 < 4. Составим разность, получим 3 − 4 = −1. Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Проверим верно ли неравенство 5 > 8. Составим разность, получим 5 − 8 = −3. Согласно правилу, число 5 будет больше числа 8, если разность 5 − 8 окажется положительной. У нас разность равна −3, то есть она не является положительной. А значит число 5 не больше числа 8. Иными словами, неравенство 5 > 8 не является верным.
Строгие и нестрогие неравенства
Неравенства, содержащие знаки >, < называют строгими. А неравенства, содержащие знаки ≥, ≤ называют нестрогими.
Примеры строгих неравенства мы рассматривали ранее. Таковыми являются неравенства 5 > 3, 7 < 9.
Нестрогим, например, является неравенство 2 ≤ 5. Данное неравенство читают следующим образом: «2 меньше или равно 5».
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
2 < 5 или 2 = 5
Тогда становится очевидным, что неравенство 2 ≤ 5 состоит из двух условий: «два меньше пять» и «два равно пять».
Нестрогое неравенство верно в том случае, если выполняется хотя бы одно из его условий. В нашем примере верным является условие «2 меньше 5». Значит и само неравенство 2 ≤ 5 верно.
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Пример 3. Неравенство 5 ≤ 2 не является верным, поскольку не выполняется ни одно из его условий: ни 5 < 2 ни 5 = 2.
Двойное неравенство
Число 3 больше, чем число 2 и меньше, чем число 4. В виде неравенства это высказывание можно записать так: 2 < 3 < 4. Такое неравенство называют двойным.
Двойное неравенство может содержать знаки нестрогих неравенств. К примеру, если число 5 больше или равно, чем число 2, и меньше или равно, чем число 7, то можно записать, что 2 ≤ 5 ≤ 7
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Например, неравенство x > 2 содержит переменную x. Обычно такое неравенство нужно решить, то есть выяснить при каких значениях x данное неравенство становится верным.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
3 > 2
4 > 2
5 > 2
Число 2, располагающееся в правой части неравенства x > 2, будем называть границей данного неравенства. В зависимости от знака неравенства, граница может принадлежать множеству решений неравенства либо не принадлежать ему.
В нашем примере граница неравенства не принадлежит множеству решений, поскольку при подстановке числа 2 в неравенство x > 2 получается не верное неравенство 2 > 2. Число 2 не может быть больше самого себя, поскольку оно равно самому себе (2 = 2).
Неравенство x > 2 является строгим. Его можно прочитать так: «x строго больше 2″. То есть все значения, принимаемые переменной x должны быть строго больше 2. В противном случае, неравенство верным не будет.
Если бы нам было дано нестрогое неравенство x ≥ 2, то решениями данного неравенства были бы все числа, которые больше 2, в том числе и само число 2. В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
Решая уравнения мы выполняли тождественные преобразования до тех пор, пока в левой части уравнения не оставалась переменная, а в правой части значение этой переменной (например: x = 2, x = 5). Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Итак, нужно найти такие значения x, при подстановке которых в 2x > 6 получится верное неравенство.
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
В левой части осталась переменная x, а правая часть стала равна 3. Получилось равносильное неравенство x > 3. На этом решение завершается, поскольку в левой части осталась переменная, а в правой части граница неравенства.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
4 > 3
5 > 3
6 > 3
7 > 3
Отметим, что неравенство x > 3 является строгим. «Переменная x строго больше трёх».
А поскольку неравенство x > 3 равносильно исходному неравенству 2x > 6, то их решения будут совпадать. Иначе говоря, значения, которые подходят неравенству x > 3, будут подходить и неравенству 2x > 6. Покажем это.
Возьмём, например, число 5 и подставим его сначала в полученное нами равносильное неравенство x > 3, а потом в исходное 2x > 6.
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат числовому промежутку от трёх до плюс бесконечности.
Иначе говоря, все числа, начиная от трёх до плюс бесконечности являются решениями неравенства x > 3. Знак ∞ в математике означает бесконечность.
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
x ∈ [ 2 ; 8 ]
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Обратим внимание на то, что ответ записан с помощью квадратных скобок, поскольку границы неравенства 2 ≤ x ≤ 8, а именно числа 2 и 8 принадлежат множеству решений этого неравенства.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
Здесь границы числового промежутка 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8.
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
Открытыми их называют по той причине, что числовой промежуток остаётся открытым из-за того, что его границы не принадлежат этому числовому промежутку. Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой луч
Числовым лучом называют числовой промежуток, который задаётся неравенством x ≥ a, где a — граница данного неравенства, x — решение неравенства.
Пусть a = 3. Тогда неравенство x ≥ a примет вид x ≥ 3. Решениями данного неравенства являются все числа, которые больше 3, включая само число 3.
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Здесь точка 3 соответствует границе неравенства x ≥ 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≥ 3.
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
[ a ; +∞ )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
x ∈ [ 3 ; +∞ )
В этом выражении говорится, что переменная x, входящая в неравенство x ≥ 3, принимает все значения от 3 до плюс бесконечности.
Иначе говоря, все числа от 3 до плюс бесконечности, являются решениями неравенства x ≥ 3. Граница 3 принадлежит множеству решений, поскольку неравенство x ≥ 3 является нестрогим.
Закрытым числовым лучом также называют числовой промежуток, который задаётся неравенством x ≤ a. Решениями неравенства x ≤ a являются все числа, которые меньше a, включая само число a.
К примеру, если a = 2, то неравенство примет вид x ≤ 2. На координатной прямой граница 2 будет изображаться закрашенным кружком, а вся область, находящаяся слева, будет выделена штрихами. В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
Здесь точка 2 соответствует границе неравенства x ≤ 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≤ 2.
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
x ∈ ( −∞ ; 2 ]
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытым числовым лучом называют числовой промежуток, который задаётся неравенством x > a, где a — граница данного неравенства, x — решение неравенства.
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
Пусть a = 3. Тогда неравенство примет вид x > 3. Решениями данного неравенства являются все числа, которые больше 3, за исключением числа 3
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Здесь точка 3 соответствует границе неравенства x > 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x > 3. Точка 3, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x > 3 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x > a, обозначается следующим образом:
( a ; +∞ )
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
x ∈ ( 3 ; +∞ )
В этом выражении говорится, что все числа от 3 до плюс бесконечности, являются решениями неравенства x > 3. Граница 3 не принадлежит множеству решений, поскольку неравенство x > 3 является строгим.
Открытым числовым лучом также называют числовой промежуток, который задаётся неравенством x < a, где a — граница данного неравенства, x — решение неравенства. Решениями неравенства x < a являются все числа, которые меньше a, исключая число a.
К примеру, если a = 2, то неравенство примет вид x < 2. На координатной прямой граница 2 будет изображаться пустым кружком, а вся область, находящаяся слева, будет выделена штрихами:
Здесь точка 2 соответствует границе неравенства x < 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x < 2. Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x < a, обозначается следующим образом:
( −∞ ; a )
Запишем ответ к неравенству x < 2 с помощью обозначения открытого числового луча:
x ∈ ( −∞ ; 2 )
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x < 2. Граница 2 не принадлежит множеству решений, поскольку неравенство x < 2 является строгим.
Отрезок
Отрезком называют числовой промежуток, который задаётся двойным неравенством a ≤ x ≤ b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x ≤ b примет вид 2 ≤ x ≤ 8. Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8. Точки 2 и 8, являющиеся границами отрезка, изображены в виде закрашенных кружков, поскольку границы неравенства 2 ≤ x ≤ 8 принадлежат множеству его решений.
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
[ a ; b ]
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8 включительно, являются решениями неравенства 2 ≤ x ≤ 8.
Интервал
Интервалом называют числовой промежуток, который задаётся двойным неравенством a < x < b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a < x < b примет вид 2 < x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая числа 2 и 8.
Изобразим интервал на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x < 8. Точки 2 и 8, являющиеся границами интервала, изображены в виде пустых кружков, поскольку границы неравенства 2 < x < 8 не принадлежат множеству его решений.
На письме интервал, заданный неравенством a < x < b, обозначается следующим образом:
( a ; b )
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 < x < 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, исключая числа 2 и 8, являются решениями неравенства 2 < x < 8.
Полуинтервал
Полуинтервалом называют числовой промежуток, который задаётся неравенством a ≤ x < b, где a и b — границы данного неравенства, x — решение неравенства.
Полуинтервалом также называют числовой промежуток, который задаётся неравенством a < x ≤ b.
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x < b ему (полуинтервалу) принадлежит левая граница.
А в ситуации с полуинтервалом a < x ≤ b ему принадлежит правая граница.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x < b примет вид 2 ≤ x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, включая число 2, но исключая число 8.
Изобразим полуинтервал 2 ≤ x < 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x < 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x < 8 принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x < 8 не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x < b, обозначается следующим образом:
[ a ; b )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x < 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, включая число 2, но исключая число 8, являются решениями неравенства 2 ≤ x < 8.
Аналогично на координатной прямой можно изобразить полуинтервал, заданный неравенством a < x ≤ b. Пусть a = 2, b = 8. Тогда неравенство a < x ≤ b примет вид 2 < x ≤ 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая число 2, но включая число 8.
Изобразим полуинтервал 2 < x ≤ 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x ≤ 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 < x ≤ 8 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 < x ≤ 8 принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a < x ≤ b, обозначается так: ( a ; b ]. Запишем ответ к неравенству 2 < x ≤ 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8, исключая число 2, но включая число 8, являются решениями неравенства 2 < x ≤ 8.
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5 < x < 1
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
Неравенством вида a < x < b, задаётся интервал. В данном случае переменная a равна −5, а переменная b равна единице. Неравенство −5 < x < 1 строгое, поэтому границы −5 и 1 будут изображаться в виде пустых кружка. Нас интересуют все значения x, которые больше −5, но меньше единицы, поэтому вся область между точками −5 и 1 будет выделена штрихами:
Пример 5. Изобразить на координатной прямой числовые промежутки [-1; 2] и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка.
Квадратными скобками с обеих сторон обозначаются отрезки. Границы отрезка принадлежат ему, поэтому границы отрезков [-1; 2] и [2; 5] будут изображаться на координатной прямой в виде закрашенных кружков. Вся область между ними будет выделена штрихами.
Чтобы хорошо увидеть промежутки [−1; 2] и [2; 5], первый можно изобразить на верхней области, а второй на нижней. Так и поступим:
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax < b), будем называть линейным неравенством с одной переменной.
В линейном неравенстве ax > b, x — это переменная, значения которой нужно найти, а — коэффициент этой переменной, b — граница неравенства, которая в зависимости от знака неравенства может принадлежать множеству его решений либо не принадлежать ему.
Например, неравенство 2x > 4 является неравенством вида ax > b. В нём роль переменной a играет число 2, роль переменной b (границы неравенства) играет число 4.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Получившееся неравенство x > 2 также является неравенством вида ax > b, то есть линейным неравенством с одной переменной. В этом неравенстве роль переменной a играет единица. Ранее мы говорили, что коэффициент 1 не записывают. Роль переменной b играет число 2.
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7 < 0
Прибавим к обеим частям неравенства число 7
x − 7 + 7 < 0 + 7
В левой части останется x, а правая часть станет равна 7
x < 7
Путём элементарных преобразований мы привели неравенство x − 7 < 0 к равносильному неравенству x < 7. Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Когда неравенство приведено к виду x < a (или x > a), его можно считать уже решённым. Наше неравенство x − 7 < 0 тоже приведено к такому виду, а именно к виду x < 7. Но в большинстве школ требуют, чтобы ответ был записан с помощью числового промежутка и проиллюстрирован на координатной прямой.
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x < a и обозначается как ( −∞ ; a)
x ∈ ( −∞ ; 7 )
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Для проверки возьмём любое число из промежутка ( −∞ ; 7 ) и подставим его в неравенство x < 7 вместо переменной x. Возьмём, например, число 2
2 < 7
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
4 < 7
Получилось верное числовое неравенство. Значит решение верное.
А поскольку неравенство x < 7 равносильно исходному неравенству x − 7 < 0, то решения неравенства x < 7 будут совпадать с решениями неравенства x − 7 < 0. Подставим те же тестовые значения 2 и 4 в неравенство x − 7 < 0
2 − 7 < 0
−5 < 0 — Верное неравенство
4 − 7 < 0
−3 < 0 Верное неравенство
Пример 2. Решить неравенство −4x < −16
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Мы привели неравенство −4x < −16 к равносильному неравенству x > 4. Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
3y − 6y> 1 − 1
Приведём подобные слагаемые:
−3y > 0
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y < 0 являются все числа, меньшие нуля. Изобразим множество решений неравенства y < 0 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства являются все числа, которые меньше . Граница принадлежит множеству решений, поскольку неравенство является нестрогим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
После приведения подобных слагаемых, получим неравенство 6x > 1. Разделим обе части этого неравенства на 6. Тогда получим:
Решениями неравенства являются все числа, которые больше . Граница не принадлежит множеству решений, поскольку неравенство является строгим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 6. Решить неравенство
Умножим обе части на 6
После приведения подобных слагаемых, получим неравенство 5x < 30. Разделим обе части этого неравенства на 5
Решениями неравенства x < 6 являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x < 6 строгим.
Изобразим множество решений неравенства x < 6 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 8. Решить неравенство 4 < 4x < 20
Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.
Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4 < 4x < 20
Решениями неравенства 1 < x < 5 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 < x < 5 является строгим.
Изобразим множество решений неравенства 1 < x < 5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 9. Решить неравенство −1 ≤ −2x ≤ 0
Разделим все члены неравенства на −2
Получили неравенство 0,5 ≥ x ≥ 0. Двойное неравенство желательно записывать так, чтобы меньший член располагался слева, а больший справа. Поэтому перепишем наше неравенство следующим образом:
0 ≤ x ≤ 0,5
Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.
Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 10. Решить неравенство
Умножим обе неравенства на 12
Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 2
Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 11. Решить неравенство
Умножим все части неравенства на 3
Теперь из каждой части получившегося неравенства вычтем 6
Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.
Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Существуют неравенства, которые не имеют решений. Таковым, например, является неравенство 6x > 2(3x + 1). В процессе решения этого неравенства мы придём к тому, что знак неравенства > не оправдает своего местоположения. Давайте посмотрим, как это выглядит.
Раскроем скобки в правой части данного неравенство, получим 6x > 6x + 2. Перенесем 6x из правой части в левую часть, изменив знак, получим 6x − 6x > 2. Приводим подобные слагаемые и получаем неравенство 0 > 2, которое не является верным.
Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:
Получили неравенство 0x > 2. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль не может быть больше, чем число 2. Значит неравенство 0x > 2 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x > 2, то не имеет решений и исходное неравенство 6x > 2(3x + 1).
Пример 2. Решить неравенство
Умножим обе части неравенства на 3
В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:
Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x < −8 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x < −8, то не имеет решений и исходное неравенство .
Ответ: решений нет.
Когда решений бесконечно много
Существуют неравенства, имеющие бесчисленное множество решений. Такие неравенства становятся верными при любом x.
Пример 1. Решить неравенство 5(3x − 9) < 15x
Раскроем скобки в правой части неравенства:
Перенесём 15x из правой части в левую часть, изменив знак:
Приведем подобные слагаемые в левой части:
Получили неравенство 0x < 45. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль меньше, чем 45. Значит решением неравенства 0x < 45 является любое число.
А если приведённое равносильное неравенство 0x < 45 имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) < 15x имеет те же решения.
Ответ можно записать в виде числового промежутка:
x ∈ ( −∞; +∞ )
В этом выражении говорится, что решениями неравенства 5(3x − 9) < 15x являются все числа от минус бесконечности до плюс бесконечности.
Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x
Раскроем скобки в левой части неравенства:
Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Получили неравенство 0x > −31. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль больше, чем −31. Значит решением неравенства 0x < −31 является любое число.
А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.
Запишем ответ в виде числового промежутка:
x ∈ ( −∞; +∞ )
Задания для самостоятельного решения
Задание 1. Решите неравенство:
Задание 2. Решите неравенство:
Задание 3. Решите неравенство:
Задание 4. Решите неравенство:
Задание 5. Решите неравенство:
Задание 6. Решите неравенство:
Задание 7. Решите неравенство:
Задание 8. Решите неравенство:
Задание 9. Решите неравенство:
Задание 10. Решите неравенство:
Задание 11. Решите неравенство:
Задание 12. Решите неравенство:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Решение квадратных неравенств через выделение квадрата двучлена
Квадратные неравенства можно решать несколькими разными способами. Для лучшего понимания сути этих выражений полезно знать их все. Помимо привычного метода интервалов или графического способа существует и метод решения через выделение квадрата двучлена, о котором мы вам расскажем в данном материале.
Выделив квадрат двучлена в левой части, можно легко решить практически любое квадратное неравенство. Сейчас мы разберем данный метод по порядку, иллюстрируя каждый шаг решениями задач.
Основа метода выделения квадрата двучлена
Для начала объясним основную суть данного подхода на примере условного квадратного неравенства a·x2+b·x+c <0. Между выражениями при этом может стоять и знак ≤, и ≥, и >, это не принципиальный момент. Суть метода заключается в переходе от исходного неравенства к равносильному, которое имеет вид (x−p)2<q (≤,>, ≥), при этом p и q могут быть произвольными числами. Для этого мы используем равносильные преобразования, подробно описанные в одной из предыдущих статей. По полученному равенству можно будет судить о решении исходного.
Теперь перейдем к объяснению следующих двух моментов: как именно привести заданное в условии равенство к нужному виду и как потом его нужно решать.
Как преобразовать исходное равенство в
(x−p)2<q (≤,>, ≥)
Для этого нам нужно последовательно выполнить несколько шагов. Вот они:
Определение 1
- Если мы имеем коэффициент a, который не равен 1, то нам нужно разделить на него правую и левую часть равенства. Если он меньше 0, то знак неравенства остается прежним, а если больше, то нужно поменять его на противоположный. В итоге у нас должно получиться равенство с коэффициентом при x2, которое будет равносильно исходному. Если коэффициент при x2равен единице, то первый шаг нужно пропустить.
- Далее смотрим на коэффициент при x. Если он не равен нулю, то мы можем слева выделить нужный нам квадрат двучлена. Если же слагаемое с x в первой степени у нас отсутствует совсем, то этот шаг мы тоже пропускаем.
- После этих действий нужно перенести оставшееся слагаемое-число направо с противоположным знаком.
Мы получили неравенство нужного нам вида. Разберем решения конкретных задач, чтобы увидеть преобразования на практике.
Пример 1
Допустим, у нас есть неравенство x2≥0. Видим, что коэффициент при x2 – единица, значит, первый и второй шаги можно пропустить. Получается, что и на третьем шаге ничего не нужно переносить, ведь слагаемого-числа с левой стороны нет. Из этого заключаем, что имеющееся у нас неравенство уже имеет нужный нам вид (x−p)2≥q, только p=0 и q=0.
Ответ: имеющееся у нас неравенство уже имеет нужный нам вид (x−p)2≥q
Возьмем пример чуть сложнее.
Пример 2
Так, у нас есть квадратное неравенство 5·x2<0. Выполняем первый шаг, разделив обе части на старший коэффициент, равный пяти. Поскольку 5 больше нуля, знак равенства при этом не меняется. После этого неравенство приобретает вид x2<0, что соответствует нужным условиям при p=0 и q=0. Два следующих шага можно пропустить.
Ответ: x2<0
Пример 3
Если у нас есть квадратное неравенство -3·x2-4>0, то сначала мы должны выполнить деление обоих частей на -3. Поскольку делитель является отрицательным числом, то нужно будет поменять знак равенства на противоположный. У нас получится x2+43<0. Избавившись от иррациональности в знаменателе, запишем x2+43<0. Коэффициента при x у нас нет, поэтому второй шаг пропускаем. На последнем этапе переносим оставшийся свободный член вправо и получаем x2<-433. Полученное равенство соответствует нужному нам виду (x−p)2<q, причем p=0, и q=-433.
Ответ: x2<-433
Пример 4
Разберем преобразование неравенства 13×2+2·x+3≤0. Первым делом разделим обе части на одну треть. Это действие аналогично умножению на три. Сохранив знак неравенства, получим x2+6·x+9≤0. Поскольку слагаемое с x у нас есть, нам нужно выделить квадрат двучлена: (x+3)2≤0. Последний шаг мы не выполняем, поскольку числового слагаемого не осталось. Таким образом, мы заменили исходное квадратное неравенство на равносильное ему (x−p)2≤q, где p=−3 и q=0.
Ответ: (x+3)2≤0
Пример 5
Посмотрим еще один пример с квадратным неравенством 4·x2−4·x−1<0. Начнем с деления на коэффициент при x2, т.е. на четыре. У нас получится x2-x-14<0. Выделяем квадрат двучлена: x2-2·12·x+122-122-14<0 и далее x-122-12<0. Осталось перенести оставшееся свободное слагаемое в правую часть с другим знаком. Итоговое равносильное неравенство имеет вид x-122<12, где p=12, q=12.
Ответ: x-122<12
Решение полученного неравенства (
x−p)2<q (≤,>, ≥)
Мы разобрали, как правильно преобразовывать имеющиеся неравенства для приведения их к исходному виду. Далее рассмотрим, как найти их решение. Разберем три основных случая, когда q больше 0, меньше 0 или равно 0.
Решение при q, меньшем 0
В этом случае в основе решения лежит свойство степени: любое число, возведенное в квадрат, является неотрицательным. Мы помним также, что квадрат числа, не равного нулю, всегда положителен, а квадрат нуля равен 0 только в том случае, если 0 лежит в основании степени. В буквенном виде это можно записать как d2≥0 для любого d, d2>0 при любом d≠0, и d2=0 только тогда, когда d=0.
Допустим, что в основании лежит отрицательное число. Значение (x−p)2, согласно указанным выше свойствам квадрата, не может быть отрицательным. Следовательно, будут справедливы неравенства (x−p)2<p и (x−p)2≤p, причем x может быть любым. Таким образом, любое действительное число может считаться решением этих неравенств.
А вот (x−p)2<p и (x−p)2≤p не будут справедливыми ни при каких значениях x. Из этого можно сделать вывод, что решений у них нет.
Пример 6
Условие: найдите решение квадратного неравенства x2+4·x+5>0.
Решение
Cначала нам нужно выделить полный квадрат с левой стороны.
x2+2·2·x+22−22+5>0, (x+2)2+1>0
После этого переносим 1 вправо: (x+2)2> −1.
У нас получилось равенство, равносильное исходному. Для него любое действительное число может стать решением, поскольку выражение слева будет неотрицательным всегда, при любом значении x. То же можно сказать и о (x+2)2> −1. Значит, решением неравенства, заданного в условии, может быть любое действительное число.
Ответ: любое действительное число.
Пример 7
Условие: вычислите 9·x2+6·x+28≤0.
Решение
Для данного квадратного неравенства подходит метод решения с помощью выделения квадрата двучлена. Для начала разделим левую и правую часть неравенства на девять и выделим нужный квадрат. У нас осталось одно слагаемое, которое надо перенести в правую часть с противоположным знаком.
x2+23·x+289≤0x2+2·13·x+132-132+289≤0x+132+3≤0x+132≤-3
Выражение в левой части будет неотрицательным при любом значении x. Это значение также не может быть равно -3 или быть меньше него. Получается, что итоговое равенство не имеет решения, следовательно, и исходное равенство, которое равносильно ему, также решений иметь не будет.
Ответ: решений у данного неравенства нет.
Решение при q, равном 0
Допустим, что значение q равно 0, тогда нам нужно рассмотреть неравенства (x−p)2<0, (x−p)2≤0, (x−p)2>0 и (x−p)2≥0). Зная свойства числа, возведенного в квадрат, мы можем заключить, что значение (x−p)2будет больше нуля при таких значениях x, которые будут соответствовать условию x−p≠0, и будет равно нулю, если x−p=0.
Подытожим:
- (x−p)2>0 будет верным неравенством при таких значениях переменной x, когда x−p≠0, то есть при x≠p.
- (x−p)2≥0 не будет верным равенством ни при одном действительном x, если x−p=0.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 8
Условие: выясните, есть ли решения у квадратного неравенства −0,2·x2+4·x−20≥0.
Решение
Начнем с необходимых равносильных преобразований.
x2−20·x+100≤0(x−10)2≤0.
Получившееся в итоге равенство будет справедливым лишь в том случае, если x−10=0. Получается, что нужное нам значение x равно 10. Следовательно, это число и будет единственным решением исходного неравенства.
Ответ: есть единственное решение 10.
Пример 9
Условие: найти решение 16·x2+40·x+25>0.
Решение
Начнем с деления на 16, после чего нужно выделить квадрат двучлена.
x2+52·x+2516>0x+542>0x+114>0
Это неравенство имеет решения. Оно будет верным для всех значений x, за исключением такого, которое обратит основание степени в 0, т.е. x≠-114.
Ответ: -∞, -114∪-114, +∞
Решение при q, большем 0
Последний случай, который нам нужно разобрать, – это решение неравенств (x−p)2<q, (x−p)2≤q, (x−p)2>q и (x−p)2≥q при значении q больше 0.
Для этого нам понадобится вспомнить другие свойства корня: неравенство u<v (≤, >, ≥) можно преобразовать в u<v при любых положительных u и v; для любого положительного t является верным равенство t2=t.
Первое свойство позволяет нам перейти от обычного квадратного неравенства к иррациональному, а второе – к неравенству с модулем. В обоих случаях полученные неравенства будут равносильными исходному.
Чтобы решить неравенство с модулем, нужно раскрыть этот модуль. Так, мы можем преобразовать x-p<q в две системы неравенств без модуля x-p≥0x-p<q и x-p<0-x-p<q. Покажем пример решения задачи.
Пример 10
Условие: вычислите x2−6·x−7>0, предварительно выделив квадрат двучлена.
Решение
Выделив нужный квадрат, получим x2−2·3·x+32−32−7>0, (x−3)2−16>0. Теперь перенесем слагаемое -16 вправо с положительным знаком и получим (x−3)2>16. Теперь запишем равносильное ему иррациональное неравенство x-32>16,далее |x−3|>4. Теперь преобразуем его в совокупность двух систем неравенств, чтобы избавиться от модуля.
x-3≥0x-3>4x-3<0-(x-3)>4 x≥3x>7x<3x<-1 x>7x<-1
У нас получилось, что решением исходного квадратного неравенства будет x <−1, x>7.
Ответ: x <−1, x>7.
Существует еще один удобный и наглядный способ решения неравенств x-p<q (≤, >, ≥). С его помощью можно обойтись без введения систем. Для его применения необходимо понимать геометрический смысл модуля.
В рамках геометрических представлений модуль |x−p| представляет собой расстояние то точки с координатой x до точки с координатой p, отложенное по оси координат. Отсюда можно сделать следующие выводы:
- Решениями неравенства x-p<q будут координаты таких точек, расстояние от которых до точки с координатой p будет меньшим, чем значение q. См. на иллюстрацию:
Таким образом, данному неравенству будут удовлетворять значения переменных из интервала p-q, p+q.
- Решением неравенства x-p≤q будут все те значения x, при которых расстояние от точки с координатой p будет меньше или равно q. Графически это можно представить так:
Следовательно, решением данного неравенства будут числа из интервала p-q, p+q
- Если нам нужно найти решение x-p>q, то мы должны взять точки, расстояние от которых до точки p будет больше q. См. на иллюстрацию:
Решения данного неравенства будут лежат в интервале -∞, p-q∪p+q, +∞.
Вернемся к решению предыдущей задачи, чтобы наглядно показать эти выкладки.
Пример 11
Условие: найдите решения квадратного неравенства x2−6·x−7>0.
Решение: выполним все необходимые равносильные преобразования, выделив квадрат двучлена слева, и приведем исходное неравенство к нужному нам виду (x−3)2>16. Далее запишем:
(x-3)2>16x-3>4
Полученному неравенству будут удовлетворять координаты всех точек, расположенных от точки с координатой 3 на расстоянии больше 4. Покажем на рисунке:
Здесь видно решение:
x <−1, x>7.
Ответ: x <−1, x>7.
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Модуль числа, решение неравенств с модулем, свойства, как раскрыть, чему равен модуль отрицательного числа, как решать уравнения с модулем, примеры графиков
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
- Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
- Если абсолютные значения содержат выражения противоположных значений, они равны:
- Значение числа не превышает величину его модуля:
- Правило раскрытия при произведении:
- Правило, применимое при делении:
- При возведении в степень:
- Сумма величин:
- Двойной модуль:
Модуль комплексного числа
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x| <, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Далее простая арифметика − нужно решить два равенства относительно x.
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.
Ответ: 2 и −2.
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.
Это означает, что –2 – поворотная точка.
Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.
Разделим интервал на 2 части:
- для x + 2 ≥ 0
Общим ответом для этих двух неравенств является интервал [−1, + ∞).
- для х + 2 <, 0
Общим ответом для этих двух неравенств является интервал (−∞, –3].
Окончательное решение – объединение ответов отдельных частей:
x ∈ (–∞, –3] ∪ [–1, + ∞).
Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).
Уравнения вида |x| = |y|
Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ: x1 = 3, x2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:
Решение:
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке .
Ответ: x = 0.
Модуль суммы
Модуль разности
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Известно свойство:
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение: из рисунка видно, что график симметричен относительно оси Y.
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
- Приравнять каждое выражение к нулю.
- Найти значения переменных.
- Нанести на числовую прямую точки, полученные в пункте 2.
- Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
- Решить неравенства с полученными знаками.
Пример 1. Решить методом интервалов.
Решение:
Результатом будет сумма всех подходящих интервалов.
Модуль в модуле
Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.
Лучше всего понять принцип на примере.
Пример 1. Решить
Решение:
Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:
В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:
Нужно упростить два уравнения:
Далее каждое из равенств разделяется еще на два:
Получено четыре результата:
Заключение
Самое важное, что нужно знать: модуль не может быть отрицательным.
Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.
В качестве итогов, напомним все свойства, которые помогут в решении задач:
- когда положительное число находится внутри модуля, достаточно просто избавиться от него,
- если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
- если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.
Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.
2 $, деление и извлечение квадратного корня дает решение $ x \ le \ frac {-1} {\ sqrt {5}} $ или $ x \ ge \ frac {1} {\ sqrt {5}} $. В сочетании с условиями реальности числителя дает
$$ \ frac {-1} {2} \ le x \ le \ frac {-1} {\ sqrt {5}} \; \ text {или} \; \ frac {1} {\ sqrt {5}} \ le x \ le \ frac {1} {2} \ tag {2} \ label {eq2} $$
Вы также можете объединить эти неравенства в 2 доллара, если хотите, чтобы получить эквивалент
$$ \ frac {1} {\ sqrt {5}} \ le | x | \ le \ frac {1} {2} \ tag {3} \ label {eq3} $$
Чтобы убедиться, что этот диапазон работает, обратите внимание на $ | x | = \ frac {1} {\ sqrt {5}} $, что левая часть \ eqref {eq1} равна $ 1 $.Когда $ | x | $ увеличивается до $ \ frac {1} {2} $, числитель уменьшается до $ 0 $, а знаменатель увеличивается. Таким образом, дробь стремится к $ 0 $ и, таким образом, остается $ \ le 1 $, поэтому неравенство в \ eqref {eq1} всегда выполняется.
Что касается ссылок на общий набор правил неравенства, то при поиске в Интернете выявляется ряд довольно хороших, таких как Правила решения неравенств. Что касается ваших конкретных опасений по поводу возведения в квадрат неравенства, включающего отрицательные количества (или, по крайней мере, возможно, отрицательные количества), есть несколько онлайн-ресурсов, которые вы можете использовать, причем сообщение MSE, на которое я ссылался выше, является хорошим, а также другие, такие как Следует ли поменять знак, если я возведу обе стороны неравенства в квадрат?
Решение уравнений, содержащих абсолютное значение
Решение уравнений, содержащих абсолютное значение
Чтобы решить уравнение, содержащее абсолютное значение, выделите абсолютное значение на одной стороне уравнения. Затем установите его содержимое равным как положительному, так и отрицательному значению числа с другой стороны уравнения и решите оба уравнения.
Пример 1
Решить | x | + 2 = 5.
Выделите абсолютное значение.
Установите содержание части абсолютного значения равным +3 и –3.
Ответ: 3, –3
Пример 2
Решить 3 | x — 1 | — 1 = 11.
Выделите абсолютное значение.
Установите содержание части абсолютного значения равным +4 и –4.
Решение для x,
Ответ: 5, –3
Решение неравенств, содержащих абсолютные значения и построение графиков
Для решения неравенства, содержащего абсолютное значение , начните с тех же шагов, что и для решения уравнений с абсолютным значением.Создавая сравнения как с +, так и с — другой стороны неравенства, измените направление неравенства при сравнении с отрицательным.
Пример 3
Решите и изобразите ответ: | x — 1 | > 2.
Обратите внимание, что выражение абсолютного значения уже изолировано.
| x — 1 | > 2
Сравните содержимое части абсолютного значения как с 2, так и с –2. Обязательно измените направление неравенства при сравнении с –2.
Решите для x .
Изобразите ответ в виде графика (см. Рисунок 1).
Рисунок 1. Графическое решение | x — 1 | > 2.
Пример 4
Решите и изобразите ответ: 3 | x | — 2 ≤ 1.
Выделите абсолютное значение.
Сравните содержимое части абсолютного значения как с 1, так и с –1. Обязательно измените направление неравенства при сравнении с –1.
Изобразите ответ в виде графика (см. Рисунок 2).
Рис. 2. Построение графика решения 3 | x | — 2 ≤ 1.
Пример 5
Решите и изобразите ответ: 2 | 1 — x | + 1 ≥ 3.
Выделите абсолютное значение.
Сравните содержимое части абсолютного значения как с 1, так и с –1. Обязательно измените направление неравенства при сравнении с –1.
Решите для x .
(не забудьте переключить направление неравенства при делении на минус)
Изобразите ответ в виде графика (см. Рисунок 3).
Рис. 3. Построение графика решения 2 | 1 — x | + 1 ≥ 3.
College Algebra WTAMU > Виртуальная математическая лаборатория> Алгебра колледжа Цели обучения
Введение
Учебник
Практические задачи
|
Как доказать неравенство. Методы, которые помогут доказать, что a
Когда вы разовьете интерес к математике и начнете работать с материалом, который серьезно относится к доказательству, рано или поздно вы будете пытаться найти доказательства неравенства. Доказать, что что-то равно другому, обычно несколько проще. Вы манипулируете обеими сторонами одинаково, пока не придете к рассматриваемому уравнению. Возможно, вам придется сделать несколько умных замен, но вы можете сделать очень многое. Неравенства могут быть немного сложнее из-за транзитивности. Если вы хотите показать для некоторых Давайте рассмотрим примеры обоих случаев, мы начнем с «простого» случая, для которого нам не нужно изобретать промежуточные звенья. Все числа в примерах являются действительными числами. Учитывая действительные числа Давайте сначала потратим время на то, чтобы развить интуицию в отношении того, что он говорит. Давайте выберем несколько чисел для Хорошо, понятно.Я могу согласиться с этим. Итак, как нам доказать, что это всегда правда? Чтобы сравнить дроби, полезно расширить их до тех же знаменателей. Нам нужно будет расширить левую сторону с помощью . Давайте сделаем это и посмотрим, где мы находимся. Теперь, когда знаменатели сравнялись, оказалось, что от них можно избавиться. Мы знаем, что и Нам не нужно менять направление неравенства, поскольку известно, что число, на которое мы умножаем, положительное. Я бы сказал, прогресс. Давай сделаем это. Остается: Умножив суммы, мы обнаружим, что в итоге получаем общий член с обеих сторон: Чтобы представить формальное доказательство, мы просто обратим наши исследовательские шаги, поэтому рассуждения имеют смысл при чтении сверху вниз. Наше доказательство, каждый шаг, оправданный данными, является противоположностью наших исследовательских шагов Доказательство было простым - в некотором смысле - потому что не требовало от нас творчества с какими-либо промежуточными выражениями. Мы могли бы справиться с доказательством очень похоже на доказательство равенства. Давайте перейдем к чему-то более требовательному. Учитывая любые два действительных числа О, мальчик. Этот выглядит немного более требовательным. Во-первых, давайте разберемся, о чем он говорит. Возьмем Хорошо, попробуем другую пару: Хорошо, похоже, мы всегда будем оставаться ниже 1 с левой стороны, даже ниже 0.Правая часть может вырасти выше 1 и никогда не опустится ниже 0, потому что отдельные члены никогда не станут отрицательными. Обратите внимание, что когда мы выбираем Хорошо, мы немного интуитивно понимаем, что происходит. Посмотрим, сможем ли мы это доказать. В правой части указана сумма дробей. Мы можем попробовать сформировать сумму, чтобы увидеть, как она соотносится с левой частью.Нам нужно расширить левый член до Хорошо. Вот как это выглядит, когда мы суммируем правую часть. Неравенство, которое необходимо доказать, принимает следующий вид: Доказывая неравенства, вам часто приходится вводить один или несколько дополнительных членов, которые находятся между двумя, которые вы уже рассматриваете. Это часто означает убирать или добавлять что-то, так что появляется третий термин. Всегда проверяйте свой учебник на предмет неравенства, о котором вы должны знать, и посмотрите, не кажутся ли какие-то из них полезными.Упражнения часто дополняют друг друга. Иногда результат упражнения а) является ключевым в упражнении б). Так что не забывайте о своих предыдущих результатах. В нашем случае мы видим, что обе стороны похожи на наш знакомый образец Давайте посмотрим, что нужно, чтобы заставить обе стороны соответствовать нашему доказанному неравенству, чтобы мы могли его использовать. Давайте посмотрим на нашу левую часть. Если мы возьмем абсолютное значение числителя Итак, у нас есть: Похоже, мы закончили с левой стороны. Давайте посмотрим на нашу правую часть. Что нам нужно сделать, чтобы получить желаемую форму Если подставить Таким образом, мы имеем: И мы пришли к желаемой форме Мы преобразовали обе стороны в Если мы можем показать, что Мы подставили Отлично! Мы знаем Мы сделали это! Наши начальные значения для левой и правой сторон было трудно сравнивать напрямую. Но мы могли бы поместить между ними несколько терминов, которые мы знали, как сравнивать, таким образом сформировав цепочку, подтверждающую наше первоначальное утверждение. При доказательстве неравенства полезно искать способы контролируемого сокращения или увеличения сроков, чтобы они соответствовали известным неравенствам и формировали транзитивные цепочки. Если вы чувствуете, что у вас все в порядке, почему бы не проверить себя и не попытаться доказать оба неравенства с нуля? Вы только что прочитали решения, так что… насколько это может быть сложно? Вот они снова. Первое неравенство: Второе неравенство: Вы получили это! Есть два основных правила для неравенств GMAT : 1.Добавление или вычитание одного и того же выражения к обеим сторонам неравенства не меняет знака неравенства . Итак, если a a + k В более простых способах наблюдения, если у A больше денег, чем у B, и 3 доллара добавляются на счет как A, так и B. , A ВСЕ ЕЩЕ будет иметь больше денег, чем B, и знак «больше» останется неизменным. То же самое верно, если с каждого отнять по 3 доллара. Знак «больше» остается прежним. Умножение или деление одного и того же положительного числа на обе стороны неравенства не изменяет неравенство . 2. Умножение или деление одного и того же отрицательного числа на обе стороны неравенства обращает неравенство на противоположное - это также называется правилом переворота неравенств . Давайте теперь попробуем понять эти два правила неравенства, используя приведенные ниже примеры. Правило 1 неравенства GMAT Добавление или вычитание одного и того же выражения к обеим сторонам неравенства не изменяет неравенство . И Умножение или деление одного и того же положительного числа на обе стороны неравенства не изменяет неравенство . Если рассматривать истинное неравенство, 4 <8 Сложение 2 с обеих сторон 6 <10 (знак неравенства верен) Как видно из приведенного выше примера, сложение, вычитание, умножение или деление обе стороны неравенства с одинаковым положительным числом не меняют неравенства. Знак неравенства верен во всех четырех случаях. Мы надеемся, что теперь вы понимаете это правило неравенства GMAT. 🙂 Правило неравенства GMAT 2: Умножение или деление одного и того же отрицательного числа на обе стороны неравенства обращает неравенство - это также называется правилом переворота неравенств. Принимая во внимание истинное неравенство, которое мы использовали для объяснения первого правила здесь: 4 <8 Умножение обеих сторон на -2-8> -16 (знак неравенства меняется на противоположный) Деление обеих сторон на -2-2> -4 (знак неравенства меняется на противоположный) Есть вопросы? Теперь, когда мы закончили с основными правилами неравенства GMAT, мы уверены, что у вас возникнет несколько вопросов.Итак, воспользуемся случаем, чтобы ответить им. Вот несколько вопросов о неравенстве GMAT, которые заставят вас задуматься. В этом калькуляторе абсолютного значения мы предоставляем всю необходимую информацию о функции абсолютного значения и ее неравенствах, и, разумеется, мы помогаем вам вычислить абсолютное значение любого числа. Чтобы помочь вам лучше понять, что такое абсолютное значение, мы включили несколько графиков абсолютных значений, а также несколько практических примеров решения уравнений абсолютных значений.Так что приходите и наслаждайтесь изучением нового об абсолютной ценности! Давайте начнем с начала, не так ли? Термин «абсолютное значение» может иметь разное значение в зависимости от контекста, но здесь, , в математическом мире это очень четко определено . Определение абсолютного значения - это просто значение числа, независимо от знака. Это определение абсолютного значения не является самым техническим, но оно наверняка никого не запутает при объяснении того, что такое абсолютное значение. Мы не забыли о вас для тех, кто любит технические детали в математических определениях: Абсолютное значение или модуль | x | действительного числа x является неотрицательным значением x независимо от его знака. А именно | x | = x для положительного x, | x | = −x для отрицательного x (в этом случае −x положительно) и | 0 | = 0. Теперь, когда вы знаете, что такое абсолютное значение, мы можем поговорить о том, как его записать и оперировать математическими терминами.Математический символ для абсолютного значения: Чтобы вычислить абсолютное значение числа , вы просто «снимаете знак» с числа. Можно также думать об этом как о «превращении числа в положительное». Если вы хотите казаться более привлекательным, вы всегда можете придумать свой собственный способ объяснения, в зависимости от того, что вы хотите вычислить, например: «вы найдете расстояние между интересующим вас числом и значением 0 (ноль) ". Важно знать, что операция абсолютного значения не ограничивается только числами . Его можно применять к таким выражениям и уравнениям: Позже мы объясним, как вычислить абсолютное значение уравнений или абсолютное значение графика / функции. А пока пойдем по шагам. Вы уверены, что это так! Ой! Думаю, вам нужны причины и примеры того, для чего нужна абсолютная величина, верно? Что ж, давайте начнем с самого простого: любой ситуации, в которой нас интересуют различия и только различия , например, когда мы говорим о расстоянии между двумя вещами.Очевидным является расстояние между двумя точками для расчета общего расстояния, пройденного объектом (типичная физическая проблема). Например, если автомобиль стартует с Мы также можем использовать абсолютное значение как способ , сокращая нашу запись .Например, если нам нужна функция, которая выдает только положительные числа, мы могли бы написать набор условий «if ... else», но это было бы слишком долго. Здесь на помощь приходит абсолютное значение: мы можем просто заключить нашу функцию в знаки абсолютного значения, чтобы получить постоянные положительные значения. Это означает, что И эта полезность приводит непосредственно к графикам абсолютных значений и абсолютным значениям внутри функций .Обе простые вещи в теории, но обе сложны вначале. Начнем с самой простой функции абсолютного значения: a и b , что a , это может показаться очень трудным. Если очевидного решения нет, может потребоваться найти c , для которого вы можете показать a a . r и s , покажите следующее: Развитие интуиции
r и s и посмотрим, что получится: 1/2 <2/3 <3/4 <9/10 <99/100
Разложить до того же знаменателя
(1 + s) и правую сторону с помощью (1 + r) (1 + r), , и (1 + s) являются положительными числами, поэтому мы знаем, что их произведение (1 + r) (1 + s) является положительным числом.То же самое и обратное значение 1 / ((1 + r) (1 + s)) . Мы можем умножить обе части на обратное, избавившись от дробей. Упростим суммы в скобках
rs . Мы вычитаем его с обеих сторон, придя к истинному утверждению согласно нашим данным. Переверните ваши шаги, чтобы обеспечить простое доказательство
x и y , покажите, что следующее: Развитие интуиции
x = y = 2 , получим: 4/5 <= 2/3 + 2/3
x = 2, y = -3 -1 / 2 <= 2/3 + 3/4
x = 0 или y = 0 , левая и правая стороны становятся равными. Разложить до знаменателя
1+ | y | и правильный член с 1+ | x | Ищите известные неравенства
something / (1 + something) , с которым мы только что имели дело в нашем первом доказательстве. Увеличение левой части
x + y , мы можем заменить r = | x + y | , а наша левая часть будет иметь вид r / (1 + r) . Это наверняка увеличит срок. Абсолютное значение x + y либо больше - в случае x + y <0 - либо равно - в случае x + y≥0 . Усадка правой части
с / (1 + с) ? s = | x | + | y | + | x || y | , мы получаем (s + | x || y |) / (1 + s) . Есть еще один лишний | x || y | В числителе присутствует . Если мы отбросим его, наш член либо останется прежним - это было бы так, если бы x или y равнялись 0 , - либо он уменьшится. Потому что, если ни x , ни y не равны 0 , тогда | x || y | положительное число, поэтому мы уменьшаем числитель в значении. с / (1 + с) Собираем наших уток в ряд
r / (r + 1 ) и с / (с + 1) образуют соответственно. Это термины, которые мы хотим вставить между нашей начальной левой и правой стороной. 0 ≤ r , мы можем использовать наш первый результат r / (r + 1)
r = | x + y | и s = | x | + | y | + | x || y | .Мы сразу видим, что 0≤r , потому что это абсолютное значение. Из неравенства треугольника мы знаем, что | x + y | ≤ | x | + | y | верно, поэтому можем показать: 0 ≤ r ≤ s и можем использовать r / (r + 1) ≤ s / (s + 1) . Мы можем привести в порядок все наши условия. (ТОЛЬКО) Окончательное руководство по неравенствам GMAT
Вычитание 2 с обеих сторон 2 <6 (знак неравенства верен)
Умножение обоих сторон на +2 8 <16 (верен знак неравенства)
Деление обеих сторон на +2 2 <4 (верен знак неравенства) Калькулятор абсолютных значений | Неравенства, функции, решение уравнений ...
Что такое «абсолютное значение»: определение
| x | , где x будет обозначать любое число, которое нам нужно абсолютное значение. Например, абсолютное значение 3 записывается как | 3 | , а абсолютное значение -5,3 будет записано как | -5,3 | . | -3x + 3 | , где x - неизвестное значение. Полезно ли абсолютное значение?
[конец раздела] x = 5 и движется к x = 2 , как далеко он проехал? Вы можете просто сказать, что это 5 - 2 = 3 , но это технически неверный , поскольку расстояние на самом деле является абсолютной величиной разницы между начальным финишем и конечной точкой. В этом случае уравнение для решения этой задачи будет выглядеть следующим образом: | 2 - 5 | = | -3 | = 3 , которые дают нам тот же результат, что и раньше, но гораздо больше технических возможностей для демонстрации;) | f (x) | всегда положителен независимо от значения f (x) . Функции абсолютных значений и графики абсолютных значений
f (x) = | x | . Прежде чем мы подумаем о его форме, мы уже знаем, что эта функция абсолютного значения может иметь значения только выше и на оси x, то есть f (x) имеет только положительные и нулевые значения.
Копнув немного глубже, мы можем начать с положительной части, x> 0 . В данном случае f (x) = x , поэтому мы получаем прямую под углом 45º, которая делит пополам первый квадрант декартовой оси.Часть для отрицательного x, x <0 , может быть переписана как f (x) = -x , что дает линию, симметричную положительной части x, с осью y, действующей как ось симметрии. Эта часть делит второй квадрант пополам и образует угол 135º с осью x. Для полноты картины добавим, что f (0) = | 0 | = 0 , завершая симметрию.
Все становится немного сложнее, когда мы получаем более сложное выражение внутри абсолютного значения.Пока абсолютное значение окружает все выражение, мы можем использовать небольшой трюк . Если мы посмотрим на f (x) = | x | как модификация f (x) = x , мы видим, что разница в том, что отрицательная часть f (x) = x была изменена, чтобы иметь положительные значения. Точнее, то, что мы сделали, - это перевернуло его вокруг оси x, так что теперь это зеркальное отражение оригинальной детали на .
Этот же прием можно использовать для любой функции абсолютного значения.Просто нарисуйте функцию, игнорируя абсолютное значение, и затем переверните любую часть ниже y = 0 , которую вы можете рассчитать с помощью нашего калькулятора угла наклона. Результатом является идеальное представление графика абсолютных значений без каких-либо проблем. Взгляните на примеры на рисунках, включенных в этот раздел, включая график синусоид и график квадратного корня.
В качестве примечания для заинтересованных, любой график абсолютных значений является таким же непрерывным, как и неабсолютный график , но также будет иметь резкую, недифференцируемую точку везде, где значения начали меняться с положительных на отрицательные.Например, в функции f (x) = | x | мы получаем острие при f (0) = 0 .
Для более сложного выражения, в котором функция абсолютного значения находится внутри выражения (например, в f (x) = 2x + 3 / | x | ), все усложняется и требует более тщательного математического анализа . Это не невозможно сделать, и это больше связано с трудом, чем со сложностью. Однако это выходит за рамки данного калькулятора, поэтому мы остановимся на этом и быстро перейдем к уравнениям и неравенствам для абсолютных значений.
Уравнения абсолютных значений и неравенства абсолютных значений
Абсолютные значения обычно находят при решении уравнений абсолютных значений (или любых других уравнений). Уравнения, которые имеют абсолютные значения, известны как уравнения абсолютных значений ; если вместо знака равенства = у нас есть знак больше (> ), меньше ( <), больше или равно ( ≥ ), меньше или равно ( ≤ ), то мы имеем то, что называется неравенством абсолютных значений .
Способ работы с абсолютными значениями в обоих случаях аналогичен. При решении уравнений абсолютного значения вы хотите оперировать и максимально упростить вещи, избегая при этом касаться части абсолютного значения до тех пор, пока вам не придется абсолютно (каламбур).
Как только мы достигаем точки, в которой нам нужно иметь дело с абсолютным значением, мы изолируем его на одной стороне знака и разлагаем на возможные варианты: положительные и отрицательные. Этот процесс одинаков как для уравнений абсолютного значения, так и для неравенств абсолютного значения.
Давайте посмотрим, как это будет выглядеть на очень простом примере. Представьте, что вам удалось все упростить до такой степени, что у вас есть следующее уравнение:
4x + 1 = | 2x - 3 |
Мы знаем, что деталь | 2x - 3 | всегда будет положительным, но 2x - 3 может быть положительным ИЛИ отрицательным. Если положительный, уравнение будет:
4x + 1 = 2x - 3
, пока он отрицательный, абсолютное значение изменит знак, дав нам:
4x + 1 = - (2x - 3) => 4x + 1 = 3 - 2x
Оба уравнения представляют собой потенциальные решения исходного уравнения и дают:
а) Положительный: x = -2
б) Отрицательный: x = 1/3
Если мы внимательно посмотрим, то увидим, что мы не закончили , так как x = -2 означает, что 2x - 3 = -4-3 = -7 .Поскольку результатом является отрицательное число, это нарушает сделанное нами предположение, что | 2x - 3 | > 0 , поэтому мы знаем, что x = -2 не может быть решением . Это подтвердится, если мы проверим это:
4 * (- 2) + 1 = | 2 * (- 2) - 3 | => -8 + 1 = | -4 - 3 | => -7 = +7
Это математический абсурд.
Тот же самый процесс разделения уравнения абсолютного значения или неравенства абсолютного значения с последующей проверкой того, какие решения имеют смысл, очень полезен и стандартен.Вы можете использовать его при решении любого уравнения абсолютного значения (даже если это квадратное уравнение), и ваш успех практически гарантирован.
Мы использовали здесь очень простой пример, чтобы быть кратким, но те же методы можно использовать для решения очень сложных неравенств или поиска важных точек в функциях абсолютного значения, чтобы вы могли нарисовать графики абсолютных значений, которые мы упоминали ранее.
Как пользоваться калькулятором абсолютных значений
Использовать калькулятор абсолютных значений настолько просто, насколько это возможно.Как математическая операция, абсолютное значение очень легко найти само по себе, но мы попытаемся рассказать вам пару советов, которые могут вам помочь.
Прежде всего, калькулятор абсолютного значения работает, превращая любое введенное вами число в положительное число, которое на самом деле является абсолютным значением. Таким образом, вы должны ввести число в поле ввода калькулятора, и в результате вы получите его абсолютное значение.
Вы можете использовать этот инструмент для проверки определенных точек вашего графика абсолютных значений и уравнения, чтобы убедиться, что ваш эскиз, рисунок или решение верны.
Это очень простой калькулятор, и именно поэтому мы предоставили всю информацию выше : превратить этот простой калькулятор абсолютных значений в инструмент для получения дополнительных знаний, который обязательно будет полезен в вашей жизни (или, по крайней мере, в вашей жизни). математический класс).
Функция модуля | Исчисление | Графики | Примеры | Решения
Функция модуля дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения.
В этом мини-уроке мы узнаем об определении модульной функции, вычислении модуля для чисел, переменных и многочленов, а также о решенных примерах и вопросах о модульной функции.
Попробуйте калькулятор функции mod, чтобы найти модуль числа!
План урока
Что такое функция модуля?
Модуль функции, который также называется абсолютным значением функции, дает величину и абсолютное значение числа независимо от того, положительное или отрицательное число. Он всегда дает неотрицательное значение любого числа или переменной.
Представляется как
\ (\ begin {align} y = | x | \ end {align} \)
или
\ (\ begin {align} f (x) = | x | \ end {align} \)
, где \ (\ begin {align} f: R \ rightarrow R \ end {align} \) и \ (\ begin {align} x \ in R \ end {align} \)
\ (\ begin {align} | x | \ end {align} \) - модуль \ (\ begin {align} x \ end {align} \), где \ (\ begin {align} x \ end { align} \) - неотрицательное число.
Если \ (\ begin {align} x \ end {align} \) положительное значение, то \ (\ begin {align} f (x) \ end {align} \) будет иметь то же значение \ (\ begin {align } х \ конец {выравнивание} \). Если \ (\ begin {align} x \ end {align} \) отрицательное значение, то \ (\ begin {align} f (x) \ end {align} \) будет величиной \ (\ begin {align} х \ конец {выравнивание} \).
Подводя итог вышеприведенным строкам,
Это означает, что если значение \ (\ begin {align} x \ end {align} \) больше или равно 0, то функция модуля принимает фактическое значение, но если \ (\ begin {align} x \ end {align} \) меньше 0, тогда функция берет минус фактического значения 'x'.
Как рассчитать функцию модуля?
Шаги по вычислению функций модуля приведены ниже.
, если \ (\ begin {align} x = -3 \ end {align} \), то
\ (\ begin {align} y = f (x) = f (-3) = - (-3) = 3 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) меньше 0
, если \ (\ begin {align} x = 4 \ end {align} \), то
\ (\ begin {align} y = f (x) = f (4) = 4 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) больше 0
, если \ (\ begin {align} x = 0 \ end {align} \), то
\ (\ begin {align} y = f (x) = f (0) = 0 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) равно 0
Подводя итог, можно сказать, что модуль отрицательного числа и положительного числа - это одно и то же число.
График функции модуля
Теперь давайте посмотрим, как построить график для функции модуля и найти ее область и диапазон.
Рассмотрим x как переменную, принимающую значения от -5 до 5
| x | -5 | -4 | -3 | -2 | –1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y = f (x) | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | 5 |
При вычислении модуля упругости для положительных значений 'x' линия на графике имеет вид 'y = x'
, а для отрицательных значений «x» линия на графике имеет вид «y = -x».
Обратите внимание, что мы можем применить модуль к любому действительному числу. Диапазон функции модуля - это набор неотрицательных целочисленных переменных, который обозначается как \ (\ begin {align} (0, \ infty) \ end {align} \), а область определения функции модуля - R (где R относится к набору всех положительных действительных чисел)
Поскольку мы обсуждали модуль - это неотрицательное значение, и в соответствии с этой интерпретацией мы также можем сказать, что модуль - это квадратный корень из квадрата переменной. 2} \ end {align} \)
Есть несколько других неотрицательных выражений, которые перечислены ниже.{2n} \ end {align} \) где \ (\ begin {align} n \ in Z \ end {align} \)
\ (\ begin {align} y = 1 - sin \: x; y = 1 - cos \: x \: as \: sin \: x ≤1 \: и \: cos \: x ≤1 \ end { align} \)
Функция Signum
Signum функция определяется как математическая функция, которая дает знак действительного числа. Сигнум-функция выражается следующим образом.
График сигнум-функции выглядит следующим образом.
Модуль комплексного числа
Комплексное число - это число, имеющее форму \ (\ begin {align} a + bi \ end {align} \), где 'a' и 'b' - действительные числа, а 'i' - мнимая единица.2} \ end {align} \)
Важные свойства функции модуля
Недвижимость 1:
Модуль и равенство
Функция модуля всегда возвращает неотрицательное число для всех действительных значений «x». Также некорректно приравнивать функцию модуля к отрицательному числу.
\ (\ begin {align} | f (x) | = a; \: a> 0⇒f (x) = ± a \\ | f (x) | = a; \: a = 0⇒f (x ) = 0 \\ | f (x) | = a; a <0 \ end {align} \)
Недвижимость 2:
Модуль и неравенство
Случай 1: (Если a> 0)
Неравенство отрицательного числа
\ (\ begin {align} | f (x) | Неравенство для положительного числа \ (\ begin {align} | f (x) |> a; a> 0 \ Rightarrow -a Случай 2: (Если <0) \ (\ begin {align} | f (x) | \ (\ begin {align} | f (x) |> a; a <0 \ Rightarrow \ end {align} \) - это действительно для всех реальных значений f (x). Недвижимость 3: Если x, y - действительные переменные, то \ (\ begin {align} | -x | = | x | \ end {align} \) \ (\ begin {align} | x − y | = 0⇔x = y \ end {align} \) \ (\ begin {align} | x + y | ≤ | x | + | y | \ end {align} \) \ (\ begin {align} | x − y | ≥ || x | - | y || \ end {align} \) \ (\ begin {align} | xy | = | x | \ times | y | \ end {align} \) \ (\ begin {align} | \ dfrac {x} {y} | = \ dfrac {| x |} {| y |}; | y | \ neq 0 \ end {align} \) Теперь давайте рассмотрим некоторые решенные вопросы о модульных функциях, чтобы лучше понять их.
Найдите модуль x для
Решение
а) х = -4
\ (\ begin {align} | x | = | -4 | = - (-4) = 4 \ end {align} \)
б) х = 6
\ (\ begin {align} | x | = | 6 | = 6 \ end {align} \)
Для x = -4, \ (\ begin {align} | -4 | = 4 \ end {align} \) и для x = 6 \ (\ begin {align} | 6 | = 6 \ end {align} \) |
Решить \ (\ begin {align} | x + 3 | = 8 \ end {align} \)
Решение
Сформируем два уравнения следующим образом.
Корпус 1:
Значение функции модуля отрицательное.
\ (\ begin {align} | x + 3 | = 8 \ end {align} \)
\ (\ begin {align} - | x + 3 | = 8 \ end {align} \)
\ (\ begin {align} x + 3 = -8 \ end {align} \)
\ (\ begin {align} x = -8 - 3 \ end {align} \)
\ (\ begin {align} x = -11 \ end {align} \)
Дело 2:
Значение функции модуля положительное.
\ (\ begin {align} | x + 3 | = 8 \ end {align} \)
\ (\ begin {align} x + 3 = 8 \ end {align} \)
\ (\ begin {align} x = 8 - 3 \ end {align} \)
\ (\ begin {align} x = 5 \ end {align} \)
Следовательно, возможные значения x в модульной функции:
\ (\ begin {align} x = 5, -11 \ end {align} \)
| x может иметь значения \ (\ begin {align} x = 5, -11 \ end {align} \) |
Нарисуйте график для \ (\ begin {align} y = | x +2 | \ end {align} \)
Решение
Согласно определению функции модуля, мы имеем,
\ (\ begin {align} y = | x + 2 | = x + 2, если \: x \ geq 1 \\ - 2 - x, если \: x <1 \ end {align} \)
Изобразим таблицу с положительными и отрицательными значениями 'x'.
| x | y = | x + 2 | |
| -7 | | -7 + 2 | = | -5 | = 5 |
| -6 | | -6 + 2 | = | -4 | = 4 |
| -5 | | -5 + 2 | = | -3 | = 3 |
| -4 | | -4 + 2 | = | -2 | = 2 |
| -3 | | -3 + 2 | = | -1 | = 1 |
| -2 | | -2 + 2 | = | 0 | = 0 |
| -1 | | -1 + 2 | = | 1 | = 1 |
| 0 | | 0 + 2 | = | 2 | = 2 |
| 1 | | 1 + 2 | = | 3 | = 3 |
| 2 | | 2 + 2 | = | 4 | = 4 |
| 3 | | 3 + 2 | = | 5 | = 5 |
| 4 | | 4 + 2 | = | 6 | = 6 |
Строя график с различными значениями \ (\ begin {align} x \ end {align} \) и \ (\ begin {align} -x \ end {align} \), мы получаем график для модуля функция, как показано ниже,
| Это график для функции модуля x + 2 |
Решить \ (\ begin {align} | 2x - 4 | = 5 - x \ end {align} \)
Решение
Согласно определению функции модуля имеем
В зависимости от функции модуля могут быть две возможности.
Корпус 1:
\ (\ begin {align} - | 2x - 4 | = 5 - x \ end {align} \)
\ (\ begin {align} 2x - 4 = - (5 - x) \ end {align} \)
\ (\ begin {align} 2x - 4 = -5 + x \ end {align} \)
\ (\ begin {align} 2x - x & = -5 + 4 \\ x & = -1 \ end {align} \)
Корпус 2:
\ (\ begin {align} | 2x - 4 | = 5 - x \\ 2x - 4 = 5 - x \\ 2x + x = 5 + 4 \\ 3x = 9 \ x = 3 \ end {align} \)
| \ (\ begin {align} x = -1 \: and \: x = 3 \ end {align} \) |
- Модуль неотрицательного числа и отрицательного числа положительный.| -5 | 5 и | 5 | тоже 5.
- Для решения уравнений модуля типа | x-2 | = 5, составьте два уравнения типа x-2 = -5 & и x - 2 = 5, чтобы найти решение.
Интерактивные вопросы
Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Урок был посвящен увлекательной концепции модульной функции, ее области и диапазона.Надеюсь, вам понравилось их изучать. Просматривая решенные примеры и решая неэффективные вопросы, вы получите больше знаний по предмету. Вы также можете попробовать калькулятор функции модуля, чтобы проверить модуль числа.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы по модульной функции
1. Что такое уравнение модуля?
Уравнение, которое дает модуль или величину данного числа, называется уравнением модуля. Обозначается как y = | x |.
2. Что означает модуль?
Модуль означает определение положительного или отрицательного числа.
3. Как вы решаете проблемы модуля?
Применение модуля к неотрицательному и отрицательному числу всегда приводит к одному и тому же числу.
4. Как нарисовать модульную функцию?
Взяв отрицательные значения, такие как (-1, -2, -3), и положительные значения, такие как (1,2,3), в соответствии с заданным уравнением модуля, мы можем нарисовать функцию модуля.
5. Почему мы используем Mod?
Функция модуля используется для определения величины положительного или отрицательного числа.
6. Всегда ли модуль упругости положителен?
Модуль положительного числа положителен.
