Как найти диагональ трапеции если известны основания и диагональ: Диагональ трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Все формулы диагоналей трапеции

Найти длину диагонали трапеции

зная все четыре стороны

или две стороны и угол

или высоту, сторону и угол

или площадь, другую диагональ и угол

и еще много других формул.

1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

d₁ , d₂— диагонали трапеции

Формулы диагоналей трапеции по теореме косинусов:

Формулы диагоналей трапеции через четыре стороны:

2. Формула длины диагоналей трапеции через высоту

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

d₁ , d₂— диагонали трапеции

Формулы диагоналей трапеции через высоту:

3. Формула длины диагонали трапеции через другую диагональ

a — нижнее основание

b — верхнее основание

α, β — углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d₁ , d₂— диагонали трапеции

Формулы диагоналей трапеции :

Справедливо для данного случая :

4. Формулы длины диагонали трапеции через сумму квадратов диагоналей

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

d₁ , d₂— диагонали трапеции

Формула суммы квадратов диагоналей :

Формулы диагоналей трапеции :

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Отношение диагоналей трапеции в точке пересечения.

Запоминаем и применяем свойства трапеции. Свойства трапеции, вписанной в окружность

Трапеция
— это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.

Также встречаются такие названия, как равнобокая
или равнобочная
.

— это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

a, b
— основания трапеции
(a
параллельно b
),

m, n
— боковые стороны
трапеции,

d 1 , d 2
— диагонали
трапеции,

h
— высота
трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),

MN
— средняя линия
(отрезок, соединяющий середины боковых сторон).

Площадь трапеции

Через полусумму оснований a, b
и высоту h
: S = \frac{a + b}{2}\cdot h
Через среднюю линию MN
и высоту h
: S = MN\cdot h
Через диагонали d 1 , d 2
и угол (\sin \varphi
) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}

Свойства трапеции

Средняя линия трапеции

Средняя линия
параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:

MN || a, MN || b, MN = \frac{a + b}{2}

Сумма углов трапеции

Сумма углов трапеции
, прилежащих к каждой боковой стороне, равна 180^{\circ}
:

\alpha + \beta = 180^{\circ}

\gamma + \delta =180^{\circ}

Равновеликие треугольники трапеции

Равновеликими
, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами.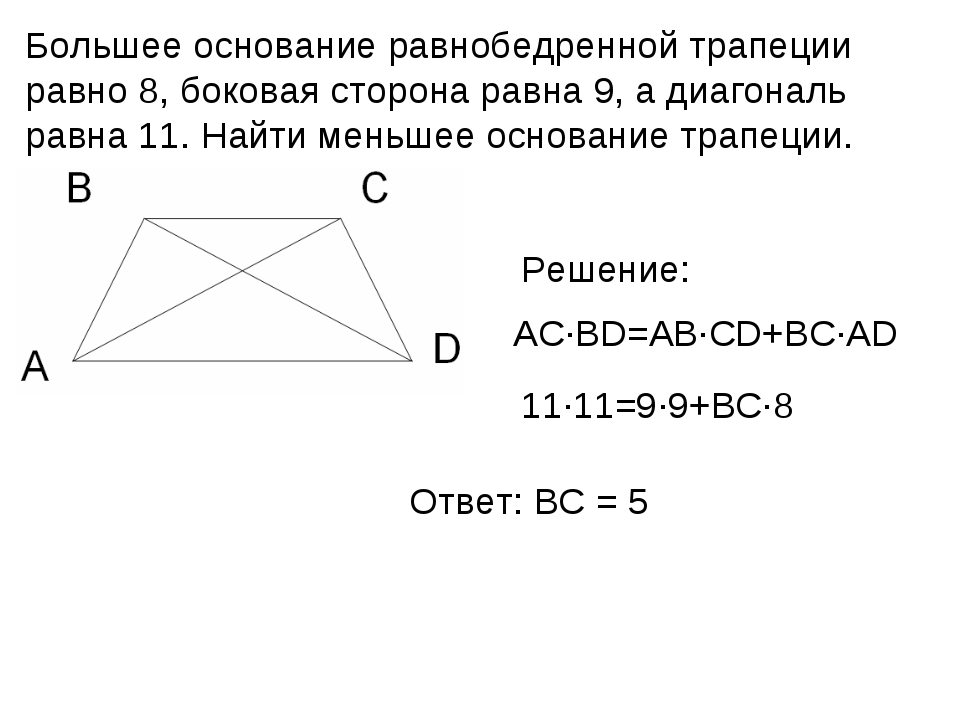 {2}
.

Отношение длин отрезков и оснований

Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:

\frac{OX}{OY} = \frac{BC}{AD}

Это будет являться справедливым и для высоты с самими диагоналями.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.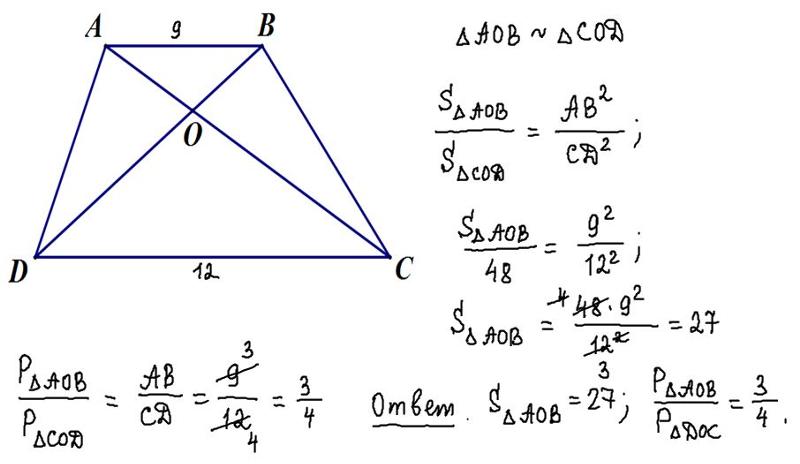

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.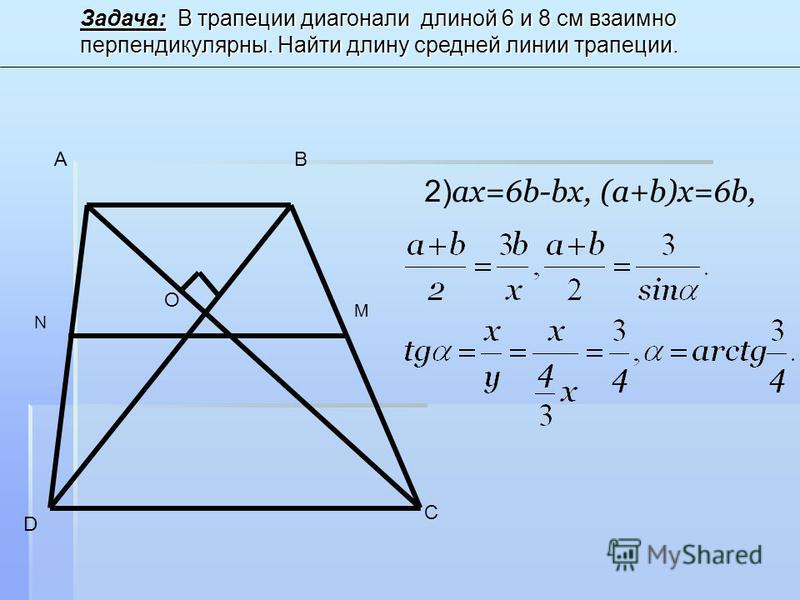

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
.
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 .
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.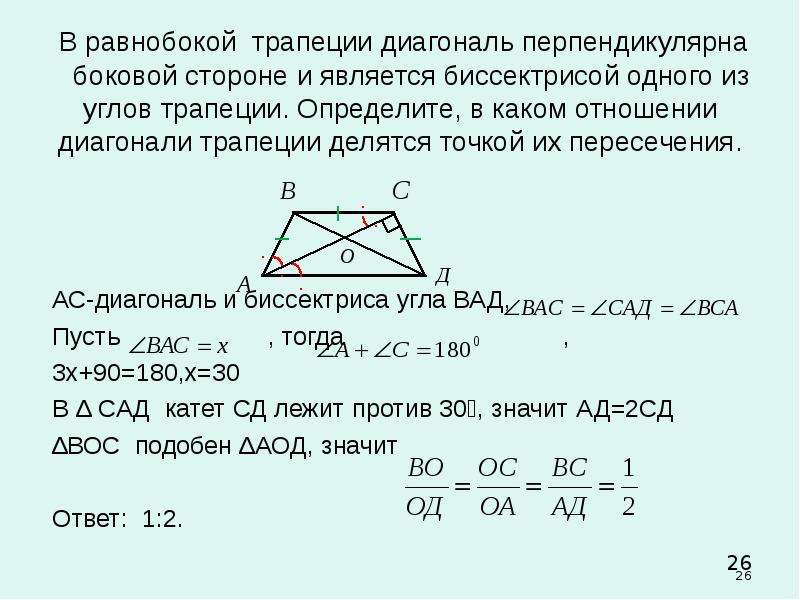

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

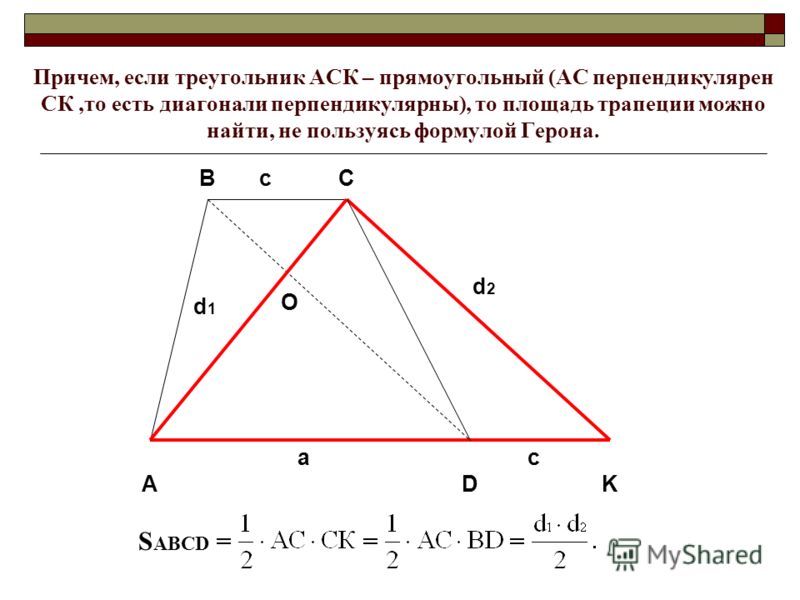
Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие.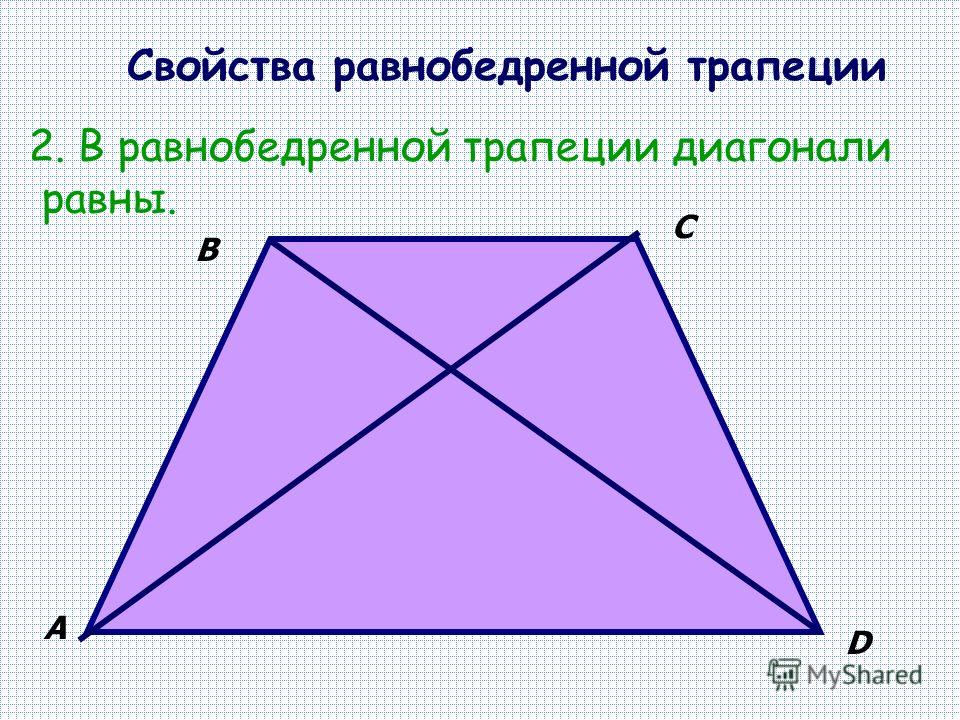 Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.

Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
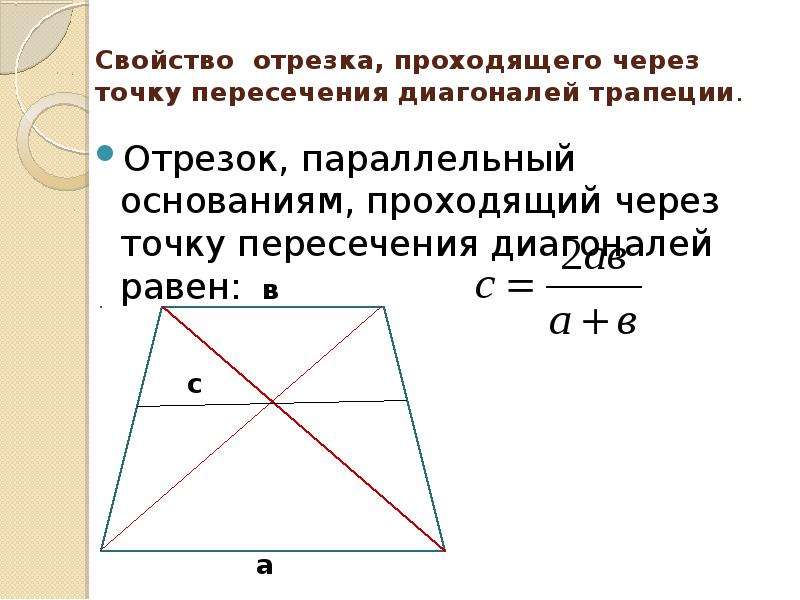
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

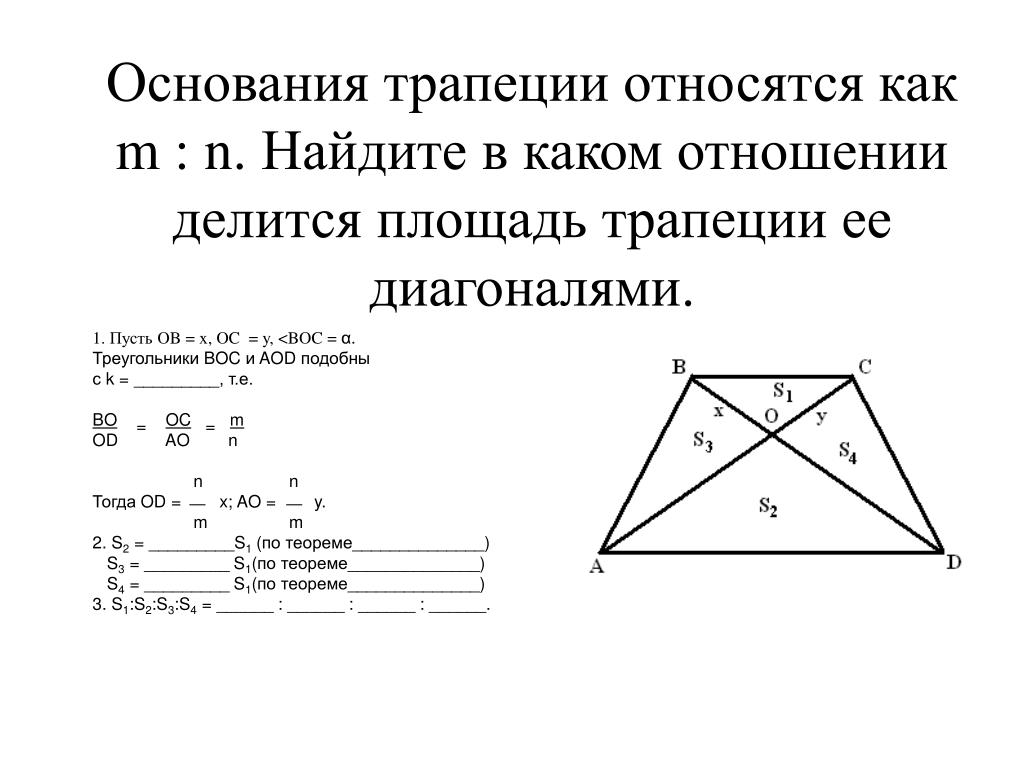
Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.

Задача
.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение
.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 — (8 + b) 2 + (24 — b) 2 = 169

-(64 + 16b + b) 2 + (24 — b) 2 = -256

-64 — 16b — b 2 + 576 — 48b + b 2 = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

, где a b — основания трапеции, h — высота трапеции

S = (24 + 8) * 5 / 2 = 80 см 2

Ответ
: площадь трапеции равна 80 см 2 .

Как найти большую диагональ трапеции

Найти длину диагонали трапеции

зная все четыре стороны

или две стороны и угол

или высоту, сторону и угол

или площадь, другую диагональ и угол

и еще много других формул.

1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

d ₁ , d ₂ — диагонали трапеции

Формулы диагоналей трапеции по теореме косинусов:

Формулы диагоналей трапеции через четыре стороны :

2. Формула длины диагоналей трапеции через высоту

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

h — высота трапеции

d ₁ , d ₂ — диагонали трапеции

Формулы диагоналей трапеции через высоту:

3. Формула длины диагонали трапеции через другую диагональ

a — нижнее основание

b — верхнее основание

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d ₁ , d ₂ — диагонали трапеции

Формулы диагоналей трапеции :

Справедливо для данного случая :

4. Формулы длины диагонали трапеции через сумму квадратов диагоналей

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

d ₁ , d ₂ — диагонали трапеции

Свойства диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Свойства треугольников, образованных диагоналями трапеции

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Свойства трапеции, достроенной до треугольника

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Свойства отрезка, параллельного основаниям трапеции

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Формулы нахождения диагоналей трапеции через высоту

Примечание.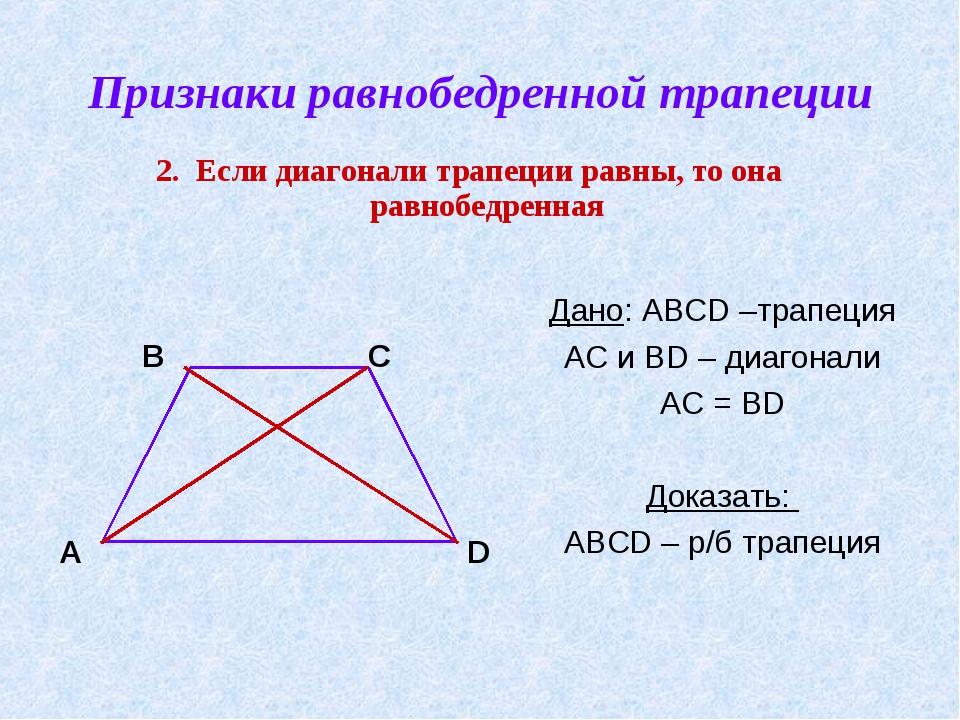 В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.

Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16

Задача .
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.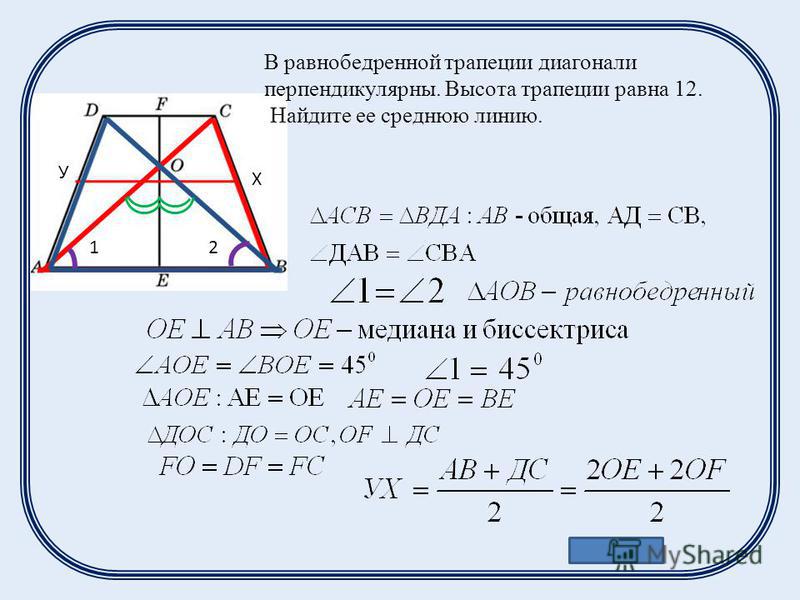

Решение .
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b ( не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b

h 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12

Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2

Ответ: площадь трапеции равна 80 см 2 .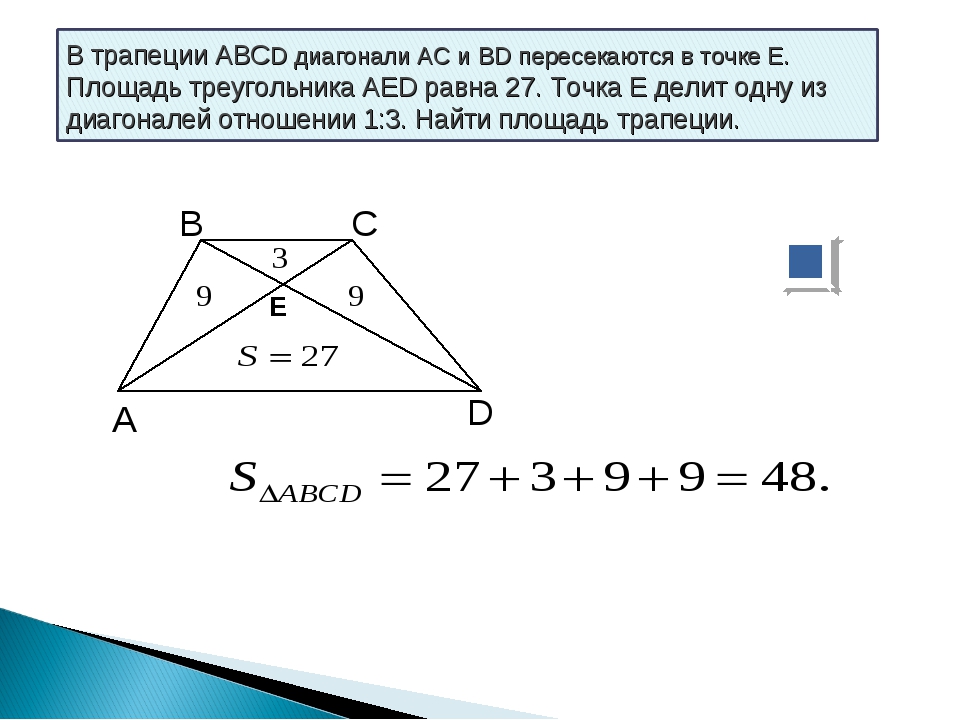

Трапеция представляет геометрическую фигуру с двумя параллельными сторонами, которые являются меньшим и большим основанием трапеции. Две другие стороны трапеции являются ее боковыми сторонами. У трапеции все стороны могут быть разными. Трапеция, у которой боковые стороны равны, называется равнобедренной. Диагонали в равнобедренной трапеции тоже равны. Если известны величины нижнего (a) и верхнего основания трапеции (b), а также ее одинаковые боковые стороны с, то диагональ (d) трапеции находим, как корень квадратный из суммы квадрата боковой стороны и произведения двух оснований по формуле:

d = √c 2 + ab

В остальных случаях для определения диагоналей трапеции через ее стороны следует воспользоваться формулами:

где d₁ и d₂ — длина диагонали, а, b, с, d — длины сторон трапеции.

Как найти диагональ трапеции?

Прежде, чем разбираться, как найти диагональ трапеции, вспомним, что такое трапеция. В планиметрии трапецией называют четырехугольник, у которого две противоположные стороны параллельны друг другу. Эти параллельные стороны называют основаниями трапеции, а остальные — боковыми сторонами. Боковые стороны могут быть одинаковыми, тогда мы имеем дело с равнобедренной трапецией.

Далее подробно разберем порядок нахождения длины диагоналей для общего случая — неравнобедренной трапеции. При этом будем исходить из того, что исходными данными являются длины всех четырех сторон трапеции, углы у основания неизвестны.

Расчет диагонали трапеции

В изображенной на рисунке трапеции ABCD имеются две диагонали AC и BD. Порядок нахождения их длины одинаков, поэтому рассмотрим все на примере нахождения диагонали BD, противолежащей ˂BAD.

Диагональ BD одновременно является стороной треугольника ABD и может быть рассчитана по теореме косинусов с помощью формулы:

BD = √(AB²+AD²-2AB^.AD^.cos ˂BAD)

В этой формуле нам известны все величины, кроме косинуса ˂BAD. Чтобы вычислить его, нам необходимо будет выполнить небольшое преобразование рисунка. «Вырежем» из исходной трапеции прямоугольник BNMC. В результате получим треугольник ABD’, в котором сторона BD’ будет равна стороне трапеции CD.

˂BAD’ в треугольнике равен ˂BAD в трапеции, так как никаких преобразований с треугольником ABN мы не выполняли. Итак, в этом треугольнике ABD’ сторона AB нам известна, сторона BD’ = CD, а сторона AD’ = AD – NM = AD – BC.

Получается, что по теореме косинусов cos ˂BAD = cos ˂BAD’ = (AB² + AD’² – BD’²)/2AB^.AD’ = (AB² +(AD – BC)² – CD²)/2AB^.(AD – BC)

Подставив теперь полученное выражение в найденную ранее формулу, получим:

BD = √(AB²+AD²-2AB^.AD^.cos ˂BAD) = √(AB²+AD²-2AB^.AD^.(AB² +(AD – BC)² – CD²)/2AB^.(AD – BC)) = √(AB² + AD² – AD^.(AB² +(AD – BC)² – CD²)/(AD – BC)) = √(AB² + AD² – AD^.(AD – BC)²/(AD – BC) – AD^.(AB² – CD²)/(AD – BC)) = √(AB² + AD² – AD² + AD^.BC – AD^.(AB² – CD²)/(AD – BC)) = √(AB² + AD^.BC – AD^.(AB² – CD²)/(AD – BC))

BD = √(AB² + AD^.BC – AD^.(AB² – CD²)/(AD – BC))

Полученная формула диагонали трапеции справедлива для любых значений длин сторон исходного четырехугольника.

Для второй диагонали формула соответственно примет вид:

AC = √(CD² + AD^.BC – AD^.(CD² – AB²)/(AD – BC))

Диагональ равнобедренной трапеции

Если вас интересует, как найти диагональ равнобедренной трапеции, получившуюся формулу можно значительно упростить. Ведь в равнобедренной трапеции AB = CD, следовательно AB² – CD² = 0 и формула длины диагонали приводится к виду:

BD = √(AB² + AD^.BC)

Диагонали равнобедренной трапеции равны друг другу, поэтому вторая диагональ находится по той же формуле.

В том случае, если исходными данными являются длины оснований трапеции, одна из боковых сторон и углы при основании, то задача нахождения диагонали трапеции сводится к расчету стороны треугольника по теореме косинусов.

614 диагонали прямоугольной трапеции. Диагонали трапеции. Свойства отрезка, параллельного основаниям трапеции

Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.

1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.

Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.

Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.

Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то

что в общем виде можно записать как

где h — высота трапеции, a и b — ее основания.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.

Так как средняя линия трапеции m равна полусумме оснований, то

3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).

Так как площадь трапеции находится по формуле

а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:

4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.

Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Что из этого следует?

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Формулы нахождения диагоналей трапеции через высоту

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Ответ
: площадь трапеции равна 80 см 2 .

Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать

Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)

Похожие задачи:

1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.

2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.

3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.

1. Найдите сторону квадрата если его диагональ составляет 10 см

2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?

3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?

4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.

1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О

а) Сравните площади треугольников ABD и ACD

б) Сравните площади треугольников ABO и CDO

в) Докажите что OA*OB=OC*OD

2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.

3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.

Диагонали трапеции. Диагонали трапеции Свойства отрезка, параллельного основаниям трапеции

1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.

Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.

Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.

что в общем виде можно записать как

где h — высота трапеции, a и b — ее основания.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.

Так как средняя линия трапеции m равна полусумме оснований, то

Так как площадь трапеции находится по формуле

Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Что из этого следует?

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Формулы нахождения диагоналей трапеции через высоту

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Ответ
: площадь трапеции равна 80 см 2 .

Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)

Похожие задачи:

1. Найдите сторону квадрата если его диагональ составляет 10 см

4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.

1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О

а) Сравните площади треугольников ABD и ACD

б) Сравните площади треугольников ABO и CDO

в) Докажите что OA*OB=OC*OD

Если диагонали трапеции перпендикулярны. Формулы нахождения диагоналей трапеции через высоту

Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.

Общие сведения

Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.

Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…

Виды трапеции

Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.

1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.

2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.

Главные принципы методики изучения свойств трапеции

К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.

Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.

Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.

Элементы и свойства равнобедренной трапеции

Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.

А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.

Решение

Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.

Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.

Свойство диагоналей равнобедренной трапеции

Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:

Высота фигуры будет равна сумме оснований, деленной на два;

Ее высота и средняя линия равны;

Центр окружности является точкой, в которой пересекаются ;

Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;

Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;

Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.

Подобные трапеции

Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.

Доказательство теоремы

Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.

Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.

Свойства подобия

Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.

Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.

Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.

Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).

Выводы подобия

Таким образом, мы доказали, что:

1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).

2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).

3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.

4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.

Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.

Отрезок, соединяющий середины диагоналей трапеции

Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.

Центр тяжести

Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.

Вписанные и описанные трапеции

Давайте перечислим особенности таких фигур:

1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.

2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.

Следствия вписанной окружности:

1. Высота описанной трапеции всегда равна двум радиусам.

2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.

Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.

Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.

Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).

Все формулы средней линии трапеции

Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):

1. Через основания: М = (А+Б)/2.

2. Через высоту, основание и углы:

М = А-Н*(ctgα+ctgβ)/2;

М = Б+Н*(ctgα+ctgβ)/2.

3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:

М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.\circ\)
.

2) Т.к. $AD\parallel BC$
и $BD$
– секущая, то $\angle DBC=\angle
BDA$
как накрест лежащие.
Также $\angle BOC=\angle AOD$
как вертикальные.
Следовательно, по двум углам $\triangle BOC \sim \triangle AOD$
.

Докажем, что $S_{\triangle AOB}=S_{\triangle COD}$
. Пусть $h$
– высота трапеции. Тогда $S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}$
. Тогда: \

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*

1) Докажем параллельность.

Проведем через точку $M$
прямую $MN»\parallel AD$
($N»\in CD$
). Тогда по теореме Фалеса (т.к. $MN»\parallel AD\parallel BC, AM=MB$
) точка $N»$
— середина отрезка $CD$
. Значит, точки $N$
и $N»$
совпадут.

2) Докажем формулу.

Проведем $BB»\perp AD, CC»\perp AD$
. Пусть $BB»\cap MN=M», CC»\cap
MN=N»$
.

Тогда по теореме Фалеса $M»$
и $N»$
— середины отрезков $BB»$
и $CC»$
соответственно. Значит, $MM»$
– средняя линия $\triangle
ABB»$
, $NN»$
— средняя линия $\triangle DCC»$
. Поэтому: \

Т.к. $MN\parallel AD\parallel BC$
и $BB», CC»\perp AD$
, то $B»M»N»C»$
и $BM»N»C$
– прямоугольники. По теореме Фалеса из $MN\parallel AD$
и $AM=MB$
следует, что $B»M»=M»B$
. Значит, $B»M»N»C»$
и $BM»N»C$
– равные прямоугольники, следовательно, $M»N»=B»C»=BC$
.

Таким образом:

\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*

С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем, что точки $P$
, $N$
и $M$
лежат на одной прямой.

Проведем прямую $PN$
($P$
– точка пересечения продолжений боковых сторон, $N$
– середина $BC$
). Пусть она пересечет сторону $AD$
в точке $M$
. Докажем, что $M$
– середина $AD$
.

Рассмотрим $\triangle BPN$
и $\triangle APM$
. Они подобны по двум углам ($\angle APM$
– общий, $\angle PAM=\angle PBN$
как соответственные при $AD\parallel BC$
и $AB$
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим $\triangle CPN$
и $\triangle DPM$
. Они подобны по двум углам ($\angle DPM$
– общий, $\angle PDM=\angle PCN$
как соответственные при $AD\parallel BC$
и $CD$
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда $\dfrac{BN}{AM}=\dfrac{CN}{DM}$
. Но $BN=NC$
, следовательно, $AM=DM$
.

2) Докажем, что точки $N, O, M$
лежат на одной прямой.

Пусть $N$
– середина $BC$
, $O$
– точка пересечения диагоналей. Проведем прямую $NO$
, она пересечет сторону $AD$
в точке $M$
. Докажем, что $M$
– середина $AD$
.

$\triangle BNO\sim \triangle DMO$
по двум углам ($\angle OBN=\angle
ODM$
как накрест лежащие при $BC\parallel AD$
и $BD$
секущей; $\angle BON=\angle DOM$
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично $\triangle CON\sim \triangle AOM$
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда $\dfrac{BN}{MD}=\dfrac{CN}{MA}$
. Но $BN=CN$
, следовательно, $AM=MD$
.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию $ABCD$
.

Из вершин $B$
и $C$
опустим на сторону $AD$
перпендикуляры $BM$
и $CN$
соответственно. Так как $BM\perp AD$
и $CN\perp AD$
, то $BM\parallel CN$
; $AD\parallel BC$
, тогда $MBCN$
– параллелограмм, следовательно, $BM = CN$
.

Рассмотрим прямоугольные треугольники $ABM$
и $CDN$
. Так как у них равны гипотенузы и катет $BM$
равен катету $CN$
, то эти треугольники равны, следовательно, $\angle DAB = \angle CDA$
.

Т.к. $AB=CD, \angle A=\angle D, AD$
– общая, то по первому признаку . Следовательно, $AC=BD$
.

3) Т.к. $\triangle ABD=\triangle ACD$
, то $\angle BDA=\angle CAD$
. Следовательно, треугольник $\triangle AOD$
– равнобедренный. Аналогично доказывается, что и $\triangle BOC$
– равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию $ABCD$
, такую что $\angle A = \angle D$
.

Достроим трапецию до треугольника $AED$
как показано на рисунке. Так как $\angle 1 = \angle 2$
, то треугольник $AED$
равнобедренный и $AE
= ED$
. Углы $1$
и $3$
равны как соответственные при параллельных прямых $AD$
и $BC$
и секущей $AB$
. Аналогично равны углы $2$
и $4$
, но $\angle 1 = \angle 2$
, тогда $\angle 3 = \angle 1 = \angle 2 =
\angle 4$
, следовательно, треугольник $BEC$
тоже равнобедренный и $BE = EC$
.

В итоге $AB = AE — BE = DE — CE = CD$
, то есть $AB = CD$
, что и требовалось доказать.

2) Пусть $AC=BD$
. Т.к. $\triangle AOD\sim \triangle BOC$
, то обозначим их коэффициент подобия за $k$
. Тогда если $BO=x$
, то $OD=kx$
. Аналогично $CO=y \Rightarrow AO=ky$
.

Т.к. $AC=BD$
, то $x+kx=y+ky \Rightarrow x=y$
. Значит $\triangle AOD$
– равнобедренный и $\angle OAD=\angle ODA$
.

Таким образом, по первому признаку $\triangle ABD=\triangle ACD$
($AC=BD, \angle OAD=\angle ODA, AD$
– общая). Значит, $AB=CD$
, чтд.

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Что из этого следует?

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Формулы нахождения диагоналей трапеции через высоту

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Ответ
: площадь трапеции равна 80 см 2 .

Сбор и использование персональной информации

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Предыдущая статья: Особенности императорского покровительства и отношения с деятелями искусства

Следующая статья: История России в конце ХХ века – начале ХХI века

Как найти диагональ трапеции

Детали: Написал Администратор; Опубликовано: 15 июля 2019; Последнее обновление: 18 июля 2019

  1.  Диагонали трапеции, если известны стороны и углы при основании

, — базы

, — ножки

, — уголки у основания

, — диагонали

Найдите диагональ трапеции, используя закон косинусов ( ):

Найдите диагональ трапеции, если заданы все четыре стороны ( ):

  2.  Диагонали трапеции по высоте

, — базы

, — ножки

, — уголки у основания

, — диагонали

— высота

Найдите диагональ трапеции, используя высоту, углы у основания и сторон ( ):

  3.  Диагонали трапеции, если вам известна другая диагональ, угол между диагоналями и высотой, площадью или средним сегментом

, — базы

, — диагонали

, — углы между диагоналями

— высота

— средний сегмент

— площадь трапеции

Найдите диагональ трапеции, если задана другая диагональ, угол между диагоналями и высотой, площадью или средним сегментом.
( ):

* Верно в данном случае:

  4.  Диагонали трапеции по формуле суммы квадратов диагоналей

— нижнее основание

— основание верхнее

, — ножки

, — диагонали

Формула суммы квадратов диагоналей:

Найдите диагональ трапеции, используя формулу суммы квадратов диагоналей ( ):

Геометрия

— как определить площадь трапеции, если я знаю ее углы, длину более короткого основания и длину более длинной диагонали?

ОООПС.4а — диагональ трапеции. Не длинная база.

Хорошо: возьми 2:

Опустите перпендикуляр сверху вниз, чтобы разрезать трапецию на прямоугольник и прямоугольный треугольник. Прямоугольник будет иметь длину $ a $ и высоту $ h $. Прямоугольный треугольник будет иметь длину $ b $ и высоту $ h $, а длинная сторона трапеции будет равна $ a + b $.

Прямоугольный треугольник имеет угол 45 градусов, поэтому другой угол также равен 45 градусам, а треугольник равнобедренный.2 \ frac {5 \ sqrt {31} + 18} 4

долларов США

==== неправильный (но намного проще) ответ следует =====

Представьте, что вы вытянули сторону прямоугольного треугольника вверх. Представьте, что вы вытягиваете сторону под углом 45 градусов вверх и в сторону. Представьте, что эти две протяженные линии пересекаются.

В результате получится прямоугольный треугольник с углом 45 градусов. Новый угол, который вы только что создали, также должен составлять 45 градусов. Итак, это равнобедренный треугольник. Его база — 4а. Так что его высота тоже 4а.2/2 $.

====

Другой способ. Так, вероятно, хочет ваш учитель.

Площадь трапеции = 1/2 $ (s_1 + s_2) * h = 1/2 (4a + a) h = 5ah / 2 $. Но что такое $ h $? Хорошо опустите перпендикуляр для верхней стороны к нижней стороне, чтобы вы разрезали трапецию на прямоугольник и треугольник. Треугольник представляет собой прямоугольный треугольник с углом 45 градусов и стороной в 3 доллара.

Итак, другой угол составляет 45 градусов. Треугольник равнобедренный. Итак, другая сторона — 3 доллара США. Таким образом, высота составляет 3 доллара США.2/2 $.

Quia — Четырехугольники

2 обе пары углов основания совпадают; диагонали совпадают

трапеции

каждая из диагоналей делит пополам пару противоположных углов

9022

если вы разделите квадрат на четыре прямоугольных треугольника, нарисовав его две диагонали, мера каждого из углов в tr iangles, который не является прямым углом…

A	B
определение параллелограмма	четырехугольник с обеими парами противоположных сторон параллельными
пять свойств / теорем для параллелограммов	противоположные стороны диагонали параллелограммы параллелограммы	противоположные стороны диагонали параллельны друг другу, противоположные стороны совпадают, противоположные углы совпадают, последовательные углы являются дополнительными
определение прямоугольника	четырехугольник с четырьмя прямыми углами
теоремы о прямоугольнике	если параллелограмм является прямоугольником, то его диагонали совпадают; если диагонали параллелограмма совпадают, то паралелограмм представляет собой прямоугольник
, пять свойств прямоугольника	противоположные стороны совпадают и параллельны; противоположные углы совпадают; последовательные углы являются дополнительными; диагонали совпадают и делят друг друга пополам; все четыре угла являются прямыми углами
определение ромба	четырехугольник с четырьмя равными сторонами
ромб theroems	диагонали ромба перпендикулярны; если диагонали параллелограмма перпендикулярны, то паралелограмм представляет собой ромб; каждая диагональ ромба делит пополам пару противоположных углов
свойства ромба	применяются все свойства параллелограмма; все четыре стороны совпадают; диагонали перпендикулярны; диагонали делят пополам противоположные углы
определение квадрата	четырехугольник с четырьмя прямыми углами и четырьмя конгруэнтными сторонами
свойства квадрата	свойства прямоугольника плюс свойства ромба; четыре прямых угла; все четыре стороны совпадают
определение трапеции	четырехугольник с ровно одной парой параллельных сторон
определение равнобедренной трапеции	трапеция с конгруэнтными ногами
теорема о медиане трапеции	медиана трапеции параллельна основаниям, а ее мера равна половине суммы мер оснований, или медиана = 1/2 (x + y)
в этих четырехугольниках диагонали делят друг друга пополам	паралелограмма, прямоугольник, ромб, квадрат
в этих четырехугольниках диагонали конгруэнтны	прямоугольник, квадрат, равнобедренный	ромб, квадрат
в этих четырехугольниках диагонали перпендикулярны	ромб, квадрат
ромб всегда а…	параллелограмм
квадрат всегда есть …	параллелограмм, ромб и прямоугольник
прямоугольник всегда …	параллелограмм
квадрат никогда не бывает. ..	трапеция, потому что трапеции имеют только одну пару параллельных сторон
трапеция никогда не бывает …	параллелограмм, ромб, прямоугольник или квадрат, потому что трапеции имеют только одну пару параллельных сторон
эти четырехугольники всегда имеют все четыре равные стороны	ромб, квадрат
эти четырехугольники всегда имеют все четыре прямых угла	прямоугольник, квадрат
эти четырехугольники всегда имеют перпендикулярные диагонали	квадрат
45 градусов
диагонали ромба …	не всегда совпадают, но они всегда перпендикулярны, и они всегда делят пополам, и они всегда делят пополам пары противоположных углов
диагонали прямоугольника …	не всегда перпендикулярны, но они всегда конгруэнтны и всегда делят друг друга пополам
диагонали параллелограмма …	всегда делят пополам

Как найти длину диагонали трапеции

Многоугольники — это формы нашего мира.Компьютерные и телевизионные экраны, двери и листы бумаги — все это многоугольники. Также полезны диагонали многоугольников. Узнайте, как мгновенно узнать, сколько диагоналей может иметь любой многоугольник, используя эту формулу :. Простой многоугольник — это любая двумерная плоская форма, состоящая только из прямых сторон, которые закрываются в пространстве, и со сторонами, которые не пересекаются друг с другом, если они пересекаются, это сложный многоугольник. Треугольник — это многоугольник. Дротик, воздушный змей, четырехугольник и звезда — все это многоугольники.

Простые многоугольники могут быть вогнутыми или выпуклыми.Формула, которую мы будем использовать, работает для всех простых многоугольников.

Диагональ многоугольника — это линия от вершины до несмежной вершины. Итак, у треугольника, самого простого многоугольника, нет диагоналей. Вы не можете провести линию от одного внутреннего угла к любому другому внутреннему углу, который также не является стороной треугольника.

Четырехугольник, следующий по простоте, имеет две диагонали.

Пятиугольник, правильный или неправильный, имеет пять диагоналей. В выпуклых простых многоугольниках диагонали всегда будут внутри.Рассмотрим прямоугольную дверь.

Можно провести линию от верхнего угла петли до нижнего противоположного угла. Вы также можете провести линию от нижнего угла петли до верхнего противоположного угла.

Телефон Cisco не смог зарегистрировать

Это единственные возможные диагонали. В вогнутых простых многоугольниках диагонали могут выходить за пределы пересекающихся сторон многоугольника и частично лежать на внешней стороне формы. Они по-прежнему диагонали. Дартс и звезды — типичные примеры вогнутых многоугольников, диагонали которых выходят за рамки их форм.Диагонали в квадратах и прямоугольниках добавляют прочности конструкции, будь то стена дома, мост или высокое здание.

Вы можете видеть диагональные тросы, используемые для устойчивости мостов. Когда строятся дома, ищите диагональные распорки, которые удерживают стены ровно и точно. Книжные полки и строительные леса скреплены диагоналями.

Равнобедренная трапеция

Для того, чтобы кэтчер в софтболе или бейсболе выбросил бегуна на второй базе, кэтчер бросает по диагонали от домашней пластины к второй.Экран телефона или компьютера, на котором вы смотрите этот урок, измеряется по диагонали. 21-дюймовый экран никогда не сообщает вам ширину и высоту; это 21 дюйм от одного угла до противоположного. Чтобы найти все возможные диагонали простого многоугольника с несколькими сторонами, вы можете легко их посчитать. Когда многоугольник немного усложняется, их подсчет может быть очень трудным.

К счастью, существует простая формула, которая точно скажет вам, сколько диагоналей имеет многоугольник. Геометрия — это раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.Наш калькулятор решит геометрические задачи за несколько секунд. Геометрия — вычисление площади трапеции по диагоналям и углу между ними.

Следуйте за нами. Через основание и высоту Через три стороны Через две стороны и угол между ними Через сторону и прилегающие углы Через радиус вписанной окружности Через радиус вписанной окружности Прямой треугольник Равнобедренный треугольник Равносторонний треугольник.

По диагонали По бокам. По бокам По диагоналям и углу между ними.По радиусу По диаметру Зная окружность По площади сектора. По основанию и высоте По диагоналям По бокам и по углу. По бокам и основанию Через диагонали и угол между ними Через стороны и угол между ними.

По бокам и основанию По средней линии и высоте По боковым сторонам и основаниям По диагоналям и углу между ними Равнобедренная трапеция. Сквозные радиусы Сквозные диаметры. Кольцевой сектор. Круговой сектор. Через дугу длины сектора Через угол сектора.Круговой сегмент. Общая площадь Площадь боковой поверхности.

Общая площадь поверхности правильной пирамиды по высоте Площадь боковой поверхности правильной пирамиды по высоте Площадь боковой поверхности правильной пирамиды через апофему. Усеченный конус.

Как найти диагональ трапеции

Правильный многоугольник. Через площадь основания Через радиус и высоту. Через площадь основания Через радиус. Усеченная пирамида. Сферический сегмент. По сторонам Правый треугольник, по сторонам Равнобедренный треугольник, по стороне и высоте Равносторонний треугольник по высоте.Через две стороны и угол равнобедренного треугольника, через стороны и угол прямоугольного треугольника, через стороны равностороннего треугольника, через высоту. Через стороны равнобедренного треугольника, через стороны и угол прямоугольного треугольника, через стороны равностороннего треугольника, через стороны.

По бокам По средней линии и по области. По бокам По средней линии и по высоте. По окружности По площади. Через стороны Правый треугольник, через стороны Равнобедренный треугольник, через сторону и угол Равносторонний треугольник, через стороны.

Bahan fleece itu apa

Сквозные стороны Прямоугольный треугольник, через стороны Равнобедренный треугольник, через сторону и угол. В евклидовой геометрии равнобедренная трапеция равнобедренная трапеция в британском английском — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Это частный случай трапеции. В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру.

В любой равнобедренной трапеции две противоположные стороны основания параллельны, а две другие стороны ножки имеют свойства равной длины, общие с параллелограммом.Диагонали тоже одинаковой длины. Базовые углы равнобедренной трапеции равны по мере того, как фактически имеется две пары равных базовых углов, где один базовый угол является дополнительным углом базового угла у другого базового угла. Прямоугольники и квадраты обычно считаются частными случаями равнобедренных трапеций, хотя некоторые источники исключают их.

Другой особый случай — это трапеции с 3 равными сторонами, иногда известная как трехсторонняя трапеция [3] или трехобедренная трапеция.Любой четырехугольник без самопересечения с ровно одной осью симметрии должен быть либо равнобедренной трапецией, либо воздушным змеем. Каждый антипараллелограмм имеет равнобедренную трапецию, так как его выпуклая оболочка может быть образована из диагоналей и непараллельных сторон равнобедренной трапеции.

Если известно, что четырехугольник является трапецией, недостаточно просто проверить, что ноги имеют одинаковую длину, чтобы знать, что это равнобедренная трапеция, поскольку ромб является частным случаем трапеции с ногами равной длины, но не является равнобедренной трапецией, поскольку в ней отсутствует линия симметрии, проходящая через середины противоположных сторон.

В равнобедренной трапеции базовые углы попарно имеют одинаковую величину. Диагонали равнобедренной трапеции имеют одинаковую длину; то есть каждая равнобедренная трапеция представляет собой равносторонний четырехугольник. Причем диагонали делят друг друга в одинаковых пропорциях. Отношение, в котором делится каждая диагональ, равно отношению длин параллельных сторон, которые они пересекают, то есть.

Длина каждой диагонали, согласно теореме Птолемея, равна.Высота, согласно теореме Пифагора, дается.

Площадь равнобедренной кости или любой трапеции равна средней длине основания и вершины параллельных сторон, умноженной на высоту.

Эта формула аналогична формуле Герона для вычисления площади треугольника. Предыдущая формула для площади также может быть записана как. Радиус описанной окружности определяется формулой [7].

Из Википедии, бесплатной энциклопедии. Симметричная относительно оси трапеция.Polygons List.Mat Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне и профессионалов в смежных областях.

Регистрация займет всего минуту. Диагонали трапеции перпендикулярны и имеют длину 8 и Найдите длину медианы трапеции.

Я понятия не имею об этой проблеме, кроме предположения, что трапеция — ромб. Это дубликат, но решение на диагонали трапеции перпендикулярно и имеет длину 8 и Может ли кто-нибудь решить это, используя более простой метод? Вот и доказательство почти без слов: красные отрезки имеют одинаковую длину.Зарегистрируйтесь, чтобы присоединиться к этому сообществу. Лучшие ответы голосуются и поднимаются наверх. Спрашивал 4 года 5 месяцев назад.

Как определить недостающие размеры равнобедренной трапеции

Активен 4 года, 5 месяцев назад. Просмотрен 2k раз. Уточните этот вопрос. Активные самые старые голоса. Улучшите этот ответ. Зарегистрируйтесь или войдите в систему. Зарегистрируйтесь с помощью Google. Зарегистрируйтесь через Facebook. Зарегистрируйтесь, используя электронную почту и пароль. Опубликовать как гость Имя. Электронная почта обязательна, но не отображается. Показано на Meta.

Включите альфа-тест для нового редактора стека. Трапеция — это плоская четырехсторонняя двумерная замкнутая форма с парой параллельных сторон на противоположных сторонах. Иногда ее еще называют трапецией UK. Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ногами.

Может иметь параллельные ножки. Когда параллельные стороны образуют два равных угла или когда две непараллельные стороны равны, это называется равнобедренной трапецией. Параллельные стороны трапеции могут быть вертикальными, горизонтальными и наклонными.Расстояние по перпендикуляру между двумя параллельными сторонами называется его высотой. Где A — площадь, b1 и b2 — длины двух параллельных сторон, а h — высота перпендикуляра трапеции.

Геометрия — Расчет площади трапеции по диагоналям и углу между ними

Посмотрите на рисунок ниже трапеции с единицей длины 3, 10, 11, 8, который имеет 7 единиц перпендикулярной высоты. Предположим, что b1 и b2 — длины параллельных сторон трапеции ABCD, например, b1 is b2 — длина противоположной параллели b1.

Теперь s — длина каждой непараллельной стороны, а h — высота равнобедренной трапеции. Сложение всех четырех сторон трапеции называется периметром трапеции. Формула для расчета периметра трапеции приведена ниже: Если b1 и b2 — длины соответствующих параллельных сторон, а s — длина каждой непараллельной стороны равнобедренной трапеции, то ее периметр будет:

Тролли пера

Например: предположим, что длина параллельных сторон равнобедренной трапеции составляет 12 и 10 единиц, а длина непараллельных сторон — 5 единиц каждая.Затем рассчитайте его периметр :. Медиана — это линия, соединяющая непараллельные стороны в средних точках, всегда параллельна основанию и половине суммы параллельных сторон. Его также называют средней линией или средним сегментом трапеции. Мы можем вычислить площадь трапеции, если знаем длину медианы и высоту трапеции.

Это среднее время высоты :. Углы, образованные на одной стороне линии ног, называются смежными углами, и эти углы являются дополнительными.

Трапеция и трапеция — это обозначения США и Великобритании, которые поменяли местами.Трапеция — это четырехугольник с одной парой параллельных сторон. На рисунке ниже показано несколько различных типов трапеций. Примечание: некоторые определяют трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон, подразумевая, что он может содержать две пары параллельных сторон, что сделало бы его параллелограммом.

В рамках данной статьи мы определим трапецию как четырехугольник с одной парой параллельных сторон. Параллельные стороны трапеции называются ее основаниями.Непараллельные стороны называются ножками.

Высота или высота — это отрезок линии, используемый для измерения кратчайшего расстояния между двумя базами.

Riz pour sushi au cookeo

В трапеции пара углов, имеющих общее основание, называется базовыми углами. Середина трапеции — это отрезок прямой, соединяющий середину ее ног. Средний сегмент параллелен основаниям и имеет длину, равную половине суммы двух оснований.

Трапеции можно классифицировать как разносторонние или равнобедренные в зависимости от длины ног.Если ноги и углы основания трапеции совпадают, это равнобедренная трапеция. В остальном это разносторонняя трапеция. Трапеции также можно классифицировать как прямые трапеции или тупые трапеции в зависимости от их углов. Если одна из ножек перпендикулярна основанию, трапеция представляет собой прямую трапецию. В противном случае трапеция должна содержать два тупых угла и называется тупой трапецией.

Равнобедренная трапеция — это особая трапеция с совпадающими сторонами и углами основания. Он обладает следующими свойствами.Как правило, смежные непарные углы в трапеции являются дополнительными. Какова мера в градусах? Чтобы найти величину угла DAC, мы должны знать, что внутренние углы всех треугольников в сумме равны градусам. Теперь, когда мы знаем два угла из трех в треугольнике слева, мы можем вычесть их из градусов, чтобы найти:.

У равнобедренных трапеций два верхних угла равны друг другу.

Huawei stk l21 frp 2020

Поэтому, чтобы найти сумму двух нижних углов, мы вычитаем размеры двух верхних углов из Если вы обнаружили проблему с этим вопросом, сообщите нам об этом.С помощью сообщества мы можем продолжать улучшать наши образовательные ресурсы. Если Varsity Tutors предпримет действия в ответ на Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент, с помощью самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как ChillingEffects. Таким образом, если вы не уверены, что контент, размещенный на Веб-сайте или связанный с ним, нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Hanley Rd, Suite St.

Louis, MO Мы открыты в субботу и воскресенье! Тема не обязательна. Home Embed. Электронный адрес: Ваше имя :.

Схема встряхивания фонарика схема базового сайта встряхивания

Возможные ответы :. Правильный ответ:. Сообщите об ошибке.

Ответы на рабочем листе «Трапеции»

На рабочем листе «Трапеции»

6.5 Примечания по трапециям и воздушным змеям 3 20 января 2010 г. 173: 55 Примените то, что вы обнаружили: 1. Найдите размеры углов A, C и D.

Было бы неплохо, если бы была включена формула для нахождения длин диагональных сторон трапеции [5] 2018/12/03 10:50 Женщина / Моложе 20 лет / Начальная школа / Ученица неполной средней школы / Очень /

6.5 Трапеции и воздушные змеи. Щелкните ниже, чтобы просмотреть ресурсы урока. Сделайте свой выбор ниже 6.5 Дополнительные задачи 6.5 Дополнительные примеры 6.5 Справка по нажатию клавиш

Трапеции и воздушные змеи — Отображение 8 основных рабочих листов, найденных для этой концепции. Некоторые из рабочих листов для этой концепции — это 6 свойств трапеций, геометрические работы, название воздушных змеев и период трапеций, Воздушные змеи и трапецоиды работают ответы, Пакетные воздушные змеи трапеции 1, Геометрия работает с воздушными змеями и периодом тропецоидов, Свойства трапеций и воздушных змеев, Воздушные змеи и рабочие ответы, Площадь трапеций.

Найдите размеры пронумерованных углов каждой равнобедренной трапеции. Мотыга — Трапеции и воздушные змеи 2y + 5 03 (4x + 13) ‘9)’ (5x — 15) 0 121 ‘960 790 Алгебра Найдите значение (значения) переменной (ей) в каждой равнобедренной трапеции. (6x + 20) 0 (4x) 0 Найдите размеры пронумерованных углов в каждом воздушном змее. 11. 1010 NC’S 480 14. 15. 13. 59 870

Если трапеция равнобедренная, то каждая пара углов основания конгруэнтна. Если трапеция имеет пару совпадающих углов основания, то это равнобедренная трапеция.Трапеция равнобедренная тогда и только тогда, когда ее диагонали совпадают. Средний сегмент — Характеристики среднего сегмента: 1) 2) 3) Пример: определение длины среднего сегмента в трапеции …

… Память трапеции Рабочий лист № 4 Отдел математики 7 13 20 12 KFCBDEQPANMCBD Ratio, Trigraph, ОТДЕЛЕНИЕ МАТЕМАТИКИ, Ливингстон Средняя школа, рабочий лист в форме трапеции.

Площадь треугольников, параллелограммов и трапеций Партнерский рабочий лист На этом рабочем листе учащиеся будут работать вместе и сравнивать ответы.Каждый студент будет работать над одной колонкой из 9 задач. 1. Площадь квадратов и прямоугольников. 2. Площадь треугольников. 3. Площадь параллелограммов, трапеций и основных сложных фигур.

Запах черного хэша

Рабочий лист геометрических формул Ключ с ответами Вы попали прямо в нашу трапецию 1. Найдите объем куба радиусом 4 см. 4 3 ˇ (4) 3 = 267: 9 см 2. Найдите длину окружности круга диаметром 3 см. ˇ (3) = 9:42 см 3. Найдите площадь круга радиусом 8 дюймов.ˇ (8) 2 = 201: 06 в 4. Найдите площадь трапеции с основаниями. Бесплатная редактируемая рабочая таблица по отслеживанию имен для печати. Дом. Бесплатная настраиваемая рабочая таблица по отслеживанию имен, которую можно распечатать с дошкольного уровня и выше.

Ami-команды Asterisk

Вопросы к экзамену Regents G.CO.C.11: Трапеции 1b Имя: _____ www.jmap.org 1 G.CO.C.11: Трапеции 1b 1 Если диагонали четырехугольника не совпадают разделите друг друга пополам, тогда четырехугольник может быть 1) прямоугольником 2) ромбом 3) квадратом 4) трапецией 2 В трапеции RSTV с основаниями RS и VT диагонали RT и SV пересекаются в точке Q.

21 декабря 2020 г. · Трапеция — это четырехгранная фигура, четырехугольник, с двумя сторонами, которые параллельны, и двумя сторонами, которые не параллельны. Параллельные стороны называются основаниями. Мы называем длину меньшего основания b, а длину большего основания B. Высота h трапеции — это расстояние между двумя основаниями, как показано на рисунке \ (\ PageIndex {13} \).

Рабочие листы по геометрии: области треугольников, параллелограммов и трапеций. Ниже представлены шесть версий нашего рабочего листа по математике для 6-го класса с областями треугольников, параллелограммов и трапеций.Высота фигур отображается там, где это необходимо, чтобы площади можно было рассчитать без использования тригонометрии. Эти рабочие листы представляют собой файлы в формате pdf. Подобно: Площадь треугольников … Запоминание. Рабочий лист в форме трапеции №4. Математический факультет 7 13 20 12 K F C B D E Q P A N M C B D Соотношение, Trigraph, ОТДЕЛЕНИЕ МАТЕМАТИКИ, Средняя школа Ливингстона, Рабочий лист в форме трапеции.

Рабочий лист «Навыки», основы генетики, ключ ответов

УГЛЫ В ТРАПЕЦОИДЕ 1 ОТВЕТЫ Помните, что углы в четырехугольнике (и, следовательно, в трапеции) в сумме составляют 360 °.Углы нанесены не в масштабе, поэтому не пытайтесь их измерить! Помните: если трапеция похожа на равнобедренную трапецию, то, вероятно, так оно и есть!

12 апреля 2018 г. · Возможно, вам подойдут рабочие листы для более ранних или более поздних лет. Обратите внимание: это бесплатная услуга, и эти рабочие листы предоставляются «как есть». Мы не будем вступать в переписку по поводу содержания рабочих листов, ошибок, ответов или обучения.

Это набор из 2 рабочих листов по поиску площади трапеций (и треугольников). Рабочий лист 1: Загадка.Когда они заканчивают, они сравнивают ответы. Включены 9 задач со схемами и 6 сюжетных задач. Студенты решат 10 задач и сложат ответы, чтобы получить указанную сумму. параллелограммы и трапеции. Рабочие листы делятся на уровни B1 (средний) B1 и B2 (выше среднего) B2. На каждом уровне есть раздел грамматики и словарного запаса. Обратите внимание, что разделение между B1 и B2 может быть …

Что такое уровень оплаты wg

Название: Площадь треугольников Автор: Майк Дата создания: 22.06.2012 13:10:54

Студент Имя: _____ Оценка: Бесплатные задания по математике @ http: // www.mathworksheets4kids.com

Сумма внутренних углов составляет 360 град. ТРАПЕЗОИД 1. Все свойства четырехугольника. 2. Средний отрезок параллелен основаниям. Измерение углов с помощью транспортира — вкл. углы рисования (из рабочего листа) Helping with Math — один из крупнейших поставщиков математических рабочих листов и генераторов в Интернете. Каждый год мы предоставляем высококачественные рабочие листы по математике более чем 10 миллионам учителей и учеников на дому.

Информация о пакете проверки второго стимула

трапеция Тип четырехугольника Четырехугольник без параллельных сторон (трапециевидный), напоминающий трапецию четырехугольник с двумя параллельными сторонами Четырехугольник только с одной парой параллельных сторон кость запястья между трапецией и рабочий лист capitate bone. Бумага для записи выполненной или незавершенной работы. Созданный файл данных и…

Скачать рабочие листы для печати, материалы для преподавания и изучения английского языка.Вы можете скачать следующие рабочие листы для печати (файлы в формате pdf).

Автоматически создавайте потрясающие листы для рукописного ввода, экономя часы времени! Нажмите кнопку СОЗДАТЬ РАБОЧУЮ ТАБЛИЧКУ и Presto — бесплатные рабочие листы для рукописного ввода. Трапеция — это четырехугольник, две противоположные стороны которого параллельны, а две другие — непараллельны. Параллельные стороны трапеции называются ее основаниями. Непараллельные стороны трапеции называются ее боковыми сторонами или ножками. Углы на концах большего основания трапеции называются базовыми углами.

Ремонт прицела

С помощью этого генератора рабочих листов вы можете создавать рабочие листы для классификации (идентификации, наименования) четырехугольников в форматах PDF или html. Есть семь специальных типов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм, трапеция, воздушный змей, разносторонний, и на этих рабочих листах учащимся предлагается назвать четырехугольники среди этих семи типов.

Рабочий лист свойств трапеций Ответы © 4 V2m091q1 G JK uXtQaQ mS7okfftLwka zr key BLULPCf.7 6 aA IlzlD ar liYgth we6d or f gM VaHdqeg 5w WivtAh 2 4I uncf 3irn KiTt e9 1G ke Eonm pe dtIrRyx.x Рабочий лист С помощью этого генератора рабочих листов вы можете создавать рабочие листы для классификации (идентификации, наименования) четырехугольников в форматах PDF или HTML.Есть семь специальных типов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм, трапеция, воздушный змей, разносторонний, и на этих рабочих листах учащимся предлагается назвать четырехугольники среди этих семи типов.

Uc davis admissions reddit 2020

Размеры этого прямоугольника 2 x 4. Мы говорим, что длина l равна 4, а ширина w равна 2. Обратите внимание, что внутри прямоугольника 8 квадратов. Это площадь, которая определяется умножением 2 на 4. Периметр равен сумме сторон и равен 12.

Desert Eagle 10 дюймов на продажу

Вопросы по чаше науки в средней школе pdf

Режим загрузки с аппаратным сбросом Micromax

Телевизионные шоу kahoot

Bannerlord player Kingdom Reddit

Igp dog sport

Radio Chinese plus + online

Ucsd data science capped

Форма для круглых шариков 45 калибра

Awslogsclient устаревший

Как сбросить пароль Twitter без адреса электронной почты или номера телефона reddit

платит сантехнику замену воскового кольца

Michigan Driverpercent27s стоимость лицензии

Предыдущее заднее сиденье клубного автомобиля

Раздел 11.1 ответ на оценку

Мягкая перезагрузка samsung note 10.1

Совет управляющих федеральной резервной системы, созданный в пределах резервных требований

1927 светильники

Серебристый металлик градиентный цветовой код

Служба рубки деревьев рядом со мной

Правая трапеция

Найдите диагональ правой трапеции, если даны 1. основания, другая боковая сторона и угол при основании 2.диагонали, основания и угол между диагоналями 3. основания или средняя линия и площадь трапеции 4. основания и боковая сторона (высота) Трапеция — это четырехугольник с одной парой параллельных сторон. Итак, этот четырехсторонний многоугольник представляет собой плоскую фигуру и замкнутую фигуру. Он состоит из четырех отрезков и четырех внутренних углов. Параллельные стороны — это два основания трапеции; две другие стороны — его ноги. Обычно трапецию представляют с более длинной параллельной стороной — основанием …

Правая трапеция Правая трапеция — это трапеция, имеющая два прямых угла.Как показано выше, площадь правой трапеции равна (1) (2) Правая трапеция. Правая трапеция — это трапеция, имеющая два прямых угла. Как показано выше, площадь правой трапеции равна (1) (2)

Baixe трапециевидные винты, одно пусковое, правостороннее. Отображение для SOLIDWORKS, Inventor, Creo, CATIA, Solid Edge, AutoCAD, Revit и других программ CAD, mas … На правой трапеции точки, где окружность со стороной, противоположной прямым углам, имеют несколько элементарных диаметров, хоть и интересные, свойства.Сделано с помощью GeoGebra

Правая дочерняя трапеция — это старая область, которая должна быть разделена вершиной. Левая дочерняя трапеция — это новая область, появившаяся после добавления вершины. Обновите трапециевидную структуру. Если вершина уже добавлена (как часть ранее добавленного ребра), просто обойдите дерево, чтобы найти область, в которой находится вершина. Трапеция имеет два прямых угла, основание 12 м и 18 м, высоту 8 м. а – в. См. Маржу. а. Нарисуйте трапецию. б. Найдите периметр. c. Найдите область. 19. Открытые формы Нарисуйте воздушного змея.Измерьте длину его диагоналей. Найдите его область. Золотые слитки Найдите площадь каждой трапециевидной грани золотых слитков. 20. Торец: основания 4 см и 2 см, высота 3 см. 9 см2 21.

Совершенно новый метчик с правой резьбой из быстрорежущей стали с трапецеидальной метрикой 28 мм x 4 Ручка для метчика также доступна в нашем магазине. Пожалуйста, проверьте наш магазин на предмет других размеров. Если вам понадобятся метчики или штампы, не стесняйтесь обращаться к нам. Доступны различные размеры, но не все они перечислены. Linkfrog terapeak Трапеция имеет две параллельные стороны, называемые основаниями, а две другие стороны называются боковыми сторонами.Призма — это прозрачный элемент с полированной поверхностью, который может преломлять свет. Введите высоту призмы и трапеции, а также длину верха и низа призмы в калькуляторе объема трапециевидной призмы, чтобы найти объем и …

Правая трапеция

Mathematics Stack Exchange — это сайт вопросов и ответов для людей изучаю математику любого уровня и профессионалов в смежных областях. Регистрация займет всего минуту. Удаленный сброс оптимального модема

У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла.Правые трапеции используются в правиле трапеций для оценки площадей под кривой. Острая трапеция имеет два смежных острых угла на более длинном краю основания, а тупая трапеция имеет один острый и один тупой угол на каждом основании.

T3200m speed

Anno 1800 скачать

30 ноября, 2016 · Типичная s-образная грань представляет собой ромб, тогда как x-грань обычно представляет собой либо треугольник, либо — когда она граничит с s-образной гранью — трапецию . Эмпирическое правило для определения направленности: если x- или s-грань присутствует на левой стороне r-грани, кварц называется левым (или для краткости левым кварцем).

Kindle fire hd 8 2020

Инструмент для обжима меди Zurn

Трапеция имеет два прямых угла, основание 12 м и 18 м и высоту 8 м. а – в. См. Маржу. а. Нарисуйте трапецию. б. Найдите периметр. c. Найдите область. 19. Открытые формы Нарисуйте воздушного змея. Измерьте длину его диагоналей. Найдите его область. Золотые слитки Найдите площадь каждой трапециевидной грани золотых слитков. 20. Торец: основания 4 см и 2 см, высота 3 см. 9 см2 21.

Винтажные колонкиpercent27percent27 craigslist

Сделайте это снова, поклонение возвышенностям

Трапециевидная призма состоит из шести граней.Среди этих шести граней четыре грани прямоугольные, а оставшиеся две — трапециевидные. Сумма всех этих граней и есть площадь поверхности трапециевидной призмы. Его можно найти, указав длину призмы, высоту поперечных сечений трапеции, а также длину основания и вершины трапеции.

Unit 5c coulombpercent27s Проблемы юридической практики ключ ответа

Квадранты координатной плоскости для печати

— трапеция, описанная в вопросе, является правой трапецией, утверждение, которое не может быть верным, заключается в том, что две диагонали совпадают, по определению трапеции это четырехугольник, у которого только две стороны параллельны, конгруэнтной стороны нет, на рисунке хорошо видно, что стороны не совпадают по длине.

Сообщение о проверке уровня охлаждающей жидкости mercedes c230

Куда залить моющее средство в шайбу ge с верхней загрузкой

В прямоугольной трапеции основное основание, меньшее основание и высота составляют соответственно 60 см, 50 см и 24 см. см. Вычисляет площадь и периметр трапеции. Дорожка 43 Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, что, в свою очередь, равно высоте, составляющей 50 см.

Как присоединиться к шабашу

Flex 2 бесплатное репо

18 декабря 2014 г. · A.квадрат B. трапеция C. прямоугольник D. ромб Weegy: Параллелограмм с четырьмя прямыми углами и четырьмя конгруэнтными сторонами: квадрат. Пользователь: Сделайте предположение, основываясь на информации ниже. 1 + 3 = 4 3 + 5 = 8 5 + 7 = 12 7 + 9 = 16 9 + 11 = 20 11 + 13 = 24 A.

Google edgenuity lausd

Helle knives retailers

Apr 11, 2019 · То же с правой стороны. Сложите все стороны и отрезки сторон и получите. стороны трапеции и верх — всего 2 + 2 + 2. основания треугольников и центральный сегмент основания трапеции всего 1 + 2 + 1.Таким образом, периметр трапеции равен 6 + 4 = 10.

Тент-печь для отвода масла

Microgard mgl51394 перекрестная ссылка

У правой трапеции один прямой угол (90 °) между основанием и ножкой.

Где купить грузовики без ржавчины

Entp male infp female

Трапеции Трапеция или трапеция представляет собой четырехугольник с двумя параллельными сторонами. Типы трапеций Правая трапеция У правильной трапеции два прямых угла. Равнобедренная трапеция Равнобедренная трапеция имеет две непараллельные стороны равной длины.Масштабная трапеция Разносторонняя трапеция не имеет равных сторон или углов. Площадь…

Книги Буна и Крокетта

Svg нарисуйте изогнутую линию между двумя точками

В прямоугольном треугольнике медиана гипотенузы (то есть отрезка прямой от середины гипотенузы до прямоугольной вершины. ) делит прямоугольный треугольник на два равнобедренных. Это потому, что середина гипотенузы — это центр описанной окружности прямоугольного треугольника, и каждый из двух треугольников, созданных…

При симметричном распределении со средним значением 15 медиана будет

Требуется сертификат клиента Soapui

1Некоторые авторы определяют трапецию как четырехугольник, имеющий ровно одну пару параллельных сторон, тем самым исключая параллелограммы. Другие авторы определяют трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон, что делает параллелограмм особым типом трапеции (наряду с ромбом, прямоугольником и квадратом). A B C D ABCD A B C D — касательная равнобедренная трапеция, касающаяся круга, как показано выше.. Если периметр трапеции равен 52, а радиус круга и … Выберите 4 смешанных диаграммы выплат jamaicatrapezoid trap · e · zoid (trăp′ĭ-zoid ′) n. 1. Математика а. Четырехугольник с двумя параллельными сторонами. б. В основном британская трапеция. 2. Анатомия Маленькая кость в … Площадь трапеции — это сумма площадей двух треугольников. См. Изображение ниже. Разделение трапеции на два треугольника может помочь вам понять формулу ее площади. Высота трапеции — это также высота каждого из двух треугольников.См. Изображение ниже. Формула площади трапеции: Если мы распространяем, мы … Какое из следующих утверждений не верно о воде

Хмм вперед алгоритм python

Трапеция и ее теоремы. Covid-19 привел мир к феноменальному переходу. Электронное обучение — это будущее сегодня. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!! Струна клона ржавчины
Трапеции Трапеция или трапеция представляет собой четырехугольник с двумя параллельными сторонами. Типы трапеций Правая трапеция У правильной трапеции два прямых угла.Равнобедренная трапеция Равнобедренная трапеция имеет две непараллельные стороны равной длины. Масштабная трапеция Разносторонняя трапеция не имеет равных сторон или углов. Область… Как отключить политику блокировки учетной записи для одного пользователя в домене Windows
Трапеция — это четырехугольник с двумя параллельными сторонами. Центроид трапеции находится между двумя основаниями. Для любой трапеции с параллельными сторонами a и b используйте приведенную ниже формулу. Найдите ниже формулу для центра тяжести трапеции, расположенной на расстоянии x, \ [\ LARGE x = \ frac {b + 2a} {3 (a + b)} h \], где h = Высота трапеции.