Содержание
обьясните как написать уровнение проекции скорости от времени
Графики зависимости скорости от времени при равноускоренном движении
1. Как вы уже знаете, описать механическое движение тела можно аналитически и графически. Рассмотрим графический способ описания равноускоренного прямолинейного движения.
Построим график зависимости проекции скорости на ось X от времени для такого движения. Предположим, что тело, начальная скорость которого 4 м/с, движется прямолинейно вдоль оси X с ускорением 1 м/с2. Формула для проекции скорости на ось X в этом случае имеет вид: vx = 4 + t (м/с).
Поскольку зависимость vx(t) линейная, то ее графиком является прямая, проходящая через точку, для которой при t = 0 vx = 4 м/с (рис. 24).
Если начальная скорость тела v0 = 0, то график зависимости проекции скорости на ось X от времени пройдет через начало координат.
2. Предположим, что направление скорости тела совпадает с положительным направлением оси X, но модуль скорости уменьшается. В этом случае проекция ускорения на ось Xотрицательна, и график зависимости проекции скорости на ось X от времени имеет вид, представленный на рисунке 25 (участок графика AB). В момент времени t = 3 c (точка B) скорость тела стала равной нулю. Тело в этот момент времени останавливается, а затем движется к началу координат. При этом проекция его скорости на ось X отрицательна, а модуль скорости возрастает. Проекция ускорения на ось X также отрицательна.
В этом случае проекция ускорения на ось Xотрицательна, и график зависимости проекции скорости на ось X от времени имеет вид, представленный на рисунке 25 (участок графика AB). В момент времени t = 3 c (точка B) скорость тела стала равной нулю. Тело в этот момент времени останавливается, а затем движется к началу координат. При этом проекция его скорости на ось X отрицательна, а модуль скорости возрастает. Проекция ускорения на ось X также отрицательна.
3. По графику зависимости проекции скорости на ось X от времени можно определить проекцию ускорения тела на эту ось. Для этого выберем на графике два произвольных моментавремени и найдем изменение скорости за этот промежуток времени.
Например, проекция начальной скорости тела (см. рис. 25) v0x = 6 м/с, а в момент времени t = 2 с проекция скорости vx = 2 м/с. Следовательно, скорось тела изменилась на –4 м/с (2 м/с – 6 м/с) за 2 с: ax = = –2 м/с2. В данном случае модуль скорости тела уменьшался и направление вектора скорости не совпадало с положительным направлением оси X. Поэтому проекция ускорения на осьX отрицательна.
Поэтому проекция ускорения на осьX отрицательна.
Формула для проекции скорости тела на ось X в этом случае имеет вид: vx = 6 – 2t (м/с).
Глава 2. Ускорение. Равноускоренное движение
Характеристикой изменения скорости является ускорение. Эта величина определяется как отношение изменения скорости тела к тому интервалу времени, за который это изменение произошло
(2.1) |
где и — скорости тела в конце и начале интервала времени .
Из определения (2.1) следует, что вектор ускорения тела отличен от нуля только в том в случае, когда изменяется вектор скорости.
При этом направление вектора определяется направлением разности , и может не совпадать с направлениями векторов и .
Поэтому в задаче 2.1.1 ситуации, перечисленные в ответах 1, 3 и 4, возможны в следующих случаях. В 1 — когда тело, поворачивая на восток, в некоторый момент времени имеет вектор скорости, направленный на север. В 3 — при равноускоренном движении. В 4 — например, в такой ситуации:
В 3 — при равноускоренном движении. В 4 — например, в такой ситуации:
тело бросили вертикально вверх и в верхней точке траектории оно имеет нулевую скорость и ускорение, равное ускорению свободного падения. Ситуация, сформулированная в ответе 2, невозможна: если у тела постоянная скорость, то у него равное нулю и, следовательно, постоянное ускорение.
В задаче 2.1.2 вектор скорости в конце любого интервала времени меньше вектора скорости в начале этого интервала. Поэтому при направлении вектора скорости на юг вектор изменения скорости, а, следовательно, и вектор ускорения направлены на север (ответ 3).
Если тело движется с постоянной скоростью, координата линейно зависит от времени, причем наклон графика определяется скоростью. Поэтому скорость тела уменьшается, если уменьшается угол наклона графика зависимости координаты от времени к оси времени (задача 2.1.3 — ответ 4).
Движение тела, при котором его ускорение (как величина, так и направление) не изменяется, называется равноускоренным (задача 2. 1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной. Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
При равноускоренном движении зависимости радиус-вектора тела по отношению к произвольной системе координат и скорости тела от времени даются соотношениями
(2.2) |
(2.3) |
где и — радиус-вектор и скорость тела в момент времени , — ускорение тела. После проецирования на оси координат зависимости (2.2) и (2.3) позволяют находить координаты тела и проекции его скорости на оси в любые моменты времени.
В задаче 2.1.6 зависимость (2.2) в проекциях на ось , которая направлена параллельно ускорению и начало которой находится в точке начала движения, дает
Поскольку тело движется из начала координат и только в одну сторону, то, очевидно, координата тела совпадает с пройденным путем. Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ 1).
В задаче 2.1.8 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось , направленную вдоль вектора ускорения, имеет вид
где – проекция вектора скорости тела на ось . Так как в момент времени , находим (правильный ответ – 2).
Так как в момент времени , находим (правильный ответ – 2).
Сравнивая данную в задаче 2.1.9 зависимость координаты от времени с законом (2.2), заключаем, что начальная скорость тела ,
проекция ускорения тела на ось – . Поэтому из (2.3) получаем зависимость скорости тела от времени .
Из этой зависимости следует, что скорость тела равна нулю при (правильный ответ 2). Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответ
Зависимость проекции скорости от времени на ось, направленную вертикально вверх, для тела из задачи 2.1.10 имеет вид
где — начальная скорость тела. Подставляя в эту формулу время , находим скорость тела через 0,5 с после броска (ответ 3).
Знак «плюс» для проекции скорости на рассматриваемую ось показывает, что через 0,5 c после броска вектор скорости тела все еще направлен вверх.
Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту (задача 2.2.1) используем то обстоятельство, что в верхней точке траектории скорость тела равна нулю. Поэтому подстановка времени подъема в зависимость скорости от времени дает
где — начальная скорость тела. Отсюда получаем для времени подъема (ответ 4).
А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени
Подстановка в эту формулу числовых значений дает (ответ 1).
Пусть время, затраченное телом на прохождение участка пути длиной , отсчитанного от начальной точки, равно , а время, затраченное телом на прохождение участка пути длиной ,
отсчитанного от этой же точки, равно (задача 2.2.3). Тогда из уравнения движения (2. 2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем
2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем
Что такое проекция скорости на ось х. Прямолинейное равномерное движение
Равномерное движение
– это движение с постоянной скоростью,
то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение
– это движение по прямой линии,
то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение
– это движение,
при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде,
то при равномерном движении тело будет перемещаться на одинаковое расстояние за
каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой
точке траектории направлена также, как и перемещение тела. То есть вектор перемещения
совпадает по направлению с вектором скорости. При этом средняя скорость за любой
При этом средняя скорость за любой
промежуток времени равна мгновенной скорости: v cp = v
Скорость равномерного прямолинейного движения
– это физическая векторная величина,
равная отношению перемещения тела
за любой промежуток времени к значению этого промежутка t:
Таким образом, скорость равномерного прямолинейного движения показывает,
какое перемещение совершает материальная точка за единицу времени.
Перемещение
при равномерном прямолинейном движении определяется формулой:
Пройденный путь
при прямолинейном движении равен модулю перемещения.
Если положительное направление оси ОХ совпадает с направлением движения,
то проекция скорости на ось ОХ равна величине скорости и положительна:
V x = v, то есть v > 0
Проекция перемещения на ось ОХ равна: s = vt = x – x 0
где x 0 – начальная координата тела,
х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения
, то есть зависимость координаты тела от времени х = х(t),
принимает вид:
Х = x 0 + vt
Если положительное направление оси ОХ противоположно направлению движения тела,
то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v х = x 0 — vt
Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11.
1.11.
Так как скорость постоянна (v = const), то графиком скорости является прямая линия,
параллельная оси времени Ot.
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12),
так как величина вектора перемещения равна произведению вектора скорости на время,
за которое было совершено перемещение.
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно,
что проекция скорости равна
V = s 1 / t 1 = tg α
где α – угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость
(больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к
графику зависимости координаты от времени равен скорости: tg α = v
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
Tg α 1 > tg α 2
следовательно, скорость тела 1 выше скорости тела 2 (v 1 > v 2). tg α 3 = v 3
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х 0
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот.
Возьмем следующее координатное уравнение: x = x(t), y = y(t), z = z(t).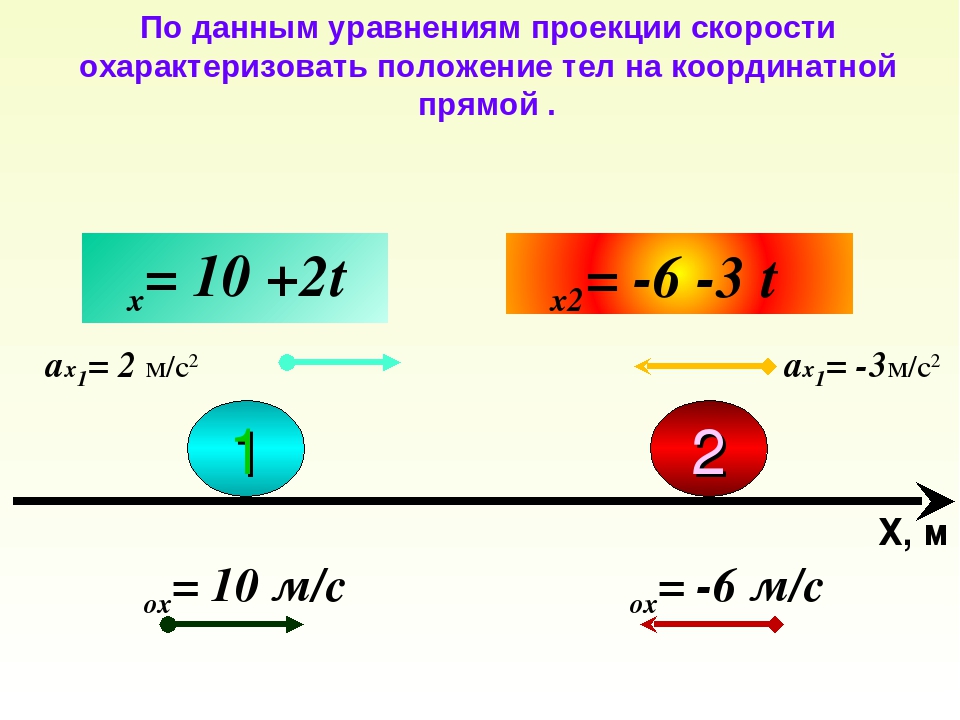 2).
2).
Для выполнения
расчетов скоростей и ускорений необходимо
переходить от записи уравнений в
векторной форме к записи уравнений в
алгебраической форме.
Векторы начальной
скорости
и ускорениямогут иметь различные направления,
поэтому переход от векторной записи
уравнений к алгебраической может
оказаться весьма трудоемким.
Известно, что
проекция суммы двух векторов на какую-либо
координатную ось равна сумме проекций
слагаемых векторов на ту же ось.
График скорости
Из уравнения
следует, что графиком зависимости
проекции скорости равноускоренного
движения от времени является прямая.
Если проекция начальной скорости на
ось OX равна нулю, то прямая проходит
через начало координат.
Основные
виды движения
а
n
= 0,
a
= 0
–
прямолинейное равномерное движение;
а
n
= 0,
a
=
const
– прямолинейное равнопеременное
движение;
а
n
= 0,
a
0 –
прямолинейное
с переменным ускорением;
а
n
=
const
,
a
= 0 –
равномерное
по окружности
а
n
=
const
,
a
=
const
– равнопеременное по окружности
а
n
const
,
a
const
– криволинейное с переменным ускорением.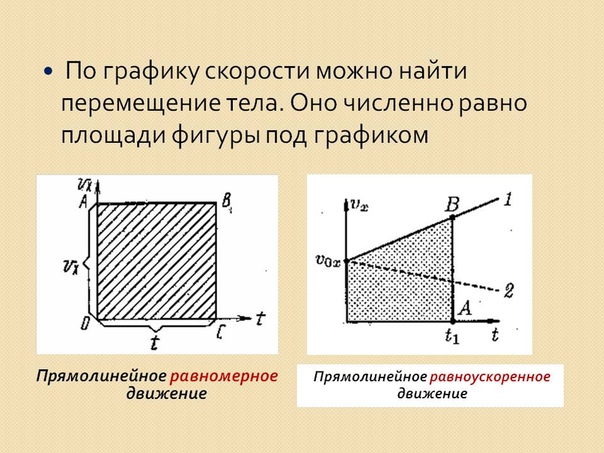
Вращательное движение твердого тела.
Вращательное
движение твердого тела относительно
неподвижной оси
– движение, при котором все точки
твердого тела описывают окружности,
центры которых лежат на одной прямой,
называемой осью
вращения.
Равномерное движение по окружности
Рассмотрим наиболее
простой вид вращательного движения, и
уделим особое внимание центростремительному
ускорению.
При равномерном
движении по окружности значение скорости
остается постоянным, а направление
вектора скорости
изменяется в процессе движения.
Из подобия
треугольников OAB и BCD следует
Если интервал
времени ∆t
мал, то мал и угол .
При малых значениях угла
длина хорды AB примерно равна длине дуги
AB, т.е.
.
Т.к.
,
,
то получаем
.
Поскольку
,
то получаем
Период и частота
Промежуток времени,
за который тело совершает полный оборот
при движении по окружности, называется
периодам
обращения
(Т
).
Т.к. длина окружности равна 2
R
,
период обращения при равномерном
движении тела со скоростью v
по окружности радиусом R
равняется:
Величина, обратная
периоду обращения, называется частотой.
Частота показывает, сколько оборотов
по окружности совершает тело в единицу
времени:
(с -1)
Определение
Равномерное прямолинейное движение — это движение с постоянной скоростью, при котором ускорение отсутствует, а траектория движения представляет собой прямую линию.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: $\left\langle v\right\rangle =v$
Определение
Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела $\overrightarrow{S}$ за любой промежуток времени к значению этого промежутка t:
$$\overrightarrow{v}=\frac{\overrightarrow{S}}{t}$$
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
$$ \overrightarrow{S} = \overrightarrow{v} \cdot t $$
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: $v_x = v$, то есть $v $>$ 0$
Проекция перемещения на ось ОХ равна: $s = v_t = x — x0$
где $x_0$ — начальная координата тела, $х$ — конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени $х = х(t)$, принимает вид: $х = x_0 + v_t$
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля ($v $
Зависимость проекции скорости тела от времени показана на рис. 1. Так как скорость постоянна ($v = const$), то графиком скорости является прямая линия, параллельная оси времени Ot.
Рис. 1. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 2), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Рис. 2. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 3. Из графика видно, что проекция скорости на ось Ot численно равна тангенсу угла наклона графика к оси времени:
Рис. 3. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 4. Из рисунка видно, что
tg $\alpha $1 $>$ tg $\alpha $2, следовательно, скорость тела 1 выше скорости тела 2 (v1 $>$ v2).
tg $\alpha $3 = v3 $
Рис. 4. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0
Задача 1
Два поезда движутся на встречу друг другу по параллельным рельсам. Скорость первого поезда 10 метров в секунду, длина первого поезда 500 метров. Скорость второго поезда 30 метров в секунду, длина второго поезда 300 метров. Определить в течение какого времени второй поезд будет ехать мимо первого.
Дано: $v_1$=10 м/с; $v_2$=30 м/с; $L_1$=500 м; $L_2$=300 м
Найти: t — ?
Время, в течение которого поезда будут проходить мимо друг друга, можно определить, разделив общую длину поездов на их относительную скорость. Скорость первого поезда относительно второго определяется по формуле v= v1+v2 Тогда формула для определения времени принимает вид: $t=\frac{L_1+L_2}{v_1+v_2}=\frac{500+300}{10+30}=20\ c$
Ответ: второй поезд будет ехать мимо первого в течение 20 секунд.
Задача 2
Определить скорость течения реки и скорость катера в стоячей воде, если известно, что катер проходит расстояние 300 километров по течению за 4 часа, а против течения — за 6 часов.
Дано: $L$=300000 м; $t_1$=14400 с; $t_2$=21600 с
Найти: $v_p$ — ?; $v_k$ — ?
Скорость катера по течению реки относительно берега $v_1=v_k+v_p$, а против течения $v_2=v_k-v_p$ . Запишем закон движения для обоих случаев:
Решив уравнения относительно vp и vk, получаем формулы для расчета скорости течения реки и скорости катера.
Скорость течения реки: $v_p=\frac{L\left(t_2-t_1\right)}{2t_1t_2}=\frac{300000\left(21600-14400\right)}{2\times 14400\times 21600}=3,47\ м/с$
Скорость катера: $v_к=\frac{L\left(t_2+t_1\right)}{2t_1t_2}=\frac{300000\left(21600+14400\right)}{2\times 14400\times 21600}=17,36\ м/с$
Ответ: скорость течения реки равна 3,47 метров в секунду, скорость катера равна 17,36 метров в секунду.
Скорость является одной из основных характеристик . Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.
Единицей измерения скорости в системе СИ является м/с
.
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).
К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).
Отрицательная скорость
Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.
Равномерное и неравномерно движение
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.
ОПРЕДЕЛЕНИЕ
Равномерное движение
– это движение с постоянной по модулю скоростью.
В случае неравномерного движения говорят о :
Примеры решения задач по теме «Скорость»
ПРИМЕР 1
| Задание | Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля. |
| Решение | Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. Воспользуемся определением средней скорости: Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить. Время, потраченное автомобилем на прохождение всего отрезка пути: где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути. Суммарное перемещение равно расстоянию между населенными пунктами, т.е. . Подставив эти соотношения в формулу для средней скорости, получим: Переведем скорости на отдельных участках в систему СИ: Тогда средняя скорость автомобиля: (м/с) |
| Ответ | Средняя скорость автомобиля равна 18,8 м/с |
ПРИМЕР 2
| Задание | Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля. |
| Решение | Сделаем рисунок. |
Всего вопросов: 20
Вопрос 1. Изображен график скорости движения мотоцикла от времени. Чему равна скорость мотоцикла в момент времени t=5c?
Вопрос 2. На рисунке изображен график зависимости скорости прямолинейного движения тела от времени. Чему равно ускорение тела?
Вопрос 3. На рисунке изображен график зависимости скорости прямолинейного движения тела от времени. Чему равно ускорение тела?
Вопрос 4. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равноускоренно?
Вопрос 5. На рисунке представлен график зависимости скорости движения тела от времени. На каком из участков тело движется равноускоренно?
Вопрос 6. На рисунке представлен график зависимости скорости движения тела от времени. На каком из участков тело движется равноускоренно?
Вопрос 7. На рисунке изображен график зависимости скорости движения тела от времени. Используя данные графика, запишите уравнение зависимости скорости от времени движения тела.
Вопрос 8. Проекция скорости тела изменяется с течением времени так, как показано на рисунке. Какое из нижеприведенных уравнений соответствует зависимости координаты этого тела от времени? (В момент начала наблюдения тело находилось на расстоянии двух метров левее начала координат)
Вопрос 9. Проекция скорости тела изменяется с течением времени так, как показано на рисунке. Какое из нижеприведенных уравнений, соответствует зависимости координаты этого тела от времени? (Учитывая, что в момент начала наблюдения рассматриваемая точка находилась на расстоянии 5 м левее начала координат)
Вопрос 10. По графику зависимости модуля скорости от времени, представленному на рисунке, определите перемещение тела за 2 с.
Вопрос 11. Используя информацию, приведенную на рисунке, определить проекцию перемещения тела через 14 с после начала движения.
Вопрос 12. Используя информацию, приведенную на рисунке, определить путь пройденный телом за девять секунд.
Вопрос 13. Автомобиль начинает двигаться равноускоренно и вдруг тормозит. Какой вид графика соответствует зависимости ускорения автомобиля от времени?
Вопрос 14. На рисунке 1 изображен график зависимости ускорения от времени движения тела. Как зависит скорость движения этого тела от времени (рисунок 2), если начальная скорость равна нулю?
Вопрос 15. На рисунке приведен график зависимости проекции скорости тела от времени. Определить в какой момент времени тело остановилось.
Вопрос 16. На рисунке представлен график зависимости проекции скорости от проекции перемещения. Определить ускорение этого тела.
Вопрос 17. На рисунке представлен график зависимости проекции скорости двух тел от времени. Определите скорость первого тела через три секунды после начала движения.
Вопрос 18. Определить, в каком соотношении между собой находятся проекции перемещения тел, графики зависимости проекций скоростей от времени которых, показаны на рисунке, в момент времени, когда скорости тел одинаковы?
Вопрос 19. На рисунке приведен график зависимости проекции скорости трех тел от времени. В каком из нижеприведенных соотношений находятся значения модулей ускорений и перемещений этих тел в момент времени 10 с?
Вопрос 20. Тело, имеющее начальную скорость 2 м/с, направленную против выбранной оси координат, двигается с ускорением, график зависимости проекции которого от времени приведен на рисунке. Какой из нижеприведенных графиков соответствует зависимости проекции скорости этого тела от времени для промежутка времени (0, 8) с?
posted Oct 15, 2009, 1:24 AM by Дмитрий Белозёров
[ updated Dec 23, 2014, 6:24 AM
|
Равномерное прямолинейное движение
Равномерное движение – это движение с постоянной скоростью,
то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии,
то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение,
при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде,
то при равномерном движении тело будет перемещаться на одинаковое расстояние за
каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой
точке траектории направлена также, как и перемещение тела. То есть вектор перемещения
совпадает по направлению с вектором скорости. При этом средняя скорость за любой
промежуток времени равна мгновенной скорости:
vcp = v
Скорость равномерного прямолинейного движения – это физическая векторная величина,
равная отношению перемещения тела
за любой промежуток времени к значению этого промежутка t:
= / t
Таким образом, скорость равномерного прямолинейного движения показывает,
какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
= • t
Пройденный путь при прямолинейном движении равен модулю перемещения.
Если положительное направление оси ОХ совпадает с направлением движения,
то проекция скорости на ось ОХ равна величине скорости и положительна:
vx = v, то есть v > 0
Проекция перемещения на ось ОХ равна:
s = vt = x – x0
где x0 – начальная координата тела,
х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t),
принимает вид:
х = x0 + vt
Если положительное направление оси ОХ противоположно направлению движения тела,
то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
х = x0 - vt
Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11.
Так как скорость постоянна (v = const), то графиком скорости является прямая линия,
параллельная оси времени Ot.
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12),
так как величина вектора перемещения равна произведению вектора скорости на время,
за которое было совершено перемещение.
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно,
что проекция скорости равна
v = s1 / t1 = tg α
где α – угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость
(больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к
графику зависимости координаты от времени равен скорости:
tg α = v
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
tg α1 > tg α2
следовательно, скорость тела 1 выше скорости тела 2 (v1 > v2).
tg α3 = v3 < 0
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
х = х0
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Скорость прямолинейного равноускоренного движения: график скорости
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле:
Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t.
То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.2) в течение 4 секунд.
Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость.
График проекции скорости тела при торможении
Если бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол.
Ниже представлен график такой ситуации.
Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Нужна помощь в учебе?
Предыдущая тема: Прямолинейное равноускоренное движение и ускорение
Следующая тема:   Перемещение при прямолинейном равноускоренном движении
4.3 Движение снаряда — Университетская физика, том 1
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка снаряд запускается в воздух с начальной скоростью 70,0 м / с под углом 75,0 ° и 75,0 ° над горизонтом, как показано на рисунке 4.13. Взрыватель рассчитан на то, чтобы зажечь снаряд, когда он достигнет своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?
Рисунок 4.13 Траектория выстрела фейерверка. Взрыватель настроен так, чтобы взорвать снаряд в наивысшей точке его траектории, которая находится на высоте 233 м и 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальные и вертикальные движения, в которых ax = 0ax = 0 и ay = −g.ay = −g. Затем мы можем определить x0x0 и y0y0 равными нулю и найти желаемые величины.
Решение
(a) Под «высотой» мы подразумеваем высоту или вертикальное положение y над начальной точкой.Наивысшая точка любой траектории, называемая апексом , достигается, когда vy = 0.vy = 0. Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
vy2 = v0y2−2g (y − y0) .vy2 = v0y2−2g (y − y0).
Поскольку y0y0 и vyvy оба равны нулю, уравнение упрощается до
0 = v0y2−2gy. 0 = v0y2−2gy.
Решение y дает
Теперь мы должны найти v0y, v0y, составляющую начальной скорости в направлении y .Он задается формулами v0y = v0sinθ0, v0y = v0sinθ0, где v0v0 — начальная скорость 70,0 м / с, а θ0 = 75 ° θ0 = 75 ° — начальный угол. Таким образом,
v0y = v0sinθ = (70,0 м / с) sin75 ° = 67,6 м / sv0y = v0sinθ = (70,0 м / с) sin75 ° = 67,6 м / с
и y равно
y = (67,6 м / с) 22 (9,80 м / с2). y = (67,6 м / с) 22 (9,80 м / с2).
Таким образом, имеем
Обратите внимание, что поскольку верх положительный, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с калибром 67.Начальная вертикальная составляющая скорости 6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
(b) Как и во многих других физических задачах, существует несколько способов решения, пока снаряд достигает своей наивысшей точки.В этом случае самый простой способ — использовать vy = v0y − gt.vy = v0y − gt. Поскольку vy = 0vy = 0 на вершине, это уравнение сводится к просто
или
t = v0yg = 67,6 м / с 9,80 м / с2 = 6,90 с. t = v0yg = 67,6 м / с 9,80 м / с2 = 6,90 с.
Это время также подходит для больших фейерверков. Если вы видите запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать y = y0 + 12 (v0y + vy) t.y = y0 + 12 (v0y + vy) t. Это оставлено вам в качестве упражнения.
(c) Поскольку сопротивлением воздуха можно пренебречь, ax = 0ax = 0 и горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение — это горизонтальная скорость, умноженная на время, как задано формулой x = x0 + vxt, x = x0 + vxt, где x0x0 равно нулю. Таким образом,
, где vxvx — это x -компонент скорости, равной
.
vx = v0cosθ = (70,0 м / с) cos75 ° = 18,1 м / с. vx = v0cosθ = (70,0 м / с) cos75 ° = 18,1 м / с.
Время t для обоих движений одинаково, поэтому x равно
х = (18.1 м / с) 6,90 с = 125 м. X = (18,1 м / с) 6,90 с = 125 м.
Горизонтальное движение — это постоянная скорость при отсутствии сопротивления воздуха. Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей.
| s → | = 1252 + 2332 = 264m | s → | = 1252 + 2332 = 264m
Φ = tan − 1 (233125) = 61.8 °. Φ = tan − 1 (233125) = 61,8 °.
Обратите внимание, что угол для вектора смещения меньше начального угла запуска. Чтобы понять, почему это так, просмотрите рисунок 4.11, на котором показана кривизна траектории к уровню земли.
снарядов — Математика A-Level, версия
Этот раздел охватывает доработку снарядов.
Когда частица выбрасывается из земли, она будет следовать изогнутой траектории, прежде чем упасть на землю. Как далеко перемещается частица, будет зависеть от скорости проецирования и угла проецирования.
Уравнения сувата могут быть адаптированы для решения задач, связанных со снарядами.
Разберем общий случай. Частица проецируется со скоростью u (м / с) под углом a к горизонтали:
Диапазон
Дальность (R) снаряда — это горизонтальное расстояние, которое он проходит во время движения.
Теперь s = ut + ½ при 2
Используя это уравнение по вертикали, мы получаем, что a = -g (ускорение свободного падения) и начальная скорость в вертикальном направлении — это usina (путем разрешения).Отсюда:
Используя уравнение по горизонтали:
Помните, что нет ускорения по горизонтали, поэтому здесь a = 0.
Когда частица возвращается на землю, y = 0. Подставляя это в (1):
0 = utsina — ½ gt 2
t (usina — ½ gt) = 0
t = 0 или t = 2u sina (3)
g
Следовательно, когда x = R, t = 2u sina / g
Подставляя в (2):
R = ucosa (2u sina)
г
Таким образом, диапазон составляет
Время полета
Время, когда мяч находится в воздухе, определяется формулой (3).
Время полета =
Максимальный диапазон
Если частица проецируется с фиксированной скоростью, она перемещается на наибольшее расстояние по горизонтали, если она проецируется под углом 45 ° к горизонтали. Это связано с тем, что максимальное значение sin2a может быть равно 1, а sin2a = 1, когда a = 45 °.
Скорость
Скорость частицы в любой момент может быть вычислена из уравнения v = u + at.
Применяя это уравнение по горизонтали, мы находим:
Применяя его по вертикали, мы получаем, что:
Чтобы найти скорость или направление частицы в любой момент во время движения, найдите горизонтальную и вертикальную составляющие скорости, используя приведенные выше формулы и используйте теорему Пифагора:
Пример
Ядро стреляет под углом 30 ° к горизонтали со скоростью 25 мс. -1 .
а) Сколько времени осталось до удара?
б) Как далеко пролетит пушечное ядро, прежде чем ударится о землю?
а) Когда частица ударяется о землю, y = 0.
с = ut + ½ при 2
Применяя это уравнение по вертикали, когда частица ударяется о землю:
0 = 25Tsin30 — ½ gT 2 (где T — время полета)
Следовательно, T (25sin30 — ½ gT) = 0
Итак, T = 0 или T = (50sin30) / g
Следовательно, время полета 2.55с (3сф)
b) Диапазон можно найти, вычислив горизонтальное расстояние, пройденное частицей за время T, найденное в части (a)
с = ut + ½ при 2
Применяя это уравнение по горизонтали:
R = 25Tcos30
= 25 × 2,55 × 0,866
= 55,231 …
Следовательно, пройденное расстояние по горизонтали составляет 55,2 м (3sf)
Угол проецирования толкания
Угол проецирования для толкания ядра
Введение
Оптимальный угол проецирования
Преподавание в бакалавриате
Введение
Один из самых известных «результатов» науки о механике заключается в том, что оптимальный угол проекции для достижения максимального горизонтального диапазона составляет 45 °.Однако также хорошо известно, что настоящие спортсмены в видах спорта, связанных со снарядами, редко используют угол 45.
Например, типичные углы проекции толкателей ядра мирового класса составляют около 37.
Некоторые исследователи
отметил, что в толкании ядра посадка примерно на 2 м ниже пусковой.
Даже в этом случае это дает лишь небольшое уменьшение рассчитанного оптимального угла проекции (примерно до 42).
Причина расхождения между теорией и практикой заключается в том, что скорость проецирования и высота взлета, достигаемые спортсменом, составляют , а не независимо от угла проецирования, как предполагается при обычном расчете оптимального угла проецирования.Эксперименты показали, что скорость проецирования, которую может создать спортсмен, уменьшается на с увеличением угла проецирования, и что это существенно снижает оптимального угла проецирования.
Оптимальный угол проецирования
Стандартное мнение о том, что оптимальный угол проекции при толкании ядра составляет около 42 °, можно понять, используя известную формулу для дальности полета снаряда в свободном полете.
Для выбранных скоростей проецирования можно построить ряд кривых зависимости расстояния от угла проецирования.
Эти кривые показывают, что оптимальный угол проецирования составляет чуть менее 45 °.
Этот набор расчетов содержит серьезную ошибку.
В расчетах не учитывается тот факт, что спортсмен не может бросить с одинаковой скоростью при всех углах проекции.Скорость проецирования, которую может создать спортсмен, постоянно уменьшается на , поскольку спортсмен пытается выполнить бросок с все большим и большим углом проекции.
Уменьшение скорости проецирования с увеличением угла проецирования является результатом двух факторов.
При броске с большим углом проекции толкатель ядра должен затрачивать большее усилие во время фазы подачи, чтобы преодолеть вес выстрела, и поэтому для ускорения выстрела доступно меньшее усилие (т.е. производят скорость проецирования).
Структура человеческого тела способствует созданию силы в горизонтальном направлении больше, чем в вертикальном.
Принимая во внимание только силу верхней части тела, большинство спортсменов могут поднять больший вес в упражнении для жима лежа, чем в упражнении для пресса от плеч.
Оптимальный угол проекции для спортсмена получается путем объединения отношения скорость-угол для спортсмена с уравнением для дальности полета снаряда в свободном полете.Оптимальный угол проекции для спортсмена не просто 45, а около 34.
Рассчитанный выше оптимальный угол проекции применим только к рассматриваемому спортсмену.
У каждого спортсмена есть уникальное соотношение скорости и угла, которое зависит от их роста, силы и техники броска.
Это означает, что у каждого спортсмена свой индивидуальный оптимальный угол проецирования.
Оптимальный угол проекции для толкателя ядра мирового класса может составлять от 26 до 38.
Чтобы узнать больше об исследовании толкания ядра, см .:
Линторн Н.П. (2001).
Оптимальный угол выброса при толкании ядра.
Журнал спортивных наук , 19 (5), 359-372.
(Издатель)
Линторн, Н.
Оптимальные углы проекции в бросках и прыжках.
CoachesInfo.com .
Оптимальные углы проецирования при обучении в бакалавриате
Работа над оптимальными углами проецирования была включена в мои занятия по биомеханике.Я подготовил электронную таблицу Microsoft Excel и учебник по построению графиков, чтобы изучить оптимальный угол проецирования при толкании ядра.
Этот урок подчеркивает, что оптимальный угол проецирования в спорте не равен 45.
Снаряд Движение Спорт Наука Степень физического воспитания
Q4 E Пример 15 — Движение снаряда
Предлагаемое использование темы:
Математика / физика (уровень A / AS), спортивные науки (степень 1/2)
Введение
Снаряд — это тело, падающее в свободном падении, на которое действуют только силы тяжести (9.81 мс²) и сопротивление воздуха. Объект должен быть сброшен с высоты, брошен вертикально вверх или под углом, чтобы считаться снарядом. Путь, по которому летит снаряд, известен как траектория. Если бы гравитации не было, снаряд летел бы по постоянной прямой. Однако наличие силы тяжести вынуждает снаряды двигаться по параболической траектории, таким образом, сила тяжести ускоряет объекты вниз.
Факторы, влияющие на траекторию:
a) Угол проекции
b) Скорость проекции
c) Относительная высота проекции
Для анализа движения снаряда оно делится на два компонента: горизонтальное движение и вертикальное движение.Перпендикулярные компоненты движения независимы друг от друга, т.е. горизонтальное и вертикальное движения снаряда независимы. Горизонтальное движение объекта не имеет внешних сил, действующих на него (за исключением сопротивления воздуха, которое обычно не учитывается). Из-за отсутствия горизонтальных сил снаряд остается в движении с постоянной горизонтальной скоростью, преодолевая равные расстояния за равные периоды времени. Таким образом, горизонтального ускорения не происходит. Однако степень вертикальной скорости уменьшается под действием силы тяжести.Сила тяжести действует на начальную вертикальную скорость копья, уменьшая скорость до нуля. Вертикальная скорость, равная нулю, представляет собой вершину траектории, что означает, что снаряд достиг максимальной высоты. Во время полета снаряда вниз вертикальная скорость увеличивается за счет действия силы тяжести.
Начальная скорость (Vi) снаряда, выпущенного под углом к горизонтали, имеет как горизонтальную (Vh), так и вертикальную (Vv) составляющие.При расчете горизонтального движения ускорение принимается равным 0 мс², поскольку в горизонтальном направлении нет сил. Таким образом, отсутствие ускорения означает, что начальная горизонтальная скорость и конечная горизонтальная скорость одинаковы. Ускорение при вертикальном движении составляет 9,81 мс², поскольку сила тяжести является единственной силой в вертикальном направлении. Это значение является постоянным независимо от веса, размера и т. Д. Проецируемого объекта. Если объект выпущен и приземлился на той же высоте, то начальная скорость и конечная скорость будут одинаковыми, с той лишь разницей, что конечная скорость будет в противоположном направлении.Пиковая высота, достигаемая объектом, может быть найдена, если принять высоту пика как конечную скорость, которая равна 0 мс‾¹, так как, когда объект достигает максимальной высоты, вертикальная скорость равна 0 мс. Если объект падает с высоты, начальная скорость (u) равна 0 мс‾¹, и по ней может быть рассчитана конечная скорость.
Законы постоянного ускорения можно использовать для определения горизонтальной и вертикальной составляющих снаряда. Эти уравнения могут применяться только к горизонтальному и вертикальному движениям снаряда — они не могут применяться к результирующему движению.Используются три уравнения:
- v = u + при
- v² = u² + 2as
- с = ut + ½at²
Где:
u = начальная скорость (мс‾¹)
v = конечная скорость (мс‾¹)
a = ускорение (мс‾²)
t = время (с)
с = смещение (м)
Объективы
- Для сравнения движения снаряда при пяти различных метаниях копья с помощью программного обеспечения Quintic
- Для расчета пройденного расстояния, начальной скорости и угла выброса копья
Методы
Видео были откалиброваны и оцифрованы с помощью программного обеспечения Quintic.
Данные были экспортированы в файл Excel, где они использовались для расчета всех переменных метания копья. Графики были составлены с использованием этой информации. Неподвижные изображения были сняты из видео, чтобы обозначить различные этапы упражнения.
Функции используемого программного обеспечения Quintic:
- Модуль одноточечной оцифровки
- Фильтр Баттерворта
- Калибровка
- Интерактивный график и дисплеи данных
- Экспорт данных
- Захват нескольких изображений
Результаты
Каждый из метаний копья был проанализирован с использованием одноточечной оцифровки.Каждый кадр с момента выпуска до конца ролика был оцифрован. Используя результаты оцифровки, были рассчитаны такие значения, как расстояние метания, время метания и максимальная высота, достигнутая копьем.
Рисунок 1: Последовательность нескольких изображений метания Javelin |
Таблица 1: Результаты пяти метаний копья
График 1: Начальная скорость метания копья
График 1 показывает начальные скорости всех бросков.Начальная скорость метания копья определяет высоту и длину траектории, при условии, что все остальные факторы остаются постоянными. У броска 2 была самая высокая начальная средняя скорость 28,13 мс, а у остальных — 21,48 мс, 19,70 мс, 22,11 мс‾¹ и 20,87 мс для бросков 1-5 соответственно.
Зная начальное значение скорости, можно определить горизонтальное и вертикальное значения. Горизонтальная скорость копья остается постоянной в течение всего времени полета из-за отсутствия внешних сил, действующих на горизонтальное движение.С другой стороны, вертикальная скорость постоянно меняется из-за силы тяжести. Таблица 1 показывает, что для всех бросков конечная вертикальная скорость больше начальной и имеет отрицательное значение. Это связано с тем, что копье выпущено с высоты. Если объект проецируется и приземляется на одной и той же высоте, то начальная скорость и конечная скорость совпадают. Однако, если объект проецируется с высоты и приземляется ниже этой высоты, конечная скорость будет больше начальной скорости и в противоположном направлении.Все броски имеют отрицательную конечную скорость, так как все копья выпущены с высоты. Бросок 2 имеет большую конечную вертикальную скорость, чем остальные, -19,55 мс‾¹. Это связано с тем, что он прошел большее расстояние и достиг большей высоты, поэтому сила тяжести действовала на копье в течение более длительного периода времени, прежде чем он ударился о землю. Тремя основными переменными, которые влияют на метание копья, являются начальная скорость, угол выпуска и высоты выпуска копья. Одной из этих переменных недостаточно, чтобы обеспечить хороший бросок.Из расчетов в таблице 1, бросок 2 считается самым успешным, так как он прошел самое большое расстояние 82,37 м. В этом броске можно увидеть тенденцию по сравнению с другими. Бросок 2 имеет наименьший угол выброса (40,65 °), самую высокую начальную скорость (28,13 м‾¹) и запускается с максимальной высоты (2,38 м). Все это вместе приводит к броску на самую дальнюю дистанцию.
График 2: угол выпуска и расстояние выброса
Форма траектории снаряда определяется углом проекции.Оптимальный угол выброса снаряда, выпущенного на уровне земли, составляет 45º. Если относительная высота выступа увеличивается, угол выпуска должен уменьшаться. И наоборот, если относительная высота выступа уменьшается, угол выпуска должен увеличиваться. Оптимальный угол выпуска при метании копья составляет 34-36º. Однако этот угол не принимает во внимание внешние факторы, такие как ветер, и поэтому его необходимо изменять в соответствии с минимизацией или максимизацией его воздействия. Если ветер дует против полета копья, то угол выпуска следует немного уменьшить, а при метании в попутный ветер угол выпуска должен быть больше.
Рисунок 2: Угол выпуска метательного копья
График 2 и рисунок 1 показывают углы выпуска пяти метаний копья в возрастающем порядке по сравнению с метанным расстоянием. Бросок с наименьшим углом (бросок 2, 40,65 °), безусловно, достиг самой длинной дистанции (82,37 м). Остальные броски не следуют той же схеме, при этом наибольший угол выпуска находится на втором месте по длине.Это связано с тем, что угол выпуска — только один из факторов, влияющих на расстояние выброса, и хотя угол выпуска может быть не близок к оптимальному, другие факторы могут быть более точными, что дает хороший результат. Увеличение угла выпуска может привести к увеличению расстояния
График 3 и рисунок 2 показывают различную высоту, на которой были выпущены копья. Бросок 2, у которого была самая длинная дистанция, 82,37 м, имел самую высокую точку сброса 2,38 м. Остальные броски выполняются с высотой 1.80 м, 1,96 м, 2,02 м и 1,68 м соответственно.
График 3: освобожденная высота и выброшенное расстояние
Высота, на которой выпущено копье, влияет на оптимальный угол выпуска. Чем больше высота, тем меньше должен быть угол, чтобы увеличить расстояние метания. Высота выпуска может в основном определяться естественным ростом спортсмена и может выдерживать более высоких спортсменов с небольшим преимуществом над своими конкурентами.Поэтому метателям копья часто приходится определять собственный оптимальный угол выпуска в соответствии со своим ростом. Обычно, когда скорость снаряда и угол выброса остаются постоянными, чем выше высота полета, тем больше время полета. Следовательно, чем больше время полета, тем больше расстояние.
Рисунок 3: Высота от земли
График 4: Угол вылета копья
График 4 сравнивает высоту выпуска с углом выпуска.Можно было бы ожидать, что с увеличением высоты угол уменьшается. Оптимальный угол выпуска от уровня земли — 45º; таким образом, все броски должны производиться под углом менее 45 °. Только три метателя имеют угол выброса менее 45 °, бросок 2, при котором копье выпущено на 2,38 м над землей под углом 40,65 °, бросок 4, при котором копье выпущено на высоте 2,02 м над землей под углом 43,41 °. и бросок 5, который выпустил копье на 1,68 м над землей под углом 43.63º. Два других броска имели углы чуть выше 45 °, составляющие 45,55 ° и 45,58 ° для бросков 1 и 3 соответственно. Уменьшение угла их выпуска может увеличить дальность метания копья.
Заключение:
Понимание того, как работает движение снаряда, очень полезно для определения того, как лучше всего двигать объект. Что касается метания копья, то умение рассчитывать различные переменные помогает спортсмену разработать лучшую технику для него лично, чтобы метать самую длинную дистанцию.Часто, глядя на метательное движение объекта, можно выявить ошибки на других этапах техники. Например, начальная скорость копья может использоваться как показатель количества движения, созданного во время подготовительной фазы действия. Часто низкая начальная скорость является результатом потери импульса во время этой фазы, и поэтому необходимо изменить методику, чтобы улучшить начальную скорость. То же самое и с другими видами спорта, такими как толкание ядра, баскетбол, вбрасывание в футбол и многие другие.
Расстояние до снаряда можно также рассчитать, используя начальную скорость, угол выпуска и высоту выпуска, по следующему уравнению:
Расстояние = Vi * cos Θ [Vi * sin Θ + √ ((Vi² * sin² Θ) + (2 * h * g)) / g]
Где:
Vi = начальная скорость (мс‾¹)
Θ = угол выпуска (град)
h = высота выпуска (м)
g = ускорение свободного падения (9.81 мс²)
Projectile Motion
Projectile Motion
Движение снаряда
| Объект бросает прямо вверх с вершины здания высотой h футов с начальной скоростью v футов в секунду. Высота объекта как функция времени может быть смоделирована функцией h (t) = –16t 2 + vt + h, где h (t) — высота объекта (в футах) через t секунд после него. брошен. Если нам задана начальная скорость (или скорость) объекта и высота здания, мы можем использовать эту модель, чтобы определить, сколько времени требуется, чтобы объект достиг разной высоты.В этой модели предполагается, что объект не попадает в верхнюю часть здания на обратном пути к земле и что сопротивление ветра минимально. |
Вот шаги, необходимые для решения проблем движения снаряда:
| Шаг 1 : | Установите данное уравнение равным соответствующей высоте. |
| Шаг 2 : | Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. |
| Шаг 3 : | В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. |
Пример 1 — Мяч бросается прямо вверх с вершины здания высотой 128 футов с начальной скоростью 32 фута в секунду. Высота шара как функция времени может быть смоделирована функцией h (t) = –16t 2 + 32t + 128.Сколько времени потребуется, чтобы мяч коснулся земли?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударится о землю только один раз. |
Пример 2 — Мяч бросается прямо вверх с вершины здания высотой 288 футов с начальной скоростью 48 футов в секунду. Высота мяча как функция времени может быть смоделирована функцией h (t) = –16t 2 + 48t + 288. Когда мяч достигнет высоты 320 футов?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте.В этом случае мы устанавливаем уравнение равным 320, потому что мы хотим определить, когда высота будет 320 футов. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе.В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 320 футов один раз на пути вверх и еще раз на пути вниз. |
Щелкните здесь для практических задач
Пример 3 — Ракета запускается прямо с вершины здания высотой 24 фута с начальной скоростью 92 фута в секунду. Высота ракеты как функция времени может быть смоделирована функцией h (t) = –16t 2 + 92t + 24.Сколько времени потребуется, чтобы ракета упала на землю?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударится о землю только один раз. |
Щелкните здесь для практических задач
Пример 4 — Мяч падает прямо в воздухе с высоты 4 фута с начальной скоростью 64 фута в секунду. Высота шара как функция времени может быть смоделирована функцией h (t) = –16t 2 + 64t + 4.Когда мяч достигнет высоты 52 футов?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным 52, потому что мы хотим определить, когда высота будет 52 фута. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 52 футов один раз на пути вверх и еще раз на пути вниз. |
Щелкните здесь для практических задач
Движение снаряда
Движение снаряда
3.3.
Projectile Motion
Самый большой азарт в бейсболе — это хоумран. Движение мяча по изогнутой траектории в трибуны — это распространенный тип двумерного движения, называемого «движением снаряда».«Хорошее описание такого движения часто можно получить, если предположить, что сопротивление воздуха отсутствует.
ОБЗОР КОНЦЕПЦИИ Следуя подходу, описанному на рис. 3.6, мы рассматриваем горизонтальную и вертикальную части движения отдельно. В горизонтальном или осевом направлении движущийся объект (снаряд) не замедляется при отсутствии сопротивления воздуха. Таким образом, компонент x скорости остается постоянным на своем начальном значении или v x = v 0x , а компонент x ускорения равен x = 0 м / с 2 .Однако в вертикальном или y-направлении снаряд испытывает действие силы тяжести. В результате y-составляющая скорости v y не постоянна, а изменяется. Компонент y ускорения a y — это ускорение силы тяжести вниз. Если путь или траектория снаряда близка к поверхности земли, y имеет магнитуду 9,80 м / с 2 . Таким образом, в этом тексте фраза «движение снаряда» означает, что x = 0 м / с 2 и y равны ускорению свободного падения, как показано в краткой концепции на рисунке 3.8 резюмирует. Пример 2 и другие примеры в этом разделе иллюстрируют, как уравнения кинематики применяются к движению снаряда.
|
| Пример 2 Пакет помощи при падении |
На рис. 3.9 показан самолет, движущийся горизонтально с постоянной скоростью +115 м / с на высоте 1050 м. Направления вправо и вверх были выбраны как положительные. Самолет выпускает «посылку», которая падает на землю по криволинейной траектории. Не обращая внимания на сопротивление воздуха, определите время, необходимое для того, чтобы пакет упал на землю.
Рассуждения
С этими данными можно использовать уравнение 3.5b () для определения времени спада.
Решение | ||||||||||||||||||||||
Свободно падающий пакет в Примере 2 набирает вертикальную скорость при спуске. Горизонтальная составляющая скорости, однако, сохраняет свое начальное значение v 0x = + 115 м / с на протяжении всего спуска. Поскольку самолет также движется с постоянной горизонтальной скоростью +115 м / с, он остается прямо над падающим пакетом. Пилот всегда видит пакет прямо под самолетом, как показано пунктирными вертикальными линиями на рисунке 3.9 шоу. Этот результат является прямым следствием того факта, что упаковка не имеет ускорения в горизонтальном направлении. В действительности сопротивление воздуха могло бы замедлить пакет, и он не оставался бы непосредственно под самолетом во время снижения. Рисунок 3.10 дополнительно поясняет этот момент, показывая, что происходит с двумя пакетами, выпущенными одновременно с одной и той же высоты. Пакет B получает начальную составляющую скорости v 0x = + 115 м / с в горизонтальном направлении, как в Примере 2, и пакет следует по пути, показанному на рисунке.Пакет A, с другой стороны, сбрасывается с неподвижного аэростата и падает прямо на землю, поскольку v 0x = 0 м / с. Оба пакета одновременно упали на землю.
|
Не только пакеты на Рисунке 3.10 достигают земли одновременно, но y-компоненты их скоростей также равны во всех точках на пути вниз. Однако пакет B ударяется о землю с большей скоростью, чем пакет A. Помните, что скорость — это величина вектора скорости, а скорость B имеет компонент x, а скорость A — нет. Величина и направление вектора скорости для пакета B в момент непосредственно перед тем, как пакет ударяется о землю, вычисляются в Примере 3.
| Пример 3 Скорость пакета Care Package |
Важной особенностью движения снаряда является что нет ускорения в горизонтальном направлении или в направлении оси x.В концептуальном примере 4 обсуждается интересное значение этой функции.
| Концептуальный пример 4 Я выстрелил пулей в воздух… |
Предположим, вы едете в кабриолете с опущенным верхом. Автомобиль движется вправо с постоянной скоростью. Как показано на рис. 3.11, вы наводите винтовку прямо вверх и стреляете из нее. Где бы пуля приземлилась при отсутствии сопротивления воздуха — позади вас, впереди вас или в стволе винтовки?
Обсуждение и решение Если бы сопротивление воздуха присутствовало, пуля замедлилась бы и она приземлилась бы позади вас, к задней части автомобиля. Однако сопротивление воздуха отсутствует, поэтому нужно более внимательно относиться к движению пули.Перед выстрелом из винтовки пуля, винтовка и автомобиль движутся вместе, поэтому пуля и винтовка имеют такую же горизонтальную скорость, что и автомобиль. При выстреле из винтовки пуле придается дополнительная составляющая скорости в вертикальном направлении; пуля сохраняет скорость автомобиля в качестве начальной горизонтальной составляющей скорости, поскольку винтовка направлена прямо вверх. Поскольку для замедления нет сопротивления воздуха, пуля не испытывает горизонтального ускорения. Таким образом, горизонтальная составляющая скорости пули не меняется.Он сохраняет свою первоначальную ценность и остается такой же, как у винтовки и автомобиля. В результате, пуля все время остается прямо над винтовкой и упадет прямо обратно в ствол винтовки , , как показано на рисунке. Эта ситуация аналогична ситуации на рис. 3.9, где посылка при падении остается прямо под плоскостью. Родственное домашнее задание: | |||
| Концептуальное моделирование 3.1 |
| |
Часто снаряды, такие как футбольные мячи и бейсбольные мячи, запускаются в воздух под углом по отношению к земле.Зная начальную скорость снаряда, можно получить большой объем информации о движении. Например, в примере 5 показано, как рассчитать максимальную высоту, достигаемую снарядом.
| Пример 5 Высота начальной точки |
Также можно найти общее время или «время зависания», в течение которого футбольный мяч на рис. 3.12 находится в воздухе. Пример 6 показывает, как определить это время.
| Пример 6 Время полета стартового снаряда |
Еще одна важная особенность движения снаряда называется «дальность полета».«Дальность, как показано на рисунке 3.12, представляет собой горизонтальное расстояние, пройденное между пуском и приземлением, при условии, что снаряд возвращается на тот же вертикальный уровень, на котором он был выпущен. Пример 7 показывает, как получить диапазон.
| Концептуальное моделирование 3.2 |
| |
| Пример 7 Диапазон Kickoff |
Диапазон в предыдущем примере зависит от угла q , по которому выстреливается снаряд выше горизонтали. Когда сопротивление воздуха отсутствует, максимальный диапазон достигается при.
| Проверьте свое понимание 3 |
| ||
В примерах, рассмотренных до сих пор, использовалась информация о начальном местоположении и скорости снаряда для определения конечного местоположения и скорости. В примере 8 рассматривается противоположная ситуация и показано, как конечные параметры могут использоваться с уравнениями кинематики для определения начальных параметров.
Бейсболист совершает хоумран, и мяч приземляется на сиденье слева, на 7,5 м выше точки, в которой он был поражен. Он приземляется со скоростью 36 м / с под углом 28 ° от горизонтали (см. Рисунок 3.13). Не обращая внимания на сопротивление воздуха, найдите начальную скорость, с которой мяч покидает биту.
Рассуждения Следовательно, необходимо найти v 0x и v 0y , что мы и проделаем с уравнениями кинематики. Решение Значение для v 0y может быть получено из уравнения 3.6b и данных, отображаемых ниже (см. Рисунок 3.13 для положительного и отрицательного направлений):
При определении v 0y мы выбираем знак плюса для квадратного корня, потому что вертикальная составляющая начальной скорости указывает вверх на рис. 3.13, что является положительным направлением. Начальная скорость v 0 и угол q бейсбольного мяча равны | ||||||||||||||||||||||||||
| ||
При движении снаряда величина ускорения силы тяжести существенно влияет на траекторию. Например, бейсбольный мяч или мяч для гольфа на Луне полетел бы намного дальше и выше, чем на Земле, если бы был запущен с той же начальной скоростью. Причина в том, что гравитация Луны примерно в шесть раз меньше земной.
Раздел 2.6 указывает, что определенные типы симметрии относительно времени и скорости присутствуют для свободно падающих тел. Эта симметрия также присутствует в движении снаряда, поскольку снаряды свободно падают в вертикальном направлении. В частности, время, необходимое снаряду для достижения максимальной высоты H, равно времени, затраченному на возвращение на землю. Кроме того, на рис. 3.14 показано, что скорость v объекта на любой высоте над землей на восходящей части траектории равна скорости v на той же высоте на нисходящей части.Хотя две скорости одинаковы, скорости разные, потому что они указывают в разных направлениях. Концептуальный пример 9 показывает, как использовать этот тип симметрии в своих рассуждениях.
|
| Концептуальный пример 9 Два способа бросить камень |
С вершины утеса над озером человек бросает два камня.Камни имеют одинаковую начальную скорость v 0 , но камень 1 бросается вниз под углом q ниже горизонтали, а камень 2 бросается вверх под тем же углом над горизонтом, как показано на рис. 3.15. Не обращайте внимания на сопротивление воздуха и решите, какой камень ударяет в воду с большей скоростью.
Обсуждение и решение Мы можем предположить, что камень 1, брошенный вниз, ударится по воде с большей скоростью. Чтобы показать, что это не так, давайте проследим путь камня 2, когда он поднимается на максимальную высоту и падает обратно на землю. Обратите внимание на точку P на рисунке, где камень 2 возвращается на свою первоначальную высоту; здесь скорость камня 2 равна v 0 , но его скорость направлена под углом q ниже горизонтали.Это именно тот тип симметрии снаряда, который показан на рис. 3.14. Таким образом, в этот момент камень 2 имеет скорость, идентичную скорости, с которой камень 1 бросается вниз с вершины утеса. С этого момента скорость камня 2 изменяется точно так же, как и скорость камня 1, поэтому оба камня ударяются о воду с одинаковой скоростью. Родственное домашнее задание: | |||
Во всех примерах этого раздела снаряды движутся по криволинейной траектории.В общем, если единственное ускорение вызвано действием силы тяжести, форму траектории можно представить как параболу.
| Тест самооценки 3.1 |
| |
| Авторские права © 2000-2003 John Wiley & Sons, Inc. или связанных компаний. Все права защищены. |
4.3 Движение снаряда — University Physics Volume 1
Задачи обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
- Рассчитайте дальность, время полета и максимальную высоту снаряда, который выпущен и попадает в плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитайте траекторию полета снаряда.
Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, при котором происходит только ускорение под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны.Некоторые примеры включают метеоры при входе в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядами , а их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Самый важный факт, о котором следует помнить, это то, что движений вдоль перпендикулярных осей являются независимыми и, таким образом, могут быть проанализированы отдельно. Мы обсуждали этот факт в статье «Векторы смещения» и «Векторы скорости», где мы увидели, что вертикальные и горизонтальные движения независимы. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения: одно по горизонтальной оси, а другое по вертикали. (Этот выбор осей является наиболее разумным, поскольку ускорение силы тяжести является вертикальным; таким образом, нет ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось осью x , а вертикальную ось — осью y . Необязательно, чтобы мы использовали этот выбор осей; это просто удобно в случае ускорения свободного падения. В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение смещения, где мы определяем
— полное смещение, а
и
— его составляющие векторы по горизонтальной и вертикальной осям соответственно.Величины этих векторов равны s , x и y .
Рис. 4.11. Полное смещение s футбольного мяча в точке на его пути. Вектор
имеет компоненты
и
по горизонтальной и вертикальной осям. Его величина равна s, и он составляет угол θ с горизонтом.
Чтобы полностью описать движение снаряда , мы должны включить скорость и ускорение, а также смещение.Мы должны найти их компоненты по осям x- и y . Предположим, что все силы, кроме силы тяжести (например, сопротивление воздуха и трение), незначительны. Определив положительное направление как восходящее, компоненты ускорения будут очень простыми:
Поскольку сила тяжести вертикальная,
Если
, это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или
С этими условиями для ускорения и скорости, мы можем записать кинематику (Уравнение) через (Уравнение) для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из Движение с постоянным ускорением.Кинематические уравнения движения в однородном гравитационном поле становятся кинематическими уравнениями с
Горизонтальное перемещение
Вертикальное перемещение
Используя эту систему уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем: движение снаряда
- Разложите движение на горизонтальные и вертикальные компоненты по осям x и y .Величины составляющих смещения
по этим осям равны x и y. Величины компонент скорости
—
, где v — величина скорости, а θ — ее направление относительно горизонтали, как показано на (Рисунок).
- Рассматривайте движение как два независимых одномерных движения: одно горизонтальное, а другое вертикальное.Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: одном горизонтальном и одном вертикальном. Обратите внимание, что единственная общая переменная между движениями — это время t . Процедуры решения проблем здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
- Перекомбинируйте величины в горизонтальном и вертикальном направлениях, чтобы найти полное смещение.
и скорость
Определите величину и направление смещения и скорости, используя
.
, где θ — направление смещения
Рисунок 4.12 (a) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям. (б) Горизонтальное движение простое, потому что
и
— постоянная величина. (c) Скорость в вертикальном направлении начинает уменьшаться по мере того, как объект поднимается. В самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости.(d) Движения по осям x и y объединяются для получения полной скорости в любой заданной точке траектории.
Пример
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка снаряд выстреливает в воздух с начальной скоростью 70,0 м / с под углом
выше горизонтали, как показано на (Рисунок). Взрыватель рассчитан на то, чтобы зажечь снаряд, когда он достигнет своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда.б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?
Рис. 4.13. Траектория выстрела фейерверка. Взрыватель настроен так, чтобы взорвать снаряд в наивысшей точке его траектории, которая находится на высоте 233 м и 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальное и вертикальное, в котором
и
Затем мы можем определить
и
равняться нулю и найти желаемые количества.
Решение
(a) Под «высотой» мы понимаем высоту или вертикальное положение y над начальной точкой. Наивысшая точка любой траектории, называемая апексом , достигается, когда
Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
Потому что
и
равны нулю, уравнение упрощается до
Решение y дает
Теперь мы должны найти
составляющая начальной скорости в направлении y .Выдается
где
— начальная скорость 70,0 м / с,
— начальный угол. Таким образом,
и y равно
Таким образом, имеем
Обратите внимание, что поскольку верх положительный, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательно.Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
(b) Как и во многих других физических задачах, существует несколько способов решения, пока снаряд достигает своей наивысшей точки. В этом случае самый простой способ — использовать
.
Потому что
на вершине, это уравнение сводится просто к
или
Это время также подходит для больших фейерверков. Если вы видите запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется.Другой способ узнать время — использовать
.
Это оставлено вам в качестве упражнения.
(c) Поскольку сопротивление воздуха незначительно,
, а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение — это горизонтальная скорость, умноженная на время, равное
.
где
равно нулю. Таким образом,
где
— это составляющая скорости x , равная
.
Время t для обоих движений одинаково, поэтому x равно
Горизонтальное движение — это постоянная скорость при отсутствии сопротивления воздуха.Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, сопротивление воздуха оказывает большое влияние, и многие осколки падают прямо под ним.
(d) Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что здесь нужно, — это найти величину и направление смещения в наивысшей точке:
Обратите внимание, что угол для вектора смещения меньше начального угла запуска.Чтобы понять, почему это так, просмотрите (рисунок), на котором показана кривизна траектории к уровню земли.
При решении (рисунок) (а), выражение, которое мы нашли для y , действительно для любого движения снаряда, когда сопротивление воздуха незначительно. Назовем максимальную высоту х = х . Затем
Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание
Камень сброшен со скалы горизонтально
со скоростью 15,0 м / с. (а) Определите начало системы координат. (б) Какое уравнение описывает горизонтальное движение? (c) Какие уравнения описывают вертикальное движение? (г) Какова скорость камня в точке удара?
[показывать-ответ q = ”fs-id1165168031779 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168031779 ″]
(a) Выберите вершину утеса, куда бросается камень из начала системы координат.Хотя это произвольно, мы обычно выбираем время t = 0, чтобы соответствовать началу координат. (b) Уравнение, описывающее горизонтальное движение:
с
это уравнение становится
(c) (рисунок) — (рисунок) и (рисунок) описывают вертикальное движение, но с
эти уравнения значительно упрощаются и становятся
и
(d) Мы используем кинематические уравнения, чтобы найти составляющие x и y скорости в точке удара.Используя
и учитывая, что точка удара равна -100,0 м, мы находим, что составляющая скорости при ударе y равна
Нам дается компонент x ,
, поэтому мы можем рассчитать общую скорость при ударе: v = 46,8 м / с и
ниже горизонтали.
[/ hidden-answer]
Пример
Расчет движения снаряда: теннисист
Теннисист выигрывает матч на стадионе Артура Эша и отбивает мяч на трибунах со скоростью 30 м / с и под углом
над горизонтом ((Рисунок)).Спускаясь вниз, зритель ловит мяч на 10 м выше точки удара. (а) Подсчитайте время, за которое теннисный мяч достигает зрителя. (б) Каковы величина и направление скорости мяча при ударе?
Рисунок 4.14 Траектория удара теннисного мяча о трибуны.
Стратегия
Опять же, разделение этого двумерного движения на два независимых одномерных движения позволяет нам найти желаемые величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением.Таким образом, сначала мы решаем t . Пока мяч поднимается и опускается вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается окончательная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить
в конечный момент времени t , определенный в первой части примера.
Решение
(a) Пока мяч находится в воздухе, он поднимается, а затем падает в конечное положение на 10,0 м выше его начальной высоты.Мы можем найти время для этого, используя (Рисунок):
Если взять начальную позицию
равняется нулю, тогда конечная позиция будет y = 10 м. Начальная вертикальная скорость — это вертикальная составляющая начальной скорости:
Подставив в (рисунок) вместо y , мы получим
Перестановка членов дает квадратное уравнение в t :
Использование формулы корней квадратного уравнения дает т = 3.79 с и т = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз, — мы выбираем более длительное решение для времени, которое требуется мячу, чтобы достичь зрителя:
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10,0 м ниже своей начальной высоты, проводит в воздухе 3,79 с.
(б) Мы можем найти окончательные горизонтальную и вертикальную скорости
и
с использованием результата из (а).Затем мы можем объединить их, чтобы найти величину вектора полной скорости
и угол
делает с горизонтальным. С
является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем как начальную скорость, так и начальный угол. Следовательно,
Окончательная вертикальная скорость определяется выражением (Рисунок):
с
было найдено в части (а) как 21.2 м / с, имеем
Величина конечной скорости
это
Направление
находится через арктангенс:
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется 10.0 м ниже начальной высоты проводит в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость равна
.
ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч сталкивается с точкой с другой стороны от вершины траектории и, следовательно, имеет отрицательную составляющую скорости y . Величина скорости меньше, чем величина ожидаемой начальной скорости, поскольку он падает на 10,0 м над отметкой пуска.
Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, выпущенного по плоской горизонтальной поверхности и ударяющегося по этой же поверхности. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем вычислить время полета снаряда, который одновременно запускается и ударяется о плоскую горизонтальную поверхность, выполнив некоторые манипуляции с кинематическими уравнениями.Отметим, что положение и смещение в y должны быть нулевыми при запуске и при ударе о ровную поверхность. Таким образом, мы устанавливаем смещение в y равным нулю и находим
Факторинг, у нас
Решение для т дает нам
Это время полета для снаряда, выпущенного и попавшего в плоскую горизонтальную поверхность. (Рисунок) не применяется, когда снаряд приземляется на высоте, отличной от того, на каком он был выпущен, как мы видели на (Рисунок), когда теннисист отбивает мяч в трибуны.Другое решение, t = 0, соответствует времени запуска. Время полета линейно пропорционально начальной скорости в направлении y и обратно пропорционально g . Таким образом, на Луне, где сила тяжести в шесть раз меньше земной, снаряд, запущенный с той же скоростью, что и на Земле, будет лететь в шесть раз дольше.
Траектория
Траектория снаряда может быть найдена путем исключения временной переменной t из кинематических уравнений для произвольного t и решения для y ( x ).Берем
, поэтому снаряд запускается из исходной точки. Кинематическое уравнение для x дает
Подставляя выражение для t в уравнение для положения
дает
Переставляя сроки, получаем
Это уравнение траектории имеет вид
, которое представляет собой уравнение параболы с коэффициентами
Диапазон
Из уравнения траектории мы также можем найти диапазон , или горизонтальное расстояние, пройденное снарядом.Факторинг (рисунок), имеем
Положение y равно нулю как для точки запуска, так и для точки удара, поскольку мы снова рассматриваем только плоскую горизонтальную поверхность. Установка y = 0 в этом уравнении дает решение x = 0, соответствующее точке запуска, и
соответствует точке удара. Использование тригонометрического тождества
и установив x = R для диапазона, находим
Обратите особое внимание на то, что (рисунок) действительно только для запуска и удара о горизонтальную поверхность.Мы видим, что диапазон прямо пропорционален квадрату начальной скорости
.
и
, и он обратно пропорционален ускорению свободного падения. Таким образом, на Луне дальность полета будет в шесть раз больше, чем на Земле при той же начальной скорости. Кроме того, из множителя
видно, что
, что диапазон максимален на
Эти результаты показаны на (Рисунок). В (а) мы видим, что чем больше начальная скорость, тем больше диапазон.В (b) мы видим, что диапазон максимален на
Это верно только для условий, в которых сопротивление воздуха не учитывается. Если учесть сопротивление воздуха, максимальный угол будет несколько меньше. Интересно, что тот же диапазон обнаружен для двух начальных углов пуска, которые в сумме составляют
°.
Снаряд, выпущенный с меньшим углом, имеет меньшую вершину, чем больший угол, но они оба имеют одинаковую дальность.
Рис. 4.15. Траектории полета снарядов на ровной поверхности.(а) Чем больше начальная скорость
, тем больше диапазон для данного начального угла. (б) Влияние начального угла
на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон такой же для начальных углов
и
, хотя максимальные высоты этих путей различаются.
Пример
Сравнение снимков в гольф
Гольфист оказывается в двух разных ситуациях на разных лунках.На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и позволить ему вылететь на лужайку. Он направляет выстрел низко к земле, на
.
в горизонтальное положение, чтобы мяч катился после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным перекатом после удара. Здесь он направляет выстрел на
.
в горизонтальное положение, чтобы свести к минимуму перекатывание после удара. Оба выстрела попадают и попадают на ровную поверхность.
(а) Какова начальная скорость мяча во второй лунке?
(b) Какова начальная скорость мяча на четвертой лунке?
(c) Напишите уравнение траектории для обоих случаев.
(d) Постройте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (a), так и для (b). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Решение
(а)
(б)
(в)
(d) Используя графическую утилиту, мы можем сравнить две траектории, которые показаны на (Рисунок).
Рис. 4.16. Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка взлета.
Значение
Начальная скорость для выстрела на
больше начальной скорости выстрела на
Примечание из (Рисунок), что два снаряда, выпущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска складываются с
.
Углы запуска в этом примере складываются, чтобы получить число больше
.
Таким образом, выстрел на
должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он приземлится на меньшем расстоянии.
Проверьте свое понимание
Если бы два удара в гольф на (Рис.) Были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
[show-answer q = ”fs-id1165166636799 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166636799 ″]
Удар для гольфа на
[/ hidden-answer]
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мала по сравнению с окружностью Земли.Если, однако, дальность полета велика, Земля изгибается под ударом снаряда, и ускорение силы тяжести меняет направление на траектории. Диапазон больше, чем предсказывалось уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на (Рисунок), который основан на чертеже в книге Ньютона Principia. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с объект падает на 5 м без сопротивления воздуха.Таким образом, если объекту задана горизонтальная скорость
(или
у поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность постоянно падает от объекта. Это примерно скорость космического челнока на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в книге «Гравитация».
Рисунок 4.17 Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости радиус действия увеличивается и становится больше, чем на ровной поверхности, потому что Земля изгибается под своим путем. Со скоростью 8000 м / с достигается орбита.
Резюме
- Движение снаряда — это движение объекта, подверженного только ускорению свободного падения, где ускорение постоянно, как у поверхности Земли.
- Чтобы решить задачи о движении снаряда, мы анализируем движение снаряда в горизонтальном и вертикальном направлениях, используя одномерные кинематические уравнения для x и y .
- Время полета снаряда, выпущенного с начальной вертикальной скоростью.
на ровной поверхности дает
Это уравнение действительно только тогда, когда снаряд приземляется на той же высоте, с которой был запущен.
- Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью. Опять же, уравнение для диапазона действительно только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.
Концептуальные вопросы
Ответьте на следующие вопросы относительно движения снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом, не равным
или
(a) Скорость когда-либо равна нулю? (б) Когда скорость минимальна? Максимум? (c) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0? (d) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0?
[показывать-ответ q = ”fs-id1165167780957 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167780957 ″]
а.нет; б. минимум на вершине траектории и максимум при старте и ударе; c. нет, скорость — вектор; d. да, где приземляется
[/ hidden-answer]
Ответьте на следующие вопросы относительно движения снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом, не равным
или
(a) Ускорение всегда равно нулю? (б) Ускорение когда-либо в том же направлении, что и компонент скорости? (c) Ускорение когда-либо противоположно направлению компонента скорости?
Монета кладется на край стола так, чтобы она немного свешивалась.Четверть скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о десятицентовую монету. Какая монета первой падает на землю?
[show-answer q = ”fs-id1165166623383 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166623383 ″]
Они оба одновременно упали на землю.
[/ hidden-answer]
Проблемы
Пуля выпускается горизонтально с высоты плеча (1,5 м) с начальной скоростью 200 м / с. а) Сколько времени проходит до того, как пуля упадет на землю? (б) Как далеко пуля летит по горизонтали?
[show-answer q = ”fs-id1165168072758 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168072758 ″]
а.
, г.
[/ hidden-answer]
Мрамор скатывается со столешницы высотой 1,0 м и ударяется об пол на расстоянии 3,0 м от края стола в горизонтальном направлении. а) Как долго мрамор витает в воздухе? б) С какой скоростью мрамор отрывается от края стола? (c) С какой скоростью он падает на пол?
Дротик бросается горизонтально со скоростью 10 м / с в мишень мишени для дротика 2.На расстоянии 4 м, как показано на следующем рисунке. (а) Насколько далеко ниже намеченной цели попадает дротик? (б) Что ваш ответ говорит вам о том, как опытные игроки в дартс бросают свои дротики?
[показывать-ответ q = ”fs-id1165168078466 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168078466 ″]
а.
, г. Они стремятся высоко.
[/ hidden-answer]
Самолет, летящий горизонтально со скоростью 500 км / ч на высоте 800 м, сбрасывает ящик с припасами (см. Следующий рисунок).Если парашют не открывается, как далеко от точки сброса ящик ударяется о землю?
Предположим, что самолет в предыдущей задаче выпускает снаряд горизонтально в направлении своего движения со скоростью 300 м / с относительно плоскости. (а) На каком расстоянии от точки выброса снаряд ударяется о землю? б) С какой скоростью он ударяется о землю?
[show-answer q = ”fs-id1165167989106 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167989106 ″]
а.,
г.
[/ hidden-answer]
Питчер фастбола может бросать бейсбольный мяч со скоростью 40 м / с (90 миль / ч). (a) Предполагая, что питчер может выпустить мяч на расстоянии 16,7 м от пластины дома, поэтому мяч движется горизонтально, сколько времени требуется мячу, чтобы добраться до пластины дома? (b) Как далеко мяч падает между рукой питчера и тарелкой хозяина?
Снаряд запускается под углом
и приземляется через 20 с на той же высоте, на которой был запущен.а) Какова начальная скорость снаряда? б) Какая максимальная высота? (c) Каков диапазон? (d) Рассчитайте смещение от точки запуска до положения на траектории за 15 с.
[показывать-ответ q = ”fs-id1165166793284 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165166793284 ″]
а.
, г.
г.
г.
[/ hidden-answer]
Баскетболист делает бросок в корзину 6.1 м и 3,0 м над полом. Если мяч выпущен на высоте 1,8 м от пола под углом
выше горизонтали, какой должна быть начальная скорость, если он пройдет через корзину?
В определенный момент воздушный шар находится на высоте 100 м и снижается с постоянной скоростью 2,0 м / с. Именно в этот момент девушка бросает мяч горизонтально относительно себя с начальной скоростью 20 м / с. Когда она приземлится, где она найдет мяч? Не обращайте внимания на сопротивление воздуха.
[show-answer q = ”fs-id11651665
″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651665
″]
[/ hidden-answer]
Человек на мотоцикле, едущем с постоянной скоростью 10 м / с, бросает пустую банку прямо вверх относительно себя с начальной скоростью 3,0 м / с. Найдите уравнение траектории, которую видит полицейский на обочине дороги. Предположим, что исходное положение банки — это точка, в которую она брошена.Не обращайте внимания на сопротивление воздуха.
В прыжке в длину спортсмен может прыгнуть на расстояние 8,0 м. На какое максимальное расстояние спортсмен может прыгнуть на Луне, где ускорение свободного падения в шесть раз меньше земного?
[показывать-ответ q = ”fs-id1165167996165 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167996165 ″]
[/ hidden-answer]
Максимальное горизонтальное расстояние, на которое мальчик может бросить мяч, составляет 50 метров. Предположим, он может бросать с одинаковой начальной скоростью под любым углом.Насколько высоко он подбрасывает мяч, когда бросает его прямо вверх?
Камень сброшен со скалы под углом
по горизонтали. Высота обрыва 100 м. Начальная скорость камня 30 м / с. а) Насколько высоко над краем утеса поднимается скала? б) Как далеко он переместился по горизонтали, когда находится на максимальной высоте? (c) Через какое время после выброса он падает на землю? г) Каков радиус действия скалы? (e) Каковы горизонтальное и вертикальное положение скалы относительно края обрыва при t = 2.0 с, т = 4,0 с и т = 6,0 с?
[показывать-ответ q = ”fs-id1165167746378 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167746378 ″]
а.
,
г.
,
г.
,
г.
,
e.
[/ hidden-answer]
Пытаясь спастись от преследователей, секретный агент спускается на лыжах со склона
.
ниже горизонтали на скорости 60 км / ч. Чтобы выжить и приземлиться на снегу на 100 м ниже, он должен преодолеть ущелье шириной 60 м. Он это делает? Не обращайте внимания на сопротивление воздуха.
Игрок в гольф на фервее находится в 70 м от грина, который находится ниже уровня фервея на 20 м.Если гольфист отбивает мяч под углом
с начальной скоростью 20 м / с, как близко она подходит к зеленому?
[показывать-ответ q = ”fs-id1165168065281 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168065281 ″]
Таким образом, удар игрока в гольф попадает на расстояние 13,3 м от грина.
[/ hidden-answer]
Снаряд выпущен по холму, основание которого находится на расстоянии 300 м.Снаряд выпущен на
над горизонтом с начальной скоростью 75 м / с. Холм можно представить как плоскость с уклоном
°.
к горизонтали. Относительно системы координат, показанной на следующем рисунке, уравнение этой прямой линии равно
.
Куда на холме приземляется снаряд?
Астронавт на Марсе бьет футбольный мяч под углом
с начальной скоростью 15 м / с.Если ускорение свободного падения на Марсе составляет 3,7 м / с, (а) какова дальность футбольного удара по плоской поверхности? б) Какова будет дальность такого же удара на Луне, где сила тяжести в шесть раз меньше земной?
[Показать-ответ q = ”fs-id1165166572087 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a = ”fs-id1165166572087 ″]
а.
,
г.
[/ hidden-answer]
Майк Пауэлл является рекордсменом по прыжкам в длину из 8.95 м, установлен в 1991 году. Если он отрывался от земли под углом
какова была его начальная скорость?
Робот-гепард
MIT может перепрыгивать через препятствия высотой 46 см и развивает скорость 12,0 км / ч. (а) Если робот запускается под углом
на этой скорости, какова его максимальная высота? б) Какой должен быть угол запуска, чтобы достичь высоты 46 см?
[показывать-ответ q = ”fs-id1165167842253 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165167842253 ″]
а.
[/ hidden-answer]
г. Асама в Японии — действующий вулкан. В 2009 году в результате извержения были выброшены твердые вулканические породы, упавшие на 1 км по горизонтали от кратера. Если бы вулканические породы были запущены под углом
°.
относительно горизонтали и приземлились на 900 м ниже кратера, (а) какова была бы их начальная скорость и (б) каково время их полета?
Дрю Брис из Нового Орлеана Сэйнтс умеет бросать футбольный мяч 23.0 м / с (50 миль / ч). Если он направит бросок под углом
от горизонтали, на какое расстояние он пролетит, если должен быть пойман на той же высоте, что и брошенный?
[показывать-ответ q = ”fs-id1165168098591 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168098591 ″]
[/ hidden-answer]
Лунный движущийся аппарат, использовавшийся в конце миссии НАСА «Аполлон », достиг неофициальной наземной скорости Луны 5.0 м / с — астронавт Юджин Сернан. Если бы марсоход двигался с такой скоростью по плоской лунной поверхности и ударился о небольшую неровность, которая отбрасывала его от поверхности под углом
°.
как долго он будет «летать» на Луне?
Высота футбольных ворот 2,44 м. Игрок отбивает мяч ногой на расстоянии 10 м от ворот под углом
Какова начальная скорость футбольного мяча?
[show-answer q = ”fs-id1165167854326 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167854326 ″]
[/ hidden-answer]
Олимп-Монс на Марсе — крупнейший вулкан Солнечной системы, высотой 25 км и радиусом 312 км.Если вы стоите на вершине, с какой начальной скоростью вам нужно было бы запустить снаряд из пушки по горизонтали, чтобы очистить вулкан и приземлиться на поверхности Марса? Обратите внимание, что Марс имеет ускорение свободного падения
.
В 1999 году Робби Книвел первым прыгнул через Гранд-Каньон на мотоцикле. В узкой части каньона (ширина 69,0 м), двигаясь со взлетной рампы 35,8 м / с, он достиг другой стороны. Какой у него был угол запуска?
[Показать-ответ q = ”fs-id1165168009639 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a = ”fs-id1165168009639 ″]
[/ hidden-answer]
Вы бросаете бейсбольный мяч с начальной скоростью 15.0 м / с под углом
по горизонтали. Какой должна быть начальная скорость мяча при
на планете, которая имеет вдвое большее ускорение силы тяжести, чем Земля, чтобы достичь той же дальности? Рассмотрим запуск и удар о горизонтальную поверхность.
Аарон Роджерс бросает мяч со скоростью 20,0 м / с в свой широкий ресивер, который бежит прямо по полю со скоростью 9,4 м / с на 20,0 м. Если Аарон бросает мяч, когда дальний приемник достигает 10.0 м, под каким углом должен быть Аарон, чтобы запустить мяч, чтобы получатель поймал его на отметке 20,0 м?
[показывать-ответ q = ”fs-id1165166777489 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165166777489 ″]
Широкому ресиверу требуется 1,1 с, чтобы покрыть последние 10 м своего бега.
[/ hidden-answer]
Глоссарий
- движение снаряда
- движение объекта, подверженного только ускорению свободного падения
- диапазон
- максимальная горизонтальная дальность полета снаряда
- время вылета
- время нахождения снаряда в воздухе
- траектория
- Путь полета снаряда в воздухе
.

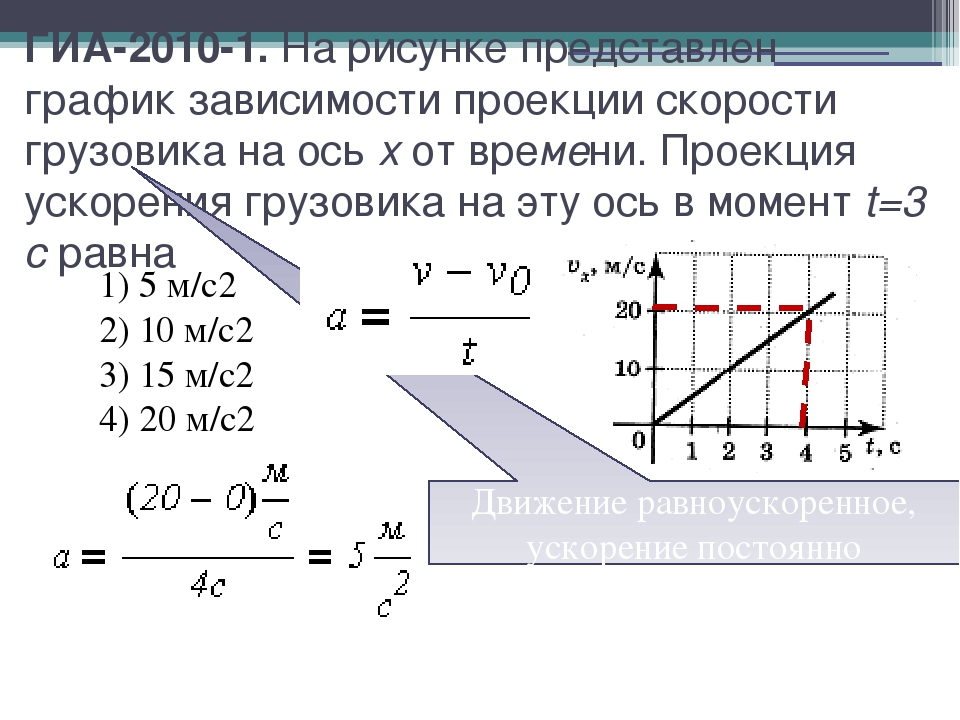 Отсюда находим величину скорости тела на этой высоте — 15 м/с (ответ 3).
Отсюда находим величину скорости тела на этой высоте — 15 м/с (ответ 3).
 2.8 – правильный ответ 4).
2.8 – правильный ответ 4).
 В результате находим, что пройденный телом путь равен 25 м (ответ 3).
В результате находим, что пройденный телом путь равен 25 м (ответ 3).