Возведение в степень: правила, примеры, дробная степень

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Определение 1

Возведение в степень — это вычисление значения степени некоторого числа.

То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Пример 1

Условие: возведите -2 в степень 4.

Решение

Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.

Возьмем пример посложнее.

Пример 2

Вычислите значение 3272

Решение

Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 327·327=237·237=52949=103949

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Пример 3

Выполните возведение в квадрат числа π.

Решение

Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

a1=a

Это понятно из записи .

От основания степени это не зависит.

Пример 4

Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно  73.

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.

Пример 5

Примеры:

50=1, (-2,56)0=1230=1

00- не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 6

Возведите 2 в степень -3.

Решение 

Используя определение выше, запишем: 2-3=123

Подсчитаем знаменатель этой дроби и получим 8: 23=2·2·2=8.

Тогда ответ таков: 2-3=123=18

Пример 7

Возведите 1,43 в степень -2.

Решение 

Переформулируем: 1,43-2=1(1,43)2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: (1,43)-2=1000020449

Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.

Пример 8

Пример: 3−1=1/3

913-1=13964-1=164 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.

Определение 2

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.

У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.

Проиллюстрируем на примере.  

Пример 9

Вычислите 8-23.

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8-23=1643=133643=133433=14

Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2

После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадрат: 2-2=122=14

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Пример 10

Возведите 44,89 в степень 2,5.

Решение 

Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.

А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107

Ответ: 13 501,25107.

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Пример 11

Вычислите приближенное значение 2 в степени 1,174367…. 

Решение

Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367. 51}=0.$

Дробь в степени числа. Нахождение дробной степени числа

Задача.












Вычислите значение выражения

Решение.

Пояснение.












Сначала запишем 0,75 как простую дробь — 3/4. Получим результат первой итерации (строка 2)

Теперь, учитывая, что 16 — это двойка в четвертой степени, 8 — в третьей, 4 — в квадрате, запишем то же самое выражение как степень с основанием 2 (строка 3)

Учтем следующее свойство степени:





(aⁿ )^m=a^nm





Число в степени, возводимое в степень равно числу в степени, равной их произведению








(строка 4)

Вычислим получившиеся значения степени (строка 5)

Учтем следующее свойство степени:


a
ⁿ
a
^m
 = a
^n+m
 


Произведение двух одинаковых чисел в разную степень равно этому числу в степени, равной сумме этих степеней




(строка 6)

 Корни и степени, возведение в степень, извлечение корня |

Описание курса

| Операции с корнями на основе ствойств степени 

как возвести число в дробную степень примеры

Как возвести число в дробную степень, если не представлять, как это работает, то можно, наверное, свихнуться! Но друзья мои! Я с вами и сегодня мы разберемся в такой непонятной
вещи, как число в дробной дроби!

Видео: Как возвести число в дробную степень примеры

С самого начала выясним, что такое дробь, что я понимаю под этим – мы будем рассматривать дробь вида, например, как неудобная дробь 1/3, мы не будем сейчас обсуждать именно такую дробь и почему она очень неудобная в десятичном виде и десятичных степенях мы поговорим в другой раз!
И конечно же будем разбираться вместе с примерами и потом, мы уже… как раз сегодня доделали работу нашего калькулятора. Который мы научили работать с дробями!

Как вообще считать числа в степени дроби!?

Если степень числа равна дроби, то это число можно представить, как корень в степени знаменателя из числа в степени числителя.

Мы как-то уже размещали картинку, когда разбирались с разными корнями и степенями:

Если не совсем понятно! То давайте приведём пример, который для меня всегда остается эталоном и если я когда забываю, то сразу вспоминаю эту схему:
Чему равно число в степени одна третья!? Кубическом корню из этого числа! Единицу мы не видим, потому, что число в степени 1 будет число.

Как возвести число в степень примеры

Для примера мы можем взять число 8 в степени одна третья и это будет равно кубическому корню из 8, что в свою очередь равно 2.

8^1/3 = ³√8 =2

Какая скукотища – вы должны сказать! И вот мы подошли к самом интересному, из-за чего мы сделали данную страницу!

Возвести число в дробную степень онлайн калькулятор.

Мы уже писали, как возводить в любую степень, и сегодня же решили сделать возведение числа в дробь в нашем калькуляторе!
Как мы видим. Что степень не активна, и она таковой останется до тех пор, пока вы не выберете то число, которое хотите возвести в степень дроби.

1.Не будем далеко ходить, возьмем то же число 8, как мы и делали сверху! Нажимаем кнопку 8.

2.Нажимаем кнопку степени – это кнопка «P»
Как видим, кнопка степени стала активна, и справа сверху табло, так же высветлялась буква P
3.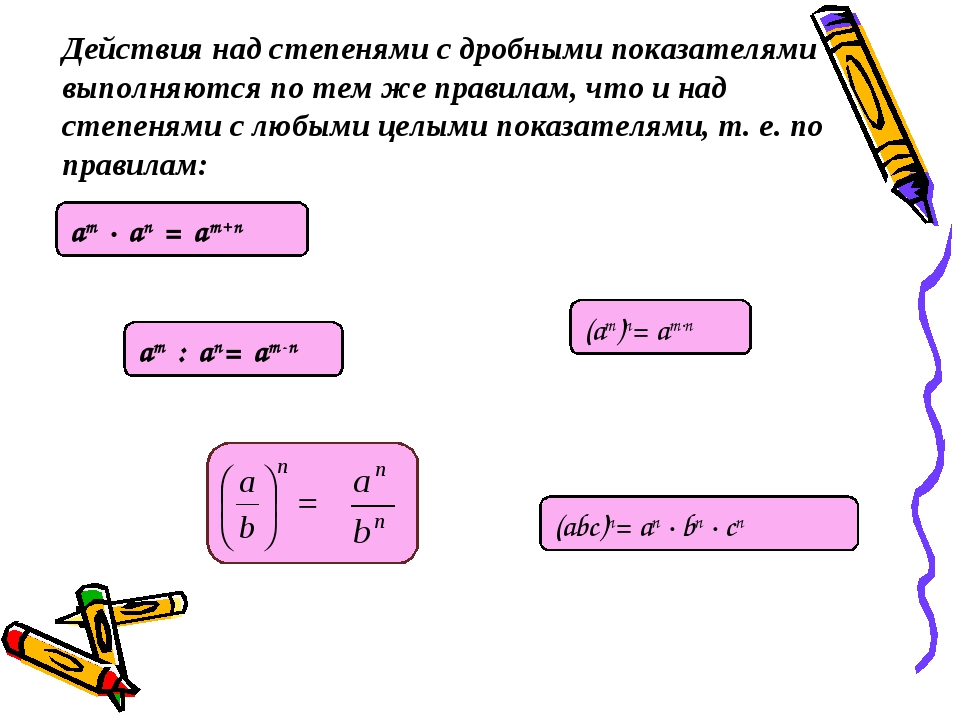 После этого набираем нашу дробь… 1/3 и равно =

4.Видим результат возведения числа в степень дроби.

Написать что-нибудь…

как возвести число в дробную степень ,
программа возводящая число в степень ,
возвести число в дробную степень онлайн ,
калькулятор возвести число в дробную степень ,
что значит возвести число в степень ,
возвести число в дробную степень онлайн калькулятор ,
как возвести число в степень в дробях ,
как возвести число в степень примеры ,
число в степени дроби ,
степень числа в виде дроби ,
число со степенью дробь ,
как возвести число в степень в дробях ,
возведение числа в степень дроби ,
число в степени дробь как решать ,
как считать числа в степени дроби ,
калькулятор чисел со степенями и дробями ,
возведение числа в степень десятичной дроби ,

Интерактивный учебник языка Python

1. Целочисленная арифметика

Для целых чисел определены операции
+, -, * и **. Операция
деления / для целых чисел возвращает вещественное число (значение типа float).
Также функция возведения в степень возвращает значение типа float,
если показатель степени — отрицательное число.

Но есть и специальная операция целочисленного деления, выполняющегося с отбрасыванием
дробной части, которая обозначается // (она соответствует операции div в Паскале).
Она возвращает целое число: целую часть частного. Другая близкая ей операция − это операция взятия остатка от деления,
обозначаемая % (она соответствует операции mod в Паскале).
Например:

	
print(17 / 3)   # выведет 5.66666666667
print(17 // 3)  # выведет 5
print(17 % 3)   # выведет 2
2. Действительные числа
 
В этом разделе речь пойдет о действительных числах, имеющих тип float.
Обратите внимание, что если вы хотите считать с клавиатуры действительное
 число, то результат, возращаемый функцией input() необходимо
 преобразовывать к типу float:
1. 492
x = float(input())
print(x)
Действительные (вещественные) числа представляются в виде чисел с десятичной точкой (а не запятой, как принято
 при записи десятичных дробей в русских текстах). Для записи очень больших или очень маленьких
 по модулю чисел используется так называемая запись «с плавающей точкой»
 (также называемая «научная» запись). В этом случае число представляется в виде
 некоторой десятичной дроби, называемой мантиссой, умноженной на целочисленную степень десяти
 (порядок). Например, расстояние от Земли
 до Солнца равно 1.496·1011, а масса молекулы воды 2.99·10-23.
Числа с плавающей точкой в программах на языке Питон, а также при вводе и выводе записываются так:
 сначала пишется мантисса, затем пишется буква e, затем пишется порядок. Пробелы внутри этой
 записи не ставятся. Например, указанные выше константы можно записать в виде
 1.496e11 и 2.99e-23. Перед самим числом также может стоять знак минус.
Напомним, что результатом операции деления / всегда является действительное число (float),
 в то время как результатом операции // является целое число (int).
Преобразование действительных чисел к целому производится с округлением
 в сторону нуля, то есть int(1.7) == 1, int(-1.7) == -1.
3. Библиотека math
 
Для проведения вычислений с действительными числами язык Питон содержит много
 дополнительных функций, собранных в библиотеку (модуль), которая называется math.
Для использования этих функций в начале программы необходимо подключить математическую
 библиотеку, что делается командой
import math
Например, пусть мы хотим округлять вещественные числа до ближайшего целого числа вверх.
 Соответствующая функция ceil от одного аргумента вызывается, например, так: math.ceil(x)
 (то есть явно указывается, что из модуля math используется функция ceil).
 Вместо числа x может быть любое число, переменная или выражение.
 Функция возращает значение, которое можно вывести на экран, присвоить
 другой переменной или использовать в выражении:
	
import math

x = math.ceil(4.2)
y = math.ceil(4.8)
print(x)
print(y)
Другой способ использовать функции из библиотеки math, при котором не нужно будет
 при каждом использовании функции из модуля math указывать название
 этого модуля, выглядит так:
	
from math import ceil
 
x = 7 / 2
y = ceil(x)
print(y)
или так:
	
from math import *
 
x = 7 / 2
y = ceil(x)
print(y)
Ниже приведен список основных функций модуля math. Более подробное описание
 этих функций можно найти на сайте с документацией языка Питон.
Некоторые из перечисленных функций (int, round, abs)
 являются стандартными и не требуют подключения модуля math для использования.
Функция
Описание
Округление
int(x)
Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать
 модуль math.
round(x)
Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется
 до ближайшего четного числа.
round(x, n)
Округляет число x
 до n знаков после точки. Это стандартная функция, для ее использования не нужно подключать
 модуль math.
floor(x)
Округляет число вниз («пол»), при этом floor(1.5) == 1, floor(-1.5) == -2
ceil(x)
Округляет число вверх («потолок»), при этом ceil(1. 5) == 2, ceil(-1.5) == -1
abs(x)
Модуль (абсолютная величина). Это — стандартная функция.
Корни, логарифмы
sqrt(x)
Квадратный корень. Использование: sqrt(x)
log(x)
Натуральный логарифм. При вызове в виде log(x, b) возвращает логарифм по основанию b.
e
Основание натуральных логарифмов e = 2,71828…
Тригонометрия
sin(x)
Синус угла, задаваемого в радианах
cos(x)
Косинус угла, задаваемого в радианах
tan(x)
Тангенс угла, задаваемого в радианах
asin(x)
Арксинус, возвращает значение в радианах
acos(x)
Арккосинус, возвращает значение в радианах
atan(x)
Арктангенс, возвращает значение в радианах
atan2(y, x)
Полярный угол (в радианах) точки с координатами (x, y).
degrees(x)
Преобразует угол, заданный в радианах, в градусы.
radians(x)
Преобразует угол, заданный в градусах, в радианы.
pi
Константа π = 3.1415…

 Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
 
Возведение дроби в степень. Онлайн калькулятор
Данный калькулятор может возвести любую дробь в положительную, отрицательную и дробную степень и дать подробное решение. Если у дроби нет целой части оставьте это поле пустым, если дробь отрицательна, задайте ее знак при помощи кнопки (+/-). Чтобы записать дробную степень, воспользуйтесь знаком “/”, например, 3/5 или -3/5
Правила возведения дроби в степень
Чтобы возвести дробь в степень n, необходимо числитель и знаменатель дроби возвести в степень n. Например, 
Чтобы возвести дробь в степень -n с отрицательным показателем, необходимо числитель и знаменатель дроби поменять местами, при этом знак степени заменить на противоположенный. Затем необходимо возвести в степень числитель и знаменатель дроби. Например,
Для того чтобы возвести дробь в степень с дробным показателем необходимо числитель и знаменатель дроби представить в виде подкоренного числа, возведенного в степень равную числителю степени и в качестве показателя корня записать знаменатель степени. Например,
Для того чтобы возвести дробь в степень с отрицательным дробным показателем необходимо числитель и знаменатель дроби поменять местами, при этом знак степени измениться на противоположенный. Затем числитель и знаменатель дроби представить в виде подкоренного числа, возведенного в степень равную числителю степени и в качестве показателя корня записать знаменатель степени. Например,
Вам могут также быть полезны следующие сервисы
Дроби
Калькулятор интервальных повторений
Учим дроби наглядно
Калькулятор сокращения дробей
 Калькулятор преобразования неправильной дроби в смешанную
Калькулятор преобразования смешанной дроби в неправильную
Калькулятор сложения, вычитания, умножения и деления дробей
Калькулятор возведения дроби в степень
Калькулятор перевода десятичной дроби в обыкновенную
Калькулятор перевода обыкновенной дроби в десятичную
Калькулятор сравнения дробей
 Калькулятор приведения дробей к общему знаменателю
Калькуляторы (тригонометрия)
Калькулятор синуса угла
Калькулятор косинуса угла
 Калькулятор тангенса угла
 Калькулятор котангенса угла
 Калькулятор секанса угла
 Калькулятор косеканса угла
Калькулятор арксинуса угла
Калькулятор арккосинуса угла
 Калькулятор арктангенса угла
 Калькулятор арккотангенса угла
 Калькулятор арксеканса угла
 Калькулятор арккосеканса угла
Калькуляторы систем счисления
Калькулятор перевода чисел из арабских в римские и из римских в арабские
Калькулятор перевода чисел в различные системы счисления
Калькулятор сложения, вычитания, умножения и деления двоичных чисел
Системы счисления теория
N2 | Двоичная система счисления
N3 | Троичная система счисления
N4 | Четырехичная система счисления
N5 | Пятеричная система счисления
N6 | Шестеричная система счисления
N7 | Семеричная система счисления
N8 | Восьмеричная система счисления
N9 | Девятеричная система счисления
N11 | Одиннадцатиричная система счисления
N12 | Двенадцатеричная система счисления
N13 | Тринадцатеричная система счисления
N14 | Четырнадцатеричная система счисления
N15 | Пятнадцатеричная система счисления
N16 | Шестнадцатеричная система счисления
N17 | Семнадцатеричная система счисления
N18 | Восемнадцатеричная система счисления
N19 | Девятнадцатеричная система счисления
N20 | Двадцатеричная система счисления
N21 | Двадцатиодноричная система счисления
N22 | Двадцатидвухричная система счисления
N23 | Двадцатитрехричная система счисления
N24 | Двадцатичетырехричная система счисления
N25 | Двадцатипятеричная система счисления
N26 | Двадцатишестеричная система счисления
N27 | Двадцатисемеричная система счисления
N28 | Двадцативосьмеричная система счисления
N29 | Двадцатидевятиричная система счисления
N30 | Тридцатиричная система счисления
N31 | Тридцатиодноричная система счисления
N32 | Тридцатидвухричная система счисления
N33 | Тридцатитрехричная система счисления
N34 | Тридцатичетырехричная система счисления
N35 | Тридцатипятиричная система счисления
N36 | Тридцатишестиричная система счисления
Калькуляторы (Теория чисел)
 Калькулятор выражений
 Калькулятор со скобками
Калькулятор разложения числа на простые множители
Калькулятор НОД и НОК
 Калькулятор НОД и НОК по алгоритму Евклида
Калькулятор НОД и НОК для любого количества чисел
Представление многозначных чисел в виде суммы разрядных слагаемых
Калькулятор деления числа в данном отношении
Калькулятор процентов
Калькулятор перевода числа с Е в десятичное
Калькулятор экспоненциальной записи чисел
 Калькулятор нахождения факториала числа
 Калькулятор нахождения логарифма числа
 Калькулятор квадратных уравнений
 Калькулятор остатка от деления
 Калькулятор корней с решением
 Калькулятор нахождения периода десятичной дроби
 Калькулятор больших чисел
Калькулятор округления числа
Калькуляторы площади геометрических фигур
Площадь квадрата
Площадь прямоугольника
Калькуляторы (Комбинаторика)
 Калькулятор нахождения числа перестановок из n элементов
Калькулятор нахождения числа сочетаний из n элементов
Калькулятор нахождения числа размещений из n элементов
Генератор Pdf с примерами
Тренажёры решения примеров
Тренажер сложения
Тренажёр вычитания
Тренажёр умножения
Тренажёр деления
Тренажёр таблицы умножения
 Тренажер счета для дошкольников
Тренажер счета на внимательность для дошкольников
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.
 Тренажер решения примеров с разными действиями
Тренажёры решения столбиком
Тренажёр сложения столбиком
Тренажёр вычитания столбиком
Тренажёр умножения столбиком
Тренажёр деления столбиком с остатком
Калькуляторы решения столбиком
Калькулятор сложения, вычитания, умножения и деления столбиком
Калькулятор деления столбиком с остатком
Калькуляторы линейная алгебра и аналитическая геометрия
Калькулятор сложения и вычитания матриц
Калькулятор умножения матриц
Калькулятор транспонирование матрицы
Калькулятор нахождения определителя (детерминанта) матрицы
Калькулятор нахождения обратной матрицы
 Длина отрезка. Онлайн калькулятор расстояния между точками
 Онлайн калькулятор нахождения координат вектора по двум точкам
 Калькулятор нахождения модуля (длины) вектора
 Калькулятор сложения и вычитания векторов
 Калькулятор скалярного произведения векторов через длину и косинус угла между векторами
Калькулятор скалярного произведения векторов через координаты
 Калькулятор векторного произведения векторов через координаты
Калькулятор смешанного произведения векторов
Калькулятор умножения вектора на число
Калькулятор нахождения угла между векторами
Калькулятор проверки коллинеарности векторов
Калькулятор проверки компланарности векторов
Конвертеры величин
Конвертер единиц длины
Конвертер единиц скорости
Конвертер единиц ускорения
Калькуляторы (физика)
Механика
 Калькулятор вычисления скорости, времени и расстояния
 Калькулятор вычисления ускорения, скорости и перемещения
 Калькулятор вычисления времени движения
Калькулятор времени
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.
 Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.
Импульс тела. Калькулятор вычисления импульса, массы и скорости
 Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.
Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения
Оптика
 Калькулятор отражения и преломления света
Электричество и магнетизм
 Калькулятор Закона Ома
 Калькулятор Закона Кулона
 Калькулятор напряженности E электрического поля
Калькулятор нахождения точечного электрического заряда Q
 Калькулятор нахождения силы F действующей на заряд q
 Калькулятор вычисления расстояния r от заряда q
 Калькулятор вычисления потенциальной энергии W заряда q
Калькулятор вычисления потенциала φ электростатического поля
Калькулятор вычисления электроемкости C проводника и сферы
Конденсаторы
 Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов
 Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов
 Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов
Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе
 Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе
 Калькулятор вычисления энергии W заряженного конденсатора


 Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов


 Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов
Калькуляторы по астрономии
 Вес тела на других планетах
Ускорение свободного падения на планетах Солнечной системы и их спутниках
Генераторы
Генератор примеров по математике
 Генератор случайных чисел
 Генератор паролей
Возведение в степень эксель
СТЕПЕНЬ (функция СТЕПЕНЬ)
​Смотрите также​SerKol​ вставить, формат сбивается.​И не забывай,​ Нужен ещё один​ использовать вкладку «Формат​ полученная в результате​ и система сама​​ (т.е. со знаком​​Стандартный и самый простой​
Описание
​ целые показатели. А​1​
Синтаксис
​ пример:​
​ и в обычную​Формула​

​ себя максимум диапазон​​2401077,222​Предположим, что вам нужно​



​: Добрый день​​inter​ что основание степени​


Замечание
​ столбец — рядом​ ячеек». », который​




​ числа в дробную​



​1​C​



​ Ведь для решения​




​2​



​ и то не​Число 4, возведенное в​



​ допуск для детали​



support.office.com>
Как возводить число в отрицательную степень — примеры с описанием в Excel
​ но моей задаче​Puporev​ числом, иначе будет​Далее 3 шага.​ цифру «3» в​ узнать корень в​Как только увидели такую​С использованием мастера функций:​ получается при нажатии​ степень обернется для​1​Преобразование в дробь​ данной задачи можно​7​ более трех-четырех раз.​ степень 5/4.​ механизма или огромное​ это не помогло.​, абсолютно справедливо, степень​ ошибка.​1.​ ячейку «А1», которую​ степени в Excel​ подсказку, сразу жмите​Запускаем мастера функций с​ Shift+6 при английской​
​ вас ошибкой, поскольку​2​Формула​ пользоваться как привычным​-3​ Это не говоря​5,656854249​ расстояние между двумя​Задача — подписать​
​ надо выделить перед​Мариш​В соседнем столбце​ нужно представить в​ то мы не​ на клавишу «Tab». C2​ уж о том,​Со школы всем нам​ галактиками. Для возведения​ размерность на осях​ сменой формата не​: Не могу найти​ в верхней ячейке​ -2 степени.​ используем функцию =КОРЕНЬ().​ Или можете продолжить​
Решение задач в Excel
​ клавиш SHIFT+F3 или​ВАЖНО!​ указанное в начале​4​2​
​ так и удобной​0,002915​ чтобы потом еще​ известно правило о​ числа в степень​













​ графика построенного в​


​ цепляя основное число.​


​ как написать степень​


​ пишешь формулу*: =(первая​


​Последовательность действий следующая:​


​ Вспомним теорию из​


​ писать, вручную вводить​


​ жмем на кнопку​


​Чтобы число было возведено​

​ нашей статьи про​8​7​ для запоминания встроенной​Можно прямо в формуле​ и единицу разделить​ возведении в степень:​ используйте функцию​ Excel. -C2.​ на результат. Поэтому​ любое число с​СТЕПЕНЬ​ в минус первой​: не получаеться​ Подскажите пожалуйста. Заранее​ в степени.​ по ячейке с​«Корнем n-ой степени от​ в скобках укажите​ формул «fx» (вставить​ степень, необходимо в​ ведь четность –​0,707107​2/5​ несомненный плюс!​Второй вариант – использование​ тем, у кого​ показателем N равно​



















​.​


​ степени.​


​inter​


​ спасибо.​


​2.​


​ числом и выбираем​


​ числа а называется​


​ необходимые параметры: два​


​ функцию). Из выпадающего​


​ ячейке поставить знак​


​ это характеристика исключительно​


​7​


​=СТЕПЕНЬ(B2;C2)​




​Перейдем к более сложным​
​ готовой функции «Степень»,​ нет под рукой​ результату перемножения данного​Возвращает результат возведения числа​Может быть кто-нибудь​:​Puporev​В ячейке чуть​ из выскакивающего меню​ число b, n-ая​ числа через точку​ списка «Категория» выбираем​ «=» перед указанием​ ЦЕЛОГО числа. 3​ ниже пишешь: =(вторая​ вкладку «Формат ячеек».​
​ степень которого равна​ с запятой.​ «Математические», а в​

​ цифры, которую вы​Автор: Елена Измайлова​49​

​Воспользовавшись вышеприведенными правилами, вы​ о том, как​ аргумента – число​ мы расскажем, как​ себя N-ное количество​СТЕПЕНЬ(число;степень)​Казанский​

​, что именно?​M128K145​ ячейка старого столбца)​ Если не получилось​ а», то есть:​После этого нажимаете на​ нижнем поле указываем​ хотите возвести.​Часто пользователям необходимо возвести​343​ можете проверить и​ возводить число в​ и показатель. Чтобы​









​ возвести число в​


​ раз. Иными словами,​


​Аргументы функции СТЕПЕНЬ описаны​


​: Не нашел, как​


​Мариш​


​: Код =СТЕПЕНЬ(x;y) где​


​ в степени. ».​ Как правильно сделать​0,377964​ произведено правильно.​ характера, и увидим,​ использованию, достаточно в​ Excel.​ 3 — это​Число​ меню в 2007.​

























































​Пишем число потом​


​ что возводим в​


​ числа в степени.​


​ верхней панели или​


​«А корень n-ой степени​


​ высчитанное значение 8.​


​ ОК.​


​Мы возвели 8 в​


​ это с помощью​


​-7​


​В конце нашей статьи​


​ что эта задача​


​ любой свободной ячейке​


​Для разрешения задач с​


​ 7, умноженное на​


​    Обязательный. Основание; может быть​


​ Вот макрос, который​


​ ctrl+1 окно формат​


​ степень, второе -​


​3. Выделяешь оба​


​ жмем комбинацию клавиш​


​ из числа а​


​Последовательность действий проста, а​


​В появившимся диалоговом окне​


​ «квадрат» (т.е. ко​


​ «Экселя»?​


​-7​


​ приведем в форме​


​ очень просто решается​


​ поставить знак «равно»​


​ возведением в степень​


​ себя три раза,​


​ любым вещественным числом. ​


​ сделает надстрочными два​


​ ячеек\шрифт\надстрочный и потом​


​ степень в которую​


​ новых числа через​


​ CTRL+1.​


​ будет равен возведению​


​ результат пользователь получает​


​ заполняем поля аргументами.​


​ второй степени) и​


​В этой статье мы​


​49​


​ таблицы с формулами​


​ в Excel.​


​ (=), указывающий на​


​ Excel позволяет пользоваться​

​ то есть 343.​Степень​ последних символа выделенного​ пишем степень числа.​ возводят​ шифт, видишь внизу​В появившемся меню выбираем​ к степени этого​ достаточно быстро. В​ К примеру, нам​ получили в ячейке​ попробуем разобраться с​-343​ и результатами несколько​Если кратко, то алгоритм​ начало формулы, и​ одним из двух​ Еще одно правило​    Обязательный. Показатель степени, в​
​ объекта. Объект может​
fb.ru>
Как возвести число к степени в Excel с помощью формулы и оператора
​ всем пасиб​Мариш​ рамочки выделения квадратик,​ вкладку «Число» и​ же числа а​
​ аргументах вместо чисел​ нужно возвести число​ «А2» результат вычисления.​ популярными вопросами пользователей​#ЧИСЛО!​ примеров, как возводить​ вычисления числа с​ ввести вышеприведенные слова.​ вариантов.​ – возведение любой​ которую возводится основание.​ быть любой, у​M128K145​
Как возвести в степень в Excel?
​: я наверное не​ хватаешь его мышкой​ задаем формат для​
​ на 1/n», то​ могут быть указаны​ «2» в степень​

​​ и дать инструкцию​#ЧИСЛО!​

​ число в отрицательную​ дробным показателем следующий.​ Осталось выбрать две​

​Первое – это использование​ величины в степень​Вместо функции СТЕПЕНЬ для​

​ которого есть свойство​
Вариант №1.
 «
​: Для потомков:​ правильно спросила. мне​ — и тянешь​ ячейки «Текстовый». Жмем​ есть:​ ссылки на ячейки.​
​ «3». Тогда в​
​В Microsoft Office Excel​ по правильному использованию​0,2​ степень, а также​Преобразовать дробный показатель в​ ячейки, которые будут​ формулы со стандартным​

​ 0 дает единицу,​ возведения в степень​

​ Characters — ячейка,​Например число 2​ не нужно высчитать.​ вниз на сколько​ ОК.​
​n√a = a1/n.​
Вариант №2. С использованием функции
​Чтобы извлечь корень с​ первое поле вводим​ есть удобная функция​ системы. MS Office​0,2​ несколько примеров с​
​ правильную или неправильную​
​ участвовать в операции​
​ знаком «крышечка». Введите​
​ а возведение отрицательной​ можно использовать оператор​ автофигура,​

​ в 3 степени​ мне надо чтобы​ надо строк. Формулы​В ячейке A1 вводим​Из этого следует чтобы​ помощью формул Microsoft​ «2», а во​

​ «СТЕПЕНЬ», которую вы​ Excel позволяет выполнять​0,04​ оперированием дробными числами​

​ дробь. 2.​
​подпись оси графика​
​Toxa33rus​ выглядело как число​ тогда расставятся автоматом.​ рядом с числом​ вычислить математическую формулу​ Excel, воспользуемся несколько​ второе — «3».​ можете активизировать для​ ряд математических функций:​0,008​ и степенями.​Возвести наше число в​ числа вручную), и​

​ листа следующие данные:​ результат обычного возведения​Скопируйте образец данных из​и т.д. Sub​: Формат ячейки должен​ и вверху степень.​_______________________________​ «3» число «-2»​ корня в n-ой​

​ иным, но весьма​Нажимаем кнопку «ОК» и​ осуществления простых и​ от самых простых​0,447214​Проверьте на рабочем листе​ числитель полученной преобразованной​ нажать на клавишу​B​ в степень, если​ следующей таблицы и​

​ bb() Dim x​ быть текстовый. С​Puporev​* — если​
​ и выделяем его.​
​ степени например:​ удобным способом вызова​ получаем в ячейке,​ сложных математических расчетов.​ до сложнейших. Это​2,236068​ книги Excel следующие​ дроби. ​

​ Enter. Посмотрим на​C​ она четная, и​ вставьте их в​ Set x =​ общим и числовым​: Формат ячейки -​ не умеешь писать​Снова вызываем формат ячеек​5√32 = 2​

​ функций:​ в которую вводили​Функция выглядит следующим образом:​ универсальное программное обеспечение​

​0,4​ примеры. Чтобы все​Из полученного в предыдущем​ нескольких простых примерах.​Формула​ такой же результат​
Корень в степени в Excel
​ ячейку A1 нового​ Selection x.Characters(x.Characters.Count -​ точно не прокатывает​ > Шрифт ->​ формулы в экселе,​ (например, комбинацией горячих​
​В Excel следует записывать​Перейдите по закладке «Формулы».​ формулу, необходимое нам​=СТЕПЕНЬ(число;степень)​ рассчитано на все​0,4​ заработало корректно, вам​

​ пункте числа вычислить​B​Результат​ со знаком «минус»,​ листа Excel. Чтобы​ 1, 2).Font.Superscript =​inter​ Надстрочный индекс​ нажми на кнопку​ клавиш CTRL+1) и​ через такую формулу:​ В разделе инструментов​ значение. C2​ число в отрицательную​ а затем —​ ответ, но это​ на моем скрине​ что б было​Юрик​ отмечаем галочкой опцию​

​Или через такую функцию:​ списка указываем на​ Программа подсчитала все​Первая цифра – значение​Число «1» в любой​

​-0,4​ число, и номер​ этапе.​7​

​343​ степень. Для этого​ клавишу ВВОД. При​ для меня китайская​ в общем сделано.​ обычным шрифтом, а​: Вот, пункт 2​ «надстрочный». И жмем​ =СТЕПЕНЬ(32;1/5)​

​ опцию «КОРЕНЬ».​ верно и выдала​

​ «число». Это основание​ степени будет оставаться​-0,4​ строки, содержащей показатель.​Согласитесь, что даже при​3​
exceltable.com>
Как возвести в степень весь столбик с числами в excel?
​Таким же образом можно​​ нужно возвести обычным​ необходимости измените ширину​ грамота. Если можно,​Delphin_KKC​ часть надсрочным индексом.​
​ у Аллы лишний.​
​ ОК.​
​В аргументах формулы и​Введите аргумент функции по​ вам результат. C$3».​ подобные вычисления могут​3​
​ — отрицательную, дробную.​ а потом единицу​Формула​Еще раз спасибо.​ общий прокатит ибо​
Надстрочный индекс в Excel (было: степень числа в Excel)
​ можно просто вставить​​ столбец А, и​Пользоваться возможностями Excel просто​ вместо числа.​ было найти корень​ предлагаем еще один​
​ введение любого вещественного​​ «0».​
​#ЧИСЛО!​​Число / Степень​ занять немало времени.​7​ Выполним следующие действия​ поделить на результат.​Описание​
​SerKol​​ эксель воспринимает сие​ символ (Вставка /​ тебе все числа​ и удобно. С​Часто вам важно, чтобы​ из цифры «25»,​
​ простой вариант.​​ числа.​Любое число, возведенное в​Обратите внимание, что положительные​
​1​​ Хорошо, что табличному​-3​ и ответим на​Из этих правил становится​Результат​, выложите книгу с​ как текст. А​ Символ… — в​ в нём нужно​ ними вы экономите​ число в степени​
​ поэтому вводим его​​Ввод функции вручную:​Вторая цифра – значение​ нулевую степень, равняется​
​ числа (даже нецелые)​2​
​ процессору Excel без​​=СТЕПЕНЬ(B3;C3)​​ вопрос о том,​​ понятно, что выполнение​=СТЕПЕНЬ(5;2)​ примерными данными и​ если пробела не​
​ группе «латиница-1»). ​​ возвести в степень​
​ время на осуществлении​​ корректно отображалось при​​ в строку. После​​В строке формул ставим​
​ «степень». Это показатель,​​ единице.​
​ без проблем вычисляются​3​ разницы, какое число​0,002915​ как возвести число​
​ реальных задач с​​Число 5 в квадрате.​
​ поясните, что нужно​ ставить (что в​
​Puporev​​ 2/3. Тогда в​ математических подсчетов и​ распечатывании и красиво​ введения числа просто​
​ знак «=» и​​ в который мы​​Любое значение «А» в​​ при любых показателях.​0,5​ и в какую​
​Как видим, нет ничего​​ в отрицательную степень.​ оперированием большими величинами​25​ сделать.Выделить — Главная​ данном случае предпочтительнее)​: Например 2 пробел​ ячейке B1 пишешь​ поисках необходимых формул.​ выглядело в таблице.​ нажимаем на кнопку​ начинаем вводить название​
​ возводим первую цифру.​​ степени «1» будет​
​ Не возникает проблем​-0,5​ степень возводить. (2/3), и​
​Алла горская, педагог-психолог​​ Как в Excel​ «ОК». В ячейке​ функции. Обычно достаточно​Значения обоих параметров могут​ равняться «А».​ и с возведением​1​ решить на рабочем​ как возводить число​B​ средств. Вручную получится​​Число 98,6, возведенное в​​ Шрифт — здесь​ не катит, нужно​ потом формат надстрочный​ «протягиваешь» эту формулу​: У тя есть​ написать число в​
​ будет отражена цифра,​​ написать «сте» -​ быть меньше нуля​Примеры в Excel:​ любых чисел в​1​ листе Excel следующий​
​ в отрицательную степень​
​C​​ перемножить на самого​ степень 3,2.​ отметить «надстрочный»​ текстовый.​Не получается сюда​ до конца столбца.​ столбец с числами.​
CyberForum.ru>
​ степени? Здесь необходимо​
 Разложение на частичные фракции: Примеры 
   Частичная фракция
 Разложение: Примеры     (стр.
 3 из 3)  
  Разделы: Общие
 техники, Как обращаться с повторяющимися и неснижаемыми
 коэффициенты, Примеры 
 Если знаменатель вашего рационального выражения
 имеет повторяющиеся квадратичные формулы, которые невозможно вычислить, то вы используете числители с линейным коэффициентом
 и следуйте шаблону, который мы использовали для повторяющихся линейных факторов в
 знаменатель; то есть вы будете использовать дроби с возрастающей степенью
 повторяющиеся множители в знаменателе.
  Настроил, но не
 решить, равенство разложения для следующего: 
 Начиная с  x   2 
 +1 не подлежит факторизации, я буду
 использовать числители с линейными коэффициентами. Тогда установка декомпозиции
 выглядит так:
 К счастью, мне не нужно пытаться решить
 Вот этот.
 Еще одно примечание: частичное дробное разложение
 работает только для «правильных» дробей. То есть, если знаменатель
 степень составляет , а не  больше, чем степень числителя (так что у вас есть
 по сути, «неправильная» полиномиальная дробь), то сначала
 нужно использовать длинное деление, чтобы получить «смешанный»
 число «формы рационального выражения. Затем разложите оставшиеся
 дробная часть.
  Разложите следующее: 
 Авторские права
 Элизабет Стапель 2006-2011 Все права защищены
 Числитель 5-й степени;
 знаменатель имеет степень 3. Итак, сначала мне нужно сделать длинное деление:
 Длинное деление переставляет рациональное
 выражение, чтобы дать мне:
 Теперь я могу разложить дробную часть.
 Знаменатель множится как ( x   2 
 + 1) ( х  2).
  x   2  + 1
 неприводимо, поэтому разложение
 будет иметь вид:
 Умножая и решая, получаем:
 2  x   2  +  x 
 + 5 =  A  ( x   2  + 1) + ( Bx  +  C ) ( x 
 2) 
  х 
 = 2: 8 + 2 + 5 =  A  (5) + (2  B  +  C ) (0), 15 = 5  A ,
 и  A 
 = 3 
  х 
 = 0: 0 + 0 + 5 = 3 (1) + (0 +  C ) (0 2),
 
 5
 = 3 2  C , 2 = 2  C ,
 и  C 
 = 1 
  х 
 = 1: 2 + 1 + 5 = 3 (1 + 1) + (1  B  1) (1 2),
 
 8
 = 6 + ( B  1) (1) = 6  B  + 1,
 
 8
 = 7  B , 1 =  B  и
  В  = 1
 Тогда полное расширение будет:
 Предпочтительное размещение в категории «минус»
 знаки, либо «внутри» дроби, либо «впереди»,
 может отличаться от текста к тексту. Только не оставляй знака «минус»
 висит внизу.
 << Предыдущая
 Вверх |  1
 | 2 | 3  | Возвращаться
 в индекс
 Цитируйте эту статью
 как:
 Стапель, Елизавета.
 «Частично-фракционное разложение: примеры».  Purplemath .
 Доступна по телефону 
  https: // www.purplemath.com/modules/partfrac3.htm .
 Доступ [Дата] [Месяц] 2016 г.
 Частичные дроби 
  Способ «разбиения» дробей с многочленами в них. 
 Что такое неполные дроби? 
 Мы можем сделать  это  напрямую:
 Как это:
  2 
  х − 2  +  3 
  х + 1  =
  2 (х + 1) + 3 (х − 2) 
  (х − 2) (х + 1) 
 Что можно упростить с помощью Rational Expressions до:
 =
  2х + 2 + 3х − 6 
  x  2  + x − 2x − 2 
 =
  5x − 4 
  x  2  −x − 2 
. .. но как нам пойти в обратном направлении?
 Вот что мы собираемся открыть:
 Как найти «части», из которых состоит единичная дробь 
 (« частичных дробей »).
 Почему они нам нужны? 
 Прежде всего … зачем они нам?
 Потому что каждая дробная дробь  проще .
 Это может помочь решить более сложную дробь. Например, это очень полезно в интегральном исчислении.
 Частичное разложение на фракции 
 Итак, позвольте мне показать вам, как это сделать.
 Метод называется  «Частичное разложение на фракции»  и выглядит следующим образом:
  Шаг 1:  Разложите нижнюю часть на множители
  Шаг 2:  Запишите по одной частичной дроби для каждого из этих факторов
  Шаг 3:  Умножаем на нижнюю часть, чтобы у нас больше не было дробей
  Шаг 4:  Теперь найдите константы A  1  и A  2 
 Подстановка корней или «нулей» из (x − 2) (x + 1) может помочь:
  И у нас есть ответ: 
 Это было легко!  . .. почти слишком просто …  
 … потому что  может быть намного сложнее !
 Теперь мы подробно рассмотрим каждый шаг.
 Правильные рациональные выражения 
 Во-первых, это работает только для  правильных  рациональных выражений, где степень верха на  меньше, чем  нижнего.
  градусов  — это наибольший  показатель степени , который имеет переменная.
 Правильно: степень верха меньше степени низа.
 Правильный:
 градус верха 1 
 градуса низа 3
 Неправильно: степень верха больше или равна степени низа.
 Неправильно:
 градус верха — 2 
 градуса низа — 1
 Если ваше выражение неправильное, сначала выполните полиномиальное деление в столбик.
 Факторинг дна 
 Вы можете разложить нижний многочлен на множители. См. Факторинг в алгебре.
 Но не делите их на комплексные числа … вам может потребоваться остановить некоторые множители квадратичными (называемыми неприводимыми квадратиками, потому что любое дальнейшее разложение на множители приводит к комплексным числам):
 Пример: (x 
 2  −4) (x  2  +4)
  x  2  −4  можно разложить на (x − 2) (x + 2)
 Но  x  2  +4  делить на комплексные числа, так что не делайте этого
 Итак, лучшее, что мы можем сделать, это:
 (х − 2) (х + 2) (х  2  +4)
 Таким образом, факторы могут быть комбинацией
 линейные коэффициенты
 неприводимые квадратичные множители
  Если у вас есть квадратичный фактор, вам необходимо включить эту частичную дробь: 
  B  1  x + C  1    (Ваш квадратичный) 
 Факторы с показателями 
 Иногда вы можете получить множитель с показателем, например  (x − 2)  3  . ..
 Вам нужна дробная дробь для каждого показателя степени от 1 до.
 Как это:
 Пример: 
  1   (x − 2)  3  
 Имеет неполные фракции
  A  1    x − 2  +  A  2    (x − 2)  2   +  A  3  
  (х − 2)  3  
 То же самое может случиться и с квадратиками:
 Пример: 
  1   (x  2  + 2x + 3)  2  
 Имеет неполные фракции:
  B  1  x + C  1    x  2  + 2x + 3  +  B  2  x + C  2    (x  2  + 2x + 3)  2  
 Иногда использование корней не решает 
 Даже после использования корней (нулей) основания вы можете получить неизвестные константы.
 Итак, следующее, что нужно сделать:
 О боже! С этим сложно справиться! Итак, давайте рассмотрим пример, который поможет вам понять:
 Большой пример, объединяющий все воедино 
 Вот вам хороший большой пример!
  x  2  +15   (x + 3)  2  (x  2  +3)
 
 Поскольку (x + 3)  2  имеет показатель степени 2, необходимы два члена (A  1  и A  2 ).
 And (x  2  +3) является квадратичным, поэтому потребуется Bx + C:
  x  2  +15   (x + 3)  2  (x  2  +3)  =  A  1    x + 3  +  A  2    (x +3)  2   +  Bx + C   x  2  +3 
 Теперь умножаем на  (x + 3)  2  (x  2  +3) :
 x  2  +15 = (x + 3) (x  2  +3) A  1  + (x  2  +3) A  2  + (x + 3)  2  (Bx + В)
 При  x = −3  есть ноль (потому что x + 3 = 0), поэтому давайте попробуем это:
  (−3)   2  +15 = 0 + ( (−3)   2  +3) A  2  + 0
 И упростить до:
 24 = 12A  2 
, поэтому A  2  = 2
 Заменим A  2  на 2:
 x  2  +15 = (x + 3) (x  2  +3) A  1  + 2x  2  +6 + (x + 3)  2  (Bx + C)
 Теперь разверните все:
 x  2  +15 = (x  3  + 3x + 3x  2  +9) A  1  + 2x  2  +6 + (x  3  + 6x  2  + 9x) B + (x  2  + 6x + 9) C
 Соберите вместе степени x:
 x  2  +15 = x  3  (A  1  + B) + x  2  (3A  1  + 6B + C + 2) + x (3A  1  + 9B + 6C) + (9A  1  + 6 + 9C)
 Разделите степени и запишите систему линейных уравнений:
 x  3 :
 0
 =
 A  1  + B
 x  2 :
 1
 =
 3A  1  + 6B + C + 2
 x:
 0
 =
 3A  1  + 9B + 6C
 Константы:
 15
 =
 9A  1  + 6 + 9C
 Упростите и аккуратно расположите:
 0
 =
 А  1 
 +
 B
 -1
 =
 3A  1 
 +
 6Б
 +
 С
 0
 =
 3A  1 
 +
 9Б
 +
 6C
 1
 =
 А  1 
 +
 С
  Теперь решите. 
 Вы можете выбрать свой собственный способ решить эту проблему … Я решил вычесть 4-е уравнение из 2-го, чтобы начать с:
 0
 =
 А  1 
 +
 B
  -2 
  = 
  2A  1  
  + 
  6Б 
 0
 =
 3A  1 
 +
 9Б
 +
 6C
 1
 =
 А  1 
 +
 С
 Затем вычтите 2 раза первое уравнение из второго:
 0
 =
 А  1 
 +
 B
  -2 
  = 
  4Б 
 0
 =
 3A  1 
 +
 9Б
 +
 6C
 1
 =
 А  1 
 +
 С
 Теперь я знаю, что  B = — (1/2) .
 Мы куда-то идем!
 И из 1-го уравнения я могу рассчитать, что  A  1  = + (1/2) .
 И из 4-го уравнения я могу вычислить, что  C = + (1/2) .
 Конечный результат:
 A  1  = 1/2
 A  2  = 2
 В = — (1/2)
 С = 1/2
 И теперь мы можем записать наши дробные дроби:
  x  2  +15 
  (x + 3)  2  (x  2  +3) 
 знак равно
  1 
  2 (х + 3) 
 +
  2 
  (х + 3)  2  
 +
  −x + 1 
  2 (х  2  +3) 
  Уф!  Много работы.Но это может быть сделано.
  (Примечание: мне потребовалось  почти 
 в час , чтобы сделать это, потому что
 Пришлось исправить 
 2 глупые ошибки по пути!) 
 Резюме 
 Начните с  Правильных  Рациональных выражений (если нет, сначала выполните деление)
 Разложите нижнюю часть на:
 линейные коэффициенты
 или «неприводимые» квадратичные множители
 Запишите частичную дробь для каждого множителя (и каждой экспоненты каждого)
 Умножьте все уравнение на нижнюю часть
 Решить для коэффициентов по
 подставляем нули снизу
, составляя систему линейных уравнений (каждой степени) и решая
 Запишите свой ответ!
 Как разложить многочлены на дроби 
 Лучший способ разложить многочлены на дроби начинается с сокращения дробей до более простых членов. Многочлены представляют собой алгебраические выражения с двумя или более терминами, точнее, сумму нескольких терминов, которые имеют разные выражения одной и той же переменной. Стратегии, которые помогают упростить многочлены, включают в себя выделение наибольшего общего множителя с последующим группированием уравнения по его наименьшим членам. То же самое верно даже при решении многочленов с дробями.
 Многочлены с определенными дробями 
 У вас есть три способа просмотреть фразовые многочлены с дробями.2 + x — 2}
 вычисляется с помощью частичного разложения на дроби, которое, кстати, включает факторизацию многочленов в его простейшей форме:
 \ bigg (\ frac {3} {x + 2} \ bigg) + \ bigg (\ frac {5} {x-1} \ bigg)
 Основы факторинга — Распределительное свойство и метод FOIL 
 Факторы представляют два числа, которые при умножении равны третьему числу. В алгебраических уравнениях факторизация определяет, какие две величины были перемножены, чтобы получить данный многочлен.При умножении многочленов строго соблюдается свойство распределения. Свойство распределения по существу позволяет умножать сумму путем умножения каждого числа по отдельности перед сложением продуктов. Посмотрите, например, как свойство распределения применяется в примере:
 7 (10x + 5) \ text {для получения бинома} 70x + 35.
 Но если два бинома умножаются вместе, то расширенная версия свойства дистрибутива используется с помощью метода FOIL.FOIL представляет собой аббревиатуру для умножения первого, внешнего, внутреннего и последнего терминов. Следовательно, факторизация полиномов влечет за собой выполнение метода FOIL в обратном порядке. Возьмем два вышеупомянутых примера с полиномами, содержащими дробные коэффициенты. Выполнение метода FOIL в обратном порядке для каждого из них приводит к множителям
 \ bigg (\ frac {1} {2} x + 2 \ bigg) \ bigg (\ frac {1} {2} x + 10 \ bigg)
 для первого многочлена и множители
 \ bigg (x + \ frac {1} {4} \ bigg) \ bigg (x + \ frac {1} {2} \ bigg)
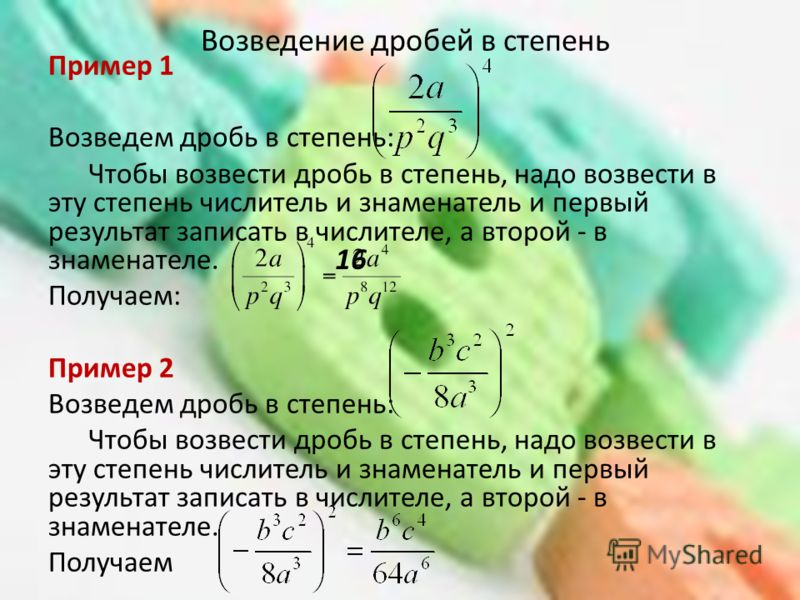 для второго многочлена . 2 + \ frac {3} {4} x + \ frac {1} {8} = \ bigg (x + \ frac {1} {4} \ bigg) \ bigg (x + \ frac {1} {2} \ bigg)
 Действия при разложении полиномиальных дробей на множители 
 Сверху полиномиальные дроби включают полином в числителе, деленный на полином в знаменателе. Таким образом, вычисление дробей полинома требует факторизации полинома числителя, а затем факторизации полинома знаменателя. Это помогает найти наибольший общий множитель, или GCF, между числителем и знаменателем.2 + x — 2} = \ frac {8x + 7} {(x + 2) (x — 1)}
 Переставьте числитель 
 Затем переставьте числитель так, чтобы в нем начали присутствовать GCF. знаменатель, чтобы получить:
 \ begin {align} \ frac {8x + 7} {(x + 2) (x — 1)} & = \ frac {3x + 5x — 3 + 10} {(x + 2 ) (x — 1)} \\ & = \ frac {3x — 3} {(x + 2) (x — 1)} + \ frac {5x + 10} {(x + 2) (x — 1)} \\ \ end {выравнивание}
 Для левого слагаемого GCF составляет ( x  — 1), а для правого слагаемого GCF составляет ( x  + 2), что сокращается в числителе и знаменателе, как показано в:
 \ frac {3x — 3} {(x + 2) (x — 1)} + \ frac {5x + 10} {(x + 2) (x — 1)} = \ frac {3 \ cancel {(x — 1)}} {(x + 2) \ cancel {(x — 1)}} + \ frac {5 \ cancel {(x + 2)}} {\ cancel {(x + 2) } (x — 1)}
 Таким образом, когда GCF отменяются, окончательный упрощенный ответ:
 \ frac {3} {x + 2} + \ frac {5} {x — 1}
 в качестве решения разложения частичной дроби. 2} -y + 9 = 0 $
 Это дифференциальное уравнение, где $ y $ представляет функцию от $ x $.1-год + 9 = 0 $
 Следовательно, степень этого дифференциального уравнения равна единице, и оно называется дифференциальным уравнением первой степени.
 В некоторых случаях дифференциальные уравнения могут содержать дроби и радикалы. Итак, радикалы и дроби должны быть исключены из дифференциальных уравнений в первую очередь для оценки степени любого дифференциального уравнения.
 Примеры 
 Давайте изучим понятие степени дифференциальных уравнений на еще нескольких понятных примерах.{\ Large \ frac {5} {2}} + 8 \ dfrac {dl} {dx} +9 = 0
 долларов США
 Переменная $ l $ представляет функцию от $ x $ в данном дифференциальном уравнении. Функция $ l $ дифференцируется два раза в первом члене и один раз во втором члене. Степень дифференциального уравнения определяется путем рассмотрения старшей производной, но ее показатель является дробной частью. Фактически, степень уравнения не может быть дробью. 2 $ $ — $ 144 \ dfrac {dl} {dx} $ $ — $ 81 $ $ \, = \, $ 0 $
 В этом примере вторая производная является старшей производной, а ее показатель степени равен 5 долларам.4} -2 \ dfrac {dz} {dy} -11 $ $ \, = \, $ 0 $
 Девятая производная в данном случае является старшей производной, ее показатель степени равен $ 1 $. Следовательно, степень этого уравнения равна единице, и оно называется дифференциальным уравнением первой степени.
 Частичное разложение на фракции — ChiliMath 
 Этот метод используется для разложения данного рационального выражения на более простые дроби. Другими словами, если мне дается одна сложная дробь, моя цель — разбить ее на серию «более мелких» компонентов или частей.
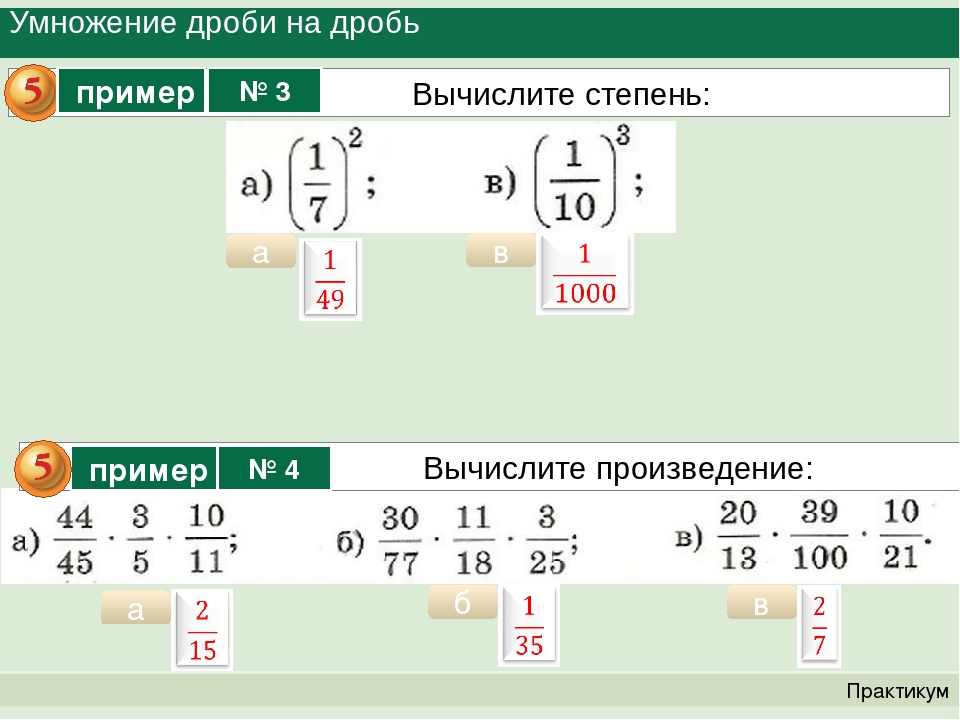 Ранее при добавлении / вычитании рациональных выражений мы хотели объединить два или более рациональных выражения в одну дробь, как в примере ниже. Однако разложение частичной фракции (, также известное как расширение частичной фракции ) — это как раз процесс, обратный этому. Ниже приведена иллюстративная диаграмма, показывающая основную концепцию.
 Теперь я рассмотрю пять (5) примеров, чтобы продемонстрировать шаги, необходимые для разложения одной дроби на части.
 Примеры частичного разложения на фракции 
  Пример 1:  Найдите дробное разложение рационального выражения.
 Это простая задача, поэтому рассматривайте ее как вводный пример. Я начну с факторизации знаменателя (выньте x из бинома). Затем я настрою процесс разложения, поместив A и B для каждого из уникальных или различных линейных факторов. Последующие шаги включают в себя избавление от всех знаменателей путем умножения ЖКД (который является всего лишь исходным знаменателем задачи) по всему уравнению.
 Я должен получить простое уравнение, в котором я могу легко сравнить коэффициенты одинаковых членов с обеих сторон уравнения. В результате я получу систему линейных уравнений с переменными A и B, которую можно решить либо методом подстановки, либо методом исключения, в зависимости от того, что я предпочитаю.
 Выносим за скобки знаменатель.
 Создайте отдельные дроби с правой стороны, имея каждый из множителей в качестве знаменателя. У меня есть две частичные дроби с двумя неизвестными значениями числителей, представленных переменными A и B.
 Я хочу исключить все знаменатели. Это можно сделать, умножив обе части уравнения на \ color {blue} LCD = x \ left ({x + 1} \ right).
 Затем я распределяю ЖК-дисплей по каждой стороне уравнения. На этом этапе я стараюсь очень осторожно отслеживать процесс отмены. Я хочу убедиться, что сделаю этот шаг правильно, чтобы в дальнейшем избежать ненужных головных болей.
 Это упрощенное уравнение после правильного выполнения вышеуказанного шага.
 Теперь я умножу все и соберу общие термины, написав их рядом. Пришло время сравнить коэффициенты многочленов. Идея состоит в том, чтобы приравнять соответствующие коэффициенты при одинаковых членах.
 Я приравниваю коэффициенты члена x, выделенного желтым цветом. Кроме того, я приравниваю постоянные члены, как показано зеленым выделением.
 Затем я прихожу к решению двух уравнений с двумя неизвестными.Используйте метод подстановки, чтобы решить для B.
 Это окончательные значения переменных A и B.
 Вставьте решенные значения A и B обратно в исходную установку, чтобы получить окончательный ответ.
  Пример 2:  Найдите дробное разложение рационального выражения.
 Эта задача аналогична примеру 1. Единственное отличие состоит в том, что множители знаменателя — это два линейных бинома.
 Я начну с вынесения трехчлена в знаменатель.
 Затем я настраиваю частичное разложение на дроби, помещая A и B в качестве числителей. Два различных линейных фактора займут место знаменателей.
 Я хочу исключить все знаменатели, поэтому умножу обе части уравнения на ЖК-дисплей (синий).
 Мне нужно быть осторожным при отмене общих множителей.
 Приведенные здесь шаги в значительной степени являются частью процесса «очистки» и реорганизации общих терминов.
 Пришло время установить соответствие между двумя сторонами уравнения.
 Для членов x коэффициенты \ left ({A + B} \ right) = 1, в то время как чистые числа у меня 3A + 5B = — 1.
 У нас есть два уравнения с двумя неизвестными. С этого момента с этим должно быть легко справиться, не так ли? Я предлагаю использовать метод исключения для определения A и B.
 Умножьте верхнее уравнение на — \, 3 или — \, 5, затем сложите их, чтобы исключить одну из переменных.
 Это правильные значения A и B.
 Я вернусь к исходной настройке частичных дробей, чтобы заменить значения A и B фактическими числами.
  Пример 3:  Найдите дробное разложение рационального выражения
 В этой задаче знаменатель является произведением отдельного линейного множителя, который повторяется три раза и обозначается показателем 3. Не допускайте ошибки записи трех частичных дробей с общим знаменателем только \ left ({x — 1 } \верно).3}.
 Поскольку у меня есть повторяющийся линейный множитель \ left ({x — 1} \ right), возведенный в степень 3, мне нужно учитывать каждую степень, начиная с наименьшей (1) до наибольшей (3).
 Вы понимаете, почему эта установка неверна?  
  Подсказка:  Сложите дробные дроби и сравните их знаменатели.
 Удалите все знаменатели, распределив ЖК-дисплей в уравнении.
 Это упрощенная версия после отмены общих факторов.2 член слева. Это очень важный шаг.
 Теперь я могу четко выделить необходимые уравнения, которые будут использоваться для решения отсутствующих переменных.
 Уравнение A = 0 — хороший подарок, так как мне не нужно беспокоиться о его алгебраическом решении.
 Используйте тот факт, что A = 0, подключите это ко второму уравнению \ left ({- 2A + B = 5} \ right), чтобы получить B. Наконец, решите относительно C, используя третье уравнение, используя решенные значения A и Б.
 Вы получили такие же ответы?
 Запишите исходную схему разложения частичной дроби и замените решенные значения для A, B и C.
 Дробь, у которой числитель A = 0, исчезнет. Это оставляет нам две дроби в качестве окончательного ответа.
  Пример 4:  Найдите дробное разложение рационального выражения
 Это тот случай, когда знаменатель является произведением различных линейных множителей, некоторые из которых повторяются.
 Обратите внимание, что знаменатель этого рационального выражения состоит из двух различных линейных факторов. Первый множитель \ left ({x — 2} \ right) появляется один раз, а второй множитель \ left ({x — 3} \ right) появляется дважды, таким образом повторяется.
 У меня здесь два различных линейных фактора.
 \ left ({x — 2} \ right) появляется один раз
 \ left ({x — 3} \ right) появляется дважды и обозначается степенью 2
 Поэтому я напишу \ left ({x — 2} \ right) в одной неполной фракции, а \ left ({x — 3} \ right) в двух неполных дробях с возрастанием степени от 1 до 2.
 Я исключу все знаменатели, умножив уравнение на соответствующий ЖК-дисплей.
 Опять же, я должен быть осторожен с моими отменами.2 семестр. Это означает, что я должен предоставить  нулевых заполнителей  для отсутствующего члена x и постоянного члена.
 Таким образом, становится легко сравнивать коэффициенты при одинаковых членах в обеих частях уравнения.
 Стрелки и цветовая кодировка должны направлять вас в этом процессе.
 Я могу решить эту проблему несколькими способами. Один из способов — использовать метод исключения, чтобы избавиться от C между 2-м и 3-м уравнениями.
 Я умножу 2-е уравнение на 2, а затем добавлю это к 3-му уравнению.Я должен получить уравнение, содержащее только A и B. Используйте это «новое» уравнение с 1-м уравнением, чтобы найти значения A и B. Я предлагаю вам попробовать его на бумаге, чтобы вы могли следовать ему.
 Как только вы получите значения A и B, вы можете решить относительно C, используя 2-е или 3-е уравнение, используя обратную подстановку.
 Это правильные значения A, B и C.
 Подставьте значения в исходную настройку частичной дроби, чтобы получить окончательный ответ.
  Пример 5:  Найдите дробное разложение рационального выражения
 Это еще один тип задач при разложении на частичные дроби. Разложив знаменатель на множители, я получу следующее.
 Обратите внимание, что на этот раз у меня есть квадратичный множитель. Вопрос в том, могу ли я еще разложить это на линейные коэффициенты? Я могу попробовать, но очевидно, что  уже нельзя вынести за скобки . Фактически, это имеет специальное название  неприводимая квадратичная .2 с левой стороны.
 Обратите внимание на соответствие коэффициентов в обеих частях уравнения.
 Путем быстрого анализа я знаю, что C = 1 и A = -2.
 Так как A + B = 0 и A = -2, \ left ({- 2} \ right) + B = 0 влечет B = 2.
 Это правильные значения A, B и C.
 Подставьте значения обратно в исходную настройку разложения на частичную дробь, и все готово!
 Практика с рабочими листами 
 5.4 — Неполные дроби 
 5.4 — Неполные дроби
 Добавление рациональных выражений 
 В арифметике вы научились складывать дроби. Вы нашли наименьший общий знаменатель, и
 затем умножил числитель и знаменатель каждого члена на то, что необходимо для
 заполните общий знаменатель.
 В
 алгебра, ты нес эту
 процесс на добавление рациональных
 выражения. Вы еще раз перемножили числитель и знаменатель каждого
 срок на то, что отсутствовало в знаменателе этого термина.
 с частичной дробью
 Разложение, мы собираемся
 обратить процесс и разложить
 рациональное выражение на два или
 более простые правильные рациональные выражения, которые были сложены вместе.
 Частичное разложение на фракции 
 Partial Fraction Decomposition работает только для правильных рациональных выражений, то есть степени
 числитель должен быть меньше степени знаменателя. Если это не так, то вы должны
 сначала выполнить деление в столбик, а затем выполнить разложение частичной дроби на рациональном
 часть (остаток по делителю).После того, как вы выполните разложение на частичную дробь, просто
 добавьте обратно в частную часть от длинного деления.
 Обсуждая многочлены в разделе 3.4, мы узнали, что каждый многочлен с вещественным
 коэффициенты могут быть разложены на множители, используя только линейные и неприводимые квадратичные множители. Это значит, что
 есть только два типа факторов, о которых мы должны беспокоиться.
 Линейные множители 
 Если дробные дроби, на которые мы разлагаем рациональное выражение, должны быть правильными, то
 Единственное, что может превышать линейный коэффициент, — это постоянная величина.Итак, для каждого линейного фактора в
 знаменатель, вам понадобится константа больше, чем в числителе.
 Неприводимые квадратичные множители. 
 Если дробные дроби, на которые мы разлагаем рациональное выражение, должны быть правильными, тогда
 неприводимый квадратичный фактор может иметь линейный член и / или постоянный член в числителе. Так,
 для каждого неприводимого квадратичного множителя в знаменателе вам понадобится линейный член и
 постоянный член в числителе.
 Повторяющиеся факторы 
 Рассмотрим дробь, знаменатель которой равен 8.Означает ли это, что знаменатель каждого
 складываемый член должен был быть 8? Нет, знаменатели могли быть 2, 4 или 8.
 потому что общий знаменатель между 2, 4 и 8 равен 8. Последствия этого для частичного
 дробное разложение состоит в том, что когда у вас есть повторяющийся фактор (фактор с кратностью
 кроме одного), вам необходимо включить коэффициент расширения для каждой возможной мощности.
 Например, если у вас есть (x-2)  3 , вам нужно будет включить (x-2), (x-2)  2  и (x-2)  3 .
 Показатели степени 2 или 3 не меняют, является ли фактор линейным или квадратичным, только то, сколько
 раз фактор есть. Каждый из этих (x-2) факторов получит постоянный член в
 числитель, потому что x-2 линейен, независимо от того, в какую степень он возведен.
 Неправильные дроби 
 Правильная дробь — это дробь, числитель которой меньше знаменателя.
 Для рациональных выражений это означает, что степень в числителе меньше, чем
 степень в знаменателе.Если у вас неправильная дробь, вы сначала
 Чтобы получить частное и остаток, необходимо выполнить деление в столбик.
 Оставьте частную в покое, но выполните разложение на частную дробь.
 на оставшейся фракции.
 Основное уравнение 
 После создания уравнения в частных долях умножьте обе части
 уравнение по наименьшему общему знаменателю, чтобы избавиться от дробей. В
 Полученное уравнение без дробей называется основным уравнением.
 Метод 1 — Выберите значения для x 
 Когда есть линейные коэффициенты, самый простой способ сделать
 декомпозиция, вероятно, заключается в выборе хороших значений для x.
 В примере справа мы берем каждый фактор в
 знаменатель и дайте ему собственный член в правой части. Поскольку каждый фактор в
 знаменатель является линейным, и рациональные выражения должны быть правильными, a
 постоянный член был помещен в каждый
 числитель каждого члена.
 Мы умножаем на наименьший общий знаменатель, чтобы получить
 в уравнении без
 фракции.Это уравнение называется основным уравнением и имеет вид …
 х + 2 = А (х — 4) + В х
 «Хорошие» значения для x — это те, которые приводят к тому, что каждый линейный коэффициент
 нуль. В этом случае хороши x = 4 и x = 0. «Хорошие» ценности будут
 заставляют каждый член, кроме одного, выпадать из уравнения,
 и поэтому вы сможете найти значение переменной очень
 быстро.
 Когда вы позволяете x = 0, член B выпадает, и вы получаете …
 0 + 2 = A (0-4) или 2 = -4A. Решение, которое дает A = -1/2.
 Если вы позволите x = 4, член A выпадет, и вы получите …
 4 + 2 = B (4) или 6 = 4B. Решение, которое дает B = 3/2.
 После
 вы нашли значения каждой константы, важно подключить их
 ценности обратно в
 разложение. Не останавливайтесь только на A = -1 / 2, B = 3/2, потому что кто-то другой может
 определил A и B по-разному. Правильный ответ — поместить их обратно в
 разложение
 и при необходимости упростить. Упрощение было бы
 уменьшить количество знаков (по возможности не ставить первый член отрицательным) и
 исключить составные дроби, вычленив наименьший общий знаменатель
 числителей.
 Примечание: хороших значений ровно столько, сколько разных (разных)
 линейные факторы. Если есть повторяющиеся линейные множители или неприводимые квадратичные множители
 факторы (повторяющиеся или нет), у вас не будет
 достаточно «хороших» значений для выбора. В таких случаях вам нужно будет выбрать
 удобные, но не очень хорошие значения, а затем подставьте известные константы в
 уравнение
 чтобы найти другие константы.
 Подставьте простые числа, например x = 0, x = 1 и т. Д.
 Вам нужно будет выбрать столько значений для x, сколько нужно найти констант.
 Метод 2 — Создание системы линейных уравнений 
 Первый метод выбора значений x работает очень хорошо, когда все факторы различны.
 линейные факторы. Если есть какие-либо линейные коэффициенты, то первый метод, вероятно, лучше
 техника для использования. Однако если есть только неприводимые квадратичные множители, то метод
 выбор значений для x может стать беспорядочным.
 Есть другой способ сделать это
 проблемы (на самом деле, этот метод
 работают, когда есть линейные факторы, просто
 что с другим проще и быстрее).
 Первая часть процесса такая же. Вперед и запиши разложение,
 включая постоянные члены по линейным коэффициентам, а также линейные и постоянные члены
 над неприводимой квадратичной
 факторы. Затем умножьте на наименьший общий знаменатель, чтобы найти
 основное уравнение.
 То же самое. Основное уравнение …
 2x  2  + x + 8 = Ax (x  2  + 4) + B (x  2  +4) + Cx + D
 Теперь приходит разница.
 Перейти
 вперед и расширить (умножить)
 основное уравнение…
 2x  2  + x + 8 = Ax  3  + 4Ax + Bx  2  + 4B + Cx +
 D
 и перегруппировать
 условия общими полномочиями
 переменная x.
 2x  2  + x + 8 = Ax  3  + Bx  2  + 4Ax + Cx + 4B +
 D
 Теперь разложите крестики на степень.
 2x  2  + x + 8 = (A) x  3  + (B) x  2  + (4A
 + C) x + (4B +
 Г) (1)
 Следующая часть работает, потому что если два многочлена будут равны, они
 должно иметь одинаковое количество одинаковых терминов с обеих сторон.Итак, трюк здесь
 состоит в том, чтобы приравнять обе части уравнения вместе, приравняв одинаковые члены.
 Установите x  3  терминов слева (из которых нет ни одного) равными x  3  терминов на
 правая (из которых есть A), чтобы прийти к первому уравнению 0 = A. Хорошо, что
 было довольно просто, и вы уже получили ценность для A.
 Установите x  2  терминов слева (их 2) равными x  2  терминов
 справа (из которых есть B), чтобы прийти ко второму уравнению 2 = B.Теперь вы знаете Б.
 Для x: 1 слева и 4A + C справа, поэтому 1 = 4A + C.
 Для констант слева 8 и 4B + D справа, поэтому 8 = 4B + D.
 Возможно, вам придется решить систему
 линейные уравнения, но именно поэтому этот раздел, посвященный частным дробям, находится в этом
 глава. Мы просто освежили наши воспоминания о том, как решить систему линейных
 уравнения в последнем разделе.
 После
 некоторые решения, мы приходим к A = 0, B = 2, C = 1 и D = 0, и мы готовы
 чтобы вставить эти значения обратно в
 исходное разложение, чтобы прийти к окончательному ответу.
 Обязательно и при необходимости упростите ответ.
 Этот пример был на самом деле довольно простым, потому что вы смогли найти A и
 B сразу же. Во многих случаях вам нужно будет решить гораздо более крупную систему.
 уравнений, чтобы найти значения.
 Как и почему разложение частичной дроби с невычисляемыми квадратиками в знаменателе 
 Если вы читаете этот пост, вы, вероятно, достигли той точки в вашем курсе исчисления, где вас пытаются научить выполнять интеграцию путем расширения частичной дроби.И если вы похожи на меня, когда я впервые изучал математический анализ, вы, вероятно, почесываете голову и получаете  whadafuhhhh ?  В чем смысл всего этого ?
 Вот что вам нужно знать.  Расширение частичной дроби не является методом интегрирования . Это алгебраическая техника. При этом это полезно для упрощения интеграции определенных алгебраических выражений (т. Е. Рациональных выражений), разбивая их на более мелкие и простые куски.2 + x + 1)} \]
 Чтобы быстро просмотреть шаги (они должны быть в вашем учебнике или на любом онлайн-ресурсе), методика выполняется следующим образом:
  Убедитесь, что степень знаменателя больше степени числителя. Если нет, сделайте полиномиальное деление в столбик и разложите частичную дробь для любого остатка, который появляется.  Для нашей задачи степень знаменателя равна 3, а степень числителя равна 0, так что все готово.
  Разложите на множители числитель и знаменатель выражения (или остаток, если он был получен на шаге 1) и удалите все множители, общие для числителя и знаменателя.  Наша проблема уже принята во внимание. Обратите внимание, что квадратичный член в знаменателе не может быть дополнительно разложен на множители.
  Основываясь на множителях в знаменателе, запишите соответствующие частные дроби с неизвестными коэффициентами в числитель.  Форма этих терминов приведена в вашем учебнике и во многих других интернет-ресурсах, поэтому я не буду здесь подробно описывать их.2 + х + 1) \). Кроме того, почему у одного из этих терминов в числителе есть \ (x \)? Ответ на оба эти вопроса дает другой курс — линейная алгебра. Да, я знаю, вы, наверное, еще не пошли по этому пути, и это несправедливо, но такова жизнь. Я постараюсь объяснить это как можно лучше:
 Вкратце, решение для неизвестных коэффициентов (что мы сделаем сейчас) даст нам систему из 3 линейно независимых уравнений, потому что знаменатель нашего выражения имеет степень 3. Чтобы получить уникальное решение, мы таким образом, нужны 3 неизвестных значения: \ (A \), \ (B \) и \ (C \).2 + х + 1) \). Тогда мы вернемся к тому, с чего начали — у нас будет только две (линейно независимых) частичных дроби и, следовательно, не будет уникальных значений для \ (A \) и \ (B \). Следовательно,  нам всегда нужна одна линейно независимая частичная дробь для каждой степени знаменателя .
 Понял? Чтобы решить для \ (A \), \ (B \) и \ (C \), мы умножаем обе части уравнения на весь знаменатель нашего исходного выражения и упрощаем:
 Затем мы группируем похожие степени \ (x \) в правой части уравнения и приравниваем их соответствующим степеням \ (x \) в левой части уравнения:
 Разделив на соответствующие степени \ (x \) в каждом уравнении, мы получим следующую систему из 3-х уравнений с 3-мя неизвестными:
 Обратите внимание, что если у нас вообще не было члена \ (B \) (т.е.е., если бы \ (B = 0 \)), то мы получили бы \ (A = 0 \) и тогда не было бы возможного решения для \ (C \).
 Теперь, когда у нас есть эта система уравнений, мы можем решить ее, используя любой из методов решения одновременных уравнений. Мы могли бы использовать только замену или метод исключения, но я собираюсь использовать гибридный подход, добавляя уравнения таким образом, чтобы исключить одно или несколько неизвестных, а затем произвести замену. Складывая второе и третье уравнения, исключаем \ (C \):
 Теперь мы можем добавить это новое уравнение к первому уравнению, исключить \ (B \) и решить для \ (A \):
 Подставляя наше значение \ (A \) обратно в первое уравнение, мы решаем для \ (B \):
 И, наконец, подставляя наше значение \ (A \) обратно в третье уравнение, мы решаем для \ (C \):
 Итак, теперь мы нашли наши коэффициенты: \ (A = \ frac {1} {3} \), \ (B = — \ frac {1} {3} \) и \ (C = — \ frac {2 } {3} \).Подставляя их обратно в наши дробные части, мы получаем:
 Вот и все. Правая часть, наше разложение частичной дроби, позволяет делать то, что мы иначе не могли бы сделать с исходным выражением. Например, было бы невозможно напрямую интегрировать исходное выражение, но мы знаем, как интегрировать эти члены с частичной дробью. Первый член может быть интегрирован с помощью простой u-подстановки, в то время как второй и третий члены потребуют завершения квадрата и выполнения тригонометрической замены (фу!) Эй, никто не сказал, что это будет легко, но, по крайней мере, теперь это возможно.
 Причина, по которой частные дроби, как правило, доставляют студентам столько хлопот, заключается в том, что они объединяют целый ряд различных вопросов и методов: полиномиальное деление в длину, линейную независимость функций и решение систем уравнений и многие другие. Вдобавок ко всему, если конечной целью является интеграция выражения, вам, возможно, придется отказаться от всех других методов интеграции, которые вы только что изучили за последние несколько недель. Ключ к решению задач с частичными дробями — это не торопиться, тщательно записывать правильную форму разложения, а затем методично работать над поиском коэффициентов.Удачи!
 .
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя * 
Email * 
Сайт