| Образовательные задачи
этапа урока | Содержание этапа урока,
методы и приемы обучения |
| Организационный этап | |
| Организация внимания школьников. Раскрытие
| — Проверка готовности класса к уроку. -
— Повторение темы предыдущего урока.
— Побуждение учащихся к целеполаганию, т. е. к
|
| Подготовка учащихся к работе
на основном этапе. | |
| Обеспечить мотивацию учения
школьников, принятие ими целей урока.  Актуализация
Постановка перед учащимися учебной проблемы.
Формулирование вместе с учениками темы урока,
| Решение задач на повторение (Слайд 6, 7
и 8) Установите соответствие между условиями
Задача 1. Для компота взяли 300 г яблок, а
Задача 2. Для компота взяли 2 части
Задача 3. Для компота взяли 300 г яблок и
Учащимся предлагается выделить среди
Учащиеся устно решают эти задачи.
И далее с помощью учителя они формулируют тему
|
| Этап усвоения новых знаний и
способов действий. | |
| Обеспечить восприятие и осмысленное
усвоение изучаемого материала. Научить
Содействовать построению самими учащимися
Создать условия для усвоения учащимися этого
| Используем электронное приложение к
учебнику: Интерактивные модули. Задачи на части. Задача 2. Для детских новогодних
Моделируя на компьютере краткое условие этой
Осмысливая ход решения этой задачи, учащиеся с
|
| Физкультминутка. (Слайд
10). | |
| Этап применения и
закрепления новых знаний и способов действий. | |
| Обеспечить закрепление в памяти
учащихся знаний и способов действий. Создать
Организация деятельности учащихся по
| 1) Придумайте по рисунку (Слайд 11)
задачу на части и решите её. 2) Работа в
Каждой группе предлагается решить задачу
Базовый уровень — № 190 б;
Повышенный уровень — № 191 а;
Высокий уровень — № 192 а.
Через 5-7 мин. представители групп отчитываются,
Учащиеся с помощью учителя поводят итог этого
|
| Этап контроля, самоконтроля
и коррекции знаний и способов действий. | |
| Выявление уровня и качества усвоения
учащимися знаний и способов действий. .Выявить
Откорректировать выявленные пробелы в знаниях
Развивать у школьников способности к
| Учащимся предлагаются 3 задачи (Слайд
13): 1.
2. В первой пачке 20 тетрадей, что в 4 раза меньше,
3. В двух пачках 20 тетрадей. Во второй пачке
Из этих задач они должны выбрать задачу на
Фронтальная устная работа по решению следующих
№4. Миша решал задачу: “У брата и сестры 20 марок,
У него получилось, что у брата 15 марок, а у
а) Докажите, что Миша не прав.
б) Дайте верный ответ.
(Слайд 16)
№5.
“Дед старше внука в 10 раз, а вместе им 60 лет.
Маша подумала и сказала, что такой ситуации
а) Согласны ли вы с Машей? Почему?
б) Исправьте какое-нибудь данное задачи.
|
| Этап информации о домашнем
задании. | |
| Обеспечить понимание учащимися цели,
содержания и способов выполнения домашнего задания. | (Слайд 17) Подробные рекомендации
|
| Этап подведения итогов
урока. | |
| Дать качественную оценку работы класса
и отдельных учащихся.  | Вернуться к сформулированным в начале
урока целям и оценить степень их достижения. |
| Этап рефлексии. | |
| Инициировать рефлексию учащихся по
поводу своего психо-эмоционального состояния, мотивации своей деятельности и взаимодействия с учителем и одноклассниками. | (Слайд 18) “Незаконченные
Предложить учащимся продолжить незаконченные
|
«Задачи на части» — математика, уроки
5класс. Математика .По учебнику Никольского.
Тема «Задачи на части».
Цели: познакомиться с задачами на части , формирование навыка решения задач на части.
Ход урока.
I.Организационный момент.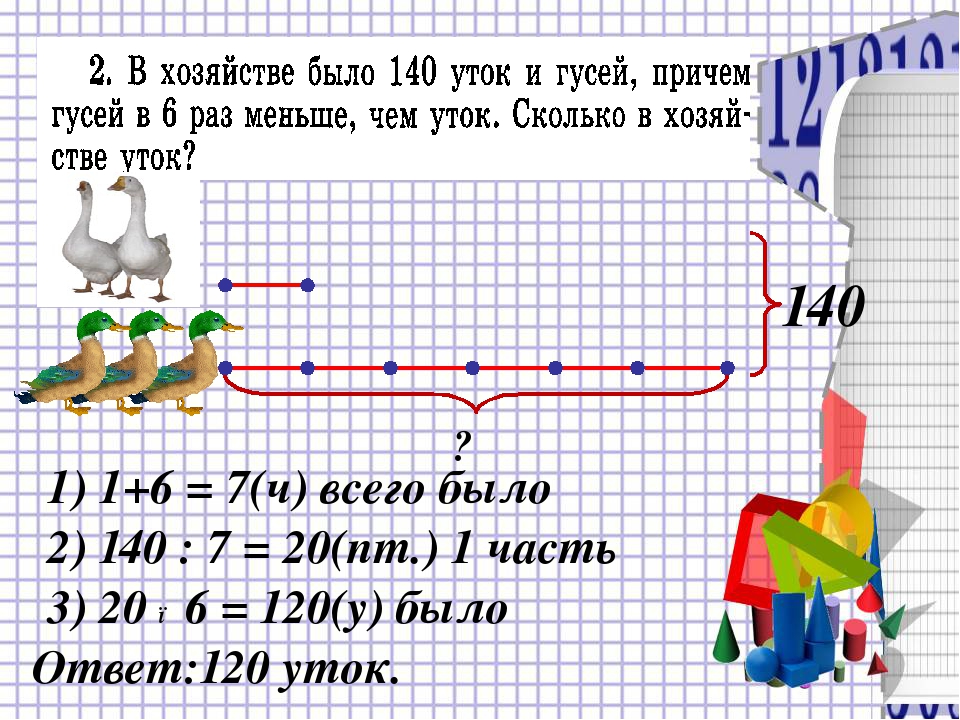
II. Устная работа.
Равенство а·(в·с)=(а·в) ·с является
1) переместительным б) сочетательным в) другим свойством умножения?
произведение 4·222·5 равно
а) 8885 б) 4445 в) 4440.
Вычислите удобным способом:
14·4+16·4 18·3+12·3 5·5·8·8
74·16-74·15 33·52-31·52 12·4·5·5
Собственная скорость лодки 7 км/ч. Скорость течения реки 2 км/ч. Найдите:
-скорость лодки по течению реки
— скорость лодки против течения реки
— путь, пройденный лодкой по течению реки за 2 часа
— путь, пройденный лодкой против течения реки за 3 часа.
III. Актуализация знаний и мотивация.
Мы решали с вами задачи на движение, а сейчас познакомимся с задачами другого типа.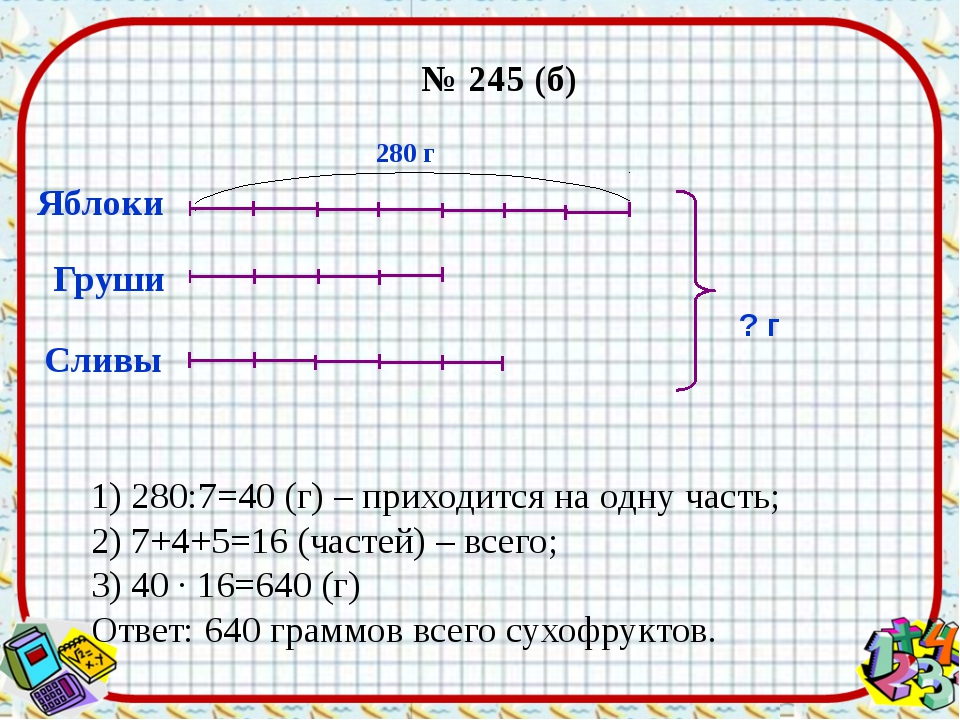
Задача 1. Чтобы сварить гречневую кашу, надо взять 2 части крупы и 3 части воды. Сколько потребуется воды, если в кастрюлю положили 150 г крупы?
Что нужно сделать, чтобы ответить на вопрос задачи?
Необходимо 150:2=75(г)-1 часть
75·3=225(г)-3 части
Ответ: требуется взять 225 г воды.
Задача 2. В сплаве содержится 2 части меди и 1 часть цинка. Сколько меди и цинка содержится в 450 г сплава?
План решения.
1) Сколько всего частей приходится на весь сплав?
2)Каков вес одной части?
3) Сколько граммов меди содержится в сплаве ( сколько граммов приходится на 2 части)?
4) Сколько граммов цинка содержится в сплаве?
1) 2+1=3 (частей) весь сплав
2)450:3= 150 (г) на одну часть
3) 150·2=300(г) меди
Ответ: 300г меди, 150 г цинка.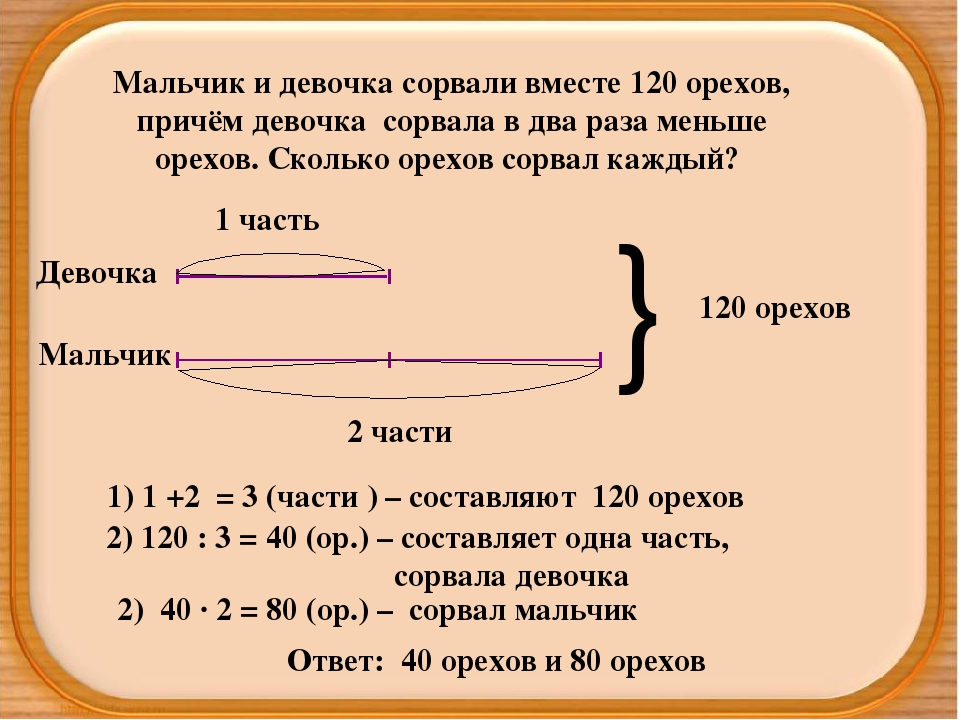
IV. Формирование умений и навыков.
Решим задачи из учебника.
№425(а). Для варенья из вишни на 2 части ягод берут 3 части сахара. Сколько сахара следует взять для 2 кг 600 г ягод?
Решение.
1) 2600:2= 1300(г) на одну часть
2) 1300·3=3900(г) на 3 части сахара
Ответ: 3кг 900г сахара.
№426. Требуется смешать 3 части песка и 2 части цемента. Сколько цемента и песка в отдельности надо взять, чтобы получить 30 кг смеси?
Решение.
1)3+2=5(частей) вся смесь
2)30:5=6(кг) на одну часть
3)3·6=18(кг) песка
4)2·6=12(кг) цемента
Ответ: 18кг песка и 12кг цемента.
Стр.41 из дидактического материала №4. Мороженое содержит 5 частей воды, 2 части молочного жира и 3 части сахара.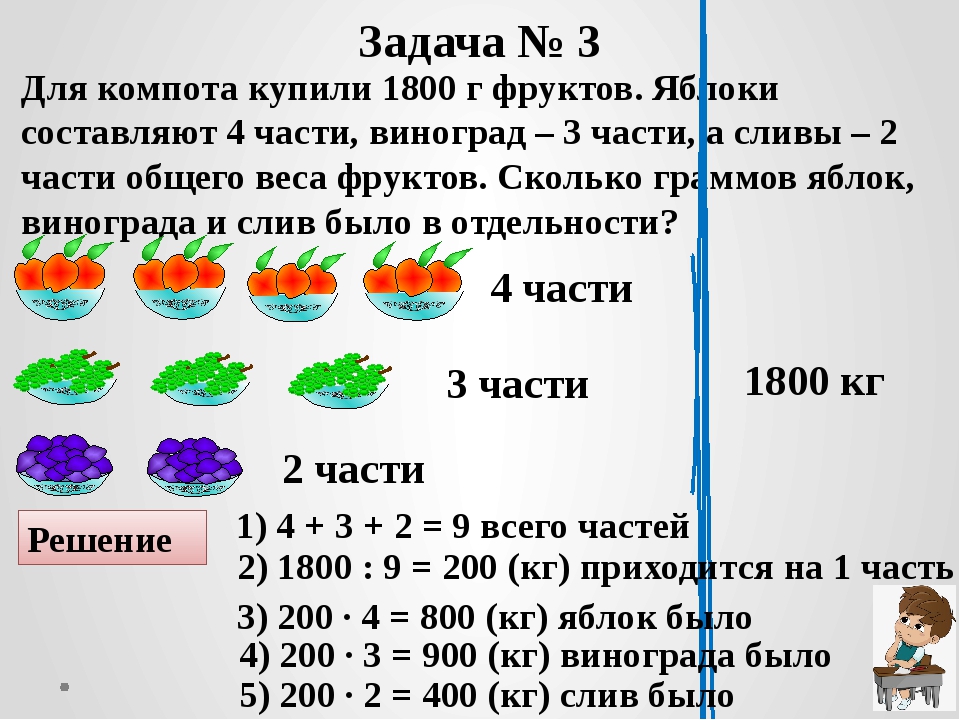 Сколько надо воды, молочного жира и сахара, чтобы приготовить 1кг мороженого?
Сколько надо воды, молочного жира и сахара, чтобы приготовить 1кг мороженого?
1) 5+2+3=10(частей)
2)1000:10=100(г) на одну часть
3)100·5=500(г) воды
4)100·2=200(г) жира
5)100·3=300(г) сахара.
Ответ:500г воды,200г жира,300гсахара.
V . Итог урока.
Обучающая самостоятельная работа.
№2(а). Для приготовления рисовой каши надо взять 2 части риса,3 части молока и 5 частей воды. Сколько молока и сколько воды понадобится, если взять 220 г риса?
1)220:2=110(г) на одну часть
2)110·3=330(г) молока
3)110·5=550 (г) воды.
Ответ:330г молока и 550г воды.
Взаимопроверка решения задачи.
Домашнее задание: п.4.3,№425(б).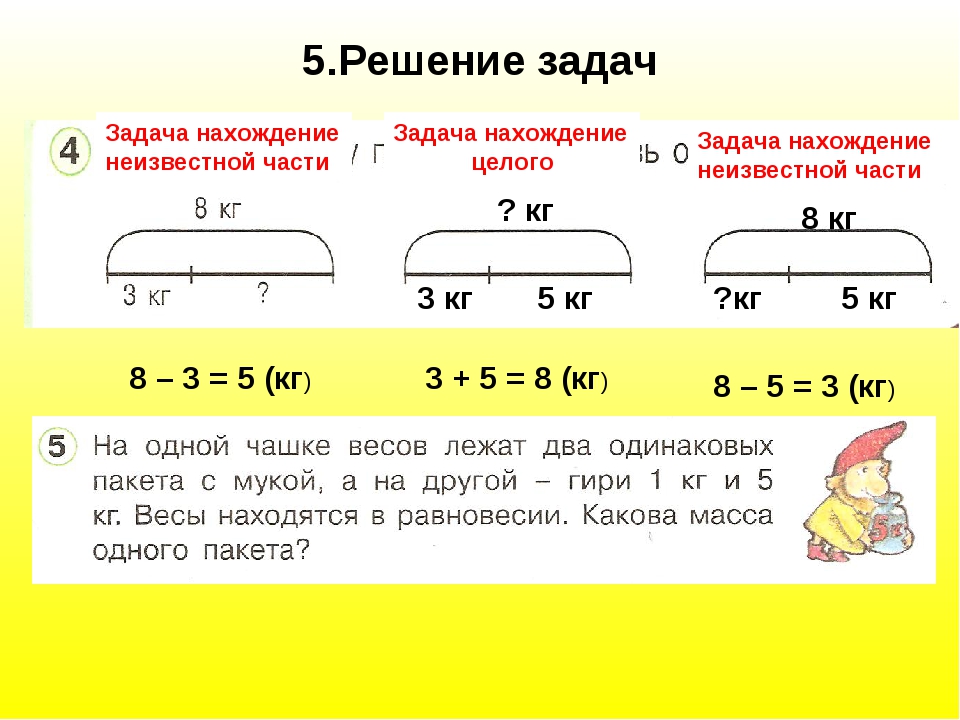
Урок математики по теме: «Задачи на части» для 5 класса (ФГОС)
Цели урока как планируемые результаты обучения, планируемый уровень достижения целей:
Вид планируемых учебных действий
Учебные действия
Планируемый уровень достижения результатов обучения
Предметные
уметь в процессе реальной ситуации использовать понятие «часть», «части»
3 — 4 уровень — понимание, адекватное употребление в речи, выборочно — воспроизведение
умение решать основные типы задач «на части» , грамотно оформлять решение задачи
3 — 4 уровень — понимание, адекватное употребление в речи, выборочно — воспроизведение
Регулятивные
самостоятельно ставят новые учебные задачи путем задавания вопросов о неизвестном
2 уровень — самостоятельное действие учащихся по заданному алгоритму
планируют собственную деятельность, определяют средства для ее осуществления
2 уровень — совместное с учителем действие учащихся на основе знания видов источников информации и способов работы с ними
Познавательные
формируют навыки и умения применять алгоритмы при решении задач « на части»; систематизируют знания, обобщают и углубляют знания при решении задач по теме: «Задачи «на части»
2 уровень — совместное с учителем действие учащихся на основе знания видов источников информации и способов работы
Коммуникативные
умение слушать и вступать в диалог; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе.
2 уровень — совместные действия учащихся в условиях взаимопомощи и взаимоконтроля
Личностные
формировать внимательность и аккуратность в вычислениях; требовательное отношение к себе и своей работе.
2 уровень — самостоятельное выполнение действий с опорой на известный алгоритм
Автор: Алексеева Татьяна Михайловна
Математика 5 класс. Сложные задачи на дроби. Дидактика репетитора
Предлагаю репетиторам по математике специально подготовленный комплект базовых сложных задач на дроби, рассчитанный для учащихся 5 класса. Ориентировочное время на его проработку на уроке — 60 минут. Регулярно использую данный комплект в ситуациях, когда родителям нужна олимпиадная помощь репетитора по математике (подготовка в Курчатовскую школу, в лицей «Вторая школа» и др.) Большинство задач составлены мной по мотивам известных классических номеров повышенной сложности. Комплект можно также использовать в работе с сильным учеником 4 класса, параллельно осваивающим с репетитором по математике программу учебника Петерсона.
Для подготовки к олимпиадам по математике в 5 классе. Задачи на дроби.
1) Тетя Нюра пожарила блинчики. Ира съела половину приготовленных блинчиков и еще один блинчик. Максим съел половину остатка и еще один блинчик, а Никита съел половину последнего остатка и последний блинчик. Сколько блинчиков пожарила тетя Нюра?
2) Мама испекла пирожки. Маша съела всех испеченных пирожков и еще один. После этого Антон съел всех оставшихся пирожков и еще один. И, наконец, Вера съела последнего остатка и последний пирожок. Сколько пирожков испекла мама?
3) Папа пошел в магазин. На первую покупку он истратил всех своих денег и еще одну монету. На вторую покупку он истратил остатка и еще одну монету. На последнюю покупку он снова истратил остатка и последнюю монету. Сколько монет было у папы?
4) Андрей прочитал книгу за 2 дня. Во второй день он прочел того, что он прочитал в первый день. Сколько страниц он прочитал во второй день, если во всей книге 80 страниц?
5) Турист проехал намеченный путь за 2 дня. В первый день он проехал того, что проехал во второй. Сколько километров он проехал во второй день, если весь путь составил 140км?
В первый день он проехал того, что проехал во второй. Сколько километров он проехал во второй день, если весь путь составил 140км?
6) Столб врыт в землю. Часть столба, находящаяся в земле, составляет той части, которая находится над землей. Найдите глубину, на которую врыт столб, если его длина составляет 3м40см.
7) Полина прочитала книги, а Софья — такой же книги. Сколько страниц в этой книге, если Полина прочла больше Софьи на 63 страницы?
8) В первый день в магазине продали всей завезенной вишни, а во второй — всей завезенной вишни. Сколько килограммов вишни завезли, если во второй день продали на 90 кг больше, чем в первый?
9) Имеются две одинаковые бочки с водой. Из первой вылили бочки, а из второй — бочки. Сколько литров воды было в каждой бочке, если из второй бочки вылили на 220литров воды больше, чем из первой.
10) Количество отсутствующих учеников в классе составляет числа присутствующих. Когда из этого класса вышло 6 учеников, число отсутствующих составило числа присутствующих. Сколько всего учеников в этом классе?
Сколько всего учеников в этом классе?
11) Преподаватель по математике проверял тетради с итоговой контрольной работой за 6 класс. До обеда число проверенных работ составляло числа не проверенных. После обеда он проверил еще 4 работы, и число проверенных составило от числа не проверенных. Сколько всего имелось работ?
12) В коробке лежат красные и белые шары. Количество красных шаров составляет числа белых. После того как 12 белых шаров покрасили в красный цвет, количество красных составило числа белых. Сколько шаров в коробке?
13) После того как почтальон проехал 1 км и еще половину оставшегося пути до почты, ему осталось проехать всего пути и еще 1 км. Чему равен путь почтальона?
14) После того как черепаха проползла 10 см и еще оставшегося пути, ей осталось проползти всей дистанции и последние 10 см. Чему равна длина дистанции черепахи?
15) После того как туристы проехали 2 км на машине и еще остатка всего маршрута, им осталось до конца маршрута проехать всего пути и последние 3 км. Найдите длину туристического маршрута?
Найдите длину туристического маршрута?
Пояснение репетитора по математике: данные задачи представляют собой полноценный комплект упражнений для одного урока с сильным учеником 4 — 5 класса по теме: «задачи на дроби». Он представлен пятью блоками полуолимпиадных номеров, рассчитанных на решение без применения уравнений. Рекомендую репетиторам по математике разбирать одну задачу самостоятельно, другую оставлять для самостоятельную работы ученика в присутствии репетитора, а еще одну задавать на дом. В каждом блоке для этого имеется соответствующее количество задач.
Колпаков А.Н Репетитор по математике в Москве. Строгино
|
I.Организационный момент.
II. Актуализация знаний:
Повторение и систематизация знаний при выполнении устных упражнений:
– Какую тему мы изучали на двух предыдущих уроках?
Слайд 1.
1. Из маленьких квадратиков составьте квадрат, в котором ¼ часть оранжевая, а ¾ зелёная.
Проверьте себя!
Слайд 2.
Слайд 3.
2. Из зелёных и белых полос сложите прямоугольник, в котором 1/5 часть зелёная; 2/5 части зелёные; 5/5 части зеленые.
Проверь себя!
Слайд 4.
– Что означает 5/5 и 4/4? (Вся фигура, одно целое).
– Как найти ½ часть? 1/3? 1/5? 3/5? 5/5?
Слайд 5.
3. Решите анаграмму
Слайд 6.
Проверим.
Слайд 7.
III. Введение новых знаний.
Тема нашего урока
«Решение задач на нахождение части от целого и целого по его части».
Сегодня на уроке мы продолжаем изучение обыкновенных дробей, рассмотрим основные виды задач на дроби с которыми мы будем встречаться не только на уроках математики, но и в жизни.
– Какие цели мы поставим перед собой на урок? (Записываем цели на дополнительной доске).
– Запишите тему урока в тетрадь.
Слайд 8.
«Если вы хотите научиться плавать, то смело входите в воду,
Слайд 9.
Рассмотрим схему
Слайд 10.
– Какие задачи можно составить, исходя из этой схемы?
Слайд 11.
Решим задачу.
Работа с ЭОР
Модуль 1.
Задание в картинках по теме «Задача на нахождение части от целого». К1
– Рассмотрим несколько задач и определим, к какому виду задач их можно отнести.
Слайд 12.
Рассмотрим решение задач:
Работа с ЭОР
Модуль 2.
Отыскание одной доли от целого и целого по одной доле
– Ребята, можно ли утверждать, что задачи 1 и 2 взаимно–обратные?
IV. Физкультминутка.
V. Работа в парах. Проговорите правила друг другу.
– Распределите задачи из списка по видам. Разложите на парте 6 квадратиков так, что
— Зелёный квадратик – задача на нахождение целого по его части
— Оранжевый квадратик – задача на нахождение части от целого
– Проверьте себя! Слайд 15.
Вывод: Обратить внимание на слова
«что», «это».
Слайд 16.
Решите задачу самостоятельно:
Работа с ЭОР
Модуль 3.
Задание в картинках по теме «Задача на составление целого из равных частей». П5
VI. Подведение итогов урока:
VII.
Выполняя задания на уроке, вы показали умение самостоятельно мыслить, делать выводы, правильно оформлять решение задач.
Посмотрите домашние задачи:
– решить по 3 задачи из списка на выбор;
Слайд 17.
Слайд 18.
Спасибо за работу на уроке
|
Приветствие.
Проверка готовности учащихся.
Задает вопросы
Следит за верностью выполнения задания
Следит за верностью выполнения задания
Задает вопросы. Следит за правильностью рассуждений.
Следит за правильностью рассуждений и ответами учащихся
Сообщение темы урока.
Задаёт вопросы, следит за правильностью рассуждений.
После ответа на вопросы на экране появляется графическая иллюстрация.
Следит за грамотностью рассуждений.
Совместно с учащимися выбирает метод решения, следит за грамотным решением у доски.
Задает вопросы. Следит за правильностью рассуждений учащихся
Задает вопросы, следит за правильностью формулировок правил
Задает вопросы учащимся. Следит за правильностью формулировок правил.
Организует работу в парах. Следит за работой учащихся за партами.
После выполнения задания учащимися на вопросы на экране появляется таблица правильного ответа.
Обращает внимание учащихся на слова «что», «это»
в задачах.
Следит за решением задачи в тетради
Выставляет оценки (с обоснованием), подводит итог урока.
Раздает карточки с домашним заданием.
|
Отвечают на вопросы
Составляют фигуры на парте, после обсуждения на экране высвечивается правильный ответ.
Составляют фигуры на парте, после обсуждения на экране высвечивается правильный ответ.
Отвечают на вопросы.
Решают анаграмму
Записывают число и тему урока. Формулируют цели урока.
Отвечают на вопрос (задачи:
— нахождение части от целого;
— целого по его части;
— соотношения части и целого
Предлагают и обсуждают решение задачи.
Один ученик записывает решение на доске, остальные в тетрадь.
Отвечают устно с места
Решают задачи. Отвечают на вопросы
Ученики с места формулируют правила: нахождение части от целого; целого по его части
Раскладывают квадратики согласно заданию по цветам.
Проверяют себя
Делают вывод.
Записывают задание и решение в тетрадь.
Отвечают на вопросы, делают выводы.
Задают вопросы по выполнению домашнего задания.
|
8
5
7
|
Страница 76 №244-251 ГДЗ к учебнику «Математика» 5 класс Бунимович, Дорофеев, Суворова
Ответы к упражнениям учебника
Задачи на части
Задание 244. Купили 1 кг 800 г сухофруктов из яблок, груш и слив. Яблок в них 4 части, груш − 3 части, слив − 2 части. Сколько граммов яблок, груш и слив в сухофруктах в отдельности?
Указание.
Выразите массу сухофруктов в граммах.
Решение задачи
1 кг 800 г = 1800 г
1) 3 + 4 + 2 = 9 (частей) − всего;
2) 1800 : 9 = 200 (г) − составляет одна часть;
3) 200 * 4 = 800 (г) − яблок в сухофруктах;
4) 200 * 3 = 600 (г) − груш в сухофруктах;
5) 200 * 2 = 400 (г) − слив в сухофруктах.
Ответ: 400 г слив, 600 г груш, 800 г яблок.
Задание 245. В сухофруктах яблоки составляют 7 частей, груши − 4 части, сливы − 5 частей. Сколько всего сухофруктов, если в них:
а) 160 г груш;
б) 280 г яблок;
в) 225 г слив?
Решение
а) 1) 160 : 4 = 40 (г) − составляет одна часть;
2) 7 * 40 = 280 (г) − яблок в сухофруктах;
3) 5 * 40 = 200 (г) − слив в сухофруктах;
4) 160 + 280 + 200 = 640 (г) − сухофруктов всего.
Ответ: 640 гб) 1) 280 : 7 = 40 (г) − составляет одна часть;
2) 40 * 4 = 160 (г) − груш в сухофруктах;
3) 40 * 5 = 200 (г) − слив в сухофруктах;
4) 280 + 160 + 200 = 640 (г) − сухофруктов всего.
Ответ: 640 гв) 1) 225 : 5 = 45 (г) − составляет одна часть;
2) 7 * 45 = 315 (г) − яблок в сухофруктах;
3) 4 * 45 = 180 (г) − груш в сухофруктах;
4) 225 + 315 + 180 = 720 (г) − сухофруктов всего.
Ответ: 720 г.
Задание 246. При пайке изделий из жести применяют сплав, содержащий 2 части свинца и 5 частей олова. Сколько свинца и олова содержит кусок сплава, в котором олова на 360 г больше, чем свинца?
Решите эту задачу по плану:
1) Сколько частей составляют 360 г?
2) Сколько граммов приходится на 1 часть?
3) Сколько свинца в сплаве?
4) Сколько олова в сплаве?
Решение
1) 5 − 2 = 3 (части) − составляют 360 г;
2) 360 : 3 = 120 (г) − приходится на 1 часть;
3) 120 * 2 = 240 (г) − свинца в сплаве;
4) 120 * 5 = 600 (г) − олова в сплаве.
Ответ: 240 г свинца и 600 г олова.
Задание 247. Купили 60 тетрадей, причем тетрадей в клетку в 2 раза больше, чем тетрадей в линейку (рис. 4.3). Сколько частей приходится на тетради в линейку? на тетради в клетку? на все тетради? Сколько купили тетрадей в линейку? Сколько − в клетку?
Решение задачи
1) 1 * 2 = 2 (части) − составляют тетради в клетку;
2) 1 + 2 = 3 (части) − всего;
3) 60 : 3 = 20 (тетрадей) − в линейку;
4) 20 * 2 = 40 (тетрадей) − в клетку.
Ответ: 20 тетрадей в линейку; 40 тетрадей в клетку.
Задание 248. а) На двух полках вместе 120 книг, причем на первой полке книг в 3 раза больше, чем на второй. Сколько книг на каждой полке?
б) В плацкартном вагоне в 3 раза больше спальных мест, чем в мягком вагоне. Всего в этих вагонах 72 места. Сколько спальных мест в мягком вагоне?
Решение задач
а) 1) 1 * 3 = 3 (части) − книг на первой полке;
2) 1 + 3 = 4 (части) − всего;
3) 120 : 4 = 30 (книг) − на второй полке;
4) 30 * 3 = 90 (книг) − на первой полке.
Ответ: 90 книг и 30 книг.б) 1) 1 * 3 = 3 (части) − спальных мест в плацкартном вагоне;
2) 1 + 3 = 4 (части) − всего;
3) 72 : 4 = 18 (мест) − в мягком вагоне;
4) 18 * 3 = 54 (места) − в плацкартном вагоне.
Ответ: 18 мест в мягком вагоне, 54 места в плацкартном вагоне.
Задание 249. а) Коля и Таня рвали в лесу орехи. Всего они сорвали 10 орехов. Таня сорвала в 2 раза меньше орехов, чем Коля. Сколько орехов было у Коли и сколько у Тани?
б) Алина прочитала в 3 раза меньше страниц, чем ей осталось прочитать. Всего в книге 176 страниц. Сколько страниц прочитала Алина?
Подсказка.
Переформулируйте каждую задачу, используя слово «больше».
Решение задач
а) Если Таня сорвала в 2 раза меньше орехов, то Коля собрал в 2 раз орехов больше, тогда:
1) 1 * 2 = 2 (части) − орехов собрал Коля;
2) 1 + 2 = 3 (части) − всего;
3) 120 : 3 = 40 (орехов) − собрала Таня;
4) 40 * 2 = 80 (орехов) − собрал Коля.
Ответ: 40 орехов собрала Таня; 80 орехов собрала Коля.б) Если Алина прочитала в 3 раза меньше страниц, чем ей осталось прочитать, то значит Алене осталось прочить в 3 раза больше, чем она прочитала, тогда:
1) 1 * 3 = 3 (части) − осталось прочитать Алине;
2) 1 + 3 = 4 (части) − всего;
3) 176 : 4 = 44 (страницы) − прочитала Алина.
Ответ: 44 страницы.
Задание 250. Дочка младше мамы в 4 раза и младше бабушки в 9 раз. Сколько лет каждой, если вместе им 98 лет?
Решение задачи
1) 1 + 4 + 9 = 14 (частей) − всего;
2) 98 : 14 = 7 (лет) − дочке;
3) 7 * 4 = 28 (лет) − маме;
4) 7 * 9 = 63 (года) − бабушке.
Ответ: 7 лет дочек, 28 лет маме, 63 года бабушке.
Задание 251. У Сережи в коллекции в 3 раза меньше марок, чем у Васи, а у Андрея в 2 раза больше, чем у Васи. Сколько марок у каждого, если у Андрея на 80 марок больше, чем у Сережи?
Решение задачи
1) 3 * 2 = 6 (раз) − больше у Андрея марок, чем у Сережи;
2) 6 − 1 = на 5 (частей) − больше у Андрея марок, чем у Сережи;
3) 80 : 5 = 16 (марок) − у Сережи;
4) 16 * 3 = 48 (марок) − у Васи;
5) 16 * 6 = 96 (марок) − у Андрея.
Ответ: 16 марок у Сережи, 48 марок у Васи, 96 марок у Андрея.
Решение задач на части (5-й класс)
Цели урока:
- обобщить и систематизировать знания, полученные по данной теме,
- закрепление навыков решения задач на части несколькими способами,
- закрепление решения уравнений,
- расширение круга задач, выходящих за рамки учебника,
- развитие речи, мышления, внимания, познавательной активности учащихся.
Тип урока: урок обобщения и систематизации знаний.
Оборудование:
- слайды с задачами в форме компьютерной презентации
(Приложение 1) на интерактивной доске, - карточки с заданиями на каждой парте.
Ход урока
1-й этап. Мотивационно-ориентировочный: разъяснение цели деятельности
учащихся.
Учитель: (слайд 1) Сегодня у нас урок решения задач на части.
Будем решать задачи, выходящие за рамки школьного учебника. Цель – отработать
арифметический и алгебраический способы решения задач, повторить решение
уравнений.
Эпиграфом к этому уроку будут слова Д. Пойа (слайд2):
“Крупное научное открытие даст решение крупной проблемы, но в решении любой
задачи присутствует крупица открытия”.
Надеюсь, сегодня вы также для себя что-то откроете.
2-й этап. Актуализация опорных знаний.
1) Устно решить следующие задачи.
1. Витя Верхоглядкин записал выражение 25 · х · 4. Потом он вместо х стал
подставлять в это выражение по очереди числа 13, 21, 39, 47. Найдя значение
каждого произведения, он очень удивился тому, что все числа оказались круглыми.
Не могли бы вы объяснить, почему? Сколько нулей будет стоять в конце каждого
полученного числа?
Слайд 3: 25 · х · 4
13, 21, 39, 47
2. Слайд 4: Н.Носов “Витя Малеев в школе и дома”
Мальчик и девочка рвали в лесу орехи. Всего они сорвали 120 штук. Девочка
сорвала в два раза меньше мальчика. Сколько орехов было у мальчика и девочки в
отдельности.
Ответ: 40 орехов у девочки, 80 орехов у мальчика.
3. Слайд 5: Сплав содержит 1 часть свинца и 2 части олова. Во сколько
раз в этом сплаве олова больше, чем свинца?
4. Слайд 6: Сплав содержит олова в 3 раза больше, чем свинца. Сколько
частей олова приходится на 1 часть свинца?
2) Фронтальный опрос:
- Сформулируйте определение уравнения? (Уравнение – это равенство,
содержащее букву.) - Что называется корнем уравнения? (Значение буквы, при котором из
уравнения получается верное числовое равенство, называют корнем уравнения.) - Что значит решить уравнение? (это значит найти все его корни или
доказать, что их нет.)
3-й этап. Решение задач.
1. Слайд 7: Какой улов был у тебя вчера? – спросил
сосед соседа-рыбака. “ Я поймал два крупных леща да щуку общим весом 15 кг. Щука
хороша! Она тяжелее каждого леща в три раза”. “Сколько весит щука?” – спросил
сосед. “Посчитай сам!” – улыбнулся рыбак. Попробуйте вы ответить на вопрос
соседа.
Решение:
Арифметический способ:
- 15 : (2 + 3) = 3 (кг) – лещ.
- 3 · 3 = 9 (кг) – щука.
Ответ: 9 кг.
Алгебраический способ:
Лещ – х кг,
Щука – 3х кг.
х + х + 3х = 15,
5х = 15,
х = 3.
3х = 3 · 3 = 9 (кг)
Ответ: 9 кг вес щуки.
Деятельность учащихся: два ученика решают задачу на доске разными
способами.
2. Слайд 8: При пайке изделий из жести применяется сплав,
содержащий 2 части свинца и 5 частей олова. Сколько граммов свинца и олова в
отдельности содержит кусок сплава, в котором олова на 360 г больше, чем свинца.
Решение:
Арифметический способ:
- 360 : (5 – 2) · 2 = 240 (г) – свинца.
- 360 : (5 – 2) · 5 = 600 (г) – олова.
Ответ: 240 г свинца, 600 г олова.
Алгебраический способ:
Пусть х г – 1 часть.1
Свинец – 2х г,
Олово – 5х г.
5х – 2х = 360,
3х = 360,
х = 120.
Если х = 120, то 2х = 2 · 120 = 240,
5х = 5 · 120 = 600.
Ответ: 240 г свинца, 600 г олова.
Деятельность учащихся: два ученика решают задачу на доске разными
способами.
3. Слайд 9: Для компота взяли 6 частей яблок, 5 частей груш
и 3 части слив. Оказалось, что груш и слив вместе взяли 2 кг 400 г. Определите
массу взятых яблок; массу всех фруктов.
Решение:
Арифметический способ:
- 2400 : (5 + 3) · 6 = 1800 (г) – яблок.
- 1800 + 2400 = 4200 (г) – фруктов.
Ответ: 1800 г яблок, 4200 фруктов.
Алгебраический способ:
Пусть х г – 1 часть.
Яблоки – 6х г,
груши – 5х г,
сливы – 3х г.
5х + 3х = 2400,
8х = 2400,
х = 300.
Если х = 300, то 6х = 6 · 300 = 1800,
1800 + 2400 = 4200.
Ответ: 1800 г яблок, 4200 фруктов
Деятельность учащихся: задача дается на самостоятельное решение с
дальнейшим обсуждением. Один из способов решения показан на слайде (слайд 10)
4-й этап: Подведение итогов урока.
Задание на дом: (Слайд 11)
- Для изготовления фарфора берут 25 частей глины, 1 часть гипса, 2 части
песка. Какова масса фарфоровой чашки, если она содержит глины на 184 г
больше, чем песка? - Составить и решить задачу по уравнению 7х – 2х + 4х = 270.
Если возможно, решить задачу несколькими способами. Оформить решение на листе
А4, можно сделать иллюстрацию.
Заключение.
Учитель: закончить наш урок я хочу закончить словами Д. Пойа (слайд
12): Приложение 1
“Недостаточно лишь понять задачу, необходимо желание решить ее.
Без сильного желания решить трудную задачу невозможно, но при наличии такого
возможно.
Где есть желание, найдется путь”
Литература:
- Совайленко В. К., Лебедева О. В. Сборник развивающих задач с
решениями по математике для 5–6-х классов. Ростов-на-Дону: Легион, 2005. - Шуба М.Ю. Занимательные задачи в обучении математике: Кн. для
учителя. – 2-е изд. М.: Просвещение, 1995. - Дышинский Е. А. Игротека математического кружка. Пособие для
учителя. М.: Просвещение, 1972.
8 способов помочь ученикам успешно решать задачи со словами в старших классах начальной школы
Задачи со словами могут быть действительно трудными для учеников старших классов начальной школы. Сложность словесных задач увеличивается, длина самих задач увеличивается, числа становятся больше и абстрактнее, а часто ключевые слова просто не работают.
Сегодня я хочу поделиться с вами восемью способами помочь учащимся, у которых возникают проблемы со словами в старших классах начальной школы.
Мой первый совет: выберите аббревиатуру, которая либо поможет вашим ученикам понять и продумать математическую задачу, либо выберите аббревиатуру, которая поможет обеспечить ясность и полноту их работы и ответов.Лично я предпочитаю использовать аббревиатуру, которая помогает студентам осмыслить проблему и адекватно показать всю свою работу и организовать свои мысли.
Имея это в виду, около четырех лет назад я создал аббревиатуру «ЛЮБОВЬ» и использовал ее во всех смыслах. ЛЮБОВЬ помогает студентам организовать свою работу, свои мысли, одновременно помогая обеспечить, чтобы студенты давали достаточно, чтобы поддержать их ответ. Шаги, встроенные в процесс, также помогают учащимся разобраться в словесной проблеме, поскольку они вынуждены использовать модели, ярлыки и т. Д.
-> Узнайте больше об использовании LOVE, чтобы помочь своим ученикам решить проблемы со словами, и получите несколько бесплатных подарков, щелкнув здесь.
Выберите закладки, показанные на картинке выше, нажав ЗДЕСЬ.
Это изменило правила игры для моих учеников. Около пяти лет я перестал учить ключевые слова и перешел к обучению ситуациям. Мы смотрим на общие ситуации и какие операции используются в этих ситуациях. Я даже предоставляю своим ученикам таблицу, на которую они могут ссылаться и добавлять при необходимости.
Когда мои ученики решают словесную задачу, они обращаются к диаграмме ситуаций, чтобы помочь им определить, какая операция необходима. Это помогает им сформировать концептуальное понимание математических операций и помогает справляться со словесными задачами. Чтобы узнать больше о том, как я учу своих студентов решать задачи со словами, не полагаясь на ключевые слова (и возьмите плакат ниже и несколько практических задач, которые я использую), щелкнув здесь.
Когда я представляю новую математическую концепцию, я всегда представляю ее в контексте проблемы или ситуации.Это помогает учащимся осмыслить математику, увидеть связь с реальным миром и лучше осмыслить новую математику.
-> Прочтите, как я делаю это для введения частичного деления на частные, нажав здесь.
Я признаю, что одна ошибка, которую я совершил, будучи учителем первого года обучения, заключалась в том, что я обучал вычислительным навыкам в первой половине года, а затем втиснул задачи со словами перед нашей государственной оценкой. Мне не удавалось регулярно включать их в нашу обычную практику и домашние задания.Я создал массу проблем со словами во многих интересных и целенаправленных форматах, так что это больше никогда не повторится. Моим ученикам нравятся наши интерактивные задачи со словами из записной книжки, а мне нравятся задачи со словами повседневной рутины, которые мы выполняем каждый день.
Щелкните здесь, чтобы узнать больше о задачах дня и получить БЕСПЛАТНЫЕ стартовые пакеты для задач 4 и 5 классов.
Когда я пишу задачи для своего класса, я всегда использую имена моих учеников, их местонахождение и опыт, которые им знакомы.Это помогает по нескольким причинам:
- Они сразу же начинают решать проблему со словом, когда видят знакомое имя, место или опыт.
- Шансы на то, что они запомнят ситуацию (чтобы применить ее к новым ситуациям), выше.
- Вам будет легче вернуться к предыдущим задачам со словами, чтобы помочь учащимся сформировать эшафот, когда они столкнутся с новыми или более сложными задачами со словами.
Совет: я использую свои уже созданные задачи слов (или купленные задачи слов) и просто меняю имена или местоположения, когда пишу их на диаграммах привязки.
Это очень похоже на мою стратегию сверху. Я не только использую знакомые имена и опыт, но и использую глупые словесные задачи со своими учениками. Я использовал персонажей мультфильмов или словесные задачи, которые просто глупо думают о зомби и другие темы из научной фантастики.
Вот пример некоторых тематических задач со словами зомби (ничего страшного или предполагающего, что они настоящие), которые мы использовали для проверки умножения и деления. Нажмите здесь, чтобы получить БЕСПЛАТНУЮ доску выбора словесных задач на тему зомби.
Мы регулярно решаем задачи по словесности или математические задания для всего класса в моем классе. Иногда мы решаем их вместе, как класс. Чаще учащиеся самостоятельно решают словесные задачи, а затем мы делимся и обсуждаем используемые стратегии. Раз в неделю я стараюсь выделять 15-20 минут специально для того, чтобы делиться идеями и стратегиями по заданной проблеме со словом. Узнайте больше о том, как я это делаю, нажав здесь.
Иногда нам нужно предложить больше поддержки нашим ученикам в решении текстовых задач.Есть несколько способов сделать это в моем классе.
1. Пошаговые органайзеры — Я использую текстовые задачи с пошаговым органайзером, чтобы помочь студентам продумать задачу и организовать свою работу. На рисунке ниже показан пример этого с использованием моего Задачи вмешательства для 5-го класса (щелкните здесь для 4-го класса).
Щелкните здесь, чтобы получить БЕСПЛАТНЫЕ пошаговые органайзеры задач со словами, которые работают с любой задачей со словами.
2. Основы предложений — Я также помогаю поддерживать своих студентов, предоставляя им основы предложений, которые они могут использовать при написании ответа на словесную проблему (и обосновывают свой ответ — подробнее читайте здесь). Я обнаружил, что повторение вопроса для студентов помогает им понять, о чем они спрашивают. На картинке ниже показан пример того, как я это делаю, используя свои дифференцированные многоэлементные математические задачи для 5-го класса.
Надеюсь, эти стратегии и советы дадут вам несколько идей, которые помогут вам решать проблемы со словами с учениками старших классов начальной школы. Есть ли у вас какие-либо другие стратегии, которые вы используете, чтобы помочь своим ученикам?
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
Сохранить
стратегий решения проблем со словами
Простое добавление этих слов увеличивает сложность (а иногда и математическую тревогу) примерно на 100!
Как вы можете помочь своим ученикам научиться уверенно решать задачи со словами? Обучая своих учеников решать текстовые задачи поэтапно и организованно, вы дадите им инструменты, необходимые для более эффективного решения текстовых задач.
Вот семь стратегий, которые я использую, чтобы помочь студентам решать задачи со словами.
1. Прочитать все слово Задача
Прежде чем учащиеся будут искать ключевые слова и пытаться понять, что им делать, им нужно немного замедлиться и прочитать всю текстовую задачу один раз (а еще лучше, дважды). Это помогает детям получить более широкую картину, чтобы понять ее немного лучше.
2. Подумайте о проблеме со словами
Студенты должны задавать себе три вопроса каждый раз, когда они сталкиваются с проблемой со словами.Эти вопросы помогут им составить план решения проблемы.
Вот вопросы:
A. В чем именно заключается вопрос?
В чем проблема? Часто составители учебных программ включают в задачу дополнительную информацию без видимых на то веских причин, за исключением, может быть, для того, чтобы научить детей игнорировать эту постороннюю информацию (грррр!). Студенты должны быть в состоянии оставаться сосредоточенными, игнорировать эти лишние детали и выяснять, в чем реальный вопрос конкретной проблемы.
B. Что мне нужно, чтобы найти ответ?
Студентам необходимо сузить круг вопросов, даже больше, чтобы выяснить, что необходимо для решения задачи, будь то сложение, вычитание, умножение, деление или их комбинация. Им потребуется общее представление о том, какая информация будет использоваться (или не использоваться) и что они будут делать.
Здесь очень помогают ключевые слова. Когда учащиеся учатся распознавать, что одни слова означают сложение (например, всего вместе, вместе ), в то время как другие означают вычитание, умножение или деление, это помогает им решить, как поступить немного лучше
Вот таблица ключевых слов, которую я люблю использовать при обучении задачам со словами.Раздаточный материал можно было скопировать в меньшем размере и вклеить в интерактивные тетради по математике. Его можно поместить в математические папки или в подшивки под математическим разделом, если ваши ученики используют подшивки.
Однажды я сделал огромные математические знаки (символы сложения, вычитания, умножения и деления) и написал ключевые слова вокруг символов. Они служили постоянным напоминанием о ключевых словах для словесных задач в классе.
Если вы хотите скачать БЕСПЛАТНЫЙ раздаточный материал по ключевым словам, нажмите здесь:
С.Какая информация у меня уже есть?
Здесь учащиеся сосредоточатся на числах, которые будут использоваться для решения задачи.
3. Задача о словах
Этот шаг укрепляет мышление, имевшее место на втором шаге. Студенты используют карандаш или цветные карандаши, чтобы записывать информацию на рабочих листах (конечно, не в книгах, если они не расходные материалы). Есть много способов сделать это, но вот что я люблю делать:
- Обведите любые числа, которые вы хотите использовать.
- Слегка вычеркните любую ненужную информацию.
- Подчеркните фразу или предложение, в котором точно указано, что вам нужно найти.
4. Нарисуйте простую картинку и назовите ее
Рисование картинок с использованием простых форм, таких как квадраты, круги и прямоугольники, помогает учащимся визуализировать проблемы. Также помогает добавление номеров или имен в качестве меток.
Например, если в словарной задаче говорится, что было пять коробок и в каждой коробке было по 4 яблока, дети могут нарисовать пять квадратов с числом четыре в каждом квадрате.Мгновенно дети могут увидеть ответ намного легче!
5. Оцените ответ, прежде чем решать
Имея общее представление о приблизительном ответе на проблему, учащиеся узнают, является ли их реальный ответ разумным или нет. Эта быстрая приблизительная оценка — хорошая математическая привычка. Это помогает учащимся по-настоящему задуматься о точности своего ответа, когда проблема, наконец, будет решена.
6. Проверьте свою работу, когда закончите
Эта стратегия соответствует пятой стратегии.Одна из фраз, которые я постоянно использую во время математических занятий: Разумный ли ваш ответ ? Я хочу, чтобы учащиеся делали больше, чем просто вычисляли числа, но на самом деле думали о значении этих чисел.
Кроме того, когда учащиеся приобретают привычку проверять работу, они более склонны замечать небрежные ошибки, которые часто являются причиной неправильных ответов.
7. Часто повторяйте проблемы со словами
Точно так же, как требуется практика, чтобы научиться играть на кларнете, вести мяч в футболе и реалистично рисовать, чтобы стать мастером решения словесных задач, требуется практика.
Когда студенты отрабатывают задачи со словами, часто происходит несколько вещей. Проблемы со словами становятся менее страшными (нет, правда).
Они начинают замечать сходство типов проблем и могут быстрее понять, как их решать. Они обретут уверенность, даже когда будут иметь дело с новыми типами задач со словами, зная, что они успешно решали многие задачи со словами в прошлом.
Если вы ищете карточки с задачами со словами, у меня их довольно много для учащихся 3-5 классов.
В этом наборе карточек с заданиями по математике для 3-го класса есть задачи со словами почти в каждом из 30 наборов карточек с заданиями.
Существуют также специальные наборы, посвященные задачам со словами и двухэтапным задачам со словами. Мне это нравится, потому что для каждого стандарта есть карточки с заданиями.
НАЖМИТЕ ЗДЕСЬ, чтобы посмотреть 3-й класс:
В этом наборе карточек с заданиями по математике для 4-х классов также есть множество задач со словами почти в каждом из 30 наборов карточек с заданиями.Эти карты идеально подходят для центров, всего класса и для один на один.
НАЖМИТЕ ЗДЕСЬ, чтобы увидеть 4-й класс:
Этот комплект карточек с заданиями по математике для 5-х классов также содержит задачи со словами, чтобы ваши ученики могли целенаправленно практиковаться.
НАЖМИТЕ ЗДЕСЬ, чтобы посмотреть 5 класс:
Хотите попробовать БЕСПЛАТНЫЙ набор карточек с заданиями по математике, чтобы узнать, что вы думаете?
3-й класс: округление целых чисел в карточках
4-й класс: преобразование дробей и десятичных знаков
5-й класс: карточки задач «Чтение, запись и сравнение десятичных знаков»
Спасибо, что заглянули!
Решение дробей в 5-м классе с помощью математических историй: часть 4 — Чартерная школа Род-Айленда
Стеф Примиани, директор STEM, и Алисия Куомо, Стажер по политике в области городского образования Университета Брауна
Что, если бы я сказал вам, что студенты могут бороться, выражать математическое мышление высокого уровня и их подталкивают к развитию своих нынешних знаний… и все это в течение 20 минут?
Студенты и учителя Blackstone Valley Prep используют для этого протокол 20-минутных историй по математике .
В последнем сообщении блога я обсуждал, как преподаватели Blackstone Valley Prep используют протокол планирования уроков каждый раз, когда планируют урок по математике. Учителя следуют четырехэтапному процессу: выявить больших идеи , предвидеть представления нескольких учеников , предвидеть возможные неправильные представления и спланировать целевых вопросов для обсуждения, чтобы обозначить ключевой момент .
Но что на самом деле происходит за эти 20 минут? Каков протокол урока математических историй?
Возьмем, к примеру, эту задачу-рассказ:
Молли проходит 1 ½ миль каждый день в течение 5 дней.Тревонте проходит 2 ½ миль каждый день в течение 5 дней. Насколько дальше Тревонте прошел за эти 5 дней, чем Молли?
Шаг 1. Вопрос
Учитель читает задачу дважды ученикам. Карандаши опущены, и учеников просят визуализировать или сделать мысленный фильм о проблеме рассказа.
Затем ученики запишут вопрос , на который они пытаются ответить.
Шаг 2. Запишите информацию, смоделируйте и решите
- Учащиеся записывают имеющуюся у них информацию и информацию, необходимую им для решения задачи.
- Студенты моделируют и решают задачу без каких-либо указаний.
Суть Math Stories заключается в том, что учащиеся моделируют задачу, используя любую стратегию представления, которая им понятна. Например, учащиеся могут выбрать представление количества миль, пройденных Молли и Тревонте, соответственно, за 5 дней, используя модель с дискретными дробями, числовые линии , ленточные диаграммы или что-то еще .
Образец модели:
- Четко обозначено визуальных изображения пройденных расстояний Молли и Тревонте.
- Ярлыки специфичны, чтобы другие ученые могли ясно видеть, где информация из проблемы представлена в модели.
- Решает проблему с помощью визуальной модели, написав алгоритм , который соответствует их модели, когда это имеет смысл.
- Записывает окончательный ответ в виде полного предложения.
Модели:
Стратегии решения:
Учащиеся считают / складывают, чтобы найти итоги, и вычитают:
1 ½ + 1 ½ + 1 ½ + 1 ½ + 1 ½ = 7 ½
2 ½ + 2 ½ + 2 ½ + 2 ½ + 2 ½ = 12 ½
12 ½ — 7 ½ = 5
Тревонте прошел на 5 миль больше, чем Молли.
Учащиеся умножают и вычитают:
1 ½ x 5 = 7 ½
2 ½ x 5 = 12 ½
12 ½ — 7 ½ = 5
Тревонте прошел на 5 миль больше, чем Молли.
Студенты обводят «лишние» мили Тревонте и добавляют:
Тревонте проходит на 1 милю больше, чем Молли каждый день в течение 5 дней. Тревонте проходит на 5 миль больше, чем Молли.
Шаг 3: Turn-and-Talk
Студенты делятся своей моделью и решением с партнером на языке математических рассказов:
«Во-первых, я… потому что в задаче… я решил…»
Шаг 4: Решение
Учитель, который активно следил за тем, как ученики моделировали и решали, использует трекер данных , чтобы решить, какой из 3 способов ответить на данные ученика .
Измеряя, какая часть класса точно моделирует и решает, учитель может провести целевое обсуждение, которое подтолкнет учащихся к эффективности , используя более сложную стратегию и / или опровергнув распространенное заблуждение .
Ученики Поворот и разговор , чтобы обсудить целевой вопрос, а учитель стратегически способствует общеклассному обсуждению, работая над тем, чтобы ученики пришли к заранее спланированному образцу ответа.
Наконец, учитель четко описывает ключевой момент и то, как он связывает с моделями и решением.
Шаг 5. Решите проблему
Учащиеся используют новые знания из обсуждения, чтобы исправить свое решение или записать новый способ решения.
Щелкните здесь, чтобы получить копию шаблона протокола Math Stories.
Студенческий дискурс
Протокол «Математические рассказы» дает студентам возможность заниматься математикой в контексте без тренировочных колес прямого обучения или индивидуального обучения.
Одним из наиболее ценных компонентов является решение The Decision , в котором преподаватели используют актуальные данные, чтобы задать содержательный вопрос для обсуждения, основанный на текущих знаниях учащихся. Использование текущих данных является частью когнитивно управляемой инструкции , в которой в центре дискурса находится мышление ученика, а не учитель. 1 Кроме того, ученики учителей, которые хорошо осведомлены о своем мышлении, имеют более высокий уровень успеваемости. 2
Посмотреть протокол Math Stories в действии:
В следующих нескольких публикациях мы рассмотрим важность визуализации и возможность обучения у ваших коллег.
Есть вопросы? Свяжитесь со Стефом Примиани, директором BVP по STEM, [email protected] и подпишитесь на меня в Twitter @stephprimiani
Ресурсы
1 Кларк, Дуг. «Меняющаяся роль учителя математики», 1997 г.
2 Carpenter et al. «Когнитивно управляемое обучение: основанная на исследованиях программа профессионального развития учителей математики в начальной школе», 2000 г.
Решение дробей в 5-м классе с помощью математических историй: Часть 42018-10-182018-10-22https: //blackstonevalleyprep.org/wp-content/uploads/2016/03/logo-mobile.png Чартерная школа Род-Айленда | Академия подготовки мэров в долине Блэкстоун дайте студентам возможность попрактиковаться в сложении и вычитании денег и единиц измерения.Студенты будут складывать или вычитать трех-, четырех- и пятизначные числа для решения этих реальных задач.
Помогите своим ученикам попрактиковаться в сложении и вычитании с помощью этих реальных словесных задач с уравнениями, используя деньги, время,
и измерения.
Развивайте у учащихся навыки решения повседневных текстовых задач. Студенты будут складывать и вычитать деньги и единицы измерения для решения этих задач.
Учащиеся будут применять навыки сложения и вычитания к реальным задачам со словами, связанным с измерениями. Напомните учащимся, что нужно проявлять осторожность при преобразовании единиц измерения.
Проверьте арифметические навыки учащихся с помощью реальных словесных задач, связанных с единицами измерения. Студенты должны умножать, складывать или вычитать целые числа, десятичные дроби и дроби для решения задач из этого математического листа.
Чтобы решить уравнения на этих листах, ученики должны будут реализовать сложение и вычитание для многозначных задач.
Применяйте математические навыки к реальным задачам, связанным с десятичными числами, деньгами и измерениями. Студенты должны выбрать операцию (умножение, деление, сложение или вычитание) для решения каждой задачи со словом. Для решения большинства этих текстовых задач требуется два шага.
Эти реальные проблемы со словами связаны с десятичными числами, деньгами и измерениями. Студенты должны выбрать операцию (умножение, сложение или вычитание) для решения каждой задачи со словом. Для решения одной из этих словесных проблем требуется два шага.
Дает студентам возможность попрактиковаться в умножении и делении для решения задач со словами. Для решения задач на этом математическом листе учащиеся будут использовать варианты формулы Расстояние = Скорость x Время.
Для решения этих задач со словом «скорость» учащиеся используют предоставленную информацию и варианты формулы «Расстояние = скорость x время». Этот рабочий лист по математике дает студентам возможность попрактиковаться в умножении, делении и работе с формулами.
Бесплатные задания по математике для пятиклассников
Ученики пятого класса, возможно, уже запомнили факты умножения в более ранних классах, но к этому моменту они должны понимать, как интерпретировать и решать словесные задачи.Задачи со словами важны в математике, потому что они помогают учащимся развивать мышление в реальном мире, одновременно применять несколько математических концепций и мыслить творчески, отмечает ThinksterMath. Задачи со словами также помогают учителям оценить истинное понимание математики учащимися.
Задачи для пятиклассников включают умножение, деление, дроби, средние значения и множество других математических понятий. В разделах №№ 1 и 3 представлены бесплатные рабочие листы, которые студенты могут использовать, чтобы практиковаться и оттачивать свои навыки решения текстовых задач.В разделах № 2 и 4 приведены соответствующие ключи ответов к этим рабочим листам для упрощения выставления оценок.
Math Word Задачи Mix
Распечатать PDF: Смешать математические задачи со словами
Этот рабочий лист представляет собой хорошее сочетание задач, включая вопросы, требующие от студентов демонстрации своих навыков умножения, деления, работы с долларовыми суммами, творческого мышления и нахождения среднего. Помогите своим пятиклассникам понять, что задачи со словами не должны быть пугающими, разрешив им хотя бы одну задачу.
Например, в задаче №1 спрашивается:
«Во время летних каникул ваш брат подрабатывает стрижкой газонов. Он косит шесть газонов в час, и ему нужно косить 21 газон. Сколько времени это у него займет?»
Брат должен быть Суперменом, чтобы косить шесть газонов в час. Тем не менее, поскольку это именно то, что указывает проблема, объясните учащимся, что они должны сначала определить, что они знают и что они хотят определить:
- Твой брат может косить шесть газонов в час.
- Ему нужно покосить 21 газон.
Чтобы решить задачу, объясните учащимся, что они должны записать ее в виде двух дробей:
6 газонов / час = 21 газон / x час
Затем они должны умножиться. Для этого возьмите числитель первой дроби (верхнее число) и умножьте его на знаменатель второй дроби (нижнее число). Затем возьмите числитель второй дроби и умножьте его на знаменатель первой дроби следующим образом:
6x = 21 час
Затем разделите каждую сторону на 6 , чтобы найти x:
6x / 6 = 21 час / 6
х = 3.5 часов
Итак, вашему трудолюбивому брату потребуется всего 3,5 часа, чтобы косить 21 газон. Он быстрый садовник.
Микс задач по математике: решения
Распечатайте PDF-файл: Смешивание задач со словами по математике: решения
В этом рабочем листе представлены решения проблем, с которыми учащиеся работали, в печатной форме на слайде № 1. Если вы видите, что учащиеся испытывают трудности после сдачи своей работы, покажите им, как решить одну или две задачи.
Например, проблема No.6 на самом деле представляет собой простую задачу деления:
«Твоя мама купила тебе годовой абонемент на плавание за 390 долларов. Она делает 12 выплат, сколько денег нужно заплатить за абонемент?»
Объясните, что для решения этой проблемы вы просто разделите стоимость годичного плавательного пропуска, 390 долларов , на количество выплат, 12 , следующим образом:
390 долл. США / 12 = 32,50 долл. США
Таким образом, стоимость каждого ежемесячного платежа вашей мамы составляет 32,50 доллара.Обязательно поблагодарите маму.
Другие математические задачи со словами
Распечатать PDF-файл: другие задачи по математике
Этот рабочий лист содержит задачи, которые немного сложнее, чем те, что были в предыдущей печатной форме. Например, проблема №1 гласит:
«Четверо друзей едят личную пиццу. У Джейн осталось 3/4, у Джилл осталось 3/5, у Синди осталось 2/3, а у Джеффа осталось 2/5. У кого осталось больше всего пиццы?»
Объясните, что сначала вам нужно найти наименьший общий знаменатель (ЖКД), нижнее число в каждой дроби, чтобы решить эту проблему.Чтобы найти ЖК-дисплей, сначала умножьте разные знаменатели:
4 х 5 х 3 = 60
Затем умножьте числитель и знаменатель на число, необходимое для каждого, чтобы получить общий знаменатель. (Помните, что любое число, разделенное само по себе, равно единице.) Итак, у вас будет:
- Джейн: 3/4 x 15/15 = 45/60
- Джилл: 3/5 x 12/12 = 36/60
- Синди: 2/3 x 20/20 = 40/60
- Джефф: 2/5 x 12/12 = 24/60
У Джейн осталось больше всего пиццы: 45/60, или три четверти.У нее будет много еды сегодня вечером.
Другие задачи с математическими словами: решения
Распечатайте PDF-файл: Дополнительные задачи с математическими словами: решения
Если учащиеся все еще не могут найти правильные ответы, пора применить несколько разных стратегий. Вы можете просмотреть все задачи на доске и показать учащимся, как их решать. Как вариант, разбейте студентов на группы — на три или шесть групп, в зависимости от того, сколько у вас студентов.Затем попросите каждую группу решить одну или две задачи, пока вы ходите по комнате, чтобы помочь. Совместная работа может помочь студентам мыслить творчески, когда они обдумывают одну или две проблемы; часто, как группа, они могут прийти к решению, даже если они изо всех сил пытались решить проблемы самостоятельно.
Вы здесь: Главная → Задания → 5 класс Это исчерпывающий набор бесплатных распечатываемых рабочих листов по математике для 5 класса, организованных по таким темам, как сложение, вычитание, алгебраическое мышление, разряд, умножение, деление, разложение на простые множители, десятичные дроби, дроби, измерения, координатная сетка и геометрия.Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа. Рабочие листы подходят для любой математической программы для пятого класса, но особенно хорошо подходят для программы IXL по математике для 5-го класса и их новых уроков внизу страницы. Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не умещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати. Все рабочие листы содержат ключ ответа, расположенный на 2-й странице файла. АлгебраМатематика для начальных классов Эдвард Заккаро Хорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем.Включает главы по следующим темам: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы в каждой главе разбиты на четыре уровня: легкий, несколько сложный, сложный и очень сложный. Сложение и вычитание по столбцам (числа друг под другом)Место и округлениеПропускной счет
Округление
УмножениеУмножение умственных способностей Длинное умножение (в столбцах) ДивизияПсихологическое отделение Длинное деление
Следующие четыре типа рабочих листов выходят за рамки ФакторингДробное сложение и вычитаниеКак дроби / дробные части В отличие от дробей / дробных частей
Умножение на дробиФракционное делениеСледующие типы рабочих листов выходят за рамки стандартов Common Core. Преобразование дробей в смешанные числа и наоборотЭквивалентные дроби и упрощенные дробиЗаписывать дроби как десятичные и наоборот В приведенных ниже таблицах ключ ответа не дает дроби в упрощенной форме. Сложение десятичных дробейМентальная математика От 0 до 1 десятичных цифр От 0 до 2 десятичных цифр Добавление колонки Десятичное вычитаниеМентальная математика От 0 до 1 десятичных цифр От 0 до 2 десятичных цифр Задачи: ментальная математика Вычитание по столбцу Вызовы: алгебраическое мышление Десятичное умножениеМентальная математика
Умножить по столбцам Десятичное делениеМентальная математика Длинное деление Единицы измеренияОбычная система
Метрическая система
Сетка координатГеометрия Если вы хотите иметь больший контроль над такими параметрами, как количество проблем, размер шрифта, интервал проблем или диапазон чисел, просто |
Решение задач умножением и делением дробей и смешанных чисел
Задачи на дробные слова с помощью интерактивных упражнений
Пример 1. Если для изготовления платья требуется 5/6 ярдов ткани, то сколько ярдов потребуется для изготовления 8 платьев?
Анализ: Чтобы решить эту проблему, мы преобразуем целое число в неправильную дробь.Затем мы умножим две дроби.
Решение:
Ответ: Для изготовления 8 платьев потребуется 6 и 2/3 ярда ткани.
Пример 2: У Рене была коробка кексов, половину которой она отдала своему другу Хуану. Хуан отдал 3/4 своей доли своей подруге Елене. Какая дробная часть оригинальной коробки кексов досталась Елене?
Анализ: Чтобы решить эту проблему, мы умножим эти две дроби.
Решение:
Ответ: Елене досталось 3/8 оригинальной коробки кексов.
Пример 3: Класс математики Нины имеет длину 6 и 4/5 метра и ширину 1 и 3/8 метра. Какая площадь классной комнаты?
Анализ: Чтобы решить эту проблему, мы умножим эти смешанные числа. Но сначала мы должны преобразовать каждое смешанное число в неправильную дробь.
Решение:
Ответ: Площадь аудитории 9 и 7/20 квадратных метров.
Пример 4: Плитка шоколада имеет длину 3/4 дюйма. Если его разделить на части длиной 3/8 дюйма, то сколько это будет частей?
Анализ: Чтобы решить эту задачу, мы разделим первую дробь на вторую.
Решение:
Ответ: 2 шт.
Пример 5: У электрика есть кусок провода длиной 4 и 3/8 сантиметра. Она делит проволоку на кусочки длиной 1 и 2/3 сантиметра. Сколько у нее штук?
Анализ: Чтобы решить эту проблему, мы разделим первое смешанное число на второе.
Решение:
Ответ: Электрик имеет 2 и 5/8 куска провода.
Пример 6: На складе 1 и 3/10 метров ленты. Если они разделят ленту на куски длиной 5/8 метров, то сколько кусков у них получится?
Анализ: Чтобы решить эту проблему, мы разделим первое смешанное число на второе. Сначала мы преобразуем каждое смешанное число в неправильную дробь.
Решение:
Ответ: На складе будет 2 и 2/25 кусков ленты.
Резюме: В этом уроке мы узнали, как решать задачи со словами, связанные с умножением и делением дробей и смешанных чисел.
Упражнения
Указания: вычтите смешанные числа в каждом упражнении ниже. Обязательно упростите ваш результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание. Чтобы написать смешанное число четыре и две трети, введите в форму 4, пробел и затем 2/3.
| 1. | Одна партия печенья содержит 1 и 3/4 стакана растопленного шоколада. Сколько чашек растопленного шоколада нужно для изготовления 8 партий печенья? |
| 2. | Тодд выпил 5/8 банки сока объемом 24 унции. Лайла выпила на треть меньше сока, чем Тодд. Сколько унций выпила Лила? |
| 3. | Прямоугольный коврик имеет длину 3 и 2/3 фута и ширину 2 и 3/4 фута. Какова площадь коврика? |
| 4. | У Джанет 5 и 3/4 сантиметра лакричника. Она делит лакрицу на кусочки длиной 1 и 7/8 сантиметра. Сколько кусочков солодки у нее будет? |
| 5. | Кусок дерева длиной 15 футов.Сколько 3/4 фута можно вырезать из него? |
.

 Что в них общего? Чем они отличаются? Можно ли
Что в них общего? Чем они отличаются? Можно ли
 Сколько было куплено
Сколько было куплено
 е. значение меньшей
е. значение меньшей

 В первой пачке 20 тетрадей, а во второй — в 4
В первой пачке 20 тетрадей, а во второй — в 4
 Петя придумал для Маши задачу:
Петя придумал для Маши задачу:


 Домашнее задание.
Домашнее задание.