Содержание
Основные понятия кинематики | План-конспект урока по физике (9 класс) по теме:
Урок №1 Основные понятия механики
- Что такое механическое движение?
- Механическое движение — это изменение положеия тела в прострастве относительно других тел.
- NB! Всякое движение относительно. Нет абсолютного покоя или абсолютного движения. Обязательно надо указывать относительно ЧЕГО движется тело.
- Тело отсчета (ТО).
За ТО может быть принято любое тело. Мы просто в данной задаче считаем его неподвижным.
- В чем заключается основная задача механики (ОЗМ)?
Определить положение тела в любой момент времени.
- Большинство материальных тел имеют совершенно определенные размеры. Поэтому возникает вопрос: «положение какой точки тела требуется определить в ОЗМ»?
Проблему можно решить если тело можно будет считать точкой, а это возможно, если выполняются следующие условия:
- размеры тела малы по сравнению с расстояниями, про которые идет речь в задаче,
- все точки тела движутся по одинаковым траекториям — поступательное движение.

Вывод: тело, размерами которого в данной задаче можно пренебречь, называется материальной точкой (МТ).
МТ — это модель реального тела, которую мы будем очень часто использовать.
Но надо учитывать, что корректное использование модели материальной точки требует тщательного анализа условия конкретной задачи.
Например.
Если мы изучаем движение Земли вокруг Солнца, то в этой задаче Землю можно считать материальной точкой, так как размер Земли (d=6400км) гораздо меньше радиуса земной орбиты (R=150 000 000 км).
Если мы изучаем движение материков, то Земля уже никак не может считаться материальной точкой.
Мы будем различать два вида движения: поступательное и вращательное.
Поступательное движение — все точки тела движутся по одинаковым траекториям. Например, движение лифта, движение кабины колеса обозрения и др.
Вращательное движение — все точки тела движутся по окружностям, центры которых лежат на прямой, которая называется ось вращения.
Любое движение можно представить, как сумму поступательного и вращательного.
Мы примем это утверждение без доказательства.
Урок №2 Способы описания движения материальной точки. Система отсчета.
- Проблема
Какие числовые данные нужно иметь, чтобы можно было утверждать, что мы решили ОЗМ?
Решим проблему, рассматривая частные случаи движения, и попытаемся сделать правильные выводы.Из геометрии известно, что для того, чтобы определить положение точки, нужно знать ее координаты.
- Способ описания движения с помощь. координат, конечно, называется координатный.
Рассмотрим самое простое движение: мотоциклист (материальная точка — МТ) движется вдоль прямой. | Для описания положения МТ достаточно одной координатной оси OX. | Для решения ОЗМ надо знать данные таблички (числовые данные в ней это просто пример):
или зависимость координаты от времени (это в математике называется функцией). Записывается это в физике так: X=X(t) (в математике это выглядит так).
Для описания движения вдоль прямой и решения ОЗМ нам потребовалось знать координату x в любой момент времени. Такое движение называется одномерным. | ||||||||||
Рассмотрим самое более сложное движение:лодка (МТ) плывет по поверхности озера. | Для описания положения МТ необходимо иметь две координатные оси OX и OY. | Для решения ОЗМ нужно знать данные двух табличек, например таких: или эти таблички можно записать как две функции: x=x(t), y=y(t) Для описания движения на плоскости и решения ОЗМ нам потребовалось знать координаты x и y в любой момент времени. | ||||||||||
И наконец, рассмотрим самый общий случай движения: ракета (МТ) движется в пространстве. |
| Для решения ОЗМ нужно знать теперь данные уже трех табличек, например таких:
или эти таблички можно записать как три функции: x=x(t), y=y(t), z=z(t) движения в пространстве и решения ОЗМ нам потребовалось знать координаты x , y, z в любой момент времени. Такое движение называется трехмерным. |
Вывод: Таким образом, в координатном методе описания движения, для решения ОЗМ необходимо знать три функции зависимости координат от времени:
x=x(t), y=y(t), z=z(t)
Какой способ определения положения точки известен в геометрии?
- Задать положение точки можно еще с помощью вектора. Такой способ описания движения называется векторный
Рассмотрим движение МТ по плоскости. | В механике вектор, задающий положение точки, начинается, например, в 0 системы координат и заканчивается в той точке, в которой находится тело. Этот вектор называется — радиус-вектор. Чтобы решить ОЗМ надо знать
или
или
Связь координатного и векторного способа описания движения.
В прямоугольном треугольнике АВО нам известны два катета. Поэтому по теореме Пифагора мы можем найти гипотенузу ОА или модуль радиус-вектора: r2=x2+y2 Направление вектора мы узнаем, если вычислим угол АОВ. А для этого нам надо знать какую-нибудь его тригонометрическую функцию, например: sin =y/r В дальнейшем нам очень пригодятся подпольные математические правила. | |
Теперь легко можно все понять для движения в трехмерном пространстве. | Как ответить на аналогичные вопросы в трехмерном случае — догадайтесь сами. |
Тело отсчета, система координат и приборы для измерения времени (часы) — называется системой отсчета.
Фактически, система отсчета — это просто лаборатория, в которой есть приборы для измерения положения тел и времени.
Упражнение
Определите координаты точек А, B, C, D, K, M.
Урок №3 Перемещение.
- Что надо знать, чтобы вычислить положение мат. точки в любой момент времени?
Для ответа на этот вопрос воспользуемся векторным способом описания движения.
- Какие у пермещения есть замечательные свойства?
- Так как перемещение — вектор, то если тело совершило подряд два перемещения, то
| |
| |
|
- результирующее перемещение можно найти простым сложением первых двух:
S=S1 + S2
- Если нам каким-нибудь образом удастся его узнать, то мы сможем рещить основную задачу механики!!!! Действительно, из определения и правила сложения вектров следует:
r(t)=ro + S
- Путь и перемещение, конечно, в общем случае не совпадают!
Задания.
- Попробуйте перечислить ??? отличия перемещения и пути.

Решение
|
Урок №4 Средняя скорость. Опрос.
Проблема
Чтобы решить основную задачу механики необходимо знать перемещение S материальной точки. Но как узнать пермещение?
Это в 7 классе и раньше | Так мы это будем понимать теперь в 9 классе |
V=S/t где S — путь пройденный телом за время t
Мы не будем забывать это определение и в 9 классе, но чтобы не путаться будем в дальнейшем называть эту скорость среднепутевой и тогда эта формула может быть использована для любых траекторий.
| Теперь мы рассматриваем не только прямолинейное движение и путь не совпадает с модулем перемещения. Поэтому скорость мы определим так:
|
Опрос «Основные понятия мехнаики».
- Механическое движение и его относительность.
- Материальная точка.
- Тело отсчета.
- Поступательное и вращательное движение. Примеры.
- Основная задача механики.
- Координатный способ описания движения.

- Векторный способ описания движения.
- Связь векторного и координатного способов.
- Система отсчета.
- Перемещение.
- Путь.
- Траектория.
Урок №5 Правило сложения скоростей
Проблема
Мы знаем, что всякое движение относительно. Для описания движения необходимо указать систему отсчета, относительно которой рассмативается движение. Следовательно, физические величины, описывающие движение: радиус-вектор, перемещение, скорость, должны меняться при изменении сситемы отсчета. Например, относительно класса (система отсчета «класс»), парты имеют скорость равную нулю, а относительно Солнца (система отсчета «Солнце») они движутся со скоростью примерно 30 км/с! Это мы хорошо знали еще в 7 классе.
На практике очень часто приходится пересчитывать кинематические величины при переходе из одной системы отсчета в другую. Например, в 7 классе, мы умели вычислять скорость лодки относительно берега и относительно воды (в стоячей воде).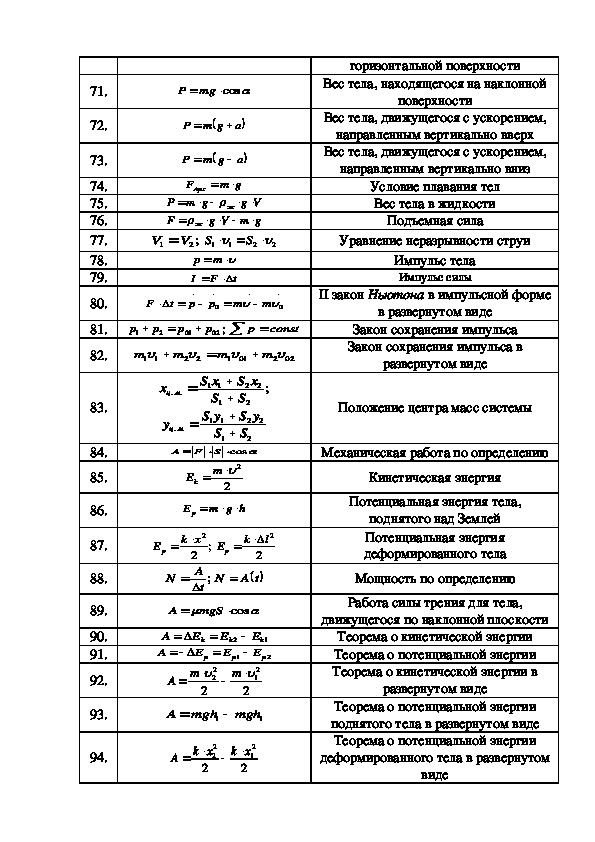
Наша задача в 9-м классе найти математические законы, по которым можно пересчитать скорость, перемещение и др. физические величины при переходе из одной системы отсчета в другую.
Решение проблемы
Сделать это очень просто.
Систему К мы будем считать неподвижной, а систему отсчета К1, движущейся со скоростью V относительно системы К | |
Рассмотрим материальную точку А, которая движется относительно обеих систем отсчета. Построим радиус-вектора в начальный момент времени точки А:
Очевидно соотношение между этими векторами: (*) | |
Через некоторое время материальная точка и система отсчета К1 изменят свое положение относительно друг друга. (**) |
Вычтем из второго уравнения первое и сгруппируем слогаемые:
Заменим разность радиус-векторов на соответствующие перемещения (мы используем уже известную нам формулу для решения основной задачи механики: r(t)=ro + S, из которой следует, что S=r(t) — ro. Получим:
(***)
где вектор S — перемещение мат. точки относительно системы отсчета К,
вектор s’ — перемещение мат. точки относительно системы отсчета К1,
вектор S — перемещение системы отсчета К1 относительно К.
Уравнение (***) дает нам возможность считать перемещение в разных ситемах отсчета. Эта математическая запись того факта, что перемещение относительно.
Разделим правую и левую часть уравнения (***) на время, получим:
(****)
где:
вектор v- скорость мат. точки относительно системы К (неподвижной ситемы отсчета),
вектор v’ — скорость материальной точки относительно подвижной системы отсчета (система К1),
вектор V — скорость системы K1 относительно системы К (скорость подвижной системы относительно неподвижной).
- Уравнение (****) называется «Правило сложения скоростей».
- По этому уравнению можно легко сосчитать скорость в разных системах отсчета.
- Это уравнение годится для любых движений (не слишком быстрых).
- Это математическая запись того факта, что скорость относительна.
Урок №6 Мгновенная скорость. Равномерное движение.
Проблема
Для решения основной задачи механики необходимо знать перемещениеS:
Для вычисления перемещения к моменту времени t мы можем воспользоваться средней скоростью Vср:
Но по этой формуле можно вычислить лишь перемещение к моменту времени t!
Например, пусть шофер перед тем, как отправиться в рейс заехал в кафе пообедать и просидел там 1 час, а потом проехал 100 км за 1 час. Таким образом его средняя скорость составила 100км/2ч=50км/ч. Зная эту скорость мы можем правильно вычислить положение автомобиля через 2 часа, т.е. за тот промежуток времени, за который эта средняя скорость определена.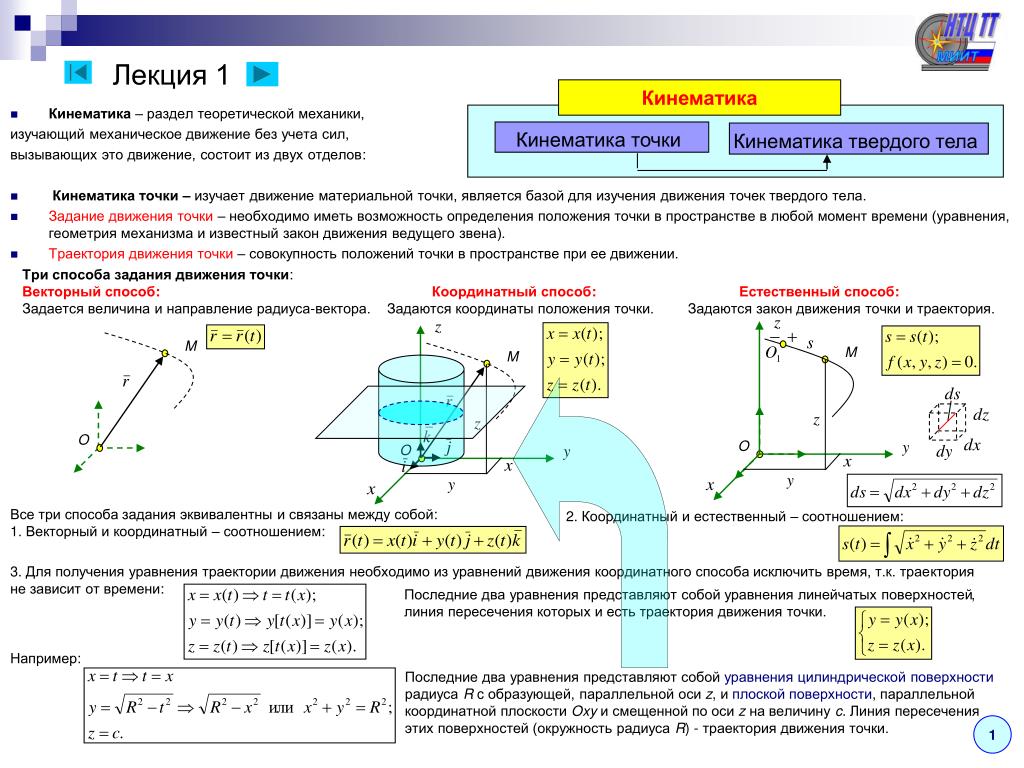 Но диспетчер здорово ошибется, если попробует по этой средней скорости вычислить положение автомобиля через 1 час движения: 50км/ч*1ч=50км (ведь мы же знаем, что в это время шофер только вышел из кафе, которое находилось за углом автобазы!!!)
Но диспетчер здорово ошибется, если попробует по этой средней скорости вычислить положение автомобиля через 1 час движения: 50км/ч*1ч=50км (ведь мы же знаем, что в это время шофер только вышел из кафе, которое находилось за углом автобазы!!!)
Получается, что средней скорости недостаточно, чтобы узнать положение мат. точки в любой момент времени: она теряет информацию о движении. Как же поступить???
Решение проблемы
Идея!
Ошибка диспетчера была бы невозможна, если бы он имел полную информацию о движении мат. точки, т.е. знал как двигалось тело в каждой точке траектории!
Как осуществить эту идею?
- Разобьем все время движения на очень маленькие отрезки.
- Отрезки должны быть настолько малы, чтобы можно было считать движение на них прямолинейным и равномерным.
- Определим среднюю скорость на каждом маленьком отрезке времени.
Средняя скорость на очень маленьком отрезке времени называется мгновенной скоростью движения мат. точки.
точки.
- Зная мгновенную скорость в каждой точке можно вычислить соответствующие перемещения:
Теперь не составляет труда найти полное перемещение за любое конечное время!!!!
и, наконец-то, решить основную задачу механики:
Как пользоваться таким громоздким способом решения основной задачи механики?
Пример: “равномерное движение”.
Пусть все мгновенные скорости равны между собой и равны некоторой постоянной величине V:
Движение, при котором мгновенная скорость не изменяется (по величине и направлению) называется равномерным.(V=const)
Легко вычисляем перемещение:
Получилась очень знакомая формула! Что и следовало ожидать! Теперь решим основную задачу механики для равномерного движения:
Для других движений этот расчет, конечно, труднее… но мы попытаемся этому научиться
Урок №7 Ускорение. Равноускоренное движение.
Как мы уже поняли, для решения основной задачи механики необходимо знать перемещение S:
(1)
А для вычисления перемещения нужно знать мгновенную скорость в каждый момент времени:
(2)
Тогда можно вычислить правую часть уравнения:
(3)
Проблема
Но где взять мгновенную скорость? К сожалению, ее нельзя вычислить из других законов природы!!!
Приходится поступать следующим образом. Для того, чтобы вычислить скорость в момент времени t нужно сложить начальную скорость vo (скорость в момент времени 0, в начале движения) и изменение скорости Δv:
Для того, чтобы вычислить скорость в момент времени t нужно сложить начальную скорость vo (скорость в момент времени 0, в начале движения) и изменение скорости Δv:
(4)
Но как найти Δv?
Эта задача очень похожа на проблему поиска перемещения. Введем новую для нас физическую величину ускорение (точнее, среднее ускорение) по формуле:
(5)
Здесь мы воспользовались тем обстоятельством, что из формулы (4) следует
(6)
Раз это новая физическая величина, то необходимо указать ед. измерения:
[a]=м/c/c=м/c2
Что показывает нам ускорение?
Пусть t=1, тогдаa= Δv (численно)
Ускорение показывает изменение скорости за единицу времени.
Направление ускорения совпадает с направлением изменения скорости Δv :
Например:
а) “Разгон” (начальная скорость меньше конечной)
б) “Торможение” (конечная скорость меньше начальной)
Теперь можно вычислить мгновенную скорость, т.е. решить нашу проблему:
Эта формула верна для равноускоренного движения.
Равноускоренное движение это такое движение, при котором ускорение мат. точки постоянно. Записывается это так:
Новая проблема.
Но где взять ускорение???
Решение проблемы.
Мир устроен так, что ускорение можно узнать из других законов природы.
Теперь понятно как решать основную задачу механики:
Еще одна проблема.
Как сосчитать что-нибудь по этим формулам? Ведь они векторные!!!
Разберем все на примерах.
Пример №1
“Разгон” вдоль прямой. Все вектора направлены в одну сторону и можно просто написать:
v=vo+at
“Торможение” вдоль прямой.
Вектора скорости направлены против вектора ускорения, поэтому, наверное, надо написать так:
v=vo-at
Но по этой формуле можно получить отрицательный результат. Что это будет означать??? Совершенно очевидно, что это будет означать, что мат. точка движется в сторону противоположную начальной скорости.
Но здесь могут возникнуть проблемы формального характера, которые потом, в более сложных случаях, может привести к ошибкам
Мы уже поняли, что для решения основной задачи механики необходимо знать перемещение , тогда мы сможем узнать положение мат.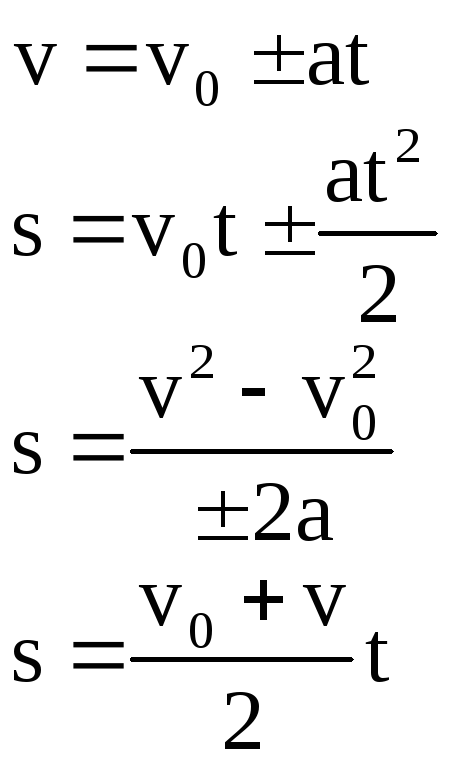 точки в любой момент времени по формуле:
точки в любой момент времени по формуле:
Чтобы узнать перемещение , надо поступить так: разбить все время движения на очень маленькие интервалы (настолько малые, чтобы можно было считать движения на них равномерным) и вычислить маленькие перемещения за эти промежутки времени, а потом сложить все полученные результаты:
Эту сумму мы уже умеем вычислять для равномерного движения (v=const, ускорение ). Наша задача сегодня научиться вычислять эту сумму для равноускоренного движения, когда ускорение а скорость меняется по закону .
Попробуем это сделать так, рассмотрим самый простой случай равноускоренного движения и для него все посчитаем, а потом попытаемся угадать, что будет в более сложных ситуациях.
Итак, рассмотрим движение вдоль прямой. Причем начальная скорость vo и ускорение a направлены в одну сторону.
Совершенно очевидно, что в этом случае невозможно изменение направление вектора скорости и следовательно можно все вычисления проводить для модулей векторов:
Первый способ (Ну очень простой!!!)
Рассмотрим на графике эту зависимость:
Так как скорость меняется по линейному закону, то легко очевидно, что средняя скорость движения равна средней арифметической в начальный и в конечный момент времени:
Подставим в эту формулу значение скорости в момент времени t и получим:
Теперь, зная среднюю скорость, легко вычислить модуль перемещения:
Ура! Мы получили правильную формулу!
Второй способ (более высоконаучный)
В первом способе мы приняли без доказательства тот факт, что средняя скорость при равноускоренном движении равна среднему арифметическому скоростей в начале и в конце промежутка времени.
Теперь мы попробуем рассуждать немного иначе.
Равномерное движение | Равноускоренное движение |
Рассмотрим график скорости равномерного движения: Перемещение при равномерном движении вычисляется по формуле: S=Vо*t Но если посмотреть на график, то можно легко увидеть, что фигура под графиком скорости — прямоугольник, а площадь прямоугольника равна произведению его сторон, поэтому имеем: площадь прям.=Vо*t=перемещение(S)
| Рассмотрим график скорости равноускоренного движения: Примем (пока без доказательства), что площадь под графиком скорости при равноускоренном движении тоже равна перемещению. Тогда получаем:
S=Vot+at2/2
|
А что делать если ускорение и скорость направлены в противоположные стороны?
График скорости будет убывать и скорость может поменять знак (тело остановилось и поехало в противоположном напрвлении). |
Легко догадаться, что знаки перед начальной скоростью и ускорением будут разными:
S=Vot-at2/2
Но в этом случае перемещение может стать отрицательным. Это надо понимать перемещение в сторону противоположную начальной скорости Vo.
Урок №9 «Ускорение свободного падения»
- Историческая справка
- Эксперимент
- Выводы
- Задачи
Проблема.
Рассмотрим свободное падение тел вблизи поверхности Земли.
Историческая справка
Во времена Аристотеля считалось, что все тела падают на Землю, так стремятся занять на ней свое «естественное положение», скорость падения зависит от массы тела: чем больше масса тела, тем быстрее падает тело. Действительно, наблюдения показывают, что перышко парит в воздухе гораздо дольше падающего камня. | Аристотель (384 — 322 гг. до н.э.) |
Первым усомнился в правильности взглядов Аристотеля великий Галилео Галилей. Галилею удалось доказать, что
| Галилео Галилей (1564 — 1642). |
Эксперимент
Давайте убедимся в том, что в отсутствии воздуха и легкие и тяжелые тела падают с одинаковой скоростью. Для этого мы воспользуемся трубкой Ньютона. В трубке находится три тела: дробинка, кусочек паралоновой губки и легкая перышко.
Если трубку поставить вертикально, то быстрее всех будет падать дробинка, а последней достигнет дна трубки перышко.
Теперь откачаем насосом воздух из трубки (конечно, откачать весь воздух мы не можем, но сделать его весьма разреженным по нашим силам). Повторим эксперимент — все тела падают с одинаковой скоростью (практически).
Мы можем записать движение свободно падающего тела, например, учебника физики с помощью компьютерной лабортаории. Проанализировав запись, мы приходим к следующим выводам:
- свободное падение является равноускоренным движением (если не учитывать сопротивление воздуха),
- в нашем эксперименте ускорение примерно равно 10м/с2.
Выводы
Все тела, независимо от массы, падают с одинаковым постоянным ускорением, которое называется ускорением свободного падения. и обозначается g.
Ускорение свободного падения равно 9,81м/с2.
Ускорение свободного падения всегда, при любых движениях тела, направлено вертикально вниз.
Все формулы для равноускоренного движения годятся для свободного падения. Надо только в них вместо ускорения а, написать g=9,8м/с2.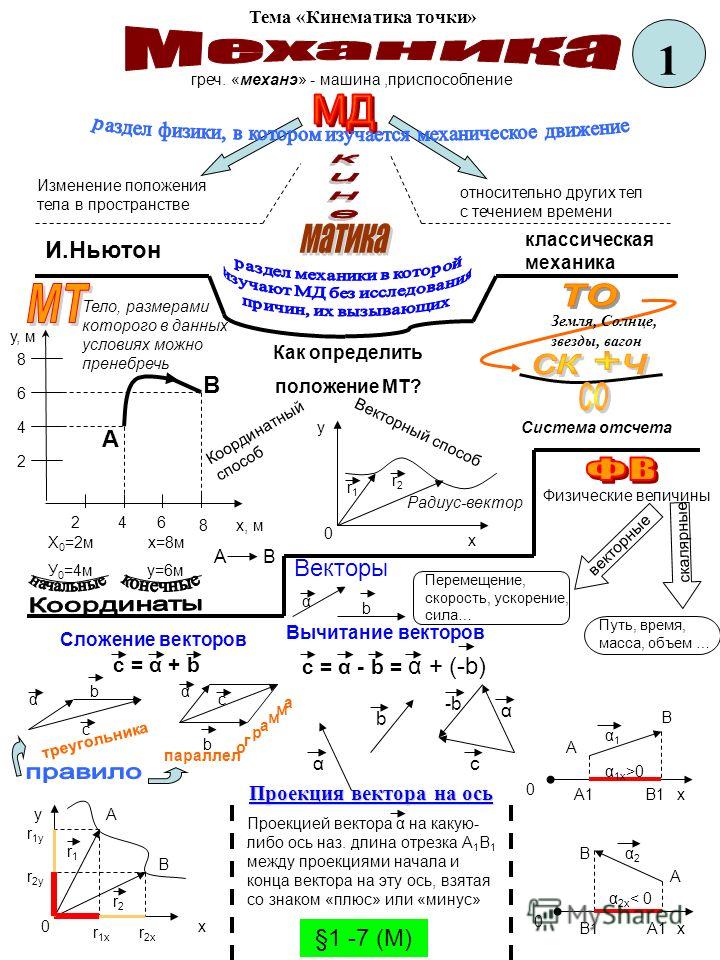
Наши любимые формулы получаются такими:
а)тело бросили вниз (начальная скорость и ускорение свободного падения направлены в одну сторону), тело только «разгоняется»:
б)тело бросили вверх (начальная скорость и ускорение свободного падения направлены в разные стороны), тело летит вверх — тормозится, достигает верхней точки, летит вниз — «разгоняется»:
А если не хочется все время мучительно думать о знаках в формулах, то можно написать все в векторном виде:
В таком виде формулы будут правильными для ЛЮБЫХ свободных падений.
Задачи
Камень свободно падает на землю с высоты 80м. Какова скорость камня в момент падения на землю? Сколько времени длилось свободное падение?
Решение
Все очень просто. Свободное падение — это равноускоренное движение с ускорением g=9,8м/с2. Начальная скорость равна 0м/с, так ничего про нее не сказано. Поэтому можно написать:
(1)
(2)
Теперь составим уравнения, подставив конкретные данные в эти функции:
где x — время полета.
Отсюда получаем: x=4c.
Теперь мы знаем время полета и можем найти скорость. Если подставить данные в формулу (2), то получим:
v(4c)=10м/с2*4с=40м/с
Теперь сами.
Столкните резинку со своего письменного стола. Сколько времени продолжается падение? Какая будет скорость резинки в конце полета?
Урок №10 Скорость и ускорение при движении по окружности
Направление скорости при движении по окружности.
Проблема
Почему искры во время заточки ножа на точильном круге летят по касательной к окружности? |
Решение проблемы.
Направление мгновенной скорости при движении по окружности.
Рассмотрим самой простой случай: пусть материальная точка движется по окружности с постоянной по модулю скоростью. (такая модель для нас удобна, так как нас интересует только то, что происходит с направлением мгновенной скорости).
Как направлен вектор мгновенной скорости при таком движении?
Движение по окружности — это криволинейное движение. | |
Но движение по 4-м хордам совсем не похоже на движение по окружности, поэтому давайте увеличим количество этих хорд и сократим их величину. | |
Теперь, легко догадалась Юлик, чтобы получить «настоящее» движение по окружности надо еще больше сократить размер хорд и еще больше увеличить их число: при этом крошечные хорды практичски станут точками окружности, а направление векторов скорости совпадет с направлением касательной в данной точке к окружности.
|
Выводы.
- Таким образом, мгновенная скорость при движении по окружнсти направлена по касательной, (Поэтому искры точильного летят тоже по касательной).
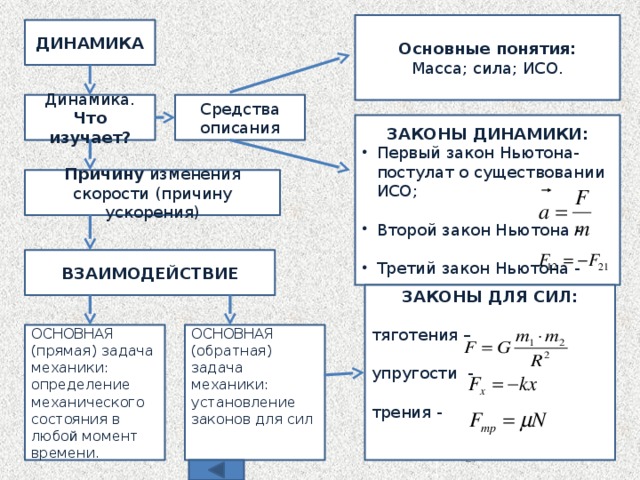
- Так как мы не использовали в наших рассждениях тот факт, что мат. точка не меняет величину скорости, то можно считать, что наш вывод будет верен и для движения по окружности, когда величина скорости меняется.
Ускорение при движении по окружности с постоянной по модулю скоростью.
Величина ускорения при движении тела по окружности с постоянной скоростью.
Ускорение равно , чтобы найти модуль этого вектора надо вычислить величину
Рассмотрим движение мат. точки на очень маленьком участке траектории АВ. Точки А и В расположены очень близко друг к другу, но мы их на чертеже разнесли подальше, чтобы лучше разобраться в чертеже. Вектора скорости имеют разное направление, но одинаковую величину. | |
Построим вектор изменения скорости . Для этого перенесем вектор V2 в точку А. Построим разность векторов . | |
Рассмотрим треугольники АОВ и ACD.
Следовательно, эти треугольники подобны. Поэтому имеем следующее соотношение: Хорда АВ практически равна дуге АВ, так как точки А и В очень близки друг к другу. Поэтому вместо величины хорды АВ можно подставить величину дуги АВ, которая равна vt. Поэтому имеем: отсюда получаем Теперь получаем то, что хотели: | |
|
|
Направление ускорения при движении по окружности с постоянной по модулю скоростью.
Направлено ускорение к центру окружности, поэтому и называют его центростремительным. |
День Сибстрина пройдет под знаком экологии Уважаемые преподаватели, сотрудники, студенты, выпускники и партнеры!
|
Идет запись на вакцинацию от COVID-19 Всем желающим пройти вакцинацию, которая будет проходить на территории НГАСУ (Сибстрин), необходимо подать информацию до 20.05.2021г. по своим подразделениям:
|
Представители Сибстрина отличились на международной студенческой конференции в Республике Беларусь Поздравляем студентов института строительства и института архитектуры и градостроительства НГАСУ (Сибстрин), которые под научным руководством кафедры строительной механики успешно выступили на IX Международной студенческой научной конференции «Традиции, современные проблемы и перспективы развития строительства», проходившей на базе Гродненского государственного университета имени Янки Купалы (Республика Беларусь).
|
Студенты НГАСУ (Сибстрин) помогли сажать молодой лес в Новосибирской области 8 мая 2021 года студенты инженерно-экологического факультета НГАСУ (Сибстрин) приняли участие в акции по высадке леса, которая прошла на территории Искитимского лесничества.
|
ОГЭ по физике: материалы для подготовки
Главная » 2016 » Июнь » 5 » Материалы для подготовки к ОГЭ по физике
21:05 Материалы для подготовки к ОГЭ по физике | |
| На сайте появились новые материалы для подготовки к ОГЭ по физике! Сборник по физике содержит следующие материалы: ● теория по разделам: 1. Механика 2. Тепловые явления 3. Электрические и магнитные явления 4. Световые явления. Строение атома и атомного ядра ● основные формулы; ● теория в формате .docx; ● формулы и определения за 7-й, 8-й и 9-й классы; ● таблицы по разделам: 1. Механика, кинематика и динамика 2. Законы сохранения в механике. Механические колебания и волны 3. Термодинамика 4. Электростатика. Законы постоянного тока 5. Электрический ток в различных средах 6. Электромагнитные колебания и волны 7.  Молекулярная физика Молекулярная физика 8. Оптика и СТО (Специальная теория относительности) 9. Квантовая физика 10. Физика атомного ядра ● все формулы и определения по разделам: 1. Кинематика; 2. Динамика; 3. Законы сохранения. Работа и мощность 4. Статика и гидростатика; 5. Тепловые явления; 6. Электростатика; 7. Постоянный ток; 8. Магнитные явления; 9. Колебания и волны; 10. Оптика + бонус: Для того, чтобы сдать ОГЭ 2020 по физике на пятёрку, мы рекомендуем: | |
| Просмотров: 34039 | | Теги: теория, физика, шпаргалки, шпоры, таблицы, скачать, 9 класс, формулы, определения, ОГЭ, материалы, бесплатно | |
| Равномерное движение | ||
| Путь | \(S=Vt\) | метр |
| Скорость | \(V=\frac{S}{t}\) | метр/секунда |
| Ускорение | \(a=0\) | метр/сек2 |
| Координата | \(x = x_0 + vt\) | |
| Равноускоренное движение | ||
| Ускорение | \(а=\frac{V-V_0}{t}\) | метр/сек2 |
| Координата | \(x=x_0+V_0t+\frac{at^2}{2}\) | |
| Путь | \(S=V_0t+\frac{at^2}{2} = V^2-\frac{{V_0}^2}{2a}\) | метр |
| Криволинейное движение по окружности | ||
| Ускорение | \(a_{цс}=\frac{v^2}{r}=w^2r\) | метр/сек2 |
| Угловая скорость | \(w=\frac{2π}{T}\) | радиан/секунда |
| Вещество | ||
| Масса | \(m=pv\) | килограмм |
| Силы | ||
| Равнодействующая сила | \(F=ma\) | Ньютон |
| Сила тяжести, вес | \(F=mg\) | Ньютон |
| Сила трения | \(F = \mu N\) | Ньютон |
| Сила упругости | \(F_{упр}=-kx\) | Ньютон |
| Закон Архимеда | \(F = p_ж V_т g\) | Ньютон |
| Закон всемирного тяготения | \(F=G\frac{m_1 m_2}{R^2}\) | Ньютон |
| Момент силы | \(M=Fl\) | Ньютон*метр |
| Давление | ||
| Давление твердых тел | \(p=\frac{F}{S}\) | Паскаль |
| Давление в жидкостях | \(p=\rho gh\) | Паскаль |
| Гидравлический пресс | \(\frac{F_1}{F_2}=\frac{S_2}{S_1}\) | |
| Работа, энергия, мощность | ||
| Механическая работа | \(A=FScos a\) | Джоуль |
| Мощность | \(N=\frac{A}{t}\) | Ватт |
| \(КПД=\frac{А_п}{A_з}100\%=\frac{Q_п}{Q_з}100\%\) | % | |
| Кинетическая энергия | \(E=\frac{mv^2}{2}\) | Джоуль |
| Потенциальная энергия | \(E=mgh\) | Джоуль |
| Количество теплоты | \(Q=cm(t_2-t_1)\) | Джоуль |
| Теплота сгорания | \(Q=qm\) | Джоуль |
| Теплота парообразования | \(Q=Lm\) | Джоуль |
| Тепловое действие тока | \(Q=I^2 Rt\) | Джоуль |
| Работа тока | \(A=IUt\) | Джоуль |
| Мощность тока | \(P=\frac{A}{t}=UI\) | Ватт |
| Энергия пружины | \(E=\frac{kx^2}{2}\) | Джоуль |
| Закон сохранения энергии | \(E_{const}=E_{кин} + E_{пот} + E_{внутр}\) | Джоуль |
| Импульс | ||
| Импульс | \(p=mv\) | кг*метр/сек2 |
| Закон сохранения импульса | \(mv_1+mv_2={mv_1}’+{mv_2}’\) | кг*метр/сек2 |
| Ток | ||
| Закон Ома | \(I=\frac{U}{R}\) | Ампер |
| Сопротивление проводника | \(R=\frac{p l}{s}\) | Ом |
| Последовательное соединение проводников | ||
| Сила тока | \(I=I_1=I_2\) | Ампер |
| Напряжение | \(U=U_1+U_2\) | Вольт |
| Сопротивление | \(R=R_1+R_2\) | Ом |
| Параллельное соединение проводников | ||
| Сила тока | \(I=I_1+I_2\) | Ампер |
| Напряжение | \(U=U_1=U_2\) | Вольт |
| Сопротивление | \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\) | Ом |
Зачет 1 по темам «Кинематика.
 Динамика». Вопросы к зачету: 1. Что изучает кинематика? 2. Основные понятия кинематики: механическое движение,
Динамика». Вопросы к зачету: 1. Что изучает кинематика? 2. Основные понятия кинематики: механическое движение,
Обучающие задания на тему «ДИНАМИКА»
Обучающие задания на тему «ДИНАМИКА» 1(А) Автобус движется прямолинейно с постоянной скоростью. Выберете правильное утверждение. 1) На автобус действует только сила тяжести. ) Равнодействующая всех приложенных
Подробнее
Банк заданий по физике 10 класс
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
Подробнее
Подготовка к ОГЭ ЧАСТЬ 1
Подготовка к ОГЭ ЧАСТЬ 1 МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ-1 1.Кинематика 1. Буксирный катер за ч проплыл 5 км. Определите скорость катера..тело, двигаясь из состояния покоя, равноускоренно за первую секунду проходит
Подробнее
Динамика. Три закона Ньютона
Динамика Три закона Ньютона Обучающие вопросы и задания 140. Как направлена равнодействующая сил, приложенных к свободно падающему телу? 141. Тело равномерно движется по окружности. Как направлена равнодействующая
Подробнее
Динамика А) mg F ; В) mg-f; С) F F mg. ; Д) ; Е) F-mg.
Динамика 008.Сила, возникающая между приводным ремнем и шкивом при его движении, является силой А) натяжения. В) трения скольжения. С) трения качения. D) упругости. Е) трения покоя. . Равнодействующая трех
. Равнодействующая трех
Подробнее
ИТТ Вариант 2 ОСНОВЫ ДИНАМИКИ
ИТТ- 10.2.2 Вариант 2 ОСНОВЫ ДИНАМИКИ 1. Единицей измерения какой физической величины является килограмм? А. Силы Б. Массы В. Работы Г. Энергии Д. Мощности 2. Кто открыл закон инерции? А. Аристотель Б.
Подробнее
Кинематика 1 1) 1 2) 2 3) 3 4) 4
Кинематика 1 1 Точка движется по окружности радиусом 2 м, и ее перемещение равно по модулю диаметру. Путь, пройденный телом, равен 1) 2 м 2) 4 м ) 6,28 м 4) 12,56 м 2 Камень брошен из окна второго этажа
Подробнее
10Ф Раздел 1. Понятия, определения
10Ф Раздел 1. Понятия, определения 1.1 Закончите определение. «Явление сохранения скорости тела постоянной при отсутствии действия на него других тел называется.». 1.2 Сила- это физическая величина, являющаяся
Подробнее
СБОРНИК ВОПРОСОВ И ЗАДАЧ ПО ФИЗИКЕ
А. Ф. Кавтрев И. Б. Хаздан СБОРНИК ВОПРОСОВ И ЗАДАЧ ПО ФИЗИКЕ Базовый уровень образования Пособие для учащихся 9 11 классов ИЗДАТЕЛЬСТВО МОСКВА 2005 1 ОСНОВЫ ДИНАМИКИ 7. Инерция. Первый закон Ньютона.
Ф. Кавтрев И. Б. Хаздан СБОРНИК ВОПРОСОВ И ЗАДАЧ ПО ФИЗИКЕ Базовый уровень образования Пособие для учащихся 9 11 классов ИЗДАТЕЛЬСТВО МОСКВА 2005 1 ОСНОВЫ ДИНАМИКИ 7. Инерция. Первый закон Ньютона.
Подробнее
ДИНАМИКА задания типа В Страница 1 из 6
ДИНМИК задания типа В Страница 1 из 6 1. Спутник движется вокруг Земли по круговой орбите радиусом R. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. (M
Подробнее
ПРОГРАММА ПО ФИЗИКЕ Механика
ПРОГРАММА ПО ФИЗИКЕ Механика Что такое механика? Классическая механика Ньютона и границы ее применимости Кинематика Кинематика точки. Основные понятия кинематики Движение тела и точки Прямолинейное движение
Подробнее
Материальная точка. Система отсчета
Неравномерное Учебник Касьянов В. А. Автор: Шипкина Е.А. 10 класс. Модуль 1 по теме «Кинематика» — 15 часов Материальная точка Система отсчета Механическое движение Равномерное Периодическое Криволинейное
А. Автор: Шипкина Е.А. 10 класс. Модуль 1 по теме «Кинематика» — 15 часов Материальная точка Система отсчета Механическое движение Равномерное Периодическое Криволинейное
Подробнее
Индивидуальное задание 6. Вариант 1.
Вариант 1. 1. Легкоподвижную тележку массой 3 кг толкают с силой 6 Н. Определите ускорение тележки.. Мяч массой 0,5 кг после удара, длящегося 0,0 с, приобретает скорость 10 м/с. Найти среднюю силу удара.
Подробнее
д) F1=5H 60 o F3=5H F2=5H F1=4H a) F2=6H F1=2H F2=3H
Урок 1. Лекция: «Основы теории относительносит». Урок 2. Работа с текстом: Г.Гамов «Приключение мистера Томпкинса». Урок 4. Лекция: Принцип относительности Галилея. Инерция. Неотличимость покоя и равномерного
Подробнее
Инерция. Законы Ньютона. Силы в механике
Физика. 9 класс. Тренинг «Инерция. Законы Ньютона. Силы в механике» 1 Инерция. Законы Ньютона. Силы в механике Вариант 1 1 Металлический брусок подвешен к пружине и целиком погружён в сосуд с водой, находясь
9 класс. Тренинг «Инерция. Законы Ньютона. Силы в механике» 1 Инерция. Законы Ньютона. Силы в механике Вариант 1 1 Металлический брусок подвешен к пружине и целиком погружён в сосуд с водой, находясь
Подробнее
если υ 0 а — движение ускоренное
Кинематика Механическое движение изменение положения тела в пространстве с течением времени относительно других тел. Поступательное движение движение, при котором все точки тела проходят одинаковые траектории.
Подробнее
Задания к контрольной работе
Задания к контрольной работе Контрольная работа проводится по двум главам: «Законы движения» и «Силы в механике». Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
Подробнее
Образовательный портал «РЕШУ ЕГЭ» (
Объяснение явлений 1. На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным
Подробнее
БАНК ЗАДАНИЙ 9 КЛАСС. ДИНАМИКА
БАНК ЗАДАНИЙ 9 КЛАСС. ДИНАМИКА 1.1 Первый закон Ньютона 1. Свойство тела сохранять свою скорость при отсутствии воздействий называется 1) инертностью)инерцией3) энергией4)мощностью. Из предложенных формулировок
Подробнее
ИТТ Вариант 1 ОСНОВЫ ДИНАМИКИ
ИТТ- 10.2.1 Вариант 1 ОСНОВЫ ДИНАМИКИ 1. Единицей измерения какой физической величины является ньютон? А. Силы Б. Массы В. Работы Г. Энергии Д. Мощности 2. Кто открыл закон инерции? А. Гераклит Б. Аристотель
Подробнее
ИТТ Вариант 2 ЗАКОНЫ СОХРАНЕНИЯ
ИТТ- 10.3.2 Вариант 2 ЗАКОНЫ СОХРАНЕНИЯ 1. Как называется физическая величина, равная произведению массы тела на вектор его мгновенной скорости? 2. Как называется физическая величина, равная половине произведения
Как называется физическая величина, равная произведению массы тела на вектор его мгновенной скорости? 2. Как называется физическая величина, равная половине произведения
Подробнее
ПРОБНЫЙ ЭКЗАМЕН по теме 1. КИНЕМАТИКА
ПРОБНЫЙ ЭКЗАМЕН по теме. КИНЕМАТИКА Внимание: сначала попытайтесь ответить на вопросы и решить задачи самостоятельно, а потом проверьте свои ответы. Указание: ускорение свободного падения принимать равным
Подробнее
Образовательный минимум
триместр предмет физика класс 9т Образовательный минимум Основные понятия Движения тела по вертикали, брошенного под углом к горизонту, горизонтально. Движение по с постоянной по модулю скоростью. Центростремительное
Подробнее
ИТТ Вариант 2 ОСНОВЫ КИНЕМАТИКИ
ИТТ- 10.1.2 Вариант 2 ОСНОВЫ КИНЕМАТИКИ 1.Предложены две задачи: 1) Определить среднюю скорость самолёта по известному расстоянию между двумя городами и времени полёта. 2) Определить путь, пройденный самолётом
Подробнее
Примеры решения задач
Примеры решения задач Пример 1 Через вращающийся вокруг горизонтальной оси блок (рис1а) перекинута невесомая нерастяжимая нить к концам которой привязаны грузы 1 и Найдите силу давления X N F блока на
Подробнее
ИТТ Вариант 1 ОСНОВЫ КИНЕМАТИКИ
ИТТ- 10.1.1 Вариант 1 ОСНОВЫ КИНЕМАТИКИ 1.Предложены две задачи: 1) Рассчитать период обращения вокруг Земли искусственного спутника шара радиусом 20 м. 2) Рассчитать силу Архимеда, действующую в воде
Подробнее
F в этой системе отсчёта равно
Отложенные задания (88) Мяч, брошенный вертикально вверх со скоростью υ, через некоторое время упал на поверхность Земли. Какой график соответствует зависимости проекции скорости на ось ОХ от времени движения?
Подробнее
Формулы прямолинейного равноускоренного движения
☰
При прямолинейном равноускоренном движении тело
- двигается вдоль условной прямой линии,
- его скорость постепенно увеличивается или уменьшается,
- за равные промежутки времени скорость меняется на равную величину.
Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с2.
Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.
Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:
v = at
При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:
v = gt
Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:
a = v/t
Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с2. Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:
v = v0 + at
Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:
v = v0 – at
Получим из этих формул формулы ускорения. В случае ускорения:
at = v – v0
a = (v – v0)/t
В случае торможения:
at = v0 – v
a = (v0 – v)/t
В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:
a = v0/t
Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:
t = v0/a
Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении. Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.
При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.
Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:
s = ½ * (v0 + v) * t
Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v0 + at). Поэтому в формуле пути мы можем заменить v:
s = ½ * (v0 + v0 + at) * t = ½ * (2v0 + at) * t = ½ * t * 2v0 + ½ * t * at = v0t + 1/2at2
Итак, пройденный путь определяется по формуле:
s = v0t + at2/2
(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)
Если тело начало двигаться равноускоренно из состояния покоя (v0 = 0), то формула пути упрощается до s = at2/2.
Если вектор ускорения был противоположен скорости, то произведение at2/2 надо вычитать. Понятно, что при этом разность v0t и at2/2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v0/a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле:
s = v02/(2a)
Что не так с физикой в современной школе / Newtonew: новости сетевого образования
Начинаем серию статей о проблемах и устаревших концепциях в школьной программе и предлагаем порассуждать о том, зачем школьникам нужна физика, и почему сегодня её преподают не так, как хотелось бы.
Для чего современный школьник изучает физику? Или для того, чтобы ему не надоедали родители и учителя, или же затем, чтобы успешно сдать ЕГЭ по выбору, набрать нужное количество баллов и поступить в хороший вуз. Есть ещё вариант, что школьник физику любит, но эта любовь обычно существует как-то отдельно от школьной программы.
В любом из этих случаев преподавание ведётся по одинаковой схеме. Оно подстраивается под систему собственного контроля — знания должны преподноситься в такой форме, чтобы их можно было легко проверить. Для этого и существует система ГИА и ЕГЭ, а подготовка к этим экзаменам в результате и становится главной целью обучения.
Как устроено ЕГЭ по физике в его сегодняшнем варианте? Задания экзамена составляются по специальному кодификатору, куда входят формулы, которые, по идее, должен знать каждый ученик. Это около сотни формул по всем разделам школьной программы — от кинематики до физики атомного ядра.
Большая часть заданий — где-то 80% — направлена именно на применение этих формул. Причем другие способы решения использовать нельзя: подставил формулу, которой нет в списке — недополучил какое-то количество баллов, даже если ответ сошелся. И только оставшиеся 20% — это задачи на понимание.
В результате главная цель преподавательской работы сводится к тому, чтобы ученики знали этот набор формул и могли его применять. А вся физика сводится к несложной комбинаторике: прочитай условия задачи, пойми, какая формула тебе нужна, подставь нужные показатели и просто получи результат.
В элитарных и специализированных физико-математических школах обучение, конечно, устроено иначе. Там, как и при подготовке к всевозможным олимпиадам, присутствует какой-то элемент творчества, а комбинаторика формул становится намного сложнее. Но нас здесь интересует именно базовая программа по физике и её недостатки.
Об истории советских физ-мат школ в программе Льва Лурье: «Этих людей учили тому, что всякое утверждение нужно доказывать, — довольно сомнительный тезис с точки зрения советской действительности».
Источник: 5-tv.ru
Стандартные задачи и абстрактные теоретические построения, которые должен знать обычный школьник, очень быстро выветриваются из головы. В результате физику после окончания школы уже никто не знает — кроме того меньшинства, которому это почему-то интересно или нужно по специальности.
Получается, что наука, главной целью которой было познание природы и реального физического мира, в школе становится донельзя абстрактной и удаленной от повседневного человеческого опыта. Физику, как и другие предметы, учат зубрёжкой, а когда в старших классах объём знаний, который необходимо усвоить, резко возрастает, всё зазубрить становится просто невозможно.
Наглядно о «формульном» подходе к обучению.
Но это было бы и необязательно, если бы целью обучения было не применение формул, а понимание предмета. Понимать — это, в конечном счёте, намного легче, чем зубрить.
Формировать картину мира
Посмотрим, к примеру, как работают книжки Якова Перельмана «Занимательная физика», «Занимательная математика», которыми зачитывались многие поколения школьников и после-школьников. Почти каждый параграф перельмановской «Физики» учит ставить вопросы, которые каждый ребенок может себе задать, отталкиваясь от элементарной логики и житейского опыта.
Задачки, которые нам здесь предлагают решить — не количественные, а качественные: нужно не подсчитать какой-то абстрактный показатель вроде коэффициента полезного действия, а поразмышлять, почему вечный двигатель невозможен в реальности, можно ли выстрелить из пушки до луны; нужно провести опыт и оценить, каким будет эффект от какого-либо физического взаимодействия.
Пример из «Занимательной физики» 1932 года: задача о крыловских лебеде, раке и щуке, решённая по правилам механики. Равнодействующая (OD) должна увлекать воз в воду.
Одним словом, заучивать формулы здесь не обязательно — главное понимать, каким физическим законам подчиняются предметы окружающей действительности. Проблема только в том, что знания такого рода куда сложнее поддаются объективной проверке, чем наличие в голове школьника точно определённого набора формул и уравнений.
Поэтому физика для обычного ученика оборачивается тупой зубрежкой, а в лучшем случае — некой абстрактной игрой ума. Формировать у человека целостную картину мира — совсем не та задача, которую де факто выполняет современная система образования. В этом отношении, кстати, она не слишком отличается от советской, которую многие склонны переоценивать (потому что раньше мы, мол, атомные бомбы разрабатывали и в космос летали, а сейчас только нефть умеем продавать).
По знанию физики ученики после окончания школы сейчас, как и тогда, делятся примерно на две категории: те, кто знает её очень хорошо, и те, кто не знает совсем. Со второй категорией ситуация особенно ухудшилась, когда время преподавания физики в 7-11 классе сократилось с 5 до 2 часов в неделю.
Большинству школьников физические формулы и теории действительно не нужны (что они прекрасно понимают), а главное — неинтересны в том абстрактном и сухом виде, в котором они преподносятся сейчас. В итоге массовое образование не выполняет никакой функции — только отнимает время и силы. У школьников — не меньше, чем у учителей.
Attention: неправильный подход к преподаванию точных наук может иметь разрушительные последствия
Если бы задачей школьной программы было формирование картины мира, ситуация была бы совершенно иной.
Конечно, должны быть и специализированные классы, где учат решать сложные задачи и глубоко знакомят с теорией, которая уже не пересекается с повседневным опытом. Но обычному, «массовому» школьнику было бы интереснее и полезнее знать, по каким законам работает физический мир, в котором он живет.
Лекция Уолтера Левина — хороший пример того, как можно соединить физические теории и формулы с конкретными наблюдениями.
Источник: youtube.com
Дело, конечно, не сводится к тому, чтобы школьники вместо учебников читали Перельмана. Нужно изменить сам подход к преподаванию. Многие разделы (например, квантовую механику) можно было бы изъять из школьной программы, другие — сократить или пересмотреть, если бы не вездесущие организационные трудности, принципиальный консерватизм предмета и образовательной системы в целом.
Но позволим себе немного помечтать. После этих изменений, может быть, повысилась бы и общая социальная адекватность: люди бы меньше верили всяческим торсионным аферистам, спекулирующим на «защите биополя» и «нормализации ауры» с помощью нехитрых приспособлений и кусков неведомых минералов.
Все эти последствия порочной системы образования мы уже наблюдали в 90-е, когда самые удачливые мошенники даже пользовались немалыми суммами из госбюджета, — наблюдаем и сейчас, хотя и в меньших масштабах.
Знаменитый Григорий Грабовой не только уверял, что может воскрешать людей, но и отводил астероиды от Земли силой мысли и «экстрасенсорно диагностровал» правительственные самолёты. Ему покровительствовал не кто-нибудь, а генерал Георгий Рогозин, заместитель начальника Службы безопасности при президенте РФ.
Источник: vk.com
Ведь теперешний школьник — это будущий президент, чиновник, бизнесмен или бухгалтер. Пусть лучше он не знает все формулы из кодификатора, но хотя бы понимает, что нельзя лазером извлечь энергию из камня, использовать для энергоснабжения вихревые генераторы, которым не писан закон сохранения энергии, и не боится, что телевизоры и компьютеры с помощью электромагнитных полей манипулируют его нервной системой.
Большая часть мыслей, высказанных выше, основана на мнениях практикующих преподавателей. Особая благодарность за рассказ и консультацию — Антону Шейкину, ассистенту кафедры физики высоких энергий и элементарных частиц СПбГУ и преподавателю физики в 10 классе.
В оформлении статьи использовано изображение «Команда мечты физиков», Flickr.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Уравнения кинематики — определение, параметры и ответы на часто задаваемые вопросы
Целью этого первого раздела, являющегося классной комнатой по физике, было исследование разнообразия средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы уже изучили и исследовали, также включает словесные представления, которые являются графическими представлениями, а также числовые представления и графические представления, которые представляют собой графики положения-времени и графики скорости-времени.
Определение кинематических уравнений
Ветвь физики, которая обычно определяет движение, относящееся к времени и пространству и игнорирующее причину этого движения, известна как кинематика. Уравнение, которое называется кинематикой, представляет собой набор уравнений, которые могут вывести неизвестный аспект движений тела, если другие аспекты предоставлены.
Эти уравнения связывают пять кинематических переменных:
Смещение, обозначаемое Δx.
Начальная скорость, которая задается как v 0 , которая называется Конечной скоростью и обозначается v Временной интервал, обозначаемый t Постоянное ускорение, обозначаемое a.
По сути, мы можем сказать, что уравнения кинематики могут выводить одну или несколько из этих переменных, если другие заданы. Эти уравнения, которые мы видели, определяют движение либо с постоянной скоростью, либо с постоянным ускорением. Поскольку мы можем сказать, что уравнения кинематики применимы только при постоянном ускорении или постоянной скорости, мы не можем использовать их, если одно из двух меняется.
Параметры кинематического уравнения
Знание каждой из различных величин обычно обеспечивает описательную информацию о движении объекта.Например, мы можем сказать, что если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, север в течение 12,0 секунд для смещения на север, которое составляет 264 метра. Тогда можно сказать, что движение автомобиля полностью описано.
Если мы возьмем вторую машину, то известно, что она ускоряется из положения покоя с ускорением на восток 3,0 м / с. 2 в течение 8,0 секунд, а конечная скорость — 24 м / с. . Направление смещения на восток и на восток составляет 96 метров, и тогда мы можем сказать, что движение этой машины полностью описано.
Эти два утверждения, которые мы видели, предназначены для полного описания движения объекта. Однако можно сказать, что такая полнота не всегда известна.
Часто бывает, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, мы можем сказать, что по мере приближения к светофору мы можем узнать, что автомобиль имеет скорость 22 м / с, движется в восточном направлении и способен к заносу 8,0 м / с 2 и в западном направлении.Однако мы не знаем, какое смещение испытала бы наша машина, если бы мы резко нажали на тормоза и занесло до полной остановки. а затем, после этого, мы не знаем, сколько времени потребуется, чтобы остановиться. В таком случае, как этот, мы можем сказать, что неизвестные параметры, которые могут быть определены с использованием физических принципов и математических уравнений, являются кинематическими уравнениями.
Что такое кинематическое уравнение?
Уравнения, которые можно использовать для любого движения, которое в целом можно описать как постоянное движение, которое имеет скорость движения, которая является ускорением 0 м / с / с, или мы можем сказать движение с постоянным ускорением.Можно сказать, что они никогда не будут использоваться в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из уравнений, которые являются кинематическими уравнениями, включает четыре переменные. Если нам известны значения трех из четырех переменных, то можно просто вычислить значение четвертой переменной.
Таким образом, мы можем сказать, что уравнение, которое является кинематическим уравнением, обеспечивает полезное средство прогнозирования информации о движении объекта, если другая информация нам уже известна.Например, мы можем сказать, что если значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля известны, то мы можем сказать, что смещение автомобиля и время можно предсказать с помощью кинематических уравнений. {2} + 2 \ times a \ times d \]
\ [v_ {f} = v_ {i} + a \ times t \] \ [ d = \ frac {v_ {i} + v_ {f}} {2} \ times t \]
В приведенных выше уравнениях используются различные символы.Каждый символ, который мы видели, имеет свое особое значение. d обозначает смещение объекта, t обозначает время, в течение которого объект перемещался, a обозначает ускорение объекта, v обозначает скорость объекта, v указывает, что значение скорости является начальным, а vf указывает, что значение скорости является окончательным.
Каждое из этих четырех уравнений, которые мы видели, надлежащим образом описывает математическую взаимосвязь между параметрами движения объекта.Таким образом, мы можем сказать, что их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. В следующей части мы исследуем процесс этого.
Что такое кинематика? Простые ответы по физике
Это сообщение в блоге является первым из серии о том, как понимать и решать проблемы кинематики. Он призван дополнить ваш класс и учебник. Я сосредоточусь на практических приложениях, способах решения проблем и типичных ошибках, которые делают студенты.Если вы хотите изучить основы кинематики, я рекомендую учебник, но если вы хотите получить более глубокое понимание, избежать путаницы и научиться решать проблемы, примите красную таблетку и присоединяйтесь к нам!
Кинематика — это просто изучение движения. Буквально это слово означает: кинезис (движение) + тики (изучение. Подумайте о математике, политике, пиццатике). На более практическом уровне кинематика, которую вы изучаете на вводном уроке физики, — это изучение положения, скорости и импульса.На самом практическом уровне кинематика — это изучение того, что происходит, когда вы подбрасываете мяч. Это означает, что если вы можете подбрасывать мяч, вы можете изучить кинематику — к вашему сведению, любой, кто когда-либо видел, как я занимаюсь спортом, знает, обратное неверно.
Итак, кинематика — это изучение трех вещей, но что именно это за три вещи?
Позиция :
Где находится объект. Его месторасположение. В физических задачах это обозначается как x, y, z p, r или d. У каждого учителя есть свои предпочтения, поэтому изучите свои, но для этого блога мы будем использовать x и y.Нас также часто интересует изменение положения, известное как смещение, которое обозначается как Δx, Δy, Δp, Δd или иногда просто x, y или d, чтобы запутать ситуацию. Положение и перемещение обычно измеряются в метрах или м.
Скорость :
Как быстро объект движется и в каком направлении: то есть как расстояние меняется с течением времени. В физических задачах скорость почти всегда обозначается буквой v. Скорость обычно измеряется в метрах в секунду или м / с.Когда скорость постоянна, это можно описать уравнением v = Δx / Δt (изменение положения, деленное на изменение во времени).
Разгон :
Как меняется скорость объекта. Если Ferrari разгоняется до 100 км / ч за 2,4 секунды, значит, он ускоряется. Если водитель пугается и врезается в стену, которая останавливает автомобиль, значит, он также разогнался. Ускорение всегда обозначается буквой a и измеряется в метрах в секунду в секунду или м / с 2 .
Когда ускорение постоянное, его можно описать уравнением a = Δv / Δt (изменение положения, деленное на изменение во времени). Вы могли заметить, что это уравнение очень похоже на уравнение для скорости. Это не совпадение: оно отражает фундаментальную физику, которая определяет все в мире.
Положение, смещение и расстояние легко спутать, и учителя физики часто проводят тесты, чтобы убедиться, что вы понимаете разницу. Положение измеряется от некоторой исходной точки и определяет местоположение объекта — в кинематике мы часто определяем исходную точку как начальное местоположение объекта, чтобы упростить задачу.Расстояние измеряет общее расстояние, пройденное объектом. Смещение измеряет, насколько далеко объект от того места, где он был начат.
Чтобы понять разницу, представьте сценарий, в котором вы начинаете на 3 метра вправо от исходной точки и идете на 2 метра влево, затем на 4 метра вправо. Ваша позиция в начале — 3 метра, а в конце — 5 метров. Ваше расстояние составляет 6 метров, потому что именно столько вы прошли. Однако ваше смещение в конце составляет 2 метра, потому что вы находитесь всего в 2 метрах от того места, откуда начали.
В обычной жизни мы используем слова скорость и скорость как синонимы, но в физике мы этого не делаем. Скорость — это то, насколько быстро что-то движется, скорость — это насколько быстро оно движется И в каком направлении (мы называем это понятие величины + направления вектором). Это означает, что объект может изменять скорость без изменения скорости, например, автомобиль, движущийся по круговой трассе. Это также означает, что скорость может увеличиваться, а скорость снижаться. Если скорость отрицательная, а ускорение отрицательное, то скорость будет все более и более отрицательной величиной, поэтому скорость будет уменьшаться (с -60 м / с до -120 м / с), но скорость увеличится (с 60 м / с. до 120 м / с).
Студенты, плохо знакомые с физикой, часто озадачены идеей, что ускорение и скорость могут идти в разных направлениях. Когда объект ускоряется, он должен лететь быстрее, верно? Не обязательно. Например, если вы подбрасываете объект в воздух, он начинает с положительной восходящей скорости, но ускорение отрицательное и нисходящее. В конце концов, объект перестает подниматься и падает обратно на землю, при этом ускорение и скорость идут в одном направлении. Однако в любой момент ускорение может быть в любом направлении — ускорение определяет изменение скорости, а НЕ саму скорость.
Итак, теперь мы понимаем основы кинематики, но как нам их использовать? В моем следующем блоге я расскажу о стандартных уравнениях кинематики и о том, как их использовать для решения задач в одномерном измерении.
следили за обновлениями! То же время летучей мыши, тот же канал летучей мыши.
Вы заинтересованы в работе с Джейкобом — в Нью-Йорке или в Интернете — над своими физическими работами?
Для более релевантного чтения ознакомьтесь с другими сообщениями в блогах, написанными нашими преподавателями физики в Нью-Йорке и Бостоне:
Свободное падение с примерами
БЕСПЛАТНАЯ ПАДЕНИЕ
Свободное падение — это движение, которое каждый может наблюдать в повседневной жизни.Мы случайно или намеренно что-то роняем и видим его движение. Вначале он имеет низкую скорость, до конца набирает скорость, а перед столкновением достигает максимальной скорости. Какие факторы влияют на скорость объекта в свободном падении? Как мы можем рассчитать расстояние, которое требуется, и время, которое требуется во время свободного падения? Мы занимаемся этими предметами в этом разделе. Во-первых, позвольте мне начать с источника увеличения скорости во время падения. Как вы можете догадаться, вещи падают из-за силы тяжести.Таким образом, наши объекты набирают скорость примерно 10 м / с в секунду при падении из-за гравитации. Мы называем это ускорение в физике ускорением свободного падения и обозначаем буквой «g». Значение g составляет 9,8 м / с², однако в наших примерах мы предполагаем, что оно составляет 10 м / с² для простых вычислений. Пришло время сформулировать сказанное выше. Мы говорили об увеличении скорости, которое равно количеству g в секунду. Таким образом, нашу скорость можно найти по формуле;
В = г.t , где g — ускорение свободного падения, а t — время.
Посмотрите на приведенный ниже пример и попытайтесь понять, что я пытался объяснить выше.
Пример Мальчик роняет мяч с крыши дома, которому требуется 3 секунды, чтобы упасть на землю. Рассчитайте скорость до того, как мяч упадет на землю. (g = 10 м / с²)
Скорость есть;
V = g.t
В = 10 м / с². 3с = 30 м / с
Мы научились определять скорость объекта в данный момент времени.Теперь мы научимся определять расстояние, пройденное во время движения. Я даю несколько уравнений для расчета расстояния и других величин. Галилей в своих экспериментах нашел уравнение для расстояния.
Это уравнение;
Используя это уравнение, мы можем найти высоту дома в приведенном выше примере. Давайте узнаем, с какой высоты был брошен мяч? Мы используем 10 м / с² для g.
Я думаю, что формула теперь немного яснее для вас.Решим еще задачи, связанные с этой темой. Теперь представьте, что если я брошу мяч прямо вверх с начальной скоростью. Когда он останавливается и падает обратно на землю? Ответим на эти вопросы сейчас.
На рисунке показаны величины скорости внизу и вверху. Как вы можете видеть, мяч подбрасывается вверх с начальной скоростью v, вверху его скорость становится равной нулю, он меняет направление и начинает падать вниз, что является свободным падением.Наконец, в нижней части перед столкновением он достигает максимальной скорости, обозначенной буквой V ’. Мы говорили о том, насколько увеличивается скорость свободного падения. Он увеличивается на 9,8 м / с каждую секунду из-за ускорения свободного падения. В этом случае также есть g, но мяч направлен вверх; поэтому знак g отрицательный. Таким образом, наша скорость уменьшается на 9,8 м / с каждую секунду, пока скорость не станет равной нулю. Вверху из-за нулевой скорости мяч меняет направление и начинает свободное падение.Перед тем, как решать задачи, хочу привести графики свободного падения.
Как вы видите на графиках, наша скорость линейно увеличивается с ускорением «g», вторые графики говорят нам, что ускорение постоянно и составляет 9,8 м / с², и, наконец, третий график представляет изменение нашего положения. Вначале у нас есть положительное смещение, а со временем оно уменьшается и, наконец, становится равным нулю. Теперь мы можем решать проблемы, используя эти графики и пояснения.
Пример Джон бросает мяч прямо вверх, и через 1 секунду он достигает максимальной высоты, а затем совершает свободное падение, которое занимает 2 секунды. Рассчитайте максимальную высоту и скорость мяча до того, как он упадет на землю. (g = 10 м / с²)
Пример Объект движется в свободном падении. Он падает на землю через 4 секунды. Рассчитайте скорость объекта через 3 секунды до того, как он упадет на землю.С какой высоты может быть брошен?
Два приведенных выше примера пытаются показать, как использовать уравнения свободного падения. Мы можем найти скорость, расстояние и время по заданным данным. Теперь я приведу еще три уравнения и завершу предмет 1D кинематики. Уравнения:
Первое уравнение используется для определения скорости объекта, имеющего начальную скорость и ускорение.Второй используется для расчета расстояния до объекта, имеющего начальную скорость и ускорение. Третье и последнее уравнение — это вневременное уравнение скорости. Если расстояние, начальная скорость и ускорение объекта известны, вы можете найти конечную скорость объекта. Теперь давайте решим некоторые проблемы, используя эти уравнения, чтобы лучше понять предмет.
Пример. Рассчитайте скорость автомобиля с начальной скоростью 24 м / с и ускорением 3 м / с² через 15 секунд.
Мы используем первое уравнение для решения этого вопроса.
Пример Автомобиль, который изначально находится в состоянии покоя, развивает ускорение 7 м / с² и пролетает 20 секунд. Найдите расстояние, которое он преодолеет за этот период.
Экзамены по кинематике
| Движение с графиками <Назад | Далее> Физические формулы Свободное падение / Шпаргалка |
|---|
Освоение физических решений Глава 2 Одномерная кинематика
Освоение физических решений Глава 2 Одномерная кинематика
Освоение физических решений
Глава 2 Одномерная кинематика Q.1CQ
Вы с собакой идете гулять в ближайший парк По дороге. ваша собака совершает много коротких боковых походов, чтобы погоняться за белками, исследовать пожарные гидранты. и так далее. Когда вы приедете в парк, у вас и вашей собаки одинаковое смещение? Вы прошли такое же расстояние? Объяснять.
Решение:
Смещение одинаково для собаки и для нас. а расстояние, пройденное собакой, больше, чем пройденное нами расстояние
Глава 2 Одномерная кинематика Q.1P
Обращаясь к рисунку, вы идете из дома в библиотеку, а затем в парк (а) Какое расстояние вы прошли? б) Каково ваше перемещение?
Решение:
Расстояние определяется как скалярная величина, равная тому, сколько земли покрыло объект во время своего движения. Смещение — это векторная величина, которая определяется как расстояние, на которое объект переместился от своего начального положения.
Расстояние измеряет фактический путь объекта, который принимает в своем движении, а смещение измеряет общее расстояние от начального и конечного положения объекта.
Глава 2 Одномерная кинематика Q.2CQ
Измеряет ли одометр в автомобиле расстояние или смещение? Объяснять.
Решение:
Одометр в автомобиле измеряет расстояние, потому что он не сообщает нам направление, в котором мы движемся.
Глава 2 Одномерная кинематика Q.2P
Решение:
Глава 2 Одномерная кинематика Q.3CQ
Можете ли вы управлять автомобилем таким образом, чтобы расстояние, которое он преодолевал, было (а) больше, (б) равно или (в) меньше, чем величина смещение? В каждом случае приведите пример, если ваш ответ «да», объясните, почему нет, если ваш ответ отрицательный.
Решение:
(A) Да.
Если мы проедем полный круг, пройденное нами расстояние будет равно длине окружности круга, а наше смещение равно нулю.
(B) Да.
Если мы едем по прямой, расстояние и смещение равны.
(C) №
Любое отклонение от прямой приводит к расстоянию, превышающему величину смещения.
Глава 2 Одномерная кинематика Q.3P
Решение:
Глава 2 Одномерная кинематика Q.4CQ
Арт-космонавт вращается вокруг Земли в космическом корабле. На одной полной орбите величина смещения равна пройденному расстоянию? Объяснять.
Решение:
№
В этой ситуации смещение равно нулю, потому что начальное и конечное положения совпадают (смещение = конечное положение — начальное положение). Расстояние, пройденное космонавтом, равно 2◊R, где R — радиус орбиты.
Глава 2 Одномерная кинематика Q.4P
На рис. 2-20 вы идете из парка в дом своего друга, а затем обратно в свой дом. Каково ваше (а) пройденное расстояние и (б) перемещение?
Решение:
Глава 2 Одномерная кинематика Q.5CQ
После теннисного матча игроки бросаются к сетке, чтобы поздравить друг друга. Если они оба бегут со скоростью 3 м / с, равны ли их скорости? Объяснять.
Решение:
№
Их скорости различаются, потому что они движутся в разных направлениях.
Глава 2 Одномерная кинематика Q.5P
Решение:
Глава 2 Одномерная кинематика Q.6CQ
Измеряет ли спидометр скорость или скорость? Объяснять.
Решение:
Спидометр показывает нам скорость, с которой мы движемся. Он не сообщает нам, в каком направлении мы движемся. Таким образом, спидометр измеряет, а не скорость.
Глава 2 Одномерная кинематика Q.6П
ИП Ребенок катается на пони по круговой дорожке радиусом 4,5 м. (a) Найдите пройденное расстояние и смещение после того, как ребенок прошел половину пути. (b) Пройденное расстояние увеличивается, уменьшается или остается неизменным, когда ребенок завершает один круг дорожки? Объясните: (c) Смещение увеличивается, уменьшается или остается неизменным, когда ребенок завершает один круг дорожки? Объясните: (г) Найдите расстояние и смещение после полного обхода пути.
Решение:
Глава 2 Одномерная кинематика Q.7CQ
Может ли машина двигаться по гоночной трассе с постоянной скоростью? Может ли он делать это с постоянной скоростью? Объяснять.
Решение:
(i) №
Поскольку машина движется по трассе, ее направление движения должно меняться. Следовательно, его скорость меняется, и поэтому она не постоянна.
(ii) Да.
Скорость (величина) автомобиля постоянна во время гонки.
Глава 2 Одномерная кинематика Q.7P
CE Прогноз / объяснение Вы ведете машину по прямой со скоростью 15 м / с на протяжении 10 километров, затем со скоростью 25 м / с еще 10 километров, (а) Ваша средняя скорость за всю поездку больше, меньше или равна 20 м / с? (b) Выберите лучшее объяснение из следующего:
I. Больше времени тратится на 15 м / с, чем на 25 м / с.
II. Среднее значение 15 м / с и 25 м / с составляет 20 м / с.
III. На скорости 15 м / с затрачивается меньше времени, чем на скорости 25 м / с.
Решение:
Глава 2 Одномерная кинематика Q.8CQ
Друзья рассказывают вам, что в недавнем путешествии их средняя скорость составляла +20 м / с. Возможно ли, чтобы их мгновенная скорость была отрицательной в какой-либо момент во время поездки? Объяснять.
Решение:
Да.
Например, ваши друзья могли выехать со стоянки в какой-то момент поездки, дав отрицательную скорость на короткое время.
Глава 2 Одномерная кинематика Q.8P
CE Прогноз / объяснение Вы ведете машину по прямой со скоростью 15 м / с в течение 10 минут, затем со скоростью 25 м / с в течение еще 10 минут. (A) Ваша средняя скорость за всю поездку больше, меньше чем или равно 20 м / с ?, (b) Выберите лучшее объяснение из следующего:
I. Для движения со скоростью 15 м / с требуется больше времени, чем при 25 м / с.
II. На скорости 25 м / с преодолевается меньшее расстояние, чем на скорости 15 м / с.
III. Равное время уходит на 15 м / с и 25 м / с.
Решение:
Глава 2 Одномерная кинематика Q.9CQ
Для какого движения мгновенная и средняя скорости равны?
Решение:
Для движения с постоянной скоростью, т. Е. Прямолинейного движения с постоянной скоростью, мгновенная и средняя скорости равны.
Глава 2 Одномерная кинематика Q.9P
Джозеф ДеЛоч из США установил олимпийский рекорд в 1988 году в беге на 200 метров со временем 19,75 секунды. Какая у него была средняя скорость? Ответьте в метрах в секунду и в милях в час.
Решение:
Глава 2 Одномерная кинематика Q.10CQ
Если положение объекта равно нулю, должна ли его скорость быть нулевой? Объяснять.
Решение:
№
Если вы бросаете мяч вверх, например, вы можете выбрать точку сброса y = 0.
Это не меняет того факта, что начальная скорость движения вверх не равна нулю.
Глава 2 Одномерная кинематика Q.10P
В 1992 году Чжуан Юн из Китая установила женский олимпийский рекорд в заплыве на 100 метров вольным стилем со временем 54.64 секунды. Какая у нее была средняя скорость в м / с и миль / ч?
Решение:
Глава 2 Одномерная кинематика Q.11CQ
Предположим, что тормоза в вашем автомобиле создают постоянное замедление, независимо от того, насколько быстро вы едете по дуге. Если вы удвоите скорость движения, как это повлияет на (а) время, необходимое для остановки, и (б) расстояние, необходимое для остановки?
Решение:
Глава 2 Одномерная кинематика Q.11P
BIO Kangaroo развивают скорость 65 км / ч.
(a) Как далеко может прыгнуть кенгуру за 3,2 минуты с такой скоростью?
(b) Сколько времени потребуется кенгуру, чтобы прыгнуть 0,25 км с такой скоростью?
Решение:
Глава 2 Одномерная кинематика Q.12CQ
Скорость объекта равна нулю в данный момент времени. (A) Возможно ли, чтобы ускорение объекта равнялось нулю в это время? Объясните: (б) Возможно ли, чтобы ускорение объекта было ненулевым в это время? Объяснять.
Решение:
(A) Да.
Для тела в состоянии покоя мгновенная скорость равна нулю, и мгновенное ускорение также равно нулю.
(B) Да.
Когда тело бросается вверх, в самой высокой точке тело имеет нулевую скорость, но ускорение в этой точке равно ускорению свободного падения (g).
Глава 2 Одномерная кинематика Q.12
Резиновые утки Сильный шторм 10 января 1992 года привел к тому, что грузовое судно у Алеутских островов выбросило в океан 29 000 резиновых уток и других игрушек для ванн.Десять месяцев спустя сотни резиновых уток начали появляться вдоль береговой линии недалеко от Ситки, Аляска, примерно в 1600 милях от них. Какова была примерная средняя скорость океанического течения, которое доставило уток к берегу в м / с (а) и в милях / ч (б)? (Резиновые утки от того же разлива начали появляться на побережье штата Мэн в июле 2003 года.)
Решение:
Глава 2 Одномерная кинематика Q.13CQ
Если скорость объекта отлична от нуля, может ли его ускорение быть нулевым? Приведите пример, если ваш ответ «да», объясните, почему бы и нет, если ваш ответ отрицательный.
Решение:
Да, если объект движется с постоянной скоростью.
Глава 2 Одномерная кинематика Q.13P
Радиоволны распространяются со скоростью света, приблизительно 186 000 миль в секунду. Сколько времени нужно, чтобы радиосообщение отправилось с Земли на Луну и обратно? (Необходимые данные см. На внутренней стороне задней обложки.)
Решение:
Глава 2 Одномерная кинематика Q.14CQ
Может ли объект иметь нулевую среднюю скорость в течение заданного интервала времени, но все же ускоряться в течение этого интервала? Приведите пример, если ваш ответ «да», объясните, почему бы и нет, если ваш ответ отрицательный.
Решение:
Да, мяч, брошенный прямо вверх и пойманный, когда он возвращается в точку сброса, имеет нулевую среднюю скорость, но он все время ускоряется.
Глава 2 Одномерная кинематика Q.14P
Была темная и бурная ночь, когда вы внезапно увидели вспышку молнии. Через три с половиной секунды вы услышали гром. Учитывая, что скорость звука в воздухе составляет около 340 м / с, как далеко находилась молния?
Решение:
Скорость звука в воздухе v = 340 м / с
Время, затраченное на то, чтобы услышать гром от шторма t = 3.5 с
Расстояние d = vt
= (340 м / с) (3,5 с)
= 1190 м
Глава 2 Одномерная кинематика Q.15CQ
Тесто попадает в поп-муху прямо вверх. (а) Отличается ли ускорение мяча на пути вверх от его ускорения при спуске? (b) Отличается ли ускорение мяча на вершине полета от его ускорения перед приземлением?
Решение:
(A) Нет
(B) Нет
Глава 2 Одномерная кинематика Q.15P
BIO Нервные импульсы Нервная система человека может передавать нервные импульсы со скоростью около 102 м / с. Оцените время, за которое нервный импульс, генерируемый при прикосновении пальца к горячему объекту, попадает в мозг.
Решение:
Глава 2 Одномерная кинематика Q.16CQ
Человек на батуте подпрыгивает вверх с начальной скоростью 4,5 м / с. Какова скорость человека, когда он возвращается к своему первоначальному росту?
Решение:
Используя кинематические соотношения, показано, что скорость человека, когда он возвращается на ту же высоту, равна 4.5 м / с.
Глава 2 Одномерная кинематика Q.16P
Оцените скорость роста ваших волос в милях в час.
Решение:
Глава 2 Одномерная кинематика Q.17CQ
После победы в бейсбольном матче один игрок роняет перчатку, а другой подбрасывает перчатку в воздух. Как сравнить ускорения двух перчаток?
Решение:
При отсутствии сопротивления воздуха обе перчатки имеют одинаковое ускорение.
Глава 2 Одномерная кинематика Q.17P
Зяблик едет на спине галапагосской черепахи, которая шагает со скоростью 0,060 м / с. Через 1,2 минуты зяблик устает от медленной скорости черепахи и летит в том же направлении еще 1,2 минуты со скоростью 12 м / с. Какова была средняя скорость зяблика за этот 2,4-минутный интервал?
Решение:
Глава 2 Одномерная кинематика Q.18CQ
Вулкан стреляет лавовой бомбой прямо вверх.Зависит ли смещение лавовой бомбы от (а) вашего выбора начала координат для вашей системы координат или (б) вашего выбора положительного направления? Объясняйте в каждом конкретном случае.
Решение:
(A) Нет, смещение — это изменение положения, поэтому оно не зависит от местоположения, выбранного для начала координат.
(B) Да, чтобы узнать, является ли смещение объекта положительным или отрицательным, нам нужно знать, какое направление было выбрано в качестве положительного.
Глава 2 Одномерная кинематика Q.18P
Вы бежите 8,0 км трусцой со скоростью 9,5 км / ч, затем запрыгиваете в машину и проезжаете еще 16 км. С какой средней скоростью вы должны вести машину, если ваша средняя скорость за все 24 км должна составлять 22 км / ч?
Решение:
Глава 2 Одномерная кинематика Q.19P
Собака бегает вперед и назад между двумя хозяевами, идущими навстречу друг другу (рис. 2-24). Собака начинает бежать, когда хозяева находятся на расстоянии 10,0 м друг от друга. Если собака бежит со скоростью 3.0 м / с, и каждый хозяин идет со скоростью 1,3 м / с, как далеко проехала собака, когда хозяева встречаются?
Решение:
Глава 2 Одномерная кинематика Q.20P
IP Вы едете по прямой со скоростью 20,0 м / с в течение 10,0 минут, затем со скоростью 30,0 м / с еще 10,0 минут. (A) Ваша средняя скорость составляет 25,0 м / с. с, более 25,0 м / с или менее 25,0 м / с? Объясните: (б) Проверьте свой ответ на пункт (а), вычислив среднюю скорость.
Решение:
Глава 2 Одномерная кинематика Q.21P
В час пик вы едете по прямой со скоростью 12 м / с в течение 1,5 минут, затем вам нужно остановиться на 3,5 минуты и, наконец, вы едете со скоростью 15 м / с еще 2,5 минуты, (a) Участок График зависимости положения от времени для этого движения. Ваш график должен простираться от t = 0 до t = 7,5 минут. (B) Используйте график из части (a), чтобы вычислить среднюю скорость между t = 0 и t = 7,5 минут.
Решение:
Глава 2 Одномерная кинематика Q.22P
IP 10,0 миль вы едете по прямой со скоростью 20,0 м / с, затем еще 10,0 миль со скоростью 30,0 м / с. (A) Ваша средняя скорость 25,0 м / с, более 25,0 м / с или менее 25,0 м / с? Объясните: (б) Проверьте свой ответ на пункт (а), вычислив среднюю скорость.
Решение:
Глава 2 Одномерная кинематика Q.23P
IP Будущий отец ходит взад и вперед, создавая график зависимости положения от времени, показанный на рис. 2-25. Не выполняя вычислений, укажите, является ли скорость отца положительной, отрицательной или нулевой на каждом из следующих сегментов графика: (a) A, (b) B, (c) C и (d) D.Вычислите числовое значение скорости отца для сегментов (e) A, (f) B, (g) C и (h) D и покажите, что ваши результаты подтверждают ваши ответы на части (a) — (d).
Решение:
Глава 2 Одномерная кинематика Q.24P
Положение частицы как функция времени определяется выражением x = (-5 м / с) t + (3 м / с2) t2. (a) Постройте график зависимости x d от t для t = 0 — t = 2s. (б) Найдите среднюю скорость частицы от t = 0 до t = 1 с.(c) Найдите среднюю скорость от t = 0 до t = 1 с.
Решение:
Глава 2 Одномерная кинематика Q.25P
Положение частицы как функция времени определяется выражением x = (6 м / с) t + (-2 м / с2) t2. (a) Постройте график зависимости x от t при t = 0 до t = 2 с. (б) Найдите среднюю скорость частицы от t = 0 до t = 1 с. (c) Найдите среднюю скорость от t = 0 до t = 1 с.
Решение:
Глава 2 Одномерная кинематика Q.26P
IP Теннисистка движется вперед и назад вдоль базовой линии, ожидая подачи соперником, создавая график зависимости положения от времени, показанный на рис. 2-26. (a) Не выполняя вычислений, укажите, на каком из сегментов графика, A, B или C, игрок имеет наибольшую скорость. Вычислите скорость игрока для (b) сегмента A, (c) сегмента B и (d) сегмента C и покажите, что ваши результаты подтверждают ваши ответы на часть (a).
Решение:
Глава 2 Одномерная кинематика Q.27P
В день свадьбы вы отправляетесь в церковь за 30 минут до начала церемонии, что должно быть достаточно времени, поскольку церковь находится всего в 10 километрах от вас. Однако по дороге вам придется сделать неожиданную остановку для строительных работ на дороге. В результате ваша средняя скорость в первые 15 минут составляет всего 5,0 миль / ч. Какая средняя скорость вам нужна на оставшуюся часть поездки, чтобы вовремя добраться до церкви?
Решение:
Глава 2 Одномерная кинематика Q.28P
CE График положения лодки в зависимости от времени, стоящей рядом с доком, показан на Рисунке 2-27. Расположите шесть точек, указанных на графике, в порядке увеличения значения скорости v, отмечая наибольшее отрицательное значение. Обозначьте ложь знаком равенства.
Решение:
Глава 2 Одномерная кинематика Q.29P
Положение частицы как функция времени определяется выражением x = (2,0 м / с) t + (-3,0 м / с3) t3.(a) Постройте график зависимости x от t для времени от t = 0 до t = 1,0 с. (b) Найдите среднюю скорость частицы от t = 0,35 с до t = 0,45 с. (c) Найдите среднюю скорость от t = 0,39 с до t = 0,41 с. (d) Ожидаете ли вы, что мгновенная скорость при t = 0,40 с будет ближе к 0,54 м / с, 0,56 м / с или 0,58 м / с? Объяснять.
Решение:
Глава 2 Одномерная кинематика Q.30P
Положение частицы как функция времени определяется выражением x = (-2.00 м / с) t + (3,00 м / с3) t3. (a) Постройте график зависимости x от t для времени от t = 0 до t = 1,00 с. (b) Найдите среднюю скорость частицы от t = 0,150 с до t = 0,250 с. (c) Найдите среднюю скорость от t = 0,190 с до t = 0,210 с. (d) Ожидаете ли вы, что мгновенная скорость при t = 0,200 с будет ближе к -1,62 м / с или -1,66 м / с? Объяснять.
Решение:
Глава 2 Одномерная кинематика Q.31P
CE Прогноз / объяснение Два лука стреляют одинаковыми стрелами с одинаковой скоростью пуска.Для этого тетива в луке 1 должна быть оттянута дальше назад, когда она стреляет из стрелы, чем тетива в луке 2. (a) Ускорение стрелы, выпущенной из лука 1, больше, меньше или равно ускорению стрелы, выпущенной из лука 2? (b) Выберите лучшее объяснение из следующего:
I. Стрела в луке 2 ускоряется в течение большего времени.
II. Обе стрелки стартуют из состояния покоя.
III. Стрела в луке 1 ускоряется на большее время.
Решение:
Изобразите проблему:
Две одинаковые стрелы выпущены из двух луков.Стрела из лука 1 отводится дальше, чем из лука 2.
Стратегия:
Для двух луков с одинаковой начальной скоростью после выстрела ускорение стрелы обратно пропорционально времени.
(a) Поскольку лук 1 отводится дальше, ускорение стрелы из лука 1 меньше, чем из лука 2.
(b) Поскольку стрела из лука 1 перемещается на большее расстояние по сравнению с стрелой из лука 2 , чтобы достичь той же скорости, стрела из лука 1 будет ускоряться на большее время.Поэтому объяснение III является лучшим.
Глава 2 Одномерная кинематика Q.32P
Авиалайнер 747 достигает взлетной скорости 173 миль / ч за 35,2 с. Какова величина его среднего ускорения?
Решение:
Глава 2 Одномерная кинематика Q.33P
У скворечника бегун ускоряется со скоростью 1,9 м / с2 за 5,2 с. Ускорение бегуна до конца забега равно нулю. Какая скорость бегуна (а) при t = 2.0 с, и (б) в конце гонки?
Решение:
Глава 2 Одномерная кинематика Q.34P
Реактивный самолет совершает посадку, летя строго на восток, со скоростью 115 м / с. Если струя останавливается через 13,0 с, каковы величина и направление ее среднего ускорения?
Решение:
Глава 2 Одномерная кинематика Q.35P
Автомобиль движется строго на север со скоростью 18,1 м / с. Найдите скорость автомобиля после 7.50 с, если его ускорение равно (а) 1,30 м / с2 на севере или (b) 1,15 м / с2 на юге.
Решение:
Глава 2 Одномерная кинематика Q.36P
Мотоцикл движется в соответствии с графиком зависимости скорости от времени, показанным на Рисунке 2-28. Найдите среднее ускорение мотоцикла во время каждого из следующих сегментов движения: (a) A, (b) B и (c) C
Решение:
Глава 2 Одномерная кинематика Q.37P
Человек верхом на лошади движется в соответствии с графиком зависимости скорости от времени, показанным на Рисунке 2-29. Найдите смещение человека для каждого из следующих сегментов движения: (a) A, (b) B и (c) C.
Решение:
Глава 2 Одномерная кинематика Q.38P
При беге с начальной скоростью +11 м / с лошадь имеет среднее ускорение -1,81 м / с2. Сколько времени нужно лошади, чтобы снизить скорость до +6.5 м / с?
Решение:
Глава 2 Одномерная кинематика Q.39P
IP Предположим, что тормоза вашего автомобиля создают постоянное замедление 4,2 м / с2 независимо от того, насколько быстро вы едете. Если вы удвоите скорость движения с 16 до 32 м / с, (а) увеличится ли время, необходимое для остановки, в два или четыре раза? Объяснять. Проверьте свой ответ на часть (а), рассчитав задерживающую известку для начальных скоростей (b) 16 м / с и (c) 32 м / с.
Решение:
Глава 2 Одномерная кинематика Q.40P
IP В предыдущей задаче: (а) увеличивается ли расстояние, необходимое для остановки, в два или четыре раза? Объяснять. Проверьте свой ответ на часть (а), рассчитав тормозной путь для начальной скорости (b) 16 м / с и (c) 32 м / с.
Решение:
Глава 2 Одномерная кинематика Q.41P
Когда поезд ускоряется от станции, он достигает скорости 4.7 м / с за 5,0 с. Если ускорение поезда остается постоянным, какова его скорость по прошествии дополнительных 6,0 с?
Решение:
Глава 2 Одномерная кинематика Q.42P
Частица имеет ускорение +6,24 м / с2 в течение 0,300 с. По истечении этого времени скорость частицы составляет +9,31 м / с. Какова была начальная скорость частицы?
Решение:
Глава 2 Одномерная кинематика Q.43P
Посадка со скоростью 81.9 м / с, и летя прямо на юг, самолет останавливается через 949 м. Предполагая, что струя замедляется с постоянным ускорением, найдите величину и направление ее ускорения.
Решение:
Глава 2 Одномерная кинематика Q.44P
Когда вы видите, что светофор становится красным, вы нажимаете на тормоза, пока не остановитесь. Если ваша начальная скорость была 12 м / с, и вы двигались строго на запад, какова была ваша средняя скорость при торможении? Предположим постоянное замедление.
Решение:
Глава 2 Одномерная кинематика Q.45P
Aball выпущен в точке x = 2 м на наклонной плоскости с ненулевой начальной скоростью. После выпуска мяч движется с постоянным ускорением. Ускорение и начальная скорость мяча описываются одним из следующих четырех случаев: случай 1, a> 0, u0 <0; случай 2, a> 0, u0 <0; случай 3, a <0, u0> 0; случай 4, a <0, u0 <0. (a) В каком из этих случаев мяч определенно пройдет мимо x = 0 через некоторое время? (b) В каком из этих случаев требуется больше информации, чтобы определить, пересечет ли мяч x = 0? (c) В каком из этих случаев мяч остановится на мгновение во время своего движения?
Решение:
Глава 2 Одномерная кинематика Q.46P
Предположим, что машина в задаче 44 останавливается через 35 метров. Сколько на это нужно времени?
Решение:
Глава 2 Одномерная кинематика Q.47P
Начиная с покоя, лодка увеличивает свою скорость до 4,12 м / с с постоянным ускорением. (A) Какова средняя скорость лодки? (b) Если лодка развивает эту скорость за 4,77 с, как далеко она ушла?
Решение:
Глава 2 Одномерная кинематика Q.48P
IP BIO Гепард может разогнаться до 25,0 м / с за 6,22 с. Предполагая постоянное ускорение, (а) как далеко пробежал гепард за это время? (b) После спринта всего за 3,13 с скорость гепарда составляет 12,5 м / с, более 12,5 м / с или менее 12,5 м / с? Объясните: (c) Какова средняя скорость гепарда в первые 3,11 секунды спринта? На вторые 3,11 секунды спринта? (d) Рассчитайте расстояние, пройденное гепардом за первые 3,11 с и за вторые 3,11 с.
Решение:
Глава 2 Одномерная кинематика Q.49P
Ребенок спускается с холма на тобоггане с ускорением 1,8 м / с2. Если она начинает в состоянии покоя, как далеко она прошла за (а) 1,0 с, (б) 2,0 с и (в) 3,0 с?
Решение:
Глава 2 Одномерная кинематика Q.50P
Детонатор Во время поездки под названием «Детонатор» в Worlds of Fun в Канзас-Сити пассажиры ускоряются прямо вниз из состояния покоя до 45 миль / ч за 2,2 секунды. Каково среднее ускорение пассажиров в этой поездке?
Решение:
Глава 2 Одномерная кинематика Q.51P
Подушки безопасности Подушки безопасности срабатывают за 10 мс. Оцените ускорение передней поверхности сумки при ее расширении. Выразите свой ответ в терминах ускорения свободного падения g.
Решение:
Глава 2 Одномерная кинематика Q.52P
Жюль Верн В своем романе «С Земли на Луну» (1866) Жюль Верн описывает космический корабль, который выстреливает из пушки, названной «Колумбиадой», со скоростью 12000 единиц. ярдов / с.Колумбиада имеет длину 900 футов, но часть ее заполнена порошком, поэтому космический корабль ускоряется на расстояние всего 700 футов. Оцените ускорение, которое испытывают находящиеся в космическом корабле люди во время запуска. Ответьте в м / с2. (Верн понимал, что «путешественники… столкнутся с сильной отдачей», но он, вероятно, не знал, что люди обычно теряют сознание, если испытывают ускорение более 7g ~ 70 м / с2.)
Решение:
Глава 2 Одномерная кинематика Q.53P
BIO Бактериальное движение Примерно 0,1% бактерий в кишечнике взрослого человека — это кишечная палочка. Было замечено, что эти бактерии движутся со скоростью до 15 мкм / с и максимальным ускорением 166 мкм / с2. Предположим, бактерия E. coli в вашем кишечнике начинается в состоянии покоя и ускоряется со скоростью 156 мкм / с2. Сколько (а) времени и (б) расстояния требуется, чтобы бактерия достигла скорости 12 мкм / с?
Решение:
Глава 2 Одномерная кинематика Q.54П
По прямой трассе едут две машины. В момент времени t = 0 машина 1 проезжает отметку мили 0, двигаясь строго на восток со скоростью 20,0 м / с. В то же время вагон 2 находится в 1,0 км к востоку от отметки 0 мили и движется со скоростью 30,0 м / с на запад. Автомобиль 1 ускоряется с ускорением величиной 2,5 м / с2, а вагон 2 замедляется с ускорением величиной 3,2 м / с2. (A) Напишите уравнения движения x-против-t для обеих машин, взяв восток как положительное направление, (б) В какое время машины проезжают рядом друг с другом?
Решение:
Глава 2 Одномерная кинематика Q.55P
Удар метеорита 9 октября 1992 года 27-фунтовый метеорит упал на автомобиль в Пикскилле, штат Нью-Йорк, оставив вмятину глубиной 22 см в багажнике. Если метеорит доставит автомобиль со скоростью 130 м / с, какова будет величина его замедления, если предположить, что оно постоянное?
Решение:
Глава 2 Одномерная кинематика Q.56P
Ракета взлетает и движется прямо вверх от стартовой площадки с постоянным ускорением. Через 3,0 с ракета находится на высоте 77 м.а) Каковы величина и направление ускорения ракеты? б) Какова его скорость в это время?
Решение:
Глава 2 Одномерная кинематика Q.57P
IP Вы едете по городу со скоростью 12,0 м / с, как вдруг перед вами катится мяч. Вы нажимаете на тормоз и начинаете замедляться со скоростью 3,5 м / с2. (A) Как далеко вы проехали до остановки? (b) Когда вы проехали только половину расстояния в части (а), ваша скорость равна 6.0 м / с, более 6,0 м / с или менее 6,0 м / с? Подтвердите свой ответ расчетом.
Решение:
Глава 2 Одномерная кинематика Q.58P
IP Вы едете по городу со скоростью 16 м / с, как вдруг перед вами выезжает машина. Вы нажимаете на тормоз и начинаете замедляться со скоростью 3,2 м / с2. (A) Сколько времени нужно, чтобы остановиться? (b) После торможения половина времени, указанного в части (а), ваша скорость составляет 8,0 м / с, больше 8,0 м / с или меньше 8.0 м / с? Подтвердите свой ответ расчетом: (c) Если автомобиль, выезжающий задним ходом, первоначально находился в 55 м перед вами, каково максимальное время реакции, которое вы можете иметь, прежде чем нажать на тормоза и все же избежать столкновения с автомобилем?
Решение:
Глава 2 Одномерная кинематика Q.59P
IP BIO Ускорение языка Когда хамелеон захватывает насекомое, его язык может вытянуться на 16 см за 0,10 с. (а) Найдите величину ускорения языка, считая его постоянным, (б) В первом 0.050 с, длина языка составляет 8,0 см, более 8,0 или менее 8,0 см? Подтвердите свой вывод расчетом
Решение:
Глава 2 Одномерная кинематика Q.60P
IP Двигаясь по инерции на запад на вашем велосипеде со скоростью 8,4 м / с, вы встречаетесь с песчаным участком дороги шириной 7,2 м. Когда вы покидаете песчаный участок, ваша скорость снижается на 2,0 м / с до 6,4 м / с. а) Если предположить, что песок вызывает постоянное ускорение, каково было ускорение велосипеда на песчаном участке? Укажите величину и направление. (Б) Сколько времени потребовалось, чтобы пересечь песчаный участок? (c) Предположим, вы въезжаете на песчаный участок со скоростью всего 5.4 м / с. Ваша конечная скорость в данном случае составляет 3,4 м / с, больше 3,4 м / с или меньше 3,4 м / с? Объяснять.
Решение:
Глава 2 Одномерная кинематика Q.61P
BIO Пережив сильное замедление 13 июля 1977 года, во время тест-драйва на британском ипподроме Сильверстоун, дроссельная заслонка на машине Дэвида Перли застряла настежь. В результате аварии Перли подвергся воздействию величайшей «перегрузки», когда-либо существовавшей у человека — он замедлился, разогнавшись до 173 км / ч, до нуля на расстоянии всего около нуля.66 мес. Вычислите величину ускорения, испытываемого Перли (считая, что оно постоянное), и выразите свой ответ в единицах ускорения свободного падения, g = 9,81 м / с2.
Решение:
Глава 2 Одномерная кинематика Q.62P
IP Лодка движется по прямой с постоянной скоростью 2,6 м / с при переключении на нейтраль. После прохождения 12 м по инерции двигатель снова включается, и лодка продолжает движение с пониженной постоянной скоростью, равной 1.6 м / с. Предполагая постоянное ускорение при движении накатом, (а) сколько времени потребовалось лодке, чтобы преодолеть 12 м? б) Какое ускорение было у лодки при движении накатом? (c) Когда лодка прошла курсом 6,0 м, была ли ее скорость 2,1 м / с, более 2,1 м / с или менее 2,1 м / с? Объяснять.
Решение:
Глава 2 Одномерная кинематика Q.63P
Модель ракеты поднимается с постоянным ускорением на высоту 3,2 м, при этом ее скорость равна 26.0 м / с. а) Сколько времени нужно, чтобы ракета достигла этой высоты? б) Какова была величина ускорения ракеты? (c) Найдите высоту и скорость ракеты через 0,10 с после запуска.
Решение:
Глава 2 Одномерная кинематика Q.64P
Печально известный цыпленок мчится к своей тарелке со скоростью 5,8 м / с, когда решает удариться о землю. Цыпленок скользит в течение 1,1 с, едва достигнув тарелки при остановке (конечно, безопасно). (А) Каковы величина и направление ускорения курицы? б) Как далеко ускользнула курица?
Решение:
Глава 2 Одномерная кинематика Q.65P
Велосипедист заканчивает ремонт спущенной шины, когда его друг едет с постоянной скоростью 3,5 м / с. Через две секунды велосипедист запрыгивает на свой байк и разгоняется со скоростью 2,4 м / с2, пока не догонит своего друга. (А) Сколько времени требуется, чтобы он догнал своего друга? б) Как далеко он прошел за это время? в) Какова его скорость, когда он догоняет?
Решение:
Глава 2 Одномерная кинематика Q.66P
Автомобиль в пробках трогается с места и движется вперед на 13 м за 8.0 с, затем снова переходит в состояние покоя. График зависимости скорости от времени для этого автомобиля приведен на рисунке 30. Какое расстояние автомобиль преодолевает за (а) первые 4,0 секунды своего движения и (б) последние 2,0 секунды своего движения? (c) Какова постоянная скорость V, характеризующая среднюю часть его движения?
Решение:
Глава 2 Одномерная кинематика Q.67P
Автомобиль и грузовик движутся прямо навстречу друг другу по прямой и узкой улице, но они избегают лобового столкновения, одновременно применяя тормоза при t = 0.Полученные графики зависимости скорости от времени показаны на рисунке 31. Каково расстояние между автомобилем и грузовиком, когда они остановились, учитывая, что в t = 0 автомобиль находится на x = 15 м, а грузовик — на x = -35 м? (Обратите внимание, что эта информация определяет, какая линия на графике соответствует какому автомобилю.)
Решение:
Глава 2 Одномерная кинематика Q.68P
В физической лаборатории ученики измеряют время, за которое небольшая тележка перемещается на расстояние 1.00 м по ровной дороге, наклоненной под углом θ к горизонту. Их результаты представлены в следующей таблице.
θ 10,0 ° 20,0 ° 30,0 °
время, с 1,08 0,770 0,640
а) Найдите величину ускорения тележки для каждого угла.
(b) Покажите, что ваши результаты для части (a) полностью согласуются с формулой a = g sin θ. (Мы выведем эту формулу в главе 5.)
Решение:
Глава 2 Одномерная кинематика Q.69P
CE На краю крыши вы бросаете мяч с начальной скоростью u0; мгновение спустя вы бросаете мяч 2 вниз с той же начальной скоростью.Мячи приземляются одновременно. Какое из следующих утверждений верно в момент непосредственно перед тем, как шары коснулись земли? A. Скорость мяча 1 больше, чем скорость мяча 2; B. Скорость мяча 1 равна скорости мяча 2; C. Скорость мяча 1 меньше скорости мяча 2. 70. Легенда гласит, что Исаака Ньютона ударило по голове падающее яблоко, что вызвало у нее мысли о гравитации. Предполагая, что история правдива, оцените скорость яблока, когда оно ударилось о Ньютона.
Решение:
Поскольку смещение двух шаров одинаково и начальные скорости также одинаковы, поэтому два шара ударяются о землю с одинаковой скоростью.
Итак, вариант (В) верен.
Глава 2 Одномерная кинематика Q.70P
Легенда гласит, что Исаака Ньютона ударило по голове падающее яблоко, что вызвало у него мысли о гравитации. Предполагая, что история правдива, оцените скорость яблока, когда оно ударилось о Ньютона.
Решение:
Глава 2 Одномерная кинематика Q.71P
В мультфильме изображена машина в свободном падении. Верно ли заявление, сделанное в мультфильме? Обосновать ответ.
Решение:
Глава 2 Одномерная кинематика Q.72P
Ссылаясь на рисунок в задаче 71, сколько времени потребуется автомобилю, чтобы разогнаться от 0 до 30 миль / ч?
Решение:
Глава 2 Одномерная кинематика Q.73P
Прыжок Джордана Вертикальный прыжок Майкла Джордана составляет 48 дюймов.Какая у него скорость взлета? Дайте свой ответ m метров в секунду.
Решение:
Глава 2 Одномерная кинематика Q.74P
BIO Часто наблюдают, как быков сбрасывают моллюсков и других моллюсков с высоты на скалы внизу, чтобы открыть раковины. Если чайка роняет снаряд с высоты 14 м, с какой скоростью движется снаряд, когда он ударяется о камни? 75. Вулкан запускает лавовую бомбу прямо вверх с начальной скоростью 28 м / с.Взяв за положительное направление вверх, найдите скорость и направление движения лавовой бомбы (а) через 2,0 секунды и (б) через 3,0 секунды после ее запуска.
Решение:
Глава 2 Одномерная кинематика Q.75P
Вулкан запускает лавовую бомбу прямо вверх с начальной скоростью 28 м / с. Взяв за положительное направление вверх, найдите скорость и направление движения лавовой бомбы (а) через 2,0 секунды и (б) через 3,0 секунды после ее запуска.
Решение:
Глава 2 Одномерная кинематика Q.76P
Внеземной вулкан Первый действующий вулкан, наблюдаемый за пределами Земли, был обнаружен в 1979 году на одной из лун Юпитера. Было замечено, что вулкан выбрасывает материал на высоту примерно 2,00 x 105 м. Учитывая, что ускорение свободного падения на lo составляет 1,80 м / с2, найдите начальную скорость выброшенного материала.
Решение:
Глава 2 Одномерная кинематика Q.77P
BIO Измерьте время своей реакции Вот кое-что, что вы можете попробовать дома — эксперимент по измерению времени вашей реакции. Попросите друга держать линейку за один конец так, чтобы другой конец свисал вертикально. На нижнем конце держите большой и указательный пальцы по обе стороны от линейки, готовые схватить ее. Пусть ваш друг отпустит линейку без предупреждения. Поймай его как можно быстрее. Если вы поймаете линейку на 5,2 см с нижнего конца, какое у вас время реакции?
Решение:
Глава 2 Одномерная кинематика Q.78P
Плотник на крыше здания случайно уронил молоток. Когда молот падает, он проходит через два окна одинаковой высоты, как показано на рисунке. (a) Увеличение скорости молота, когда он падает за окно, больше, меньше или равно увеличению скорости, когда он падает за окно 2? (b) Выберите лучшее объяснение из следующего:
I. Большая скорость в окне 2 приводит к большему увеличению скорости.
II. Постоянное ускорение означает, что молот увеличивает скорость на одинаковую величину для каждого окна.
III. Молот тратит больше инея, падая за окно 1.
Решение:
Глава 2 Одномерная кинематика Q.79P
CE Predict / Explain На рис. 33 показан график зависимости u-t от t для молотка, брошенного плотником в задаче 78. Обратите внимание, что время, когда молот проходит мимо двух окон, обозначены заштрихованными областями: (a) Является ли площадь заштрихованной области, соответствующей окну 1, больше, меньше или равна площади заштрихованной области, соответствующей окну 2? (b) Выберите лучшее объяснение из следующего:
I.Заштрихованная область окна 2 выше, чем у. заштрихованная область окна 1.
II. Окна одинаковые по высоте.
III. Заштрихованная область для окна 1 шире, чем заштрихованная область для окна 2.
Решение:
(a) Площадь заштрихованной области, соответствующей окну 1, равна площади заштрихованной области, соответствующей окну 2.
(b) Поскольку площадь графика время — скорость показывает расстояние, пройденное объектом, и поскольку два окна имеют одинаковую высоту, следовательно, площади равны.
Итак, вариант II — лучшее объяснение.
Глава 2 Одномерная кинематика Q.80P
Решение:
Глава 2 Одномерная кинематика Q.81P
Билл сходит с трамплина высотой 3,0 м и падает в воду. В то же время Тед прыгает вверх со скоростью 4,2 м / с с трамплина высотой 1,0 м. Выбрав начало координат на поверхности воды, а вверх в качестве положительного направления x, напишите уравнения движения x-против-t как для Билла, так и для Теда.
Решение:
Глава 2 Одномерная кинематика Q.82P
Повторите предыдущую задачу, на этот раз с исходной точкой. 3,0 м над водой и вниз в качестве положительного направления оси x.
Решение:
Глава 2 Одномерная кинематика Q.83P
В жаркий летний день в штате Вашингтон во время каякинга я увидел, как несколько пловцов прыгнули с железнодорожного моста в реку Снохомиш внизу, пловцы сошли с моста, и я по оценкам, они попали в воду 1.Спустя 5 секунд: (а) Какова высота моста? б) Как быстро пловцы двигались, когда попадали в воду? (c) Каким было бы время падения пловцов, если бы мост был вдвое выше?
Решение:
Глава 2 Одномерная кинематика Q.84P
Самый высокий водный фонтан Самый высокий в мире водный фонтан находится, что весьма уместно, в Фаунтин-Хиллз, Аризона. Фонтан поднимается на высоту 560 футов (на 5 футов выше монумента Вашингтона). (А) Какова начальная скорость воды? б) Сколько времени нужно, чтобы вода достигла вершины фонтана?
Решение:
Глава 2 Одномерная кинематика Q.85P
Разъяренный баскетболист, ошибочно объявивший фолом, бросает мяч прямо на пол. Если мяч отскакивает прямо вверх и возвращается на пол через 2,8 секунды после первого удара, какова максимальная высота мяча над полом?
Решение:
Глава 2 Одномерная кинематика Q.86P
Чтобы отпраздновать победу, питчер бросает перчатку вверх с начальной скоростью 6,0 м / с. а) Сколько времени нужно, чтобы перчатка вернулась к питчеру? б) Сколько времени нужно, чтобы перчатка достигла максимальной высоты?
Решение:
Глава 2 Одномерная кинематика Q.87P
IP Стоя на краю обрыва высотой 32,5 м, вы бросаете мяч. Позже вы бросаете второй мяч вниз с начальной скоростью 11,0 м / с. (а) Какой мяч имеет большее увеличение скорости, когда он достигает основания обрыва, или оба шара ускоряются на одинаковую величину? (б) Проверьте свой ответ на часть (а) расчетами.
Решение:
Глава 2 Одномерная кинематика Q.88P
Вы стреляете стрелой в воздух.Через две секунды (2,00 с) стрела улетела прямо вверх на высоту 30,0 м над точкой запуска. (A) Какова была начальная скорость стрелы?
(b) Сколько времени потребовалось стрелке, чтобы сначала достичь высоты 15,0 м над точкой запуска?
Решение:
Глава 2 Одномерная кинематика Q.89P
Когда вы едете на лифте, спускающемся с постоянной скоростью 3,0 м / с, вы случайно уроните книгу из-под руки. (а) Сколько времени нужно, чтобы книга поднялась на этаж лифта, 1.2 м ниже руки? б) Какова скорость книги относительно вас, когда она падает на этаж лифта?
Решение:
Глава 2 Одномерная кинематика Q.90P
Воздушный шар опускается со скоростью 2,0 м / с, когда пассажир роняет камеру. Если при падении камера находится на высоте 45 м над землей, (а) сколько времени требуется камере, чтобы достичь земли, и (б) какова ее скорость непосредственно перед приземлением? Пусть вверх будет положительное направление для этой проблемы.
Решение:
Глава 2 Одномерная кинематика Q.91P
IP Стоя рядом, вы и ваш друг в разное время ступаете с моста и падаете на 1,6 секунды в воду внизу. Ваша подруга идет первой, а вы следуете за ней после того, как она снизилась на 2,0 м. а) Когда ваш друг ударяется о воду, расстояние между вами составляет 2,0 м, меньше 2,0 м или больше 2,0 м? (б) Проверьте свой ответ на часть (а) расчетами.
Решение:
Глава 2 Одномерная кинематика Q.92P
Модель ракеты взлетает и движется вверх с ускорением 12 м / с2, пока не достигает высоты 26 м, после чего ее двигатель выключается, и она продолжает полет. в свободном падении.
(а) Какая максимальная высота достигает ракеты?
(b) Какова скорость ракеты непосредственно перед тем, как она упадет на землю?
(c) Какова общая продолжительность полета ракеты?
Решение:
Глава 2 Одномерная кинематика Q.93P
Попадание в «высокий ударник» Молодая женщина на карнавале подходит к «высокому ударнику», популярному испытанию на силу, когда участник ударяет молотком по одному концу рычага, толкая небольшую металлическую пробку вверх к колокол. Она сильно взмахивает молотком и направляет пробку в верхнюю часть ударника, где он звонит в колокольчик. На рисунке 34 показан соответствующий график зависимости положения от времени для пробки. Используя информацию, представленную на графике, ответьте на следующие вопросы: (а) Какова средняя скорость пробки во время ее движения вверх? б) Насколько уменьшается скорость пробки во время ее движения вверх? (c) Какова начальная скорость вилки? (Предположим, что свеча во время восходящего движения находится в свободном падении без влияния сопротивления воздуха или трения.)
Решение:
Глава 2 Одномерная кинематика Q.94P
Сидя на ветке дерева на высоте 10,0 м над землей, вы уроните каштан. Когда каштан упал на 2,5 м, вы бросаете второй каштан прямо вниз. Какую начальную скорость вы должны дать второму каштану, если они оба должны коснуться земли одновременно?
Решение:
Глава 2 Одномерная кинематика Q.95GP
В известном романе Жюля Верна Филеас Фогг путешествует вокруг света за 80 дней.Какова была примерная средняя скорость мистера Фогга во время его приключения?
Решение:
Глава 2 Одномерная кинематика Q.96GP
Астронавт на Луне бросает камень прямо вниз с высоты 1,25 м. Если ускорение свободного падения на Луне составляет 1,62 м / с2, какова скорость камня перед приземлением?
Решение:
Глава 2 Одномерная кинематика Q.97GP
Вы прыгаете с вершины валуна на землю 1.5 м ниже. Оцените ваше замедление при приземлении.
Решение:
Глава 2 Одномерная кинематика Q.98GP
Сверхзвуковой водопад Геологам известны периоды в прошлом, когда закрывался Гибралтарский пролив, а Средиземное море высыхало и превращалось в пустыню. Позже, когда пролив вновь открылся, был создан массивный водопад с соленой водой. По словам геологов, вода в этом водопаде была сверхзвуковой; то есть он падал со скоростью, превышающей скорость звука.Если не учитывать сопротивление воздуха, какова минимальная высота, необходимая для создания сверхзвукового водопада? (Скорость звука можно принять равной 340 м / с.)
Решение:
Глава 2 Одномерная кинематика Q.99GP
CE На краю крыши вы бросаете мяч A из состояния покоя, а затем бросаете мяч B вниз с начальной скоростью v0. Будет ли увеличение скорости непосредственно перед тем, как шары приземлятся, больше для мяча A, больше для мяча B или одинаково для каждого мяча?
Решение:
Глава 2 Одномерная кинематика Q.100GP
Предположим, что два мяча, описанные в задаче 99, выпущены в одно и то же время, при этом мяч A выпадает из состояния покоя, а мяч B брошен вниз с начальной скоростью υ0. Определите, какой из пяти графиков, показанных на рис. 2-35, соответствует (a) шару A и (b) шару B.
Задача 99
На краю крыши вы бросаете шар A из состояния покоя, а затем бросаете шар B вниз с помощью начальная скорость υ0. Будет ли увеличение скорости непосредственно перед тем, как шары приземлятся, больше для шара A, больше для бейла B или одинаково для каждого шара?
Решение:
Поскольку шары падают с постоянным ускорением, график временной скорости представляет собой прямую линию с одинаковым наклоном, а начальная точка каждой прямой соответствует их начальной скорости.
(a) Следовательно, для мяча A график представлен графиком 3
(b) А для шара B график представлен графиком 2.
Глава 2 Одномерная кинематика Q.101GP
Астронавты на далекой планете бросают камень прямо вверх и записывают его движение с помощью видеокамеры. После оцифровки своего видео они могут построить график зависимости высоты y от времени t, показанный на рис. 2-36. а) Каково ускорение свободного падения на этой планете? б) Какова была начальная скорость камня?
Решение:
Глава 2 Одномерная кинематика Q.102GP
Drop Tower НАСА эксплуатирует 2,2-секундную башню для сброса в Исследовательском центре Гленна в Гевеланде, штат Огайо. На этом объекте экспериментальные пакеты сбрасываются с вершины башни на 8-м этаже здания. В течение 2,2 секунд свободного падения участники экспериментов испытывают микрогравитацию, аналогичную условиям космического корабля на орбите. а) Какова дальность падения башни 2,2 с? б) Как быстро перемещаются эксперименты, когда они попадают в воздушные подушки внизу башни? (c) Если экспериментальный пакет останавливается на расстоянии 0.75 м после удара о подушку безопасности, какое среднее ускорение при торможении?
Решение:
Глава 2 Одномерная кинематика Q.103GP
Мальчик подпрыгивает на батуте прямо вверх и вниз. Предположим, она удвоила свою начальную скорость с 2,0 м / с до 4,0 м / с. а) В какой степени увеличивается время ее пребывания в воздухе? б) Во сколько раз увеличивается ее максимальный рост? (c) Проверьте свои ответы на части (a) и (b) с точным расчетом.
Решение:
Глава 2 Одномерная кинематика Q.104GP
На 18-м грине Открытого чемпионата США вам нужно сделать 20,5-футовый удар, чтобы выиграть турнир с ничьей. Когда вы ударяете по мячу с начальной скоростью 1,57 м / с, он останавливается на расстоянии 6 футов от лунки. (а) Если предположить, что замедление, вызванное травой, постоянно, какой должна быть начальная скорость, чтобы просто сделать удар? (b) Какая начальная скорость вам нужна, чтобы сделать оставшийся удар длиной 6 футов?
Решение:
Глава 2 Одномерная кинематика Q.105GP
Популярным развлечением на некоторых карнавалах является бросание одеяла (см. Фото, стр. 39). а) Если человека подбрасывают на высоту не более 28 футов над одеялом, сколько времени он проводит в воздухе? (b) Является ли количество времени, в течение которого человек находится на высоте 14,0 футов, больше, меньше или равно количеству времени, в течение которого человек находится ниже высоты 14,0 футов? Объяснять. (c) Проверьте свой ответ на часть (b) расчетами.
Решение:
Глава 2 Одномерная кинематика Q.106GP
Ссылаясь на концептуальную контрольную точку 2-5, найдите расстояние между породами при (a) t = 1,0 с, (b) t = 2,0 с и (c) t = 3,0 с, где время отсчитывается от момента времени. второй камень упал. (d) Убедитесь, что расстояние увеличивается линейно со временем.
Решение:
Глава 2 Одномерная кинематика Q.107GP
Сизокрылая чайка, поднимающаяся прямо вверх со скоростью 5,20 м / с, взлетает над раковиной, когда она находится на высоте 12,5 м над землей.а) Каковы величина и направление ускорения снаряда сразу после того, как он выпущен? (b) Найдите максимальную высоту снаряда над землей. (c) Сколько времени требуется, чтобы снаряд достиг земли? (г) Какова скорость снаряда в это время?
Решение:
Глава 2 Одномерная кинематика Q.108GP
Врач, готовясь сделать пациенту инъекцию, впрыскивает небольшое количество жидкости прямо вверх из шприца.Если жидкость выходит со скоростью 1,5 м / с, (а) сколько времени нужно, чтобы она вернулась на уровень шприца? б) Какова максимальная высота жидкости над шприцем?
Решение:
Глава 2 Одномерная кинематика Q.109GP
Воздушный шар только что поднялся в воздух и поднимается с постоянной скоростью 2,0 м / с. Внезапно одна из пассажиров понимает, что оставила камеру на земле. Друг поднимает его и подбрасывает прямо вверх с начальной скоростью 13 м / с.Если при подбрасывании камеры пассажир находится на 2,5 м выше подруги, насколько высоко она будет, когда камера достигнет ее?
Решение:
Глава 2 Одномерная кинематика Q.110GP
В предыдущей задаче, какова минимальная начальная скорость камеры, если она должна просто достичь пассажира? (Подсказка: когда камеру бросают с минимальной скоростью, ее скорость при достижении пассажира равна скорости пассажира.)
Решение:
Глава 2 Одномерная кинематика Q.111GP
Old Faithful Наблюдая за извержением Old Faithful, вы замечаете, что требуется время t, чтобы вода вышла из основания гейзера и достигла максимальной высоты. (а) Какова высота гейзера и (б) какова начальная скорость воды? Оцените свои выражения для (c) высоты и (d) начальной скорости для измеренного времени 1,65 с.
Решение:
Глава 2 Одномерная кинематика Q.112GP
Мяч подбрасывается вверх с начальной скоростью υ0.Когда он достигает вершины своего полета, на высоте h, второй шар подбрасывается вверх с той же начальной скоростью. (а) Нарисуйте график зависимости x от t для каждого шара. (b) Из вашего графика решите, пересекаются ли шары в точках h / 2, выше h / 2 или ниже h / 2. (c) Найдите высоту, на которой пересекаются пути.
Решение:
Глава 2 Одномерная кинематика Q.113GP
Гири привязаны к каждому концу 20,0-сантиметровой струны. Вы держите одну гирю в руке, а другую позволяете висеть вертикально на высоте h над полом.Когда вы отпускаете гирю в руке, два гиря ударяются о землю один за другим с слышимым стуком. Найдите значение h, для которого время между выпуском и первым ударом равно времени между первым и вторым ударом.
Решение:
Глава 2 Одномерная кинематика Q.114GP
Мяч, брошенный из состояния покоя, преодолевает три четверти расстояния до земли в последнюю секунду своего падения. а) С какой высоты упал мяч? б) Сколько было всего времени падения?
Решение:
Глава 2 Одномерная кинематика Q.115GP
Сталактит на крыше пещеры с постоянной скоростью капает в бассейн на 4,0 м ниже. Одна капля воды попадает в бассейн, вторая падает в воздух, а третья просто отрывается от сталактита. а) Каковы положение и скорость второй капли, когда первая капля попадает в лужу? б) Сколько капель в минуту попадает в бассейн?
Решение:
Глава 2 Одномерная кинематика Q.116GP
Вы бросаете лыжную перчатку с высоты h на свежий снег, и она опускается на глубину d, прежде чем остановиться.(а) С точки зрения g и h, какова скорость перчатки, когда она достигает снега? б) Каковы величина и направление ускорения перчатки при движении по снегу, если предположить, что оно постоянное? Дайте свой ответ в виде g, h и d.
Решение:
Глава 2 Одномерная кинематика Q.117GP
Чтобы определить высоту воздушной линии электропередачи, вы бросаете мяч прямо вверх. Мяч пересекает линию на пути вверх после 0.75 с, и снова передает его по пути вниз через 1,5 с после того, как он был подброшен. Какова высота линии электропередачи и начальная скорость мяча?
Решение:
Глава 2 Одномерная кинематика Q.118GP
Решение:
Глава 2 Одномерная кинематика Q.119GP
Стрела выстреливает со скоростью 20,0 м / с по блоку пенополистирола, лежащему на гладкой поверхности. Стрелка проникает в блок на определенное расстояние, прежде чем остановиться относительно него.Во время этого процесса замедление стрелки составляет 1550 м / с2, а ускорение блока — 450 м / с2. (a) Сколько времени нужно, чтобы стрелка перестала двигаться с rcspeet к блоку? б) Какова общая скорость стрелки и блока, когда это происходит? (c) Как далеко проникает стрела в блок?
Решение:
Глава 2 Одномерная кинематика Q.120GP
Сидя в квартире на втором этаже, физик замечает шар, движущийся вверх прямо за ее окном.Мяч виден в течение 0,25 с, когда он перемещается на расстояние 1,05 м от нижней части до верхней части окна. (а) Сколько времени нужно, прежде чем мяч снова появится? б) Какая наибольшая высота шара над верхним краем окна?
Решение:
Глава 2 Одномерная кинематика Q.121GP
Решение:
Глава 2 Одномерная кинематика Q.122PP
Бам! — Аполлон 15 приземляется на Луне
Первое слово, сказанное на поверхности Луны после высадки Аполлона 15 30 июля 1971 года, было «Бац!» Это была непроизвольная реакция Джеймса Ирвина на их довольно резкое приземление.«Мы действительно пострадали сильнее, чем любой другой рейс!» — говорит Ирвин. «И я, очевидно, был поражен, когда сказал:« Бац! »˝
Причина« твердой посадки »Аполлона-15, как позже охарактеризовал его пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше планировалось, когда посадочный модуль все еще находился на высоте 4,30 фута над поверхностью Луны и двигался вниз со скоростью 0,500 фут / с. С этого момента посадочный модуль спустился в условиях свободного падения Луны с ускорением 1,62 м / с2. В результате посадочная скорость Аполлона 15 была безусловно самой большой из всех миссий Аполлона.Для сравнения, посадочная скорость Нила Армстронга на Аполлоне-11 была самой низкой — 1,7 фута / с — он не выключал двигатель до тех пор, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлялись со скоростью от 3,0 до 3,5 футов / с.
Чтобы лучше понять спуск Аполлона 15, мы показываем его траекторию на заключительных этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) мы показываем различные графики зависимости скорости от времени.
Решение:
Глава 2 Одномерная кинематика Q.123PP
Бам! — Аполлон 15 приземляется на Луне
Первое слово, сказанное на поверхности Луны после приземления Аполлона 15 30 июля 1971 года, было «Бам!» Это была непроизвольная реакция Джеймса Ирвина на их довольно резкое приземление. «Мы действительно пострадали сильнее, чем любой другой рейс!» — говорит Ирвин. «И я был, очевидно, поражен, когда сказал:« Бац! »
Причина« твердого приземления »Аполлона-15, как позже охарактеризовал его пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше, чем планировалось, когда посадочного модуля было еще 4.30 футов над поверхностью Луны и движется вниз со скоростью 0,500 фут / с. С этого момента посадочный модуль спустился в условиях свободного падения Луны с ускорением 1,62 м / с2. В результате посадочная скорость Аполлона 15 была безусловно самой большой из всех миссий Аполлона. Для сравнения, посадочная скорость Нила Армстронга на Аполлоне-11 была самой низкой — 1,7 фута / с — он не выключал двигатель до тех пор, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлялись со скоростью от 3,0 до 3,5 футов / с.
Чтобы лучше понять спуск Аполлона 15, мы показываем его траекторию на заключительных этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) мы показываем различные графики зависимости скорости от времени.
Решение:
Глава 2 Одномерная кинематика Q.124PP
Бам! — Аполлон 15 приземляется на Луне
Первое слово, сказанное на поверхности Луны после высадки Аполлона 15 30 июля 1971 года, было «Бац!» Это была непроизвольная реакция Джеймса Ирвина на их довольно резкое приземление.«Мы действительно пострадали сильнее, чем любой другой рейс!» — говорит Ирвин. «И я, очевидно, был поражен, когда сказал:« Бац! »˝
Причина« твердой посадки »Аполлона-15, как позже охарактеризовал его пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше планировалось, когда посадочный модуль все еще находился на высоте 4,30 фута над поверхностью Луны и двигался вниз со скоростью 0,500 фут / с. С этого момента посадочный модуль спустился в условиях свободного падения Луны с ускорением 1,62 м / с2. В результате посадочная скорость Аполлона 15 была безусловно самой большой из всех миссий Аполлона.Для сравнения, посадочная скорость Нила Армстронга на Аполлоне-11 была самой низкой — 1,7 фута / с — он не выключал двигатель до тех пор, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлялись со скоростью от 3,0 до 3,5 футов / с.
Чтобы лучше понять спуск Аполлона 15, мы показываем его траекторию на заключительных этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) мы показываем различные графики зависимости скорости от времени.
РИСУНОК 2-37
Решение:
Поскольку скорость линейно увеличивается со временем, график B представляет график зависимости скорости от времени.
Глава 2 Одномерная кинематика Q.125PP
Бам! — Аполлон 15 приземляется на Луне
Первое слово, сказанное на поверхности Луны после приземления Аполлона 15 30 июля 1971 года, было «Бац!» Это была непроизвольная реакция Джеймса Ирвина на их довольно резкое приземление. «Мы действительно пострадали сильнее, чем любой другой рейс!» — говорит Ирвин. «И я был, очевидно, поражен, когда сказал:« Бац! »
Причина« твердого приземления »Аполлона-15, как позже охарактеризовал его пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше, чем планировалось, когда посадочного модуля было еще 4.30 футов над поверхностью Луны и движется вниз со скоростью 0,500 фут / с. С этого момента посадочный модуль спустился в условиях свободного падения Луны с ускорением 1,62 м / с2. В результате посадочная скорость Аполлона 15 была безусловно самой большой из всех миссий Аполлона. Для сравнения, посадочная скорость Нила Армстронга на Аполлоне-11 была самой низкой — 1,7 фута / с — он не выключал двигатель до тех пор, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлялись со скоростью от 3,0 до 3,5 футов / с.
Чтобы лучше понять спуск Аполлона 15, мы показываем его траекторию на заключительных этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) мы показываем различные графики зависимости скорости от времени.
РИСУНОК 2-37
Решение:
В этом случае ускорение направлено вверх. Это противоположно направлению его скорости. Следовательно, скорость спускаемого аппарата линейно уменьшается. Следовательно, график C описывает ситуацию, заданную в задаче
.
Глава 2 Одномерная кинематика Q.126IP
Ссылаясь на пример 2-9. Предположим, что спидер (красная машина) движется с постоянной скоростью 25 м / с, и что максимальное ускорение полицейской машины (синяя машина) составляет 3,8 м / с2. Если полицейская машина должна стартовать с места и догнать спидер за 15 с или меньше, какова максимальная дистанция старта, которую может преодолеть спидер? Измерьте время с момента запуска полицейской машины.
Решение:
Глава 2 Одномерная кинематика Q.127IP
Ссылаясь на Пример 2-9 Спидер проезжает мимо полицейской машины с постоянной скоростью 15 м / с.Полицейская машина сразу трогается с места и преследует спидер с постоянным ускорением. Какое ускорение должна иметь полицейская машина, если она должна догнать спидер за 7,0 с? Измерьте время с момента запуска полицейской машины.
Решение:
Глава 2 Одномерная кинематика Q.128IP
IP Ссылаясь на Пример 2-12 (a) В Примере 2-12 мешок с песком выпускается на высоте 20,0 м и достигает максимальной высоты 22 м. Если бы сумку выпустили в 30.0 м, при том, что все остальное остается прежним, будет ли его максимальная высота 32 м, больше 32 м или меньше 32 м? (b) Найдите скорость мешка непосредственно перед его приземлением, когда он выпущен с высоты 30,0 м.
Решение:
Глава 2 Одномерная кинематика Q.129IP
Ссылаясь на пример 2-12. Предположим, что воздушный шар опускается с постоянной скоростью 4,2 м / с, когда мешок с песком высвобождается на высоте 35 м.а) Как долго мешок находится в воздухе? (b) Какова скорость мешка, когда он находится на высоте 15 м над землей?
Решение:
Движение в двух измерениях — AP Physics 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Онлайн-математические заметки Пауля
Показать общее уведомление
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Пол
6 мая 2021 г.
Кажется, вы используете устройство с «узкой» шириной экрана (, то есть , вероятно, вы используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Добро пожаловать в мои онлайн-уроки и заметки по математике. Цель этого сайта — предоставить полный набор бесплатных онлайн (и загружаемых) заметок и / или руководств для классов, которые я преподаю в Университете Ламара.Я попытался написать заметки / учебные пособия таким образом, чтобы они были доступны для всех, кто хочет изучить предмет, независимо от того, посещаете ли вы мои классы или нет. Другими словами, они не предполагают, что у вас есть какие-либо предварительные знания, кроме стандартного набора обязательных материалов, необходимых для этого класса. Другими словами, предполагается, что вы знаете алгебру и триггер до чтения заметок по исчислению I, знаете исчисление I до чтения заметок по исчислению II, и т. Д. . Предположения о вашем прошлом, которые я сделал, приводятся с каждым описанием ниже.
Я хотел бы поблагодарить Шейна Ф., Фреда Дж., Майка К. и Дэвида А. за все опечатки, которые они нашли и прислали мне! Я пытался проверить эти страницы и отловить как можно больше опечаток, однако невозможно отловить их все, если вы также являетесь тем, кто написал материал. Фред, Майк и Дэвид поймали довольно много опечаток, которые я пропустил, и были достаточно любезны, чтобы отправить их мне. Еще раз спасибо, Фред, Майк и Дэвид!
Если вы один из моих нынешних студентов и ищете здесь домашние задания, у меня есть набор ссылок, которые приведут вас на нужные страницы, перечисленные здесь.
В настоящее время я получил онлайн-заметки / учебные пособия по моей алгебре (Math 1314), Calculus I (Math 2413), Calculus II (Math 2414), Calculus III (Math 3435) и Дифференциальные уравнения (Math 3301). У меня также есть пара обзоров / дополнений. Среди обзоров / дополнений, которые у меня есть, есть обзор алгебры / триггера для моих студентов, изучающих математику, учебник по комплексным числам, набор общих математических ошибок и несколько советов по изучению математики.
Я также сделал большинство страниц этого сайта доступными для загрузки.Эти загружаемые версии представлены в формате pdf. Каждая тема на этом сайте доступна для полной загрузки, и в случае очень больших документов я также разделил их на более мелкие части, которые в основном соответствуют каждой из отдельных тем. Чтобы получить загружаемую версию любой темы, перейдите к этой теме, а затем в меню Загрузить вам будет предложена возможность загрузить тему.
Вот полный список всех тем, которые в настоящее время доступны на этом сайте, а также краткие описания каждой из них.
Шпаргалки по алгебре — это столько общих фактов, свойств, формул и функций алгебры, которые я мог придумать. Также есть страница с распространенными алгебраическими ошибками. Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия — это уменьшенная версия, которая содержит точно такую же информацию, что и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне и две страницы печатаются на обратной стороне одного листа бумаги.Шпаргалки по триггерам
— Вот набор общих фактов, свойств и формул триггеров. Также включен единичный круг (полностью закрашенный). Доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия — это уменьшенная версия, которая содержит точно такую же информацию, что и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне и две страницы печатаются на обратной стороне одного листа бумаги.
Шпаргалки по исчислению — это серия шпаргалок по исчислению, охватывающая большую часть стандартного курса «Исчисление I» и несколько тем из курса «Исчисление II».Здесь есть четыре разных шпаргалки. Один содержит всю информацию, другой — только информацию о ограничениях, один — только информацию о производных, а последний — только информацию об интегралах. Каждая шпаргалка представлена в двух версиях. Один полноразмерный, а другой уменьшенный, с точно такой же информацией, что и полноразмерная версия, печатающая две страницы на лицевой и / или оборотной сторонах каждой страницы.
Общие производные и интегралы — это набор общих производных и интегралов, которые довольно часто используются в классе «Исчисление I» или «Исчисление II».Также включены напоминаний о нескольких методах интеграции. вот доступны две версии шпаргалки. Один полноразмерный и в настоящее время состоит из четырех страниц. Другая версия — это уменьшенная версия, которая содержит точно такую же информацию, что и полная версия, за исключением того, что она только что была уменьшена, поэтому две страницы печатаются на лицевой стороне и две страницы печатаются на обратной стороне одного листа бумаги.
Таблица преобразований Лапласа — вот список преобразований Лапласа для класса дифференциальных уравнений.В этой таблице приведены многие из часто используемых преобразований и формул Лапласа. В настоящее время он состоит из двух страниц, первая страница — это преобразования Лапласа, а вторая — некоторая информация / факты о некоторых записях.
Все классы, за исключением дифференциальных уравнений, содержат практические задачи (с решениями), которые вы можете использовать на практике, а также набор задач с заданиями (без решений / ответов), которые преподаватели могут использовать, если они того пожелают.
Алгебра (математика 1314) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:
- Предварительные сведения — свойства экспоненты, рациональные показатели, отрицательные показатели, радикалы, полиномы, факторинг, рациональные выражения, комплексные числа
- Решение уравнений и неравенств — линейные уравнения, квадратные уравнения, завершение квадрата, квадратичная формула, приложения линейных и квадратных уравнений, приводимые к квадратичной форме, уравнения с радикалами, линейные неравенства, полиномиальные и рациональные неравенства, уравнения абсолютных значений и неравенства.
- Графики и функции — Графические линии, окружности и кусочные функции, определение функций, обозначение функций, композиция функций, обратные функции.
- Общие графы — параболы, эллипсы, гиперболы, абсолютное значение, квадратный корень, постоянная функция, рациональные функции, сдвиги, отражения, симметрия.
- Полиномиальные функции — деление многочленов, нули / корни многочленов, поиск нулей многочленов, отображение многочленов, частичные дроби.
- Экспоненциальные и логарифмические функции — экспоненциальные функции, логарифмические функции, решение экспоненциальных функций, решение логарифмических функций, приложения.
- Системы уравнений — метод подстановки, метод исключения, расширенная матрица, нелинейные системы.
Примечания / учебник по алгебре предполагают, что вы имели некоторое представление об основах алгебры. В частности, предполагается, что разделы показателей и факторинга будут для вас в большей степени обзором.Также предполагается, что вы ознакомились с основами построения графиков уравнений. Построение графиков конкретных типов уравнений подробно рассматривается в примечаниях, однако предполагается, что вы понимаете основную систему координат и способы построения точек.
Calculus I (Math 2413) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:
- Обзор алгебры / триггера — триггерные функции и уравнения, экспоненциальные функции и уравнения, логарифмические функции и уравнения.
- Пределы — концепции, определение, вычисления, односторонние ограничения, непрерывность, ограничения, связанные с бесконечностью, Правило L’Hospitals
- Производные — определение, интерпретации, формулы производных, правило степени, правило произведения, правило факторного, цепное правило, производные высшего порядка, неявное дифференцирование, логарифмическое дифференцирование, производные триггерных функций, экспоненциальные функции, логарифмические функции, обратные триггерные функции и гиперболические функции Функции.
- Приложения производных финансовых инструментов — связанные ставки, критические точки, минимальные и максимальные значения, функции увеличения / уменьшения, точки перегиба, вогнутость, оптимизация
- Интегрирование — определение, неопределенные интегралы, определенные интегралы, правило подстановки, вычисление определенных интегралов, основная теорема исчисления
- Приложения интегралов — среднее значение функции, площадь между кривыми, тела вращения, работа.
Заметки / учебник по исчислению I предполагают, что у вас есть практические знания алгебры и триггера. Есть некоторый обзор нескольких тем по алгебре и триггерам, но по большей части предполагается, что у вас есть приличный опыт в алгебре и триггерах. Эти заметки не предполагают никаких предварительных знаний о математическом анализе.
Calculus II (Math 2414) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:
- Методы интеграции — интеграция по частям, интегралы с участием триггера
Функции, подстановки триггеров, интегрирование с использованием дробных дробей, интегралы
С участием корней, интегралов с участием квадратичных структур, стратегии интеграции, несобственные
Интегралы, сравнительный тест для несобственных интегралов и аппроксимация определенных
Интегралы. - Применение интегралов — длина дуги, площадь поверхности, центр масс / центроид, гидростатическое давление и сила, вероятность.
- Параметрические уравнения и полярные координаты — параметрические уравнения и кривые, расчет с параметрическими уравнениями (касательные, площади, длина дуги и площадь поверхности), полярные координаты, расчет с полярными координатами (касательные, площади, длина дуги и площадь поверхности).
- Последовательности и серии — Последовательности, серии, сходимость / расхождение серий, абсолютная серия, интегральный тест, сравнительный тест, предельный сравнительный тест, чередующийся последовательный тест, коэффициент соотношения, корневой тест, оценка значения серии, степенная серия, серия Тейлора , Биномиальный ряд
- Векторы — основы, величина, единичный вектор, арифметика, точечное произведение, крест
Продукт, Проекция - Трехмерная система координат — уравнения линий, уравнения плоскостей, квадратичные поверхности, функции нескольких переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, векторы нормалей, бинормальные векторы, кривизна, цилиндрические координаты, сферические Координаты
Заметки / учебник по исчислению II предполагают, что у вас есть рабочие знания по исчислению I, включая ограничения, производные и интеграцию (вплоть до базовой замены).Также предполагается, что вы достаточно хорошо знакомы с Trig. Некоторые темы сильно зависят от триггеров и знания триггерных функций.
Calculus III (Math 3435) [Примечания] [Практические задачи] [Проблемы с назначением] — В этот набор примечаний / учебного пособия включены следующие темы:
- Трехмерная система координат — уравнения линий, уравнения плоскостей, квадратичные поверхности, функции нескольких переменных, векторные функции, пределы, производные и интегралы векторных функций, касательные векторы, векторы нормалей, бинормальные векторы, кривизна, цилиндрические координаты, Сферические координаты
- Частные производные инструменты — лимиты, частичные производные инструменты, частичные производные высшего порядка
Производные, дифференциалы, цепное правило, производные по направлениям, градиент. - Приложения частных производных — касательная плоскость, нормальная линия, относительные экстремумы, абсолютные экстремумы, оптимизация, множители Лагранжа.
- Кратные интегралы — повторяющиеся интегралы, двойные интегралы, двойные интегралы в полярных координатах, тройные интегралы, тройные интегралы в цилиндрических координатах, тройные интегралы в сферических координатах, изменение переменных, площадь поверхности.
- Линейные интегралы — векторные поля, линейные интегралы относительно длины дуги, линейные интегралы относительно x и y , линейные интегралы векторных полей, фундаментальная теорема линейных интегралов, консервативные векторные поля, потенциальные функции, теорема Грина, Curl, Дивергенция.
- Поверхностные интегралы — параметрические поверхности, поверхностные интегралы, поверхностные интегралы векторных полей, теорема Стокса, теорема о расходимости.
Заметки / учебники по Calculus III предполагают, что у вас есть рабочие знания Calculus I, включая ограничения, производные и интеграцию. Также предполагается, что читатель хорошо знаком с несколькими темами Calculus II, включая некоторые методы интеграции, параметрические уравнения, векторы и знание трехмерного пространства.
Дифференциальные уравнения (Math 3301) [Примечания] — В этот набор примечаний / учебного пособия включены следующие темы:
- Дифференциальные уравнения первого порядка — линейные уравнения, разделимые уравнения, точные уравнения, равновесные решения, задачи моделирования.
- Дифференциальные уравнения второго порядка — однородные и неоднородные дифференциальные уравнения второго порядка, основной набор решений, неопределенные коэффициенты, изменение параметров, механические колебания
- Преобразования Лапласа — определение, обратные преобразования, ступенчатые функции, функции Хевисайда, дельта-функция Дирака, решение IVP, неоднородная IVP, IVP с непостоянным коэффициентом, интеграл свертки.
- Системы дифференциальных уравнений — форма матрицы, собственные значения / собственные векторы, фазовая плоскость, неоднородные системы, преобразования Лапласа.
- — серийные решения, дифференциальные уравнения Эйлера.
- Дифференциальные уравнения высшего порядка — n th дифференциальные уравнения, неопределенные коэффициенты, изменение параметров, системы дифференциальных уравнений 3 x 3.
- Краевые задачи и ряды Фурье — Краевые задачи, собственные значения и собственные функции, ортогональные функции, ряды синуса Фурье, ряды косинусов Фурье, ряды Фурье.
- Уравнения в частных производных — уравнение теплопроводности, волновое уравнение, уравнение Лапласа, разделение переменных.
Решения серии
Эти примечания не предполагают предварительного знания дифференциальных уравнений. Однако требуется хорошее владение математическим анализом. Сюда входит практическое знание дифференциации и интеграции.
Algebra / Trig Review — это обзор алгебры и Trig Review
это было первоначально написано для моих студентов Calculus I. Это все еще в основном
по направлению к студентам, изучающим математику, с случайными комментариями о том, как
будет использоваться в классе Calculus.Однако любой, кому нужен обзор некоторых
основной алгебры, триггеры, экспоненциальные функции и логарифмы должны найти
информация об использовании.
Не все темы, затронутые в классе алгебры или триггера, охвачены в этом
рассмотрение. В основном я затрагивал темы, которые имеют особое значение для студентов.
в классе исчисления. Я включил пару тем, которые не так важны
в класс по математике, но у студентов, кажется, иногда возникают проблемы.
Если позволит время, я буду добавлять и другие разделы.
Обзор представляет собой набор задач с первым решением, содержащий подробную информацию о том, как работать с этим типом проблемы. Более поздние решения обычно не столь подробны, но могут содержать дополнительную / новую информацию по мере необходимости.
Учебник по комплексным числам — это краткое введение в некоторые из основных идей, связанных с комплексными числами. Обсуждаемые темы — это краткий обзор арифметики с комплексными числами, комплексного сопряжения, модуля, полярной и экспоненциальной формы, а также вычислительных мощностей и корней комплексных чисел.
Обратите внимание, что этот учебник предполагает, что вы хотя бы видели некоторые комплексные числа перед чтением. Цель этого документа — выйти за рамки того, что большинство людей видит, когда впервые знакомится с комплексными числами, скажем, на уроках алгебры в колледже. Кроме того, этот документ никоим образом не предназначен для того, чтобы дать полное представление о комплексных числах, и я не охватываю все задействованные концепции (это целый класс сам по себе).
Распространенные математические ошибки — как и в случае с алгеброй / триггером, просмотрите это.
изначально был написан для моего класса по исчислению I.Однако только один из пяти
Разделы, которые я привел здесь, напрямую относятся к теме исчисления. В
другие четыре раздела относятся к более общим ошибкам или охватывают ошибки алгебры и триггера.
В первых четырех разделах есть пара примеров исчисления, но в
Во всех этих случаях я также пытался привести примеры, не относящиеся к исчислению.
Эта часть сайта должна быть интересна всем, кто ищет общие
математические ошибки. Если вы не изучаете математику или не изучали математику, вы
следует просто игнорировать последний раздел.
Как изучать математику — это небольшой раздел с некоторыми советами
о том, как лучше всего изучать математику.
Таблицы формул по физике для 9-го класса
Формулы физики — одна из самых сложных вещей для запоминания при изучении книги или при перелистывании уроков один за другим, чтобы найти, какая формула относится к какой главе. Приближаются экзамены 9-го класса CBSE, и студенты уже начали подготовку к ключевому экзамену в своей жизни. Формулы по физике — это общие формулы, которые не только важны для подготовки к 9-му классу, но и образуют основу для концепций физики более высокого уровня.Формулы физики также играют важную роль в таких областях, как инженерия, медицина, информатика, механика, электричество, программное обеспечение, оборудование и т. Д.
Таблицы формул по физике для 9-го класса — мудрые формулы
Запоминание всех формул физики может быть сложной задачей , но с помощью вручную подобранных таблиц формул по физике для класса 9 от Gradeup вы можете легко запомнить все формулы из всех глав, которые помогут вам сдать экзамен по физике CBSE Class 9 2021.
Формулы 9-го класса CBSE по физике включают формулы, относящиеся к Движение, сила и законы движения, гравитация, звук.Эти формулы по физике для 9-го класса будут чрезвычайно полезны для учащихся, чтобы они могли быстрее и точнее решать вопросы.
Пожалуйста, перейдите по следующей ссылке, чтобы загрузить PDF-файл с таблицами физических формул для 9-го класса:
Загрузите таблицы с физическими формулами для 9-го класса здесь
Преимущества таблиц физических формул для 9-го класса:
Physics Formula Таблицы могут помочь студентам в мгновение ока решить сложную задачу.Запоминание каждой формулы из каждой главы может считаться большой проблемой для студентов, которым просто необходимы некоторые стратегии для легкого запоминания формул. На этом этапе Gradeup предлагает Таблицы формул по физике для класса 9, чтобы учащиеся могли легко загрузить PDF-файл со всеми формулами с веб-сайта или приложения без каких-либо проблем.

 д.
д. Такое движение называется двумерным
Такое движение называется двумерным


 Изменятся, соответственно, и радиус-вектора, но соотношение между ними останется в силе:
Изменятся, соответственно, и радиус-вектора, но соотношение между ними останется в силе:
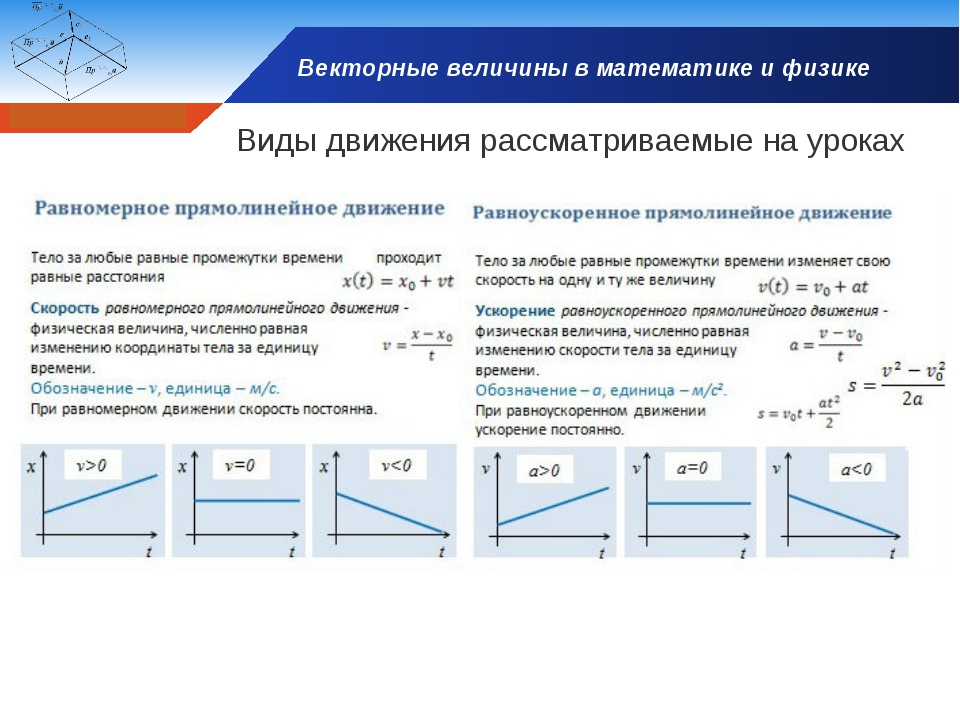 Как гласит легенда, Галилей сбрасывал с Пизанской башни тела различной массы, а его ассистент фиксировал время их падения. В этоми знаменитом эксперименте, выяснилось, что тела различной массы падают с одинаковой скоростью.
Как гласит легенда, Галилей сбрасывал с Пизанской башни тела различной массы, а его ассистент фиксировал время их падения. В этоми знаменитом эксперименте, выяснилось, что тела различной массы падают с одинаковой скоростью. Оно, конечно, гораздо сложнее чем прямолинейное, которым мы занимались все это время. Поэтому Юлик Левкович правильно предложила попробовать рассмотреть движение по хордам окружности. При этом на каждой хорде частица движется с постоянной скоростью и по величине и по напрвлению. Вектор скорости лежит на хорде.
Оно, конечно, гораздо сложнее чем прямолинейное, которым мы занимались все это время. Поэтому Юлик Левкович правильно предложила попробовать рассмотреть движение по хордам окружности. При этом на каждой хорде частица движется с постоянной скоростью и по величине и по напрвлению. Вектор скорости лежит на хорде.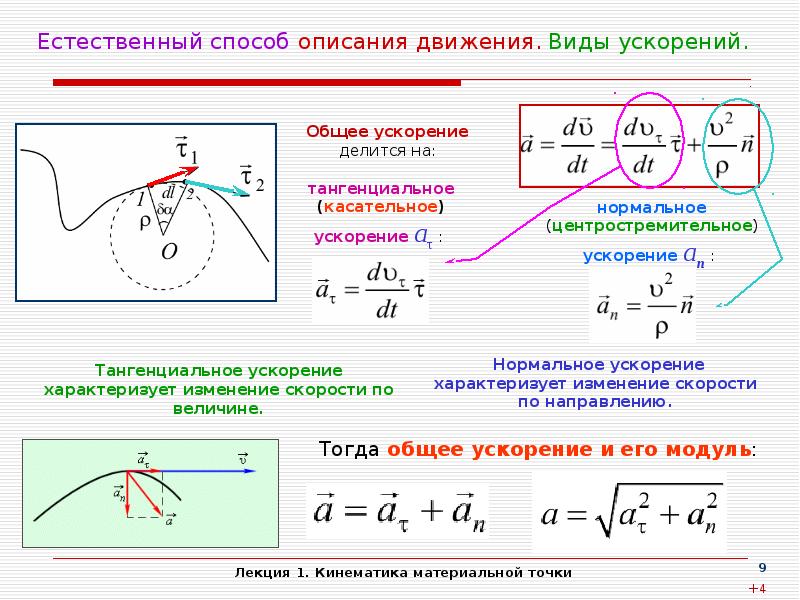
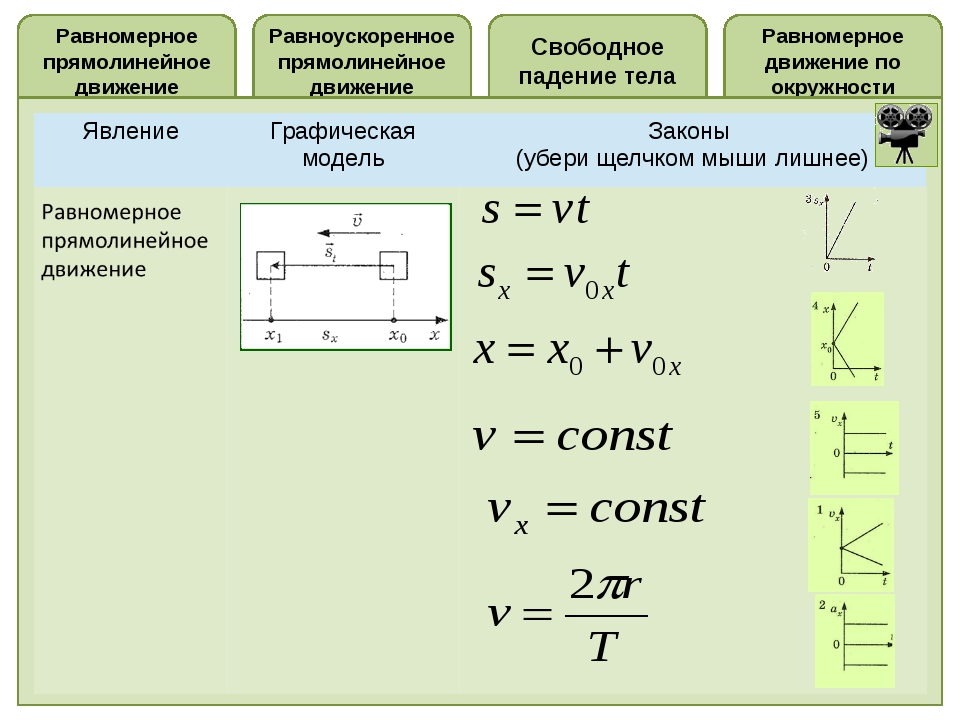 Приглашаем присоединиться к мероприятиям, посвященным празднованию Дня Сибстрина!
Приглашаем присоединиться к мероприятиям, посвященным празднованию Дня Сибстрина!

 Этот год не стал исключением. Наши студенты стали участниками IX Международной студенческой научной конференции «Традиции, современные проблемы и перспективы развития строительства», которая прошла 13-14 мая 2021 года.
Этот год не стал исключением. Наши студенты стали участниками IX Международной студенческой научной конференции «Традиции, современные проблемы и перспективы развития строительства», которая прошла 13-14 мая 2021 года.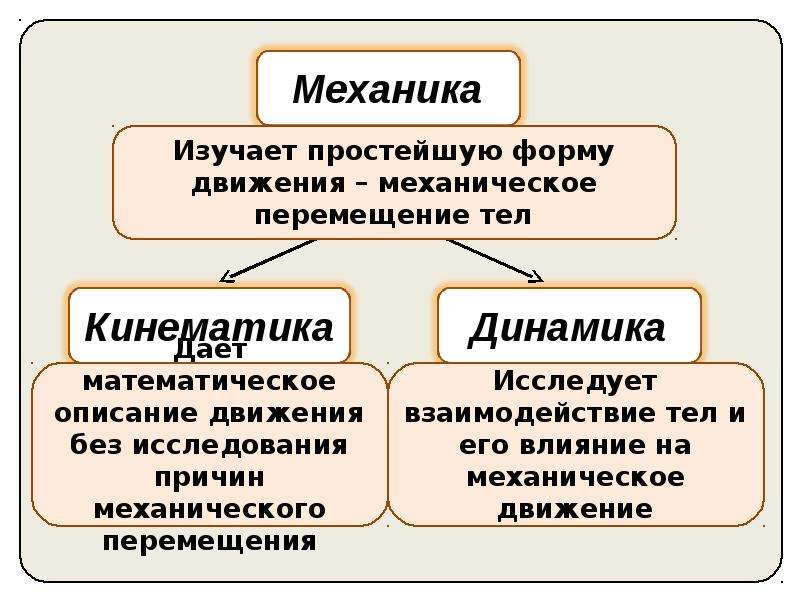 ..
..