Содержание
Конспект урока по геометрии 8 класс «Трапеция»
Конспект урока по геометрии 8 класс по теме «Трапеция». К учебнику «Геометрия 7-9» для общеобразовательных организаций/ Авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. Москва «Просвещение» 2015г.
Просмотр содержимого документа
«Подготовка к изучению нового материала»
Просмотр содержимого документа
«Трапеция_урок1»
Просмотр содержимого презентации
«Трапеция_урок1»
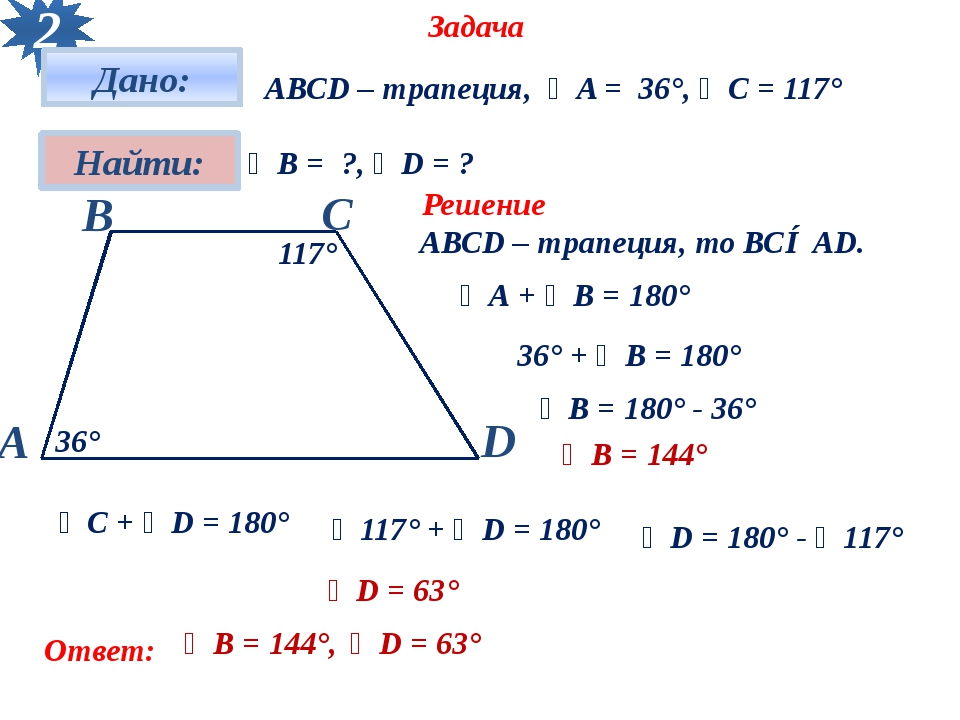
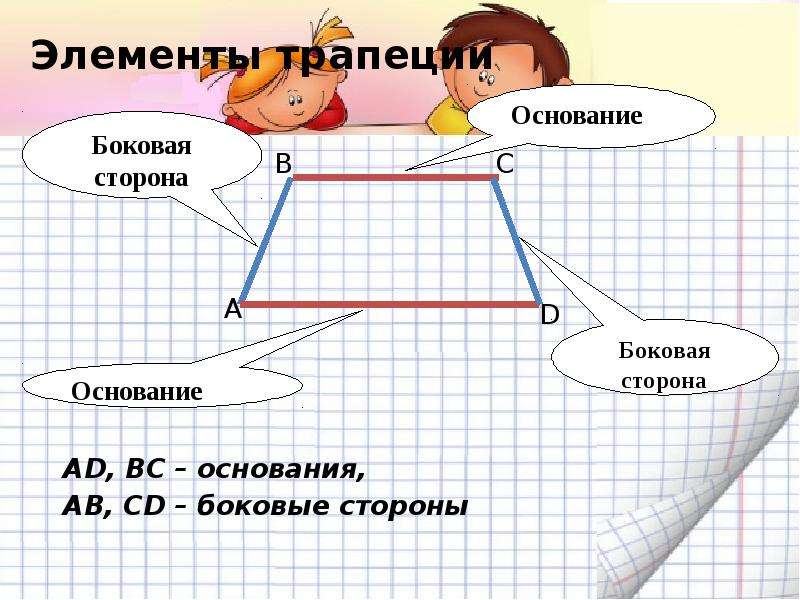
Трапеция
боковая сторона
боковая сторона
Четырехугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией.
Параллельные стороны называются
основаниями.
Не параллельные стороны называются
боковыми сторонами .
основание
основание
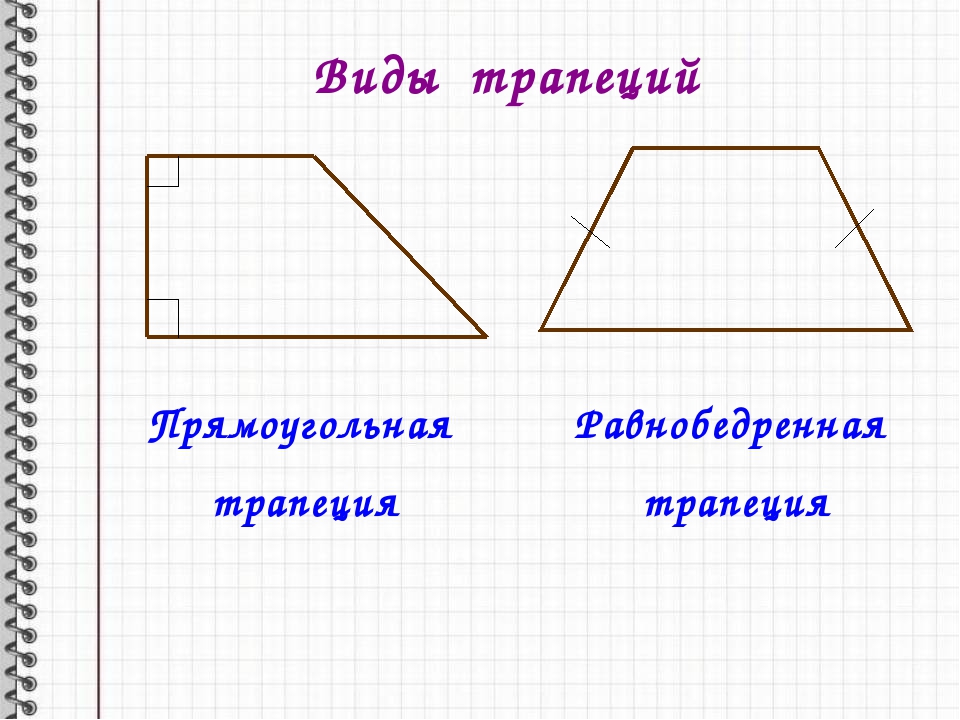
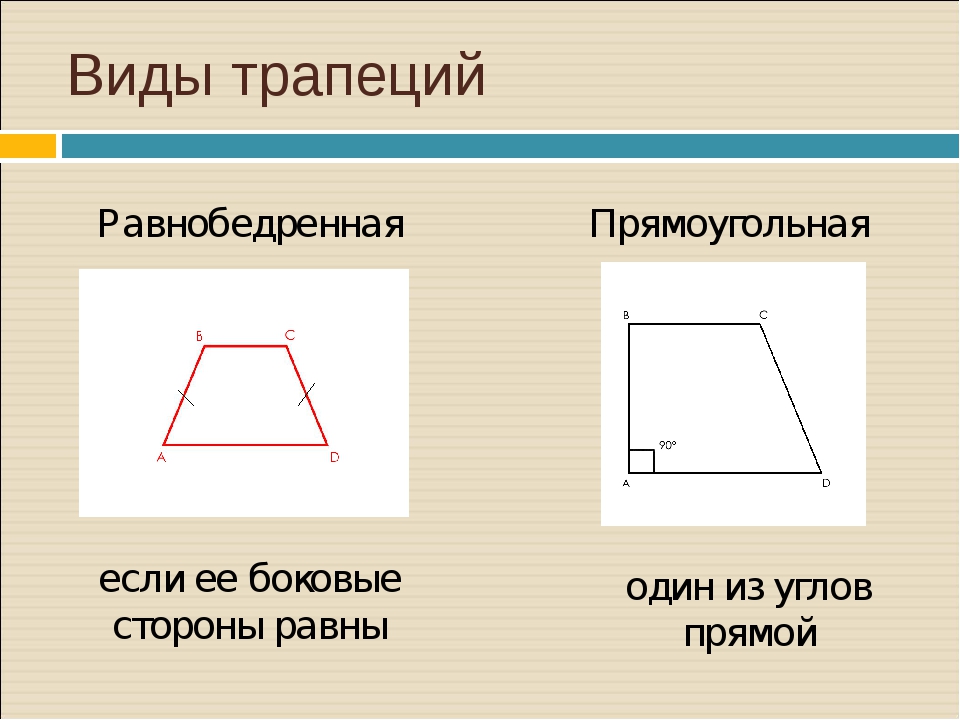
Виды трапеций
Трапеция, у которой боковые стороны равны, называется
равнобедренной.
Трапеция, один из углов которой прямой, называется
прямоугольной.
А
D
H
А
Какие четырехугольники на рисунке являются трапециями? Назовите их основания и боковые стороны.
1
В
2
Р
С
0
110
T
S
0
70
М
О
R
N
С
3
В
Q
К
Средняя линия трапеции
В
С
MN – средняя линия трапеции
M
N
D
А
Отрезок, соединяющий середины боковых сторон трапеции, называется
средней линией трапецией
MN= (BC+AD): 2 – свойство средней линии трапеции
Свойства равнобедренной трапеции
1
У равнобедренной трапеции углы при основании равны.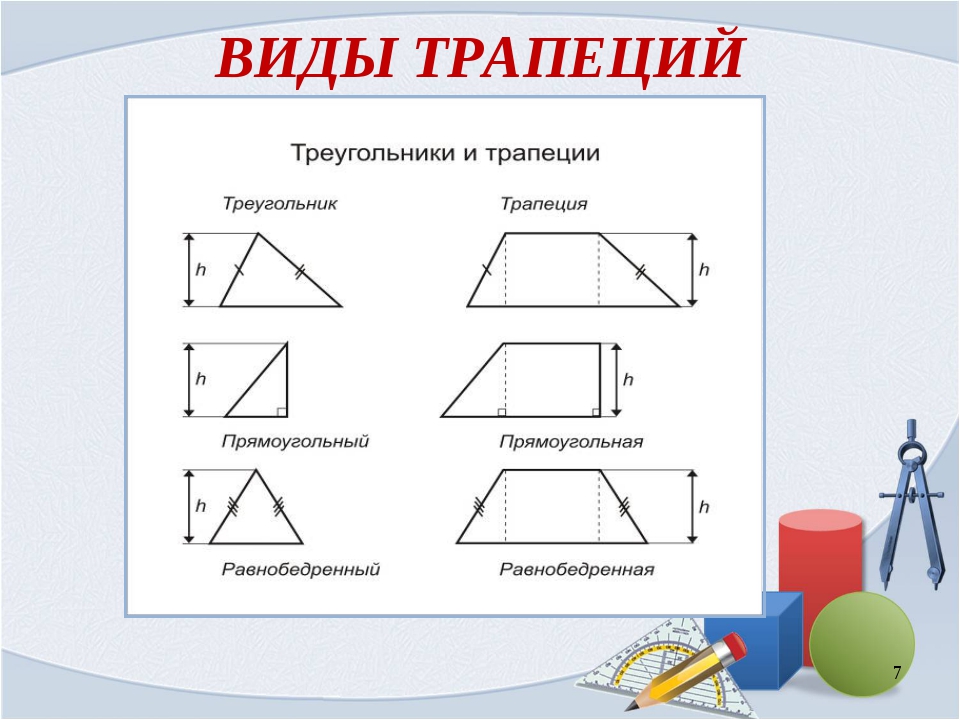
В
С
2
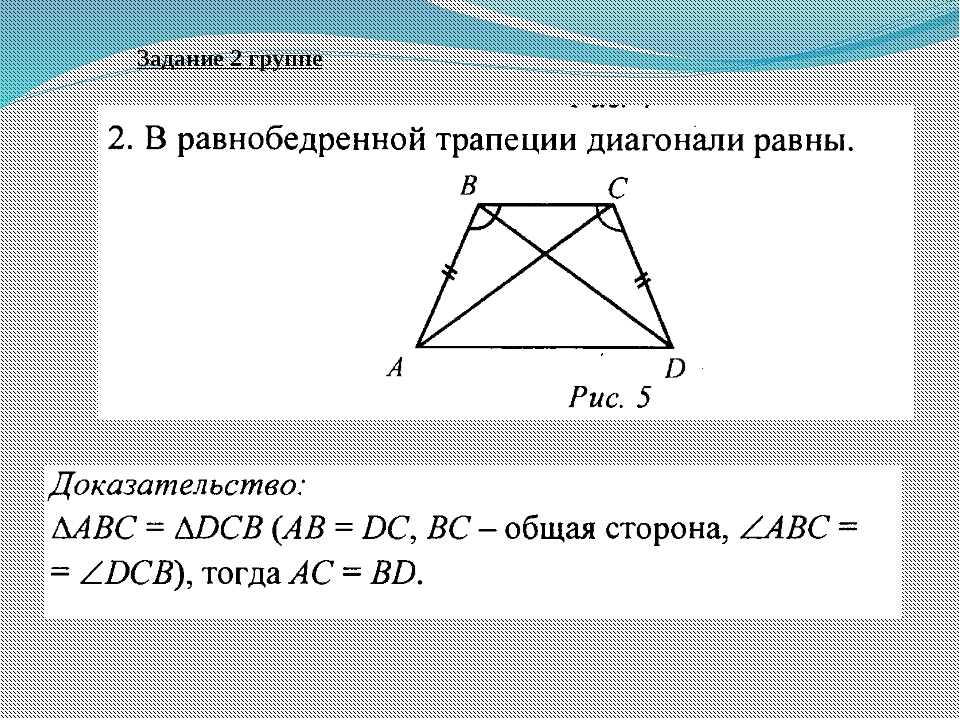
В равнобедренной трапеции диагонали равны.
АС=ВD
D
А
Признаки равнобедренной трапеции
Если углы при основании трапеции равны, то она равнобедренная.
1
Если в трапеции диагонали равны, то она равнобедренная.
2
Урок 23. площадь криволинейной трапеции. интеграл и его свойства — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №23.Площадь криволинейной трапеции. Интеграл и его свойства.
Перечень вопросов, рассматриваемых в теме
1) Нахождение определенного интеграла
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
Формула Ньютона – Лейбница
Основная литература:
Колягин Ю.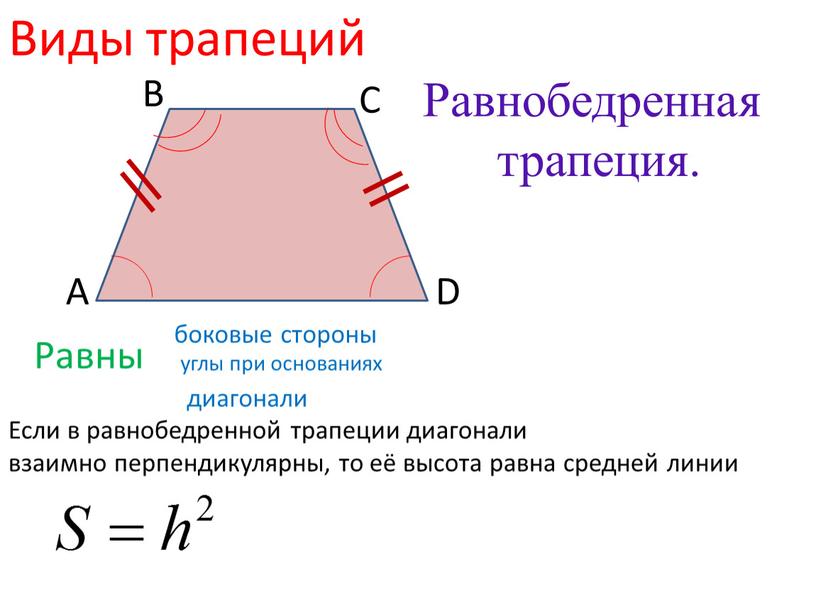 М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).
Примеры и разбор решения заданий тренировочного модуля
№1.Найти площадь криволинейной трапеции, изображенной на рисунке
Решение
Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.
Ответ:
№2. Вычислить определенный интеграл:
Решение: Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) — F(а), это и будет ответ.
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).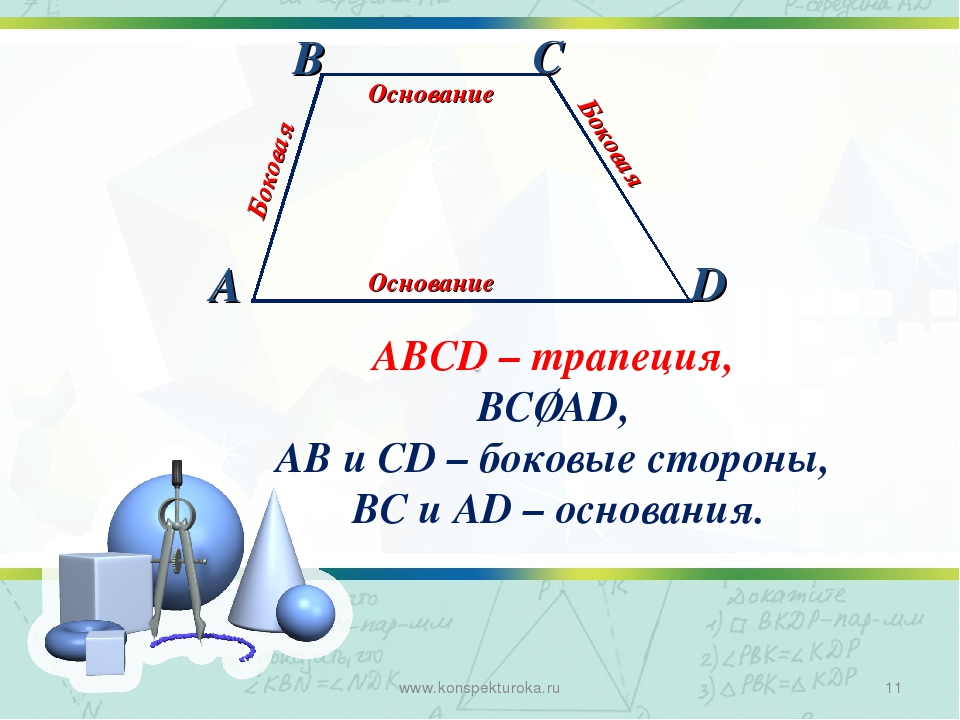
Рассчитываем разность F(b) — F(а), это и будет ответ.
Конспект урока «Трапеция и средняя линия трапеции» по математике
Тема: Трапеция и средняя линия трапеции
Цели:
а) повторить и закрепить знания по теме, формирование навыков решения задач на нахождение элементов трапеции, создание условий контроля (самоконтроля) знаний и умений;
б) формирование и развитие навыков диалогического обучение, взаимообучение
развитие речи, внимания, памяти;
в) формирование интереса к математике, содействие воспитанию активности, организованности, умению участвовать в диалоге с товарищами и учителями, развитие внимания и умения анализировать полученное решение.
1. Организационный момент
Ученикам необходимо прослушать следующие высказывания и выяснить, о какой фигуре пойдет речь на уроке, свой ответ надо обосновать:
— Это фигура четырехугольник;
— сумма ее внутренних углов равна 360 °;
— Две противолежащие стороны параллельны?
— данная фигура хорошо разбивается на параллелограмм и треугольник.
После обсуждения учитель прикрепляет на доску магнитом «королеву урока» — трапецию.
2.Работа в парах по повторению теории
Ученики в течение 5–7 минут отвечают в парах на вопросы, которые появляются на экране. Хорошо, если пары учащихся будут разноуровневыми, тогда один из учеников является консультантом и помогает вспомнить нужный материал товарищу в случае затруднения.
Вопросы
— Трапеция – это …
— Какие стороны трапеции называются : а) основаниями? б) боковыми сторонами?
— Высота треугольника – это ….
— Диагональю трапеции называют …
— Какая трапеция называется
а) равнобедренной б) прямоугольной
— Что называется средней линией трапеции?
— Чему равна средняя линия трапеции?
3. Математический диктант:
Четырехугольник, у которого две стороны равны –это трапеция?
Могут ли углы, прилежащие к основанию трапеции, быть один острым, а другой тупым?
Верно ли, что если два угла трапеции равны, то она равнобедренная?
Может ли у трапеции быть три прямых угла?
Верно ли, что если два угла при основании трапеции равны, то она равнобедренная?
Верно ли, что если диагонали трапеции равны, то она равнобедренная?
Верно ли что, сумма углов, прилежащих к одной стороне трапеции равна 180 градусов
Взаимноконтроль: пары друг-друга проверяют
4. Составление постера:
Составление постера:
1 группа
На координатной плоскости по данным точкам построить трапецию: А(-5;-1), В(-2;3), С(2;3), Д(5;-1). Определить вид трапеции.
2 группа
На координатной плоскости по данным точкам построить трапецию: А(-3;-2), В(-3;2), С(1;2), Д(4;-2). Определить вид трапеции.
5.Работа с учебником.
№ 93 и 99
6. Дифференцированные задания: (по парам выполняют)
1 вариант
Средняя линия трапеции равна 30 см, а меньшее основание равно 20 см. Найдите большее основание.
Основания трапеции относятся как 2 : 3, а средняя линия равна 5 м. Найдите основания.
Определите углы трапеции, если отношение углов равно 2:4:5:7.
Найдите периметр равнобедренной трапеции, если средняя линия равна 5 см, а бокавая сторона – 3 см.
2 вариант
Найдите среднюю линию трапеции, если сумма двух оснований равна 24 см.
Основания трапеции относятся как 1 :4, а средняя линия равна 5 м.
 Найдите основания.
Найдите основания.Определите углы трапеции, если отношение углов равно 3:2:6:7.
Найдите периметр и основания трапеции, если сумма двух боковых сторон равна 5 см, средняя линия – 2 см.
Оценочный лист
№ | ФИО учащихся | Вопросы | Математический диктант | Карточка | Итоговая оценка |
1 |
7. Итог урока. Оценивание. Рефлексия.
8. Домашнее задание . №101,102
Конспект занятия по математике в старшей группе на тему Знакомство с трапецией.
Государственное бюджетное образовательное учреждение
СОШ №717 дошкольное отделение.
Конспект занятия по математике в старшей группе на тему «Знакомство с трапецией».
Педагог: Беспалова Е.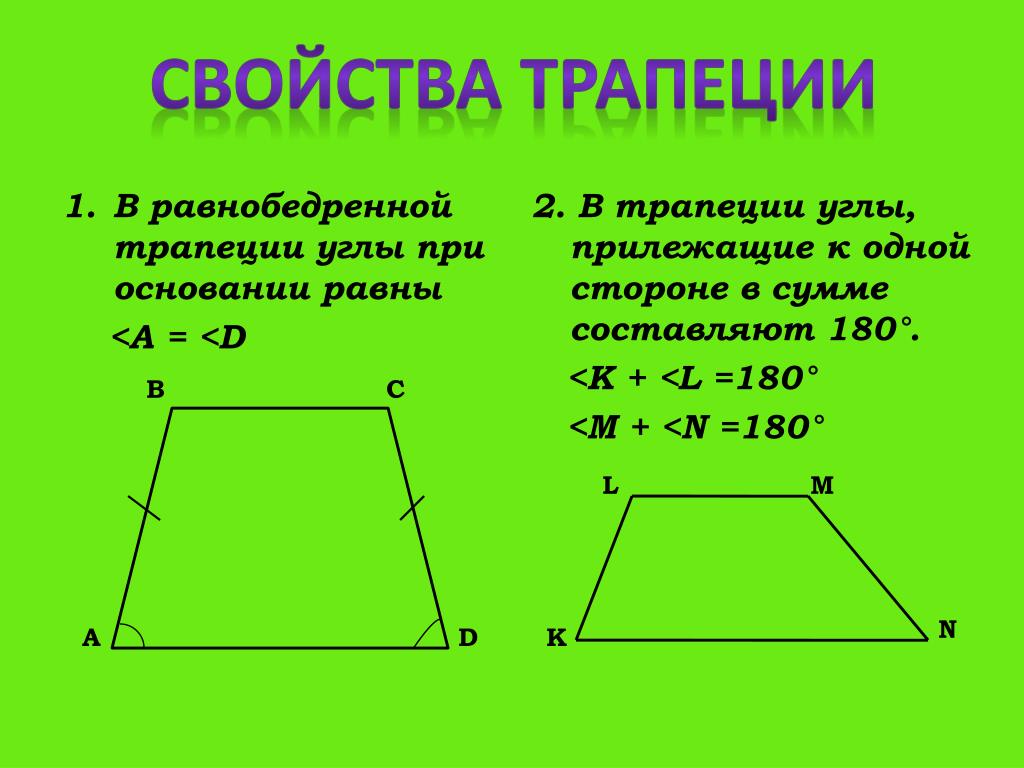 Ю.
Ю.
Чорноус Е. Н.
Москва – 2015г.
Воспитатель — Начнём наше занятие с повторения счёта. Воспитатель указывает на цифру, а дети повторяют хором (счёт от 1 до 8 и обратный счёт).
Воспитатель – А сейчас называет цифру, на которую я покажу тот, чьё имя я назову (цифры называются в разнобой).
Воспитатель демонстрирует коробку, с объёмными геометрическими фигурами.
Воспитатель – Посмотрите, что у меня лежит в коробке?
Ответы детей (в коробке лежат геометрические фигуры).
Воспитатель– Объёмные фигуры или плоские?
Ответы детей (объёмные геометрические фигуры).
Затем воспитатель показывает плоский конструктор.
Воспитатель – А эти фигуры плоские или объёмные?
Ответы детей (плоские геометрические фигуры).
Воспитатель предлагает детям дать название геометрическим фигурам в сравнении, для этого он демонстрирует сразу две фигуры: плоскую и объёмную.
1.Квадрат и куб.
2.Треугольник и треугольная призма.
3..Круг и шар.
4.Прямоугольник и параллелепипед.
Если у детей возникают затруднения, то воспитатель совместно с детьми сравнивает фигуры и находит отличия.
Воспитатель – Ребята вы, наверное, устали, давайте проведем физкультурную минутку.
Раз, два, три. Четыре, пять (шагают на месте)
Застилаю я кровать (имитируют движения).
Чищу зубы, чищу уши, пять минут стою под душем (имитируют движения)
Раз, два, три, четыре, пять (шагают на месте).
Рано я люблю вставать (шагают на месте).
Воспитатель надевает колпак, и « превращается в волшебника».
Воспитатель – Вы знаете кто я?
Дети– Волшебник.
Воспитатель– правильно, волшебник. А что умеют делать волшебники?
Дети – Всякие чудеса.
Воспитатель — Я предлагаю вам стать моими помощниками и превратить вот эту фигуру (демонстрирует квадрат) в прямоугольник, но сначала скажите, как она называется?
Ответы детей – квадрат.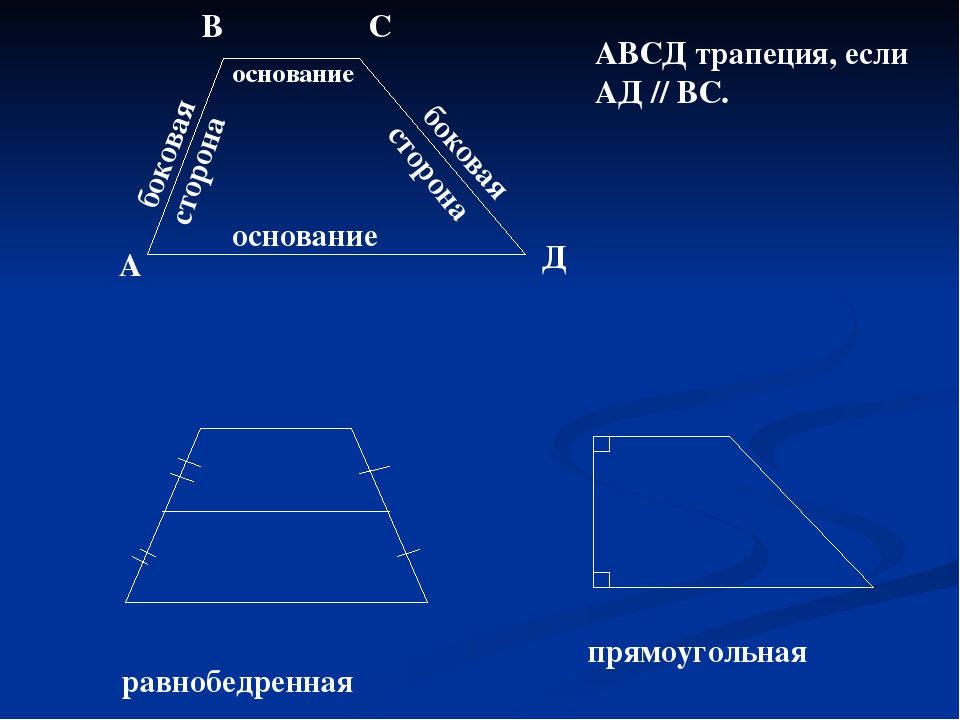
Воспитатель – правильно, квадрат. Подумайте, как это можно сделать?
Ответы детей (нужно сложить квадрат пополам, совместив две стороны квадрата).
Воспитатель – Превратите квадрат в прямоугольник. Дети выполняют задание.
Воспитатель— А теперь превратите прямоугольник в квадрат поменьше.
Дети складывают большую сторону пополам и получают маленький квадрат.
Воспитатель – У меня есть ещё задание для вас. Возьмите другой квадрат со стола, и превратите квадрат в треугольник.
Дети складывают квадрат по диагонали, если задание у некоторых вызывает затруднение, то воспитатель «волшебник» помогает им.
Воспитатель– Какие вы молодцы, очень талантливые волшебники, справились со всеми заданиями. Но у меня есть ещё одна фигура (показывает детям трапецию). Кто знает, как она называется?
Ответы детей – Трапеция (если дети не знают название фигуры, то воспитатель называет её сам).
Воспитатель – Правильно, эта фигура называется трапеция. Давайте все вместе скажем трапеция.
Давайте все вместе скажем трапеция.
(дети повторяют слово трапеция). Воспитатель вывешивает трапецию на доску (закрепляет фигуру при помощи магнита).
Воспитатель– А сейчас самое сложное задание. Нужно этот треугольник (воспитатель держит его в руках) превратить в трапецию. Кто хочет попробовать? Воспитатель предлагает одному из желающих выйти и превратить треугольник в трапецию.
Ребёнок загибает угол треугольника так, чтобы сторона была параллельна стороне треугольника (получается трапеция).
Воспитатель – Возьмите в руки треугольник и превратите его в трапецию, как это сделал Миша (дети самостоятельно выполняют задания, если задание вызывают у некоторых затруднения, то воспитатель помогает им).
Воспитатель – Что вы сегодня делали на занятии?
Ответы детей – Называли геометрические фигуры (объёмные и плоские), считали от одного до восьми и обратно, так же просто называли цифры; проводили физкультурную минутку; стали волшебниками и превращали квадрат в разные фигуры.
Воспитатель – С какой фигурой вы познакомились сегодня на занятии?
Ответы детей — Мы познакомились с трапецией.
Воспитатель – На этом наше занятие закончилось.
Занятие по математике (ФЭМП) в старшей группе.
Тема: «Знакомство с трапецией».
Цель: Закрепить знания детей об объёмных и плоских геометрических фигурах, познакомить с трапецией.
Задачи:
1. Продолжать учить считать в пределах восьми (от 1-8, обратный счёт, счёт в разнобой). Закрепить знания об объёмных и плоских геометрических фигурах. Познакомить с трапецией.
2.Развивать интерес к математике, умение сравнивать геометрические фигуры и делать выводы.
3.Воспитывать усидчивость, самостоятельность.
Материалы.
1.Набор объёмных и плоских геометрических фигур.
2.Цифры от 1 до 8(на магнитах), магнитная доска.
3.Колпачёк волшебника (для игрового момента).
4.Два квадрата размером 15×15 сантиметров на каждого ребёнка, и квадрат размером 20х20 сантиметров. Бумажный треугольник, трапеция.
Бумажный треугольник, трапеция.
5.Магнит.
Ход занятия:
1.Повторение счёта в пределах 8 (от 1-8 и обратно, и в разнобой).
2.Повторение названий геометрических фигур (объёмных и плоских).
3.Физкультурная минутка.
4.Игровой момент (появление волшебника), « превращение квадрата в другие фигуры».
5.Знакомство с трапецией.
Тема: «Трапеция» Учитель: Синиченкова Галина Алексеевна
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этап урока Деятельность учителя Деятельность ученика 1 2 4 5 Организационный момент Актуализация знаний. Целеполагание и мотивация Изучение нового материала. Закрепление изученного материала. Решение задач.
Подробнее
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Предмет: геометрия 9 Б 9 Д 9 Е Номер урока в КТП: 56 Преподаватель: УМК, учебник: Геометрия: Учебник для 7-9 классов общеобразовательных учреждений /А. В. Погорелов. М.: Просвещение,
В. Погорелов. М.: Просвещение,
Подробнее
Урок по теме «Треугольник». 7-й класс
Урок по теме «Треугольник». 7-й класс Николаева Наталия Геннадьевна Цели урока: Образовательные: o ввести определение треугольника и его элементов, периметра треугольника, понятие равных треугольников.
Подробнее
Подробный конспект урока.
Подробный конспект урока. Тема урока Предмет Класс Автор урока (ФИО, должность) Образовательное учреждение Город/поселение Тип урока Цели урока Организационная информация Площадь параллелограмма геометрия
Подробнее
Повышение качества знаний.
Повышение качества знаний. Открытый урок по геометрии в 8 классе Тема урока: Прямоугольник. Ромб. Квадрат. Автор: Напцок Сулиет Чемальевна, учитель математики, МБОУ СШ 5, п.яблоновский Цель: сформировать
Подробнее
СУММА УГЛОВ ТРЕУГОЛЬНИКА
ТЕМА УРОКА: СУММА УГЛОВ ТРЕУГОЛЬНИКА ТИП УРОКА: УРОК ФОРМИРОВАНИЯ НОВЫХ ЗНАНИЙ Данилова Светлана Леонидовна учитель математики МБОУ Лицея 1 г. Сургут ЦЕЛЕВАЯ НАПРАВЛЕННОСТЬ УРОКА Данный урок является первым
Сургут ЦЕЛЕВАЯ НАПРАВЛЕННОСТЬ УРОКА Данный урок является первым
Подробнее
Решение задач с помощью двумерных диаграмм
Муниципальное бюджетное общеобразовательное учреждение «Основная общеобразовательная школа 3» Киселёвского городского округа Решение задач с помощью двумерных диаграмм Занятие элективного курса по математике
Подробнее
D
Открытый урок по геометрии в 0 классе Тема: «Расстояния между прямыми и плоскостями в прямоугольном параллелепипеде» Цели урока: ) Образовательные: вспомнить и систематизировать те знания, которые ученики
Подробнее
Конспект открытого урока
Конспект открытого урока «11» мая 2013 г. Класс 10 «А» Предмет математика Учитель Новгородова Н.И. Цель посещения в рамках обобщения опыта работы Тема урока «Построение сечений многогранников» Тип урока:
Подробнее
Технологическая карта урока
Технологическая карта урока Учитель: Кривцовой О. И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Школьное математическое образование ставит следующие цели обучения: овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения
Подробнее
Технологическая карта урока
Технологическая карта урока Тема: Площадь прямоугольного треугольника. Класс: 4 класс. Предмет: математика. УМК (авторы): УМК «Перспектива», автор Л.Г. Петерсон Тип урока: открытие нового знания. Планируемые
Подробнее
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ. Эта тема считается трудной. Если работать на обычной доске, много времени уходит на построение рисунков, условие задачи не всегда позволяет
Эта тема считается трудной. Если работать на обычной доске, много времени уходит на построение рисунков, условие задачи не всегда позволяет
Подробнее
«Цилиндр. Площадь поверхности цилиндра»
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 49 Петродворцового района Санкт-Петербурга имени Героя Российской Федерации М.Ю. Малофеева Методическая разработка
Подробнее
«Смежные и вертикальные углы»
Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа 92 г. Тюмень учитель математики: Гобец Елена Ивановна Методическая разработка урока по теме «Смежные и вертикальные
Подробнее
Задачи: Обучающие: Развивающие:
Технологическая карта урока (7 класс ). Ф.И. О. учителя: Стихина Ольга Николаевна 2. Класс: 7 Предмет:Геометрия 3. Тема урока: Призгаки параллельности прямых Тип урока: Урок изучения нового материала Геометрия
О. учителя: Стихина Ольга Николаевна 2. Класс: 7 Предмет:Геометрия 3. Тема урока: Призгаки параллельности прямых Тип урока: Урок изучения нового материала Геометрия
Подробнее
ПЛАН-КОНСПЕКТ УРОКА 1. ФИО
ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г.о. Чапаевск 3. Должность Учитель математики 4. Предмет
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
8 класс геометрия ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Школьное математическое образование ставит следующие цели обучения: овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности,
Подробнее
Технологическая карта урока по геометрии
Технологическая карта урока по геометрии Автор: Турукина Светлана Ивановна, учитель математики, МБОУ «СОШ 6» города Обнинска Предмет: Геометрия Класс: 9 класс Тип урока: урок «открытия нового знания» Тема:
Подробнее
«Волжский городской лицей»
Министерство образования республики Марий Эл «Волжский городской лицей» РАЗРАБОТКА УРОКА ПО ТЕМЕ: «СУММА УГЛОВ ТРЕУГОЛЬНИКА» Выполнила: Казакова С.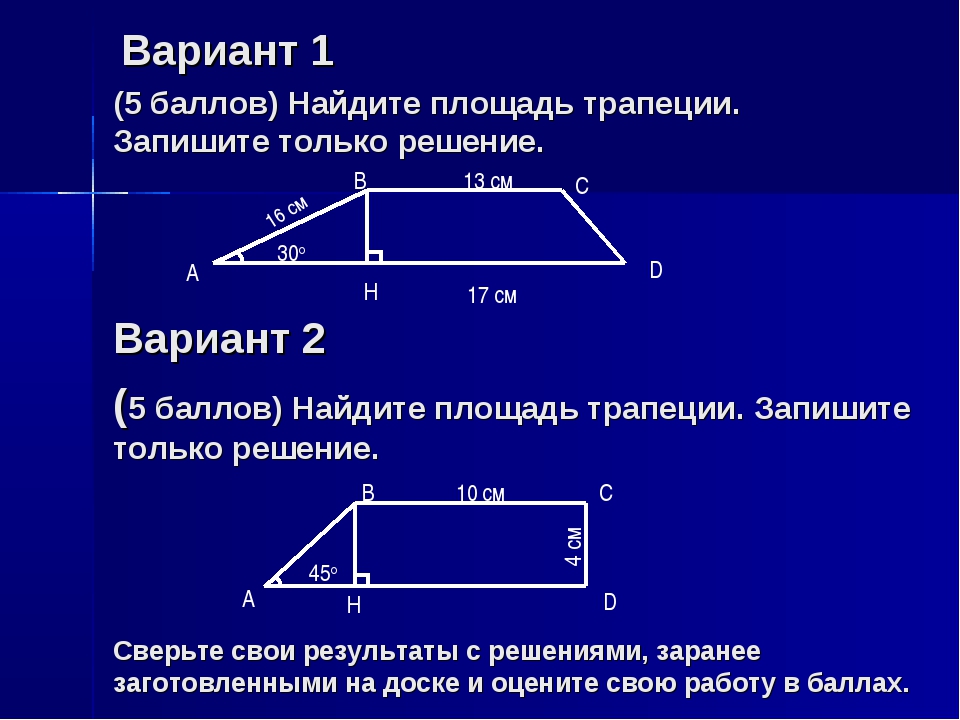 В. учитель математики г. Волжск 2016 г. 1 Методическая
В. учитель математики г. Волжск 2016 г. 1 Методическая
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося, виды контроля, а также компьютерное
Подробнее
Технологическая карта урока
Технологическая карта урока Учитель: Стекольникова О.А., МБОУ Школа 176, учитель математики и информатики Предмет: геометрия Класс: 7Б Тема урока: Сумма углов треугольника Тип урока: урок изучения нового
Подробнее
Урок геометрии в 8 классе
Урок геометрии в 8 классе Тема: «Итоговое повторение курса геометрии 8 класса» Продолжительность урока: 90 минут Цели урока: обучающие: обобщение знаний по курсу геометрии 8 класса; развивающие: развитие
Подробнее
Пояснительная записка
Количество уроков на год всего 68 ч.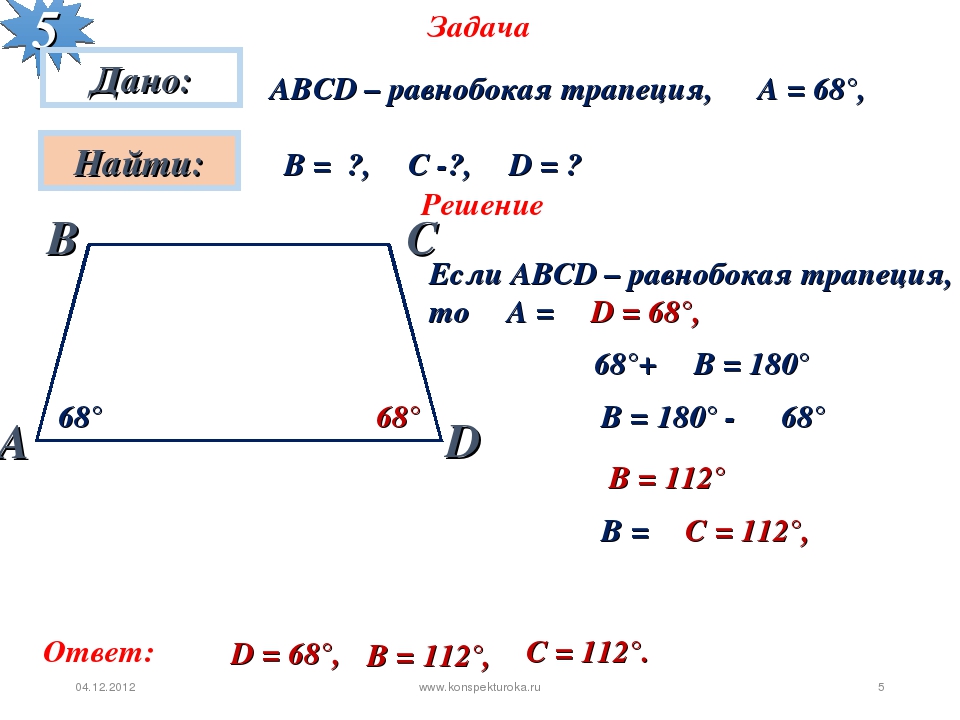 В неделю ч. Контрольных работ — 5. Пояснительная записка Цели и задачи программы: формирование представлений о математике как универсальном языке науки, средстве моделирования
В неделю ч. Контрольных работ — 5. Пояснительная записка Цели и задачи программы: формирование представлений о математике как универсальном языке науки, средстве моделирования
Подробнее
Математика 4 класс программа «Перспектива»
Математика 4 класс программа «Перспектива» Нахождение площади прямоугольного треугольника Цель урока: развивать у учащихся пространственное воображение и логическое мышление путем изучения площади треугольника
Подробнее
«УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ» 10 КЛАСС
УРОК ГЕОМЕТРИИ ПО ТЕМЕ: «УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ» 10 КЛАСС — 1 ЦЕЛИ: Образовательная введение нового понятия; отработка знаний, умений и навыков по нахождению угла между прямой и плоскостью; умение
Подробнее
Параллелограмм и трапеция. Основные свойства и признаки.
 — Математика
— Математика
Выпуклые четырехугольники
Выпуклый четырехугольник — четырехугольник, который расположен по одну сторону от любой из своих сторон.
Сумма углов выпуклого четырехугольника равна 360˚.
Средняя линия — отрезок прямой, соединяющий середины противоположных сторон.
Теоремы:
Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы сумма длин противоположных сторон были равны друг другу. Центр окружности — точка пересечения биссектрис.
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противоположных углов были равны. Центр окружности — точка пересечения серединных перпендикуляров к сторонам четырехугольника.
Параллелограмм, его признаки и свойства
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.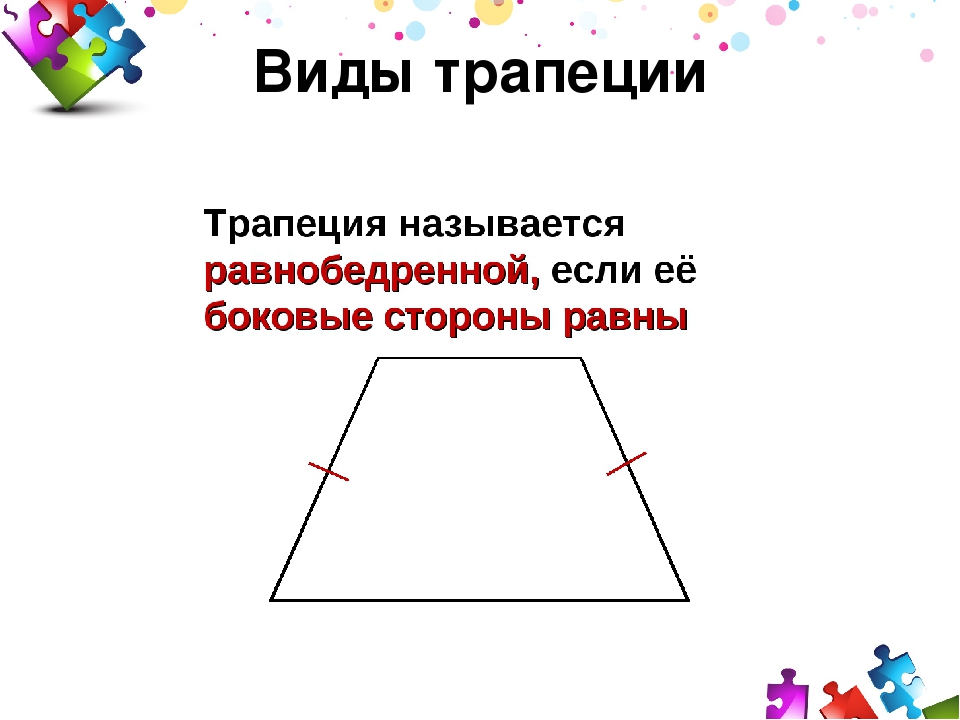
Теоремы (свойства параллелограмма):
В параллелограмме противоположные стороны равны и противоположные углы равны: AB=CD, BC=AD, ,.
Диагонали параллелограмма точкой пересечения делятся пополам: AO=OC, OB=OD.
Углы, прилежащие к любой стороне, в сумме равны 180˚.
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC² + BD² = 2AB² + 2BC .
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Дополнительно:
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,L,M,N являются вершинами параллелограмма Вариньона.
Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника ABCD. Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.
Прямоугольник, его признаки и свойства
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства:
Признак прямоугольника: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Помним: Вокруг прямоугольника всегда можно описать окружность.
Ромб, его признаки и свойства
Ромб — параллелограмм, у которого все стороны равны.
Свойства:
Все свойства параллелограмма.
Диагонали ромба взаимно перпендикулярны.
Диагонали ромба делят углы ромба пополам.
Признаки ромба:
Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
Если в параллелограмме диагонали делят углы пополам, то этот параллелограмм — ромб.
Помним: В ромб всегда можно вписать окружность.
Квадрат, его признаки и свойства
Квадрат – параллелограмм, у которого все стороны равны и все углы — прямые; или прямоугольник, у которого все стороны равны; или ромб, у которого все углы — прямые.
Свойства:
Трапеция, ее признаки и свойства
Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие —боковыми сторонами.
Высота трапеции — расстояние между прямыми, на которых лежат основания трапеции, любой общий перпендикуляр этих прямых.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон.
Свойство трапеции:
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон: a + b = c + d , а средняя линия равна полусумме боковых сторон: m = (c+d): 2 .
Равнобедренная трапеция — трапеция, у которой боковые стороны равны AB = CD. Тогда равны диагонали AC = BD и углы при основании , .
Из всех трапеций только около равнобедренной трапеции можно описать окружность, так как окружность можно описать около четырехугольника, только если сумма противоположных углов равна 180˚.
В равнобедренной трапеции расстояние от вершины одного основания, до проекции противоположной вершины на прямую, содержащую это основание равно средней линии.
Прямоугольная трапеция — трапеция, у которой один из углов при основании равен 90˚.
Теоремы о площади четырехугольника
Любой четырехугольник можно разбить на треугольники, и его площадь будет равна сумме площадей треугольников.

Если в четырехугольник можно вписать окружность, то его площадь равна: S=pr.
Если четырехугольник вписан в окружность,то его площадь будет равна
.
Если диагонали выпуклого четырехугольника равны и и образуют угол, то площадь четырехугольника равна: .
Следствие: Площадь ромба равна: .
Площадь прямоугольника: .
Площадь параллелограмма: .
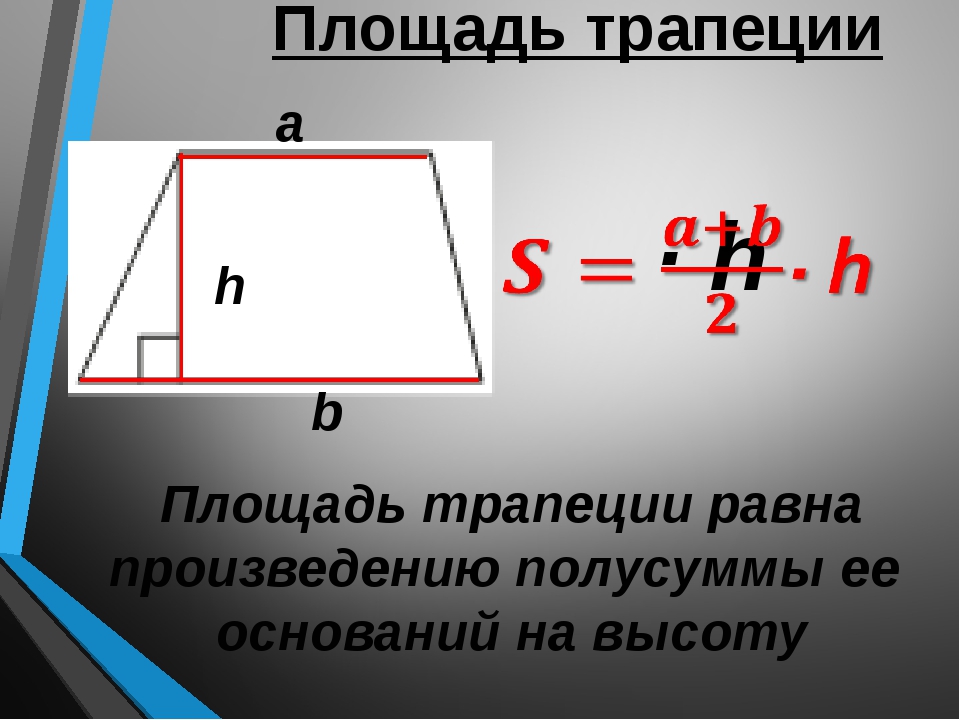
Площадь трапеции: .
Трапеция – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Трапеция – четырехугольник, у которого две стороны попарно параллельны, а две другие не параллельны. Параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. 2\).
2\).
Свойства и признаки равнобедренной трапеции
-
В равнобедренной трапеции углы при любом основании равны.
- В равнобедренной трапеции длины диагоналей равны.
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
- Около равнобедренной трапеции можно описать окружность.
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом \(r\) и она делит боковую сторону точкой касания на два отрезка – \(a\) и \(b\), то \(r=\sqrt{ab}\).
Сумка через плечо
Trapezoid
— КОКОН
Трапециевидная сумка через плечо среднего размера с чистой золотой сужающейся рамкой — идеальный размер, чтобы вместить все самое необходимое! Дно специально усилено, чтобы носить с собой более тяжелые предметы, сохраняя при этом стильную форму и легкий вес.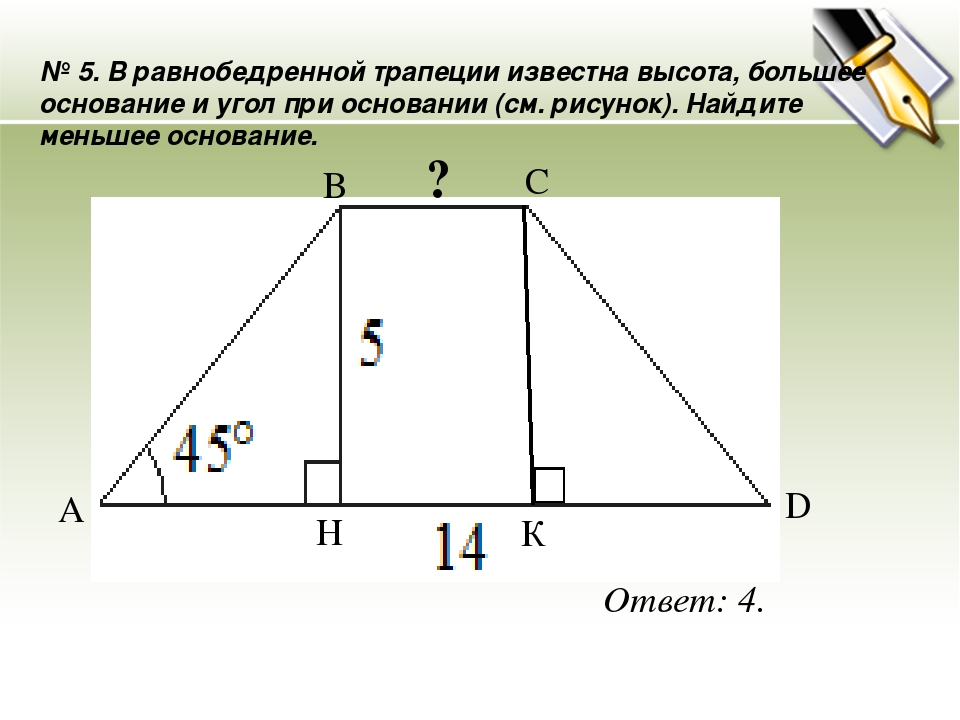 Внутри сумки также есть небольшой карман для хранения мелких вещей, например карточек и ключей.
Внутри сумки также есть небольшой карман для хранения мелких вещей, например карточек и ключей.
Сумка через плечо Trapezoid разработана с учетом универсальности.Съемный кожаный ремешок хорошо удерживает вес ваших вещей. После отсоединения он также выглядит хорошо как сцепление. Сумка на все случаи жизни!
Каждая сумка снабжена изысканной золотой биркой с логотипом COCOONESE сбоку. Простой дизайн, винтажный и стильный одновременно, отличная сумка для молодого офисного работника, который отправляется по делам или на обед!
🔖 Описание:
— Каждая сумка сделана вручную в Сингапуре .
— Дизайн и производство Cocoonese
📐Размеры приблизительные:
— Длина: 20 см
— Ширина: 10 см
— Высота: 24 см
— Ремешок: 107-125 см (регулируемый)
— Цвет: синий
🔎Спецификация товара:
— Материал: хлопчатобумажная ткань
— Ремешок: кожа
— Материал рамы: Гальванические сплавы с латунным покрытием
Примечание 1: 1 дюйм = 2.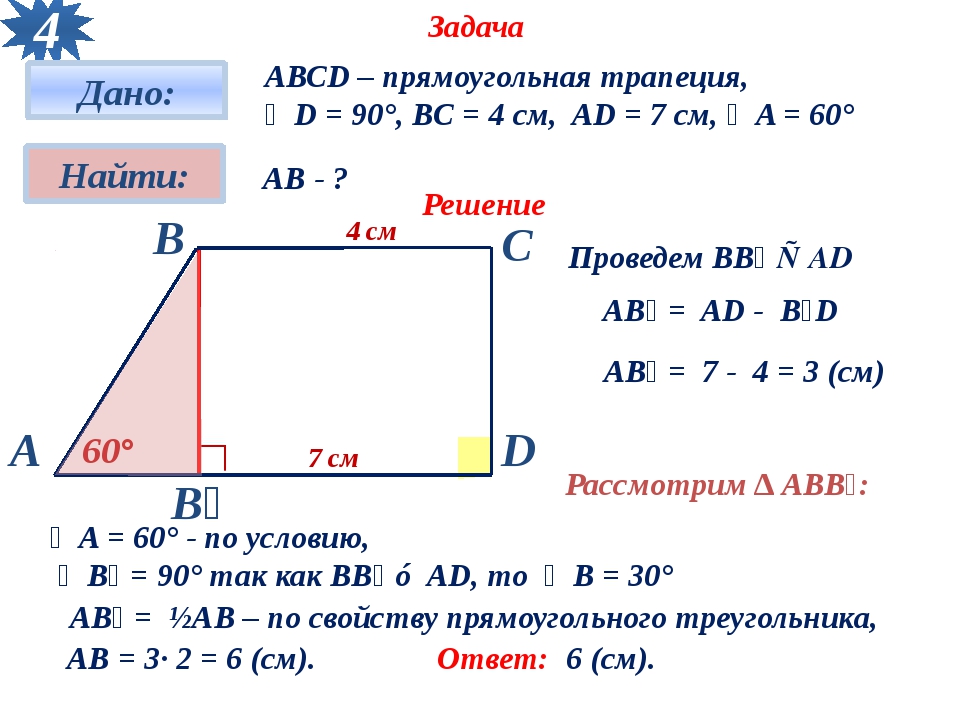 54 см, 1 см = 0,39 дюйма
54 см, 1 см = 0,39 дюйма
Примечание 2: цвет может немного отличаться из-за настроек монитора компьютера.
Примечание 3: Все сумки изготавливаются вручную, допускается отклонение в размере на 1-3 см.
✈️Поставка:
a. Все пакеты будут отправлены аккуратно сложенными и упакованными.
г. Заказ будет отправлен в течение 1-3 рабочих дней после оплаты.
г. Все сумки отправляются обычной почтой с номером для отслеживания.
Спасибо, что посетили COCOONESE. Если у вас есть вопросы, отправьте нам сообщение.
Используйте стрелки влево / вправо для навигации по слайд-шоу или проведите пальцем влево / вправо при использовании мобильного устройства
абстрактный фон технологии трапеции Клипарты, векторы, и Набор Иллюстраций Без Оплаты Отчислений. Изображение 41957899.
абстрактный фон технологии трапеции Клипарты, векторы, и Набор Иллюстраций Без Оплаты Отчислений. Изображение 41957899.
Изображение 41957899.
Абстрактный фон технологии трапеции
M
L
XL
EPS
Таблица размеров
| Размер изображения | Идеально подходит для |
| S | Интернет и блоги, социальные сети и мобильные приложения. |
| M | Брошюры и каталоги, журналы и открытки. |
| л | Внутренние и наружные плакаты и печатные баннеры. |
| XL | Фоны, рекламные щиты и цифровые экраны. |
Используете это изображение на предмете перепродажи или шаблоне?
Распечатать
Электронный
Всесторонний
5000 x 3533 пикселей
|
42.3 см x
29,9 см |
300 точек на дюйм
|
JPG
Масштабирование до любого размера • EPS
5000 x 3533 пикселей
|
42,3 см x
29,9 см |
300 точек на дюйм
|
JPG
Скачать
Купить одно изображение
6 кредитов
Самая низкая цена
с планом подписки
- Попробовать 1 месяц на 2209 pyб
- Загрузите 10 фотографий или векторов.
- Нет дневного лимита загрузок, неиспользованные загрузки переносятся на следующий месяц
221 ру
за изображение любой размер
Цена денег
Ключевые слова
Похожие векторы
Нужна помощь? Свяжитесь с вашим персональным менеджером по работе с клиентами
@ +7 499 938-68-54
Мы используем файлы cookie, чтобы вам было удобнее работать. Используя наш веб-сайт, вы соглашаетесь на использование файлов cookie, как описано в нашей Политике использования файлов cookie
Используя наш веб-сайт, вы соглашаетесь на использование файлов cookie, как описано в нашей Политике использования файлов cookie
.
Принимать
Иллюстративная математика
Задача
Ниже представлены изображения четырех четырехугольников: квадрата, прямоугольника, трапеции и параллелограмма.
Для каждого четырехугольника найдите и проведите все линии симметрии.
Комментарий IM
Это задание дает студентам возможность поэкспериментировать с отражениями плоскости и их воздействием на определенные типы четырехугольников.Это оба
Интересно и важно, что эти типы четырехугольников можно отличить по линиям симметрии. С этой точки зрения здесь отсутствуют только изображения ромба и общего четырехугольника, которые не попадают ни в одну из рассматриваемых здесь специальных категорий.
Это задание лучше всего подходит для обучения, хотя его можно адаптировать для оценивания. Если учащиеся еще не выучили терминологию для трапеций и параллелограммов, учитель может начать с объяснения значения этих терминов. В пункте 4.G.2 говорится, что учащиеся должны классифицировать фигуры на основе наличия или отсутствия параллельных и перпендикулярных линий, поэтому эта задача будет хорошо работать в подразделении, отвечающем всем стандартам кластера 4.G.A.
В пункте 4.G.2 говорится, что учащиеся должны классифицировать фигуры на основе наличия или отсутствия параллельных и перпендикулярных линий, поэтому эта задача будет хорошо работать в подразделении, отвечающем всем стандартам кластера 4.G.A.
Студенты должны сначала попытаться визуализировать линии симметрии, а затем они могут сделать или получить вырезы четырех четырехугольников или обвести их на кальке. Студентам полезно поэкспериментировать и увидеть, что идет не так, например, при отражении прямоугольника (который не является квадратом) по диагонали.Это упражнение помогает развить навыки визуализации, а также получить опыт работы с различными формами и их поведением при отражении.
Учащимся следует вернуться к этой задаче как в средней, так и в старшей школе, чтобы проанализировать ее с более сложной точки зрения по мере того, как они разрабатывают инструменты для этого. В восьмом классе четырехугольникам можно дать координаты, и ученики могут изучить свойства отражений в системе координат. В старших классах учащиеся могут использовать абстрактные определения отражений и различных четырехугольников, чтобы доказать, что эти четырехугольники на самом деле характеризуются количеством линий симметрии, которые у них есть.
В старших классах учащиеся могут использовать абстрактные определения отражений и различных четырехугольников, чтобы доказать, что эти четырехугольники на самом деле характеризуются количеством линий симметрии, которые у них есть.
Решение
Линии симметрии для каждого из четырех четырехугольников показаны ниже:
Когда геометрическая фигура складывается по линии симметрии, две половинки совпадают, поэтому, если у учащихся есть копии четырехугольников, они могут проверить линии симметрии, сложив их. Что касается квадрата, его можно сложить пополам по диагонали, горизонтальному сегменту, разрезающему квадрат пополам, или вертикальному сегменту, разрезающему квадрат пополам.Итак, у квадрата четыре линии симметрии. Прямоугольник их всего два, так как его можно сложить пополам по горизонтали или вертикали: учеников следует поощрять попытаться сложить прямоугольник пополам по диагонали, чтобы понять, почему это не работает. Трапеция имеет только вертикальную линию симметрии. У параллелограмма нет линий симметрии, и, как и в случае с прямоугольником, ученики должны поэкспериментировать со складыванием копии, чтобы увидеть, что происходит с линиями через диагонали, а также с горизонтальными и вертикальными линиями.
У параллелограмма нет линий симметрии, и, как и в случае с прямоугольником, ученики должны поэкспериментировать со складыванием копии, чтобы увидеть, что происходит с линиями через диагонали, а также с горизонтальными и вертикальными линиями.
Указанные линии симметрии — единственные для фигур. Один из способов показать это — заметить, что для четырехугольника линия симметрии должна либо соответствовать двум вершинам на одной стороне линии с двумя вершинами на другой, либо проходить через две из вершин, а затем через две другие пары вершин. в сложенном виде по строчке. Это ограничивает количество возможных линий симметрии, и тогда эксперименты покажут, что единственно возможными являются те, которые показаны на рисунках.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.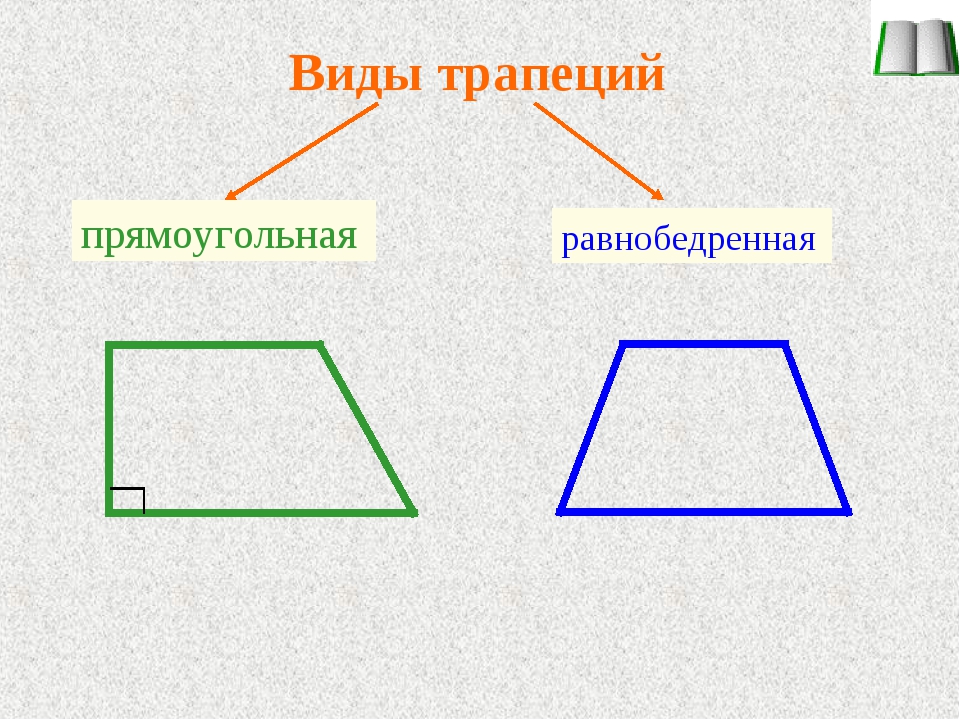 Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.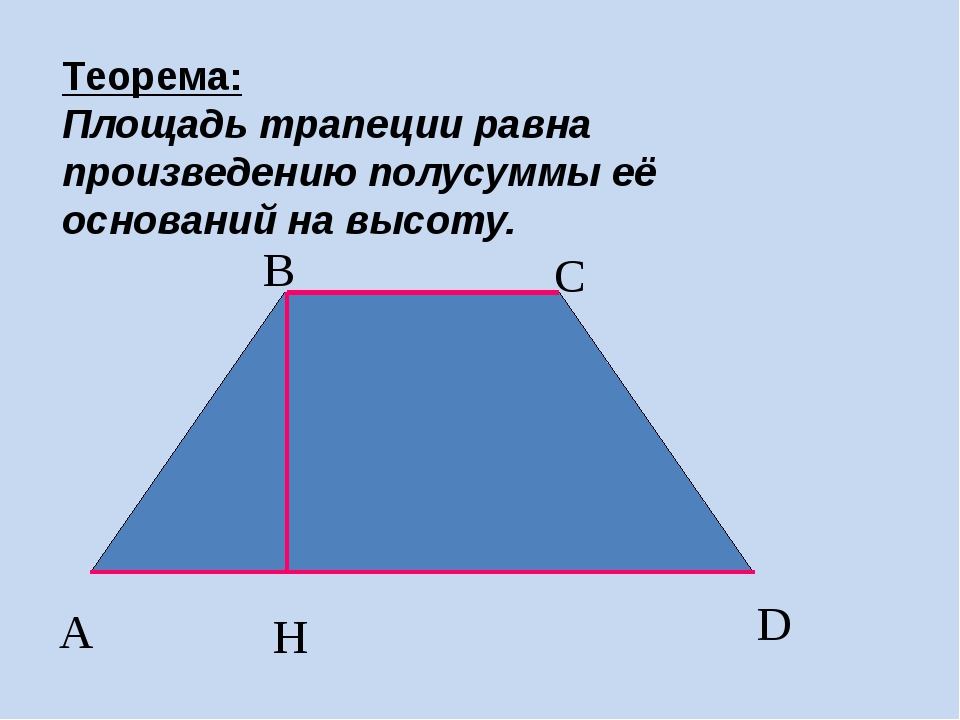
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.

 Обнаружено асимметричное динамическое поведение доменной стенки в зависимости от направления распространения во внешнем магнитном поле. Когда доменные стенки распространяются в противоположном направлении вдоль длинной оси нанополоски, поля пробоя Уокера, а также средние скорости различаются. Асимметричный ландшафт энергий размагничивания, который возникает из трапециевидной геометрии, является основной причиной асимметричного поведения распространения. Кроме того, нанополоска с поперечным сечением трапеции станет нанотрубкой, если ее искусственно свернуть вдоль своей длинной оси, и, таким образом, двумерная поперечная доменная стенка станет трехмерной.Интересно, что обнаружено, что асимметричное поведение, наблюдаемое в двумерных нанополосках с трапециевидным поперечным сечением, аналогично некоторым динамическим свойствам, имеющимся в трехмерных нанотрубках.
Обнаружено асимметричное динамическое поведение доменной стенки в зависимости от направления распространения во внешнем магнитном поле. Когда доменные стенки распространяются в противоположном направлении вдоль длинной оси нанополоски, поля пробоя Уокера, а также средние скорости различаются. Асимметричный ландшафт энергий размагничивания, который возникает из трапециевидной геометрии, является основной причиной асимметричного поведения распространения. Кроме того, нанополоска с поперечным сечением трапеции станет нанотрубкой, если ее искусственно свернуть вдоль своей длинной оси, и, таким образом, двумерная поперечная доменная стенка станет трехмерной.Интересно, что обнаружено, что асимметричное поведение, наблюдаемое в двумерных нанополосках с трапециевидным поперечным сечением, аналогично некоторым динамическим свойствам, имеющимся в трехмерных нанотрубках.
 Почта:
Почта: 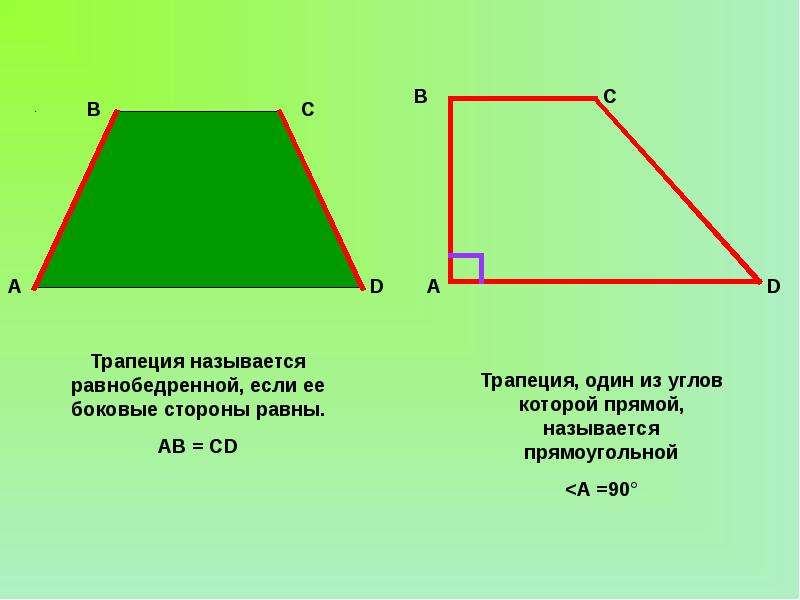 П. 2002 Science 296 2003
П. 2002 Science 296 2003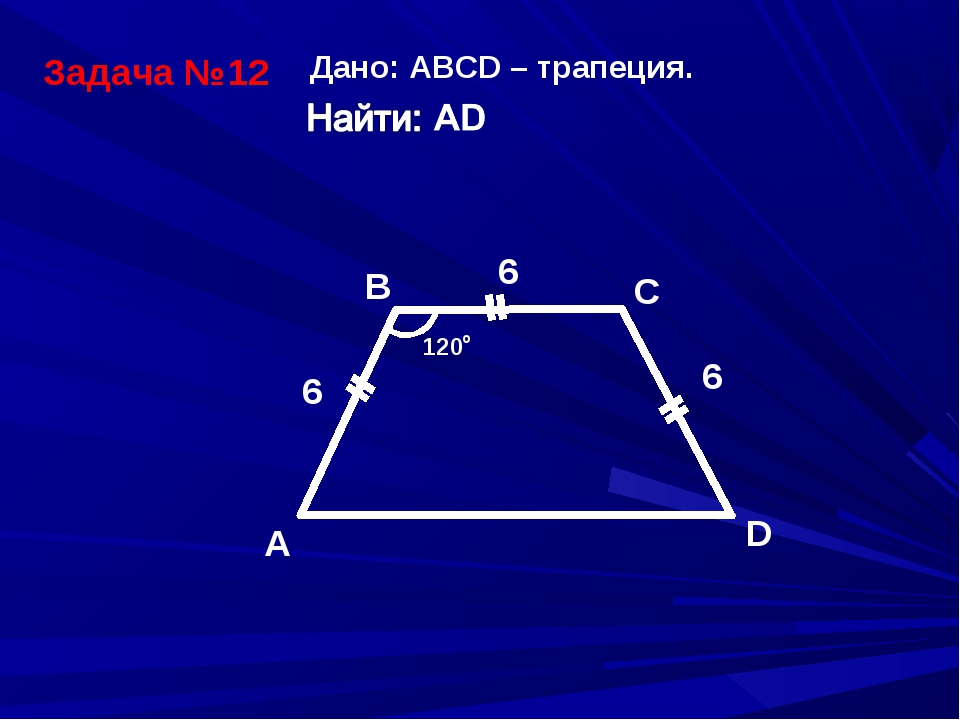 Appl. Phys. 45 5406
Appl. Phys. 45 5406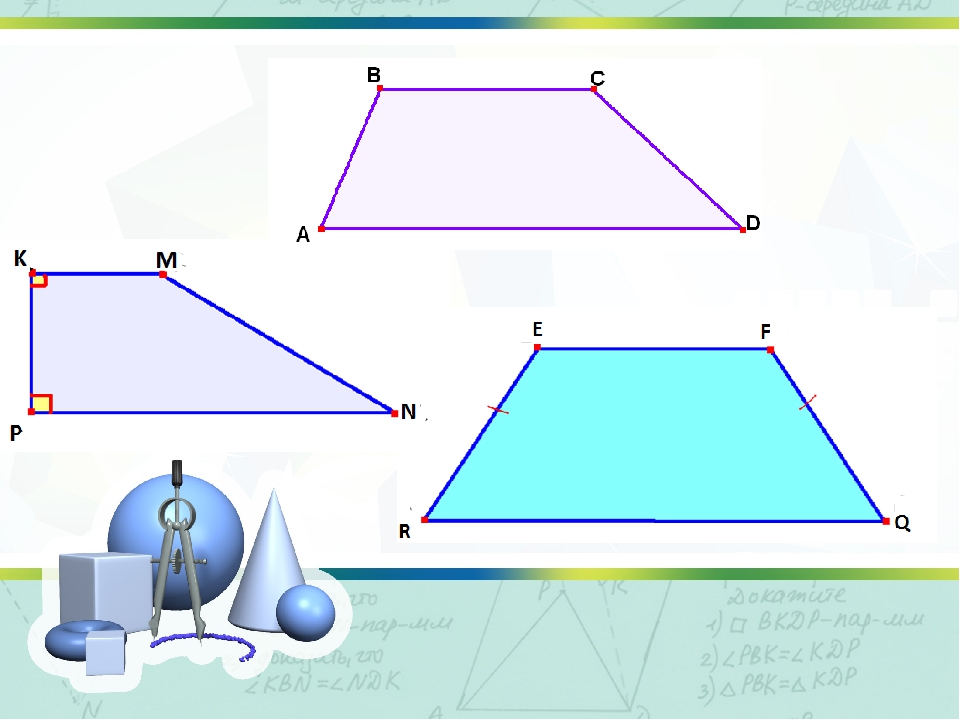 , Чой С., Кан Х. К. и Чанг С. Международная конференция по электронным устройствам, 2011 г. (Вашингтон, округ Колумбия, США, 5-7 декабря 2011 г.) стр.24.1.1
, Чой С., Кан Х. К. и Чанг С. Международная конференция по электронным устройствам, 2011 г. (Вашингтон, округ Колумбия, США, 5-7 декабря 2011 г.) стр.24.1.1 и Шефер Р. 1998 Магнитные домены: анализ магнитных микроструктур (Гейдельберг: Springer-Verlag), гл.3 шт. 223
и Шефер Р. 1998 Магнитные домены: анализ магнитных микроструктур (Гейдельберг: Springer-Verlag), гл.3 шт. 223