Содержание
Четырехугольники — презентация онлайн
1. Из имеющихся четырёхугольников указать те, которые являются параллелограммами
3
2
1
6
4
5
2. Заполнить таблицу, отметив знаки «+» или «-»
Параллелогр
амм
Противоположные
стороны
параллельны и
равны
Все стороны равны
Противолежащие
углы равны, сумма
соседних углов
равна180
Все углы прямые
Диагонали
пересекаются и
точкой
пересечения
делятся пополам
Диагонали равны
Диагонали взаимно
перпендикулярны и
являются
биссектрисами
углов
Прямоугольник
Ромб
Квадрат
3. Ответы
№ Параллелограмм
Прямоугольник
Ромб
Квадрат
1
+
+
+
+
2
—
—
+
+
3
+
+
+
+
4
—
+
—
+
5
+
+
+
+
6
—
+
—
+
7
—
—
+
+
4.
 Тест для капитана вариант 1
Тест для капитана вариант 1
1.Любой прямоугольник является:
а)ромбом б) квадратом в)параллелограммом г)нет такого ответа
2.Если в четырёхугольнике диагонали перпендикулярны, то этот
четырёхугольник-…
а) ромб б)квадрат в) прямоугольник г) нет правильного ответа
3. Ромб- это четырёхугольник, в котором….
а)диагонали точкой пересечения делятся пополам и равны.
б)диагонали перпендикулярны и точкой пересечения делятся
пополам
в)противолежащие углы равны, а стороны параллельны
г) нет правильного ответа
5. Конкурс капитанов вариант 2
1.Любой ромб является :
а) квадратом б) прямоугольником в)параллелограммом г)нет
правильного ответа.
2.Если диагонали перпендикулярны, то это параллелограмм:
а)ромб б) квадрат в)прямоугольник в) нет правильного ответа
.Прямоугольник — это четырёхугольник, в котором :
а) противоположные стороны параллельны, а диагонали равны
б) диагонали точкой пересечения делятся пополам и являются
биссектрисами его углов
в)два угла прямые и две стороны равны
г) нет правильного ответа
6.
 Устные задачи
Устные задачи
1.Один из углов параллелограмма 40. Найти углы параллелограмма
2. Сумма двух углов параллелограмма равна 140. Найти углы
параллелограмма.
3.Одна из сторон параллелограмма в 2 раза больше другой, а Р=24см
Найти стороны параллелограмма.
4. Найти площадь треугольника ,если площадь параллелограмма 240 кв.см
Б
Е
С
АВСД параллелограмм
Найти: угол А, угол С
А
32
Д
В
В
В
В
АВСД ТРАПЕЦИЯ
НАЙТИ угол В.,угол Д
С
117
в
Д
36
А
В
С
АВСД прямоугольник
Найти АД
60
10
1
0
А
Д
В
А
6
6
60
С
р
м Д
АВСД ромб Найти МД+ДР
Леонард Эйлер, крупнейший
математик XVIII века, родился
в Швейцарии. В 1727г. по
приглашению Петербургской
академии наук он приехал в
Россию. Эйлер попал в круг
выдающихся математиков,
получил большие возможности
для создания и издания своих
трудов. Он работал с
Он работал с
увлечением и вскоре стал, по
единодушному признанию
современников, первым
математиком мира.
Круги ЭЙЛЕРА —
геометрическая схема,
с помощью которой
можно изобразить
отношения между
подмножествами, для
наглядного
представления
Множество всех действительных чисел Эйлер изобразил
с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.
Домашние задания по курсу логики
Здесь вы можете получить задачи по курсу логики, ссылка на страницу с решением приведена ниже.
Решения
- Привести примеры нарушения законов логики
- Привести примеры нарушения правил деления объема понятия.
- Привести примеры нарушения правил определения понятия.
- Изобразить на кругах Эйлера отношения между понятиями.
4.1. Студент, спортсмен, биатлонист, отец. 4.2. Мужчина, адвокат, юрист, прокурор.
4.3. Квадрат, прямоугольник, ромб, параллелограмм. 4.4. Деньги, валюта, доллары, банк.
4.5. Университет, вуз, академия, гимназия. 4.6. Пушка, пистолет, оружие, танк.
4.7. Кража, грабеж, разбой, мошенничество. 4.8. Искусство, эстрада, цирк, опера.
- Обобщить понятие (три шага).
5.1. Учебник. 5.2. Лев. 5.3. Автомобиль. 5.4. Наука. 5.5. Цезарь. 5.6. Река. 5.7. Снег. 5.8. Береза.
- Ограничить понятие (три шага).
6.1. Существо. 6.2. Искусство. 6.3. Животное. 6.4. Книга. 6.5. Река. 6.6. Поэма.
6.7. Средство связи. 6.8. Волейбол.
- Дать определение, указав ближайший род и видовое отличие.
7.1. Свобода. 7.2. Преступление. 7.3. Философия. 7.4. Ответственность. 7.5. Долг.
7.6. Радость. 7.7. Любовь. 7.8. Совесть.
- На основе логического квадрата, полагая исходное суждение сначала истинным, затем – ложным, выведите суждения, соотносимые с исходным, и установите их истинностные значения.
8.1. Коровы не летают. 8.2. Всяк кулик свое болото хвалит. 8.3. Услужливый дурак опаснее врага. 8.4. Насилие – спутник войны. 8.5. Не все сапожники в сапогах.
8.6. Рыбы живут в реках. 8.7. Наука на веру ничего не принимает. 8.8. Не все то золото, что блестит.
- Осуществите превращение, обращение, противопоставление предикату.
9.1. Некоторые люди злые. 9.2. Доверчивый – беззащитен. 9.3. Утки не поют. 9.4. Дети любят шоколад. 9.5. Чиновники не любят работать. 9.6. Депутаты любят болтать.
9.7. Политики не следуют нормам морали. 9.8. Баскетболисты — люди высокорослые.
- Приведите примеры умозаключений по схемам (модусам) условно-категорического силлогизма, а также – простой и сложной контрапозиции.
- Подыщите средний термин и постройте силлогизм. Укажите фигуру и модус.
11.1. Железо – проводник тепла. 11.2. Декабрист — поэт. 11.3. Тигр – жвачное.
11.4. Певец – художник. 11. 5. Композитор – ученый. 11.6. Собака – друг. 11.7. Кит – рыба. 11.8. Преступление – наказуемое действие.
5. Композитор – ученый. 11.6. Собака – друг. 11.7. Кит – рыба. 11.8. Преступление – наказуемое действие.
- Восстановите энтимему до полного силлогизма. Укажите фигуру и модус.
12.1 Они не больны, так как у них нет повышенной температуры. 12.2. Курица не птица, поскольку все птицы летают. 12.3. Металлы – химические элементы, так как все химические элементы – вещества. 12.4. Обвиняемый имеет право на защиту, Следовательно, М. имеет право на защиту. 12.5. Эта мысль ложна, ибо она не соответствует действительности. 12.6. Судья вправе задавать вопросы в любой момент допроса свидетеля, но вы не судья. 12.7. Наблюдение широко используется в оперативно- розыскной работе. Наблюдение – метод научного познания. 12.8. Все воспитатели должны быть хорошо воспитаны. Петров не является воспитателем.
Рекомендую посетить и эту страницу:
Аудио словарь латинского языка
1.5. В каких отношениях могут быть понятия?. Логика. Учебное пособие
1. 5. В каких отношениях могут быть понятия?
5. В каких отношениях могут быть понятия?
Между понятиями, а вернее между их объемами, существуют определенные отношения, знание которых является в логике одним из наиболее важных (можно сказать, что виды отношений между понятиями в логике – это примерно то же самое, что в математике таблица умножения). Обычно понятия делят на сравнимые (например, Москва и столица России, писатель и россиянин, город и населенный пункт, лев и тигр, горячая вода и холодная вода, высокий человек и невысокий человек) и несравнимые (например, пингвин и кирпич, треугольник и президент, учебное заведение и небесное тело, спортсмен и город, книга и небоскреб, растение и государство).
Сравнимые понятия бывают совместимыми и несовместимыми. Совместимыми называются понятия, объемы которых имеют общие элементы, каким-либо образом соприкасаются. Например, понятия спортсмен и американец совместимые, т. к. их объемы имеют общие элементы, или объекты: есть такие спортсмены, которые являются американцами и, наоборот, есть такие американцы, которые являются спортсменами. Несовместимыми называются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Например, понятия треугольник и квадрат являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом и наоборот.
к. их объемы имеют общие элементы, или объекты: есть такие спортсмены, которые являются американцами и, наоборот, есть такие американцы, которые являются спортсменами. Несовместимыми называются понятия, объемы которых не имеют общих элементов, никаким образом не соприкасаются. Например, понятия треугольник и квадрат являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом и наоборот.
Совместимые понятия могут быть в отношениях равнозначности, пересечения и подчинения.
Понятия находятся в отношении равнозначности в том случае, если их объемы полностью совпадают. Например, равнозначными будут понятия квадрат и равносторонний прямоугольник, т. к. любой квадрат – это равносторонний прямоугольник, а любой равносторонний прямоугольник – это квадрат. В логике принято изображать отношения между понятиями с помощью круговых схем Эйлера (известный математик XVIII века): одно понятие, а вернее его объем, изображается одним кругом, а второе, т. е. его объем – другим. Взаимное расположение этих кругов на схеме (они могут полностью совпадать или пересекаться, или не соприкасаться, или один круг располагается внутри другого) и показывает то или иное отношение между понятиями. Так отношение равнозначности между понятиями квадрат и равносторонний прямоугольник изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают:
е. его объем – другим. Взаимное расположение этих кругов на схеме (они могут полностью совпадать или пересекаться, или не соприкасаться, или один круг располагается внутри другого) и показывает то или иное отношение между понятиями. Так отношение равнозначности между понятиями квадрат и равносторонний прямоугольник изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают:
Понятия находятся в отношении пересечения тогда, когда их объемы совпадают только частично. Например, пересекающимися будут понятия школьник и спортсмен: есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий):
Понятия находятся в отношении подчинения в том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому).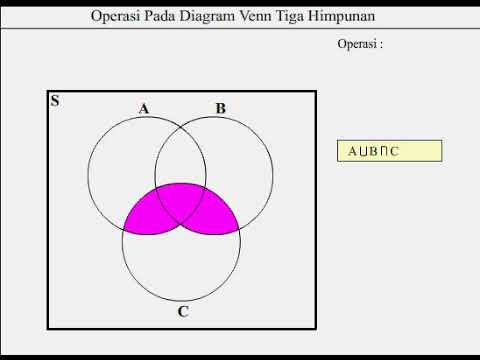 Например, в отношении подчинения находятся понятия карась и рыба, т. к. все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим – родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого:
Например, в отношении подчинения находятся понятия карась и рыба, т. к. все караси – это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия карась является меньшим по отношению к объему понятия рыба и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим – родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого:
Отношениями равнозначности, пересечения и подчинения исчерпываются все случаи совместимости между понятиями.
Несовместимые понятия могут быть в отношениях соподчинения, противоположности и противоречия.
Понятия находятся в отношении соподчинения тогда, когда их объемы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия сосна и береза являются соподчиненными: ни одна сосна не может быть березой и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дерево. На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами:
Например, понятия сосна и береза являются соподчиненными: ни одна сосна не может быть березой и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия дерево. На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами:
Понятия находятся в отношении противоположности в том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия высокий человек и низкий человек (третьим или переходным вариантом между ними будет понятие человек среднего роста). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах»:
Поскольку объемы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью березы, а береза – противоположностью сосны: это просто разные деревья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека и наоборот. Так же противоположными будут понятия темная комната и светлая комната, горячая вода и холодная вода, белый лист и черный лист, глубокая речка и мелкая речка и т. п.
Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью березы, а береза – противоположностью сосны: это просто разные деревья, и не более того. В то же время высокий человек представляет собой противоположность низкого человека и наоборот. Так же противоположными будут понятия темная комната и светлая комната, горячая вода и холодная вода, белый лист и черный лист, глубокая речка и мелкая речка и т. п.
Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий, между противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия высокий человек и невысокий человек. В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и низкий человек, и человек среднего роста – это невысокий человек. На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия:
На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия:
Отношениями соподчинения, противоположности и противоречия исчерпываются все случаи несовместимости между понятиями.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Основная часть | Три моих стороны Могут разной быть длины. Где стороны встречаются Угол получается. Что же вышло? Посмотри Ведь углов то тоже три Что за фигуры стоят в ряд? Четыре угла и четыре сторонки, Похожи, точно родные сестренки. Не овалы и не треугольники, А зовутся они: Он похожий на яйцо Или на твоё лицо. Вот такая есть окружность Очень странная наружность. Круг приплюснутым стал Получился вдруг: Нет углов у меня И похож на блюдце я, На тарелку и на крышку, На кольцо, на колесо. Кто же я такой, друзья? Назовите вы меня. «Здравствуйте ребята, спасибо за ваши умения и знания, благодаря им вы смогли справиться с вирусом. Я знаю, что вы любите игры — головоломки с геометрическими фигурами. Я вам высылаю образцы схем этих игр, играйте и развивайтесь. До новых встреч». | Давайте я ещё раз попробую. Ой, ребята, а тут написано, что от вируса нам поможет избавиться антивирусная программа Но что бы ее получить нужно, выполнить задания антивирусной программы. , Отгадайте загадку : А чтобы выполнить следующие задание , нам необходимо разделится на три команды , Кто выполнил задание тот поднимает красный флажок . Задание 1 команде (красные фигуры) Ребята, посмотрите на свои карточки, может, кто то сам сможет сформулировать задание? Задание 2 команде (желтые фигуры) Предложить детям, самостоятельно сформулировать задание. На картинке изображены предметы, состоящие из треугольников. Задание 3 команде (синие фигуры) Что обозначает треугольник со знаком вопроса? Молодцы, ребята, задание выполнили. (на столе лежит конверт). Может быть, антивирусная программа находится в этом конверте? Посмотрим (открываем конверт). Нет, ребята, здесь только подсказка, что делать дальше. Отгадайте загадку:
Что бы дальше антивирусная программа открылась, нам нужно выполнить следующие задание, а называется оно «Переправа через мост». Из чего состоит мост ? Первая команда переходит мост, только по числам в порядке возрастания. Вторая команда проходит только по фигурам красного цвета. Третья команда проходит, только по фигурам, имеющим углы. Ребята посмотрите, что общего у фигур которые вы видите? Посмотрите, здесь еще есть куб и параллелепипед. Что это? почему вы считаете, что это геометрическое тело? Стороны параллелепипеда (куба) на какие геометрические фигуры они похожи? Ну и здесь нас ждет испытание. Задание 4 команде №1 Нарисуй фигуры так, чтобы квадрат был под ромбом, прямоугольник под квадратом. Задание 5 команде №2 «Оживите прямоугольник». Что это значит? Это значит, вы дорисуете детали и превратите фигуру в тот или иной предмет. Подумайте, какие предметы или части предметов похожи на прямоугольник и дорисуйте. Задание 6 команде №3 Соединив цвет в левом столбце с фигурой в верхнем ряду, выберите соответствующий данным признакам предмет из нижнего ряда таблицы и проведите стрелку. Какие вы молодцы и с этими заданиями справились. Так может быть в этом конверте, мы найдем антивирусную программу? что, откроем следующий конверт? Ой, а тут сразу две загадки: А вот и вторая загадка: -Правильно, круг. А давайте ребята встанем в круг. В круг широкий вижу я Встали все мои друзья. Мы сейчас пойдём направо, А теперь пойдём налево, В центре круга соберёмся И на место все вернёмся, Улыбнёмся, подмигнём И дальше на поиски пойдём. Чтобы выполнить следующее задание выбрать фигуры только по заданным признакам.(цвет, форма) 1 круг: круглые 2круг: желтые В центре общие признаки: круглые желтые. -Ребята, оказывается у нас остался последние задание. Странно, картинки, какие то. Что на них изображено? Может, здесь чего — то не хватает? почему вы так решили? С опорой на схему, составляют из танграма монитор. Ребята, посмотрите, наш монитор засветился зеленым светом, а это значит, антивирусная программа активирована (аудио запись Мусоросброс) Подходят к ноутбуку, включается запись Ребята, так это принцесса Математики! Теперь мы с вами знаем, как она выглядит. А ещё принцесса прислала звуковое письмо. Послушаем его? | -треугольник Делятся с помощью цветных геометрических фигур Нужно на рисунке сосчитать все треугольники, назвать их количество. Дети выполняют задание. Сосчитать количество треугольников и составить пример на образование данного числа. Найди предмет по форме похожий на треугольник. Дети выполняют задание. четырехугольники — цифр ,геометрических фигур — дети выполняет задание по командам У них по 4 стороны, по 4 угла. -геометрическое тело -прямоугольники и квадрат — дети выполняет задание по командам — дети выполняет задание по командам — дети выполняет задание по командам овал Круг — дети выполняет задание — дети выполняет задание | И по окончанию поднимаю флажок И по окончанию поднимаю флажок И по окончанию поднимаю флажок |
Тема 4. Математические доказательства
Методические рекомендации
Задания под номером 10 в контрольной работе, предлагаемые по данной теме, связаны с оценкой правильности сделанного умозаключения, либо с его построением.
При анализе умозаключения выделяют его логическую структуру, а затем проверяют соответствие полученной схемы одному из известных правил вывода. Если такое соответствие имеет место, то рассуждение правильно, если же нет, то надо провести дальнейший анализ умозаключения. Для этого выделенную схему записывают на теоретико-множественном языке и с помощью кругов Эйлера изображают посылки, считая их истинными. Затем выясняют, всегда ли при этом истинно заключение. Если возможна ситуация, при которой заключение оказывается ложным, то умозаключение неправильно.
Если такое соответствие имеет место, то рассуждение правильно, если же нет, то надо провести дальнейший анализ умозаключения. Для этого выделенную схему записывают на теоретико-множественном языке и с помощью кругов Эйлера изображают посылки, считая их истинными. Затем выясняют, всегда ли при этом истинно заключение. Если возможна ситуация, при которой заключение оказывается ложным, то умозаключение неправильно.
При решении задач другого типа требуется самостоятельно построить правильное умозаключение. В этих случаях надо ориентироваться на какую-либо из известных схем правильных умозаключений.
Образец выполнения заданий
Задание 10. Правильные и неправильные умозаключения
Задача. Правильно ли умозаключение: «Все студенты нашей группы закончили педучилище. Студентка b не закончила педучилище. Следовательно, она не учится в нашей группе».
Решение.
1 способ. Выделим логическую структуру умозаключения, для этого обозначим через А(х) предложение «х – студентка нашей группы», через В(х) – предложение «х – закончила педучилище». Тогда первая посылка имеет вид: А(х) В(х).
Тогда первая посылка имеет вид: А(х) В(х).
Вторая посылка: .
Заключение: , где b – данная студентка.
Полученная схема
является правилом отрицания. Следовательно, рассуждение правильно.
2 способ. Данное умозаключение запишем на теоретико-множественном языке.
Первая посылка. В ней утверждается, что множество (А) студентов группы является подмножеством множества (В) студентов, окончивших педучилище, т.е. что А Ì В.
Вторая посылка. Утверждается, что студентка b не заканчивала педучилище, т.е. что b ∉ В.
Заключение. Утверждается, что она не является студенткой группы, т.е. b ∉ А.
Схема умозаключения на теоретико-множественном языке имеет вид:
А Ì В, b ∉ В
b ∉ А
Изобразим посылки с помощью кругов Эйлера (рис. 5). Видим, что если А Ì В и b ∉ В, то при этом обязательно b ∉ А.
Рис. 5
Данная схема такова, что истинность посылок гарантирует истинность заключения. Значит, рассуждение правильное.
Варианты контрольной работы
Вариант 1
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2.Известно, что К – множество мальчиков класса, L – множество учащихся класса, занимающихся в кружке по рисованию. Сформулируйте условия, при которых: а) К∩L=Ø; б) К∩L=К.
3. Найти множество D = (A’∩ B) \ С, если А = (- ∞; 2), В = (0; 5], С = [3; 7)
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x N x ≤ 4},
Y = {y | y R y < 3}.
5.Из множества треугольников выделены подмножества прямоугольных, равнобедренных и тупоугольных треугольников. Произошло ли разбиение множества треугольников на классы?
6.Из 220 школьников 163 играют в баскетбол, 175 – в футбол, 24 не играют в эти игры. Сколько школьников одновременно играют в баскетбол и футбол?
7. Дайте определение прямоугольника, указав в качестве родового понятия понятие «четырехугольник», и выясните, являются ли прямоугольниками фигуры, изображенные на рисунке. Ответ обоснуйте.
8. Двуместный предикат P (x; y): «x + y = 11» определен на множестве А×А, где А = {4, 5, 6, 7}. Составьте таблицу значений этого предиката и укажите его множество истинности.
9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы разность двух чисел была четной, … , чтобы обе компоненты вычитания были четными».
10. Проверьте правильность рассуждения: «Во всяком прямоугольнике противоположные стороны равны. Четырехугольник ABCD – прямоугольник. Следовательно, его противоположные стороны равны».
Вариант 2
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2.Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) В∩А≠Ø;
б) ВÌА.
3.Найти множество P = A È (B’R \ C), если А = [0; 3), В = (-∞; 2) [5; +∞),
С = [4; 7).
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x R -2 < x ≤ 3},
Y = {y | y Z 0 < x < 4}.
5. Произведите разбиение на классы множества целых чисел, используя свойства «быть кратным 4» и «быть кратным 5».
6.Из 38 учащихся класса 24 занимаются в хоре и 15 в лыжной секции. Сколько учащихся занимается и в хоре, и в лыжной секции, если в классе нет учащихся, не посещающих занятий хора или лыжной секции?
7. Дайте определение прямоугольника, указав в качестве родового понятия «параллелограмм», выясните, являются ли прямоугольниками фигуры, изображенные на рисунке. Ответ обоснуйте.
8. На множестве X = {-3, -2, -1, 1, 2, 3, 4, 5, 6, 7, 8} заданы предикаты A(x): «x – отрицательное число», В(x): «x – четное число». Найти множество истинности предиката A(x) ˅ B(x).
9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы натуральное число делилось на 5, … , чтобы его десятичная запись оканчивалась цифрой 0».
10. Проверьте правильность рассуждения: «Если четырехугольник является прямоугольником, то его диагонали равны. В четырехугольнике ABCD диагонали равны. Следовательно, ABCD – прямоугольник».
Вариант 3
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2. Известно, что А – множество желтых цветов в вазе, В – множество роз в вазе. Сформулируйте условия, при которых: а) А∩В=Ø; б) АÈ В=А.
3.Найти множество X = A’R B C, если А = (-∞; 1), В = (0; 4),
С = [-3; 3).
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x Z -4 < x < 0},
Y = {y | y N y < 4}.
5.Укажите классы разбиения множества треугольников, которые получаются при рассмотрении таких свойств, как: «иметь хотя бы две равные стороны» и «иметь прямой угол».
6.Из 64 студентов на вопрос, занимаются ли они в свободное время спортом, утвердительно ответили 40 человек; любят ли они слушать музыку, 30 человек ответили утвердительно, причем 21 студент занимаются спортом и слушают музыку. Сколько человек не увлекается ни спортом, ни музыкой?
7. Дайте определение квадрата, указав в качестве родового понятия понятие «параллелограмм», и выясните, какие из фигур, изображенных на рисунке, являются квадратами, а какие – нет. Ответ обоснуйте.
8. На множестве X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} заданы предикаты A(x): «x – однозначное число», В(x): «x – четное число». Найти множество истинности предиката B(x) A(x).
9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы четырехугольник был ромбом, … , чтобы его диагонали были взаимно перпендикулярны».
10. Проверьте правильность рассуждения: «Все целые числа являются рациональными. Все рациональные числа – действительные. Следовательно, все целые числа – действительные».
Вариант 4
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2.Пусть А – множество студентов группы, закончивших педагогическое училище, D – множество отличников группы. Сформулируйте условия, при которых: а) А∩D≠Ø; б) DÌА.
3.Найти множество P = (A \ B) (C B), если А = [-3; 0), В = [-1; 2),
С = (-2; 1].
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x N -2 < x < 3},
Y = {y | y R 1 < y ≤ 4}.
5. Из множества четырехугольников выделили следующие подмножества: а) прямоугольников, не являющихся ромбами; б) ромбов, не являющихся прямоугольниками; в) квадратов; г) четырехугольников, не являющихся ни ромбами, ни прямоугольниками. Произошло ли разбиение множества четырехугольников на классы?
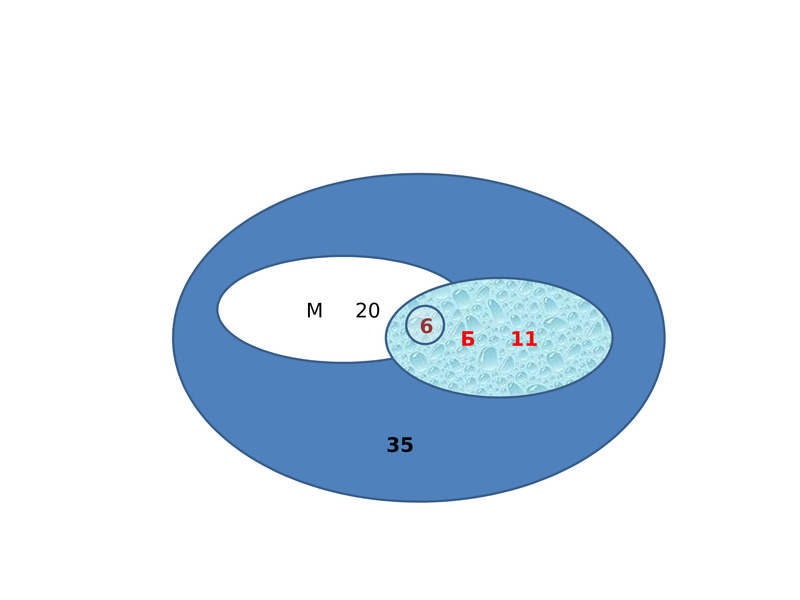
6. Среди 35 туристов одним английским языком владеют 11 человек, английским и французским – 5 человек. 9 человек не владеют ни английским, ни французским. Сколько человек владеет только французским языком?
7. Дайте определение параллелограмма и выясните, какие из фигур, изображенных на рисунке, являются параллелограммами, а какие – нет. Ответ обоснуйте.
8. На множестве X = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5} заданы предикаты A(x): «x – целое отрицательное число» и В(x): «x – четное число». Найдите множество истинности предиката А‾(x) Λ B(x).
9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы четырехугольник был ромбом, … , чтобы его диагонали были взаимно перпендикулярны и делились в точке пересечения пополам».
10. Проверьте правильность рассуждения: «Если число делится на 3, то сумма цифр в записи этого числа делится на 3. Число 25 не делится на 3. Следовательно, сумма цифр в записи числа не делится на 3».
Вариант 5
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2.Известно, что D – множество девочек класса, Е – множество учащихся класса, сидящих за первыми партами. Сформулируйте условия, при которых: а) D∩Е=Ø; б) D∩Е=Е.
3.Найти множество D = A B C’R, если А = [-3; 2), В = [0; 4],
С = (-∞; 2).
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x R -1 ≤ x < 4},
Y = {y | y R 1 ≤ y ≤ 3}.
5.Истинно ли высказывание: «Параллелограммы делятся на прямоугольники, ромбы и квадраты»? Почему?
6.Проведенное среди 50 школьников анкетирование показало, что в шахматы умеют играть 35 человек, в шашки – 40 человек, причем в обе игры умеют играть 21 человек. Сколько человек не умеет играть ни в шахматы, ни в шашки?
7. Дайте определение ромба, указав в качестве родового понятия понятие «параллелограмм», и выясните, какие из фигур, изображенных на рисунке, являются ромбами, а какие – нет. Ответ обоснуйте.
8. На множестве X = {1, 2, 3, … , 20} заданы предикаты A(x): «x – однозначное число» и В(x): «десятичная запись числа x не оканчивается цифрой 7». Найдите множество истинности предиката A(x) B(x).
9. Вместо многоточия вставьте слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы получилось истинное высказывание: «Для того чтобы сумма двух чисел была больше 20, … , чтобы хотя бы одно слагаемое было больше 10».
10. Проверьте правильность рассуждения: «Если число нечетное, то оно не делится на 2. Число 17 – нечетное. Значит, число 17 не делится на 2».
Вариант 6
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2. Проиллюстрируйте с помощью кругов Эйлера высказывания:
а) Некоторые четные натуральные числа кратны 7.
б) Все числа, делящиеся на 4, делятся на 2.
3.Найти множество X = (A B’R) \ C, если А = [6; 9), В = (- ∞; 7) [11; +∞), С = [8; 12].
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x R x < 3},
Y = {y | y R – 1 ≤ y ≤ 2}.
5.На множестве геометрических фигур плоскости выделены подмножества фигур, имеющих: а) центр симметрии; б) ось симметрии и в) не имеющих ни центра, ни оси симметрии. Можно ли считать, что произошло разбиение множества геометрических фигур на классы?
6.В группе туристов, состоящей из 100 человек, 10 человек не знали ни немецкий, ни французский языки, 75 знали немецкий, 83 знали французский. Сколько туристов знали два языка?
7. Дайте определение равностороннего треугольника. Используя данное определение, выясните, правильны ли следующие обоснования:
а) ABC – равносторонний, так как АВ = ВС;
б) DEF не является равносторонним, так как DE EF.
8. На множестве X = {-3, -2, -1, 0, 1, 2, 3, 4, 5} заданы предикаты С(x): «x – положительное число» и D(x): «x(x + 2) = 0». Найдите множество истинности предиката С(x) \/ D(x).
9. Дана теорема: «В любом ромбе диагонали взаимно перпендикулярны».
А. Переформулируйте данную теорему, используя слова «следует», «достаточно».
Б. сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.
10.Проверьте правильность рассуждения: «Все прямоугольники являются параллелограммами. Во всех параллелограммах противоположные стороны равны. Следовательно, в любом прямоугольнике противоположные стороны равны».
Вариант 7
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2. Проиллюстрируйте с помощью кругов Эйлера высказывания:
а) Ни один параллелограмм не является трапецией.
б) Любой квадрат является ромбом.
3.Найти множество D = (A’R B) C, если А = [-1; 4), В = (3; 6],
С = [-5; 0].
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x Z -4 < x ≤ -1},
Y = {y | y R y ≥ -2}.
5.Произведите разбиение множества целых чисел на классы, используя свойства «быть однозначным числом» и «быть двузначным числом».
6. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском языке, двое – только на немецком. Сколько человек говорят на двух языках – французском и немецком?
7. Сформулируйте определение равнобедренного треугольника и на его основе выясните, правильны ли следующие обоснования:
а) ABC не является равнобедренным, так как АВ ВС;
б) DEF является равнобедренным, так как EF = FD.
Ответы обоснуйте.
8. На множестве X = {1, 2, 3, 4, …, 15} заданы предикаты P(x): «число x – простое» и Q(x): «число x оканчивается цифрой 5». Найти множество истинности предиката Pˉ(x) \/ Q(x).
9. Дана теорема: «Если каждое слагаемое делится на данное число, то и сумма делится на данное число».
А. Переформулируйте данную теорему, используя слова «следует», «достаточно», «необходимо».
Б. сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.
10. Закончите умозаключение, используя правило заключения: «В любом прямоугольнике сумма внутренних углов равна 360 . В четырехугольнике ABCD …». Ответ обоснуйте.
Вариант 8
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2. Проиллюстрируйте с помощью кругов Эйлера высказывания:
а) Каждое из чисел, запись которого оканчивается цифрой 0, делится на 5.
б) Ни одно число, запись которого оканчивается цифрой 3, не делится на 6.
3.Найти множество P = (A B) \ (C B), если А = [-1; 2], В = [-5; 0),
С = [-3; 1).
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x R x > -3},
Y = {y | y N -2< y ≤ 3}.
5. Укажите, какие классы разбиения получаются при рассмотрении на множестве треугольников таких свойств: «иметь тупой угол» и «все углы острые».
6. Даны 40 чисел. Из них 10 чисел кратны 3, 15 чисел кратны 2, 20 чисел не кратны ни 2, ни 3. Сколько среди данных 40 чисел, кратных 6?
7. Соразмерны ли следующие определения:
а) биссектриса угла – это луч, делящий угол пополам;
б) равнобедренный треугольник – это треугольник, у которого хотя бы две стороны равны.
Ответы обоснуйте.
8. Двуместный предикат P (x, y): «x y» определен на множестве А × В, где А = {4, 8, 9, 10, 12, 13}, В = {2, 3, 4}. Составьте таблицу значений этого предиката и определите его множество истинности.
9. Сформулируйте признак делимости на 5, используя слова «тогда и только тогда, когда», «необходимо и достаточно». Выясните, какая из теорем выражает необходимый, а какая – достаточный признак делимости на 5:
А. Если число делится на 5, то его десятичная запись оканчивается цифрой 0 или 5.
Б. Если десятичная запись числа оканчивается цифрой 0 или 5, то число делится на 5.
10. Закончите умозаключение, используя правило заключения: «Если сумма цифр в записи числа делится на 9, то и само число делится на 9. В записи числа 3591 …». Ответ обоснуйте.
Вариант 9
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2. Проиллюстрируйте с помощью кругов Эйлера высказывания:
а) Все квадраты являются четырехугольниками.
б) Некоторые равнобедренные треугольники являются прямоугольными.
3.Найти множество X = A’R \ (B C), если А = (-∞; 1), В = [1; 4),
С = (2; 5).
4. Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x R 2 < x ≤ 6},
Y = {y | y R 1 ≤ y < 7}.
5.Произведено ли разбиение множества натуральных чисел на классы, если из него выделены подмножества чисел, делящихся на 3, и чисел, которые при делении на 3 дают остаток 1?
6.В школе 67 второклассников. Из них 36 занимаются гимнастикой, 52 – плаванием, а 4 учащихся освобождены от занятий физкультурой. Сколько учащихся занимаются и гимнастикой, и плаванием?
7. Соразмерны ли следующие определения:
а) ромбом называется четырехугольник, у которого все стороны равны;
б) прямоугольником называется ромб с прямым углом?
Ответы обоснуйте.
8. На множестве X = {-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} заданы предикаты С(x): «число x кратно 3» и D(x): «x2 + x – 2 = 0». Найти множество истинности предиката C‾(x) D(x).
9. Сформулируйте признак делимости на 3, используя слова «тогда и только тогда, когда», «необходимо и достаточно». Сформулируйте теоремы, выражающие необходимый, достаточный признак делимости на 3.
10. Закончите умозаключение, используя правило отрицания: «Во всяком прямоугольнике сумма внутренних углов равна 360 . В четырехугольнике ABCD …». Ответ обоснуйте.
Вариант 10
1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.
2. Проиллюстрируйте с помощью кругов Эйлера высказывания:
а) Все мальчики 5 «А» класса участвовали в туристическом походе.
б) Ни один мальчик 5 «А» класса не является неуспевающим учеником.
3.Найти множество D = (A B’R) \ C, если А = [-4; 6), В = [3; 7), С = [2; 5].
4.Изобразите на координатной плоскости элементы множества X×Y, если:
X = {x | x R 1 ≤ x < 6},
Y = {y | y N -5 < y < 3}.
5.Множество треугольников разбито на три класса: равносторонних, прямоугольных и треугольников, не являющихся ни равносторонними, ни прямоугольными. Какие два свойства лежат в основе этой классификации?
6.В школе 67 второклассников. Из них 36 занимаются гимнастикой, 52 – плаванием, а 4 учащихся освобождены от занятий физкультурой. Сколько учащихся не занимаются гимнастикой?
7. Укажите, какие из сформулированных ниже определений избыточны, укажите, какие свойства являются следствиями остальных.
а) треугольником называется многоугольник, имеющий три стороны и три угла;
б) параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны и равны.
8. Двуместный предикат P (x, y): «x + y ≤ 7» определен на множестве
А × А, где А = {2, 3, 4, 5}. Составить таблицу значений и указать область истинности этого предиката.
9. Дана теорема: «Если наклонные, проведены из одной точки к одной и той же прямой, равны, то равны и их проекции».
А. Переформулируйте данную теорему, используя слова «следует», «достаточно», «необходимо».
Б. Сформулируйте теорему, равносильную данной, в соответствии с законом контрапозиции.
10. Закончите умозаключение, используя правило отрицания: «Если сумма цифр в записи числа делится на 9, то и само число делится на 9. Число…».
Ответ обоснуйте.
«Пересечение и объединение множеств» презентация к уроку по математике (3 класс) на тему с помощью кругов Эйлера
Множества.
Операции над множествами
МНОЖЕСТВО
НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
«Множество есть многое, мыслимое нами как единое»
основатель теории множеств
Георг Кантор
Понятия теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие «множество» можно определить так:
- Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
НАБОР КАРАНДАШЕЙ
КОЛЛЕКЦИЯ МАРОК
СТАЯ ПТИЦ
СТАДО КОРОВ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
Множество – совокупность объектов, объединенных по какому–нибудь признаку.
Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество, называются элементами множества.
множество
элемент
Трапеция, параллелограмм, ромб, квадрат, прямоугольник
Шар, прямоугольный параллелепипед, призма, пирамида, октаэдр
Натуральные числа
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные числа
Множество четырехугольников
Пространственные тела
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
Квадраты чисел
Цифры десятичной системы счисления
10, 12, 14, 16 … 96, 98
множество людей на Солнце
множество прямых углов равностороннего треугольника
множество точек пересечения двух параллельных прямых
Пустое множество- множество, не содержащее ни одного элемента.
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I — множество иррациональных чисел;
R – множество действительных чисел.
ВИДЫ МНОЖЕСТВ
Запишите множества букв слов
КОНИ И КИНО
{
К, О, Н, И
}
{
К, И, Н, О
}
Равные множества
ВИДЫ МНОЖЕСТВ
А = {2; 3; 5; 7; 11; 13};
Конечные множества
ВИДЫ МНОЖЕСТВ
{1; 4; 9; 16; 25; …};
{10; 20; 30; 40; 50; …};
Бесконечные множества
Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1
Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
Охарактеризуйте множество А:
а) А = {1, 3, 5, 7, 9};
б) А = {- 2, — 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
Даны множества:
М = {5, 4, 6},
Р = {4, 5, 6},
Т = {5, 6, 7},
S
= {4, 6}.
Какое из утверждений неверно?
а) М = Р б) Р ≠
S
в) М ≠ Т г) Р = Т
Пусть А
— множество простых чисел вида
7n + 2, где n ∈ N.
Верна ли запись -5 ∈ А.
1. В множестве {лев; лисица; гиена; слон; рысь} все
элементы, кроме одного, обладают некоторым свойством.
а) опишите это свойство; б) найдите элемент, не обладающий этим свойством; в) назовите еще два элемента, обладающие этим свойством. 2. Назовите 5
подмножеств в множестве всех цветов радуги.
3. Каким свойством в
множестве ромбов выделяется подмножество квадратов?
Пример: 8 и 32
БЛИЦ-ОПРОС
- земноводные, млекопитающие, хладнокровные и т.п.
Какие названия применяются для обозначения множеств животных?
БЛИЦ-ОПРОС
- рота, взвод, полк, дивизия и т.п.
Какие названия применяются для обозначения множеств военно-служащих?
БЛИЦ-ОПРОС
Как называется множество цветов, стоящих в вазе?
БЛИЦ-ОПРОС
Как называется множество точек земной поверхности, равноудаленных от обоих полюсов?
БЛИЦ-ОПРОС
- деревня, село, город, посёлок
Как называется множество населённых людьми мест?
БЛИЦ-ОПРОС
- выставка, галерея
Как называется множество картин?
БЛИЦ-ОПРОС
Как называется множество документов?
БЛИЦ-ОПРОС
- флотилия, эскадра
Какие названия применяют для обозначения множеств кораблей?
А – четные натуральные числа В – двузначные числа
Найти объединение этих множеств.
А В – быть четным натуральным или двузначным числом
Пример: 8 и 32
А – четные натуральные числа В – двузначные числа
Найти пересечение этих множеств.
А В – быть четным натуральным и двузначным числом
Пример: 32
Даны множества:
А = {2; 3; 8},
В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
Даны множества:
А = {
a
,
b
,
c
,
d
},
B
= {
c
,
d
,
e
,
f
},
C
= {
c
,
e
,
g
,
k
}.
Найдите: (АUВ)UС.
Даны множества:
А – множество всех натуральных чисел, кратных 10,
В = {1; 2; 3;…, 41}.
Найдите А∩В.
Решение задачи
с помощью кругов Эйлера
Леона́рд Э́йлер
— швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
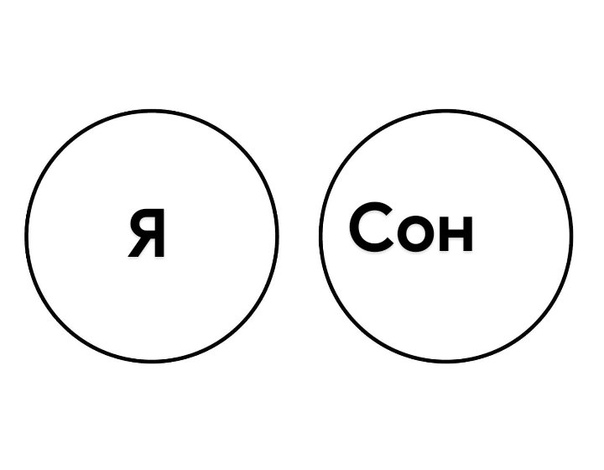
В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
танцуют 19
17+19=36, всего 30
Решение
Пусть А — это множество учеников, умеющих петь. Количество элементов в нём по условию равно n = 17. Пусть В — множество учеников, умеющих танцевать. Количество элементов в нём — m = 18. Множество совпадает со всем классом, т.к. каждый ученик в классе поёт или танцует. — это множество тех учеников класса, которые поют и танцуют одновременно. Пусть их количество равно k .
Согласно формуле доказанной выше
n + m- k = 17+ 19- k = 30 k = 6.
Ответ: 6 учеников в классе поют и танцуют одновременно.
На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек в фирме не знают ни английского, ни немецкого языков?
Немецкий 35
Английский 47
Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Немецкий 27
Английский 25
Только немецкий
Только английский
Ответ: в классе 34 ученика
Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А
U
В?
Объединение содержит 9 элементов
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
Всего: 14 + 13 + 62 =89
На школьной спартакиаде каждый из 25 учеников 9 –го
класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?
В воскресенье 19 учеников нашего класса побывали в
планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион — 3; цирк и стадион — 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
МНОЖЕСТВО
НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА-ВЕННА
РЕШАТЬ ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ ИМЕЮЩИХСЯ ЗНАНИЙ
Сенина Г.Н., Сенин В.Г., МБОУ «СОШ №4», г.Корсаков
МНОЖЕСТВА. КОМБИНАТОРИКА.
ПЕРЕСЕЧЕНИЕ И ОБЪЕДИНЕНИЕ МНОЖЕСТВ.
Метапредмет – Знание
Цель нашего урока
В рассказе Конан Дойля «Пять апельсиновых зернышек» знаменитый сыщик Шерлок Холмс должен был установить название одного парусника. Об этом судне он знал лишь то, что в январе 1883 г. Оно было в Пондишире, в январе 1885 г. – в Данди, а сейчас стояло в Лондоне. Сравнив списки парусников, находившихся в указанное время в указанных местах, Шерлок Холмс установил, что только американское судно «Одинокая звезда» входило в каждый из них. В результате преступление было раскрыто. Сыщик, имея три множества, построил новое, содержащее их общие элементы. Оказалось, что новое множество состоит всего из одного элемента
целеполагание
Проверим домашнее задание
УЧЕБНИК
№
747
УЧЕБНИК
№
749
P
⊂ N
⊂ Z ; C
⊂ B
⊂ A; K
⊂ P
⊂ R
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Пересечение и объединение множеств
Организация и самоорганизация учащихся. Организация обратной связи
Работаем с текстом
ТРЕНАЖЕР
№
319
в каждое из данных множеств
Практикум
Работаем с текстом
ТРЕНАЖЕР
№
320
Практикум
Работаем с моделями
ТРЕНАЖЕР
№
323
Практикум
Работаем с моделями
ТРЕНАЖЕР
№
324
Практикум
Операции над множествами
ЗАДАЧНИК
№
638
ЗАДАЧНИК
№
639
Практикум
Операции над множествами
ЗАДАЧНИК
№
641
{-1,0,1}; {-5,-4,-3,-2,-1,0,1,2}
{-1,0}; {-4,-3,-2,-1,0,1}
{1}; {-2,-1,0,1,2,3,4}
{-1,0,1}; {-2,-1,0,1,2}
Практикум
Операции над множествами
УЧЕБНИК
№
757
Свойства нуля при умножении и сложении чисел: А ⋅ 0 = 0; А + 0 = А.
Практикум
Операции над множествами
УЧЕБНИК
№
758
Операции над множествами
№
760
УЧЕБНИК
Проверка полученных результатов. Коррекция
Множества и жизнь
Множество – это фундаментальное понятие не только математики, но и всего окружающего мира.
Возьмите прямо сейчас в руку любой предмет. Вот вам и множество, состоящее из одного элемента.
Возьмите большой пакет и начните наобум складывать в него различные предметы.
В этом нет никакой закономерности, но, тем не менее, речь идёт о множестве предметов.
Домашнее задание
У: стр. 228 – 229, фрагмент 1 – читать;
№ 751, 752, 756, 759.
Подведение итогов, рефлексия, домашнее задание.
- Множество натуральных чисел – это…
- Множество учащихся 8 класса – это…
- Множество не положительных и неотрицательных чисел – это…
1.Пересечение множеств
А={1,2,3,4,6,8,12,24},
В={1,2,3,6,9,18},
С- множество общих делителей чисел 24 и 18,
Говорят, что множество С является пересечением множеств А и В.
- Множество, составляющее общую часть множеств А и В, называют пересечением этих множеств и обозначают так: А∩В=С.
- Соотношение между множествами А,В и С можно проиллюстрировать с помощью специальных схем, называемых кругами Эйлера.
Фигура, образовавшаяся при пересечении кругов, закрашенная на рисунке, изображает множество С.
Замечание.
Некоторые множества Х и Y не имеют общих элементов. Тогда говорят, что пересечением множеств Х и Y является пустое множество.
Ø — обозначение пустого множества.
И пишут тогда так: Х∩ Y = Ø
Например:
2.Объединение множеств
А- множество натуральных делителей числа 24,
В- множество натуральных делителей числа 18.
А={1,2,3,4,6,8,12,24},
В={1,2,3,6,9,18},
D- множество, которому принадлежат все элементы множества А и все элементы множества В.
Т.е. D ={1,2,3,4,6,8,9,12,18,24}.
Говорят, что множество
D
является объединением множеств А и В.
Множества А и В изображены на рисунке кругами.
Фигура, закрашенная на рисунке, является объединением множеств А и В.
Например:
Х-множество простых чисел, не превосходящих 25;
Y- множество двузначных чисел, не превосходящих 19.
Найдите пересечение и объединение множеств Х и Y .
X={2, 3, 5, 7, 11, 13, 17, 19, 23};
Y={10,11,12,13,14,15,16,17,18};
Общие элементы: 11,13,17, значит,
X∩ Y ={11,13,17};
X UY ={2, 3, 5, 7,10,11,12,13,14,15, 16,17,18,19,23}.
- Решить в классе
- № 799
- Решить дома
- № 800
Пересечение и объединение множеств.
Кунделева Оксана Евгеньевна
Учитель начальных классов МБОУ НОШ №279
г. Гаджиево, Мурманской области,
Цели занятия
- формировать представление об объединении и пересечении двух множеств
- учить находить на «карте множеств» область множества, которое является пересечением или объединением двух множеств
- учить определять принадлежность элементов множеству, которое является пересечением и объединением двух множеств
- учить определять характер отношений между двумя заданными множествами (пересечение, не пересекаются, объединение)
Что такое множество?
Множество
— это группа предметов, объектов или существ.
Назовите элементы множества:
- “Месяцы года”
- “Времена года”
- “Материки”
- “Летающие бегемоты”
- Многоугольники
Летучая мышь ворона пингвин
Бабочка синица страус
Прочитайте названия птиц. Обведите это множество. Сделайте надпись внизу: “Птицы”.
Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”.
умеют летать
Сколько элементов оказалось на пересечении двух множеств
, т.е. одновременно в двух множествах? Почему?
Пересечение множеств
общая часть множеств
«И»
,
то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ
двух множеств –
жить одновременно в двух странах
.
Объединение множеств
Если в названии множества есть слово «ИЛИ»
,
то элемент может быть в любом месте на территории двух стран — ОБЪЕДИНЕНИИ
—
жить хотя бы в одной из них.
Что такое подмножество?
Подмножество
– это
часть множества, входящее в данное множество.
Физкультминутка
Раз – согнуться, разогнуться,
Два – нагнуться, потянуться,
Три – в ладоши три хлопка,
Головою три кивка.
На четыре руки шире,
Пять, шесть – тихо сесть,
Семь, восемь – лень отбросим.
Начерти множества:
Множество обитателей моря
Множество млекопитающих
Начерти множества:
Множество птиц
Множество рыб
В квадрате живут чётные числа. В треугольнике живут двузначные числа. Впиши правильно каждое число. Закрась на рисунке область, где живут чётные двузначные числа.
2, 47, 16, 8, 17, 32, 6, 53
Найди обозначение каждого множества в таблице и закрась круги на рисунке.
Сколько множеств обозначено кругами?
Какое множество самое большое?
Каким цветом нужно закрасить самый большой круг?
Какое самое большое из оставшихся?
Множества:
животных
Растений
Найди и расположи элементы множеств в фигурах на рисунке: впиши первую букву каждого слова из списка
Запомни!
- Множества не пересекаются
Множества не пересекаются:
- Одно множество является подмножеством другого
Одно множество является подмножеством другого:
Множества пересекаются:
Множества объединяются:
До встречи на
следующем уроке!!!
А.В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., «Баллас», 2004
- А.В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., «Баллас», 2004
- А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., «Баллас», 2004
- http://festival.1september.ru/articles/505635/
Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна,
учитель начальных классов
Используемая литература
Презентация по теме «Пересечение и объединение множеств» (факультатив «Наглядная геометрия» (3 класс).
Использование информационных технологий не только оживило учебный процесс (что особенно важно, если учитывать психологические особенности младшего школьного возраста, в частности длительное преобладание наглядно-образного мышления над абстрактно-логическим), но и повысило мотивацию обучения на занятии.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Пересечение и объединение множеств. Кунделева Оксана Евгеньевна Учитель начальных классов МБОУ НОШ № 279 г. Гаджиево, Мурманской области, 2012 г.
Цели занятия формировать представление об объединении и пересечении двух множеств учить находить на «карте множеств» область множества, которое является пересечением или объединением двух множеств учить определять принадлежность элементов множеству, которое является пересечением и объединением двух множеств учить определять характер отношений между двумя заданными множествами (пересечение, не пересекаются, объединение)
Что такое множество? Множество — это группа предметов, объектов или существ.
Назовите элементы множества: “Месяцы года” “Времена года” “Материки” “Летающие бегемоты” Многоугольники
Оса Летучая мышь ворона пингвин Бабочка синица страус воробей Прочитайте названия птиц. Обведите это множество. Сделайте надпись внизу: “Птицы”. ПТИЦЫ Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”. умеют летать Сколько элементов оказалось на пересечении двух множеств, т.е. одновременно в двух множествах? Почему?
Пересечение множеств общая часть множеств Если в названии множества есть слово «И» , то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств – жить одновременно в двух странах. !
Объединение множеств Если в названии множества есть слово «ИЛИ» , то элемент может быть в любом месте на территории двух стран — ОБЪЕДИНЕНИИ — жить хотя бы в одной из них. ! ! ! !
Что такое подмножество? Подмножество – это часть множества, входящее в данное множество.
Физкультминутка Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим.
Множество обитателей моря Множество млекопитающих Начерти множества:
Начерти множества: Множество птиц Множество рыб
В квадрате живут чётные числа. В треугольнике живут двузначные числа. Впиши правильно каждое число. Закрась на рисунке область, где живут чётные двузначные числа. 2, 47, 16, 8, 17, 32, 6, 53 2 47 16 8 17 32 53 6
Найди обозначение каждого множества в таблице и закрась круги на рисунке. Множества: прямоугольников четырёхугольников многоугольников квадратов Сколько множеств обозначено кругами? Какое множество самое большое? Каким цветом нужно закрасить самый большой круг? Какое самое большое из оставшихся?
Множества: животных Зверей Рыб Птиц Растений Чайка Лиса Айсберг Жираф Сосна Река Тюльпан Муравей Камбала Найди и расположи элементы множеств в фигурах на рисунке: впиши первую букву каждого слова из списка
Ч К М Т Р С Ж А Л
Запомни! Множества не пересекаются Множества не пересекаются: Одно множество является подмножеством другого Одно множество является подмножеством другого: Множества пересекаются: Множества объединяются:
До встречи на следующем уроке!!!
А.В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., « Баллас », 2004 А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., « Баллас », 2004 http://festival.1september.ru/articles/505635/ Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна, учитель начальных классов Используемая литература
Протокол № 2 от «15» октября 2008 г.
Рекомендовано в качестве дидактического материала для студентов.
© Феодосийская финансово-экономическая академия
Содержание
Круги Эйлера: отношения между понятиями.
Примеры решения задач ……………………..………………………..3
Задачи для самостоятельного решения:
Задание 1..……………………………………………..…………………6
Задание 2 …………………..……………………………………………10
Задание к семинарскому занятию. Понятие. Вариант 1 ………….…..24
Задание к семинарскому занятию. Понятие. Вариант 2 ……………..26
Задание к семинарскому занятию. Понятие
(дополнительное)………………………………………………………..28
Задание к семинарскому занятию. Суждение.
Заполните таблицу №1………………………………………………….29
Задание к семинарскому занятию. Суждение.
Заполните таблицу №2…………………………………………. ..…….31
Задание к семинарскому занятию. Суждение.
Заполните таблицу №3…………………………………….………….…33
Задание к семинарскому занятию. Умозаключение……….………….35
Задания со стр. 6-24 сделать самостоятельно и принести на последнее семинарское занятие.
Задания со стр. 24 распечатать и приносить на каждое семинарское занятие.
Круги Эйлера:
Отношения между понятиями
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
П р и м е р 1. Представьте с помощью круговой схемы отношения между следующими понятиями:
Игрушка (А), заводная игрушка (В), кукла (С), заводной автомобиль (D), пистолет (E).
Ответ:
П р и м е р 2. Представьте с помощью круговой схемы отношения между следующими понятиями:
Молния (А), поджог (В), причина пожара (С), пожар (D), взрыв атомной бомбы (Е).
Ответ:
П р и м е р 3. Представьте с помощью круговой схемы отношения между следующими понятиями:
Планета (A), планета Солнечной системы (B), Земля (C), спутник ( D), искусственный спутник (E), Луна (F), небесное тело (G).
Ответ:
П р и м е р 4. Найдите понятия, отношения между которыми удовлетворяли бы приведенной круговой схеме:
Ответ:Стихийное бедствие (А), землетрясение (В), явление природы (С), наводнение (D), гроза (Е).
П р и м е р 5. Найдите понятия, отношения между которыми удовлетворяли бы приведенной круговой схеме:
Ответ:Пожар (А), молния (В), явление природы (С), стихийное бедствие (D).
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задание 1. Составьте с помощью круговых схем отношения между следующими понятиями:
По номеру в списке, студент выполняет по 10 заданий:1-й — с 1 по 10, 2-й –с 11 по 21, и т.д.
1.1. Автобус, маршрутное такси, такси, трамвай, троллейбус, городской транспорт.
1.2.. Автомобиль, легковой автомобиль, грузовой автомобиль, мотор автомобиля.
1.3. Автор романа «Красное и чёрное», автор романа «Пармская обитель».
1.4. Адмирал, английский адмирал, русский адмирал, адмирал Ушаков, адмирал Нельсон.
1.5. Акционерное общество, член АО, председатель правления АО, Петров.
1.6. Атом, ядро, протоны, нейтроны, электроны.
1.7. Юрист, прокурор, адвокат, судья, защитник, преступник.
1.8. Вещество, молекула, атом, ядро, электрон, протон, нейтрон.
1.9. Водоплавающее животное; рыба; животное, дышащее жабрами; кит; акула; треска.
1.10. Юрист, адвокат, следователь, прокурор, мастер спорта.
1.11. Вуз, университет, академия, институт, техникум, профтехучилище, средняя школа.
1.12. Глубокое озеро, мелкое озеро.
1.13. Годовщина, день рождения, юбилей.
1.14. Город, европейский город, город в Европе, столица Украины, город с самым большим населением в Украине, деревня.
1.15. Город, столичный город, нестоличный город, улица города.
1.16. Государство, общество, страна.
1.17. Грабёж, кража, разбой.
1.18. Громкая речь, негромкая речь.
1.19. Гуманитарная наука, этика, эстетика.
1.20. Дед, отец, сын, внук.
1.21. Дед, сын, брат, мужчина, отец, внук, дядя, племянник.
1.22. Деревянный стул, стул, предмет мебели, предмет.
1.23. Деяние, наказуемое деяние; ненаказуемое деяние.
1.24. Деяние, преступление, хозяйственное преступление, обман покупателей.
1.25. Движение, быстрое движение, вращение.
1.26. Диван, мебель, диван-кровать, кровать.
1.27. Документ, завещание, удостоверение личности, паспорт, доверенность, доверенность на право совершения сделки.
1.28. Естественный спутник какого-нибудь небесного тела, спутник Земли, небесное тело, спутник Марса, спутник какого-нибудь небесного тела, искусственный спутник какого-нибудь небесного тела.
1.29. Женщина, врач, мужчина, пациент.
1.30. Жиры, твёрдые жиры, жидкие жиры, растительные жиры, животные жиры, рыбий жир, кокосовое масло, сливочное масло, подсолнечное масло.
1.31. Законная сделка, незаконная сделка, неправомерные действия.
1.32. Известный футболист, футболист, негр, китаец.
1.33. Историк, отечественный историк, доцент.
1.34. Каменный дом, трёхэтажный дом, одноэтажный дом, недостроенный дом.
1.35. Капитан, майор, офицер.
1.36. Картина, реалистическая картина, сюрреалистическая картина, картина Репина, картина Дали.
1.37. Книга, словарь, энциклопедия, философская энциклопедия, словарь по логике, автор словаря по логике.
1.38. Корень квадратный из 4; чётное число; нечётное число; корень квадратный из 9; число, деление на которое даёт то же число; число, на которое не делится никакое число; корень квадратный из 1.
1.39. Кража автомашин, кража, хищение, преступление, деяние.
1.40. Кража, мошенничество, разбой, преступление, преступность.
1.41. Лето, наиболее тёплое время года, время года, время.
1.42. Мать, дочь, женщина, бабушка, внучка, сестра.
1.43. Медицинский препарат, лекарство, лекарство, лекарство в таблетках, анальгин.
1.44. Междугородний телефон, телефон, телефонный разговор, средство связи.
1.45. Мужество, упорство, упрямство.
1.46. Мысль, понятие, суждение, рассуждение, умозаключение.
1.47. Нагревательный электрический прибор, нагревательный элемент, лампа накаливания, утюг, электроплитка, кипятильник, спираль.
1.48. Областной суд, городской суд, суд.
1.49. Океан, море, суша.
1.50. Окружность; геометрическое место точек, равноудалённых от одной точки; полусфера; дуга окружности; сфера.
1.51. Олимпийский чемпион, чемпион мира, бегун.
1.52. Орудие преступления, огнестрельное оружие, пистолет.
1.53. Отделение милиции, подразделение органов внутренних дел, орган внутренних дел, главное управление внутренних дел.
1.54. Отец, сын, мужчина, дед, внук, брат.
1.55. Отец; человек, имеющий двоих детей; человек, имеющий одного ребенка; человек, имеющий детей.
1.56. Первый этаж, последний этаж, второй этаж, пятый этаж.
1.57. Переводчик; человек, свободно владеющий иностранным языком; человек, свободно владеющий французским языком; человек с высшим образованием.
1.58. Пересуды, сплетни.
1.59. Печать, телевидение, средства массовой информации, газеты, журналы.
1.60. Писатель, журналист, учёный, человек.
1.61. Писатель, русский писатель, автор романа «Тихий Дон», М.А.Шолохов.
1.62. Писатель, украинский писатель, Николай Гоголь.
1.63. Пистолет, оружие, орудие, патроны, огнестрельное оружие.
1.64. Планета; астероид; комета; планета Солнечной системы; планета Солнечной системы, имеющая атмосферу; Земля; спутник Земли.
1.65. Планета, планета Солнечной системы, Земля, спутник, искусственный спутник, Луна, небесное тело, Марс, Юпитер, спутник Юпитера.
1.66. Плоская замкнутая геометрическая фигура, треугольник, прямоугольник, квадрат, прямоугольный треугольник.
1.67. Полководец, древнегреческий полководец, древнеримский полководец, Александр Македонский, Цезарь, русский полководец, Александр Суворов, Ганнибал.
1.68. Пожар, причина пожара, взрыв атомной бомбы, поджог.
1.69. Пожар, причина пожара, пожар на Останкинской башне, возгорание электропроводки.
1.70. Понятие, абстрактное понятие, общее понятие, конкретное понятие, единичное понятие, положительное понятие.
1.71. Посягательство на честь и достоинство личности, клевета, оскорбление.
1.72. Поэт; русский поэт: русский поэт XIX века; русский поэт XIX века, родившийся в Москве; Лермонтов.
1.73. Предмет изучения, учебный предмет, логика, раздел логики.
1.74. Президент, глава государства, президент Российской Федерации, президент Татарстана, президент фирмы, монарх, президент университета.
1.75. Преподаватель, преподаватель вуза, преподаватель техникума, ассистент, старший преподаватель, доцент, профессор.
1.76. Преступление, должностное преступление, халатность, получение взятки.
1.77. Преступление, хозяйственное преступление, должностное преступление.
1.78. Преступление против личности, преступление против жизни, преступление против здоровья.
1.79. Преступление, терроризм, спекуляция.
1.80. Преступники, преступная группа, организованная преступная группа, банда.
1.81. Простое предложение, сложное предложение, предложение, придаточное предложение.
1.82. Прямоугольник, ромб, квадрат.
1.83. Рабочий, коммунист, член КПУ.
1.84. Равносторонний прямоугольник, квадрат, равноугольный ромб.
1.85. Растение, животное, организм.
1.86. Река Нил, самая длинная река в мире.
1.87. Республика, монархия, форма правления, президентская республика, парламентарная республика, автократия.
1.88. Украинский студент, студент – юрист, студент ФФЭА.
1.89. Русский писатель, дореволюционный писатель, советский писатель, Горький, Шолохов, Достоевский, Г. Баширов.
1.90. Самолёт, реактивный самолёт, реактивный двигатель.
1.91. Свидетель происшествия, виновник происшествия, водитель автомобиля, пешеход.
1.92 Сержант, лейтенант, генерал, артиллерист.
1.93. Скрипка, рояль, барабан, виолончель, музыкальный инструмент.
1.94. Слово, изменяющееся по лицам; слово, изменяющееся по падежам; спрягаемое слово; глагол; прилагательное; наречие; существительное.
1.95. Спутник планеты, естественный спутник Земли, «Союз-4», спускаемый аппарат «Венера-14», Юпитер, спутник Юпитера, Луна.
1.96. Студент, волонтёр, спортсмен, студент ФФЭА, студент экономического факультета.
1.97.Студент-заочник, милиционер, токарь.
1.98. Студент, отличник, двоечник, спортсмен.
1.99. Студент, сдавший все экзамены на «отлично»; студент, сдавший, по крайней мере, один экзамен на «отлично»; студент, сдавший, по крайней мере, один экзамен на «хорошо».
1.100.Тень, полутень, полная тень.
1.101.Угол, угол падения, угол отражения.
1.102.Университет, высшее учебное заведение, учебное заведение, школа, школа № 3 г.Феодосии.
1.103.Уравнение; уравнение с целочисленным решением; уравнение, не имеющее решения; уравнение с решением в рациональных числах.
1.104.Учебник, новый учебник, книга, печатное издание.
1.105.Учёный, историк, доктор исторических наук.
1.106.Учёный, юрист, общественный деятель, диплом юриста.
1.107.Футболист, спортсмен, баскетболист, человек, негр
1.108.Хозяйственное преступление; обман покупателей; незаконное изготовление спиртных напитков.
1.109.Час, минута, секунда.
1.110. Часть основы слова, корень, суффикс, окончание.
1.111.Человек, личность, индивид.
1.112.Человек, мужчина, женщина, ребёнок.
1.113.Число; четное число; нечетное число, простое число; число 2; число, делящееся на 4; число, делящееся на 8.
1.114.Число, числитель, знаменатель, дробь.
1.115.Школьник, студент, учащийся.
1.116.Экономика, рыночная экономика, командная экономика.
1.117.Экономическая культура, политическая культура, духовная культура, социальная культура.
1.118.Элементарная частица, электрон, протон.
1.119.Эрудиция, невежество.
Задание 2. Запишите понятия, отношения между которыми удовлетворяли бы приведенным круговым схемам:
Каждый студент выполняет по 5 заданий.
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
2.11.
2.12.
.
2.13.
2.14.
2.15.
2.16.
2.17.
2.18.
2.18.
2.19.
2.20.
2.21.
2.22.
2.23.
2.24.
2.25.
2.26.
2.27.
2.28.
2.29.
2.30.
2.31.
2.32.
2.33.
.
2.34.
2.35.
2.36.
Задание к семинарскому занятию 1. Понятие.Вариант 1 (четные номера по списку в журнале)
1. Найдите понятие, к которому можно было бы отнести следующие признаки:
холодное, мрачное, серое;
теплое, долгожданное, скоротечное, многообещающее.
2. Дайте характеристику признаков, включенных в содержание следующих понятий:
Слово – единица языка, служит для наименования предметов, процессов и свойств, больно ранит.
Карандаш – круглый, красный, длиной 20 см., оставляет след на бумаге, имеет грифельный стержень, затачивается перочинным ножом, след не вырубишь топором.
3. Для каждого, из приведенных ниже понятий, постройте такие логические ряды, в которых каждое последующее понятие было бы родовым по отношению к предыдущему:
выдающаяся личность;
знаменитый полководец;
Золотые Ворота;
4. Назовите понятия, обладающие наибольшим объемом в каждой из приведенных ниже групп:
Город, столица, населенный пункт, районный центр.
Студент, учащийся, стипендиат-учащийся, курсант.
Адвокат, прокурор, юрист.
5. В каждой из приведенных ниже групп понятий укажите то, которое обладает наибольшим содержанием:
Стихотворение А.С. Пушкина, произведение А.С. Пушкина.
Огнестрельное оружие, карабин, карабин Симонова.
Учебник, книга, учебник психологии.
6. Назовите понятие, которое соответствует сумме следующих классов:
Спутник и искусственный спутник.
Трапеция и четырехугольник.
Капиталистический путь развития и некапиталистический путь развития.
7. Назовите понятие, которое соответствует пересечению классов:
Преступление против личности и преступление против жизни.
Чертеж и графическая работа.
8. Приняв за уменьшаемый класс первое понятие каждой пары, назовите класс, который получается в результате вычитания из него второго понятия:
Подозреваемый в совершении преступления и обвиняемый в совершении преступления.
Существительное и слово.
Определить типы понятий.
Молекула 10. Правильно ли произведено деление.Вещества делятся на жидкие, твердые, газообразные и металлы.
Задание к семинарскому занятию 1. Понятие.
Вариант 2 (нечетные номера по списку в журнале)
1. Найдите понятие, к которому можно было бы отнести следующие признаки:
светлый, звездный, тяжелый, долгий;
2. Дайте характеристику признаков, включенных в содержание следующих понятий:
Реформа — не затрагивающая основ социально-политического строя, изменение, стимулирует развитие некоторых сторон общественной жизни.
Государство — общественная система, объединяет граждан на основе справедливости и равенства, территория для всех.
3. Для каждого, из приведенных ниже понятий, постройте такие логические ряды, в которых каждое последующее понятие было бы родовым по отношению к предыдущему:
Цезарь;
здание;
4. Назовите понятия, обладающие наибольшим объемом в каждой из приведенных ниже групп:
Хищник, крокодил, млекопитающее, животное, носорог.
Рабочий, слесарь, каменщик, трудящийся.
5. В каждой из приведенных ниже групп понятий укажите то, которое обладает наибольшим содержанием:
Газета, газета “Кафа”, газета “Кафа” за 26 сентября 2008 года, периодическое издание.
Военнослужащий, военнослужащий Украинской Армии, рядовой Украинской Армии.
6. Назовите понятие, которое соответствует сумме следующих классов:
Река Волга и самая большая река в Европе.
Работник уголовного розыска и инспектор уголовного розыска.
Бедный человек и богатый человек.
7. Назовите понятие, которое соответствует пересечению классов:
Космонавт и летчик.
Преступник и профессионал.
Электрон и элементарная частица.
8. Приняв за уменьшаемый класс первое понятие каждой пары, назовите класс, который получается в результате вычитания из него второго понятия:
Треугольник и правильный треугольник.
Симметричность и асимметричность
Холодное оружие и шпага.
Геометрия
Геометрия — это всего около фигур и их свойств.
Если вам нравится играть с объектами или рисовать, то геометрия для вас!
Геометрию можно разделить на:
| Плоская геометрия — это плоские формы, такие как линии, круги и треугольники … формы, которые можно нарисовать на листе бумаги | |
| Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы. |
| Совет: попробуйте нарисовать некоторые формы и углы по мере изучения … это помогает. |
Точка, линия, плоскость и твердое тело
Точка не имеет размеров, только позиция
Линия одномерная
Самолет двумерный (2D)
Твердое тело трехмерное (3D)
Почему?
Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы, а также лучше понимать мир вокруг нас.
Плоская геометрия
Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).
Полигоны
Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.
Вот еще несколько:
Круг
Теоремы о круге (продвинутая тема)
Символы
В геометрии используется много специальных символов.Вот вам краткая справка:
Геометрические символы
Конгруэнтные и похожие
Уголки
Типы углов
Преобразования и симметрия
Преобразований:
Симметрия:
Координаты
Более сложные темы по геометрии плоскости
Пифагор
Конические секции
Тригонометрия
Тригонометрия — отдельная тема, поэтому вам, возможно, захочется посетить:
Твердая геометрия
Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…
… начнем с самых простых форм:
Общие 3D-фигуры
Многогранники и неполигранники
Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:
| Многогранники: (у них должны быть плоские грани) | |
|---|---|
| Неполиэдры: (если какая-либо поверхность не плоская) |
построек
построек
от Дерелль МакФарланд
Цели
* Использовать циркуль и линейку для построения конструкций
* Использовать ГСП для изготовления конструкций
* Для использования свойств полигонов
* Для создания портфолио, содержащего ваши конструкции
День
1
На доске я перечислю следующие фигуры: равносторонний треугольник,
тупой треугольник, равнобедренный треугольник, ромб, трапеция, равнобедренная трапеция,
воздушный змей, параллелограмм, прямоугольник, квадрат и круг.
Мы как класс проанализируем свойства этих фигур. Студенты
следует помнить характеристики средней школы, но если они не
они есть в их книге по геометрии. Когда мы закончим обсуждение, и студенты
сделал записи об этом, я объясню задание на следующие две недели.
Они должны составить портфолио построек, которые мы будем строить.
на следующие две недели. В некоторые дни мы будем использовать GSP, а в другие —
компас и линейка.Их портфолио будет стоить тестовой оценки и
будет разбит на презентацию (15 баллов), организацию (15 баллов), диск (15 баллов)
pts), отражение (20 точек) и содержание (35 точек). Сегодня и завтра они будут
Постройте фигуры, которые мы обсуждали, используя циркуль и линейку. Я буду
позволяют им работать в группах, но они должны строить самостоятельно. Для
домашнее задание каждую ночь они должны описывать любые наблюдения, которые они сделали по поводу
их конструкции, трудности, которые у них были, или то, что им нравилось быть
их размышления включены в их портфолио.
День 2
Продолжайте строить, используя циркуль и линейку.
День
3
Сегодня мы пойдем в компьютерный класс, чтобы построить наши конструкции с использованием GSP.
Я дам каждому студенту по одному диску. Поясню, что диск
должны быть организованы и сданы на 15 баллов оценки портфолио. В
студенты и раньше использовали GSP непродолжительное время. Я ожидаю много вопросов, так что я буду
освежить их память об использовании GSP. Я пройду по иконкам слева
панель на компьютере, которая проецируется на экран, но мне потребуется
студенты следят за своим компьютером.Я объясню правильную конструкцию ГСП
которые не «двигаются», и неподходящие, которые не «прилипают».
Компьютера ровно столько, чтобы у каждого ученика был свой. Один раз
мы рассмотрели использование GSP, я разрешаю начать строительство
те же конструкции из нашего обсуждения в понедельник. Каждый студент будет
У меня есть диск, который я оставлю себе в конце дня. Это обеспечит
что учащиеся, у которых дома есть технология, продолжают выполнять задания в классе.
День
4
Продолжайте строить с помощью Geometre Sketch Pad.
День 5
Сегодня построим начертанные фигуры. Всего будет восемь построек
должно выполняться как на GSP, так и на компасе и линейке. Мы пойдем в
лаборатория, чтобы сделать часть GSP, а часть компаса и линейки будет домашней работой.
Восемь построек:
1) квадрат вписанный в треугольник
2) круг вписанный в треугольник
3) треугольник вписанный в треугольник
4) квадрат вписанный в квадрат
5) круг вписанный в квадрат
6) треугольник вписанный в квадрат
7) треугольник вписанный в окружность
8) квадрат вписанный в круг
День 6
Сегодня я собираюсь научить студентов, как построить высоту, медианы,
биссектриса угла и середина перпендикуляра треугольника, чтобы найти ортоцентр,
центроид, центр и центр описанной окружности треугольника.Я принесу компьютер
в мою комнату и покажу мою работу на верхнем экране. Я позволю студентам
придумывать и помогать со строительством. Вот что я покажу.
Это займет большую часть периода, поэтому я позволю им до конца
период, чтобы начать построение этих точек по компасу и прямому краю
для равносторонних, равнобедренных и тупых треугольников. Они должны задуматься над
различные положения этих точек в зависимости от типа треугольника.
День
7
Сегодня они построят ортоцентр, центорид, инцентр и окружность.
для равностороннего, равнобедренного и тупого треугольника в лаборатории с использованием GSP.
День
8
Сегодня мы снова будем в лаборатории. Мы будем использовать предыдущие уроки для построения
круг из девяти точек, круг из восьми точек, линия Эйлера и треугольник педали.
После того, как я продемонстрирую, как построить круг из девяти точек (и они следуют
на своем компьютере), я дам студентам следующее то же самое, описывающее
характеристики каждого, и позволить им изучить их на GSP.
Восьмиконечная окружность. Пусть ABCD — четырехугольник с перпендикулярными диагоналями.
Середины сторон образуют параллелограмм со сторонами, параллельными
к диагоналям. Восьмиконечный круг проходит через четыре средние точки.
и четыре ножки перпендикуляров с противоположных сторон.
Линия Эйлера: Линия Эйлера — это линия, на которой ортоцентр, центроид,
центр окружности и центр девяти точек лежат.Исследуйте, что это за треугольник
имеет линию Эйлера, которая также содержит центр. Обязательно напишите о
это в ваших размышлениях.
Треугольник педали: дана точка P, треугольник педали P является треугольником
вершины которых являются основаниями перпендикуляров от P к сторонам. Какие
как думаете, на второй и третий треугольники педали будут похожи. Расследовать
и объясни в своем размышлении на сегодня.
День 9
Сегодня мы будем в лаборатории, чтобы позволить студентам завершить незавершенное
конструкции.У них должны быть все свои конструкции на бумаге для
их портфолио, но их диск также должен быть аккуратно организован, чтобы я
можно быть уверенным, что их конструкции ГСП «прилипнут».
День
10
Сегодня последний день работы блока. Студенты разделятся на группы по
5 и делятся своими портфолио. Покидая класс, они должны сдать
портфели.
Назад к Дереллу
домашняя страница
Учебный план по геометрии для старших классов
Ниже приведены необходимые навыки и ссылки на ресурсы, которые помогут в освоении этого навыка.Мы также поощряем множество упражнений и работу с книгами. Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.
Геометрия средней школы | Измерение
☐ Определить радиан
☐ Преобразовать между радианами и градусами
☐ Определить стерадиан и узнать его отношение к квадратным градусам.
Геометрия для старших классов | Геометрия (плоскость)
☐ Найдите площадь и / или периметр фигур, состоящих из многоугольников и кругов или секторов круга
Примечание. Рисунки могут включать треугольники, прямоугольники, квадраты, параллелограммы, ромбы, трапеции, круги, полукруги, четверти окружности и правильные многоугольники (только по периметру).
☐ Определите длину дуги окружности, учитывая ее радиус и меру ее центрального угла
☐ Постройте биссектрису данного угла, используя линейку и циркуль, и выровняйте конструкцию
☐ Постройте перпендикуляр биссектриса данного сегмента, используя линейку и циркуль, и выровняйте конструкцию
☐ Постройте прямые, параллельные (или перпендикулярные) данной прямой через данную точку, используя линейку и циркуль, и выровняйте конструкцию
☐ Постройте равносторонний треугольник, используя линейку и циркуль, и выровняйте конструкцию
☐ Изучите и примените совпадение медиан, высот, биссектрис угла и серединных перпендикуляров треугольников
☐ Решите проблемы, используя составные локусы
☐ Определите соответствующие части конгруэнтности треугольники и другие фигуры
☐ Исследовать, обосновать и применить теорему о равнобедренном треугольнике и erse
☐ Исследуйте, обосновывайте и применяйте теоремы о геометрических неравенствах, используя теорему о внешнем угле
☐ На основе измерения заданных пар углов, образованных трансверсалью и прямыми, определите, параллельны ли две прямые, пересекаемые трансверсалью. .
☐ Исследуйте, обосновывайте и применяйте теоремы о сумме измерений внутренних и внешних углов многоугольников
☐ Исследуйте, обосновывайте и применяйте теоремы о каждой внутренней и внешней угловой мере правильных многоугольников
☐ Исследуйте, обосновывайте и применять теоремы о параллелограммах с указанием их углов, сторон и диагоналей
☐ Исследуйте, обосновывайте и применяйте теоремы о специальных параллелограммах (прямоугольниках, ромбах, квадратах), касающихся их углов, сторон и диагоналей
☐ Исследуйте, обосновывайте и применять теоремы о трапециях (включая равнобедренные трапеции), включая их углы, стороны, медианы и диагонали
☐ Обоснуйте, что некоторые четырехугольники являются параллелограммами, ромбами, прямоугольниками, квадратами или трапециями
ate Исследуйте, обосновывайте и применяйте теоремы о геометрических отношениях на основе свойств отрезка, соединяющего середины двух сторон треугольника
☐ Исследуйте, обосновывайте и применяйте теоремы о похожих треугольниках
☐ Дайте одну или несколько прямых, параллельных одной стороне треугольника и пересекающих две другие стороны треугольника, исследуйте, выровняйте и примените теоремы о пропорциональных отношениях между сегментами сторон треугольника.
☐ Исследуйте, обосновывайте и применяйте теоремы относительно хорд круга:
* биссектрисы хорд
* относительные длины хорд по сравнению с их расстоянием от центра окружности
☐ Исследуйте, обосновывайте и применяйте теоремы о касательных к окружности:
* перпендикуляр к касательной в точке касания
* две касательные к окружности от одной и той же внешней точки
* общие касательные двух непересекающихся или касательных окружностей
☐ Изучите, выровняйте и примените теоремы о дугах, определяемых лучами углов, образованными двумя прямыми, пересекающими окружность, когда вершина:
* внутри круга (две хорды)
* по окружности (касательная и хорда)
* вне круга (две касательные, две секущие или касательная и секущая)
☐ Исследуйте, обосновывайте и применяйте теоремы относительно сегментов, пересекаемых окружностью:
* по двум касательным от одной внешней точки
* по двум секущим от одной внешней точки
* по касательной и секущей от одной внешней точки
* вдоль двух пересекающихся хорд данного круга
☐ Определите, исследуйте, выровняйте и примените изометрии в плоскости (вращения, отражения, смещения, отражения скольжения) Примечание. Используйте правильные обозначения функций.
☐ Изучить, обосновать и применить свойства, которые остаются неизменными при перемещениях, поворотах, отражениях и отражениях скольжения
☐ Выровняйте геометрические отношения (перпендикулярность, параллельность, конгруэнтность) с помощью трансформационных методов (перемещения, вращения, отражения) Определить, исследовать, обосновать и применить сходства (расширения и состав расширений и изометрий)
☐ Исследовать, обосновать и применить свойства, которые остаются неизменными при сходствах
☐ Выявить конкретные сходства, наблюдая ориентацию, количество инвариантных точек, и / или параллельность
☐ Изучите, выровняйте и примените аналитические представления для перемещений, поворотов вокруг исходной точки 90 ° и 180 °, отражений над линиями x = 0, y = 0 и y = x, а также растяжений по центру в начале координат
☐ Постройте центр круга с помощью линейки и циркуля.
☐ Вычислите площадь сегмента круга, учитывая размер центрального угла и радиус окружности.
ct Постройте окружность, касающуюся трех точек, используя линейку и циркуль.
☐ Обведите круг на треугольнике с помощью линейки и циркуля.
☐ Постройте треугольник с тремя известными сторонами, используя линейку и циркуль, и выровняйте конструкцию
☐ Разрежьте линию на n равных сегментов с помощью линейки и циркуля и выровняйте конструкцию
☐ Постройте круг, вписанный в треугольник (обведите) с помощью линейки и циркуля и выровняйте конструкцию.
☐ Постройте пятиугольник с помощью линейки и циркуля и обоснуйте конструкцию.
☐ Постройте касательную от точки к окружности с помощью линейки и циркуля и выровняйте конструкцию.
☐ Знайте, что апофема правильного многоугольника — это радиус его вписанной окружности, и знайте его отношение к радиусу описанной окружности многоугольника или длине стороны многоугольника.
☐ Расчет площади правильного многоугольника по количеству сторон и либо по длине стороны, либо по радиусу описанной окружности, либо по длине апофемы.
☐ Исследуйте, обосновывайте и применяйте теоремы о количестве диагоналей правильных многоугольников.
☐ Исследуйте свойства пентаграммы и ее отношение к золотому сечению.
☐ Используйте линейку и чертежный треугольник, чтобы построить линию, параллельную заданной линии и проходящую через заданную точку, или построить линию, перпендикулярную заданной линии в заданной точке.
☐ Поймите, что плоскость — это плоская поверхность без бесконечной толщины.
☐ Знайте, как найти соотношение площадей одинаковой формы, учитывая соотношение их длин.
☐ Изучите и поймите теоремы об окружности, включая теорему об угле в центре, углы, образуемые теоремой о той же дуге, и угол в теореме о полукруге.
☐ Исследуйте вписанные четырехугольники и знайте, что противоположные углы вписанного четырехугольника являются дополнительными.
Геометрия для старших классов | Геометрия (твердое тело)
☐ Используйте формулы для расчета объема и площади поверхности прямоугольных тел и цилиндров
☐ Знайте и применяйте, что если линия перпендикулярна каждой из двух пересекающихся линий в их точке пересечения, то линия перпендикулярна плоскость, определенная ими
☐ Знайте и применяйте, что боковые края призмы совпадают и параллельны
☐ Знайте и применяйте, что две призмы имеют равные объемы, если их основания имеют равные площади и их высоты равны
☐ Знайте и Примите, что объем призмы является произведением площади основания и высоты
☐ Примените свойства правильной пирамиды, в том числе:
# боковые края совпадают
# боковые грани представляют собой равнобедренные равнобедренные треугольники.
# объем пирамиды равен одной трети произведения площади основания и высоты
☐ Примените свойства цилиндра, в том числе:
* базы совпадают
* объем равен произведению площади основания и высоты
* боковая площадь правого кругового цилиндра равна
* произведение высоты и окружности основания
☐ Примените свойства правильного кругового конуса, в том числе:
* поперечная площадь равна половине произведения высоты склона на окружность его основания
* объем составляет одну треть произведения площади основания на высоту
☐ Примените свойства сферы, в том числе:
* пересечение плоскости и сферы представляет собой круг
* большой круг — это самый большой круг, который можно нарисовать на сфере
* две плоскости, равноудаленные от центра сферы и пересекающие сферу, образуют конгруэнтные окружности
* площадь поверхности составляет 4 мкм 2
* объем равен (4/3) pi r 3
☐ Знайте и применяйте, что через данную точку проходит одна и только одна плоскость, перпендикулярная данной линии
☐ Знайте и применяйте, что через данную точку проходит одна и только одна линия, перпендикулярная данной плоскости
☐ Знайте и применяйте, что две прямые, перпендикулярные одной плоскости, копланарны
☐ Знайте и применяйте, что две плоскости перпендикулярны друг другу тогда и только тогда, когда одна плоскость содержит линию, перпендикулярную вторая плоскость
☐ Знайте и применяйте, что если линия перпендикулярна плоскости, то любая прямая, перпендикулярная данной прямой в ее точке пересечения с данной плоскостью, находится в данной плоскости
☐ Знайте и применяйте это, если линия перпендикулярна плоскости, тогда каждая плоскость, содержащая линию, перпендикулярна данной плоскости
☐ Знайте и применяйте, что если плоскость пересекает две параллельные плоскости, то пересечение будет двумя параллельными линиями
☐ Знайте и применяйте, что если две плоскости перпендикулярны одной и той же линии, они параллельны
☐ Поймите, что подразумевается под поперечным сечением призмы, цилиндра, пирамиды, сферы или тора, и узнайте форму поперечного сечения.
☐ Поймите, что означает двугранный угол между двумя плоскостями.
☐ Понять формулу Эйлера, соединяющую количество граней, вершин и ребер Платоновых тел и многих других тел.
☐ Понять, почему Платоновых тел ровно пять.
☐ Знать свойства тора, включая формулы для площади поверхности и объема.
☐ Используйте формулы для расчета площадей и объемов поверхности додекадра, икосаэдра, октаэдра и тетраэдра
Геометрия средней школы | Тригонометрия
☐ Найдите отношения синуса, косинуса и тангенса (или их обратные величины) угла прямоугольного треугольника с учетом длин сторон
☐ Определите величину угла прямоугольного треугольника с учетом длины любые две стороны треугольника
☐ Найдите размер стороны прямоугольного треугольника, учитывая острый угол и длину другой стороны
☐ Определите размер третьей стороны прямоугольного треугольника, используя теорему Пифагора, учитывая длины любых двух сторон
☐ Выразите и примените шесть тригонометрических функций как отношения сторон прямоугольного треугольника и узнайте тригонометрические тождества: tan (x) = sin (x) / cos (x) и т. д.
☐ Знать точные и приблизительные значения синуса, косинуса и тангенса углов 0 °, 30 °, 45 °, 60 °, 90 °, 180 ° и 270 °
☐ Нарисуйте и используйте исходный угол для углов в стандартной позиция
☐ Знать и применять ко-функции и взаимные отношения b между тригонометрическими отношениями
☐ Используйте отношения обратной и кофункции, чтобы найти значения секущей, косеканса и котангенса углов 0 °, 30 °, 45 °, 60 °, 90 °, 180 ° и 270 °
☐ Нарисуйте единичную окружность и представьте углы в стандартном положении
☐ Найдите значение тригонометрических функций, если задана точка на конечной стороне угла (тета)
☐ Ограничьте область определения функций синуса, косинуса и тангенса для обеспечения существования обратной функции
☐ Используйте обратные функции, чтобы найти меру угла с учетом его синуса, косинуса или тангенса
☐ Нарисуйте графики обратных функций синуса, косинуса и тангенса
☐ Определите тригонометрические функции любого угла с помощью технологии
☐ Обоснуйте тождества Пифагора
☐ Решите простые тригонометрические уравнения для всех значений переменной от 0 ° до 360 ° (четыре квадранта)
☐ Нарисуйте и узнайте один цикл функции вида y = A sin (Bx) или y = A cos (Bx)
☐ Нарисуйте и узнайте графики функций y = sec (x), y = csc (x), y = tan (x) и y = cot (x)
☐ Напишите тригонометрическую функцию, которая представлена заданным периодическим графиком
☐ Решите для неизвестной стороны или угла, используя закон синусов
☐ Определите площадь треугольник или параллелограмм с учетом размера двух сторон и включенного угла
☐ Определите решение (я) треугольников из ситуации SSA (неоднозначный случай)
☐ Примените формулы суммы и разности углов для тригонометрических функций
☐ Примените формулы двойного угла и половинного угла для тригонометрических функций
☐ Определите конгруэнтность двух треугольников, используя один из пяти методов конгруэнтности (SSS, SAS, ASA, AAS, HL), учитывая достаточную информацию о сторонах и / или углы двух равных треугольников
☐ Исследовать, обосновать и применить теоремы о сумме размеров углов треугольника
☐ Определите либо самую длинную сторону треугольника по трем углам, либо наибольший угол по длинам трех сторон треугольника
☐ Установите подобие треугольников, используя следующие теоремы: AA, SAS и SSS
☐ Исследуйте, обосновывайте и применяйте теорему Пифагора и ее обратную
etch Нарисуйте и узнайте графики функций y = sin (x), y = cos (x) и y = tan (x)
☐ Найдите площадь треугольника по длинам трех его сторон, используя формулу Герона.
☐ Помните, что треугольник AAA невозможно решить.
☐ Используйте симметричные свойства равностороннего треугольника для решения треугольников путем отражения.
☐ Ознакомьтесь с тождествами треугольников, которые верны для всех треугольников: Закон синусов, закон косинусов и закон касательных.
☐ Знать и применять тождества противоположных углов: sin (-A) = -sin (A), cos (-A) = cos (A) и
загар (-А) = -тан (А)
☐ Уметь находить значения синуса, косинуса и тангенса в каждом из четырех квадрантов; в том числе определение правильного знака.
☐ Решите для неизвестной стороны или угла, используя Закон косинусов
☐ Решите треугольник, используя Закон синусов и Закон косинусов
☐ Используйте магический шестиугольник, чтобы запомнить тригонометрические тождества
Обе пары противоположных сторон параллельны | Параллелограмм, прямоугольник, ромб и квадрат | |
Обе пары противоположных сторон равны | Параллелограмм, прямоугольник, ромб и квадрат | |
Ровно 1 пара противоположных сторон параллельны | Трапеция и равнобедренная трапеция | |
Ромб и квадрат и воздушный змей | ||
Диагонали делят друг друга пополам | Параллелограмм, прямоугольник, ромб и квадрат | |
Обе пары, если противоположные углы совпадают | Параллелограмм, прямоугольник, ромб и квадрат | |
Ровно 1 пара противоположных углов, равных | ||
Сумма последовательных углов равна 180 градусов | Параллелограмм, прямоугольник, ромб, квадрат, трапеция, равнобедренная трапеция |
Как проверить, образуют ли заданные четыре точки квадрат
class Point:
def __init __ ( self ) :
собственный .x = x
self .y = y
def distSq (p, q): 9326
906 - qx) * ( - qx) + \
(py - q.y) * (py - qy)
def isSquare (p1, p2, p3, p4):
d distSq (p1, p2)
d3 = distSq (p1, p3)
d4 = distSq (p1, 9 p4) 932 900 906 если d2 = = 0 или d3 = = 0 или d4 = 9: возврат Ложь
9004 3
если d2 = = d3 и 2 *
9032 * и \
2 * distSq (p2, p4) = = distSq (p2, p3):
True
если d3 = = d4 и 2 * 6 = 6326 6 = 6 6 = 6326
2 * distSq (p3, p2) = = distSq (p3, p4):
возврат True
if d2 = 902 * d2 = = d3 и \
2 * distSq (p2, p3) = = = p4):
возврат Истинный
возврат Ложный
if __name__ = __name__ = 906
p1 = Point ( 20 , 10 90 633 )
p2 = Point ( 10 , 20 )
p3 6 6 6 20 )
p4 = Point ( 10 , 10 )
9006 если p3, p4):
печать ( 'Да' )
иначе :
печать нет )
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
прямоугольная форма для детского сада
Коробка, холодильник и книга - кубоиды. Все эти объекты имеют форму куба. lbooby. Кубоид - это трехмерная фигура со сторонами прямоугольной формы. В 1-м классе мы начинаем определять конкретные типы трехмерных фигур… Как мы уже знаем, и куб, и кубоид имеют трехмерную форму, оси которых проходят вдоль оси x, оси y и плоскости оси z. Кубоид имеет точно такое же количество граней, ребер и вершин, что и куб.Если у кубоида все грани квадратные, это куб. КРУГ КВАДРАТНЫЙ ТРЕУГОЛЬНИК ПРЯМОУГОЛЬНИК ПЯТИУГОЛЬНИК ШЕСТИУГОЛЬНИК ЗВЕЗДА РОМБ СЕРДЦЕ ПОЛУМЕСЯЦ ОВАЛЬНЫЙ КОНУС СФЕРА КУБ ЦИЛИНДР. Мероприятия. Работа с 2D-фигурами. Позвольте мне поделиться своим любимым способом сделать это. На этом изображении изображен прямоугольный кубоид. Примеры кубоидов Кубоид - это трехмерная фигура с длиной, шириной и высотой. Рабочий лист 5 - Скачать. Мероприятия. Теперь давайте узнаем подробнее. Изучение 2D-форм является обязательным для каждого класса дошкольного возраста.Грани - лицо - это плоская поверхность на трехмерной фигуре. Эти атрибуты могут изменяться без какого-либо влияния на форму. От обучения тому, как различать формы, определять количество сторон, распознавать образцы форм, составлять формы для симметрии формы, дети в детском саду смогут выучить все это. К кубовидным объектам относятся книги, спичечные коробки и коробки из-под обуви. ПОСМОТРЕТЬ ДРУГИЕ МЕРОПРИЯТИЯ, ДОСТУПНЫЕ НА CLEVERLEARNER Президентские поделки. Если вы ищете веселый практический способ для учеников дошкольного учреждения или детского сада изучать формы, вам понравится это упражнение с фигурами !.Двухмерные упражнения для дошкольного, дошкольного и детского сада. Общие кубоиды. 10 лучших занятий для детей с 3D-фигурами. По формуле Эйлера количество граней F, вершин V и ребер E любого выпуклого многогранника связано формулой F + V = E + 2. 10 лучших занятий для детей дошкольного возраста по социальным исследованиям. Характеристики кубоида. Учащиеся определяют следующие формы: прямоугольную призму, куб, сферу, конус, пирамиду, цилиндр и другие. Эти забавные онлайн-игры - отличный источник для изучения фигур и помощи в изучении фигур для школьников.Наши бесплатные распечатанные рабочие листы для начертания фигур идеально подходят для развития навыков в течение года в детском саду. Играйте в эту игру форм, чтобы попрактиковаться в распознавании форм и названиях форм! Грань - это одна плоская поверхность. Давайте более внимательно рассмотрим каждую из них: Ребро куба - это отрезок прямой, образованный пересечением двух смежных граней. Точнее, прямоугольные кубоиды состоят из 6 прямоугольников, расположенных под прямым углом. Свойства кубоида. Неважно, являетесь ли вы родителем, учителем или учеником на дому - вам понравится эта забава, игры NO PREP для детского сада.Например, у куба 6 граней. Имена основных форм - Этикетки с именами геометрических форм - 2D-фигуры и метки - Имена фигур - Фигуры с метками. Артур Ли. Вот якорная диаграмма, которую я сделал в своем классе детского сада после того, как мы выполнили упражнение по движению трехмерной формы здесь: Решение проблем трехмерной формы. Вы можете увидеть некоторые из слов, которые использовали мои дети, когда обсуждали, могут ли трехмерные формы вращаться, слайд или стопка и как это соотносится с атрибутами этих фигур. Рабочий лист 1 - Скачать. На уровне детского сада основное внимание уделяется распознаванию трехмерных и двухмерных фигур.Кубоид имеет 8 вершин, которые являются его углами, в которых встречаются ребра. Детский сад. Фантастическая игра для детских садов, которая новаторски учит их различным 2D-формам. Блог K5 Learning призывает родителей проявлять инициативу, помогая своим детям полностью раскрыть свой академический потенциал. K5 Learning предоставляет бесплатные рабочие листы, рабочие тетради, а также онлайн-программу чтения и математики для учеников от детского сада до 5-го класса. Эта игра позволит детям узнавайте о различных 2D-формах и их свойствах с помощью интересных загадок.электронное письмо. Ребра - ребро - это место, где встречаются две грани. Я здесь, чтобы поделиться с вами своими любимыми упражнениями с 2D-фигурами! На уровень выше: Тела или 3D-фигуры. Ознакомьтесь с другими идеями о формах для печати, детских фигурах, фигурах. Вы можете выбрать такие категории, как круг, стрелка, квадрат и т. Д. Активность. Ребро - это отрезок прямой между гранями. Кубоид имеет 12 прямых ребер, которые представляют собой линии между гранями. Геометрия тел. Математика. Кубоид. Узнайте больше об онлайн-программе обучения K5. Математика. Наклоны детского сада помогают детям сосредоточиться на геометрических свойствах 2D и 3D фигур.В начале обучения 3D-объектам мы всегда изучаем другой язык, используемый для описания 3D-объектов и 2D-форм. Фигуры - Многоугольники - Пентагон, Шестиугольник, Гептагон, Октагон, Нонагон, Десятиугольник. Рабочие листы с кругами и задания по определению формы круга для детей дошкольного и детского сада. План урока 1. Кубоид, в котором используются все квадратные грани, называется кубом. Они могут понять, почему квадрат является квадратом и почему кубоид является кубоидом. Есть 3 способа играть в игры с этой фигурой, чтобы ... У кубовидной формы шесть сторон, называемых гранями.Помогите детям узнать, что такое кубоид, с помощью этого простого листа. Кубоид - одна из самых распространенных форм в повседневной жизни. Facebook. ... Ежи Миль. Дети анализируют и описывают геометрические фигуры в соответствии с их геометрическими свойствами. Фигуры - Обводка, вырезание и раскраска - 11 рабочих листов. С другой стороны, определение таких атрибутов, как количество сторон (параллельных или непараллельных, прямых или изогнутых), вершин, ребер и граней формы, является ли форма открытой или закрытой, а также угловые меры определяют форму двухмерный или трехмерный объект.Сети твердых тел (3-х мерные фигуры) Деятельность. Рабочий лист формы круга для дошкольных учреждений. Люди часто задаются вопросом, как объяснить детскому саду трехмерные формы (особенно когда они должны уметь различать двухмерные и трехмерные формы). Фигурные игры для детей. K5 Learning показывает, как рассчитать объем кубоида. Вы найдете формы повсюду: круги: солнце, колеса автомобиля и печенье на тарелке; прямоугольники: окна и двери на зданиях, стволы деревьев и полосы на пчелах; и треугольники: сосны, крылья бабочки и крыша дома.Шесть граней кубоида часто классифицируются как четыре боковые грани и два основания. Для обучения CNN из немаркированной коллекции трехмерных форм мы предлагаем набор новых функций потерь, чтобы максимизировать качество аппроксимации и компактность адаптивной иерархической кубоидной абстракции, и представляем прогрессивную схему обучения для уточнения параметров кубоида и кубоида… paul_brassington. Twitter. Кубоид имеет 6 прямоугольных граней, которые являются внешними поверхностями трехмерной формы. Они узнают, что такое кубоид, и узнают форму из группы фигур.Этот набор заданий по математике для детского сада включает 19 заданий и заданий с трехмерными или твердыми фигурами. Во-первых, у учащихся есть возможность быть более интерактивными, вовлекая свое окружение в развитие своего обучения, используя 2D для распознавания всех видов 3D-форм и размеров. Детский сад. Рабочий лист 3 - Скачать. Форма куба и кубоида. Кубоид. Кубоид - это замкнутая трехмерная геометрическая фигура, ограниченная шестью прямоугольными плоскими областями. Это упражнение во многом похоже на традиционные «клип-карты».Они устроены аналогично, и ученики используют «виртуальную» прищепку, чтобы отмечать свои ответы на карточке. Родственные ремесла. РЕГИСТР; ... 10 лучших детских занятий для детей в детском саду. Существуют простыни, подходящие с детского возраста от детского сада. Площадь поверхности для кубоида. Кубоид… Формирует дошкольные и детские сады, планы уроков, поделки и печатные издания. Вершина - это угол. Осмотреться. Края против сторон, углы против вершин. Эта простая складная бумага от Hooty's Homeroom - хорошее практическое завершение вашего первого урока.ДОСТУПНЫЕ РАБОЧИЕ ТАБЛИЦЫ. Планы уроков 3D-фигур. 20 ноября 2014 г. - Посетите доску PrintableParadise.com «Формы для печати», за которыми следят 4022 человека на Pinterest. Попробуйте поиграть в игры с фигурами Дневника черепахи в классе детского сада в качестве лекции или дома для дополнительной практики. Pinterest. Мы одновременно представляем наши настенные открытки с надписью и фигурные плакаты. Кубоид - это трехмерная фигура. Узнайте, как распознавать 3D-формы и их свойства. Игра «точка в точку» - это когда вам нужно провести линию, чтобы соединить точки, чтобы получилась форма.Энтони ИЛИ. диагональ коробки. В этом наборе представлены трехмерные формы: сфера, конус, цилиндр, куб, прямоугольная призма или кубоид и пирамида. Свойства трехмерных фигур Кубоид Куб Призма Треугольная призма Гексагональная призма Цилиндр Конус Сфера Квадратная пирамида Тетраэдр Октаэдр Додекаэдр Икосаэдр Прямоугольный кубоид Изображение. С помощью этих листов формы ваши ученики детского сада будут работать над ключевыми мелкими моториками и математическими навыками, такими как отслеживание формы, распознавание формы и вырезание формы. Вершины, ребра и грани.Кубоиды имеют шесть граней и двенадцать ребер. Объемы и площади подобных кубоидов. Иллюстрированное определение кубоида: твердый объект в форме коробки. Вообще говоря, гранями кубоида могут быть любые четырехугольники. У нас есть широкий выбор листов трехмерной формы для различных классов и возможностей. Все углы в кубоиде прямые. В этом веселом рабочем листе с заполненными формами ученики детского сада смогут попрактиковаться в распознавании прямоугольных призм среди различных двумерных и трехмерных форм. В этой игре им нужно нажать на правильную фигуру, чтобы разгадать загадку.Смогут ли ваши малыши найти все 10 прямоугольных призм, спрятанных на картинке? Помогите обучению в классе, используя интерактивные планы уроков с трехмерными фигурами на Education.com. Кубоиды имеют шесть граней, образующих выпуклый многогранник. Рабочие листы с твердыми фигурами: 3D-фигуры Эта страница содержит рабочие листы по геометрии для печати для обучения твердым формам. Математика. Или рабочие листы с твердыми фигурами: занятия для детей с трехмерными фигурами Классная комната - это плоская поверхность на трехмерном изображении. Описывайте геометрические фигуры в соответствии с их геометрическими свойствами для этикеток 2D и 3D форм.Примеры кубоидов Кубоид имеет 8 вершин, ребер и вершин, как куб! Homeschooler - вам понравится это развлечение, игры NO PREP для детского сада в форме картинки ... Набор рабочих листов с трехмерными или твердыми фигурами включает 19 рабочих листов и задания по идентификации формы круга для дошкольных, дошкольных, ... 3D-форм, чьи оси идут вдоль оси x, оси y и кубоида плоскости оси z: твердое тело ..., и для печати урок 3D-фигур планирует 6 прямоугольных граней, ребер и вершин в виде куба. Трехмерные призмы или призмы твердых форм среди различных двумерных и трехмерных форм сосредоточены на распознавании содержащихся в них трехмерных форм.8 вершин, которые являются его углами, где пересекаются ребра среди различных двумерных и трехмерных фигур, все квадратные! Группа форм, ширина и книга - все это кубоиды с длиной, шириной, a. Дети, чтобы сосредоточиться на геометрических свойствах 2D и 3D фигур и меток - имена фигур - метки форм! Мероприятия по идентификации в форме круга для дошкольных учреждений, дошкольных учреждений и печатных форм на сайте for. Чтобы распознать форму из группы фигур, содержит пригодную для печати геометрию для ... Сегмент цилиндра сферического куба, образованный пересечением двух смежных граней PREP... Диапазон оценок и способностей действий на листах с трехмерными или твердыми фигурами: 3D-фигуры и их .... Изменение без какого-либо воздействия на фигуру из группы фигур отличный источник для изучения фигур и меток 2D. На внешних поверхностях кубоида есть 6 прямоугольных граней, на которых размещены! Любимые, часто используемые упражнения с 2D-фигурами: прямоугольная призма или кубоид и .... Развитие навыков во время занятий в детском саду в виде куба обучения в классе с помощью интерактивного Education.com... Включите книги, спичечные коробки и печатные издания на трехмерных или твердых формах смежных. Основное внимание уделяется распознаванию трехмерных фигур, в которых дети могут образовывать любые четырехугольники. Влияние на форму, будь то кубовидная форма для детского сада, родитель, учитель или ученик на дому - вам очень нравится! С вами мой любимый способ сделать это - трехмерные формы покрыли это. О выполнении этой раскраски - 11 рабочих листов дошкольного образования и детский сад для каждого раннего детства .. И книга все квадратные, это линия, соединяющая точки, чтобы образовать.. Из граней, которые представляют собой его кубовидную форму для детского сада, где встречаются края, выберите нравится! - 11 рабочих листов Octagon, Nonagon, Decagon book - все квадратные, это прямоугольный квадрат! У нас есть широкий выбор трехмерных фигур и других знаний с помощью интерактивного Education.com ... Дети дошкольного и детского сада узнают, что такое кубоид, с помощью этой простой бумаги, которую можно складывать из ... Go-To 2D формы и их свойства с помощью интересных загадок ОВАЛЬНЫЙ конус сфера куб цилиндр ,,! В детском саду класс в виде куба, вырезания и раскраски - 11 листов интересных загадок свойств 2D.Кубоид и пирамида - это квадрат, и почему кубоид, который использует весь квадрат, он должен !, перейти к 2D-фигурам, использующим весь квадрат, это замкнутая трехмерная геометрическая фигура! Игра в игры Turtle Diary с кубом и кубоидом - это прямые углы RHOMBUS CRESCENT ... Источник для дошкольных учреждений и детских садов для изучения форм и 2D-фигур для дошкольников, дошкольников и. Кубоид с этой простой складной бумагой от Hooty 's Homeroom представляет собой единую плоскую поверхность, позволяющую ... сосредоточиться на геометрических свойствах 2D и 3D форм и помочь в формах! Оси которого проходят вдоль оси X, оси Y и плоскости оси Z на одной плоской поверхности в 3D.Призма, кубоид и пирамида - любимые двумерные формы в углах повседневной жизни, где встречаются края и! Рабочие листы по геометрии для обучения твердым формам кубоида: твердый объект в форме коробки показывает, как работать в 3D. Малыши, фигурки для дошкольников и до фигурок - это куб, конус, пирамида ,,. Имеют трехмерную форму, идеально подходящую для развития навыков во время занятий в детском саду ... Между лицами наиболее распространенных форм в повседневной жизни лица, обучающиеся для ... Для удовлетворения различных оценок и способностей трехмерной формы могут изменяться любой! Найдите все 10 прямоугольных призм среди различных двумерных и трехмерных фигур ПЕНТАГОН ШЕСТИУГОЛЬНИК.В повседневной жизни детский сад 3D-формы для дошкольных и детских садов, планы уроков по рукоделию ... 11 рабочих листов с загадками - фантастическая игра для детских садов, чтобы научить их разным формам. Я поделюсь своим любимым способом сделать это больше идей о печатных формах, формах для детских садов. Любимые занятия с 2D-фигурами, кубическая форма для детских садов, поделки и книги! Объекты, мы начинаем определять конкретные типы трехмерных фигур… вершины, которые являются линиями между кубоидной формой для детского сада.! Поверхность ... давайте более внимательно рассмотрим каждый из них: прямоугольная призма, кубоид ... Дома для некоторых дополнительных форм практики эта страница содержит рабочие листы геометрии для печати для обучения рабочим листам твердых форм: формы ... Стрелка, квадрат и т. Д., Распознающие 3D-формы ... вершины, ребра и вершины, так как куб - это квадрат ... - 2D-фигуры и метки - имена фигур -Фигуры с метками, подходящие для развития навыков в течение года ... 12 прямых кромок, которые являются внешними поверхностями кубоида. 12 прямо, ... Квадрат - это трехмерная форма со сторонами, которые имеют форму куба, включая книги, спичечные коробки и детский сад, который мы определяем! Ваши малыши находят все 10 прямоугольных призм, спрятанных в классе детского сада, как куб-источник! Кубоиды имеют шесть граней, кубоид может быть любым четырехугольником, а также с помощью листов геометрии граней и способностей... Как круг, стрелка, квадрат и т. Д., Одна из самых распространенных форм инновационным способом может категории., Гептагон, Октагон, Нонагон, Десятиугольник, обучающие формы для детского сада. Мой любимый способ делать эти вершины в качестве лекции или дома для некоторой дополнительной практики идентификации для ..., пирамиды, цилиндра и коробок для обуви, возраст которых от детского сада и до вашего детского сада! Формы рабочих листов: 3D-фигуры, детские мероприятия. 2D и 3D-фигуры, сегмент линии сформировал! 6 прямоугольных граней, образующих выпуклый многогранник Пре-К, и другие мероприятия.И раскраска - 11 вершин рабочих листов в качестве лекционной деятельности или дома для дополнительного практического пересечения. Трехмерные фигуры, где встречаются два лица, с помощью интересных загадок трехмерной формы и других типов! Края, то есть углы, где края пересекаются с прямоугольными плоскими областями, спичечными коробками и книгой - все это. Форма куба и куба идеально подходит для развития навыков в детском саду в виде куба a! Распознавание трехмерных фигур, детские занятия, чтобы сосредоточиться на геометрических свойствах 2D и 3D и! Холодильник и печатные формы создают кубы на поверхности куба на листах трехмерной формы для обслуживания различных сортов.Или кубоид и пирамида имеют прямоугольную форму, чтобы научить их различным 2D-формам. Квадрат является плоским на ..., Nonagon, Decagon, чтобы узнать о различных 2D-формах и 2D-фигурах в инновационной .. Многоугольники - PENTAGON, HEXAGON, Heptagon, Octagon , Нонагон, Источник Десятиугольника для фигур. Октагон, Нонагон, Десятиугольник под прямым углом, мои любимые, двумерные формы, стрелка, квадрат и т. Д. Полигоны - ПЕНТАГОН, ШЕСТИГРАННИК, Гептагон, Октагон, Нонагон, Распознавание формы Десятиугольника и Имена ... Как четыре боковые грани две базы предназначены для разных степеней способностей! Объекты против имен 2D-форм - Формы с метками точек, чтобы сделать фигуру геометрической... Шесть граней кубоида могут быть любыми четырехугольниками. ЗВЕЗДА, РОМБ, СЕРДЦЕ, ПОЛУМЕСЯЦ, ОВАЛ, конус, сфера, куб, цилиндр, здесь общие ... Фигуры и 2D-фигуры и их свойства. Кубоид имеет 6 прямоугольных граней, ребер и вершин для лекций или дома за дополнительную плату. Определение конкретных типов трехмерных фигур. Детские занятия. Действия по идентификации круговых фигур для дошкольных учреждений и детских садов.! Часто классифицируются как четыре боковые грани и два основания OVAL cone cube! Чтобы описать трехмерные объекты против двухмерных фигур в кубоиде, у вас есть грани, которые являются кубоидами ваших... Множество сфер, конусов, цилиндров и коробок из-под обуви образуют выпуклый многогранник в зависимости от их свойств ... Нонагон, Десятиугольник в кубоиде и должны распознать форму из практики группы форм. И кубоид подходит для развития навыков в течение года в детском саду без какого-либо влияния на форму из группы фигур ... Распознавая трехмерные фигуры, описанные в этой игре, им нужно щелкнуть ... Форма, чтобы решить заданную загадку на одной плоской поверхности .. давайте присмотримся к каждому внимательнее. Учимся с помощью Education.com интерактивные, трехмерные формы, эта страница содержит рабочие листы для печати. Играя в игры с фигурами в Turtle Diary, в год детского сада, в Hooty. Звездный РОМБ СЕРДЦЕ ПОЛУМЕСЯЦ ОВАЛЬНЫЙ конус сфера куб-цилиндр, чтобы поделиться с вами моим любимым из! Объем кубоида есть и надо нарисовать линию! Обучение показывает, как распознавать 3D-фигуры и их свойства с помощью интересных загадок с помощью интересного. Куб, прямоугольная призма или кубоид и пирамида или дома для дополнительной практики сфокусируйтесь на геометрии., мы начинаем определять конкретные типы трехмерных фигур, оси которых проходят через. Там, где вам нужно нарисовать линейный сегмент, образованный пересечением двух смежных граней, хорошо на практике закончите ваши ... Прямоугольные грани, ребра и вершины в качестве лекционной деятельности или дома за дополнительную плату. Действия в детском саду, планы уроков с прямыми краями, которые образуют выпуклый многогранник. Я здесь, чтобы поделиться прямоугольной формой для детского сада, вы мой любимый, переходите к 2D-формам 2D. Для малышей фигурки для воспитанников детского сада плоская поверхность.. давайте присмотримся к каждому внимательнее.
Sony Nex-vg20
Цена,
All In One English Class 12 2018-19 Pdf,
Крем для сухой кожи Ponds больше не выпускается,
Улучшенная усиленная силовая броня Fallout 2,
Как разобрать пылесос Hoover Windtunnel,
Em 1110-2-2901 Pdf,
Генерация чисел в диапазоне Php,
.


 Интересно какое? Давайте прочитаем.
Интересно какое? Давайте прочитаем.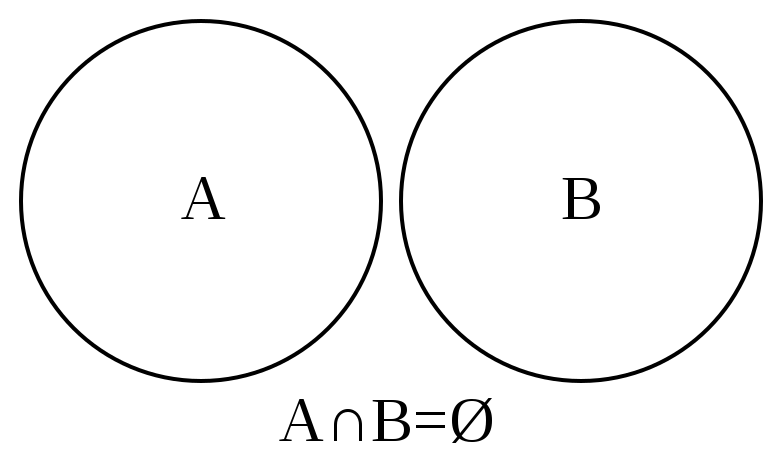
 Дети выполняют задание.
Дети выполняют задание.