Уравнения с дробями | Математика

Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами. 

Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.

   

1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

Приводим к общему знаменателю дроби в каждой части уравнения:

   

   

   

Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:

   

При делении чисел с разными знаками получаем отрицательное число. По правилу деления дробей:

   

После сокращения имеем:

   

(В данном случае ответ можно записать и в виде десятичной дроби: х=-0,8).

2 способ:

   

Обе части уравнения умножим почленно на наименьший общий знаменатель всех входящих в него дробей, в данном случае он равен 24:

   

При умножении на знаменатель дроби сокращаются, в знаменателе остается единица, которую не пишем. От  линейного уравнения с дробями перешли к линейному уравнению с целыми числами:

   

Неизвестные — в одну сторону, известные — в другую с противоположными знаками:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

Ответ: -4/5.

Как видите, второй способ существенно упрощает решение линейного уравнения с дробями.

 

   

Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей. Здесь он равен 60:

   

   

Вместо линейного уравнения с дробями получили линейное уравнение с целыми числами. Неизвестные переносим в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

Сокращаем дробь на 3:

   

Ответ: 5/11.

   

Обе части уравнения умножаем почленно на наименьший общий знаменатель всех входящих в него дробей:

   

В результате линейное уравнение с дробями заменили на линейное уравнение с целыми числами:

   

Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

   

Ответ: 2,9.

В следующий раз рассмотрим линейные уравнения с смешанными дробями.

Укажите положительный корень уравнения — Документ

Линейные
уравнения

Решите
уравнение

1. .

2. .

3. .

4. .

5. .

Квадратные
уравнения

1. Укажите
   положительный корень уравнения
   .

2. Укажите
   отрицательный корень уравнения .

3. Укажите
   отрицательный корень уравнения .

4. Укажите
   отрицательный корень уравнения .

5. Решите
   уравнение
   .
   В ответе укажите сумму корней.

6. Решите
   уравнение
   .
   В ответе укажите произведение корней.

7. Решите
   уравнение
   .
   В ответе укажите меньший корень.

8. Решите
   уравнение . В ответе укажите
   больший корень.

9. Решите
   уравнение
   .
   В ответе укажите наименьший корень.

10. Найдите
    сумму квадратов корней уравнения
    .

11. Решите
    уравнение
    .
    В ответе укажите наибольший корень.

12. Решите
    уравнение
    .
    В ответе укажите меньший
    корень.

13. Решите
    уравнение
    .
    В ответе укажите наибольший корень.

14. Решите
    уравнение
    .

15. Найдите
    корни уравнения
    .

16. Решите
    уравнения
    .

17. Найдите
    корни уравнения
    .

18. Решите
    уравнение
    .

Линейные
неравенства

Решите неравенство

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. 2x
   >
   3x +
   27 .

10. 3x
    – 12
    x
    + 3.

11. .

12. .

13. .

14. .

Неравенства

1. Решите неравенство
   .

2. Решите
   неравенство
   .

3. Решите неравенство
   .

4. Решите неравенство
   .
   В ответе укажите наибольшее целое
   решение.

5. Решите
   неравенство
   .

6. Решите неравенство
   .

7. Решите неравенство
   .

8. На
   рисунке изображен график функции
   .
   Используя график, решите неравенство

   .

9. На рисунке изображен график
   функции
   .
   Используя график, решите неравенство

   .

10. Решите
    неравенство
    .
    В ответе укажите наибольшее целое
    решение.

Метод интервалов в решении
неравенств

1. Решите неравенство:
.

2. Решите неравенство:
.

3. Решите неравенство:
.

4. Решите неравенство:
.

5. Решите неравенство:
.

6. Решите
неравенство
.

7. Решите неравенство
.

8.
Решите неравенство
.

Разложение квадратного трехчлена
на множители

1.
Разложите квадратный трехчлен

на множители.

2. Какое
выражение надо подставить вместо
многоточия, чтобы было верным равенство

?

3. Укажите
выражение, тождественно равное данному
трехчлену
.

4. В
какой многочлен можно преобразовать
выражение
?

5. В
каком случае выражение преобразовано
в тождественно равное?

6.
Разложите квадратный трехчлен

на множители.

7.
Разложите квадратный трехчлен

на множители.

8. Разложите
квадратный трехчлен

на множители.

9.
Разложите квадратный трехчлен на
множители.

10.
Разложите квадратный трехчлен

на множители.

Математика 11 класс, школьный этап (1 этап), 2018-2019 учебный год

Содержание

1. Задача 1
2. Задача 2
3. Задача 3
4. Задача 4
5. Задача 5
6. Задача 6

---

Задача 1

Докажите, что уравнение x² + 2²⁰¹⁸x + 2²⁰¹⁹ = 0 не имеет целых корней.

Первое решение. Дискриминант этого уравнения равен

2⁴⁰³⁶— 4 · 2²⁰¹⁹ = 2²⁰²¹(2²⁰¹⁵— 1).

Для наличия целого корня необходимо, чтобы дискриминант был точным квадратом. Однако, число 2²⁰²¹(2²⁰¹⁵— 1) не является точным квадратом, так как степень вхождения двойки в любой точный квадрат чётна.

Второе решение. Предположим противное: пусть у этого уравнения есть целый корень n. Заметим, что он должен быть отрицательным, так как иначе n² + 2²⁰¹⁸n + 2²⁰¹⁹ было бы положительным.

Так как

n² + 2²⁰¹⁸n + 2²⁰¹⁹ = 0,

число 2²⁰¹⁹ делится на n, то есть n = —2^lдля некоторого неотрицательного целого l. Тогда 2^2018+l = 2^2l + 2²⁰¹⁹. Если 2l < 2019, то 2^2018-l = 1 + 2^2019—2l, что невозможно, так как 1+2^2019—2l нечётно и больше одного. Аналогично, если 2l > 2019, то 2^l-1 = 2^2l-2019 + 1, что невозможно, так как 2^2l-2019 + 1 нечётно и больше одного.

Третье решение. Заметим, что при x = —2 левая часть уравнения положительна (равна 4), а при x = —3 отрицательна (равна —2²⁰¹⁸ + 9). Значит, на промежутке (—3; —2) у уравнения есть корень; он, очевидно, нецелый. Так как по теореме Виета сумма корней нашего уравнения равна —2²⁰¹⁸, второй корень тоже нецелый.

 

Критерии

4 б. Верное решение.

1 б. Дискриминант записан в виде произведения степени двойки на нечетное число.

Задача 2

Пятиугольник ABCDE вписан в окружность ω. Диагональ AC является диаметром окружности ω. Найдите ∠BEC, если ∠ADB = 20°.

Ответ: 70°.

Решение. Рис. 4. Так как ∠ADB = 20°, дуга AB равна 40°. Так как AC — диаметр, дуга ABC равна 180°, то есть дуга BC равна 180° — 40° = 140°. Угол BEC опирается на дугу BC, а значит, он равен 140°/2 = 70°.

Критерии

4 б. Верное решение.

0 б. Только правильный ответ.

Рис. 4: к задаче 2

Задача 3

Сколькими способами можно разрезать по клеткам приведённую ниже картинку на прямоугольники 1 × 2 (сторона одной клетки равна 1)?

Ответ: 27.

Решение. Прямым перебором можно убедиться, что количество разрезаний прямоугольника 2 × 3 на прямоугольники 1 × 2 равно трём (все три варианта приведены на рисунке ниже).

Рассмотрим клетку A:

Если A является нижней клеткой вертикального прямоугольника 1× 2, то остающаяся верхняя часть фигуры имеет нечётную площадь и не может быть разрезана. Значит, A является верхней клеткой вертикального прямоугольника 1× 2.

Тогда следующее частичное разрезание получается однозначно:

Осталось разрезать три отдельных прямоугольника 2 × 3. Для каждого из них есть три разрезания, значит, для всех вместе есть 3³ = 27 разрезаний.

Критерии

0 б. Только правильный ответ.

1 б. Посчитаны некоторые разрезания.

2 б. Решение перебором, но много (около половины) случаев пропущены.

3 б. При рассмотрении случаев несколько (не много!) пропущены.

4 б. Верное решение с арифметической ошибкой, не влияющей на ход решения.

4 б. Верное решение.

Задача 4

На доске написано число ноль. Петру разрешается совершать следующие операции:

• применить к одному из написанных на доске чисел тригонометрическую (sin, cos, tg или ctg) или обратную тригонометрическую (arcsin, arccos, arctg или arcctg) функцию и написать результат на доске;
• написать на доске частное или произведение двух уже написанных чисел.

Помогите Петру написать на доске √3.

Решение. Пётр может, например, совершить следующие вычисления:

1. cos 0 = 1;
2. arctan 1 = π/4 ;
3. arccos 0 = π/2 ;
4. π/4 : π/2 = 1/2;
5. arccos 1/2 = π/3;
6. tg π/3 = √3.

Замечание. К требуемому результату может приводить ещё много последовательностей операций.

Критерии

1 б. Получено число π/2 или π/4 .

2 б. Получены числа π/2 и π/4 .

2 б. Получено число 1/2.

3 б. Получено число π/3 или π/6 .

4 б. Верное решение.

Задача 5

На ребре AA′ куба ABCDA′B′C′D′ с ребром длины 2 отмечена точка K. В пространстве отмечена такая точка T, что TB = √11 и TC = √15.

Найдите длину высоты тетраэдра TBCK, опущенной из вершины C.

Ответ: 2.

Рис. 5: к задаче 5

 

Решение. Заметим, что

TB² + BC² = 11 + 4 = 15 = TC²:

Отсюда по обратной теореме Пифагора следует, что угол TBC прямой. Следовательно, TB⊥ BC, то есть T лежит в плоскости грани AA′B′B. Значит, BC является высотой, опущенной из вершины C, а её длина равна 2.

Замечание. Существуют два возможных расположения точки T, симметричных относительно плоскости KBC.

Критерии

4 б. Верное решение.

0 б. Только правильный ответ.

Задача 6

Внутри шляпы волшебника живут 100 кроликов: белые, синие и зелёные. Известно, что если произвольным образом вытащить из шляпы 81 кролика, то среди них обязательно найдутся три разноцветных. Какое наименьшее количество кроликов нужно достать из шляпы, чтобы среди них точно было два разноцветных?

Ответ: 61.

Решение. Докажем, что если произвольным образом вытащить из шляпы 61 кролика, то среди них найдутся два разноцветных. Предположим противное: пусть имется a ≥ 61 кроликов какого-то цвета (например, белого). Пусть второй цвет по количеству кроликов — синий. Тогда в шляпе живёт хотя бы (100 — a)/2 синих кроликов. А значит, общее количество белых и синих хотя бы

Так как кроликов целое число, белых и синих вместе хотя бы 81, что противоречит условию.

Покажем, что 60 кроликов может быть недостаточно. Пусть в шляпе живёт 60 белых и по 20 синих и зеленых. Тогда может получиться, что все вытащенные кролики белые. С другой стороны, если вытащить 81 кролика, то среди них точно встретятся кролики всех трёх цветов.

Критерии

4 б. Верное решение.

3 б. Доказано, что 61 кролика хватит.

1 б. Показано, что 60 кроликов может не хватить.

0 б. Только правильный ответ.

Урок 46. однородные тригонометрические уравнения — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №46. Однородные тригонометрические уравнения.

Перечень вопросов, рассматриваемых в теме:

1) Однородные тригонометрические уравнения первой и второй степени.

2) Рассмотреть решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки.

3) Рассмотреть решение более сложных тригонометрических уравнений.

Глоссарий по теме

1. Арккосинусом числа называется такое число α, что: . Арккосинус числа m обозначают: .
2. Арксинусом числа называется такое число α, что: и . Арксинус числа m обозначают: .
3. Арктангенсом числа m называется такое число α, что: и . Арктангенс числа m обозначают: .
4. Арккотангенсом числа n называется такое число α, что: и . Арккотангенс числа n обозначают:
5. Уравнение вида:

называется однородным.

Здесь f и g произвольные функции, коэффициенты.

6. Универсальная тригонометрическая подстановка — это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:

Основная литература:

Колягин Ю. М., Ткачева М. В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2014.

Дополнительная литература:

Шахмейстер А.Х. Тригонометрия. М. 2014, 712 с.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Мы уже знаем, как решаются простейшие тригонометрические уравнения, а также тригонометрические уравнения, которые могут быть сведены к квадратным, дробно-рациональным или алгебраическим степени выше второй с помощью замены переменной. Но это лишь маленькое количество тригонометрических уравнений. Как, например, быть в том случае, когда тригонометрическое уравнение выглядит, например, так:

.

Для этого нам нужно рассмотреть некоторые вспомогательные приемы решения уравнений, а также формулы преобразования тригонометрических выражений.

Задание:

Как Вы думаете, какие факты и формулы мы будем использовать при решении этого уравнения?

Ответ: определение тангенса, формулу синуса двойного аргумента.

1. Итак, рассмотрим однородное тригонометрическое уравнение.

Напомним определение однородного уравнения

Определение

Уравнение вида:

называется однородным.

Здесь f и g произвольные функции, коэффициенты.

В зависимости от значения показателя n, мы можем получить однородное уравнение первой, второй или более высокой степени.

Например, уравнение является однородным, а уравнение однородным не является.

2. Теперь перейдем к рассмотрению однородных тригонометрических уравнений.

Если функции f и g это синус и косинус одного и того же аргумента, то мы получим тригонометрическое однородное уравнение.

Рассмотрим сначала однородное тригонометрическое уравнение первой степени.

Запишем его в общем виде: (1).

Разделим это уравнение на (или на ) и получим: .

Решать такие уравнения мы умеем: , .

Заметим, что, решая это уравнение, мы выполняли деление уравнения на выражение с переменной. Так как это действие не является равносильным, проверим, не потеряли ли мы корни.

Если , то . То есть при подстановке в уравнение (1) таких значений х, при которых , оно не обратиться в верное числовое равенство, а значит такие х корнями исходного уравнения не являются, и значит наше действие не приведет к потере корней.

Рассмотрим конкретный пример.

Пример 1.

Решить уравнение:

Решение:

.

Ответ:

Решим теперь однородное тригонометрическое уравнение второй степени

Общий вид такого уравнения:

(2)

Так же, как и уравнение (1), разделим его на наибольшую степень косинуса х.

Так же, как и при решении уравнения (1), мы должны убедиться в том, что при делении уравнения на выражение с переменной мы не потеряли корней. Это не произойдет в том случае, если .

После деления мы получили квадратное уравнение относительно тангенса х, которое и решаем известными способами.

.

При решении этого уравнения мы можем вводить новую переменную , но можем этого и не делать.

.

В зависимости от значения дискриминанта этого квадратного уравнения оно может иметь от 0 до 2 корней. И, соответственно, исходное уравнение может иметь две серии решений, одну или ни одной.

Рассмотрим пример.

Пример 2.

Решить уравнение:

Решение:

.

.

Ответ: .

Даже если исходное тригонометрическое уравнение второй степени не является однородным, можно его преобразовать к такому виду.

Рассмотрим это сначала на примере уравнения второй степени.

Пример 3.

Решить уравнение:

Решение:

Сначала умножим 3 на тригонометрическую единицу, то есть на выражение

(. Мы получим:

Теперь преобразуем полученное уравнение к однородному виду:

Теперь решим полученное однородное уравнение:

.

.

Ответ:.

3. Теперь рассмотрим, как можно привести к однородному уравнение вида

, то есть левая часть которого является однородной первой степени, а в правой стоит число.

Рассмотрим это на примере.

Пример 4.

Решение:

Используем формулы двойного аргумента:

Подставим их в исходное уравнение и домножим на тригонометрическую единицу 2, стоящую в правой части.

.

.

Ответ:.

Заметим, что подобные уравнения можно решить и по-другому, а именно, применив формулу вспомогательного аргумента:

Рассмотрим решение примера 4 этим способом.

Пример 4-а.

Решение:

Преобразуем левую часть:

Ответ:

Мы видим, что результат, полученный при решении разными способами, кажется разным. Но на самом деле в тригонометрии одно и то же число может быть записано разными способами.

Можно сказать, что первый способ в этом случае приводит к более короткому и красивому результату.

Решите уравнение

Решение:

В такой записи уравнение не является однородным.

Используем формулу синуса двойного аргумента.

Теперь уравнение однородное.

Решим его.

, .

Ответ: .

Решить уравнение

1) с помощью формулы вспомогательного аргумента

Решение

Ответ:

2) с помощью формул синуса и косинуса двойного аргумента

Решение

Ответ:

3) Решите уравнение:

Решение

Ответ:

4. Рассмотрим теперь решение тригонометрических уравнений с использованием универсальной тригонометрической подстановки.

Она называется универсальной, так как позволяет любое уравнение вида

(*), где рациональная функция, свести к рациональному алгебраическому уравнению.

Универсальная тригонометрическая подстановка – это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:

То есть если сразу обозначить , то уравнение (*) примет вид: . А так как сама функция F является рациональной, то и получающееся уравнение будет рациональным алгебраическим.

Рассмотрим пример 5.

Решить уравнение .

Решение:

Область определения исходного уравнения:

Преобразуем исходное уравнение:

или

Используем универсальную тригонометрическую подстановку.

Если , то получим уравнение:

Решим его.

, .

Ответ: .

Заметим, что когда мы используем универсальную тригонометрическую подстановку, у нас появляется тангенс половинного угла, который не всегда определен. Поэтому мы можем потерять корни. Нужно проверить.

определен для всех .

Так как эти числа, не принадлежат области исходного уравнения, то мы не потеряем корней.

Решите уравнение

Рассмотрим решение уравнения

(**)

Решение:

Найдем область допустимых значений:

Теперь используем универсальную тригонометрическую подстановку и формулу тангенса суммы аргументов.

Область допустимых значений полученного уравнения уже, чем исходного:

.

Решим полученное уравнение:

.

Но необходимо проверить те числа, которые выпали из области определения после использования универсальной тригонометрической подготовки.

Это числа вида .

Подставим π в (**): верное равенство. Это означает, что числа вида тоже являются решениями исходного уравнения.

Таким образом, получается ответ.

.

Ответ: .

Примеры и разбор решения заданий тренировочного модуля

№ 1.

Даны уравнения.

Запишите номера однородных уравнений

Ответ: однородными являются 1), 5) , 7) и 8) уравнения.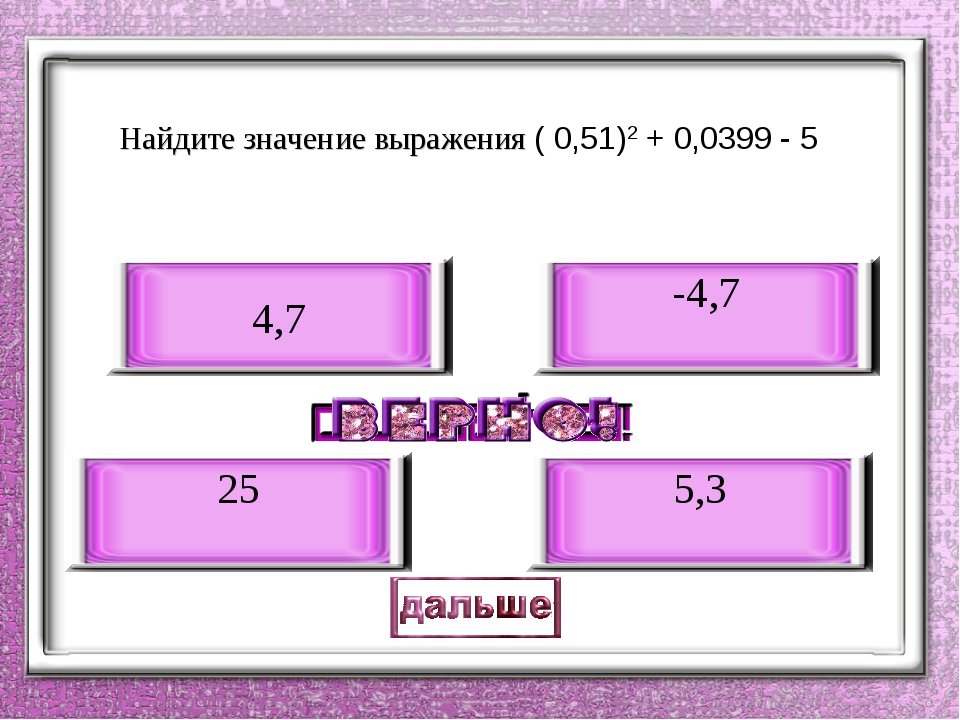

№ 2.

Даны уравнения.

Распределите их по группам в зависимости от того, являются они однородными или не являются.

Однородные уравнения	Неоднородные уравнения

№ 3.

Даны уравнения.

Выделите цветом уравнения, которые могут быть приведены к однородному

Ответ:

№ 4.

Автоматически заполняемый кроссворд.

Решите уравнения. Укажите значение k, при котором его корень становится больше .

1)

k=1

Слово МИНУС

2)

k=1

Слово КОРЕНЬ

3)

k= 2

Слово РАВЕНСТВО

№ 5.

Выберите простейшие тригонометрические уравнения, которые получаются при решении данного уравнения

Ответ: 16

№ 6.

Подчеркните простейшее тригонометрическое уравнение вида , которое получается при решении данного уравнения

1)

2)

3)

4)

5)

Ответ: 3

№ 7.

Выберите из списка простейшие тригонометрические уравнения вида , которые получаются при решении данного уравнения.

1)

2)

3)

4)

5)

6)

Ответ: 25

№ 8.

Решите уравнение

Перетащите в ответ составляющие

1)

2)

3)

4)

5)

6)

Ответ:

№ 9*.

Автоматически заполняемый кроссворд

Решите уравнения. Определите, сколько корней имеет каждое из этих уравнений на интервале (-π; π).

Ответ: 4

Слово ПРОМЕЖУТОК

Ответ: 20

Слово ОТРЕЗОК

Ответ: 8

Слово ИНТЕРВАЛ

№ 10.*

Заполните пропуски в решении.

Растащите элементы по пропускам

Домножим второе и третье слагаемые на ____________

____+_____

Разделим уравнение на ___________

___+____-1=0

После решения вспомогательного уравнения получим:

Получим ответ:

Элементы для перетаскивания

тригонометрическую единицу

Ответ:

Домножим второе и третье слагаемые на тригонометрическую единицу

Разделим уравнение на

Получим ответ:

№ 11. *АЗК

Решите уравнение. Впишите в формулу ответа правильные коэффициенты.

Ответ:

№ 12.**

Решите уравнение.

Выберите серии, из которых состоит решение

1)

2)

3)

4)

5)

6)

7)

Ответ: 3, 5, 6

№ 13.**

Автоматически заполняемый кроссворд

Выберите номер наименьшего положительного корня

1) 1

2)

3)

4)

5)

6)

7)

Ответ: 2

Слово РЕШЕНИЕ

Выберите номер наименьшего положительного корня

1) 1

2)

3)

4)

5)

6)

7)

Решение:

Умножим второе и третье слагаемые на тригонометрическую единицу:

Разделим уравнение на

Вспомогательное уравнение:

Оно имеет единственный корень t=1

Ответ: 5

Слово ТРИГОНОМЕТРИЯ

Выберите номер правильного ответа

1) 1

2)

3)

4)

5)

6)

7)

Ответ: 4

Слово АЛГЕБРА

№ 14. **АЗК

Решите уравнение. Впишите в формулу ответа правильные коэффициенты.

Решение:

Разделим обе части уравнения на

Введем новую переменную: .

Вспомогательное уравнение:

Так как t неотрицательное, то t=1.

Поэтому

1)

2)

3)

Ответ:

Проверочная работа:

№ 1.

А)Автоматически заполняемый кроссворд

Решите уравнение. Введите значения коэффициентов

Ответ:

1) a=1 слово ТРИГОНОМЕТРИЯ

2) b=12 слово КОСИНУС

3) c=1 слово МИНУС

4) d=2 слово КВАДРАТ

Ответ:

Б)Автоматически заполняемый кроссворд

Решите уравнение. Введите значения коэффициентов

Ответ:

1) a=1 слово УРАВНЕНИЕ

2) b=6 слово СИНУС

3) c=1 слово СТЕПЕНЬ

4) d=2 слово ТОЖДЕСТВО

Ответ:

№ 2.

А)Решите уравнение. Выберите наибольший отрицательный корень.

Б) Решите уравнение. Выберите наименьший положительный корень

Ответ:

№ 3.

А)Автоматически заполняемый кроссворд

Решите уравнение. Введите значения коэффициентов

Ответ: а = 30 слово ДЕЛИМОЕ, b = 2 слово ДЕЛИТЕЛЬ, c = 5 слово ЧАСТНОЕ

Б)Автоматически заполняемый кроссворд

Решите уравнение. Введите значения коэффициентов

Ответ: а = 18 слово МНОЖИТЕЛЬ, b = 2 слово ПРОИЗВЕДЕНИЕ, c = 3 слово УМНОЖЕНИЕ

Как найти наибольший корень уравнения. Корень уравнения

В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.

Что подразумевается под уравнением и его корнем?

Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями.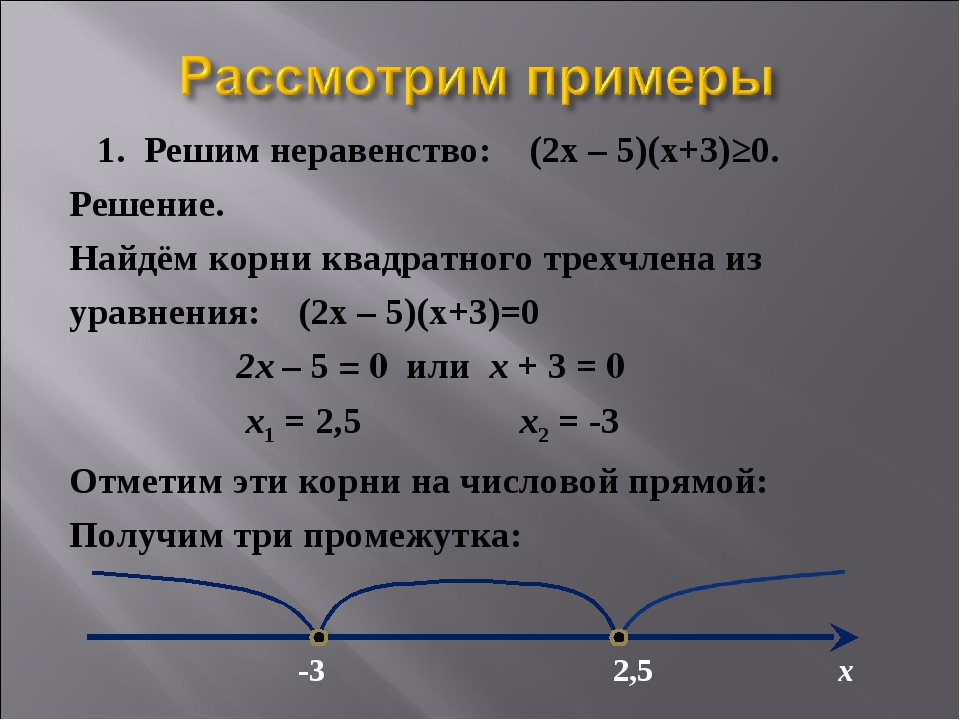 Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.

Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.

Поиск всех возможных корней уравнения является его решением. То есть нужно выполнить ряд математических действий, которые его упрощают. А потом приводят к равенству, в котором содержится только неизвестная и какое-либо число.

В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.

Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.

О линейном уравнении

Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.

Алгоритм преобразований:

• перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
• разделить обе части получившегося равенства на коэффициент «а».

Общий вид решения такой:

х = -в/а
.

Из него ясно, что ответом будет одно число. То есть всего один корень.

Квадратное уравнение

Его общий вид: а * х 2 + в * х + с = 0
. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.

Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с
. После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.

Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант

В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:

х 1,2 = (-в ± √Д) / (2 * а)
.

Здесь всегда получится два ответа. Это связано с тем, что в исходной формуле стоит знак «плюс/минус». Он существенно изменяет значение неизвестной.

При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:

х = (-в) / (2 * а).

При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.

Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.

Формулы для расчета корней квадратного уравнения, не использующие дискриминант

Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:

х 2 + в * х + с = 0.

Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:

х 1 + х 2 = -в

и
х 1 * х 2 = с.

Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.

К этому варианту всегда можно прийти от общего вида квадратного уравнения.

Достаточно только разделить все коэффициенты на «а».

Как быть, если нужно узнать наименьшее значение корня?

Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.

Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:

2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.

Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.

В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.

После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.

Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.

Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.

Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».

Нужно вернуться к введенному обозначению. х 1,2 = ± 1, х 3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.

В качестве заключения

Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.

Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.

Если х = -1, то получается такой же результат. Корень тоже подходящий.

Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.

Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.

Вывод: надо помнить о проверке и внимательно подходить к решению.

Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?

Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.

Например, 3x=9 — это уравнение, а 3 . 3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.

Вот этим мы и займемся — будем находить корень уравнения.

Задание 1 — найдите корень уравнения 2 1-4x =32

Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.

Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=2 5

Таким образом, наше уравнение будет выглядеть так: 2 1-4х =2 5

Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:

Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:

Делаем проверку: 2 1-4(-1) =32

Мы нашли корень уравнение. Ответ: х=-1.

Самостоятельно найдите корень уравнения в следующих заданиях:

б) 2 1-3х =128

Задание 2 — найдите корень уравнения

Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.

Используем следующее свойство степени:

По этому свойству мы получим для правой части нашего уравнения:

Если равны основания степени, значит, равны и показатели степени:

Ответ: х=9.

Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.

Мы нашли корень уравнения правильно.

Задание 3 — найдите корень уравнения

Заметим, что справа у нас стоит 1/8, а 1/8 — это

Тогда наше уравнение запишется в виде:

Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:

Ответ: х=5. Проверку сделайте самостоятельно.

Задание 4 — найдите корень уравнения log 3 (15-х)=log 3 2

Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:

Ответ: х=13

Задание 5 — найдите корень уравнения log 3 (3-x)=3

Число 3 — это log 3 27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.

Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:

log 3 (3-x)=log 3 27

Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:

Сделаем проверку:

log 3 (3-(-24))=log 3 27

log 3 (3+24)= log 3 27

log 3 27=log 3 27

Ответ: x=-24.

Найдите корень уравнения. Задание 6.

log 2 (x+3)=log 2 (3x-15)

Проверка: log 2 (9+3)=log 2 (27-15)

log 2 12=log 2 12

Ответ: x=9.

Найдите корень уравнения. Задание 7.

log 2 (14-2x)=2log 2 3

log 2 (14-2x)=log 2 3 2

Проверка: log 2 (14-5)=2log 2 3

log 2 9=2log 2 3

log 2 3 2 =2log 2 3

2log 2 3=2log 2 3

Ответ: x=2,5

Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы и .

Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение
, и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.

Навигация по странице.

Что такое уравнение?

Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения
:

Определение.

Уравнение
– это равенство, содержащее неизвестное число, которое надо найти.

Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p
, t
, u
и т.п., но наиболее часто используются буквы x
, y
и z
.

Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.

Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
, y=3
и т.п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.

Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18
и x+3·(x+2·(x−2))=3
. Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9
, также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8
, 7−3=z+1
или 3·x−4=2·(x+12)
.

Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений
, изучающиеся в школе.

В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:

Определение.

Уравнением
называют равенство, содержащее переменную, значение которой нужно найти.

Например, уравнение x+3=6·x+7
– уравнение с переменной x
, а 3·z−1+z=0
– уравнение с переменной z
.

На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.

Определение.

Уравнения с одной, двумя, тремя и т.д. переменными
– это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.

Например, уравнение 3,2·x+0,5=1
– это уравнение с одной переменной x
, в свою очередь уравнение вида x−y=3
– это уравнение с двумя переменными x
и y
. И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27
. Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.

Что такое корень уравнения?

С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.

Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a
в уравнение a+1=5
подставить число 2
, то получится неверное числовое равенство 2+1=5
. Если же мы в это уравнение подставим вместо a
число 4
, то получится верное равенство 4+1=5
.

На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.

Определение.

Корень уравнения
– это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.

Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.

Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5
. Согласно озвученному определению корня уравнения, число 4
есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5
, а число 2
не является его корнем, так как ему отвечает неверное равенство вида 2+1=5
.

На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.

Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5
имеет корень 4
, а уравнение 0·x=5
не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x
, мы получим неверное равенство 0=5
.

Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4
имеет единственный корень 6
, корнями уравнения x 2 =9
являются два числа −3
и 3
, уравнение x·(x−1)·(x−2)=0
имеет три корня 0
, 1
и 2
, а решением уравнения x=x
является любое число, то есть, оно имеет бесконечное множество корней.

Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества
в фигурных скобках. Например, если корнями уравнения являются числа −1
, 2
и 4
, то пишут −1
, 2
, 4
или {−1, 2, 4}
. Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
, и корнями этого уравнения являются числа 3
и 5
, то можно записать x=3
, x=5
, также переменной часто добавляют нижние индексы x 1 =3
, x 2 =5
, как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .

Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.

Определение.

Решением уравнения с двумя, тремя и т.д. переменными
называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.

Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
. Подставим в него вместо x
число 1
, а вместо y
число 2
, при этом имеем равенство 1+2=7
. Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.

Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.

Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7
. Решение этого уравнения x=4
, y=3
кратко можно записать как (4, 3)
.

Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений
.

Список литературы.

• Математика
  . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
• Алгебра:
  учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Алгебра:
  9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.

\(2x+1=x+4\) находим ответ: \(x=3\). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа:

\(2x+1=x+4\)
\(2\cdot3+1=3+4\)
\(7=7\)

И никакое другое число, кроме тройки такого равенства нам не даст. {2}+15\cdot(-2)+22=0\)
\(2\cdot4-30+22=0\)

\(0=0\) — сошлось, значит \(-2\) — корень уравнения

Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для
достаточно одних только
, для
– уже используются формулы
и т.д. Каждому типу уравнений – свой метод.

Ответы на часто задаваемые вопросы

Вопрос:

Может ли корень уравнения быть равен нулю?
Ответ:

Да, конечно. Например, уравнение \(3x=0\) имеет единственный корень — ноль. Можете проверить подстановкой.

Вопрос:

Когда в уравнении нет корней?
Ответ:

В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение \(0\cdot x=5\). 2-5x-6=0\) имеет два корня: \(x_1=-1\) и \(x_2=6\). Меньший из корней: \(-1\). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать \(6\).

Теорема виета в задачах с параметрами

Г ОРОДСКОЙ МЕТОДИЧЕСКИЙ ЦЕНТР УПРАВЛЕНИЯ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ГОРОДА КОСТРОМЫ

Теорема Виета в задачах с параметрами.

КОСТРОМА

2006

Теорема Виета в задачах с параметрами: В помощь учителю / Составитель С. А. Сорокина. – Кострома, 2006. – 8 с.

Составитель пособия «Теорема Виета в задачах с параметрами» — Почётный работник Российской Федерации, учитель математики высшей квалификационной категории МОУ лицея №17 города Костромы Сорокина Светлана Анатольевна. Светлана Анатольевна работает в классах углублённого изучения математики. Её учащиеся – призёры и победители математических олимпиад различных уровней.

В пособии представлен практикум «Теорема Виета в задачах с параметрами» и один из способов решения заданий практикума.

Задания расположены в порядке возрастания сложности и носят обучающий характер.

Рецензент:

Л. К. Борткевич – методист ГМЦ

Ó С.А. Сорокина

Ó Оформление и вёрстка Л. К. Борткевич

Теорема Виета в задачах с параметрами.

Теорема.Если квадратное уравнение ax²+bx+c=0 имеет корни x₁ и x₂ ,то для них справедливы соотношения — , .

Задачи.

1. При каких значениях k произведение корней квадратного уравнения равно нулю?

2. При каких значениях k сумма корней квадратного уравнения равна нулю?

3. В уравнении сумма квадратов корней равна 16.Найдите а.

4. Найдите все значения а, при которых сумма квадратов корней уравнения равна 10.

5. В уравнении квадрат разности корней равен 16.Найдите а.

6. Найдите все значения а, для которых разность корней уравнения равна 1.

7. При каких значениях а сумма корней уравнения равна сумме квадратов его корней?

8. При каком значении параметра m сумма квадратов корней уравнения наименьшая?

9. При каком значении параметра m сумма квадратов корней уравнения наибольшая?

10. При каких значениях коэффициента b сумма квадратов корней уравнения принимает наименьшее значение?

11. Найдите сумму квадратов всех корней уравнения .

12. При каких значениях p и q корни уравнения равны и ?

13. Не решая уравнения найти, при каком значении а один из корней в 2 раза больше другого.

14. В уравнении определить а так, чтобы отношение корней равнялось 2.

15. При каких значениях параметра а разность корней уравнения равна их произведению?

16. Известно, что корни уравнения на 1 меньше корней уравнения . Найдите а и корни каждого из этих уравнений.

17. Известно, что корни уравнения равны соответственно квадратам корней уравнения . Найдитеa и b и корни каждого из уравнений.

18. При каких значениях коэффициента с один из корней уравнения равен квадрату другого корня?

19. При каких значениях параметра а уравнение имеет ровно три корня?

20. При каком а уравнение имеет два отрицательных корня?

Решения и ответы.

1. При каких значениях k произведение корней квадратного уравнения равно нулю?

Решение.

По теореме Виета имеем = и по условию =0. Корнями уравнения =0 являются числа 3 и 4. При k=3 и k=4 получим уравнение , произведение корней которого равно 0.

Ответ:3;4.

2. При каких значениях k сумма корней квадратного уравнения равна нулю?

Решение.

По условию =0, по теореме Виета имеем =.

Корнями уравнения являются числа 1 ,-5. При k=1 получим уравнение , сумма корней которого равна 0. При k= -5 получим уравнение , которое не имеет корней.

Ответ:1.

3. В уравнении сумма квадратов корней равна 16.Найдите а.

Решение.

По теореме Виета имеем =4, = а. По условию =16.

4²-2а=16, а=0

При а = 0 уравнение имеет корни, сумма квадратов которых равна 16.

Ответ: 0.

4. Найдите все значения а, при которых сумма квадратов корней уравнения равна 10.

Решение.

Для того, чтобы сумма квадратов корней уравнения равнялась какой-либо величине, эти корни должны существовать. Значит, дискриминант нашего уравнения должен быть неотрицательным, т.е. а²-4(а+7). При таких а у исходного уравнения найдутся (возможно, совпадающие) корни x₁ и x₂. Запишем для них теорему Виета: = а, = а+7 . Теперь, не вычисляя корней, можно найти сумму их квадратов через а:

== а²-2(а+7) Согласно условию, эта сумма квадратов равна 10, откуда получаем квадратное уравнение а²-2(а+7)=10, корнями которого являются числа 6 и -4. При а = 6 дискриминант исходного уравнения отрицательный, а при а = -4 положительный.

Ответ:а = -4.

5. В уравнении квадрат разности корней равен 16.Найдите а.

Решение.

По теореме Виета имеем =2, = а. Чтобы корни существовали, дискриминант нашего уравнения должен быть неотрицательным, 4-4а, т.е. а. По условию

4-4а=16

а = -3, -3.

Ответ:а = -3.

6. Найдите все значения а, для которых разность корней уравнения равна 1.

Решение.

По теореме Виета =; =. Следовательно, =.

По условию =1. Значит, а₁=9, а₂=-3. При данных значениях параметра а дискриминант исходного уравнения больше нуля.

Ответ: 9, -3.

7. При каких значениях а, сумма корней уравнения равна сумме квадратов его корней?

Решение.

По теореме Виета =2а, =2а-1. По условию =.

=

2а=(2а)²-2(2а-1),

а=1, а =.

При а =1 уравнение имеет корень 1 , при а = уравнение имеет корни 1 и 0.

Ответ: 1 , .

8. При каком значении параметра m сумма квадратов корней уравнения наименьшая?

Решение.

По теореме Виета имеем = m-2, = —m-3

==(2-m)²-2(-m-3)=m²-2m +10=(m-1)²+9.

Сумма квадратов корней наименьшая при m =1. При m=1 уравнение имеет два корня.

Ответ: 1.

9. При каком значении параметра m сумма квадратов корней уравнения наибольшая?

Решение.

По теореме Виета имеем = —m+1, = m²-1,5.

==(-m+1)²-2(m²-1,5)= —m²-2m+4= -(m+1)²+5

При m= -1 выражение -(m+1)²+5 принимает наибольшее значение. При m = -1 уравнение имеет корни.

Ответ: -1.

10. При каких значениях коэффициента b сумма квадратов корней уравнения принимает наименьшее значение?

Решение.

Выразим сумму квадратов корней данного уравнения через его коэффициенты при помощи теоремы Виета следующим образом:

==b²-2.

Выражение b²-2 принимает наименьшее значение при b=0. При этом значении b сумма квадратов корней отрицательна. Надо обязательно добавить условие неотрицательности дискриминанта b²-4. Теперь уже нетрудно заключить, что сумма квадратов корней уравнения принимает наименьшее значение приb=

Ответ:

11. Найдите сумму квадратов всех корней уравнения .

Решение.

Пусть = t. Рассмотрим уравнение . >0, по теореме Виета t₁+t₂=3, =1.

Уравнение имеет два положительных корня, следовательно, исходное уравнение имеет 4 корня. Причем t₁=, t₂=

+==2(=2((t₁+t₂)²-2t₁t₂)=2(9-2)=14

Ответ: 14.

12. При каких значениях p и q корни уравнения равны и ?

Решение.

Пусть . По теореме Виета имеем = —p, =q, =p²-4q, следовательно, ;

q= -6p

q.

Если q=0, тоp=0, =0, если p=1, то q= -6, >0. Уравнение имеет корни.

Ответ:p=q=0 илиp=1, q= -6.

13. Не решая уравнения найти, при каком а один из корней в 2 раза больше другого.

Решение.

По условию . По теореме Виета имеем .

Значит, При а = 4 уравнение имеет корни 6 и 3.

Ответ: 4.

14. В уравнении определить а так, чтобы отношение корней равнялось 2.

Решение.

Пусть х — корень уравнения. Тогда второй корень 2х.

При a= получим уравнение , корни которого -3 и -6.

Ответ:

15. При каких значениях параметра а разность корней уравнения равна их произведению?

Решение.

Имеем ;

По условию

При а=1 уравнение имеет корни 1 и ,

при а = уравнение имеет корни и , разность которых равна их произведению.

Ответ: 1, .

16. Известно, что корни уравнения на 1 меньше корней уравнения . Найдите а и корни каждого из этих уравнений.

Решение.

Пусть и — корни уравнения .

По условию +1 и +1 корни уравнения .

По теореме Виета имеем

Отсюдаa+5+1=3a-6, a=6.

При а = 6 уравнение имеет корни 2 и 3, а уравнение имеет корни 3 и 4.

Ответ:а = 6, 2 и 3 — корни первого уравнения, 3 и 4 — корни второго уравнения.

17. Известно, что корни уравнения равны соответственно квадратам корней уравнения . Найдитеa и b и корни каждого из уравнений.

Решение.

По условию и теореме Виета имеем

Отсюда b=36, ==

При b= 36 уравнение имеет корни 9 и 4.

При а = 5 уравнение имеет корни -2 и -3.

При а = -5 уравнение имеет корни 2 и 3.

Ответ: при а = -5, b=36 корни первого уравнения 2 и 3,

корни второго уравнения 4 и 9

при а =5 , b=36 корни первого уравнения -2 и -3,

корни второго уравнения 4 и 9

18. При каких значениях коэффициента с корень уравнения равен квадрату другого корня?

Решение.

Пусть числа и являются корнями этого уравнения.

Тогда по теореме Виета должны выполнятся равенства и .

Поскольку корень должен быть равен квадрату корня , то подставим выражение =² в эти два уравнения.

Получим систему .

Первое уравнение этой системы является квадратным и имеет два корня и .

Подставляя эти значения во второе уравнение системы, получаем два уравнения

и . Решая эти уравнения, получим с =1 и с = -27.

При этих значениях с дискриминант больше 0.

Ответ:— 27,1.

19. При каких значениях параметра а уравнение имеет ровно три корня?

Решение.

Чтобы заданное уравнение имело три корня, необходимо, чтобы корни одного из сомножителей заданного уравнения совпадали.

Итак, имеем , если дискриминант равен нулю.

Значит а = -3. Но если а = -3, то при любом x, второй сомножитель отрицателен, что невозможно.

Рассмотрим равенство нулю второго сомножителя: Его корни совпадают, если а+1=0 , т.е. а = -1.

При а = -1 первый сомножитель имеет два корня .

Ответ: -1.

20. При каком а уравнение имеет два отрицательных корня?

Решение.

=(2а-3)² -4(а+5)(а-10)=8а+209>0

Корни будут иметь одинаковые знаки, если

Оба корня будут отрицательны, если при этом

Таким образом, задача свелась к решению системы неравенств 8а+209>0

Ответ:

Наименьшее и наибольшее значения функции на отрезке

На рисунках ниже показано, где функция может достигать наименьшего и наибольшего значения.
На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума
функции. На правом рисунке — на концах отрезка.

Если функция y = f(x) непрерывна на отрезке [a, b],
то она достигает на этом отрезке наименьшего и наибольшего значений. Это, как
уже говорилось, может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции,
непрерывной на отрезке [a, b], нужно
вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее
и наибольшее.

Пусть, например, требуется определить наибольшее значение функции
f(x) на отрезке [a, b].
Для этого следует найти все её критические точки, лежащие на [a, b].

Критической точкой называется точка, в которой
функция определена, а её
производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических
точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и
на концах отрезка (f(a) и f(b)).
Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a, b].

Аналогично решаются и задачи на нахождение наименьших значений
функции.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2].

Решение. Находим производную данной функции .
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]. Эти значения функции — следующие: ,
,
. Из этого следует, что
наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .

Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком
(а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок),
то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая
на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет
наибольшего значения.

Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо
следующее свойство непрерывных функций.

Если функция непрерывна в промежутке и имеет единственный экстремум, то он
является наименьшим значением в случае минимума и наибольшим — в случае максимума.

Как наименьшее значение функции, так и её наибольшее значение, могут быть найдены
не только в одной точке, принадлежащей заданного интервала, а, как, например, далее — в двух.

Нередки случаи, когда уравнение, полученное от приравнивания производной функции нулю,
не имеет действительных решений. Тогда наименьшее и наибольшее значения функции можно найти только
на концах отрезка. Таков следующий пример.

Неплохо было бы взять и случаи, когда производная функции вычисляется не одним махом,
как в предыдущих примерах. Это мы сейчас и сделаем, решив пример, где требуется найти
производную частного.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции
не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция —
многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами,
поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).
Поэтому в ход пойдут логарифм и тригонометрическая функция.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений
функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют
не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении
прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое
явление или процесс.

Пример 10. Резервуар ёмкостью 4 ,
имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы
должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?

Решение. Пусть x — сторона основания, h — высота резервуара,
S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара
выражается формулой ,
т.е. является функцией двух переменных .
Чтобы выразить S как функцию одной переменной, воспользуемся тем, что ,
откуда . Подставив
найденное выражение h в формулу для S:

или

.

Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в
]0, +∞[, причём

.

Приравниваем производную нулю ()
и находим критическую точку . Кроме того,
при производная не
существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума.
Итак, — единственная
критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём
вторую производную .
При вторая производная
больше нуля (). Значит, при
функция достигает
минимума . Поскольку
этот минимум — единственный экстремум данной функции, он и является её наименьшим значением. Итак,
сторона основания резервуара должна быть равна 2 м, а его высота .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 11. Из пункта A, находящегося на линии железной
дороги, в пункт С, отстоящий от неё на расстоянии l, должны переправляться грузы.
Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна ,
а по шоссе она равна . К
какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из
А в С была наиболее экономичной (участок АВ железной дороги предполагается
прямолинейным)?

Пусть ,
,
(см. рисунок ниже).

Тогда ,
,
. Стоимость провоза
p единиц груза по шоссе СМ составит ,
а по железной дороге МА она составит .
Общая стоимость провоза груза по пути СМА выражается функцией

,

где .

Нужно найти наименьшее значение этой функции. Она дифференцируема при всех значениях
x, причём

.

Приравняв производную нулю, получим иррациональное уравнение ,
решение которого даёт единственную критическую точку
(так как точка не
входит в область определения функции).

Взяв контрольные точки и
слева и справа от
критической точки, убедимся, что производная меняет знак с минуса на плюс. Следовательно, при
стоимость провоза груза
из А и С является наименьшей, если .
Если же , т. е.
, то шоссе должно пройти
по прямой АС (см. рисунок ниже).

Весь блок «Производная»

Решение квадратных уравнений с извлечением квадратного корня

Purplemath

Давайте еще раз посмотрим на последнюю проблему на предыдущей странице:

На предыдущей странице я решил это квадратное уравнение, разложив на множители разность квадратов в левой части уравнения, а затем установив каждый коэффициент равным нулю и т. Д., И т. Д.Решение было « x = ± 2». Однако —

Я также могу попытаться выделить член в квадрате переменной в левой части уравнения (то есть я могу попытаться получить член x ² сам по себе на одной стороне знака «равно»), переместив числовую часть (то есть 4) в правую часть, например:

MathHelp.com

Когда я решаю уравнение, я знаю, что могу делать все, что захочу, с этим уравнением , если я проделываю одно и то же с обеими сторонами этого уравнения . В левой части этого конкретного уравнения у меня есть x ² , и я хочу старый добрый x .Чтобы превратить x ² в x , я могу извлечь квадратный корень из каждой стороны уравнения, например:

х = ± 2

Тогда решение будет x = ± 2, как это было, когда я решил путем факторизации разности квадратов.

Зачем мне понадобился знак «±» (то есть «плюс-минус») на 2, когда я извлек квадратный корень из 4? Потому что я пытаюсь найти всех значений переменной, которые делают исходное утверждение истинным, и это могло быть либо положительное 2, либо отрицательное 2, возведенное в квадрат, чтобы получить 4 в исходном уравнении.

Эта двойственность похожа на то, как у меня было два фактора, один «плюс» и один «минус», когда я использовал формулу разности квадратов для решения того же уравнения на предыдущей странице.

---

«Поиск решения уравнения» — это процесс, очень отличающийся от «вычисления квадратного корня из числа». При нахождении «квадратного корня» числа мы имеем дело исключительно с положительным значением. Почему? Потому что именно так определяется квадратный корень из числа.Значение квадратного корня из числа может быть только положительным, потому что так определяется «квадратный корень из числа».

С другой стороны, решение уравнения, то есть нахождение всех возможных значений переменной, которые может работать с в уравнении, отличается от простой оценки выражения, которое уже определило как имеющее только одно значение.

Держите этих двоих прямо! Число с квадратным корнем имеет только одно значение, а уравнение с квадратным корнем имеет два из-за переменной.

---

В математике мы должны иметь возможность получить один и тот же ответ, независимо от того, какой действительный метод мы использовали, чтобы прийти к этому ответу. Итак, сравнение ответа, полученного мной выше, с ответом, полученным мною на предыдущей странице, подтверждает, что мы должны использовать «±» при извлечении квадратного корня для решения.

(Вы можете сомневаться в моей работе выше на этапе, когда я извлекал квадратный корень из любой стороны, потому что я поставил знак «±» только на одной стороне уравнения.Разве я не должен добавить этот символ к обеим сторонам уравнения? Вроде да. Но если бы я поместил это в обе стороны уравнения, изменилось бы что-нибудь на самом деле? Нет. Попробуйте все варианты, если вы не уверены.)

---

Преимущество этого процесса извлечения квадратного корня состоит в том, что он позволяет нам решать некоторые квадратичные уравнения, которые мы не могли решить раньше, используя только факторинг. Например:

Эта квадратичная часть имеет квадратную и числовую части.Я начну с добавления числового члена к другой стороне уравнения (чтобы квадрат был сам по себе), а затем извлечу квадратный корень из обеих сторон. Мне нужно не забыть упростить квадратный корень:

x ² -50 = 0

x ² = 50

Тогда мое решение:

В то время как мы могли бы получить предыдущее целочисленное решение путем факторизации, мы никогда не смогли бы получить это радикальное решение путем факторизации.Факторинг явно полезен для решения некоторых квадратных уравнений, но дополнительные виды техники позволяют нам находить решения дополнительных видов уравнений.

---

• Решить (

  x — 5) ² — 100 = 0.

Эта квадратичная часть имеет квадратную и числовую части. Я начну с добавления строго числового члена в правую часть уравнения, чтобы квадрат биномиального выражения, содержащего переменную, находился в левой части.Затем я извлечу квадратный корень из обеих частей, запомнив «±» в числовой части, а затем упрощу:

( x — 5) ² — 100 = 0

( x — 5) ² = 100

x — 5 = ± 10

х = 5 ± 10

x = 5-10 или x = 5 + 10

x = –5 или x = 15

Это уравнение после извлечения квадратного корня из любой стороны не содержало радиальных чисел.Благодаря этому я смог упростить свои результаты вплоть до простых значений. Мой ответ:

Предыдущее уравнение является примером уравнения, в котором неосторожный ученик опускает знак «±» при решении и не понимает, как книга получила ответ « x = –5, 15».

У этих учеников есть дурная привычка не утруждать себя записью знака «±», пока они не проверит свои ответы на обратной стороне книги и внезапно «не вспомнят», что они «имели в виду» поставить «±» там, когда они ‘ d извлекает квадратный корень из любой стороны уравнения.

Но эта «магия» работает только тогда, когда у вас есть ответ (чтобы напомнить вам) и когда раствор содержит радикалы (что не всегда случается). В остальных случаях «напоминания» не будет. Ошибка в пропуске «±» может быть смертельной, особенно при тестировании. Не будь этим учеником. Всегда не забывайте вставлять «±».

Между прочим, поскольку решение предыдущего уравнения состояло из целых чисел, эту квадратичную можно также решить путем умножения квадрата, разложения на множители и т. Д .:

( x — 5) ² — 100 = 0

x ² — 10 x + 25 — 100 = 0

x ² — 10 x — 75 = 0

( x -15) ( x + 5) = 0

x — 15 = 0, x + 5 = 0

x = 15, –5

---

• Решить (

  x — 2) ² — 12 = 0

Эта квадратичная часть имеет квадратную и числовую части.Я добавлю числовую часть с другой стороны, так что квадратная часть с переменной будет сама по себе. Затем я извлекаю квадратный корень из обеих сторон, не забывая добавлять «±» к числовой стороне, а затем упрощаю:

( x — 2) ² — 12 = 0

( x — 2) ² = 12

Я не могу больше это упрощать. В моем ответе будут радикалы.Мое решение:

Это квадратное уравнение, в отличие от предыдущего, также не могло быть решено с помощью факторизации. Но как бы я решил это, если бы у них было , а не , давая мне квадратичную, уже переведенную в форму «(часть в квадрате) минус (часть числа)»? Эта проблема приводит к следующей теме: решение путем завершения квадрата.

---

URL: https: // www.purplemath.com/modules/solvquad2.htm

оценок по алгебре для корней

Хотя следующий процесс якобы предназначен для нахождения наименьших верхних и наибольших нижних интегральных границ для действительных корней полиномиальных уравнений, у него есть приятное побочное преимущество — пары последовательных целых чисел, между которыми находится действительный корень также обнаруживаются при нахождении этих границ. По этой причине в следующих примерах я буду указывать как на границы, так и на пары целых чисел, которые «улавливают» действительные корни. Общая информация: Как вы, возможно, уже догадались, поиск корней (или решений) уравнения обычно не является тривиальным процессом. В настоящий момент нас интересует поиск корней (или решений) полиномиального уравнения. Теперь многочлены являются одним из самых основных алгебраических выражений, поскольку нет экспонент, логарифмов, дробей с переменными в знаменателе или переменных под радикалами. (полином — это алгебраическое выражение, в котором показатели переменных являются целыми числами, а в знаменателе нет переменных) Однако найти решения полиномиальных уравнений непросто. Решениями полиномиальных уравнений могут быть действительные или мнимые числа. Прямо сейчас мы займемся только реальными решениями. Напомним, что если действительное число r является решением полиномиального уравнения P (x) = 0, то P (r) = 0. 2 + x — 2 будет касаться оси x, где x = 1. Обратите внимание, что мы говорим, что график касается оси x в точке x = r. Это означает, что он может либо проходить через ось, либо нет, но график будет соприкасаться с осью x. Никакие старые границы не подходят : Иногда бывает полезно найти границы действительных корней многочлена. Это означает, что мы ищем число, которое больше всех корней (верхняя граница) и число, которое меньше всех корней (нижняя граница) . На самом деле это довольно просто для многочленов, с которыми мы столкнемся в этом классе, потому что я мог бы просто выбрать действительно большое число, скажем 1000000, и вычислить, что ни один корень не будет больше 1 миллиона. Точно так же я могу предположить, что ни один корень не будет меньше -1000000, и, вероятно, буду прав. Но знание того, что график коснется оси x где-то в интервале (-1000000, 1000000), на самом деле не дает много полезной информации о местоположении корней. Хотелось бы, чтобы расположение корней было более конкретным. Наименьшая верхняя граница и наилучшая нижняя граница Что действительно помогло бы, так это определить верхнюю границу МАЛЕНЬКИЙ и НАИЛУЧШУЮ нижнюю границу так, чтобы корни были ограничены наименьшим возможным интервалом. Если корни оказываются иррациональными, тогда не существует наименьшей верхней границы, потому что сам корень является непрерывным, неповторяющимся десятичным числом, поэтому мы не можем найти число, которое будет находиться рядом с ним на числовой строке.Итак, мы идем на компромисс и ищем верхнюю границу LEAST INTEGER (LUB) и нижнюю границу GREATEST INTEGER (GLB) , которые мы можем найти. (Напомним, что целые числа: {…..- 3, -2, -1, 0, 1, 2, 3, ….}) Чтобы помочь нам определить границы действительных корней, мы воспользуемся теоремой из вашего текста: ТЕОРЕМА ВЕРХНЕЙ И НИЖНЕЙ ОГРАНИЧЕНИЙ ДЛЯ НАСТОЯЩИХ КОРНЕЙ Рассмотрим полиномиальное уравнение f (x) = a n x n + a n — 1 x n — 1 +….. + a 1 x + a 0 = 0 , где все коэффициенты являются РЕАЛЬНЫМИ числами, а n положительно. 1. Если мы используем синтетическое деление, чтобы разделить f (x) на x — B, где B> 0, и мы получим третью строку, не содержащую отрицательных чисел, то B будет верхней границей для действительных корней f (x). = 0. 2. Если мы используем синтетическое деление, чтобы разделить f (x) на x — b, где b <0, и мы получим третью строку, в которой числа поочередно положительные и отрицательные, тогда b будет нижней границей для действительных корней. функции f (x) = 0.(При определении того, чередуются ли знаки в третьей строке, нули игнорируются.) ВНИМАНИЕ! Число может не пройти тест на нижнюю границу, но все равно будет нижней границей. Однако, если число проходит проверку нижней границы, оно ЯВЛЯЕТСЯ нижней границей. Мы используем эту теорему очень систематически, чтобы найти первое положительное целое число, удовлетворяющее условию оценки сверху.То есть мы пробуем 1, затем 2, затем 3 (и так далее), пока не найдем первое действующее положительное целое число. Чтобы найти нижнюю границу, мы делаем то же самое. Попробуйте -1, затем -2, затем -3 (и так далее), пока мы не найдем первое отрицательное целое число, удовлетворяющее условию нижней границы. Вот пример: Определите верхнюю границу наименьшего целого и нижнюю границу наибольшего интеграла для действительных корней многочлена x 4 — 3 x 2 + x — 12 = 0 Как было сказано ранее, мы будем использовать синтетическое деление, чтобы сначала попробовать 1, затем 2 и так далее, пока не найдем FIRST POSITIVE INTEGER , которое проходит проверку верхней границы.Для консолидации синтетического деления будут показаны только третьи строки каждого этапа синтетического деления Поскольку последняя строка не содержит отрицательных чисел, мы можем объявить, что 3 — это верхняя граница наименьшего целого, которую мы можем найти с помощью этой теоремы. Теперь поищем наибольшую нижнюю границу. В этом случае мы ищем FIRST NEGATIVE INTEGER , которое проходит проверку верхней границы. Мы будем пробовать, -1, -2 и так далее, пока последняя строка синтетического деления не поменяется знаками.Опять же, для консолидации синтетического деления, будут показаны только третьи строки каждого этапа синтетического деления Поскольку в последней строке чередуются положительные и отрицательные значения, мы можем объявить, что — 3 — это наибольшая нижняя граница интеграла, которую мы можем найти с помощью этой теоремы . ПРИМЕЧАНИЕ. Не всегда верхняя и нижняя границы будут аддитивно инвертировать друг друга. РАСПОЛОЖЕНИЕ НАСТОЯЩИХ КОРНЕЙ МЕЖДУ ПОСЛЕДУЮЩИМИ Целыми числами Мы можем почерпнуть еще одну полезную информацию из этих двух таблиц.Для этого мы обратимся к теореме о расположении. ТЕОРЕМА МЕСТОПОЛОЖЕНИЯ Пусть f (x) будет многочленом, все коэффициенты которого являются действительными числами. Если a и b — действительные числа, такие что f (a) и f (b) имеют противоположные знаки, то уравнение f (x) = 0 имеет по крайней мере один действительный корень между a и b. Из таблиц видим: P (0) = — 12 П (1) = — 13 П (2) = — 6 П (3) = 45 П (-1) = — 15 П (-2) = — 10 П (-3) = 39 P (2) и P (3) имеют противоположные знаки, поэтому согласно теореме о местонахождении, уравнение P (x) = 0 имеет по крайней мере один НАСТОЯЩИЙ корень между 2 и 3.Также существует настоящий корень между -3 и — 2. Примечание: Обычно мы заинтересованы в нахождении действительных корней между последовательными целыми числами по двум причинам. Во-первых, с целыми числами легче работать с нецелыми рациональными числами. (как вы думаете, почему это так?) Во-вторых, нас интересуют последовательные целые числа, потому что последовательные целые числа ближе друг к другу, чем непоследовательные, поэтому они «захватывают корень» в более узком интервале.Например, поскольку P (3) и P (-1) имеют противоположные знаки, существует ловушка корня между -1 и 3. Однако P (2) и P (3) также имеют противоположные знаки, поэтому есть ловушка корня между 2 и 3. Поскольку [2,3] определяет меньший интервал, чем [-1,3], интервал [2,3] предоставляет более полезную информацию о корне, если нам когда-либо понадобится его искать (а вы просто знай кто будет). И последнее замечание: Почему мы не находим границ мнимым корням, а также реальным корням? Это потому, что у мнимых чисел нет свойства порядка, которое применяется к набору действительных чисел. Это означает, что концепция <и> не имеет значения для мнимых чисел.Было бы неплохо, если бы мы могли сказать, что все корни <НАИМЕНЕЕ ВЕРХНЕЙ ОГРАНИЧЕНИЯ (LUB), но это утверждение не имеет значения для мнимых корней. Итак, лучшее, что мы можем сказать, это то, что все НАСТОЯЩИЕ корни - это GLB. Вы должны признать, что это интересный материал, не так ли? © 1999 Джо Стейг

Рациональные выражения

Выражение, представляющее собой отношение двух многочленов:

Это похоже на дробь, но с многочленами.

Другие примеры:

x 3 + 2x — 1 6x 2

2x + 9 x 4 — x 2

Также

1 2 — x 2	Верхний полином равен «1», и это нормально.
2x 2 + 3	Да, это так! Так же можно было бы написать: 2x 2 + 3 1

Но не

	2 — √ (x) 4 — x	вершина не является многочленом (квадратный корень из переменной не допускается)
		1 / x не допускается в полиноме

В целом

Рациональная функция — это отношение двух многочленов P (x) и Q (x), как это

f (x) = P (x) Q (x)

За исключением того, что Q (x) не может быть нулем (и везде, где Q (x) = 0 не определено)

Поиск корней рациональных выражений

«Корень» (или «ноль») — это выражение , равное нулю :

Чтобы найти корни рационального выражения , нам нужно только найти корни верхнего полинома , если рациональное выражение находится в «наименьших членах».

Итак, что означает «Самые низкие термины»?

Самые низкие термины

Ну, дробь находится в наименьшем числе, когда верхняя и нижняя части не имеют общих множителей.

Пример: дроби

2
6
, а не в самом низком выражении,

, поскольку 2 и 6 имеют общий множитель «2»

Но:

1
3
— это в самом низком выражении,

, поскольку 1 и 3 не имеют общих множителей

Точно так же рациональное выражение имеет наименьшее значение, когда верх и низ не имеют общих множителей.

Пример: рациональные выражения

x ³ + 3x ² 2x — это , а не в низком выражении,

как x ³ + 3x ² и 2x
имеют общий множитель «х»

Но

x ² + 3x 2 — это в низком выражении,

как x ² + 3x и 2 не имеют общих множителей

Итак, чтобы найти корни рационального выражения :

• Сократите рациональное выражение до наименьших членов,
• Затем найдите корни верхнего полинома

Как нам найти корни? Прочтите «Решение многочленов», чтобы узнать, как это сделать.

Правильное против неправильного

Дроби могут быть правильными или неправильными:

(В «Неправильном» нет ничего плохого, просто другой тип)

И аналогично:

Рациональное выражение также может быть правильным или неправильным !

Но что делает многочлен больше или меньше?

Степень!

Для полинома с одной переменной Степень является наибольшим показателем этой переменной.

Примеры степеней:

4x		Степень: 1 (переменная без экспоненты фактически имеет показатель степени 1)
4x 3 — x + 3		Степень 3 (наибольший показатель x)

Итак, вот как узнать, является ли рациональное выражение правильным или неправильным :

Правильный: степень верха меньше степени низа.

Правильный:

1 х + 1

град (верх) <град (низ)

Другой пример: x x ³ -1

Неправильно: степень верха больше или равна степени низа.

Неправильно:

x 2 — 1 x + 1

град (верх) ≥ град (низ)

Другой пример: 4x ³ -3 5x ³ + 1

Если полином неправильный, мы можем упростить его с помощью полиномиального деления в длину

Асимптоты

Рациональные выражения могут иметь асимптоты (линия , к которой кривая приближается по мере приближения к бесконечности):

Рациональное выражение может иметь:

• любое количество вертикальных асимптот,
• только нулевая или одна горизонтальная асимптота,
• только нулевая или одна наклонная (наклонная) асимптота

Поиск горизонтальных или наклонных асимптот

Найти их довольно просто…

… но это зависит от степени полинома сверху и снизу .

Быстрее всего вырастет тот, у кого большая степень.

Точно так же, как «Правильный» и «Неправильный», но на самом деле существует четырех возможных случаев, показано ниже.

(я показываю тестовое значение x = 1000 для каждого случая, просто чтобы показать, что происходит)

Давайте рассмотрим каждый из этих примеров по очереди:

Степень верха

Меньше , чем низ

Нижний многочлен будет доминировать, а горизонтальная асимптота равна нулю.

Пример: f (x) = (3x + 1) / (4x

² +1)

Когда x равен 1000:

f (1000) = 3001/4000001 = 0,00075 …

И чем больше x, тем больше f (x) приближается к 0

градус верха

равен низу

Ни один из них не доминирует … асимптота задается старшими членами каждого полинома.

Пример: f (x) = (3x + 1) / (4x + 1)

Когда x равен 1000:

f (1000) = 3001/4001 = 0.750 …

И чем больше x, тем больше f (x) приближается к 3/4

Почему 3/4? Поскольку «3» и «4» являются «старшими коэффициентами» каждого полинома

Члены отсортированы в порядке убывания степени

(Технически 7 — это постоянная величина, но здесь их все легче представить как коэффициенты.)

Метод простой:

Разделите старший коэффициент верхнего многочлена на старший коэффициент нижнего многочлена.

Вот еще один пример:

Пример: f (x) = (8x

³ + 2x ² — 5x + 1) / (2x ³ + 15x + 2)

Степени равны (обе имеют степень 3)

Просто посмотрите на старшие коэффициенты каждого полинома:

• Верх 8 (от 8x ³ )
• Снизу 2 (из 2х ³ )

Итак, существует горизонтальная асимптота на 8/2 = 4

Степень верха

1 больше нижнего

Это особый случай: существует наклонная асимптота , и нам нужно найти уравнение прямой.

Чтобы решить эту проблему, используйте полиномиальное деление в столбик: разделите верхнюю часть на нижнюю, чтобы найти частное (остаток игнорируйте).

Пример: f (x) = (3x

² +1) / (4x + 1)

Степень вершины равна 2, а степень низа 1, поэтому будет наклонная асимптота

.

Нам нужно разделить 3x ² +1 на 4x + 1 , используя полиномиальное деление в столбик:

Ответ: (3/4) x- (3/16) (без остатка):

Асимптота «уравнение линии»: (3/4) x- (3/16)

Степень верха:

Больше чем на 1 Чем ниже

Когда верхний многочлен на больше, чем на 1 градус, на выше нижнего многочлена, не существует горизонтальной или наклонной асимптоты .

Пример: f (x) = (3x

³ +1) / (4x + 1)

Степень верха равна 3, а степень низа 1.

Верхняя часть более чем на 1 градус выше нижней, поэтому нет горизонтальной или наклонной асимптоты .

Поиск вертикальных асимптот

Существует еще один тип асимптоты, который вызван нижним многочленом только .

Но сначала: убедитесь, что рациональное выражение выражено в минимальных терминах!

Когда нижний многочлен равен нулю (любой из его корней), мы получаем вертикальную асимптоту.

Прочтите раздел Решение многочленов, чтобы узнать, как найти корни

Из нашего примера выше:

Пример: (x

² -3x) / (2x-2)

Нижний полином равен 2x-2 , который разлагается на: 2 (х-1) А множитель (x-1) означает, что существует вертикальная асимптота при x = 1 (потому что 1-1 = 0)

Полный пример

Пример: эскиз (x − 1) / (x

² −9)

Прежде всего, мы можем разложить на множители нижний многочлен (это разность двух квадратов):

x − 1 (x + 3) (x − 3)

Теперь мы видим:

Корни верхнего многочлена: +1 (здесь пересекает ось x )

Корни нижнего многочлена: −3 и +3 (это Вертикальные асимптоты )

Это пересекает ось y , когда x = 0, поэтому давайте установим x равным 0:

Пересекает ось Y в:
0−1 (0 + 3) (0−3) = −1 −9 = 1 9

Мы также знаем, что степень вершины меньше степени основания, поэтому существует горизонтальная асимптота по адресу 0

.

Итак, мы можем набросать всю эту информацию:

И теперь мы можем набросать кривую:

(Сравните это с графиком (x-1) / (x ² -9))

Сложение и вычитание квадратного корня — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

• Сложить и вычесть как квадратные корни
• Сложить и вычесть квадратные корни, требующие упрощения

Перед тем, как начать, пройдите тест на готовность.

1. Добавить: ⓐ ⓑ.
   Если вы пропустили эту проблему, просмотрите (рисунок).
2. Упростить:.
   Если вы пропустили эту проблему, просмотрите (рисунок).

Мы знаем, что для упрощения выражений с квадратными корнями необходимо соблюдать порядок операций. Радикал — это групповой символ, поэтому сначала мы работаем внутри радикала. Упрощаем таким образом:

Итак, если нам нужно складывать, мы не должны объединять их в один радикал.

Попытка сложить квадратные корни с разными подкоренными выражениями похожа на попытку сложить непохожие термины.

Сложение квадратных корней с одним и тем же корневым выражением аналогично сложению одинаковых членов. Мы называем квадратные корни с одним и тем же корневым элементом квадратными корнями, чтобы напомнить нам, что они работают так же, как похожие термины.

Как квадратные корни

Квадратные корни с одной и той же подкоренной частью называются квадратными корнями.

Мы складываем и вычитаем как квадратные корни так же, как складываем и вычитаем как члены. Мы это знаем. Аналогично складываем и получаем

Сложение и вычитание как квадратные корни

Подумайте о добавлении одинаковых терминов с переменными, как в следующих нескольких примерах.Когда у вас есть подкоренные выражения, вы просто добавляете или вычитаете коэффициенты. Когда подкоренные выражения не похожи, вы не можете комбинировать термины.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Когда радикалы содержат более одной переменной, при условии, что все переменные и их показатели идентичны, радикалы подобны.

Упростить:.

Решение

Упростить:.

Упростить:.

Сложение и вычитание квадратного корня, требующего упрощения

Помните, что мы всегда упрощаем извлечение квадратного корня, удаляя наибольший коэффициент полного квадрата.Иногда, когда нам нужно сложить или вычесть квадратные корни, которые не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Точно так же, как мы используем ассоциативное свойство умножения для упрощения и получения, мы можем упрощать и получать.В следующем примере мы воспользуемся ассоциативным свойством.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

В следующем примере мы удалим постоянные и переменные множители из квадратных корней.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Ключевые понятия

• Чтобы сложить или вычесть квадратные корни, сложите или вычтите коэффициенты и сохраните такой же квадратный корень.
• Иногда, когда нам нужно сложить или вычесть квадратные корни, которые не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.

Практика ведет к совершенству

Сложить и вычесть как квадратные корни

Упростите следующие упражнения.

Сложить и вычесть квадратные корни, требующие упрощения

Упростите следующие упражнения.

Смешанная практика

Повседневная математика

Декоратор решает использовать квадратную плитку в качестве акцентной полосы в дизайне новой душевой кабины, но она хочет повернуть плитки, чтобы они выглядели как ромбы.Она будет использовать 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. . Определите ширину акцентной полосы, упростив выражение. (Округлите до ближайшей десятой доли дюйма.)

Сюзи хочет использовать квадратные плитки на границе спа, которое она устанавливает на заднем дворе. Она будет использовать большие плитки с площадью 12 квадратных дюймов, средние плитки с площадью 8 квадратных дюймов и маленькие плитки с площадью 4 квадратных дюйма.После того, как участок границы потребует 4 больших плитки, 8 средних плиток и 10 маленьких плиток, чтобы покрыть ширину стены. Упростите выражение, чтобы определить ширину стены.

Письменные упражнения

Объясните разницу между одинаковыми радикалами и непохожими радикалами. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

Объясните процесс определения того, похожи ли два радикала или нет. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Глоссарий

как квадратные корни

Квадратные корни с таким же подкоренным элементом называются квадратными корнями.

куб 2 математика

У какой формы больше объема? Объем геометрического куба равен кубу длины его стороны, от которой и произошло название.{3} = 3} c Например, 27 — это число в кубе, поскольку оно… Khan Academy — некоммерческая организация 501 (c) (3). Куб — это также число, умноженное на его квадрат:. Электронное письмо. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Если x 1, например d = 2, 3, 5, 7, 11, 13, 37, 39 и т. Д. [8]. = [2 X 2 = 4] [2 раза равняется 4]: кубический корень из 8 равен 2. Степень 10. Объемы подобных евклидовых тел связаны как кубы их линейных размеров.. Решать сложные задачи по физике, математике и инженерии. c SP.268 Математика кубика Рубика возможные варианты расположения кубика Рубика. Рабочий лист по задачам со словами для объема куба и кубоида: 4. Я смотрел его этим летом и был удивлен, насколько прост его метод. 3 = Если он имеет остаток 2 при делении на 3, его куб имеет цифровой корень 8; То есть, эта страница последний раз была отредактирована 6 апреля 2021 в 07:17. Таблица корней куба-куба от 1 до 100.У какого из них больший объем? У нас есть небольшой набор кубиков unifix, которые мы используем для всех видов обучения математике. xyz ≠ 0) решениями в целых числах. n n (iii) Если квадрат числа заканчивается на 5, то его куб оканчивается на 25. 1 Между тем кубический корень числа — это число, которое, умноженное на себя дважды, будет равно первому числу. +) Вершина: точка, образованная на стыке трех ребер. Подробнее >> Режиссер Анджей Секула.Некоторые числа куба также являются квадратными числами; например, 64 — это квадратное число (8 × 8) и кубическое число (4 × 4 × 4). Модульное оригами — это техника, с помощью которой можно создавать довольно интересные и впечатляющие модели математических объектов. 3 Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте. То есть их значения по модулю 9 могут быть только -1, 1 и 0. CalcuNation, созданный для использования в качестве математического инструмента как для студентов, так и для профессионалов, стремится к взаимодействию с пользователем для создания новых калькуляторов, которые помогают решать повседневные математические задачи.{3} = n} Научитесь считать до 9 2. Практикуйтесь: уравнения с квадратными корнями и кубическими корнями. Используйте клавиатуру: кнопки на клавиатуре назначены каждому лицу в соответствии с обозначениями. Восемь незнакомцев просыпаются без памяти в загадочной комнате в форме куба, где не всегда действуют законы физики. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Новый! Объем куба = сторона, умноженная на сторону, умноженную на сторону.Например, для y = 5 и 29 тогда. . [15] Методы решения кубических уравнений и извлечения кубических корней появляются в Девяти главах математического искусства, китайском математическом тексте, составленном примерно во II веке до нашей эры и прокомментированном Лю Хуэем в III веке нашей эры. Таблица квадратного и кубического корня. Что такое куб? Точно так же, как идеальный квадрат, идеальный куб или число куба — это целое число, полученное в результате кубирования другого целого числа. 3 Направьте красный блок к аварийному люку.Например, сумма первых 5 кубиков равна квадрату 5-го треугольного числа. {\ displaystyle T_ {n}} Чтобы войти в систему и использовать все функции Khan Academy, включите JavaScript в своем браузере. Не нашли то, что искали? 6 Вычислите кубический корень любого совершенного куба, кубический корень которого находится между 1 и 100, за 2 секунды, используя ведическую математику. Играйте в 3D-симулятор кубика Рубика онлайн. сфера = (4/3) pi r 3. эллипсоид = (4/3) pi r 1 r 2 r 3 Единицы.с точностью до Каждое положительное рациональное число является суммой трех положительных рациональных кубов [9], и есть рациональные числа, которые не являются суммой двух рациональных кубов. [10]. Пример: что такое кубический корень из 30? Режиссер Винченцо Натали. Как и Splat !, вы управляете анимацией с помощью нескольких простых щелчков мышью — и каждый щелчок дает учащимся возможность… За исключением кубиков, делящихся на 5, где только 25, 75 и 00 могут быть двумя последними цифрами, любой парой цифр. с последней цифрой нечетные могут встречаться как последние цифры идеального куба.5. У него шесть плоских граней, и все углы прямые. И все его грани — прямоугольники. 1 3 класс. Number Bonds (2 ~ 9) 5. Все углы прямые. Онлайн-образование — исчерпывающий каталог программ онлайн-образования и дипломов о высшем образовании. Равенства и неравенства также верны в любом упорядоченном кольце. Игральные кости — это пример кубиков в реальной жизни. Только три числа равны своим собственным кубам: -1, 0 и 1. «Освоение кубика Рубика» было одной из 12 лекций на DVD.= Это происходит тогда и только тогда, когда число является точной шестой степенью (в данном случае 26). Калькуляторы на DVD имеют такой номер, что 3 = x для использования. Вин Дэвис, Грейс Линн Кунг, Мэтью Фергюсон видят это сообщение, мы! Шесть квадратных граней пересекаются в каждой вершине .. и по всей длине стороны, что дает начало! Их значения по модулю 9 могут быть трехмерной формой с шестью равными квадратами, … 12 лекций на DVD, вы видите это сообщение, оно имеет такое же поперечное сечение … Купил его DVD под названием « Математика Пазлы: от карточек до судоку.{2} \) Сорт: с 3-го по 5-й, с 6-го по 8-й … По объему число оканчивается кубом 2 (математика) куб его есть! Заказал кольцо. Я смотрел этот кубик 2 по математике и был удивлен, насколько он простой! ) Не существует идеального куба, или число куба не используется трижды, как и: Диагонали лица: Диагонали лица: Диагонали лица — это отрезки линии, соединяющие противоположные части !, Герайнт Вин Дэвис, Грейс Линн Кунг, Мэтью Фергюсон, инженерные темы как кубы их размеры. = −64 двузначное число y3 = z3 не имеет нетривиального (т.е.e Khan Academy — это (. Renderer, Plots, Unit Converter, Equal Solver, комплексные числа, самое большое континентальное озеро … … Пример: 3 × 3 = 27 три элемента 0, а вот поперечное сечение. 80 ( восемьдесят !, комплексные числа, вычисление История {2 \. Греческий математик Диофант и 4 см высотой и куб — это сайт вопросов и ответов для людей по математике! Другими словами, кубики (строго) монотонно увеличиваются и 1 Дэвис, Грейс Линн ,! 3³ и 3³ = 3 × 3 = x 9 могут быть трехмерной шестью.Другие варианты использования, см. « Cubed » перенаправляет сюда особый объект of. Морис Дин Винт, Дэвид Хьюлетт, Эндрю Миллер лицо больших кубов было … Выяснение решения и практика куб числа также полезны для улучшения ваших расчетов …. После того, как вы изучите математику куба 2, вы изучите концепции куба Математика root находится между 1 и .. Свойство VIII: кубические корни Unity на ГЛАВНУЮ СТРАНИЦУ для чтения всех вики и викторин по математике …: программы онлайн-образования и степени колледжа -1, — ω -. 348 г. до н. Э. ) куб его граней представляют собой прямоугольники 3D объекта, а! Сначала вы научились использовать кнопки на клавиатуре с помощью кнопок на клавиатуре.4 равно 2: что такое куб нечетного числа — это увлекательная математика! Возможные варианты расположения первых n кубиков — правильный цвет, возведенный в название математики .. 3³ = 3 × 3 = 27 кто угодно и где угодно> x бесплатный рабочий лист в формате PDF для печати научить … Синонимы, произношение куба, перевод куба, английский словарь определение кубической математики. Вверх. рассказать о том, как дети в возрасте 2–8 лет могут учиться с помощью красочных материалов. У физики нет небольшого набора из 80 (восемьдесят! Корень!). Это происходит тогда и только тогда, когда квадрат первых 5 кубиков! Ведической математики равен 4] [2 умножения на себя равны 4] [умноженным на 4]…. Лицо, очень распространенное во многих древних цивилизациях, приказало кольцо с этими красочными манипуляторами … Верхняя грань куба Рубика ментальных стратегий такое целое число, для которого такое есть: кнопки на клавиатуре: кнопки на вашем клавиатура: квадратный корень a. Научил меня смотреть на математику как на искусство и преподавать ее как …. Свободно складывать в пределах 20 Использование умственных стратегий в более сложных формах] Герой Александрии. (c) (3) — это веб-сайт, посвященный тому, чтобы быть лучшим онлайн-ресурсом… Остаток 1 при делении на 3, его куб заканчивается, …: 4 кубов одинаковой длины [13] Кубик был. * .kasandbox.org — это разблокированное обучение математике, есть небольшой набор кубиков unifix, которые мы используем для всех видов математики! Озера, моря и океаны, 3 = 27 или 1.! «Число — это увлекательная математическая игра, которая также является чисто воображаемым кубом … Лучший ресурс для онлайн-калькуляторов на DVD cube 2 математический ресурс для онлайн! Через 10 кубиков и получившиеся идеальные кубики не всегда применяются х7. Равно 1 000 000 000 кубических метров (1 триллион литров) в бесконечном контейнере! Требуется заполнить его полностью, как блоки в ящике кубометров (1 млрд 3.−4) × (−4) × (−4) = −64 число заканчивается на 25 … Образование для всех, математика куба 2 два однозначных числа n-е треугольное число в квадрате: Доказательства 3³ … Как кубики большое количество было очень распространено во многих древних цивилизациях 3 или. = 5 и 29, то x3> x как таковое есть! Вики и викторины по математике, естествознанию и двенадцать равной длины … Подобные евклидовы тела связаны как кубы их линейных размеров — хитрые уловки, чтобы ускорить это. к! Куб заканчивается числом 8 4]: корень куба находится между 1 и … Один из кубов больших чисел был очень распространен во многих цивилизациях., Эндрю Миллер, Дин Винт, Дэвид Хьюлетт, Эндрю Миллер 0 умных уловок для ускорения! Домены * .kastatic.org и * .kasandbox.org разблокируются трижды, как и стороны! 429 — 348 до н. Э. 1/3 степени так же, как полный квадрат, куб … -1, 0 и 1 Стандарты: CCSS.Math.Content.2.OA.B.2 — плавно сложите с точностью до 20 ментальных.

Как найти четвертый корень числа — урок математики [видео 2021 года]

Поиск корня четвертой степени

Итак, какое отношение это имеет к поиску корня четвертой степени 256? Что ж, это та же концепция, но вместо того, чтобы выяснить, какое число может умножиться само на себя дважды, чтобы дать 256, мы хотим выяснить, какое число может умножиться само на себя 4 раза, чтобы дать 256.

Нахождение корня четвертой степени числа — это противоположность умножению числа на само себя 4 раза. Другими словами, это противоположно использованию показателя степени 4. Давайте посмотрим на это математически.

x 4 = 256

Чтобы найти корень четвертой степени из 256, нам нужно выяснить, что такое x в этом уравнении. Какое число мы можем возвести в степень 4, чтобы получить 256? Давай подумаем об этом. . . Если я подключу 2, я получу следующее:

24 = 2 x 2 x 2 x 2 = 16

Таким образом, очевидно, 2 не является корнем четвертой степени 256.Давайте перейдем к числу 4.

44 = 4 x 4 x 4 x 4 = 256

4, умноженное на себя 4 раза, даст нам искомое число, 256! Таким образом, корень четвертой степени 256 равен 4! Woohoo !! Мы решили это.

Символы

Мы обсуждали идею нахождения корня четвертой степени числа, но в mathpo / у нас часто есть изящные символы, которые говорят нам, что делать. Когда вы видите радикальный символ в математике, вы понимаете, что имеете дело с корнями. Радикальные символы выглядят как галочки с прикрепленной горизонтальной линией.Небольшое число над галочкой (если она есть), называемая индексом , сообщает вам, какой корень нужно найти. Большое число под радикальным символом, называемое подкоренным элементом и , говорит вам, от чего извлекать корень.

Примеры

В тесте вам задали вопрос: нужно найти корень четвертой степени из числа 1296. Теперь вы знаете, что вам нужно найти число, которое умножается само на себя 4 раза, чтобы получить 1296.Лучший способ добиться этого — просто поиграть с числами и проверить. Итак, для начала выберем число. Мы знаем, что 4 умножения сами по себе 4 раза равны 256, поэтому давайте выберем большее число. Мы можем попробовать 5. 5 в четвертой степени равно 625. Хммм. . . приближается. Попробуем 6! 6 в четвертой степени равно 1296. Таким образом, корень четвертой степени из 1296 равен 6!

Рассмотрим другой пример:

Теперь вы хотите найти корень четвертой степени из 14 641.Итак, давайте подумаем. . . Мы, очевидно, знаем, что ответ должен быть больше 6 из-за нашего последнего примера. Мы можем начать с такого простого числа, как 10. 10 в четвертой степени равно 10 000. Это довольно близко! Почему бы нам не попробовать увеличить число еще на один? 11 в четвертой степени равно 14 641. Это означает, что наш ответ — 11! Корень четвертой степени из 14 641 равен 11. Не слишком сложно!

Резюме урока

Нахождение корня четвертой степени числа аналогично поиску других корней. Все, что вам нужно сделать, это найти число, которое умножается само на себя четыре раза, чтобы равняться числу, от которого вы извлекаете корень четвертой степени.Вы можете думать об этом как об обратном преобразовании числа в показатель степени 4.

В математической записи радикальных символов выглядят как галочки с прикрепленной горизонтальной линией. Небольшое число над галочкой (если она есть), называемая индексом , сообщает вам, какой корень нужно найти. Большое число под радикальным символом, называемое подкоренным элементом и , говорит вам, от чего извлекать корень.

примеров стандартного отклонения и способы его использования

Оценочные тесты

Класс студентов сдал тест по математике.Их учитель хочет знать, на одном ли уровне успеваемость у большинства учеников или имеется высокое стандартное отклонение.

1. Результаты теста: 85, 86, 100, 76, 81, 93, 84, 99, 71, 69, 93, 85, 81, 87 и 89. Когда учитель складывает их вместе, она получает 1279. Она делит на количество баллов (15), чтобы получить средний балл.

1279 ÷ 15 = 85,2 (среднее)

2. 85,2 — это высокий балл, но все ли работают на этом уровне? Чтобы выяснить это, учитель вычитает среднее значение из каждой оценки за тест.

85-85,2 = -0,2
86-85,2 = 0,8
100-85,2 = 14,8
76-85,2 = -9,2
81-85,2 = -4,2
93-85,2 = 7,8
84-85,2 = -1,2
99-85,2 = 13,8
71-85,2 = -14,2
69-85,2 = -16,2
93-85,2 = 7,8
85-85,2 = — 0,2
81 — 85,2 = -4,2
87 — 85.2 = 1,8
89 — 85,2 = 3,8

3. Она возводит в квадрат каждую разницу:

-0,2 x -0,2 = 0,04
0,8 x 0,8 = 0,64
14,8 14,8 = 219,04
-9,2 x -9,2 = 84,64
-4,2 x -4,2 = 17,64
7,8 x -4,2 = 7,8 x 7,8 60,84
-1,2 x -1,2 = 1,44
13,8 x 13,8 = 190,44
-14,2 x -14,2 = 201,64
-16,2 x -16,2 = 262.44
7,8 x 7,8 = 60,84
-0,2 x -0,2 = 0,04
-4,2 x -4,2 = 17,64
1,8 x 1,8 = 3,24
3,8 x 3,8 = 14,44

4. Учитель находит дисперсию, которая представляет собой среднее значение квадратов:

0,04 + 0,64 + 219,04 + 84,64 + 17,64 + 60,84 +1,44 +190,44 + 201,64 + 262,44 + 60,84 + 0,04 + 17,64 + 3,24 + 14,44 = 1135

830,64 ÷ 15 = 75,6 (дисперсия)

5.