Нод в математике что значит: Наибольший общий делитель. Взаимно простые числа — урок. Математика, 6 класс. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Признаки делимости, НОД, НОК — Математика в колледже

Наименьшее общее кратное

Отправлено 9 февр. 2015 г., 16:20 пользователем Ksenija Borska

[

обновлено 9 февр. 2015 г., 23:50
]

Общее кратное. Наименьшее общее кратное.

Общим кратным нескольких чисел называется число, котороеделится на каждое из этих чисел. Например, числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 – тоже их общие кратные.Среди всех общих кратных всегда есть наименьшее, в данномслучае это 90. Это число называется наименьшим общимкратным (НОК).

Чтобы найти наименьшее общее кратное (НОК) нескольких чисел надо:

1) представить каждое число как произведение его простых множителей, например:

504 = 2 · 2 · 2 · 3 · 3 · 7 ,

2) записать степени всех простых множителей:

504 = 2 · 2 · 2 · 3 · 3 · 7 = 2³ · 3² · 7¹,

3) выписать все простые делители (множители) каждого из этих чисел;

4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;

5) перемножить эти степени.

П р и м е р . Найти НОК чисел: 168, 180 и 3024.

Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 2³ · 3¹ · 7¹ ,

180 = 2 · 2 · 3 · 3 · 5 = 2² · 3² · 5¹ ,

3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2⁴ · 3³ · 7¹ .

Выписываем наибольшие степени всех простых делителей

и перемножаем их:

НОК = 2⁴ · 3³ · 5¹ · 7¹ = 15120 .

Наибольший Общий Делитель

Отправлено 9 февр. 2015 г., 15:57 пользователем Ksenija Borska

Общий делитель. Наибольший общий делитель.

Общим делителем нескольких чисел называется число, котороеявляется делите-лем каждого из них. Например, числа 36, 60, 42 имеют общие делители 2, 3 и 6. Среди всех общих делителей всегда есть наибольший, в данном случае это 6. Это и естьнаибольший общий делитель (НОД).

Чтобы найти наибольший общий делитель (НОД) нескольких чисел надо:

1) представить каждое число как произведение его простых множителей, например:

360 = 2 · 2 · 2 · 3 · 3 · 5 ,

2) записать степени всех простых множителей:

360 = 2 · 2 · 2 · 3 · 3 · 5 = 2³ · 3² · 5¹,

3) выписать все общие делители (множители) этих чисел;

4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях;

5) перемножить эти степени.

П р и м е р . Найти НОД чисел: 168, 180 и 3024.

Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 2³ · 3¹ · 7¹ ,

180 = 2 · 2 · 3 · 3 · 5 = 2² · 3² · 5¹ ,

3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2⁴ · 3³ · 7¹ .

Выпишем наименьшие степени общих делителей 2 и 3

и перемножим их:

НОД = 2² · 3¹ = 12 .

Множители

Отправлено 9 февр. 2015 г., 15:54 пользователем Ksenija Borska

Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называютсяпростыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами. Простых чисел – бесконечное множество. Ниже приведены простые числа, не превосходящие 200:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Всякое составное число может быть единственным образом представлено в виде произведения простых множителей. Например,

48 = 2 · 2 · 2 · 2 · 3, 225 = 3 · 3 · 5 · 5, 1050 = 2 · 3 · 5 · 5 · 7 .

Для небольших чисел это разложение легко делается на основетаблицы умножения. Для больших чисел рекомендуем пользоваться следующим способом, который рассмотрим на конкретном примере. Разложим на простые множители число 1463. Для этого воспользуемся таблицей простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Перебираем числа по этой таблице и останавливаемся на том числе, которое является делителем данного числа. В нашем примере это 7. Делим 1463 на 7 и получаем 209. Теперь повторяем процесс перебора простых чисел для 209 и останавливаемся на числе 11, которое является его делителем (см. параграф «Признаки делимости»). Делим 209 на 11 и получаем 19, которое в соответствии с этой же таблицей является простым числом. Таким образом, имеем: 1463 = 7 ∙ 11 ∙ 19, т.е. простыми делителями числа 1463 являются 7, 11 и 19. Описанный процесс можно записать следующим образом:

Делимое       Делитель
—————————-
1463                  7
  209                11
    19              19
—————————-

Признаки делимости

Отправлено 9 февр. 2015 г., 15:45 пользователем Ksenija Borska

Признаки делимости на 2, 4, 8, 3, 9, 6, 5, 25, 10, 100, 1000, 11.

Признак делимости на 2. Число делится на 2, если его последняя цифра — ноль или делится на 2. Числа, делящиеся на два, называются чётными, не делящиеся на два – нечётными.

Признак делимости на 4. Число делится на 4, если две егопоследние цифры — нули или образуют число, которое делится на 4.

Признак делимости на 8. Число делится на 8, если три егопоследние цифры — нули или образуют число, которое делится на 8.

Признаки делимости на 3 и 9. Число делится на 3, если егосумма цифр делится на 3. Число делится на 9, если его сумма цифр делится на 9.

Признак делимости на 6. Число делится на 6, если оно делится на 2 и на 3.

Признак делимости на 5. Число делится на 5, если его последняя цифра — ноль или 5.

Признак делимости на 25. Число делится на 25, если две егопоследние цифры — нули или образуют число, которое делится на 25.

Признак делимости на 10. Число делится на 10, если егопоследняя цифра — ноль.

Признак делимости на 100. Число делится на 100, если две егопоследние цифры – нули.

Признак делимости на 1000. Число делится на 1000, если триего последние цифры – нули.

Признак делимости на 11. На 11 делятся только те числа, у которых сумма цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, делящееся на 11.

Существуют признаки делимости и для некоторых других чисел, однако они более сложные и в программе средней школы не рассматриваются.

П р и м е р . Число 378015 делится на 3, так как сумма его цифр равна:

3 + 7 + 8 + 0 + 1 + 5 = 24, а это число делится на 3. Данное

число делится на 5, так как его последняя цифра 5.Наконец,

это число делится на 11, так как суммы его нечётных цифр:

3 + 8 + 1 = 12 и чётных цифр 7 + 0 + 5 = 12 равны.

Но это число не делится на 2, 4, 6, 8, 9, 10, 25, 100 и 1000, так как …

Математика. НОД и НОК: наибольший общий делитель и наименьшее общее кратное

Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) >

<< Назад | Оглавление | Далее >>

Множество делителей

Рассмотрим такую задачу: найти делитель числа 140. Очевидно, что у числа 140 не один делитель, а несколько. В таких случаях говорят, что задача имеет множество решений. Найдем их все. Прежде всего разложим данное число на простые множители:

140 = 2 ∙ 2 ∙ 5 ∙ 7.

Теперь мы без труда можем выписать все делители. Начнем с простых делителей, то есть тех, которые присутствуют в разложении, приведенном выше:

2, 5, 7.

Затем выпишем те, которые получаются попарным умножением простых делителей:

2∙2 = 4, 2∙5 = 10, 2∙7 = 14, 5∙7 = 35.

Затем — те, которые содержат в себе три простых делителя:

2∙2∙5 = 20, 2∙2∙7 = 28, 2∙5∙7 = 70.

Наконец, не забудем единицу и само разлагаемое число:

1, 140.

Все найденные нами делители образуют множество делителей числа 140, которое записывается с помощью фигурных скобок:

Множество делителей числа 140 =

{1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}.

Для удобства восприятия мы выписали здесь делители (элементы множества) в порядке возрастания, но, вообще говоря, это делать необязательно. Кроме того, введем сокращение записи. Вместо «Множество делителей числа 140» будем писать «Д(140)». Таким образом,

Д(140) = {1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}.

Точно так же можно найти множество делителей для любого другого натурального числа. Например, из разложения

105 = 3 ∙ 5 ∙ 7

мы получаем:

Д(105) = {1, 3, 5, 7, 15, 21, 35, 105}.

От множества всех делителей следует отличать множество простых делителей, которые для чисел 140 и 105 равны соответственно:

ПД(140) = {2, 5, 7}.

ПД(105) = {3, 5, 7}.

Следует особо подчеркнуть, что в разложении числа 140 на простые множители двойка присутствует два раза, в то время как во множестве ПД(140) — только один. Множество ПД(140) — это, по своей сути, все ответы на задачу: «Найти простой множитель числа 140». Ясно, что один и тот же ответ не следует повторять больше одного раза.

Сокращение дробей. Наибольший общий делитель

Рассмотрим дробь

105 / 140.

Мы знаем, что эту дробь можно сократить на такое число, которое одновременно является и делителем числителя (105) и делителем знаменателя (140). Взглянем на множества Д(105) и Д(140) и выпишем их общие элементы.

Д(105) = {1, 3, 5, 7, 15, 21, 35, 105};

Д(140) = {1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}.

Общие элементы множеств Д(105) и Д(140) =

{1, 5, 7, 35}.

Последнее равенство можно записать короче, а именно:

Д(105) ∩ Д(140) = {1, 5, 7, 35}.

Здесь специальный значок «∩» («мешок отверстием вниз») как раз и указывает на то, что из двух множеств, записанных по разные стороны от него, надо выбрать только общие элементы. Запись «Д(105) ∩ Д(140)» читается «пересечение множеств Дэ от 105 и Дэ от 140».

[Заметим по ходу дела, что с множествами можно производить разные бинарные операции, почти как с числами. Другой распространенной бинарной операцией является объединение, которое обозначается значком «∪» («мешок отверстием вверх»). В объединение двух множеств входят все элементы как того, так и другого множества:

ПД(105) = {3, 5, 7};

ПД(140) = {2, 5, 7};

ПД(105) ∪ ПД(140) = {2, 3, 5, 7}. ]

Итак, мы выяснили, что дробь

105 / 140

можно сократить на любое из чисел, принадлежащих множеству

Д(105) ∩ Д(140) = {1, 5, 7, 35}

и нельзя сократить ни на какое другое натуральное число. Вот все возможные способы сокращения (за исключением неинтересного сокращения на единицу):

105	=	105/5	=	21	;
140		140/5		28

105	=	105/7	=	15	;
140		140/7		20

105	=	105/35	=	3	.
140		140/35		4

Очевидно, что практичнее всего сокращать дробь на число, по возможности большее. В данном случае это число 35, про которое говорят, что оно является наибольшим общим делителем (НОД) чисел 105 и 140. Это записывается как

НОД(105, 140) = 35.

Впрочем, на практике, если нам даны два числа и требуется найти их наибольший общий делитель, мы вовсе не должны строить какие-либо множества. Достаточно просто разложить оба числа на простые множители и подчеркнуть те из этих множителей, которые являются общими для обоих разложений, например:

105 = 3 ∙ 5 ∙ 7;

140 = 2 ∙ 2 ∙ 5 ∙ 7.

Перемножая подчеркнутые числа (в любом из разложений), получаем:

НОД(105, 140) = 5 ∙ 7 = 35.

Разумеется, возможен случай, когда подчеркнутых множителей окажется больше двух:

168 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 7;

396 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 11.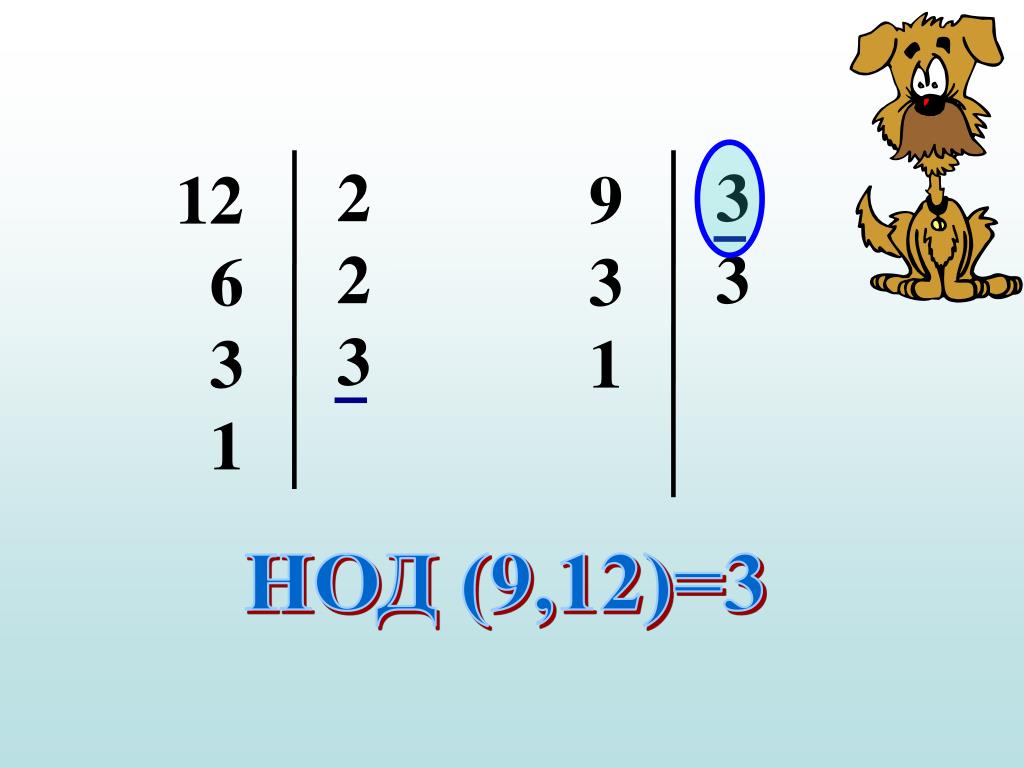

Отсюда видно, что

НОД(168, 396) = 2 ∙ 2 ∙ 3 = 12.

Особого упоминания заслуживает ситуация, когда общих множителей совсем нет и подчеркивать нечего, например:

42 = 2 ∙ 3 ∙ 7;

55 = 5 ∙ 11.

В этом случае,

НОД(42, 55) = 1.

Два натуральных числа, для которых НОД равен единице, называются взаимно простыми. Если из таких чисел составить дробь, например,

42 / 55,

то такая дробь является несократимой.

Вообще говоря, правило сокращения дробей можно записать в таком виде:

a	=	a / НОД(a, b)	.
b		b / НОД(a, b)

Здесь предполагается, что a и b — натуральные числа, а вся дробь положительна.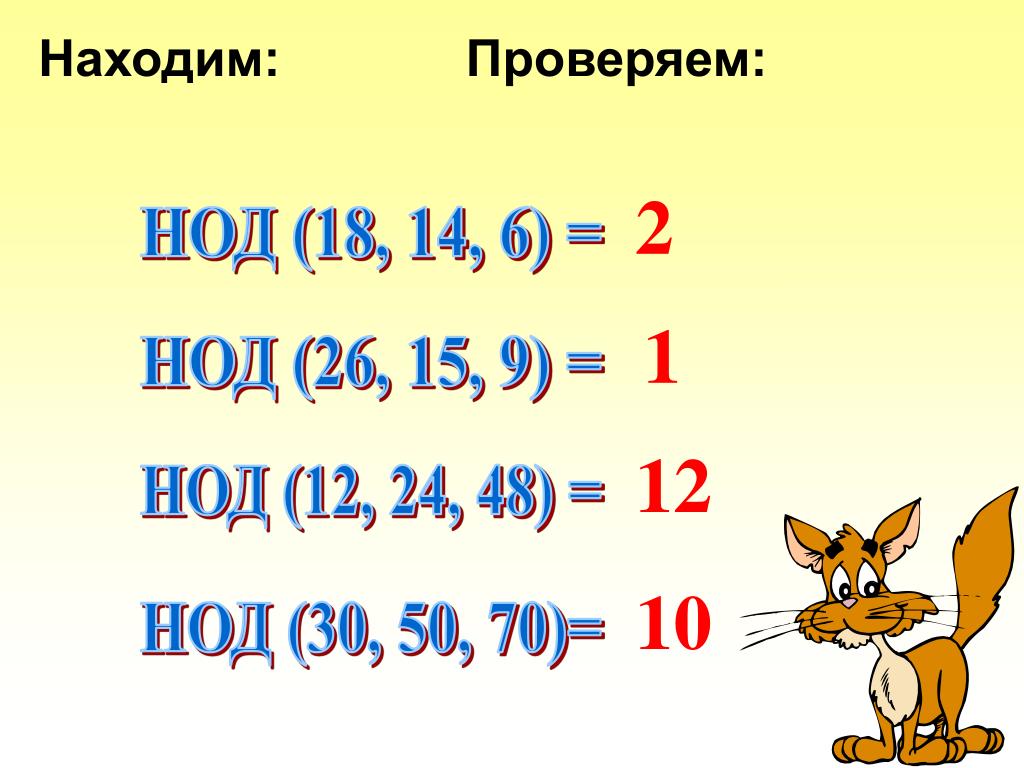 Если мы теперь припишем знак «минус» к обоим частям этого равенства, то получим соответствующее правило для отрицательных дробей.

Сложение и вычитание дробей. Наименьшее общее кратное

Пусть требуется вычислить сумму двух дробей:

1	+	1	.
105		140

Мы уже знаем, как раскладываются на простые множители знаменатели:

105 = 3 ∙ 5 ∙ 7;

140 = 2 ∙ 2 ∙ 5 ∙ 7.

Из этого разложения сразу следует, что, для того чтобы привести дроби к общему знаменателю, достаточно числитель и знаменатель первой дроби умножить на 2 ∙ 2 (произведение неподчеркнутых простых множителей второго знаменателя), а числитель и знаменатель второй дроби — на 3 («произведение» неподчеркнутых простых множителей первого знаменателя). В результате знаменатели обеих дробей станут равны числу, которое можно представить так:

2 ∙ 2 ∙ 3 ∙ 5 ∙ 7 = 105 ∙ 2 ∙ 2 = 140 ∙ 3 = 420.

Нетрудно видеть, что оба исходных знаменателя (как 105, так и 140) являются делителями числа 420, а число 420, в свою очередь, кратно обоим знаменателям, — и не просто кратно, оно является наименьшим общим кратным (НОК) чисел 105 и 140. Это записывается так:

НОК(105, 140) = 420.

Приглядевшись повнимательнее к разложению чисел 105 и 140, мы видим, что

105 ∙ 140 = НОК(105, 140) ∙ НОД(105, 140).

Точно так же, для произвольных натуральных чисел b и d:

b ∙ d = НОК(b, d) ∙ НОД(b, d).

Теперь давайте доведем до конца суммирование наших дробей:

1	+	1	=
105		140

1	+	1	=
3 ∙ 5 ∙ 7		2 ∙ 2 ∙ 5 ∙ 7

2 ∙ 2	+	3	=
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7		2 ∙ 2 ∙ 3 ∙ 5 ∙ 7

4 + 3	=
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7

7	=
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7

1	=
2 ∙ 2 ∙ 3 ∙ 5

Подобным же образом можно посчитать разность:

1	−	1	=
105		140

4	−	3	=
105 ∙ 4		140 ∙ 3

4	−	3	=
420		420

Из «бесконечного» сборника типовых упражнений

Задачи, где требуется разлагать числа на простые множители

Примечание. Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа a называется число a, помноженное само на себя, то есть a∙a. (Как нетрудно видеть, оно равно площади квадрата со стороной a).

Что такое НОД и НОК: вспомните математику 6 класса ? | Математика не для всех

Приветствую Вас, уважаемые Читатели! Сегодня хочу еще раз окунуться в школьную математику и напомнить Вам о понятиях наибольший общего делителя (НОД) и наименьшего общего кратного (НОК) — простых вещах, настоящем основании теории чисел, которое изучают в 6 классе. Поехали!

Источник: https://w7.pngwing.com/pngs/261/1019/png-transparent-two-children-writing-on-chalkboard-illustration-teacher-mathematics-estudante-math-class-teacher-and-student-child-class-text.png

Наибольший общий делитель

Пусть а и b — некие положительные числа, тогда наибольшее из целых чисел, на которое делится и а и b называется наибольшим общим делителем (НОД). Пример:

Последняя строчка — особенная, ведь из неё следует, что числа 9 и 16 не имеют общих делителей, кроме 1. Такие числа называются взаимно простыми.

Ввел это понятие Евклид, авторству которого принадлежит теорема о бесконечности простых чисел, которую, например, Г.Г. Харди в своей «Апологии математики» причисляет к красивейшим плодам чистой математики.

Наименьшее общее кратное

Если НОД «подпирает» числа a и b снизу, то наименьшее общее кратное — наоборот, является наименьшим числом, которое делится на a и b без остатка. Пример:

Как видно из примеров, НОД для небольших чисел находить проще, чем НОК. Естественно, что придуманы алгоритмы, которые призваны облегчить нахождение этих величин.

Естественно, НОК И НОД определены и более, чем для двух чисел

Алгоритмы нахождения

Самый простой алгоритм, который фактически реализуется, когда мы подбираем на глазок НОД и НОК, на самом деле основан на основной теореме арифметики, которая утверждает, что каждое натуральное число единственно представимо в виде произведения простых чисел с точностью до порядка сомножителей (подробнее — тут).

Чтобы найти НОК и НОд как раз необходимо это знать каноническое разложение чисел a и b. Давайте разберем на примере чисел 42 и 188, которые уже на «глазок» не раскусить. Итак:

Исходя из этого разложения существует простая формула:

Я выбираю именно такую формулу, сознательно уходя от объяснения на пальцах : если для НОД — это совсем просто (подчеркнуть наибольший общий множитель в обоих разложениях), то для НОК уже надо запоминать некий алгоритм. Лучше знать и понимать одну универсальную формулу.

Там, где простые числа присутствуют в разложении лишь одного числа, пишем нулевую степень. Наименьшее общее кратное вычисляется диаметрально противоположно:

Здесь, описка: вместо НОК написан НОД. Вручную подбор бы затянулся

Как видно, процесс вычисления НОК и НОД требует проведения подготовительного этапа — факторизации, который для больших чисел уже не является тривиальной задачей. Однако, к счастью, для более эффективного вычисления НОД (а, значит, и НОК, ведь их можно выразить друг через друга) еще Евклидом был придуман особый алгоритм. названный его именем. Этот алгоритм по праву считается золотым достоянием математики. О нём поговорим в одной из следующих заметок. Спасибо за внимание!

Читайте также:

Что такое вероятность: взрослому и ребенку
Простое объяснение пропорций
TELEGRAM и Facebook — там я публикую не только интересные статьи, но и математический юмор и многое другое.

84, 85. Наибольший общий делитель

Это надо знать

Наибольший общий делитель (НОД) двух и более чисел — это самое большее натуральное число, на которое эти числа делятся без остатка.

Пример:

Найти наибольший общий делитель чисел 15 и 35.

Найдем делители каждого числа:

15: 1, 3, 5, 15.

35: 1, 5, 7, 35.

Общие делители чисел 15 и 35: 1 и 5. Наибольший их общий делитель равен 5.

Ответ: НОД (15, 35) = 5.

Правило нахождения наибольшего общего делителя (НОД)

1) разложить числа на простые множители;

2) подчеркнуть одинаковые множители , входящие в каждое разложение этих чисел;

3) выписать подчеркнутые множители из первого разложения, найти их произведение — это и есть наибольший общий делитель.

Пример:

Найти НОД (100, 140).

Разложим оба числа на простые множители:

100 | 2 140 | 2

50 | 2 70 | 2

25 | 5 35 | 5

5 | 5 7 | 7

1 1

НОД (100, 140) = 2 ∙ 2 ∙ 5 = 20.

Ответ: НОД (100, 140) = 20.

Видеоурок

Домашнее задание

К уроку 84 (на 15.01)

П. 5.6

№ 1.221 стр. 43

Сформулируйте правило нахождения наибольшего общего делителя чисел А и В, если:
1) числа А и В взаимно простые;
2) число А кратно числу В;
3) число А является делителем числа В.
Приведите примеры!!!

№ 1.221

Найдите наибольший общий делитель чисел:
1) 72 и 35; 2) 120 и 77; 3) 55 и 165; 4) 328 и 8; 5) 60, 240 и 20; 6) 1620, 135 и 15.

К уроку 85 (на 18.01)

П. 5.6

№ 5.108 стр. 122

Срезали 48 цветков розовых, 64 цветка белых цикламентов и 80 декоративных веточек. Какое наибольшее число одинаковых букетов можно составить из этих растений?

№ 5.109 стр. 122

Для новогодних гирлянд школьники подготовили флажки разного цвета: 960 красных, 480 желтых, 720 синих и 680 зеленых. Какое наибольшее количество одинаковых гирлянд можно изготовить из этих флажков, если флажков каждого цвета во всех гирляндах будет поровну?

№ 5.342 стр. 173 Задача на повторение

Из двух городов, находящихся на расстоянии 700 км друг от друга, одновременно навстречу друг другу выехали два поезда. Скорость одного из поездов 80 км/ч. Найдите скорость другого поезда, если через 2 ч после начала движения между поездами было 200 км.

Зачем вводить понятия «Наибольший общий делитель (НОД)» и «Наименьшее общее кратное (НОК)» чисел в школьный курс математики?

С понятиями наибольшего общего делителя(НОД) и
наименьшего общего кратного(НОК) учащиеся
средней школы, встречаются в шестом классе.
Данная тема всегда трудна для усвоения. Дети
часто путают эти понятия, не понимают, зачем их
нужно изучать. В последнее время и в
научно-популярной литературе встречаются
отдельные высказывания о том, что данный
материал нужно исключить из школьной программы.
Думаю, что это не совсем верно, и изучать его
нужно если не на уроках, то во внеурочное время на
занятиях школьного компонента обязательно, так
как это способствует развитию логического
мышления школьников, повышению скорости
вычислительных операций , умению решать задачи
красивыми методами.

При изучении темы «Сложение и вычитание дробей
с разными знаменателями» мы учим детей находить
общий знаменатель двух или более чисел. Например,
нужно сложить дроби 1/3 и 1/5. Учащиеся без труда
находят число, делящееся без остатка на 3 и 5 . Это
число 15. Действительно , если числа небольшие, то
их общий знаменатель найти легко, зная хорошо
таблицу умножения . Кто-то из ребят замечает, что
это число является произведением чисел 3 и 5. У
детей складывается мнение, что всегда таким
образом можно найти общий знаменатель для чисел.
К примеру вычитаем дроби 7/18 и 5/24. Найдем
произведение чисел 18 и 24 . Оно равно 432. Получили
уже большое число, а если дальше нужно
производить какие-то вычисления(особенно это
касается примеров на все действия), то
вероятность ошибки возрастает. А вот найденное
наименьшее общее кратное чисел (НОК), что в этом
случае равнозначно наименьшему общему
знаменателю (НОЗ)-число 72 -значительно облегчит
вычисления и приведет к более быстрому решению
примера, а тем самым сэкономит время, отведенное
на выполнение данного задания, что играет
немаловажную роль при выполнении итоговых
тестовых, контрольных работ, особенно во время
итоговой аттестации.

При изучении темы «Сокращение дробей» можно
двигаться последовательно деля числитель и
знаменатель дроби на одно и то же натуральное
число, используя при этом признаки делимости
чисел, получив в конечном итоге несократимую
дробь. Например, нужно сократить дробь 128/344.
Разделим сначала числитель и знаменатель дроби
на число 2, получим дробь 64/172. Ещё раз поделим
числитель и знаменатель полученной дроби на 2,
получим дробь 32/86. Поделить ещё раз числитель и
знаменатель дроби на 2 , получим несократимую
дробь 16/43. Но сокращение дроби можно выполнить
гораздо проще , если мы найдем наибольший общий
делитель чисел 128 и 344. НОД(128, 344) = 8. Разделив
числитель и знаменатель дроби на это число,
получим сразу несократимую дробь.

Нужно показать детям разные способы нахождения
наибольшего общего делителя (НОД) и наименьшего
общего кратного (НОК)чисел. В простых случаях
удобно находить наибольший общий делитель (НОД) и
наименьшее общее кратное (НОК)чисел путем
простого перебора. Когда числа становятся
больше, можно использовать разложение чисел на
простые множители. В учебнике шестого класса
(автор Н.Я.Виленкин)показан следующий способ
нахождения наибольшего общего делителя
(НОД)чисел. Разложим числа на простые множители:

16 = 2*2*2*2

120 = 2*2*2*3*5

Затем из множителей, входящих в разложение
одного из этих чисел, вычеркиваем те, которые не
входят в разложение другого числа. Произведение
оставшихся множителей и будет являться
наибольшим общим делителем этих чисел. В данном
случае это число 8. На своем опыте убедилась в том,
что детям более понятно, если мы подчеркиваем
одинаковые множители в разложениях чисел , а
затем в одном из разложений находим произведение
подчеркнутых множителей. Это и есть наибольший
общий делитель данных чисел. В шестом классе дети
активны и любознательны. Можно поставить перед
ними следующую задачу: попробуйте описанным
способом найти наибольший общий делитель чисел
343 и 287. Сразу не видно, как разложить их на простые
множители. И вот здесь можно рассказать им про
замечательный способ, придуманный древними
греками, позволяющий искать наибольший общий
делитель(НОД)без разложения на простые
множители. Этот метод отыскания наибольшего
общего делителя впервые описан в книге Евклида
«Начала». Его называют алгоритмом Евклида.
Заключается он в следующем : Вначале делят
большее число на меньшее. Если получается
остаток, то делят меньшее число на остаток. Если
снова получается остаток, то делят первый
остаток на второй. Так продолжают делить до тех
пор, пока в остатке не получится нуль. Последний
делитель и есть наибольший общий делитель
(НОД)данных чисел.

Вернемся к нашему примеру и для наглядности
запишем решение в виде таблицы.

Делимое	Делитель	Частное	Остаток
343	287	1	56
287	56	5	7
56	7	8	0

Итак, НОД(344,287) = 7

А как найти наименьшее общее кратное (НОК) тех
же чисел? Нет ли и для этого какого-нибудь
способа, не требующего предварительного
разложения этих чисел на простые множители?
Оказывается, есть, и притом очень простой.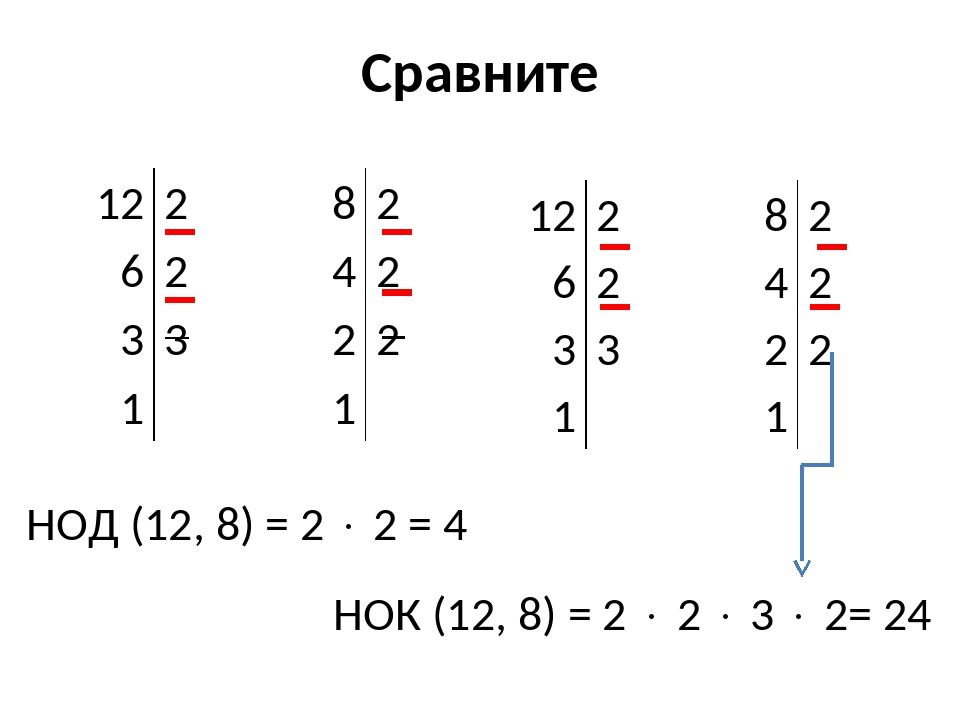 Нужно
перемножить эти числа и разделить произведение
на найденный нами наибольший общий делитель(НОД).
В данном примере произведение чисел равно 98441.
Делим его на 7 и получаем число 14063. НОК(343,287) = 14063.

Одной из трудных тем в математике является
решение текстовых задач. Нужно показать учащимся
, как с помощью понятий «Наибольший общий
делитель (НОД)» и «Наименьшее общее кратное
(НОК)» можно решать задачи, которые порой трудно
решить обычным способом. Здесь уместно
рассмотреть с учащимися наряду с задачами,
предложенными авторами школьного учебника ,
старинные и занимательные задачи, развивающие
любознательность детей и повышающие интерес к
изучению данной темы. Умелое владение этими
понятиями позволяет учащимся увидеть красивое
решение нестандартной задачи. А если у ребенка
после решения хорошей задачи поднимается
настроение-это признак успешной работы.

Таким образом, изучение в школе таких понятий ,
как «Наибольший общий делитель(НОД)» и
«Наименьшее общее кратное (НОК)»чисел

— позволяет экономить время, отводимое на
выполнение работы, что приводит к значительному
увеличению объема выполненных заданий;

— повышает скорость и точность выполнения
арифметических операций, что ведет к
значительному уменьшению количества
допускаемых вычислительных ошибок;

— позволяет находить красивые способы решения
нестандартных текстовых задач;

— развивает любознательность учащихся,
расширяет их кругозор;

— создает предпосылки для воспитания
разносторонней творческой личности.

Наибольший общий делитель / Обыкновенные дроби / Справочник по математике 5-9 класс

Число 36 имеет такие делители: 1, 2, 4, 6, 9, 12, 18, 36.

Число 126 имеет такие делители: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.

Синим цветом мы выделили числа 1, 2, 6, 9, 18, которые являются общими делителями чисел 36 и 126. Наибольшим из данных множителей является 18.

Наибольший общий делитель чисел и обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.

Найдем НОД(240; 165).

240 = 222235 165 = 3511.

Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.

Найдем НОД(2520; 4620).

2 520 = 2223357 4 620 = 2235711.

Рассмотрев разложения данных чисел, мы можем заметить, что некоторые простые множители повторяются, например, число 2 в разложении числа 2520 повторяется трижды, а в разложении числа 4620 — дважды. Заметим, что число 4 = 22 является делителем и числа 2520, и числа 4620, а число 8 = 222, является делителем только числа 2520. Так же число 3 является множителем рассматриваемых чисел, а число 9 = 33 является только делителем числа 2520. Кроме чисел 4 и 3, общими делителями данных чисел являются числа 5 и 7.

Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.

Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).

Таким же образом можно найти НОД трех и более чисел.

Чтобы найти НОД нескольких натуральных чисел, надо:

разложить их на простые множители;
из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
найти произведение оставшихся множителей.

Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.

Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.

Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:

2 520 = 2³3²5¹7¹

4 620 = 2²3¹5¹7¹11¹.

Тогда НОД мы можем найти по следующему правилу:

Определить степени, основания которых являются общими простыми делителями данных чисел.
Из каждой пары степеней с одинаковыми основаниями выбрать степень с меньшим показателем.
Перемножить выбранные степени. Полученное произведение является искомым наибольшим общим делителем.

Найдем НОД(2520; 4620):

Выписываем общие основания: 2, 3, 5, 7.
Выбираем наименьшие показатели данных степеней: 2², 3¹, 5¹, 7¹.
Находим произведение данных степеней, то есть искомый наибольший общий делитель: НОД(2520; 4620) = 2²3¹5¹7¹ = 420.

Линейное представление НОД. Простые и составные числа

Теорема. Пусть – целые числа, НОД. Число можно представить в виде

, где — целые числа

Доказательство. Пусть — множество всех чисел, которые можно получить из и с помощью сложения и вычитания. Тогда, если , то . Так как в алгоритме Евклида

Но .

Следствия.

1. НОД двух чисел делится на любой общий делитель этих чисел.

2. Уравнение , где — целые коэффициенты, — целочисленные неизвестные, разрешимо в том и только в том случае, если делится на НОД.

Простые и составные числа

Определение. Целое число называется составным, если оно делится на какое-нибудь целое число, отличное от и , и .

Целое число называется простым, если оно не является составным и не равно .

Замечание. Здесь необходимо отметить, что общепринятым является другое определение простых и составных чисел. Обычно простыми числами называются только натуральные числа. По этому поводу читайте здесь. В этом есть свои удобства и неудобства. В любом случае, когда возникнут сомнения, какие числа имеются в виду, всегда можно задать вопрос.

Теорема. Всякое составное натуральное число можно представить в виде произведения простых натуральных чисел.

Доказательство. Пусть есть такие составные натуральные числа, которые нельзя представить в виде произведения простых. Выберем из этих чисел самое маленькое и обозначим его через . Так как — составное число, то у него есть делитель , который больше 1 и меньше .

Числа натуральные. Каждое из чисел либо является простым, либо это составное, меньшее , которое поэтому раскладывается на простые множители. Но тогда и раскладывается на простые множители. Получили противоречие.

Теорема. Если – целые числа, — простое число, , то или .

Доказательство. Пусть ни , ни не делятся на . Тогда
НОД,НОД. Следовательно, можно подобрать такие целые числа и и такие целые числа и , что

Перемножим эти равенства почленно:

Каждое слагаемое в левой части равенства делится на , а . Получили противоречие.

Теорема. Пусть — составное натуральное число и

где — простые натуральные числа. Пусть

Тогда и .

Доказательство.

Если в левой и правой части есть равные сомножители, сократим на них и получим равенство такого же вида, в котором ни один сомножитель в левой части не равен ни одному сомножителю в правой части (если не все сомножители сократятся).

Правая часть равенства делится на . Так как — простое число, то хотя бы один сомножитель в правой части делился на (по предыдущей теореме). В то же время все сомножители в правой части — это простые числа, не равные . Следовательно, они не делятся на . Противоречие.

Пусть

— канонические разложения чисел и .

В каноническое разложение НОД входят те и только те простые числа, которые входят в оба разложения, причем из двух показателей выбирается меньший.

Простое число входит в каноническое разложение числа с показателем, равным

где суммирование ведется до тех пор, пока целая часть не станет равной нулю.

Задачи.

1. Доказать, что делится на 30 для любого целого .

2. Доказать, что для любого целого .

3. Доказать, что сумма кубов трех последовательных чисел кратна 9.

4. Доказать, что для любого целого неотрицательного

5. Доказать, что для любого целого неотрицательного

6. Доказать, что при любом простом натуральном число .

7. Доказать, что для любого натурального

8. Доказать, что для любого натурального нечетного

9. Какие остатки могут давать при делении на 9 кубы целых чисел?

10. Доказать, что для любого целого

11. Доказать, что для любого натурального

12. Доказать, что ни при каком целом не делится на 169.

13. Доказать, что если , то целые числа и также делятся на 3.

14. Доказать, что для любого целого

не имеют общих делителей, отличных от 1.

15. Два двузначных числа, оканчивающихся одной и той же цифрой, таковы, что при делении на 9 частное каждого из них равно остатку другого. Найти все числа, удовлетворяющие этим условиям.

16. Доказать, что в любой из последовательностей

а)

б)

содержится бесконечно много составных чисел.

17. Разложить число на два натуральных множителя, каждый из которых не меньше 1000.

18. Доказать, что число составное.

19*. Натуральные числа такие, что . Доказать, что число

— составное.

20. Доказать, что число ( нулей и единиц) составное .

21. Доказать, что число

(цифр там, где отмечено фигурной скобкой, по ) составное.

22. Представить в каноническом виде, найти НОД

а) и ;

б) и .

23. Доказать, что для любого натурального

24. Доказать, что для любого натурального

25. Доказать, что нечетная степень , увеличенная на , кратна .

26. Найти все простые , для которых и также являются простыми.

27. Натуральные числа таковы, что ,

Доказать, что .

28. На какую наибольшую степень числа делится произведение всех четных четырехзначных чисел?

3.2 Строительные блоки графов: ребра и узлы

Строительные блоки графов: ребра и узлы

Существует математическое определение графика, которое является немного более техническим. График представляет собой набор , обычно обозначаемый заглавной буквой G . Из математики средней школы вы, возможно, помните, что математическое определение набора — это просто набор сущностей, некоторые из которых могут быть упорядочены, а некоторые из которых сами могут быть другими наборами (набор может иметь наборы в качестве своих членов).В случае графов, сущностями внутри коллекции являются узлов и ребер Таким образом, граф представляет собой набор, содержащий два набора в качестве своих членов: набор узлов (обычно представленный заглавной буквой V ) и набор ребер (обычно обозначается заглавной буквой E ). В формальной записи:

\ [\ begin {уравнение}
G = {V, E}
\ tag {2.1}
\ end {Equation} \]

Набор узлов обычно представляет участников реальной социальной сети. Точечные и линейные диаграммы (например, показанные на рисунке 1) используются для представления графиков, которые, в свою очередь, представляют реальную социальную сеть. На этих диаграммах узлы (представляющие актеров) изображены в виде круга. В анализе социальных сетей участниками часто являются либо отдельные лица, либо организации, но в более широких применениях сетевых изображений в физических и биологических науках (обычно идущих под знаменем network science ) узлы могут представлять все, что связано с другими аналогичные объекты в более крупной системе.В их число входят электростанции и дома, серверы и компьютеры, животные в экосистеме, города, на самом деле все существенное, на что мы можем определить какие-то отношения или из которого можно обмениваться некоторым типом контента.

Ребра представляют наличие соединения или отношения между двумя узлами. В анализе социальных сетей это обычно какой-то тип социальной связи . Мы определим, что такое социальные связи, сколько их типов и каковы их свойства, в следующей главе.На данный момент мы можем сказать, что в анализе социальных сетей эти связи представляют собой отношения между узлами, а ребра в графе предназначены для их представления. В теории графов ребра лучше всего рассматривать как набор из пар узлов, где два члена пары являются узлами, участвующими в фокальной взаимосвязи. Таким образом, если узел A связан с узлом B посредством некоторой связи R , тогда AB является ребром в соответствующем графе.

Фигура 2.3: простая сеть.

В случае электростанций и домов края могут представлять линии электропередач. Между тем, серверы и компьютеры соединены интернет-кабелями и Wi-Fi, а города соединены дорогами. Наличие границ сигнализирует о возможности распространения контента, будь то мощность, компьютерные данные или люди в машинах. В случае социальных сетей контент, передаваемый между двумя узлами, представляет собой отношения определенного типа.

Рисунок 2.3 показан пример графа с тремя узлами и двумя ребрами. Узлы A , B и C — это круги, представляющие актеров A , B и C , социальные отношения которых в реальном мире мы заинтересованы в изучении. Простые линии, проведенные между A и B , а также между B и C , представляют собой ребра, указывающие на наличие взаимосвязи, и ребра, AB и BC на графике.Отсутствие границы между узлами A и C отражает отсутствие взаимосвязи между субъектами с именами A и C в реальном мире.

Хотя в этой книге в основном используются термины узел и ребро, когда речь идет о графах, это не единственные термины, используемые теми, кто использует методы сетевого анализа. Дополнительные имена для узлов включают вершину или точку . Связи между двумя узлами, помимо того, что они называются ребрами, называются связями или связями .

Математика	Вершина	Край
Социометрия	Узел	Галстук / звено