Содержание
Трапеция вписана в окружность
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.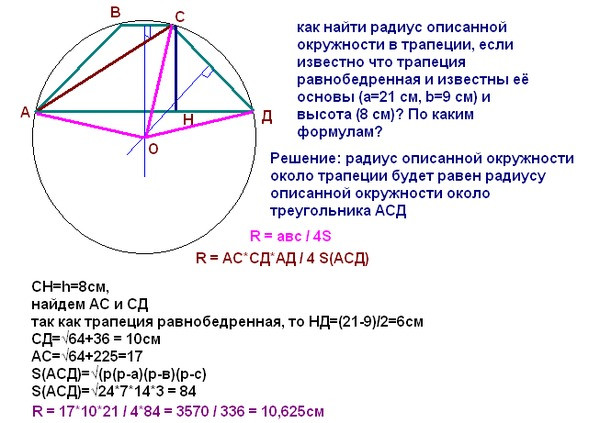
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
По формуле нахождения площади четырехугольника через его диагонали
В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним:
Отсюда
Описанная окружность и трапеция
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
1. Свойство сторон четырёхугольника описанного около окружности.
2. Теорему Пифагора. *Куда мы без неё )
3. Понятие средней линии трапеции.
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь.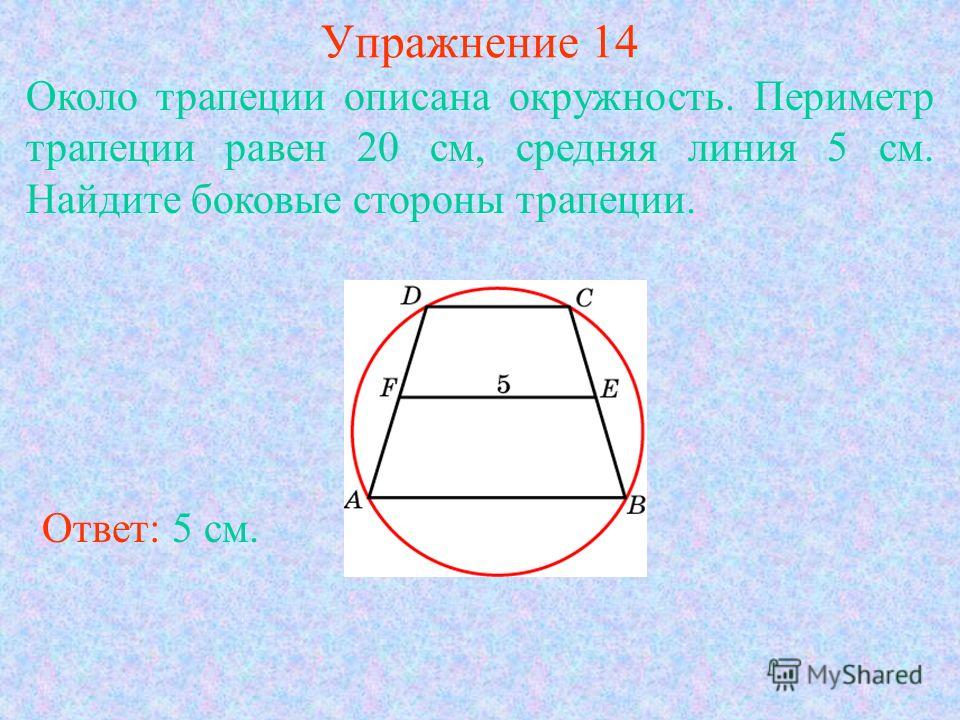
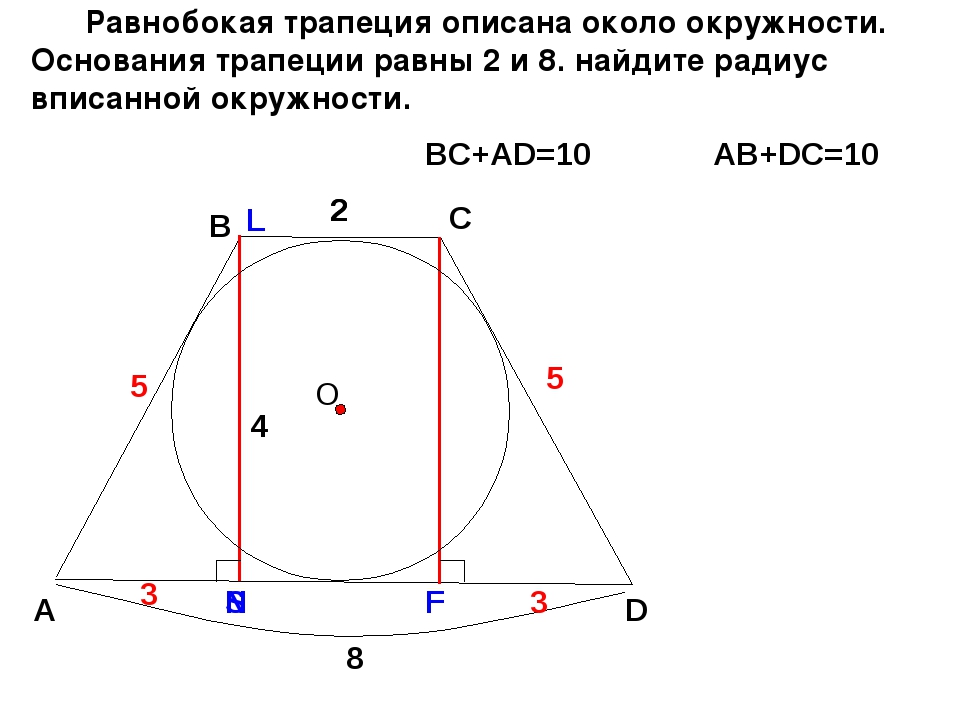
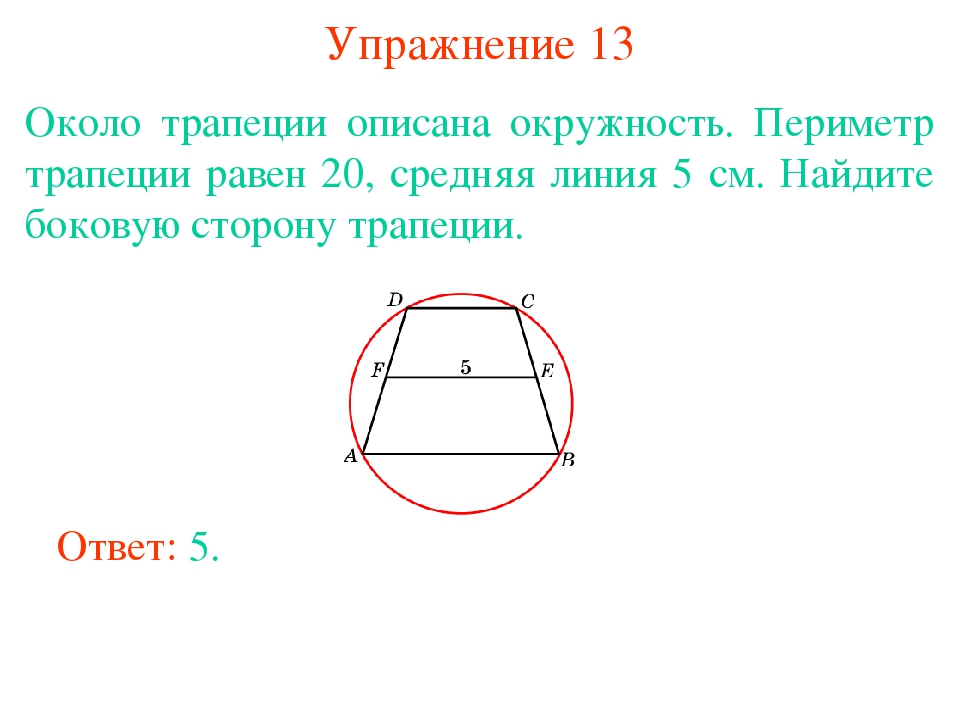
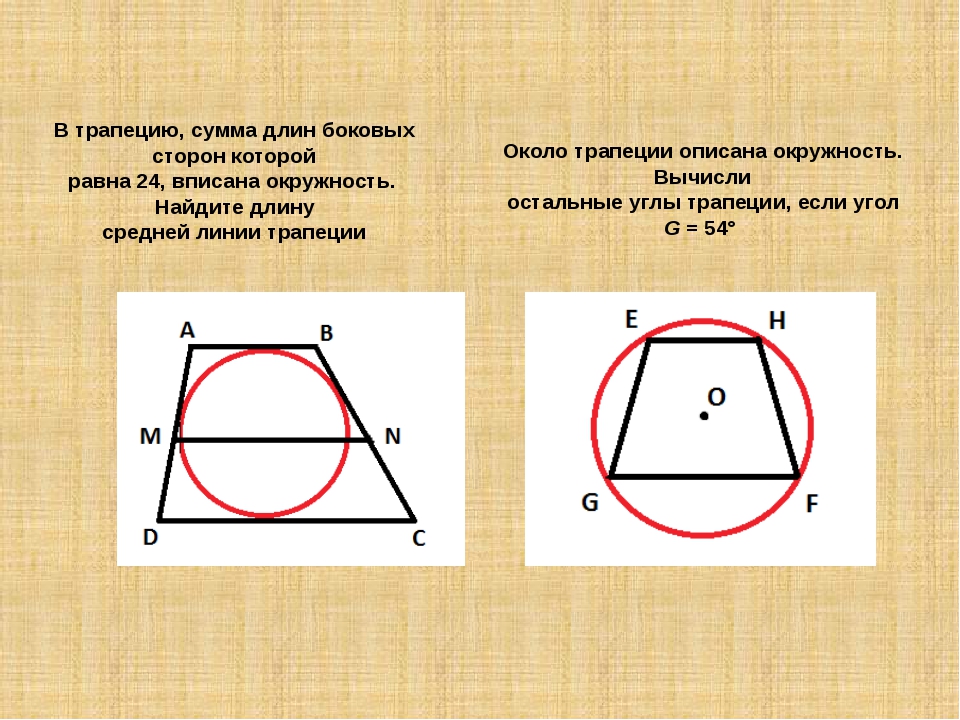
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
Ответ: 6
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 600, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 600 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
*Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 1800 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
Ответ: 6
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC).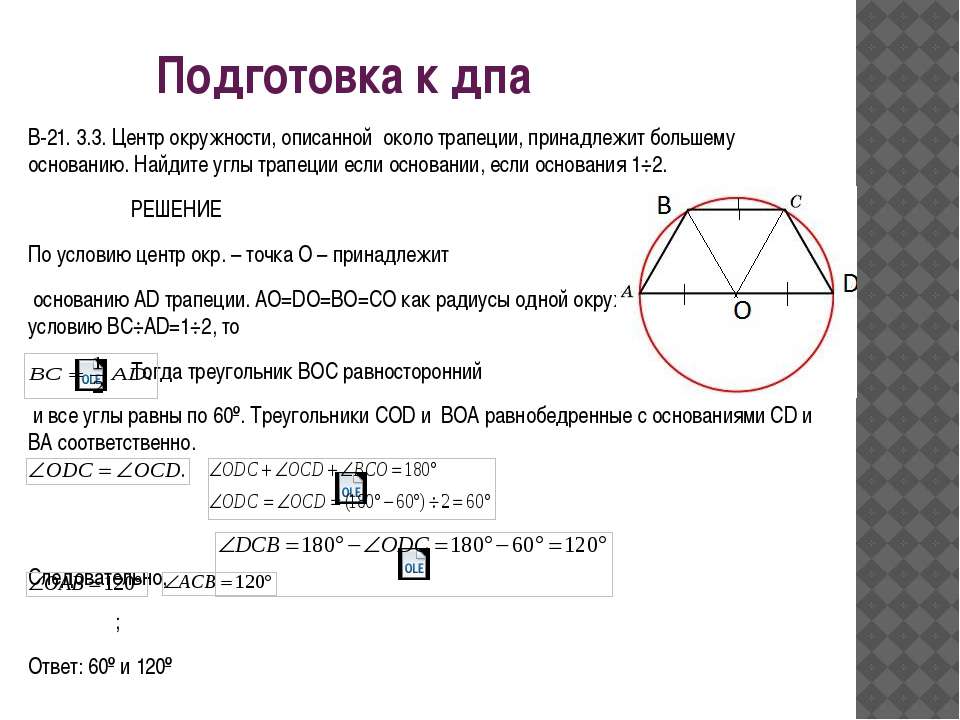 По теореме Пифагора можем вычислить OF:
По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Ответ: 7
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Значит
А средняя линия равна половине суммы оснований, то есть 10.
Ответ: 10
27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:
Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.
Таким образом, радиус будет равен 2.
Ответ: 2
27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.
Посмотреть решение
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
*Расскажите о сайте в социальных сетях.
Радиус описанной окружности трапеции | Треугольники
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
или
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
Свойства трапеции, описанной около окружности: формулы и теоремы
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».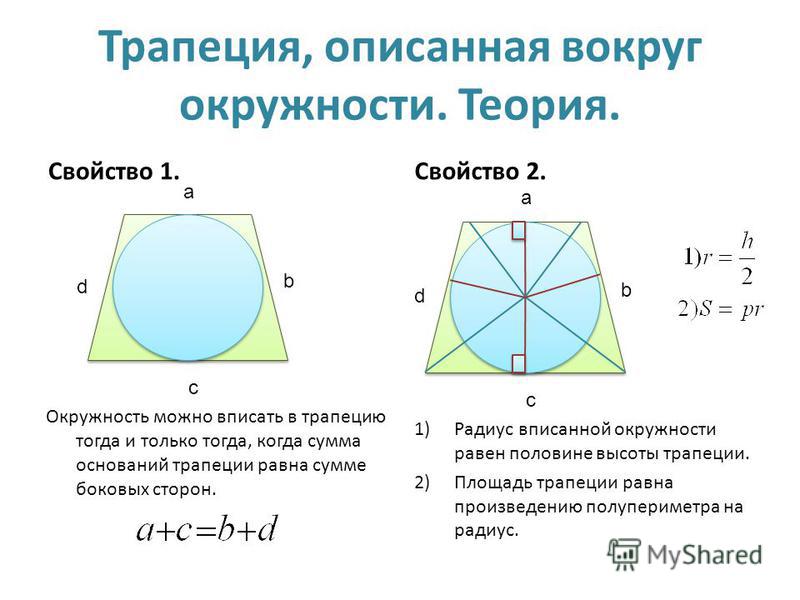
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.

- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией.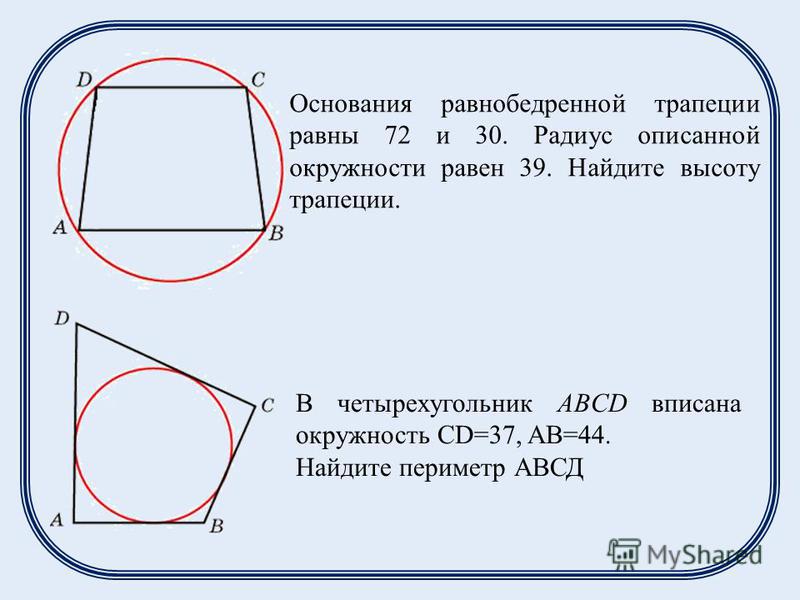 Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Вписанные четырёхугольники и их свойства
Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.
Рис.1
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Доказательство. Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.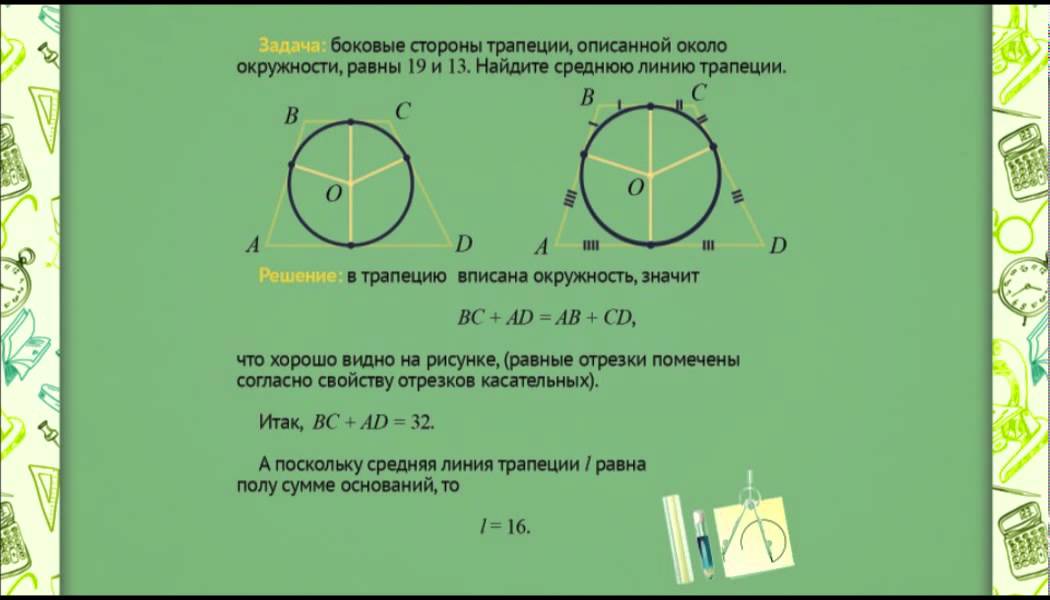 1). Поэтому величина угла ABC равна половине угловой величины дуги ADC. Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.
1). Поэтому величина угла ABC равна половине угловой величины дуги ADC. Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.
Если рассмотреть углы BCD и BAD, то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A, B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис. 2).
2).
Рис.2
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E, и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180°. При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC. Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC, не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |
| Окружность, описанная около ромба | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, |
| Окружность, описанная около параллелограмма | |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. | |
| Окружность, описанная около ромба | |
| Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. | |
| Окружность, описанная около трапеции | |
| Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. | |
| Окружность, описанная около дельтоида | |
| Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. | |
| Произвольный вписанный четырёхугольник | |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, | |
| Окружность, описанная около параллелограмма |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, |
Теорема Птолемея
Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.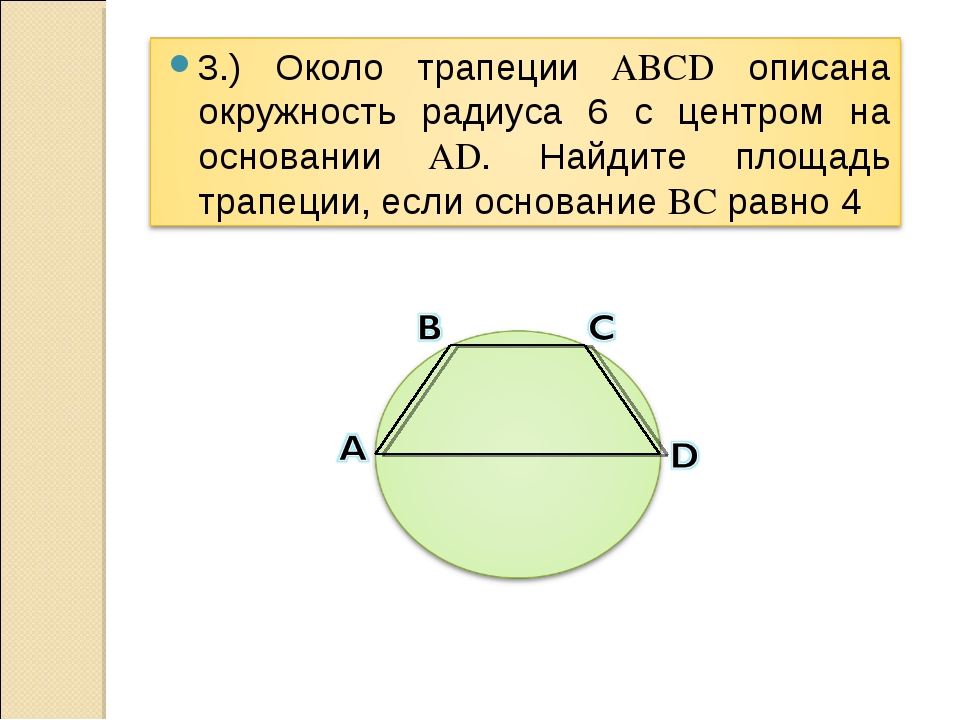
Доказательство. Рассмотрим произвольный четырёхугольник ABCD, вписанный в окружность (рис.3).
Рис.3
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Рис.4
Заметим, что треугольник ABD подобен треугольнику BCE. Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (1) |
Заметим, что треугольник ABE подобен треугольнику BCD. Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу).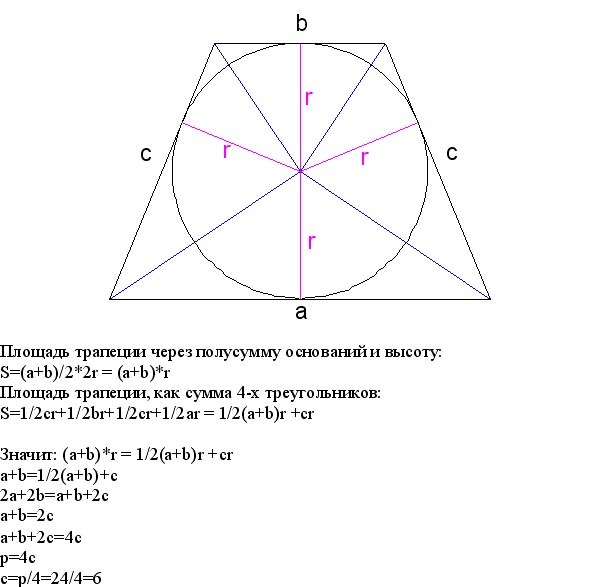 Следовательно, справедлива пропорция:
Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (2) |
Складывая равенства (1) и (2), получаем:
Теорема Птолемея доказана.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти центр окружности описанной около трапеции. Материал по геометрии на тему «трапеция и ее свойства»
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Свойства трапеции, описанной около окружности
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.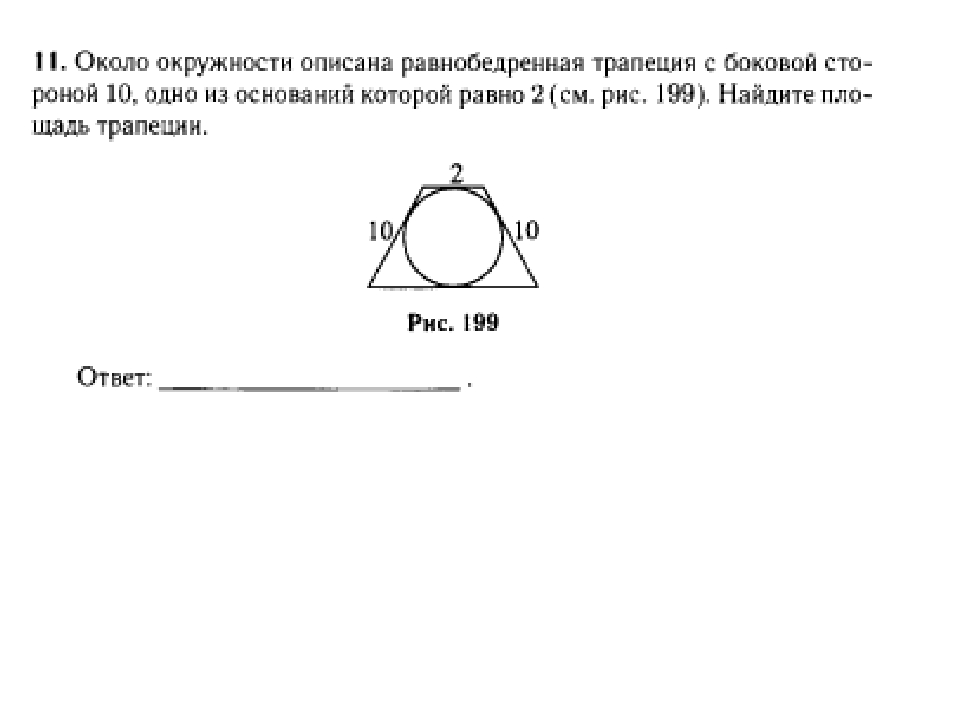
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
. - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
. - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
. - Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
. - Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
. - Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
. - Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
. - У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
. - Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
. - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
ФГКОУ «МКК «Пансион воспитанниц МО РФ»
«УТВЕРЖДАЮ»
Руководитель отдельной дисциплины
(математика, информатика и ИКТ)
Ю. В. Крылова _____________
«___» _____________ 2015 г.
«Трапеция и ее свойства
»
Методическая разработка
преподавателя математики
Шаталиной Елены Дмитриевны
Рассмотрено и
на заседании ПМО от _______________
Протокол №______
Москва
2015 год
Оглавление
Введение 2
Определения 3
Свойства равнобедренной трапеции 4
Вписанные и описанные окружности 7
Свойства вписанных и описанных трапеций 8
Средние величины в трапеции 12
Свойства произвольной трапеции 15
Признаки трапеции 18
Дополнительные построения в трапеции 20
Площадь трапеции 25
10. Заключение
Список используемой литературы
Приложение
Доказательства некоторых свойств трапеции 27
Задачи для самостоятельных работ
Задачи по теме «Трапеция» повышенной сложности
Проверочный тест по теме «Трапеция»
Введение
Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.
Трапеция.
Определения
Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.
Трапеция, у которой есть прямые углы при боковой стороне, называется
прямоугольной
.
Отрезок, соединяющий середины боковых сторон, называется
средней линией трапеции
.
Расстояние между основаниями называется высотой
трапеции
.
2
. Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны.
4
1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
3. Вписанная и описанная окружность
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
Е
сли трапеция равнобедренная, то около неё можно описать окружность.
4
. Свойства вписанных и описанных трапеций
2.Если в равнобедренную
трапецию можно вписать окружность, то
сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.
4
.
Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
Е
сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m
и n,
тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.
1
0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.
5.
Средние величины в трапеции
Среднее геометрическое
В любой трапеции с основаниями
a
и
b
для
a
>
b
справедливо неравенство
:
b
˂
h
˂
g
˂
m
˂
s
˂
a
6.
Свойства произвольной трапеции
1
. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.
2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.
5.
При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).
6.
Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
d
1
2
+
d
2
2
=
c
2
+
d
2
+ 2
ab
7
.
В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований
d
1
2
—
d
2
2
=
a
2
–
b
2
8
. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.
7
. Признаки трапеции
8
. Дополнительные построения в трапеции
1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.
2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.
3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.
4
. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.
6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований
7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.
8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
9. Биссектриса угла трапеции отсекает равнобедренный треугольник.
1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.
13.
Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.
9. Площадь трапеции
1
. Площадь трапеции равна произведению полусуммы оснований на высоту
S
= ½(a
+
b
)
h
или
П
лощадь трапеции равна произведению средней линии трапеции на высоту S
=
m
h
.
2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
Площадь равнобедренной трапеции с радиусом вписанной окружности равным
r
и углом при основании
α:
10.
Заключение
ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?
Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.
Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.
Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.
Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.
Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн
В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.
Список используемой литературы
Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.
Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004
Гордин Р.К. Планиметрия. Задачник.
Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN
5-89155-188-3
Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).
Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.
Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.
Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.
Приложение
1.Доказательство некоторых свойств трапеции.
1.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках
K
и
L
.
Доказать, что если основания трапеции равны
а
и
b
, то
длина отрезка
KL
равна среднему геометрическому оснований трапеции.
Доказательство
Пусть
О
— точка пересечения диагоналей,
AD
=
а, ВС
=
b
.
Прямая
KL
параллельна основанию
AD
, следовательно,
K
О
║
AD
,
треугольники
В
K
О
и
BAD
подобны, поэтому
(1)
(2)
Подставим (2) в (1)
, получим KO =
Аналогично LO
= Тогда K
L
=
KO
+
LO
=
В
о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.
Доказательство: Пусть продолжения боковых сторон пересекаются в точке
К.
Через точку
К
и точку
О
пересечения диагоналей
проведём прямую
КО.
K
Окажем, что эта прямая делит основания пополам.
Обозначим
ВМ
=
х, МС
=
у,
AN
=
и,
ND
=
v
.
Имеем:
∆
ВКМ
~
∆AKN
→
M
x
B
C
Y
∆
MК
C
~
∆NKD
→
→
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
. - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
. - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
. - Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
. - Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
. - Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
. - Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
. - У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
. - Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
. - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной.\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\)
. Пусть \(h\)
– высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\)
. Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\)
прямую \(MN»\parallel AD\)
(\(N»\in CD\)
). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\)
) точка \(N»\)
— середина отрезка \(CD\)
. Значит, точки \(N\)
и \(N»\)
совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\)
и \(N»\)
— середины отрезков \(BB»\)
и \(CC»\)
соответственно. Значит, \(MM»\)
– средняя линия \(\triangle
ABB»\)
, \(NN»\)
— средняя линия \(\triangle DCC»\)
. Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\)
и \(BB», CC»\perp AD\)
, то \(B»M»N»C»\)
и \(BM»N»C\)
– прямоугольники. По теореме Фалеса из \(MN\parallel AD\)
и \(AM=MB\)
следует, что \(B»M»=M»B\)
. Значит, \(B»M»N»C»\)
и \(BM»N»C\)
– равные прямоугольники, следовательно, \(M»N»=B»C»=BC\)
.
Таким образом:
\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\)
(\(P\)
– точка пересечения продолжений боковых сторон, \(N\)
– середина \(BC\)
). Пусть она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Рассмотрим \(\triangle BPN\)
и \(\triangle APM\)
. Они подобны по двум углам (\(\angle APM\)
– общий, \(\angle PAM=\angle PBN\)
как соответственные при \(AD\parallel BC\)
и \(AB\)
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\)
и \(\triangle DPM\)
. Они подобны по двум углам (\(\angle DPM\)
– общий, \(\angle PDM=\angle PCN\)
как соответственные при \(AD\parallel BC\)
и \(CD\)
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\)
. Но \(BN=NC\)
, следовательно, \(AM=DM\)
.
2) Докажем, что точки \(N, O, M\)
лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\)
по двум углам (\(\angle OBN=\angle
ODM\)
как накрест лежащие при \(BC\parallel AD\)
и \(BD\)
секущей; \(\angle BON=\angle DOM\)
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\)
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\)
. Но \(BN=CN\)
, следовательно, \(AM=MD\)
.
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\)
и \(C\)
опустим на сторону \(AD\)
перпендикуляры \(BM\)
и \(CN\)
соответственно. Так как \(BM\perp AD\)
и \(CN\perp AD\)
, то \(BM\parallel CN\)
; \(AD\parallel BC\)
, тогда \(MBCN\)
– параллелограмм, следовательно, \(BM = CN\)
.
Рассмотрим прямоугольные треугольники \(ABM\)
и \(CDN\)
. Так как у них равны гипотенузы и катет \(BM\)
равен катету \(CN\)
, то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\)
.
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\)
– общая, то по первому признаку . Следовательно, \(AC=BD\)
.
3) Т.к. \(\triangle ABD=\triangle ACD\)
, то \(\angle BDA=\angle CAD\)
. Следовательно, треугольник \(\triangle AOD\)
– равнобедренный. Аналогично доказывается, что и \(\triangle BOC\)
– равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\)
, такую что \(\angle A = \angle D\)
.
Достроим трапецию до треугольника \(AED\)
как показано на рисунке. Так как \(\angle 1 = \angle 2\)
, то треугольник \(AED\)
равнобедренный и \(AE
= ED\)
. Углы \(1\)
и \(3\)
равны как соответственные при параллельных прямых \(AD\)
и \(BC\)
и секущей \(AB\)
. Аналогично равны углы \(2\)
и \(4\)
, но \(\angle 1 = \angle 2\)
, тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\)
, следовательно, треугольник \(BEC\)
тоже равнобедренный и \(BE = EC\)
.
В итоге \(AB = AE — BE = DE — CE = CD\)
, то есть \(AB = CD\)
, что и требовалось доказать.
2) Пусть \(AC=BD\)
. Т.к. \(\triangle AOD\sim \triangle BOC\)
, то обозначим их коэффициент подобия за \(k\)
. Тогда если \(BO=x\)
, то \(OD=kx\)
. Аналогично \(CO=y \Rightarrow AO=ky\)
.
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\)
(\(AC=BD, \angle OAD=\angle ODA, AD\)
– общая). Значит, \(AB=CD\)
, чтд.
ОГЭ по математике. Вычисление длин
Задачи для ОГЭ с ответами и решениями
Вычисление длин II
перейти к содержанию задачника
- Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 132.
- Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 15.
- Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
- Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус окружности, описанной около этого треугольника.
- В треугольнике АВС АС равно 7,5, ВС равно 4, угол С равен 90o. Найдите радиус вписанной окружности.
- Боковые стороны равнобедренного треугольника равны 569, основание равно 462. Найдите радиус вписанной окружности.
- Боковые стороны равнобедренного треугольника равны 656, основание равно 288. Найдите радиус вписанной окружности.
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 12 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
- Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 15 и .
- Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 27 и .
- Найдите радиус окружности, описанной около квадрата со стороной, равной .
- Найдите радиус окружности, описанной около квадрата со стороной, равной .
- Сторона ромба равна , острый угол равен 60o. Найдите радиус вписанной в этот ромб окружности.
- Найдите высоту трапеции, в которую вписана окружность радиуса 28.
- Найдите высоту трапеции, в которую вписана окружность радиуса 24.
- Около трапеции описана окружность. Периметр трапеции равен 116, средняя линия равна 54. Найдите боковую сторону трапеции.
- Основания равнобедренной трапеции равны 48 и 20. Радиус описанной окружности равен 26. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции.
- Основания равнобедренной трапеции равны 120 и 50. Радиус описанной окружности равен 65. Найдите высоту трапеции, если известно, что центр описанной окружности лежит внутри трапеции.
- Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
- Около окружности описана трапеция, периметр которой равен 128. Найдите среднюю линию трапеции.
- Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 29. Найдите радиус окружности.
- В четырехугольник ABCD вписана окружность, АВ = 17, CD = 22. Найдите периметр четырехугольника.
- Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 7 и 25. Найдите большую из оставшихся сторон.
- В четырехугольник ABCD вписана окружность, АВ = 7, ВС = 12 и CD = 9. Найдите четвертую сторону четырехугольника.
- В четырехугольник ABCD вписана окружность, АВ = 7, ВС = 1 и CD = 19. Найдите четвертую сторону четырехугольника.
- Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1 : 3 : 9. Найдите большую сторону этого четырехугольника, если его периметр равен 20.
- Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
- Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
- Сторона АВ треугольника АВС равна 11. Противолежащий ей угол С равен 30o. Найдите радиус окружности, описанной около этого треугольника.
- Угол С треугольника АВС, вписанного в окружность радиуса 10, равен 30o. Найдите сторону АВ этого треугольника.
- Угол С треугольника АВС, вписанного в окружность радиуса 12, равен 30o. Найдите сторону АВ этого треугольника.
перейти к содержанию задачника
Ответы
- 44
- 5
- 16,5
- 3,125
- 1,5
- 150,15
- 115,2
- 22
- 28
- 10
- 16
- 27
- 14
- 25,5
- 56
- 48
- 4
- 34
- 85
- 5,5
- 32
- 10,5
- 78
- 21
- 4
- 25
- 9
- 32
- 58
- 11
- 10
- 12
Метки ОГЭ. Смотреть запись.
Дан полукруг радиуса r. Какой максимум
площадь любой трапеции, вписанной в полукруг?
Щелкните здесь, чтобы вызвать анимацию GSP
чтобы увидеть, как изменяется площадь вписанной трапеции.Предполагается, что трапеция максимальной площади будет
имеют самое длинное основание по диаметру полукруга. Какие
про трапеции ориентированы как на следующей картинке? Какие
Можно ли привести аргумент, чтобы показать, что они никогда не занимают максимальную площадь?
Нажмите ЗДЕСЬ , чтобы вызвать анимацию GSP
Чтобы увидеть площадь вписанной трапеции, варьируйте .
Рассмотрение случая
полукруг с единичным радиусом. Максимальная площадь любой трапеции
вписанные в полукруг радиуса r, будут раз
максимальная площадь трапеции, вписанной в полукруг единицы
радиус. (ПОЧЕМУ?)
1. Используйте таблицу для оценки
максимальная площадь. Один из подходов заключается в следующем. Самая длинная база
имеет длину 2r (на диаметре полукруга) и
мы можем позволить столбцу A содержать меры высоты h
от 0 до р.Тогда размер другой базы будет
.
, и эти значения можно поместить в столбец B. В столбце C может накапливаться
расчетная площадь трапеций. кликните сюда
чтобы увидеть таблицу Excel для r = 10, где высота
увеличивается с шагом 0,25. График серии 2 представляет
области трапеций.На какой высоте максимальная площадь? Какая длина
чем короче база в этом месте?
2.Напишите функцию для площади и используйте графическую программу
чтобы показать кривую и оценить максимальную площадь. Используйте график
калькулятор или компьютерная программа для построения графиков.Подсказка (при необходимости).
3. Используйте неравенство среднего арифметического и среднего геометрического, чтобы найти
точную площадь и доказать, что это максимум.Подсказка : Пусть x будет длиной более короткого основания.
Справка , если необходимо.
4. Чтобы не думать об этом, используйте исчисление. Настроить функцию
для области и установите первую производную на ноль, чтобы найти
относительный максимум.
5. Используйте геометрию. Рассмотрим отражение полукруга и
вписанная трапеция в диаметр полукруга. Трапеция
и его отражение объединяются в шестиугольник, вписанный в круг
. . .
Известно ли, что из всех шестиугольников, вписанных в круг,
максимальная площадь будет, когда шестиугольник правильный? Если да, то это
Проблема решена.Если нет, то как это доказать?
Рассмотрите периметр трапеции, где более короткое основание
колеблется от 2р до 0. Есть ли максимальный периметр? Если так,
что это? Какая длина самой короткой базы при периметре
есть максимум?Пусть x будет длиной кратчайшего основания. См. ниже.
Подобные треугольники ACB и AKC дадут легко вычисляемую длину.
для наклонной стороны s через r и x.
Помощь по периметру , если
в розыске.
Вернуться к EMAT
4400/6600 Страница
| |||||||||||||||||||||
swift — Как нарисовать текст трапецией (или кругом)?
Здесь вам нужно будет перейти на уровни CoreText. Хорошая новость в том, что вы сможете рисовать текст практически любой формы!
extension NSAttributedString {
public func draw (в пути: CGPath) {
let context = UIGraphicsGetCurrentContext ()!
let transform = CGAffineTransform (scaleX: +1, y: -1)
пусть flippedPath = CGMutablePath ()
flippedPath.addPath (путь, преобразование: преобразование)
let range = CFRange (расположение: 0, длина: 0)
let framesetter = CTFramesetterCreateWithAttributedString (self)
let frame = CTFramesetterCreateFrame (framesetter, range, flippedPath, nil)
context.saveGState ()
// Отладка: заполнить путь.
context.setFillColor (красный: 1,0, зеленый: 0,0, синий: 0,0, альфа: 0,5)
context.beginPath ()
context.addPath (путь)
context.fillPath ()
context.concatenate (преобразовать)
CTFrameDraw (фрейм, контекст)
контекст.restoreGState ()
}
}
А можно так использовать:
let string = NSAttributedString (строка: «Lorem ipsum dolor sit amet, conctetur adipiscing elit. Lorem ipsum dolor sit amet, conctetur adipiscing elit.»)
пусть границы = CGRect (x: 0, y: 0, ширина: 120, высота: 120)
пусть путь = CGMutablePath ()
path.move (в: CGPoint (x: 10, y: 10))
path.addLine (to: CGPoint (x: 110, y: 10))
path.addLine (to: CGPoint (x: 90, y: 110))
path.addLine (to: CGPoint (x: 30, y: 110))
дорожка.closeSubpath ()
UIGraphicsBeginImageContextWithOptions (bounds.integral.size, true, 0)
отложить {UIGraphicsEndImageContext ()}
let context = UIGraphicsGetCurrentContext ()!
context.setFillColor (UIColor.white.cgColor)
context.fill (. бесконечный)
string.draw (in: путь)
let image = UIGraphicsGetImageFromCurrentImageContext ()!
Плохая новость в том, что это решение не отображает многоточие в конце. Если вы действительно этого хотите, вам может потребоваться внести некоторые изменения в последнюю строку, которую дает вам фреймсеттер.
Polygons — Площадь многоугольников и окружностей
Площадь всегда
положительное число. Он представляет собой количество квадратных единиц, необходимых для покрытия
фигура, например многоугольник или круг. Обычно мы используем формулы для расчета
области.
Площадь: прямоугольник | квадратный
| параллелограмм | треугольник | трапеция
| круг
Площадь
прямоугольника
Прямоугольник — это хорошая и простая форма для начала.Площадь прямоугольника
равна произведению длины основания на длину и высоту.
Высота — это отрезок, перпендикулярный основанию. Для прямоугольника
основание и высоту часто называют «длиной» и «шириной», а иногда
высота называется «высотой».
Давайте найдем
площадь этого прямоугольника с основанием 4 фута и высотой
6 футов. Используя формулу, мы умножаем 4 фута на 6 футов, чтобы получить 24 квадратных метра.
ноги.
Площадь
Квадрата
Квадрат — это особый прямоугольник, площадь которого можно определить с помощью прямоугольника.
формула. Однако, поскольку основание и высота всегда одинаковы для
квадрат, мы их обычно называем «сторонами». Площадь квадрата равна
длина одной стороны в квадрате.
Если
длина одной стороны этого квадрата 4 сантиметра, какова площадь?
Подставляем в формулу значение «4 см» и находим площадь равной
16 квадратных сантиметров.
Площадь
параллелограмма
Чтобы найти площадь параллелограмма, мы можем использовать ту же формулу, что и мы.
для площади прямоугольника, умножив длину основания на
длина высоты.
Давайте найдем
площадь параллелограмма с основанием 23 см и высотой 7 см. Если
подставляем значения в формулу, находим, что параллелограмм
имеет площадь 161 квадратный сантиметр.
Площадь
треугольника
А как насчет треугольников? Этот набросок четырехугольника показывает нам, что одна диагональ
разделяет внутреннее пространство на две равные части.
The
Следовательно, площадь треугольника составляет половину площади четырехугольника, который
это базовая длина, умноженная на высоту. Какова площадь треугольника с
длина основания 23 фута и высота 16 футов? Подставьте значения в
формула, и мы находим площадь 184 квадратных фута.
Площадь
трапеции
Чтобы найти площадь трапеции, мы можем нарисовать диагональ так, чтобы трапеция была
разделен на два треугольника.
Вы
видно, что площадь трапеции DEFG равна сумме площадей
двух треугольников EFG и DEG.
Площадь
треугольника EFG = & frac12bh = & frac12 (base1) h
Площадь треугольника DEG = & frac12bh = & frac12 (base2) h
Площадь
трапеции DEFG = & frac12 (base1) h + & frac12 (base2) h.Поскольку высота
треугольника EFG и DEG одинаковы, мы можем написать формулу для площади
трапеции (в любом случае правильно):
Если трапеция
DEFG имеет высоту 8 дюймов, основание DG составляет 12 дюймов, а базовое EF — размеры.
7 дюймов, какова площадь трапеции? Если подставить значения в
по формуле, мы находим площадь 76 квадратных дюймов.
Площадь
круга
Наконец, мы посмотрим, как найти площадь круга.Чтобы помочь нам понять
площадь круга лучше, сначала нарисуем квадрат, и впишем в него круг,
что означает нарисовать круг внутри квадрата так, чтобы круг только касался
каждую сторону квадрата.
ср
можно найти площадь этого квадрата, сначала найдя площадь четырех меньших
квадраты — каждый со сторонами, равными r , радиус круга — и
складывая их вместе.
Обратите внимание, что
стороны квадрата вдвое длиннее радиуса круга.Ты
также можно найти площадь квадрата, умножив сторону на сторону,
или 2r x 2r, что также равно 4r 2 .
Вы можете увидеть
что площадь круга должна быть меньше площади четырех квадратов.
Но насколько меньше? Мы могли бы сделать обоснованное предположение и сказать, что площадь
круг может быть немного больше трех меньших квадратов.
Фактическое число
мы ищем (от 3 до 4) специальный номер, называемый
пи, представленный греческой буквой.Пи примерно равно 3,14.
Символ вы
см. здесь означает «примерно равно». Пи на самом деле имеет бесконечное число
десятичных знаков, но 3,14 обычно достаточно близко для наших расчетных целей.
Пи — это отношение диаметра окружности к окружности.
The
Окончательная формула для площади круга показана здесь.
Допустим, ваш
циферблат имеет диаметр 1 дюйм, поэтому его радиус равен или 0.5. Мы можем найти
его площадь такая:
назад
наверх
Площадь трапеции
Площадь трапеции , формулы и калькулятор для расчета площади онлайн. Формулы приведены для всех типов трапеций и частных случаев для равнобедренных трапеций.
Таблица с формулами трапеции площади (в конце страницы)
— Вычисление (показано)
(скрыта)
— примечания (показаны)
(скрыта)
Площадка для всех типов трапеций
1
Площадь трапеции по высоте и два основания
… подготовка …
a — базовая
b — цоколь
h — высота
2
Площадь трапеции по высоте и средней линии
… подготовка …
м — средняя линия
h — высота
3
Площадь трапеции с четырех сторон
… подготовка …
a — базовая
b — цоколь
c — боковая
d — боковой
4
Площадь трапеции по диагонали и угол между диагоналями
… подготовка …
d 1 — диагональ
d 2 — диагональ
α ° — Угол между диагоналями
5
Площадь трапеции через основание и углы у основания
… подготовка …
a — базовая
b — цоколь
α ° — угол при основании
β ° — угол при основании
Площадь равнобедренной трапеции
6
Площадь равнобедренной трапеции по бокам
… подготовка …
a — боковой
b — боковой
c — боковая
7
Площадь равнобедренной трапеции через малое основание, боковую сторону и угол с большим основанием
… подготовка …
a — базовая
c — боковая
α ° — угол при основании
8
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол с большим основанием
… подготовка …
b — цоколь
c — боковая
α ° — угол при основании
9
Площадь равнобедренной трапеции через основание и угол при основании
… подготовка …
a — базовая
b — цоколь
α ° — угол при основании
10
Площадь равнобедренной трапеции по диагоналям и угол между диагоналями
… подготовка …
d — диагональ
α ° — Угол между диагоналями
11
Площадь равнобедренной трапеции по средней линии, бокам и углу у основания
… подготовка …
м — средняя линия
c — боковая
α ° — угол между сторонами
12
Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами
Эта формула применима только для равнобедренных трапеций, в которые можно вписать круг.
… подготовка …
r — радиус вписанной окружности
α ° — угол между сторонами
13
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности
Эта формула применима только для равнобедренных трапеций, в которые можно вписать круг.
… подготовка …
a — базовая
b — цоколь
r — радиус вписанной окружности
14
Площадь равнобедренной трапеции через основание и угол с большим основанием
Эта формула применима только для равнобедренных трапеций, в которые можно вписать круг.
… подготовка …
a — базовая
b — цоколь
α ° — угол при основании
15
Площадь равнобедренной трапеции по бокам
Эта формула применима только для равнобедренных трапеций, в которые можно вписать круг.
… подготовка …
a — базовая
b — цоколь
c — боковая
16
Площадь равнобедренной трапеции через основание и среднюю линию
Эта формула применима только для равнобедренных трапеций, в которые можно вписать круг.
… подготовка …
a — базовая
b — цоколь
м — средняя линия
Примечание:
Если в исходных данных угол указан в радианах, то для преобразования в градусы можно использовать формулу: 1 радиан × (180 / π) ° = 57,296 °
Таблица с формулами трапеции площади
В зависимости от известных исходных данных и типа трапеции площадь трапеции можно рассчитать по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула | |
| Площадка для всех типов трапеций | |||
| 1 | высота и два основания | ||
| 2 | высота и средняя линия | ||
| 3 | четыре стороны | ||
| 4 | и угол между ними | ||
| 5 | основания и уголки у одного из оснований | ||
| Площадь равнобедренной трапеции | |||
| 6 | стороны | ||
| 7 | основание, стороны и угол у основания | ||
| 8 | основание, стороны и угол у основания | ||
| 9 | основания и уголки у одного из оснований | ||
| 10 | и угол между ними | ||
| 11 | средняя линия, стороны и углы между основанием и сторонами | ||
| 12 | радиус вписанной окружности и угол при основании | ||
| 13 | основание и радиус вписанной окружности | ||
| 14 | основания и уголки у одного из оснований | ||
| 15 | основания и борта | ||
| 16 | базовая и средняя линия | ||
9.5 Решайте геометрические приложения: круги и неправильные фигуры — Prealgebra 2e
Задачи обучения
К концу этого раздела вы сможете:
- Используйте свойства окружностей
- Найдите площадь неправильных фигур
Будьте готовы 9,13
Перед тем, как начать, пройдите тест на готовность.
Вычислить x2x2, когда x = 5.x = 5.
Если вы пропустили эту проблему, просмотрите Пример 2.15.
Будьте готовы 9.14
Используя 3.143.14 для π, π, аппроксимируйте (a) длину окружности и (b) площадь круга с радиусом 88 дюймов.
Если вы пропустили эту проблему, просмотрите Пример 5.39.
Будьте готовы 9.15
Упростим 227 (0,25) 2227 (0,25) 2 и округлим до ближайшей тысячной.
Если вы пропустили эту проблему, просмотрите Пример 5.36.
В этом разделе мы продолжим работу с геометрическими приложениями. Мы добавим несколько новых формул в нашу коллекцию формул.Чтобы помочь вам в выполнении примеров и упражнений в этом разделе, мы покажем здесь стратегию решения проблем для геометрических приложений.
Стратегия решения проблем для геометрических приложений
- Шаг 1. Прочтите задачу и убедитесь, что вы понимаете все слова и идеи. Нарисуйте фигуру и напишите на ней указанную информацию.
- Шаг 2. Определите то, что вы ищете.
- Шаг 3. Назовите то, что вы ищете.Выберите переменную для представления этого количества.
- Шаг 4. Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Шаг 5. Решите уравнение, используя хорошие методы алгебры.
- Шаг 6. Отметьте ответ в задаче и убедитесь, что он имеет смысл.
- Шаг 7. Ответьте на вопрос полным предложением.
Используйте свойства кругов
Вы помните свойства кругов из «Десятичных знаков и дробей вместе»? Мы покажем их здесь снова, чтобы указать, как мы используем их для решения приложений.
Свойства кругов
- rr — длина радиуса
- dd — длина диаметра
- d = 2rd = 2r
- Окружность — периметр круга. Формула окружности
- Формула площади круга:
Помните, что мы аппроксимируем ππ с помощью 3,143,14 или 227227 в зависимости от того, задан ли радиус круга в виде десятичной или дробной части. Если вы используете кнопку ππ на своем калькуляторе для выполнения вычислений в этом разделе, ваши ответы будут немного отличаться от показанных.Это потому, что клавиша ππ использует более двух десятичных знаков.
Пример 9.41
Круглая песочница имеет радиус 2,52,5 фута. Найдите окружность и ⓑ площадь песочницы.
Решение
| ⓐ Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | окружность круга |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть c = длина окружности |
| Шаг 4. Translate. Напишите соответствующую формулу Замените | C = 2πrC = 2πr C = 2π (2.5) C = 2π (2.5) |
| Шаг 5. Решите уравнение. | C≈2 (3,14) (2,5) C≈2 (3,14) (2,5) C≈15 футовC≈15 футов |
| Шаг 6. Проверка. Имеет ли смысл этот ответ? Да.Если мы нарисуем квадрат вокруг круга, его стороны будут равны 5 футам (удвоенному радиусу), поэтому его периметр будет 20 футов. Это немного больше, чем длина окружности круга, 15,7 фута. | |
| Шаг 7. Ответьте на вопрос. | Окружность песочницы составляет 15,7 футов. |
| ⓑ Шаг 1. Прочтите , в чем проблема. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | площадь круга |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть A = площадь круга |
| Шаг 4. Translate. Напишите соответствующую формулу Замените | A = πr2A = πr2 A = π (2,5) 2A = π (2,5) 2 |
| Шаг 5. Решите уравнение. | A≈ (3.14) (2,5) 2A≈ (3,14) (2,5) 2 A≈19,625 кв. ftA≈19,625 кв. фут |
| Шаг 6. Проверка. Да. Если мы нарисуем квадрат вокруг круга, его стороны будут 5 футов, как показано в части ⓐ. Таким образом, площадь квадрата будет 25 кв. Футов. Это немного больше, чем площадь круга, 19,625 кв. Футов. | |
| Шаг 7. Ответьте на вопрос. | Площадь круга составляет 19,625 квадратных футов. |
Попробуй 9.81
Круглое зеркало имеет радиус 55 дюймов. Найдите окружность и ⓑ площадь зеркала.
Попробуйте 9,82
Круглый бассейн имеет радиус 4,54,5 фута. Найдите окружность и ⓑ площадь спа.
Обычно мы видим формулу длины окружности через радиус rr окружности:
Но поскольку диаметр окружности в два раза больше радиуса, мы могли бы записать формулу длины окружности в единицах d.ofd.
C = 2πr Используя свойство коммутативности, мы получаем C = π · 2r Затем подставляем d = 2rC = π · dSoC = πdC = 2πr Используя свойство коммутативности, получаем C = π · 2r Затем подставляем d = 2rC = π · dSoC = πd
Мы будем использовать эту форму окружности, когда нам дается длина диаметра вместо радиуса.
Пример 9.42
Круглый стол имеет диаметр четыре фута. Какова окружность стола?
Решение
| Шаг 1. Прочтите , в чем проблема. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | окружность стола |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть c = окружность стола |
| Шаг 4. Translate. Напишите формулу, соответствующую ситуации. Запасной. | C = πdC = πd C = π (4) C = π (4) |
| Шаг 5. Решите уравнение, используя 3,14 для π.π. | C≈ (3,14) (4) C≈ (3,14) (4) C≈12,56 футов C≈12,56 футов |
| Шаг 6. Проверка: Если мы обведем круг квадратом, его сторона будет равна 4. Периметр будет равен 16. Имеет смысл, что длина окружности круга, 12,56, немного меньше 16. | |
| Шаг 7. Ответьте на вопрос. | Диаметр стола 12,56 квадратных футов. |
Попробуйте 9,83
Найдите окружность круглой костровой ямы диаметром 5,55,5 футов.
Попробуйте 9,84
Если диаметр круглого батута составляет 1212 футов, какова его окружность?
Пример 9.43
Найдите диаметр круга с длиной окружности 47,147,1 см.
Попробуйте 9,85
Найдите диаметр круга с окружностью 94,294,2 см.
Попробуйте 9,86
Найдите диаметр круга с окружностью 345,4345,4 фута.
Найдите площадь неправильных фигур
Итак, мы нашли область для прямоугольников, треугольников, трапеций и кругов. Неправильная фигура — это фигура, не имеющая стандартной геометрической формы.Его площадь не может быть рассчитана ни по одной из стандартных формул площади. Но некоторые неправильные фигуры состоят из двух или более стандартных геометрических фигур. Чтобы найти площадь одной из этих неправильных фигур, мы можем разбить ее на фигуры, формулы которых нам известны, а затем сложить площади фигур.
Пример 9,44
Найдите область затененной области.
Решение
Данная фигура неправильная, но мы можем разбить ее на два прямоугольника. Площадь заштрихованной области будет суммой площадей обоих прямоугольников.
Синий прямоугольник имеет ширину 1212 и длину 4,4. Красный прямоугольник имеет ширину 2,2, но его длина не обозначена. Правая часть рисунка — это длина красного прямоугольника плюс длина синего прямоугольника. Поскольку правая сторона синего прямоугольника составляет 44 единицы, длина красного прямоугольника должна быть 66 единиц.
Площадь рисунка 6060 кв.
Есть ли другой способ разбить эту фигуру на два прямоугольника? Попробуйте и убедитесь, что у вас такая же площадь.
Попробуйте 9,87
Найдите площадь каждой заштрихованной области:
Попробуйте 9,88
Найдите площадь каждой заштрихованной области:
Пример 9.45
Найдите область затененной области.
Решение
Мы можем разбить эту неправильную фигуру на треугольник и прямоугольник. Площадь фигуры будет суммой площадей треугольника и прямоугольника.
Прямоугольник имеет длину 88 единиц и ширину 44 единицы.
Нам нужно найти основание и высоту треугольника.
Поскольку обе стороны прямоугольника равны 4,4, вертикальная сторона треугольника равна 33, что составляет 7−47−4.
Длина прямоугольника 8,8, поэтому основание треугольника будет 33, что составляет 8−48−4.
Теперь мы можем добавить области, чтобы найти площадь неправильной фигуры.
Площадь рисунка 36 536,5 кв.
Попробуйте 9,89
Найдите площадь каждой заштрихованной области.
Попробуйте 9,90
Найдите площадь каждой заштрихованной области.
Пример 9.46
Трасса средней школы имеет форму прямоугольника с полукругом (полукругом) на каждом конце. Прямоугольник имеет длину 105105 метров и ширину 6868 метров. Найдите область, ограниченную дорожкой. Округлите ответ до ближайшей сотой.
Решение
Разобьем фигуру на прямоугольник и два полукруга. Площадь фигуры будет суммой площадей прямоугольника и полукругов.
Прямоугольник имеет длину 105105 м и ширину 6868 м. Полукруги имеют диаметр 6868 м, поэтому каждый имеет радиус 3434 м.
Попробуйте 9.91
Найдите область:
Попробуйте 9.92
Найдите область:
Раздел 9.5 Упражнения
Практика ведет к совершенству
Используйте свойства окружностей
В следующих упражнениях решайте, используя свойства окружностей.
217.
Крышка ведра с краской представляет собой круг радиусом 77 дюймов. Найдите окружность и ⓑ площадь крышки.
218.
Пицца очень большого размера — это круг радиусом 88 дюймов. Найдите окружность и ⓑ площадь пиццы.
219.
Распылитель на ферме разбрасывает воду по кругу радиусом 8,58,5 футов. Найдите окружность и ⓑ площадь red политого круга.
220.
Круглый коврик имеет радиус 3,53,5 фута. Найдите окружности и ⓑ площади ковра.
221.
Отражающий бассейн имеет форму круга диаметром 2020 футов. Какова окружность бассейна?
222.
Поворотный стол — это круг диаметром 1010 дюймов. Какова окружность проигрывателя?
223.
Циркулярная пила имеет диаметр 1212 дюймов. Какая окружность пилы?
224.
Круглая монета имеет диаметр 33 сантиметра. Какая окружность у монеты?
225.
Гриль для барбекю представляет собой круг диаметром 2.22,2 футов. Какова окружность гриля?
226.
Верхняя часть формы для пирога представляет собой круг диаметром 9,59,5 дюйма. Какая окружность верха?
227.
Окружность окружности составляет 163,28163,28 дюйма. Найдите диаметр.
228.
Окружность окружности составляет 59,6659,66 фута. Найдите диаметр.
229.
Окружность окружности составляет 17,2717,27 метра. Найдите диаметр.
230.
Окружность окружности равна 80.0780,07 см. Найдите диаметр.
В следующих упражнениях найдите радиус круга с заданной длиной окружности.
231.
Окружность окружности составляет 150,72150,72 фута.
232.
Окружность круга составляет 251,2251,2 сантиметра.
233.
Окружность окружности составляет 40,8240,82 мили.
234.
Окружность окружности составляет 78,578,5 дюйма.
Найдите площадь неправильной фигуры
В следующих упражнениях найдите площадь неправильной фигуры.Округлите ответы до ближайшей сотой.
236.
238.
240.
242.
244.
246.
248.
250.
252.
254.
В следующих упражнениях решите.
255.
Городской парк занимает один квартал плюс части еще четырех кварталов, как показано. Блок представляет собой квадрат со сторонами 250–250 футов в длину, а треугольники представляют собой равнобедренные прямоугольные треугольники. Найдите территорию парка.
256.
Подарочная коробка будет сделана из прямоугольного куска картона размером 1212 на 2020 дюймов, с квадратами, вырезанными по углам сторон, как показано.Стороны квадратов 33 дюйма. Найдите участок картона после вырезания углов.
257.
Перри нужно поставить новый газон. Его участок представляет собой прямоугольник длиной 120120 футов и шириной 100100 футов. Дом прямоугольной формы и имеет размеры 5050 на 4040 футов. Его подъездная дорога имеет прямоугольную форму и, как показано, имеет размеры 2020 на 3030 футов. Найдите участок лужайки Перри.
258.
Дениз планирует поставить колоду на заднем дворе. Палуба будет представлять собой прямоугольник размером 20 футов 20 футов на 12 футов 12 футов с полукругом диаметром 66 футов, как показано ниже.Найдите площадь колоды.
Повседневная математика
259.
Площадь стола Юки купила кухонный стол с откидной створкой. Прямоугольная часть таблицы представляет собой прямоугольник размером 1 фут1 фут на 3 фут3 фута с полукругом на каждом конце, как показано. Ⓐ Найдите область стола одним листом вверх. Ⓑ Найдите область стола обоими листами вверх.
260.
Картина Леора хочет расписать детскую в своем доме. Детская представляет собой прямоугольник размером 8 футов 8 футов на 10 футов 10 футов, а высота потолка составляет 88 футов.На одной стене есть дверь размером 3 фута на 6,5 фута 6,5 фута, дверь туалета размером 3 фута на 6,5 футов 6,5 фута на другой стене и одна дверь размером 4 фута на 3,5 фута. -ft3.5 ft окно на третьей стене. В четвертой стене нет дверей и окон. Если она будет красить только четыре стены, а не потолок или двери, сколько квадратных футов ей нужно будет красить?
Письменные упражнения
261.
Опишите два разных способа найти площадь этой фигуры, а затем покажите свою работу, чтобы убедиться, что оба способа дают одинаковую площадь.
262.
Круг имеет диаметр 1414 футов. Найдите площадь круга ⓐ, используя 3.143.14 для ππ ⓑ, используя 227227 для π.π. Ⓒ Какой расчет сделать предпочтительнее? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.