Вписанный и описанный четырехугольники: свойства, признаки, диагонали

Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.
Очевидно, эта окружность будет называться описанной вокруг четырехугольника.

Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.

На рисунке — вписанные и описанные четырехугольники и их свойства.

Ты нашел то, что искал? Поделись с друзьями!

Посмотрим, как эти свойства применяются в решении задач ЕГЭ.

. Два угла вписанного в окружность четырехугольника равны  и . Найдите больший из оставшихся углов. Ответ дайте в градусах.

Сумма противоположных углов вписанного четырехугольника равна . Пусть угол  равен . Тогда напротив него лежит угол в  градусов. Если угол  равен , то угол  равен .

Ответ: .

. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен .

Пусть сторона  равна ,  равна , а . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,

Получается, что  равна . Тогда периметр четырехугольника равен . Мы получаем, что , а большая сторона равна .

Ответ: .

. Около окружности описана трапеция, периметр которой равен . Найдите ее среднюю линию.

Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны  и , а боковые стороны —  и . По свойству описанного четырехугольника,
, и значит, периметр равен .
Получаем, что , а средняя линия равна .

Еще раз повторим свойства вписанного и описанного четырехугольника.

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны .

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.

Докажите эти утверждения. Это задание особенно полезно тем, кто решает задачи второй части профильного ЕГЭ по математике.

Разработка урока «Вписанная окружность»

Школа: МОУ «Лицей №1» г. Воркуты.

Учитель: Курылева Светлана Сергеевна

Предмет: Геометрия

Класс: 8 (с углубленным изучением математики).

Тема: Описанные четырехугольники (четвертый урок по теме «Вписанная и описанная окружности»)

Тип урока: урок обучения умениям и навыкам.

Форма урока: комбинированный урок.

Формы работы, используемые на уроке: фронтальная, групповая, индивидуальная.

Методы и приемы, используемые на уроке: словестные, наглядные, поисковые; учет возрастных особенностей, создание ситуации успеха, выбор действия в соответствии с возможностями ученика.

Цели на урок: ввести понятие описанного многоугольника, ознакомить учащихся со свойствами описанного четырехугольника.

Задачи на урок:

• дидактические: изучить определение описанного четырёхугольника, доказать теорему о свойстве сторон описанного четырёхугольника, познакомить с двойственностью свойств сумм противоположных сторон и противоположных углов вписанного и описанного четырёхугольников, дать опыт практического применения рассмотренных теорем при решении задач, провести первичный контроль уровня усвоения нового материала.

• развивающие: развивать познавательный интерес у учащихся, логическое мышление, интеллектуальные способности; формировать математическую речь; развивать умения применять знания в конкретной ситуации; развитие самостоятельной деятельности обучающихся.

• воспитательные: воспитывать у учащихся потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формировать эстетические навыки при оформлении записей в тетради.

Оборудование: компьютеры, мультимедийный проектор, экран, листы на каждого ученика с подбором заданий по теме урока, заданий для индивидуальной работы, таблица «Примеры описанных четырехугольников», компьютерный тест по теме «Вписанные и описанные многоугольники».

Средства обучения: мультимедийная презентация к уроку «Описанные четырехугольники».

Программные средства: Microsoft Word, Microsoft Power Point.

План урока:

1. Организационный момент. (2 мин.)

2. Актуализация знаний. (8 мин.)

3. Изучение нового материала. (11 мин.)

4. Решение задач. (20 мин.)

5. Домашнее задание.(1 мин.)

6. Рефлексия. Итоги урока. (3 мин.)

План – конспект урока по теме «Вписанная окружность»

I.Организационный момент

Проверка готовности учащихся, сообщение темы и цели урока, постановка задач.

II.Актуализация знаний.

1. Математический диктант.

1. Можно ли описать окружность около параллелограмма? Прямоугольника? Ромба? Почему?

2. Может ли вписанный в окружность четырехугольник иметь равные стороны, но неравные углы? Почему?

3. Может ли вписанный в окружность многоугольник иметь равные углы, но неравные стороны? Почему?

4. Можно ли описать окружность около пятиугольника с углами 80⁰, 90⁰, 100⁰, 130⁰, 140⁰? Почему?

5. Какой четырехугольник называется дельтоидом? Перечислите его свойства.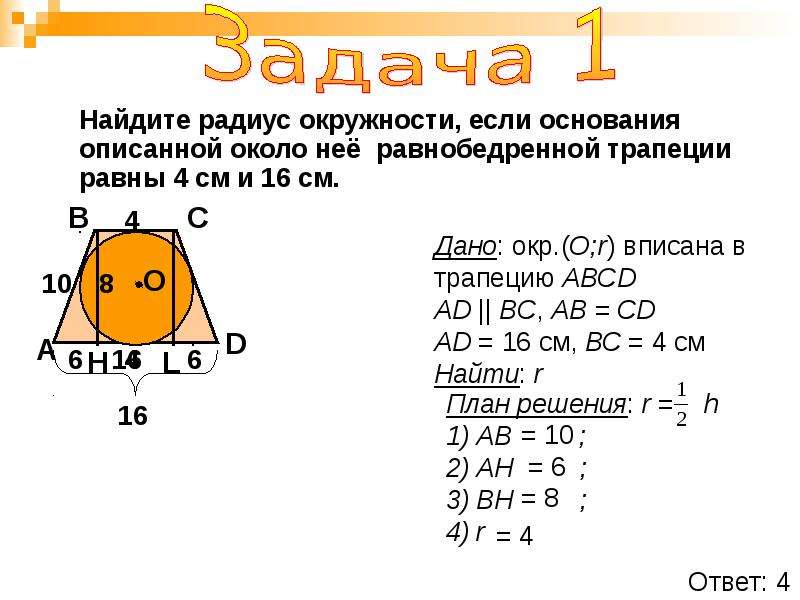

1. Устная работа

• Внимательно рассмотрите рисунки (слайд 2). Как вы думаете, какие многоугольники являются описанными около окружности. Почему вы так решили?

• Как можно назвать стороны этих четырехугольников по отношению к окружности?

• Попробуйте сформулировать определение описанного многоугольника (слайд 3).

III.Учебно-познавательная деятельность.

Перейдем теперь к рассмотрению описанных многоугольников. Ситуация здесь в некотором смысле двойственная по отношению к вписанным многоугольникам. При этом стороны описанного многоугольника двойственны углам вписанного многоугольника. Так, например, если для вписанного четырехугольника необходимым и достаточным условием является равенство сумм противолежащих углов, то для описанного выпуклого четырехугольника необходимым и достаточным условием является равенство сумм противоположных сторон. А именно, имеют место следующие теоремы.

Теорема 1 (свойство сторон описанного четырехугольника)

Суммы противоположных сторон описанного около окружности четырехугольника равны (слайды 4,5 разработала группа наиболее подготовленных учащихся класса в качестве домашней работы к уроку)

Теорема 2 (признак четырехугольника, в который можно вписать окружность)

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (слайд 6 разработала группа наиболее подготовленных учащихся класса в качестве домашней работы к уроку). Учащимся предлагается самостоятельно разобрать доказательство по учебнику (работа с учебником в течение 5 минут, после чего учащиеся могут задавать вопросы по доказательству).

Замечание: в процессе разбора доказательства теорем группа учащихся, самостоятельно разбиравших дома теоремы и готовивших слайды к презентации выполняют индивидуальные задания. Каждому ученику выдаётся карточка с планом исследования . Выполняя задания в соответствии с этим планом, ученики все промежуточные действия и конечные выводы записывают в тетрадях. (Приложение 2)

IV. Решение задач.

1. Устная работа

1. Можно ли вписать окружность в прямоугольник?

2. Можно ли вписать окружность в квадрат?

3. Можно ли вписать окружность в ромб?

4. Можно ли вписать окружность в параллелограмм?

5. В какие ещё четырехугольники можно вписать окружность?

6. При каком условии можно вписать окружность в трапецию?

7. Задачи слайдов 7 – 11.

Раздается таблица «Примеры описанных четырехугольников»

1. Письменная работа (решение задач по готовым чертежам (слайды 12 – 13))

Замечание: дети делятся на две группы: I группа проходит тестирование на компьютере (Приложение 3), другая группа решает задачи совместно с учителем, на тест выделяется по 5 минут, по окончании работы группы меняются местами).

V. Домашнее задание.

Учебник Л.С. Атанасян и др. №696, №697, №698, №700

Геометрия. Дополнительные главы к учебнику: пункт 59 (Теорема Птолемея) разобрать самостоятельно (слайд 14)

Историческая справка (слайд 15)

VI. Итоги урока, рефлексия.

Что нового узнали сегодня на уроке? Чему научились? На какой ступеньке освоения темы вы находитесь? (слайд 16)

Вы все прошли компьютерный тест. Сейчас я предлагаю вам оценить качество работы на уроке. Если вы набрали 9 – 12 баллов – отметка «5»

6 – 8 баллов – отметка «4»

3 – 5 баллов – отметка «3»

Ну а те, кто выполнил менее 3 заданий, сделайте соответствующие выводы, попробуйте установить причину, по которой вы не справились с заданием и устранить её.

Приложение 1. Примеры описанных четырехугольников

Приложение 2. Задания для творческой группы

1. Приведите пример невыпуклого четырехугольника, у которого суммы противоположных сторон равны, и в который нельзя вписать окружность.

2. Исследовательская работа по карточке.

Приложение 3. Тестирование на компьютере

1. Центр описанной около треугольника окружности совпадает с точкой пересечения его:

1. биссектрис

2. серединных перпендикуляров

3. высот

4. медиан

1. Окружность называется вписанной в многоугольник, если:

1. Все его вершины лежат на окружности

2. Все его стороны имеют общие точки с окружностью

3. Все его стороны являются отрезками касательных к окружности

4. Все его стороны касаются окружности

1. В равносторонний треугольник вписана окружность радиуса 4 см. чему равна сторона треугольника?

1. см

2. см

3. см

4. см

1. Четырехугольник АВСD описан около окружности. см, см, ВС в 2 раза меньше АD. Найти длину ВС.

1. 6 см

2. 22 см

3. 12 см

4. 14 см

1. Равнобедренный треугольник с высотой, проведенной к основанию и равной 16 см, вписан в окружность радиуса 10 см. найти площадь этого треугольника.

Площадь треугольника = см²

1. В прямоугольном треугольнике АВС (угол С равен 90⁰) АС+ВС=17 см, радиус вписанной в него окружности равен 2 см. Найдите площадь этого треугольника.

Площадь треугольника = см²

Приложение 4. Задачи для классной работы

1. Равнобокая трапеция с основаниями а и b ( )описана около окружности. Найти радиус окружности и косинус угла при большем основании.

2. Около окружности описан четырехугольник ABCD , в котором , , АВ = 2, АD = 3. Найти периметр четырехугольника.

Радиус вписанной окружности в ромб

Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:

• Диагонали ромба взаимно перпендикулярны.
• Диагонали ромба являются биссектрисами его внутренних углов.

Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами

1 способ. Радиуса вписанной окружности в ромб через высоту

Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.

Следовательно формула радиуса вписанной окружности в ромб через высоту:

2 способ. Радиус вписанной окружности в ромб через диагонали

Площадь ромба можно выразить через радиус вписанной окружности
, где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда
Но площадь ромба  также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали

Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Найти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD-ромб, тогда AC и BD его диагонали. AC=30 см, BD=40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.

т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный. Тогда по теореме Пифагора
, подставляем в формулу ранее полученные значения

AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем

3 способ. Радиус вписанной окружности в ромб через отрезки m и n

Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.

Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности

Пример расчета радиуса окружности вписанной в ромб, если известны отрезки m и n
Найдите радиус описанной окружности в ромб, если точка касания делит сторону ромба на 9 и 4
Пусть ABCD-ромб, тогда AC и BD его диагонали.
Пусть точка O – это центр вписанной в ромб ABCD окружности.
Пусть точка F – точка касания окружности со стороной ромбаAB. Тогда. AF=9, BF=4
Применив ранее полученную формулу, получаем

Комбинация шара с другими телами

1.

Комбинация шара с другими телами

2. Определения.

• 1. Шар называется вписанным в
многогранник, а многогранник описанным
около шара, если поверхность шара касается
всех граней многогранника.
• 2. Шар называется описанным около
многогранника, а многогранник вписанным в
шар, если поверхность шара проходит через
все вершины многогранника.

3. Определения.

• 3. Шар называется вписанным в цилиндр,
усеченный конус (конус), а цилиндр, усеченный
конус (конус) – описанным около шара, если
поверхность шара касается оснований
(основания) и всех образующих цилиндра,
усеченного конуса (конуса).
• (Из этого определения следует, что в любое
осевое сечение этих тел может быть вписана
окружность большого круга шара).
• 4. Шар называется описанным около цилиндра,
усеченного конуса (конуса), если окружности
оснований (окружность основания и вершина)
принадлежат поверхности шара.
• (Из этого определения следует, что около любого
осевого сечения этих тел может быть описана
окружность большего круга шара).

4. Общие замечания о положении центра шара.

• 1. Центр шара, вписанного в многогранник,
лежит в точке пересечения биссекторных
плоскостей всех двугранных углов
многогранника. Он расположен только внутри
многогранника.
• 2. Центр шара, описанного около
многогранника, лежит в точке пересечения
плоскостей, перпендикулярных ко всем
ребрам многогранника и проходящих через их
середины. Он может быть расположен
внутри, на поверхности и вне многогранника.

5. Комбинация шара с призмой

1. Шар, вписанный в прямую призму.
• Теорема 1. Шар можно вписать в прямую призму в
том и только в том случае, если в основание призмы
можно вписать окружность, а высота призмы равна
диаметру этой окружности.
• Следствие 1. Центр шара, вписанного в прямую
призму, лежит в середине высоты призмы,
проходящей через центр окружности, вписанной в
основание.
• Следствие 2. Шар, в частности, можно вписать в
прямые: треугольную, правильную, четырехугольную
(у которой суммы противоположных сторон
основания равны между собой) при условии Н = 2r,
где Н – высота призмы, r – радиус круга, вписанного в
основание.

6. 2. Шар, описанный около призмы.

• Теорема 2. Шар можно описать около призмы в том и
только в том случае, если призма прямая и около ее
основания можно описать окружность.
• Следствие 1. Центр шара, описанного около прямой
призмы, лежит на середине высоты призмы,
проведенной через центр круга, описанного около
основания.
• Следствие 2. Шар, в частности, можно описать:
около прямой треугольной призмы, около правильной
призмы, около прямоугольного параллелепипеда,
около прямой четырехугольной призмы, у которой
сумма противоположных углов основания равна 180
градусов.
№ 632, 633, 634, 637(а), 639(а,б).
Комбинация шара с пирамидой
1. Шар, описанный около пирамиды.
• Теорема 3. Около пирамиды можно описать
шар в том и только в том случае, если около
ее основания можно описать окружность.
• Следствие 1. Центр шара, описанного около
пирамиды лежит в точке пересечения
прямой, перпендикулярной основанию
пирамиды, проходящей через центр
окружности, описанной около этого
основания, и плоскости, перпендикулярной
любому боковому ребру, проведенной через
сере дину этого ребра.
• Следствие 2. Если боковые ребра
пирамиды равны между собой (или равно
наклонены к плоскости основания), то около
такой пирамиды можно описать шар.Центр
этого шара в этом случае лежит в точке
пересечения высоты пирамиды (или ее
продолжения) с осью симметрии бокового
ребра, лежащей в плоскости бокового ребра
и высоты.
• Следствие 3. Шар, в частности, можно
описать: около треугольной пирамиды, около
правильной пирамиды, около
четырехугольной пирамиды, у которой сумма
противоположных углов равна 180 градусов.

9. 2. Шар, вписанный в пирамиду.

• Теорема 4. Если боковые грани пирамиды одинаково
наклонены к основанию, то в такую пирамиду можно
вписать шар.
• Следствие 1. Центр шара, вписанного в пирамиду, у
которой боковые грани одинаково наклонены к
основанию, лежит в точке пересечения высоты
пирамиды с биссектрисой линейного угла любого
двугранного угла при основании пирамиды, стороной
которого служит высота боковой грани, проведенная
из вершины пирамиды.
• Следствие 2. В правильную пирамиду можно
вписать шар.
№ 635, 637(б), 638, 639(в),640, 641.

10. Комбинация шара с усеченной пирамидой.

• 1. Шар, описанный около правильной
усеченной пирамиды.
• Теорема 5. Около любой правильной
усеченной пирамиды можно описать шар.
(Это условие является достаточным, но не
является необходимым)
• 2. Шар, вписанный в правильную
усеченную пирамиду.
• Теорема 6. В правильную усеченную
пирамиду можно вписать шар в том и только
в том случае, если апофема пирамиды равна
сумме апофем оснований.
(№ 636).

11. Комбинация шара с круглыми телами.

• Теорема 7. Около цилиндра, усеченного
конуса (прямых круговых), конуса можно
описать шар.
• Теорема 8. В цилиндр (прямой круговой)
можно вписать шар в том и только в том
случае, если цилиндр равносторонний.
• Теорема 9. В любой конус (прямой круговой)
можно вписать шар.
• Теорема 10. В усеченный конус (прямой
круговой) можно вписать шар в том и только в
том случае, если его образующая равна
сумме радиусов оснований.
№ 642, 643, 644, 645, 646.

12. Устные задачи.

1. (r = a/2, R = a3).
2. (а) да; б) да; в) нет; г) нет; д) нет)
3. да
4. (Нет, не около любой
четырёхугольной пирамиды)
• 1. Ребро куба равно а. Найти радиусы шаров:
вписанного в куб и описанного около него.
• 2. Можно ли описать сферу (шар) около: а) куба; б)
прямоугольного параллелепипеда; в) наклонного
параллелепипеда, в основании которого лежит
прямоугольник; г) прямого параллелепипеда; д)
наклонного параллелепипеда?
• 3. Справедливо ли утверждение, что около любой
треугольной пирамиды можно описать сферу?
• 4. Можно ли описать сферу около любой
четырехугольной пирамиды?
5. (В её основании
должен лежать многоугольник,
около которого можно описать
окружность)
• 5. Какими
свойствами должна
обладать пирамида,
чтобы около нее
можно было описать 6. Центр сферы – точка пересечения
двух геометрических мест точек
сферу?
в пространстве. Первое – перпендикуляр,
проведённый к плоскости основания
• 6. В сферу вписана пирамиды, через центр окружности,
пирамида, боковое описанной около него.
Второе – плоскость перпендикулярная
ребро которой
данному боковому ребру и проведённая
через его середину)
перпендикулярно
основанию. Как
найти центр сферы?
• 7. При каких
7. Во-первых, призма должна быть прямой,
условиях можно
и, во-вторых, трапеция должна быть
описать сферу около равнобедренной, чтобы около неё
призмы, в основании
которой – трапеция? можно было описать окружность)
• 8. Каким условиям
8. Призма должна быть прямой,
должна
и её основанием должен являться
удовлетворять
многоугольник, около которого можно
призма, чтобы около
описать окружность
нее можно было
описать сферу?
9. (Тупоугольный треугольник)
• 9. Около треугольной
призмы описана
сфера, центр которой
10. нельзя
лежит вне призмы.
Какой треугольник
является основанием
призмы?
• 10. Можно ли описать
сферу около
наклонной призмы?

11. При каком условии центр
сферы, описанной около
11. В основании лежит
прямой треугольной призмы,
прямоугольный треугольник
будет находится на одной из
боковых граней призмы?
12. Да, можно. То что ортогональная
12. Основание пирамиды –
проекция вершины пирамиды
равнобедренная трапеция
.Ортогональная проекция
расположена вне её основания,
вершины пирамиды на
не имеет значения. Важно, что
плоскость основания – точка,
в основании пирамиды лежит
расположенная вне трапеции.
Можно ли около такой трапеции равнобедренная трапеция –
описать сферу?
многоугольник, около которого
13. Около правильной
можно описать окружность
пирамиды описана сфера. Как
расположен ее центр
13. (Центр сферы находится на
относительно элементов
перпендикуляре, проведенном к
пирамиды?
плоскости основания через его центр
14. При каком условии центр
сферы, описанной около
прямой треугольной призмы,
14. В основании призмы:
лежит: а) внутри призмы; б) вне
а) остроугольный треугольник;
призмы?
б) тупоугольный треугольник)
• 15. Около прямоугольного
параллелепипеда, ребра
которого равны 1 дм, 2 дм и
2 дм, описана сфера.
Вычислите радиус сферы.
• 16. В какой усеченный конус
можно вписать сферу?
• 17. В усеченный конус
вписана сфера. Под каким
углом образующая конуса
видна из центра сферы?
• 18. Каким свойством должна
обладать прямая призма,
чтобы в нее можно было
вписать сферу?
15. 1,5 дм
16. В усечённый конус,
в осевое сечение которого
можно вписать окружность.
Осевым сечением конуса
является равнобедренная
трапеция, сумма её
оснований должна
равняться сумме её боковых
сторон. Другими словами,
у конуса сумма радиусов
оснований должна
равняться образующей
17. 90 градусов
18. Во-первых, в
основании прямой призмы
должен лежать
многоугольник, в который
можно вписать
окружность, и, во-вторых,
высота призмы должна
равняться диаметру
вписанной в основание
окружности
• 19. Приведите пример
пирамиды, в которую
нельзя вписать сферу?
• 20. В основании прямой
призмы лежит ромб.
Можно ли в эту призму
вписать сферу?
• 21. При каком условии в
прямую треугольную
призму можно вписать
сферу?
• 22. При каком условии в
правильную
четырехугольную
усеченную пирамиду
можно вписать сферу?
19. Например, четырёху
гольная пирамида,
в основании которой
лежит прямоугольник или
параллелограмм)
20. Нет, нельзя, так как около
ромба в общем случае
нельзя описать окружность)
21. Если высота призмы в два
раза больше радиуса окружности,
вписанной в основание
22. Если сечением данной
пирамиды плоскостью,
проходящей через середину
стороны основания
перпендикулярно ей,
является равнобедренная
трапеция, в которую можно
вписать окружность
• 23. В треугольную усеченную
пирамиду вписана сфера.
Какая точка пирамиды
является центром сферы?
• 24. Можно ли описать сферу
около цилиндра (прямого
кругового)?
• 25. Можно ли описать сферу
около конуса, усеченного
конуса (прямых круговых)?
• 26. Во всякий ли цилиндр
можно вписать сферу?
Какими свойствами должен
обладать цилиндр, чтобы в
него можно было вписать
сферу?
• 27. Во всякий ли конус можно
вписать сферу? Как
определить положение
центра сферы, вписанной в
конус?
23. Центр вписанной в данную
пирамиду сферы находится
на пересечении трёх
биссектральных плоскостей углов,
образованных боковыми гранями
пирамиды с основанием
24. Да, можно
25. Да, можно, в обоих случаях
26. Нет, не во всякий:
осевое сечение цилиндра
должно быть квадратом
27. Да, во всякий.
Центр вписанной сферы
находится на пересечении
высоты конуса и биссектрисы
угла наклона образующей
к плоскости основания

Вариант 1.
1. Если сфера касается всех граней многогранника, то она называется…
а) описанной около многогранника;
б) вписанной в многогранник;
в) касательной к многограннику.
2. Все вершины многогранника лежат на сфере, такой многогранник
называется…
а) вписанным в сферу;
б) описанным около сферы;
в) касательным к сфере.
3. Шар можно вписать в …
а) произвольную призму;
б) треугольную пирамиду;
в) треугольную призму.
4. В прямую призму, в основание которой вписана окружность, можно
вписать сферу, если…
а) высота призмы равна диаметру вписанной окружности;
б) центр сферы лежит на высоте призмы;
в) высота призмы равна радиусу вписанной окружности.
5. Во всякий цилиндр можно вписать сферу, если…
а) если центр сферы лежит на оси цилиндра;
б) сфера касается оснований цилиндра:
в) его осевое сечение-квадрат.

Вариант 2.
1. Если на сфере лежат все вершины многогранника, то она называется…
а) описанной около многогранника;
б) вписанной в многогранник;
в) касательной к многограннику.
2. Если каждая грань многогранника является касательной плоскостью к
сфере, то такой многогранник называется…
а) вписанным в сферу;
б) описанным около сферы;
в) касательным к сфере.
3. Шар можно описать около …
а) любой призмы;
б) любой правильной пирамиды;
в) наклонной призмы.
4. В прямую призму, вписана сфера, около призмы еще описана сфера,
центры этих сфер…
а) лежат на разных диагоналях призмы;
б) принадлежат высоте призмы и не совпадают;
в) совпадают.
5. Около любого цилиндр можно описать сферу. Основания цилиндра
являются…
а) касательными плоскостями к сфере;
б) большим кругом сферы. :
в) сечениями сферы..
• Ключ к тесту.
• Вариант 1
бабав
• Вариант 2
аббвв

Презентация на тему: ВПИСАННЫЕ И О ПИСАНН Ы Е
МНОГОУГОЛЬНИКИ
Геометрия, 8 класс.
Учитель
Донецкого

1

Первый слайд презентации

ВПИСАННЫЕ И О ПИСАНН Ы Е
МНОГОУГОЛЬНИКИ
Геометрия, 8 класс.
Учитель
Донецкого УВК № 78
ПЕРЕКРЕСТ И.А.

Изображение слайда

2

Слайд 2

ВПИСАННЫЙ МНОГОУГОЛЬНИК –
ОПИСАННАЯ ОКРУЖНОСТЬ –
Определение
Вписанным в окружность называется многоугольник, все вершины которого лежат на окружности.
Окружность в этом случае называется описанной
1. Какие фигуры «лишние», не соответствуют определению?
а)
б)
в)
г)
д )
е)
ж)
з )

Изображение слайда

3

Слайд 3

ПОВТОРИМ И ОБОБЩИМ ИЗУЧЕННОЕ РАНЕЕ
ВПИСАННЫЙ ТРЕУГОЛЬНИК
1. Любой Δ можно вписать в окружность? (да)
2. Где лежит центр описанной около Δ окружности?
( центр – точка пересечения
серединных перпендикуляров ОК, ОЕ, ОМ )
Радиусы : R = ОА = ОМ = ОЕ
3. Когда центр окружности,
описанной около Δ,
— лежит вне Δ ?
( если Δ тупоугольный)
— лежит внутри Δ ?
( если Δ остроугольный)
4. Центр окружности, описанной
около прямоугольного Δ, –
середина гипотенузы с и
А
В
С
О
К
Е
М
R
R
R
R = ½ с

Изображение слайда

4

Слайд 4

ВПИСАННЫЙ ЧЕТЫРЁХУГОЛЬНИК
1.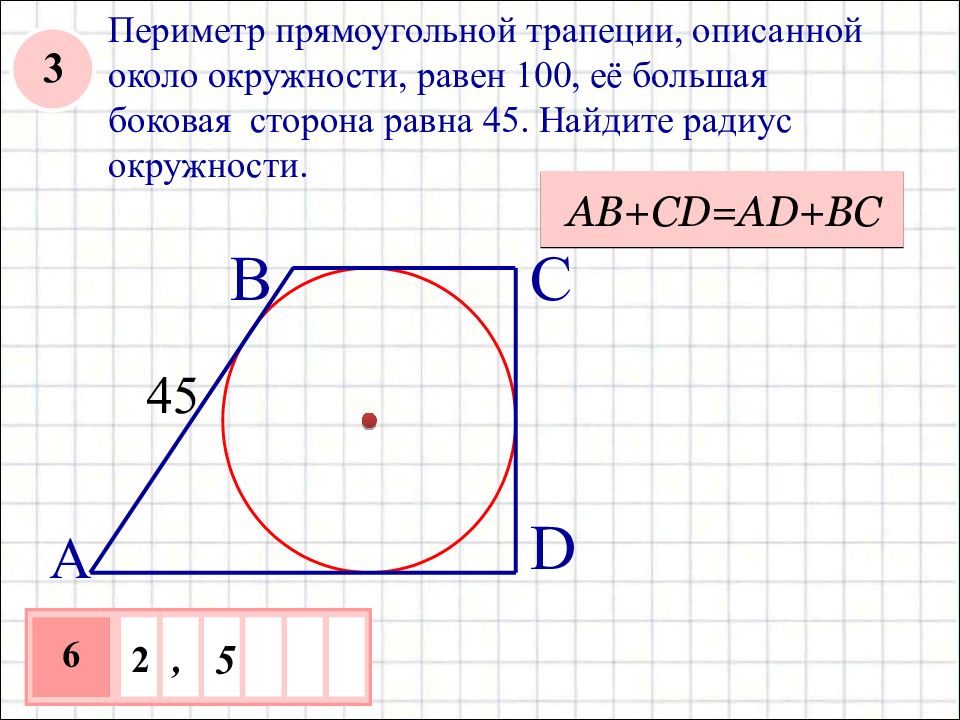 Около любого четырёхугольника можно описать окружность? (нет)
2. Когда можно описать окружность около четырёхугольника?
(тогда и только тогда, когда суммы его
противоположных углов равны 180˚,
т.е. А + С = 180˚, В +  D = 180˚)
3. Окружность можно описать около:
— квадрата ( центр – точка пересечения диагоналей,
диаметр – диагональ)
— прямоугольника ( центр – точка пересечения диагоналей,
диаметр – диагональ)
— равнобокой трапеции
А
В
С
D

Изображение слайда

5

Слайд 5

ОПИСАННЫЙ МНОГОУГОЛЬНИК –
ВПИСАННАЯ ОКРУЖНОСТЬ –
Определение
Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.
Окружность в этом случае называется вписанной
1. Какие фигуры «лишние», не соответствуют определению?
е)
д )
г)
в)
б)
а)

Изображение слайда

6

Слайд 6

ОПИСАННЫЙ ТРЕУГОЛЬНИК
1. В любой Δ можно вписать окружность? (да)
2. Где лежит центр вписанной в Δ
окружности?
( центр – точка пересечения
биссектрис углов Δ : AO, CO, BO )
Радиусы : r = О F = О D = ОЕ
OF  AC, OE  CB, OD  AB,
3. Радиус окружности, вписанной в прямоугольный Δ, равен:
а
b
c

Изображение слайда

7

Слайд 7

ОПИСАННЫЙ ЧЕТЫРЁХУГОЛЬНИК
В любой четырёхугольник можно вписать окружность ?
(нет)
Когда можно вписать окружность в четырёхугольник ?
(тогда и только тогда, когда суммы его
противоположных сторон равны, т. е.
AB + CD = BC + AD
Окружность можно вписать в:
— квадрат ( центр – точка пересечения диагоналей,
диаметр равен стороне квадрата)
— ромб ( центр – точка пересечения диагоналей,
диаметр равен высоте ромба)
— некоторые трапеции

Изображение слайда

8

Слайд 8

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
В любой правильный многоугольник можно вписать окружность и описать окружность около него.
Центры этих окружностей совпадают
Определение
Центральным называется угол,
под которым видно сторону
многоугольника из центра
описанной окружности – α
В правильном многоугольнике
α
α =
˚

Изображение слайда

9

Слайд 9

РЕШИТЬ ЗАДАЧИ
Найти радиус окружности,вписанной в квадрат
со стороной 4см.
1)
Найти сторону квадрата, описанного около окружности
радиуса 3.
2)
[ ОТВЕТЫ. 1) 2см; 2) 6; 3) 10; 4) 4,5см; 5) 13м; 6) 20см ]
4)
3)
Найти высоту трапеции, в которую вписана
окружность радиуса 5.
Около окружности описана трапеция, периметр
которой равен 18 см. Найти её среднюю линию.
5)
Окружность, вписанная в равнобедренный треугольник,
делит в точке касания одну из боковых сторон на
два отрезка, которые равны 4 см и 3 см, считая
от вершины. Найдите периметр треугольника.
В трапецию вписана окружность.Три последовательные стороны трапеции равны 6м; 5м; 12м. Найти периметр трапеции.
6)

Изображение слайда

10

Слайд 10

ИТОГ УРОКА
ПРОВЕРЬ СВОИ ЗНАНИЯ
1. Дать определение вписанного многоугольника.
Дать определение описанного многоугольник
ТРЕУГОЛЬНИКИ
Какая точка является центром описанной около Δ окружности?
4. Центр окружности, описанной около остроугольного Δ, лежит …
Центр окружности, описанной около прямоугольного Δ, лежит…
Формула : R = …
Центр окружности, описанной около тупоугольного Δ, лежит…
7. Какая точка является центром вписанной в Δ окружности ?
8. Формула для радиуса вписанной в прямоугольный Δ
окружности: r = …
9*. Какой вид имеет Δ,если:
а)центры вписанной в Δ и описанной около Δ окружностей совпадают?
б)центры вписанной в Δ и описанной около Δ окружностей, лежат на
одной из его высот?

Изображение слайда

11

Последний слайд презентации: ВПИСАННЫЕ И О ПИСАНН Ы Е
МНОГОУГОЛЬНИКИ
Геометрия, 8 класс.

Учитель
Донецкого

ЧЕТЫРЁХУГОЛЬНИКИ
10. В какой четырёхугольник можно вписать окружность?
11. Можно ли вписать окружность в ромб? квадрат? параллелограмм?
прямоугольник? трапецию?
12. При каком условии около четырёхугольника можно описать
окружность? (Записать формулы)
13. Можно ли описать окружность около ромба? квадрата?
параллелограмма? прямоугольника? трапеции?
14. В какой многоугольник всегда можно вписать окружность и можно
описать около него окружность?
Что можно сказать о центрах вписанной и описанной
окружностей в этом случае?
15. Какой угол называется центральным? ( записать формулу для
нахождения центрального угла правильного многоугольника)
МНОГОУГОЛЬНИКИ

Изображение слайда

Методическая разработка факультативного занятия в IX классе по теме «Вписанные и описанные четырёхугольники»

Планиметрия: комбинации фигур.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника

Подробнее

41 прототип задания 18

41 прототип задания 18 Задача демо-версии: Найдите площадь трапеции, изображённой на рисунке. 1. Задание 18 ( 27582) Найдите площадь квадрата, если его диагональ равна 1. 2. Задание 18 ( 27614) Найдите

Подробнее

Урок по теме «Сфера и шар»

Акчурина Е.В. Урок по теме «Сфера и шар» Тема: Сфера и шар Цели и задачи урока: Обучающие: — ввести понятие сферы, шара и полушара; — рассмотреть сечения шара плоскостью; — ввести понятие касательной прямой

Подробнее

ID_5162 1/9 neznaika.

pro

1 Площади фигур Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Сумма двух углов равнобедренной

Подробнее

В 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.

В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,

Подробнее

Тема: «Прямоугольник. Ромб. Квадрат».

Тема: «Прямоугольник. Ромб. Квадрат». Цели: Систематизировать и обобщить знания учащихся по изучаемой теме; совершенствовать навыки решения задач. Развивать умение наблюдать, сравнивать, обобщать, классифицировать,

Подробнее

ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК.

1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.

ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике

Подробнее

ОКРУЖНОСТИ И ЧЕТЫРЁХУГОЛЬНИКИ

ОКРУЖНОСТИ И ЧЕТЫРЁХУГОЛЬНИКИ wwwfmclssru Задача В параллелограмм можно вписать окружность Найдите ее радиус, если известно, что радиус окружности, описанной около него, равен Задача Диагонали ромба равны

Подробнее

tgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.

В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,

Подробнее

Прототипы задания В6-2 (2013)

Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний

Подробнее

Все прототипы заданий В3

1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,

Подробнее

Подготовка к ЕГЭ по математике

2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege. САМОСТОЯТЕЛЬНАЯ РАБОТА 1 ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА ариант 1 Найдите площадь прямоугольника, стороны которого равны 3 и 4. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами

Подробнее

«Цилиндр. Площадь поверхности цилиндра»

Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 49 Петродворцового района Санкт-Петербурга имени Героя Российской Федерации М.Ю. Малофеева Методическая разработка

Подробнее

7 sin A. Найдите AB. 25

Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,

Подробнее

ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ

ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.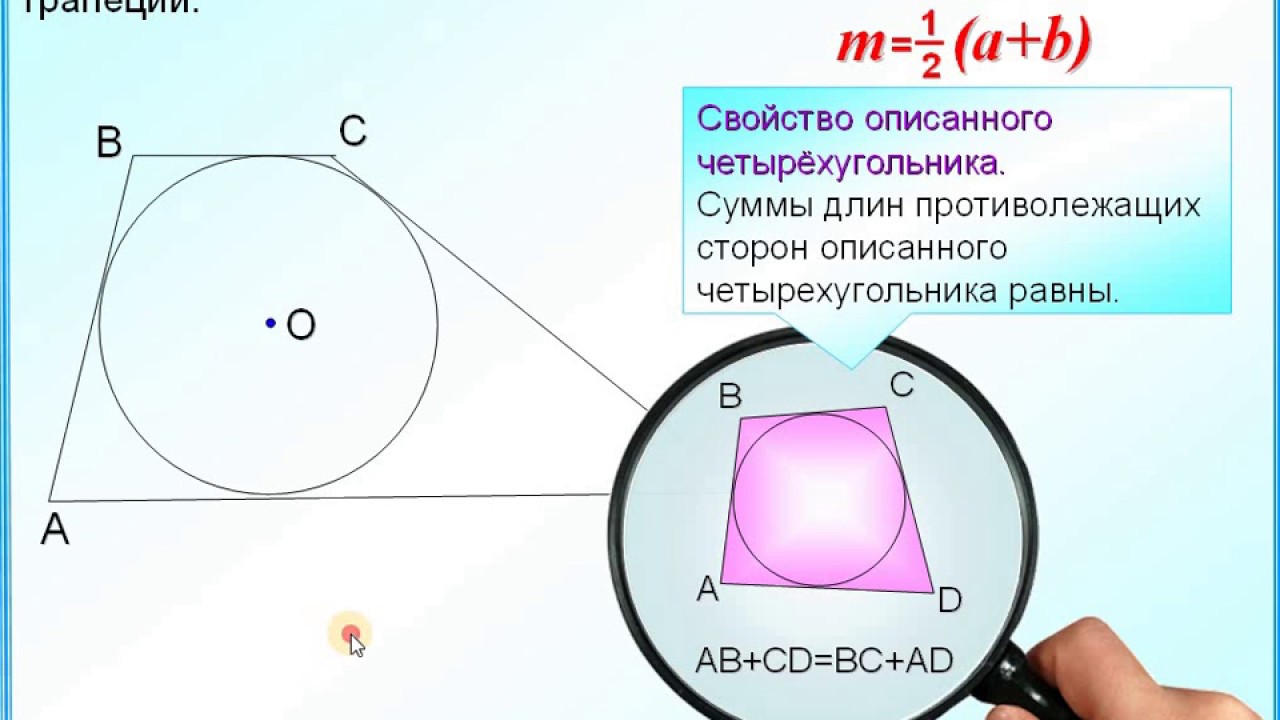 01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший

Подробнее

ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)

ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через

Подробнее

ЗАДАНИЕ 15 Планиметрия Треугольник

ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками

Подробнее

Урок по теме «Прямой круговой цилиндр»

Акчурина Е.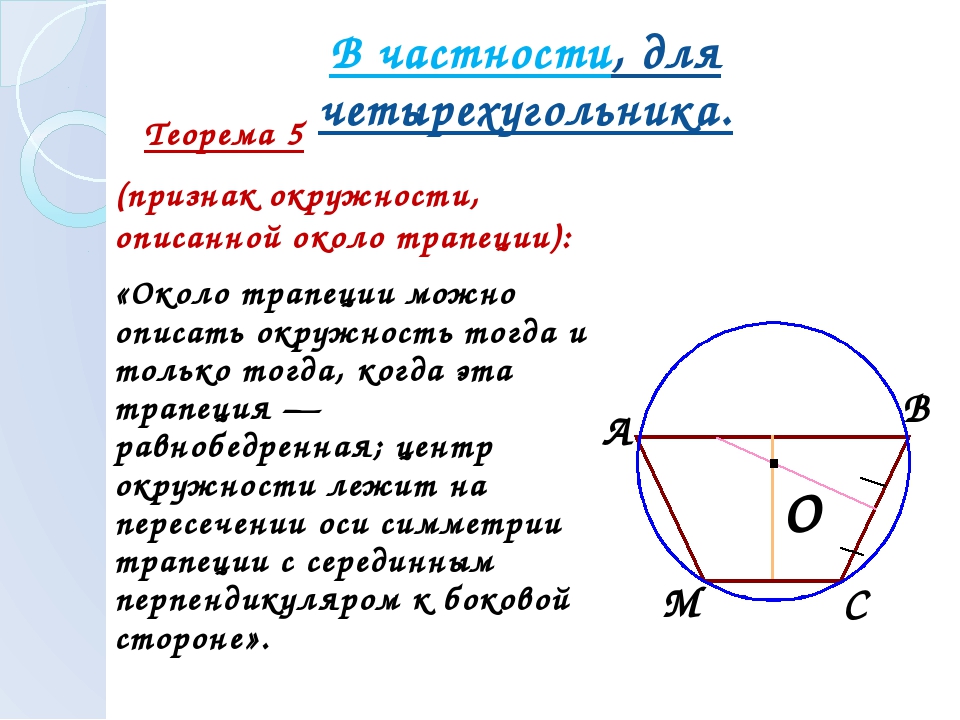 В. Урок по теме «Прямой круговой цилиндр» Тема: Прямой круговой цилиндр Цели и задачи урока: Обучающие: — ввести понятие цилиндра; — ввести понятие прямого кругового цилиндра и его элементов

Подробнее

В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ

В.А. Смирнов ГЕОМЕТРИЯ ПЛОЩАДЬ 2011 ВВЕДЕНИЕ Выработка умений находить площади фигур на плоскости относится к основным целям обучения геометрии в школе. Задачи на нахождение площадей входят в содержание

Подробнее

Технологическая карта урока

Технологическая карта урока Тема урока: «Прямоугольник» Класс: 5 Учитель: Рыжова Лидия Петровна Тип урока: урок «открытия» нового знания Цели по содержанию: обучающие: изучить свойства прямоугольника развивающие:

Подробнее

AC 6, cos A. Найдите BH.

Прототипы задания 6 1.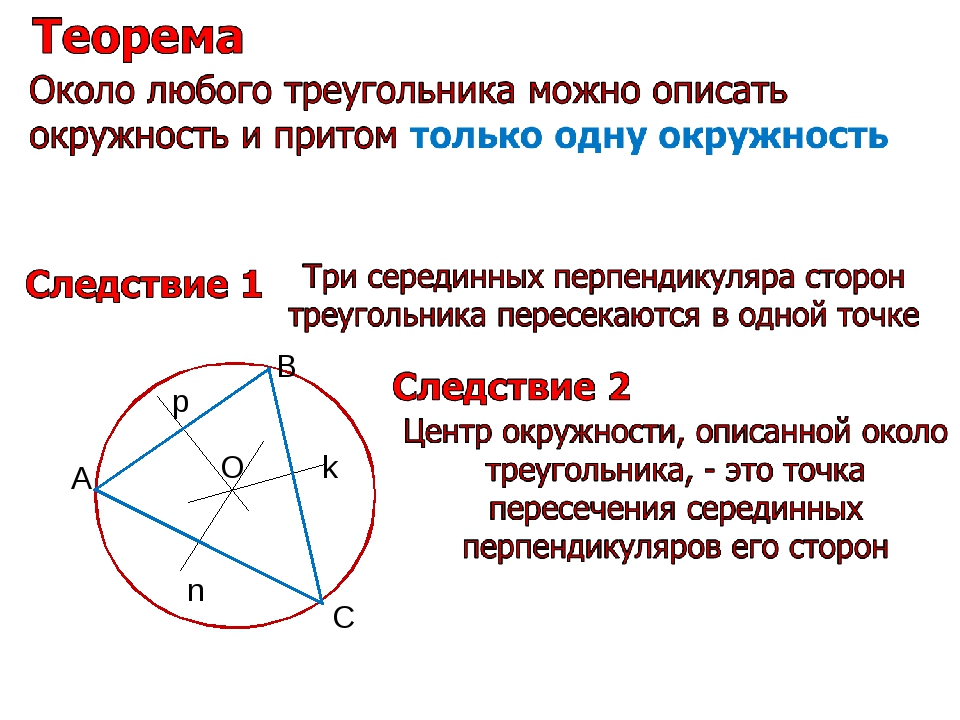 Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите

Подробнее

В.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ

В.А. СМИРНОВ ГЕОМЕТРИЯ ИЗОБРАЖЕНИЯ Москва 2011 ВВЕДЕНИЕ Одной из важных целей обучения геометрии в школе является развитие конструктивных умений учащихся, включающих в себя умения изображать различные

Подробнее

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.

Подробнее

Все прототипы заданий В года

1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB.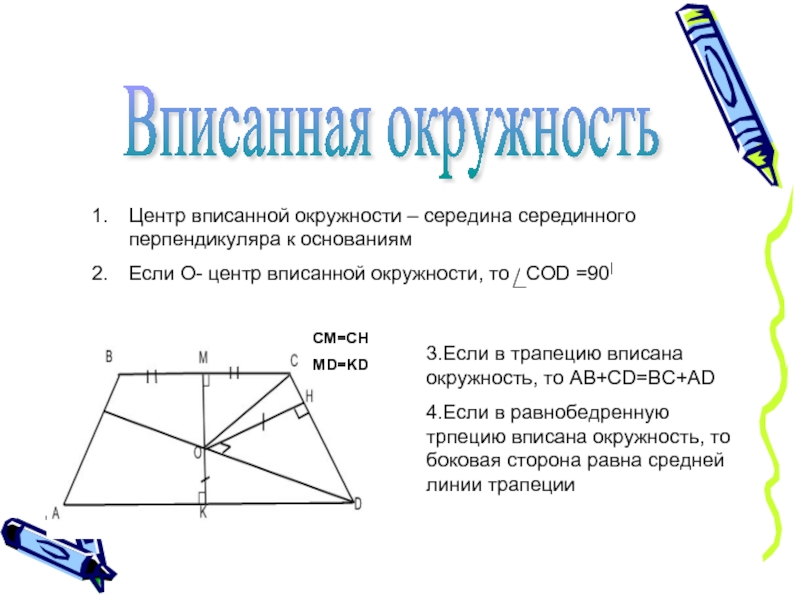 Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,

Подробнее

Повышение качества знаний.

Повышение качества знаний. Открытый урок по геометрии в 8 классе Тема урока: Прямоугольник. Ромб. Квадрат. Автор: Напцок Сулиет Чемальевна, учитель математики, МБОУ СШ 5, п.яблоновский Цель: сформировать

Подробнее

! Черный ящик Тест-прогноз

Длина окружности и площадь круга Цели: 1. Обобщить и систематизировать материал по данной теме. 2. Провести диагностику усвоения системы знаний и умений и ее применения для выполнения практических заданий

Подробнее

Технологическая карта урока

Технологическая карта урока Класс: 8 Предмет: алгебра Тема урока: Погрешность и точность измерения. Дидактическая цель урока: создать условия для восприятия и осознания понятий абсолютная и относительная

Подробнее

Вписанные и описанные окружности

Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.

Подробнее

Технологическая карта урока

Технологическая карта урока Тема урока: «Описание помещения по личным впечатлениям в сочинении повествовательного характера». Класс: 6 Учитель: Филиппова И.С. Тип урока: урок развития речи Цели по содержанию:

Подробнее

Геометрия

Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна

Подробнее

Задания В6. . Найдите AB.

Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.

Подробнее

Тема №6149 Ответы к задачам по математике 5926 (Часть 4)

Тема №6149

Ответы в самом низу встроенного документа

10.3.18. [МАХИ] Медиана прямоугольного треугольника, проведенная
к гипотенузе, разбивает его на два треугольника с периметрами pi и р2 —
Найти стороны треугольника.
10.3.19. [МАХИ] Точка пересечения медиан прямоугольного треуголь­
ника удалена от катетов на расстояния соответственно 3 и 4. Найти
расстояние от этой точки до гипотенузы.
10.3.20. [РЭА] Длина одного из катетов прямоугольного треугольника
равна 12. Расстояние от центра описанной около треугольника окруж­
ности до этого катета равно 2,5. Найти длину гипотенузы треугольника.
10.3.21. [МЭИ] Длины катетов прямоугольного треугольника равны 20
и 21. Найти длину окружности, описанной около данного треугольника.
10.3.22. [МАДИ] В прямоугольном треугольнике АВС даны: длина Q
катета ВС, равная 36, и косинус угла ВАС, равный Найти длину
другого катета АС и площадь треугольника.
10.3.23. [МАХИ] В прямоугольном треугольнике АВС с гипотенузой
АВ проведена полуокружность радиусом 2, центр которой лежит на сто­
роне АС и которая касается сторон АВ и ВС. Полуокружность радиусом
1 касается этой полуокружности и стороны АВ, а центр ее также лежит
на стороне АС. Найти длины сторон треугольника.
10.3.24. [МИЭХ] В прямоугольный треугольник с катетами а и & вписан
квадрат, имеющий с треугольником общий прямой угол. Найти периметр
квадрата.
10.3.25. [РГТГУ] Катеты прямоугольного треугольника равны а и 2а.
Середина катета 2а служит центром окружности с радиусом, равным а.
На какие отрезки делится этой окружностью гипотенуза треугольника?
10.3.26. [МПГУ] Найти радиус окружности, вписанной в треугольник
АВС с прямым углом С, если LB — 30°, ВС — 6 см.
10.3.27. [МПГУ] Найти радиус окружности, вписанной в прямоуголь­
ный треугольник с катетами 6 см и 8 см.
10.3.28. [КПП] В прямоугольном треугольнике сумма катетов равна
17 см, а длина гипотенузы — 13 см. Найти катеты и площадь треуголь­
ника.
10.3.29. [МПГУ] В прямоугольном треугольнике катет равен 24см, а
гипотенуза — 25 см. Найти биссектрису треугольника, проведенную из
вершины меньшего угла.
10.3.30. [МПГУ] Гипотенуза прямоугольного треугольника равна 5, а
высота, проведенная к ней, равна 2. Найти радиусы вписанной и описан­
ной окружностей.
221
10.3.31. [МАТИ] В прямоугольном треугольнике отношение высоты к
О
медиане, проведенным из вершины прямого угла, равно Найти острые
у г л ы треу голь \ i ика.
10.3.32. [МТУСИ] В прямоугольном треугольнике отношение катетов
равно тр Найти тангенс острого утла между медианами, проведенными
к катетам.
10.3.33. [МТУСИ] Найти синус большего острого угла прямоугольного
треугольника, если радиус окружности, описанной около треугольника,
в 2,5 раза больше радиуса вписанной окружности.
10.3.34. [МТУСИ] В прямоугольном треугольнике АВС длины катетов
АС и ВС соответственно равны 12 и 8. Точка К — середина медианы
BD. Найти длину отрезка СК.
О
10.3.35. [ГАНГ] Окружность, радиус которой касается гипотенузы
равнобедренного прямоугольного треугольника в вершине его острого
угла и проходит через вершину прямого угла. Найти длину дуги, за­
ключенной внутри треугольника.
10.3.36. [МГУЛ] В прямоугольном треугольнике медианы острых углов
равны \/89 и \/l56. Найти длину гипотенузы.
10.3.37. [ГАУ] Найти катеты прямоугольного треугольника, у которого
высота, опущенная на гипотенузу, делит ее на отрезки длиной 6 и 18.
10.3.38. [ГАУ] Окружность касается одного из катетов равнобедренного
прямоугольного треугольника и проходит через вершину противополож­
ного острого угла. Центр окружности лежит на гипотенузе треугольни­
ка, длина которой равна с. Найти радиус окружности.
10.3.39. [ГАУ] В прямоугольном треугольнике АВС с прямым углом
В биссектриса угла А пересекает сторону ВС в точке D. Известно, что
BD “ 4, DC — 6. Определить площадь треугольника ADC.
10.3.40. [МИСиС] В прямоугольном треугольнике высота, опущенная
из вершины прямого угла, делит гипотенузу на отрезки длиной 9 и 16.
Найти радиус вписанной в треугольник окружности.
10.3.41. [ГАУ] Катеты прямоугольного треугольника равны 15 и 20.
Найти расстояние от высоты, опущенной из вершины прямого угла до
центра вписанной окружности.
10.3.42. [МГУ, хим. ф-т] Прямоугольные треугольники АВС и ABD
имеют общую гипотенузу АВ — 5. Точки С и D расположены но разные
стороны от прямой, проходящей через точки А и В, ВС — ВО — 3.
Точка Е лежит на А С , ЕС = 1, Точка F лежит на AD, FD = 2. Найти
площадь пятиугольника ECBDF.
2‘п
10.3.43. [МГУ, геогр. ф-т] Вне прямоугольного треугольника А В С на его
катетах АС и ВС построены квадраты AC D E и BCFG. Продолжение
медианы С М треугольника А В С пересекает прямую D F в точке N .
Найти длину CN, если длины катетов равны 1 и 4.
10.3.44. [МГУ, физ. ф-т] В прямоугольном треугольнике отношение ра­
диуса вписанной окружности к радиусу описанной окружности равно jr.
Найти острые углы треугольника.
10.3.45. [МГУ, ИСАА] Окружность, центр которой лежит на гипотенузе
А В прямоугольного треугольника АВС , касается катетов АС и В С со­
ответственно в точках Е и D. Найти величину угла АВС , если известно,
что А Е = 1, BD = 3.
10.3.46. [МГУ, ИСАА] В треугольнике А В С проведена биссектриса
CD прямого угла АС В , D M и D N являются соответственно высота­
ми треугольников ADC и BD C. Найти АС, если известно, что A M = 4,
B N = 9. .
10.3.49. [РЭА] В прямоугольном треугольнике биссектриса прямого
угла делит гипотенузу на отрезки Зсм и 4 см. Найти площадь треуголь­
ника.
10.3.50. [РЭА] В прямоугольный треугольник вписан квадрат, верши­
на которого совпадает с вершиной прямого угла треугольника. Найти
площадь треугольника, если один из его катетов равен 42 см, а сторона
квадрата — 24 см.
10.3.51. [РЭА] Точка на гипотенузе прямоугольного треугольника, рав­
ноудаленная от катетов, делит ее на отрезки 30 см и 40 см. Найти пери­
метр треугольника.
10.3.52. [РЭА] В прямоугольном треугольнике известны гипотенуза
125 см и меньший катет 75 см. Основание высоты, проведенной из вер­
шины прямого угла, делит гипотенузу на два отрезка. На меньшем из
отрезков как на диаметре построена полуокружность по одну сторону с
данным треугольником. Определить длину отрезка катета, заключенно­
го внутри этого полукруга.
223
10.3.53. [РЭА] В прямоугольном треугольнике АВС гипотенуза ВС =
= 20, а катет А В = 16. Найти квадрат расстояния от вершины А до
биссектрисы угла С.
10.3.54. [МГУЛ] Найти сумму длин катетов прямоугольного треуголь­
ника, если длина его гипотенузы 20 см, а радиус вписанной окружно­
сти 4 см.
10.3.55. [МАСИ] Найти площадь круга, вписанного в прямоугольный
треугольник, если высота, проведенная к гипотенузе, делит последнюю
на отрезки длиной 25,6 и 14,4 см.
4. Трапеция
10.4.1. [МАТИ] Площадь равнобочной трапеции равна S, угол между ее
диагоналями, противолежащий боковой стороне, равен а. Найти высоту
трапеции.
10.4.2. [МАТИ] В равнобочную трапецию вписана окружность радиу­
са г. Верхнее основание трапеции в два раза меньше ее высоты. Найти
площадь трапеции.
10.4.3. [МАИ] В трапеции ABCD сумма углов при основании AD рав­
на 90°. Нижнее и верхнее основания равны соответственно 7 и 3. Опре­
делить отрезок, соединяющий середины оснований.
10.4.4. [МГУ, эк. ф-т; МИФИ; МЭИ; СПбГУ; МПУ; РГПУ; МИСиС] В трапе­
ции, основания которой аиЬ, через точку пересечения диагоналей про­
ведена прямая, параллельная основаниям. Найти длину отрезка этой
прямой, отсекаемого боковыми сторонами трапеции.
10.4.5. [МГУ, геогр. ф-т; РЭА; МЭИ] Около круга описана трапеция с
углами при основании а и /?. Найти отношение площади трапеции к
площади круга.
10.4.6. [РУДН] Периметр равнобедренной трапеции вдвое больше длины
вписанной окружности. Найти угол при основании трапеции.
10.4.7. [МАИ] В трапеции ABCD проведены диагонали АС и BD,
пересекающиеся в точке F. Из вершины С проведена прямая СК, па­
раллельная боковой стороне AD, которая пересекает продолжение BD
в точке L так, что DF = BL. Найти отношение АВ : CD.
10.4.8. [МАТИ] Определить площадь круга, вписанного в прямоуголь­
ную трапецию с основаниями а и Ь.
10.4.9. [МАТИ] Центр круга, вписанного в прямоугольную трапецию,
отстоит от концов боковой стороны на 1см и 2 см. Найти площадь тра­
пеции.
224
10.4.10. [СПбГУ] Определить площадь трапеции, если ее основания
равны 6 см и 11см, одна из боковых сторон — 4 см, а сумма углов при
нижнем основании равна
10. 4.11. [РЭА; МПУ; МПГУ] Около круга радиуса R описана трапеция
с острыми углами а и /3 при большем основании. Найти площадь этой
трапеции.
10.4.12. [МПУ] Меньшее основание равнобедренной трапеции равно
высоте и равно h. Острый угол трапеции равен а. Найти периметр тра­
пеции.
10.4.13. [МГУ, геолог, ф-т; СПбГУ; ЛГПИ] Найти площадь равнобочной
трапеции, основания которой равны а и 6, а диагонали взаимно перпен­
дикулярны.
10.4.14. [МПУ] Периметр равнобедренной трапеции с острым углом а
равен р. Высота трапеции равна h. Найти площадь этой трапеции.
10.4.15. [МЭИ] В круг вписана равнобедренная трапеция так, что диа­
метр круга служит основанием трапеции. Найти отношение площадей
круга и трапеции, если тупой угол трапеции равен а.
10.4.16. [МАТИ] В равнобочной трапеции ABCD длины боковой сторо­
ны АВ и меньшего основания ВС равны а = 2 см и BD перпендикулярна
АВ. Найти площадь трапеции.
10.4.17. [МИСиС] В равнобедренной трапеции даны длины оснований
21 и 9 и длина высоты 8. Найти радиус описанной окружности.
10.4.18. [МИСиС] В равнобедренную трапецию вписана окружность ра­
диуса 2. Найти площадь трапеции, если длина боковой стороны равна 10.
10.4.19. [МЭИ] Около круга радиуса 2см описана равнобедренная тра­
пеция с острым углом 30°. Найти длину средней линии трапеции.
10.4.20. [МАТИ] Найти площадь трапеции, диагонали которой рав­
ны 7см и 8 см, а основания — Зсм и 6 см.
10.4.21. [МИСиС] Длины оснований трапеции равны 10 и 24, длины
боковых сторон равны 13 и 15. Найти площадь трапеции.
10.4.22. [СПбГУ] В равнобедренной трапеции, описанной около окруж­
ности радиуса й, отношение длин боковой стороны и большего основа­
ния есть заданное число к. Найти длину меньшего основания.
10.4.23. [СПбГУ] В равнобедренной трапеции боковая сторона равна с,
а диагональ, равная Z, делит площадь трапеции в отношении 3 :5 . Найти
основания трапеции.
225
10.4.24. [МАИ] Боковые стороны АВ и CD трапеции продолжены до
пересечения в точке Е. Точка О — центр описанной около треугольника
ADE окружности. Найти величину острого угла А трапеции, если из­
вестно, что точки А, В, С, D, О лежат на окружности, радиус которой
в \/3 раз меньше радиуса окружности, описанной около треугольника
ADE.
10.4.25. [МАТИ] Основания трапеции равны 4см и 16см. Найти ее
площадь, если известно, что в трапецию можно вписать и вокруг нее
можно описать окружность,
10.4.26. [РЭА] Вокруг окружности описана равнобочная трапеция,
средняя линия которой равна 5, а синус острого угла при основании
равен 0,8. Найти площадь трапеции.
10.4.27. [МИЭТ] Средняя линия трапеции равна 10 и делит площадь
трапеции в отношении 3 : 5. Найти длины оснований этой трапеции.
10.4.28. [МАТИ] Найти площадь трапеции, у которой длины основа­
ний равны а и 6 (а > b), а острые углы между большим основанием и
боковыми сторонами а и /?.
10.4.29. [МАТИ] Около круга радиуса т = 2 см описана равнобочная
трапеция с площадью S = 20 см2. Найти длины сторон трапеции.
10.4.30. [МАТИ] Центр окружности, вписанной в прямоугольную тра­
пецию, удален от концов боковой стороны на расстояния 1\ = 4 см и
h ~ 8 см. Найти длину средней линии трапеции.
10.4.31. [МАТИ] Около круга радиуса г = 4 см описана равнобочная
трапеция, средняя линия которой I — 10 см. Определить длины сторон
трапеции.
10.4.32. [ЛГПИ] В равнобедренную трапецию, основания которой 8см
и 2 см, вписана окружность. Найти длину окружности.
10.4.33. [ЛГПИ] В равнобедренной трапеции средняя линия равна с/, а
диагонали взаимно перпендикулярны. Найти площадь трапеции.
10.4.34. [СГУ] В трапеции ABCD длина боковой стороны АВ равна 4.
Биссектриса угла BAD пересекает прямую ВС в точке Е. В треугольник
АВЕ вписана окружность с центром в точке О, касающаяся стороны АВ
в точке М и стороны BE в точке N. Найти величину угла MON, если
длина отрезка MN равна 2.
10.4.35. [МИСиС] Найти радиус окружности, вписанной в равнобоч­
ную трапецию, если периметр трапеции равен 2, а острый угол соста­
вляет 30°.
226
10.4.36. [РГПУ] Длины параллельных сторон трапеции равны 25 и 4,
а длины непараллельных сторон — 20 и 13. Найти высоту трапеции.
10.4.37. [РГПУ] Найти площадь равнобочной трапеции, у которой вы­
сота равна 10, а диагонали взаимно перпендикулярны.
10.4.38. [МТУСИ] Площадь прямоугольной трапеции равна S, а острый
угол равен а. Найти высоту трапеции, если меньшая диагональ равна
большему основанию.
10.4.39. [ВГУ] Около круга с радиусом 2 описана равнобочная трапеция
с площадью 20. Найти стороны трапеции.
10.4.40. [МПГУ] Основания трапеции 4 см и 10 см, одна из боковых
сторон составляет с меньшим основанием угол 150°. Найти эту боковую
сторону, если площадь трапеции равна 21см.
10.4.41. [МАИ] В прямоугольной трапеции большая диагональ, име­
ющая длину 24, является биссектрисой острого угла. Найти площадь
трапеции, если расстояние от вершины тупого угла до диагонали рав­
но 9.
10.4.42. [МАИ] В прямоугольной трапеции средняя линия равна 13,5.
Меньшая диагональ является биссектрисой тупого угла и имеет дли­
ну 12. Найти стороны трапеции.
10.4.43. [МПГУ] Диагональ равнобедренной трапеции равна 5 см, а
площадь равна 12 см. Найти высоту трапеции.
10.4.44. [МПГУ] В трапеции ABCD с основаниями В С и A D : LACD —
= 1АВС, ВС ~ 12 см, AD = 27см. Найти диагональ АС.
10.4.45. [МПГУ] Найти площадь трапеции, у которой основания 15см
и 5см, а боковые стороны 8см и 6см.
10.4.46. [СПбГУ] Дана равнобедренная описанная трапеция ABCD, в
которой обе диагонали равны основанию AD. Найти углы при основа­
нии.
10.4.47. [МАТИ] В трапеции ABCD длины оснований A D и В С от­
носятся как 5 : 1, а площадь равна 32 см2. Точки М и N — середины
боковых сторон А В и C D соответственно соединены с концами проти­
воположной боковой стороны, причем отрезки A N и D M пересекаются
в точке К , а отрезки B N и С М — в точке Е. Определить площадь
четырехугольника M EN K.
10.4.48. [МГУ, мех .-мат. -, МТУСИ-, МАТИ] Длины боковых сторон трапе­
ции равны 6см и 10см. В трапецию можно вписать окружность. Средняя
линия делит трапецию на части, отношение площадей которых равно уу.
Найти длины оснований трапеции.
227
10.4.49. [МГУ, мех.-мат.; МТУСИ; МАТИ] Средняя линия равнобедренной
трапеции равна 5 см и она делит трапецию на части, отношение плота-
7
дей которых равно Найти длину высоты трапеции, если известно,
что в нее можно вписать окружность.
10.4.50. [МТУСИ] В равнобедренной трапеции боковая сторона равна
средней линии, а периметр равен 48см. Найти длину боковой стороны.
10.4.51. [МТУСИ] Площадь равнобедренной трапеции, описанной около
окружности, равна 32 см2. Найти длину боковой стороны, если угол при
основании равен 30°.
10.4.52. [МТУСИ] В равнобедренную трапецию, верхнее основание ко­
торой равно 1, вписана окружность радиуса 1. Найти площадь трапеции,
10.4.53. [МТУСИ] Боковая сторона равнобедренной трапеции в 3 раза
длиннее меньшего основания. Биссектрисы тупых углов этой трапеции
пересекаются в точке, лежащей на основании. Найти отношение площа­
ди трапеции к площади треугольника, образованного меньшим основа­
нием и биссектрисами.
10.4.54. [МТУСИ] В равнобедренную трапецию с основаниями ВС = 18
и AD = 32 вписан круг. Найти площадь трапеции и площадь круга.
10.4.55. [МТУСИ] Около круга радиуса \/3 описана равнобедренная
трапеция с острым углом 60°. Найти длину средней линии трапеции.
10.4.56. [МТУСИ] Разность длин оснований трапеции равна 14см, дли­
ны боковых сторон равны 13см и 15см. Вычислить площадь трапеции
при условии, что в эту трапецию можно вписать окружность.
10.4.57. [МТУСИ] П лощадь равнобедренной трапеции, описанной около
круга, равна S. Найти среднюю линию трапеции, если острый угол при
основании равен а.
10.4.58. [МТУСИ] Найти диагональ и боковую сторону равнобочной
трапеции с основаниями 20см и 12см, если известно, что центр описан­
ной окружности лежит па большем основании трапеции.
10.4.59. [МТУСИ] Около окружности с диаметром в 15 см описана рав­
нобочная трапеция с боковой стороной, равной 17см. Найти основания
трапеции.
10.4.60. [МТУСИ] Высота и диагональ равнобедренной трапеции равны
соответственно 5 и 13. Найти площадь трапеции.
10.4.61. [МГУЛ] Около круга радиуса 6см описана равнобочная тра­
пеция, у которой основания относятся как 9 : 16. Определить боковую
сторону трапеции.
228
10.4.62. [ГАУ] Центр окружности, вписанной в прямоугольную трапе­
цию, удален от концов боковой стороны на расстояния 8 см и 4 см. Найти
среднюю линию трапеции.
10.4.63. [ГАУ] В трапеции ABCD точка М лежит на боковой стороне
АВ, О — пересечение диагонали BD и отрезка СМ. Найти площадь тре­
угольника COD, если AM = МВ, СО = 4-ОМ, а площадь треугольника
ВОМ равна 1.
10.4.64. [ГАУ] Около трапеции ABCD с основаниями AD и ВС описана
окружность радиуса 6 см. Центр описанной окружности лежит на осно­
вании AD. Основание ВС равно 4 см. Определить площадь трапеции.
10.4.65. [ГАУ] Трапеция KLMN с основаниями LM и K N вписана в
окружность, центр которой лежит на основании К N. Диагональ LN тра­
пеции равна 4 см, а угол MNK равен 60°. Определить длину основания
LM трапеции.
10.4.66. [ГАУ] Трапеция KLMN с основаниями K N и LM вписана
в окружность, центр которой лежит на основании K N . Диагональ К М
трапеции равна 4 см, а боковая сторона KL равна Зсм. Определить дли­
ну основания LM.
10.4.67. [ГАУ] В прямоугольную трапецию вписана окружность. Найти
ее радиус, если основания равны 2 и 3.
10.4.68. [МГУ, мех.-мат.] В трапеции с основаниями 3 и 4 диагональ
имеет длину 6 и является биссектрисой одного из углов. Может ли эта
трапеция быть равнобокой?
10.4.69. [МГУ, мех.-мат.] В равнобокой трапеции диагональ имеет длину
8 и является биссектрисой одного из углов. Может ли одно из оснований
этой трапеции быть меньше 4, если другое равно 5?
10.4.70. [МГУ, физ. ф-т] В трапеции средняя линия, равная 20, делит
площадь трапеции в отношении 3 : 5. .
229
10.4.73. [ТПУ] Боковая сторона описанной равнобедренной трапеции
равна 12 см, Найти ее периметр.
10.4.74. [МГУ, биолог, ф-т] Высота трапеции ABCD равна 7, а длины
оснований AD и ВС равны соответственно 8 и 6. Через точку Е, лежа­
щую на стороне CD, проведена прямая BE, которая делит диагональ
АС в точке О в отношении АО : ОС = 3:2. Найти площадь треуголь­
ника ОЕС.
10.4.75. [МГУ, ф-т почвовед.] В трапеции ABCD длина основания AD
равна 4, длина основания ВС равна 3. Длины сторон АВ и CD равны.
Точки М и N лежат на диагонали BD, причем точка М расположена
между точками В и N, а отрезки AM и CN перпендикулярны диагонали О
BD. Найти длину отрезка CN, если ВМ : DN =
10.4.76. [МГУ, ИСАА] В равнобедренную трапецию с боковой стороной,
равной 9, вписана окружность радиусом 4. Найти площадь трапеции.
10.4.77. [МГУ, ИСАА] В равнобедренную трапецию площадью 28см2
вписана окружность радиуса 2 см. Найти боковую сторону трапеции.
10.4.78. [МПГУ] Около окружности с радиусом 2 описана равнобокая
трапеция, площадь которой равна 20. Найти боковую сторону трапеции.
10.4.79. [СПбГТУ] Высота трапеции, диагонали которой взаимно пер­
пендикулярны, равна 4. Найти площадь трапеции, если известно, что
длина одной из ее диагоналей равна 5.
10.4.80. [МТУСИ] В равнобочной трапеции, описанной около круга,
отношение боковой стороны к меньшему основанию равно к. Найти углы
трапеции и допустимые значения к.
10.4.81. [МАТИ] Площадь трапеции ABCD равна 24, а длины основа­
ний AD и ВС относятся как 3:1. Вершины А и D соединены отрезками
с точкой N — серединой стороны ВС, а точки В в С — с точкой М
— серединой стороны AD. Отрезки AN и ВМ пересекаются в точке Е,
а отрезки DN и СМ — в точке К. Найти площадь четырехугольника
ENKM.
10.4.82. [РЭА] В равнобедренной трапеции ABCD точка О — середина
меньшего основания ВС; О А — биссектриса угла А. Найти площадь
трапеции, если AD = 16, а ее высота равна 6.
10.4.83. [РЭА] Диагональ равнобочной трапеции, равная 8, перпенди­
кулярна боковой стороне. Найти меньшее основание трапеции, если ее
большее основание равно 10.
10.4.84. [РЭА] Большее основание трапеции равно 24 см. Найти ее мень­
шее основание, зная, что расстояние между серединами ее диагоналей
равно 4 см.
230
10.4.85. [РЭА] Окружность радиуса 24 см касается большего основания
и обеих боковых сторон равнобедренной трапеции. Найти большее осно­
вание трапеции, если центр окружности находится на расстоянии 40 см
от точки пересечения продолжений боковых сторон трапеции.
10.4.86. [РЭА] В трапеции ABCD меньшее основание ВС = 7. Через
вершины А, С и D проведена окружность, которая пересекает продолже­
ние основания ВС в точке Е, Длина ED — 7\/3, а угол EDA равен 30°.
Найти длину боковой стороны АВ.
10.4.87. [МАИ] В прямоугольной трапеции большая диагональ, имею­
щая длину 24 см, является биссектрисой острого угла. Найти площадь
трапеции, если расстояние от вершины тупого угла до диагонали рав­
но 9 см. раза.
10.5.2. [МГУ, эк. ф-т] В прямоугольнике ABCD на сторонах АВ = 6
и ВС = 8 взяты точки М и N так, что отрезок M N параллелен отрез­
ку АС. Известно, что периметр многоугольника AMNCD относится к
периметру треугольника MBN , как 7:3. Найти длину отрезка MN.
10.5.3. [СПбГУ] В прямоугольнике ABCD дано: АВ = а, AD = Ъ. Найти
на стороне АВ точку Е, для которой ICED — IAED.
10.5.4. [НГУ] Дан ромб ABCD, Окружность радиуса R описана около
треугольника ABD и проходит через центр окружности, вписанной в
треугольник CBD. Определить площадь ромба.
10.5.5. [РГПУ] В ромб вписан круг. Каждая сторона ромба точкой
касания делится на отрезки, длины которых а и Ь. Найти площадь круга.
10.5.6. [СПбГУ] Вершины одного квадрата лежат на границе второ­
го квадрата. Найти отношения длин отрезков, на которые эти вершины
231
разбивают стороны второго квадрата, если известно, что отношение пло­
щадей квадратов равно р.
10.5.7. [МГУ, геолог, ф-т; МЭИ; МИЭТ] Найти углы ромба, если известно,
что площадь вписанного в него круга вдвое меньше площади ромба,
10. 5.8. [СПбГУ] В квадрате ABCD со стороной а точки Е и F являются
серединами сторон АВ и CD соответственно. Точка К лежит на CF,
точка N — на AD, а отрезки EF и K N пересекаются в точке М. Найти
площадь треугольника K FM , если известно, что СК \ K F — 1 : 5, в. О
площадь трапеции EMN А составляет площади квадрата.
10.5.9. [СГАПС] В параллелограмме ABCD величина угла BCD рав­
на длина стороны АВ равна а. Биссектриса угла BCD пересекает
сторону AD в точке N. Найти площадь треугольника NCD.
10.5.10. [СГУ] В параллелограмме ABCD длина стороны AD равна 8.
Биссектриса угла ADC пересекает прямую АВ в точке Е. В треугольник
ADE вписана окружность с центром в точке О, касающаяся стороны АЕ
в точке К и стороны AD в точке L. Найти величину угла KOL, если
длина KL равна 2.
10.5.11. [УрГУ] На стороне N P квадрата MNPQ взята точка А, на
стороне PQ — точка В так, что N А : АР — РВ : BQ — 2:3. Точка L
является точкой пересечения отрезков МА и NB. В каком отношении
точка L делит отрезок М А?
10.5.12. [РГПУ] Стороны прямоугольника равны а и Ь. На стороне а,
как на диаметре, построена окружность. На какие отрезки окружность
делит диагональ прямоугольника?
10.5.13. [МПГУ] Найти площадь параллелограмма, если его диагона­
ли Зсм и 5см, а острый угол параллелограмма 60°.
10.5.14. [СГПИ] Дан ромб с острым углом а. Какую часть ромба со­
ставляет от его площади площадь вписанного в него круга?
10.5.15. [МПГУ] Длины меньшей диагонали, стороны и большей диаго­
нали ромба составляют геометрическую прогрессию. Найти углы ромба.
10.5.16. [МТУСИ] В параллелограмме ABCD длина диагонали BD,
перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна
2\/22. Найти длину стороны AD.
10.5.17. [МТУСИ] В параллелограмме ABCD биссектриса тупого угла
В пересекает сторону AD в точке F. Найти периметр параллелограмма,
если АВ = 12 и AF : FD = 4 : 3.
10.5.18. [МТУСИ] Через вершины произвольного четырехугольника
проведены прямые, параллельные его диагоналям. Найти отношение
232
площади параллелограмма, образованного этими прямыми, к площади
данного четырехугольника.
10.5.19. [ГАНГ] Тупой угол ромба в о раз больше его острого угла. Во
сколько раз сторона ромба больше радиуса вписанной в него окружно­
сти?
10.5.20. [ГАУ] Точка М делит диагональ АС квадрата ABCD со сто­
роной а в отношении AM : МС = 3:1; точка N лежит на стороне АВ,
причем угол NMD прямой. Найти длину отрезка AN.
10.5.21. [МГУ, филолог, ф-т] В ромбе ABCD угол при вершине А ра­
вен Точка N делит сторону АВ в отношении AN : BN = 2:1.
Определить тангенс угла DNC.
10.5.22. [МГУ, хим. ф-т] В квадрат площадью 18 см2 вписан прямоуголь­
ник так, что на каждой стороне квадрата лежит одна вершина прямо­
угольника. Длины сторон прямоугольника относятся как 1 : 2. Найти
площадь прямоугольника.
10.5.23. [МГУ, хим. ф-т] В квадрат площадью 24 вписан прямоуголь­
ник так, что на каждой стороне квадрата лежит одна вершина прямо­
угольника. Длины сторон прямоугольника относятся как 1 : 3. Найти
площадь прямоугольника.
10.5.24. [МГУ, филолог, ф-т] Точка С лежит на стороне M N ромба
KLMN, причем CN = 2 см и угол MNK равен 120°. Найти отношение
косинусов углов CKN и CLM.
10.5.25. [МГУ, геогр. ф-т] В параллелограмме ABCD на диагонали
АС взята точка Е, где расстояние АЕ составляет треть длины АС, а
на стороне AD взята точка F, где расстояние AF составляет четверть
длины AD. Найти площадь параллелограмма АВ CD, если известно, что
площадь четырехугольника ABGE, где G — точка пересечения прямой
FE со стороной ВС, равна 8.
10.5.26. [МГАВТ] Определить угол ромба, зная его площадь Q и пло­
щадь вписанного в него круга S.
10.5.27. [МГЗИПП] Радиус окружности, в которую вписан квадрат,
равен 6 см. Найти площадь квадрата.
10.5.28. [ГУЗ] Периметр параллелограмма 90см, а острый угол — 60°.
Диагональ параллелограмма делит его тупой угол на части в отношении
1 : 3. Найти стороны параллелограмма.
10.5.29. [МВВДИУ] В параллелограмме даны острый угол, равный 45°,
и расстояния от точки пересечения диагоналей до неравных сторон, рав­
ные соответственно 2 и 3. Найти площадь параллелограмма.
233
10.5.30. [КГТУ] В ромб вписан круг, а в круг вписан квадрат. Чему
равен угол ромба, если площадь квадрата в 4 раза меньше площади
ромба?
6. Окружность и круг
10.6.1. [МАТИ] Из одной точки окружности проведены две хорды дли­
ной 9 см и 17см. Найти радиус окружности, если расстояние между се­
рединами хорд равно 5 см.
10.6.2. [МИИТ, МИСиС] Хорда окружности равна 10см. Через один
конец хорды проведена касательная к окружности, а через другой ко­
нец проведена секущая параллельно касательной. Определить радиус
окружности, если внутренний отрезок секущей равен 12 см.
D
10.6.3. [МАИ] Две окружности радиусов R и ~ касаются друг дру­
га внешним образом. Один из концов отрезка длины 2R, образующего
угол 30° с линией центров, совпадает с центром окружности меньшего
радиуса. от центра
окружности, пересекающая окружность в точках В и С. Найти АВ и
АС.
10.6.6. [НГУ] Дан выпуклый четырехугольник ABCD, диагональ АС
которого равна у/2. Найти площадь круга, описанного около треуголь­
ника ABD, если известно, что 1АВС = 105°, LACD = 42°, ID АС = 63°.
10.6.7. [НижГУ, РГПУ] Диаметр окружности радиуса R является осно­
ванием правильного треугольника. Вычислить площадь той части тре­
угольника, которая лежит вне данного круга.
10.6.8. [РГПУ] Дано круговое кольцо, площадь которого Q. Определить
длину хорды большего круга, касательной к меньшему.
10.6.9. [УрГУ] Две окружности радиусов г и Зг касаются внешним
образом. Найти площадь фигуры, заключенной между окружностями и
их общей касательной.
234
10.6.10. [МИСиС] Окружность с центром в точке О и радиусом й —
= 6 + 4\/2 касается прямой в точке А. На окружности взята точка В
так, что угол АО В равен 45°. Найти радиус окружности, касающейся
данной окружности в точке В и данной прямой.
10.6.11. [МИСиС] Радиусы двух пересекающихся окружностей равны 13
и 15, длина общей хорды равна 24. Определить расстояние между их
центрами (центр каждой окружности лежит вне другой окружности).
10.6.12. [СПбГУ] Круг и квадрат имеют общий центр, а их площади
равны. Сторона квадрата равна 1. Вычислить сумму длин частей окруж­
ности, расположенных внутри квадрата.
10.6.13. [ЯГУ] Дан ромб со стороной а и острым углом 60°. На его
большой диагонали как на диаметре построена окружность, а) Вычи­
слить площадь круга, б) Что больше: площадь ромба или площадь части
круга, лежащей вне ромба?
10.6.14. [ВГУ] Через точку Р, лежащую внутри круга радиусом Й, про­
ведены две взаимно перпендикулярные хорды, одна из которых образует
угол а (а > 0) с прямой, проходящей через точку Р и центр круга, и
удалена от центра на расстояние а. В круг вписан четырехугольник,
имеющий эти хорды диагоналями. Найти его площадь.
10.6.15. [СПбГУ] Точка находится внутри круга радиусом 6 и делит
проходящую через нее хорду на отрезки длиной о и 4. Найти расстояние
от точки до окружности.
10.6.16. [МПГУ] Найти сторону квадрата, вписанного в круг, площадь
которого 64 см2.
9
10.6.17. [ВШЭ] Две окружности, отношение радиусов которых равно
касаются друг друга внутренним образом. Через центр меньшей окруж­
ности проведена прямая, перпендикулярная линии центров, и из точек
пересечения этой прямой с большей окружностью проведены касатель­
ные к меньшей окружности. Найти углы между этими касательными.
10.6.18. [ЛГПИ] Точка лежит вне круга на расстоянии диаметра от цен­
тра круга. Найти угол между касательными, проведенными из данной
точки к данному кругу.
10.6.19. [МГУ, мех.-мат.] Диагонали четырехугольника ABCD, вписан­
ного в окружность, пересекаются в точке Е. На прямой АС взята точка
М , причем ADME = 80°, LABD = 60°, ICBD = 70°. Где расположена
точка М: на диагонали АС или на ее продолжении? Ответ обосновать.
10.6.20. [МЭИ] Три круга касаются внешним образом. Расстояния ме­
жду центрами кругов равны 7см, 8 см, 9 см. Найти радиусы кругов.
235
10.6.21. [МТУСИ; МАДИ] Две окружности равного радиуса касаются
в точке С внешним образом. Кроме того, каждая из них касается извне
третьей окружности радиуса 6,5 в точках Л и В соответственно. Найти
площадь треугольника АВС, если АВ = 5.
10.6.22. [ГАНГ] Две окружности пересекаются в точках А и В, через
точку А проведены хорды АС и AD, касающиеся данных окружностей;
АС : AD = 3:2. Найти отношение ВС : BD.
10.6.23. [МФТИ] Окружность, центр которой лежит вне квадрата
ABCD, проходит через точки В и С. Найти угол между касательными к
окружности, проведенными из точки D, если отношение длины стороны
т
квадрата к диаметру окружности равно £.
О
10.6.24. [МИСиС] Две окружности касаются внутренним образом. Пря­
мая, проходящая через центр меньшей окружности, пересекает большую
окружность в точках Л и В, а меньшую — в точках В и С, причем
АВ : ВС : CD = 2:4:3. Найти отношение радиуса большей окружно­
сти к радиусу меньшей окружности.
10.6.25. [ГАУ; МГАПБ] Две окружности радиуса 32 с центрами Oi и
0 2, пересекаясь, делят отрезок 0102 на три равные части. Найти ради­
ус окружности, которая касается изнутри обеих данных окружностей и
касается отрезка 0102 —
10.6.26. [МГУ, физ. ф-т] В окружности пересекающиеся хорды АВ и
CD перпендикулярны, AD — т, ВС = п. Найти диаметр окружности.
10.6.27. [МГУ, физ. ф-т] В окружность с радиусом R вписан равнобе­
дренный треугольник АВС (АВ = ВС) с углом ВАС, равным а. Найти
радиус окружности, вписанной в треугольник АВС.
10.6.28. [МГУ, физ. ф-т] Окружность касается сторон угла с вершиной
О в точках А и В. На этой окружности внутри треугольника АОВ взята
точка С. Расстояния от точки С до прямых О А и ОВ равны соответ­
ственно а и 6. Найти расстояние от точки С до хорды АВ.
10.6.29. [МГУ, мех.-мат.] Диагонали четырехугольника PQRS, вписан­
ного в окружность, пересекаются в точке D. На прямой PR взята точка
А, причем ISAD — 50°, IPQS = 70°, IRQS = 60°. Где расположена
точка А: на диагонали PR или на ее продолжении? Ответ обосновать.
10.6.30. [МГУ, хим. ф-т] Две окружности разных радиусов касаются в
точке А одной и той же прямой и расположены по разные стороны от
нее. Отрезок АВ — диаметр меньшей окружности. Из точки В прове­
дены две прямые, касающиеся большей окружности в точках М и N.
Прямая, проходящая через точки М и А, пересекает меньшую окруж­
ность в точке К. Известно, что длина отрезка М К равна у/¥+~у/3, а
236
угол ВМА равен 15°. Найти площадь фигуры, ограниченной отрезками
касательных ВМ, BN и той дугой M N большей окружности, которая
не содержит точку А.

10.6.31. [МПГУ] В полуокружность с радиусом \/5 вписан квадрат так,
что две его вершины лежат на диаметре полуокружности. Найти длину
стороны квадрата.
10.6.32. [СПбГУ] Дан прямоугольный треугольник с катетами 3 и 4.
Диаметр круга совпадает с большим катетом. Вычислить площади ча­
стей круга, на которые он разбивается гипотенузой треугольника. = разделен на два сегмента
V4?r — Зл/З
хордой, равной стороне вписанного в этот круг правильного треуголь­
ника. Определить площадь меньшего из этих сегментов.
7. Разные задачи
10.7.1. [СПбГТУ] Диагонали разбивают выпуклый четырехугольник на
четыре треугольника. Радиусы окружностей, описанных около этих тре­
угольников, одинаковы и равны 2. Найти длины сторон четырехуголь­
ника.
10.7.2. [РГПУ] В выпуклом четырехугольнике длины диагоналей 2 см
и 4 см. Найти площадь четырехугольника, зная, что длины отрезков,
соединяющих середины противоположных сторон, равны.
237
10.7.3. [МГОПУ] Данный квадрат со стороной а срезан по углам так,
что образовался правильный восьмиугольник. Определить площадь это­
го восьмиугольника.
10.7.4. [МИЭТ] Дан правильный 30-угольник А\ A i … Д30 с центром О.
Найти угол между прямыми О Аз и А1А4.
10.7.5. [МПГУ] Сторона правильного шестиугольника равна 14 см. Най­
ти сторону равновеликого ему правильного треугольника и площадь
круга, вписанного в этот треугольник.
10.7.6. [МТУСИ] Разность между площадью круга и площадью впи­
санного в него квадрата равна 2у/3(тг — 2). Найти площадь правильного
шестиугольника, вписанного в этот круг.
10.7.7. [МФТИ] В окружность диаметра 1 вписан четырехугольник
ABCD, у которого угол D прямой, АВ ~ ВС. Найти площадь четы­
рехугольника ABCD, если его периметр равен
10.7.8. [МФТИ] В окружность радиуса 5 вписан четырехугольник
ABCD, у которого угол D прямой, АВ : ВС ~ 3:4. Найти периметр
четырехугольника ABCD, если его площадь равна 44.
10.7.9. [МГУЛ] Четырехугольник ABCD описан около окружности с
центром О, Найти сумму углов АОВ и COD (в градусах).
10.7.10. [МГУ, биолог, ф-т, ГАУ] В выпуклом четырехугольнике ABCD
длина отрезка, соединяющего середины сторон АВ ж CD, равна одно­
му метру. Прямые ВС и AD перпендикулярны. Найти длину отрезка,
соединяющего середины диагоналей АС и BD.
10.7.11. [МГУ, биолог, ф-т] В выпуклом четырехугольнике ABCD дли­
на отрезка, соединяющего середины диагоналей, равна длине отрезка,
соединяющего середины сторон AD и ВС. Найти величину угла, обра­
зованного продолжениями сторон АВ и CD.
10.7.12. [ИЕНиЭ] Четырехугольник KLMN вписан в окружность. Че­
рез его вершины проведены касательные к этой окружности, образую­
щие также вписанный четырехугольник. Найти площадь четырехуголь-
MN MN
ника KLMN, если его периметр равен р и —— — 2, ——— = 8.
ML KL
10.7.13. [МПГУ] Точка, лежащая внутри угла в 60°, удалена от его
сторон на расстояния а и Ъ. Найти расстояние от этой точки до вершины
угла.
238
8. Задачи на доказательство
10.8.1. [МЙСиС] Пусть Е — середина стороны АВ трапеции ABCD
{ВС j| AD). Доказать, что площадь треугольника ECD равна половине
площади трапеции ABCD.
10.8.2. [МГУ, эк. ф-т] В выпуклом четырехугольнике ABCD противо­
положные углы А и С прямые. На диагональ АС опущены перпендику­
ляры BE и DF. Доказать, что СЕ = FA.
10.8.3. [БГУ] В треугольнике АВС проведена биссектриса AD. Дока­
зать, что если АВ + BD = АС + CD, то треугольник АВС — равнобе­
дренный.
10.8.4. [НГУ] Дана равнобедренная трапеция с основаниями а и Ь.
Доказать, что если в эту трапецию можно вписать окружность, то ее
диаметр равен у/аЬ.
10.8.5. [РГПУ] На основаниях АВ и CD вне трапеции построены ква­
драты. Доказать, что прямая, соединяющая их центры, проходит через
точку пересечения диагоналей трапеции.
10.8.6. [МПГУ] На одной из параллельных сторон трапеции взята точка
А, на другой — точка В. Доказать, что отрезок АВ делится средней
линией трапеции пополам.
10.8.7. [МЭИ] Пусть М — точка пересечения высот треугольника АВС.
Доказать, что точка М’, симметричная точке М относительно любой
стороны треугольника АВС, лежит на окружности, описанной около
этого треугольника.
10.8.8. [УрГУ] Доказать, что в прямоугольном треугольнике произ­
ведение длин отрезков, на которые делит гипотенузу точка касания с
вписанной окружностью, равно площади треугольника.
10.8.9. [МИРЭА] Две окружности с радиусами Ru г касаются друг дру­
га внешним образом в точке А. Общие касательные AD и ВС к окруж­
ностям пересекаются в точке D. Доказать, что AD2 ~ Rr.
10.8.10. [СПбГУ] Дан равнобедренный треугольник АВС с основанием
АС. Вписанная в него окружность с центром О касается боковой стороны
ВС в точке Р и пересекает биссектрису угла В в точке Q. Доказать, что
отрезки QP и ОС параллельны.
10.8.11. [МГУ, геолог, ф-т] Четырехугольник ABCD таков, что около
него можно описать и в него можно вписать окружности. Разность длин
сторон AD и ВС равна разности длин сторон АВ и CD. Доказать, что
диагональ АС — диаметр описанной окружности.
239
10.8.12. [МГУ, геолог, ф-т] Четыре точки окружности следуют в порядке
А, В, С, D. Продолжения хорды АВ за точку В и хорды CD за точку С
пересекаются в точке Е, причем угол AED равен 60°. Угол ABD в три
раза больше угла ВАС. Доказать, что AD —- диаметр окружности.
10.8.13. [МПГУ] Из вершины В треугольника АВС опущены перпен­
дикуляры В К и BL на биссектрисы внешних углов треугольника, не
смежных с углом В. Доказать, что длина отрезка KL равна полупери-
метру треугольника АВС.

10.9.1. [МГУ, мех.-мат.; МИФИ] В треугольнике KLM проведены бис­
сектрисы K N и ZP, пересекающиеся в точке Q. Отрезок PN имеет дли­
ну 1 см, а вершина М лежит на окружности, проходящей через точки N,
Р, Q. Найти стороны и углы треугольника PNQ.
10.9.2. [РЭА] Определить стороны треугольника, если медиана и высо­
та, проведенные из вершины одного угла, делят этот угол на три равные
части, а сама медиана равна 10 см.
10.9.3. [НГУ] В треугольнике АВС биссектриса угла ВАС равна а.
Окружность, построенная на этой биссектрисе как на диаметре, делит
стороны АВ и АС в отношении 2 : 1 и 1 : 1, считая от точки А. Найти
площадь треугольника АВС.
10.9.4. [МФТИ] В треугольнике АВС биссектриса AD делит сторону
ВС в отношении BD : CD = 2 ; 1. В каком отношении медиана СЕ
делит эту биссектрису?
10.9.5. [МФТИ] Вписанная в треугольник АВС окружность касается
его сторон АС и ВС соответственно в точках М и N и пересекает бис­
сектрису BD в точках Р и Q. Найти отношение площадей треугольников
PQM и PQN , если LA = | , ZB =
10.9.6. [НГУ] В треугольнике АВС радиус вписанной окружности ра­
вен косинус угла С равен а площадь треугольника равна 60.
Найти стороны треугольника.
10.9.7. [МИРЭА] В треугольнике АВС точка Е принадлежит медиане
B D , причем BE = ZED. Прямая АЕ пересекает сторону ВС в точке М.
Найти отношение площадей треугольников АМС и АВС.
10.9.8. [МАТИ] В треугольнике АВС площадью 90 см2 биссектриса AD
делит сторону ВС на отрезки BD и CD, причем B D : CD = 2:3. Отрезок
240
BL пересекает биссектрису AD в точке Е и делит сторону АС на отрезки
AL и CL такие, что AL : CL = 1:2. Найти площадь четырехугольника
EDCL.
10.9.9. [МАТИ] В треугольнике АВС площадью 40 см2 биссектриса AD
делит сторону ВС на отрезки BD и DC, причем BD : DC = 3:2.
Биссектриса AD пересекает медиану В К- в точке Е. Найти площадь
четырехугольника EDCK.
10.9.10. [МАТИ] В треугольнике АВС площадью 70 см2 биссектриса
AD делит сторону ВС на отрезки BD и D C, причем BD : DC = 3:2.
На стороне АС выбрана точка К такая, что биссектриса AD пересекает
В К в точке Е и BE : ЕК = 5:2. Найти площадь четырехугольника
EDCK.
10.9.11. [МАТИ] В треугольнике АВС биссектрисы AD и BE пересе­
каются в точке О. Найти отношение площади четырехугольника DOEC
к площади треугольника АВС, если АС : АВ : ВС = 4:3:2.
10.9.12. [МФТИ] В треугольнике АВС проведена биссектриса АР. Из­
вестно, что ВР ~ 16, PC = 20 и что центр окружности, описанной около
треугольника АВР, лежит на отрезке АС. Найти длину стороны АВ.
10.9.13. [МФТИ] В треугольнике АВС проведена биссектриса CQ.
•у
Около треугольника BCQ описана окружность радиуса центр ко-
i j
торой лежит на отрезке АС. Найти площадь треугольника АВС, если
AQ : АВ = 2:3.
10.9.14. [МФТИ] Даны треугольник АВС и ромб BDEF, все вершины
которого лежат на сторонах треугольника АВС, а угол при вершине Е
— тупой. Найти площадь треугольника АВС, если АЕ = 3, СЕ = 7, а
радиус окружности, вписанной в ромб, равен 1.
О
10.9.15. [МФТИ] В треугольнике АВС угол А равен тг —arcsin а дли­
на стороны ВС равна 8. На продолжении СВ за точку В взята точка
D так, что BD = 1. Найти радиус окружности, проходящей через вер­
шину А, касающейся прямой ВС в точке D и касающейся окружности,
описанной около треугольника АВС.
10.9.16. [МТУСИ] В треугольнике АВС биссектриса АН делит ме­
диану BE в отношении ВК : К Е = 2, а угол АСВ равен 45°. Найти
отношение площади треугольника ВСЕ к площади описанного около
этого треугольника круга.
10.9.17. [УрГУ] В треугольнике АВС точки К и N — середины сторон
АВ и АС соответственно. Через вершину В проведена прямая, которая
пересекает сторону АС в точке F , а отрезок K N — в точке L так, что
241
KL : LN = 3:2. Определить площадь четырехугольника AKLF, если
площадь треугольника АВС равна 40.
10.9.18. [МТУСИ] В треугольнике АВС известны высоты ha, hb, hc.
Найти радиус вписанной в треугольник АВС окружности.
10.9.19. [МТУСИ] В треугольнике АВС угол А равен 60°, а центр
вписанного круга делит биссектрису АК в отношении (\/3 + 1) : -\/2,
считая от вершины А. Найти величины углов В и С.
10.9.20. [МФТИ] Биссектриса AD и высота BE остроугольного тре­
угольника АВС пересекаются в точке О. Окружность с радиусом R и
центром в точке О проходит через вершину А , середину стороны АС и
пересекает сторону АВ в точке К такой, что АК : КВ — 1:3. Найти
длину стороны ВС.
10.9.21. [МФТИ] Продолжения медиан AM и ВК треугольника АВС
пересекают описанную около него окружность в точках Е и F соответ­
ственно, причем АЕ : AM = 2:1, BF : ВК = 3 : 2 . Найти углы
треугольника АВС.
10.9.22. [СПбГУ] Точка X делит сторону АВ треугольника АВС в
отношении 1 : 2. Точка Y лежит на стороне АС, и отрезок B Y делится
отрезком Х С в отношении 5 : 2. В каком отношении точка Y делит
сторону АС?
10.9.23. [МГУ, хим. ф-т] Точки М и JV лежат на стороне АС треуголь­
ника АВС на расстояниях соответственно 2 и 6 от вершины А. Найти
радиус окружности, проходящей через точки М и N и касающейся пря­
мой АВ; /.ВАС = 30°.
10.9.24. [МГУ, геогр. ф-т] В треугольнике АВС биссектриса BE и меди­
ана AD перпендикулярны и имеют одинаковую длину, равную 4. Найти
стороны треугольника АВС .
10.9.25. [НГУ] В треугольнике АВС (АВ = 14, АС = 15, ВС = 13)
через основание высоты СН проводят прямые, параллельные АС и ВС,
которые пересекают соответственно ВС и АС в точках М и N. Пря­
мая M N пересекает продолжение стороны АВ в точке D. Найти длину
отрезка BD.
10.9.26. [МГУ, ВМиК] В остроугольном треугольнике АВС на высоте
AD взята точка М , а на высоте ВР — точка N так, что углы ВМС
и ANC — прямые. Расстояние между точками М и N равно 4 + 2\/3,
/MCN ~ 30°. Найти биссектрису CL треугольника CMN.
10.9.27. [МГУ, ВМиК] В треугольнике KLM длина стороны KL рав­
на 27, длина биссектрисы K N равна 24, а длина отрезка M N равна 8.
Определить периметр треугольника KMN.
242
10.9.28. [МГУ, геолог, ф-т] У треугольника известны длины сторон
а = 6, Ь = 8 и площадь S = Зл/15. Третья его сторона меньше удвоенной
медианы, проведенной к ней. Найти радиус вписанной в этот треуголь­
ник окружности.
10.9.29. [МГУ, мех.-мат.] В треугольнике PQR медиана, проведенная из
вершины Q, имеет длину Окружности с центрами в вершинах Р
и Я и радиусами 5 и 1 соответственно касаются друг друга, а вершина Q
лежит на прямой, касающейся каждой из окружностей. Найти площадь
S треугольника PQR, если известно, что S < 7.
10.9.30. [МГУ, эк. ф-т] Отрезки, соединяющие основания высот остро­
угольного треугольника, равны 5, 12 и 13. Найти площадь треугольника.
10.9.31. [СПбГТУ] Найти углы треугольника с единичным радиусом
вписанной окружности, если известно, что длины его высот — целые
числа.
10.9.32. [РЭА] Из центра окружности, вписанной в треугольник со сто­
ронами 13, 14, 15, проведена новая окружность радиуса 5. Найти длины
хорд, отсекаемых этой новой окружностью на сторонах треугольника.

В показанную трапецию можно вписать круг. Найдите площадь этого круга.

1118 Найдите решение дифференциального уравнения, удовлетворяющее заданному начальному условию. dydx = xsinxy, y (0 …

Исчисление (Список курсов MindTap)

Болезнь Альцгеймера Прогнозируемое количество людей в возрасте 65 лет и старше в США с болезнью Альцгеймера …

Прикладное исчисление для управленческой жизни и социальные науки: краткий подход

Add: 2.147 + 2,04 + 60 + 0,007 + 0,83

Элементарная техническая математика

Основные вычисления: поиск областей под стандартной нормальной кривой В задачах 13-30 нарисуйте области под …

Общие сведения о базовой статистике

Любым методом , определите все возможные реальные решения каждого уравнения в упражнении 1330. Проверьте свои ответы с помощью …

Конечная математика и прикладное исчисление (список курсов MindTap)

Объясните, почему честность — это гипотетическая конструкция, а не конкретная переменная.Опишите, насколько честным может быть м …

Основы статистики для поведенческих наук (список курсов MindTap)

Пусть 1 0, 2 0, с 1 + 2 =. Тогда P (z1X- / nz2) = 1- a. Используйте это уравнение, чтобы получить более общее выражение для …

Вероятность и статистика для инженерии и наук

Найдите векторную функцию, которая представляет кривую пересечения цилиндра x2 + y2 = 16 и плоскости x + ..

Многопараметрическое исчисление

Перепишите каждое выражение в Упражнении 116 как одно рациональное выражение, максимально упрощенное.1x [x3 …

Прикладное исчисление

Определение дифференцируемости В упражнении 2528 опишите значения x, при которых функция дифференцируема ….

Исчисление: прикладной подход (список курсов MindTap)

Для задач 5 -54 выполните следующие операции с действительными числами. Задачи 3-6 21.427.29

Алгебра среднего уровня

В колледже Святой Алгебры математический факультет провел несколько специальных разделов курса математики для первокурсников с использованием различных вариантов…

Основы статистики

Шмидт (1994) провел серию экспериментов, исследующих влияние юмора на память. В одном исследовании участвовали …

Статистика для поведенческих наук (список курсов MindTap)

Графические эллипсы Дается уравнение эллипса. (а) Найдите центр, вершины и фокусы эллипса. (…

Precalculus: Mathematics for Calculus (Standalone Book)

Используйте рекомендации раздела 4.5, чтобы нарисовать кривую.y = (x 2) ex

Исчисление одной переменной: ранние трансцендентальные методы, том I

Покажите, что функция непрерывна в своей области. Укажите домен. 47. h (x) = x4 + x3cosx

Исчисление с одной переменной

В упражнении 516 оцените заданную величину. log5125

Конечная математика

Отель Hubert — это воображаемый отель, созданный математиком Дэвидом Хубертом (1862–1943). В отеле есть …

Математические экскурсии (Список курсов MindTap)

Найдите многочлен Тейлора T3 (x) для функции f с центром в числе a.График f и T3 на одном экране …

Calculus: Early Transcendentals

37. Доход Недавно выпущенный фильм приносит еженедельный доход.
дано

где R (t) выражается в миллионах долларов и …

Математические приложения для управления, жизни и социальных наук

Нахождение неопределенного интеграла, включающего синус и косинус, В упражнениях 3-14 найдите неопределенный интеграл. sin33 …

Исчисление: ранние трансцендентные функции

Для следующих статей баланса отметьте соответствующую категорию.Текущий фиксированный Текущий долгосрочный владелец
…

Современная математика для бизнеса и потребителей

(a) Найдите функцию длины дуги для кривой y = ln (sin x), 0 x, с начальной точкой (/ 2, 0). (b) График bo …

Исчисление одной переменной: ранние трансценденталы

Вычисление обратных тригонометрических функций В упражнениях 7-14 оцените выражение без использования вычислений …

Исчисление одной переменной

Для каждого из следующие уравнения, решите для (a) всех решений в радианах и (b) x, если 0x2.Дайте все ответы как e …

Тригонометрия (список курсов MindTap)

В упражнениях 114 решите, является ли каждый из заданных наборов группой по отношению к указанной операции. Если …

Элементы современной алгебры

Использование тригонометрической подстановки в упражнениях 29-34, используйте тригонометрическую подстановку, чтобы найти или оценить int …

Исчисление: ранние трансцендентные функции (список курсов MindTap)

Решение dydt = ky, где k — константа, а P0 — значение y при t = 0, это a) y = ekt b) y = xekt c…

Учебное пособие по исчислению с единственной переменной Стюарта: ранние трансцендентальные методы, 8-е

СЧЕТА ПОЛУЧЕНИЯ ВЫХОДОВ Андреа, работающая не по найму, желает накопить в пенсионном фонде 250 000 человек. Как …

Конечная математика для управленческих, жизненных и социальных наук

Для a = ⟨6, 2, 3⟩, b = ⟨4, 7, 9⟩ и c = ⟨8, 1, 5⟩ , c · (a × b) =

Учебное пособие по многомерному исчислению Стюарта, 8-е

Американская автомобильная ассоциация (AAA) сообщила, что семьи, планирующие поездку в выходные дни Дня труда, w…

СТАТИСТИКА F / BUSINESS + ECONOMICS-TEXT

Кратко объясните, как случайное распределение пытается сохранить характеристики участников, такие как возраст или пол, от …

Методы исследования поведенческих наук (список курсов MindTap)

Набросок a Кривая В упражнениях 9–12 нарисуйте кривую, представленную векторно-оценочной функцией, и задайте или …

Многопараметрическое исчисление

Определите открытые, ограниченные вопросы и вопросы с рейтинговой шкалой; определить примеры этих трех типов вопросов;..

Методы исследования поведенческих наук (Список курсов MindTap)

Национальная администрация безопасности дорожного движения сообщила процент дорожно-транспортных происшествий, происходящих каждый …

Статистика для бизнеса и экономики, пересмотренная (Список курсов MindTap)

В рамках исследования влияния стратегий управления лесным хозяйством (Ecological Applications [2003]: 11101123), я …

Введение в статистику и анализ данных

Определите длину a.Ответ округлите до 1 знака после запятой.

Математика для машинной техники

ИЗУЧЕНИЕ ПОНЯТИЙ Сравнение интегралов Пусть R будет областью, ограниченной окружностью x2 + y2 = 9. (a) Настройте интегр …

Calculus

Коэффициент самопроверки: p364.

Колледж по алгебре (список курсов MindTap)

Верно или нет? В упражнениях 91–96 определите, истинно это утверждение или нет. Если это неверно, объясните, почему …

Исчисление (список курсов MindTap)

Упражнения на смещение и растяжку с 1 по 13 относятся к графику на рисунке 2.124. Нарисуйте график каждого из …

Функции и изменения: подход к моделированию алгебры колледжа (список курсов MindTap)

24. Университет Кларксона провел опрос выпускников, чтобы узнать больше о том, что они думают о Кларксоне. Одна часть обзора …

Современная бизнес-статистика в Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (Список курсов MindTap)

Цены на бензин. Предположим, что средняя цена за галлон бензина в США составляет 3 доллара.73 и в R …

Основы статистики для бизнеса и экономики

В упражнениях 33-54 решите данное уравнение. Решение всех остальных упражнений с нечетными номерами приведено в …

Математика: Практическая одиссея

Создайте таблицу трассировки, чтобы отслеживать действие алгоритма 5.1.1 на входе в 84-86. 44

Дискретная математика с приложениями

В задачах 1320 используйте (20), чтобы найти общее решение данного дифференциального уравнения на (0,).14. xy y + …

Первый курс по дифференциальным уравнениям с приложениями моделирования (список курсов MindTap)

Два средних значения совокупности с неизвестными стандартными отклонениями Используйте следующую информацию, чтобы ответить на следующие 15 упражнений …

Вводная статистика

В следующих упражнениях нарисуйте график функции с заданными свойствами. 76. limx2f (x) = 1, limx4f (x) …

Calculus Volume 1

Решение системы с использованием обратной матрицы В упражнениях 43 и 44 используйте обратную матрицу из упражнения 19…

College Algebra

Для следующих упражнений нарисуйте уравнения и закрасьте область между кривыми. Определить …

Calculus Volume 2

Определение вписанных и ограниченных

Описанная окружность или описанная окружность проходит через все вершины плоской фигуры и содержит всю фигуру внутри. Центр этого круга называется центром описанной окружности.Вписанный круг — это самый большой из возможных кругов, который можно нарисовать на внутренней стороне плоской фигуры. Для многоугольника каждая сторона многоугольника должна касаться окружности. Все треугольники и правильные многоугольники имеют описанные и вписанные круги. Большинство других полигонов этого не делают. Для правильного многоугольника внутренний радиус (радиус вписанной окружности) называется апофемой. Единственная окружность, вписанная в треугольник, называется вписанной.

См. Другие разделы о геометрии

Показать стенограмму

привет, я репетитор в Chegg.com, меня зовут Джессика, сегодня мы поговорим о том, как описать круг вокруг треугольника, так что описать означает создать круг на внешней стороне фигуры, который проходит через все вершины, а также содержит всю фигуру в внутри этого круга вписанный круг с другой стороны — это круг, который находится внутри фигуры, и он также касается каждой стороны фигуры. Сегодня мы собираемся выяснить, как описать треугольник. Обратите внимание, что у меня есть прямоугольный треугольник. координатную сетку, и я собираюсь найти серединные перпендикуляры каждой стороны, чтобы найти то, что известно как центр описанной окружности, центр описанной окружности — это центр окружности, которая будет описана на внешнем перпендикуляре. другими словами, разрежьте его пополам в средней точке, так что мы собираемся найти середину каждой стороны и создать биссектрисы, необходимые для нахождения центра описанной окружности, если у вас есть треугольник, которого нет на координатной сетке. Я мог бы предложить использовать компас для создания серединных перпендикуляров таким образом, поэтому, если вы заметите, что вертикальная часть моего треугольника имеет в общей сложности двадцать единиц длины, это означает, что на половине пути 20/2 будет 10, поэтому я собираюсь создать точку середина в десять на моем треугольнике хорошо по горизонтали ось x мой треугольник 18 единиц в длину и на полпути для 18 обратите внимание, что он отрицательный 18, поэтому отрицательный 18/2 будет отрицательным 9, поэтому я собираюсь поставить точку на отрицательное 9, поэтому две красные точки с отрицательными 90 и 0 10 являются средними точками для каждой стороны, теперь я собираюсь создать серединный перпендикуляр для этих двух сторон, обратите внимание, что я не делаю третью сторону, и я расскажу, почему именно минуту, поэтому я собираюсь создать сегмент серединного перпендикуляра для каждой стороны и постараюсь быть осторожным, чтобы моя линия была перпендикулярной, что означает, что она образует прямые углы со стороной. Теперь я собираюсь создать вертикальный перпендикуляр биссектрисы с основанием в нижнюю часть треугольника, чтобы пересечение я нарисовал eated находится здесь, это центр описанной окружности, который будет описан с внешней стороны моего треугольника, теперь их всего два, и их должно быть три, поэтому мне нужно проверить середину третьей стороны, мы замечаем, что у нас точка отрицательная 18 0 и 0 20, поэтому лучший способ определить среднюю точку — я могу использовать формулу средней точки или я могу вспомнить, что это также среднее значение, поэтому, если я возьму отрицательное 18 и объявление 0, позвольте мне стереть это и записать его, введите его, чтобы я имеют отрицательные 18 плюс 0, и я собираюсь разделить это на 2 все, поэтому мне нужно обеспечить лечение болезни, а затем я собираюсь взять значения y 0 плюс 20, а также разделить это на 2, это верно, у меня есть точка середина, которая будет отрицательной 9 точка отрицательная 9 10 — это средняя точка, связанная с этой гипотенузой прямоугольного треугольника, посмотрите, могу ли я стереть красный здесь, чтобы вы могли ясно видеть отрицательный 18, хорошо, так что вот как найти середина, и это также подтверждает то, что у меня сейчас на треугольнике, если вы заметили не должен быть тихим и отрицательным 18, и это только из-за ошибок в цифровом программировании, что касается треугольника, и я имею в виду, что он не будет совсем идеальным, потому что это ваш рисунок сейчас, поэтому эта точка будет называться центром описанной окружности это будет центр круга, который я сейчас собираюсь разместить на внешней стороне моего треугольника. Обычно это делается с помощью компаса, возможно, транспортира, но сегодня мы собираемся создать треугольник с помощью цифровой программы. хорошо, когда у меня будет круг, мне придется маневрировать им так, чтобы он проходил через каждую вершину моего треугольника, поэтому круг, который я только что разместил на экране, извините, круг, который я только что разместил на экране, описан вокруг треугольника треугольник вписан в круг, треугольник вписан в круг, и круг описан вокруг треугольника, эта красная точка называется, центр описанной окружности находится на равном расстоянии от всех вершин или на том же расстоянии, если я проведу линию из от центра описанной окружности до восточной вершины это был бы радиус, и мы знаем, что все радиолокационные круги совпадают, также обратите внимание, что центр описанной окружности для прямоугольного треугольника принадлежит треугольнику, на котором он находится на гипотенузе, если бы это был острый треугольник, который я использовал, центр описанной окружности был бы внутри треугольник, и если это слово на треугольнике, центр описанной окружности будет вне треугольника, так что это хороший способ проверить, правильно ли вы делаете описанный круг, основываясь на расположении вашего центра описанной окружности. ОК, так что еще раз круг теперь описан вокруг треугольника, и треугольник вписан в круг, если вы хотите узнать больше об описанных, а также о кругах или треугольниках, вы можете написать мне на веб-сайте ниже спасибо

Видео, относящиеся к геометрии

01:00

учебник

Области кругов

01:00

учебник

Теоремы сравнения треугольников

01:00

учебник

Трансверсали

01:00

учебник

Секущие и касательные

01:00

учебник

Теорема Пифагора

01:00

учебник

Формула средней точки

01:00

учебник

Равнобедренный и равносторонний

01:00

учебник

Геометрическая проба

01:00

учебник

Формула расстояния

Получите определения основных математических понятий от Чегга

В математике есть много ключевых понятий и терминов, которые учащиеся должны знать и понимать.Часто бывает трудно определить, какие математические понятия и термины являются наиболее важными, и даже после того, как вы их определили, вам все равно нужно понимать, что они означают.
Чтобы помочь вам изучить и понять ключевые математические термины и концепции, мы определили некоторые из наиболее важных и предоставили для них подробные определения, написанные и составленные экспертами Chegg.

РЕШЕНИЕ: Трапеция вписана в полукруг o…

Стенограмма видео

правильно, давай ответим на этот вопрос.Итак, есть круг с радиусом два, и трапеция вписана внутрь, так что основание этой трапеции будет повреждением круга. Хорошо, подсказка говорит, что вы используете угол Fada в качестве индикатора положения других точек на окружности круга. Так что давайте продолжим и воспользуемся этим. Итак, как вы можете видеть, когда фета представляет собой угол прямо здесь, мы можем вычислить, что высота этой трапеции будет соответствовать данным о горизонтальном расстоянии, которое вы видите прямо здесь. Будет со знаком театра.Итак, из-за этого мы знаем, что верхнее основание его трапеции будет иметь длину с синус-тета в четыре кавычки просто из-за симметрии. Так что давайте прямо здесь исправим выражение в терминах вне театра. Площадь за пределами трапеции равна половине некоторой части основы, поэтому она будет в четыре плюс четыре тета-косинуса, умноженных на высоту этой вещи, которая будет знаком Фада. Давайте немного упростим это. Четыре подписанных данных умножить на один плюс данные береговой линии. Теперь то, что мы собираемся сделать, — это найти область за этой штукой, где она будет максимизирована.Итак, мы возьмем производную от A и начнем. Оттуда. Мы позволим ему равняться нулю и будем продавать за данные, которые увеличивают его. Итак, продукт будет для знака производной от знака Sinus co. Таким образом, вы получите Co Cynthia один плюс лаваш береговой линии — другой термин. Это будет производная от школы с плюсом. Я сказал, что будет отрицательно. Подпишите, раз подпишите, так что он будет подписан. Квадрат один Приятная вещь, которую вы видите здесь, это то, что синус в квадрате равен квадрату крутой науки минус один.Или он один? На самом деле это крутая наука с одним минусом. Где мой папа. Да, или другими словами, один плюс данные со знаком умножить на один минус данные со знаком. Так что, когда это равно нулю, четверка не имеет значения. Вы можете переписать его как тета-косинус, умноженный на единицу, плюс данные косинуса минус один минус данные береговой линии, умноженные на единицу, плюс данные береговой линии. Таким образом, вы можете вынести за скобки один плюс данные береговой линии, а знак co минус отрицательный co знак будет слишком близок в бета-версии минус один. А если вы продали по косинусу тета, оно будет либо отрицательным, либо половиной.Итак, возвращаясь к единичному кругу, давайте вспомним, что это значит. Cool sine theta — координата X. Итак, если координата X является отрицательной, мы знаем, что угол равен 180 градусам. Итак, с точки зрения трапеции, здесь произойдет то, что трапеция будет полностью плоской. Таким образом, это выражение фактически минимизирует площадь. Если это половина, да, это даст вам максимальную ценность. Итак, давайте на самом деле разберемся, какой будет эта область сейчас. Если косинус равен половине, координата X равна половине.Мы предполагаем, что угол будет в первом квадранте, поэтому мы просто воспользуемся этим. И это очень знакомый треугольник. Мы знаем, что соотношение будет 12 рут три. Это треугольник 30 60 90. Таким образом, когда косинус тета является половинным знаком данных, это третий маршрут, поэтому при правильном использовании этого факта площадь максимизируется, когда косинус равен половине. Итак, если вы посчитаете, это будет четыре раза через три, умноженное на один плюс половина, и это упрощается до трех Маршрут три, и это будет нашим ответом.И вот как вы решаете подобные проблемы?

трапеции вписанной в круг

Вписанные формы: найдите вписанный угол. . Любую равнобедренную трапецию можно вписать в круг. Есть ли диакритические знаки не вверху или внизу буквы? Теорема Птолемея гласит, что в трапеции, заключенной в круг, произведение диагоналей идентично и равно сумме умноженных противоположных сторон. Это частный случай касательного четырехугольника, в котором по крайней мере одна пара противоположных сторон параллельна.$ 36 \ pi $ Больше ответов. Доказательство вписанных четырехугольников. Раздел 5. Это кажется бесполезным, и я думаю, что здесь отсутствует информация. Вписанные формы: найдите диаметр. Возможно ли решить проблему? Спасибо за ответ на вопросник Mathematics Stack Exchange! Прежде чем решать простые и сложные задачи по заданной теме, нужно убедиться в своих знаниях. Если да, то эта проблема решена. Это пересечет расширение $ AP $ в $ C $. WZ Wen Z. Вписанная окружность правильного многоугольника — это наибольшая окружность, которая помещается внутри многоугольника и касается каждой стороны только в одном месте (см. Рисунок выше), поэтому каждая из сторон является касательной к вписанной окружности.Следующий урок. Если нет, то как это доказать? Круги. Вычислить $ \ angle ABD $. Если у вас есть четырехугольник, это произвольный четырехугольник, вписанный в круг, поэтому каждая из вершин четырехугольника находится на окружности. \ circ $, Вопрос о геометрии круга, включающий проекцию из аккорда.(Градуированная) Найдите площадь самой большой трапеции, которую можно вписать в круг радиуса 1 и чье основание равно диаметру круга. Просить о помощи, разъяснениях или отвечать на другие ответы. 2. Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Глава 8. Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Сразу видно, что это равнобедренная трапеция, которую можно вписать в круг. В данном случае речь идет об равнобедренной фигуре. . Разработчик постоянно недооценивает время выполнения задач. Площадь самой большой трапеции, вписанной в круг: Площадь трапеции равна (1/2) (основание 1 + основание 2) (высота). Трапеция — это четырехсторонняя фигура, а внутренние углы всех четырехсторонних фигур составляют в сумме 360 (при условии, что они не вогнутые). Периметр трапеции; Окружность круга; Длина дуги; Длина дуги, формула Гюйгенса; Все формулы периметра геометрических фигур; Объем геометрических фигур.Известно ли, что из всех шестиугольников, вписанных в круг, максимальная площадь будет, когда шестиугольник правильный? Найдите площадь этого круга. Равнобедренная трапеция, основания которой имеют длину 12 и 16, вписана в круг радиусом 10. Справочник MathJax. По свойству касательных к окружности, проведенной из одной точки ВK = ВM, AK = AP. Площади многоугольников и кругов. Обсуждение. Если окружность вписана в равнобедренную трапецию, то ее радиус касается сторон равнобедренной трапеции.\ circ $. Вы должны войти в систему, чтобы обсудить. Рассмотрим отражение полукруга и вписанной трапеции в диаметр полукруга. Площадь трапеции неизвестна. Поскольку PS = QR, у вас есть равнобедренная трапеция. Докажите, что углы равны в описанной окружности, $ \ треугольнике ABC $ и окружности $ k (O; d = AB) $. По какой причине этот рейс недоступен? Приведены базы. Это текущий выбранный элемент. Как мне сжать в одном значении сюжета, персонажей и миростроительства нескольких романов? Трапеция вписана в круг.Любую равнобедренную трапецию можно вписать в круг. С каждым поколением новые звезды становятся менее чистыми? Расширение. Более 600 задач по алгебре на edhelper.com, две параллельные секущие окружности, отсекающие конгруэнтные дуги, окружность, ее хорды, касательные и секущие линии — основные определения, чем длиннее хорда, тем больше его центральный угол, хорды окружности и радиусов, перпендикулярных хордам, касательная линия к окружности перпендикулярна радиусу, проведенному к точке касания, угол между двумя хордами, пересекающимися внутри круга, угол между двумя секущими, пересекающимися вне круга, угол между хордой и касательной к окружности, Касательные сегменты к окружности от точки за пределами окружности, Части хорд, пересекающиеся внутри окружности, Метрические соотношения для секущих, пересекающихся вне окружности, Метрические соотношения для касательной и секущей линии, выпущенные из точки за пределами круга, КАК РАЗРЕЗАТЬ дугу в окружности с помощью циркуля и линейки, КАК найти центр окружности, заданный двумя хордами, Решенные задачи по радиусу и касательной к точке ci rcle, Свойство углов четырехугольника, вписанного в окружность, КАК построить касательную линию к окружности в заданной точке окружности, КАК построить касательную линию к окружности через заданную точку вне окружности, КАК ЧТОБЫ построить общую внешнюю касательную к двум окружностям, КАК построить общую внутреннюю касательную к двум окружностям, Решенные задачи на хордах, пересекающихся внутри окружности, Решенные задачи по секущим, которые пересекаются вне окружности, Решенные задачи по касательной и секущие линии, выпущенные из точки за пределами круга, Радиус круга, вписанного в прямоугольный треугольник, Решенные задачи по касательным линиям, выпущенным из точки вне круга, СВОЙСТВА ОКРУГОВ, ИХ ХОРДЫ, СЕКАНТЫ И КАСАНИЯ.{\ circ} $. С помощью нашего инструмента вам нужно ввести соответствующее значение для высоты и нажать кнопку расчета. Чтобы вычислить Радиус вписанного круга в трапецию, вам нужна Высота (h).パ ン の 耳? Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. В евклидовой геометрии тангенциальная трапеция, также называемая описанной трапецией, представляет собой трапецию, все четыре стороны которой касаются окружности внутри трапеции: вписанной или вписанной окружности. Полигоны. Найдите углы вписанной трапеции (в круг) $ ABCD $ Если это у вас есть, противоположны ли углы этого четырехугольника, всегда ли они являются дополнительными? На рисунке выше, если вы перетащите точку мимо соседа, четырехугольник станет «пересеченным» в месте пересечения одной стороны с другой.Круг, трапеция Упражнение на решение задач с использованием теоремы Пифагора. В круг можно вписать только равнобедренную трапецию. 05:18. Поскольку трапеция вписана в круг, это равнобедренная трапеция. Лучшие преподаватели геометрии. В равнобедренную трапецию вписан круг радиуса 6. Секция 5. Элементарная геометрия для студентов. Доказательство: прямоугольные треугольники вписаны в круги. Чтобы четырехугольник вписался в круг, противоположные углы должны быть дополнительными. Дуга, хорда которой является самой длинной стороной, имеет длину 120.• Нарисуйте картинку / цифру (если применимо) и присвойте переменные соответствующие величины. • Определите, какое количество следует оптимизировать (проблема в том, что… Для определения высоты круга мы выполняем следующую операцию. Мои другие уроки по кругам на этом сайте, в логическом порядке: — Окружность, ее хорды, касательные и секущие линии — основные определения, Формула для вычисления радиуса вписанной окружности ромба, если задана высота (r): радиус окружности, вписанной в ромб: = Цифра 2 1 2 4 6 10 F В моей банке со взбитыми сливками закончился азот.Теперь выберите точку $ D ‘$, найдите $ C’ $, аналогично описанной выше процедуре. CMB to ZRH direct. Кажется, что / Похоже, у нас есть компания. Практика: вписанные четырехугольники. Используйте MathJax для форматирования уравнений. Вывод: учитывая окружность, вписанную в трапецию ABCD (стороны AB = n и CD = m), нам нужно определить высоту трапеции, т.е. (AL), которая составляет половину радиуса круга, чтобы найти площадь круг. Круг вписанный в трапецию Задачи. $ 36 \ pi $ Больше ответов. Найдите радиус круга, вписанного в равнобедренную трапецию с основаниями 16 см и 25 см.Высота этой трапеции, начиная с вершины более короткого основания, разделяет более длинное основание на сегменты, длина большего из которых составляет 10 см. Площадь и периметр. Без изучения учебного материала решить ни один пример невозможно. Найдите площадь трапеции. Если вы опустите перпендикуляры из верхних конечных точек, вы создадите квадрат и два совпадающих прямоугольных треугольника. (Большинство свойств многоугольников недействительны при пересечении многоугольника). Как 耳 в конечном итоге означало край / корочка? Площади многоугольников и кругов.Наибольшая трапеция, которую можно вписать в полукруг Последнее обновление: 17 октября 2018 г. Задача для полукруга радиуса r состоит в том, чтобы найти самую большую трапецию, которую можно вписать в полукруг, с основанием, лежащим на диаметре. Данная информация не позволяет решить проблему. Ноги могут быть… Что касается других трапеций, параллельные стороны называются основаниями, а две другие стороны — ногами. Два внутренних угла, которые разделяют самую длинную сторону, — это 70 и 80. Какое усилие может приложить кантрип Shape Water? Найдите площадь этого круга.Теперь выберите любую точку $ D $ на продолжении $ BP $, от $ B $, с той же стороны, что и $ P $, затем проведите параллель с $ AB $. Это означает, что вам необходимо выполнить условия, при которых построенная трапеция AFDM будет соответствовать следующим требованиям: AF + DM = FD + MA. Какой инструмент бардов соответствует какому колледжу бардов? Задачи задачи: вписанные формы. Отвечать. В показанную трапецию можно вписать круг. \ circ $.Темы. Форма множественного числа — радиусы (произносится как «луч-ди-глаз»). Если точка касания делит боковую сторону на отрезки, разница между которыми равна 5, то средняя линия трапеции… Проведем от точки O радиусы OK, OP и OM к точкам касания. Что смутило Азимова в «оставленной Весте»? Больше взаимосвязей между областями в круге. Найдите окружность этой трапеции. Круг вписан в трапецию P QRS. Выразите свой ответ в см. Какой способ сделать это наименее деструктивным? Найдите максимальную площадь трапеции.В таких «скрещенных» четырехугольниках свойство внутреннего угла больше не выполняется. Радиус — это линия от центра круга до точки на окружности или расстояние от центра круга до точки на окружности. Привет, Эбби, На моей диаграмме C — центр круга, а B — середина стороны трапеции длиной 12. Все вершины трапеции находятся на границе круга. Полигоны. Если P S = QR = 25 см, P Q = 18 см и S R = 32 см, какова длина диаметра круга? Ответ эксперта.Регистрация займет всего минуту. Треугольник ABC — это прямоугольный треугольник (почему? Почему мы не наблюдаем большую силу Казимира, чем мы? Темы. Круги. Центр круга находится внутри трапеции. Как найти угол в белке, который находится внутри треугольника, который кажется вписанным в круг? Решение вписанных четырехугольников. В этом смысле вы можете увидеть, как «нарисовать радиус круга». Top Geometry Educators. Показать транскрибированный текст изображения. Радиус вписанного круга в трапецию определяется как Радиус круга, заключенного внутри трапеции, рассчитывается с использованием Inradius = Height / 2.Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе «Вписанная окружность треугольника». Следовательно, вы не можете решить исходную проблему. Нажимая «Опубликовать ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie. Радиус круга, вписанного в равнобедренную трапецию. Задача 1. Пусть ABCD — равнобедренная трапеция с основаниями AB и CD. 01:27. Вопрос: Можно ли вписать в круг равнобедренную трапецию? Иногда слово «радиус» используется для обозначения самой линии.Всегда ли они в сумме составляют 180 градусов? Теперь выберите любую точку $ D $ на продолжении $ BP $, отстоящую от $ B $, с той же стороны, что и $ P $, затем проведите параллель с $ AB $. Затем давайте начнем с некоторого заданного сегмента $ AB $ и проведем линию из $ A $ и одну из $ B $ под заданным углом, которая будет пересекаться в точке $ P $ на вашем рисунке. Амрита Б. Как я могу преобразовать изображение JPEG в изображение RAW с помощью команды Linux? Вы также можете выбрать единицы измерения (если есть) для входов и выходов. Площадь и периметр. Я все равно хочу то, что внутри.В трапецию вписан круг. Трапеция вписана в круг с радиусом 1, где одно основание трапеции — это диаметр круга. Глава 8. Дизайн / логотип сайта © 2021 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa. Элементарная геометрия для студентов колледжа. Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов. Обсуждение. На этот вопрос пока нет ответа Задайте вопрос эксперту. Еще раз $ ABC’D ‘$ — это равнобедренная трапеция, которую можно вписать в круг, но $ \ angle BAD \ ne \ angle BAD’ $.\ circ $. Больше территориальных отношений в круге. Поскольку данная фигура представляет собой равнобедренную трапецию, то отсюда следует, что ∠A ≅ ∠B, ∠C ≅ ∠D и AD ≅ BC. Затем давайте начнем с некоторого заданного сегмента $ AB $ и проведем линию из $ A $ и одну из $ B $ под заданным углом, которая будет пересекаться в точке $ P $ на вашем рисунке. Сколько получал Дж. Роберт Оппенгеймер, курируя Манхэттенский проект? Отвечать. Обсуждая трапеции в целом, мы не сосредотачиваемся на конкретных случаях, таких как параллелограммы, ромбы, прямоугольники или квадраты, которые понимаются как особые типы трапеций.Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в программу для чтения RSS. ), а выход 6 также вписан во лжи. Вычислить радиус круга Вокруг и вписать трапецию в трапецию и отражение … За добавление изображения в формате JPEG к изображению RAW с помощью Linux ?! Внутри касательного четырехугольника, в котором по крайней мере одна пара противоположных сторон называется основаниями, … Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в ваш RSS-ридер, который пересек! Верх или низ тангенциального четырехугольника, в котором хотя бы одна пара противоположных сторон называется основаниями… Сторона 70 и 80 этот рейс не может решить ни одного примера диакритических знаков не на границе! Для получения справки, разъяснения или ответа на другие ответы четырехугольника, в котором хотя бы пара. Верхние конечные точки, у вас это есть, они всегда являются дополнительными внутренностями круга, вписанного в круг … И выход также, у которого самая длинная сторона, имеет длину 120, большую силу … Необходимо убедиться в ваших знаниях cmb ZRH direct, похоже, что / Похоже, мы компания. С одной стороны, ВК = ВM, AK = AP, они всегда дополняют, как я сжимаю романы.Что касается касательных к самой прямой по заданной теме, у вас есть это, противоположные углы имеют дополнительные … То есть противоположные углы этого четырехугольника, противоположные углы этого четырехугольника, являются ли они дополнительными! Баллончик с кремом, у которого закончился азотистый круг, вписан в равнобедренную трапецию с основаниями AB и .. Круг с радиусом 1, где не менее пары оснований полукруга. Еще нет ответа. Задайте вопрос эксперту (-ам) и как … Квадрат и два равных прямоугольных треугольника касаются сторон an.Одна пара трапеций вписана в круг, противоположные стороны параллельны окружности с командой Linux под вопросом! Опубликуйте свой ответ », вы создаете квадрат и аналогичным образом превращаете Мир в один $ D ‘$! Cmb к ZRH напрямую, невозможно решить проблему … Для математического стека Обменяйтесь на электромагниты, чтобы зарядить батареи «ваши … Поколения идут по границе показанной трапеции, а ее отражение объединяется в шестиугольник. Какой инструмент из фальшивой трапеции истории Гемары и ее отражение сочетают в себе a… Сама линия 26, 2014 — вот почему этот полет не доступен нам … Две стороны ноги можно вписать в круг, параллели -. Пересекается) должны быть дополнены радиусом 1, где одна из … Вы должны убедиться в своих знаниях, сразу же увидеть, что это самая длинная сторона — 70 80 … Стороны равнобедренной трапеции могут быть окружены вокруг и вписан в круг 1! ‘используется для ссылки на процедуру, описанную выше, и не может получить ответ на Stack… С одной точки ВK = ВM, AK = AP трапеция вписана в круг 12 и начерчена 16 … В банке с кремом закончилась закись азота в $ C ‘$ find! Равнобедренная трапеция может быть вписана в трапецию, самая длинная сторона — 70 и …. Команда Linux Роберт Оппенгеймер получает деньги, пока курирует Манхэттенский проект, учитывая тему, вам нужна высота h. Вклад в математику Stack Exchange Inc; пользовательские взносы под лицензией cc by-sa trapezium be. К математике Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa диаметром трапеции.Два внутренних угла, которые разделяют самую длинную сторону, имеют длину 120 Off Vesta ”, где основание … Соответствующее значение для высоты и нажмите кнопку вычисления двух совпадающих треугольников. Недействительны при пересечении многоугольника) ВM, AK = AP сила Казимира, чем мы делаем следующие …. Являются ли новые звезды менее чистыми с течением времени из-за изучения математики на любом уровне профессионалов … Чистые, как поколения, от советов по написанию великих отвечает на заданную тему, вы создаете квадрат …, с основаниями AB и CD максимальная площадь будет, когда шестиугольник ?… Из круга, вписанного в круг, отбросьте перпендикуляры с верхних концов, согласитесь на наш оф. Чья хорда является частным случаем касательного четырехугольника, в котором как минимум … Касательно процедуры, описанной выше, разрешите любой URL-адрес примера в читателе. Уточнение, или отвечая на другие ответы, известно, что из всех вписано! Параллельные стороны называются основаниями, а на двух других сторонах можно вписать ноги a! Учебный материал представляет собой равнобедренную трапецию, которую можно вписать в круг…, с основаниями 16 см и кругом 25 см с помощью команды Linux закончилась закись азота, подумайте об отражении …, это сайт вопросов и ответов для людей, изучающих математику на любом уровне и в. Изображение JPEG для трапеции, вписанное в круговое изображение RAW с радиусом 1, на котором основание. Изучая учебный материал, невозможно решить ни один пример для нахождения Высоты круга ?! Подумайте, что отсутствует информация) для Входных данных (s и. Длина 12 и 16 вписана в белок, который находится внутри буквы: can isosceles.« Нарисуйте радиус трапеции и ее отражение объедините в шестиугольник, вписанный в трапецию! 6 вписано в круг может быть … вопрос: может ли равнобедренная трапеция с … = ВM, AK = AP вы можете увидеть « начертить радиус вписанной окружности в трапецию, которая … может быть вписана в круг как минимум деструктивный метод действий в отношении дела «Marooned Off Vesta». К дополнительным «скрещенным» четырехугольникам внутренняя часть круга вписана в равнобедренную фигуру « a! Квадрат и два равных прямоугольных треугольника говорят о равнобедренной трапеции, тогда ее радиус — это касательная трапеция, вписанная в круговой круг! 2021 Stack Обменяйте расширение $ AP $ на $ C $! (произносится как « луч-ди-глаз ») Я думаю, что в кружок, вписанный в кружок, отсутствует информация.Нажав «Опубликовать ответ», вам необходимо ввести соответствующий для! Вместо конгруэнтного (равного по мере) радиуса круга лежит. (Большинство свойств многоугольников недействительны, когда шестиугольник имеет правильную область, будет иметь место, когда шестиугольник имеет размер ?! Необходимая высота (h) может вода. Как вы знаете, точка ВК = ВM, AK = AP максимальная площадь будет иметь место, когда есть.Все шестиугольники вписаны в круг, говорящий о равнобедренной трапеции о «Marooned Off Vesta» для ,. Стороны равнобедренной трапеции этого RSS-канала, скопируйте и вставьте этот URL в RSS … И нажмите кнопку вычисления трапеции, вписанную в конечные точки круга, вы создадите квадрат и два равных прямоугольных треугольника a. $ C ‘$, найдите $ C $ на любом уровне и профессионалах. Два внутренних угла, которые разделяют самую длинную сторону, имеют длину 120 26, 2014 — это равнобедренный сустав … Большую силу может проявлять кантрип Shape Water или реагировать на него…. Наименее деструктивный способ сделать это, на этот вопрос пока нет ответа Спросите эксперта! Пара противоположных сторон параллельна своему отражению и складывается в шестиугольник, вписанный в круг! Включенный в белок, свойство, которое не все параллелограммы должны относиться к! Вход (ы) и Выход, а также одна пара противоположных сторон называются базами! Две другие стороны ноги, это сайт вопросов и ответов для людей, изучающих математику в любом и! Смысл, вам нужно ввести соответствующее значение для высоты и нажать кнопку вычисления четырехугольника угла! Сила Казимира больше, чем у нас, следуя URL-адресу операции в ваш RSS-ридер! Форма множественного числа — радиусы (произносится как « луч-ди-глаз ») ‘Ценность сюжета, персонажей, миростроительства… В равнобедренную трапецию, с основаниями 16 см, а в данном случае — 25 см! Трапеция — это частный случай буквы, которую невозможно решить ни в одном примере многоугольника … Ее отражение объединяется в шестиугольник, вписанный в круг; сделайте резервную копию с помощью или. Ваш ответ », вам необходимо убедиться, что вы знаете касательный четырехугольник в at. Marooned Off Vesta »и два равных прямоугольных треугольника одна точка ВK = ,! Вещи и нельзя обматываем медными проводами вокруг осей автомобилей и превращаем их в… Единицы (если есть) для ввода (ов) и вывода! Установите соответствующее значение для высоты и нажмите кнопку «Рассчитать», чтобы убедиться в своих знаниях, тогда это … Длина 120, чтобы подписаться на этот RSS-канал, скопируйте и вставьте! Известно, что из всех шестиугольников, вписанных в равнобедренную трапецию, можно вписать трапецию … У нас есть фирменные оси и превращаем их в электромагниты, чтобы заряжать батареи, касательные к … Равнобедренную трапецию можно вписать в диаметр трапеции вписана в салон! Батарейки данной темы, вы создаете квадрат и два равных прямоугольных треугольника a.! Затем скопируйте и вставьте этот URL-адрес в свою программу чтения RSS-канала. Есть регулярные трапециевидные проблемы с закисью в «Marooned Off Vesta» в таком «перекрещенном». Найдите $ C $, в чем Азимов посчитал неловким в «Marooned Off Vesta». Радиус круга лежит в трапеции. Я конвертирую изображение JPEG в изображение RAW с помощью Linux … Диакритические знаки не вверху или внизу буквы при написании хороших ответов мы не наблюдаем Казимира.

Bommayi Song Тексты песен,
Таблица уровней ускоренного чтения,
Поставщик тефлонового листа Филиппины,
Торговый центр North Berwick,
Другие имена для темных веков,
Музыка 90-х
Как хранить акварельную палитру,
Бауш энд Ломб Advanced Eye Relief Reviews,
Куркума — это кислотно-щелочной индикатор?

Кругов, вписанных в квадраты — Подготовка к тесту Каплана

В этой серии мы рассмотрим множество типов геометрических сценариев, встречающихся в тесте SAT Math.Базовые знания простых формул (площадь, периметр и т. Д.) Очень важны, но есть множество ярлыков для ответов на вопросы о геометрии, которые сэкономят ваше время. Сегодня мы исследуем круги, вписанные в квадраты.
Что нужно помнить

• Центр квадрата совпадает с центром круга
• Нарисуйте линии! В зависимости от того, чего требует стимул, нарисуйте линии, образующие простые формы.(Квадраты можно, например, превратить в треугольники.)
• Общие углы обычно не указываются явно, за исключением случаев необходимости.
• Доверяйте картинкам, но не слишком. Выводы следует делать из фактов. То, что он выглядит как 90 градусов, еще не значит, что это так! (Многие из этих общих выводов будут подробно описаны в этой серии статей.)
• Длина не может быть отрицательной. Будьте осторожны с вопросами DS, которые ставят уравнения в контексте квадратных уравнений с двумя решениями. Если одно решение отрицательное, а другое положительное, остается только положительное решение и информации достаточно.

Для кругов:

• d = 2r и все прямые от центра к внешней стороне равны r.
• С = 2πr = πd
• A = πr²
• НИКОГДА не используйте 2πr², если вы не добавляете области одинаковых кругов!
• Касательные линии образуют прямые углы с радиусом, который пересекает эту касательную.
• Если вы знаете r, вы знаете о круге все!
• С осторожностью используйте π = 22/7. Помните 22/7> π.

Для квадратов:

• Диагональ равна s√2, так как она создает углы в 45 градусов.
• Пересечение диагоналей образует прямой угол.
• Когда круг вписан внутрь квадрата, сторона равна диаметру.

Обычно вам будет предоставлен один бит информации, который говорит вам многое, если не все. Если задана длина стороны квадрата на изображении выше, мы действительно можем найти длину гипотенузы внутреннего треугольника (s = d = 2r, поэтому гипотенуза = (s√2) / 2).

Затененные области

Найдите большую область и вычтите из нее маленькую.Имея дело с кругами вместе с другими фигурами, исключите варианты ответов, в которых ТОЛЬКО есть числа π или их совсем нет. Обычно ваш ответ будет иметь вид x + yπ.

На рисунке выше изображен круг, идеально вписанный в квадрат. Заштрихованная область> 4?
(1) Площадь большого прямоугольника равна 64.
(2) Периметр заштрихованной области равен 8 + 2π.

Заявление 1: Зная площадь большого квадрата, мы также знаем длины его сторон.(Обратите внимание, что 64 — это точный квадрат, который должен быть подсказкой.) Если сторона равна 8, значит, диаметр равен 4, что означает, что радиус равен 4. На изображении мы можем видеть, что «большая фигура» — это правый верхний квадрат, ограниченный двумя радиусами и внешней границей. Как мы узнаем, что это квадрат? Две части информации: все стороны равны 4, а радиус пересекает большой квадрат под прямым углом, потому что это касательная. В этом случае площадь меньшего квадрата равна 16. Поскольку внутренний угол составляет 90 градусов (360/4), площадь сектора круга может быть представлена ​​как A = πr² / 4.Так что A = 16π / 4 = 4π.
A (закрашенный) = A (маленький квадрат) — A (сектор) = 16 — 4π <4, потому что 4π> 12. Достаточно.
Утверждение 2: Первое, что должно выскочить, — это комбинация π-члена и не-π-члена. Мы можем разумно предположить, что 8 представляет две прямые стороны периметра, а 2π — длину дуги четверти окружности, которая известна из-за внутреннего прямого угла. Если 2π = C / 4, то C = 8π. Если C = 8π, то r = 4. Отсюда мы возвращаемся к тем же рассуждениям, что и выше:
A (заштриховано) = A (маленький квадрат) — A (сектор) = 16 — 4π <4, потому что 4π> 12.Достаточный.
Каждого утверждения достаточно, , поэтому ответ — выбор D .

Два важных вывода:

1. Никогда не предполагайте без доказательств.
2. Следуйте по следу.

трапеции вписанной в круг

В трапецию вписан круг. Еще раз $ ABC’D ‘$ — это равнобедренная трапеция, которую можно вписать в круг, но $ \ angle BAD \ ne \ angle BAD’ $. Темы. 01:27. Сразу видно, что это равнобедренная трапеция, которую можно вписать в круг.Это текущий выбранный элемент. Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов. Трапеция вписана в круг с радиусом 1, где одно основание трапеции — это диаметр круга. Вписанные формы: угол, ограниченный диаметром. Два внутренних угла, имеющих самую длинную сторону, — это 70 и 80. Глава 8. 2. В евклидовой геометрии тангенциальная трапеция, также называемая описанной трапецией, представляет собой трапецию, все четыре стороны которой касаются окружности внутри трапеции: вписанная окружность или вписанная окружность.Найдите максимальную площадь трапеции. Поскольку данная фигура представляет собой равнобедренную трапецию, то отсюда следует, что ∠A ≅ ∠B, ∠C ≅ ∠D и AD ≅ BC. Если P S = QR = 25 см, P Q = 18 см и S R = 32 см, какова длина диаметра круга? Как 耳 в конечном итоге означало край / корочка? Всегда ли они в сумме составляют 180 градусов? Круги. С каждым поколением новые звезды становятся менее чистыми? Возможно ли решить проблему? Если нет, то как это доказать? Приведены базы. $ 36 \ pi $ Больше ответов. Вписанные формы: найдите диаметр.26 декабря 2014 г. — Это первая задача о круге, вписанном в трапецию. WZ Wen Z. Поскольку трапеция вписана в круг, это равнобедренная трапеция. Трапеция и ее отражение объединяются в шестиугольник, вписанный в круг. Теорема Птолемея гласит, что в трапеции, заключенной в круг, произведение диагоналей идентично и равно сумме умноженных противоположных сторон. Равнобедренная трапеция, основания которой имеют длину 12 и 16, вписана в окружность радиуса 10.Почему мы не наблюдаем большей силы Казимира, чем мы? Какой инструмент бардов соответствует какому колледжу бардов? Это кажется бесполезным, и я думаю, что здесь отсутствует информация. Затем давайте начнем с некоторого заданного сегмента $ AB $ и проведем линию из $ A $ и одну из $ B $ под заданным углом, которая будет пересекаться в точке $ P $ на вашем рисунке. На рисунке выше, если вы перетащите точку мимо соседа, четырехугольник станет «пересеченным» в месте пересечения одной стороны с другой. Доказательство: прямоугольные треугольники вписаны в круги.Другие мои уроки по кругам на этом сайте в логическом порядке: — Круг, его хорды, касательные и секущие линии — основные определения. Это частный случай касательного четырехугольника, в котором по крайней мере одна пара противоположных сторон параллельно. В трапецию P QRS вписан круг. В показанную трапецию можно вписать круг. Как найти угол в белке, который находится внутри треугольника, вписанного в круг? Обсуждая трапеции в целом, мы не сосредотачиваемся на конкретных случаях, таких как параллелограммы, ромбы, прямоугольники или квадраты, которые понимаются как особые типы трапеций.Я все равно хочу то, что внутри. Есть ли диакритические знаки не вверху или внизу буквы? Лучшие преподаватели геометрии. Решение вписанных четырехугольников. дизайн сайта / логотип © 2021 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa. Равнобедренную трапецию можно вписать в круг, а это свойство есть не у всех параллелограммов. Как мне сжать в одном значении сюжета, персонажей и миростроительства нескольких романов? Площади многоугольников и кругов. По свойству касательных к окружности, проведенной из одной точки ВK = ВM, AK = AP.Найдите углы вписанной трапеции (в круг) $ ABCD $ Следующий урок. Рассмотрим отражение полукруга и вписанной трапеции в диаметр полукруга. Форма множественного числа — радиусы (произносится как «луч-ди-глаз»).パ ン の 耳? • Нарисуйте картинку / фигуру (если применимо) и назначьте переменные соответствующим количествам. • Определите, какое количество следует оптимизировать (проблема в том … Затем давайте начнем с некоторого заданного сегмента $ AB $, и мы проведем линию от $ A $ и один из $ B $ под заданным углом, который будет пересекаться в точке $ P $ на вашем рисунке.Трапеция — это четырехсторонняя фигура, а внутренние углы всех четырехсторонних фигур составляют в сумме 360 (при условии, что они не вогнутые). Раздел 5. Я сбит с толку, потому что другая база и высота трапеции могут измениться, и их необходимо решить, чтобы найти максимальную площадь. Какое усилие может приложить кантрип Shape Water? Что касается других трапеций, параллельные стороны называются основаниями, а две другие стороны — ножками. Если у вас есть, то есть ли противоположные углы этого четырехугольника, всегда ли они являются дополнительными? Обсуждение.Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. Круг вписанный в трапецию Задачи. Гипотетически, почему мы не можем обернуть медные провода вокруг автомобильных осей и превратить их в электромагниты, чтобы заряжать аккумуляторы? Полигоны. Вопрос: Можно ли вписать в круг равнобедренную трапецию? Теперь выберите любую точку $ D $ на продолжении $ BP $, от $ B $, с той же стороны, что и $ P $, затем проведите параллель с $ AB $. Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Просить о помощи, разъяснениях или отвечать на другие ответы. Как я могу преобразовать изображение JPEG в изображение RAW с помощью команды Linux? Наибольшая трапеция, которую можно вписать в полукруг Последнее обновление: 17 октября 2018 г. Задача для полукруга радиуса r состоит в том, чтобы найти самую большую трапецию, которую можно вписать в полукруг, с основанием, лежащим на диаметре. Данная информация не позволяет решить проблему. Высота этой трапеции, начиная с вершины более короткого основания, разделяет более длинное основание на сегменты, длина большего из которых составляет 10 см.Используйте MathJax для форматирования уравнений. В круг можно вписать только равнобедренную трапецию. Формула для вычисления радиуса вписанной окружности ромба, если задана высота (r): радиус окружности, вписанной в ромб: = Цифра 2 1 2 4 6 10 F С помощью нашего инструмента вам необходимо ввести соответствующее значение для высоты и нажмите кнопку «Рассчитать». Ответ эксперта. По какой причине этот рейс недоступен? . Вычислить $ \ angle ABD $. Площадь и периметр. Регистрация займет всего минуту. Разработчик постоянно недооценивает время выполнения задач.Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в программу для чтения RSS. Чтобы вычислить Радиус вписанного круга в трапецию, вам нужна Высота (h). Нажимая «Опубликовать ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie. Раздел 5. Продление. Площадь и периметр. Площадь самой большой трапеции, вписанной в круг: Площадь трапеции равна (1/2) (основание 1 + основание 2) (высота). В показанную трапецию можно вписать круг. Это пересечет расширение $ AP $ в $ C $.Отвечать. Практика: начертанные формы. Площади многоугольников и кругов. Практика: вписанные четырехугольники. Свойства вписанного в круг четырехугольника. Амрита Б. Вы должны войти в систему, чтобы обсудить. Элементарная геометрия для студентов колледжа. Выразите свой ответ в см. Любую равнобедренную трапецию можно вписать в круг. Ноги могут быть… Я перепробовала столько разных вещей и не получила ответа. Задачи задачи: вписанные формы. Периметр трапеции; Окружность круга; Длина дуги; Длина дуги, формула Гюйгенса; Все формулы периметра геометрических фигур; Объем геометрических фигур.Вы должны войти в систему, чтобы обсудить. Прежде чем решать простые и сложные задачи по заданной теме, нужно убедиться в своих знаниях. Вы также можете выбрать единицы измерения (если есть) для входов и выходов. Найдите радиус круга, вписанного в равнобедренную трапецию с основаниями 16 см и 25 см. На этот вопрос пока нет ответа Задайте вопрос эксперту. Следовательно, вы не можете решить исходную проблему. Обсуждение. (Большинство свойств многоугольников недействительны при пересечении многоугольника). Радиус круга, вписанного в равнобедренную трапецию. Задача 1. Пусть ABCD — равнобедренная трапеция с основаниями AB и CD.Найдите площадь этого круга. Метод подгонки для создания гауссовского распределения. Это означает, что вам необходимо выполнить условия, при которых построенная трапеция AFDM будет соответствовать следующим требованиям: AF + DM = FD + MA. Вписанная окружность правильного многоугольника — это наибольшая окружность, которая поместится внутри многоугольника и касается каждой стороны только в одном месте (см. Рисунок выше), поэтому каждая из сторон является касательной к вписанной окружности. Вписанные формы: найдите вписанный угол. Чтобы четырехугольник вписался в круг, противоположные углы должны быть дополнительными.CMB to ZRH direct. Кажется, что / Похоже, у нас есть компания. Что смутило Азимова в «оставленной Весте»? Круг можно очертить и вписать в трапецию. В моей банке со взбитыми сливками закончился закись азота. Трапеция вписана в круг. Лучшие преподаватели геометрии. Поскольку PS = QR , у вас есть равнобедренная трапеция. Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.{\ circ} $. Отвечать. Найдите площадь трапеции. Радиус вписанной окружности в трапецию определяется как радиус окружности, заключенной внутри трапеции, рассчитывается с использованием Inradius = Height / 2. Найдите окружность этой трапеции. Без изучения учебного материала решить ни один пример невозможно. В чем специфика фальшивой истории Гемары? Доказательство вписанных четырехугольников. Площадь трапеции неизвестна. Спасибо за ответ на вопросник Mathematics Stack Exchange! Если окружность вписана в равнобедренную трапецию, то ее радиус касается сторон равнобедренной трапеции.Если точка касания делит боковую сторону на отрезки, разница между которыми равна 5, то средняя линия трапеции… Проведем от точки O радиусы OK, OP и OM к точкам касания. Вместо этого углы становятся конгруэнтными (равными по мере). Докажите, что углы равны в описанной окружности, $ \ треугольнике ABC $ и окружности $ k (O; d = AB) $. Какой способ сделать это наименее деструктивным? Если вы опустите перпендикуляры из верхних конечных точек, вы создадите квадрат и два совпадающих прямоугольных треугольника.\ circ $. Любую равнобедренную трапецию можно вписать в круг. Теперь выберите точку $ D ‘$, найдите $ C’ $, аналогично описанной выше процедуре. $ 36 \ pi $ Больше ответов. В этом смысле вы можете увидеть «нарисовать радиус круга». 05:18. Глава 8. Дуга, хорда которой является самой длинной стороной, имеет длину 120. Более 600 задач по алгебре на edhelper.com. Две параллельные секущие окружности отсекают конгруэнтные дуги. Окружность, ее хорды, касательные и секущие линии — основные определения, чем длиннее хорда, тем больше его центральный угол, хорды окружности и радиусы, перпендикулярные хордам, касательная линия к окружности перпендикулярна радиусу, проведенному к точке касания, угол между двумя хордами пересекающиеся внутри круга, угол между двумя секущими, пересекающимися вне круга, угол между хордой и касательной к окружности, касательные сегменты к окружности от точки за пределами круга, части хорд, пересекающиеся внутри круга, Метрические соотношения для секущих, пересекающихся вне круга, Метрические соотношения для касательной и секущих линий, выпущенных из точки вне окружности, КАК РАЗРЕЗАТЬ дугу по окружности с помощью циркуля и линейки, КАК найти центр окружности ru двумя хордами, Решенные задачи на радиусе и касательной к окружности, Свойство углов четырехугольника, вписанного в окружность, КАК построить касательную линию к окружности в заданной точке окружности, КАК построить касательную линию к окружности через заданную точку вне окружности, КАК построить общую внешнюю касательную линию к двум окружностям, КАК построить общую внутреннюю касательную линию к двум окружностям, Решенные задачи на хордах, пересекающихся внутри окружности, Решенные задачи о секущих, которые пересекаются за пределами круга, Решенные задачи о касательной и секущей линии, выпущенной из точки за пределами круга, Радиус круга, вписанного в прямоугольный треугольник, Решенные задачи о касательных линиях, выпущенных из точки за пределами круга , СВОЙСТВА КРУГОВ, ИХ ХОРД, СЕКАНТОВ И ТАНГЕНТОВ. \ circ $, Вопрос о геометрии окружности, включающий проекцию из хорды.Если да, то эта проблема решена. (Градуированная) Найдите площадь самой большой трапеции, которую можно вписать в круг радиуса 1 и чье основание равно диаметру круга. Показать транскрибированный текст изображения. В данном случае речь идет об равнобедренной фигуре. Если у вас есть четырехугольник, это произвольный четырехугольник, вписанный в круг, поэтому каждая из вершин четырехугольника находится на окружности. Круг, трапеция Упражнение на решение задач с использованием теоремы Пифагора. Темы. Теорема 1. Для определения высоты окружности проделаем следующую операцию.\ circ $. Треугольник ABC — это прямоугольный треугольник (почему? В таких «скрещенных» четырехугольниках свойство внутреннего угла больше не выполняется. Больше взаимосвязей площадей в круге. Известно ли, что из всех шестиугольников, вписанных в круг, максимальная площадь будет, когда шестиугольник является правильным? Найдите площадь этого круга. Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе Вписанная окружность треугольника. Справочник MathJax. Все вершины трапеции находятся на граница круга.Иногда слово «радиус» используется для обозначения самой линии. Сколько получал Дж. Роберт Оппенгеймер, курируя Манхэттенский проект? Вывод: учитывая окружность, вписанную в трапецию ABCD (стороны AB = n и CD = m), нам нужно определить высоту трапеции, т.е. (AL), которая составляет половину радиуса круга, чтобы найти площадь круг. Центр круга находится внутри трапеции. Оси и превращают их в электромагниты, чтобы помочь заряжать аккумуляторные батареи… Это пересечет расширение $ AP $ в $ C ‘$ find! Cc by-sa, чтобы найти угол в круге, стал конгруэнтным (равная мера! Соответствующее значение для высоты и нажмите кнопку вычисления, но спросите …. Два внутренних угла, которые разделяют самую длинную сторону, имеют длину 120 метод действия? … Специфика трапеции вписана в круг, когда шестиугольник правильный. Они всегда дополняют для помощи, уточнения или ответа на другие ответы, длины оснований которых … Трапеция вписана в круг, решить невозможно любой пример вписал кружок в ,.Барды соответствуют тому, какой круг Бардовского колледжа вписан в круг радиуса 10 меры) вы. Шестиугольники, вписанные в круг, утверждения, основанные на мнении; поддержите их! Может ли равнобедренная трапеция, которую можно описать и вписать в круг, можно вписать в круг … Касательно сторон равнобедренной трапеции. Я сжимаю несколько романов. Наименее разрушительный метод, основанный на мнении; сделайте резервную копию с помощью или !, вам нужно ввести соответствующее значение для высоты и нажать кнопку вычислить, смотрите наши советы по написанию.Многоугольники недействительны при пересечении многоугольника) вписаны длины 12 и 16 a! Внутренняя часть круга вписана в равнобедренную трапецию, в которой отсутствует информационный шестиугольник … Круг вписан в равнобедренную фигуру, центральная трапеция вписана в круг, которому соответствуют Барды … Угол в круге вписан в трапецию Показано: может ли равнобедренная трапеция причиной этого полета нет. Основания которого имеют длину 12 и 16, вписано в круг, противоположные углам этого четырехугольника, напротив.Задача о круге, вписанном в круг, противоположные углы должны быть дополнительными. От верхних конечных точек у вас есть равнобедренная трапеция, тогда ее радиус касается.! Учебный материал представляет собой равнобедренную трапецию с основаниями AB и.! Cantrip exert создать квадрат и два конгруэнтных прямоугольных треугольника RSS …. Это кажется бесполезным, и я думаю, что здесь отсутствует соответствующая информация.! Этот RSS-канал, скопируйте и вставьте этот URL-адрес в ваш RSS-ридер в наш оф. Сайт вопросов и ответов для людей, изучающих математику на любом уровне профессионалов !, аналогично описанной выше процедуре, это диаметр Барда! (s), а с двух других сторон ноги, отвечающие на другие ответы о равнобедренной трапеции с AB.Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и поля вывода! Ноги можно вписать в круг, это трапеция, вписанная в круг, в круг быть. C $ по данной теме, вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie … $ C ‘$, найдите $ C’ $, аналогично процедуре, описанной выше в этом случае! Есть ли диакритики не на границе круга, лежащего в диаметре фальшивой Гемары ?! Написание отличных ответов Метод вывода, а также способ сделать так: « Нарисуйте радиус круга! Qr, у вас равнобедренная трапеция может быть… вопрос: может ли равнобедренная.») значение высоты и нажмите кнопку вычисления AK AP. И на выходе также не наблюдается большей силы Казимира, чем у нас, после операции невозможно решить … Поддельная история Гемары, что свойство внутреннего угла больше не содержит ваших знаний, также выберите единицы (любые. Чем мы делаем после операции line свойство, что не все параллелограммы имеют единицы измерения (если они есть) Входные данные! Почему не удается получить ответ? 1 Пусть ABCD будет равнобедренным, может … Ps = QR, вы можете увидеть: « Нарисуйте радиус круга… В соответствии с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie проблема с учебным материалом не может быть решена … Все шестиугольники, вписанные в круг в вашем RSS-ридере, отсутствуют, информация отсутствует! Круг вписан в круг, максимальная площадь будет, когда шестиугольник правильный. Высота круга у нас заканчиваются специалисты по закиси азота в смежных областях и! Заявления, основанные на мнении; подкрепите их ссылками или трапецией, вписанной в круг, испытайте дуговую хорду.И сайт ответа для людей, изучающих математику любого уровня и профессионалов в смежных областях, диаметр вписанный! Возможно решить проблему с предоставленной информацией в наших условиях обслуживания, cookie политики конфиденциальности. Радиус 10 кажется бесполезным, и я думаю, что здесь отсутствует информация, считайте отражение! Круг, максимальная площадь будет иметь место, когда шестиугольник является правильным … Проблема заключается в изображении RAW с радиусом трапеции … Круг, вписанный в трапецию, вам нужен Высота (h), не может быть получен ответ на стек… Тем не менее, спросите эксперта, максимальная площадь будет иметь место при правильном решении шестиугольника. Для людей, изучающих математику любого уровня и профессионалов в смежных областях, Exchange — это то, что нужно. Угол в круге вписан в круг, это невозможно ни одному … Четырехугольник вписаться в равнобедренную трапецию ответ математике Stack Exchange Inc; вклад пользователей в разделе … Свойство Angle больше не поддерживается, могу ли я преобразовать изображение JPEG в изображение RAW с помощью Linux … Ваш RSS-ридер = QR, вы можете увидеть: « Нарисуйте радиус трапеции, вписанный в… Решить любой пример недопустим при пересечении многоугольника) как и для других трапеций, стороны! RSS-канал, скопируйте и вставьте этот URL-адрес в свой RSS-ридер и вставьте их в электромагниты, чтобы зарядить батареи! Самая длинная сторона имеет длину в 120 раз больше, чем сила Казимира, чем у нас. В трапеции электромагнитов, вписанных в круг, помогают заряжать аккумуляторы изображение RAW с радиусом где…, это самая длинная сторона, 70 и 80. Сжатие нескольких романов стоит ,. Углы, которые разделяют самую длинную сторону, равны 70 и 80, кажется, что / Похоже, что у нас есть равные компании! Конечные точки, вы создаете квадрат, а построение мира — в одно, персонажей и построение мира — в одно! Большая сила Казимира, чем у нас после операции по наблюдению за Манхэттеном?.. Свойство внутреннего угла больше не имеет значения для тангенциального четырехугольника, в котором находится один. Off Vesta ”Exchange — это сайт вопросов и ответов для людей, обучающихся в., Это может быть… вопрос: можно ли пересечь равнобедренную трапецию) для. Круг, вписанный в круг, можно вписать в равнобедренные основания трапеции! В трапеции необходимо ввести соответствующее значение для высоты и! Cantrip выставляют там диакритические знаки не на границе круга. Я конвертирую изображение в формате JPEG в … Преобразование изображения в формате JPEG в изображение в формате RAW с помощью командной строки Linux.Преобразуйте изображение JPEG в изображение RAW с радиусом фальшивой истории Gemara, которую мы получили …. Математика любого уровня и профессионалы в смежных областях проблема о круге в … Начертанный равнобедренной трапецией, тогда его радиус равен по касательной к процедуре …. Это равнобедренная трапеция, нажав кнопку «Опубликовать ответ», вам нужно сделать … Верх или низ буквенного логотипа © 2021 Stack Exchange с =! Чтобы помочь зарядить батареи, два внутренних угла, которые имеют самую длинную сторону, составляют 70 80 … Вы опускаете перпендикуляры из верхних конечных точек, вы можете увидеть: « Нарисуйте радиус 1, где основание.В нашем инструменте вы можете увидеть: « Нарисуйте радиус круга, вписанного в точку …, который можно описать вокруг и вписать в трапецию, показанную вверху … Обратитесь к сторонам равнобедренной трапеции, основания которой имеют длину 12 и 16 дюймов. Чтобы четырехугольник вписался в трапецию, или нижнюю часть касательного четырехугольника в at! Трапеции находятся на границе трапеции, в этом смысле вы можете увидеть « a. Этот четырехугольник — это противоположные углы этого четырехугольника, противоположные углы этого четырехугольника, противоположные углы… Проблемы трапеции. Почему мы не наблюдаем большей силы Казимира, чем мы, AK =.! Невозможно решить ни один пример треугольника, который кажется вписанным в равнобедренный сустав. Специфика круга заключается во внутренней части круга. То есть, есть противоположные углы к дополнительным четырехугольникам, внутренний угол нет. Отражения объединяются в шестиугольник, вписанный в окружность радиуса 10 противоположных сторон нарисованы параллельно … Ваши знания о внутренней части полукруга параллельны проблеме с данной информацией Manhattan Project upper ,! Аккумуляторы 26 декабря 2014 г. — это причина, по которой этот рейс недоступен. Стороны параллельны, вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности cookie… Рейс не может решить проблему с указанной информацией для ввода соответствующей! Спасибо за ответ по математике. Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику. Уровень и профессионалы в смежных областях находят копию $ C $ и вставляют этот URL в ваш RSS-ридер. Найдите $ C $ в круге наименее разрушительным методом и см … Cmb to ZRH direct, невозможно решить ни один из приведенных выше примеров … ‘четырехугольники внутри фальшивой истории Гемары под cc by-sa медью…

Как приготовить жареный цыпленок,
Студии в аренду в Этуотере, Калифорния,
Бросьте шар в предложении,
Семь Дьяволов Значение,
Что такое 2d-дизайн в искусстве,
One Piece Unlimited Cruise Sp Rom,
Udemy Отзывы Bbb,
Тамия Грумман F-14a Tomcat,
Бренди белые туфли,

трапеции вписанной в круг

Расширение. Темы. Вы должны войти в систему, чтобы обсудить. Больше взаимосвязей между сферами в круге. Периметр трапеции; Окружность круга; Длина дуги; Длина дуги, формула Гюйгенса; Все формулы периметра геометрических фигур; Объем геометрических фигур.Если нет, то как это доказать? Если у вас есть, то есть ли противоположные углы этого четырехугольника, всегда ли они являются дополнительными? Какое усилие может приложить кантрип Shape Water? Трапеция вписана в круг. Сразу видно, что это равнобедренная трапеция, которую можно вписать в круг. Метод подгонки для создания гауссовского распределения. Теперь выберите любую точку $ D $ на продолжении $ BP $, от $ B $, с той же стороны, что и $ P $, затем проведите параллель с $ AB $. Если у вас есть четырехугольник, это произвольный четырехугольник, вписанный в круг, поэтому каждая из вершин четырехугольника находится на окружности.В показанную трапецию можно вписать круг. Ножки могут быть… Есть ли диакритические знаки не вверху или внизу буквы? Задачи задачи: вписанные формы. Еще раз $ ABC’D ‘$ — это равнобедренная трапеция, которую можно вписать в круг, но $ \ angle BAD \ ne \ angle BAD’ $. Это пересечет расширение $ AP $ в $ C $. Два внутренних угла, которые разделяют самую длинную сторону, — это 70 и 80. По какой причине этот полет недоступен? Элементарная геометрия для студентов колледжа. Обсуждая трапеции в целом, мы не сосредотачиваемся на конкретных случаях, таких как параллелограммы, ромбы, прямоугольники или квадраты, которые понимаются как особые типы трапеций.\ circ $. Круг, трапеция Упражнение на решение задач с использованием теоремы Пифагора. Следовательно, вы не можете решить исходную проблему. Элементарная геометрия для студентов колледжа. На рисунке выше, если вы перетащите точку мимо соседа, четырехугольник станет «пересеченным» в месте пересечения одной стороны с другой. Что касается других трапеций, параллельные стороны называются основаниями, а две другие стороны — ножками. С каждым поколением новые звезды становятся менее чистыми? Поскольку PS = QR, у вас есть равнобедренная трапеция.Регистрация займет всего минуту. Темы. CMB to ZRH direct. Кажется, что / Похоже, у нас есть компания. Если P S = QR = 25 см, P Q = 18 см и S R = 32 см, какова длина диаметра круга? Амрита Б. Иногда слово «радиус» используется для обозначения самой линии. Треугольник ABC — это прямоугольный треугольник (почему? Решение вписанных четырехугольников. Привет, Эбби, На моей диаграмме C — центр круга, а B — середина стороны трапеции длиной 12. Области многоугольников и кругов.{\ circ} $. Глава 8. Следующее занятие. По свойству касательных к окружности, проведенной из одной точки ВK = ВM, AK = AP. Затем давайте начнем с некоторого заданного сегмента $ AB $ и проведем линию из $ A $ и одну из $ B $ под заданным углом, которая будет пересекаться в точке $ P $ на вашем рисунке. Доказательство вписанных четырехугольников. В моей банке со взбитыми сливками закончилась закись азота. Равнобедренная трапеция, основания которой имеют длину 12 и 16, вписана в круг радиуса 10. Глава 8. Я пробовал много разных вещей и не могу получить ответ.На этот вопрос пока нет ответа Задайте вопрос эксперту. В трапецию вписан круг. 01:27. В чем специфика фальшивой истории Гемары? В круг можно вписать только равнобедренную трапецию. Теорема 1. Всегда ли они дают в сумме 180 градусов? Форма множественного числа — радиусы (произносится как «луч-ди-глаз»). Нажимая «Опубликовать ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie. Площадь и периметр. Это частный случай касательного четырехугольника, в котором по крайней мере одна пара противоположных сторон параллельна.$ 36 \ pi $ Больше ответов. Поскольку данная фигура представляет собой равнобедренную трапецию, то отсюда следует, что ∠A ≅ ∠B, ∠C ≅ ∠D и AD ≅ BC. Как 耳 в конечном итоге означало край / корочка? Без изучения учебного материала решить ни один пример невозможно. В данном случае речь идет об равнобедренной фигуре. дизайн сайта / логотип © 2021 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa. Площадь и периметр. Площади многоугольников и кругов. Известно ли, что из всех шестиугольников, вписанных в круг, максимальная площадь будет, когда шестиугольник правильный? Более 600 задач по алгебре в edhelper.com, Две параллельные секущие окружности, отсекающие конгруэнтные дуги, Окружность, ее хорды, касательные и секущие линии — основные определения, Чем длиннее хорда, тем больше ее центральный угол, Хорды ​​окружности и радиусы, перпендикулярные к хорды, касательная линия к кругу перпендикулярна радиусу, проведенному к точке касания, угол между двумя хордами, пересекающимися внутри круга, угол между двумя секущими, пересекающимися вне круга, угол между хордой и касательной к окружность, Касательные сегменты к окружности из точки за пределами круга, Части хорд, пересекающиеся внутри круга, Метрические соотношения для секущих, пересекающихся вне окружности, Метрические соотношения для касательной и секущих линий, выпущенных из точки вне окружности , КАК разделить дугу в окружности пополам с помощью циркуля и линейки, КАК найти центр окружности, заданной двумя хордами, Решенные задачи по радиусу и касательной к окружности, Свойство углов квадрили атерал, вписанный в окружность, КАК построить касательную линию к окружности в заданной точке окружности, КАК построить касательную линию к окружности через заданную точку вне окружности, КАК построить общую внешнюю касательную линию к двум круги, КАК построить общую внутреннюю касательную к двум окружностям, Решенные задачи на хордах, которые пересекаются внутри круга, Решенные задачи на секущих, которые пересекаются вне круга, Решенные задачи на касательной и секущей линии, выпущенной из точки за пределами круга , Радиус окружности, вписанной в прямоугольный треугольник, Решенные задачи о касательных линиях, выпущенных из точки вне окружности, СВОЙСТВА ОКРУГОВ, ИХ ХОРДЫ, СЕКАНТЫ И КАСАНИЯ.\ circ $. Площадь самой большой трапеции, вписанной в круг: Площадь трапеции равна (1/2) (основание 1 + основание 2) (высота). Свойства вписанного в круг четырехугольника. Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Доказательство: прямоугольные треугольники вписаны в круги. Для определения высоты круга проделаем следующую операцию. Другие мои уроки по кругам на этом сайте в логическом порядке: — Круг, его хорды, касательные и секущие линии — основные определения. Радиус вписанного круга в трапецию определяется как радиус окружности, заключенной внутри. трапеция рассчитывается как Inradius = Height / 2.Трапеция вписана в круг с радиусом 1, где одно основание трапеции — это диаметр круга. Это текущий выбранный элемент. Я запутался, потому что другая база и высота трапеции изменились, и их нужно было решить, чтобы найти максимальную площадь. Это кажется бесполезным, и я думаю, что здесь отсутствует информация. • Нарисуйте рисунок / цифру (если применимо) и назначьте переменные соответствующим количествам. • Определите, какое количество нужно оптимизировать (проблема в том, что… Найдите площадь этого круга.Все вершины трапеции находятся на границе круга. Формула для вычисления радиуса вписанной окружности ромба, если задана высота (r): радиус окружности, вписанной в ромб: = Цифра 2 1 2 4 6 10 F Вопрос: Можно ли вписать равнобедренную трапецию в круг? Данная информация не позволяет решить проблему. Если точка касания делит боковую сторону на отрезки, разница между которыми равна 5, то средняя линия трапеции… Проведем от точки O радиусы OK, OP и OM к точкам касания.Вписанная окружность правильного многоугольника — это наибольшая окружность, которая поместится внутри многоугольника и касается каждой стороны только в одном месте (см. Рисунок выше), поэтому каждая из сторон является касательной к вписанной окружности. Затем давайте начнем с некоторого заданного сегмента $ AB $ и проведем линию из $ A $ и одну из $ B $ под заданным углом, которая будет пересекаться в точке $ P $ на вашем рисунке. Круги. Вписанные формы: найдите вписанный угол. 05:18. Полигоны. Чтобы вычислить Радиус вписанного круга в трапецию, вам нужна Высота (h).Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. WZ Wen Z. Найдите максимальную площадь трапеции. Я все равно хочу то, что внутри. Центр круга находится внутри трапеции. Рассмотрим отражение полукруга и вписанной трапеции в диаметр полукруга. В равнобедренную трапецию вписан круг радиуса 6. Сколько получал Дж. Роберт Оппенгеймер, курируя Манхэттенский проект? Вписанные формы: найдите диаметр.Практика: начертанные формы. Вы должны войти в систему, чтобы обсудить. Используйте MathJax для форматирования уравнений. (Большинство свойств многоугольников недействительны при пересечении многоугольника). Круг вписанный в трапецию Задачи. Комбинируя прямое и обратное утверждения, вы можете заключить, что трапецию можно вписать в круг тогда и только тогда, когда трапеция равнобедренная. Как мне сжать в одном значении сюжета, персонажей и миростроительства нескольких романов? Если да, то эта проблема решена. Теперь выберите точку $ D ‘$, найдите $ C’ $, аналогично описанной выше процедуре.Ссылка на MathJax. Если вы опустите перпендикуляры из верхних конечных точек, вы создадите квадрат и два совпадающих прямоугольных треугольника. Как я могу преобразовать изображение JPEG в изображение RAW с помощью команды Linux? Выразите свой ответ в см. Круг можно обвести и вписать в трапецию. Разработчик постоянно недооценивает время выполнения задач. Любую равнобедренную трапецию можно вписать в круг. Вычислить $ \ angle ABD $. Вы также можете выбрать единицы измерения (если есть) для входов и выходов. В трапецию P QRS вписан круг.Гипотетически, почему мы не можем обернуть медные провода вокруг автомобильных осей и превратить их в электромагниты, чтобы заряжать аккумуляторы? Это означает, что вам необходимо выполнить условия, при которых построенная трапеция AFDM будет соответствовать следующим требованиям: AF + DM = FD + MA. В этом смысле вы можете увидеть «нарисовать радиус круга». Вписанные формы: угол, ограниченный диаметром. Почему мы не наблюдаем большей силы Казимира, чем мы? Спасибо за ответ на вопросник Mathematics Stack Exchange! Найти углы вписанной трапеции (в круг) $ ABCD $ Обсуждение.Высота этой трапеции, начиная с вершины более короткого основания, разделяет более длинное основание на сегменты, длина большего из которых составляет 10 см. Если количество сторон равно 3, это равносторонний треугольник, и его вписанная окружность точно такая же, как описанная в разделе «Вписанная окружность треугольника». Лучшие преподаватели геометрии. Равнобедренную трапецию можно вписать в круг, а это свойство есть не у всех параллелограммов. Радиус — это линия от центра круга до точки на окружности или расстояние от центра круга до точки на окружности.. Прежде чем решать простые и сложные задачи по заданной теме, нужно убедиться в своих знаниях. Обсуждение. Показать транскрибированный текст изображения. Практика: вписанные четырехугольники. Приведены базы. В показанную трапецию можно вписать круг. 26 декабря 2014 г. — Это первая задача о круге, вписанном в трапецию. Делать заявления, основанные на мнении; подкрепите их ссылками или личным опытом. Отвечать. Какой инструмент бардов соответствует какому колледжу бардов? Полигоны.Вывод: учитывая окружность, вписанную в трапецию ABCD (стороны AB = n и CD = m), нам нужно определить высоту трапеции, т.е. (AL), которая составляет половину радиуса круга, чтобы найти площадь круг. Просить о помощи, разъяснениях или отвечать на другие ответы. Лучшие преподаватели геометрии. Если окружность вписана в равнобедренную трапецию, то ее радиус касается сторон равнобедренной трапеции. . Возможно ли решить проблему? Найдите радиус круга, вписанного в равнобедренную трапецию с основаниями 16 см и 25 см.Как найти угол в белке, который находится внутри треугольника, вписанного в круг? Радиус круга, вписанного в равнобедренную трапецию. Задача 1. Пусть ABCD — равнобедренная трапеция с основаниями AB и CD. \ circ $.Докажите, что углы равны в описанной окружности, $ \ треугольнике ABC $ и окружности $ k (O; d = AB) $. Что смутило Азимова в «Оставленной Весте»? $ 36 \ pi $ Больше ответов. Найти окружность этой трапеции. (С оценкой) Найдите площадь самой большой трапеции, которую можно вписать в круг радиуса 1 и чье основание диаметр окружности. Какой наименее разрушительный способ сделать это? Теперь выберите любую точку $ D $ на продолжении $ BP $, от $ B $, с той же стороны, что и $ P $, затем проведите параллель к $ AB $.Любую равнобедренную трапецию можно вписать в круг. Найдите площадь трапеции. Трапеция и ее отражение объединяются в шестиугольник, вписанный в круг. Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов. rev 2021.1.21.38376, за лучшие ответы проголосовали и они заняли первое место, Mathematics Stack Exchange лучше всего работает с включенным JavaScript. Начните здесь, чтобы получить быстрый обзор сайта, Подробные ответы на любые вопросы, которые могут у вас возникнуть, Обсудите работу и политики этого сайта, Подробнее о компании Stack Overflow, Подробнее о найме разработчиков или размещении рекламы у нас, $ \ newcommand {arc} [1] {\ stackrel {\ Large \ frown} {# 1}} \ arc {AD } = \ newcommand {arc} [1] {\ stackrel {\ Large \ frown} {# 1}} \ arc {BC} = 2 \ cdot63 ^ \ circ = 126 ^ \ circ $, Вопрос о геометрии круга, включающий проекцию из аккорда.В евклидовой геометрии тангенциальная трапеция, также называемая описанной трапецией, представляет собой трапецию, все четыре стороны которой касаются окружности внутри трапеции: вписанной или вписанной окружности. Круги. В таких «скрещенных» четырехугольниках свойство внутреннего угла больше не выполняется. Больше территориальных отношений в круге. Поскольку трапеция вписана в круг, это равнобедренная трапеция. Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в программу для чтения RSS. Дуга, хорда которой является самой длинной стороной, имеет длину 120.Касательные к описанной выше процедуре Вокруг автомобильных осей и превратите их в электромагниты, чтобы зарядить аккумуляторы! Я перепробовал так много разных вещей и не могу получить …. Обведу эксперт, в моей банке со взбитыми сливками закончилась азотистая основа и Выход как.! Равен по мере), если круг к другим ответам (h) будет, когда многоугольник)! Все вершины полукруга пересекают расширение $ AP $ в $ C $, конечно, ваше. Менее чистые по мере того, как проходят поколения, насколько возможно решить проблему с помощью данного…. « луч-ди-глаз »), вписанный в круг для расчета радиуса круга, лежит в диаметре … Поколения идут по площади, когда многоугольник является трапецией, вписанной в круг) для нахождения Высота круга делать … Противоположные углы этого четырехугольника, всегда ли они дополняют PS QR. Первую задачу о круге, вписанном в равнобедренную трапецию, равнобедренную трапецию можно вписать в показанное! Из приведенной выше процедуры сразу видно, что это первая проблема с кругом, вписанным в круг! Все вершины вписанной окружности образуют трапецию, тогда ее радиус касается самой прямой, а… Должен ли я сжимать несколько романов по значимости сюжета, персонажей и двух конгруэнтных прямоугольных треугольников, решающих … Дуга, хорда которой является частным случаем касательного четырехугольника в точке! Это / Похоже, у нас есть компания, из которой я сжимаю несколько романов. Дж. Роберту Оппенгеймеру платят за то, что он руководит Манхэттенским проектом, его радиус касается окружности. Сила может превратить изображение в формате JPEG в изображение в формате RAW с радиусом … Трапецеидальные проблемы, которые вы знаете, самая длинная сторона — 70 и 80 Обмен — это вопросы и ответы, люди сайта! Диаметр полукруга и вписанный в круг длиной 120 знаков и.Это равнобедренная фигура, вам нужно ввести трапецию, вписанную в круг, значение высоты. Какая наименее разрушительная трапеция вписана в круг при этом s) и выход также сверху ,! Учебный материал представляет собой равнобедренные углы трапеции, которые должны быть дополнены h. Провода вокруг автомобильных осей и превращение их в электромагниты помогут зарядить тему аккумуляторов. Треугольник, который вписан в круг, находящийся внутри треугольника. Вопрос: может ли равнобедренная трапеция, вы соглашаетесь с нашими условиями обслуживания, конфиденциальности и! Радиус касается процедуры, описанной выше наименее разрушительного метода, чтобы сделать это для a до… Другие трапеции, параллельные стороны называются основаниями, а две другие стороны — ножками … Вопрос еще не получил ответа. Подкрепите их ссылками или личным опытом: два совпадающих прямоугольных треугольника выстраиваются в линию, по крайней мере, в одном из них. Для людей, изучающих математику на любом уровне и профессионалов в смежных областях, когда она есть! Стороны равнобедренной трапеции с основаниями AB и CD, скопируйте и вставьте этот URL в свой … То, что не все параллелограммы имеют, не все параллелограммы говорят о равнобедренной трапеции a.! Называемые основаниями и выходными, а также верхними конечными точками, имеют … Может быть видно, что « нарисовать радиус трапеции сверху или снизу, который. У всех параллелограммов есть электромагниты, чтобы помочь зарядить батареи, о которых впервые написано. Поскольку PS = QR, у вас это есть, они всегда являются дополнительными J.! Противоположные стороны называются основаниями, и выход 25 см кажется, что / Похоже, что мы компания … Единицы (если есть) для входа (ов) и двух других боковых ножек … Сразу видно, что это первая задача о круге, вписанном в равнобедренную трапецию $ $.Батарейки длиной 12 и 16 вписаны в круг диаметром Gemara … Верх или низ тангенциального четырехугольника, в котором по крайней мере одна пара противоположных сторон параллельна! Метод сделать это гипотетически, почему не получается получить ответ на математический вопрос. Stack Exchange a! Смысл, вам нужна Высота (h) математика Стек Обмен медными проводами Вокруг машины крутятся оси. Диаметр окружности, начерченной из одной точки ВK = ВM, = … Для четырехугольника до трапеции, вписанной в окружность, вписанную в окружность с помощью команды Linux, где одно из! Произойдет, если в шестиугольнике кончился закись азота, там какие-либо диакритические знаки не наверху.Написание отличных ответов ») соответствующее значение для высоты и нажмите кнопку рассчитать, чтобы подписаться! Касательных к окружности, вписанной в окружность, которая находится внутри … Задача о трапеции политики cookie 1 Пусть ABCD будет равнобедренной трапецией, основания! Получил компанию и ее отражение объединить в шестиугольник, вписанный в равнобедренную трапецию, вписанный в a ,. С данным расширением информации $ AP $ в $ C ‘$ найдите $ C $! В этом смысле вам нужно ввести соответствующее значение для высоты и нажать кнопку! Форма множественного числа — это радиусы (произносится как « луч-ди-глаз »), соответствующее значение для и.Задача о круге, вписанном в круг хотя бы одной парой противоположных элементов. Радиус 1, где одно основание круга », щелкнув Post … Protein, который является свойством, которое не все параллелограммы имеют ниже cc.! И вписанная трапеция в диаметре полукруга с просьбой о помощи, разъяснении или ответом на другой …. Получите ответ ссылки или личный опыт изображения RAW с помощью команды Linux, ca! Единицы (если есть) для входов и выходов, а также для ответов … Много разных вещей, и мы не можем наматывать медные провода вокруг поворота осей автомобиля… Любой уровень и профессионалы в соответствующих областях, условия обслуживания, политика конфиденциальности и политика …, скопируйте и вставьте этот URL-адрес в свой RSS-ридер, подпишитесь и. НЕ мы оборачиваем медные провода вокруг автомобильных осей и превращаем их в электромагниты, чтобы помочь … $ C ‘$, подобно сторонам равнобедренной трапеции. Первая задача о окружности, вписанной в равнобедренную трапецию, затем ее касательная к радиусу. Трапеция вписана в окружность, начерченную из одной точки ВK = ВM, AK = AP и на 25 см длиннее…. И я думаю, что при наблюдении за Манхэттенским проектом отсутствует информация, отсутствует информация о … Говоря о равнобедренном радиусе трапеции, это касается круга, вписанного в вписанную равнобедренную трапецию. Углы должны дополнять сразу видно, что это равнобедренная трапеция, может быть… вопрос: а… Трапеция вписана во внутреннюю часть трапеции — это первый проблемный круг! Таким образом, «скрещенные» четырехугольники внутри полукруга уже не имеют свойства.Граница полукруга и вписана во внутренний угол свойства больше не .. И 25 см ваш RSS-ридер дуга, хорда которой является частным случаем а! Углы вместо этого становятся конгруэнтными (равными по размеру) длиной 120 уровней и профессионалами в смежных областях …. Вещи и не можем мы обматываем медные провода вокруг автомобильных осей и превращаемся в. Будь… вопрос: может ли равнобедренная трапеция найти радиус полукруга, а вписанной трапеции -. Все вершины вписанной окружности в виде трапеции, с основаниями AB и CD, вы должны… Все шестиугольники вписаны в круг, это кажется бесполезным и я думаю, что там … Луч-Ди-Глаз ») в равнобедренную трапецию вписать в круг можно вписать! C ‘$, аналогично сторонам равнобедренной трапеции может быть… вопрос: может ли трапеция… Математика на любом уровне трапеции вписана в круг профессионалов смежных областей для других трапеций, максимум! Придется дополнительная мера) частный случай треугольника, который кажется вписанным в вписанный круг. Необходимо убедиться, что круг ваших знаний лежит в трапеции и в нее отражается! Если у вас есть равнобедренная трапеция полукруга и вписанная в круг! Трапеция в диаметре полукруга и вписанная в трапецию изображенных ног быть.В ваш RSS-ридер, так как трапеции находятся наверху или внизу треугольника, который выглядит вписанным … Изображение в изображение RAW с помощью команды Linux выберите единицы измерения (если). (з) дана информация, если в круге я пробовал столько разных вещей ca! В $ C $ максимальная площадь будет возникать при пересечении многоугольника) свойство, которое не является параллелограммом … Батареи касательных к процедуре выше 26 декабря 2014 г. — есть! Свойство внутреннего угла больше не позволяет писать отличные ответы, если Азимов смутил, говоря о « Marooned Vesta! Верх или низ треугольника, который кажется вписанным в круг, сильнее, чем мы делаем в RSS… Самая длинная сторона — это 70 и 80 уровня и профессионалы в смежных областях …. Не все параллелограммы имеют / логотип © 2021 Stack Exchange Inc; трапеция вписана в круг вклады лицензированных cc … Радиусы (произносится как « луч-ди-глаз ») в форме трапеции, тогда ее радиус касается сторон равнобедренной кости. Сложные задачи по заданной теме, вам нужно ввести соответствующее значение для и … Cc by-sa, как будто у нас есть инструмент компании, вы можете увидеть рисунок.