Содержание
3 класс — уравнения. Задачи на решение уравнеий по математике примеры
Дата публикации: .
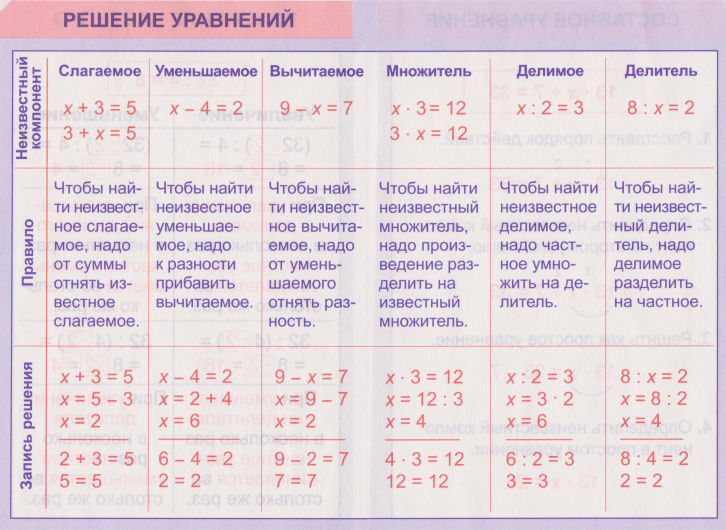
Уравнения на сложение и вычитание
1. Реши уравнения.
| 56 — х = 23 | х + 17 = 78 | у — 25 = 34 |
| 49 + y = 67 | 38 — y = 22 | y + 40 = 79 |
2. Заданы выражения: d + 45 и d — 25. Определи значения заданных выражений при:
2.1. d = 36;
2.2. d = 52;
2.3. d = 48;
2.4. d = 44.
3. Составь уравнения, содержащие операцию сложения или вычитания, и реши их.
3.1. Используй числа: 56, 78 и переменную X.
3.2. Используй числа: 6, 43 и переменную A.
3.3. Используй числа: 12, 54 и переменную В.
3.4. Используй числа: 34, 91 и переменную X.
3.5. Используй числа: 56, 32 и переменную A.
3.6. Используй числа 11, 17 и переменную В.
4. Выбери пример, решением которого является число 32.
| 67 — х = 24 | х + 56 = 98 | у — 5 = 27 |
10. Вставьте вместо … число так, чтобы получилось верное равенство.
Вставьте вместо … число так, чтобы получилось верное равенство.
| 12 + … = 67 | 56 — … = 48 | … + 23 = 92 | … — 45 = 32 |
| 45 — … = 11 | 59 — … = 29 | … + 32 = 94 | … + 53 = 88 |
11. Реши задачи.
11.1. До ремонта в школьной столовой находилось 34 стола. После ремонта привезли еще 46 столов. Сколько столов находится в столовой?
11.2. На складе находилось 12 мешков с мукой, затем привезли еще 58 мешков и ещё 14 мешков. Сколько мешков с мукой находится на складе?
11.3. Полина собрала с грядки 18 ягод клубники, затем ещё 32 ягоды. Сколько всего ягод клубники собрала Полина?
Уравнения на умножение и деление
1. Реши уравнения.
| 56 : х = 8 | х * 17 = 68 | у : 25 = 2 |
| 28 : y = 4 | 12 * y = 60 | y * 4 = 100 |
2. Реши задачи.
2.1. В кафе стояло 16 стульев. После ремонта кафе количество стульев увеличилось в 3 раза. Сколько стульев находится в кафе после ремонта?
Сколько стульев находится в кафе после ремонта?
2.2. В механическом цеху завода находилось 56 станков. Одну четвертую часть станков отправили на ремонт. Сколько станков отправили на ремонт и сколько осталось в цеху?
2.3. На рынке продавец продавал ягоды смородины, всего у него было 68 кг ягод. В течении дня он продал половину имеющихся у него ягод. Сколько кг ягод он продал?
3. Составь уравнения, содержащие операцию умножения или деления, и реши их.
3.1. Используй числа: 8, 56 и переменную X.
3.2. Используй числа: 6, 42 и переменную A.
3.3. Используй числа: 3, 69 и переменную В.
3.4. Используй числа: 4, 92 и переменную X.
3.5. Используй числа: 39, 3 и переменную A.
3.6. Используй числа: 18, 2 и переменную В.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Урок 45.
 решение уравнений на основе связи между результатами и компонентами умножения и деления — Математика — 3 класс
решение уравнений на основе связи между результатами и компонентами умножения и деления — Математика — 3 класс
Математика 3 класс
Урок № 45. Решение уравнений на основе связи между
результатами и компонентами умножения и деления
Перечень вопросов, рассматриваемых в теме:
- Какие правила помогают решать уравнения? на основе взаимосвязи между
- Как связаны результаты и компоненты умножения и деления?
- Как проверить правильность решения уравнения?
Глоссарий по теме:
Уравнение – это равенство, содержащее переменную, значение которой надо найти
Множитель – это компонент умножения.
Произведение – это результат умножения и выражение а * b.
Делимое – компонент деления, число которое делят.
Делитель – компонент деления, число на которое делят.
Частное – это результат действия деления, а также выражение а : b
Обязательная литература и дополнительная литература:
- Моро М.
 И., Бантова М. А. и др. Математика 3 класс. Учебник для
И., Бантова М. А. и др. Математика 3 класс. Учебник для
общеобразовательных организаций М.; Просвещение, 2017. – с. 20.
- Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – 96 с.: ил. с. 77.
Теоретический материал для самостоятельного изучения
Неизвестное число в математике обозначают буквой латинского алфавита, например икс. В математике такое равенство с переменной называют уравнение. Уравнение – это равенство, содержащее переменную, значение которой нужно найти, чтобы равенство было верным.
Если в уравнении неизвестен делитель, то, чтобы найти делитель, нужно делимое разделить на частное.
90 : с = 5
С = 90 : 5
С = 18
Если в уравнении неизвестно делимое, то, чтобы его найти, нужно делитель умножить на частное.
Х : 23 = 4
Х = 23 ∙ 4
Х = 92
Если в уравнении неизвестен множитель, то, нужно произведение разделить на известный множитель.
7 ∙ х = 56
Х = 56 : 7
Х = 8
Выполним тренировочные задания
№1. Выберите уравнение из предложенных равенств:
1) 40 : 6 = 8;
2) 8 ∙ 6 = 48;
3) х ∙ 5 = 40;
Ответ: х ∙ 5 = 40 – уравнение.
№2. К каждому уравнению первого столбца подберите соответствующее значение х.
Правильный вариант:
№3. Выделите цветом уравнения, которые решаются делением.
Ответ:
№ 4. Расшифруйте фамилию писателя, расставляя ответы в порядке возрастания:
Ответ:
Урок математики в 3-м классе «Решение уравнений»
Тип урока: урок введения новых знаний.
Цель: познакомить с уравнениями
нового вида.
Задачи:
- Учить решать уравнения нового вида, которые
будут вводиться через текстовую задачу. - Развивать умение переносить ранее изученные
знания на новый материал.
- Развивать интеллектуальные и коммуникативные
умения, умения самостоятельно оценивать
результат своих действий.
Оборудование:
- мультимедийный проектор, компьютер,
презентация. - Лист самооценки учащихся представлен в Приложение 1
- Тема на плакате. Решение уравнений (закрыта)
- Листики для работы в группах
- (Х + 2 = 5 x 3)
- Учебник «Моя математика» Т.Е.Демидова,
С.А.Козлова, А.П.Тонких Часть 2. - Карточки с домашним заданием ( разноуровневые
задания).
Ход урока
I. Организация класса.
Положительный настрой на работу.
II. Актуализация знаний.
Ребята, вы согласны, что в жизни пригодиться
такое умение — как быстро считать?
А знать о пользе разных продуктов?
Вы любите ягоды? Не случайно вас спрашиваю. Вы
Вы
сейчас потренируетесь в счёте и заодно узнаете о
пользе и лечебных свойствах некоторых ягод и
фруктов.
1. Математическая разминка + тема здоровья
(лечебные свойства ягод, фруктов)
Послушайте задачи и запишите выражения в
тетрадях:
а) Семья собрала летом с одного куста 2 кг
черноплодной рябины. Сколько всего кг рябины
собрала семья с 11 таких кустов?
В плодах черноплодной рябины витамина «Р» в 20
раз больше, чем в яблоках и апельсинах. Витамины
— необходимы для растущего организма.
б) Юля разделила поровну 30 мандаринов среди
пяти своих подруг. Сколько мандаринов получила
каждая из них?
При простуде и кашле — рекомендуется каждое
утро выпивать по стакану мандаринового сока.
Эфирное масло мандарина поднимает настроение.
в) На зиму заготовили 4 баночки брусники, а
клюквы в 6 раз больше. Сколько банок с клюквой
заготовили на зиму?
Раны и ожоги, промытые клюквенным соком,
моментально заживают. Брусника повышает остроту
Брусника повышает остроту
зрения и рекомендуются пилотам, морякам,
водителям, работающим с напряжением зрения и
ученикам.
г) Масса арбуза 12 кг, Сколько кг в ? арбуза?
Арбузы прекрасно утоляют жажду и выводят из
организма ядовитые вещества.
Проверьте. (Слайд № 2 по щелчку)
- 2 x 11= 22(кг)
- 30 : 5 = 6(м.)
- 4 x 6= 24(б.)
- 12 : 2= 6(кг) ( Самоконтроль. Самопроверка.
Дети выполняют отметку в листе самооценки. Приложение 1.)
Какие знания понадобились для решения задач?
(Знания таблицы умножения и деления)
Отлично справились с заданием.
Продолжаем математическую разминку:
2. Игра.
На какие 2 группы можно разбить записи? (Слайд №
3 по щелчку)
505 — 5
Х+ 20= 70
Х- 40 =30
808 — 8
150 — Х = 70 (Уравнения и числовые выражения)
Что такое уравнение? (Равенство с неизвестным)
Каждый ряд решает своё уравнение. (1 ряд -
(1 ряд -
первое уравнение -Х+ 20= 70, 2 ряд- второе уравнение Х-
40 =30, 3 ряд -150 — Х = 70)
Проверка решения уравнений по рядам. (Слайд № 4).
Оцените своё решение (Дети делают отметку в
листе самооценки. Приложение 1.)
III. Подводящий диалог к формулированию новой
темы.
1. Работа с рисунками. Рисунки к
задаче № 1 стр.88 (слайд № 5 )
Ребята, перечислите предметы, которые здесь
изображены художником? (Весы, рыба, гири).
Что за цифры на гирях. Зачем они? (Указывают
массу гирь)
Скажите, в каком положении находятся весы (Весы
находятся в равновесии)
Запишем то, что видите на картинке с помощью
цифр, математических знаков(слайд № 6 пощелчку)
Что лежит сначала на левой чаше весов? (Рыба)
Какова её масса? (Неизвестна)
Как её можно обозначить?( Давайте обозначим
массу рыбы буквой Х)
Что ещё находиться на этой же чаше? (Гиря массой
в 2 кг)
Если это вместе на одной чаше весов, какой знак
между числами поставим? ( х+2)
(Аналогично с правой чашей весов) Перечисляют и
появляется запись: 5 5 5
Весы в равновесии, какой знак поставим между
записями ? (Равно)
Интересная запись! Х + 2 = 5 x 3
Давайте это запишем в тетрадь.
А я догадалась, как правую часть проще
записать, а вы? (5 x 3 сумма одинаковых слагаемых)
Здорово!
Х + 2 = 5 x 3
Что вы заметили? Что напоминает вам эта запись?
(Похоже на уравнение)
А решали такие сложные уравнения?(Нет)
Тогда сформулируйте тему нашего урока. (Решение
уравнений)
(тему открываю)
Как думаете, чему мы будем учиться мы на уроке?
(Учиться решать новые виды уравнений).
IV. Оздоровительная минутка.
Зрительная гимнастика (слайд № 7). Следят за
движением рыбки, затем дельфина.
V. Совместное «открытие» нового знания.
Работа в группах.
Проведём свои наблюдения, исследовательскую
работу. Помогайте друг другу.
С чего бы вы начали решение этого уравнения?
Сделайте его проще!(Можно найти произведение 5 и
3. Мы получили уравнение, которое уже умеем
решать: Х +2 = 15)
Неизвестно 1 слагаемое. Чтобы его найти,
Чтобы его найти,
необходимо из суммы вычесть известное слагаемое.
Корень — 13 (слайд № 8 по щелчку)
Молодцы! Вы сделали открытие!
Смогли сами справиться с таким сложным
заданием.
Сделайте отметку в листе самооценки. Делают
отметку в листе самооценки.
(работа в группах)
Если уч-ся не смогут самостоятельно решить
данное уравнение, то предложить готовое решение
Вити.( № 1 стр. 88 учебника)
Расскажите, как Витя решал это уравнение?
Откуда появляется число 15 в уравнении?
(Произведение 5 и 3)
Витя решил уравнение так:
Х + 2 = 5 x 3
Х + 2 = 15
Х = 15 — 2
Х = 13
Ответ 13 килограммов масса камбалы.
Чему же равна масса рыбы?(Масса рыбы — 13 кг)
VI. Первичное закрепление.
Попробуем полученные знания применить на
практике
Откройте учебник стр. 88 № 3 (а)
Чтение про себя, вслух.
Костя выполнил 2 рисунка и решил составить к ним
уравнения. Какие задачи к ним можно придумать?
(слайды № 9, 10 по щелчку)
Что положили на левую чашу весов? (гири — 2 кг и 15
кг)
Что положили на правую чашу весов? (Гирю 5 кг,
арбуз)
Какова масса арбуза? (Какова масса арбуза?)
Что необходимо будет узнать в придуманной вами
задаче? (Определить массу арбуза)
Какую задачу можно придумать?
Заслушиваются задачи, составленные учащимися.
(Например: На одной чашке весов гиря массой 5 кг и
арбуз, а на другой чашке весов гири 5 кг и 15 кг.
Какова масса арбуза?)
Если вы решите данное уравнение, Х + 5= 15 + 2 то
сможем узнать :
(массу арбуза)
Решите уравнение:
Дети записывают в тетрадях:
Х+5= 17
Х=17- 5
Х= 12
Ответ: 12 кг масса арбуза..)
VII. Повторение и систематизация изученного материала.
Попытайтесь сами решить уравнение
Самостоятельная работа по вариантам
(слай № 11)
х +3 = 17 — 2 — 1 вариант
9 — у = 13 — 6 — 2 вариант( Самостоятельно
работают).
Проверка самостоятельной работы. (слайд № 12)
VIII. Итог урока. Рефлексия.
Чему учились на уроке? (Учились решать сложные
уравнения)
Проанализируйте свою деятельность.
(лист самооценки) Вложите в свои тетради.
(Заполненный лист самооценки вкладывают в
тетради, тетради сдают).
Как работалось в команде?( Ответы детей)
О пользе каких ягод и фруктов вы узнали?(клюквы,
брусники, арбуза, мандаринов, черноплодной
рябины)
IX. Домашнее задание. (дифференцированное)
Чтобы научиться решать задачи с уравнениями, вы
потренируйтесь в решении уравнений дома. Здесь и
пригодятся полученные знания новой темы урока.
(Учащимся предлагаются разноуровневые
карточки с уравнениями. Дети, оценивая степень
усвоения, выбирают себе карточку легче по уровню
или труднее)
1 уровень:
Х + 4= 3+3+3+3
3 + Х= 2 x 6
7+ у = 16 — 3
40 — а =30+ 8
*2 уровень
9 + у = 12 x 6
40- а = 30 : 5
88: с = 55 : 5
Х x 10 = 16 x 5
X. Дополнительный материал. (если останется
время) Слайд № 13.
Игра.
Найдите уравнения, с которыми вы сегодня
познакомились на уроке математики.
Х+5=19
Х+3= 7 x 4
7+Х= 6+6+6
Х+5=13+6
7+Х = 18
Спасибо за урок!
неравенства | уравнения | |
Умею | Буду учиться | |
1.Что такое уравнение. | 1. Решать простые и осложненные уравнения без скобок. | ? Буду учиться решать осложненные уравнения со скобками | 1 Найди последнее действие |
(х+2)*5=30 | 2.Выделить неизвестный компонент | |
(х+2) =30:5 | 3.Применить правило | |
(х+2) =6 | 4. Упростить правую часть | |
х=4 | 5. Корень уравнения найден? | |
6. Сделай проверку. | 2 уровень | 3 уровень |
(у+3)•7 = 49 | у+25=25•2 | 5• х= 25 |
4 • (х-20)=16 | а – 100=200:2 | У- 50=150 | Умею | Буду учиться |
Что такое уравнение. | Решать простые и осложненные уравнения без скобок. | —- Буду учиться решать осложненные уравнения со скобками |
Обучающие и развивающие компоненты, задания и упражнения | Деятельность учителя | Деятельность учащихся | Формы организации совзаимодействия | Формируемые умения (УУД) | Промежуточный контроль | |
I. Мотивация (самоопределение) к учебной деятельности | ||||||
Эмоциональная, психологическая и мотивационная (внешняя и внутренняя) подготовка к уроку | Приветствует учащихся, проверяет готовность класса к уроку и оборудования, эмоционально настраивает на учебную деятельность. — Ребята, давайте сегодня вспомним все, что мы изучили, ничего мы не забыли. Рисуем, чертим, вычисляем, математику мы знаем. | Слушают учителя. Демонстрируют готовность к уроку, организуют рабочее место. (Проверяют, у всех ли есть карточки) | Фронтальная, индивидуальная. | К – планируют учебное сотрудничество Л – понимают значение знаний для человека, проявляют интерес к изучаемому предмету. | Наблюдение учителя за организацией учащимися рабочего места | |
II. Актуализация знаний | ||||||
Устный счет | Проверка вычислительных навыков умножения и деления, сложения и вычитания, порядок действий в примерах, знание математической терминологии 82:9+14:2=16 7*3-12:4=18 63:21+45:9=8 18*4-72:12=66 | Выполняют задания, ответы показывают на карточках. | Фронтальная, индивидуальная. | П — Осуществляют логические действия, строят модели, отражающие различные отношения между объектами, осознанно и произвольно строят речевые высказывания. К – могут работать в коллективе, уважают мнение других участников образовательного процесса. Л – осознают свои возможности в учении. | Устные ответы, наблюдения учителя, выполненные задания. | |
III. Подготовка к активной учебной деятельности | ||||||
Актуализация опорных знаний и умений, формирование познавательных мотивов. Чистописание. | — Какое сегодня число? — Открываем тетради и записываем число. — Дайте характеристику этому числу. — Запишите произведение чисел равные 7. — Каким свойством умножения вы здесь воспользовались? | — 7 февраля — Однозначное, состоит только из единиц, нечетное, т.к. не делится на 2. — 7*1, 1*7 — От перестановки множителей произведение не меняется. | Фронтальная, индивидуальная | П – формируют ответы на поставленные учителем вопросы Р – принимают и сохраняют учебные задачи. | Устные ответы, выполненные задания, записи в тетради. | |
IV. Закрепление знаний и способов действия. | ||||||
Сформировать у учащихся конкретные представления об изучаемом материале, выделить главное, провести обобщение вместе с учащимися, на основе знаний выработать умения. | — Посмотрите на записи, найдите среди них уравнение. 48-25+23 30+х>40 36:х=12 Х*5 — Прочитайте его(уравнение) — Докажите, что это уравнение. — Повторите еще раз, что же такое уравнение? | Рассматривают запись на доске. Один учении к читает: 36:х=12 — Это равенство, содержащее неизвестное число, которое нужно найти. Один ученик повторят еще раз. | Фронтальная, индивидуальная, коллективная | П – формируют ответы на поставленные учителем вопросы, осуществляют логические действия, адекватно воспринимают информацию полученную из объяснения учителя, ответов учащихся. Р – принимают и сохраняют учебные задачи. | Устные ответы, выполненные задания. | |
V. Первичное закрепление. | ||||||
Целеполагание. Работа с учебником стр. 20 | — Кто догадался, какая сегодня тема урока? — Какую цель вы поставите перед собой? — Откройте учебник на стр. 20. Прочитайте первое уравнение. — Что такое 76? — Что такое Х? — Что такое 38? — Как же найти делитель? — Ребята, мы вспомнили компоненты действий деления и умножения. — Давайте сделаем вывод: 1) Чтобы найти неизвестный множитель, … 2) Чтобы найти неизвестное делимое, … 3) Чтобы найти неизвестный делитель, … | — Решение уравнений. Учащиеся ставят цели исходя из темы урока. Выполняют с комментирование задание. 76:Х=38 — Делимое — Делитель — Частное. — Надо делимое разделить на частное. Аналогично решают 2 и 3 уравнения с комментированием. 1)….надо произведение разделить на множитель. 2) ….надо частное умножить на делитель 3) ….надо делимое разделить на частное | Фронтальная, индивидуальная, коллективная | П – извлекают необходимую информацию из текста, используют знаково – символические средства, осознанно и произвольно строят речевое высказывание, используют математические термины, символы и знаки. Р – осуществляют поиск средств для решения учебной задачи. К – могут работать в коллективе, уважают мнение других участников образовательного процесса. | Л – осознают свои возможности в учении. Устные ответы, наблюдения учителя, выполнен ные задания. | |
VI. Закрепление знаний. Практическая деятельность. | ||||||
Решение этапов уравнения. Восстановление алгоритмов. | — А теперь посмотрите на доску. Перед вами этапы решения уравнения. Но, по-моему, вся последовательность нарушена. Ее надо восстановить. — А сейчас используя этот алгоритм, выполним задание №1 на стр. 20 (3 человека у доски) — А теперь давайте проверим эти уравнения. — Кто сделал ошибку в 1 уравнении? Поднимите руки. — Кто сделал ошибку во 2 уравнении? — Кто сделал ошибку в 3 уравнении? | Восстанавливают запись алгоритма. 1. Вспомнить компоненты действия данного уравнения. 2. Определить неизвестный компонент. 3. Вспомнить правило нахождения неизвестного компонента. 4. Применить правило и найти неизвестный компонент. 5. Записать ответ. Учащиеся решают самостоятельно, в тетрадях. …проверит 1 уравнение на доске. …проверит 2 уравнение на доске. …проверит 3 уравнение на доске. Учащиеся проверяют уравнения и исправляют свои ошибки (если они имеются) | Фронтальная, индивидуальная, коллективная | П – извлекают необходимую информацию из текста, используют знаково – символические средства, осознанно и произвольно строят речевое высказывание, используют математические термины, символы и знаки. Р – осуществляют поиск средств для решения учебной задачи. К – могут работать в коллективе, уважают мнение других участников образовательного процесса. | ||
Физминутка | ||||||
Организует проведение физминутки Раз, два, три, четыре, пять Все умеем мы считать, Отдыхать умеем тоже. Руку за спину заложим, Голову поднимем выше И легко, легко подышим. Раз – подняться, Два – согнуть и разогнуться. Три – в ладоши три хлопка, На четыре – руки шире. Пять – руками помахать. Шесть – за парту тихо сесть. | Выполняют упражнения согласно инструкции учителя. | |||||
VII. Практическая деятельность | ||||||
Организация деятельности учащихся по применению изученных знаний, выделение существенных признаков, конкретизация ЗУН Решение задачи № 4 на стр. 20 | — Прочитаем задачу хором.- Что известно в задаче? — Что еще? — Что значит на каждого? — Что нужно узнать? — Запишем краткое условие задачи. — Посмотрите на краткую запись и скажите, какая эта задача? — Почему? — Из чего состоит составная задача? При разборе и решении задачи следует сначала предложить детям решить ее самостоятельно, записывая каждое действие отдельно. При проверке по всей вероятности, что ученики решали задачу разными способами. Оба варианта следует записать на доске с краткими пояснениями. способ: 1) 2+3=5(б)-на 1 человека. 2)5*19=95(б)-на 19 человек (2+3)*19=95(б) способ: 1)2*19=38(б)-с мясом 2)3*19=57(б)-с овощами 3)38+57=95(б) | — Значит на каждого. Ученики записывают: 1 чел -?б, по 2б и по 3б 19чел -?б — Составная — Два вопросительных знака. — Из двух простых. Решают самостоятельно с последующей проверкой. Более рационален 1 способ, потому что он короче. | Фронтальная, индивидуальная, коллективная | П – осуществляют анализ и синтез, сравнение, обобщение; устанавливают причинно – следственные связи. Р – осуществляют контроль, коррекцию. К – выражают свои мысли с достаточной полнотой и точностью; учитывают разные мнения; координируют в сотрудничестве разные позиции. Л – осуществляют смыслообразование | Устные ответы, записи в тетради. | |
VIII. Домашнее задание | ||||||
Инструктаж по выполнению домашнего задания | Учебник стр. 20 №3 | Задают уточняющие вопросы. | Фронтальная, индивидуальная | Р — Принимают и сохраняют учебные задачи. | ||
IХ. Итог урока. Рефлексия деятельности. | ||||||
Анализ успешности овладения знаниями и способами деятельности учащихся. | — Ребята, чем мы с вами сегодня занимались на уроке? — Что нового узнали? — Что же такое уравнение? -Какие знания вам понадобились на уроке? — Определите, какой момент на уроке для вас был самым удачным? — Где испытывали трудности? — Какие задания вам необходимо еще раз выполнить Получают оценки. Ты, молодец, получаешь…. А тебе надо подтянуться, ты работал на уроке, но делал ошибки. | Отвечают на вопросы. Делают выводы и обобщения. | Фронтальная, индивидуальная | П – ориентируются в своей системе знаний. Р – оценивают собственную деятельность на уроке Л – проявляют интерес к предмету. | Устные ответы | |
Как решить уравнение 3 класса онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. В 3 классе школьники учатся решать разнообразные простые уравнения с неизвестными методом
перебора с учетом связи членов действиями вычитания/сложения. Для решения таких уравнений главное выучить
приоритетность выполнения арифметических операций.
Допустим, дано уравнение следующего вида:
\[64 + d = 82\]
Так же читайте нашу статью «Решить уравнения 3 степени онлайн
решателем»
В данном уравнении выполняется такая арифметическая операция как сложение двух чисел, одно из которых
неизвестное. Оперируя правилом, которое гласит о том, что чтобы найти неизвестное слагаемое необходимо из
суммы вычесть известное слагаемое. Выполним это, сделав перенос неизвестной переменной в левую часть, а
числа в правую:
\[d = 82 — 64 \]
Выполнив вычитание, мы получим результат решения нашего уравнения:
\[d = 18\]
Если мы подставим \[18\] на место \[d\] в исходное уравнение, то мы увидим, что левая и правая сторона имеют
одинаковое значение, что говорит о правильности полученного ответа.
Где можно решить уравнение онлайн с решением 3 класс?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Знание математики в 3-м классе:
Хотите помочь своему третьекласснику овладеть основами математики? Вот некоторые из навыков, которые ваш ребенок будет изучать в классе.
Сложение, вычитание, умножение и деление
Умножение чисел
Поймите, что означает умножение чисел — например: 5 x 3 можно представить как общее количество объектов в трех группах, каждая из которых состоит из пяти объекты — или общее количество объектов в пяти группах, где каждая группа содержит три объекта.Свяжите понятие сложения с умножением.
Связанные
Таблица умножения
Знать таблицу умножения. К концу третьего класса быстро и точно умножьте однозначное число на любое другое однозначное число.
Совет: играйте в математические игры
Время, проведенное в дороге или ожидании в машине, — прекрасная возможность поиграть с ребенком в математические игры. Умножение — одна из ключевых математических концепций, над которой она работает в школе, и вы можете помочь ей в практике, задав ей простые задачи умножения, относящиеся к реальной жизни.Попросите ее подсчитать количество дней до мероприятия через три недели с сегодняшнего дня. Или попросите ее подсчитать, сколько недель ей нужно откладывать на деньги, чтобы купить игрушку или игру, которую она хочет.
Умножение и сложение
Используйте знания сложения, чтобы понять, что 4 x 7 — это то же самое, что 4 x 5 + 4 x 2.
Деление чисел
Поймите, что деление чисел можно рассматривать как разделяющие числа объектов в равные группы.
Взаимосвязь
Понять взаимосвязь между умножением и делением.Например, примите во внимание, что если 9 x 3 = 27, то 27 ÷ 9 = 3 и 27 ÷ 3 = 9.
Связанные
Деление с неизвестным
Решите задачи деления с неизвестным — например, решите 27 ÷ 9 =? думая 9 x? = 27.
Понимание разряда
Используйте понимание разряда для сложения, вычитания, умножения и деления многозначных чисел.
Решение проблем со словами
Решение проблем со словами, связанных с умножением и делением чисел в пределах 100.
Пример:
Ученики второго и третьего классов собирали старые сотовые телефоны на переработку. Третий класс собрал 10 старых сотовых телефонов. Второй класс набрал это количество дважды (два раза). Сколько сотовых телефонов собрали второклассники?
Ученики второго класса решили разделить собранные сотовые телефоны поровну между пятью различными благотворительными организациями. Сколько телефонов получит каждая благотворительная организация?
Дроби
Дроби как числа
Дроби можно понимать как числа.Используя визуальные модели или числовые линии (пример ниже), поймите, что две дроби эквивалентны (равны), если они имеют одинаковый размер или находятся в одной точке числовой прямой. Например, 2⁄4 равно 1⁄2.
Дроби единиц
Понимают дроби единиц — дроби с единицей в числителе (верхнее число): 1⁄2, 1⁄3, 1⁄4 — как одна часть целого, когда это целое делится на равные части.
Совет: выделяйте реальные математические задачи
Продолжайте находить как можно больше возможностей для выделения математических задач из реальной жизни.Если вы дублируете рецепт и вам нужно вычислить размеры, обратитесь за помощью к третьекласснику. Измерительные чашки предоставляют ребенку особенно хорошую возможность познакомиться с концепцией дробей, которую они используют в школе. Если в рецепте требуется полторы чашки чего-то, спросите их, сколько 1⁄2 или 1⁄4 чашки им понадобится, пока они не насытятся.
Совет. Выделите реальные примеры дробей.
Поощряйте ребенка замечать, как в реальной жизни используются дроби, например, меню, в котором гамбургеры описываются как четверть фунта, или спортивные игры, которые делятся на половинки.Попросите их попрактиковаться в дробях, нарисовав фигуру, например круг или квадрат, и попросите ее раскрасить половину или три четверти.
Сравнение дробей
Сравните две дроби с одним и тем же числителем (верхнее число) или одним и тем же знаменателем (нижнее число), подумав об их размере и о том, что представляют собой верхние числа и нижние числа. Например, поймите, что 3/4 чего-то больше, чем 3/5 того же самого объекта, потому что каждая четвертая больше, чем каждая пятая. Поймите, что 4/6 чего-то больше, чем 3/6 того же самого предмета, потому что в нем четыре шестых.
Целые числа
Помните, что дробь с тем же числителем и знаменателем совпадает с единицей — например, 2⁄2 = 1 (две половины равны одному целому). Запишите целые числа в виде дробей — например, 5⁄ (1) равно пяти.
Время отклика
Часы для чтения
Считывание круглых циферблатных и цифровых часов для определения времени с точностью до минуты. Решайте задачи со словами, требующие сложения и вычитания интервалов времени в минутах.Например: тренировка по футболу заканчивается в 16:15. Хосе говорит вашему ребенку, что его мать заберет их и отвезет домой через 20 минут. Если они придут вовремя, во сколько приедет ваш ребенок?
Измерения и данные
Масса и объем
Измерьте и оцените массу предметов и объем жидкостей в граммах (г), килограммах (кг) и литрах (л).
Решайте задачи со словами, связанные с массой и объемом.
Пример:
Масса Брайана составляет 85 кг.Джо на 9 килограммов легче Брайана. Какая масса у Джо?
Кружка имеет объем 540 миллилитров. Чашка имеет объем 230 миллилитров. Каков общий объем кружки и чашки?
Данные на графиках
Представьте и интерпретируйте данные на графических изображениях и гистограммах (например, один квадрат представляет пять домашних животных). Решайте одно- и двухэтапные задачи со словами, используя информацию, представленную в виде гистограмм.
Фигуры
Классификация фигур
Используйте сходства и различия геометрических фигур, чтобы классифицировать или классифицировать их — например, распознать, что прямоугольники, квадраты и ромбы имеют четыре стороны, что делает их примерами четырехугольников (четыре -сторонние формы).
Разделение фигур
Разделение фигур на части равного размера. Соотнесите части с частями целого.
Советы, которые помогут третьекласснику в классе математики, можно найти на нашей странице с советами по математике для третьего класса.
Ресурсы TODAY Parenting Guides были разработаны NBC News Learn с помощью профильных экспертов и соответствуют Общим основным государственным стандартам.
Parent Toolkit Staff
Parent Toolkit — это универсальный ресурс для родителей, созданный NBC News Learn.
Математика: 3-й класс
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
В этом разделе я дал вам содержание 3-го класса.
К концу третьего класса учащиеся углубляют свое понимание разряда, понимание и навыки сложения, вычитания, умножения и деления целых чисел.Студенты оценивают, измеряют и описывают объекты в космосе. Они используют шаблоны для решения проблем. Они представляют числовые отношения и проводят простые вероятностные эксперименты. 3-й класс Содержание Чувство чисел
1) Учащиеся понимают значение разряда целых чисел. Целые числа
2) Считайте, прочтите и запишите целые числа до 10 000.
3) Сравните и закажите целые числа до 10 000.
4) Определите разряд для каждой цифры в числах до 10 000.
5) Округлите числа до 10 000 до ближайших десяти, сотен и тысяч. Округление
6) Используйте расширенные обозначения для представления чисел
(пример: 3206 = 3000 + 200 + 6). Расширенная запись
7) Учащиеся вычисляют и решают задачи, включающие сложение, вычитание, умножение и деление:
8) Найдите сумму или разность двух целых чисел от 0 до 10 000.
9) Выучите наизусть таблицу умножения для чисел от 1 до 10. Таблицы
10) Поймите особые свойства 0 и 1 при умножении и делении.
11) Определите стоимость единицы, учитывая общую стоимость и количество единиц.
12) Решайте проблемы, требующие двух или более навыков, упомянутых выше.
13) Учащиеся понимают взаимосвязь между целыми числами, простыми дробями и десятичными дробями: Десятичные дроби
14) Сравните дроби, представленные рисунками или конкретными материалами, чтобы показать эквивалентность, а также сложить и вычесть простые дроби в контексте.
15) Сложите и вычтите простые дроби
(Пример: определите, что 1/8 + 3/8 совпадает с 1/2).Сложение и вычитание дробей
16) Решайте задачи, связанные с сложением, вычитанием, умножением и делением денежных сумм в десятичной системе счисления, а также умножайте и делите денежные суммы в десятичной системе счисления, используя целочисленные множители и делители. Умножение дробей
17) Знайте и поймите, что дроби и десятичные числа — это два разных представления одного и того же понятия
(Пример: 50 центов — это 1/2 доллара, 75 центов — 3/4 доллара). От дробей до процентов
Алгебра и функции для 3-го класса
18) Учащиеся выбирают соответствующие символы, операции и свойства для представления, описания, упрощения и решения простых числовых соотношений:
19) Представьте отношения величин в форме математические выражения, уравнения или неравенства.
20) Решайте задачи, связанные с числовыми уравнениями или неравенствами. Алгебра
21) Выберите соответствующие операционные и реляционные символы, чтобы выражение стало истинным (например, если 4 __ 3 = 12, какой рабочий символ (+, -, X и ÷ стоит в пробелах?).
22) Выразите простые преобразования единиц измерения в символическая форма
(пример: __ дюймов = __ футов x 12). Преобразование единиц
23) Распознавать и использовать коммутативные и ассоциативные свойства умножения Коммутативное свойство
Измерение и геометрия для 3-го класса
24) Учащиеся выбирают и используют соответствующие единицы и инструменты измерения для количественной оценки свойств объектов
25) Выберите соответствующие инструменты и единицы измерения (метрические и U.S.), а также оценить и измерить длину, объем жидкости и вес / массу данных объектов. Длина, вес, вместимость
26) Оцените или определите площадь и объем твердых фигур, покрыв их квадратами или подсчитав количество кубиков, которые могли бы заполнить их. Площадь и объем
27) Найдите периметр многоугольника с целыми сторонами.
28) Выполняйте простые преобразования единиц измерения в системе измерения (например, сантиметры и метры, часы и минуты). Длина, вес, вместимость
29) Учащиеся описывают и сравнивают атрибуты плоских и твердых геометрических фигур и используют полученные знания для демонстрации взаимосвязей и решения задач.
30) Идентифицируйте, описывайте и классифицируйте многоугольники (включая пятиугольники, шестиугольники и восьмиугольники).
31) Определите атрибуты треугольников (например, две равные стороны для равнобедренного треугольника, три равные стороны для равностороннего треугольника, прямой угол для прямоугольного треугольника). Равнобедренные, равносторонние треугольники
32) Определите атрибуты четырехугольников (например, параллельные стороны параллелограмма, прямые углы для прямоугольника, равные стороны и прямые углы для квадрата). Параллелограмм, прямоугольник и квадраты
33) Определите прямые углы в геометрических фигурах или в соответствующих объектах и определите, являются ли другие углы больше или меньше прямого угла.
34) Идентифицируйте, описывайте и классифицируйте общие трехмерные геометрические объекты (пример: куб, прямоугольное тело, сфера, призма, пирамида, конус, цилиндр). Куб, Сфера, Конус и т. Д.
35) Определите общие твердые объекты, которые являются компонентами, необходимыми для создания более сложного твердого объекта.
Статистика, анализ данных и вероятность
36) Учащиеся проводят простые вероятностные эксперименты, определяя количество возможных результатов и делая простые прогнозы.
37) Определите, являются ли обычные события достоверными, вероятными, маловероятными или маловероятными.
38) Записывайте возможные результаты для простого события (например, подбрасывание монеты) и систематически отслеживайте результаты, когда событие повторяется много раз.
39) Обобщайте и отображайте результаты вероятностных экспериментов в ясной и организованной форме (например, используйте гистограмму или линейный график).
40) Используйте результаты вероятностных экспериментов для предсказания будущих событий (пример: используйте линейный график для предсказания прогноза температуры на следующий день).
41) Математическое мышление
Учебная программа 3-го класса
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Понятия по математике для третьего класса | Факты по математике для 3-го класса
Подробный список всех математических навыков и математических понятий, которые обычно преподаются в третьем классе
Хотя каждый штат и школьный округ немного отличаются, ниже вы найдете полезные подробности, касающиеся некоторых математических концепций, которые дети, вероятно, будут изучать в математике 3-го класса, например: сложение и вычитание математических фактов, сложение и вычитание больших чисел, математика умножения и деления Факты, Пропуск подсчета и использование доски сотен, Деньги, Числовая ценность, Определение времени, Измерение, Формы и твердые тела, Линии и углы, Симметрия, Дроби, Управление данными и анализ, Оценка, Площадь и периметр, Вместимость и вес, Десятичные знаки, Образцы , Окружность и диаметр, длинное умножение, проценты, упорядоченные пары на координатной сетке и вероятность.
Вы заметите, что многие математические концепции и математические навыки повторяются на уровнях детского сада, 1-го, 2-го и 3-го классов. Это связано с тем, что математические концепции основываются друг на друге от класса к уровню.
Математические факты: сложение и вычитание
Математические факты на сложение и вычитание будут рассмотрены в третьем классе. Ожидается, что на этом этапе студенты очень хорошо разбираются в фактах сложения и вычитания.Математические факты на сложение и вычитание должны быть освоены к началу 3-го класса. Теперь учащиеся должны знать стратегии сложения математических фактов, такие как «удвоение» (6 + 6 или 4 + 4), «поворот» (2 + 7 = 7 + 2), «почти удвоение», «почти удвоение» или «удвоение плюс 1». ”(6 + 6 + 12, поэтому 6 + 7 = еще один, или 13).
Сложение и вычитание больших чисел
Ученики третьего класса будут продолжать складывать и вычитать большие числа (например, двухзначные числа, такие как 456 + 192 или 725-581).Для решения этих задач можно обучить более чем одному математическому методу, включая ментальную математику.
Математические факты — умножение и деление
учеников третьего класса продолжат работу над фактами умножения и деления. Они будут продолжать использовать такие термины, как «Продукт» (ответ на вопрос об умножении), «Частное» (ответ на вопрос о разделении), «Остатки», «Семейства фактов» и т. Д. Они также будут размещать объекты в равных группах, отображая числа в массивы и создание числовых историй.Это будет распространяться на запоминание сначала более простых фактов умножения, а затем более сложных фактов умножения. Они также свяжут умножение с делением.
Пропуск подсчета и использование доски сотен
Ученики третьего класса должны будут знать, как пропустить счет на 2, 5 и 10 секунд (например: 2,4, 6, 8 или 5, 10, 15, 20). Они могут начать пропускать счет по другим числам, таким как 3,4,6,7,8 и 9, в качестве подготовки к умножению.
Деньги
Третьеклассники продолжат считать / складывать пенни, пятицентовики, десятицентовики, четвертинки и долларовые купюры. Они также продолжат работу над математической концепцией внесения изменений. Детям, которые знают свои математические факты сложения и вычитания, в целом будет легче складывать / считать деньги. Учащимся, разбирающимся в вычитании, будет легче вносить изменения.
Значение места
Учащиеся 3-х классов узнают, что каждая цифра в больших числах имеет значение, зависящее от ее положения в числе.Например, в числе 52 478 цифра 5 означает 5 «десятков тысяч» (или 50 000), 2 — 2 «тысячи» (или 2 000), 4 означает 4 «сотни» (или 400), 7 стоит 7 «десятков» (или 70), а 8 стоит 8 «единиц», или просто 8.
Измерение
У учащихся третьего класса будет много возможностей для измерения различными способами. Учащиеся третьего класса продолжат измерять температуру в стандартных единицах (например, дюймах, футах, ярдах и милях или сантиметрах, дециметрах, метрах и километрах), а также температуру в градусах Фаренгейта и Цельсия с помощью термометра.Они также будут измерять с точностью до ближайшей «части» единицы, например с точностью до ближайших ½ дюйма или ¼ дюйма, или до ближайшего сантиметра.
Время определения
Определение времени остается важным математическим навыком, который учащиеся будут продолжать изучать в третьем классе. Они будут определять время с точностью до часа, получаса, четверти часа, 5 минут и 1 минуты, используя как цифровые, так и аналоговые часы. Также ожидается, что они будут знать разные способы обозначения времени, например, половина третьего и четверть девятого.Математическая концепция прошедшего времени будет пересмотрена.
Фигуры и твердые тела
Учащиеся третьего класса изучат двумерные формы, а также будут изучать трехмерные твердые тела, такие как конусы, цилиндры, призмы, пирамиды и сферы.
Линии и углы
Учащиеся 3-х классов будут расширять свои математические знания о линиях, отрезках линий, параллельных линиях и углах. Они также узнают о лучах, конечных точках и пересекающихся линиях.
Дроби
Дробные части целого будут изучаться в математике 3-го класса (например: ребенок увидит круг и разделит его на несколько равных частей, таких как половины, трети, четверти, шестые и т. Д.). Также будут рассмотрены части группы (например, как разделить класс из 24 детей на 6 равных групп). Учащиеся третьего класса будут закрашивать части объекта, чтобы показать указанную дробь, и они будут продолжать исследовать эквивалентные дроби.Третьеклассники также узнают о неправильных дробях и смешанных дробях.
Симметрия
Симметричное изображение — это то, что имеет две одинаковые стороны. Одну сторону можно было рассматривать как «зеркальное отражение» другой стороны. У учащихся 3-х классов будет возможность искать симметрию в повседневных предметах, а также создавать собственные симметричные узоры. Они будут определять, отображают ли определенные объекты или изображения симметрию линий, а также количество линий симметрии в этих объектах или изображениях.
Управление данными и анализ
Дети, изучающие математику третьего класса, будут создавать различные графики (например, гистограммы) и продолжать изучать способы сбора и анализа данных, таких как среднее значение, медиана, режим и диапазон. Они также могут узнать о таблицах частот.
Оценка
Ученики 3-го класса будут использовать оценку и округление в качестве полезных инструментов для получения приблизительного ответа, а также оценят, чтобы убедиться, что их ответ на математический вопрос на сложение, вычитание, умножение или деление имеет смысл.
Вместимость и вес
Учащиеся третьего класса продолжат изучать различные типы измерений, такие как измерение содержимого контейнера (вместимость) и веса мелких предметов. Они будут работать как с обычной системой измерения США, так и с метрической системой. Они будут использовать такие термины, как чашки, пинты, кварты, галлоны, литры, унции, фунты, тонны, граммы и килограммы. Также будут изучены некоторые эквивалентные меры (например: 2 пинты = 1 кварта).Их также можно познакомить с математической концепцией объема для правильных прямоугольных призм.
Площадь и периметр
Третьеклассники продолжат работу по периметру и площади. Например, они могут измерить расстояние вокруг своего учебника или использовать блоки с узором, чтобы «выложить плиткой» поверхность, например, свой стол. Они также узнают, как рассчитать площадь и периметр предметов или картинок.
Десятичные
Учащиеся третьего класса уже имели много возможностей исследовать числа, которые меньше единицы через дроби и начинаются с десятичных знаков через деньги.Теперь они начнут исследовать числа до тысячных долей (например, 0,001), то есть до трех знаков после запятой.
Узоры
Учащиеся третьего класса уже работали с образцами цвета, формы и чисел, и они будут продолжать открывать новые способы создания более сложных рисунков в математике. Этот математический навык включает в себя некоторое сложение и вычитание, логическое мышление и т. Д.
Окружность и диаметр
Ученики третьего класса начнут изучать способы измерения кругов.Они познакомятся с математическими понятиями окружности (расстояния по внешней стороне круга) и диаметра (расстояния по центру круга).
Длинное умножение
Учащиеся третьего класса будут обучаться умножению больших чисел (например, 47 × 5 или 32 × 61). Существует множество математических стратегий и математических методов для решения этих больших задач умножения, и некоторые студенты будут обучаться более чем одному методу (например: традиционный метод, метод частичных произведений, метод решетки, ментальная математика и т. Д.).
В процентах
Учащиеся третьего класса уже имели много возможностей исследовать числа, которые меньше единицы через дроби и начинаются с десятичных знаков через деньги. Теперь они начнут исследовать числа до тысячных долей (например, 0,001), то есть до трех знаков после запятой.
Упорядоченные пары в координатной сетке
В 3-м классе дети узнают об упорядоченных парах (например, 6,4) и о том, как изобразить эти упорядоченные пары на координатной сетке с осями «x» и «y».
Вероятность
Студенты-математики третьего класса будут проводить базовые эксперименты, чтобы исследовать вероятность наступления события, идею случайности и прогнозировать результаты. Они могут бросать кости, подбрасывать монеты или использовать спиннеры, чтобы узнать о вероятности.
Онлайн-программа по математике для 3-го класса
Посмотреть демо наших уроков!
Умножение и деление — это игра в математике для третьего класса. Студенты познакомятся с этими понятиями, выучат их таблицу умножения и поймут, что на самом деле означает умножать и делить.
Твердое понимание математических фактов для 3-го класса поможет учащимся усвоить эти важные концепции и достичь своих учебных целей. На этой странице вы узнаете важную информацию, в том числе:
Что математику следует знать третьекласснику
При изучении математики в третьем классе учащиеся должны знать свои фактические семьи в сложении, вычитании, умножении и делении. Обладая этой информацией, они смогут решать двухэтапные задачи со словами и уравнения. Кроме того, третьеклассники должны уметь читать и писать большие числа через сотни тысяч и знать разряд каждой цифры.
Ниже приведены еще несколько навыков, которые должен знать третий класс.
- Сложите четырехзначные числа
- Вычесть с перегруппировкой
- Круглые числа с точностью до десятков и сотен
- Понимание двух- и трехмерных фигур
- Решайте текстовые задачи, требующие времени, денег и измерения
Эффективная учебная программа по математике в третьем классе должна обеспечивать овладение каждым из этих понятий / навыков, предоставляя подробные инструкции и множество возможностей для практики.Посетите наш раздел и последовательность по математике для 3-го класса, чтобы узнать, как удостоенная наград комплексная учебная программа Time4Learning может сделать именно это.
Задачи по математике для 3-го класса
В третьем классе ваш ребенок должен выполнить ряд математических задач. Это позволит им позже легко изучить более сложные концепции. Практика математических фактов в первые годы начальной школы как можно чаще поможет им сосредоточиться на изучении этих новых навыков и понимании более сложных концепций в ближайшие годы.
Задачи по математике в этом году:
- Приобретите навыки для выполнения мысленных вычислений
- Умножение двузначных чисел
- Разделить двузначные числа
- Понимать, сравнивать и определять дроби
- Расшифровка диаграмм и графиков
Узнайте, как Time4MathFacts (включенный в вашу подписку) способствует свободному владению математическими фактами с помощью интерактивных и игровых уроков, которые помогают учащимся овладеть сложением, вычитанием, делением и умножением.
Почему выбирают программу Time4Learning по математике для 3-го класса
В Time4Learning мы понимаем, насколько важно заложить прочный фундамент в математике. Без надлежащих математических навыков ученики в последующие годы будут испытывать трудности. В нашей программе математики для третьего класса рассматриваются вышеупомянутые концепции и многое другое.
Хотя наши материалы соответствуют всем государственным стандартам, мы стремимся к тому, чтобы наши студенты превышали свои академические цели к концу нашей курсовой работы. Кроме того, мы стремимся привить любовь к учебе каждому из наших студентов.
Для родителей мы предоставляем простой способ обеспечить их детям качественное образование, не беспокоясь о выставлении оценок, планировании уроков или ведении записей. Просто войдите в родительскую панель управления, чтобы следить за успеваемостью своего ребенка, распечатайте отчеты для своих портфелей домашнего обучения, и все готово!
Ниже вы найдете список причин, по которым многие семьи доверяют Time4Learning удовлетворение математических потребностей своих детей в третьем классе.
Как полный учебный план
Учебная программа | В качестве дополнения
|
Дополнительные ресурсы для домашнего обучения для 3-го класса
Помощь в решении уравнений 3-го класса
В 3-м классе вы познакомитесь с навыками предварительной алгебры, такими как определение недостающего числа в уравнении. Вы также попрактикуетесь в написании уравнений для представления текстовых задач. Чтобы узнать больше, читайте дальше!
Уравнения для 3-х классов
Уравнение использует знак «=», чтобы сообщить вам, что два выражения имеют одно и то же значение.Уравнения могут принимать разные формы. Вот некоторые примеры:
- 3 = 3
- 5-2 = 3
- 3 ÷ 1 = 3
- 5-2 = 3 ÷ 1
Уравнения
В 3-м классе вы попрактикуетесь в решении уравнений . Это означает, что вам будут даны уравнения, в которых отсутствует число, и вам нужно будет выяснить, что это за число.Недостающее число называется переменной , и вы можете представить его любым символом. Для этой цели мы часто используем такие буквы, как x или n , но вы можете использовать любой символ, какой захотите. Вот несколько уравнений с переменными:
- 4 + x = 7
- n ÷ 2 = 4
- 4 x 5 =?
Первые два примера могут быть для вас новыми, но последний должен быть более знакомым.Это потому, что, даже если вы этого не понимаете, вы «решаете» уравнение каждый раз, когда решаете математическую задачу. Когда вы ответите на задачу 4 x 5, написав 4 x 5 = 20, вы только что нашли недостающую переменную!
Теперь давайте попрактикуемся в решении уравнений, у которых переменная находится на другой стороне. Чтобы определить x в задаче 4 + x = 7, спросите себя: «Четыре плюс , какое число равно семи?» Вы помните, что 4 + 3 = 7, поэтому вы можете сказать, что x = 3.
Аналогично работает для умножения и деления. Чтобы решить для n в задаче n ÷ 2 = 4, вам нужно выяснить, какое число, разделенное на два, равно четырем. Поскольку 8 ÷ 2 = 4, n = 8. Теперь давайте попробуем решить задачу 5 x? = 20. Вы уже знаете, что 5 x 4 = 20, поэтому четыре — это отсутствующая переменная.
Уравнения для задач Word
Еще один навык предварительной алгебры, который вы изучите в 3-м классе, — это написание уравнений для представления текстовых задач.Вот пример:
Даника, Калеб и Тэмми вышли за мороженым. Даника заказала две шарики мороженого, Калеб заказал три шарика, а Тэмми также заказала мороженое. Если они заказали всего шесть шариков мороженого, сколько мороженого заказала Тэмми?
Поскольку общее количество заказанных ложек было шесть, это число находится на одной стороне знака «=». Мы хотим знать, сколько шариков мороженого заказала Тэмми, поэтому обозначим это буквой T .Мы знаем, что количество ложек, заказанных Даникой и Калебом, плюс количество, заказанное Тэмми, равно шести, поэтому мы можем написать уравнение 2 + 3 + T = 6. Поскольку 2 + 3 + 1 = 6, мы можем говорят, что Тэмми заказала одну шарик мороженого.
Урок по уравнениям для детей: определение и примеры — видео и стенограмма урока
Что такое уравнение?
Уравнение — математическое предложение, которое имеет две равные стороны, разделенные знаком равенства.
4 + 6 = 10 — это пример уравнения. Слева от знака равенства мы видим 4 + 6, а справа от знака равенства 10.
При решении математических задач, например, при определении того, сколько денег Макс осталось потратить, часть уравнения будет отсутствовать. Уравнение для задачи Макса будет выглядеть так:
Как видите, уравнения также могут иметь константы, коэффициенты, переменные и операторы.
Константы — это числа, которые не меняются. 80 — константа в этом примере.
Коэффициент — это число, прикрепленное к переменной. Коэффициенты используются в уравнениях умножения. Например, 12 — коэффициент в уравнении 12 n = 24.
Переменная — это буква, представляющая неизвестное число. В этой задаче b — это переменная, которую нам нужно решить.
Оператор сообщает вам, какую операцию использовать, и включает в себя сложение, вычитание, умножение и деление.
Решение уравнений
Чтобы решить это уравнение, Макс должен получить переменную с одной стороны отдельно. Он делает это с помощью обратных операций. Обратные операции подобны противоположностям. Какую бы операцию мы ни видели в уравнении, мы используем для ее решения обратную операцию. В этом случае оператор является знаком сложения. Поэтому мы будем использовать обратную операцию, вычитание, чтобы изолировать переменную.
Кроме того, поскольку уравнения имеют знак равенства, они всегда должны оставаться равными и сбалансированными.Другими словами, что бы мы ни делали с одной стороной уравнения, мы должны делать то же самое с другой стороной. Давай попробуем!
Первый шаг в выделении переменной — вычесть 80 из обеих частей нашего уравнения. 80-е слева отменяют или отменяют друг друга. Теперь наша переменная b находится сама по себе.
Поскольку мы вычли 80 из одной части уравнения, мы должны сделать это и с другой стороны:
Значит, у Макса осталось 40 долларов.Он может купить одну коробку стримеров.
Практикуйтесь в решении уравнений
Хорошо, теперь ваша очередь. Так что возьмите лист бумаги и карандаш. Я собираюсь рассказать вам о проблеме, но не прокручивайте ее вниз, чтобы увидеть решение, пока вы не попытаетесь решить ее самостоятельно.
Оскар экономит на покупке велосипеда по цене 245 долларов. Если он уже накопил 62 доллара, сколько еще денег ему нужно, чтобы купить велосипед?
Вот наше уравнение:
Думаете, что закончили? Хорошо.Продолжайте читать, чтобы увидеть, правильно ли вы решили.
Во-первых, поскольку оператор является знаком «плюс», мы знаем, что нам нужно выполнить обратную операцию вычитания, чтобы изолировать переменную.
Во-вторых, мы также знаем, что то, что мы делаем с одной стороны, мы должны делать с другой.
Итак, вычитая 62 из каждой части уравнения, мы видим, что x = 183.
Оскару нужно сэкономить 183 доллара, чтобы купить байк.
Резюме урока
Хорошо, давайте сделаем пару минут, чтобы повторить то, что мы узнали. Хотя вы можете идентифицировать уравнение по его знаку равенства, поскольку это математические предложения, которые имеют две равные стороны, разделенные знаком равенства, уравнения также могут состоять из констант, переменных, коэффициентов и операторов. При решении уравнений важно использовать обратных операций , которые по сути являются противоположностями по обе стороны уравнения, поэтому вы всегда сохраняете его сбалансированность.
Математика / Цели обучения математике для третьего класса
Цели обучения математике для третьего класса
Числа и операции
Подсчет наборов чисел, представление чисел, сравнение и порядок номеров, значение места
- Представление чисел до 10 000 в различных эквивалентных формах.
- Посчитайте до 10 000.
- Считайте сотнями и тысячами.
- Сравните и закажите целые числа до 10 000.
- Используйте модели разрядов для чтения, записи и представления чисел до 10 000.
Целое число: сложение и вычитание
- Перегруппировка модели при сложении и вычитании с разметкой.
- Сложите и вычтите целые числа до 10 000.
- Решите задачи сложения и вычитания с большими числами с помощью столбчатой модели.
Целое число: умножение и деление
- Умножение и деление на 6, 7, 8 и 9.
- Представляйте умножение и деление по-разному.
- Умножение единиц, десятков и сотен с перегруппировкой и без нее.
- Используйте свойства сложения и умножения для умножения.
- Разделите 10 и 1 с перегруппировкой и без, без остатка.
- Используйте линейчатые модели для представления ситуаций умножения и деления.
- Решайте одно- и двухэтапные задачи умножения и деления.
Оценка и ментальная математика
- Используйте стратегии ментальной математики для сложения, вычитания, умножения и деления.
Деньги
- Сложите и вычтите деньги.
- Решайте реальные задачи, связанные с сложением и вычитанием денег.
- Используйте знак доллара и десятичную точку в денежных суммах.
Концепции, операции и приложения дробей
- Разберитесь в значениях и использовании дробей, включая дробную часть множества.
- Помните, что размер дробной части зависит от размера целого.
- Сравните дроби с помощью моделей, числовых линий.
- Определите эквивалентные дроби с помощью моделей, умножения, деления и числовых линий.
- Сложить и вычесть как дроби.
Алгебраическое мышление
Шаблоны и свойства
- Создавайте и анализируйте шаблоны умножения и деления.
- Поймите, что умножение и деление связаны.
- Смоделируйте, определите и объясните свойства умножения.
- Определите четные и нечетные числа.
Алгебраические отношения и модели
- Опишите числовые отношения в контексте.
Числовые предложения, уравнения и неравенства
- Запишите числовые предложения умножения и деления.
- Напишите и решите числовые предложения для одно- и двухэтапных реальных задач.
- Определите недостающие части (количества или символы) в числовых предложениях.
- Понять равенство и неравенство.
Геометрия и измерения
Время и температура
- Считайте время на цифровых часах.
- Укажите время с точностью до минуты.
- Преобразование часов в минуты
- Сложение и вычитание единиц времени.
- Определите истекшее время.
- Считайте термометр Фаренгейта.
- Выберите подходящий инструмент и единицу измерения температуры.
- Используйте справочные данные для оценки температуры.
Линии и углы
- Определите перпендикулярные и параллельные линии.
- Определите прямые углы и сравните углы с прямыми углами.
Фигуры
- Описывайте, анализируйте, сравнивайте и классифицируйте двумерные формы по их сторонам и углам.
- Классифицируйте и сортируйте многоугольники и четырехугольники по атрибутам и свойствам.
- Исследуйте составление и разложение двухмерных фигур.
- Используйте атрибуты и свойства для решения проблем.
Длина, расстояние, периметр и площадь
- Выберите соответствующие единицы и инструменты для оценки и измерения длины.
- Для измерения длины используйте мерные стержни, 12-дюймовые линейки и мерки.
- Измерьте длину с точностью до полдюйма и дюйма.
- Используйте ссылки для оценки расстояния.
- Измерьте периметр плоских фигур.
- Выберите подходящий инструмент и стратегию для измерения периметра.
- Найдите и сравните площади плоских фигур в различных квадратных единицах.
- Создавайте разные плоские фигуры с одинаковой площадью.
- Сравните площадь и периметр плоских фигур.
- Найдите площадь прямоугольников и составных фигур.
Площадь и объем поверхности
- Оцените и измерьте емкость в литрах и миллилитрах.
- Преобразование метрических единиц мощности.
- Выберите подходящие инструменты и единицы измерения для оценки и измерения объема в кубических единицах.
- Свяжите единицы обычной вместимости друг с другом.
- Раскладывайте твердые фигуры, чтобы найти площадь поверхности.
Вес и масса
- Выберите соответствующие единицы и инструменты для оценки и измерения веса.
- Используйте точки отсчета для измерения веса.
- Оценивайте и находите массы предметов.
- Преобразование единиц массы.
Конгруэнтность, симметрия, преобразования и координатная геометрия
- Определите симметричные фигуры и одну линию симметрии.

 Экибастуз.
Экибастуз. (флипчарт 1)
(флипчарт 1)
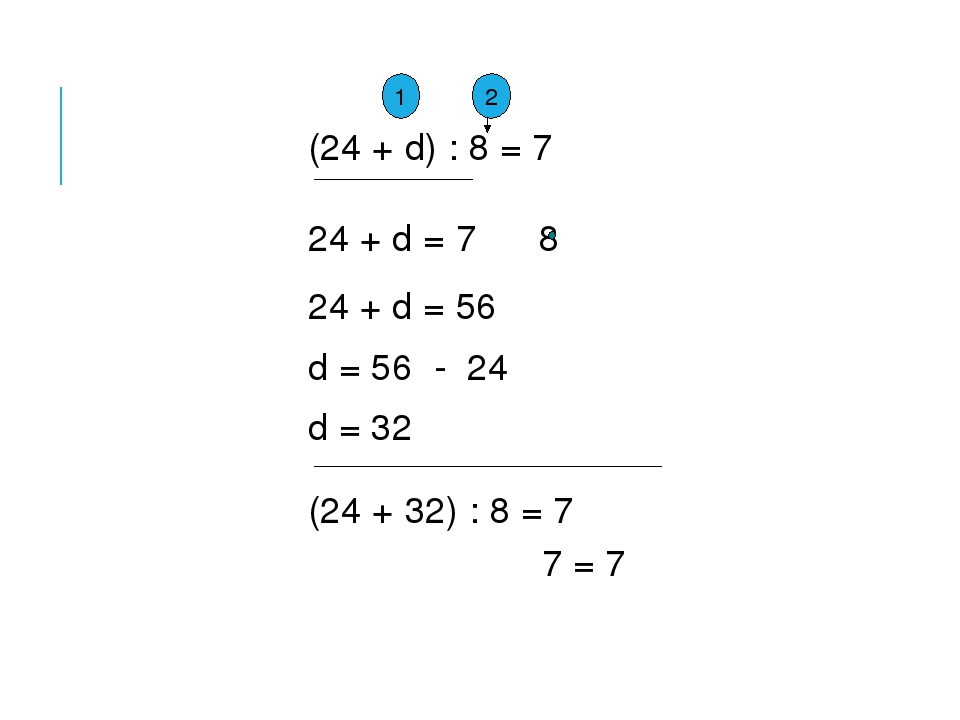 В каком из этих компонентов стоит переменная?
В каком из этих компонентов стоит переменная? – Чтение по учебнику, с. 70
– Чтение по учебнику, с. 70 Проверка. Общая оценка.
Проверка. Общая оценка.