Содержание
Диагонали трапеции. Диагонали трапеции Формулы для нахождения диагоналей трапеции
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.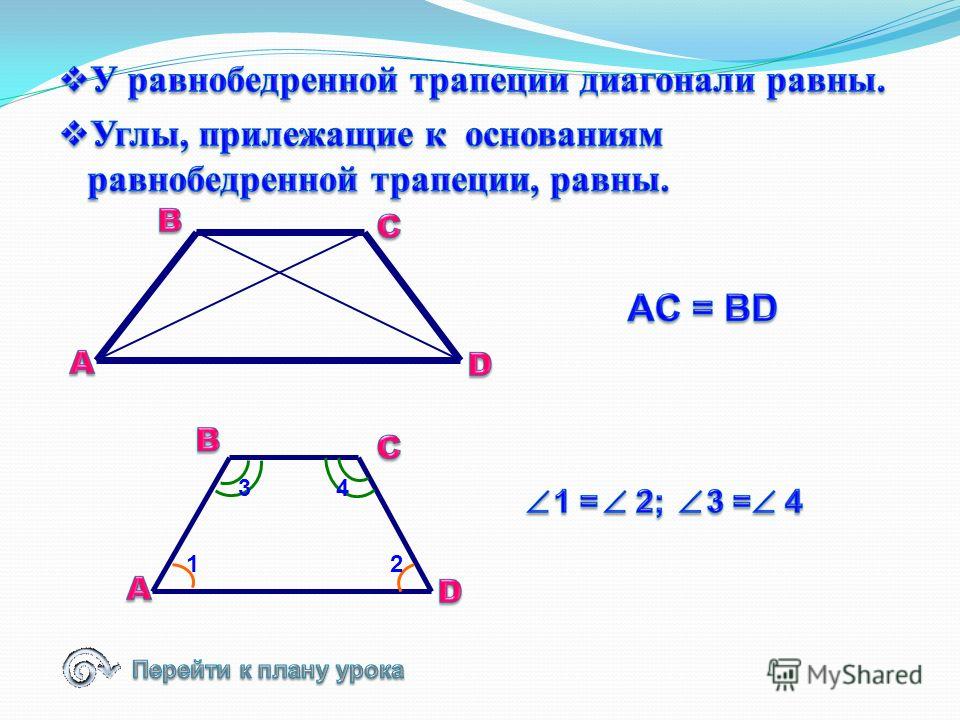
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
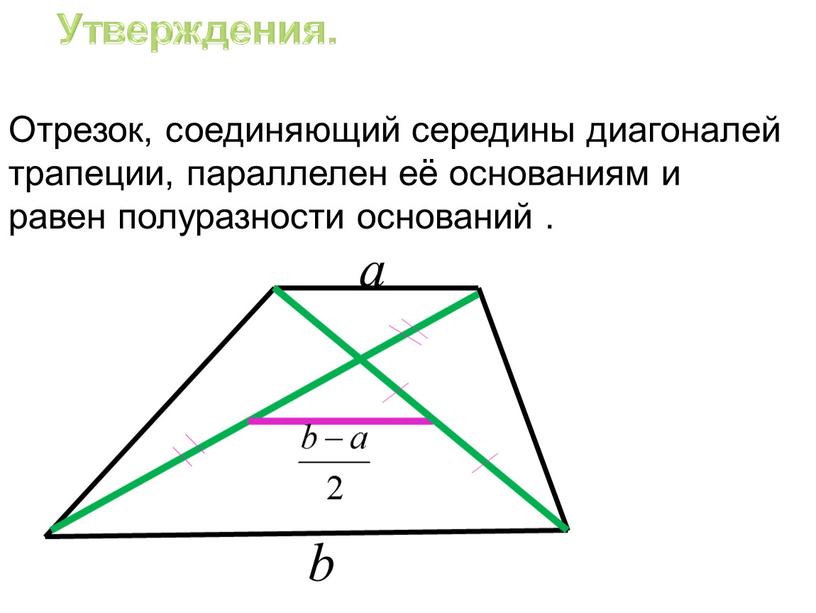
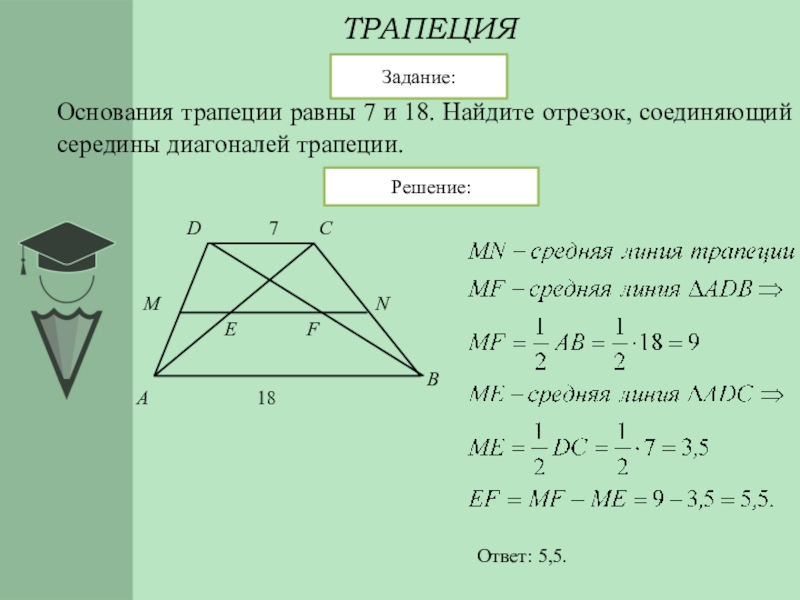
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.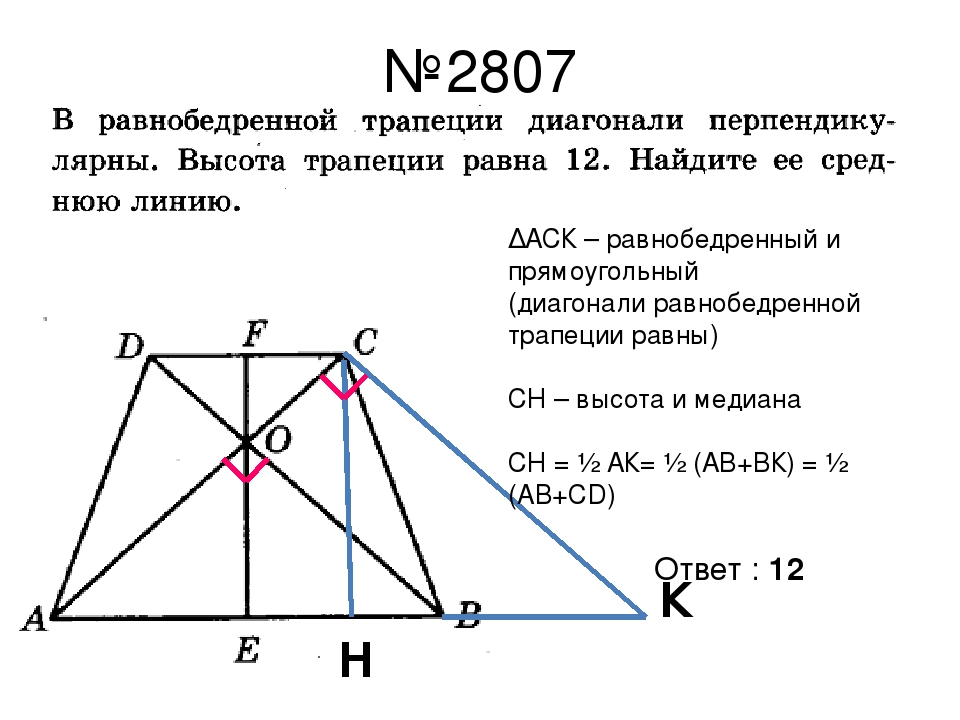
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.
Данный отрезок параллелен основаниям трапеции
.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.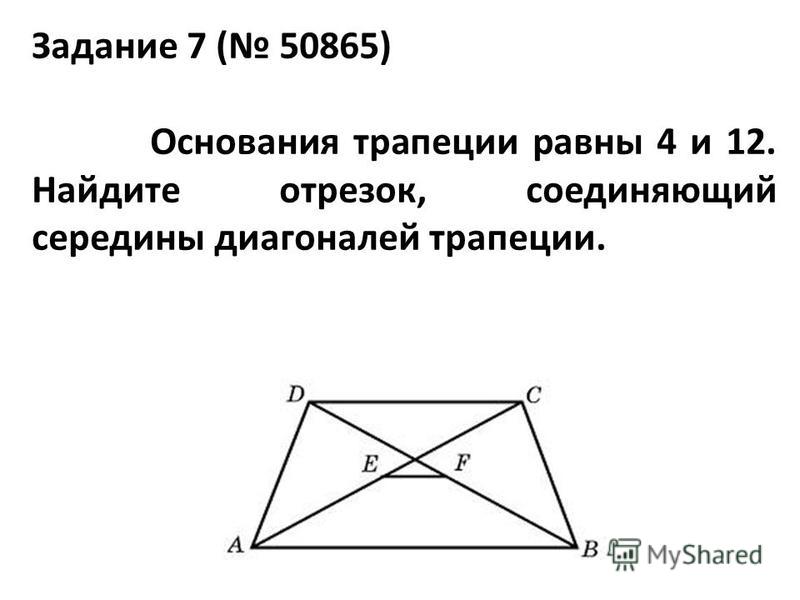
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b
— основания трапеции
c, d
— боковые стороны трапеции
d1 d2
— диагонали трапеции
α β
— углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.
Задача
.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение
.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ
: 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты.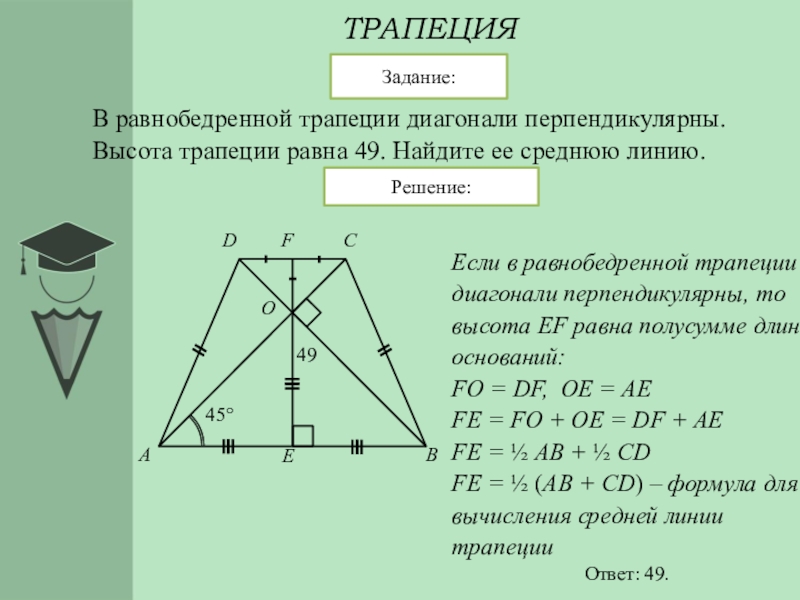 Поскольку трапеция неравнобокая — то обозначим
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ
: площадь трапеции равна 80 см 2 .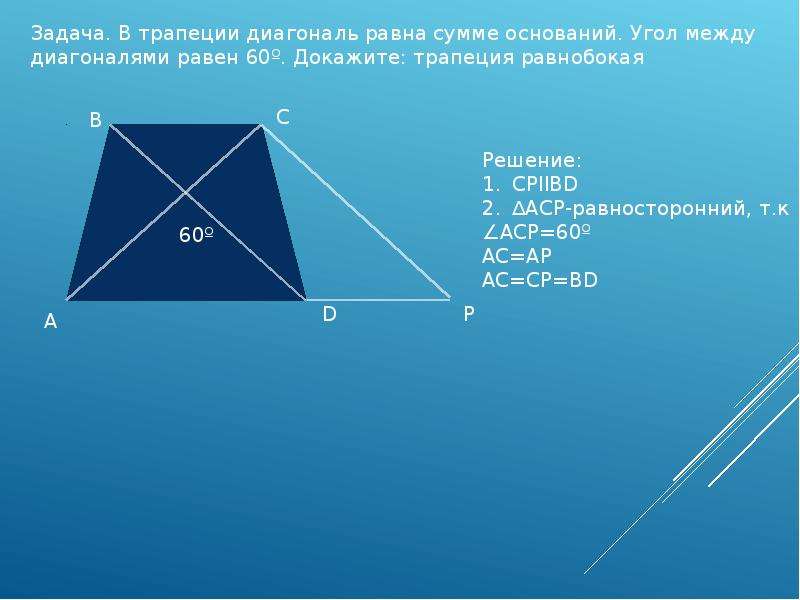
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.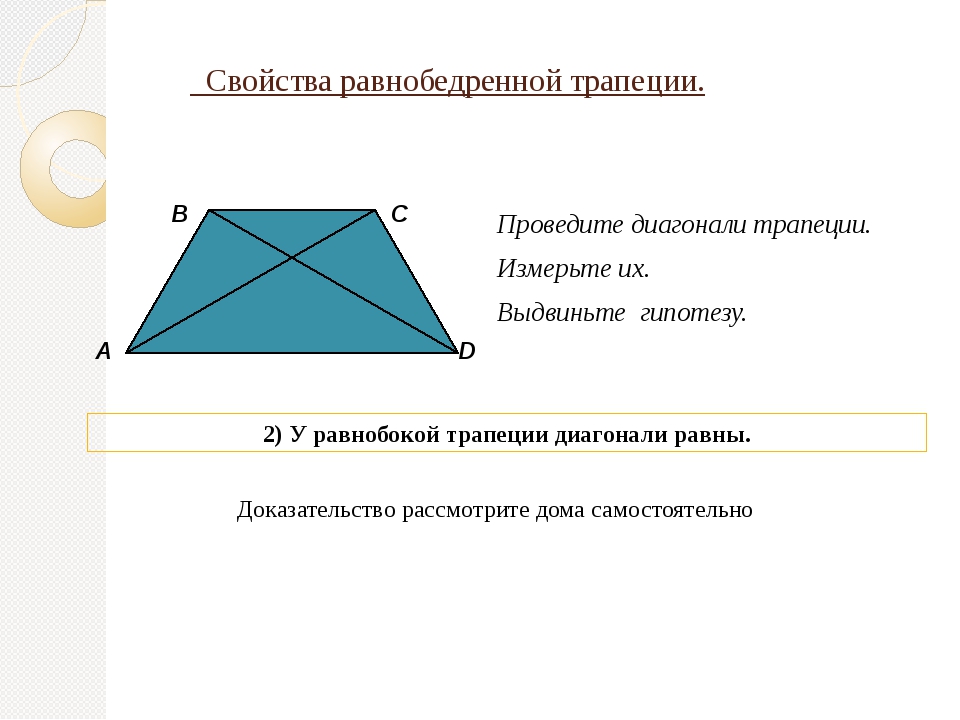
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
Диагонали трапеции. Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.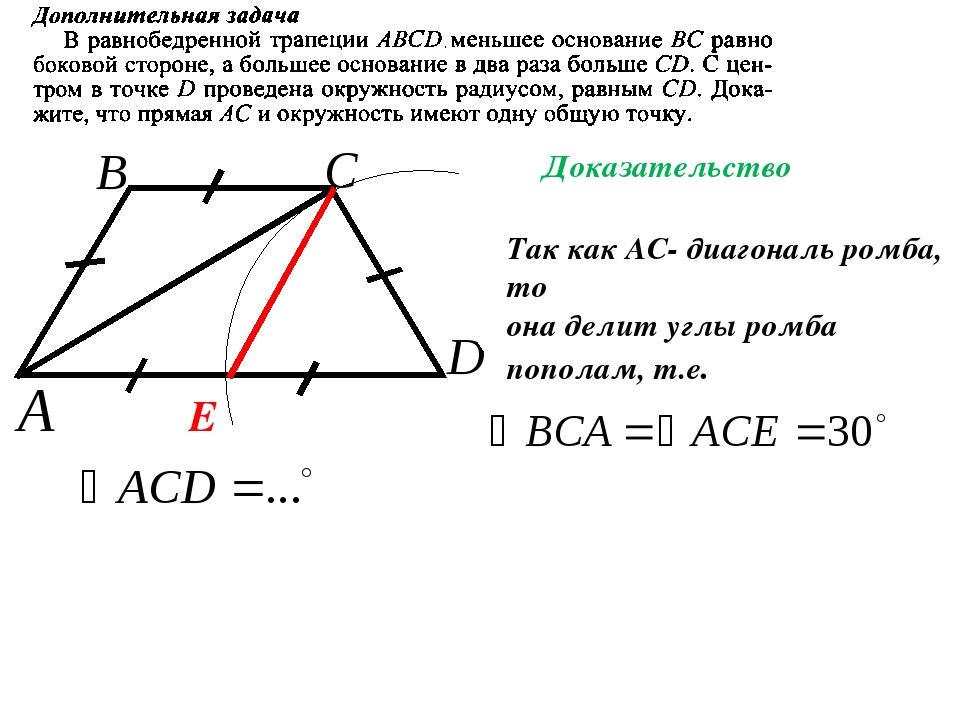
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние
;
— равнобокие
;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции
параллельна основаниям и равна их полусумме - Отрезок, соединяющий середины диагоналей
, равен половине разности оснований и лежит на средней линии. Его длина
Его длина - Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции
, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника) - Треугольники, лежащие на основаниях
трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции - Треугольники, лежащие на боковых сторонах
трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади) - В трапецию можно вписать окружность
, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований) - Отрезок, параллельный основаниям
и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые
.
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые
, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему
по длине основанию, а острые – большему
основанию.
Любую трапецию можно рассматривать как усеченный треугольник
, у которого линия сечения параллельна основанию треугольника.
Важно
. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.
Свойства параллелограмма
1. Противолежащие стороны равны.
На рис. 11 AB
= CD
; BC
= AD
.
2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A
= ∠C
; ∠B
= ∠D
.
3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.
На рис. 11 отрезки AO
= OC
; BO
= OD
.
Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.
Параллельные стороны называются ее основаниями
, а две другие стороны — боковыми сторонами
.
Виды трапеций
1. Трапеция
, у которой боковые стороны не равны,
называется разносторонней
(рис.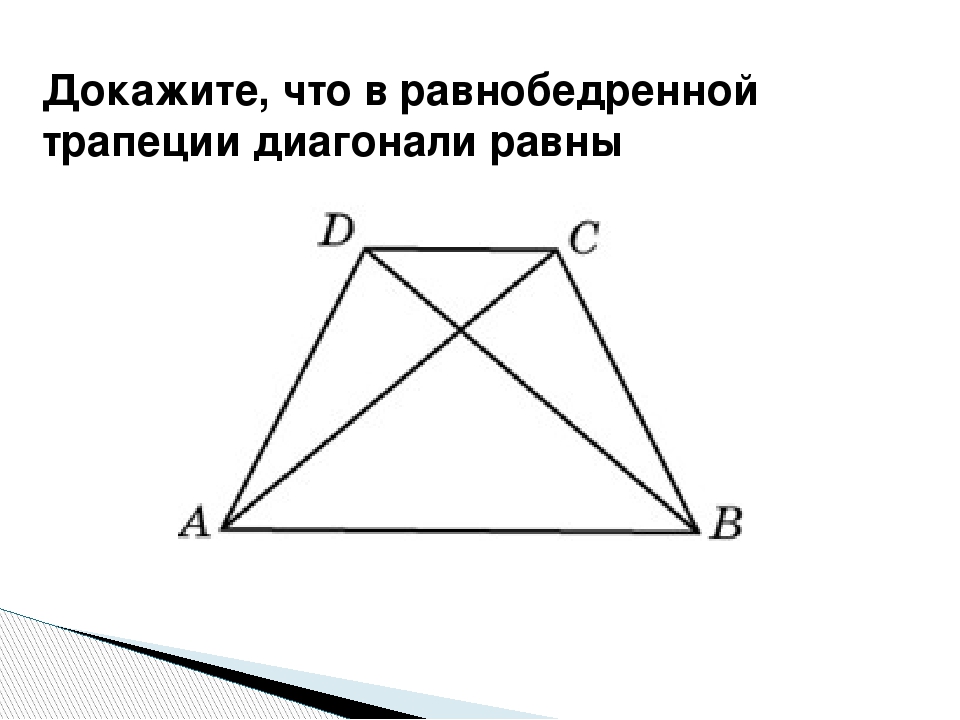 12).
12).
2. Трапеция, у которой боковые стороны равны, называется равнобокой
(рис. 13).
3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной
(рис. 14).
Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN
). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).
Площадь параллелограмма и трапеции
Правило. Площадь параллелограмма
равна произведению его стороны на высоту, проведенную к этой стороне.
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции
О свойствах фигуры было известно еще в Древней Греции
, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Вконтакте
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей.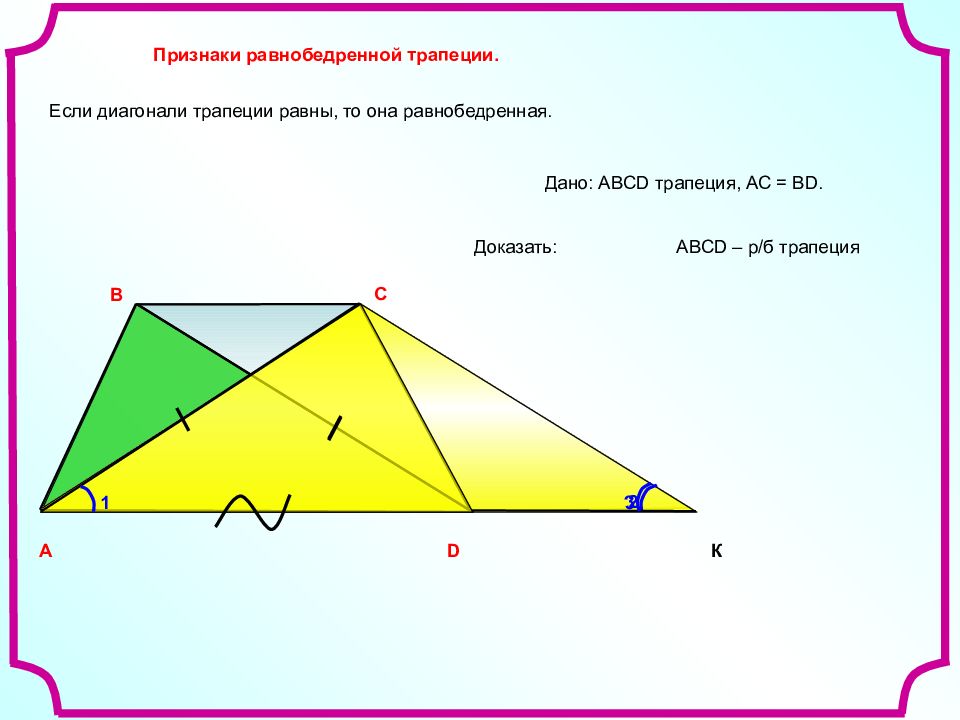
Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника
ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет . Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции.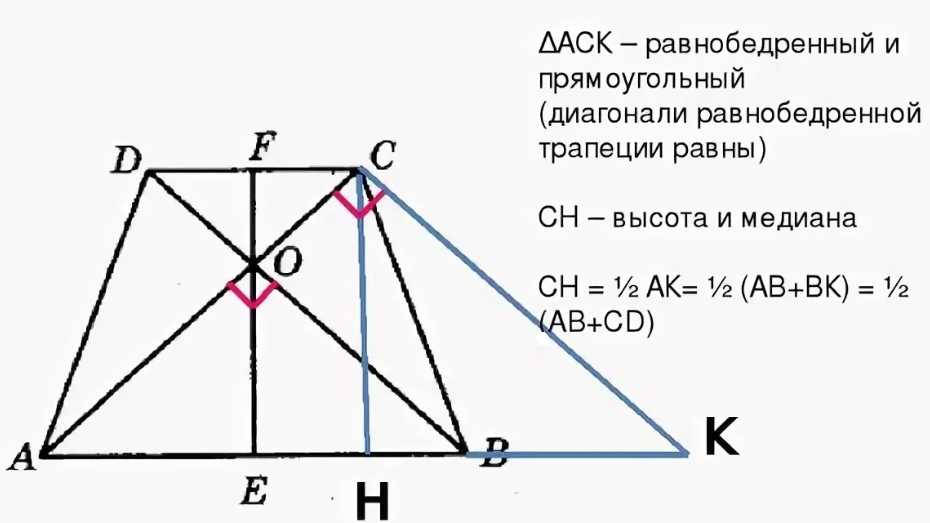 Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
Важно!
При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная
. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.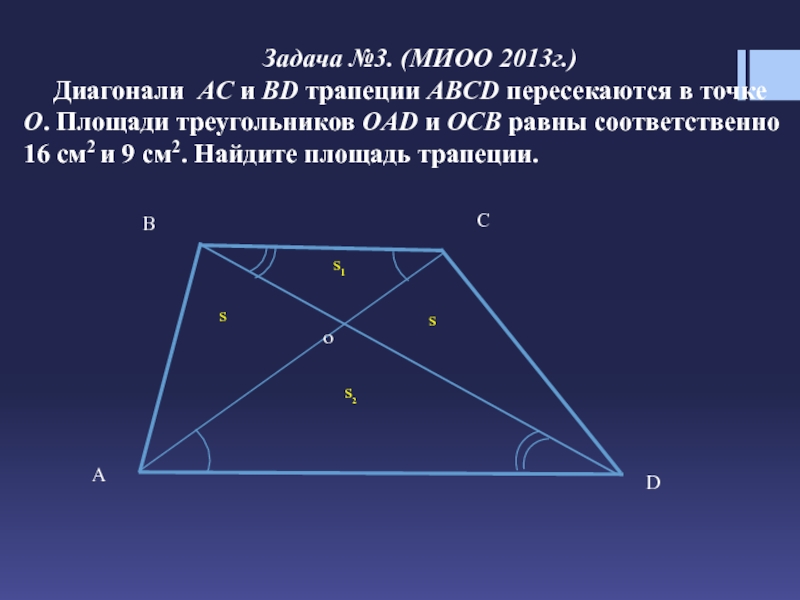
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить .
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции
:
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может,
Двух боковых сторон с углами при основании быть не может,
потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией.
Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно!
Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции,
следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис. 5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников.
Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Важно!
В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как
:
- средняя линия;
- площадь;
- высота;
- диагонали.

Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь
.
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее
*Центр шестиугольника и центр окружности совпадают, подробнее
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB).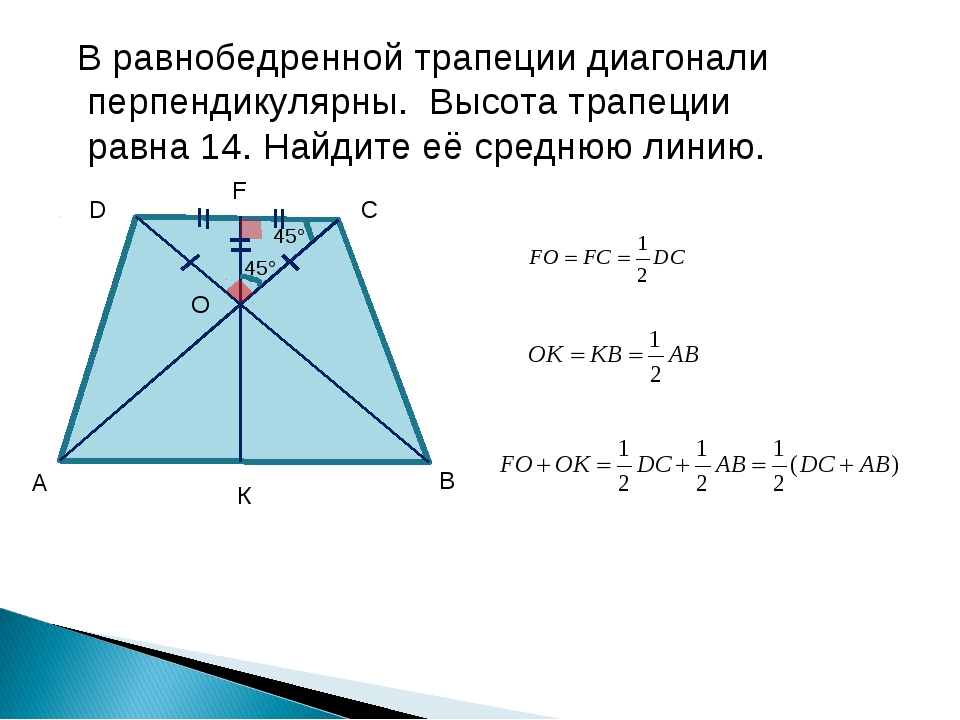 По теореме Пифагора можем вычислить OE:
По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием).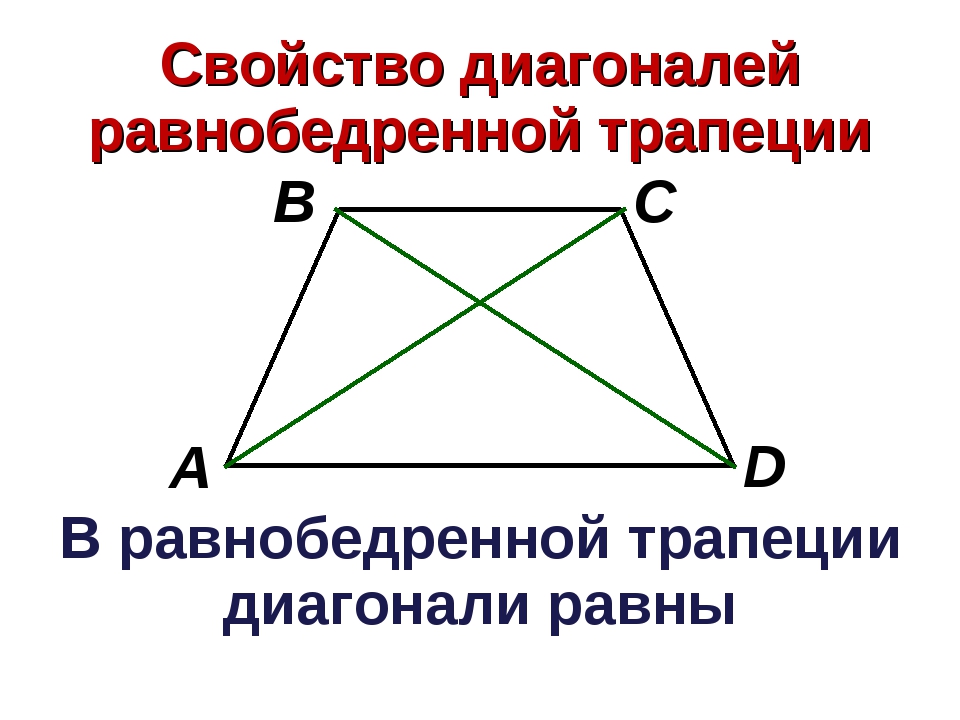 Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
— (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка
Трапеция
— Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь
трапеция
— четырехугольник, снаряд, перекладина Словарь русских синонимов. трапеция сущ., кол во синонимов: 3 перекладина (21) … Словарь синонимов
трапеция сущ., кол во синонимов: 3 перекладина (21) … Словарь синонимов
ТРАПЕЦИЯ
— (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия
ТРАПЕЦИЯ
— (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь
ТРАПЕЦИЯ
— ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь
ТРАПЕЦИЯ
— ТРАПЕЦИЯ, трапеции, жен. (от греч. trapeza стол). 1. Четырехугольник с двумя параллельными и двумя непараллельными сторонами (мат.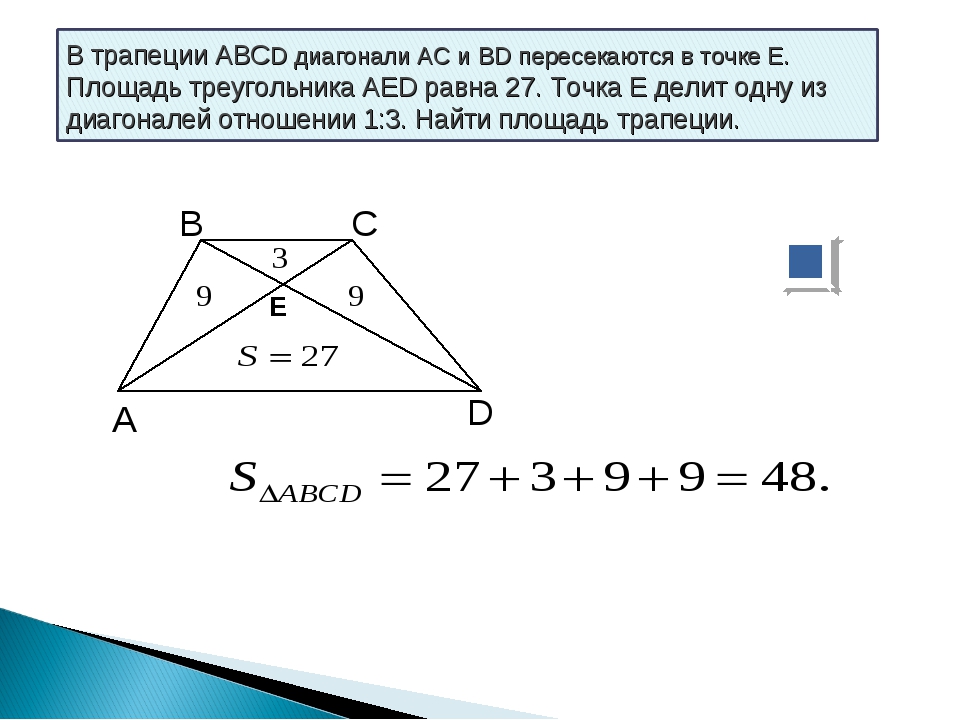 ). 2. Гимнастический снаряд, состоящий из перекладины, подвешенной на двух веревках (спорт.). Акробатические… … Толковый словарь Ушакова
). 2. Гимнастический снаряд, состоящий из перекладины, подвешенной на двух веревках (спорт.). Акробатические… … Толковый словарь Ушакова
ТРАПЕЦИЯ
— ТРАПЕЦИЯ, и, жен. 1. Четырёхугольник с двумя параллельными и двумя непараллельными сторонами. Основания трапеции (её параллельные стороны). 2. Цирковой или гимнастический снаряд перекладина, подвешенная на двух тросах. Толковый словарь Ожегова. С … Толковый словарь Ожегова
ТРАПЕЦИЯ
— жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ТРАПЕЦИЯ
— (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино
Трапеция
— четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны.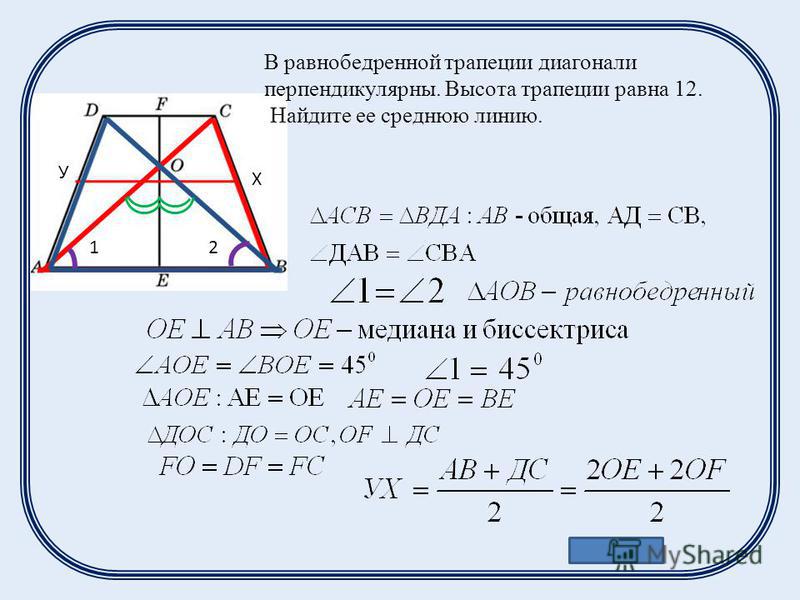 Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона
Если диагонали трапеции делятся точкой пересечения в отношении 1 : 3
Решение:
Сначала вспомним теорию.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.Трапеция
Трапеция называется равнобедренной трапецией, если ее боковые стороны равны.
Равнобедренная трапеция
Трапеция, один из углов которой прямой, называется прямоугольной трапецией.
Прямоугольная трапеция
Также будет полезно вспомнить следующую теорему:
Трапеция разбивается диагоналями на два равновеликих треугольник (примыкающих к боковым сторонам) и два подобных треугольника (примыкающих к основаниям).
А также будет полезно вспомнить свойство трапеции:
Любой отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в отношении:
Свойство трапеции
Это справедливо, в том числе , для самых диагоналей и высоты.
Снова обратимся к рисунку.
Так как треугольники AOD и BOC подобны, то справедливы следующие соотношения:
По условию диагонали трапеции делятся точкой пересечения в отношении 1 : 3, значит
Далее вспомним еще одно определение.
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме. На приведенном ниже рисунке это отрезок MN.
MN — средняя линия трапеции
Из соотношения:
следует, что 3BC = AD, значит:
MN = (AD + BC) : 2 = (3BC + BC): 2 = 4BC: 2 = 2BC
Таким образом, средняя линия трапеции в два раза больше меньшего основания.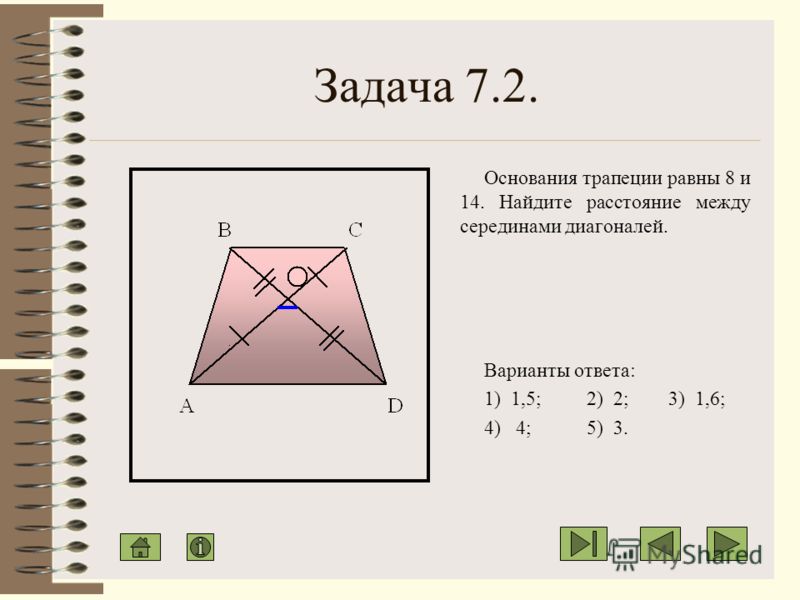 Утверждение верное.
Утверждение верное.
Ответ: утверждение верно.
В прямоугольной трапеции диагонали взаимно. Диагонали трапеции
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.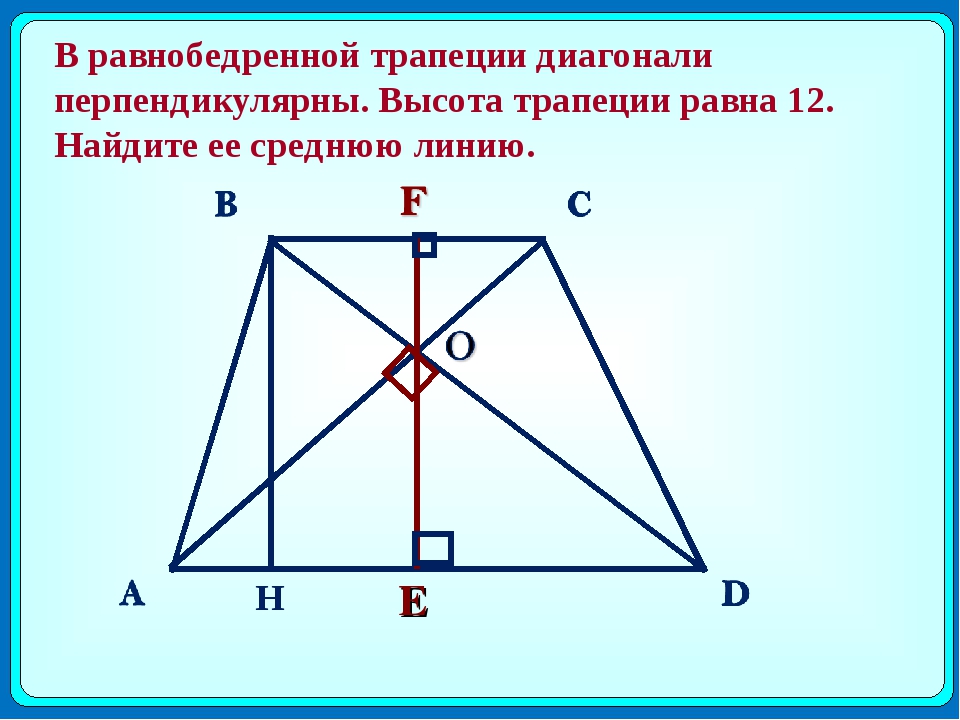
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.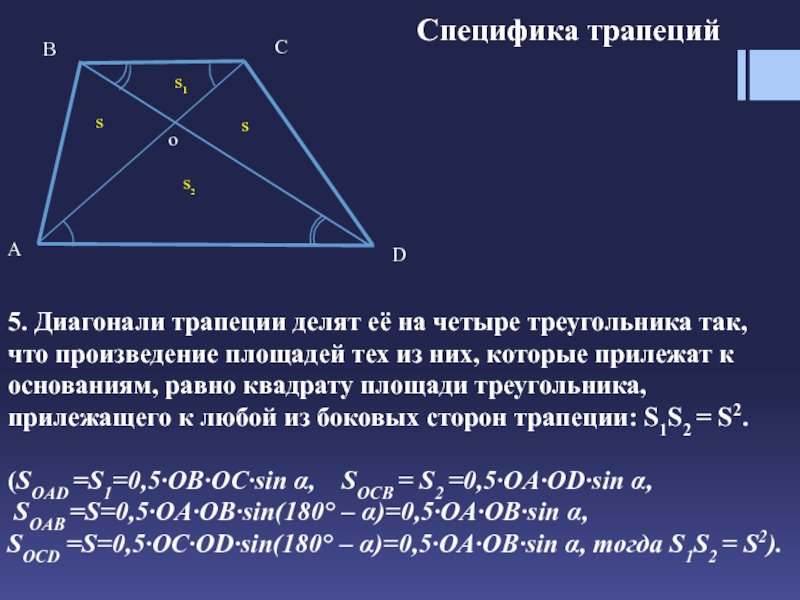 х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с.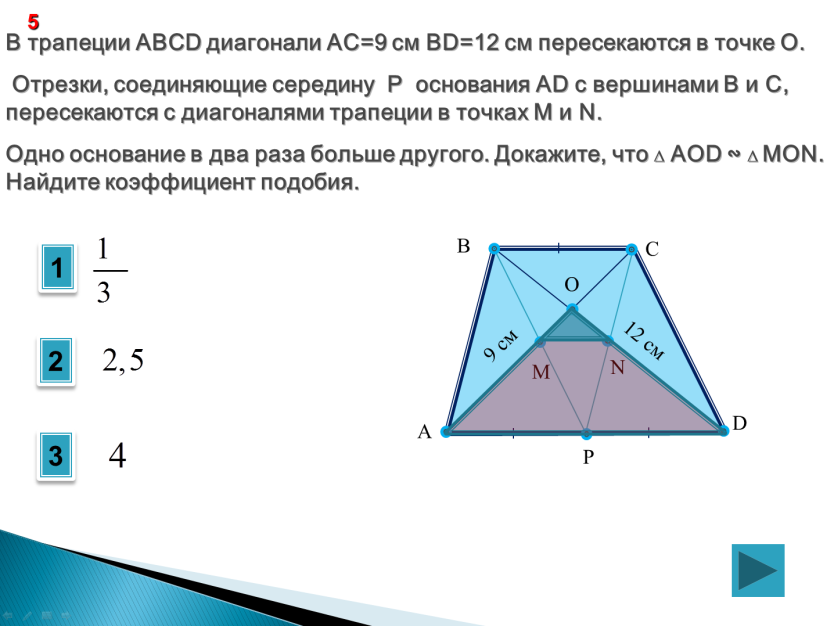 Найдите объем призмы.
Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.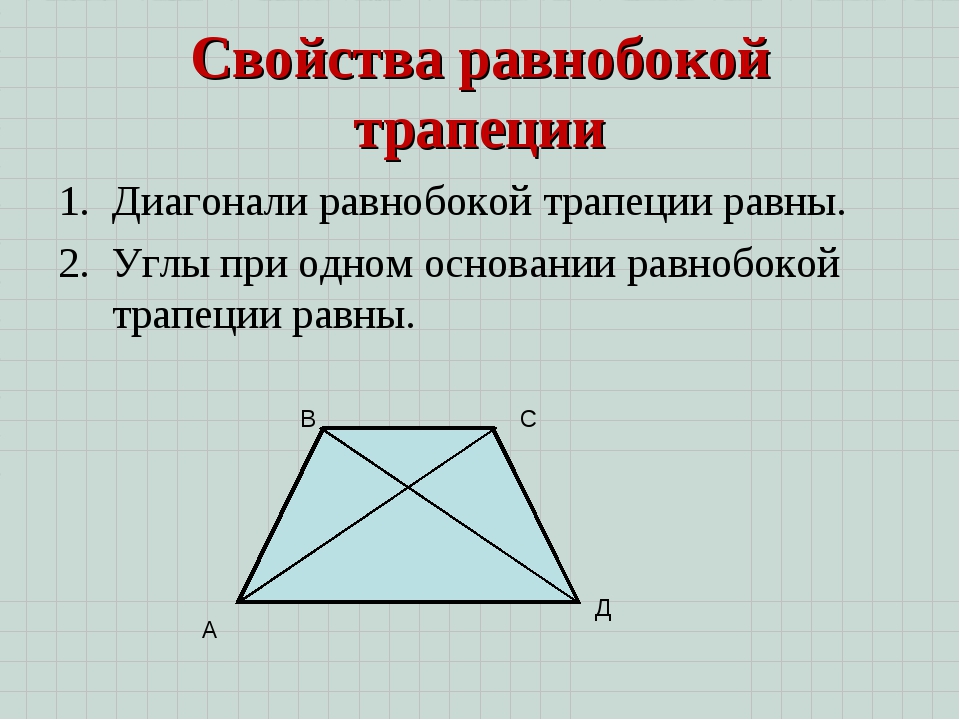
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.
Данный отрезок параллелен основаниям трапеции
.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.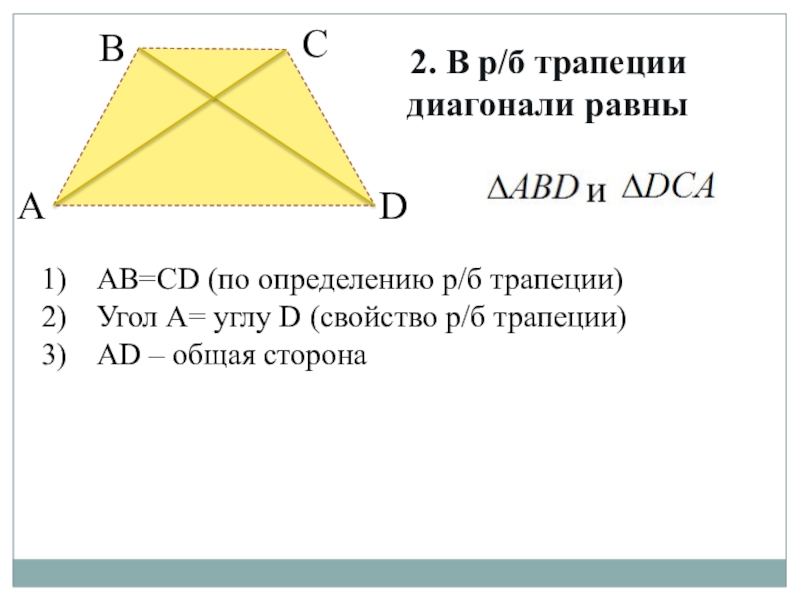
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.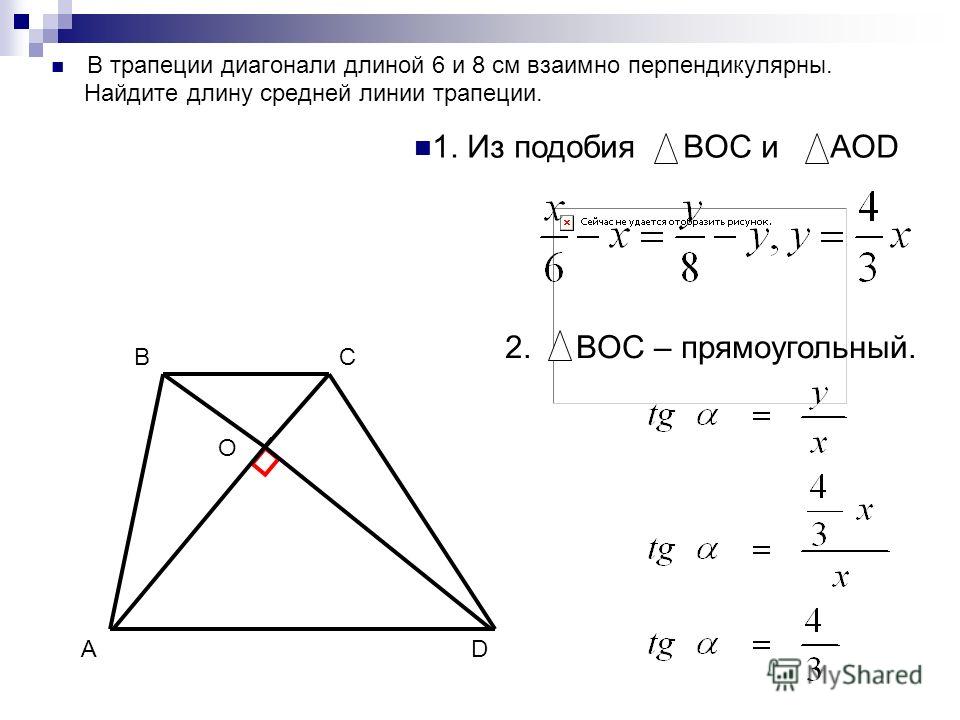
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b
— основания трапеции
c, d
— боковые стороны трапеции
d1 d2
— диагонали трапеции
α β
— углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.
Задача
.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение
.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ
: 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты.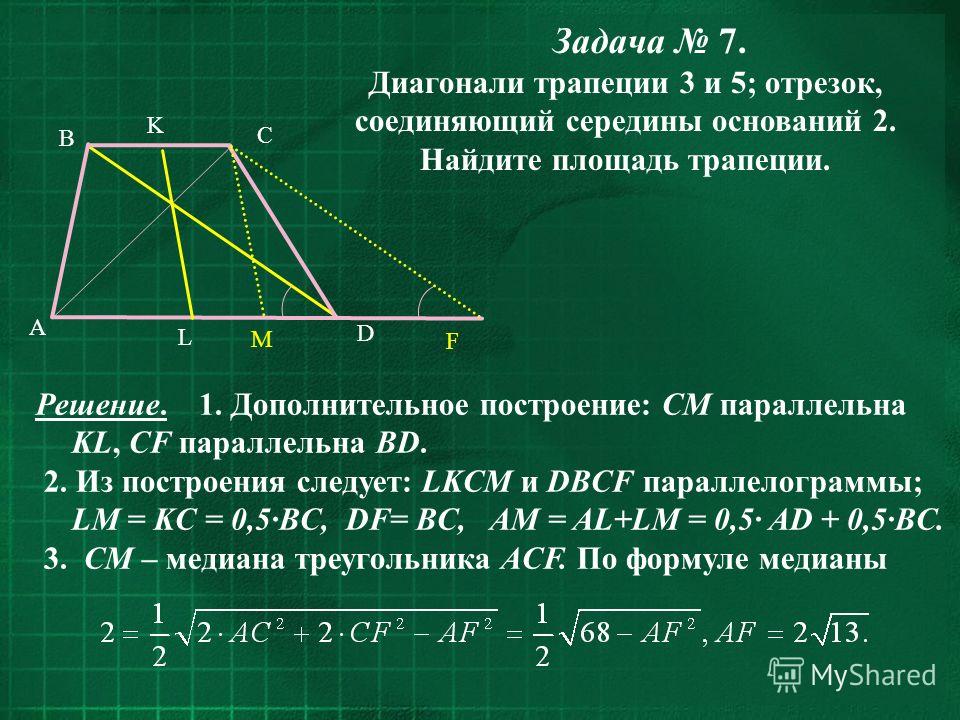 Поскольку трапеция неравнобокая — то обозначим
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ
: площадь трапеции равна 80 см 2 .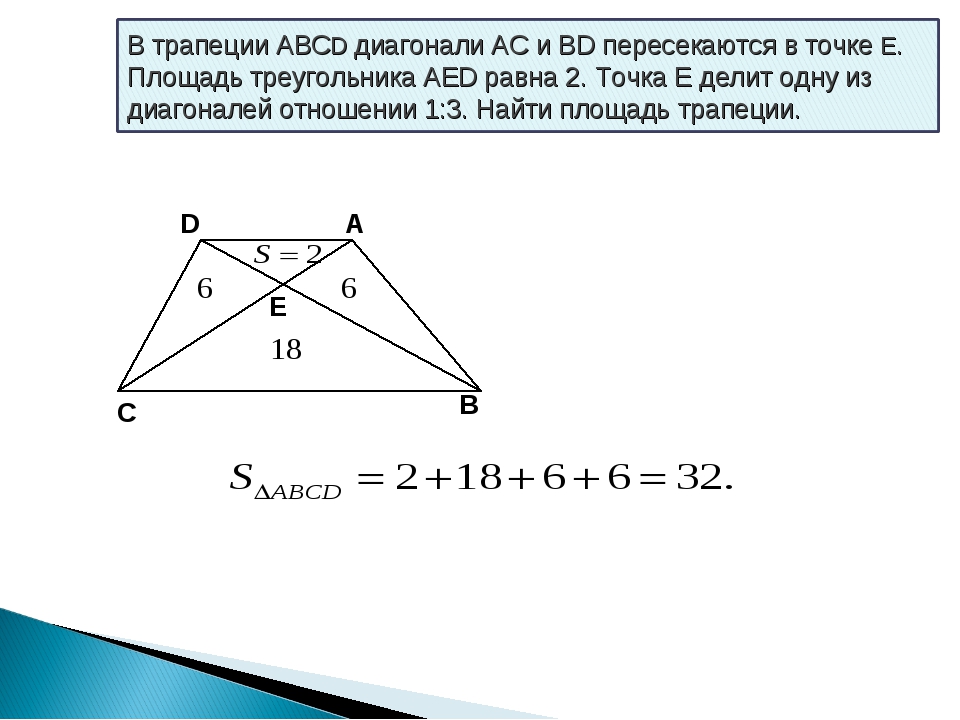 \circ$.
\circ$.
Свойства равнобедренной трапеции
Углы при основании равнобедренной трапеции равны.
Диагонали равнобедренной трапеции равны.
Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $\angle A=\angle D$.
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $\triangle ABE$ и $\triangle CFD$ равны по катету и гипотенузе ($AB=CD,
BE=CF$).
Следовательно, $\angle A=\angle D$.
Докажем второй пункт теоремы.
В равнобедренной трапеции $ABCD$ рассмотрим треугольники $\triangle ABD$ и $\triangle ACD$.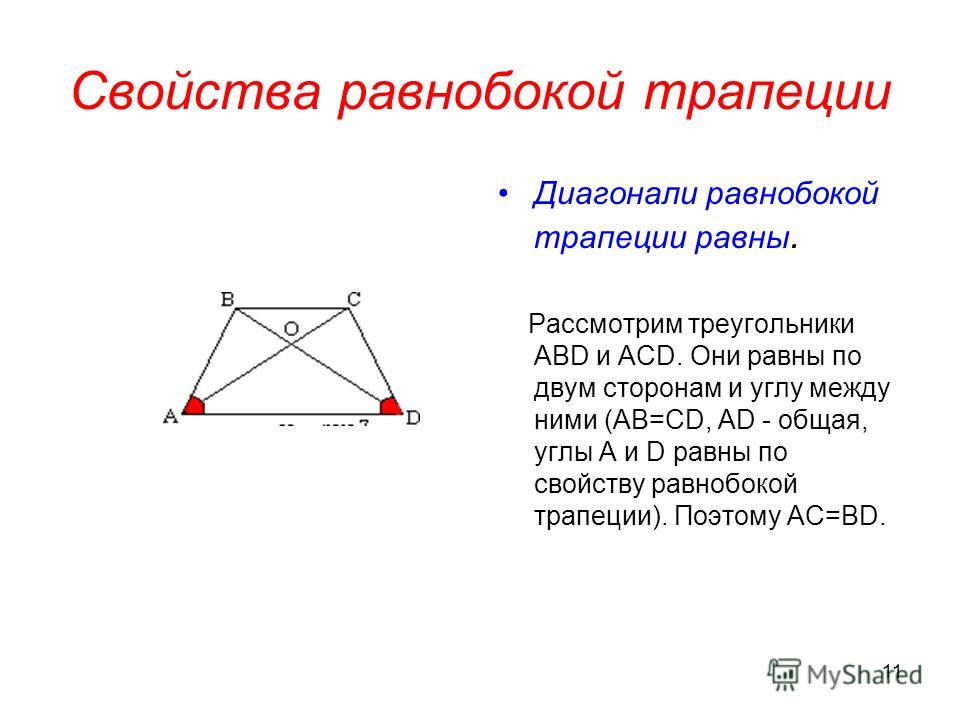
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $\angle A=\angle D$ по
первому пункту).
Следовательно, $AC=BD$.
Докажем третий пункт теоремы.
Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $\triangle AOD$ и $\triangle BOC$ – равнобедренные, а треугольники $\triangle AOB$ и $\triangle COD$ равны.
Действительно, во втором пункте уже было доказано, что $\triangle ABD=\triangle ACD$.
Следовательно, $\angle 1=\angle 2$, а так как они накрест лежащие с углами $\angle 3$ и $\angle 4$ соответственно, то $\angle 3=\angle 4$, что
и означает, что треугольники $\triangle AOD$ и $\triangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $\triangle AOB=\triangle COD$ по
третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как $\triangle AEB=\triangle CFD$ (по катету и
гипотенузе), то $AE=FD$.
Кроме того, $EF=BC$, следовательно, $AE=\dfrac{AD-BC}{2}$ и
$AF=\dfrac{AD-BC}{2}+BC=\dfrac{AD+BC}{2}$.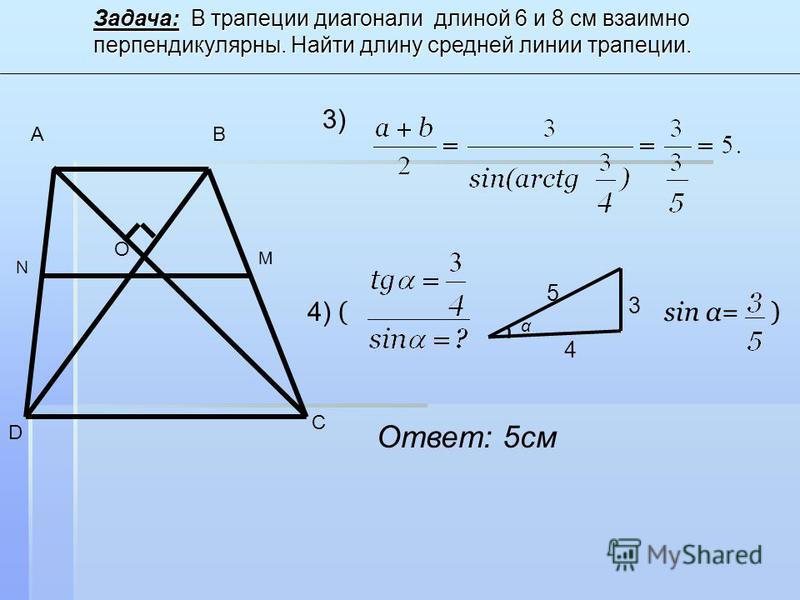
Признаки равнобедренной трапеции
Если углы при основании трапеции равны, то она равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим трапецию $ABCD$, в которой $\angle A=\angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $\angle A=\angle CED$, как соответственные углы.
Следовательно, $\angle CED=\angle D$, а тогда $\triangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.
Докажем второй пункт теоремы.
Рассмотрим трапецию $ABCD$, у которой $AC=BD$.
Докажем, что тогда $AB=CD$.
Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.
Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.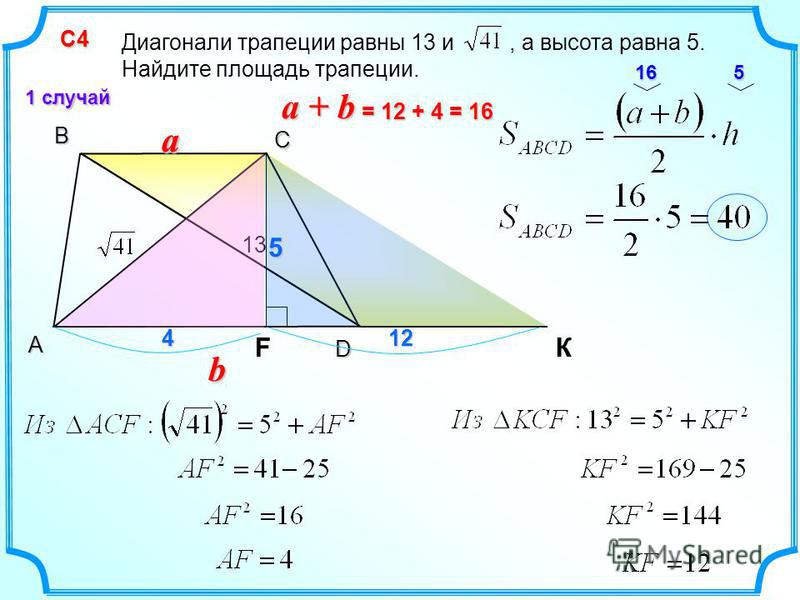 \circ$. Тогда $\triangle AHC$ – равнобедренный, то есть $AH=CH$.
\circ$. Тогда $\triangle AHC$ – равнобедренный, то есть $AH=CH$.
Но отрезок $AH$ равен полусумме оснований.
math-public/trapeciya.txt · Последнее изменение: 2016/04/13 23:56 — labreslav
Диагонали прямоугольной трапеции взаимно перпендикулярны. Диагонали трапеции. Формулы для нахождения диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.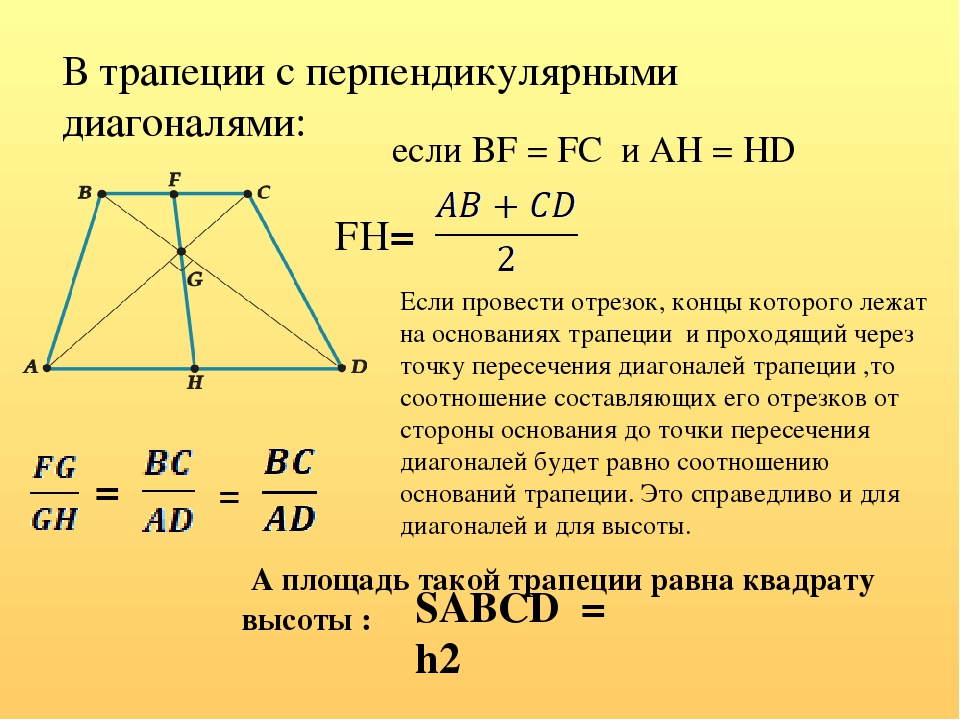
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.
Данный отрезок параллелен основаниям трапеции
.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b
— основания трапеции
c, d
— боковые стороны трапеции
d1 d2
— диагонали трапеции
α β
— углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.
Задача
.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение
.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ
: 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты.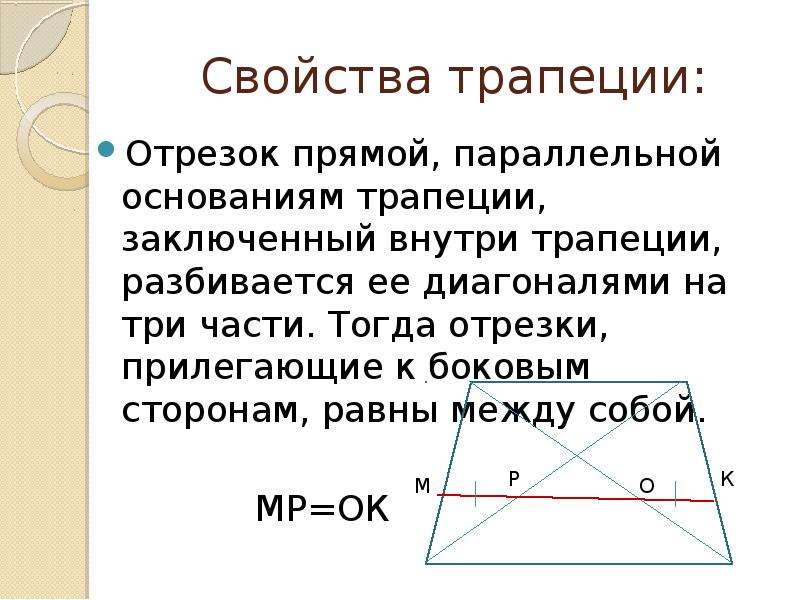 Поскольку трапеция неравнобокая — то обозначим
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ
: площадь трапеции равна 80 см 2 .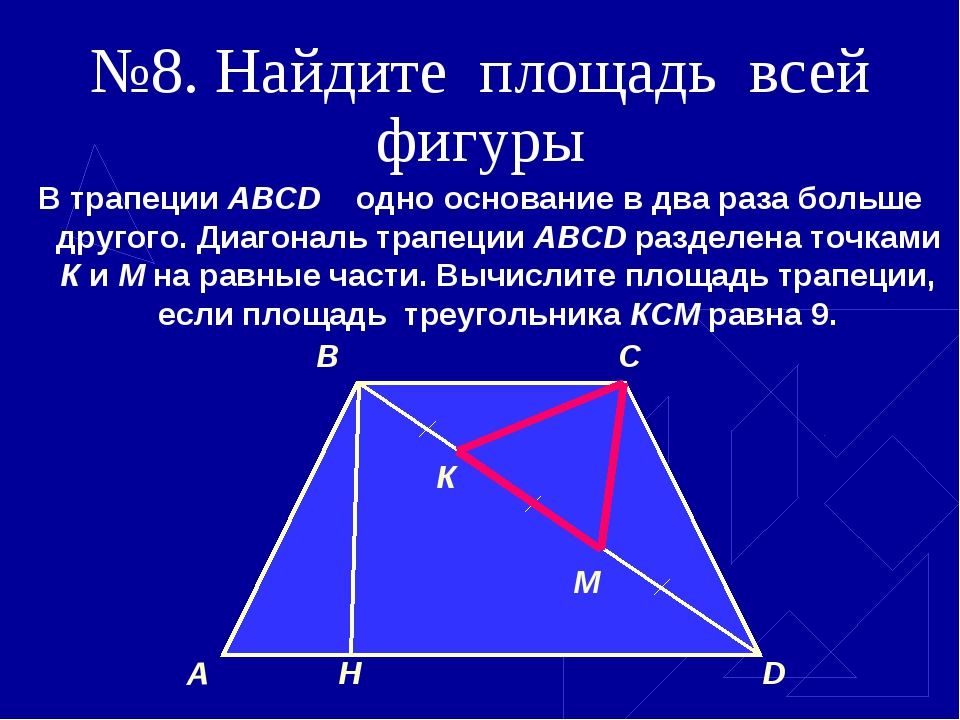
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Поделитесь статьей с друзьями:
Похожие статьи
Как найти длину диагонали в трапеции?
Диагональ трапеции
Найти диагональ трапеции можно несколькими способами. В основе первого способа лежит теорема косинусов в треугольнике, который получается внутри трапеции при проведении диагонали. Если известны одно из оснований трапеции и прилежащая к нему боковая сторона, а также угол между ними, то формула диагонали будет такая же, как и для параллелограмма:
Можно вычислить диагональ трапеции через стороны.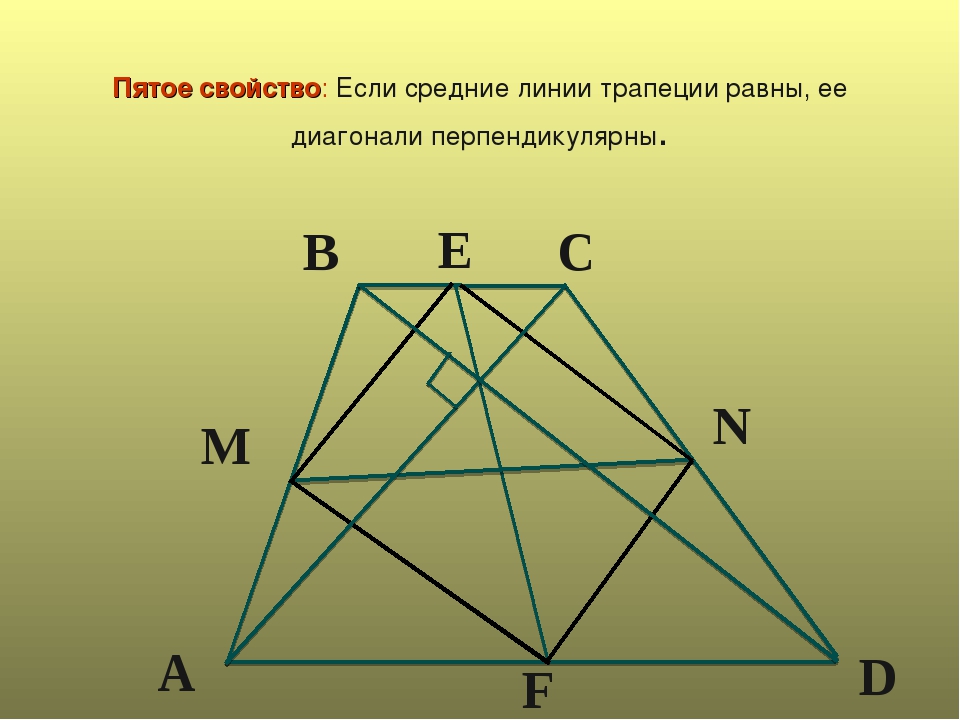 Для этого необходимо знать все четыре стороны. Выведение этой формулы основано на параллельности оснований трапеции, и прямоугольными треугольниками, которые образует высота, проведенная из вершин верхнего основания.
Для этого необходимо знать все четыре стороны. Выведение этой формулы основано на параллельности оснований трапеции, и прямоугольными треугольниками, которые образует высота, проведенная из вершин верхнего основания.
Третий способ нахождения диагонали трапеции, если даны высота и средняя линия, актуален для равнобокой трапеции, то есть когда ее боковые стороны равны. Нужно начертить высоту и диагональ таким образом, чтобы они образовывали прямоугольный треугольник, тогда диагональ можно будет найти в нем по теореме Пифагора. Так как катет треугольника, лежащий на большем основании трапеции, состоит из меньшего основания и половины разности двух оснований по свойствам равнобокой трапеции, то он будет равен по значению средней линии:
Подставляя известные значения в теорему Пифагора, получаем:
d2=h3+m2
Прямоугольная трапеция
Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований.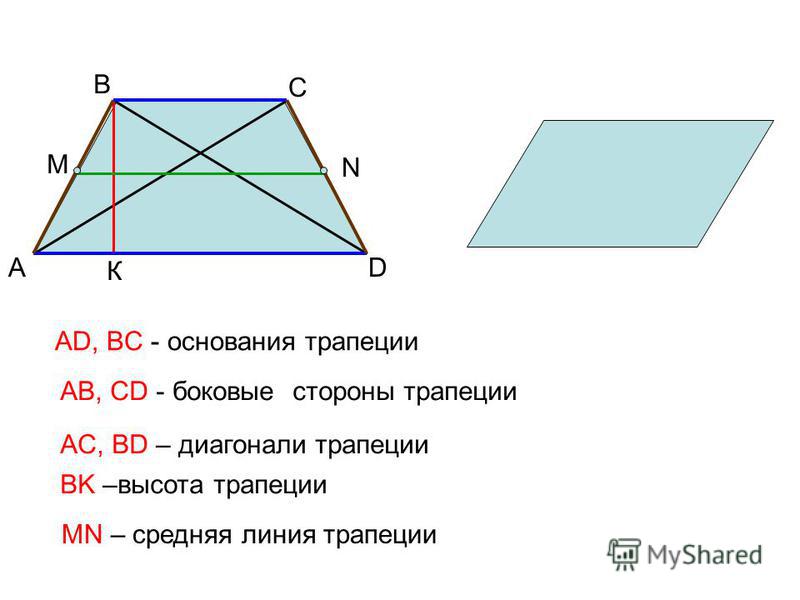 2 )
2 )
Если боковые стороны прямоугольной трапеции в сумме дают то же, что и основания, то внутри такой трапеции можно вписать окружность. Радиусом вписанной окружности будет служить половина высоты или, в данном случае, половина квадратного корня из произведения оснований. r=√bc/2
Вокруг прямоугольной трапеции нельзя описать окружность, для этого она должна стать либо равнобокой трапецией, либо прямоугольником
Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12см, если известно,что центр описанной окружности лежит на большом основании трапеции
Дан треугольник ABC. AC= 29,4 см; ∢ B= 60°; ∢ C= 45°AB=…√… см? Прямая проходит через точки а 5 0 и в 5 3 проходит ли эта прямая через точку с 5 5. СРОЧНО УМАЛЯЮ Дан треугольник ABC и координаты вершин этого треугольника. Определи длины сторон треугольника и укажи вид этого треугольника. A(3;0), B(0;4) и C(3;8) AB=?BC=?AC=?Треугольник:Равносторонний?Равнобедренный?Разносторонний? Что означает слово «библия» в переводе с греческого языка Площа бічної поверхні правильної чотирикутної призми зі стороною основи 5 см і бічним ребром 8 см. Дан треугольник Ac = 28,8 Угол B = 60 Угол С = 45 Ав = ___ корень ___ Помогите пожалуйста!!! Напиши данному тригонометрическому выражение тождественное выражение, которое содержит острый угол( в первом окошке пиши знак + или -) Sin90 = Sin Помогите пожалуйста решитес объяснением пожалуйста 35 БАЛЛОВ!СРОЧНО, + НАРИСОВАТЬ ОКРУЖНОСТЬ! Точки A и B делят окружность с центром O на дуги AMB и ACB так, что дуга ACB на 40(градусов) меньше дуги AM B. AM – диаметр окружности. Найдите углы AMB, ABM, ACB.
Дан треугольник Ac = 28,8 Угол B = 60 Угол С = 45 Ав = ___ корень ___ Помогите пожалуйста!!! Напиши данному тригонометрическому выражение тождественное выражение, которое содержит острый угол( в первом окошке пиши знак + или -) Sin90 = Sin Помогите пожалуйста решитес объяснением пожалуйста 35 БАЛЛОВ!СРОЧНО, + НАРИСОВАТЬ ОКРУЖНОСТЬ! Точки A и B делят окружность с центром O на дуги AMB и ACB так, что дуга ACB на 40(градусов) меньше дуги AM B. AM – диаметр окружности. Найдите углы AMB, ABM, ACB.
Все формулы диагоналей трапеции
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
Формула длины диагоналей трапеции через высоту
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
карточек с геометрией | Quizlet
Четырехсторонний правильный многоугольник со всеми сторонами равными и всеми внутренними углами 90 °
Свойства и советы
• Если диагонали ромба равны, то этот ромб должен быть квадратом. Диагонали квадрата (примерно в 1,414) раза больше длины стороны квадрата.
• Квадрат также можно определить как прямоугольник со всеми равными сторонами, или ромб со всеми равными углами, или параллелограмм с равными диагоналями, которые делят углы пополам.
• Если фигура представляет собой прямоугольник (прямые углы) и ромб (равные длины ребер), то это квадрат.(Прямоугольник (четыре равных угла) + Ромб (четыре равные стороны) = Квадрат)
• Если круг описан вокруг квадрата, площадь круга в π / 2 (примерно 1,57) раз больше площади квадрата.
• Если круг вписан в квадрат, площадь круга в π / 4 (примерно 0,79) раз больше площади квадрата.
• Квадрат имеет большую площадь, чем любой другой четырехугольник с таким же периметром.
• Как и у большинства четырехугольников, площадь равна длине одной стороны, умноженной на высоту перпендикуляра.2/2, где dd — длина любой диагонали.
• Каждая диагональ квадрата является серединным перпендикуляром другой. То есть каждая разрезает другую на две равные части, и они пересекаются под прямым углом (90 °).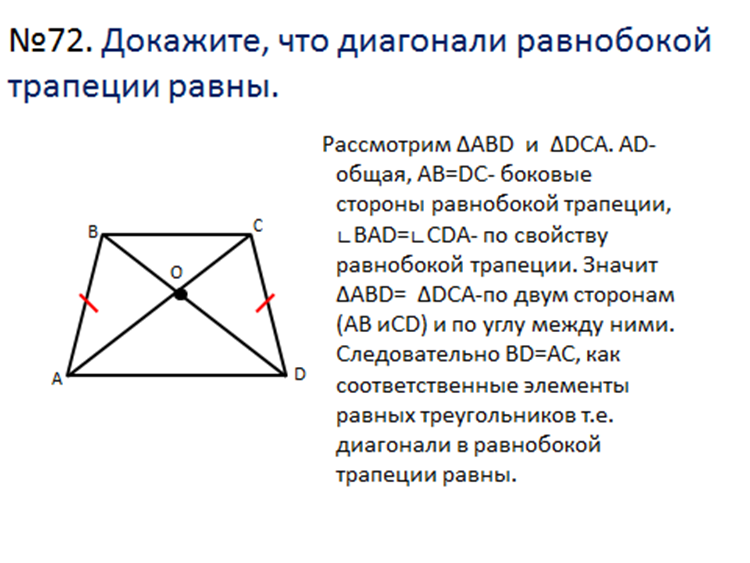
• Длина каждой диагонали равна s квадратный корень из 2, где s — длина любой одной стороны.
Квадрат одновременно является ромбом (равные стороны) и прямоугольником (равные углы) и, следовательно, обладает всеми свойствами обеих этих форм, а именно:
Диагонали квадрата делят друг друга пополам.
• Диагонали квадрата делят его углы пополам.
• Диагонали квадрата перпендикулярны.
• Противоположные стороны квадрата параллельны и равны.
• Все четыре угла квадрата равны. (Каждый равен 360/4 = 90 градусов, поэтому каждый угол квадрата — прямой угол.)
• Диагонали квадрата равны.
Квадрат можно рассматривать как частный случай других четырехугольников, например
• прямоугольник, но со смежными сторонами равными
• параллелограмм, но с равными соседними сторонами и всеми углами 90 °
• ромб, но со всеми углами 90 °
Соотношение площадей треугольников в трапеции
В сегодняшнем уроке мы будем использовать аналогичные треугольники и треугольники одинаковой высоты, чтобы найти соотношение между площадями треугольников, образованных пересечением диагоналей трапеции.
Диагонали трапеции образуют 2 одинаковых треугольника. и два других набора треугольников с одинаковым основанием и высотой. Это свойство используется во многих геометрических задачах, которые требуют от вас определения соотношения площадей этих треугольников или соотношения сторон.
Вот один пример.
Задача
ABCD — это трапеция (AB || CD). Его диагонали AC и BD пересекаются в точке O. Отношение площадей треугольников △ ABO и △ CDO составляет 16:25. Найдите отношение площади △ AOD к площади трапеции.
Стратегия
Задачи, требующие определения соотношения площадей или соотношения отрезков линий, часто основываются на использовании похожих треугольников и того факта, что если ΔABC∼ ΔDEF, то AB / DE = BC / EF = AC / DF.
В других случаях, если мы просто сравниваем площади треугольников, они часто используют тот факт, что отношение площадей треугольников с одинаковым основанием равно отношению их высот, а отношение площадей треугольников с одинаковым основанием.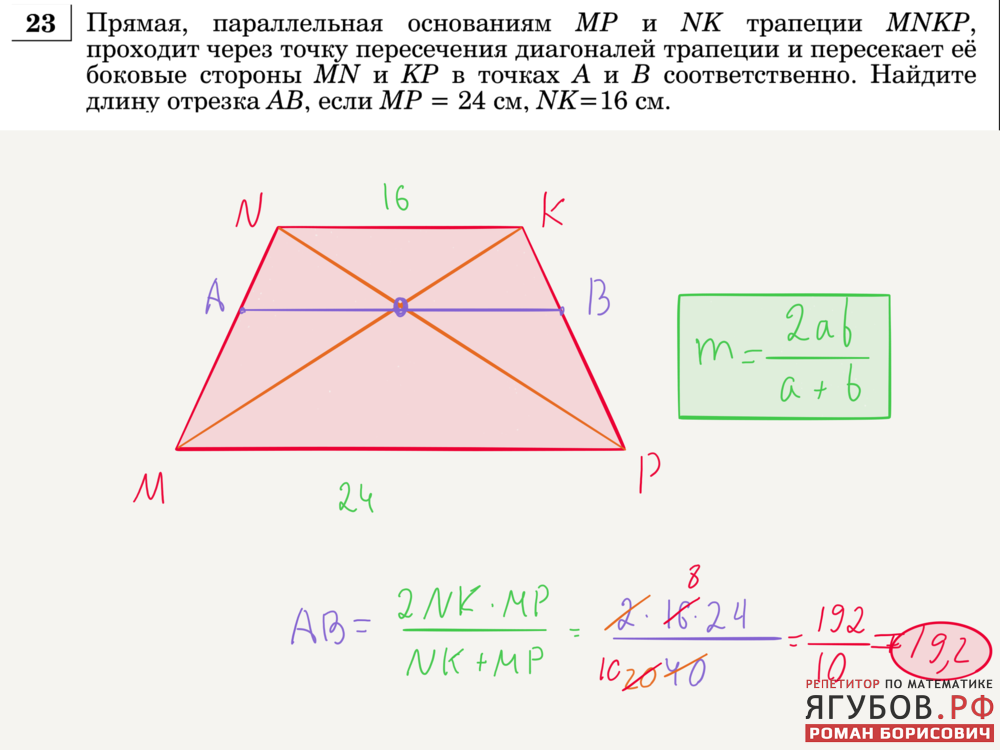 высота равна соотношению их оснований.Пример такой проблемы можно найти на этой странице.
высота равна соотношению их оснований.Пример такой проблемы можно найти на этой странице.
Так что в этой проблеме — у нас есть оба! Диагонали трапеции образуют два одинаковых треугольника (△ ABO и △ CDO) и несколько пар треугольников с одинаковым основанием (△ ACD и △ BDC; △ DBA и △ CAB) или одинаковой высоты (△ ABO и △ ADO; △ BAO и △ BOC).
И еще один намек в постановке задачи заключается в том, что соотношение между двумя треугольниками △ ABO и 16: CDO составляет 16:25.
Это и подсказка, на которую похожи треугольники (△ ABO и △ CDO), и каков масштабный коэффициент — поскольку мы знаем, что отношение площадей подобных треугольников есть коэффициент масштабирования в квадрате, и как 16, так и 25 равны. квадраты целых чисел (4 и 5 соответственно).
Proof
(1) AB || CD // Учитывая
(2) ∠ACD≅ ∠CAB // Чередующиеся внутренние углы между двумя параллельными линиями
(3) ∠ABD ≅ ∠BDC // Чередующиеся внутренние углы между двумя параллельными линии
(4) ∠BOA ≅ ∠DOC // Вертикальные углы
(5) ΔABO∼ ΔCDO // (2), (3), (4), угол-угол-угол
(6) Площадь ABO / Площадь CDO = 16/25 // Дано
(7) AO / OC = BO / OD = √ (16/25) = & frac45; // Отношение площадей одинаковых треугольников — это квадрат масштабного коэффициента
(8) Площадь ABO / Площадь ADO = & frac45; // Соотношение площадей треугольников одинаковой высоты одинаково s отношение их оснований
(9) Площадь ABO / Площадь BOC = & frac45; // Соотношение площадей треугольников одинаковой высоты одинаково s отношение их оснований
Установить площадь ABO = 16k. Тогда Area CDO = 25k, а Area ADO = Area BOC = 20k.
Тогда Area CDO = 25k, а Area ADO = Area BOC = 20k.
(10) Площадь ABCD = Площадь ABO + Область ADO + Область CDO + Площадь BOC = 16k + 20k + 25k + 20k = 81k |
(11) Площадь AOD / Площадь ABCD = 20k / 81k = 20/81
Докажите, что диагонали трапеции равны
Равнобедренные трапеции
Ирен только что купила дом и очень взволнована по поводу заднего двора. Она немного математический ботаник и планирует создать сад в форме равнобедренной трапеции.Она красит лужайку в белый цвет там, где будет ее будущая грядка.
В геометрии трапеция — это четырехугольник, у которого есть по крайней мере одна пара параллельных сторон. Трапеция, у которой непараллельные стороны равны, называется равнобедренной трапецией.
ABCD — это равнобедренная трапеция, у которой AB параллельна CD (мы записываем ее так в математике: AB || CD), а прямая AD равна прямой BC.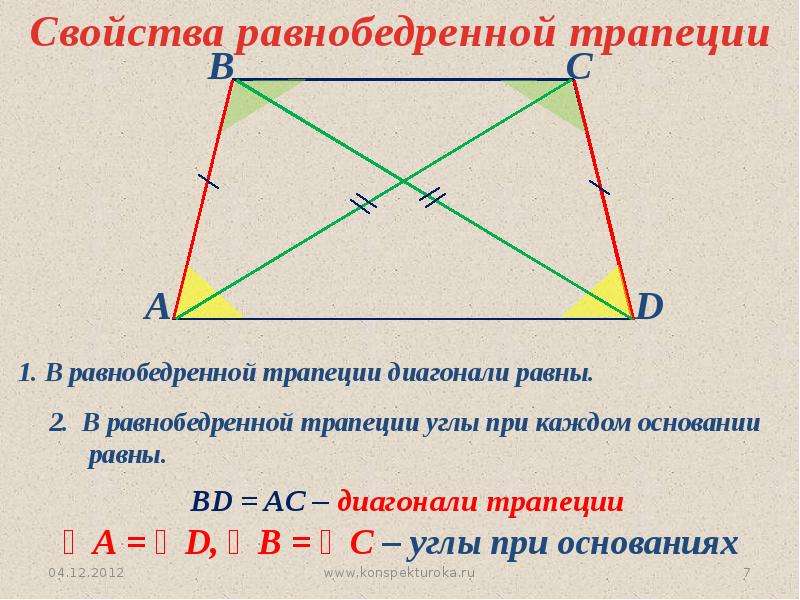
Равнобедренная трапеция
Равнобедренная трапеция
Но как Ирэн может доказать, что ее сад — это равнобедренная трапеция? Давайте посмотрим на некоторые важные теоремы, связанные с равнобедренной трапецией, чтобы помочь ей.
Базовые углы
Углы, образованные между непараллельными сторонами и параллельными сторонами, называемые базовыми углами, равны в равнобедренной трапеции. В трапеции ABCD на газоне Ирен углы C и D равны.
Базовые углы равны
Чтобы доказать эту теорему, давайте проведем линию CE, параллельную AD, так что ADCE станет параллелограммом.
Параллелограмм ADCE
Параллелограмм ADCE
В этом параллелограмме мы знаем, что линия AD = линия CE. Мы также знаем, что линия AD = линия BC, поэтому мы также знаем, что линия BC = линия CE.
Теперь, когда прямые BC и CE равны, треугольник BCE становится равнобедренным. Следовательно, углы CBE и CEB равны.
Мы понимаем, что линия AD и линия CE параллельны, а линия AE является поперечной.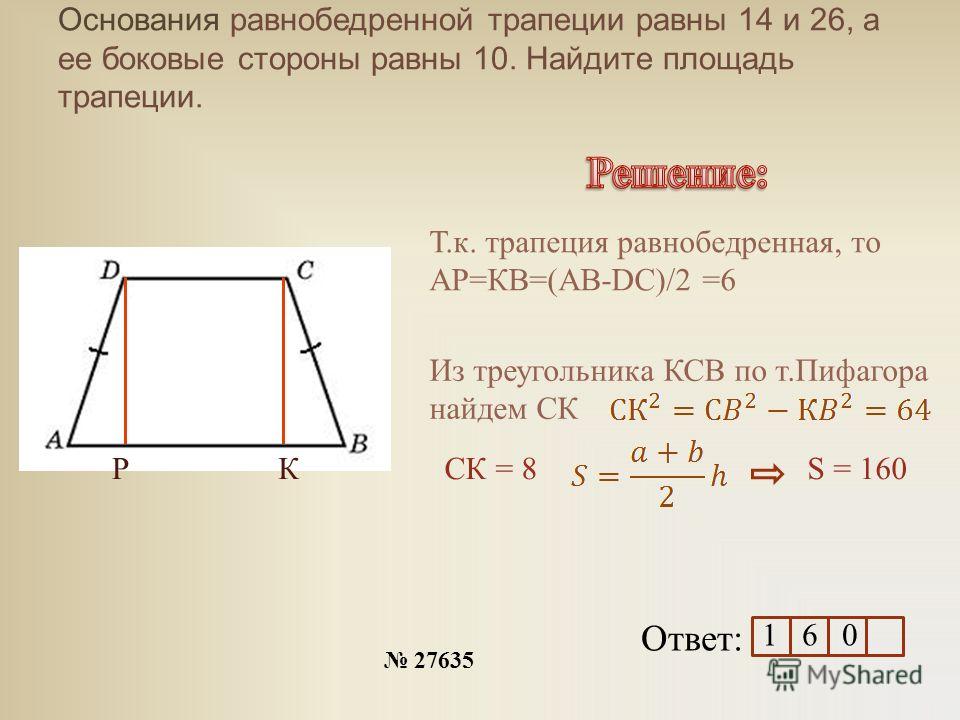 Итак, сумма внутренних углов на одной стороне, угла DAE и угла CEA составляет 180 градусов
Итак, сумма внутренних углов на одной стороне, угла DAE и угла CEA составляет 180 градусов
Итак,
Следовательно, углы DAB и CBA равны.
Далее мы знаем, что ADCE — параллелограмм, поэтому противоположные углы будут равны.
Теперь углы CBE и BCD будут равны, потому что они являются альтернативными внутренними углами для параллельных прямых AE и CD.
Мы уже знаем, что углы CEB и CEB равны. Следовательно,
Таким образом, доказано, что базовые углы в равнобедренной трапеции равны.
Если большее основание равнобедренной трапеции соответствует математике класса 10, CBSE
Подсказка: Прежде всего нарисуйте фигуру в соответствии с информацией, приведенной в приведенной выше задаче.Поскольку данная трапеция является равнобедренной трапецией, это означает, что ее нижние углы основания совпадают с верхними углами основания. И обе диагонали трапеции также совпадают. Допустим, меньшее основание диагонали обозначено буквой «s», а более длинное основание — буквой «l». Тогда длина диагоналей станет «l», а высота трапеции станет «s», потому что задано, что большее основание равнобедренной трапеции равно диагонали, а меньшее основание равно высоте. После этого, используя теорему Пифагора и основную геометрию, мы можем найти соотношение «s» и «l».
И обе диагонали трапеции также совпадают. Допустим, меньшее основание диагонали обозначено буквой «s», а более длинное основание — буквой «l». Тогда длина диагоналей станет «l», а высота трапеции станет «s», потому что задано, что большее основание равнобедренной трапеции равно диагонали, а меньшее основание равно высоте. После этого, используя теорему Пифагора и основную геометрию, мы можем найти соотношение «s» и «l».
Полный пошаговый ответ:
На приведенной ниже диаграмме мы показали равнобедренную трапецию ABCD с большим и меньшим основанием в виде «l» и «s» и двумя диагоналями AD и BC.
Теперь мы собираемся нарисовать две высоты AE и BF на основании CD трапеции.
Возьмем два треугольника AEC и BFD, и мы собираемся доказать конгруэнтность этих двух треугольников.
В $ \ Delta AEC \ And \ Delta BFD $,
$ AE = BF $
Равнобедренная трапеция имеет одинаковые высоты.{\ circ}} $ с нижним основанием трапеции.
$ \ angle ACE = \ angle BDF $
Указанные выше углы равны, потому что свойство равнобедренной трапеции состоит в том, что нижние углы основания равны.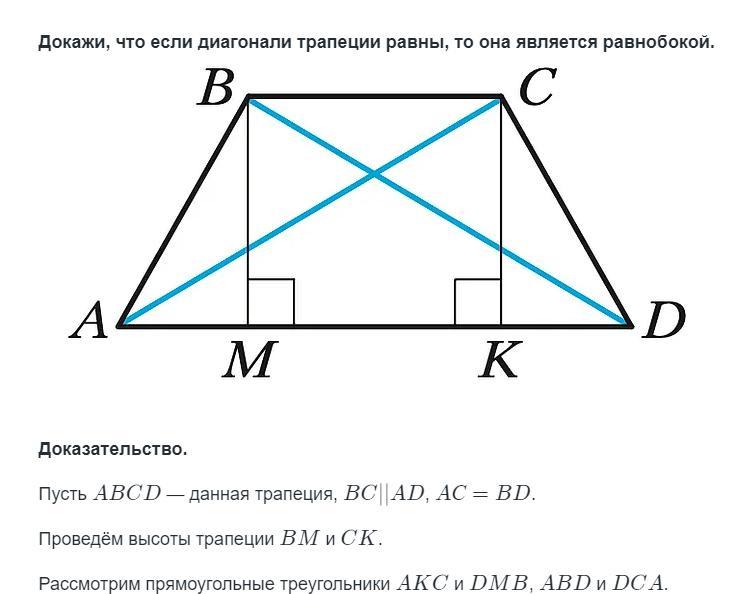
Следовательно, по сравнению с AAS $ \ Delta AEC \ cong \ Delta BFD $.
Мы знаем, что если два треугольника конгруэнтны, то согласно CPCT (соответствующая часть конгруэнтных треугольников) стороны CE и DF равны.
Как мы доказали выше, что:
$ CE = DF $
Предположим, что длины CE и DF равны x.
Итак, сумма CE, EF и FD равна «l».
Длина стороны EF равна «s» на рисунке.
Добавляя CE, EF и FD и приравнивая их к «l», получаем
$ \ begin {align}
& CE + EF + FD = l \\
& \ Rightarrow x + s + x = l \\
& \ Rightarrow 2x + s = l \\
& \ Rightarrow x = \ dfrac {ls} {2} \\
\ end {align} $
Мы снова рисуем диаграмму, которую мы нарисовали выше для лучшего понимания решение.
Теперь возьмем прямоугольный треугольник AED.
$ \ Delta AED $ содержит стороны AE, ED и AD, и мы знаем длины сторон AE как «s» и AD как «l», но мы не знаем длину стороны ED, которая решается следующим образом:
$ \ begin {align}
& ED = EF + FD \\
& \ Rightarrow ED = s + \ dfrac {ls} {2} \\
& \ Rightarrow ED = \ dfrac {2s + ls} {2} \ \
& \ Rightarrow ED = \ dfrac {s + l} {2} \\
\ end {align} $
Теперь, применяя теорему Пифагора в этом прямоугольном треугольнике, мы получаем
$ {{\ left (Hypotenuse \ right )} ^ {2}} = {{\ left (Перпендикуляр \ вправо)} ^ {2}} + {{\ left (Base \ right)} ^ {2}} $
Подставляя гипотенузу как «l», перпендикулярную как «S» и основание как $ » \ dfrac {s + l} {2} » $ в приведенном выше уравнении мы получаем
$ {{\ left (l \ right)} ^ {2}} = {{\ left (s \ right)} ^ {2}} + {{\ left (\ dfrac {s + l} {2} \ right)} ^ {2}} $
$ \ Rightarrow 4 {{l} ^ {2 }} — 4 {{s} ^ {2}} = {{s} ^ {2}} + {{l} ^ {2}} + 2ls $
$ \ Rightarrow 3 {{l} ^ {2}} -5 {{s} ^ {2}} — 2ls = 0 $
Переписывая приведенное выше уравнение, мы получаем
$ \ begin {align}
& 3 {{l} ^ {2}} — 2ls-5 {{s } ^ {2}} = 0 \\
& \ Rightarrow 3 {{l} ^ {2}} — 5ls + 3ls-5 {{s} ^ {2}} = 0 \\
& \ Rightarrow l \ left (3l-5s \ right) + s \ left (3l-5s \ right) = 0 \\
\ end {align} $
Принимая $ 3l-5s $, как обычно, мы получаем
$ \ left (l + s \ right) \ left (3l-5s \ right) = 0 $
Решая приведенное выше уравнение, приравнивая каждую скобку к 0, мы получаем
$ \ begin {align}
& l + s = 0 \\
& \ Rightarrow l = -s.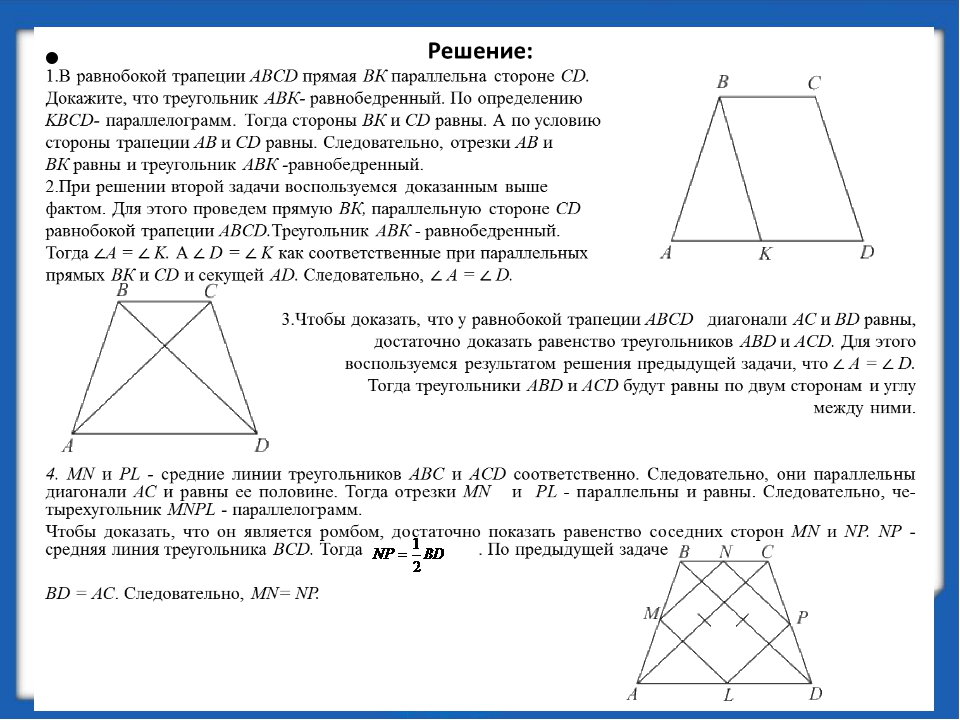 ……… Уравнение (1) \\
……… Уравнение (1) \\
& 3l-5s = 0 \\
& \ Rightarrow 3l = 5s \\
& \ Rightarrow \ dfrac {3} {5} = \ dfrac { s} {l} ………. Уравнение (2) \\
\ end {align} $
Поскольку «l» и «s» представляют стороны трапеции, которые не могут быть отрицательными, поэтому экв. (1) отклоняется, и решение, которое мы получаем, равно:
$ \ dfrac {3} {5} = \ dfrac {s} {l} $
Следовательно, мы получили отношение меньшего основания к большему, равное в $ \ dfrac {3} {5} $.
Итак, правильный ответ — «Вариант D».{2}} = 0 $
Мы получаем два решения:
$ l = -s $
$ \ dfrac {3} {5} = \ dfrac {s} {l} $
Мы отклонили первое решение, потому что стороны трапеции не могут быть отрицательными.
Геометрия: четырехугольники — Magoosh Math
Что такое четырехугольники? В этом видео мы исследуем этот и другие вопросы. Наслаждайтесь — а затем обязательно посмотрите другие наши видеоролики о геометрии!
Теперь можно говорить о четырехугольниках.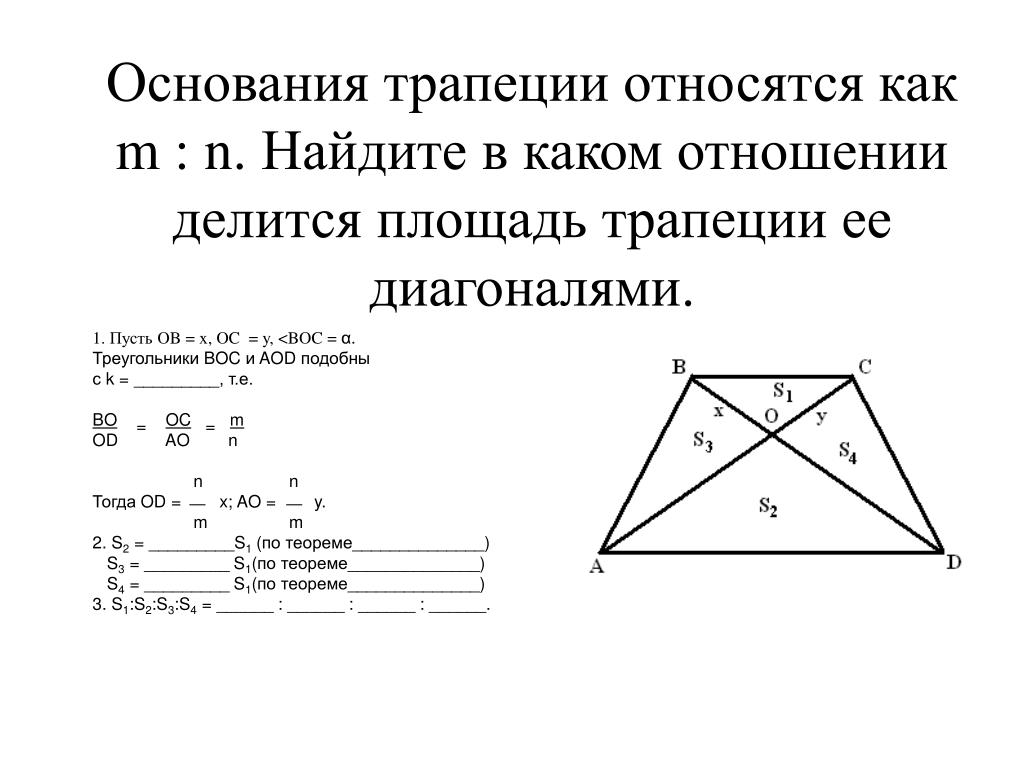 Фигура с четырьмя сторонами, состоящими из отрезков прямой, представляет собой четырехугольник .
Фигура с четырьмя сторонами, состоящими из отрезков прямой, представляет собой четырехугольник .
Итак, у нас четыре случайных четырехугольника. На самом деле это неправильных четырехугольников . Может ли такой четырехугольник иметь четыре совершенно разных длины стороны и четыре совершенно разных угла?
Иногда тест спрашивает про неправильный четырехугольник. Тест, скорее всего, спросит об очень симметричных четырехугольниках. И мы поговорим о них также в этом видео.
Итак, это неправильные четырехугольники.Набор четырехугольников также содержит некоторые элитные симметричные элементы, трапецию, параллелограмм, прямоугольник, ромб и самый элитный из всех — квадрат.
И это заслуживает комментария. Мы поговорим об этом еще раз, когда дойдем до площадей. Но самое забавное в квадрате, если подумать, это одна из первых форм, которую вы выучите в детстве. Так что это очень знакомая форма. А из-за того, что он настолько знаком, трудно оценить, насколько он особенный и элитный.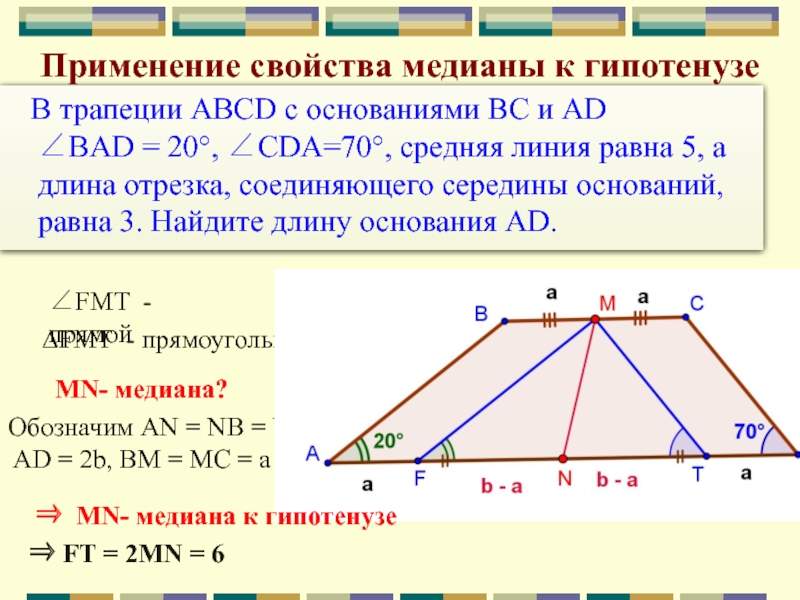
Очень сложно доказать, что что-то представляет собой квадрат. Квадрат — невероятно элитная форма. И мы поговорим об этом подробнее, когда дойдем до этого.
Что верно для всех четырехугольников
Прежде всего, давайте поговорим о том, что верно для всех четырехугольников, абсолютно для каждого члена этого множества. Для каждого четырехугольника сумма четырех внутренних углов составляет 360 градусов , что вам необходимо знать.
Изображение от WhiteDragon
Один из способов понять это — увидеть, что каждый четырехугольник можно разделить на два треугольника.Итак, у нас есть случайный четырехугольник. И мы проводим линию от B к D. И мы видим, что у нас есть два треугольника. В треугольнике ABD у нас есть три синих угла, их нужно складывать до 180.
В треугольнике BCD у нас есть три красных угла, их нужно складывать в 180. И действительно, углы во всем четырехугольнике ABCD , это просто сумма красных углов плюс синие углы. Итак, красный плюс синий должны равняться 180, то есть 360. Вот почему сумма углов каждого четырехугольника равна 360.Теперь эта линия, которую мы провели от одной вершины к противоположной вершине, называется диагональю.
Итак, красный плюс синий должны равняться 180, то есть 360. Вот почему сумма углов каждого четырехугольника равна 360.Теперь эта линия, которую мы провели от одной вершины к противоположной вершине, называется диагональю.
У треугольников нет диагоналей, но у каждого четырехугольника ровно две диагонали. Итак, вот четырехугольник с двумя нарисованными диагоналями. Сегменты EG и FH являются диагоналями четырехугольника EFGH. Как мы увидим, у некоторых четырехугольников есть диагонали с особыми свойствами. Теперь мы можем начать говорить об особых четырехугольниках, более элитных четырехугольниках, которые чаще встречаются на тесте, параллелограмме.
Свойства параллелограмма большой четверки
Все параллелограммы обладают следующими четырьмя свойствами:
- Номер свойства 1 : противоположные стороны параллельны. Это своего рода определение параллелограмма. Итак, AB параллельна CD, а AD параллельна BC.
- Номер объекта 2 : противоположные стороны равны.
 Таким образом, AB равно CD, а BC равно AD.
Таким образом, AB равно CD, а BC равно AD. - Номер объекта 3 : противоположные углы равны. Таким образом, красные углы равны, а синие углы равны.
- И номер свойства 4 : диагонали делят друг друга пополам. Таким образом, их точка пересечения M на самом деле является серединой каждой диагонали. Итак, мы можем сказать, что AM = MC и отдельно BM = MD.
Итак, эти четыре свойства действительно важны.
Я буду называть их свойствами большого четырех параллелограмма . И вот что интересно, они всегда собираются вместе. Они всегда идут в комплекте, то есть, если одно из них истинно, это автоматически означает, что остальные три должны быть правдой.И если одно из них не соответствует действительности, остальные три автоматически становятся неверными.
Итак, совершенно невозможно построить четырехугольник, в котором есть некоторые из большой четверки, но нет других. Либо четырехугольник должен иметь все четыре из них, либо не иметь ни одного из четырех. Вот почему они так важны. И любой четырехугольник, в котором все четыре верны, является параллелограммом.
Вот почему они так важны. И любой четырехугольник, в котором все четыре верны, является параллелограммом.
Опять же, эти четыре свойства параллельны противоположным сторонам, равны противоположным сторонам, равны противоположным углам, а диагонали делят друг друга пополам.Таким образом, любой из них автоматически делает остальные три истинными.
Ромб
Теперь можно говорить о ромбах. Ромбы — это равносторонние четырехугольники, то есть четырехугольник с четырьмя равными сторонами.
Изображение Ольги Стасевич
Некоторые люди воспринимают это как форму ромба, особенно если мы так сориентируем. Ориентируем его четырьмя точками, указывающими горизонтально и вертикально. Алмаз — это просто случайный или разговорный способ обозначения ромба.Итак, ромбы — это параллелограммы, поэтому они автоматически обладают четырьмя большими свойствами. Каждый ромб имеет четыре основных свойства, о которых мы только что говорили.
Два особых свойства ромба
Кроме того, есть два особых свойства ромба.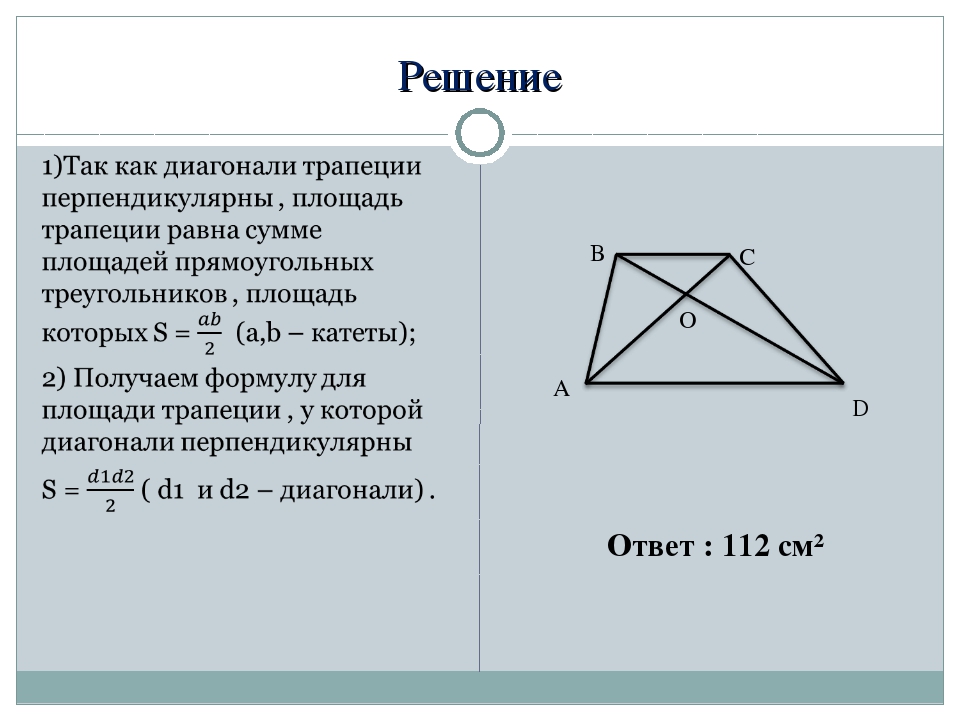 Все четыре стороны равны, а диагонали перпендикулярны. Итак, если у вас есть параллелограмм с перпендикулярными диагоналями, это должен быть ромб. Я отмечу, однако, что возможен неправильный четырехугольник с перпендикулярными диагоналями.
Все четыре стороны равны, а диагонали перпендикулярны. Итак, если у вас есть параллелограмм с перпендикулярными диагоналями, это должен быть ромб. Я отмечу, однако, что возможен неправильный четырехугольник с перпендикулярными диагоналями.
Это свойство диагонали отделимо от других. Таким образом, у вас может быть неправильный четырехугольник, у которого нет большой четверки, у него нет равных сторон, но у него есть перпендикулярные диагонали. Только это свойство можно отделить от остальных четырех. Это не похоже на четыре больших объекта недвижимости, которые всегда объединяются. Прямоугольники, прямоугольники — это четырехугольники с четырьмя углами 90 градусов.
Равносторонние четырехугольники
Мы могли бы назвать их равносторонними четырехугольниками.Это очень интересно с треугольником, единственный равносторонний треугольник — равносторонний, а единственный равносторонний треугольник — равносторонний. Эти двое всегда должны соединяться треугольниками. Но мы можем разделить эти два, как только мы получим два четырехугольника или любые более высокие многоугольники, которые могут иметь равностороннюю форму без равносторонней формы.
Итак, у прямоугольников все углы равны. Фактически, один из этих прямоугольников, EFGH, представляет собой золотой прямоугольник. Прямоугольники — это параллелограммы, и для них справедливы свойства четырех больших параллелограммов.Кроме того, есть два специальных свойства прямоугольника. Очевидно, что все четыре угла равны друг другу, а диагонали совпадают, поэтому QS = PR.
И снова это диагональное свойство, это может быть отделено от других. У нас мог бы быть неправильный четырехугольник, у которого нет ни одной большой четверки, у него нет прямых углов, но у него есть совпадающие диагонали. Так что это свойство можно отделить от остальных четырех. Это важно ценить. Наконец, среди этого набора мы поговорим о квадратах.
Что такого особенного в квадратах?
Квадраты — самые элитные четырехугольники, форма с наибольшим количеством особых свойств. Квадрат — это прямоугольник, квадрат — это ромб, а квадрат — это параллелограмм. Итак, у него есть все свойства прямоугольника, все свойства параллелограмма, все свойства ромба. Так что это очень, очень особенная форма.
Так что это очень, очень особенная форма.
Если нам говорят, что фигура представляет собой квадрат, это просто потрясающе. Если в тестовой задаче на самом деле говорится, что эта форма является квадратом, они дают нам массу информации.И это действительно важная вещь, которую нужно знать. Мы знаем все виды геометрических фактов, если просто располагаем информацией о том, что фигура представляет собой квадрат.
Не обманывайте себя!
Но доказать, что что-то является квадратом, очень сложно. Не будьте легковерны, предполагая, что фигура представляет собой квадрат, если у вас нет для этого достаточно информации. Это одна из самых распространенных ловушек на тестах. Если форма близка к квадрату, но не совсем квадрат, она не обязательно имеет какие-либо свойства квадрата.
Вот две нарисованные в масштабе диаграммы. Оба они выглядят как квадраты, но ни то, ни другое. Итак, тот, что слева, EFGH, оказывается ромбом. Четыре стороны равны, но один угол немного меньше 90 градусов, другой угол будет немного больше 90 градусов. Так что это не совсем квадрат.
Так что это не совсем квадрат.
У другого три равные стороны, а затем одна сторона немного меньше, KL немного меньше. Похоже, что угол M равен 90 градусам, но угол K больше 90 градусов, а два других немного меньше и не равны друг другу.Итак, это совершенно неправильный четырехугольник. Но в масштабе он выглядит как квадрат.
Просто факт, что даже если у нас что-то нарисовано в масштабе и выглядит как квадрат, нет гарантии, что это квадрат.
Практическая задача
Вот практическая задача. Поставьте видео на паузу, а потом мы поговорим об этом.
Хорошо, это очень странный формат вопроса. Можем ли мы определить, что ABCD является квадратом, если мы знаем одно из них?
Итак, BC = CD, а угол B равен 90 градусам.Итак, это факт номер 1. AD = AB и угол D = 90 градусов. Итак, вопрос заключается в использовании только одного из них, можем ли мы определить, что это квадрат? Если мы сложим их вместе, достаточно ли этого, чтобы определить, что это квадрат? Или, даже если мы сложим их вместе, этого недостаточно, чтобы доказать, что что-то является квадратом.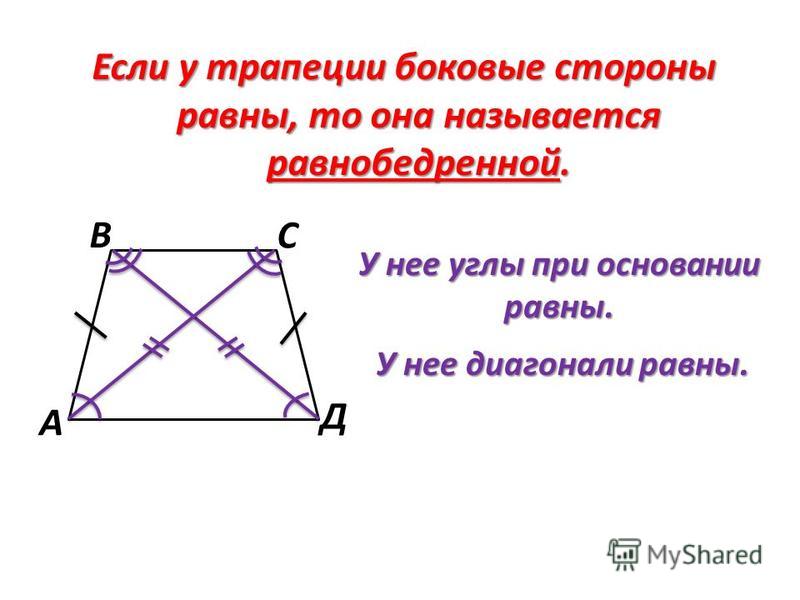
Оказывается, если даже оба факта вместе верны, это не гарантирует, что форма является квадратом. Это могут быть просто два равных прямоугольных треугольника, прикрепленных к гипотенузе, вот так.Итак, на этой диаграмме верно, что BC = CD, верно, что AD = AB, и у нас есть прямые углы в точках B и D, и все же ABCD не является квадратом.
На самом деле, это вообще не какой-то особенный четырехугольник. Всей этой информации недостаточно, чтобы определить, что ABCD — квадрат, и ответ на вопрос — C.
Четырехугольники: трапеции
Теперь мы можем поговорить о трапециях. У трапеции ровно одна пара параллельных сторон. Итак, это трапеции.
ПРАВЫЙ УГОЛ ТРАПЕЗОИДА
Изображение от icon99
Трапеция может иметь два прямых угла на одной из ножек.Две параллельные стороны называются основаниями, а непараллельные — ножками. Два угла на ножке всегда дополняют друг друга. Итак, один из них — 90 градусов, другой — 90 градусов. Всегда верно, что, например, A + B = 180 и C + D = 180. И это из-за основных свойств параллельных прямых.
И это из-за основных свойств параллельных прямых.
У некоторых трапеций две равные ножки. Мы называем эти симметричные трапеции, или иногда более формальное название для них — равнобедренные трапеции, любой термин подходит. Если две стороны параллельны, и если KJ = LM, стороны равны, то мы знаем, что углы на противоположных сторонах должны быть равны.По сути, форма становится полностью симметричной.
Таким образом, угол K = угол L, угол J = угол M, а также диагонали имеют одинаковую длину.
Практическая задача
Вот практическая задача. Поставьте видео на паузу, а потом мы поговорим об этом.
Хорошо, ABCD — это трапеция указанной длины. Найдите диагональ AC. Что ж, прямой формулы нет.
Невозможно просто вставить четыре числа, которые у нас есть, и найти диагональ. Нам нужно будет найти это шаг за шагом.По сути, мы будем работать над теоремой Пифагора. Как правило, в любой геометрической задаче, где вас просят найти длину наклонной линии, очень и очень велики шансы, что теорема Пифагора где-то скрыта в этой задаче.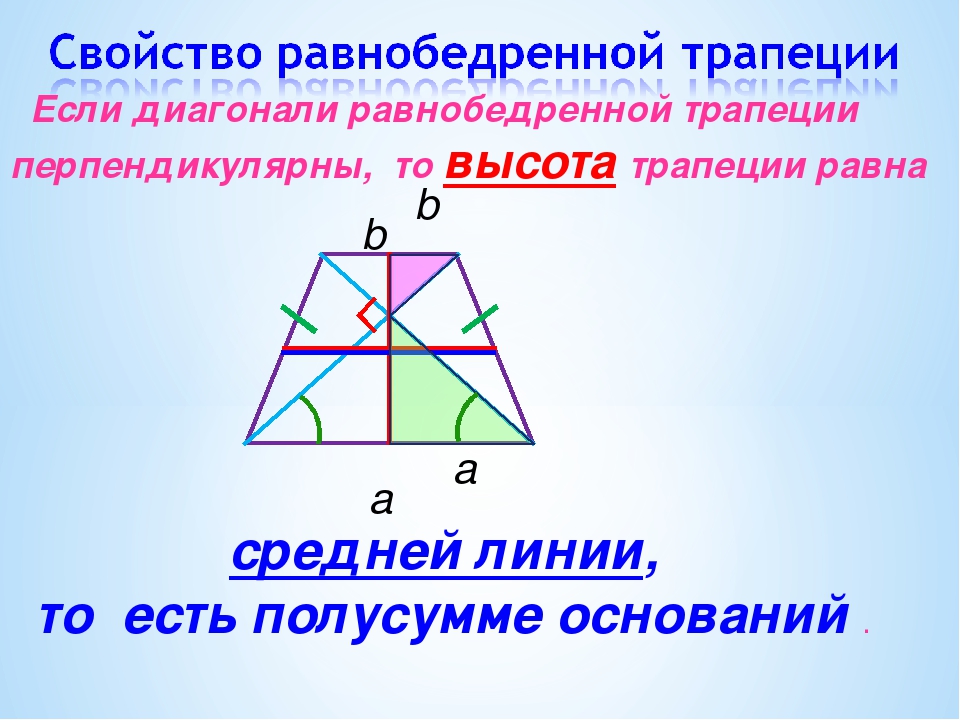
И ваша задача — просто выяснить, как использовать теорему Пифагора. Это действительно отличная идея. Итак, вот что мы собираемся сделать, это опустить перпендикулярные сегменты от B, C вниз к основанию. Итак, что мы создаем, у нас есть какой-то прямоугольник посередине, похоже, он может быть близок к квадрату, но это не совсем квадрат.
И тогда у нас есть два симметричных прямоугольных треугольника с каждой стороны. Итак, мы знаем, что сторона, противоположная BC, EF, тоже должна быть 11. Ну, вся база равна 21. И мы знаем, что AE и FD, две маленькие стороны треугольника, должны быть равны друг другу. , потому что эти треугольники совпадают. Таким образом, должно быть верно, что каждая из них имеет длину 5.
Итак, мы разделили площадь основания, 5, 11, 5, и это в сумме составляет 21. Что ж, теперь обратите внимание на эти прямоугольные треугольники, у нас есть 5 пустой 13.Это должно прозвучать в колокол. Это треугольник 5-12-13, поэтому должно быть верно, что BE и CF = 12.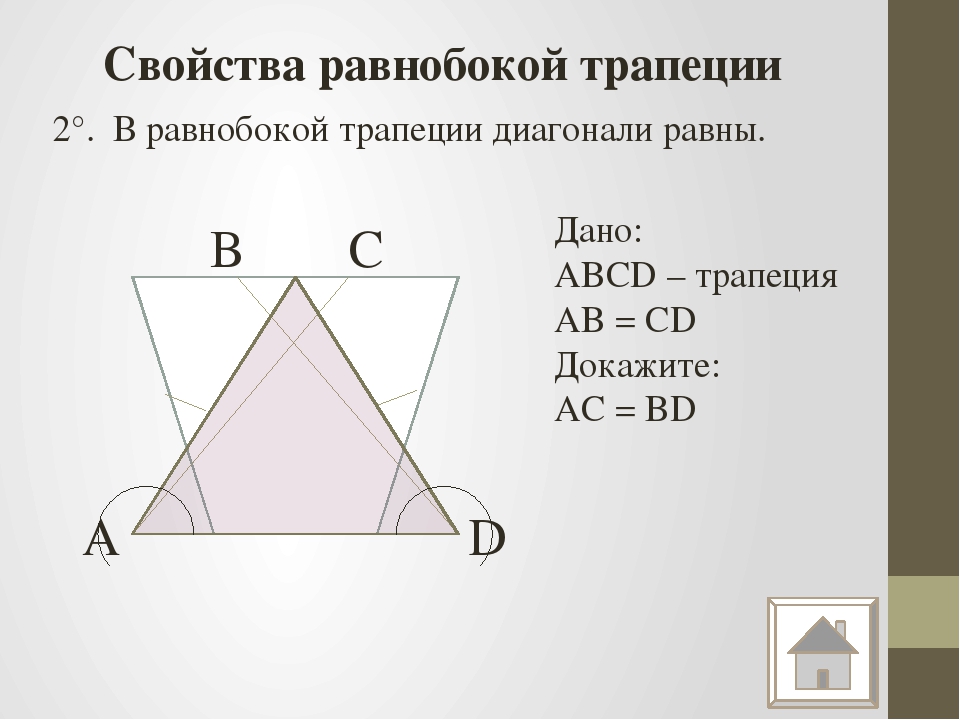 Итак, теперь мы знаем длину высоты. Теперь мы можем подумать об этой диагонали. Эта диагональ AC — гипотенуза прямоугольного треугольника ACF.
Итак, теперь мы знаем длину высоты. Теперь мы можем подумать об этой диагонали. Эта диагональ AC — гипотенуза прямоугольного треугольника ACF.
И мы знаем, что AF — это 5 плюс 11, 16, а CF — 12. Ну, это треугольник 3, 4, 5, увеличенный в 4 раза. Это треугольник 12, 16, 20. Итак, гипотенуза AC равна 20, это длина диагонали. Итак, снова обратите внимание, что мы нашли все, используя теорему Пифагора.Опять же, всякий раз, когда вам нужно найти длину диагонали или длину почти любой наклонной линии, очень, очень высоки шансы, что это проблема теоремы Пифагора.
Концептуальные отношения между четырехугольниками
На этой диаграмме показаны концептуальные отношения между четырехугольниками. Во-первых, есть много четырехугольников, которые не являются ни параллелограммами, ни трапециями. Это просто неправильные четырехугольники, которые находятся за пределами двух больших кругов.Внутри круга параллелограмма все, что находится в этом круге, имеет свойства больших четырех параллелограммов.
И ничто за пределами окружности параллелограмма не может иметь ни одного из этих свойств. Внутри круга параллелограмма у нас есть ромбы, прямоугольники, а затем квадраты — это пересечение ромбов и прямоугольников. Потому что квадраты — это и прямоугольники, и ромбы. И, конечно же, они тоже параллелограммы. Отдельно трапеции.
Внутри трапеций мы имеем область симметричных трапеций, частный случай.И снова, в тесте больше всего нравится спрашивать о более элитных, более цивилизованных, более симметричных и особых типах четырехугольников. Потому что у них больше свойств. Так что есть еще о чем спросить, вот почему они нравятся тесту. Таким образом, это верно для всех четырехугольников, если сумма углов составляет 360 градусов.
Очень важно знать свойства четырех больших параллелограммов: параллельные противоположные стороны, равные противоположные стороны, равные противоположные углы и диагонали, разделяющие друг друга пополам. Эти четверо всегда собираются вместе.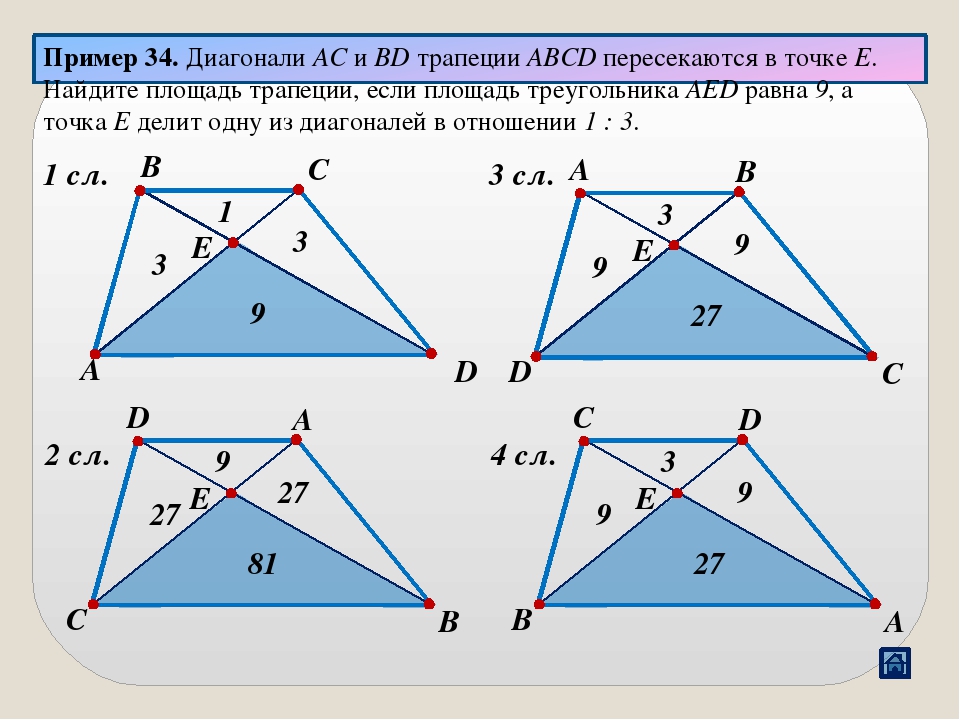 Таким образом, у вас не может быть формы, в которой одни из этих истинных, а другие — ложные.
Таким образом, у вас не может быть формы, в которой одни из этих истинных, а другие — ложные.
Они либо все четыре верны, либо все четыре неверны относительно определенной формы. У ромба четыре равные стороны плюс большая четыре, также у него перпендикулярные диагонали. Прямоугольник имеет углы 90 градусов плюс большая четверка. Он также имеет совпадающие диагонали.
Квадрат — это прямоугольник и ромб. Итак, квадрат имеет все свойства прямоугольника, все свойства ромба и все свойства параллелограмма.У трапеции ровно одна пара параллельных сторон. А симметричная трапеция или равнобедренная трапеция имеют равные длины. Это означает, что у него равные углы с каждой стороны и равные диагонали.
Параллельно через пересечение диагоналей.
Параллель через пересечение диагоналей.
Необязательно, чтобы трапеция была равнобедренной.
Возьмите любую трапецию
ABCD с диагоналями AC и BD , пересекающимися в точке E .Пусть a = AB и b = CD . Пусть c будет длиной
отрезка FG параллельно двум основаниям трапеции. Наш
Проблема состоит в том, чтобы выразить c через a и b .———————————
Вытяните стороны DA и CB так, чтобы они встретились в точке H. Постройте линию A, параллельную стороне.
DA через G и продолжается до места пересечения AB в точке J (внешней по отношению к AB)
и CD в K (внутренний для CD).
Это дает следующие подобных треугольников: HAB, HDC, GJB,
GKC. Обратите внимание, что в терминах a , b и c , BJ = c
— a и CK = b — cСледовательно, учитывая треугольники GJB и HAB, отношение подобия
есть и учитывая треугольники GKC и HDC, отношение подобия.
Следовательно, у нас есть отношение, включающее a, b и c, которое мы можем решить для
c.Если три числа таковы, что по любой части наибольшее
срок превышает средний срок, а средний срок превышает третий срок
та же часть третьего и среднего члена — это среднее гармоническое
первого и третьего. Это соотношение показано в этом уравнении.
Обычно отношение записывается в одной из следующих форм, чтобы показать, что
c — среднее гармоническое положительных чисел a и b :или же
Таким образом, длина отрезка параллельной прямой через точку пересечения
диагоналей — это гармоническое среднее оснований трапеции.
Возврат
Четырехугольники
Четырехугольник — это замкнутая плоская фигура, ограниченная четырьмя линиями
сегменты. Например, фигура ABCD , показанная здесь, является
Например, фигура ABCD , показанная здесь, является
четырехугольник.
Отрезок, проведенный от одной вершины четырехугольника к противоположной.
вершиной называется диагональ четырехугольника.Например, AC — это диагональ четырехугольника ABCD , и поэтому BD .
Типы четырехугольников и их свойства
Четырехугольники бывают шести основных типов:
1. Прямоугольник
- Противоположные стороны параллельны и равны.
- Все углы 90.
- Диагонали пересекают друг друга.
2. Квадрат
- Противоположные стороны параллельны и все стороны равны.
- Все углы 90.

- Диагонали пересекают друг друга под прямым углом.
3. Параллелограмм
- Противоположные стороны параллельны и равны.
- Противоположные углы равны.
- Диагонали пересекают друг друга.
4. Ромб
- Все стороны равны, а противоположные стороны параллельны.
- Противоположные углы равны.
- Диагонали пересекают друг друга под прямым углом.
5.Трапеция
- Трапеция имеет одну пару параллельных противоположных сторон.
- У правильной трапеции непараллельные стороны равны, а углы основания
равны, как показано на следующей диаграмме.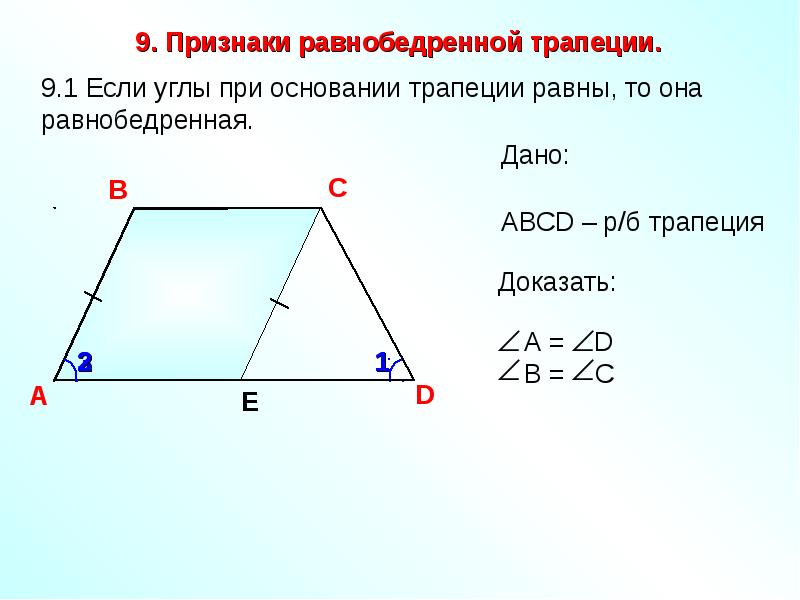
6. Воздушный змей
- Две пары смежных сторон равны.
- Одна пара противоположных углов равна.
- Диагонали пересекаются под прямым углом.
- Самая длинная диагональ делит самую короткую диагональ пополам на две равные части.
части.
Теорема 3
Докажите, что сумма углов четырехугольника равна 360.
Проба:
Следовательно, сумма углов четырехугольника равна 360.
Применение свойств углов в четырехугольниках
Доказанные теоремы можно использовать для доказательства других теорем. Они
также может использоваться для поиска значений местоимений в задаче.
Пример 14
Найдите значение местоимения x на прилагаемой диаграмме.
Обоснуйте свой ответ.
Решение:
Пример 15
Найдите значение каждого местоимения в показанном здесь воздушном змее.Назови причины
за ваши ответы.
Решение:
Пример 16
Найдите значение каждого местоимения на прилагаемой диаграмме. Дайте
причины для ваших ответов.
Решение:
Пример 17
Найдите значение местоимения на прилагаемой диаграмме.Дайте
причины вашего ответа.


