Содержание
Решение квадратных уравнений онлайн
С помощю этого онлайн калькулятора можно найти решение (корни) квадратного уравнения. Дается подробное решение с пояснениями. Для нахождения решений квадратного уравнения введите коэффициенты уравнения и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Корни квадратного уравнения − теория примеры и решения
Квадратным уравнением называется уравнение следующего вида:
где x−переменная, а a, b, c некоторые числа (a≠0). Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.
Коэффицинт c называется свободным членом.
Если a=1, то квадратное уравнение называется приведенным. Заметим, что любое квадратное уравнение можно привести к приведенному виду, разделив обе части уравнения на a. Действительно:
Если в квадратном уравнении (1) один из коэффициентов b, c равен нулю или оба коэффициента b, c равны нулю, то квадратное уравнение называется неполным.
Рассмотрим разные виды неполных квадратных уравнений.
1. При b=0 имеем:
Для решения этого уравнения свободный член перенесем в правую часть уравнения:
Решая последнее уравнение относительно x получим корни квадратного уравнения (3):
Если , то квадратное уравнение не имеет действительных корней.
2. При c=0 имеем:
Разложим левую часть последнего уравнения на множители:
Из (4) следует x=0 или ax+b=0. Следовательно имеем следующие решения:
3. При b=0, c=0 имеем:
При b=0, c=0 имеем:
и, следовательно
Рассмотрим, далее, алгоритм решения квадратных уравнений общего вида (1). Разделим обе части уравнения на a:
Сделаем эквивалентные преобразования уравнения (5):
Легко догадаться, что первые три слагаемые уравнения (6) образуют квадрат следующей суммы:
Тогда
Обозначим
D− называется дискриминантом квадратного уравнения (1). Так как a≠0, то 4a2>0. Знак правой части уравнения (7) определяется знаком дискриминанта D.
Учитывая (8) запишем (7) в следующем виде:
При решении последнего уравнения возможны следующие варианты:
1. При D>0, имеем
Таким образом, при D>0, квадратное уравнение (1) имеет две корни:
2.При D=0, имеем
То есть, при D=0 квадратное уравнение (1) имеет единственный корень:
3. При D<0, правая часть уравнения (9) отрицательна, а так как квадрат числа не может быть отрицательным числом, то квадратное уравнение (1) не имеет корней.
При D<0, правая часть уравнения (9) отрицательна, а так как квадрат числа не может быть отрицательным числом, то квадратное уравнение (1) не имеет корней.
Пример 1. Решить квадратное уравнение
| . | (10) |
Решение. Запишем коэффициенты квадратного уравнения (10):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант положительное число. Следовательно квадратное уравнение (10) имеет два решения.
Найдем решение квадратного уравнения используя следующую формулу:
| . | (11) |
Подставляя значения коэффициентов a, b, c, D в (11), получим:
| , |
| . |
Ответ:
Пример 2. Решить следующее квадратное уравнение:
| . | (12) |
Решение. Запишем коэффициенты квадратного уравнения (12):
Вычислим дискриминант квадратного уравнения:
. |
Дискриминант равен нулю. Следовательно квадратное уравнение (12) имеет единственное решение. Найдем решение квадратного уравнения используя следующую формулу:
| . | (13) |
Подставляя значения коэффициентов a, b, c, D в (13), получим:
| , |
Ответ:
| . |
Пример 3. Решить следующее квадратное уравнение:
| . | (14) |
Решение. Запишем коэффициенты квадратного уравнения (14):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант отрицательное число. Следовательно квадратное уравнение (14) не имеет действительных корней.
Ответ: Квадратное уравнение не имеет действительных корней.
Квадратные уравнения. Примеры решения
Задачи на квадратное уравнение изучаются и в школьной программе и в ВУЗах. 2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения.
2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения.
Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х). Из этого следует, что есть три возможных случая:
1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) парабола имеет одну точку пересечения с осью Ох. Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2 и осуществим преобразование
2 и осуществим преобразование
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0.
2+x-6=0.
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см2.
Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х2-18х+77=0.
Найдем дискриминант уравнения
Вычисляем корни уравнения
Если х=11, то 18-х=7, наоборот тоже справедливо (если х=7 , то 21-х=9).
Задача 6. Разложить квадратное 10x2-11x+3=0 уравнения на множители.
Решение: Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество.
Квадратное уравнение с параметром
Пример 1. При каких значениях параметра а, уравнение (а-3)х2+(3-а)х-1/4=0 имеет один корень?
Решение: Прямой подстановкой значения а=3 видим, что оно не имеет решения. Далее воспользуемся тем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Выпишем дискриминант
упростим его и приравняем к нулю
Получили квадратное уравнение относительно параметра а, решение которого легко получить по теореме Виета. Сумма корней равна 7, а их произведение 12. Простым перебором устанавливаем, что числа 3,4 будут корнями уравнения. Поскольку решение а=3 мы уже отвергли в начале вычислений, то единственным правильным будет — а=4. Таким образом, при а=4 уравнение имеет один корень.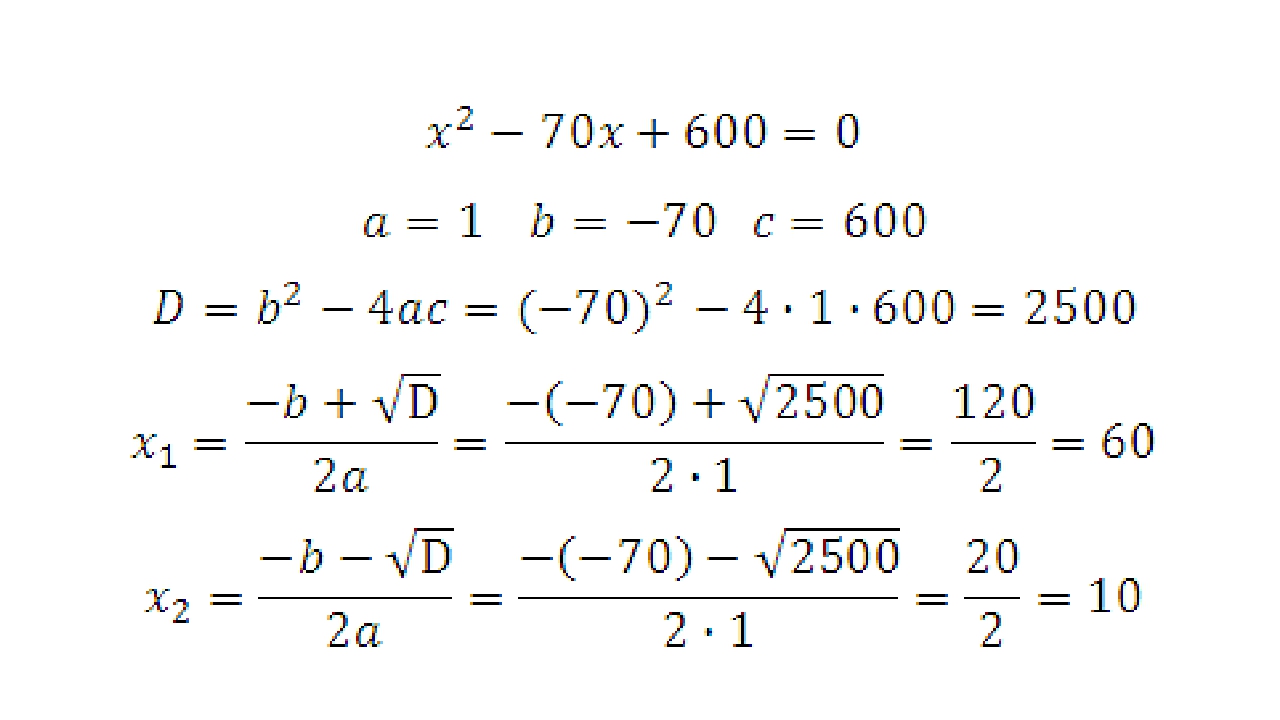 2+(2а+6)х-3а-9=0 имеет более одного корня?
2+(2а+6)х-3а-9=0 имеет более одного корня?
Решение:Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3. При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0.
Вычислим дискриминант
и найдем значения а при котором оно положительно
С первого условия получим а>3. Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0. Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0, которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа. Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||
Решение полных квадратных уравнений
Покажем, как вывести эти формулы:
Последнюю формулу можно существенно упростить в случае, если b делится на 2, то есть b = 2k. Тогда формула для корней квадратного уравнения будет иметь вид
Тогда формула для корней квадратного уравнения будет иметь вид
,
где k =
.
Полученную формулу для корней квадратного уравнения в случае четного коэффициента b можно переписать и без использования буквы k:
или
, где D1 = (
)2 — ac.
Очевидно, полученные формулы для корней полных квадратных уравнений можно использовать и для решения неполных уравнений, хотя проще использовать способы решения неполных квадратных уравнений.
Пример 1. Решить квадратное уравнение 4x2 -28x + 49 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.
Так как b = -28 — четное число, то вычислим дискриминант D1 :
D1 = (
)2 — ac = (-14)2 — 4*49 = 196 — 196 = 0, следовательно, уравнение имеет единственный корень
x = .
Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
4x2 -28x + 49 = 0 (2x — 7)2 = 0 2x = 7 x =
.
Ответ:
.
Пример 2. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть уравнения:
Умножив обе части уравнения на -6, получим x2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
.
Ответ: -3,0.
Пример 3. Решить уравнение .
Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:
.
Умножив обе части уравнения на 15, получим:
6x2 + 3x = 20x-10 6x2 + 3x — 20x + 10 = 0 6x2 — 17x + 10 = 0.
Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10,
D = b2 — 4ac = (-17)2 — 4*6*10 = 289 — 240 = 49 > 0, следовательно, уравнение имеет два действительных корня.
Ответ:
, 2.
Пример 4. Решить уравнение .
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.
Так как b = 2√2, то есть b делится на 2 (
= √2), вычислим дискриминант D1:
D1 = (
)2 — ac = (√2)2 — 1*1 = 1 > 0. Cледовательно, уравнение имеет два действительных корня.
Cледовательно, уравнение имеет два действительных корня.
Ответ: -√2-1, -√2+1.
Пример 5. Решить уравнение .
Решение.
Умножим левую и правую части уравнения на 6:
Вычислим дискриминант полученного квадратного трехчлена. У нас a = 3, b = -6, c = 2.
Так как b = -6, то есть b делится на 2 (
= 3), вычислим дискриминант D1:
D1 = (b/2)2 — ac = 32 — 3*2 = 3 > 0. Cледовательно, уравнение имеет два действительных корня.
Ответ:
Решение квадратных уравнений: формула корней, дискриминант, график
Квадратное уравнение – это математическое уравнение, которое в общем виде выглядит так:
ax2 + bx + c = 0
Это многочлен второго порядка с 3 коэффициентами:
- a – старший (первый) коэф., не должен быть равен 0;
- b – средний (второй) коэф.;
- c – свободный элемент.
Решением квадратного уравнения является нахождение двух чисел (его корней) – x1 и x2.
Формула для вычисления корней
Для нахождения корней квадратного уравнения используется формула:
Выражение внутри квадратного корня называется дискриминантом и обозначается буквой D (или Δ):
D = b2 – 4ac
Таким образом, формула для вычисления корней может быть представлена разными способами:
1. Если D>0, у уравнения есть 2 корня:
2. Если D=0, уравнение имеет всего один корень:
3. Если D<0, вещественных корней нет, но есть комплексные:
Решений квадратных уравнений
Пример 1
3x2+5x+2 = 0
Решение:
a = 3, b = 5, c = 2
x1 = (-5 + 1)/6 = -4/6 = -2/3
x2 = (-5 – 1)/6 = -6/6 = -1
Пример 2
3x2-6x+3 = 0
Решение:
a = 3, b = -6, c = 3
x1 = x2 = 1
Пример 3
x2+2x+5 = 0
Решение:
a = 1, b = 2, c = 5
В данном случае нет вещественных корней, а решением являются комплексные числа:
x1 = -1 + 2i
x2 = -1 – 2i
График квадратичной функции
Графиком квадратичной функции является парабола.
f(x) = ax2 + bx + c
- Корни квадратного уравнения – это точки пересечения параболы с осью абцисс (X).
- Если корень один – парабола касается оси в одной точке, не пересекая ее.
- При отсутствии вещественных корней (наличии комплексных), график с осю X не соприкасается.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Квадратным трёхчленом относительно переменной x называют многочлен
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
ax2 + bx + c = 0,
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1. Решить уравнение
5x2 = 0 .
Решение.
Ответ: 0 .
Пример 2. Решить уравнение
Решение. Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ: .
Пример 3. Решить уравнение
Решить уравнение
2x2 – 5 = 0 .
Решение.
Ответ: .
Пример 4. Решить уравнение
Решение. Поскольку левая часть уравнения (5) положительна при всех значениях переменной x, а правая часть равна 0, то уравнение решений не имеет.
Ответ: .
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
| (6) |
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
| (8) |
Разложение квадратного трёхчлена на множители
Утверждение. В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D < 0, квадратный трехчлен нельзя разложить на линейные множители.
Доказательство. В случае, когда D = 0, формула (8) и является разложением квадратного трехчлена на линейные множители:
| (9) |
В случае, когда D > 0, выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0, разложение квадратного трехчлена (1) на линейные множители имеет вид
| (10) |
В случае, когда D < 0, выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание. В случае, когда D < 0, квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0, из формулы (9) получаем:
Следовательно, в случае, когда D = 0, уравнение (1) обладает единственным корнем, который вычисляется по формуле
| (11) |
В случае, когда D > 0, из формулы (10) получаем:
Таким образом, в случае, когда D > 0, уравнение (1) имеет два различных корня, которые вычисляются по формулам
| (12) | |
| (13) |
Замечание 1. Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
| (14) |
Замечание 2. В случае, когда D = 0, обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0, квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
| (15) |
Замечание 3. В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0, разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax2 + bx + c = = a (x – x1)2. | (16) |
В случае, когда D > 0, разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax2 + bx + c = = a (x – x1) (x – x2) .  | (17) |
Замечание 4. В случае, когда D = 0, корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
ax2 + bx + c =
= a (x – x1) (x – x2) =
= a [x2 – (x1 + x2) x + x1x2] =
= ax2 – a(x1 + x2) x + ax1x2 .
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
ax2 + bx + c
равны соответствующим коэффициентам многочлена
ax2 – a (x1 + x2) x + a x1x2 .
Таким образом, справедливы равенства
следствием которых являются формулы
| (18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета).
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. 2-4*a*c.
2-4*a*c.
2. В зависимости от значения дискриминанта вычислить корни по формулам:
D<0, корней нет.
D=0, x=(-b/(2*a)
D>0, x=(-b+√D)/(2*a), x=(-b-√D)/(2*a)
Данный алгоритм универсален и подходит для решения любых квадратных уравнений. Полных и не полных, приведенных и неприведенных.
Нужна помощь в учебе?
Предыдущая тема: Решение квадратных уравнений выделением квадрата двучлена
Следующая тема:   Решение задач с помощью квадратных уравнений: алгоритм и примеры
Использование и понимание дискриминанта — стало проще
”Привет! Пришло время снова сыграть в любимую викторину
СТЕНА СЛАВЫ! »
»Первая участница сегодняшнего шоу — Тереза!
Надеюсь, вы готовы сыграть в СТЕНУ СЛАВЫ! »
Прежде чем мы начнем сегодняшнюю игру, давайте быстро рассмотрим наши правила игры. Тереза, ты собираешься увидеть сегодняшнюю стену. На стене 5 секретных дверей с одним уравнением , написанным над каждой дверью. Во время игры вы сможете открыть 3 из этих дверей.За каждую выбранную дверь вы получите приз, равный количеству решений уравнения. Если каждая дверь, которую вы выбираете, открывает приз, вы вернетесь на шоу завтра и получите шанс выиграть еще больший приз!
Во время игры вы сможете открыть 3 из этих дверей.За каждую выбранную дверь вы получите приз, равный количеству решений уравнения. Если каждая дверь, которую вы выбираете, открывает приз, вы вернетесь на шоу завтра и получите шанс выиграть еще больший приз!
Понимание дискриминанта
Секрет этой игры в том, что понимает и , используя дискриминант . Если Тереза придумает, как использовать этот инструмент, у нее будет шанс выиграть все призы и вернуться завтра! Давайте взглянем на сегодняшнюю СТЕНУ СЛАВЫ! уравнений , которые мы имеем сегодня:
Уравнение 1: x-квадрат минус 10x плюс 34.
Уравнение 2: 3 квадрата x минус 4x плюс 10.
Уравнение 3: квадрат x минус 3x плюс 5.
Уравнение 4: квадрат x плюс 2 корня 2x плюс 2.
Уравнение 5: квадрат x плюс 6x минус 16
В качестве первого выбора Тереза выбирает дверь номер 4. Помните, мы говорили, что можем использовать дискриминант , чтобы быстро определить, выиграла ли Тереза один из наших невероятных призов. Дискриминант происходит от квадратной формулы , и ее формула представляет собой квадрат b минус 4ac, где a, b и c относятся к коэффициентам и константе квадратного уравнения в стандартной форме .
Дискриминант происходит от квадратной формулы , и ее формула представляет собой квадрат b минус 4ac, где a, b и c относятся к коэффициентам и константе квадратного уравнения в стандартной форме .
Когда дискриминант положительный , наше уравнение будет иметь 2 решения ; когда дискриминант равен 0 , наше уравнение имеет 1 решение , а когда дискриминант отрицательный , наше уравнение не будет иметь решений . Давайте посмотрим на уравнение , которое только что выбрала Тереза. В уравнении, которое только что выбрала Тереза, «a» равно 1, «b» равно двукратному квадратному корню из 2, а «c» равно 2.
Рассчитаем дискриминант ! Величина, умноженная на квадратный корень из 2 в квадрате, будет равна 8. 8 минус 8 будет равно 0. Поскольку дискриминант равен 0, это уравнение будет иметь одно решение. Тереза, вы только что выиграли 1 новенького единорога! Разве она не выглядит счастливой ?! Это самое хорошее начало, о котором вы можете мечтать!
Тереза, вы только что выиграли 1 новенького единорога! Разве она не выглядит счастливой ?! Это самое хорошее начало, о котором вы можете мечтать!
Второй пример
При втором выборе Тереза выбирает пятое уравнение. Давайте посмотрим внимательнее! В этом уравнении «a» равно 1, «b» равно 6, а «c» равно отрицательному 16.Рассчитаем дискриминант! Подставляя наши значения, мы получаем 6 в квадрате минус 4 умножить на 1 отрицательное 16.
Используя PEMDAS , мы получаем 36 плюс 64, что равно 100. Вау! Посмотри на это! Тереза только что выиграла пару фигурок Позитрона и Негатрона! 2 приза за уравнение с 2 решениями! У Терезы пока все отлично! Если она сможет выбрать дверь с еще одним призом, ее снова пригласят на завтрашнее шоу и шанс выиграть главный приз!
И, сделав последний выбор, Тереза выбирает уравнение двери номер 2! Давайте посмотрим на ее уравнение! В этом уравнении «a» равно 3, «b» равно отрицательному 4, а «c» равно 10.Рассчитаем дискриминант! Подставляя значений , мы получаем отрицательные 4 в квадрате минус 4 умноженные на 3 умноженные на 10. Вычисляя с нашим по математике , мы получаем 16 минус 120, что равно отрицательному 104. Как вы думаете, что это означает? Не только в отношении того, сколько решений имеет наше уравнение, но и в отношении шансов Терезы вернуться завтра?
Сводка
Помните, когда наш дискриминант на больше 0 , это означает, что уравнение будет иметь 2 решения .Когда наш дискриминант равен 0 , наше уравнение будет иметь 1 решение . И когда наш дискриминант равен отрицательному , наше уравнение не будет иметь реальных решений .
Ну, ребята! Это также означает, что приза нет! Хотя Тереза будет разочарована, по крайней мере, у нее есть фигурки и новый Единорог! Хотя тот Единорог выглядит немного подозрительно … И волосы хозяина тоже выглядят подозрительно!
Квадратичные уравнения без реального решения Учебное пособие
Транскрипция видео
Скачать PDF
Сегодня мы поговорим о решении квадратных уравнений с невещественными решениями.Итак, мы собираемся начать с рассмотрения того, что значит быть квадратным уравнением без реального решения, а затем мы рассмотрим несколько примеров, решающих квадратные уравнения.
Итак, давайте начнем с того, что посмотрим, что значит иметь нереальное решение квадратного уравнения. У меня есть квадратная формула, которая, если вы помните, является одним из методов решения квадратного уравнения. И в нашей формуле мы можем специально посмотреть на выражение, которое находится под символом квадратного корня. Мы называем это дискриминантом.И дискриминант скажет вам, действительно ли ваше решение уравнения или нет.
Если значение дискриминанта равно 0 или больше 0, то у вас будет реальное решение квадратного уравнения или реальные решения квадратного уравнения. Если значение дискриминанта меньше 0, строго меньше 0, тогда у вас будет нереальное решение для вашего квадратного уравнения.
Итак, если у нас есть квадратное уравнение с ненастоящим решением, это не означает, что квадратное уравнение не имеет решения.Это просто означает, что решение — не действительные числа. Мы называем нереальные числа мнимыми числами. И мы можем определить термин «i» как квадратный корень из отрицательного 1. Итак, i определяется как квадратный корень из отрицательного 1. И мы говорим, что i мнимый, потому что нет действительного числа, возведенного в квадрат, или нет действительного числа, умноженного на сам по себе, что даст вам значение отрицательное 1. Таким образом, квадратный корень из отрицательного 1 является мнимым. Это не настоящее число.
Итак, у нас есть способы писать условные термины.Так, например, если у нас есть квадратный корень из отрицательных 5, мы знаем, что это будет мнимое число, и поэтому я могу переписать квадратный корень из отрицательных 5 как квадратный корень из 5, умноженный на квадратный корень из отрицательного числа. 1, используя мое свойство продукта радикалов. И я могу упростить квадратный корень из отрицательной 1 до просто i. Таким образом, это выражение становится квадратным корнем из 5 i.
Другой пример — квадратный корень из отрицательного 16. Итак, это снова мнимое число. Я могу переписать его как квадратный корень из 16, умноженный на квадратный корень из отрицательной 1, и снова подставив i вместо квадратного корня из отрицательной 1, я получу квадратный корень из 16 i.А квадратный корень из 16 равен 4, поэтому это выражение становится 4i.
Итак, давайте рассмотрим пример решения квадратного уравнения, которое не имеет реального решения. Итак, если бы мне пришлось решить квадратное уравнение «0 равно 2x в квадрате минус 4x плюс 4», я сначала знаю, что если бы мне пришлось изобразить уравнение «y равно 2x в квадрате минус 4x плюс 4», график будет выглядеть следующим образом . Итак, мы можем видеть, что из-за отсутствия пересечений по оси x мы уже знаем из графика, что реальных решений не существует.
Теперь давайте посмотрим, как мы можем проверить это, используя формулу корней квадратного уравнения для решения этого уравнения. Итак, в моем квадратном уравнении мне нужны значения для a, b и c. Итак, я вижу, что мое значение для a будет 2, b будет отрицательным 4, а c будет положительным 4. Таким образом, подставив эти три значения в мою квадратную формулу, я получу отрицательное b, поэтому отрицательное отрицательное 4 станет положительным 4 , плюс или минус квадратный корень из b в квадрате, поэтому отрицательный 4 в квадрате, минус 4 раза мое значение a, поэтому в 2 раза мое значение c, поэтому положительное 4, и это более чем в 2 раза больше моего значения для a.
Теперь я сначала упрощу это, упростив под квадратным корнем. Так что у меня будет 4 … о, извините. 4 плюс-минус квадратный корень из отрицательных 4 в квадрате будет положительным 16, минус … Я могу умножить эти три числа вместе. 4 умножить на 2 равно 8, умножить на 4 даст мне 32, так что у меня будет 16 минус 32. Сверху — я собираюсь пойти дальше и упростить знаменатель, так что это даст мне 4.
Затем, продолжая упрощать под моим квадратным корнем, я получил 16 минус 32, что даст мне отрицательное значение 16, и поскольку я знаю, что могу переписать квадратный корень из отрицательных 16 как квадратный корень из 16, умноженный на квадратный корень из отрицательное 1, и что квадратный корень из 16 равен 4, а квадратный корень из отрицательного 1 равен i, я могу переписать это как 4i.Таким образом, это будет 4 плюс-минус 4i вместо 4.
Теперь я могу упростить это, потому что у меня есть общий фактор во всех моих терминах. Так что, если бы я вычленил 4 из членов числителя, у меня был бы 1 плюс или минус 1i, или просто i. И тогда эти две четверки будут отменены, и у меня останется только 1 плюс-минус i для моего решения.
Теперь это решение записано в виде комплексного числа. Комплексные числа имеют как действительную, так и мнимую составляющую числа. Таким образом, 1 будет моей составляющей действительного числа, а i — моей составляющей воображаемого числа.В общем, комплексные числа можно записать как «плюс или минус bi», где a и b могут быть любыми действительными числами.
Итак, давайте рассмотрим наши ключевые моменты сегодняшнего дня. В квадратной формуле, если дискриминант больше или равен 0, то решениями квадратного уравнения будут действительные числа. Если дискриминант меньше 0, уравнение не имеет реального решения. Глядя на график квадратного уравнения, если парабола не пересекает или не пересекает ось x, то уравнение не имеет реального решения.И отсутствие реального решения не означает, что решения нет, но что решения не являются действительными числами.
Итак, я надеюсь, что эти ключевые моменты и примеры помогли вам немного больше понять о решении квадратных уравнений без реального решения. Продолжайте использовать свои записи и продолжайте практиковаться, и скоро вы станете профессионалом. Спасибо за просмотр.
Квадратичная формула — Бесплатная справка по математике
Что такое квадратное уравнение?
Квадратичная формула используется для решения очень специфического типа уравнения, называемого квадратным уравнением .4 \) термины и т. Д. В них могут присутствовать или не присутствовать все три члена (\ (Bx \) или \ (C \) могут отсутствовать). Есть несколько вариантов решения квадратного уравнения относительно x, включая факторизацию или завершение квадрата. В этом уроке мы будем использовать метко названную квадратную формулу , которая принимает три коэффициента (A, B и C) и предоставляет до двух решений, если они существуют.
Первым шагом к использованию квадратной формулы будет определение трех коэффициентов: A, B и C. В приведенном выше уравнении они удобно расположены на одной стороне упрощенного уравнения.2 + 5x = -8 $$
Решение уравнения для x
Как бы вы решили это уравнение относительно x? Мы упростили его до стандартной формы, но нет очевидного способа преобразовать это уравнение в форму x =. Вот здесь и пригодится квадратичная формула!
Квадратичная формула
Квадратичная формула — это инструмент, который мы можем использовать для решения квадратных уравнений для любых возможных решений. В конце концов мы обнаружим, что на самом деле может быть несколько уникальных решений, а может и не быть ни одного.2-4ac}} {2a} $$
Я знаю, это выглядит очень сложно. Как только вы будете использовать его много, вы выучите формулу наизусть, но до тех пор продолжайте практиковаться. На самом деле с использованием не так уж и сложно — просто введите свои номера шаг за шагом. Мы уже научились находить три коэффициента A, B и C, и я сказал, что мы на полпути к решению. Теперь мы просто вставляем значения для A, B и C, и у нас остается два возможных решения для x, если они существуют. Почему два? Обратите внимание, что в формуле есть знак плюс / минус.2 + 12}} {2} $$
$$ x = \ frac {-2 \ pm \ sqrt {16}} {2} $$
$$ x = \ frac {-2 \ pm 4} {2} $$
$$ x = \ frac {-2 + 4} {2} = 1 \ text {OR} $$
$$ x = \ frac {-2-4} {2} = -3 $$
Как видите, у нас есть два решения для этого уравнения. Может показаться странным, что x может быть двумя разными значениями, но попробуйте их оба в исходном уравнении, и вы увидите, что оба они работают! Как такое возможно? Квадратное уравнение — это не прямая линия, соединяющая каждый x с одним значением y. Если вы посмотрите на график этого типа уравнения, вы поймете, почему может быть 0, 1 или 2 решения.2 + 2x-3 = y \), поэтому мы можем изобразить его на графике. Если мы сделаем это, мы увидим, что квадратные уравнения на графике выглядят как параболы, и парабола, безусловно, может пересекать ось x дважды (что означает y = 0 в двух местах). Например, следующее изображение представляет собой график уравнения, которое мы только что решили. Видите, как он дважды пересекает ось абсцисс? Для двух разных значений x значение y равно 0. Это два решения. Если кончик параболы просто касается оси x, то у нас есть единственное решение. Если он никогда не пересечется, у нас нет решений.2-x + 1 \) и нарисуйте график, мы увидим почему. Нет случаев, когда y = 0:
Квадратичная формула сложна, но если вы просто будете следовать инструкциям, у вас не будет проблем. Обязательно проверьте дискриминант, чтобы знать, сколько решений ожидать, и не забудьте знак +/-. Запоминание самой формулы может занять некоторое время, но это очень пригодится.
Попробуйте дополнительные уроки с других сайтов: PurpleMath, SOSMath, wikipedia. Подумайте о том, чтобы попросить дополнительную помощь на нашей бесплатной доске объявлений — лучше всего подойдет начальная алгебраическая категория.
Использование дискриминантного видео | Shmoop
Дискриминант является частью формулы корней квадратного уравнения, но это не значит, что он не важен сам по себе; фактически, однажды он даже принимал гостей The Tonight Show . Дискриминант определяет количество решений в квадратной формуле. Если дискриминант положительный, есть два решения. Если дискриминант равен нулю, будет одно реальное решение. Если он отрицательный, реальных решений не будет.
| Язык | Английский язык |
| Квадратичные уравнения | Квадратные уравнения |
Транскрипт
Если b2 — 4ac положительный и больше нуля, будет два вещественных решения.
Если b2 — 4ac равно нулю, будет одно отличное реальное решение.
Но, если b2 — 4ac отрицательно и меньше нуля, реальных решений нет.
Нет. Даже не пытайся придумать. Этого не случится.
Давайте рассмотрим квадратичную формулу для пары примеров.
Наш первый пример — квадрат x плюс три x плюс пять равняется нулю.
Подставляя этих плохих парней в дискриминант, b в квадрате минус 4ac, мы получаем три в квадрате
минус четыре раза-один-пять.
Это упрощается до девяти минус двадцать, что является минус одиннадцать.
Это меньше нуля… реальных решений нет.
Что означает «нет реальных решений»? Если мы посмотрим на график, парабола
не касается оси x ни при каком значении x.
Для нашего второго примера у нас есть уравнение…
x-квадрат минус шесть-x минус десять равняется нулю.
Если вставить это в дискриминант, это выглядит так …
шесть в квадрате минус четыре раза отрицательные, десять раз один.
Это тридцать шесть плюс сорок, то есть семьдесят шесть.
Семьдесят шесть больше нуля. Итак, есть два различных реальных решения этой проблемы.
Посмотрев на график, мы можем увидеть, что есть два реальных решения, потому что парабола
касается оси x при двух различных значениях x. Итак, Magic Discriminant Ball может
не помочь вам с некоторыми из самых важных вопросов жизни …
… но использование дискриминанта может помочь вам в следующем. тест по математике.
Квадратные уравнения: сводка
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-7: Квадратные уравнения: сводка
В предыдущих двух разделах мы довольно много говорили о решении квадратных уравнений.Здесь возникает логичный вопрос: какой метод мы должны использовать для решения данного квадратного уравнения? К сожалению, ответ зависит от обстоятельств.
Если ваш инструктор указал метод, который следует использовать, то это, конечно, тот метод, который вам следует использовать. Однако, если ваш инструктор НЕ указал метод, который следует использовать, нам придется принять решение самостоятельно. Вот общий набор рекомендаций, которые может помочь при определении того, какой метод использовать.
- Очевидно ли, что это проблема свойства квадратного корня? Другими словами, состоит ли уравнение ТОЛЬКО из квадрата и константы.Если это так, то, вероятно, проще всего использовать свойство квадратного корня.
- Это фактор? Если так, то, вероятно, это лучший вариант. Обратите внимание, что вам не следует тратить много времени на то, чтобы определить, учитывается ли квадратное уравнение. Посмотрите на уравнение, и, если вы можете быстро определить, что в нем учитывается, примените его. Если вы не можете быстро определить, что это за факторы, не беспокойтесь об этом.
- Если вы достигли этой точки, значит, вы определили, что уравнение имеет неправильную форму для свойства квадратного корня и не учитывает множители (или вы не можете быстро увидеть, что оно множится).Итак, на данный момент единственный реальный вариант — это квадратичная формула.
Как только вы решите достаточное количество квадратных уравнений, приведенный выше набор рекомендаций станет для вас почти второй натурой, и вы обнаружите, что проходите их почти не задумываясь.
Также обратите внимание, что нигде в наборе руководящих указаний не было завершение упомянутого квадрата. Причина в том, что это долгий метод, который может привести к ошибкам, если вы торопитесь.Квадратичная формула также всегда будет работать, и ее использование намного короче. В общем, вы должны использовать квадрат только в том случае, если ваш инструктор требует, чтобы вы его использовали.
В качестве метода решения завершение квадрата всегда должно быть вашим последним выбором. Однако это не означает, что это не важный метод. Мы увидим, как завершение квадратного процесса возникает в нескольких разделах следующих глав. Интересно, что когда мы увидим этот процесс в следующих разделах, мы не будем решать уравнения! Этот процесс очень полезен во многих ситуациях, решение которых — только одно.2} + bx + c = 0 \]
мы получим один из следующих трех возможных наборов решений.
- Два реальных различных (, т. Е. не равных) решений.
- Двойной корень. Вспомните, это возникает, когда мы можем разложить уравнение на полный квадрат. 2} — 4ac = 0 \).2} — 4 \ left ({49} \ right) \ left ({81} \ right) = 0 \]
В этом случае мы получим двойной корень, поскольку дискриминант равен нулю. Вот она,
\ [x = — \ frac {9} {7} \]
Дискриминант: определение и объяснение | Study.com
Это формула для нахождения дискриминанта. Использование дискриминанта
Дискриминант сообщает вам, сколько возможных решений имеет конкретное квадратное уравнение.Однако, прежде чем мы сможем использовать квадратное уравнение, мы сначала должны изменить его на стандартную форму . Стандартная форма — это когда все переменные и константы находятся на одной стороне уравнения, а другая сторона равна нулю. Выглядит это так:
Это квадратное уравнение в стандартной форме. Когда у вас есть квадратное уравнение в стандартной форме, вы можете пометить числа соответствующими буквами и вставить значения в формулу для поиска дискриминанта.Результат вашего дискриминанта говорит вам, сколько решений имеет ваша квадратичная.
Примеры
Давайте посмотрим на пример:
Пример 1 В нашем примере квадратное уравнение дает нам 1 для буквы a , 5 для буквы b и 4 для буквы c . Мы берем эти значения и вставляем их в соответствующие места в формуле дискриминанта, и мы обнаруживаем, что наш дискриминант равен 9, положительному числу.Это говорит нам о том, что у нашего квадратного уравнения есть два возможных вещественных решения. Реальные решения — это решения, которые можно вычислить по формуле корней квадратного уравнения. Когда вы изобразите это квадратное уравнение, вы увидите, что кривая пересекает ось x в двух местах, именно там, где находятся ваши решения.
Хотя дискриминант сообщает нам количество возможных решений, он не говорит нам, что это за решения. Но это дает нам представление о том, сколько решений нам нужно искать.
Помните, что если перед переменными нет чисел, предполагается, что перед ними стоит 1. Мы не пишем 1, потому что это математическое соглашение и потому что это выглядит аккуратнее, особенно когда у вас много букв, с которыми нужно работать.
Рассмотрим другой пример:
Пример 2 Мы присвоили нашим буквам соответствующие значения. После вставки соответствующих значений в нашу дискриминантную формулу мы обнаруживаем, что наш дискриминант -31, отрицательное число.Хм … что это могло значить? Когда дискриминант отрицательный, это означает, что реальных решений нет. Это означает, что при построении графика уравнения вы увидите, что оно никогда не пересекает ось x и поэтому не имеет реальных решений.
Есть еще одна возможная ситуация — когда дискриминант равен 0. Когда вы видите это, это означает, что существует только одно возможное реальное решение. На графике уравнение касается оси x только в одной точке.
Вот таблица, которая поможет вам запомнить возможные дискриминантные ситуации и их значение:
Дискриминант Количество решений > 0 Два реальных решения = 0 Одно реальное решение <0 Реальных решений нет Резюме урока
Подводя итог, дискриминант помогает вам, сообщая вам, сколько возможных решений имеет квадратное уравнение.Формулу можно найти, посмотрев на квадратный корень в формуле квадратного корня. Возможны три сценария. Если дискриминант положительное число, то есть два реальных решения. Если дискриминант равен 0, то существует только одно реальное решение. Если дискриминант отрицательное число, то реальных решений нет.
Результаты обучения
После этого урока вы сможете:
- Определить дискриминант и вспомнить его назначение
- Объясните, как найти дискриминант
- Опишите возможные сценарии использования дискриминанта
Дискриминант квадратичной формулы
Дискриминант — это часть квадратичной формулы.

 Дискриминант. Формула дискриминанта. Теорема Виета. Версия для печати.
Дискриминант. Формула дискриминанта. Теорема Виета. Версия для печати.
 Введите свой запрос:
Введите свой запрос: