Содержание
Урок 7. тетраэдр и параллелепипед — Геометрия — 10 класс
Геометрия, 10 класс
Урок №7. Тетраэдр и параллелепипед
Перечень вопросов, рассматриваемых в теме
- понятие тетраэдра;
- понятие параллелепипеда;
- свойства ребер, граней, диагоналей параллелепипеда;
- определение сечения в фигуре;
- метод следа.
Глоссарий по теме
Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
Сечением поверхности геометрических тел называется – плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.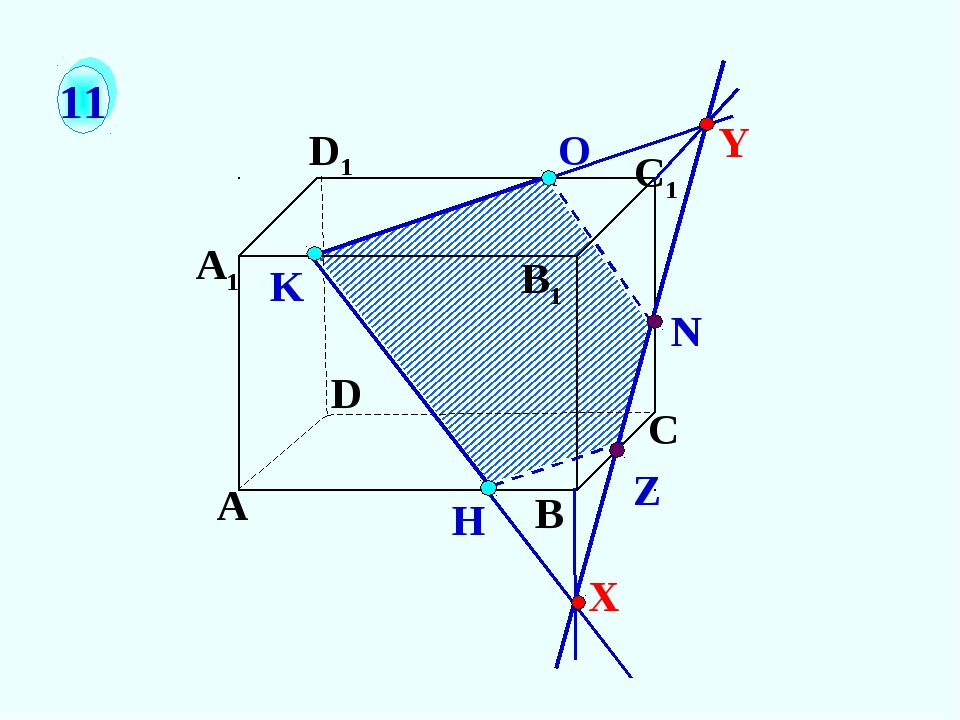
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Учебник Геометрия 10-11 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.
Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.
Открытый электронный ресурс:
Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru
Теоретический материал для самостоятельного изучения
В дельнейшем несколько уроков нашего курса будет посвящены многогранникам- поверхностям геометрических тел, составленным из многоугольников. Но до более подробного изучения многогранников мы познакомимся с двумя из них- тетраэдром и параллелепипедом. Нам данные тела дадут возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей.
Давайте вспомним, что мы понимали под многоугольником в планиметрии. Многоугольник мы рассматривали либо как замкнутую линию без самопересечений, либо как часть плоскости, ограниченную этой линией, включая ее саму.
Мы будем использовать второе толкование многоугольника при рассмотрении поверхностей и тел в пространстве. При таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность.
Давайте рассмотрим изображенную фигуру и ответим на несколько вопросов.
Итак, поверхность данной фигуры состоит из четырёх треугольников DАВ, DВС, DАС и АВС.
Тетраэдр состоит:
- из вершин- их у него 4- А, B, C, D;
- из ребер- их у него 6- AB, BC, AC, AD, BD, CD;
- из граней- их у него 4- треугольники ∆АВС, ∆DАС, ∆DВС, ∆DАВ.
Мы с вами выяснили из элементов состоит наша фигура тетраэдр. Теперь сформулируем определение.
Определение. Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.
Говорят, что рёбра АD и ВС, АВ и CD, и т.д.- противоположные.
Считается АВС — основание, остальные грани — боковые.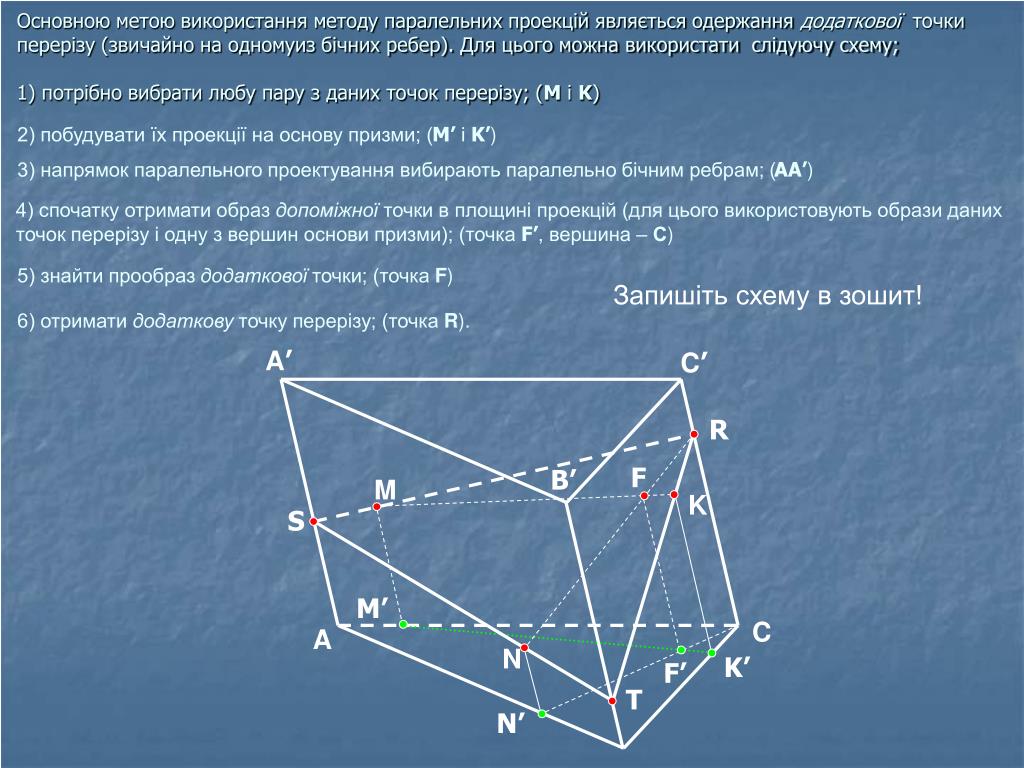
Изображается тетраэдр обычно так (рис. 1).
Рисунок 1 – изображение тетраэдра.
Математика, в частности геометрия, является мощнейшим инструментом в познании мира. Различные геометрические формы находят свое практическое приспособление в различных областях знания: архитектуре, скульптуре, живописи. И тетраэдр тому доказательство. Так же мы можем наблюдать тетраэдр в повседневной жизни (рис. 2).
Форма пакета молока | Архитектурные решения | Солнечные панели |
Рисунок 2 — тетраэдр в повседневной жизни
Параллелепипед.
Прежде чем начать изучать параллелепипед вспомним определение параллелограмма и его свойства.
Определение. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом (рис. 3).
Рисунок 3 – параллелограмм
Свойства параллелограмма
1. Противоположные стороны параллелограмма равны: AB=DC, BC=AD | |
2. ∟A=∟C, ∟B=∟D | |
3. Диагонали параллелограмма точкой пересечения делятся пополам: BO=OD, AO=OC | |
треугольники ABC и CDA равны. | |
| |
6. Накрест лежащие углы при диагонали равны: ∟BAC=∟ACD, ∟BCA=∟CAD |
А теперь перейдем к параллелепипеду.
Рассмотрим два равных параллелограмма ABCD и A1B1C1D1, расположенных в параллельных плоскостях так, что отрезки AA1, BB1, CC1 и DD1 параллельны.
АВСDА1В1С1D1 — параллелепипед.
Давайте рассмотрим изображенную фигуру (рис. 4).
4).
Рисунок 4 – параллелепипед и его диагонали
АВСDA1B1C1D1: поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1, лежащих в параллельных плоскостях и четырёх параллелограммов.
Все параллелограммы — грани, их стороны — рёбра, их вершины — вершины параллелепипеда.
Считается: АВСD и A1B1C1D1 — основания, остальные грани — боковые.
Определение. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда:
A1C, D1B, AC1, DB1.
Параллелепипед – слово греческого происхождения, параллел – идущий рядом, епипед – плоскость.
Определение.Параллелепипед- этошестигранник с параллельными и равными противоположными гранями.
Следует отметить, что многоугольник в пространстве представляет собой плоскую поверхность, а тетраэдр и параллелепипед – поверхности, составленные из плоских поверхностей (соответственно треугольников и параллелограммов).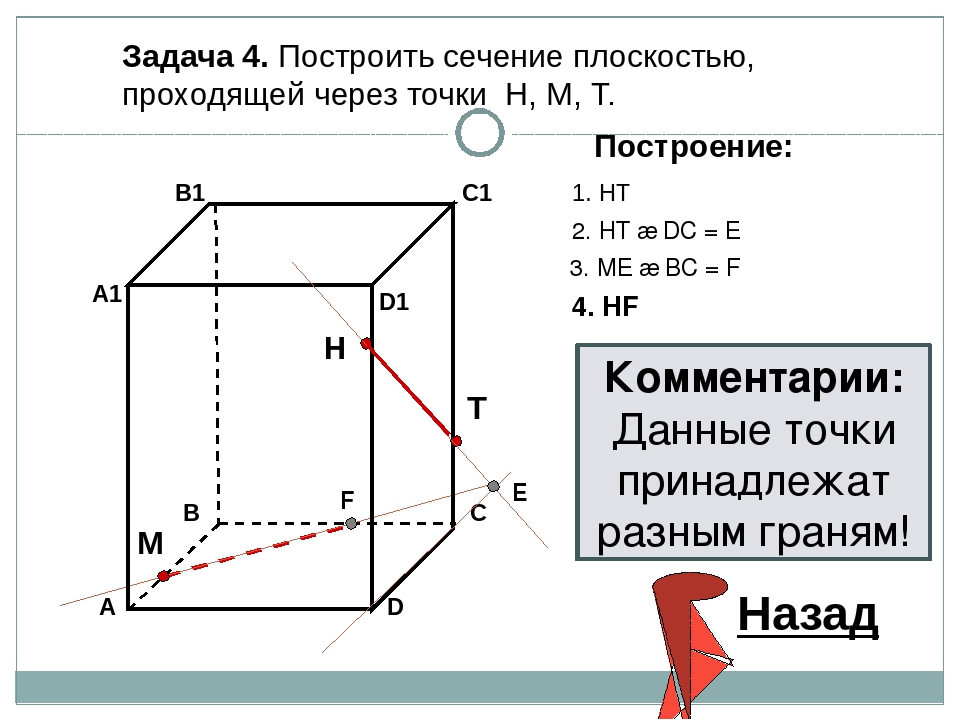
Способы изображения параллелепипеда
Параллелепипед, в основании которого лежит ромб | |
Параллелепипед, в основании которого лежит квадрат | |
Параллелепипед,в основании которого лежит прямоугольник или параллелограмм | |
Параллелепипед, у которого все грани — равные квадраты |
Можно сделать вывод, что параллелепипеды делятся на (рис. 5)
Рисунок 5 – виды параллелепипедов
Свойства параллелепипеда
- Противоположные грани параллелепипеда параллельны и равны.
- Все четыре диагонали пересекаются в одной точке и делятся в ней пополам.
Доказательство 1
В параллелепипеде ABCDA1B1C1D1грани ВВ1С1С и AA1D1D параллельны (рис. 6), потому что две пересекающиеся прямые ВВ1 и В1С1 одной грани параллельны двум пересекающимся прямым АА1 и A1D1 другой; эти грани и равны, так как В1С1 = A1D1, В1В= А1А (как противоположные стороны параллелограммов) и ∟ ВВ1С1= ∟АA1D1.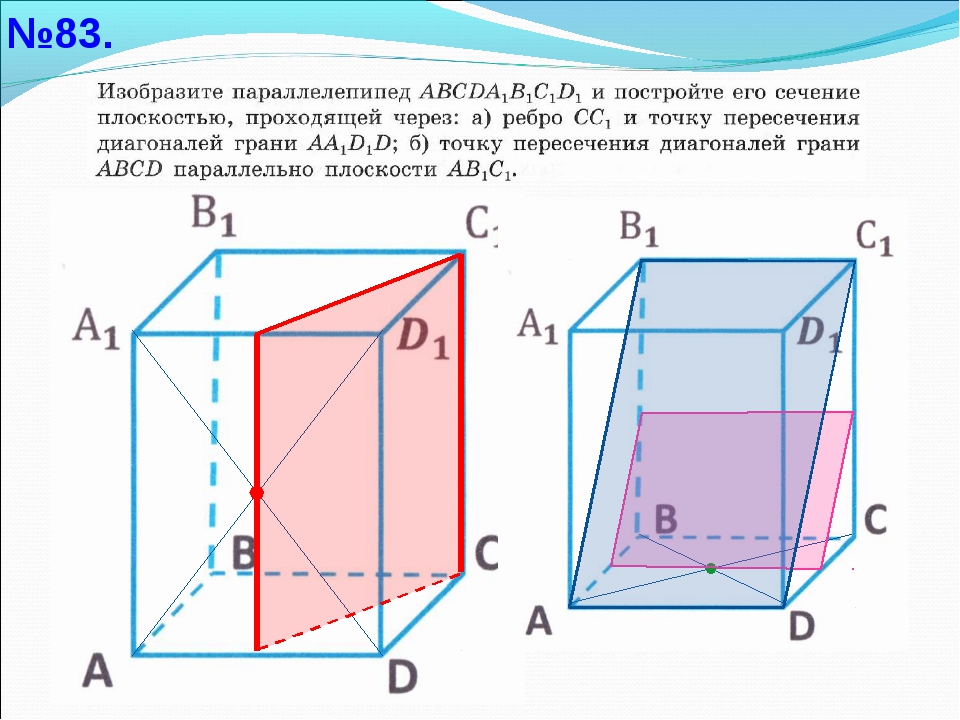
Рисунок 6 – чертеж к доказательству свойства 1
Доказательство 2
Возьмём какие-нибудь две диагонали, например АС1 и ВD1, и проведём вспомогательные прямые АD1 и ВС1 (рис. 7).
Так как рёбра АВ и D1С1 соответственно равны и параллельны ребру DС, то они равны и параллельны между собой; вследствие этого фигура АD1С1В есть параллелограмм, в котором прямые С1А и ВD1 —диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам.
Возьмём теперь одну из этих диагоналей, например АС1, с третьей диагональю, положим, с В1D. Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B1D и АС1 и диагонали АС1 и BD1(которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали
АС1. Наконец, взяв эту же диагональ АС1 с четвёртой диагональю А1С, мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали АС1. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.
Наконец, взяв эту же диагональ АС1 с четвёртой диагональю А1С, мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали АС1. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.
Рисунок 7 – чертеж к доказательству свойства 2
Задачи на построение сечений.
Определение. Сечением поверхности геометрических тел называется — плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.
Взаимное расположение многогранника и секущей плоскости:
- Многогранник и плоскость не имеют общих точек.
- Многогранник и плоскость имеют одну общую точку-вершину многогранника.
- Многогранник и плоскость имеют общую грань.
- Многогранник и плоскость имеют общий отрезок-ребро многогранника.

Виды сечений:
- сечение параллельное плоскости основания,
- диагональное сечение,
- сечение, параллельное плоскости грани,
- произвольное сечение.
Фигуры, которые получаются в результате сечения:
- треугольник;
- четырехугольник;
- пятиугольник;
- шестиугольник.
Один из методов построения сечений, который мы рассмотрим- метод следа.
Рассмотрим метод следов, применяемый при построении сечений многогранников, а именно при построении сечения куба плоскостью.
Что такое метод следов? При построении сечений многогранников в качестве вспомогательной прямой часто используется след секущей плоскости (в плоскости грани, удобной для рассмотрения). Такой метод построения сечений называется методом следа.
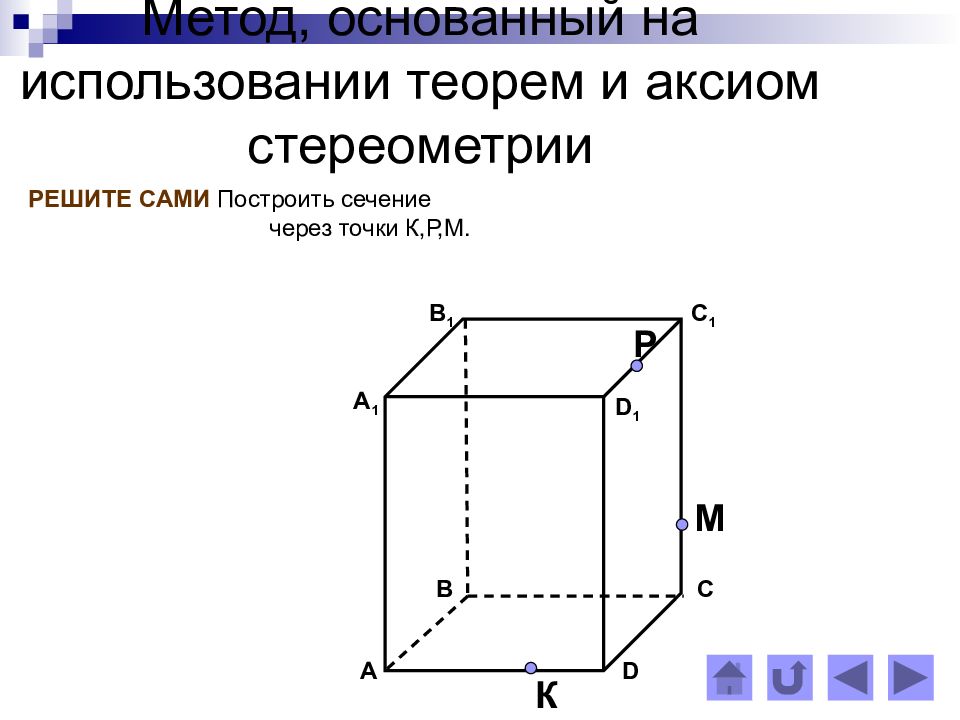
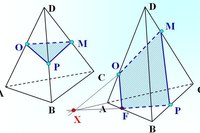
Задача №1.
Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R (рис.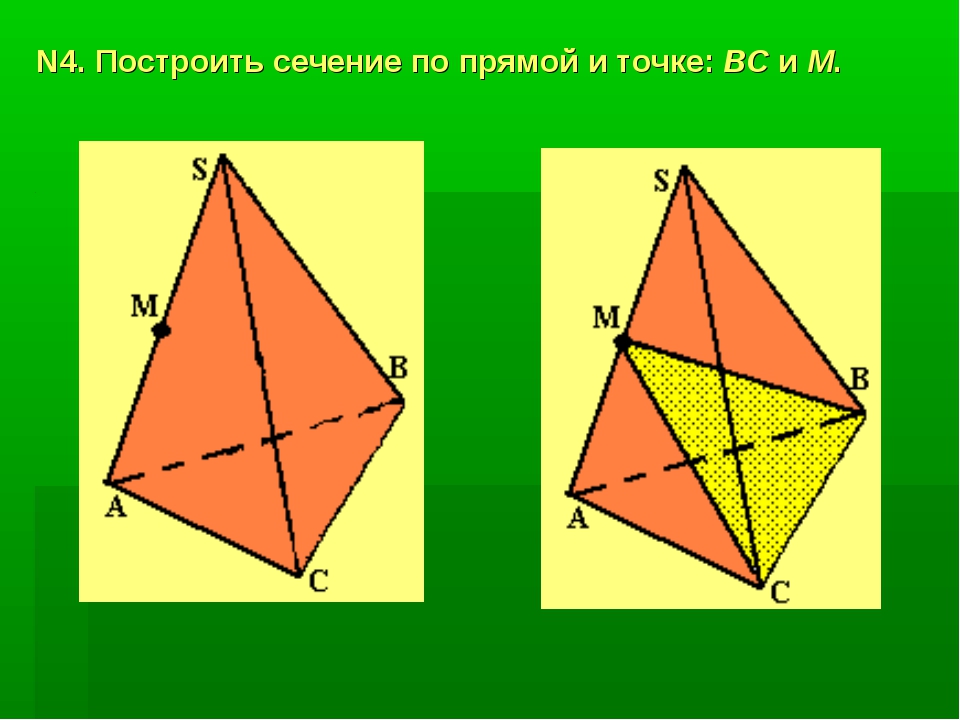 8).
8).
Решение.
Рисунок 8 –чертеж к задаче №1
- Построим след секущей плоскости на плоскость нижнего основания параллелепипеда. Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
- Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S1, принадлежащую следу.
- Аналогично получаем точку S2 пересечением прямых QR и BC.
- Прямая S1S2 — след секущей плоскости на плоскость нижнего основания параллелепипеда.
- Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА1D1D. Аналогично получаем TU и RT.
- PQRTU – искомое сечение.
Основные правила построения сечений методом следа:
- Если даны (или уже построены) две точки плоскости сечения на одной грани многогранника, то след сечения этой плоскости – прямая, проходящая через эти три точки.
- Если дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определенной боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью ( точка пересечения данного следа с общей прямой основания и данной боковой грани)
- Точку пересечения плоскости сечения с основанием можно определить как точку пересечения какой-либо прямой в плоскости сечения с ее проекцией на плоскость основания.
То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.
Задача №2.
Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС.
N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС.
Рисунок 9 – чертеж к задаче №2
Решение:
Для решения построим вспомогательную плоскость DМN (рис. 10). Пусть прямая DМ пересекает прямую АВ в точке К. Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.
Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС (рис. 11). В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.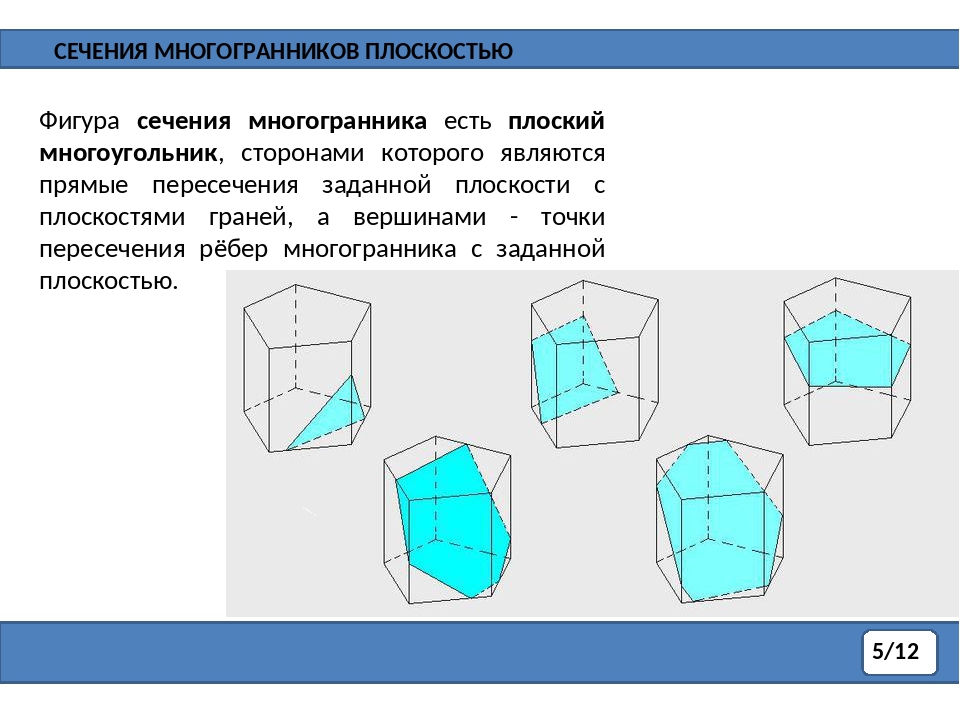 е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.
е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.
Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р1 и Р2. Соединяем Р1 и М и на продолжении получаем точку М1. Соединяем точку Р2 и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.
Рисунок 10 – чертеж к примеру 1 (первый случай)
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС (рис. 12). Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямая Р1Р2 параллельна данной прямой MN.
Теперь проведем прямую Р1М и получим точку М1. Р1Р2NМ1 – искомое сечение.
Рисунок 11 – чертеж к примеру 1 (второй случай)
Пример 2.
Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите, что эта плоскость пересекает грани SAB и SBC по параллельным прямым.
Доказательство
Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N (рис. 13).
По теореме (о параллельных прямых) линия пересечения параллельна SB.
В плоскость SBC через т. N проходит NQ||SB.
Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. M (прямая MP). По теореме (о параллельных прямых) линия пересечения параллельна SB.
следовательно, PM||NQ.Утверждение доказано.
Рисунок 12 — чертеж к примеру 2
Построение сечений многогранников ( 10 класс, геометрия)
Урок геометрии в 10 классе
Тема: «Построение сечений многогранников»
Автор: Учитель математики
МАОУ СОШ №45
г. Калининграда
Калининграда
Маврина Т.В.
Учебно-методическое обеспечение: Атанасян Л.С. и др. Геометрия 10-11 класс.
Оборудование и материалы для урока: компьютер, проектор, экран, презентация для сопровождения урока, раздаточный материал учащимся.
Цель урока: углубление, обобщение, систематизация, закрепление полученных знаний и развитие их в перспективе (изучить метод следов)
Задачи урока:
1. Сформировать у школьников мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для получения новых знаний.
3. Развивать у учащихся мышление (умение выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач и навыки исследовательской работы над задачей.
Знания, умения, навыки и качества, которые закрепят ученики в ходе урока:
умение пользоваться опорными знаниями, для получения новых знаний;
умение выделять существенные признаки и делать обобщения;
навыки творческого подхода к решению задач на построение сечений
План урока:
1. Сформирование у школьников мотивации к изучению данной темы.
Сформирование у школьников мотивации к изучению данной темы.
2. Проверка домашнего задания. Исторические сведения.
3. Повторение опорных знаний (аксиоматика, способы задания плоскости).
4. Применение знаний в стандартной ситуации.
5. Изучение и закрепление нового материала: метод следов.
6. Самостоятельная работа.
7. Подведение итога урока.
8. Домашнее задание.
Ход урока:
I этап – Вводная беседа.
Проверка домашнего задания. (6-7 мин)
Формы и методы работы
учителя
Виды деятельности
учащихся
1.Мотивация
Вводная беседа (1 мин)
Слушают учителя
2. Проверка домашнего задания
Комментирует мини-выступления учащихся
Слушают выступления товарищей, задают вопросы
II этап – Актуализация знаний (10 мин)
(повторение теоретического материала)
Формы и методы работы
учителя
Виды деятельности
учащихся
1. Повторение аксиом стереометрии
Повторение аксиом стереометрии
Работа по готовым слайдам (фронтальный опрос учащихся)
Устные ответы на вопросы учителя
2. Повторение: взаимное расположение в пространстве прямых и плоскостей
3. Обобщение теории
Вывод о способах задания плоскости
Запись вывода в тетрадь
4. Повторение понятия многогранника и сечения многогранника плоскостью
Опрос учащихся
Устные ответы на вопросы учителя
III этап – Применение знаний в стандартной ситуации(6-7 мин)
(работа по готовым чертежам)
Формы и методы работы
учителя
Виды деятельности
учащихся
Решение типовых задач по готовым чертежам (каждому ученику выдается рабочий листок с условием задачи и чертежом для построения сечения).
Объяснение предстоящей работы.
Совместное решение первой задачи (подробное комментирование шагов решения и записи оформления в рабочий лист).
Изучение условия задачи, работа по готовым чертежам, с последующим разбором решения по слайдам.
IV этап –Свойства параллельных плоскостей (6 мин)
1. Повторение темы «Параллельность плоскостей».
2. Решение задач
Работа по готовым слайдам (фронтальный опрос учащихся)
Проверка правильности выполнения задания
Устные ответы на вопросы учителя
Построение сечений в рабочем листе.
Ответы у доски.
V этап — Выход на получение новых знаний: «Метод следов»(6 мин)
Формы и методы работы
учителя
Виды деятельности
учащихся
1. Изучение нового материала
2. Закрепление нового материала
Объяснение нового материала. Показ учебного фрагмента учебного фильма «Как построить сечение куба?»
Показ учебного фрагмента учебного фильма «Как построить сечение куба?»
Работа по готовым чертежам у доски (с последующим комментированием этапов построения сечения по слайду)
Слушают объяснение учителя. Просмотр учебного фильма. Анализ видеофрагм., запись образца решения.
Двое учащихся решают у доски, остальные в рабочем листе
VI этап — Самостоятельная работа (4-5 мин)
Формы и методы работы
учителя
Виды деятельности
учащихся
Самостоятельная работа обучающего характера
Объяснение предстоящей работы.
Проверка выполнения задания.
Выполнение самостоятельной работы (по готовым чертежам).
Самопроверка по готовым слайдам.
VII этап – подведение итогов урока (4 мин)
Формы и методы работы
учителя
Виды деятельности
учащихся
1. Подведение итогов
Подведение итогов
2. Творческое домашнее задание
Беседа по итогам урока с использованием слайдов
Проецируется на экран
Устные ответы на вопросы учителя
Запись в дневники
ХОД УРОКА
Вступительная беседа. Исторические сведения.
Учитель: Здравствуйте, ребята! Тема нашего урока «Построение сечений многогранников на основе аксиоматики». (Слайд№1 ).
На уроке мы обобщим и систематизируем пройденный теоретический материал, и применим его к практическим задачам на построение сечений, с выходом на новый более сложный уровень трудности задач.
Главная цель нашего урока в углублении, систематизации, закреплении полученных знаний и развитии их в перспективе.
В качестве домашнего задания вам было предложено написание рефератов или небольших выступлений об истории развития геометрии, о жизни великих математиков, об их знаменитых открытиях и теоремах.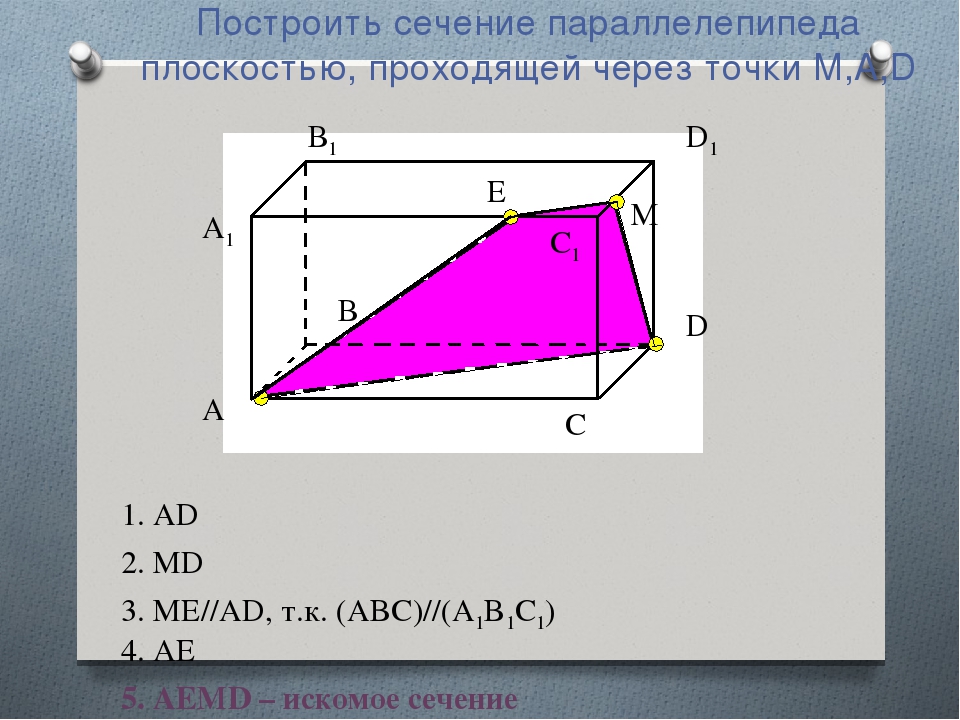 Доклады и рефераты получились очень интересные, но на уроке мы заслушаем только три мини-выступления, отвечающие на вопрос, что изучает стереометрия, как возникла и развивалась и где находит своё применение?
Доклады и рефераты получились очень интересные, но на уроке мы заслушаем только три мини-выступления, отвечающие на вопрос, что изучает стереометрия, как возникла и развивалась и где находит своё применение?
1 ученик. Понятие стереометрии, что изучает. (2 мин) (Слайд №2)
2 ученик. Евклид – основоположник геометрии, греческая архитектура. (2 мин)
3 ученик. Математическая теория живописи. «Золотое сечение» — формула совершенного человеческого тела по Леонардо да Винчи. (2 – 3 мин)
В стереометрии изучаются красивые математические объекты. Их формы находят своё применение в искусстве, архитектуре, строительстве. « Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии, а греческая архитектура – внешнее выражение геометрии Евклида», — писал архитектор Корбюзье.
Прошли века, но роль геометрии не изменилась. Она по прежнему остается «грамматикой архитектора». Геометрические формы находят своё применение в искусстве, архитектуре, строительстве.
Она по прежнему остается «грамматикой архитектора». Геометрические формы находят своё применение в искусстве, архитектуре, строительстве.
Математическая теория живописи – это теория перспективы, представляющая, по словам Леонардо да Винчи, «тончайшее исследование и изобретение, основанное на изучении математики, которое силой линий заставляло казаться отдаленным то, что близко, и большим то, что невелико». Развернувшееся в эпоху Возрождения строительство инженерных сооружений возродило и расширило применявшиеся в античном мире приёмы проекционных изображений. Архитекторы и скульпторы встали перед необходимостью создания учения о живописной перспективе на геометрической основе. Многочисленные примеры построения перспективных изображений имеются в работах гениального итальянского художника и выдающегося ученого Леонардо да Винчи. Он впервые говорит о сокращении масштаба разных отрезков удаляющихся в глубь картины, кладет начало панорамной перспективе, указывает правила распределения теней, высказывает уверенность в существовании некой математической формулы красоты отношения размеров человеческого тела – формулы «золотого сечения».
Таким образом мы плавно подошли к теме нашего урока, и мостиком в его следующий этап будут слова Леонардо да Винчи :
«Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет». (Слайд №3)
Это высказывание определяет следующий этап нашего урока: повторение теоретического материала.
II. Актуализация знаний (повторение теоретического материала)
2.1. Аксиомы стереометрии (таблицы остаются учащимся для работы).
В ходе беседы выделяются существенные моменты теории:
а) разъяснить содержание аксиом и иллюстрировать на модели;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
г) запись содержания с помощью символов. (Слайды №4-№6)
2.2. Следствия из аксиом стереометрии. (Слайды № 7-№ 9)
(Слайды № 7-№ 9)
2.3. Взаимное расположение в пространстве прямых и плоскостей.
а) двух прямых (прямые параллельны, пересекаются, скрещиваются) (Слайд №10)
б) прямой и плоскости (прямая лежит в плоскости, пересекает плоскость, параллельна плоскости). (Слайды №11,№12)
в) двух плоскостей (плоскости пересекаются либо параллельны). (Слайд №13)
В ходе беседы выделяются существенные моменты теории:
а) Признак параллельности прямой и плоскости: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
б) Признак параллельности плоскостей: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Учитель: Обобщая все сказанное, приходим к выводу о способах задания плоскости.
2.5. Понятие многогранников. Сечение.
Многогранником называется тело, ограниченное конечным числом плоскостей. Поверхность многогранника состоит из конечного числа многоугольников.
Многоугольник, полученный при пересечении многогранника и плоскости, называется сечением многогранника указанной плоскостью ( Слайды №14,№15)
III. Применение знаний в стандартной ситуации.
Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики. (Слайд №16)
Примеры и их решение приводят учащиеся (под руководством учителя).
(Слайды №17-20)
IV. Построение сечений с использованием свойств параллельных плоскостей.
Учитель: Для решения следующей группы задач нам необходимо повторить свойства параллельных плоскостей. (Слайды №21-№24)
V. Выход на получение новых знаний: «Метод следов».
(Слайды №25,№26)
Просмотр учебного фильма.
Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»
Применение полученных знаний (решение учащимися двух задач у доски с последующим просмотром правильного решения и записи оформления).
VI — Самостоятельная работа. (Слайды №27,№28)
с последующей взаимопроверкой (по слайду с готовым решением).
VII. Подведение итогов урока
Что нового вы узнали на уроке?
Каким образом строится сечение тетраэдра?
Какие многоугольники могут быть сечением тетраэдра?
Какие многоугольники могут получиться в сечении параллелепипеда?
Что вы можете сказать о методе следов?
Творческое домашнее задание. Составить две задачи на построение сечений многогранников с использованием полученных знаний. (
Слайды №29, №30)
Атанасян Л.С. и др. Геометрия 10-11 класс. Учебное пособие.
Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»
Электронное издание «Решебник по геометрии. Пособие для абитуриентов. Полный курс за 7-11 классы»
Построение сечений многогранников — PDF Free Download
Сечения многогранников
Сечения многогранников Цель работы Показать как решать задачи на построение сечений Задачи работы Объяснить понятие плоского сечения Что значит построить сечение Методы построения сечений многогранников
Подробнее
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ. Эта тема считается трудной. Если работать на обычной доске, много времени уходит на построение рисунков, условие задачи не всегда позволяет
Подробнее
Параллельность плоскостей
Параллельность плоскостей Рассмотрим две плоскости α и β. В пространстве они могут располагаться следующим образом: 1. Совпадать, если они имеют три общие точки, не принадлежащие одной прямой. α=β 2. Пересекаться,
Подробнее
Построение сечений многогранников
Построение сечений многогранников Секущей плоскостью геометрической фигуры называется такая плоскость, по обе стороны от которой есть точка данной фигуры. Сечением называется фигура, состоящая из всех
Подробнее
C 1 сентября по 30 декабря
Тематическое планирование по геометрии (заочное отделение) в 10 классе Учебник: Л.С. Атанасян, Геометрия 10-11 классы, Просвещение, 2011г. Дидактические материалы по геометрии 10 класс Б.Г. Зив, Просвещение,
Подробнее
2. Сечения многогранников
. Сечения многогранников Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью (секущей плоскостью). Мы будем заниматься решением
Подробнее
Задание 8, 14. Стереометрия
Задание 8, 4. Стереометрия Основные определения Аксиомы стереометрии Теорема. Через любые три точки, не лежащих на одной прямой, проходит плоскость, и притом только одна. Теорема. Если две точки прямой
Подробнее
УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАРЕЛИЯ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ РЕСПУБЛИКИ КАРЕЛИЯ «КОЛЛЕДЖ ТЕХНОЛОГИИ И ПРЕДПРИНИМАТЕЛЬСТВА» (ГАПОУ РК «Колледж технологии
Подробнее
Многогранники. Призма
Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,
Подробнее
параллелепипеда АD=а, АВ=b, АА 1 =с. (Ответ: V a b
c Государственное автономное образовательное учреждение общеобразовательная школа-интернат Республики Коми «Коми республиканский лицей-интернат для одаренных детей из сельской местности» Елизарова Н.Г.,
Подробнее
Основные определения, теоремы и формулы планиметрии.
Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне
Подробнее
Тема 62 «Сечения многогранников»
Тема 6 «Сечения многогранников» 1. Способы задания плоскости: тремя точками, не лежащими на одной прямой; прямой и точкой, не лежащей на прямой; двумя параллельными прямыми; двумя пересекающимися прямыми..
Подробнее
Правильные многогранники
Правильные многогранники Правильные многогранники были описаны еще в Древней Греции. Эти многогранники носят название «платоновых тел», по имени древнегреческого философа Платона (48 348 до н.э.). Правильным
Подробнее
Подготовка к ЕГЭ 2013, стереометрия
1 Подготовка к ЕГЭ 2013, стереометрия Интерактивный комплект 2. Параллельность и перпендикулярность 2.1. Параллельность в пространстве Пособие содержит описание основных понятий, методов расчёта, примеры
Подробнее
РАБОЧАЯ ПРОГРАММА ПО ГЕОМЕТРИИ. 10 класс
РАБОЧАЯ ПРОГРАММА ПО ГЕОМЕТРИИ. 0 класс п/п РАЗДЕЛ / ТЕМА КОЛ- ВО ЧАСОВ КОМПЕТЕНЦИИ ПРИМЕЧАНИЕ НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ 2 ПЛАНИМЕТРИИ Углы и отрезки, связанные с окружностью 4 Должен знать: Вписанные и центральные
Подробнее
Стереометрия: пирамиды.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: пирамиды. 27069. Стороны основания правильной
Подробнее
МАТЕМАТИКА Сечения многогранников
Агентство образования администрации Красноярского края Красноярский государственный университет Заочная естественно-научная школа при КрасГУ Математика: Модуль 5 для 11 класса. Учебно-методическая часть./
Подробнее
А. В. ПОГОРЕЛОВ «ГЕОМЕТРИЯ КЛАССЫ»
А. В. ПОГОРЕЛОВ «ГЕОМЕТРИЯ. 0 КЛАССЫ» Базовый уровень (,5 ч в неделю) Номера пункта Содержание материала Кол-во часов Характеристика основных видов деятельности ученика (на уровне учебных действий). Аксиомы
Подробнее
12+ УДК 373:51 ББК 22.1я72 Г68
УДК 373:51 ББК 22.1я72 Г68 Г68 Гордин Р. К. ЕГЭ 2018. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) / Под ред. И. В. Ященко. М.: МЦНМО, 2018. 128 с. ISBN 978-5-4439-1214-1 Пособия
Подробнее
Аксиомы стереометрии
Аксиомы стереометрии Аксиома (греч. αχιομα авторитетное предложение «то, что приемлемо») утверждение, принимаемое без доказательства. Теорема (греч. τεορεμα рассматривать, обдумывать) утверждение, требующее
Подробнее
Геометрия, ХI ГЕОМЕТРИЯ
ГЕОМЕТРИЯ Геометрия, ХI Экзамен по геометрии экзамен по выбору, форма проведения которого может быть различной: ответ по билету, защита реферата, собеседование, тестовая проверка. Предлагаемые экзаменационные
Подробнее
Анализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Подробнее
Календарно-тематическое планирование
Данная программа курса по геометрии в 10 классе разработана на основе Федерального государственного образовательного стандарта основного общего образования, утв. Приказом Минобрнауки России от 17.12.2010
Подробнее
Тест 250. Отрезок. Длина
Тест 250. Отрезок. Длина Длина отрезка равна 1, если он является: 1. высотой равностороннего треугольника со стороной 2; 2. третьей стороной треугольника, в котором две другие стороны равны 1 и 2, а угол
Подробнее
Аффинные преобразования.
Аффинные преобразования. Методологический паспорт. Тема: Аффинные преобразования плоскости. Проблема: Изучение понятия аффинных преобразований плоскости, их свойств, особенностей и применения на практике.
Подробнее
ОТВЕТЫ НОРМЫ ВЫСТАВЛЕНИЯ ОЦЕНОК
АТЕАТИКА, класс Ответы и критерии, Январь 0 ОТВЕТЫ Вариант/ задания В В В В4 В5 В6 В7 С,5 0 4,5 940 0-5 4 4600 4,5 7 0,65 4,8 50 0 98 0,,4 4 4,5 0,5 4 7,5 5 96 7,5 950 6,5 90 6 97,8 45 0,5 500-0,5 455
Подробнее
Подготовка к ЕГЭ 2013, стереометрия
1 Подготовка к ЕГЭ 2013, стереометрия Интерактивный комплект 3. Проекции и расстояния 3.1. Проекции Пособие содержит описание основных понятий, методов расчёта, примеры объяснений, как использовать интерактивный
Подробнее
Операции над векторами. Сложение векторов
Операции над векторами К линейным действиям над векторами относят сложение, вычитание векторов и умножение вектора на число Сложение векторов Суммой двух векторов и называется вектор, начало которого совпадает
Подробнее
Развертки поверхностей
Развертки поверхностей Разверткой поверхности называется плоская фигура, полученная в результате совмещения всех точек поверхности с одной плоскостью. Между поверхностью и ее разверткой устанавливается
Подробнее
ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС
ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС ПРОВЕРОЧНАЯ РАБОТА 1 1) Найти площадь равнобедренного треугольника с углом при основании, если а) боковая сторона равна с; б) основание равно р 2) Стороны параллелограмма
Подробнее
Угол между прямой и плоскостью
Угол между прямой и плоскостью Углом между прямой, не перпендикулярной плоскости, и плоскостью называется угол между прямой и ее прямоугольной проекцией на данную плоскость. Теорема. Угол между прямой
Подробнее
Построение сечений многогранника. 10 класс
1. ГЕОМЕТРИЯ 10 класс
Построение сечений
многогранника.
Дано:
Пирамида MABCD.
Постройте сечение пирамиды,
проходящее через точки P, Q, R.
Известно, что точка P MB,
точка R MA,
точка Q DC.
M
p
N
R
B
F
C
A
Е
D
Q
1) PR AB=F;
2) FQ AD=E;
3)FQ BC=T;
4)PT MC=N;
5)PREQNP – ИСКОМОЕ СЕЧЕНИЕ
T
4. Сечение куба
Прямоугольный параллелепипед, у
которого все три измерения равны,
называется кубом.
Куб имеет 6 граней. Его сечениями
могут быть треугольники,
четырехугольники, пятиугольники
и шестиугольники.
5. Дано:
ABCDА1B1C1D1 -куб,
точка К
принадлежит
ребру A1В1, точка L
принадлежит
ребру В1C1 , точка
М принадлежит
ребру DC.
Построить:
сечение куба
плоскостью.
6. Решение:
Проведем
прямую КL и
отметим точки ее
пересечения с
продолжениями
соответствующи
х ребер куба.
Получим еще
две точки,
лежащие в
плоскости
сечения и на
продолжениях
ребер куба.
Проводя
аналогичным
образом прямые
в плоскостях
других граней
куба мы
построим все
сечение.
9. Дано:
ABCDA1B1C1D1 – куб.
Точки PNKQ
принадлежат
ребрам.
Построить сечение
куба плоскостью.
10. Решение:
Соединим точки P и
N
М – точка
пересечения
прямых PQ и DD1
Проведем прямую
МК
Соединим точки
NК.
NPQFK – искомое
сечение.
14. Задание:
На ребрах
взяты точки K,
L и M, как
показано на
рисунках.
Постройте
сечение куба
плоскостью,
проходящей
через эти
точки.
15. Ответ к заданию:
«Правильных многогранников вызывающе мало,
но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных
наук»
Л.Кэрролл
За каждым многогранником
закреплено его значение, НАПРИМЕР:
Тетраэдр является огнём!
куб-земля
октаэдр-воздух
21. Даже пчёлы знакомы с понятием многогранник!!!
Многогранники в архитектуре.
Александрийский
маяк
Великая пирамида в
Гизе
Презентация «Построение сечений многогранников» | Презентация к уроку по геометрии (10 класс) на тему:
Слайд 1
Учитель математики МАОУ лицей №3 г. Кропоткин Краснодарского края Зозуля Елена Алексеевна
Слайд 2
Цель урока: повторить основные методы сечения многогранников, определенного тремя точками пространства; формулы для вычисления площадей плоских многоугольников; Оборудование: интерактивная доска
Слайд 3
Вопросы к классу: — Что значит построить сечение многогранника плоскостью? — Как могут располагаться относительно друг друга многогранник и плоскость? — Как задается плоскость? — Когда задача на построение сечения многогранника плоскостью считается решенной?
Слайд 4
Постройте сечение четырехугольной призмы плоскостью, проходящей через три точки на боковых ребрах призмы.
Слайд 5
1. Соединим точки M и K (т.к. они лежат в одной плоскости)
Слайд 6
2. Соединим точки M и N (т.к. они лежат в одной плоскости)
Слайд 7
3. Продлим прямую CD до пересечения с прямой MN (CD MN = L)
Слайд 8
4 . Продлим прямую CB до пересечения с прямой MK (CB MK = P)
Слайд 9
5 . Соединим точки L и P (LP AD = E ; LP AB = = F)
Слайд 10
6 . Соединим точки B и F ( т.к. они лежат в одной плоскости)
Слайд 11
7. Соединим точки E и N (т.к. они лежат в одной плоскости)
Слайд 12
8. ( KMNEF) – искомая плоскость (сечение)
Слайд 13
Постройте сечение четырехугольной призмы плоскостью, проходящей через три точки на боковых ребрах призмы.
Слайд 14
1. Соединим точки M и K (т.к. они лежат в одной плоскости)
Слайд 15
2. Соединим точки M и N (т.к. они лежат в одной плоскости)
Слайд 16
3. Продлим прямую CB до пересечения с прямой MK (CB MK = P)
Слайд 17
4. Продлим прямую CD до пересечения с прямой MN (CD MN = L)
Слайд 18
5 . Соединим точки L и P
Слайд 19
6. Продлим прямую AB до пересечения с прямой LP ( AB LP = F)
Слайд 20
7. Проведем прямую KF ( KF AA 1 = E)
Слайд 21
8. Соединим точки E и N (т.к. они лежат в одной плоскости)
Слайд 22
9 . ( KEMN) – искомая плоскость (сечение)
Слайд 23
На ребре AB куба ABCDA 1 B 1 C 1 D 1 взята точка P — середина этого ребра, а на ребре DD 1 — точка Q 1 такая, что DQ 1 : Q 1 D 1 = 1 : 2. Построить сечение куба плоскостью C 1 Q 1 P. Найти его площадь, считая ребро куба равным a .
Слайд 24
1. Соединим точки С и Q 1 (т.к. они лежат в одной плоскости)
Слайд 25
2. Продлим прямую CD до пересечения с прямой CQ 1 (CD CQ 1 = O)
Слайд 26
3. Проведем прямую PO (PO AD = M)
Слайд 27
4. Соединим точки P и Q 1 (т.к. они лежат в одной плоскости)
Слайд 28
5. Продлим прямую CB до пересечения с прямой OP ( CB OP =L )
Слайд 29
6. Проведем прямую C 1 L ( C 1 L BB 1 = N )
Слайд 30
7. Соединим точки P и N (т.к. они лежат в одной плоскости)
Слайд 31
8. ( C 1 Q 1 MPN) – искомая плоскость (сечение)
Слайд 32
Задача 3 (для самостоятельного решения). Построить сечение куба ABCDA1B1C1D1 со стороной а плоскостью, проходящей через точки B, M и N, где Ь – середина ребра АА1, а N – середина ребра СС1. Решение. Сечение строим методом следов. Площадь сечения находим с помощью теоремы о площади ортогональной проекции многоугольника. Ответ: S = 1/2 · a 2 .
Урок по теме «Сечение многогранников» / Открытый урок
Цель: углубление, обобщение, систематизация, закрепление полученных знаний и навыков построения сечений
Задачи:
1. Сформировать у школьников мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для получения новых знаний.
3. Развивать у учащихся мышление (умение выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач и навыки
исследовательской работы над задачей.Оборудование: Атанасян Л. С. и др. Геометрия 10-11 класс (М.Просвещение.2010), компьютер,
проектор, экран, презентация для сопровождения урока, раздаточный материал учащихся,
СD: Виртуальнаяшкола Кирилла и Мефодия (Уроки геометрии 10класс)
План урока: 1. Организационныймомент (1мин)
2. Проверка домашнегозадания (4-5мин)
3. Актуализация (3-4мин)
4. Применение знаний встандартной ситуации (закрепление) (21-23мин)
5. Самостоятельнаяработа (10мин)
6. Домашнеезадание (2мин)
7. Подведение итогаурока (2мин)
1. Организационный момент (приветствие,сообщение темы, целей и плана урока)
2. Проверка домашнего задания (задачи №1, 2, презентация слайд № 3, 4) разборрешения задач домашней работы по этапам, с объяснением теоретической составляющей)
3. Актуализация (блиц-опрос)
Что называется многогранником
Что называется сечением многогранника (слайд № 5)
Что является базовым при построениисечений (слайд № 6)
Какие методы построения сеченийиспользуются при решении задач
4. Закрепление: Просмотр решения задачи (анимация №3 «сечение параллелепипеда»,урок №13 по теме «Многогранники», СD Виртуальная школа Кирилла и Мефодия, Уроки геометрии 10 класс), обсуждение
Решение задач (обсуждение плана построения, построение каждым в тетради и проверка с помощью подготовленной презентации, слайды 7-10)
1. Построить сечение,определяемое параллельными прямыми АА1 и СС1
2. Построитьсечение куба плоскостью, проходящей через М и прямую АС3.
Построть сечение куба, проходящее через точки Р,М,К
4.Определить вид сечениякуба АВСДА1В1С1Д1 плоскостью,проходящей через ребро А1Д1 и середину ребраВВ1
5. Самостоятельнаяработа на построение сечений, проходящих через данные точки, по готовым чертежам с взаимопроверкой (слайд №11-условие, №12-решение)
6. Домашнеезадание: № 84,85 [1,с.32] дополнительно: Составить две задачи на построение сечений многогранников с использованием полученных знаний. (творческое задание)
7. Итог урока:
Что нового вы узнали на уроке?
Каким образом строится сечение параллелепипеда?
Какие многоугольники могутполучиться в сечении параллелепипеда?
Литература:
1. Атанасян Л.С. и др. Геометрия. /Учебник для 10-11классов общеобразовательных учрежденийМ.Просвещение.20102.
2. Смирнов В.А.,Смирнова И.М. Геометрия / Учебник для 10-11 классов. М.Мнемозина.20083.
3. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»
4. Электронное издание«Решебник по геометрии. Пособие для абитуриентов. Полный курс за 7-11 классы»
5. Электронное издание«Виртуальная школа Кирилла и Мефодия: Уроки геометрии 10 класс»
Сечения многогранников
Сечение многогранников
В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно (геометрическое) тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Многогранник — это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называетсявыпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины — вершинами многогранника.
Сечением многогранника плоскостью называется геометрическая фигура, представляющая собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости; плоскость при этом называется секущей плоскостью.
Поскольку плоскость определяется:
Тремя точками;
Прямой и точкой;
Двумя параллельными прямыми;
Двумя пересекающимися прямыми,
построение плоскости сечения проходит в зависимости от задания этой плоскости.
Поверхность многогранника состоит из ребер – отрезков и граней – плоских многоугольников. Так как прямая и плоскость могут пересекаться только в одной точке, а две плоскости – по прямой, то сечением многогранника плоскостью является плоский многоугольник. Вершинами этого многоугольника служат точки пересечения секущей плоскости с ребрами многогранника, а сторонами — отрезки, по которым секущая плоскость пересекает его грани. Это означает, что для построения искомого сечения данного многогранника плоскостью α достаточно построить точки её пересечения с ребрами многогранника или прямыми, содержащими эти ребра. Затем, последовательно соединив отрезками прямых эти точки, необходимо выделить сплошными линиями видимые, и штриховыми – невидимые стороны полученного многоугольника-сечения.
Рассмотрим основные методы построений сечений:
1. Построение сечений многогранников на основе системы аксиом и теорем стереометрии. (Аксиоматический метод)
Примеры сечений, построенных аксиоматическим способом:
В качестве примера рассмотрим решение следующих задач:
Задача 1-4. Построить сечение тетраэдра плоскостью, заданной тремя точками
2. Метод следов
Прямая, по которой секущая плоскость α пересекает плоскость основания многогранника, называется следом плоскости α в плоскости этого основания.
Из определения следа получаем: в каждой его точке пересекаются прямые, одна из которых лежит в секущей плоскости, другая – в плоскости основания. Именно это свойство следа используют при построении плоских сечений многогранников методом следов. Причем в секущей плоскости удобно использовать такие прямые, которые пересекают ребра многогранника.
Задача 1.Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.
Задача 2. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.
Задача 3.
3. Метод внутреннего проектирования.
Метод внутреннего проектирования называют еще методом соответствий, или методом диагональных сечений.
При применении этого метода каждая заданная точка проектируется на плоскость основания. Существует два возможных вида проектирования: центральное и параллельное. Центральное проектирование, как правило, используется при построении сечений пирамид, вершина пирамиды при этом является центром проекции. Параллельное проектирование используется при построении сечений призм.
При применении этого метода каждая заданная точка проектируется на плоскость основания. Существует два возможных вида проектирования: центральное и параллельное. Центральное проектирование, как правило, используется при построении сечений пирамид, вершина пирамиды при этом является центром проекции. Параллельное проектирование используется при построении сечений призм.
Сущность метода внутреннего проектирования рассмотрим на примере построения сечения призмы.
Задача 1. Постройте сечение призмы ABCDE плоскостью α, заданной точками M є B,P є , Q є E (рис 10).
Рис. 10
Решение. Плоскость нижнего основания призмы обозначим β. Для построения искомого сечения построим точки пересечения плоскости α с ребрами призмы..
ПятиугольникMNPQR – искомое сечение.
Задача 2.
4.Метод вспомогательных сечений.
Этот метод построения сечений многогранников является в достаточной мере
универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь в виду, что построения, выполняемые при использовании этого метода, зачастую получаются «искусственное». Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
Задача.На ребре BM пирамиды MABCD зададим точку Р. Построим сечение пирамиды плоскостью PQR, точку R которой зададим на грани АMD,аQ на грани DMC.
5. Координатный метод.
Суть координатного метода заключается в вычислении координат точек пересечения ребер или многогранника с секущей плоскостью, которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется на основе условий задачи.
Любую плоскость можно задать уравнением первой степени вида
A x + B y + C z + D = 0 (общее уравнение плоскости), где A, B и C не могут быть одновременно равны нулю.
Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то можно записать уравнение плоскости в отрезках
Уравнение плоскости, проходящей через точку M(x0, y0, z0), перпендикулярно вектору нормали n (A; B; C) имеет вид: A(x — x0) + B(y — y0) + C(z — z0) = 0.
Если заданы координаты трех точек A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3), лежащих на плоскости, уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой можно найти по следующей формуле:
Задача. В правильной треугольной призме АВСА1В1С1 все ребра которой равны, точка К — середина В1С1. Найти угол между плоскостью АВС и плоскостью В1КР, где Р — середина АА1.
Решение.
Пусть ребро заданной призмы равно 2. Введем декартову систему координат. Выберем начало координат в точке О — середине ребра АВ. Ось направим по ОС, ось у — по ОВ, ось — по ОО1; О1 — середина А1В1. При выбранной системе координат и длине ребра призмы найдем координаты нужных точек:
Ясно, что уравнение плоскости АВС будет иметь вид: , а плоскость В1КР пройдет через точку С1 , т.е. совпадет с плоскостью В1С1Р.
Уравнение плоскости В1С1Р будем искать в виде Пусть Найдем значения и методом неопределенных коэффициентов.
Искомое уравнение имеет вид: или
Угол между плоскостями АВС и В1С1Р равен углу между их нормальными векторами и соответственно Для отыскания угла (так обозначим искомый угол) воспользуемся определением скалярного произведения двух векторов:
Ответ: 30º.
Комбинированный метод.
Сущность комбинированного метода построения сечений многогранников состоит в том, что искомое сечение строится с помощью метода следов или метода внутреннего проектирования или метода вспомогательных сечений, при этом дополнительно используются свойства данного многогранника.
Для иллюстрации применения этого метода рассмотрим задачи:
Задача 1. Постройте сечение куба, проходящее через точки P,R,Q.
Задача 2.
Задачи с решениями по теме
«Сечения многогранников»
(Задание 8 № 324451)
В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1.
Решение.
Противоположные стороны сечения являются соответственно средними треугольников, лежащих в основании, и прямоугольников, являющихся боковыми гранями призмы. Тем самым, сечение представляет собой прямоугольник со сторонами 1 и 5, площадь которого равна 5.
Ответ: 5.
(Задание 8 № 513339)
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 16, AD = 21, AA1 = 28. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
Решение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение — параллелограмм. Кроме того, ребро перпендикулярно граням и Поэтому углы и — прямые. Поэтому сечение — прямоугольник.
Из прямоугольного треугольника найдем
Тогда площадь прямоугольника равна:
Ответ: 560
3. (Задание 8 № 76613)
Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.
Решение.
В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, и поэтому вдвое меньше параллельного ей ребра. Значит, сечением является квадрат со стороной 19. Тогда площадь сечения равна 361.
Ответ: 361.
(Задание 8 № 524067)
В правильной четырёхугольной пирамиде все рёбра равны 70. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
Решение.
Каждая из сторон сечения является средней линией боковой грани. Поэтому стороны сечения образуют квадрат со стороной 35, площадь которого равна 1225.
Ответ: 1225.
(Задание 8 № 505383)
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро BC = 4, ребро ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
Решение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому четырехугольник — параллелограмм. Кроме того, ребро перпендикулярно граням и , поэтому углы и — прямые. Следовательно, сечение — прямоугольник.
Из прямоугольного треугольника по теореме Пифагора найдем
Тогда площадь прямоугольника равна:
Ответ:20.
(Задание 8 № 508229)
В правильной треугольной призме ABCA1B1C1 стороны оснований равны боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, и A1B1и точку С.
Решение.
Введём обозначения как показано на рисунке. Треугольник правильный, следовательно, медиана является биссектрисой и высотой. Из прямоугольного треугольника по теореме Пифагора найдём
Площадь искомого сечения — это площадь прямоугольника найдём её:
Ответ: 15.
7. Задание 14 № 507887
В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
Решение.
а) Проведём через точку N прямую, параллельную прямой AB, до пересечения с прямой B1C1 в точке K. Трапеция ABKN — искомое сечение.
б) Имеем A1N= 3, так как точка N — середина ребра A1C1. Значит, Аналогично BK = 5.
Далее NK = 3, как средняя линия треугольника A1B1C1. Следовательно, искомый периметр сечения равен 6 + 5 + 5 + 3 = 19.
Ответ: 19.
(Задание 14 № 508233)
В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
Решение.
а) В плоскости ABP через точку K проведем прямую, параллельную прямой PB до пересечения ее с прямой AB в точке L— середине AB. В основании ABCD через точку L проведем прямую, параллельную прямой BC до пересечения ее с ребром СDв точке M — его середине. По признаку параллельности прямой и плоскости плоскость KLM параллельна прямым PB и BC. Прямая LM параллельна прямой AD, следовательно, она параллельна плоскости APD, а, значит, плоскость KLM пересекает плоскость APD по прямой, параллельной LM и пересекает ребро PD в его середине N.
Таким образом, искомое сечение ― трапеция KLMN.
б) Отрезки KL и MN равны, как средние линии равных правильных треугольников ABP и DCP, а отрезок LM ― средняя линия квадрата ABCD, следовательно, построенное сечение ― равнобедренная трапеция, в которой LM = 4, KL = KN = MN = 2. Проведем высоту KFэтой трапеции. Тогда и из прямоугольного треугольника KLF находим
Окончательно получаем
Ответ:
СПИСОК ЛИТЕРАТУРЫ
Потоскуев Е.В., Звавич Л.И. Геометрия. 10 кл.: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики. — М.: Дрофа, 2008.
Потоскуев Е.В., Звавич Л.И. Геометрия. 10 кл.: Задачник для общеобразовательных учреждений с углубленным и профильным изучением математики. — М.: Дрофа, 2008.
Потоскуев Е.В. Изображение пространственных фигур на плоскости. Построение сечений многогранников. Учебное пособие для студентов физико-математического факультета педвуза. — Тольятти: ТГУ, 2004.
Научно-практический журнал для старшеклассников «Математика для школьников»,-2009,№2/№3,1-64.
Смирнов В.А. ЕГЭ 2011. Математика. Задача С2. Геометрия. Стереометрия: пособ. для подготовки к ЕГЭ / под ред. А.Л. Семенова и И.В. Ященко. — М.: МЦНМО, 2009. — 272 с.
https://ege.sdamgia.ru/
ege.fipi.ru/os11/xmodules/qprint/index.php?theme_guid=f6ec29149541e311bacb001fc68344c9&proj_guid=AC437B34557F88EA4115D2F374B0A07B
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/407220-sechenie-mnogogrannikov
Урок 8.1A: Трехмерные объекты, сети и сечения
Презентация на тему: «Урок 8.1A: Трехмерные объекты, сети и сечения» — стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
Урок 8.1A: Трехмерные объекты, сети и поперечные сечения
Цель: R.4.G.8 Рисование, исследование и классификация поперечных сечений трехмерных объектов
2
Словарь Многогранник — это трехмерное твердое тело с плоскими поверхностями и прямыми краями. Каждый многоугольник — это грань многогранника. Ребро — это сегмент, образованный пересечением двух граней. Вершина — это точка пересечения трех или более ребер.Сетка — это двухмерный узор, который можно сложить в трехмерную фигуру. Одна из самых простых таких фигур — куб — многогранник с шестью гранями, каждая из которых представляет собой квадрат.
3
Словарь Призмы: многогранник с 2 конгруэнтными и параллельными гранями, называемыми основаниями. Пирамида: многогранник, в котором одна грань представляет собой многоугольник, а остальные — треугольники … подходит к вершине. Цилиндр: трехмерная фигура с 2 конгруэнтными и параллельными основаниями, которые представляют собой круги. Конус: имеет 1 круглое основание и выходит на вершину.
4
Словарь сечений:
Пересечение твердого тела и плоскости.В результате получился многоугольник.
5
Определение сети
6
Определение сети
7
Определение сети
8
Рисование сетки упаковки
Нарисуйте сетку для коробки с крекером Грэма.Обозначьте сетку ее размерами.
9
Рисование сети
10
Поперечные сечения Поперечное сечение — это форма, образующаяся при пересечении плоскостью трехмерной фигуры. Представьте себе очень тонкий кусок твердого тела. Основания — это противоположные грани, параллельные и конгруэнтные. Чтобы описать взаимосвязь между плоскостью и твердым телом, это будет либо: Параллельно основанию, либо Перпендикулярно основанию. Поперечные сечения могут быть многоугольниками и кругами. Укажите форму, которую оно создает, когда вы разрезаете твердое тело.
11
Параллельные сечения
12
Параллельные сечения
13
Перпендикулярные поперечные сечения
14
Перпендикулярные поперечные сечения
15
Плоскость разрезает цилиндр ниже, параллельно основанию
Плоскость разрезает цилиндр ниже, параллельно основанию.Какое в результате сечение?
16
Плоскость разрезает прямоугольную призму ниже, параллельно основанию. Какое в результате сечение?
17
Плоскость разрезает конус, и в результате получается треугольник. Опишите отношения между плоскостью и конусом.
18
Учитывая конус высотой 6 м и радиусом 4 м, какова площадь поперечного сечения, если плоскость разрезает конус перпендикулярно основанию через центр? 6м 4м
19
Найдите площадь заштрихованного поперечного сечения угловой призмы
20
Плоскость пересекает сферу на расстоянии 3 дюймов от центра сферы.Радиус сферы 5 дюймов. Какова площадь поперечного сечения с точностью до десятых?
Трехмерные формы | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. У трехмерной твердой формы тоже есть глубина. Трехмерные формы по своей природе имеют внутреннюю и внешнюю стороны, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как твердые тела с прямыми сторонами, называемые многогранниками, которые основаны на многоугольниках, так и твердые тела с кривыми, такие как глобусы, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) — это твердые формы с прямыми сторонами. Многогранники основаны на многоугольниках, двухмерных плоских формах с прямыми линиями.
См. Нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.
Многогранники определяются как имеющие:
- Прямые кромки .
- Плоские стороны называются , грани .
- углов, называемых вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые у них есть, а также тем, имеют ли их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках). Многогранники также могут быть вогнутыми или выпуклыми.
Один из самых простых и известных многогранников — это куб.Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных тел — это особый класс многогранников, все грани которых идентичны, причем каждая грань представляет собой правильный многоугольник. Платоновы тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью гранями пятиугольника.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
См. Диаграмму выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, у которого есть два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно концу, ее поперечное сечение будет одинаковым — вы получите две призмы.Стороны призмы равны параллелограммам — четырехгранным формам с двумя парами сторон равной длины.
Антипризмы похожи на обычные призмы, их концы совпадают. Однако стороны антипризм состоят из треугольников, а не параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с основанием многоугольника , который соединяется с вершиной (верхняя точка) прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, подобных тем, что строили древние египтяне, на самом деле они могут иметь любое основание многоугольника, правильное или неправильное. Кроме того, пирамида может иметь вершину в прямом центре своего основания, Правая пирамида , или может иметь вершину вне центра, когда это наклонная пирамида .
Более сложные многогранники
Есть еще много типов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано) представляет собой архимедово твердое тело с 14 гранями. 6 граней — правильные восьмиугольники, а остальные 8 — правильные (равносторонние) треугольники. У фигуры 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с закругленными или закругленными краями не являются многогранниками. Многогранники могут иметь только прямые стороны.
Многие из окружающих вас объектов будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными изогнутыми телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца в форме круга или овала.Несмотря на то, что цилиндры похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера, имеющая форму шара или земного шара, представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Обычный кольцевой тор в форме кольца, шины или бублика образуется путем вращения меньшего круга вокруг большего круга. Есть также более сложные формы торов. |
Площадь
На нашей странице «Расчет площади» объясняется, как рассчитать площадь двумерных фигур, и вам необходимо понимать эти основы, чтобы рассчитать площадь поверхности трехмерных фигур.
Для трехмерных форм мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двумерных форм для вычисления площади поверхности трехмерной формы, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы прорабатываете площадь каждой грани, а затем складываете их вместе.
Как и в случае плоских форм, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба — это площадь одной грани (длина х ширина), умноженная на 6, потому что все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба 10 × 10 см = 100 см 2 .Умножив на 6 количество граней куба, мы находим, что площадь поверхности этого куба равна 600 см 2 .
Другие правильные многогранники
Точно так же площадь поверхности других правильных многогранников (платоновых тел) можно вычислить, найдя площадь одной стороны и затем умножив ответ на общее количество сторон — см. Диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на общее количество сторон (12), чтобы получить ответ 264 см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Затем проработайте площадь одной стороны (треугольник). Измерьте ширину по основанию, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Затем вы можете либо разделить полученный ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножить на 4, чтобы получить площадь поверхности всех четырех сторон, либо просто умножьте площадь поверхности одного треугольника на 2.
Наконец, сложите площадь основания и стороны вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы рассчитать площадь поверхности для других типов пирамид, сложите вместе площадь основания (известную как площадь основания) и площадь сторон (боковая площадь), вам может потребоваться измерить стороны по отдельности.
Диаграммы сети
Геометрическая сеть — это двухмерный «узор» для трехмерного объекта. Сетки могут быть полезны при определении площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды. Если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о сетевых диаграммах см. Нашу страницу 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два конца одинаковые и плоские стороны параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа (концы × стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если отрезать сторону по длине и приплюснуть, получится прямоугольник. Поэтому вам нужно найти площадь двух кругов и прямоугольника.
Сначала проработайте область одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
Предполагая радиус 5 см, площадь одного из кругов составляет 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как есть два круга 157см 2
Площадь стороны цилиндра равна периметру окружности, умноженному на высоту цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4
Измерьте высоту цилиндра — в этом примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314см 2 .
Общую площадь поверхности можно определить, сложив вместе площади кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона = 10 см
Конус
При расчете площади поверхности конуса необходимо использовать длину «склона», а также радиус основания.
Однако вычислить относительно просто:
Площадь круга у основания конуса равна π (пи) × радиус 2 .
В этом примере сумма равна 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь боковой части, наклонного участка, может быть найдена по следующей формуле:
π (пи) × радиус × длина уклона.
В нашем примере сумма равна 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте основание к боковой области, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
Площадь поверхности сферы — это относительно простое разложение формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто легче измерить диаметр — расстояние по сфере. Затем вы можете найти радиус, равный половине диаметра.
Диаметр стандартного теннисного мяча — 2.6 дюймов. Следовательно, радиус составляет 1,3 дюйма. Для формулы нам понадобится радиус в квадрате. 1,3 × 1,3 = 1,69.
Таким образом, площадь теннисного мяча составляет:
.
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площади поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На схеме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаковый для каждой детали.
Формула: площадь поверхности = (2πR) (2πr)
Для определения площади поверхности примера тора.
(2 × π × R) = (2 × 3.14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Умножьте два ответа вместе, чтобы найти общую площадь поверхности примера тора.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Заполнение твердого тела: Том
Для трехмерных фигур вам также может потребоваться знать, какой объем у них составляет .
Другими словами, если вы наполните их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Призмы с примерами
Перейти к площади или объему поверхности.
Призма — это твердый объект с:
- одинаковые концы
- плоские поверхности
- и тот же сечение по всей длине!
Поперечное сечение — это форма, полученная прямым разрезом объекта.
Поперечное сечение этого объекта — треугольник …
.. одинаковое поперечное сечение по всей длине …
… значит, это треугольная призма .
images / prism-grow.js
Попробуйте нарисовать фигуру на листе бумаги А теперь представьте, что он выходит из листа бумаги … |
Без кривых!
Призма — это многогранник, а это значит, что все грани плоские!
Например, цилиндр не является призмой , потому что у него изогнутые стороны.
Базы
Концы призмы параллельны
, и каждый из них называется основанием.
Стороны
Боковые грани призмы — параллелограммы
(четырехсторонние формы с параллельными противоположными сторонами)
Это все призмы:
и более!
Пример: гексагональный кристалл льда.
Похоже на шестиугольник, но из-за некоторой толщины это на самом деле шестиугольная призма!
Фотография НАСА / Алексей Клятов.
Обычная и неправильная призмы
Все предыдущие примеры — это призмы Regular , потому что поперечное сечение является правильным (другими словами, это форма с равными длинами кромок и равными углами).
Вот пример неправильной призмы :
| Неправильная пятиугольная призма: | ||
| Поперечное сечение | ||
| Он «неправильный», потому что поперечное сечение не имеет «правильной» формы. | ||
Правая и наклонная призма
Когда два конца идеально выровнены, это правая призма, в противном случае — наклонная призма:
Площадь призмы
Площадь поверхности = 2 × площадь основания
+ периметр основания × длина
Пример: Какова площадь поверхности призмы, у которой площадь основания 25 м
2 , периметр основания 24 м, а длина 12 м:
Площадь поверхности = 2 × Площадь основания + Периметр основания × Длина
= 2 × 25 м 2 + 24 м × 12 м
= 50 м 2 + 288 м 2
= 338 м 2
(Примечание: у нас есть инструмент для расчета площади)
Объем призмы
Объем призмы — это площадь одного конца, умноженная на длину призмы.
Объем = Базовая площадь × длина
Пример: каков объем призмы с площадью основания 25 м
2 и длиной 12 м:
Объем = Площадь × Длина
= 25 м 2 × 12 м
= 300 м 3
Поиграй с этим здесь. Формула также работает, когда он «наклоняется» ( наклон ), но помните, что высота находится под прямым углом к основанию:
И вот почему:
Стек может наклоняться, но имеет тот же объем
Подробнее о боковых гранях
Боковые грани призмы — параллелограммы (четырехсторонняя форма с параллельными противоположными сторонами)
Призма может наклоняться в одну сторону, что делает ее наклонной призмой , но два конца по-прежнему параллельны, а боковые грани по-прежнему параллелограммы!
Но если два конца не параллельны , это не призма .
639 640 863, 1826, 1827 864, 3379, 3377, 3378, 7649
Многогранники (3D-формы) | NZ Maths
Назначение
В этом разделе учащиеся создают и исследуют различные многогранники (трехмерные объекты), уделяя особое внимание созданию сетей.
Конкретные результаты обучения
- Создавайте модели многогранников из структурированных или повседневных материалов.
- Используйте термины грани, ребра и вершины для описания моделей многогранников.
Описание математики
Многоугольник — это двумерная фигура с прямыми сторонами. Многогранник — это полностью замкнутый трехмерный объект, грани которого представляют собой многоугольники. Существует много различных семейств многогранников, включая призмы, пирамиды и Платоновы тела.
Термины, обычно используемые для описания атрибутов многогранников, включают:
- Грань: один многоугольник в твердой фигуре
- Edge: линия, где две грани соединяются
- Вершина: точка пересечения граней — угол
В 1750-х годах Леонард Эйлер обнаружил известную связь между этими тремя владениями.Количество вершин плюс количество граней, отведенных от двух, равно количеству ребер.
E = V + F — 2
Возможности адаптации и дифференциации
Учебные действия в этом разделе можно дифференцировать, варьируя предоставленные строительные леса или изменяя сложность задач, чтобы сделать возможности обучения доступными для широкого круга учащихся. Способы поддержки студентов включают:
- предоставляет готовые версии моделей, на которые студенты могут ссылаться при создании своих собственных
- предоставляет сети, которые студенты могут использовать для изготовления моделей
- , ограничивающее количество моделей, которые просят сделать учащиеся.
Этот модуль ориентирован на построение определенных геометрических фигур и поэтому не установлен в реальном контексте. Есть способы адаптировать его к интересам и опыту ваших учеников. Например, учащимся может быть предоставлена возможность украсить модель своего любимого твердого тела многогранника в стиле, который они выберут для демонстрации в классе. Это могут быть как культурные мотивы, так и любимые цвета, узоры или изображения.
Деятельность
Начало работы
- Покажите студентам PowerPoint One.На первом слайде показан футбольный мяч из пятиугольников и шестиугольников.
Что вы знаете об этой твердой форме? - Попросите студентов обратить внимание на формы, составляющие твердое тело.
Какие формы вы видите? (Пентагоны и шестиугольники)
Посмотрите на вершины (углы). Сколько фигур встречаются в одной вершине? Эта комбинация одинакова для каждой вершины? (Два шестиугольника и один пятиугольник пересекаются в каждой вершине.) - На втором слайде показан куб. Покажите учащимся куб, который вы построили из пластиковых многоугольников (полидронов, геоформ и т. Д.) Или карты (см. Ниже).
Как называется эта сплошная форма? (куб)
Из каких форм он сделан? (квадраты)
Сколько таких фигур необходимо? (шесть)
Как можно сосчитать лица, чтобы проверить, пересчитаете ли вы их все? (например, сверху и снизу, четыре грани по центру) Объясните, что углы можно назвать вершинами.
Сколько вершин у куба? (восемь)
Как вы их посчитали?
Сколько ребер у куба? (12)Задайте себе задачу:
Сколько различных твердых тел вы можете сделать, используя только равносторонние треугольники или квадраты? Давайте попробуем построить твердые тела, которые выглядели бы сбалансированными.
При необходимости вернитесь к примеру с футбольным мячом, чтобы показать пример симметричного сбалансированного твердого тела.Дайте студентам время построить твердые тела. После того, как подходящая коллекция будет сформирована, соберите класс вместе. Ищите тетраэдр и октаэдр.
Что общего в этих двух твердых телах? (состоит только из треугольников)Твердое тело слева называется тетраэдром. Что означает тетра? (четыре)
Твердое тело справа называется октаэдром. Что означает окта? (восемь)Отметьте, что правильные многогранники названы по количеству граней.
Есть ли у кого-нибудь другой многогранник, составленный только из треугольников?
Если ученик создал икосаэдр (икоса- означает двадцать), обратите на него внимание класса. Если нет, покажите четвертый слайд PowerPoint One.Посмотрите внимательно на каждую вершину трех многогранников, которые мы составили из треугольников.
Что вы заметили?Сосредоточьте обсуждение на последовательном шаблоне вокруг каждой вершины.Три треугольника окружают каждую вершину тетраэдра, четыре треугольника — октаэдр и пять — икосаэдр.
Можно ли окружить каждую вершину шестью треугольниками и образовать твердое тело?
Попросите учащихся проверить, работает ли это.Окружение вершины шестью треугольниками создает мозаику, покрывающую плоскость или плоскую поверхность. Внутренние углы равносторонних треугольников составляют 60 °. Шесть углов по 60 ° добавляют к 360 °, что составляет полный оборот и становится «плоским» при соединении.Следовательно, невозможно создать твердое тело с шестью равносторонними треугольниками в каждой вершине.
Один из учеников, вероятно, сделал этот многогранник, который называется треугольной дипирамидой (состоящей из двух пирамид).
Это твердое вещество не относится к ним (тетра-, окта- и икоса-). Почему нет?
Если вы посчитаете количество треугольников, окружающих каждую вершину, что вы получите?У некоторых вершин есть четыре пересекающихся треугольника (вокруг «экватора»), а у некоторых — три пересекающихся треугольника (верхний и нижний).Не существует одинакового числа, встречающегося в каждой вершине, что является требованием для Платоновых тел.
Эти твердые тела, вероятно, сделали другие студенты.
Обратите внимание учащихся на конфигурацию многоугольников вокруг каждой вершины. В пирамиде с квадратным основанием вершина окружена четырьмя треугольниками, а каждая базовая вершина имеет квадрат и два треугольника. Пирамида с квадратным основанием может быть исключена из набора сбалансированных симметричных тел, поскольку она не сбалансирована, если находится на одной из своих треугольных сторон.Для кубооктаэдра есть два квадрата и два треугольника вокруг каждой вершины. Для ромбокубооктаэдра есть один квадрат и три треугольника вокруг каждой вершины.
Для всех сбалансированных симметричных тел, состоящих из треугольников и квадратов, попросите своих учеников определить, сколько граней имеет каждое твердое тело. Для тетра-, окта- и икосаэдра префикс называет многогранник. Однако подсчитать грани кубооктаэдра и ромбокубооктаэдра немного сложнее.Поощряйте своих учеников систематически записывать свои данные:
Цельный
Количество и форма граней
Количество вершин
Количество граней
Тетраэдр
4 треугольника
Октаэдр
8 треугольников
Икосаэдр
20 треугольников
Треугольная дипирамида
6 треугольников
Кубооктаэдр
8 треугольников
6 квадратов
Ромбокубооктаэдр
8 треугольников
18 квадратов
- Ищите систематические способы подсчета количества лиц.Это может включать в себя разделение твердого тела на части или методический учет каждой вершины.
Вторая сессия
- Напомните студентам, что на предыдущем занятии им разрешалось использовать только треугольники и квадраты.
Какие твердые тела мы сделали?
Как помнят ученики, возьмите модель твердого тела и назовите ее. - Объясните, что существует особая группа многогранников, называемых Платоновыми телами, которые были найдены древними греками.Объясните, что существует два критерия платоновского твердого тела:
- Все грани твердого тела — одинаковые правильные многоугольники.
- В каждой вершине встречается одинаковое количество граней.
Обратите внимание, что правильный означает, что стороны, а следовательно, и углы многоугольника одинаковы. Используйте мел на полу, чтобы нарисовать эту диаграмму Кэрролла и поместить в нее модели. Это сложная классификация, поэтому вам может потребоваться поддержать студентов в ее выполнении.
Каждая вершина
одинаковаяВершины различаются Одна правильная форма Более одной формы Твердые тела в верхнем левом квадранте идеальны, остальные — нет.
Какие еще формы есть в вашем наборе?
Можно ли создать любые другие совершенные твердые тела с другими формами? Предложите учащимся изучить возможность других совершенных твердых тел. Существует только один, додекаэдр (dodeca- префикс двенадцати).
Студенты могли обнаружить, что шестиугольники не работают.
Почему , а не , можно сделать из шестиугольников идеальным телом?
Вокруг вершины требуется не менее трех полигонов.Внутренние углы шестиугольника составляют 120 °. Три партии по 120 ° в сумме составляют 360 °, что составляет полный оборот. Следовательно, при соединении сторон многоугольники не заполняются незаполненными углами, чтобы они оторвались от плоскости.Добавьте додекаэдр в набор совершенных тел. Включите его в таблицу вместе с другими данными.
Начнем с тетраэдра, который является простейшим платоновым телом. Поднимите модель этого твердого тела.
Представьте, если я открою тетраэдр и положу его ровно.Этот узор называется сеткой.
Как вы думаете, как это будет выглядеть?
Попросите учащихся набросать свои прогнозы для сети. Они могут проверить свои прогнозы, составив каждую сетку и сложив ее, чтобы проверить.
Есть две возможные сети:Существует также расположение треугольников, при котором работает , а не .
Почему две верхние сети работают, а нижняя — нет?
Причины, по которым сеть не работает, иногда столь же важны, как и причины, по которым сеть будет работать.Все сети состоят из четырех равносторонних треугольников. Это необходимое условие. Сети, которые складываются в тетраэдр, при складывании допускают только три угла треугольника вокруг каждой вершины. Дно позволяет сделать четыре угла вокруг центральной вершины, поэтому не будет складываться в тетраэдр.Попросите учеников исследовать:
Сколько разных сеток будет для куба?
Раздайте каждой паре студентов лист с квадратной сеткой и шесть квадратных полидронов.Дайте ученикам достаточно времени, чтобы найти и записать возможные сети.
Третья сессия
На этом занятии студенты пытаются найти набор решений для всех сетей куба.
- Предложите ученикам поработать в парах, чтобы найти все возможные сети для куба.
Сколько разных сеток можно сделать, чтобы получился куб? - После того, как ученики нарисовали несколько сетей, предложите нескольким ученикам поделиться своей любимой сеткой.Начните галерею возможных сетей. Важный вопрос — как установить, что две сети разные. Вы можете использовать следующий пример:
Эти сети одинаковые или разные?
Учащиеся могут заметить, что одну цепь можно сопоставить с другой путем отражения или вращения, а в данном случае и того и другого. Это означает, что сети не уникальны (разные в математическом смысле). - Напомните ученикам, что вы ищете полный набор сетей.
У кого-нибудь есть система поиска всех сетей? - Некоторые студенты, возможно, заметили семейство сетей, состоящих из четырех квадратов в ряд.Центральная линия четырех может оставаться постоянной, а две другие грани перемещаются, чтобы сформировать уникальные сети. Вот три сети «четыре в ряд». Таких сетей шесть.
Может возникнуть вопрос:
Можно ли сделать сетку, в которой не более трех квадратов подряд?
А как насчет двух квадратов подряд? - Пусть ученики продолжают исследовать возможные сети, пока они не решат, что нашли их все. Могут ли они обосновать, что эти сети полностью укомплектованы?
- Соберите класс и пополните галерею, попросив учащихся создать «новую» сеть.Убедитесь, что каждое предложение не является отраженной или повернутой копией другой сети. Для этого полезны модели полидронов, так как их можно поворачивать и переворачивать для сопоставления друг с другом.
Всего 11 сетей. Тщательная организация сетей может помочь учащимся увидеть общую структуру в семьях сетей. Например, вот четыре квадрата в ряду.
Обратите внимание, что четыре верхние сети фиксируют верхний левый квадрат и перемещают правый квадрат в разные положения.Следующие две сети прикрепляют левый квадрат ко второму центральному квадрату и находят две новые позиции для правого квадрата. Верхняя правая и нижняя правая позиции уже покрыты первыми четырьмя сетками.
Еще четыре сети можно найти, организовав три квадрата в ряд и манипулируя тремя другими.В финальной сетке не более двух квадратов подряд.
Попросите своих учеников проверить уникальность всех новых цепей, что означает, что новая цепь не отображается на существующую сеть путем отражения и / или вращения.Например, в этом образце работы Уильям сигнализирует о том, что новая сеть такая же, как предыдущая, заключая ее в скобки.
Ваши ученики могут попытаться найти сети для трех других Платоновых тел. Попросите их нарисовать сетку для твердого тела на бумаге с сеткой. Они могут проверить точность своей сети, сделав ее из полидронов и складывая.
У ваших учеников:
Используйте симметрию для формирования сети?
Разделить твердое тело на две половины, чтобы упростить задачу?
Зафиксируем одну грань как основание или верх и представим, что другие грани связаны с ней?
Изобразите складку лиц, чтобы правильно их расположить?
Четвертая сессия
- Покажите своим ученикам PowerPoint Two.На первом слайде показаны три разных вида октаэдра. Попросите их нарисовать различные виды, рисуя только те края и вершины, которые они могут видеть, а не рисовать те, которые скрыты. На втором слайде есть простые рисунки тех же видов. Некоторым ученикам сложно не рисовать то, что они не видят. Попросить их представить, что «увидит» цифровая камера, а затем создать рисунок, — хорошая стратегия. Сравнение рисунка с изображением, полученным с цифровой камеры, помогает учащимся понять, что именно было запечатлено.
- Попросите ваших учеников взять одно из созданных ими твердых тел и нарисовать его в трех разных ракурсах. Более сложные твердые тела, такие как икосаэдр и ромбокубооктаэдр, может быть довольно сложно нарисовать, но более простые твердые тела очень доступны.
Например, куб (шестигранник) имеет множество возможных видов. - После того, как учащиеся создали виды выбранного твердого тела, они могут передать эти виды партнеру, который пытается представить себе, с какой точки зрения было нарисовано твердое тело.
- Интересно обсудить, как перспектива меняет способ появления форм. При просмотре куба над квадратом квадрат выглядит как неквадратный прямоугольник и ромб. Квадрат также может выглядеть как трапеция под определенным углом.
Пятая сессия
На этом занятии студенты создают точные сети для двух семейств многогранников, называемых призмами и пирамидами. Они ищут свойства в сетях и учитывают относительную длину ребер / сторон.
- Покажите студентам PowerPoint Three.На первом слайде представлены три примера призм.
Чем эти твердые тела одинаковы и чем они отличаются?
Учащиеся должны заметить, что все три тела имеют прямоугольные грани, хотя их торцы разные (треугольник, квадрат и шестиугольник). Скажите учащимся, что твердые тела являются примерами призм, многогранников с постоянным поперечным сечением. Представьте себе, что каждое твердое тело было буханкой хлеба. Можно разрезать твердое тело на части одинаковой формы.
Каждая призма известна своим поперечным сечением.Например, треугольная призма имеет треугольное сечение. - Попросите ваших учеников представить сеть для прямоугольной призмы. Попросите их набросать его форму в воздухе. Сосредоточьтесь на формах, которые должны быть в сети, и соотнесите эти формы с изображением на первом слайде. Четыре прямоугольника должны охватывать торцы, которые являются квадратами. Раздайте ученикам квадратную сетку размером 1 см. Квадраты удобны для выдерживания прямых углов и измерения длины.
- Попросите студентов использовать линейку и карандаш, чтобы создать точную сетку для кубоида.Точная сетка должна складываться так, чтобы стороны точно совпадали, чтобы стать краями. Студенты могут проверить свои сети, разрезав их и сложив. Обычная проблема для учащихся заключается в том, что стороны сети, которые встречаются для образования ребер, должны быть конгруэнтными (одинаковой длины).
- После создания сетки для прямоугольной призмы сосредоточьтесь на треугольной и шестиугольной призмах.
Что нужно изменить в сети, чтобы сформировать треугольную или шестиугольную призму?
Понимают ли учащиеся, что торцы должны быть треугольниками или шестиугольниками и что количество прямоугольников должно соответствовать количеству сторон? Например, треугольная призма будет иметь только три прямоугольника.Предложите своим ученикам создать сети для других призм. Бумажная сетка по-прежнему будет полезна, хотя задача получить совпадающие стороны сложнее. - Посмотрите, как ваши ученики создают треугольники и шестиугольники, длина стороны которых равна длине короткой стороны прямоугольника.
- Соберите студентов вместе, чтобы они делили свои сети.
Что общего у всех сетей?
В чем отличия?
Представьте себе сетку для восьмиугольной призмы.Как бы это выглядело? - Вы можете создать таблицу данных о призмах и искать закономерности, или вы можете сосредоточить урок на сетях.
Призма
Количество граней
Количество граней
Количество вершин
треугольная
5
9
6
прямоугольный
6
12
8
шестиугольник
8
18
12
восьмиугольная
10
24
16
Как вариант, перейдите ко второму слайду в PowerPoint 3, чтобы обсудить общие особенности твердых тел.На всех фотографиях изображены пирамиды. Основание пирамиды называет это. Например, пирамида с квадратным основанием имеет квадратное основание. Начните с квадратной пирамиды.
Какие формы находятся в сетке этого твердого тела?
Как узнать, что треугольников будет четыре?Попросите учащихся набросать свой прогноз для сети.
Какие стороны должны быть одинаковой длины?Учащиеся могут сделать точную сеть для квадратной пирамиды или попробовать сложную пирамидальную сеть.Сеть для восьмиугольной пирамиды — отличная задача для среднего уровня. Как и в случае с призмами, вы можете создать таблицу данных и искать закономерности.
Пирамида
Количество граней
Количество граней
Количество вершин
Треугольная основа
4
6
4
Площадь из расчета
5
8
5
Гексагональный на основе
7
14
7
Восьмиугольная на базе
9
18
9
Домашняя ссылка
Дорогая семья и ванау,
На этой неделе мы изучали многогранники.Попросите учащегося объяснить, как у этих твердых форм есть грани, края и вершины. Для домашнего задания вашего ученика попросили:
- найти фотографии различных многогранников из журналов и создать страницу с плакатом для своего учебника по математике; или
- использует материалы, найденные в доме, для создания икосаэдра.
Формула многогранника Эйлера | plus.maths.org
июнь 2007
Леонард Эйлер, 1707 — 1783
Давайте начнем с представления главного героя этой истории — формулы Эйлера:
В — E + F = 2.
Хотя это может показаться простой, эта маленькая формула заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками , которые очаровывали математиков более 4000 лет. На самом деле я могу пойти дальше и сказать, что формула Эйлера говорит нам кое-что очень глубокое о форме и пространстве. Формула носит имя известного швейцарского математика Леонарда Эйлера (1707–1783), которому в этом году исполнилось бы 300 лет.
Что такое многогранник?
Прежде чем мы исследуем, что говорит нам формула Эйлера, давайте рассмотрим многогранники более подробно.Многогранник — это твердый объект, поверхность которого состоит из ряда плоских граней , которые сами по себе ограничены прямыми линиями. Каждая грань на самом деле представляет собой многоугольник , замкнутую форму на плоской 2-мерной плоскости, состоящую из точек, соединенных прямыми линиями.
Рис. 1. Знакомые треугольник и квадрат являются многоугольниками, но многоугольники могут иметь и более неправильную форму, как показано справа.
В многоугольниках не разрешается иметь отверстия, как показано на рисунке ниже: левая фигура здесь является многоугольником, а правая — нет.
Рис. 2: Фигура слева — многоугольник, а фигура справа — нет, потому что в ней есть «дыра».
Многоугольник называется правильным , если все его стороны имеют одинаковую длину и все углы между ними одинаковы; треугольник и квадрат на рисунке 1 и пятиугольник на рисунке 2 правильные.
Многогранник — это то, что вы получаете, когда перемещаетесь на одно измерение вверх. Это замкнутый твердый объект, поверхность которого состоит из множества многоугольных граней.Мы называем стороны этих граней ребрами — две грани пересекаются вдоль каждого из этих ребер. Назовем углы граней вершинами , так что любая вершина лежит как минимум на трех разных гранях. Чтобы проиллюстрировать это, вот два примера
известные многогранники.
Рис. 3. Знакомый куб слева и икосаэдр справа. Многогранник состоит из многоугольных граней , их стороны известны как ребра , а углы — как вершины .
Многогранник состоит из одной части. Например, он не может состоять из двух (или более) в основном отдельных частей, соединенных только ребром или вершиной. Это означает, что ни один из следующих объектов не является истинным многогранником.
Рисунок 4: Эти объекты не являются многогранниками, потому что они состоят из двух отдельных частей, которые встречаются только на ребре (слева) или вершине (справа).
Что нам говорит формула?
Теперь мы готовы посмотреть, что формула Эйлера говорит нам о многогранниках.Посмотрите на многогранник, например куб или икосаэдр выше, посчитайте количество вершин, которые у него есть, и назовите это число V . У куба, например, 8 вершин, поэтому V = 8 . Затем посчитайте количество ребер многогранника и назовите это число E . У куба 12 ребер, поэтому в случае
куб E = 12 . Наконец, посчитайте количество лиц и назовите его F . В случае куба F = 6 . Теперь формула Эйлера говорит нам, что
В — E + F = 2;
или, говоря словами: количество вершин минус количество ребер плюс количество граней равно двум.
В случае с кубом мы уже видели, что V = 8, E = 12 и F = 6 . Итак,
V — E + F = 8 — 12 + 6 = 14 — 12 = 2
, что и должно быть согласно формуле Эйлера. Если мы теперь посмотрим на икосаэдр, мы обнаружим, что V = 12, E = 30 и F = 20 . Сейчас,
V — E + F = 12-30 + 20 = 32-30 = 2,
как мы и ожидали.
Формула Эйлера верна для куба и икосаэдра. Оказывается, довольно красиво, что это верно для почти для каждого многогранника .Единственные многогранники, для которых это не работает, — это те, в которых есть отверстия, как показано на рисунке ниже.
Рис. 5: В многограннике сквозное отверстие. Формула Эйлера в этом случае не выполняется.
Эти многогранники называются непростыми , в отличие от многогранников без отверстий, которые называются простыми . Непростые многогранники, возможно, не первое, что приходит в голову, но их много, и мы не можем избежать того факта, что формула Эйлера не работает ни с одним из них.Однако даже этот неловкий факт стал частью совершенно новой теории космоса.
и форма.
Сила формулы Эйлера
Всякий раз, когда математики сталкиваются с инвариантным признаком, свойством, истинным для целого класса объектов, они знают, что натолкнулись на что-то хорошее. Они используют его, чтобы исследовать, какими свойствами может обладать отдельный объект, и для определения свойств, которые должны иметь все они. Формула Эйлера может сказать нам, например, что не существует простого многогранника с
ровно семь граней.Вам не нужно садиться с картоном, ножницами и клеем, чтобы узнать это — формула — это все, что вам нужно. Аргумент, показывающий, что не существует семигранного многогранника, довольно прост, так что взгляните на него, если вам интересно.
Аналогичным образом используя формулу Эйлера, мы можем обнаружить, что не существует простого многогранника с десятью гранями и семнадцатью вершинами. Призма, показанная ниже, в основе которой лежит восьмиугольник, имеет десять граней, но число вершин здесь шестнадцать. Пирамида, имеющая 9-гранное основание, также имеет десять граней, но имеет десять вершин.Но формула Эйлера говорит нам, что ни один простой многогранник не имеет
ровно десять граней и семнадцать вершин.
Рисунок 6: Оба этих многогранника имеют десять граней, но ни у одного из них нет семнадцати вершин.
Именно такие соображения приводят нас к, вероятно, самому прекрасному открытию из всех. Он включает Платоновы тела , хорошо известный класс многогранников, названный в честь древнегреческого философа Платона, в трудах которого они впервые появились.
Рисунок 7: Платоновы тела.Слева направо мы видим тетраэдр с четырьмя гранями, куб с шестью гранями, октаэдр с восемью гранями, додекаэдр с двенадцатью гранями и икосаэдр с двадцатью гранями.
Хотя их симметричная элегантность сразу бросается в глаза, когда вы смотрите на приведенные выше примеры, на самом деле не так просто описать это словами. Оказывается, это описывается двумя особенностями. Во-первых, у Платоновых тел нет шипов или провалов, поэтому они имеют красивую округлую форму.Другими словами, это означает, что всякий раз, когда вы выбираете две точки в Платоновом теле и рисуете
прямая линия между ними, этот кусок прямой линии будет полностью заключен в твердое тело — Платоново твердое тело — это то, что называется выпуклым . Вторая особенность, называемая регулярностью , заключается в том, что все грани твердого тела представляют собой правильные многоугольники с одинаковым количеством сторон и одинаковое количество ребер выходит из каждой вершины твердого тела.
Куб правильный, так как все его грани квадратные и из каждой вершины выходит ровно три ребра.Вы можете сами убедиться, что тетраэдр, октаэдр, икосаэдр и додекаэдр тоже правильные.
Теперь вы можете задаться вопросом, сколько существует различных Платоновых Тел. С момента открытия куба и тетраэдра математиков настолько привлекла элегантность и симметрия Платоновых тел, что они искали больше и пытались перечислить их все. Именно здесь на помощь приходит формула Эйлера. Вы можете использовать ее, чтобы найти все возможности для числа граней, ребер и
вершины правильного многогранника.Вы обнаружите, что на самом деле существует только пять различных правильных выпуклых многогранников! Это очень удивительно; в конце концов, количество различных правильных многоугольников не ограничено, так почему мы должны ожидать здесь ограничения? Пять Платоновых Тел — это тетраэдр, куб, октаэдр, икосаэдр и додекаэдр, показанные выше.
Доказательство
Рене Декарт,
(1596–1650)
Игра с различными простыми многогранниками покажет вам, что формула Эйлера всегда верна.Но если вы математик, этого недостаточно. Вам понадобится доказательство, водостойкий логический аргумент, который показывает, что это действительно работает для всех многогранников, включая те, которые у вас никогда не будет времени проверить.
Адриан-Мари Лежандр, (1752 — 1833)
Несмотря на название формулы, на самом деле не Эйлер предложил первое полное доказательство. Его история сложна, насчитывает 200 лет и включает в себя некоторых из величайших математиков, в том числе Рене Декарта (1596–1650), самого Эйлера, Адриана-Мари Лежандра (1752–1833) и Огюстена-Луи Коши (1789–1857).
Огюстен-Луи Коши, (1789 — 1857)
Интересно отметить, что все эти математики использовали очень разные подходы для доказательства формулы, каждый из которых поражал своей изобретательностью и проницательностью. Однако это доказательство Коши, что я хотел бы дать вам здесь представление. Его методика состоит из нескольких этапов и шагов. Первый этап включает построение так называемой сети .
Создание сети
Представьте, что вы держите свой многогранник одной стороной вверх.Теперь представьте, что вы «удаляете» только эту грань, оставляя края и вершины вокруг нее позади, так что у вас есть открытая «коробка». Затем представьте, что вы можете держаться за коробку и отодвинуть края отсутствующей грани друг от друга. Если вы потянете их достаточно далеко, коробка расплющится и превратится в сеть точек и линий.
в плоской плоскости. Приведенная ниже серия диаграмм иллюстрирует этот процесс применительно к кубу.
Рисунок 8: Превращение куба в сеть.
Как вы можете видеть на диаграмме выше, каждая грань многогранника становится областью сети, окруженной ребрами, и это то, что мы будем называть гранью сети.Это внутренних лиц сети. Также существует внешняя грань , состоящая из области вне сети; это соответствует той грани, которую мы удалили из многогранника. Итак, у сети есть вершины,
прямые края и многоугольные грани.
Рисунок 9: Сеть имеет грани, ребра и вершины.
При формировании сети вы не добавляли и не удаляли вершины, поэтому сеть имеет то же количество вершин, что и многогранник — V .Сеть также имеет такое же количество ребер — E — что и многогранник. Теперь о лицах; все грани многогранника, кроме «недостающей», оказываются «внутри» сети. Отсутствующее лицо превратилось в внешнее лицо, которое тянется
по всей сети. Итак, включая внешнюю грань, в сети насчитывается F граней. Таким образом, вы можете использовать сеть , а не сам многогранник, чтобы найти значение V — E + F . Теперь мы продолжим преобразование нашей сети, чтобы упростить вычисление этого значения.
Преобразование сети
Есть три типа операций, которые мы можем выполнять в нашей сети. Мы представим три этапа с их участием.
Шаг 1 Мы начинаем с рассмотрения полигональных граней сети и спрашиваем: существует ли грань с более чем тремя сторонами? Если есть, мы рисуем диагональ, как показано на схеме ниже, разделяя лицо на две меньшие грани.
Рисунок 10: Разделение граней.
Мы повторяем это с выбранной гранью до тех пор, пока грань не будет разбита на треугольники.
Рис. 11: В итоге у нас остались треугольные грани.
Если есть еще одна грань с более чем тремя сторонами, мы используем Шаг 1 для этой грани, пока она тоже не будет разбита на треугольные грани. Таким образом, мы можем разбить каждую грань на треугольные грани и получить новую сеть, все грани которой треугольные. Мы проиллюстрируем этот процесс, показав, как преобразовать сеть, созданную из куба.
Рисунок 12: Вот что происходит с сетью куба, когда мы многократно выполняем Шаг 1.
Мы возвращаемся к шагу 1 и смотрим на сеть, которую мы получаем после выполнения шага 1 только один раз. Теперь, нарисовав диагональ, мы добавили одно ребро. Наше исходное лицо стало двумя лицами, поэтому мы добавили одно к количеству лиц. Мы не изменили количество вершин. Теперь сеть имеет V, вершины, E + 1 ребра и F + 1 грани. Так как же
V — E + F изменилось после того, как мы выполнили Шаг 1 один раз? Используя то, что мы знаем об изменениях в V , E и F , мы можем увидеть, что V — E + F превратилось в V — (E + 1) + (F + 1) .Теперь у нас
V — (E + 1) + (F + 1) = V — E — 1 + F + 1 = V — E + F.
Итак, V — E + F имеет , не изменилось после шага 1! Поскольку каждое использование шага 1 оставляет V — E + F неизменным, оно остается неизменным, когда мы достигаем нашей новой сети, состоящей полностью из треугольников! Влияние на V — E + F при преобразовании сети, созданной из куба, показано в таблице ниже.
| Круглый | В | E | Ф | V — E + F |
| (а) | 8 | 12 | 6 | 2 |
| б) | 8 | 13 | 7 | 2 |
| (в) | 8 | 14 | 8 | 2 |
| (г) | 8 | 15 | 9 | 2 |
| д) | 8 | 16 | 10 | 2 |
| (ж) | 8 | 17 | 11 | 2 |
Теперь мы представляем шаги 2 и 3.Они будут удалять грани с внешней стороны сети, шаг за шагом уменьшая количество лиц. Как только мы начнем это делать, сеть, вероятно, больше не будет представлять собой многогранник, но важное свойство сети сохранится.
Шаг 2 Проверяем, есть ли в сети грань, которая имеет только одно ребро с внешней гранью. Если это так, мы удаляем эту грань, удаляя одно общее ребро. Область, которая была покрыта выбранной нами гранью, становится частью внешней грани, и сеть имеет новую границу.Это проиллюстрировано приведенной ниже схемой для сети, построенной из куба.
Рис. 13: Удаление граней с одной внешней кромкой.
Теперь возьмем V , E и F как числа вершин, ребер и граней, которые имела сеть, состоящая из треугольных граней, до того, как мы выполнили шаг 2. Теперь посмотрим, как число V — E + F изменился после того, как мы выполнили Шаг 2 один раз. Мы удалили одно ребро, поэтому наша новая сеть имеет E — 1 ребра.Мы не трогали вершины в
всего, так что у нас остается V вершины. Грань, которую мы использовали для шага 2, была объединена с внешней гранью, так что теперь у нас есть F — 1 граней. Итак, V — E + F превратилось в V — (E — 1) + (F — 1) и
.
V — (E — 1) + (F — 1) = V — E + 1 + F — 1 = V — E + F.
Итак, еще раз V — E + F не изменился.
Step 3 Проверяем, есть ли у нашей сети грань, у которой два ребра общие с внешней гранью.Если это так, мы удаляем эту грань, удаляя как эти общие ребра, так и их общую вершину, так что снова область, принадлежащая нашей выбранной грани, становится частью внешней грани. Это проиллюстрировано ниже в случае сети, сделанной из куба, после выполнения шага 2.
дважды.
Рисунок 14: Удаление граней с двумя внешними кромками.
Как и раньше, возьмем V , E и F в качестве количества вершин, ребер и граней сети, с которой мы начинаем.Каким образом шаг 3 повлиял на число V — E + F ? Мы удалили одну вершину — ту, которая находится между двумя ребрами, — теперь осталось V — 1 вершины. Мы удалили два ребра, так что теперь есть
E — 2 ребра. Наконец, наша выбранная грань слилась с внешней гранью, так что теперь у нас есть F — 1 граней. Итак, V — E + F превратилось в (V — 1) — (E — 2) — (F — 1) и
.
(V — 1) — (E -2) + (F — 1) = V — 1 — E + 2 + F — 1 = V — E + F.
Итак, еще раз V — E + F не изменился.
Секрет доказательства заключается в выполнении последовательности шагов 2 и 3 для получения очень простой сети. Напомним, что мы неоднократно использовали шаг 1 для создания сети только с треугольными гранями. Эта сеть определенно будет иметь грань, которая имеет ровно одно ребро с внешней гранью, поэтому мы берем эту грань и выполняем Шаг 2. Мы можем выполнить Шаг 2 на нескольких гранях, по одной, до тех пор, пока не появится
появляется грань, имеющая два ребра с внешней гранью.Затем мы можем выполнить шаг 3, используя это лицо. Мы продолжаем выполнять шаги 2 и 3 и продолжаем удалять лица таким образом.
При этом нужно соблюдать два важных правила. Во-первых, мы всегда должны выполнять Шаг 3, когда это возможно; если есть выбор между Шагом 2 и Шагом 3, мы всегда должны выбирать Шаг 3. В противном случае сеть может разбиться на отдельные части. Во-вторых, мы должны удалять лица только по одному. Если мы этого не сделаем, мы можем закончить тем, что края сами по себе будут торчать наружу.
лицо, и у нас больше не будет нормальной сети.Чтобы проиллюстрировать процесс, мы выполним несколько шагов в сети куба, продолжая с того места, где мы оставили его на последней диаграмме.
Рисунок 15: Применение нашего алгоритма к сети куба.
Теперь мы можем задать себе один или два вопроса. Останавливается ли когда-нибудь этот процесс удаления лиц, и если он останавливается, с чем мы остаемся? Небольшое размышление покажет вам, что он должен остановиться — мы можем удалить лишь конечное число граней и ребер — и что когда это произойдет, у нас останется один треугольник.Вы можете увидеть несколько диаграмм, описывающих весь процесс для сети, образованной из додекаэдра (напомним, что это было одно из Платоновых тел, представленных ранее).
Теперь посмотрите на количество вершин, ребер и граней, присутствующих в нашей окончательной сети — единственном треугольнике. У нас V = 3 , E = 3 и F = 2 — мы все равно должны включить внешнюю грань. Сейчас
V — E + F = 3 — 3 + 2 = 2.
На протяжении всего процесса, начиная с полного многогранника и заканчивая треугольником, значение V — E + F не менялось.Итак, если V — E + F = 2 для конечной сети, мы также должны иметь V — E + F = 2 для самого многогранника! Доказательство закончено!
За многогранниками
Я закончу упоминанием некоторых следствий формулы Эйлера за пределами мира многогранников. Я начну с очень маленького: компьютерных чипов. Компьютерные микросхемы — это интегральные схемы, состоящие из миллионов мельчайших компонентов, связанных миллионами проводящих дорожек. Они напоминают наши сети, приведенные выше, , за исключением , которые обычно невозможно разложить на плоскости.
без некоторых проводящих дорожек — краев — пересечения.Крестовины — плохая вещь в схемотехнике, поэтому их количество должно быть уменьшено, но найти подходящее расположение — непростая задача. Формула многогранника Эйлера с ее информацией о сетях является важным ингредиентом в поиске решений.
Теперь перейдем к самому большому: нашей вселенной. До сих пор космологи не пришли к единому мнению о его точной форме. Основным для их рассмотрения является топология , , математическое исследование формы и пространства. В 19 веке математики обнаружили, что все поверхности в трехмерном пространстве по существу характеризуются количеством отверстий, которые у них есть: наши простые многогранники не имеют отверстий, т.е.
пончик имеет одно отверстие и т. д.Формула Эйлера не работает для многогранников с дырками, но математики обнаружили захватывающее обобщение. Для любого многогранника V — E + F ровно в 2 минус 2 раза больше количества отверстий! Оказывается, это число, называемое эйлеровой характеристикой , имеет решающее значение для изучения всех трехмерных поверхностей, а не только многогранников.
Формулу Эйлера можно рассматривать как катализатор совершенно нового мышления о форме и пространстве.
Об авторе
Аби выросла на севере Англии и переехала на юг, чтобы изучать математику в Имперском колледже в Лондоне и Королеве Марии в Лондонском университете.Сейчас она преподает математику в Открытом университете. Главный математический интерес Аби — теория групп. При написании этой статьи ей очень понравилось исследовать тайны формулы Эйлера.
Первоначально опубликовано 1 июня 2007 г.
Объяснение, части, типы, счетный многогранник, проблемы и ответы на часто задаваемые вопросы
Определение многогранника гласит, что «трехмерная структура в евклидовой геометрии, состоящая из конечного числа многоугольных граней».
Граница между внутренней и внешней частью твердого тела — многогранник.
Многогранники, как правило, именуются по количеству граней.
Части многогранника
Многогранник состоит из трех частей, а именно:
Грань — это плоская поверхность, составляющая многогранник, который представляет собой правильные многоугольники.
Край — это область, где две плоские поверхности встречаются, образуя линейный сегмент.
Вершина, также известная как угол, — это точка пересечения ребер многогранника.
(Изображение будет загружено в ближайшее время)
Типы многогранников
Существует три основных типа многогранников:
Призмы
Призма — это многогранник, состоящий из n-стороннего многоугольного основания и второго основания. это переведенная копия первой, а не другие грани, которые соединяют две основы с соответствующими сторонами.
Призмам присваиваются названия в соответствии с их поперечными сечениями (гранями многогранников).
(Изображение будет скоро загружено)
(Изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
(Изображение будет скоро загружено)
Платоновы тела
Обычные выпуклые Многогранник — это платоново твердое тело в трехмерном пространстве.{3} \]
(Изображение будет загружено в ближайшее время)
Куб
У него 6 граней, 8 вершин, 12 граней.
Он состоит из трех квадратов, пересекающихся в каждой вершине.
Площадь поверхности куба = 6a2
Объем куба = a3
(Изображение будет загружено в ближайшее время)
Октаэдр
У него 8 граней, 6 вершин , 12 кром.{3} \]
(Изображение будет загружено в ближайшее время)
Пирамиды
Пирамида — это многогранник, образованный соединением многоугольного основания и точки, называемой вершиной. Треугольник, называемый боковой гранью, образован любым краем основания и вершиной. Это твердое тело конической формы с основанием из многоугольников.
Типы пирамид названы в честь основания пирамиды.
(Изображение будет загружено в ближайшее время)
(Изображение будет скоро загружено)
(Изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
Подсчет граней многогранников , Ребра и вершины
Формула Эйлера связывает количество граней, вершин и ребер любого многогранника.Эта формула используется при подсчете граней, ребер и вершин многогранников.
Формула Эйлера имеет следующий вид:
F + V — E = 2
Где F = количество граней
V = количество вершин
E = количество ребер
Задачи на гранях, ребрах и гранях многогранников Вершины
1) Многогранник имеет 6 граней и 12 ребер. Найдите количество вершин. Также назовите тип Многогранник.
Ответ: Здесь, чтобы найти количество вершин, мы воспользуемся формулой Эйлера,
F + V — E = 2
Из вопроса F = 6, E = 12, V =?.Подставляя эти значения в формулу Эйлера, мы получаем
6 + V — 12 = 2
V — 6 = 2
V = 8
Здесь мы можем заключить, что Многогранник — это Куб.
2) Многогранник имеет 5 граней и 6 вершин. Найдите количество ребер. Также назовите тип Многогранник.
Ответ: Здесь мы воспользуемся формулой Эйлера, чтобы найти количество ребер,
F + V — E = 2
Из заданных данных F = 5, V = 6, E =?. Подставляя эти значения в формулу Эйлера, мы получаем
5 + 6 — E = 2
11 — E = 2
E = 9
Следовательно, многогранник является треугольной призмой.
Интересные факты
Слово «многогранник» происходит от греческих слов «поли», означающих «многие», и «эдрон», что означает поверхность.
Многогранник означает, что для образования трехмерной формы многочисленные плоские поверхности соединяются.
Многогранник — множественное число от многогранника.
Презентация по построению сечений параллельно. Презентация по стереометрии «Построение поперечных сечений многогранников» (10 класс).Как строится поперечное сечение тетраэдра
Построение поперечных сечений многогранников
Слайд 2.
Определение сечения.
Плоскостью крепления многогранника назовем любую плоскость, по обе стороны от которой находятся точки этого многогранника. Плоскость крепления пересекает край многогранника отрезками. Многоугольник, сторонами которого являются эти отрезки, называется поперечным сечением многогранника.
Слайд 3.
Поющая плоскость A B с D M n k α
Слайд 4.
Сечение поющей плоскости A B C D M n k α
Slide 5.
На каких картинках поперечное сечение не то?
B a a a a d d d d d b b b b b c c c c c c n m m m m m n q p p q s
Slide 6.
Постройте поперечное сечение тетраэдра из трехточечных плоскостей.
P n Здание: A в C d M m n 2. Вырезать PN A V C C D M L 1. Вырезать MP Конструкция: 3. Вырезать MN MPN — желаемое сечение 1. Вырезать MN 2. Балка NP; Луч NP пересекает динамики в точке L 3.Вырезать ML MNL-Insit
Slide 7.
Здание: A C в D N P Q R e 1. Cut NQ 2. NP Cut Прямая NP пересекает AC в точке E 3. Direct EQ EQ пересекает BC в точке R NQRP — желаемый участок
Слайд 8.
Дом: A B C d M n p x k s L 1. Mn; Разрез MK 2. Mn пересекает AB в точке x 3. XP; SL MKLS Cut — Поверхностный разрез
Slide 9.
Аксиоматический метод Метод следов Суть метода заключается в построении вспомогательного прямого, представляющего собой изображение линии пересечения плоскости закрепления с плоскостью любой грани формы.Удобно построить изображение линии пересечения плоскости крепления с плоскостью нижнего основания. Эта линия называется последовательной плоскостью. С помощью следа легко построить изображения точек фиксирующей плоскости, расположенные на боковых краях фигур фигуры.
Слайд 10.
Постройте поперечное сечение пирамиды с плоскостью, проходящей через три точки M, N, P.
XY — след секулярной плоскости на базовой плоскости d c b a z y x m n p s f
Слайд 11.
XY — след вековой плоскости на базовой плоскости d c b z y x m n p s a f
Задания для строительных участков
Определения. 1. Для используемого тетраэдра плоскость (параллелепипед) — это любая плоскость, по обе стороны от которой находятся точки этого тетраэдра (параллелепипеда). 2. Германия, стороны которой представляют собой отрезки, пересекающие границу тетраэдра (параллепипеда), называется поперечным сечением тетраэдра (параллелепипедом).
Поперечные сечения тетраэдра и параллелепипед
А Б с заданием 1.Постройте поперечное сечение плоскости, проходящей через данные d, e, k. Конструкция ДЭКМФ: 2. ЭК 3. ЭК ∩ AC = F 4. FD 5. FD ∩ BC = M 6. КМ 1. ДЭ ДЭКМ — искомый участок
Пояснения к конструкции: 1. Соединить точки k и f, принадлежащей одной плоскости A 1 в 1 s 1 D 1. A d в 1 VCA 1 C 1 D 1 Задача 2. Построить поперечное сечение с плоскостью, проходящей через данные точки E, F, K. Построение KLM : 1. KF 2. Fe 3. Fe ∩ AB = L EFKNM — искомое сечение F en 4.LN ║ FK 6. EM 5. LN ∩ AD = M 7. KN Пояснения к конструкции: 2. Соединить точки F и E, принадлежащие одной плоскости AA 1 в 1 V. Пояснения к конструкции: 3. Прямые Fe и AV, лежащие в одной плоскости AA 1 в 1 V, пересекаются в точке L. Пояснения к построению: 4. Проводим прямую LN параллельно FK (если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельные отрезки). Пояснения к построению: 5. Прямая ЛС пересекает край AD в точке m.Пояснения к конструкции: 6. Соедините точки E и M, принадлежащие одной плоскости AA 1 D 1 D. Пояснения к конструкции: 7. Соедините точки к и n, принадлежащие одной плоскости ASC 1 в 1.
AD в 1 VCA 1 C 1 D 1 Задача 3. Построить сечение плоскости, проходящей через точки K, L, M. Построение KLM: 1. ML 2. ML ∩ D 1 A 1 = E 3. EK M LFKPG есть желаемое сечение FenPGT 4. EK ∩ A 1 B 1 = F 6. LM ∩ D 1 D = N 5. LF 7. E K ∩ D 1 C 1 = T 8. NT 9.NT ∩ DC = G NT ∩ CC 1 = P 10. MG 11. ПК.
A d in 1 V C A 1 C 1 D 1 Задача 4. Построить поперечное сечение плоскостью, проходящей через точки T, N, M, M∈Av. NTM Building: 1. Nm 1. MT 1. NT Выберите надежную версию:
A d in 1 VCA 1 C 1 D 1 Задача 4. Постройте поперечное сечение с плоскостью, проходящей через точки T, N, M, M∈ Средний. N T M Дом: 1. Nm Комментарии: Эти точки принадлежат разным граням! Назад
A d in 1 V C A 1 C 1 D 1 Задание 4. Построить поперечное сечение плоскостью, проходящей через точки T, N, M, M∈Av.N t m Дом: 1. m t Комментарии: Эти точки принадлежат разным граням! Назад
A d in 1 VCA 1 C 1 D 1 Задание 4. Построить поперечное сечение плоскостью, проходящей через точки N, M, T. Построение NTM: 1. NT 2. NT ∩ DC = E 2. NT ∩ BC = E Выберите верную версию:
AD 1 VCA 1 C 1 D 1 Задача 4. Построить сечение плоскости, проходящей через точки N, M, T. Построение NTM: 1. NT 2. NT ∩ Вс = e Назад Комментарии: Data Direct — пересечение! Не могут пересекаться!
A d in 1 V C A 1 C 1 D 1 Задача 4.Построить сечение плоскостью, проходящей через точки H, M, T. Построение НТМ: 1. NT 2. NT ∩ DC = EE 3. ME ∩ AA 1 = F 3. ME ∩ BC = F 3. . ME ∩ CC 1 = F Выберите верную версию:
AD в 1 VCCA 1 C 1 D 1 Задача 4. Построить сечение с плоскостью, проходящей через точки N, M, T. Построение NTM: 1 NT 3. ME ∩ AA 1 = F 2. NT ∩ DC = E e Назад Комментарии: Data Direct — Crossing! Не могут пересекаться!
A D in 1 V C C A 1 C 1 D 1 Задача 4.Построить сечение плоскостью, проходящей через точки N, M, T. Построение NTM: 1. NT 3. ME ∩ CC 1 = F 2. NT ∩ DC = E e Назад Комментарии: Data Direct — Crossing ! Не могут пересекаться!
AD в 1 VCC 1 C 1 D 1 Задача 4. Построить сечение до плоскости, проходящей через точки H, M, T. Построение NTM: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Солнце = fff 4 4 N f 4. T f 4. mt Выберите верную версию:
AD в 1 VCC 1 C 1 D 1 Задача 4. Построить сечение до плоскости, проходящей через точки H, M, Т.N T M Конструкция: 1. NT 2. NT ∩ D C = E E 3. ME ∩ Sun = F f f 4 4 N F Комментарии: Эти точки принадлежат разным граням! Назад
AD в 1 VCC 1 C 1 D 1 Задание 4. Построить сечение плоскости, проходящей через точки H, M, T. Построение NTM: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Солнце = F ff 4. Mt Комментарии: Эти точки принадлежат разным граням! Назад
A D in 1 V C C 1 C 1 D 1 Задание 4. Построить сечение плоскости, проходящей через точки H, M, T.Конструкция НТМ: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Sun = F ff 4. T f 5. T f ∩ A 1 A = k 5. T f ∩ in 1 V = k Выбрать верная версия:
AD в 1 VCC 1 C 1 D 1 Задача 4. Построить сечение до плоскости, проходящей через точки H, M, T. Построение NTM: 1. NT 2. NT ∩ DC = EE 3. Me ∩ Sun = F ff 4. T f 5. T f ∩ A 1 A = K Комментарии: Данные прямые — перекрестные! Не могут пересекаться! Назад
A D in 1 V C C 1 C 1 D 1 Задание 4. Построить сечение плоскости, проходящей через точки H, M, T.Конструкция НТМ: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Sun = F ff 4. T f 5. T f ∩ in 1 В = kk 6. MK AA 1 = L 6. NK ∩ AD = L 6. TK ∩ AD = L Выберите верную версию:
AD в 1 VCC 1 C 1 D 1 Задача 4. Построить сечение до плоскости, проходящей через точки H, M, T. Конструкция НТМ: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Sun = F ff 4. T f 5. T f ∩ in 1 V = k K 6. NK ∩ AD = L Комментарии: Данные прямые — кроссы! Не могут пересекаться! Назад
A D in 1 V C C 1 C 1 D 1 Задача 4.Построить сечение плоскости, проходящей через точки H, M, T. Построение NTM: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Sun = F ff 4. T f 5. T f ∩ в 1 В = k К 6. ТК ∩ AD = L Комментарии: Прямые данные — переточка! Не могут пересекаться! Назад
AD в 1 VCC 1 C 1 D 1 Задание 4. Построить сечение плоскости, проходящей через точки H, M, T. Построение NTM: 1. NT 2. NT ∩ DC = EE 3. Me ∩ Вс = Ф фф 4. Т ф 5. Т ф ∩ в 1 В = кк 6.MK ∩ AA 1 = LL 7. LT 7. LF 7. LH. Выберите правильный вариант:
AD в 1 VCC 1 C 1 D 1 Задача 4. Построить сечение плоскости, проходящей через точки H, M , Т. Конструкция НТМ: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Sun = F f 4. T f 5. T f ∩ in 1 V = k K 6. MK ∩ AA 1 = LL 7. Прокомментируем: эти точки принадлежат разным лицам! Назад
A D in 1 V C C 1 C 1 D 1 Задание 4. Построить сечение плоскости, проходящей через точки H, M, T.Конструкция НТМ: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Sun = F f 4. T f 5. T f ∩ in 1 В = k K 6. MK ∩ AA 1 = LL 7. LF Комментарии: Эти точки принадлежат разным лицам! Назад
AD в 1 VCC 1 C 1 D 1 Задание 4. Построить сечение плоскости, проходящей через точки H, M, T. Построение NTM: 1. NT 2. NT ∩ DC = EE 3. ME ∩ Вс = fff 4. T f 5. T f ∩ in 1 V = kk 6. MK ∩ AA 1 = LL 7. LH NT f ML — желаемый участок
И в ss задача 5.Постройте поперечное сечение плоскостью, проходящей через данные точки K, M, R, RΣAVS до m. Дом:
А в сс задание 5. Построить поперечное сечение плоскостью, проходящей через данные точек к, м, р, p∈Avs до здания МРЭНФ: 1. км 2. км ∩ Ca = E 3 ЭП 4. ЭП ∩ AB = F EP ∩ в C = N 5. MF 6. N до км фн — желаемый участок
Спасибо за внимание!
«Пять платонических тел» — Тетраэдр. Куб А сфера — это пустота. Октаэдр.Многие многогранники имеют «близнецов». Куб, будучи полностью замкнутой фигурой, символизирует ограничение. Во-первых, все грани такого тела равны по размеру. Поэтому крест, порожденный кубом, также обозначается ограничением, страданием. Додекаэдр и икосаэдр.
«Задания для многогранников» — прямоугольный треугольник. Треугольник. Многогранник. Октаэдр. База — прямая призма. Не разъединяющий многогранник. Равнобедренный треугольник. Сумма площадей всех граней. Диагональ прямоугольного параллелепипеда.Стороны в основании прямой параллелепипед. Призма. Сторона фундамента. Боковой край. Раздел.
«Многие чужие» стереометрия »- урок эпиграф. Великая пирамида в Гизе. Разрез многогранников. Звездный час многогранников. Правильная логическая цепочка. Историческая справка.« Игра со зрителями ». Многогранник. Список соответствуют геометрическим фигурам и их названиям. Задачи урока. Архимедово тело. Платоническое тело. Укажите правильное сечение.
«Геометрическое тело многогранника» — землетрясение разрушило мавзолей.Расстояние между самолетами. Элементы пирамиды. Призма. Великая пирамида. Слово. Ученые и философы Древней Греции. Фигура тела. Заявление. Лицевая сторона. Прах королевской четы. Свойства призмы. Основание пирамиды Хеопса. Октаэдр. Возведите любую диагональ в квадрат.
«Понятие многогранника» — четырехугольная призма. Определение. Прямая призма называется правильной. Ребра — лицо лицо. Что такое прямоугольный параллелепипед. Призма. Теорема. Сумма площадей всех его граней. Понятие многогранника.Что такое параллелепипед. Многогранники. Край. Высота призмы перпендикулярна. Что такое тетраэдр.
«Звездные формы многогранников» — звездчатые Кабукиэдры. Большой звездный додекаэдр. Икосаэдр усеченный звездой. Отвечать. Многогранник изображен на рисунке. Звезда Икошедра. Пики большого звездного додекаэдра. Звездный додекаэдр. Многогранник. Многогранник, полученный усечением звездообразно усеченного икосаэдра. Большой икосаэдр.
Всего по тематике 29 презентаций
Многие художники, искажая законы перспективы, рисуют необычные картины.Кстати, эти рисунки очень популярны среди математиков. В Интернете можно найти множество сайтов, где публикуются эти невозможные объекты. Популярные художники Морис Эшер, Оскар Ретерсвард, Хос де Мей и другие удивили своими картинами математиков, это интересно!
Jos de Mei «Это может нарисовать только тот, кто делает дизайн, не зная перспектив …»
«Те, кто влюбляется в практику без теории, подобны штурману, грустному для корабля без руля и компаса и поэтому никогда не знают, где он плывет.» Леонардо да Винчи
Построить поперечное сечение плоскости многогранника — это означает указать точки пересечения плоскости крепления с ребрами многогранника и соединить эти точки с участками, принадлежащими ребрам многогранника. Чтобы построить поперечное сечение многогранника, нужна плоскость в плоскости каждой грани. Укажите 2 точки, принадлежащие поперечному сечению, соедините их прямыми и найдите точки пересечения этой прямой с ребрами многогранника.
Аксиомы осаждения стереометрии 1. Каждая прямая принадлежит по крайней мере двум точкам 2. Есть по крайней мере три точки, которые не лежат на одной прямой 3. Через любые две точки проходит прямая, и только с одной. Охарактеризуйте взаимное расположение точек и прямое основное понятие геометрии «лежащее между» 4. Из трех точек прямая и только одна находится между двумя другими.А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, причем только одна А2. Если две точки прямые лежат в плоскости, то все точки прямые лежат в этой плоскости A3. Если две плоскости имеют общую точку, то у них есть общая прямая, на которой лежат все общие точки этих плоскостей.
В этом случае необходимо учитывать следующее: 1. Можно соединить только две точки, лежащие в плоскости одной грани. Для построения сечения необходимо построить точки пересечения крепежной плоскости с ребрами жесткости и совместить их с сечениями.2. Плоскость крепления пересекает параллельные грани по параллельным сегментам. 3. Если на плоскости отмечена только одна точка, принадлежащая плоскости сечения, то вам нужно построить дополнительную точку. Для этого вам нужно найти уже построенные точки пересечения с другими прямыми линиями, лежащими на тех же гранях.
А в К д А1А1 d1d1 С1С1 b1b1 n h k простых задач д р о м и в с
О и в с Д о и в с Д
A B C D A1A1 D1D1 C1C1 B1B1 Диагональные сечения A B C D A1A1 D1D1 C1C1 B1B1
Аксиоматический метод Метод следов Суть метода заключается в построении вспомогательной прямой, которая представляет собой изображение линии пересечения фиксирующей плоскости с плоскостью любой грани формы.Удобно построить изображение линии пересечения плоскости крепления с плоскостью нижнего основания. Эта линия называется последовательной плоскостью. Используя след, легко построить изображения точек плоскости крепления, расположенных на боковых гранях или формах волокон.
A B C D K L M n f G осуществляется через точки F и O прямого FO. O Cut FO — разрез кромки KLBA плоскостью крепления. Точно так же сегмент FG — это часть грани LMCB. Аксиома Если две разные плоскости имеют общую точку, они пересекаются по прямой, проходящей через эту точку (а у нас даже есть 2 точки).Теорема. Если две прямые точки принадлежат плоскости, то вся прямая принадлежит этой плоскости. Почему мы уверены, что по краям есть порезы? Постройте поперечное сечение призмы, проходящее через точки O, F, G. Шаг 1. Вырежьте грани KLBA и LMCB.
A B C D K L M N f g Шаг 2: Ищем след секулярной плоскости на базовой плоскости, проводим прямую АВ до пересечения с прямой ВО. O Получаем точку H, принадлежащую секущей плоскости, и базовой плоскости.Аналогично получаем аксиому точки R. Если две разные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже есть 2 точки). Теорема. Если две прямые точки принадлежат плоскости, то вся прямая принадлежит этой плоскости. H R через точки H и R осуществляют прямой HR — след светской плоскости. Почему мы уверены, что прямой HR — это след светской плоскости на базовой плоскости?
E S A B C D K L M N F G Шаг 3. Делаем надрезы на других гранях. Поскольку прямая HR пересекает нижнюю линию многогранника, мы получаем точку E на входе и выходе.O Итак, отрезок ES имеет разрез грани ABCD. Аксиома Если две разные плоскости имеют общую точку, они пересекаются по прямой, проходящей через эту точку (а у нас даже есть 2 точки). Теорема. Если две прямые точки принадлежат плоскости, то вся прямая принадлежит этой плоскости. H R выполняют отрезки OE (разрез края KNDA) и GS (разрез лица MNDC). Почему мы уверены, что все делаем правильно?
A1A1 A в B1B1 с C1C1 D D1D1 Mn 1.Построить сечение параллелепипеда к плоскости, проходящей через точки в 1, m, no to e p правило 1. MN 2. Проведение Mn, Ba 4. через 1 o 6. км 7. Продолжим Mn и BD. 9. В 1 E 5. В 1 o и 1 A = K 8. Mn Bd = E 10. B 1 E D 1 D = P, PN 3. MN BA = O
Правила самоконтроля: Вершины сечения находятся только на ребрах. Раздел партии только на грани многогранника. Фиксирующая плоскость пересекает лицо или плоскость лица, то только один раз.
44 1.Танасян Л.С. и др. Геометрия — М .: Просвещение, Литвиненко В.Н., Многогранники. Задачи и решения. — М .: Вита-Пресс, Смирнов В.А., Смирнова И.М., Эге 100 баллов. Геометрия. Сечение многогранников. — М .: Экзамен, учебно-методическое приложение к газете «Первое сентября» «Математика». Федотова О., Кабакова Т. Комплексное занятие «Построение разрезов призмы», 9 / Зив Б.Г. Дидактические материалы по геометрии для 10 класса. — М., Просвещение, электронное издание «1С: Школа.Математика, 5-11 кл. Мастерская »7. ML
Чудуева Елена Владимировна, учитель математики,
МОУ «Инсарская средняя школа № 1»,
инсар, Республика Мордовия
Построение сечений многогранников
Учебно-методическое обеспечение:
Атанасян Л.С. и другие. Геометрия 10-11 класс.
Оборудование и материалы к уроку : компьютер, проектор, экран, презентация для сопровождения урока, раздача материалов учащимся.
Цель занятия: углубление, обобщение, систематизация, закрепление полученных знаний и развитие их в перспективе (изучение метода следов)
Задания урока:
1. Сформировать мотивация к изучению данной темы у школьников.
2. Развивайте способность использовать вспомогательные знания учащихся для получения новых знаний.
3. Развивать мышление учащихся (умение выделять существенные признаки и делать обобщения).
4. Развивать в школе навыки творческого подхода к решению задач и навыков исследовательской работы Над задачей.
Знания, навыки, навыки и качества, которые закрепят учащиеся во время урока:
умение использовать вспомогательные знания для получения новых знаний;
умение выделять существенные признаки и делать обобщения;
навыки творческого подхода к решению задач по сечениям
План урока:
1.Для формирования у школьников мотивации к изучению данной темы.
2. Проверка домашнего задания. Историческая справка.
3. Повторение поддерживающих знаний (аксиоматика, способы постановки плоскости).
4. Применение знаний в стандартной ситуации.
5. Изучение и закрепление нового материала: метод следов.
6. Самостоятельная работа.
7. Подведение итогов урока.
8. Домашнее задание.
На занятиях: И.
Этап — вступительный разговор.
Проверьте свою домашнюю работу. (6-7 мин)
Формы и методы работы
Мероприятия
учеников
1. Расчет
Вводная беседа (1 мин)
Слушайте учителей
2. Проверка домашних заданий
Комментарии к мини-выступлениям учеников Слушайте
товарищам, задавайте вопросы
II.
этап — Актуальное знание знаний (10 мин)
(повторение теоретического материала)
Формы и методы работы
Мероприятия
студенты
1. Повторение аксиомы стереометрии
2. Повторение: взаимное расположение в пространстве прямой и плоскости
3. Обобщение теории
Заключение о Способы настройки плоскости
Запись с помощью тетради
4.Повторение концепции многогранника и сечения плоскости многогранника
Опрос студентов
Устные ответы на вопросы учителя
III
этап — Применение знаний в стандартной ситуации (6-7 мин)
(работа по готовым чертежам)
Формы и методы работы
Задания
учеников
Решение типовых задач по готовым чертежам (каждому ученику выдается рабочая памятка с условием задания и чертеж для построения раздела).
Совместное решение первой задачи (подробное комментирование шагов решения и написание дизайна в рабочий лист).
Изучение условий задачи, работа по готовым чертежам с последующим анализом твердого решения.
IV
этап — из военные параллельные плоскости (6 мин)
Формы и методики учителя
Виды деятельности учащихся
1. Повторение темы «Параллельность плоскостей.«
2. Решение задач
Работа над готовыми слайдами (фронтальный опрос студентов)
Проверка правильности задания
Устные ответы на вопросы учителя
Построение разделов в рабочем листе.
Ответы у доски
V Этап — доступ к новым знаниям: «Метод следов» (6 мин)
Формы и методы работы
Мероприятия
студенты
1.Изучение нового материала
2. Крепление нового материала
Пояснение к новому материалу. Покажите обучающий фрагмент из обучающего фильма «Как построить поперечное сечение Кубы?»
Работа по готовым чертежам у доски (с последующим комментированием этапов построения поперечного сечения слайда)
Выслушайте объяснение учителя. Просмотр обучающего фильма. Анализ видеофрагм., Запись пробы раствора.
Два студента решают за доской, остальные в рабочем листе
VI этап — самостоятельная работа (4-5 мин)
Формы и методы работы
Мероприятия
студентов
Самостоятельная работа учебного характера
Разъяснение предстоящей работы.
Проверка задачи.
Выполнение самостоятельной работы (по готовым чертежам).
Самопроверка готовых слайдов.
VII
этап — подведение итогов урока (4 мин)
Формы и методы работы
Занятия
учеников
1. Подведение итогов
2. Творческое домашнее задание
Разговор По итогам урока с использованием слайдов
На экране
Устные ответы на вопросы учителя
Письмо дневники
ВО ВРЕМЯ КЛАССОВ
Открытие разговора.Историческая справка.
Учитель : Привет, ребята! Тема нашего урока «Построение сечений многогранников на основе аксиоматики». На уроке мы обобщаем и систематизируем пройденный теоретический материал и применяем его к практическим заданиям на построение разделов, с выходом на новый, более сложный уровень сложности заданий.
основная цель наш урок в углублении, систематизации, закреплении полученных знаний и развитии их в перспективе .
В качестве домашнего задания вас попросили написать рефераты или небольшие доклады об истории развития геометрии, о жизни великих математиков, об их знаменитых открытиях и теоремах. Доклады и аннотации получились очень интересными, но на уроке мы услышали всего три мини-спектакля, отвечающих за вопрос, изучающий стереометрию, по мере возникновения, развития и развития и где находит свое применение?
1 студент. Понятие стереометрии, которое изучается.(2 минуты)
2 студента. Евклидов — основоположник геометрии, греческой архитектуры. (2 минуты)
3 студента. Математическая теория. Картина. «Золотое сечение» — формула идеального человеческого тела по Леонардо да Винчи. (2-3 мин)
IN
стереометрия
Изучаются красивые математические объекты. Их формы находят применение в искусстве, архитектуре, строительстве. «Не случайно пирамида Геопса — это тупой трактат о геометрии, а греческая архитектура — внешнее выражение евклидовой геометрии», — писал архитектор Корбюзье.
Прошло столетие, но роль геометрии не изменилась. Она по-прежнему остается «архитектором грамматики». Геометрические формы находят применение в искусстве, архитектуре, строительстве.
Математическая теория живописи —
Это теория перспективы, представляющая, по словам Леонардо да Винчи, «тончайшее исследование и изобретение, основанное на изучении математики, из-за которого линия линий кажется далекой от того, что близко, и большим — с того, что мало». Возрождение разработало в эпоху инженерных сооружений Возрождение и расширение проекционных изображений, использовавшихся в древнем мире.Архитекторы и скульпторы стояли перед необходимостью создать ученицу живописную перспективу на геометрической основе. Многочисленные примеры построения многообещающих образов есть в творчестве гениального итальянского художника и выдающегося ученого Леонардо да Винчи. Он впервые говорит об уменьшении масштаба различных участков снимков, удаляющихся вглубь, ставит начало панорамной перспективы, указывает правила распределения теней, выражает уверенность в существовании некой математической формулы красоты изображения. природа размеров человеческого тела — формула золотого сечения.
Таким образом, мы плавно подошли к теме нашего урока, и слова Леонардо да Винчи станут мостом на его следующем этапе:
«Те, кто влюбляются в практику без теории, похожи на мореплавателя. , грустно кораблю без руля и компаса и поэтому никогда не знаешь, где он плывет ».
Это утверждение определяет следующий этап нашего урока: повторение теоретического материала.
II. Актуализация знаний (повторение теоретического материала)
2.1. Аксиомы стереометрии (таблицы остаются студентами для работы).
а) пояснить содержание аксиомы и проиллюстрировать на модели;
б) чтение текста аксиомы;
в) выполнение чертежа;
2.2. Следствия аксиомы стереометрии.
2.3. Взаимное расположение в пространстве прямых и плоскостей.
а) две прямые (прямые параллели пересекаются, пересекаются)
б) прямая и плоская (прямая лежит в плоскости, пересекает плоскость параллельно плоскости)
в) две плоскости (плоскости пересекаются или параллельны).
В ходе разговора выделяются значимые моменты теории:
а) признак прямой и плоскопараллельности: Если прямая, не лежащая в этой плоскости, параллельная какой-то прямой, лежащей в этой плоскости, то она параллельна этот самолет.
б) признак параллельности плоскостей: Если две пересекающиеся прямые одна плоскости соответственно параллельны двум пересекающимся прямым другим плоскостям, то эти плоскости параллельны.
Учитель: Обобщая все это, приходим к выводу о способах постановки самолета.
2.5. Понятие о многогранниках. Раздел.
Многогранник
Его называют телом, ограниченным конечным числом плоскостей. Поверхность многогранника состоит из конечного числа многоугольников.
M.
фрагмент, полученный при пересечении многогранника и плоскости, называется сечение
заданная плоскость многогранника
.
III. Применение знаний в стандартной ситуации.
Используя полученные знания, мы применяем их для построения поперечных сечений многогранников на основе аксиоматики.
Примеры и их решение приводят ученики (под руководством преподавателя).
IV. Построение сечений с использованием свойств параллельных плоскостей.
Учитель: Для решения следующей группы задач нам необходимо повторить свойства параллельных плоскостей.
В ..
Выход для получения новых знаний: «Метод следов».
Посмотреть обучающий фильм.
Электронное издание
Применение полученных знаний (решение студентами двух заданий на доске с последующим просмотром правильного решения и записью).
VI — Самостоятельная работа
с последующей взаимной проверкой (согласно слайду с готовым решением).
VII.Подведение итогов урока
Что нового вы узнали на уроке?
Каково поперечное сечение тетраэдра?
Какие многоугольники могут быть поперечным сечением тетраэдра?
Какие многоугольники могут попасть в поперечное сечение параллелепипеда?
Что вы можете сказать о методе трассировки?

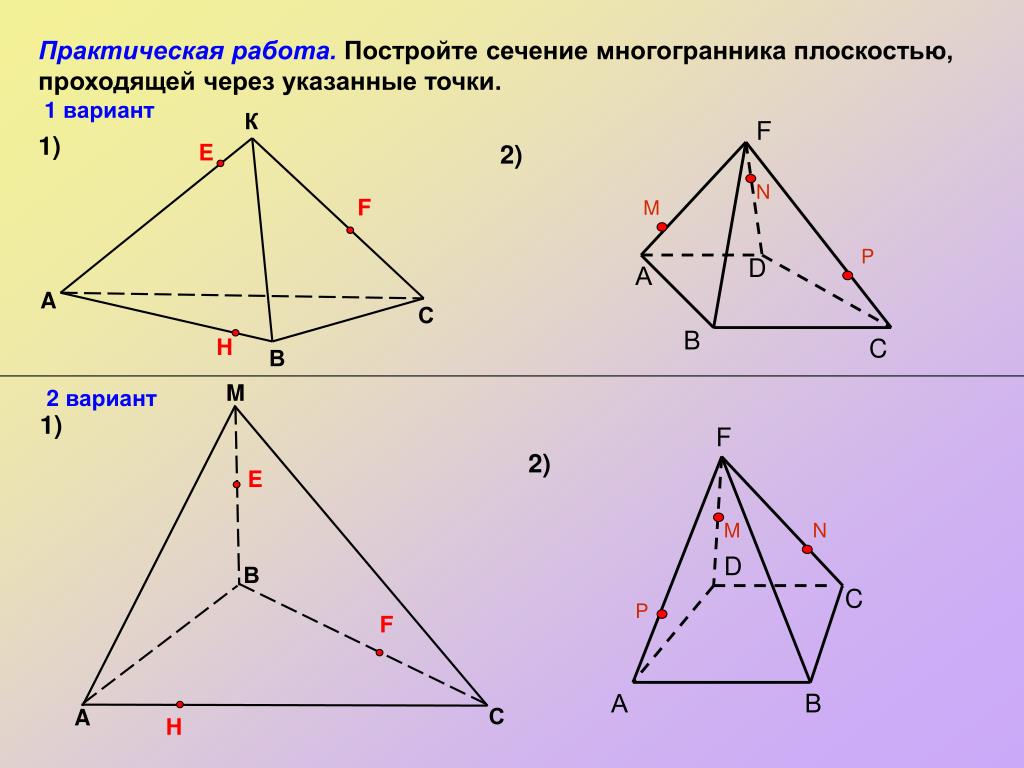 Противоположные углы параллелограмма равны:
Противоположные углы параллелограмма равны: