Содержание
Теорема косинусов. Следствия из теоремы косинусов
Цель урока:
- Повторить ранее изученный теоретический материал, изучить теорему косинусов и её следствия, учить делать теоретические обобщения.
- Развивать логику мышления при решении специально подобранных задач.
- Воспитывать потребность в доказательстве высказанной гипотезы.
Тип урока: урок ознакомления с новым материалом.
Оборудование урока: ноутбук, мультимедийный проектор, интерактивная доска.
Ход урока
I. Сообщение темы, цели и задач урока. Мотивация учебной деятельности.
II. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний
(Фронтальная работа с классом)
III.
Изучение нового материала.
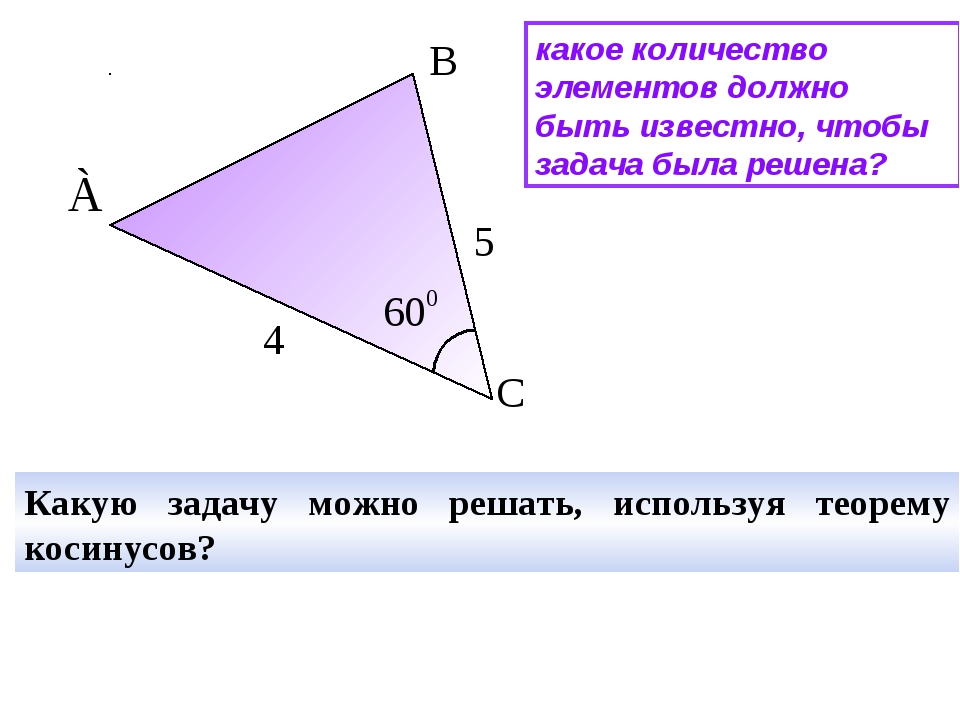
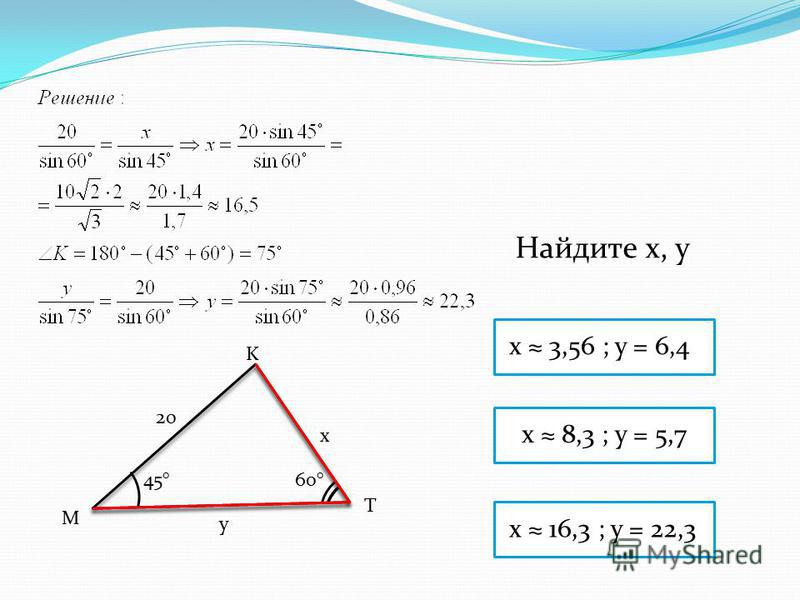
Учащимся предлагается задача на готовом чертеже. Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.
Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.
Первый способ решения задачи. (Устно)
Дано:
ABC,
AC = b, AB = c.
A
__________________
Найти:
BC = a = ? | Проведём CH – высоту.
1) Прямоугольный ACH:
AH = bcosA, CH =
или CH = bsinA
BH = AB – AH.
CB2 = a2 = CH2 + BH2
a = . | Рис. 4 |
Второй способ решения задачи. Координатный метод.
1. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату.
Решение записывают все учащиеся. | |
2. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA).
3. Найдём квадрат стороны BC:
| Рис.  5 5 |
Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
По теореме косинусов можно найти любую сторону треугольника, зная длины двух других сторон и угол между ними.
Теорему косинусов иногда называют обобщённой теоремой Пифагора. Почему? Объясните.
Если С = 90°, то cosC = 0 и 2abcosC = 0, тогда c2 = a2 + b2.
Вывод: Теорема Пифагора является частным случаем теоремы косинусов.
Рассмотрим следствия из теоремы косинусов.
| 1 следствие. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дано:
ABC
AC = b,
AB = c,
AH = bc
__________________
Найти: a | Решение:
Возможны 2 случая:
а) A – острый, то cosA > 0,
б) A – тупой, то cosA < 0,
а) Если A – острый, тогда
по теореме косинусов
a2 = b2 + c2 – 2bccosA | Рис. 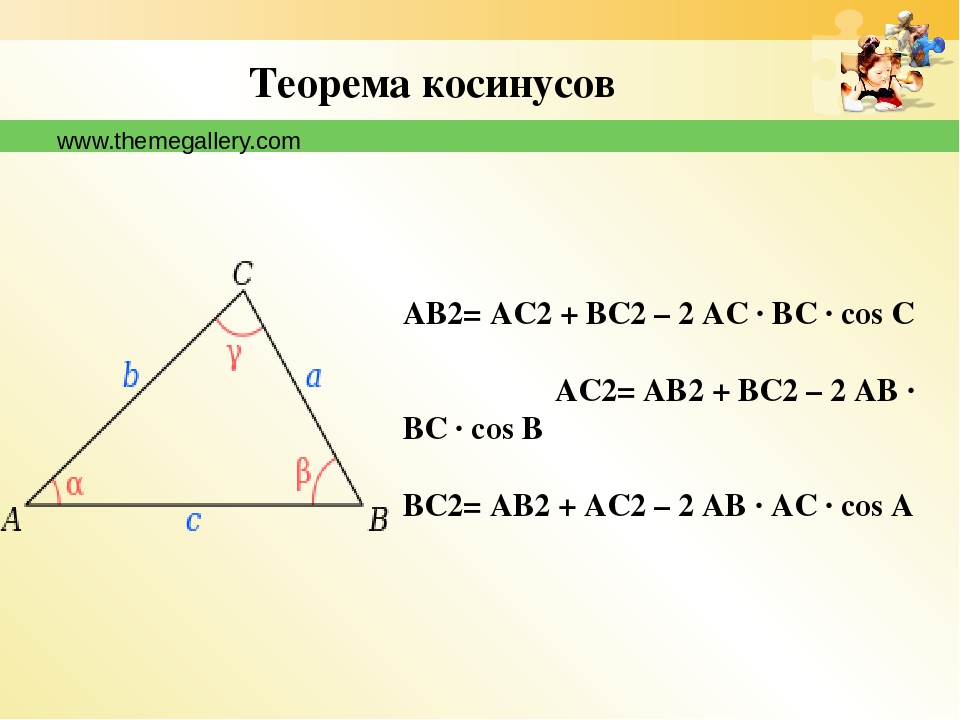 6 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В прямоугольном ACH: bc = bcosA. Так как A – острый, то cosA > 0, тогда a2 = b2 + c2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой.
Случай, когда угол, лежащий против неизвестной стороны тупой рассмотреть самостоятельно. Следующий урок начнём с проверки этого задания. (т.к. cosA < 0, то a2 = b2 + c2 + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 следствие. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дано:
ABCD – параллелограмм,
AB = CD =a,
BC = AD = b.
__________________
Найти: d12 + d22 . | Решение:
ABC: d12 = a2 + b2 – 2abcosB.
ABD: d22 = a2 + b2 – 2abcosA = a2 + b2 – 2abcos(180° — B) = a2 + b2 + 2abcosB.
d12 + d22 = a2 + b2 – 2abcosB + a2 + b2 + 2abcosB = a2 + b2 + a2 + b2.
d12 + d22 = 2 a2 + 2 b2. | Рис. 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 следствие. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дано:
ABC,
AB = c,
AC = b,
BC = a.
__________________
Найти: ma | Решение:
Достроим ABC до параллелограмма ABA1C.
AA12 + BC2 = 2b2 + 2c2 . BC = a, 2ma = AA1.
(2ma)2 + a2 = 2b2 + 2c2
4ma2 = 2(b2 + c2) – a2
ma2 =
ma =
mb =
mc = | Рис. 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывод: В любом треугольнике со сторонами a, b и c длины медиан ma, mb, mc вычисляются по формулам: ma = , mb = , mc = . Теорема косинусов является обобщением теоремы Пифагора. В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её Тогда $$A B=\sqrt{247}$$ Ответ. $A B=\sqrt{247}$ Теорема Косинусов и Синусов треугольника. Формулы и примерыФормулировка и доказательство теоремы косинусовДля начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Формула Теоремы Пифагора: a2> + b2> = c2>, где a, b — катеты, с — гипотенуза. Из формулы следует: a2 = c2 — b2 К полученному выражению прибавим и отнимем квадрат второго катета: Но так как b = c * cos α, то Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.
Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу: BC2 = (x2 — x1)2 + (y2 — y1)2 В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0). BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2 cos2α + sin2α = 1 — основное тригонометрическое тождество. b2(cos2α + sin2α) — 2bc cos α + c2 = b2 + c2 — 2bc cos α Что и требовалось доказать. Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:
Запоминаем Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора. Сформулируем еще одно доказательство теоремы косинусов. Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
либо
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше. Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольникаТеорема косинусов справедлива для всех сторон треугольника, то есть: a2 = b2 + c2 — 2bc cos α b2 = c2 + a2 — 2ca cos β c2 = a2 + b2 — 2ab cos γ Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника. Описание формулы косинуса угла из теоремы косинусовТеорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов: Аналогично: Определение угла с помощью косинусаА теперь обратим внимание на углы. Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса). Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM. Рассмотрение пределов изменения cos α и sin αРассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°. Предел изменения косинуса: -1 < cos α < 1. Предел изменения синуса: 0 < sin α ≤ 1.
Примеры решения задачПри помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи. Пример 1. Дан треугольник АВС. Найти длину СМ. ∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ. Как решаем:
Ответ: СМ = √33. Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол. Как доказываем:
Что и требовалось доказать. Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в онлайн-школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок математики вместе с ребенком и попробуйте сами! Материал по математике «Теорема косинусов и ее следствия»
Конспект урока геометрии в 9 классе на тему «Теорема косинусов. Следствия из теоремы косинусов»Урок 26 05.12.2019 Тема «Теорема косинусов. Следствия из теоремы косинусов» Цель урока:
Тип урока: урок ознакомления с новым материалом Оборудование урока: ноутбук, мультимедийный проектор, интерактивная доска. Ход урока
(Фронтальная работа с классом)
Рис.1
Рис.2
Рис.3
Учащимся предлагается задача на готовом чертеже. Первый способ решения задачи. (Устно) Рис.4 Дано: Проведём CH – высоту. ABC, 1) Прямоугольный ACH: AC = b, AB = c. AH = bcosA, CH = A или CH = bsinA __________________ BH = AB – AH. Найти: CB2 = a2 = CH2 + BH2 BC = a = ? a = . Второй способ решения задачи. Координатный метод.
Решение записывают все учащиеся. Рис.5
B(c; 0) ; C(bcosA; bsinA).
BC2 = a2 = (bcosA — c)2 + (bsinA)2 = = b2cos2A – 2bccosA + c2 + b2sin2A = = b2(cos2A + sin2A) + c2 – 2bccosA = = b2 + c2 – 2bccosA. a2 = b2 + c2 – 2bccosA — теорема косинусов b2 = a2 + c2 – 2accosB c2 = b2 + a2 – 2abcosC Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними. По теореме косинусов можно найти любую сторону треугольника, зная длины двух других сторон и угол между ними. Теорему косинусов иногда называют обобщённой теоремой Пифагора. Почему? Объясните. Если С = 900, то cosC = 0 и 2abcosC = 0, тогда c2 = a2 + b2. Вывод: Теорема Пифагора является частным случаем теоремы косинусов. Закрепление №1025(д) Если осталось время Рассмотрим следствия из теоремы косинусов. Рис.6 1 следствие. Дано: Решение: ABC Возможны 2 случая: AC = b, а) A – острый, то cosA > 0, AB = c, б) A – тупой, то cosA < 0, AH = bc а) Если A – острый, тогда Найти: a по теореме косинусов a2 = b2 + c2 – 2bccosA В прямоугольном ACH: bc = bcosA. Случай, когда угол, лежащий против неизвестной стороны тупой рассмотреть самостоятельно. Следующий урок начнём с проверки этого задания. (т.к. cosA < 0, то a2 = b2 + c2 + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой. 2 следствие. Рис.7 Дано: ABCD – параллелограмм, AB = CD =a, BC = AD = b. Найти: d12 + d22 . Решение: ABC: d12 = a2 + b2 – 2abcosB. ABD: d22 = a2 + b2 – 2abcosA = a2 + b2 – 2abcos(1800 — B) = a2 + b2 + 2abcosB. d12 + d22 = a2 + b2 – 2abcosB + a2 + b2 + 2abcosB = a2 + b2 + a2 + b2. d12 + d22 = 2 a2 + 2 b2. Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. 3 следствие. Рис.8 Дано: ABC, AB = c, AC = b, BC = a. Найти: ma . Решение: Достроим ABC до параллелограмма ABA1C. AA12 + BC2 = 2b2 + 2c2 . BC = a, 2ma = AA1 . (2ma)2 + a2 = 2b2 + 2c2 4ma2 = 2(b2 + c2) – a2 ma2 = mb= ma = mc = Вывод: В любом треугольнике со сторонами a,b и c длины медиан ma, mb, mc вычисляются по формулам: ma = , mb= , mc = .
Задача: В треугольнике две стороны равны 20 см и 21 см, а синус угла между ними равен 0,6 . Найти третью сторону. Сколько решений имеет задача? Рис.9 Дано: Решение: sin = 0,6 , sin = 0,6 может быть острым AB = 20 см, или тупым. AC = 21 см. 1 случай: — острый Найти: BC. BC2 = AB2 + AC2 – 2ABACcos. Так как — острый, то cos>0. Тогда cos = = = = 0.8 BC = = = 13(см). 2 случай: — тупой. BC2 = AB2 + AC2 – 2ABACcosРис.10 Так как — тупой, то cos<0 cos = -= — = -0.8 BC = = (см). Ответ: 1) BC = 13 см. 2) BC = см. 5. Домашняя работа: п. 98 №1025( в, е). 6. Подведение итогов урока. Теорема косинусов: формулировка, следствия, доказательство и примерыТеорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними. Формула косинуса:
Например: Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны. Решение по формуле a² = b² + c² – 2b.c.cosα: b = 12 см c = 8 см cos α = cos 120º = — 1/2 (это значение можно найти в таблицах) a² = 12² + 8² – 2×12×8×(- 1/2) a² = 144 + 64 – (–96) a² = 304 a = √304 a ≈ 17,436 Длина третьей стороны — примерно 17,436 см. СледствияСледствие косинуса угла треугольникаПри помощи теоремы косинусов можно найти косинус угла треугольника. Формула: Либо Либо Например: сторона c = 6 сторона b = 7 сторона a = 8 Используйте теорему косинусов, чтобы найти угол β. Решение: Будем использовать эту версию формулы: cos β = (6² + 8² − 7²) / 2×6×8 = (36 + 64 − 49) / 96 = 51 / 96 = 0,53125 = cos¯¹(0,53125) ≈ 57,9° Следствие верхней части формулы cos αЧтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
Доказательство теоремы косинусовНужно доказать, что c² = a² + b² − 2a.b.cos C 1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.cos C. 2. Вычитаем это из стороны b, так мы получим DA: DA = b − a.cosC 3. Мы знаем из определения синуса, что в том же треугольнике BCD: sin C = BD/a <=> BD = a.sinC. 4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA² 5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)² 6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C 6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC 7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC 8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C Q.E.D. Теорема косинусов для равнобедренного треугольникаВ равнобедренном треугольнике:
Рассмотрим пример: Используем формулу теоремы косинусов a² = b² + c² – 2b.c.cosα Подставляем все известные: x² = 8² + 8² – 2×8×8×cos140º x² = 64 + 64 – 128 × (-0,766) x² ≈ √226,048 x ≈ 15,035. Теорема синусовТеорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике: Узнайте также, что такое Теорема Пифагора и Теорема Менелая. Терема косинусов на занятиях с репетитором по математике — Колпаков Александр НиколаевичФормулировка: Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для произвольного треугольника ABC и его сторон a,b и с (противолежащих к соответствующим вершинам) это равенство можно записать и для двух других сторон: Теорема косинусов используется для решения треугольников в двух главных ситуациях: 1) Когда даны две стороны и угол между ними, а требуется найти последнюю сторону: 2) Когда даны все три стороны треугольника, а требуется найти его углы: Иногда репетитор по математике рекомендует использовать теорему косинусов в задаче с двумя данными сторонами и углом, не лежащим между ними. В этом случае а) придется решать квадратное уравнение и отбирать среди полученных корней длину реальной стороны. б) такая ситуация не характерна для задач с ЕГЭ по математике, так как не всегда однозначно задает треугольник. Если угол не лежит между сторонами, то циркулем и линейкой можно построить двух разных треугольника с такими элементами. Теорема косинусов иногда называют расширенной теоремой Пифагора или обобщением теоремы Пифагора, ибо при угле 90 градусов из указанных выше равенств получается . Как любое обобщение она намного универсальнее и эффективнее частного случая и применяется к большему числу реальных ситуаций (в отличае от искусственных задач ГИА и ЕГЭ по математике, расчитанных на программу 8 класса). Доказательство теоремы косинусовВсе известные мне доказательства связаны с векторами и координатами. В учебнике Атанасяна оно проводится через координаты точек, а в учебнике Погорелове используется понятие «скалярное произведение векторов». Проведем доказательство по Атанасяну. Оно, как мне кажется больше всего подходит репетитору по математике для работы, так как имеет меньшую зависимость от соседних тем. Докажем равенство для стороны а и угла А. Для этого введем систему координат как показано на рисунке (ось Ох направляется вдоль стороны АС). Точка B при этом получит координаты B (cCosA;cSinA). Это единственный сложный для слабого или среднего ученика факт, который репетитор по математике, работающий по учебнику Атанасяна, должен отдельно рассмотреть. Cложным он является часто по причине того, что не подкреплен в программе достаточным количеством задач и после изучения теоремы косинусов не используется. В случае с данным расположеним точек (когда — острый) репетитору по математике достаточно обратиться к определению косинуса и синуса острого угла в прямоугольных треугольниках с пунктирными сторонами. Даленейшее доказательство строится на алгебраических и тригонометрических выкладках. К ним необходимо добавить знание формулы расстояния между двумя точками. Применяем формулу сокращенного усножения к квадрату суммы: Выносим за скобку: . Используем основное тригонометрическое тождество и получаем и в итоге Любознательному ученику репетитор по математике может показать редкое доказательство теоермы косинусов. Проведем в треугольнике ABC высоту BH и запишем АВ=АН+НВ или с=bCosA+aCosB. Если угол B — тупой, то АВ=АН-НВ и с учетом того, что косинусы смежных углов противоположны, снова получим равенство с=bCosA+aCosB. Поэтому оно не зависит от вида треугольника. запишем аналогичные формулы для а и b: Торема косинусов позволяет объяснить весьма полезное на практике свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов длин его сторон. Для того, чтобы в этом убедиться достаточно записать теорему косинусов для каждой диагонали и сложить полученные равенства. Примеры задач, в которых так или иначе можно (или нужно) использовать теорему косинусов: 1) В треугольнике со сторонами 2,3 и 4 найдите длину медианы, проведенную к большей стороне. Полноценная подготовка к ЕГЭ по математике невозможна без решения задач на теорему косинусов. В варианте ЕГЭ она может встретится или в номере B4 или в C4. Постепенно я буду переносить на страницу интересные задачи С4 из моей дидактической базы и с пробных экзаменов. Репетиторы, не забудьте, что в ГИА, как на ЕГЭ, теорема косинусов может проявиться и в первой и во второй части варианта. Колпаков Александр Николаевич, Несколько следствий из теоремы ПифагораТеорема Пифагора играет важную роль в геометрии и математике в целом. На этой странице я постараюсь собрать несколько утверждений, некоторые из которых основаны на теореме Пифагора. Арифметика — Неравенство геометрических среднихДля положительных $ a $ и $ b $ $ (a + b) / 2 ≥ \ sqrt {ab}, $ с равенством тогда и только тогда, когда $ a = b. $ Для доказательства предположим, что $ a> b $ и построим прямоугольный треугольник с гипотенузой $ (a + b) / 2 $ и одной стороной, равной $ (a-b) / 2.{2} = 4ab. $ В этом случае теорема Пифагора дает интуитивно понятную геометрическую иллюстрацию. Просто нарисуйте два соприкасающихся круга с радиусами $ a / 2 $ и $ b / 2 $, как на схеме. $ (a + b) / 2 $ известен как среднее арифметическое чисел $ a $ и $ b; $ \ sqrt {ab} $ — их среднее геометрическое, также известное как среднее арифметическое , потому что если $ k = \ sqrt {ab} $, тогда $ a / k = k / b $ и наоборот. Как и в случае изопериметрического неравенства, неравенство AM-GM также допускает две эквивалентные экстремальные задачи:
В обоих случаях экстремальное значение достигается при совпадении двух чисел. Последний факт имеет красивую геометрическую иллюстрацию, которая также предлагает другое доказательство неравенства среднего арифметического — среднего геометрического. Первое часто переписывают в другом виде: (1) Для $ x> 0 выполняется $ $ x + 1 / x \ ge 2, $ с равенством тогда и только тогда, когда $ x = 1. $ Среднее арифметическое — среднее геометрическое неравенство для последовательностей чисел было впервые доказано, когда длина последовательности была степенью 2 $, а отсюда и для произвольного целого числа.(1) также распространяется на произвольное количество положительных чисел: Пусть $ x_ {i}> 0, $ $ i = 1,2, \ ldots, n. $ Тогда $ x_ {1} / x_ {2} + x_ {2} / x_ {3} + \ ldots + x_ { n} / x_ {1} \ ge n. $ На самом деле верно больше. Для положительных $ x_ {i} $ пусть p — произвольная перестановка набора индексов $ \ {1, \ ldots, n \}. $ Тогда $ x_ {1} / x_ {p (1)} + x_ {2} / x_ {p (2)} + \ ldots + x_ {n} / x_ {p (n)} \ ge n. $ Правило косинусаПравило косинусов — очевидное обобщение теоремы Пифагора.{2} = \ mbox {const}. $ Только что полученный результат можно переформулировать следующим образом: Пусть $ \ mathcal {O} (X) $ — степень точки $ X $ относительно $ (O), $ $ \ mathcal {o} (X) $ степень точки $ X $ относительно $ (o $ Тогда геометрическое место точки $ X $, для которой $ \ mathcal {O} (X) — \ mathcal {o} (X) $ является постоянным, является прямой, параллельной радикальной оси двух окружностей. Теорема СтюартаКокстер и Грейцер отмечают, что приведенная ниже теорема была названа в честь М. Стюарта, сформулировавшего ее в 1746 году, но, вероятно, была обнаружена Архимедом около 300 г. до н. Э.{2} $ Это просто еще один способ записать формулу Герона. Таким образом, два факта: теорема Пифагора и формула Герона имеют независимое доказательство. Но, кроме того, каждое из них может быть получено из другого. ЗамечаниеДоктор С. Броди любезно подготовил демонстрацию того, как теорема Пифагора используется для построения правильного пятиугольника. Он также заметил, что теорема эквивалентна знаменитому параллельному (или пятому) постулату. Наконец, есть интересное, только недавно обнаруженное приложение теоремы и интересная загадка, которую теорема помогает решить.{2}. $ Чтобы понять, почему это так, нарисуйте радиусы двух окружностей, чтобы получился прямоугольный треугольник. Примените теорему Пифагора. Можно утверждать независимо от теоремы Пифагора, что площадь, охватываемая отрезком фиксированной длины, одинакова, независимо от того, вращается ли он вокруг одной из своих точек или скользит по касательной к данной кривой. Получение этого результата даст дополнительное доказательство теоремы Пифагора. Список литературы
| Контакты | Copyright © 1996-2018 Александр Богомольный Синус, косинус и теорема ПтолемеяИз теоремы Птолемея следует теорема Пифагора. Последний служит основой тригонометрии, раздела математики, который занимается отношениями между сторонами и углами треугольника.{2} (A) = 1, $ , где $ A $ — один из внутренних углов прямоугольного треугольника. Если гипотенуза треугольника имеет длину $ 1, $, то $ \ sin (A) $ — длина стороны, противоположной углу $ A, $ $ \ cos (A) $ — длина соседней стороны. Теорема Птолемея также предоставляет элегантный способ доказательства других тригонометрических тождеств. Через некоторое время я докажу формулы сложения и вычитания для синуса : . (1) $ \ sin (A + B) = \ sin (A) \ cos (B) + \ cos (A) \ sin (B) $ (2) $ \ sin (A — B) = \ sin (A) \ cos (B) — \ cos (A) \ sin (B).$ Но сначала давайте рассмотрим простое доказательство закона синуса . Предложение III.20 из Элементов Евклида говорит: В круге угол в центре вдвое больше угла на окружности, когда углы имеют ту же длину окружности, что и основание. Более распространенная формулировка утверждает, что угол, описанный в окружности, равен половине центрального угла, который образует ту же хорду.(Как следствие, отсюда следует, что все описанные углы, соединяющие одну и ту же дугу, равны независимо от их положения на окружности. Это предложение III.21) На диаграмме $ \ angle BOC = 2 \ angle BAC (= 2A .) $ Опустите перпендикуляр из $ O $ на сторону $ BC. $ Предполагая, что радиус окружности равен $ R, $ $ OB = OC = R. $ Кроме того, $ \ angle BOP = \ angle POC. $ In $ \ Delta BOP, $ $ \ sin (\ angle BOP) = BP / OB = BC / 2R. $ Следовательно, $ BC / \ sin (\ angle BOP) = 2R. $ Когда угол $ A $ тупой, центр $ O $ находится вне $ \ Delta ABC $, и диаграмма выглядит иначе.Однако в результате идентичность остается прежней. Повторяя эти шаги с двумя другими углами $ B $ и $ C $ в $ \ Delta ABC $, мы получаем закон синусов , который в стандартных обозначениях отображается как (3) $ \ displaystyle \ frac {a} {\ sin (A)} = \ frac {b} {\ cos (B)} = \ frac {c} {\ sin (A)} = 2R. $ В случае, когда диаметр описанной окружности равен 1, мы имеем $ a = \ sin (A), $ $ b = \ sin (B), $ и $ c = \ sin (C). $ Это все, что нам нужно, чтобы применить теорему Птолемея.Это, конечно, полезно для запоминания определения функций синуса и косинуса. В прямоугольном треугольнике синус острого угла — это отношение противоположного катета к гипотенузе; его косинус — это отношение соседнего катета к гипотенузе. Рассмотрим четырехугольник $ ABDC $, вписанный в окружность диаметра $ 1 $, так что диагональ $ BC $ служит диаметром. Из определения синуса и косинуса мы определяем стороны четырехугольника. Закон синуса определяет длину оставшейся диагонали.Формула сложения для синуса — это просто переформулировка теоремы Птолемея. Для доказательства формулы вычитания пусть сторона $ BC $ служит диаметром. Как следствие, получаем формулы для синуса (за один шаг) и косинуса (за два шага) дополнительных углов: $ \ begin {align} Из этих формул и формул сложения для синуса нетрудно вывести формулы сложения для косинуса: $ \ begin {align} (Есть дополнительные простые доказательства этих формул.) Список литературы
Тригонометрия | Контакты | Copyright © 1996-2018 Александр Богомольный Геометрия — Доказательство теоремы Стюарта без триггера Прежде всего, см. Статью в Википедии Теорема Стюарта .2 \ cdot AB + BC \ cdot CA \ cdot AB = 0 ~, Доказательство. Доказательство простыми вычислениями. Обратите внимание, что теорема верна также в частично вырожденных ситуациях, когда некоторые из точек $ A $, $ B $, $ C $ совпадают или точка $ P $ находится на прямой $ l $. Замечание. Тождество $ (1) $ является общим полиномиальным тождеством , что означает, что оно является тождеством в кольце $ \ mathbb {Z} [a, b, c, x] $ многочленов от (формальных) переменных $ a $, $ b $, $ c $, $ x $ с целочисленными коэффициентами и, следовательно, создает экземпляр тождества, когда переменные заменяются элементами произвольного коммутативного кольца.Это наблюдение говорит нам, что теорема Стюарта верна в «геометрии евклидовой плоскости» над любым коммутативным кольцом, в частности над любым полем. теорем, следствий, лемм. Что это все за штуки? Они звучат так впечатляюще! Ну, в основном это всего лишь фактов : какой-то результат, который был достигнут.
ПримерыВот пример из Geometry: Пример: теорема и следствиеТеорема:Углы на одной стороне прямой всегда составляют 180 °. Следствие:Следуя этой теореме, мы находим, что там, где две прямые пересекаются, углы друг напротив друга (называемые вертикальными углами) равны , равным (на диаграмме a = c и b = d). Угол a = угол c Проба:Углы a и b складываются в 180 °, потому что они расположены вдоль линии: а + Ь = 180 ° а = 180 ° — б Аналогично для углов b и c б + с = 180 ° c = 180 ° — b А поскольку и a, и c равны 180 ° — b, то а = с И немного более сложный пример из Geometry: Пример: теорема, ее следствие, а также лемма!Теорема: Вписанный угол a ° равен половине центрального угла 2a ° Доказательство: соедините центр O с A. Треугольник ABO равнобедренный (две равные стороны, два равных угла), поэтому: Угол OBA = Угол BAO = b ° И, используя углы треугольника, прибавляем к 180 °: Угол AOB = (180 — 2b) ° Треугольник ACO равнобедренный, поэтому: Угол OCA = Угол CAO = c ° И, используя углы треугольника, прибавляем к 180 °: Угол AOC = (180 — 2c) ° И, используя углы вокруг точки, добавьте к 360 °: Угол BOC = 360 ° — (180 — 2b) ° — (180 — 2c) ° = 2b ° + 2c ° = 2 (Ь + с) ° Заменим b + c на a , получаем: Угол BAC = a ° и угол BOC = 2a ° И мы доказали теорему. (Это был «главный» результат, как и теорема.) Следствие(Это называется «Углы, подчиненные той же дуговой теореме », но на самом деле это просто следствие из «Угол в центре теоремы» ) Сохранение конечных точек фиксированными … … угол a ° всегда один и тот же, независимо от того, где он находится на окружности: Итак, углы, образуемые одной и той же дугой, равны. Лемма(Иногда это называют «Угол в теореме о полукруге» , но на самом деле это просто лемма к «Угол в теореме о центре» ) В особом случае, когда центральный угол образует диаметр окружности: 2a ° = 180 °, поэтому a ° = 90 ° Таким образом, угол, вписанный в полукруг, всегда является прямым. (Это был «маленький» результат, так что это лемма.) Другой пример, связанный с теоремой Пифагора: Пример:ТеоремаЕсли m и n — любые два целых числа и
, затем a 2 + b 2 = c 2 Доказательство : a 2 + b 2 = (m 2 — n 2 ) 2 + (2mn) 2 = м 4 — 2 м 2 n 2 + n 4 + 4 м 2 n 2 = м 4 + 2 м 2 n 2 + n 4 = (m 2 + n 2 ) 2 = с 2 (Это был «главный» результат.) Следствиеa, b и c, как определено выше, являются тройной пифагорейской Доказательство : Из теоремы a 2 + b 2 = c 2 , (Этот результат «последовал» из предыдущей теоремы.) ЛеммаЕсли m = 2 и n = 1, то получаем тройку Пифагора 3, 4 и 5 Доказательство : Если m = 2 и n = 1, то
(Это был «маленький» результат.) Треугольник 30 ° -60 ° -90 °. Темы по тригонометрии.Темы | Дом 4 В тригонометрии ЕСТЬ ДВА особых треугольника. Один из них — треугольник 30 ° -60 ° -90 °. Другой — равнобедренный прямоугольный треугольник. Они особенные, потому что с помощью простой геометрии мы можем узнать соотношение их сторон. Теорема. В треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении Мы докажем это ниже. (Определение углов измерения «градусами» см. В теме 12.) Обратите внимание, что наименьшая сторона, 1, противоположна наименьшему углу, 30 °; в то время как самая большая сторона, 2, противоположна наибольшему углу, 90 °. (Теорема 6). (Поскольку, 2 больше, чем. Кроме того, хотя 1:: 2 правильно соответствует сторонам, противоположным 30 ° -60 ° -90 °, многие считают, что последовательность 1: 2: легче запомнить.) Приведенные теоремы взяты из Приложения, Некоторые теоремы плоской геометрии. Вот примеры того, как мы пользуемся знанием этих соотношений. Во-первых, мы можем оценить функции 60 ° и 30 °. Пример 1. Оценить cos 60 °. Ответ . Для решения любой задачи, связанной с треугольником 30 ° -60 ° -90 °, ученик не должен использовать стол. Учащийся должен нарисовать треугольник и указать числа отношения. Поскольку косинус — это отношение смежной стороны к гипотенузе, вы можете видеть, что cos 60 ° = ½. Пример 2. Оценить sin 30 °. Ответ . По свойству совместных функций (Тема 3), Вы можете видеть это прямо на рисунке выше. Задача 1. Оценить sin 60 ° и tan 60 °. Чтобы увидеть ответ, наведите указатель мыши на цветную область. Синус — это отношение противоположной стороны к гипотенузе.
Урок 5 алгебры Касательная — это отношение противоположной стороны к соседней.
Задача 2. Оценить кроватку 30 ° и cos 30 °. Котангенс — это отношение соседней стороны к противоположной.
=. Или, проще говоря, раскладушка 30 ° = загар 60 °. Проблема 1 Что касается косинуса, то это отношение смежной стороны к гипотенузе. Следовательно,
Прежде чем мы перейдем к следующему примеру, вот как мы соотносим стороны и углы треугольника: Если угол обозначен заглавной буквой A, то противоположная сторона будет обозначена малым a .Аналогично для угла B и стороны b , угла C и стороны c . Пример 3. Решите прямоугольный треугольник ABC, если угол A равен 60 °, а сторона c равна 10 см. Решение. Решить треугольник — значит знать все три стороны и все три угла. Поскольку это прямоугольный треугольник, а угол A равен 60 °, то оставшийся угол B является его дополнением, 30 °. Теперь в каждом треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:, как показано справа.Когда мы знаем отношения сторон, мы можем решить треугольник методом подобных фигур. Итак, в треугольнике ABC сторона, соответствующая 2, была умножена на 5. Следовательно, каждая сторона будет умножена на 5. Сторона b будет 5 × 1, или просто 5 см, а сторона a будет равна 5 см. . В качестве альтернативы мы могли бы сказать, что сторона, прилегающая к 60 °, всегда равна половине гипотенузы. Следовательно, сторона b будет 5 см.Теперь сторона b — это сторона, соответствующая 1. И она была умножена на 5. Следовательно, сторона nI> a также должна быть умножена на 5. Она будет равна 5 см. Всякий раз, когда мы знаем числа отношения, ученик должен использовать этот метод подобных фигур для решения треугольника, а не тригонометрическую таблицу. (В теме 6 мы будем решать прямоугольные треугольники, отношения сторон которых нам неизвестны.) Задача 3. В прямоугольном треугольнике DFE угол D равен 30 °, а сторона DF — 3 дюйма.Какова длина сторон d и f ? Ученик должен нарисовать подобный треугольник в той же ориентации. Затем убедитесь, что сторона, соответствующая значению, была умножена на. Урок 26 алгебры Задача 4. В прямоугольном треугольнике PQR угол P равен 30 °, а сторона r равна 1 см. Какова длина сторон p и q ? Сторона, соответствующая 2, была разделена на на 2.Следовательно, каждая сторона должна быть разделена на 2. Сторона p будет равна 1/2, а сторона q будет равна 1/2. Задача 5. Решите прямоугольный треугольник ABC, если угол A равен 60 °, а гипотенуза равна 18,6 см. Сторона, прилегающая к 60 °, всегда равна половине гипотенузы, поэтому сторона b равна 9,3 см. Пример 4. ABC — равносторонний треугольник, высота AD которого равна 4 см. Найдите длину стороны x . Решение 1 . Поскольку треугольник равносторонний, он также равносторонний, поэтому угол в точке B равен 60 ° Высота треугольника — это прямая линия, проведенная от вершины под прямым углом к основанию.Следовательно, треугольник ADB — это треугольник 30-60-90. Для этой задачи будет удобно формировать пропорцию дробными символами:
Это означает
Приблизительно 1 . 732,
Сторона, соответствующая умноженной, стала 4. Как она умножалась?
Сравните предыдущий раздел.
, что опять же примерно 4 . 619 см. Проблема 6. Проверьте значения 30 °, 60 ° и 45 ° — то есть посмотрите на два треугольника — — и в каждом уравнении решите, какой из этих углов имеет значение x .
Пример 5.Решите это уравнение относительно угла x :
Итак, синус какого угла равен ½?
Задача 7. Решите это уравнение для угла x :
Задача 8. Доказательство: Площадь A равностороннего треугольника со стороной s равна . A = ¼ с 2 . Площадь A любого треугольника равна половине синуса любого угла, умноженному на произведение двух сторон, составляющих угол. (Тема 2, проблема 6.) В равностороннем треугольнике каждая сторона равна s , а каждый угол равен 60 °.Следовательно, A = ½ sin 60 ° s 2 . Так как sin 60 ° = ½, Проблема 1 A = ½ · ½ с 2 = ¼ с 2 . Задача 9. Доказательство: Площадь A равностороннего треугольника, вписанного в круг радиуса r, равна
Три радиуса делят треугольник на три равных треугольника. Боковая сторона Боковая Следовательно, каждый радиус делит каждую вершину пополам на два угла по 30 °. Теорема 2 Triangle OBD, следовательно, треугольник 30-60-90. Следовательно, с = r , так что с 2 = 3 r 2 . Теперь площадь A равностороннего треугольника равна . A = ¼ с 2 . Задача 8 Следовательно,
Это то, что мы хотели доказать. Задача 10. Доказательство: Биссектрисы равностороннего треугольника пересекаются в точке, которая составляет две трети расстояния от вершины треугольника до основания. Пусть ABC — равносторонний треугольник, AD, BF, CE — биссектрисы углов A, B, C соответственно; тогда эти биссектрисы пересекаются в точке P, так что AP составляет две трети AD. Во-первых, треугольники BPD, APE равны. Поскольку, поскольку треугольник равносторонний, а BF, AD — биссектрисы, тогда углы PBD, PAE равны и каждый Теорема 2 Углы PDB, AEP тогда прямые и равны. Следовательно, Уголок боковой треугольника BPD, APE равны.
Задача 2 Следовательно, BP = 2PD. Но AP = BP, потому что треугольники APE, BPD соприкасаются, и это стороны, противоположные равным углам. Следовательно, AP составляет две трети всего AD. Доказательство Вот доказательство того, что в треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:. Он основан на том факте, что треугольник 30 ° -60 ° -90 ° равен половине равностороннего треугольника. Нарисуйте равносторонний треугольник ABC. Тогда каждый из его равных углов равен 60 °. (Теоремы 3 и 9) Проведите прямую AD, разделяющую угол A пополам на два угла по 30 °. Теперь, поскольку BD равно DC, то BD составляет половину BC. Это означает, что BD также является половиной AB, потому что AB равно BC. То есть BD: AB = 1: 2 Из теоремы Пифагора мы можем найти третью сторону AD:
Следовательно, в треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:; что мы и пытались доказать. Следствие. Квадрат, нарисованный на высоте равностороннего треугольника, составляет три четверти квадрата, нарисованного сбоку. Следующая тема: Равнобедренный прямоугольный треугольник Темы | Дом Сделайте пожертвование, чтобы TheMathPage оставалась в сети. Авторские права © 2021 Лоуренс Спектор Вопросы или комментарии? Эл. Почта: [email protected]
Единичный круг: функции синуса и косинусаЧтобы определить наши тригонометрические функции, мы начнем с рисования единичного круга, круга с центром в начале координат и радиусом 1, как показано на рисунке 2.Угол (в радианах), который пересекает [latex] t [/ latex], образует дугу длиной [latex] s [/ latex]. Используя формулу [latex] s = rt [/ latex] и зная, что [latex] r = 1 [/ latex], мы видим, что для единичной окружности , [latex] s = t [/ latex]. Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемых квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление, в котором развернется положительный угол. Четыре квадранта обозначены I, II, III и IV. Для любого угла [латекс] t [/ латекс] мы можем обозначить пересечение конечной стороны и единичного круга его координатами, [латекс] \ left (x, y \ right) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f \ left (t \ right) = \ cos t [/ latex] и [latex] f \ left (t \ right) = \ sin t [/ latex] соответственно. Это означает [латекс] x = \ cos t [/ latex] и [латекс] y = \ sin t [/ latex]. Рис. 2. Единичная окружность с центральным углом [латекс] t [/ латекс] радиан A Общее примечание: Unit CircleЕдиничная окружность имеет центр [латекс] \ влево (0,0 \ вправо) [/ латекс] и радиус [латекс] 1 [/ латекс].В единичном круге длина перехваченной дуги равна радианам центрального угла [латекс] 1 [/ латекс]. Пусть [latex] \ left (x, y \ right) [/ latex] будет конечной точкой единичной окружности дуги длиной [латекс] s [/ latex]. Координаты [latex] \ left (x, y \ right) [/ latex] этой точки могут быть описаны как функции угла. Определение функций синуса и косинусаТеперь, когда у нас есть помеченная единичная окружность, мы можем узнать, как координаты [latex] \ left (x, y \ right) [/ latex] соотносятся с длиной дуги и углом .Синусоидальная функция связывает действительное число [латекс] t [/ латекс] с координатой y точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [латекс] t [/ латекс] равен значению y конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 2 синус равен [latex] y [/ latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — координата y соответствующей точки на единичной окружности. Функция косинуса угла [латекс] t [/ latex] равна значению x конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 3 косинус равен [латекс] х [/ латекс]. Рисунок 3 Поскольку понятно, что синус и косинус являются функциями, нам не всегда нужно записывать их в скобках: [latex] \ sin t [/ latex] то же самое, что [latex] \ sin \ left (t \ right) [ / latex] и [latex] \ cos t [/ latex] то же самое, что и [latex] \ cos \ left (t \ right) [/ latex].{2} [/ латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают сокращенную запись. В случае сомнений используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер. Общее примечание: функции синуса и косинусаЕсли [латекс] t [/ latex] является действительным числом и точка [латекс] \ left (x, y \ right) [/ latex] на единичном круге соответствует углу [латекса] t [/ latex] , затем [латекс] \ cos t = x [/ латекс] [латекс] \ sin t = y [/ латекс] Как сделать: по точкеP [латекс] \ left (x, y \ right) [/ latex] на единичной окружности, соответствующей углу [латекс] t [/ latex], найдите синус и косинус.
Пример 1: Поиск значений функции для синуса и косинусаТочка [латекс] P [/ латекс] — это точка на единичной окружности, соответствующая углу [латекс] t [/ латекс], как показано на рисунке 4. Найдите [латекс] \ cos \ left (t \ right) \\ [/ latex] и [latex] \ text {sin} \ left (t \ right) \\ [/ latex]. Рисунок 4 РешениеМы знаем, что [latex] \ cos t [/ latex] — это координата x соответствующей точки на единичном круге, а [latex] \ sin t [/ latex] — координата y соответствующей точка на единичной окружности. Итак: [латекс] \ begin {массив} {l} \ begin {array} {l} \\ x = \ cos t = \ frac {1} {2} \ end {array} \ hfill \\ y = \ sin t = \ frac {\ sqrt {3}} {2} \ hfill \ end {array} \\ [/ latex] Попробуй 1Определенный угол [латекс] t [/ латекс] соответствует точке на единичной окружности в [латекс] \ left (- \ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex], как показано на рисунке 5. {2} t = 1 [/ латекс] Как сделать: учитывая синус некоторого угла [латекс] t [/ латекс] и его положение в квадранте, найдите косинус [латекс] t [/ латекс].
Пример 3: Нахождение косинуса из синуса или синуса из косинусаЕсли [латекс] \ sin \ left (t \ right) = \ frac {3} {7} \\ [/ latex] и [latex] t [/ latex] находится во втором квадранте, найдите [latex] \ cos \ left (t \ right) \\ [/ латекс].{2} \ left (t \ right) = \ frac {40} {49} \ hfill \\ \ text {cos} \ left (t \ right) = \ pm \ sqrt {\ frac {40} {49}} = \ pm \ frac {\ sqrt {40}} {7} = \ pm \ frac {2 \ sqrt {10}} {7} \ hfill \ end {array} \\ [/ latex] Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицательный. Итак, Попробовать 3Если [латекс] \ cos \ left (t \ right) = \ frac {24} {25} \\ [/ latex] и [latex] t [/ latex] находится в четвертом квадранте, найдите [latex] \ text {грех} \ влево (т \ вправо) \\ [/ латекс].Треугольник \ circ [/ latex] — это равнобедренный треугольник, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны. Рисунок 9 При [latex] t = \ frac {\ pi} {4} [/ latex], что составляет 45 градусов, радиус единичной окружности делит пополам угол первого квадранта . Это означает, что радиус лежит вдоль линии [латекс] y = x [/ latex].{2} = \ frac {1} {2} \\ \ text {} x = \ pm \ frac {1} {\ sqrt {2}} \ end {array} \\ [/ latex] В квадранте I [латекс] x = \ frac {1} {\ sqrt {2}} \\ [/ latex]. \ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex].\ circ [/ latex], как показано на рисунке 12. Рисунок 11 Рисунок 12 Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [латекс] 2y [/ latex], и, поскольку все стороны равны, мы также можем сделать вывод, что [latex] r = 2y [/ latex] или [latex] y = \ frac {1} {2 } г [/ латекс]. Поскольку [латекс] \ sin t = y [/ latex], [латекс] \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} r \\ [/ latex] А поскольку [latex] r = 1 [/ latex] в нашем единичном круге , [латекс] \ begin {array} {l} \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} \ left (1 \ right) \ hfill \\ \ текст {} = \ frac {1} {2} \ hfill \ end {array} \\ [/ latex] Используя тождество Пифагора, мы можем найти значение косинуса.\ circ [/ латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс] ABC [/ латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1. Рисунок 13 Угол наклона [латекс] ABD [/ латекс] составляет 30 °. Так, если двойной, угол [латекс] ABC [/ латекс] равен 60 °. [latex] BD [/ latex] — это серединный перпендикуляр к [latex] AC [/ latex], поэтому он разрезает [latex] AC [/ latex] пополам. Это означает, что [latex] AD [/ latex] — это [latex] \ frac {1} {2} [/ latex] радиус или [latex] \ frac {1} {2} [/ latex].\ circ [/ latex] — это [латекс] \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \\ [/ latex], поэтому мы можем найти синус и косинус. [латекс] \ begin {array} {l} \ left (x, y \ right) = \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \ hfill \\ x = \ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \ hfill \\ \ cos t = \ frac {1} {2}, \ sin t = \ гидроразрыв {\ sqrt {3}} {2} \ hfill \ end {array} \\ [/ latex] Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.
На рисунке 14 показаны общие углы в первом квадранте единичной окружности. Рисунок 14 Использование калькулятора для поиска синуса и косинусаЧтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Будьте внимательны : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы для входного значения. Когда мы вычисляем [латекс] \ cos \ left (30 \ right) [/ latex] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в радианном режиме. Как сделать: если задан угол в радианах, используйте графический калькулятор, чтобы найти косинус.
Пример 4: Использование графического калькулятора для поиска синуса и косинусаВычислить [латекс] \ cos \ left (\ frac {5 \ pi} {3} \ right) \\ [/ latex] с помощью графического калькулятора или компьютера.\ circ [/ latex], например, включив коэффициент преобразования в радианы как часть входных данных: SIN (20 × π ÷ 180) ВВОД Попробовать 4Вычислить [латекс] \ sin \ left (\ frac {\ pi} {3} \ right) \\ [/ latex]. Решение
Определение области и диапазона функций синуса и косинусаТеперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области и диапазоны. Каковы области определения функций синуса и косинуса? То есть, какие наименьшие и наибольшие числа могут быть входами функций? Поскольку углы меньше 0 и углы больше [латекс] 2 \ pi [/ latex] все еще могут быть нанесены на единичный круг и имеют реальные значения [латекс] x, y [/ latex] и [латекс] r [/ latex], не существует нижнего или верхнего предела углов, которые могут входить в функции синуса и косинуса.Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число. Каковы диапазоны функций синуса и косинуса? Каковы наименьшие и наибольшие возможные значения их производительности? Мы можем увидеть ответы, исследуя единичную окружность , как показано на рисунке 15. Границы координаты x равны [латекс] \ слева [-1,1 \ справа] [/ латекс]. Границы координаты y также равны [latex] \ left [-1,1 \ right] [/ latex].Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex]. Рисунок 15 Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса является координатой y на единичной окружности, другой угол с таким же синусом будет иметь то же значение y , но будет иметь противоположное значение x .Следовательно, его значение косинуса будет противоположным значению косинуса первого угла. Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с таким же косинусом будет иметь одинаковое значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположным значению синуса исходного угла. Как показано на рисунке 16, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны.Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны. [латекс] \ begin {array} {lll} \ sin \ left (t \ right) = \ sin \ left (\ alpha \ right) \ hfill & \ text {and} \ hfill & \ cos \ left (t \ right ) = — \ cos \ left (\ alpha \ right) \ hfill \\ \ sin \ left (t \ right) = — \ sin \ left (\ beta \ right) \ hfill & \ text {и} \ hfill & \ cos \ left (t \ right) = \ cos \ left (\ beta \ right) \ hfill \ end {array} [/ latex] Рисунок 16 Напомним, что опорный угол угла — это острый угол [латекс] t [/ латекс], образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. \ circ \ mathrm {-t} | [/ latex].\ circ [/ latex] Попробуй 5Найдите опорный угол [латекса] \ frac {5 \ pi} {3} [/ latex]. Решение Использование опорных угловА теперь давайте вернемся к колесу обозрения, представленному в начале этого раздела. Предположим, всадник делает снимок, остановившись на высоте двадцати футов над уровнем земли. Затем всадник совершает поворот на три четверти по кругу. Какая у всадника новая высота? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов, или при отрицательном угле .Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для поиска координат [latex] \ left (x, y \ right) [/ latex] для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла. Использование опорных углов для оценки тригонометрических функцийМы можем найти косинус и синус любого угла в любом квадранте, если мы знаем косинус или синус его опорного угла.Абсолютные значения косинуса и синуса угла такие же, как и у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака значений x в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений y в этом квадранте. Общее примечание: Использование опорных углов для определения косинуса и синусаУглы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы.Знак (положительный или отрицательный) можно определить по квадранту угла. Как: для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
Попробуй 6а.\ circ \ right) [/ латекс]. г. Используйте опорный угол [латекс] — \ frac {\ pi} {6} [/ latex], чтобы найти [латекс] \ cos \ left (- \ frac {\ pi} {6} \ right) [/ latex] и [латекс] \ sin \ left (- \ frac {\ pi} {6} \ right) [/ latex]. Использование опорных углов для поиска координатТеперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности.Они показаны на рисунке 19. Найдите время, чтобы узнать координаты [latex] \ left (x, y \ right) [/ latex] всех основных углов в первом квадранте. В дополнение к изучению значений специальных углов, мы можем использовать опорные углы, чтобы найти координаты [latex] \ left (x, y \ right) [/ latex] любой точки на единичной окружности, используя то, что мы знаем об опорных углах. вместе с удостоверениями [латекс] \ begin {array} {l} x = \ cos t \ hfill \\ y = \ sin t \ hfill \ end {array} [/ latex] Сначала мы находим опорный угол, соответствующий данному углу.Затем мы берем значения синуса и косинуса опорного угла и даем им знаки, соответствующие значениям квадранта y и x . Как сделать: учитывая угол точки на окружности и радиус окружности, найдите координаты [latex] \ left (x, y \ right) [/ latex] точки.
Пример 6: Использование единичной окружности для поиска координатНайдите координаты точки на единичной окружности под углом [latex] \ frac {7 \ pi} {6} [/ latex]. РешениеМы знаем, что угол [латекс] \ frac {7 \ pi} {6} [/ латекс] находится в третьем квадранте. Во-первых, давайте найдем опорный угол, измерив угол к оси x .Чтобы найти опорный угол угла, конечная сторона которого находится в квадранте III, мы находим разность угла и [латекс] \ pi [/ латекс]. [латекс] \ frac {7 \ pi} {6} — \ pi = \ frac {\ pi} {6} [/ latex] Далее мы найдем косинус и синус опорного угла: [латекс] \ cos \ left (\ frac {\ pi} {6} \ right) = \ frac {\ sqrt {3}} {2} \ sin \ left (\ frac {\ pi} {6} \ right ) = \ frac {1} {2} [/ латекс] Мы должны определить соответствующие знаки для x и y в данном квадранте.Поскольку наш исходный угол находится в третьем квадранте, где оба [latex] x [/ latex] и [latex] y [/ latex] отрицательны, косинус и синус отрицательны. [латекс] \ begin {array} {l} \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {\ sqrt {3}} {2} \ hfill \\ \ sin \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {1} {2} \ hfill \ end {array} [/ latex] Теперь мы можем вычислить координаты [latex] \ left (x, y \ right) [/ latex], используя тождества [latex] x = \ cos \ theta [/ latex] и [latex] y = \ sin \ theta [ /латекс]. Координаты точки: [latex] \ left (- \ frac {\ sqrt {3}} {2}, — \ frac {1} {2} \ right) [/ latex] на единичной окружности.{2} t = 1 [/ латекс] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом 1 единица.
- Используя единичную окружность, синус угла [латекс] t [/ latex] равен значению y конечной точки единичной окружности дуги длиной [латекс] t [/ латекс], тогда как косинус угол [latex] t [/ latex] равен значению x конечной точки.
- Значения синуса и косинуса наиболее точно определяются, когда соответствующая точка единичной окружности попадает на ось.
- Когда синус или косинус известен, мы можем использовать пифагорову тождество, чтобы найти другое. Пифагорейская идентичность также полезна для определения синусов и косинусов особых углов.
- Калькуляторы и программное обеспечение для построения графиков полезны для поиска синусов и косинусов, если известна правильная процедура ввода информации.
- Все функции синуса и косинуса являются действительными числами.
- Диапазон функций синуса и косинуса: [latex] \ left [-1,1 \ right] [/ latex].
- Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус его опорного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла — это размерный угол [латекс] t [/ латекс],
, образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. - Опорные углы можно использовать для определения синуса и косинуса исходного угла.
- Опорные углы также можно использовать для определения координат точки на окружности.
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 1
- синусоидальная функция
- значение y точки на единичной окружности, соответствующее заданному углу
- единичный круг
- круг с центром в [latex] \ left (0,0 \ right) [/ latex]
и радиусом
Раздел упражнения
- 1.Опишите единичный круг.
- 2. Что обозначают координаты x- и y- точек на единичной окружности?
3. Обсудите разницу между котерминальным углом и опорным углом.
4. Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
5. Объясните, чем синус угла во втором квадранте отличается от синуса его опорного угла в единичной окружности.
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором лежит конечная точка, определяемая [latex] t [/ latex].
6. [латекс] \ text {sin} \ left (t \ right) <0 [/ latex] и [latex] \ text {cos} \ left (t \ right) <0 [/ latex]
7. [латекс] \ text {sin} \ left (t \ right)> 0 [/ latex] и [latex] \ cos \ left (t \ right)> 0 [/ latex]
8. [латекс] \ sin \ left (t \ right)> 0 [/ latex] и [латекс] \ cos \ left (t \ right) <0 [/ latex]
9.[латекс] \ sin \ left (t \ right) <0 [/ latex] и [латекс] \ cos \ left (t \ right)> 0 [/ latex]
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
10. [латекс] \ sin \ frac {\ pi} {2} [/ латекс]
11. [латекс] \ sin \ frac {\ pi} {3} [/ латекс]
12. [латекс] \ cos \ frac {\ pi} {2} [/ латекс]
13. [латекс] \ cos \ frac {\ pi} {3} [/ латекс]
14. [латекс] \ sin \ frac {\ pi} {4} [/ латекс]
15. [латекс] \ cos \ frac {\ pi} {4} [/ латекс]
16.\ circ [/ latex]
28. [латекс] \ frac {5 \ pi} {4} [/ латекс]
29. [латекс] \ frac {2 \ pi} {3} [/ латекс]
30. [латекс] \ frac {5 \ pi} {6} [/ латекс]
31. [латекс] \ frac {-11 \ pi} {3} [/ латекс]
32. [латекс] \ frac {-7 \ pi} {4} [/ латекс]
33. [латекс] \ frac {- \ pi} {8} [/ латекс]
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла. Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.\ circ [/ latex]
42. [латекс] \ frac {5 \ pi} {4} [/ латекс]
43. [латекс] \ frac {7 \ pi} {6} [/ латекс]
44. [латекс] \ frac {5 \ pi} {3} [/ латекс]
45. [латекс] \ frac {3 \ pi} {4} [/ латекс]
46. [латекс] \ frac {4 \ pi} {3} [/ латекс]
47. [латекс] \ frac {2 \ pi} {3} [/ латекс]
48. [латекс] \ frac {5 \ pi} {6} [/ латекс]
49. [латекс] \ frac {7 \ pi} {4} [/ латекс]
Найдите требуемое значение для следующих упражнений.
50. Если [латекс] \ text {cos} \ left (t \ right) = \ frac {1} {7} [/ latex] и [latex] t [/ latex] находится в квадранте 4 -го , найдите [латекс] \ text {sin} \ left (t \ right) [/ latex].
51. Если [латекс] \ text {cos} \ left (t \ right) = \ frac {2} {9} [/ latex] и [latex] t [/ latex] находится в квадранте 1 st , найдите [латекс] \ text {sin} \ left (t \ right) [/ latex].
52. Если [латекс] \ text {sin} \ left (t \ right) = \ frac {3} {8} [/ latex] и [latex] t [/ latex] находится в квадранте 2 nd , найдите [латекс] \ text {cos} \ left (t \ right) [/ latex].
53. Если [латекс] \ text {sin} \ left (t \ right) = — \ frac {1} {4} [/ latex] и [latex] t [/ latex] находится в квадранте 3 rd найдите [латекс] \ text {cos} \ left (t \ right) [/ latex].\ circ [/ латекс].
56. Найдите координаты точки на окружности с радиусом 8, соответствующей углу [латекс] \ frac {7 \ pi} {4} [/ latex].
57. Найдите координаты точки на окружности с радиусом 16, соответствующей углу [латекс] \ frac {5 \ pi} {9} [/ latex].
58. Укажите область определения функций синуса и косинуса.
59. Укажите диапазон функций синуса и косинуса.
Для следующих упражнений используйте данную точку на единичном круге, чтобы найти значение синуса и косинуса [латекс] t [/ латекс].
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
Для следующих упражнений используйте графический калькулятор для оценки.\ circ [/ latex]
90. [латекс] \ sin \ left (\ frac {11 \ pi} {3} \ right) \ cos \ left (\ frac {-5 \ pi} {6} \ right) [/ latex]
91. [латекс] \ sin \ left (\ frac {3 \ pi} {4} \ right) \ cos \ left (\ frac {5 \ pi} {3} \ right) [/ latex]
92. [латекс] \ sin \ left (- \ frac {4 \ pi} {3} \ right) \ cos \ left (\ frac {\ pi} {2} \ right) [/ latex]
93. [латекс] \ sin \ left (\ frac {-9 \ pi} {4} \ right) \ cos \ left (\ frac {- \ pi} {6} \ right) [/ latex]
94. [латекс] \ sin \ left (\ frac {\ pi} {6} \ right) \ cos \ left (\ frac {- \ pi} {3} \ right) [/ latex]
95.[латекс] \ sin \ left (\ frac {7 \ pi} {4} \ right) \ cos \ left (\ frac {-2 \ pi} {3} \ right) [/ latex]
96. [латекс] \ cos \ left (\ frac {5 \ pi} {6} \ right) \ cos \ left (\ frac {2 \ pi} {3} \ right) [/ latex]
97. [латекс] \ cos \ left (\ frac {- \ pi} {3} \ right) \ cos \ left (\ frac {\ pi} {4} \ right) [/ latex]
98. [латекс] \ sin \ left (\ frac {-5 \ pi} {4} \ right) \ sin \ left (\ frac {11 \ pi} {6} \ right) [/ latex]
99. [латекс] \ sin \ left (\ pi \ right) \ sin \ left (\ frac {\ pi} {6} \ right) [/ latex]
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту.Ребенок входит в точку [latex] \ left (0,1 \ right) [/ latex], то есть в правильном положении на север. Предположим, карусель вращается против часовой стрелки.
100. Какие координаты ребенка через 45 секунд?
101. Какие координаты ребенка через 90 секунд?
102. Какие координаты ребенка через 125 секунд?
103. Когда у ребенка будут координаты [latex] \ left (0.707, -0.707 \ right) [/ latex], если поездка длится 6 минут? (Есть несколько ответов.)
104. Когда у ребенка будут координаты [latex] \ left (-0,866, -0,5 \ right) [/ latex], если поездка продлится 6 минут?
.

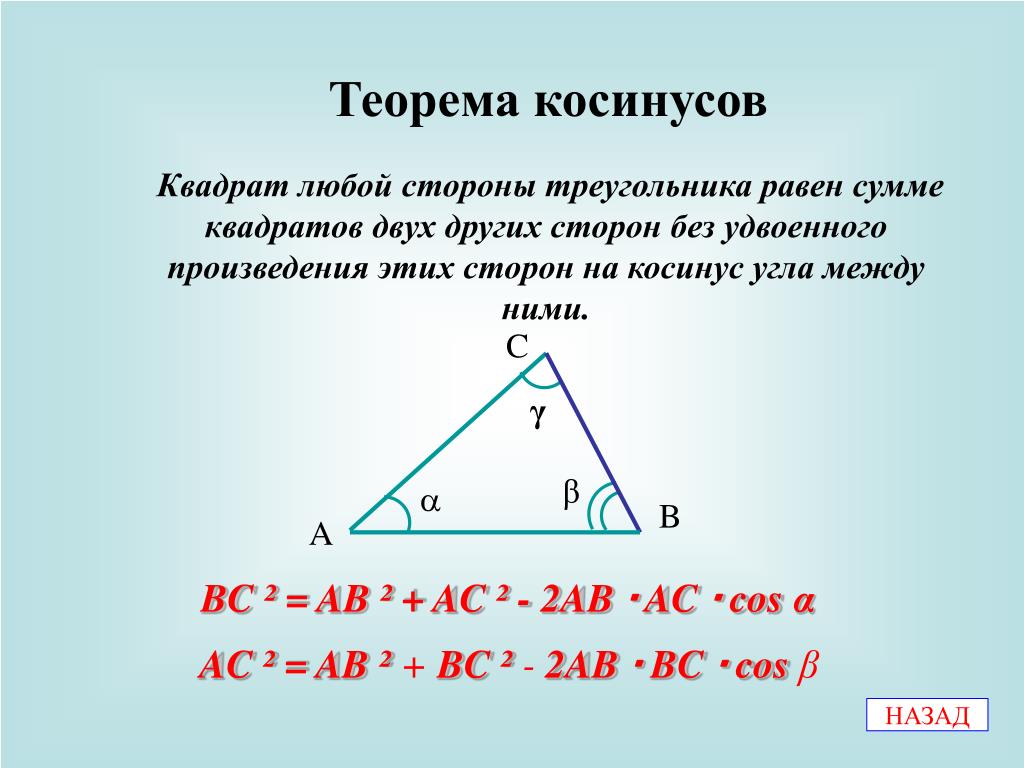
 {2}-2 b c \cos \alpha$
{2}-2 b c \cos \alpha$ {\circ}=289+196-238=24$$
{\circ}=289+196-238=24$$




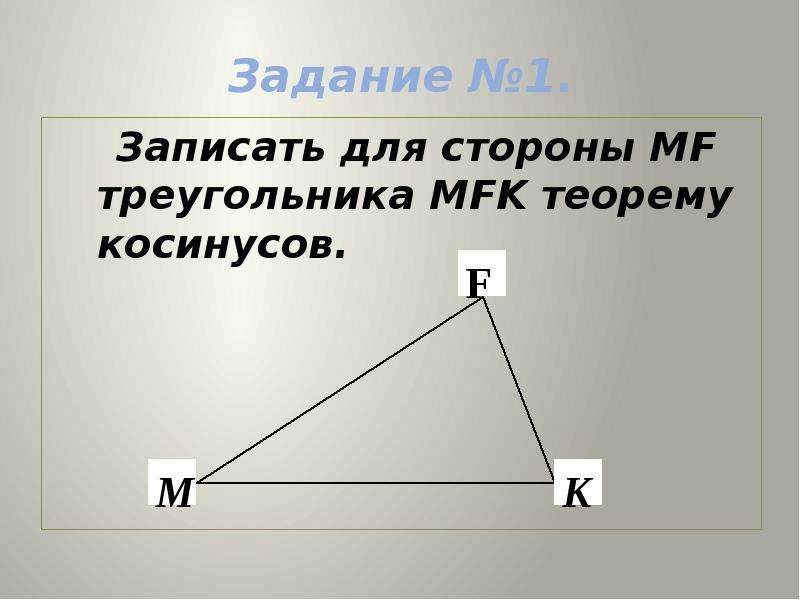
 Алгебраической символики тогда не существовало. Доказал теорему косинусов Евклид в 325 году до н.э.
Алгебраической символики тогда не существовало. Доказал теорему косинусов Евклид в 325 году до н.э.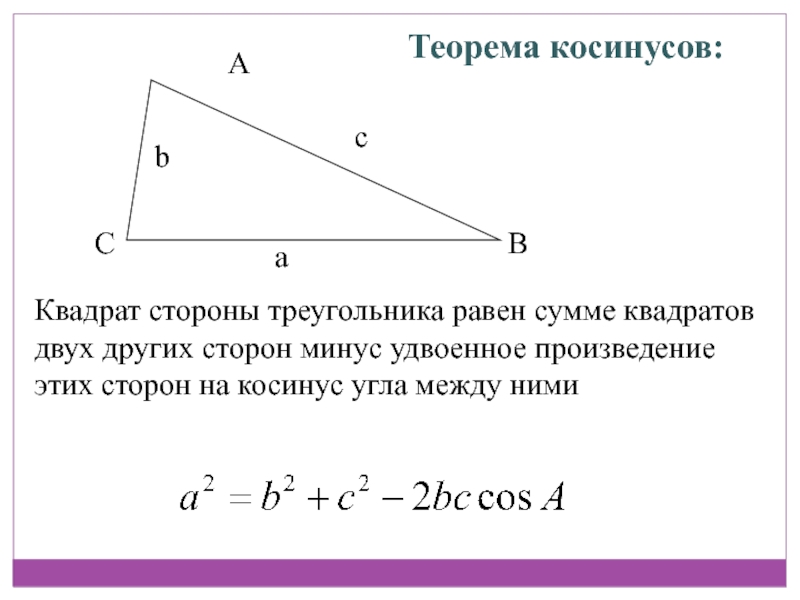
 1) АВ2=АС2+ВС2–2 АD*AС; а. 2) АС2= АВ2+ВС2-2ВС*СD.
1) АВ2=АС2+ВС2–2 АD*AС; а. 2) АС2= АВ2+ВС2-2ВС*СD.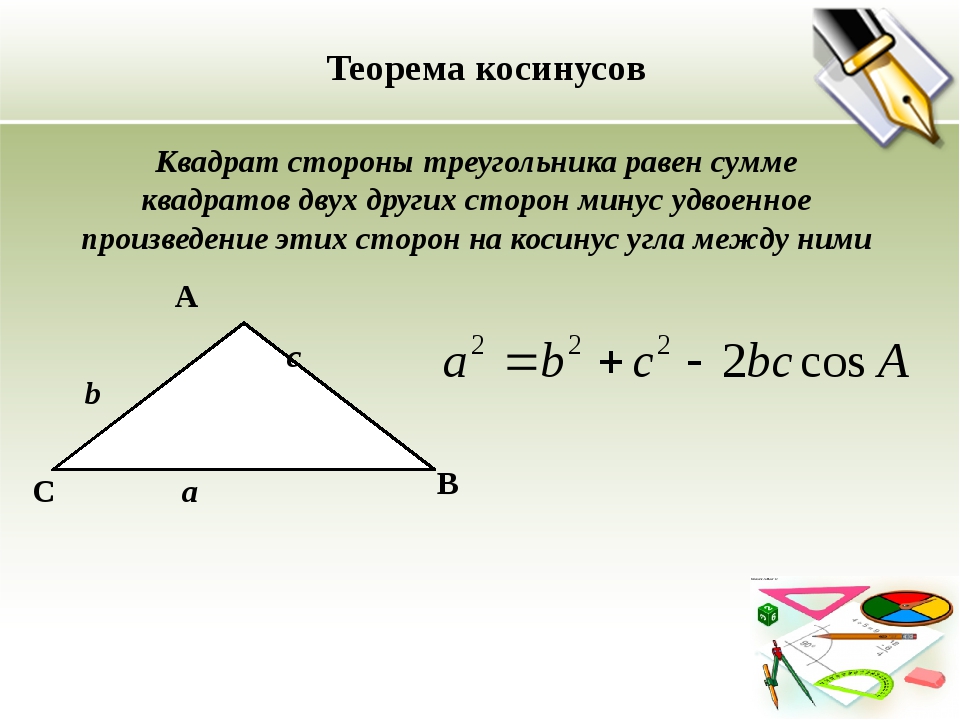
 Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.
Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.

 Так как A – острый, то cosA > 0, тогда a2 = b2 + c2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой.
Так как A – острый, то cosA > 0, тогда a2 = b2 + c2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой.