Содержание
Относительность механического движения — урок. Физика, 9 класс.
Чтобы разобраться в относительности механического движения, зададимся вопросом:
«Мы сейчас, в настоящий момент времени, движемся или находимся в состоянии покоя?»
Ты, конечно же, ответишь, что всё зависит от того, что мы делаем.
Просто сидим на месте или двигаемся куда-нибудь.
Однако это не совсем верно.
Дело в том, что даже когда ты сидишь, стоишь или лежишь на одном и том же месте —
ты всё равно движешься!
Как это понять? Да всё очень просто. Я предполагаю, что ты сейчас находишься на планете Земля, так вот знай: она движется вокруг Солнца, таким образом, и ты движешься вместе с Землёй вокруг Солнца.
Магазины и деревья на улице не стоят на месте? Стоя возле них, мы же видим, что они никуда не движутся. Так движутся или нет?
Со всем разобраться поможет слово «относительно».
Пример:
Если ты находишься в движущемся вагоне трамвая, то относительно двери того же трамвая ты не движешься, а относительно растущих деревьев ты движешься.
Давайте примем дом за неподвижное тело. Правильно оно называется тело отсчёта. Относительно него стоящие рядом деревья находятся на месте, то есть не движутся. А пролетающие рядом птицы и едущие по дороге автомобили находятся в движении.
Чтобы найти скорость движения одного тела относительно другого, необходимо сложить векторы этих скоростей.
Классический закон сложения скоростей гласит:
скорость тела относительно неподвижной системы отсчёта равна геометрической сумме двух скоростей — скорости тела относительно подвижной системы отсчёта и скорости подвижной системы отсчёта относительно неподвижной.
Вспомним, как складываются векторы. Пусть это будут векторы скорости V→1 и V→2.
Вот они направлены в одну сторону, например, так:
Для того чтобы их сложить, нужно выстроить их друг за другом.
Это называется сложением векторов по правилу треугольника.
Должно получиться так:
В результате сложения таких векторов должен получиться один результирующий.
Покажем его красным цветом. Это вектор V→.
Он получился, когда мы соединили начало первого вектора с концом последнего.
Два вектора V→1 и V→2 сложились, и получился один вектор V→. Всё просто.
Бывает, что векторы могут быть направлены в разные стороны. Скажем, вот так:
Будем пробовать их складывать по известному правилу — правилу треугольника.
Выстроим векторы друг за другом. Должно получиться примерно так:
Снова соединим начало первого вектора с концом последнего.
Чтобы было лучше видно, изобразим результирующий вектор красным цветом.
Два вектора V→1 и V→2 сложились, и получился один вектор V→.
Может случиться, что векторы лежат не так ровно, а, скажем, под углом \(90°\) друг к другу.
Например:
Перед нами два вектора — V→1 и V→2. Как же их сложить?
Снова выстраиваем их друг за другом, чтобы получились стороны треугольника.
Или соединяем начала этих векторов — тогда получится правило параллелограмма.
Правило треугольника нам уже знакомо. Просто соединяем начало первого вектора с концом последнего.
Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.
Результат сложения не зависит от выбранного правила сложения — правила треугольника или правила параллелограмма.
Должен получиться один и тот же вектор V→. Изобразим его красным.
Теперь можно приступать к решению задач на относительное движение.
Теория «Относительность движение и сложение скоростей для 9 кл. по физике»
В общем случае, при движениях систем отсчета с ускорением друг относительно друга, ускорения тела в различных системах отсчета оказываются различными.
В случае, когда вектора относительной скорости v ′ и переносной скорости v0 параллельны друг другу, закон сложения скоростей можно записать в скалярной форме:
Относительность механического движения.
1. Механическое движение можно наблюдать только относительно других тел. Обнаружить изменение положения тела, если не с чем сравнивать невозможно.
Обнаружить изменение положения тела, если не с чем сравнивать невозможно.
2. В различных системах отсчета физические величины (скорость, ускорение, перемещение и т.д.), характеризующие движение одного и того же тела, могут быть различными.
3. Характер движения, траектория движения и т.п. могут быть различны в разных системах отсчета для одного и того же тела могут быть различны.
Пусть две СО движутся друг относительно друга с постоянной скоростью . Положение точки А в неподвижной системе К задано вектором , а в движущейся системе К1 — вектором . Из чертежа видим, что . Это уравнение позволяет переходить из одной СО в другую.
При этом мы считаем, что время течет в обеих СО одинаково.
Будем условно называть систему К неподвижной, а систему К1 — движущейся.
Тогда для случая, когда координаты y и z не меняются, получим:
— преобразования Галилея.
Из этих уравнений следует:
— расстояние между двумя точками абсолютно, т.е. не зависит от выбора СО. Пусть в неподвижной СО координаты точек x и x‘, а в подвижной соответственно x1 и x1‘. Тогда ;
Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение.
Получим:
— закон сложения скоростей. Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной.
Скорость подвижной СО относительно неподвижной наз. переносной скоростью.
При решении задач часто бывает удобно принимать одно из движущихся относительно Земли тел за неподвижное. Тогда скорость Земли в этой СО будет равна по величине и противоположна по направлению скорости данного тела.
Тогда скорость Земли в этой СО будет равна по величине и противоположна по направлению скорости данного тела.
Если скорости v1 и u сонаправлены (тела сближаются), то их проекции складываются, если противоположно направлены (тела удаляются) – вычитаются.
Если скорости направлены под прямым углом — ,
если угол произвольный, то необходимо пользоваться теоремой косинусов: .
Эти выводы справедливы для скоростей много меньших скорости света в вакууме (3.108м/с).
Презентация «Классический закон сложения скоростей и перемещений» | Презентация к уроку по физике (9, 10 класс) на тему:
Слайд 1
Относительность движения. Классический закон сложения скоростей и перемещений.
Слайд 2
Классический закон сложения перемещений.
Слайд 3
Скорость тела параллельна скорости ПСО
Слайд 4
Y0X — неподвижная система координат Y I 0 I X I — подвижная система координат Перемещение тела относительно неподвижной системы отсчета Перемещение тела относительно подвижной системы отсчета Перемещение подвижной системы относительно неподвижной системы отсчета
Слайд 5
X 0 Y Y 0 X X l Y l
Слайд 6
Перемещение тела относительно неподвижной системы отсчета (абсолютное) равно векторной сумме перемещения тела относительно подвижной системы отсчета (относительное) и перемещения подвижной системы отсчета относительно неподвижной (переносное). Классический закон сложения перемещений
Классический закон сложения перемещений
Слайд 7
X 0 y y 0 X X l Y l
Слайд 8
Если тело и подвижная система отсчета движутся в одном направлении , перемещение относительно неподвижной системы отсчета равно сумме перемещений подвижной системы отсчета и перемещения тела в подвижной системе отсчета. Частный случай:
Слайд 9
X 0 Y Y 0 X X l Y l
Слайд 10
x 0 y y 0 x X l Y l
Слайд 11
Если тело и подвижная система отсчета движутся в противоположных направлениях , перемещение относительно неподвижной системы отсчета равно разности перемещений подвижной системы отсчета и перемещения тела в подвижной системе отсчета. Частный случай:
Слайд 12
Классический закон сложения скоростей.
Слайд 13
Скорость тела относительно неподвижной системы отсчета Скорость тела относительно подвижной системы отсчета Скорость подвижной системы относительно неподвижной системы отсчета
Слайд 14
Скорость тела относительно неподвижной системы отсчета (абсолютная) равна векторной сумме скорости тела относительно подвижной системы отсчета (относительная) и скорости подвижной системы отсчета относительно неподвижной (переносная).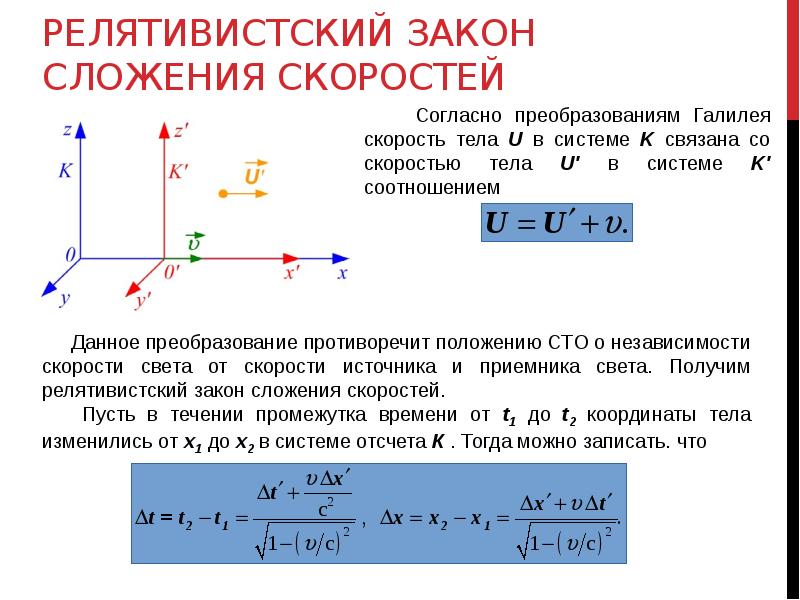 Классический закон сложения скоростей
Классический закон сложения скоростей
Слайд 15
X 0 Y Y 0 X X l Y l
Слайд 16
Если тело и подвижная система отсчета движутся в одном направлении , скорость относительно неподвижной системы отсчета равна сумме скоростей подвижной системы отсчета и тела в подвижной системе отсчета. Частный случай:
Слайд 17
X 0 Y Y 0 X X l Y l
Слайд 18
Если тело и подвижная система отсчета движутся в противоположных направлениях , скорость относительно неподвижной системы отсчета равна разности скоростей подвижной системы отсчета и тела в подвижной системе отсчета. Частный случай:
Слайд 19
Задача
Слайд 20
Сколько времени потребуется, чтобы на катере пройти расстояние 1,5км туда и обратно по реке, скорость течения которой V 1 =2км/ч, и по озеру(в стоячей воде), если скорость катера относительно воды в обоих случаях V 2 =8км/ч? Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение:
Слайд 21
Y 1 O 1 X 1 Y O X По течению
Слайд 23
Y 1 O 1 X 1 Y O X Против течения
Слайд 25
Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение:
Слайд 26
Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение:
Слайд 27
Y 1 O 1 X 1 Y O X По озеру туда
Слайд 28
Y 1 O 1 X 1 Y O X По озеру обратно
Слайд 29
Дано: S =1,5км V 1 =2км/ч V 2 =8км/ч t 1 — ? t 2 — ? Решение: Ответ: время движения по реке составляет 0,4 часа, по озеру 0,375 часа
Слайд 30
Скорость тела направлена под углом к скорости ПСО
Слайд 31
Y l 0 X l Y 0 X
Закон сложения скоростей
Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.
В этом определении ключевой является фраза «относительно других тел». Каждый из нас относительно какой-либо поверхности неподвижен, но относительно Солнца мы совершаем вместе со всей Землей орбитальное движение со скоростью 30 км/с, то есть движение зависит от системы отсчета.
Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение.
Например, описывая движения пассажиров в салоне автомобиля, систему отсчета можно связать с придорожным кафе, а можно с салоном автомобиля или с движущимся встречным автомобилем, если мы оцениваем время обгона
Преобразование координат и времени
Закон сложения скоростей является следствием преобразований координат и времени.
Пусть частица в момент времени t’ находится в точке (x’, y’, z’), а через малое время Δt’ в точке (x’ + Δx’, y’ + Δy’, z’ + Δz’) системы отсчета K’. Это два события в истории движущейся частицы. Имеем:
Это два события в истории движущейся частицы. Имеем:
Δx’ = vx’Δt’,
где
vx’ — x-я компонента скорости частицы в системе K’.
Аналогичные соотношения имеют место для остальных компонент.
Разности координат и промежутки времени (Δx, Δy, Δz, Δt) преобразуются так же, как координаты:
Δx = Δx’ + VΔt’,
Δy = Δу’,
Δz = Δz’,
Δt = Δt’.
Отсюда следует, что скорость той же частицы в системе K будет иметь компоненты:
vx = Δx / Δt = (Δx’ + VΔt’) / Δt = vx’ + V,
vy = vy’,
vz = vz’.
Это закон сложения скоростей. Его можно выразить в векторной форме:
Его можно выразить в векторной форме:
v̅ = v̅’ + V
(координатные оси в системах K и K’ параллельны).
Закон сложения скоростей
Если тело движется относительно системы отсчета К1 со скоростью V1, а сама система отсчета К1 движется относительно другой системы отсчета К2 со скоростью V, то скорость тела (V2) относительно второй системы отсчета К2 равна геометрической сумме векторов V1 и V.
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.
\( \vec{V_2} = \vec{V_1} + \vec{V} \)
где всегда
К2 — неподвижная система отсчета
V2 — скорость тела относительно неподвижной системы отсчета (К2)
К1 — подвижная система отсчета
V1 — скорость тела относительно подвижной системы отсчета (К1)
V — скорость подвижной системы отсчета (К1) относительно неподвижной системы отсчета (К2)
Закон сложения ускорений для поступательного движения
При поступательном движении тела относительно подвижной системы отсчёта и подвижной системы отсчёта относительно неподвижной, вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС}$ (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ${\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН}$ (относительного ускорения) и вектора ускорения подвижной системы отсчёта относительно неподвижной ${\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР}$ (переносного ускорения):
\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}\]
В общем случае, когда движение материальной точки (тела) является криволинейным, его в каждый момент времени можно представить как комбинацию поступательного движения материальной точки (тела) относительно подвижной системы отсчёта со скоростью \( {\overrightarrow{v}}_r \), и вращательного движения подвижной системы отсчёта относительно неподвижной с угловой скоростью \( {\overrightarrow{\omega }}_e \). В этом случае, при сложении ускорений, наряду с относительным и переносным ускорением необходимо учитывать и ускорение Кориолиса \( a_c=2{\overrightarrow{\omega }}_e\times {\overrightarrow{v}}_r \), которое характеризует изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.
В этом случае, при сложении ускорений, наряду с относительным и переносным ускорением необходимо учитывать и ускорение Кориолиса \( a_c=2{\overrightarrow{\omega }}_e\times {\overrightarrow{v}}_r \), которое характеризует изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.
Теорема Кориолиса
Вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта \( \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС} \) (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета \( {\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН} \) (относительного ускорения), вектора ускорения подвижной системы отсчёта относительно неподвижной \( {\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР} \) (переносного ускорения), и кориолисова ускорения \( a_c=2{\overrightarrow{{\mathbf \omega }}}_e\times {\overrightarrow{v}}_r={\overrightarrow{a}}_{КОР} \):
\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}+{\overrightarrow{a}}_{КОР}\]
Абсолютное перемещение равно сумме относительного и переносного перемещений.
Перемещение тела в неподвижной системе отсчета равно сумме перемещений: тела в подвижной системе отсчета и самой подвижной системы отсчета относительно неподвижной.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Сложение скоростей
1. Релятивистская механика
В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические электромагнитные процессы. По существу произошёл конфликт между двумя идеями классической механики первая — Пространство-время теории Ньютона, вторая — принцип относительности, перенесёнными в новую область — теорию электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями.
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое, электродинамическим эффектам? Интуиция довольно явным образом связанная с классическим принципом относительности говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Специальная теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Одновременно специальная теория относительности кардинально изменяет представления о пространстве и времени. Правило сложения скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
v r e l = v 1 + v 2 1 + v 1 v 2 c 2. {\displaystyle v_{rel}={\frac.}
{\displaystyle v_{rel}={\frac.}
Можно заметить, что в случае, когда v / c → 0 {\displaystyle v/c\rightarrow 0}, преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что механика в специальной теории относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся специальная теория относительности и классическая механика — первая является обобщением второй.
Правила сложения перемещений и скоростей
п.1. Правило сложения перемещений при прямолинейном движении
Рассмотрим движение катера по реке.
Можно говорить о движении катера как относительно реки, так и относительно берега.
При этом сама река также движется относительно берега.
Как было показано в §5 данного справочника, для описания движения необходимо указать тело отсчета и ввести связанную с ним систему отсчета.
Введем две системы отсчета.
Берег неподвижен. Назовем систему отсчета, связанную с берегом, неподвижной системой отсчета (НСО). Перемещение тела в НСО назовем абсолютным перемещением, \(\overrightarrow{r_a}.\)
Перемещение тела в НСО назовем абсолютным перемещением, \(\overrightarrow{r_a}.\)
Река подвижна. Назовем систему отсчета, связанную с рекой, подвижной системой отсчета (ПСО). Перемещение тела в ПСО назовем относительным перемещением, \(\overrightarrow{r_o}.\)
Перемещение реки относительно берега – это перемещение подвижной системы отсчета относительно неподвижной. Перемещение ПСО относительно НСО назовем переносным перемещением, \(\overrightarrow{r_п}.\)
Правило сложения перемещений
Абсолютное перемещение равно векторной сумме относительного и переносного перемещений: $$ \overrightarrow{r_a}=\overrightarrow{r_o}+ \overrightarrow{r_п} $$
Чтобы найти сумму двух векторов, нужно от конца первого вектора отложить второй вектор (см. §6 данного справочника).
При прямолинейном движении все перемещения направлены вдоль одной прямой. В этом случае сумму векторов найти проще.
Пример: правило сложения перемещений при движении катера по реке
Пусть катер плывет по течению реки.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в одну сторону, и модуль абсолютного перемещения равен сумме модулей векторов-слагаемых:
$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|+ |\overrightarrow{r_п}| $$
Теперь пусть катер плывет против течения.
В этом случае векторы \(\overrightarrow{r_o}\) и \(\overrightarrow{r_п}\) направлены в противоположные стороны, и модуль абсолютного перемещения равен разности модуля большего и модуля меньшего вектора:
$$ |\overrightarrow{r_a}|=|\overrightarrow{r_o}|- |\overrightarrow{r_п}| $$
п.2. Правило сложения скоростей при прямолинейном движении
Напомним, что:
Скорость – векторная величина, равная отношению перемещения ко времени, за которое это перемещение было совершено: $$ \overrightarrow{v}=\frac{\overrightarrow{r}}{t} $$
Тогда из закона сложения перемещений получаем: $$ \overrightarrow{r_a}=\overrightarrow{r_o} +\overrightarrow{r_п} \Rightarrow \frac{\overrightarrow{r_a}}{t}=\frac{\overrightarrow{r_o}}{t} +\frac{\overrightarrow{r_п}}{t}\Rightarrow \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Правило сложения скоростей
Абсолютная скорость равна векторной сумме относительной и переносной скоростей: $$ \overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п} $$
Если при описании движения выбрать направление координатной оси ОХ, то можно ввести проекции скоростей \(v_x\) (см. §8 данного справочника) и получить еще одно очень полезное при решении задач правило сложения:
§8 данного справочника) и получить еще одно очень полезное при решении задач правило сложения:
Правило сложения проекций скоростей при прямолинейном движении
Проекция абсолютной скорости на координатную ось ОХ равна сумме проекций относительной и переносной скоростей: $$ v_{ax}=v_{ox}+v_{пx} $$
п.3. Абсолютная скорость при движении катера по реке
Пусть собственная скорость катера (скорость относительно реки) равна \(v\), скорость течения (переносная скорость) равна \(u\).
Направим ось ОХ в направлении скорости катера, тогда её проекция будет положительной: \(v_{ox}=v\). Если катер плывет по течению, скорость течения также направлена по ОХ и её проекция положительна: \(v_{пx}=u\). Проекция абсолютной скорости равна сумме: $$ v_{ax}=v_{ox}+v_{пx}=v+u $$
Если катер плывет против течения, при сохранении направления оси OX скорость течения направлена противоположно и её проекция отрицательна: \(v_{пx}=-u\). Проекция абсолютной скорости равна разности $$ v_{ax}=v_{ox}+v_{пx}=v-u $$ Если \(v\gt u\), проекция абсолютной скорости положительна, \(v_{ax}\gt 0\), катер поднимается вверх по реке.
При недостаточной скорости катера \(v\lt u\), проекция абсолютной скорости отрицательна, \(v_{ax}\lt 0\). Катер не сможет подниматься вверх по реке, его будет сносить вниз.
Внимание!
При описании прямолинейного движения выбор направления оси ОХ, определение знаков проекций скоростей и перемещений важны для правильного хода решения задачи и объяснения полученных результатов.
Всегда помните: скорость и перемещение – это вектора, у которых есть не только величина, но и направление.
п.4. Задачи
Задача 1. По заданным векторам относительной и переносной скоростей найдите вектор абсолютной скорости. Какой путь пройдет тело в подвижной и неподвижной системе отсчета за 5 с?
a)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму:
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=4\ \text{м/с}\) — скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=3\ \text{м/с}\) — скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=4\cdot 5=20\ \text{м}\) — путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=3\cdot 5=15\ \text{м}\) — путь тела в неподвижной СО
Ответ: 20 м и 15 м
б)
Вектор абсолютной скорости равен сумме векторов: \(\overrightarrow{v_a}=\overrightarrow{v_o} +\overrightarrow{v_п}\)
Находим сумму:
Пользуясь заданным масштабом, получаем:
\(\overrightarrow{v_o}=|\overrightarrow{v_o}|=30\ \text{м/с}\) — скорость тела в подвижной СО
\(\overrightarrow{v_a}=|\overrightarrow{v_a}|=50\ \text{м/с}\) — скорость тела в неподвижной СО
Путь тела в разных СО:
\(s_о=v_о t;\ \ s_о=30\cdot 5=150\ \text{м}\) — путь тела в подвижной СО
\(s_a=v_a t;\ \ s_a=50\cdot 5=250\ \text{м}\) — путь тела в неподвижной СО
Ответ: 150 м и 250 м
Задача 2. Между двумя катерами, которые движутся навстречу друг другу со скоростями 10 км/ч и 12 км/ч, летает альбатрос с постоянной скоростью 15 км/ч. Сколько километров он пролетит до момента встречи катеров, если первоначальное расстояние между ними равнялось 99 км.
Между двумя катерами, которые движутся навстречу друг другу со скоростями 10 км/ч и 12 км/ч, летает альбатрос с постоянной скоростью 15 км/ч. Сколько километров он пролетит до момента встречи катеров, если первоначальное расстояние между ними равнялось 99 км.
Дано:
\(v_1=10\ \text{км/ч}\)
\(v_2=12\ \text{км/ч}\)
\(v=15\ \text{км/ч}\)
\(d=99\ \text{км}\)
_______________
\(s-?\)
Пусть первый катер – неподвижное тело отсчета. Тогда второй катер приближается к нему со скоростью, равной сумме скоростей \((v_1+v_2)\). Время, через которое катера встретятся: $$ t=\frac{d}{v_1+v_2} $$ За это время альбатрос пролетит расстояние: $$ s=vt=v\cdot\frac{d}{v_1+v_2}=\frac{v}{v_1+v_2}d $$ Подставляем: $$ s=\frac{15}{10+12}\cdot 99=67,5\ (\text{км}) $$ Ответ: 67,5 км
Задача 3. В подрывной технике используют бикфордов шнур, пламя по которому распространяется со скоростью 0,8 см/с. Какой длины шнур понадобится подрывнику, чтобы он успел отбежать на расстояние 300 м после того, как его подожжет?
Скорость бега равна 5 м/с.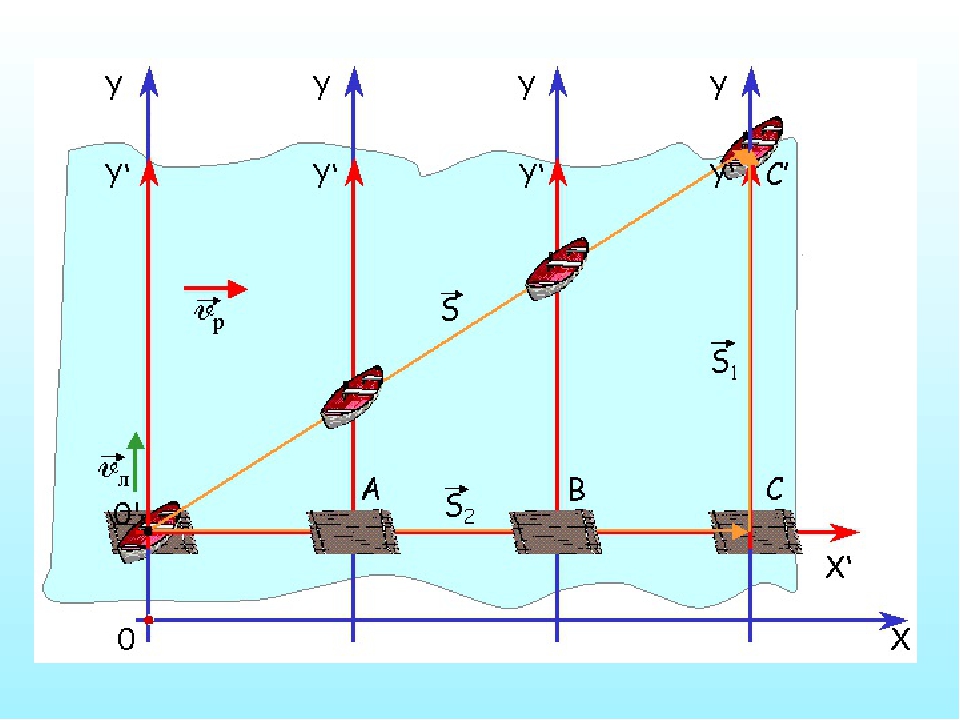
Дано:
\(u=0,8\ \text{см/с}=0,008\ \text{м/с}\)
\(v=5\ \text{м/c}\)
\(s=300\ \text{м}\)
_______________
\(L-?\)
На чертеже объект, который нужно взорвать, находится в точке B. Подрывник находится в точке O и бежит в точку A, длина шнура L=OB, расстояние AB=s.
Скорости \(u\) и \(v\) направлены противоположно. Время, за которое шнур догорит и подрывник добежит, определяется суммой скоростей \((u+v)\): $$ t=\frac{s}{u+v} $$ Длина шнура определяется временем и скоростью сгорания: $$ L=tu=\frac{su}{u+v} $$ Подставляем: $$ L=\frac{300\cdot 0,008}{5+0,008}\approx 0,48\ (\text{м})=48\ (\text{см}) $$ Ответ: 48 см
Задача 4. Из городов A и B, расстояние между которыми d=9 км, одновременно навстречу друг другу выехало два велосипедиста. В направлении от A к B дует ветер со скоростью \(v_0\). Первый велосипедист проехал расстояние между городами за 30 минут, а второй – за 45 минут. Найдите скорость ветра \(v_0\) и скорость велосипедистов в безветренную погоду, если она у них одинакова.
Найдите скорость ветра \(v_0\) и скорость велосипедистов в безветренную погоду, если она у них одинакова.
Пусть \(v\) — скорость велосипедистов в тихую погоду.
Переведем время в часы: \begin{gather*} t_1=30\ \text{мин}=\frac{30}{60}\text{ч}=\frac12\text{ч}\\ t_2=45\ \text{мин}=\frac{45}{60}\text{ч}=\frac34\text{ч} \end{gather*} Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й велосипедист, из А в Б | \(v+v_0\) | \(\frac12\) | \(\frac12(v+v_0)\) |
| 2й велосипедист, из Б в А | \(v-v_0\) | \(\frac34\) | \(\frac34(v-v_0)\) |
Расстояние: $$ d=\frac12(v+v_0)=\frac34(v-v_0)=9 $$ Получаем систему: $$ \begin{cases} \frac12(v+v_0)=9\\ \frac34(v-v_0)=9 \end{cases} \Rightarrow \begin{cases} v+v_0=9\cdot 2=18\\ v-v_0=9\cdot\frac43=12 \end{cases} \Rightarrow \begin{cases} 2v=18+12\\ 2v_0=18-12 \end{cases} \Rightarrow \begin{cases} v=\frac{30}{2}=15\\ v_0=\frac62=3 \end{cases} $$
Ответ:
Скорость ветра \(v_0=3\) км/ч
Скорость велосипедистов в тихую погоду \(v=15\) км/ч
Задача 5. Катер проходит расстояние между двумя пристанями по течению реки за 2 ч, а против течения – за 4 ч. За какое время от одной пристани к другой проплывет плот?
Катер проходит расстояние между двумя пристанями по течению реки за 2 ч, а против течения – за 4 ч. За какое время от одной пристани к другой проплывет плот?
Пусть \(v\) — скорость катера относительно реки (относительная скорость), \(u\) — скорость реки относительно берега (переносная скорость).
Составим таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Катер по течению | \(v+u\) | 2 | \(2(v+u)\) |
| Катер против течения | \(v-u\) | 4 | \(4(v-u)\) |
| Плот | \(u\) | \(t\) | \(s\) |
Расстояние во всех случаях одно и то же: $$ s=2(v+u)=4(v-u)\Rightarrow (v+u)=2(v-u)\Rightarrow u+2u=2v-v\Rightarrow 3u=v $$ Скорость катера в 3 раза больше скорости течения (скорости плота).
Тогда расстояние \(s=2(v+u)=2(3u+u)=8u\)
Время для плота: $$ t=\frac su=\frac{8u}{u}=8\ (\text{ч}) $$
Ответ: 8 ч
Задача 6*. 3}=\frac16\ \text{ч}=10\ \text{мин}\)
3}=\frac16\ \text{ч}=10\ \text{мин}\)
Второй корабль подбирает контейнеры каждые 10 мин.
Значит, в течение часа второй корабль подберет еще \(N=\frac{60\ \text{мин}}{10\ \text{мин}}=6\) контейнеров.
Ответ: 6 контейнеров
Задача 7*. Автомобиль, движущийся со скоростью 72 км/ч, был пробит пулей, летевшей перпендикулярно его движению. Отверстие в дальней стенке оказалось смещено относительно отверстия в ближней стенке на 4 см. Ширина салона 1,5 м. Считая, что пуля в салоне не изменила траекторию, определите её скорость.
Дано:
\(u=72\ \text{км/ч}=20\ \text{м/с}\)
\(d=4\ \text{cм}=0,04\ \text{м}\)
\(a=1,5\ \text{м}\)
_______________
\(v-?\)
Построим чертеж движения, вид сверху. Направим ось ОХ по движению автомобиля относительно земли, ось ОУ – по движению пули относительно земли.
Если перейти в систему отсчета, связанную с автомобилем, земля «побежит» в обратном направлении со скоростью \(–u\), и траектория пули в салоне сместится (пунктирная линия на чертеже). Смещение на расстояние \(d\) за счет движения автомобиля происходит за время, в течение которого пуля пролетает от одной стенки салона к другой: $$ d=ut,\ \ t=\frac av $$ Откуда: $$ v=\frac ad u $$ Подставляем: $$ v=\frac{1,5}{0,04}\cdot 20=750\ (\text{м/с}) $$ Ответ: 750 м/с
Смещение на расстояние \(d\) за счет движения автомобиля происходит за время, в течение которого пуля пролетает от одной стенки салона к другой: $$ d=ut,\ \ t=\frac av $$ Откуда: $$ v=\frac ad u $$ Подставляем: $$ v=\frac{1,5}{0,04}\cdot 20=750\ (\text{м/с}) $$ Ответ: 750 м/с
Закон сложения скоростей в классической механике
Классическая механика использует понятие абсолютной скорости точки. Она определяется как сумма векторов относительной и переносной скоростей этой точки. Подобное равенство содержит утверждение теоремы о сложении скоростей. Принято представлять, что скорость движения определенного тела в неподвижной системе отсчета является равной векторной сумме скорости такого же физического тела относительно подвижной системе отсчета. В этих координатах находится непосредственно тело.
сложения скоростей. Автор24 — интернет-биржа студенческих работ»>
Рисунок 1. Классический закон сложения скоростей. Автор24 — интернет-биржа студенческих работ
Примеры закона сложения скоростей в классической механике
Рисунок 2. Пример сложения скоростей. Автор24 — интернет-биржа студенческих работ
Пример сложения скоростей. Автор24 — интернет-биржа студенческих работ
Существует несколько основных примеров сложения скоростей, согласно установленным правилам, взятым за основу в механической физике. В качестве простейших объектов при рассмотрении физических законов может быть взят человек и любое движущееся тело в пространстве, с которым происходит прямое или косвенное взаимодействие.
Пример 1
Например, человек, который движется по коридору пассажирского поезда со скоростью пять километров в час, при этом состав двигается со скоростью 100 километров в час, то он относительно окружающего пространства двигается со скоростью 105 километров в час. При этом направление движения человека и транспортного средства должны совпадать. Такой же принцип действует и при движении в обратном направлении. В этом случае человек будет перемещаться относительно земной поверхности со скоростью 95 километров в час.
Если значения скорости двух объектов относительно друг друга будут совпадать, то они станут неподвижными с точки зрения движущихся объектов. При вращении скорость изучаемого объекта равна сумме скоростей движения объекта относительно движущейся поверхности другого объекта.
При вращении скорость изучаемого объекта равна сумме скоростей движения объекта относительно движущейся поверхности другого объекта.
Принцип относительности Галилея
Ученые смогли сформулировать основные формулы для ускорений объектов. Из нее следует, что движущаяся система отсчета удаляется относительно другой без видимого ускорения. Это закономерно в тех случаях, когда ускорение тел происходит одинаково в разных системах отсчета.
Подобные рассуждения берут начало еще во времена Галилея, когда сформировался принцип относительности. Известно, что по второму закону Ньютона ускорение тел имеет принципиальное значение. От этого процесса зависит относительное положение двух тел в пространстве, скорость физических тел. Тогда все уравнения можно записать одинаковым образом в любой инерциальной системе отсчета. Это говорит о том, что классические законы механики не будут иметь зависимость от положения в инерциальной системе отсчета, как принято действовать при осуществлении исследования.
Наблюдаемое явление также не имеет зависимость от конкретного выбора системы отсчета. Подобные рамки в настоящее время рассматриваются как принцип относительности Галилея. Он вступает в некоторые противоречия с иными догмами физиков-теоретиков. В частности, теория относительности Альберта Эйнштейна предполагает иные условия действия.
Принцип относительности Галилея базируется на нескольких основных понятиях:
- в двух замкнутых пространствах, которые движутся прямолинейно и равномерно относительно друг друга, результат внешнего воздействия всегда будет иметь одинаковое значение;
- подобный результат будет действителен только для любого механического действия.
В историческом контексте изучения основ классической механики, подобная трактовка физических явлений сформировалась во многом, как результат интуитивного мышления Галилея, что подтвердилось в научных трудах Ньютона, когда тот представил свою концепцию классической механики. Однако подобные требования по Галилею могут накладывать на структуру механики некоторые ограничения. Это влияет на ее возможные формулировки, оформление и развитие.
Это влияет на ее возможные формулировки, оформление и развитие.
Закон движения центра масс и закон сохранения импульса
Рисунок 3. Закон сохранения импульса. Автор24 — интернет-биржа студенческих работ
Одной из общих теорем в динамике стала теорема центра инерции. Ее также называют теоремой о движении центра масс системы. Подобный закон можно вывести из общих законов Ньютона. Согласно ему, ускорение центра масс в динамической системе не является прямым следствием внутренних сил, которые действуют на тела всей системы. Оно способно связать процесс ускорения с внешними силами, которые действуют на такую систему.
Рисунок 4. Закон движения центра масс. Автор24 — интернет-биржа студенческих работ
В качестве объектов, о которых идет речь в теореме, выступают:
- импульс материальной точки;
- система тел.
Эти объекты можно описать как физическую векторную величину. Она является необходимой мерой воздействия силы, при этом полностью зависит от времени действия силы.
При рассмотрении закона сохранения количества движения утверждается, что векторная сумма импульсов всех тел система полностью представляется как постоянная величина. При этом векторная сумма внешних сил, которые действуют на всю систему, должна быть равна нулю.
При определении скорости в классической механике также используют динамику вращательного движения твердого тела и момент импульса. Момент импульса имеет все характерные признаки количества вращательного движения. Исследователи используют это понятие как величину, которая зависит от количества вращающейся массы, а также как она распределена по поверхности относительно оси вращения. При этом имеет значение скорости вращения.
Вращение также можно понимать не только с точки зрения классического представления вращения тела вокруг оси. При прямолинейном движении тела мимо некой неизвестной воображаемой точки, которая не лежит на линии движения, тело также может обладать моментом импульса. При описании вращательного движения момента импульса играет самую существенную роль. Это очень важно при постановке и решении разнообразных задач, связанных с механикой в классическом понимании.
Это очень важно при постановке и решении разнообразных задач, связанных с механикой в классическом понимании.
В классической механике закон сохранения импульса является следствием ньютоновской механики. Он наглядно показывает, что при движении в пустом пространстве импульс сохраняется во времени. Если существует взаимодействие, то скорость его изменения определяется суммой приложенных сил.
дополнительных приемов для увеличения вашей скорости | Бретт Берри | Math Hacks
Серия мысленных математических вычислений, часть 2
Сегодня мы рассмотрим несколько простых методов, позволяющих улучшить вашу способность мысленно суммировать числа. Давайте начнем наш урок с некоторых специальных пар чисел.
Q: Что общего у этих пар чисел?
A: Все они добавляют к 10.
Это может показаться очевидным, но это важный первый шаг.Мы будем использовать эти пары чисел для тестирования и перегруппировки. Поэтому всякий раз, когда вы видите одну из этих пар, я автоматически хочу, чтобы вы думали «10».
Поэтому всякий раз, когда вы видите одну из этих пар, я автоматически хочу, чтобы вы думали «10».
При добавлении однозначного числа к другому я предпочитаю использовать технику тестов. Тест — удобное число, которое мы можем использовать в качестве точки отдыха в середине проблемы, обычно кратное десяти.
Предположим, мы хотим сложить 15 + 8.
Мы будем использовать число 20 в качестве ориентира, поэтому разбиваем 8 на 5 + 3.
Сначала объедините 15 + 5, чтобы получить наш тестовый показатель 20.
Затем завершите сложение.
Давайте попробуем другую задачу с помощью тестов.
Для этой задачи 70 будет эталоном, поскольку он является следующим кратным десяти после 63. Нам нужно добавить 7 к 63, чтобы получить эталонное значение 70. Итак, разбейте 9 на 7 + 2 и сложите их время.
Теперь мы — эталон.
Наконец, добавьте 2.
Другой пример:
В этой задаче 120 является эталоном.Поскольку 7 + 3 = 10, разделите 6 на 3 + 3.
Чтобы решить эту проблему, мы разделим числа по разрядам. Помните, что десятичная система значений знаков — это структура под каждым числом.
Двенадцать эквивалентны 1 десятке и 2 единицам, а восемьдесят восемь эквивалентны 8 десяткам и 8 единицам. Используя значения разряда, мы можем представить сложение в развернутом виде.
Добавление коммутативное , что означает, что мы можем изменить порядок без изменения ответа. Это позволяет нам перемещать числа по мере необходимости.
Сгруппируйте десятки и единицы вместе соответственно.
Уведомление 8 + 2 = 10.
На этом этапе вы можете считать по десяткам.
Конечно, это не единственный способ разбить числа на части. Мы также можем отделить 2 от 12 и сначала прибавить их к 88.
9 быстрых математических уловок для ускорения вычислений
Одно лишь упоминание математики означает проблемы и напряжение для некоторых людей, особенно детей. Здесь мы предлагаем 9 быстрых математических приемов, которые действительно ускорят ваши арифметические вычисления. Знание этих математических приемов поможет вам очень быстро производить вычисления в уме и, что более важно, уменьшить ваш страх перед математикой. Но большая часть математики связана с практикой. Итак, в статье мы также поделились ссылками на некоторые действительно интересные ресурсы для практики, которые вы можете использовать.
Знание этих математических приемов поможет вам очень быстро производить вычисления в уме и, что более важно, уменьшить ваш страх перед математикой. Но большая часть математики связана с практикой. Итак, в статье мы также поделились ссылками на некоторые действительно интересные ресурсы для практики, которые вы можете использовать.
Итак, давайте возьмем нашу волшебную палочку и извлечем некоторые быстрые вычисления из нашей математической шляпы. Скорость, с которой вы сможете действовать, другим покажется не чем иным, как волшебством.
Быстрый математический трюк 1: умножение в степень или возведение в квадрат числа, заканчивающегося на 5
Здесь скорость действительно поразит вас.Попробуйте найти в своей голове квадрат 85. Сколько времени это заняло у вас? А теперь попробуйте этот быстрый математический трюк.
- Игнорировать 5 на месте единиц
- Возьмите цифру в разряде десятков, т. Е. 8, и умножьте ее на следующую, т.
 Е. 8 + 1 = 9. Результат: 72
Е. 8 + 1 = 9. Результат: 72 - Просто поставьте 25 в конце результата, т.е. 7225. Вот и все. 7225 — это квадрат 85. Это ваш ответ.
Разве это не быстрый математический трюк? Этот математический трюк можно использовать в любое время, когда вам нужно найти квадрат числа, заканчивающегося на 5.Он также работает с 3-значными числами. Итак, квадрат 135 равен ….. сначала умножьте 13 на его преемника, т.е. 14 = 182. Теперь прибавьте 25 в конце. Ваш ответ 18225.
Скорость умножения зависит от знания таблиц умножения и фактов. Попробуйте эту настольную игру на умножение, чтобы освоить столы. В наших тестах со школьниками было доказано, что он очень эффективен в улучшении практики и улучшении запоминания.
Быстрый математический трюк 2: Умножение на 11
Как умножить число на 11? Возьмем пример.Предположим, вам нужно умножить 35 на 11. Просто выполните 3 следующих шага.
- Запишите 35 как 3 () 5 (где () — пробел для новой цифры, которая будет вставлена посередине)
- Найдите среднюю цифру как 3 (3 + 5) 5.
 Средняя цифра — это сумма первых двух цифр
Средняя цифра — это сумма первых двух цифр - Число 385. Это так просто и быстро.
Но что, если сумма первых двух цифр больше 9, то есть двузначное число? Возьмем еще раз пример. Скажем, число 59 нужно умножить на 11
.
- Запишите 59 как 5 () 9
- Найдите среднюю цифру как 5 (5 + 9) 9 = 5 (14) 9.Так как средняя цифра на самом деле не цифра, а двухзначное число, поэтому добавьте 10 к первой цифре и сохраните 4 в середине
- Число 5 + 1 (4) 9 = 649. Так быстро, как это
Быстрый математический трюк 3: Умножение на 5
Умножить любое число на 5 — это то же самое, что умножить его на 10 и разделить на 2. Верно? Мы можем использовать это правило, чтобы ускорить умножение на 5. Итак, вот трюк. Допустим, вы хотите умножить 236 на 5.
- Разделите число на 2 i.е. 118
- Теперь добавьте 0 в конце. Ответ 1180
Это была быстрая математика что ли! Но подождите, а что, если ответ будет десятичным? Правило все еще остается в силе. Попробуйте умножить 1305 на 5
Попробуйте умножить 1305 на 5
- Разделите число на 2, т. Е. 652,5
- Теперь умножьте его на 10, т.е. 6525. Это то же самое, что добавить 0 в конце или переместить десятичную точку на один шаг вправо.
Быстрый математический трюк 4: Умножение на 9
Предположим, вы хотите умножить число на 9, есть ли быстрый способ? Что ж, есть кое-что, что поможет, когда вы имеете дело с большими числами, особенно если вы быстро вычитаете.Допустим, вам нужно умножить 81 на 9.
- 0 в конце числа, например 810
- Вычтите исходное число из нового числа, т. Е. 810-81 = 729
Это правило работает каждый раз. Единственное, что это становится немного громоздким, когда вы имеете дело с числами среднего размера, скажем, с 4-значным числом или около того. Но этот математический трюк по-прежнему ускоряет умножение на 9 и снижает вероятность ошибок для большинства из нас. Это был наш быстрый математический трюк для умножения на 9
.
Уловки — это нормально, и они помогают.Но в центре внимания должна быть практика. Практикуйте эти математические методы до тех пор, пока числа не начнут выскакивать из вашей головы, как на изображении ниже. Чем больше вы практикуетесь, тем быстрее вы становитесь и более заинтересованы.
Быстрый математический трюк 5: Умножение на 25
Что делать, если вам нужно умножить двузначное число на 25. Скажем, вам нужно умножить 57 на 25. Можете ли вы быстро посчитать? Сможете ли вы сделать это в уме, не хватаясь за ручку и бумагу? Мы научим вас быстрому математическому трюку, чтобы делать эти вычисления в уме
- Добавьте два 0 в конце числа i.е. 5700
- Теперь найдите половину этого числа, то есть разделите его на 2. Итак, вы получите 2850
- Делим еще раз на 2, т.е. получаем половину. 1425. Это ваш ответ. т.е. 1425 — это произведение 57 и 25. Не верьте мне, проверьте свой калькулятор.
Это также будет работать для больших чисел и будет столь же эффективным. Так что попробуйте с 185. Найдите произведение 185 и 25
Так что попробуйте с 185. Найдите произведение 185 и 25
- Добавьте два нуля в конце. Итак 18500
- Теперь разделите его на 2. Итак, вы получите 9250
- Делим еще раз на 2.Итак, вы получаете 4625. Это ваш ответ.
Быстро и легко выполняется в уме. Так что это был еще один быстрый математический трюк. Хотите узнать больше способов ускорить арифметические вычисления? Продолжай читать.
Быстрый математический трюк 6: разделить на 5
Хватит трюков с умножением. Что, если вам нужно разделить на 5. Предположим, вы хотите разделить 565 на 5. Просто выполните этот двухэтапный математический трюк.
- Удвойте число, то есть умножьте его на 2. Итак, вы получите 1130
- Теперь переместите десятичную точку на один шаг влево i.е. уменьшить единицу 0. Итак, ответ 113.
Работает с любыми числами, даже с десятичными. Так что попробуйте с 142.3
- Увеличьте число вдвое. Получается 284,6
- Теперь переместите десятичную точку влево на 1 позицию.
 Итак, вы получаете 28,46. Это ваш ответ
Итак, вы получаете 28,46. Это ваш ответ
Один из способов улучшить свои расчеты — это познакомить вас с числами. Опять же, мы нашли неплохой забавный способ — это математическая стратегическая игра, которую нам прислали для испытания. Игра требовала много размышлений.Хотя производители говорят, что он должен быть возрастом от 7 лет и старше, мы рекомендуем его взрослым в течение 9 лет. Если вам нравятся мыслительные игры, вам стоит попробовать эту игру.
Быстрый математический трюк 7: вычитание из 1000
Что делать, если вам нужно вычесть число из 1000? Скажем, число 739. Здесь много переходящих остатков, поэтому сделать это в уме не так-то просто. Но, возможно, этот изящный математический трюк поможет ускорить ваши вычисления и повысить точность. Попробуйте и скажите мне, быстро ли это было для вас.
- Вычтите цифры в позиции единиц из 10 и вычтите цифру в позиции сотни из 9. Это ваш ответ. Итак, у нас есть 9-7, 9-3, 10-9. Итак, ответ — 261.
 Вот и все. Это всего лишь один шаг.
Вот и все. Это всего лишь один шаг.
Это был быстрый трюк с вычитанием за один шаг. Этот математический трюк для вычитания работает для любых чисел, таких как 10, 100, 1000, 10000, 100000 и так далее. Просто вычтите все цифры из 10 и последнюю цифру, то есть цифру с наибольшим разрядным значением из 9.Это ваш ответ.
Быстрый математический трюк 8: Умножение на 15
Что такое 15? Помните, 15 равно 10 + половина от 10. Поэтому, если вам нужно умножить любое число на 15, этот трюк или простое математическое правило поможет улучшить скорость арифметических вычислений. Допустим, вам нужно найти произведение 67 на 15.
- Напишите 0 в конце числа. Здесь 670
- Разделите это на 2. Итак, мы имеем 335
- Сложите 2 числа i.е. 335 + 670 = 1005
Быстрый математический трюк 9: Быстрое сложение двухзначных чисел
Что, если вам нужно сложить 67 и 24. Сможете ли вы сделать это в уме? Ты умеешь делать это быстро? Попробуйте этот арифметический трюк и посмотрите, поможет ли он в ваших расчетах.
- Сложите числа в разряде ДЕСЯТКИ. т.е. 6 + 2 = 8
- Теперь внесите одно из чисел в место ЕДИНИЦ после 8. Допустим, мы вводим 7. Итак, ваш номер 87.
- Теперь посчитайте от 87 на 4, то есть другое число на месте ЕДИНИЦЫ.Итак, вы поднялись на 4 места из 87, то есть 88, 89, 90 и 91. 91 — ваш ответ.
Давайте попробуем еще раз. Складываем 75 и 89.
- Сложите числа в разряде ДЕСЯТКИ. Получаем 7 + 8 = 15
- Введите одно из чисел на место UNITs. Получаем 159.
- Сосчитайте 5 разрядов из 159. Итак, ответ — 160, 161, 162, 163 и 164. Ваш ответ — 164.
Этот трюк особенно полезен для маленьких детей, которые изучают сложение двух цифр в своем классе.Это поможет им делать математику намного быстрее и, следовательно, побудит их больше интересоваться математикой. Опять же, самый надежный и универсальный способ повысить сложность — это практиковать больше мысленных вычислений. Мы нашли эту действительно потрясающую игру-дополнение. За одну игровую сессию мы отработали около 60-75 задач сложения, и это было огромным развлечением для нас и детей.
За одну игровую сессию мы отработали около 60-75 задач сложения, и это было огромным развлечением для нас и детей.
Необходимо знать и понимать, что эти «уловки» на самом деле не что иное, как применение основных математических правил.Например, умножение на 9 похоже на умножение на (10-1), что означает умножение на 10 и вычитание числа из самого себя и т. Д. Если у вас есть еще несколько математических трюков, вы можете поделиться ими ниже. Мы включим лучших в этот блог с вашим именем. Кто знает, это может помочь многим людям делать свои математические вычисления быстрее и лучше. В конечном итоге секрет быстрой математики — это практика. Практикуйте свои математические навыки, избегайте использования калькуляторов, и вы увидите, что ваши навыки улучшатся.
Если вам понравилось то, что вы прочитали, поделитесь этой статьей в твиттере / фейсбуке /…. и помогать другим извлекать из этого пользу.
Советы и хитрости по добавлению
Вот множество «приемов мышления», которые вы можете использовать, чтобы упростить сложение.
Используйте те, которые вам понятны!
Считайте от числа вверх
Пример: 6 + 3
Think «6 … 7, 8, 9»
Подсказка: начните с большего числа.
Пример: 2 + 6
2 + 6 Сложнее: «2… 3, 4, 5, 6, 7, 8 «
6 + 2 Проще: «6 … 7, 8»
Вместо этого введите 6 + 2 (вы получите тот же ответ).
Стратегия прыжков
Мы также можем считать по 2 или 10 или делать любые «прыжки», которые нам нужны, чтобы помочь нам выполнить расчет.
Пример: 4 + 12
Думайте «4 … 14 … 15, 16»
Сложение до десяти
Посмотрите, добавляются ли какие-нибудь числа к 10.Им не обязательно находиться рядом друг с другом.
Пример: 7 + 8 + 3 + 2 + 5
7 + 3 это 10,
8 + 2 — это еще 10, что составляет 20,
плюс 5 это 25
Сделай десятки последних
Разбейте большие числа на Десятки и Единицы, сложите Единицы, затем сложите Десятки.
Пример: 14 + 5
Разбейте число «14» на десятки и единицы: 10 + 4
Сложите единицы: 4 + 5 = 9
Теперь сложите десятки: 10 + 9 = 19
Думайте, что «4 плюс 5 равно 9, плюс 10 равно 19»
Другой пример: 14 + 12
Разбивка на десятки и единицы: 10 + 4 + 10 + 2
Сложите единицы: 4 + 2 = 6
Теперь добавьте десятки: 6 + 10 + 10 = 26
Целься в десятку
Когда число близко к десяти, мы можем «позаимствовать» у другого числа, так что оно достигнет десяти.
Пример: 9 + 79 находится всего в 1 от 10 | |
поэтому возьмите 1 из 7: 9 + 1 + 6 Подумайте: «9 плюс 1 равно 10 … 7 минус 1 равно 6 … вместе то есть 16 « | |
Пример: 8 + 5
8 + 2 = 10, поэтому возьмем 2 из 5: 8 + 2 + 3
и дадим его 8: 10 + 3 = 13
Мы также можем переместить назад с на десять, увеличив другое число по мере необходимости:
Пример: 12 + 7
Уменьшить 12 на 2: 12 — 2 = 10
Увеличить 7 на 2: 7 + 2 = 9
12 + 7 = 10 + 9 = 19
Метод компенсации
«Компенсация» — это округление числа (для облегчения сложения), а затем убирать лишнее после добавления.
Пример 19 + 16
Легче сделать 20 + 16 = 36
Затем уберите лишнюю 1 (которая превратила 19 в 20), чтобы получить: 35
Пример 395 + 126
Легче сделать 400 + 126 = 526
Затем уберите лишние 5 (которые превратили 395 в 400) и получите: 521
Двойное при совпадении чисел
Пример 5 + 5 = 2 x 5 = 10
Удвойте, если числа близки, то исправьте
Пример: 5 + 6 — это почти две пятерки, но 6 на 1 больше 5, поэтому:
5 + 6 = две пятерки + 1 = 10 + 1 = 11
Пример: 7 + 9 похоже на две восьмерки, но 7 на 1 меньше 8, а 9 на 1 больше 8.Итак,
ровно две восьмерки , потому что 1 меньшая и 1 большая взаимно компенсируют друг друга:
7 + 9 = «8 минус 1» + «8 прибавить 1» = две восьмерки = 16
Таблица сложения
Мы также можем использовать Таблицу сложения, чтобы помочь нам.
Рабочие листы для дополнений
Добро пожаловать на страницу дополнительных листов на Math-Drills. com, где мы добавим много положительных качеств к вашему обучению! На этой странице вы найдете рабочие листы сложения из фактов сложения и добавление двузначных чисел к добавлению столбцов и добавление с играми.В первый раздел мы включили несколько дополнительных печатных форм, которые должны помочь начинающему студенту. Обучение дополнительным фактам лучше всего проводить с помощью некоторых интересных обучающих стратегий.
com, где мы добавим много положительных качеств к вашему обучению! На этой странице вы найдете рабочие листы сложения из фактов сложения и добавление двузначных чисел к добавлению столбцов и добавление с играми.В первый раздел мы включили несколько дополнительных печатных форм, которые должны помочь начинающему студенту. Обучение дополнительным фактам лучше всего проводить с помощью некоторых интересных обучающих стратегий.
Некоторые учителя и родители используют манипуляторы сложения, чтобы помочь ученикам понять основные факты сложения. Например, добавление групп «яблочных валетов» (хлопьев для завтрака) путем подсчета быстро приведет учащихся к пониманию концепции сложения. Чем раньше вы познакомите своих учеников с десятью базовыми блоками, тем лучше.Если вы еще не использовали их для подсчета, используйте их для базового сложения и покажите студентам, как работает перегруппировка.
Самые популярные дополнительные рабочие листы на этой неделе
Дополнительные таблицы фактов
Бесспорно, не лучший способ узнать дополнительные факты, но, несомненно, отличный способ подвести итоги. Таблицы дополнительных фактов являются бесценным ресурсом в любом домашнем или школьном классе.
Таблицы дополнительных фактов являются бесценным ресурсом в любом домашнем или школьном классе.
Дополнительные таблицы
Сложение очень хорошо работает как таблица, поскольку слагаемые могут быть последовательными.Призовите студентов искать закономерности и научите их различным стратегиям усвоения фактов сложения. Для учащихся, которые еще не запомнили свои факты сложения, но которым необходимо знать их для более сложного урока математики, такого как сложение двузначных чисел, предоставьте им таблицу фактов сложения, чтобы они могли быстро найти факты сложения. Через некоторое время они, скорее всего, узнают факты, используя таблицу, и станут меньше полагаться на нее. Чтобы столы были более прочными, распечатайте их на картоне и ламинируйте.Их можно отобразить на экране или увеличить и распечатать на плакатной бумаге для использования всем классом.
Таблицы пятиминутного безумия
Пятиминутные диаграммы безумия — это сетки 10 на 10 для практики сложения фактов. В каждом квадрате учащиеся записывают сумму номера столбца и номера строки.
В каждом квадрате учащиеся записывают сумму номера столбца и номера строки.
Кто-то называет безумными минутами или рассчитанными на время упражнениями, пятиминутное безумие предназначено для того, чтобы добавить немного больше азарта к отработке фактов сложения. Они идеально подходят для повышения способности ученика быстро вспоминать дополнительные факты, что дает всевозможные преимущества в дальнейшей школьной жизни, включая предотвращение жалоб учителей старших классов на то, «что их ученики не могут даже складывать однозначные числа без использования калькулятора. .«
Общая цель — заполнить одну таблицу менее чем за пять минут и набрать 98 процентов или выше, однако мы рекомендуем устанавливать личные цели для учащихся на основе первоначального теста. Если они бьются головой об стену через пару минут и заданы лишь несколько вопросов, им действительно не следует в данный момент завершать тренировку по сложению фактов по времени. Им еще предстоит кое-чему научиться. На этом этапе мы бы рекомендовали отказаться от манипуляторов.Если они ответят на вопросы за 1,5 минуты и ответят почти на все вопросы, они, вероятно, готовы к чему-то более сложному.
На этом этапе мы бы рекомендовали отказаться от манипуляторов.Если они ответят на вопросы за 1,5 минуты и ответят почти на все вопросы, они, вероятно, готовы к чему-то более сложному.
Five Minute
Addition Frenzies , которые включают по одной таблице сложения на странице
Безумное добавление одной страницы на страницу — не самое эффективное использование бумажных ресурсов, но они являются хорошей отправной точкой, особенно для младших школьников, которые недостаточно освоили свой почерк, чтобы уместить свои числа в меньшую таблицу.Они также отлично подходят для отображения на экранах или мониторах при групповых занятиях. Например, вы можете использовать интерактивную доску для заполнения таблицы.
Five Minute
Addition Frenzies , которые включают четыре дополнительных диаграммы на странице
Более разумное использование ограничений на количество бумаги и фотокопий, наличие четырех таблиц на странице позволяет выполнять многодневную практику, совместную работу или использовать резак для бумаги — быструю стопку страниц для практики для студентов, которые заканчивают раньше.
Рабочие листы для сложения однозначных чисел
Большинство людей согласятся, что умение быстро и мысленно складывать однозначные числа является важным навыком для успеха в математике. Различные дополнительные рабочие листы в этом разделе сосредоточены на навыках, которые учащиеся будут использовать на протяжении всей своей жизни. Эти рабочие листы не будут волшебным образом заставить ученика учиться, но они ценны для подкрепления и практики, а также могут использоваться в качестве инструментов оценки.
Вертикально расположенное сложение одной цифры
Итак, вам нужны практические листы для дополнения фактов? Вы их нашли.Используйте их для практики, оценки, игр или просто для развлечения.
Сложение однозначных чисел с горизонтальным расположением
Не торопитесь? Эти дополнительные рабочие листы помогут учащимся, испытывающим трудности, делать это шаг за шагом, не беспокоясь о перегруппировке. Просто кучка красивых однозначных сумм.
Make Ten Дополнительная стратегия
Стратегия сложения «сделать десять» включает «разделение» второго слагаемого на две части.Первая часть объединяется с первым добавлением, чтобы получить десять, а вторая часть — это оставшаяся сумма. Эта стратегия помогает студентам быстро складывать в уме суммы более десяти. Например, складывая 8 + 7, ученики сначала понимают, что им нужно прибавить 2 к 8, чтобы получить 10, поэтому они делят 7 на 2 + 5. 8 + 2 дает 10, а еще 5 составляют 15. Навык может быть расширен. Во многих ситуациях, например, складывая 24 + 9, учащиеся понимают, что им нужно еще 6, чтобы получить 30, а 9 можно разделить на 6 + 3, поэтому 24 + 6 = 30 и еще 3 дает 33.Продолжая, учащиеся могут работать над распознаванием «дополнений» других важных чисел (см. Раздел ниже) для дальнейшей разработки этой стратегии.
Однозначные вопросы на сложение с
фокусными числами
Некоторым учащимся необходимо уделять внимание одному числу за раз. Может быть, они перегружены информацией, и им нужно добиваться успеха маленькими шагами.
Может быть, они перегружены информацией, и им нужно добиваться успеха маленькими шагами.
Рабочие листы для сложения нескольких цифр
Для изучения сложения многозначных чисел можно использовать различные стратегии; не стоит полагаться только на бумажные и карандашные методы.Базовые десять блоков могут помочь учащимся осмыслить сложение. Обучение студентов навыку сложения в уме слева направо поможет им в будущих исследованиях математики и жизни в целом. Например. 34 + 78 будет 30 + 70 = 100, 100 + 4 = 104, 104 + 8 = 112. Не забывайте об использовании оценок с этими листами.
Сложение нескольких цифр с перегруппировкой
НЕКОТОРЫЕ
Классические таблицы сложения, некоторые этапы которых требуют перегруппировки, а другие нет.Версии со ВСЕМИ перегруппировками и БЕЗ перегруппировки следуют за этим разделом. Версии с разделителями тысяч находятся немного дальше по странице.
Сложение нескольких цифр с перегруппировкой
ВСЕ
Перегруппировка — вот в чем суть длинного сложения; эти рабочие листы дают студентам много практики, поскольку каждый шаг требует перегруппировки.
Сложение нескольких цифр с
NO перегруппировкой
Если вы еще не освоили все факты сложения или длинный алгоритм сложения, этот раздел может быть для вас.Эти рабочие листы не требуют перегруппировки, поэтому они предоставляют дополнительный промежуточный навык для студентов, которым требуется немного больше руководства.
Горизонтально сложение
Горизонтальное сложение может побудить учащихся использовать в уме математические или другие стратегии для сложения чисел. Одна из наиболее распространенных стратегий сложения в уме — это стратегия сложения слева направо (также называемая внешним интерфейсом). Это включает в себя сначала добавление более высоких разрядов.Другие стратегии для добавления многозначных чисел включают использование десятичных блоков или других манипуляций, числовых линий, разложение чисел и сложение частей, а также использование калькулятора.
Добавление
номеров фокусировки больше 9
Эти рабочие листы включают числа больше, чем те, которые расположены дальше по странице.
Сложение нескольких цифр с
тысячами, разделенными запятыми
Использование запятой для разделения тысяч — наиболее распространенный способ форматирования больших чисел в английском мире.
Сложение нескольких цифр с
тысячами, разделенными пробелами
Использование пробела для разделения тысяч больших чисел распространено в некоторых языках. В английском мире вы, скорее всего, встретите канадцев, форматирующих свои числа таким образом.
Сложение нескольких цифр с
тысячами, разделенными точками
Использование точки в качестве разделителя тысяч обычно не встречается в англоязычных странах, но, поскольку есть люди со всего мира, которые используют эти рабочие листы сложения, они включены.
Сложение многозначных цифр крупным шрифтом
По разным причинам иногда требуются дополнительные вопросы, выделенные более крупным шрифтом. Они должны соответствовать всем требованиям.
Они должны соответствовать всем требованиям.
Различные другие рабочие листы для дополнений
Столбец Дополнительные рабочие листы
Добавление столбцов — это не только упражнение в бухгалтерском учете, оно также развивает умственные навыки сложения, которые пригодятся в повседневной жизни. Для добавления столбцов чисел доступны различные стратегии.Традиционный метод — использовать карандаш и бумагу, также известный как сложение справа налево, когда учащиеся складывают и перегруппировываются, начиная с наименьшего места (в данном случае с единиц), и переходят к наибольшему месту. Мысленный подход может включать в себя учеников, идущих слева направо, где сначала добавляется большее место. Это легче уследить в голове, но время от времени требуется корректировка в предыдущих ответах. Например, сложите 345 + 678 + 901. Сначала сложите 300, 600 и 900, чтобы получить 1800, затем добавьте по очереди 40, 70 и 0, чтобы получить 1910, затем обработайте 5, 8 и 1, чтобы получить 1924. Попутно вам приходилось корректировать итоговую сумму, но держать ее в голове намного проще, чем переносить в голову метод карандаша и бумаги.
Попутно вам приходилось корректировать итоговую сумму, но держать ее в голове намного проще, чем переносить в голову метод карандаша и бумаги.
Добавление с поддержкой сетки
Добавление с поддержкой сетки помогает учащимся, у которых возникают проблемы с составлением значений разрядов. Возможно, немного попрактиковавшись, они смогут лучше понять не только выстраивание значений разряда, но и то, почему это делается. Например, указание на то, что 5 из 659 означает 50, полезно для того, чтобы помочь учащимся понять значение разряда в том, что касается сложения.
Добавление с помощью
игр
Эти дополнительные рабочие листы также помогают учащимся развивать умственные навыки сложения, но используют игровой контекст для знакомства и интереса. В рабочих листах с игральными картами валет считается за 11, королева — за 12, король — за 13, а туз — за 1. Игра в математические игры, наслаждаясь общением с друзьями, — отличный способ развить стратегическое мышление и свободное владение математикой у детей.
Добавление дополнений различных сумм
Поиск дополнительных чисел может очень помочь учащимся в развитии умственных арифметических навыков и углублении понимания чисел.
Сложение
двойников чисел
Использование стратегии сложения удвоений может помочь учащимся быстрее обрабатывать дополнительные вопросы с помощью мысленной математики. Чтобы использовать эту стратегию, учащиеся должны понимать, что два числа близки к одному и тому же значению (обычно на одно или два). Они также должны распознавать, насколько оно больше или меньше первого слагаемого. Типичный диалог с вопросом 15 + 16 может быть таким: «Я вижу, что второе число больше первого на 1.Если я удвою первое число и добавлю 1, я получу свой ответ. 15 удвоенных — 30 плюс один — 31. 15 + 16, следовательно, 31 ».
Добавление
в другие системы счисления
Не обычно преподают в современных школах, добавление в другие системы счисления может расширить умы учащихся и найти немало важных приложений, особенно в сфере технологий. Например, вы обнаружите, что двоичная, восьмеричная и шестнадцатеричная системы довольно часто используются в компьютерных технологиях.Четвертичные числа могут использоваться в генетике для хранения последовательностей ДНК. Двенадцатеричная система иногда предлагается как система, превосходящая десятичную
Например, вы обнаружите, что двоичная, восьмеричная и шестнадцатеричная системы довольно часто используются в компьютерных технологиях.Четвертичные числа могут использоваться в генетике для хранения последовательностей ДНК. Двенадцатеричная система иногда предлагается как система, превосходящая десятичную
.
Рабочие листы Math Minute — Безумные минуты
Дополнение Основные факты Безумные минутные упражнения
В этом практическом листе есть изображения дружественных детям монстров. Первое дополнение для каждой задачи — 0, 1 или 2. Второе добавление — от 0 до 9.
От детского сада до 2-го класса
Зарегистрированные участники могут использовать картотеку Super Teacher Worksheets, чтобы сохранять свои любимые рабочие листы.
Быстрый доступ к наиболее часто используемым файлам И настраиваемым рабочим листам!
Пожалуйста, войдите в свою учетную запись или станьте участником и присоединяйтесь к нашему сообществу сегодня, чтобы воспользоваться этой полезной функцией.
Практикуйте сорок три факта сложения на этом листе. Первое добавление находится между 0 и 3. На листе есть графика в виде американских горок.
От детского сада до 2-го класса
Еще одна основная таблица дополнительных упражнений. На этот раз первое слагаемое находится между 0 и 4.Графика лошади украшает этот рабочий лист.
От детского сада до 2 класса
Первое дополнение к каждой задаче на этом листе находится между 0 и 5. На листе есть изображения игривых обезьян.
От детского сада до 2-го класса
Рабочий лист основных фактов, в котором первое добавление находится в диапазоне от 0 до 6. Рабочий лист содержит графику гоночных автомобилей.
1–3 классы
Первое добавление к каждому факту на этой печатной форме — от 0 до 7. С очаровательными картинками котят.
1–3 классы
Еще более важные факты сложения. На этот раз первое добавление для каждой задачи — от 0 до 8. Симпатичные картинки волшебника.
1–3 классы
Базовый рабочий лист для сложения. Первое дополнение — от 0 до 9. Включает мультяшные изображения лягушек.
1–3 классы
Основные факты вычитания (0–18) Безумные минутные упражнения
Сколько из этих 25 фактов на вычитание (0–18) могут выполнить ваши ученики за одну минуту?
1-й класс
Еще 25 фактов вычитания (0–18) для учеников.
1-й класс
Ищете более 25 фактов? Попробуйте этот рабочий лист. Их 50!
От детского сада до 2 класса
10 хитростей для быстрого выполнения математических расчетов в голове
Не нужно быть учителем математики, чтобы знать, что многие ученики — и, вероятно, многие родители (это было давно!) — боятся математических задач, особенно если они включают большое количество.Изучение методов быстрого выполнения математики может помочь учащимся развить большую уверенность в математике, улучшить математические навыки и понимание, а также преуспеть в продвинутых курсах.
Получайте релевантные учебные материалы и обновления прямо на ваш почтовый ящик. Подпишитесь сегодня!
Присоединиться
Если это ваша работа — обучать их, вот вам отличное напоминание.
Инфографика быстрых математических приемов
10 уловок для быстрой математики
Вот 10 быстрых математических стратегий, которые учащиеся (и взрослые!) Могут использовать, чтобы вычислить в уме.Освоив эти стратегии, учащиеся должны иметь возможность точно и уверенно решать математические задачи, которые они когда-то боялись решать.
1. Сложение больших чисел
Сложить в уме большие числа. Этот метод показывает, как упростить этот процесс, сделав все числа кратными 10. Вот пример:
644 + 238
Хотя с этими числами сложно бороться, округление их в большую сторону сделает их более управляемыми. Итак, 644 становится 650, а 238 становится 240.
Теперь сложите 650 и 240 вместе. Итого 890. Чтобы найти ответ на исходное уравнение, необходимо определить, сколько мы прибавили к числам, чтобы округлить их в большую сторону.
650 — 644 = 6 и 240 — 238 = 2
Теперь сложите 6 и 2, чтобы получить 8
Чтобы найти ответ на исходное уравнение, нужно вычесть 8 из 890.
890 — 8 = 882
Итак, ответ на 644 +238 — 882.
2. Вычитаем из 1 000
Вот основное правило вычитания большого числа из 1000: вычтите все числа, кроме последнего, из 9 и вычтите последнее число из 10.
Например:
1 000–556
Шаг 1: вычтем 5 из 9 = 4
Шаг 2: вычтем 5 из 9 = 4
Шаг 3: вычтем 6 из 10 = 4
Ответ 444.
3. 5-кратное умножение любого числа
Умножив число 5 на четное, можно быстро найти ответ.
Например, 5 x 4 =
- Шаг 1: Возьмите число, умноженное на 5, и разрежьте его пополам, в результате число 4 станет числом 2.
- Шаг 2: Добавьте ноль к числу, чтобы найти ответ. В данном случае ответ — 20.
5 х 4 = 20
При умножении нечетного числа на 5 формула немного отличается.
Например, рассмотрим 5 x 3.
- Шаг 1: Вычтите единицу из числа, умноженного на 5, в этом случае число 3 становится числом 2.
- Шаг 2: Теперь уменьшите число 2 вдвое, и оно станет числом 1. Сделайте 5 последней цифрой. Произведено число 15, и это и есть ответ.
5 x 3 = 15
4. Уловки деления
Вот быстрый способ узнать, когда число может быть равномерно разделено на эти определенные числа:
- 10, если номер заканчивается на 0
- 9, когда цифры складываются и сумма делится на 9
- 8, если последние три цифры делятся на 8 без остатка или равны 000
- 6, если это четное число и когда цифры складываются, ответ делится без остатка на 3
- 5, если он заканчивается на 0 или 5
- 4, если он заканчивается на 00 или двузначное число, которое делится на 4 без остатка.
- 3, когда цифры складываются и результат делится без остатка на 3
- 2, если он заканчивается на 0, 2, 4, 6 или 8
без остатка.
5.Умножение на 9
Это простой метод, который помогает умножить любое число на 9. Вот как это работает:
Давайте возьмем пример 9 x 3.
Шаг 1 : Вычтите 1 из числа, которое умножается на 9.
3 — 1 = 2
Число 2 — это первое число в ответе на уравнение.
Шаг 2 : Вычтите это число из числа 9.
9–2 = 7
Число 7 — второе число в ответе на уравнение.
Итак, 9 x 3 = 27
6. 10 и 11-кратные фокусы
Уловка для умножения любого числа на 10 состоит в том, чтобы добавить ноль в конец числа. Например, 62 x 10 = 620.
Существует также простой способ умножить любое двузначное число на 11. Вот оно:
11 х 25
Возьмите исходное двузначное число и поставьте между цифрами пробел. В данном примере это число 25.
2_5
Теперь сложите эти два числа и поместите результат в центр:
2_ (2 + 5) _5
2_7_5
Ответ на 11 x 25 — 275.
Если числа в центре складываются в число из двух цифр, вставьте второе число и прибавьте 1 к первому. Вот пример уравнения 11 x 88
8_ (8 +8) _8
(8 + 1) _6_8
9_6_8
Есть ответ на 11 x 88: 968
7. В процентах
Найти процентное значение числа может быть несколько сложно, но правильное понимание этого числа значительно упрощает понимание. Например, чтобы узнать, что составляет 5% от 235, воспользуйтесь этим методом:
- Шаг 1: Переместите десятичную запятую на одну позицию, 235 станет 23.5.
- Шаг 2: Разделите 23,5 на число 2, получится 11,75. Это также ответ на исходное уравнение.
8. Быстро возведите в квадрат двузначное число, которое заканчивается на 5
Давайте возьмем число 35 в качестве примера.
- Шаг 1. Умножьте первую цифру на себя плюс 1.
- Шаг 2: Поставьте 25 в конце.
35 в квадрате = [3 x (3 + 1)] & 25
[3 x (3 + 1)] = 12
12 и 25 = 1225
35 в квадрате = 1225
9.Сложное умножение
При умножении больших чисел, если одно из чисел четное, разделите первое число пополам, а затем удвойте второе число. Этот метод быстро решит проблему. Например, рассмотрим
20 х 120
Шаг 1: разделите 20 на 2, получится 10. Удвойте 120, что равно 240.
Затем умножьте свои два ответа вместе.
10 х 240 = 2400
Ответ на 20 x 120: 2400.
10. Умножение чисел, оканчивающихся на ноль
Умножение чисел, оканчивающихся на ноль, на самом деле довольно просто.Это включает в себя умножение других чисел вместе, а затем добавление нулей в конце. Например, рассмотрим:
200 х 400
Шаг 1: Умножьте 2 на 4
2 х 4 = 8
Шаг 2: Поместите все четыре нуля после 8
80 000
200 x 400 = 80 000
Выполнение этих быстрых математических приемов может помочь как ученикам, так и учителям улучшить свои математические навыки и укрепить свои знания математики — и не бояться работать с числами в будущем.
Присоединяйтесь к Resilient EducatorПодпишитесь на нашу рассылку, чтобы получать контент на свой почтовый ящик. Щелкните или коснитесь кнопки ниже. |
Вы также можете прочитать
Теги: Математика и естественные науки, Математика
7 практических советов по ментальной математике (которые может использовать ЛЮБОЙ!)
Скорее всего, вы слышали о ментальной математике — способности производить вычисления в уме — и о том, как важно для детей ее выучить.Но почему это важно? Потому что ментальная математика связана с ЧУМСТВОМ ЧИСЛОВ: способностью манипулировать числами в голове различными способами для выполнения вычислений. В свою очередь было доказано, что чувство числа предсказывает успехи студента в алгебре. По сути, то, что мы делаем с переменными в алгебре, аналогично тому, что учащиеся могут научиться делать с числами в младших классах.
Люди с пониманием чисел гибко используют числа . Они могут разбирать их и складывать различными способами для проведения расчетов.Это очень похоже на умение «ИГРАТЬ» словами, чтобы составлять интересные предложения, или на умение играть с аккордами и мелодиями, чтобы сочинять песни.
Но математика / числовое чутье не только для «математических гениев» — как раз наоборот! Выучить основы может КАЖДЫЙ, и это значительно упростит изучение математики и алгебры! Мы ожидаем, что наши дети выучат много английских слов и смогут складывать эти слова разными способами в предложения, так почему бы не ожидать, что они сделают то же самое с числами? И они могут, если им покажут основы и покажут примеры того, как это происходит.Итак, давайте перейдем к практической части этого письма: математические стратегии для ВСЕХ.
- «Девятка».
Чтобы прибавить 9 к любому числу, сначала прибавьте 10, а затем вычтите 1. В моих книгах по Math Mammoth я рассказываю детям эту сюжетную линию, где девять очень сильно хотят быть 10… поэтому он просит это другое число вместо «единицы». Другое число становится на единицу меньше. Например, мы меняем сложение 9 + 7 на 10 + 6, что намного проще решить.
Но этот «трюк» расширяется.Можете ли вы придумать простой способ сложить 76 + 99? Измените его на 75 + 100. Как насчет 385 + 999?
Как бы вы сложили в голове 39 + 28? Пусть 39 станет 40… что уменьшает 28 до 27. Теперь сложение составляет 40 + 27. Еще один способ — подумать о компенсации: 39 — это на единицу меньше 40, а 28 — на два меньше, чем 30. Итак, их сумма на три меньше чем 70.
- Двухместные + 1.
Поощряйте детей запоминать двойные числа от 1 + 1 до 9 + 9. После этого у них под рукой появляется множество других фактов сложения: те, которые мы можем назвать «двойные плюс еще один».Например, 5 + 6 на единицу больше, чем 5 + 5, или 9 + 8 просто на единицу больше, чем 8 + 8.
- Используйте факты сложения при сложении больших чисел.
Как только вы узнаете, что 7 + 8 = 15, вы также сможете делать все эти сложения в уме:
- 70 + 80 это 15 десятков, или 150
- 700 + 800 это 15 сотен, или 1500
- 27 + 8 — это 20, а 15 — 35. Или подумайте так: поскольку 7 + 8 на пять больше, чем десять, то 27 + 8 на пять больше, чем следующие десять.
- Вычесть сложением.
Это очень важный принцип, основанный на связи между сложением и вычитанием. Детям действительно не нужно запоминать факты вычитания как таковые, если они могут использовать этот принцип. Например, чтобы найти 8-6, подумайте: «Шесть плюс какое число дает 8?» Другими словами, подумайте о сложении отсутствующего числа 6 + ___ = 8. Ответ на это также является ответом на 8 — 6.
Этот принцип особенно удобен с вычитаниями, такими как 13-7, 17-8, 16-9 и другими основными фактами вычитания, где уменьшаемое значение находится между 10 и 20.Но вы также можете использовать его во множестве других ситуаций. Например, число 63–52 легче решить сложением: 52 + 11 дает 63, поэтому ответ на 63–52 — 11.
- Пять умноженное на число.
Теперь обратим внимание на умножение. Вот изящный трюк, о котором вы, возможно, не знали. Чтобы найти любое число в 5 раз, сначала умножьте это число на десять, а затем возьмите половину этого числа. Например, 5 × 48 можно найти, умножив 10 × 48 = 480 и взяв половину результата, что дает нам 240.Конечно, вы также можете использовать эту стратегию для таких фактов умножения, как 5 × 7 или 5 × 9.
- Четыре и восемь чисел.
Если вы умеете удваивать числа, значит, это у вас уже есть! Чтобы найти четырехкратное число, удвойте это число дважды. Например, что такое 4 × 59? Сначала найдите удвоение 59, что составляет 118. Затем удвойте это, и вы получите 236.
Точно так же восемь умноженное на число означает просто трижды удвоение. Например, найти 8 × 35 означает удвоить 35, чтобы получить 70, удвоить 70, чтобы получить 140, и (еще раз) удвоить 140, чтобы получить 280.
