Степени числа 7: Урок 2. степень числа — Алгебра — 7 класс

alexxlab

Урок 2. степень числа — Алгебра — 7 класс

Алгебра

7 класс

Урок № 2

Степень числа

Перечень вопросов, рассматриваемых в теме:

Понятие степени числа.

Свойства степеней.

Тезаурус

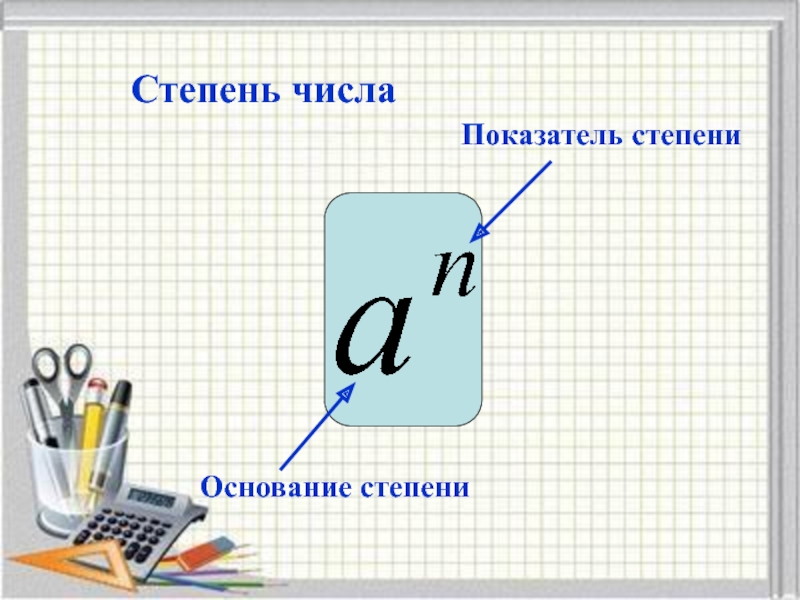
Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований.

Произведение степеней с одним и тем же основанием – это степень с тем же основанием и показателем, равным сумме показателей этих степеней.

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С.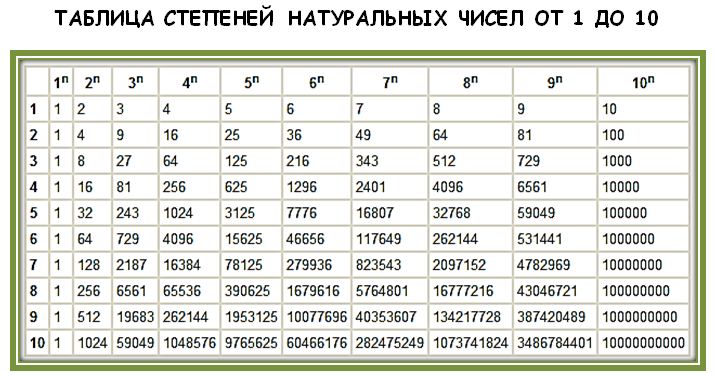 М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Макарычев Ю. Н. Алгебра: 7 класс. // Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. – М.: Просвещение, 2019. – 256 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Произведение шести множителей, каждый из которых равен 8, называют шестой степенью числа 8 и обозначают 86, т.е.

8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 ∙ 8 = 86.

При этом число 8 называют основанием степени, а число 6 – показателем степени.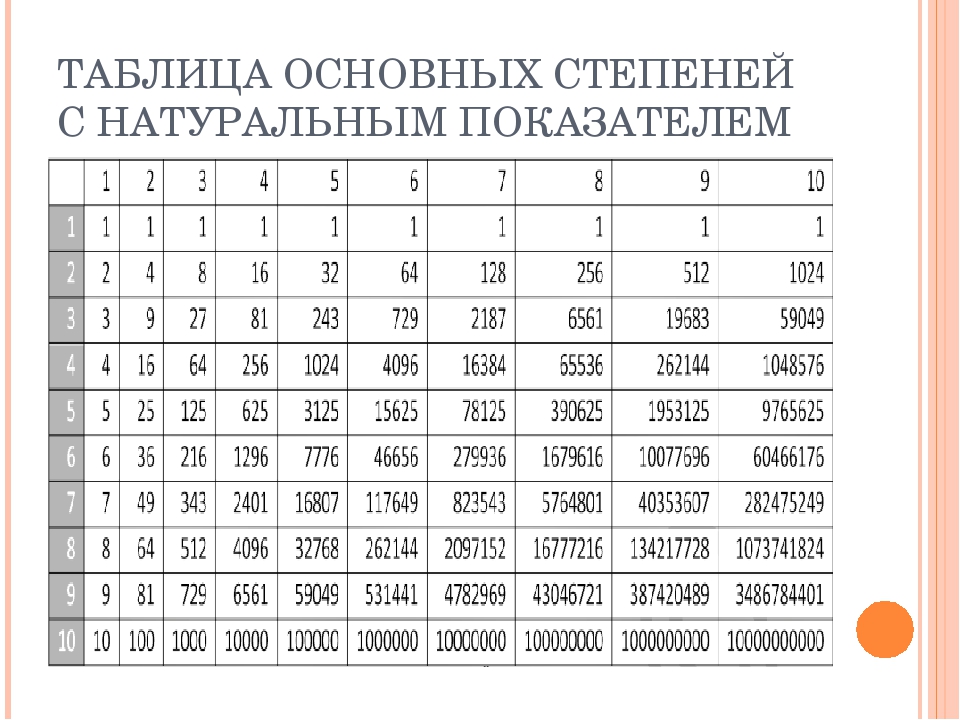

А теперь давайте сформулируем общее определение степени числа, опираясь на предыдущий пример:

степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Запись an читается как: а в степени n, или n-ая степень числа a.

А вот следующие записи можно произносить по-разному:

a2– её можно произносить «а в квадрате» или «а во второй степени»;

a3 – её можно произносить «а в кубе» или «а в третьей степени».

Стоит отметить, что особые случаи возникают, если показатель степени равен нулю или единице:

степенью числа а с показателем n = 1 является само это число:

a1 = a;

любое число в нулевой степени равно единице:

a0 = 1;

ноль в любой натуральной степени равен нулю:

0n = 0;

единица в любой степени равна 1:

1n = 1.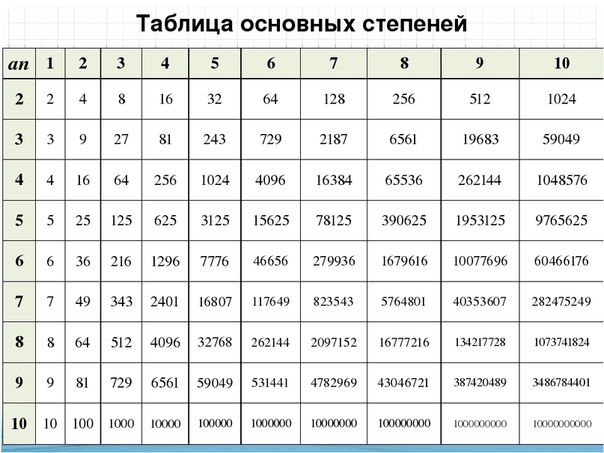

Выражение 00 (ноль в нулевой степени) считают неопределенным.

Примеры. Возведём в степени:

(−91)0 = 1

0144 = 0

1236 = 1.

При решении задач, нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Рассмотрим несколько примеров.

Возведём в степень

25 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32

2,53 = 2,5 ∙ 2,5 ∙ 2,5 = 15,625

Основание степени может быть любым числом – положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа, в результате может получиться как положительное число, так и отрицательное число. Это зависит от того, чётным или нечётным числом был показатель степени.

Например, (-2)5.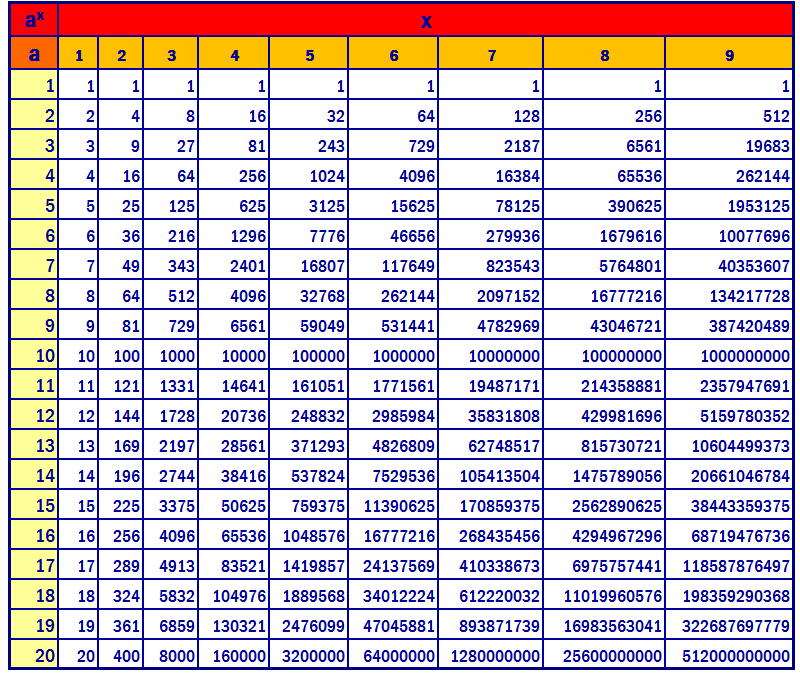 Ответ будет отрицательным, так как показатель степени, 5- нечётное число. (-2)5 = (-2) ∙ (-2) ∙ (-2) ∙ (-2) ∙ (-2) = -32.

(-5)4. А вот в этом примере ответ будет положительным, так как показатель степени, 4 – чётное число.

(-5)4 = (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625.

Рассмотрим такой пример: 42 ∙ 52 = 4 ∙ 4 ∙ 5 ∙ 5 = (4 ∙ 5) ∙ (4 ∙ 5) = (4 ∙ 5)2 = 202 = 400.

Данный пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований:

an∙ bn = (a ∙ b)n

Приведём еще такой пример: 52 ∙ 55 = (5 ∙ 5) ∙ (5 ∙ 5 ∙ 5 ∙ 5 ∙ 5) = 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 = 57.

Этот пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же основанием это степень с тем же основанием и показателем, равным сумме показателей этих степеней, т.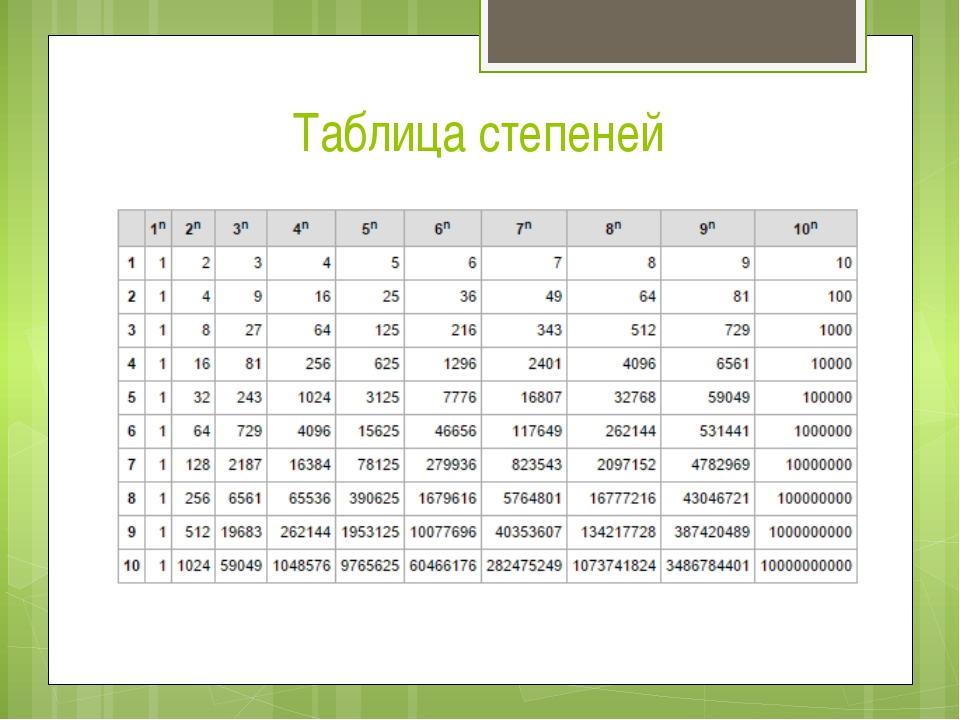 е.

an ∙ am = an+m

Наконец, рассмотрим равенство:

(72)3 = (7 ∙ 7)3 = (7 ∙ 7) ∙ (7 ∙ 7) ∙ (7 ∙ 7) = 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 = 76.

Это равенство подтверждает справедливость следующего свойства степеней:

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней, т.е.

(an)m = an∙m

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

Число

Основание

Показатель степени

1.

255

2.

1113

3.

1356

Для заполнения пропусков вспомним, что такое основание и показатель степени.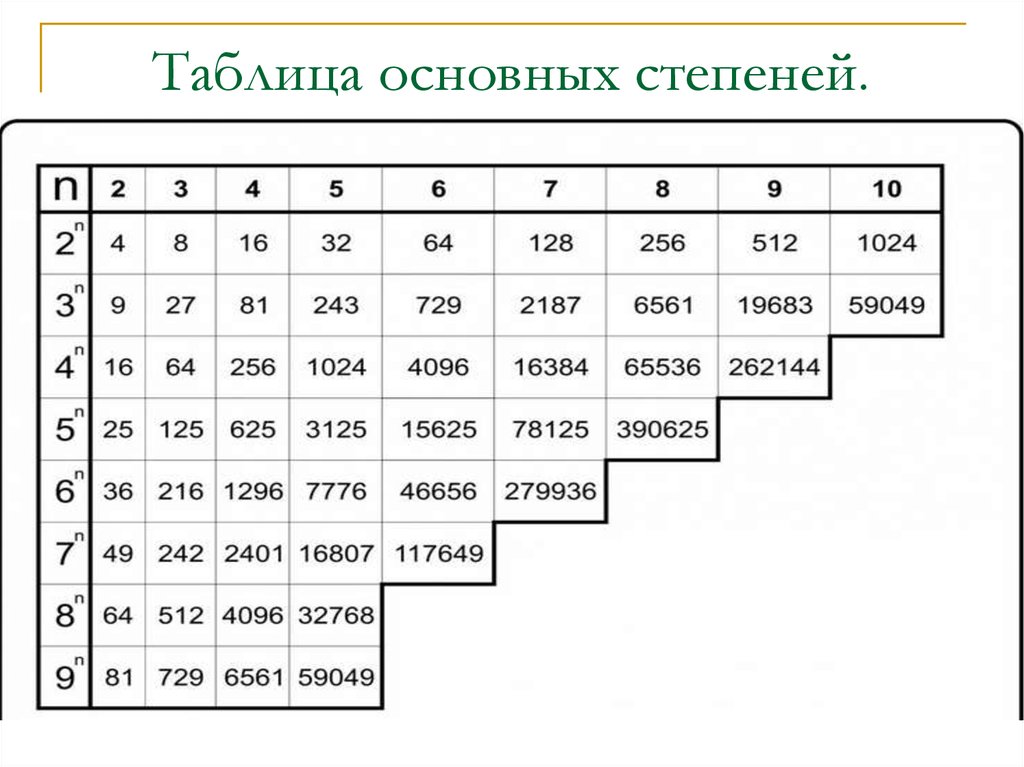

Число

Основание

Показатель степени

1.

255

25

5

2.

1113

11

13

3.

1356

135

6

№2. Тип задания: Чему равно произведение 54 ∙ 511 ∙ 42 ∙ 413?

Варианты ответов:

(4 ∙ 5)15

413 ∙ 514

(4 ∙ 5)30

415 ∙ 530

Для решения задания, воспользуемся свойствами степеней: an∙am= an+m и an∙bn= (a ∙ b)n

54 ∙ 511 ∙ 42 ∙ 413 = 515 ∙ 415 = (4 ∙ 5)15.

Верный ответ: (4 ∙ 5)15.

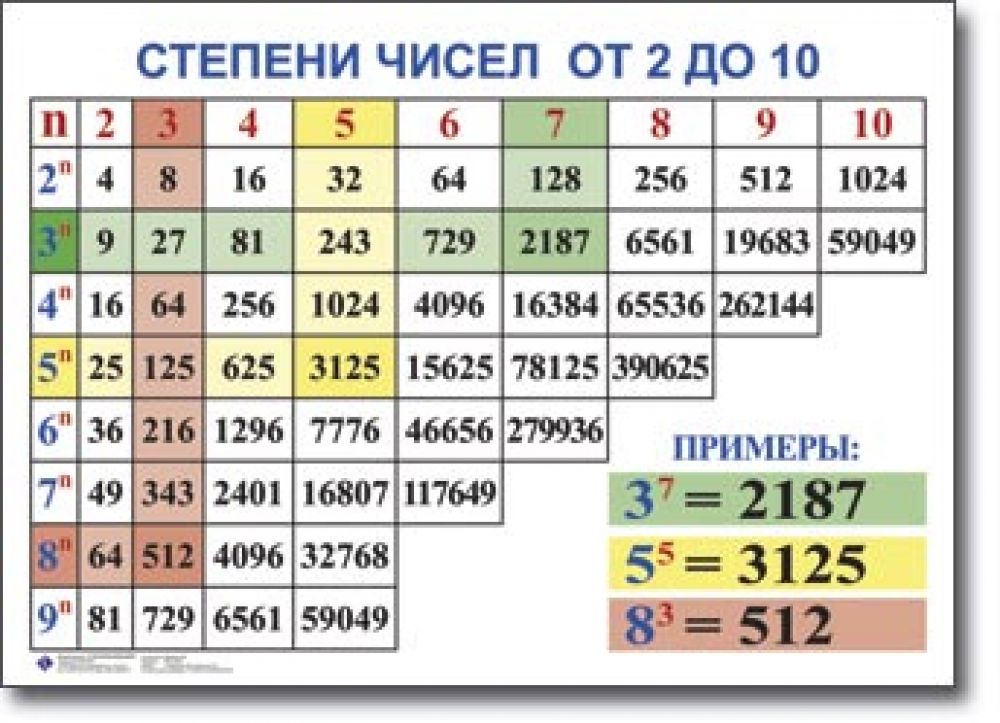
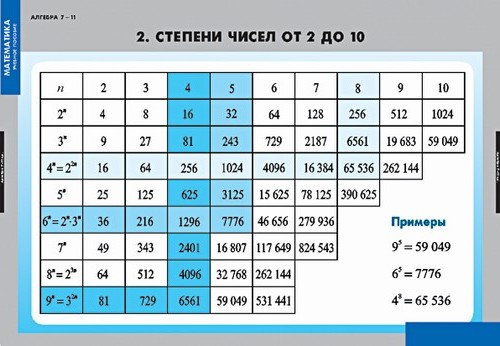
Таблица степеней по алгебре

На этой странице размещена таблица степеней от 2 до 10 для натуральных чисел от 1 до 20. Пример использования: находим в таблице число 9 (слева), затем во втором столбике видим квадрат числа, который равен 81. В третьем столбце таблицы значения кубов. Смотрите также: таблица квадратов, таблица корней.

https://uchim.org/matematika/tablica-stepenej — uchim.org

Таблица степеней

Пример: 23=8

Степень:
Число2345678910
2481632641282565121 024
3927812437292 1876 56119 68359 049
416642561 0244 09616 38465 536262 1441 048 576
5251256253 12515 62578 125390 6251 953 1259 765 625
6362161 2967 77646 656279 9361 679 61610 077 69660 466 176
7493432 40116 807117 649823 5435 764 80140 353 607282 475 249
8645124 09632 768262 1442 097 15216 777 216134 217 7281 073 741 824
9817296 56159 049531 4414 782 96943 046 721387 420 4893 486 784 401
101001 00010 000100 0001 000 00010 000 000100 000 0001 000 000 00010 000 000 000
111211 33114 641161 0511 771 56119 487 171214 358 8812 357 947 69125 937 424 601
121441 72820 736248 8322 985 98435 831 808429 981 6965 159 780 35261 917 364 224
131692 19728 561371 2934 826 80962 748 517815 730 72110 604 499 373137 858 491 849
141962 74438 416537 8247 529 536105 413 5041 475 789 05620 661 046 784289 254 654 976
152253 37550 625759 37511 390 625170 859 3752 562 890 62538 443 359 375576 650 390 625
162564 09665 5361 048 57616 777 216268 435 4564 294 967 29668 719 476 7361 099 511 627 776
172894 91383 5211 419 85724 137 569410 338 6736 975 757 441118 587 876 4972 015 993 900 449
183245 832104 9761 889 56834 012 224612 220 03211 019 960 576198 359 290 3683 570 467 226 624
193616 859130 3212 476 09947 045 881893 871 73916 983 563 041322 687 697 7796 131 066 257 801
204008 000160 0003 200 00064 000 0001 280 000 00025 600 000 000512 000 000 00010 240 000 000 000
214419 261194 4814 084 10185 766 1211 801 088 54137 822 859 361794 280 046 58116 679 880 978 201
2248410 648234 2565 153 632113 379 9042 494 357 88854 875 873 5361 207 269 217 79226 559 922 791 424
2352912 167279 8416 436 343148 035 8893 404 825 44778 310 985 2811 801 152 661 46341 426 511 213 649
2457613 824331 7767 962 624191 102 9764 586 471 424110 075 314 1762 641 807 540 22463 403 380 965 376
2562515 625390 6259 765 625244 140 6256 103 515 625152 587 890 6253 814 697 265 62595 367 431 640 625

Свойства степени — 2 части

Таблица основных степеней по алгебре в компактном виде (картинка, удобно, чтобы распечатать), сверху числа, сбоку степени:

(можно открыть в новом окне, нажав на картинку)

Полную математическую таблицу можно бесплатно скачать, просто сохранив картинку выше с помощью правой кнопки мыши.

Всё для учебы » Математика в школе » Таблица степеней по алгебре

📝Таблица чисел от 1 до 25 в степени от 1 до 10

При решении разных математических упражнений часто приходится заниматься возведением числа степень, в основном от 1 до 10. И для того, что бы быстрее находить эти значения и нами создана таблицу степеней по алгебре, которую я опубликую на этой странице.

Также у нас вы можете посмотреть таблицы квадратов и кубов.

Для начала рассмотрим числа от 1 до 6. Результаты здесь ещё не очень большие все из них вы можете проверить на обычном калькуляторе.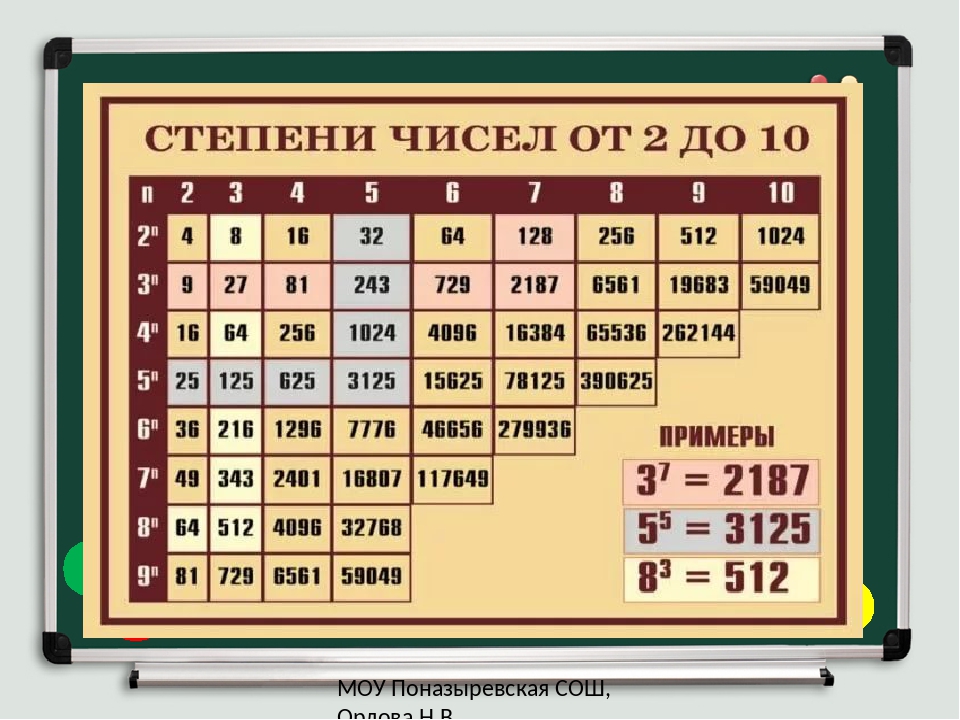

  • 1 и 2 в степени от 1 до 10
    11= 1
    12= 1
    13= 1
    14= 1
    15= 1
    16= 1
    17= 1
    18= 1
    19= 1
    110= 1    		21= 2
    22= 4
    23= 8
    24= 16
    25= 32
    26= 64
    27= 128
    28= 256
    29= 512
    210= 1 024
  • 3 и 4 в степени от 1 до 10
    3 1 = 3
    3 2 = 9
    3 3 = 27
    3 4 = 81
    3 5 = 243
    3 6 = 729
    3 7 = 2 187
    3 8 = 6 561
    3 9 = 19 683
    3 10 = 59 049    		4 1 = 4
    4 2 = 16
    4 3 = 64
    4 4 = 256
    4 5 = 1 024
    4 6 = 4 096
    4 7 = 16 384
    4 8 = 65 536
    4 9 = 262 144
    4 10 = 1 048 576
  • 5 и 6 в степени от 1 до 10
    5 1 = 5
    5 2 = 25
    5 3 = 125
    5 4 = 625
    5 5 = 3 125
    5 6 = 15 625
    5 7 = 78 125
    5 8 = 390 625
    5 9 = 1 953 125
    5 10 = 9 765 625    		6 1 = 6
    6 2 = 36
    6 3 = 216
    6 4 = 1 296
    6 5 = 7 776
    6 6 = 46 656
    6 7 = 279 936
    6 8 = 1 679 616
    6 9 = 10 077 696
    6 10 = 60 466 176
  • 7 и 8 в степени от 1 до 10
    7 1 = 7
    7 2 = 49
    7 3 = 343
    7 4 = 2 401
    7 5 = 16 807
    7 6 = 117 649
    7 7 = 823 543
    7 8 = 5 764 801
    7 9 = 40 353 607
    7 10 = 282 475 249    		8 1 = 8
    8 2 = 64
    8 3 = 512
    8 4 = 4 096
    8 5 = 32 768
    8 6 = 262 144
    8 7 = 2 097 152
    8 8 = 16 777 216
    8 9 = 134 217 728
    8 10 = 1 073 741 824
  • 9 и 10 в степени от 1 до 10
    9 1 = 9
    9 2 = 81
    9 3 = 729
    9 4 = 6 561
    9 5 = 59 049
    9 6 = 531 441
    9 7 = 4 782 969
    9 8 = 43 046 721
    9 9 = 387 420 489
    9 10 = 3 486 784 401    		10 1 = 10
    10 2 = 100
    10 3 = 1 000
    10 4 = 10 000
    10 5 = 100 000
    10 6 = 1 000 000
    10 7 = 10 000 000
    10 8 = 100 000 000
    10 9 = 1 000 000 000
    10 10 = 10 000 000 000
  • 11 и 12 в степени от 1 до 10
    11 1 = 11
    11 2 = 121
    11 3 = 1 331
    11 4 = 14 641
    11 5 = 161 051
    11 6 = 1 771 561
    11 7 = 19 487 171
    11 8 = 214 358 881
    11 9 = 2 357 947 691
    11 10 = 25 937 424 601    		12 1 = 12
    12 2 = 144
    12 3 = 1 728
    12 4 = 20 736
    12 5 = 248 832
    12 6 = 2 985 984
    12 7 = 35 831 808
    12 8 = 429 981 696
    12 9 = 5 159 780 352
    12 10 = 61 917 364 224
  • 13 и 14 в степени от 1 до 10
    13 1 = 13
    13 2 = 169
    13 3 = 2 197
    13 4 = 28 561
    13 5 = 371 293
    13 6 = 4 826 809
    13 7 = 62 748 517
    13 8 = 815 730 721
    13 9 = 10 604 499 373
    13 10 = 137 858 491 849    		14 1 = 14
    14 2 = 196
    14 3 = 2 744
    14 4 = 38 416
    14 5 = 537 824
    14 6 = 7 529 536
    14 7 = 105 413 504
    14 8 = 1 475 789 056
    14 9 = 20 661 046 784
    14 10 = 289 254 654 976
  • 15 и 16 в степени от 1 до 10
    15 1 = 15
    15 2 = 225
    15 3 = 3 375
    15 4 = 50 625
    15 5 = 759 375
    15 6 = 11 390 625
    15 7 = 170 859 375
    15 8 = 2 562 890 625
    15 9 = 38 443 359 375
    15 10 = 576 650 390 625    		16 1 = 16
    16 2 = 256
    16 3 = 4 096
    16 4 = 65 536
    16 5 = 1 048 576
    16 6 = 16 777 216
    16 7 = 268 435 456
    16 8 = 4 294 967 296
    16 9 = 68 719 476 736
    16 10 = 1 099 511 627 776
  • 17 и 18 в степени от 1 до 10
    17 1 = 17
    17 2 = 289
    17 3 = 4 913
    17 4 = 83 521
    17 5 = 1 419 857
    17 6 = 24 137 569
    17 7 = 410 338 673
    17 8 = 6 975 757 441
    17 9 = 118 587 876 497
    17 10 = 2 015 993 900 449    		18 1 = 18
    18 2 = 324
    18 3 = 5 832
    18 4 = 104 976
    18 5 = 1 889 568
    18 6 = 34 012 224
    18 7 = 612 220 032
    18 8 = 11 019 960 576
    18 9 = 198 359 290 368
    18 10 = 3 570 467 226 624
  • 19 и 20 в степени от 1 до 10
    19 1 = 19
    19 2 = 361
    19 3 = 6 859
    19 4 = 130 321
    19 5 = 2 476 099
    19 6 = 47 045 881
    19 7 = 893 871 739
    19 8 = 16 983 563 041
    19 9 = 322 687 697 779
    19 10 = 6 131 066 257 801    		20 1 = 20
    20 2 = 400
    20 3 = 8 000
    20 4 = 160 000
    20 5 = 3 200 000
    20 6 = 64 000 000
    20 7 = 1 280 000 000
    20 8 = 25 600 000 000
    20 9 = 512 000 000 000
    20 10 = 10 240 000 000 000
  • 21 и 22 в степени от 1 до 10
    21 1 = 21
    21 2 = 441
    21 3 = 9 261
    21 4 = 194 481
    21 5 = 4 084 101
    21 6 = 85 766 121
    21 7 = 1 801 088 541
    21 8 = 37 822 859 361
    21 9 = 794 280 046 581
    21 10 = 16 679 880 978 201    		22 1 = 22
    22 2 = 484
    22 3 = 10 648
    22 4 = 234 256
    22 5 = 5 153 632
    22 6 = 113 379 904
    22 7 = 2 494 357 888
    22 8 = 54 875 873 536
    22 9 = 1 207 269 217 792
    22 10 = 26 559 922 791 424
  • 23 и 24 в степени от 1 до 10
    23 1 = 23
    23 2 = 529
    23 3 = 12 167
    23 4 = 279 841
    23 5 = 6 436 343
    23 6 = 148 035 889
    23 7 = 3 404 825 447
    23 8 = 78 310 985 281
    23 9 = 1 801 152 661 463
    23 10 = 41 426 511 213 649    		24 1 = 24
    24 2 = 576
    24 3 = 13 824
    24 4 = 331 776
    24 5 = 7 962 624
    24 6 = 191 102 976
    24 7 = 4 586 471 424
    24 8 = 110 075 314 176
    24 9 = 2 641 807 540 224
    24 10 = 63 403 380 965 376
  • 25 в степени от 1 до 10
    25 1 = 25
    25 2 = 625
    25 3 = 15 625
    25 4 = 390 625
    25 5 = 9 765 625
    25 6 = 244 140 625
    25 7 = 6 103 515 625
    25 8 = 152 587 890 625
    25 9 = 3 814 697 265 625
    25 10 = 95 367 431 640 625

Хочу напомнить:

Для того, что бы возвести число «a» в степень «b» надо «a» умножить само на себя «b» раз!

Вот, например, в начале изучения компьютера мы рассматриваем двоичный код – то есть язык, на котором «разговаривает» компьютер. И там часто используются разные степени двойки, которые надо знать. От вы знаете, сколько будет два в восьмой?

Материалы по теме:

Поделиться с друзьями:

Загрузка…

ПОСЛЕДНЯЯ ЦИФРА СТЕПЕНИ

ПОСЛЕДНЯЯ ЦИФРА СТЕПЕНИ

Старцев Д.В. 1

1МБОУ СОШ № 77

Кулагина О.А. 1

1МБОУ СОШ № 77


Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF


 Введение



«Математику уже затем учить следует,



что она ум в порядок приводит»



М. В. Ломоносов



Эти слова раскрывают сущность предмета математика, так как именно она, прежде всего, учит нас мыслить, рассуждать, анализировать, делать выводы, умозаключения и подводить итоги. Математика является одним из основных школьных предметов, потому, что все перечисленные качества необходимы не только математику, но и представителю любой другой науки. Развитием этих качеств занимается, прежде всего, математика. Существуют специальные задачи, которые направлены на формирование названных умений. Готовясь к различным математическим конкурсам, мы столкнулись с таким заданием « Какой будет последняя цифра числа ?» На первый взгляд эта задача может показаться достаточно сложной и я принялся за вычисления…



В ходе решения этой задачи возникла идея исследовать, а какой будет последняя цифра любого натурального числа в любой степени, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа?



Цели работы



Составить опорную таблицу «Последние цифры степени», найти закономерности в них, научится вычислять последние цифры степеней.



Актуальность темы исследования обусловлена насущной необходимостью поиска быстрых алгоритмов решения практически важных задач, отработки навыков устного счета.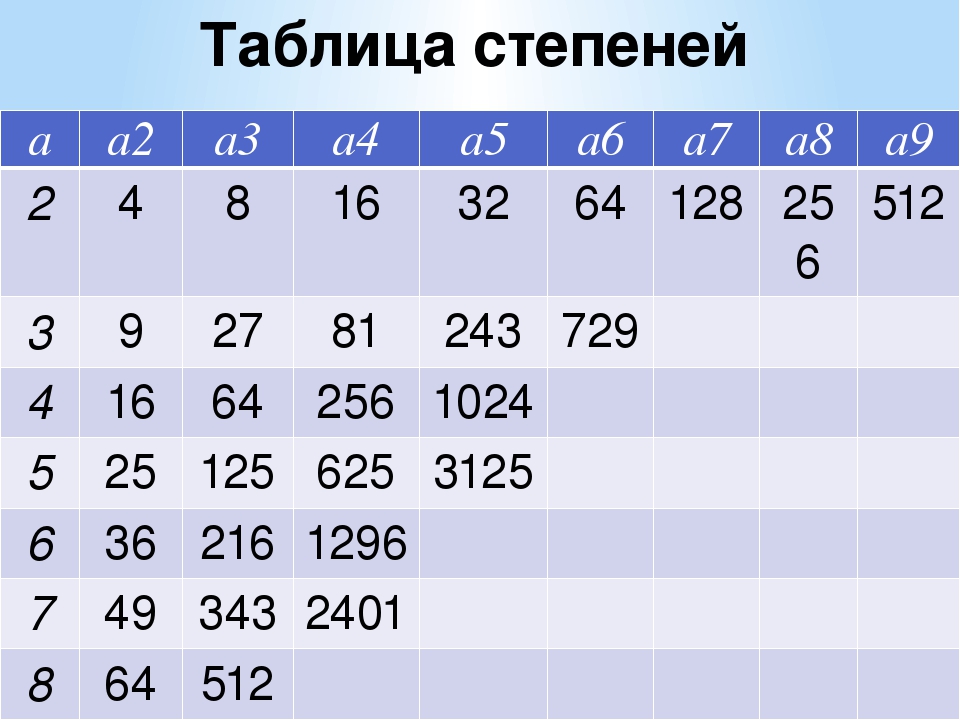



2. Последняя цифра степени



Выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа , где N , n – натуральные числа, с изменением показателя n. Для этого составим таблицу:

















N n


1


2


3


4


5


6


7


8


9


10


11


12


13


1


1


1


1


1


1


1


1


1


1


1


1


1


1


2


2


4


8


16


32


64


128


256


512


1024


2048


4096


8192


3


3


9


27


81


243


729


2187


6561


19683


59049


177147


531441


1594323


4


4


16


64


256


1024


4096


16384


65536


262144


1048576


4194304


16777216


67108864


5


5


25


125


625


3125


15625


78125


390625


1953125


9765625


48828125


244140625


1220703125


6


6


36


216


1296


7776


46656


279936


1679616


10077696


60466176


362797056


2176782336


13060694016


7


7


49


343


2401


16807


117649


823543


5764801


40353607


282475249


1977326743


13841287201


96889010407


8


8


64


512


4096


32768


262144


2097152


16777216


134217728


1073741824


8589934592


68719476736


549755813888


9


9


81


729


6561


59049


531441


4782969


43046721


387420489


3486784401


31381059609


282429536481

 


10


10


100


1000


10000


100000


1000000


10000000


100000000


1000000000


10000000000


100000000000


1000000000000

 


11


11


121


1331


14641


161051


1771561


19487171


214358881


2357947691


25937424601


285311670611

  


12


12


144


1728


20736


248832


2985984


35831808


429981696


5159780352


61917364224


743008370688

  


13


13


169


2197


28561


371293


4826809


62748517


815730721


10604499373


137858491849

   


Для наглядности составим таблицу, где будут записаны цифры, которыми оканчиваются записи натуральных чисел:


















N n


1


2


3


4


5


6


7


8


9


10


1


1


1


1


1


1


1


1


1


1


1


2


2


4


8


6


2


4


8


6


2


4


3


3


9


7


1


3


9


7


1


3


9


4


4


6


4


6


4


6


4


6


4


6


5


5


5


5


5


5


5


5


5


5


5


6


6


6


6


6


6


6


6


6


6


6


7


7


9


3


1


7


9


3


1


7


9


8


8


4


2


6


8


4


2


6


8


4


9


9


1


9


1


9


1


9


1


9


1


10


0


0


0


0


0


0


0


0


0


0


11


1


1


1


1


1


1


1


1


1


1


12


2


4


8


6


2


4


8


6


2


4


13


3


9


7


1


3


9


7


1


3


9


14


4


6


4


6


4


6


4


6


4


6


Заполняя столбики получаем такой результат: пятая и девятая и т.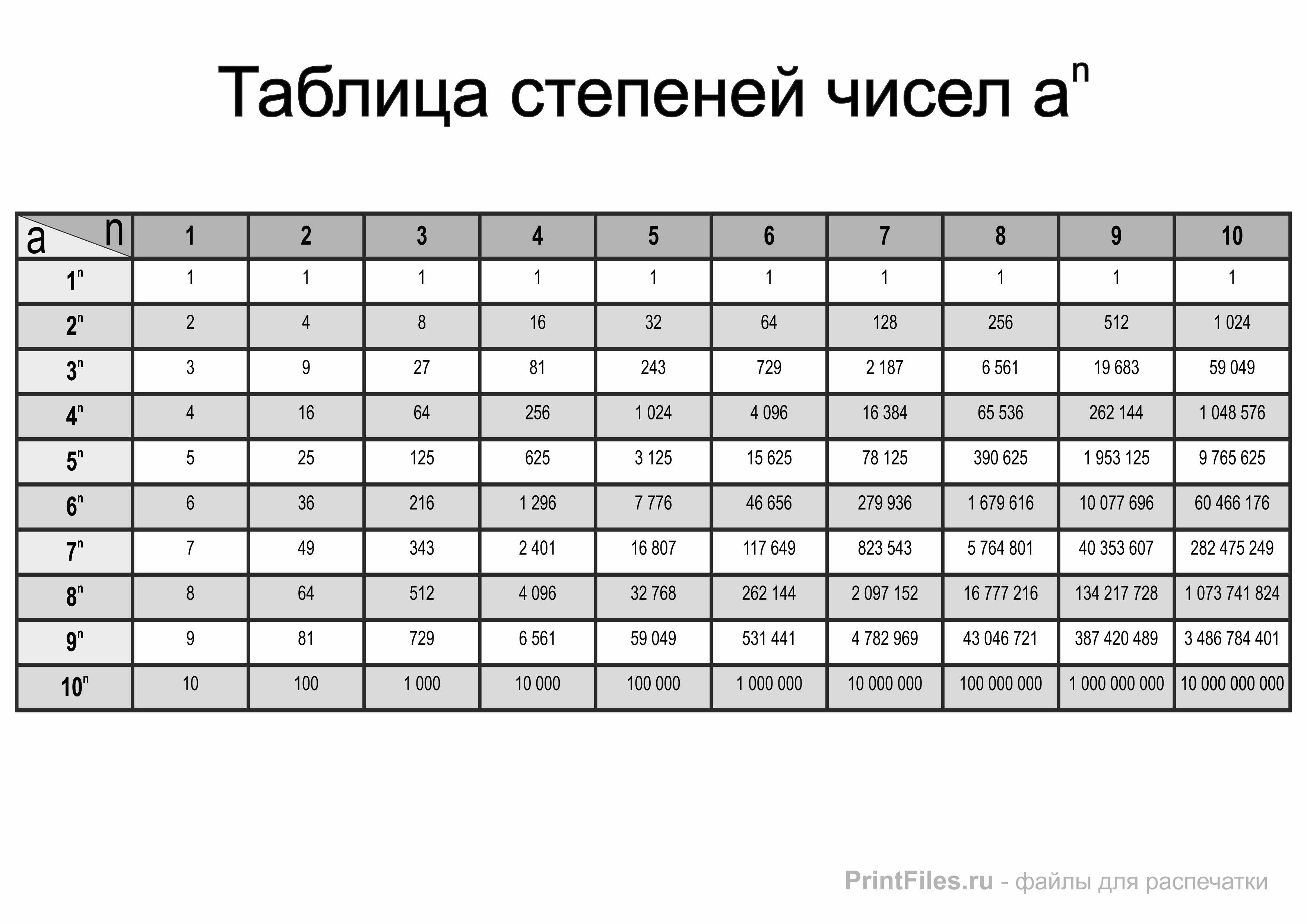 д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.



3. Закономерности возведения в степень



Результаты в таблице повторяются через каждые четыре столбца.



Про числа 1 и 10 писать не будем, т.к. результат всегда будет 1 или 0 соответственно.



Любая степень чисел 5 и 6 оканчивается соответственно на 5 и на 6.



Последние цифры степеней чисел 4 и 9 повторяются через каждые два шага, при возведении в четную степень последняя цифра не меняется, будет соответственно 4 или 9, при возведении в нечетную степень изменится на 6 или 1 соответственно.



Квадрат любого натурального числа может оканчиваться на 0, 1,4, 5, 6 и 9,



Куб натурального числа может оканчиваться любой цифрой



Используя полученные результаты попробуем найти последние цифры степени по остатку от деления её показателя на 4






 


24: 4=5(остаток 0)


1

 


48:4=12(остаток 0)


1

 


2016:4=504(остаток0)


6

 


28:4=7(остаток0)


6


Если остаток равен 0 и основание нечетное, то число будет оканчиваться на 1(кроме чисел оканчивающихся на цифру 5), если основание четное (кроме круглых чисел), то числа будут оканчиваться на цифру 6.



Теперь будем подбирать такие числа, что при делении показателя степени на 4 будут давать остатки 1, 2, 3








 


45:4=11 (остаток 1)


7

 


37:4=9 (остаток 1)


2

 


18:4=4 (остаток 2)


1

 


102:4=25 (остаток 2)


6

 


31:4=7(остаток3)


2

 


1199:4=299(остаток3)


9


Если остаток равен 1, то последняя цифра степени будет равна последней цифре в записи основания степени;



Если остаток равен 2, то последняя цифра степени будет равна последней цифре в записи квадрата основания;



Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.



Значит чтобы найти последнюю цифру степени натурального числа с натуральным показателем, нужно найти остаток от деления показателя степени на 4.



Последние цифры степеней чисел 2 , 12, 22 и т. д. (3, 13, 23 и т.д.) и т. д. будут совпадать.



4. Последние две цифры степени



Мы видим, что последняя цифра рано или поздно будет повторяться, а как будет обстоять дело с 2-мя и 3-мя последними цифрами ? Вероятно, они тоже будут повторяться. Для наглядности составим таблицу, где будут записаны две цифры, которыми оканчиваются записи натуральных чисел:

























N n


1


2


3


4


5


6


7


8


9


10


11


12


13


14


15


16


17


18


19


20


21


22


23


24


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


1


2


2


4


8


16


32


64


28


56


12


24


48


96


92


84


68


36


72


44


88


76


52


04


08


16


3


3


9


27


81


43


29


87


61


83


49


47


41


23


69


07


21


63


89


67


01


03


09


27


81


4


4


16


64


56


24


96


84


36


44


76


04


16


64


56


24


96


84


36


44


76


04


16


64


56


5


5


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


25


6


6


36


16


96


76


56


36


16


96


76


56


36


16


96


76


56


36


16


96


76


56


36


16


96


7


7


49


43


01


07


49


43


01


07


49


43


01


07


49


43


01


07


49


43


01


07


49


43


01


8


8


64


12


96


68


44


52


16


28


24


92


36


88


04


32


56


48


84


72


76


08


64


12


96


9


9


81


29


61


49


41


69


21


89


01


09


81


29


61


49


41


69


21


89


01


09


81


29


61


10


10


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


11


11


21


31


41


51


61


71


81


91


01


11


21


31


41


51


61


71


81


91


01


11


21


31


41


12


12


44


28


36


32


84


08


96


52


24


88


56


72


64


68


16


92


04


48


76


12


44


28


36


13


13


69


97


61


93


09


17


21


73


49


37


81


53


89


57


41


33


29


77


01


13


69


97


61


14


14


96


44


16


24


36


04


56


84


76


64


96


44


16


24


36


04


56


84


76


64


96


44


16


15


15


25


75


25


75


25


75


25


75


25


75


25


75


25


75


25


75


25


75


25


75


25


75


25


16


16


56


96


36


76


16


56


96


36


76


16


56


96


36


76


16


56


96


36


76


16


56


96


36


17


17


89


13


21


57


69


73


41


97


49


33


61


37


29


93


81


77


09


53


01


17


89


13


21


18


18


24


32


76


68


24


32


76


68


24


32


76


68


24


32


76


68


24


32


76


24


24


32


76


19


19


61


59


21


99


81


39


41


79


01


19


61


59


21


99


81


39


41


76


01


19


61


59


21


20


20


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


00


21


21


41


61


81


01


21


41


61


81


01


21


41


61


81


01


21


41


61


81


01


21


41


61


81


Глядя на таблицу, замечаем что последние две цифры тоже повторяются, только период повторения увеличивается, кроме того у некоторых чисел 1-е не входит в период, так например:



Но начиная с 21 степени по 40 последние две цифры будут повторяться.



Последние цифры чисел 3,13 и 8 тоже будут повторятся с периодом 20, но последние две цифры чисел 3 и 13 совпадать не будут, не будут совпадать последние две цифры для степеней чисел 4 и 14 и т.д.



Последние цифры чисел 4 и 9 будут повторяться с периодом 10,последние цифры числа 6 будут повторятся с периодом 5, но число 6 не входит в период, последние цифры числа 7 будут повторятся с периодом – 4. Любая степень числа 5 (начиная со 2 –ой) и 25 будет оканчиваться на 25, а число 15 в четной степени будет оканчиваться на 25, а в нечетной на 75. Период чисел 11, тоже будет равен 10, но здесь есть еще одна закономерность:



Для числа 11 в степени – число десятков будет равно показателю степени



Для числа 21 – период равен 4, а число десятков будет равно числу, полученному , если число 2 умножить на показатель степени



.



5. Заключение



Определить последнюю цифру степени числа не сложно, мы легко составили алгоритм, для двух последних цифр степени числа такой алгоритм уже не составишь, закономерности есть , но их меньше. Считаю, что таблицу с тремя последними цифрами составлять не имеет смысла – не рационально.



Мы провели большую работу: составили таблицы для последней и двух последних цифр степеней и получили интересные с нашей точки зрения выводы. Результаты работы могут быть использованы на занятиях математического кружка и факультативах в 5- 7 классах для развития интереса к математике у учащихся, а так же для индивидуальной работы с теми учениками, кто интересуется математикой. Кроме того, данными выводами можно воспользоваться при подготовке к различным олимпиадам и конкурсам. Кроме того сам процесс проведённого исследования позволил нам ещё раз убедиться в своих возможностях.



6. Задачи



  1. Определите последнюю цифру в записи числа (ответ 8)


  2. Найдите последнюю цифру числа 2017 в степени 4207. 41 .


(8+3=11, последняя цифра 1)



  1. Найдите последнюю цифру суммы степеней числа 2 с показателями, равными 32, 69, 469, 1995, 19951995.


(6+2+2+8+8=26 последняя цифра 6)



  1. В книге рекордов Гиннеса написано, что наибольшее известное простое число равно (− 1). Не опечатка ли это?


(опечатка. Число 23021337 оканчивается единицей Поэтому последняя цифра числа (23021337 − 1) равна 0, а значит, это число делится на 10 и потому составное.)



  1. Делится ли число+ на 10 ?


(Число 4730 оканчивается цифрой 9, а число 3950 — цифрой 1 Значит, их сумма оканчивается на 0 и потому делится на 10.)



  1. Найдите последнюю цифру числа . Степени считаются сверху вниз: =


Последние две цифры числа 77 образуют число 43 (это можно вычислить непосредственно, отбрасывая при каждом умножении все цифры результата, кроме последних двух). Значит, число 77 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 77 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).



  1. Найдите 2 последние цифры числа 81989 .


В таблице 2-х последних цифр, у числа 8 период 20, (1989:20=99 остаток 9 , число 8 в 9 степени оканчивается цифрами 28, последние 2 цифры числа 81989 – 28).



  1. На контрольной работе по перекрашиванию юный хамелеон перекрашивается по очереди из красного -> в желтый -> зелёный -> синий -> фиолетовый -> красный -> жёлтый -> зелёный и т.д. перекрасился он 2010 раз и начав с красного он в конце стал синим, но известно что он допустил ошибку, покраснел в тот момент, когда должен был приобрести другой цвет.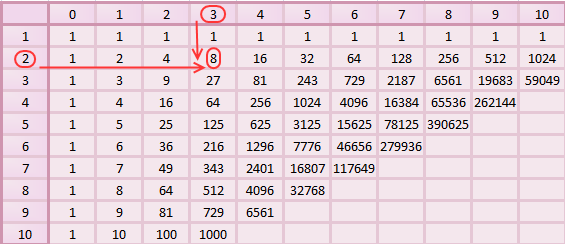 Какого он был цвета перед этим покраснением?


(Заметим, что здесь период повторения цветов равен 5. Красный цвет будет встречаться на числах оканчивающихся на 0 и 5. Значит и должен он был закончить снова на красном. Поэтому чтобы найти ошибку перейдём сразу к 2005 перекрашиванию. Теперь просто будем считать по очереди меняя цвета до 2010-го. Сразу же смотрим что он сделал ошибку допустим после жёлтого, тогда получается 2005-красный, 2006 – жёлтый 2007- снова красный (это его ошибка), 2008 — жёлтый, 2009 -зелёный, 2010 – синий, перед ошибочным покраснением хамелеон был жёлтым).



  1. Сейчас на часах 10:00. Какое время они будут показывать через 102938475 часов?


(У часов период повторения равен 24, значит число 102938475 разделить на 24 = 4289103,12… 102938475 — (4289103 * 24) = 3. Значит время которое часы будут показывать через 102938475 часов равно 10+3 = 13 часов, через 102938475 часы будут показывать 13:00).



11. Доказать, что число кратно 2.



12. Доказать, что -1 кратно 5 (при натуральном n).



13. Верно ли, что 1,6*( -1 ) – целое число при любом (натуральном) n. 14. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?



7. Использованная литература



1. «Все задачи «Кенгуру» 1994-2008- Санкт-Петербург, 2008.



2. «Задачи для подготовки к олимпиадам. Математика 5-8 классы» сост. Н.В. Заболотнева. – Волгоград: Учитель, 2007.- 99с.



3. Лихтарников Л.М. Занимательные логические задачи. (Для учащихся начальной школы) Оформление С. Григорьева — СПб.: Лань, МИК, 1996.- 125с.



4. Л.М.Лоповок 1000 проблемных задач по математике. Книга для учащихся Москва : Просвещение, 1995



5. Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.



6. Чулков П.В. Математика. Школьные олимпиады: методическое пособие. 5- кл./ П.В. Чулков.- М.: Издательство НЦ ЭНАС, 2007.- 88с. (Портфель учителя).



7. Шуба М.Ю. Занимательные задачи в обучении математике: Книга для учителя. — 2-е изд.-М.: Просвещение, 1995.- 22с.



4


Просмотров работы: 42866

Последняя цифра степени числа — математика, прочее

Последняя цифра степени.

Приведем небольшое исследование: выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа 2n, где n – натуральное число, с изменением показателя n. Для этого рассмотрим таблицу:

21 = 2

25 = 32

29 = 512

22 = 4

26 = 64

210 = 1024

23 = 8

27 = 128

211 = 2048

24 = 16

28 = 256

212 = 4096

Мы видим, что через каждые четыре шага последняя цифра повторяется. Заметив это, нетрудно определить последнюю цифру степени 2n для любого показателя n.

В самом деле, возьмем число 2100. Если бы мы продолжили таблицу, то оно попало бы в столбец, где находятся степени 24, 28, 212, показатели которых кратны четырем. Значит, число 2100, как и эти степени, оканчивается цифрой 6.

Возьмем к примеру, 222, если проверить, просто посчитав, то получится 4194304 – последняя цифра 4.

Теперь попробуем пользоваться таблицей, но в таблице 4 числа, а показатель степени 22, однако, после последнего числа этот «круг» начинается заново. Поэтому, показатель степени 22 делим на 4, получаем число 5 и остаток 2 т.е мы сделаем 5 «кругов», и отсчитаем ещё 2 в перед, а второе число – это 4, значит, таблица работает.

А теперь посмотрим, можно ли составить таблицы для остальных чисел. Все описывать не буду, лишь скажу, что у меня получилось составить таблицу для всех чисел от 1 до 10, а далее будет повторяться, допустим, у 12 последние числа будут такие же, как и у 2, а у 25 – так же, как и у 5.

Закономерности возведения в степень:

    • Запись числа, являющегося полным квадратом, может оканчиваться только цифрами 0, 1, 4, 5, 6 или 9.

    • Если запись числа оканчивается цифрой 0, 1, 5 или 6,то возведение в любую степень не изменит последние цифры.

    • При возведении любого числа в пятую степень его последняя цифра не изменится.

    • Если число оканчивается цифрой 4 (или 9), то при возведении в нечетную степень последняя цифра не изменяется, а при возведении в четную степень изменится на 6 (или 1 соответственно).

    • Если число оканчивается цифрой 2, 3, 7 или 8, то при возведении в степень возможны четыре различных цифры.

    Две последних цифры степени.

    Мы теперь знаем, что последняя цифра рано или поздно будет повторяться. Но как же обстоит дело с 2-мя последними цифрами? Я осмелюсь предположить, что не только 2, но и 3 и более последних цифр будут повторяться.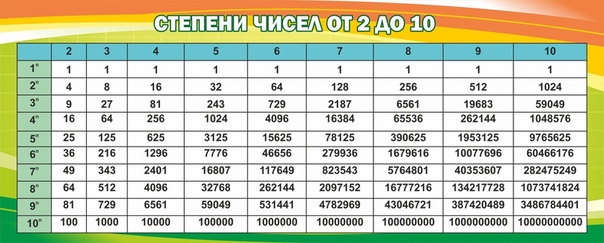 Что ж проверим это, так же я заметила, что периоды из прошлой таблицы просто увеличились в 5 раз, кроме чисел 5 и 10, а про число 1 я писать не стала, так как результат всегда будет 1.

    Степень

    02

    03

    04

    05

    06

    07

    08

    09

    10

    Х2

    04

    09

    16

    25

    36

    49

    64

    81

    00

    Х3

    08

    27

    64

    25

    16

    43

    12

    29

    00

    Х4

    16

    81

    56

    25

    96

    01

    96

    61

    Х5

    32

    43

    24

    76

    07

    68

    49

    Х6

    64

    29

    96

    56

    44

    41

    Х7

    28

    87

    84

    36

    52

    69

    Х8

    56

    61

    36

    16

    21

    Х9

    12

    83

    44

    28

    89

    Х10

    24

    49

    76

    24

    01

    Х11

    48

    47

    04

    92

    09

    Х12

    96

    41

    36

    Х13

    92

    23

    88

    Х14

    84

    69

    04

    Х15

    68

    07

    32

    Х16

    36

    21

    56

    Х17

    72

    63

    48

    Х18

    44

    89

    84

    Х20

    88

    67

    72

    Х21

    76

    01

    76

    Х22

    52

    03

    08

    Х23

    04

    Повтор

    20

    20

    10

    1

    5

    4

    20

    10

    1

    (Красным кругом выделен период)

    Заметим, что у некоторых чисел, например 1-е не входит в период, так как, например, у числа 2, после последнего числа 52, будет 04, а не 02, поэтому оно само не входит в этот период, следовательно, перед тем как вычислять последние 2 цифры надо будет вычесть из показателя степени 1.

    К сожалению, с 2-мя последними цифрами не получится как с 1-й, и последние 2 цифры 3 не будут одинаковы с 2-мя последними цифрами 13, и таблицу для остальных надо составлять отдельно.

    Степень

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    Х2

    21

    44

    69

    96

    25

    56

    89

    24

    61

    00

    Х3

    31

    28

    97

    44

    75

    96

    13

    32

    59

    00

    Х4

    41

    36

    61

    16

    25

    36

    21

    76

    21

    Х5

    51

    32

    93

    24

    76

    57

    68

    99

    Х6

    61

    84

    09

    36

    16

    69

    24

    81

    Х7

    71

    08

    17

    04

    73

    39

    Х8

    81

    96

    21

    56

    41

    41

    Х9

    91

    52

    73

    84

    97

    79

    Х10

    01

    24

    49

    76

    49

    01

    Х11

    11

    88

    37

    64

    33

    19

    Х12

    56

    81

    96

    61

    Х13

    72

    53

    37

    Х14

    64

    89

    29

    Х15

    68

    57

    93

    Х16

    16

    41

    81

    Х17

    92

    33

    77

    Х18

    04

    29

    09

    Х20

    48

    77

    53

    Х21

    76

    01

    01

    Х22

    12

    13

    17

    Х23

    Повтор

    10

    20

    20

    10

    2

    5

    20

    4

    10

    1

    Число в первой и нулевой степени

    Степень числа – это краткая запись произведения одинаковых сомножителей

    Пример.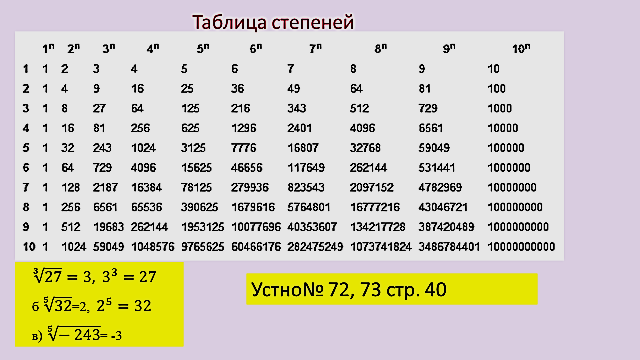

    7 · 7 · 7 · 7 = 74.

    В записи  74  число 7 — это основание степени, то есть число, повторяющееся сомножителем, а число 4 — показатель степени, то есть число, показывающее количество одинаковых сомножителей.

    Первая степень числа

    Любое число в первой степени равно самому себе, так как показатель степени  1  указывает что число берётся сомножителем всего один раз, то есть оно ни на что не умножается, а просто остаётся без изменений.

    Примеры:

    71 = 7,

    1001 = 100,

    -251 = -25.

    Нулевая степень числа

    Любое число в нулевой степени (за исключением  0)  равно  1.

    Примеры:

    70 = 1,

    1000 = 1,

    -250 = 1.

    Чтобы разобраться почему число в нулевой степени равно  1,  надо вспомнить правило деления степеней с одинаковыми основаниями:

    При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.

    Следовательно, если разделить одинаковые степени с одинаковыми основаниями, то в результате получится основание в нулевой степени:

    a3 : a3 = a3-3 = a0.

    Так как два одинаковых числа, взятых в одной и той же степени, равны, по сути, они являются одним и тем же числом, то при их делении в частном получается единица. Значит:

    a3 : a3 = 1.

    Следовательно, любое число в нулевой степени равно единице. Это можно легко доказать, проведя проверку деления умножением, умножив частное на делитель:

    a0 · a3 = a0+3 = a3

    или

    1 · a3 = a3.

    Как определить последнюю цифру числа в степени

    Разделы: Математика

    Основная часть

    I.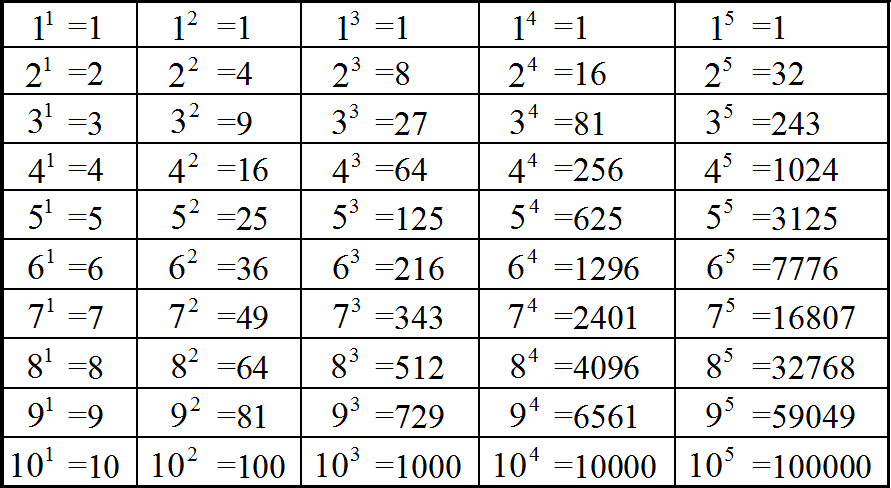 Нахождение последней цифры в записи степени натурального числа.

    После изучения темы “Степень с натуральным показателем” была предложена такая задача: найти последнюю цифру степеней:

    а) , , , , ;

    б) , .

    Мы заметили, что в первом случае показатели степеней составные числа, а во втором случае показатели степеней простые числа. В обоих случаях есть основания четные и нечетные. Мы сначала попробовали представить степени в виде произведения степеней с тем же основанием и одинаковыми показателями, затем воспользовались со свойствами степеней с натуральными показателями

    Например, = *** или

    В первом случае узнали последнюю цифру степени . Это 3. А дальше определили искомую цифру как последнюю цифру числа . Получили 1. Во втором случае сначала нашли последнюю цифру степени . Это 1. А 1 в любой степени -1. Второй способ нам понравился больше. Аналогично нашли последнюю цифру остальных степеней.

    В ходе решения таких задач мы поняли, чтовсегда оканчивается (при натуральном) n на 6.

    Но вторая задача достаточно сложная, так как показатели степеней простые числа и мы не можем представить эти степени в виде произведения степеней с одинаковыми показателями, как делали раньше. Но мы нашли способы решения.

    Значит, последняя цифра степени равна 3.

    Мы решили найти более удобный, универсальный способ нахождения последней цифры степени.

    Решили заполнить таблицу, где в первой строке написаны цифры, которыми оканчиваются записи натуральных чисел. Во – второй строке – цифры, которыми оканчиваются соответствующие квадраты, в третьей – кубы и т.д.

    Мы заполнили пятую строку, затем шестую и удивились. Оказывается, пятая степень числа оканчивается той же цифрой, что и первая степень числа; а шестая степень числа оканчивается той же цифрой, что и вторая степень этого числа; седьмая степень – что и третья степень этого числа.

    К нашему удивлению, результаты в таблице повторяются через каждые четыре строки.

    После решения этих примеров и заполнения таблицы мы пришли к выводу, что:

    • Во-первых, квадрат натурального числа может оканчиваться любой цифрой;
    • Во-вторых, куб натурального числа может оканчиваться любой цифрой;
    • В-третьих, четвертая степень натурального числа может оканчиваться одной из цифр: 0, 1, 5, 6;
    • В-четвертых, пятая степень натурального числа оканчивается той же цифрой, что и само число;
    • В-пятых, если запись натурального числа оканчивается на 1, на 5, на 6, то любая степень этого числа оканчивается соответственно на 1, на 5, на 6;
    • В-шестых, нечетные степени числа 4 оканчиваются цифрой 4, а четные – цифрой 6.

    Мы поставили перед собой такую задачу, а нельзя ли найти способ определения последней цифры степени по остатку от деления ее показателя на 4.

    II. Составление алгоритма нахождения последней цифры степени по остатку от деления ее показателя на 4.

    Вернулись к нашим же примерам.

    Найти последнюю цифру степеней: , , , ;.

    Итак, мы заметили, что если остаток равен 0, то для всех нечетных оснований, кроме чисел, оканчивающихся на 5, искомая цифра равна 1, а для четных, искомая цифра равна 6.

    Далее мы начали подбирать такие степени, когда при делении показателя степени на 4 получаются остатки 1, 2, 3.

    Например, .

    5: 4= 1 (остаток 1)2
    1989:4 = 497 (остаток 1)3

    Если остаток равен 1, то искомая цифра будет равна последней цифре основания степени.

    22: 4 = 5 (остаток 2)4
    18: 4 = 4 (остаток 2)9

    Если остаток равен 2, то искомая цифра будет равна последней цифре в записи квадрата основания.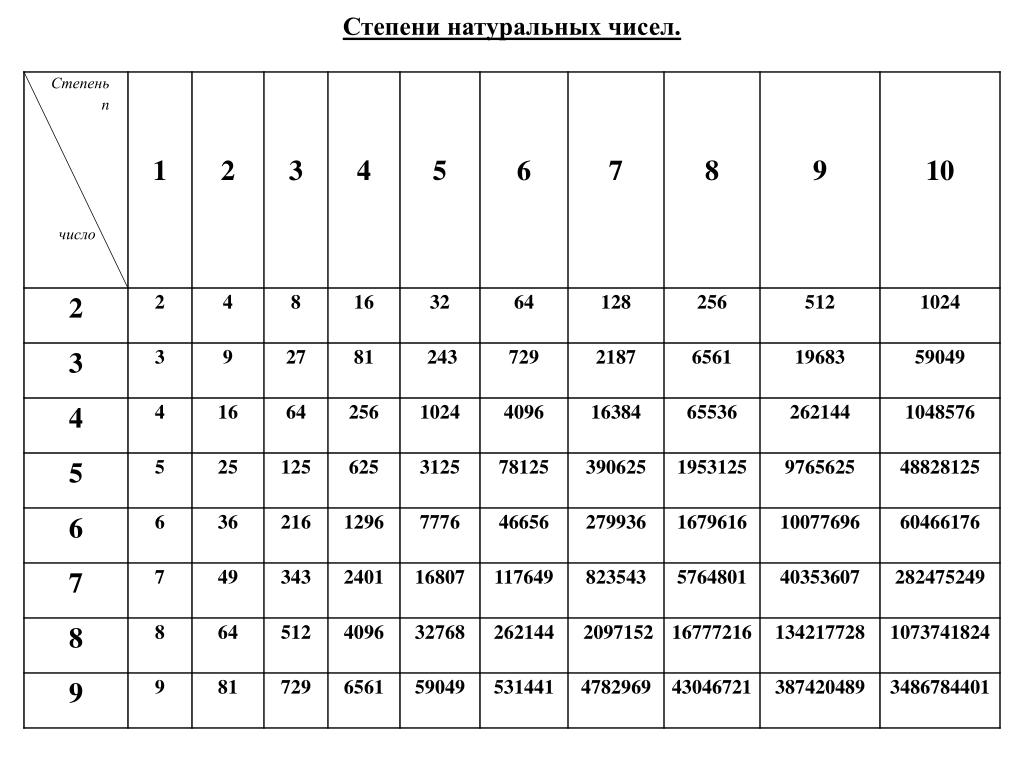

    43: 4 = 10 (остаток 3)3
    19: 4 = 4 (остаток 3)8

    Если остаток равен 3, то искомая цифра будет равна последней цифре в записи куба основания.

    А если степени с очень большими показателями?

    Например,

    Мы легко справились и с этой задачей.

    Итак, мы получили алгоритм нахождения последней цифры степени натурального числа.

    Чтобы найти последнюю цифру степени натурального числа с натуральным показателем, надо:

    Найти остаток от деления показателя степени на 4;

    Если остаток равен

    а) 1, то искомая цифра будет совпадать с последней цифрой основания степени;

    б) 2, то искомая цифра будет равна последней цифре в записи квадрата основания;

    в) 3, то искомая цифра будет равна последней цифре в записи куба основания;

    г) 0, то для всех нечетных оснований, кроме чисел, оканчивающихся на 5, искомая цифра равна 1, а для четных, кроме круглых чисел, искомая цифра равна 6.

    Мы научились быстро находить последнюю цифру степени и попробовали расширить круг знаний. Например, мы составили такие задачи.

    III. Составление упражнений на применение алгоритма.

    1. Доказать, что число кратно 2.

    2. Доказать, что -1 кратно 5 (при натуральном n).

    3. Верно ли, что 1,6*( -1 ) – целое число при любом (натуральном) n.

    4. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?

    Введение

    «Математику уже затем учить следует,

    что она ум в порядок приводит»

    Эти слова раскрывают сущность предмета математика, так как именно она, прежде всего, учит нас мыслить, рассуждать, анализировать, делать выводы, умозаключения и подводить итоги. Математика является одним из основных школьных предметов, потому, что все перечисленные качества необходимы не только математику, но и представителю любой другой науки. Развитием этих качеств занимается, прежде всего, математика. Существуют специальные задачи, которые направлены на формирование названных умений. Готовясь к различным математическим конкурсам, мы столкнулись с таким заданием « Какой будет последняя цифра числа ?» На первый взгляд эта задача может показаться достаточно сложной и я принялся за вычисления…

    В ходе решения этой задачи возникла идея исследовать, а какой будет последняя цифра любого натурального числа в любой степени, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа?

    Составить опорную таблицу «Последние цифры степени», найти закономерности в них, научится вычислять последние цифры степеней.

    Актуальность темы исследования обусловлена насущной необходимостью поиска быстрых алгоритмов решения практически важных задач, отработки навыков устного счета.

    2. Последняя цифра степени

    Выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа , где N , n – натуральные числа, с изменением показателя n. Для этого составим таблицу:

    Для наглядности составим таблицу, где будут записаны цифры, которыми оканчиваются записи натуральных чисел:

    Заполняя столбики получаем такой результат: пятая и девятая и т. д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.

    3. Закономерности возведения в степень

    Результаты в таблице повторяются через каждые четыре столбца.

    Про числа 1 и 10 писать не будем, т.к. результат всегда будет 1 или 0 соответственно.

    Любая степень чисел 5 и 6 оканчивается соответственно на 5 и на 6.

    Последние цифры степеней чисел 4 и 9 повторяются через каждые два шага, при возведении в четную степень последняя цифра не меняется, будет соответственно 4 или 9, при возведении в нечетную степень изменится на 6 или 1 соответственно.

    Квадрат любого натурального числа может оканчиваться на 0, 1,4, 5, 6 и 9,

    Куб натурального числа может оканчиваться любой цифрой

    Используя полученные результаты попробуем найти последние цифры степени по остатку от деления её показателя на 4

    Если остаток равен 0 и основание нечетное, то число будет оканчиваться на 1(кроме чисел оканчивающихся на цифру 5), если основание четное (кроме круглых чисел), то числа будут оканчиваться на цифру 6.

    Теперь будем подбирать такие числа, что при делении показателя степени на 4 будут давать остатки 1, 2, 3

    45:4=11 (остаток 1)

    102:4=25 (остаток 2)

    Если остаток равен 1, то последняя цифра степени будет равна последней цифре в записи основания степени;

    Если остаток равен 2, то последняя цифра степени будет равна последней цифре в записи квадрата основания;

    Если остаток равен 3, то последняя цифра степени будет равна последней цифре в записи куба основания.

    Значит чтобы найти последнюю цифру степени натурального числа с натуральным показателем, нужно найти остаток от деления показателя степени на 4.

    Последние цифры степеней чисел 2 , 12, 22 и т. д. (3, 13, 23 и т.д.) и т. д. будут совпадать.

    4. Последние две цифры степени

    Мы видим, что последняя цифра рано или поздно будет повторяться, а как будет обстоять дело с 2-мя и 3-мя последними цифрами ? Вероятно, они тоже будут повторяться. Для наглядности составим таблицу, где будут записаны две цифры, которыми оканчиваются записи натуральных чисел:

    Глядя на таблицу, замечаем что последние две цифры тоже повторяются, только период повторения увеличивается, кроме того у некоторых чисел 1-е не входит в период, так например:

    Но начиная с 21 степени по 40 последние две цифры будут повторяться.

    Последние цифры чисел 3,13 и 8 тоже будут повторятся с периодом 20, но последние две цифры чисел 3 и 13 совпадать не будут, не будут совпадать последние две цифры для степеней чисел 4 и 14 и т.д.

    Последние цифры чисел 4 и 9 будут повторяться с периодом 10,последние цифры числа 6 будут повторятся с периодом 5, но число 6 не входит в период, последние цифры числа 7 будут повторятся с периодом – 4. Любая степень числа 5 (начиная со 2 –ой) и 25 будет оканчиваться на 25, а число 15 в четной степени будет оканчиваться на 25, а в нечетной на 75. Период чисел 11, тоже будет равен 10, но здесь есть еще одна закономерность:

    Для числа 11 в степени – число десятков будет равно показателю степени

    Для числа 21 – период равен 4, а число десятков будет равно числу, полученному , если число 2 умножить на показатель степени

    5. Заключение

    Определить последнюю цифру степени числа не сложно, мы легко составили алгоритм, для двух последних цифр степени числа такой алгоритм уже не составишь, закономерности есть , но их меньше. Считаю, что таблицу с тремя последними цифрами составлять не имеет смысла – не рационально.

    Мы провели большую работу: составили таблицы для последней и двух последних цифр степеней и получили интересные с нашей точки зрения выводы. Результаты работы могут быть использованы на занятиях математического кружка и факультативах в 5- 7 классах для развития интереса к математике у учащихся, а так же для индивидуальной работы с теми учениками, кто интересуется математикой. 41 .

    (8+3=11, последняя цифра 1)

    Найдите последнюю цифру суммы степеней числа 2 с показателями, равными 32, 69, 469, 1995, 19951995.

    (6+2+2+8+8=26 последняя цифра 6)

    В книге рекордов Гиннеса написано, что наибольшее известное простое число равно (− 1). Не опечатка ли это?

    (опечатка. Число 23021 337 оканчивается единицей Поэтому последняя цифра числа (23021 337 − 1) равна 0, а значит, это число делится на 10 и потому составное.)

    Делится ли число+ на 10 ?

    (Число 4730 оканчивается цифрой 9, а число 3950 — цифрой 1 Значит, их сумма оканчивается на 0 и потому делится на 10.)

    Найдите последнюю цифру числа . Степени считаются сверху вниз: =

    Последние две цифры числа 7 7 образуют число 43 (это можно вычислить непосредственно, отбрасывая при каждом умножении все цифры результата, кроме последних двух). Значит, число 7 7 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 7 7 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).

    Найдите 2 последние цифры числа 8 1989 .

    В таблице 2-х последних цифр, у числа 8 период 20, (1989:20=99 остаток 9 , число 8 в 9 степени оканчивается цифрами 28, последние 2 цифры числа 8 1989 – 28).

    На контрольной работе по перекрашиванию юный хамелеон перекрашивается по очереди из красного -> в желтый -> зелёный -> синий -> фиолетовый -> красный -> жёлтый -> зелёный и т.д. перекрасился он 2010 раз и начав с красного он в конце стал синим, но известно что он допустил ошибку, покраснел в тот момент, когда должен был приобрести другой цвет. Какого он был цвета перед этим покраснением?

    (Заметим, что здесь период повторения цветов равен 5. Красный цвет будет встречаться на числах оканчивающихся на 0 и 5. Значит и должен он был закончить снова на красном. Поэтому чтобы найти ошибку перейдём сразу к 2005 перекрашиванию. Теперь просто будем считать по очереди меняя цвета до 2010-го. Сразу же смотрим что он сделал ошибку допустим после жёлтого, тогда получается 2005-красный, 2006 – жёлтый 2007- снова красный (это его ошибка), 2008 – жёлтый, 2009 -зелёный, 2010 – синий, перед ошибочным покраснением хамелеон был жёлтым).

    Сейчас на часах 10:00. Какое время они будут показывать через 102938475 часов?

    (У часов период повторения равен 24, значит число 102938475 разделить на 24 = 4289103,12… 102938475 – (4289103 * 24) = 3. Значит время которое часы будут показывать через 102938475 часов равно 10+3 = 13 часов, через 102938475 часы будут показывать 13:00).

    11. Доказать, что число кратно 2.

    12. Доказать, что -1 кратно 5 (при натуральном n).

    13. Верно ли, что 1,6*( -1 ) – целое число при любом (натуральном) n. 14. Какой цифрой оканчивается произведение всех двузначных чисел, каждое из которых оканчивается на 7?

    7. Использованная литература

    1. «Все задачи «Кенгуру» 1994-2008- Санкт-Петербург, 2008.

    2. «Задачи для подготовки к олимпиадам. Математика 5-8 классы» сост. Н.В. Заболотнева. – Волгоград: Учитель, 2007.- 99с.

    3. Лихтарников Л.М. Занимательные логические задачи. (Для учащихся начальной школы) Оформление С. Григорьева – СПб.: Лань, МИК, 1996.- 125с.

    4. Л.М.Лоповок 1000 проблемных задач по математике. Книга для учащихся Москва : Просвещение, 1995

    5. Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы – М.: Просвещение, 1990.- 224 с.: ил.

    6. Чулков П.В. Математика. Школьные олимпиады: методическое пособие. 5- кл./ П.В. Чулков.- М.: Издательство НЦ ЭНАС, 2007.- 88с. (Портфель учителя).

    7. Шуба М.Ю. Занимательные задачи в обучении математике: Книга для учителя. – 2-е изд.-М.: Просвещение, 1995.- 22с.

    МОУ «Шербакульская средняя общеобразовательная школа №1»

    Научное сообщество учащихся «Поиск»

    Тема: « Последняя цифра степени. »

    Выполнила: ученица 7 «б» класса

    Руководитель: Пушило Т.Л.

    2010 – 2011 уч. год

    · Последняя цифра степени.

    · Закономерности возведения в степень

    · Две последних цифры степени.

    Однажды, листая страницы книги «Тысяча проблемных задач по математике», я увидела с первого взгляда очень трудную задачу, точнее сказать пример надо было найти последнюю цифру суммы

    1 1989 + 2 1989 + 3 1989 + 4 1989 + 5 1989 +…+ 1989 1989 .

    Потом я подумала, а ведь должен же быть, какой-нибудь рациональный способ вычисления и тут я принялась считать…

    Гипотеза: Можно ли сказать какой будет последняя цифра у любой степени?

    · Узнать, можно ли построить таблицу последних цифр различных степеней.

    · Найти закономерность в них.

    · Используя таблицу практиковаться на более легких задачах и решить вышеупомянутый пример и если получится более сложные.

    Последняя цифра степени.

    Приведем небольшое исследование: выясним есть ли какая-нибудь закономерность в том, как меняется последняя цифра числа 2 n , где n – натуральное число, с изменением показателя n . Для этого рассмотрим таблицу:

    2 1 = 2 2 5 = 32 2 9 = 5122 2 = 4 2 6 = 64 2 10 = 10242 3 = 8 2 7 = 128 2 11 = 20482 4 = 16 2 8 = 256 2 12 = 4096

    Мы видим, что через каждые четыре шага последняя цифра повторяется. Заметив это, нетрудно определить последнюю цифру степени 2 n для любого показателя n .

    В самом деле, возьмем число 2 100 . Если бы мы продолжили таблицу, то оно попало бы в столбец, где находятся степени 2 4 , 2 8 , 2 12 , показатели которых кратны четырем. Значит, число 2 100 , как и эти степени, оканчивается цифрой 6.

    Возьмем к примеру, 2 22 , если проверить, просто посчитав, то получится 4194304 – последняя цифра 4.

    Теперь попробуем пользоваться таблицей, но в таблице 4 числа, а показатель степени 22, однако, после последнего числа этот «круг» начинается заново. Поэтому, показатель степени 22 делим на 4, получаем число 5 и остаток 2 т.е мы сделаем 5 «кругов», и отсчитаем ещё 2 в перед, а второе число – это 4, значит, таблица работает.

    А теперь посмотрим, можно ли составить таблицы для остальных чисел. Все описывать не буду, лишь скажу, что у меня получилось составить таблицу для всех чисел от 1 до 10, а далее будет повторяться, допустим, у 12 последние числа будут такие же, как и у 2, а у 25 – так же, как и у 5.

    Закономерности возведения в степень:

      • Запись числа, являющегося полным квадратом, может оканчиваться только цифрами 0, 1, 4, 5, 6 или 9.
      • Если запись числа оканчивается цифрой 0, 1, 5 или 6,то возведение в любую степень не изменит последние цифры.
      • При возведении любого числа в пятую степень его последняя цифра не изменится.
      • Если число оканчивается цифрой 4 (или 9), то при возведении в нечетную степень последняя цифра не изменяется, а при возведении в четную степень изменится на 6 (или 1 соответственно).
      • Если число оканчивается цифрой 2, 3, 7 или 8, то при возведении в степень возможны четыре различных цифры.

      Две последних цифры степени.

      степеней семи | NZ Maths

      Конкретные результаты обучения

      Решите задачи, связанные с нахождением степеней числа

      Описание математики

      В этой задаче учащиеся работают со степенями чисел и, как следствие, приходят к пониманию того, что происходит с числами.

      Студенты также видят, как кажущиеся огромными и трудные вычисления можно разбить на управляемые части.Студенты должны понять, что при возведении 7 в степень можно получить только ограниченное количество цифр единицы. Кроме того, эти конкретные цифры «циклически повторяются» по мере увеличения степени 7. Это цикл 7, 9, 3, 1, 7, 9,…

      То же самое и с цифрой в разряде десятков.

      Требуемые ресурсные материалы

      Деятельность

      Проблема

      Подумайте о числе 7 1999 . Теперь подумайте об этом после того, как оно было умножено. Какова его единица измерения?

      Последовательность обучения

      1. Расскажите о проблеме классу. Убедитесь, что учащиеся понимают, как возвести число в степень и как найти степень с помощью функций калькулятора.
      2. Найдите способы решения проблемы.
      3. По мере того, как учащиеся работают над проблемой индивидуально или в небольших группах, убедитесь, что они записывают свои решения таким образом, чтобы они могли искать закономерности.Старайтесь не указывать , чтобы искали закономерность в цифрах.
      4. Поделиться решениями.
      Продолжение проблемы

      Как насчет разряда десятков?
      Можете ли вы узнать здесь общую картину. Независимо от того, какое число вы увеличиваете до 7, можете ли вы с минимальными вычислениями сказать, какова его единица измерения?

      Повторите эту задачу с номерами, отличными от 7.

      Решение

      Ответ будет найден, если вы поищете закономерности в степенях 7.
      7 1 = 7
      7 2 = 4 9
      7 3 = 34 3
      7 4 = 240 1
      7 5 = 1680 7
      7 6 = 11764 9
      7 7 = 82354 3
      7 8 = 576480 1
      7 9 = 4435360 7
      7 10 = 28247524 9

      Цикл разряда единиц — 7, 9, 3, 1, 7, 9…
      7 1999 Цифра единиц = 3

      Решение для расширения

      Цикл для разряда десятков: 4, 4, 0, 0, 4, 4, 0 …

      7 Power Table

      7 Power Table

      Вы ищете другие числовые диаграммы, воспользуйтесь этим калькулятором

      Число

      Поднятый силой

      Равно

        от 1 до 10

      1. 7 1 = 7
      2. 7 2 = 49
      3. 7 3 = 343
      4. 7 4 = 2401
      5. 7 5 = 16807
      6. 7 6 = 117649
      7. 7 7 = 823543
      8. 7 8 = 5764801
      9. 7 9 = 40353607
      10. 7 10 = 282475249

        11-20

      1. 7 11 = 1977326743
      2. 7 12 = 13841287201
      3. 7 13 = 9688
        07
      4. 7 14 = 678223072849
      5. 7 15 = 4747561509943
      6. 7 16 = 332329305696021

        7. 7

      7. 7

          1. 7 18 = 1628413597

            9

          1. 7 19 = 11398895185373144
          2. 7 20 = 797

            297612000

            21 до 30

          1. 7 21 = 5585458640832840 00
          2. 7 22 = 3

            1048582988000

          3. 7 23 = 27368747340080

            0

          4. 7 24 = 1231380566400000
          5. 7 25 = 1. 341068619663965e + 21
          6. 7 26 = 9,387480337647754e + 21
          7. 7 27 = 6,571236236353428e + 22
          8. 7 28 = 4,5998653654474e + 23
          9. 7 29 = 3,2278 9007 30 = 2,2539340226e + 25

            от 31 до 40

          1. 7 31 = 1,5777538203484584e + 26
          2. 7 32 = 1,1044276742439208e + 27
          3. 7 33 70 + 2772771945e 2772771945 7 34 = 5.411695603795212e + 28
          4. 7 35 = 3,788186

            66484e + 29

          5. 7 36 = 2,651730845859654e + 30
          6. 7 37 = 1,8562115758e + 31

            7. 32

          7. 7 38

            7 7 9001 22930 900 39 = 9.095436801298613e + 32

          8. 7 40 = 6.366805760e + 33

            41 до 50

          1. 7 41 = 4.45676403263632e + 34
          2. 7 42 = 3.119734822845 7 43 = 2.1838143759e + 36
          3. 7 44 = 1,5286700631942579e + 37
          4. 7 45 = 1,07006

            5. 359805e + 38

          5. 7 46 = 7,4
          6. 309651864e + 38
          7. 7 47
          8. 622 = 5,2430 900 48 = 3,6703368217294133e + 40
          9. 7 49 = 2,56
            752105895e + 41
          10. 7 50 = 1,7984650426474127e + 42

            51 до 60

          1. 7 51 = 1,25828925529 7 52 = 8. 812478708972323e + 43
          2. 7 53 = 6,168735096280626e + 44
          3. 7 54 = 4,318114567396438e + 45
          4. 7 55 = 3,0226801971775067e + 46
          5. 7 56 8024 7,115876 57 = 1,4811132966169783e + 48
          6. 7 58 = 1,0367793076318848e + 49
          7. 7 59 = 7,257455153423194e + 49
          8. 7 60 = 5,080218607396236e + 50

            3

          9. до 7 61 = 3.556153025177365e + 51
          10. 7 62 = 2.4893071176241554e + 52
          11. 7 63 = 1.7425149823369089e + 53
          12. 7 64 = 1.2197604876358363e + 54 3
          13. 7 6576358363e + 54 3
          14. 7 6513422 = 8.5383 66 = 5,976826389415598e + 55
          15. 7 67 = 4,1837784725
            e + 56
          16. 7 68 = 2,9286449308136425e + 57
          17. 7 69 = 2,0500514515695498e + 58 8 1 = 2,0500514515695498e + 58 8 1 +59

            71 по 80

          1. 7 71 = 1. 00452521126e + 60
          2. 7 72 = 7,031676478883556e + 60
          3. 7 73 = 4,3535218489e + 61
          4. 7 74 = 3,4455214746529423e + 62
          5. 7 75 25 = 2,4119650 76 = 1.6883055225799416e + 64
          6. 7 77 = 1.181813865805959e + 65
          7. 7 78 = 8,272697060641714e + 65
          8. 7 79 = 5,7

            9424492e + 6621 80402 = 4,7

            9424492e + 6621 80424492e +67

            от 81 до 90

          1. 7 81 = 2.8375350

            1083e + 68

          2. 7 82 = 1,9862745642600758e + 69
          3. 7 83 = 1,3194982053e + 70
          4. 7 84 = 9,732745364874371e + 70
          5. 7 85

            41 720,812 = 620,812 900 86 = 4,76287884414e + 72

          6. 7 87 = 3,338331660151909e + 73
          7. 7 88 = 2,3368321621063364e + 74
          8. 7 89 = 1,6357825134744355e + 75
          9. 7104

          10. +76

            91-100

          1. 7 91 = 8. {2011} $ слишком велико, чтобы его можно было вычислить даже с помощью калькулятора.{2011} $.
          2. Определение шаблона в последних двух цифрах последовательных степеней 7 (которые, надеюсь, быстро появятся!).

            3. Как только учащиеся увидят, что последние две цифры последовательных степеней 7 соответствуют образцу, они могут легко угадать правильный ответ. Полное объяснение того, почему мы знаем, что эта закономерность сохранится, вероятно, не найдет шестиклассник, но, поскольку он основан на разряде, его могут понять шестиклассники, хорошо разбирающиеся в десятичной системе счисления.

            Было бы интересно заменить показатель 2011 на текущий год, который никак не меняет сути проблемы. Это задание предназначено только для учебных целей и было бы совершенно неуместным для оценивания с высокими ставками (на случай, если кому-то интересно).

            Это задание было адаптировано из задачи № 22 теста 8 Американской математической олимпиады (AMC) 2011 года. Для AMC 8 2011 года, который прошли 153 485 студентов, ответы с несколькими вариантами ответов на задачу, в которой учащимся предлагалось найти десятичную цифру в размере 7 ^ {2011} $, имели следующее распределение:

            Выбор Ответ Процент ответов
            (А) 0 16
            (В) 1 16
            (К) 3 14
            (D) * 4 21
            (E) 7 21
            Пропустить — 12

            Из 153485 учеников: 72 648 (47%) были в 8-м классе, 50 433 (33%) были в 7-м классе, а остальные были младше 7-го класса. {2011} $ мы снова умножаем на 7, получая 43 в качестве последних двух цифр.

          Таблицы и модели экспонент

          В таблицах степеней целых чисел можно найти много интересных закономерностей.


          Полномочия

          2


          Полномочия

          3


          Полномочия

          4

          2

          1

          знак равно

          2

          3

          1

          знак равно

          3

          4

          1

          знак равно

          4

          2

          2

          знак равно

          4

          3

          2

          знак равно

          9

          4

          2

          знак равно

          16

          2

          3

          знак равно

          8

          3

          3

          знак равно

          27

          4

          3

          знак равно

          64

          2

          4

          знак равно

          16

          3

          4

          знак равно

          81 год

          4

          4

          знак равно

          256

          2

          5

          знак равно

          32

          3

          5

          знак равно

          243

          4

          5

          знак равно

          1024

          2

          6

          знак равно

          64

          3

          6

          знак равно

          729

          4

          6

          знак равно

          4096

          2

          7

          знак равно

          128

          3

          7

          знак равно

          2187

          4

          7

          знак равно

          16384

          2

          8

          знак равно

          256

          3

          8

          знак равно

          6561

          4

          8

          знак равно

          65536

          2

          9

          знак равно

          512

          3

          9

          знак равно

          19683

          4

          9

          знак равно

          262144

          2

          10

          знак равно

          1024

          3

          10

          знак равно

          59049

          4

          10

          знак равно

          1048576

          Одна вещь, которую вы можете заметить, — это закономерности в цифрах.В полномочиях

          2

          таблица, единичные цифры образуют повторяющийся узор

          2

          ,

          4

          ,

          8

          ,

          6

          ,

          2

          ,

          4

          ,

          8

          ,

          6

          ,

          …

          . В полномочиях

          3

          таблица, единичные цифры образуют повторяющийся узор

          3

          ,

          9

          ,

          7

          ,

          1

          ,

          3

          ,

          9

          ,

          7

          ,

          1

          ,

          …

          . Мы предоставляем вам разобраться, почему это происходит!

          В полномочиях

          4

          таблица, чередуются единицы цифр:

          4

          ,

          6

          ,

          4

          ,

          6

          . Фактически, вы можете видеть, что полномочия

          4

          такие же, как четные степени

          2

          :

          4

          1

          знак равно

          2

          2

          4

          2

          знак равно

          2

          4

          4

          3

          знак равно

          2

          6

          и т.п.

          Такая же связь существует между

          полномочия

          3

          и

          полномочия

          9

          :


          Полномочия

          3


          Полномочия

          9

          3

          1

          знак равно

          3

          9

          1

          знак равно

          9

          3

          2

          знак равно

          9

          9

          2

          знак равно

          81 год

          3

          3

          знак равно

          27

          9

          3

          знак равно

          729

          3

          4

          знак равно

          81 год

          9

          4

          знак равно

          6561

          3

          5

          знак равно

          243

          9

          5

          знак равно

          59 049

          3

          6

          знак равно

          729

          9

          6

          знак равно

          531 441

          3

          7

          знак равно

          2187

          9

          7

          знак равно

          4,782,969

          3

          8

          знак равно

          6561

          9

          8

          знак равно

          43 046 721

          3

          9

          знак равно

          19 683

          9

          9

          знак равно

          387 420 489

          3

          10

          знак равно

          59 049

          9

          10

          знак равно

          3 486 784 401

          В

          полномочия

          10

          легко, потому что мы используем

          база

          10

          : для

          10

          п

          просто напишите »

          1

          » с участием

          п

          нули после него.Для

          отрицательные силы

          10

          —

          п

          , написать »

          0.

          » с последующим

          п

          —

          1

          нули, а затем

          1

          . Полномочия

          10

          широко используются в

          научная нотация

          , так что будет неплохо с ними освоиться.


          Полномочия

          10

          10

          1

          знак равно

          10

          10

          0

          знак равно

          1

          10

          2

          знак равно

          100

          10

          —

          1

          знак равно

          0.1

          10

          3

          знак равно

          1000

          10

          —

          2

          знак равно

          0,01

          10

          4

          знак равно

          10 000

          10

          —

          3

          знак равно

          0,001

          10

          5

          знак равно

          100 000

          (сто тысяч)

          10

          —

          4

          знак равно

          0.0001

          (одна десятитысячная)

          10

          6

          знак равно

          1,000,000

          (один миллион)

          10

          —

          5

          знак равно

          0,00001

          (стотысячная)

          10

          7

          знак равно

          10 000 000

          (десять миллионов)

          10

          —

          6

          знак равно

          0.000001

          (одна миллионная)

          10

          8

          знак равно

          100 000 000

          (сто миллионов)

          10

          —

          7

          знак равно

          0,0000001

          (одна десятимиллионная)

          10

          9

          знак равно

          1 000 000 000

          (один миллиард)

          10

          —

          8

          знак равно

          0.00000001

          (стомиллионная)

          10

          10

          знак равно

          10 000 000 000

          (десять миллиардов)

          10

          —

          9

          знак равно

          0,000000001

          (одна миллиардная)

          Нажмите

          здесь

          для получения дополнительных имен для

          действительно большие и очень маленькие числа

          .

          Еще одно последствие использования нами

          база

          10

          хороший образец между отрицательными степенями

          2

          и полномочия

          5

          .


          Степень 2


          Степень 5

          2

          —

          5

          знак равно

          1

          32

          знак равно

          0.03125

          5

          —

          5

          знак равно

          1

          3125

          знак равно

          0,00032

          2

          —

          4

          знак равно

          1

          16

          знак равно

          0,0625

          5

          —

          4

          знак равно

          1

          625

          знак равно

          0.0016

          2

          —

          3

          знак равно

          1

          8

          знак равно

          0,125

          5

          —

          3

          знак равно

          1

          125

          знак равно

          0,008

          2

          —

          2

          знак равно

          1

          4

          знак равно

          0.25

          5

          —

          2

          знак равно

          1

          25

          знак равно

          0,04

          2

          —

          1

          знак равно

          1

          2

          знак равно

          0,5

          5

          —

          1

          знак равно

          1

          5

          знак равно

          0.2

          2

          0

          знак равно

          1

          5

          0

          знак равно

          1

          Таблица мощности

          5 9 = 1953125

          5 10 = 9765625

          800022 = 282475249

          1 1 = 1

          1 2 = 1

          1 3 = 1

          1 4 = 1

          1 5 = 1

          1 6 = 1

          1 7 = 1

          1 8 = 1

          1 9 = 1

          1 10 = 1

          2 1 = 2

          2 2 = 4

          2 3 = 8

          2 4 = 16

          2 5 = 32

          2 6 = 64

          2 7 = 128

          2 8 = 256

          2 9 = 512

          2 10 = 1024

          3 1 = 3

          3 2 = 9

          3 3 = 27

          3 4 = 81

          3 5 = 243

          3 6 = 729

          3 7 = 2187

          3 8 = 6561

          3 9 = 19683

          3 10 = 59049

          4 1 = 4

          4 2 = 16

          4 3 = 64

          4 4 = 256

          4 5 = 1024

          4 6 = 4096

          4 7 = 16384

          4 8 = 65536

          4 9 = 262144

          4 10 = 1048576

          5 1 = 5

          5 2 = 25

          5 3 = 125

          5 4 = 625

          5 5 = 3125

          5 6 = 15625

          5 7 = 78125

          5 8 = 3

          6

          = 6 2 = 36

          6 3 = 216

          6 4 = 1296

          6 5 = 7776

          6 6 = 46656

          6 7 = 279936

          6 8 = 1679616

          6

          2 = 1679616

          6

          2 = 1679616

          6

          2 =

          6 10 = 60466176

          7 1 = 7

          7 2 = 49

          7 3 = 343

          7 4 = 2401

          7 5 = 16

          7 6 = 117649

          7 7 = 823543

          7 8 = 5764801

          7 9 = 40353607

          7 10 = 282475249

          900

          8 2 = 64

          8 3 = 512

          8 4 = 4096

          8 5 = 32768

          8 6 = 262144

          8 7 = 2097152

          8 8 = 16777216

          900 02 8 9 = 134217728

          8 10 = 1073741824

          9 1 = 9

          9 2 = 81

          9 3 = 729

          9 4 2 = 6561

          9 4 2 = 6561

          9 5 = 59049

          9 6 = 531441

          9 7 = 4782969

          9 8 = 43046721

          9 9 = 387420489

          9 4 104075221

          10 1 = 10

          10 2 = 100

          10 3 = 1000

          10 4 = 10000

          10 5 = 100000

          10 6 = 1000000

          10 7 = 10000000

          10 8 = 100000000

          10 9 = 1000000000

          10 10 = 10000000000

          Степени и экспоненты

          A power является продуктом умножение числа на само себя.


          Обычно степень представлена ​​ базовым числом и показателем степени. Базовое число сообщает , какое число умножается. Показатель степени , — небольшое число, написанное выше и справа от основного числа, сообщает , сколько раз умножается базовое число.

          Например,? 6 в 5-й степени? можно записать как? 6 5 .? Здесь базовое число 6, а показатель степени 5.Это означает, что 6 умножается само на себя 5 раз: 6 x 6 x 6 x 6 x 6

          6 x 6 x 6 x 6 x 6 = 7,776 или 6 5 = 7,776

          915

          базовое число 2-я степень 3-я степень 4-я степень 5-я степень
          1 1 1 1 1
          2 886
          3 9 27 81 243
          4 16 64 256 1,024

          		 905
          6 36 216 1,296 7,776
          7 49 343 2,401 16,807
          4 512 4,096 32,768
          9 81 729 6,561 59,049
          10 10075 121 1,331 14,641 161,051
          12 144 1,728 20,736 248,832

          Формальные числа и правила для множителей Purplemath

          Purplemath

          Экспоненты — это сокращение для многократного умножения одного и того же самого на себя.Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5) (5) (5) = 5 3 . «Показатель», равный 3 в этом примере, означает, сколько раз умножается значение. То, что умножается (в этом примере 5), называется «базой».

          Этот процесс использования экспонент называется «возведением в степень», где показатель — это «степень». Выражение «5 3 » произносится как «пять в третьей степени» или «пять в третьей степени».

          MathHelp.com

          Есть две специально названные степени: «до второй степени» обычно произносится как «в квадрате», а «до третьей степени» обычно произносится как «в кубе».Таким образом, «5 3 » обычно произносится как «пять кубов».

          Когда мы имеем дело с числами, мы обычно просто упрощаем; мы предпочли бы иметь дело с «27», чем с «3 3 ». Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x 6 », чем с « x‍x‍x‍x‍x‍x ».

          У экспонентов есть несколько правил, которые мы можем использовать для упрощения выражений.

          Чтобы упростить это, я могу думать в терминах того, что означают эти показатели.«До третьей» означает «умножение трех копий», а «до четвертой» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме. Сначала я расширяюсь:

          ( x 3 ) ( x 4 ) = ( x‍x‍x ) ( x‍x‍x‍x )

          Теперь я могу убрать скобки и сложить все множители:

          ( x‍x‍x ) ( x‍x‍x‍x ) = x‍x‍x‍x‍x‍x‍x

          Это семь копий переменной.«Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:

          x‍x‍x‍x‍x‍x‍x = x 7

          Собираем все вместе, шаги следующие:

          ( x 3 ) ( x 4 ) = ( x‍x‍x ) ( x‍x‍x‍x )

          = x‍x‍x‍x‍x‍x‍x

          = х 7

          Тогда упрощенная форма ( x 3 ) ( x 4 ) будет:

          Обратите внимание, что x 7 также равно x (3 + 4) .Это демонстрирует первое основное правило экспоненты:

          Всякий раз, когда вы умножаете два члена с одинаковым основанием, вы можете складывать экспоненты:

          ( x м ) ( x n ) = x (m + n)

          Однако мы НЕ можем упростить ( x 4 ) ( y 3 ), потому что основания разные: ( x 4 ) ( y 3 ) = x‍x‍x‍xyyy = ( x 4 ) ( y 3 ).Ничего не сочетается.

          Теперь, когда я знаю правило (а именно, что я могу добавлять силы к одной и той же базе), я могу начать с перемещения баз, чтобы расположить все одинаковые базы рядом друг с другом:

          ( a 5 b 3 ) ( a b 7 ) = ( a 5 ) ( a ) ( b 3 ) ( б 7 )

          Теперь я хочу добавить мощности на a и b .Однако у второго или , похоже, нет мощности. Что мне добавить для этого срока?

          Все, что не имеет силы, в техническом смысле «возведено в степень 1». Все, что находится в степени 1, является самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:

          ( a 5 ) ( a ) ( b 3 ) ( b 7 ) = ( a 5 ) ( a 1 ) ( b 3 ) ( б 7 )

          Теперь могу комбинировать:

          ( a 5 ) ( a 1 ) ( b 3 ) ( b 7 ) = a 5 + 1 b 3 + 7 = a 6 b 10

          Если сложить все вместе, моя ручная работа будет выглядеть так:

          ( a 5 b 3 ) ( a b 7 ) = ( a 5 a 1 ) ( b 3 b 7 ) =

          В следующем примере есть две силы, одна из которых в некотором смысле «внутри» другой.

          Чтобы сделать упрощение, я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, заключенного в круглые скобки. В этом случае база четвертой степени равна x 2 . Умножение четырех копий этой базы дает мне:

          Каждый фактор в приведенном выше расширении — это «умножение двух копий» переменной.Это расширяется как:

          ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 ) = ( x‍x ) ( x‍x ) ( x‍x ) ( x‍x )

          Убрав скобки, получим:

          ( x‍x ) ( x‍x ) ( x‍x ) ( x‍x ) = x‍x‍x‍x‍x‍x‍x‍x

          Это строка из восьми копий переменной.«Умножение восьми копий» означает «в восьмой степени», поэтому это означает:

          x‍x‍x‍x‍x‍x‍x‍x = x 8

          Собираем все вместе:

          ( x 2 ) 4 = ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 )

          = ( x‍x ) ( x‍x ) ( x‍x ) ( x‍x )

          = x‍x‍x‍x‍x‍x‍x‍x

          = х 8

          Обратите внимание, что ( x 2 ) 4 = x 8 , и что 2 × 4 = 8.Это демонстрирует правило второй степени:

          Всякий раз, когда у вас есть выражение в степени, которое возведено в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:

          Если в круглых скобках указан продукт, а в скобках — мощность, то питание идет на каждый элемент внутри. Например:

          ( xy 2 ) 3 = ( xy 2 ) ( xy 2 ) ( xy 2 )

          = ( x‍x‍x ) ( y 2 y 2 y 2 )

          = ( x‍x‍x ) ( yyyyyy )

          = x 3 y 6

          = ( x ) 3 ( y 2 ) 3

          Другой пример:

          Предупреждение. Это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяются» по сложению.

          Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильный. На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25.

          Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x — 2) 2 , не пытайтесь делать это в уме.Вместо этого запишите это; «в квадрате» означает «умножение двух копий», поэтому:

          ( x -2) 2 = ( x -2) ( x -2)

          = x ( x -2) — 2 ( x -2)

          = xx -2 x -2 x + 4

          = x 2 — 4 x + 4.

          Ошибка в виде ошибочной попытки «распределить» экспоненту чаще всего совершается, когда ученик пытается делать все в своей голове, вместо того, чтобы показать свою работу.Делайте все аккуратно, и вы вряд ли совершите эту ошибку.

          Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. (Мне нужно помнить, что для c в скобках это «в степени 1».)

          ( a 2 ) 4 ( b 3 ) 4 ( c 1 ) 4

          = ( a 2 × 4 ) ( b 3 × 4 ) ( c 1 × 4 )

          = a 8 b 12 c 4

          Партнер

          Есть еще одно правило, которое может или не может быть рассмотрено в вашем классе на данном этапе:

          Все, что находится в нулевой степени, равно «1» (пока «что-нибудь» не является нулем само по себе).

          Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:

          • Упростить [(3

            x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0

          Кого волнует эта фигня в квадратных скобках? Я точно не знаю, потому что нулевая мощность снаружи означает, что значение всего этого равно 1.Ха!

          [(3 x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0 = 1

          Между прочим, как только ваш класс охватит «до нуля», вы должны ожидать упражнения, подобного приведенному выше, на следующем тесте.Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.

          Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с помощью экспонент. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите здесь множество отработанных примеров.)

          Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.

          URL: https://www.purplemath.com/modules/exponent.htm

          .

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *