Содержание
Урок 13. теорема пифагора. — Геометрия — 8 класс
Рассмотрим прямоугольный треугольник.
Соотношение между катетами и гипотенузой было известно еще в Древнем Египте и Вавилоне. Сегодня нам это соотношение известно как теорема Пифагора.
В современной формулировке теорема Пифагора звучит так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Для доказательства теоремы Пифагора рассмотрим прямоугольный треугольник ABC с прямым углом C, катетами а, b и гипотенузой с
Достроим треугольник до квадрата со стороной a + b
S(большого квадрата) = (a + b)2
S(большого квадрата) = 4 ∙ SABC + c2
S(большого квадрата) = 4 ∙ 1/2 ab + c2
(a + b)2 = 4 ∙ 1/2 ab + c2
a2 + 2ab + b2 = 2ab + c2, c2 = a2 + b2
Для теоремы Пифагора обратное утверждение также верно: если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.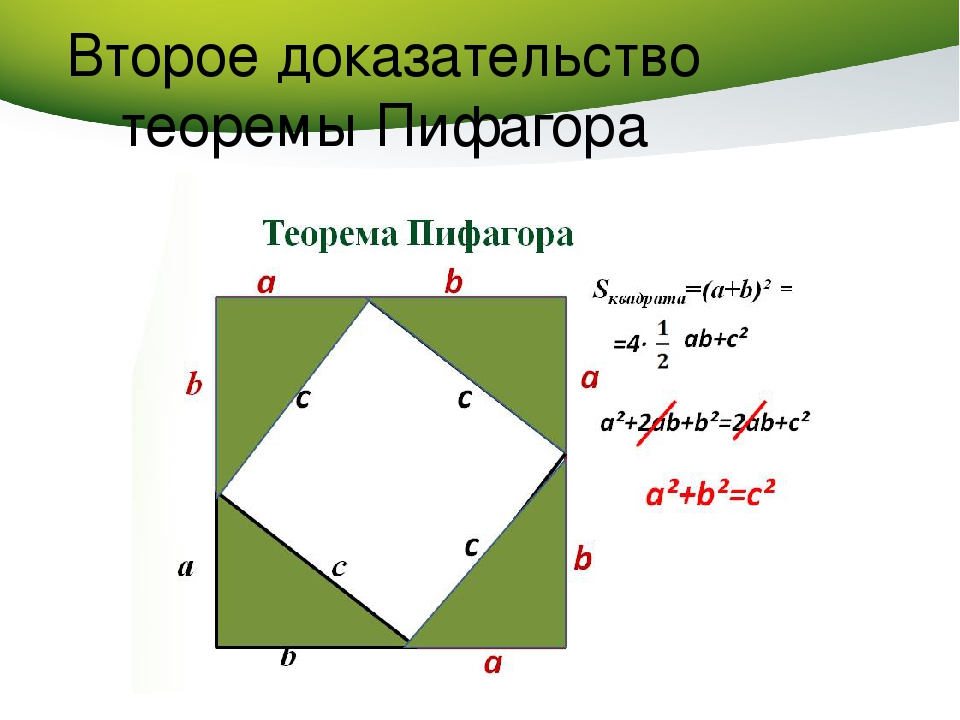
Для доказательства рассмотрим треугольник А1В1С1, такой, что угол С1 прямой, стороны A1C1 = АС, B1C1 = ВС.
По теореме Пифагора A1B12 = A1C12 + B1C12
Из равенства сторон следует A1B12 = A1C12 + B1C12 = AC2 + BC2 = AB2, поэтому
A1B12 = AB2
A1B1 = AB
Таким образом треугольники ABC и А1B1C1 равны по трем сторонам, т. к. угол С1 – прямой, то угол С также прямой. Треугольник ABC – прямоугольный.
к. угол С1 – прямой, то угол С также прямой. Треугольник ABC – прямоугольный.
Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называют пифагоровыми треугольниками.
Теорема Пифагора
Вернемся к нашему прямоугольнику, который мы начали рассматривать в предыдущей статье. Нас интересует соотношение длин сторон прямоугольника и длин диагонали, то есть мы решаем ту же задачу, что и греческие математики в древности. Поскольку прямоугольник разделяется диагональю на две абсолютно симметричные части, мы можем упростить задачу и отбросить одну половину фигуры, предположим, левую. У нас остался так называемый прямоугольный треугольник.
Еще за много столетий до наших дней египтяне на основе практического опыта установили, что если одна сторона прямоугольного треугольника равна 3 единицам, а другая — 4 единицам, то длина гипотенузы составит 5 единиц. В этом случае соотношение гипотенузы и одной из сторон равно $\frac54$ для более длинной стороны и 5$\frac53$ для более короткой.
Греки подошли к задаче с более общих позиций. Им важно было найти закономерность, то есть соотношение длин сторон прямоугольника и длин диагонали для любого прямоугольного треугольника.
Как гласит история, великий греческий математик Пифагор такую закономерность открыл. Он установил, что для любого прямоугольного треугольника верно следующее утверждение:
сумма квадратов сторон равна квадрату гипотенузы.
Это утверждение получило название теоремы Пифагора. Теорема до сих пор носит имя великого грека, хотя теперь мы знаем, что еще за 600 лет до Пифагора древним китайцам уже было известно это соотношение.
Проверим теорему для треугольника со сторонами 3 и 4. Квадрат одной из сторон равен 3×3=9, квадрат другой стороны равен 4х4=16. Сумма квадратов равна: 9+16=25, то есть квадрат гипотенузы равен 25, следовательно, гипотенуза равна 5.
Рассмотрим другой треугольник со сторонами 5 и 12.
Сумма квадратов сторон этого треугольника равна 5х5+12х12=25+144=169. Следовательно, 169 — это квадрат гипотенузы. Тогда гипотенуза равна $\sqrt{169}$, или 13 поскольку 13х13=169.
Следовательно, 169 — это квадрат гипотенузы. Тогда гипотенуза равна $\sqrt{169}$, или 13 поскольку 13х13=169.
Для этого треугольника соотношение гипотенузы к стороне равно $\frac{13}{5}$ для короткой стороны и $\frac{13}{12}$ для длинной стороны.
Используя теорему Пифагора, можно найти соотношение гипотенузы и любой из сторон любого прямоугольного треугольника. Математики Древней Греции могли вздохнуть спокойно, задача была решена. Самое главное заключалось в том, что теорема распространялась на все прямоугольные треугольники, в том числе, разумеется, и на равносторонние, то есть на прямоугольные треугольники, у которых обе стороны равны. А нас сейчас интересуют именно такие треугольники.
Один из них представлен на рисунке слева.
Максимально упростим задачу и предположим, что стороны треугольника равны 1. Тогда квадрат стороны равен 1х1, а сумма квадратов сторон равна 1х1+1х1=2. Согласно теореме Пифагора квадрат гипотенузы равен 2, а гипотенуза равна соответственно $\sqrt{2}$.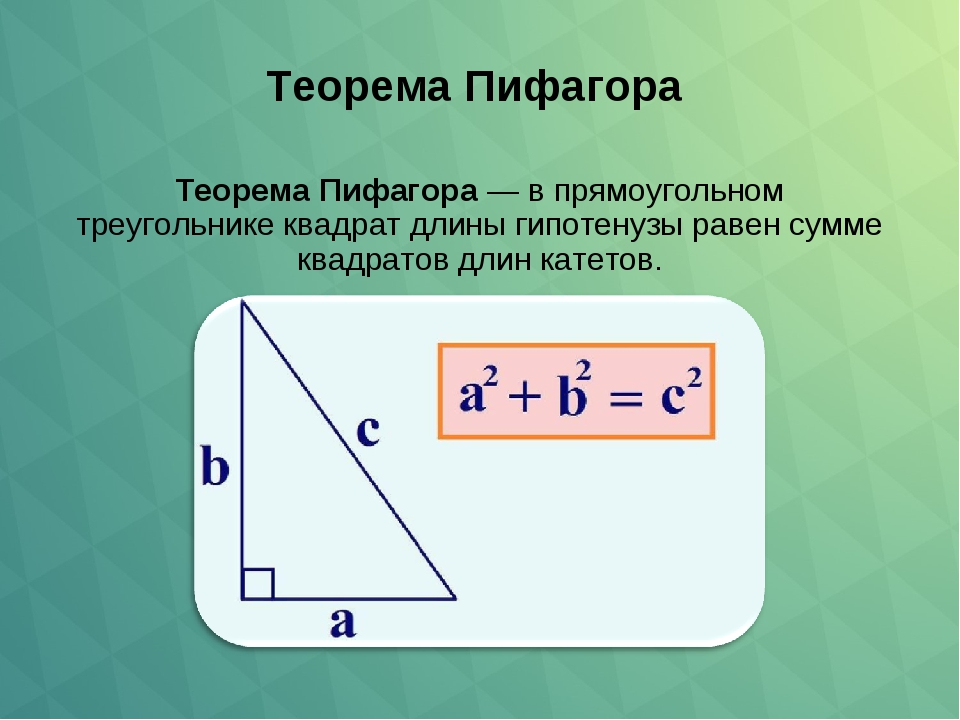
Казалось бы, теперь грекам осталось сделать совсем немного. Надо было только найти такую дробь, которая являлась бы $\sqrt{2}$, а потом представить ее в виде соотношения целых чисел, и можно праздновать победу. Но все оказалось гораздо сложнее. Почему — читайте в следующей статье.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Применение теоремы Пифагора в повседневной жизни | Математика, Алгебра, Геометрия
Применение теоремы Пифагора в повседневной жизни
Автор: Гасанова Елена Николаевна
Организация: МБОУ СОШ №35 им. Героя Советского Союза Д.Ф. Чеботарёва
Населенный пункт: Воронежская область, г. Воронеж
С помощью теоремы Пифагора, которая рассматривается в школьном курсе геометрии, можно решать не только задачи математические, но и задачи, связанные с повседневной жизнью.
Поэтому я бы хотела показать различные области применения теоремы Пифагора.
Формулировка теоремы Пифагора
Площадь квадрата гипотенузы равна сумме квадратов его катетов.
Изучение вавилонских клинописных табличек и древнекитайских рукописей (древних рукописных копий и того более) показало, что знаменитая теорема была известна задолго до Пифагора, возможно несколько тысячелетий до него.
Есть такое понятие, как «египетский треугольник». Его особенностью считается строгое соотношение сторон в прямоугольном треугольнике 3:4:5. Это соотношение было известно египтянам около 2300 лет до н.э. 32+42=52. Одни предполагают, что Пифагор дал теореме полноценное доказательство, а другие отказывают ему в этой заслуге.
Применение в жизни
Задачи в курсе физики средней школы требуют знания теоремы Пифагора.
Задача из курса физики за 9 класс:
Когда биатлонист стреляет по мишени, он делает «поправку на ветер». Если ветер дует справа, а спортсмен стреляет по прямой, то пуля уйдёт влево. Чтобы попасть в цель, надо сдвинуть прицел вправо на расстояние смещения пули. Для них составлены специальные таблицы (на основе следствий из т. Пифагора). Биатлонист знает, на какой угол смещать прицел при известной скорости ветра.
Чтобы попасть в цель, надо сдвинуть прицел вправо на расстояние смещения пули. Для них составлены специальные таблицы (на основе следствий из т. Пифагора). Биатлонист знает, на какой угол смещать прицел при известной скорости ветра.
Сотовая телефонная связь.
Все понимают, что сейчас мобильный телефон очень важный атрибут жизни современного человека. Каждому абоненту важна качественная сотовая связь. А качество зависит от высоты антенны мобильного оператора. Чтобы рассчитать, в каком радиусе можно принимать передачу, задействуем теорему Пифагора.
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
Решение:
Пусть AB = x, BC=R= 200 км, OC= r =6380 км.
OB=OA; AB+OB = r + x.
С помощью теоремы Пифагора получим 2,3 км.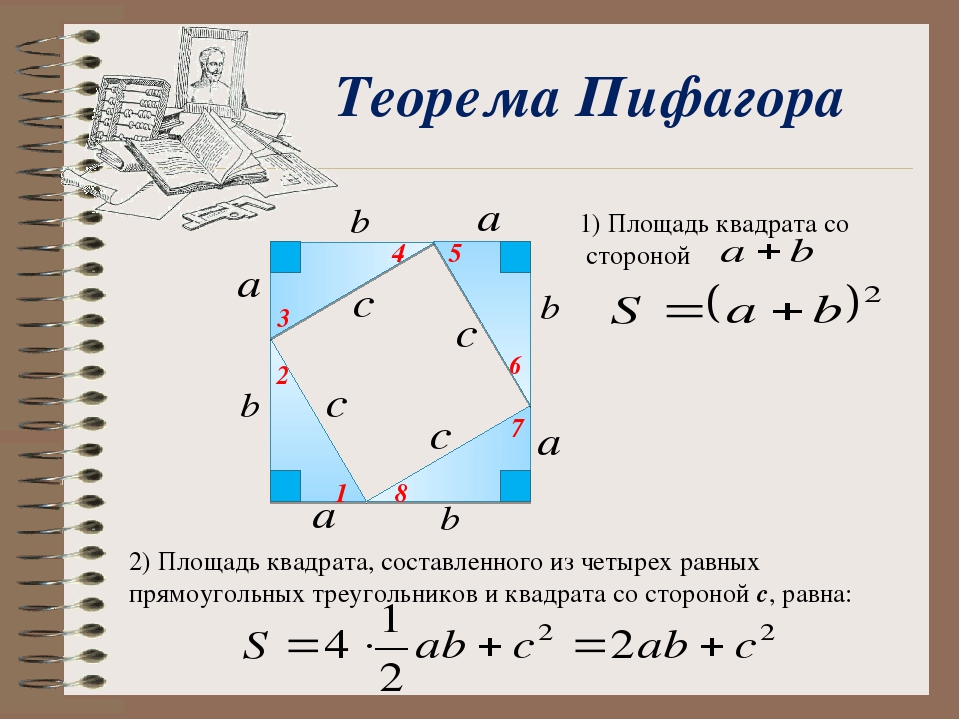
Как определить длину лестничного косоура?
Нужно знать отметки высот лестничных площадок и их расстояние друг от друга, тогда можно найти длину косоура (гипотенузу).
Например, отметки высот лестничных площадок +1,200 и +3,700, а расстояние между ними 3 м. Тогда по теореме Пифагора получим, что 2,52+32=(3,905)2 м.
Как рассчитать длину лестницы при пожаре?
Нужно определить на каком расстоянии будет опираться лестница от возгорания и на какой высоте произошло возгорание. После, применяя теорему Пифагора, необходимо вычислить длину лестницы (гипотенуза).
Например, возгорание произошло на втором этаже, будем считать, что на высоте 7 м, лестницу отстоит от здания на 2,5 м, значит необходимая длина лестницы равняется 7,44 м.
Заключение
Теорема Пифагора нашла применение во многих аспектах нашей жизни. Сейчас невозможно представить как без неё можно обойтись.
Сейчас невозможно представить как без неё можно обойтись.
Изучение информации о теореме Пифагора показало, что:
а) теорема очень важная и проста для понимания;
б) теорема Пифагора – является уникальной теоремой и занесена в книгу рекордов Гиннесса;
в) область применения теоремы огромна и очень тяжело раскрыть ее в полной мере;
г) загадки теоремы Пифагора продолжают удивлять людей и поэтому у всех есть возможность их раскрыть.
Список используемой литературы:
1. «Успехи математических наук», 1962, т. 17, № 6 (108)
2. Геометрия: Учеб. Для 7 – 11 кл. сред.шк./ Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова. – М.: Просвещение, 1992
Опубликовано: 31.08.2018
Малоизвестное обобщение теоремы Пифагора / Хабр
Теорема Пифагора — пожалуй, самая известная из математических теорем. Сколько существует оригинальных доказательств! Сколько применений она находит в технике! Сколькими благами цивилизации мы обязаны этой великой теореме! Однако, совсем недавно, я открыл для себя совершенно новую, ранее неизвестную грань этой теоремы, которая значительно расширяет область ее применения. Именно этим открытием я и хочу поделиться с вами, уважаемые читатели Geektimes. Пожалуйста, не судите строго, если описанные с статье факты, вам известны. Это скроее развлекательная история с научно-популярным элементом, чем строгая математика.
Именно этим открытием я и хочу поделиться с вами, уважаемые читатели Geektimes. Пожалуйста, не судите строго, если описанные с статье факты, вам известны. Это скроее развлекательная история с научно-популярным элементом, чем строгая математика.
Геометрическое доказательство теоремы Пифагора
Вокруг да около
История теоремы Пифагора уходит в века и тысячелетия. В этой статье, мы не будем подробно останавливаться на исторических темах. Для интриги, скажем только, что, по-видимому, эту теорему знали еще древне-египетские жрецы, жившие более 2000 лет до нашей эры. Для тех, кому любопытно, вот ссылка на статью в Википедии.
Прежде всего, хочется для полноты изложения привести здесь доказательство теоремы Пифагора, которое, по моему мнению, наиболее элегантно и очевидно. На рисунке выше изображено два одинаковых квадрата: левый и правый. Из рисунка видно, что слева и справа площади закрашенных фигур равны, так как в каждом из больших квадратов закрашено по 4 одинаковых прямоугольных треугольника. А это означает, что и незакрашенные (белые) площади слева и справа тоже равны. Замечаем, что в первом случае площадь незакрашенной фигуры равна , а во втором — площадь незакрашенной области равна . Таким образом, . Теорема доказана!
А это означает, что и незакрашенные (белые) площади слева и справа тоже равны. Замечаем, что в первом случае площадь незакрашенной фигуры равна , а во втором — площадь незакрашенной области равна . Таким образом, . Теорема доказана!
Зарождение идеи
В этой статье я хочу не только рассказать что-то новое и познавательное о теореме Пифагора, но и поделиться своей историей о том, как в моей голове зародилась интересная идея, которую я сумел сформулировать, доказать и даже предположил возможность обобщения на более высокую размерность. Но обо всем по порядку.
Египетские треугольники
С давних времен науке известны так называемые египетские треугольники. Это такие прямоугольные треугольники, у которых катеты и гипотенуза выражаются целыми числами. Можно сказать и иначе: египетские треугольники — это такие тройки натуральных чисел , которые образуют прямоугольный треугольник. Мы все, наверняка, хоть раз встречались с ними в школе на уроках геометрии. Для примера привожу несколько таких троек:
Во-первых, это красивые математические объекты.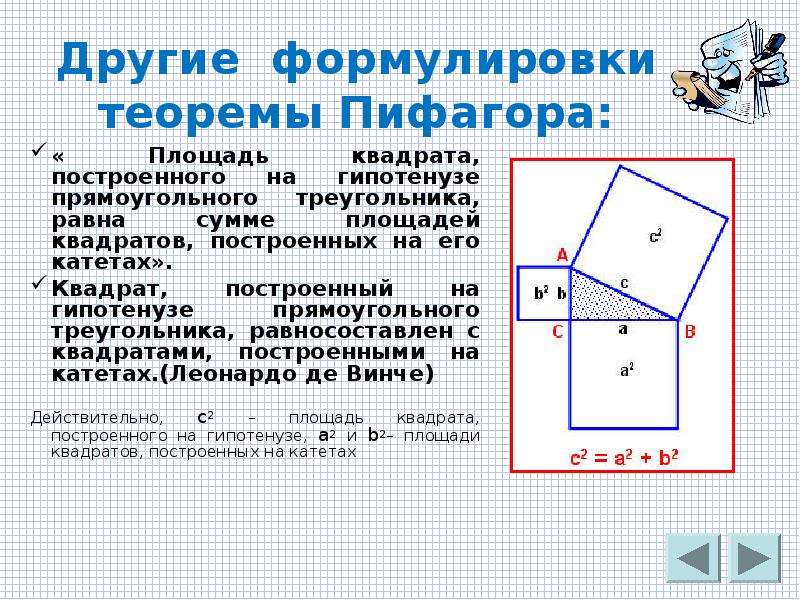 А во-вторых, с ними очень удобно решать задачи! Нет никаких квадратных корней и иррациональных чисел в ответе.
А во-вторых, с ними очень удобно решать задачи! Нет никаких квадратных корней и иррациональных чисел в ответе.
Загадочные четверки
И вот, году этак в 2004 — 2005, в пору подготовки к ЕГЭ, когда я сутками напролет решал просто какую-то бесконечную прорву хитро-вычурных задач из части С, мне то и дело стали попадаться не тройки, а уже четверки чисел, которые обладали похожими свойствами: а именно, сумма квадратов трех из них давала полный квадрат четвертого. Этот факт заинтриговал меня настолько, что я до сих пор наизусть помню некоторые из них. На самом деле, таких четверок бесконечно много и только в пределах чисел до 1000 их существует около 84 000. А вот, к примеру, пять таких четверок, из тех, что компьютер нашел перебором, пока я писал эту статью:
Заметив такое удивительное совпадение, я стал думать. Вопрос, который меня занимал в связи с этим загадочным обстоятельством, наличием не только троек, но и четверок, обнаруживающих свойства египетского треугольника, был таков: «А что бы это все могло значить?» Я перебирал варианты, какие только приходили в голову. В фантазии себя никак не ограничивал. Много раз садился за стол, выписывал известные мне наборы четверок и вдумчиво на них смотрел… часами… без перерыва… и… ничего не происходило. У меня был школьный товарищ Саня, с которым я как-то поделился своими идеями. Но его больше интересовали гуманитарные науки. Он стал юристом и сейчас служит в звании майора милиции. Саня сказал мне примерно следующее:«Вот странный ты человек. Делать тебе больше нечего. Мало тебе задают домашек? Хватит думать о всякой ерунде!». А, надо сказать, думал я, не переставая, и думал много лет, время от времени возвращаясь к этой загадке. Еще будучи школьником, я сделал вывод, что это, вероятнее всего, имеет отношение к великой теореме Ферма (на которую я тоже много раз подолгу смотрел). Шли годы. Ничего не получалось. Озарение не приходило. И я понял, что, вероятно, дальше чем «что-то связанное с теоремой Ферма» я никуда уже не продвинусь. Но не тут то было
В фантазии себя никак не ограничивал. Много раз садился за стол, выписывал известные мне наборы четверок и вдумчиво на них смотрел… часами… без перерыва… и… ничего не происходило. У меня был школьный товарищ Саня, с которым я как-то поделился своими идеями. Но его больше интересовали гуманитарные науки. Он стал юристом и сейчас служит в звании майора милиции. Саня сказал мне примерно следующее:«Вот странный ты человек. Делать тебе больше нечего. Мало тебе задают домашек? Хватит думать о всякой ерунде!». А, надо сказать, думал я, не переставая, и думал много лет, время от времени возвращаясь к этой загадке. Еще будучи школьником, я сделал вывод, что это, вероятнее всего, имеет отношение к великой теореме Ферма (на которую я тоже много раз подолгу смотрел). Шли годы. Ничего не получалось. Озарение не приходило. И я понял, что, вероятно, дальше чем «что-то связанное с теоремой Ферма» я никуда уже не продвинусь. Но не тут то было
Шерлок нашел зацепку
Итак, в 2014 году ехал я в автобусе по Новосибирску. А может быть это было метро. Дорога не близкая. Заняться нечем. И в очередной раз решил я подумать о моей школьной загадке. И вот что я подумал.
А может быть это было метро. Дорога не близкая. Заняться нечем. И в очередной раз решил я подумать о моей школьной загадке. И вот что я подумал.
Как же назвать эти числа? Треугольниками не назовешь, ведь четыре числа никак не могут образовать треугольник. И тут! Как гром среди ясного неба
Раз есть такие четверки чисел, значит должен быть геометрический объект с такими же свойствами, отраженными в этих числах!
Теперь осталось только подобрать какой-то геометрический объект под это свойство, и все встанет на свои места! Конечно, предположение было чисто гипотетическое, и никакого подтверждения под собой не имело. Но что если это так!
Начался перебор объектов. Звезды, многоугольники, правильные, неправильные, с прямым углом и так далее и тому подобное. Опять ничего не подходит. Что делать? И в этот момент Шерлок получает свою вторую зацепку.
Надо повысить размерность! Раз тройке соответствуют треугольник на плоскости, значит четверке соответствует нечто трехмерное!
О нет! Опять перебор вариантов! А в трехмерии гораздо, гораздо больше всевозможных геометрических тел. Попробуй перебрать их все! Но не все так плохо. Есть же еще прямой угол и другие зацепки! Что мы имеем? Египетские четверки чисел (пусть будут египетские, надо же их как-то называть), прямой угол (или углы) и некий трехмерный объект. Дедукция сработала! И… Полагаю, что догадливые читатели уже поняли, что речь идет о пирамидах, у которых при одной из вершин все три угла — прямые. Можно даже назвать их прямоугольными пирамидами по аналогии с прямоугольным треугольником.
Попробуй перебрать их все! Но не все так плохо. Есть же еще прямой угол и другие зацепки! Что мы имеем? Египетские четверки чисел (пусть будут египетские, надо же их как-то называть), прямой угол (или углы) и некий трехмерный объект. Дедукция сработала! И… Полагаю, что догадливые читатели уже поняли, что речь идет о пирамидах, у которых при одной из вершин все три угла — прямые. Можно даже назвать их прямоугольными пирамидами по аналогии с прямоугольным треугольником.
Новая теорема
Итак, у нас есть все что нужно. Прямоугольные (!) пирамиды, боковые грани-катеты и секущая грань-гипотенуза. Пришло время нарисовать еще одну картинку.
Теорема Пифагора для прямоугольной пирамиды
На картинке изображена пирамида с вершиной в начале прямоугольных координат (пирамида как бы лежит на боку). Пирамида образована тремя взаимно-перпендикулярными векторами, отложенными из начала координат вдоль координатных осей. То есть каждая боковая грань пирамиды — это прямоугольный треугольник с прямым углом при начале координат.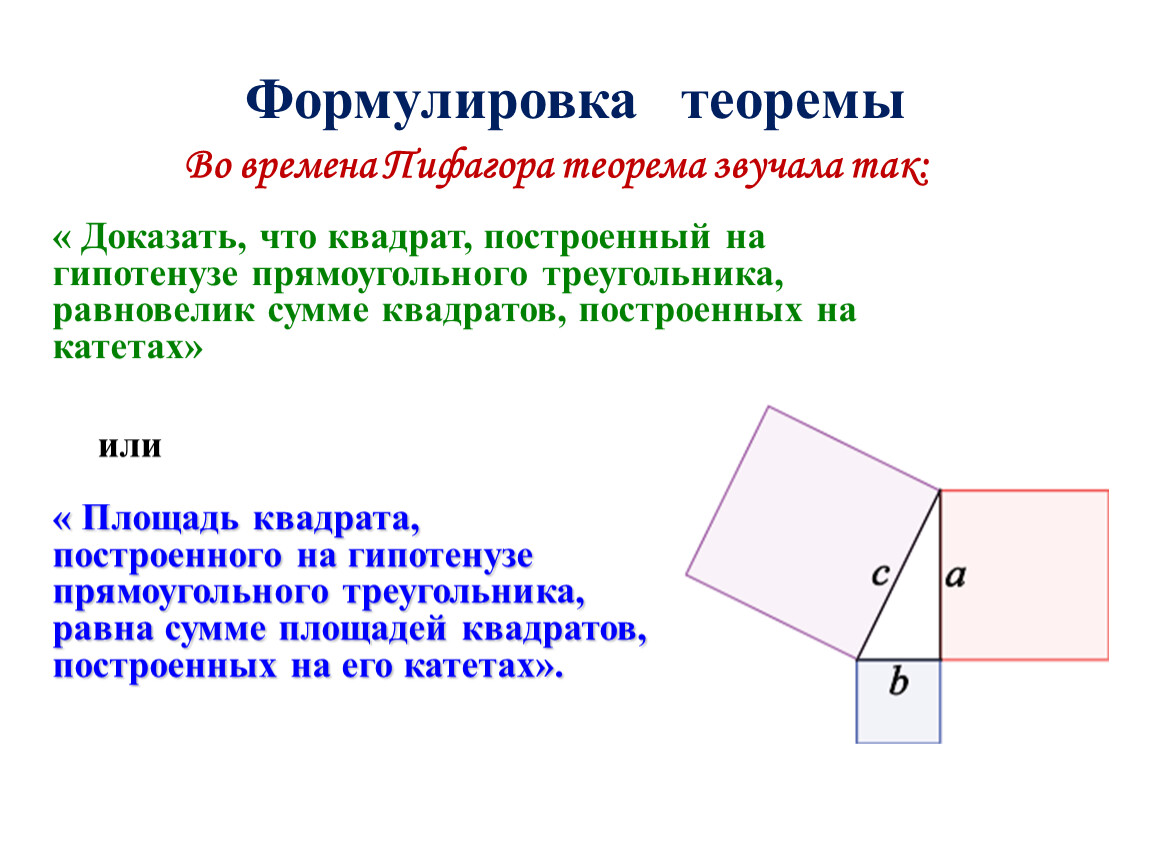 Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.
Концы векторов определяют секущую плоскость и образуют грань-основание пирамиды.
Теорема
Пусть есть прямоугольная пирамида, образованная тремя взаимно-перпендикулярными векторами , у которой площади граней-катетов равны — , и площадь грани-гипотенузы — . ТогдаАльтернативная формулировка: У четырехгранной пирамиды, у которой при одной из вершин все плоские углы прямые, сумма квадратов площадей боковых граней равна квадрату площади основания.
Разумеется, если обычная теорема Пифагора формулируется для длин сторон треугольников, то наша теорема формулируется для площадей сторон пирамиды. Доказать эту теорему в трех измерениях очень просто, если вы немного знаете векторную алгебру.
Доказательство
Выразим площади через длины векторов .
где .Площадь представим как половину площади параллелограмма, построенного на векторах и
Как известно, векторное произведение двух векторов — это вектор, длина которого численно равна площади параллелограмма, построенного на этих векторах.
Поэтому
Таким образом,
Что и требовалось доказать!
ЭВРИКА!
Моему восторгу не было границ! Я буквально прыгал от счастья. Конечно, это не бог весть какая сложная теорема, и доказательство очень простое, но ведь сам. И до меня — никто! Я был в этом искренне убежден в течение около года. Попытки найти хоть какие-то свидетельства о том, что это уже известно и доказано терпели неудачу одна за другой, и я думал, что совершил открытие. Это непредаваемое чувство! Я хотел поделиться этой теоремой со всем миром. Говорил о ней друзьям, знакомым математикам, просто знакомым с техническим/математическим образованием и без. Никто не разделял моего восторга и энтузиазма. Всем было попросту безразлично. Будто бы я не придумал и доказал теорему, а просто в магазин за хлебом сходил. Ну и что тут такого? Вот уж действительно… Как говорится, «Как скучно мы живём! В нас пропал дух авантюризма, мы перестали лазить в окна к любимым женщинам, мы перестали делать большие хорошие глупости. » (из фильма «Ирония судьбы»).
» (из фильма «Ирония судьбы»).
Конечно, как у человека, профессионально занимающегося исследованиями, подобное в моей жизни уже случалось, и не раз. Но этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя. От зарождения мысли, кристализации идеи, нахождения доказательства — до полного непонимания и даже неприятия, которое встретили мои идеи у моих друзей, знакомых и, как мне тогда казалось, у целого мира. Это было уникально! Я словно почувствовал себя в шкуре Галлилея, Коперника, Ньютона, Шредингера, Бора, Эйнштейна и многих многих других открывателей.
Послесловие
В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!
Вот ссылка на статью:
Amir-Moéz, Ali R., Robert E. Byerly, and Robert R. Byerly. «Pythagorean theorem in unitary spaces. » Publikacije Elektrotehničkog fakulteta. Serija Matematika (1996): 85-89.
» Publikacije Elektrotehničkog fakulteta. Serija Matematika (1996): 85-89.
Статья опубликована издательством Техасского технического университета. Авторы, профессиональные математики, ввели терминологию (которая, кстати, во многом совпала с моей) и доказали также и обобщенную теорему справедливую для пространства любой размерности большей единицы. Что же произойдет в размерностях более высоких, чем 3? Все очень просто: вместо граней и площадей будут гиперповерхности и многомерные объемы. А утверждение, конечно, останется все тем же: сумма квадратов объемов боковых граней равна квадрату объема основания, — просто количество граней будет больше, а объем каждой из них станет равен половине произведения векторов-образующих. Вообразить это почти невозможно! Можно только, как говорят философы, помыслить!
Что удивительно, узнав о том, что такая теорема уже известна, я ничуть не расстроился. Где-то в глубине души я подозревал, что вполне возможно, я был не первый, и понимал, что нужно быть всегда к этому готовым. Но тот эмоциониальный опыт, который я получил, зажег во мне искру исследователя, которая, я уверен, теперь уже не угаснет никогда!
Но тот эмоциониальный опыт, который я получил, зажег во мне искру исследователя, которая, я уверен, теперь уже не угаснет никогда!
P.S.
Эрудированный читатель в комментариях прислал ссылку
Теорема де Гуа
Выдержка из Википедии
В 1783 году теорема была представлена Парижской академии наук французским математиком Ж.-П. де Гуа, однако ранее она была известна Рене Декарту[3] и до него Иоганну Фульгаберу (англ.), который, вероятно, первым открыл её в 1622 году[4]. В более общем виде теорему сформулировал Шарль Тинсо (фр.) в докладе Парижской академии наук в 1774 году[4]
Так что я опоздал не на 18 лет, а как минимум на пару веков!
Источники
Читатели указали в комментариях несколько полезных ссылок. Вот эти и некоторые другие ссылки:
- Теорема де Гуа
- Теорема Пифагора
- Пифагорова тройка
- Пифагорова четверка
- Равенство Парсеваля
Открытый урок на тему: «Теорема Пифагора» | План-конспект урока по алгебре (8 класс):
Слайд 2
Старинная задача На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
Слайд 3
Переведем задачу на математический язык Дано: АС=30, ВД=20, АВ=50.
Слайд 4
Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике. Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора .
Слайд 5
Биография Пифагора Пифагор-это не имя, а прозвище, данное ему за то , что он высказывал истину также постоянно, как дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции. О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
Слайд 6
Пифагорейская школа Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Так на юге Италии, которая была тогда греческой колонией, возникла пифагорейская школа.
Слайд 7
Пифагорейская школа Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. В школ существовал декрет, по которому авторство всех математических работ приписывалось Пифагору. Звездчатый пятиугольник, или пентаграмма, — пифагорейский символ здравия и тайный опознавательный знак
Слайд 8
Заповеди Пифагора и его учеников актуальны и сейчас и могут быть приемлемы для любого здравомыслящего человека. Вот они!
Слайд 9
Заповеди пифагорийцев Делать то, что впоследствии не огорчит тебя и не принудит раскаиваться; Не делай никогда того, что не знаешь, но научись всему, что следует знать; Не пренебрегай здоровьем своего тела; Приучайся жить просто и без роскоши.
Слайд 10
Физминутка
Слайд 11
Построим на сторонах прямоугольного треугольника квадраты со стронами а, в,с
Слайд 12
Попробуйте сформулировать теорему!
Слайд 13
Так звучала теорема во времена Пифагора Площадь квадрата построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на его катетах.
Слайд 14
А так звучит современная формулировка: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 15
1 ученик. Квадраты построенные на катетах, состоят из 2-х одинаковых треугольников. А квадрат, построенный на гипотенузе состоит из 4-х такаих треугольников
Слайд 16
2-й ученик. Еслизакрасить 4 треугольника на одном рисунке, то останется квадрат площадью с 2 , а если закрасить такие же 4 треугольника на втором рисунке, то останутся квадраты площадью a2 и b2 Вот и получится с 2 = a2 + b2
Слайд 17
3-й ученик Я использовал этот же прием, но по-другому. Поставил рядом квадраты площадью a 2 и b 2. Теперь отрежем от них два одинаковых треугольника с катетами a и b и гипотенузой с, и переложим так, как показано на рисунке. Получим квадрат площадью с2 . Значит, опять получается, что a 2+ b 2= c 2 .
Поставил рядом квадраты площадью a 2 и b 2. Теперь отрежем от них два одинаковых треугольника с катетами a и b и гипотенузой с, и переложим так, как показано на рисунке. Получим квадрат площадью с2 . Значит, опять получается, что a 2+ b 2= c 2 .
Слайд 19
4 ученик. А я не смог сделать неочевидное очевидным, но я доказал теорему, используя уже известные, ранее доказанные факты. Дано: ΔАВС – прямоугольный. Угол с-прямой; АС=в, АВ=с, ВС=а. Доказать: а2+в2=с2 .
Слайд 20
В чем достоинство этого способа доказательства? Этот способ доступен пониманию каждого, кто занимается геометрией. Для того, чтобы его освоить, не надо обладать воображением или еще какими-то особенными способностями.
Слайд 21
А сейчас вернемся к нашей задаче На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами.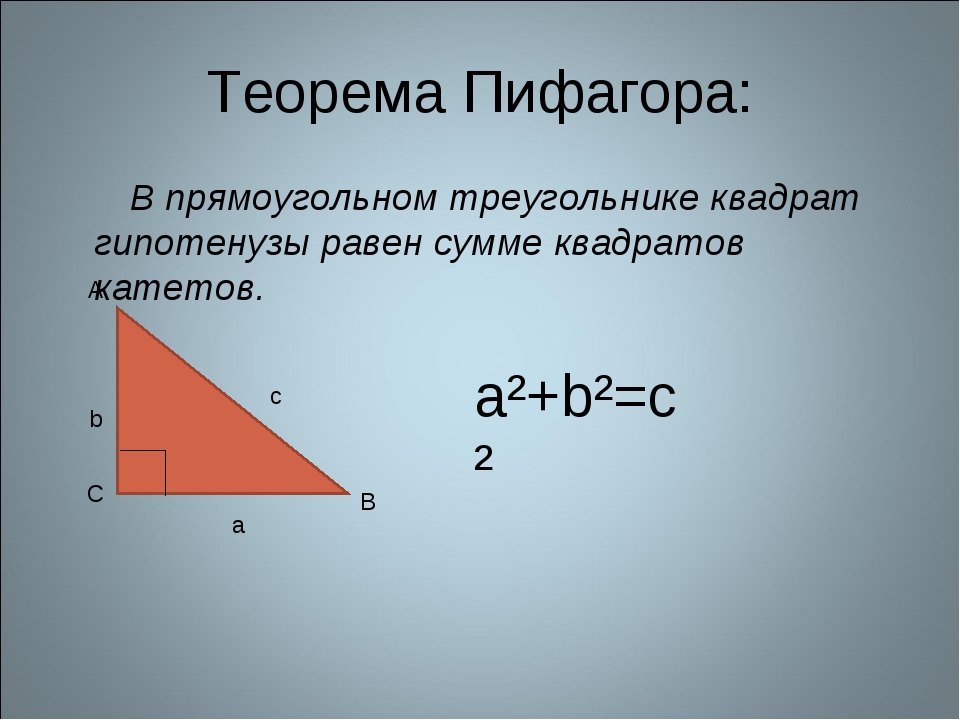 Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
Слайд 22
Дано: АС=30, ВД=20, АВ=50.
Слайд 23
Рассмотрим еще одну задачу, для решения которой нам необходимо знать теорему Пифагора. Над озером тихим, С полфута размером, Высился лотоса цвет. Он рос одиноко. И ветер порывом Отнес его в сторону. Нет боле цветка над водой. Нашел же рыбак его ранней весной В двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода глубока?
Слайд 24
Решение СД – глубина озера СД – Х, СВ=2 фута АД=ВД=Х+0,5 Треугольник ВСД прямоуг. ВД2-ВС2=СД2 Х2=(Х+0,5)2 — 22 Х2=Х2+Х+0,25-4 Х=3,75 футов Ответ: 3,75 футов
Слайд 25
Итог. 1 . Возможно было решение задач данного типа без знания теоремы Пифагора? Почему? 2. В чем суть теоремы Пифагора? 3. О чем надо помнить, применяя теорему Пифагора?
Слайд 26
4 . Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5. Правильно ли они поступали?
По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5. Правильно ли они поступали?
Слайд 27
Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
Слайд 28
Вам, наверное, известны также детские стишки о пифагоровых штанах. Данный рисунок подтверждает их содержание. Пифагоровы штаны Во все стороны равны.
Слайд 29
До нас дошли и другие шуточные рисунки к теореме
Слайд 30
Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим И таким простым путём К результату мы придём.
Слайд 31
Спасибо за урок!
Презентация к уроку по теме:Теорема Пифагора
Теорема Пифагора
2 . Найдите площадь прямоугольного треугольника
с катетами 3 см и 4 см; 2 ,2 м и 5 см; а см и b см.
3. Чему равна площадь домика?
S
= 5 см 2 ; S
= 20 см 2 .
Ответ: 30 см 2
«Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!»
«Золотые стихи» Пифагора
- Не делай никогда того, чего не знаешь, но научись
всему тому, что хочешь знать
— Либо молчи, либо говори то, что ценнее молчания
— Изнурять своё тело ты не должен, но старайся пищи, питья и упражнений давать ему в меру — дабы тело твоё укрепилось, не зная ни излишеств, ни лени!
— Делай лишь то, что тебя ни теперь, ни потом не погубит! И потому обдумывай прежде каждый свой шаг и поступок.
«Геометрия владеет
двумя сокровищами:
одно из них – это
теорема Пифагора»
Иоганн Кеплер
«Пифагоровы штаны во все стороны равны»
Современная формулировка
теоремы Пифагора
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов ».
Во времена Пифагора формулировка теоремы звучала так:
«Квадрат, построенный на гипотенузе прямо — угольного треугольника, равновелик сумме квадратов, построенных на катетах ».
И. Дырченко
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
Теорема Пифагора
В прямоугольном треугольнике
квадрат гипотенузы равен
сумме квадратов катетов .
a
b
b
а 2 + b 2 =с 2
c
a
c
Доказательство:
S
=( а+ b ) 2
S
c
a
c
b
а 2 +2а b + b 2 = с 2 +2а b
b
a
а 2 + b 2 = с 2
Задача №1 Найдите гипотенузу прямоугольного треугольника, если катеты равны 6 см и 8 см.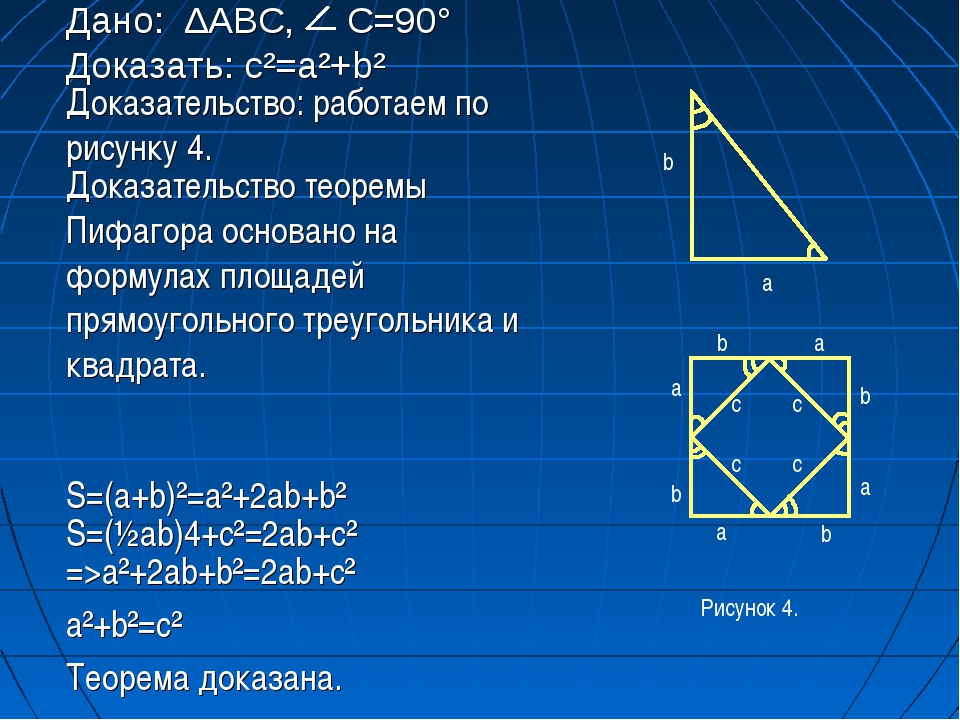
Задача №2 Найдите катет прямоугольного треугольника, если гипотенуза равна 13 см, а второй катет – 12 см.
Задача №3 Три стороны четырехугольника имеют длины 4см, 7 см и 8 см; два противоположных угла прямые. Найдите длину четвертой стороны.
Задача №4 В прямоугольный треугольник с углом60° вписан ромб со стороной 6 см так, что угол 60° -общий и все вершины ромба лежат на сторонах треугольника. Найдите стороны треугольника.
Домашнее задание п.54 прочитать, знать теорему стр.129-131 483бв, 484ав, 486вг
УРОК «ТЕОРЕМА ПИФАГОРА» (8 КЛАСС)
УРОК «ТЕОРЕМА ПИФАГОРА» (8 КЛАСС)
Автор: Подкопаева В.Е.
Методическая копилка —
Математика
УРОК «ТЕОРЕМА ПИФАГОРА»
(8 КЛАСС)
Цели: 1. Образовательная — познакомить учащихся с теоремой Пифагора и научить ее применять к решению задач.
2.Развивающая — развивать мыслительные способности учащихся посредством вовлечения их в обсуждение проблемы.
3. Воспитательная – прививать устойчивый интерес к изучению математики, воспитывать культуру общения, умение вести дискуссию.
Девиз урока: «Учится можно весело… .Чтобы переваривать знания,надо поглощадь их с аппетитом.»
План урока
1. Организационный момент.
2. Актуализация знаний.
3. Создание проблемной ситуации.
4 Сообщение учащегося о жизни Пифагора Самосского.
5 Историческая справка о теореме Пифагора.
6. Работа над теоремой.
7. Решение задач с применением теоремы.
8 Подведение итога урока.
9. Домашнее задание.
Оборудование:
1. Персональный компьютер
2. Проектор, экран
3. Презентация для урока
4. Чертежные инструменты
5 «Раскладушка»: легенды о Пифагоре, нравственные заповеди пифагорей-
цев, пентаграмма, исторические задачи, пифагорова головоломка, пифа-
горовы тройки…
6 Рисунки к устным задачам
Ход урока
1.Организационный момент.
2.Повторение
Самостоятельная работа с целью повторения формул площадей квадрата и прямоугольного треугольника
1Вычислите площадь квадрата a==8;0,7;1,3
2 Вычислите площадь прямоугольного треугольника a=13;2,5; b =7;6
3.Начало урока: Наш урок мы начнем с решения одной старинной задачи. Слайд
Задача. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от более высокой пальмы появилась рыба?
Переведем задачу на математический язык.
Дано: АС=30, ВД=20, АВ=50.
Учитель: Что означает, что птицы летели с одинаковой скоростью и догнали рыбу одновременно?
1 ученик: Это означает, что до рыбы они пролетели одинаковое расстояние, т.е. СЕ=ДЕ.
Учитель: Что требуется найти в задаче?
2 ученик: Найти АЕ.
Учитель: Какой способ для решения задачи вы предлагаете?
3 ученик: С помощью уравнения. За Х можно принять расстояние АЕ. Тогда ВЕ=50-Х.
Учитель: Какие величины надо выразить через Х, чтобы мы могли составить уравнение?
4 ученик: Надо выразить СЕ и ДЕ.
Учитель: Можем ли мы это сделать?
1 ученик: Нет, мы не можем это сделать.
Учитель: Что мы можем сказать о треугольниках АСЕ и ВДЕ?
2 ученик: Они прямоугольные.
Учитель: Как называются стороны АС и АЕ в треугольнике АСЕ, ВД и ВЕ в треугольнике ВДЕ?
3 ученик: Они называются катетами.
Учитель: Как называются стороны СЕ и ДЕ?
4 ученик Они называются гипотенузами.
Учитель: Значит, нам надо знать зависимость между катетами и гипотенузой в прямоугольном треугольнике.
Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора. Послушайте историческую справку.
Пифагор- это не имя а прозвище, данное ему за то, что он высказывал истину также постоянно, дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции (родился он в 580 г. до н.э., умер в 500 г. до н.э.). О жизни этого ученого известно немного, зато с его именем связан ряд легенд. Рассказывают, что он много путешествовал: был в Индии, Египте, Вавилоне; изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В пифагорейский союз, который имел свой кодекс чести, принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения своего основателя. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. Авторство всех работ приписывалось Пифагору. Заповеди Пифагора и его учеников актуальны и сейчас и могут быть приемлемы для любого здравомыслящего человека. Вот они:
— делать то, что впоследствии не огорчит тебя и не принудит раскаиваться;
— не делай никогда того, что не знаешь, но научись всему, что следует знать;
— не пренебрегай здоровьем своего тела;
— приучайся жить просто и без роскоши.
Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд.
Учитель: К настоящему времени известно более 200 способов доказательства этой теоремы. Мы рассмотрим современную формулировку теоремы и её доказательство.
Ребята, может быть, вы что-нибудь слышали о теореме Пифагора? (…)
. А ещё? (Пифагоровы штаны во все стороны равны.) Слайд
Действительно, это шуточная формулировка теоремы.
Такие стишки придумывали учащиеся средних веков при изучении тео-
ремы; рисовали шаржи. Вот, например, такие (слайд)
В современных учебниках теорема сформулирована так: «В прямоуголь-
ном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
. Как записать терему Пифагора для прямоугольного треугольника
D АВС с катетами а, b и гипотенузой с (рис.)?
c2 = a2 + b2
Предполагают, что во времена Пифагора теорема звучала по-другому:
«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника,
равна сумме площадей квадратов, построенных на его катетах». Действительно,
с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов ,построенных на катетах b2,a2 Слайд
c2 = a2 + b2.
Вероятно, факт, изложенный в теореме Пифагора, был сначала установ-
лен для равнобедренных прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка 9 видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах. Слайд
Рис.
Формулировка теоремы: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»
Учитель доказывает теорему.
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
III. Учитель: А сейчас вернемся к нашей задаче.
Условие задачи сохранилось на доске.
Итак, в треугольнике АСЕ: СЕ2=АС2+АЕ2=302+Х2=900+Х2;
в треугольнике ВДЕ: ДЕ2=ВД2+ВЕ2=202+(50-Х)2==400+2500- 100Х+Х2=2900-100Х+Х2.
По СЕ=ДЕ СЕ2=ДЕ2=900+Х2=2900-100+Х2
100Х=2000
Х=20, АЕ=20.
Значит, рыба была на расстоянии 20 локтей от большой пальмы.
4.Первоначальное закрепление.
Заполнить таблицу
а в с
6 8 ?
1 1 ?
8 15 ?
Теорема Пифагора – одна из главных теорем геометрии, потому что с её
помощью можно доказать много других теорем и решить множество задач.
Особенностью теоремы Пифагора является то, что она неочевидна. На-
пример, свойства равнобедренного треугольника можно увидеть непосредст-
венно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак
не увидишь, что его стороны находятся в соотношении с2 = а2 + b2.
Значение теоремы Пифагора состоит в том, что из нее или с ее помощью
можно вывести большинство теорем геометрии и решить множество задач. К
следующему уроку вы должны выучить теорему Пифагора с доказательством,так как мы будем учиться применять её к решению более сложных задач.
Популярность теоремы столь велика, что её доказательства встречаются
даже в художественной литературе, например в рассказе известного английского писателя Хаксли «Юный Архимед». Такое же доказательство, но для частного случая равнобедренного прямоугольного треугольника приводится в диалогеПлатона «Менон». Этой теореме даже посвящены стихи.
За 2000 лет до н.э., т.е. задолго до Пифагора был известен практический способ построения египетского треугольника. Пифагор же предложил первое, стройное с точки зрения математики доказательство теоремы, поэтому вся слава досталась ему.
На эту тему существует легенда о том, что, открыв теорему, Пифагор принес в жертву богам 100 быков. Послушаем стихотворение А.Шамиссо.
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношение
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков
Поэтому всегда, с тех самых пор
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед,
Они не в силах свету помешать,
А могут лишь, закрыв глаза дрожать
От страха, что вселил в них Пифагор.
Ребята, Д.Пойа говорил: «Если вы хотите плавать , то смело входите в воду,а если хотите научиться решать задачи,то решайте их.»
Решим устно несколько задач.
Задача №1
Р е ш е н и е.
D АВС — прямоугольный с гипотенузой АВ,
по теореме Пифагора: АВ2 = АС2 + ВС2,
АВ2 = 82 + 62,
8 ? АВ2 = 64 + 36,
АВ2 = 100,
АВ = 100 ,
АВ = 10. АС, значит, D ABD и D CBD – прямоуголь-
ные.
2) По теореме Пифагора для D ABD: АВ2 = AD2 + BD2, отсюда
BD2 = AB2 – AD2,
BD2 = 202 – 162,
BD2 = 400 – 256,
BD2 = 144,
BD = 144 ,
BD = 12 см.
3) По теореме Пифагора для D СBD: ВС2 = ВD2 + DС2, отсюда
BC2 = 122 + 92,
BC2 = 144 + 81,
BC2 = 225,
BC = 225 ,
BC = 15 см.
О т в е т: ВС = 15 см.
Итак, сегодня на уроке мы познакомились с одной из главных теорем
геометрии — теоремой Пифагора и её доказательством, с некоторыми сведениями из жизни учёного, имя которого она носит, решили несколько простейших задач.
Для тех, кто желает больше узнать о Пифагоре, прочитать о нём легенды,
выяснить, почему союз пифагорейцев был тайным, почему авторство работ
приписывалось учителю и о многом другом, советую прочитать книгу А.В. Волошинова «Пифагор».
А познакомившись с материалами «раскладушки», вы можете узнать о
нравственных заповедях пифагорейцев, прочитать несколько легенд, связанных
с именем Пифагора, попробовать решить несколько исторических задач и разгадать пифагорову головоломку.
Запишите домашнее задание: выучить материалы п. 63, 64, ответить
на контрольный вопрос
IV. Итог.
1. Возможно было решение задач данного типа без знания теоремы Пифагора? Почему?
2. В чем суть теоремы Пифагора?
3. О чем надо помнить, применяя теорему Пифагора?
4. Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей – 5. Правильно ли они поступали?
Треугольник со сторонами 3,4,5 теперь мы называем египетским.
А закончить урок мне хочется словами великого Иоганна Кеплера: «Геометрия владеет многими сокровищами, но одно из главных сокровищ – это теорема Пифагора». Сегодня мы прикоснулись к этому сокровищу, и теперь оно будет помогать нам при решениизадач по геометрии.
ВСЕМ СПАСИБО ЗА УРОК!
Решение задач, связанных с теоремой Пифагора
Решение задач, связанных с теоремой Пифагора
Вот шаги, необходимые для решения комбинированных вариационных задач:
| Шаг 1 : | Нарисуйте прямоугольный треугольник и снова прочтите задачи, чтобы определить длину катетов и гипотенузу. |
| Шаг 2 : | Используйте теорему Пифагора (a 2 + b 2 = c 2 ), чтобы написать уравнение, которое нужно решить.Помните, что a и b — это катеты, а c — гипотенуза (самая длинная сторона или сторона, противоположная углу 90º). |
| Шаг 3 : | Упростите уравнение, распределяя и комбинируя одинаковые члены по мере необходимости. |
| Шаг 4 : | Решите уравнение. Если уравнение содержит x 2 , приравняйте уравнение к нулю и решите уравнение на множители. Если уравнение не содержит x 2 , решите уравнение, получив переменные с одной стороны и числа с другой. |
| Шаг 5 : | Ответьте на вопрос, заданный в исходном вопросе, и убедитесь, что ответ имеет смысл. Не забудьте указать единицы в своем окончательном ответе. |
Пример 1 — Гипотенуза прямоугольного треугольника на 1 дюйм длиннее его более длинного катета. Более короткая нога на 7 дюймов короче более длинной. Найдите длину гипотенузы.
Пример 2 — Кэрри работает в счет к югу от своей квартиры.Ее подруга Сара работает к востоку от квартиры. Они уходят на работу одновременно. К тому времени, как Кэрри находится в 5 милях от их квартиры, расстояние между ними на 1 милю больше, чем расстояние Сары от квартиры. Как далеко от квартиры Сара?
Щелкните здесь, чтобы просмотреть практические задания
Пример 3 — Оттяжка прикреплена к телефонной опоре. Расстояние от точки соприкосновения провода с землей до основания телефонной опоры на 4 фута меньше длины провода.На каком расстоянии от телефонного столба расположен провод, если расстояние от земли до места, где провод прикреплен к столбу, на 2 фута меньше длины провода?
Щелкните здесь, чтобы просмотреть практические задания
Пример 4 — Основание лестницы находится на расстоянии 10 футов от стены. Лестница на 2 фута длиннее, чем высота, которую она достигает на стене. Какая длина лестницы?
Щелкните здесь, чтобы просмотреть практические задания
Читайте: Теорема Пифагора | Промежуточная алгебра
Прочтите и поймите: Мы знаем длины всех сторон треугольника через одну сторону.2-4x-12 = 0 \ end {array} [/ latex]
Это превратилось из запутанной проблемы во что-то многообещающее. Мы можем разложить на множители, используя ярлык:
[латекс] -6 \ cdot {2} = — 12, \ text {и} -6 + 2 = -4 [/ латекс]
Итак, мы можем построить наши биномиальные множители с помощью [latex] -6 [/ latex] и [latex] 2 [/ latex]:
[латекс] \ влево (x-6 \ вправо) \ влево (x + 2 \ вправо) = 0 [/ латекс]
Установить каждый коэффициент равным нулю:
[латекс] x-6 = 0, x = 6 [/ латекс]
[латекс] x + 2 = 0, x = -2 [/ латекс]
Интерпретация: Хорошо, не имеет смысла иметь длину, равную [латекс] -2 [/ латекс], поэтому мы можем спокойно выбросить это решение.2 \\ 36 + 64 = 100 \\ 100 = 100 \ end {array} [/ latex]
Наше решение прошло проверку.
Ответ
Стороны прямоугольного треугольника имеют длину [латекс] 6, 8 [/ латекс] и [латекс] 10 [/ латекс].
2.4: Теорема Пифагора — математика LibreTexts
- Последнее обновление
- Сохранить как PDF
Без заголовков
Теорема Пифагора связывает длины катетов прямоугольного треугольника и гипотенузы.{2} \), где \ (c \) — длина гипотенузы, а \ (a \) и \ (b \) — длины катетов. Однако вам придется измерить каждый такой треугольник, чтобы узнать его абсолютную истину, что, конечно, невозможно. Поэтому мы хотели бы найти способ увидеть, что это верно для всех прямоугольных треугольников. Утверждение теоремы Пифагора можно увидеть, рассмотрев следующую конструкцию. Начните с треугольника (так можно сориентировать любой прямоугольный треугольник)
затем постройте три других треугольника того же размера и формы, что и первый (т.{2} \ nonumber \]
\ (\ квадрат \)
Теорема Пифагора
The
Теорема Пифагора (стр.
1 из 2)
Когда вы впервые изучали квадрат
корни и как решать радикальные уравнения,
вы, вероятно, познакомились с чем-то, что называется «пифагорейским
Теорема ».Эта теорема связывает длины трех сторон
любой прямоугольный треугольник.
Катеты прямоугольного треугольника (две стороны
треугольника, которые пересекаются под прямым углом) обычно обозначаются
как имеющие длину « a »
и « b «,
и гипотенуза (длинная сторона треугольника, противоположная правой
угол) имеет длину « c «.
Длины связаны следующим уравнением:
a 2 + b 2 = c 2
Это уравнение позволяет найти длину
стороны прямоугольного треугольника, когда они дали вам длину для
две другие стороны, и, идя в другую сторону, позволяет определить
если треугольник — это прямоугольный треугольник, когда они дали вам длину для
со всех трех сторон.
- Учитывая прямоугольные треугольники
как показано ниже, найдите длины оставшихся сторон.
а) Сторона, противоположная прямому углу
— c ;
как я назову две другие стороны, на самом деле не имеет значения. Я подключу
значений в теорему и решите:
80 2 = 48 2 + b 2
6400 = 2304 + б 2
4096 = б 2
Авторские права
© Элизабет Стапель 2010-2011 Все права защищены
64
= б
Обычно мне нужны оба ответа, от
«плюс / минус», чтобы решить квадратное уравнение, взяв
квадратные корни.В этом случае, однако, я знал, что буду
необходимо найти положительное значение для длины третьего
сторону, поэтому я могу игнорировать отрицательное решение.
б) Этот треугольник работает так же
как сделал (а):
- Учитывая треугольники
ниже определите, правильны ли треугольники.
а) Мне нужно посмотреть, есть ли квадраты
катеты равны квадрату гипотенузы:
Треугольник для (а)
НЕ является прямоугольным треугольником.
б) Этот работает так же, как для (а):
Треугольник для (б)
— прямоугольный треугольник.
Верх | 1 | 2 | Возвращаться
к указателю След. >>
Цитируйте эту статью | Стапель, Элизабет.«Теорема Пифагора». Пурпурная математика . Доступна с |
Выучите теорему Пифагора | Найти недостающую сторону прямоугольного треугольника
В этом видео мы рассмотрим, как найти недостающую сторону прямоугольного треугольника с помощью теоремы Пифагора.После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.
Теорема Пифагора
где a и b — длины катетов прямоугольного треугольника,
и c — длина гипотенузы.
Например:
Чтобы решить следующее уравнение:
Подставьте переменные, где 3 заменяет a и 4 заменяет b
Решить для и
Добавьте 9 и 16 вместе, оставляя нас с:
Найдите квадратные корни с обеих сторон
Оставив нас с:
Итак, гипотенуза равна 5
Примеры теоремы Пифагора
Пример 1
Используйте уравнение теоремы Пифагора
Подставьте переменные, где заменяет и заменяет
Решите для и
Сложите и вместе, получив:
Найдите квадратные корни с обеих сторон
Итак, гипотенуза равна к
Пример 2
Используйте уравнение теоремы Пифагора 90 057
Подставьте переменные, где заменяет и заменяет
Решите для и
Вычтите из, оставив:
Найдите квадратные корни с обеих сторон
Итак, равно
Стенограмма видео-урока
В этом уроке , мы обсудим теорему Пифагора.
Очень важно отметить, что теорема Пифагора применима только для прямоугольных треугольников. Вы не можете использовать эту теорему в других типах треугольников.
Прямоугольный треугольник имеет угол.
Давайте сначала рассмотрим терминологию.
Сторона, противоположная прямому углу, называется гипотенузой.
Две другие стороны называются ножками.
В этом прямоугольном треугольнике есть уравнение, которое связывает измерение катетов с измерением гипотенузы.
Это уравнение просто
Где гипотенуза, а катеты и.
Что касается ножек, то неважно, с какой стороны поставить или. Это ваш вызов.
Это уравнение называется теоремой Пифагора.
Давайте рассмотрим пример и применим это уравнение.
Вот прямоугольный треугольник с измерением вертикального отрезка и отрезка горизонтального отрезка. А гипотенуза неизвестна или.
Давайте начнем с нашего уравнения
Опять же, поскольку не имеет значения, какая нога или.
Давайте просто выберем вертикальную опору и горизонтальную опору.
Чтобы найти значение, мы должны выполнить обратную операцию — квадратный корень.
Итак, наша гипотенуза
Алгебраические и геометрические доказательства теоремы Пифагора
Теорема Пифагора утверждает, что если прямоугольный треугольник имеет длины сторон и, где — гипотенуза, то сумма квадратов двух более коротких длин равна квадрату длины гипотенузы.
Рис. 1. Прямоугольный треугольник со сторонами a, b и c.
Обращаясь к уравнению, получаем
.
Например, если прямоугольный треугольник имеет стороны и, то длина его гипотенузы равна, поскольку.
Упражнение 1: Что такое гипотенуза треугольника со сторонами , и ?
Верно и обратное утверждение теоремы. Если длины сторон треугольника удовлетворяют уравнению, то треугольник правильный.Например, треугольник с длинами сторон удовлетворяет уравнению, следовательно, это прямоугольный треугольник.
Геометрически теорема Пифагора утверждает, что в прямоугольном треугольнике со сторонами и где — гипотенуза, если построены три квадрата, одна из сторон которых является стороной треугольника, как показано на рисунке 2, то площадь двух меньших квадратов при сложении равняется площади самого большого квадрата.
Рис. 2. Геометрическая интерпретация теоремы Пифагора утверждает, что площадь зеленого квадрата плюс площадь красного квадрата равна площади синего квадрата.
Один конкретный случай показан на рисунке 3: площади двух меньших квадратов равны и квадратным единицам, а площадь самого большого квадрата — квадратным единицам.
Exercise 2: Используя единичные квадраты, убедитесь, что площадь самого большого квадрата на рисунке 3 составляет 25 квадратных единиц.
Рисунок 3 — Прямоугольный треугольник с длинами сторон 3, 4 и 5.
Точно так же треугольники с длинами сторон и являются прямоугольными треугольниками. Если все стороны прямоугольного треугольника являются целыми числами, мы называем их пифагоровыми тройками .Следовательно, и являются пифагоровыми тройками.
Упражнение 3. Приведите другие примеры троек Пифагора .
Упражнение 4. Докажите, что пифагоровых троек бесконечно много.
Доказательства теоремы Пифагора
Имеется более 300 доказательств теоремы Пифагора. На сайте Cut-The-Knot представлено более 70 доказательств. Ниже приведены два доказательства. Обратите внимание, что при доказательстве теоремы Пифагора мы хотим показать, что для любого прямоугольного треугольника с гипотенузой, сторонами и выполняется следующее соотношение:.
Геометрическая проба
Сначала мы рисуем треугольник с длинами сторон, как показано на рисунке 1. Затем мы создаем 4 идентичных ему треугольника и с помощью треугольников формируем квадрат со сторонами, как показано на рисунке 4-A. Обратите внимание, что площадь белого квадрата на рис. 4-A равна.
Рисунок 4 — Геометрическое доказательство теоремы Пифагора.
Переставив треугольники, мы также можем сформировать еще один квадрат с такой же длиной стороны, как показано на рисунке 4-B.Это означает, что площадь белого квадрата на Рисунке 4-A равна сумме площадей белых квадратов на Рисунке 4-B (Почему?). То есть это именно то, что мы хотим показать. * И поскольку мы всегда можем сформировать (большой) квадрат, используя четыре прямоугольных треугольника с любым размером (в высшей математике мы говорим, что мы можем выбрать произвольную длину и длину стороны прямоугольного треугольника), это означает, что приведенное выше уравнение всегда true независимо от размера треугольника.
Упражнение 5. Докажите, что четырехугольник со стороной C на рис. 4-A является квадратом.
Алгебраическое доказательство
Во втором доказательстве мы теперь рассмотрим желтые треугольники вместо квадратов. Рассмотрим рисунок 4-A. Мы можем вычислить площадь квадрата со сторонами, используя два метода: (1) мы можем возвести в квадрат длины сторон и (2) мы можем добавить площадь четырех равных треугольников, а затем добавить их к площади белого квадрата, который является . Если мы допустим площадь квадрата со стороной, то при вычислении мы получим
Метод 1:
Метод 2:
Методы 1 и 2 вычисляют площадь одного и того же квадрата, поэтому они должны быть равны.Это означает, что мы можем приравнять оба выражения. Приравнивая имеем,
— это именно то, что мы хотим показать.
Теорема Пифагора — определение математического слова
Теорема Пифагора — определение математического слова — Math Open Reference
| c 2 = a 2 + b 2 |
Попробуйте это Перетащите оранжевые точки на каждую вершину
прямоугольного треугольника ниже. Соответственно изменится формула, показывающая вычисление теоремы Пифагора.
Хотя к этой теореме добавлено имя Пифагора,
на самом деле он был известен вавилонянам за много веков до него.
Есть много доказательств этой теоремы,
некоторые графические по своей природе, а другие с использованием алгебры.
См. Графическое доказательство теоремы Пифагора для одного такого доказательства.
На сайте «Разрезанный узел» автор собирает доказательства теоремы Пифагора, а по состоянию на
в этом сочинении перечислено более 70, но на самом деле известны сотни.
Решение прямоугольного треугольника
Термин «решение треугольника» означает, что если мы начнем с прямоугольного треугольника и знаем любые две стороны, мы можем найти или «решить для» неизвестную сторону.Это включает в себя простую перестановку формулы теоремы Пифагора, чтобы поместить неизвестное в левую часть уравнения.
Найдите гипотенузу
Если мы знаем два катета прямоугольного треугольника, мы можем найти гипотенузу по формуле:
где a и b — длины двух катетов треугольника, а
h — гипотенуза.
Найдите ногу
Если мы знаем гипотенузу и один катет, мы можем найти другой катет, используя формулу:
где a — отрезок, который мы хотим найти.
b — известный отрезок
h — гипотенуза.
Обращение теоремы Пифагора
Верно и обратное утверждение этой теоремы. То есть, если треугольник удовлетворяет теореме Пифагора, то это прямоугольный треугольник.
Другими словами, только прямоугольных треугольников удовлетворяют теореме.
Что попробовать
- На рисунке выше нажмите «Сброс».
- Установите один из флажков «скрыть».
- Отрегулируйте треугольник, перетащив оранжевую точку.
- Используйте теорему Пифагора, чтобы найти недостающую сторону.
- Снимите флажок «скрыть», чтобы проверить свой ответ.
Другие темы треугольника
Общий
Периметр / Площадь
Типы треугольников
Центры треугольника
Конгруэнтность и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
