Точки экстремума функции, необходимые и достаточные условия экстремума

Содержание:

Определение

Точка $x_{0}$ называется точкой локального максимума
функции $f(x)$, если существует такая окрестность
этой точки, что для всех $x$ из этой окрестности
выполняется неравенство: $f(x) \leq f\left(x_{0}\right)$.

Точка $x_{0}$ называется точкой локального минимума
функции $f(x)$, если существует такая окрестность этой
точки, что для всех $x$ из этой окрестности
$f(x) \geq f\left(x_{0}\right)$.

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума —
локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка $x_{0}$ называется точкой строгого локального
максимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет справедливо
строгое неравенство $f(x) \lt f\left(x_{0}\right)$. {2}+1}=-1$.

Ответ. $y_{\min }=y(0)=-1$

Читать дальше: наибольшее и наименьшее значение функции.

Точки экстремума — rajak.rs

Экстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума.
Точка ${x_0}$ называется точкой локального максимума функции $f$, если выполняется условие: $\exists {U_\delta }\left( {{x_0}} \right):\forall x \in {U_\delta }\left( {{x_0}} \right)$  $f\left( {{x_0}} \right) \geqslant f\left( x \right).$
Аналогично точка ${x_0}$ называется точкой локального минимума функции $f$ , если выполняется условие: $\exists {U_\delta }\left( {{x_0}} \right):\forall x \in {U_\delta }\left( {{x_0}} \right)$ $f\left( {{x_0}} \right) \leqslant f\left( x \right).$

Точки, в которых производная равна нулю, называются стационарными точками.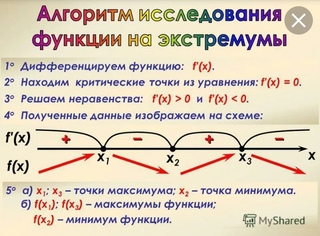
Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическими точками.

Теорема (необходимое условие экстремума)

Если точка ${x_0}$ – точка экстремума функции $f$, то она критическая.

Замечаниe:

Не всякая критическая точка является точкой экстремума.

Теорема (первое достаточное условие экстремума в терминах первой производной)

Пусть функция $f$ определена и дифференцируема в некоторой окрестности точки ${x_0}$, кроме, быть может, самой точки ${x_0}$ и непрерывна в этой точке. Тогда:

1. Если производная ${f’}$ меняет знак с » — » на «+» при переходе через точку ${x_0}$: $\forall x \in \left( {{x_0} — \delta ;{x_0}} \right)$ $f’\left( x \right) < 0$ и $\forall x \in \left( {{x_0};{x_0} + \delta } \right)$ $f’\left( x \right) > 0$, то ${x_0}$ – точка строго минимума функции $f$.
2. Если производная ${f’}$ меняет знак с «+» на » — » при переходе через точку ${x_0}$: $\forall x \in \left( {{x_0} — \delta ;{x_0}} \right)$ $f’\left( x \right) > 0$ и $\forall x \in \left( {{x_0};{x_0} + \delta } \right)$ $f’\left( x \right) < 0$, то ${x_0}$ – точка строго максимума функции $f$.

Замечание:

Если ${x_0}$ – точка строго экстремума, то из этого не следует, что производная ${f’}$ меняет знак при переходе через точку ${x_0}$.

Теорема (второе достаточное условие строгого экстремума в терминах второй производной)

Пусть дана функция $f$, она определена в некоторой окрестности точки ${x_0}$, ее первая производная $f’\left( x \right) = 0$  и пусть существует $f»\left( {{x_0}} \right)$, тогда:

1. Если $f»\left( {{x_0}} \right) > 0$, то точка ${x_0}$ – точка строгого минимума;
2. Если $f»\left( {{x_0}} \right) < 0$, то точка ${x_0}$ – точка строгого максимума.

Замечаниe:

Если $f’\left( x \right) = 0$ и $f»\left( x \right) = 0$ , то функция $f$ может и не иметь экстремум в точке ${x_0}$.

Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)

Пусть функция $f$ определена в некоторой окрестности точки ${x_0}$, и в этой точке существуют производные до n-го порядка пусть существует ${f^{\left( n \right)}}\left( {{x_0}} \right)$, n>2 и  \[f’\left( {{x_0}} \right) = f»\left( {{x_0}} \right) = . {\left( n \right)}}\left( {{x_0}} \right) > 0$, то ${x_0}$ – точка локального минимума;

Экстремумы функции (Лекция №9)

Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке.

Значение функции в точке x₁ будет больше значений
функции во всех соседних точках как слева, так и справа от x₁. В
этом случае говорят, что функция имеет в точке x₁ максимум. В точке x₃ функция, очевидно,
также имеет максимум. Если рассмотреть точку x₂, то в ней значение функции
меньше всех соседних значений. В этом случае говорят, что функция имеет в точке
x₂ минимум.
Аналогично для точки x₄.

Функция y=f(x) в точке x₀ имеет максимум, если значение функции в этой точке больше, чем ее
значения во всех точках некоторого интервала, содержащего точку x₀, т. е. если существует такая
окрестность точки x₀, что для всех x≠x₀,
принадлежащих этой окрестности, имеет место неравенство f(x)<f(x₀).

Функция y=f(x) имеет минимум в точке x₀, если существует такая окрестность
точки x₀, что
для всех x≠x₀, принадлежащих этой окрестности, имеет
место неравенство f(x)>f(x₀.

Точки, в которых функция
достигает максимума и минимума, называются точками экстремума, а значения
функции в этих точках экстремумами функции.

Обратим внимание на то,
что функция, определенная на отрезке, может достигать максимума и минимума
только в точках, заключенных внутри рассматриваемого отрезка.

Отмети, что если функция
имеет в точке максимум, то это не означает, что в этой точке функция имеет
наибольшее значение во всей области определения. На рисунке, рассмотренном выше,
функция в точке x₁ имеет максимум, хотя
есть точки, в которых значения функции больше, чем в точке x₁. В частности, f(x₁) < f(x₄)
т.е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.

Теорема 1. (Необходимое условие
существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x₀
экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно
малых приращениях Δx имеем f(x₀+ Δx)<f(x₀), т.е. Но тогда

Переходя в этих
неравенствах к пределу при Δx→ 0 и учитывая, что производная f ‘(x₀)
существует, а следовательно предел, стоящий слева, не
зависит от того как Δx → 0,
получаем: при Δx → 0
– 0 f’(x₀)
≥ 0 а при Δx → 0
+ 0 f’(x₀)
≤ 0. Так как f ‘(x₀)
определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x₀) = 0.

Доказанная
теорема утверждает, что точки максимума и минимума могут находиться только
среди тех значений аргумента, при которых производная обращается в нуль.

Мы рассмотрели случай,
когда функция во всех точках некоторого отрезка имеет производную. Как же
обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.

Примеры.

1. y=|x|.

   Функция не имеет
   производной в точке x=0 (в этой точке график функции не имеет определенной касательной),
   но в этой точке функция имеет минимум, так как y(0)=0,
   а при всех x≠ 0y > 0.

2.  

   Функция не имеет производной
   при x=0, так как обращается в
   бесконечность приx=0. Но в этой точке функция имеет максимум.

3.  

   Функция не имеет производной при x=0, так как при x→0. В
   этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0.

   Таким образом, из
   приведенных примеров и сформулированной теоремы видно, что функция может иметь
   экстремум лишь в двух случаях: 1) в точках, где производная существует и равна
   нулю; 2) в точке, где производная не существует.

   
   

   Однако, если в некоторой точке x₀ мы знаем,
   что f ‘(x₀)=0, то отсюда нельзя делать вывод, что в
   точке x₀ функция
   имеет экстремум.

   Например. .

   Но точка x=0 не является
   точкой экстремума, поскольку слева от этой точки значения функции расположены
   ниже оси Ox, а справа выше.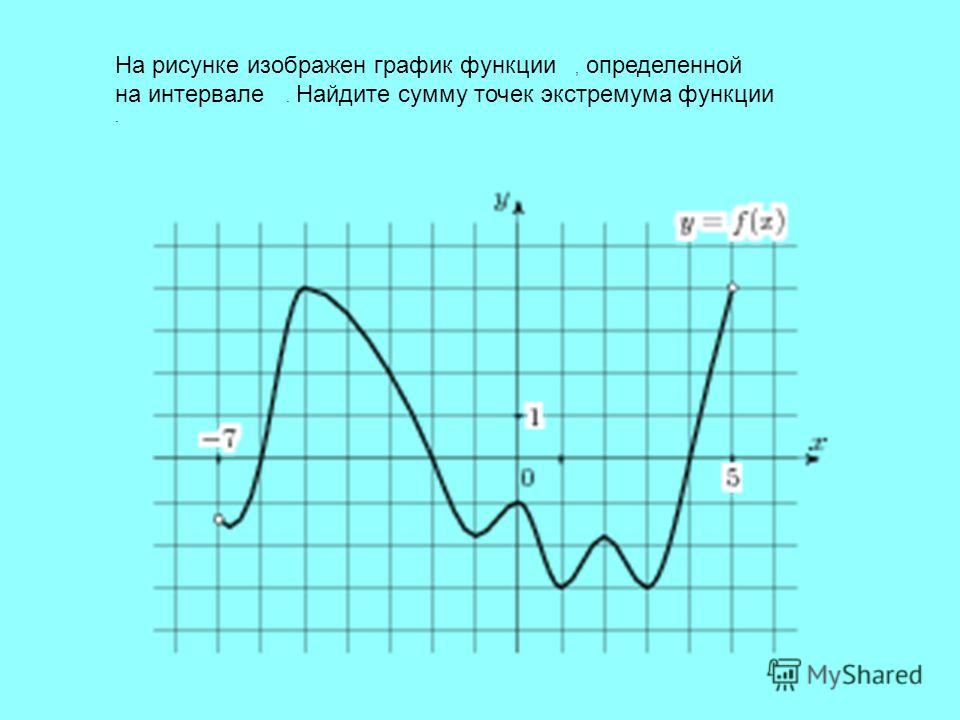

   Значения аргумента из
   области определения функции, при которых производная функции обращается в нуль
   или не существует, называются критическими
   точками.

   Из всего вышесказанного
   следует, что точки экстремума функции находятся среди критических точек, и,
   однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы
   найти экстремум функции, нужно найти все критические точки функции, а затем
   каждую из этих точек исследовать отдельно на максимум и минимум. Для этого
   служит следующая теорема.

   Теорема 2. (Достаточное
   условие существования экстремума.) Пусть функция непрерывна на некотором
   интервале, содержащем критическую точку x₀, и дифференцируема
   во всех точках этого интервала (кроме, быть может, самой точки x₀). Если при
   переходе слева направо через эту точку производная меняет знак с плюса на
   минус, то в точке x = x₀
   функция имеет максимум. Если же при переходе через x₀
   слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
   точке минимум.

   Таким образом, если

   1. f ‘(x)>0 при x<x₀ и f ‘(x)<0 при x> x₀, то x₀ – точка максимума;
   2. при x<x₀
      и f ‘(x)>0 при x> x₀, то x₀ – точка минимума.

   Доказательство. Предположим сначала, что при переходе
   через x₀ производная меняет знак с плюса на минус, т.е.
   при всех x, близких к точке x₀f ‘(x)>0 для x< x₀, f ‘(x)<0 для x> x₀. Применим теорему
   Лагранжа к разности f(x) — f(x₀) = f ‘(c)(x- x₀), где c лежит между x и
   x₀.

   1. Пусть x < x₀. Тогда c< x₀ и f ‘(c)>0. Поэтомуf ‘(c)(x- x₀)<0и, следовательно,

      f(x) — f(x₀)<0,т.е. f(x)< f(x₀).

   2. Пусть x > x₀. Тогда c> x₀
      и f ‘(c)<0. Значитf ‘(c)(x- x₀)<0. Поэтому f(x) — f(x₀)<0,т.е.f(x) < f(x₀).

   Таким образом, для всех
   значений x достаточно близких к x₀f(x) < f(x₀). А это значит, что в точке x₀ функция
   имеет максимум.

   Аналогично доказывается
   вторая часть теоремы о минимуме.

   Проиллюстрируем
   смысл этой теоремы на рисунке. Пусть f ‘(x₁)=0 и для любых x, достаточно близких к x₁, выполняются неравенства

   f ‘(x)<0 при x< x₁, f ‘(x)>0 при x> x₁.

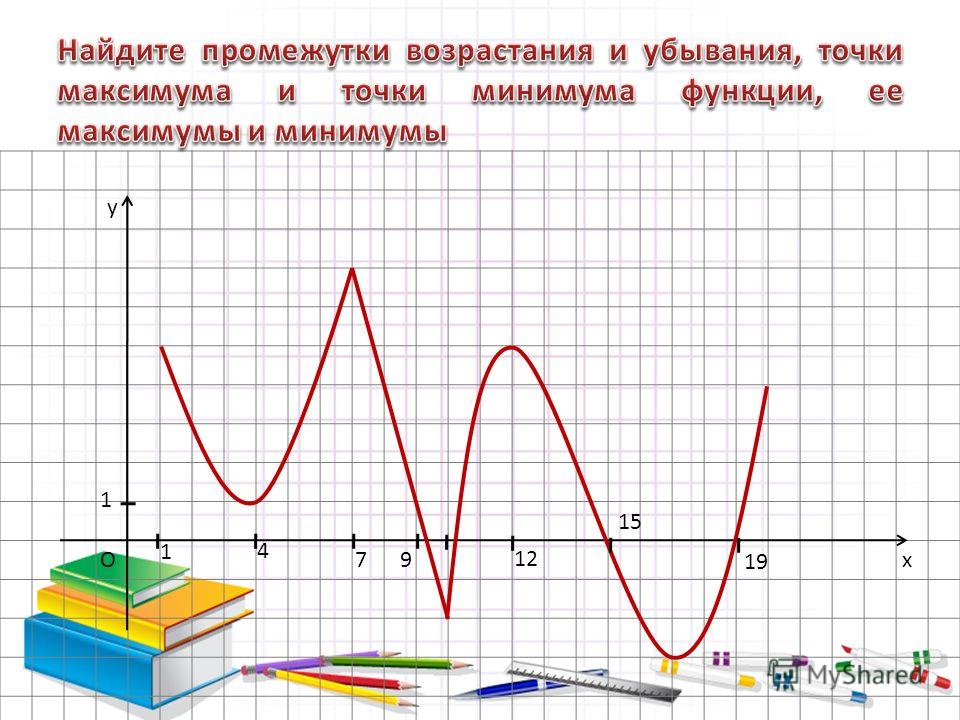
   Тогда слева от точки x₁ функция возрастает, а
   справа убывает, следовательно, при x = x₁
   функция переходит от возрастания к убыванию, то есть имеет максимум.

   Аналогично можно рассматривать
   точки x₂ и x₃.

   
   Схематически все вышесказанное можно изобразить на картинке:

   Правило исследования
   функции y=f(x) на экстремум

   1. Найти область определения
      функции f(x).
   2. Найти первую
      производную функции f ‘(x).
   3. Определить критические
      точки, для этого:
      1. найти действительные корни уравнения f ‘(x)=0;
      2. найти все значения x при которых производная f ‘(x) не существует.

   4. Определить знак
      производной слева и справа от критической точки. Так как знак производной
      остается постоянным между двумя критическими точками, то достаточно определить
      знак производной в какой-либо одной точке слева и в одной точке справа от
      критической точки.
   5. Вычислить значение
      функции в точках экстремума.

   Примеры. Исследовать функции на
   минимум и максимум.

   1. . Область определения функции D(y)=R.

      Найдем
      производную заданной функции

      Определим
      критические точки . Производная не существует при х₂= 0. Следовательно,
      критические точки: 0 и 2/5. Нанесем их на числовую ось и определим знак
      производной на каждом из полученных промежутков.

   2.  

      Критическая точка функции x =3. Точка x= –1 не входит в область определения функции.

   НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ

   Наибольшим значением функции на отрезке называется самое
   большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

   Рассмотрим функцию y=f(x) непрерывную
   на отрезке [a, b].
   Как известно, такая функция достигает своего наибольшего и наименьшего
   значений, либо на границе отрезка, либо внутри него. Если наибольшее или
   наименьшее значение функции достигается во внутренней точке отрезка, то это
   значение является максимумом или минимумом функции, то есть достигается в
   критических точках.

   Таким образом,
   получаем следующее правило нахождения
   наибольшего и наименьшего значений функции на отрезке[a, b]:

   1. Найти все
      критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
   2. Вычислить
      значения функции на концах отрезка при x = a, x = b.
   3. Из всех полученных
      значений выбрать наибольшее и наименьшее.

   Примеры.

   1. Найти наибольшее и наименьшее значения функции на отрезке [–2; –0,5].

      Найдем
      критические точки функции.

      Вычислим
      значения функции в найденной точке и на концах заданного отрезка.

      Итак,

   2. Найти
      наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].

   
   

   3. Чему равна наименьшая площадь боковой поверхности
      прямого кругового конуса объема 3π?

      По теореме Пифагора

      .

      Следовательно, .

      .

      Найдем
      критические точки функции S: S‘ = 0, т.е.

      Покажем, что при
      найденном значении h функция S_бок
      достигает минимума.

      .

   4. Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.

      Пусть r – радиус основания цилиндра, h – высота.

      Нам нужно
      максимизировать объем цилиндра .

      Используя
      условие задачи, найдем связь между r и h. По теореме
      Пифагора из треугольника ABC следует,
      что . Отсюда .

      , по смыслу задачи 0≤h≤2R.

      .

      Покажем, что при
      найденном значении h
      функция V принимает наибольшее
      значение.

Внеклассный урок — Экстремум функции

Экстремум функции

Определения:

Экстремумом называют максимальное или минимальное значение функции на заданном множестве.

Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.

Точка максимума – это точка, в которой достигается максимальное значение функции.

Точка минимума – это точка, в которой достигается минимальное значение функции.

Пояснение.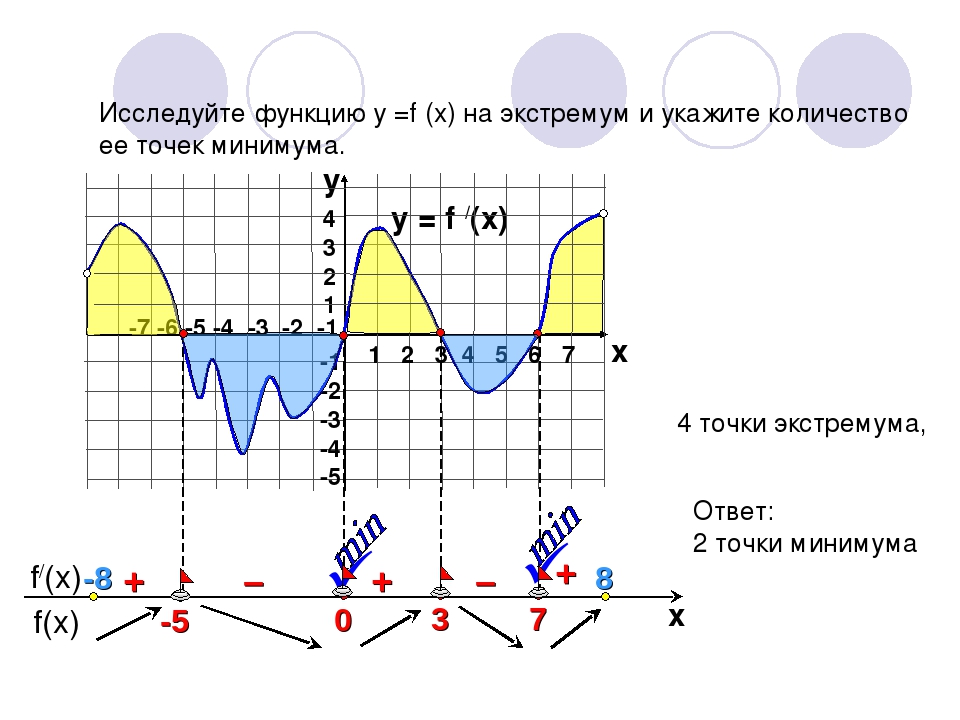

На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:

x_max = 3,  x_max = 8.

В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:

x_min = 5.

Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.

Критические и стационарные точки функции:

Необходимое условие экстремума:

Достаточное условие экстремума:

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:

Точки экстремума, наибольшее и наименьшее значение на промежутке

Экстремумы функции

Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.

Определение 1

Точка $x’$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.

Определение 2

Точка $x’$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\le f(x'{\rm \ })$.

Определение 3

Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\ge f(x'{\rm \ })$.

Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.

Определение 4

Точка $x’$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:

1. Точка $x’$ является внутренней точкой для области определения данной функции;
2. $f’\left(x'{\rm \ }\right)=0$ или не существует.

Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.

Теорема 1

Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.

Теорема 2

Пусть точка $x’$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $\left(a,x'{\rm \ }\right)\ и\ (x'{\rm \ },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:

1. Если в $(a,x'{\rm \ })$ $f’\left(x\right) >0$, а в $(x'{\rm \ },b)$ $f’\left(x\right)
2. Если в $(a,x'{\rm \ })$ $f’\left(x\right)0$, то $x’$ —будет точкой минимума для этой функции.
3. Если и в $(a,x'{\rm \ })$, и в $(x'{\rm \ },b)$ производная $имеет\ один\ и\ тот\ же\ постоянный\ знак$, то $x’$ не будет точкой экстремума для этой функции.

На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.

Рисунок 1.

Примеры точек экстремумов вы можете видеть на рисунке 2.

Рисунок 2.

Правило исследования на экстремум

1. Найти $D(f)$;
2. Найти $f'(x)$;
3. Найти точки, где $f’\left(x\right)=0$;
4. Найти точки, где $f'(x)$ не будет существовать;
5. Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
6. Определить знак $f'(x)$ на полученных промежутках;
7. Используя теорему 2, сделать заключение по поводу всех найденных точек.

Понятие наибольшего и наименьшего значений

Определение 5

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’\in X$, если выполняется

\[f\left(x\right)\le f(x’)\]

Определение 6

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’\in X$, если выполняется

\[f\left(x\right)\ge f(x’)\]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

1. Найти $f'(x)$;
2. Найти точки, в которых $f’\left(x\right)=0$;
3. Найти точки, в которых $f'(x)$ не будет существовать;
4. Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
5. Вычислить значения в оставшихся точках и на концах $[a,b]$;
6. Выбрать из этих значений наибольшее и наименьшее. 2}{x-2}=x-2,\ x\ne 2\]

   1. $f’\left(x\right)=(x-2)’=1$;

      Точек экстремума нет.

   2. Значения:

      \[f\left(-1\right)=-3\] \[f\left(1\right)=-1\]

   Ответ: $max=-1,\ min=-3$.

   Необходимое условие экстремума функции | matematicus.ru

   Достаточное и необходимое условие существования экстремума функции

   Экстремум функции — это максимум и минимум непрерывной функции y=f(x) непрерывна в критической точке x₀.

   Условие максимума функции

   Если производная от функции больше нуля при

   f′(x)>0 при x<x₀, x₀ — точка максимума

   Если производная от функции меньше нуля при

   f′(x)<0 при x>x₀, x₀ — точка максимума

   Условие минимума функции

   Если производная от функции меньше нуля при

   f′(x)<0 при x<x₀, x₀ — точка максимума

   Если производная от функции больше нуля при

   f′(x)>0 при x>x₀, x₀ — точка максимума

   Условие экстремума функции через нахождения второй производной

   При f′′(x₀)≠0 и f′′(x₀)<0 — максимум
   При f′′(x₀)≠0 и f′′(x₀)>0 — минимум
   С помощью второй производной определяется вогнутость и выпуклость функции

   ---

   Пример
   Найти экстремумы функции

   $y=\frac{x^{4}}{4}-2x^{2}+4$

   Решение
   Найдём производную от функции

   y′=x³–4x

   Определите количество точек экстремума функции
   Найдём критические точки функции

   x(x²–4)=0

   x(x–2)(x+2)=0

   Отсюда
   x₁=–2; x₂=0; x₃=2
   Точки экстремума функции на отрезке

   Точками экстремума функции являются:
   f(–2)=0 — минимум;
   f(0)=4 — максимум;
   f(2)=0 — минимум.
   Получается три точки экстремума функции.
   Построим график функции онлайн здесь
   Пунктирной линией на графике показана производная функция

   Определение

   Точка называется точкой Локального максимума (Минимума) функции , Если для любого числа в некоторой окрестности точки выполнено неравенство .

   Термины «локальный минимум» и «локальный максимум» объединены общим названием «Локальный экстремум».

   Теорема

   (Необходимое условие существования локального экстремума). Для того чтобы функция имела экстремум в точке , необходимо, чтобы ее Производная в этой точке равнялась нулю или не существовала.

   Геометрический смысл теоремы заключается в следующем: если в точках локальных экстремумов существуют касательные, то они параллельны оси .

   Точки, в которых выполнено необходимое условие экстремума называют Критическими или Стационарными (а также Точками возможного экстремума). Очевидно, что эти точки должны входить в ОДЗ функции. Таким образом, если в какой–либо точке имеется экстремум, то эта точка критическая, однако обратное утверждение неверно: критическая точка вовсе не обязана быть точкой экстремума.

   Это можно показать на примерах функций . Для первой функции точка является точкой экстремума, а для второй – нет.

   Сформулируем достаточные условия существования локального экстремума.

   Теорема (Первое достаточное условие экстремума)

   Пусть функция Дифференцируема в некоторой окрестности точки . Если при переходе через точку слева направо производная Меняет знак с плюса на минус, то в точке функция имеет Локальный максимум, а если с Минуса на плюс, то – точка Минимума. Если же не меняет знака в Окрестности точки , то данная функция Не имеет локального экстремума в этой точке.

   Геометрический смысл теоремы иллюстрирует Рис. 5.9.1.

   Отметим также, что дифференцируемость в самой точке Вовсе не обязательна. Например, функция имеет экстремум (минимум) в точке , но не дифференцируема в ней.

   Рис. 5.9.1

   Схема исследования функции на локальный экстремум

   1. Найти производную .

   2. Найти критические точки функции, в которых производная или не существует.

   3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

   4. Найти экстремумы функции.

   Пример

   Исследовать на экстремум функцию .

   Решение

   Найдем производную и приравняем нулю:.

   Нули производной: . Исследуем знаки первой производной.

   Так как при переходе через точку производная меняет знак с минуса на плюс, то точка является точкой минимума. При переходе через точку производная знак не меняет, поэтому точка не является точкой экстремума.

   Теорема (Второе достаточное условие экстремума)

   Если первая производная дважды дифференцируемой функции Равна нулю в некоторой точке , а Вторая производная в этой точке положительна , то точка есть Точка минимума функции ; если Вторая производная отрицательна – , то – точка Максимума.

   Второе достаточное условие экстремума утверждает, что если в критической точке , то в этой точке имеется экстремум. Обратное утверждение неверно – экстремум в критической точке может быть и при равенстве нулю в ней второй производной, например, для функции и критической точки .

   При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке .

   Ранее отмечалось, что если функция непрерывна на отрезке , то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значения функции могут достигаться как в точках экстремума, так и на концах отрезка.

   Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:

   1. Найти производную .

   2. Найти критические точки функции, в которых или не существует.

   3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.

   < Предыдущая		Следующая >

   Extremum Point — обзор

   ВВЕДЕНИЕ

   На протяжении почти трех тысячелетий элемент Fe и его сплавы были наиболее часто используемыми конструкционными металлами и остаются предпочтительными материалами для значительной части всех инженерных сооружений и устройств. Это верно по трем основным причинам. Во-первых, Fe распространен в земной коре и относительно легко извлекается из ее руд. Во-вторых, Fe обладает разумной внутренней прочностью, его можно легировать или обрабатывать, чтобы он стал еще прочнее.В-третьих, Fe (или сталь) — очень гибкий материал, который можно сделать мягким для формовки или твердым для прочности конструкции путем довольно простых изменений в способе его обработки. Сила Fe является обязательным условием. Если бы он не позволял создавать сплавы, «прочные, как сталь», он не получил бы широкого распространения.

   Прогресс в вычислительной технике и вычислительных машинах недавно позволил вычислить идеальную прочность кристаллического материала — напряжение, которое приводит к нестабильности самой кристаллической решетки и устанавливает верхний предел прочности, которую материал может иметь [1,2 ].Когда эти методы применяются к Fe, как это было впервые сделано в работе [3,4], возникает пара сюрпризов. Во-первых, Fe на самом деле не так уж и силен. Во-вторых, удивительно, что Fe такое сильное.

   Эти утверждения могут быть основаны на простой модели, которая выводится из доминирующей роли симметрии в определении идеальной прочности, что хорошо установлено расчетами из первых принципов [2,5]. Энергия деформированного кристалла зависит от шести независимых компонентов деформации и, следовательно, представляет собой 6-мерную гиперповерхность в 7-мерном пространстве.Локальные экстремумы и седловые точки на этой гиперповерхности почти всегда соответствуют структурам с высокой симметрией. Наибольший интерес представляют конфигурации седловых точек на энергетической поверхности, которые соседствуют с начальным состоянием. Для заданной геометрии нагрузки (напряженного состояния) кристалл деформируется по определенной траектории на поверхности энергии деформации по мере увеличения нагрузки. Напряжение, необходимое для привода системы, связано с локальным наклоном энергетической поверхности в направлении движения. Идеальная прочность определяется самым крутым уклоном на пути между начальным состоянием и первой седловой точкой.

   Самый крутой уклон соответствует максимальному напряжению; кристалл становится упруго неустойчивым, как только проходит точка максимального напряжения.

   Чтобы понять идеальную прочность, необходимо определить соответствующие конструкции седловой точки. Четыре такие структуры были идентифицированы при исследовании идеальной прочности ОЦК-металлов: ГЦК-структура, простая кубическая (sc) структура, объемно-центрированная тетрагональная (ОЦТ) структура и базоцентрированная орторомбическая структура [6–8].Например, расслабленный сдвиг ОЦК-металла в «легком» направлении <111> на плоскости {112} или {110} создает ОЦК-структуру без напряжений [8]. Поскольку система сдвига <111> {112} не является симметричной по знаку направления сдвига, также можно перейти от ОЦК-структуры к ромбической структуре с центром в основании путем сдвига в «жестком» направлении. Одноосное растяжение в направлении <111> переводит ОЦК-структуру в НЦК [6,8], а растяжение <001> перемещает ее из ОЦК либо в ГЦК (преобразование Бейна на рис.1 [2]) или к bct (та же самая свободная от напряжений структура bct, встречающаяся при сдвиге [7]). Конкуренция между двумя возможными путями, которые могут быть достигнуты с помощью натяжения <001>, приводит к тому, что, в то время как большинство ОЦК-кристаллов (Mo, W) регулируются нестабильностью, связанной с ГЦК-структурой, и, в идеале, не выдерживают разрушения, по крайней мере, one (Nb) становится нестабильным относительно эволюции к седловой точке bct и терпит неудачу при сдвиге [7].

   Рис. 1. Кристаллическая структура ОЦК становится структурой ГЦК после удлинения вдоль & lt; 100 & gt; направление.

   Ab initio расчеты полной энергии идеальной прочности на растяжение свободных ОЦК-металлов показывают, что они являются самыми слабыми при растяжении в направлении <001> [2] (неудивительно, что {001} является доминирующей плоскостью спайности в ОЦК-металлах). Постоянная объемная деформация растяжения вдоль <001> преобразует ОЦК структуру в ГЦК при инженерной деформации около 0,26 («деформация Бейна», рис. 1). Поскольку обе конструкции не подвергаются напряжению в силу симметрии, растягивающее напряжение должно проходить по крайней мере через один максимум на пути трансформации.Если мы последуем Оровону [9] в предположении единственного экстремума (сплошная линия на рис. 2) и подгоним кривую напряжения-деформации с синусоидой, которая имеет правильный модуль упругости при низкой деформации, идеальная прочность на растяжение будет примерно

   2. Энергия как функция деформации имеет экстремум в ГЦК-структуре, который может быть локальным максимумом (сплошная линия) или минимумом (пунктирная линия). При синусоидальной форме точка перегиба, определяющая идеальную прочность, в последнем случае приходится на гораздо меньшую деформацию, а идеальная прочность значительно меньше.

   (1) σm = 0,08E <100>

   в хорошем соответствии с расчетами ab initio (например, σ _м = 30 ГПа = 0,072 E _<100> для W [10]). Поскольку модуль Fe значительно меньше, чем у других переходных металлов, таких как W, Mo и Ta, верхняя граница его прочности также меньше.

   Но вторая проблема возникает, когда мы расширяем этот анализ на железо [3]. Известно, что ГЦК-фаза в Fe лишь немного превышает энергию ОЦК-фазы и, по крайней мере, является метастабильной при низкой температуре.Фактически, термомеханическая обработка, которая используется для обработки конструкционной стали (в частности, включая многие из них, разработанные или исследованные Гаретом Томасом), зависит от простоты преобразования ее из ОЦК в ГЦК и обратно. Если мы предположим, что метастабильная ГЦК-фаза связана непрерывной кривой деформации-энергии (пунктирная линия на рис.2), неустойчивость при растяжении проявляется при гораздо меньшей деформации, и идеальная прочность должна составлять всего около 6 ГПа (по сравнению с 12 ГПа на основе расчетов). на нестабильной ГЦК). Это число слишком мало, чтобы в него можно было поверить.Поскольку растягивающие напряжения, которые в несколько раз превышают предел текучести, возникают перед вершинами трещин в упругопластических материалах, стали с пределом текучести намного выше 1 ГПа обязательно будут хрупкими. Фактически, стали с гораздо большим пределом текучести обладают высокой вязкостью разрушения и значительной пластичностью.

   Возможное разрешение этого парадокса предлагается в работе Herper et al. [11]. Они вычислили энергии Fe для различных магнитных состояний и деформаций решетки. Их расчеты показывают, что энергия ферромагнетика Fe монотонно возрастает, если он искажается в сторону нестабильной ферромагнитной ГЦК, которую можно стабилизировать, переходя в сложное антиферромагнитное состояние.Следствием этого является то, что низкоэнергетическая антиферромагнитная ГЦК-фаза является минимумом, а не седловой точкой на поверхности энергии деформации Fe. В то время как Herper, et al. [11] не исследовали этот вопрос (у них были другие интересы), это предполагает возможность того, что ферромагнитный Fe может стать механически нестабильным при напряжении <100> до того, как столкнется с магнитным переходом, который преобразует его в антиферромагнитное состояние, которое стабилизирует ГЦК. В этом случае Fe может иметь механическое поведение типичного металла с ОЦК-решеткой, но при этом иметь метастабильную структуру с ГЦК-решеткой, которая стабилизируется поздним магнитным переходом.То есть он может быть как прочным, так и простым в обработке.

   Как мы покажем ниже, это очевидное объяснение того факта, что Fe имеет как полезную прочность на разрыв, так и фазу ГЦК, которая облегчает обработку. Идя дальше, мы установим, что Fe естественно разрушается при расщеплении на плоскостях {100}, и вычислим его прочность на растяжение и сдвиг. Наконец, мы рассмотрим, как на прочность Fe влияет наложенное гидростатическое напряжение, которое встречается, например, на вершине острой трещины.

   Точка локального экстремума — Исчисление

   Определение

   Точка локального экстремума относится к точке внутри области функции, которая является либо точкой локального максимума , либо точкой локального минимума . Оба они определены ниже.

   Точка местного максимума

   Точка внутри области функции — это точка локального максимума , если выполняется следующее:

   Значение называется локальным максимальным значением .

   Точка местного минимума

   Точка внутри области функции — это точка локального минимума , если выполняется следующее:

   Значение называется локальным минимальным значением .

   Варианты

   Варианты, применимые во всех случаях (не обязательно, чтобы они были функцией одной переменной)

   Вариации, относящиеся к функции одной переменной

   Факты

   Заявление	Устанавливает ли он необходимое условие для локального экстремума или достаточное условие для локального экстремума?	Он односторонний или двусторонний, или есть версии для обоих?	Каковы условия непрерывности / дифференцируемости и другие допущения, чтобы тест был применимым и окончательным?	Неубедительные дела	Заключительные дела
   Локальный максимум слева подразумевает, что левая производная неотрицательна, если она существует (аналог: [ПОКАЗАТЬ БОЛЬШЕ])	Необходимое условие	Односторонний, но имеет двусторонние следствия	Соответствующая односторонняя дифференцируемость	Односторонняя производная не существует	Не применимо
   Точка локального экстремума подразумевает критическую точку	Необходимое условие	Двусторонний, но следует из односторонних результатов	Нет	Не применимо	Не применимо
   Тест первой производной	Достаточное условие, а в двустороннем случае необходимое условие (но не необходимое и достаточное условие )	Односторонняя и двусторонняя	Непрерывный (односторонний или двусторонний) в точке, дифференцируемый около точки (односторонний или двусторонний), производная имеет постоянный знак с одной стороны (или, возможно, неравные постоянные знаки с обеих сторон)	не непрерывна в точке, не дифференцируема вблизи точки, производная колеблется (по знаку) около точки	изолированных критических точек всегда верны для функций с алгебраической производной, включая многочлены и рациональные функции.Также убедительно для локально аналитических функций.
   Односторонний производный тест	Достаточное условие, а в двустороннем случае необходимое условие (но не необходимое и достаточное условие )	Односторонняя и двусторонняя	Дифференцируемый (односторонний или оба односторонний, но не обязательно двусторонний) в точке, с ненулевым значением производной	Критические точки односторонней производной неопределенной или односторонней производной, равной нулю, тип	не является окончательным в большинстве интересующих нас случаев
   Односторонняя версия теста второй производной	Достаточное условие, а в двустороннем случае необходимое условие (но не необходимое и достаточное условие )	Односторонняя и двусторонняя	Дважды дифференцируемые (односторонние или оба односторонние, но не обязательно двусторонние) в точке, при этом первая односторонняя производная равна нулю, а вторая односторонняя производная отлична от нуля	Критические точки односторонней второй производной неопределенной или односторонней второй производной, равной нулю, тип	не является окончательным в большинстве интересующих нас случаев
   Тест второй производной	Достаточное состояние Только	Двусторонний только (но есть односторонний вариант)	дважды дифференцируемые в точке, первая производная равна нулю, вторая производная отлична от нуля	Критические точки, которые также являются критическими точками для производной	заключительный для функций с критическими точками, которые являются только нулями кратности производной.
   Односторонняя версия теста высшей производной	Достаточное условие, а в двустороннем случае необходимое условие (но не необходимое и достаточное условие )	Односторонняя и двусторонняя	Первая производная равна нулю в точке, функция может быть дифференцирована (односторонняя) в точке достаточно раз, чтобы можно было получить ненулевую одностороннюю высшую производную	Односторонняя первая производная не определена, односторонние производные перестают определяться до того, как станут отличными от нуля, односторонние производные всегда остаются равными нулю в точке	заключительных для многочленов, рациональных функций и функций с алгебраической производной, функций этого типа кусочно и т. Д.
   Тест высшей производной	Достаточное состояние и необходимое состояние (но не необходимое и достаточное условие )	двусторонний (но есть односторонний вариант)	Первая производная равна нулю в точке, функция может быть дифференцирована (односторонняя) в точке столько раз, чтобы можно было получить ненулевую производную с нулевым знаком	первая производная не определена, производные перестают определяться до того, как станут отличными от нуля, производные всегда остаются нулевыми в точке	заключительный для непостоянных многочленов, рациональных функций и функций с алгебраической производной, функций кусочно этого типа, локально непостоянных локально аналитических функций и т. Д.

   Точка абсолютного экстремума — Исчисление

   Определение

   Точка абсолютного экстремума относится к точке в области определения функции, которая является либо точкой абсолютного максимума , либо точкой абсолютного минимума . Оба они определены ниже.

   Точка абсолютного максимума

   Точка в области определения функции определяется как точка абсолютного максимума , если для всех в области определения функции.

   Значение называется абсолютное максимальное значение .

   Обратите внимание, что для данной функции может быть более одной точки абсолютного максимума, но значение абсолютного максимума должно быть одинаковым во всех точках абсолютного максимума.

   Точка абсолютного минимума

   Точка в области определения функции определяется как точка абсолютного минимума , если для всех в области определения функции.

   Значение называется абсолютным минимальным значением .

   Обратите внимание, что для данной функции может быть более одной точки абсолютного минимума, но значение абсолютного минимума должно быть одинаковым во всех точках абсолютного минимума.

   Связь с точкой локального экстремума

   Абсолютный экстремум подразумевает локальный экстремум или экстремум конечной точки для функций на интервалах

   Верны следующие утверждения:

   • Любая точка абсолютного максимума, находящаяся внутри области определения функции, является точкой локального максимума.Точно так же любая точка абсолютного минимума, которая находится внутри области определения функции, является точкой локального минимума.
   • Если точка абсолютного максимума для функции одной переменной находится в конечной точке домена с функцией, определенной на одной стороне, это точка максимума конечной точки, что означает, что это точка одностороннего локального максимума. Например, если абсолютный максимум происходит в правой конечной точке, то эта точка является точкой локального максимума слева. Точно так же, если абсолютный максимум происходит в левой конечной точке, то эта точка является точкой локального максимума справа.Аналогично для минимумов.
   • Для функции, домен которой является интервалом, любая точка абсолютного максимума должна быть либо точкой локального максимума, либо точкой максимума конечной точки. Точно так же любая точка абсолютного минимума должна быть либо точкой локального минимума, либо точкой минимума конечной точки.

   Наличие абсолютных экстремумов

   Рассмотрим непрерывную функцию на замкнутом ограниченном интервале вида с. Затем, по теореме об экстремальном значении, достигает своего абсолютного максимального значения и своего абсолютного минимального значения.Таким образом, имеет хотя бы одну точку абсолютного максимума и хотя бы одну точку абсолютного минимума. Способствовать:

   • Каждая точка абсолютного максимума является либо точкой локального максимума, либо точкой максимума конечной точки.
   • Каждая точка абсолютного минимума является либо точкой локального минимума, либо точкой минимума конечной точки.

   Объединяя вышесказанное с тем фактом, что точка локального экстремума подразумевает критическую точку, получаем, что:

   Каждая точка абсолютного экстремума является либо критической точкой, либо одной из двух конечных точек.

   Относительный экстремум — исчисление 1

   Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
   или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
   в
   информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
   ан
   Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
   средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

   Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
   в виде
   ChillingEffects.org.

   Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
   искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
   на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

   Чтобы отправить уведомление, выполните следующие действия:

   Вы должны включить следующее:

   Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
   Идентификация авторских прав, которые, как утверждается, были нарушены;
   Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
   достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
   а
   ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
   к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
   Ваше имя, адрес, номер телефона и адрес электронной почты; а также
   Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
   ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
   информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
   либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

   Отправьте жалобу нашему уполномоченному агенту по адресу:

   Чарльз Кон
   Varsity Tutors LLC
   101 S. Hanley Rd, Suite 300
   St. Louis, MO 63105

   Или заполните форму ниже:

   Создание элементов экстремума

   Создание точки экстремума на кривой Вы можете создать точку экстремума на кривой в соответствии с заданными направлениями. Нажмите на экстремум на панели инструментов Каркас (дополнительная панель инструментов Точки). Откроется диалоговое окно «Определение экстремума». В поле «Элемент» выберите кривую. В поле Направление выберите направление, в котором должна находиться точка экстремума. быть идентифицированным. Нажмите ОК. Точка (обозначенная как Extremum.xxx) добавляется к дерево спецификаций. Создание экстремума Точка на поверхности Вы можете создать точку экстремума на поверхности в соответствии с заданными направлениями. Нажмите на экстремум . Откроется диалоговое окно «Определение экстремума». В поле «Элемент» выберите поверхность. В поле Направление выберите направление, в котором должен быть экстремум. идентифицированы. Если нажать ОК, грань экстремума будет созданный. В поле Направление 2 выберите второе направление. Если нажать ОК, край экстремума будет созданный. В поле Направление 3 выберите третье направление. Нажмите ОК. Точка (обозначенная как Extremum.xxx) добавляется к дерево спецификаций. Примечание: О параметры Min и Max: Max: согласно заданному направлению самая высокая точка на кривой создано Мин .: согласно тому же направлению самая низкая точка на кривой создано

   ок.классический анализ и оды — Кубический интерполирующий сплайн — количество точек экстремума

   Число локальных точек экстремума $ s (t) $ можно оценить как функцию от $ n $ (где $ n + 1 $ — количество точек интерполяции).
   Окончательная граница, которую я разработаю с помощью B-Splines, — это $ n-1 $. Я также покажу, что его связь тугая.

   Во-первых, отметим, что существует наивная оценка $ 2n $ точек экстремума, поскольку каждый сегмент сплайна между узлами представляет собой просто кубический многочлен, который имеет не более двух точек экстремума.Однако, как я сказал выше, мы можем добиться большего, используя теорию B-сплайнов.

   В ссылке в вопросе каждый интервал $ [t_i, t_ {i + 1}] $ имеет единичную длину, поэтому мы будем
   представляют $ s (t) $ с использованием однородных базисных функций B-сплайна, где $ \ {t_i \} $ — это равноотстоящие узлы, расположенные на единицу длины.
   Для простоты (и без потери общности) $ t_i = i $, однако приведенные ниже аргументы, вероятно, могут быть распространены и на неоднородные узловые векторы.

   Теперь функция представлена ​​(см., Например, Piegl, Les; Tiller, Wayne , The $ NURBS $ books.{n + 2} P_k N_ {k, 3} (t)
   $$
   Где $ N_ {k, 3} (t) $ — это базисные функции кубического B-сплайна, полученные из вектора узла, а $ P_k $ — это контрольных точек (в данном случае контрольные коэффициенты, поскольку они являются скалярами).
   Упорядоченные контрольные точки составляют контрольный многоугольник , который имеет геометрические свойства, которые мы будем использовать.
   Обратите внимание, что количество контрольных точек в представлении B-сплайна равно $ n + 3 $.

   (Я буду здесь немного свободно использовать термины контрольные точки и контрольный многоугольник.Их можно сформулировать более формально, используя параметрическую кривую B-сплайна $ (x (t) = t, y (t) = s (t)) $ графика функции, но я опускаю детали).

   Решение задачи интерполяции B-сплайна является стандартным (см., Например, главу 9 книги NURBS или здесь). Чтобы вычислить контрольные точки, вы оцениваете базисные функции в узлах для $ n + 1 $ линейных ограничений, а естественные конечные условия $ s » (t_0) = s » (t_n) = 0 $ дают вам дополнительные два ограничения.

   Как только у нас есть представление B-сплайна, у нас есть $ n + 3 $ коэффициентов $ P_k $, и мы можем использовать их геометрические свойства, чтобы дать нашу оценку.{n + 1} (P_ {k + 1} -P_k) N_ {k, 2} (t).

   $

   Второе свойство, которое мы используем, — это свойство уменьшения вариации B-сплайнов, которое мы применяем к производной функции. Это означает, что количество точек пересечения любой линии с графиком функции меньше или равно количеству пересечений этой линии с контрольным многоугольником.
   Применение его к нашему контексту означает, что ось $ x $ не пересекает график производной функции более чем $ n + 1 $ раз (поскольку в контрольном многоугольнике есть $ n + 1 $ сегментов с $ n + 2 $ контрольные точки).Следовательно, у нас есть оценка $ n + 1 $ на переход производной через нуль.
   Таким образом, у исходной функции $ s (t) $ не может быть более $ n + 1 $ экстремальных точек.

   Для естественного сплайна мы можем сделать немного лучше.
   Естественные конечные условия подразумевают, что $ P_1 $ лежит на прямой между $ P_0 $ и $ P_2 $ (и аналогично для последних конечных точек).
   Отсюда следует, что $ P_1-P_0 $ и $ P_2-P_1 $, первые контрольные точки производной, имеют одинаковый знак (и аналогично для последних точек).Следовательно, первые (и последние) два сегмента многоугольника производного контроля могут вносить не более одного пересечения нуля, и, следовательно, максимальное количество пересечений нуля составляет $ n-1 $.
   Итак (наконец), наша окончательная оценка — $ n-1 $ точек экстремума.

   Эта граница жесткая; для любого $ n $ мы можем построить следующую конфигурацию $ n + 1 $ точек, для которой естественный сплайн будет иметь $ n-1 $ точек экстремума.

   Чередующаяся последовательность точек размером $ (n + 1) $ $ \ pm 1 $ будет иметь $ n-1 $ экстремальных точек (пример с $ n = 10 $ см. На рисунке).Это можно доказать путем явного решения интерполяционных уравнений, но более простое доказательство исходит из теоремы о среднем значении. По теореме о среднем значении каждый чередующийся отрезок $ (t_i, -1), (t_ {i + 1}, 1) $ имеет положительную производную значения $ s ‘(c_i) = 2 = \ frac {1 — (- 1 )} {t_ {i + 1} -t_i} $, и его последовательный сегмент будет иметь отрицательную производную от значения $ s ‘(c_ {i + 1}) = — 2 = \ frac {(- 1) -1} {t_ {i + 2} -t_ {i + 1}} $. Таким образом, по непрерывности производной мы имеем нулевую производную в интервале $ (c_0, c_1) $, а другую — в $ (c_1, c_2) $ и т. Д.. до последнего интервала $ (c_ {n-2}, c_ {n-1}) $, всего $ n-1 $ нулевых производных.

   Заключение: Из теории B-сплайнов и их геометрических свойств следует, что
   максимальное количество точек экстремума $ s (t) $ равно $ n-1 $, и эта граница является точной, поскольку для любого $ n $ мы можем построить конфигурацию точек интерполяции, для которых эта оценка достигается.

   Одномерность точки экстремума неравенства Фридрихса в сферическом и плоском слоях

7. 1.

   G. Pólya и G. Szegö, Изопериметрические неравенства в математической физике , Princeton University Press, Princeton (1951).

   MATH

   Google Scholar

8. 2.

   Х. Брезис, Л. Ниренберг, «Положительные решения нелинейных уравнений с критическими показателями Соболева», Comm. Чистый. Прил. Математика. , , 36, , 437–477 (1983).

   MATH
   Статья

   Google Scholar

9. 3.

   К. В. Коффман, «Нелинейная краевая задача со многими положительными решениями», J. Дифференциальные уравнения. , 54 , 429–437 (1984).

   MATH
   Статья

   Google Scholar

10. 4.

    Б. Каволь, «Перестановки и выпуклость наборов уровней в PDE», Конспект лекций по математике. , № 1150 (1985).

11. 5.

    Х. Брезис, «Некоторые вариационные задачи с недостаточной компактностью», Simposia in Pure Mathematics , 45 , 165–201 (1985).

    Google Scholar

12. 6.

    А. И. Назаров, “Об“ одномерной ”экстремали в неравенстве Пуанкаре на квадрате”, Зап. Научн. Семин. ПОМИ , 259 , 167–181 (1999).

    Google Scholar

13. 7.