Содержание
Решить уравнение с х онлайн калькулятор
Для обозначения неизвестного числа используются буквенные обозначения. Именно значение этих букв и приходится
искать с помощью решений уравнения.
Так же читайте нашу статью «Решить уравнение Эйлера онлайн»
Работая над решением уравнения, мы стараемся на первых этапах привести его к более простому виду,
позволяющему получить результат с помощью простых математических манипуляций. Для этого мы выполняем перенос
слагаемых с левой стороны на правую, изменяем знаки, умножаем/делим части предложения на какое-то число,
раскрываем скобки. Но выполняем все эти действия мы только с одной целью — получения простого уравнения.
Уравнения \[rx+c=0\] — является уравнением с одной неизвестной линейного вида, в котором r и c — обозначение
для числовых значений. Чтобы решить уравнение данного вида необходимо произвести перенос его членов:
\[x=-b\div a. \]
\]
Например, нам необходимо решить такое уравнение:
\[3-2х=5-3х\]
Начинаем решение данного уравнения с переноса его членов: с \[х\] — в левую часть, остальные — в правую. При
переносе помним о том, что меняется \[+\] на \[-.\] Получим:
\[-2х+3х=5-3\]
Выполнив простые арифметические действия, получим следующий результат:
\[x=2\]
Где можно решить уравнение с х онлайн?
Решить уравнение с иксом онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн
решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео
инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте
Вступайте
в нашу группу, мы всегда рады помочь вам.
Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из
слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением
является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
.
Решение. Воспользуемся основным свойством дроби с представим левую и
правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их
числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а
следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
При решении квадратного уравнения получаем его корни:
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются
корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное
уравнение. Общий знаменатель —
.
Заменим исходное уравнение целым. Для этого умножим обе его части на
Для этого умножим обе его части на
общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к
квадратному уравнению
.
Решенив квадратное уравнение, получаем его корни:
.
Если x = -3, то
найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3.
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а,
поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное
уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Получим:
Выполнив преобразования, придём к квадратному уравнению
.
Решенив квадратное уравнение, получаем его корни:
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно,
числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив .
Получим уравнение с переменной y:
.
Корни этого уравнения:
Значит
или .
Из уравнения находим, что
.
Из уравнения находим, что
.
Итак, данное уравнение имеет четыре корня:
, .
Другие темы в блоке «Школьная математика»
Уравнение. Корень уравнения | Математика
Уравнение — это равенство, которое справедливо не при любых значениях входящих в него букв, а только при некоторых. Так же можно сказать, что уравнение является равенством, содержащим неизвестные числа, обозначенные буквами.
Например, равенство 10 — x = 2 является уравнением, так как оно справедливо только при x = 8. Равенство x2 = 49 — это уравнение, справедливое при двух значениях x, а именно, при
x = +7 и x = -7,
так как
(+7)2 = 49 и (-7)2 = 49.
Если вместо x подставить его значение, то уравнение превратится в тождество. Такие переменные, как x, которые только при определённых значениях обращают уравнение в тождество, называются неизвестными уравнения. Они обычно обозначаются последними буквами латинского алфавита x, y и z.
Они обычно обозначаются последними буквами латинского алфавита x, y и z.
Любое уравнение имеет левую и правую части. Выражение, стоящее слева от знака =
, называется левой частью уравнения, а стоящее справа — правой частью уравнения. Числа и алгебраические выражения, из которых состоит уравнение, называются членами уравнения:
Корни уравнения
Корень уравнения — это число, при подстановке которого в уравнение получается верное равенство. Уравнение может иметь всего один корень, может иметь несколько корней или не иметь корней вообще.
Например, корнем уравнения
10 — x = 2
является число 8, а у уравнения
x2 = 49
два корня — +7 и -7.
Решить уравнение – значит, найти все его корни или доказать, что их нет.
Виды уравнений
Кроме числовых уравнений, подобных приведённым выше, где все известные величины обозначены числами, существуют ещё буквенные уравнения, в которые кроме букв, обозначающих неизвестные, входят ещё буквы, обозначающие известные (или предполагаемые известные) величины.
Примеры:
x — a = b + c;
3x + c = 2a + 5.
По числу неизвестных уравнения разделяются на уравнения с 1-м неизвестным, с 2-мя неизвестными, с 3-мя и более неизвестными.
Примеры:
7x + 2 = 35 — 2x — уравнение с одним неизвестным,
3x + y = 8x — 2y — уравнение с двумя неизвестными.
Линейные уравнения
Линейные уравнения – уравнения, которые можно представить в виде \(ax+b=0\), где \(a\) и \(b\) – какие-либо числа.
Проще говоря, это такие уравнения, в которых переменные (обычно иксы) в первой степени. При этом не должно быть переменных в знаменателях дробей.
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
| |
|
|
|
|
|
Решение линейных уравнений
При решении линейных уравнений, мы стремимся найти корень, то есть такое значение для переменной, которое превратит уравнение в правильное равенство.
В простых уравнениях корень очевиден сразу или легко находиться подбором. Например, понятно, что корнем уравнения \(x+3=5\) будет число \(2\), ведь именно двойка при подстановке ее вместо икса даст \(5=5\) – верное равенство.
Однако в более сложных случаях ответ сразу не виден. И тогда на помощь приходят равносильные преобразования.
Чтобы найти корень уравнения нужно
равносильными преобразования привести данное нам уравнение к виду
\(x=[число]\)
Это число и будет корнем.
То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:
1. Прибавление или вычитание из обеих частей уравнения одинакового числа или выражения.
Например: прибавим \(5\) к обеим частям уравнения \(6x-5=1\)
\(6x-5=1\) \(|+5\)
\(6x-5+5=1+5\)
\(6x=6\)
Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».
2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.
Например: разделим уравнение \(-2x=8\) на минус два
\(-2x=8\) \(|:(-2)\)
\(x=-4\)
Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду \(ax=b\), и мы делим на \(a\), чтобы убрать его слева.
3. Использование свойств и законов математики: раскрытие скобок, приведение подобных слагаемых, сокращение дробей и т.д.
Например: раскроем скобки в уравнении \(2(3+x)=4(3x-2)-5\)
\(6+2x=12x-8-5\)
Чаще всего при решении линейного уравнения приходиться делать несколько разных преобразований.
Пример. Решить линейное уравнение \(6(4-x)+x=3-2x\)
Решение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: \(7\)
Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство — одинаковые числа слева и справа. Пробуем.
Проверка:
\(6(4-7)+7=3-2\cdot7\)
\(6\cdot(-3)+7=3-14\)
\(-18+7=-11\)
\(-11=-11\)
Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.
Не ленитесь проверять подстановкой найденные вами ответы, особенно если вы решаете уравнение на контрольной или экзамене.
Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?
Ответ прост:
Ваша цель – привести уравнение к виду \(x=[число]\), то есть, слева икс без коэффициентов и чисел, а справа – только число без переменных.
 Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.
Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.
Чтобы лучше это понять, разберем по шагам решение линейного уравнения \(x+3=13-4x\).
Давайте подумаем: чем данное уравнение отличается от \(x=[число]\)? Что нам мешает? Что не так?
Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать — вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.
\(x+3=13-4x\) \(|-3\)
\(x+3-3=13-4x-3\)
\(x=10-4x\)
Хорошо. Теперь что мешает? \(4x\) справа, ведь там должны быть только числа. \(4x\) вычитается — убираем прибавлением.
\(x=10-4x\) \(|+4x\)
\(x+4x=10-4x+4x\)
Теперь приводим подобные слагаемые слева и справа.
\(5x=10\)
Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением.
\(5x=10\) \(|:5\)
\(\frac{5x}{5}\)\(=\)\(\frac{10}{5}\)
\(x=2\)
Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.
Заметим, что чаще всего корень в линейных уравнениях только один. Однако могут встретиться два особых случая.
Особый случай 1 – в линейном уравнении нет корней.
Пример. Решить уравнение \(3x-1=2(x+3)+x\)
Решение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: нет корней.
На самом деле, то, что мы придем к такому результату было видно раньше, еще когда мы получили \(3x-1=3x+6\). Вдумайтесь: как могут быть равны \(3x\) из которых вычли \(1\), и \(3x\) к которым прибавили \(6\)? Очевидно, что никак, ведь с одним и тем же выражением сделали разные действия! Понятно, что результаты будут отличаться.
Особый случай 2 – в линейном уравнении бесконечное количество корней.
Пример. Решить линейное уравнение \(8(x+2)-4=12x-4(x-3)\)
Решение:
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
Ответ: \(x=5\)
Пример. Решить линейное уравнение \(\frac{x+2}{2}\) \(-\) \(\frac{1}{3}\) \(=\) \(\frac{9+7x}{6}\)
Решение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: \(x=-1,25\)
Смотрите также:
Линейная функция
Скачать статью
Уравнения, содержащие неизвестное в обеих частях
3x – 17 = 18 – 2x.
Мы сумеем решить уравнение такого вида, если сможем преобразовать его так, чтобы члены, содержащие неизвестное, оказались только в одной части уравнения (то есть приведем уравнение к такому виду, который мы уже умеем решать).
Воспользовавшись первым свойством уравнения, мы легко решим уравнение
3x – 17 = 18 – 2x.
Прибавив к обеим частям этого уравнения по 2x, получим уравнение, равносильное данному:
3x – 17 + 2x = 18 – 2x + 2x,
или после упрощения:
5x – 17 = 18.
Но это уравнение мы решать уже умеем, получим:
5x = 35, x = 7.
Подставив x = 7 в данное уравнение, получим:
3 * 7 – 17 = 4, 18 – 2 * 7 = 4,
4 = 4.
Корень найден верно.
Выведем некоторые следствия из первого свойства уравнений.
Возьмем уравнение:
2x – 5 + 4x = 17 + 4x.
В обеих частях этого уравнения есть один и тот же член 4x. Очевидно, если мы прибавим к обеим частям по –4x (или, что то же, вычтем 4x), то вместо этих членов в обеих частях уравнения будем иметь нули и сразу получим уравнение 2x – 5 = 17, равносильное данному.
Если в обеих частях уравнения имеются одинаковые члены, то их можно опустить.
Возьмем уравнение:
3x + 11 = 26 – 2x.
Чтобы сгруппировать в левой части члены, содержащие неизвестное, нужно к обеим частям уравнения прибавить по 2x, а чтобы сгруппировать в правой части свободные члены, надо к обеим частям прибавить по –11.
Получим:
3x + 11 + 2x – 11 = 26 – 2x + 2x – 11,
или
3x + 2x = 26 – 11.
Сравнивая это уравнение с данным, видим, что член –2x оказался в левой части, а 11 — в правой, но оба при этом изменили знак на противоположный. Отсюда правило:
Любой член уравнения можно перенести из одной части уравнения в другую, переменив его знак на противоположный.
Пример.
7x – 11 – 2x + 4 = 3x + 18 + x – 2.
Перенесем все члены, содержащие неизвестное, в левую часть, а все свободные члены — в правую, переменив у каждого из них знак на противоположный. Получим:
7x – 2x – 3x – x = 18 – 2 + 11 – 4,
или
x = 23.
Решить уравнение а x. Решение матричных уравнений
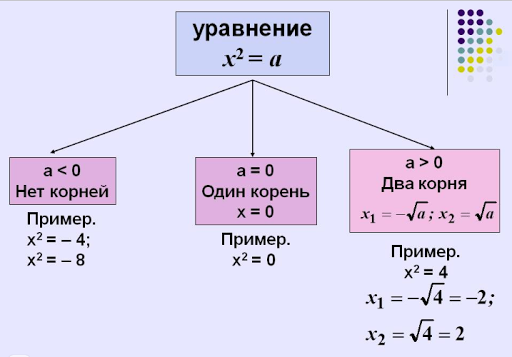
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант
.
Дискриминант
Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D
= 0, есть ровно один корень; - Если D
> 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x
2 − 8x
+ 12 = 0;- 5x
2 + 3x
+ 7 = 0;- x
2 − 6x
+ 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x
2 − 2x
− 3 = 0;- 15 − 2x
− x
2 = 0;- x
2 + 12x
+ 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D
> 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D
> 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x
2 + 9x
= 0; - x
2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b
= c
= 0. В этом случае уравнение принимает вид ax
2 = 0. Очевидно, такое уравнение имеет единственный корень: x
= 0.
Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:
Вывод:
- Если в неполном квадратном уравнении вида ax
2 + c
= 0 выполнено неравенство (−c
/a
) ≥ 0, корней будет два. Формула дана выше; - Если же (−c
/a
)
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax
2 + bx
= 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x
2 − 7x
= 0;- 5x
2 + 30 = 0;- 4x
2 − 9 = 0.
x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.
5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5.
Линейные уравнения. Решение, примеры.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Линейные уравнения.
Линейные уравнения — не самая сложная тема школьной математики. Но есть там свои фишки, которые могут озадачить даже подготовленного ученика. Разберёмся?)
Обычно линейное уравнение определяется, как уравнение вида:
ax
+
b
= 0
где а и b
– любые числа.
2х + 7 = 0. Здесь а=2,
b=7
0,1х — 2,3 = 0 Здесь а=0,1,
b=-2,3
12х + 1/2 = 0 Здесь а=12,
b=1/2
Ничего сложного, правда? Особенно, если не замечать слова: «где а и b – любые числа»
. ..
..
А если заметить, да неосторожно задуматься?) Ведь, если а=0,
b=0
(любые же числа можно?), то получается забавное выражение:
Но и это ещё не всё! Если, скажем, а=0,
а b=5,
получается совсем уж что-то несусветное:
Что напрягает и подрывает доверие к математике, да…) Особенно на экзаменах. А ведь из этих странных выражений ещё и икс найти надо! Которого нету вообще. И, что удивительно, этот икс очень просто находится. Мы научимся это делать. В этом уроке.
Как узнать линейное уравнение по внешнему виду? Это, смотря какой внешний вид.) Фишка в том, что линейными уравнениями называются не только уравнения вида ax
+
b
= 0
, но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду. А кто ж его знает, сводится оно, или нет?)
Чётко распознать линейное уравнение можно в некоторых случаях. Скажем, если перед нами уравнение, в которых есть только неизвестные в первой степени, да числа. Причём в уравнении нет дробей с делением на неизвестное
Причём в уравнении нет дробей с делением на неизвестное
,
это важно! А деление на число,
или дробь числовая – это пожалуйста! Например:
Это линейное уравнение. Здесь есть дроби, но нет иксов в квадрате, в кубе и т.д., и нет иксов в знаменателях, т.е. нет деления на икс
. А вот уравнение
нельзя назвать линейным. Здесь иксы все в первой степени, но есть деление на выражение с иксом
. После упрощений и преобразований может получиться и линейное уравнение, и квадратное, и всё, что угодно.
Получается, что узнать линейное уравнение в каком-нибудь замудрёном примере нельзя, пока его почти не решишь. Это огорчает. Но в заданиях, как правило, не спрашивают о виде уравнения, правда? В заданиях велят уравнения решать.
Это радует.)
Решение линейных уравнений. Примеры.
Всё решение линейных уравнений состоит из тождественных преобразований уравнений. Кстати, эти преобразования (целых два!) лежат в основе решений всех уравнений математики.
Другими словами, решение любого
уравнения начинается с этих самых преобразований. В случае линейных уравнений, оно (решение) на этих преобразованиях и заканчивается полноценным ответом. Имеет смысл по ссылке сходить, правда?) Тем более, там тоже примеры решения линейных уравнений имеются.
Для начала рассмотрим самый простой пример. Безо всяких подводных камней. Пусть нам нужно решить вот такое уравнение.
х — 3 = 2 — 4х
Это линейное уравнение. Иксы все в первой степени, деления на икс нету. Но, собственно, нам без разницы, какое это уравнение. Нам его решать надо. Схема тут простая. Собрать всё, что с иксами в левой части равенства, всё, что без иксов (числа) — в правой.
Для этого нужно перенести —
4х
в левую часть, со сменой знака, разумеется, а —
3
— в правую. Кстати, это и есть первое тождественное преобразование уравнений.
Удивлены? Значит, по ссылке не ходили, а зря…) Получим:
х + 4х = 2 + 3
Приводим подобные, считаем:
Что нам не хватает для полного счастья? Да чтобы слева чистый икс был! Пятёрка мешает. Избавляемся от пятёрки с помощью второго тождественного преобразования уравнений.
Избавляемся от пятёрки с помощью второго тождественного преобразования уравнений.
А именно — делим обе части уравнения на 5. Получаем готовый ответ:
Пример элементарный, разумеется. Это для разминки.) Не очень понятно, к чему я тут тождественные преобразования вспоминал? Ну ладно. Берём быка за рога.) Решим что-нибудь посолиднее.
Например, вот это уравнение:
С чего начнём? С иксами — влево, без иксов — вправо? Можно и так. Маленькими шажочками по длинной дороге. А можно сразу, универсальным и мощным способом. Если, конечно, в вашем арсенале имеются тождественные преобразования уравнений.
Задаю вам ключевой вопрос: что вам больше всего не нравится в этом уравнении?
95 человек из 100 ответят: дроби
! Ответ правильный. Вот и давайте от них избавимся. Поэтому начинаем сразу со второго тождественного преобразования
. На что нужно умножить дробь слева, чтобы знаменатель сократился напрочь? Верно, на 3. А справа? На 4. Но математика позволяет нам умножать обе части на одно и то же число
А справа? На 4. Но математика позволяет нам умножать обе части на одно и то же число
. Как выкрутимся? А умножим обе части на 12! Т.е. на общий знаменатель. Тогда и тройка сократится, и четвёрка. Не забываем, что умножать надо каждую часть целиком
. Вот как выглядит первый шаг:
Раскрываем скобки:
Обратите внимание! Числитель (х+2)
я взял в скобки! Это потому, что при умножении дробей, числитель умножается весь, целиком! А теперь дроби и сократить можно:
Раскрываем оставшиеся скобки:
Не пример, а сплошное удовольствие!) Вот теперь вспоминаем заклинание из младших классов: с иксом – влево, без икса – вправо!
И применяем это преобразование:
Приводим подобные:
И делим обе части на 25, т.е. снова применяем второе преобразование:
Вот и всё. Ответ: х
=0,16
Берём на заметку: чтобы привести исходное замороченное уравнение к приятному виду, мы использовали два (всего два!) тождественных преобразования
– перенос влево-вправо со сменой знака и умножение-деление уравнения на одно и то же число. Это универсальный способ!
Это универсальный способ!
Работать таким образом мы будем с любыми
уравнениями! Совершенно любыми. Именно поэтому я про эти тождественные преобразования всё время занудно повторяю.)
Как видим, принцип решения линейных уравнений простой. Берём уравнение и упрощаем его с помощью тождественных преобразований до получения ответа. Основные проблемы здесь в вычислениях, а не в принципе решения.
Но… Встречаются в процессе решения самых элементарных линейных уравнений такие сюрпризы, что могут и в сильный ступор вогнать…) К счастью, таких сюрпризов может быть только два. Назовём их особыми случаями.
Особые случаи при решении линейных уравнений.
Сюрприз первый.
Предположим, попалось вам элементарнейшее уравнение, что-нибудь, типа:
2х+3=5х+5 — 3х — 2
Слегка скучая, переносим с иксом влево, без икса — вправо… Со сменой знака, всё чин-чинарём… Получаем:
2х-5х+3х=5-2-3
Считаем, и. .. опаньки!!! Получаем:
.. опаньки!!! Получаем:
Само по себе это равенство не вызывает возражений. Нуль действительно равен нулю. Но икс-то пропал! А мы обязаны записать в ответе, чему равен икс.
Иначе, решение не считается, да…) Тупик?
Спокойствие! В таких сомнительных случаях спасают самые общие правила. Как решать уравнения? Что значит решить уравнение? Это значит, найти все значения икса, которые, при подстановке в исходное уравнение, дадут нам верное равенство.
Но верное равенство у нас уже
получилось! 0=0, куда уж вернее?! Остаётся сообразить, при каких иксах это получается. Какие значения икса можно подставлять в исходное
уравнение, если эти иксы всё равно посокращаются в полный ноль?
Ну же?)
Да!!! Иксы можно подставлять любые!
Какие хотите. Хоть 5, хоть 0,05, хоть -220. Они всё равно сократятся. Если не верите — можете проверить.) Поподставляйте любые значения икса в исходное
уравнение и посчитайте. Всё время будет получаться чистая правда: 0=0, 2=2, -7,1=-7,1 и так далее.
Вот вам и ответ: х — любое число.
Ответ можно записать разными математическими значками, суть не меняется. Это совершенно правильный и полноценный ответ.
Сюрприз второй.
Возьмём то же элементарнейшее линейное уравнение и изменим в нём всего одно число. Вот такое будем решать:
2х+1=5х+5 — 3х — 2
После тех же самых тождественных преобразований мы получим нечто интригующее:
Вот так. Решали линейное уравнение, получили странное равенство. Говоря математическим языком, мы получили неверное равенство.
А говоря простым языком, неправда это. Бред. Но тем, не менее, этот бред — вполне веское основание для правильного решения уравнения.)
Опять соображаем, исходя из общих правил. Какие иксы, при подстановке в исходное уравнение, дадут нам верное
равенство? Да никакие! Нет таких иксов. Чего ни подставляй, всё посократится, останется бред.)
Вот вам и ответ: решений нет.
Это тоже вполне полноценный ответ. В математике такие ответы частенько встречаются.
В математике такие ответы частенько встречаются.
Вот так. Сейчас, надеюсь, пропажа иксов в процессе решения любого (не только линейного) уравнения вас нисколько не смутит. Дело уже знакомое.)
Теперь, когда мы разобрались со всеми подводными камнями в линейных уравнениях, имеет смысл их порешать.
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям. Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ.
Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. 2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Приложение
Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений. . Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.
. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени.
Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов.
Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования.
Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции.
Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента.
Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус.
Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу.
В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом.
Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин.
В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида.
Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости.
Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера.
В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество.
По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ.
Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь.
Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям.
Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части.
Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения.
Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить.
Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
=
для решения математики. Быстро найти решение математического уравнения
в режиме онлайн
. Сайт www.сайт позволяет решить уравнение
почти любого заданного алгебраического
, тригонометрического
или трансцендентного уравнения онлайн
. При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн
. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн
займет несколько минут. Основное преимущество www. сайт при решении математических уравнений онлайн
сайт при решении математических уравнений онлайн
— это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн
, тригонометрические уравнения онлайн
, трансцендентные уравнения онлайн
, а также уравнения
с неизвестными параметрами в режиме онлайн
. Уравнения
служат мощным математическим аппаратом решения
практических задач. C помощью математических уравнений
можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений
можно найти, сформулировав задачу на математическом
языке в виде уравнений
и решить
полученную задачу в режиме онлайн
на сайте www.сайт. Любое алгебраическое уравнение
, тригонометрическое уравнение
или уравнения
содержащие трансцендентные
функции Вы легко решите
онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений
. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн
При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн
. Поэтому для решения математических уравнений онлайн
мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн
, тригонометрических уравнений онлайн
, а также трансцендентных уравнений онлайн
или уравнений
с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений
ресурса www.. Решая уравнения онлайн
самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений
на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение
, после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн
и сравнить ответы. Это поможет Вам избежать ошибок в решении
и вовремя скорректировать ответ при решении уравнений онлайн
будь то алгебраическое
, тригонометрическое
, трансцендентное
или уравнение
с неизвестными параметрами.
Уравнения равные нулю | Алгебра
Что такое «уравнения равные нулю»?
Если в левой части уравнения стоит сумма или разность одночленов или многочленов, а в правой части — нуль, то это может быть обычное линейное уравнение.
Если левая часть уравнения представляет собой произведения двух или нескольких множителей, а правая часть — нуль, то это — уравнение типа «произведение равно нулю».
В общем виде простейшие равные нулю уравнения можно записать как
(множителей может быть больше).
Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому приравниваем к нулю каждый множитель:
и решаем каждое из полученных уравнений отдельно.
Примеры.
Это — уравнение типа «произведение равно нулю».
Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Ответ: 0; 1,5; -0,8.
Ответ: 3; -2/7.
Если в уравнении, равном 0, левую часть можно разложить на множители, то такое уравнение также можно решить как уравнение типа «произведение равно 0».
Например,
Сгруппируем первое слагаемое с третьим, а четвёртое — со вторым:
Из первых скобок вынесем за скобки общий множитель x², из вторых — 4:
Общий множитель (x-3) вынесем за скобки:
Получили уравнение типа «произведение равно 0». Приравниваем к нулю каждый из множителей:
Корень первого уравнения —
Второе уравнение не имеет корней (сумма положительных чисел не может равняться нулю).
Ответ: 3.
В алгебре многие уравнения сводятся к уравнениям типа «произведение равно нулю» с помощью разложения на множители.
Множители могут линейными, квадратными, логарифмическими, тригонометрическими и т. д. уравнениями.
д. уравнениями.
Еще один важный частный случай уравнений, равных нулю, рассмотрим позже.
Решение линейных уравнений — Полный курс алгебры
9
Закон обратного
Четыре формы уравнений
Транспонирование
Логическая последовательность операторов
Транспонирование и обмен сторон
Форма ax = 0
Раздел 2 :
Отмена
Неизвестное с обеих сторон
Простые дробные уравнения
УРАВНЕНИЕ — это алгебраическое утверждение, в котором глагол «равно» =.Уравнение включает неизвестное число, обычно называемое x . Вот простой пример:
x + 4 = 10.
«Некоторое число плюс 4 равно 10.»
Мы говорим, что уравнение имеет две стороны: левую, x + 4, и правую, 10.
Поскольку x появляется в первой степени, мы называем это линейным уравнением. Линейное уравнение еще называют уравнением первой степени.
Степень любого уравнения — это наивысший показатель степени неизвестного числа. Уравнение первой степени называется линейным , потому что, как мы увидим много позже, его график представляет собой прямую линию .
Уравнение — это утверждение — станет истинным только тогда, когда неизвестное имеет определенное значение, которое мы называем решением уравнения.
Решение этого уравнения, очевидно, 6:
6 + 4 = 10.
6 — единственное значение x , для которого верно утверждение « x + 4 = 10». Мы говорим, что x = 6 удовлетворяет уравнению.
Итак, алгебра зависит от того, как все выглядит. Что касается того, как все выглядит, то мы узнаем, что решили уравнение, когда выделим x слева.
Почему налево? Потому что мы читаем слева направо. « x равно.. . «
В стандартной форме линейного уравнения — ax + b = 0 — x появляется слева.
Фактически, мы видели, что для любого уравнения, которое выглядит так:
| x + а | = | б , |
| решение всегда будет выглядеть так: | ||
| x | = | b — а . |
| Если | |||
| x + 4 | = | 10, | |
| , затем | |||
| х | = | 10–4 | |
| = | 6. | ||
Закон обратного
Есть две пары обратных операций. Сложение и вычитание, умножение и деление.
Формально, чтобы решить уравнение, мы должны изолировать неизвестное на одной стороне уравнения.
топор — b + c = d .
Мы должны переместить a, b , c на другую сторону, так что x будет один.
Вопрос:
Как перенести число из одной части уравнения
в другую?
Ответ:
Путем записи на другой стороне с помощью обратной операции.
Это закон обратного. Это следует из двух Правил 5 урока.
Пример 1. Решите это уравнение:
| a x — b + c | = | г . |
| Решение. Поскольку b — это , вычтенное из слева, мы прибавим справа: | ||
| a x + c | = | д + б . |
| Поскольку c — это , добавленное слева, мы вычтем справа: | ||
| топор | = | d + b — c . |
| И, наконец, поскольку a умножает слева, мы будем разделить справа: | ||
| x | = | d + b — c a |
Мы решили уравнение.
Четыре формы уравнений
Таким образом, решение любого линейного уравнения распадается на четыре формы, соответствующие четырем операциям арифметики.Ниже приведены основные правила решения любого линейного уравнения. В каждом случае мы будем перемещать на на другую сторону.
1. Если x + a = b , то x = b — a .
«Если число добавлено с одной стороны уравнения,
мы можем вычесть с другой стороны».
2. Если x — a = b , то x = b + a .
«Если число вычтено из на одной стороне уравнения,
мы можем прибавить на другой стороне».
| 3. Если ax = b , то x = | б а | . | |
«Если число умножает на одну сторону уравнения,
мы можем разделить на другую сторону.«
| 4. Если | x a | = b , затем x = ab . |
«Если число делит на одну сторону уравнения,
мы можем умножить на на другой стороне».
В каждом случае a были сдвинуты на другую сторону посредством обратной операции.Любое линейное уравнение можно будет решить, применив одно или несколько из этих правил.
Транспонирование
Когда используются операции сложения или вычитания (формы 1 и 2), мы называем это транспонированием.
Мы можем переместить член на другую сторону уравнения
, изменив его знак .
+ a переходит на другую сторону как — a .
— a переходит на другую сторону как + a .
Транспонирование — одна из наиболее характерных операций алгебры, и считается, что это значение слова алгебра , имеющего арабское происхождение. (Арабские математики изучали алгебру в Индии, откуда они представили ее в Европе.) Транспонирование — это техника тех, кто действительно использует алгебру в науке и математике — потому что это искусно. И, как мы скоро увидим, в нем сохраняется четкая логическая последовательность утверждений. Более того, это подчеркивает, что вы занимаетесь алгеброй глазами.Когда вы видите
| x + a | = | б , |
| тогда вы сразу увидите , что + a переходит на другую сторону как — a : | ||
| x | = | b — а . |
Однако часто учат писать — a с обеих сторон, начертить линию и сложить.
Во-первых, вы никогда не увидите этого ни в одном математическом тексте. Вы увидите логическую последовательность утверждений, к которой мы скоро подойдем.
Более того, мы доказали, что можем просто транспонировать. Нет необходимости доказывать это снова каждый раз, когда вы решаете уравнение.
(Вам нужно доказывать теорему Пифагора каждый раз, когда вы ее применяете? Нет, вы этого не сделаете.)
Если вы хотите представить, что вы вычли из с обеих сторон, хорошо. Но писать приходиться не умело.
Вот что вы увидите в своем тексте расчетов.
Логическая последовательность операторов
Рассмотрим снова уравнение из Примера 1.
топор — b + c = d .
Это алгебраическое предложение — это утверждение — логически подразумевает другие утверждения. Теперь мы увидим логическую последовательность, которая приводит к окончательному утверждению, которое и является решением.
Теперь мы увидим логическую последовательность, которая приводит к окончательному утверждению, которое и является решением.
| (1) | топор — b + c | = | г | |
| подразумевает | (2) | топор | = | d + b — c |
| подразумевает | (3) | х | = | d + b — c . а |
Исходное уравнение (1) «преобразуется» путем перестановки членов. Из утверждения (1) следует утверждение (2).
Затем этот оператор преобразуется делением на и . Из утверждения (2) следует утверждение (3), которое и является решением.
Таким образом, мы решаем уравнение, преобразовывая его — изменяя его внешний вид — оператор за оператором, строка за строкой в соответствии с правилами алгебры, пока наконец не будет выделено x слева. Так пишут книги по математике (но, к сожалению, не книги по алгебре!). Каждая строка представляет собой собственное читаемое утверждение, которое следует из строки выше — без зачеркивания.
Так пишут книги по математике (но, к сожалению, не книги по алгебре!). Каждая строка представляет собой собственное читаемое утверждение, которое следует из строки выше — без зачеркивания.
Другими словами, что такое расчет? Это дискретное преобразование символов. В арифметике преобразовываем «19 + 5» в «24». В алгебре мы преобразуем « x + a = b » в « x = b — a ».
Проблема 1.Напишите логическую последовательность операторов, которая решит это уравнение для x :
.
abcx — d + e — f = 0
Чтобы увидеть ответ, наведите указатель мыши на
слева направо над цветной областью.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| (1) | abcx — d + e — f | = | 0 | |
| подразумевает | (2) | abcx | = | d — e + f |
| подразумевает | (3) | х | = | d — e + f . abc |
Сначала транспонируйте термины . Строка (2).
Нет необходимости писать справа термин 0.
Затем разделите на коэффициент x .
Задача 2. Напишите логическую последовательность операторов, которая решит это уравнение для x :
.
| (1) | 2 x + 5 | = | 27 | |
| подразумевает | (2) | 2 х | = | 27-5 = 22 |
| подразумевает | (3) | х | = | 22 2 |
| подразумевает | (4) | х | = | 11. |
В задачах 3, 4 и 5 дано только решение. Студент должен написать логическую последовательность утверждений, которая к нему приводит.
Студент должен написать логическую последовательность утверждений, которая к нему приводит.
Задача 3. Решите для x : ( p — q ) x + r = s
Задача 4. Решите для x :
ab ( c + d ) x — e + f = 0
| х = | e — f ab ( c + d ) |
Проблема 5.Решите относительно x : 2 x + 1 = 0
х = −½
Каждое из приведенных выше уравнений имеет стандартную форму, а именно:
топор + b = 0.
a не означает a . Значит коэффициент х . И b не означает b . Это означает любые термины.
Вот почему он называется формой.Как бы то ни было, так выглядит .
Проблема 6. Решить: Решить: | топор + b | = | 0. | |
| х | = | – | б а | |
Это простое уравнение иллюстрирует выполнение алгебры глазами. ученик должен немедленно увидеть решение. Вы должны увидеть , что b перейдет на другую сторону как — b , и что a разделит.
Это навык в алгебре.
Задача 7. Решите для x : ax = 0 ( a 0).
Теперь, когда произведение двух чисел равно 0, то хотя бы одно из них должно быть 0. (Урок 6.) Следовательно, любое уравнение с такой формой имеет решение
.
х = 0.
Мы могли бы решить это формально, конечно, разделив на .
Задача 8. Решите для x :
| 4 x -2 | = | -2 |
| 4 x | = | −2 + 2 = 0 |
| x | = | 0. |
Задача 9. Напишите последовательность операторов, которая решит это уравнение:
| (1) | 6 — х | = | 9 |
| (2) | — х | = | 9–6 |
| (3) | — х | = | 3 |
| (4) | х | = | −3. |
Когда мы переходим от строки (1) к строке (2), — x остается слева. Для членов в строке (1) равны 6 и — x .
Мы «решили» уравнение, выделив слева x , а не x . Поэтому мы переходим от строки (3) к строке (4), меняя знаки с обеих сторон. (Урок 5.)
Как вариант, можно было бы исключить — x слева, сразу поменяв все знаки:
| (1) | 6 — х | = | 9 |
| (2) | −6 + х | = | −9 |
| (3) | х | = | −9 + 6 = −3. |
| Задача 10. Решите для x : | 3 — х | = | −5 |
| х | = | 8. | |
Проблема 11.Решить для x :
| 4 — (2 x — 1) | = | −11. |
| 4-2 x + 1 | = | −11. |
| 5-2 x | = | −11 |
| −2 x | = | −11 — 5 |
| 2 x | = | 16 |
| x | = | 8. |
Задача 12. Решите для x :
| 3 x -15 2x + 1 | = 0. |
( Подсказка : Сравните Урок 6, Задача 18.)
x = 5.
Транспонирование и обмен сторон
| Пример 2. | a + b = c — x |
Мы можем легко решить эту проблему — в одной строке — просто переставив x влево, а то, что слева, вправо:
x = c — a — b .
| Пример 3. | a + b = c + x |
В этом примере справа + x .Поскольку нам нужно + x слева, мы можем добиться этого, поменяв стороны:
c + x = a + b
Примечание: При обмене сторонами знаки не меняются.
После транспонирования c легко следует решение:
c + x = a + b — c .
Таким образом, когда — x справа, его можно просто транспонировать.Но когда справа + x , то стороны можно поменять местами.
Задача 13. Решите для x :
| п. + в. | = | r — x — с | |
| Транспонировать: | |||
| х | = | r — s — p — q | |
Проблема 14.Решить для x :
| p — q + r | = | с + x | |
| Сменные стороны: | |||
| с + x | = | p — q + r | |
| х | = | p — q + r — s | |
Проблема 15.Решить для x :
| 0 | = | пикселей + q | |
| пикселей + q | = | 0 | |
| пикселей | = | – | q |
| x | = | – | q p |
Проблема 16.Решить для x :
| -2 | = | −5 x + 1 |
| 5 x | = | 1 + 2 = 3 |
| x | = | 3 5 |
Проблема 17.Решить для x :
| п. | = | q — топор . |
| топор | = | q — p |
| x | = | q — p a |
Проблема 18.Решите относительно cos θ («косинус против -ta»).
Стоит увидеть, что это уравнение имеет точно такую же форму и , что и задача 17. cos θ — это неизвестное. Вы решите ее точно так же, как задачу 17.
| 2 cos θ | = | 8 — А |
| cos θ | = | 8 — А 2 |
Алгебра состоит в распознавании формы.И их только конечное число.
Раздел 2 :
Отмена
Неизвестное с обеих сторон
Простые дробные уравнения
Содержание | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Калькулятор многоступенчатых уравнений
Как решить основные линейные уравнения?
Во-первых, взгляните на этот пример:
Во-первых, упростите с обеих сторон.Слева вы можете добавить и. Тогда вы получите уравнение:
Затем вы должны переставить уравнение таким образом, чтобы x находился слева, а числа — справа. Поскольку нам не нравится x в правой части, мы вычитаем x с обеих сторон. слева.
Теперь нам нужно получить число на другой стороне. Так что прибавляем по обеим сторонам. Так как мы получаем
Теперь разделим обе стороны на число перед x:
Уравнение решено; это решение.
Вы всегда можете действовать точно так же: во-первых, максимально упростите обе части уравнения. Затем упростите с помощью преобразований эквивалентности. Вычтите число с умом с обеих сторон. Наконец, на одной стороне должно быть несколько переменных, а на другой — число. Вы делите на число перед переменной, и уравнение решается.
Как Mathepower показывает решения?
Когда вы ввели уравнение, вы получите следующее:
Набор решений: {} |
А если я хочу решить другое уравнение?
Вы используете mathepower.com. Введите уравнение выше, и оно будет решено с помощью той же процедуры. Прямо сейчас и бесплатно (mathepower финансируется за счет рекламы).
Какие частные случаи необходимо учитывать при решении уравнений?
Наиболее важными частными случаями являются уравнения с бесконечным числом решений или без решений.
Во-первых, пример уравнения с бесконечным числом решений:
Вы видите, что у вас одинаковые числа с обеих сторон. Очевидно, что это верное утверждение для любого значения x (в этом уравнении больше нет x).Таким образом, мы видим, что уравнение может иметь бесконечное число решений.
Что означает, когда уравнение имеет бесконечное количество решений? Вы можете попробовать это: возьмите любое значение для x (например, обе стороны будут одинаковыми. Он работает с любым значением для x. Причина в том, что термины на обеих сторонах эквивалентны, то есть термины с одинаковым решением с любым значение для x.
Другой частный случай — уравнение без решения:
Мы видим, что после перестановки в уравнении нет x и что уравнение явно неверно.Это связано с тем, что исходное уравнение не имеет решения.
Решение двухэтапных уравнений — ChiliMath
Нет сомнений в том, что решить двухэтапное уравнение чрезвычайно просто. Как следует из названия, двухэтапные уравнения можно решить всего за два шага. Если вы впервые сталкиваетесь с двухэтапными уравнениями, не волнуйтесь, потому что мы рассмотрим достаточно примеров, чтобы вы познакомились с процессом.
Решая уравнение в целом, мы всегда помним о том, что все, что мы делаем с одной стороной уравнения, должно быть сделано и с другой стороной, чтобы уравнение оставалось сбалансированным.
Мы знаем, что мы полностью решили двухэтапное уравнение, если переменная, обычно представленная буквой в алфавите, изолирована на одной стороне уравнения (левой или правой), а число находится на противоположной стороне.
ОБЫЧНЫЙ способ решения двухэтапного уравнения:
Примечание : Это «обычный» метод, потому что так решается большинство двухэтапных уравнений. Обратите внимание, что шаг 2 можно в качестве альтернативы заменить на шаг 3, который по сути тот же.
1) Сначала сложите или вычтите обе части линейного уравнения на одно и то же число.
2) Во-вторых, умножьте или разделите обе части линейного уравнения на одно и то же число.
3) * Вместо шага 2 всегда умножайте обе части уравнения на обратную величину коэффициента переменной.
Примеры решения двухэтапных уравнений
Пример 1: Решите приведенное ниже двухэтапное уравнение.
Как следует из названия этого линейного уравнения, для определения неизвестной переменной требуется два шага. Как правило, первый шаг заключается в том, чтобы избавиться от числа, «наиболее удаленного» от члена с решаемой переменной. Затем мы исключаем число, «ближайшее» к переменной. Число либо умножает, либо делит переменную. Его еще называют коэффициентом срока.
Здесь переменная x. Наша цель — решить x, изолировав его на одной стороне уравнения.Сохранение переменной слева или справа не имеет никакого значения. Это тебе решать! В этой задаче оставим его слева, так как он уже там.
Обратите внимание на то, что на той стороне (левая часть линейного уравнения), где находится переменная, 2 — это «ближайший» к переменной x, а 5 — «самый дальний».
Это простое наблюдение позволяет нам решить, какое число удалить в первую очередь. Очевидно, +5, потому что это дальше между двумя. Противоположность +5 равна -5, это означает, что мы вычтем обе части уравнения на 5.
После исключения 5 в левой части уравнения путем вычитания обеих частей на 5, пора избавиться от числа, ближайшего к x или непосредственно связанного с ним, которое равно 2 в 2x. Поскольку 2 — это умножение переменной x, противоположная операция — деление на 2.
Разделив обе части на 2, мы получим окончательный ответ или решение данного двухшагового линейного уравнения.
Напоминаю, что это считается решенным, потому что коэффициент переменной просто положительный, +1.
Пример 2: Решите двухэтапное уравнение ниже.
Наша цель — сохранить переменную x на одной стороне уравнения. Неважно, на какой стороне, однако это «стандартная» практика — оставлять решаемую переменную в левой части. Некоторые учителя алгебры могут потребовать, чтобы переменная оставалась слева, и с этим ничего не поделаешь. Лично я не против, где вы храните переменную, левую или правую, при условии, что изолированная переменная на одной стороне уравнения имеет коэффициент +1.
Первый шаг включает удаление числа «дальше всего» от переменной x. Обратите внимание, что -3 «ближе всего» к x, а -8 «дальше». Итак, мы можем исключить -8, добавив к его противоположности, равному +8.
Второй шаг заключается в том, чтобы избавиться от числа, ближайшего к переменной x, равного -3. Поскольку -3 умножает переменную x, его противоположная операция — деление на -3. Разделив обе части на -3, мы решили линейное уравнение.
Быстрое напоминание, -3 деленное на -3 равно +1.
Пример 3: Решите приведенное ниже двухэтапное уравнение.
Вот ситуация, когда мы можем изолировать переменную x в правой части уравнения, поскольку она уже существует.
Если посмотреть на правую часть уравнения, где находится переменная, число 3 наиболее близко к x, потому что 3 делит переменную x. С другой стороны, число 26 — «дальше». Это означает, что нам придется иметь дело с +26, вычитая обе части уравнения на 26.Причина, по которой мы вычитаем, заключается в том, что аддитивная величина, обратная +26, равна -26.
Второй шаг — избавиться от знаменателя 3. Поскольку 3 делит x, противоположная операция — умножение на 3.
После умножения обеих частей на 3 мы пришли к окончательному ответу. Вы можете переписать свой окончательный ответ как x = -9.
Пример 4: Решите уравнение для двух ниже.
Это может показаться многоступенчатым уравнением, но это не так. Это можно решить в два этапа.Не беспокойтесь о дробях, потому что с ними очень легко работать. В этом случае вы примените правило сложения дробей. Правило гласит, что если вы складываете две дроби с одинаковым знаменателем, просто сложите числители, а затем скопируйте общий знаменатель.
Вернемся к решению двухэтапного уравнения выше, чтобы удалить дробь в левой части, которая равна \ Large {- {3 \ over {10}}}, мы добавим \ Large {{3 \ over {10}}} к обеим сторонам уравнения.
Причина, по которой мы добавляем вместо вычитания, заключается в том, что аддитивная величина, обратная \ Large {- {3 \ over {10}}}, есть \ Large {+ {3 \ over {10}}}.
После добавления \ Large {{3 \ over {10}}} с обеих сторон с левой стороны остается только {\ Large {{2 \ over 5}}} x.
Для правой части уравнения имеем \ Large {{9 \ over {10}} + {3 \ over {10}} = {{12} \ over {10}}}.
Все, что я сказал выше, — это только первый шаг. Теперь переходим ко второму шагу. Посмотрите на коэффициент переменной x. Это \ Large {{2 \ over 5}}, что означает, что его обратное значение равно \ Large {{5 \ over 2}}.
Чтобы окончательно решить данное уравнение, мы умножим обе части уравнения на обратную величину коэффициента рассматриваемой переменной.Вот полное пошаговое решение:
Практика с рабочими листами
Перестановка уравнений
Уравнения как важный геологический инструмент
Профессор говорит по математике, которая может показаться другим языком! , фото Дженнифер М. Веннер.
Иногда может показаться, что ваш инструктор по геофизическим наукам говорит на другом языке, когда говорит об уравнениях или формулах. Особенно, если он / она ожидает, что вы «манипулируете» или переставляете их! Но уравнения могут предоставить мощные инструменты для описания мира природы.В науках о Земле мы можем описать поведение многих природных явлений, написав уравнение для линии ( y = mx + b ) или с помощью экспоненциальных функций ( y = e xt ). И немного алгебры, мы можем изменить эти уравнения, чтобы решить для ЛЮБОЙ из переменных в них.
Хотя это может показаться волшебством, для этого не нужно быть «математиком». Эта страница предназначена для предоставления вам некоторых инструментов, которые помогут вам изучить некоторые простые шаги, которые помогут вам решить уравнение для любой из переменных (буквы, которые представляют интересующий элемент или количество).
Зачем мне манипулировать уравнениями?
Фотография Кена Эндрюса (ученого из JPL) жонглирования. Изменено Джен Веннер.
Вы не поверите, но есть много веских причин для развития вашей способности переставлять уравнения, важные для наук о Земле. Это может сэкономить время, помочь вам с юнитами и сэкономить немного места для мозга! Вот несколько причин для развития навыков манипулирования уравнениями (в произвольном порядке):
- Уравнения легче обрабатывать до вставки чисел! И, если вы можете изолировать переменную на одной стороне уравнения, она применима к любой подобной проблеме, которую вам нужно решить для этой переменной!
- Если вы знаете, как манипулировать уравнениями, вам нужно запомнить только одно уравнение, в котором есть все рассматриваемые переменные — вы можете манипулировать им, чтобы найти любую другую переменную! Это означает меньше запоминания!
- Управление уравнениями может помочь вам отслеживать (или вычислять) единицы числа.Поскольку единицы измерения определяются уравнениями, если вы манипулируете, вставляете числа и отменяете единицы, вы получите именно те единицы измерения (для данной переменной)!
Где это используется в науках о Земле?
Если честно, манипуляции с уравнениями происходят почти во всех аспектах наук о Земле. Каждый раз, когда вы видите P, T, ρ или x (или даже =), есть уравнение, которым вы можете манипулировать. Поскольку уравнения можно использовать для описания множества важных природных явлений, возможность манипулировать ими дает вам мощный инструмент для понимания мира вокруг вас!
См. Лишь несколько примеров на странице «Практика управления уравнениями».
Обзор важных правил перестановки уравнений
Решение для y Дженнифер М. Веннер.
Вы, вероятно, выучили ряд правил работы с уравнениями в предыдущем курсе алгебры. Никогда не помешает напоминать себе о правилах. Итак, давайте рассмотрим:
- ПРАВИЛО №1: вы можете складывать, вычитать, умножать и делить на что угодно, , если вы делаете то же самое с обеими сторонами знака равенства. В уравнении знак равенства действует как точка опоры баланса: если вы добавляете 5 единиц чего-либо к одной стороне баланса, вы должны добавить такое же количество к другой стороне, чтобы баланс оставался устойчивым.То же самое и с уравнением — выполнение одной и той же операции с обеими сторонами сохраняет смысл уравнения от изменения.
Давайте воспользуемся уравнением для линии, чтобы проиллюстрировать пример того, как использовать Правило №1. Общее уравнение для линии:
Если мы хотим найти b в этом уравнении, мы должны вычесть mx из обеих частей.
Если мы произведем математические вычисления с каждой стороны (то есть вычтем mx из mx справа), мы получим уравнение, которое выглядит следующим образом:
Это уравнение также можно записать b = y — mx, если вы предпочитаете, чтобы решаемая переменная находилась слева. - ПРАВИЛО № 2: чтобы переместить или отменить величину или переменную на одной стороне уравнения, выполните «противоположную» операцию с ней на обеих сторонах уравнения. Например, если у вас было g-1 = w и вы хотите изолировать g, добавьте 1 к обеим сторонам (g-1 + 1 = w + 1). Упростим (потому что (-1 + 1) = 0) и получим g = w + 1.
Давайте воспользуемся более сложным уравнением, которое геологи могут использовать, чтобы выяснить отношение толщины к плотности плавающих веществ (например,g., кора в мантии, айсберги в воде):
, где H выше = высота объекта над поверхностью жидкости, в которой он плавает,
H всего = общая высота (или толщина) плавающего объекта
ρ объекта = плотность объекта
и ρ жидкости = плотность жидкости
Представим, что мы изучаем айсберг и хотим знать, какова его плотность. Как нам изменить уравнение для решения этой переменной? Чтобы выделить объект с ρ на одной стороне уравнения, необходимо предпринять несколько шагов.С чего начать?- Давайте начнем с выделения части уравнения в круглые скобки. Для этого нам нужно обе части разделить на H итого :
Сущность, разделенная сама по себе, равна 1:
и, поскольку 1, умноженная на что-то, равно этому чему-то, мы можем упростить, чтобы получить: - Мы еще не совсем там. Что еще нужно переместить, чтобы выделить ρ объект ? Давайте выделим содержащую его дробь, поэтому мы хотим вычесть 1 с обеих сторон:
и 1 минус 1 равно 0, поэтому мы можем избавиться от единиц в левой части.
- Нам все еще нужно проделать еще несколько операций, чтобы выделить ρ объект . Сначала умножьте обе части на ρ жидкость , чтобы очистить дробь:
Мы можем отменить ρ жидкость с каждой стороны:
- Тогда нам нужно избавиться от знака минус:
Умножьте обе части на -1, чтобы получить -ρ жидкость положительным:
Отрицательное число (или символ), умноженное на отрицательное число, является положительным числом.Поскольку мы умножаем на -1, мы просто меняем знак на всех числах и символах с обеих сторон и получаем: - Немного изменив правую часть уравнения, мы получим уравнение для определения плотности айсберга!
Несколько простых шагов для работы с уравнениями
Вот несколько простых шагов для работы с уравнениями. Под каждым шагом вы найдете пример того, как это сделать, с примером, который использует геологический контекст плотности (мера массы на единицу объема).
- Оцените, что у вас есть (для каких переменных у вас есть значения? Какие единицы измерения присутствуют? И т. Д.). НОМЕРА пока НЕ подключайте!
Например: у вас есть куб пирита размером 3 см x 3 см x 3 см. Вы знаете, что плотность пирита 5,02 г / см 3 . Можете ли вы выяснить, сколько весит этот кубик пирита (без весов)?
Во-первых, вам нужно знать, что плотность (ρ) равна массе (m), деленной на объем (v).Мы можем записать это в виде математического выражения (или уравнения, если хотите):
Какие из этих значений указаны в вопросе выше? У вас есть плотность (5,02 г / см 3 ). И с помощью информации вы можете определить объем (длина x ширина x высота).
- Определите, какие из переменных вы хотите использовать в качестве ответа. (Какой вопрос вас просят вычислить? Что такое неизвестная переменная?)
В приведенном выше вопросе вам предлагается определить массу кубика пирита (без его взвешивания / с использованием информации, указанной в задаче).Итак, в уравнении плотности вы хотите определить «массу». Помните, пока ничего не подключайте.
- Измените уравнение так, чтобы неизвестная переменная находилась по одну сторону от знака равенства (=), а все другие переменные — по другую сторону. ПРАВИЛО №1: вы можете складывать, вычитать, умножать и делить на что угодно, , если вы делаете то же самое с обеими сторонами знака равенства.
Возьмем уравнение плотности:
и переставить.Мы хотим выделить переменную для массы (м). Для этого сначала умножим обе части уравнения на объем (v).Затем мы можем отменить объем в правой части уравнения (объем Ã · объем = 1).
Обратите внимание, что эти первые два шага аналогичны перекрестному умножению. Если вы более знакомы с этим методом, вы тоже можете это сделать. Так или иначе…
В итоге мы получаем уравнение, в котором масса изолирована на одной стороне уравнения!
- СЕЙЧАС подключите номера! Замените известные переменные на их значения и не забывайте отслеживать единицы измерения!
Наше уравнение.Самое приятное в этом уравнении состоит в том, что теперь, когда мы его изменили, все известные нам переменные находятся на одной стороне, а та, которую мы не знаем, — на другой. Начнем с того, что подставим то, что мы знаем: ρ (плотность пирита) и V (объем (длина x ширина x высота) куба):
Упростите термин объема, умножив:
Отмените одни и те же единицы сверху и снизу (где вы можете), чтобы мы получили желаемые единицы (если вы не понимаете, как это сделать, см. Модуль преобразования единиц): - Определите значение неизвестной переменной, выполнив математические функции.То есть складывайте, вычитайте, умножайте и делите в соответствии с уравнением, которое вы написали для шага 2.
В данном случае это простое умножение:
И получаем массу: - Спросите себя, является ли ответ разумным в контексте того, что вы знаете о науках о Земле и сколько вещей должны весить.
Это то, что в основном требует опыта. Если вы не уверены, вы можете найти весы и взвесить куб, чтобы увидеть, правильно ли вы находитесь.Если вы держите его в руке, вы можете догадаться, кажется ли это правильным … Что еще более важно, если вы получите число вроде 135 000 г, как вы думаете, это разумно? Это 135 кг (что составляет около 300 фунтов!), И, вероятно, это неправильно. А что, если вы получите что-то вроде 0,00135 грамма? Важно уметь различать, находитесь ли вы в правильном диапазоне, больше, чем точно ли вы правы.
Другой способ подумать, правы ли вы, — это найти что-то такое же, исходя из вашего собственного опыта.На что похоже 135 г? Ну, в фунте около 450 г, так что 135 г составляют от 1/4 до 1/3 фунта. Что вы знаете, что имеет такой же вес? (Первая мысль, которая приходит мне в голову, — это гамбургеры …). Есть ли смысл в том, что куб пирита (золотого металлического минерала), имеющий примерно один дюйм с каждой стороны, будет так много весить? Используйте свой собственный опыт, чтобы разработать способ оценки веса и других мер.
Следующие шаги
Дополнительная справка по уравнениям
На химическом факультете Texas A&M есть страница математического обзора, посвященная алгебраическим манипуляциям.
На факультете экономики и бизнеса Сиднейского университета есть страница, на которой вы можете попрактиковаться в работе с уравнениями! Пройдите тесты по алгебраическим манипуляциям!
Эта страница была написана и скомпилирована доктором Дженнифер М. Веннер, геологический факультет, Ошкош Висконсинского университета, и доктором Эриком М. Бэром, геологическая программа, Общественный колледж Хайлайн
- Давайте начнем с выделения части уравнения в круглые скобки. Для этого нам нужно обе части разделить на H итого :
Решение уравнения | Энциклопедия.com
Методы решения простых уравнений
Решение более сложных уравнений
Решение уравнений с несколькими переменными
Решение уравнений второй степени и выше
Ресурсы
Решение уравнения — это набор всех значений, которые при замене неизвестных, сделать уравнение истинным. Для уравнений, имеющих одно неизвестное, возведенное в единственную степень, два фундаментальных правила алгебры, включая свойство аддитивности и свойство мультипликативности, используются для определения его решений.Решения для уравнений с несколькими неизвестными переменными находятся с использованием принципов системы уравнений. Уравнения с членами в степени, большей единицы, могут быть решены путем факторизации, а в некоторых конкретных случаях — квадратного уравнения.
Идея решения уравнений существовала со времен древних египтян и вавилонян. В то время они использовали простые алгебраические методы для поиска решений практических проблем, связанных с их повседневной жизнью.Методы, используемые древними, были сохранены в трактате, написанном арабским математиком Аль-Коваризми 825 г. н.э.). В эту работу он включает методы решения линейных уравнений, а также уравнений второй степени. Решения некоторых уравнений более высокой степени были разработаны в шестнадцатом веке итальянским математиком Джероламо Кардано (1501–1576).
Уравнение — это алгебраическое выражение, которое обычно связывает неизвестные переменные с другими переменными или константами. Например, уравнение x + 2 = 15 равно y 2 = 4.Решение или корень уравнения — это любое значение или набор значений, которые можно подставить в уравнение, чтобы сделать его истинным утверждением. Для первого примера решение для x равно 13. Во втором примере есть два значения, которые делают утверждение истинным, а именно 2 и –2. Эти значения составляют набор решений уравнения.
Используя два основных правила алгебры, можно получить решения многих простых уравнений. Первое правило гласит, что одна и та же величина может быть добавлена к обеим сторонам уравнения без изменения решения уравнения.Например, уравнение x + 4 = 7 имеет решение x = 3. Согласно первому правилу, можно добавить любое число к обеим сторонам уравнения и все равно получить то же решение. При добавлении 4 к обеим частям уравнение становится x + 8 = 11, но решение остается x = 3. Это правило известно как аддитивное свойство равенства. Чтобы использовать это свойство для поиска решения уравнения, все, что требуется, — это выбрать правильное число для добавления. Решение предыдущего примера x + 4 = 7 можно найти, прибавив –4 к обеим сторонам уравнения.Если это сделано, уравнение упрощается до x + 4 — 4 = 7 — 4 или x = 3, и уравнение решается.
Второе фундаментальное правило, известное как мультипликативное свойство равенства, гласит, что каждый член в обеих частях уравнения может быть умножен или разделен на одно и то же число без изменения решения уравнения. Например, решением уравнения y — 2 = 10 является y = 12. Используя правило мультипликативности, можно получить эквивалентное уравнение с тем же набором решений, умножив обе части на любое число, например, 2.Таким образом, уравнение принимает вид 2y– 4 = 20, но решение остается y = 12. Это свойство также можно использовать для решения алгебраических уравнений. В случае уравнения 2x = 14 решение получается путем деления обеих частей на 2. Когда это делается 2x / 2 = 14/2, уравнение упрощается до x = 7.
Часто оба этих правила должны быть используется для решения одного уравнения, такого как уравнение 4x + 7 = 23. В этом уравнении к обеим сторонам уравнения добавляется –7, и оно упрощается до 4x = 16. Обе части этого уравнения затем делятся на 4 и он упрощается до решения x = 4.
Большинство уравнений даются в более сложной форме, которую можно упростить. Рассмотрим уравнение 4x — x — 5 = 2x + 7. Первый шаг в решении этого уравнения — объединить одинаковые члены с каждой стороны уравнения. В правой части нет одинаковых терминов, но 4x и –x в левой части похожи на термины. Это уравнение в упрощенном виде становится 3x — 5 = 2x + 7. Следующим шагом является удаление неизвестного из одной части уравнения. В этом примере это достигается добавлением –2x к обеим частям уравнения, что дает x — 5 = 7.Используя свойство аддитивности, решение получается добавлением 5 к обеим сторонам уравнения, так что x = 12.
Весь процесс решения алгебраических уравнений с одной переменной можно резюмировать следующими шагами. Во-первых, удалите скобки, умножив множители. Во-вторых, добавьте одинаковые термины с каждой стороны. В-третьих, удалите неизвестное с одной стороны уравнения, используя мультипликативные или аддитивные свойства. В-четвертых, удалите постоянный член со стороны неизвестного, используя аддитивное свойство.Наконец, исключите любой коэффициент при неизвестном, используя свойство мультипликативности.
Многие алгебраические уравнения содержат более одной переменной, поэтому полный набор решений не может быть найден с помощью методов, описанных до сих пор. Уравнения с двумя неизвестными называются линейными уравнениями и могут быть представлены общей формулой ax + by = c; где a, b и c — константы, а x и y — переменные. Решением этого типа уравнения будет упорядоченная пара x и y, которая делает уравнение истинным.Например, набор решений для уравнения x + y = 7 будет содержать все пары значений x и y, которые удовлетворяют уравнению, такие как (2,5), (3,4), (4,3), и т. д. В общем, чтобы найти решение линейного уравнения с двумя переменными, уравнение переписывается и решается в терминах одной переменной. Решением уравнения x + y = 7 становится любая пара значений, которая делает x = 7 — y истинным.
Часто существует несколько линейных уравнений, связывающих две переменные в одной системе.Все уравнения, связанные с переменными, известны как система уравнений, а их решение — это упорядоченная пара, которая делает каждое уравнение истинным. Эти уравнения решаются методами построения графиков, подстановки и исключения.
Уравнения, содержащие неизвестные в степени единицы, известны как уравнения первой степени. Также существуют уравнения второй степени, которые включают:
КЛЮЧЕВЫЕ УСЛОВИЯ
Аддитивное свойство — свойство уравнения, в котором указано число, может быть добавлено к обеим сторонам уравнения, не влияя на его решение.
Факторинг — Метод сведения уравнения более высокой степени к продукту уравнений более низкой степени.
Уравнение первой степени —Алгебраическое выражение, содержащее неизвестное в первой степени.
Мультипликативное свойство — Свойство уравнения, которое устанавливает все члены в уравнении, можно умножить на то же число, не влияя на окончательное решение.
Уравнение второй степени —Алгебраическое выражение, содержащее неизвестное во второй степени.
как минимум одна переменная, возведенная в квадрат или возведенная в степень двойки. Уравнения также могут быть третьей, четвертой и т. Д. Самым известным уравнением второй степени является квадратное уравнение, которое имеет общий вид ax 2 + bx + c = 0; где a, b и c — константы, а a не равно 0. Решение этого типа уравнения часто можно найти с помощью метода, известного как факторинг.
Поскольку квадратное уравнение является произведением двух уравнений первой степени, оно может быть включено в эти уравнения.Например, произведение двух выражений (x + 2) (x — 3) дает одно квадратичное выражение x 2 — x — 6. Два выражения (x + 2) и (x — 3) называются коэффициенты квадратного выражения x 2 — x — 6. Приняв каждый коэффициент квадратного уравнения равным нулю, можно получить решения. В этом квадратном уравнении решениями являются x = –2 и x = 3.
Нахождение множителей квадратного уравнения не всегда легко. Для решения этой проблемы была изобретена квадратная формула, позволяющая решить любое квадратное уравнение.Квадратное уравнение для общего уравнения формулируется следующим образом: ax 2 + bx + c = 0
Чтобы использовать формулу корней квадратного уравнения, в уравнение подставляются числа для a, b и c, и определяются решения для x. .
См. Также Системы уравнений.
КНИГИ
Биттингер, Марвин Л. и Давик Элленбоген. Промежуточная алгебра: концепции и приложения . 7-е изд. Ридинг, Массачусетс: Издательство Аддисон-Уэсли, 2006.
Ларсон, Рон. Предварительный расчет . 7-е изд. Бостон, Массачусетс: Houghton Mifflin, 2007.
Лоренц, Фалько. Алгебра. Нью-Йорк: Springer, 2006.
Сетек, Уильям М. Основы математики . Река Аппер Сэдл, Нью-Джерси: Pearson Prentice Hall, 2005.
Perry Romanowski
Решение уравнений
Решение уравнений — повторяющаяся тема в большей части математики.
Мы изучим некоторые принципы, используемые для решения уравнений и
затем используйте уравнения для решения прикладных задач.
Решение уравнений необходимо для решения задач алгебры.
В этом разделе мы изучаем два самых важных принципа.
используется для этой задачи.
Уравнения и решения
Мы уже видели, что уравнение — это числовое предложение
заявляя, что выражения по обе стороны от знака равенства
представляют собой то же число. Некоторые уравнения, например 3 + 2 = 5 или 2x +
6 = 2 (x + 3) всегда верны, а некоторые, например, 3 + 2 = 6 или x + 2 =
x + 3 никогда не верны. В этом тексте мы сконцентрируемся на
уравнения типа 3x + 6 = 17 или 7x = 141, которые иногда верны,
в зависимости от значения замены для переменной.
Решение уравнения: Любая замена для
переменная, которая делает уравнение истинным, называется решением
уравнение. Решить уравнение — значит найти все его
решения.
Чтобы определить, является ли число решением, подставляем
это число для переменной во всем уравнении. Если
значения по обе стороны от знака равенства одинаковы, то
число, которое было подставлено, является решением.
Пример 1
Определите, является ли 7 решением x + 6 = 13
Решение
У нас
Написание уравнения.
Подставив 7 вместо x.
Обратите внимание, что решение — 7, а не 13.
Поскольку левая и правая части совпадают, 7
это решение.
Пример 2
Определите, является ли 19 решением 7x = 141.
Решение
У нас
Написание уравнения.
Подставив 19 вместо x.
Утверждение 133 = 141 неверно.
Поскольку левая и правая части различаются, 19 не
решение.
Принцип сложения
Рассмотрим уравнение x = 7.
Легко видеть, что решение этого уравнения равно 7.
Заменяя x на 7, мы получаем 7 = 7, что верно.
Теперь рассмотрим уравнение x + 6 = 13.
В примере 1 мы обнаружили, что решение x + 6 = 13 также
7. Хотя решение x = 7 может показаться более очевидным,
уравнения x + 6 = 13 и x = 7 эквивалентны.
Эквивалентные уравнения : Уравнения с одинаковыми
решения называются эквивалентными уравнениями.
Есть принципы, которые позволяют нам начать с одного уравнения
и получим эквивалентное уравнение, например x = 7, для которого
решение очевидно. Один из таких принципов касается сложения. В
уравнение a = b говорит, что a и b обозначают одно и то же число.
Предположим, что это правда, и к a добавлено некоторое число c. Мы получаем
тот же результат, если мы добавим c к b, потому что a и b одинаковы
номер.
Принцип сложения: Для любых действительных чисел
a, b и c, a = b эквивалентно a + c = b + c.
Чтобы наглядно представить принцип сложения, рассмотрим весы
похож на тот, который может использовать ювелир. (См. Рисунок.) Когда
две стороны весов имеют одинаковый вес,
баланс ровный. Если вес добавлен или удален, одинаково на обоих
стороны, баланс останется ровным.
При использовании принципа сложения мы часто говорим, что
«Добавьте одно и то же число к обеим сторонам уравнения». Мы
также может «вычесть одно и то же число с обеих сторон»,
поскольку вычитание можно рассматривать как добавление противоположного.
Пример 3
Решите: x + 5 = -7.
Решение
Мы можем добавить любое число к обеим сторонам. Поскольку это
напротив или аддитивно обратного 5, мы добавляем к каждой стороне:
х + 5 = -7
x + 5-5 = -7-5 Использование принципа сложения: прибавление -5 к
обе стороны или вычитая 5 с обеих сторон.
x + 0 = -12 Упрощение: x + 5-5 = x + 5 + (-5) = x + 0.
x = -12 Используя свойство идентичности 0.
Очевидно, что решением x = -12 является число -12.
Чтобы проверить ответ в исходном уравнении, подставим.
Чек:
Решение исходного уравнения -12.
Обратите внимание, что в примере 3, поскольку мы добавили противоположное, или
аддитивная обратная 5, левая часть уравнения упрощена
к x плюс аддитивная идентичность 0 или просто x. Эти шаги
эффективно заменил 5 слева на 0. При решении x +
a = b для x, мы просто добавляем -a (или вычитаем a) с обеих сторон.
Пример 4
Решить: -6,5 = y — 8,4
На этот раз переменная находится справа. Мы можем выделить y
прибавив 8,4 в каждую сторону:
-6,5 = y — 8,4 Это можно рассматривать как -6,5 = y + (- 8,4)
-6,5 + 8,4 = y — 8,4 + 8,4 Используя принцип сложения:
Добавление 8,4 к обеим сторонам «исключает» -8,4 справа.
боковая сторона.
1,9 = y Sice y — 8,4 + 8,4 = y + (-8,4) + 8,4 = y + 0 = y
Чек:
Решение — 1.9.
Обратите внимание, что уравнения a = b и b = a имеют одинаковый смысл.
Таким образом, -6,5 = y — 8,4 можно было бы переписать как y-8,4 = -6,5.
Пример 5
Решить:
Решение
У нас
Добавление
к
обе стороны.
Умножив на 1, чтобы получить общий знаменатель
Чек оставляется студенту. Решение есть.
Принцип умножения
Второй принцип решения уравнений касается умножения.Предположим, что a и b равны. Если a и b умножить на некоторые
число c, тогда ac и bc также будут равны.
Принцип умножения: Для любого действительного
числа a, b и c, где c 0, a = b
эквивалентно a.c = b.c.
Уравнений с «x» на обеих сторонах (рабочие листы с ответами)
Я регулярно загружаю ресурсы, которые создал за 30 лет работы учителем. По большей части это математика, но есть некоторые виды деятельности, связанные с ИКТ / вычислениями и репетиторством. Все ресурсы принадлежат мне и недоступны третьим лицам.Ресурсы менялись со временем, и у меня было много счастливых уроков и множество счастливых и успешных учеников.
В конце 2017 года TES объявил меня самым загружаемым новым автором, а в 2018 году к этому счету добавилось еще 2 миллиона.
Последнее обновление
16 января 2019
Поделиться
Эти рабочие листы ( с подробными решениями ) обеспечивают стабильное продвижение, позволяя ученикам делать первые шаги , затем укрепляют и расширяют свои навыки в решении уравнения с неизвестными с обеих сторон .
Чтобы просмотреть рабочие листы аналогичного стиля по другим темам, щелкните 👉 www.tes.com/…/worksheets
Эти листы удобны для использования в классе, но также являются отличным домашним заданием. Листы Первые шаги и Усиление хорошо подходят для индивидуального обучения и практических занятий.
«Если вам понравился этот ресурс, то поставьте ему оценку и / или оставьте комментарий».
Если кнопка ресурса на этой странице не работает, перейдите на страницу оценок, щелкнув 👉 www.tes.com/…/rate-resources…
Выберите общий рейтинг
(без рейтинга)
Ваша оценка необходима, чтобы отражать ваше счастье.
Написать отзывОтменить
Это хорошо, чтобы оставить отзыв.
Что-то пошло не так, повторите попытку позже.
Пустой ответ не имеет никакого смысла для конечного пользователя
Отправить ответОтменить
Люблю работу.



 Поэтому ответ – в этом линейном уравнении нет корней.
Поэтому ответ – в этом линейном уравнении нет корней.
 {2}+8x-6x=-6+16\)
{2}+8x-6x=-6+16\)
 .. Однако давайте избавимся от знаменателей, умножив обе части уравнения на общий знаменатель всех дробей – шестерку
.. Однако давайте избавимся от знаменателей, умножив обе части уравнения на общий знаменатель всех дробей – шестерку

