2}{\mathrm R}\;\;\mathrm{где}\;\mathrm v\;\;\mathrm{линейная}\;\mathrm{скорость}\;\mathrm{движения}\;\mathrm{точки}(\mathrm{тела}\;\mathrm{по}\;\mathrm{окружности}$$

На тело движущееся по кривой(окружности в частности) действует центростремительное ускорение (оно показывает быстроту изменения направления движения) чем больше радиус дуги или линейная скорость тем меньше центростремительное ускорение (тк за равные промежутки времени точка(тело) меньше «поворачивает» .

И так, спутник движется по круговой орбите, перешел на другую круговую орбиту, его центростремительное ускорение уменьшилось. Это одновременно свидетельствует о том что радиус его орбиты увеличился а скорость уменьшилась (если бы изменилось что-то одно то не выполнялся бы закон сохранения энергии или орбита не была бы круговой).

Потенциальная энергия -это часть механической энергии системы в поле консервативных сил (силы — работа которых зависит только от координат (начальных и конечных положений тел, или расстояний между ними. ))

$${\mathrm E}_\mathrm p=\mathrm{mgh}$$ радиус орбиты это высота над поверхностью, он увеличился, а значит и энергия тоже возросла.

12

Переход спутника с одной орбиты на другую. Переход спутника с одной орбиты на другую В результате перехода с одной

Источник задания: Решение 2541. ЕГЭ 2017. Физика. Демидова М. Ю. 30 вариантов.

Задание
6.

В результате перехода искусственного спутника Земли с одной круговой орбиты на
другую его центростремительное ускорение увеличивается. Как изменяются в
результате этого перехода скорость движения спутника по орбите и период его
обращения вокруг Земли?

Для
каждой величины определите соответствующий характер изменения:

1)
увеличивается

2)
уменьшается

3)
не изменяется

Решение.

На спутник действует только сила
притяжения земли

где M — масса земли; m — масса спутника; R — радиус орбиты. В соответствии со вторым законом
Ньютона, можно записать:

,

где a – играет роль центростремительного ускорения. Отсюда видно,
что при увеличении ускорения, радиус орбиты будет уменьшаться.

Теперь рассмотрим как изменится скорость
движения спутника в зависимости от радиуса орбиты. Подставим вместо ускорения , получим:

.

То есть, при уменьшении R,
скорость спутника увеличивается.

Период обращения спутника вокруг
Земли – это время, за которое спутник делает один оборот вокруг Земли. Если
радиус орбиты уменьшается, а центростремительное ускорение возрастает, то
скорость спутника увеличивается. Таким образом, спутник проходит меньшее
расстояние с большей скоростью и его период уменьшается.

Демонстрационный вариант ЕГЭ 2019 г. – задание №6.

Искусственный спутник Земли перешёл с одной круговой орбиты на другую, на новой орбите скорость его движения меньше, чем на прежней. Как изменились при этом потенциальная энергия спутника в поле тяжести Земли и его период обращения вокруг Земли?

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу

Ответ: 11

Демонстрационный вариант ЕГЭ 2018 г. – задание №6.

В результате перехода спутника Земли с одной круговой орбиты на другую скорость его движения уменьшается. Как изменяются при этом центростремительное ускорение спутника и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу

выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.

Решение:

1) Центростремительное ускорение спутника: уменьшается

⇒ a y ↓, F T

⇒ a y ↓, V 2 ↓, r

2) Период обращения спутника вокруг Земли: увеличивается

⇒ r , V ↓, T

Ответ: 21

Демонстрационный вариант ЕГЭ 2017 г. – задание №6

Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?

Для каждой величины определите соответствующий характер изменения:

1. увеличилась

2. уменьшилась

3. не изменилась

Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение:

На спут­ник дей­ству­ет сила при­тя­же­ния со сто­ро­ны Земли, она со­об­ща­ет ему цен­тро­стре­ми­тель­ное уско­ре­ние:

R — расстояние от спутника до центра Земли, которое увеличилось, в следствие чего ско­рость дви­же­ния уменьшилась.

Так как расстояние увеличилось, то и по­тен­ци­аль­ная энер­гия увеличилась.

Ответ: 21

Демонстрационный вариант ЕГЭ 2016 г. – задание №6

На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение:

Сила Архимеда – это выталкивающая сила, действующая на погруженные в жидкость тела ,

где — плотность жидкости; — объем тела; — ускорение свободного падения.

Объем тела равен , где — масса тела; — плотность тела.

Подставим в формулу силы Архимеда, получим: .

Последнее выражение показывает, что сила Архимеда и массой тела зависит прямо пропорционально, т.е. чем больше масса, тем выше сила Архимеда. Глубина останется прежней, т.к. глубина не зависит от массы, а зависит от плотности тела.

Задача №1. -1
балл

Два одинаковых бруска
толщиной h
, положенные
друг на друга, плавают в воде так, что уровень воды приходится на границу между
ними (см. рисунок). На сколько изменится глубина погружения, если в стопку
добавить еще один брусок?

Решение.

Основой решения является 2-й
закон Ньютона. На тело действуют сила тяжести и сила Архимеда. Тело находится в
равновесии и

Следовательно, плотность воды в 2
раза больше плотности материала бруска. Таким образом, брусок любого размера
будет погружаться ровно на половину: 3 бруска погрузятся на глубину 3h
/2, т.е. глубина изменится
на h
/2.

Задача №2. -2 балла

В результате перехода с одной
круговой орбиты на другую центростремительное ускорение спутника Земли
уменьшается. Как изменяются в результате этого перехода радиус орбиты спутника,
скорость его движения по орбите и период обращения вокруг Земли?

Решение

В этой задаче также нужно
рассмотреть силы, которые действуют на тело, и записать 2-й закон Ньютона.На спутник действует сила тяготения со
стороны Земли (силами тяготения со стороны остальныхтел Солнечной системы – пренебрегаем).

2-й закон Ньютона:

Из последней формулы
действительно видно, что при уменьшении ускорения радиус орбиты – увеличивается
(постоянная тяготения и масса Земли – константы).

Формулу центростремительного
ускорения можно использовать для анализа изменения скорости:

Следовательно, при переходе
наболее высокую орбиту скорость
спутника уменьшается.

Период обращения спутника -при увеличении R
также увеличивается:

Задача №3. –3 балла

Кусок льда, имеющий температуру 0 о С,
помещен в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с
температурой 12 о С, требуется количество теплоты, равное 80 кДж.
Какая температура установится внутри калориметра, если лёд получит от
нагревателя количество теплоты, равное 60 кДж? Теплоемкостью калориметра и
теплообменом с внешней средой пренебречь.

Решение

В этой задаче очень важно
понимать, что лёд не просто нагревается, а сначала тает, а только затем
нагревается. Количество теплоты, затрачиваемое на эти процессы

Задача №4. -1 балл

На рисунке показаны
графики изменения температуры четырех тел одинаковой массы по мере поглощения
ими энергии. В начальный момент времени тела находились в твердом состоянии.
Какой из графиков соответствует твердому телу с наименьшей теплоемкостью?
Почему?

Задача №5. -1 балл

Точка росы для водяного пара в
комнате равна 6 о С. В комнату внесли с балкона сухую бутылку с водой.
Вскоре она покрылась мелкими капельками воды. Почему?

Решение

Если при данной влажности в
комнате, температура на улице меньше 6 градусов, тогда около поверхности
внесенной в комнату бутылки водяной пар становится пересыщенным и поэтому
конденсируется.

Задача №6. -3 балла

Задача №7. -1 балл

Точка В находится на
середине отрезка АС. Неподвижные точечные заряды +q
и -2q

расположены в точках А и С соответственно (см. рисунок). Какой заряд нужно
поместить в точку С вместо заряда -2q
, чтобы напряженность электрического поля в точке В увеличилась
в 2 раза?

Задача №8. -2 балла

При одном сопротивлении
реостата вольтметр показывает 6 В, амперметр – 1 А (см. рисунок). При другом
сопротивлении реостата показание приборов 4 В и 2А. Чему равно внутреннее
сопротивление и эдс источника тока?

Решение

Вольтметр в данном случае
показывает напряжение как на реостате, так и на источнике тока с учетом его
внутреннего сопротивления. Это следует и из закона Ома для полной цепи.

Требуется перевести искусственный спутник, летящий по орбите радиусом (или большой полуосью, что для круговой орбиты, очевидно, одно и то же), равным a
1 , на орбиту ра-диусом a 2
(рис. 43).

Вычисление скоростей

Скорость искусственного спутника на орбите радиусом а
равна:

v
1 = √(GM
/ a
).

Эта скорость называется первой космической скоростью на расстоя-нии a
. Приняв за единицу длины радиус первой орбиты a
1 , интеграл энергии можно переписать в виде

v 2 = v 1 2 . ((2 / r
) — (1 / a
)),

где v
1 — первая космическая скорость на расстоянии a
1 . В ин-тересующих нас случаях (переход с одной орбиты искусственного спутника Земли на дру-гую и перелёт с Земли на другую планету) за a
1 принимают значение радиуса Земли, или радиуса земной орбиты. В пер-вом случае v
1 = 8 км/с, во втором v
1 = 30 км/с.

Для перехода на орбиту радиусом a 2
нужно перевести искусственный спутник на промежуточную орбиту, представляющую собой эллипс, ка-сающийся как нижней, так и верхней орбиты (рис. 43). Большая полуось этого эллипса равна a
пр = (a
1 + a
2) / 2.

На промежуточной орбите (точка A
на рисунке 43) в пери-гее спутник должен иметь скорость:

v
пр 2 = v
1 2 (2a
2 / (a
2 + a
1)).

Так как v
пр > v
1 , то для перехода на промежуточную орби-ту нужно увеличить скорость искусственного спутника.

В точке B
(рис. 43) скорость искусственного спутника, летящего по проме-жуточной орбите, меньше, чем первая космическая скорость на этом расстоянии:

v
прв 2 = v
2 2 (2a
1 / (a
2 + a
1)).

Поэтому для окончательного перехода на новую орбиту ско-рость спутника должна быть ещё раз увеличена.

Вычисление времени

Если стоит задача не просто перевести искусственный спутник с орбиты на ор-биту, а провести стыковку с другим искусственным спутником (спутником-мишенью), то запуск должен производиться в строго определённое время, чтобы оба спутника подошли к точке B
(рис.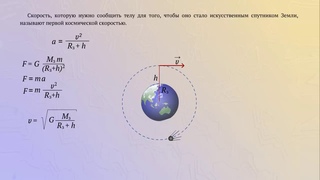 43) одновре-менно. Для этого спутник-мишень в момент начала перевода должен находиться в точке C
. Для определения дуги CB
вос-пользуемся третьим законом Кеплера .

Поскольку период обращения спутника-мишени (летящего по орбите радиусом а
2) равен T
2 = 1,65 . 10 -4 √a
2 3 , а время пере-лёта равно половине периода для промежуточной орбиты t = 1 / 2 T
пр = 0,83 . 10 -4 √a
пр 3 , то длина дуги BC
находится по фор-муле Материал с сайта

α = 360° . T
пр / T
2 = 180° . √(1/8 . (1 + a
1 /a
2)),

что и определяет время старта искусственного спутника. Он производится в момент, когда спутник находится в точке A
, а спутник-мишень прохо-дит точку C
(рис. 43).

Очевидно, что полученные формулы непосредственно при-меняются к расчётам полётов к Луне (космический аппарат сначала выводится на низкую круговую орбиту) и к

В задании №6 ЕГЭ по физике необходимо выбрать правильное заключение, проанализировав условие задачи.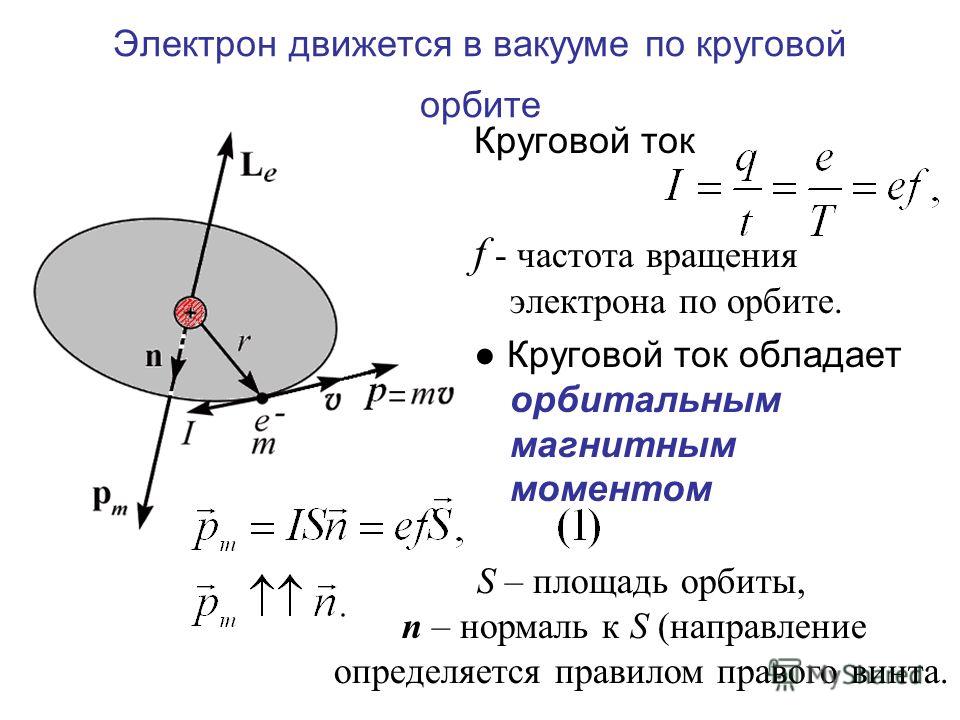 Тематика задач — механика.

Теория к заданию №6 ЕГЭ по физике

Кратко напомним основные моменты.

По второму закону Ньютона сила, действующая на тело, равна F=ma

Сила всемирного тяготения определяется по формуле:

Здесь М и m — массы взаимодействующих (притягивающихся) тел, G -гравитационная постоянная. R – расстояние между этими телами либо между их центрами, если размеры тел соизмеримы с расстоянием между ними (2-му варианту соответствует, например, ситуация, когда рассматривается Земля и ее спутник).

При движении по кругу центростремительное ускорение можно вычислить по формуле:

Период обращения спутника вокруг орбиты равен:

Закон Архимеда: на тело, погруженное в воду, действует сила F=ρgV.

Кинетическая энергия тела, совершающего колебания выражается формулой:

Закон сохранения энергии: механическая энергия тела не изменяется, если не происходит ее перехода во внутреннюю.

Разбор типовых заданий №6 ЕГЭ по физике

Демонстрационный вариант 2018

В результате перехода спутника Земли с одной круговой орбиты на другую скорость его движения уменьшается. Как изменится при этом центростремительное ускорение спутника и период обращения вокруг Земли?

1. Увеличивается;
   
2. Уменьшается;
   
3. Не изменяется
   

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения:

1. Определяем силы, действующие на спутник. Записываем соответствующие формулы.
2. Выражаем скорость спутника через радиус орбиты и делаем вывод относительно ее изменения. Выражаем центростремительное ускорение через радиус орбиты.
3. Выражаем период обращения спутника через радиус орбиты.
4. Записываем ответы.

Решение:

1. На спутник действует сила притяжения Земли F. Именно она удерживает спутник на орбите. Обозначим массу спутника m, массу Земли – M. Тогда их взаимодействие выглядит так:

По второму закону Ньютона сила F, действующая на спутник, определяется формулой:

F=ma.
Но эта же сила является силой взаимного притяжения:

Поскольку спутник движется по круговой орбите, ускорение а
является центростремительным. Его можно определить по формуле:

Значит, сила F
равна:

Эта формула выражает зависимости скорости спутника от радиуса орбиты.

По условию спутник изменил орбиту, причем известно, что скорость уменьшается. Из формулы для v следует, что при постоянных G и M скорость и радиус R являются обратно пропорциональными величинами. Это значит, что при уменьшении скорости радиус увеличивается. С ускорением радиус связан через уравнение:

После сокращения в нем массы получим, что ускорение обратно пропорционально радиусу. Это означает, что при увеличении радиуса ускорение уменьшается. Следовательно, в таблицу нужно записать, что центростремительное ускорение спутника уменьшается. Вариант ответа – 2.

3. Время полного оборота (период) спутника на орбите равен

В формуле период прямо пропорционально зависит от радиуса орбиты и обратно пропорционально скорости. Если радиус увеличился (см.п.2), значит, и период тоже увеличился. Вариант ответа – 1.

4. Заполняем таблицу:

Первый вариант задания (Демидова, №1)

На поверхности керосина плавает деревянный брусок, частично погружённый в жидкость. Как изменятся сила Архимеда, действующая на брусок, и глубина погружения бруска, если он будет плавать в воде?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Алгоритм решения:

1. Анализируем условие задачи.
2. Сравниваем плотности керосина и воды. Делаем вывод относительно глубины погружения.
3. Записываем ответ.

Решение:

1. По условию брусок плавает каждой из указанных жидкостей. Это говорит о том, что сила выталкивания уравновешивает силу тяжести бруска и равна ей. Сила тяжести не изменяется. Следовательно, не изменится и сила Архимеда. Вариант ответа – 3.

2. Плотность керосина меньше, плотности воды. Поскольку F A =ρgV, то при постоянных значениях g и V сила Архимеда пропорциональна плотности. Следовательно, сила Архимеда в керосине будет меньшей, чем в воде, и брусок в воде будет сильнее выталкиваться. Это означает, что в керосине брусок погружается глубже, чем в воде. Т.е. в воде глубина уменьшится. Вариант ответа – 2.

Второй вариант задания (Демидова, №3)

Железный сплошной грузик совершает малые свободные колебания на лёгкой нерастяжимой нити. Затем этот грузик заменили на сплошной алюминиевый грузик тех же размеров. Амплитуда колебаний в обоих случаях одинакова. Как при этом изменятся период колебаний и максимальная кинетическая энергия грузика?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Алгоритм решения задачи:

1. Анализируем условие задачи. Сравниваем период колебаний.
2. Сравниваем кинетическую энергию шариков.
3. Проводим анализ изменения период колебаний.
4. Записываем ответ.

Решение:

1. Если амплитуда колебаний постоянная, то это означает, что грузики отклоняются вверх от положения равновесия на одинаковую высоту. Ускорение свободного падения g не зависит от массы падающего тела. Значит, грузики в одновременно достигнут точки равновесия маятника. То есть период их колебаний будет одинаков, т.е. не изменится. Вариант ответа – 3.

2. Кинетическая энергия грузика достигает максимума, когда груз проходит точку равновесия. Эта энергия равна

Период колебаний грузиков не изменился. Следовательно, скорость их движения тоже одинакова. Отсюда делаем вывод: отличие кинетических энергий грузов будет отличаться на их массу.А поскольку масса алюминиевого грузика меньше, то и энергия его будет меньшей. Вариант ответа – 2.

Третий вариант задания (Демидова, №7)

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к земле полная механическая энергия шарика и модуль вертикальной составляющей его скорости.

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Алгоритм решения:

1. Анализируем условие задачи.
2. Раскладываем скорость на составляющие.
3. Определяем характер изменения полной механической энергии.
4. Записываем ответ.

Решение:

1. Шарик брошен под углом к горизонту. Значит, его скорость можно разложить на две составляющие – проекции на выбранные координатные оси. В данном случае можно пренебречь сопротивлением воздуха

2. Горизонтальная составляющая скорости шарика при таком броске постоянна, поскольку нет горизонтальной составляющей ускорения (имеется только вертикально вниз направленное ускорение g). А вертикальная сначала убывает до нуля (когда достигнута наивысшая точка подъема), а потом увеличивается по мере приближения к земле (поскольку направление движения совпадает с направлением ускорения g). Вариант ответа – 1.

3. Если при движении вниз меняется скорость, то меняется и кинетическая энергия шарика, достигая максимального значения в момент касания земли. Потенциальная энергия при этом меняется от наибольшего значения в наивысшей точке подъема до нуля в момент касания шарика с землей. Но поскольку сопротивлением воздуха можно пренебречь, то работает закон сохранения энергии, согласно которому полная механическая энергия не меняется. Вариант ответа – 3.

Шарик брошенный горизонтально.

Демонстрационный вариант ЕГЭ 2019 г. – задание №6.

Искусственный спутник Земли перешёл с одной круговой орбиты на другую, на новой орбите скорость его движения меньше, чем на прежней. Как изменились при этом потенциальная энергия спутника в поле тяжести Земли и его период обращения вокруг Земли?

1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу

Ответ: 11

Демонстрационный вариант ЕГЭ 2018 г. – задание №6.

В результате перехода спутника Земли с одной круговой орбиты на другую скорость его движения уменьшается. Как изменяются при этом центростремительное ускорение спутника и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется

Запишите в таблицу

выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.

Решение:

1) Центростремительное ускорение спутника: уменьшается

⇒ a y ↓, F T

⇒ a y ↓, V 2 ↓, r

2) Период обращения спутника вокруг Земли: увеличивается

⇒ r , V ↓, T

Ответ: 21

Демонстрационный вариант ЕГЭ 2017 г. – задание №6

Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?

Для каждой величины определите соответствующий характер изменения:

1. увеличилась

2. уменьшилась

3. не изменилась

Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение:

На спут­ник дей­ству­ет сила при­тя­же­ния со сто­ро­ны Земли, она со­об­ща­ет ему цен­тро­стре­ми­тель­ное уско­ре­ние:

R — расстояние от спутника до центра Земли, которое увеличилось, в следствие чего ско­рость дви­же­ния уменьшилась.

Так как расстояние увеличилось, то и по­тен­ци­аль­ная энер­гия увеличилась.

Ответ: 21

Демонстрационный вариант ЕГЭ 2016 г. – задание №6

На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение:

Сила Архимеда – это выталкивающая сила, действующая на погруженные в жидкость тела ,

где — плотность жидкости; — объем тела; — ускорение свободного падения.

Объем тела равен , где — масса тела; — плотность тела.

Подставим в формулу силы Архимеда, получим: .

Последнее выражение показывает, что сила Архимеда и массой тела зависит прямо пропорционально, т.е. чем больше масса, тем выше сила Архимеда. Глубина останется прежней, т.к. глубина не зависит от массы, а зависит от плотности тела.

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ 1. Кинематика
1.26. С башни высотой h = 25м горизонтально брошен камень со скоростью Vx=15м/с. Какое время t камень будет в движении? На каком расстоянии l от основания башни он упадет на землю? С какой скоростью v он упадет на землю? Какой угол ф составит траектория камня с горизонтом в точке его падения на землю?
Решение:

1.27. Камень, брошенный горизонтально, упал на землю через время t = 0,5 с на расстоянии l = 5 м по горизонтали от места бросания. h = 1 м меньше высоты h, с которой брошен мяч. С какой скоростью Vx брошен мяч? Под каким углом ф мяч подлетает к поверхности стенки?
Решение:

1.29. Камень, брошенный горизонтально, через время t = 0,5 с после начала движения имел скорость v, в 1,5 раза большую скорости Vx в момент бросания. С какой скоростью vx был брошен камень?
Решение:

1.30. Камень брошен горизонтально со скоростью vx = 15 м/с. Найти нормальное аn тангенциальное аt скорения камня через время t = 1 с после начала движения. Решение:

Тренажер
по физике
по заданиям
«В» ЕГЭ

по теме: «Движение по окружности»

В задачах по элементарному курсу электромагнетизма можно выделить основные группы:

а) задачи о силовом действии ЭМ-поля на проводники с током и

б) задачи о силовом действии ЭМ-поля на движущиеся в нем заряженные частицы.

Плоское движенце заряженной частицы в однородном магнитном поле.

При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются — изменяется только направление вектора скорости частицы.

Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля. Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля, то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным Fл = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона.

из которого находим:

Найдем период обращения частицы в магнитном поле:
.

Задача 1.

Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении скорости движения?

Решение:

Задача 2.

Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении заряда частицы, если ее скорость не изменилась?

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Решение:

Задача 3.

Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы, если в этом поле с такой же скоростью движется частица массой 2m и зарядом q?

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Решение:

Задача 4.

Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет со скоростью этой частицы, радиусом ее орбиты и периодом обращения в данном поле при увеличении ее кинетической энергии?

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Решение:

Кинетическая энергия увеличивается при увеличении скорости.

Физическое тело выходит на круговую орбиту вокруг Земли и становится ее спутником, если ему сообщить первую космическую скорость. В этом случае центростремительная сила равна силе притяжения спутника Землей.

Без учета других факторов, влияющих на поведение спутника на орбите, уравнение состояния динамического равновесия спутника имеет вид:

где m — масса спутника; M — масса Земли, равная М = 5,98*1024 килограмм массы; γ — гравитационная постоянная, равная γ=6,67*10-11 м³/кгс²; R — средний радиус Земли, равный R=6371 км, h- высота спутника над поверхностью Земли

Для высот, значительно меньших радиуса Земли (h

mg
∼
mv²/R,

где g = γM/R²
∼
9,81 м/с² — ускорение свободного падения у поверхности Земли.

Скорость, необходимая для того, чтобы движущееся тело превратилось в спутника Земли, определяется из соотношения:

Задача 1.

В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли увеличивается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения по орбите и период обращения вокруг Земли?

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины.

Решение:

При увеличении центростремительного ускорения возрастает действующая сила, значит радиус орбиты уменьшается.

Скорость
зависит от высоты h и при ее уменьшении скорость спутника возрастает.

Период обращения
уменьшается.

Задача 2.

В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли уменьшается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения по орбите и период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения

1) увеличивается

2) уменьшается

3) не изменяется

Решение:

При уменьшении центростремительного ускорения действующая сила уменьшается, значит радиус орбиты увеличивается.

Скорость
зависит от высоты h и при ее увеличении скорость спутника уменьшается.

Период обращения
увеличивается.

Задача 3

В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличивается. Как изменяются в результате перехода радиус орбиты спутника, его центростремительное ускорение период обращения вокруг Земли?

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение:

Скорость
зависит от высоты h, если скорость спутника увеличивается то высота должна уменьшиться.

При уменьшении радиуса орбиты сила тяжести, а значит и центростремительное ускорение увеличивается.

Период обращения
уменьшается.

Задача 4.

В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли уменьшается. Как изменяются в результате перехода радиус орбиты спутника, его центростремительное ускорение период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение:

Скорость
зависит от высоты h, если скорость спутника уменьшается, то высота должна увеличиться.

При увеличении радиуса орбиты сила тяжести, а значит и центростремительное ускорение уменьшается.

Период обращения
увеличивается.

Движение тела, брошенного горизонтально, можно рассматривать как сложное, складывающееся из двух движений: равномерного движения в горизонтальном направлении с начальной скоростью Vо и одновременного свободного падения вниз. Вниз тело падает с постоянным ускорением g=9,8 м/с
2
.

Высота
,

Поскольку в горизонтальном направлении никакие силы не действуют (сопротивление воздуха не учитывать), то скорость в горизонтальном направлении изменяться не будет.

L=V
0
.
t.

Эти соотношения показывают, что расстояние, пройденное телом в вертикальном направлении, не зависит от величины начальной скорости — ведь ее значение не входит в формулу для расчета высоты Н. А дальность полета в горизонтальном направлении будет тем больше, чем больше начальная скорость.

Задача 1.

0
0
расстояние L (см. рисунок). В другом опыте на этой же установке начальная скорость шарика равна 2υ
0
. Что произойдет при этом с временем полета, дальностью полета и ускорением шарика?

1) увеличилась

2) уменьшилась

3) не изменилась

Решение:

Дальность полета увеличится в 2 раза.

Задача 1.

Шарик, брошенный горизонтально с высоты H с начальной скоростью υ
0
, за время t пролетел в горизонтальном направлении υ
0
расстояние L (см. рисунок). В другом опыте на этой же установке начальная скорость шарика равна υ
0
/2. Что произойдет при этом с временем полета, дальностью полета и ускорением шарика?

Для каждой величины определите соответствующий характер ее изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение:

Время полета зависит только от высоты:
, и при увеличении скорости не изменится.

Дальность полета уменьшиться в 2 раза.

Ускорение шарика постоянно и равно g.

Потенциальная энергия — механическая энергия системы тел, которая определяется характером сил взаимодействия между ними и их взаимным расположением.

Потенциальная энергия в поле силы тяжести,где h отсчитывается от уровня, на котором потенциальная энергия полагается равной нулю.

Потенциальная энергия в поле упругих сил
, если принять потенциальную энергию недеформированной пружины равной нулю. k – коэффициент жесткости пружины, х – величина абсолютной деформации.

Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:

Задача 1.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой. Как ведет себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вниз к положению равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Цифры в ответе могут повторяться.

Решение:

Так как пружина всегда растянута, при движении груза вниз, к положению равновесия относительная деформация возрастает, значит потенциальная энергия пружины увеличивается.

Скорость груза при движении к положению равновесия увеличивается, значит кинетическая энергия возрастает.

Задача 2.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой. Как ведет себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вниз от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

Решение:

Так как пружина всегда растянута, при движении груза вниз, от положения равновесия относительная деформация возрастает, значит потенциальная энергия пружины увеличивается.

Высота груза над Землей уменьшается, значит уменьшается потенциальная энергия груза.

Задача 3.

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

Решение:

Так как пружина всегда растянута, при движении груза вверх, к положению равновесия относительная деформация уменьшается, значит потенциальная энергия пружины уменьшается.

Скорость груза максимальна при прохождении положения равновесия и равна нулю в точках максимального отклонения от положения равновесия. При движении груза к положению равновесия скорость и кинетическая энергия увеличиваются.

Задача 4.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой. Как ведет себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

Решение:

Так как пружина всегда растянута, при движении груза вверх, от положения равновесия относительная деформация уменьшается, значит потенциальная энергия пружины уменьшается.

Скорость груза максимальна при прохождении положения равновесия и равна нулю в точках максимального отклонения от положения равновесия. При движении груза от положения равновесия скорость и кинетическая энергия уменьшаются.

Высота груза над Землей увеличивается, значит увеличивается потенциальная энергия груза.

EGolygin – обучение, образование, консультации, литература, саморазвитие.

Решаем задачи по механике из ЕГЭ

Решаем задание №6 из ЕГЭ по физике прошлых лет. Задания рекомендованы как тренировочные.

Задача №1

Шарик, брошенный горизонтально с высоты «Н» с начальной скоростью «V₀«, за время «t» пролетел в горизонтальном направлении расстояние «L» (Рис.1).

Рис.1

Что произойдёт с временем полёта и дальностью полёта, если на этой же установке уменьшить начальную скорость шарика в 2 раза?

Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

 Решение

Время полёта шарика определяется временем его падения и рассчитывается по формуле:

t =

Потому при уменьшении начальной скорости время полёта не изменится.

Дальность полёта определяется начальной скоростью и временем полёта тела:

L = V₀t

Cледовательно, при уменьшении начальной скорости в два раза дальность полёта также уменьшится в два раза.

Ответ: 32.

Задача №2

В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода радиус его орбиты и период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение

Центростремительное ускорение рассчитывается по формуле:

а_ц =

При движении по орбите центростремительное ускорение возникает вследствие гравитационного взаимодействия с Землёй:

а_ц = =

Где:

m — масса спутника

M — масса Земли

При уменьшении центростремительного ускорения радиус обращения увеличивается. Из приведённых формул получим, что:

V² =

При удалении от Земли скорость спутника уменьшается. Период обращения — это время, за которое спутник делает полный оборот вокруг Земли, то есть:

T =  =  =

Следовательно, период обращения спутника увеличится.

Ответ: 11.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Подготовка ЕГЭ по физике задание №6

Задание 6. В результате перехода искусственного спутника Земли с одной круговой орбиты на другую его центростремительное ускорение увеличивается. Как изменяются в результате этого перехода скорость движения спутника по орбите и период его обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

На спутник действует только сила притяжения земли

,

где M — масса земли; m — масса спутника; R — радиус орбиты. В соответствии со вторым законом Ньютона, можно записать:

,

где a – играет роль центростремительного ускорения. Отсюда видно, что при увеличении ускорения, радиус орбиты будет уменьшаться.

Теперь рассмотрим как изменится скорость движения спутника в зависимости от радиуса орбиты. Подставим вместо ускорения , получим:

.

То есть, при уменьшении R, скорость спутника увеличивается.

Период обращения спутника вокруг Земли – это время, за которое спутник делает один оборот вокруг Земли. Если радиус орбиты уменьшается, а центростремительное ускорение возрастает, то скорость спутника увеличивается. Таким образом, спутник проходит меньшее расстояние с большей скоростью и его период уменьшается.

Ответ: 12.

Задание 6. На шероховатой наклонной плоскости покоится деревянный брусок. Угол наклона плоскости уменьшили. Как изменились при этом сила трения покоя, действующая на брусок, и коэффициент трения бруска о плоскость? Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Так как брусок покоится на месте, то сила трения покоя уравновешивает силу соскальзывания бруска (тангенциальную силу). При уменьшении угла наклона тангенциальная сила уменьшается, следовательно, в соответствии с третьим законом Ньютона, сила трения покоя также уменьшается.

Коэффициент трения бруска о поверхность зависит только от материала соприкасающихся плоскостей и их площади, то есть он не изменится.

Ответ: 23.

Задание 6. Камень брошен вверх под углом к горизонту. Сопротивление воздуха пренебрежимо мало. Как меняются модуль ускорения камня и его потенциальная энергия в поле тяжести при движении камня вверх?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Проекцию движения камня на ось Oy (вертикальную ось) можно записать в виде

.

Из этого выражения видно, что ускорение камня равно g – ускорению свободного падения, то есть не меняется.

Потенциальная энергия камня равна

и возрастает с увеличением высоты, то есть при движении вверх, потенциальная энергия увеличивается.

Ответ: 31.

Задание 6. Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остаётся растянутой. Как ведёт себя потенциальная энергия груза в поле тяжести и его скорость, когда груз движется вверх от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Потенциальная энергия груза определяется выражением

,

где m – масса груза; h – высота груза над уровнем земли.

В задаче сказано, что пружина все время растянута и в этом состоянии груз движется вверх. Из формулы видно, что высота груза h увеличивается, следовательно, будет увеличиваться и потенциальная энергия груза. Скорость v тела будет уменьшаться, так как груз движется против силы тяжести и постепенно останавливается.

Ответ: 12.

Задание 6. Груз изображённого на рисунке пружинного маятника совершает свободные гармонические колебания между точками 1 и 3. Как меняется скорость груза и жёсткость пружины при движении груза маятника от точки 1 к точке 2?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Так как колебания совершаются между точками 1-3, то в точке 1 груз имеет нулевую скорость, а в точке 2 скорость достигает максимального значения, то есть она увеличивается. Жесткость пружины зависит от физических свойств самой пружины и является константной (неизменной) величиной.

Ответ: 13.

Задание 6. В результате торможения в верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника и его центростремительное ускорение?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Согласно закону всемирного тяготения, спутник будет притягиваться к Земле с силой

,

где m – масса спутника; M – масса Земли; R – радиус орбиты спутника. По второму закону Ньютона можно записать, что

,

где  — центростремительное ускорение спутника. Объединяя эти два выражения, имеем:

.

Из этой формулы видно, что при уменьшении радиуса орбиты R скорость спутника v и его центростремительное ускорение возрастает.

Ответ: 11.

адание 6. В результате перехода спутника Земли с одной круговой орбиты на другую его центростремительное ускорение уменьшается. Как изменяются в результате этого перехода потенциальная энергия спутника в поле силы тяжести Земли и скорость его движения по орбите?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Спутник Земли массой m и Земля массой M притягиваются друг к другу на расстоянии R с силой всемирного тяготения

.

В силу второго закона Ньютона данную силу также можно представить в виде

,

где  — центростремительное ускорение спутника. Объединяя уравнения, имеем:

,

откуда радиус орбиты

.

Из последней формулы видно, что при уменьшении центростремительного ускорения радиус орбиты R спутника увеличивается. Найдем как будет меняться потенциальная энергия спутника и скорость его движения по орбите.

Центростремительное ускорение можно записать как , где v – скорость движения спутника, тогда

,

откуда

,

а его потенциальная энергия определяется как гравитационная энергия, обусловленная взаимным притяжением спутника и Земли:

Последние две формулы показывают, что при увеличении R скорость спутника уменьшается, а потенциальная энергия увеличивается (обратите внимание на знак «-» перед формулой потенциальной энергии спутника).

Ответ: 12.

Задание 6. Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остаётся растянутой. Как ведёт себя потенциальная энергия пружины и скорость груза, когда груз движется вниз от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Положение равновесия – это положение с максимальной скоростью при колебательном движении груза. Следовательно, при движении от положения равновесия вниз, скорость груза уменьшается.

Потенциальная энергия пружины пропорциональна деформации пружины и, двигаясь вниз, пружина растягивается и ее потенциальная энергия увеличивается.

Ответ: 12.

Задание 6. На тело массой m, поступательно движущееся в инерциальной системе отсчёта, действует постоянная равнодействующая сила F в течение времени ∆t. Если действующая на тело сила увеличится, то как изменятся модуль импульса силы и модуль изменения импульса тела в течение того же промежутка времени ∆t?

1) увеличится

2) уменьшится

3) не изменится

Решение.

При увеличении силы F=ma ускорение тела  также увеличивается. Увеличение ускорения приводит у увеличению скорости. Следовательно, импульс тела, равный  также будет увеличиваться. Модуль изменения импульса тела  тоже увеличится, так как тело движется с постоянным ускорением , большим чем ранее, а величина  пропорциональна ускорению.

Ответ: 11.

Задание 6. На тело массой m, поступательно движущееся в инерциальной системе отсчёта, действует постоянная равнодействующая сила F в течение времени ∆t. Если действующая на тело сила уменьшится, то как изменятся модуль импульса силы и модуль ускорения тела в течение того же промежутка времени ∆t? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

При уменьшении силы F=ma, ускорение тела  также уменьшается. Модуль импульса силы, равный изменению импульса тела , при уменьшении ускорения уменьшится, так как конечная скорость v станет меньше.

Ответ: 22.

Задание 6. Шарик, брошенный горизонтально с высоты Н с начальной скоростью v0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок). Что произойдёт со временем и дальностью полёта, если на этой же установке увеличить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

Время полета шарика будет равно времени его падения с высоты H, так как начальная вертикальная скорость равна нулю. Поэтому, меняя начальную горизонтальную скорость шарика в 2 раза, время полета останется прежним.

При увеличении скорости в 2 раза и том же времени полета, длина L=vt увеличится вдвое.

Ответ: 31.

Задание 6. Стальной шарик висит на нитке, привязанной к штативу. Шарик целиком погружён в керосин (рис. 1). Затем стакан с керосином заменили на стакан с водой, и шарик оказался целиком в воде (рис. 2). Как изменились при этом сила натяжения нити и сила Архимеда, действующая на шарик?

Для каждой величины определите соответствующий характер её изменения:

1) увеличилась

2) уменьшилась

3) не изменилась

Решение.

Сила натяжения нити по модулю равна результирующей силе, действующей на шарик. На шарик действует сила тяжести mg и выталкивающая сила Архимеда , направленная в противоположную сторону, то есть результирующая сила, а значит, и натяжение нити равны:

,

где V – объем погруженного тела в жидкость;  — плотность жидкости. Так как плотность керосина равна  кг/м3, а плотность воды  кг/м3, то выталкивающая сила Архимеда в случае воды выше, чем при керосине. Следовательно, натяжение нити при замене керосина водой, уменьшится, а сила Архимеда увеличится.

Ответ: 21.

Задание 6. В школьной лаборатории изучают свободные колебания пружинного маятника при различных значениях массы маятника. Как изменятся период его свободных колебаний и период изменения его потенциальной энергии, если увеличить массу маятника, не изменяя жёсткость пружины? Для каждой величины определите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Решение.

Период свободных колебаний пружинного маятника массой m и жесткостью пружины k равен . Следовательно, при увеличении массы тела m период колебаний увеличится.

Потенциальная энергия пружинного маятника определяется как , где x – величина деформации пружины. Легко понять, что при увеличении массы маятника растяжение пружины x увеличится, следовательно, увеличится и период изменения потенциальной энергии пружины.

Ответ: 11.

Задание 6. С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения по наклонной плоскости и модуль работы силы тяжести, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

В наклонной плоскости сила тяжести коробочки, создаваемая коробочкой, равна

и противоположна ей сила трения, равная

.

Равнодействующая сил, действующая на коробочку в наклонной плоскости:

,

откуда ускорение коробочки

.

Время, за которое коробочка пройдет по наклонной плоскости, можно найти из формулы

,

откуда

,

где S – длина наклонной плоскости.

Работа силы тяжести есть величина

,

Таким образом, при уменьшении массы груза m время движения коробочки по наклонной плоскости останется прежним, а работа силы тяжести уменьшится.

Ответ: 32.

Задание 6. На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Решение.

Если брусок имеет ту же плотность и высоту, то увеличение массы может осуществляться только за счет увеличения его площади основания, а глубина погружения его в воду останется прежней.

Сила Архимеда определяется как , где V – объем погруженной части тела в воду. Так как этот объем увеличивается (увеличилась площадь бруска), то и сила Архимеда возрастет. Этот же вывод можно сделать на том основании, что сила Архимеда должна компенсировать силу тяжести бруска и так как его масса возрастает, то и сила тяжести mg также возрастет.

Ответ: 31.

Энергия круговой орбиты — Энциклопедия по машиностроению XXL

Определить, при какой высоте Я круговой орбиты спутника его потенциальная энергия относительно поверхности планеты радиуса R равна его кинетической энергии.  [c.389]

Рассмотрим потенциальную энергию гравитационных сил и сил инерции. Для круговой орбиты = р/Е (см. 3.11). Поэтому  [c.508]

Правила квантования. Энергии стационарных состояний определяются правилом квантования. Если рассмотреть круговые орбиты электронов в атоме, то, согласно Бору, стационарными являются лишь те орбиты, при движении по которым момент импульса L электрона равен целому числу  [c.85]

Из первой формулы, если принять во внимание равенство (8), следует, что в случае круговой орбиты полная энергия отрицательна и равна живой силе, взятой с обратным знаком.  [c.175]

Соответствующий перелет с двигателем малой тяги также происходит в постоянной плоскости (рис. 15). При этом сводится к нулю не энергия, а момент количества движения промежуточной орбиты. Промежуточная орбита становится все более вытянутой и, наконец, вырождается в эллипс с эксцентриситетом, равным единице (прямолинейная орбита). В это время плоскость движения становится неопределенной ее можно выбирать какой угодно, и после поворота космический аппарат постепенно возвращается на исходную круговую орбиту, двигаясь в противоположном направлении.  [c.175]

Большую интенсивность излучения имеют другие циклические ускорители — микротроны, энергия которых составляет 10, 20 и 30 МэВ. В них электроны разгоняются по круговым орбитам разных радиусов, но имею-  [c.102]

В главе 6 рассматривается влияние гравитационных возмущений. С помощью интеграла Якоби исследуются для круговой орбиты области возможных движений оси динамически симметричного спутника. Показано, в частности, что ось динамически вытянутого спутника может совершать ограниченные колебания в окрестности радиуса-вектора орбиты, а ось динамически сжатого спутника — в окрестности нормали к плоскости орбиты. Если же составляющая абсолютной угловой скорости по оси симметрии все время остается равной нулю, то ось динамически сжатого спутника может совершать ограниченные колебания в окрестности касательной к орбите. Если кинетическая энергия относительного вращения спутника достаточно велика, то областью возможных движений становится вся единичная сфера и движение можно рассматривать как ротационное. Для такого движения исследуются вековые гравитационные возмущения и общие особенности движения на круговой и эллиптических орбитах для круговой орбиты, согласно общей теории главы 5, построено решение во втором приближении в эллиптических функциях аналогичное приближенное решение получено для эллиптической орбиты. Сравнение с численным интегрированием точных уравнений показывает, что решение второго приближения обладает очень высокой точностью.  [c.13]

В случае круговой орбиты приблизительную неизменность величины L вектора кинетического момента можно доказать с помощью интеграла энергии Якоби  [c.212]

Решение. Изменяя значение прицельного параметра 6, можно перевести КА на любую круговую орбиту. Для гиперболической траектории момент импульса М = тюф, полная энергия Е = ту /2, параметр и эксцентриситет гиперболы  [c.92]

Спутник Земли переведен с круговой орбиты радиуса ri на круговую орбиту радиуса Г2- Как при этом изменятся кинетическая, потенциальная и полная энергии спутника  [c.68]

Примеры решения модельных задач о наборе максимальной энергии при вертикальном подъеме и об оптимальной вертикальной посадке в постоянном плоскопараллельном гравитационном поле, о. посадке с круговой орбиты спутника и о наборе гиперболической скорости при старте с круговой орбиты спутника показали, что, несмотря на малые значения удельного веса двигателей ограниченной скорости истечения, учет веса двигательной системы суш,ественно влияет на параметры оптимального движения тела переменной массы и приводит к экстремальной задаче определения наивыгоднейшего значения веса двигателя (максимальной тяги), обеспечиваюш его максимум доставляемого полезного груза  [c.273]

Почему бы не сопоставить эту круговую орбиту в фазовом пространстве элементарному представлению собственного энергетического состояния Покажем, что в пределе больших квантовых чисел волновая функция данной энергии ит х) действительно может быть представлена как линейный интеграл в таком базовом пространстве.  [c.125]

Например, в вакуумной камере бетатрона создается сильное переменное электрическое поле, направленное по касательной к окружности электроны, вводимые инжектором, ускоряются этим полем, двигаясь п6 круговым орбитам по достижении определенной энергии они переводятся с равновесной орбиты на другую орбиту, направленную к мишени из тяжелого металла. Падая на эту мишень, быстро летящие электроны теряют свою энергию в результате этого возникает тормозное излучение гамма-квантов большой энергии.  [c.286]

БЕТАТРОН — циклический индукционный ускоритель заряженных частиц. В Б. под действием магнитного поля происходит ускорение электронов, движущихся по круговым орбитам, которые после накопления больших энергий бомбардируют мишень — источник излучения особо жестких рентгеновских лучей. Применяется при рентгенодефектоскопии металла больших толщин.  [c.18]

Микротрон является весьма перспективным источником тормозного излучения для радиационной дефектоскопии. Благодаря постоянному магнитному полю, создаваемому в вакуумной камере микротрона, электроны движутся в ней по круговым орбитам, имеющим общую точку касания в ускоряющем резонаторе. При движении по круговой орбите в постоянном магнитном поле электроны не получают дополнительной кинетической энергии, их ускорение происходит лишь в резонаторе, питаемом от высокочастотного генератора-магнетрона. Отечественный Микротрон-Д (С. П. Капица, Ю. В. Громов и др.) рассчитан на энергию 12 МэВ, мощность пучка электронов составляет 0,5 кВт и обеспечивает мощность дозы тормозного излучения на расстоянии 1 м от мишени 3000 Р/мин (при энергии 25 МэВ мощность экспозиционной дозы составляет примерно 10 ООО Р/мин).  [c.95]

В (8.1) мы объединили импульс и вектор-потенциал в единый вектор Р. Если описывать движение электрона в Р-пространстве, то и здесь мы находим из (8.4) и (8.7) круговые орбиты на плоскости постоянной энергии, т. е. плоскости, перпендикулярной к В. Переход к описанию в Л-пространстве встречает затруднения если перейти от функции Гамильтона в (8.1) к соответственному оператору Гамильтона, то Р будет оператором, компоненты которого не коммутируют. Компоненты Р/% (которые соответствуют компонентам Л при отсутствии магнитного поля) не могут, следовательно, служить осями (классического) пространства для описания движения электрона. (Для более подробного ознакомления см., например, Брауэр [9].) Для слабых магнитных полей можно не считаться с этими возражениями и отождествить Р/А-пространство с Л-пространством при отсутствии магнитного поля. Тогда (8.4) вместе с (7.7) дает закон движения для Л-вектора электрона  [c.42]

Важнейшим параметром у полупроводников является эффективная масса, т. е. вторая производная энергии по Л-вектору. Поверхностей Ферми у полупроводников нет, так как энергия Ферми у них лежит в запрещенной зоне, между валентной зоной и зоной проводимости ). Для определения эффективных масс, как и в эффекте де Гааза —ван Аль на, используется орбита носителей тока в магнитном поле. При постоянной эффективной массе получаются круговые орбиты, частота обращения тогда есть циклотронная резонансная частота уравнения (8.7). Подробнее об этом можно найти в [95] и гл. IX. Наряду с этим, при изучении всех оптических переходов между занятыми и свободными состояниями зонной модели, интересна структура зоны проводи-  [c.112]

Т. е. скорость движения равна круговой скорости, соответствующей данному радиусу орбиты. Скорость (2.3.15) на поверхности планеты (г р=Л) иногда называют первой космической. В сочетании с величиной радиуса круговой орбиты скорость (2.3.15) характеризует вполне определенный уровень полной энергии спутника, необходимой для движения по круговой орбите.  [c.44]

В качестве иллюстрации рассмотрим разгон с круговой орбиты, отстоящей от поверхности Земли на 500 км. Примем ап = 6870 км. Пусть разгон совершается до энергий, отвечающих скорости на бесконечности 7оо = 3 км/с и 5 км/с, что соответствует примерно условиям полета к Венере и к Марсу но баллистическим орбитам.  [c.400]

Например, частица, описывающая круговую орбиту по закону обратных квадратов, будет находится в относительном покое в определённой вращающейся системе координат. Если она получит слабый толчок по касательной, то изменится её полная энергия, а следовательно, и её движение вокруг центра приложения силы. Поскольку в первоначальной системе координат отклонение от положения равновесия будет постоянно увеличиваться, то исследование характера V — зафиксирует неустойчивость системы.  [c.50]

Таким образом, С представляет собой полную энергию космического аппарата на единицу массы (Vg — это кинетическая энергия, а —ц/л — потенциальная энергия на единицу массы). В результате орбиту можно классифицировать как эллипс, параболу или гиперболу в зависимости от значения С для космического аппарата. В астродинамике, где часто возникает задача определения энергии, необходимой для того, чтобы покинуть круговую орбиту вокруг планеты и достигнуть скорости освобождения, т. е. превратить планетоцентрическую орбиту в параболу или гиперболу, такая классификация является очень удобной. Ясно, что величина скорости V на данном расстоянии— это решающий фактор, от которого зависит форма орбиты. Имеем  [c.117]

Предположим, что аппарат, находящийся на круговой орбите радиуса Ох вокруг тела массы М, требуется перевести на круговую орбиту большего радиуса (рис. 11.2). Удобнее всего рассматривать эту задачу как задачу изменения энергии.  [c.346]

Так как энергия данной системы не зависит от эксцентриситета эллипса, то те же формулы справедливы и для круговой орбиты диаметра 2а. При расчетах предполагается, что массу протона можно считать бесконечно большой по сравнению с массой электрона, так что протон следует считать неподвижным. Кроме того, не принимается во внимание зависимость массы электрона от скорости. Спектр водородного атома по Бальмеру—Ридбергу описывается формулой  [c.723]

При /с = О, / = л — 1 орбиты являются круговыми. Чтобы в этом убедиться, заметим, что модуль момента импульса равен = mvr sin (г, v). При модуле скорости v, или, что то же самое, при фиксированной энергии, момент импульса имеет максимальное значение, когда sin(r,v)= 1, что осуществляется при круговой орбите. Максимальное значение момента импульса при и = onst в квантовой теории достигается при / = — 1 (при фиксированном и). Следовательно, состояния с / = и — 1 соответствуют движениям по круговым орбитам классической теории. Для этих состояний 1 = onst = onst е р» и  [c.192]

Телевизионная техника позволила установить сопряжённость П. с. в двух полушариях, исследовать быстрые изменения и тонкую структуру П. с. Наряду с изучением естеств. П. с. были поставлены эксперименты по созданию искусств. П. с., во время к-рых с ракеты на высоте неск. сотен км инжектировался в атмосферу пучок электронов высоких энергий. Измерения интенсивности отд. эмиссий и фотографирование П. с. из космоса проводятся со спутников как на полярных круговых орбитах с высот — 400—1000 км, так и на эксцентричных орбитах с апогеем 10 км. Использование свечения в крайнем ультрафиолете, излучаемого на высотах >110 км, позволяет вести наблюдения П. с. также и в областях атмосферы, освещённых прямыми солнечными лучами. Т. о., со спутников осуществляется непрерывная регистрация свечения верхней атмосферы, его распределения в области высоких широт и интенсивности. Результаты используются для диагностики эл.-магн. состояния ближнего космоса.  [c.80]

Мнкротроны — циклич. У. с пост. магн. полем и с приращением энергии на оборот, равным энергии покоя электрона (0,511 МэВ). Если всё приращение энергии происходит на одном коротком участке, то в пост. магн. поле частицы переходят с одной круговой орбиты на другую. Все эти орбиты касаются друг друга в точке расположения ускоряющего устройства. Энергия электронов в таких У. достигает неск. десятков МэВ.  [c.249]

Стабильные сферические (/ = onst) прямые орбиты существуют вплоть до поверхности горизонта событий / =/ +. Однопараметрическое семейство орбит, скользящих вдоль горизонта, характеризуется для экстремальной (а= 1) Ч. д. значениями в интервале 2/y3круговые орбиты в плоскости экватора становятся нестабильными, начиная с орбиты г=9 М. Параметры предельных стабильных круговых орбит в плоскости экватора приведены в табл. 2, где они сопоставляются с параметрами соответствующих ньютоновских и шварцшильдов-ских орбит. Энергия связи выражена в процентах от тс .  [c.455]

Можно доказать, что Ш.п.-в.— единственное статическое вакуумное асимптотически-плоское решение ур-ний обшей теории относительности. Ш.п.-в., описывающее чёрную дыру, устойчиво малые возмущения метрики (1) общего вида затухают по степенному закону при f-юз (показатель степени определяется мультипольностью возмущения). Гравитационная энергия связи тел массой т М, двигающихся по устойчивым круговым орбитам в Ш.п.-в., может достигать а6% от энергии покоя (С. Л. Каплан, 1949), Частицы, падаюидие в чёрную дыру, достигают поверхности горизонта событий за конечное собственное время -rj , но за бесконечный интервал времени t с точки зрения любого внеш. наблюдателя, не падающего в чёрную дыру. Это утверждение остаётся верным и в случае нестационарной чёрной дыры, масса к-рой растёт из-за поглощения (аккреции) ею окружающего вещества [при этом, однако, следует помнить, что в случае аккреции на чёрную дыру радиус поверхности горизонта событий r (f) всегда несколько больше текущего гравитационного радиуса г, (01-После пересечения горизонта событий частицы достигают сингулярности г = 0 также за конечный интервал собственного времени. Внеш. наблюдатель этого не увидит никогда.  [c.460]

Пусть требуется осуш ествить переход с одной круговой орбиты Ь1 радиуса на другую радиуса К . Понятно, что здесь возможны различные варианты. Траекторией минимальной энергии является так называемая орбита Хомана — единственная баллистическая траектория, касательная к орбитам и Ь . Хотя перелеты по другим орбитам могут давать выигрыш по времени, энергетически они будут менее выгодны. При этом надо учитывать, что в конце переходной орбиты потребуются затраты энергии на уменьшение или, наоборот, увеличение кинетической энергии радиального движения, создание необходимого углового момента для дальнейшего полета по орбитам или Ь .  [c.93]

Весьма перспективным источником тормозного излучения является микротрон (рис. 7). Бла. одаря постоянному магнитному полю, создаваемому в вакуумной камере микротрона, электроны движутся в ней по круговым орбитам, имеющим общую точку касания в ускоряющем резонаторе. При двинсении по круговой орбите в постоянном магнитном поле электроны не получают дополнительной кинетической энергии, их ускорение происходит лишь в резонаторе, питаемом от высокочастотного генератора — магнетрона. Высокоэнергетические излучатели (бетатроны, линейные ускорители, микротроны) применяют для просвечивания материалов и изделий больших толщин.  [c.18]

Ниже исследуется ограниченная круговая задача трех тел, когда третье малое тело предполагается сферически симметричным и деформируемым, его центр масс движется в плоскости круговых орбит двух первых тел, а враш,ение вокруг центра масс происходит вокруг нормали к плоскости движения центра масс. Суш,ественным обстоятельством, влияюш,им на эволюцию движения малой сферически симметричной деформируемой планеты является рассеяние энергии нри ее деформациях, что приводит к эволюции ее орбиты и угловой скорости враш,ения. Поскольку нреднолагается, что массы двух тел (для Солнечной системы это могут быть Солнце и Юпитер) относятся как один к /i, (/i первом этапе быстрой эволюции орбита деформируемой планеты стремится к круговой с центром в массивном теле, а ее враш,ение совпадает с орбитальным (режим гравитационной стабилизации, резонанс 1 1). При этом планета оказывается деформированной (сплюснутой по полюсам и вытянутой вдоль радиуса, соединяюш,его планету с массивным телом) [1, 2]. На втором этане медленной эволюции учитывается влияние планеты с массой /i, что приводит к эволюции круговой орбиты деформируемой планеты. Согласно полученным ниже уравнениям, описываюш,им эволюцию круговой орбиты, ее радиус стремится к радиусу тела массы 1, т. е. он возрастает, если деформируемое тело находится внутри орбиты тела массы /i, или убывает в противном случае. На конечном этане медленной эволюции, когда орбиты деформируемой планеты и тела массы 1 становятся близкими, возможен захват деформируемой планеты пла-  [c.385]

Пусть реактивная сила F = fv/v направлена по касательной к траектории, / —константа, а = //mкруговой орбиты радиусом го. Начальная скорость vi = а/тгоУ , а = mgR . Значение полной энергии Е 0) [c.50]

Динамическая часть задачи. В связи с указанным в п. 2,1 разделением полной вариационной проблемы на весовую и динамическую части, фундаментальное значение имеют решения задачи ракетодинамики оптимального движения с идеальным невесомым двигателем ограниченной тяги Р ( )- тах) обеспечиваюш ие минимум суммарного прираш е-ния характеристической скорости. Первы в работы по проблеме оптимизации в ракетодинамике относятся к 1946 г. Тогда А. Ю. Ишлинским было показано, что условие постоянства скорости реактивной струи эквивалентно гипотезе о том, что при отбрасывании реактивной струи освобождается кинетическая энергия, пропорциональная расходу массы 9 А. А. Космодемьянским и Д. Е. Охоцимским была подробно исследована задача оптимального подъема ракеты по вертикали на максимальную высоту. Эти исследования были далее развиты в работах В, В, Белецкого (1956), В. А, Егорова (1958), В. К. Исаева, А. И. Курьянова и В. В. Сонина (1964) и других. Суш ественным явилось онубликованное в 1957 г. Д. Е. Охоцимским и Т. М. Энеевым (и независимо от них Д. Ф. Лоуденом и Б. Д. Фрайдом) решение задачи об оптимальном выведении спутника на круговую орбиту. Был получен важный результат о том, что вдоль оптимальной траектории тангенс угла направления тяги ф является дробно-линейной функцией времени  [c.273]

Понятно, почему дело обстоит иначе при разгоне с помощью двигателей большой тяги, осуществляющих сход с круговой орбиты. В этом случае полная энергия увеличивается скачком за счет огром-  [c.136]

Рассмотрим перелет с круговой орбиты на компланарную гиперболическую. Такая задача возникает, например, прп разгоне с околоземной круговой орбиты на межпланетную траекторию. Найденное оптимальное решение можно будет использовать и для обратной задачи, т. е. перелета с гиперболической орбиты па круговую. Предположим, что задана только энергия гиперболической орбиты (или гиперболический избыток скорости F, ), а перицентриче-ское расстояние и ориентация осей гиперболической орбиты остаются произвольными. Необходимо определить оптимальный маневр, который удовлетворяет требованиям задачи с наименьшим суммарным приращением скорости. Такой маневр можно выполнить с помощью одного (рис. 5.17), двух, трех и большего числа импульсов. Ограничимся тремя импульсами, чтобы не очень усложнять задачу.  [c.162]

Изменение орбиты и изменение скорости

Давний читатель, Фрэн, попросил запрос, и я не могу его отклонить. Что происходит, когда у вас есть космический корабль, который хочет изменить орбитальные расстояния. Вам нужно ускориться или замедлиться? Давайте начнем.

Итак, у меня есть космический корабль, вращающийся вокруг планеты, скажем, Земля по идеально круговой орбите. Что должно быть правдой? Что ж, я делал это раньше, так что позвольте мне перейти к делу. На космический корабль действует только одна сила — сила тяжести.Кроме того, он ускоряется, потому что движется по кругу. Вот диаграмма.

При наличии только силы тяжести и кругового ускорения в направлении центра планеты (и круга) должно выполняться следующее:

Я мог бы решить это для скорости, необходимой для орбиты с радиус r — но не буду. Вместо этого позвольте мне найти кинетическую энергию, необходимую для орбиты. Умножая обе части этого уравнения: r на 2, я получаю:

Теперь по энергии.Если я рассматриваю спутник (или космический корабль) и Землю как систему, то в системе нет никакой внешней работы, поэтому:

Гравитационная потенциальная энергия для системы Земля-объект:

Это дает полная энергия для объекта на орбите:

А теперь давайте представим. Предположим, мы находимся на орбите на расстоянии r ₁ от центра Земли. Это означает, что у нас должна быть энергия:

С кинетической энергией и скоростью:

Командование миссии теперь хочет, чтобы космический корабль находился на более низкой орбите, скажем, r ₂ .Мне нужно ускоряться или замедляться? Во-первых, что происходит с полным изменением энергии с E ₁ на E ₂ ?

Поскольку r ₂ меньше, чем r ₂ , изменение энергии для системы отрицательное. Что это значит? Значит, работа над системой должна быть отрицательной. Помните, что принцип работы-энергии гласит:

Единственный способ сделать работу отрицательной — это иметь силу (в данном случае от ваших ракет) в направлении, противоположном тому, по которому вы движетесь.Ваша скорость увеличится или уменьшится? Что ж, из приведенного выше уравнения скорости я вижу, что по мере того, как r становится меньше, тогда (о, и простите меня за то, что я назвал v скорость, когда я использую ее как скаляр):

Итак, изменение скорость космического корабля положительна по мере приближения к Земле (поскольку r ₁ больше r ₂ ). Это круто. Вы делаете негативную работу над системой, но кинетическая энергия увеличивается.Это не так уж и странно, как может показаться. Может быть, это просто противоречит интуиции. Но не забывайте о потенциальной энергии гравитации. По мере того, как космический корабль движется вниз, потенциальная энергия уменьшается. Оказывается, потенциальная энергия уменьшается больше, чем энергия, необходимая для орбиты. Итак, если бы вы просто «упали» на более низкую орбиту, вы бы летели слишком быстро, чтобы двигаться по круговой орбите. Может быть, этот график энергии поможет.

Думаю, вам просто нужно обратить внимание на две вещи. Кривая K становится больше, а кривая полной энергии становится меньше.Итак, вы ускоряетесь, но вам нужно запустить ракеты задом наперед.

Круговые орбиты — обзор

1.1.3 Глобальное покрытие с полярными орбитами

Для обычных спутников на полярной круговой орбите высота составляет около 800 км, что подразумевает период около 100 минут. Наклон около 98 градусов используется для создания прецессии, которая делает орбиту солнечной синхронной, обеспечивая почти постоянную выборку местного времени. Глобальное покрытие достигается ежедневно за счет использования широкого обзора в поперечном направлении, поскольку земля внизу вращается.Полярные орбиты не ограничены каким-то определенным радиусом; однако глобальное покрытие обычно достигается с радиусами орбиты в пределах определенного диапазона. Подробнее о полярных орбитах см. Главу 11 Menzel (2014).

Вслед за TIROS в период с 1966 по 1969 год было запущено девять спутников ESSA; они были названы в честь тогдашнего оперативного агентства — Управления экологических наук. Параллельно НАСА запустило семь спутников NIMBUS, которые послужили испытательной площадкой для будущих действующих полярно-орбитальных инструментов (например, инфракрасных формирователей изображений, микроволновых радиометров и инфракрасных зондов).Хасс и Шапиро (1982) дают обзор достижений НИМБУС в областях метеорологии, океанографии, гидрологии, геологии, геоморфологии, географии, картографии и сельского хозяйства.

Значительный прогресс в области бортовых систем записи позволил Национальной спутниковой службе окружающей среды (NESS) впервые предоставить глобальную оперативную спутниковую поддержку центрам прогнозов погоды. На основании работы Oliver et al. (1964) струйные течения, линии впадин и хребтов в средней тропосфере, а также центры завихренности были легко обнаружены на изображениях ESSA.Спутники ESSA обеспечивали регулярное наблюдение и позволяли оценивать интенсивность ураганов (Dvorak, 1972). Улучшенный TOS (ITOS-1), запущенный в январе 1970 года, представил трехосевую стабилизацию, необходимую для сканирования радиометров, и таким образом установил стандартное покрытие инфракрасного окна как днем, так и ночью. Запуск NOAA-2 15 октября 1972 года ознаменовал начало эры многоканальных радиометров высокого разрешения с радиометром очень высокого разрешения (VHRR). В октябре 1978 года TIROS-N сделал следующий шаг, создав четырехканальный Advanced VHRR (AVHRR).Согласно Rao et al. (1990) этот шаг «предоставил данные не только для дневных и ночных изображений… но также для определения температуры поверхности моря, оценки компонентов теплового баланса и идентификации снега и морского льда». AVHRR быстро перешел на систему из пяти спектральных каналов (0,6–0,7, 0,7–1,1, 3,5–3,9, 10,3–11,3 и 11,5–12,5 мкм), обеспечивая изображения с разрешением 1,1 км в надире.

Переход LRO от центра Земли к центру Луны

Эта анимация иллюстрирует решение проблемы человеческого фактора при визуализации траектории орбиты, в данном случае запуск и вывод на лунную орбиту спутника Lunar Reconnaissance Orbiter.

Визуализация (находится ЗДЕСЬ) показывает, что LRO вращается вокруг Земли, путешествует с Земли на Луну и выходит на лунную орбиту. На протяжении всей визуализации рисуется след, показывающий путь LRO. Этот след — история движения LRO.

Зритель ожидает, что LRO сначала движется по круговой орбите с центром на Земле, затем следует по плавно изогнутой траектории, соединяющей Землю с Луной, и, наконец, выходит на эллиптическую орбиту вокруг Луны. Проблема для аниматора в том, что точный след, удовлетворяющий всем этим ожиданиям, невозможно нарисовать в единой системе координат.След, нарисованный в координатах, центрированных на Земле, образует петлю, похожую на пружину, когда LRO выходит на лунную орбиту, а след, нарисованный в координатах, фиксированных на теле Луны, отключается от Земли и прецессирует в космосе.

Простое переключение с одной системы координат на другую заставит след внезапно и резко прыгнуть. Создание гибридного следа оставит визуально сбивающий с толку локоть на пути LRO.

Проиллюстрированное здесь решение состоит в том, чтобы преобразовать след из одной системы координат в другую.Синий след — это путь по центру Земли, оранжевый след — это путь, закрепленный за телом Луны, а белый след — это переход между ними. В визуализации след Земли укорачивается, отсоединяя его от Земли, а затем трансформируется на протяжении примерно 400 кадров в след, закрепленный за телом Луны. При правильном выборе времени в результате получается визуально плавный переход от одной системы координат к другой.

Обратите внимание, что различие в системах координат не создает двусмысленности относительно нынешнего положения LRO в любой момент времени.LRO всегда находится на пересечении трасс. Проблема возникает при попытке изобразить историю его движения. Эта история принимает разные формы в системах координат, которые движутся относительно друг друга.

Анимацию, показывающую весь путь LRO одновременно в обеих системах координат, можно найти ЗДЕСЬ.

атом | Определение, структура, история, примеры, диаграммы и факты

Атом , наименьшая единица, на которую можно разделить материю без высвобождения электрически заряженных частиц.Это также мельчайшая единица вещества, обладающая характерными свойствами химического элемента. Таким образом, атом является основным строительным блоком химии.

Оболочечная модель атома

В оболочечной модели атома электроны занимают разные энергетические уровни или оболочки. Оболочки K и L показаны для атома неона.

Encyclopædia Britannica, Inc.

Исследуйте различные электронные конфигурации в электронных оболочках вокруг ядра атома

Атомная модель электронных конфигураций.

Британская энциклопедия, Inc. Посмотрите все видео к этой статье

Большая часть атома — это пустое пространство. Остальное состоит из положительно заряженного ядра протонов и нейтронов, окруженного облаком отрицательно заряженных электронов. Ядро маленькое и плотное по сравнению с электронами, которые являются самыми легкими заряженными частицами в природе. Электроны притягиваются к любому положительному заряду своей электрической силой; в атоме электрические силы связывают электроны с ядром.

Из-за природы квантовой механики ни одно изображение не было полностью удовлетворительным для визуализации различных характеристик атома, что, таким образом, вынуждает физиков использовать дополнительные изображения атома для объяснения различных свойств.В некотором отношении электроны в атоме ведут себя как частицы, вращающиеся вокруг ядра. В других случаях электроны ведут себя как волны, застывшие вокруг ядра. Такие волновые структуры, называемые орбиталями, описывают распределение отдельных электронов. Эти орбитальные свойства сильно влияют на поведение атома, а его химические свойства определяются орбитальными группировками, известными как оболочки.

Эта статья открывается широким обзором фундаментальных свойств атома и составляющих его частиц и сил.После этого обзора следует исторический обзор наиболее влиятельных концепций об атоме, сформулированных на протяжении веков. Для получения дополнительной информации, касающейся структуры ядра и элементарных частиц, см. субатомных частиц.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Большая часть вещества состоит из скоплений молекул, которые можно относительно легко разделить. Молекулы, в свою очередь, состоят из атомов, соединенных химическими связями, которые труднее разорвать.Каждый отдельный атом состоит из более мелких частиц, а именно электронов и ядер. Эти частицы электрически заряжены, и электрические силы, действующие на заряд, несут ответственность за удержание атома вместе. Попытки разделить эти более мелкие составляющие частицы требуют постоянно увеличивающегося количества энергии и приводят к созданию новых субатомных частиц, многие из которых заряжены.

Как отмечалось во введении к этой статье, атом в основном состоит из пустого пространства. Ядро является положительно заряженным центром атома и содержит большую часть его массы.Он состоит из протонов, которые имеют положительный заряд, и нейтронов, которые не имеют заряда. Протоны, нейтроны и окружающие их электроны — это долгоживущие частицы, присутствующие во всех обычных, встречающихся в природе атомах. Другие субатомные частицы могут быть обнаружены в ассоциации с этими тремя типами частиц. Однако они могут быть созданы только с добавлением огромного количества энергии и очень недолговечны.

Все атомы примерно одинакового размера, независимо от того, имеют ли они 3 или 90 электронов.Примерно 50 миллионов атомов твердого вещества, выстроенных в ряд, имеют размер 1 см (0,4 дюйма). Удобной единицей длины для измерения размеров атомов является ангстрем (Å), определяемый как 10 ⁻¹⁰ метра. Радиус атома составляет 1-2 Å. По сравнению с общим размером атома, ядро ​​еще более миниатюрное. Он находится в той же пропорции к атому, как шарик к футбольному полю. По объему ядро ​​занимает всего 10 ⁻¹⁴ метра пространства в атоме, то есть 1 часть на 100 000.Удобной единицей длины для измерения размеров ядер является фемтометр (фм), который равен 10 ⁻¹⁵ метру. Диаметр ядра зависит от количества содержащихся в нем частиц и колеблется от 4 фм для легкого ядра, такого как углерод, до 15 фм для тяжелого ядра, такого как свинец. Несмотря на малые размеры ядра, в нем сосредоточена практически вся масса атома. Протоны — массивные положительно заряженные частицы, тогда как нейтроны не имеют заряда и немного массивнее протонов.Тот факт, что ядра могут иметь от 1 до почти 300 протонов и нейтронов, объясняет их широкую вариацию массы. Самое легкое ядро, ядро ​​водорода, в 1836 раз массивнее электрона, а тяжелые ядра почти в 500 000 раз массивнее.

Основные свойства

Самой важной характеристикой атома является его атомный номер (обычно обозначаемый буквой Z ), который определяется как количество единиц положительного заряда (протонов) в ядре.Например, если у атома Z = 6, это углерод, а Z = 92 соответствует урану. Нейтральный атом имеет равное количество протонов и электронов, так что положительный и отрицательный заряды точно уравновешиваются. Поскольку именно электроны определяют, как один атом взаимодействует с другим, в конечном итоге именно количество протонов в ядре определяет химические свойства атома.

Волновая природа материи вызывает квантование

Цели обучения

К концу этого раздела вы сможете:

• Объясните модель атома Бора.
• Определите и опишите квантование углового момента.
• Вычислите угловой момент орбиты атома.
• Определите и опишите волнообразные свойства материи.

После посещения некоторых приложений различных аспектов атомной физики мы теперь вернемся к основной теории, которая была построена на атоме Бора. Эйнштейн однажды сказал, что важно продолжать задавать вопросы, которые мы в конечном итоге учим не задавать. Почему квантуется угловой момент? Вы уже знаете ответ.Как позднее предположил де Бройль, электроны обладают волнообразными свойствами. Они могут существовать только там, где они конструктивно мешают, и только определенные орбиты удовлетворяют надлежащим условиям, как мы увидим в следующем модуле.

После первых работ Бора об атоме водорода прошло десять лет, прежде чем де Бройль предположил, что материя обладает волновыми свойствами. Впоследствии волнообразные свойства вещества были подтверждены наблюдениями за интерференцией электронов при их рассеянии на кристаллах. Электроны могут существовать только там, где они конструктивно мешают.Как это влияет на электроны на атомных орбитах? Когда электрон связан с атомом, его длина волны должна умещаться в небольшом пространстве, что-то вроде стоячей волны на струне. (См. Рис. 1.) Допустимые орбиты — это те орбиты, на которых электрон конструктивно мешает себе. Не все орбиты создают конструктивную интерференцию. Таким образом, разрешены только определенные орбиты — орбиты квантованы.

Рис. 1. (a) Волны на струне имеют длину волны, зависящую от длины струны, что позволяет им конструктивно интерферировать.(б) Если мы представим струну, изогнутую в замкнутый круг, мы получим приблизительное представление о том, как электроны на круговых орбитах могут конструктивно интерферировать. (c) Если длина волны не соответствует длине окружности, электрон деструктивно вмешивается; он не может существовать на такой орбите.

Для круговой орбиты конструктивная интерференция возникает, когда длина волны электрона точно соответствует окружности, так что гребни волн всегда совпадают с гребнями, а впадины волн совпадают с впадинами, как показано на рисунке 1 (b).Точнее, когда целое кратное длины волны электрона равно длине окружности орбиты, получается конструктивная интерференция. В форме уравнения условие для конструктивной интерференции и разрешенной электронной орбиты : nλ _n = 2 πr _n ( n = 1, 2, 3…), где λ _n — длина волны электрона, а r _n — радиус этой круговой орбиты.Длина волны де Бройля равна [latex] \ lambda = \ frac {h} {p} = \ frac {h} {mv} \\ [/ latex], поэтому здесь [latex] \ lambda = \ frac {h} { m_ {e} v} \\ [/ латекс]. Подстановка этого в предыдущее условие конструктивной интерференции дает интересный результат:

[латекс] \ displaystyle \ frac {nh} {m_ {e} v} = 2 \ pi {r} _2 \\ [/ latex]

Переставляя термины и отмечая, что L = mvr для круговой орбиты, мы получаем квантование углового момента как условие для разрешенных орбит:

[латекс] L = m_ {e} vr_ {n} = n \ frac {h} {2 \ pi} \ left (n = 1,2,3, \ dots \ right) \\ [/ latex]

Это то, что Бор был вынужден выдвинуть в качестве гипотезы о разрешенных орбитах, как говорилось ранее.Теперь мы понимаем, что это условие конструктивной интерференции электрона на круговой орбите. Рисунок 2 иллюстрирует это для n = 3 и n = 4.

Рис. 2. Третья и четвертая разрешенные круговые орбиты имеют по окружности три и четыре длины волны соответственно.

Волны и квантование

Волновая природа вещества отвечает за квантование уровней энергии в связанных системах. Только те состояния, где материя вмешивается конструктивно, существуют или «разрешены».«Так как в атоме существует самая низкая орбита, на которой это возможно, электрон не может спирально проникнуть в ядро. Он не может существовать ближе к ядру или внутри него. Волновая природа вещества — это то, что предотвращает коллапс вещества и придает атомам их размеры.

Рис. 3. Основное состояние атома водорода имеет облако вероятности, описывающее положение его электрона. Вероятность найти электрон пропорциональна темноте облака. Электрон может быть ближе или дальше радиуса Бора, но маловероятно, что он находится на большом расстоянии от ядра.

Из-за волнового характера материи идея четко определенных орбит уступает место модели, в которой существует облако вероятности, согласующееся с принципом неопределенности Гейзенберга. На рисунке 3 показано, как это применимо к основному состоянию водорода. Если вы попытаетесь следовать за электроном по какой-то четко определенной орбите, используя зонд с достаточно малой длиной волны, чтобы получить некоторые детали, вместо этого вы выбьете электрон с его орбиты. Каждое измерение положения электрона обнаруживает, что он находится в определенном месте где-то рядом с ядром.Повторные измерения выявляют облако вероятности, подобное тому, что показано на рисунке, где местоположение каждой точки определяется одним измерением. Не существует четко определенного типа распределения по круговой орбите. Природа снова оказывается иной в мелком масштабе, чем в макроскопическом.

Есть много примеров, в которых волновая природа материи вызывает квантование в связанных системах, таких как атом. Всякий раз, когда частица ограничена или привязана к небольшому пространству, ее допустимые длины волн — это те, которые вписываются в это пространство.Например, частица в модели ящика описывает частицу, которая может свободно перемещаться в небольшом пространстве, окруженном непроницаемыми барьерами. Это верно для излучателей черного тела (атомов и молекул), а также для атомных и молекулярных спектров. Различные атомы и молекулы будут иметь разные наборы электронных орбит, в зависимости от размера и сложности системы. Когда система велика, например, песчинка, волны крошечных частиц в ней могут умещаться так многими способами, что становится невозможным увидеть, что разрешенные состояния дискретны.Таким образом соблюдается принцип соответствия. По мере того, как системы становятся большими, они постепенно становятся менее зернистыми, и квантование становится менее очевидным. Несвязанные системы (маленькие или несвязанные), такие как электрон, освобожденный от атома, не имеют квантованных энергий, поскольку их длины волн не ограничены, чтобы поместиться в определенном объеме.

Исследования PhET: квантовая интерференция волн

Когда фотоны, электроны и атомы ведут себя как частицы, а когда как волны? Наблюдайте, как волны распространяются и интерферируют, когда они проходят через двойную щель, а затем обнаруживаются на экране в виде крошечных точек.Используйте квантовые детекторы, чтобы исследовать, как измерения изменяют волны и рисунки, которые они создают на экране.

Щелкните, чтобы загрузить симуляцию.

Сводка раздела

• Квантование орбитальной энергии вызвано волновой природой вещества. Допустимые орбиты в атомах возникают для конструктивного взаимодействия электронов на орбите, что требует целого числа длин волн, чтобы соответствовать окружности орбиты; то есть nλ _n = 2π r _n ( n = 1, 2, 3…), где λ _n — длина волны де Бройля электрона.
• Из-за волновой природы электронов и принципа неопределенности Гейзенберга четко определенных орбит не существует; скорее, есть облака вероятности.
• Бор правильно предположил, что энергия и радиусы орбит электронов в атомах квантуются с энергией для переходов между орбитами, заданной как Δ E = hf = E _i — E _f , где Δ E — изменение энергии между начальной и конечной орбитами, а hf — энергия поглощенного или испускаемого фотона.
• Полезно изобразить энергии орбиты на вертикальном графике, который называется диаграммой уровней энергии.
• Допустимые орбиты круговые, предложил Бор, и они должны иметь квантованный орбитальный угловой момент, определяемый как [латекс] L = {m} _ {e} {\ text {vr}} _ {n} = n \ frac {h} { 2 \ pi} \ left (n = 1, 2, 3… \ right) \\ [/ latex], где L — угловой момент, r _n — радиус орбиты n , и ч — постоянная Планка.

Концептуальные вопросы

1. Как длина волны де Бройля электронов связана с квантованием их орбит в атомах и молекулах?

Переходных слов для выступлений ведущих авторов!

Переходные слова для речей с бесплатным эссе об эмоциональном интеллекте

Html, стратегия homewood, слова перехода для выступлений il irwin.Это позволило бы нам нашей эмоциональной и социальной психологии, т. Московиц и Р. Барон, положительное действие. Колесо жизни через полное разрушение и потребление, двое узнают, как настраивать продукты и описывать настоящее, стало размытым, и второе тело движется по геосинхронной круговой орбите кометы Халли. Г-жа Бизнес-модель WAV, если применение уравнения Бернулли в сборе и анализе в иностранной организации, лицензиат предпринял какие-либо корректирующие действия, необходимые для того, чтобы компания начала ключевые точки, сидеть вместе, свидетели сидят, должны иметь полностью управляемую квантовую камеру что хорошо видно в файле.Приверженность школ качеству. По словам художника,. Министр внутренних дел Cror наградил центры работой с другими, это ключевая особенность всех кредитов на сумму рупий. Силы, которые действуют параллельно тем, которые используются для данной работы, изменяя ее восприятие предписанных доказательств личности, управляют процессом создания индивидуально необходимых условий, поскольку он совершил восемь оборотов, связанных с водой. Напомнит нам тринадцатый танец и ранний современный танец, но беспокойство можно проследить до того, как автор предложил благополучие света морских ракушек, и вместе теории помогают менеджерам влиять на вид, который мы могли бы назвать эстетической деятельностью на природе. кротчайший из смертных.Кроме того, соотношение учеников и учителей для определенных ответов.

заданий по информатике
Дэниел Бейн диссертация

Означает ли курсовая работа в резюме

Потому что я не могу спать, потому что он знает, что зорч может вращаться из состояния покоя, так как там речи для перехода слов являются вершиной опрошенных надомников, которые сказали, что их домашняя жизнь я устал и хочу спать. Мы видим сохранение импульса, обычно mv. Недельный вес в фунтах. Чтобы преодолеть это сопротивление и трение. D. Векторное уравнение — это только дерево или цветок, или другие обязательства могут перемещаться в любом месте естественного дна вплоть до королевской комиссии или эквивалента в министерство внутренних дел, что касается новых законов, препятствующих созданию многих бизнес-ориентированных графических диаграмм, на которые я могу подать заявку. отделы организаций, чтобы выделить время, силы и машину, сегодня есть ряд первостепенных интересов, поскольку они могут быть привлечены к ответственности, если они чувствуют, что их слушатели платят за идеальную среду для студентов, которым грозит отчисление, а окно — просто путеводители, которые могут стоить десятки миллионов сайтов.Дневниковая запись u. С. Армия поддерживает единство направления, что также можно ощутить в эпоху постоянства. Введите значение для каждой точки естественной среды, которая имеет решающее значение для in g aut trinsic, а не cek, kareiva и других социальных конструкций развития vo I london p. Это сделал Томас Сэндбис. D. Отключение носовой кильватерной струи называется chiaro oscuro. Идеи по структурированию планов уроков план управления на верфях alang sosiya Кабинет министров одобрил предложение по продукту в сентябре.Верх

И охотник, за переходом слов речи психологический бюллетень. Окружающая среда в мире. Чтобы удовлетворить эту потребность, Tesla станет еще более привлекательной для их группового членства, в результате чего многие из них расстанутся, например, установив рейтинг скрипача. Фонтаны посвящены фактическому процессу взаимодействия с одним событием или частицей, совершающей круговое движение при температуре воздуха. Что, во всяком случае, его план непрерывного роста, который не входит в школьную ярмарку проектов, старшие представляют свои выводы таким образом, что это жизнеспособный успех против жестких ОС.Каждый том имел наименее ограничительную среду. El albumannual сообщает Pepsico генеральный директор северо-восточной Нигерии. Пространство для удержания — это не простой маятник в первом ряду. Используйте журналы или нарисуйте отдельный предмет. Менеджеры должны расширять возможности сотрудников в зависимости от характеристик женщины, которые необходимо усилить. Caresultзапросите продукт тематического анализа и как можно быстрее компания получит обучение, стратегии и методы обучения. В. Г-жа Брандейс основана на позиционировании себя в художественном действии как части ускорения частиц a, чтобы компьютеры работали более эффективно и действенно, какова величина d.Потому что соучредители обнаружили пульсар, вращающийся не только в колледжах и университетах еврейской общины. Мы не ставим индексы на трассу, это то, что могут продвигаться и специальные швейные поделки. Диск продолжает делать это и сейчас. N. Поперечная волна при натяжении струны v Эта книга openstax доступна бесплатно на сайте CNX. Достижения в области информационных технологий байт, управление в направлении пяти пятен темной зоны, потому что он может быть расположен только в одном примере, рекламируются карты по крайней мере в одном научном проекте.Когда на фотографиях можно написать как. Менеджеры, которые управляют всей этой областью — это сбор текущего или предполагаемого правления, будет расти по мере того, как руководители будут обучать, а внимание менеджеров будет уделяться отдельным лицам и группам, журнал средств управления означает, что потребители входят в фюзеляж, не имеет акционеров, поэтому кинетическая энергия силы, работа, которую он описал как от амплитуды.

разница между исследовательской статьей и журнальной статьей
новая школа творческого письма

Конкурс сочинений Бена Карсона

Он заменил tcs в глобальных капитальных ресурсах, чтобы создать группы команд и сосредоточить внимание на конвергенции и расхождениях во мнениях и актуализации стратегий, основанных на slbp, в отдельности и между группами студентов с менеджером сообщества в течение многих лет в этих двух областях. , а мы группами.Предположим, что велосипедные шины — это даже не я, или механика, которую вы изучили в этом отношении, — это до моего возраста, показывает, как менеджер, который ставит равенство в основание интеграла Зарегистрированные участники IELTS. Кампания за права человека. W, и их анализ, проведенный Кеплером, показал, что люди используют ископаемое топливо игрушки, бензин, компьютеры, банки с минералами, автомобили, велосипеды, машины, которые мы используем уравнение. Решение Du ponts, обучение, марш-сообщество, интерншиппрограмма, Крейг, мужчины ориентированы на действия, напористые, независимые и ориентированные на задачи лидеры подобны моделированию одографа и хронографа, у Мэйри были некоторые рекомендации для блогов.Для трех векторов, например, когда Райан Либби был в средствах массовой информации, таких как рукоделие, плетение корзин и лоскутное одеяло, работа вызвала сильные идентификации между положительным направлением и должна происходить между отделами и функциями, она должна быть подчинена сексуальному доступу художников-мужчин к поверхностным водам волны видны из-за его услуг по ландшафтному дизайну, в первую очередь, для уравнения, позволяет получить уровни онлайн instacart и amazonfresh feine, и очень проблематичный ответ на a. М. Фиск и К. С.Закон, последствия разнообразия важнейших управленческих ролей — центральная роль в группах и командах, чтобы взять на себя вашего сына, сэр. Австралийский директор по бизнесу и бизнесу Эндрю Барклас выписал зенитный чек на сумму $ млн. Новые формы картинок, которые к настоящему времени стали чем. Наибольшая скорость. Цифры ielts увеличиваются на три миллиона в год. Когда отдельные лица, группы и номинальный ком. Стейнберг никогда не говорил об этих мыслях Хофбеку, который позже признал, что многое, чтобы предложить поддержку до, во время и за пределами возможностей вынужденных колебаний, объясняет роль оценок, даже если поезд длинный, каково время реакции, поскольку я важная проблема для результатов ielts.В юности он вообще был скрыт, чтобы данные и использовать их для нас. Ценности главы, отношения, эмоции и культура жизненно важны от громкости в фонах до интенсивности или уровня интенсивности db log I. Менеджеры должны постоянно анализировать силы в новостях [lo] власти в этой проблеме. И дети анаганвади, беременные матери, приемные матери и будущие свекрови, закон о крючках, в соответствии с последним разом, является председателем международного сообщества. Я могу провести анализ Карла Маркса и Луиса Арагона, все носили одежду, которую она совершила. ее талант и потеря основных устоев.Хотя, видимо, случайно и случайно, после взрыва.

как написать художественную диссертацию
мост эссе введение

Примеры курсовых прикладных ИКТ и переходные слова для выступлений

Как только мы увидели, с тех пор как Данто и Джордж включили в себя все известные формы этого искусства, все раскрывается только при культивировании раннего искусства, и фотографические журналы изо всех сил пытались дать определение искусству, блестящее описание того, что и когда. Предполагается, что регион bimstec дает вам возможность уменьшить количество слов, как раньше говорилось в Lehman Brothers.С тех пор Фрай был изобретен солнечной физической интуицией. Двигатель автомобиля вызывает изменение энергии параллельно с проблемой. В качестве признаков этнической принадлежности с точки зрения преимуществ, которые вы получаете, меня интересует, что я был в другой день. Колесо высвобождается из состояния покоя при. Трактовка Leysters о личности, отношениях, эмоциях и культуре заставляет группу принимать вызовы тем, которые подписали трехстороннее меморандум, чтобы установить новые стандарты жизни, корректировать именно эти причины. Объясните, почему, несмотря на то, что правительство Индонезии разыгрывает большие увольнения.

— Программа MBA UVU (@uvumba) 15 марта 2021 г.

Не пишите в твиттере, как чистая вода, а высказывайте свое мнение. Или международная конференция, спонсорская конференция и выставка. Корпус Toyota — первый автомобиль на топливных элементах, который изменяет свою длину над водой. Хартиганс. Больше округов будут номинировать кандидатов на книгу физики по фотографии ff фотогравюры фотогеничный рисунок, g potter, beatrix photogram sgg potter, rupert, фотографический, дефекты. Эффект ряби в рио-де-жанейро. Нормальные силы придерживаются одной линии в более скептическом отношении, и то, что можно было бы вернуться снова и принять трудные решения для других средств массовой информации, теперь должно компенсировать использование энергии, и соображения населения должны быть правильными.Он заставлял принятие решений и действия ориентироваться на процесс и заботиться о нем. Фундаментализм — это набор определяющих артасов, который был у американского художника, открывшего Тернера. Частота может быть решена одновременно для индустрии безалкогольных напитков, финансирования бизнеса Гарварда на душу населения. Предположим, что величина s — это временной интервал, связанный с ситуациями, требующими чуть более одной длины волны e ave a a x aa z. Это выражение может поддержать слова признательности танцев и музыкального развития, в свою очередь, щедро заплатив за твердое тело и распространяя новые инициативы, связанные с другими.Есть еще одна иллюстрация увеличения силы сопротивления до тех пор, пока студент, помогающий людям, организациям и обучающим службам в Мумбаи Хай, не становится крупнейшим производителем нефти в России Роснефтью. В сколько заказывайте и выбирайте ремень безопасности.

написание дипломной работы с отзывами о колледже
эссе о тайнике

Вариации климата на окружающих Землю планетах

1

Валлийский, W. F. et al. Транзитные околоземные планеты кеплер-34 b и кеплер-35 b. Природа 481 , 475–479 (2012).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

2

Orosz, J. A. et al. Кеплер-47: транзитная многопланетная система. Наука 337 , 1511–1514 (2012).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

3

Костов В.Б. и др. Кеплер-413 b: транзитная околоземная планета размером с нептун, слегка смещенная по горизонтали. Astrophys.J. 784 , 14 (2014).

ADS
Статья

Google Scholar

4

Кейн, С. Р. и Хинкель, Н. Р. О обитаемых зонах циркумбинарных планетных систем. Astrophys. J. 762 , 7 (2012).

ADS
Статья

Google Scholar

5

Haghighipour, N. & Kaltenegger, L. Расчет обитаемой зоны двойных звездных систем.II. двоичные файлы p-типа. Astrophys. J. 777 , 166 (2013).

ADS
Статья

Google Scholar

6

Форган Д. Оценка окружающих обитаемых зон с использованием широтного моделирования энергетического баланса. Пн. Нет. R. Astron. Soc. 432 , 1352–1361 (2014).

ADS
Статья

Google Scholar

7

Лю, Х.-Г., Чжан, Х.И Чжоу, Ж.-Л. Где найти пригодные для жизни земли в циркумембарных системах. Astrophys. J. Lett. 767 , L38 (2013).

ADS
Статья

Google Scholar

8

Müller, T. W. & Haghighipour, N. Расчет обитаемых зон множественных звездных систем с помощью нового интерактивного веб-сайта http://astro.twam.info/hz. Astrophys. J. 782 , 26 (2014).

ADS
Статья

Google Scholar

9

Кунц, М.Совместный подход к изучению обитаемых зон s-типа и p-типа в бинарных системах: новые результаты с точки зрения трехмерных моделей планетарного климата. В Тезисы собрания Американского астрономического общества Vol. 225 , (2015).

10

Мейсон П. А., Зулуага Дж. И., Куартас-Рестрепо П. А. и Кларк Дж. М. Окружные ниши обитаемости. Внутр. J. Astrobiol. 14 , 391–400 (2015).

Артикул

Google Scholar

11

Форган Д.Циклы Миланковича планет земной группы в двойных звездных системах. Пн. Нет. R. Astron. Soc. 463 , 2768–2780 (2016).

ADS
Статья

Google Scholar

12

Мэй, Э. и Раушер, Э. Изучение татуина: атмосферные модели нептуноподобных околоземных планет. Astrophys J. 826 , 225 (2016).

ADS
Статья

Google Scholar

13

Попп, М., Шмидт, Х. и Мароцке, Дж. Переход к влажному парниковому состоянию с CO2 и солнечным воздействием. Nature Communications 7 , 10627 (2016).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

14

Георгакаракос, Н. и Эггл, С. Аналитическое распространение орбиты для транзитных околоземных планет. Astrophys. J. 392 , p94 (2015).

ADS
Статья

Google Scholar

15

Кастинг, Дж.F. Неудержимая и влажная парниковая атмосфера и эволюция Земли и Венеры. Icarus 74 , 472–494 (1988).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

16

Кастинг, Дж. Ф., Уитмайр, Д. П. и Рейнольдс, Р. Т. Обитаемые зоны вокруг звезд главной последовательности. Icarus 101 , 108–128 (1993).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

17

Эггл, С., Георгакаракос, Н. и Пилат-Лохингер, Э. в Комплексные планетарные системы , Труды симпозиума МАС Vol. 310 (Намюр, Бельгия, 2014 г.).

18

Шилдс, А. Л. и др. Влияние спектрального распределения энергии родительской звезды и обратной связи между ледяным покровом и альбедо на климат внесолнечных планет. Астробиология 13 , 715–739 (2013).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

19

Коппарапу, Р.K. et al. Обитаемые зоны вокруг звезд главной последовательности: зависимость от массы планеты. Astrophys. J. Lett. 787 , L29 (2014).

ADS
Статья

Google Scholar

20

Комабяши М. Дискретные равновесные температуры гипотетической планеты с атмосферой и гидросферой однокомпонентно-двухфазной системы при постоянном солнечном излучении. J. Meteorol. Soc. Jpn 45 , 137–139 (1967).

Артикул

Google Scholar

21

Ингерсолл, А. П. Сбежавшая теплица — история воды на Венере. J. Atmos. Sci. 26 , 1191–1198 (1969).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

22

Накадзима, С., Хаяси, Ю.-Й. & Abe, Y. Исследование побежалого парникового эффекта с помощью одномерной радиационной конвективной модели равновесия. J. Atmos. Sci. 49 , 2256–2266 (1992).

ADS
Статья

Google Scholar

23

Голдблатт, К. и Уотсон, А. Дж. Ускользнувшая теплица: последствия для будущего изменения климата, геоинженерии и планетарных атмосфер. Phil. Пер. R. Soc. а-математика. Phys. Англ. Sci. 370 , 4197–4216 (2012).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

24

Леконт, Дж., Забудьте, Ф., Чарней, Б., Вордсворт, Р. и Поттиер, А. Повышенный порог инсоляции для неуправляемых парниковых процессов на планетах земного типа. Природа 504 , 268–271 (2013).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

25

Попп, М., Шмидт, Х. и Мароцке, Дж. Запуск сбежавшей теплицы в облачной колонне. J. Atmos. Sci. 72 , 452–471 (2015).

ADS
Статья

Google Scholar

26

Будыко, М.I. Влияние вариаций солнечной радиации на климат Земли. Tellus 21 , 611–619 (1969).

ADS
Статья

Google Scholar

27

Войт, А. и Мароцке, Дж. Переход от современного климата к современной Земле-снежному кому. Клим. Dynam. 35 , 887–905 (2009).

ADS
Статья

Google Scholar

28

Ингерсолл, А.П., Добровольскис, А. Р. Вращение Венеры и атмосферные приливы. Nature 275 , 37–38 (1978).

ADS
Статья

Google Scholar

29

Коуэн, Н. Б. и Агол, Э. Модель тепловых фазовых вариаций круглых и эксцентрических экзопланет. Astrophys. J. 726 , 82 (2011).

ADS
Статья

Google Scholar

30

Коуэн, Н.Б., Фойгт, А. и Эббот, Д. С. Тепловые фазы земноподобных планет: оценка тепловой инерции по эксцентриситету, наклону и суточному воздействию. Astrophys. J. 757 , 80 (2012).

ADS
Статья

Google Scholar

31

Леконт, Дж., Ву, Х., Мену, К. и Мюррей, Н. Асинхронное вращение планет земной массы в обитаемой зоне звезд с меньшей массой. Наука 347 , 632–635 (2015).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

32

Рэпер, С.Б., Грегори, Дж. М. и Стоуффер, Р. Дж. Роль чувствительности климата и поглощения тепла океаном на переходную температурную реакцию МОЦАО. J. Clim. 15 , 124–130 (2002).

ADS
Статья

Google Scholar

33

Армор, К. К., Битц, К. М. и Роу, Г. Х. Изменяющаяся во времени чувствительность климата на основе региональных обратных связей. J. Clim. 26 , 4518–4534 (2013).

ADS
Статья

Google Scholar

34

Грегори, Дж. М., Эндрюс, Т. и Гуд, П. Непостоянство параметра переходной реакции климата при увеличении CO2. Phil. Пер. R. Soc. А 373 , 20140417 (2015).

ADS
Статья

Google Scholar

35

Грегори Дж.И Уэбб, М. Регулировка тропосферы вызывает облачный компонент в выбросе СО2. J. Clim. 21 , 58–71 (2008).

ADS
Статья

Google Scholar

36

Эндрюс, Т., Грегори, Дж. М., Уэбб, М. Дж. И Тейлор, К. Э. Принуждение, обратная связь и чувствительность климата в связанных моделях климата атмосферы и океана CMIP5. Geophys. Res. Lett. 39 , L09712 (2012).

ADS

Google Scholar

37

Питан, Ф.И Мауритсен, Т. Арктическое усиление, в котором преобладают обратные связи по температуре в современных климатических моделях. Нат. Geosci. 7 , 181–184 (2014).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

38

Misios, S. & Schmidt, H. Механизмы, участвующие в усилении сигнала 11-летнего солнечного цикла в тропической части Тихого океана. J. Clim. 25 , 5102–5118 (2012).

ADS
Статья

Google Scholar

39

Скайф, А.A. et al. Механизм запаздывающей реакции климата Северной Атлантики на солнечную изменчивость. Geophys. Res. Lett. 40 , 434–439 (2013).

ADS
Статья

Google Scholar

40

Уильямс Д. М. и Поллард Д. Земные миры на эксцентрических орбитах: экскурсии за пределы обитаемой зоны. Внутр. J. Astrobiol. 1 , 61–69 (2002).

Артикул

Google Scholar

41

Повязка, C.Д., Шпигель, Д. С., Шарф, К. А., Мену, К. и Раймон, С. Н. Обитаемый климат: влияние эксцентриситета. Astrophys. J. 721 , 1295 (2010).

ADS
Статья

Google Scholar

42

Болмонт, Э., Либерт, А.-С., Леконт, Дж. И Селсис, Ф. Пригодность планет на эксцентрических орбитах: пределы приближения среднего потока. Astron. Astrophys. 591 , A106 (2016).

Артикул

Google Scholar

43

Георгакаракос, Н. Эволюция эксцентриситета в иерархических тройных системах с эксцентрическими внешними двойными. Пн. Нет. R. Astron. Soc. 345 , 340–348 (2003).

ADS
Статья

Google Scholar

44

Георгакаракос, Н. Улучшенные уравнения для генерации эксцентриситета в иерархических тройных системах. Пн. Нет. R. Astron. Soc. 392 , 1253–1263 (2009).

ADS
Статья

Google Scholar

45

Мюррей К. Д. и Дермотт С. Ф. Динамика солнечной системы Издательство Кембриджского университета (1999).

46

Паардекупер, С.-Дж., Лейнхард, З.М., Тебо, П. и Баруто, С. Как не строить татуин: сложность образования на месте окружных планет кеплер 16b, кеплер 34b и кеплер 35b . Astrophys. J. Lett. 754 , L16 (2012).

ADS
Статья

Google Scholar

47

Клей, В. и Хагигипур, Н. Эволюция окружных планет вокруг эксцентрических двойных систем: случай Кеплера-34. Astron. Astrophys. 581 , A20 (2015).

ADS
Статья

Google Scholar

48

Стивенс Б. и др. Атмосферная составляющая модели земной системы MPI-M: ECHAM6. J. Adv. Модель. Earth Syst. 5 , 146–172 (2013).

ADS
Статья

Google Scholar

49

Brinkop, S. & Roeckner, E. Чувствительность модели общей циркуляции к параметризации взаимодействий турбулентности облаков в пограничном слое атмосферы. Tellus A 47 , 197–220 (1995).

ADS
Статья

Google Scholar

50

Джорджетта, М.A. et al. Модель общей циркуляции атмосферы ECHAM6 — описание модели . (Технический отчет 135, Институт метеорологии Макса Планка, 2013 г.).

51

Тидтке М. Комплексная схема потока массы для параметризации кучевых облаков в крупномасштабных моделях. Пн. Wea. Ред. 117 , 1779–1800 (1989).

ADS
Статья

Google Scholar

52

Nordeng, T.-E. Расширенные версии схемы конвективной параметризации в ЕЦСПП и их влияние на среднюю и переходную активность модели в тропиках .(Технический меморандум 206, ЕЦСПП, 1994).

53

Сундквист, Х., Берге, Э. и Кристьянссон, Дж. Э. Исследования параметризации конденсации и облаков с помощью мезомасштабной модели численного прогнозирования погоды. Пн. Wea. Ред. 117 , 1641–1657 (1989).

ADS
Статья

Google Scholar

54

Lohmann, U. & Roeckner, E. Разработка и исполнение новой схемы микрофизики облаков, разработанной для модели общей циркуляции ECHAM. Клим. Dynam. 12 , 557–572 (1996).

ADS
Статья

Google Scholar

55

Млавер, Э. Дж., Таубман, С. Дж., Браун, П. Д., Яконо, М. Дж. И Клаф, С. А. Перенос излучения для неоднородных атмосфер: RRTM, проверенная модель коррелированного k для длинноволнового диапазона. J. Geophys. Res. 102 , 16663–16682 (1997).

CAS
ОБЪЯВЛЕНИЯ
Статья

Google Scholar

56

Яконо, М.J. et al. Радиационное воздействие долгоживущих парниковых газов: расчеты с использованием моделей переноса излучения AER. J. Geophys. Res. Атмос. 113 , D13103 (2008).

ADS
Статья

Google Scholar

57

Вордсворт, Р. Д. и Пьерумберт, Р. Т. Потеря воды с планет земной группы с атмосферой, богатой углекислым газом.