Содержание
Смежные и вертикальные углы, их свойства.
по теме: Смежные и вертикальные углы, их свойства.
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
— понятия: смежных и вертикальных углов, перпендикулярных прямых
— различать понятия смежные и вертикальные углы
— теоремы смежных и вертикальных углов
-решать задачи с использованием свойств смежных и вертикальных углов
— свойства смежных и вертикальных углов
-строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева , А.Т. Миразова. Алматы «Атамұра». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы «Атамұра». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы «Атамұра». 2012
А.Н.Шыныбеков. Алматы «Атамұра». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы «Атамұра». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
заполнять рейтинговый лист темы.
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
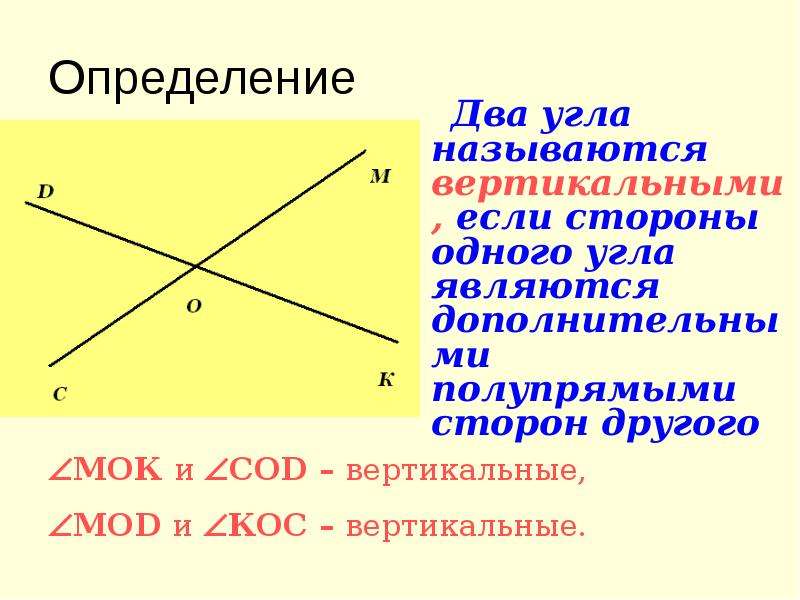
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему : (2б)
Сумма смежных углов равна 180.
- Дано:
∠АОД и ∠ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠АОД + ∠ДОВ = 180
Доказательство:
На основе аксиомы III4 :
∠АОД + ∠ДОВ = ∠АОВ.
∠АОВ — развернутый. Следовательно,
∠АОД + ∠ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения задачи:
а) Дано: ∠h k и ∠kl — смежные; ∠h k больше ∠kl на 50° .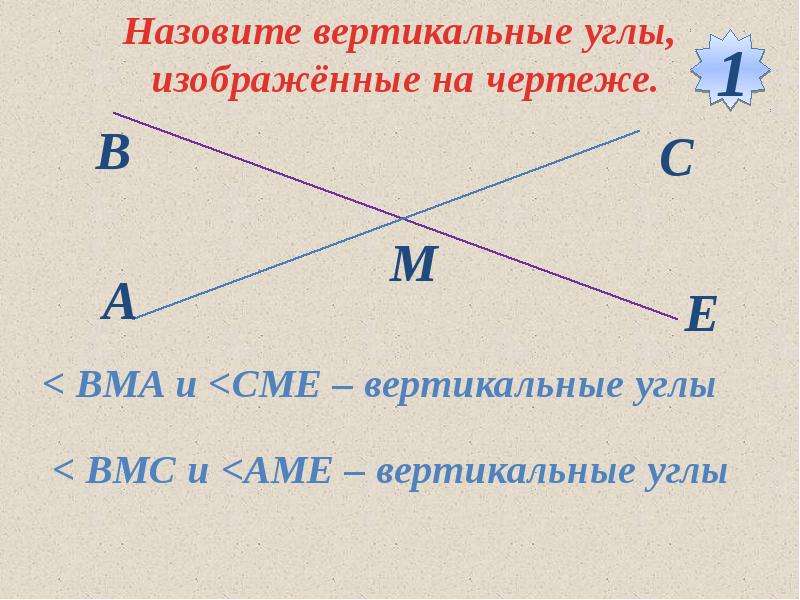
Найти: ∠h k и ∠kl.
Решение: Пусть ∠kl = х, тогда ∠h k = х + 50°. По свойству о сумме смежных углов ∠kl + ∠h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠kl = 65°; ∠h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠kl = х, тогда ∠h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠kl = 45°; ∠hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB.(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол смежный углу а, если а: острый, прямой, тупой.
Построй угол смежный углу а, если а: острый, прямой, тупой.
2. Измерь величины углов.
3.Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый ∠АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
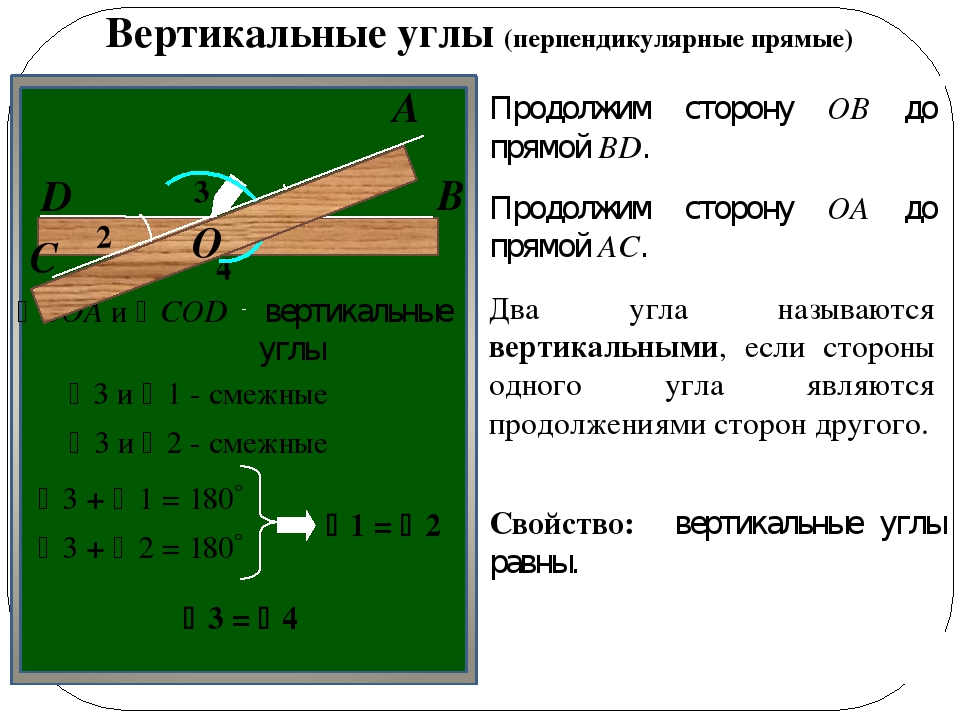
Запишите в тетради: углы∠ АОВ и ∠СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
<1 и <2, <3 и <4 вертикальные углы
Лучи OF и OA ,OC и OE являются попарно дополнительными лучами.
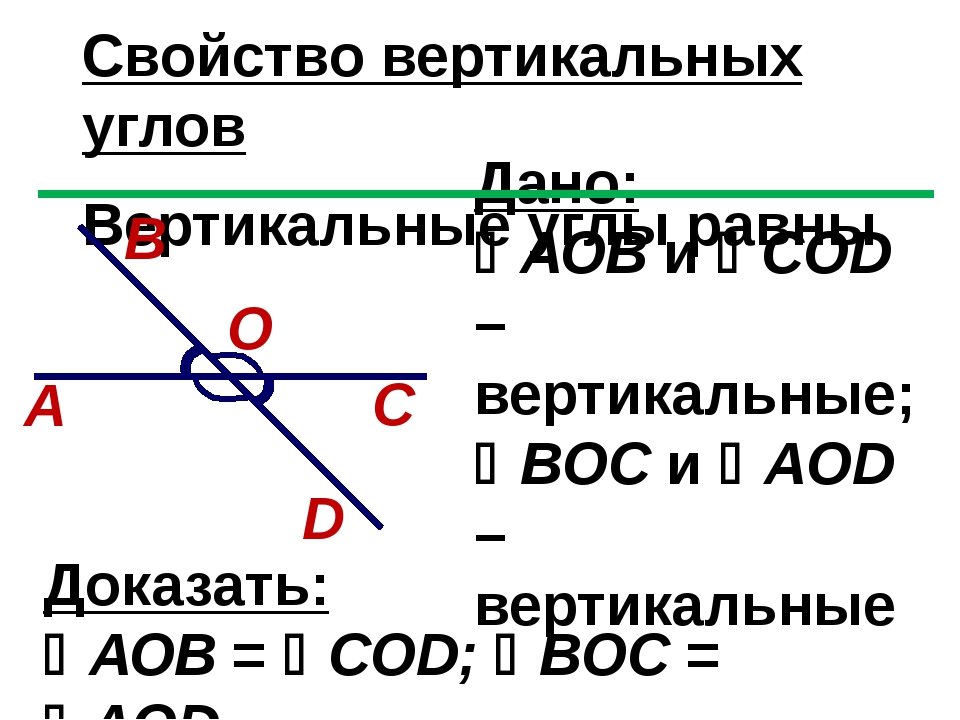
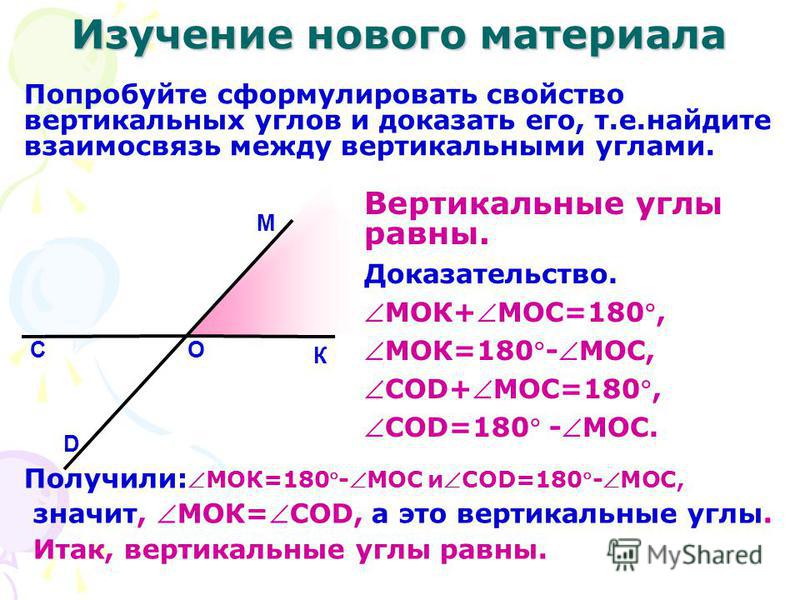
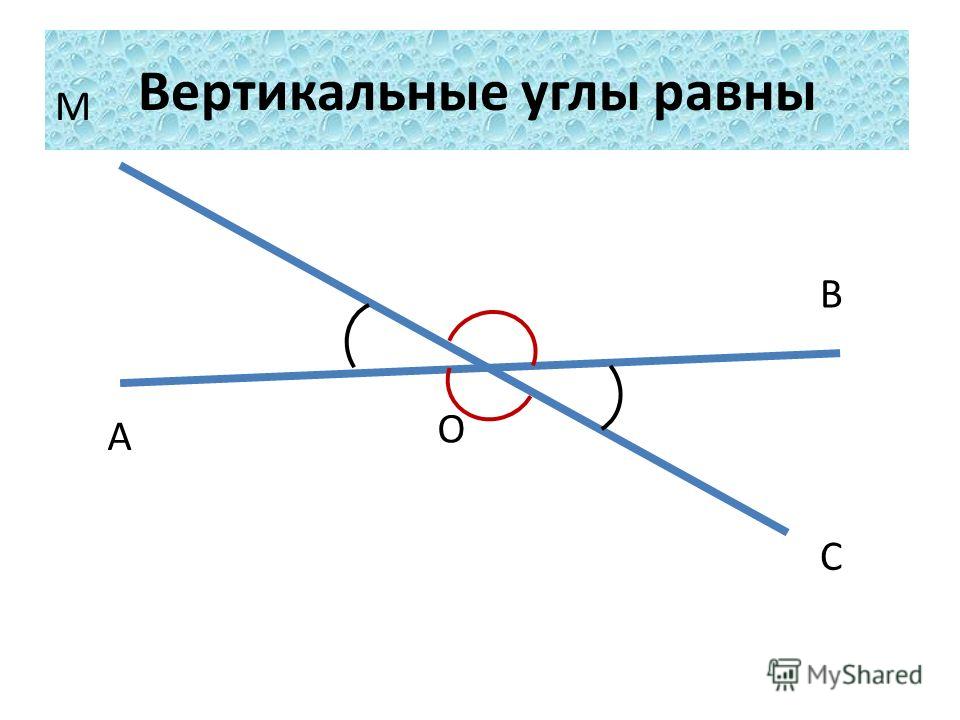
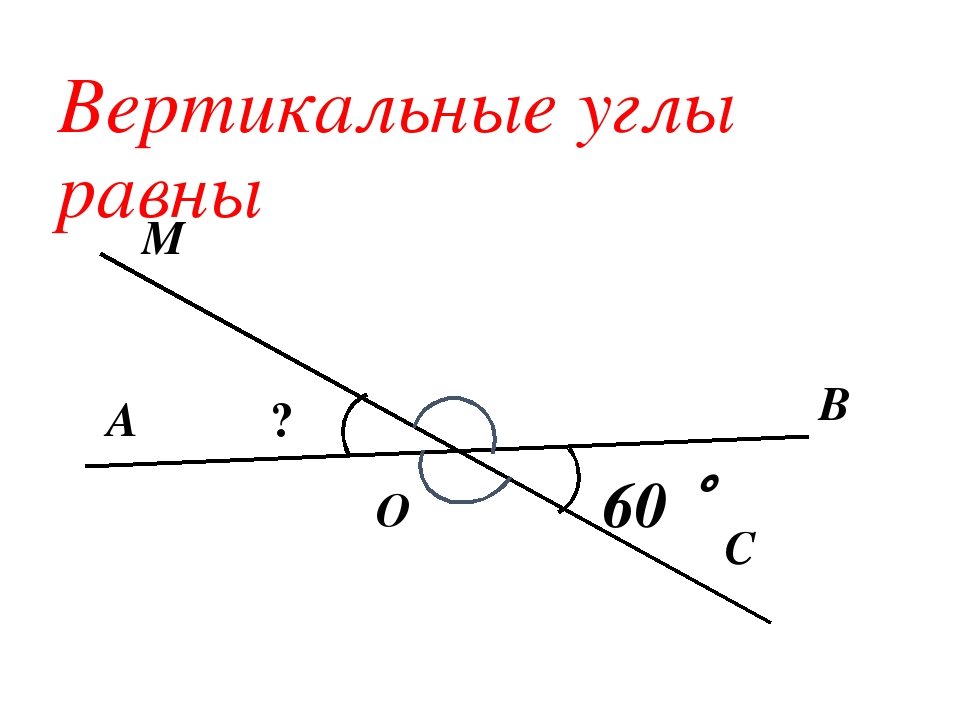
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠2 –вертикальные углы.
∠АОС-развернутый, значит ∠АОС= 180°. Однако ∠ 1+ ∠ 2=∠АОС, т.е.
∠ 3+ ∠ 1=180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ДОВ= 180°, отсюда ∠ 2+ ∠ 3=180°, или ∠ 2=180°-∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то ∠ 1=∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов :(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α, если α:
острый, прямой, тупой.
2.Измерь величины углов.
3. Данные измерений занеси в таблицу
Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов . (3б)
2) Рассмотри образец решения задачи.
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠BOC = 180° — 145° = 35°.
Значит, ∠BOC = ∠АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?
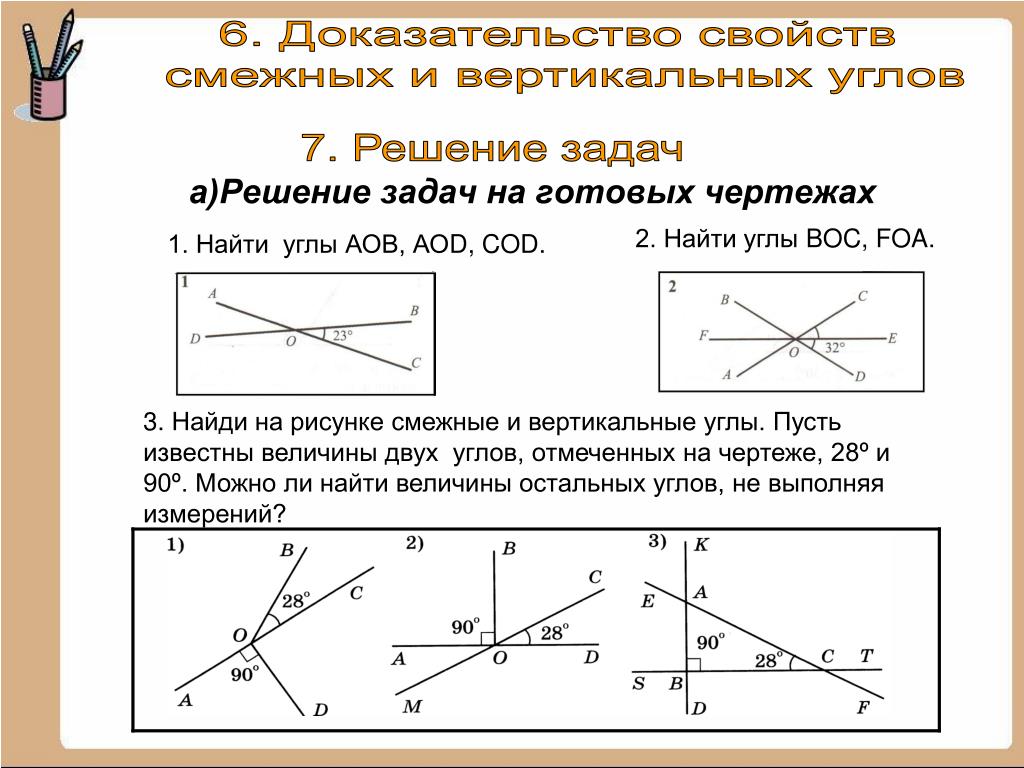
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: ( 3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
2 ) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого .Найдите каждый из углов.(3б)
3. Найдите смежные углы ,если их разность и их сумма относятся как 2:9.(3б)
Найдите смежные углы ,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
- <1 и <2,
<3 и <2,
г) <1 и <3. Какие это углы?
Смежные
д) Начертите ( на глаз) угол в 30° и <ABC, смежный с данным
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.

2. Назовите вертикальные углы на данном рисунке.
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
- <1 и <4,
<2 и <4
Д) <1 и < 3 смежные ?
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов .
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9.
 (4б)
(4б)Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других.(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов .
РЕЙТИНГОВЫЙ ЛИСТ
по теме : «Смежные и вертикальные углы, их свойства »
Ф.И. __________________________________________, класс _____
1
2 б
2 б
2 б
2 б
2б
2
2б
5б
3
3 б
4б
2б
2б
4
5б
3б
3б
3б
2б
5
7б
3б
6
3б
2б
3б
7
4б
6б
Итого
72 б
ИТОГО: 76 баллов
«5» — 72 — 60 б;
«4» — 59 — 436;
«3» — 42 – 38 б.
«2» — 38 б. и менее
Смежные и вертикальные углы — презентация онлайн
Смежные углы и их свойства.
В
С
М
А
Два угла, у которых одна сторона общая,
а две другие являются продолжением одна другой,
называются смежными
Углы АМВ и СМВ – смежные.
Сумма смежных углов равна 1800
Два угла называются вертикальными,
если стороны одного угла являются
продолжениями сторон другого.
М
А
О
В
Углы АОВ и МОN являются
N
вертикальными.
Построение вертикальных углов
М
А
О
В
Углы АОВ и МОN являются
N
вертикальными.
Тренировочные задания
Дано:
АВС и СВD – смежные,
АВС – CBD = 200
Найдите:
Угол АВС на 200
больше угла СВD
АВС, СВD
С
х
А
В
D
Тренировочные задания
Дано:
KLM и MLN – смежные,
KLM = 3 MLN
Найдите:
Угол KLM в 3 раза
больше угла MLN
KLM, MLD
M
х
K
L
D
Тренировочные задания
Дано:
PQR и RQS – смежные,
RQS = 0,8 PQR
Найдите:
Угол RQS составляет
0,8 части угла PQR
RQS, PQR
R
х
P
0,8х
Q
S
Тренировочные задания
Дано:
(ab)
и
(bc) – смежные,
(bc) : (ab) = 4 : 5
Найдите:
(ab), (bc)
b
5х
a
X – 1 часть
(bc) = 4x
(ab) = 5x
4х
c
Прямые MN и КР пересекаются в точке О,
причем сумма углов КОМ и NОР равна 1340.
Найдите величину угла КОN.
M
O
K
1130
P
670
N
Тренировочные задания
Прямая АВ разбивает плоскость на две полуплоскости.
Из точки О, принадлежащей прямой АВ, в разные
полуплоскости проведены лучи ОС и ОD, причем угол
АОD в 3 раза больше угла АОС. Найдите угол АОС,
если
ВОD = 126
0.
С
А
3x+126 = 180
x O
3x 1260
>
в 3 раза
D
Тренировочные задания
В
Угол NOK в 3 раза больше угла DОМ, а угол DOK на 120
больше угла NOK. Найдите угол СОN.
Р
M
O
С
3x
x
3x+12
на
N
Тренировочные задания
К
120
D
>
Углы АОМ и СОМ – смежные. ОК – биссектриса угла
АОМ, причем угол АОК в 4 раза меньше, чем угол СОМ.
Найдите угол КОМ.
М
в 4 раза x
А
Тренировочные задания
x
4x
O
С
Прямые АB и СD пересекаются в точке О.
ОК – биссектриса угла АОD, СОК = 1180.
Найдите угол ВОD.
А
К
620
С
Тренировочные задания
O 560
B
D
Найдите остальные углы
M
F
O
K
1400
D
Тренировочные задания
100
300
P
N
Дано: СОD – КОD =
Угол СОD на 610
больше угла КОD
Угол СОD на 530
больше угла КОС.
Тогда угол КОС на 530
меньше угла СОD
610
СОD – КОС = 530
Найти:
СОD
х+61
С
O
х+61–53
x
К
Тренировочные задания
*
1
4
одного из смежных углов и
другого составляют
7 в сумме прямой угол. Найдите4 эти смежные углы.
А
В
О
С
*
1
4
одного из смежных углов и
другого составляют
7 в сумме прямой угол. Найдите4 эти смежные углы.
4
х
7
х
В
О
1
(
х
180
)
А 4
х-180
С
*
Один из четырех углов, образовавшихся при
пересечении двух прямых, в 11 раз меньше суммы
трех остальных углов. Найдите эти четыре угла.
Найдите эти четыре угла.
M
x+11х= 360
P
O
K
x
в 11 раз
N
Тренировочные задания
*
Сумма трех углов, образовавшихся при пересечении
двух прямых, на 2800 больше четвертого угла.
Найдите эти четыре угла.
x+х+280= 360
M
на 2800 >
x+280
K
P
O
x
N
Тренировочные задания
Найди на чертеже для угла 1
вертикальный угол и щелкни по нему мышкой.
4
1
5
2
умница!
3
Найди на чертеже для угла 3 смежный угол и щелкни
по нему мышкой.
5
молодец!
3
4
6
1
2
Найди на чертеже для угла 1 вертикальный угол и
щелкни по нему мышкой.
1
3
умница!
4
2
7
5
8
6
S
440
Y
SNY, MNF
LМN, CMF
N
Смежные углы! LМN, CML
Смежные углы! LМN, NMF
DFR, NFM
Смежные углы! NFR, NFM
SNM, YNF
М
L
630
C
F 730
R
LMC, NMF
RFN, DFM
D
Найди пары вертикальных углов и щелкни по ним мышкой
1. Найти все углы, образованные при пересечении
Найти все углы, образованные при пересечении
двух прямых, если сумма углов OLA и VLZ равна 1240.
Z
O OLA =
OLZ =
L
А
V
B
A
500
O
700
F
Проверить.
E
0
ZLV=
ALV=
3.
Сумма трёх углов 1, 2, 3,
образовавшихся при
пересечении двух
прямых равна 3250.
3
O 1 2
2. Найти углы.
C AOC =
BOD =
D COE =
COD =
C
B
D
Найдите углы.
1 =
2 =
A
Смежные и вертикальные углы, их свойства
1. Тема урока: Смежные и вертикальные углы.
Школа 291
Класс 7
Автор: Алескерова И.Г.
Цели урока:
Ознакомить учащихся с понятиями
смежных и вертикальных углов,
рассмотреть их свойства;
Научить строить угол, смежный с
данным углом, изображать
вертикальные углы, находить на
рисунке вертикальные и смежные углы.
3. Давай вспомним!
Что
такое угол?
АОВ
ВОА
О
Как
обозначаются углы?
А
О
В
Какой
инструмент
Для
измерения
можно
углов
использовать для
используют
измерения углов?
транспортир .
Что называется биссектрисой угла ?
А
АOB = 700
110
100
130
60
70
90
120
140
80
70
80
60
100
120
50
150
30
140
30
150
160
20
170
170
10
180
40
130
40
160
50
110
180
0
O
20
10
0
B
Единицы измерения угла
Всего 180 частей.
1 часть – это 1 градус.
1/60 часть градуса
называется минутой,
обозначается знаком «′»
1/60 часть минуты
называется секундой,
обозначается знаком «″»
Виды углов
Название угла
Рисунок
Градусная
мера
ОСТРЫЙ УГОЛ
менее 90˚
ПРЯМОЙ УГОЛ
90˚
ТУПОЙ УГОЛ
>90˚, но
РАЗВЕРНУТЫЙ
180˚
9. Какой угол образует клюв вороны, когда: «Ворона сыр во рту держала?»
Какой угол образует клюв вороны, когда:
«Ворона сыр во рту держала?»
А когда «Ворона каркнула во все воронье
горло?»
10.
 Острый Тупой
Острый Тупой
11. В сказке об углах квадрата брат-круг отрубил ему углы. Какими они стали после этого?
В сказке об углах квадрата браткруг отрубил ему углы. Какими
они стали после этого?
К
вашим знаниям об углах
сегодня добавится еще два
вида:
13. Начертите развернутый угол АОС. Начертите произвольный луч ОB, лежащий между сторонами развернутого угла.
B
O
C
A
14. Определение смежных углов
А
а другие стороны
этих углов являются
противоположными
лучами.
О
Определение. Два
угла называются
смежными, если у
них одна сторона
общая,
В
С
ВОА и ВОС смежные
15. Являются ли смежными углы AOD и BOD AOС и DOС AOС и DOВ AOС, DOС и BOD?
Являются ли смежными углы
AOD и BOD
AOС и DOС
AOС и DOВ
AOС, DOС и BOD?
16. Построение смежных углов
1.Одну из сторон угла продолжить
за его вершину.
А
2.Получившийся угол АОС
является смежным с углом АОВ.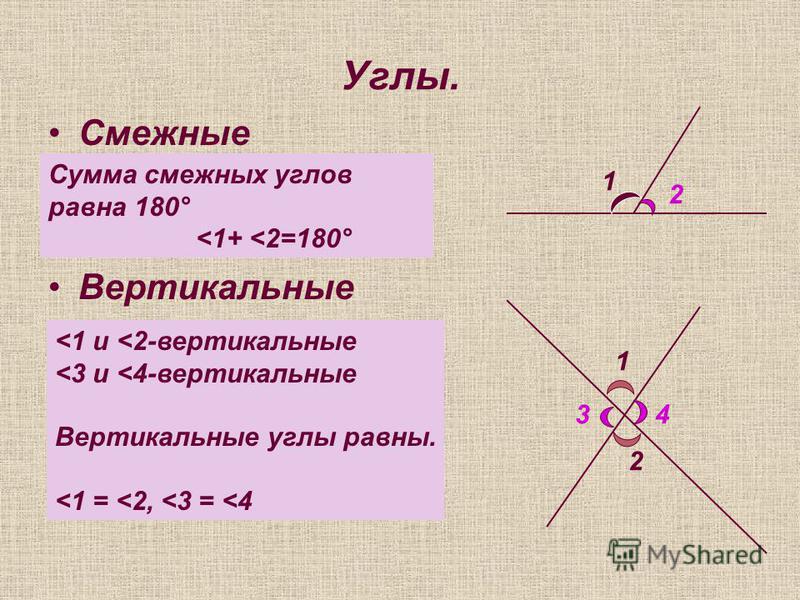
С
0
1
2
3
4
5
6
7
8
О
9
10
11
12
13
14
В
15
16
17
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Угол смежный для острого угла является тупым.
1. Одну из сторон угла
продолжить за его
вершину.
А
С
О
В
2. Получившийся угол
АОС является
смежным для угла
АОВ.
Угол смежный для тупого угла является
острым.
1.
А
2.
В
О
С
Одну из сторон угла
продолжить за его
вершину.
Получившийся угол
АОС является
смежным с углом АОВ
Угол смежный с прямым углом является прямым
20. Cвойство смежных углов
Теорема.
Сумма
смежных углов
1. Сколько углов изображено на
рисунке? Какие это углы?
2. Существует ли какая-нибудь
взаимосвязь между этими углами?
(Вспомните аксиому сложения
углов).
равна 1800
Дано: AOC и BOC –
смежные.
Доказать: AOC + BOC =
180 .
Доказательство. 1) Так как
AOC и BOC – смежные, то
лучи ОА и ОВ –
противоположные, то есть,
AOB – развернутый,
следовательно, AOB = 180 .
2) Луч OC проходит между
сторонами AOB, значит,
AOC + BOC = AOB = 180
Решите задачу по чертежу
D
?
A
C
Решение:
B
(по свойству смежных углов)
22. Начертите произвольный AOB. Постройте лучи OC и OD, противоположные к его сторонам.
Начертите произвольный AOB.
Постройте лучи OC и OD,
противоположные к его
сторонам.
D
А
В
О
Определение. Два угла
называются
вертикальными, если
стороны одного угла
являются
противоположными
лучами к сторонам
другого.
С
Найдите
вертикальные углы.
C
B
O
А
D
D
B
O
А
С
B
D
А
N
С
D
B
M
А
С
24.
 Построение вертикальных углов
Построение вертикальных углов
А
В
1. Построить угол.
2.Продлить каждую
сторону угла за его
вершину.
О
D
C
26. Свойство вертикальных углов
Теорема. Вертикальные
A
D
O
B
C
углы равны.
Дано: AOD и COB –
вертикальные.
Доказать: AOD= COB
Доказательство. Каждый из
углов AOD и COB является
смежным с углом AOB. По
свойству смежных углов:
AOD + AOB = 180
и COВ + AOB = 180 .
Имеем: AOD = 180 – AOB
и COB = 180 – AOB,
значит, AOD = COB
Решите задачу по чертежу
Решение:
(по свойству вертикальных
углов)
28. Закончи предложение
Если один из смежных углов равен 50°,
то другой равен… 130°
Угол, смежный с прямым, … прямой
Если один из вертикальных углов
прямой, то второй… прямой
Угол смежный с острым… тупой
Если один из вертикальных углов равен
25°, то второй угол равен… 25°
29.
 Задания для самопроверки Определите по рисункам:
Задания для самопроверки Определите по рисункам:
Найдите 1 и 2
?
1
50°
2
1
+
2
= 90°
Найдите 1 и 2
?
11
79°
1
_
2
2 = 70°
Дано: = 3 .
Найти: и .
ОС- биссектриса
Найти BOC
Найти BOC
1. Сумма смежных углов равна….
A
3600
B
900
C
1800
2. Как называется угол меньше 1800,
но больше 900
A острый
B
тупой
C
прямой
3. Чему равен угол, если смежный с
ним равен 470?
A 1330
B
0
47
C
0
43
4. Какой угол образуют часовая и
минутная стрелки часов, когда они
показывают 6 часов?
A
тупой
B
развернутый
C прямой
5. Найдите
С
О
A
0
77
В
А
1030
D
0
103
B
C
30
6. Найдите
A
B
С
0
54
О
0
126
А
540
D
C
0
36
В
7. Найдите смежные углы, если один
Найдите смежные углы, если один
из них в два раза больше другого.
A 900 и 1000
и
B
0
60
C
0
40 и
0
120
0
80
8. Угол равен 720. Чему равен
вертикальный ему угол?
A
0
18
0
108
B
C
720
9. Какой угол образуют часовая и
минутная стрелки часов, когда они
показывают три часа?
A
острый
B
тупой
C прямой
41. Проверь себя.
1. C
2. B
3. A
4. B
5. B
6. B
7. B
8. C
9. C
42. Образец оформления решения задачи
При пересечении двух прямых образовалось четыре
угла. Один из них равен 430. Найдите величины
остальных углов.
F
M
Дано:
МК PF = О
МОF = 43°
43 0
Найти: FOK, KOP, POM.
Решение:
O
P
МОF и KOP вертикальные, значит, по свойству
вертикальных углов, МОF = KOP , KOP = 43°
МОF + FOK = 180°, так как они смежные. Отсюда
FOK = 180°- 43°=137°
K FOK и POM вертикальные, значит FOK = POM ,
POM =137°
Ответ: 1370, 430, 1370
Задача 1. Найдите углы, полученные при пересечении
Найдите углы, полученные при пересечении
двух прямых, если один из углов равен 102 0.
Задача 2. Найдите величины смежных углов, если один из
них в 5 раз меньше другого.
Задача 3. Чему равны смежные углы, если один из них на
300 больше другого?
Задача 4. Найдите величину каждого из двух вертикальных
углов, если их сумма равна 980.
Обучающая самост оят ельная работ а
В
С
o
А
D
1. На рисунке изображены прямые АС и ВD,
пересекающиеся в точке О. Дополните записи:
ВОС и . . . — вертикальные,
ВОС и . . . — смежные,
СОD и . . . — вертикальные,
СОD и . . . — смежные.
2. Начертите угол МОК. Постройте смежный с ним: а) угол КОN; б)
угол MOR.
3. Запишите пары смежных углов, имеющиеся на рисунке:
В
А
Е
D
C
F
4. Запишите пары вертикальных углов, имеющиеся на
рисунке:
В
D
М
А
С
N
Смежные и вертикальные углы, и их свойства
Предлагаю классу рассчитаться на первый, второй.
Образовываются две смешанные группы.
1 группа: Смежные
2 группа: Вертикальные
Каждой группе дается одинаковая карточка, но с разными заданиями.
Цель обучения:7.1.1.10 доказывать и применять свойства вертикальных и смежных углов
Критерий оценивания:
-доказывают и применяют свойства вертикальных и смежных углов
Уровни мыслительных навыков: знание, понимание, применение
В С
О
А Д
Задание:
1 группа: 1)найти и написать смежные углы;
2) доказать, что они смежные.
2 группа: 1) найти и написать вертикальные углы;
2) доказать, что они веритикальные.
Дескриптор:
-определяют смежные и вертикальные углы;
-доказывают свойства смежных и вертикальных углов.
ФО. Взаимооценивание. Меняются друг с другом записями (одна группа проверяет другую группу) и проверяют по образцу на экране.
Когда проверят меняются обратно.
Прием «Светофор».
Обратная связь:
-Что было для вас сложным?
-На что нужно обратить внимание, чтобы справляться с заданием?
Дифференциация по результату
Практическая работа
Цель: 7.1.1.32 знать понятие о перпендикуляре
Критерий оценивания
-знает понятие о перпендикуляре.
Уровни мыслительных навыков: применение, анализ
Задание:
Лодка плыла на юг, затем повернула на 900.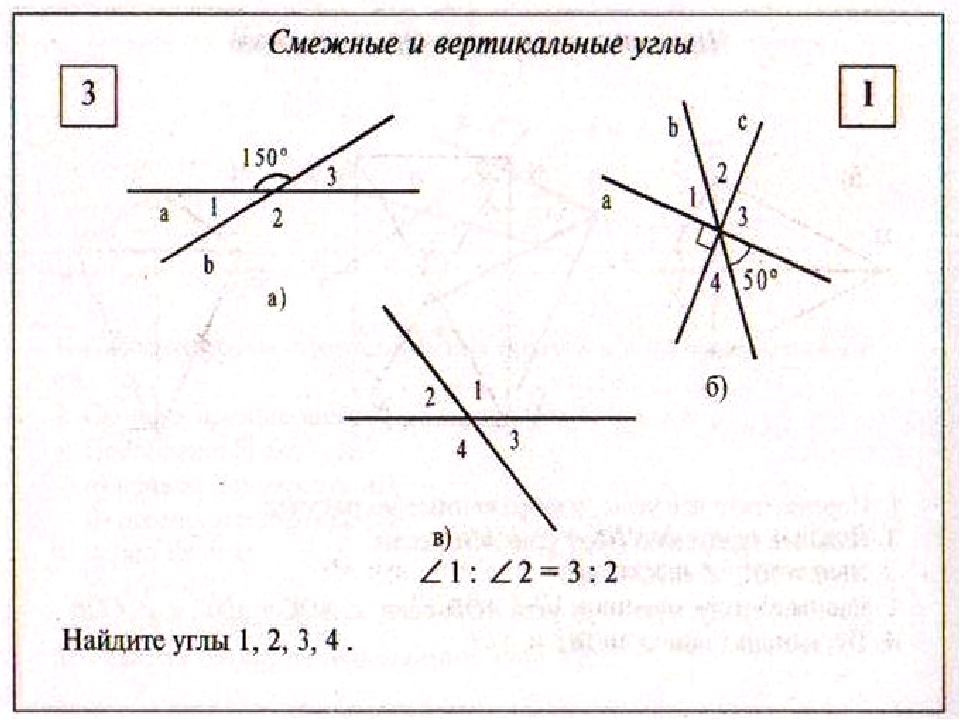 В каком направлении она теперь плывет? Сколько решений имеет задача? Сколько раз и в какую сторону должна повернуться лодка на 90, чтобы вернуться обратно? Начертите путь лодки.
В каком направлении она теперь плывет? Сколько решений имеет задача? Сколько раз и в какую сторону должна повернуться лодка на 90, чтобы вернуться обратно? Начертите путь лодки.
Дескриптор:
— выполняют чертеж;
— знают понятие о перпендикуляре;
— находят все решения.
ФО: самооценивание
Учащиеся знают направление сторон света, но также можно показать на экране, если кто-то забыл.
Прием «Углы». В четырех углах класса развесить возможные ответы. Ученики размещаются в тех углах, который считают правильным. Те ученики которые выполнили несколькими способами, становятся посередине класса.
Каждая группа формулирует свой ответ. Объясняет выполнение чертежа.
Затем обосновывает и доказывает свой ответ, те кто посередине класса. Если какая то группа соглашается, то переходит в середину класса.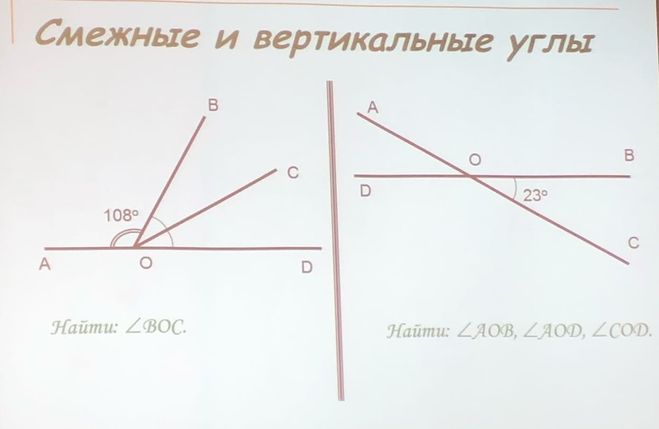
Обратная связь: —почему задача все таки имеет несколько решений?
Дифференциация по уровню сложности задания.
Цель: определять смежные и вертикальные углы;
Критерий оценивания
Обучающийся
-определяет смежные и вертикальные углы;
Уровни мыслительных навыков: знание, понимание, применение.
Задание
Уровень А
Рис.1 Рис.2
1. 1=47˚. Найдите 2.(рис1)
2. 1=15˚. Найдите 2, 3 , 4. (рис2)
3. 1+4=78˚. Найдите1,2, 3 , 4. (рис2)
Уровень В
1.Один из смежных углов в 9 раз больше другого. Найдите эти углы.
2.Сумма трех углов, образовавшихся при пересечении двух прямых, равна 240˚. Найдите все образовавшиеся углы.
Найдите все образовавшиеся углы.
Дескриптор:
-определяют смежные и вертикальные углы;
-находят вертикальные и смежные углы через составление уравнения
ФО: самооценивание по образцу на экране
Прием: «Светофор»
Покажите сигнальной карточкой кто справился, а кто нет.
— поднять зеленую, кто справился с заданием;
-желтую, кто справился, но допустил ошибки;
-красную, кто совсем не справился
Обратная связь: —какие задания были трудными?
Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия
Факт 1.
\(\bullet\) Смежные углы — два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.
Смежные углы: \(\angle AOB\) и \(\angle BOC\). \circ\).
\circ\).
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.
Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.
Факт 5.
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:
Второе свойство равнобедренного треугольника: углы при основании равны.
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.
Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
\(\bullet\) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.
Факт 11.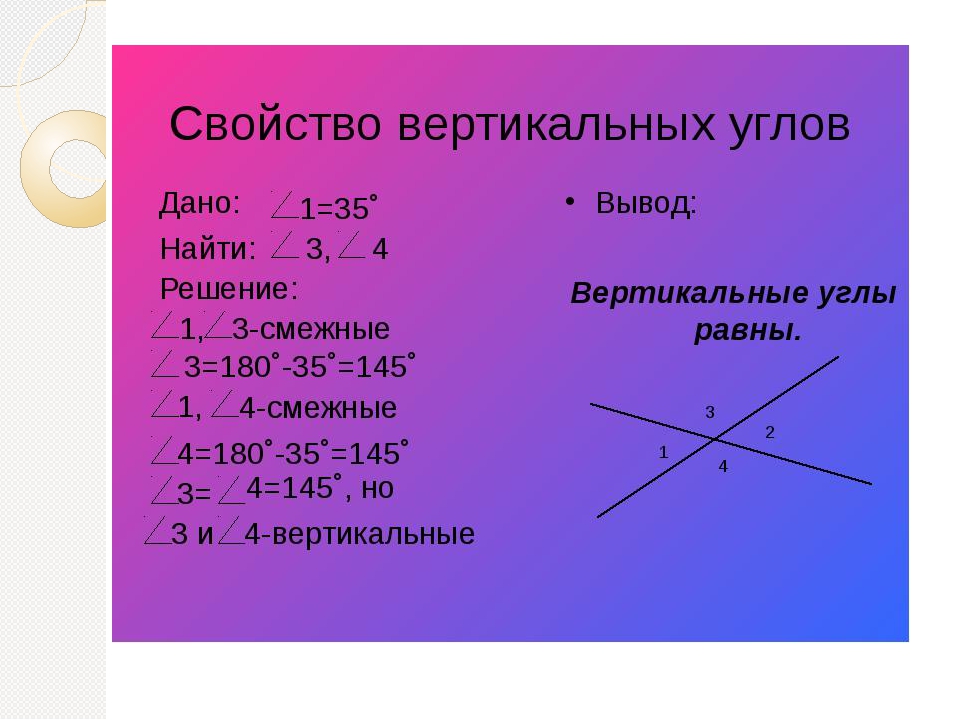
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.
\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.
Смежные и вертикальные углы и их свойства. П1
Данный модуль состоит из 5 заданий. Задания предназначены для формирования у учеников представления о смежных углах и их свойствах, о вертикальных углах и их свойствах, а также для отработки умения находить величину углов. При решении заданий Пользователю предоставляется возможность использовать подсказки. Все задания данного учебного модуля параметризированы. Это позволяет учителю формировать индивидуальные задания для каждого учащегося.
Категория пользователей
Обучаемый, Преподаватель
Дисциплины
Математика
/ Угол.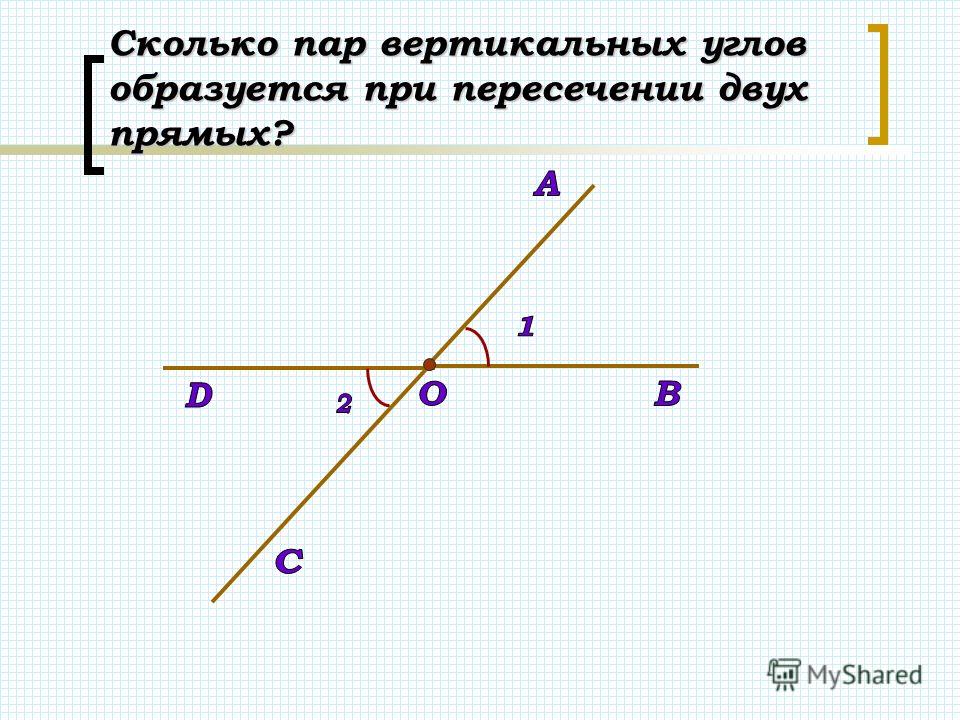 Равенство углов. Величина угла и ее свойства. Виды углов. Смежные и вертикальные углы и их свойства. Перпендикулярные прямые
Равенство углов. Величина угла и ее свойства. Виды углов. Смежные и вертикальные углы и их свойства. Перпендикулярные прямые
Уровень образования
Профессионально-техническая подготовка, повышение квалификации
Статус
Завершенный вариант (готовый, окончательный)
Тип ИР сферы образования
информационный модуль
Ключевые слова
угол, величина угла, смежные углы, вертикальные углы,
Издатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Правообладатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр. 1, ул. Пришвина, 8
1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Внимание! Для воспроизведения модуля необходимо установить на компьютере проигрыватель ресурсов.
Характеристики информационного ресурса
Тип используемых данных:
text/plain, text/html, image/jpeg
Объем цифрового ИР
1 529 871 байт
Проигрыватель
Категория модифицируемости компьютерного ИР
Признак платности
бесплатный
Наличие ограничений по использованию
нет ограничений
Рубрикация
Ступени образования
Основное общее образование
Целевое назначение
Учебное
Тип ресурса
Открытая образовательная модульная мультимедийная система (ОМС)
Классы общеобразовательной школы
7
Уровень образовательного стандарта
Федеральный
Характер обучения
Базовое
что такое в геометрии, признаки, равны или нет, теорема, как доказать
Вертикальные углы — что это такое в геометрии, определение
Определение
Вертикальные углы – пара углов с общей вершиной, которые образованы при пересечении двух прямых таким образом, что стороны одного из них являются продолжением сторон другого.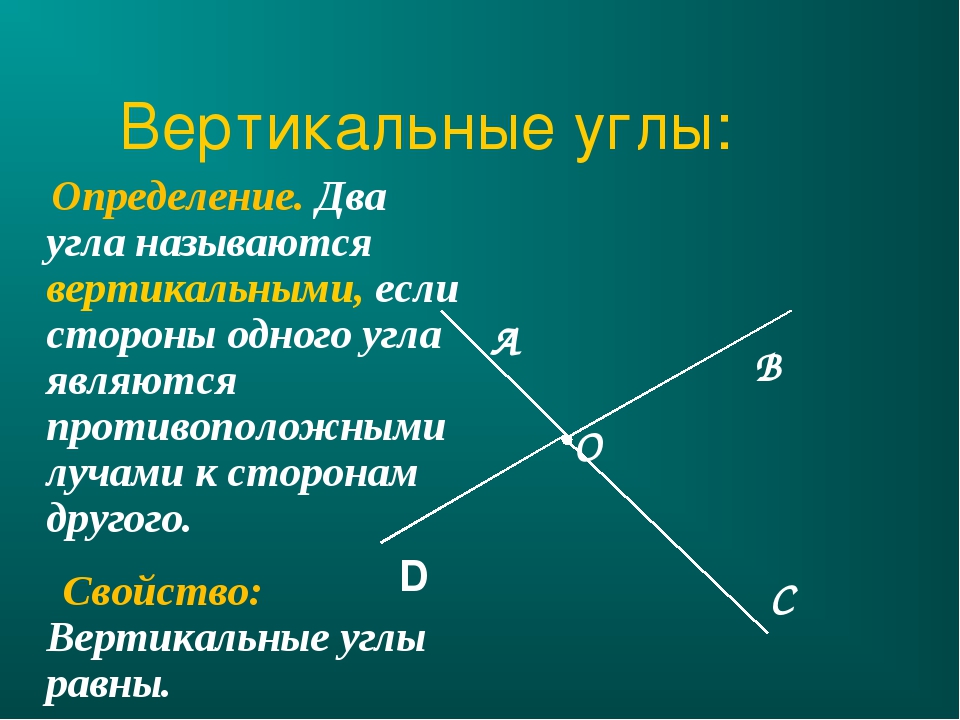 \circ\).
\circ\).
Определение и свойства треугольника — Math Open Reference
Определение и свойства треугольника — Math Open Reference
Замкнутая фигура, состоящая из трех отрезков, соединенных встык.
Трехсторонний многоугольник.
Попробуйте это Перетащите оранжевые точки на каждую вершину
чтобы изменить форму треугольника.
Недвижимость треугольника
| Вершина | Вершина (множественное число: вершины) угол треугольника. Каждый треугольник имеет три вершины. |
| База | Основанием треугольника может быть любая из трех сторон, обычно та, которая нарисована внизу. Вы можете выбрать любую сторону в качестве основы. Обычно используется как справочная сторона для расчета площадь треугольника. В равнобедренном треугольнике за основу обычно принимается неравная сторона. |
| Высота | Высота треугольника — это перпендикуляр от основания к противоположной вершине.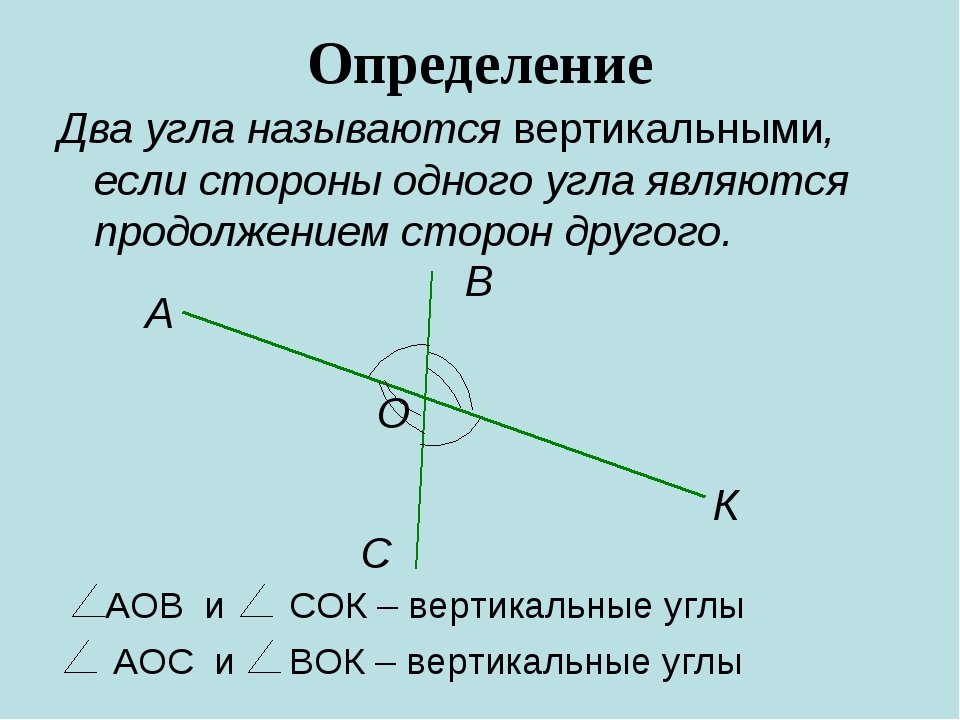 (Возможно, потребуется расширить базу). (Возможно, потребуется расширить базу).Поскольку существует три возможных базы, есть также три возможных высоты. Три высоты пересекаются в единственная точка, называемая ортоцентром треугольника. См. «Ортоцентр треугольника». На рисунке выше вы можете увидеть одну возможную базу и соответствующую высоту. |
| Медиана | Медиана треугольника — это линия от вершины до середины противоположной стороны. Три медианы пересекаются в одной точке, называемой центром тяжести треугольника.Увидеть центроид треугольника |
| Площадь | См. Площадь треугольника и Формула Герона |
| Периметр | Расстояние вокруг треугольника. Сумма его сторон. Увидеть периметр треугольника |
| Уголки внутренние | Три угла внутри треугольника в каждой вершине. См. Внутренние углы треугольника |
| Наружные углы | Угол между стороной треугольника и продолжением соседней стороны. См. Внешние углы треугольника. См. Внешние углы треугольника. |
Также:
- Самая короткая сторона всегда противоположна наименьшему внутреннему углу
- Самая длинная сторона всегда противоположна наибольшему внутреннему углу
Подробнее об этом см. Взаимосвязь стороны / угла в треугольнике.
Терминология
Обычно каждую вершину треугольника называют одной заглавной (заглавной) буквой. Стороны могут быть названы одним
маленькая (строчная) буква и названа в честь противоположного угла.Итак, на рисунке выше вы можете видеть, что сторона b противоположна вершине B, сторона c — противоположна вершине C и так далее.
В качестве альтернативы сторону треугольника можно рассматривать как
отрезок, соединяющий две вершины. Тогда сторона b будет называться
AC.
Эта форма используется на этом сайте, потому что она одинакова для всех форм, а не только для треугольников.
Свойства всех треугольников
Это некоторые хорошо известные свойства всех треугольников.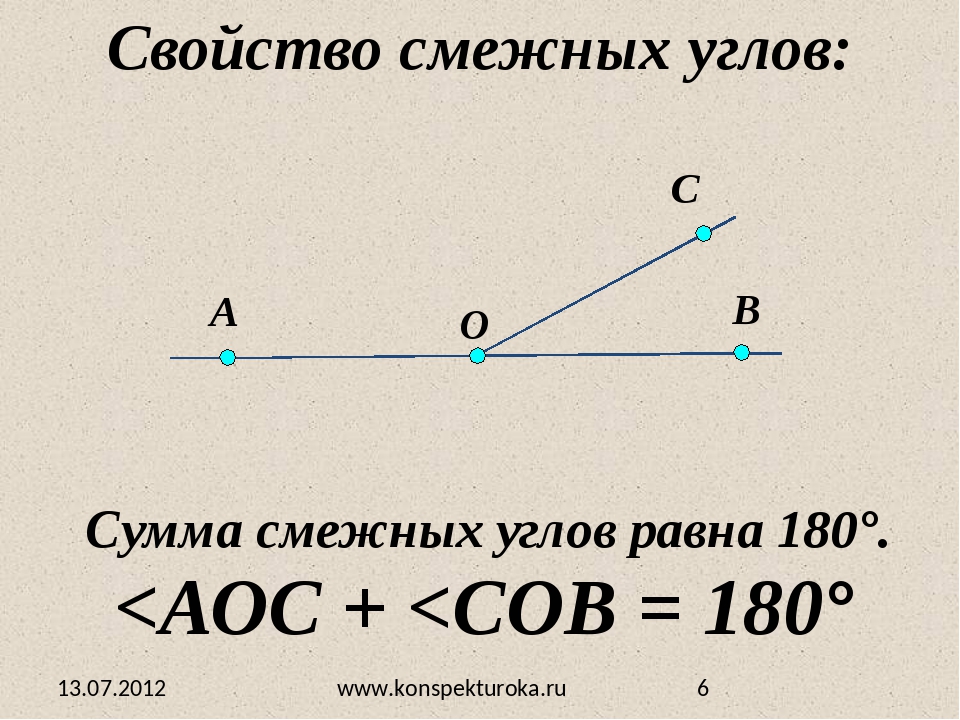 См. Полный список в разделе ниже.
См. Полный список в разделе ниже.
Типы треугольников
Ниже перечислены семь типов треугольников.Обратите внимание, что данный треугольник
может быть более одного типа одновременно.
Например, разносторонний треугольник (без сторон одинаковой длины) может иметь один внутренний угол 90 °, что делает его также прямоугольным.
Это можно было бы назвать «прямоугольным разносторонним треугольником».
Классифицирующие треугольники
Семь типов треугольников можно классифицировать двумя способами: по сторонам и по внутренним углам.
Подробнее об этом см. Классификация треугольников.
Построение треугольников
Многие типы треугольников могут быть построены с помощью циркуля и линейки с использованием традиционных
Евклидовы методы построения.Для получения дополнительной информации см. Конструкции с использованием циркуля и линейки.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Соответствие и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
свойств полигонов | SkillsYouNeed
На этой странице рассматриваются свойства двумерных или «плоских» многоугольников.Многоугольник — это любая форма, состоящая из прямых линий, которую можно нарисовать на плоской поверхности, например на листе бумаги. Такие формы включают квадраты, прямоугольники, треугольники и пятиугольники, но не круги или любую другую форму, которая включает кривую.
Понимание форм важно в математике. Вам, безусловно, потребуется изучать формы в школе, но понимание свойств форм имеет много практических применений в профессиональных и реальных ситуациях.
Многие профессионалы должны понимать свойства форм, включая инженеров, архитекторов, художников, агентов по недвижимости, фермеров и строителей.
Возможно, вам понадобится разбираться в формах, когда вы делаете ремонт дома и делаете самодельные работы, при работе в саду и даже при планировании вечеринки.
При работе с полигонами важны следующие основные свойства:
- количество сторон фигуры.

- Элемент расположен под углом между сторонами фигуры.
- Длина сторон формы.
Количество сторон
Полигоны обычно определяются количеством сторон, которые у них есть.
Трехсторонние многоугольники: треугольники
Трехсторонний многоугольник — это треугольник. Существует несколько различных типов треугольников (см. Диаграмму), в том числе:
- Равносторонний — все стороны равны по длине, а все внутренние углы равны 60 °.
- Равнобедренный — имеет две равные стороны, у третьей разной длины. Два внутренних угла равны.
- Scalene — все три стороны и все три внутренних угла разные.
Треугольники также можно описать с точки зрения их внутренних углов (см. Нашу страницу Углы для получения дополнительной информации об именах углов). Сумма внутренних углов треугольника всегда составляет 180 °.
Треугольник, имеющий только острых внутренних углов, называется острым (или остроугольным) треугольником. Один с одним тупым углом и двумя острыми углами называется тупым (тупоугольным), а другой с прямым углом известен как прямоугольный.
Каждый из них будет также либо равносторонним, равнобедренным, или разносторонним .
Четырехсторонние многоугольники — четырехугольники
Четырехсторонние многоугольники обычно называют четырехугольниками, четырехугольниками или иногда четырехугольниками. В геометрии обычно используется термин четырехугольник . Термин четырехугольник часто используется для описания прямоугольного замкнутого открытого пространства, например «новички, собранные в четырехугольнике колледжа». Термин четырехугольник соответствует многоугольнику, пятиугольнику и т. Д. Вы можете встретить его время от времени, но на практике он обычно не используется.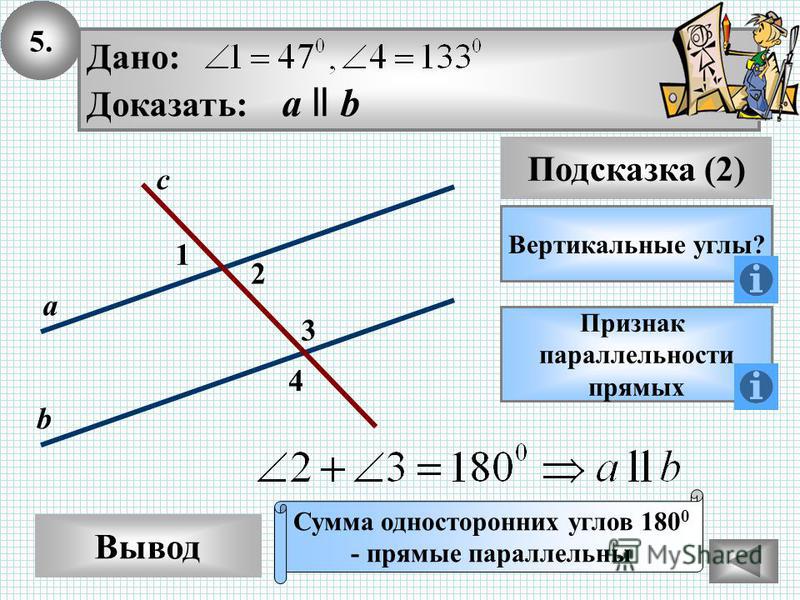
Семейство четырехугольников включает квадрат, прямоугольник, ромб и другие параллелограммы, трапецию / трапецию и воздушный змей.
Суммарные внутренние углы всех четырехугольников составляют 360 °.
Квадрат : четыре стороны равной длины, четыре внутренних прямых угла.
Прямоугольник : четыре внутренних прямых угла, противоположные стороны равной длины.
Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны.
Ромб : особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как квадрат, сдавленный в стороны.
Трапеция (или трапеция) : две стороны параллельны, а две другие — нет. Длина сторон и углы не равны.
Равнобедренная трапеция (или трапеция) : Две стороны параллельны, а углы основания равны, что означает, что непараллельные стороны также равны по длине.

Воздушный змей : две пары смежных сторон равной длины; форма имеет ось симметрии.
Неправильный четырехугольник : четырехсторонняя форма, в которой нет одинаковых сторон и внутренние углы. Все внутренние углы по-прежнему составляют 360 °, как и у всех других правильных четырехугольников.
Более четырех сторон
Пятиугольник называется пятиугольником.
Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон…
Имена многоугольников
Имена многоугольников образованы от префиксов древнегреческих чисел. Греческий числовой префикс встречается во многих названиях повседневных предметов и понятий. Иногда они могут помочь вам вспомнить, сколько сторон имеет многоугольник. Например:
- У осьминога восемь ног — у восьмиугольника восемь сторон.
- Десятилетие — это десять лет — у десятиугольника десять сторон.
- Современное пятиборье состоит из пяти видов — пятиугольник имеет пять сторон.
- Олимпийское семиборье состоит из семи этапов, семиугольник имеет семь сторон.
Префикс «поли-» просто означает «множественный», поэтому многоугольник — это фигура с множеством сторон, точно так же, как «полигамия» означает множественность супругов.
Есть имена для многих различных типов многоугольников, и обычно количество сторон более важно, чем имя формы.
Есть два основных типа многоугольника — правильный и неправильный.
Правильный многоугольник имеет стороны равной длины с равными углами между ними. Любой другой многоугольник — это неправильный многоугольник , у которого по определению есть стороны неравной длины и неравные углы между сторонами.
Окружности и формы, включающие кривые, не являются многоугольниками. — многоугольник по определению состоит из прямых линий. Смотрите наши страницы, посвященные кругам и изогнутым формам , чтобы узнать больше.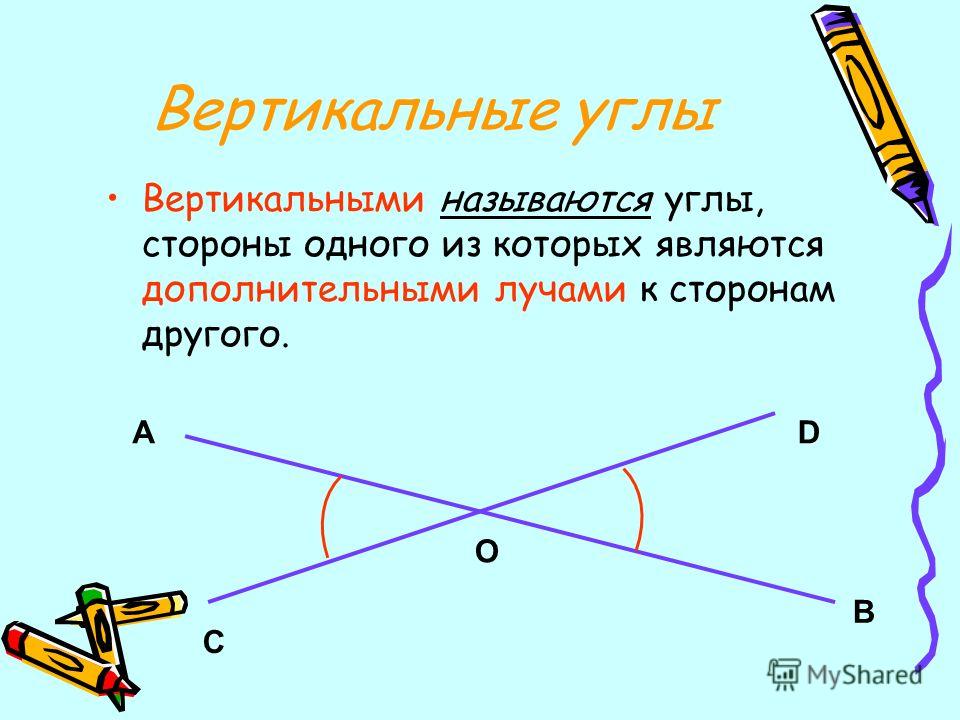
Углы между сторонами
Углы между сторонами фигур важны при определении многоугольников и работе с ними. См. Нашу страницу «Углы», чтобы узнать больше о том, как измерять углы.
Существует полезная формула для определения суммы (или суммы) внутренних углов для любого многоугольника, а именно:
(количество сторон — 2) × 180 °
Пример:
Для пятиугольника (пятиугольной формы) расчет будет:
5 — 2 = 3
3 × 180 = 540 °.
Сумма внутренних углов любого (несложного) пятиугольника составляет 540 °.
Кроме того, если форма представляет собой правильный многоугольник (все углы и длины сторон равны), вы можете просто разделить сумму внутренних углов на количество сторон, чтобы найти каждый внутренний угол.
540 ÷ 5 = 108 °.
Следовательно, правильный пятиугольник имеет пять углов, каждый равный 108 °.
Длина сторон
Помимо количества сторон и углов между сторонами, длина каждой стороны фигур также важна.
Длина сторон плоской фигуры позволяет вычислить периметр фигуры (расстояние вокруг внешней стороны фигуры) и площадь (количество пространства внутри фигуры).
Если ваша фигура представляет собой правильный многоугольник (например, квадрат в приведенном выше примере), то необходимо измерить только одну сторону, поскольку, по определению, другие стороны правильного многоугольника имеют одинаковую длину. Обычно используются деления, чтобы показать, что все стороны имеют одинаковую длину.
В примере с прямоугольником нам нужно было измерить две стороны — две неизмеренные стороны равны двум измеренным сторонам.
Некоторые размеры обычно не отображаются для более сложных форм. В таких случаях можно рассчитать недостающие размеры.
В приведенном выше примере отсутствуют две длины.
Недостающую длину по горизонтали можно вычислить. Возьмите более короткую известную длину по горизонтали из известной длины по горизонтали.
9 м — 5,5 м = 3,5 м.
По такому же принципу можно определить недостающую длину по вертикали. То есть:
3м — 1м = 2м.
Объединение всей информации: расчет площади многоугольников
Самым простым и основным многоугольником для вычисления площади является четырехугольник. Чтобы получить площадь, просто умножьте длину на высоту по вертикали.
Для параллелограммов обратите внимание, что высота по вертикали составляет НЕ длины наклонной стороны, а расстояние по вертикали между двумя горизонтальными линиями.
Это потому, что параллелограмм по сути представляет собой прямоугольник с треугольником, обрезанным с одного конца и наклеенным на другой:
Вы можете видеть, что если вы удалите левый синий треугольник и прикрепите его к другому концу, прямоугольник превратится в параллелограмм.
Площадь — это длина (верхняя горизонтальная линия), умноженная на высоту, расстояние по вертикали между двумя горизонтальными линиями.
Чтобы вычислить площадь треугольника , вы умножаете длину на высоту по вертикали (то есть высоту по вертикали от нижней линии до верхней точки) и делите ее пополам.По сути, это потому, что треугольник — это половина прямоугольника.
Чтобы вычислить площадь любого правильного многоугольника , проще всего разделить его на треугольники и использовать формулу для площади треугольника.
Итак, для шестиугольника, например:
На диаграмме видно, что имеется шесть треугольников.
Площадь есть:
Высота (красная линия) × длина стороны (синяя линия) × 0,5 × 6 (потому что треугольников шесть).
Вы также можете определить площадь любого правильного многоугольника с помощью тригонометрии, но это гораздо сложнее.
Дополнительные сведения, включая примеры, см.
На нашей странице Расчет площади .
Вы также можете определить площадь любого правильного многоугольника с помощью тригонометрии, но это гораздо сложнее. См. Нашу страницу Введение в тригонометрию для получения дополнительной информации.
Что такое четырехугольник? [Определение, факты и пример]
Четырехугольники
Определить четырехугольники
Четырехугольники — это замкнутые фигуры с 4 сторонами.Определите разные четырехугольники, такие как прямоугольники, квадраты, ромбы и параллелограммы.
охватывает Common Core Curriculum 3.G.1Играть сейчасЧетыреугольники с разной ориентацией
Квадрат — это квадрат, даже если вы перевернете его вверх ногами! Определите четырехугольники, представленные в разной ориентации.
охватывает Common Core Curriculum 3.G.1Играть сейчасПосмотреть все игры по геометрии >>
Учитесь с полной программой обучения математике K-5
Что такое четырехугольник?
Многоугольник состоит из четырех вершин или углов.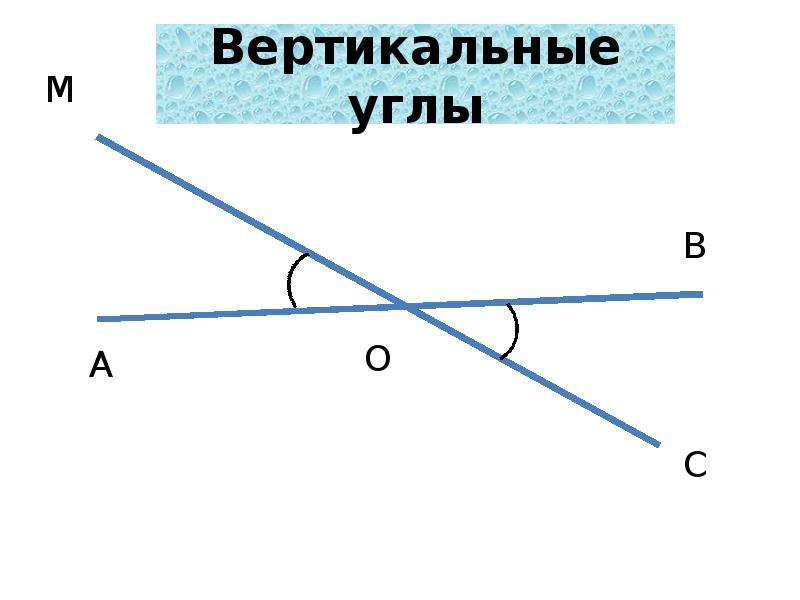
Мы можем найти форму четырехугольников в различных предметах вокруг нас, например, в шахматной доске, колоде карт, воздушном змеи, кадке с попкорном, вывеске и стрелке.
Свойства четырехугольника:
- Четырехугольник имеет 4 стороны, 4 угла и 4 вершины.
- Четырехугольник может быть правильным или неправильным.
- Сумма всех внутренних углов четырехугольника составляет 360 °.
Типы четырехугольников
Четырехугольники можно разделить на параллелограммы, квадраты, прямоугольники и ромбы.Квадрат, Прямоугольник и Ромб тоже параллелограммы.
Вот список типов четырехугольников с их названиями, изображениями и свойствами:
| Название четырехугольника: | Изображение четырехугольника: | Свойства четырехугольника: |
| Параллелограмм | Противоположные стороны параллельны. Противоположные стороны равны. Противоположные углы равны. | |
| Квадрат | Все стороны равны. Все углы равны и составляют 90 °. | |
| Прямоугольник | Противоположные стороны параллельны. Противоположные стороны равны. Все углы равны и составляют 90 °. | |
Ромб | Все стороны равны. Противоположные углы равны. | |
| Трапеция | Противоположные стороны параллельны. Смежные углы в сумме составляют 180 °. |
Интересные факты
|
Давайте споем!
Четыре стороны и, как и четыре угла,
Найдите четырехугольник на полу в ванной.
Другой вы можете увидеть в деревянной двери,
Или в лодке и веслах, у берега моря !!
Давайте сделаем это!
Вместо того, чтобы раздавать своим детям четырехугольные листы-раскраски, попросите их наблюдать и отмечать предметы в форме правильных и неправильных четырехугольников, например, в телевизоре, ноутбуке, книге или воздушном змее. Далее вы можете обсудить и показать видео, чтобы рассмотреть свойства разных четырехугольников.
Сопутствующая математическая лексика
border-top-left-radius — CSS: каскадные таблицы стилей
Свойство CSS border-top-left-radius округляет верхний левый угол элемента, указывая радиус (или радиус большой и малой полуосей) эллипса, определяющего кривизну угол.
Округление может быть кругом или эллипсом, или, если одно из значений 0, , округление не выполняется, а угол квадратный.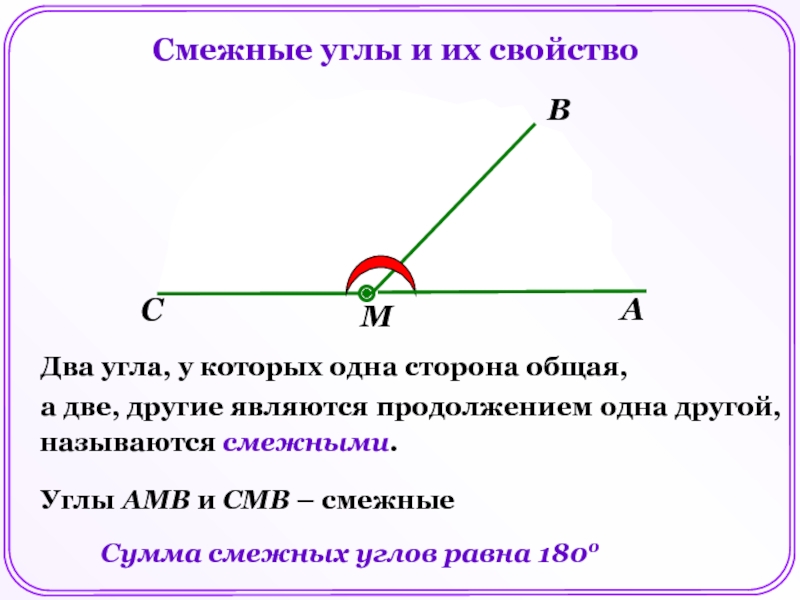
Фон, являющийся изображением или цветом, обрезается по границе, даже если она закруглена; точное место отсечения определяется значением свойства background-clip .
Примечание: Если значение этого свойства не установлено в сокращенном свойстве border-radius , которое применяется к элементу после CSS-свойства border-top-left-radius , значение этого свойства затем сбрасывается. к его начальному значению сокращенным свойством.
граница-верх-левый-радиус: 3 пикселя;
граница-верхний-левый-радиус: 0.5em 1em;
граница-верхний-левый-радиус: наследование;
С одним значением:
- значение —
<длина>или<процент>, обозначающее радиус круга, который будет использоваться для границы в этом углу.
С двумя значениями:
- первое значение — это
<длина>или<процент>, обозначающее горизонтальную большую полуось эллипса, используемую для границы в этом углу.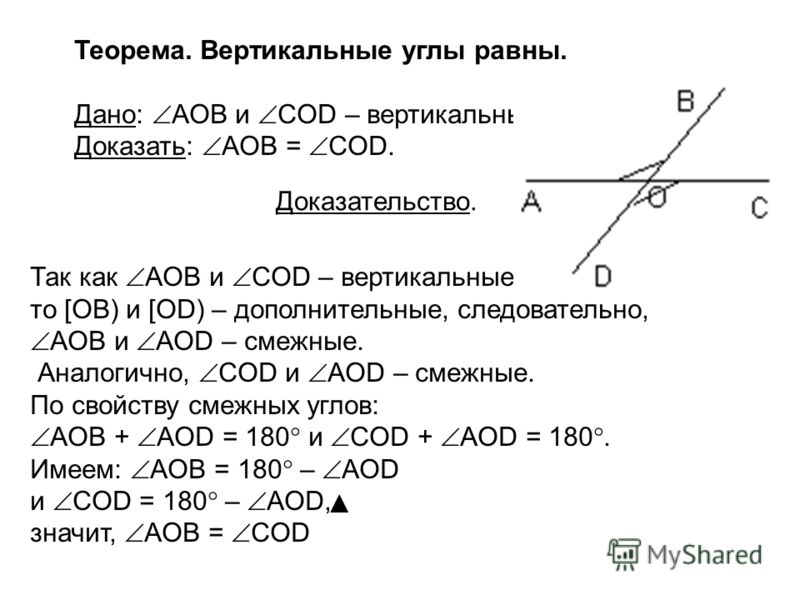
- второе значение —
<длина>или<процент>, обозначающее большую вертикальную полуось эллипса, используемую для границы в этом углу.
Значения
-
<длина-процент> - Обозначает размер радиуса окружности или большой и малой полуосей эллипса. Абсолютная длина может быть выражена в любых единицах, разрешенных типом данных CSS
Примеры различных значений радиуса border-top-left-radius
| Живой пример | Код |
|---|---|
Дуга эллипса используется в качестве границы | |
Дуга эллипса используется в качестве границы | |
Блок представляет собой квадрат: дуга круга используется в качестве границы | |
Поле не квадрат: дуга эллипса используется в качестве границы | |
Цвет фона обрезан по границе |
Таблицы BCD загружаются только в браузере
Закругленные углы | HTML Собака
Закругленные углы раньше использовались для сужения сплошных фоновых изображений или, для гибких рамок, множества фоновых изображений, по одному на угол, наложенных на несколько вложенных элементов div . Ах, некрасиво. Ну, больше нет. Теперь, с помощью простого CSS, вы можете украсить свой дизайн большим количеством кривых, чем Мэрилин Монро.
Ах, некрасиво. Ну, больше нет. Теперь, с помощью простого CSS, вы можете украсить свой дизайн большим количеством кривых, чем Мэрилин Монро.
Радиус границы?
Ага. Радиус границы. Но не бойтесь — вам не обязательно иметь границы. Свойство border-radius можно использовать для добавления угла к каждому углу блока.
#maryn {
фон: #fff;
ширина: 100 пикселей;
высота: 100 пикселей;
радиус границы: 20 пикселей;
}
И вот оно.Закругленные углы, понимаете? Хорошо, если у вас есть разумный браузер (см. Примечание ниже).
Углы вырезаются вокруг соответствующих четвертей круга (или эллипса) с заданным радиусом.
Конечно, если вы хотите, чтобы граница…
#ok_a_border_then {
граница: 5px solid # 8b2;
ширина: 100 пикселей;
высота: 100 пикселей;
радиус границы: 5 пикселей;
}
Woop.
Новый раздел примеров!
Посмотрите на весь этот код в действии и поиграйте с ним.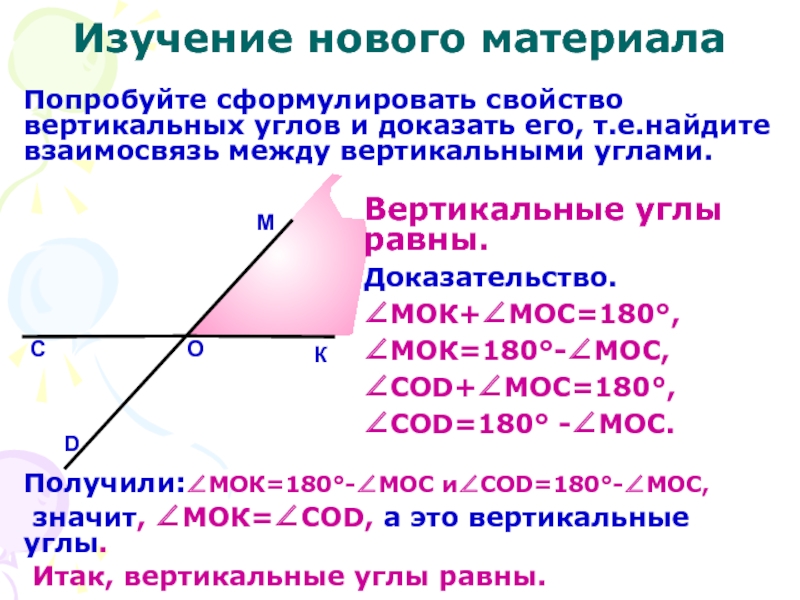
Несколько значений
border-top-left-radius , border-top-right-radius , border-bottom-right-radius и border-bottom-left-radius также можно использовать для нацеливания на определенные углы.
Когда-либо это было немного менее ужасно многословным, вы также можете определить все угловые радиусы (какое замечательное слово) индивидуально с помощью списка значений, разделенных пробелами, работая по часовой стрелке от верхнего левого угла, как и другие сокращенные свойства:
#monroe {
фон: #fff;
ширина: 100 пикселей;
высота: 100 пикселей;
border-radius: 6px 12px 18px 24px;
}
Граничный радиус с несколькими значениями.
Curvy.
Используя два значения вместо четырех, вы нацеливаете верхний левый и нижний правый угол на первую длину (или процент), а верхний правый + нижний левый — на второй. Три ценности? Верхний левый, затем верхний правый + нижний левый, затем нижний правый.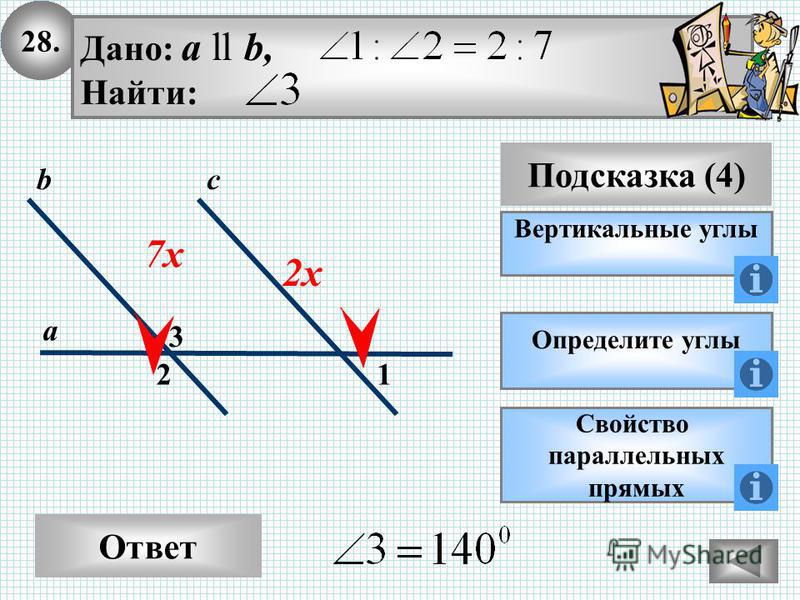 Разрушение.
Разрушение.
Гах! Просто должны быть проблемы с браузером, не так ли? Будь прокляты, браузеры.
Internet Explorer версии 8 и ниже не поддерживает border-radius . Единственный способ справиться с этим — либо довольствоваться дизайном в тех браузерах, у которого нет закругленных углов (большинство людей могут с этим смириться), либо вернуться к старым фоновым изображениям.
Вы также можете наткнуться на похожие проприетарные свойства, такие как -webkit-border-radius и -moz-border-radius , которые предназначены для более старых, мало используемых версий Safari и Firefox соответственно. Наш тщательно сформулированный профессиональный совет? К черту их.
Эллипсы
Круги для вас слишком квадратные? Вы можете указать разные радиусы по горизонтали и вертикали, разделив значения знаком «/».
#nanoo {
фон: #fff;
ширина: 100 пикселей;
высота: 150 пикселей;
радиус границы: 50 пикселей / 100 пикселей;
граница-нижний-левый-радиус: 50 пикселей;
граница-нижний-правый-радиус: 50 пикселей;
}
Наноо.
Поддержание границ лесной собственности | Публикации о расширении штата Северная Каролина
Учитывая высокую стоимость деревянных лесов на сегодняшний день, землевладельцам следует принять необходимые меры для защиты своих инвестиций. Поддержание границ и границ собственности — одна из простейших, но чаще всего упускаемых из виду форм защиты от краж, посягательств и посягательств.В этой публикации подробно рассказывается, как поддерживать или восстанавливать границы собственности, и содержится подробная информация о положениях Закона о защите землевладельцев Северная Каролина
«Поиск углов», как правило, является единственным способом, которым многие землевладельцы могут определить границы своей собственности. Хотя на жилых объектах может быть достаточно простого определения местоположения и отметки углов, этого недостаточно для лесных участков, где углы могут находиться на расстоянии тысячи футов друг от друга.Как лесовладелец, установление и поддержание хорошо размеченных линий может сэкономить вам деньги, снизить ответственность и сократить судебные разбирательства. Следующие ниже события требуют или поддерживаются хорошо обозначенными и разнесенными линиями собственности.
Хотя на жилых объектах может быть достаточно простого определения местоположения и отметки углов, этого недостаточно для лесных участков, где углы могут находиться на расстоянии тысячи футов друг от друга.Как лесовладелец, установление и поддержание хорошо размеченных линий может сэкономить вам деньги, снизить ответственность и сократить судебные разбирательства. Следующие ниже события требуют или поддерживаются хорошо обозначенными и разнесенными линиями собственности.
Продажа древесины
Продажа древесины предполагает точное определение границ продажи для проведения законной и законной коммерческой сделки. Часто затраты, связанные с обновлением границ, могут быть самыми высокими затратами на проведение продажи древесины. Однако затраты на обследование для восстановления границ могут быть вычтены как затраты на продажу.Обследование, проведенное в год без продажи древесины, должно быть капитализировано (добавлено к базе земли).
Подразделение или передача имущества
Каждый раз, когда недвижимость продается, передается или разделяется, зарегистрированный землемер должен проводить обследование для проверки местоположения, протяженности и границ собственности.
Соглашения и ограничения
Многие земельные участки несут ограничения на размещение зданий, отступы от заборов или другие ограничения на застройку.Определение точных границ собственности может помочь владельцу соблюдать эти ограничения.
Управленческая деятельность
Заготовка древесины, подготовка участка и предписанные операции по сжиганию должны проводиться в пределах своей собственности. Четко определенные границы собственности помогут избежать конфликтов и потенциальных посягательств на прилегающие земли.
Взлом
Нежелательное вторжение и браконьерство можно свести к минимуму, пометив и разместив строки собственности.В случае охоты преследование за незаконное владение может иметь место только в отношении земель, на которых «вывешены» объявления. Закон Северной Каролины гласит, что земля должна размещаться с интервалом не более 200 футов. Закон о защите землевладельцев Северной Каролины от 2011 года позволяет сотрудникам службы охраны дикой природы применять законы о несанкционированном проникновении, в которых границы, окрашенные в пурпурный цвет, используются вместо вывесок. (Подробности см. В конце публикации.)
(Подробности см. В конце публикации.)
Неблагоприятное владение
Неотмеченные границы собственности могут привести к потере земли.Земельные границы, которые не оспариваются в течение всего семи лет, могут привести к потере земли первоначальным владельцем.
Кража древесины
Имущество без опознавательных знаков может быть уязвимо для кражи древесины (незаконного проникновения древесины). Лучшая защита от кражи древесины — это четко обозначенная и поддерживаемая граница, которая часто проверяется на предмет посягательств.
Ответственность
Право собственности на собственность связано с множеством обязанностей и обязательств перед приглашенными и незваными пользователями.Четко обозначенные или обозначенные границы могут помочь минимизировать ответственность землевладельца, особенно в случаях отдыха и использования троп, когда плата не взимается.
Сервировка стола и права прохода
Часто некоторые права собственности на землю переходят к другой стороне.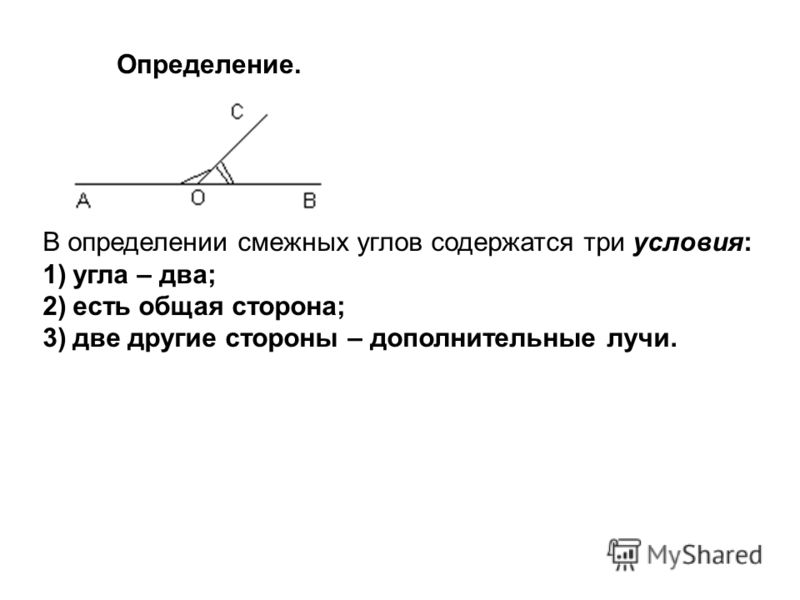 Сервитут или отвод, который дает правообладателю право въезжать на чью-либо землю или использовать ее в определенных целях, является наиболее распространенным явлением. Четкое размещение сервитута и соблюдение этих «внутренних» границ может свести к минимуму проблемы с держателем сервитута (часто с коммунальной компанией).
Сервитут или отвод, который дает правообладателю право въезжать на чью-либо землю или использовать ее в определенных целях, является наиболее распространенным явлением. Четкое размещение сервитута и соблюдение этих «внутренних» границ может свести к минимуму проблемы с держателем сервитута (часто с коммунальной компанией).
Самый эффективный способ сохранить границы владений — начать после завершения недавнего обследования, обычно во время приобретения. Поскольку многие лесные владения оставались в одной семье на протяжении десятилетий, это не всегда может быть практичным. Следующий лучший вариант — начать поддержание линии вдоль недавно обследованного или вырубленного прилегающего участка, поскольку смежные владения имеют по крайней мере одну общую границу.Последующие строки могут быть отмечены после обследования продажи или передачи древесины. Стоимость обследования может быть вычтена как расходы на продажу в год продажи древесины и только для той части обследования, которая определяет площадь продажи древесины.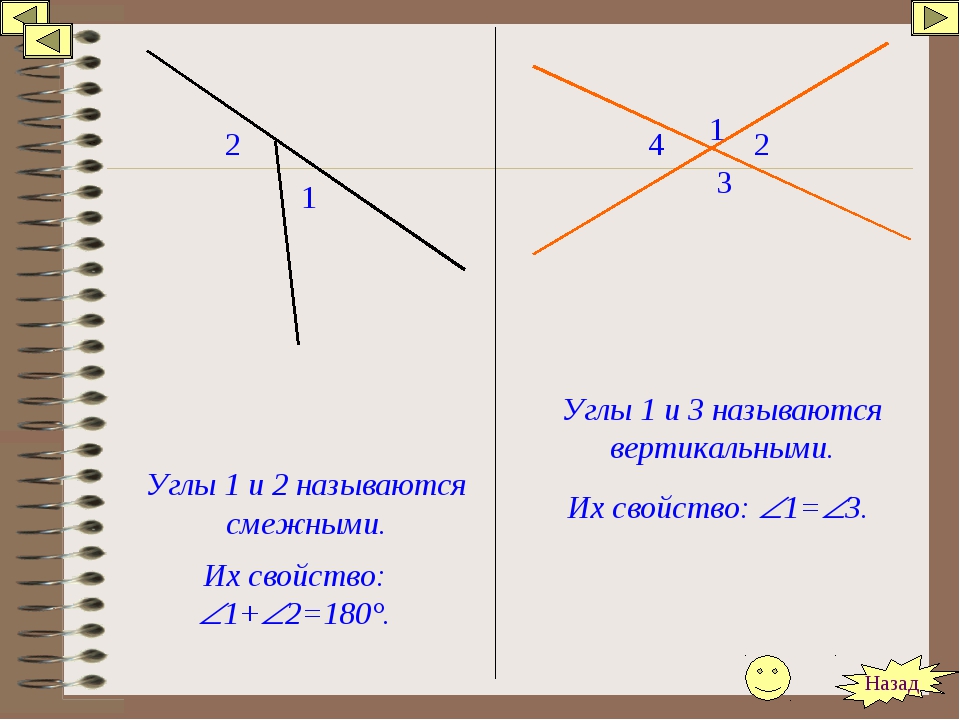 Для получения дополнительной информации о налоговых последствиях обследования как расхода на продажу древесины см. Публикацию IRS 225, Справочник по налогам для фермеров .
Для получения дополнительной информации о налоговых последствиях обследования как расхода на продажу древесины см. Публикацию IRS 225, Справочник по налогам для фермеров .
В отсутствие недавнего обследования расположение углов собственности, расстояния и пеленги можно получить из описания документа, доступного в офисе реестра документов округа (рис. 1).В описании собственности должно быть указано приблизительное расположение большинства углов. Затем с помощью компаса, помощника и ленты из стекловолокна можно определить местонахождение собственности. Одно предостережение для тех, кто занимается своими руками: хотя любой землевладелец или консультант по лесному хозяйству может восстановить линию собственности, они должны делать это с пониманием того, что они несут ответственность и, следовательно, несут ответственность за ущерб из-за любого ошибочного местоположения. Если есть какие-либо сомнения относительно линии собственности, единственный выход — профессиональный осмотр.(Обратите внимание, что закон штата запрещает уничтожение или перемещение любого участка собственности, даже если землевладелец считает, что он размещен неправильно.)
Если есть какие-либо сомнения относительно линии собственности, единственный выход — профессиональный осмотр.(Обратите внимание, что закон штата запрещает уничтожение или перемещение любого участка собственности, даже если землевладелец считает, что он размещен неправильно.)
Рис. 1. Платная карта типичного лесного участка (включая полосы отвода, пеленги и расстояния).
Землемеры обычно «чистят» или очищают границы участков во время съемки границ.Обычно валок расчищают с помощью мачете или бензопилы, чтобы обеспечить четкую линию обзора между точками или станциями съемки. Во время «зачистки» границ владений деревьям, находящимся непосредственно внутри, часто наносят от одной до трех косых черт на коре бензопилой (рис. 2). Эти отметки легко найти, если знать, что искать. Комбинация мазков кистью и косой чертой позволяет землевладельцам проследить за геодезистом и нарисовать или вывесить линию собственности.
Во время «зачистки» границ владений деревьям, находящимся непосредственно внутри, часто наносят от одной до трех косых черт на коре бензопилой (рис. 2). Эти отметки легко найти, если знать, что искать. Комбинация мазков кистью и косой чертой позволяет землевладельцам проследить за геодезистом и нарисовать или вывесить линию собственности.
Рисунок 2.Свидетельства следов обследования или рубцов на линейных деревьях, сделанных с помощью мачете или топора. Если освежить или снова открыть их, они будут видны на долгие годы.
Нож или мачете используются для соскабливания гладкой 5–6-дюймовой полосы на внешней коре примерно на уровне глаз.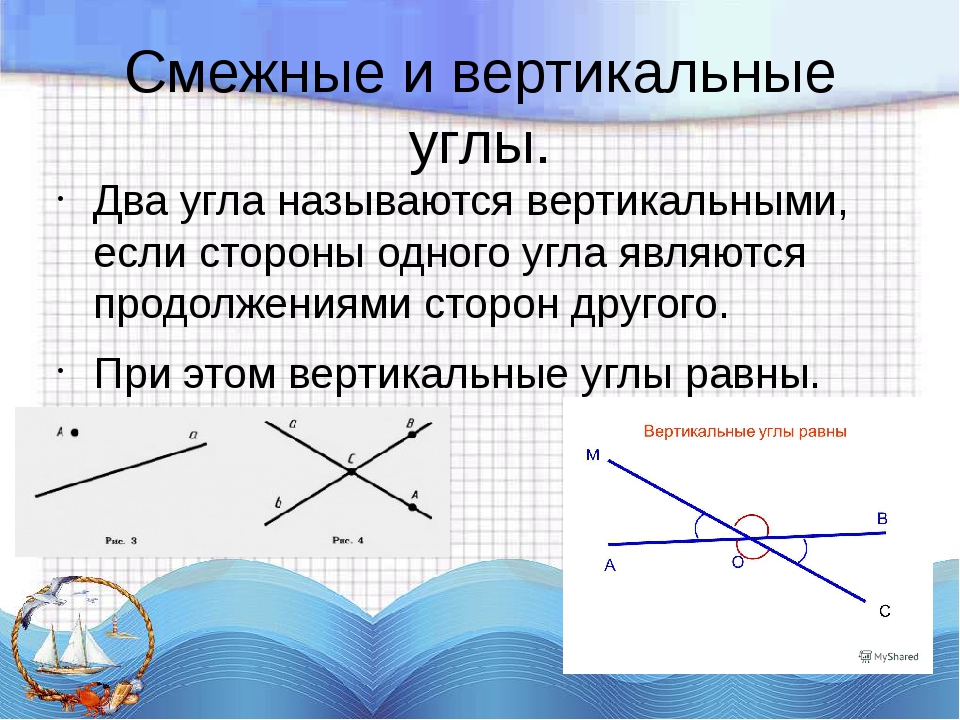 Работая в бригаде из двух человек, скребок может быстро подготовить каждое дерево для художника, следующего непосредственно за ним.
Работая в бригаде из двух человек, скребок может быстро подготовить каждое дерево для художника, следующего непосредственно за ним.
Один из широко используемых методов рисования границ участков — это использование ряда окрашенных полос или полос для обозначения положения линий и углов. Этот метод включает следующие компоненты:
- Вертикальная линия для осевых деревьев (расположена на линии собственности) (рисунок 3).
- Одна полоса для внутренних деревьев, прилегающая к линии собственности (обращенная к линии) (Рисунок 4).
- Две полосы для изменения линии (в сторону изменения) (Рисунок 5).
- Три полосы для обозначения угла участка (обращенного к углу) (Рисунок 6). Иногда дерево, расположенное прямо на углу, также отмечается большим X.
Закрашивание половины каждой линии или углового дерева позволяет легко видеть и определять направление линий собственности. Для максимальной стойкости всегда используйте наружную краску на масляной основе. Специально подготовленная красящая краска, срок годности которой составляет 10 лет и более, испытанная на практике, доступна в цветах с высокой видимостью (белый, желтый, оранжевый, красный и синий).
Для максимальной стойкости всегда используйте наружную краску на масляной основе. Специально подготовленная красящая краска, срок годности которой составляет 10 лет и более, испытанная на практике, доступна в цветах с высокой видимостью (белый, желтый, оранжевый, красный и синий).
Хорошо обозначенные границы владений могут сохраняться в течение многих лет, но их следует проверять на целостность ежегодно и чаще, когда поблизости случаются сильные штормы, ураганы или лесные пожары. К другим событиям, которые требуют частой проверки границ участка, относятся уборка урожая поблизости, а также вспышки насекомых и болезней.Хорошо обозначенная и патрулируемая граница собственности — ваша лучшая защита от вторжений и вторжений. Часто используемые инструменты для обслуживания границ выделены на Рисунке 7.
Рис. 3. Осевые деревья окрашиваются вертикальной меткой 2 x 6 дюймов в точке, где дерево пересекает линию собственности.
3. Осевые деревья окрашиваются вертикальной меткой 2 x 6 дюймов в точке, где дерево пересекает линию собственности.
Рисунок 4.Деревья внутренней линии получают одну полосу шириной от 3 до 4 дюймов, обращенную к линии собственности. (Раскрасьте только половину дерева, обращенную к линии.)
Рис. 5. Деревья, указывающие на изменение направления, получают двойную полосу шириной от 3 до 4 дюймов, нарисованную на той стороне дерева, к которой линия собственности меняет направление.
Рис. 6. Угловые деревья, расположенные в пределах 5 футов от угла, получают тройную полосу шириной 2 дюйма на стороне дерева, непосредственно обращенной к угловой стойке или стойке.
Рисунок 7.Инструменты для разметки линий включают мачете, бензопилу, нож, крюк или втулочный топор, кисть и консервную банку, малярную кисть и вывешенные знаки.
Закон о защите землевладельцев Северной Каролины (принят в 2011 году) усиливает существующий закон о посягательстве на частную собственность, разъясняя общие законы о посягательстве и правоприменении.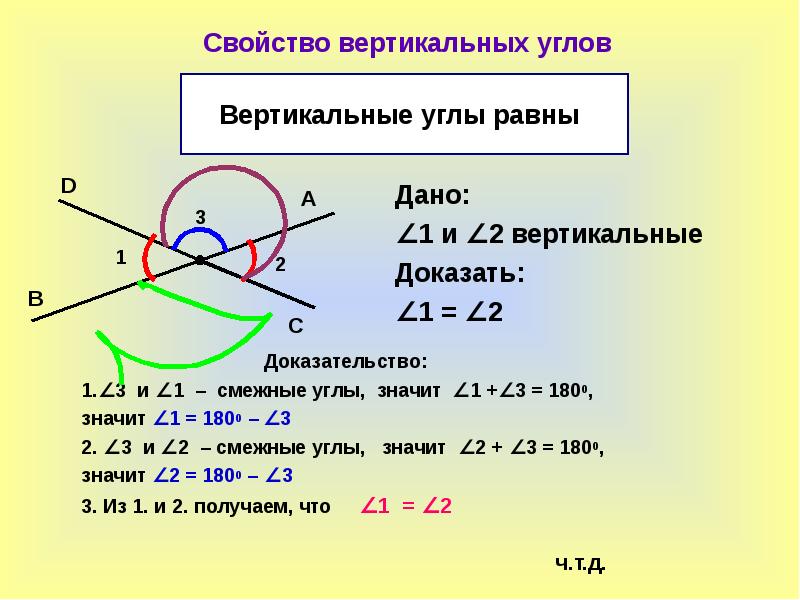 Закон предоставляет землевладельцам упрощенный способ вывесить свою собственность пурпурной краской. Землевладелец может нарисовать вертикальную линию пурпурной краской на деревьях или столбах вокруг границ собственности или участков, предназначенных для запрещения вторжения (рис. 8).
Закон предоставляет землевладельцам упрощенный способ вывесить свою собственность пурпурной краской. Землевладелец может нарисовать вертикальную линию пурпурной краской на деревьях или столбах вокруг границ собственности или участков, предназначенных для запрещения вторжения (рис. 8).
Закон о защите землевладельцев Северной Каролины также определяет требования, касающиеся письменного разрешения на охоту, ловлю рыбы или ловлю на размещенных землях:
- Письменное разрешение должно быть выдано в течение последних 12 месяцев.
- Разрешение должно быть подписано землевладельцем, арендатором или агентом этой земли.
- Письменное согласие должно быть у посетителя при нахождении на территории и предоставлено по запросу любого сотрудника правоохранительных органов.
Закон о защите землевладельцев штата Северная Каролина позволяет сотрудникам службы охраны дикой природы обеспечивать соблюдение законов о нарушении прав владения на территории. Кроме того, это позволяет землевладельцам размещать земельные участки, используя отметки фиолетовой краской и / или размещая знаки запрета вторжения, как это было разрешено до 2011 года.
Кроме того, это позволяет землевладельцам размещать земельные участки, используя отметки фиолетовой краской и / или размещая знаки запрета вторжения, как это было разрешено до 2011 года.
Для получения более подробной информации о Законе о защите землевладельцев Северной Каролины, в том числе о том, как разместить пурпурные знаки на частных землях, получить ответы на часто задаваемые вопросы о Законе о защите землевладельцев и просмотреть образцы разрешительных писем, посетите Комиссию по ресурсам дикой природы Северной Каролины.
Подробнее на NC State Extension Forestry.
Рис. 8. Правильное размещение пурпурных пятен краски в соответствии с требованиями к размещению в Акте о защите землевладельцев штата Северная Каролина.
Создание и обслуживание участков собственности — это стоящая инвестиция, которая может принести много ценных дивидендов владельцам недвижимости. Поддерживайте очереди сразу после обследования для получения максимальной выгоды и наименьших затрат. Практическое знание законодательных актов Северной Каролины, касающихся посягательств и ответственности, также может значительно улучшить ваши усилия по защите собственности. Проконсультируйтесь с профессиональным консультантом по лесному хозяйству, лицензированным геодезистом и адвокатом при решении вопросов, связанных с территорией собственности, поскольку они влияют на ваши лесные угодья.
Поддерживайте очереди сразу после обследования для получения максимальной выгоды и наименьших затрат. Практическое знание законодательных актов Северной Каролины, касающихся посягательств и ответственности, также может значительно улучшить ваши усилия по защите собственности. Проконсультируйтесь с профессиональным консультантом по лесному хозяйству, лицензированным геодезистом и адвокатом при решении вопросов, связанных с территорией собственности, поскольку они влияют на ваши лесные угодья.
- Марк Мегалос
Дополнительный специалист по лесному хозяйству
Лесное хозяйство и экологические ресурсы
- Рик Гамильтон
Руководитель отдела повышения квалификации — специалист
Лесное хозяйство и экологические ресурсы
- Эндрю Бранан
Ассистент-профессор (сельскохозяйственное и экологическое право)
Экономика сельского хозяйства и природных ресурсов
Дополнительную информацию можно найти на следующих веб-сайтах NC State Extension:
Дата публикации: 8 апреля 2019 г.
WON-35
Н.C. Cooperative Extension запрещает дискриминацию и домогательства независимо от возраста, цвета кожи, инвалидности, семейного и семейного положения, гендерной идентичности, национального происхождения, политических убеждений, расы, религии, пола (включая беременность), сексуальной ориентации и статуса ветерана.
3D-фигуры — Maths GCSE Revision
3D-фигура описывается ее ребрами, гранями и вершинами (вершина — это особая форма вершин).
Это видео и изображения ниже объясняют грани, вершины и края обычных трехмерных форм.
Грань — это двумерная форма, которая составляет одну поверхность трехмерной формы, кромка — это место, где встречаются две грани, а вершина — это точка или угол геометрической формы.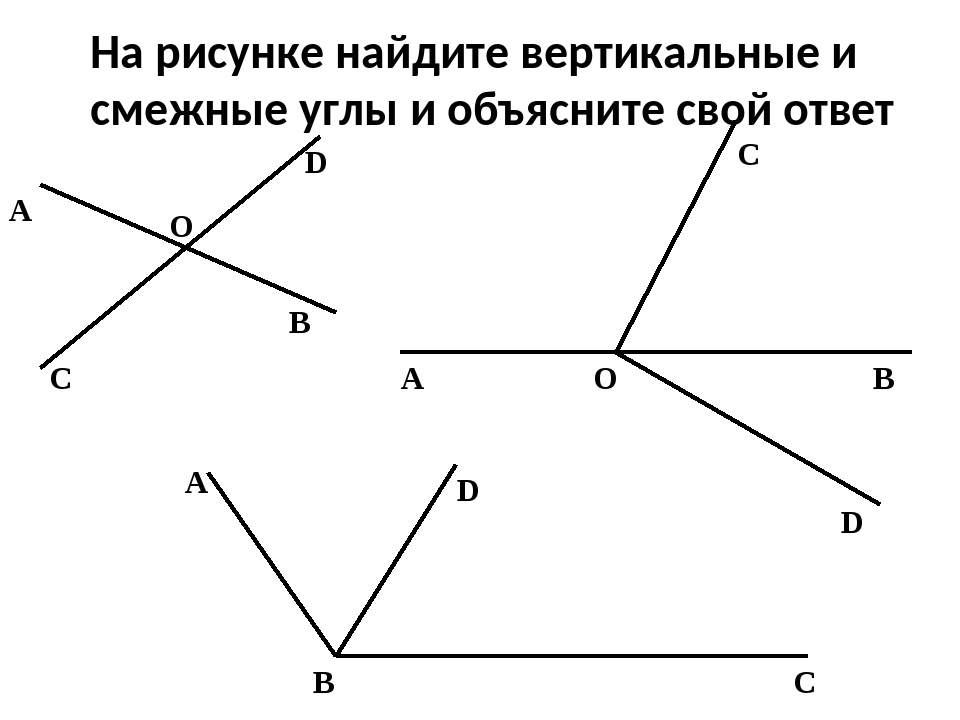
Чтобы определить площадь грани трехмерной формы, вы используете квадратные единицы, такие как см 2 , поскольку грань трехмерной формы сама по себе является двумерной фигурой (грань пирамиды образует треугольник или ее основание квадрата). Вы можете узнать, как проработать область фигуры здесь.
Чтобы определить объем всей трехмерной формы, вы использовали кубические единицы, например, см 3 .Чтобы узнать, как вычислить объем 3D-фигур, нажмите здесь.
Свойства трехмерных форм — призмы
Куб
Количество кромок: 12
Количество лиц: 6
Количество вершин: 8
Кубоид
Количество кромок: 12
Количество лиц: 6
Количество вершин: 8
Цилиндр
Количество кромок: 2
Количество лиц: 3
Количество вершин: 0
Треугольная призма
Количество кромок: 9
Количество лиц: 5
Количество вершин: 6
Восьмиугольная призма
Количество кромок: 24
Количество лиц: 10
Количество вершин: 16
Свойства трехмерных фигур — пирамиды
Тетраэдр
Количество кромок: 6
Количество граней: 4
Количество вершин: 4
Пирамида на основе квадрата
Количество кромок: 8
Количество лиц: 5
Количество вершин: 5
Пирамида с шестиугольным основанием
Количество кромок: 12
Количество лиц: 7
Количество вершин: 7
Свойства 3D-форм — изогнутые грани
Конус
Количество кромок: 1
Количество лиц: 2
Количество вершин: 1
Фрустум
Количество кромок: 2
Количество лиц: 3
Количество вершин: 0
Сфера
Количество кромок: 0
Количество граней: 1
Количество вершин: 0
.