Содержание
Как вынести число из-под корня
Как выносить из под корня число
Часто вынесение множителя (числа) из под знака корня может быть необходимо для совершения каких-либо арифметических операций, например, для сокращения дроби или вынесения общего множителя и дальнейшего преобразования выражения.
Давайте рассмотрим основные арифметические правила и определения, необходимые для того, чтобы понять, как вынести число из под корня.
Необходимые операции и определения
Разложение выражения на множители — это преобразование этого числа в произведение нескольких сомножителей без изменения значения исходного выражения.
Это довольно частая операция, необходимая для вынесения множителя из-под знака корня.
Для разложения на множители используются следующие приёмы:
- Вынесение за скобки общего множителя;
- Группировка множителей;
- Применение формул сокращённого умножения;
- Комбинация вышеизложенных методов.
При вынесении за скобки общего множителя для начала нужно определить множитель, который можно вынести, а затем разделить всё выражение на этот множитель и записать результат частного рядом со множителем как произведение, например:
$6x^2 – 8xy +4x = 2x \cdot 3x — 2x \cdot 4y + 2x \cdot 2 = 2x \cdot (3x — 4y + 2)$. 2$.
2$.
Оба продемонстрированных выше метода можно комбинировать.
Свойства корня
Теперь перейдём к более детальному рассмотрению корня.
Определение 1
Корнем $n$-нной степени из числа $b$ называют число, которое нужно возвести в $n$-нную степень чтобы получить число $b$:
$\sqrt[n]{b}= m$.
Замечание 1
Процесс получения корня называется его извлечением.
Левая часть равенства вида $\sqrt[n]{b} = m$ называется радикалом, то, что стоит непосредственно под знаком корня — подкоренным выражением, а число, стоящее слева сверху перед знаком корня называется показателем корня.
Правая же часть равенства после знака «равно» называется корнем $n$-нной степени из числа $b$.
При извлечении числа из-под корня нужно учитывать то, что в случае с корнем нечётной степени возможен лишь один ответ, математически это запишется так: $\sqrt[n]{x} = b$, тогда как в случае с извлечением корня чётной степени ответа будет два, причём один с положительным знаком, а другой с отрицательным, это записывается так: $\sqrt[n]{x} = ±b$. 2} = x (a+b)\sqrt{7x}$.
2} = x (a+b)\sqrt{7x}$.
Как вынести множитель из-под знака корня: теория, примеры, решения
В данном материале мы продолжим рассказывать о том, как преобразовывать рациональные выражения, а конкретно о том, как правильно выносить множитель из-под знака корня. В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
Что такое вынесение множителя из-под знака корня
Чтобы лучше понять суть подобного преобразования, нужно сначала сформулировать, что такое вообще вынесение множителя из-под знака корня. Сформулируем определение:
Определение 1
Вынесение множителя из-под знака корня представляет собой замену выражения Bn·Cn на произведение B·Cn с условием, что n – нечетное число, или же на произведение B·C – где n – четное число, а B и C – другие числа и выражения.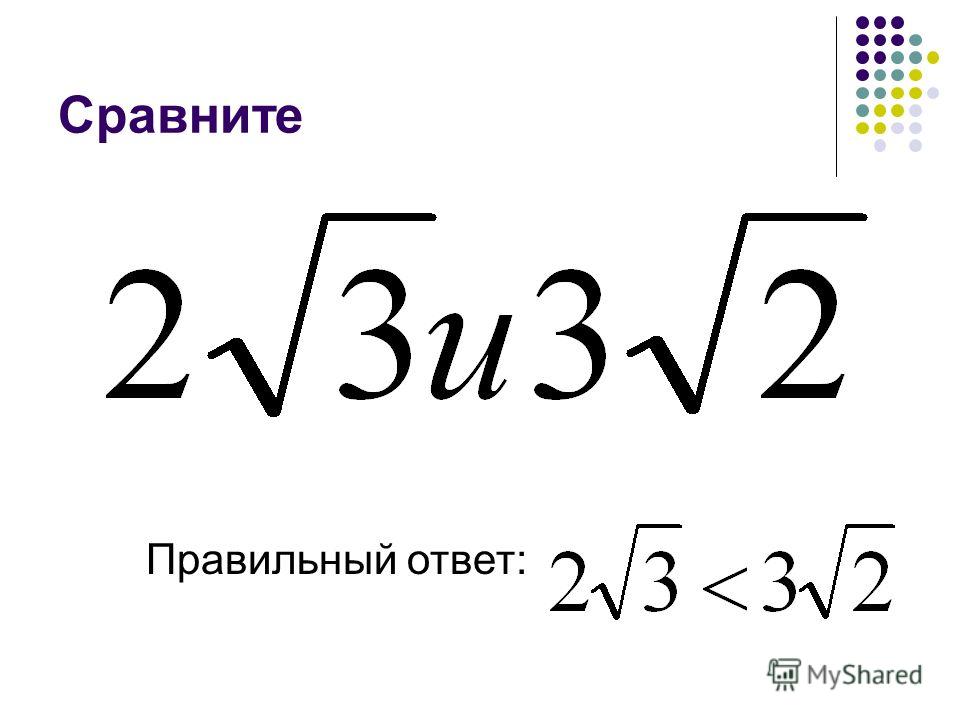
Если мы имеем в виду только квадратный корень, то есть число n равно двум, то процесс вынесения множителя можно свести к замене выражения B2·C на произведение B·C. Отсюда и название данного преобразования: после того, как оно было проведено, множитель Byоказывается свободным от знака корня.
Приведем примеры, поясняющие данное определение. Так, допустим, у нас есть выражение 22·3. Оно аналогично B2·C, где B равно двум, а C – трем. Заменив данный корень на произведение 2·3 и опустив знаки модулей (это можно сделать, поскольку оба множителя являются положительными числами), мы получим 2·3. Мы вынесли множитель 22 из-под знака корня.
Приведем еще один пример подобного преобразования. У нас есть выражение (x2-3·x·y·z)2·x=x2-3·x·y·z·x. Здесь из-под корня был вынесен не просто числовой множитель, а целое выражение с переменными (x2−3·x·y·z)2.
Оба примера относятся к случаю вынесения множителя из-под квадратного корня. Можно также производить данные преобразования и для корней n-ной степени. Вот пример с кубическим корнем: (3·a2)3·2·a23=3·a2·2·a23
Вот пример с кубическим корнем: (3·a2)3·2·a23=3·a2·2·a23
Пример с корнем шестой степени: 12·x2+y26·5·(x2+y2)6 можно преобразовать в произведение 12·x2+y2·5·(x2·y2)6, которое, в свою очередь, упрощается до 12·(x2+y2)·5·(x2+y2)6. В данном случае мы выносим множитель 12·x2+y26.
Мы выяснили, что такое вынесение множителя из-под знака корня. Теперь перейдем к доказательствам, т.е. поясним, почему произведение, полученное в итоге данного преобразования, равнозначно исходному выражению.
Почему возможно заменить корень на произведение
В этом пункте мы будем разбираться, как возможна такая замена и почему корень Bn·Cn равнозначен произведениям B·Cn и B·Cn. Обратимся к ранее изученным теоретическим положениям.
Когда мы разбирали преобразование иррациональных выражений, у нас получились некоторые важные результаты, которые мы собрали в таблицу. Здесь нам будут нужны только два из них:
1. Выражение A·Bn при условии нечетности n может быть заменено на An·Bn, а для четных n – An·Bn.
2. Выражение Ann при нечетном значении n может быть преобразовано в A, а при четном – в |A|.
Определение 2
Используя эти результаты и зная основные свойства модуля, мы можем вывести следующее:
- при четном n: Bn·Cn=Bnn·Cn=B·Cn;
- при нечетном n: Bn·Cn=Bnn·Cn=Bnn·Cn=B·Cn.
Эти выражения лежат в основе преобразований, которые мы проводим, вынося множитель из-под знака корня.
Следовательно, можно вывести две формулы:
Определение 3
- B1n·B2n·…·Bkn·Cn=B1·B2·…·Bk·Cn для нечетного n;
- B1n·B2n·…·Bkn·Cn=B1·B2·…·Bk·Cn для четного n.
Здесь B1, B2, и др. могут быть как числами, так и выражениями.
С помощью данных формул можно выполнить вынесение из-под корня сразу нескольких множителей.
Основное правило вынесения множителя из-под корня
Когда нам нужно решать примеры с подобными преобразованиями, чаще всего приходится предварительно приводить подкоренное выражение к виду Bn·C. С учетом этого момента мы можем записать следующие правила.
Определение 4
Для вынесения множителя из-под корня в выражении An нужно предварительно привести корень к виду Bn·Cn и после этого перейти к произведению B·Cn (при нечетном показателе) или к B·Cn (при четном показателе, при необходимости раскрываем модули).
Таким образом, схема решения подобных задач выглядит следующим образом:
An→Bn·Cn→B·Cn, если n-нечетноеB·Cn, если n-четное
Если нам надо вынести несколько множителей, то действуем так:
An→B1n·B2n·…·Bkn·Cn→B1·B2·…·Bk·Cn, если n-нечетноеB1·B2·…·Bk·Cn, если n-четное
Теперь можно переходить к решению задач.
Задачи на вынесение множителя из-под знака корня
Пример 1
Условие: выполните вынесение множителя за знак корня в трех выражениях: 22·7, -1232·5, (-0,4)7·117.
Решение
Мы видим, что подкоренные выражения во всех трех случаях уже имеют нужный нам вид. Поскольку в первых двух примерах показателем корня является четное число, а в третьем – нечетное, записываем следующее:
- Показатель корня равен 2.
 Берем правило вынесения множителя для четного показателя и вычисляем: 22·7=2·7=2·7
Берем правило вынесения множителя для четного показателя и вычисляем: 22·7=2·7=2·7 - Во втором выражении показатель тоже четный, значит, -1232·5=-123·5=123·5
В этом случае мы можем сначала преобразовать выражения, исходя из основных свойств корня:
-1232·5=-12·1232·5=1232·5
А потом уже выносить множитель: 1232·5=123·5=123·5. - Последнее выражение имеет нечетный показатель, поэтому нам понадобится другое правило: (-0,4)7·117=-0,4·117.
Возможен и такой вариант расчета:
-0,47·117=(-1)7·0,47·117==-0,47·117=-0,47·117=-0,4·117
Или такой:
-0,47·117=(-1)7·0,47·117==-0,47·117=0,47·-117=0,4·-117=-0,4·117
Ответ: 1) 2·7; 2) 123·5; 3) -0,4·117.
Пример 2
Условие: преобразуйте выражение (-2)4·(0,3)4·74·114.
Решение:
При помощи схемы, приведенной во втором пункте статьи, мы можем вынести из-под корня сразу три множителя.
(-2)4·(0,3)4·74·114==-2·0,3·7·114=4,2·114
Можно сделать преобразование в несколько шагов, вынося множителя по одному, но так будет гораздо дольше.
Есть и другой способ. Преобразуем само выражение, приведя его к виду Bn·C. После этого уже будем выносить множители:
(-2)4·(0,3)4·74·114==(-2·0,3·7)4·114=(-4,2)4·114==-4,2·114=4,2·114
Ответ: (-2)4·(0,3)4·74·114=-4,2·114=4,2·114.
Разберем более подробно тот случай, когда подкоренное выражение требует предварительного преобразования. Здесь есть несколько моментов, которые нужно дополнительно пояснить.
Предварительное преобразование подкоренного выражения
Мы уже отмечали, что выражение под корнем не всегда имеет удобный для нас вид. Часто корень дан как An, и множитель, который нужно вынести, не представлен в явном виде. Иногда это обозначено в условии, но довольно часто множитель приходится определять самостоятельно. Посмотрим, как надо действовать в этих случаях.
Допустим, нам надо вынести заранее определенный множитель B. Естественно, подкоренное выражение должно быть таким, чтобы эта операция была возможна. Тогда для преобразования An в Bn·Cn достаточно определить второй множитель, т. е. вычислить значение C из выражения A=Bn·C.
е. вычислить значение C из выражения A=Bn·C.
Пример 3
Условие: есть выражение 24·x3. Вынесите из-под знака корня множитель 23.
Решение
Здесь мы имеем n=3, A=24·x, B3=23. Тогда из A=Bn·С вычисляем C=A:(Bn) =24·x:(23) =3·x.
Значит, 24·x3=23·3·x3. Подкоренное выражение имеет нужный нам вид, и мы можем воспользоваться правилом для нечетного показателя и подсчитать: 24·x3=23·3·x3=2·3·x3.
Ответ: 24·x3=2·3·x3.
А как быть в случае, если множитель, который нужно вынести, не указан? Тогда у нас есть определенная свобода выбора, и мы можем использовать несколько подходов к решению задачи.
Допустим, нам дано выражение, под корнем у которого стоит степень или произведение нескольких степеней. В таком случае, зная основные свойства степени, мы можем преобразовать выражение в удобный для нас вид с очевидно указанными множителями для вынесения.
Пример 4
Условие: необходимо вынести множитель из-под корня в трех выражениях – 24·54, 27·54, 222·54.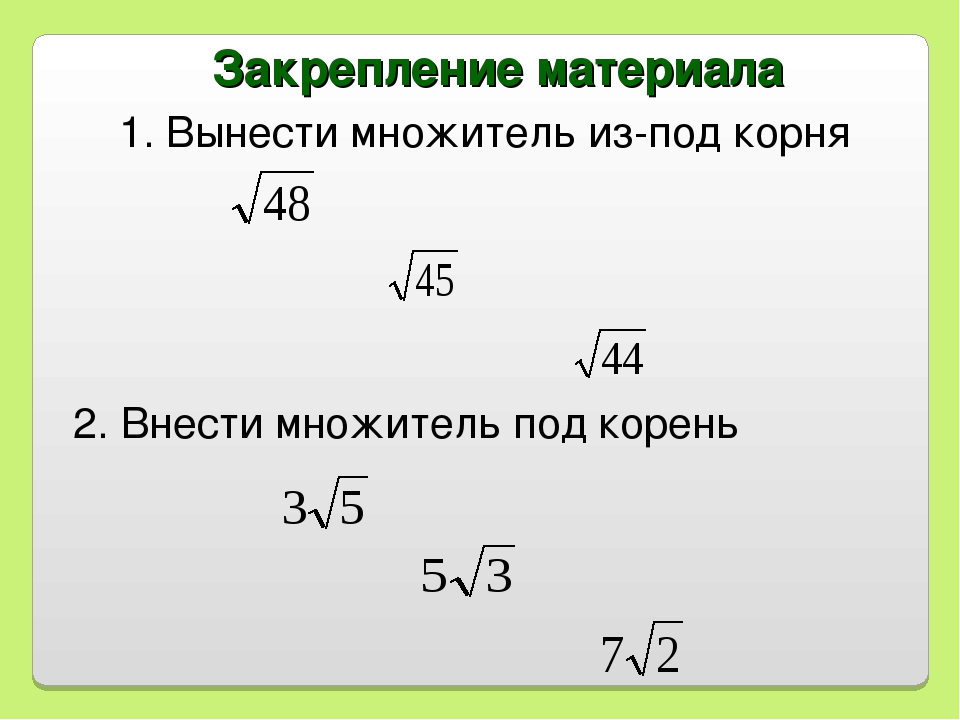
Решение
Преобразование первого выражения не представляет особой сложности, т.к. подобные примеры мы уже разбирали. Сразу вычисляем: 24·54=2·54=2·54.
Во втором примере легко догадаться, как преобразовать подкоренное выражение: нужно просто представить 27 как 24·23.
27·54=24·23·54=24·404=2·404=2·404
В последнем примере также нужно начать с преобразования подкоренного выражения. Сразу отметим, что итоговый вид будет таким:
254·22·54
Теперь покажем, как именно прийти к этому виду. Сначала выполняем деление 22 на 4, получаем 5 с остатком 2 (если нужно, повторите, как правильно выполнять деление с остатком). Иначе говоря, 22 можно рассматривать как 4·5+2. Используя свойства степени, можем записать:
222+25·4+2=25·4·22=(25)4·22
Таким образом:
222·54=(25)4·22·54=(25)4·204==25·204=32·204
Ответ: 1) 24·54=2·54, 2) 27·54=2·404, 3) 222·54=32·204.
Если выражение под корнем не является степенью или произведением степеней, надо попробовать представить его в таком виде. Чаще всего встречаются следующие случаи.
Чаще всего встречаются следующие случаи.
Подкоренное выражение – натуральное составное число. Тогда мы сразу можем увидеть нужные множители, которые надо вынести из-под знака корня, предварительно разложив данное число на простые множители.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 5
Условие: выполните вынесение множителя из-под знака корня в следующих выражениях: 1) 45; 2) 135; 3) 3456; 4) 102.
- Выполняем разложение 45 на простые множители.
451551335
То есть 45=3·3·5=32·5, а 45=32·5. В этом выражении видно, что выносить мы будем множитель 32. Вычисляем:
32·5=3·5=3·5
- Теперь представим в нужном виде число 135 и получим: 135=3·3·3·5=33·15. Иначе можно записать, что 32·3·5=32·15. Следовательно, 135=32·15. Мы видим, что вынесению из-под знака корня подлежит множитель 32:
32·15=3·15=3·15
- Разложим на простые множители число 3456:
3456172886443221610854279312222222333
У нас получилось, что 3456=27·33 , а 3456=27·33. Поскольку 27=23·2+1=(23)2·2 и 33=32·3, то 27·33=(23)2·2·32·3=(23)2·32·6==23·3·6=24·6
Поскольку 27=23·2+1=(23)2·2 и 33=32·3, то 27·33=(23)2·2·32·3=(23)2·32·6==23·3·6=24·6
- Представим натуральное число 102 как произведение простых множителей и получим 2·3·17. Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.
Ответ: 1) 45=3·5; 2) 135=3·15; 3) 3456=24·6; 4) 102.
Теперь разберем, как решать примеры, у которых подкоренное выражение представлено в виде обыкновенной дроби. В этом случае следует числитель и знаменатель разложить на простые множители и посмотреть, можно ли вынести какие-то из них за знак корня. Если у нас есть десятичная дробь или смешанное число, предварительно заменяем их обыкновенными дробями, после чего переходим от корня отношения к отношению корней.
Пример 6
Условие: выполните вынесение множителя за корень в выражении 200·0,000189·x3 и упростите его.
Решение
Для начала перейдем от десятичной дроби к обыкновенной и разложим ее числитель и знаменатель на простые множители.
0,189=1891000000=33·726·56
Используя свойства степени, перепишем выражение в следующем виде:
322·523·7
Подставим получившееся выражение в исходное и получим:
200·0,000189·x3==200·322·523·7·x3==200·322·52·7·x3=6·7·x3
К такому же ответу можно прийти и с помощью других преобразований:
200·0,000189·x3==200·1891000000·x3=200·18910000003·x3==200·189310000003·x3=200·33·7310033·x3==200·3·73100·x3=6·73·x3=6·7·x3
Ответ: 200·0,000189·x3=6·7·x3.
Иными словами, для обнаружения множителя, который можно вынести за знак корня, можно преобразовывать подкоренное выражение любыми допустимыми способами.
Пример 7
Условие: выполните упрощение иррационального выражения 2·(3+2·2).
Решение
Мы можем преобразовать выражение в скобках как 2+2·2+1 и далее как 22+2·2·1+12.
То, что у нас получилось, можно свернуть в квадрат суммы с помощью формулы сокращенного умножения: 22+2·2·1+1=2+12.
В итоге: 2·3+2·2=2·2+12. Теперь выносим 2+12 за знак корня и упрощаем выражение:
2·2+12=2·2+1==2·2+1=2+2
Ответ: 2·3+2·2=2+2.
Теперь посмотрим, как вынести из-под знака корня выражение, содержащее переменные. В целом можно сказать, что для этого используются те же методы, что и при работе с числами.
Пример 8
Условие: вынесите множитель из-под знака корня в выражениях (x-5)54 и (x-5)64.
Решение
- Выполняем преобразование в первом примере.
(x-5)54=(x-5)4·x-54=x-5·x-54
Знак модуля можно опустить. Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство (x−5)5≥0. Для его решения выбираем метод интервалов и получаем x≥5. Если значение x принадлежит области допустимых значений, то значением выражения x-5 будет неотрицательное число. Значит, можем записать следующее:
Значит, можем записать следующее:
x-5·x-54=x-5·x-54
- (x-5)64=(x-5)4·x-524==x-5·(x-5)24=x-5·x-524
Выполним сокращение показателей корня и степени на два. Обратимся к таблице результатов из статьи о преобразовании иррациональных выражений, о которой мы говорили выше. Возьмем из нее следующий результат: выражение Amn·m можно заменить на An при условии, что m и n – натуральные числа. Следовательно,
x-5·x-524=x-5·x-5
Нужно ли здесь убирать знак модуля? Посмотрим на область допустимых значений данного выражения: ее составляют все действительные числа, поскольку (x−5)6≥0 для любого x. При этом значения x−5 могут быть больше 0, если x>5, равными 0 или отрицательными. Значит, оставляем выражение в виде x-5·x-5 или представляем его в виде системы уравнений
(x-5)·x-5, x≥5(5-x)·5-x, x<5
Ответ: 1) (x-5)54=(x-5)·x-54; 2) (x-5)64=x-5·x-5.
Пример 9
Условие: выполните упрощение выражения x5+2·x4·y+x3·y2.
Решение
Выносим за скобки x3 и получаем x3·(x2+2·x·y+y2). Выражение в скобках можно представить в виде квадрата суммы: x3·(x2+2·x·y+y2)=x3·(x+y)2.
Теперь видим множители, подлежащие вынесению из-под корня: x3·(x+y)2=x2·x·(x+y)2=x·x+y·x
Также мы можем убрать знаки модуля, в которых находится x, поскольку область допустимых значений будет определена условием x5+2·x4·y+x3·y2≥0. Оно равносильно x3·(x+y)2≥0, а из него можно сделать вывод, что x≥0. У нас получилось, что x·x+y·x.
Ответ: x5+2·x4·y+x3·y2=x·x+y·x.
Это все, что мы хотели бы вам рассказать о вынесении множителя за знак корня. В следующей статье мы разберем обратное действие – внесение множителя под корень.
Как вынести из под корня число
Извлечь из данного числа корень какой-нибудь степени значит найти такое число, которое при возведении в эту степень, будет равно данному числу.
Из правил знаков при возведении в степень следует, что:
- Корень нечётной степени из положительного числа есть число положительное, а из отрицательного – отрицательное.
, так как (+3) 3 =27
, так как (-3) 3 =-27
Корень чётной степени из положительного числа может быть как положительным, так и отрицательным числом.
, так как (+3) 2 =+9 и (-3) 2 =+9
, так как (+4) 4 =+256 и (-4) 4 =+256
Извлечение корня из произведения, степени и дроби
Чтобы извлечь корень из произведения, надо извлечь его из каждого множителя отдельно.
Так же можно сказать, что корень произведения равен произведению корней всех его множителей:
Чтобы извлечь корень из степени, следует показатель степени разделить на показатель корня:
Чтобы извлечь корень из дроби, следует извлечь его отдельно из числителя и из знаменателя:
Вынесение множителя из-под знака корня
Когда нельзя извлечь корень из всего подкоренного числа или выражения, то подкоренное число или выражение раскладывают на множители и извлекают корень только из тех множителей, из которых это возможно сделать.
Внесение множителя под корень
Если нужно внести множитель под знак корня, то его следует возвести в степень, равную показателю корня.
Как выносить из под корня число
Часто вынесение множителя (числа) из под знака корня может быть необходимо для совершения каких-либо арифметических операций, например, для сокращения дроби или вынесения общего множителя и дальнейшего преобразования выражения.
Давайте рассмотрим основные арифметические правила и определения, необходимые для того, чтобы понять, как вынести число из под корня.
Необходимые операции и определения
Разложение выражения на множители — это преобразование этого числа в произведение нескольких сомножителей без изменения значения исходного выражения.
Это довольно частая операция, необходимая для вынесения множителя из-под знака корня.
Для разложения на множители используются следующие приёмы:
- Вынесение за скобки общего множителя;
- Группировка множителей;
- Применение формул сокращённого умножения;
- Комбинация вышеизложенных методов.
 2$.
2$.Оба продемонстрированных выше метода можно комбинировать.
Свойства корня
Теперь перейдём к более детальному рассмотрению корня.
Корнем $n$-нной степени из числа $b$ называют число, которое нужно возвести в $n$-нную степень чтобы получить число $b$:
Процесс получения корня называется его извлечением.
Левая часть равенства вида $sqrt[n] = m$ называется радикалом, то, что стоит непосредственно под знаком корня — подкоренным выражением, а число, стоящее слева сверху перед знаком корня называется показателем корня.
Правая же часть равенства после знака «равно» называется корнем $n$-нной степени из числа $b$.
Задай вопрос специалистам и получи
ответ уже через 15 минут!При извлечении числа из-под корня нужно учитывать то, что в случае с корнем нечётной степени возможен лишь один ответ, математически это запишется так: $sqrt[n] = b$, тогда как в случае с извлечением корня чётной степени ответа будет два, причём один с положительным знаком, а другой с отрицательным, это записывается так: $sqrt[n]= ±b$.

Также существует ещё одна теорема, которую нужно знать при вынесении множителя из-под знака корня:
Для извлечения корня $n$-ой степени из произведения, моно извлечь его из каждого сомножителя отдельно, а результаты перемножить. Математически это запишется так: $sqrt[n]=sqrt[n]sqrt[n]sqrt[n]left(1
ight)$.Докажем эту теорему для случая если под корнем стоит положительное число, а степень $n$ является нечётной.
Применим эту логику к равенству $(1)$.
Для этого возведём в степень правую часть равенства. Но для того чтобы сделать это, необходимо возвести в степень произведение, а для этого нужно возвести в степень каждый сомножитель и затем перемножить их все между собой:
Получилось выражение, стоящее под знаком корня, а это значит, что теорема доказана.
Правила вынесения множителя из под знака корня
Вынесение множителя из-под знака корня $n$-ой степени — это упрощение выражения с помощью записи какого-либо множителя, являющегося частью подкоренного выражения, перед знаком корня.
 Например, $sqrt[6] <192>= sqrt[6] <64 cdot 3>= 2 sqrt[6]<3>$.
Например, $sqrt[6] <192>= sqrt[6] <64 cdot 3>= 2 sqrt[6]<3>$.Для вынесения множителей из-под знака корня необходимо показатель выносимого множителя разделить на показатель корня и разместить перед корнем этот множитель с тем показателем степени, который получится в результате этого деления:
В частном случае, если приходится иметь дело с квадртным корнем, степень множителя, который необходимо вынести, нужно разделить на два, а сам множитель записать перед знаком корня:
В случае если приходится иметь дело с множителем-дробью, можно извлечь по отдельности корень из числителя и знаменателя, например:
Общий порядок вынесения множителя из под корня такой:
- Сначала подкоренное значение раскладывается на множители непосредственно под знаком корня, а у этих множителей выделяются показатели степени.
- Затем показатель степени при множителе делится на показатель корня, а сам выносимый множитель записывается слева от радикала.
Вынесите множитель из-под знака корня в следующих выражениях:
Так и не нашли ответ
на свой вопрос?Просто напиши с чем тебе
нужна помощьВ данном материале мы продолжим рассказывать о том, как преобразовывать рациональные выражения, а конкретно о том, как правильно выносить множитель из-под знака корня.
 В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.Что такое вынесение множителя из-под знака корня
Чтобы лучше понять суть подобного преобразования, нужно сначала сформулировать, что такое вообще вынесение множителя из-под знака корня. Сформулируем определение:
Вынесение множителя из-под знака корня представляет собой замену выражения B n · C n на произведение B · C n с условием, что n – нечетное число, или же на произведение B · C – где n – четное число, а B и C – другие числа и выражения.
Если мы имеем в виду только квадратный корень, то есть число n равно двум, то процесс вынесения множителя можно свести к замене выражения B 2 · C на произведение B · C . Отсюда и название данного преобразования: после того, как оно было проведено, множитель B y оказывается свободным от знака корня.

Приведем примеры, поясняющие данное определение. Так, допустим, у нас есть выражение 2 2 · 3 . Оно аналогично B 2 · C , где B равно двум, а C – трем. Заменив данный корень на произведение 2 · 3 и опустив знаки модулей (это можно сделать, поскольку оба множителя являются положительными числами), мы получим 2 · 3 . Мы вынесли множитель 2 2 из-под знака корня.
Приведем еще один пример подобного преобразования. У нас есть выражение ( x 2 – 3 · x · y · z ) 2 · x = x 2 – 3 · x · y · z · x . Здесь из-под корня был вынесен не просто числовой множитель, а целое выражение с переменными ( x 2 − 3 · x · y · z ) 2 .
Оба примера относятся к случаю вынесения множителя из-под квадратного корня. Можно также производить данные преобразования и для корней n -ной степени. Вот пример с кубическим корнем: ( 3 · a 2 ) 3 · 2 · a 2 3 = 3 · a 2 · 2 · a 2 3
Пример с корнем шестой степени: 1 2 · x 2 + y 2 6 · 5 · ( x 2 + y 2 ) 6 можно преобразовать в произведение 1 2 · x 2 + y 2 · 5 · ( x 2 · y 2 ) 6 , которое, в свою очередь, упрощается до 1 2 · ( x 2 + y 2 ) · 5 · ( x 2 + y 2 ) 6 .
 В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .
В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .Мы выяснили, что такое вынесение множителя из-под знака корня. Теперь перейдем к доказательствам, т.е. поясним, почему произведение, полученное в итоге данного преобразования, равнозначно исходному выражению.
Почему возможно заменить корень на произведение
В этом пункте мы будем разбираться, как возможна такая замена и почему корень B n · C n равнозначен произведениям B · C n и B · C n . Обратимся к ранее изученным теоретическим положениям.
Когда мы разбирали преобразование иррациональных выражений, у нас получились некоторые важные результаты, которые мы собрали в таблицу. Здесь нам будут нужны только два из них:
1. Выражение A · B n при условии нечетности n может быть заменено на A n · B n , а для четных n – A n · B n .
2. Выражение A n n при нечетном значении n может быть преобразовано в A , а при четном – в | A | .
Используя эти результаты и зная основные свойства модуля, мы можем вывести следующее:
- при четном n : B n · C n = B n n · C n = B · C n ;
- при нечетном n : B n · C n = B n n · C n = B n n · C n = B · C n .

Эти выражения лежат в основе преобразований, которые мы проводим, вынося множитель из-под знака корня.
Следовательно, можно вывести две формулы:
- B 1 n · B 2 n · . . . · B k n · C n = B 1 · B 2 · . . . · B k · C n для нечетного n ;
- B 1 n · B 2 n · . . . · B k n · C n = B 1 · B 2 · . . . · B k · C n для четного n .
Здесь B 1 , B 2 , и др. могут быть как числами, так и выражениями.
С помощью данных формул можно выполнить вынесение из-под корня сразу нескольких множителей.
Основное правило вынесения множителя из-под корня
Когда нам нужно решать примеры с подобными преобразованиями, чаще всего приходится предварительно приводить подкоренное выражение к виду B n · C . С учетом этого момента мы можем записать следующие правила.
Для вынесения множителя из-под корня в выражении A n нужно предварительно привести корень к виду B n · C n и после этого перейти к произведению B · C n (при нечетном показателе) или к B · C n (при четном показателе, при необходимости раскрываем модули).

Таким образом, схема решения подобных задач выглядит следующим образом:
A n → B n · C n → B · C n , е с л и n – н е ч е т н о е B · C n , е с л и n – ч е т н о е
Если нам надо вынести несколько множителей, то действуем так:
A n → B 1 n · B 2 n · . . . · B k n · C n → B 1 · B 2 · . . . · B k · C n , е с л и n – н е ч е т н о е B 1 · B 2 · . . . · B k · C n , е с л и n – ч е т н о е
Теперь можно переходить к решению задач.
Задачи на вынесение множителя из-под знака корня
Условие: выполните вынесение множителя за знак корня в трех выражениях: 2 2 · 7 , – 1 2 3 2 · 5 , ( – 0 , 4 ) 7 · 11 7 .
Решение
Мы видим, что подкоренные выражения во всех трех случаях уже имеют нужный нам вид. Поскольку в первых двух примерах показателем корня является четное число, а в третьем – нечетное, записываем следующее:
- Показатель корня равен 2 . Берем правило вынесения множителя для четного показателя и вычисляем: 2 2 · 7 = 2 · 7 = 2 · 7
- Во втором выражении показатель тоже четный, значит, – 1 2 3 2 · 5 = – 1 2 3 · 5 = 1 2 3 · 5
В этом случае мы можем сначала преобразовать выражения, исходя из основных свойств корня:
– 1 2 3 2 · 5 = – 1 2 · 1 2 3 2 · 5 = 1 2 3 2 · 5
А потом уже выносить множитель: 1 2 3 2 · 5 = 1 2 3 · 5 = 1 2 3 · 5 .
- Последнее выражение имеет нечетный показатель, поэтому нам понадобится другое правило: ( – 0 , 4 ) 7 · 11 7 = – 0 , 4 · 11 7 .
Возможен и такой вариант расчета:
– 0 , 4 7 · 11 7 = ( – 1 ) 7 · 0 , 4 7 · 11 7 = = – 0 , 4 7 · 11 7 = – 0 , 4 7 · 11 7 = – 0 , 4 · 11 7
Или такой:
– 0 , 4 7 · 11 7 = ( – 1 ) 7 · 0 , 4 7 · 11 7 = = – 0 , 4 7 · 11 7 = 0 , 4 7 · – 11 7 = 0 , 4 · – 11 7 = – 0 , 4 · 11 7
Ответ: 1 ) 2 · 7 ; 2 ) 1 2 3 · 5 ; 3 ) – 0 , 4 · 11 7 .
Условие: преобразуйте выражение ( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 .
Решение:
При помощи схемы, приведенной во втором пункте статьи, мы можем вынести из-под корня сразу три множителя.
( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 = = – 2 · 0 , 3 · 7 · 11 4 = 4 , 2 · 11 4
Можно сделать преобразование в несколько шагов, вынося множителя по одному, но так будет гораздо дольше.
Есть и другой способ. Преобразуем само выражение, приведя его к виду B n · C .
 После этого уже будем выносить множители:
После этого уже будем выносить множители:( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 = = ( – 2 · 0 , 3 · 7 ) 4 · 11 4 = ( – 4 , 2 ) 4 · 11 4 = = – 4 , 2 · 11 4 = 4 , 2 · 11 4
Ответ: ( – 2 ) 4 · ( 0 , 3 ) 4 · 7 4 · 11 4 = – 4 , 2 · 11 4 = 4 , 2 · 11 4 .
Разберем более подробно тот случай, когда подкоренное выражение требует предварительного преобразования. Здесь есть несколько моментов, которые нужно дополнительно пояснить.
Предварительное преобразование подкоренного выражения
Мы уже отмечали, что выражение под корнем не всегда имеет удобный для нас вид. Часто корень дан как A n , и множитель, который нужно вынести, не представлен в явном виде. Иногда это обозначено в условии, но довольно часто множитель приходится определять самостоятельно. Посмотрим, как надо действовать в этих случаях.
Допустим, нам надо вынести заранее определенный множитель B . Естественно, подкоренное выражение должно быть таким, чтобы эта операция была возможна.
 Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т.е. вычислить значение C из выражения A = B n · C .
Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т.е. вычислить значение C из выражения A = B n · C .Условие: есть выражение 24 · x 3 . Вынесите из-под знака корня множитель 2 3 .
Решение
Здесь мы имеем n = 3 , A = 24 · x , B 3 = 2 3 . Тогда из A = B n · С вычисляем C = A : ( B n ) = 24 · x : ( 2 3 ) = 3 · x .
Значит, 24 · x 3 = 2 3 · 3 · x 3 . Подкоренное выражение имеет нужный нам вид, и мы можем воспользоваться правилом для нечетного показателя и подсчитать: 24 · x 3 = 2 3 · 3 · x 3 = 2 · 3 · x 3 .
Ответ: 24 · x 3 = 2 · 3 · x 3 .
А как быть в случае, если множитель, который нужно вынести, не указан? Тогда у нас есть определенная свобода выбора, и мы можем использовать несколько подходов к решению задачи.
Допустим, нам дано выражение, под корнем у которого стоит степень или произведение нескольких степеней. В таком случае, зная основные свойства степени, мы можем преобразовать выражение в удобный для нас вид с очевидно указанными множителями для вынесения.

Условие: необходимо вынести множитель из-под корня в трех выражениях – 2 4 · 5 4 , 2 7 · 5 4 , 2 22 · 5 4 .
Решение
Преобразование первого выражения не представляет особой сложности, т.к. подобные примеры мы уже разбирали. Сразу вычисляем: 2 4 · 5 4 = 2 · 5 4 = 2 · 5 4 .
Во втором примере легко догадаться, как преобразовать подкоренное выражение: нужно просто представить 2 7 как 2 4 · 2 3 .
2 7 · 5 4 = 2 4 · 2 3 · 5 4 = 2 4 · 40 4 = 2 · 40 4 = 2 · 40 4
В последнем примере также нужно начать с преобразования подкоренного выражения. Сразу отметим, что итоговый вид будет таким:
2 5 4 · 2 2 · 5 4
Теперь покажем, как именно прийти к этому виду. Сначала выполняем деление 22 на 4 , получаем 5 с остатком 2 (если нужно, повторите, как правильно выполнять деление с остатком). Иначе говоря, 22 можно рассматривать как 4 · 5 + 2 . Используя свойства степени, можем записать:
2 22 + 2 5 · 4 + 2 = 2 5 · 4 · 2 2 = ( 2 5 ) 4 · 2 2
2 22 · 5 4 = ( 2 5 ) 4 · 2 2 · 5 4 = ( 2 5 ) 4 · 20 4 = = 2 5 · 20 4 = 32 · 20 4
Ответ: 1 ) 2 4 · 5 4 = 2 · 5 4 , 2 ) 2 7 · 5 4 = 2 · 40 4 , 3 ) 2 22 · 5 4 = 32 · 20 4 .

Если выражение под корнем не является степенью или произведением степеней, надо попробовать представить его в таком виде. Чаще всего встречаются следующие случаи.
Подкоренное выражение – натуральное составное число. Тогда мы сразу можем увидеть нужные множители, которые надо вынести из-под знака корня, предварительно разложив данное число на простые множители.
Условие: выполните вынесение множителя из-под знака корня в следующих выражениях: 1 ) 45 ; 2 ) 135 ; 3 ) 3456 ; 4 ) 102 .
- Выполняем разложение 45 на простые множители.
45 15 5 1 3 3 5
То есть 45 = 3 · 3 · 5 = 3 2 · 5 , а 45 = 3 2 · 5 . В этом выражении видно, что выносить мы будем множитель 3 2 . Вычисляем:
3 2 · 5 = 3 · 5 = 3 · 5
- Теперь представим в нужном виде число 135 и получим: 135 = 3 · 3 · 3 · 5 = 3 3 · 15 . Иначе можно записать, что 3 2 · 3 · 5 = 3 2 · 15 . Следовательно, 135 = 3 2 · 15 . Мы видим, что вынесению из-под знака корня подлежит множитель 3 2 :
3 2 · 15 = 3 · 15 = 3 · 15
- Разложим на простые множители число 3456 :
3456 1728 864 432 216 108 54 27 9 3 1 2 2 2 2 2 2 2 3 3 3
У нас получилось, что 3456 = 2 7 · 3 3 , а 3456 = 2 7 · 3 3 .
 Поскольку 2 7 = 2 3 · 2 + 1 = ( 2 3 ) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = ( 2 3 ) 2 · 2 · 3 2 · 3 = ( 2 3 ) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6
Поскольку 2 7 = 2 3 · 2 + 1 = ( 2 3 ) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = ( 2 3 ) 2 · 2 · 3 2 · 3 = ( 2 3 ) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6- Представим натуральное число 102 как произведение простых множителей и получим 2 · 3 · 17 . Видим, что все множители имеют показатель, равный единице, а показатель корня в этом примере равен двум. Следовательно, в данном примере ни один множитель не нужно выносить из-под знака корня, то есть такое действие для 102 нецелесообразно.
Ответ: 1 ) 45 = 3 · 5 ; 2 ) 135 = 3 · 15 ; 3 ) 3456 = 24 · 6 ; 4 ) 102 .
Теперь разберем, как решать примеры, у которых подкоренное выражение представлено в виде обыкновенной дроби. В этом случае следует числитель и знаменатель разложить на простые множители и посмотреть, можно ли вынести какие-то из них за знак корня. Если у нас есть десятичная дробь или смешанное число, предварительно заменяем их обыкновенными дробями, после чего переходим от корня отношения к отношению корней.

Условие: выполните вынесение множителя за корень в выражении 200 · 0 , 000189 · x 3 и упростите его.
Решение
Для начала перейдем от десятичной дроби к обыкновенной и разложим ее числитель и знаменатель на простые множители.
0 , 189 = 189 1000000 = 3 3 · 7 2 6 · 5 6
Используя свойства степени, перепишем выражение в следующем виде:
3 2 2 · 5 2 3 · 7
Подставим получившееся выражение в исходное и получим:
200 · 0 , 000189 · x 3 = = 200 · 3 2 2 · 5 2 3 · 7 · x 3 = = 200 · 3 2 2 · 5 2 · 7 · x 3 = 6 · 7 · x 3
К такому же ответу можно прийти и с помощью других преобразований:
200 · 0 , 000189 · x 3 = = 200 · 189 1000000 · x 3 = 200 · 189 1000000 3 · x 3 = = 200 · 189 3 1000000 3 · x 3 = 200 · 3 3 · 7 3 100 3 3 · x 3 = = 200 · 3 · 7 3 100 · x 3 = 6 · 7 3 · x 3 = 6 · 7 · x 3
Ответ: 200 · 0 , 000189 · x 3 = 6 · 7 · x 3 .
Иными словами, для обнаружения множителя, который можно вынести за знак корня, можно преобразовывать подкоренное выражение любыми допустимыми способами.

Условие: выполните упрощение иррационального выражения 2 · ( 3 + 2 · 2 ) .
Решение
Мы можем преобразовать выражение в скобках как 2 + 2 · 2 + 1 и далее как 2 2 + 2 · 2 · 1 + 1 2 .
То, что у нас получилось, можно свернуть в квадрат суммы с помощью формулы сокращенного умножения: 2 2 + 2 · 2 · 1 + 1 = 2 + 1 2 .
В итоге: 2 · 3 + 2 · 2 = 2 · 2 + 1 2 . Теперь выносим 2 + 1 2 за знак корня и упрощаем выражение:
2 · 2 + 1 2 = 2 · 2 + 1 = = 2 · 2 + 1 = 2 + 2
Ответ: 2 · 3 + 2 · 2 = 2 + 2 .
Теперь посмотрим, как вынести из-под знака корня выражение, содержащее переменные. В целом можно сказать, что для этого используются те же методы, что и при работе с числами.
Условие: вынесите множитель из-под знака корня в выражениях ( x – 5 ) 5 4 и ( x – 5 ) 6 4 .
Решение
- Выполняем преобразование в первом примере.
( x – 5 ) 5 4 = ( x – 5 ) 4 · x – 5 4 = x – 5 · x – 5 4
Знак модуля можно опустить.
 Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство ( x − 5 ) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x – 5 будет неотрицательное число. Значит, можем записать следующее:
Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство ( x − 5 ) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x – 5 будет неотрицательное число. Значит, можем записать следующее:x – 5 · x – 5 4 = x – 5 · x – 5 4
- ( x – 5 ) 6 4 = ( x – 5 ) 4 · x – 5 2 4 = = x – 5 · ( x – 5 ) 2 4 = x – 5 · x – 5 2 4
Выполним сокращение показателей корня и степени на два. Обратимся к таблице результатов из статьи о преобразовании иррациональных выражений, о которой мы говорили выше. Возьмем из нее следующий результат: выражение A m n · m можно заменить на A n при условии, что m и n – натуральные числа. Следовательно,
x – 5 · x – 5 2 4 = x – 5 · x – 5
Нужно ли здесь убирать знак модуля? Посмотрим на область допустимых значений данного выражения: ее составляют все действительные числа, поскольку ( x − 5 ) 6 ≥ 0 для любого x .
 При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x – 5 · x – 5 или представляем его в виде системы уравнений
При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x – 5 · x – 5 или представляем его в виде системы уравнений( x – 5 ) · x – 5 , x ≥ 5 ( 5 – x ) · 5 – x , x 5
Ответ: 1 ) ( x – 5 ) 5 4 = ( x – 5 ) · x – 5 4 ; 2 ) ( x – 5 ) 6 4 = x – 5 · x – 5 .
Условие: выполните упрощение выражения x 5 + 2 · x 4 · y + x 3 · y 2 .
Решение
Выносим за скобки x 3 и получаем x 3 · ( x 2 + 2 · x · y + y 2 ) . Выражение в скобках можно представить в виде квадрата суммы: x 3 · ( x 2 + 2 · x · y + y 2 ) = x 3 · ( x + y ) 2 .
Теперь видим множители, подлежащие вынесению из-под корня: x 3 · ( x + y ) 2 = x 2 · x · ( x + y ) 2 = x · x + y · x
Также мы можем убрать знаки модуля, в которых находится x, поскольку область допустимых значений будет определена условием x 5 + 2 · x 4 · y + x 3 · y 2 ≥ 0 . Оно равносильно x 3 · ( x + y ) 2 ≥ 0 , а из него можно сделать вывод, что x ≥ 0 .
 У нас получилось, что x · x + y · x .
У нас получилось, что x · x + y · x .Ответ: x 5 + 2 · x 4 · y + x 3 · y 2 = x · x + y · x .
Это все, что мы хотели бы вам рассказать о вынесении множителя за знак корня. В следующей статье мы разберем обратное действие – внесение множителя под корень.
Извлечение корня. Внесение и вынесения множителя из под корня
Извлечь из данного числа корень какой-нибудь степени значит найти такое число, которое при возведении в эту степень, будет равно данному числу.
Из правил знаков при возведении в степень следует, что:
- Корень нечётной степени из положительного числа есть число положительное, а из отрицательного – отрицательное.
Примеры:
3√+27 = +3, так как (+3)3 = 27;
3√-27 = -3, так как (-3)3 = -27.
- Корень чётной степени из положительного числа может быть как положительным, так и отрицательным числом.

Примеры:
√+9 = ±3, так как (+3)2 = +9 и (-3)2 = +9;
4√+256 = ±4, так как (+4)4 = +256 и (-4)4 = +256.
- Корень чётной степени из отрицательного числа является невозможным выражением, потому что любое положительное или отрицательное число при возведении в чётную степень даёт только положительный результат. Таким образом,
√-49 , 4√-256 , 6√-64 — это невозможные выражения.
Невозможные выражения иначе называют мнимыми.
Извлечение корня из произведения, степени и дроби
Чтобы извлечь корень из произведения, надо извлечь его из каждого множителя отдельно.
Так же можно сказать, что корень произведения равен произведению корней всех его множителей:
Чтобы извлечь корень из степени, следует показатель степени разделить на показатель корня:
Чтобы извлечь корень из дроби, следует извлечь его отдельно из числителя и из знаменателя:
Примеры:
Вынесение множителя из-под знака корня
Когда нельзя извлечь корень из всего подкоренного числа или выражения, то подкоренное число или выражение раскладывают на множители и извлекают корень только из тех множителей, из которых это возможно сделать.

Внесение множителя под корень
Если нужно внести множитель под знак корня, то его следует возвести в степень, равную показателю корня.
Примеры:
Корни и степени. Квадратный корень, кубический корень.
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя..
Возвести число в куб — значит умножить его само на себя три раза.

.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени.
 Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .

Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
 n\times b}\) на произведение \(a\times\sqrt[n]b\), если n — нечетное число, и на произведение \(\left|a\right|\times\sqrt{\left|b\right|}\), если n — четное число.
n\times b}\) на произведение \(a\times\sqrt[n]b\), если n — нечетное число, и на произведение \(\left|a\right|\times\sqrt{\left|b\right|}\), если n — четное число.Вынесение числа (или множителя) из-под корня позволяет упрощать выражения, например, сокращать дроби или выносить общий множитель.
Смысл вынесения множителя из-под корня заключается в том, чтобы разложить число под корнем на несколько, хотя бы одно из которых можно освободить от знака корня. Однако выноситься из-под корня может неограниченное количество множителей.
Обычно число выносят из-под корня с помощью разложения числа на произведение. Рассмотрим, почему такое действие в принципе возможно.
Почему возможно заменить корень на произведение
Теория преобразования иррациональных выражений дает сформулировать два основных положения:
- Нечетное выражение \(\sqrt[n]{a\times b}\) можно заменить на \(\sqrt[n]a\times\sqrt[n]b\).
 n\times b}\) и после перейти к произведению \(a\times\sqrt[n]b\), если n — нечетное число, или к \(\left|a\right|\times\sqrt[n]{\left|b\right|}\), если n — четное число.
n\times b}\) и после перейти к произведению \(a\times\sqrt[n]b\), если n — нечетное число, или к \(\left|a\right|\times\sqrt[n]{\left|b\right|}\), если n — четное число.В целом, единственное отличие выражений с четным показателем от выражений с нечетным — наличие модуля, который при необходимости раскрывают.
Необходимые операции и определения
После того как нам стало известно основное определение, перейдем к более детальному рассмотрению процесса вынесения множителя из-под корня.
Вспомним, что основой вынесения числа из-под корня является разложение на множители. Для этого используются следующие приемы:
- Вынесение общего множителя за скобки. При использовании данного метода мы находим число, на которое можно поделить каждую составляющую выражения, непосредственно делим на него выражение и выносим это число за скобки.
- Группировка множителей. При использовании данного метода мы объединяем определенные множители в группы и правильно расставляем скобки.
 3}\)
3}\)Возведение в степень и извлечение корня из числа онлайн.
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .

Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби .
 Обратная операция также верна ,
Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Как вычислить квадратный корень вручную (с иллюстрациями)
Резюме статьиX
Чтобы вычислить квадратный корень вручную, сначала оцените ответ, найдя 2 полных квадратных корня, между которыми находится это число.
 Идеальный квадратный корень — это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата.Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней. Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение.Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходного среднего, сложив их и разделив на 2.
Идеальный квадратный корень — это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата.Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней. Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение.Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходного среднего, сложив их и разделив на 2. Например, сначала вы разделите 7, число, с которого вы начали, на 2,16, среднее, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали.В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы должны просто повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеальный квадрат, используя это число и старое среднее значение, чтобы найти новое среднее, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом. Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью!
Например, сначала вы разделите 7, число, с которого вы начали, на 2,16, среднее, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали.В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы должны просто повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеальный квадрат, используя это число и старое среднее значение, чтобы найти новое среднее, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом. Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью!Спасибо всем авторам за создание страницы, которую прочитали 2111920 раз.
Как избавиться от квадратного корня в уравнении
Обновлено 20 ноября 2020 г.

Лиза Мэлони
Когда вы впервые узнали о квадратных числах, таких как 3 2 , 5 2 и x 2 , вы, вероятно, узнали об обратной операции возведения в квадрат числа, то есть о квадратном корне. Эта обратная связь между возведением чисел в квадрат и квадратными корнями важна, потому что на простом английском языке это означает, что одна операция отменяет действие другой.Это означает, что если у вас есть уравнение с квадратными корнями в нем, вы можете использовать операцию «возведения в квадрат» или экспоненты, чтобы удалить квадратные корни. Но есть некоторые правила, как это сделать, а также потенциальная ловушка ложных решений.
TL; DR (слишком долго; не читал)
Чтобы решить уравнение с квадратным корнем, сначала выделите квадратный корень на одной стороне уравнения. Затем возведите обе части уравнения в квадрат и продолжайте поиск переменной. Не забудьте в конце проверить свою работу.
Простой пример
Перед рассмотрением некоторых потенциальных «ловушек» решения уравнения с квадратными корнями в нем рассмотрим простой пример: Решите следующее уравнение для x :
\ sqrt {x } + 1 = 5
Используйте арифметические операции, такие как сложение, вычитание, умножение и деление, чтобы выделить выражение квадратного корня на одной стороне уравнения.
 Например, если ваше исходное уравнение было √ x + 1 = 5, вы вычли бы 1 из обеих частей уравнения, чтобы получить следующее:
Например, если ваше исходное уравнение было √ x + 1 = 5, вы вычли бы 1 из обеих частей уравнения, чтобы получить следующее:\ sqrt {x} = 4
Возведя в квадрат обе стороны уравнение исключает знак квадратного корня.2
x = 16
Вы удалили знак квадратного корня и , у вас есть значение x , так что ваша работа здесь сделана. Но подождите, есть еще один шаг:
Проверьте свою работу, подставив найденное вами значение x в исходное уравнение:
\ sqrt {16} + 1 = 5
4 + 1 = 5
5 = 5
Поскольку это вернуло допустимый оператор (5 = 5, в отличие от недопустимого оператора, такого как 3 = 4 или 2 = -2, решение, которое вы нашли на шаге 2, является действительным.В этом примере проверка вашей работы кажется тривиальной. Но этот метод устранения радикалов иногда может давать «ложные» ответы, которые не работают в исходном уравнении. Так что лучше иметь привычку всегда проверять свои ответы, чтобы убедиться, что они возвращают действительный результат, начиная с этого момента.

Немного сложнее
Что делать, если под знаком корня (квадратного корня) стоит более сложное выражение? Рассмотрим следующее уравнение. Вы по-прежнему можете применить тот же процесс, что и в предыдущем примере, но это уравнение выделяет пару правил, которым вы должны следовать.2
y — 4 = 576
Теперь, когда вы исключили радикальный или квадратный корень из уравнения, вы можете изолировать переменную. Чтобы продолжить пример, добавив 4 к обеим сторонам уравнения, вы получите:
y = 580
Как и раньше, проверьте свою работу, подставив найденное вами значение y обратно в исходное уравнение. Это дает:
\ sqrt {580 — 4} + 5 = 29
\ sqrt {576} + 5 = 29
Упрощение радикала дает:
24 + 5 = 29
29 = 29
истинное утверждение, указывающее на действительный результат.
Математическая сцена — Корни — Урок 1
Математическая сцена — Корни — Урок 1
2007 Rasmus ehf и Jhann sak Ptursson Корни
Печать Урок
1Квадрат
корниЕсли мы извлечем квадратный корень из числа, а затем
возьмите квадрат результата, мы снова получим исходное число.
например 4 = 2
и 2 2 = 4.Можно сказать, что квадратный корень и квадрат
уравновешивают друг друга. Они противоположны друг другу.Если у нас есть число, записанное с индексом 2 (
в квадрате), то извлечение квадратного корня просто означает, что мы не учитываем 2 (это
применяется только к положительным числам).Таким образом, мы можем взять в квадрат любые числа, которые
находятся под знаком квадратного корня из-под знака корня, опуская
мощность 2.Пример 1
Упростите следующее с помощью
извлечение наибольшего возможного значения из квадратного корня .:а)
ср
начните с факторизации числа под знаком корня. Появляются как 2, так и 9
дважды. Таким образом, извлечение квадратного корня оставляет нам только 2 и 9.
В
во втором примере только 9 появляется дважды, поэтому 3 должно оставаться под
корень.б)
в)
г)
д)
Большинство квадратных корней — иррациональные числа. Этот
означает, что мы не можем указать их точное значение в
дроби или десятичные дроби.Из-за этого, когда мы используем калькуляторы, чтобы найти
квадратные корни мы получаем только приблизительные значения. Если оставить в расчетах квадратный корень, мы получим то, что
называются точными значениями.При работе с дробями и квадратными корнями
в знаменателе принято не оставлять квадратных корней.Упрощение удаления квадратных корней из
знаменатель называется Рационализация знаменателя.
В простейших примерах просто умножаем числитель
а знаменатель — тем же квадратным корнем.Пример
2Рационализировать знаменатели
в следующих примерах:а)
Умножить
числитель и знаменатель на
2
.Затем получаем (
2) 2
= 2 в знаменателе.б)
Когда
мы умножаем два квадратных корня, чтобы получить оба числа под одним и тем же
знак квадратного корня.Мы тоже можем решить проблему
как это:Положить
оба термина под одним и тем же знаком квадратного корня и отменить.Если в
знаменатель мы используем правило о сопряжении
сроки избавиться от корней.
(a + b) и (a − b) являются сопряженными членами и:а 2 — б 2
= (а + б) (а б)Умножаем числитель
а знаменатель — путем сопряжения знаменателя,то есть либо по (a — b), либо по (a + b).
Пример
3Рационализируем знаменатель:
а)
В
сопряженный o fэто
б)
Попробуйте пройти тест 1 по корням.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.
Как найти квадратный корень вручную
Как вручную найти квадратный корень
Как найти квадратный корень вручную
Вот почти забытое искусство: с появлением электронных
калькуляторы, скорее всего, доживут до XXI века только на бумаге и
в воспоминаниях стариков.Из какого числа вы хотите найти квадратный корень?
Вот один из них, который мы будем использовать:46656
Сначала разделите число, которое нужно извлекать из квадратного корня, на пары цифр,
начиная с десятичной точки. То есть никакая пара цифр не должна пересекаться
десятичная точка. (Например, разделите 1225 на «12 25», а не на
«1 22 5»; 6.5536 на «6,55 36», а не на «6,5 53 6».)Затем вы можете поместить несколько линий на каждую пару цифр и полосу на
слева, что-то вроде длинного деления.+ --- ---- ---- | 4 66 56Найдите наибольшее число, квадрат которого меньше или равен ведущему
пара цифр. В этом случае первая пара цифр — 4; самое большое число
квадрат которого меньше или равен 4 равен 2.Поместите это число слева, и над первой парой цифр.
2 + --- ---- ---- 2 | 4 66 56Теперь возведите это число в квадрат и вычтите из пары первых цифр.
2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 0Выдвинуть левую скобу; умножьте последнюю (и единственную) цифру левой
число на 2, поместите его слева от разницы, которую вы только что вычислили, и
оставьте рядом с ним пустой десятичный знак.2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0Затем опустите следующую пару цифр и поместите ее вправо
разницы.2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0 66Найдите наибольшее число для этого пустого десятичного разряда, чтобы
число, умноженное на уже существующее число плюс десятичный разряд, будет меньше
чем текущая разница. Например, если 1 * 41 равно ≤ 66, то 2 * 42
≤ 66 и т. Д. В данном случае это 1. Поместите это число в оставленное вами поле,
и в следующем десятичном разряде в строке результатов вверху.2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66Теперь вычтите продукт, который вы только что нашли.
2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 25Теперь повторите, как раньше: возьмите число в левом столбце (здесь 41) и
удвойте его последнюю цифру (что даст вам 42). Скопируйте это ниже в левый столбец и
оставьте рядом с ним пустое место. (Двойная последняя цифра с переносом: для
Например, если у вас было не 41, а 49, что составляет 40 + 9, вы должны скопировать 40 + 18
что равно 58.) Также опустите следующую пару цифр справа.2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 42_ 25 56Теперь найдите самую большую цифру (назовите ее #) такую, что 42 # * # ≤ 2556. Здесь
получается, что 426 * 6 = 2556 точно.2 1 6 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 426 | 25 56 | - 25 56 + ------------- 0Когда разница равна нулю, у вас есть точный квадратный корень, и вы
Выполнено.В противном случае вы можете продолжать находить больше десятичных знаков до тех пор, пока
как ты хочешь.Вот еще один пример с меньшим количеством аннотаций.
7. 2 8 0 1 ... + ---------------------- 7 | 53. 00 00 00 00 00 | 49 + ---------------------- 142 | 4 00 | 2 84 + ---------------------- 1448 | 1 16 00 | 1 15 84 + ---------------------- 14560 | 16 00 | 0 + ---------------------- 145601 | 16 00 00 | 14 56 01 + ---------------------- | 1 43 99 00 ...Джон Керл
john dot r dot kerl at lmco точка com
Июль 1998 г.Текущий адрес (по состоянию на 2005 г.):
[email protected]
← Прочие документыMath 1010 on-line — корни и радикалы
Math 1010 on-line — Корни и радикалы
Кафедра математики
—
Колледж наук
—
Университет Юты
Корни и радикалы
Корни и радикалы заслуживают отдельной главы и домашнего задания, потому что
они часто встречаются в приложениях.Пусть будет
натуральное число, и пусть будет
настоящий номер . Корень -й степени из
это число, которое удовлетворяет
Номер обозначаетсяНапример,
с тех пор, и
поскольку .
Символ
называется радикальным символом , и
выражение, включающее его, называется радикалом (выражение) .Если тогда — квадратный корень из , и это число обычно опускается. Например,
Если, то это кубический корень из.Например,
кубический корень из есть, а кубический из is.Если четное и положительное, то есть два -го числа.
корни, каждый из которых является отрицательным по отношению к другому. Например,
поскольку
есть два квадратных корня из. В
в этом случае условно символ
означает положительный
-й корень, и он называется главный (-й) корень
из .Если отрицательное и нечетное, то есть только корень 1/4, и он также отрицательный. Например,
На этом этапе нам неизвестен корень -й степени, если он даже
и отрицательный.Это приводит к теме
комплексные числа, которые мы рассмотрим позже в этом курсе.Радикалы — это просто частные случаи полномочий , и вы
Помните об этом факте, что может упростить ваше мышление:Непосредственно из этого наблюдения и свойств
полномочия, которыеРешение радикальных уравнений
Уравнение, включающее радикалы, называется радикальным уравнением
(естественно).
Чтобы решить эту проблему, вы просто применяете нашу общую
принцип:Чтобы решить уравнение, выясните, что вас беспокоит, и сделайте то же самое.
вещь по обе стороны уравнения, чтобы избавиться от него.Чтобы избавиться от радикала, вы приводите его к власти, которая изменит
рациональный показатель до натурального числа. Это будет работать, если
радикал сам по себе находится на одной стороне уравнения .Давайте посмотрим на несколько простых примеров :
Предполагать
Действуем следующим образом:
Вот немного более сложная проблема:
Мы получаем
Наш последний пример показывает, как избавиться от более чем одного радикала:
Чтобы избавиться от квадратных корней, мы изолируем их и возведем в квадрат
время:В каждом случае мы проверяем наш ответ, подставляя его в исходный.
уравнение.Например, в последнем уравнении получаем:Позже в курсе мы рассмотрим более сложные случаи
радикальные уравнения.Числовые значения
Все радикалы в приведенных выше примерах были натуральными числами.
Это связано только с разумным подбором примеров. Часто корни
в приложениях встречаются иррациональные числа с десятичными разложениями, которые никогда не повторяются и не заканчиваются. В следующей таблице приведены приблизительные значения
несколько специфических радикалов.Некоторые радикалы (приблизительно)
Калькулятор корня
— получение n-го радикала числа
Добро пожаловать в калькулятор корня , где мы рассмотрим теорию и практику вычисления корня , как вычислить n-й корень числа , также называемого n-м. радикал , вместе. Мы начнем с краткого объяснения того, что такое корень в математике, и приведем несколько простых примеров, которые вы, возможно, уже видели, например, квадратный корень из 2, квадратный корень из 3 или кубический корень из 4.Но что, если вы хотите найти , корень четвертой степени ? Предыдущие были довольно простыми, но что такое, скажем, корень 4-й степени из 81? Не беспокойтесь, мы вам скоро покажем!
Устройтесь поудобнее, расслабьтесь и наслаждайтесь поездкой по миру радикалов !
Что такое корень
в математике?
Мы все знаем умножение, верно? Как
12 * 4 = 48? Если мы хотим умножить одно и то же число несколько раз, то мы можем записать его в упрощенном виде :12 * 12 * 12 * 12 * 12 = 12⁵,, где малое число
5называется показателем степени и означает, сколько копий большого числа (в данном случае12) мы берем.Мы также называем эту операцию , принимая5-ю степень12.Корень — это обратная операция. Чтобы связать это с биологическим значением, когда мы смотрим на выросшее дерево, мы видим его листья и ствол, но все это построено на его корнях . И история очень похожа с числами: когда мы видим число
125, то, взяв его корень, мы увидим крошечное зерно, которое оно выросло из . В этом примере он покажет нам, что начальное число —5, потому что5³ = 125.Формально, корень
nчислаaявляется числомb, так что:bⁿ =.Например, давайте внимательнее посмотрим на , что является квадратным корнем из некоторого числа . Предположим, вы копаете бассейн на заднем дворе. Вы хотели бы, чтобы он был таким же длинным, как и широким, и в целом занимал площадь в
256квадратных футов. Как определить , какой длины должны быть стороны ? Правильно — вычислением радикала! В этом случае это должен быть квадратный корень из площади, т.е.е., квадратный корень из256.И каков квадратный корень из этого числа? Что ж, давайте посмотрим, как его найти и как вообще вычислить квадратный корень.
Как вычислить квадратный корень
Иногда вычисление корня в математике может напоминать игру в угадывание . Но это не то же самое, что бросать кости с закрытыми глазами и гадать, что получится. Это больше расчетное предположение . В конце концов, как только мы узнаем, что
3⁴ = 81, мы можем с уверенностью сказать, что корень 4-й степени из81равен3.Но сначала мы должны это знать.Итак, что мы можем сделать, если мы забыли дома нашу удобную таблицу первых ста чисел и их первых нескольких степеней ? Это безнадежное дело? К счастью, нет. Не совсем, но мы вернемся к этому через секунду.
В качестве примера мы покажем , как вычислить квадратный корень из
72. Нашим основным инструментом здесь будет разложение на простые множители, то есть разделение72на самые маленькие возможные части.В процедуре разложения на простые множители мы берем число (в нашем случае
72) и находим наименьшее простое число, которое делит его . Напомним, что простое число — это целое число, которое имеет только два делителя:1,и само себя. Достаточно легко увидеть, что для нас это будет2с.
72/2 = 36.Следующий шаг — найти наименьшее простое число результата деления числа на простое число, т.е.е., номер
36. Если мы продолжим это, пока не достигнем1, мы получим следующие простые числа:2,2,2,3,3. Это разложение на простые множители72, и это означает, что72 = 2 * 2 * 2 * 3 * 3.Теперь, если мы найдем пары среди одинаковых чисел, мы увидим, что у нас осталось пара
2, пара3и одно2.Это позволяет нам записать квадратный радикал72как√72 = √ (2 * 2 * 2 * 3 * 3) = √ (2² * 3² * 2) = 2 * 3 * √2 = 6√2.Внимательный взгляд заметит, что единственные числа, которые остаются под корнем, — это ровно одиночек, которые не нашли пару .
А как насчет
2? Что такое квадратный корень из2? Ну, вот что такое « не совсем ». Квадратный корень из2, квадратный корень из3или любого другого простого числа возвращает нас к игре в угадайку.К счастью, мы можем использовать наш калькулятор корня , чтобы вычислить, что√2 ≈ 1,4142, что дает нам√72 = 6√2 ≈ 6 * 1,4142 = 8,4852.По сути, когда нас спрашивают: « каков квадратный корень из …, », мы должны сначала выполнить разложение на простые множители , чтобы решить проблему, и если (как указано выше) у нас останется маленькая цифра в конце, нам просто нужно использовать такой инструмент, как , калькулятор корня , чтобы найти его.
« А как насчет высших радикалов? Что, если мне понадобится, например.г., корень четвертой степени числа? «Ну, как удобно с вас спросить! Именно с этой проблемой мы и поговорим в следующем разделе.
Кубический корень, корень четвертой степени, корень n-й степени
Вспомните, как вы хотели вырыть бассейн в первой секции. Теперь предположим, что вы хотите, чтобы все это было кубом, вмещающим
1728кубических футов воды. (Не спрашивайте нас, почему. Возможно, что-либо выше облагается налогом по-другому?)Как найти бортик такого бассейна? Ага — вычислением кубического корня числа (отсюда и произошло название кубический корень ).Он сообщит нам, что длина должна быть
∛1,728 = 12футов в длину.Но как мы туда попали? К счастью, основной инструмент здесь тот же: разложение на простые множители . Если мы применим процедуру к
1,728, мы получим1,728 = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3.Теперь другое дело — вместо пар, мы группируем числа в тройки . Это то, что предполагает маленький
3в корневом символе — нам нужно третьих степеней .Обратите внимание, что квадратные корни на самом деле являются радикалами порядка2, но мы не пишем2, потому что … Ну, , если нам не нужно делать это из одного типа корня, это с таким же успехом может быть самый простой . Это просто условность и традиция. Думайте об этом как о математическом эквиваленте запекания индейки на День Благодарения.В любом случае, возвращаясь к нашей проблеме, группировка позволяет нам написать
∛1,728 = ∛ (2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3) = ∛ (2³ * 2³ * 3³) = 2 * 2 * 3 = 12.Если мы поднимемся выше с порядком радикала, применяется то же правило . При вычислении корня четвертой степени мы группируем простые числа в , четверные . Например, если вам нужен 4-й корень из
81, вы сначала заметите, что81 = 3 * 3 * 3 * 3,, поэтому у нас есть четыре
3. Это означает, что корень 4-й степени из81равен3. И если нам нужен n-й корень , мы берем группы изnэлементов.И, если что-то останется после факторизации, мы просто найдем с помощью какого-либо внешнего инструмента, такого как наш калькулятор корня .Хорошо, после того, как вы все это время читали теорию, самое время взглянуть на реальный пример и увидеть калькулятор корня в действии , вам не кажется?
Пример: использование калькулятора корня
Поздравляю, это мальчик! Теперь, когда вы стали родителем, вы решили начать с начала и откладывать немного денег, когда он пойдет в колледж.Вы решаете взять хорошую часть своих сбережений и оставить ее в банке на следующие восемнадцать лет , чтобы сумма росла вместе с вашим ребенком.
Предположим, вам удалось отложить на твердые 8000 долларов . К сожалению, вы как-то забыли процентную ставку по вложениям, но что сделано, то сделано. Сумма в конце будет для вас такой же неожиданностью, как и для вашего сына .
Время идет, годы идут, и, наконец, пришло время подарить вашему ребенку деньги, которые вы сэкономили .Вы звоните в банк, и выясняется, что на счету
$ 12 477,27. Неплохо, правда? Кажется, ты сможешь осуществить мечты своего сына.Но, только для себя, просто из чистого любопытства, можем ли мы рассчитать процентную ставку по имеющимся у нас числам?
Конечно, можем , и калькулятор корня нам поможет!
Предположим, что проценты начислялись на счет в конце каждого года и что деньги вообще не облагались налогом (да, мы знаем, что здесь мы немного надуманы).Тогда сумма, которую мы получаем в итоге , описывается формулой
end_amount = начальная_ сумма * (1 + процентная ставка) ¹⁸,, где
18-я степень исходит от восемнадцати лет, что деньги потрачены в банке. В нашем случае это означает.
12 477,27 долларов США = 8 000 долларов США * (1 + процентная ставка)9.Если мы разделим обе стороны на
8000, мы получим12 477,27 долл. США / 8 000 долл. США = (1 + процентная_ ставка)¹⁸или приблизительно
1.5597 = (1 + процентная ставка)¹⁸.Итак, если у нас есть
18-я степень справа, нам нужно найти18-й радикал числа слева . Это что-то немного более сложное, чем квадратный корень из 3, не так ли?Обратимся к нашему вычислителю корня . Там у нас есть два числа:
n. Когда мы смотрим на символическое изображение там, мы видим, чтоn— это порядок корня , поэтому мы вводимn = 18.В свою очередь,a— это число под корнем , поэтому мы беремa = 1,5597. Это заставляет калькулятор корня выдавать ответ.
1 + процентная ставка = 1,025.Если перевести десятичную дробь в проценты, получим
процентная ставка = 0,025 = 2,5%.Кажется довольно маленьким, но о, , как он вырос за восемнадцать лет!
Хорошо, любопытство удовлетворено , пора вернуться к праздничному торту.Будем надеяться, что ваш сын хорошо распорядится деньгами и продолжит учебу.
Как вычислить квадратный корень
Понимание того, как вычислять математические задачи вручную, является важным навыком. Одна математическая концепция, которая иногда используется в бизнес-анализе, — извлечение квадратного корня. Вычисление квадратного корня вручную позволяет понять, как работает формула.
В этой статье мы описываем, как используются квадратные корни, и объясняем три способа их вычисления вручную.
Связано: 10 лучших навыков и методов обучения
Использование квадратного корня
Квадратные корни используются для нахождения хвостов при нормальном распределении, которое представляет собой график, показывающий, где будет находиться большинство чисел в наборе данных. . Они особенно полезны для определения ключевых показателей эффективности (KPI), понимания того, насколько хорошо люди справятся с тестом и насколько вероятен результат.
Нормальное распределение основано на стандартных отклонениях или блоках оценок от среднего всех оценок.Хвосты нормального распределения обычно представляют собой наивысшие и самые низкие 5% оценок, при этом большинство оценок попадают в одно стандартное отклонение по обе стороны от среднего.
Связано: Важность когнитивных способностей в вашей карьере
Как вычислить квадратные корни вручную
Есть несколько способов вычислить квадратный корень. Решение квадратного корня — это умноженное на само число число, равное числу под символом квадратного корня, которое выглядит как √.Почти все калькуляторы имеют функцию извлечения квадратного корня, которую вы можете использовать. Вот несколько способов, которыми вы можете вычислить это вручную:
- Факторинг по квадратам
- Факторинг в длинной форме
- Метод деления в столбик
Факторинг по квадратам
Факторинг квадратного корня означает, что вы находите самые близкие числа которые умножаются вместе. Самые простые квадратные корни — это те, которые делятся непосредственно на квадраты, например √100, но более сложные включают несколько квадратных корней, например √225.Вот шаги, чтобы найти квадратный корень с помощью факторизации:
- Найдите множители . Факторы — это числа, которые вы умножаете, чтобы найти итог под символом квадратного корня. Для √100 множители будут √ (10 x 10). Коэффициент √225 будет равен √ (25 x 9).
- Разделите множители на их собственные квадратные корни . Поскольку оба множителя √100 равны 10, квадратный корень из 100 равен 10. Для √225 вы должны разделить множители под их собственными знаками квадратного корня, так что формула будет √25 x √9.
- Решите для отдельных квадратов . Затем вы найдете квадраты каждого из отдельных факторов. √25 = 5 и √9 = 3. Оставшаяся формула будет иметь вид 5 x 3.
- Завершите решение уравнения . Теперь, когда вы знаете, что такое упрощенные квадраты, вы обнаружите, что 5 x 3 = 15. Итак, √225 = 15.
Фактор в длинной форме
Иногда вы не знаете, какие множители квадратного корня квадраты. Вы можете разбить квадратный корень на каждый отдельный фактор, а затем решить его.Например, для длинного форм-фактора √225 выполните следующие действия:
- Найдите множители. Самый очевидный множитель 225 — пять, поэтому вы должны начать с √225 = √ (5 x 45). Вы бы упростили еще больше, найдя множители 45: √ (5 x 5 x 9). Последний коэффициент, который вы можете упростить, — это 9, поэтому ваш окончательный коэффициент длинной формы будет выглядеть как √ (5 x 5 x 3 x 3).
- Вытяните повторяющиеся факторы. Когда вы видите одно и то же число дважды в качестве множителя, вы указываете его один раз за пределами символа квадратного корня.В данном случае у нас есть две пятерки и две тройки, поэтому уравнение будет иметь вид 5 x 3.
- Решите оставшееся уравнение. Последний шаг — завершить решение уравнения. В этом случае 5 x 3 = 15.
Метод деления в столбик
Бывают случаи, когда вы можете не сразу распознать множители. Метод длинного деления позволяет найти квадратный корень без оценки. Для этого метода мы найдем √361. Вот шаги к методу длинного деления:
- Разделите основание квадратного корня на пары .Начиная справа, сгруппируйте числа в пары. В нашем примере 361 будет 3 61.
- Найдите наибольший квадрат, который делится на первое число или пару . Это даст вам первое число в вашем ответе. Первое число слева — 3. Наивысший квадрат, входящий в него, равен единице, потому что 1 x 1 = 1, а 2 x 2 = 4.
- Вычтите квадрат из первого числа или пары. Вычитание квадрата из первого числа даст вам остаток, который будет включен в следующий шаг.В этом примере 3 — 1 = 2.
- Перейдите к следующей паре. Следующее число, с которым вы будете работать, будет комбинацией вычтенного квадрата и следующей пары. В этом случае они составили бы трехзначное число. Когда вы опускаете 61 вниз, число, которое вы будете использовать для нахождения следующей цифры в квадратном корне, будет 261.
- Умножьте первую цифру квадрата на два. Это будет первая цифра в множителе для нахождения второй цифры квадратного корня.В этом примере первая цифра квадратного корня — единица.

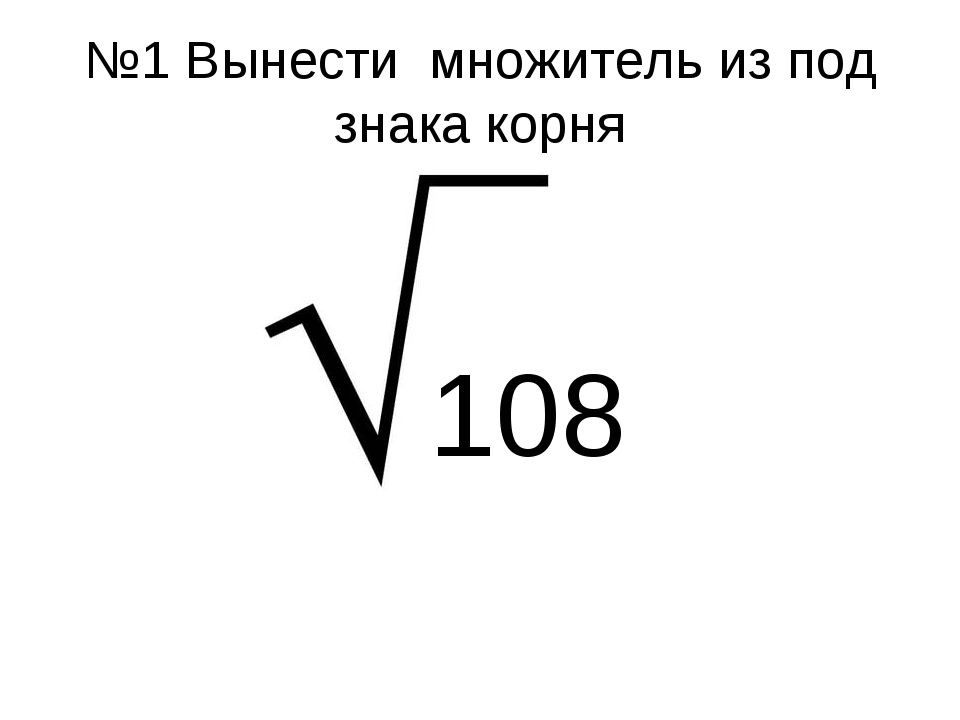 Берем правило вынесения множителя для четного показателя и вычисляем: 22·7=2·7=2·7
Берем правило вынесения множителя для четного показателя и вычисляем: 22·7=2·7=2·7 2$.
2$.
 Например, $sqrt[6] <192>= sqrt[6] <64 cdot 3>= 2 sqrt[6]<3>$.
Например, $sqrt[6] <192>= sqrt[6] <64 cdot 3>= 2 sqrt[6]<3>$. В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
В первом пункте объясним, зачем нужно такое преобразование, далее покажем, как именно оно делается и сформулируем общее для всех случаев правило. Далее покажем, какие существуют методы, чтобы привести подкоренное выражение к удобному для преобразования виду, и разберем примеры решений задач.
 В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .
В данном случае мы выносим множитель 1 2 · x 2 + y 2 6 .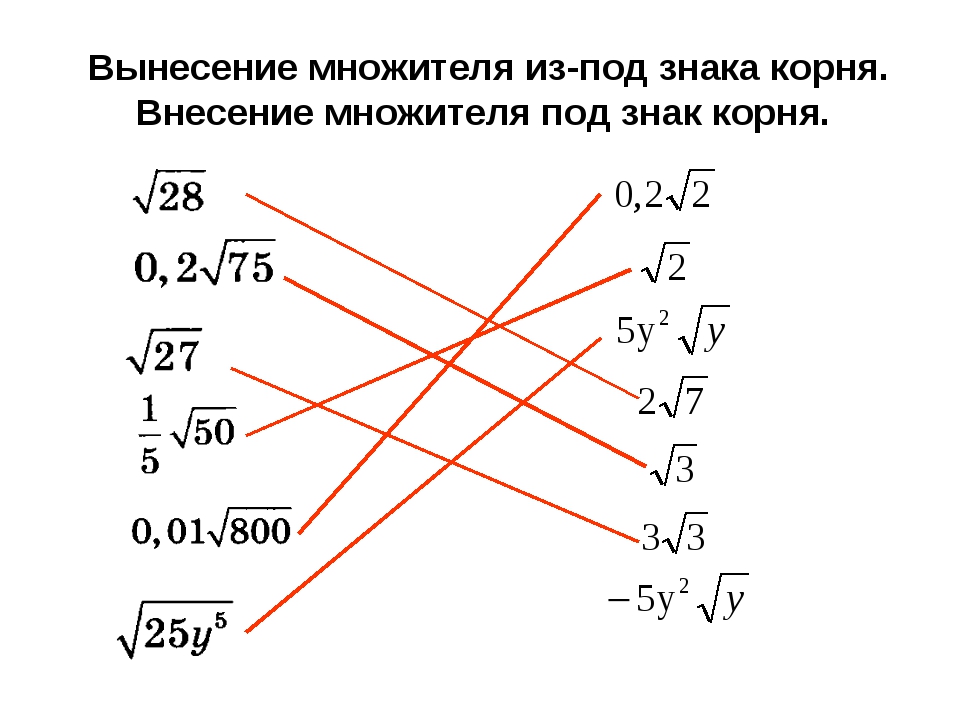


 После этого уже будем выносить множители:
После этого уже будем выносить множители: Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т.е. вычислить значение C из выражения A = B n · C .
Тогда для преобразования A n в B n · C n достаточно определить второй множитель, т.е. вычислить значение C из выражения A = B n · C .

 Поскольку 2 7 = 2 3 · 2 + 1 = ( 2 3 ) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = ( 2 3 ) 2 · 2 · 3 2 · 3 = ( 2 3 ) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6
Поскольку 2 7 = 2 3 · 2 + 1 = ( 2 3 ) 2 · 2 и 3 3 = 3 2 · 3 , то 2 7 · 3 3 = ( 2 3 ) 2 · 2 · 3 2 · 3 = ( 2 3 ) 2 · 3 2 · 6 = = 2 3 · 3 · 6 = 24 · 6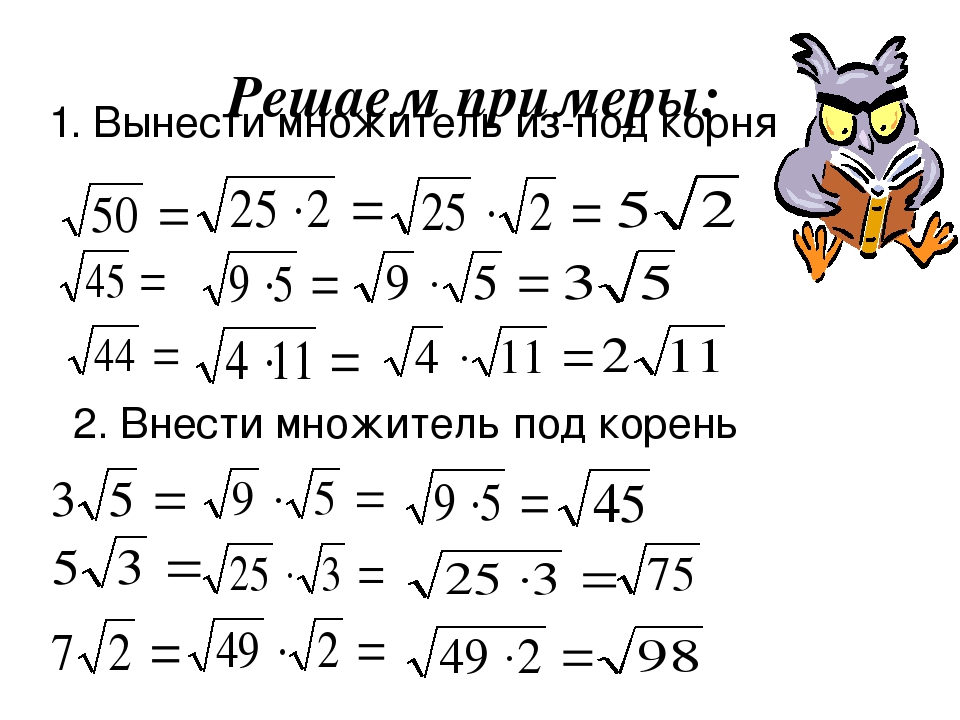
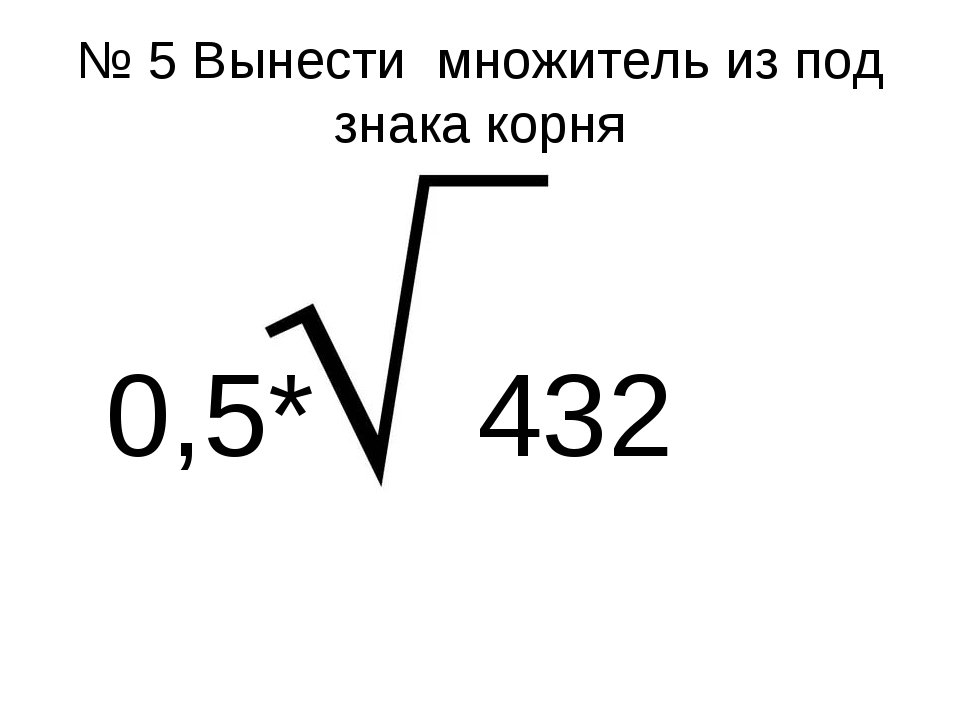
 Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство ( x − 5 ) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x – 5 будет неотрицательное число. Значит, можем записать следующее:
Посмотрим, каким условием определяется область допустимых значений переменной для исходного выражения. Таким условием будет неравенство ( x − 5 ) 5 ≥ 0 . Для его решения выбираем метод интервалов и получаем x ≥ 5 . Если значение x принадлежит области допустимых значений, то значением выражения x – 5 будет неотрицательное число. Значит, можем записать следующее: При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x – 5 · x – 5 или представляем его в виде системы уравнений
При этом значения x − 5 могут быть больше 0 , если x > 5 , равными 0 или отрицательными. Значит, оставляем выражение в виде x – 5 · x – 5 или представляем его в виде системы уравнений У нас получилось, что x · x + y · x .
У нас получилось, что x · x + y · x .


 Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
 n\times b}\) на произведение \(a\times\sqrt[n]b\), если n — нечетное число, и на произведение \(\left|a\right|\times\sqrt{\left|b\right|}\), если n — четное число.
n\times b}\) на произведение \(a\times\sqrt[n]b\), если n — нечетное число, и на произведение \(\left|a\right|\times\sqrt{\left|b\right|}\), если n — четное число. n\times b}\) и после перейти к произведению \(a\times\sqrt[n]b\), если n — нечетное число, или к \(\left|a\right|\times\sqrt[n]{\left|b\right|}\), если n — четное число.
n\times b}\) и после перейти к произведению \(a\times\sqrt[n]b\), если n — нечетное число, или к \(\left|a\right|\times\sqrt[n]{\left|b\right|}\), если n — четное число. 3}\)
3}\)
 Обратная операция также верна ,
Обратная операция также верна , Идеальный квадратный корень — это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата.Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней. Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение.Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходного среднего, сложив их и разделив на 2.
Идеальный квадратный корень — это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата.Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней. Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение.Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходного среднего, сложив их и разделив на 2. Например, сначала вы разделите 7, число, с которого вы начали, на 2,16, среднее, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали.В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы должны просто повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеальный квадрат, используя это число и старое среднее значение, чтобы найти новое среднее, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом. Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью!
Например, сначала вы разделите 7, число, с которого вы начали, на 2,16, среднее, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали.В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы должны просто повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеальный квадрат, используя это число и старое среднее значение, чтобы найти новое среднее, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом. Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью!
 Например, если ваше исходное уравнение было √ x + 1 = 5, вы вычли бы 1 из обеих частей уравнения, чтобы получить следующее:
Например, если ваше исходное уравнение было √ x + 1 = 5, вы вычли бы 1 из обеих частей уравнения, чтобы получить следующее:
