2
…
+4y при y = 60
4 Если x/y = B, y/z= 1/в, то чему равно x/z?
No1. Вказати з поясненням вид множини(скінченна, нескінченна, порожня)А- множина парних натуральних чиселВ- множина коренів рівняння х 25С- множина ра
…
діусів, що можна провести у коліз однієї точки
помогите пожалуйста,второене надо я его сдела,только 1 и 3
*помогите СРОЧНО!!!!!!*
По учебнику пункт 34 страница 72 выполнить краткий конспект с темой урока и с выполнением чертежей . Составить по одной задаче на каждое свойство
…
и покажите их решения. Пожалуйста срочно помогите хоть кто-нибудь ответьте !!!!!!
Постройте график функции y =-х²-4х+3 Найдите с помощью графика значение у при х =1, 5 значение X при которых у=-2 значение X при которых у меньше 0 пр
…
омежуток в котором функция возрастает
4хів 8/%-тоозчину?, а друг29. Розв’язування задач за допомогою систем лінійних рівнянь 2091080. (Задача з оповідання «Репетитор» А. П. Чехова. Купец-к
…
упив 138 аршинів- чорного та синього сукна за 540 рублівЗапитання: скільки аршинів він купив того й другого, яксинє коштувало 5 рублів за аршин, а чорне — 3 рублі?1081. Група із 46 туристів вирушила в похід на 10 човнах, частиз яких були чотиримісними, а рештачовнів кожного виду було в туристів?1082. Щоб нагодувати 4 коней і 12 корів, потрібно 120 кгЗнайдіть денну норму сіна для коня та для корови.на день, а щоб нагодувати з коней і 20 корів1083° За перший день 2 гусеничних трактори й один колісниЗнайдіть, скільки гектарів землі може зорювати щоднярали 22 га, а за другий день з гусеничних і 8 Коліснихгусеничний трактор і скільки один колісний,167 кг с0,0871. Отже,1084. Двоє робітників виготовили 135 деталей. Перший ро12 днів. Скільки деталей вляв щодня кожний робітник, якщо перший за 3 дні зрпрацював 7 днів, а другийі пругиза 4 дні?
Група із 46 туристів вирушила в похід на 10 човнах, частиз яких були чотиримісними, а рештачовнів кожного виду було в туристів?1082. Щоб нагодувати 4 коней і 12 корів, потрібно 120 кгЗнайдіть денну норму сіна для коня та для корови.на день, а щоб нагодувати з коней і 20 корів1083° За перший день 2 гусеничних трактори й один колісниЗнайдіть, скільки гектарів землі може зорювати щоднярали 22 га, а за другий день з гусеничних і 8 Коліснихгусеничний трактор і скільки один колісний,167 кг с0,0871. Отже,1084. Двоє робітників виготовили 135 деталей. Перший ро12 днів. Скільки деталей вляв щодня кожний робітник, якщо перший за 3 дні зрпрацював 7 днів, а другийі пругиза 4 дні?
Принадлежит ли графику функции y=39x точка B(11;−8)?
Помогите пожалуйста, срочно!!!
Решите пожалуйста, я в 7 классе
Содержание
y x 2 2x 3 график функции
Вы искали y x 2 2x 3 график функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и график функции y x 2 2x 3, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y x 2 2x 3 график функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 2 2x 3 график функции,график функции y x 2 2x 3,график функции y x2 2x 3,построить график функции y x2 2x 3,постройте график функции y x 2 2x 3,постройте график функции y x 2 3x 2,постройте график функции y x 2x 3,постройте график функции y x2 2x 3. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y x 2 2x 3 график функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, график функции y x2 2x 3).
Где можно решить любую задачу по математике, а так же y x 2 2x 3 график функции Онлайн?
Решить задачу y x 2 2x 3 график функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
График x 2 2x 3. Квадратичная и кубическая функции
Урок на тему: «График и свойства функции $y=x^3$.
 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.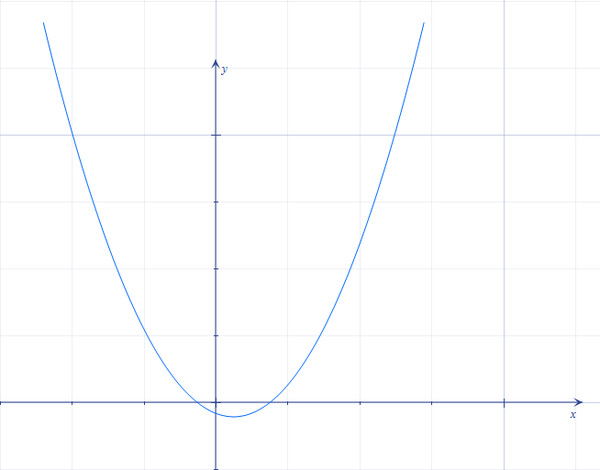 ).
).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика:
|
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.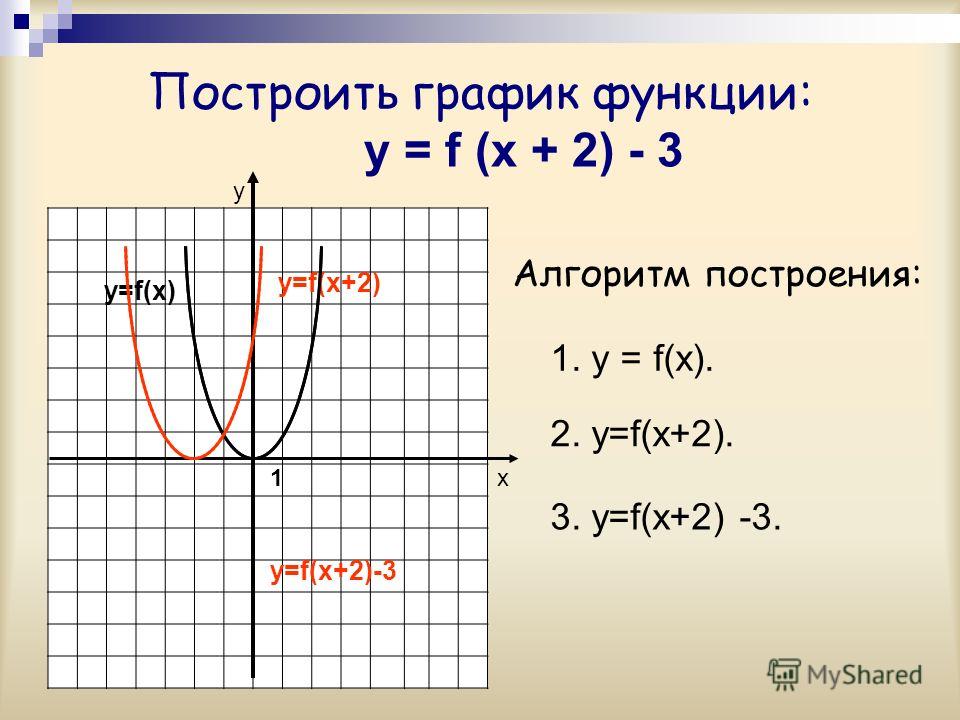
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2
, изображен пунктиром).
2.
Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1
).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3)
.
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4)
.
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис.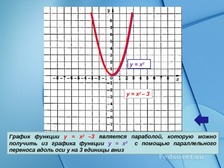 6)
6)
.
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7)
.
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8)
.
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9)
.
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11)
.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).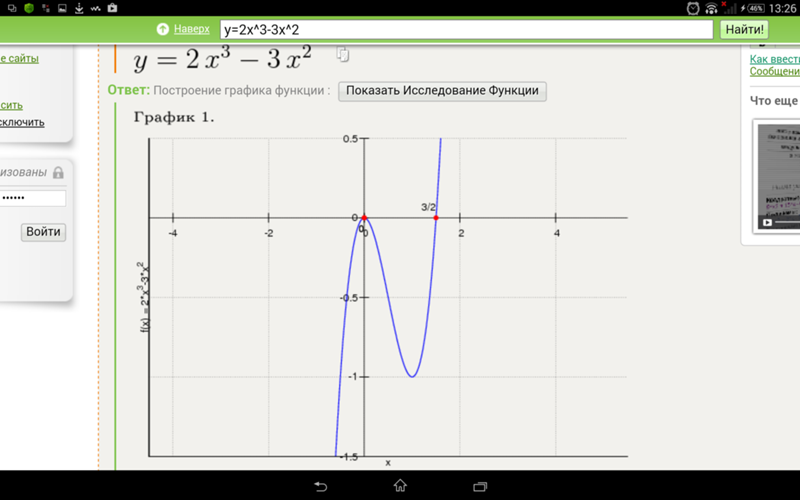
y=—
(x-3)-(—
(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—
(x-3)-(+
(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+
(x-3)-(+
(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|.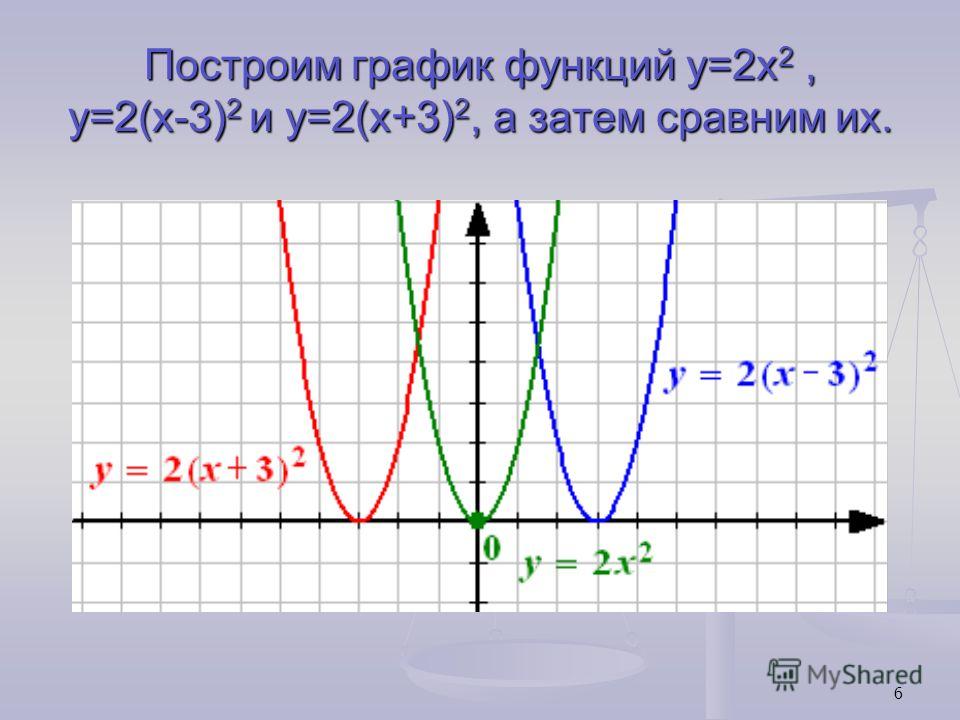 2.
2.
Решение.
- Функция степенная без каких-либо ограничений, поэтому область определения будет вся числовая прямая. Значения функции — вся числовая прямая.
- Четная или нечетная функция.
Подставим вместо переменной х значение —х и по результату сделаем вывод:
В результате получили, что функция не является ни четной, ни нечетной.
- Функция должна пересекаться с координатными осями. Вычислим точки пересечения функции с ними.
Для вычисления точек пересечения с осью Ох, подставим в функцию вместо переменной х число 0:
Функция пересекается с осью Ох в точке с координатами (0; 0).
Вычислим точку пересечения с осью Оу. Для этого подставим вместо переменной у значение 0 и решим полученное уравнение:
или
или
Функция пересекается с осью Оу в двух точках, первая— это пересечение с осью Ох, так как это начало координат — (0; 0). У второй точки координаты (1; 0).
У второй точки координаты (1; 0).
- Поскольку функция степенная, то должна иметь экстремумы. Вычислим их, рассчитав производную:
Запишем производную, как равную нулю, и вычислим корни уравнения:
или
или
Проверим полученные точки на экстремум. Для этого возьмем какую-нибудь точку из каждого полученного промежутка между найденными точками и найдем знак производной на всех полученных промежутках.
Первый промежуток от минус бесконечности до 0. Возьмем точку —1 и рассчитаем для нее производную:
— функция возрастает.
Второй промежуток от 0 до 2/3. Выберем точку 0,5 и вычислим от нее производную:
— функция убывает.
Третий промежуток от 2/3 до + бесконечности. Возьмем точку 1 и вычислим от нее производную:
— функция возрастает на этом промежутке.
Когда функция переходит через точку с абсциссой 0, она изменяет знак производной с + на —. Значит, это точка максимума, а при переходе через точку 2/3 знак производной меняется с — на +, значит, это точка минимума.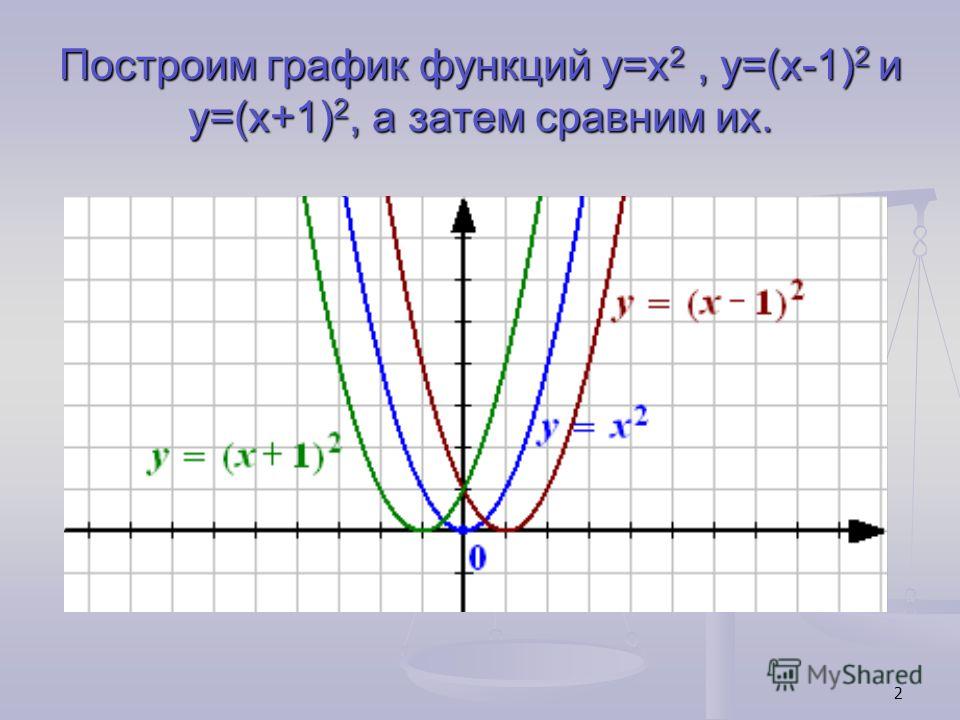 2 — 2x — 3′)
2 — 2x — 3′)
plt.ylabel(‘Ось y’)
plt.xlabel(‘Ось x’)
plt.grid()
plt.axis([-10, 16, -10, 10])
plt.scatter(x1, y1, s = 1, c = ‘b’)
plt.scatter(x1, -y1, s = 1, c= ‘b’)
plt.plot(x2, y2, ‘r—‘)
plt.plot(x2, -y2, ‘r—‘)
plt.show()
Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
Поскольку |y| может быть только больше нуля, нам нужно выделить значения функции, которые >= 0 и нарисовать в основной части графика только их. Для этого мы делаем булевую маску для всех значений f(x) (в моём коде это значение обозначено как y, но мой y это не y из вашей формулы).
ind = y >= 0
Более понятно можно записать так:
ind = (y >= 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y >= 0 и False, где y < 0.
Далее, мы отбираем по этой маске значения из наших массивов x и y:
x1 = x[ind]
y1 = y[ind]
А также мы отбираем остальные значения x и y, для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x[~ind]
y2 = y[~ind]
После этого мы рисуем основной график, причём два раза — один раз используя f(x), а другой раз -f(x) (по формуле |y| = f(x) получается, что у нас есть два графика: y = f(x) и y = -f(x)).
И затем рисуем псевдо-график там, где функция f(x) могла бы продолжаться, но из-за условия равенства модулю |y| она в этом месте прерывается.
Постройте график функции и найдите значение k
Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.
Решение:
Разберем как строить график с модулем.
y=|x-3|-|x+3|
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—(x-3)-(—(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—(x-3)-(+(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.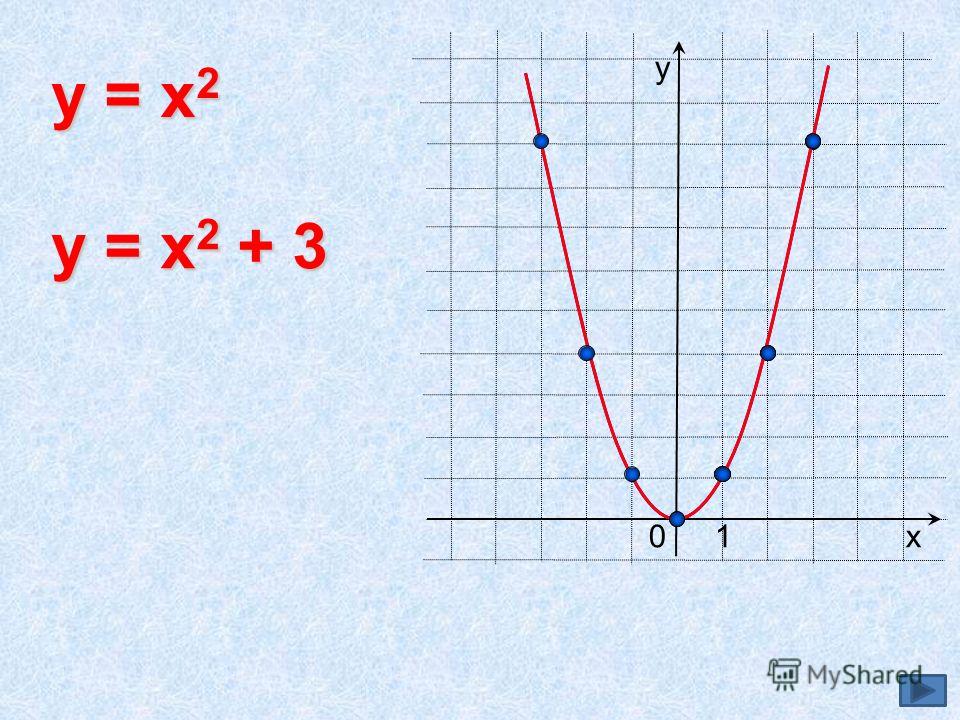 Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+(x-3)-(+(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.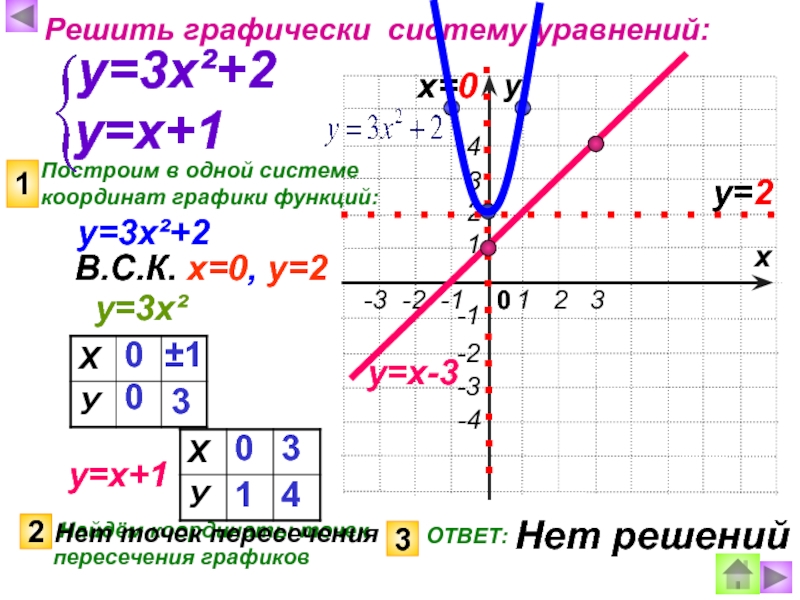 Этот вариант нам подходит.
Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
y = x2-2x-3 и как вы его изобразите?
Содержание:
Шаг 1: Поиск вершины
Шаг 2: Поиск двух точек слева от оси симметрии
Шаг 3: Отражение двух точек для получения точек справа от оси симметрии
Шаг 4: Построение точек (с таблицей)
Шаг 5: Построение параболы
Чтобы построить график, мы можем выполнить следующие шаги:
Шаг 1) Найдите вершину (вершина — это либо самая высокая, либо самая низкая точка на графике).Также вершина находится на оси симметрии параболы (т.е. делит ее пополам).
Шаг 2) Когда у вас есть вершина, найдите две точки слева от оси симметрии (линия, которая вертикально проходит через вершину).
Шаг 3) Отразите эти две точки над осью симметрии, чтобы получить еще две точки справа от оси симметрии.
Шаг 4) Постройте все найденные точки (включая вершину).
Шаг 5) Проведите кривую через все точки, чтобы построить параболу.
Давайте подробно рассмотрим эти шаги
Перейти к началу страницы
Шаг 1)
Нахождение вершины:
Чтобы найти вершину, нам сначала нужно найти x-координату вершины.
Чтобы найти координату x вершины, используйте эту формулу:.
Начните с данной формулы.
Из, мы видим, что, и.
Подключите и.
Отменить получить.
Умножаем 2 и получаем.
Разделить.
Итак, координата x вершины. Примечание: это означает, что ось симметрии тоже.
Теперь, когда мы знаем координату x вершины, мы можем использовать ее, чтобы найти координату y вершины.
Начните с данного уравнения.
Подключите.
Квадрат
пр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, y-координата вершины.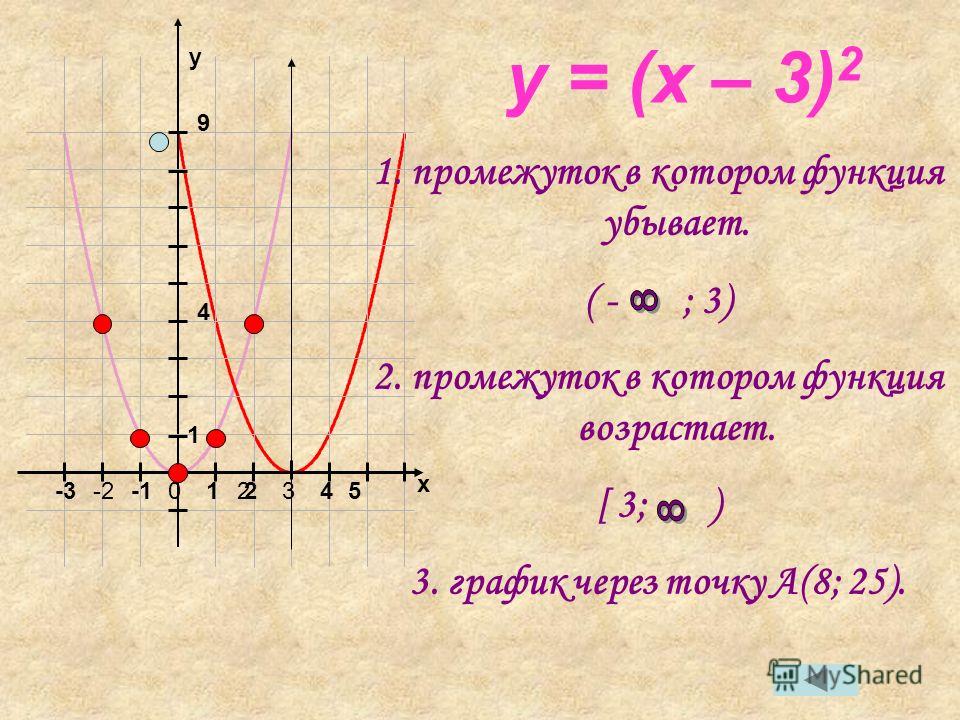
Так вершина есть.
———————————————— ———————
Перейти к началу страницы
Шаг 2)
Найдите две точки слева от оси симметрии:
Давайте найдем значение y, когда
Начнем с данного уравнения.
Подключите.
Квадрат
пр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, первая точка слева от оси симметрии (-1,0)
———————
Давайте найдем значение y, когда
Начнем с данного уравнения.
Подключите.
Квадрат
пр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, вторая точка слева от оси симметрии (0, -3)
———————————————— ———————
Перейти к началу страницы
Шаг 3)
Отражение двух точек по оси симметрии:
Теперь запомните, парабола симметрична относительно оси симметрии (которая есть)
Это означает, что значение y для (которое находится на расстоянии одной единицы от оси симметрии) равно значению y (которое также находится на расстоянии одной единицы от оси симметрии). Итак, когда, что дает нам точку (2, -3). Таким образом, мы по существу отразили точку (0, -3) на (2, -3).
Итак, когда, что дает нам точку (2, -3). Таким образом, мы по существу отразили точку (0, -3) на (2, -3).
Кроме того, значение y для (которое находится в двух единицах от оси симметрии) равно значению y (которое также находится на расстоянии двух единиц от оси симметрии). Итак, когда, что дает нам точку (3,0). Таким образом, мы по существу отразили точку (-1,0) на (3,0).
———————————————— ———————
Перейти к началу страницы
Шаг 4)
Нанесение точек:
Теперь давайте составим таблицу вычисленных нами значений:
Построение графиков квадратных уравнений на GRE
Некоторые математические вопросы GRE связаны с графиками квадратных уравнений.Квадратное уравнение может иметь вид y = ax 2 + bx + c, где a не равно 0, а a, b и c — константы.
График такого уравнения имеет форму параболы. Если a положительно, парабола открывается вверх, а вершина — это самая низкая точка на графике.![]()
И наоборот, если a отрицательно, парабола открывается вниз, а вершина — это самая высокая точка на графике.
Чтобы найти точки пересечения по оси x на графике, запишите уравнение в следующей форме:
ax
2 + bx + c = 0
Решите это для x, и вы получите две точки пересечения по оси x.Парабола симметрична относительно вертикальной линии, проходящей через ее вершину. X-точки пересечения равноудалены от этой линии.
Рассмотрим квадратное уравнение y = x 2 — 2x — 3 из Официального руководства.
1. Запишите уравнение в форму:
x 2 — 2x — 3 = 0
2. Решите относительно x, чтобы найти точки пересечения по оси x
x 2 — 2x — 3 = 0
→ (x — 3) (x + 1) = 0
→ x = 3 или -1
Следовательно, точки пересечения по оси x нашей параболы равны -1 и 3.
Чтобы вычислить координаты вершины, сначала определите x-координату вершины. Координата X вершины находится на полпути между точками пересечения по оси x. На полпути между -1 и 3 будет 1. Координата x вершины, следовательно, 1.
На полпути между -1 и 3 будет 1. Координата x вершины, следовательно, 1.
Чтобы определить координату y вершины, поместите координату x в квадратное уравнение:
y = x 2 — 2x — 3
Замените x на 1 и решите относительно y:
→ y = (1) 2 -2 (1) — 3
→ y = 1-2-3 = -4
Теперь квадратное уравнение может быть нарисованным с вершиной в точке (1, -4) и пересечениями по оси x в точках -1 и 3.
Этот пошаговый процесс упрощает работу с графиками квадратных уравнений. Хотя вам не нужно рисовать параболу на тесте, вам может потребоваться вычислить точку, в которой находится вершина, или точки пересечения по оси x. Теперь у вас есть способ сделать это.
Стандартная и вершинная форма уравнения параболы и ее связь с графиком параболы.
Уравнение параболы может быть выражено в стандартной или вершинной форме, как показано на рисунке ниже.
Вершинная форма уравнения
Вершинная форма уравнения параболы обычно выражается как: y = a (x-h) 2 + k
- (h, k) — это вершина , как вы можете видеть на рисунке ниже
- Если a положительно, то парабола открывается вверх, как правильная буква «U».
- Если a отрицательно, то график открывается вниз, как вверх ногами «U».
Практика Задачи
Вершина и Уравнение формы направление-вершина
Часть I
Проблема 1
Каков график следующей параболы y = (x – 1) ² + 1?
Покажи ответ
Вершиной параболы является точка (1,1).
Проблема 2
Каков график следующей параболы y = — (x – 1) ² + 1?
Покажи ответ
Задача 3
Каков график следующей параболы y = (x + 2) ² –3?
Покажи ответ
Определение вершины в форме вершины
Задача 4.1
Какова вершина следующей параболы: y = (x + 3) ² + 4
Покажи ответ
Вершиной является точка (-3,4)
Задача 4.2
Найдите вершину следующей параболы: y = (x — 3) ² + 4
Покажи ответ
Задача 4.3
Какова вершина параболы, уравнение формы вершины которой имеет вид y = (x — 2) ² — 3
Покажи ответ
Часть II
Задача 5.1
Какова вершина параболы со следующим уравнением:
у = 2 (х-3) 2 +4? Парабола открывается вверх или вниз?
Покажи ответ
Вершина — (3,4), и она открывается вверх, поскольку a положительно (это 2), она открывается вверх.
Проблема 5.2
Если уравнение параболы имеет вид y = 3 (x + 3) 2 +4, какова его вершина? Куда он открывается?
Покажи ответ
Vertex = (-3, 4), и открывается вверх, поскольку a положительно.
Проблема 5.3
У параболы есть уравнение y = -22 (x — 9) 2 + 5. Какова ее вершина? В какую сторону открывается парабола?
Покажи ответ
Vertex = (9, 5) и поскольку a отрицательно (это -22), открывается вниз.
Эта страница:
Связанные страницы:
Системы линейных и квадратных уравнений
| Линейное уравнение — это уравнение линии . | |
| Квадратичное уравнение — это уравнение параболы , имеющее по крайней мере одну переменную в квадрате. (например, x 2 ) | |
| И вместе они образуют Систему линейного и квадратного уравнений |
A Систему этих двух уравнений можно решить (найти, где они пересекаются) либо:
- Графически (путем нанесения их обоих на график функций и увеличения)
- или используя Алгебра
Как решить с помощью алгебры
- Преобразуйте оба уравнения в формат «y =»
- Приравняйте их друг к другу
- Упростить в формат «= 0» (как стандартное квадратное уравнение)
- Решите квадратное уравнение!
- Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x, y) точек в качестве ответов
Поможет пример:
Пример: Решите эти два уравнения:
- y = x 2 — 5x + 7
- y = 2x + 1
Преобразуйте оба уравнения в формат y =:
Они оба в формате «y =», поэтому сразу переходите к следующему шагу
Приравнять их друг к другу
x 2 — 5x + 7 = 2x + 1
Упростить до формата «= 0» (как стандартное квадратное уравнение)
Вычтем 2x с обеих сторон: x 2 — 7x + 7 = 1
Вычтем 1 с обеих сторон: x 2 — 7x + 6 = 0
Решите квадратное уравнение!
(самая сложная часть для меня)
Вы можете прочитать, как решать квадратные уравнения, но здесь мы будем учитывать квадратное уравнение:
Начать с: x 2 — 7x + 6 = 0
Записать -7x как -x-6x: x 2 — x — 6x + 6 = 0
Тогда: x (x-1) — 6 (x-1) = 0
Тогда: (x-1) (x-6) = 0
Что дает нам решения x = 1 и x = 6
Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x, y) точек в качестве ответов
Соответствующие значения y (см. Также график):
- для x = 1 : y = 2x + 1 = 3
- для x = 6 : y = 2x + 1 = 13
Наше решение: две точки: (1,3) и (6,13)
Я рассматриваю это как три этапа:
Объедините в квадратное уравнение ⇒ Решите квадратичное уравнение ⇒ Вычислите точки
Решения
Возможны три случая:
- Нет реальное решение (случается, когда они никогда не пересекаются)
- Одно реальное решение (когда прямая только касается квадратичной)
- Два реальных решения (как в примере выше)
Время для другого примера!
Пример: Решите эти два уравнения:
- y — x 2 = 7 — 5x
- 4 года — 8x = -21
Преобразуйте оба уравнения в формат y =:
Первое уравнение: y — x 2 = 7 — 5x
Добавьте x 2 к обеим сторонам: y = x 2 + 7 — 5x
Второе уравнение: 4y — 8x = -21
Добавьте 8x к обеим сторонам: 4y = 8x — 21
Разделить все на 4: y = 2x — 5.25
Приравнять их друг к другу
x 2 — 5x + 7 = 2x — 5,25
Упростить до формата «= 0» (как стандартное квадратное уравнение)
Вычтем 2x с обеих сторон: x 2 — 7x + 7 = -5,25
Добавьте 5,25 к обеим сторонам: x 2 — 7x + 12,25 = 0
Решите квадратное уравнение!
Использование квадратичной формулы из квадратных уравнений:
- x = [-b ± √ (b 2 -4ac)] / 2a
- х = [7 ± √ ((- 7) 2 -4 × 1 × 12.25)] / 2 × 1
- x = [7 ± √ (49 -49)] / 2
- x = [7 ± √0] / 2
- х = 3,5
Всего одно решение! («Дискриминант» равен 0)
Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x, y) точек в качестве ответов
Соответствующее значение y:
- для x = 3,5 : y = 2x-5,25 = 1,75
Наше решение: (3.5,1.75)
Пример из реального мира
Кабум!
Ядро летит в воздухе по параболе: y = 2 + 0,12x — 0,002x 2
Земля наклонена вверх: y = 0,15x
Куда приземляется пушечное ядро?
Оба уравнения уже имеют формат «y =», поэтому установите их равными друг другу:
0,15x = 2 + 0,12x — 0,002x 2
Упростить в формат «= 0»:
Переместите все термины влево: 0.002x 2 + 0,15x — 0,12x — 2 = 0
Упростить: 0,002x 2 + 0,03x — 2 = 0
Умножить на 500: x 2 + 15x — 1000 = 0
Решите квадратное уравнение:
Разделить 15x на -25x + 40x: x 2 -25x + 40x — 1000 = 0
Тогда: x (x-25) + 40 (x-25) = 0
Тогда: (x + 40) (x-25) = 0
x = -40 или 25
Отрицательный ответ можно проигнорировать, поэтому x = 25
Используйте линейное уравнение для вычисления совпадающего значения «y»:
у = 0.15 х 25 = 3,75
Итак, пушечное ядро попадает в склон под углом (25, 3,75)
.
Вы также можете найти ответ графически, используя Function Grapher:
.
Обе переменные в квадрате
Иногда можно возвести в квадрат ОБЕ члены квадратичной:
Пример: найти точки пересечения
Окружность x 2 + y 2 = 25
А прямая 3у — 2х = 6
Сначала введите строку в формате «y =»:
Переместите 2x вправо: 3y = 2x + 6
Разделить на 3: y = 2x / 3 + 2
СЕЙЧАС. Вместо преобразования круга в формат «y =» мы можем использовать замену на (заменить «y» в квадратичном выражении на линейное):
Положите y = 2x / 3 + 2 в уравнение круга: x 2 + (2x / 3 + 2) 2 = 25
Развернуть: x 2 + 4x 2 /9 + 2 (2x / 3) (2) + 2 2 = 25
Умножить все на 9: 9x 2 + 4x 2 + 2 (2x) (2) (3) + (9) (2 2 ) = (9) (25)
Упростить: 13x 2 + 24x + 36 = 225
Вычтем 225 с обеих сторон: 13x 2 + 24x — 189 = 0
Теперь он находится в стандартной квадратичной форме, давайте решим его:
13x 2 + 24x — 189 = 0
Разделить 24x на 63x-39x: 13x 2 + 63x — 39x — 189 = 0
Тогда: x (13x + 63) — 3 (13x + 63) = 0
Тогда: (x — 3) (13x + 63) = 0
Итак: x = 3 или -63/13
Теперь рассчитаем y-значения:
Подставляем x = 3 в линейное уравнение:
- 3 года — 6 = 6
- 3 года = 12
- г = 4
- Итак, одна точка (3, 4)
Подставляем x = -63/13 в линейное уравнение:
- 3 года + 126/13 = 6
- г + 42/13 = 2
- y = 2 — 42/13 = 26/13 — 42/13 = -16/13
- Итак, другая точка — (-63/13, -16/13)
Решите квадратные уравнения x ^ 2-2x-3 = 0 Tiger Algebra Solver
Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1.1 Факторинг x 2 -2x-3
Первый член x 2 , его коэффициент равен 1.
Средний член, -2x, его коэффициент равен -2.
Последний член, «константа», равен -3
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -3 = -3
Шаг-2: Найдите два множителя -3, сумма которых равен коэффициенту среднего члена, равному -2.
| -3 | + | 1 | = | -2 | Вот и все |
Шаг 3: Перепишите полиномиальное разделение двух найденных средних членов шаг 2 выше, -3 и 1
x 2 — 3x + 1x — 3
Шаг 4: сложите первые 2 члена, извлекая одинаковые множители:
x • (x-3)
Сложите последнее 2 члена, извлекая общие множители:
1 • (x-3)
Шаг 5: сложите четыре члена шага 4:
(x + 1) • (x-3)
Какое будет желаемое разложение на множители
Уравнение в конце шага 1:
(x + 1) • (x - 3) = 0
Шаг 2:
Теория — Корни продукта:
2.1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте
Любое решение для члена = 0 также решает продукт = 0.
Решение уравнения с одной переменной:
2.2 Решите: x + 1 = 0
Вычтите 1 из обеих частей уравнения:
x = -1
Решение уравнения с одной переменной:
2.3 Решите: x-3 = 0
Добавьте 3 к обеим сторонам уравнения:
x = 3
Дополнение: Решение квадратного уравнения напрямую
Решение x 2 -2x-3 = 0 напрямую
Ранее мы разложили этот многочлен на множители, разделив средний член. Давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Парабола, найдя вершину:
3.1 Найдите вершину y = x 2 -2x-3
Параболы имеют наибольшее или самая низкая точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 1.0000
Подставляя в формулу параболы 1,0000 для x, мы можем вычислить координату y:
y = 1,0 * 1,00 * 1,00 — 2,0 * 1,00 — 3,0
или y = -4,000
Парабола, графическая вершина и пересечение по оси X:
Корневой график для: y = x 2 -2x-3
Ось симметрии (пунктирная линия) {x} = {1,00}
Вершина в точке {x, y} = {1,00, -4,00}
x -Переходы ( Roots):
Корень 1 при {x, y} = {-1.00, 0.00}
Корень 2 при {x, y} = {3.00, 0.00}
Решите квадратное уравнение, заполнив квадрат
3.2 Решение x 2 -2x-3 = 0, завершив Квадрат.
Добавьте 3 к обеим сторонам уравнения:
x 2 -2x = 3
Теперь умный бит: возьмите коэффициент при x, равный 2, разделите его на два, получив 1, и возведите его в квадрат, получив 1
Добавьте 1 к обеим частям уравнения:
В правой части мы имеем:
3 + 1 или, (3/1) + (1/1)
Общий знаменатель двух дробей равен 1 Сложение (3 / 1) + (1/1) дает 4/1
Таким образом, прибавляя к обеим сторонам, мы, наконец, получаем:
x 2 -2x + 1 = 4
Добавление 1 завершило левую часть в полный квадрат:
x 2 -2x + 1 =
(x-1) • (x-1) =
(x-1) 2
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x 2 -2x + 1 = 4 и
x 2 -2x + 1 = (x-1) 2
, то согласно закону транзитивности
(x-1) 2 = 4
Мы будем называть это уравнение уравнением. # 3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-1) 2 равен
(x-1) 2/2 =
(x-1) 1 =
x-1
Теперь, применяя Принцип квадратного корня для уравнения.# 3.2.1 получаем:
x-1 = √ 4
Добавьте 1 к обеим сторонам, чтобы получить:
x = 1 + √ 4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — 2x — 3 = 0
имеет два решения:
x = 1 + √ 4
или
x = 1 — √ 4
Решите квадратное уравнение с помощью квадратичной формулы
3.3 Решение x 2 -2x-3 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = -2
C = -3
Соответственно B 2 — 4AC =
4 — (-12) =
16
Применение квадратичной формулы:
2 ± √ 16
x = —————
2
Можно ли упростить √ 16?
Да! Разложение на простые множители 16 равно
2 • 2 • 2 • 2
Чтобы иметь возможность удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).
√ 16 = √ 2 • 2 • 2 • 2 = 2 • 2 • √ 1 =
± 4 • √ 1 =
± 4
Итак, теперь мы смотрим на:
x = (2 ± 4) / 2
Два реальных решения:
x = (2 + √16) / 2 = 1 + 2 = 3.000
или:
x = (2-√16) / 2 = 1-2 = -1,000
Два были найдены решения:
- x = 3
- x = -1
Quadratics
Квадраты — это многочлены степени 2.
Они бывают разных форм, но всегда имеют квадрат.
Примеры
Квадратичное выражение:
Квадратное уравнение:
Квадратичная функция:
Квадратичный график:
Квадратичное неравенство:
Квадратичное отображение:
Квадратичные графики
Квадратичные графики имеют отличительную U-образную форму
называется параболой.
Положительная парабола улыбка:
у = ах 2
Отрицательные параболы нахмурились!
у = — ах 2
Рисование парабол вида y = ax
2
Выберите значения для x и поместите их в таблицу.
Разработайте соответствующий для y.
Постройте эти точки и соедините их плавной кривой.
Пример
Заполните таблицу значений для
уравнение y = x 2
Построение этих точек и объединение их плавной кривой дает
Обратите внимание, насколько симметричен график!
Пример
Заполните таблицу значений для
уравнение y = -5x 2
Построение этих точек и объединение их плавной кривой дает
Снова обратите внимание на симметричность графика!
Работа назад
Пример
Найдите уравнение следующей параболы
вида y = ax 2
График имеет вид y = ax 2
Данная координата (2, 1)
Итак, x = 2 и y = 1 находятся на кривой
.
Подставить и решить
Параболы формы y = a (x-b)
2
Пример
Заполните таблицу значений для
уравнение y = (x-2) 2
Нанесение этих точек и объединение их плавной кривой дает
На этот раз график симметричен, когда x = 2
Точка поворота (2,0)
Ось симметрии b
в уравнении y = a (x-b) 2
Пример
Найдите уравнение следующей параболы
вида y = a (x-b) 2
График имеет вид y = a (x-b) 2
Данная координата (2, 3)
Итак, x = 2 и y = 3 находятся на кривой
.
Подставляем и решаем
Параболы вида y = a (x-b)
2 + c
Пример
Заполните таблицу значений уравнения
у = -2 (х + 3) 2 + 2
Обратите внимание, что ось симметрии x = — 3
Работа в обратном направлении
Пример
Найдите уравнение следующей параболы
вида y = a (x-b) 2 + c
График имеет вид y = a (x-b) 2 + c
Данная координата (-3, -2)
Итак, x = -3 и y = -2 находятся на кривой
.
На графике b = -2, поскольку это ось симметрии.
Заменить x = -3, y = -2 и b = -2
Точка (-2, -5) также находится на кривой.
Итак, c = -5
Заменить на -2 = a + c
Подставив a, b и c в исходное уравнение
у = а (х-б) 2 + с
Ось симметрии
Это квадрат в законченной квадратной форме.
Завершение площади
Параболы формы y = ax
2 + bx + c
Пример
Заполните таблицу значений
для уравнения y = 2x 2 + 3x — 2
Поворотные моменты
Положительные параболы имеют минимальную точку поворота.
Пример
Найдите точку поворота квадратичной
y = x 2 + 3x + 2
Точка поворота находится на оси симметрии.
Отрицательные параболы имеют максимальную точку поворота.
Корни
Корень уравнения — это значение, которое удовлетворяет
уравнение, когда его выражение установлено равным нулю.
Например, 0 = x 2 + 2x -3
Максимально возможное количество корней
совпадает со степенью многочлена,
поэтому у квадратичной может быть не более двух корней.
Не все квадраты имеют корни.
Чтобы найти корни квадратичной,
Нарисуйте график и посмотрите, где он пересекает ось x.
или
Установить y = 0 и разложить на множители (если возможно)
Пример
Из графика видно, что уравнение y = x 2 + 2x –3 имеет корни
х = -3 и х = 1
Это то же самое, что установить y на ноль и разложить на множители: —
Любая скобка может равняться 0, поэтому необходимо учитывать обе:
Таблица Excel
Построение парабол
Чтобы нарисовать график
y = ax 2 + bx + c
- Определите форму как U (a> 0) или ∩ (a <0)
- Найдите корни уравнения.
(ах 2 + bx + c = 0)
- Отметьте корни на оси.
- Отметьте точку (0, c) на вашей оси.
- Найдите ось симметрии.
(½ пути между корнями)
- Используйте это значение x, чтобы найти точку поворота.
- Соедините значения плавной кривой.
Пример
Эскиз y = x 2 — 2x — 3
Это будет U-образная форма, так как a = 1
Он обрежет ось Y в точке (0, -3)
Пример
Эскиз y = 3-2x-x 2
Это будет фигура, так как a = -1
Он обрежет ось Y в точке (0,3)
Квадратные уравнения
Стандартная форма Квадратные уравнения имеют вид
Чтобы найти решение квадратного уравнения:
Перепишем выражение в стандартной квадратичной форме
Факторизуйтесь, если можете:
{Не забудьте найти общие множители и разницу двух квадратов}
Используйте квадратные формулы
Примеры
Решить 3x — 6x 2 = 0
Решить 49 — 9x 2 = 0
Решить 15x 2 — x — 6 = 0
Решить 15x 2 — x + 1 = 7
Факторизация квадратичных расчетов
Квадратичная формула
Если квадратичный коэффициент не факторизуется,
попробуйте квадратную формулу:
Пример
Решить 2 + 4x -5x 2 = 0
Дайте свой ответ в виде сурда.
Пример
Найдите корни 2 + 4x -5x 2
Ответьте правильно с точностью до двух десятичных знаков.
Не все квадраты разложить на множители
Дискриминант
Примеры
Дискриминант
б 2 — 4ac
= 3 2 — 4x1x4
= 9–16
= — 7
b 2 — 4ac <0
Нет настоящих корней
b 2 — 4ac
= 3 2 — 4x1x (-2)
= 9 +8
= 17
b 2 — 4ac> 0
Два отличных настоящих корня
б 2 — 4ac
= 6 2 — 4x1x9
= 36–36
= 0
b 2 — 4ac = 0
Корни равные и настоящие
Работа в обратном направлении
Пример
Корни (x — 1) (x + k) = -4 равны.
Найдите значения k.
Сначала разложим скобки
Касание
Касательная к кривой касается кривой только в одной точке.
Чтобы проверить касание, установите две функции равными друг другу
и найдем получившийся дискриминант.
Если b 2 — 4ac> 0, линия обрывается в двух разных точках.
Это не касательная.
Если b 2 — 4ac <0, линия не касается кривой.
Это не касательная.
Если b 2 — 4ac = 0, линия касается кривой только в одной точке.
Это касательная.
Примеры
© Александр Форрест
Нахождение x-точек пересечения функции
Для графика любой функции пересечение по оси x — это просто точка или точки, в которых график пересекает ось x.Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько x-точек пересечения. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции. Вы также можете прокрутить вниз до примера видео ниже.
Содержание
- Использование графика для поиска пересечений по оси x
- Использование алгебры для поиска пересечений по оси x
- Пример видео (в том числе при отсутствии x-перехватов)
- Дополнительная литература
реклама
Нахождение пересечений по оси x или x с помощью графика
Как упоминалось выше, функции могут иметь одно, ноль или даже множество x-точек пересечения.Их можно найти, посмотрев, где график функции пересекает ось x, которая является горизонтальной осью в плоскости координат xy. Вы можете увидеть это на графике ниже. Эта функция имеет единственную точку пересечения по оси x.
На графике ниже функция имеет два пересечения по оси x. Обратите внимание, что форма точки всегда \ ((c, 0) \) для некоторого числа \ (c \).
Наконец, на следующем графике показана функция без пересечений по оси x. Вы можете видеть это, потому что он ни в какой точке не пересекает ось абсцисс.
Более подробное обсуждение этих идей можно увидеть здесь: Нули многочлена.
Нахождение точки пересечения по оси x или точки пересечения с использованием алгебры
Общее правило для поиска точки пересечения по оси x или точки пересечения любой функции состоит в том, чтобы положить \ (y = 0 \) и решить для \ (x \). Это может быть несколько легко или действительно сложно, в зависимости от функции. Давайте рассмотрим несколько примеров, чтобы понять, почему это так.
Пример
Найдите точку пересечения по оси x функции: \ (y = 3x — 9 \)
Решение
Пусть \ (y = 0 \) и решит относительно \ (x \). 2 + 2x — 8 \)
Решение
Как и раньше, пусть \ (y = 0 \) и решит относительно \ (x \).2 + 2x — 8 \\ 0 & = (x + 4) (x — 2) \\ x & = -4, 2 \ end {align} \)
Ответ: Эта функция имеет два пересечения по оси x: –4 и 2. Они расположены в \ ((- 4, 0) \) и \ ((2, 0) \).
Для более сложных уравнений часто бывает полезен графический калькулятор, по крайней мере, для оценки местоположения любых точек пересечения.
объявление
Видео примеры
В следующем видео вы можете увидеть, как найти точки пересечения по оси x трех различных функций.Это также включает в себя пример, в котором нет x-перехватов.
Продолжайте изучение графиков
Вы можете продолжить изучение графиков в следующих статьях.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
