2

y x 2 y 0 x 2 найти площадь

Вы искали y x 2 y 0 x 2 найти площадь? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить площадь фигуры ограниченной линиями x 2 y 2, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y x 2 y 0 x 2 найти площадь».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x 2 y 0 x 2 найти площадь,вычислить площадь фигуры ограниченной линиями x 2 y 2,найдите площадь фигуры ограниченной линиями y 2 x 2,найдите площадь фигуры ограниченной линиями y x 2 y 0 x 2,найдите площадь фигуры ограниченной линиями y x 2 y 0 x 3,найдите площадь фигуры ограниченной линиями y x 3 y 0 x 2,найдите площадь фигуры ограниченной линиями y x 3 y 0 y 2,найти площадь фигуры ограниченной линиями y 2 x 2,найти площадь фигуры ограниченной линиями y x 2 x y 2,найти площадь фигуры ограниченной линиями y x 2 y 0 x 2,найти площадь фигуры ограниченной линиями y x 2 y x. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y x 2 y 0 x 2 найти площадь. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найдите площадь фигуры ограниченной линиями y 2 x 2).

Где можно решить любую задачу по математике, а так же y x 2 y 0 x 2 найти площадь Онлайн?

Решить задачу y x 2 y 0 x 2 найти площадь вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Угол между прямыми

Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.

Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + b₁,
y = k₂x + b₂,

то угол между ними можно найти, используя формулу:

tg γ = k₁ — k₂1 + k₁·k₂

Если знаменатель равен нулю (1 + k₁·k₂ = 0), то прямые перпендикулярны.

Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX

tg α = k₁
tg β = k₂

Соответственно легко найти угол между прямыми

γ = α — β

tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k₁ — k₂1 + k₁·k₂

Угол между прямыми через направляющие векторы этих прямых

Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано параметрически

x = l t + ay = m t + b

то вектор направляющей имеет вид {l; m}

Если уравнение прямой задано как

A x + B y + C = 0

то для вычисления направляющего вектора, можно взять две точки на прямой.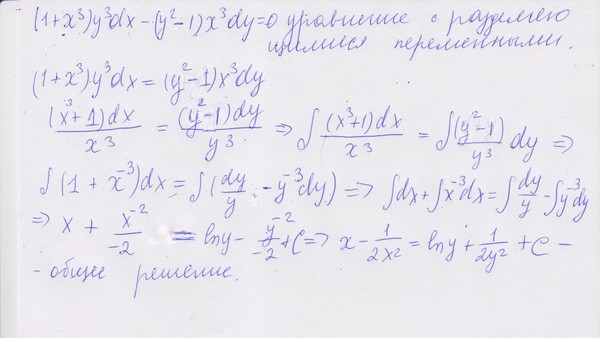

Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m

то вектор направляющей имеет вид {l; m}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}

Угол между прямыми через векторы нормалей этих прямых

Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано как

A x + B y + C = 0

то вектор нормали имеет вид {A; B}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то вектор нормали имеет вид {1; -k}

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

sin φ = |a · b||a| · |b|

Примеры задач на вычисления угла между прямыми на плоскости

Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k₁ — k₂1 + k₁·k₂ = 2 — (-3)1 + 2·(-3) = 5-5 = 1

Ответ. γ = 45°

Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}

cos φ = |1 · 2 + 2 · 1|1² + 2² · 2² + 1² = 45 · 5 = 0.8

Ответ. φ ≈ 36.87°

Пример 3 Найти угол между прямыми 2x + 3y = 0 и x — 23 = y4.

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2x + 3y = 0 => y = -23x   (k₁ = -23)

x — 23 = y4 => y = 43x — 83   (k₂ = 43)

tg γ = k₁ — k₂1 + k₁·k₂ = -23 — 431 + (-23)·43 = -631 — 89 = 18

Ответ. γ ≈ 86.82°

Угол между прямыми в пространстве

Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m = z — z₀n

то направляющий вектор имеет вид {l; m; n}

Если уравнение прямой задано параметрически

x = l t + ay = m t + bz = n t + c

то направляющий вектор имеет вид {l; m; n}

Пример 4. Найти угол между прямыми x = 2t + 1y = tz = -t — 1 и x = t + 2y = -2t + 1z = 1.

Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0² = 06 · 5 = 0

Ответ. φ = 90°

Пример 5 Найти угол между прямыми x — 23 = y4 = z — 35 и -x — 22 = 1 — 3y = 3z — 52.

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.

Преобразуем второе уравнение к каноническому вид.

-x — 22 = x — 2-2

1 — 3y = 1 + y-1/3 = y — 1/3-1/3

3z — 52 = z — 5/32/3

Получено уравнение второй прямой в канонической форме

x — 2-2 = y — 1/3-1/3 = z — 5/32/3

{-2; -13; 23} — направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)² = -6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49 = -450 · 41/9 = 12582 = 682205

Ответ. φ ≈ 74. 63°

Объем тела вращения вокруг оси Ox, Oy

Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y₁(x) и y₂(x) — непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций y_i(x) по переменной x

Объем тела V, образованного вращением вокруг оси Oy фигуры , , где y(x) — однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле

Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко. 

Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример. 2, y=0 
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:

И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:

б) Вычислим объем тела вращения вокруг оси Oy:

В этом примере интегралы легко берутся и нет потребности объяснять детали операций.

Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)

а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:

Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:

б) Выполняем вычисление объема тела при вращении вокруг оси Oy:

Замена переменных помогает найти последний интеграл.

Пример 2.142 (2475) Найти объем тела, образованного вращением кривой
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Чтобы записать подинтегральную функцию найдем разницу квадратов заданных функций:
а)
б) для тела, образованного вращением вокруг оси Oy подинтегральная функция имеет вид

Из условия равенства функций y₁(x)=y₂(x) определяем пределы интегрирования

x₁=0, |x|=a поэтому
Пределы интегрирования :
а)  
б)
При :
поэтому принимая во внимание симметрию имеем неравенство .

а) Вычисляем объем тела вращения вокруг оси Ox:

б) Через следующий интеграл определяем объем тела вращения вокруг оси Oy:

Здесь нет сложных моментов при вычислении интеграла.

Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e^{— x}, y=0,
а) вокруг оси Ox; б) вокруг оси Oy.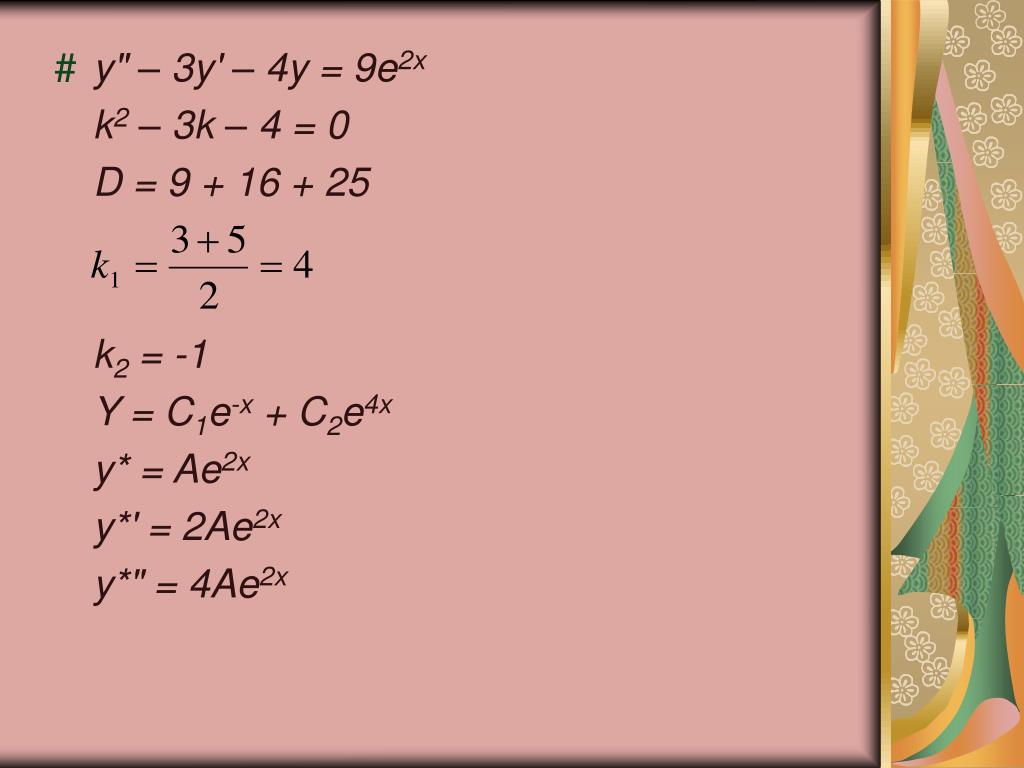
Решение: Уравнение подинтегральных функций :
а) y²=e^-2x;
б) x*y (x) =xe^-x.
Запишем пределы интегрирования (известно за условием):

а) Находим объем тела вращения вокруг оси Ox:

б) Найдем объем тела вращения вокруг оси Oy:

Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.

Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x²+(y-b)²=a², , вокруг оси Ox.
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:

При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:

Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:

Внимательно разберите приведенный пример.

Пример 2.145 (2478) Найти объем тела, образованного вращением кривой x²-xy+y²=a², вокруг оси Ox.
Решение: Сведем кривую к каноническому виду (методами из аналитической геометрии) устанавливаем, что заданная линия является эллипсом
— уравнение в канонической системы координат.
В приведенной системе координат уравнения эллипса имеет вид:

Прямая y=x/2 является осью симметрии этой фигуры.
Запишем подинтегральную функцию:

Найдем пределы интегрирования из условия равности функций y₂(x)=y₁(x):

или двукратный объем на интервале

Но тогда еще нужно отнять объем тела в пределах

(которая не принадлежит эллипсу) и ограничена первой кривой

и результат умножить на 2 (симметрия).

Последним шагом вычисляем объем тела вращения вокруг оси Ox:

Формула интеграла вышла достаточно длинным, однако его удобно читать пользователям, которые заходят на сайт из мобильных устройств.

Пример 2.146 (2479) Найти объем тела, образованного вращением кривой вокруг оси Ox.
Решение: Запишем подинтегральную функцию:
y²(x)=e^-2x*sin (x).
Установим пределы интегрирования: при , где k=0,1,2.
Таким образом имеем бесконечный ряд промежутков интегрирования.
При нахождении объема тела вращения вокруг оси Ox получим бесконечный ряд интегралов, который совпадает:

Здесь вычислили интеграл дважды выполнив замену переменных:

тому
— это числовой ряд.
В данном случае бесконечно нисходящая геометрическая прогрессия, у которой b₁=1, b₂=e^-4Pi, поэтому q=e^{— 4Pi}, а сумма прогрессии равна

Пример 2480 Найти объем тела, образованного вращением кривой x=a (t — sin (t)), y=a (1 — cos (t)), , y=0.
а) вокруг оси Ox; б) вокруг оси Oy;
в) вокруг прямой y=2a.
Решение: Вычислим подинтегральную функцию и дифференциал по аргументу:
y²=a²(1-cos (t))², dx=a(1-cos(t)) dt.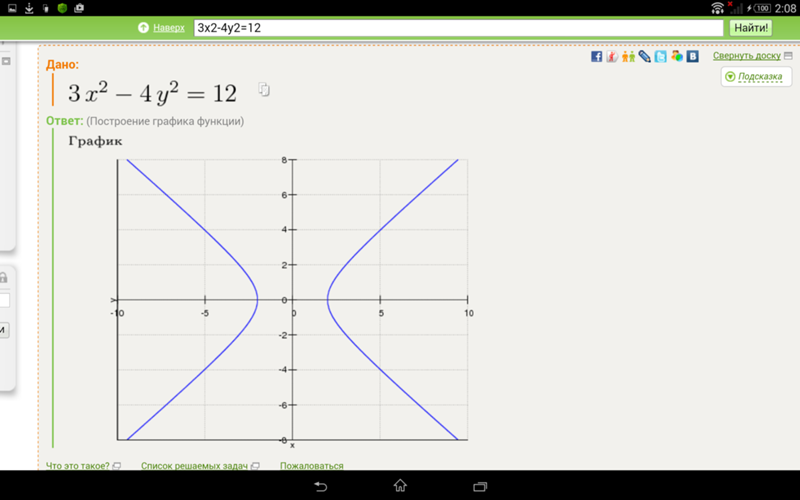
Пределы интегрирования известны из начального условия: tє[0;2pi].
Переходим к применению формул объемов:
а) Первым вычислим объем тела вращения вокруг оси Ox:

Здесь применили замену переменных и условие

б) Следующим найдем объем тела вращения вокруг оси Oy:

Его попробуйте расписать самостоятельно.

в) Последним вычислим объем тела вращения вокруг прямой y=2a:
Перейдем к новой системе координат по формулам y₁=y-2a, x₁=x.
Тогда искомый объем V=V₁-V₂, где V₁ — объем колового цилиндра с высотой H=2pi*a и радиусом основы R=2a, поэтому объем цилиндра равен
куб. од.
Второй объем находим интегрированием

Как и в предыдущих задачах здесь использовали замену переменных под интегралом.
Напоследок находим разницу объемов
куб. од.

Объем тела, образованного вращением вокруг полярной оси плоской фигуры

Чтобы найти объем тела V, образованного в результате вращением вокруг полярной оси плоской фигуры r(phi)
необходимо вычислить определенный интеграл по формуле

Пример 2483 Найти объем тела, образованного вращением кривой r=a (1+cos (phi)), , y=0
а) вокруг полярной оси;
б) вокруг прямой

Решение: Чтобы достать подинтегральную функцию подносим к кубу заданную функцию:

Пределы интегрирования записываем из начального условия:

а) Сначала найдем объем тела вращения вокруг полярной оси:

Для упрощения вычислений переходим к новой переменной под интегралом.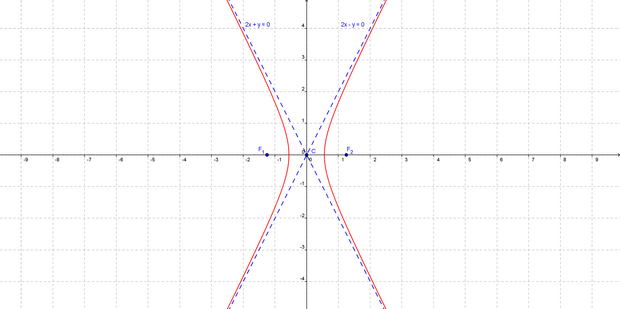
б) Перейдем к новым координатам с помощью формул: x₁=y, y₁=-x-a/4.
Определяем пределы интегрирования:
при росте угла от 0 к Pi/2 координата x₁ растет от 0 к , при росте от Pi/2 к Pi переменная x₁ спадает от к 0, поэтому пределы ограничены интервалом

Запишем подинтегральную функцию:
Уравнения перехода между системами координат имеют вид

Подстановкой в уравнение получим:
,
Найдем объем тела вращения вокруг прямой :

откроем скобки, возведем подобные слагаемые и, приняв во внимание, что интеграл равен нулю получим

Здесь последние интегралы выражаются через факториалы

(смотри пример 2.59, часть І).
Парные факториалы вычисляем по правилу

Пример 2484.1 Найти объем тела, образованного вращением кривой r=a*phi (a>0)вокруг полярной оси.
Решение: Запишем подинтегральную функцию:

С пределами интегрирования проблем нет:

Чтобы найти объем тела вращения вокруг полярной оси выполняем ряд манипуляций с интегралами:

Внимательно проанализируйте, как находится этот «тригонометрический» интеграл.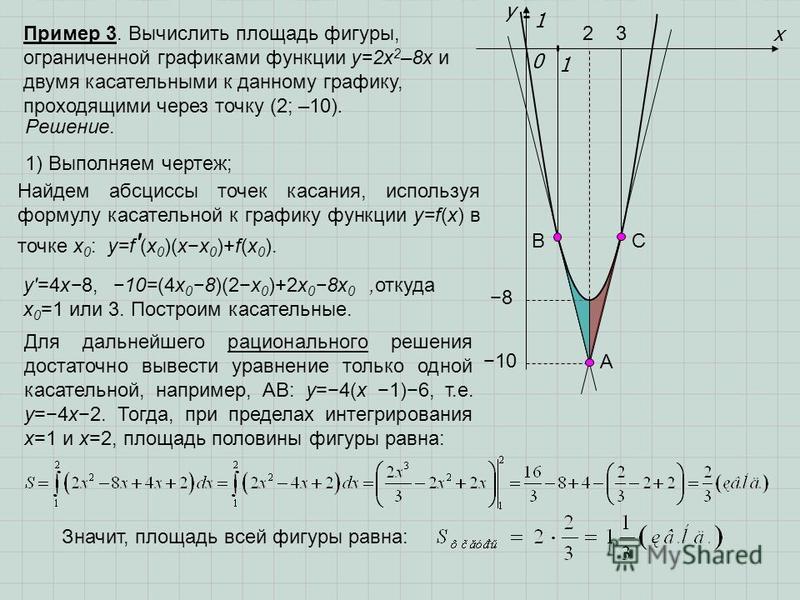 2

Решить свойства прямой линии y-x-3 = 0 Решатель алгебры тигра

Решить свойства прямой линии y-x-3 = 0 Решатель алгебры тигра

Этот сайт лучше всего просматривать с помощью Javascript.Если вы не можете включить Javascript, нажмите здесь.

Вход камеры не распознается!

Мы думаем, что вы написали:

y-x-3 = 0

Это касается свойств прямой линии.

Наклон = 2.000 / 2.000 = 1.000

Наклон = 2.000 / 2.000 = 1.000

xi «ntercept = 3 / -1 = -3,00000

xi» ntercept = 3 / -1 = -3,00000

yi «ntercept = 3/1 = 3,00000

yi «ntercept = 3/1 = 3,00000

Пошаговое решение

Шаг 1:

 
 Уравнение прямой 
 
 1.1 Решите y-x-3 = 0 
 
 Тигр понимает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании). 
 
 «y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.  
 
 В этой формуле: 
 
 y сообщает нам, как далеко идет линия. 
 x сообщает нам, как далеко вдоль 
 м находится наклон или градиент, т.е. насколько крута линия. 
 b — это точка пересечения оси Y i.е. где линия пересекает ось Y 
 
 Пересечения X и Y и наклон называются свойствами линии. Теперь мы построим график линии yx-3 = 0 и вычислим ее свойства. 
 
 График прямой линии: 
 
 
 Вычислите точку пересечения Y: 
. Обратите внимание, что когда x = 0, значение y равно 3/1, поэтому эта линия «разрезает» ось y в точке y = 3.00000
 y-intercept = 3/1 = 3.00000 
 Вычислите точку пересечения X: 
 Когда y = 0, значение x равно 3 / -1 Следовательно, наша линия » обрезает «ось x при x = -3.00000
 x-intercept = 3 / -1 = -3.00000 
 Вычислить наклон: 
 Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно 3.000, а для x = 2.000 значение y равно 5. 000. Итак, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 5.000 — 3.000 = 2.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = RISE / RUN)
 Наклон = 2.000 / 2.000 = 1.000 
 Геометрическая фигура: прямая 
 Наклон = 2.000 / 2.000 = 1.000
 пересечение по оси x = 3 / -1 = -3,00000
 пересечение по оси y = 3/1 = 3,00000
 Зачем это изучать 
 Термины и темы 
 Ссылки по теме 
 Поиск точек пересечения с помощью уравнения 
  X Intercept : график уравнения пересекает ось x
  Y Intercept : где график уравнения пересекает ось Y
 Чтобы найти перехватчики:
 Если вы хотите, чтобы  x перехватывал  (x, 0):
 Установите y = 0, затем решите относительно x
 Если вы хотите, чтобы  y перехватывал  (0, y):
 Установите x = 0, затем решите относительно y
 Пример: найти точки пересечения y = x 
 2 -4
  x пересечение: установить y = 0 
 0 = х  2 -4
 x  2  = 4
 x =  2  или  −2 
 Точки:  (2,0)  и  (−2,0) 
  y пересечение: установить x = 0 
 y = 0  2 -4
 г =  −4 
 Точка  (0, -4) 
 А вот график x  2 -4, чтобы подтвердить то, что мы нашли:
 Пример: найти точки пересечения x 
 2  — 5x + y  2  + 3y = 0
  x пересечение: установить y = 0 
 x  2  — 5x + 0  + 0 = 0
 х (х − 5) = 0
 x =  0  и  5 
 Точки:  (0,0)  и  (5,0) 
  y пересечение: установить x = 0 
 0  — 0 + y  2  + 3y = 0
 y (y + 3) = 0
 y =  0  или  −3 
 Точки:  (0,0)  и  (0, −3) 
 Итак, всего 3 точки:
 (0,0), (5,0) и (0, −3)
 А вот и график. {3},…
 Стенограмма видео 
 Итак, нас просят найти. Итак, мы даем тело. База определяется как таковая. Вот почему это X. У нас есть почему X равно X в кубе. Итак, давайте нарисуем некоторые из этих границ. Так почему же равен нулю? Это одна из границ. У нас есть еще одна граница, которая говорит, что почему равно X в кубе? У нас есть еще одна граница. То есть, извините. Не поэтому равно нулю. Вот почему равно нулю.Ага. Я просто пришел сюда по телефону. Ага. Итак, это Ах, вот почему он равен нулю. Так что это просто ось X. По сути. Итак, мы смотрим на всю территорию здесь. Итак, если бы мы изобразили это трехмерно, у нас были бы поперечные сечения, перпендикулярные оси Y, которые у нас есть. Почему? X и Z. И если у нас есть что-то похожее на это. Хорошо, я сделаю это немного преувеличенным, чтобы было легче сначала увидеть, мы собираемся иметь. Ну, он перпендикулярен оси Y, так что он будет первым.У нас будут такие квадраты, и по мере продвижения они будут становиться все меньше. Верно. Так что у него будет такая глубина. Итак, а затем мы будем гореть полукругами. Так что это будет примерно так. И тогда у нас будут равносторонние треугольники, которые будут выглядеть вот так. Это будет похоже на сплошное сужение. И, наконец, у нас будут эллипсы, которые вы знаете, что такое эллипс, что такое губы. Итак, мы собираемся быть. Первое, что мы хотим сделать, это то, что мы хотим найти так, типа, что? Какие полоски мы делаем? Какие полоски берем? Гм, как мы собираемся это сократить и как мы собираемся это интегрировать? Итак, мы хотим найти область всех этих вещей.Мы хотим взять твердые тела перпендикулярно оси Y. Итак, мы будем брать такие куски. Теперь, когда мы возьмем такие куски, это будет нашим базовым eso. Если мы хотим интегрироваться в этом направлении, мы хотим сделать это с точки зрения d y. Итак, если это d y, то мы должны поставить это. Каковы значения X в терминах выкл. Почему? Так почему же X в кубе? И почему тогда эта строка равна X Cube? Это означает, что X равно почему в одной третьей степени, Верно. Итак, если X равно y в степени одной трети, следующее, что мы собираемся сделать, это сказать: как мы собираемся найти объем этого твердого тела? Итак, мы собираемся интегрировать от нуля до конца, почему будет равно единице? Поскольку это X равно единице, это означает, что если мы подключили это сюда, то это означает, что это также почему равно единице.Итак, это были границы нашего интеграла или интегрирования между почему равно нулю и почему равно единице, верно? Почему равно нулю? Y равен единице. Это означает, что границы вне интеграла будут равны нулю и единице. Далее нам нужно уравнение для площади. Таким образом, площадь, ммм, и воображаемое количество, которое было множеством языков по толщине, скорее, это D y. Итак, это будет D Y. Итак, какова площадь квадрата для квадрата? Площадь квадрата равна квадрату основания глаз.Итак, мы знаем, что база — это X. А, мы знаем, что база будет одной. Это X равно одному минус X равно. Почему до одной трети. Значит, площадь равна одному минусу. Почему? До одной трети. Итак, теперь давайте поместим это здесь ноль умноженное на единицу, Эм, и это будет возведено в квадрат, Конечно. Так что это будет, ну ладно. Во-первых, давайте расширим это. Так что, если мы сорвем это, мы получим один минус два ширины до одной трети минус или плюс почему до двух третей. Итак, у нас будет один минус два y на одну треть плюс, почему две трети d y? И как только мы это интегрируем, мы поймем, почему минус три половины.Почему две трети сейчас? Почему четыре трети хорошо? Что я говорю? Ах, я всегда забываю, как интегрироваться, а это очень плохо. Так почему? К одной трети добавляется еще один. Итак, это станет Почему четыре трети, и мы будем умножать, чтобы купить инверсию этой новой силы, чтобы получить шесть, никогда не будет слишком коротким. Итак, это три половинки. И тогда это станет Смотри, почему до пяти третей. Так что это будет сделано. 3/5, и это будет между единицей и нулем.Итак, если вы подключите одну сюда, мы получим одну мину, три абс плюс 3/5, что равно 1/10. Значит, объем первой части составляет одну палатку. Так что давайте избавимся от этого материала. Мы можем оставить это, потому что это важно. Ослабьте. Тем не менее, примените это к следующей части. Это будет для квадратных поперечных сечений. Эм, теперь мы собираемся найти, мм, площадь полукруга равна пи. Время равно или пи больше двух, потому что это половина круга пи переходит в квадрат r. Итак, что у нас здесь? То, что мы обнаружили раньше, — это радиус между здесь и здесь, на самом деле это не радиус, а длина основания, так что она называется.Этот B равен одному минусу. Почему? До одной трети. Итак, в этом случае база будет, если у нас будет круг, как это, на нашей основе. Мы хотим, чтобы половина этой базы давала нам радиус. Верно? Значит, больше двух даст нам радиус. Так что у нас есть. Это равно пи. Более двух раз. Быть больше двух в квадрате. Теперь мы перейдем к Пи. Это тоже превратится в квадраты, превратится в пи в четыре раза больше, чем B в квадрате. Итак, теперь мы собираемся получить интеграл A от числа пи больше четырех. Единица минус умноженная на единицу минус у равна одной трети. Это квадрат D y. Таким образом, мы могли бы просто взять это число больше четырех. А теперь у нас будет то, что должно быть вам хорошо знакомо, потому что мы только что это сделали. Итак, теперь мы просто умножим предыдущий ответ на одно из моих высказываний: это будет Форд, а это умножится на два. Итак, это будет восемь вещей. Я поймал свою ошибку там. А теперь мы просто умножим наш предыдущий ответ. Это полукруг в поперечном сечении.Мы просто умножим наш предыдущий объем на число пи больше восьми. Таким образом, B будет равно числу пи раз больше 80. Так что хорошо. Теперь мы можем использовать ту же информацию и технику, чтобы найти О, не хочу, чтобы найти поперечные сечения равностороннего треугольника. Таким образом, площадь треугольника равна половине основания, умноженному на высоту. Итак, если у нас есть неравный боковой треугольник, правый, мы разделим его пополам. А это наш рост, правда? И мы знаем, что это основа. Так что все кончено и внутренние углы будут равны 60. И поскольку это также угол в 60 градусов, который был разделен пополам, мы знаем, что это 60. Треугольник 30 90 даст нам, ну, эта сторона будет квадратным корнем из трех величин. Это квадрат, умноженный на 3/2 B, и это высота. Итак, теперь у нас есть половина, умноженная на квадрат, умноженная на 3/2, умноженная на B, так что это даст нам квадрат 3/4 умноженной на b в квадрате. И снова мы собираемся получить что-то, что должно показаться вам очень знакомым, потому что этот коэффициент будет выходить за пределы интеграла, и мы собираемся получить, ммм, тот же самый интеграл, что и раньше.Итак, теперь, если мы, э-э, снова интегрируем это, мы получим квадрат 3/4, умноженный на 1 10. Итак, это будет квадрат 3/40. Итак, теперь у нас есть другой ответ. Далее мы собираемся найти то же самое. Но на этот раз наша площадь поперечного сечения представляет собой эллипс. Таким образом, область эллипса в губах выглядит так, как будто эта правая область губ задается двумя параметрами: один из них а, а другой -. Итак, мы знаем, что это вдвое больше. Так на самом деле, позвольте себе вызвать море, чтобы не запутаться.Итак, C равно половине B. Это означает, что здесь есть половина. Значит, a будет равно, гм, это значение, время увидеть значение, умноженное на пи, которое будет равно пи, умноженному на значение, умноженное на половину b. Итак, это будет равно. Мы знаем, что a равно см. Итак, у нас есть пирог, равный, чтобы увидеть, умноженный на половину b, и мы знаем, что c равно, чтобы быть. Итак, это означает, что это равно пи, умноженное на четыре b, умноженное на половину b. Это означает, что это равно двум пи умноженным на говядина. Итак, теперь мы будем скорее возведены в квадрат.Итак, теперь у нас есть интеграция между нулем и единицей. Коэффициент равен двум пи, и мы снова имеем один минус. Почему я написал одну половину, оказалось, что 31 третья, эм, почему больше одной трети? Почему до одной трети, и это г-н. И снова получим этот коэффициент. Это будет два пи умножить на 1/10. Два пи умножить на 1/10, то есть пи больше пяти, и это наши полукруги. Посмотрите на нас, Кора, поперечное сечение
 Д Х 3 Д 0 Х 2 
 график log3 журнал графики
 x3 факторизуйте идентичность y3, используя
 график
 вершина 2x квадратичный тони связанный
 линейные уравнения класса ex уравнение пары классов решить заданные решения viii vii следующие переменные ncert maths сокращение
 3x 2y нарисовать линейные уравнения из пары графиков
 2y 3x рисовать линейные уравнения графики ex class check пара переменных Глава
 2y 3x 3xy dx dy дифференциал раствора
 6x графиков
 xy условия серии решений
 2y 3y 4e решить дифференциальное уравнение
 Рисование таблицы графиков с использованием градиента пересечения
 значение средний интервал 2sqrt введите
 2y 2xy сокращение заказа
 2y 2x dx dy решить
 å¯¾æ • ° é– æ • ° â‘¡ î €€ yî ​​€ = logx / î €€ xî € 㠮㠂° ム© ム• å —é¨« ã ® 月
 dx dy решить socratic
 График 3x пример строки
 графики график математика алгебра статистика наука kwiznet геометрия ags средний наблюдение выше
 sqrt vk
 2x найти матрицы ex class сложение глава
 объем найти область замкнутые кривые ось вокруг повернуть ответ математика повернуть подумать проверьте вправо
 dy dx 2y решить ответ
 уравнение касательной линии график синус заданных точек градиент sin кривая точка pi решение значение пересечение формы производные уравнения ниже после
 2 года
 dx x2 dy y2 2xy ex однородные уравнения дифференциального класса channel teachoo
 пример решить примеры уравнения линейная пара класс глава
 sans diffmbre second avec
 dx dy xy решение найти уравнение дифференциальное ex заданные уравнения класс переменная разделение на чай
 5x 2x найти нули
 Кривая dx dy найти исчисление касательных xy с учетом p-линий
 Найдите объем, полученный при вращении данной области вокруг указанной линии.
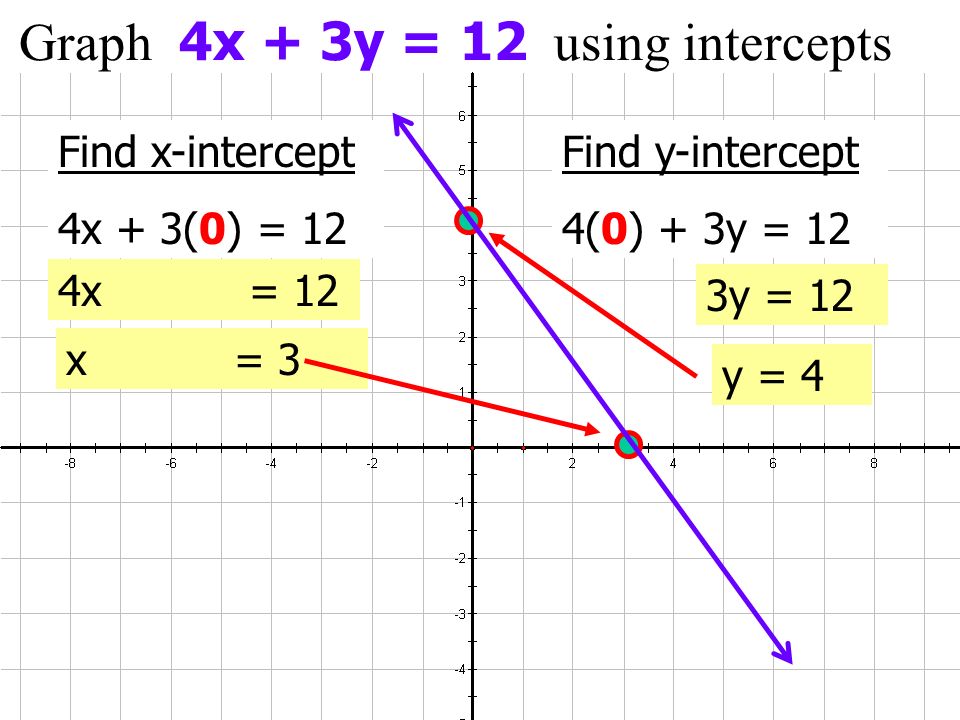 r2 about y 1
 … область, ограниченная данными кривыми относительно указанной линии. y = 2e − x, y = 2, x = 6; о y Нарисуйте регион. y = 2e-x и y = 4 пересекаются, когда 2e-x = 4. Решая уравнение, получаем x = -ln2. Найдите онлайн-репетитора сейчас. Выберите эксперта и познакомьтесь онлайн. Нет пакетов или подписок, платите …
 Обратитесь к рисунку и найдите объем, генерируемый вращением данной области вокруг указанной строки. примерно OA 3 примерно OC 217 примерно AB примерно BC // YR 2 примерно OA примерно OC примерно AB примерно BC (1,1 A (110) примерно OA s.R3 около OC около AB около BC
 Найдите объем V твердого тела, полученный вращением области, ограниченной данными кривыми, вокруг указанной прямой. V = (Нет отклика) Нарисуйте область, затем на собственном эскизе твердое тело и типичный диск или шайбу. Решение или объяснение Щелкните, чтобы просмотреть Решение y = 4 / x, y = 0, x = 1, x = 5; около y = −1
 Найдите объем твердого тела, образованного вращением вокруг линии y = 2 области в первый квадрант, ограниченный этими параболами и осью ординат.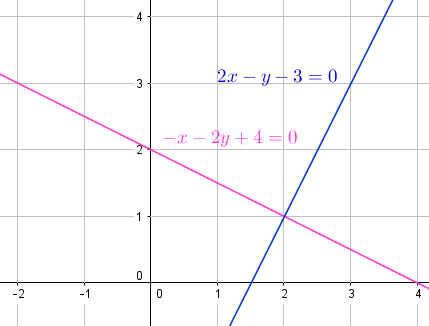 30B Сухой остаток. ПРИМЕР 8 Ниже показан регион R. Установите интеграл для объема, полученного вращением R вокруг данной линии. a) …
 Marlin — это огромная программа на C ++, состоящая из множества файлов, но здесь мы будем говорить только о двух файлах, которые содержат все параметры конфигурации Marlin во время компиляции: Configuration.h содержит основные настройки для выбор оборудования, языка и контроллера …
 Найдите объем V твердого тела, полученный вращением области, ограниченной заданными кривыми, вокруг заданной линии.V = (Нет отклика) Нарисуйте область, затем на собственном эскизе твердое тело и типичный диск или шайбу. Решение или объяснение Щелкните, чтобы просмотреть решение y = 4 / x, y = 0, x = 1, x = 5; около y = −1
 найдите материалы с сайта «example.com». URL: текст. (4) Для тем, по которым уже было опубликовано несколько видеороликов, новые видеоролики на ту же тему должны содержать новую важную информацию, новые перспективы и / или более высокое качество видеопроизводства.
 Уравнение с двумя точками kuta 
 28 августа 2014 г. · © R t230 C1I3x cK qu Itlad ZSjobfptIw dahr geJ DLwLKC1.v W 3A gl3l v 9r Biyg qhXtusL или Eets meZrJv MeHdF. f 3 1MwaTd 0eF Vw0iHtwhY SINnlf ViHnAiqtReP HAClCgBefb lr Ta0 z2 f.f Рабочий лист Kuta Software LLC Напишите уравнение прямой, проходящей через заданные точки, в форме пересечения наклона. (Подсказка: используйте формулу наклона и форму «точка-наклон»)
 Начиная с двух точек (x 1, y 1) и (x 2, y 2), калькулятор наклона подставляет значения в это уравнение для расчета «подъема» сверху и «бег» снизу. При выборе между двумя точками не имеет значения, какая точка используется как (x 1, y 1) или (x 2, y 2), но очень важно, чтобы вы постоянно использовали…
 Уравнения с логарифмами — Кута L 1 lMYaEdje P awWiztGhE MIHnyfYiCn7iPtxe v tA SlZg ieWbDr4ai K2r. m Рабочий лист ООО «Кута Софтвер» Kuta Software — Бесконечная алгебра 2 Имя _____ Экспоненциальные уравнения, не требующие логарифмов Дата _____ Период ____ Решите каждое уравнение. 1) 42 x + 3 = 1 2) 53 — 2x = 5 − x 3) 31 — 2x = 243 4) 32a = 3 − a …
 Форма точечного уклона. Стенограмма видео. Линия проходит через точки (-1, 6) и (5, 4). Какое уравнение линии? Давайте просто попробуем это представить себе.Я перехожу к отрицательному 4, я опустился на 10, или если вы просто хотите использовать эту формулу, она даст вам то же самое. Мы закончили с отрицательными 4, мы закончили с …
 Введите 3 точки, чтобы сформировать квадратное уравнение: <- Введите точку 1 <- Введите точку 2 <- Введите точку 3. Учитывая 3 точки, которые вы ввели: (6,24), (8,23) и (22,22), вычислите квадратное уравнение. по этим 3 очкам. Вычислите буквы a, b, c, d из точки 1 (6, 24)
 Рабочий лист от Kuta Software LLC Назовите все углы, у которых V является вершиной.13) JV 14) F 6 5 EH 15) 2 VD 16) TV 3 2 IFE 1 3 SR 4 VD 17) 18) MHGL 4 3 1 VK 23 VF 19) IV 43 FI 20) E 2 FDH 3 G 4 5 VC Укажите, является ли данная точка внутренней, внешней или угловой. 21) 22) P P 23) 24) P P 25) 26) P P
 Уравнения с логарифмами — Кута L 1 lMYaEdje P awWiztGhE MIHnyfYiCn7iPtxe v tA SlZg ieWbDr4ai K2r.