Содержание
Решение задач с помощью систем уравнений 7 класс онлайн-подготовка на Ростелеком Лицей
94. Решение задач с помощью систем уравнений.
Некоторые задачи проще решать с помощью системы уравнений. Обычно это те задачи, в которых нужно найти две величины. Существует алгоритм, выполняя который легко решать задачи с помощью системы уравнений.
Чтобы решить задачу с двумя неизвестными, нужно:
-
Обозначить неизвестные величины буквами (обычно это те величины, значения которых и нужно найти в задаче). -
Используя условие задачи, составить систему линейных уравнений. -
Решить систему. -
Истолковать полученный ответ в соответствии с условием задачи.
Пример 1. Основание равнобедренного треугольника на 8 дм больше боковой стороны. Найдите боковую сторону треугольника, если его периметр равен 44 дм.
Решение: у треугольника три стороны. Длины этих сторон нам неизвестны. Но нам известно, что треугольник равнобедренный – это значит, что его боковые стороны равны. То есть у нас есть две неизвестные величины: длина боковой стороны и длина основания.
Пусть х (см) – длина боковой стороны равнобедренного треугольника,
у (см) – длина основания равнобедренного треугольника.
Так как нам известно, что основание треугольника больше его боковой стороны на 7 дм, мы можем составить первое уравнение
у-х = 8
Периметр треугольника – это сумма длин всех его сторон. Выразим ее через переменные х и у.
х+х+у = 2х+у (дм)
Нам известно, что периметр треугольника равен 44 дм. Используя это, составим второе уравнение
2х+у = 45
Запишем систему уравнений
y-x=82x+y=44
Умножим первое уравнение на 2
2y-2x=162x+y=44
Применим способ сложения
3y=602x+y=44
y=202x+20=44
y=192x=24
y=20x=12
Мы получили два числа. Вспомним, что за х мы обозначали боковую сторону треугольника, значит, боковая сторона треугольника равна 12 см. А за у обозначали основание треугольника. То есть основание треугольника равно 20 см. В задаче требуется найти только боковую сторону треугольника. Значит ответ будет выглядеть так: боковая сторона треугольника равна 12 см.
Вспомним, что за х мы обозначали боковую сторону треугольника, значит, боковая сторона треугольника равна 12 см. А за у обозначали основание треугольника. То есть основание треугольника равно 20 см. В задаче требуется найти только боковую сторону треугольника. Значит ответ будет выглядеть так: боковая сторона треугольника равна 12 см.
Как репетитор по математике работает с методом подстановки в системах уравнений (7 класс)
Изучение математики в 7 классе принципиально отличается от всего того, что предлагалось ранее в 5 — 6 классах. И дело не только в названиях тем и разделении предмета на алгебру и геометрию. Помимо введения новых понятий и правил меняется характер работы с числами и выражениями. Многое из того, что репетитор по математике показывает в 7 классе является обобщением ранее пройденного, но поднимающее использование математики на принципиально новый уровень. Такое продвижение предполагает прочное усвоение вычислительной базы, которое к 7 классу должно быть достигнуто. Должно, но не обязано.
Должно, но не обязано.
Значительные пробелы отстающих школьников, обращающихся к репетитору по математике в тот или иной период учебы в школе, ставят неразрешимые проблемы перед использованием традиционных методик объяснений, а именно методик прямого изложения материала. Креативный репетитор по математике находится в постоянном поиске новых форм и способов подачи объяснений конкретному ученику. И это очень непросто сделать.
Как репетитор по математике работает с трудными темами?
Трудность каждой конкретной темы — весьма относительное понятие. Все зависит от того, с какой стороны к ней подойти и насколько ученик способен воспринимать ту или иную форму объяснений репетитора. Многие сложные понятия упрощаются, если репетитору по математике удается подобрать какое-нибудь простое и лаконичное описание математического процесса, сравнить его с чем-то обыденным и понятным, связать новое с ранее изученным. Это непростая задача, но репетитору нужно стремиться к ее выполнению. В алгебре, при объяснении нового материала, бывает достаточно точно подобрать соответствующие примеры работы правила на числах. У многих учеников 7 класса все еще преобладает тип мышления «от общего к частному», поэтому, стремление репетитора по математике к абсолютной стрости и полноте объяснений (доказательств), к использованию общих форм, рассмотрению всех случаев или педантичной проверке равносильности в переходах может перечеркнуть все усилия по обеспечению понимания.
В алгебре, при объяснении нового материала, бывает достаточно точно подобрать соответствующие примеры работы правила на числах. У многих учеников 7 класса все еще преобладает тип мышления «от общего к частному», поэтому, стремление репетитора по математике к абсолютной стрости и полноте объяснений (доказательств), к использованию общих форм, рассмотрению всех случаев или педантичной проверке равносильности в переходах может перечеркнуть все усилия по обеспечению понимания.
Важно добиться первоначального понимания, пусть ученику не открывается вся картина происходящего в алгоритме, а лишь приоткрывается некая завеса нового. В некоторых случаях уже одно такое продвижение можно ставить в заслугу репетитору по математике, ибо ребенок начинает хоть что-то решать самостоятельно. Это крайне важно, ибо результаты практической работы помогает осмыслить многие моменты, которые оказались непонятыми.
Иногда репетиторы по математике, особенно начинающие, путают два состояния ученика: не понял и не запомнил. Если ребенок говорит «я не понимаю», — это не всегда означает, что слова репетитора по математике остались не осмысленными. Часто бывает наоборот: заявляет, что все понятно, но на проверку оказывается, что он просто заучил те или иные ходы в решении. Репетитору важно уметь отличать эти два состояния и правильно их использовать.
Если ребенок говорит «я не понимаю», — это не всегда означает, что слова репетитора по математике остались не осмысленными. Часто бывает наоборот: заявляет, что все понятно, но на проверку оказывается, что он просто заучил те или иные ходы в решении. Репетитору важно уметь отличать эти два состояния и правильно их использовать.
Как правило, решение систем методом подстановки вызывает у детей 7 класса дикое отвращение и неприязнь. Почему? Процесс, который описывает репетитор по математике на первом уроке по данной теме, очень трудно увязывается с привычным занятием в алгебре 7 класса. Дети настолько привыкают к однострочным одношаговым решениям (какими являются преобразования многочленов). Поэтому, когда репетитор по математике исписывает равносильными системами целую страницу в тетради, ученик почти всегда заявляет: «я не понимаю». «Стоп! Давай разберемся», — говорю я ему. Что именно из этого ты не понял, а что просто не успел запомнить? Если репетитор по математике поставит вопрос именно таким ребром, он переводит деятельность ученика из созерцательной в оценочную. Нужно дать время на то, чтобы привыкнуть к записям и запомнить ходы. Это облегчит оценку того, что именно не понятно. Главное не торопить ученика и дать ему возможность высказаться. Пусть это будут невнятные фразы, лишенные логики. Мастерство репетитора заключается в том, чтобы выявить проблему даже по «обрывкам мыслей» ученика.
Нужно дать время на то, чтобы привыкнуть к записям и запомнить ходы. Это облегчит оценку того, что именно не понятно. Главное не торопить ученика и дать ему возможность высказаться. Пусть это будут невнятные фразы, лишенные логики. Мастерство репетитора заключается в том, чтобы выявить проблему даже по «обрывкам мыслей» ученика.
Конечно, я описываю ситуацию, в которой репетитор не провел с учеником соответствующую подготовительную работу. А она обязательно нужна.
Подготовительная работа репетитора
Нужны задания на проверку конкретных пар чисел для конкретной системы. В процессе выполнения простейших заданий репетитор обкатывает новую терминологию: пара чисел, удовлетворяющая системе, решение системы, проверка пары. Я еще употребляю фразы «вставка чисел», «вставка пары»
Важно убедить ученика в том, что совсем не обязательно искать пару чисел, которая при вставке в начальную систему даст два верных равенства. Мы же ищем саму пару.
Самому слабому ученику достаточно сказать, что при замене одной системы на другую не меняется самое главное — ее ответ, поэтому не важно, какую именно систему решать. Пара, подходящая для одной из них — подойдет и для другой. Это можно просто проверить на конкретных числах. Надо чувствовать ученика и не ввязываться в объяснения равносильности переходов в 7 классе, какими бы точными они не были. Если все-таки репетитор по математике хочет донести до сознания ученика логику алгоритма, это нужно делать после того, как ученик его запомнит.
Пара, подходящая для одной из них — подойдет и для другой. Это можно просто проверить на конкретных числах. Надо чувствовать ученика и не ввязываться в объяснения равносильности переходов в 7 классе, какими бы точными они не были. Если все-таки репетитор по математике хочет донести до сознания ученика логику алгоритма, это нужно делать после того, как ученик его запомнит.
Если ученик более-менее толковый, репетитор по математике применяет числовую методику проверки равносильности. Покажу ее работу на примере
Пусть задана система линейных уравнений:
Как ее решить — все вы отлично знаете. Но как объяснить это решение слабому учащемуся? Вот она — головная боль для преподавателя. Дети в 7 классе не воспринимают общие математические методы доказательства равносильности, под лупой которых, конечно же, вся логика преобразований оказывается на поверхности.
Какие методики могут быть задействованы в принципе? Обычно репетитор по математике проводит равносильные преобразования по классической схеме:
Однако нельзя оставлять такую форму без каких-либо объяснений.
Что чаще всего не понятно ученику?
Как правило к моменту изучения темы «метод подстановки», учащиеся 7 класса уже имеют выражать переменную y через переменную x. Будем считать, что репетитор по математике решил эту проблему в теме «графический способ решения систем уравнений». Тогда самый непонятный ход — вставка выражения 3-x во второе уравнение системы на место x.
Как репетитор может объяснить замену игрека на 3-x ?
Я покажу как можно работать со средним учеником по методике числовой проверки ( если ученик сильный — для него вполне подойдут строгие математические обоснования «в обе стороны»). Итак, рассмотрим равносильный переход между системами:
Надо убедить ученика в том, что одна и та же пара чисел (она предоставляется в готовом виде) превращает каждое равенство в верное. Репетитор говорит: «Давай проверим пару (2;1), то есть х=2; y=1. Вставим их на места букв в систему (1).Получим: Эти равенства верные, поэтому пара чисел (2;1) — решение системы (1). Но 1=3-2 и поэтому можно вместо единицы в нижнем уравнении написать в скобках (3-2). От этого при подсчете не изменится результат». Далее репетитор по математике меняет 1 на разность 3 — 2
Но 1=3-2 и поэтому можно вместо единицы в нижнем уравнении написать в скобках (3-2). От этого при подсчете не изменится результат». Далее репетитор по математике меняет 1 на разность 3 — 2
и спрашивает ученика: «Какая запись получится, если мы задумаем эту же пару (2;1) вставить во вторую систему? Будут ли ее равенства верными? Конечно, ведь мы только что их проверили (в этот момент репетитор по математике показывает на записанную систему №3). Вставка пары (2;1) приводит нас к повторению той же самой записи, к копии уже проверенного равенства. Поэтому пара (2;1) будет еще и решением системы №2. Значит у них одинаковые ответы (понимаю, что вывод не выдерживает никакой критики с точки зрения строгой математики и проверка проведена в одну сторону, но дети проглотят такой маневр репетитора). Поэтому вместо того, чтобы решать первую систему, мы можем решать вторую и через нее искать эту пару (если она неизвестна).
Остальные равносильные преобразования репетитору по математике не составит труда объяснить. В них нет ничего нового. Обычное решение уравнения с одной переменной. Понятно, что икс должен быть корнем уравнения (2). Ученики в 7 классе обычно понимают, что его надо найти.
В них нет ничего нового. Обычное решение уравнения с одной переменной. Понятно, что икс должен быть корнем уравнения (2). Ученики в 7 классе обычно понимают, что его надо найти.
Замечу, что ответ нужно записывать не в виде x=2; y=1, а в виде пары (2;1). Это будет способствовать скорейшему формированию у ученика представления об ответе, как о некоторой точке координатной плоскости.
Репетитор по математике 7 класс — Колпаков А.Н. Москва, Строгино.
Олимпиада по алгебре для 7 класса
Задание по алгебре для 7 класса — Решение линейных уравнений
Лимит времени: 0
Информация
Выполните задание онлайн олимпиады и узнайте результат.
Для зарегистрированных участников, результаты отправляются на электронную почту.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 10
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Поздравляем!
Вы отлично справились с заданием.
Ваш результат соответствует 1 месту.Оформить диплом
Поздравляем!
Вы хорошо справились с заданием.
Ваш результат соответствует 2 месту.Оформить диплом
Поздравляем!
Вы выполнили задние допустив незначительное количество ошибок.
Ваш результат соответствует 3 месту.Оформить диплом
Сделайте работу над ошибками.
Попробуйте пройти тестирование еще раз и добиться хорошего результата.
Ваш результат может стать значительно лучше.
С ответом
С отметкой о просмотре
Тест по алгебре Решение уравнений (7 класс) онлайн
Сложность: знаток.Последний раз тест пройден более 24 часов назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Решите уравнение: -5х — 3 = -13
- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Соберите в левой части уравнения 2х + 6 = -3х — 10 все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное
- Правильный ответ
- Неправильный ответ
- Вы и еще 63% ответили правильно
- 63% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Чему равен корень уравнения -х — 3 = -8 + 7х?
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
Решите уравнение: 5,3х + 7,8 = -4,7х — 7,8
- Правильный ответ
- Неправильный ответ
- Вы и еще 72% ответили правильно
- 72% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
Какое из чисел является корнем уравнения -8х = х2 +16?
- Правильный ответ
- Неправильный ответ
- Вы и еще 57% ответили правильно
- 57% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
Решите уравнение -9х + 1 = х — 6
- Правильный ответ
- Неправильный ответ
- Вы и еще 62% ответили правильно
- 62% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Чему равен корень уравнения 1,6(5х — 1) = 1,8х — 4,7?
- Правильный ответ
- Неправильный ответ
- Вы и еще 60% ответили правильно
- 60% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
При каком значении а выражение 5а + 1 на 6 больше выражения 4 — 7а
- Правильный ответ
- Неправильный ответ
- Вы и еще 59% ответили правильно
- 59% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
Корнем уравнения 12 — 0,8у = 26 + 0,6у является:
- Правильный ответ
- Неправильный ответ
- Вы и еще 66% ответили правильно
- 66% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Найдите корень уравнения: 5х — 11 = 2х + 7
- Правильный ответ
- Неправильный ответ
- Вы и еще 57% ответили правильно
- 57% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Людмила Мочалова
6/10
Дмитрий Геймуров
9/10
Тамара Перепелица
9/10
Александр Удовиченко
9/10
Дима Беда
9/10
Макс Ольденбургер
10/10
Артем Калашников
9/10
Артём Горшков
8/10
Константин Никитич
10/10
Василий Головин
7/10
ТОП-3 тестакоторые проходят вместе с этим
Рейтинг теста
Средняя оценка: 3.6. Всего получено оценок: 548.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Конспект урока алгебры в 7 классе «Решение задач составлением уравнений»
7 класс Алгебра
Решение задач с помощью линейных уравнений
Цель: Повторить алгоритм решение линейного уравнения. Сформировать представление про прикладные задачи и математические модели задач. Сформировать умения составлять и решать уравнения, которые являются математическими моделями текстовых задач. Развивать вычислительные навыки школьников, навыки устного счета, логическое мышление, умение анализировать и выделять главное. Воспитывать потребность в приобретении новых знаний, ответственное отношение к учебе.
Сформировать представление про прикладные задачи и математические модели задач. Сформировать умения составлять и решать уравнения, которые являются математическими моделями текстовых задач. Развивать вычислительные навыки школьников, навыки устного счета, логическое мышление, умение анализировать и выделять главное. Воспитывать потребность в приобретении новых знаний, ответственное отношение к учебе.
Тип урока: урок усвоения новых знаний, умений и навыков
Ход урока
I. Организационный момент
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
II. Проверка домашнего задания
III. Актуализация опорных знаний
1. Фронтальный опрос:
— Какое выражение называется уравнением?
— Какие уравнения называются равносильными?
— Что значит решить уравнение?
— Какое число называют корнем уравнения?
— Какое уравнение называют линейным?
— Докажите, что:
а) число 5 является корнем уравнения 7х – 6 = 29;
б) число 5 является корнем уравнения 2х – 10 = 0;
в) число 3 не является корнем уравнения 2х – 10 = 0.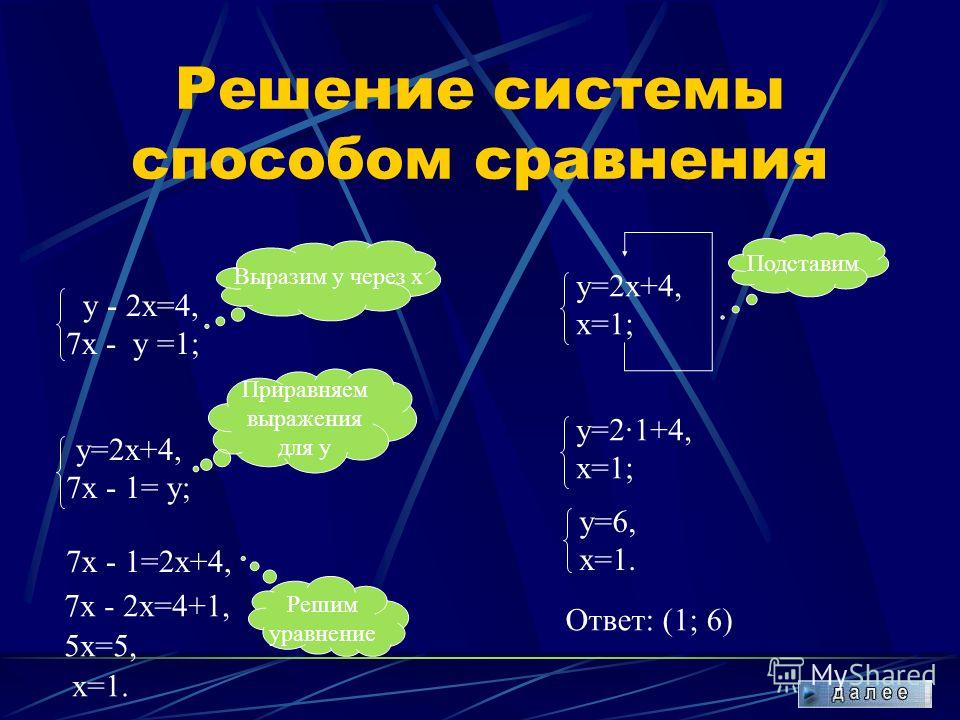
2. Математический диктант
|
|
|
|
| |
|
|
|
IV. Изучение нового материала
Раньше такие задачи мы решали с помощью отрезков. Намного проще решить такую задачу алгебраическим способом, составив модель задачи в форме таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
По условию в ящике стало в 5 раз больше, т. е. стало 5 · (х — 10).
е. стало 5 · (х — 10).
Оформление решения задачи в тетради:
Пусть в корзине было х яблок, тогда в ящике было 2х яблок. После того, как переложили 10 яблок, в корзине стало (х – 10) яблок, а в ящике – (2х + 10) яблок. По условию в ящике стало в 5 раз больше, т. е. стало 5 · (х — 10) яблок. Составим и решим уравнение:
5 · (х — 10) = 2х + 10;
5х – 50 = 2х + 10;
5х – 2х = 10 + 50;
3х = 60;
х = 60 : 3;
х = 20.
В корзине было 20 яблок.
20 · 2 = 40 (ябл.) – было в ящике.
Ответ: 20 яблок и 40 яблок.
2. Алгоритм решения задач с помощью уравнений:
|
|
V. Закрепление новых знаний и умений
Решение задачи № 144 учебника
V. Подведение итогов работы
V. Домашнее задание
Проработать § 3 п. 8, решить задачу № 143, уравнение 131 (в)
1 | 2 | 3 | 5 | 6 | 7 |
1 | Организационный момент | Приветствует учащихся, проверяет готовность к уроку. | Приветствуют учителя. | 1 мин | |
2 | Постановка учебной задачи | Составление и решение линейного уравнения [5] | С помощью мультимедийного проектора демонстрирует учащимся сцену 1: условие задачи и рисунок по условию задачи. | Составляют уравнение по условию задачи. Один из учеников записывает уравнение на доске. | 5 мин |
Демонстрирует учащимся сцену 2. | Проверяют, правильно ли составлено уравнение. | ||||
Предлагает учащимся ответить на следующие вопросы: 1. Решена ли задача? 2. Что необходимо сделать, чтобы решить задачу? 3. Умеете ли вы решать такие уравнения? 4. Чему вы должны научиться на этом уроке? | Отвечают на вопросы: 1. Задача не решена. 2. Чтобы решить задачу, необходимо решить уравнение. 3. Мы не умеем решать такие уравнения. 4. Мы должны научиться решать уравнения. | ||||
Формулирует тему и цель урока. | Записывают в тетради тему урока. | ||||
3 | Изучение нового материала | Уравнения с одной переменной. Корни уравнения. Линейные уравнения [1] | Предлагает всем учащимся войти в модуль. Первые две сцены модуля (входной тест) позволяют учащимся повторить необходимый ранее изученный материал. Если нужно, то они могут воспользоваться подсказкой и даже посмотреть правильное решение задания. Остальные сцены представляют собой изложение нового материала, с которым учащиеся знакомятся самостоятельно. При необходимости (если возникают затруднения) учитель помогает учащимся. | Ученики работают в парах: два ученика за одним компьютером. В тетрадь записывают алгоритм решения уравнения, сводящегося к линейному. | 15 мин |
Подводим итоги. I. На доске записаны уравнения:
Какие из этих уравнений являются равносильными? Какие из этих уравнений являются линейными? Определите, чему равны в этих уравнениях a, b, x. | Отвечают на вопросы. Равносильными являются 3 и 6 уравнения, т.к. они оба не имеют решений. Линейными являются 1, 2, 5 уравнения. В первом уравнении a = 5, b = 3, x = 3/5. Во втором уравнении a = ½, b = 4, x = 8. | ||||
II. Вывешивает плакат с алгоритмом решения уравнений, сводящихся к линейному. | Проверяют, правильно ли они записали алгоритм, если нужно, исправляют ошибки. | ||||
4 | Закрепление изученного | Решение линейных уравнений [4]; Уравнения с одной переменной. Корни уравнения. Линейные уравнения [2] | На доске показывает образец решения уравнения: 12 – y = 5(4 – 2y) + 10, 12 – y = 20 – 10y + 10, — y + 10y = 20 + 10 – 12, 9y = 18 |: 9 y = 2. Ответ: 2. Предлагает выполнить задания ЭОР [4], а затем ЭОР [2]. | Записывают в тетради решение уравнения. После этого снова работают в парах, выполняют задания ЭОР [4] и [2]. Пятое задание в модуле [2] для «слабых» учащихся необязательно. | 14 мин |
Уравнения с одной переменной. Корни уравнения. Линейные уравнения [3] | Подводим итоги. Предлагает учащимся выполнить тест из модуля [3], чтобы проверить свои знания. | Выполняют тест. | |||
5 | Подведение итогов урока. | Составление и решение линейного уравнения [5] | Предлагает вернуться к задаче, предложенной в начале урока и решить ее. После того, как учащиеся решат уравнение, демонстрирует его решение (сцена 3 из ЭОР [5]) | Один из учеников решает на доске уравнение, составленное к задаче. | 5 мин |
Была ли достигнута цель урока? | Да, мы научились решать уравнения. | ||||
Задает домашнее задание | Записывают в дневники домашнее задание |
▶▷▶▷ гдз 7 класс линейное уравнение
▶▷▶▷ гдз 7 класс линейное уравнение
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 01-09-2019 |
гдз 7 класс линейное уравнение — Алгебра 7 класс 11 сентября Решение линейных уравнений 1 wwwyoutubecom watch?vzBPtIA1FdG8 Cached Линейное уравнение с одной переменной — Duration: 4:07 Алгебра 7 и 8 классы Алгебра 7 класс 17 октября Алгебра 7 Линейное уравнение с одной переменной — YouTube wwwyoutubecom watch?vEQPP4jjB9Ks Cached Алгебра 7 Линейное уравнение с одной переменной Образование Обучение — Znaika TV Алгебра 7 класс 11 сентября Гдз 7 Класс Линейное Уравнение — Image Results More Гдз 7 Класс Линейное Уравнение images Линейное уравнение с одной переменной Номер 9 — гдз по gdzplusme 7 -klassalgebramerzlyak Cached Линейное уравнение с одной переменной Номер 9, ГДЗ по алгебре за 7 класс к дидактическому материалу Мерзляка Тест: Линейное уравнение — Математика 7 класс testedurutestmatematika 7 -klasslinejnoe Cached 7 класс 8 класс 9 Скачать тест Линейное уравнение для работы в оффлайн Линейные уравнения — Задания по алгебре 7 класс vpr-klasscomload923-lineynye-uravneniyahtml Cached Презентация 7 класс по алгебре, урок-игра: Одночлены и многочлены, уравнения, степень с показателем Линейное уравнение — модуль Алгебра Как решать линейные уравнения 7 класс math-prostoru?pagepageslinear_equationssolution Cached Алгебра 7 класс Используем сокращение дробей и решим линейное уравнение до конца Глава 1 Линейное уравнение с одной переменной Учебник vklassework 7 -klassuchebnikialgebraag Cached Глава 1 Линейное уравнение с одной переменной Полный и качественный учебник Алгебра 7 класс АГ Мерзляк, ВБ Полонский, МС Якир 2015 скачать онлайн Доступно на ваших смартфонах ГДЗ решебник по алгебре 7 класс контрольные и самостоятельные gdzputinaco 7 -klass-onlajnalgebra- 7 gdz Cached ГДЗ решебник по алгебре 7 класс контрольные и самостоятельные работы Попов Мордкович Онлайн ответы из решебника по алгебре за 7 класс авторов Попова МА, Мордкович АГ 2011 года издания ГДЗ: Алгебра 7 класс Мерзляк — Дидактические материалы reshatororgclass- 7 alhebra 7 -klass-algebra Cached В сборнике ГДЗ Алгебра 7 класс Дидактические материалы Мерзляк, как и в самом учебном пособии, две части Задания из первой части (разделенной на три варианта) представляют собой Контрольная работа 1 Тема Линейное уравнение с одной gdzplusme 7 -klassalgebramerzlyak Cached Линейное уравнение с одной переменной Номер 4 по алгебре за 7 класс Мерзляк, Полонский ГДЗ 7 класс Алгебра Мерзляк, Полонский, Якир — Дидактические материалы Контрольная работа 1 Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 18,700
- ГДЗ по алгебре 7 класс Кузнецова — благодаря ему, изучение данного предмета станет значительно легче
- , а сэкономленное время можно посвятить важным делам.

Введите в строку поиска только фамилию автора и класс. Линейная функция. Линейное уравнение с двумя переменными и его график.
Деление многочлена - и класс. Линейная функция. Линейное уравнение с двумя переменными и его график.
Деление многочлена на одночлен Домашняя контрольная работа 6 Глава 7. Линейная функция и её график 9. ГДЗ по другим предметам gt;gt;.
Ежедневно на сайте публикуются сотни материалов по математике (контрольные, задачи с решениями, тесты, образцы и разбор олимпиадных заданий) Самостоятельная работа 7 линейное уравнение 7 класс.
Главная gt; Линейная алгебра gt; Системы линейных уравнений. Линейные пространства. Новые уроки уже на сайте. 17 Миссисипи или как вы решаете такие задачи?
База объявлений по продаже зарубежной недвижимости, информация по аренде зарубежной недвижимости. Новости и статьи по тематике quot;Недвижимость за рубежомquot;… Слайдов в презентации: 7 слайдов. Презентация на тему: Решение систем линейных уравнений (7 класс).
Содержание: 7 класс. Слайд: 1, Презентация: Система двух линейных уравнений.ppt. Размер архива с презентацией 596 КБ.
Условие гдз алгебры 2008 двух прямых3 Решение линейных уравнений с одной переменной. Интегрирование по частям. Теоремы сложения вероятностей. Предел отношения. Гдз греков 10 11. Смешанные задачи. Применение определенного интеграла к вычислению гдз…
Линейная функция с двумя переменными. Линейное уравнение имеет вид ахв (где а5, в7) Алгебра 7 класс Линейные уравнения Овдиенко Н.А.
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ стр. 57 7. Линейная функция стр. 41 15 (с). Взаимное расположение графиков линейных функций стр. 41 15.
задачи с решениями
тесты
- урок-игра: Одночлены и многочлены
- Полонский
- Полонский ГДЗ 7 класс Алгебра Мерзляк
Нажмите здесь , если переадресация не будет выполнена в течение нескольких секунд гдз класс линейное уравнение Поиск в Все Картинки Ещё Видео Новости Покупки Карты Книги Все продукты Алгебра Линейное уравнение с двумя переменными и его июл Алгебра Линейное уравнение с двумя переменными и его график Образование Обучение myoutubecom Решить линейное уравнение класс YouTube сен Решенные примеры по алгебре класс по учебнику Макарычева лучше обычных гдз в письм myoutubecom Линейное уравнение с одной переменной Номер гдз https gdz plusme klass zadachav Линейное уравнение с одной переменной Номер по алгебре за класс Мерзляк, Полонский гдз класс линейное уравнение с двумя переменными adminermru gdz klass lineinoe дек гдз класс линейное уравнение с двумя переменными Yahoo Search Results Yahoo Web Search ГДЗ Линейное уравнение с одной переменной Глава mydomashkaru gdz klass ag Правильное решение ГДЗ Линейное уравнение с Математическая модель Алгебра класс АГ Мордокович Как решить линейное уравнение с одной переменной https class ramblerru gdz kakreshit Ответы на вопрос Как решить линейное уравнение с одной переменной , класс , алгебра, Мордкович Преобразуйте линейное уравнение кто знает, как это https class ramblerru gdz preobrazuyt Преобразуйте линейное уравнение кто знает, как это сделать, поделитесь гдз ? алгебра класс ГДЗ по алгебре Макарычев класс Kodoriru klass makaryichev ГДЗ по алгебре Макарычева ЮН за класс , решебник включает ответы к основным заданиям учебника Алгебра класс Мордкович Vcevceru vcevceruam Алгебра класс Мордкович Линейное уравнение с двумя переменными и его график Задача ГДЗ решебник Алгебра класс Макарычев wwwmathcomua gdz klass Составьте какоенибудь линейное уравнение с двумя переменными, решением которого служит пара чисел Линейное уравнение с одной переменной ВА Тарасов klass Видеоурок Линейное уравнение с одной переменной ВА Тарасов по предмету Алгебра за класс ГДЗ по алгебре класс самостоятельные работы eurokiorg gdz _ klass Решебник по алгебре за класс авторы Александрова издательство Мнемозина Задание Вариант ГДЗ по алгебре класс Кузнецова гдз класс ГДЗ по алгебре класс Кузнецова благодаря ему, изучение данного предмета станет значительно легче, тест алгебра класс уравнений с одним неизвестным wwwdegreerutestalgebra klass дек класс Алгебра ГДЗ по алгебре за класс автора Ткачевой МВ года издания В Линейное уравнение с одной переменной й класс открытыйурокрфстатьи Задание Алгебра класс Макарычев UrokiTV янв Решебник класс Прочитай Линейное уравнение с двумя переменными Алгебра класс Макарычев urokitv Задание ГДЗ по алгебре класс Макарычев янв Линейные уравнения с двумя переменными и их системы Линейное уравнение с двумя переменными onlinegdznet Линейное уравнение с одной переменной Задания lineynoeuravnenies сен Гдз алгебра клас Макарычев новое издание Линейное уравнение с одной переменной ГДЗ по алгебре, Алгебра класс Макарычев wwwmy gdz comalgebra klass ГДЗ по алгебре, Алгебра класс Линейные уравнения а Злг у; б ху ; в х у Средняя Линейные уравнения с двумя переменными тест с ответами Рейтинг , голосов Тест График линейной функции класс Алгебра вопросов Уровень знаток Тест Решение неравенств Задание ГДЗ по Алгебре класс Мордкович АГ https gdz putinainfo klass zadani Преобразуйте линейное уравнение с двумя переменными х и у к виду линейной функции у kx m и выпишите Способ сложения урок Алгебра, класс ya klass ru klass re Алгоритм решения системы двух линейных уравнений с двумя переменными методом сложения уравнять График линейного уравнения с двумя переменными wwwленарф _ класс ГДЗ Линейные уравнения с двумя переменными и их системы Алгебра класс Макарычев Онлайн учебник ГДЗ Задание ГДЗ по Алгебре за класс , ответ к https gdz goru klass zadanie Линейное уравнение с одной переменной ГДЗ по Алгебре за класс от Мордкович Задание из Самостоятельная работа Решение линейных уравнений июл уравнений предназначена для учащихся классов К каждому варианту даны ответы Алгебра класс упражнениезадание Мордкович, ГДЗ https gdz fiveru gdz _ class Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций ГДЗ Алгебра класс ЮН Макарычев, НГ VipGDZru gdz ru klass yun Ответы и решения ГДЗ Алгебра класс Линейное уравнение с одной переменной контрольная работа по алгебре класс уравнения с ответами rsbispbrukontrolnaiarabotapo ноя контрольная работа по алгебре класс уравнения с ответами уравнений ответы контрольная работа по алгебре класс линейные уравнения ответы контрольная работа К уравнению x y подберите второе линейное gdz com klass uprazhnenie ГДЗ на Упражнение по учебнику АГ Мерзляк, ВБ Полонский, МС Якир Учебник по алгебре класса Картинки по запросу гдз класс линейное уравнение Алгебра класс Правила Задания Решения class _algebra Алгебра класс , Интерактивный учебник Задачи на составление линейных уравнений с одной переменной ГДЗ самостоятельные работы по алгебре класс https gdz georu gdz klass kim Решебник ГДЗ ответы к самостоятельным работам по алгебре класс Александрова С Линейное уравнение с двумя переменными и его график С Линейная функция и её график Решебник по Алгебре класс Мордкович Онлайн ГДЗ prepodtop gdz algebra klass правильные ГДЗ по Алгебре класс Мордкович Опытные Линейное уравнение с одной переменной ГДЗ по математике класс Ключникова рабочая тетрадь https gdz putinainfo klass gdz po Рейтинг , голоса Линейное уравнение с двумя переменными и его график Линейная функция и ее график АЛГЕБРА Контрольные работы класс Мерзляк Контроль контрользнанийрфalgebrakontrolnye апр Контрольная КР Системы линейных уравнений с двумя Вы смотрели АЛГЕБРА Контрольные работы класс Мерзляк Дидактические материалы Ответы Вернуться ГДЗ номер К Системы линейных уравнений УРОКУНЕТ yrokynet gdz otvethtml Системы линейных уравнений с двумя переменными ГДЗ Самостоятельные и Контрольные Класс класс ГДЗ к рабочей тетради по алгебре за класс Мерзляка , klass merzlyak ГДЗ по алгебре за класс к рабочей тетради Мерзляка часть , Линейное уравнение с одной переменной ГДЗ решебник по алгебре класс Звавич, Кузнецова reshatorcom gdz klass algebrazvavich Тогда ГДЗ по алгебре класс Звавич Дидактические материалы отличная возможность исправить ситуацию и начать хорошо Решение уравнений , сводящихся к линейным ; ; ; ; ; PDF Самостоятельные и контрольные работы по алгебре класс schtegiedusiterusamostoyatel В сборник включены также ответы к за даниям его усвоения Книга адресована учителям математики класса и школьникам Приказом Линейное уравнение с одной переменной Глава ЛИНЕЙНАЯ ФУНКЦИЯ Решебник ГДЗ Алгебра klass evip klass glava Полный и качественный решебник ГДЗ Алгебра класс АГ Мордкович Линейное уравнение с двумя переменными и его график Линейная функция и ее график Урок алгебры класс Решение задач с помощью уравнений klass фев класс Урок алгебры Ответы на вопросы по домашнему заданию разбор нерешенных задач Устная в определение линейного уравнения с одной переменной, Упр Appendix Математика ГДЗ Enjoy English класс Решение онлайн Упр ГДЗ Enjoy English класс Are you good at math с система линейных уравнений Составьте линейное уравнение с двумя переменными https gdz expert klass ГДЗ по алгебре за класс Мордковича Упражнения решение задания Составьте линейное уравнение с двумя Поурочное планирование по алгебре класс compendiumsu Подробное планирование уроков алгебры в классе ; план уроков Работа с учебником под руководством Тест Решение линейных уравнений класс iqu Решение линейных уравнений класс Пройдите тест, узнайте свой уровень и посмотрите правильные ответы ! ГДЗ к дидактическому материалу по алгебре класс к gdz onlinecom klass merzlyak ГДЗ к дидактическому материалу по алгебре за класс Мерзляк онлайн Линейное уравнение с двумя переменными и его график Системы уравнений с двумя ГДЗ по алгебре класс рабочая тетрадь Ключникова Я ГДЗ gdz com klass gdz po ГДЗ решебник рабочая тетрадь Алгебра класс Е М Ключниковой, И В Комиссаровой к учебнику АГ Контрольная по алгебре класс контрольные работы с klass Алгебра за класс , контрольные работы по учебнику Мордковича с ответами за , Линейное уравнение с двумя переменными, Линейная функция, Системы Ответы на задания контрольной работы на тему Числовые и Линейное уравнение с одной переменной й класс открытыйурокрфarticles Линейное уравнение с одной переменной й класс Бардаш Марина Васильевна работ с последующей взаимопроверкой проверкой; ответы будут отображены на интерактивной доске Ответы литейные уравнения с переменной класс Ответы литейные уравнения с переменной класс алгебра учиру Обсудить Задание Отметь все линейные уравнения с одной переменной Ответ х; t; Ответ на ГДЗ самостоятельные и контрольные работы по алгебре gdz bestruonlinealgebradefaulthtm ГДЗ для самостоятельных и контрольных работ по алгебре для класса Глазков работа Линейное уравнение с одной переменной Итоговое повторение курса алгебры го класса Запросы, похожие на гдз класс линейное уравнение линейные уравнения с двумя переменными класс уравнения класс с ответами линейные уравнения класс тест линейные уравнения с двумя переменными и их системы решение уравнений класс с дробями как решать линейные уравнения класс линейные уравнения класс самостоятельная работа решение уравнений класс калькулятор След Войти Версия Поиска Мобильная Полная Конфиденциальность Условия Настройки Отзыв Справка
ГДЗ по алгебре 7 класс Кузнецова — благодаря ему, изучение данного предмета станет значительно легче, а сэкономленное время можно посвятить важным делам.
Введите в строку поиска только фамилию автора и класс. Линейная функция. Линейное уравнение с двумя переменными и его график.
Деление многочлена на одночлен Домашняя контрольная работа 6 Глава 7. Линейная функция и её график 9. ГДЗ по другим предметам gt;gt;.
Ежедневно на сайте публикуются сотни материалов по математике (контрольные, задачи с решениями, тесты, образцы и разбор олимпиадных заданий) Самостоятельная работа 7 линейное уравнение 7 класс.
Главная gt; Линейная алгебра gt; Системы линейных уравнений. Линейные пространства. Новые уроки уже на сайте. 17 Миссисипи или как вы решаете такие задачи?
База объявлений по продаже зарубежной недвижимости, информация по аренде зарубежной недвижимости. Новости и статьи по тематике quot;Недвижимость за рубежомquot;… Слайдов в презентации: 7 слайдов. Презентация на тему: Решение систем линейных уравнений (7 класс).
Содержание: 7 класс. Слайд: 1, Презентация: Система двух линейных уравнений.ppt. Размер архива с презентацией 596 КБ.
Условие гдз алгебры 2008 двух прямых3 Решение линейных уравнений с одной переменной. Интегрирование по частям. Теоремы сложения вероятностей. Предел отношения. Гдз греков 10 11. Смешанные задачи. Применение определенного интеграла к вычислению гдз…
Линейная функция с двумя переменными. Линейное уравнение имеет вид ахв (где а5, в7) Алгебра 7 класс Линейные уравнения Овдиенко Н.А.
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ стр. 57 7. Линейная функция стр. 41 15 (с). Взаимное расположение графиков линейных функций стр. 41 15.
Модель баланса для обучения линейным уравнениям: систематический обзор литературы | International Journal of STEM Education
Почему использовалась модель баланса?
Обоснование использования балансовой модели дано в 26 статьях. Можно выделить три основных класса обоснований, все из которых связаны с конкретными особенностями контекста модели баланса. В статьях, составляющих класс обоснований «Равенство», все непосредственно ссылались на использование весов для улучшения понимания учащимися концепции равенства. Прямые ссылки на равенство прямо сосредоточены на математическом равенстве, подчеркивая аналогию между моделью баланса и равенством в уравнении. Статьи в оставшихся двух классах обоснований содержат более косвенных ссылок на использование модели баланса для улучшения понимания учащимися равенства. Косвенные ссылки на равенство — это, например, предложение студентам физических переживаний при манипулировании моделью баланса и, таким образом, через опыт балансирования ощущать концепцию равенства.Такие статьи, в которых упоминались предыдущие или сопутствующие физические переживания, связанные с моделью баланса, попадали в класс логических обоснований «Физический опыт». Статьи, которые попали в класс обоснований «Модели и представления», касались использования моделей и представлений для улучшения концептуального понимания учащимися при решении линейных уравнений. Наконец, были устранены ограничения использования модели баланса для обучения решению линейных уравнений.
Прямые ссылки на равенство прямо сосредоточены на математическом равенстве, подчеркивая аналогию между моделью баланса и равенством в уравнении. Статьи в оставшихся двух классах обоснований содержат более косвенных ссылок на использование модели баланса для улучшения понимания учащимися равенства. Косвенные ссылки на равенство — это, например, предложение студентам физических переживаний при манипулировании моделью баланса и, таким образом, через опыт балансирования ощущать концепцию равенства.Такие статьи, в которых упоминались предыдущие или сопутствующие физические переживания, связанные с моделью баланса, попадали в класс логических обоснований «Физический опыт». Статьи, которые попали в класс обоснований «Модели и представления», касались использования моделей и представлений для улучшения концептуального понимания учащимися при решении линейных уравнений. Наконец, были устранены ограничения использования модели баланса для обучения решению линейных уравнений.
Обоснования, связанные с концепцией равенства
В большинстве из 15 статей (три из одного и того же исследовательского проекта) упоминались основания для использования модели баланса, связанной с концепцией равенства. Часто заявлялось, что понимание концепции равенства можно улучшить, используя модель баланса (например, Gavin & Sheffield, 2015; Leavy et al., 2013; Mann, 2004; Taylor-Cox, 2003; Warren et al. др., 2009). Поскольку обе стороны модели баланса имеют равную ценность и, следовательно, взаимозаменяемы, модель была описана как очень подходящая для демонстрации идеи равенства или равновесия (Figueira-Sampaio et al., 2009) и количественного сходства (например, Warren & Cooper , 2005).В соответствии с этим несколько авторов ссылались на использование модели баланса для улучшения понимания знака равенства как символа, обозначающего равенство (например, Vlassis, 2002; Warren & Cooper, 2009). Соответственно, модель баланса часто описывается как подходящая для демонстрации стратегии выполнения одного и того же действия по обе стороны уравнения, в котором решающее значение имеет концепция баланса (например, Andrews & Sayers, 2012; Figueira-Sampaio et al. al., 2009; Marschall & Andrews, 2015), тем самым помогая студентам сформировать, согласно Влассису (2002), мысленную картину операций, которые они должны применить.
Часто заявлялось, что понимание концепции равенства можно улучшить, используя модель баланса (например, Gavin & Sheffield, 2015; Leavy et al., 2013; Mann, 2004; Taylor-Cox, 2003; Warren et al. др., 2009). Поскольку обе стороны модели баланса имеют равную ценность и, следовательно, взаимозаменяемы, модель была описана как очень подходящая для демонстрации идеи равенства или равновесия (Figueira-Sampaio et al., 2009) и количественного сходства (например, Warren & Cooper , 2005).В соответствии с этим несколько авторов ссылались на использование модели баланса для улучшения понимания знака равенства как символа, обозначающего равенство (например, Vlassis, 2002; Warren & Cooper, 2009). Соответственно, модель баланса часто описывается как подходящая для демонстрации стратегии выполнения одного и того же действия по обе стороны уравнения, в котором решающее значение имеет концепция баланса (например, Andrews & Sayers, 2012; Figueira-Sampaio et al. al., 2009; Marschall & Andrews, 2015), тем самым помогая студентам сформировать, согласно Влассису (2002), мысленную картину операций, которые они должны применить. Еще одним упомянутым преимуществом модели баланса является возможность отслеживать «всю числовую взаимосвязь, выражаемую уравнением, пока оно подвергается преобразованиям» (Linchevski & Herscovics, 1996, p. 52), что делает ее пригодной для демонстрации отмена идентичных членов с обеих сторон уравнения (см. также Filloy & Rojano, 1989).
Еще одним упомянутым преимуществом модели баланса является возможность отслеживать «всю числовую взаимосвязь, выражаемую уравнением, пока оно подвергается преобразованиям» (Linchevski & Herscovics, 1996, p. 52), что делает ее пригодной для демонстрации отмена идентичных членов с обеих сторон уравнения (см. также Filloy & Rojano, 1989).
Обоснования, связанные с физическим опытом
Второй класс обоснований, который был идентифицирован и упомянут в 11 статьях (все из различных исследовательских проектов), был связан с обучением через физические переживания.В нескольких статьях упоминались предыдущие физические переживания, связанные с поддержанием равновесия. Araya et al. (2010) утверждали, что процесс поддержания баланса имеет первичную биологическую основу и, следовательно, является общим физическим знанием для всех людей. Используя модель баланса, это биологически первичное знание можно связать с абстрактной идеей поддержания равенства в уравнении. Другие подчеркивали сходство модели и качели (или качели) и ссылались на (игровой) опыт детей с этим предметом (Alibali, 1999; Kaplan & Alon, 2013).
В других статьях отмечалось, что одновременный физический опыт с моделью баланса способствует изучению линейных уравнений. Уоррен и Купер (2009) подчеркнули важность движения (например, отыгрыша баланса) и жестов во время учебной траектории для развития ментальных моделей математических идей. Они утверждали, что обращение к этому опыту на более поздних этапах процесса обучения может быть полезным. Кроме того, в нескольких статьях упоминалась важность физического опыта с конкретными объектами для развития понимания линейных уравнений.Предоставление молодым студентам опыта манипулирования весами равновесия, поскольку посредством этих манипуляций можно признать, определить, создать и поддерживать равенство, могло бы улучшить понимание студентами этой концепции (Taylor-Cox, 2003). Сух и Мойер (2007) отметили, что использование управляемых конкретных объектов имеет смысловую функцию, соединяя процедурные знания (манипуляции с объектами) и концептуальные знания алгебраических уравнений. Однако в то же время эти авторы указали, что осторожность с использованием таких манипуляторов для обучения решению формальных уравнений необходима, потому что не все студенты автоматически связывают свои действия с манипуляторами с их манипуляциями с абстрактными символами.Также Орлов (1971) отметил, что модель баланса как физический инструмент может помочь в формировании абстрактного математического мышления, поскольку представляет собой промежуточную степень между непосредственными сенсорными данными и математической абстракцией. В этой же строке Fyfe et al. (2015) рекомендовали последовательность, основанную на увядающей конкретности, где инструкция начинается с конкретного материала и превращается в абстрактные математические символы. Обратная связь в реальном времени, обеспечиваемая некоторыми моделями о балансе, которая позволяет учащимся проверять результаты своих манипуляций и процессов рассуждения и, как таковые, конструировать знания, также считалась важной (Austin & Vollrath, 1989).
Однако в то же время эти авторы указали, что осторожность с использованием таких манипуляторов для обучения решению формальных уравнений необходима, потому что не все студенты автоматически связывают свои действия с манипуляторами с их манипуляциями с абстрактными символами.Также Орлов (1971) отметил, что модель баланса как физический инструмент может помочь в формировании абстрактного математического мышления, поскольку представляет собой промежуточную степень между непосредственными сенсорными данными и математической абстракцией. В этой же строке Fyfe et al. (2015) рекомендовали последовательность, основанную на увядающей конкретности, где инструкция начинается с конкретного материала и превращается в абстрактные математические символы. Обратная связь в реальном времени, обеспечиваемая некоторыми моделями о балансе, которая позволяет учащимся проверять результаты своих манипуляций и процессов рассуждения и, как таковые, конструировать знания, также считалась важной (Austin & Vollrath, 1989). Говорят, что в сочетании с социальным опытом физический опыт также способствует формированию знаний (Фигейра-Сампайо и др., 2009), например, потому что он создает общий смысл между учителем и учениками (Перри и др., 1995).
Говорят, что в сочетании с социальным опытом физический опыт также способствует формированию знаний (Фигейра-Сампайо и др., 2009), например, потому что он создает общий смысл между учителем и учениками (Перри и др., 1995).
Обоснования, связанные с обучением с помощью моделей и представлений
Третий класс обоснований, упомянутый в восьми статьях (четыре из того же исследовательского проекта), включает более общую аргументацию и относится к обучению с использованием моделей и представлений.Согласно Филлою и Рохано (1989), такие модели, как модель баланса, могут предоставить возможность семантически и синтаксически заложить основу для решения линейных уравнений. Здесь значение равенства и алгебраических операций может быть сначала выведено из контекста, а после того, как учащиеся прошли через процесс абстракции, значение на синтаксическом уровне связано с этим значением контекста. Исследователи, участвующие в австралийском проекте раннего алгебраического мышления (Cooper & Warren, 2008; Warren & Cooper, 2009), утверждали, что с помощью моделей математические идеи представляются извне как конкретный материал, с помощью иконических представлений, языка или символов, а их понимание идеи возникают внутри, в ментальных моделях или внутренних когнитивных представлениях математических идей, лежащих в основе внешних представлений. С этой точки зрения математическое понимание определяется количеством и силой связей во внутренней сети представлений учащегося. Также поддерживалось использование множественных представлений при обучении абстрактным математическим концепциям или стратегиям (например, Berks & Vlasnik, 2014), потому что испытание различных способов представления и установление связей между этими различными способами представления и внутри них могло бы улучшить глубокое математическое понимание (Suh & Vlasnik, 2014). Мойер, 2007).Смысловая функция представлений была развита Каглайаном и Оливом (2010), которые пришли к выводу, что студенты могут понять абстрактные символические уравнения, связав это символическое уравнение с уравнением, выраженным его представлением.
С этой точки зрения математическое понимание определяется количеством и силой связей во внутренней сети представлений учащегося. Также поддерживалось использование множественных представлений при обучении абстрактным математическим концепциям или стратегиям (например, Berks & Vlasnik, 2014), потому что испытание различных способов представления и установление связей между этими различными способами представления и внутри них могло бы улучшить глубокое математическое понимание (Suh & Vlasnik, 2014). Мойер, 2007).Смысловая функция представлений была развита Каглайаном и Оливом (2010), которые пришли к выводу, что студенты могут понять абстрактные символические уравнения, связав это символическое уравнение с уравнением, выраженным его представлением.
Также были предложены другие причины для использования представлений балансовой модели. Например, он может создать общую языковую базу, которую студенты могут использовать при объяснении своих решений (Berks & Vlasnik, 2014; Warren et al. , 2009; Warren & Cooper, 2005) или что он должен снизить когнитивную нагрузку учащихся в процессе решения уравнений (см. Araya et al., 2010). Последнее контрастирует с Boulton-Lewis et al. (1997), которые выдвинули гипотезу об увеличении нагрузки обработки, вызванной использованием конкретных представлений. Это может зависеть от опыта учащихся и типа задач с уравнениями, которые им приходится решать: если учащимся больше не нужна помощь в конкретном представлении модели баланса, и они по-прежнему должны ее использовать, это действительно может увеличить нагрузку на обработку. .
, 2009; Warren & Cooper, 2005) или что он должен снизить когнитивную нагрузку учащихся в процессе решения уравнений (см. Araya et al., 2010). Последнее контрастирует с Boulton-Lewis et al. (1997), которые выдвинули гипотезу об увеличении нагрузки обработки, вызванной использованием конкретных представлений. Это может зависеть от опыта учащихся и типа задач с уравнениями, которые им приходится решать: если учащимся больше не нужна помощь в конкретном представлении модели баланса, и они по-прежнему должны ее использовать, это действительно может увеличить нагрузку на обработку. .
Ограничения модели баланса
Ограничения модели баланса описаны в восьми статьях (все из разных исследовательских проектов). В своей известной статье Влассис (2002) описала, как восьмиклассников учили решать формальные линейные уравнения с использованием модели баланса, и пришла к выводу, что, хотя модель баланса способна предоставить учащимся «оперативный мысленный образ» (стр. 355) применяемых стратегий решения уравнений, эта модель также имела некоторые недостатки. Например, модель бесполезна для уравнений, содержащих отрицательные числа, или для других уравнений, которые «отделены от модели» (стр. 354) и больше не относятся к конкретной модели. Кроме того, в нескольких других статьях говорится об ограниченных возможностях модели для представления уравнений с отрицательными величинами или вычитаниями (например, Filloy & Rojano, 1989; Linchevski & Herscovics, 1996). Как только используются отрицательные значения, например, в случае уравнения x + 5 = 3, или уравнения с вычитанием, например 2 x — 3 = 5, решение трудно выразить в терминах физических величин. веса, который затрудняет построение смысла для этих уравнений (Caglayan & Olive, 2010).
Например, модель бесполезна для уравнений, содержащих отрицательные числа, или для других уравнений, которые «отделены от модели» (стр. 354) и больше не относятся к конкретной модели. Кроме того, в нескольких других статьях говорится об ограниченных возможностях модели для представления уравнений с отрицательными величинами или вычитаниями (например, Filloy & Rojano, 1989; Linchevski & Herscovics, 1996). Как только используются отрицательные значения, например, в случае уравнения x + 5 = 3, или уравнения с вычитанием, например 2 x — 3 = 5, решение трудно выразить в терминах физических величин. веса, который затрудняет построение смысла для этих уравнений (Caglayan & Olive, 2010).
Обсуждение выводов относительно того, почему была использована модель
Хотя все три класса обоснований имеют уникальные характеристики, на основе которых их можно дифференцировать, они также взаимосвязаны. Наиболее часто упоминаемое обоснование было связано с равенством; понимание равенства считается одним из основных концептуальных требований, связанных с решением линейных уравнений (например, Kieran et al. , 2016). Неотъемлемые свойства баланса были связаны с концепцией равенства и стратегиями, которые можно применять при сохранении баланса.Два оставшихся довода упоминались реже. Эти обоснования содержали косвенные ссылки на использование модели баланса для улучшения понимания учащимися равенства в уравнении посредством ссылки на обучение через физический опыт или на обучение через модели и представления.
, 2016). Неотъемлемые свойства баланса были связаны с концепцией равенства и стратегиями, которые можно применять при сохранении баланса.Два оставшихся довода упоминались реже. Эти обоснования содержали косвенные ссылки на использование модели баланса для улучшения понимания учащимися равенства в уравнении посредством ссылки на обучение через физический опыт или на обучение через модели и представления.
Статьи в классе обоснований, связанных с физическими переживаниями, относящимися либо к биологической основе поддержания равновесия, либо к другим физическим переживаниям с равновесием (например, с колебаниями), которые с помощью модели баланса могут быть связаны с идея поддержания баланса в уравнении.Эти предыдущие физические опыты с равновесием могут способствовать пониманию учащимися равенства в уравнении. Это можно объяснить с точки зрения теории воплощенного познания, утверждающей, что связь перцептивного и физического опыта, который мы испытываем, когда мы взаимодействуем с миром, имеет фундаментальное значение для развития концептуальных знаний и процессов когнитивного обучения (например, Barsalou, 2008; Wilson, 2002 ). Перцептуомоторные переживания считаются необходимыми для развития математических концепций (например,г., Алибали и Натан, 2012; Núñez, Edwards, & Matos, 1999), а математические рассуждения неразрывно связаны с воплощенными действиями (Abrahamson, 2017; Alibali & Nathan, 2012). При применении теории воплощенного познания к обучению и решению линейных уравнений предполагается, что перцептуомоторные знания о действии балансировки являются необходимой основой для развития понимания математической концепции равенства (например, Antle, Corness, & Bevans, 2013 ).Это перцептуомоторное знание строится на очень распространенных физических переживаниях, которые мы испытываем с балансированием с раннего возраста (Гиббс-младший, 2006), посредством ходьбы без падений, вставания и сидения или удерживания предметов разного веса (Алессандрони, 2018). Кроме того, в других статьях этого класса обоснований подчеркивается вклад одновременного физического опыта с моделью баланса в изучение линейных уравнений.
Перцептуомоторные переживания считаются необходимыми для развития математических концепций (например,г., Алибали и Натан, 2012; Núñez, Edwards, & Matos, 1999), а математические рассуждения неразрывно связаны с воплощенными действиями (Abrahamson, 2017; Alibali & Nathan, 2012). При применении теории воплощенного познания к обучению и решению линейных уравнений предполагается, что перцептуомоторные знания о действии балансировки являются необходимой основой для развития понимания математической концепции равенства (например, Antle, Corness, & Bevans, 2013 ).Это перцептуомоторное знание строится на очень распространенных физических переживаниях, которые мы испытываем с балансированием с раннего возраста (Гиббс-младший, 2006), посредством ходьбы без падений, вставания и сидения или удерживания предметов разного веса (Алессандрони, 2018). Кроме того, в других статьях этого класса обоснований подчеркивается вклад одновременного физического опыта с моделью баланса в изучение линейных уравнений. Управляя моделью, учащиеся узнают, как сохранить ее равновесие; эти стратегии для поддержания баланса модели могут позже быть связаны со стратегиями для поддержания равенства в уравнении.Это также согласуется с теорией воплощенного познания: предложение учащимся возможности оживить базовые перцептуомоторные знания посредством использования модели баланса, с помощью которой они могут представить (или заново испытать) ситуацию уравновешивания, может быть полезным для поддержки понимание студентами равенства в уравнении и, следовательно, для обучения решению линейных уравнений.
Управляя моделью, учащиеся узнают, как сохранить ее равновесие; эти стратегии для поддержания баланса модели могут позже быть связаны со стратегиями для поддержания равенства в уравнении.Это также согласуется с теорией воплощенного познания: предложение учащимся возможности оживить базовые перцептуомоторные знания посредством использования модели баланса, с помощью которой они могут представить (или заново испытать) ситуацию уравновешивания, может быть полезным для поддержки понимание студентами равенства в уравнении и, следовательно, для обучения решению линейных уравнений.
В статьях класса обоснований, связанных с обучением с помощью моделей и представлений, были включены более общие аргументы в пользу более глубокого понимания учащимися равенства в уравнении.Однако эти доводы частично совпадают с доводами, связанными с физическими переживаниями. Оба класса связаны с перцептуомоторными переживаниями с равновесием. В случае с классом «Модели и представления» этот опыт больше связан с тем, как выглядит баланс. Весы как устройство с двумя рычагами и точкой опоры посередине можно использовать для представления уравнения, в котором по обе стороны от знака равенства находится выражение равного значения. Обучение с помощью моделей и представлений может быть связано с идеями реалистичного математического образования (RME).Одним из основных учебных принципов RME является использование дидактических моделей с целью преодоления разрыва между неформальными, контекстно-зависимыми методами решения и более формальными, и, таким образом, стимулировать учащихся к достижению более высоких уровней понимания ( например, Van den Heuvel-Panhuizen, 2003).
Весы как устройство с двумя рычагами и точкой опоры посередине можно использовать для представления уравнения, в котором по обе стороны от знака равенства находится выражение равного значения. Обучение с помощью моделей и представлений может быть связано с идеями реалистичного математического образования (RME).Одним из основных учебных принципов RME является использование дидактических моделей с целью преодоления разрыва между неформальными, контекстно-зависимыми методами решения и более формальными, и, таким образом, стимулировать учащихся к достижению более высоких уровней понимания ( например, Van den Heuvel-Panhuizen, 2003).
Какие типы балансовых моделей использовались?
В рассмотренных статьях были выделены три типа внешнего вида балансовых моделей: физический, виртуальный и нарисованный балансовый.Модели физического баланса — это конкретные весы баланса. На этих шкалах учащиеся могут представлять уравнения, помещая реальные объекты, обозначающие известные и неизвестные, по обе стороны модели. Для этих моделей характерно то, что они динамичны, что означает, что учащиеся могут оперировать ими и получать обратную связь о своих действиях в режиме реального времени. В моделях виртуального баланса баланс реализован в цифровой среде. Эти модели в основном динамичны в том смысле, что баланс наклоняется в ответ на (цифровые) манипуляции студентов и, таким образом, дает обратную связь в реальном времени.В нарисованных моделях баланса схематическая версия баланса представлена на бумаге или на доске. Представления этих моделей баланса статичны: учащиеся не могут ими манипулировать и не могут получать обратную связь в реальном времени. В то время как в большинстве статей использовался только один тип внешнего вида модели баланса, в других статьях использовались разные типы (например, Figueira-Sampaio et al., 2009) или была представлена последовательность различных представлений, начиная с использования физического модель, за которой следует нарисованная модель баланса (например,г., Файф и др.
Для этих моделей характерно то, что они динамичны, что означает, что учащиеся могут оперировать ими и получать обратную связь о своих действиях в режиме реального времени. В моделях виртуального баланса баланс реализован в цифровой среде. Эти модели в основном динамичны в том смысле, что баланс наклоняется в ответ на (цифровые) манипуляции студентов и, таким образом, дает обратную связь в реальном времени.В нарисованных моделях баланса схематическая версия баланса представлена на бумаге или на доске. Представления этих моделей баланса статичны: учащиеся не могут ими манипулировать и не могут получать обратную связь в реальном времени. В то время как в большинстве статей использовался только один тип внешнего вида модели баланса, в других статьях использовались разные типы (например, Figueira-Sampaio et al., 2009) или была представлена последовательность различных представлений, начиная с использования физического модель, за которой следует нарисованная модель баланса (например,г., Файф и др. , 2015).
, 2015).
Модели физического баланса
Модели физического равновесия опубликованы в 14 статьях (три из одного исследовательского проекта). Мы нарисовали схематические версии некоторых из этих моделей физического баланса. Эти чертежи показаны на рис. 2. Весы, показанные на рис. 2а, были использованы Файфом и др. (2015), чтобы представить, например, 3 + 2 = 1 + 1 + __. Здесь ученики могут поставить трех красных и двух желтых медведей с левой стороны, одного красного и одного желтого медведя справа, а затем добавить недостающее число, чтобы сбалансировать весы (для аналогичных моделей см. Также e.г., Уоррен и др., 2009). В модели баланса Остина и Воллрата (1989; рис. 2b) уравнение 3 x + 5 = 11 изображается с левой стороны тремя контейнерами с неизвестным содержимым и пятью шайбами и 11 шайбами с правой стороны (для аналогичные модели, см. также, например, Andrews, 2003). Более сложный пример весов был использован Орловым (1971; рис. 2в). Его модель содержит четыре шкалы, по две с каждой стороны. Например, если положить груз на левый лоток левой части весов, левый рычаг весов поднимется вверх.Таким образом, эта модель также может обрабатывать отрицательные числа и неизвестные. Последний тип описанной модели физического баланса — это модель баланса, в которой расстояние от объектов до точки опоры может быть адаптировано для представления линейных уравнений, таких как 8 + 4 + 2 = 4 + 4 + __ (Perry et al., 1995; Рис. 2d; аналогичную модель см. Также Smith, 1985). Здесь все объекты имеют одинаковый вес, но, помещая их в определенное положение на балке, они представляют определенную ценность.
Например, если положить груз на левый лоток левой части весов, левый рычаг весов поднимется вверх.Таким образом, эта модель также может обрабатывать отрицательные числа и неизвестные. Последний тип описанной модели физического баланса — это модель баланса, в которой расстояние от объектов до точки опоры может быть адаптировано для представления линейных уравнений, таких как 8 + 4 + 2 = 4 + 4 + __ (Perry et al., 1995; Рис. 2d; аналогичную модель см. Также Smith, 1985). Здесь все объекты имеют одинаковый вес, но, помещая их в определенное положение на балке, они представляют определенную ценность.
Рис. 2
Физические модели баланса, примеры из четырех статей ( a — d )
Виртуальные модели баланса
Виртуальные модели баланса появились в трех статьях (из разных исследовательских проектов).Чертежи используемых моделей виртуального баланса показаны на рис. 3. Большинство из этих моделей имеют шкалу баланса, очень похожую на модели физического баланса. Однако цифровая среда дает больше возможностей в представлении и функциях модели.
Однако цифровая среда дает больше возможностей в представлении и функциях модели.
Рис. 3
Виртуальные модели баланса, примеры из двух статей ( a — b )
В цифровой модели, используемой Фигейра-Сампайо и его коллегами (2009; Рис. 3a), уравнение 5 x + 50 = 3 x + 290 представлено банками с буквой X , обозначающей неизвестные величины, и маленькими обозначенными гирями (например.г., 50 г, 100 г) с изображением цифр (для аналогичной модели см. также Suh & Moyer, 2007). Здесь, пока студенты манипулируют виртуальной шкалой баланса, соответствующее уравнение отображается в формальных алгебраических символах, что делает явной связь между этими манипуляциями и изменениями в соответствующем символьном уравнении. Еще один тип модели виртуального баланса был обнаружен в статье Каплана и Алона (2013; рис. 3b). В этой модели учащиеся могут исследовать взаимосвязи между различными формами неизвестных и находить новые уравнения на основе заданных. Например, на основе уравнений ▲▲ = ●●● и ▲▲ = ●● ■■ можно создать третье уравнение.
Например, на основе уравнений ▲▲ = ●●● и ▲▲ = ●● ■■ можно создать третье уравнение.
Модели баланса
Модели баланса представлены в 26 статьях (четыре и три из тех же исследовательских проектов). Чертежи использованных нарисованных моделей баланса показаны на Рис. 4. Здесь заметно, что одни нарисованные модели баланса изображены более реалистично (Рис. 4a – c), а другие — более схематично (Рис. 4d – f), с изображениями объекты или символические выражения для представления известных и неизвестных.
Рис. 4
Нарисованные модели баланса, примеры из шести статей ( a — f )
Хотя нарисованные модели баланса присутствовали во многих статьях (например, Brodie & Shalem, 2011; Mann, 2004; Vlassis, 2002), способы представления уравнений в этих моделях сильно различались. В модели баланса, приведенной в статье Влассиса (2002; рис. 4a), уравнение 7 x + 38 = 3 x + 74 представлено квадратами для каждых x и кружками, в которых указаны числа. указано.Неизвестные в этой модели изображены в развернутом виде (т.е. 7 x и 3 x представлены как семь отдельных x и три отдельных x ). В то время как в большинстве моделей все неизвестные изображаются отдельно, в модели Linchevski and Herscovics (1996) неизвестные и известные в уравнении 8 n + 11 = 5 n + 50 частично показаны в развернутом, соответственно разложенном виде. Таким образом, получаем уравнение 5 n + 3 n + 11 = 5 n + 11 + 39.Таким образом, учащиеся могут видеть, что члены 5 n и 11 появляются с обеих сторон уравнения, что может компенсировать друг друга. В балансах Маршалла и Эндрюса (2015; рис. 4b) и Уоррена и Купера (2009; рис. 4c) также могут быть представлены уравнения с отрицательными значениями и вычитаниями. На рис. 4b вычитание в уравнении 4 x — 3 = 2 x + 5 представлено стрелкой, идущей вниз от одной из шкал, так что действие «удаления» становится видимым.В качестве альтернативы, на рис.
указано.Неизвестные в этой модели изображены в развернутом виде (т.е. 7 x и 3 x представлены как семь отдельных x и три отдельных x ). В то время как в большинстве моделей все неизвестные изображаются отдельно, в модели Linchevski and Herscovics (1996) неизвестные и известные в уравнении 8 n + 11 = 5 n + 50 частично показаны в развернутом, соответственно разложенном виде. Таким образом, получаем уравнение 5 n + 3 n + 11 = 5 n + 11 + 39.Таким образом, учащиеся могут видеть, что члены 5 n и 11 появляются с обеих сторон уравнения, что может компенсировать друг друга. В балансах Маршалла и Эндрюса (2015; рис. 4b) и Уоррена и Купера (2009; рис. 4c) также могут быть представлены уравнения с отрицательными значениями и вычитаниями. На рис. 4b вычитание в уравнении 4 x — 3 = 2 x + 5 представлено стрелкой, идущей вниз от одной из шкал, так что действие «удаления» становится видимым.В качестве альтернативы, на рис. 4c включен знак минус.
4c включен знак минус.
Другой способ, которым нарисованные модели баланса появлялись в статьях, — это абстрактный рисунок. Здесь баланс выступает в качестве метафоры, чтобы привлечь внимание студентов к концепции равенства. В Rystedt et al. (2016, рис. 4d) уравнение 4 x + 4 = 2 x + 8 представлено прямоугольниками для неизвестных и точками для чисел. В статьях, в которых присутствовало такое метафорическое использование модели баланса (например,g., Caglayan & Olive, 2010), это использование часто сопровождалось указанием, что баланс в уравнении должен быть , поддерживаемым при решении уравнения (Boulton-Lewis et al., 1997), или жестами. представляет собой шкалу баланса (Rystedt et al., 2016). Использование нарисованной модели баланса, особенно для моделей с абстрактным рисунком, часто сопровождалось использованием манипуляторов. Например, в модели Бултона-Льюиса и его коллег (1997; рис. 4e) схематически обозначенное уравнение 2 x + 3 = 7 представлено двумя белыми чашками и тремя зелеными счетчиками с левой стороны (обозначено by LHS) и семь зеленых счетчиков с правой стороны (обозначены RHS), в то время как другие цветные чашки и счетчики используются для представления вычитаний или отрицательных неизвестных и чисел (аналогичный подход см. в e.г., Suh & Moyer, 2007). Другим примером является нарисованная модель баланса, использованная Caglayan и Olive (2010; рис. 4f), где в уравнении 4 x — 3 = x + 6 «- 3» представлено серыми плитками вместо черных. . Более того, в этой модели прямо представлен знак равенства.
в e.г., Suh & Moyer, 2007). Другим примером является нарисованная модель баланса, использованная Caglayan и Olive (2010; рис. 4f), где в уравнении 4 x — 3 = x + 6 «- 3» представлено серыми плитками вместо черных. . Более того, в этой модели прямо представлен знак равенства.
Обсуждение результатов относительно типов используемых моделей баланса
Нарисованные модели появлялись больше всего, а виртуальные модели меньше всего, в то время как использование физической модели часто сопровождалось использованием рисованной модели.При изучении взаимосвязи между обоснованиями и внешним видом моделей кажется, что использование модели физического баланса чаще всего сочетается с обоснованиями, связанными с обучением через физический опыт и аспектом равенства. Для виртуальных моделей все обоснования появляются более или менее одинаково, а нарисованные модели баланса чаще всего сочетаются с обоснованием аспекта равенства и обоснованиями, связанными с обучением через модели и представления. За исключением обоснований, связанных с обучением через физический опыт, оставшиеся два класса обоснований чаще всего сочетаются с использованием нарисованной модели баланса.Нарисованная модель оказалась наиболее гибкой, а это значит, что она использовалась со всеми классами обоснований.
За исключением обоснований, связанных с обучением через физический опыт, оставшиеся два класса обоснований чаще всего сочетаются с использованием нарисованной модели баланса.Нарисованная модель оказалась наиболее гибкой, а это значит, что она использовалась со всеми классами обоснований.
Хотя все три внешнего вида модели имеют баланс как базовую концепцию, они различаются по своей природе. В то время как модель физического баланса и частично виртуальный баланс имеют динамическую природу и, как таковые, могут предоставлять учащимся обратную связь в реальном времени об их действиях, нарисованная модель баланса является статической. Нарисованные модели, представленные на бумаге или на доске, тем не менее, могут быть расширены динамическими аспектами с помощью манипуляторов.Для всех трех типов внешнего вида модели применяется, что большинство моделей состоит как минимум из точки опоры, горизонтальной балансировочной балки и шкалы с обеих сторон. В дополнение к этой конфигурации модели баланса, в других моделях добавлены дополнительные функции. Благодаря добавлению этих функций досягаемость модели баланса расширяется, чтобы представлять более широкий круг проблем. Например, дополнительные шкалы в физической модели Орлова (1971; рис. 2в), стрелка, идущая вниз от шкал нарисованной модели баланса в статье Маршалла и Эндрюса (2015; рис.4b), а манипуляторы разного цвета, добавленные к нарисованной модели Бултона-Льюиса и его коллег (1997; рис. 4e), — все это примеры вариаций модели баланса, позволяющие представлять отрицательные числа и неизвестные. Такие дополнительные функции обеспечивают решение ограниченных возможностей, которыми обладает эта модель (например, Vlassis, 2002), например, позволяя представлять уравнения с отрицательными величинами или вычитаниями. Фактически, эта гибкость модели баланса — это именно то, как модели должны работать.При использовании в качестве дидактических моделей (Van den Heuvel-Panhuizen, 2003) модели должны быть гибкими, а не только подходящими для решения одного типа уравнений. Одним из способов обеспечения такой гибкости является возможность адаптации без потери своей основной функции.
Благодаря добавлению этих функций досягаемость модели баланса расширяется, чтобы представлять более широкий круг проблем. Например, дополнительные шкалы в физической модели Орлова (1971; рис. 2в), стрелка, идущая вниз от шкал нарисованной модели баланса в статье Маршалла и Эндрюса (2015; рис.4b), а манипуляторы разного цвета, добавленные к нарисованной модели Бултона-Льюиса и его коллег (1997; рис. 4e), — все это примеры вариаций модели баланса, позволяющие представлять отрицательные числа и неизвестные. Такие дополнительные функции обеспечивают решение ограниченных возможностей, которыми обладает эта модель (например, Vlassis, 2002), например, позволяя представлять уравнения с отрицательными величинами или вычитаниями. Фактически, эта гибкость модели баланса — это именно то, как модели должны работать.При использовании в качестве дидактических моделей (Van den Heuvel-Panhuizen, 2003) модели должны быть гибкими, а не только подходящими для решения одного типа уравнений. Одним из способов обеспечения такой гибкости является возможность адаптации без потери своей основной функции. Однако, принимая во внимание концепцию модели для… — модели для… (Streefland, 2003), дидактические модели не предназначены как инструмент, который должен постоянно использоваться для решения проблем на конкретном, контекстно-зависимом уровне. Вместо этого идея состоит в том, что на более позднем этапе учебного процесса, когда закладывается основа для решения линейных уравнений и учащиеся должны решать более сложные уравнения, мышление учащегося все еще может поддерживаться моделью и связываться с ней без конкретное представление уравнения в физической модели.
Однако, принимая во внимание концепцию модели для… — модели для… (Streefland, 2003), дидактические модели не предназначены как инструмент, который должен постоянно использоваться для решения проблем на конкретном, контекстно-зависимом уровне. Вместо этого идея состоит в том, что на более позднем этапе учебного процесса, когда закладывается основа для решения линейных уравнений и учащиеся должны решать более сложные уравнения, мышление учащегося все еще может поддерживаться моделью и связываться с ней без конкретное представление уравнения в физической модели.
Когда использовалась балансовая модель?
Ситуации, в которых модель баланса использовалась в статьях при описании обучения решению линейных уравнений, значительно варьировались в зависимости от уровня обучения учащихся, продолжительности вмешательства с моделью, типа задач с уравнениями. над которыми работали студенты, и тип инструкций, которые были предоставлены студентам.
Уровни обучения и продолжительность вмешательства
Балансовая модель использовалась для обучения решению линейных уравнений учащихся от детского сада до 9 класса. Учащиеся до 6-го класса, не имеющие предыдущего опыта в алгебре, впервые столкнулись с линейными уравнениями через модель баланса, которая использовалась в различных исследованиях (например, Warren & Cooper, 2005). В исследованиях с учениками 7–9 классов, которые уже имеют некоторый базовый опыт решения линейных уравнений (за исключением учеников седьмого класса в исследовании Araya et al., 2010), модель баланса была представлена как инструмент для решения уравнений (Vlassis, 2002) или используется для иллюстрации метода баланса (т.е. проделайте одинаковые операции с обеими сторонами уравнения; Нгу и Фан, 2016). Продолжительность интервенций, в которых использовалась модель баланса, также была очень разнообразной. Самые короткие интервенции включали одно мероприятие или один урок (например, Figueira-Sampaio et al., 2009; Rystedt et al., 2016), тогда как в других исследованиях модель баланса была интегрирована в многолетнюю траекторию обучения (например, Орлов, 1971; Уоррен и Купер, 2009).
Учащиеся до 6-го класса, не имеющие предыдущего опыта в алгебре, впервые столкнулись с линейными уравнениями через модель баланса, которая использовалась в различных исследованиях (например, Warren & Cooper, 2005). В исследованиях с учениками 7–9 классов, которые уже имеют некоторый базовый опыт решения линейных уравнений (за исключением учеников седьмого класса в исследовании Araya et al., 2010), модель баланса была представлена как инструмент для решения уравнений (Vlassis, 2002) или используется для иллюстрации метода баланса (т.е. проделайте одинаковые операции с обеими сторонами уравнения; Нгу и Фан, 2016). Продолжительность интервенций, в которых использовалась модель баланса, также была очень разнообразной. Самые короткие интервенции включали одно мероприятие или один урок (например, Figueira-Sampaio et al., 2009; Rystedt et al., 2016), тогда как в других исследованиях модель баланса была интегрирована в многолетнюю траекторию обучения (например, Орлов, 1971; Уоррен и Купер, 2009).
Типы задач по уравнениям
С очень маленькими учениками (например,g., Kindergarten, 1-2 классы), модель баланса в основном использовалась для исследования первых идей равенства и знака равенства (например, Taylor-Cox, 2003; Warren et al., 2009). Задача студентов заключалась, например, в том, чтобы взвесить разные предметы, чтобы определить, какие из них одинаковые, а какие разные. Для учащихся старшего возраста (например, 3–6 классов) модель баланса, например, использовалась, чтобы помочь им в решении простых задач сложения, таких как 8 = __ + 3 (например, Leavy et al., 2013). Здесь восемь предметов были помещены на левую сторону весов, а три — на правую, и задача учеников заключалась в том, чтобы выяснить, что они могут сделать, чтобы уравнять обе стороны.Модель также использовалась для представления алгебраических символов студентам, не имеющим предшествующего опыта алгебры, чтобы они могли связать модель с абстрактными символами. Тогда задача студентов заключалась, например, в том, чтобы манипулировать объектами на весах таким образом, чтобы они могли определить вес неизвестного объекта, в то время как в цифровой среде было показано соответствующее символическое уравнение (например, Figueira-Sampaio et al. al., 2009, см. рис. 3a; Suh & Moyer, 2007). В исследованиях со студентами с некоторым опытом алгебры (т.е., начиная с 7 класса), задача учеников заключалась, например, в представлении символьных уравнений с использованием модели баланса и использовании этого представления для преобразования и решения уравнений (Caglayan & Olive, 2010; см. рис. 4f). Или задача студентов заключалась в том, чтобы решить уравнение, используя модель физического баланса, а затем представить уравнение и этапы решения символически (Andrews, 2003). Были также статьи, в которых одновременно были представлены две модели баланса с разными неизвестными, чтобы создать систему уравнений и вызвать алгебраическую стратегию подстановки (например,г., Austin & Vollrath, 1989; Berks & Vlasnik, 2014). Здесь задача студентов заключалась в том, чтобы объединить информацию уравнений, чтобы найти значения неизвестных.
В большинстве исследований задачей студентов было определить ценность неизвестного (-ых). Однако были и статьи, основной целью которых было обнаружение различных возможностей для поддержания баланса модели, не сосредотачиваясь на поиске значений неизвестных. Например, в исследовании Каплана и Алона (2013) цель состояла в том, чтобы создать несколько сбалансированных шкал и проанализировать отношения между неизвестными (см.рис.3б). Также в других статьях модель баланса использовалась для обнаружения различных возможностей поддержания равенства (Орлов, 1971) или для обнаружения «законных ходов» (Раймонд и Лейненбах, стр. 288), которые можно было бы сделать, не нарушая равновесия.
Наконец, между исследованиями, касающимися поддержания модели баланса при обучении уравнениям, было большое количество различий. Например, в Уоррене и Купере (2005) сначала использовалась модель физического баланса, а затем нарисованная модель баланса, чтобы моделировать уравнения, содержащие положительные значения и аддитивные операции (например,грамм.,? + 7 = 11). После некоторых уроков эти студенты также решили уравнения, содержащие вычитание (например,? — 4 = 13), но эти уравнения не были представлены с помощью модели баланса. В других исследованиях использование модели баланса сохранялось дольше в процессе обучения. Например, один из учителей в исследовании Маршалла и Эндрюса (2015) не только использовал модель для обучения уравнениям, содержащим положительные значения и сложение, но и расширил использование модели для представления таких уравнений, как 4 x — 3. = 2 x + 5 (см. Рис.4b; для использования модели для других типов уравнений см. также, например, Boulton-Lewis et al., 1997, см. рис. 4e; Орлов, 1971, см. Рис. 2в).
Тип обучения
При работе с моделью баланса учащиеся либо получали инструкции в классе от учителя (например, Warren & Cooper, 2009), либо через обучающий фильм (Araya et al., 2010), либо получали индивидуальные инструкции. учителем (например, Perry et al., 1995), через инструкции (Ngu, Chung, & Yeung, 2015) или работая индивидуально или в паре с весами (e.г., студенты, работающие с виртуальным балансом в Фигейра-Сампайо и др., 2009). Обучение в классе часто связано с тем, что учитель манипулирует моделью баланса перед классом (например, учащиеся, работающие с моделью физического равновесия в Figueira-Sampaio et al., 2009), в то время как во время индивидуального обучения учащиеся чаще получают возможность активно работать с сами модели баланса (например, Suh & Moyer, 2007).
Обсуждение результатов, касающихся того, когда использовалась модель баланса
В разных исследованиях, в каких ситуациях использовалась модель баланса, было очень много различий.Для решения задач с уравнениями использовалась модель баланса, как оказалось, связано с опытом студентов в решении линейных уравнений. Для учащихся до 6 класса, не имеющих предыдущего опыта в алгебре, большинство задач было сосредоточено на изучении основных идей баланса и решении простых уравнений (например, 8 = __ + 3), что сопровождалось обоснованием того, что такие действия могут быть полезно для развития понимания равенства и относительного понимания знака равенства. Физические и виртуальные модели баланса относительно часто использовались для обучения решению линейных уравнений студентам, не имеющим предшествующего опыта алгебры.В большинстве этих исследований уравнения содержали только положительные значения и аддитивные операции. Исследования, проведенные со студентами без предварительного опыта в целом, подтвердили использование модели баланса для обучения решению линейных уравнений более тщательно, чем исследования со студентами, имеющими некоторый опыт алгебры. Обоснование, которое относительно часто упоминалось в связи с обучением студентов без предварительного опыта алгебры, — это обоснование, связанное с физическим опытом, которое соответствует использованию модели физического равновесия для обучения этих студентов.Это также согласуется с общей тенденцией использования конкретных материалов для обучения молодых студентов, а не для обучения студентов старшего возраста, и с исследованиями, показывающими, что использование конкретных материалов в математическом образовании особенно полезно для детей в возрасте 7–11 лет в математических областях дроби и алгебра (Карбонно, Марли и Селиг, 2013).
Что касается исследований, проводимых с учащимися с предшествующим опытом алгебры (в основном учащиеся с 7 классов и выше), задачи учащихся при работе с моделью баланса чаще всего заключались в моделировании, преобразовании и решении уравнений с помощью балансовой модели.Также в этих исследованиях наиболее заметным было обоснование, связанное с аспектом равенства. Напротив, большинство исследований, в которых не было предоставлено никакого обоснования для использования модели, также проводились со студентами с предшествующим опытом алгебры. В большинстве исследований, в которых упоминалось об ограничении использования модели баланса, участвовали эти студенты. Нарисованные модели баланса в основном использовались для обучения студентов с предшествующим опытом алгебры, и более чем в половине этих исследований студенты также обучались уравнениям, содержащим отрицательные значения и вычитание.
Результаты обучения
В девятнадцати статьях оценивались результаты обучения студентов, связанные с использованием модели баланса. План исследования этих исследований и наиболее важные результаты обучения сведены в Таблицу 1. Большинство исследований носили описательный характер, и менее чем в одной трети исследований использовался план до и после тестирования в сочетании с группой сравнения. Как описано в разделе «Когда использовалась модель баланса?» В разделе, исследования показали большие различия в отношении возраста и алгебраического опыта учащихся в их выборке, продолжительности вмешательства, задач, над которыми учащиеся работали, и типа обучения, полученного учащимися.Подобные вариации были обнаружены при изучении результатов обучения в различных исследованиях. Например, Araya et al. (2010) обнаружили очень положительные результаты использования обучающего фильма с нарисованной моделью баланса в 7-м классе с учащимися, не имеющими опыта алгебры. Эти студенты превзошли студентов из группы сравнения, получивших инструкции по решению символьных линейных уравнений. Кроме того, Сух и Мойер (2007) сообщили о положительных эффектах использования моделей баланса для обучения учащихся третьего класса решению линейных уравнений.Напротив, Boulton-Lewis et al. (1997) обнаружили, что учащиеся восьмых классов испытывали трудности с моделированием и решением линейных уравнений при использовании модели баланса. Эти студенты предпочли не использовать модель. Исследования Ngu et al. (2015), 2016, 2018) неизменно демонстрировали аналогичные или более низкие результаты у учеников 7–9 классов, которые использовали метод выполнения одних и тех же операций с обеих сторон уравнения, чему учили с использованием лист инструкций с моделью баланса — по сравнению со студентами, которые использовали обратный метод, — который учили как обращение к стороне изменения, правилу изменения знака — для решения уравнений.В этом последнем подходе, в котором, например, x — 4 = 6 становится x = 6 + 4, учащиеся могут концептуализировать обратную операцию превращения — 4 в + 4 как средство сохранения равенства уравнений. Поэтому понимание этого обратного принципа на структурном уровне считается очень важным для изучения студентами алгебраического мышления (см., Например, Ding, 2016). Интересно отметить, что, хотя при поверхностном рассмотрении, метод баланса отличается от обратного метода, этот последний метод очень похож на «выполнение одного и того же действия с обеих сторон».Если взять пример x — 4 = 6, то это правило означает, что с обеих сторон нужно добавить 4. Это составляет x — 4 + 4 = 6 + 4, что после упрощения результатов до x = 6 + 4. Другими словами, основная разница между «делать одно и то же с обеих сторон» и «менять стороны, менять знак »предполагает, что к результату можно сразу перейти, пропустив промежуточный шаг добавления 4 с обеих сторон. Однако, несмотря на тесную взаимосвязь между этими двумя подходами и соответствующими основополагающими принципами, только в нескольких статьях нашего обзорного исследования, когда авторы ссылаются на использование модели баланса, они также ссылаются на обратный метод.Это указывает на то, что не было проведено много исследований, в которых оба подхода были бы сопоставлены или противопоставлены.
Большой разброс между исследованиями, в которых использовалась модель баланса, и отсутствие исследований с экспериментальным планом исследования очень затрудняют однозначные выводы о влиянии использования модели баланса на результаты обучения студентов. Тем не менее, некоторые тенденции можно выделить. В целом, наиболее неоднозначные и отрицательные результаты получены при обучении с учениками старшего возраста (7–9 классы), которые уже имели некоторый (базовый) опыт решения линейных уравнений (например,г., Нгу, Фан, Йунг и Чунг, 2018; Влассис, 2002). Основными причинами этого вывода могло быть то, что модели баланса в этих исследованиях, которые все были нарисованы, использовались для обучения широкому кругу уравнений, включая более сложные уравнения, такие как уравнения, содержащие отрицательные числа и неизвестные (например, Boulton-Lewis et al. al., 1997; Caglayan & Olive, 2010; Vlassis, 2002). В целом, более положительные результаты были обнаружены в исследованиях, проведенных с младшими школьниками (например, Suh & Moyer, 2007; Warren & Cooper, 2005) или со студентами, не имеющими предварительных знаний о решении уравнений (например, Suh & Moyer, 2007; Warren & Cooper, 2005).г., Арая и др., 2010). В этих исследованиях чаще использовалась физическая модель (например, Perry et al., 1995; см. Рис. 2d) или виртуальная модель (например, Figueira-Sampaio et al., 2009; см. Рис. 3a), которые в за некоторыми случаями на более поздних стадиях последовала нарисованная модель (например, Warren & Cooper, 2005). В большинстве этих исследований модель баланса использовалась для обучения линейным уравнениям, содержащим только положительные значения и сложение. Однако были и исключения. Например, Орлов (1971) обнаружил положительные результаты при обучении восьмиклассников различным типам линейных уравнений (включая отрицательные значения и вычитание) с помощью модели физического равновесия (см.рис.2в).
Обсуждение результатов обучения
В целом, модель баланса, кажется, имеет более положительное влияние на результаты обучения, связанные с решением линейных уравнений для (младших) студентов, не имеющих предварительных знаний о решении линейных уравнений. Возможное объяснение может заключаться в том, что для младших школьников модель баланса используется для создания концептуальной основы для решения линейных уравнений, в то время как для старших школьников, которые уже имеют такую основу для решения линейных уравнений, модель чаще используется для оживления этого. основание.У младших школьников есть свой первый опыт изучения концепции равенства и решения линейных уравнений с помощью модели баланса. Задачи старшеклассников при работе с балансовой моделью чаще заключаются в моделировании, преобразовании или решении уравнений. Другими словами, модель баланса затем используется, чтобы оживить их знания о решении линейных уравнений и помочь в решении всех видов новых уравнений. Уоррен и Купер (2005) приводят пример использования модели баланса для поддержки учащихся в решении уравнений, содержащих вычитание.В своей учебной последовательности они сначала использовали физическую модель, чтобы позволить ученикам развить понимание концепции равенства как «баланса» и стратегии выполнения одних и тех же действий с обеих сторон. Позже студенты могли использовать эту стратегию для решения задач с символическими обозначениями на бумаге, которые также содержали вычитание.
Иллюстративная математика для ускоренного курса 7 класс, Раздел 5.14 — Учителя
Иногда проще решить систему уравнений без графического построения уравнений и поиска точки пересечения.В общем, всякий раз, когда мы решаем систему уравнений, записанную как
\ (\ Displaystyle \ begin {case} y = \ text {[кое-что]} \\ y = \ text {[кое-что]} \ end {case} \)
мы знаем, что ищем пару значений \ ((x, y) \), которая делает оба уравнения истинными. В частности, мы знаем, что значение \ (y \) будет одинаковым в обоих уравнениях. Это означает, что
\ (\ displaystyle \ text {[некоторые вещи]} = \ text {[некоторые другие вещи]} \)
Например, посмотрите на эту систему уравнений:
\ (\ Displaystyle \ begin {case} y = 2x + 6 \\ y = \ text-3x — 4 \ end {cases} \)
Поскольку значение \ (y \) решения одинаково в обоих уравнениях, мы знаем, что \ (\ displaystyle 2x + 6 = \ text-3x -4 \)
Мы можем решить это уравнение относительно \ (x \):
\ (\ begin {align} 2x + 6 & = \ text-3x-4 && \\ 5x + 6 & = \ text-4 \ && \ text {add \ (3x \) с каждой стороны} \\ 5x & = \ text-10 \ && \ text {вычтите 6 с каждой стороны} \\ x & = \ text-2 \ && \ text {разделите каждую сторону на 5} \ \ end {align} \)
Но это только половина того, что мы ищем: мы знаем значение для \ (x \), но нам нужно соответствующее значение для \ (y \).Поскольку оба уравнения имеют одинаковое значение \ (y \), мы можем использовать любое уравнение, чтобы найти значение \ (y \):
\ (\ Displaystyle у = 2 (\ текст-2) + 6 \)
или
\ (\ Displaystyle у = \ текст-3 (\ текст-2) -4 \)
В обоих случаях находим \ (y = 2 \). Итак, решение системы — \ ((\ text-2,2) \). В этом можно убедиться, построив оба уравнения на координатной плоскости.
Развернуть изображение
Описание:
График из двух линий, начало координат O, с сеткой.Горизонтальная ось, x, масштабирование от 4 до 1 с шагом 1 с. Вертикальная ось, y, масштабирование от 1 до 4 с шагом 1. Линии пересекаются в точке минус 2, запятая 2.
В общем, система линейных уравнений может иметь:
- Нет решений. В этом случае линии, соответствующие каждому уравнению, никогда не пересекаются.
- Ровно одно решение. Линии, соответствующие каждому уравнению, пересекаются ровно в одной точке.
- Бесконечное количество решений.Графики двух уравнений — одна и та же линия!
Учебная программа по математике для 7-го класса — задания, онлайн-задания по математике и викторины
Каждая тема разбита на более мелкие навыки, и учащиеся овладевают этими навыками, изучая и практикуясь с помощью интерактивных заданий и рабочих листов. В конце каждой темы учащимся назначаются интерактивные викторины для оценки
уровень понимания.
Целые числа
- Практика целочисленных операций (сложение и вычитание) — II
- Свойства сложения целых чисел
- Свойства вычитания целых чисел
- Умножение целых чисел
- Деление целых чисел
- Свойства умножения целых чисел
- Свойства деления целых чисел
Фракции — Обзор
- Умножение дроби на целое число — II
- Умножение двух дробей — II
- Ответная дробь
- Деление дроби на число
- Деление числа на дробь
- Деление дроби на дробь
Decimals — Обзор
- Умножение десятичного числа на целое
- Умножение двух десятичных чисел
- Как разделить десятичную дробь на целое число
- Разделение десятичной дроби на десятичную дробь
- Расчетная сумма и разность десятичной дроби
- Умножение и деление чисел на 0.1 и 0,01
- Оценка умножения и деления десятичных знаков (с точностью до сотых)
- Word Задачи с использованием десятичных операций
Рациональные числа
- Введение в рациональные числа
- Рациональные числа на числовой строке
- Эквивалентные рациональные числа
- Стандартная форма рациональных чисел
- Рациональные номера для заказа
- Абсолютное значение рациональных чисел
- Сложение рациональных чисел при одинаковых знаменателях
- Сложение рациональных чисел, когда один знаменатель кратен другому
- Вычитание рациональных чисел
- Умножение рациональных чисел
- Деление рациональных чисел
- Завершающие десятичные и рациональные числа
- Повторяющиеся десятичные и рациональные числа
Показатели
- Показатели только натуральных чисел
- Законы экспонент
- Научная запись
- Применение законов экспонент в простых повседневных задачах
Алгебраические выражения
- Термины алгебраического выражения
- Условия как и отличия
- Алгебраическое выражение со степенями
- Степень алгебраического выражения с одной переменной
- Степень алгебраического выражения — Несколько переменных
- Упрощение алгебраических выражений
- Вычисление алгебраического выражения
- Получение и использование формулы
Введение в многочлены
- Типы многочленов
- Факторы одночлена
Операции с многочленами
- Сложение и вычитание многочленов
Линейные уравнения
- Линейные уравнения с неизвестными по обе стороны
- Решение простого линейного уравнения с односторонними переменными
- Реальное решение через алгебраические выражения — I
Соотношения и пропорции
- Простейшая форма соотношения
- Коэффициенты пропорциональности
- Пропорциональны ли соотношения?
- Применение соотношений и пропорций
- Прямая пропорциональность через унитарную
Процент и его применение
- Введение в проценты
- Преобразование дробей, десятичных знаков и процентов
- Расчет процентов
- Определить целое в процентах
- Применение: выразить одно в процентах от другого количества
- Увеличение или уменьшение в процентах
- Процент прибыли и убытков
Простой процент
- Введение в простые проценты
- Расчет простых процентов
Линии и углы
- Пары уголков
- Пары углов — Дополнительные и Дополнительные уголки
- Параллельные и поперечные линии
Свойства треугольника
- Медиана и высота треугольника
- Свойства углов треугольника
- Свойство сторон треугольника
- Теорема Пифагора
Симметрия — Обзор
- Симметрия отражения
- Линии симметрии
- Симметрия вращения
Визуализация твердых форм
- Призмы и пирамиды
- Вершины, ребра и грани 3D-объектов
- Виды сплошного — II
Конструкции
- Построение параллельных и перпендикулярных прямых
- Постройте треугольник с тремя заданными сторонами
- Треугольник с двумя сторонами и углом дан
- Треугольник с двумя углами и общей стороной
Конгруэнтность треугольников
- Соответствие геометрических форм
- Условия сравнения
- Соответствующие части равных треугольников (CPCT)
Периметр и площадь
- Периметр и площадь прямоугольника и квадрата
- Площадь треугольника — II
- Площадь и периметр параллелограмма
- Окружность круга
- Площадь круга
- Площадь между двумя окружностями
Обработка данных
- Среднее, медиана и мода
- Представление с использованием гистограмм
- Интерпретировать гистограмму (вертикальную) — I
- Интерпретация двойной гистограммы
Вероятность
- Расчет вероятности простых событий
- Экспериментальная и теоретическая вероятность
Оценка: 7 — Алгебра и функции 2
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования.Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для математиков, испытывающих трудности | |
|---|---|
Стратегии | Примеры |
Вовлечение в стратегии исполнительного функционирования |
|
Примерные примеры |
|
Поощряйте и моделируйте математическую беседу |
|
Проверить понимание при использовании «математических правил»; объясните почему |
|
Обучение математике — ключевые слова |
|
Используйте сокращения, чтобы помочь учащимся запомнить шаги / процессы |
|
7.Руководство для учителя EE.4 | ilteachandtalk_1
Использование переменных для представления величин, ведущих к уравнениям или неравенствам
Каждый из стандартов выражений и уравнений для 7-го класса посвящен обучению учащихся составлению и решению уравнений. 7.EE.1 — это решение с использованием свойств. 7.EE.2 фокусируется на написании уравнений и выражений в нескольких формах для улучшения понимания, а 7.EE.3 объединяет 1 и 2 вместе для решения реальных проблем. 7.EE.4 также начинает включать неравенство.
Также 7.EE.4 ожидает, что студенты будут представлять неизвестное с помощью переменной, потому что по мере усложнения задач алгебраические методы становятся более ценными.
Например:
Два велосипедиста едут навстречу друг другу по дороге (каждый с постоянной скоростью). В 8 утра их разделяет 63 мили. Встречаются в 11 утра. Если один велосипедист едет со скоростью 12,5 миль в час, какова скорость другого велосипедиста?
Первое решение: первый велосипедист путешествует 3 x 12.5 = 37,5 миль. Второй путь составляет 63 — 37,5 = 25,5 миль, поэтому проходит
.
= 8,5 миль в час.
Другое решение использует ключевую скрытую величину, скорость, с которой велосипедисты приближаются друг к другу, для упрощения вычислений: поскольку = 21, велосипедисты приближаются друг к другу со скоростью 21 миля в час, поэтому другой велосипедист едет со скоростью 21 — 12,5 = 8,5 миль в час.
Шаги решения уравнения отражают шаги численного решения.По мере того, как проблемы становятся более сложными, алгебраические методы становятся более ценными. Например, в приведенной выше задаче велосипедиста численное решение требует некоторого понимания, чтобы контролировать когнитивную нагрузку расчетов. В отличие от этого, выбирая букву s для обозначения неизвестной скорости, учащиеся составляют уравнение, складывая расстояния, пройденные за три часа (3 с и 3 x 12,5), и устанавливая их равными 63, чтобы получить 3 с + 3 (12,5) = 63.
Стоит изучить два возможных следующих шага в решении этого уравнения:
3x + 37.5 = 63 и 3 (x + 12,5) = 63
Первый предлагает стандартный подход к решению линейных уравнений; второй предлагается путем сравнения с численным решением, описанным ранее.
Студенты также создают и решают неравенства, осознавая, что процесс их решения похож на процесс решения линейных уравнений:
Как продавцу, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата составляла не менее 100 долларов.Напишите неравенство для количества продаж, которые вам нужно сделать, и опишите решение.
Студенты также осознают одно важное новое соображение при решении вопросов неравенства: умножение или деление обеих сторон неравенства на отрицательное число меняет порядок сравнения, которое оно представляет. Полезно представить контексты, которые позволят учащимся понять это.
Например,
Если билет на школьный концерт стоит p долларов, то посещение 1000-50 пенсов.Какой диапазон цен обеспечивает присутствие не менее 600 человек?
Студенты признают, что требование минимум 600 человек приводит к неравенству 1000 — 50 пенсов 600. Перед тем как решить неравенство, они, руководствуясь здравым смыслом, ожидают, что ответ будет в форме p .)
Группа разработки общих основных стандартов. (2011, 22 апреля).
Прогрессии для Общих государственных стандартов по математике (проект). 6-8, Выражения и уравнения. Тусон, Аризона: Институт математики и образования, Университет Аризоны.
Примеры
Студенты изобразили неравенство и осмыслили неравенство в контексте. Неравенства могут иметь отрицательные коэффициенты. Проблемы могут быть использованы для поиска максимального или минимального значения в контексте. Примеры
· У Эми было 26 долларов, которые она могла потратить на школьные принадлежности.После покупки 10 ручек у нее осталось 14,30 доллара. Сколько стоила каждая ручка?
· Сумма трех последовательных четных чисел равна 48. Какое наименьшее из этих чисел?
· Решить: + 5 = 20.
· Флоренсия может потратить не более 60 долларов на одежду. Она хочет купить джинсы за 22 доллара, а остальное потратить на футболки. Каждая футболка стоит 8 долларов. Запишите неравенство для количества футболок, которые она может купить.
· У Стивена 25 долларов. Он потратил 10,81 доллара, включая налоги, на покупку нового DVD.Ему нужно выделить 10 долларов на обед на следующей неделе. Если арахис стоит 0,38 доллара за упаковку, включая налоги, какое максимальное количество упаковок Стивен может купить?
Напишите уравнение или неравенство для моделирования ситуации. Объясните, как вы определили, писать ли уравнение или неравенство, а также свойства действительной системы счисления, которую вы использовали для поиска решения.
Решите x + 3 и изобразите решение на числовой прямой.
Канзасская ассоциация учителей математики (KATM) Flipbooks.Вопросы или отправить отзыв:.
Получено из Math Flipbooks.
В отличие от простых линейных выражений, которые они видят в 6-м классе, более сложные выражения, которые учащиеся видели в 7-м классе, позволяют изменить точку зрения, особенно из-за их опыта работы с отрицательными числами: например, ученики могут видеть 7 — 2 (3 — 8x ) как 7 — (2 (3 — 8x)) или как 7 + (-2) (3 + (-8) x) (MP7).
По мере того, как учащиеся приобретают опыт использования нескольких способов написания выражений, они также узнают, что разные способы написания выражений могут служить разным целям и обеспечивать разные способы видения проблемы.Например,
a + 0,05a = 1,05a означает, что «увеличить на 5%» — это то же самое, что «умножить на 1,05». 7.EE.2 В приведенном ниже примере связь между выражениями и рисунком подчеркивает, что все они представляют то же число и связь между структурой каждого выражения и методом вычисления подчеркивают тот факт, что выражения строятся из операций с числами.
Стратегии обучения:
Чтобы помочь учащимся оценить разумность ответов, особенно проблемных ситуаций, связанных с дробными или десятичными числами, используйте целочисленные аппроксимации для вычислений, а затем сравните их с фактическими вычислениями.Здесь уместны связи между выполнением обратной операции и отменой операций. Уместно ожидать, что студенты покажут шаги в своей работе. Студенты должны уметь объяснять свое мышление, используя правильную терминологию для свойств и операций. Продолжайте развивать понимание и применение учащимися написания и решения одношаговых уравнений от проблемной ситуации до многоэтапных проблемных ситуаций. В этом контексте студенты также могут практиковаться в использовании рациональных чисел, включая целые числа, а также положительные и отрицательные дроби и десятичные дроби.По мере того как учащиеся анализируют ситуацию, им необходимо определить, какая операция должна быть завершена в первую очередь, а затем значения для этого вычисления. Каждый набор необходимых операций и значений определяется по порядку. Наконец, записывается уравнение, соответствующее порядку операций. Например, Бонни идет поесть и покупает еду по цене 12,50 долларов, включая налог в 0,75 доллара. Она хочет оставить только чаевые, исходя из стоимости еды. В этой ситуации учащиеся должны понимать, что налог необходимо вычесть из общей стоимости, прежде чем умножить на процент чаевых, а затем добавить обратно, чтобы получить окончательную стоимость.
C = (12,50 — 0,75) (1 + T) + 0,75 = 11,75 (1 + T) + 0,75, где C = стоимость, а T = чаевые. Предоставьте учащимся множество возможностей для работы с многоэтапными проблемными ситуациями, которые имеют несколько решений и поэтому могут быть представлены неравенством. Студенты должны знать, что ценности могут удовлетворять неравенству, но не соответствовать ситуации, что ограничивает решения этой конкретной проблемы.
Канзасская ассоциация учителей математики (KATM) Flipbooks.Вопросы или отправить отзыв:.

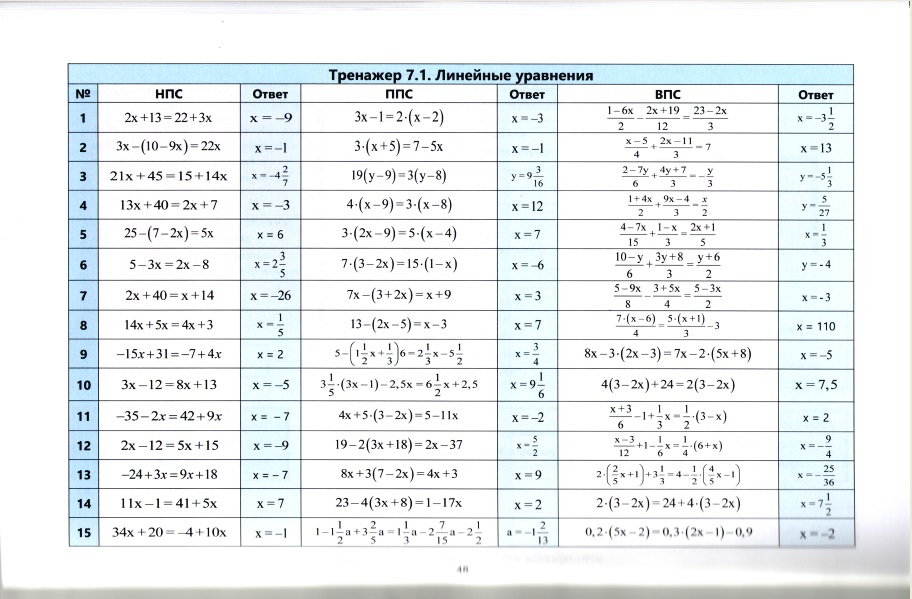

 Задачи:
Задачи: Затем предлагает составить уравнение по условию задачи, обозначив неизвестное время буквой t.
Затем предлагает составить уравнение по условию задачи, обозначив неизвестное время буквой t.

 В пятом уравнении a = 1/3, b = 2/7, x = 6/7.
В пятом уравнении a = 1/3, b = 2/7, x = 6/7. При необходимости (если возникают затруднения) учитель помогает учащимся.
При необходимости (если возникают затруднения) учитель помогает учащимся.