2
Содержание
Отвод 48,3х2,6 (Ду-40) стальной 90 градусов 1 исп ГОСТ 17375
- Внешний диаметр по торцам: 48,3 мм.
- Внутренний диаметр по торцам: 43,1 мм.
- Температура: от минус 70°С до плюс 450°С
- Номинальное (условное) давление: до 63 кгс/см2 (6,3 МПа)
- Радиус изгиба: R = 1,5DN
- Тип отвода: крутоизогнутый 3D
- Тип конструкции: бесшовный приварной
- Стандарт: ГОСТ 17375-2001 (ИСО 3419-81)
| DN, мм | D, мм | Т, мм | F, мм | R, мм | B, мм | Масса, кг |
| 40 | 48,3 | 2,6 | 57 | 57 | 82 | 0,26 |
В ГОСТ 17375-2201 применяют следующие обозначения:
PN(Pу) — номинальное (условное) давление по ГОСТ 356 и ГОСТ 26349;
DN — условный проход (номинальный размер) по ГОСТ 28338;
D — наружный диаметр торцов отводов;
T — толщина стенки деталей на торцах диаметра D;
F — размер между плоскостью одного торца и центром другого торца отводов;
R — радиус кривизны осевой линии (радиус изгиба) отводов;
B — размер между плоскостью торцов и наиболее удаленной от нее точкой наружной поверхности отводов;
Отвод 48,3х2,6 стальной (ст20) 90 градусов крутоизогнутый (к/з) приварной бесшовный ГОСТ 17375-2001 по низкой цене и с бесплатной доставкой по Москве и МО. Доставка по России Деловыми Линиями или любой другой транспортной компанией по желанию заказчика. Данные отводы производятся в России и отвечают высоким стандартам качества московской объединённой энергетической компании (МОЭК) и Мосводоканала.
Доставка по России Деловыми Линиями или любой другой транспортной компанией по желанию заказчика. Данные отводы производятся в России и отвечают высоким стандартам качества московской объединённой энергетической компании (МОЭК) и Мосводоканала.
Чтобы оформить заказ пришлите заявку с контактами и реквизитами на [email protected] или воспользуйтесь формой заказа на сайте. В ответ вышлем счет на оплату и уточним адрес доставки. В случае, если на данный момент товара нет на складе, в комментарии к счету указывается срок комплектации в рабочих днях для каждой отсутствующей позиции.
Швейцария — Турция, 20 июня
Все! Финальный свисток! Швейцарцы обыграли турков 3:1, но не сумели занять второе место в группе. Сборная Турции же покидает турнир без единой победы — в три поражения в трех матчах и 1:8 по разнице мячей
Мбабу совершил грубый фол! И опять без желтой!
Три минуты добавил арбитр к основному времени матча
Мюльдюр в касание пробил с центра штрафной после прострела — Зоммер спас!
Замена у турков! Токез вместо Чалханоглу
Двойная замена у Швейцарии! Мехмеди и Бенито появились на поле вместо Цубера и Эмболо
Йылмаз высоко выпрыгнул и пробил головой после подачи с углового — мимо!
Двойная замена у турков! Кекчю и Караман вышли вместо Ундера и Кахведжи
Джака получил карточку за споры с арбитром!
Момент! Джака со штрафного плотно пробил низом — мяч угодил в штангу!
Еще одна желтая у турков! Сеюнджю сфолил на Джаке
Двойная замена у Швейцарии! Вместо Сеферовича выходит Бенито, а Шакири поменял Варгас
Челик получил желтую за срыв атаки
Желтую карточку получил Чалханоглу после фола!
Дубль Шакири! Забивает швейцарец третий мяч своей сборной! Получил мяч в штрафной после передачи Цубера и пробил точно под перекладину
Цубер бил по воротам! Выше мяч пролетел
Вторая замена у турков! Туфан заменил Языджи
И первая замена в матче! Йокушлу выходит вместо Айхана
Гол! Турки отыгрывают один мяч! Кахведжи забивает с паса Чалханоглу!
Сеферович! Нанес хороший удар после сольного прохода — Чакыр потащил
Шкаф-купе 3-х дверный Хит-24-18/2-777-17, 2400х1770х620, фотопечать «Абстракция №1» Дуб млечный в Белгороде заказать с доставкой
Характеристики шкаф-купе 3-х дверный Хит-24-18/2-777-17, 2400х1770х620, фотопечать «Абстракция №1» Дуб млечный
| Категория | Детские шкафы |
|---|---|
| Тип шкафа | Шкаф купе |
| Назначение шкафа | Для одежды |
| Ширина | 177 см |
| Глубина | 62 см |
| Высота | 240 см |
| Расположение шкафа | Напольный |
| Материал | ДСП |
| Тип поверхности | Матовая |
| Количество дверей | Три |
| Особенности шкафа | С фотопечатью |
| Стиль | Современный |
| Цвет | Разноцветный, Бежевый |
| Производитель | Россия |
| Гарантия производителя | 18 месяцев |
| Особенности | Длинные детские шкафы |
| Вес / Объем | Расчитать для доставки |
Описание шкаф-купе 3-х дверный Хит-24-18/2-777-17, 2400х1770х620, фотопечать «Абстракция №1» Дуб млечный
Шкаф-купе ХИТ выполнен из ДСП.
Для изготовления шкафа-купе мы разработали собственную уникальную запатентованную Алюминиевую систему раздвижных дверей FUTURUM, цвет – серебро. Серебряные профили гармонично впишутся в любой интерьер современной квартиры. Эргономичная форма профиля удобна для ежедневного использования.
Полноцветная печать. Фотопечать производится на японском оборудовании, что обеспечивает высокое качество и четкость изображения.
Информация о доставке шкаф-купе 3-х дверный Хит-24-18/2-777-17, 2400х1770х620, фотопечать «Абстракция №1» Дуб млечный
| Способ доставки | Описание |
|---|---|
| Самовывоз | Бесплатно — самостоятельный вывоз с пункта выдачи. Пункт выдачи расположен по адресу г. Белгород, ул. Коммунальная, 18. Режим работы: пн — пт, c 09:00 по 18:00, сб, c 10:00 по 14:00. Всего пунктов: 3 получения готовой мебели (посмотреть) |
| Доставка до подъезда дома из пункта выдачи | Время доставки согласуется дополнительно. Выгрузка из машины и подъём на нужный этаж осуществляется Вами лично, либо за дополнительную плату после согласования с менеджером. Выгрузка из машины и подъём на нужный этаж осуществляется Вами лично, либо за дополнительную плату после согласования с менеджером. |
| Доставка по РФ | Рассчитывается индивидуально после оформлении заказа на сайте |
*Дополнительную информацию о том, как купить шкаф-купе 3-х дверный Хит-24-18/2-777-17, 2400х1770х620, фотопечать «Абстракция №1» Дуб млечный в Белгороде уточняйте у нашего менеджера по телефону 8800-333-58-61
Найдите наибольшее значение функции
В прошлой статье мы рассмотрели задания на определение точек максимума (минимума) степенной функции. Здесь представлено 7 примеров со степенной функцией. Требуется определить наибольшее (или наименьшее) значение функции на интервале. На блоге уже рассматривались подобные примеры функций с числом е, логарифмические, тригонометрические, рациональные.
Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии.
Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии.
Советую поступать немного по-другому. Почему? Писал об этом здесь.
Предлагаю решать такие задания следующим образом:
1. Находим производную.
2. Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).
В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать производные элементарных функций.
Рассмотрим примеры:
77422. Найдите наибольшее значение функции у=х3–3х+4 на отрезке [–2;0].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = –1.
Вычисляем значения функции в точках –2, –1 и 0:
Наибольшее значение функции равно 6.
Ответ: 6
77425. Найдите наименьшее значение функции у = х3 – 3х2 + 2 на отрезке [1;4].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = 2.
Вычисляем значения функции в точках 1, 2 и 4:
Наименьшее значение функции равно –2.
Ответ: –2
77426. Найдите наибольшее значение функции у = х3 – 6х2 на отрезке [–3;3].
Найдём производную заданной функции:
Найдем нули производной:
Указанному в условии интервалу принадлежит точка х = 0.
Вычисляем значения функции в точках –3, 0 и 3:
Наименьшее значение функции равно 0.
Ответ: 0
77429. Найдите наименьшее значение функции у = х3 – 2х2 + х +3 на отрезке [1;4] .
Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х2 – 4х + 1 = 0
Получим корни: х1 = 1 х1 = 1/3.
Указанному в условии интервалу принадлежит только х = 1.
Найдём значения функции в точках 1 и 4:
Получили, что наименьшее значение функции равно 3.
Ответ: 3
77430. Найдите наибольшее значение функции у = х3 + 2х2 + х + 3 на отрезке [– 4; –1].
Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х2 + 4х + 1 = 0
Получим корни:
Указанному в условии интервалу принадлежит корень х = –1.
Находим значения функции в точках –4, –1, –1/3 и 1:
Получили, что наибольшее значение функции равно 3.
Ответ: 3
77433. Найдите наименьшее значение функции у = х3 – х2 – 40х +3 на отрезке [0;4].
Найдём производную заданной функции:
Найдем нули производной, решаем квадратное уравнение:
3х2 – 2х – 40 = 0
Получим корни:
Указанному в условии интервалу принадлежит корень х = 4.
Находим значения функции в точках 0 и 4:
Получили, что наименьшее значение функции равно –109.
Ответ: –109
Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).
77437. Найдите наименьшее значение функции у=7+12х–х3 на отрезке [–2;2].
Подставляем точки от –2 до 2:
у(–2)=7+12 (–2) – (–2)3 = – 9
у(–1)=7+12 (–1) – (–1)3 = – 6
у(0)=7+12∙0 – 03 = 7
у(1)=7+12∙1 – 13 = 18
у(2)=7+12∙2 – 23 = 23
Наименьшее значение равно –9.
Ответ: –9
77441. Найдите наименьшее значение функции у=9х2–х3 на отрезке [–2;2].
Подставляем точки от –2 до 2:
у(–2)=9 (–2)2 – (–2)3 = 44
у(–1)=9 (–1)2 – (–1)3 = 10
у(0)=9∙02 – 03 = 0
у(1)=9∙12 – 13 = 8
у(2)=9∙22 – 23 = 28
Наименьшее значение равно 0.
Ответ: 0
77442. Найдите наибольшее значение функции у=9х2–х3 на отрезке [2;10].
Подставляем точки от 2 до 10. В данном примере интервал большой и вычислений будет больше, но способ вполне применим.
Ответ: 108
*Чем меньше интервал, тем быстрее решите задачу.
77421. Найдите наименьшее значение функции у=х3 –27х на отрезке [0;4].
Посмотреть решение
77434. Найдите наибольшее значение функции у=х3 + 2х2 – 4х + 4 на отрезке [–2;0].
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| ax3 + bx2 + bx + a = 0, | (1) |
где a, b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
ax2 + (b – a) x + a = 0.
Пример 1. Решить уравнение
| 2x3 + 7x2 + 7x + 2 = 0. | (2) |
Решение. Разложим левую часть уравнения (2) на множители:
Ответ:.
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| ax4 + bx3 + cx2 + + bx + a = 0, | (3) |
а также уравнения вида
| ax4 + bx3 + cx2– – bx + a = 0, | (4) |
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение (3), разделим его на x2. В результате получится уравнение
| (5) |
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
| (6) |
Если теперь обозначить
| (7) |
то уравнение (6) станет квадратным уравнением:
| ay2 + by + c – 2a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x2. В результате получится уравнение
В результате получится уравнение
| (9) |
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
| (10) |
Если теперь обозначить
| (11) |
то уравнение (10) станет квадратным уравнением:
| ay2 + by + c + 2a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (4) завершено.
Пример 2. Решить уравнение
| 2x4 – 3x3 – x2 – – 3x + 2 = 0.  | (13) |
Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на x2. В результате получится уравнение
| (14) |
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
| (15) |
Если теперь обозначить
| (16) |
то уравнение (15) станет квадратным уравнением:
| 2y2 – 3y – 5 = 0. | (17) |
Решим уравнение (17):
| (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ:
Пример 3. Решить уравнение
| 6x4 – 25x3 + 12x2 + + 25x + 6 = 0. | (19) |
Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на x2. В результате получится уравнение
| (20) |
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
| (21) |
Если теперь обозначить
| (22) |
то уравнение (21) станет квадратным уравнением:
6y2 – 25y + 24 = 0.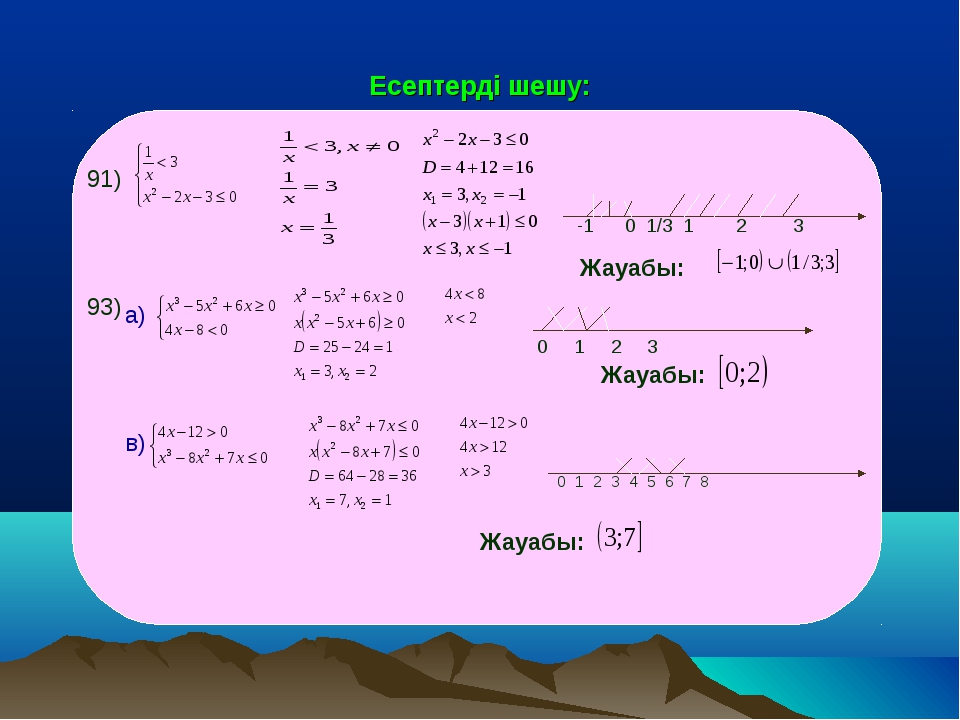 | (23) |
Решим уравнение (23):
| (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ:
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
| (25) |
где a, b, c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x2. В результате получится уравнение
| (26) |
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
| (28) |
то уравнение (27) станет квадратным уравнением:
| (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (25) завершено.
Пример 4. Решить уравнение
| 2x4 – 15x3 + 35x2 – – 30 x + 8 = 0. | (30) |
Решение. Введем для коэффициентов уравнения (30) следующие обозначения
a = 2 , b =– 15,
c = 35, d = – 30,
и найдем значение выражения
Поскольку
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение
| (31) |
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
| (32) |
Если теперь обозначить
| (33) |
то уравнение (32) станет квадратным уравнением:
2y2 – 15y + 27 = 0. | (34) |
Решим уравнение (34):
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Интерактивный учебник языка Python
1. Целочисленная арифметика
Для целых чисел определены операции
+, -, * и **. Операция
деления / для целых чисел возвращает вещественное число (значение типа float).
Также функция возведения в степень возвращает значение типа float,
если показатель степени — отрицательное число.
Но есть и специальная операция целочисленного деления, выполняющегося с отбрасыванием
дробной части, которая обозначается // (она соответствует операции div в Паскале).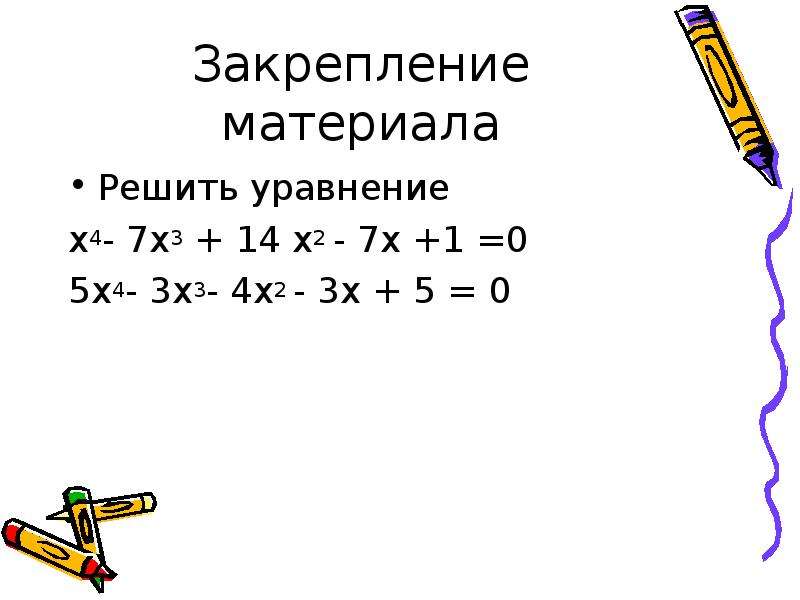
Она возвращает целое число: целую часть частного. Другая близкая ей операция − это операция взятия остатка от деления,
обозначаемая % (она соответствует операции mod в Паскале).
Например:
print(17 / 3) # выведет 5.66666666667 print(17 // 3) # выведет 5 print(17 % 3) # выведет 2
2. Действительные числа
В этом разделе речь пойдет о действительных числах, имеющих тип float.
Обратите внимание, что если вы хотите считать с клавиатуры действительное
число, то результат, возращаемый функцией input() необходимо
преобразовывать к типу float:
1.492
x = float(input()) print(x)
Действительные (вещественные) числа представляются в виде чисел с десятичной точкой (а не запятой, как принято
при записи десятичных дробей в русских текстах). Для записи очень больших или очень маленьких
по модулю чисел используется так называемая запись «с плавающей точкой»
(также называемая «научная» запись). В этом случае число представляется в виде
В этом случае число представляется в виде
некоторой десятичной дроби, называемой мантиссой, умноженной на целочисленную степень десяти
(порядок). Например, расстояние от Земли
до Солнца равно 1.496·1011, а масса молекулы воды 2.99·10-23.
Числа с плавающей точкой в программах на языке Питон, а также при вводе и выводе записываются так:
сначала пишется мантисса, затем пишется буква e, затем пишется порядок. Пробелы внутри этой
записи не ставятся. Например, указанные выше константы можно записать в виде
1.496e11 и 2.99e-23. Перед самим числом также может стоять знак минус.
Напомним, что результатом операции деления / всегда является действительное число (float),
в то время как результатом операции // является целое число (int).
Преобразование действительных чисел к целому производится с округлением
в сторону нуля, то есть int(1.7) == 1, int(-1.. 7) == -1
7) == -1
3. Библиотека math
Для проведения вычислений с действительными числами язык Питон содержит много
дополнительных функций, собранных в библиотеку (модуль), которая называется math.
Для использования этих функций в начале программы необходимо подключить математическую
библиотеку, что делается командой
import math
Например, пусть мы хотим округлять вещественные числа до ближайшего целого числа вверх.
Соответствующая функция ceil от одного аргумента вызывается, например, так: math.ceil(x)
(то есть явно указывается, что из модуля math используется функция ceil).
Вместо числа x может быть любое число, переменная или выражение.
Функция возращает значение, которое можно вывести на экран, присвоить
другой переменной или использовать в выражении:
import math x = math.ceil(4.2) y = math.ceil(4.8) print(x) print(y)
Другой способ использовать функции из библиотеки math, при котором не нужно будет
при каждом использовании функции из модуля math указывать название
этого модуля, выглядит так:
from math import ceil x = 7 / 2 y = ceil(x) print(y)
или так:
from math import * x = 7 / 2 y = ceil(x) print(y)
Ниже приведен список основных функций модуля math. Более подробное описание
Более подробное описание
этих функций можно найти на сайте с документацией языка Питон.
Некоторые из перечисленных функций (int, round, abs)
являются стандартными и не требуют подключения модуля math для использования.
| Функция | Описание |
|---|---|
| Округление | |
int(x) | Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать модуль math. |
round(x) | Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется до ближайшего четного числа. |
round(x, n) | Округляет число xдо n знаков после точки. Это стандартная функция, для ее использования не нужно подключатьмодуль math. |
floor(x) | Округляет число вниз («пол»), при этом floor(1.5) == 1, floor(-1.5) == -2 |
ceil(x) | Округляет число вверх («потолок»), при этом ceil(1.5) == 2, ceil(-1.5) == -1 |
abs(x) | Модуль (абсолютная величина). Это — стандартная функция. |
| Корни, логарифмы | |
sqrt(x) | Квадратный корень. Использование: sqrt(x) |
log(x) | Натуральный логарифм. При вызове в виде log(x, b) возвращает логарифм по основанию b. |
e | Основание натуральных логарифмов e = 2,71828… |
| Тригонометрия | sin(x) | Синус угла, задаваемого в радианах |
cos(x) | Косинус угла, задаваемого в радианах |
tan(x) | Тангенс угла, задаваемого в радианах |
asin(x) | Арксинус, возвращает значение в радианах |
acos(x) | Арккосинус, возвращает значение в радианах |
atan(x) | Арктангенс, возвращает значение в радианах |
atan2(y, x) | Полярный угол (в радианах) точки с координатами (x, y). |
degrees(x) | Преобразует угол, заданный в радианах, в градусы. |
radians(x) | Преобразует угол, заданный в градусах, в радианы. |
pi | Константа π = 3.1415… |
Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
2 + 1 (пример графика),
4x + 2 = 2 (x + 6) (пример решения)
Калькулятор алгебры — это калькулятор, который дает пошаговую помощь по задачам алгебры.
Посмотреть другие примеры »
Заявление об отказе от ответственности:
Этот калькулятор не идеален. Пожалуйста, используйте на свой страх и риск и сообщите нам, если что-то не работает. Спасибо.
Как пользоваться калькулятором
Введите задачу по алгебре в текстовое поле.
(экспонента: «в степень»)
sqrt (квадратный корень) (пример: sqrt (9))
Другие математические символы
Учебное пособие
Прочтите полное руководство, чтобы узнать, как построить графики уравнений и проверить свое домашнее задание по алгебре.Учебное пособие по калькулятору
»
Мобильное приложение
Загрузите мобильное приложение MathPapa! Работает офлайн!
Обратная связь
(Для студентов 13+)
Пожалуйста, используйте эту форму обратной связи, чтобы отправить свой отзыв. Спасибо!
Нужно больше практических задач?
Попробуйте MathPapa
Математическая практика
Учебное пособие по калькулятору алгебры — MathPapa
Это учебное пособие по использованию калькулятора Algebra Calculator , пошагового калькулятора для алгебры.
Решение уравнений
Сначала перейдите на главную страницу Калькулятора алгебры. В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить.
Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле.
После того, как вы введете выражение, Калькулятор алгебры распечатает пошаговое объяснение того, как решить 3x + 2 = 14.
Примеры
Чтобы увидеть больше примеров задач, которые понимает калькулятор алгебры, посетите
Страница примеров.2.
Вычисление выражений
Калькулятор алгебры может вычислять выражения, содержащие переменную x.
Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите вставить для x.
Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6.
Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y. Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4).
Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4).
Проверка ответов для решения уравнений
Так же, как калькулятор алгебры можно использовать для вычисления выражений,
Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x.
В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Поскольку ответ правильный, в калькуляторе алгебры отображается зеленый знак равенства.
Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно».
Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенные точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Пример: x + y = 7; х + 2у = 11 @ (3,4).
Пример: x + y = 7; х + 2у = 11 @ (3,4).
Режим планшета
Если вы используете планшет, например iPad, войдите в Режим планшета, чтобы отобразить сенсорную клавиатуру.
Статьи по теме
Вернуться к калькулятору алгебры »
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Fractions — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Fractions — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Дроби: умножение и деление дробей
Урок 4: Умножение и деление дробей
/ ru / fractions / сложение-и-вычитание-дроби / content /
Умножение дробей
Дробь — это часть из целого . На последнем уроке вы узнали, как складывать и вычитать дроби.Но это не единственная математика, которую вы можете выполнять с дробями. Бывают случаи, когда будет полезно умножить и дроби.
Щелкните слайд-шоу, чтобы узнать, как написать задачу умножения с дробями.
Попробуй!
Попробуйте настроить задачу умножения ниже. Пока не беспокойтесь о ее решении!
Рецепт требует 2/3 стакана молока. Вы хотите разрезать рецепт пополам.
Примечание : Хотя наш пример говорит, что правильный ответ — 2/3 x 1/2, помните, что порядок умножения не имеет значения.1/2 x 2/3 тоже будет правильным.
Решение задач умножения на дроби
Теперь, когда мы знаем, как ставить задачи умножения с дробями, давайте попрактикуемся в решении некоторых. Если вы чувствуете себя комфортно, умножая целые числа, вы готовы умножать дроби.
Щелкните слайд-шоу, чтобы узнать, как умножить две дроби.
Попробуй!
Попробуйте решить приведенные ниже задачи умножения.
Умножение дроби на целое число
Умножение дроби и целого числа аналогично умножению двух дробей.Есть только один дополнительный шаг: прежде чем вы сможете умножить, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать.
Щелкните слайд-шоу, чтобы узнать, как умножить дробь на целое число.
Умножим 2 раза на 1/3. Помните, это просто еще один способ спросить: «Что такое 1/3 из 2?»
Прежде чем мы начнем, мы должны убедиться, что эти числа готовы к умножению.
Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 как дробь.
Как вы узнали из «Введение в дроби», мы также можем записать 2 как 2/1, потому что 2 можно дважды разделить на 1.
Теперь мы готовы к умножению!
Сначала мы умножим числителей: 2 и 1.
2 умножить на 1 равно 2. Мы выровняем 2 вместе с числителями.
Затем умножим знаменатели : 1 и 3.
1 умножим на 3 равно 3.Совместим тройку со знаменателями.
Итак, 2/1 умноженное на 1/3 равно 2/3. Мы также можем сказать, что 1/3 от 2 — это 2/3.
Давайте попробуем другой пример: 4 раза по 1/5.
Перед тем, как мы начнем, нам нужно записать 4 в виде дроби.
Перепишем 4 как 4/1. Теперь мы готовы к размножению.
Сначала умножим числители: 4 и 1.
4 раза 1 равно 4, поэтому числитель нашего ответа равен 4.
Затем мы умножим знаменатели: 1 и 5.
1 умножить на 5 равно 5, поэтому 5 является знаменателем нашего ответа.
Итак, 4/1 умноженное на 1/5 равно 4/5.
Попробуй!
Попробуйте решить приведенные ниже задачи умножения.
Разделение на дроби
За последние несколько страниц вы узнали, как умножить дробей. Вы, наверное, догадались, что тоже можно разделить на дробей.Вы делите дроби, чтобы увидеть, сколько частей чего-то приходится на чего-то другого. Например, если вы хотите узнать, сколько четвертей дюйма в четырех дюймах, вы можете разделить 4 на 1/4.
Попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваша мерная чашка вмещает только 1/3, или 1/3 чашки. Сколько третей стакана нужно добавить?
Нам нужно узнать, сколько третей чашки находится в трех чашках.Другими словами, нам нужно разделить три на одну треть.
Задачу запишем так:
3 ÷ 1/3
Попробуй!
Попробуйте поставить эти задачи деления на дроби. Пока не беспокойтесь о их решении!
Рецепт требует 3/4 стакана воды. У вас есть только 1/8 мерного стакана.
Решение задач деления на дроби
Теперь, когда мы знаем, как писать задачи деления, давайте попрактикуемся в решении нескольких. Деление дробей во многом похоже на умножение.Требуется всего лишь один дополнительный шаг. Если вы умеете умножать дроби, вы можете и их делить!
Щелкните слайд-шоу, чтобы узнать, как разделить целое число на дробь.
Разделим 3 на 1/3. Помните, это просто еще один способ спросить: «Сколько третей в 3?»
В нашем уроке о делении вы научились писать знак деления следующим образом (/).
При делении дробей полезно использовать другой символ для деления (÷), чтобы не ошибочно принять его за дробь.
Как и умножение, мы начнем с поиска любых целых чисел в нашей задаче. Там один: 3.
Помните, 3 — это то же самое, что и 3/1.
Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.
Мы заменим числителем и знаменателем дроби, которую мы делим на на: 1/3 в этом примере.
Таким образом, 1/3 становится 3/1.
Это называется нахождением , обратного , или мультипликативного , обратного , дроби.
Поскольку мы меняем исходную дробь, мы также изменим знак деления (÷) на знак умножения (x).
Это потому, что умножение — это , обратное делению.
Теперь мы можем рассматривать это как обычную задачу умножения.
Сначала мы умножим числители: 3 и 3.
3 раза 3 равно 9, поэтому мы напишем это рядом с числителями.
Затем мы умножим знаменатели: 1 и 1.
1 умножить на 1 равно 1, поэтому мы запишем 1 рядом со знаменателем.
Как видите, 3/1 x 1/3 = 9/1.
Помните, любая дробь больше 1 также может быть выражена как целое число .Итак, 9/1 = 9.
3 ÷ 1/3 = 9. Другими словами, в 3.
.
Давайте попробуем другой пример: 5 разделить на 4/7.
Как всегда, мы перепишем любые целые числа, так что 5 станет 5/1.
Далее мы найдем , обратное 4/7. Это дробь, на которую мы делим.
Для этого мы заменим числителем и знаменателем , так что 4/7 станет 7/4.
Затем мы изменим знак деления (÷) на знак умножения знак (x).
Теперь мы можем умножать как обычно. Сначала мы умножим числители: 5 и 7.
5 умножим на 7 равно 35, так что запишем это рядом с числителями.
Затем мы умножим знаменатели: 1 и 4.
1 умножить на 4 равно 4, поэтому мы запишем это рядом со знаменателями.
Итак, 5/1 x 4/7 = 35/4.
Как вы узнали ранее, мы можем преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.
35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4.
Попробуй!
Попробуйте решить эти проблемы с разделением. Не беспокойтесь о сокращении ответа на данный момент.
На две дроби
Мы только что научились делить целое число на дробь .Вы можете использовать тот же метод, чтобы разделить на две дроби .
Щелкните слайд-шоу, чтобы узнать, как разделить на две дроби.
Давайте попробуем задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.
Сначала мы найдем , обратное дроби, которую мы делим на: 3/4.
Для этого мы поменяем местами числитель и знаменатель.Итак, 3/4 становится 4/3.
Затем мы изменим знак деления (÷) на знак умножения знак (x).
Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.
Затем мы умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами.
Итак, 2/3 x 4/3 = 8/9.
Мы также можем записать это как 2/3 ÷ 3/4 = 8/9.
Давайте попробуем другой пример: 4/7 разделить на 2/9.
Целых чисел нет, поэтому мы найдем , обратное дроби, на которую мы делим. Это 2/9.
Для этого мы поменяем местами числитель и знаменатель. Таким образом, 2/9 становится 9/2.
Теперь мы изменим знак деления (÷) на знак умножения знак (x) и умножим как обычно.
Сначала умножим числители. 4 x 9 = 36.
Затем мы умножим знаменатели. 7 x 2 = 14.
Итак, 4/7 x 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.
Итак, 4/7 ÷ 2/9 = 2 8/14.
Попробуй!
Попробуйте решить эти проблемы с разделением. Не беспокойтесь о сокращении ответа на данный момент.
Умножение и деление смешанных чисел
Как бы вы решили такую проблему?
Как вы узнали на предыдущем уроке, всякий раз, когда вы решаете задачу со смешанным числом , вам нужно сначала преобразовать его в неправильную дробь .Затем вы можете как обычно умножать или делить.
Использование отмены для упрощения задач
Иногда вам может понадобиться решить такие проблемы:
Обе эти дроби включают больших чисел . Эти дроби можно умножать так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить себе 21/50 или двадцать одна пятидесятая , ?
21/50 x 25/14 = 525/700
Даже ответ кажется сложным.Это 525/700, или пятьсот двадцать пять семисотых . Какой полный рот!
Если вам не нравится работать с большими числами, вы можете упростить такую задачу, используя метод под названием отмена . Когда вы отменяете дробей в задаче, вы сокращаете их обеих одновременно.
Поначалу отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз посмотрим на только что рассмотренный пример.
Шаг 1
Сначала посмотрите на числитель первой дроби и знаменатель второй. Мы хотим увидеть, можно ли разделить на на одно и то же число.
В нашем примере 21 и 14 можно разделить на 7.
Шаг 2
Затем мы разделим 21 и 14 на 7. Сначала разделим наше верхнее число слева: 21.
21 ÷ 7 = 3
Затем разделим нижнее число справа: 14.
14 ÷ 7 = 2
Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, запишем 3 вместо 21. 14 ÷ 7 равно 2, поэтому напишем 2 вместо 14. Мы можем зачеркнуть или отменить , числа, с которых мы начали.
Наша задача теперь выглядит намного проще, не так ли?
Шаг 3
Давайте посмотрим на другие числа дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй.Можно ли их разделить на на одно и то же число?
Обратите внимание, что их можно разделить на 25! Вы также могли заметить, что их можно разделить на 5. Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце.
Шаг 4
Затем мы отменим , как мы это делали на шаге 2.
Мы разделим наше нижнее число слева: 50.
50 ÷ 25 = 2
Затем разделим верхнее число справа: 25.
25 ÷ 25 = 1
Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили.
Шаг 5
Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножаем числители:
3 х 1 = 3
Затем умножьте знаменатели:
2 х 2 = 4
Итак, 3/2 x 1/2 = 3/4, или три четверти .
Шаг 6
Наконец, давайте еще раз проверим нашу работу. 525/700 был бы нашим ответом, если бы мы решили проблему без отмены. Если мы разделим 525 и 700 на 175, мы увидим, что 525/700 равно 3/4.
Можно также сказать, что мы уменьшаем 525/700 до 3/4. Помните, что отмена — это еще один способ уменьшить дроби перед решением проблемы. Вы получите один и тот же ответ, независимо от того, когда вы их уменьшите.
/ ru / фракции / преобразование-десятичные-дроби-и-дроби / содержание /
Как найти 1/2 из 2/3 — Видео и стенограмма урока
Проверка вашей работы
Если мы хотим убедиться, что наши вычисления верны, мы можем проверить нашу работу, используя тот факт, что умножение и деление противоположны друг другу.В некотором смысле они уничтожают друг друга. Например, если мы разделим 15 на 5, чтобы получить 3, мы можем отменить операцию, умножив 3 на 5, чтобы получить 15. В общем, следующие два факта позволяют нам проверить нашу работу в обоих наших методах решения.
- Если a * b = c и a и b не равны 0, то c / a = b и c / b = а
- Если r / s = t , то r = ts
Если мы решим найти 1/2 от 2/3 путем умножения 2/3 на 1/2, мы получим 1/2 * 2/3 = 1/3.Мы можем использовать первый факт, чтобы проверить это. Поскольку 1/2 * 2/3 = 1/3, должно быть так, что 1/3, разделенная на 2/3, дает 1/2, а 1/3, разделенная на 1/2, дает 2/3. Чтобы разделить дроби , мы умножаем числитель на обратную величину знаменателя, где обратная величина числа просто меняет местами числитель и знаменатель числа.
Если мы решим найти 1/2 от 2/3, разделив 2/3 на 2, мы получим (2/3) / 2 = 1/3.Чтобы проверить наше решение, мы можем использовать второй факт. Поскольку (2/3) / 2 = 1/3, должно быть, что 1/3 * 2 = 2/3.
Конечно, как и ожидалось, это подтверждается.
Реальные приложения
Давайте рассмотрим реальное приложение задачи «найти 1/2 из 2/3». Предположим, вы готовите овсяное печенье. По вашему рецепту получается 36 печенек, но вам не нужно так много. Итак, вы решили уменьшить количество печенья, уменьшив вдвое все ингредиенты в рецепте.Рецепт требует 2/3 стакана сахара. поэтому нам просто нужно умножить 2/3 на 1/2 или разделить 2/3 на 2. В любом случае мы знаем, что 1/2 от 2/3 равно 1/3. Следовательно, для рецепта требуется 1/3 стакана сахара.
Рассмотрим другое приложение. Представьте, что вы решили заняться бегом. В парке возле вашего дома есть петля длиной 2/3 мили. Вы делаете половину пути по петле и хотите знать, как далеко вы прошли, или что составляет 1/2 от 2/3. Опять же, мы знаем, что ответ — 1/3. Это говорит нам о том, что вы пробежали 1/3 мили.Отличная работа!
Нахождение 1/2 числа — математическая задача, с которой мы часто сталкиваемся в повседневной жизни. Изучив шаги, необходимые для нахождения 1/2 из 2/3, как мы сделали в этом уроке, вы теперь знакомы с процессом и можете распространить его на другие числа.
Ввод математических задач на этом сайте
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансовМатематика, Практика полиномов по математике, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
.
