1 х в степени: Решите уравнение x^(1/4)=2 (х в степени (1 делить на 4) равно 2) — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — Формулы сокращенного умножения

Формулы сокращенного умножения включают в себя следующие группы формул:

Степень суммы

Группа формул «Степень суммы» составляет Таблицу 1. Эти формулы можно получить, выполняя вычисления в следующем порядке:

(x + y)² = (x + y)(x + y) ,
(x + y)³ = (x + y)²(x + y) ,
(x + y)⁴ = (x + y)³(x + y)

и т.д.

Группу формул «Степень суммы» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.

Таблица 1. – Степень суммы

Название формулы	Формула
Квадрат (вторая степень) суммы	(x + y)² = x² + 2xy + y²
Куб (третья степень) суммы	(x + y)³ = x³ + 3x²y + 3xy² + y³
Четвертая степень суммы	(x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴
Пятая степень суммы	(x + y)⁵ = x⁵ + 5x⁴y + 10x³y² + 10x²y³ + 5xy⁴ + y⁵
Шестая степень суммы	(x + y)⁶ = x⁶ + 6x⁵y + 15x⁴y² + 20x³y³ + 15x²y⁴ + 6xy⁵ + y⁶
…	…

Квадрат (вторая степень) суммы

(x + y)² = x² + 2xy + y²

Куб (третья степень) суммы

(x + y)³ =
= x³ + 3x²y + 3xy² + y³

Четвертая степень суммы

(x + y)⁴ = x⁴ + 4x³y +
+ 6x²y² + 4xy³ + y⁴

Пятая степень суммы

(x + y)⁵ = x⁵ + 5x⁴y +
+ 10x³y² +
+ 10x²y³ +
+ 5xy⁴ + y⁵

Шестая степень суммы

(x + y)⁶ = x⁶ + 6x⁵y +
+ 15x⁴y² +
+ 20x³y³ +
+ 15x²y⁴ + 6xy⁵ + y⁶

…

Общая формула для вычисления суммы

(x + y)ⁿ

с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.

Степень разности

Если в формулах из Таблицы 1 заменить y на – y , то мы получим группу формул «Степень разности» (Таблица 2.):

Таблица 2. – Степень разности

Название формулы	Формула
Квадрат (вторая степень) разности	(x – y)² = x² – 2xy + y²
Куб (третья степень) разности	(x – y)³ = x³ – 3x²y + 3xy²– y³
Четвертая степень разности	(x – y)⁴ = x⁴ – 4x³y + 6x²y² – 4xy³ + y⁴
Пятая степень разности	(x – y)⁵ = x⁵ – 5x⁴y + 10x³y² – 10x²y³ + 5xy⁴– y⁵
Шестая степень разности	(x – y)⁶ = x⁶ – 6x⁵y + 15x⁴y² – 20x³y³ + 15x²y⁴ – 6xy⁵ + y⁶
…	…

Квадрат (вторая степень) разности

(x – y)² = x² – 2xy + y²

Куб (третья степень) разности

(x – y)³ =
= x³ – 3x²y + 3xy²– y³

Четвертая степень разности

(x – y)⁴ = x⁴ – 4x³y +
+ 6x²y² – 4xy³ + y⁴

Пятая степень разности

(x – y)⁵ = x⁵ – 5x⁴y +
+ 10x³y² –
– 10x²y³ +
+ 5xy⁴– y⁵

Шестая степень разности

(x – y)⁶ = x⁶ – 6x⁵y +
+ 15x⁴y² –
– 20x³y³ +
+ 15x²y⁴ – 6xy⁵ + y⁶

…

Квадрат многочлена

Следующая формула применяется достаточно часто и называется «Квадрат многочлена»:

Словами эту формулу можно выразить так: — «Квадрат многочлена равен сумме квадратов всех его членов плюс сумма всевозможных удвоенных произведений его членов».

Куб трехчлена

Следующая формула называется «Куб трехчлена»:

(x + y + z)³ =
= x³ + y³ + z³ + 3x²y +
+ 3x²z + 3xy² +
+ 3xz² +
+ 3y²z + 3yz² + 6xyz .

Другие формулы сокращенного умножения приведены в разделе «Формулы сокращенного умножения: сумма степеней, разность степеней» нашего справочника.

Mathway | Популярные задачи

1	Trovare la Derivata — d/dx	натуральный логарифм x
2	Вычислим интеграл	интеграл натурального логарифма x по x
3	Trovare la Derivata — d/dx	e^x
4	Вычислим интеграл	интеграл e^(2x) относительно x
5	Trovare la Derivata — d/dx	1/x
6	Trovare la Derivata — d/dx	x^2
7	Trovare la Derivata — d/dx	1/(x^2)
8	Trovare la Derivata — d/dx	sin(x)^2
9	Trovare la Derivata — d/dx	sec(x)
10	Вычислим интеграл	интеграл e^x относительно x
11	Вычислим интеграл	интеграл x^2 относительно x
12	Вычислим интеграл	интеграл квадратного корня x по x
13	Trovare la Derivata — d/dx	cos(x)^2
14	Вычислим интеграл	интеграл 1/x относительно x
15	Вычислим интеграл	интеграл sin(x)^2 относительно x
16	Trovare la Derivata — d/dx	x^3
17	Trovare la Derivata — d/dx	sec(x)^2
18	Вычислим интеграл	интеграл cos(x)^2 относительно x
19	Вычислим интеграл	интеграл sec(x)^2 относительно x
20	Trovare la Derivata — d/dx	e^(x^2)
21	Вычислим интеграл	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
22	Trovare la Derivata — d/dx	sin(2x)
23	Trovare la Derivata — d/dx	tan(x)^2
24	Вычислим интеграл	интеграл 1/(x^2) относительно x
25	Trovare la Derivata — d/dx	2^x
26	График	натуральный логарифм a
27	Trovare la Derivata — d/dx	cos(2x)
28	Trovare la Derivata — d/dx	xe^x
29	Вычислим интеграл	интеграл 2x относительно x
30	Trovare la Derivata — d/dx	( натуральный логарифм x)^2
31	Trovare la Derivata — d/dx	натуральный логарифм (x)^2
32	Trovare la Derivata — d/dx	3x^2
33	Вычислим интеграл	интеграл xe^(2x) относительно x
34	Trovare la Derivata — d/dx	2e^x
35	Trovare la Derivata — d/dx	натуральный логарифм 2x
36	Trovare la Derivata — d/dx	-sin(x)
37	Trovare la Derivata — d/dx	4x^2-x+5
38	Trovare la Derivata — d/dx	y=16 корень четвертой степени 4x^4+4
39	Trovare la Derivata — d/dx	2x^2
40	Вычислим интеграл	интеграл e^(3x) относительно x
41	Вычислим интеграл	интеграл cos(2x) относительно x
42	Trovare la Derivata — d/dx	1/( квадратный корень x)
43	Вычислим интеграл	интеграл e^(x^2) относительно x
44	Вычислить	e^infinity
45	Trovare la Derivata — d/dx	x/2
46	Trovare la Derivata — d/dx	-cos(x)
47	Trovare la Derivata — d/dx	sin(3x)
48	Trovare la Derivata — d/dx	1/(x^3)
49	Вычислим интеграл	интеграл tan(x)^2 относительно x
50	Вычислим интеграл	интеграл 1 относительно x
51	Trovare la Derivata — d/dx	x^x
52	Trovare la Derivata — d/dx	x натуральный логарифм x
53	Trovare la Derivata — d/dx	x^4
54	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
55	Вычислим интеграл	интеграл от x^2 натуральный логарифм x по x
56	Trovare la Derivata — d/dx	f(x) = square root of x
57	Trovare la Derivata — d/dx	x^2sin(x)
58	Вычислим интеграл	интеграл sin(2x) относительно x
59	Trovare la Derivata — d/dx	3e^x
60	Вычислим интеграл	интеграл xe^x относительно x
61	Trovare la Derivata — d/dx	y=x^2
62	Trovare la Derivata — d/dx	квадратный корень x^2+1
63	Trovare la Derivata — d/dx	sin(x^2)
64	Вычислим интеграл	интеграл e^(-2x) относительно x
65	Вычислим интеграл	интеграл натурального логарифма квадратного корня x по x
66	Trovare la Derivata — d/dx	e^2
67	Trovare la Derivata — d/dx	x^2+1
68	Вычислим интеграл	интеграл sin(x) относительно x
69	Trovare la Derivata — d/dx	arcsin(x)
70	Оценить предел	предел (sin(x))/x, если x стремится к 0
71	Вычислим интеграл	интеграл e^(-x) относительно x
72	Trovare la Derivata — d/dx	x^5
73	Trovare la Derivata — d/dx	2/x
74	Trovare la Derivata — d/dx	натуральный логарифм 3x
75	Trovare la Derivata — d/dx	x^(1/2)
76	Trovare la Derivata — d/d@VAR	f(x) = square root of x
77	Trovare la Derivata — d/dx	cos(x^2)
78	Trovare la Derivata — d/dx	1/(x^5)
79	Trovare la Derivata — d/dx	кубический корень x^2
80	Вычислим интеграл	интеграл cos(x) относительно x
81	Вычислим интеграл	интеграл e^(-x^2) относительно x
82	Trovare la Derivata — d/d@VAR	f(x)=x^3
83	Вычислим интеграл	интеграл 4x^2+7 от 0 до 10 относительно x
84	Вычислим интеграл	интеграл от ( натуральный логарифм x)^2 по x
85	Trovare la Derivata — d/dx	логарифм x
86	Trovare la Derivata — d/dx	arctan(x)
87	Trovare la Derivata — d/dx	натуральный логарифм 5x
88	Trovare la Derivata — d/dx	5e^x
89	Trovare la Derivata — d/dx	cos(3x)
90	Вычислим интеграл	интеграл x^3 относительно x
91	Вычислим интеграл	интеграл x^2e^x относительно x
92	Trovare la Derivata — d/dx	16 корень четвертой степени 4x^4+4
93	Trovare la Derivata — d/dx	x/(e^x)
94	Оценить предел	предел arctan(e^x), если x стремится к 3
95	Вычислим интеграл	интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x
96	Trovare la Derivata — d/dx	3^x
97	Вычислим интеграл	интеграл xe^(x^2) относительно x
98	Trovare la Derivata — d/dx	2sin(x)
99	Вычислить	sec(0)^2
100	Trovare la Derivata — d/dx	натуральный логарифм x^2

Таблица производных простых функций

Пояснение:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.

3. Производная переменной и множителя равна этому множителю
сx´ = с

Пример:

(3x)´ = 3

(2x)´ = 2
Пояснение:

В данном случае, при каждом изменении аргумента функции (х) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.

Откуда следует, что
(cx + b)’ = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).

4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|’ = x / |x| при условии, что х ≠ 0
Пояснение:

Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.

5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
( x^c )’= cx^c-1, при условии, что x^c и сx^c-1,определены а с ≠ 0

Пример:

(x² )’ = 2x

(x³)’ = 3x²
Для запоминания формулы:

Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x² — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x³ — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x² .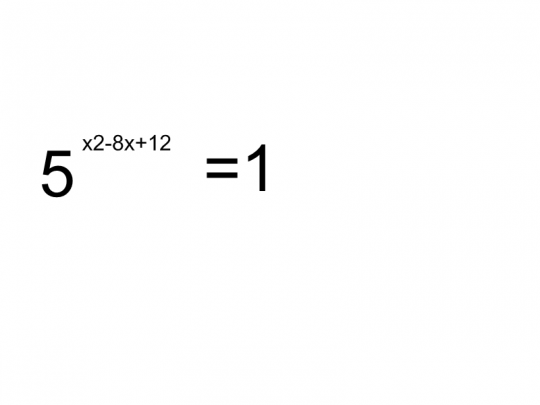 Немного «не научно», но очень просто запомнить.

6. Производная дроби 1/х
(1/х)’ = — 1 / x²

Пример:

Поскольку дробь можно представить как возведение в отрицательную степень

(1/x)’ = (x^-1 )’ , тогда можно применить формулу из правила 5 таблицы производных

(x^-1 )’ = -1x^-2 = — 1 / х²

7. Производная дроби с переменной произвольной степени в знаменателе
( 1 / x^c )’ = — c / x^c+1

Пример:

( 1 / x² )’ = — 2 / x³

8. Производная корня (производная переменной под квадратным корнем)
( √x )’ = 1 / ( 2√x ) или 1/2 х^-1/2

Пример:

( √x )’ = ( х^1/2 )’ значит можно применить формулу из правила 5

( х^1/2 )’ = 1/2 х^-1/2 = 1 / (2√х)

9. Производная переменной под корнем произвольной степени
( ⁿ√x )’ = 1 / ( n ⁿ√x^n-1 )

.

Приведенная здесь таблица производных простых функций содержит только основные преобразования, которые (по большому счету) следует запомнить наизусть. Нахождение более сложных производных приведены в соответствующих таблицах других уроков:

1 3 в степени x

Вы искали 1 3 в степени x? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 3 в степени x 1, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 3 в степени x».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 3 в степени x,1 3 в степени x 1,3 в степени 1 x,3 в степени 1 х,3 в степени x,3 в степени x 1,3 в степени x равно 1 в степени 3,x 1 в степени 3,степень x 1,х 1 в 3 степени. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 3 в степени x. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 3 в степени 1 x).

Где можно решить любую задачу по математике, а так же 1 3 в степени x Онлайн?

Решить задачу 1 3 в степени x вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. {3x}=1$.

1.2. Корень n-й степени

В 8-м классе изучались квадратные корни из действительных чисел (их называют также
корнями 2-й степени).

Перейдем к изучению корней степени n для
произвольного натурального числа n≥2.

Определение. Пусть n≥2 и n∈N.

Корнем

n-й степени

из числа a
называется такое число t, n-я степень
которого равна a

Таким образом, утверждение «t —
корень n-й степени из a» означает, что
tn=a.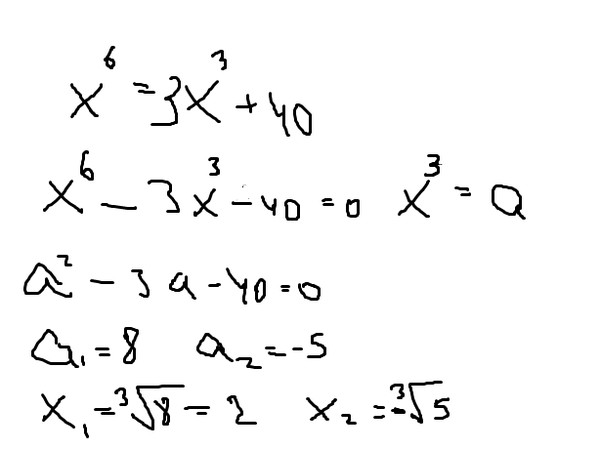

Корень 3-й степени называется также кубическим.

Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.

Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.

Во множестве действительных чисел существует единственный
корень нечетной степени n из любого числа a. Этот корень
обозначается

Например, 1253=5,−1287=−2,07=0.

Стр. 11

Утверждение о существовании корня нечетной степени из любого числа мы
принимаем без доказательства.

Согласно определению, когда n нечетное, то при любом
значении а верно равенство

Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.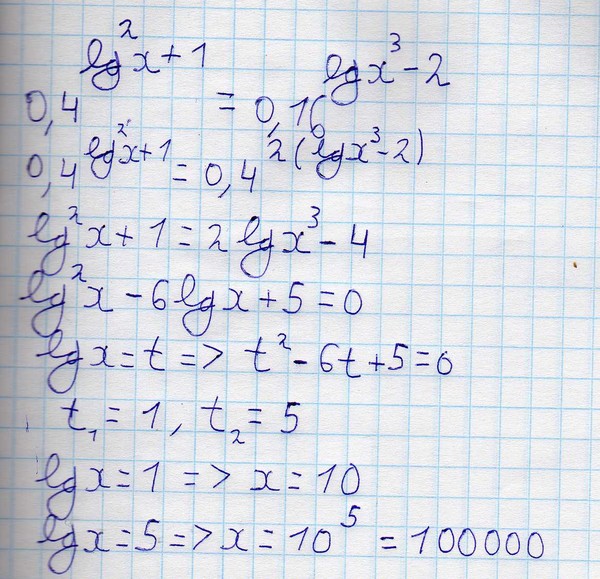

Заметим, что 0 — это единственное число, n-я степень
которого равна 0. Поэтому

при любом натуральном n≥2 существует единственный корень n-й степени
из 0 — это число 0, т. е. 0n=0.

Примерами корней четной степени могут служить квадратные корни: −7 и 7 —
квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров.
Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.

Во множестве действительных чисел существует ровно два
корня четной степени n из любого положительного числа а, их модули равны, а
знаки противоположны. Положительный корень обозначается

Например, 814=3,646=2.

Утверждение о существовании корня четной степени из любого положительного
числа мы принимаем без доказательства.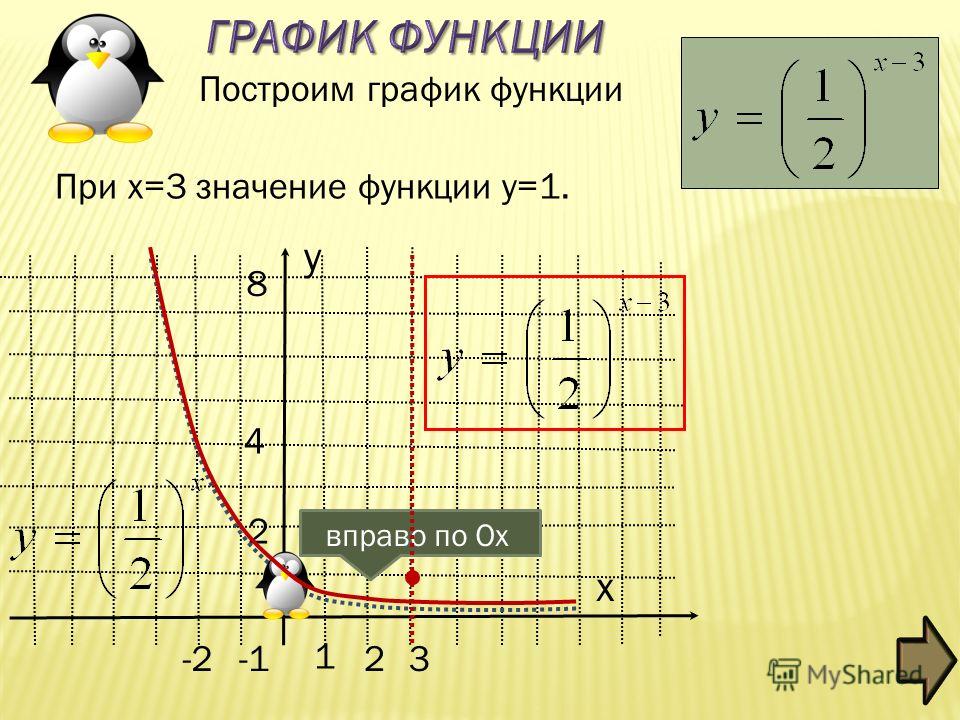 Согласно определению, когда n четное, то при любом положительном значении а верно
равенство

Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.

Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й
степени из числа −81 не существует. И вообще, поскольку не существует такого числа,
четная степень которого была бы отрицательной, то

Стр. 12

не существует корня четной степени из отрицательного
числа.

Определение.

Неотрицательный корень n-й степени из числа
a
называется

арифметическим корнем n-й степени из a
.

При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении
записи an слово «арифметический» обычно пропускают).

Выражение, стоящее под знаком корня, называется подкоренным выражением.

Извлечь корень n-й степени
из числа a — это значит найти значение выражения an.

Так как корня четной степени из отрицательного числа не существует, то выражение
an при четном n и отрицательном а не имеет смысла.

Например, не имеют смысла выражения −814 и −646.

Как мы установили, при любом значении а, при котором
выражение an имеет смысл, верно равенство

Поэтому равенство
(1)
является тождеством.

В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования
в алгебраическую символику. В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так,
выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.

Знак корня в современном виде был предложен в 1525 г. чешским математиком К.
Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился
знаменитый математик Л. Эйлер.

Знак еще называют радикалом.

Стр. 13

Пример 1. Верно
ли, что:

а) (−2)44=−2;

б) (−2)77=−2?

Решение. а) По определению арифметический корень
n-й степени из неотрицательного числа a (n — четное число) является
неотрицательным числом, n-я степень которого равна
подкоренному выражению a.

Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.

б) По определению корень n-й степени из числа
а (n — нечетное
число) является числом, n-я степень которого равна
подкоренному выражению а.

Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.

Пример 2. Решить
уравнение:

а) x3=7;

б) x4=5.

Решение. а) Решением этого уравнения является такое
значение х, 3-я степень которого равна 7, т. е. по
определению кубического корня имеем:

б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного
числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют
противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т. е. x=±54.

Ответ: а) 73; б) ±54.

В тетради решение уравнения б) (аналогично и а)) можно записать так:

Решение: x4=5 ⇔ x=±54.

Ответ: ±54.

Пример 3. Решить
уравнение:

а) (x8)8=x;

б) (x13)13=x.

Стр. 14

Решение. а) Число 8 — четное, значит, данное
равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х
является решением (корнем) уравнения (x8)8=x.

б) Число 13 — нечетное, значит, данное равенство является тождеством при любом
значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R —
множество всех его корней.

Ответ: а) [0;+∞); б) R.

Пример 4. Решить
уравнение

Решение. Обозначим x6=t, тогда получим уравнение

Корни этого уравнения

Таким образом, имеем

откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).

Ответ: ±2.

1Какое число называется корнем n-й степени из
числа а?

2Сколько существует корней четной степени n
из положительного числа а?

3Корень какой степени существует из любого числа а?

4Какой корень n-й степени из числа а называется арифметическим?

5При каких значениях а верно равенство (an)n=a, если:

а) n — нечетное число;

б) n — четное число?

Упражнения

1. 24°

1.24°Используя определение арифметического корня n-й
степени, докажите, что:

1) 2564=4;

2) 102410=2;

3) 7296=3;

4) 65618=3;

5) 409612=2;

6) 14 6414=11.

1.24°

Стр. 15

1.25°

1.25°Верно ли, что:

1) число −4 является корнем четвертой степени из числа 256;

2) число −0,3 является корнем четвертой степени из числа −0,0081?

1.25°

1.26°

1.26°Верно ли, что:

1) −17283=−12;

2) −33753=15;

3) −16 8075=7;

4) −77765=−6?

1.26°

1.27°

1.27°Найдите арифметический квадратный корень из числа:

1) 16;

2) 49;

3) 0;

4) 1;

5) 0,81;

6) 0,25;

7) 2,25;

8) 1,21;

9) 36169;

10) 144289;

11) 169100;

12) 81256.

1.27°

1.28°

1.28°Найдите кубический корень из числа:

1) 1;

2) 0;

3) 343;

4) 8;

5) 127;

6) 0,027;

7) 0,001;

8) 64125.

1.28°

1.29°

1.29°Найдите арифметический корень четвертой степени из числа:

1) 0;

2) 1;

3) 16;

4) 0,0016;

5) 1681;

6) 256625;

7) 0,0001;

8) 0,1296.

1.29°

Вычислите (1.30—1.42).

1.30°

1.30°1) 9,16,25,49,81,100;

2) 0,16,0,09,0,01,0,04,0,0025,0,0001;

3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;

4) 164,6254,10 0004,0,00814,0,000000164,24014;

5) 325,10245,2435,0,031255,100 0005,0,000015;

6) 646,7296,15 6256,40966,0,0466566,1 000 0006.

1.30°

1.31°

1.31°1) −10003;

2) −115;

3) −643;

4) −10245;

5) −1273;

6) −3433;

7) −272163;

8) −31255;

9) −0,000325.

1.31°

Стр. 16

1.32

1.321) ⎛⎝−33⎞⎠3;

2) ⎛⎝−145⎞⎠5;

3) ⎛⎝−307⎞⎠7;

4) ⎛⎝−1511⎞⎠11;

5) ⎛⎝−69⎞⎠9;

6) ⎛⎝−9915⎞⎠15.

1.32

1.33

1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;

2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.

1.33

1.34

1.341) ⎛⎝53⎞⎠6;

2) ⎛⎝0,14⎞⎠12;

3) ⎛⎝1125⎞⎠10;

4) ⎛⎝2136⎞⎠18;

5) ⎛⎝567⎞⎠21;

6) ⎛⎝239⎞⎠36.

1.34

1.35

1.351) ⎛⎝35⎞⎠10;

2) ⎛⎝534⎞⎠48;

3) ⎛⎝7610⎞⎠120;

4) ⎛⎝643⎞⎠12;

5) ⎛⎝108⎞⎠16;

6) ⎛⎝1294⎞⎠36.

1.35

1.36°

1.36°1) ⎛⎝10⎞⎠2;

2) ⎛⎝53⎞⎠3;

3) ⎛⎝−124⎞⎠4;

4) −1244;

5) ⎛⎝−35⎞⎠5;

6) ⎛⎝323⎞⎠3;

7) ⎛⎝−444⎞⎠4;

8) ⎛⎝−157⎞⎠7;

9) −5555;

10) ⎛⎝−36⎞⎠6;

11) ⎛⎝−229⎞⎠9;

12) −488.

1.36°

1.37°

1.37°1) 325+−83;

2) 6254−−1253;

3) 12−60,1253;

4) 1+100,00814;

5) 3164−4273;

6) −3383+2,25;

7) 83−643;

8) 164−643.

1.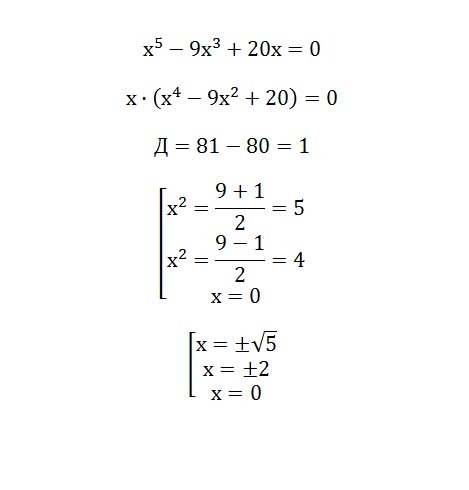 37°

1.38°

1.38°1) 9+4;

2) 36−164;

3) 0,81+0,0013;

4) 0,0273−0,04;

5) 5−2564;

6) 7+83;

7) −325+164;

8) −273+814.

1.38°

1.39°

1.39°1) (1−2)⎛⎝1+2⎞⎠;

2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;

3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;

4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;

5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;

6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.

1.39°

Стр. 17

1.40

1.401) 1225244⋅15−1382−2323;

2) 58+442−26235;

3) 90+31⎛⎝572−262⎞⎠83;

4) 2364+⎛⎝482−3225⎞⎠−13.

1.40

1.41

1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;

2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;

3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;

4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).

1.41

1.42

1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;

2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;

3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;

4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.

1.42

Найдите естественную область определения выражения (1.43—1.44).

1.43

1.431) x+4;

2) −9+2×4;

3) 5×2−6×10;

4) 8x−4×212;

5) x+33;

6) x−75;

7) x2−47;

8) 2×2−329.

1.43

1.44

1.441) 34x−112;

2) −48x−314;

3) 2−59−5×8;

4) 3−1016−7×6;

5) 2+x4−2(8−6x)3;

6) 12−6×2−7x+(3x−1)·25;

7) −x22(x−2)−5⎛⎝1−3x)−24;

8) 3(x+4)−6(2−x)+9×428.

1.44

Стр. 18

1.45

1.45Найдите длину ребра куба, если его объем равен:

1) 27 см³;

2) 64 мм³;

3) 0,125 дм³;

4) 0,216 м³.

1.45

Решите уравнение (1.46—1.54).

1.46°

1.46°1) x2=0,49;

2) x2=121;

3) x3=0,008;

4) x3=1000;

5) x3=−64 000;

6) x3=216;

7) x4=0,0625;

8) x4=−16.

1.46°

1.47

1.471) x3=−27;

2) x5=−132;

3) x7=−1;

4) x9=−512;

5) x3=−0,027;

6) x11=0.

1.47

1.48°

1.48°1) x2=11;

2) x4=19;

3) x8=27;

4) x3=25;

5) x7=38;

6) x9=−2;

7) x15=−6;

8) x17=4;

9) x13=−13.

1.48°

1.49

1.491) x2=25 600;

2) x2=0,0196;

3) x2+1=1,0016;

4) 5×2−20=0;

5) x2+25=0;

6) x2+179=0;

7) x2·4=0;

8) −6×2=0;

9) 113×2−12=0;

10) 13×2−1=0.

1.49

1.50

1.501) 4×3+4125=0;

2) 8×3+27=0;

3) −0,1×4=−0,00001;

4) 16×4−81=0;

5) 12×5+16=0;

6) 132×6−2=0.

1.50

1.51

1.511) x4+2=7;

2) x5−3=30;

3) x6−7=19;

4) x3+5=5.

1.51

1.52

1.521) (x+1)4=16;

2) (x−2)6=64;

3) (2x+1)3=27;

4) (3x−1)5=32.

1.52

1. 53

1.531) x10−31×5−32=0;

2) x8−15×4−16=0;

3) x4−12×2+27=0;

4) x6−7×3−8=0;

5) x8−82×4+81=0;

6) x4+2×2−15=0.

1.53

Стр. 19

1.54

1.541)° (x6)6=x;

2)° (x10)10=x;

3)° (x3)3=x;

4)° (x5)5=x;

5) ⎛⎝x−14⎞⎠4=x−1;

6) ⎛⎝x+212⎞⎠12=x+2;

7) ⎛⎝1×7⎞⎠7=1x;

8) ⎛⎝1x−211⎞⎠11=1x−2.

1.54

Степенная функция, линейная функция, квадратичная, кубическая и y=1/х 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 14.

Функция y=xⁿ , четные и нечетные функции.

Сравним значения функции fx=18×4-x2 при двух противоположных значениях аргумента, например x=3 и x=-3:

f3=18∙34-32=18∙81-9=118

f-3=18∙(-3)4-(-3)2=18∙81-9=118

Получим f3=f-3.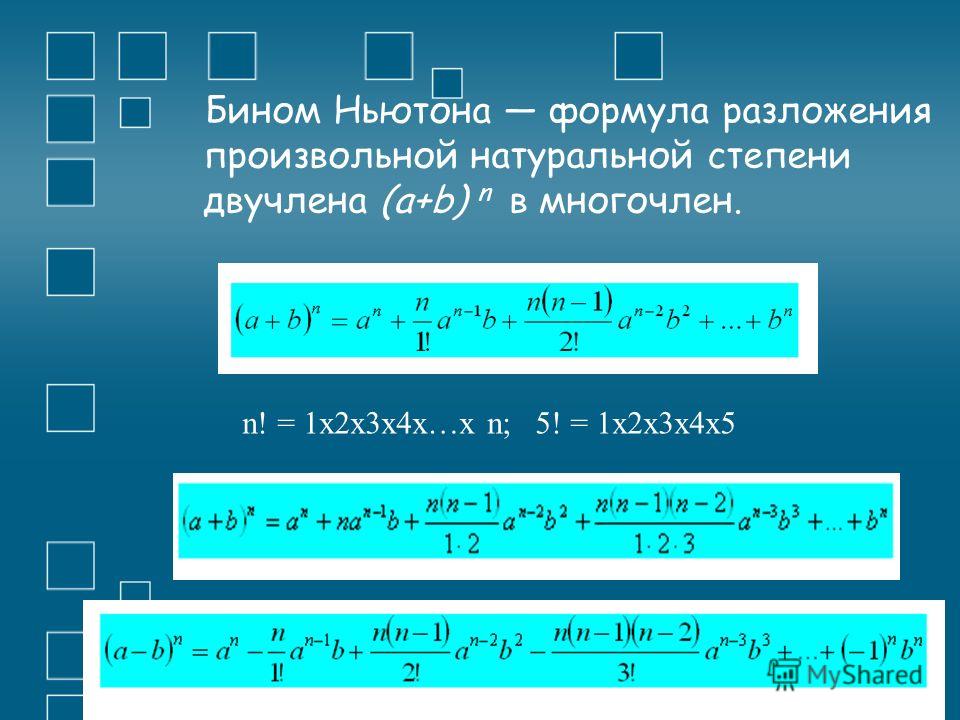 Значения этой функции равны и при любых других противоположных значениях аргумента. Действительно,

f-x=18∙(-x)4-(-x)2=18∙x4-x2, то есть

f-x=fx

При этом рассматриваемая функция такова, что для каждого значения аргумента х противоположное ему число (–х) так же принадлежит ее области определения. В таких случаях говорят, что область определения функции симметрична относительно нуля.

Функции, обладающие такими свойствами, называют четными функциями.

Определение: Функция y=fx называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство

f-x=fx

График любой четной функции симметричен относительно оси ординат.

Определение: Функция y=fx называется нечетной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство

f-x=-fx

Заметим, что не всякая функция является четной или нечетной.

График любой нечетной функции симметричен относительно начала координат.

Давай проверим на четность и нечетность функции:

fx=3×4-x2+5

Для этого подставим в нашу функцию вместо переменной х (-х), получим:

f-x=3(-x)4—x2+5=3×4-x2+5

Значит, f-x=fx, следовательно, функция является четной.

fx=x2+x+1

f-x=(-x)2+(-x)+1=x2-x+1

Эта функция является ни четной, ни нечетной.

Свойства функции y = xⁿ при четном n аналогичны свойствам функции y = x².

Степенные функции при n=1, 2 и 3, то есть функции y=x, y = x², y = x³ тебе уже знакомы. Их свойства и графики нам известны.

Выясним теперь свойства степенной функции и особенности ее графика при любом натуральном n.

Рассмотрим случай, когда n – четное число.

Свойства функции y = xⁿ при четном n аналогичны свойствам функции y = x².

Выражение xⁿ, где n – натуральное число, имеет смысл при любом x. Поэтому областью определения функции является множество всех действительных чисел.

Область значений функции есть множество неотрицательных чисел.

Если х=0, то у=0. График функции проходит через начало координат.

Если Если x ≠ 0, то y > 0. Это следует из того, что четная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях.

Функция является четной, график функции симметричен относительно оси ординат.

Функция возрастает в промежутке 0;+∞) и убывает в промежутке (-∞;0.

Рассмотрим теперь случай, когда n – нечетное число.

Свойства функции y = xⁿ при нечетном n аналогичны свойствам функции y = x³.

По графику этой функции перечислим ее свойства.

Выражение xⁿ, где n – натуральное число, имеет смысл при любом x. Поэтому областью определения функции является множество всех действительных чисел.

Область значений функции есть множество всех действительных чисел.

Если х=0, то у=0. График функции проходит через начало координат.

Если x > 0, то y > 0, если x < 0, то y < 0 График функции расположен в первой и третьей координатных четвертях

Функция является нечетной. График функции симметричен относительно начала координат.

Функция возрастает на всей области определения.

Определение степени и ведущего коэффициента многочленов

Только что найденная формула является примером полинома , который представляет собой сумму или разность членов, каждый из которых состоит из переменной, возведенной в неотрицательную целую степень. {2} + {a} _ {1} x + {a} _ {0 } [/ latex]

Каждое действительное число a _i называется коэффициентом .{i} [/ latex] — это член полинома . Наивысшая степень переменной, входящей в полином, называется степенью полинома . Старший член — это член с наивысшей степенью, а его коэффициент называется старшим коэффициентом .

Практическое руководство. Для данного полиномиального выражения определите степень и старший коэффициент.

Найдите наибольшую степень x , чтобы определить градус.

Определите член, содержащий наибольшую степень x , чтобы найти главный член.3 6 Решить для? cos (x) = 1/2 7 Решить относительно x sin (x) = — 1/2 8 Преобразование из градусов в радианы 225 9 Решить для? cos (x) = (квадратный корень из 2) / 2 10 Решить относительно x cos (x) = (квадратный корень из 3) / 2 11 Решить относительно x sin (x) = (квадратный корень из 3) / 2 12 График г (x) = 3/4 * корень пятой степени x 13 Найдите центр и радиус х ^ 2 + у ^ 2 = 9 14 Преобразование из градусов в радианы 120 градусов 15 Преобразование из градусов в радианы 180 16 Найдите точное значение желто-коричневый (195) 17 Найдите степень е (х) = 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2 18 Решить для? tan (x) = квадратный корень из 3 19 Решить для? sin (x) = (квадратный корень из 2) / 2 20 Найдите центр и радиус х ^ 2 + у ^ 2 = 25 21 Найдите центр и радиус х ^ 2 + у ^ 2 = 4 22 Решить относительно x 2cos (x) -1 = 0 23 Решить относительно x 6x ^ 2 + 12x + 7 = 0 24 Найдите домен х ^ 2 25 Найдите домен е (х) = х ^ 2 26 Преобразование из градусов в радианы 330 градусов 27 Разверните логарифмическое выражение натуральный логарифм от (x ^ 4 (x-4) ^ 2) / (квадратный корень из x ^ 2 + 1) 28 Упростить ((3x ^ 2) ^ 2y ^ 4) / (3y ^ 2) 29 Упростить (csc (x) кроватка (x)) / (sec (x)) 30 Решить для? tan (x) = 0 31 Решить относительно x х ^ 4-3x ^ 3-х ^ 2 + 3x = 0 32 Решить относительно x cos (x) = sin (x) 33 Найдите точки пересечения x и y х ^ 2 + у ^ 2 + 6х-6у-46 = 0 34 Решить относительно x квадратный корень из x + 30 = x 35 Упростить детская кроватка (x) коричневый (x) 36 Найдите домен у = х ^ 2 37 Найдите домен квадратный корень из x ^ 2-4 38 Найдите точное значение грех (255) 39 Оценить бревно, база 27 из 36 40 Преобразовать из радианов в градусы 2п 41 Упростить (F (x + h) -Fx) / час 42 Решить для? 2sin (x) ^ 2-3sin (x) + 1 = 0 43 Решить относительно x tan (x) + квадратный корень из 3 = 0 44 Решить относительно x sin (2x) + cos (x) = 0 45 Упростить (1-cos (x)) (1 + cos (x)) 46 Найдите домен х ^ 4 47 Решить для? 2sin (x) + 1 = 0 48 Решить относительно x х ^ 4-4x ^ 3-х ^ 2 + 4x = 0 49 Упростить 9 / (х ^ 2) + 9 / (х ^ 3) 50 Упростить (детская кроватка (x)) / (csc (x)) 51 Упростить 1 / (с ^ (3/5)) 52 Упростить квадратный корень из 9a ^ 3 + квадратный корень из 53 Найдите точное значение желто-коричневый (285) 54 Найдите точное значение cos (255) 55 Преобразовать в логарифмическую форму 12 ^ (x / 6) = 18 56 Разверните логарифмическое выражение (основание 27 из 36) (основание 36 из 49) (основание 49 из 81) 57 Найдите недвижимость x ^ 2 = 12 лет 58 Найдите недвижимость х ^ 2 + у ^ 2 = 25 59 График f (x) = — натуральный логарифм x-1 + 3 60 Найдите значение, используя единичную окружность арксин (-1/2) 61 Найдите домен корень квадратный из 36-4x ^ 2 62 Упростить (корень квадратный из x-5) ^ 2 + 3 63 Решить относительно x х ^ 4-2x ^ 3-х ^ 2 + 2x = 0 64 Решить относительно x у = (5-х) / (7х + 11) 65 Решить относительно x х ^ 5-5x ^ 2 = 0 66 Решить относительно x cos (2x) = (квадратный корень из 2) / 2 67 График г = 3 68 График f (x) = — логарифм по основанию 3 из x-1 + 3 69 Найдите корни (нули) f (x) = 3x ^ 3-12x ^ 2-15x 70 Найдите степень 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2 71 Решить относительно x квадратный корень из x + 4 + квадратный корень из x-1 = 5 72 Решить для? cos (2x) = — 1/2 73 Решить относительно x основание журнала x 16 = 4 74 Упростить е ^ х 75 Упростить (cos (x)) / (1-sin (x)) + (1-sin (x)) / (cos (x)) 76 Упростить сек (x) sin (x) 77 Упростить кубический корень из 24 кубический корень из 18 78 Найдите домен квадратный корень из 16-x ^ 2 79 Найдите домен квадратный корень из 1-x 80 Найдите домен у = грех (х) 81 Упростить квадратный корень из 25x ^ 2 + 25 82 Определить, нечетно ли, четно или нет е (х) = х ^ 3 83 Найдите домен и диапазон f (x) = квадратный корень из x + 3 84 Найдите недвижимость x ^ 2 = 4y 85 Найдите недвижимость (x ^ 2) / 25 + (y ^ 2) / 9 = 1 86 Найдите точное значение cos (-210) 87 Упростить кубический корень из 54x ^ 17 88 Упростить квадратный корень из квадратного корня 256x ^ 4 89 Найдите домен е (х) = 3 / (х ^ 2-2x-15) 90 Найдите домен квадратный корень из 4-x ^ 2 91 Найдите домен квадратный корень из x ^ 2-9 92 Найдите домен е (х) = х ^ 3 93 Решить относительно x e ^ x-6e ^ (- x) -1 = 0 94 Решить относительно x 6 ^ (5x) = 3000 95 Решить относительно x 4cos (x-1) ^ 2 = 0 96 Решить относительно x 3x + 2 = (5x-11) / (8y) 97 Решить для? sin (2x) = — 1/2 98 Решить относительно x (2x-1) / (x + 2) = 4/5 99 Решить относительно x сек (4x) = 2 100 Решите для n (4n + 8) / (n ^ 2 + n-72) + 8 / (n ^ 2 + n-72) = 1 / (n + 9)

Алгебра — многочлены

Показать мобильное уведомление

Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 1-4: Многочлены

В этом разделе мы начнем рассматривать полиномы.{23}} \ hspace {0,5 дюйма} & \ hspace {0,5 дюйма} & {\ mbox {степень:}} \, \, 23 \\ & 5x — 7 & \ hspace {0,5 дюйма} & {\ mbox {степень :}} \, \, 1 \\ & — 8 & \ hspace {0,5 дюйма} & {\ mbox {степень:}} \, \, 0 \ end {align *} \]

Итак, многочлен не обязательно должен содержать все степени \ (x \), как мы видим в первом примере. Кроме того, полиномы могут состоять из одного члена, как мы видим в третьем и пятом примерах. 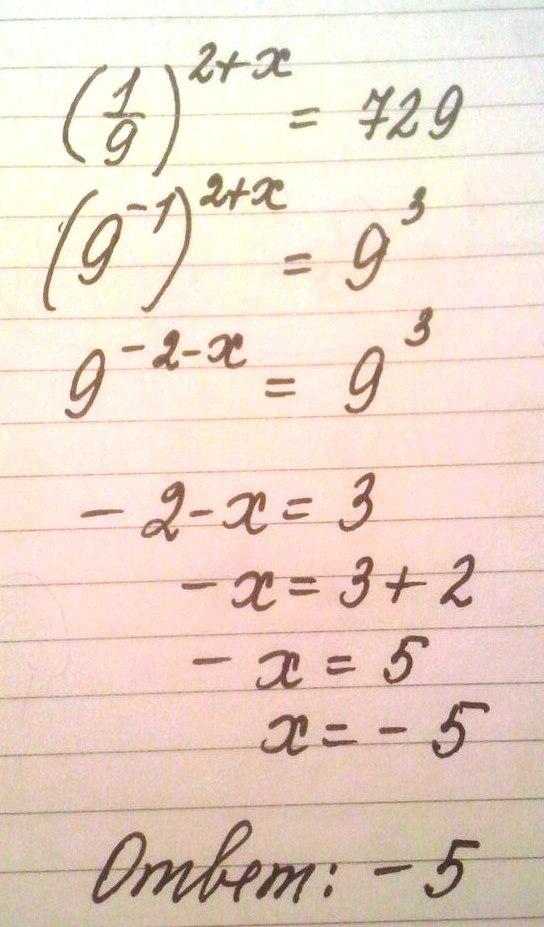m} \).3} + 3x — 11y & \ hspace {0,5 дюйма} & {\ mbox {степень: 14}} \ end {align *} \]

В полиномах такого типа не каждый член должен содержать в себе как \ (x \), так и \ (y \), на самом деле, как мы видим в последнем примере, им не нужно иметь никаких терминов, которые содержат как \ (x \), так и \ (y \). Кроме того, степень полинома может быть получена из членов, содержащих только одну переменную. Также обратите внимание, что несколько терминов могут иметь одинаковую степень.

Мы также можем говорить о многочленах от трех переменных, четырех переменных или любого количества переменных, которое нам нужно.Подавляющее большинство полиномов, которые мы увидим в этом курсе, являются полиномами от одной переменной, поэтому большинство примеров в оставшейся части этого раздела будут полиномами от одной переменной.

Далее нам нужно избавиться от некоторой терминологии. Моном — это многочлен, состоящий ровно из одного члена. Бином — это многочлен, состоящий ровно из двух членов. Наконец, трехчлен — это многочлен, состоящий ровно из трех членов.Мы будем использовать эти термины время от времени, так что вы, вероятно, должны хотя бы немного с ними ознакомиться.

Теперь нам нужно поговорить о сложении, вычитании и умножении многочленов. Обратите внимание, что мы не учли деление многочленов. Это будет обсуждаться в следующем разделе, где мы будем довольно часто использовать деление многочленов.

Прежде чем фактически начать это обсуждение, мы должны вспомнить закон распределения. Это будет многократно использоваться в оставшейся части этого раздела.2} — 9x + 4} \ right) \]

В этом случае скобки не требуются, поскольку мы складываем два многочлена. Они существуют просто для того, чтобы прояснить операцию, которую мы выполняем. Чтобы сложить два полинома, все, что мы делаем, это , объединяем аналогичные термины . 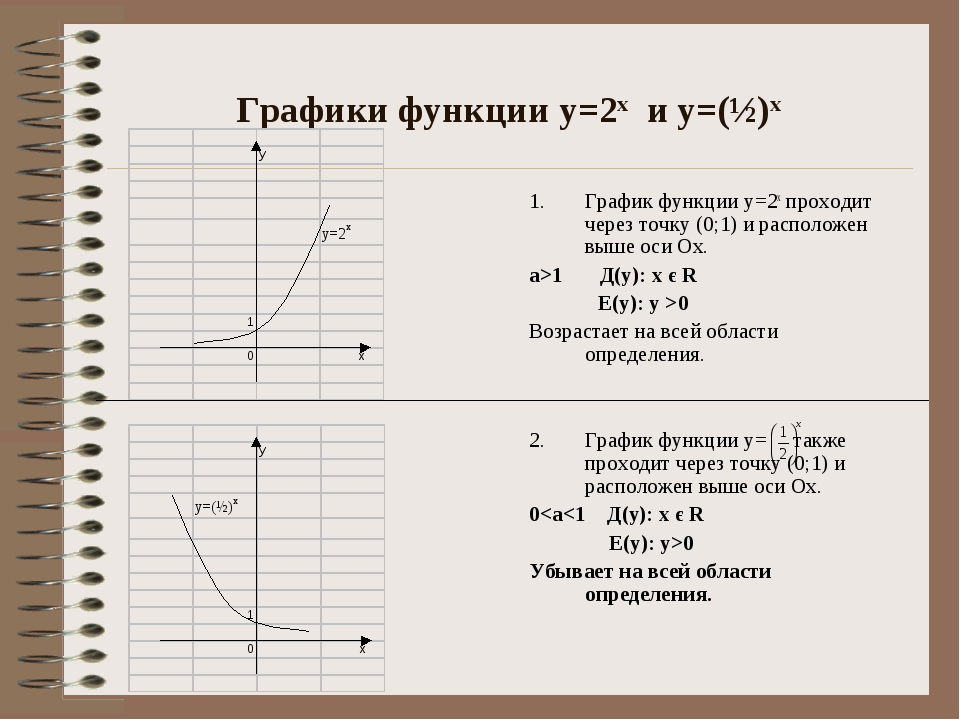2} + x + 1 \).2} + x — 3} \ right) \]

На этот раз скобки вокруг второго члена обязательны. Мы вычитаем весь многочлен, и скобки должны быть там, чтобы убедиться, что мы действительно вычитаем весь многочлен.

При выполнении вычитания первое, что мы сделаем, это поставим знак минус через круглые скобки. Это означает, что мы изменим знак у каждого члена второго многочлена. Обратите внимание, что все, что мы на самом деле здесь делаем, это умножение «-1» на второй многочлен, используя закон распределения.2} \ end {align *} \]

Это очень распространенные ошибки, которые студенты часто совершают, когда только начинают учиться умножать многочлены.

Примеры одночленов и многочленов

Одночлен — это выражение в алгебре, содержащее один член, например 3xy. Мономы включают: числа, целые числа и переменные, которые умножаются вместе, и переменные, которые умножаются вместе. Многочлен — это сумма одночленов, где каждый одночлен называется термом.

Идентификация монома

Любое число само по себе является мономом, например 5 или 2700. Моном также может быть переменной, например «m» или «b». Это также может быть их комбинация, например 98b или 78xyz. Он не может иметь дробную или отрицательную экспоненту. Это не одночлены: 45x + 3, 10 — 2a или 67a — 19b + c.

Два правила о мономах:

Моном, умноженный на одночлен, также является одночленом.
Моном, умноженный на константу, также является одночленом.

Рассматривая примеры одночленов, вы должны понимать различные виды многочленов. Ниже приводится объяснение многочленов, двучленов, трехчленов и степеней многочлена.

Полиномы

Многочлен — это алгебраическое выражение с конечным числом членов. Эти термины имеют форму «axn», где «a» — действительное число, «x» означает умножение, а «n» — неотрицательное целое число. Примеры: 7a2 + 18a — 2, 4m2, 2×5 + 17×3 — 9x + 93, 5a-12 и 1273.

Биномы

Бином — это многочлен с двумя членами. 3x + 1, 2×3 — 5x, x4 — 4, x — 19 — примеры биномов.

Трехчлены

Трехчлен — это многочлен с тремя членами. Примеры трехчленов: 2×2 + 4x — 11, 4×3 — 13x + 9, 7×3 — 22×2 + 24x и 5×6 — 17×2 + 97.

Степени многочленов

Степень полинома — это наивысшая степень переменной в этом полиноме, если есть только одна переменная. Степень многочлена 7×3 — 4×2 + 2x + 9 равна 3, потому что наибольшая степень переменной «x» равна 3.В 18s12 — 41s5 + 27 степень равна 12. Степень этого многочлена 8z + 2008 равна 1, потому что «z» находится в первой степени.

Если многочлен имеет более одной переменной, то степень этого одночлена равна сумме показателей этих переменных. В этом многочлене 24xyz степень равна 3, потому что сумма степеней x, y и z равна 1 + 1 + 1 = 3. Степень этого многочлена 12x4y2z7 равна 13, потому что 4 + 2 + 7 = 13. 14×3 + 27xy — y имеет степень 6, потому что 3 + 1 + 1 + 1 = 6. Итак, по сути, вы складываете показатели переменных вместе.

Термины по алгебре

Поначалу это может показаться немного запутанным при просмотре примеров одночленов, двучленов и трехчленов. Это просто классификация разных многочленов с разным количеством членов. Многочлен второй степени также называется «квадратичным». Примеры: 4×2, x2 — 9 или 6×2 + 13x + c.

Ради интереса, полином третьей степени называется «кубикой», полином четвертой степени — «квартикой», а полином пятой степени — «квинтикой».

Вы можете задаться вопросом, откуда произошло слово «квадриатический», потому что приставка «квад» обычно означает четыре. Слово происходит от латинского слова «делать квадрат». Итак, в этом случае «четырехугольник» относится к четырем углам квадрата, например, когда вы умножаете шесть футов на шесть футов, вы получаете 36 квадратных футов.

История алгебры

Алгебра — это раздел чистой математики. Чистая математика отличается от других дисциплин, потому что она не обязательно применяется к какой-либо конкретной ситуации, но исследуются концепции и красота математики. Греки создали геометрическую алгебру, изображающую стороны предметов линиями и буквами. В III веке нашей эры Диофант, которого называют «отцом алгебры», написал несколько книг под названием Arithmetica . В них он объяснил, как решать алгебраические уравнения.

Слово «алгебра» на самом деле происходит от арабского и означает «восстановление». На самом деле алгебра началась с вавилонян, которые были продвинутыми математиками, имевшими дело с квадратными и линейными уравнениями. Другие цивилизации в то время все еще решали проблемы геометрически.

полиномов

Проект «Улучшение математического образования в школах» (TIMES)

вернуться к индексу

Предполагаемые знания

Мотивация

Полиномы представляют следующий уровень алгебраической сложности после квадратичных. В самом деле, квадратичный — это многочлен степени 2. Мы можем разложить квадратные выражения на множители, решить квадратные уравнения и построить график квадратичных функций; возникает очевидный вопрос:
, как эти вещи могут быть выполнены с помощью алгебраических выражений более высокой степени.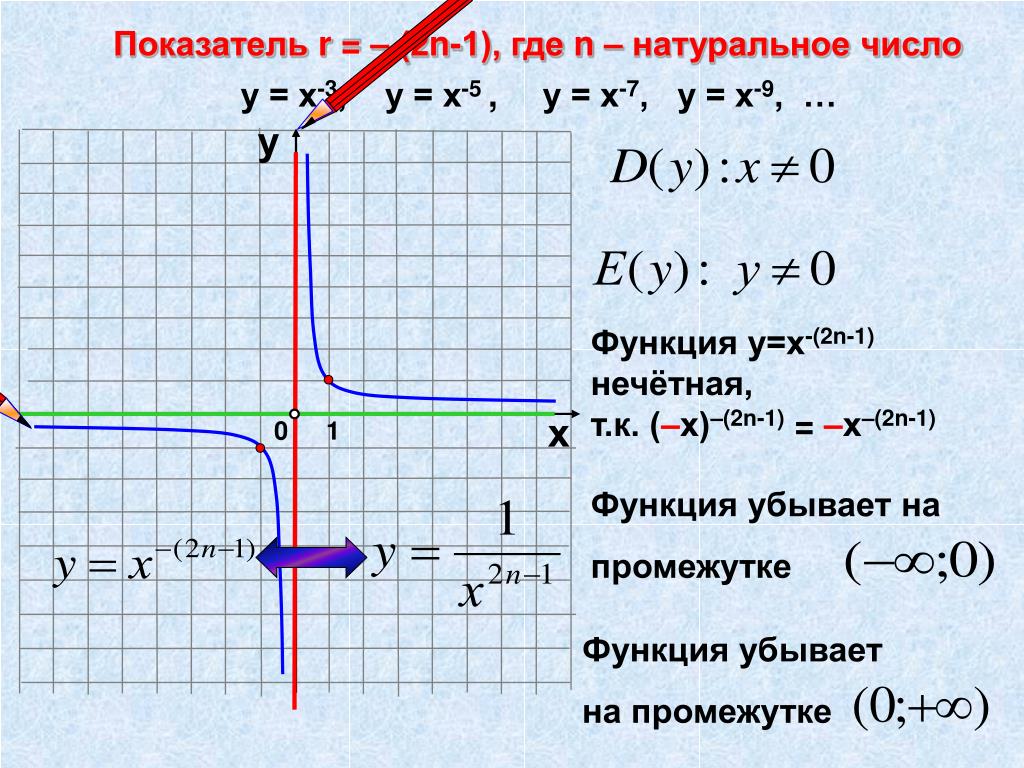

Квадратичный x2 — 5x + 6 множится как (x — 2) (x — 3). Следовательно, уравнение x2 — 5x + 6 = 0
имеет решения x = 2 и x = 3.

Аналогичным образом мы можем разложить на множители кубику x3 — 6×2 + 11x — 6 как (x — 1) (x — 2) (x — 3), что позволяет нам показать, что решения x3 — 6×2 + 11x — 6 = 0 являются x = 1, x = 2 или x = 3. В этом модуле мы увидим, как получить эту факторизацию.

Полиномы во многих отношениях ведут себя как целые или целые числа. Мы можем складывать, вычитать и умножать два или более многочлена вместе, чтобы получить еще один многочлен.Так же, как мы можем разделить одно целое число на другое, получая частное и остаток, мы можем разделить один многочлен на другой и получить частное и остаток, которые также являются многочленами.

Квадратное уравнение вида ax2 + bx + c имеет 0, 1 или 2 решения, в зависимости от того, какой дискриминант отрицательный, нулевой или положительный. Количество решений этого уравнения помогло нам построить график квадратичной функции y = ax2 + bx + c. Точно так же информация о корнях полиномиального уравнения позволяет нам дать грубый набросок соответствующей полиномиальной функции.

Помимо того, что полиномы являются интересными по своей сути объектами, они имеют важные приложения в реальном мире. Одно из таких приложений для кодов исправления ошибок обсуждается в Приложении к этому модулю.

Содержимое

Терминология

Многочлен — это такое выражение, как x5 — 2×3 + 8x + 3 или x4 — x2 + 1. Может быть любое количество членов, но каждый член должен быть кратным степени целого числа x. Таким образом, 2×3 — x не является многочленом.

Член с наибольшей степенью называется старшим членом, а его коэффициент — старшим коэффициентом. Если старший коэффициент равен 1, то многочлен называется моническим. Индекс главного члена называется степенью полинома. Термин, не зависящий от, называется постоянным членом.

Таким образом, x5 — 2×3 + 8x + 3 является моническим многочленом степени 5 с постоянным членом 3, а
x4 — x2 + 1 является немоническим многочленом степени 4 со старшим коэффициентом и постоянным членом 1.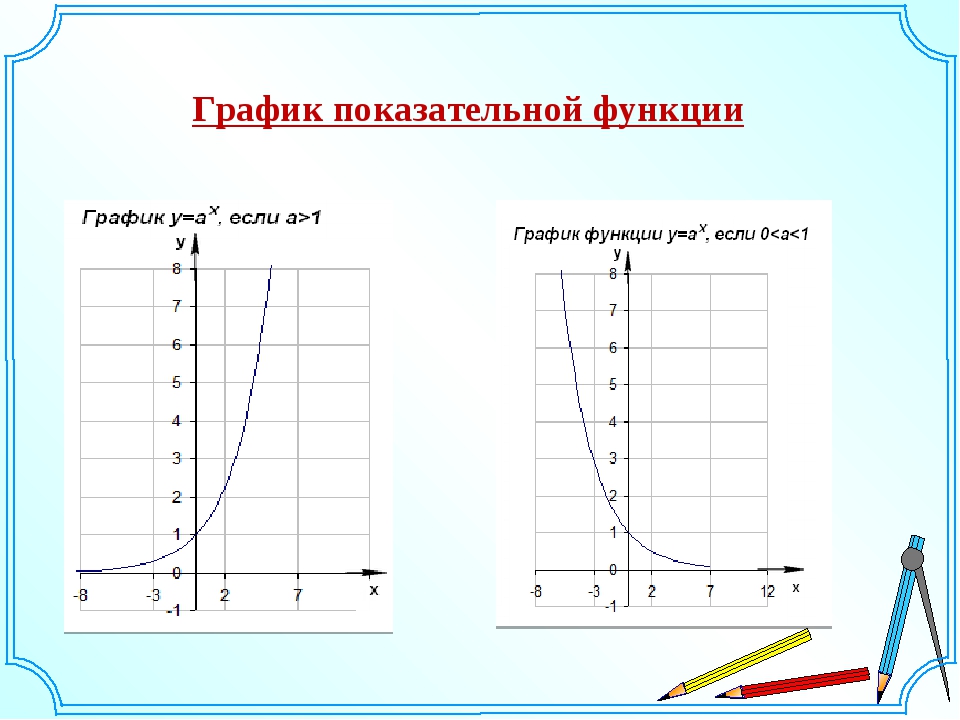

В первом полиноме все коэффициенты являются целыми числами, а во втором полиноме есть иррациональный коэффициент. По большей части мы будем рассматривать только многочлены первого типа, но многое из того, что следует ниже, одинаково хорошо применимо и ко второму.

Для именования полиномов мы будем использовать обозначение функций, например p (x) или q (x). Таким образом, мы можем записать p (x) = x5 — 2×3 + 8x + 3 или q (x) = x4 — x2 + 1. Это позволяет нам удобно подставлять значения x, когда это необходимо.

Общий многочлен имеет вид

p (x) = тревога — an — 1xn — 1 + … + a1x + a0,

, где 0, а n — целое число. Коэффициенты, как правило, являются действительными числами.

УПРАЖНЕНИЕ 1

Запишите главный член, старший коэффициент, степень и постоянный член в приведенном выше общем полиноме.

Для полиномов малой степени мы используем следующие имена.

полином степени 1 называется линейным
полином степени 2 называется квадратичным
полином степени 3 называется кубикой
полином четвертой степени называется квартикой
полином 5-й степени называется квинтикой

Многочлен, состоящий только из ненулевой константы, называется постоянным многочленом и имеет степень 0. Многочлен p (x) = 0 называется нулевым многочленом.В нем нет терминов, и поэтому нет ведущего термина. Лучше не определять степень нулевого многочлена. В некоторых книгах его степень обозначается как −1 или −∞.

Сложение, вычитание и умножение многочленов

Чтобы сложить или вычесть два многочлена, мы собираем одинаковые члены.

Обратите внимание, что мы обычно пишем члены многочлена от наибольшей к наименьшей степени. Иногда это называют стандартной формой многочлена.

Чтобы умножить два полинома, мы умножаем каждый член в первом полиноме на второй полином и собираем похожие члены.

ПРИМЕР

Многочлены P (x), Q (x) и R (x) задаются формулами P (x) = x3 — 2×2 + x — 1, Q (x) = 3×3 — 2×2 и R (x) = −x4 + 2×3 — 3×2. Находят:

а P (x) Q (x) b Q (x) R (x)

Решение

	P (x) Q (x)	= (x3 — x2 + x — 1) (3×3 — 2×2)
		= x3 (3×2 — 2×2) — x2 (3×3 — 2×2) + x (3×3 — 2×2) — (3×3 — 2×2)
		= 3×6 — 2×5 — 3×5 + 2×4 + 3×4 — 2×3 — 3×3 + 2×2
		= 3×6 — 5×5 + 5×4 — 5×3 + 2×2

б	Q (x) R (x)	= (3×3 — 2×2) (- x4 + 2×3 — 3×2)
		= 3×3 (−x4 + 2×3 — 3×2) — 2×2 (−x4 + 2×3 — 3×2)
		= −3×7 + 6×6 — 9×5 + 2×6 — 4×5 + 6×4
		= −3×7 + 8×6 — 13×5 + 6×4

Делительные многочлены

При делении одного целого числа на другое образуется частное и остаток. Таким образом дает 7 остаток 2. Есть разные способы записать этот результат.

37 ÷ 5 равно 7 остаток 2
37 ÷ 5 = 7
37 = 7 × 5 + 2

В выписке 37 ÷ 5 равно 7, остаток 2

число 5, на которое мы делим, называется делителем
число 37, на которое мы делим, называется делимым
число 7 называется частным
число 2 называется остатком

Ключевым моментом в отношении остатка является то, что он неотрицателен, но строго меньше делителя.Таким образом, используя третье представление, когда мы разделим два целых числа p и d> 0, мы можем написать

p = dq + r, где 0 ≤ r ≤ d.

Если остаток равен нулю, то мы говорим, что d является множителем p.

Эти основные утверждения, касающиеся арифметики, имеют аналоги, когда мы начинаем делить один многочлен на другой. Мы будем использовать ту же терминологию при обсуждении полиномиального деления. Это делается по образцу деления в столбик.

Деление многочлена p (x) на многочлен d (x) также дает частное q (x) и остаток r (x), поэтому мы можем записать

п (х) = d (х) q (х) + г (х).

Ключевой идеей при выполнении деления является продолжение работы с ведущими терминами, как показано в следующем примере.

ПРИМЕР

Мы разделим многочлен p (x) = 5×4 −7×3 + 2x — 4 на многочлен d (x) = x — 2, а затем выразим деление в виде p (x) = d (x) q (x ) + г (х).

Решение

	5×3	+	3×2	+	6x	+	14
х — 2	5×4	–	7×3			+	2x	–	4	(Разделите x на 5×4, получив 5×3. )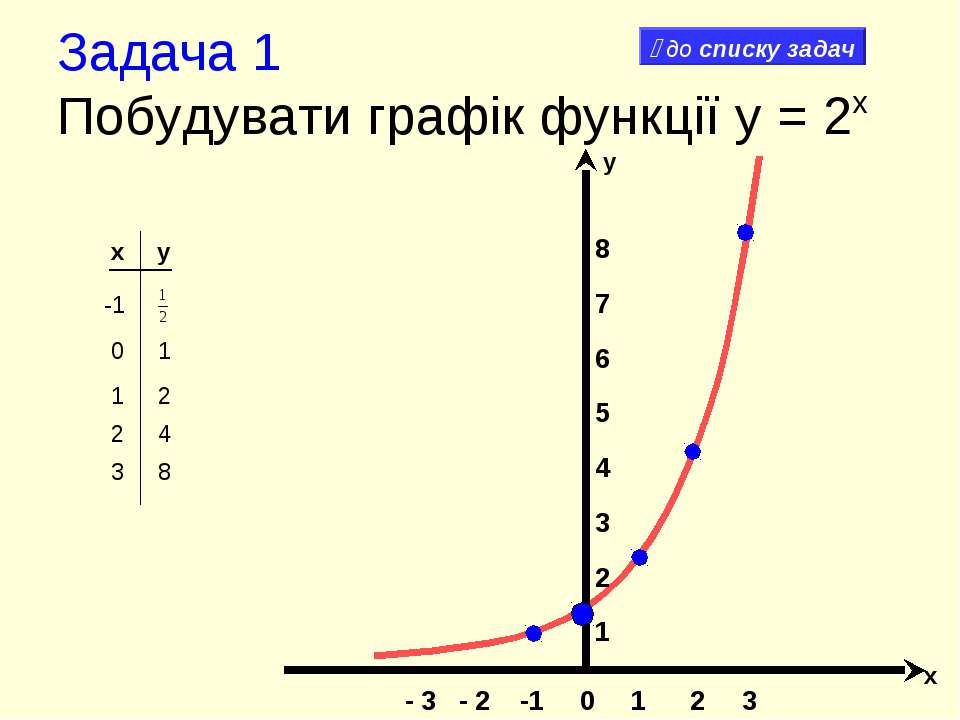
	5×4	–	10×3							(Умножьте x — 2 на 5×3, а затем вычтите.)
			3×3			+	2x	–	4	(Разделите x на 3×3, получив 3×2.)
			3×3	–	6×2					(Умножьте x — 2 на 3×2, а затем вычтите. )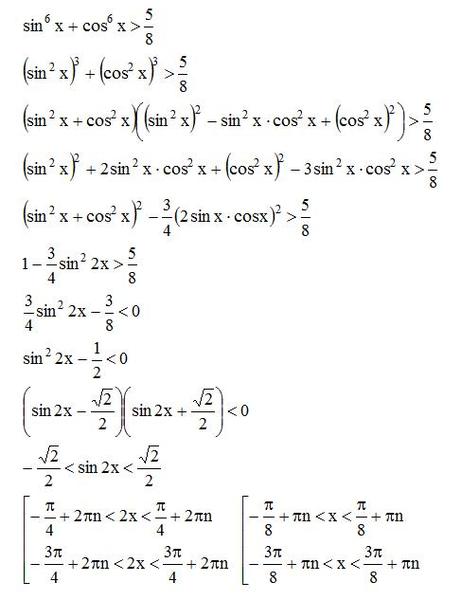
					6×2	+	2x	–	4	(Разделите x на 6×2, получив 6x.)
					6×2	–	12x			(Умножьте x — 2 на 6x, а затем вычтите.)
							14x	–	4	(Разделите x на 14x, получим 14. )
							14x	–	28	(Умножьте x — 2 на 14, а затем вычтите.)
									24	(Это последний остаток.)

Отсюда 5×4 — 7×3 + 2x — 4 = (x — 2) (5×3 + 3×2 + 6x + 14) + 24. 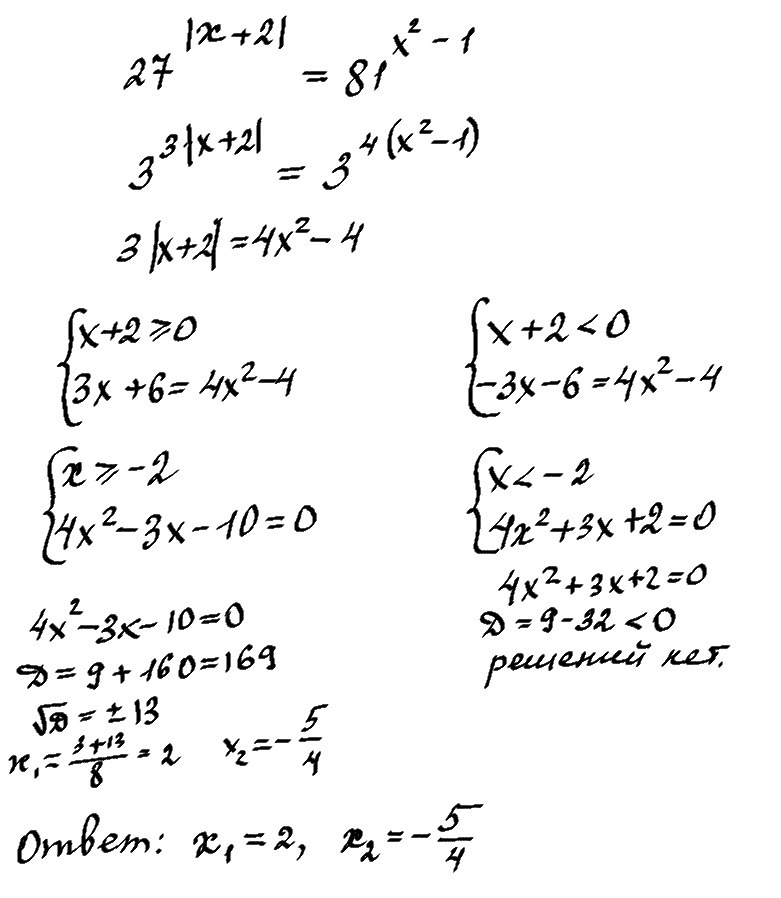(1)

В этом примере мы видим, что частное q (x) = 5×3 + 3×3 + 6x — 14, а остаток равен r (x) = 24.

Мы можем выполнить частичную проверку, подставив x = 2 в последнюю строку.

Из приведенного выше примера видно, что степень остатка меньше степени делителя, так как в противном случае мы могли бы продолжить деление.Таким образом, в случае линейного множителя остаток будет константой, и мы можем записать его как.

В общем, теперь мы можем написать p (x) = d (x) q (x) + r (x), где r (x) = 0, или, 0 ≤ степень (r (x)) <степень (d (Икс)).

УПРАЖНЕНИЕ 3

Разделите p (x) = 5×4 — 7×3 + 2x — 4 на d (x) = x2 — 2. Выразите результат в виде
p (x) = d (x) q (x) + r (x), где степень r (x) меньше степени d (x).

Обратите внимание, что в этом случае, поскольку делитель имеет степень 2, остаток будет либо равен 0, либо иметь степень не выше 1.

Теорема об остатке

Деление многочленов в длину — громоздкий процесс, и в некоторых случаях нас интересует только остаток. Это не появляется до конца вычислений. Когда мы делим многочлен p (x) на линейный множитель (x — a), мы можем довольно легко найти остаток.

Поскольку делитель линейный, p (x) = (x — a) q (x) + r, где r — постоянная. Подставляя x = a в обе части, получаем r = p (a).

Таким образом, остаток равен полиному, вычисленному при x = a.

Этот удивительный результат называется теоремой об остатке. Мы должны иметь в виду, что он вообще ничего не говорит о частном q (x) и работает только тогда, когда мы делим на линейный множитель (x — a).

УПРАЖНЕНИЕ 4

Многочлен p (x) = x5 — 7×3 + ax + 1 имеет остаток 13 после деления на x — 1. Найдите значение коэффициента a.

Фактор теорема

Квадратичное разложение на множители — важный метод, который мы использовали для решения квадратных уравнений.Подобным образом мы хотели бы разработать некоторые методы факторизации многочленов.

Если линейный многочлен (x — a) является множителем многочлена p (x), то мы можем записать
p (x) = q (x) (x — a) и, таким образом, остаток от деления p (x) by (x — a) равно 0.
Используя теорему об остатке, мы доказали:

Теорема

(x — a) является множителем многочлена p (x), если p (a) = 0. Если p (a) ≠ 0, то

(x — a) не является множителем p (x).

Число a, которое дает p (a) = 0, называется нулем многочлена.

Обратите внимание, что, поскольку (x — 2) и (x — 1) являются множителями p (x), то и их произведение равно
(x — 2) (x — 1) = x2 — 3 x + 2. Таким образом, мы могли бы найти третий множитель путем деления в столбик.
Деление p (x) на x2 — 3x + 2 дает (x — 3) в качестве третьего множителя, и поэтому мы получаем
после факторизации,

p (x) = x3 — 6×2 + 11x — 6 = (x — 1) (x — 2) (x — 3).

Альтернативный метод

Поскольку p (2) = 0 и p (1) = 0, а p (x) имеет степень 3, мы можем записать p (x) = (x — 2) (x — 1) (x — a)

Где a — число, которое предстоит определить. Поскольку p (0) = −6, имеем −2a = −6, поэтому a = 3.

УПРАЖНЕНИЕ 5

Многочлен p (x) = 3×6 — 5×3 + ax2 + bx + 10 делится на x + 1 и x — 2. Найдите значения коэффициентов a и b.

Факторинговые многочлены

Наша цель — взять многочлен с целыми коэффициентами и записать его как произведение многочленов меньшей степени, которые также имеют целые коэффициенты. Этот процесс называется факторингом по целым числам.

Теорема о факторах позволяет нам проверить, имеет ли многочлен p (x) линейный фактор (x — a). Если это так, то мы можем использовать длинное деление, чтобы найти многочлен q (x) такой, что p (x) = (x — a) q (x) и q (x) имеет степень на единицу меньше, чем степень p (x ). Таким образом, мы сможем повторять процесс над q (x) и так далее как можно чаще, чтобы получить полную факторизацию p (x).

Например,

Начнем с полинома p (x) = x3 + 4×2 — 7x — 10.

Мы систематически ищем один линейный фактор, проверяя числа a = 1, — 1, 2, −2,…, пока не найдем целое значение a такое, что p (a) = 0.

p (1) = −12 ≠ 0, p (−1) = 0, поэтому (x + 1) факторный.

Затем мы используем длинное деление, чтобы разделить p (x) на (x + 1), чтобы получить p (x) = (x + 1) (x2 + 3x — 10).

Теперь квадратичная величина q (x) = x2 + 3x — 10 может быть разложена на множители, используя наши знания о квадратиках, как (x + 5) (x — 2), и поэтому полная факторизация p (x) равна

п (х) = (х + 1) (х + 5) (х — 2).

Чтобы помочь нам найти целое число нуль многочлена, мы используем следующий результат.

Теорема

Если многочлен

p (x) = тревога + an − 1xn − 1 +… + a1x + a0

имеет целое число ноль a, тогда a является множителем постоянного члена a0.

Таким образом, в приведенном выше примере единственными возможными целыми нулями являются ± 1, ± 2, ± 5 или ± 10.

УПРАЖНЕНИЕ 6

Объясните, почему приведенная выше теорема верна.

ПРИМЕР

Разложите многочлен p (x) = x4 — 2×3 — 8x + 16 на множители.

Решение

Нам нужно только проверить положительный и отрицательный множители 16.
P (1) = 1-2-8 + 16 ≠ 0, поэтому x — 1 не является множителем p (x).
P (−1) = 1 + 2 + 8 + 16 ≠ 0, поэтому x + 1 не является множителем p (x).
P (2) = 16-16-16 + 16 = 0, поэтому x — 2 является множителем.
После деления p (x) на x — 2, p (x) = (x — 2) (x3 — 8)
Пусть Q (x) = x3 — 8.
x — 1 и x + 1 не являются факторами Q (x), поскольку P (x) = (x — 2) Q (x), и они не являются факторами P (Икс).
Однако Q (2) = 8-8 = 0, поэтому x — 2 также является множителем Q (x).
После деления Q (x) на x — 2, Q (x) = (x — 2) (x2 + 2x + 4).
Квадратичный x2 + 2x + 4 не может быть разложен на множители, см. Ниже.
Следовательно, P (x) = (x — 2) 2 (x2 + 2x + 4) — полная факторизация P (x).

Обратите внимание, что квадратичный x2 + 2x + 4 = (x + 1) 2 + 3, который всегда больше или равен 3, следовательно, квадратичный не имеет множителей.

УПРАЖНЕНИЕ 7

Сначала удалите очевидный общий множитель, разложите на множители многочлен
p (x) = 2×5 — 22×4 + 78×3 — 90×2.

Полиномиальные уравнения

Одним из основных методов решения квадратных уравнений был метод факторизации. Точно так же одно из основных приложений факторизации многочленов — решение полиномиальных уравнений.

ПРИМЕР

Решить x3 + 4 x2 — 7x — 10 = 0

Решение

В предыдущем примере мы разложили многочлен
p (x) = x3 + 4 x2 — 7x — 10 = 0 как (x + 1) (x + 5) (x — 2).

Таким образом, уравнение x3 + 4 x2 — 7x — 10 = 0 принимает вид (x + 1) (x + 5) (x — 2) = 0

Поскольку произведение трех множителей равно нулю, мы можем приравнять каждый множитель к нулю, чтобы найти решения. Таким образом, x + 1 = 0 или x — 2 = 0, или x + 5 = 0, что дает x = −1, x = 2 или x = −5.

Примечание: полином p (x) = (x — 1) (x — 2) 2 (x — 4) 3 имеет степень 6, но полиномиальное уравнение (x — 1) (x — 2) 2 (x — 4) 3 = 0 имеет только 3 (различных) решения x = 1 или x = 2 или x = 4.Таким образом, количество (различных) решений может быть меньше степени, но никогда не может превышать степень.

УПРАЖНЕНИЕ 8

Воспользуйтесь факторизацией p (x) = 2×5 — 22×4 + 78×3 −90×2 из приведенного выше упражнения, чтобы решить уравнение 2×5 — 22×4 + 78×3 — 90×2 = 0.

В некоторых ситуациях факторизация приводит к квадратному уравнению без реальных решений или без иррациональных решений. В этом случае нам может потребоваться завершить задачу, используя формулу корней квадратного уравнения.

ПРИМЕР

Решить x4 + 7×3 — 2×2 — 7x + 1 = 0

Решение

Многочлен x4 + 7×3 — 2×2 — 7x + 1 имеет факторизацию (x — 1) (x + 1) (x2 + 7x — 1).

Следовательно, уравнение принимает вид (x — 1) (x + 1) (x2 + 7x — 1) = 0.

Таким образом, решения x = 1, x = −1 и решения x2 + 7x — 1 = 0.

Используя формулу корней квадратного уравнения, b2 — 4ac = 49 + 4 = 53, поэтому квадратичная формула имеет решения
x = и x =.

Следовательно, квартика имеет четыре решения x = 1, −1 и x =.

Обратите внимание, что существуют полиномиальные уравнения с иррациональными корнями, которые нельзя решить с помощью описанной выше процедуры. Например, многочлен p (x) = x5 — 3×3 — 2×2 + 6 множится как
(x2 — 3) (x3 — 2), и поэтому уравнение x5 — 3×3 — 2×2 + 6 = 0 имеет решения, x =, x = — и x =.

В общем, факторизация многочленов по целым числам является сложной задачей. Например, многочлен
x3-2 не может быть разложен на целые числа, но у него есть одно действительное решение, x =.

Построение полиномиальных функций

Полиномиальная функция — это функция вида y = p (x), где p (x) — полином.

В модуле Квадратичные функции мы увидели, как нарисовать график квадратичного
, указав

перехватывает
нахождение вершины.

Вершина — это пример точки поворота.

Для многочленов степени больше 2 поиск точек поворота не является элементарной процедурой и обычно требует использования исчисления:

Чтобы найти точку пересечения оси y, положим x = 0.
Чтобы найти точки пересечения по оси x, мы полагаем y = 0 и решаем соответствующее полиномиальное уравнение, если это возможно.

Возьмем многочлен y = x3 + x2 — 6x = x (x — 2) (x — 3).

Перехват по оси Y равен 0, а пересечение по оси x происходит, когда x (x — 2) (x — 3) = 0, то есть когда x = 0, 2 и 3.

Чтобы получить представление об общей форме кривой, мы можем подставить несколько контрольных точек.

Мы можем представить знак y с помощью диаграммы знаков:

С этой информацией мы можем начать набросок графика y = x (x — 2) (x + 3).

Знаковая диаграмма говорит нам, что график пересекает ось x в точках x = −3, 0 и 2, а также находится ли график выше или ниже оси a с каждой стороны этих точек. Он не сообщает нам максимальное и минимальное значения y между нулями.

Обратите внимание, что если x — большое положительное число, то p (x) также большое и положительное число. Например, если x = 10, то y = 1040. Если x — большое отрицательное число, то p (x) также является большим отрицательным числом. Например, если x = −10, то y = −840.

УПРАЖНЕНИЕ 9

Нарисуйте график y = (x + 2) (x + 1) (x — 1) (x — 2).

Графики многочленов с повторяющимися множителями

Полиномиальные функции, такие как p (x) = 3 (x — 1) 2 (x + 3) 5 (x — 4), которые содержат повторяющиеся множители, требуют особой осторожности.

Если мы рассмотрим, например, размер x4 для различных значений x, мы заметим

x4 положительно как для положительного, так и для отрицательного значения x
для значений x от -1 до 1 размер x4 меньше, чем значение x.

Графически это говорит нам, что график y = x4 имеет минимум при x = 0 и что около x = 0 график довольно плоский, но начинает резко увеличиваться при x> 1 и x <−1.

Графики y = x2 и y = x4 показаны для сравнения.

Оба этих графа имеют минимум при x = 0. В случае параболы мы называем это вершиной, но обычно мы не используем это слово для многочленов более высокой степени. Вместо этого мы говорим о поворотной точке и далее классифицируем ее как максимум или минимум.

Каждый график y = −x2 и y = −x4 имеет максимум при x = 0.

Четные степени

То же самое явление происходит для всех положительных четных степеней x и для четных степеней (x — a). Следовательно, около нуля многочлена, который возникает из множителя с четной степенью, график имеет минимум или максимум и является «плоским» около этого нуля.

Нечетные степени

График y = (x — 2) пересекает ось x в точке x = 2, но не имеет там максимума или минимума. Так как это прямая линия, график в этой точке не плоский, он действительно имеет градиент 45 °. С другой стороны, график y = (x — 2) 3 ведет себя немного иначе при
x = 2. В Далее мы будем рассматривать нечетные степени, равные или равные 3.

Поскольку нечетная степень отрицательного числа отрицательна, знаковая диаграмма показывает, что
значения y графика y = x3 меняются от отрицательного к положительному, когда значения x перемещаются от -1 к 1. Как и выше, график имеет вид квартира возле начала координат.

Следовательно, график y = x3 выглядит так:

В начале у нас нет ни максимума, ни минимума. Точка x = 0 называется точкой заражения кривой.

ПРИМЕР

Постройте график y = 2×3 (x — 2) 2.

Решение

График проходит через начало координат и срезает ось x в точках x = 0 и x = 2. При x = 0 график имеет точку перегиба, а при x = 2 — минимум. Знаковая схема есть.

График:

УПРАЖНЕНИЕ 10

Нарисуйте график полиномиальной функции p (x) = (x + 3) 3 (x — 1) 3. (Вы должны обнаружить, что график симметричен относительно x = −1, вы понимаете, почему?)

Ссылки вперед

Основная теорема алгебры

Нули полинома также называют корнями соответствующего полиномиального уравнения.

Полиномиальное уравнение x2− 4 = 0 имеет два целых корня, x = 2, x = −2, а уравнение x2-2 = 0 имеет два действительных корня, x =, x = -. С другой стороны, уравнение x2 + 2 = 0 не имеет действительных корней. Кроме того, уравнение x3 — 1 = 0, которое множится как (x — 1) (x2 + x + 1 = 0), имеет только один действительный корень, поскольку квадратное уравнение x2 + x + 1 = 0 не имеет решений.

Чтобы правильно понять, сколько решений может иметь полиномиальное уравнение, нам нужно ввести комплексные числа. Комплексное число — это число в форме a + ib, где a, b — действительные числа и i2 = — 1. Комплексное число i часто называют мнимым числом. Обратите внимание, что если мы положим b = 0, мы получим действительное число, поэтому комплексные числа содержат набор всех действительных чисел.

Таким образом, хотя уравнение x2 + 1 = 0 не имеет вещественных решений, у него есть два комплексных решения, x = i и x = −i, и многочлен x2 + 1 может быть разложен на множители как (x — i) (x + i).

Великий математик Гаусс (1777–1855) дал первое доказательство следующего удивительного результата, который стал известен как Основная теорема алгебры.

Теорема

Каждое полиномиальное уравнение степени больше 0 имеет хотя бы одно комплексное решение.

Учитывая этот результат, нетрудно показать, что:

Следствие

Каждое полиномиальное уравнение степени n больше 0 имеет ровно n решений с учетом кратности над комплексными числами.

УПРАЖНЕНИЕ 11

Объясните, как следствие можно вывести из теоремы.

Следовательно, каждый многочлен степени n, больше 0, можно разложить на n линейных множителей, используя комплексные числа.

Обратите внимание, что выражение, учитывающее кратность, означает, что при заданном полиномиальном уравнении (x — 2) 3 (x + 1) 2 = 0, например, мы говорим, что корни равны x = 2, 2, 2, −1, −1 . Таким образом, мы говорим, что x = 2 — корень кратности 3, а x = −1 — корень кратности 2. Однако уравнение имеет только два (различных) корня.

Поворотные точки

Вершина параболы — пример точки поворота.Координата x точки поворота параболы y = ax2 + bx + c задается как x = -. Координаты x точек поворота многочлена не так просто найти и требуют использования дифференциального исчисления, которое изучается в высшей математике.

Корни многочлена

Предположим, что мы можем разложить на множители моническую квадратичную x2 + bx + c как (x — α) (x — β). Раскрывая их, мы видим, что сумма корней α + β равна −b, а произведение корней ab равно c.

Аналогичное упражнение можно выполнить на монических кубиках. То есть, если корни кубики
x3 + bx2 + cx + d равны α, β, γ, то можно показать, что

α + β + γ = −b, αβ + αγ + βγ = c и αβγ = −d,

Эти тождества определяют отношения между корнями многочлена и его коэффициентами.

УПРАЖНЕНИЕ 12

Выведите приведенные выше формулы.

История

Изучение уравнений степени больше двух восходит к арабской математике.Омар Хайям (1048–1141) большую часть своей жизни провел, пытаясь решить различные случаи кубического уравнения. Только в эпоху Возрождения было получено общее решение кубики. Точные детали отрывочны, но итальянский математик Кардано (1501–1576) сумел раскрыть секрет решения кубической формы своего соотечественника Тартальи и включил его в свою работу Ars Magna (Великое искусство), опубликованную в 1545 году.

Кубик

Кардано показал, как привести любое кубическое уравнение к виду x3 + px + c = 0, а затем, сделав замену x = u — v, свести задачу к решению квадратичной. На практике проще положить x = u + v.

УПРАЖНЕНИЕ 13

Положим x = y — в уравнение x3 + ax2 + bx + c = 0, чтобы показать, что полученное уравнение не содержит членов степени 2.

ПРИМЕР

Решите x3 + 3x — 1 = 0, используя замену x = u + v.

Решение

Переставляя уравнение и подставляя, получаем

(u + v) 3 = −3 (u + v) + 1.

Теперь мы расширяем левую часть и множим 3uv из двух членов, чтобы получить

u3 + v3 + 3uv (u + v) = 1 −3 (u + v).

Приравнивая коэффициенты при (u + v) с обеих сторон и приравнивая оставшиеся члены,
получаем

u3 + v3 = 1, 3uv = −3.

Кубирование второго уравнения дает

u3 + v3 = 1, u3v3 = -1,

На этом этапе у нас есть два числа u3, v3, сумма и произведение которых нам известны. Следовательно,
они будут удовлетворять квадратному уравнению z2 — z — 1 = 0, которое имеет решения z = или
z =. Эти решения представляют числа u3 + v3 в любом порядке, поэтому, взяв кубические корни, мы получим следующее решение исходного уравнения

х = и + v = +.

Это единственное реальное решение уравнения.

УПРАЖНЕНИЕ 14

Воспользуйтесь калькулятором, чтобы выразить это в десятичной форме, и убедитесь, что оно удовлетворяет исходному уравнению
.

Квартик

Решение общего уравнения четвертой степени было вскоре найдено учеником Кардано и протеже Феррари. Он открыл метод, позволяющий свести задачу решения
квартики к задаче решения кубики.

В обоих случаях можно выразить решение данного уравнения, используя квадратные и более высокие корни и обычные арифметические операции (сложение, вычитание, умножение и деление). Такой раствор часто называют раствором с использованием радикалов.Решениями квадратного уравнения ax2 + bx + c = 0 являются x = и x = -, поэтому квадратное уравнение также может быть решено с использованием радикалов.

Потребовалось несколько сотен лет, прежде чем Абель (1802-1829) и Галуа (1811-1832) осознали, что невозможно найти решение общего уравнения пятой степени или общего уравнения более высокой степени с использованием радикалов. . Очевидно, что некоторые уравнения более высокой степени могут быть решены с использованием радикалов, например x5 — 32 = 0, но в общем случае это невозможно.

Корни многочленов

Хотя работа Кардано была большим прорывом, оставалось много безответных вопросов относительно полиномов. В 17 веке Декарт нашел тест, известный как правило знаков Декарта, для определения количества положительных действительных корней многочлена, в то время как Ньютон открыл так называемые тождества Ньютона, которые находят и связывают формулы для суммы k-й степени корней многочлена. В XVIII и XIX веках великие математики Эйлер, Лагранж, Эйзенштейн и Гаусс еще больше расширили наше понимание полиномов и полиномиальных уравнений.Это привело к развитию того, что сегодня называется современной алгеброй, которая занимается изучением алгебраических структур.

Факторинговые многочлены

Выше мы видели, что когда мы изучаем многочлен, нам нужно указать, какие решения / факторы мы ищем. В частности, предположим, что p (x) — многочлен со степенью больше 0 и действительными коэффициентами

по комплексным числам p (x) делить на линейные множители
над действительными числами p (x) имеет все свои множители либо линейные, либо квадратичные
над рациональными числами, можно найти полиномы сколь угодно большой степени
, которые являются неприводимыми, то есть они не могут быть выражены как произведение
двух полиномов с рациональными коэффициентами, каждый меньшей степени.

Основная теорема алгебры используется для доказательства первого из этих утверждений. Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые комплексные корни будут встречаться парами, известными как сопряженные пары. То есть, если a + ib — корень, то a — ib тоже. Этот факт можно использовать для доказательства второго утверждения.

УПРАЖНЕНИЕ 15

(Для этого нужно немного знать комплексные числа.)

Предположим, что все коэффициенты многочлена p (x) = dancingn — an — 1xn — 1 + … + a1x + a0 действительны.

a: Если α = a + ib является решением полиномиального уравнения, p (x) = dancingn — an — 1xn — 1 + … + a1x + a0 = 0, покажите, что = a — ib также является решением.
б: Покажите, что если x — α является множителем p (x), где α = a + ib — комплексное число, то квадратичный (x — α) (x -) также является множителем p (x) и что (x — α) (x -) имеет действительные коэффициенты.
c: Выведите, что каждый многочлен с действительными коэффициентами теоретически может быть разложен на множители как произведение линейных и / или квадратичных множителей с действительными коэффициентами. (Обратите внимание, что на практике это может быть очень сложной задачей.)

Эйзенштейн (ок. 1850 г.) придумал следующий остроумный тест на несводимость многочленов над рациональными числами.

Рассмотрим многочлен p (x) = тревогу — an — 1xn — 1 + … + a1x + a0, где все коэффициенты являются целыми числами.Предположим, что мы можем найти простое число p, которое не делит старший коэффициент an, но которое делит все остальные коэффициенты. Тест говорит, что если квадрат того же простого числа не делит константный член, то есть p2 + a0, то p (x) неприводимо по рациональным числам.

ПРИМЕР

Многочлен p (x) = 5×7 + 6×6 — 15x 4 + 12x — 21 удовлетворяет критерию Эйзенштейна с простым p = 3, и поэтому p (x) не может быть выражено как произведение двух многочленов меньшей степени с целыми коэффициентами. То есть p (x) неприводимо.

УПРАЖНЕНИЕ 16

Объясните, как построить многочлен сколь угодно большой степени, который нельзя разложить на рациональные числа.

Маклорен серии

В 17-м и 18-м веках математики сделали замечательное открытие, что такие функции, как y = sin x и y = cos x, могут быть выражены с помощью «бесконечных многочленов», то есть многочленов, степени x которых продолжаются бесконечно.Это называется степенным рядом. Так, например,

sin x = x — + — +…,

, где очевидная закономерность продолжается вечно. Обозначение n! (читается как факториал n) — это сокращение от n (n — 1) (n — 2)… 3.2.1. Таким образом 5! = 5 × 4 × 3 × 2 × 1 = 120. Эти бесконечные ряды часто называют рядами Маклорена и имеют очень широкое применение как в математике, так и в физике.

На сегодняшний день остаются нерешенными проблемы, связанные с многочленами. В приложении ниже в общих чертах обсуждается замечательное применение полиномов в современных телекоммуникациях.

Приложение

Применение полиномов к кодам с исправлением ошибок

Оцифровка информации

Информация обычно оцифровывается путем преобразования ее в последовательность нулей и единиц. Например, код ASCII для цифры 1 и буквы A — «1» 1000110 и «A» 1000001. Здесь мы предположим, что все рассматриваемые сообщения представляют собой конечные последовательности нулей и единиц.

Когда ваш мобильный телефон отправляет или принимает сообщения, или данные отправляются со спутников в глубоком космосе, информация может быть потеряна или повреждена по пути к месту назначения.

Поскольку информация отправляется как последовательности из 0 и 1, «поврежденный» 0 становится 1 и наоборот.

Простая проверка на наличие ошибок — это добавить контрольную цифру, чтобы в строке было четное число единиц, и, следовательно, сумма цифр была четной.

Таким образом, мы кодируем 1 как 10001101 и A как 10000010.

Теперь, если байт передан и один из битов поврежден, то количество единиц становится нечетным, и поэтому получатель может запросить повторную передачу.

Этот код может обнаружить одну ошибку, но не может ее исправить.

Полиномы по модулю 2

Полином по модулю 2 — это полином, коэффициенты которого равны 0 или 1. Затем арифметические операции выполняются по модулю 2, так что 0 + 1 = 1 + 0 = 1 и 1 + 1 = 2 = 0.

Производим сложение по модулю 2.

ПРИМЕР

Если p (t) = t3 + 1 + 1, q (t) = t4 + t3 + t2 + 1

Тогда p (t) + q (t) = t4 + 2t3 + t2 + 2t + 2 = t4 + t2.

Умножение производится аналогично.

Решение

p (t) = t3 + 1 + 1, q (t) = t + 1, тогда

p (t) × q (t) = (t3 + t + 1) (t + 1) = t4 + t3 + t2 + 2t + 1 = t4 + t3 + t2 + 1

Кодировка

Зафиксируем многочлен m1 (t) = t3 + t + 1.

Этот многочлен не может быть разложен на множители по модулю 2, поскольку единственные возможные корни — это 0 и 1, и ни один из них не работает.

Предположим теперь, что многочлен m1 (t) имеет корень a. То есть a имеет свойство
α3 + α + 1 = 0 или α3 = α + 1 (напомним, что по модулю 2, −1 = 1)

Это число α очень интересно, и, используя приведенное выше уравнение, мы можем составить таблицу его степеней.

Мощность | Упрощенная форма

	α	\| α
	α2	\| α2
	α3	\| α + 1
	α4	\| α2 + α
	α5	\| α2 + α + 1
	α6	\| α2 + 1
	α7	\| 1

Например, чтобы получить α5, мы умножаем α4 = α2 + α на α5 = α3 + α2 и заменяем α3 на α + 1, чтобы получить α5 = α + 1 + α2.

Таким образом, мы можем записать все степени α как комбинации 1, α и α2 (!!)

Теперь о кодах.

Мы начинаем с сообщения (a, b, c, d) в двоичном формате длиной 4, добавляем 3 контрольных цифры, чтобы получить
(a, b, c, d, x, y, z). Мы используем их как коэффициенты многочлена

p (t) = at6 + bt5 + ct4 + dt3 + xt2 + yt + z.

Цифры x, y, z выбраны так, чтобы p (t) делилось на многочлен m1 (t) = t3 + t + 1

Поскольку a является корнем m1 (t), он также является корнем p (t), и поэтому p (a) = 0.

ПРИМЕР

Возьмите сообщение (1, 0, 0, 1) и закодируйте его как (1, 0, 0, 1, x, y, z). Преобразуя в полином, получаем

	п (т)	знак равно t6 + t3 + xt2 + yt + z.
Подставляя t = a и используя таблицу для упрощения, получаем
	п (а)	= a6 + a3 + xa2 + ya + z.
		= (a2 + 1) + (a + 1) + xa2 + ya + z
		= а2 (х + 1) + а (у + 1) + z.

Теперь, если мы возьмем x = 1, y = 1, z = 0, тогда p (a) будет равно нулю.Следовательно, мы кодируем сообщение
(1, 0, 0, 1) как (1, 0, 0, 1, 1, 1, 0). Мы будем называть многочлен, соответствующий отправленному сообщению, C (t), поэтому C (a) = 0.

Исправление ошибок

Предположим, что одна ошибка возникает в пятом числе слева, поэтому мы получаем сообщение (1, 0, 1, 1, 1, 1, 0).

Таким образом, коэффициент t4 неверен и полином для полученного сообщения равен

R (t) = C (t) + t4

Подставляя t = α, получаем

R (α) = C (α) + α4 = α4

и поэтому мы знаем, где ошибка.

В общем, если бы в 1-й цифре была ровно одна ошибка, мы бы получили

R (t) = C (t) + ti.

Тогда R (α) = C (α) + αi = αi, и поэтому вычисление R (a) дает позицию неправильной цифры.

Если R (α) = 0, то ошибок не было. Этот процесс, конечно, предполагает, что произошло не более 1
ошибок.

ПРИМЕР

Предполагая, что не более одной ошибки, исправьте и расшифруйте сообщение (1, 0, 0, 1, 0, 0, 1).

Решение

Преобразуя в полиномы, получаем

R (t) = t6 + t3 + 1

и т. Д.

R (α) = α6 + α3 + 1 = α2 + 1 + α + 1 + 1 = α2 + α + 1 = α5

Итак, исправленное сообщение было (1, 1, 0, 1, 0, 0, 1), которое декодируется как (1, 1, 0, 1).

Исправление более одной ошибки

Процедура кодирования и исправления, описанная выше, работает только в том случае, если при передаче возникла не более одной ошибки.

Полиномиальный метод может быть расширен для обнаружения и исправления более чем одной ошибки.
Детали этих кодов немного сложнее, но в них используются те же идеи, которые были развиты выше.

Коды, используемые для исправления множественных ошибок, называются кодами BCH и были открыты (независимо) Бозом и Чаудхури (в 1960 г. ) и Хоккенгемом (в 1959 г.) — отсюда и название BCH.

В то время как арифметика теперь становится очень сложной, она легко выполняется компьютером, и могут быть созданы коды, которые могут обнаруживать и исправлять произвольное количество ошибок.

Современные коды исправления ошибок, используемые в технологии мобильных телефонов, снова более сложны, но в основном используют те виды оборудования, которые я описал выше.

В последнее время коды Рида-Соломона, которые представляют собой тип кода BCH, использовались в таких приложениях, как спутниковая связь, проигрыватели компакт-дисков, DVD-диски и дисководы.

ОТВЕТЫ НА УПРАЖНЕНИЯ

УПРАЖНЕНИЕ 1

Ведущий термин: тревога

Ведущий коэффициент:

Степень: n

Постоянный член: a0

УПРАЖНЕНИЕ 2

а 4×6 — 4×4 + 4×3 + x2 — 2x + 1

b i….сумма степеней полиномов

ii… произведение констант

УПРАЖНЕНИЕ 3

5×4 — 7×3 + 2x — 4 = (x2 — 2) (5×2 — 7x + 10) + (−12x + 16)

УПРАЖНЕНИЕ 4

а = 18

УПРАЖНЕНИЕ 5

a = -33 и b = -15

УПРАЖНЕНИЕ 6

Если P (a) = 0, то a0 = — anan — an − 1an − 1…. − A1a. Следовательно, a делит a0.

УПРАЖНЕНИЕ 7

2×2 (x — 3) 2 (x — 5)

УПРАЖНЕНИЕ 8

x = 0 или x = 3 или x = 5

УПРАЖНЕНИЕ 9

УПРАЖНЕНИЕ 10

УПРАЖНЕНИЕ 11

Для полиномиального уравнения P (x) = 0 существует решение x = a по теореме.Следовательно, x — a является фактором P (x) и P (x) = (x — a) Q (x). Уравнение Q (x) = 0 также имеет решение, поэтому с помощью теоремы можно найти новый линейный множитель.

УПРАЖНЕНИЕ 12

(x — α) (x — β) (x — γ) = x3 — (α + β + γ) x2 + (αβ + αγ + βγ) x + αβγ = x3 + bx2 + cx + d

Следовательно, результат b = — (α + β + γ), c = (αβ + αγ + βγ) и d = αβγ

УПРАЖНЕНИЕ 13

y3 — + — + d

УПРАЖНЕНИЕ 14

a: Возьмите конъюгаты с обеих сторон.Сопряжение с действительным — это то же самое, что и реальное.
б: Непосредственное следствие a и теоремы о факторах, а также того факта, что сумма и произведение комплексного числа и его сопряженного действительны.
c: Основная теорема и b дает результат

Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.

Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений австралийского правительства.

© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Непортированная лицензия.
https://creativecommons.org/licenses/by-nc-nd/3.0/

Как решать полиномиальные уравнения

Резюме:
В алгебре вы тратите много времени на решение многочлена
уравнения или факторизации многочленов (что одно и то же).
Было бы легко потеряться во всех техниках, но эта статья
связывает их все вместе в единое целое.

Генеральный план

Убедитесь, что вас не смущает терминология. Все это
то же:

Решение полиномиального уравнения p ( x ) = 0
Нахождение корней полиномиального уравнения p ( x ) = 0
Нахождение нулей полиномиальной функции p ( x )
Факторизация полиномиальной функции p ( x )

Есть коэффициент для каждого корня, и наоборот.
( x — r ) является фактором тогда и только тогда, когда r является корнем. Это
Теорема о факторах : поиск корней или факторов
по сути то же самое. (Основное различие заключается в том, как вы относитесь к
постоянный коэффициент.)

точное или приблизительное значение?

Чаще всего, когда мы говорим о решении уравнения или факторизации
многочлен, мы имеем в виду точное (или аналитическое) решение . В
другой тип, приблизительное (или числовое) решение , является
всегда возможно, а иногда и единственно возможный.

Когда найдешь, точное решение лучше .
Вы всегда можете найти численное приближение к точному решению,
но пойти другим путем намного труднее. Эта страница тратит больше всего
своего времени на методы точных решений, но также расскажет, что нужно
делать, когда аналитические методы не работают.

Шаг за шагом

Как найти множители или нули многочлена (или корни
полиномиального уравнения)? В основном вы сточите . Каждый раз
вы вычеркиваете множитель или корень из многочлена, у вас остается
полином на одну степень проще.Используйте этот новый уменьшенный
полином, чтобы найти оставшиеся факторы или корни.

На любом этапе процедуры, если вы попадете в
кубическое или четвертое уравнение (степень 3 или 4), у вас есть выбор
продолжения факторинга или использования
кубические или четвертичные формулы. Этих формул много
работы, поэтому большинство людей предпочитают продолжать факторинг.

Выполните эту процедуру, шаг за шагом:

При решении уравнения запишите его в стандартную форму с 0
с одной стороны и упрощают .[ подробности ]
Знайте , сколько корней ожидать.
[ подробности ]
Если у вас есть линейное или квадратное уравнение
(степень 1 или 2), решите осмотром или по формуле корней квадратного уравнения.
[ подробности ]

Затем переходите к шагу 7.
Найдите один рациональный множитель или корень. Это самая сложная часть,
но есть много методов, которые могут вам помочь.
[ подробности ]

Если вы можете найти фактор или корень, перейдите к шагу 5 ниже; если
не можете, переходите к шагу 6.
Разделите на коэффициент . Это оставляет вас с новым
приведенный многочлен , степень которого на 1 меньше.
[ подробности ]

Для остальной части проблемы вы будете работать с уменьшенным
многочлен, а не оригинал. Продолжите с шага 3.
Если вы не можете найти множитель или корень , обратитесь к
численные методы.
[ подробности ]

Затем переходите к шагу 7.
Если нужно было решить это уравнение, запишите корни .
Если это был многочлен для факторизации, запишите его в факторизованной форме ,
включая любые постоянные факторы, которые вы вывели на шаге 1.

Это пример алгоритма , набор шагов
что приведет к желаемому результату за конечное количество операций.
Это итеративная стратегия , потому что средние шаги
повторять столько, сколько необходимо.

Кубические и четвертые формулы

Приведенные здесь методы находят рациональный корень и
использовать синтетическое деление проще всего.
Но если вы не можете найти рациональный корень, есть специальные методы для
кубические уравнения (степень 3) и
уравнения четвертой степени (степень 4), оба в Mathworld.Альтернативный подход предоставляется
Дик Никаллс в PDF для
кубический
а также
четвертичная
уравнения.

Шаг 1. Стандартная форма и упрощение

К сожалению, это легко не заметить.
Если у вас есть полиномиальное уравнение , отложите все члены в одну сторону
и 0 с другой.
И независимо от того, является ли это проблема факторинга или уравнение, которое нужно решить, положите
ваш многочлен в стандартной форме, от до наименьшей степени .

Например, вы не можете решить это уравнение в такой форме:

x + 6 x + 12 x = −8

Вы должны изменить его на эту форму:

x + 6 x + 12 x + 8 = 0

Также убедитесь, что вы упростили, исключив любые
общие факторы .Это может включать в себя вычитание −1
так что наивысшая степень имеет положительный коэффициент. Пример: в коэффициент

7-6 x -15 x —
2 x

начнем с его стандартной формы:

−2 x — 15 x — 6 x + 7

, а затем вычтите −1

— (2 x + 15 x + 6 x — 7)
или же
(−1) (2 x + 15 x + 6 x -7)

Если вы решаете уравнение, вы можете выбросить любых
общий постоянный множитель.Но если вы факторизуете многочлен, вы должны
сохранить общий множитель .

Пример: решить
8 x + 16 x + 8 = 0, вы можете
разделите левую и правую на общий множитель 8. Уравнение
x + 2 x + 1 = 0
имеет те же корни, что и исходное уравнение .

Пример: Фактор
8 x + 16 x + 8, вы узнаете
общий множитель 8 и перепишем многочлен в виде
8 ( x + 2 x + 1), что является
идентичен исходному многочлену .(Хотя это правда, что вы
сосредоточит ваши дальнейшие усилия по факторингу на
x + 2 x + 1, это будет ошибкой
написать, что исходный многочлен равен
x + 2 x + 1.)

Ваш общий фактор может быть
дробь, потому что вы должны вычесть любые дроби, чтобы
многочлен имеет целых коэффициентов.

Пример: решить
(1/3) x + (3/4) x — (1/2) x + 5/6 = 0,
вы узнаете общий множитель 1/12 и разделите обе стороны на 1/12.Это в точности то же самое, что и распознавание и умножение на
наименьший общий знаменатель из 12. В любом случае вы получите
4 x + 9 x — 6 x + 10 = 0,
которое имеет те же корни, что и исходное уравнение .

Пример: Фактор
(1/3) x + (3/4) x — (1/2) x + 5/6,
вы узнаете общий множитель 1/12 (или наименьший общий
знаменатель 12) и вычитаем 1/12. Ты получаешь
(1/12) (4 x + 9 x — 6 x + 10),
что идентично исходному многочлену .

Шаг 2. Сколько корней?

Многочлен степени n будет иметь n корней, некоторые из которых могут быть
множественные корни.

Как узнать, что это правда? В
Основная теорема алгебры говорит вам, что многочлен
имеет хотя бы один корень. Теорема о факторах говорит вам, что если r
является корнем, тогда ( x — r ) является фактором. Но если разделить многочлен
степени n на коэффициент ( x — r ), степень которого равна 1, вы получите
полином степени n −1.Неоднократно применяя Фундаментальный
Теорема и теорема о множителях дают вам n корней и n факторов.

Правило знаков Декарта

Правило знаков Декарта может сказать вам , сколько положительных и
сколько отрицательных действительных нулей многочлен. Это
большое трудосберегающее устройство, особенно когда вы решаете, какой
возможные рациональные корни, которые нужно искать.

Чтобы применить Правило знаков Декарта, вам необходимо понимать термин
изменение знака .Когда многочлен расположен в
стандартная форма, вариация в
знак возникает, когда знак коэффициента отличается от знака
предыдущего коэффициента. (Нулевой коэффициент игнорируется.) Для
пример,

p ( x ) = x ⁵ —
2 x ³ + 2 x ² — 3 x + 12

имеет четыре варианта знака.

Правило знаков Декарта:

Число положительных корней из p ( x ) = 0 равно
количество вариаций знака p ( x ), или меньшее, чем на четное
номер.
Число отрицательных корней из p ( x ) = 0 либо равно
количество вариаций знака p (- x ), или меньшее, чем на четное
номер.

Пример: рассмотрим p ( x ) выше. Поскольку у него четыре варианта
в знаке должно быть либо четыре положительных корня, либо два положительных корня,
или нет положительных корней.

Теперь сформируйте p (- x ), заменив x на (- x ) в
выше:

p (- x ) = (- x ) ⁵ — 2 (- x ) ³ + 2 (- x ) ² — 3 (- x ) + 12

p (- x ) = — x ⁵ + 2 x ³ + 2 x ² + 3 x + 12

p (- x ) имеет один вариант знака, поэтому
оригинал p ( x ) имеет один минус
корень.Поскольку вы знаете, что p ( x ) должен иметь отрицательный корень, но он может
или может не иметь положительных корней, сначала ищите отрицательные
корнеплоды.

p ( x ) — полином пятой степени, поэтому он должен иметь пять нулей.
Поскольку x не является фактором, вы знаете, что x = 0 не является
нуль полинома. (Для полинома с действительными коэффициентами, например
в этом случае комплексные корни встречаются парами.)
Следовательно, есть три возможности:

	положительный	отрицательный	комплексный не настоящий
	количество нулей , которые равны
первая возможность	4	1		1	вторая возможность 2	1	2
третий вариант	0	1	4

Сложные корни

Если полином имеет действительных коэффициентов , то либо все
корни настоящие или есть
четное число невещественных комплексных корней в сопряженных парах .

Например, если 5 + 2i является нулем многочлена с вещественными
коэффициентов, то 5−2i также должен быть нулем этого многочлена.
В равной степени верно и то, что если ( x −5−2i) является множителем, то
( x −5 + 2i) также является фактором.

Почему это правда? Потому что, когда у вас есть фактор с воображаемым
часть и умножьте ее на комплексное сопряжение, вы получите реальную
результат:

( x −5−2i) ( x −5 + 2i) =
x −10 x + 25−4i =
x −10 x +29

Если ( x −5−2i) было фактором, но
( x −5 + 2i) не было, тогда полином будет иметь
воображаемые в его коэффициентах, независимо от других факторов
возможно.Если многочлен имеет только действительные
коэффициентов, то любые комплексные корни должны входить в сопряженные пары.

Иррациональные корни

По аналогичным причинам, если многочлен имеет
рациональных коэффициентов то иррациональные корни, содержащие
квадратный
корни встречаются (если вообще встречаются) в сопряженных парах.
Если ( x −2 + √3) является множителем многочлена с рациональными
коэффициентов, то ( x −2 − √3) также должен быть
фактор. Чтобы понять почему, вспомните, как вы рационализируете бином
знаменатель; или просто проверьте, что происходит, когда вы умножаете эти два
факторы.(1/3) и два
сложные корни.

Интересная проблема, нет ли иррациональности
с четными корнями порядка ≥4 также должны встречаться в сопряженных
пары. У меня нет немедленного ответа. Я работаю над
пруф, как я успеваю.

Множественные корни

Когда данный коэффициент ( x — r ) встречается в полиноме m раз, r равен
называется кратным корнем или корнем кратности м .

Если кратность м — четное число, график касается
Ось x при x = r , но не пересекает ее.
Если кратность м — нечетное число, график пересекает
Ось x при x = r . Если кратность равна 3, 5, 7 и т. Д., График имеет вид
горизонтально в точке пересечения оси.

Примеры: сравните эти два многочлена и их графики:

f ( x ) =
( x −1) ( x −4) ² =
x ³ — 9 x ² +
24 x — 16

г ( x ) =
( x −1) ³ ( x −4) ² =
x ⁵ — 11 x ⁴ + 43 x ³
— 73 x ² + 56 x -16

Эти многочлены имеют одинаковые нули, но корень 1 встречается
с разной кратностью.Посмотрите на графики:

Оба полинома имеют нули только в точках 1 и 4. f ( x ) имеет степень 3,
что означает три корня. Вы видите из факторов, что 1 является корнем
кратность 1 и 4 является корнем из кратности 2. Следовательно, граф
пересекает ось в точке x = 1 (но не горизонтально там) и касается в точке
x = 4 без пересечения.

Напротив, g ( x ) имеет степень 5. ( g ( x ) = f ( x ) раз
( x −1) ².) Из пяти корней 1 встречается с
кратность 3: график пересекает ось при x = 1 и является горизонтальным
там; 4 встречается с кратностью 2, и график касается
ось x = 4 без пересечения.

Шаг 3. Квадратичные множители

Когда у вас есть квадратичные множители (Ax + Bx + C), он может или не может
можно будет их дополнительно проанализировать.

Иногда вы можете просто увидеть факторы, как в случае с
x — x −6 = ( x +2) ( x −3).В других случаях не так очевидно,
квадратичный можно разложить на множители. Вот когда квадратная формула
(показан справа) ваш друг.

Например, предположим, что у вас есть коэффициент
12 x — x −35. Можно ли это еще раз проанализировать? Судом и
ошибка вам придется перепробовать много комбинаций! Вместо этого используйте факт
что факторов соответствуют корням , и примените формулу к
найти корни 12 x — x −35 = 0, вот так:

x = [- (- 1) √1 — 4 (12) (- 35)] / 2 (12)

x = [1 √1681] / 24

√1681 = 41, следовательно,

x = [1 41] / 24

x = 42/24 или -40/24

x = 7/4 или −5/3

Если 7/4 и −5/3 являются корнями, то ( x −7/4) и ( x +5/3)
факторы.Следовательно,

12 x — x −35 =
(4 x −7) (3 x +5)

А как насчет x −5 x +7? Этот выглядит как лучший,
но как ты можешь быть уверен? Снова примените формулу:

x = [- (- 5) √25 — 4 (1) (7)] / 2 (1)

x = [5 √ − 3] / 2

Что с этим делать, зависит от исходной проблемы. Если это
должен был разложить на множители реалы, тогда x −5 x +7 — простое число.Но если
этот фактор был частью уравнения, и вы должны были найти все
сложные корни, у вас их два:

x = 5/2 + (√3 / 2) i, x = 5/2 — (√3 / 2) i

Поскольку исходное уравнение имело действительные коэффициенты, эти
сложные корни встречаются в сопряженной паре.

Шаг 4. Найдите один фактор или корень

Этот шаг является сердцем факторизации многочлена или решения
полиномиальное уравнение. Есть много методов, которые могут вам помочь
найти фактор.

Иногда можно найти факторы путем осмотра (см. Первые два
следующие разделы). Это отличный способ быстрого доступа, поэтому проверьте
легкие факторы, прежде чем начинать более напряженные
методы.

Мономиальные множители

Всегда начинайте с поиска любых мономиальных множителей, которые вы видите. Например,
если ваша функция

f ( x ) = 4 x ⁶ + 12 x ⁵ + 12 x ⁴ + 4 x ³

, вы должны немедленно разложить его на

f ( x ) = 4 x ³ ( x ³ + 3 x ² + 3 x + 1)

Получение числа 4 упрощает оставшиеся числа,
x ³ дает вам корень x = 0 (с кратностью
3), и теперь у вас есть только кубический многочлен (степени 3) вместо
sextic (степень 6).Фактически, теперь вы должны распознать эту кубику как
особый продукт, идеальный куб
( x +1) ³.

Когда вы вычитаете множитель общей переменной, убедитесь, что вы
помните об этом в конце, когда перечисляете фактор или корни.
x +3 x +3 x +1 = 0 имеет определенные корни, но
x ( x +3 x +3 x +1) = 0 имеет те же корни и
также корень x = 0 (с кратностью 3).

Особые продукты

Будьте внимательны к применению специальных продуктов .Если вы сможете применить их, ваша задача станет намного проще. Специальный
Продукты

идеальный квадрат (2 формы): A 2 A B + B = ( A B )
сумма квадратов: A + B не может быть разложено на множители в целом (для исключительных случаев см. Как разложить сумму квадратов на множители)
разность квадратов: A — B = ( A + B ) ( A — B )
идеальный куб (2 формы): A 3 A B + 3 A B B = ( A B )
сумма кубов: A + B = ( A + B ) ( A — A B + B )
разница кубов: A — B = ( A — B ) ( A + A B + B )

Выражения для суммы или разности двух кубиков выглядят так:
хотя они должны учитывать дополнительные факторы, но они этого не делают. A A B + B — простое число над реалами.

Рассмотрим

p ( x ) = 27 x — 64

Вы должны узнать это как

p ( x ) = (3 x ) — 4

Вы умеете множить разницу двух кубов:

p ( x ) = (3 x −4) (9 x +12 x +16)

Бинго! Как только вы дойдете до квадратичной, вы можете применить
Квадратичная формула, и все готово.

Вот другой пример:

q ( x ) = x ⁶ + 16 x ³ + 64

Это просто идеальный квадратный трехчлен, но в x ³ вместо
из x . Вы учитываете это точно так же:

q ( x ) = ( x ³) ² + 2 (8) ( x ³) + 8 ²

q ( x ) = ( x ³ + 8) ²

И вы можете легко разложить ( x ³ +8) ² как
( x +2) ² ( x ² −2 x +4) ².

Рациональные корни

Предполагая, что вы уже учли простые
мономиальные факторы и
специальные продукты, что делать, если
у вас все еще есть многочлен степени 3 или выше?

Ответ — Rational Root Test .
Он может показать вам некоторые корни кандидатов
когда вы не видите, как разложить полином на множители, как показано ниже.

Рассмотрим многочлен стандартной формы, записанный с высшей степени
до самого низкого и всего с целочисленными коэффициентами :

f ( x ) = a _n x ⁿ +… + a _o

Теорема о рациональном корне говорит вам, что , если
многочлен имеет рациональный нуль
, затем , это должна быть дробь p / q ,
где p — коэффициент конечной константы a _o и
q — множитель ведущего коэффициента a _n.

Пример:

p ( x ) = 2 x ⁴ — 11 x ³ — 6 x ² + 64 x + 32

Коэффициенты старшего коэффициента (2) равны 2 и 1.В
коэффициенты постоянного члена (32) равны 1, 2, 4, 8, 16 и 32.
Следовательно, возможные рациональные нули: 1, 2, 4, 8, 16 или
32 разделить на 2 или 1:

любой из 1/2, 1/1, 2/2, 2/1, 4/2, 4/1, 8/2, 8/1, 16/2, 16/1, 32/2, 32/1

уменьшенный: любой из, 1, 2, 4, 8, 16, 32

Что мы имеем в виду, когда говорим, что это список всех
возможных рациональных корня ? Мы имеем в виду, что никакое другое рациональное число,
как или 32/7, может быть нулем этого конкретного многочлена.

Осторожно : Не делайте Rational Root Test
больше, чем есть.Это не означает, что рациональные числа являются корнями , просто
что никакие другие рациональные числа не могут быть корнями. И это не говорит
вы что-нибудь о том, есть ли какие-то иррациональные или даже сложные корни
существовать. Rational Root Test — это только отправная точка.

Предположим, у вас есть многочлен с нецелыми коэффициентами.
Вы застряли? Нет, вы можете исключить наименее распространенные
знаменатель (LCD) и получите многочлен с целыми коэффициентами, которые
способ. Пример:

(1/2) x — (3/2) x + (2/3) x — 1/2

ЖК-дисплей 1/6.Вынося за скобки 1/6, получаем многочлен

(1/6) (3 x — 9 x + 4 x — 3)

Эти две формы эквивалентны, и поэтому имеют одинаковые
корнеплоды. Но вы не можете применить Rational Root Test к первой форме,
только ко второму. Тест говорит вам, что единственно возможное рациональное
корни — любые из 1/3, 1, 3.

После того, как вы определили возможных рациональных нулей, как
вы можете их проверить? Метод грубой силы заключался бы в том, чтобы взять каждый
возможное значение и замените его на x в полиноме: если
результат равен нулю, тогда это число является корнем.Но есть лучше
способ.

Используйте Synthetic Division, чтобы узнать,
кандидат делает полином равным нулю. Это лучше на троих
причины. Во-первых, это проще в вычислительном отношении, потому что вам не нужно
вычислить высшие степени чисел. Во-вторых, в то же время он сообщает
независимо от того, является ли данное число корнем, он производит
сокращенный многочлен , который вы будете использовать, чтобы найти оставшийся
корнеплоды. Наконец, результаты синтетического деления могут дать вам
верхняя или нижняя граница, даже если число
тестирование оказывается не рутом.

Иногда правило знаков Декарта может
поможет вам в дальнейшем выявить возможные рациональные корни. Например,
Rational Root Test сообщает, что если

q ( x ) = 2 x ⁴ + 13 x ³ + 20 x ² + 28 x + 8

имеет какие-либо рациональные корни, они должны происходить из списка
любой из, 1, 2, 4, 8. Но не начинайте с замены или
синтетическое разделение. Поскольку нет изменений знаков, нет
положительные корни.Есть ли отрицательные корни?

q (- x ) = 2 x ⁴-13 x ³ + 20 x ²-28 x + 8

имеет четыре смены знака. Следовательно, может быть целых четыре
отрицательные корни. (Также может быть два отрицательных корня или ни одного.)
Нет гарантии, что какой-либо из корней является рациональным, но любой корень
рациональное должно происходить из списка -, −1,
−2, −4, −8.

(Если у вас есть
графического калькулятора, вы можете предварительно просмотреть рациональные корни, построив график
полином и увидеть, где он, кажется, пересекает ось x .Но ты
по-прежнему необходимо проверить корень алгебраически, чтобы увидеть, что f ( x )
ровно 0, а не почти 0.)

Помните, что Rational Root Test гарантирует нахождение всех
рациональных корней. Но он полностью упустит настоящие корни, которых нет.
рациональные, как корни x −2 = 0, которые
√2, или корни x + 4 = 0, которые
2i.

Наконец, помните, что Rational Root Test работает, только если все
коэффициенты — целые числа.Посмотрите еще раз на эту функцию, которая
на графике справа:

p ( x ) = 2 x ⁴ — 11 x ³ — 6 x ² + 64 x + 32

Теорема о рациональном корне говорит вам, что единственно возможный рациональный
нули — это 1, 2, 4, 8, 16, 32. Но предположим, что вы
вычтите 2 (как я когда-то сделал в классе), написав эквивалент
функция

p ( x ) = 2 ( x ⁴ — (11/2) x ³ — 3 x ² + 32 x + 16)

Эта функция аналогична предыдущей, но вы не можете
дольше применять Rational Root Test, потому что коэффициенты не
целые числа.По сути — это ноль p ( x ), но это не так
появляются, когда я (незаконно) применил Rational Root Test к
вторая форма. Моя ошибка заключалась в том, что я забыл, что применима теорема о рациональном корне.
только когда все коэффициенты многочлена равны
целые числа.

Графические подсказки

Построив график функции вручную или с помощью графика
Вы можете понять, где находятся корни,
примерно, и сколько существует настоящих корней.

Пример: Если Rational Root Test
говорит вам, что 2 возможных рациональных корня, вы можете посмотреть на
график, чтобы увидеть, пересекает ли он (или касается) ось x в точках 2 или
−2.Если да, используйте синтетическое деление, чтобы
убедитесь, что предполагаемый корень на самом деле является корнем. Да ты всегда
нужно проверить по графику, вы никогда не можете быть уверены
является ли перехват на ваш возможный рациональный корень или
просто около это.

Границы корней

Некоторые методы не сообщают вам конкретное значение корня, но
скорее, что корень существует между двумя значениями или что все корни
меньше определенного числа больше определенного числа. Этот
помогает сузить область поиска.

Теорема о промежуточном значении

Эта теорема говорит вам, что если график многочлена находится выше
ось x для одного значения x и ниже оси x для
другое значение x , оно должно пересекать ось x где-то посередине.
(Если вы можете построить график функции, пересечения
обычно будет очевидным.)

Пример:

p ( x ) = 3 x + 4 x -20 x −32

Рациональные корни
(если есть) должны быть из списка
любой из 1/3, 2/3, 1, 4/3, 2, 8/3, 4, 16/3, 8, 32/3, 16, 32.Естественно, сначала вы посмотрите на целые числа, потому что арифметика
Полегче. Пробуя синтетическое деление, вы
найти p (1) = −45, p (2) = −22 и
p (4) = 144. Поскольку p (2) и p (4) имеют противоположные знаки, вы
знайте, что график пересекает ось между x = 2 и x = 4, поэтому
хотя бы один корень между этими числами. Другими словами, либо 8/3 — это
корень или корень от 2 до 4 иррациональны. (По факту,
синтетическое деление показывает, что 8/3 — это корень.)

Теорема о промежуточном значении может сказать вам, где находится
root, но он не может сказать вам, где нет root. Например,
считать

q ( x ) = 4 x — 16 x + 15

q (1) и q (3) положительные, но это вам не говорит
может ли график касаться или пересекать ось между ними. (Это на самом деле
дважды пересекает ось, при x = 3/2 и
x = 5/2.)

Верхняя и нижняя границы

Одним из побочных эффектов синтетического деления является
что даже если число, которое вы тестируете, окажется не корневым, оно может
сказать вам, что все корни меньше или больше этого
номер:

Если вы выполните синтетическое деление на положительное число , a , и каждое
число в нижней строке положительное или нулевое, тогда , — это
верхняя граница для корней, что означает, что все действительные корни
≤ a .
Если вы делаете синтетическое деление на
отрицательное число b , а числа в нижнем ряду чередуются
знак, тогда b — это нижняя граница для корней, что означает, что все
настоящие корни ≥ b .
Что делать, если нижняя строка содержит нули? Более полный
утверждение состоит в том, что чередующихся неотрицательных и неположительных знаков ,
после синтетического деления на отрицательное число показать нижнюю границу
корень. Следующие два примера поясняют это.

(Кстати, правило для нижних оценок следует
из правила для верхних оценок.
Нижние пределы корней p ( x ) равны верхним пределам
корни p (- x ), и деление на (- x + r ) аналогично
деление на — ( x — r ).)

Пример:

q ( x ) = x ³ + 2 x ² — 3 x — 4

Использование Rational Root
Тест, вы определяете единственно возможные рациональные корни как
4, 2 и 1.Вы решаете попробовать −2 в качестве
возможный корень, и вы тестируете его с синтетическим делением:

        -2 | 1 2 -3-4
            | -2 0 6
            | ------------------
               1 0–3 2

−2 не является корнем уравнения f ( x ) = 0.
В третьей строке чередуются знаки, и вы делили на
отрицательное число; однако этот ноль все портит.
Напомним, что у вас есть нижняя граница, только если знаки в нижнем ряду
чередовать неположительный и неотрицательный.1 положительный
(неотрицательный), и 0 может считаться неположительным, но
−3 не считается неотрицательным. Чередование
битая, а ты не знаешь есть ли корни
меньше -2. (Фактически, графический или
численные методы покажут корень около -2,5.)
Следовательно, вам нужно попробовать нижний возможный рациональный корень, −4:

        -4 | 1 2 -3-4
            | -4 8-20
            | ------------------
               1–2 5–24

Здесь знаки чередуются; поэтому вы знаете, что нет
корни ниже −4.(Остаток −24 показывает, что
−4 сам по себе не является корнем.)

Вот другой пример:

r ( x ) = x + 3 x — 3

Rational Root Test сообщает вам
что возможные рациональные корни — 1 и 3. С синтетическим
деление на −3:

        -3 | 1 3 0-3
            | -3 0 0
            | ------------------
               1 0 0-3

−3 не является корнем, но знаки здесь чередуются, так как
первый 0 считается неположительным, а второй — неотрицательным.Следовательно, −3 — это нижняя граница корней, а это означает, что
уравнение не имеет вещественных корней ниже −3.

Коэффициенты и корни

Существует интересная взаимосвязь между коэффициентами
многочлен и его нули. Я упомянул об этом последним, потому что он больше подходит
для формирования многочлена, который имеет нули с желаемыми свойствами,
вместо нахождения нулей существующего многочлена. Однако если вы
знать все корни многочлена, кроме одного или двух, вы можете легко использовать это
техника, чтобы найти оставшийся корень.

Рассмотрим многочлен

f ( x ) =
a _n x ⁿ +
a _{n −1} x ^{n −1} +
a _{n −2} x ^{n −2} + … +
а ₂ x ² +
а ₁ x +
a _o

Существуют следующие отношения:

— a _{n −1} a _n = сумма всех корней
+ a _{n − 2} a _n = сумма произведений корней
взяты по два за раз
— a _{n −3} a _n = сумма произведений корней
взято по три за раз
и так далее, пока
(−1) ⁿ a ₀ a _n = произведение всех корней

Пример: f ( x ) = x ³ — 6 x ² —
7 x — 8 имеет степень 3 и, следовательно, не более трех реальных нулей.Если
записываем настоящие нули как r ₁, r ₂,
r ₃, то сумма корней равна
r ₁ + r ₂ + r ₃ = — (- 6) = 6; в
сумма произведений корней, взятых по два за раз, равна
r ₁ r ₂ + r ₁ r ₃ + r ₂ r ₃ =
−7, а произведение корней равно
r ₁ r ₂ r ₃ =
(-1) ³ (-8) = 8.

Пример: Учитывая, что многочлен

г ( x ) = x ⁵ — 11 x ⁴ + 43 x ³-73 x ² + 56 x — 16

имеет тройной корень x = 1, найдите два других корня.

Решение: Пусть два других корня будут c и d .
Тогда вы знаете, что сумма всех корней равна 1 + 1 + 1 + c + d =
— (- 11) = 11, или c + d = 8.Ты
также знайте, что продукт всех корней
111 c d =
(−1) ⁵ (−16) = 16, или
c d = 16. c + d = 8,
c d = 16; поэтому c = d =
4, поэтому оставшиеся корни представляют собой двойной корень с размером x = 4.

Дополнительные коэффициенты и корни

Есть еще несколько теорем о соотношении
между коэффициентами и корнями.
Статья в Википедии
Свойства корней полиномов
дает хорошее, хотя и несколько краткое изложение.

Шаг 5. Разделите на множитель

Помните, что r является корнем тогда и только тогда, когда x — r является фактором;
это факторная теорема. Так что если ты хочешь
чтобы проверить, является ли r корнем, вы можете разделить многочлен на
x — r и посмотрите, выходит ли ровным (остаток от 0).
Элизабет Стапель
пример деления многочленов делением в столбик.

Но делать синтетическое деление проще и быстрее.Если твой
синтетическое деление немного заржавело, вы можете взглянуть на Dr.
Математика короткая
Учебник по синтетическому дивизиону;
если вам нужен более длинный учебник, Элизабет Стейплс
Синтетический дивизион отличный.
(У доктора Мата также есть страница о
почему работает Synthetic Division.)

Синтетическое подразделение также имеет некоторые побочные преимущества. Если вы подозреваете
корень на самом деле корень, синтетическое деление дает вам
приведенный многочлен . А иногда и тебе везет, и
синтетическое деление показывает вам верхнюю или нижнюю
связаны на корнях.

Вы можете использовать синтетическое деление при делении на
бином вида x — r для константы r . Если вы делите на
x −3, вы проверяете, является ли 3 корнем, и вы синтетическое деление
на 3 (не на −3). Если вы делите на x +11, вы проводите тестирование
является ли −11 корнем, и вы синтетически делите на −11 (не
11).

Пример:

p ( x ) = 4 x ⁴ — 35 x ² — 9

Вы подозреваете, что x −3 может быть фактором, и проверяете это с помощью
синтетическое деление, например:

        3 | 4 0-35 0-9
           | 12 36 3 9
           | --------------------
              4 12 1 3 0

Поскольку остаток равен 0, вы знаете, что 3 является корнем
p ( x ) = 0, а x −3 является множителем p ( x ).Но ты знаешь
более. Поскольку 3 положительно и нижняя строка синтетического деления
все положительные или нулевые, вы знаете, что все корни
p ( x ) = 0 должно быть ≤ 3. И вы также знаете
что

p ( x ) = ( x −3) (4 x ³ + 12 x ² + x + 3)

4 x ³ + 12 x ² + x + 3
— это приведенный многочлен .Все его факторы также
коэффициентов исходного p ( x ), но его степень на единицу ниже , поэтому его
с ним легче работать.

Шаг 6. Численные методы

Когда у вашего уравнения больше нет рациональных корней (или
многочлен не имеет более рациональных множителей) можно перейти к числовым
методы нахождения приблизительного значения иррациональных корней:

Статья в Википедии
Алгоритм поиска корней
имеет достойное резюме с указателями на конкретные методы.
Многие графические калькуляторы имеют
Команда Root или Zero, которая поможет вам найти
приблизительные корни. Например, на ТИ-83 или ТИ-84 вы
график
функцию, а затем выберите [2nd] [Calc] [zero].

Полный пример

Решить для всех сложных корней:

4 x + 15 x — 36 = 0

Шаг 1. Уравнение уже в стандартной форме, с
только ноль с одной стороны и степень x от наибольшей к наименьшей.Там
нет общих факторов.

Шаг 2. Так как уравнение имеет степень 3, будет 3
корнеплоды. Есть одна вариация знака, а от
Правило знаков Декарта, которое, как вы знаете, должно
быть одним положительным корнем. Изучите многочлен с заменой — x
x :

−4 x -15 x -36

Знаков нет, значит, нет
отрицательные корни. Следовательно, два других корня должны быть сложными,
и конъюгаты друг друга.

Шаги 3 и 4. Возможные рациональные корни
к сожалению, довольно много: любые из 1, 2, 3, 4, 6, 9, 12, 18, 36
делится на любое из 4, 2, 1. (перечислены только положительные корни, потому что вы
уже определили, что для этого нет отрицательных корней
уравнение.) Вы решаете сначала попробовать 1:

        1 | 4 0 15 -36
           | 4 4 19
           | -----------------
              4 4 19-17

1 не является корнем, поэтому вы проверяете 2:

        2 | 4 0 15 -36
           | 8 16 62
           | -----------------
              4 8 31 26

Увы, 2 тоже не рут.Но обратите внимание, что
f (1) = −17 и f (2) = 26. У них противоположные
знаки, что означает, что график пересекает ось x между x = 1
и x = 2, а корень находится между 1 и 2. (В данном случае это единственный
root, поскольку вы определили, что существует один положительный корень и
нет отрицательных корней.)

Единственный возможный рациональный корень между 1 и 2 — 3/2, и
следовательно, либо 3/2 является корнем, либо корень иррационален. Вы пытаетесь 3/2
по синтетическому отделению:

        3/2 | 4 0 15 -36
             | 6 9 36
             | -----------------
                4 6 24 0

Ура! 3/2 — это корень.Приведенный полином равен
4 x + 6 x + 24. Другими словами,

(4 x + 15 x — 36)
( x −3/2) =
4 x + 6 x + 24

Приведенный многочлен имеет степень 2,
так что нет необходимости в большем
методом проб и ошибок, и вы переходите к шагу 5.

Шаг 5. Теперь вы должны решить

4 x + 6 x + 24 = 0

Сначала разделите общий множитель 2:

2 x + 3 x + 12 = 0

Нет смысла пытаться множить этот квадратичный коэффициент, потому что
вы определили, используя Правило знаков Декарта, что больше нет
настоящие корни.Итак, вы используете квадратичный
формула:

x = [−3 √9 — 4 (2) (12)] / 2 (2)

x = [−3 √ − 87] / 4

x = −3/4 (√87 / 4) i

Шаг 6. Помните, что вы нашли корень в
более ранний шаг! Полный список корней —

3/2, −3/4 + (√87 / 4) я,
−3/4 — (√87 / 4) я

Что нового

19 октября 2020 г. : преобразовано в HTML5. Переменные, выделенные курсивом и
имена функций; выделил мнимое i.
3 ноября 2018 г. : Некоторые изменения форматирования для ясности,
особенно с радикалами. Здесь отметили, что 0
является тройным корнем в этом примере.
(промежуточные изменения подавлены)
15 февраля 2002 г. : Первая публикация.

Классифицирующие полиномы

Полиномы можно классифицировать двумя разными способами — по количеству членов и по их степени.

1. Количество терминов.

Одночлен состоит только из одного члена. Например, 4x ². Помните, что термин содержит как переменную (и), так и ее коэффициент (число перед ним). Таким образом, это всего лишь один член.

Бином имеет два члена. Например: 5x ² -4x

Трехчлен состоит из трех членов. Например: 3y ² + 5y -2

Любой многочлен с четырьмя или более членами просто называется многочленом.Например: 2y ⁵ + 7y ³ — 5y ² + 9y -2

Практикуйте классификацию этих многочленов по количеству членов:

1. 5y.

2. 3x ² -3x + 1

3. 5y-10

4. 8xy

5. 3x ⁴ + x ² -5x + 9

Ответы: 1) Monomial 2 ) Трехчлен 3) бином 4) моном 5) полином

2.Степень. Степень полинома определяется по члену с наивысшим показателем в его переменной (-ах) .

Примеры:

5x ² -2x + 1 Наивысший показатель степени равен 2, так что это трехчлен 2 ^и градусов.

3x ⁴ + 4x ² Наивысший показатель степени равен 4, так что это 4 ^{-й бином} градусов.

8x-1 Хотя кажется, что показатель степени отсутствует, у x есть понятый показатель степени 1; следовательно, это бином на 1 ^{градуса и} градусов.

5 Переменной нет вообще. Следовательно, это моном 0 степени. Это 0 градусов, потому что x ⁰ = 1. Таким образом, технически 5 может быть записано как 5x ⁰.

3x ² y ⁵ Поскольку обе переменные являются частью одного и того же члена, мы должны сложить их показатели вместе, чтобы определить степень. 2 + 5 = 7, так что это моном степени 7 ^-я.

Классифицируйте эти многочлены по степени.

1,7x ³ +5 ² +1

2.6y ⁵ + 9y ² -3y + 8

3.8x-4

4.9x ² y + 3

5.12x ²

Ответы 1) 3 ^rd градусов 2) 5 ^-я градусов 3) 1 ^-я градусов 4) 3 ^-я градусов 5) 2 ^-я градусов

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — Формулы сокращенного умножения

Степень суммы

Степень разности

Квадрат многочлена

Куб трехчлена

Mathway | Популярные задачи

Таблица производных простых функций

1 3 в степени x

Где можно решить любую задачу по математике, а так же 1 3 в степени x Онлайн?

1.2. Ко­рень n-й сте­пе­ни

1.2. Ко­рень n-й сте­пе­ни

Упраж­не­ния

Степенная функция, линейная функция, квадратичная, кубическая и y=1/х 9 класс онлайн-подготовка на Ростелеком Лицей |

Определение степени и ведущего коэффициента многочленов

Практическое руководство. Для данного полиномиального выражения определите степень и старший коэффициент.

Алгебра — многочлены

Раздел 1-4: Многочлены

Примеры одночленов и многочленов

Идентификация монома

Полиномы

Биномы

Трехчлены

Степени многочленов

Термины по алгебре

История алгебры

полиномов

Как решать полиномиальные уравнения

Генеральный план

точное или приблизительное значение?

Шаг за шагом

Кубические и четвертые формулы

Шаг 1. Стандартная форма и упрощение

Шаг 2. Сколько корней?

Правило знаков Декарта

Сложные корни

Иррациональные корни

Множественные корни

Шаг 3. Квадратичные множители

Шаг 4. Найдите один фактор или корень

Мономиальные множители

Особые продукты

Рациональные корни

Графические подсказки

Границы корней

Теорема о промежуточном значении

Верхняя и нижняя границы

Коэффициенты и корни

Дополнительные коэффициенты и корни

Шаг 5. Разделите на множитель

Шаг 6. Численные методы

Полный пример

Что нового

Классифицирующие полиномы

Добавить комментарий Отменить ответ

1.2. Корень n-й степени

1.2. Корень n-й степени

Упражнения