Содержание
2 в степени x больше или равно 2
Вы искали 2 в степени x больше или равно 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 в степени х больше или равно 2, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «2 в степени x больше или равно 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 2 в степени x больше или равно 2,2 в степени х больше или равно 2. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 2 в степени x больше или равно 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 2 в степени x больше или равно 2).
Где можно решить любую задачу по математике, а так же 2 в степени x больше или равно 2 Онлайн?
Решить задачу 2 в степени x больше или равно 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Функция EXP — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel. ).
).
Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
|
|
|
|---|---|---|
|
=EXP(1)
|
Приблизительное значение e
|
2,71828183
|
|
=EXP(2)
|
Основание натурального логарифма e, возведенное в квадрат
|
7,3890561
|
причины, симптомы и методы диагностики
Тугоухость-это частичное нарушение слуха, которое характеризуется ухудшением способности обнаруживать и понимать звуки.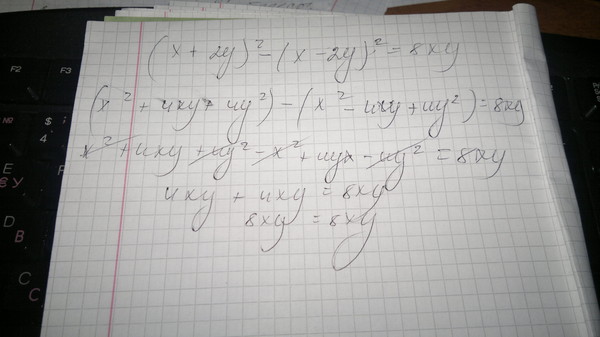 В зависимости от степени нарушения слуха человек перестает слышать некоторые части речевого сигнала, в результате чего нарушается разборчивость речи. Тугоухость может возникнуть неожиданно или развиваться постепенно. Она может появиться в результате нарушений в слуховой системе и отразиться на различных участках частотного диапазона.
В зависимости от степени нарушения слуха человек перестает слышать некоторые части речевого сигнала, в результате чего нарушается разборчивость речи. Тугоухость может возникнуть неожиданно или развиваться постепенно. Она может появиться в результате нарушений в слуховой системе и отразиться на различных участках частотного диапазона.
Различают следующие типы тугоухости в зависимости от места возникновения и нарушения в ухе:
- Нейросенсорная (или сенсоневральная) тугоухость;
- Кондуктивная тугоухость;
- Смешанная (комбинированная) тугоухость;
- Слуховая (аудиторная нейропатия).
Посмотрите видео, чтобы узнать больше о типах нарушения слуха.
Нейросенсорная (или сенсоневральная) тугоухость
Это нарушение слуха, вызванное поражением звуковоспринимающего аппарата: внутреннего уха, преддверно-улиткового нерва или слуховых центров головного мозга. Сначала происходит повреждение наружных волосковых клеток, что значительно затрудняет восприятие тихих звуков. В результате чего человеку, страдающему нейросенсорной тугоухостью, кажется, что звук в 50 дБ звучит тихо, в то время как нормально слышащий человек воспринимает этот звук вполне комфортно.
Сначала происходит повреждение наружных волосковых клеток, что значительно затрудняет восприятие тихих звуков. В результате чего человеку, страдающему нейросенсорной тугоухостью, кажется, что звук в 50 дБ звучит тихо, в то время как нормально слышащий человек воспринимает этот звук вполне комфортно.
Существуют следующие причины развития нейросенсорной тугоухости:
- Свинка
- Менингит
- Рассеянный склероз
- Неврит слухового нерва
- Возрастное снижение слуха
- Сильный шум без защиты от него
- Краснуха матери во время беременности
- Нарушение кровоснабжения слухового нерва
- Определенные лекарства (цисплатин, хинин, ряд антибиотиков)
- Повышение давления жидкостей внутреннего уха (болезнь Меньера).
Нейросенсорная тугоухость, к сожалению, не подлежит ни оперативному, ни медикаментозному лечению и может быть компенсирована с помощью подбора слуховых аппаратов.
Кондуктивная тугоухость
Это нарушение слуха, связанное с проблемами при передачи звука либо в самом слуховом проходе, либо в среднем ухе. Кондуктивная тугоухость возникает на уровне наружного слухового прохода или среднего уха. Среди причин возникновения кондуктивной тугоухости выделяют:
Кондуктивная тугоухость возникает на уровне наружного слухового прохода или среднего уха. Среди причин возникновения кондуктивной тугоухости выделяют:
- На уровне наружного уха: опухоли, наружный отит, пороки развития, серные пробки.
- На уровни среднего уха: отосклероз, повреждение слуховых косточек, острые и хронические средние отиты, нарушения функции слуховой (евстахиевой) трубы.
В некоторых случаях кондуктивная тугоухость лечится медикаментозно или хирургическим путем. В других случаях для этого используют слуховые аппараты, поскольку кортиев орган в улитке продолжает функционировать нормально и главной проблемой становится лишь преодоление препятствия в наружном или среднем ухе.
Смешанная (комбинированная) тугоухость
Смешанная тугоухость-это сочетание у одного человека кондуктивной и нейросенсорной тугоухости. Данный тип тугоухости корректируется использованием слухового аппарата и медицинским лечением.
Слуховая (аудиторная нейропатия)
При слуховой нейропатии окончания слухового нерва чаще всего остаются неповрежденными и могут воспринимать окружающие звуки в полном объеме.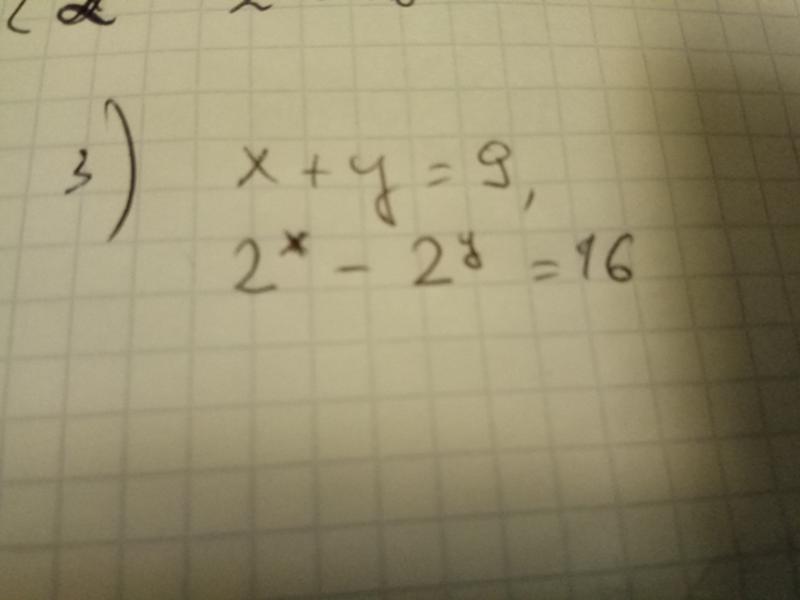 Однако при проведении нервных импульсов по слуховому нерву в головной мозг звуковая информация декодируется и искажается. Именно поэтому обнаружение и коррекция данного типа снижения слуха настолько сложны.
Однако при проведении нервных импульсов по слуховому нерву в головной мозг звуковая информация декодируется и искажается. Именно поэтому обнаружение и коррекция данного типа снижения слуха настолько сложны.
Больше информации о развитии слуховой нейропатии у детей Вы найдете здесь.
Степени снижения слуха
Как правило, при тугоухости слух снижается постепенно, иногда на протяжении нескольких лет. Различают стабильную и прогрессирующую стадию хронической тугоухости. Для определения степени тугоухости выполняют ряд исследований слуха- аудиометрию. Для этого испытуемому надо различить звуки основных частот. Чем большая громкость звука требуется для того, чтобы тестируемый человек его услышал, тем большая степень тугоухости у него имеется.
В Беларуси принята следующая классификация степеней нарушения слуха:
| Степень нарушения слуха | Описание степени нарушения слуха |
| Нормальный слух | 0-25 дБ |
| I Степень | 26-40 дБ Неспособность слышать тихие звуки, трудности с разборчивостью речи в шумной обстановке. |
| II Степень | 41-55 дБ Неспособность слышать тихие звуки и звуки средней громкости, значительные трудности с разборчивостью речи, особенно при фоновом шуме. |
| III Степень | 56-70 дБ Неспособность слышать большинство звуков. Чтобы быть услышанным, говорящему приходится значительно повышать голос. Общение в группе людей проблематично и требует существенных усилий. |
| IV Степень | 71-90 дБ Различимы только очень громкие звуки, общение без использования жестового языка или слухового аппарата практически невозможно. |
| Полная потеря слуха | Свыше 90 дБ |
Получите консультацию сурдолога в ближайший к Вам Центре хорошего слуха, чтобы быть уверенным, что с вашим слухом все в порядке. Записаться вы можете одним из следующих способов:
— оставить заявку на сайте;
— написать онлайн-консультанту;
— позвонить или написать в любой мессенджер на номер единой линии + 375 29 320-33-36.
Засенко Ирина Леонидовна
Врач оториноларинголог-сурдолог первой категории. Главный врач Центров хорошего слуха. Стаж работы: 20 лет. Ведет прием взрослых и детей с рождения.
Ведет прием взрослых и детей:
Минск, ул. Плеханова, 27 Центр хорошего слуха
Степени и возведение в степень, вторая, третья, четвёртая степени
Когда число умножается само на себя, произведение называется степенью.
Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.
Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.
И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a
Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.
Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения.
Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель. Это число или буква называется показателем степени или степенью числа. Так, а2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a3 означает aaa, то есть здесь a повторяется три раза как множитель.
Показатель первой степени есть 1, но он обычно не записывается. Так, a1 записывается как a.
Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a. Но a4 = a.a.a.a
Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении ax, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень. Так, bm и dn возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда bm = b3; но если m = 5, тогда bm=b5.
Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)3 есть (a + b + d). (a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a3 + 3a2b + 3a2d + 3ab2 + 6abd + 3ad2 + b3 + d3.
Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.
Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a5, a4, a3, a2, a1;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.
Tак a.a = a2, второй член. И a3.a = a4
a2.a = a3, третий член. a4.a = a5.
a4.a = a5.
Если мы начнем слева делить на a,
мы получим a5:a = a4 и a3:a = a2.
a4:a = a3 a2:a = a1
Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.
Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.
Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.
Или a5, a4, a3, a2, a, 1, 1/a, 1/a2, 1/a3.
Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.
Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a3) = a3.
Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
Так, для a + b, мы получим множество,
(a + b)3, (a + b)2, (a + b), 1, 1/(a + b), 1/(a + b)2, 1/(a + b)3.
Для удобства используется еще одна форма записи обратных степеней.
Согласно этой форме, 1/a или 1/a1 = a-1. И 1/aaa или 1/a3 = a-3.
1/aa или 1/a2 = a-2. 1/aaaa или 1/a4 = a-4.
А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a0.
Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a4, a3, a2, a1, a0, a-1, a-2, a-3, a-4.
Или a+4, a+3, a+2, a+1, a0, a-1, a-2, a-3, a-4.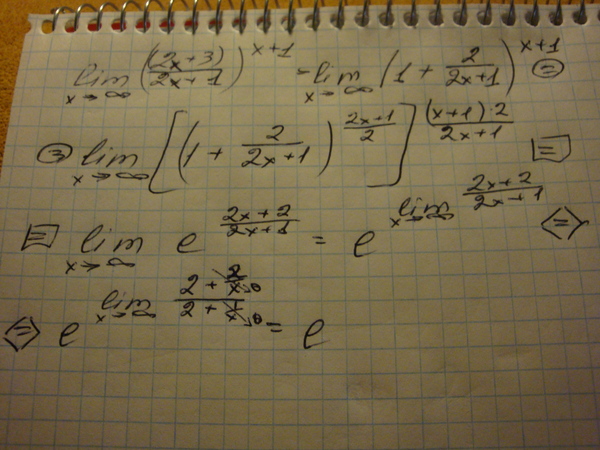
А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.
Корень степени может выражен более чем одной буквой.
Так, aa.aa или (aa)2 есть второй степенью aa.
И aa.aa.aa или (aa)3 есть третьей степенью aa.
Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.
Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:
Умножайте величину саму на себя столько раз, сколько указано в степени числа.
Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.
Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.
Четвертая степень a есть a4 или aaaa. (Art. 195.)
Шестая степень y есть y6 или yyyyyy.
N-ая степень x есть xn или xxx….. n раз повторенное.
Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.
Tак (ay)2 =a2y2; (ay)2 = ay.ay.
Но ay.ay = ayay = aayy = a2y2.
Так, (bmx)3 = bmx.bmx.bmx = bbbmmmxxx = b3m3x3.
Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.
Пример 1. Четвертая степень dhy есть (dhy)4, или d4h4y4.
Пример 2. Третья степень 4b, есть (4b)3, или 43b3, или 64b3.
Пример 3. N-ая степень 6ad есть (6ad)n или 6nandn.
Пример 4. Третья степень 3m.2y есть (3m.2y)3, или 27m3.8y3.
Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,
(a + b)1 = a + b, первая степень.
(a + b)1 = a2 + 2ab + b2, вторая степень (a + b).
(a + b)3 = a3 + 3a2b + 3ab2 + b3, третья степень.
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4, четвертая степень.
Квадрат a — b, есть a2 — 2ab + b2.
3 + 3a2 + 3a + 1.
Квадрат a + b + h есть a2 + 2ab + 2ah + b2 + 2bh + h2
Упражнение 1. Найдите куб a + 2d + 3
Упражнение 2. Найдите четвертую степень b + 2.
Упражнение 3. Найдите пятую степень x + 1.
Упражнение 4. Найдите шестую степень 1 — b.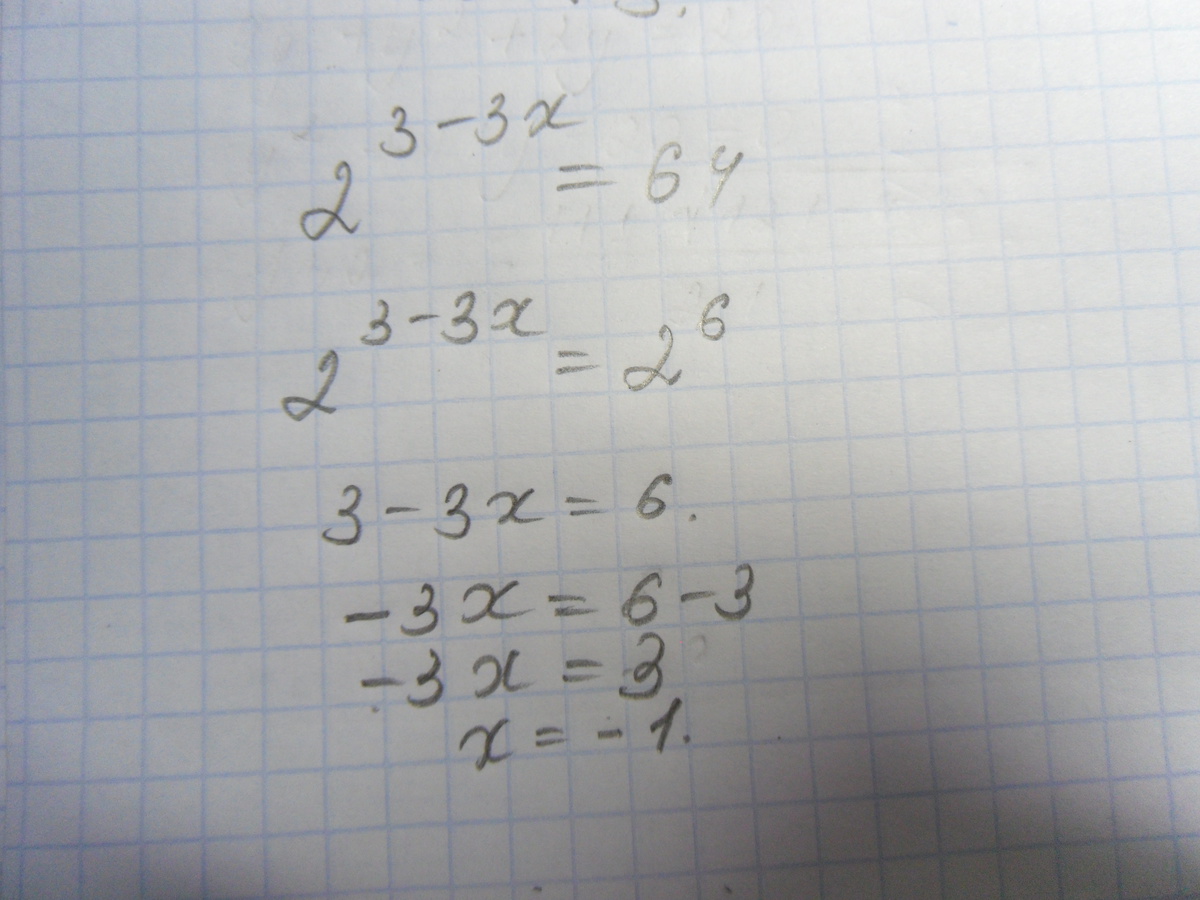
Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.
Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a2 + 2ah + h2 также, (a — h)(a — h) = a2 — 2ah + h2.
Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.
Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.
Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.
Пример 1. Квадрат 2a + b, есть 4a2 + 4ab + b2.
Пример 2. Квадрат ab + cd, есть a2b2 + 2abcd + c2d2.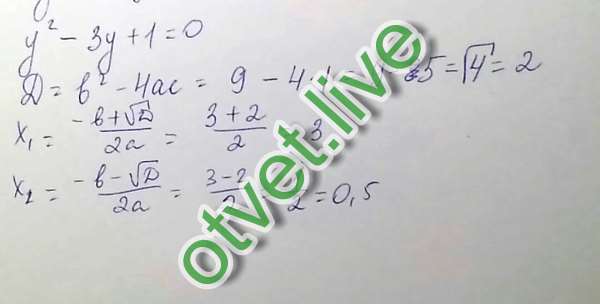
Пример 3. Квадрат 3d — h, есть 9d2 + 6dh + h2.
Пример 4. Квадрат a — 1 есть a2 — 2a + 1.
Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.
Во многих случаях является эффективным записывать степени без умножения.
Так, квадрат a + b, есть (a + b)2.
N-ая степень bc + 8 + x есть (bc + 8 + x)n
В таких случаях, скобки охватывают все члены под степенью.
Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.
Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]2 или (a + b)2.(c + d)2.
Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.
Куб a. (b + d), есть [a.(b + d)]3, или a3.(b + d)3.
(b + d), есть [a.(b + d)]3, или a3.(b + d)3.
Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.
Вторая степень (- a) есть +a2
Третья степень (-a) есть -a3
Четвёртая степень (-a) есть +a4
Пятая степень (-a) есть -a5
Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a2
И -a.-a = +a2
Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.
Третья степень a2 есть a2. 3 = a6.
3 = a6.
Для a2 = aa; куб aa есть aa.aa.aa = aaaaaa = a6; что есть шестой степенью a, но третьей степенью a2.
Четвертая степень a3b2 есть a3.4b2.4 = a12b8
Третья степень 4a2x есть 64a6x3.
Пятая степень (a + b)2 есть (a + b)10.
N-ая степень a3 есть a3n
N-ая степень (x — y)m есть (x — y)mn
(a3.b3)2 = a6.b6
(a3b2h4)3 = a9b6h12
Правило одинаково применяется к отрицательным степеням.
Пример 1. Третья степень a-2 есть a-3.3=a-6.
Для a-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a6 = a-6
Четвертая степень a2b-3 есть a8b-12 или a8/b12.
Квадрат b3x-1, есть b6x-2.
N-ая cтепень ax-m есть x-mn или 1/x.
Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.
Пример 1. Квадрат -a3 есть +a6. Квадрат -a3 есть -a3.-a3, которое, согласно правилам знаков при умножении, есть +a6.
2. Но куб -a3 есть -a9. Для -a3.-a3.-a3 = -a9.
3. N-ая степень -a3 есть a3n.
Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.
Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.
Квадрат a/b есть a2/b2. Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a2b2
Вторая, третья и n-ая степени 1/a есть 1/a2, 1/a3 и 1/an.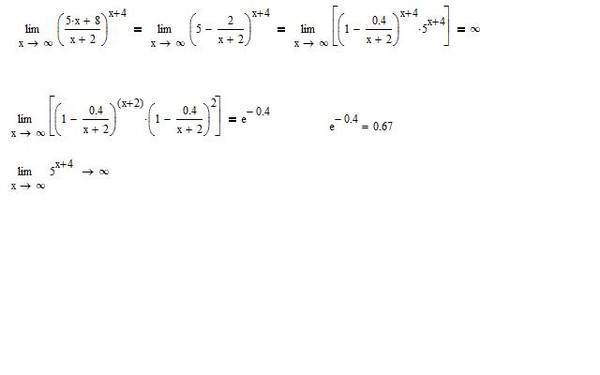
Примеры двочленов, в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)2 = x2 + 2.x.(1/2) + 1/22 = x2 + x + 1/4
(x — 1/2)2 = x2 — 2.x.(1/2) + 1/22 = x2 — x + 1/4
2. Квадрат a + 2/3 есть a2 + 4a/3 + 4/9.
3. Квадрат x + b/2 = x2 + bx + b2/4.
4 Квадрат x — b/m есть x2 — 2bx/m + b2/m2.
Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.
Так, в дроби ax-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax-2/y = (a/y).x-2 = (a/y).(1/x2 = a/yx2.
В дроби a/by3 мы можем переместить у из знаменателя в числитель.
Тогда a/by2 = (a/b).(1/y3) = (a/b).y-3 = ay-3/b.
Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.
Так, ax3/b = a/bx-3. Для x3 обратным есть x-3, что есть x3 = 1/x-3.
Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.
Так, a/b = 1/ba-1, or ab-1.
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Степень с натуральным показателем
Предварительные навыки
Что такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
23 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 53, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.
Число, которое повторяется называют основанием степени. В выражении 53 основанием степени является число 5.
А число, которое надписано над числом 5 называют показателем степени.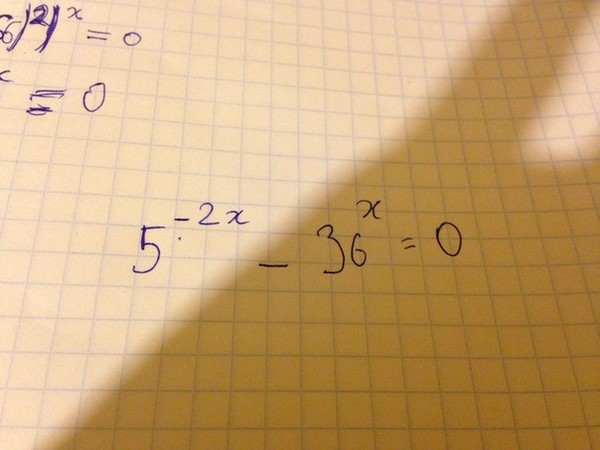 В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень.
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 00 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.
Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
32 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
24 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
23 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
Сначала запишем само число 10 и в качестве показателя укажем число 2
102
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
102 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
102 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
103 = 1000
Пример 3. Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
104 = 10000
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
101 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 101
10 = 101
Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 102
100 = 102
Пример 3. Представим число 1 000 в виде степени с основанием 10.
1 000 = 103
Пример 4. Представим число 10 000 в виде степени с основанием 10.
10 000 = 104
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2)2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −22, которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −22 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −22 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−22 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2)3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5)3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1. Найти значение выражения 2 + 52
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 52 = 2 + 25 = 27
Пример 10. Найти значение выражения −62 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−62 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−62 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 22
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 22 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.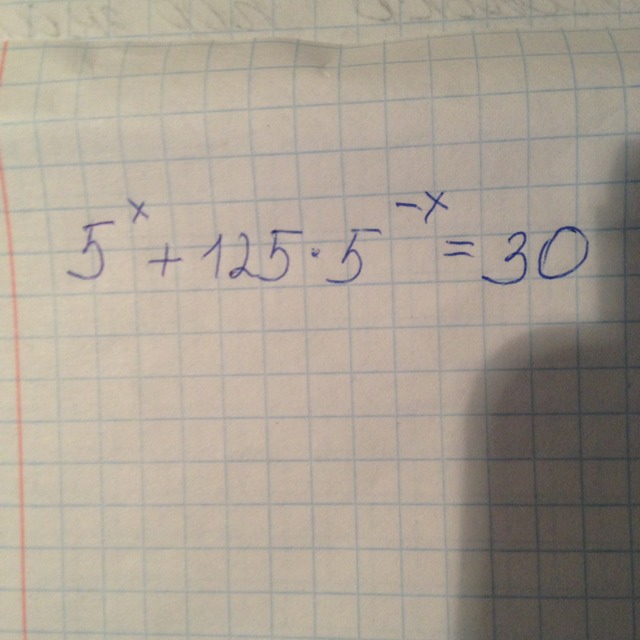
Пример 12. Найти значение выражения (32 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 53 + 5 × 23
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (23)2. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(23)2это произведение двух степеней, каждая из которых равна 23
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (23)2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (23)2 можно перемножить и записать это произведение над основанием 2
Получили 26. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 23 это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:
(an)m = an × m
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (32)2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 34. А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 22 на 33.
22 это число 4, а 33 это число 27. Перемножаем числа 4 и 27, получаем 108
22 × 33 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 22 на 23
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 22 и 23. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 25. Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 22 это произведение 2 × 2, а 23 это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2.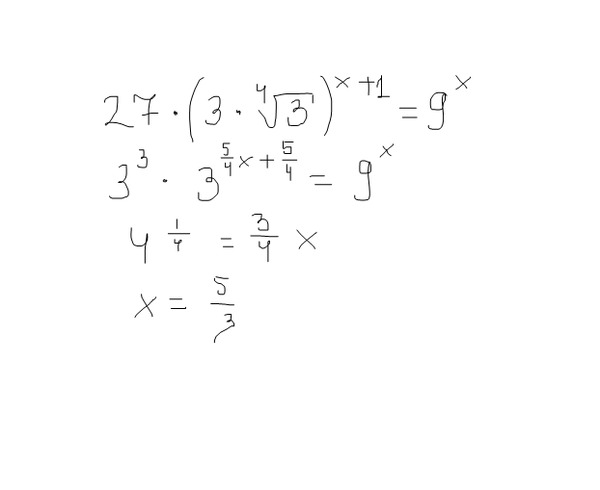 Это произведение представимо в виде 25
Это произведение представимо в виде 25
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 21 × 22 × 23. Основание 2 оставим без изменений, а показатели сложим:
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 58 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 58 × 25 получилась одна степень.
Число 25 можно представить в виде 52. Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 58 × 25 в виде одной степени, а именно в виде степени 510.
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 29 × 32
Число 32 можно представить в виде 25. Тогда получим выражение 29 × 25. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 31 и 31
31 × 31
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
31 × 31 = 32
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
31 × 31 = 32 = 9
Пример 4. Вычислите произведение 2 × 2 × 32 × 33, используя основное свойство степени.
Произведение 2 × 2 заменим на 21 × 21, затем на 21 + 1, а затем на 22. Произведение 32 × 33 заменим на 32 + 3, а затем на 35
Далее вычисляем значение каждой степени и находим произведение:
Пример 5. Выполнить умножение x × x
Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7. Выполнить умножение y3y2y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8. Выполнить умножение aa3a2a5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9. Представить степень 38 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 38 в виде произведения степеней 35 и 33
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 35 × 33 можно записать как 35 + 3, откуда 38.
Конечно можно было представить степень 38 в виде произведения других степеней. Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x12 в виде различных произведений степеней с основаниями x.
Воспользуемся основным свойство степени. Представим x12 в виде произведений с основаниями x, и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2
Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 22, а произведение 3 × 3 можно заменить на 32. Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 22 × 32.
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4)2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz)3
Возведём в третью степень каждый множитель данного произведения:
(3xyz)3 = 33x3y3z3
Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 52 × 32. Возведем каждое число во вторую степень и перемножим полученные результаты:
52 × 32 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)2. Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
52 × 32 = (5 × 3)2 = (15)2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)n = an × bn, то an × bn = (a × b)n. То есть левая и правая часть равенства поменялись местами.
То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(an)m = an × m
К примеру, выражение (23)2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(23)2 = 23 × 2 = 26
Далее вычислить степень 26, которая равна 64
(23)2 = 23 × 2 = 26 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (23)2. Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
(2 × 2 × 2)2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2)2 = 22 × 22 × 22
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
Как и раньше получили 26. Значение этой степени равно 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (22 × 32)3. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 21 × 41. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
У нас должен получиться тот же результат:
Пример 2. Найти значение выражения (33)2
Основание оставляем без изменений, а показатели перемножаем:
Получили 36. Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax)3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)3 — получится −8. Буквенная часть останется без изменений:
Буквенная часть останется без изменений:
Пример 6. Выполнить возведение в степень в выражении (10xy)2
Пример 7. Выполнить возведение в степень в выражении (−5x)3
Пример 8. Выполнить возведение в степень в выражении (−3y)4
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
Пример 10. Упростите выражение x5 × (x2)3
Степень x5 пока оставим без изменений, а в выражении (x2)3 выполним возведение степени в степени:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Теперь выполним умножение x5× x6.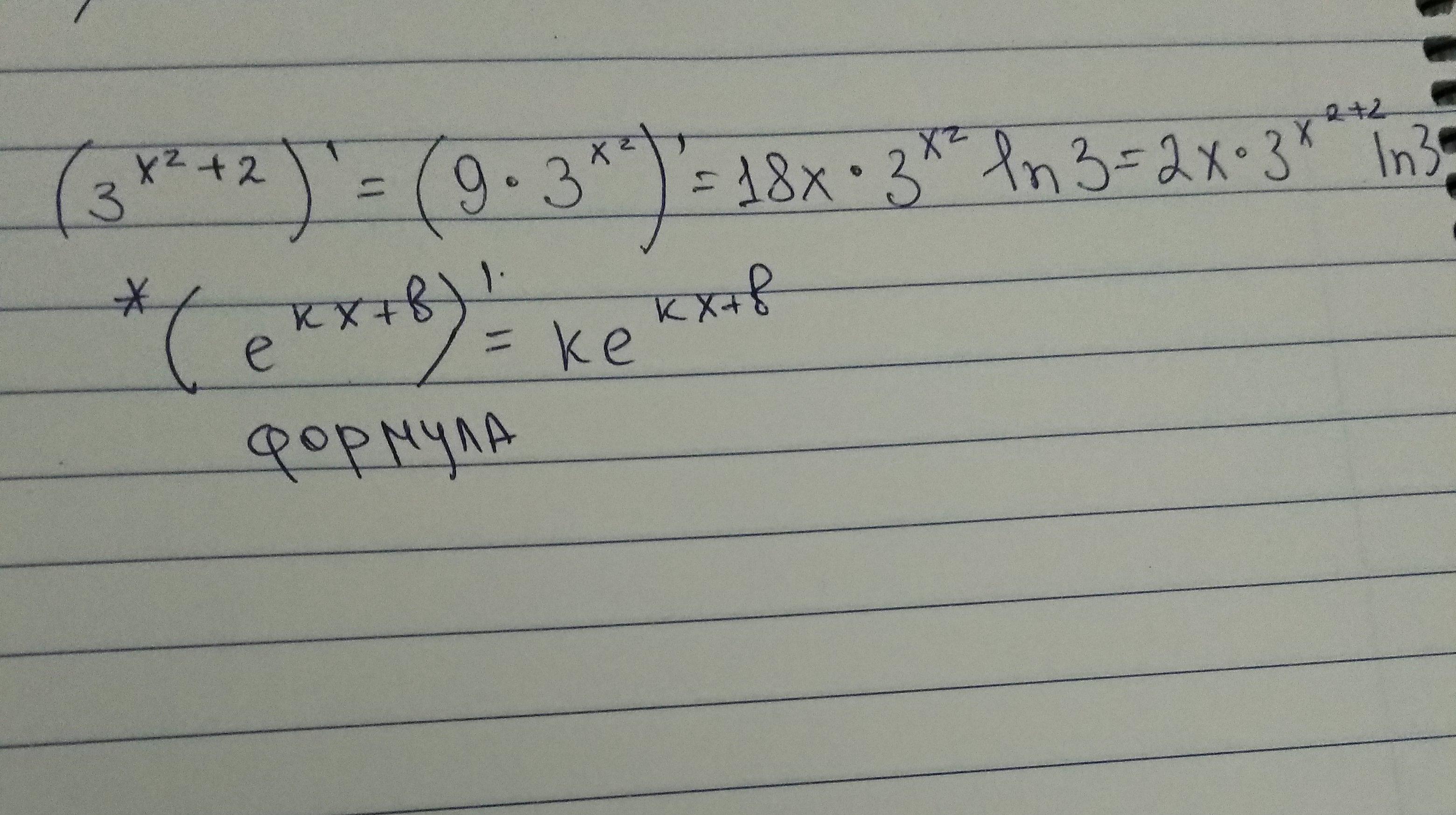 Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Пример 9. Найти значение выражения 43 × 22, используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 43. Основание у этой степени есть число 4, которое можно представить в виде 22. Тогда исходное выражение примет вид (22)3 × 22. Выполнив возведение степени в степень в выражении (22)3, мы получим 26. Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 43 на 22.
Вычислим 43, получим 64. Вычислим 22, получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 23 : 22
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 23 : 22 равно 2.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 23 : 22. Здесь делимое это 23, а делитель 22.
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 23 на 22 означает найти такую степень, которая при умножении на делитель 22 даст в результате 23. А какую степень можно умножить на 22, чтобы получить 23 ? Очевидно, что только степень 21. Из основного свойства степени имеем:
Убедиться, что значение выражения 23 : 22 равно 21 можно непосредственно вычислив само выражение 23 : 22. Для этого сначала найдём значение степени 23, получим 8. Затем найдём значение степени 22, получим 4. Разделим 8 на 4, получим 2 или 21, поскольку 2 = 21.
23 : 22 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
Например, найдём значение выражения 22 : 22. Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 22 : 22 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 22 и 22 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 22 : 22 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 412 : 410
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
412 : 410 = 412 − 10 = 42 = 16
Пример 3. Представить частное x3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Пример 4. Представить частное x3 : x2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x3 можно записать как x × x × x, а степень x2 как x × x. Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x2. Чтобы сократить дробь на x2 нужно числитель и знаменатель дроби разделить на x2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5. Выполнить деление x12 : x3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 72
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (23)4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями:
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 43 запишем в виде возведения степени в степень (22)3. Тогда получим следующее выражение:
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (22)3
В числителе и в знаменателе получившегося выражения содержится степень 26, которую можно сократить на 26
Видим, что в результате осталась единственная степень 32, значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 75 × 45 можно представить в виде степени с одним показателем (7 × 4)5. Далее перемножим выражение в скобках, получим 285. В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
Значит, значение выражения равно 28. Запишем решение полностью:
Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности
Значит обыкновенная дробь во второй степени равна дроби .
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 22 и 32 соответственно:
Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби
Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
Далее вычислим значение получившегося выражения:
Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
Пример 2. Найти значение степени (−1,5)3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
Пример 3. Найти значение степени (−2,4)2
Показатель степени является чётным числом. Значит ответ будет положительным:
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Представьте в виде степени произведение:
Решение:
Задание 8. Представьте в виде степени произведение:
Решение:
Задание 9. Представьте в виде степени произведение:
Решение:
Задание 10. Представьте в виде степени произведение:
Решение:
Задание 11. Представьте в виде степени произведение:
Решение:
Задание 12. Представьте в виде степени произведение:
Решение:
Задание 13. Представьте в виде степени частное:
Решение:
Задание 14. Представьте в виде степени частное:
Решение:
Задание 15. Представьте в виде степени частное:
Решение:
Задание 16. Представьте в виде степени частное:
Решение:
Задание 17. Представьте в виде степени частное:
Решение:
Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2
Решение:
Задание 19. Представьте в виде степени частное:
Решение:
Задание 20. Сократите дробь на c¹
Решение:
Задание 21. Представьте в виде степени следующее произведение:
Решение:
Задание 22. Представьте в виде степени следующее произведение:
Решение:
Задание 23. Представьте в виде степени следующее произведение:
Решение:
Задание 24. Представьте в виде степени следующее произведение:
Решение:
Задание 25. Представьте в виде степени следующее произведение:
Решение:
Задание 26. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 27. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 28. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 32. Представьте в виде степени следующее выражение:
Решение:
Задание 33. Представьте в виде степени следующее выражение:
Решение:
Задание 34. Представьте в виде степени следующее выражение:
Решение:
Задание 35. Представьте в виде степени следующее выражение:
Решение:
Задание 36. Представьте в виде степени следующее выражение:
Решение:
Задание 37. Представьте в виде степени следующее выражение:
Решение:
Задание 38. Найдите значение следующего выражения:
Решение:
Задание 39. Найдите значение следующего выражения:
Решение:
Задание 40. Найдите значение следующего выражения:
Решение:
Задание 41. Найдите значение следующего выражения:
Решение:
Задание 42. Найдите значение следующего выражения:
Решение:
Задание 43. Найдите значение следующего выражения:
Решение:
Задание 44. Найдите значение следующего выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
симптомы, причины, диагностика, лечение и профилактика
Гонартроз представляет собой артроз коленного сустава деформирующего вида. Болезнь поражает гиалиновый хрящ в поверхности суставов костей большой берцовой и бедренной. Патология протекает в хронической прогрессирующей форме.
Клиническая симптоматика гонартроза суставов заключается в наличии усиливающейся в процессе движения боли, скоплении жидкости в суставе и ограниченности движений. Поздние стадии гонартоза характеризуются отсутствием опоры на ногу. Диагностика основывается на сборе жалоб и анамнестических данных, рентгенографии и данных физикального осмотра. Лечение гонартроза коленного сустава предполагает протезирование в случае отсутствия эффекта от консервативного лечения.
Гонартроз в дословном переводе означает коленный сустав. Патология протекает в виде деформирующего артроза. Это означает, что происходит поражение хряща внутри сустава физиологически дистрофическим способом, а не воспалительным процессом. Патология протекает в прогрессирующей форме. Данная патология является наиболее распространенным видом артроза. В группу риска с наибольшей степенью вероятности входят женщины среднего и пожилого возраста. В молодом возрасте патология возникает в качестве посттравматического осложнения. Профилактика имеет огромное значение в рамках предупредительной терапии.
Очаги отложенных солей кальция в сухожилиях и аппарате связок и сухожилий обладают вторичной ролью в формировании гонартроза коленного сустава.
Симптомы и признаки
Гонартроз суставов развивается постепенно. Первые стадии болезни практически не тревожат пациентов, разве что незначительные боли при спуске или подъеме по лестнице. Более чувствительные пациенты указывают чувство скованности в суставах или подколенной области.
Отличительные симптомом гонартроза 1 степени является стартовый порог боли – это болевые ощущения, сопровождающие первые шаги после сидячего положения. Далее в процессе ходьбы боль сходит на нет или значительно притупляется. Ее новое появление будет ознаменовано какими-либо физическими нагрузками значительной тяжести.
Внешние симптомы гонартроза появляются редко. В основном к ним относится отечность. Сопровождение патологии скоплением жидкости приводит к синовиту. В данном случае сустав раздувается до шарообразного вида и движения становятся скованными, а больной ощущает тяжесть.
Каждая степень гонартроза имеет свои отличительные признаки. Гонартроз 2 степени отличает интенсивная боль при ходьбе и умеренных физических нагрузках. Прогрессирование гонартроза приводит к постепенному обездвиживанию сустава. При этом сгибание и разгибание коленного сустава приводит к хрусту и резким болевым ощущениям.
Гонартроз 3 степени сопровождается постоянным болевым синдромом. При этом движение сустава практически парализуется и больной не может распрямить ногу. Сустав увеличивается в размере и деформируется. Появляются внешние признаки патологии – неустойчивость походки, переваливающийся характер движений или отсутствие возможности ходить без дополнительной опоры.
У вас появились симптомы гонартроза?
Точно диагностировать заболевание может только врач.
Не откладывайте консультацию — позвоните по телефону
+7 (495) 775-73-60
Причины возникновения и развития
Практически всегда патология развивается на фоне комплексного воздействия ряда факторов:
- травмы – переломы голени, поврежденные мениски, надрывы или разрывы связок. Болезнь возникает в период от 2 месяцев до 5 лет после травмирования;
- физические нагрузки – занятия спортом полезны в том случае если комплекс упражнений и их интенсивность соответствуют возрастному положению пациента;
- лишний вес – ожирение приводит к чрезмерной нагрузке на суставы и их преждевременному износу, в группе риска особенно находятся пациенты с варикозным расширение вен.
Пути заражения и факторы риска
Гонартроз 1 степени – нарушение кровообращения внутри мелких костных сосудов приводит к утрате способности хряща к скольжению.
Гонартроз 2 степени – изменение вязкости и густоты суставной жидкости, начинается дегенерация хряща из-за недостатка питания, усиливается трение между костями и болезнь прогрессирует.
Гонартроз 3 степени – кости практически вдавлены друг в друга, ограничивается движение сустава, и хрящ как таковой уже не существует.
Среди факторов риска развития болезни можно назвать:
- артриты любого характера;
- наследственную слабость связок;
- нарушенный обмен веществ;
- нарушенную иннервацию в ряде неврологических болезней;
- черепно-мозговые травмы;
- травмы позвоночника.
Классификация
Исходя из путей появления болезни, существует:
- первичный гонартроз – возникает сам по себе, зачастую носит характер двустороннего гонартроза;
- вторичный гонартроз колена – развивается на фоне травм или иных патологий коленного сустава, бывает двух видов: правосторонний гонартроз на правой ноге и левосторонний гонартроз на левой ноге.
От степени гонартроза зависит яркость выражения симптомов:
- 1 стадия – тупые боли, легкая отечность сустава, отсутствие деформации;
- 2 стадия – усиление симптоматики и болевого синдрома, наличие хруста, умеренная ограниченность движения и легкая деформация;
- 3 стадия – максимум клинической симптоматики, нарушение походки и сильные постоянные боли, ограниченная подвижность и видимая деформация сустава.
Осложнения
Безусловно, отсутствие грамотного и своевременного лечения гонартроза приводит к разрушению и деформации коленного сустава, полной ограниченности движения и инвалидности. Однако осложнения после запущенного лечения гонартроза могут распространиться на прочие элементы опорно-двигательного аппарата, наиболее весомым считается позвоночный столб.
Лечение гонартроза суставов необходимо для адекватности нагрузки на позвоночный столб, ведь ограничение движения коленного сустава увеличивает нагрузку на позвоночник до 75%. Поэтому среди последствий патологии назовем следующие:
- искривления позвоночника;
- радикулит;
- стеноз межпозвоночных каналов;
- грыжи межпозвоночные;
- остеохондроз;
- нестабильность позвонков.
Таким образом, отсутствие актуального лечения гонартроза суставов приводит к последующим патологиям и их осложнениям, нарастающим будто снежный ком.
Такое развитие событий приведет к длительному лечению посредством ряда хирургических операций не только на коленном суставе. Прочие суставы в рамках принимают на себя нагрузку поврежденного коленного сустава, в результате чего происходит их преждевременный износ.
Еще одним видом осложнения болезни считается наличие воспалительного процесса и большие количества жидкости, способные вытечь за пределы коленного сустава, принося новые разрушения и деформации, а также образование грыжи или опухоли.
Когда следует обратиться к врачу
При наличии малейшего дискомфорта при движении или болях в коленном суставе необходимо обращаться к врачу-травматологу или ортопеду, можно также обратиться за первичной консультацией к хирургу.
В АО «Медицина» (клиника академика Ройтберга) работают врачи 66 медицинских специальностей, которые имеют большой стаж работы, постоянно повышают свою квалификацию. Записаться на прием и выбрать доктора можно на сайте, по телефону +7 (495) 775-73-60 или у администраторов в клинике: Москва 2-й Тверской-Ямской переулок д.10.
Диагностика
Осуществляет диагностику гонартроза врач травмотолог-ортопед или хирург. Первоначально проводится детальный врачебный осмотр и рентгенография.
В ходе первичного осмотра обнаружить признаки можно только на 2 и 3 стадии патологии за счет деформации костей и суставов, искривлении конечностей кости и грубости ее контуров. Пальпация позволяет понятие о наличии и характере болевых ощущений.
Рентгенография относится к числу классических методов обследования. Она дает возможность уточнения диагноза и разграничения с прочими патологиями, дает представление о глубине поражений и динамике развития процесса. При этом начальная стадия, как правило, просматривается тяжело. У пожилых людей изменения присутствуют ввиду возрастного ценза и при отсутствии клинической симптоматики не влекут постановку диагноза гонартроз.
Современные методами исследования являются КТ и МРТ, которые используются крайне редко.
Лечение
Как лечить гонартроз? Существует две группы методов лечения консервативные и хирургические.
Консервативные методы применяются травматологами и ортопедами. Их успешность зависит от своевременности начала лечения – чем раньше, тем успешнее. Периоды обострения необходимо проводить в состоянии полного покоя. Данная терапия включает:
- гимнастику при гонартрозе и лечебную физкультуру, подразумевающую выполнение упражнений при гонартрозе;
- грязелечение;
- физиопроцедуры – электрофорез с новокаином, магнитные и лазерные токи, диадинамические токи, УВЧ;
- медикаментозные средства – осуществляется введение посредством уколов при гонартрозе следующих групп препаратов: хондопротекторов, стрероидных гормонов;
- санаторно-курортное лечение.
Важно соблюдать некоторые правила – разгрузить коленный сустав за счет трости или ортезов, подбор удобной обуви и стелек, контроль веса, правильный режим дня.
Хирургические методы используются на третьей стадии болезни, когда стандартная терапия не принесла видимого эффекта и улучшений. Хирургическое лечение основано на эндопротезировании коленного сустава. Назначается людям молодого и среднего возраста для компенсации ограничения двигательной активности. Период реабилитации и полного восстановления длится от трех месяцев до полугода.
Профилактика
Профилактические меры при гонартрозе имеют огромное значение в рамках предупредительной терапии. К таким мероприятиям относятся:
- поддержание массы тела на уровне средней;
- тренировка мышц нижних конечностей;
- исключение травмирования суставов;
- своевременность лечения воспалений в суставах;
- умеренность и посильность физических нагрузок;
- соблюдение правил здорового образа жизни – правильное питание, активность в соответствии с возрастным цензом, соблюдение режима сна и отдыха;
- укрепление иммунитета.
Решение экспоненциальных уравнений из определения
Purplemath
Чтобы решить экспоненциальные уравнения без логарифмов, вам необходимо иметь уравнения со сравнимыми экспоненциальными выражениями по обе стороны от знака «равно», чтобы вы могли сравнивать степени и решать. Другими словами, у вас должно быть «(некоторая база) к (некоторой степени) равняется (та же основа) (некоторой другой степени)», где вы устанавливаете две степени равными друг другу и решаете полученное уравнение.Например:
Так как основания («5» в каждом случае) одинаковы, то единственный способ, при котором два выражения могут быть равны, — это одинаковые степени. То есть:
MathHelp.com
Это решение демонстрирует логическую основу того, как решается весь этот класс уравнений: если основания одинаковы, то мощности также должны быть равны; это единственный способ, чтобы две части уравнения были равны друг другу.Поскольку степени должны быть одинаковыми, мы можем установить две степени равными друг другу и решить полученное уравнение.
Поскольку основания одинаковы, я могу приравнять силы и решить:
1 — x = 4
1–4 = x
–3 = x
Тогда мое решение:
Не все экспоненциальные уравнения даны с одинаковым основанием по обе стороны от знака «равно».Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какую-то другую базу, прежде чем мы сможем установить степени равными друг другу. Например:
Поскольку 9 = 3 2 , это действительно просит меня решить:
Преобразовав 9 в 3 2 , я преобразовал правую часть уравнения в то же самое основание, что и левая часть. Поскольку базы теперь такие же, я могу установить две степени равными друг другу:
В данном случае у меня экспонента с одной стороны от знака «равно» и число с другой.Я могу решить уравнение, если могу выразить «27» как степень 3. Поскольку 27 = 3 3 , то я могу преобразовать и продолжить решение:
3 2 x –1 = 27
3 2 x –1 = 3 3
2 x — 1 = 3
2 x = 4
х = 2
Если я не уверен в своем ответе или если я хочу проверить его перед тем, как сдать его (скажем, на тест), я могу проверить его, вставив обратно в исходное упражнение.Степень в левой части исходного уравнения упростится как:
И 3 3 = 27, что является правой частью исходного уравнения. Тогда мое (подтвержденное) решение:
Как вы, наверное, догадались, вам нужно будет хорошо освоить свои силы чисел, такие как степени от 2 до 2 6 = 64, степени от 3 p до 3 5 = 243, степени От 4 до 4 4 = 256, от 5 до 5 4 = 625, от 6 до 6 3 = 216, и все квадраты.
Не планируйте полагаться на свой калькулятор во всем, потому что необходимость находить каждое значение в вашем калькуляторе может напрасно тратить много времени. К тому времени, как вы дойдете до теста, вы захотите иметь определенную степень удобства (то есть определенную степень осведомленности и скорости), поэтому ознакомьтесь с меньшими способностями сейчас.
Примечание по форматированию: HTML обычно не «любит» вложенные надстрочные индексы, поэтому выше для обозначения степени используется нотация «каратов».2–3 x = 3 4
x 2 — 3 x = 4
x 2 — 3 x — 4 = 0
( x — 4) ( x + 1) = 0
x = –1, 4
Итак, мой ответ:
Это уравнение похоже на предыдущие два, но не совсем то же самое, потому что 8 не является степенью 4.2 + 4 x = 2 3
4 x 2 + 4 x = 3
4 x 2 + 4 x — 3 = 0
(2 x — 1) (2 x + 3) = 0
x = 1 / 2 , –3 / 2
Отрицательные показатели степени могут использоваться, чтобы указать, что основание принадлежит другой стороне дробной линии.Поскольку 64 = 4 3 , то я могу использовать отрицательные показатели для преобразования дроби в экспоненциальное выражение:
Используя это, я могу решить уравнение:
4 x +1 = 1 / 64
4 x +1 = 4 –3
x + 1 = –3
x = –4
Чтобы решить эту задачу, мне сначала нужно вспомнить, что квадратные корни — это то же самое, что и половинные степени, и преобразовать радикал в экспоненциальную форму.Тогда я могу решить уравнение:
8 x –2 = sqrt [8]
8 x –2 = 8 1/2
x — 2 = 1/2
x = 2 + 1 / 2 = 5 / 2
Тогда мой ответ:
Ниже приводится пример распространенного типа вопроса с подвохом:
Подумайте об этом: какая степень на положительном числе «2» может дать , возможно, , дать отрицательное число ? Число никогда не может перейти от положительного к отрицательному, принимая полномочия; Я никогда не смогу превратить положительные два в отрицательные , любые , четыре или другие, умножая два на себя, независимо от того, сколько раз я это умножаю.Возведение в степень просто не работает. Итак, ответ здесь:
URL: https://www.purplemath.com/modules/solvexpo.htm
Правило мощности
Правило мощности, одно из наиболее часто используемых производных правил, гласит:
Производная x n равна nx (n − 1)
Пример: Какая производная от x
2 ?
Для x 2 мы используем правило мощности с n = 2:
| Производная от x 2 | = | 2x (2-1) |
| = | 2x 1 | |
| = | 2x |
Ответ: производная от x 2 равна 2x
«Производная от» может быть обозначена этой маленькой «тире»: ’
Используя эту метку, мы можем записать Правило мощности следующим образом:
f ’(x n ) = nx (n − 1)
Пример: Какая производная от x
3 ?
f ’(x 3 ) = 3x 3−1 = 3x 2
«Производная от» также может быть представлена как
г
dx
Пример: Что такое
г
dx
(1 / х)?
1 / x также x -1
Использование правила мощности с n = −1 :
г
dx
x n = nx n − 1
г
dx
x -1 = −1x -1−1 = −x -2
Как помнить
«умножить на мощность
, затем уменьшить мощность на 1″
A Короткий стол
Вот правило мощности с некоторыми примерными значениями.Видите узор?
| из | f ’(x n ) = nx (n − 1) | f ’ |
|---|---|---|
| х | 1x (1−1) = x 0 | 1 |
| x 2 | 2x (2−1) = 2x 1 | 2x |
| x 3 | 3x (3−1) = 3x 2 | 3x 2 |
| x 4 | 4x (4−1) = 4x 3 | 4x 3 |
| и т. Д… | ||
| А для отрицательных показателей: | ||
| x -1 | −1x (−1−1) = −x -2 | −x -2 |
| x -2 | −2x (−2−1) = −2x -3 | −2x -3 |
| x -3 | −3x (−3−1) = −3x -4 | −3x -4 |
| и т. Д… | ||
чисел — экспоненты — подробно
Показатель говорит
сколько раз базовое число используется в качестве множителя. База из пяти поднятых
во второй степени называется «пять в квадрате» и означает «пять».
умножить на пять ». Пять в третьей степени называют« пятью в кубе ».
и означает «пять раз по пять раз». База может быть любой
число — целое число, десятичное число или дробь могут быть возведены в
власть.
Здесь
это несколько простых правил для использования с показателями.
- a 1 =
Любое число, возведенное в степень единицы, равно самому числу. - Для любого
число a, кроме 0, a 0 = 1
Любое число, возведенное в степень нуля, кроме нуля, равно единице. - Для любого
числа a, b и c,
a b x a c = a b + c
Это правило умножения говорит нам, что мы можем просто сложить экспоненты, когда
умножение двух степеней с одинаковым основанием.
ВНИМАНИЕ!
Это ошибки, которые студенты часто допускают при работе с экспонентами.
Ошибка!
Не умножайте основание и показатель степени. 2 6 не равно 12,
это 64!
Ошибка!
Правило умножения применяется только к выражениям с одинаковым основанием. Четыре
квадрат, умноженный на два в кубе — это не то же самое, что 8 в степени два плюс
три.
Ошибка!
Правило умножения применяется только к произведению, а не к сумме двух
числа.
Научный
Обозначение
Что происходит, когда вы используете калькулятор и ваш ответ слишком длинный, чтобы
влезть в окно? Воспользуйтесь калькулятором, чтобы умножить эти 2 числа:
60 000 000 000 000
х 20 000 000 000
Вы откроете для себя короткий способ написания очень длинных чисел.Это называется научным
обозначение или обозначение E на калькуляторе («E» означает «Exponent»).
Число, записанное в научных обозначениях, записывается как произведение числа
между 1 и 10 и степенью 10.
Например,
чтобы записать 127 680 000 в экспоненциальном представлении, замените число на число
от 1 до 10, переместив десятичную запятую на 8 разрядов влево. Затем умножьте
на 10 в степени количества знаков, на которое вы должны были переместить десятичную дробь
точка — то есть 108:
127 680 000
= 1.2768 х 10 8
В окне вашего калькулятора основание 10 не отображается; буква E означает «10»
возведен в следующую степень. «
Примеры
7 х 7 х 7 х 7 =? 7 4
2 х 2 х 2 х 2 х 2 х 2 =? 2 6
1 10 = 1
5 3 = 5 x 5 x 5 = 125
Напишите следующее
числа в экспоненциальной записи.
565 000
= 5.65 х 10 5
7,325,000 = 7,325 x 10 6
91 247 000 000 = 9,1247 x 10 10
назад
наверх
Решение экспоненциальных уравнений с использованием логарифмов
На нашем предыдущем уроке вы узнали, как решать экспоненциальные уравнения без логарифмов. На этот раз мы хотим решить экспоненциальные уравнения , требующие использования логарифмов . Почему? Причина в том, что мы не можем манипулировать экспоненциальным уравнением, чтобы иметь одинаковую или общую основу для обеих сторон уравнения.Если вы столкнулись с проблемой такого типа, выполните следующие действия:
Шаги для решения экспоненциальных уравнений с использованием логарифмов
1) Держите экспоненциальное выражение отдельно от одной стороны уравнения.
2) Найдите логарифмы обеих частей уравнения. Вы можете использовать любых баз для логов.
3) Найдите переменную. Ответьте точно или используйте десятичные дроби. В дополнение к шагам, описанным выше, обязательно ознакомьтесь с основными правилами логарифмирования, потому что вы будете использовать их так или иначе.{2x}} = 21.
Преимущество этого уравнения в том, что экспоненциальное выражение уже выделено в левой части. Теперь мы можем логарифмировать обе части уравнения. Не имеет значения, какое основание логарифма использовать. Окончательный ответ должен быть таким же. Наилучший выбор для базы логарифмической операции — 5, поскольку она является базой самого экспоненциального выражения. Однако мы также будем использовать в вычислениях общую основу 10 и естественную основу \ color {red} e (обозначенную \ color {blue} ln), чтобы показать, что в конечном итоге все они имеют одинаковые ответы. .{x — 5}}} \ right) = 12.
Как видите, экспоненциальное выражение слева не само по себе. Мы должны исключить число 2, которое умножает экспоненциальное выражение. Для этого разделите обе части на 2. В результате мы получим только экспоненциальное выражение слева и 6 справа после упрощения.
Пора взять бревно с обеих сторон. Поскольку экспоненциальное выражение имеет основание 3, это удобное основание для работы с журналом. Кроме того, мы также решим эту проблему, используя естественное основание e, чтобы сравнить, согласуются ли наши окончательные результаты.{x — 2}}}}}}} \ right) — 7 = 13.
Сначала это похоже на беспорядок. Однако, если вы знаете, с чего начать, решение этой проблемы становится простым. В первую очередь нам следует упростить выражение внутри скобок. Используйте правило деления экспоненты, скопировав общее основание числа е и вычтя верхнюю на нижнюю степень.
Теперь выделите экспоненциальное выражение, сложив обе части на 7, а затем разделив все уравнение на 2.
Возьмите логарифм обеих сторон.х} + 3 = 53.
Обратите внимание, что экспоненциальное выражение возводится в x. Упростите это, применив Силу к Правилу Силы. Сделайте это, скопировав основание 10 и умножив его показатель на внешний показатель. После этого он должен выглядеть так.
Теперь мы можем выделить экспоненциальное выражение, вычтя обе части на 3, а затем умножив обе стороны на 2.
Возьмите логарифм обеих сторон с основанием 10. Если вы просто видите журнал \ color {red} без какой-либо конкретной основы, предполагается, что его основание равно 10.{2x} $ в степенях $ \ left (x-1 \ right) $ означает?
Вы спросили:
Я не понимаю, что мы делаем во всем этом процессе
, и это справедливый вопрос. Я этого тоже не понимал, когда впервые узнал об этом. Но это важно как с практической инженерией, так и с теоретико-математической.
Прежде чем мы продолжим, давайте посмотрим, что ваше предложение — неправильный ответ на этот вопрос, потому что это правильный ответ, но на другой вопрос.9 $$
Если мы сделаем это, мы получим 7,3887, что не так уж и далеко. Но работы было много! И мы обнаруживаем, что по мере удаления $ x $ от нуля приведенный выше ряд становится все менее и менее точным. Например, возьмите $ x = 3,1 $, формула с четырьмя членами дает нам 66,14 $, что совершенно неверно. Даже если мы используем десять терминов, мы получим 444,3 доллара, что все еще далеко. Правильный ответ — 492,7 доллара.
Что нам с этим делать? Просто добавить дополнительные термины? Это может потребовать много работы, и это может не привести нас туда, куда нам нужно.i $, и когда $ x = 3,1 $, они , а не малые, они очень большие! Они увеличивают до по мере увеличения $ i $, и очень быстро. ($ I! $ В знаменателе, в конце концов, побеждает, но этого не происходит для многих членов.) Если мы пропустим эти многие большие члены, мы получим неверные результаты.
Краткий ответ на ваш вопрос:
Ряды Маклорена подходят только для вычисления функций, когда $ x $ близко к $ 0 $, и становятся неточными по мере удаления $ x $ от нуля.Но ряд Тейлора вокруг $ a $ имеет «центр» около $ a $ и наиболее точен, когда $ x $ близко к $ a $.
делим x в степени 3-6x в степени 2+ 2x -4 на 1-2x
Лучше переставить делитель в той же нисходящей форме, что и делимое.
-1 / 2x 2 + 11 / 4x + 3/8
-2x + 1) x 3 -6 x 2 + 2x + 4
x 3 — 1/2 x 2 (1)
-11/2 х 2 + 2 х
-11/2 x 2 + 11 / 4x (2)
-3/4 х + 4
-3/4 х +3/8 (3)
R 29/8
Пояснение:
(1) Делим (x 3 ) на (-2x).Ответ (-1 / 2x 2 ). Это первый член полиномиального ответа.
Далее умножаем (-1 / 2x 2 ) и (-2x +1). Ответ: (x 3 -1 / 2x 2 ).
Как и при числовом делении в столбик, вычитаем:
x 3 — 6x 2
–
x 3 — 1 / 2x 2
Результат вычитания (-11/2 x 2 )
(2) Сбиваем (+ 2х) и повторяем процесс из (1).
Делим (-11 / 2x 2 ) на (-2x). Ответ (11/4 x). Это следующий член полиномиального ответа.
Умножаем (11/4 x) на делитель (-2x + 1) и вычитаем (я сделаю это на одной строке).
-11/2 x 2 + 2x — (-11/2 x 2 + 11 / 4x) = 2x — 11 / 4x = -3 / 4x.
(3) Сбиваем (+4) и повторяем процесс из (1) еще раз.
Делим (-3 / 4x) на (-2x). Ответ (+3/8).
Умножаем (+3/8) на делитель (-2x + 1) и вычитаем (я сделаю это на одной строке).
-3 / 4x +4 — (- 3 / 4x +3/8) = 4 — 3/8 = 29/8. {2x-1} = 3375 $
Это уравнение экспоненциальной формы в сочетании как арифметической, так и алгебраической формы, и его можно решить в математике, используя правила экспонент для получения значения $ x $.3 $. Значит, их показатели математически равны.
Следовательно, $ x + 1 = 3 $ и $ 2x-1 = 3 $.
$ \ подразумевает x = 3-1 $ и $ 2x = 3 + 1 $.
$ \ подразумевает x = 2 $ и $ 2x = 4 $.
$ \ подразумевает x = 2 $ и $ x = \ dfrac {4} {2} $.
Следовательно, $ x = 2 $ и $ x = 2 $.
Два уравнения дали одинаковый результат. Следовательно, значение $ x $ равно $ 2 $.
.

