Содержание
Задачи на скорость, время и расстояние: примеры и решение
Скорость — это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Разные объекты имеют разную скорость. Например, средняя скорость пешехода составляет 5 километров в час, скорость велосипедиста — 12 км в час, а автомобиля — 80 км в час. При записи скорости, предлог в заменяют наклонной чертой — км/ч (например, 15 км/ч).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным. Далее будут рассмотрены задачи только на равномерное движение.
Нахождение скорости
Чтобы найти скорость по данному пути (расстоянию) и времени, надо путь разделить на время.
скорость = расстояние : время
Задача 1. Поезд проехал 320 км за 4 часа. Чему равна скорость поезда?
Чему равна скорость поезда?
Решение: Чтобы найти скорость поезда, надо расстояние, которое прошёл поезд (320 км), разделить на время поезда в пути (4 ч):
320 : 4 = 80 (км).
Ответ: Скорость поезда равна 80 км/ч.
Задача 2. Турист за 3 часа прошёл 12 км, а велосипедист за 2 часа проехал 24 км. Во сколько раз турист движется медленнее велосипедиста?
Решение: Чтобы узнать во сколько раз скорость туриста меньше, чем у велосипедиста, надо узнать их скорость, разделив пройденные расстояния на затраченное время:
12 : 3 = 4 (км/ч) — скорость туриста,
24 : 2 = 12 (км/ч) — скорость велосипедиста.
Теперь осталось узнать на сколько медленнее движется турист, для этого надо большее число разделить на меньшее:
12 : 4 = 3.
Ответ: Турист движется в 3 раза медленнее, чем велосипедист.
Нахождение времени
Чтобы найти время по данному расстоянию и скорости, надо расстояние разделить на скорость.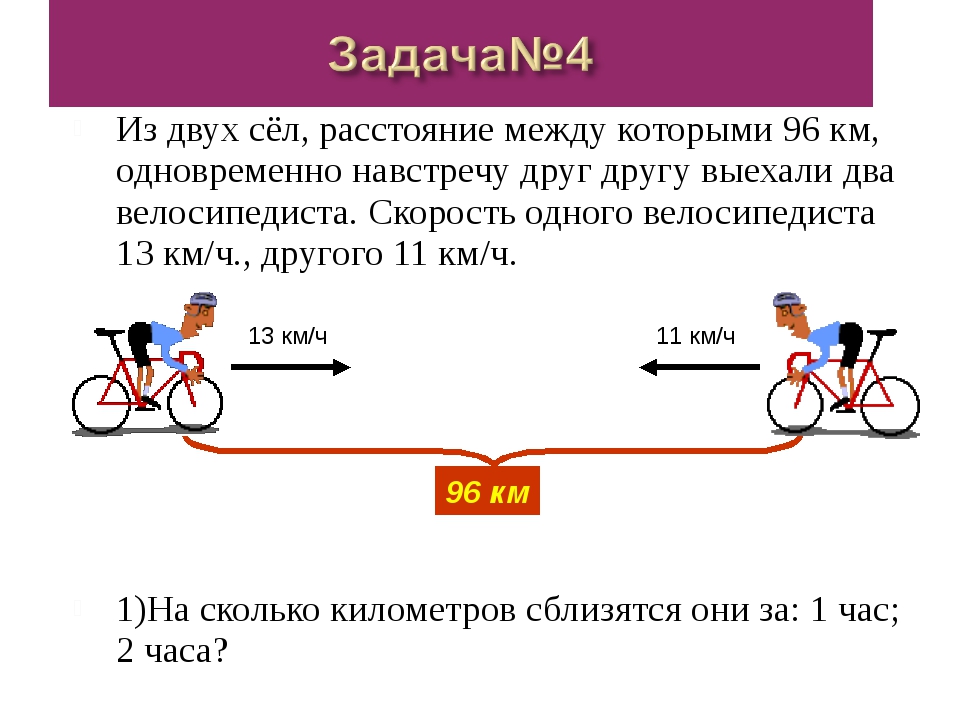
время = расстояние : скорость
Задача. Лодка преодолела путь в 100 км со скоростью 20 км/ч. Сколько времени плыла лодка?
Решение:
100 : 20 = 5 (ч).
Ответ: Лодка плыла 5 часов.
Нахождение расстояния
Чтобы найти расстояние по данным скорости и времени, надо скорость умножить на время.
расстояние = скорость · время
Задача. Грузовик ехал 12 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение:
70 · 12 = 840 (км).
Ответ: Грузовик за 12 часов проехал 840 км.
Задачи на движение: скорость, время и расстояние.
Скорость – это физическая величина, показывающая какое расстояние пройдет объект за единицу времени.
Сегодня мы будем решать задачи на:
- движение
- скорость \(v=s/t\)
- время \(t=s/v\)
- расстояние \(s=v*t\)
Расстояние — путь, который нужно преодолеть во время движения.
Время — промежуток действия движения.
Скорость — характеристика движения.
Для решения задач необходимо ввести неизвестную, верно составить и решить уравнение.
Задача 1. Легковая машина прошла расстояние в \(160\) км за два часа. С какой скоростью двигалась машина?
Решение.
\(160/2=80\) км/час
Ответ: \(80.\)
Задача 2. Из города Минск в Смоленск, расстояние между которыми \(346\) км, отправились одновременно велосипедист и автомобилист. Скорость автомобиля \(20\) м/с, а велосипедиста \(20\) км/ч. Какое расстояние будет между ними через \(2\) часа?
Решение.
Мы не можем складывать разные единицы измерения, поэтому надо перевести м/с в км/ч. Как нам перевести км/ч в м/с? В км – 1000 м, в \(1\) ч \(-3600\), в \(1\) км/час\(-1000/3600\) м/c, то есть в \(1\) км/c \(-3600/1000\) м/c. \(20*\frac{3600}{1000}=72\). Итого скорость автомобиля \(72\) км/ч.
Как нам перевести км/ч в м/с? В км – 1000 м, в \(1\) ч \(-3600\), в \(1\) км/час\(-1000/3600\) м/c, то есть в \(1\) км/c \(-3600/1000\) м/c. \(20*\frac{3600}{1000}=72\). Итого скорость автомобиля \(72\) км/ч.
Так как автомобилист и велосипедист выехали из одного места и двигаются в одном направлении, расстояние между ними будет нарастать со скоростью:
- 72-20=52(км/ч)
- 52∗2=104 (км) – расстояние между ними через два часа.
Ответ: \(104\) км.
В таких задачах важно понимать:
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
Задача 3. Из А в В тронулись в одно время турист пешком, а второй турист – на велосипеде. В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
10 * 3 = 30 (км) – мотоциклист от А через 3 часа.
3* 4 = 12 (км) – мотоциклист от А через 4 часов.
30 – 12 = 18 (км/ч) – скорость автомобиля.
10 + 18 = 28 (км/ч) – скорость сближения мотоциклиста и велосипедиста.
28 * 3 = 84 (км) – расстояние от А до В.
Ответ: 84 км.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Логарифмы (урок)
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Данный урок посвящен задачам на движение.
Предварительные навыки
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.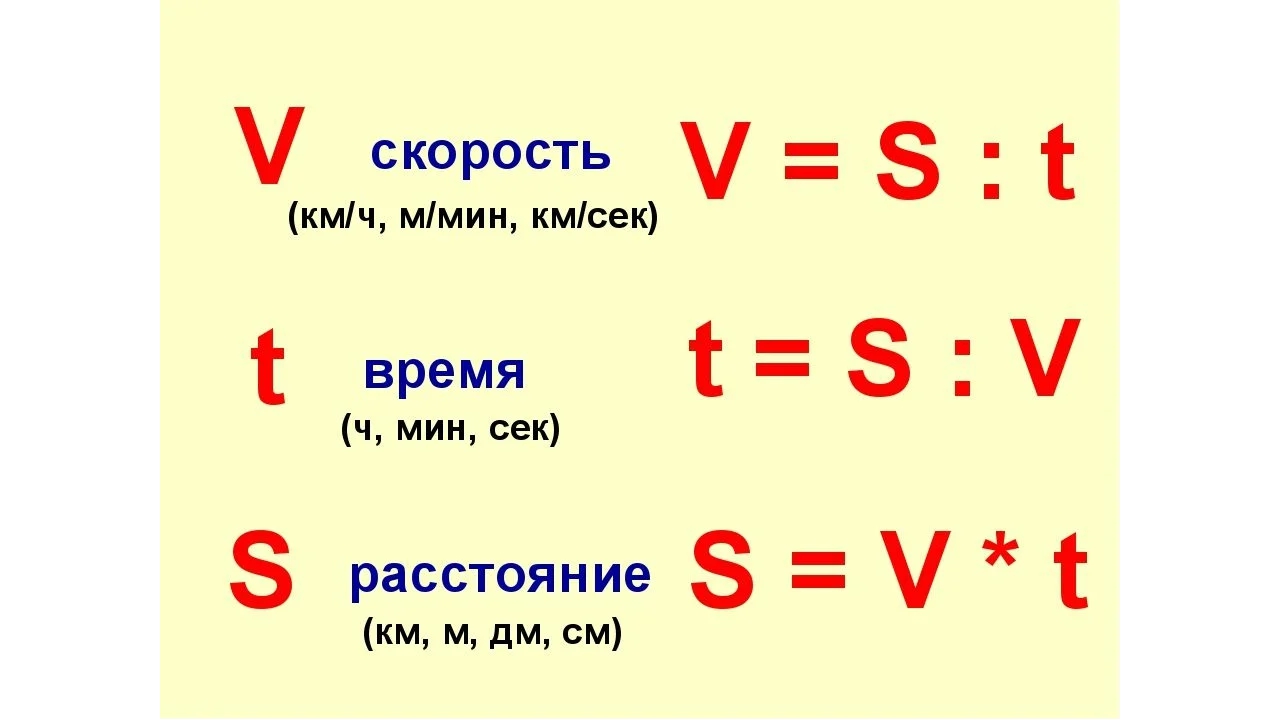
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.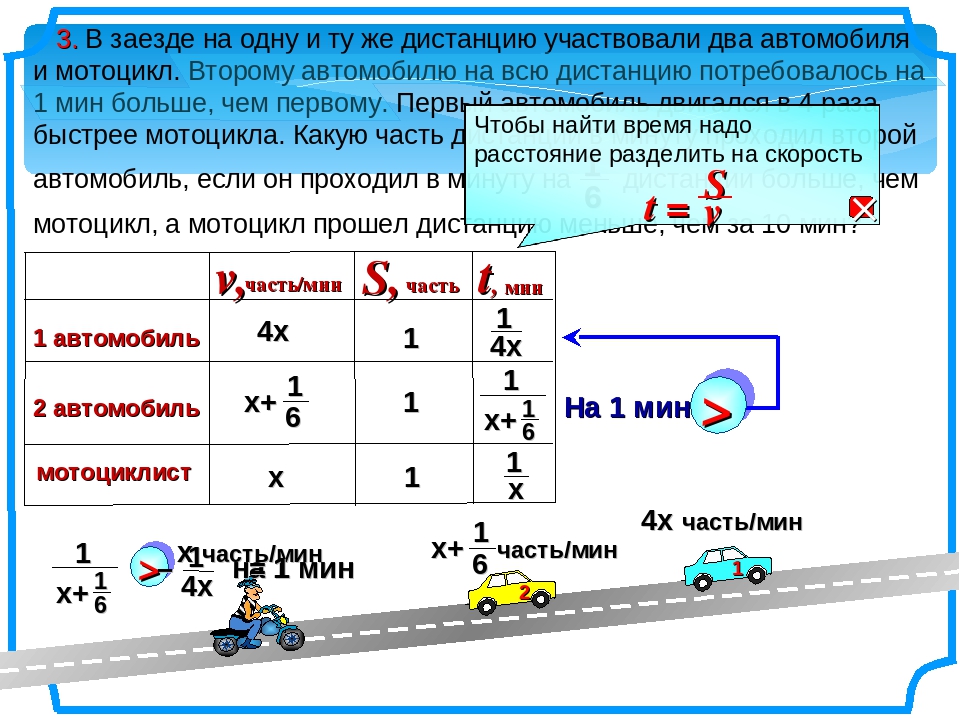
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1.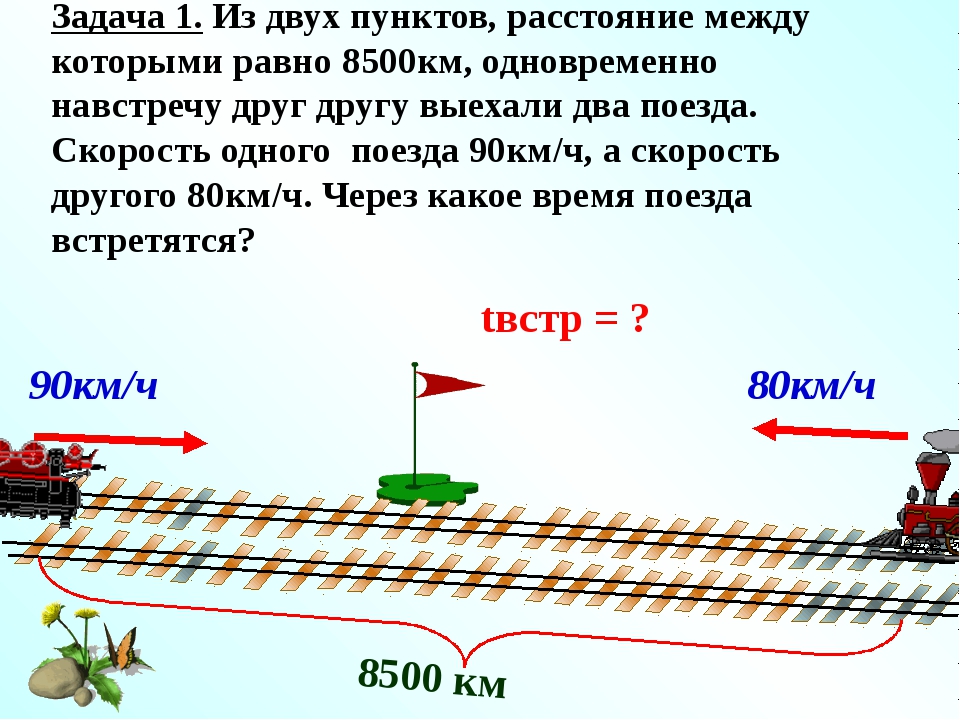 Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.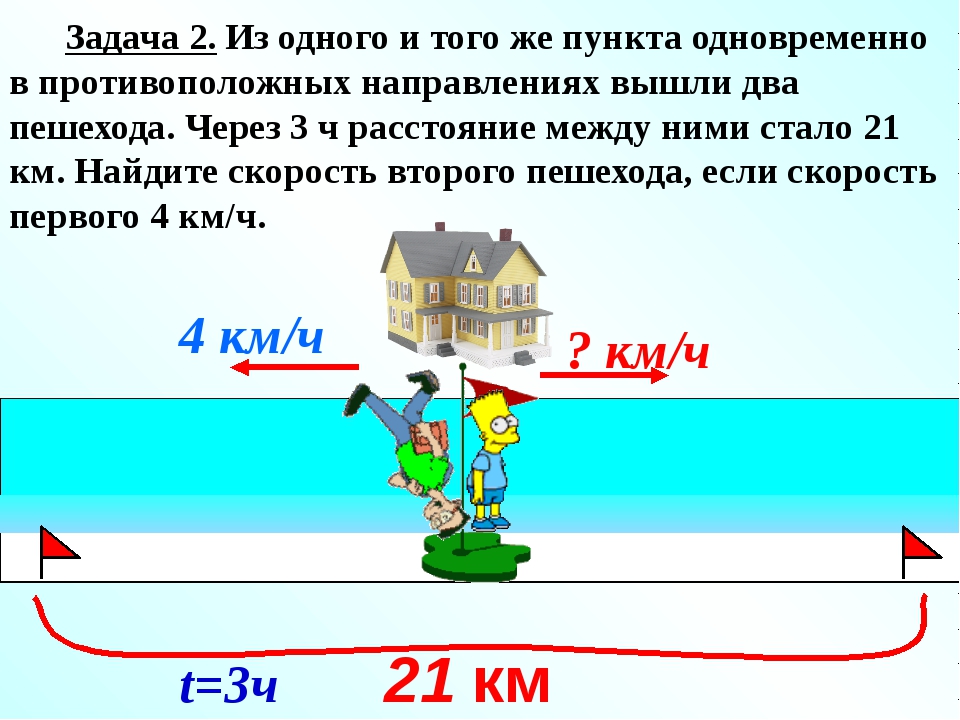
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров.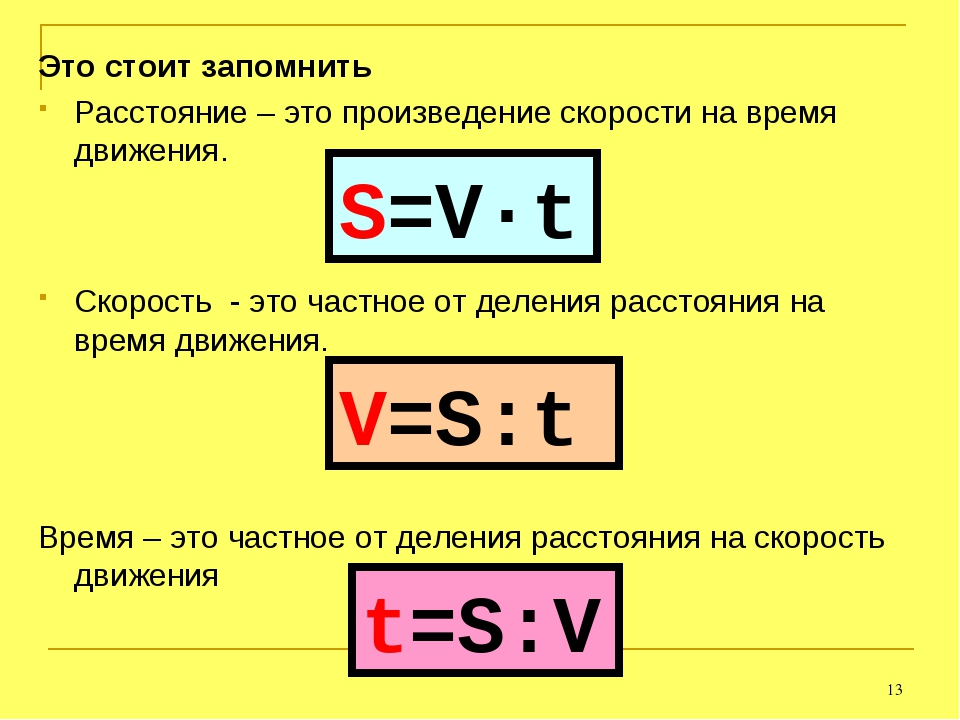 Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как найти Время, Скорость и Расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой S.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: S = V * T |
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: V = S/T |
Показатели скорости чаще всего выражаются в м/сек; км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Единицами времени могут быть секунды, минуты, часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: T = S/V |
Эта формула пригодится, если нужно узнать за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 15 минут
s = v × t = 50 × 15 = 750
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.
Ответ: первый школьник добежал быстрее.
Если известна скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Урок 36. связь между скоростью, временем и расстоянием — Математика — 4 класс
Математика, 4 класс
Урок № 36. Связь между скоростью, временем и расстоянием
Перечень вопросов, рассматриваемых в теме:
— как скорость взаимосвязана с величинами время, расстояние?
— как определить скорость по известному расстоянию и времени движения?
— как определить расстояние по известной скорости и времени движения?
— как определить время движения по известному расстоянию и скорости?
Глоссарий по теме:
Скорость — это расстояние, пройденное за единицу времени.
Скорость, расстояние и время можно измерять и сравнивать, значит это величины.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Чтобы узнать расстояние, нужно скорость умножить на время.
Чтобы найти время, нужно расстояние разделить на скорость.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.6-8.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.15.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54.
Теоретический материал для самостоятельного изучения
В таблицах даны скорости вороны и комара, льва и кенгуру. Определи, какое расстояние пролетит ворона за 2 мин, а комар за 3 с. Какой путь преодолеет лев за 4 ч, а кенгуру за 30 мин?
Мотоциклист едет со скоростью 41 км/ч. Какое расстояние он преодолеет за 5 ч, если будет двигаться с той же скоростью?
Для того чтобы узнать расстояние, необходимо скорость, 41 км в час умножить на время, 5 часов. Таким образом, расстояние, которое преодолел мотоциклист равно 205 км.
41 · 5 = 205 км
Чтобы найти расстояние, нужно скорость умножить на время.
Будем учиться записывать задачи в таблицу и решать их.
Задача 1.
Черепаха двигалась со скоростью 5 м/ мин. Какое расстояние прошла она за 3 минуты?
Задача 2.
Слон двигался со скоростью 100 м/мин. Какое расстояние он прошёл за 10 мин?
Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения.
Составим таблицу и рассмотрим, как можно найти расстояние, зная скорость и время движения. Расстояние, которое прошли черепаха и расстояние, которое прошёл слон, нам неизвестны. Поставим в таблице знаки «вопрос».
5 м/мин – это скорость черепахи, 100 м/мин – это скорость слона. Запишем данные в колонку «Скорость». 3 минуты это время движения черепахи, 10 минут — время, которое находился в пути слон. Запишем эти данные в третью колонку.
Скорость | Время | Расстояние | |
Черепаха | 5 м/мин | 3 мин | ? |
Слон | 100 м/мин | 10 мин | ? |
Мы теперь знаем, чтобы найти расстояние, нужно скорость умножить на время. Запишем решение и ответ.
Скорость 5 м/мин умножим на время 3 мин, получится 15 метров. Это расстояние, которое прошла черепаха.
Скорость 100 м/мин умножим на время 10 мин, получится 1000 метров. Это расстояние, которое прошёл слон.
5 · 3 = 15 (м)
100 · 10 = 1000 (м)
Ответ: черепаха за 3мин прошла 15 м, а слон за 10 мин прошёл 1000 м.
Итак, чтобы найти расстояние, нужно скорость умножить на время.
А теперь рассмотрим задачу на нахождение времени.
Расстояние от города до посёлка 20 км. Из города вышел пешеход со скоростью 5 км/ч. Сколько времени потребуется пешеходу, чтобы пройти весь путь?
Это задача на движение, значит, речь идет о величинах скорость, время, расстояние. Заполним таблицу.
В задаче нужно узнать время движения пешехода. Оно нам неизвестно, поставим знак вопроса. Известно, что расстояние, которое нужно пешеходу равно 20 км.5 км/ч это скорость движения.
Скорость | Время | Расстояние |
5 км/ч | ? | 20 км |
Правило: чтобы найти время, нужно расстояние разделить на скорость. Запишем решение:
20 : 5 = 4 (ч)
Ответ: пешеход будет в пути 4 часа.
Запоминаем правило нахождения времени: чтобы узнать время, расстояние разделить на скорость.
Задания тренировочного модуля:
1. Заполните кроссворд.
Решите кроссворд.
По горизонтали:
2. Плот проплыл 630 м со скоростью 90 м/мин. Чему равно время движения плота?
3. Анника за 6 мин проехала на велосипеде 600 м. Чему равно время движения Анники?
По вертикали:
1. За 7 мин улитка проползла 7 дм. Чему равна скорость движения улитки?
Правильные ответы:
По горизонтали: 2.семь. 3. сто.
По вертикали: 1. десять.
2. Распределите единицы измерения величин по группам. Перенесите данные в соответствующие столбики.
Варианты ответа:
1. 85 см/мин
2. 120 с
3. 548 км
4. 12 мин
5. 850 м/с
6. 600 км/ч
7. 10 ч
8. 2500 м
9. 41 дм
Правильный вариант:
Скорость | Время | Расстояние |
85 см/мин 850 м/с 600 км/ч | 120 с 12 мин 10 ч | 548 км 2500 м 41 дм |
3. Вставьте пропущенное слово, выбирая из списка правильный ответ.
Как пройденный путь зависит от скорости?
Если скорость движения увеличить в несколько раз, то пройденный путь_______ во столько же раз.
Варианты ответа: уменьшится, увеличится.
Правильный вариант: увеличится.
|
1. |
Заполни таблицу
|
1,5 |
|
2. |
Кто быстрее?
|
1 |
|
3. |
Задача с картинками
|
1 |
|
4. |
Скорость при различных видах движения
|
2 |
|
5. |
Найди время на обратный путь
|
2 |
|
6. |
Два пешехода идут навстречу друг другу
|
2 |
|
7. |
Теплоходы движутся в разных направлениях
|
3 |
|
8. |
Маршрутное такси и автобус
|
4 |
|
9. |
Собака гонится за зайцем
|
3 |
Подборка задач на путь, скорость и расстояние для 4 класса. | Тренажёр по математике (4 класс) по теме:
Задачи на путь, скорость и расстояние для 4 класса по программе «Школа России».
№1
Караван верблюдов шёл в первый день 8 ч со скоростью 9 км/ч, во второй день – 6 ч со скоростью 8 км/ч, а в третий день – 9 ч со скоростью 7 км/ч. Какое расстояние прошёл караван за 3 дня?
№2
Вертолёт пролетает 840 км за 3 ч, а автомобиль проходит это же расстояние за 7 ч. У кого из них скорость больше и на сколько?
№3
Поезд проходит 320 км за 5 ч. Какое расстояние он пройдёт за 8 ч, двигаясь с этой же скоростью?
№4
Туристы решили пройти за день 30 км. Они уже прошли 3 ч со скоростью 6 км/ч. Какое расстояние им осталось пройти?
За сколько времени они пройдут это расстояние, двигаясь с прежней скоростью?
№5
Ира прошла 15 км за 3 ч, а Петя – 16 км за 4ч. У кого из ребят скорость больше и на сколько?
№6
Автомобиль за 6 ч проехал 480 км. Какое расстояние мог бы проехать автомобиль за это же время, если бы увеличил скорость на 12 км/ч?
№7
Первый лыжник за 3 ч пробежал 51 км, а второй лыжник пробежал за это же время на 6 км больше. На сколько километров в час скорость второго лыжника больше скорости первого?
№8
Расстояние от посёлка Солнечное до Тучково 18 км, а от Тучково до Маросейкино – в 4 раз больше. За сколько времени пройдёт автобус расстояние от Солнечного до Маросейкино, если скорость его движения 45 км/ч?
№9
Стоянка геологов находится на расстоянии 250 км от города. Чтобы добраться до стоянки, геологи сначала ехали из города 3 ч на машине со скоростью 72 км/ч, затем 2 ч ехали на лошадях со скоростью 9 км/ч, а после этого 4 ч шли пешком. С какой скоростью они шли пешком?
№10
Орёл за 9 с пролетел 270 м, а сокол за это время пролетел 189 м. На сколько метров в секунду скорость сокола меньше скорости орла?
№11
Катер идёт от одной пристани к другой со скоростью 30 км/ч, а возвращается обратно со скоростью на 10 км/ч большей. За сколько времени катер пройдёт весь путь туда и обратно, если расстояние между пристанями 240 км/ч.
№12
Волк гонится за Зайцем. Сначала Заяц бежал 2 ч со скоростью 24 км/ч, затем он 3ч ехал на велосипеде, а после этого 5 ч ехал на поезде со скоростью 48 км/ч. Всего Заяц пробежал и проехал 357 км. С какой скоростью он ехал на велосипеде?
Используемая литература
Л.Г. Петерсон. «Математика 3 класс».
Скорость, дистанция, время задания
Продолжаем изучать элементарные математические задания. Этот урок о задачах движения.
Продолжаем изучать элементарные математические задания. Этот урок о скорости, расстоянии, времени.
Задание на определение расстояния, скорости, времени
Задача 1. Автомобиль движется со скоростью 80 км / ч. Сколько километров он проедет за 3 часа?
Решение
Если автомобиль преодолеет 80 километров за час, он проедет в три раза больше за три часа.Чтобы найти расстояние, умножьте скорость автомобиля (80 км / ч) на время в пути (3 часа)
.
80 × 3 = 240 км
Ответ: машина проедет 240 километров за три часа.
Задача 2. Автомобиль проехал 180 км с той же скоростью за 3 часа. Рассчитайте скорость автомобиля.
Решение
Скорость — это расстояние, которое проходит тело за единицу времени. Единица измерения — 1 час, 1 минута или 1 секунда.
Если автомобиль проехал 180 километров за 3 часа с той же скоростью, то разделив 180 километров на 3 часа, мы определим расстояние, которое автомобиль проехал за один час.А это скорость передвижения. Чтобы определить скорость, нам нужно разделить пройденное расстояние на время в пути:
180: 3 = 60 км / ч
Ответ: скорость автомобиля 60 км / ч
Задача 3. За 2 часа машина проехала 96 км, а велосипедист проехал 72 км за 6 часов. Во сколько раз машина проехала быстрее велосипедиста?
Решение
Определите скорость автомобиля. Для этого нужно разделить пройденное расстояние (96 км) на время его движения (2ч)
.
96: 2 = 48 км / ч
Определите скорость велосипедиста.Для этого разделите пройденное расстояние (72 км) на время его движения (6ч).
72: 6 = 12 км / ч.
Узнайте, во сколько раз автомобиль проехал быстрее велосипедиста. Для этого найдите отношение 48 к 12
Ответ: машина была в 4 раза быстрее велосипедиста.
Задача 4. Вертолет пролетел 600 км со скоростью 120 км / ч. Как долго он был в полете?
Решение
Если вертолет может пролететь 120 километров за 1 час, то нам нужно узнать, сколько часов вертолет провел на этих 600 километрах.Чтобы найти время, разделите пройденное расстояние на скорость движения
.
600: 120 = 5 часов
Ответ: Вертолет летел 5 часов.
Задание 5. Вертолет летел 6 часов со скоростью 160 км / ч. На какое расстояние он прошел за это время?
Решение
Если вертолет преодолел 160 км за 1 час, то за 6 часов полета он пролетел в шесть раз больше. Чтобы определить расстояние, умножьте скорость на время
160 × 6 = 960 км
Ответ: вертолет преодолел 960 км за 6 часов.
Задание 6. Автомобиль проехал из Перми в Казань (723 км) за 13 часов. Первые 9 часов он двигался со скоростью 55 км / ч. Определите скорость автомобиля за оставшееся время.
Решение
Определите, сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость, с которой он ехал в течение первых 9 часов (55 км / ч), на 9
.
55 × 9 = 495 км
Давайте определим расстояние, которое осталось проехать.Для этого вычтите из общего расстояния (723 км) расстояние, которое он проехал за первые девять часов
.
723 — 495 = 228 км
Автомобиль проехал 228 км за оставшиеся 4 часа. Чтобы определить скорость автомобиля за оставшееся время, разделите 228 километров на 4 часа:
228: 4 = 57 км / ч
Ответ: скорость автомобиля в оставшееся время составила 57 км / ч
Две машины (транспортные средства) — математическая задача
Например, если два пешехода начинают идти из двух точек навстречу друг другу, и скорость первого составляет 100 метров / мин, а второго пешехода — 105 метров / мин, то оба пешехода преодолевают 205 метров / мин.Это означает, что каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость схождения, сложите скорости объектов.
Предположим, пешеходы встретились через три минуты после того, как начали идти. Зная, что они встретились через три минуты, мы можем вычислить расстояние между двумя точками.
Каждую минуту пешеходы преодолевали расстояние в двести пять метров. Через три минуты они встретились.Итак, умножив сумму скоростей на время движения, мы можем определить расстояние между двумя точками:
205 × 3 = 615 метров.
Вы также можете использовать другой способ определения расстояния между точками. Для этого найдите расстояние, которое прошел каждый пешеход перед встречей.
Например, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, поэтому за 3 минуты он прошел 100х3 метра
.
100 × 3 = 300 метров.
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метра.
105 × 3 = 315 метров.
Теперь мы можем сложить результаты и определить расстояние между двумя точками:
300 м + 315 м = 615 м
Задание 1. Два велосипедиста одновременно выехали из двух населенных пунктов навстречу друг другу. Скорость первого велосипедиста составляет 10 км / ч, а скорость второго велосипедиста — 12 км / ч.Они встретились через 2 часа езды. Определите расстояние между двумя населенными пунктами.
Решение
Найдем скорость, с которой велосипедисты приблизились
10 км / ч + 12 км / ч = 22 км / ч.
Определите расстояние между населенными пунктами. Для этого мы умножаем скорость ближайшего сближения на время в пути.
22 × 2 = 44 км
Решите эту проблему вторым способом. Для этого найдите расстояния, пройденные каждым из них, и сложите результаты.
Найдите расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложите полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами 44 км.
Задача 2. Два велосипедиста одновременно выехали из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу. Скорость первого велосипедиста составляет 14 км / ч, а скорость второго велосипедиста — 16 км / ч.Через сколько часов они встретились?
Решение
Найдем скорость, с которой велосипедисты приблизились друг к другу:
14 км / ч + 16 км / ч = 30 км / ч
За час расстояние между велосипедистами сокращается на 30 км. Чтобы определить, через сколько часов они встретятся, разделите расстояние между двумя поселениями на скорость их приближения:
60:30 = 2 часа
Итак, велосипедисты встретились через два часа.
Ответ: Велосипедисты встретились через два часа.
Задача 3. Два велосипедиста одновременно выехали из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км / ч. Определите скорость второго велосипедиста.
Решение
Определите расстояние, пройденное первым велосипедистом. Как и второй велосипедист, он провел в дороге два часа. Умножив скорость первого велосипедиста на 2 часа, мы можем узнать, сколько километров он проехал до встречи
.
12 × 2 = 24 км
За два часа первый велосипедист проехал 24 км.За час он прошел 24: 2, то есть 12 км. Изобразим это графически
Вычтите расстояние, пройденное первым велосипедистом (24 км), из общего расстояния (56 км). Это определит, сколько километров преодолел второй велосипедист:
56 км — 24 км = 32 км
Второй велосипедист, как и первый велосипедист, ехал два часа. Если разделить пройденное им расстояние на 2 часа, мы узнаем, с какой скоростью он проехал:
32: 2 = 16 км / ч.
Следовательно, скорость второго велосипедиста — 16 км / ч.
Ответ: Скорость второго велосипедиста 16 км / ч.
Давайте возьмем пример двух пешеходов, которые начали идти из одной и той же точки в противоположных направлениях, причем первый пешеход двигался со скоростью 4 км / ч, а второй — со скоростью 6 км / ч, затем мы добавляем скорости (потому что они идут в противоположных направлениях). ), что составляет 10 км / ч.
Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость двух объектов, движущихся в противоположных направлениях, сложите скорости объектов .
Значит, в первый час расстояние между пешеходами будет 10 километров. На следующем рисунке вы можете увидеть, как это происходит
Видно, что первый пешеход прошел 4 километра за первый час. Второй пешеход за первый час тоже прошел 6 километров. В первый час расстояние между ними было 4 + 6, т.е.е., 10 километров.
Через два часа расстояние между пешеходами будет 10 × 2, то есть 20 километров. На следующем рисунке вы можете увидеть, как это происходит:
Задача 1. Товарный поезд и Пассажирский экспресс отправились с одной станции одновременно в противоположных направлениях. Скорость товарного поезда составляла 40 км / час, скорость экспресса — 180 км / час. Какое расстояние между этими поездами будет через 2 часа?
Решение
40 + 180 = 220 км / ч.
Эта скорость показывает, что за час расстояние между поездами увеличится на 220 км. Чтобы узнать, какое расстояние будет между поездами через два часа, умножьте 220 на 2.
220 × 2 = 440 км.
Ответ: через два часа расстояние между поездами составит 440 км.
Задание 2. Велосипедист и мотоциклист покинули точку одновременно в противоположных направлениях. Скорость велосипедиста — 16 км / ч, мотоциклиста — 40 км / ч.Какое расстояние между велосипедистом и мотоциклистом будет через 2 часа?
Решение
16 км / ч + 40 км / ч = 56 км / ч.
Эта скорость показывает, что за один час расстояние между велосипедистом и мотоциклистом увеличится на 56 км.
Определите расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого умножьте (56 км / ч) на 2 часа
56 × 2 = 112 км
Ответ: Через 2 часа расстояние между велосипедистом и мотоциклистом составит 112 км.
Задание 3. Велосипедист и мотоциклист покинули точку одновременно в противоположных направлениях. Скорость велосипедиста — 10 км / ч, мотоциклиста — 30 км / ч. Через сколько часов между ними будет расстояние 80 км?
Решение
10 км / ч + 30 км / ч = 40 км / ч.
За час расстояние между велосипедистом и мотоциклистом увеличивается на 40 км. Чтобы узнать, сколько часов будет расстояние между ними 80 км, мы должны определить, сколько раз в 80 км содержится 40 км
80: 40 = 2
Ответ: Через 2 часа после начала движения между велосипедистом и мотоциклистом будет 80 километров.
Задание 4. Велосипедист и мотоциклист покинули точку одновременно в противоположных направлениях. Через 2 часа расстояние между ними составило 90 км. Скорость велосипедиста составляла 15 км / ч. Рассчитайте скорость мотоциклиста.
Решение
Определите расстояние, пройденное велосипедистом за 2 часа. Для этого умножьте его скорость (15 км / ч) на 2 часа
15 × 2 = 30 км
На рисунке показано, что велосипедист преодолевает 15 километров каждый час => 30 километров за два часа.
Вычтем расстояние, пройденное велосипедистом (30 километров), из общего расстояния (90 километров). Это покажет нам, сколько километров проехал велосипедист:
90 км — 30 км = 60 км
Мотоциклист проехал 60 км за два часа. Если разделить пройденное им расстояние на два часа, мы узнаем, с какой скоростью он проехал:
60: 2 = 30 км / ч.
Значит, скорость мотоциклиста составила 30 км / ч.
Ответ: скорость мотоциклиста 30 км / ч.
Задание на движение в одном направлении.
В предыдущей задаче мы рассматривали задачи, в которых объекты (люди, машины, лодки) движутся либо навстречу друг другу, либо в противоположных направлениях. Мы обнаружили разные расстояния, которые менялись между объектами с течением времени.
В первом случае мы нашли связанные скорости — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшилось на определенное расстояние
Во втором случае это была ситуация, когда два объекта двигались в противоположных направлениях.За единицу времени расстояние между объектами увеличилось на определенное расстояние
Но объекты также могут двигаться в одном направлении и с разной скоростью. Например, велосипедист и мотоциклист могут одновременно выезжать из одной точки, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке показано, что мотоциклист опережает велосипедиста на двадцать километров.Это потому, что он проезжает на 20 километров в час больше, чем велосипедист. Таким образом, каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров .
В данном случае 20 км / ч — это разница в скорости между мотоциклистом и велосипедистом.
Через два часа расстояние, пройденное велосипедистом, составит 40 км. Мотоциклист преодолеет 80 километров и отодвинется от велосипедиста еще на 20 километров — общее расстояние между ними составит 40 километров.
Чтобы найти скорость, с которой один объект удаляется от другого при движении в одном направлении, вы должны вычесть меньшую скорость из более высокой.
В приведенном выше примере скорость одного объекта, удаляющегося от другого, составляет 20 км / ч. Его можно найти, вычтя скорость велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км / ч, а скорость мотоциклиста — 40 км / ч. Скорость мотоциклиста больше, поэтому мы вычитаем 20 из 40
40 км / ч — 20 км / ч = 20 км / ч
Задача 1. Автомобиль и автобус выехали из города в одном направлении. Скорость автомобиля составляет 120 км / ч, а скорость автобуса — 80 км / ч. Какое расстояние между ними будет через 1 час? 2 часа?
Решение
120 км / ч — 80 км / ч = 40 км / ч.
Каждый час легковой автомобиль отъезжает на 40 км от автобуса. Через час расстояние между автомобилем и автобусом составит 40 км. За 2 часа это вдвое больше:
40 × 2 = 80 км
Ответ: через час расстояние между автомобилем и автобусом будет 40 км, через два часа 80 км.
Рассмотрим ситуацию, в которой объекты начали движение с разных точек, но в одном направлении.
Предположим, есть дом, школа и аттракцион. От дома до школы 700 метров
Задача 6 Два пешехода проехали одновременно. Первый пешеход проехал от дома со скоростью 100 метров в минуту, а второй пешеход проехал по дороге от школы со скоростью 80 метров в минуту.Какое будет расстояние между пешеходами через 2 минуты? Через сколько минут после старта первый пешеход догонит второго пешехода?
Ответим на первый вопрос задачи: Какое расстояние между пешеходами через 2 минуты?
Определите расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдёт вдвое больше, то есть 200 метров.
100 × 2 = 200 метров
Определите расстояние, пройденное вторым пешеходом за 2 минуты.Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет вдвое больше — 160 метров.
80 × 2 = 160 метров
Теперь нам нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, вы можете прибавить расстояние, пройденное вторым пешеходом (160 м) к расстоянию от дома до школы (700 м), и вычесть из результата расстояние, пройденное первым пешеходом (200 м).
700 м + 160 м = 860 м
860 м — 200 м = 660 м
Либо вычтите расстояние, пройденное первым пешеходом (200 м) из расстояния от дома до школы (700 м), и добавьте к результату расстояние, пройденное вторым пешеходом (160 м).
700 м — 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами составит 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Посмотрим, какая была ситуация в начале пути — когда пешеходы еще не начали движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров.Но через минуту после начала движения расстояние между ними составит 680 метров, потому что первый пешеход движется на 20 метров быстрее, чем второй:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м — 100 м = 780 м — 100 м = 680 м
Через две минуты после начала движения расстояние уменьшится еще на 20 метров и составит 660 метров. Это был наш ответ на первый вопрос проблемы:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м — 200 м = 860 м — 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и составит уже 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м — 300 м = 940 м — 300 м = 640 м
Мы видим, что каждую минуту первый пешеход будет приближаться ко второму пешеходу на 20 метров и в итоге догонит его.Можно сказать, что скорость двадцать метров в минуту — это скорость сближения пешеходов. Правила определения скорости приближения и удаления в одном направлении идентичны.
Чтобы определить скорость схождения при движении в одном направлении, вы должны вычесть меньшую скорость из более высокой.
А поскольку каждую минуту 700 метров уменьшается на те же 20 метров, мы можем узнать, сколько раз 700 метров содержат по 20 метров каждый, тем самым определяя, через сколько минут первый пешеход догонит второго
700: 20 = 35
Итак, через 35 минут после начала движения первый пешеход догонит второго.Ради интереса узнайте, сколько метров к этому времени прошел каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3 500 метров, второй прошел 2 800 метров. Первый прошел еще 700 метров, потому что шел из дома.Если мы вычтем эти 700 метров из 3500 метров, мы получим 2800 метров.
Задача 7 Рассмотрим ситуацию, когда объекты движутся в одном направлении, но один из объектов начал движение раньше другого.
Предположим, есть дом и школа. Первый пешеход пошел в школу со скоростью 80 метров в минуту. Через 5 минут второй пешеход последовал за ним в школу со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого пешехода?
Второй пешеход ушел через 5 минут.К тому времени первый пешеход уже прошел некоторое расстояние. Найдем это расстояние. Для этого умножьте его скорость (80 м / м) на 5 минут
80 × 5 = 400 метров
Первый пешеход находится в 400 метрах от второго пешехода. Следовательно, в момент начала движения второго пешехода между ними будет эти 400 метров.
Но второй пешеход движется со скоростью 100 метров в минуту. То есть он движется на 20 метров быстрее первого пешехода, а это значит, что с каждой минутой расстояние между ними будет уменьшаться на 20 метров.Наша задача — узнать, через сколько минут это произойдет.
Например, через минуту расстояние между пешеходами составит 380 метров. Первый пешеход пройдет еще 80 метров в дополнение к своим 400 метрам, а второй пешеход пройдет 100 метров.
Принцип такой же, как и в предыдущей задаче. Расстояние между пешеходами во время движения второго пешехода необходимо разделить на скорость приближения пешеходов.Скорость приближения в этом случае — двадцать метров. Следовательно, чтобы определить, через сколько минут второй пешеход догонит первого пешехода, разделите 400 метров на 20
.
400: 20 = 20
Итак, через 20 минут второй пешеход догонит первого.
Задание 2. Автобус и велосипедист выехали из двух сел, расстояние между которыми 40 км, одновременно в одном направлении. Скорость велосипедиста — 15 км / ч, а скорость автобуса — 35 км / ч.Через сколько часов автобус догонит велосипедиста?
Решение
Найдите скорость сходимости
35 км / ч — 15 км / ч = 20 км / ч.
Сколько часов потребуется автобусу, чтобы обогнать велосипедиста?
40: 20 = 2
Ответ: Автобус догонит велосипедиста через 2 часа.
Проблема с движением реки, лодки и ручья
Суда движутся по реке с разной скоростью. Они могут двигаться как вниз, так и вверх по потоку.В зависимости от того, как они движутся (вверх или вниз по потоку), скорость будет меняться.
Предположим, что скорость реки 3 км / ч. Если вы впустите лодку в реку, река унесет лодку со скоростью 3 км / ч.
Если вы спустите лодку в стоячую воду, в которой нет потока, лодка также будет стоять. Скорость лодки в этом случае будет равна нулю.
Если лодка идет в стоячей воде без течения, считается, что лодка движется со своей скоростью .
Например, если моторная лодка движется по стоячей воде со скоростью 40 км / ч, то собственная скорость моторной лодки считается 40 км / ч.
Как узнать скорость корабля?
Если судно плывет вниз по течению, вы должны добавить скорость реки к собственной скорости судна.
Например, если моторная лодка движется со скоростью 30 км / ч по реке и скорость речного потока составляет 2 км / ч, то к собственной скорости катера (30 км / ч) необходимо добавить скорость реки. ручей (2 км / ч)
30 км / ч + 2 км / ч = 32 км / ч
Речной поток, можно сказать, помогает моторной лодке с дополнительной скоростью, равной двум километрам в час.
Если корабль идет против течения реки, вы должны вычесть скорость течения реки из скорости корабля.
Например, если моторная лодка плывет со скоростью 30 км / ч против течения реки , а скорость речного течения составляет 2 км / ч, то исходя из скорости моторной лодки (30 км / ч) вы должны вычесть скорость речного потока (2 км / ч)
30 км / ч — 2 км / ч = 28 км / ч
Речной поток в данном случае не позволяет катеру свободно двигаться вперед, снижая его скорость на два километра в час.
Задача 1. Скорость лодки 40 км / час, скорость потока 3 км / час. С какой скоростью лодка будет двигаться вниз по течению реки? Против течения реки?
Ответ:
Если бы лодка двигалась вниз по течению реки, ее скорость была бы 40 + 3, то есть 43 км / ч.
Если лодка движется против течения реки, ее скорость будет 40-3, то есть 37 км / ч.
Задача 2. Скорость катера на стоячей воде — 23 км / ч.Скорость речного потока — 3 км / ч. По какому пути будет плыть корабль через 3 часа вниз по течению реки? Против течения?
Решение
Фактическая скорость корабля — 23 км / ч. Если корабль движется вниз по течению, его скорость будет 23 + 3, то есть 26 км / ч. За три часа он проедет втрое больше
26 × 3 = 78 км
Если корабль движется против течения реки, его скорость будет 23 — 3, то есть 20 км / ч. За три часа он проедет втрое больше
20 × 3 = 60 км
Задача 3. Судно преодолело расстояние от точки A до точки B за 3 часа 20 минут, а расстояние от точки B до A за 2 часа 50 минут. В каком направлении течет река: от А к Б или от Б к А, если известно, что скорость лодки не менялась во время поездки?
Решение
Скорость лодки не изменилась. Давайте выясним, в каком направлении реки прошло больше времени: путь от A до B или путь от B до A. Самый длинный путь, по которому течет река против лодки
3 часа 20 минут более 2 часов 50 минут.Это означает, что течение реки снизило скорость лодки, и это отразилось на времени в пути. 3 часа 20 минут — время, которое потребовалось, чтобы добраться из пункта А в пункт Б. Итак, река течет из пункта Б в пункт А
.
Задача 4. За какое время при движении против течения реки корабль пробежит 204 км при собственной скорости 15 км / ч, а скорость течения в 5 раз меньше скорости корабля. ?
Решение
Найдите время, за которое корабль преодолеет 204 километра против течения реки.Скорость корабля — 15 км / ч. Он движется против течения реки, поэтому нам нужно определить его скорость в этом движении.
Чтобы определить скорость против течения реки, вычтите скорость корабля (15 км / ч) из его собственной скорости (15 км / ч). Условие гласит, что скорость речного течения в 5 раз меньше скорости лодки, поэтому сначала определите скорость речного течения. Для этого уменьшите 15 км / ч в пять раз
15: 5 = 3 км / ч
Скорость ручья 3 км / ч.Вычтем эту скорость из скорости лодки
.
15 км / ч — 3 км / ч = 12 км / ч.
Теперь определите время, необходимое кораблю для прохождения 204 км со скоростью 12 км / ч. Корабль движется со скоростью 12 км в час. Чтобы узнать, сколько часов пройдет 204 км, определите, сколько раз в 204 км содержится 12 км
.
204: 12 = 17 ч
Ответ: корабль пройдет 204 километра за 17 часов
Задание 5. Двигаясь по течению реки, лодка
за 6 часов преодолела 102 км.Определите собственную скорость лодки,
, если скорость потока составляет 4 км / ч.
Решение
Найдите скорость, с которой лодка двигалась по реке. Разделите пройденное расстояние (102 км) на время в пути (6 ч).
102: 6 = 17 км / ч.
Определим собственную скорость лодки. Это делается путем вычитания скорости потока (4 км / ч) из скорости, с которой лодка двигалась по реке (17 км / ч)
17-4 = 13 км / ч
Задача 6. Двигаясь против течения, лодка
за 5 часов прошла 110 км. Определите собственную скорость лодки,
, если скорость потока составляет 4 км / ч.
Решение
Найдите скорость, с которой лодка двигалась по ручью. Это делается путем деления пройденного расстояния (110 км) на время поездки (5 ч).
110: 5 = 22 км / ч.
Определим собственную скорость лодки. В условии указано, что лодка двигалась против течения реки. Скорость речного потока составляла 4 км / ч.Это означает, что собственная скорость лодки уменьшилась на 4. Наша задача — прибавить 4 км / ч и найти собственную скорость лодки
.
22 + 4 = 26 км / ч.
Ответ: собственная скорость лодки 26 км / ч
Задача 7. Сколько времени потребуется, чтобы лодка, движущаяся против течения реки
, прошла 56 км, если скорость потока была 2 км / ч, а собственная скорость лодки была
Собственная скорость 8 км / ч больше текущей скорости?
Решение
Определите собственную скорость лодки.Условие гласит, что она на 8 км / ч больше скорости ручья. Поэтому добавим еще 8 км / ч к скорости потока (2 км / ч), чтобы найти собственную скорость лодки
.
2 км / ч + 8 км / ч = 10 км / ч
Лодка идет против течения реки, поэтому давайте вычтем скорость реки (2 км / ч) из собственной скорости лодки (10 км / ч)
10 км / ч — 2 км / ч = 8 км / ч
Узнайте, сколько времени займет лодка, чтобы преодолеть 56 км. Для этого разделим расстояние (56 км) на скорость лодки:
56: 8 = 7 ч
Ответ: Если лодка идет вверх по течению, она преодолеет 56 км за 7 часов.
Упражнения
Задание 1. Сколько времени займет пешеход, чтобы пройти 20 км, если его скорость 5 км / ч?
Решение
За час пешеход проходит 5 километров. Чтобы определить, сколько времени ему потребуется, чтобы пройти 20 км, нужно узнать, сколько раз в 20 км содержится 5 км. Или воспользуйтесь правилом определения времени: разделите пройденное расстояние на скорость
.
20: 5 = 4 часа
Задача 2. Велосипедист ехал из пункта A в пункт B в течение 5 часов со скоростью 16 км / ч, а обратно по тому же маршруту он ехал со скоростью 10 км / ч. Сколько времени потребовалось велосипедисту, чтобы ехать обратно?
Решение
Определите расстояние от точки A до точки B . Для этого умножьте скорость, с которой велосипедист проехал от точки A до точки B (16 км / ч), на время в пути (5 ч)
.
16 × 5 = 80 км
Узнайте, сколько времени велосипедист потратил на обратный путь.Для этого расстояние (80 км) разделите на скорость (10 км / ч)
.
80:10 = 8 ч
Задача 3. Велосипедист ехал 6 часов с определенной скоростью. После того, как он проехал еще 11 км с той же скоростью, его путь стал 83 км. С какой скоростью ехал велосипедист?
Решение
Найдите расстояние, которое велосипедист преодолеет за шесть часов. Вычитаем из 83 км расстояние, пройденное за шесть часов (11 км).
83 — 11 = 72 км
Определите, насколько быстро велосипедист ехал в течение первых 6 часов.Для этого 72 км разделите на 6 часов
72: 6 = 12 км / ч
Поскольку условие проблемы состоит в том, что велосипедист проехал оставшиеся 11 км с той же скоростью, на которой он ехал в течение первых 6 часов, скорость 12 км / ч является решением проблемы.
Ответ: велосипедист ехал со скоростью 12 км / ч.
Задача 4. Двигаясь против течения реки, корабль преодолевает расстояние 72 км за 4 часа, а плот — такое же расстояние за 36 часов.За сколько часов лодка будет преодолевать расстояние в 110 км, если она плывет вниз по течению?
Решение
Найдите скорость течения реки. Условие гласит, что плот может преодолеть 72 километра за 36 часов. Плот не может двигаться против течения реки. Таким образом, скорость, с которой плот преодолевает 72 километра, и есть скорость течения реки. Чтобы найти эту скорость, разделите 72 километра на 36 часов.
72:36 = 2 км / ч
Найдем скорость лодки.Сначала мы узнаем ее скорость против течения реки. Для этого делим 72 километра на 4 часа
72: 4 = 18 км / ч
Если скорость корабля против течения реки 18 км / ч, то его собственная скорость будет 18 + 2, т.е. 20 км / ч. А ниже по течению — 20 + 2, т. Е. 22 км / ч
.
Собственная скорость корабля 20 + 2, т. Е. 22 км / ч.
Разделив расстояние 110 км на скорость движения судна в речном потоке (22 км / ч), вы узнаете, сколько часов требуется судну, чтобы преодолеть расстояние 110 км
110: 22 = 5 ч
Ответ: по течению реки корабль преодолеет 110 километров за 5 часов.
Задача 5. Два велосипедиста одновременно выехали из одной точки в противоположных направлениях. Один из них ехал со скоростью 11 км / ч, а другой — со скоростью 13 км / ч. Какое расстояние между ними за 4 часа?
Решение
Найдите скорость удаления велосипедистов
11 + 13 = 24 км
Узнать расстояние между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами составит 96 км.
Задача 6. Два теплохода вышли из двух причалов, чтобы встретиться друг с другом одновременно, и они встретились через 6 часов. Какое расстояние прошло каждое судно до встречи друг с другом и какое расстояние между пристанями для яхт, если одно судно двигалось со скоростью 21 км / ч, а другое — 24 км / ч?
Решение
Найдите расстояние, пройденное первым кораблем. Для этого умножаем его скорость (21 км / ч) на время в пути до встречи (6 ч).
21 × 6 = 126 км
Определите расстояние, пройденное вторым кораблем. Для этого умножьте его скорость (24 км / ч) на время в пути до встречи (6 ч)
24 × 6 = 144 км
Определите расстояние между опорами. Для этого складываем расстояния, пройденные первым и вторым судами
.
126 км + 144 км = 270 км
Ответ: первое судно прошло 126 км, второе судно 144 км. Расстояние между причалами — 270 км.
Задача 7. Два поезда вышли из Нью-Йорка и Орландо одновременно. Через 16 часов они встретились. Поезд из Нью-Йорка двигался со скоростью 51 км / ч. С какой скоростью ехал поезд, уходивший из Орландо, если расстояние между Нью-Йорком и Орландо составляло 1520 км? Какое расстояние было между поездами через 5 часов после встречи?
Решение
Узнайте, сколько километров поезд покинул Нью-Йорк до встречи. Для этого умножьте его скорость (51 км / ч) на 16 часов
51 × 16 = 816 км
Давайте узнаем, сколько километров проехал поезд, вышедший из Орландо, до встречи.Для этого мы вычитаем расстояние, пройденное поездом, вышедшим из Нью-Йорка, из расстояния между Нью-Йорком и Орландо (1520 км).
1520 — 816 = 704 км
Найдите скорость, с которой поезд покинул Орландо. Для этого разделите расстояние, которое он проехал до встречи, на 16 часов
704: 16 = 44 км / ч
Найдем расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдите скорость поездов и умножьте эту скорость на 5
.
51 км / ч + 44 км / ч = 95 км / ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Орландо, ехал со скоростью 44 км / ч. Через пять часов после встречи поездов расстояние между ними составит 475 км.
Задача 8. Два автобуса выехали из одной точки одновременно в противоположных направлениях. Скорость одного автобуса — 48 км / ч, другого — на 6 км / ч. Через сколько часов расстояние между автобусами составит 510 км?
Решение
Найдите скорость второго автобуса. Это на 6 км / ч больше скорости первого автобуса
.
48 км / ч + 6 км / ч = 54 км / ч
Найдите скорость удаления автобусов.Для этого добавьте их скорости:
48 км / ч + 54 км / ч = 102 км / ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать, через сколько часов расстояние между ними составит 510 км, нам нужно узнать, сколько раз в 510 км содержится 102 км / ч
510: 102 = 5 ч
Ответ: Между автобусами 510 км будет через 5 часов.
Задание 9. Расстояние от Чикаго до Нью-Йорка 1230 км.Два поезда вышли из Нью-Йорка и Чикаго навстречу друг другу. Поезд из Нью-Йорка движется со скоростью 63 км / ч, а скорость чикагского поезда совпадает со скоростью поезда Нью-Йорка. На каком расстоянии от Чикаго встретятся поезда?
Решение
Найдем скорость чикагского поезда. Это
скорости нью-йоркского поезда. Итак, чтобы определить скорость чикагского поезда, нам нужно найти 63 км.
63: 21 × 20 = 3 × 20 = 60 км / ч
Найдем скорость закрытия поездов
63 км / ч + 60 км / ч = 123 км / ч
Определите, через сколько часов поезда встретят
12:30: 123 = 10 часов
Давайте найдем расстояние, на котором поезда будут встречаться из Чикаго.Для этого достаточно найти расстояние, которое проехал чикагский поезд до встречи
.
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Чикаго.
Задача 10. Две моторные лодки одновременно вышли из двух причалов, расстояние между ними 75 км, навстречу друг другу. Одна двигалась со скоростью 16 км / ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние между лодками через 2 часа?
Решение
Найдите скорость второй лодки.Это 75% скорости первой лодки. Следовательно, для определения скорости второй лодки нам потребуется 75% от 16 км
.
16 × 0,75 = 12 км / ч
Найдите скорость схождения лодок
16 км / ч + 12 км / ч = 28 км / ч
Расстояние между лодками будет уменьшаться на 28 км каждый час. Через 2 часа это будет 28 × 2, то есть 56 км. Чтобы определить расстояние между лодками в это время, мы вычтем 56 км из 75 км
.
75 км — 56 км = 19 км
Ответ: через два часа между лодками будет 19 км.
Задача 11. Автомобиль со скоростью 62 км / ч догоняет грузовик со скоростью 47 км / ч. За сколько времени и на каком расстоянии от начала движения автомобиль догонит грузовик, если исходное расстояние между ними составляло 60 км?
Решение
Найдите скорость приближения
62 км / ч — 47 км / ч = 15 км / ч
Если изначально расстояние между автомобилями составляло 60 км, то каждый час это расстояние будет уменьшаться на 15 км, и в конечном итоге легковой автомобиль догонит грузовик.Чтобы узнать, через сколько часов это произойдет, определите, сколько раз в 60 км содержится 15 км
.
60:15 = 4 ч
Выясним, на каком расстоянии от начала движения легковой автомобиль догнал грузовик. Для этого умножаем скорость автомобиля (62 км / ч) на время его движения до встречи (4 ч)
62 × 4 = 248 км
Ответ: легковой автомобиль догонит грузовик за 4 часа. На момент встречи легковой автомобиль будет находиться на расстоянии 248 км от места начала движения.
Задача 12. Два мотоциклиста одновременно выехали из одной точки в одном направлении. Скорость одного составляла 35 км / ч, а скорость другого — 80% скорости первого мотоциклиста. Какое расстояние между ними будет через 5 часов?
Решение
Найдите скорость второго мотоциклиста. Это 80% скорости первого мотоциклиста. Следовательно, чтобы найти скорость второго мотоциклиста, нам нужно найти 80% от 35 км / ч
35 × 0.80 = 28 км / ч
Первый мотоциклист движется со скоростью 35-28 км / ч
35 км / ч — 28 км / ч = 7 км / ч
За час первый мотоциклист проезжает еще 7 километров. С каждым часом он будет приближаться ко второму мотоциклисту на эти 7 километров.
За 5 часов первый мотоциклист преодолеет 35 × 5, т.е. 175 км, а второй мотоциклист — 28 × 5, то есть 140 км. Определим расстояние между ними. Для этого из 175 км
вычитаем 140 км.
175 — 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами составит 35 км.
Задача 13. Мотоциклист со скоростью 43 км / ч догоняет велосипедиста со скоростью 13 км / ч. За сколько часов мотоциклист догонит велосипедиста, если исходное расстояние между ними составляло 120 км?
Решение
Найдите скорость приближения:
43 км / ч — 13 км / ч = 30 км / ч
Если изначально расстояние между мотоциклистом и велосипедистом составляло 120 км, то каждый час это расстояние будет уменьшаться на 30 км, и со временем мотоциклист догонит велосипедиста.Чтобы узнать, через сколько часов это произойдет, определите, сколько раз в 120 км содержится 30 км
.
120: 30 = 4 часа
Так за 4 часа мотоциклист догонит велосипедиста
На рисунке показано движение мотоциклиста и велосипедиста. Вы можете видеть, что после 4 часов езды они выровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист со скоростью 12 км / ч догоняет велосипедиста, скорость которого составляет 75% от его скорости.Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое было исходное расстояние между велосипедистами?
Решение
Найдите скорость велосипедиста, едущего впереди. Для этого найдите 75% скорости велосипедиста, едущего сзади:
12 × 0,75 = 9 км / ч — скорость велосипедиста, едущего впереди
Давайте узнаем, сколько километров проехал каждый велосипедист, прежде чем второй велосипедист догнал первого:
12 × 6 = 72 км — тот, кто едет сзади
9 × 6 = 54 км — тот, кто едет впереди
Давайте выясним начальную дистанцию между велосипедистами.Для этого мы вычитаем расстояние, пройденное вторым велосипедистом (который догонял), из расстояния, пройденного первым велосипедистом (который догонял)
72 км — 54 км = 18 км
Ответ: между велосипедистами изначально было 18 км.
Задача 15. Автомобиль и автобус выехали из одной точки в одном направлении в одно и то же время. Скорость автомобиля — 53 км / час, скорость автобуса — 41 км / час. Через сколько часов после выхода машина будет на 48 км впереди автобуса?
Решение
Определите скорость движения машины от автобуса
53 км / ч — 41 км / ч = 12 км / ч
Автомобиль будет отходить от автобуса на 12 км каждый час.На рисунке показано положение автомобилей после первого часа
Видно, что машина опережает автобус на 12 км.
Чтобы узнать, за сколько часов автомобиль будет на 48 км впереди автобуса, необходимо определить, сколько раз 48 км содержат 12 км
48:12 = 4 ч
Ответ: Через 4 часа после выезда машина будет на 48 километров впереди автобуса.
Скорость, расстояние и время — третий / четвертый уровень | Счисления и математика | Ресурсы для практиков | Scotland Learns
Цель деятельности
Понимание и применение связей между математическими понятиями — важный навык, который необходимо развивать в математике и арифметике.Поощрение молодых людей к размышлению о связи между скоростью, расстоянием и временем поможет им развить этот навык. Для них важным навыком будет делиться своими идеями и мыслями с кем-то дома. Это может быть взрослый или старший брат или сестра.
Учебная программа для повышения квалификации (CfE) уровни: Третий уровень
- Используя простые периоды времени, я могу вычислить, сколько времени займет поездка, пройденную скорость или пройденное расстояние, используя свои знания о связи между временем, скоростью и расстоянием.(MTH 3-10a)
Учебная деятельность
При разработке учебных мероприятий подумайте о круге учащихся в вашем классе и их индивидуальных обстоятельствах. Рассмотрим следующее учебное задание, которое можно адаптировать для ваших учащихся:
Вот полезное напоминание о скорости, расстоянии и времени.
Это задание попросит учащихся исследовать время, которое требуется свету, чтобы пройти от Солнца до каждой из планет нашей солнечной системы. Для этого им потребуется калькулятор.Для облегчения расчетов расстояния, скорости и время округлены. Примечание: мс -1 означает метры в секунду.
Часть 1
- Возьмем скорость света 300000000 мс -1 .
- Расстояние от Солнца до Земли 149 600 000 км.
- Сколько времени нужно, чтобы свет, покидающий Солнце, достиг Земли? Дайте ответ, округленный до ближайшей минуты.
Часть 2
- Сколько времени требуется солнечному свету, чтобы достичь других планет в нашей солнечной системе? Вам нужно будет выбрать наиболее подходящие единицы времени для каждого из ваших ответов.
- Вы можете попросить своих молодых людей заполнить эту таблицу:
Планета | Расстояние до Солнца в километрах (км) | Время |
Меркурий | 57 900 000 | |
Венера | 108 200 000 | |
Земля | 149 600 000 | |
Марс | 227 900 000 | |
Юпитер | 778 600 000 | |
Сатурн | 1 433 500 000 | |
Уран | 2 872 500 000 | |
Нептун | 4 495 100 000 | |
Плутон | 5 906 400 000 |
Источник: https: // nssdc.gsfc.nasa.gov/planetary/factsheet/index.html
Часть 3
- Скорость света приближается к 299792458 мс -1 . Объясните, как это изменит ваше время, рассчитанное в части 1 и части 2.
Часть 4
- Если свету требуется 1,275 секунды, чтобы добраться от Земли до Луны, как далеко он в километрах от Земли до Луны? Возьмем скорость света 300000000 мс -1 .
Часть 5 — Расширение (требуется знание научных обозначений)
- Световой год — это мера того, как далеко свет проходит за один год.Подсчитайте, как далеко уходит свет за год, с точностью до ближайшего километра.
Национальные ориентиры
В зависимости от индивидуальной стадии развития молодых людей и их предыдущего обучения они будут работать над этими национальными ориентирами к концу третьего уровня.
Третий уровень
- Прикладные знания о взаимосвязи между скоростью, расстоянием и временем для определения каждой из трех переменных.
Возможный подход к оценке обучения
Получение примеров домашнего обучения от молодых людей поможет вам понять, как они справляются с поставленными вами задачами, и предоставит некоторую обратную связь.Независимо от того, какие подходы ваша школа использует для общения с молодыми людьми, некоторые из следующих могут быть полезны для того, чтобы помочь вам оценить и отметить их успехи:
- Молодые люди могут захотеть загрузить фотографии, видео или комментарии в свой учебный онлайн-дневник. В этом случае вы можете побудить их поделиться своими мыслями или решениями.
- Вы могли бы побудить молодых людей рассказать, как они пришли к этой задаче. Насколько легко им это удалось? Было ли что-нибудь, что им мешало?
- В зависимости от вашей платформы для домашнего обучения у молодых людей могут быть возможности обсудить и совместно работать над этим заданием.
Рабочие листы скорости, времени и расстояния
Вы здесь: Главная страница → Рабочие листы → Скорость, время и расстояние
Создавайте настраиваемые рабочие листы о постоянной (или средней) скорости, времени и расстоянии для курсов предварительной алгебры и алгебры 1 курсов (6–9 классы). Доступны как PDF, так и html форматы. Вы можете выбрать типы текстовых задач на листе, количество задач, метрические или обычные единицы, способ выражения времени (часы / минуты, дробные или десятичные часы) и объем рабочего пространства для каждой задачи.
Существует СЕМЬ различных типов задач со словами, от простых до сложных, так что вы можете создавать самые разные рабочие листы. Семь типов проблем подробно объясняются в реальном генераторе ниже.
Все рабочие листы включают ключ ответа на 2-й странице файла.
Воспользуйтесь быстрыми ссылками ниже, чтобы создать некоторые распространенные типы рабочих листов.
Простая таблица скорости, времени и расстояния 1: Как далеко можно пройти или сколько времени займет поездка — на полчаса или полчаса
Простая таблица скорости, времени и расстояния 2: Как далеко он может уйти, сколько времени занимает поездка или какова средняя скорость — с использованием целых или получасовых часов
Рабочий лист 3: скорость, время и расстояние: Как далеко он может уйти, сколько времени занимает поездка или какова средняя скорость — с использованием четверти часа
Рабочий лист скорости, времени и расстояния 4: Как далеко можно пройти, сколько времени займет поездка или какова средняя скорость — время до 5-минутных интервалов
Рабочий лист 5: скорость, время и расстояние: задачи включают преобразование минут в часы.
Найдите среднюю скорость: время дается до четверти часа.
Найдите среднюю скорость: время дается с точностью до двенадцатой части часа.
Найдите среднюю скорость: задачи связаны с преобразованием единицы времени
Скорость, время и расстояние: более сложные задачи 1
Скорость, время и расстояние: более сложные задачи 2
Алгебра реального мира Эдвард Заккаро
Алгебра часто преподается абстрактно, практически без акцента на том, что такое алгебра и как ее можно использовать для решения реальных задач.Подобно тому, как английский можно переводить на другие языки, текстовые задачи можно «переводить» на математический язык алгебры и легко решать. Алгебра реального мира объясняет этот процесс в удобном для понимания формате с использованием мультфильмов и рисунков. Это упрощает самообучение как для ученика, так и для любого учителя, который никогда не понимал алгебру. Включает главы по алгебре и деньгам, алгебре и геометрии, алгебре и физике, алгебре и рычагам и многому другому. Предназначен для детей 4–9 классов с более высокими математическими способностями и интересами, но может использоваться также учениками старшего возраста и взрослыми.Содержит 22 главы с инструкциями и задачами трех уровней сложности.
=> Узнать больше
Navigation NAU 102 Урок 12. Время, скорость, расстояние Расчет времени, скорости и расстояния Ежедневная задача для навигатора. Расчет требует точности.
Презентация на тему: «Навигация НАУ 102 Урок 12. Время, скорость, расстояние Расчет времени, скорости и расстояния Ежедневная задача для навигатора. Расчет требует точности.»- стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
Навигация НАУ 102 Урок 12
2
Время, скорость, расстояние Расчет времени, скорости и расстояния Ежедневная задача для навигатора.Расчет требует точности и скорости. Когда я туда доберусь? Как быстро я должен идти?
3
Единица измерения скорости — это узел (узлы, узлы или узлы) из узлового журнала скорости.
4
Единица измерения скорости — узел (узлы, узлы или узлы) 1 узел = 1 морская миля / час Скорость = расстояние / время
5
Расчет Несколько методов Мысленный расчет «Правило 6 минут» Логарифмическая шкала Номограмма Математическая формула
6
Мысленный расчет Решите, используя простые соотношения единиц времени.например ½, ⅓, ¼ Ваша скорость 20 узлов. Как далеко вы уедете за 30 минут? Вы преодолеете 6 морских миль за 20 минут. Какая у тебя скорость? 10 морских миль 18 узлов
7
«Правило 6 минут» 6 минут — это 1/10 часть часа. Каждые 6 минут вы проезжаете расстояние, равное 1/10 вашей скорости. Переместите десятичную запятую на 1 место влево или вправо.
8
«Правило шести минут» E.грамм. Если ваша скорость составляет 15 узлов, сколько вы проедете за 6 минут? 15,0 1,50 нм
9
«Правило шести минут». Какова ваша скорость, если вы преодолеете 2,7 морских миль за 6 минут? 2.7 27 узлов.
10
«Правило 6 минут». Вы также можете использовать значение, кратное 6 минутам. 6 минут = 0,1 час 12 минут = 0,2 часа 18 минут = 0,3 часа и т. Д.
11
«Правило шести минут». Если ваша скорость составляет 15 узлов, сколько вы проедете за 18 минут? 15,0 1,50 нм x 3 = 4,5 нм
12
Логарифмическая шкала На некоторых диаграммах и радиолокационных чертежах.
13
Номограмма На некоторых графиках и досках маневрирования.
14
Номограмма Например. Как далеко вы проедете за 16 минут на скорости 13 узлов?
15
Номограмма Например. Сколько времени потребуется, чтобы проехать 2,5 морских мили на скорости 16 узлов?
16
Математическая формула Расстояние = Скорость x Время D = S x T S = D / T T = D / S
17
ETA Расчетное время прибытия Во сколько я доберусь туда? Для коротких рейсов: время в пути = расстояние / скорость, время в пути + время отправления = расчетное время прибытия.
18
Пример расчетного времени прибытия. Вы вылетаете из точки A в 08:00 и двигаетесь через 60 морских миль до точки B со скоростью 13 узлов.Какое ваше расчетное время прибытия в точку B? Время прохождения = 60 нм / 13 узлов = 4,6154 часа = 4 часа + 0,6154 часа * 60 мин / час = 4 часа 37 минут + 0800 = 1237
19
Расчетное время прибытия Для дальних путешествий нам необходимо знать часовые пояса.
20
Часовые пояса Земля разделена на 24 часовых пояса. Время отличается на час от соседних зон. У всех в зоне одинаковое время.
21 год
Часовые пояса
22
Ширина каждого часового пояса составляет 15 ° долготы. 360 ° / 24 = 15 ° Зоны пронумерованы («описания зон») от 0 до -12 по восточной долготе, от 0 до +12 по западной долготе.
23
Часовые пояса Сначала вычислите центральный меридиан зоны E.грамм. Зоны ZD +4 простираются на 7,5 ° к востоку и западу от центра. Границы зоны 15 ° x описание зоны 4 x 15 ° = 60 ° з.д.
24
Часовые пояса
25
Чтобы найти зону определенного местоположения: разделите на 15 Округлите до ближайшего целого числа Преобразуйте долготу в градусы и десятые доли
26 год
Часовые пояса ZD = -9 141.5 ° / 15 = 9,43 141 ° 30 ’= 141,5 ° Например. Что такое ZD для 141 ° 30 ’E (- E / + W) ZD = -10142,66 ° / 15 = 9,51 142 ° 40’ = 142,66 ° Например. Что такое ZD у 142 ° 40 ’E?
27
Часовые пояса, а иногда и зулусское время, всемирное координированное время (UTC), известное как среднее время по Гринвичу (GMT) ZD 0 — отправная точка для мировой системы времени. Мы должны иметь возможность конвертировать часовые пояса.
28 год
Часовые пояса E.грамм. Когда в Вальехо (ZD +8) 08:15, сколько сейчас времени по Гринвичу? Добавьте ZD к местному времени. Чтобы преобразовать местное время в GMT 0815 + (+8) = 1615 GMT
29
Часовые пояса Например. Когда по ZD +4 22:30, сколько сейчас времени по Гринвичу? 2230 + (+4) = 2630 GMT 2630 = 02:30 на следующий день
30
Часовые пояса Например. Когда в ZD -4 22:30, сколько сейчас времени по Гринвичу? 22:30 + (-4) = 18:30 по Гринвичу
31 год
Часовые пояса E.грамм. Когда 7 октября 02:30 в ZD -4, сколько сейчас времени по Гринвичу? 0230 + (-4) =? 0230 = 2630 06 октября 26:30 + (-4) = 2230 06 октября
32
Часовые пояса Например. Когда сейчас 08:15 по Гринвичу, сколько времени в Вальехо (ZD +8)? вычесть ZD из GMT Чтобы преобразовать GMT в местное время 08:15 — (+8) = 0015 Местное время
33
Часовые пояса E.грамм. Когда сейчас 08:15 по Гринвичу, сколько времени по ZD -8? вычесть ZD из GMT Чтобы преобразовать GMT в местное время 08:15 — (-8) = 1615 Местное время
34
Часовые пояса Например. Летнее время в Вальехо (ZD +7) Зоны сохраняют время следующей зоны на восток. Переход на летнее время Обычно с 1-го воскресенья апреля по последнее воскресенье октября.
35 год
Часовые пояса Переход на летнее время 2007: со 2-го воскресенья марта по первое воскресенье ноября.Примечание. В некоторых странах летнее время не используется. Смотрите в маршруте плавания
36
Введение в вопросы по навигации?
Скорость Расстояние Время Рабочий лист и математические ресурсы KS3 и KS4
ССЫЛКИ НА ПРОГРАММУ
АНГЛИЯ
KS3 NC Science
Физика, описывающая движение:
Скорость и количественное соотношение между средней скоростью, расстоянием и временем (скорость = расстояние ÷ время).
Изображение путешествия на графике расстояние-время.
GCSE Science
Edexcel
2.6 Вспомните и используйте эти уравнения (средняя) скорость = расстояние ÷ время, пройденное расстояние = средняя скорость x время.
2.7 Анализируйте графики расстояния / времени, включая определение скорости по уклону.
Вспомните некоторые типичные скорости, которые встречаются в повседневной жизни для ветра и шума, а также для ходьбы, бега, езды на велосипеде и других транспортных систем.
AQA
Скорость движущегося объекта редко бывает постоянной.Когда люди ходят, бегают или путешествуют на машине, их скорость постоянно меняется.
Типичные значения могут быть приняты как: ходьба ̴ 1,5 м / с, бег ̴ 3 м / с, езда на велосипеде ̴ 6 м / с. Учащиеся должны уметь вспоминать типичные значения скорости человека, идущего, бегающего и велосипедного, а также типичные значения скорости для различных типов транспортных систем.
Для объекта, движущегося с постоянной скоростью, расстояние, пройденное за определенное время, можно рассчитать с помощью уравнения: пройденное расстояние = скорость × время s = v t.
Если объект движется по прямой линии, расстояние до определенной точки можно представить в виде графика «расстояние – время».
Скорость объекта можно вычислить по градиенту его графика расстояние – время.
Комбинированный шлюз OCR
P2.1b описывает, как измерять расстояние и время и использовать их для расчета скорости.
P2.1e связывает изменения и различия в движении с соответствующими графиками расстояние-время и скорость-время; интерпретировать линии и уклоны.
P2.1g вычислить среднюю скорость для неравномерного движения.
KS3 NC Maths
Соотношение, пропорция и скорость изменения; algebra:
Используйте составные единицы измерения, такие как скорость, для решения задач.
Моделируйте ситуации или процедуры с помощью графиков.
Находите приближенные решения контекстных проблем на основе заданных графиков различных функций, включая кусочно-линейные, экспоненциальные и обратные графики.
KS4 NC Maths
Алгебра; соотношение, пропорция и скорость изменения:
Постройте и интерпретируйте графики (включая взаимные графики {и экспоненциальные графики}) и графики нестандартных функций в реальных контекстах, чтобы найти приблизительные решения таких проблем, как простые кинематические задачи, связанные с расстоянием, скоростью и ускорение.
Используйте составные единицы, такие как скорость.
Свободно переключаться между соответствующими стандартными единицами (например, время, длина) и составными единицами (например, скоростью) в числовом и алгебраическом контекстах.
GCSE Mathematics
AQA
G3.7 Понимание и использование составных мер.
N6.12 Обсудить, построить и интерпретировать, например, графики расстояния-времени (которые могут быть графиками. Нелинейными), моделирующие реальные ситуации.
Edexcel
A14 строит и интерпретирует нестандартные функции в реальном контексте, а также графики для поиска приблизительных решений таких проблем, как простые кинематические задачи, связанные с расстоянием, скоростью и ускорением.
A15 вычисляет или оценивает градиенты графиков и областей под графиками и интерпретирует результаты в таких случаях, как графики расстояния-времени, графики скорости-времени.
R1 Свободное переключение между соответствующими стандартными единицами (например, время, длина) и составными единицами (например, скоростью) в числовом и алгебраическом контекстах.
R11 использует составные единицы, такие как скорость.
OCR
A4.3 Интерпретация информации, представленной в виде линейных и нелинейных графиков, включая графики перемещения (расстояние / время).NB расчет скорости не требуется.
S7.8 Понимать и использовать нормы и составные меры, например скорость.
WALES
KS3 Science
Поймите силы в устройствах и их связь с выполненной работой и мощностью.
GCSE Physics
WJEC
Учащиеся должны быть в состоянии продемонстрировать и применить свои знания и понимание движения с использованием скорости, скорости и ускорения.
ШОТЛАНДИЯ
Четвертый уровень Наука
Используйте соответствующие методы для измерения, расчета и графического отображения скорости объекта и покажите, как эти методы могут использоваться в выбранном приложении.
Свяжите движение объекта с действующими на него силами, сделав точные измерения скорости и ускорения.
National 4 Physics
Использование соответствующей взаимосвязи для решения задач, связанных со скоростью, расстоянием и временем.
Определение средней и мгновенной скорости. Интерпретация графиков скорость-время для описания движения, включая расчет расстояния.
СЕВЕРНАЯ ИРЛАНДИЯ
KS3 Science & Technology
Установите связи между двумя наборами данных или событий и опишите отношения между ними своими словами, например, скорость, тормозной путь и т. Д .; как бы изменились отношения, если бы что-то изменилось.
GCSE Physics
1.1.1 экспериментально исследовать количественные отношения между средней скоростью, расстоянием и временем.
1.1.3 рассчитать скорость изменения скорости (ускорение) как изменение скорости, деленное на затраченное время.
Математика, 6 класс, курс, по курсу для определения скорости и расстояния
Кластер: понимание концепций соотношений и использование их рассуждений для решения проблем
Стандарт
: понять концепцию единичной ставки a / b, связанной с соотношением a: b, где b 0 (b не равно нулю), и использовать язык ставок в контексте отношения отношения.Например, «В этом рецепте соотношение 3 стакана муки к 4 стаканам сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки». «Мы заплатили 75 долларов за 15 гамбургеров, что составляет 5 долларов за гамбургер». (Ожидания для удельных ставок в этом классе ограничены несложными дробями.)
Кластер: понимание концепций соотношений и использование их рассуждений для решения проблем
Стандарт: используйте рассуждения о соотношении и скорости для решения реальных и математических задач, e.g., рассуждая о таблицах эквивалентных соотношений, ленточных диаграммах, линейных диаграммах с двойными числами или уравнениях.
Кластер: понимание концепций соотношений и использование их рассуждений для решения проблем
Standard: Решение проблем с удельной стоимостью, включая проблемы, связанные с ценообразованием и постоянной скоростью. Например, если для стрижки 4 газонов потребовалось 7 часов, то при такой скорости, сколько газонов можно было бы косить за 35 часов? С какой скоростью косили газон?
Кластер: понимание концепций соотношений и использование их рассуждений для решения проблем
Стандарт: используйте рассуждение о соотношении для преобразования единиц измерения; соответствующим образом манипулировать и преобразовывать единицы при умножении или делении величин.
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем
Индикатор
: понять концепцию единичной ставки a / b, связанной с соотношением a: b с b äĘ 0 (b не равно нулю), и использовать язык ставки в контексте отношения отношения. Например, «В этом рецепте соотношение 3 стакана муки к 4 стаканам сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки.«Мы заплатили 75 долларов за 15 гамбургеров, что составляет 5 долларов за гамбургер». (Ожидаемые расценки для этого сорта ограничены несложными дробями.)
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем
Индикатор
: используйте рассуждения о соотношении и скорости для решения реальных и математических задач, например, рассуждая о таблицах эквивалентных соотношений, ленточных диаграммах, линейных диаграммах с двойными числами или уравнениях.
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем
Индикатор
: Решите проблемы с удельной стоимостью, включая проблемы, связанные с установлением цены за единицу и постоянной скоростью. Например, если для стрижки 4 газонов потребовалось 7 часов, то при такой скорости, сколько газонов можно было бы косить за 35 часов? С какой скоростью косили газон?
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем
Показатель: Используйте рассуждение о соотношении для преобразования единиц измерения; соответствующим образом манипулировать и преобразовывать единицы при умножении или делении величин.
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем.
Индикатор
: понять концепцию единичной ставки a / b, связанной с соотношением a: b, где b 0, и использовать язык ставки в контексте отношения отношения.
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем.
Индикатор: Используйте рассуждения о соотношении и скорости для решения реальных и математических задач.
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем.
Индикатор
: Решите проблемы с удельной стоимостью, включая проблемы, связанные с установлением цены за единицу и постоянной скоростью.
Область обучения: соотношения и пропорциональные отношения
Стандарт: понимание концепций соотношений и использование их рассуждений для решения проблем.
Показатель: Используйте рассуждение о соотношении для преобразования единиц измерения; конвертируйте единицы измерения соответствующим образом при умножении или делении величин.
Компромисс скорости и точности — обзор
2.4 Декомпозиция латентности
Этапы принятия решения о перцепционном сенсорном и моторном планировании имеют место между появлением стимула и началом саккады (Cutsuridis, 2010; Gomez et al., 2007; Hutton, 2008; Ноорани, 2014; Ван Руллен, Торп, 2001). В этом смысле интервал задержки отражает время, затрачиваемое процессом принятия решения на приведение саккады к конкретной желаемой цели из набора потенциальных альтернатив (Hutton, 2008; Noorani, 2014).Процесс влечет за собой поток информации, переходящий от механизмов кодирования стимулов низкого уровня к механизмам планирования действий высокого уровня (Van Rullen and Thorpe, 2001), так что сначала обнаруживается визуальный стимул (процесс восприятия), затем определяется цель и саккада к выбранному размещению планируется и инициируется (процесс сенсомоторного принятия решения) (Cutsuridis, 2010; Hutton, 2008).
Согласно нашей гипотезе, мозжечок должен был модулировать движения глаз посредством видимого действия во время принятия решения.Поэтому функция распределения Экс-Вальда (Schwarz, 2001) использовалась для разложения временного ряда задержки на время принятия решения (DT, этап сенсомоторно-принятия решения) и остаточное время (RT, этап компонента без принятия решения) (рис. ).
Рис. 1. Сенсорная карта-планирование-действие. Большая часть задержки (около 97%) покрывается временем принятия решения (DT), которое отражает диффузный процесс восприятия стимула и решения траектории. Остаточная часть (RT) воплощает сенсорный процесс нейронного кодирования визуального сигнала и синаптические задержки двигательной команды (до и после процесса принятия решения, соответственно).
DT — время для восприятия визуального стимула, распознавания цели и планирования траектории саккады. RT, напротив, включает нейронное кодирование: время преобразования стимула в нервный сигнал для его сенсорного обнаружения, время перехода моторной команды для достижения группы мышц и время для подавления рефлексивных реакций (Гомес и Переа , 2014; Luce, 1986; Schwarz, 2001; Voss et al., 2015; White et al., 2010).
Плотность вероятности Экс-Вальда — это четырехпараметрическая (μ, σ, a, γ) функция, заданная сверткой обратной гауссовой и независимой экспоненциальной случайной величины.Среднее значение и дисперсия случайной величины x, распределенной по бывшему Вальду, показаны в уравнениях. (1-2):
(1) Ex = aμ + 1γ
(2) varx = a · σ2μ3 + 1γ2
Взаимодействие между μ, σ и a определяет компромисс между скоростью и точностью во время принятия решения. процесс:
- •
μ оценивает среднюю скорость дрейфа (т. е. накопление свидетельств в единицу времени), и это относится к сложности задачи и перцепционной неопределенности в отношении стимула, так что если стимул легко классифицируется (высокое качество информации) скорость дрейфа увеличивается;
- •
σ — параметр масштабирования, который измеряет изменчивость скорости дрейфа;
- •
— это поглощающая граница, которая указывает количество доказательств, необходимых для принятия решения, и отражает осторожность при ответе, то есть априорную уверенность в наилучшем выборе.
Экспоненциальный параметр распределения Экс-Вальда, γ , выражает остаточную стадию латентного периода (McGill, 1963; Palmer et al., 2011; Schwarz, 2001; White et al., 2010).
Параметры Ex-Wald были рассчитаны с применением процедуры оценки максимального правдоподобия, основанной на алгоритме симплексного поиска Нелдера-Мида (Lagarias et al., 1998), с начальными значениями μ 0 , выбранными случайным образом в пределах [- 5, + 5 ], σ 0 = 1, a 0 , равное медиане временного ряда с задержкой, и γ 0 = 0.0025. Оцененные параметры распределения Экс-Вальда были впоследствии использованы для оценки DT и RT. Средние значения DT и RT были рассчитаны по формуле. 1 как первое отношение (a / μ) и второе отношение (1 / γ) соответственно.
После этого было выполнено моделирование для оценки взаимосвязи между амплитудой, DT, RT и длительностью в каждой группе. Т-копула использовалась для генерации 200 коррелированных многомерных данных о задержке, продолжительности и амплитуде за 1000 итераций.
