Построить график y 3x 2. Квадратичная и кубическая функции

Разберем как строить график с модулем.

Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=—

(x-3)-(—

(x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2.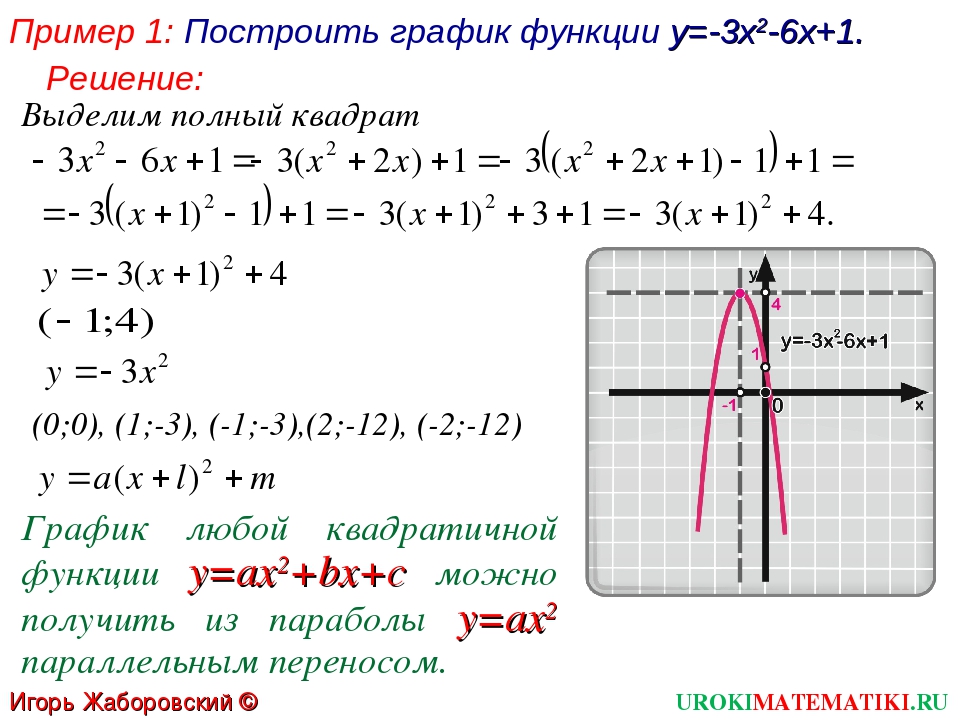 Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=—

(x-3)-(+

(x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+

(x-3)-(+

(x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4.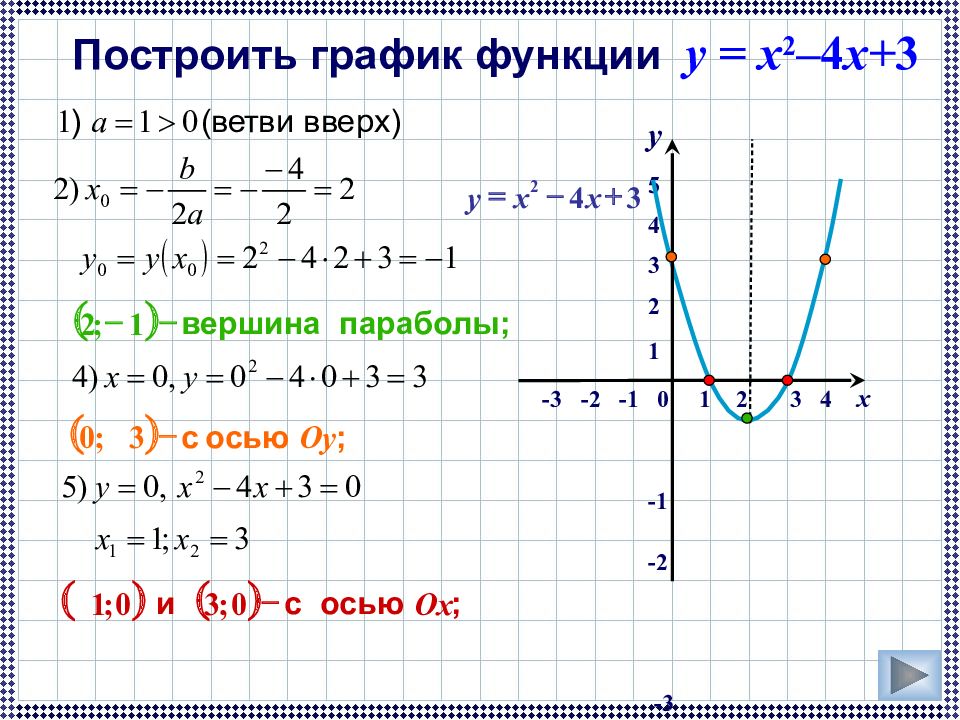 Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.

На интервале (-3;3) строим график линейной функции (прямой) у=-2х.

Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три. 2-2x-3) и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Функция состоит из трех квадратных трехчленов. разложим их на множители по формуле

ax² + bx + c = a(x — x₁)(x — x₂), где х₁ и х₂ — корни квадратных уравнений.

Все три квадратных уравнения приведенные. Это значит, что можно найти их корни по теореме Виета. Именно поэтому я сразу напишу разложения этих трехчленов на множители. Конечно, решать через дискриминант никто не запрещал и ошибкой это не будет.

Итак, после разложения на множители функция примет такой вид:

Видно невооруженным глазом, что скобки из знаменателя сокращаются со скобками из числителя. Это просто супер-пупер! Но надо обязательно оговориться, что знаменатель не может быть равен нулю, а значит, что x ≠ -1 и x ≠ 3. Эти исключения подразумевают выколотые точки на нашем будущем графике.

После сокращения раскрываем оставшиеся скобки.

О, чудо! Это квадратичная функция! График — парабола!

Ищем ее вершину О (m; n).

Первая координата m, которую мы будем отмечать на оси Ох, находится по формуле.

А чтобы найти вторую координату надо m подставить в упрощенную ранее функцию и посчитать.

В общем, вершина параболы имеет координаты (-0,5; -2,25).

Чертим координатную плоскость и отмечаем вершину.

Мастера по рисованию парабол могут ее начертить, не прибегая к таблице по нахождению координат других точек. А вот тем, кто не в очень теплых отношениях с параболами, придется ее рисовать.

Поскольку я мастер — обойдусь без таблицы 🙂

Не забываем про выколотые точки!

В условии задачи сказано, что некоторая прямая y = m должна иметь одну общую точку с параболой. Эта прямая будет параллельна оси Ох и одну общую точку она будет иметь в выколотых точках и вершине параболы.

Ответ: 10; -2; -2,25.

P.S. Бывает так, что график нарисован очень криво.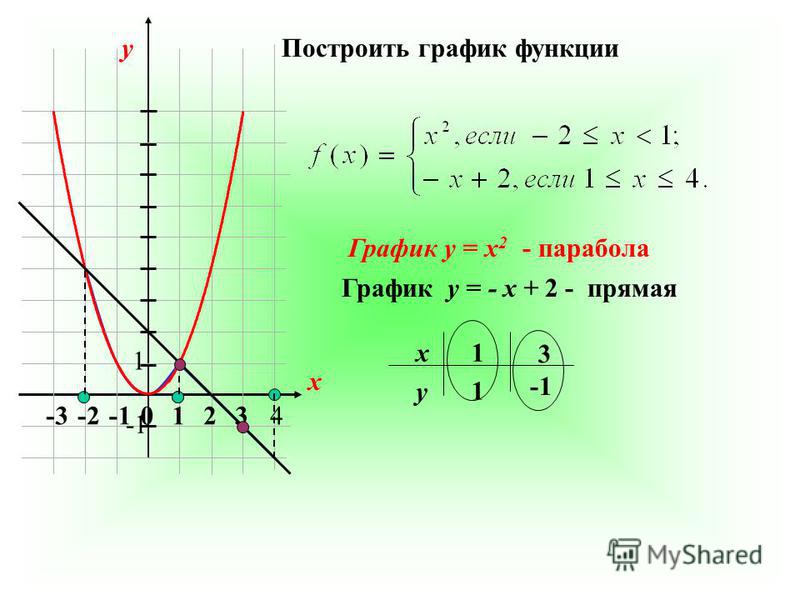 Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).

Постройте график функции y 3x 2 6x. Постройте график функции y=

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.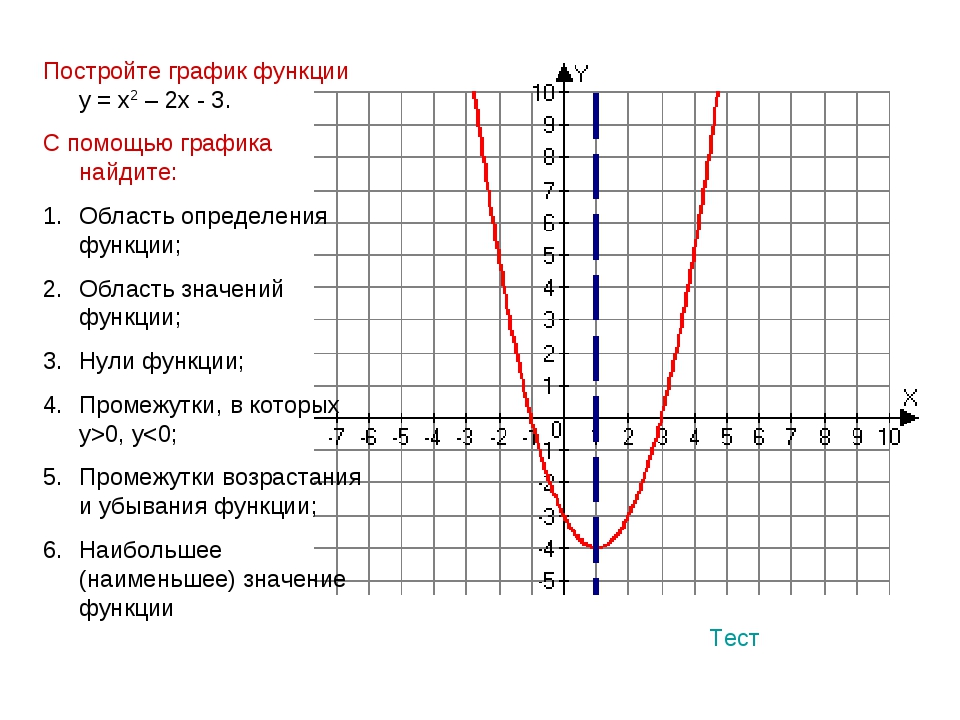

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2
, изображен пунктиром).

2.
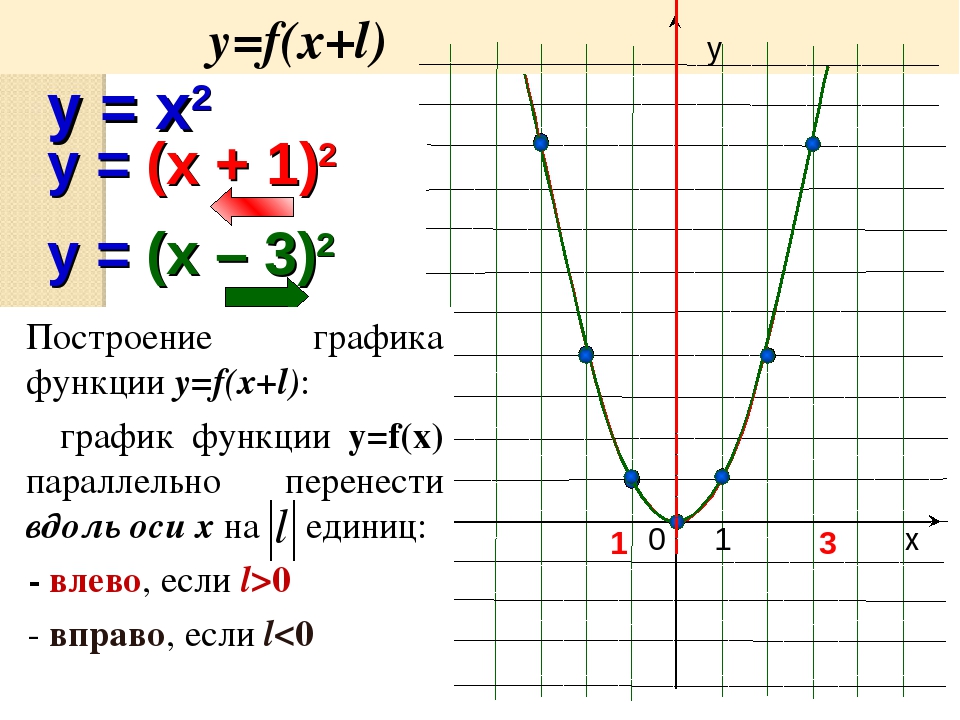
Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1
).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.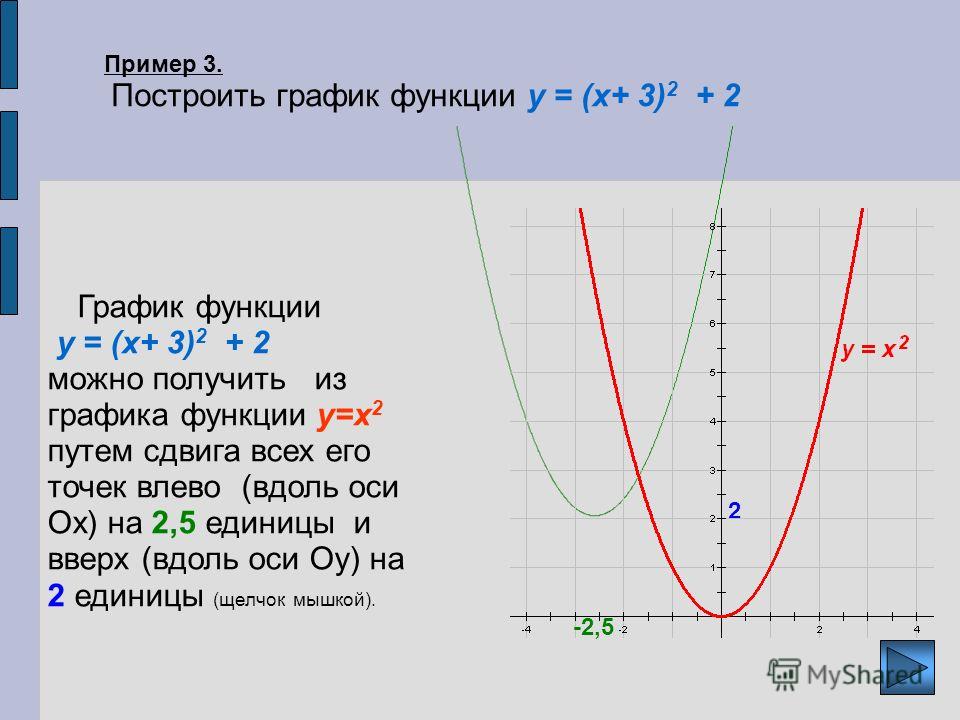

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3)
.

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4)
.

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).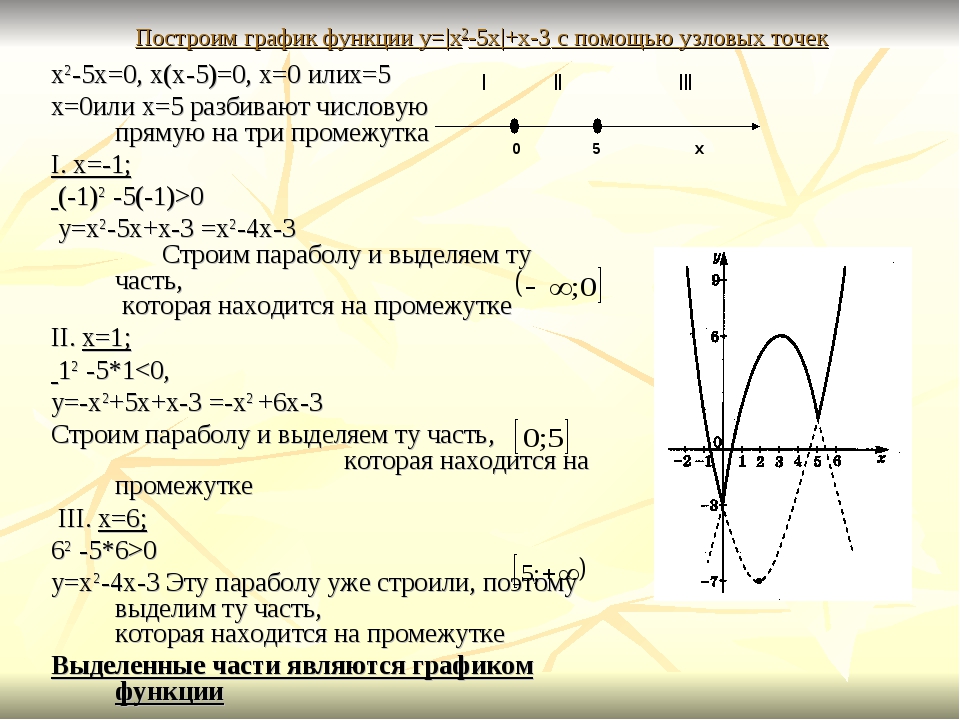

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6)
.

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7)
.

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8)
.

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3).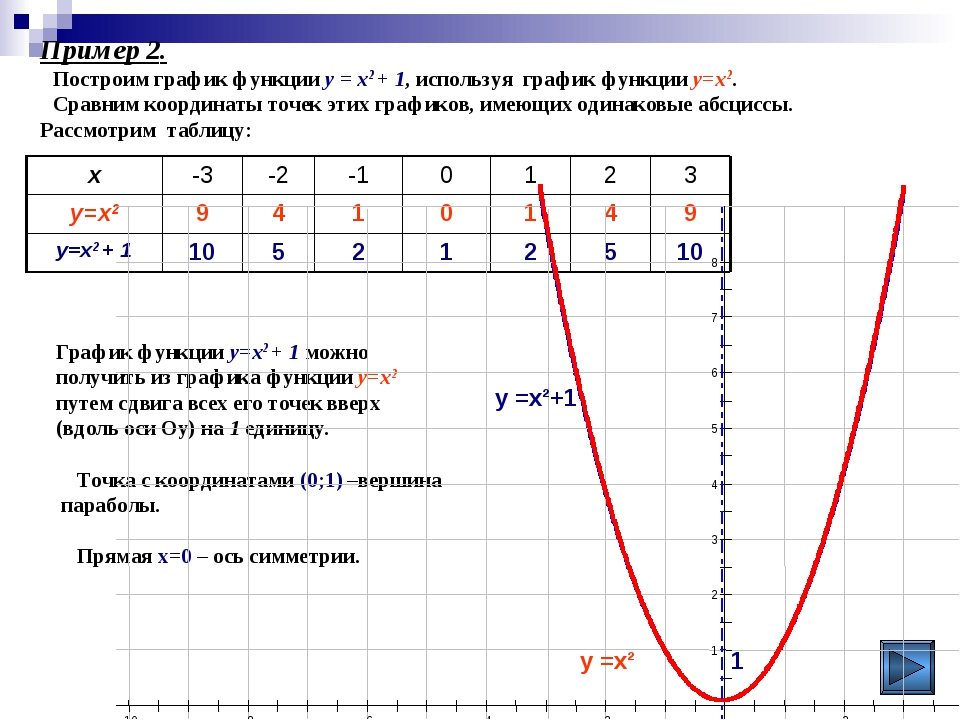 Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9)
.

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11)
.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Разберем как строить график с модулем.

Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞).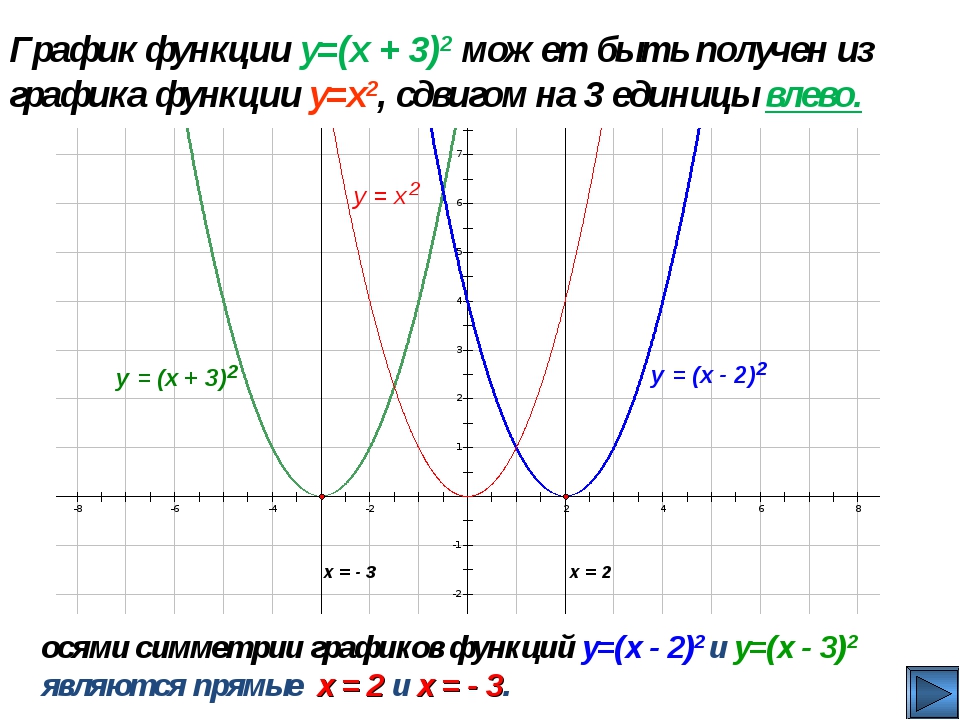 На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=—

(x-3)-(—

(x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=—

(x-3)-(+

(x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+

(x-3)-(+

(x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.

На интервале (-3;3) строим график линейной функции (прямой) у=-2х.

Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.

Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно. Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }

Y 1 3x 2 график. Как построить график функции. Графический способ построения функции

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2
, изображен пунктиром).

2.
Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1
).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3)
.

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4)
.

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).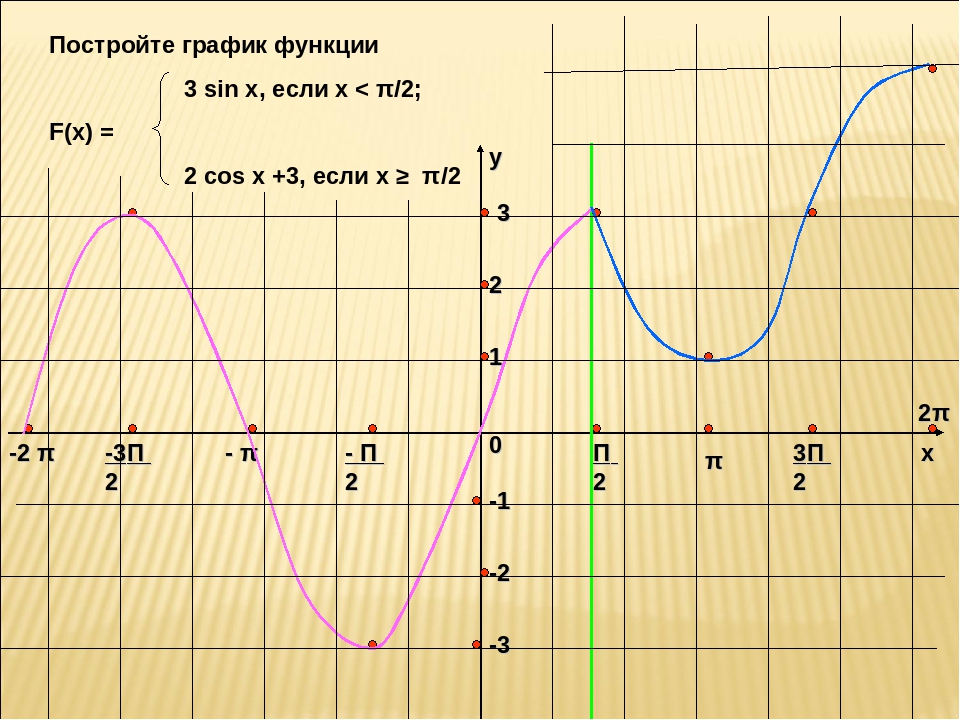

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6)
.

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7)
.

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8)
.

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3).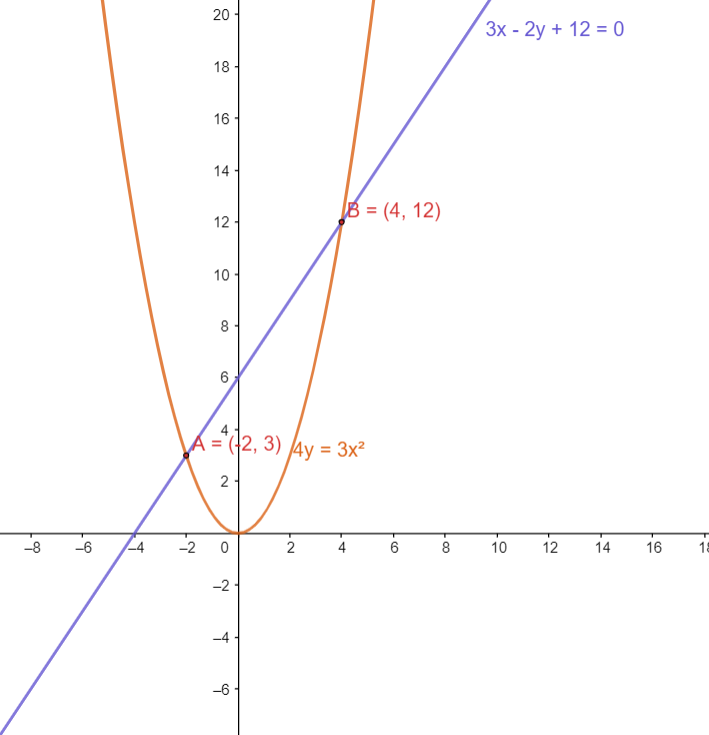 3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.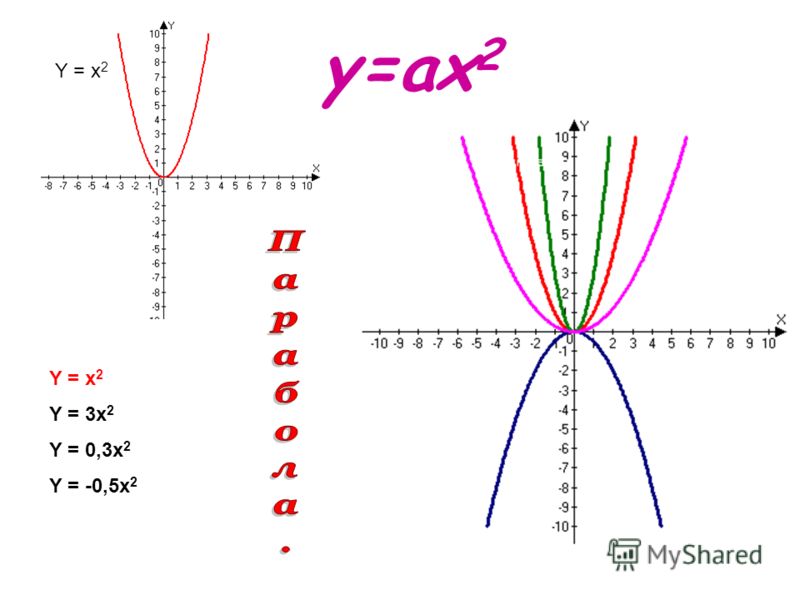

На рисунке мы видим график функции y = x
. Это прямая и у каждой ее точки есть свои координаты на оси X
и на оси Y
. Исходя из определения, если мы подставим координату X
некоторой точки в данное уравнение, то получим координату этой точки на оси Y
.

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график»
   .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить»
   .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:»
   .
4. Нажмите кнопку «Построить»
   .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. 3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

Составим таблицу значений функции

Мы видим, что при (куб положительного числа положителен), а при (куб отрицательного числа отрицателен). Следовательно, график расположится на координатной плоскости в I и III четвертях. Заменим значение аргумента х противоположным значением тогда и функция примет противоположное значение; так как если , то

Значит, каждой точке графика соответствует точка того же графика, расположенная симметрично относительно начала координат.

Таким образом, начало координат является центром симметрии графика.

График функции изображён на чертеже 81. Эта линия называется кубической параболой.

В I четверти кубическая парабола (при ) «круто» поднимается

вверх (значения у «быстро» возрастают при возрастания х. см. таблицу), при малых значениях х линия «тесно» подходит к оси абсцисс (при «малых» значение у «весьма мало», см.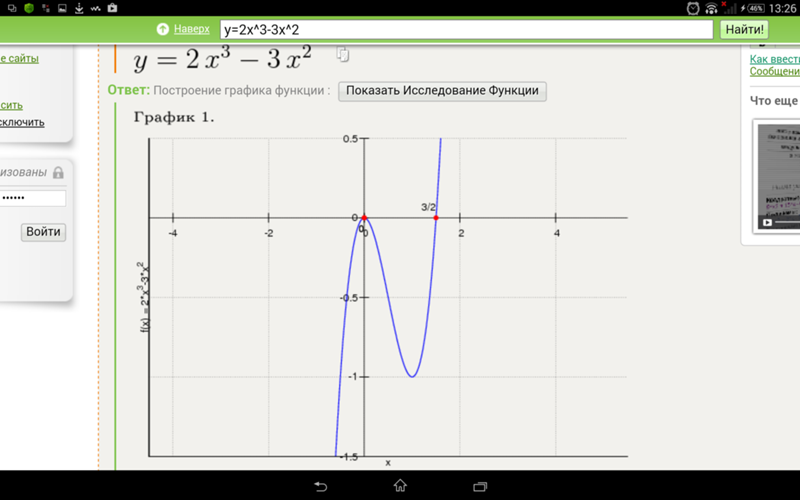 таблицу). Левая часть кубической параболы (в III четверти) симметрична правой относительно начала координат.

Аккуратно вычерченный график может служить средством приближённого возведения чисел в куб. Так, например, положив найдём по графику

Для приближённого вычисления кубов составлены специальные таблицы.

Такая таблица имеется и в пособии В. М. Брадиса «Четырёхзначные математические таблицы».

Эта таблица содержит приближённые значения кубов чисел от 1 до 10, округлённые до 4-х значащих цифр.

Устройство таблицы кубов и правила пользования ею такие же, как и таблицы квадратов. Однако при увеличении (или уменьшении) числа в 10, 100 и т. д. раз его куб увеличивается (или уменьшается) в 1000, 1000 000 и т. д. раз. Значит, при пользовании таблицей кубов надо иметь в виду следующее правило переноса запятой:

Если в числе перенести запятую на несколько цифр, то в кубе этого числа надо перенести запятую в ту же сторону на утроенное количество цифр.

Поясним сказанное примерами:

1) Вычислить 2,2353. По таблице находим: ; прибавляем к последней цифре поправку 8 на последний знак:

2) Вычислить . Так как то находим

По таблице найдем перенеся запятую, получим

Приближённые формулы. Если в тождестве

число а мало по сравнению с единицей, то, отбросив члены с получим приближённые формулы:

По этим формулам легко найти приближённые кубы чисел, близких к единице, например: точный куб: 1,061208;

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2
, изображен пунктиром).

2.
Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см.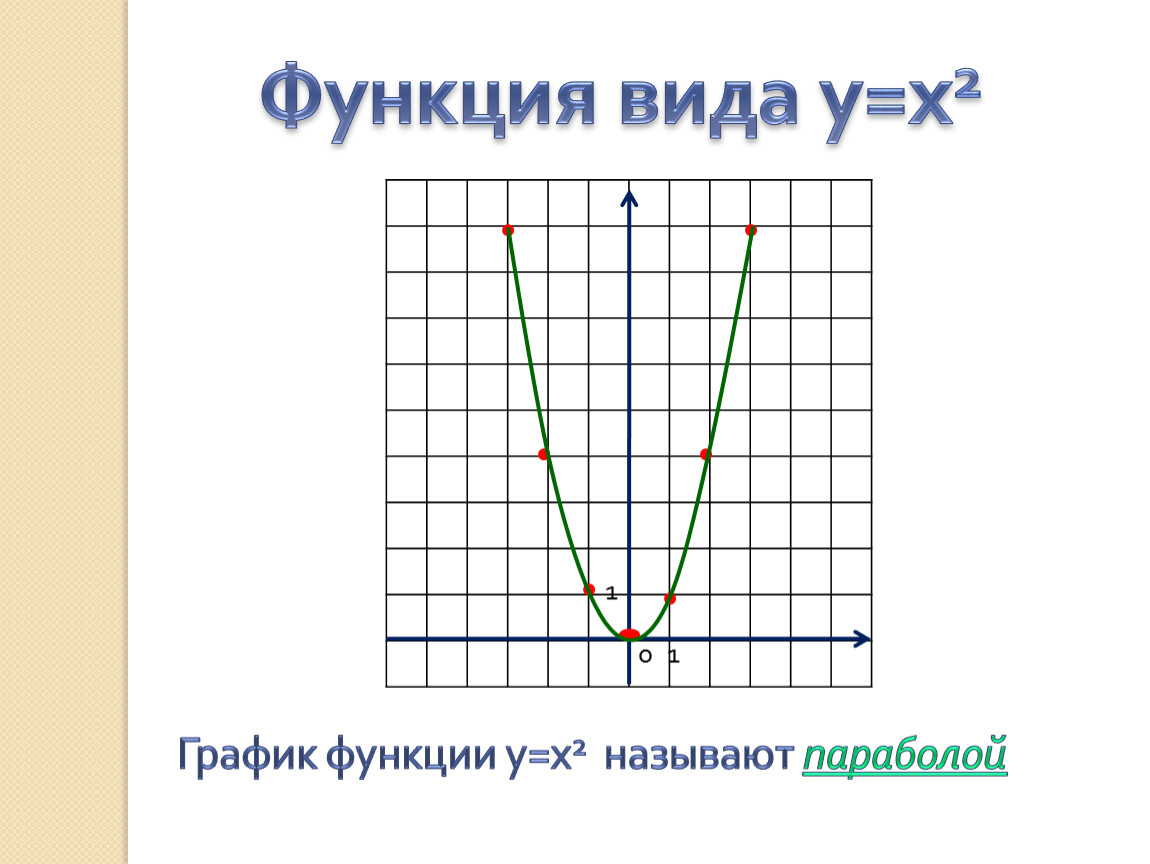 также рис. 1
).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3)
.

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4)
.

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6)
.

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7)
.

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8)
.

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9)
.

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11)
.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Разберем как строить график с модулем.

Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=—

(x-3)-(—

(x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=—

(x-3)-(+

(x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+

(x-3)-(+

(x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.

На интервале (-3;3) строим график линейной функции (прямой) у=-2х.

Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.

Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }

Lighting & Studio 3×2.5m Photography Backdrops Seamless Wedding Floral Photo Backdrops Birthday Party Wedding Background for Photography Purple Flower Wall Photo Booth Background KP-521 Video Studio

Ежегодно количество людей, которые хотят получать стабильный заработок, увеличивается. К ним не относятся миллионеры или депутаты, это обычные люди, которые желают обеспечивать собственную семью и детей. К сожалению, в Украине отсутствует желаемое количество профессий, которые приносили бы достойный заработок. Именно поэтому большинство украинцев ищут работу за границей.

Единственное, что останавливает граждан нашей страны – отсутствие языковых знаний. Люди думают, что за границей везде понадобится иностранный язык. Но это не так проблематично, в современном мире иностранные компании ищут дешевую рабочую силу. В их стране зарплата – минимальная, но если сравнить ее с Киевской, заработной платой в Днепре или других городах Украины, то она — намного выше.

Поиск работы за границей

Если вы все же хотите отправиться на работу за рубеж и найти высокооплачиваемую работу, то рекомендуем вам отнестись к этому вопросу очень внимательно. Вы можете попасть на человека, который не захочет устраивать вас на работу официально. Соответственно, вы можете не получить оплату за собственный труд.

Сейчас существуют мошеннические кадровые агентства, которые привлекают украинцев в организацию, а после того, как человек отработал, забирают его деньги и исчезают.

Именно поэтому, если вы выбираете агентство по трудоустройству, то рекомендуем вам обращать внимание лишь на официальные документы организаций. Те их них, которые имеют все сертификаты, и могут предоставить качественные услуги. Например, компания «BWG» предлагает официальное трудоустройство в Европе. Она соблюдает все правила Трудового законодательства, а также имеет лицензию, выданную Министерством социальной политики Украины. Агентство имеет представительства на территории США, Польши, Чехии и Германии, именно из этих стран поступают актуальные вакансии на работу за границей.

Работа за границей для украинцев без знания иностранного языка

Высокооплачиваемые работы за рубежом требуют хотя бы минимального знания языка, но также можно найти и другие профессии. Чаще всего это работа на лето, и она связана с сельским хозяйством. Сюда входит:

• сбор урожая;
• уборка территории;
• уход за животными и т.д.

Как правило, тут не требуется знание языка, а организации обеспечивают человека жилой площадью. Также изредка встречаются вакансии на различных заводах, сюда могут входить:

1. Мясоперерабатывающая фабрика.
2. Различные промышленности.
3. Работа на заводе.

Такие профессии подходят больше для мужчин, так как они связаны с физической деятельностью, но некоторые заводы примут вас и со 2 половинкой.

Девушки, которые не так хорошо знают иностранный язык, могут стать:

• няней;
• уборщицей;
• парикмахером;
• массажистом;
• поваром и т.д.

Вы сможете пойти на любую работу, если будете обладать минимальным знанием языка.  Если вы все еще обучаетесь в университете и хотите устроиться на работу на лето, то предлагаем вам воспользоваться услугой Work and Travel.

В какую страну поехать

Чтобы определиться с выбором страны, стоит опираться на собственные языковые знания. Если вы обладаете лишь родным языком, то рекомендуем вам рассмотреть страны, в которых больше всего нуждаются в работниках. В ряд таких стран входит Польша, Чехия, Германия и Словакия так как они нуждаются в рабочей силе. Здесь больше всего нуждаются в нянях, уборщицах и сиделках. Именно поэтому, эти страны наиболее подходят для трудоустройства  за рубежом.

В Австралии и Англии не хватает специалистов в сфере медицины, образования, а также инженеров. Если у вас есть диплом, а также вы обладаете минимальными знаниями языка, то не раздумывайте и соглашайтесь на выгодную сделку.

Вы можете выбрать высокооплачиваемую работу в Польше, Чехии, Словакии, Германии и Финляндии, но тут требуется физический труд. Более того, языки – довольно легкие и могут быть понятны вам.

Почему стоит обратиться в фирму «WBG»?

Данное агентство уже длительное время осуществляет помощь при трудоустройстве украинцев за границей и уже успело завоевать сердца клиентов. Наши специалисты помогут не только найти работу за рубежом, но и оформить туристическую, гостевую и даже Шенгенскую визу.

Если вы желаете узнать больше информации о нашей организации, то рекомендуем вам связаться с нами по телефону, указанному на сайте. Наши сотрудники предоставят всю необходимую информацию о работе за рубежом и расскажут о нюансах сотрудничества.

Kitchen & Dining Trevi Fountain fridge magnet 3×2 Rome Italy travel souvenir Kitchen Utensils & Gadgets

Ежегодно количество людей, которые хотят получать стабильный заработок, увеличивается. К ним не относятся миллионеры или депутаты, это обычные люди, которые желают обеспечивать собственную семью и детей. К сожалению, в Украине отсутствует желаемое количество профессий, которые приносили бы достойный заработок. Именно поэтому большинство украинцев ищут работу за границей.

Единственное, что останавливает граждан нашей страны – отсутствие языковых знаний. Люди думают, что за границей везде понадобится иностранный язык. Но это не так проблематично, в современном мире иностранные компании ищут дешевую рабочую силу. В их стране зарплата – минимальная, но если сравнить ее с Киевской, заработной платой в Днепре или других городах Украины, то она — намного выше.

Поиск работы за границей

Если вы все же хотите отправиться на работу за рубеж и найти высокооплачиваемую работу, то рекомендуем вам отнестись к этому вопросу очень внимательно. Вы можете попасть на человека, который не захочет устраивать вас на работу официально. Соответственно, вы можете не получить оплату за собственный труд.

Сейчас существуют мошеннические кадровые агентства, которые привлекают украинцев в организацию, а после того, как человек отработал, забирают его деньги и исчезают.

Именно поэтому, если вы выбираете агентство по трудоустройству, то рекомендуем вам обращать внимание лишь на официальные документы организаций. Те их них, которые имеют все сертификаты, и могут предоставить качественные услуги. Например, компания «BWG» предлагает официальное трудоустройство в Европе. Она соблюдает все правила Трудового законодательства, а также имеет лицензию, выданную Министерством социальной политики Украины. Агентство имеет представительства на территории США, Польши, Чехии и Германии, именно из этих стран поступают актуальные вакансии на работу за границей.

Работа за границей для украинцев без знания иностранного языка

Высокооплачиваемые работы за рубежом требуют хотя бы минимального знания языка, но также можно найти и другие профессии. Чаще всего это работа на лето, и она связана с сельским хозяйством. Сюда входит:

• сбор урожая;
• уборка территории;
• уход за животными и т.д.

Как правило, тут не требуется знание языка, а организации обеспечивают человека жилой площадью. Также изредка встречаются вакансии на различных заводах, сюда могут входить:

1. Мясоперерабатывающая фабрика.
2. Различные промышленности.
3. Работа на заводе.

Такие профессии подходят больше для мужчин, так как они связаны с физической деятельностью, но некоторые заводы примут вас и со 2 половинкой.

Девушки, которые не так хорошо знают иностранный язык, могут стать:

• няней;
• уборщицей;
• парикмахером;
• массажистом;
• поваром и т.д.

Вы сможете пойти на любую работу, если будете обладать минимальным знанием языка.  Если вы все еще обучаетесь в университете и хотите устроиться на работу на лето, то предлагаем вам воспользоваться услугой Work and Travel.

В какую страну поехать

Чтобы определиться с выбором страны, стоит опираться на собственные языковые знания. Если вы обладаете лишь родным языком, то рекомендуем вам рассмотреть страны, в которых больше всего нуждаются в работниках. В ряд таких стран входит Польша, Чехия, Германия и Словакия так как они нуждаются в рабочей силе. Здесь больше всего нуждаются в нянях, уборщицах и сиделках. Именно поэтому, эти страны наиболее подходят для трудоустройства  за рубежом.

В Австралии и Англии не хватает специалистов в сфере медицины, образования, а также инженеров. Если у вас есть диплом, а также вы обладаете минимальными знаниями языка, то не раздумывайте и соглашайтесь на выгодную сделку.

Вы можете выбрать высокооплачиваемую работу в Польше, Чехии, Словакии, Германии и Финляндии, но тут требуется физический труд. Более того, языки – довольно легкие и могут быть понятны вам.

Почему стоит обратиться в фирму «WBG»?

Данное агентство уже длительное время осуществляет помощь при трудоустройстве украинцев за границей и уже успело завоевать сердца клиентов. Наши специалисты помогут не только найти работу за рубежом, но и оформить туристическую, гостевую и даже Шенгенскую визу.

Если вы желаете узнать больше информации о нашей организации, то рекомендуем вам связаться с нами по телефону, указанному на сайте. Наши сотрудники предоставят всю необходимую информацию о работе за рубежом и расскажут о нюансах сотрудничества.

Графические уравнения и системы уравнений с пошаговым решением математических задач

ВВЕДЕНИЕ В КВАДРАТИКУ

Цели

В этом разделе вы будете складывать, вычитать, умножать и строить графики квадратов.

Словарь : Стандартный формат квадратного уравнения : y = ax ² + bx + c ; a, b, c — постоянные; x — независимая переменная, а y — зависимая переменная. Квадраты также называются полиномами второй степени , потому что наивысший показатель степени равен 2.Уравнение углового пересечения из второй главы y = mx + b называется полиномом первой степени , потому что наивысший показатель степени равен единице.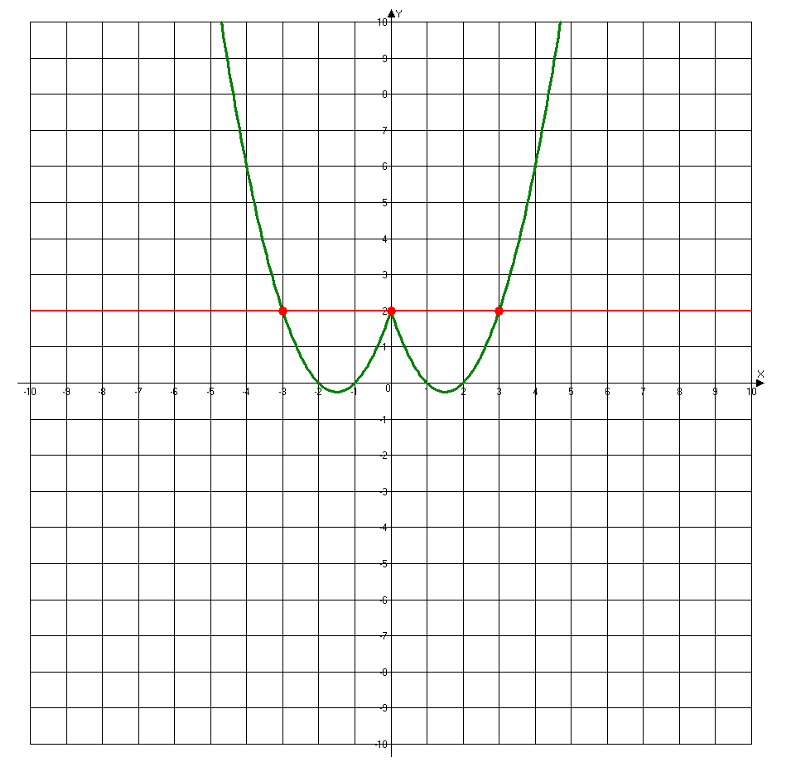

Зачем изучать квадратичность? Графики квадратных уравнений приводят к параболам (U-образные графики, открывающиеся вверх или вниз). Эта особенность квадратичности делает их хорошими моделями для описания пути объекта в воздухе или описания прибыли компании (примеры чего вы можете увидеть в конечной математике или микроэкономике.)

Пример 1. Мальчик, лежащий на спине, выстрелом из пращи выстрелил в воздух камнем с начальной скоростью (силой, которую мальчик использует для выстрела камня) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно

.

ч = -16т ² + 64т.

а. Найдите высоту камня при t = 0.

В формуле h = -16t ² + 64t, заменить t на 0.

h = -16 (0) ² +64 (0)
h = 0

Камень находится на нулевом уровне в воздухе за 0 секунд.(Это момент прямо перед тем, как он стреляет камнем в воздух.)

г. Найдите высоту камня при t = 1.

В формуле h = -16t ² + 64t, заменить t на 1.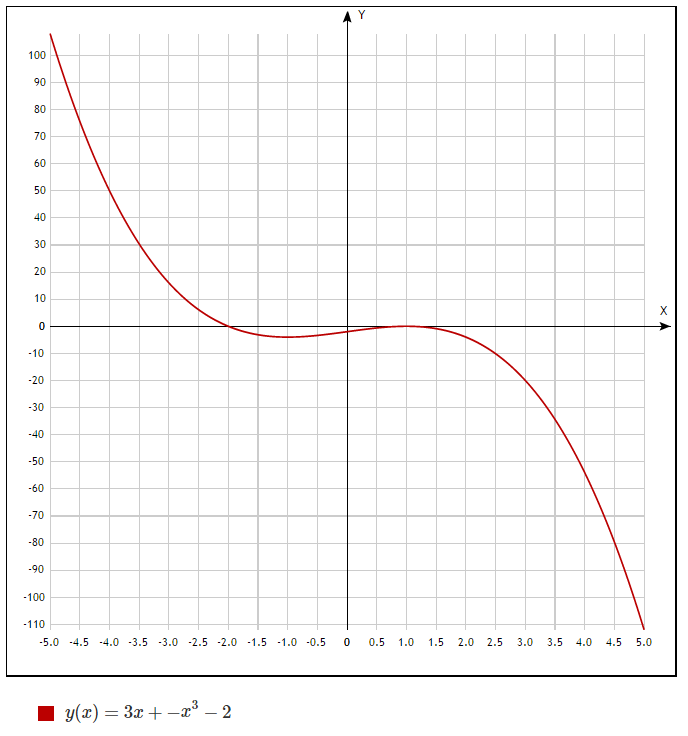

Камень поднимается на высоту 48 футов за одну секунду.

Объяснение : Возводится в квадрат только «1». -16 умножается на 1 ²

г. Найдите высоту камня при t = 2.

В формуле h = -16t ² + 64t заменить t на 2.

Камень находится на высоте 64 фута за 2 секунды.

Объяснение : Порядок операций требует применения экспонент перед умножением.

г. Найдите высоту камня при t = 3.

В формуле h = -16t ² + 64t, заменить t на 3.

Камень находится на высоте 48 футов за 3 секунды.

e. Найдите высоту камня при t = 4.

В формуле h = -16t ² + 64t заменить t на 4.

Камень находится на нулевом уровне в воздухе за 4 секунды; то есть камень ударился о землю.

ф. Постройте график точек, полученных в частях от a до e.

Высота камня зависит от времени, поэтому h — зависимая переменная, а t — независимая переменная.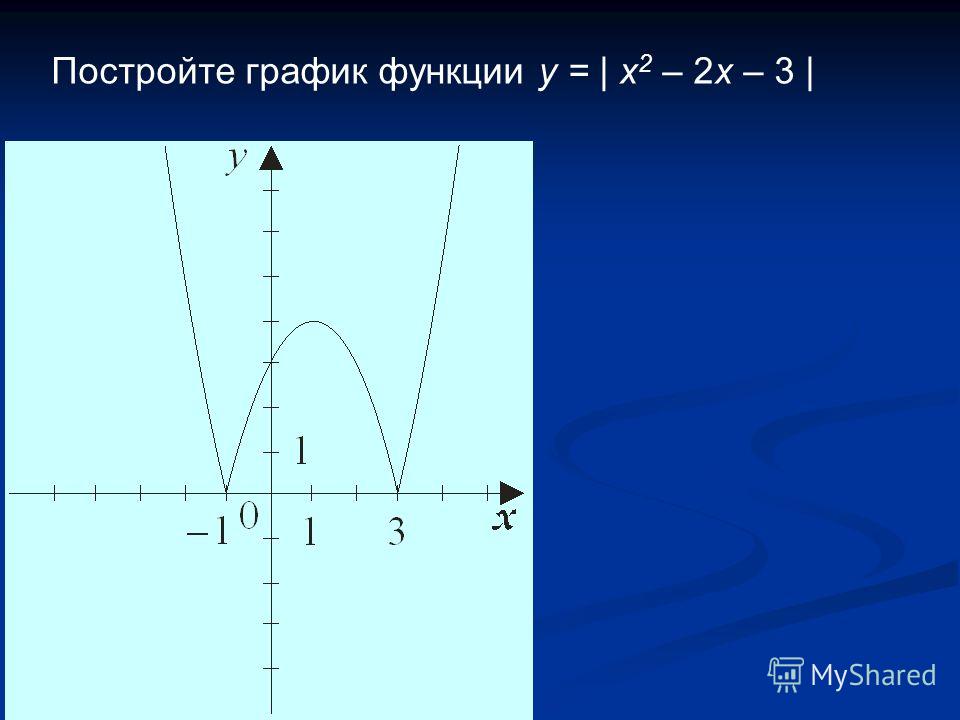 Точки имеют вид (t, h).

Согласно графику, скала достигает максимальной высоты за 2 секунды. Максимальная высота — 64 фута. Точка максимума или минимума квадратичной называется вершиной.Вы узнаете, как найти вершину в Разделе 4.3, Квадратичные приложения и графики.

Согласно графику, камень оказывается на земле в 0 секунд (прямо перед тем, как мальчик стреляет в него) и в 4 секунды (когда камень приземляется). Эти точки являются отсечками времени. Вы узнаете, как их найти, в следующем разделе 4.2, «Приложения квадратичной формулы».

Сложение и вычитание квадратичных:

Словарь : Чтобы добавить или вычесть квадратичные, объедините одинаковые термины. Подобные термины , первоначально представленные в разделе 1.3, «Упрощение алгебраических выражений», имеют одинаковую переменную и одинаковый показатель степени. Например, 2x ² и 5x ² являются подобными терминами, а 3x ² и 7x — нет.

Коэффициент , первоначально представленный в Разделе 1.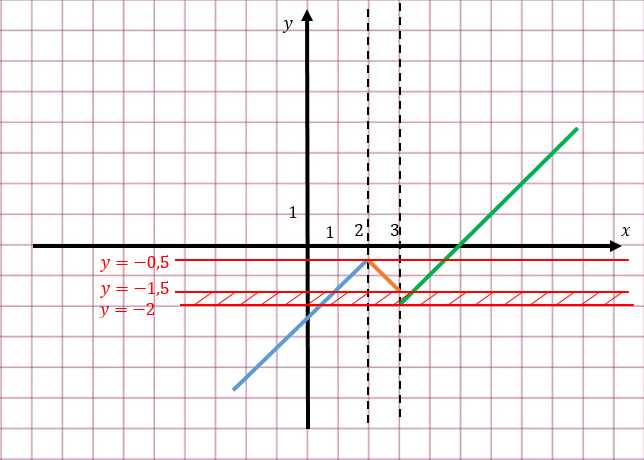 3, «Упрощение алгебраических выражений», является числом, умножающим переменную. Например, коэффициент 2x равен 2, а коэффициент -x ² равен -1.

Правило: Чтобы объединить одинаковые термины, сложите их коэффициенты

Вспомните распределительное свойство : определение a (b + c) = ab + ac.

Не удалось объединить непохожие термины в скобках, поэтому мы использовали свойство распределения. После этого мы умножили 6x на 3, а затем -5 на 3.

Использовали свойство распределения и объединили похожие термины.

Пример 5. Уравнение прибыли: Прибыль = Выручка — Затраты

Если уравнение дохода компании:

, а уравнение затрат:

найти уравнение прибыли для компании.

Подставил уравнения доходов и затрат в формулу для расчета прибыли. Необходимо использовать скобки.

Использовал свойство распределения и умножил уравнение доходов на 1 и уравнение затрат на -1.

Комбинированные одинаковые термины.

Подставил уравнения доходов и затрат в формулу прибыли. Необходимо использовать круглые скобки. Использовал распределительное свойство.
Умножил уравнение доходов на 1 и уравнение затрат на -1. Сочетание подобных терминов.

Умножение двух биномов.

Словарь : У бинома есть два члена (точно так же, как у велосипеда есть два колеса).

Правило: Чтобы умножить два бинома, умножьте каждый член первого члена на каждый член второго.

Пример 7. Умножаем (x + 2) (5x + 3).

Умножить x на 5x и 3 и умножить 2 на 5x и 3.

Объединить похожие термины.

FOIL — это простая мнемоника, чтобы запомнить, как умножить два бинома.

Пример 8.Умножьте (8x + 6) (x + 7).

Совет для изучения: Напишите карточку с объяснением мнемонической ФОЛЬГИ. Часто просматривайте карту.

Сводка

Квадраты — важные уравнения в физике и микроэкономике. Техника сложения и вычитания квадратиков такая же, как и мы практикуем весь семестр; то есть складывать или вычитать похожие термины. Для умножения используйте свойство распределения или FOIL. Вершина квадратичного будет объяснена более подробно в разделе «Графики квадратичной графики и приложения».«Вершина — это точка максимума или минимума на квадратичном графике.

ПРИМЕНЕНИЕ КВАДРАТИЧЕСКОЙ ФОРМУЛЫ

Цель

В этом разделе показано, как решать квадратные уравнения.

Словарь : квадратное уравнение — это ax ² + bx + c = 0. a, b и c — константы, а x — переменная.

Квадратичная формула ,, используется для решения квадратного уравнения.

Анализируем

Учебный совет: Напишите квадратное уравнение и квадратную формулу на карточках для заметок, чтобы вы могли ссылаться на них при выполнении домашнего задания.

Пример 1. Предположим, вы стоите на вершине утеса на высоте 375 футов над дном каньона и подбрасываете в воздух камень с начальной скоростью 82 фута в секунду. Уравнение, моделирующее высоту скалы над дном каньона:

ч = -16т ² + 82т + 375.

Узнайте, сколько времени требуется камню, чтобы упасть на дно каньона.

Найдите t, когда h = 0.
Решите 0 = -16t ² + 82t + 375.
Определите константы a, b и c.

Объяснение : Одна часть квадратного уравнения должна быть равна нулю.

a = -16, b = 82, c = 375

Пояснение :
a — коэффициент переменной, возведенный в квадрат.
b — коэффициент переменной в первой степени.
c — постоянная.

Используйте формулу корней квадратного уравнения

с a = -16, b = 82 и c = 375.

T = -2,916 — бессмысленный ответ, поскольку t — это время, за которое камень ударится о дно каньона, и время не может быть отрицательным.

T = 8,041 секунды — это время, за которое камень ударится о дно каньона.

Камень ударится о дно каньона за 8,041 секунды.

Пример 2. У владельца ранчо есть 500 ярдов ограждения, чтобы ограждать два соседних загона для свиней, которые упираются в сарай. Если площадь двух ручек должна составлять 20 700 квадратных ярдов, каковы должны быть размеры ручек?

L — длина обоих ручек.

а. Воспользуйтесь таблицей, чтобы найти уравнение для площади ручек.

г. Упростите уравнение для площади.

г. Найдите W, когда A = 20700.

Ширина 76,67 или 90 ярдов.

г. Найдите длину ручек.

Из таблицы в Части a, L = 500 — 3W. Подставляем W = 76,67 и W = 90 в уравнение для длины, L = 500 — 3w.

Размеры загона для свиней, площадь которого составляет 20 700 квадратных ярдов, составляют 76,67 на 270 ярдов и 90 на 230 ярдов.

Пример 3. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,

T = 0,26 м ² -4,1 м + 7,9

, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент. Определите, когда температура кислорода составляет 0 градусов Цельсия.

Задача просит вас найти m при T = 0.

Температура кислорода будет 0 градусов Цельсия через 2.246 минут 13,52 минуты.

Совет для исследования: Ключевая идея, продемонстрированная в примере 3, заключается в том, как обрабатывать отрицательное b в квадратном уравнении.

Сводка

В этом разделе показано, как решить новый тип уравнения — квадратное. У них есть важные приложения во многих областях, таких как бизнес, физика и инженерия. Учить
разница между квадратным уравнением и квадратной формулой.

Квадратное уравнение: ax ² + bx + c = 0.

• Одна часть уравнения должна быть равна нулю.
• a — коэффициент при x.
• b — коэффициент при x.
• c — постоянный член.

Квадратичная формула решает квадратное уравнение.

• Формула дает два решения.
• Калькулятор используется для поиска ответов.
• Первым шагом в вычислении формулы является упрощение квадратного корня.

КВАДРАТИЧЕСКИЕ ПРИЛОЖЕНИЯ И ГРАФИКИ

Цели

В этом разделе исследуются дополнительные ключевые точки квадратичного графика, вершины и пересечений.Эти пункты будут интерпретированы в приложениях.

Пример 1. Мальчик, лежащий на спине, выстрелом из пращи выстрелил камнем в воздух с начальной скоростью (силой, которую мальчик использует, чтобы выстрелить в камень) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно

.

ч = -16т ² + 64т.

(Этот пример взят из Раздела 4.1 «Введение в квадратику», стр. 317.)

На странице 318 мы сгенерировали следующие значения:

Мы использовали точки, чтобы получить график ниже.Вершина и пересечения также отмечены на графике.

Объяснение : Точка (0, 0) — это время и высота пересечения.

Вершина , (2,64) представляет максимальную высоту скалы.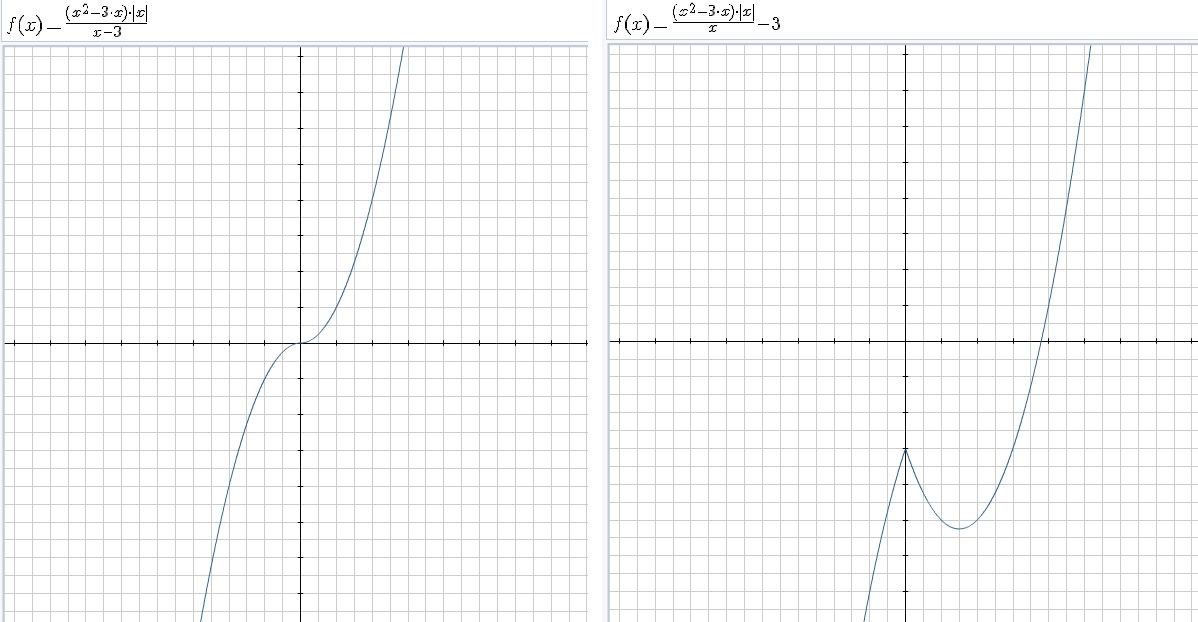 Скала достигает максимальной высоты 64 фута за 2 секунды.

Временные точки , (0, 0) и (4, 0) представляют, когда камень находится на земле. Камень оказывается на земле за 0 секунд до выстрела (это Высота Intercept ) и через 4 секунды, когда он возвращается на землю.

Чтобы построить квадратичный график, указанный уравнением, y = ax ² + bx + c, усвойте следующие термины:

Словарь : Вершина: Вершина — это максимальная или минимальная точка на графике. Чтобы найти вершину:

а. Найдите координату x:
b. Найдите координату y: подставьте значение x, полученное в части a, в формулу y = ax ² + bx + c.

X intercept : установите y = 0 и решите 0 = ax ² + bx + c, используя формулу корней квадратного уравнения,

Пересечение Y : установите x = 0 и найдите y.y всегда будет c, константой.

Учебный совет: Напишите процедуру и определения на трех карточках для удобного использования.

Пример 2. Компания D +++ производит компьютерные игры. Стоимость создания игр g в месяц составляет C = 0,4g ² — 32g + 625. Выручка от продажи игр g в месяц составляет R = -0,6g ² + 52g. Единицы измерения g — сотни, C и R — тысячи долларов.

а. Найдите уравнение прибыли.

г.Найдите вершину и объясните, что эта вершина означает с точки зрения создания компьютерных игр.

Формула для координаты g:

Из уравнения прибыли a = -1, b = 84.

Вершина (42,1139). Если D +++ продаст 4200 игр, то они получат максимальную прибыль в размере 1 139 000 долларов США.

г. Найдите g перехватывает и объясните, что они означают с точки зрения создания компьютерных игр.

Чтобы найти точку пересечения g, установите P = 0.

Решить 0 = -g ² + 84g — 625.

Используйте формулу корней квадратного уравнения, a = -1, b = 84, c = -625.

Перехваты g: (8. 251, 0) и (75.75, 0).

Если они продадут 825 или 7 575 игр, они выйдут на уровень безубыточности.

г. Найдите P перехватчики и объясните, что они означают с точки зрения создания компьютерных игр.

Чтобы найти точку пересечения с P, установите g = 0.
P = -0 ² + 84 * 0-625
P = -625
Перехват по оси P равен (0, -625).
Стартовые затраты компании составляют 625 000 долларов.

e. Постройте график функции.

Постройте точки:
Вершина. (42, 1139).
Данный перехватывает. (8,251, 0) и (75,75, 0).
Перехват P. (0, -625).

Объяснение : Одно из объяснений того, что прибыль имеет две точки безубыточности, заключается в том, насколько эффективно компания производит продукт. Изготовление очень небольшого количества предметов обычно неэффективно. В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много предметов, компания становится неэффективной в производстве своей продукции.

Помните, что единицы измерения g — сотни, а единицы P — тысячи.

Предположим, D +++ должен получать прибыль в размере 500 000 долларов (P = 500) в месяц. Нарисуйте эту линию на графике, полученном в Части b, и найдите, где линия пересекает график квадратичного. Напишите предложение, объясняющее, что означают ответы.

Эскиз P = 500 на предыдущем графике.

P = 500 — горизонтальная линия.

Если D +++ хочет получить прибыль в размере 500 000 долларов, им необходимо сделать и продать 1 672 или 6 728 игр.

Объяснение : График дает оценку того, где пересекаются горизонтальная линия P = 500 и уравнение прибыли P = -g ² + 84g-625. Алгебра дает точную точку их пересечения.

г. Используя график и ответы к Части c, определите, сколько компьютерных игр необходимо сделать и продать, чтобы гарантировать прибыль более 500 000 долларов.

Компания получит прибыль более 500 000 долларов, если график прибыли находится выше горизонтальной линии P = 500.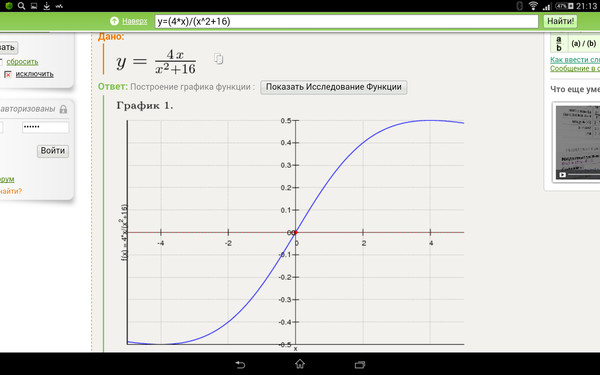 Эта проблема аналогична примеру 2d на стр. 203 в Разделе 2.9 «Приложения графиков».

Это происходит между точками g = 16,72 и g = 67,28 или

.

16,72

Компания заработает более 500 000 долларов, если будет производить и продавать от 1 672 до 6 728 компьютерных игр.

Пример 3. Оператор питомника хочет поставить три соседние загоны для собак одинакового размера у стены. У него 96 метров забора.

а. Найдите формулу для площади.

Объяснение : Самая трудная часть таблицы — найти значение длины.Если фермер использует 10 метров для ширины загона, а есть 4 ширины, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений осталось на эту длину, вычтите 40 из 96 — общего количества ограждений, доступных фермеру.

Формула площади загона для собак:

г. Найдите вершину и объясните, что это означает с точки зрения загонов для собак.

Формула для координаты W:

Из уравнения прибыли a = -4, b = 96.

Вершина равна (12, 576).

Вершина , (12, 576) представляет максимальную площадь трех загонов для собак. Когда W = 12, максимальная площадь будет 576. (Длина всех трех загонов будет 48 или длина одного загона для собак будет 16.) Будет три загона для собак, каждая размером 12 на 16 метров.

г. Найдите W перехватывает и объясните, что они означают в терминах загонов для собак.

Чтобы найти точку пересечения с W, установите A = 0.

Решить 0 = -4 Вт ² + 96 Вт.

Используйте формулу корней квадратного уравнения, a = -4, b = 96, c = 0.

W-точки перехвата: (0, 0) и (24, 0).

Перемычки W, (0, 0) и (24, 0) представляют ширину загонов для собак, которые дадут нулевую площадь.

г. Найдите точку перехвата A и объясните, что это означает с точки зрения загонов для собак.

Чтобы найти точку пересечения A, установите W = 0.

Объяснение : Если ширина прямоугольника равна нулю, то площадь должна быть равна нулю.

Перехватчик A равен (0, 0).

Перехватчик A, (0, 0) — это область, когда W = 0.

e. Изобразите уравнение

Постройте точки:
Вершина. (12, 576).
W перехватывает. (0, 0) и (24, 0).
Перехват. (0, 0).

ф. Предположим, общая площадь должна быть 400 квадратных метров. На графике A = 400 найдите размеры загонов для собак.

Эскиз A = 400 на предыдущем графике.

A = 400 — горизонтальная линия.

Поскольку W, ширина, известна, длину L можно определить по формуле A = LW.

Решите относительно L, разделив обе части на W.

Размеры загонов для собак, которые дадут площадь 400 квадратных метров, составляют 5,367 на 74,53 и 18,63 на 21,47.

Пример 4. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,

Т = 0.26 м ² -4,1 м + 7,9

, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент. Постройте уравнение, найдя вершину и точки пересечения. Обозначьте эти точки на графике и объясните, что означают вершина и пересечения с точки зрения модели.

Вернуться назад: Это та же модель, что использовалась в примере 3 на стр. 332. Этот пример работал при нулевой температуре.

Найдите вершину из T = 0.26 м ² — 4,1 м + 7,9.

Формула для координаты m вершины:

Вершина равна (7,885, -8,263).

Найдите точки пересечения м T = 0,26 м ² -4,1 м + 7,9

Чтобы найти точки пересечения m, установите T = 0.

Решить 0 = 0,26 м ² -4,1 м + 7,9.

Используйте формулу корней квадратного уравнения, a = 0,26, b = -4,1, c = 7,9.

M точек пересечения (13.52, 0) и (2.246, 0).

Найдите точки пересечения T T = 0,26 м ² — 4,1 м + 7,9

Чтобы найти точку пересечения с Т, установите m = 0.

Т-образная точка пересечения (0, 7.9).

Vertex: Минимальная температура составляет 7,885 минут. Минимальная температура составит -8,263 градуса по Цельсию.

м пересекает: Температура будет ноль градусов Цельсия на отметках 2.246 и 13.52 мин.

T intercept: Температура в начале эксперимента составляла 7,9 градусов Цельсия.

Подсказки: Квадраты представляют собой U-образные графики. В некоторых случаях они имеют U-образную форму, как в примере выше, или форму, как в примерах с 1 по 3. Если a в уравнении, y = ax ² + bx + c, положительно, тогда график имеет U-образную форму, что есть, открываясь. Если a отрицательно, график имеет форму, то есть раскрывается вниз. Этот факт следует записать на карточке для заметок.

Сводка

Графики квадратиков появляются по таким разнообразным предметам, как микроэкономика и физика. В этом разделе кратко излагаются основные идеи устройства.

Чтобы построить квадратичный график y = ax ² + bx + c, вы должны найти:

• Вершина .
  Формула для координаты x:

  Чтобы найти координату y, подставьте свой ответ вместо координаты x в уравнение y = ax ² + bx + c.

• x перехватывает .Установите y = 0 и решите уравнение 0 = ax ² + bx + c, используя формулу корней квадратного уравнения

.

• Перехватчик y .
  Установите x = 0 в уравнении, y = ax ² + bx + c, и найдите y. Обратите внимание, когда x = 0, y = c.
• Если a отрицательное , график обычно выглядит так:
• Если a положительное значение , обычно график выглядит следующим образом:

ФАКТОРИНГ

Цели

Факторинг — это алгебраический метод, используемый для разделения выражения на составные части.Когда составные части перемножаются, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг — важный навык в MAT 100, Intermediate Algebra.

Словарь : алгебраическое выражение учитывается, если последней операцией при вычислении выражения является умножение.

Пример 1. Какое выражение подвергается факторизации , x ² — 5x — 24 или (x — 8) (x + 3)?

Выберите значение x и подставьте его в выражение.

Пусть x = 3.

Поскольку последней операцией для (x — 8) (x + 3) было умножение, то факторизуется (x — 8) (x + 3).

Объяснение : Менее формально, алгебраическое выражение факторизуется, если оно заключено в круглые скобки.

Словарь : Распределительное свойство — это a (b + c) = ab + ac. Левая часть подвергается факторизации, и a является общим множителем.

У вас должна быть возможность проверить с помощью свойства distributive.

Объяснение : Хотя 8x ³ + 4x равно как 2x (4x ² + 2), так и 4 (2x ³ + x), ни один из них не считается полностью разложенным, потому что в обоих случаях общее кратное 2, в 2x (4x ² +2) и x в 4 (2x ³ + x) по-прежнему могут быть факторизованы из членов в скобках.

Факторинг трехчленов: (Трехчлен состоит из трех членов.) Чтобы разложить на множители трехчлены, вспомните аббревиатуру FOIL.

Совет для изучения: Проверьте свои карточки для заметок на предмет определения ФОЛЬГИ.

Пример 4. Умножаем (x + 3) (x + 5).

(x + 3) (x + 5) учитывается, а x ² + 8x +15 — нет. Чтобы разложить на множители трехчлены, вам нужно знать, как были вычислены 8x и 15. 8x произошло от сложения 5x и 3x, а 15 — от умножения 5 и 3.

Пример 5. Множитель x ² + 8x +15. (Это из Примера 4.)

Нам нужны два числа, которые при сложении равны 8, а при умножении равны 15. 3 и 5 в сумме дают 8, а при умножении — 15.

Таким образом, x ² + 8x +15 = (x + 3) (x + 5)

Пример 6. Коэффициент x ² -4x- 12.

Нам нужны два числа, которые при сложении равны -4, а при умножении равны -12. -6 и 2 в сумме дают -4, а при умножении -12.

Итак, x ² -4x -12 = (x-6) (x + 2).

Пример 7. Коэффициент x ² — 64.

Это не трехчлен, но он может стать одним, добавив 0x.

x ² -64 = x ² + 0x -64

Нам нужны два числа, которые при сложении равны 0, а при умножении равны -64.

-8 и 8 складываются в 0, а при умножении получается -64.

Итак, x ² -64 = (x-8) (x + 8).

Этот пример называется факторизацией разности полных квадратов, и вы снова увидите это, если возьмете MAT 100, промежуточную алгебру.

Словарь : a ² — b ² — это разность полных квадратов .
Разность полных квадратов имеет специальную формулу факторизации: a ² — b ² = (a — b) (a + b)

Решение квадратных уравнений с помощью факторинга:

Если вы умножаете две величины и результат равен нулю, то вы знаете, что одна из величин должна быть равна нулю.В математической записи

, если a.b = 0, то a = 0 или b = 0.

Прежде чем вы подумаете, что разложение на множители для решения квадратичных уравнений намного проще, чем использование формулы квадратов, вы должны знать, что разложение на множители не всегда работает. Рассмотрите возможность изменения примера 8 всего на единицу до x ² — 11x + 31 = 0. Вы не можете найти два целых числа, которые при сложении равны -11, а при умножении равны 31. Чтобы множить x ² — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как разложить на множители любое квадратное уравнение в Precalculus I, MAT 161.

Сводка

В этом модуле представлены два метода факторинга. Первый — это общие факторы, использующие свойство распределения, ab + ac = a (b + c). Другой — факторизация трехчленов. Чтобы разложить на множители трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, промежуточную алгебру, вы увидите больше факторинга.

ОБЗОР ГЛАВЫ 4

Эта глава познакомила вас с квадратиками. Две основные темы — это квадратичная формула и квадратичные графики.Эти темы имеют множество приложений в бизнесе, физике и геометрии. Факторинг — важная тема в MAT 100, Intermediate Algebra.

Раздел 4.1: Введение в квадратичность

Раздел 4.2: Приложения квадратичной формулы

Определение: ax ² + bx + c = 0 — квадратное уравнение.

Определение: квадратная формула.

Пример 4. Фермер хочет ограждать два соседних курятника напротив сарая.У него 125 футов забора. Какие должны быть размеры, если он хочет, чтобы общая площадь составляла 700 квадратных футов.

а. Заполните таблицу, чтобы найти уравнение для площади.

г. Найдите W, когда A = 700.

Размеры курятника, который даст площадь 700 квадратных футов, составляют 35 на 20 футов и 6,667 на 105 футов.
(Чтобы получить длину, разделите 700 на 6,667 и 35.)

Раздел 4.3: Квадратичные приложения и графики

Для построения квадратичного графика y = ax ² + bx + c необходимо найти:

1. Вершина:
   Координата x вычисляется по формуле
   Координата y вычисляется путем замены координаты x на y = ax ² + bx + c.
2. Пересечение x:
   Установите y = 0 и решите 0 = ax ² + bx + c, используя формулу корней квадратного уравнения.
3. Пересечение оси y:
   Замените x = 0 на y = ax ² + bx + c. Обратите внимание, что когда x = 0, y = c.

Пример 5. Уравнение затрат на изготовление коробок для сока: C = 0,6B ² — 24B + 36, а уравнение дохода — R = -0,4B ² + 18B. B выражается в миллионах, а C и R — в тысячах долларов.

а. Найдите уравнение прибыли.

г. Изобразите уравнение прибыли и объясните, что точки пересечения B и P означают с точки зрения проблемы.

Вершина — (21, 405).

Найдите точку пересечения B. Установите P = 0.

Перехваты B — это (0.875, 0) и (41.13, 0).

Найдите точку пересечения P. Установите B = 0.

Перехватчик P равен (0, -36).

г. Предположим, компании нужно заработать 200 000 долларов прибыли (P = 200).Изобразите линию P = 200 и найдите, сколько коробок из-под сока нужно сделать компании, чтобы заработать 200 000 долларов.

Чтобы получить прибыль в размере 200 000 долларов, компании необходимо произвести 6 682 или 35,32 миллиона ящиков для сока.

Вершина (21,405) представляет максимальную прибыль. Компания получит максимальную прибыль в размере 405 000 долларов, продав 21 миллион коробок сока.

Перехватчики B (0,875, 0) и (41,13, 0) говорят нам, что компания сломается, даже если они продадут.875 или 41,13 миллиона ящиков сока.

Перехват P (0–36) представляет начальные затраты компании в размере 36 000 долларов.

Раздел 4.4: Факторинг

Общие факторы:

Триномы:

Решение квадратных уравнений на множители.

Если a. b = 0, тогда a = 0 или b = 0

Советы по обучению:

1. Практикуйте повторный тест, начиная со следующей страницы, поместив себя в реалистичные условия экзамена.2 — 6x — 5 График на координатной плоскости

   Уравнение: y = -3 x ² — 6 x — 5

   Вышеупомянутое квадратное уравнение представляет собой стандартную форму параболы y = ax ² + bx + c .

   a = — 3, b = -6, c = -5.

   Ось симметрии x = — b /2 a = 6 / -6 = -1.

   Чтобы найти вершину, замените значение x в y = -3 x ² — 6 x — 5.

   y = -3 + 6-5 = -2

   Вершина = (-1, -2)

   Составьте таблицу значений, чтобы найти упорядоченные пары, удовлетворяющие уравнению.

   Выберите значения для x и найдите соответствующие значения для y .

   x	y = -3x 2 — 6x — 5	( x , y )
   — 1	y = -3 (- 1) ^ 2-6 (- 1) -5 = -3 + 6-5 = -2	(- 1, -2)
   — 2	y = -3 (- 2) ^ 2-6 (- 2) — 5 = -12 +12-5 = -5	(- 2, -5)
   0	y = -3 (0) ^ 2-6 (0) — 5 = -5	(0, -5)
   1	y = -3 (1) ^ 2-6 (1) — 5 = -3-6-5 = -14	(1, -14)
   2	y = -3 (2) ^ 2-6 (2) — 5 = -12-12-5 = -29	(2, -29)

   1.Нарисуйте координатную плоскость.

   2. Постройте координатные точки.

   3. Затем нарисуйте график, соединив точки плавной кривой.

   На графике мы можем наблюдать вершину ( x , y ) = (-1, — 2)

   Пересечения параболы x нет.

   y — точка пересечения (0, -5).

   Математическая сцена — Уравнения III — Урок 3

   Математическая сцена — Уравнения III — Урок 3 — Квадратные уравнения

   2008 Rasmus ehf и Jhann sak

   Уравнения III

   Урок
   3
   Пересечение
   точек графиков

   ---

   Как приступить к поиску точек, в которых два графика
   y = f (x) и y = g (x) пересекаются?

   Мы уже знаем, где найти график
   f (x) пересекает ось x.Здесь y = 0. Мы вычисляем его, решая
   уравнение f (x) = 0.
   Когда графики y = f (x) и y =
   g (x) пересекаются, оба графа имеют
   точно такие же значения x и y. Итак, мы можем найти точку или точки
   пересечения путем решения уравнения f (x)
   = g (x). Решение этого уравнения даст нам значение (я) x
   точка (и) пересечения. Затем мы можем найти значение y, поместив значение для
   x, который мы нашли в одном из исходных уравнений.То есть путем расчета
   либо f (x), либо g (x).

   Пример 1

   Рассчитать точку
   пересечение двух прямых f (x) = 2x — 1 и g (x) = x + 1. Сначала
   давайте посмотрим на график двух функций. Мы видим смысл
   пересечение есть (2, 3).

   Рассчитываем точку пересечения по
   решение уравнения f (x) = g (x). То есть:

   2х — 1 = х + 1

   2х — х = 1 + 1

   х = 2

   Координата Y теперь может быть найдена
   вычисление f (2):

   f (2) = 2 × 2 — 1 =
   3

   Точка пересечения — (2,
   3) .

   Пример показывает, что мы можем найти точку
   пересечения двумя способами.
   Либо графически, нарисовав два графика в одной системе координат, либо
   алгебраически, решив уравнение, такое как в приведенном выше примере.

   Решить уравнение графически легко с помощью
   графический калькулятор или компьютерная программа, например Excel.
   Некоторые уравнения нельзя решить алгебраически, но мы можем найти решения, которые
   исправляем до любого количества значащих цифр, используя компьютеры и
   калькуляторы.

   Пример 2

   Решите уравнение x ² — 2x — 3 = 2x — 3 сначала графически, затем алгебраически.

   Рисуем графики f (x) = x ² —
   2x — 3 и g (x) = 2x — 3, составив таблицу значений и построив график
   точки. Как из графика, так и из таблицы значений видно, что
   графики пересекаются при x = 0 и x = 4 .

   Решает алгебраически:

   x ² — 2x — 3 = 2x — 3

   x ² — 4x = 0

   х (х — 4) = 0

   Получение решений x = 0 и x = 4 .

   Пример 3

   Решите уравнение x ² — 1 = 2x — 3

   Сначала переместите все термины
   перейдите к левой части уравнения и упростите.

   Это дает x ² — 2x + 2 = 0

   Используем квадратичную формулу с a = 1, b =
   −2 и c = 2.

   Число под знаком квадратного корня:
   отрицательный, что означает, что это уравнение не имеет решения.
   Чтобы понять, почему это так, мы рисуем графики левой части оригинала.
   уравнение

   f (x) = x ² — 1 и правая часть g (x) = 2x — 3.

   Мы видим, что парабола
   f (x) и прямая g (x) не пересекаются.Легко видеть, что мы
   не может вычислить точку пересечения просто потому, что такой точки нет.

   Пример 4

   Решите уравнение x ³ — 3x + 2 = x ² —
   2x + 1

   Как и в предыдущем примере, мы перемещаем все
   слагаемые в левую часть уравнения.

   x ³ — 3x + 2 = x ² — 2x + 1

   x ³ — x ² — x + 1 = 0

   (x ³ — x ² ) — (x — 1) = 0

   x ² (x — 1) — (x — 1) = 0

   (х — 1) (х ² —
   1) = 0

   (х — 1) (х — 1) (х
   + 1) = 0

   Расчеты показывают, что их всего два
   решений, x = 1 и x = −1, но кубическое уравнение может иметь три
   решения.График показывает нам, что происходит.

   Графики f (x) =
   x ² — 2x + 1 и g (x)
   = x ³ — 3x + 2 пересекаются
   только в двух местах, где x = −1 и x = 1, которые были решениями
   уравнение.

   Пример 5

   Решите уравнение x ² = x

   Легко видеть, что x = 0 и x = 1 являются
   решения уравнения, но есть ли еще решения? Это не очень
   вероятно, но давайте посмотрим на графики.

   Назовите левую часть f (x) = x ² и правую часть g (x) = x.
   Помните, что g (x) не может принимать отрицательные значения x, поэтому не может быть никаких
   отрицательные точки пересечения.

   На графике видно, что точек всего две
   пересечения и, следовательно, только два решения уравнения. х = 0 и х =
   1.
   Вот как решить уравнение расчетом:

   x 2 = x х 4 = х х 4 — х = 0 х (х 3 — 1) = 0

   Квадрат обе стороны уравнения, чтобы избавиться от квадратного корня .

   Это дает решение x = 0 и x = 1 .

   Пример 6

   Решите уравнение ln x = x ² — 1

   Это уравнение не так-то просто решить. Если мы
   помните определение логарифма, мы видим, что x = 1 делает обе стороны
   уравнение равно 0 и, следовательно, является одним решением уравнения. Мы рисуем
   графики, чтобы увидеть, есть ли другие решения.

   График показывает нам, что есть два
   решения. Одно решение — это ровно x
   = 1, поскольку e ⁰ = 1.

   Обратите внимание, что мы выбираем значения x так, чтобы значения y
   становятся все ближе и ближе друг к другу в таблице значений. Таким образом мы
   можем выбрать значение x, чтобы получить желаемую точность.

   Пример 7

   EXCEL

   Если мы воспользуемся графическим калькулятором, то сможем найти
   решение уравнения ln x = x ² — 1 намного проще. 2 − ln (B2)

   Теперь выберите Инструменты
   а затем «Поиск цели» в строке меню.В
   на экране появляется следующее:

   Пишем D2,
   1 и B2 в промежутках, как показано. Мы просим Excel сделать значение ячейки D2 равным
   к значению 1, изменив значение в B2.

   Когда
   нажимаем ОК, появляется следующая информация.

   Это говорит нам о том, что
   аппроксимация x ≈ 0,45, которую мы нашли графически в примере 6, довольно
   хорошо.Решение x ≈ 0.4500289, найденный с помощью EXCEL, не намного лучше.

   ---

   Попробуйте пройти тест 3 по уравнениям III.

   Не забудьте использовать контрольный список для
   следите за своей работой.

   Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

   Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения.Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся достаточно точек для распознавания шаблона, а затем соединить точки, чтобы включить все точки.

   Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.

   ---

   Пример

   Постройте функцию y = x + 2

   Начните с выбора пары значений для x e.грамм. -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.

   х	Y = х + 2	Заказанная пара
   -2	-2 + 2 = 0	(-2, 0)
   -1	-1 + 2 = 1	(-1, 1)
   0	0 + 2 = 2	(0, 2)
   1	1 + 2 = 3	(1, 3)
   2	2 + 2 = 4	(2, 4)

   Теперь вы можете просто нанести пять упорядоченных пар на координатную плоскость

   На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.

   Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.

   Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y).

   Стандартная форма линейного уравнения —

   $$ Ax + By = C, \: \: A, B \ neq 0 $$

   Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.

   $$ 2y-4x = 8 $$

   $$ 2y-4x \, {\ color {green} {+ \, 4x}} = 8 \, {\ color {green} {+ \, 4x}} $$

   $$ 2y = 4x + 8 $$

   $$ \ frac {2y} {{\ color {green} 2}} = \ frac {4x} {{\ color {green} 2}} + \ frac {8} {{\ color {green} 2}}

   $

   $$ y = 2x + 4 $$

   Отсюда вы можете построить уравнение, как в примере выше.

   График y = a представляет собой горизонтальную линию, где прямая проходит через точку (0, a)

   В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)

   ---

   Видеоурок

   Постройте график линейного уравнения y = 3x — 2

   Содержит ли линия с уравнением y = 3x + 2 в плоскости xy точку (r, s)?

   Содержит ли линия с уравнением y = 3x + 2 в плоскости xy точку (r, s)?

   (1) (3r + 2 − s) (4r + 9 − s) = 0
   (2) (4r − 6 − s) (3r + 2 − s) = 0

   Это сложный вопрос по геометрии и системе уравнений / алгебре из подготовительных тестов GMAT 1 и 2.Мы довольно часто видим это на репетиторских занятиях по GMAT, поэтому не только вам нужна помощь. Важно помнить, что с геометрией GMAT часто аспект геометрии является легкой частью, а не обязательно основной темой вопроса.

   Определите вопрос: содержит ли линия с уравнением y = 3x + 2 точку (r, s)?

   В принципе, находится ли (r, s) на линии y = 3x + 2? Другой способ взглянуть на это: можем ли мы заменить r вместо x и s вместо y? Так что, s = 3r + 2? Это то, что мы хотим выяснить.Нам не нужно искать отдельные значения r и s.

   Упорядочить информацию

   Я бы, наверное, не стал строить график. Почему? Потому что этот вопрос касается уравнений / алгебры. Кажется, что у него нет аспекта пространственного мышления.

   Просто чтобы убедиться, что вы знаете, как это сделать: вот график y = 3x + 2

   Нам это может не понадобиться, но для полноты картины y = 3x + 2. Используйте пересечения x и y, чтобы упростить задачу.

   Для точки пересечения x сделайте y = 0

   3x + 2 = 0

   х = -2/3

   Для точки пересечения y сделайте x = 0

   г = 2

   Таким образом, точка пересечения по оси x равна -2/3, 0

   точка пересечения по оси y 0,2

   Утверждение 1: (3r + 2 − s) (4r + 9 − s) = 0

   Вы редко хотите перемножать трехчлены.Это создаст беспорядок. Что мы можем из этого получить? Либо:

   3r + 2 — s = 0

   или

   4r + 9 — s = 0

   или они оба равны нулю.

   Давайте вернемся к нашему вопросу, чтобы посмотреть, сможем ли мы что-нибудь сопоставить.

   Мы ищем доказательства: s = 3r + 2

   Это что-нибудь из этого?

   Да! Это то же самое: 3r + 2 — s = 0

   Так что вполне возможно, что r и s действительно стоят на очереди.

   Однако это не обязательно, потому что 4r + 9 — s может равняться 0, а 3r + 2 — s может равняться чему угодно.

   Итак, у нас нет однозначного ответа.

   Недостаточно .

   Утверждение 2: (4r − 6 − s) (3r + 2 − s) = 0

   Здесь та же проблема. Недостаточно.

   Заявление 1 + Заявление 2

   Теперь все становится интересно.

   Оба эти уравнения равны нулю, поэтому равны друг другу.

   (3r + 2 − s) (4r + 9 − s) = (4r − 6 − s) (3r + 2 − s)

   Давайте отложим все в сторону, чтобы мы могли вынести за скобки общий термин 3r + 2 — s

   (3r + 2 — s) (4r + 9 — s — 4r + 6 + s) = 0

   Объединить похожие термины

   (3r + 2 — с) (15) = 0

   Мы знаем, что 15 не равно нулю, поэтому (3r + 2 — s) должно быть равно 0

   3r + 2 — s = 0

   переставить, что немного

   с = 3r + 2

   Знакомо?

   Они совпадают.Значит, должно быть, что r и s находятся на линии y = 3x + 2.

   Альтернативное (и более быстрое) решение

   (3r + 2 − s) (4r + 9 − s) = 0

   (4r − 6 − s) (3r + 2 − s) = 0

   Давайте посмотрим на вышесказанное в более крупном / практическом плане.

   Если оба этих утверждения равны нулю, тогда должно быть 3r + 2 — s = 0.

   Почему?

   Потому что одна из двух круглых скобок в каждом из операторов должна равняться нулю.

   Таким образом, либо 3r + 2 — s равно нулю, либо ОБА 4r + 9 — s И 4r — s — 6 должны быть равны нулю.

   Учитывая, что 4r + 9 — s и 4r — s — 6 не равны друг другу (вычтите их, и вы обнаружите, что разница равна 15), нет никакого способа, чтобы они оба были равны нулю.

   Вот очень простой пример, почему оба они не могут быть равны нулю:

   Могут ли оба x + 1 и x + 2 равняться нулю? НЕТ!!! Ясно, что они не равны друг другу, поэтому не могут оба равняться нулю. То же самое с 4r + 9 — s и 4r — s — 6

   Значит, должно быть, что 3r + 2 — s равно нулю.Это соответствует нашему вопросу.

   Достаточно.

   Вот все получилось компактнее и нагляднее

   Правильный ответ: C

   Дополнительные сложные вопросы по геометрии GMAT, практические вопросы по координатной плоскости

   Вот еще один очень сложный вопрос о координатной плоскости GMAT, в котором много алгебры и вопрос о достаточности данных в стиле «да / нет».

   В плоскости xy область R состоит из всех точек (x, y) таких, что 2x + 3y ≤ 6.Находится ли точка (r, s) в области R?

   И еще один сложный вопрос о плоскости координат GMAT. Такая же достаточность данных в стиле да / нет, что и в приведенном выше.

   В каких двух точках график y = (x + a) (x + b) пересекает ось x на плоскости xy?

   А вот более фундаментальный вопрос о координатной плоскости из Вопроса дня GMAT.

   Как отразить график через ось x, ось y или начало координат?

   Это письмо недавно пришло от читателя Стюарта:

   Можете ли вы объяснить принципы построения графика, в котором y = — f ( x ) является отражением графика y = f ( x ) по оси x и график y = f (- x ) отражение графика y = f ( x ) по оси y- ?

   Спасибо

   Мой ответ

   Привет Стюарт

   Давайте посмотрим, что это означает на примере.

   Пусть f ( x ) = 3 x + 2

   Если вы не уверены, как это выглядит, вы можете построить график с помощью этого средства построения графиков.

   Вы увидите, что это прямая линия, наклон 3 (положительный, т. Е. Идет в гору, когда мы идем слева направо) и y — пересечение 2.

   Теперь рассмотрим — f ( x ).

   Это дает нам

   — f ( x ) = −3 x — 2

   Наша новая линия имеет отрицательный наклон (он уменьшается при сканировании слева направо) и проходит через −2 на оси y .

   Когда вы изобразите 2 уровня на одной и той же оси, это будет выглядеть так:

   Обратите внимание, что если вы отразите синий график ( y = 3 x + 2) по оси x , вы получите зеленый график ( y = −3 x — 2) (как показано красными стрелками).

   Что мы сделали, так это взяли каждое значение y и перевернули их вверх дном (это эффект минус спереди).

   Теперь для

   f (- x )

   Аналогично сделаем f (- x ).

   Так как f ( x ) = 3 x + 2, то

   f ( −x ) = −3 x + 2 (замените каждое « x » на « −x »).

   Теперь, построив график на тех же осях, мы имеем:

   Обратите внимание, что эффект «минуса» в f ( −x ) должен отражать синюю исходную линию ( y = 3 x + 2) по оси y , и мы получаем зеленая линия: ( y = −3 x + 2).Зеленая линия также проходит через 2 на оси y .

   Дополнительный пример

   Вот пример использования кубического графа.

   Синий график: f ( x ) = x ³ — 3 x ² + x — 2

   Отражение по оси x (зеленый): — f ( x ) = — x ³ + 3 x ² — x + 2

   Теперь отразим в оси ординат.

   Синий график: f ( x ) = x ³ — 3 x ² + x — 2

   Отражение по оси Y (зеленый): f ( −x ) = −x ³ — 3 x ² — x — 2

   Четные и нечетные функции

   Мы действительно должны упомянуть четных и нечетных функций , прежде чем покинуть эту тему.

   Для каждого из приведенных выше примеров отражения на оси x или y давали график, который составлял различных .Но иногда отражение такое же, как и на исходном графике. Мы говорим, что отражение «отображается на» оригинале.

   Четные функции

   Функция даже имеет свойство f ( −x ) = f ( x ). То есть, если мы отразим четную функцию по оси y , она будет выглядеть точно так же, как оригинал.

   Пример четной функции: f ( x ) = x ⁴ -29 x ² + 100

   Вышеупомянутая четная функция эквивалентна:

   f ( x ) = ( x + 5) ( x + 2) ( x — 2) ( x — 5)

   Обратите внимание: если мы отразим график по оси y , мы получим тот же график (или мы могли бы сказать, что он «отображается на себя»).

   Нечетные функции

   Функция с нечетным числом имеет свойство f ( −x ) = −f ( x ).

   На этот раз, если мы отразим нашу функцию в и ось x и ось y , и если она выглядит точно так же, как оригинал, то у нас будет нечетная функция.

   Этот вид симметрии называется симметрией происхождения . Нечетная функция либо проходит через начало координат (0, 0), либо отражается через начало координат.

   Пример нечетной функции: f ( x ) = x ³ — 9 x

   Вышеупомянутая нечетная функция эквивалентна:

   f ( x ) = x ( x + 3) ( x — 3)

   Обратите внимание: если мы отразим график по оси x , а затем по оси y , мы получим тот же график.

   Другие примеры четных и нечетных функций

   На этой странице есть еще несколько примеров: Четные и нечетные функции

   Знание о четных и нечетных функциях очень полезно при изучении рядов Фурье.

   Я надеюсь, что все имеет смысл, Стюарт.

   См. 8 комментариев ниже.

   График Y 2 3x 2 — Cute766

   Определите наклон и точку пересечения Y 2 3x 2

   График y = 2 3x 2. Перепишем в форме пересечения наклона. нажмите, чтобы увидеть больше шагов, форма пересечения наклона: где — наклон, а — точка пересечения по оси y. напишите в форме.Поскольку это говорит нам, что точка пересечения y — это точка пересечения с осью y, помните, что точка пересечения с y — это точка, в которой график пересекается с осью y, так что теперь у нас есть одна точка, поскольку наклон состоит из «подъема» по «пробегу», это также означает, что поскольку наклон равен, это означает: что показывает нам, что подъем равен 2, а разбег равен 3. График y = 2 3x. перепишите в форме пересечения уклона. нажмите, чтобы увидеть больше шагов, форма пересечения наклона: где — наклон, а — точка пересечения по оси y. условия повторного заказа. Y = 2 3x 2 геометрическая фигура: наклон прямой = 1.333 2.000 = 0,667 x отрезок = 6 2 = 3 1 = 3,00000 y отрезок = 6 3 = 2 переставить: переставить уравнение, вычитая что. Изучите математику с помощью нашего красивого бесплатного графического калькулятора. функции графиков, точки построения, визуализация алгебраических уравнений, добавление ползунков, анимация графиков и многое другое.

   Выбери график 3x Y 2 с умом

   Бесплатный графический калькулятор мгновенно отображает ваши математические задачи.2 3x 2 идентифицируют вершину и ось симметрии ответ графа джима томпсона 5910 (35256). обратите внимание, как вершина (,). График 3x y = 2. найти. нажмите, чтобы вычесть больше шагов из обеих частей уравнения. нарисуйте линию, используя наклон и точку пересечения оси y или точки. склон:.

   Определите наклон и точку пересечения Y = 2 3x 2 График Уравнение

   узнать, как построить график линейных уравнений, записанных в форме пересечения наклона.2 bx c, где a, b и c — константы.

   демонстрация того, как построить график уравнения в форме пересечения наклона, интерпретируя наклон при коэффициенте x и постоянный член как точку пересечения y.
   узнать, как построить график линейных уравнений, записанных в форме пересечения наклона.