4 х 2 решить уравнение: решите уравнение 4х=-2 — Школьные Знания.com — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Способы решения квадратных уравнений | Творческие проекты и работы учащихся

Варианты решения квадратных уравнений

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения (Приложение 1).

Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно остановимся на каждом из них.

1 способ: разложение левой части уравнения на множители.

Решим уравнение

х2 + 10х — 24 = 0.

Разложим левую часть на множители:

х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х — 2) = 0

Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.

2 способ: метод выделения полного квадрата.

Решим уравнение х2 + 6х — 7 = 0.

Выделим в левой части полный квадрат.

Для этого запишем выражение х2 + 6х в следующем виде:

х2 + 6х = х2 + 2• х • 3.

В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2• х • 3 + 32 = (х + 3)2.

Преобразуем теперь левую часть уравнения

х2 + 6х — 7 = 0,

прибавляя к ней и вычитая 32. Имеем:

х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16.

Таким образом, данное уравнение можно записать так:

(х + 3)2 — 16 =0, (х + 3)2 = 16.

Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.

3 способ: решение квадратных уравнений по формуле.

Умножим обе части уравнения

ах2 + bх + с = 0, а ≠ 0

на 4а и последовательно имеем:

4а2х2 + 4аbх + 4ас = 0,

((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,

(2ax + b)2 = b2 — 4ac,

2ax + b = ± √ b2 — 4ac,

2ax = — b ± √ b2 — 4ac,

Примеры. Сколько корней имеет уравнение?

а) 4х2 + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b2 — 4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1,

D > 0, два разных корня;

Таким образом, в случае положительного дискриминанта, т.е. при

b2 — 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.

б) 4х2 — 4х + 1 = 0,

а = 4, b = — 4, с = 1, D = b2 — 4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0,

D = 0, один корень;

Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение

ах2 + bх + с = 0 имеет единственный корень,

в) 2х2 + 3х + 4 = 0,

а = 2, b = 3, с = 4, D = b2 — 4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D < 0.

Данное уравнение корней не имеет.

Итак, если дискриминант отрицателен, т. е. b2 — 4ac < 0,

уравнение ах2 + bх + с = 0 не имеет корней.

Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

4 способ: решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

х2 + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x1 x2 = q,

x1 + x2 = — p

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р > 0, то оба корня отрицательны, если р < 0, то оба корня положительны.

Например, x2 – 3x + 2 = 0; x1 = 2 иx2 = 1, так какq = 2 > 0 иp = — 3 < 0;

x2 + 8x + 7 = 0; x1 = — 7 иx2 = — 1, так какq = 7 > 0 иp= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .

Пример: x2 + 4x – 5 = 0; x1 = — 5 иx2 = 1, так какq= — 5 < 0 иp = 4 > 0;

x2 – 8x – 9 = 0; x1 = 9 иx2 = — 1, так какq = — 9 < 0 иp = — 8 < 0.

5 способ: решение уравнений способом «переброски»( Приложение 2).

Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение

а2х2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению

у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а.

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример. Решим уравнение 2х2 – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у2 – 11у + 30 = 0.

Согласно теореме Виета

у1 = 5 х1 = 5/2 x1 = 2,5

у2 = 6 x2 = 6/2 x2 = 3.

Ответ: 2,5; 3.

6 способ: свойства коэффициентов квадратного уравнения (Приложение 2)

А.Пусть дано квадратное уравнение

ах2 + bх + с = 0, где а ≠ 0.

1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1

х2 = с/а.

Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x2 + b/a • x + c/a = 0.

Согласно теореме Виета

x1 + x2 = — b/a,

x1x2 = 1• c/a.

По условию а – b + с = 0, откуда b = а + с. Таким образом,

x1 + x2 = — а + b/a= -1 – c/a,

x1x2 = — 1• ( — c/a),

т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.

Примеры.

1) Решим уравнение 345х2 – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

х1 = 1, х2 = c/a = -208/345.

Ответ: 1; -208/345.

2)Решим уравнение 132х2 – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

х1 = 1, х2 = c/a = 115/132.

Ответ: 1; 115/132.

Б. Если второй коэффициент b = 2k – четное число, то формулу корней.

Пример.

Решим уравнение 3х2 — 14х + 16 = 0.

Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;

D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;

Ответ: 2; 8/3

В. Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид:

Формулу (3) особенно удобно использовать, когда р — четное число.

Пример. Решим уравнение х2 – 14х – 15 = 0.

Решение. Имеем: х1,2 =7± 8,

Ответ: х1 = 15; х2 = -1.

7 способ: Графическое решение квадратного уравнения.

Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = — px — q.

Построим графики зависимости у = х2 и у = — px — q.

График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис.1). Все данные вводим в программу«Advanced Grapher» и получаем ответы [13].

Искомая окружность пересекает ось абсцисс в точках B (х1 ;0) и D (х2 ;0), где х1 и х2 – корни уравнения ах2 + bх + с=0, и проходит через точки А (0;1) и С (0; ) на оси ординат. [5, c.34]

Возможны следующие случаи:

прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

Примеры.

1) Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2).

Решение. Запишем уравнение в виде х2 = 3х + 4.

Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = — 1 и х2 = 4.

Ответ: х1 = — 1; х2 = 4.

2) Решим графически уравнение (рис. 3) х2 — 2х + 1 = 0.

Решение. Запишем уравнение в виде х2 = 2х — 1.

Построим параболу у = х2 и прямую у = 2х — 1.

Прямую у = 2х — 1 построим по двум точкам М (0; — 1)

и N(1/2; 0). Прямая и парабола пересекаются в точке А с

абсциссой х = 1. Ответ: х = 1.

3) Решим графически уравнение х2 — 2х + 5 = 0 (рис. 4).

Решение. Запишем уравнение в виде х2 = 5х — 5. Построим параболу у = х2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.

Ответ. Уравнение х2 — 2х + 5 = 0 корней не имеет.

8 способ:: решение квадратных уравнений с помощью циркуля и линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика. Найти корни квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5). [5, c.34]

Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD.

Итак: 1) построим точки (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.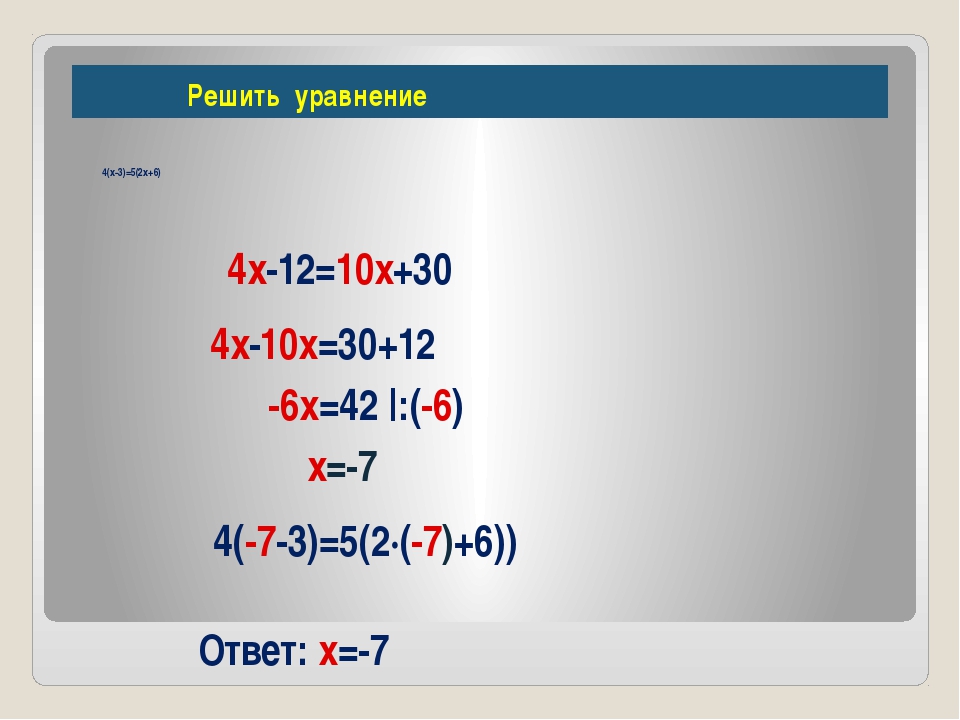

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.

2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.

Пример. Решим уравнение х2 — 2х — 3 = 0 (рис. 7).

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).

Ответ: х1 = — 1; х2 = 3.

9 способ: решение квадратных уравнений с помощью номограммы.

Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990) [ 3, c.83] .

Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис.11):

Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение

z2 + pz + q = 0,

причем буква z означает метку любой точки криволинейной шкалы.

Примеры.

1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корниz1 = 8,0 и z2 = 1,0 (рис. 12).

(рис.12)

2) Решим с помощью номограммы уравнение

2z2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение

z2 — 4,5z + 1 = 0.

Номограмма дает корни z1 = 4 иz2 = 0,5.

3) Для уравнения

z2 — 25z + 66 = 0

коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t2 — 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откудаz1 = 5t1 = 3,0 иz2 = 5t2 = 22,0.

10 способ: геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

Примеры.

1) Решим уравнение х2 + 10х = 39.

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х2 + 10х + 25. Заменяя

х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.

Решение представлено на рис. 16, где у2 + 6у = 16,

или у2 + 6у + 9 = 16 + 9.

Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис.16).

3) Решить геометрически уравнение у2 — 6у — 16 = 0.

Преобразуя уравнение, получаему2 — 6у = 16.

На рис. 17 находим «изображения» выражения у2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,

получаем: (у — 3)2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у1 = 8 и у2 = — 2.

Заключение

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней. Здесь мы остановилась на вопросе решения квадратных уравнений, а что, если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое.

Но это вопросы уже следующих работ. В результате изучения новых способов решения квадратных уравнений мы получили возможность решать уравнения не только по формуле, но и более интересными способами. Решили множество уравнений, изучили программу «Advanced Grapher». Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи.

Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт. Данная исследовательская работа может быть использована учителями математики на уроках и элективных курсах по математике при изучении темы «Квадратные уравнения» (Приложения 1-3), учениками для расширения и углубления знаний по решению квадратных уравнений. Любой учащийся, используя эту исследовательскую работу, может самостоятельно изучить данную тему (Приложения 1-2).

Литература

Алимов, Ш.А., Ильин В.А. и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981.
Арутюнян, Е.Б.Занимательная математика/ Е.Б. Арутюнян Москва «Аст – пресс» 1999.
Брадис, В. М. Четырехзначные математические таблицы для средней школы. Изд. 57-е. — М., Просвещение, 1990. С. 83.
Глейзер, Г.И. История математики в школе. 7-8 классы. – М., Просвещение, 1982.
Окунев , А.К. Квадратичные функции, уравнения и неравенства. / Пособие для учителя. — М., Просвещение, 1972.
Пресман, А.А. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.
Соломник , В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М., Высшая школа, 1973.
Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение,
Пичурин, Л.Ф. За страницами учебника алгебры/ Л.Ф. Пичурин. Москва «Просвещение» 1990г.
Энциклопедический словарь юного математика. – 2-е издание, испр. и доп. – М.:Педагогика, 1989.
Энциклопедия для детей. Т.11. Математика.- М.: Аванта+, 1999.
Ресурсы сети Интернет.
Программы «Advanced Grapher» и «Открытая математика».

Перейти к разделу: 3. Что необходимо знать для решения квадратных уравнений?

Решите уравнение:а) 4х2 + 7х + 3 = 0; б) х2 +

Решите уравнение:

а) 4х² + 7х + 3 = 0; б) х² + х — 56 = 0;
в) х² — х — 56 = 0; г) 5х² — 18x + 16 = 0;
д) 8х² + x — 75 = 0; е) 3х² — 11х — 14 = 0;
ж) 3х² + 11х — 3 4= 0; з) х² — х — 1 = 0.

Решение:

a) 4х² + 7х + 3 = 0; D = 49 — 4 • 4 • 3 = 49 — 48 = 1; x = (-7±1)/8; x₁ = -1; x₂ = -3/4;
б) х² + х — 56 = 0; D = 1 + 4 • 56 = 255; x = (-1±15)/2; x₁ = -8; x₂ = 7;
в) х² — х — 56 = 0; D = 1 + 4 • 56 = 255; x = (1±15)/2; x₁ = 8; x₂ = -7;
г) 5х² — 18x + 16 = 0; D₁ = 9² — 5 • 16 = 81 — 80 = 1; x = (9±15)/5; x₁ = 2; x₂ = 1,6;
д) 8х² + x — 75 = 0; D = 1 + 4 • 8 • 75 = 2401; x = (-1±49)/16; x₁ = 50/16 = -3 1/8; x₂ = -48/16 = 3;
e) 3х² — 11х — 14 = 0; D = 11² + 4 • 3 • 14 = 121 + 168 = 289; х = (11±17)/6; x₁ = -1; x₂ = 28/6 = 4 2/3;
ж) 3х² + 11х — 3 4= 0; D = 11² + 4 • 3 • 34 = 121 + 408 = 529; х = (-11±23)/6; x₁ = 2; х₂ = -34/6 = -5 2/3;
з) х² — х — 1 = 0; D = 1 + 4 = 5; х = (1±√5)/2.

Похожие задачи:

Не решая уравнения, выясните, имеет ли оно корни, и если имеет, то определите их знаки:
а) х² + 7х — 1 = 0; г) 19х² — 23x + 5 = 0;
б) х² — 7х + 1 = 0; д) 2х² + 5√3х + 11 = 0;
в) 5х² + 17x + 16 = 0; е) 11х² — 9х + 7 — 5√2 = 0.
1) Сформулируйте теорему, на основании которой можно определить знаки корней.
2) Распределите, кто выполняет задания а), в), д), а кто — задания б), г), е), и выполните их.
3) Проверьте друг у друга, правильно ли выполнены задания. Исправьте ошибки, если они допущены.
смотреть решение >>

4х х 2 решите уравнение

Вы искали 4х х 2 решите уравнение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решите уравнение х 2 4х, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «4х х 2 решите уравнение».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 4х х 2 решите уравнение,решите уравнение х 2 4х,х 2 4х 4. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 4х х 2 решите уравнение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, х 2 4х 4).

Где можно решить любую задачу по математике, а так же 4х х 2 решите уравнение Онлайн?

Решить задачу 4х х 2 решите уравнение вы можете на нашем сайте https://pocketteacher. ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Урок 11. многочлен p(x) и его корень. алгебраическое уравнение — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №11. Многочлен P(x) и его корень. Алгебраическое уравнение.

Перечень вопросов, рассматриваемых в теме

1) обобщенное понятие многочлена;

2) основные действия над многочленами;

3) определение алгебраического уравнения;

4) теорема Безу.

Глоссарий по теме

Многочлен P_n(x) = a _nx ⁿ+ a _{n – 1} x ^{n – 1} + a _{n – 2} x ^{n – 2} + . .. + a ₁ x + a ₀ , где a≠0, aₖ, k=0,1,2,3,…, aₖ,k=0,1,2,3,…,n — числа, x — переменная, называется многочленом n -ной степени .
Традиционно aₙ называется старшим коэффициентом, a₀ — свободным членом многочлена.

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Следствие. Если число а является корнем многочлена Р(х), то многочлен

Рₙ(х)= a₀x ⁿ+ a₁ x ^{n – 1} + … + a_{n – 1} x + a_nделится без остатка на двучлен х-а.

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0,

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнением над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Общая теория многочленов многих переменных далеко выходит за рамки школьного курса.

Мы рассмотрим многочлены одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.

Многочлен ax + b, где a≠0, a, b — числа, x — переменная, называется многочленом первой степени.
Многочлен ax²+bx+c, где a≠0, a, b, c — числа, x — переменная, называется многочленом второй степени (квадратным трёхчленом, квадратичной функцией).
Многочлен ax³+bx²+cx+d, где a≠0, a, b, c, d — числа, x — переменная, называется многочленом третьей степени.

Вообще, многочлен P_n(x) = a _nx ⁿ+ a _{n – 1} x ^{n – 1} + a _{n – 2} x ^{n – 2} + … + a ₁ x + a ₀, где a≠0, aₖ, k=0,1,2,3,…, aₖ,k=0,1,2,3,…,n — числа, x — переменная, называется многочленом n -ной степени.
Традиционно aₙ называется старшим коэффициентом, а a₀ — свободным членом многочлена.

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида

P(x₁, x₂, …, x_n)=0,

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Степенью алгебраического уравнения называют степень многочлена P.

Например, уравнение

является алгебраическим уравнением четвертой степени от трёх переменных (с тремя неизвестными) над множеством вещественных чисел.

Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Доказательство. Разделим Р(х) c остатком на (x — а).

Получим Р(х)= (x — а)·Q(х) + R; по определению остатка, многочлен r либо равен 0, либо имеет степень, меньшую степени (x — a), т.е. меньшую 1. Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях R на самом деле является числом – нулем или отличным от нуля.

Подставив теперь в равенство Р(х)= (x — а)·Q(х) + R значение x = a, мы получим Р(a)= (a — а)Q(х) + R, P(a) = R, так что действительно R = P(a).

Эту закономерность отметил и математик Безу.

Следствие. Если число а является корнем многочлена Р(х), то многочлен

Рₙ(х)= a₀x ⁿ+ a₁ x ^{n – 1} + … + a_{n – 1} x + a_nделится без остатка на двучлен х-а.

Историческая справка

Этьенн Безу — французский математик, член Парижской Академии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.

Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.

В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.

Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах.

Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.

Часть трудов Безу посвящена внешней баллистике.

Именем ученого названа одна из основных теорем алгебры.

Примеры алгебраических уравнений

алгебраическое уравнение с одним неизвестным -уравнение вида , где n- натуральное число.
Линейное уравнение от одной переменной ax+b=0, a
Квадратное уравнение ax²+bx+c=0, a.

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Разложим на множители многочлен:

Решение: )

Ответ: ))

Пример 2.

Решить уравнение: х⁴ — x³ — 6x² — x + 3 = 0.

Решение: Целые корни многочлена Р(х) = х⁴ — x³ — 6x² — x + 3 должны быть делителями свободного члена, так что это могут быть числа -1, 1, 3, -3.

Подберем корень по схеме Горнера:

х⁴ — x³ — 6x² — x + 3= (х + 1)(х³ -2х² – 4х +3) =0

	1	-2	-4	3
-1	1	-3	-1	4
1	1	-1	-5	-2
-3	1	-5	11	-30
3	1	1	-1	0

Q(x) = х³ -2х² – 4х +3=(x- 3)(x² + x -1)=0

x² + x -1 =0

D=5

Ответ: -1; 3;

Метод интервалов

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:

Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;

Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;

Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)

Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;

Отметить знаки на остальных интервалах, чередуя их.

После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.

В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

Пример 1:

Решить неравенство:

(x — 2)(x + 7) < 0

Работаем по методу интервалов.

Шаг 1: заменяем неравенство уравнением и решаем его:

(x — 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x — 2 = 0 => x = 2

x + 7 = 0 => x = -7

Получили два корня.

Шаг 2: отмечаем эти корни на координатной прямой. Имеем:

Шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000).

Получим:

f(x) = (x — 2)(x + 7)

x = 3

f(3)=(3 — 2)(3 + 7) = 1*10 = 10

Получаем, что f(3) = 10 > 0 (10 – это положительное число), поэтому в самом правом интервале ставим знак плюс.

Шаг 4: нужно отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус. Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси.

Вернемся к исходному неравенству, которое имело вид:

(x — 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

Пример 2:

Решить неравенство:

(9x²— 6x + 1)(x — 2) ≥ 0

Решение:

Для начала необходимо найти корни уравнения

(9x²— 6x + 1)(x — 2) = 0

Свернем первую скобку, получим:

(3x — 1)²(x — 2) = 0

Отсюда:

x — 2 = 0; (3x — 1)² = 0

Решив эти уравнения получим:

x₁= 2; x₂= ; x₃= ;

Нанесем точки на числовую прямую:

Т. к. x₂и x₃– кратные корни, то на прямой будет одна точка и над ней “петля”.

Возьмем любое число меньшее самой левой точки и подставим в исходное неравенство. Возьмем число -1.

(9*(-1)²— 6*(-1) + 1)(-1 — 2) = -12

Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства ≤.

Не забываем включать решение уравнения (найденные X), т.к. наше неравенство нестрогое.

Ответ: {} U [2;+∞)

Пример 3:

Решить неравенство:

(9x²— 6x + 1)(x — 2) > 0

Все, чем данное неравенство отличается от предыдущего – вместо нестрогого неравенства (≥) стоит строгое (>). Как ни странно, решение данного неравенства будет иным.

Найдем корни уравнения (9x²— 6x + 1)(x — 2) ≠ 0 (знак ≠ означает, что найденные корни не могут быть решениями нашего неравенства, т. к. оно строгое). Проделав все этапы, что и в предыдущем примере получим:

x₁= 2; x_2,3 =;

Вынесем наши решения на числовую прямую (обратите внимания, что данные точки не включены, т.к. неравенство строгое, т.е. левая часть неравенства не равна нулю)

Обратите внимание, что корни x₂ и x₃ совпадают, корень “” является кратным. Соответственно, в данной точке на числовой прямой рисуем петлю.

Возьмем число -1.

(9*(-1)²— 6*(-1) + 1)(-1 — 2) = -12

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства <.

Найденные корни не включаем в ответ.

Ответ: (2;+∞).

Курсы подготовки к ЕГЭ и ОГЭ Видное

В центре преподаются курсы по точным наукам – математике и физике. Наша основная задача – дать обучающимся теоретические знания и опыт практического взаимодействия с предметом. Это позволяет полноценно подготовиться к профессиональному обучению в высших учебных заведениях.

Мы готовим школьников к сдаче государственных экзаменов, олимпиадам, поступлению в лицеи и устраняем пробелы в знаниях. В рамках подготовительных курсов разбираются задания, соответствующие требованиям экспертных комиссий ФИПИ, дается информация о порядке проведения экзаменов. Мы используем современные технологии преподавания, особое внимание уделяется практической работе с обучающимися и широко используется интерактивное обучение.

Кроме этого, мы проводим курсы по робототехнике и ментальной арифметике для детей от 4 до 15 лет. На занятиях мы развиваем интеллектуальные и творческие способности ребенка с ранних лет: логика, воображение, скорость мыслительных процессов, мелкая моторика пальцев, усидчивость, программирование и физика. Дети знакомятся с тем, как работают математические и физические законы в окружающем мире.

Наш центр проводит подготовку школьников к сдаче ЕГЭ и ОГЭ на базе 9 — 11 классов школы и повышению успеваемости в младших классах.
Занятия проводятся в составе небольших групп до 4-х человек и индивидуально. Несмотря на то, что точные науки для многих ребят кажутся скучными предметами, мы стараемся побудить их к самостоятельному изучению. Преподавателями берутся примеры из реальной жизни. Мы уверены, что фактор любознательности является главным ключом к усвоению математики и физики.

При построении учебного процесса педагоги руководствуются принципом «от простого – к сложному». При этом каждое занятие учит детей решать понятные для них проблемы, закреплять навыки работы с информацией, критического мышления и поиска эффективных методов решения.

Занятия по физике и математике в учебном центре дают возможность выйти за рамки школьного кабинета.

Какой формат подготовки выбрать – личное дело каждого. Если вдруг у Вас есть знакомый проверенный педагог, то выбор очевиден. А если нет, приходите в SIGMA. Мы проведем для Вас бесплатное пробное занятие. Погрузитесь в атмосферу знаний и интересных уроков. Здесь начнется Ваш путь к отличной сдаче экзаменов и покорению самых высоких вершин.

4 + 4x-1 = 0 $? — Обмен математическим стеком

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

0
+0
Авторизоваться
Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил
4 года, 8 месяцев назад

Просмотрено
4к раз

$ \ begingroup $

Я знаю, что могу легко решить эту проблему с помощью уравнения 4-й степени, но разве нет более разумного способа? Это задача олимпиады, поэтому формула должна быть не формулой, а найти формулу. 2 $$
и разложить на множители.

Создан 06 сен.

Х. Х. Рух Х. Ру

31.1k11 золотых знаков1717 серебряных знаков4545 бронзовых знаков

$ \ endgroup $

$ \ begingroup $

Если вы не хотите полагаться на уловки (хотя уловки всегда полезны), более систематический подход заключается в следующем.2- \ sqrt2 x + 1 + \ sqrt2) $$

Создан 06 сен.

Адхвайта

19.4k11 золотых знаков2020 серебряных знаков4949 бронзовых знаков

$ \ endgroup $

$ \ begingroup $

Есть хитрый способ, поскольку наш многочлен можно легко записать как разность двух квадратов:
$$ (x ^ 2 + 1) ^ 2-2 (x-1) ^ 2 = \ left [x ^ 2 + x \ sqrt {2} + (1- \ sqrt {2}) \ right] \ cdot \ слева [x ^ 2-x \ sqrt {2} + (1+ \ sqrt {2}) \ right] \ tag {1} $$
следовательно, по формуле корней квадратного уравнения корни имеют вид
$$ — \ frac {1} {\ sqrt {2}} \ pm \ sqrt {\ sqrt {2} — \ frac {1} {2}}, \ qquad \ frac {1} {\ sqrt {2}} \ pm i \ sqrt {\ sqrt {2} + \ frac {1} {2}}. \ tag {2} $$

Создан 06 сен.

Джек Д’АурициоJack D’Aurizio

329k3737 золотых знаков339339 серебряных знаков763763 бронзовых знака

$ \ endgroup $

Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie

Настроить параметры

Решение уравнений по факторингу

Решение квадратных уравнений с помощью факторинга

Научиться решать уравнения — одна из наших основных целей в алгебре.До этого момента мы решали линейные уравнения степени 1. В этом разделе мы изучим технику, которую можно использовать для решения некоторых уравнений степени 2. Квадратичное уравнение Полиномиальное уравнение с одной переменной степени 2. — любое уравнение, которое можно записать в стандартной форме Квадратичное уравнение, записанное в виде ax2 + bx + c = 0.

, где a , b и c — действительные числа и ≠ 0. Ниже приведены некоторые примеры квадратных уравнений, все из которых будут решены в этом разделе:

Решение квадратного уравнения в стандартной форме называется корневым решением квадратного уравнения в стандартной форме.. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Квадратное уравнение x2 + x − 6 = 0 имеет два решения, а именно x = −3 и x = 2.

Пример 1: Убедитесь, что x = −3 и x = 2 являются решениями x2 + x − 6 = 0.

Решение: Чтобы проверить решения, подставьте значения для x , а затем упростите, чтобы увидеть, является ли результат истинным.

Ответ: Оба значения дают верные утверждения.Следовательно, они оба являются решениями уравнения.

Наша цель — разработать алгебраические методы нахождения решений квадратных уравнений. Первый метод требует свойства нулевого продукта: любой продукт равен нулю тогда и только тогда, когда хотя бы один из факторов равен нулю .:

Другими словами, если какой-либо продукт равен нулю, то один или оба переменных фактора должны быть равны нулю.

Пример 2: Решите: (x − 8) (x + 7) = 0.

Решение: Это уравнение состоит из произведения двух величин, равных нулю; следовательно, применяется свойство нулевого продукта. Одно или оба количества должны быть равны нулю.

Чтобы убедиться, что это решения, подставьте их вместо переменной x .

Обратите внимание, что каждое решение дает коэффициент, равный нулю.

Ответ: Решения 8 и −7.

Квадратное уравнение не может быть дано в его факторизованной форме.

Пример 3: Решить: x2 + 3x − 10 = 0.

Решение: Цель состоит в том, чтобы произвести продукт, равный нулю. Мы можем сделать это, факторируя трехчлен в левой части уравнения.

Затем примените свойство нулевого произведения и установите каждый коэффициент равным нулю.

Это оставляет нам два линейных уравнения, каждое из которых может быть решено относительно x.

Проверьте решения, подставив их в исходное уравнение, чтобы убедиться, что мы получаем истинные утверждения.

Ответ: Решения — 5 и 2.

Использование свойства нулевого произведения после факторизации квадратного уравнения в стандартной форме является ключом к этой технике. Однако квадратное уравнение не может быть дано в стандартной форме, и поэтому перед факторизацией могут быть предприняты некоторые предварительные шаги.Шаги, необходимые для решения путем факторизации Процесс решения уравнения, равного нулю, путем факторизации и последующего установления каждого переменного множителя равным нулю. описаны в следующем примере.

Пример 4: Решить: 2×2 + 10x + 20 = −3x + 5.

Решение:

Шаг 1: Выразите квадратное уравнение в стандартной форме. Для применения свойства нулевого продукта квадратное выражение должно быть равно нулю.Используйте свойства сложения и вычитания равенства, чтобы объединить противоположные стороны, похожие на члены, и получить ноль на одной стороне уравнения.

В этом примере прибавьте 3x и вычтите 5 с обеих сторон.

Шаг 2: Разложите квадратичное выражение на множители.

Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным нулю.

Шаг 4: Решите полученные линейные уравнения.

Ответ: Решения: −5 и −3/2. Проверка не обязательна.

Пример 5: Решить: 9×2 + 1 = 6x.

Решение: Запишите это в стандартной форме, вычтя 6x с обеих сторон.

После того, как уравнение в стандартной форме равно нулю, коэффициент.

Это трехчлен в виде полного квадрата. Следовательно, установка каждого коэффициента равным нулю приводит к повторному решению.

Повторяющееся решение называется двойным корнем Корень, который повторяется дважды. и не нужно писать дважды.

Ответ: Решение 1/3.

Попробуй! Решите: x2−3x = 28.

Ответ: x = −4 или x = 7

Не все квадратные уравнения в стандартной форме являются трехчленами. Мы часто сталкиваемся с двучленами.

Пример 6: Решите: x2−9 = 0.

Решение: Это квадратное уравнение дается в стандартной форме, где бином в левой части представляет собой разность квадратов. Фактор:

Затем установите каждый коэффициент равным нулю и решите.

Ответ: Решениями являются 3 и −3, которые также можно записать как ± 3.

Пример 7: Решить: 5×2 = 15x.

Решение: Посмотрев, мы видим, что x = 0 является решением этого квадратного уравнения.Поскольку деление на ноль не определено, мы не хотим делить обе части этого уравнения на x . В общем, мы не хотим делить обе части любого уравнения на переменную или выражение, содержащее переменную. Мы обсудим это более подробно позже. Первый шаг — переписать это уравнение в стандартной форме с нулем на одной стороне.

Затем разложите выражение на множители. Обратите внимание, что бином слева имеет GCF 5x.

Установите каждый коэффициент равным нулю.

Ответ: Решения — 0 и 3.

Пример 8: Решите: (2x + 1) (x + 5) = 11.

Решение: Это квадратное уравнение, по-видимому, учитывается; следовательно, может возникнуть соблазн установить каждый коэффициент равным 11. Однако это приведет к неверным результатам. Мы должны переписать уравнение в стандартной форме, равной нулю, чтобы мы могли применить свойство нулевого произведения.

Когда он будет в стандартной форме, мы можем разложить на множители, а затем установить каждый множитель равным нулю.

Ответ: Решения: 1/2 и −6.

Пример 9: Решить: 15×2−25x + 10 = 0.

Решение: Начнем с факторинга GCF 5. Затем разложим полученный трехчлен на множители.

Затем мы устанавливаем каждый переменный коэффициент равным нулю и решаем для x .

Обратите внимание, что коэффициент 5 не является переменным фактором и, следовательно, не влияет на набор решений.

Ответ: Решения 2/3 и 1.

Пример 10: Фактор: 52×2 + 76x − 13 = 0.

Решение: Очистите дроби, умножив обе части уравнения на ЖК-дисплей, который равен 6.

На данный момент у нас есть эквивалентное уравнение с целочисленными коэффициентами, которое можно разложить на множители, как обычно. Начнем с множителей 15 и 2.

Коэффициент при среднем члене равен 7 = 3 (−1) +5 (2).Фактор:

Установите каждый коэффициент равным нулю и решите.

Ответ: Решения — 2/3 и 1/5.

Попробуй! Решить: 4×2−9 = 0.

Ответ: −3/2 и 3/2

Нахождение уравнений с заданными решениями

Состояние нулевого продукта,

И, на самом деле, верно и обратное:

В этом случае мы можем написать следующее:

Мы используем это свойство, чтобы находить уравнения по их решениям.Для этого шаги решения путем факторинга выполняются в обратном порядке.

Пример 11: Найдите квадратное уравнение с решениями −7 и 2.

Решение: Имея решения, мы можем определить два линейных фактора.

Произведение этих линейных множителей равно нулю, когда x = −7 или x = 2:

Умножьте биномы и представьте уравнение в стандартной форме.

Ответ: x2 + 5x − 14 = 0. Мы можем проверить наше уравнение, подставив данные ответы, чтобы увидеть, получим ли мы истинное утверждение. Кроме того, приведенное выше уравнение не является уникальным, поэтому проверка становится важной, когда наше уравнение отличается от чужого. Это оставлено как упражнение.

Пример 12: Найдите квадратное уравнение с целыми коэффициентами, учитывая решения 1/2 и −3/4.

Решение: Чтобы избежать дробных коэффициентов, мы сначала очищаем дроби, умножая обе части на знаменатель.

Примените свойство нулевого произведения и умножьте.

Ответ: 8×2 + 2x − 3 = 0

Попробуй! Найдите квадратное уравнение с целыми коэффициентами при решениях −1 и 2/3.

Ответ: 3×2 + x − 2 = 0

Решение полиномиальных уравнений с помощью факторинга

Свойство нулевого произведения верно для любого числа факторов, составляющих уравнение. Если выражение равно нулю и может быть разложено на линейные коэффициенты, тогда мы сможем установить каждый коэффициент равным нулю и решить для каждого уравнения.

Пример 13: Решить: 3x (x − 5) (3x − 2) = 0.

Решение: Установите каждый переменный коэффициент равным нулю и решите.

Ответ: Решения: 0, 5 и 2/3.

Конечно, нельзя ожидать, что уравнение будет дано в факторизованной форме.

Пример 14: Решите: x3 + 2×2−9x − 18 = 0.

Решение: Начните с полного факторизации левой стороны.

Установите каждый коэффициент равным нулю и решите.

Ответ: Решения: −2, −3 и 3.

Обратите внимание, что степень многочлена равна 3, и мы получили три решения. В общем, для любого полиномиального уравнения с одной переменной степени n  основная теорема алгебры гарантирует, что будет столько же (или меньше) действительных решений многочлена с одной переменной, как его степень.гарантирует n  реальных решений или меньше. Мы видели, что многие полиномы не множатся. Это не означает, что уравнения, включающие эти неактивируемые многочлены, не имеют реальных решений. Фактически, многие полиномиальные уравнения, не учитывающие множители, действительно имеют реальные решения. Мы узнаем, как решать эти типы уравнений, продолжая изучать алгебру.

Попробуй! Решите: −10×3−18×2 + 4x = 0.

Ответ: −2, 0, 1/5

Основные выводы

Многочлен может иметь не более числа решений, равных его степени.Следовательно, квадратные уравнения могут иметь до двух вещественных решений.
Чтобы решить квадратное уравнение, сначала запишите его в стандартной форме. Как только квадратное выражение станет равным нулю, разложите его на множители, а затем установите каждый переменный множитель равным нулю. Решения полученных линейных уравнений являются решениями квадратного уравнения.
Не все квадратные уравнения можно решить с помощью факторизации. Позже в ходе курса мы узнаем, как решать квадратные уравнения, которые не учитываются.
Чтобы найти квадратное уравнение с заданными решениями, выполните процесс решения путем факторизации в обратном порядке.
Если какой-либо полином разложен на линейные множители и установлен на ноль, то мы можем определить решения, установив каждый переменный множитель равным нулю и решив каждый отдельно.

Тематические упражнения

Часть A: Решения квадратных уравнений

Определите, является ли данный набор значений решениями квадратного уравнения.

1. {−3, 5}; х2−2х − 15 = 0

2. {7, −1}; х2−6х − 7 = 0

3. {−1/2, 1/2}; х2−14 = 0

4. {−3/4, 3/4}; х2−916 = 0

5. {−3, 2}; х2-х-6 = 0

6. {−5, 1}; х2−4х − 5 = 0

Решить.

7. (x − 3) (x + 2) = 0

8. (x + 5) (x + 1) = 0

9. (2x − 1) (x − 4) = 0

10.(3x + 1) (3x − 1) = 0

11. (х − 2) 2 = 0

12. (5x + 3) 2 = 0

13. 7x (x − 5) = 0

14. −2x (2x − 3) = 0

15. (x − 12) (x + 34) = 0

16. (x + 58) (x − 38) = 0

17. (14x + 12) (16x − 23) = 0

18. (15x − 3) 2 = 0

19. −5 (x + 1) (x − 2) = 0

20. 12 (x − 7) (x − 6) = 0

21. (x + 5) (x − 1) = 0

22.(х + 5) (х + 1) = 0

23. −2 (3x − 2) (2x + 5) = 0

24. 5 (7x − 8) 2 = 0

Часть B: Решить с помощью факторинга

Решить.

25. x2 − x − 6 = 0

26. x2 + 3x − 10 = 0

27. y2−10y + 24 = 0

28. y2 + 6y − 27 = 0

29. x2−14x + 40 = 0

30. x2 + 14x + 49 = 0

31. x2−10x + 25 = 0

32.3×2 + 2x − 1 = 0

33. 5×2−9x − 2 = 0

34. 7y2 + 20y − 3 = 0

35. 9×2−42x + 49 = 0

36. 25×2 + 30x + 9 = 0

37. 2y2 + y − 3 = 0

38. 7×2−11x − 6 = 0

39. 2×2 = −15x + 8

40. 8x − 5 = 3×2

41. x2−36 = 0

42. x2−100 = 0

43. 4×2-81 = 0

44. 49×2−4 = 0

45.х2 = 4

46. 9y2 = 1

47. 16y2 = 25

48,36×2 = 25

49. 4×2−36 = 0

50. 2×2−18 = 0

51. 10×2 + 20x = 0

52. −3×2 + 6x = 0

53. 25×2 = 50x

54. х2 = 0

55. (x + 1) 2−25 = 0

56. (x − 2) 2−36 = 0

57. 5x (x − 4) = — 4 + x

58.(x − 1) (x − 10) = 22

59. (x − 3) (x − 5) = 24

60. −2x (x − 9) = x + 21

61. (x + 1) (6x + 1) = 2x

62. (x − 2) (x + 12) = 15x

63. (х + 1) (х + 2) = 2 (х + 16)

64. (x − 9) (2x + 3) = 2 (x − 9)

Очистите дроби, сначала умножив обе части на ЖК-дисплей, а затем решив.

65. 115×2 + 13x + 25 = 0

66. 114×2−12x + 37 = 0

67.32×2−23 = 0

68. 52×2−110 = 0

69. 314×2−212 = 0

70. 13×2−15x = 0

71. 132×2−12x + 2 = 0

72. 13×2 + 56x − 12 = 0

73. Стороны квадрата имеют размер x + 3 единицы. Если площадь составляет 25 квадратных единиц, найдите x .

74. Высота треугольника на 2 единицы больше его основания. Если площадь 40 квадратных единиц, то найдите длину основания.

75. Стороны прямоугольного треугольника имеют меры, являющиеся последовательными целыми числами. Найдите длину гипотенузы. (Подсказка: гипотенуза — самая длинная сторона. Примените теорему Пифагора.)

76. Прибыль в долларах от производства и продажи нестандартных ламп размером x определяется функцией P (x) = — 10×2 + 800x − 12000. Сколько ламп нужно продать и произвести, чтобы обеспечить безубыточность? (Подсказка: мы выходим на уровень безубыточности, когда прибыль равна нулю.)

Предполагая сухие дорожные условия и среднее время реакции, безопасный тормозной путь, d футов среднего автомобиля, определяется по формуле d = 120v2 + v , где v представляет скорость машина в милях в час.Для каждой приведенной ниже проблемы, учитывая тормозной путь, определите безопасную скорость.

77.15 футов

78. 40 футов

79. 75 футов

80. 120 футов

Часть C: Нахождение уравнений с заданными решениями

Найдите квадратное уравнение с целыми коэффициентами, имея следующие решения.

81. −3, 1

82.−5, 3

83. −10, −3

84. −7, −4

85. −1, 0

86,0, 3/5

87. −2, 2

88. −1/2, 1/2

89. −4, 1/3

90,2/3, 2/5

91. −1/5, −2/3

92. −3/2, 3/4

93,3, двойной корень

94. −5, двойной корень

Часть D: Решение полиномиальных уравнений

Решить.

95. 7x (x + 5) (x − 9) = 0

96. (x − 1) (x − 2) (x − 3) = 0

97. −2x (x − 10) (x − 1) = 0

98. 8x (x − 4) 2 = 0

99. 4 (x + 3) (x − 2) (x + 1) = 0

100. −2 (3x + 1) (3x − 1) (x − 1) (x + 1) = 0

101. x3 − x2−2x = 0

102. 2×3 + 5×2−3x = 0

103. 5×3−15×2 + 10x = 0

104. −2×3 + 2×2 + 12x = 0

105.3×3−27x = 0

106. −2×3 + 8x = 0

107. x3 + x2 − x − 1 = 0

108. x3 + 2×2−16x − 32 = 0

109. 8×3−4×2−18x + 9 = 0

110. 12×3 = 27x

Часть E: Темы дискуссионной доски

111. Объясните, почему 2 (x + 5) (x − 5) = 0 имеет два решения, а 2x (x + 5) (x − 5) = 0 имеет три решения.

112. Составьте собственное квадратное уравнение и разместите его вместе с решениями на доске обсуждений.

113. Объясните своими словами, как решить квадратное уравнение в стандартной форме.

ответов

1: Есть

3: Есть

5: Нет

7: -2, 3

9: 1/2, 4

11: 2

13: 0, 5

15: −3/4, 1/2

17: -2, 4

19: -1, 2

21: −5, 1

23: −5/2, 2/3

25: -2, 3

27: 4, 6

29: 4, 10

31: 5

33: -1/5, 2

35: 7/3

37: −3/2, 1

39: −8, ½

41: −6, 6

43: −9/2, 9/2

45: -2, 2

47: −5/4, 5/4

49: −3, 3

51: -2, 0

53: 0, 2

55: −6, 4

57: 1/5, 4

59: -1, 9

61: -1/2, -1/3

63: −6, 5

65: −3, −2

67: −2/3, 2/3

69: ± 7

71: 8

73: 2 шт.

75: 5 шт.

77: 10 миль в час

79: 30 миль в час

81: x2 + 2x − 3 = 0

83: x2 + 13x + 30 = 0

85: х2 + х = 0

87: x2−4 = 0

89: 3×2 + 11x − 4 = 0

91: 15×2 + 13x + 2 = 0

93: x2−6x + 9 = 0

95: −5, 0, 9

97: 0, 1, 10

99: −3, −1, 2

101: -1, 0, 2

103: 0, 1, 2

105: −3, 0, 3

107: -1, 1

109: −3/2, 1/2, 3/2

Решите квадратные уравнения по квадратичной формуле — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

Решите квадратные уравнения, используя формулу корней квадратного уравнения
Используйте дискриминант, чтобы предсказать количество решений квадратного уравнения
Определите наиболее подходящий метод решения квадратного уравнения

Перед тем, как начать, пройдите тест на готовность.

Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).

Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз предпринимали одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ — «да». В этом разделе мы выведем и воспользуемся формулой, чтобы найти решение проблемы. квадратное уровненеие.

Мы уже видели, как решить формулу для конкретной переменной «в целом», чтобы мы выполняли алгебраические шаги только один раз, а затем использовали новую формулу для нахождения значения конкретной переменной. Теперь мы рассмотрим этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x . Возможно, будет полезно взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение формы, когда вы читаете алгебраические шаги ниже, поэтому вы видите их как с числами, так и со словом «в целом».’

Последнее уравнение — квадратичная формула.

Квадратичная формула

Решения квадратного уравнения вида даются формулой:

Чтобы использовать квадратичную формулу, мы подставляем значения в выражение в правой части формулы. Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения.

Как решить квадратное уравнение с помощью квадратной формулы