|
|
Цель урока: создать условия для формирования умения решения задач с помощью уравнения. Задачи урока: -выявить основные правила решения задач способом составления уравнений, -познакомить с алгоритмом решения задач способом составления уравнений; -содействовать развитию навыков сотрудничества, самоконтроля; -совершенствовать навыки решения уравнений; -развивать умение анализировать и рассуждать; -закреплять вычислительные навыки. Планируемые результаты: Знать алгоритм решения задач с помощью уравнений. Формирование УУД: Личностные: использовать усвоенные приёмы работы для решения учебной задачи, осуществлять самоконтроль при выполнении заданий, Осознать необходимость самосовершенствования, положительного отношения к процессу познания, применять правила сотрудничества Регулятивные: планировать и принимать учебную задачу, составлять план действий, оценивать и корректировать свои действия Коммуникативные: участвовать в учебном диалоге, воспринимать различные точки зрения, сотрудничать с учащимися и учителем, выражать свою точку зрения, работать в паре и группе Познавательные: воспроизводить по памяти информацию, необходимую для решения учебной задачи, находить дополнительную информацию, обсуждать проблемные вопросы, сформировать умения при решении задач и уравнений работать со схемой Оборудование: ПК, проектор, интерактивная доска, презентация, карточки, экран настроения, экран успеха, жетоны-цветы, памятка с алгоритмом. Дата проведения: 7 апреля 2015 г
|
«Решение задач на составление уравнений»
Урок математики в 6-м классе по теме
«Решение задач на составление уравнений»
Цель деятельности учителя: создать условия для формирования навыков решения задач на составление уравнений.
Планируемые результаты изучения темы:
Личностные: осознают причины успеха/неуспеха учебной деятельности; понимают важность и необходимость знаний для человека.
Предметные: умеют составлять математическую модель реальной ситуации, решать уравнение по правилам.
Метапредметные результаты изучения темы (универсальные учебные действия):
познавательные: владеют общим приемом решения задач; умеют проводить информационно-смысловой анализ текста, приводить примеры;
регулятивные: различают способ и результат действия;
коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
Оборудование: компьютер, мультимедийный проектор.
Дидактические материалы:
Учебник авт.
 И.И. Зубарева, А.Г. Мордкович “Математика. 6 класс”. М.: Мнемозина, 2009 г.
И.И. Зубарева, А.Г. Мордкович “Математика. 6 класс”. М.: Мнемозина, 2009 г.И.И.Зубарева, М.С.Мильштейн, В.Г.Гамбарин “Мультимедийное приложение” к учебникам “Математика, 5 класс”, “Математика, 6 класс” авторов И.И.Зубаревой, А.Г.Мордковича.
Компьютерная презентация урока в POWER POINT.
Сценарий урока.
Организационный этап
Добрый день, присаживайтесь!
Этап актуализация знаний.
– Ребята. Сегодня у нас необычный урок. Мы начнём знакомство с основами математического моделирования. Узнаем, как моделирование помогает решать задачи. С моделями мы встречаемся с детства. (Примеры приводят ученики) (Слайд №1)
“Откроем тетради, запишем тему урока. В начале урока не забудьте нарисовать в тетради смайлик. Какое у вас настроение?” Вы привели несколько примеров различных моделей. Но мы будем говорить о математических моделях.
Математическая модель является приближенным представлением реальных объектов, процессов, выраженных в математических терминах и сохраняющим существенные черты оригинала. (Слайд №2)
Построение математической модели заключается в определении связей между теми или иными процессами и явлениями.
Математическое моделирование – это средство изучения реального объекта, процесса или системы путем их замены математической моделью.
– Сегодня на уроке мы научимся использовать математическое моделирование для решения задач.
Слайд №3 «Для начала мы начнем с разминки» (работа в парах с взаимной проверкой по образцу)
Один ученик получает индивидуальное задание на карточке:
Реши задачу: Мастер и ученик вместе за 1 час изготовили 120 деталей. Сколько деталей изготовил ученик за 1 час, если мастер сделал на 20 деталей больше?
Этап изучение нового материала
На прошлых уроках вы учились решать уравнения. А сегодня будите учиться решать задачи при помощи уравнения.
А сегодня будите учиться решать задачи при помощи уравнения.
Прочитаем задачу (Слайд №4)
Мастер и ученик вместе за 1 час изготовили 120 деталей. Сколько деталей изготовил ученик за 1 час, если мастер сделал на 20 деталей больше?
Решая задачи в 5 классе, с чего вы начинали? (рисовали схемы, исходя из условия задачи), т.е. переводили текст задачи на математический язык и получали математическую модель ситуации.
Ученик, работавший по карточке, объясняет решение задачи:
Ученик — ?
Мастер – на 20 деталей больше
120-20 = 100 (дет.) – делает мастер и ученик
100: 2 = 50 (дет.) – делает ученик за 1 час
Ответ: 50 деталей
Но, кроме такого способа решения задач, существует еще один способ решения таких задач. И я вам сейчас о нем расскажу. В задачах, в которых обе величины неизвестны, одну из них обозначают переменной (чаще всего это меньшая из двух величин).
Составляем краткую запись в виде таблицы.
Итак получаем уравнение.
х+х+20 = 120
Решаем, полученное уравнение и получаем ответ на вопрос задачи.
Итак, решим еще одну задачу(слайд №5)
В классе 24 ученика. Известно, что девочек в 2 раза меньше, чем мальчиков. Сколько девочек и сколько мальчиков в классе?
Мальчики — ?
Девочки — ?, в 2 раза меньше, чем мальчиков
Девочек в два раза меньше, чем мальчиков. Отсюда, одна часть учащихся – девочки, а еще две такие части приходится на мальчиков.
1 + 2 = 3 (части) – приходится на всех учеников класса;
24 : 3 = 8 (уч.) – девочки;
24 — 8 = 16(уч.) –мальчики.
Ответ : 8 девочек, 16 мальчиков.
Решим эту задачу другим способом.
Пусть х девочек в классе, тогда 2х — мальчиков.
Зная, что всего в классе 24 ученика, имеем уравнение:
2х + х = 24;
3х = 24;
х = 24:3;
х = 8.
8 девочек в классе;
24 – 8 = 16 мальчиков.
Ответ : 8 девочек, 16 мальчиков.
Сравните эти две задачи и назовите, что у них общего. Вывод делают ученики.
При решении задач: 1) Составили краткую запись, 2) Составили уравнение, 3) Решили уравнение и 4) Записали ответ.
Открываем учебники п.20, читаем «Проверь себя!» и делаем вывод.
Этап первичное осмысление и закрепление знаний
Слайд №6. Выполнение № 595(у доски и в тетради)
Физминутка (проводит физорг класса)
Дети, повторяйте: хлопать начинайте,
Дружно наклоняйтесь. Дружно покачайтесь.
Вместе покивайте, вместе поморгайте,
Ручки вы потрите, ручкой помашите!
(Читает стишок и все вместе выполняют то, что в нём говорится)
Этап закрепление изученного материала
Работа в парах. Выполните № 596 самостоятельно. По окончании поменяйтесь тетрадями с соседом и проверьте. Один ученик работает за доской.
Выполните № 596 самостоятельно. По окончании поменяйтесь тетрадями с соседом и проверьте. Один ученик работает за доской.
Решение:
Составление математической модели
х+21,6 = (х+3,4)•3
Работа с математической моделью.
1) х – 3х = 10,2 – 21,6
-2х=-11,4
х = (-11,4):-2
х =5,7 (м) – глубина 1 скважины
2) 5,7+3,4 = 9,1 (м) – глубина 2 скважины
Ответ на вопрос задачи.
Ответ: 5,7м, 9,1м.
7. Этап подведение итогов. Домашнее задание.
— Наш урок подходит к концу, с начала запишем домашнее задание, затем подведем итоги.
На доске: Домашнее задание: П. 20, № 594(разобрать по учебнику), №597, тетрадь для см.р. стр. 73, упр. 3.
— А теперь подведем итоги: Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы?
— Достигли ли вы поставленной цели?
— Давайте еще раз вспомним, как решить задачу с помощью уравнения? (Выделить три этапа математического моделирования)
Оценки за урок.
— Итог урока каждый из вас подведет с помощью телеграммы; то есть в виде одного краткого предложения, которое выразит ваше отношение к уроку
“Всем спасибо, урок окончен!”
Урок математики 4 класс Решение задач с помощью составления уравнения. Решение уравнений. Закрепление. День Независимости.
Прощалыгина Евгения Викторовна
Учитель начальных классов
ГУ «Школа – гимназия № 113»
Образование – высшее, КАЗНПУ
им . Абая
Педагогический стаж – 30 лет
Квалификационная категория – высшая.
Мое хобби — чтение научно – популярной и художественной литературы, периодики, интернет, домашние животные, туризм.
Мое педагогическое кредо – «Плохой учитель преподносит истину, хороший учит ее находить». А. Дистервег.
Я работаю учителем потому, что «Призвание учителя есть призвание высокое и благородное. Но не тот учитель, кто получает воспитание и образование учителя, а тот, у кого есть внутренняя удовлетворенность в том, что он есть, должен быть и не может быть иным».
Л.Н.Толстой.
Урок: математики 4 класс
Тема урока: Решение задач с помощью составления уравнения. Решение уравнений. Закрепление. День Независимости.
Цели урока:
образовательная: совершенствовать умения учащихся решать задачи с помощью составления уравнения.
развивающая: развитие умения анализировать и решать логические задачи.
воспитывающая: прививать чувство патриотизма, интерес к обычаям и традициям казахского народа.
Тип урока: Совершенствование знаний и способов деятельности.
Форма организации урока: заочное путешествие по карте Республики Казахстан
Дидактическое обеспечение урока: учебник, пропись, карточки для устного счета, карта Республики Казахстан, иллюстрации с изображением достопримечательностей нашей страны.
Ход урока
Организационный этап:
1. Обеспечение нормальной внешней обстановки для работы на уроке.
2. Психологически подготовить учащихся к общению:
— Сегодня у нас необычный урок. Мы отправимся с вами в путешествие по нашей стране, по карте Казахстана. Для этого нужно разделиться на 3 команды. Каждая команда выберет себе капитана и название команды. А наши гости будут представлять жюри. Они будут оценивать ваши ответы и подсчитывать балы.
2. Актуализация знаний.
Актуализировать субъектный опыт учащихся (опорные знания)
Чтобы узнать, какому празднику будет посвящен наш урок, нужно решить выражение, а ответы помогут нам найти название:
Устный счет
«Н » 3*100 = «А» 23*1000 = «С» 2000:100 = «О» 23400: 234 = «И» 2340: 10 =
«Е» 13000:1000 = «В» 1000: 500 = «И» 234000: 1000 = «С»1600: 800 =
«З» 234*10 = «И» 23400:100 = «М» 27000:100 = «Т» 2000: 400 =
н
в
з
а
е
и
т
о
с
м
300
2
2340
23000
13
234
5
100
20
270
— Какой праздник будет отмечать наша страна?
— День Независимости
— Что вы знаете об этом празднике?
— День Независимости Казахстана – высший государственный праздник страны. 16 декабря 1991 года Верховный Совет принял закон о независимости и государственном суверенитете Казахстана. Этот день считается днем памяти жертв декабрьских событий 1986 года. (На доске записываются числа 1991 и 1986)
16 декабря 1991 года Верховный Совет принял закон о независимости и государственном суверенитете Казахстана. Этот день считается днем памяти жертв декабрьских событий 1986 года. (На доске записываются числа 1991 и 1986)
Задача: Совместное с учащимися планирование работы на уроке.
Сегодня на уроке вы расскажете о достопримечательностях нашего государства и решите математические задания, а жюри будет подсчитывать очки.
3. Применение. Формирование умений и навыков.
Задание №1: Работа в тетради:
Выполнить в тетради каллиграфическую минутку. Прописать числа 1991 и 1986, дать характеристику этих чисел.
Задание № 2
Задача: применение изученного материала с учетом применения знаний о достопримечательностях Казахстана.
Первым пунктом нашего путешествия будет озеро Балхаш. Что вы можете о нем рассказать? Покажите его на карте. Сообщение ученика о достопримечательностях озера Балхаш.
Сообщение ученика о достопримечательностях озера Балхаш.
Балхаш (каз. Балқаш) — бессточное полупресноводное озеро в восточной части Казахстана, второе по величине непересыхающее солёное озеро (после Каспийского моря) и 13-е в списке крупнейших озёр в мире. Уникальность озера состоит в том, что оно разделено узким проливом на две части с различными химическими характеристиками воды — в западной части она практически пресная, а в восточной — солоноватая.Балхаш» происходит от слова «balkas»
татарского, казахского и алтайского языков, которое означает «болотистая местность, покрытая кочками» или «кочки на болоте» Согласно легенде о происхождении озера, у богатого чародея Балхаша была красавица-дочь Или. Когда пришло время выдавать Или замуж, Балхаш объявил, что выдаст её только за самого богатого, красивого и сильного.Однако был среди пожелавших попытать счастье и бедный пастух Каратал, который сразу же понравился невесте. После состязаний, из которых Каратал вышел победителем, Балхаш с негодованием выгнал его. Однако Или ночью сбежала из родного дома и ускакала с избранником от злого отца. Узнав о побеге дочери, Балхаш наложил заклятие на возлюбленных, и они превратились в две реки, стремительно несущие свои воды с гор. А чтобы реки никогда не соединились, Балхаш упал между ними и стал седым от пенных волн озером.
После состязаний, из которых Каратал вышел победителем, Балхаш с негодованием выгнал его. Однако Или ночью сбежала из родного дома и ускакала с избранником от злого отца. Узнав о побеге дочери, Балхаш наложил заклятие на возлюбленных, и они превратились в две реки, стремительно несущие свои воды с гор. А чтобы реки никогда не соединились, Балхаш упал между ними и стал седым от пенных волн озером.
Задание для первой команды. Закрепление умения детей решать задачи с помощью составления выражения.
Отправимся мы с вами туда на поезде со скоростью 40 км/час. Но нам навстречу едет другой поезд со скоростью 50 км/час. Через 40 часов они встретятся. Найдите расстояние между Алматы и Балхашом.
Решение задачи: (40+50)*40 =3600 (км)
Вторая станция: Аральское море. Что вы о нем знаете? Ара́льское море — бывшее бессточное солёное озеро в Средней Азии, на границе Казахстана и Узбекистана. С 1960-х годов XX века уровень моря (и объём воды в нём) стал быстро снижаться вследствие забора воды из основных питающих рек Амударья и Сырдарья с целью орошения, в 1989 году море распалось на два изолированных водоёма — Северное (Малое) и Южное (Большое) Аральское море.До начала обмеления Аральское море было четвёртым по величине озером в мире. Коллекторно-дренажные воды, поступающие с полей в русло Сырдарьи и Амударьи, стали причиной отложений из пестицидов и различных других сельскохозяйственных ядохимикатов, появляющихся местами на 54 тыс. км² бывшего морского дна, покрытого солью. Пыльные бури разносят соль, пыль и ядохимикаты на расстояние до 500 км. Бикарбонат натрия, хлорид натрия и сульфат натрия переносятся по воздуху и уничтожают или замедляют развитие естественной растительности и сельскохозяйственных культур.
Задание № 3 Задание для второй команды. Закрепление умения детей решать задачи при помощи составления уравнения:
В 1965 году объем Арала составлял 1070 км3 В. 2005 году объем уменьшился в 10 раз. Какой объем стал у Арала?
Решение: х*10 = 1070
х = 107 (м3)
Третья станция Байконур. Что вы о нем знаете?
Байкону́р (с каз. Байқоңыр — плодородная земля). Космодром «Байконур» — первый и крупнейший[1] в мире космодром, расположен на территории Казахстана, недалеко от поселка Тюратам. Занимает площадь 6717 км². Космодром имеет большое международное значение. С космодрома возможны запуски различных типов ракет-носителей. Один из трёх космодромов планеты, наряду с космодромами Мыс Канаверал в США и Цзюцюань в Китае, предназначенных для запуска аппаратов с космонавтами на борту. Орбита МКС была подоб-
с учётом широты Байконура — с него производятся основные запуски. «Байконур» начал строиться 12 февраля 1955 года (принятое 12 февраля 1955 года постановление Правительства СССР о строительстве полигона для проведения испытаний межконтинентальных баллистических ракет), стал космодромом в 1957. В 1970-1980-х являлся крупнейшим космодромом Советского Союза. После распада СССР в начале 1990-х космодром отошёл Казахстану. Арендуется Россией до 2050 года. Парламент Казахстана ратифицировал соглашение о продлении договора аренды до 2050 года в апреле 2010 года (соглашение было подписано президентами РФ и РК ещё в 2004 году).
Задание № 4 Задание для третьей команды. Закрепление умения детей решать выражения на внетабличное умножение и деление с комментированием.
Ученые, работающие на этой станции, прежде чем запустить космический корабль решают очень сложные задачи. Давайте и мы с вами попробуем решить выражение, состоящее из трех действий:
491645: 5 – 81208 : 8 = 88378
Дети определяют порядок действий и решают выражение по действиям с комментированием.
Четвертая станция — Астана. Что вы знаете об этом городе?
Уникальный город, сочетающий и восточную, и западную культуры, гордость Республики. Новой столицей Казахстана Астана стала в 1997 году, когда предложение Президента Назарбаева о переносе получило всеобщую поддержку. Причины переноса – важное геополитическое положение города, развитые коммуникационная и транспортная инфраструктуры, свободные земли для роста. Перенос столицы Казахстана в Астану ознаменовал новый этап в развитии города. Именно Астана стала государственным центром культурной, политической и общественной жизни. В 1999 г. Астана была удостоена премии Юнеско «Город мира», а в 2003 столицу отметило знаменитое мировое рейтинговое агентство Moody`s Investors Service. Так, город стал важным элементом «казахстанского бренда» и вошел в список 30 лучших мировых городов.
Задание № 5 Конкурс капитанов. Закрепить умение детей решать сложные уравнения с комментированием.
х*10 = 7890 – 890 40*6 + х = 9400 х- 560 : 7 = 20000
Пятая станция – город Алматы. Что вы знаете об этом городе?
С 1927 по 1936 год Алма-Ата была столицей Казахской АССР, с 1936 по 1991 годы столицей Казахской ССР, с 1991 по 1997 годы столицей Республики Казахстан. Алма-Ата была последней столицей и крупнейшим городом Казахской ССР, затем стала первой столицей и крупнейшим городом Республики Казахстан. Несмотря на утрату статуса
политико-административной столицы, город является культурным и финансово-экономическим центром республики, остаётся единственным городом-миллионером страны. Город расположен у подножия гор Заилийского Алатау на крайнем юго-востоке республики и имеет своеобразный, довольно мягкий климатический режим с непростой экологической ситуацией. В 1997 году столицу перенесли в Акмолу (с 6 мая 1998 — Астана), однако за Алма-Атой закрепляется статус Южной столицы Казахстана.
Задание № 6 Веселая разминка – соревнование между командами.
Закрепить умение детей устно решать сложные выражения на внетабличное умножение и деление, соблюдая порядок действий.
Каждой команде учитель раздает листы с заданием. Команда, которая выполнит задание первой, отдает лист жюри.
900: 3*2 = 900 : (3*2) =
(900 + 100) : 2 = 900 + 100 : 2 =
(900 — 100) * 2 = 900 – 100 * 2 =
4.Этап информации о домашнем задании:
Составить и решить сложные уравнения на нахождение неизвестного множителя и делимого.
5. Подведение итогов:
— Ребята, какие интересные задания вы выполнили на уроке?
— Какие стихи о Родине вы знаете?
Жюри подсчитывает баллы, дети читают стихи.
6. Рефлексия
— Ребята, что вам особенно понравилось на уроке? Реализация рефлексивного алгоритма: «Я», «Мы», «Дело»
1. Награждение команд 2.Угощение гостей. Казахский народный обычай: «Ша-шу».
Урок математики в 4 классе «Решение задач на движение с помощью уравнений»
Тема: Решение задач на движение с помощью уравнения.
Цель: Познакомить учащихся с решением задач на движение с помощью уравнений.
Совершенствовать навыки составления уравнений.
Умение решать уравнения усложненной структуры.
Развивать умение анализировать и обобщать.
Ход урока
1. Орг. момент
2. Актуализация опорных знаний
1) Игра «Шифровальщик»
Цель игры : Совершенствовать навыки устных вычислений в пределах 100:
а 164-8 220+135 е 44*2 н
у 160+40 58+9 р
н 90-2 200-120 и
е 102+18 60*2 е
200 | 67 | 156 | 355 | 88 | 120 | 88 | 80 | 120 |
Расшифруй тему урока
2) Составьте и решите уравнение
а) Андрей придумал задание : « Я загадал число, увеличил его в 20 раз и получил 800, какое число я задумал?»
б) Алина придумала задание : « Я загадала число, увеличила его в 20 раз, прибавила 100 и получила 900, какое число я задумала?»
в) Число 11 увеличить в 30 раз
г) Произведение чисел 10 и 20 увеличить на 100.
Вопросы: Какую из записей можно назвать уравнением?
Что такое уравнение?
Что значит решить уравнение?
3. Сообщение темы: Сегодня мы будем составлять и решать задачи с помощью уравнения.
4. Работа по книге
Зад. №1 – устно
Зад. №2 Прочитайте условия задач
Майский жук пролетел путь длиной 39 км за 3 часа. За сколько часов при такой же скорости майский жук пролетит путь длиной 65 км?
1) – О чем говорится в задаче?
— Что надо узнать в задаче? 1. За сколько часов пролетит майский жук? Можно ответить на вопрос задачи? Почему нам надо знать скорость жука?
За 3 часа – 39 км
За х ч — 65 км
Учитель объясняет: при решении задачи уравнением, надо определить вопрос задачи и обозначить неизвестное число.
Решение: Скорость жука равна 39:3 км/ч
Длина пути майского жука 65 км, этот путь надо пролететь за х ч. Тогда скорость равна 65:х км/ч. Получим уравнение :
39 : 3 = 65 : х
13=65 : х
х=65:13
х=5
Ответ: Майский жук пролетит путь длиной 65 км за 5 часов.
Дети приходят к выводу, что задачи можно решать разными способами.
5. Закрепление
1) Самостоятельная работа №2(б). Учитель предлагает решить задачу разными способами.
Рак полз 3 минуты со скоростью 18м/мин. С какой скоростью рак проползёт столько же метров пути за 9 минут?
2) Работа в парах №4
Запиши в сантиметрах: Запиши в граммах:
38м25см = 6кг600г =
162м 54см 18кг 750г =
70м 5см = 30кг 50г =
6. Работа над изученным материалом
3) Решение задачи №6
За 8с ёжик пробежал путь длиной 18м, а на обратном пути скорость была в 2 раза меньше. С какой скоростью ёжик бежал на обратном пути?
4) вычисли:
1538*2= 2025*5= 3699:3= 6555:5=
7. Рефлексия. Подведение итогов урока.
Д/з №7,8
200 | 67 | 156 | 355 | 88 | 120 | 88 | 80 | 120 |
Зад. №2 Прочитайте условия задач
Майский жук пролетел путь длиной 39 км за 3 часа. За сколько часов при такой же скорости майский жук пролетит путь длиной 65 км?
Зад.№3. Самостоятельная работа №2(б).
Рак полз 3 минуты со скоростью 18м/мин. С какой скоростью рак проползёт столько же метров пути за 9 минут?
4) Работа в парах
Запиши в сантиметрах: Запиши в граммах:
38м25см = 6кг600г =
162м 54см 18кг 750г =
70м 5см = 30кг 50г =
5) Решение задачи
За 8с ёжик пробежал путь длиной 18м, а на обратном пути скорость была в 2 раза меньше. С какой скоростью ёжик бежал на обратном пути?
6) вычисли:
1538*2= 2025*5= 3699:3= 6555:5=
Д.з. 1. Выполни действия, расписывая каждое действие столбиком! 849 +(705-450) :5= 6*(115 -21) + 721= 2. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? | Д.з. 1. Выполни действия, расписывая каждое действие столбиком! 849 +(705-450) :5= 6*(115 -21) + 721= 2. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? |
Д.з. 1. Выполни действия, расписывая каждое действие столбиком! 849 +(705-450) :5= 6*(115 -21) + 721= 2. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? | Д.з. 1. Выполни действия, расписывая каждое действие столбиком! 849 +(705-450) :5= 6*(115 -21) + 721= 2. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? |
Д.з. 1. Выполни действия, расписывая каждое действие столбиком! 849 +(705-450) :5= 6*(115 -21) + 721= 2. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? | Д.з. 1. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? |
Д.з. 1. Выполни действия, расписывая каждое действие столбиком! 849 +(705-450) :5= 6*(115 -21) + 721= 2. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? | Д.з. 1. Реши задачу с помощью уравнения: От деревни до районного центра автобус ехал 8ч со скоростью 48км/ч, а на обратном пути его скорость была 32 км/ч. За какое время автобус доехал от районного центра до деревни? |
Решение сложных уравнений (4 класс)
Слайды и текст этой онлайн презентации
Слайд 1
Урок математики 4 класс
учитель начальных классов
Сыроватская Л.Н.
МБОУ «Жиганская средняя общеобразовательная школа»
с.Жиганск – 2015 г.
Слайд 2
Математику, друзья, Не любить никак нельзя. Очень точная наука, Очень строгая наука, Интересная наука – Это математика!
Слайд 3
Устный счёт
70
70 с
15 ц
580
54
170
121
270
12 · 3 + 10
8 дм70 см = … см
5600
(30 – 9) : 3
46 + у =100
у + 23 = 50
увеличить
56 в 10 раз
1мин 10с = … с
60 – 12 :(4+2)
уменьшить
в 10 раз
число 170
Слайд 4
38 х 1 = 38 х +15 = 68 : 2 х + 34 = 50 30 > 6 х 4 2 х 4 Равенства
38 х 1 = 38
57+ 30 = 87
Уравнения
х+34=50
х +15 =68:2
Неравенства
30 > 6 х 4
2 х 4
Слайд 5
Алгоритм решения простого уравнения
х+34=50
34 — слагаемое
50 — сумма
х — слагаемое
х=50-34
х=16
____________
16+34=50
50=50
Слайд 6
Тема урока Решение сложных уравнений
Х
+
15
=
68
:
2
Х+ 15 = 34
Х = 34 — 15
Х = 19
19 + 15 = 68 : 2
34 = 34
Слайд 7
Танцевальная физминутка
Слайд 8
29+у=7х5
29+у=35
у=35-29
у=6
29+6=7х5
35=35
_________
1.Определяем неизвестный компонент.
2.Решаем правую часть и записываем ответ.
3.Решаем как простое уравнение, в котором неизвестно второе слагаемое.
4.Для этого вычтем из суммы 35 первое слагаемое 29
5.Записываем ответ уравнения 6.
6.Выполняем проверку: вместо неизвестного компонента подставляем его значение.
7.Равенство верное так как и в левой и правой части получаем 35.
Алгоритм решения сложного уравнения
Слайд 9
46-х=90-82
46-х=8
х=46-8
у=38
46-38=90-82
8=8
_________
1.Определяем неизвестный компонент.
2.Решаем правую часть и записываем ответ.
3.Решаем как простое уравнение, в котором неизвестно вычитаемое.
4.Для этого вычтем из уменьшаемого 46 разность 8
5.Записываем ответ уравнения 38.
6.Выполняем проверку: вместо неизвестного компонента подставляем его значение.
7.Равенство верное так как и в левой и правой части получаем 8.
Слайд 10
Самостоятельная работа
Х+24=67-33
Слайд 11
Рассуждаем…
Лягушка встречала гостей. Осёл пришёл раньше Барана, Волк позже Зайца, Баран раньше Зайца, Ёжик позже Волка. В каком порядке пришли гости?
Слайд 12
х+35=100-40
Домашнее задание
Слайд 13
Молодцы!
Слайд 14
Урок 54-55 Тема: Решение задачи на движение с помощью уравнения | Поурочные планы по математике 4 класс (Атамура)
Урок 54-55 Тема: Решение задачи на движение с помощью уравнения
27.05.2013
16234
0
Цель: Познакомить учащихся с решением задач на движение с помощью уравнений.
Совершенствовать
навыки составления уравнений.
Умение решать
уравнения усложненной структуры.
Развивать умение
анализировать и обобщать.
Ход урока
1.
Орг. момент
– Математику, друзья,
Не любить никак нельзя.
Очень строгая наука,
Очень точная наука.
Интересная наука –
Это математика!
2.
Актуализация опорных знаний
1)
Игра «Шифровальщик»
Цель игры :
Совершенствовать навыки устных вычислений в пределах 100:
а 164-8
220+135 е 44*2 н
у 160+40 58+9 р
н 90-2 200-120 и
е 102+18
60*2 е
200 | 67 | 156 | 355 | 88 | 120 | 88 | 80 | 120 |
у | р | а | в | н | е | н | и | е |
Расшифруй тему урока
2)
Составьте и решите уравнение
а) Андрей
придумал задание : « Я загадал число, увеличил
его в 20 раз и получил 800, какое число я задумал?»
б) Алина придумала задание : « Я
загадала число, увеличила его в 20
раз, прибавила 100 и получила 900, какое число я задумала?»
в) Число 11
увеличить в 30 раз
г) Произведение
чисел 10 и 20 увеличить на 100.
Вопросы: Какую из
записей можно назвать уравнением?
Что такое уравнение?
Что значит решить уравнение?
3.
Сообщение темы: Сегодня мы будем составлять и решать
задачи с помощью уравнения.
4.
Работа по книге
Зад. №1 – устно
Зад. №2 Прочитайте условия задачи
1)
– О чем говорится в задаче?
— Что надо
узнать в задаче? 1. За сколько часов пролетит майский жук? Можно ответить на
вопрос задачи? Почему нам надо знать скорость жука?
За 3 часа – 39 км
За х ч — 65 км
Учитель
объясняет: при решении задачи уравнением, надо определить вопрос задачи и обозначить неизвестное число.
Решение: Скорость жука равна 39:3 км/ч
Длина пути
майского жука 65 км,
этот путь надо проехать за х ч. Тогда
скорость равна 65:х км/ч. Получим уравнение :
39 : 3 = 65 :
х
13=65 : х
х=65:13
х=5
Ответ: Майский жук пролетит путь
длиной 65 км
за 5 часов.
Дети приходят к выводу, что задачи можно
решать разными способами.
5.
Закрепление
1)
Самостоятельная работа №2(б). Учитель предлагает решить
задачу разными способами
2)
Работа в парах №4
6.
Работа над изученным материалом
3)
Решение задачи №6
4)
Выполнение порядка действий №8
7.
Рефлексия. Подведение итогов урока.
Д/з №7,8
Урок для четвертого класса Используйте гистограмму и напишите уравнение
Во время этого группового задания ученики работают в парах. У каждой пары есть копия ведомости действий группы. Нарисуйте картинку. Учащиеся должны работать вместе, чтобы найти ответ на каждую словесную задачу. Студенты должны решать задачи с целыми числами и целыми числами, используя четыре операции (4.OA.A3) . Студентов направляют к концептуальному пониманию через вопросы своих одноклассников, а также меня.Студенты общаются друг с другом и согласовывают ответ на задачу. Это требует обсуждения, критики и обоснования ответов обоих студентов (MP3) . Когда пары обсуждают проблему, они должны быть точными в своем общении в своих группах, используя соответствующую математическую терминологию для этого навыка (MP6). Когда я хожу, я слушаю, как студенты используют «разговор», который приведет к ответу. Я призываю студентов нести ответственность за собственное обучение.
Во время работы я отслеживаю и оцениваю их понимание с помощью вопросов. Должно быть очевидно, что они используют подсказки, чтобы помочь им определить правильную операцию. Некоторые из вопросов, которые я задаю:
1. Есть ли какие-нибудь подсказки, которые помогут вам определить, какую операцию использовать? Если так, то кто они?
2. Что вас просят найти?
3. Почему вы выбрали именно эту операцию?
4. Как гистограмма связана с этой проблемой?
Прогуливаясь по классу, я слышал, как студенты обсуждают задание друг с другом.Я слышу классную болтовню и постоянную дискуссию среди студентов. Группы обсуждают, как использовать гистограмму в качестве инструмента для решения своих проблем. Как мы уже говорили об использовании моделей в прошлом, я слышал, как студенты говорят, что «модель должна соответствовать задаче». Это тот разговор, который я хочу услышать на этом уроке. Когда я готовлю студентов к оценке PARCC, они всегда должны быть уверены, что все их ответы на проблему (письменные, образцовые и т. Д.) Должны быть связаны друг с другом.До появления Common Core я думал, что идеальным уроком будет тихая работа над книгой. Теперь меня удивляют некоторые разговоры, происходящие в классе между студентами.
Как вы можете видеть из «Работы учеников» и «Работа учеников — нарисуйте картинку», эти ученики преуспели. В примере «Работа учащегося» показано, как учащийся использовал гистограмму для решения задачи сложения. Студент знал, что вопросительный знак вверху представляет общую сумму задачи. В примере «Работа учащегося — нарисуйте картинку» показано, как учащийся использовал гистограмму для решения задачи разделения.Учащийся знал, что уравнение состоит из 32, разделенных на 8, и это показано на гистограмме с 8 разделами с цифрой 4 в качестве частного. Благодаря нашей предыдущей практике с четырьмя операциями студенты смогли выполнить это задание. Например, очень полезно было выучить ключевые слова для решения словесных задач. Они выучили такие слова, как «левый» и «оба». Кроме того, необходимы уроки по решению задач и проблем. Как учитель, мы должны предоставлять учащимся как можно больше возможностей для отработки реальных ситуаций.Это делает ученика более разносторонним.
Мои наблюдения:
Использование столбчатых диаграмм подошло большинству студентов. Когда я прошел вокруг, чтобы контролировать, я увидел, что некоторые студенты не знают, как нарисовать гистограмму для задач деления. Один студент спросил: «Откуда вы знаете, как должна выглядеть столбиковая диаграмма?» Поскольку я заметил это с некоторыми учениками, я решил остановить класс и собрать всех учеников вместе, чтобы ответить на этот вопрос. Я указал студентам, что за проблему разделения нам дали дивиденды.Ищем частное. Делить — значит делить поровну. Я указываю студентам, что мы должны нарисовать столбчатую диаграмму, представляющую делитель. Например, если делитель 8, то нам нужна столбиковая диаграмма с 8 секциями. Я напоминаю студентам использовать умножение, чтобы решить задачу деления. В этом конкретном случае студенты будут искать 8 раз что-нибудь, чтобы получить размер дивиденда. Поделившись этой информацией со всем классом, я позволил студентам вернуться в свои группы для работы.
Любые группы, которые завершают задание раньше, могут подойти к компьютеру, чтобы попрактиковаться в этом навыке на следующем сайте, пока мы не будем готовы к совместному использованию всей группы.
Решение проблем: нарисуйте картинку
Решение проблем — критический и социально-эмоциональный навык 21 века
Стратегия «Нарисуй картинку» — это техника решения проблем, при которой учащиеся визуально представляют проблему. Этот ресурс поможет вашим ученикам научиться применять фундаментальную стратегию решения проблем, которую легко усвоят ученики всех способностей.
Ищете дополнительные ресурсы по навыкам 21 века и социально-эмоциональному обучению? Найдите их в нашем ресурсном центре FutureFit.
Страница 1 из 2
Решение проблем: нарисуйте картинку
Что это?
Стратегия «Нарисуй картинку» — это метод решения задач, при котором учащиеся визуально представляют проблему. Например, нарисовав картинку, можно решить следующую задачу:
Лягушка на дне 10-метрового колодца. Каждый день он поднимается на 3 метра.Каждую ночь он спускается на 1 метр. В какой день он достигнет вершины колодца и сбежит?
Почему это важно?
Рисование диаграммы или другого визуального представления часто является хорошей отправной точкой для решения всех видов текстовых задач. Это промежуточный этап между языком как текстом и символическим языком математики. Представляя единицы измерения и другие объекты наглядно, учащиеся могут начать думать о проблеме математически. Рисунки и диаграммы также являются хорошими способами описания решений проблем; поэтому они являются важной частью математической коммуникации.
Как это сделать?
Поощряйте студентов рисовать задачи в самом начале их математического образования. Продвигайте и укрепляйте стратегию на всех последующих этапах. Большинство студентов, естественно, будут рисовать картинки при малейшей поддержке.
Предложите учащимся задачу, для решения которой им потребуется нарисовать картинку. Например:
Мара ставит палатку для воссоединения семьи. Размер палатки — 16 на 5 футов.Каждой 4-футовой секции палатки нужна стойка, за исключением сторон 5 футов. Сколько постов ей понадобится?
Продемонстрируйте, что первым шагом к решению проблемы является ее понимание. Это включает в себя поиск ключевой информации, необходимой для выяснения ответа. Это может потребовать от студентов прочитать задачу несколько раз или изложить ее своими словами.
16 футов на 5 футов
1 столбик на каждые 4 фута, в том числе по одному в каждом углу
Нет столбов на коротких сторонах
Выберите стратегию
Чаще всего учащиеся используют стратегию рисования картинки для решения задач вовлекает пространство или организацию, но его можно применить почти ко всем математическим задачам.Также студенты используют эту стратегию при работе с новыми понятиями, такими как эквивалентные дроби или основные операции умножения и деления.
Полное руководство по задачам SAT Math Word
Примерно 25% вашего общего количества разделов SAT Math будут составлять задачи со словами, что означает, что вам придется создавать свои собственные наглядные пособия и уравнения, чтобы решать свои ответы. Хотя фактические темы по математике могут быть разными, у текстовых задач SAT есть несколько общих черт, и мы здесь, чтобы показать вам, как их лучше всего решать.
Этот пост будет вашим полным руководством по задачам по SAT Math. Мы расскажем, как преобразовывать словесные задачи в уравнения и диаграммы, различные типы математических задач со словами, которые вы встретите на тесте, и как решать свои задачи со словами в день теста.
Изображение функции: Антонио Литтерио / Викимедиа
Что такое проблемы со словами SAT Math?
Словесная задача — это любая математическая задача, в основном или полностью основанная на письменном описании. Вам не будет предоставлено уравнение, диаграмма или график для задачи со словами. Вместо этого вы должны использовать свои навыки чтения, чтобы преобразовать слова вопроса в выполнимую математическую задачу. Как только вы это сделаете, вы сможете решить эту проблему.
В разделе SAT Math вам будут предложены задачи со словами по разным причинам. Например, задача из слов проверяет ваше понимание прочитанного и вашу способность визуализировать информацию.
Во-вторых, эти типы вопросов позволяют разработчикам тестов задавать вопросы, которые невозможно было бы задать с помощью простой диаграммы или уравнения. Например, если в математическом вопросе вас просят уместить как можно больше мелких объектов в более крупный, будет сложно продемонстрировать и задать это с помощью только диаграммы.
Перевод задач с математическими словами в уравнения или рисунки
Для того, чтобы преобразовать ваши текстовые задачи SAT в действенные математические уравнения, которые вы можете решить, вам необходимо понимать и уметь использовать некоторые ключевые математические термины. Когда вы видите эти слова, вы можете перевести их в правильное математическое действие.
Например, слово «сумма» означает значение, когда два или более элементов складываются вместе. Итак, если вам нужно найти сумму a и b , вам нужно будет составить уравнение следующим образом: a + b.
Также обратите внимание, что ко многим математическим действиям имеет более одного присоединенного термина, , которые могут использоваться как взаимозаменяемые.
Вот таблица со всеми ключевыми терминами и символами, которые вы должны знать при выполнении задач по SAT Math:
| Ключевые термины | Математическое действие |
| Сумма, увеличенная, прибавленная, более чем, всего | + |
| Разница, уменьшенная, меньше чем, вычтенная из | – |
| Продукт, раз, в __ раз больше, __ раз больше (число, например.г., «втрое больше») | * или x |
| Разделено на, на, __ на столько, __ на столько (дробная часть, например, «одна треть меньше») | / или ÷ |
| Равно, есть, эквивалентно | = |
| Менее | < |
| Больше | > |
| Меньше или равно | ≤ |
| Больше или равно | ≥ |
Теперь давайте посмотрим на эти математические термины в действии на нескольких официальных примерах:
Мы можем решить эту проблему, переведя полученную информацию в алгебру. Нам известна индивидуальная цена каждого салата и напитка, а также общий доход от продажи 209 салатов, и напитков вместе взятых. Итак, давайте запишем это в алгебраической форме.
Скажем, что количество проданных салатов = S , а количество проданных напитков = D . Задача сообщает нам, что было продано 209 салатов, и напитков, что можно представить так:
S + D = 209
Наконец, нам сказали, что определенное количество S и D было продано и принесло общий доход в 836 долларов 50 центов.Мы не знаем точных цифр S и D , но мы с до знаем, сколько стоит каждая единица. Следовательно, мы можем записать это уравнение:
6,50 S + 2 D = 836,5
Теперь у нас есть два уравнения с одинаковыми переменными ( S и D ). Поскольку мы хотим знать, сколько салатов было продано, нам нужно найти D , чтобы мы могли использовать эту информацию для решения S .Первое уравнение говорит нам, что равняется S и D при сложении, но мы можем переставить это, чтобы сказать нам, что просто D равно S :
S + D = 209
Теперь просто вычтите S с обеих сторон, чтобы получить то, что D равно:
D = 209 — S
Наконец, подставьте это выражение для D в другое уравнение, а затем решите для S :
6.50 S + 2 (209 — S ) = 836,5
6,50 S + 418-2 S = 836,5
6,50 S — 2 S = 418,5
4,5 S = 418,5
S = 93
Правильный вариант ответа: (B) 93.
Эта словесная задача просит нас решить одно возможное решение (запрашивается «возможная сумма»), поэтому мы сразу знаем, что будет несколько правильных ответов.
Wyatt может очистить не менее 12 дюжин кукурузных початков и не более 18 дюжин кукурузных початков в час. Если он снимает 72 дюжины со скоростью 12 дюжин в час, это равно 72/12 = 6 часам. Таким образом, вы можете написать 6 в качестве окончательного ответа.
Если Вятт обрабатывает 72 дюжины со скоростью 18 дюжин в час (максимальная скорость, которую он может сделать), получается 72/18 = 4 часа. Вы можете написать 4 в качестве окончательного ответа.
Поскольку минимальное время, которое требуется Wyatt — 4 часа, а максимальное — 6 часов, будет правильным любое число от 4 до 6.
Хотя сейчас самые сложные задачи со словами SAT могут показаться вам латинскими, практика и изучение скоро помогут вам преобразовать их в рабочие вопросы.
Типичные проблемы со словом SAT
Проблемы со словами на тесте SAT можно разделить на по трем основным категориям:
- Задачи Word, для которых нужно просто составить уравнение
- Задачи Word, которые необходимо решить для определенного значения
- Проблемы Word, для которых необходимо определить значение значения или переменной
Ниже мы рассмотрим каждый тип мировых проблем и дадим вам примеры.
Word Тип проблемы 1: Настройка уравнения
Это довольно необычный тип задачи SAT со словами, но вы обычно видите ее хотя бы один раз в разделе «Математика». Скорее всего, вы также увидите это — первый в разделе.
Для этих задач вы должны использовать предоставленную информацию, а затем настроить уравнение. Нет необходимости искать отсутствующую переменную — это все, что вам нужно.
Почти всегда вы встретите этот тип вопросов в первых четырех вопросах в разделе SAT Math, а это означает, что College Board считает эти вопросы простыми. Это связано с тем, что вам нужно предоставить только настройку, а , а не — выполнение.
Чтобы решить эту проблему, нам нужно знать ситуации Арманда и Тайрона, поэтому давайте рассмотрим их отдельно:
Armand: Armand отправлял m текстовых сообщений каждый час в течение 5 часов, поэтому мы можем записать это как 5m — количество текстов, которые он отправил за час, умноженное на общее количество часов, в течение которых он отправлял текстовые сообщения.
Тайрон: Тайрон отправлял p текстовых сообщений каждый час в течение 4 часов, поэтому мы можем записать это как 4 p — количество отправленных им текстов в час, умноженное на общее количество часов, в течение которых он отправлял текстовые сообщения.
Теперь мы знаем, что ситуацию Армана алгебраически можно записать как 5m , а ситуацию Тайрона можно записать как 4 p . Поскольку нас спрашивают выражение, которое представляет общее количество текстов, отправленных Арманом и Тайроном, , мы должны сложить два выражения:
5м + 4 п.
Правильный ответ — выбор (C) 5 мес + 4 p
Word Тип проблемы 2: Решение отсутствующего значения
Подавляющее большинство вопросов по SAT Math попадают в эту категорию. Для этих вопросов вы должны настроить уравнение и решение для конкретной информации.
Большинство (хотя и не все) проблемных вопросов этого типа будут представлять собой сценариев или рассказов, охватывающих все виды тем SAT Math, таких как средние значения, уравнения с одной переменной и отношения. Вы почти всегда должны иметь твердое представление о математической теме, о которой идет речь, чтобы решить проблему со словами в этой теме.
Давайте попробуем обдумать эту проблему в терминах x .Если деревья типа A произвели на 20% больше груш, чем деревья типа B, мы можем записать это в виде выражения:
x + 0,2 x = 1,2 x = количество груш, произведенных типом A
В этом уравнении x — это количество груш, произведенных деревьями типа B. Если мы прибавим 20% от x (0,2 x ) к x , мы получим количество груш, произведенных деревьями типа А.
Задача говорит нам, что деревья типа А дали в общей сложности 144 груши.Поскольку мы знаем, что 1,2 x равно количеству груш, произведенных типом A, мы можем написать следующее уравнение:
1,2 x = 144
Теперь все, что нам нужно сделать, это разделить обе части на 1,2, чтобы найти количество груш, произведенных деревьями типа B:
x = 144 / 1,2
x = 120
Правильный вариант ответа: (B) 120.
Вы также можете получить геометрическую задачу в виде задачи , которая также может быть установлена или не установлена в сценарии.Вопросы о геометрии будут представлены в виде текстовых задач, как правило, потому что создатели тестов считали, что задачу было бы слишком легко решить, если бы вам дали диаграмму, или потому что задачу невозможно было бы показать с помощью диаграммы. (Обратите внимание, что геометрия составляет очень небольшой процент SAT Math. )
Это случай , проблема, которую трудно показать визуально, , поскольку x не является установленным значением в градусах, а скорее значением больше , чем 55; таким образом, это должно быть представлено как словесная проблема.
Поскольку мы знаем, что x должно быть целочисленным значением степени больше 55, позволяет присвоить ему значение. В данном случае назовем x 56 °. (Почему 56? Могут быть и другие значения x , но 56 гарантированно работает, поскольку это наименьшее целое число больше 55. В принципе, это безопасная ставка!)
Теперь, поскольку x = 56, следующий угол в треугольнике — 2 x — должен иметь следующее значение:
56 * 2 = 112
Давайте сделаем грубый (не в масштабе) набросок того, что мы знаем на данный момент:
Итак, мы знаем, что в треугольнике 180 °, , поэтому мы можем найти значение y , сказав следующее:
y = 180 — 112 — 56
и = 12
Одно из возможных значений для и — 12. (другие возможные значения: 3, 6 и 9. )
Word Тип проблемы 3: Объяснение значения переменной или значения
Проблема такого типа будет появляться хотя бы один раз. Он просит вас определить часть уравнения, представленного словом проблема — обычно значение конкретной переменной или числа.
Сначала этот вопрос может показаться сложным, но на самом деле он довольно прост.
Мы знаем, что t P — это количество телефонов, которые у Кэти осталось , , которые нужно починить, а d — это количество дней, которые она проработала в неделю. Если она проработала 0 дней (то есть, если мы подставим 0 в уравнение), вот что мы получим:
P = 108 — 23 (0)
P = 108
Это означает, что Кэти, не работая ни в какие дни недели, нужно отремонтировать 108 телефонов. Следовательно, правильный ответ: (B) Кэти начинает каждую неделю с 108 телефонов, которые нужно починить.
Чтобы помочь справиться со всеми различными задачами со словами SAT, давайте рассмотрим математические стратегии и подсказки, имеющиеся в нашем распоряжении.
Готовы выйти за рамки простого чтения о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Разработанная и написанная экспертами PrepScholar SAT , наша программа SAT настраивается в соответствии с вашим уровнем навыков по более чем 40 вспомогательным навыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший набор баллов.
Нажмите на кнопку ниже, чтобы попробовать!
Стратегии SAT по математике для задач со словами
Хотя вы увидите задачи со словами в разделе SAT Math по различным математическим темам, все же есть несколько методов, которые можно применить для решения задач со словами в целом.
# 1: Нарисуйте
Независимо от того, является ли ваша проблема проблемой геометрии или проблемой алгебры, иногда , сделав быстрый набросок сцены, может помочь вам понять, с чем именно вы работаете. Например, давайте посмотрим, как картинка может помочь вам решить словесную задачу о круге (в частности, о пицце):
Если у вас часто возникают проблемы с визуализацией подобных проблем, нарисуйте их. Мы знаем, что имеем дело с кругом, поскольку наша цель — пицца. Мы также знаем, что пицца весит 3 фунта.
Поскольку нам нужно решить вес каждого ломтика в унциях, давайте сначала переведем общий вес нашей пиццы из фунтов в унции. Нам дана конверсия (1 фунт = 16 унций), поэтому все, что нам нужно сделать, это умножить нашу трехфунтовую пиццу на 16, чтобы получить ответ:
3 * 16 = 48 унций (для целой пиццы)
А теперь нарисуем картинку. Сначала пицца делится пополам (не в масштабе):
Теперь у нас есть две части одинакового размера. Продолжаем рисовать. Тогда задача говорит, что мы делим каждую половину на три равные части (опять же, не в масштабе):
Это дает нам шесть частей одинакового размера. Поскольку мы знаем, что общий вес пиццы составляет 48 унций, все, что нам нужно сделать, это разделить на 6 (количество кусочков), чтобы получить вес (в унциях) одного кусочка пиццы:
48/6 = 8 унций за штуку
Правильный вариант ответа: (C) 8.
Что касается геометрических задач, помните, что вы можете получить текстовую задачу о геометрии, записанную в виде словесной задачи. В этом случае сделайте собственный рисунок сцены. Даже грубый набросок может помочь вам визуализировать математическую задачу и сохранить всю вашу информацию в порядке.
# 2: запомнить ключевые термины
Если вы не привыкли переводить английские слова и описания в математические уравнения, то сначала вам будет сложно понять задачи со словами SAT. Посмотрите на диаграмму, которую мы дали вам выше, чтобы вы могли научиться переводить ключевые слова в их математические эквиваленты. Таким образом, вы можете точно понять, какую проблему просит вас найти и как вы должны ее найти.
В Интернете доступны бесплатные вопросы по SAT Math, так что запомните свои термины, а затем потренируйтесь над реалистичными задачами по SAT, чтобы убедиться, что вы поняли свои определения и можете применить их к настоящему тесту.
# 3: Подчеркните и / или запишите важную информацию
Ключ к решению проблемы со словом — собрать воедино все ключевые фрагменты данной информации и поместить их в нужные места. Убедитесь, что вы выписали все эти данные на нарисованной вами диаграмме (если проблема требует диаграммы), чтобы все ваши движущиеся части были в порядке.
Один из лучших способов сохранить четкость — это подчеркнуть ключевую информацию в задаче, , а затем записать их самостоятельно, прежде чем составлять уравнение.Поэтому найдите время, чтобы выполнить этот шаг, прежде чем сосредоточиться на решении вопроса.
# 4: Обращайте пристальное внимание на то, о чем спрашивают
Это может привести в ярость, когда вы решаете неправильную переменную или записываете заданные вами значения в неправильные места. И все же это слишком легко сделать при работе с математическими задачами со словами.
Убедитесь, что вы уделяете пристальное внимание именно , что вы должны решать, и точно , какие фрагменты информации куда попадают. Ищете площадь или периметр? Значение x, 2x или y?
Всегда лучше перепроверить , что вы должны найти. до того, как вы запустите , чем через две минуты осознать, что вам придется начинать решать проблему заново.
# 5: Осветите любую конкретную математическую тему, которую вы чувствуете слабой в
Вы, вероятно, встретите и проблему с диаграммой / уравнением, и проблему со словами почти по каждой теме SAT Math в тесте.Вот почему существует так много разных типов задач со словами и почему вам нужно знать все тонкости каждой темы SAT Math, чтобы иметь возможность решить проблему со словами.
Например, если вы не знаете, как найти среднее значение по набору чисел, вы наверняка не будете знать, как решить задачу со словами, которая имеет дело со средними значениями!
Поймите, что решение словесной задачи SAT Math — это двухэтапный процесс: требует, чтобы вы оба понимали, как работают текстовые задачи и , чтобы понять рассматриваемую математическую тему.Если у вас есть какие-то слабые места в математике, сейчас хорошее время, чтобы освежить их в памяти, иначе задачи со словами SAT могут оказаться сложнее, чем вы ожидали!
Все готово? Пошли!
Проверьте свои знания задачи SAT Math Word
Наконец, пришло время проверить свои знания о задачах со словами на реальных задачах по SAT Math:
Проблемы со словами
1. Нет калькулятора
2.Калькулятор ОК
3. Калькулятор ОК
4. Калькулятор ОК
Ответы: C, B, A, 1160
Ответ объяснения
1. Для этой задачи мы должны использовать предоставленную нам информацию, чтобы составить уравнение.
Мы знаем, что Кен потратил x долларов, а Пол потратил на 1 доллар больше, чем Кен.Следовательно, мы можем написать следующее уравнение для Пола:
х + 1
Кен и Пол разделили счет поровну. Это означает, что нам придется вычислить общую сумму обоих их бутербродов, а затем разделить ее на 2. Поскольку сэндвич Кена стоит x долларов, а стоимость Пола x + 1, вот как выглядит наше уравнение, когда мы объедините два выражения:
x + x + 1
2 х + 1
Теперь мы можем разделить это выражение на 2, чтобы получить цену, которую заплатил каждый человек:
(2 x + 1) / 2
х + 0.5
Но мы еще не закончили. Мы знаем, что и Кен, и Пол также заплатили 20% чаевых по счетам. В результате мы должны умножить общую стоимость одной купюры на 0,2, а затем добавить эти чаевые к счету. Алгебраически это выглядит так:
( x + 0,5) + 0,2 ( x + 0,5)
x + 0,5 + 0,2 x + 0,1
1,2 x + 0,6
Правильный выбор ответа: (C) 1,2 x + 0.6
2. Вы должны быть знакомы со статистикой, чтобы понять, о чем идет речь.
Поскольку Ник исследовал случайную выборку своего класса первокурсников, мы можем сказать, что эта выборка точно отражает мнение (и, следовательно, те же проценты), что и весь класс первокурсников.
Из 90 опрошенных первокурсников 25,6% заявили, что хотели бы, чтобы осенний фестиваль проводился в октябре. Все, что нам нужно сделать сейчас, это найти этот процент от всего класса первокурсников (который состоит из 225 студентов) , чтобы определить, сколько всего первокурсников предпочли бы октябрьский фестиваль:
225 * 0.256 = 57,6
Поскольку вопрос спрашивает «о том, сколько студентов» — а поскольку у нас явно не может быть и доли человека! — нам придется округлить это число до ближайшего доступного варианта ответа, то есть 60, или ответа выбор (B).
3. Это одна из тех проблем, которые просят вас определить значение в данном уравнении. Это может показаться запутанным, но не бойтесь — на самом деле это не так сложно, как кажется!
Во-первых, мы знаем, что t представляет количество секунд, прошедших после того, как объект был запущен вверх.Но что, если время еще не прошло? Это будет означать, что t = 0. Вот что происходит с уравнением, когда мы подставляем 0 для t :
.
ч (0) = -16 (0) 2 + 110 (0) + 72
ч (0) = 0 + 0 + 72
ч (0) = 72
Как мы видим, еще до запуска объект имеет высоту 72 фута. Это означает, что 72 должно представлять начальную высоту объекта в футах или вариант ответа (A).
4. У вас может возникнуть соблазн нарисовать диаграмму для этой задачи, поскольку речь идет о пуле (прямоугольнике), но на самом деле быстрее просто посмотреть на приведенные числа и работать оттуда.
Мы знаем, что в настоящее время бассейн вмещает 600 галлонов воды и что вода заливается в него из шланга со скоростью 8 галлонов в минуту, в общей сложности 70 минут.
Чтобы найти количество воды в бассейне сейчас, нам нужно сначала решить количество воды, добавляемой в бассейн с помощью шланга. Мы знаем, что каждую минуту в течение 70 минут добавлялось 8 галлонов, поэтому все, что нам нужно сделать, это умножить 8 на 70:
.
8 * 70 = 560 галлонов
Это говорит о том, что 560 галлонов воды были добавлены в наш уже заполненный 600-галлонный бассейн.Чтобы найти общее количество воды, мы просто складываем эти два числа вместе:
560 + 600 = 1160
Правильный ответ — 1160.
Аааааааааа и пора вздремнуть.
Ключевые выводы: понимание задач со словами SAT Math
Задачи со словами составляют значительную часть раздела SAT Math, , поэтому неплохо понять, как они работают и как преобразовать слова на странице в правильное выражение или уравнение.Но это еще только полдела.
Хотя вы не будете знать, как решить проблему со словами, если не знаете, что такое продукт или как нарисовать прямоугольный треугольник, вы также не будете знать, как решить проблему со словами о соотношениях, если не знаете Я не знаю, как работают соотношения.
Поэтому обязательно научитесь не только подходу к математическим задачам со словами в целом, но и тому, как сузить свой фокус на любых темах SAT Math, в которых вам нужна помощь. Здесь вы можете найти ссылки на все наши руководства по SAT Math, которые помогут вам в учебе.
Что дальше?
Хотите освежить в памяти темы SAT Math? Ознакомьтесь с нашими индивидуальными руководствами по математике, чтобы получить обзор каждой темы SAT Math. От полигонов и наклонов до вероятностей и последовательностей — мы вас охватим!
Не хватает времени на SAT Math? У нас есть ноу-хау, чтобы помочь вам выиграть время и увеличить ваш счет.
Медлили с изучением SAT? Узнайте, как преодолеть желание откладывать дела на потом и составить хорошо сбалансированный план подготовки.
Пытаетесь получить высший балл за SAT? Взгляните на наше руководство по получению идеальных 800 баллов по SAT Math, написанное отличным бомбардиром.
Хотите улучшить свой результат SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.
Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.
Воспользуйтесь нашей 5-дневной бесплатной пробной версией:
6 способов помочь учащимся понять математику
Конечная цель обучения математике состоит в том, чтобы учащиеся понимали представленный материал, применяли навыки и вспоминали концепции в будущем.Мало пользы от того, что студенты вспомнят формулу или процедуру для подготовки к завтрашнему экзамену, а к следующей неделе забывают основную концепцию. Учителям необходимо сосредоточиться на том, чтобы ученики понимали материал, а не просто запоминали процедуры.
Вот шесть способов научить понимать в классе математики:
1. Создайте эффективный вводный курс.
Первые пять минут урока задают тон всему уроку.В идеале учителя должны начать с того, что поделятся повесткой дня урока, чтобы учащиеся знали, чего ожидать от того, что будет происходить. Затем учителя могут разместить и сформулировать цель обучения или основной вопрос для класса, чтобы учащиеся знали цель и в конце урока могли самостоятельно оценить, была ли цель для них достигнута. Наконец, вводный курс может включать в себя одну или несколько задач для разминки как способ проверить и оценить предыдущие знания учащихся при подготовке к ознакомлению с новым материалом.В этом видео показан вводный курс для седьмого класса урока по прямоугольным призмам:
видео
2. Представляйте темы, используя несколько представлений.
Чем больше типов представлений вы можете представить учащимся, обращаясь к их различным стилям обучения, тем с большей вероятностью они действительно поймут представляемую концепцию. Различные представления могут включать использование манипуляторов, показ изображения, рисование проблемы и предложение символического представления. Например, представляя линейные отношения с одним неизвестным, проиллюстрируйте учащимся ту же задачу, что и уравнение, на числовой прямой, словами и картинками.Учащиеся, которые подвергаются воздействию и могут распознать одни и те же отношения, представленные в различных режимах представления, с большей вероятностью будут иметь концептуальное понимание отношений и лучше справляться с оценками (PDF).
3. Решать проблемы разными способами.
В лучшей обстановке в классе учитель может показать разные способы решения одной и той же проблемы и побудить учеников придумывать свои собственные творческие способы их решения. Чем больше стратегий и подходов используют студенты, тем глубже становится их концептуальное понимание темы.Предоставление учащимся возможности создавать собственные методы решения проблем может заставить учителя нервничать. Что, если мы не будем следовать их логике? Что, если они неверны? Тем не менее, стоит рискнуть, чтобы они исследовали. После того, как один, пара или небольшая группа учащихся завершат решение классной задачи одним методом, предложите им поискать альтернативные способы найти такое же правильное решение. Когда учащиеся разрабатывают свои собственные методы, а затем делятся с классом правильными шагами, это очень мощный учебный опыт.На видео ниже показано, как учитель предлагает ученикам несколько способов решить одну и ту же задачу на прямоугольных призмах:
видео
4. Покажите приложение.
В идеальном мире мы всегда сможем продемонстрировать, как каждая концепция может быть применена к реальному миру — и, когда это возможно, это поможет улучшить понимание учащимися. Когда концепция не может быть применена таким образом, мы все равно можем рассказать, как ее можно применить в математике или другой предметной области. Другой вариант — показать, как эта концепция развивалась на протяжении истории математики.Выделите минутку из каждого урока, чтобы показать своим ученикам, где и как математику можно увидеть или использовать в жизни за пределами класса.
5. Предложите учащимся изложить свои соображения.
Студенты должны объяснять свои рассуждения при решении задач. Чтобы учитель мог определить, действительно ли каждый ученик понимает цель урока, каждому ученику необходимо общаться как устно, так и письменно. Предоставив классу десять минут, чтобы обсудить их аргументы друг с другом, изучая при этом несколько способов решения проблем, вы обеспечите отличное взаимодействие и обучение.Не всегда легко заставить учеников говорить в классе, но есть способы их поощрить (PDF).
6. Завершить занятие с аннотацией.
Каждый может заблудиться во время урока, и легко потерять счет времени, пока не прозвенит звонок и урок не закончится. Последние семь минут могут быть самыми важными для того, чтобы студенты поняли учебную цель дня. Вы можете использовать это время для выполнения трех очень важных задач:
- Быстрая формирующая оценка, чтобы определить, сколько было усвоено, например, учащиеся самостоятельно оценивают свое согласие с концепцией по шкале от 1 до 5. время урока и краткое обсуждение того, где будет проходить урок в следующий раз.
- Предварительный просмотр домашнего задания вместе, чтобы избежать путаницы.
Это лишь некоторые из заданий в конце урока.Есть как минимум 22 дополнительных действия по закрытию. В этом видео показана итоговая фаза того же урока:
видео
В разделе комментариев ниже поделитесь своими советами и приемами, которые помогут учащимся понять математику.
Весы как модель уравнения
В этой статье обсуждается, как использовать весы для моделирования простых линейных уравнений в предалгебре или алгебре 1. На этой странице мы имеем дело только с положительными целыми числами; часть 2 объясняет, как использовать баланс с уравнениями, которые включают отрицательные целые числа.
Уравнение в основном говорит, что две вещи (точнее, выражения) РАВНЫ. Поскольку в сбалансированной ситуации обе стороны весов имеют равный вес, мы можем моделировать простые уравнения с помощью весов.
На рисунках ниже каждый кружок представляет один, а блок представляет неизвестное x . Узнать, сколько весит блок, можно
Таким образом, обе стороны будут поддерживать баланс или «равенство».
х + 3 = 5 | Если это сбалансированная ситуация … |
х = 2 | … так оно и есть! (Мы сняли три круга с ОБЕИХ сторон.) |
3 x + 2 = 2x + 6 | Уберите два блока (два x ) с обоих стороны. Баланс остается сбалансированным. |
x + 2 = 6 | Уберите по 2 круга с обеих сторон. Баланс остается сбалансированным. |
x = 4 | Вот решение! |
Без масштабной модели процесс решения выглядит так:
| 3x + 2 -2x | = | 2x + 6 -2x | (уберите 2х с обеих сторон) | |
| х + 2 -2 | = | 6 -2 | (снимаем по 2 с двух сторон) | |
| x | = | 4 |
Деление
В некоторых ситуациях вам нужно разделить обе части уравнения на одно и то же число.Когда это? Это удачная ситуация, когда на одной стороне ТОЛЬКО x (блоков), но их больше одного.
2 x = 8 | Если забрать половину вещей на левая сторона, и аналогично половина вещей на правой стороне, баланс останется сбалансированным . |
x = 4 |
3 x = 9 | Подумай об этом! Если это уравновешенная ситуация… |
x = 3 | … то же самое (и наоборот)! Мы просто разделили обе стороны на 3. |
Объединение операций
Разрешенные операции:
- Добавьте одинаковое количество к обеим сторонам ( x или единицам)
- Вычтите одинаковое количество с обеих сторон ( x или единиц)
- Умножьте обе стороны на одинаковое число (но не на ноль)
- Разделите обе стороны на одинаковое число (но не на ноль)
(Есть и другие, но они не нужны в простых уравнениях.)
Цель состоит в том, чтобы ПЕРВЫЙ сложить и вычесть до тех пор, пока мы не получим ТОЛЬКО блоки (блоки) x с одной стороны и ТОЛЬКО блоки (кружки) с другой. Затем, если у вас более одного блока, вам нужно разделить , чтобы получить ситуацию только с и одним блоком с одной стороны, что является решенным уравнением!
Умножение с обеих сторон может произойти, если у вас есть дробный блок ( минус , чем один блок) с одной стороны.Например, уравнение 1 / 4x = 13 решается путем умножения обеих частей на 4. Попробуйте позволить своим ученикам смоделировать уравнение 1 / 2x + 14 = 20, используя весы; они могут решить это с его помощью. Более продвинутые студенты могут подумать, что делать с уравнением 2 / 3x = 12.
Пример вычитания и деления
В этом примере мы используем все вышеперечисленные операции: снятие с
обе стороны уравнения и разделив уравнение на одно и то же число.
4 x + 2 = 2 x + 5 | Сначала избавляемся от блоков с правой стороны убрав по два квартала с обеих сторон. |
2 x + 2 = 5 | Затем убираем кружочки с левой стороны убрав по 2 круга с обеих сторон. |
2 x = 3 | Теперь только блоки с одной стороны и только круги с другой. Узнать, что за 1 блок весит, берем половину с обеих сторон. |
x = 1 1/2 | Решение состоит в том, что 1 блок весит 1 1/2 круга. |
Попробуйте подставить это значение x = 1 1/2 в исходное уравнение 4 x + 2 = 2 x + 5 и проверьте, выполняется ли уравнение!
Примеры упражнений
Эти уравнения достаточно просты, чтобы их можно было решить с помощью модели баланса. ВСЕГДА проверяйте свое решение, подставляя его в исходное уравнение.
- 2 x + 3 = 5
- 2 x + 5 = x + 9
- 3 x + 2 = 2 x + 4
- 3 x + 3 = 5 + x
- 5 x + 4 = 3 x + 6
- 6 x + 2 = 3 x + 6
- 6 x + 3 = 2 x + 5
Продолжить до Отрицательных членов в уравнении
См. Также
Задачи с весами — видеоурок
В этом видеоуроке для 4 или 5 классов я решаю 14 различных задач на баланс, начиная от самых простых и заканчивая теми, у которых есть двойные весы.Учащиеся изучают принципы деления обеих частей уравнения на одно и то же число и удаления (вычитания) одинакового количества обеих сторон уравнения.
Приложения линейных уравнений
Равномерное движение означает движение с неизменной скоростью или скоростью. Мы можем определить пройденное расстояние, умножив среднюю скорость на время, пройденное с этой скоростью, по формуле D = r⋅t. Приложения, связанные с равномерным движением, обычно содержат много данных, поэтому помогает сначала организовать данные в виде диаграммы, а затем создать алгебраическое уравнение, моделирующее проблему.
Пример 14: Два поезда покидают станцию одновременно, двигаясь в противоположных направлениях. Один движется со скоростью 70 миль в час, а другой — со скоростью 60 миль в час. Сколько времени нужно, чтобы расстояние между ними достигло 390 миль?
Решение: Сначала определите неизвестное количество и систематизируйте данные.
Данная информация представлена в следующей таблице. Время на каждый поезд одинаковое.
Чтобы не вводить еще две переменные, используйте формулу D = r⋅t для заполнения неизвестных расстояний, пройденных каждым поездом.
Теперь мы можем полностью заполнить график.
Алгебраическая установка определяется столбцом расстояния. Задача спрашивает, сколько времени требуется, чтобы общее расстояние достигло 390 миль.
Решить относительно t .
Пример 15: Поезд, идущий без остановок к месту назначения, может двигаться со средней скоростью 72 мили в час. На обратном пути поезд делает несколько остановок и может развивать скорость только 48 миль в час. Если обратный путь занимает на 2 часа дольше, чем первоначальный путь к месту назначения, то каково время в пути в каждую сторону?
Решение: Сначала определите неизвестное количество и систематизируйте данные.
Используйте формулу D = r⋅t для заполнения неизвестных расстояний.
Используйте эти выражения для заполнения диаграммы.
Алгебраическая установка снова определяется столбцом расстояния. В этом случае расстояние до пункта назначения и обратно одинаково, и уравнение равно
Решите для t .
Обратный путь занимает t + 2 = 4 + 2 = 6 часов.
Ответ: 4 часа, чтобы прибыть в пункт назначения и 6 часов, чтобы вернуться.
Попробуй! Мэри отправляется в школу на велосипеде со средней скоростью 6 миль в час.Ее сестра Кейт, опаздывая, уезжает через 15 минут и ездит вдвое быстрее. Сколько времени понадобится Кейт, чтобы догнать Мэри? Будь осторожен! Обратите внимание на единицы, указанные в задаче.
Ответ: Кейт наверстывает упущенное.
Тематические упражнения
Часть A: Перевести
Переведите следующее в алгебраические уравнения.
1. Сумма числа и 6 составляет 37.
2.Когда из удвоенного числа вычитается 12, получается 6.
3. Четырнадцать меньше, чем 5 умноженное на число 1.
4. Из 30 вычитается дважды какое-то число, и получается 50.
5. Пять умноженное на 6, а некоторое число равно 20.
6. Сумма 5-кратного некоторого числа и 6 равно 20.
7. Когда сумма числа и 3 вычитается из 10, получается 5.
8.Сумма трех и пяти одинаковых чисел равна 24.
9. Десять вычитается из удвоенного числа, и в результате получается сумма числа и 2.
10. Шесть меньше некоторого числа, в десять раз больше суммы этого числа и 5.
Часть B: Проблемы с номерами
Составьте алгебраическое уравнение и решите его.
11. Большое целое число на 1 больше, чем удвоенное другое целое число.Если сумма целых чисел равна 25, найдите целые числа.
12. Если большее целое число на 2 больше, чем в 4 раза больше другого целого числа, и их разница равна 32, найдите целые числа.
13. Одно целое число на 30 больше другого целого числа. Если разница между большим и удвоенным меньшим равна 8, найдите целые числа.
14. Частное числа и 4 равно 22. Найдите число.
15. Восемь раз число уменьшается в три раза на то же число, что дает разницу в 20.Какой номер?
16. Одно целое число на две единицы меньше другого. Если их сумма равна −22, найдите два целых числа.
17. Сумма двух последовательных целых чисел равна 139. Найдите целые числа.
18. Сумма трех последовательных целых чисел равна 63. Найдите целые числа.
19. Сумма трех последовательных целых чисел равна 279. Найдите целые числа.
20. Разница в два раза меньшего из двух последовательных целых чисел и большего — 39.Найдите целые числа.
21. Если меньшее из двух последовательных целых чисел вычесть из двукратного большего, то получится 17. Найдите целые числа.
22. Сумма двух последовательных четных целых чисел равна 46. Найдите целые числа.
23. Сумма двух последовательных четных целых чисел равна 238. Найдите целые числа.
24. Сумма трех последовательных четных целых чисел равна 96. Найдите целые числа.
25. Если меньшее из двух последовательных четных целых чисел вычитается из 3-х кратного большего, результат будет 42.Найдите целые числа.
26. Сумма трех последовательных четных целых чисел равна 90. Найдите целые числа.
27. Сумма двух подряд идущих нечетных целых чисел равна 68. Найдите целые числа.
28. Сумма двух подряд идущих нечетных целых чисел равна 180. Найдите целые числа.
29. Сумма трех последовательных нечетных целых чисел равна 57. Найдите целые числа.
30. Если меньшее из двух последовательных нечетных целых чисел вычитается из удвоенного большего, получается 23.Найдите целые числа.
31. Дважды сумма двух последовательных нечетных целых чисел равна 32. Найдите целые числа.
32. Разница между удвоенным большим из двух последовательных нечетных целых чисел и меньшим составляет 59. Найдите целые числа.
Часть C: Проблемы геометрии
Составьте алгебраическое уравнение и решите его.
33. Если периметр квадрата 48 дюймов, найдите длину каждой стороны.
34. Длина прямоугольника на 2 дюйма больше его ширины. Если периметр 36 дюймов, найдите длину и ширину.
35. Длина прямоугольника на 2 фута меньше его ширины в два раза. Если периметр составляет 26 футов, найдите длину и ширину.
36. Ширина прямоугольника на 2 сантиметра меньше половины его длины. Если периметр 56 сантиметров, найдите длину и ширину.
37. Длина прямоугольника на 3 фута меньше его ширины в два раза.Если периметр составляет 54 фута, найдите размеры прямоугольника.
38. Если длина прямоугольника вдвое больше ширины, а его периметр составляет 72 дюйма, найдите размеры прямоугольника.
39. Периметр равностороннего треугольника составляет 63 сантиметра. Найдите длину каждой стороны.
40. Равнобедренный треугольник, основание которого составляет половину длины двух других равных сторон, имеет периметр 25 сантиметров.Найдите длину каждой стороны.
41. Каждая из двух равных катетов равнобедренного треугольника в два раза длиннее основания. Если периметр составляет 105 сантиметров, то какой длины каждая ножка?
42. У треугольника есть стороны, размеры которых являются последовательными четными целыми числами. Если периметр составляет 42 дюйма, найдите размер каждой стороны.
43. У треугольника есть стороны, размеры которых являются последовательными нечетными целыми числами. Если периметр составляет 21 дюйм, найдите размер каждой стороны.
44. У треугольника есть стороны, размеры которых являются последовательными целыми числами. Если периметр составляет 102 дюйма, найдите размер каждой стороны.
45. Длина окружности составляет 50π единиц. Найдите радиус.
46. Длина окружности составляет 10π единиц. Найдите радиус.
47. Окружность круга составляет 100 сантиметров. Определите радиус с точностью до десятых.
48.Окружность круга составляет 20 сантиметров. Найдите диаметр, округленный до сотых.
49. Диаметр круга 5 дюймов. Определите длину окружности с точностью до десятых долей.
50. Диаметр круга 13 футов. Рассчитайте точное значение окружности.
Часть D. Проблемы с процентами и деньгами
Составьте алгебраическое уравнение и решите его.
51.Подсчитайте простой процент, полученный от двухлетних инвестиций в размере 1550 долларов США при годовой процентной ставке 8¾%.
52. Рассчитайте простой процент, полученный по годовой инвестиции в размере 500 долларов США при годовой процентной ставке 6%.
53. На сколько лет необходимо инвестировать 10 000 долларов под 8½% годовых, чтобы получить 4250 долларов в виде простых процентов?
54. На сколько лет необходимо инвестировать 1 000 долларов США под 7,75% годовых, чтобы получить 503,75 долларов США в виде простых процентов?
55.По какой годовой процентной ставке нужно инвестировать 2500 долларов на 3 года, чтобы получить 412,50 долларов в виде простых процентов?
56. По какой годовой процентной ставке необходимо инвестировать 500 долларов на 2 года, чтобы получить 93,50 долларов в виде простых процентов?
57. Если простой процент, полученный за 1 год, составлял 47,25 доллара США, а годовая ставка составляла 6,3%, то какой был основной процент?
58. Если простые проценты, полученные за 2 года, составляли 369,60 долларов, а годовая ставка составляла 5¼%, то каков был основной процент?
59.Джо вложил прошлогоднюю налоговую декларацию в размере 2500 долларов в два разных счета. Он положил большую часть денег на счет денежного рынка, получая 5% простых процентов. Остальное он вложил в компакт-диск, получив 8% простых процентов. Сколько он положил на каждый счет, если общая сумма процентов за год составила 138,50 долларов?
60. Джеймс вложил 1600 долларов в два счета. Один счет приносит 4,25% простых процентов, а другой — 8,5%. Если через год процентная ставка составила 85 долларов, сколько он вложил в каждую учетную запись?
61.Джейн вложила свои сбережения в размере 5 400 долларов в два счета. Часть этих денег она хранит на компакт-диске под 3% годовых, а остальная часть — на сберегательном счете, который приносит 2% годовых. Если простые проценты, полученные с обоих счетов, составляют 140 долларов в год, то сколько у нее есть на каждом счете?
62. Марти поместил прошлогодний бонус в размере 2400 долларов на два счета. Он вложил часть в компакт-диск с годовой процентной ставкой 2,5%, а остальную часть — в фонд денежного рынка с годовой ставкой 1,3%. Его общая сумма процентов за год составила 42 доллара.00. Сколько он вложил в каждый счет?
63. Алиса кладет деньги на два счета, один с годовой процентной ставкой 2%, а другой — с годовой процентной ставкой 3%. Она инвестирует в 3 раза больше в счет с более высокой доходностью, чем в счет с более низкой доходностью. Если ее общий процент за год составляет 27,50 долларов, сколько она инвестировала в каждую учетную запись?
64. Джим вложил наследство в два отдельных банка. Один банк предложил ставку 5,5% годовых, другой — 6¼%.Он вложил в более доходный банковский счет вдвое больше, чем в другой. Если его общая простая процентная ставка за 1 год составляла 4860 долларов, то какова была сумма его наследства?
65. Если рекламируемый товар стоит 29,99 долларов плюс налог 9,25%, какова общая стоимость?
66. Если рекламируется товар, стоимость которого составляет 32,98 доллара США плюс 8¾% налога, какова его общая стоимость?
67. Товар, включая налог в размере 8,75%, стоил 46,49 долларов. Какова первоначальная стоимость товара до вычета налогов?
68.Товар, включая налог в размере 5,48%, стоил 17,82 доллара. Какова первоначальная стоимость товара до вычета налогов?
69. Если еда стоит 32,75 доллара, какова сумма после добавления 15% чаевых?
70. Сколько чаевых составляет 15% от счета в ресторане на сумму 33,33 доллара?
71. У Рэя есть пригоршня десятицентовиков стоимостью 3,05 доллара. У него на 5 центов больше, чем у него. Сколько у него каждой монеты?
72. У Джилл на 3 полдоллара меньше, чем у нее четвертей.Стоимость всех 27 ее монет составляет 9,75 доллара. Сколько каждой монеты у Джилл?
73. Кэти должна внести пяти- и десятидолларовые банкноты на 410 долларов. У нее 1 меньше, чем в три раза больше десятков, чем у нее пятидолларовых купюр. Сколько денег от каждого счета она должна внести?
74. У Билли есть стопка четвертаков, десятицентовиков и никелей стоимостью 3,75 доллара. У него на 3 центов больше, чем четвертей, и на 5 центов больше, чем четвертей. Сколько каждой монеты у Билли?
75.У Мэри есть банка с однодолларовыми банкнотами, полдолларовыми монетами и четвертаками стоимостью 14 долларов. У нее в два раза больше четвертаков, чем у нее полудолларовых монет, и столько же полудолларовых монет, как у однодолларовых банкнот. Сколько у нее каждого?
76. У Чада есть пачка одно-, пяти- и десятидолларовых банкнот на общую сумму 118 долларов. У него в 2 раза больше, чем в 3 раза больше, чем у него пятидолларовых банкнот, и на 1 банкнот меньше десяти, чем пяти долларов. Сколько каждой банкноты есть у Чада?
Часть D: Равномерное движение (проблемы расстояния)
Составьте алгебраическое уравнение и решите его.
77. Две машины выезжают из локации, двигаясь в противоположных направлениях. Если одна машина развивает в среднем 55 миль в час, а другая — 65 миль в час, то сколько времени им потребуется, чтобы преодолеть расстояние в 300 миль?
78. Из аэропорта одновременно вылетают два самолета в противоположных направлениях. Средняя скорость самолетов составляет 450 миль в час и 395 миль в час. Сколько времени потребуется самолетам, чтобы преодолеть расстояние в 1478 единиц.75 миль друг от друга?
79. Билл и Тед мчатся по стране. Билл уезжает на час раньше, чем Тед, и едет со средней скоростью 60 миль в час. Если Тед намеревается наверстать упущенное со скоростью 70 миль в час, то сколько времени это займет?
80. Два брата уезжают из одного и того же места, один на машине, а другой на велосипеде, чтобы встретиться в доме своей бабушки за ужином. Если один брат в среднем проезжает 30 миль в час в машине, а другой — 12 миль в час на велосипеде, тогда у брата на велосипеде на 1 час меньше, чем в 3 раза больше времени, чем у другого в машине.Сколько времени нужно каждому из них, чтобы совершить путешествие?
81. Пилот коммерческой авиакомпании летел со средней скоростью 350 миль в час, прежде чем был проинформирован о том, что аэродром его назначения может быть закрыт из-за плохих погодных условий. Пытаясь прибыть перед бурей, он увеличил скорость до 400 миль в час и летел еще 3 часа. Если общее расстояние полета составило 2950 миль, то сколько времени длилось путешествие?
82. Два брата проехали 2793 мили от Лос-Анджелеса до Нью-Йорка.Один из братьев, управляя автомобилем днем, мог развивать скорость в среднем 70 миль в час, а другой, двигаясь ночью, мог развивать скорость в среднем 53 мили в час. Если брат, ехавший ночью, ехал на 3 часа меньше, чем брат, ехавший днем, то сколько часов каждый из них ехал?
83. Джо и Эллен живут в 21 миле друг от друга. Отправляясь одновременно, они едут навстречу друг другу. Если у Джо в среднем 8 миль в час, а у Эллен — 6 миль в час, сколько времени у них уйдет на встречу?
84.Если дорога до автомастерской занимает 6 минут со средней скоростью 30 миль в час, то сколько времени потребуется, чтобы вернуться обратно со средней скоростью 4 мили в час?
85. Хайме и Алекс покидают то же место и едут в противоположных направлениях. Условия движения позволили Алексу в среднем разгоняться на 14 миль в час, чем Хайме. Через полтора часа их разделяет 159 миль. Найдите скорость, с которой каждый мог двигаться.
86. Джейн и Холли живут в 51 миле друг от друга и уезжают, путешествуя навстречу друг другу, чтобы встретиться за обедом.Джейн ехала по автостраде со скоростью вдвое большей, чем Холли. Они смогли встретиться через полчаса. С какой скоростью путешествовал каждый?
Часть F: Темы дискуссионной доски
87. Обсудите в уме идеи для расчета налогов и чаевых.
88. Изучите исторические методы представления неизвестных.
89. Изучите и сравните простые и сложные проценты. В чем разница?
90.Обсудите, почему алгебра — обязательный предмет.
91. Изучите способы показать, что повторяющаяся десятичная дробь рациональна. Поделитесь своими выводами на доске обсуждений.
Нахождение уравнения графической линии — Задача 1
Чтобы найти уравнение построенной на графике линии, найдите точку пересечения по оси Y и наклон, чтобы записать уравнение в форме точки пересечения по оси Y (y = mx + b). Наклон — это изменение y по сравнению с изменением x. Найдите две точки на линии и нарисуйте наклонный треугольник, соединяющий две точки.Обозначьте стороны треугольника. Это сообщит вам значение роста (изменение y, числитель) и значение пробега (изменение x, знаменатель). Пересечение оси Y происходит от точки, в которой линия пересекает ось Y. Значение Y координаты — это точка пересечения по оси Y или значение «b». Подключите наклон m и точку пересечения оси y b к форме линии пересечения с уклоном.
Задачи этого типа используются во всем курсе алгебры 1.Под типом задачи я подразумеваю, когда вам дается график и вас просят написать его уравнение. Поэтому, когда вы это делаете, есть много разных подходов к этому. Мой личный любимый способ — найти наклон и точку пересечения оси y. Особенно в таких графиках, где такие вещи бросаются в глаза. Вот что я имею в виду.
Для уравнения прямой, я думаю, y равно mx плюс форма b. Мне нужен наклон и точка пересечения по оси Y. Эта буква y и эта буква x останутся в моем уравнении, так что давайте продолжим и пощупаем пробелы.
Мой номер наклона можно найти по изменению y поверх изменения x. Один из способов сделать это — найти две любые точки, через которые проходит линия, и нарисовать наклонный треугольник. Итак, давайте посмотрим, эта линия проходит точно через эту точку, а эта точка прямо там. Итак, я хочу нарисовать треугольник наклона, который их соединяет, хорошо, а затем я помечаю стороны, которые будут говорить мне о моем подъеме и моем беге, а затем наклон — это вертикальное изменение поверх горизонтального изменения. Так что в моем случае наклон будет +3/2.Я почти закончил. +3/2, милая, не так уж и плохо. Последнее, что мне нужно из моего уравнения y равно mx плюс b, — это точка пересечения y.
Помните, что y — это вертикальная ось, поэтому точка пересечения y происходит от того места, где ваша графическая линия пересекает эту вертикальную ось. Вот и все, координаты 0 для x, 3 для y. 3 — важная часть, которая будет моим значением b для моего пересечения с y. Уравнение для линии будет y равно 3 / 2x плюс 3.
Вот и все. Когда у вас есть такой график, и особенно когда он нанесен на миллиметровую бумагу, например, графическая сетка, очень легко найти уравнение в форме Slope-Intercept.Первое, что вам нужно сделать, это найти угол наклона, второе — найти точку пересечения оси y, а затем просто подключить их.
.





 Актуализация познавательной деятельности.
Актуализация познавательной деятельности.
 Регулятивные: целеполагание, планирование
Регулятивные: целеполагание, планирование



 Выполнение задания № 283.(работа в парах)
Выполнение задания № 283.(работа в парах)
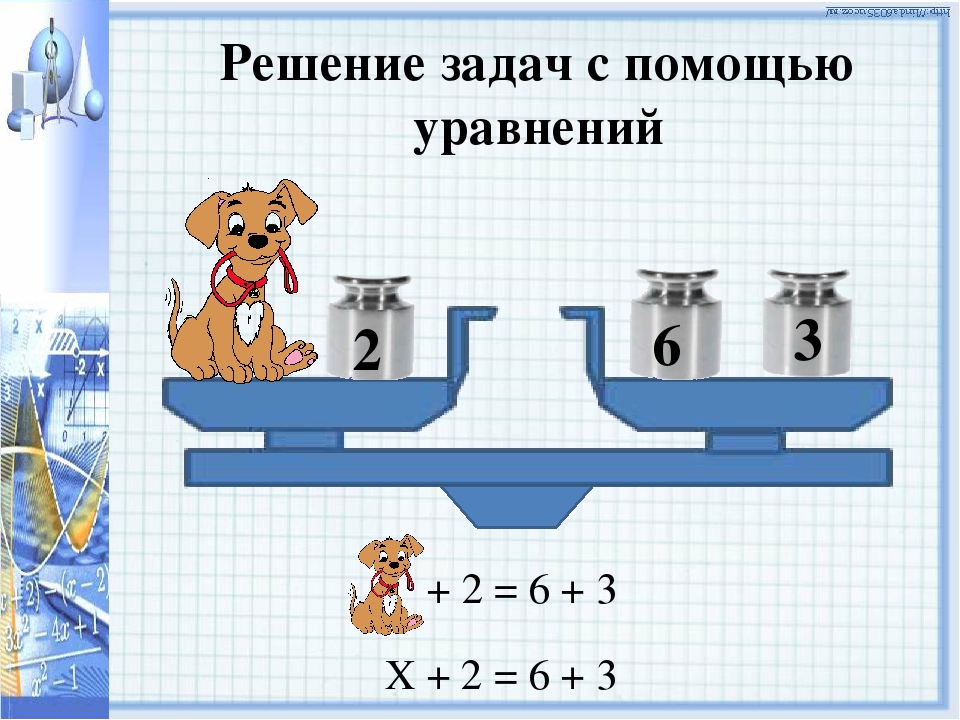




 Тестовая работа.
Тестовая работа.
 Итог урока. Рефлексия.
Итог урока. Рефлексия.


 На доске ответы к задачам.
На доске ответы к задачам.
 Решите уравнение: 45- а=29
Решите уравнение: 45- а=29
 Решите уравнение: m — 27=43
Решите уравнение: m — 27=43








 Я надеюсь вы все сделали утреннюю зарядку?
Я надеюсь вы все сделали утреннюю зарядку?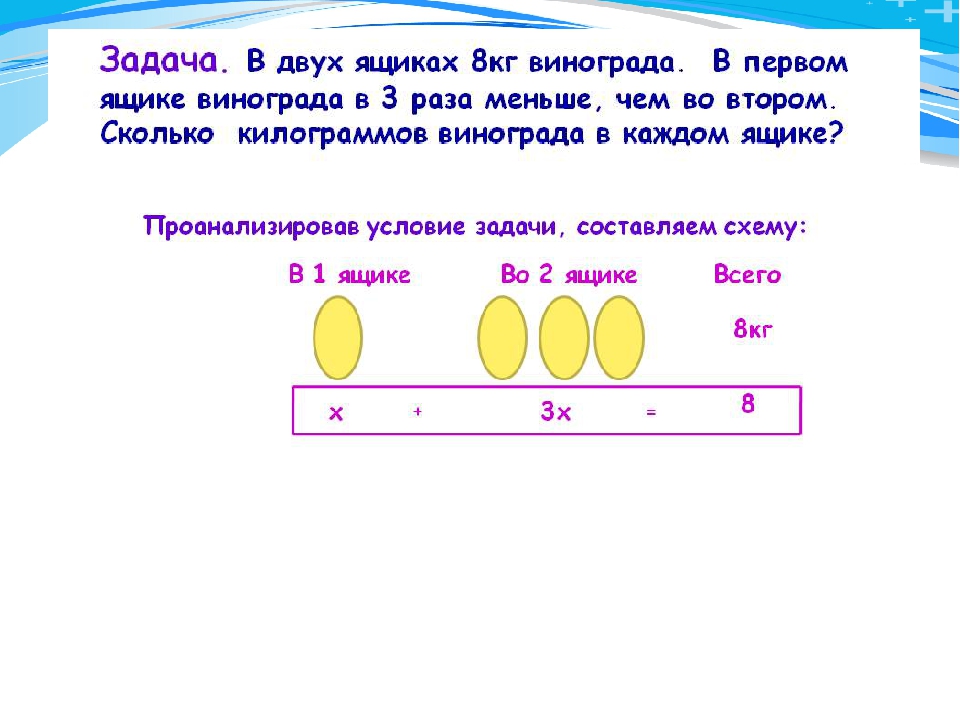 Актуализация познавательной деятельности.
Актуализация познавательной деятельности. Познавательные: формировать умение на основе анализа делать выводы.
Познавательные: формировать умение на основе анализа делать выводы.
 (прочитать, обозначить неизвестное х, записать ответ, составить уравнение, решить уравнение, записать краткую запись)
(прочитать, обозначить неизвестное х, записать ответ, составить уравнение, решить уравнение, записать краткую запись)

 Тестовая работа.
Тестовая работа.

 Решите уравнение: х-29=94
Решите уравнение: х-29=94
