Содержание
Конспект урока по математике на тему «Числовые выражения»(7 класс)
Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа № 45
Разработка урока по теме
«Числовые выражения»,
алгебра, 7 класс.
Автор: учитель математики
первой категории
МАОУ СОШ №45 г. Калининграда
Борисова Алла Николаевна.
г. Калининград
2018 – 2019 учебный год
Автор – Борисова Алла Николаевна
Образовательное учреждение – муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 города Калининграда
Предмет – математика (алгебра)
Класс – 7
Тема – «Числовые выражения»
Учебно-методическое обеспечение:
Алгебра, 7 класс: учебник для общеобразовательных организаций / Ю.
 М.Колягин и др., М.: Просвещение, 2016 г.
М.Колягин и др., М.: Просвещение, 2016 г.
Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010
Цель:
актуализация и обобщение знаний и умений по теме «Числовые выражения», введение в алгебру.
Задачи урока:
Образовательные:
обеспечить осознанное усвоение правил выполнения арифметических действий над десятичными и обыкновенными дробями, положительными и отрицательными числами;
закрепить вычислительные навыки и умения;
создать условия для систематизации, обобщения и углубления знаний обучающихся при решении заданий по теме «Числовые выражения»
Развивающие:
способствовать развитию творческой активности обучающихся;
повышать познавательный интерес к предмету;
развивать логическое и образное мышление, способность рассуждать и делать выводы.

Воспитательные:
формировать внимательность и точность в вычислениях;
воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению;
культуру учебного труда, требовательное отношение к себе и своей работе.
Оборудование и материалы для урока: проектор, экран, презентация для сопровождения урока, раздаточный материал.
Тип урока: комбинированный.
Формы организации работы: фронтальная, индивидуальная, самостоятельная.
Структура урока:
II. Актуализация опорных знаний: организация повторения изученного ранее материала. Введение в алгебру.
Давайте вспомним, чем мы занимались на уроках математики?
Повторим правила действий с обыкновенными дробями Сформулируйте правила сложения и вычитания обыкновенных дробей.
Как выполнить умножение обыкновенных дробей?
Как выполнить деление обыкновенных дробей?
Вычислите (слайд №4)
В 6 классе мы изучали положительные и отрицательные числа, умеем выполнять арифметические действия с ними.
 Вспомним правила действий с отрицательными числами, числами с разными знаками. Напомните, на что нужно обратить особое внимание? (слайд №5)
Вспомним правила действий с отрицательными числами, числами с разными знаками. Напомните, на что нужно обратить особое внимание? (слайд №5)
III. Изучение нового материала.
Введение в алгебру.
— Какой предмет вы изучали в прошлом году? (Математику).
— Чем вы занимались на уроках математики? (Проводили вычисления с целыми и дробными числами, решали уравнения, задачи, строили фигуры в координатной плоскости и т. д.)
— Все это составляло содержание предмета «Математика». Мы с вами изучили школьную арифметику, а теперь будем изучать алгебру и геометрию (слайд №6).
— Мы приступаем к изучению алгебры.
Знакомство с учебником.
Алгебра как искусство решать уравнения зародилась очень давно в связи с потребностями практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны те приёмы решения уравнений, которые вы узнали в 6- м классе. А в Индии умели решать некоторые уравнения ещё в 499 году. Большую роль в развитии алгебры сыграл математик и астроном из г.Хивы Мухаммед бен Муса аль-Хорезми (787-ок.850г.). Он написал трактат «Аль-китаб аль мухтасар фи хисаб аль-джебр ва аль-мукабала». Термин «аль-джебр» постепенно стал употребляться как «алгебра» (слайд №7).
А в Индии умели решать некоторые уравнения ещё в 499 году. Большую роль в развитии алгебры сыграл математик и астроном из г.Хивы Мухаммед бен Муса аль-Хорезми (787-ок.850г.). Он написал трактат «Аль-китаб аль мухтасар фи хисаб аль-джебр ва аль-мукабала». Термин «аль-джебр» постепенно стал употребляться как «алгебра» (слайд №7).
Современная алгебра – один из основных разделов математики и, чтобы это произошло, многие выдающиеся люди своего времени вложили свой талант и труд (слайд №8). В школе мы изучаем простейшие основы этой науки.
Совместный разбор задачи (слайд №9).
Введение понятий «числовое выражение», «значение числового выражения», «числовое равенство», «верное числовое равенство»
(слайды №10 — 12).
Повторить порядок выполнения действий в числовом выражении. (слайды №13-16).
IV. Решение упражнений (слайд №14).
Решение упражнений (слайд №14).
Все упражнения, выполняемые на этом уроке, можно разбить на группы, учитывая уровень подготовленности учащихся:
1-я группа(с низким уровнем мотивации к учебе). Нахождение значения числового выражения, представляющего собой сумму или разность, произведение или частное. Решают самостоятельно
2-я группа(средний уровень). Нахождение значения числового выражения, содержащего в записи два и более арифметических действия, а также скобки. Работают самостоятельно (по необходимости пользуются помощью учителя или соседа по парте). Двое учащихся работают на откидной доске. После окончания работы взаимопроверка.
3-я группа(высокий уровень). Работают самостоятельно в тетради. При необходимости ребята получают консультации учителя. Затем решения оформляются на доске и обсуждаются.
1-я группа
№ 1 (1, 3, 5, 7), № 2, 6(1).
2-я группа
№ 3 (1), № 5(1), № 6 (3), № 7 (1)
3-я группа
№ 3 (3), № 5(3), № 6(5), № 7 (3)
V. Подведение итогов урока.
Подведение итогов урока.
Что называется значением числового выражения?
Для чего в записи числового выражения присутствуют скобки?
Что называется значением числового выражения?
Каков порядок выполнения действий при нахождении значения числового выражения?
Выставление отметок за урок.
VIII. Домашнее задание (слайд №17).
§ 1, № 1(2,4,6,8), 3(2,4), 5(2,4), 6(2, 4)
Алгебра: 7 класс. Урок 2. Числовые выражения. Выражения с переменными. Добрый день, ребята!
ОБРАЩЕНИЕ К ЧИТАТЕЛЮ
ОБРАЩЕНИЕ К ЧИТАТЕЛЮ Дорогие друзья! Мы рады снова встретиться с вами в 6 классе! Мы предлагаем учить математику уже в привычной для вас форме: вы сможете одновременно использовать учебник, учебные книги,
Подробнее
ISBN К 22.
 14я721 ISBN
14я721 ISBN
ДК 373:512 К 22.14721 49 49 аа, аьяа Маа.. 7 9 /.М.. М : Э, 2018. 128. (. ). ISBN 978-5-04-093533-8, 7 9-. П ё -. П,. П 7 9-,, -. ДК 373:512 К 22.14я721 ISBN 978-5-04-093533-8 аа.м., 2018 О. ООО «Иаь «Э»,
Подробнее
Образовательный минимум Предмет
Четверть 1 Какие числа являются натуральными? Как прочитать число? Как записать цифрами число? Соотношения между единицами Как начертить координатный луч и отметить на этом луче точки? Формулы Числа, которые
Подробнее
Поурочное планирование
Поурочное планирование урока, число 1 2 Темы учебных занятий Обозначение натуральных чисел Стандарт темы Понятие натурального числа, позиционной десятичной системы счисления Планируемый результат обучения
Подробнее
8 класс Алгебра. Тема «Рациональные дроби»
8 класс Алгебра Тема «Рациональные дроби» 1.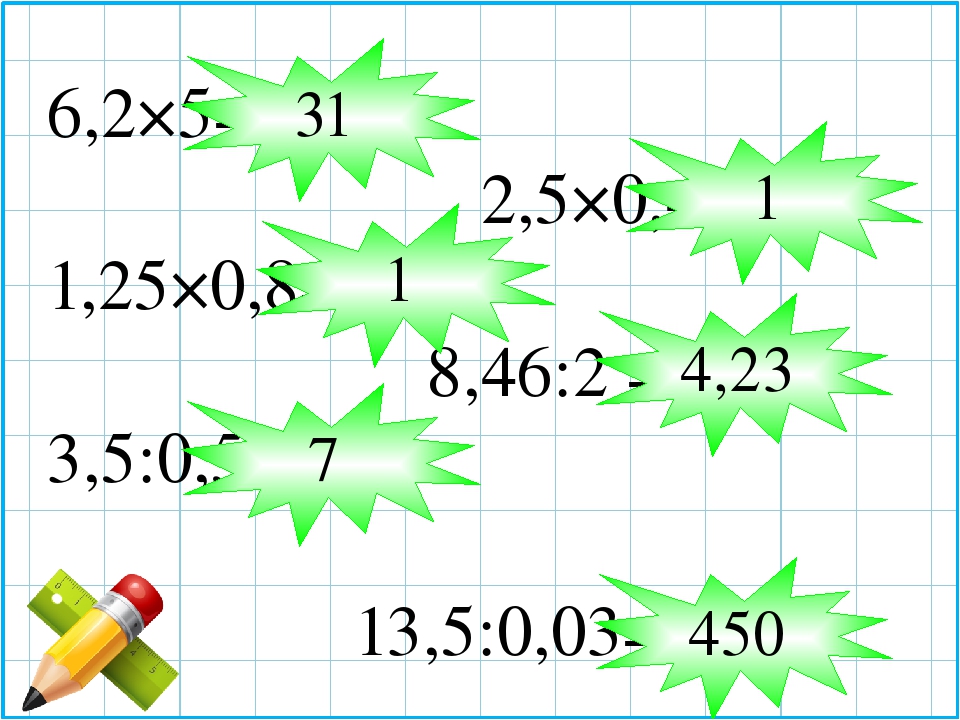 ОСНОВНЫЕ ПОНЯТИЯ Понятие алгебраической дроби знакомо вам из курса алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей.
ОСНОВНЫЕ ПОНЯТИЯ Понятие алгебраической дроби знакомо вам из курса алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей.
Подробнее
2- периметр прямоугольника;
Основные правила за курс математики 5-6 классов. Свойства сложения и вычитания: a + b = b + a переместительное; a + (b + c) = (a + b) + c = a + b + c = (a + c) + b = a + c + b сочетательное; (a + b)c =
Подробнее
Рабочая программа по математике 3 класс
Муниципальное казенное общеобразовательное учреждение «Евдаковская основная общеобразовательная школа» Каменского муниципального района Воронежской области Рассмотрено на заседании ШМО учителей начальных
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа по математике составлена на основе следующих нормативных документов и методических рекомендаций: 1. Федеральнфй государственный образовательный стандарт основного
Федеральнфй государственный образовательный стандарт основного
Подробнее
Пояснительная записка
Пояснительная записка Программа по математике разработана, в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа учебного предмета «Математика» составлена в соответствии с требованиями федерального компонента государственного стандарта общего образования и на основе программы,
Подробнее
ОГЛАВЛЕНИЕ. Предисловие… 5
ОГЛАВЛЕНИЕ Предисловие……………………………………… 5 Глава первая Арифметика и алгебра………………………………. 6 1.1. Числа и действия с ними. ……………………….
……………………….
Подробнее
Тема 1. Элементы теории погрешностей
— 1 — Тема 1 Элементы теории погрешностей 11 Источники и классификация погрешностей Численное решение любой задачи, как правило, осуществляется приближенно, те с некоторой точностью Это может быть обусловлено
Подробнее
Вопросы для повторения I
4 Вопросы для повторения I. Натуральные числа. Натуральный ряд.. Числа и цифры. Десятичная система счисления. 3. Разряды и классы. Представление числа в виде суммы разрядных слагаемых. 4. Сравнение натуральных
Подробнее
Рабочая учебная программа
Рабочая учебная программа МАТЕМАТИКА 5-6 классы 2017-2018 учебный год АННОТАЦИЯ Настоящая рабочая программа разработана в соответствии с основными положениями Федерального государственного образовательного
Подробнее
Математика.
 Пояснительная записка.
Пояснительная записка.
Математика Программа: ШКОЛА РОССИИ. Концепция и программы для Начальных классов. Часть 1. Математика. Авторы: М. И. Моро, Ю. М. Калягин, М.А,Бантова, Г. В. Бельтюкова, С. И. Волкова, С. В. Степанова. —
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по математике для 4 класса разработана на основе Федерального государственного образовательного стандарта начального общего образования, примерной программы начального
Подробнее
I. Планируемые результаты
I. Планируемые результаты предметные: умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя
Подробнее
ББК Б94 ISBN
ББК 74. 262.21 Б94 Б94 Буцко Е.В. Алгебра : 7 класс : методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский и др. М. : Вентана-Граф, 2017. 104 с. : ил. ISBN 978-5-360-08673-4 Пособие содержит
262.21 Б94 Б94 Буцко Е.В. Алгебра : 7 класс : методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б. Полонский и др. М. : Вентана-Граф, 2017. 104 с. : ил. ISBN 978-5-360-08673-4 Пособие содержит
Подробнее
СПРАВОЧНИК ПО МАТЕМАТИКЕ. 5 9 классы
СПРАВОЧНИК ПО МАТЕМАТИКЕ 5 9 классы МОСКВА «ВАКО» 201 УДК 32.851 ББК 4.262.22 С4 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ
Подробнее
Умножение и деление обыкновенных дробей.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ Название раздела, п/п тема Кол-во часов Содержание Требования к результатам обучения по темам 1 Делимость 21 Делимость натуральных. Делители и кратные числа. Признаки делимости
Подробнее
ББК я72 М52 ISBN
ББК я7 М5 Мерзляк АГ М5 Алгебра : 8 класс : cамостоятельные и контрольные работы : пособие для учащихся общеобразовательных организаций / АГ Мерзляк, ВБ Полонский, ЕМ Рабинович и др М : Вентана-Граф, 07
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данные групповые занятия по математике для учащихся 8 класса относятся к отработке навыков тем из курса 8 класса, которые наиболее трудно усваивались учащимися, а также для дополнения
Подробнее
Рабочая программа по математике
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 2» Утверждено: Директор О. А. Сорокина Приказ 371 31.08.2016 Согласовано: Зам. директора по УР Поповцева И.Ю. 30.08.2016
А. Сорокина Приказ 371 31.08.2016 Согласовано: Зам. директора по УР Поповцева И.Ю. 30.08.2016
Подробнее
Целые и рациональные числа
Тема Целые и рациональные числа Входной тест Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Запишите ответы к заданиям в поле ответа в тексте работы,
Подробнее
СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ
А. Н. РУРУКИН, Н. Н. ГУСЕВА, Е. А. ШУВАЕВА СБОРНИК ЗАДАЧ ПО АЛГЕБРЕ 7 класс МОСКВА «ВАКО» 06 УДК 7.5 ББК.4 Р87 6 Издание допущено к использованию в образовательном процессе на основании приказа Министерства
Подробнее
Выражения с переменными
Вопросы
занятия:
·
ввести понятие «выражение с переменными»;
·
ввести понятие «область определения выражения».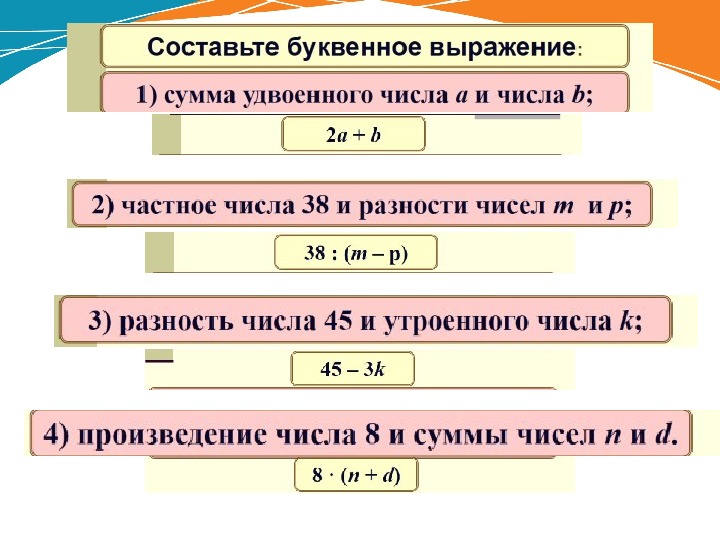
Материал
урока
Вспомним, что на прошлом уроке мы говорили о
числовых выражениях и значениях числовых выражений.
Числовым выражением
называется запись, составленная из чисел, знаков арифметических действий и
скобок, указывающих на порядок выполнения действий.
Значением числового выражения
называется число, которое получается при выполнении всех действий числового
выражения.
Определение.
Буквенным выражением
называется запись, состоящая из чисел, букв, знаков арифметических действий и
скобок, указывающих на порядок выполнения действий.
Строчные буквы латинского алфавита чаще всего
используют при записи буквенных выражений.
Следует также знать, что и одна буква является
буквенным выражением.
Давайте решим задачу.
Велосипедист двигается со скорость 15 километров в
час. Какой путь он проедет за время t?
Известно, что путь можно найти
скорость умножив на время. Тогда путь, который проедет велосипедист,
Тогда путь, который проедет велосипедист,
будет равен 15t.
Теперь, если нам нужно будет узнать, какое
расстояние проехал велосипедист, например, за 3 часа, мы подставим в выражение
15 ∙ t
вместо буквы t
число 3, то есть найдём значение выражения при t = 3, и получим 45 километров.
В нашем случае буква t называется переменой, а само выражение – выражением с переменной.
То есть, переменная – это буква, входящая в
буквенное выражение, которая может принимать различные значения.
Например,
Если мы в выражение с переменной вместо переменной
подставим число, то получим числовое выражение.
Например,
Теперь, прежде, чем перейти
к решению упражнений, вернёмся к выражению 15t, которое мы получили при решении
первой задачи. Здесь переменная t
может принимать только положительные значения, так как время не может быть
отрицательным, и это множество значений называется областью определения
выражения 15t.
Таким образом, важно помнить, что в область
определения любого выражения могут входить только те значения переменных, при
которых получается числовое равенство, имеющее смысл.
А сейчас давайте решим некоторые упражнения.
Пример.
Следующее упражнение.
Пример.
И последнее упражнение.
Пример.
Числовые выражения | Презентация к уроку по алгебре (7 класс) на тему:
Слайд 1
И снова в позолоте тополя, А школа — как корабль у причала, Где ждут учеников учителя, Чтоб новой жизни положить начало. Пусть счастье в дверь твою стучит, Открой ее скорей пошире. Путь жизни тайною покрыт, Но так прекрасно в этом мире! И пусть всегда – в окошке свет, Улыбка мамина – с порога. Пусть будет много добрых лет И в жизни легкая дорога!
Слайд 2
Есть о математике молва, Что она в порядок ум приводит. Поэтому хорошие слова Часто говорят о ней в народе.
Слайд 4
S = v· t a · b = b · a
Слайд 5
Вавилон Египет
Слайд 6
Около 4000 лет назад в Вавилоне и в Египте ученые уже умели составлять линейные уравнения, с помощью которых они решали самые разнообразные задачи землемерия, строительного искусства и военного дела. В Британском музее хранится задача из папируса Ринда (его называли также папирусом Ахмеса)
Слайд 7
В Британском музее хранится задача из папируса Ринда (его называли также папирусом Ахмеса) Найти число, если известно, что от прибавления к нему 2/3 его и вычитая от полученной суммы ее трети получается число 10.
Слайд 8
« Хисаб Ал-джебр Вал-мукабала » («Метод восстановления и противопоставления») – это была первая книга по алгебре. Ал-джебр При решении уравненья, Если в части одной, Безразлично какой, Встретится член отрицательный, Мы к обеим частям, С этим членом сличив. Равный член придадим, Только с знаком другим,— И найдем результат, нам желательный! Вал-мукабала Дальше смотрим в уравненье, Можно ль сделать приведенье, Если члены есть подобны, Сопоставить их удобно. Вычитая равный член из них, К одному приводим их.
Вычитая равный член из них, К одному приводим их.
Слайд 10
Алгебра уравнение число тождество функция Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные вычисления, но и учит его делать это как можно быстрее, рациональнее.
Слайд 11
Тема урока: «Числовые выражения» Повторить и углубить умение учащихся находить значения числовых выражений; Запомнить, что выражение, содержащее действие деление на нуль, не имеет смысла; Развить познавательный интерес учащихся к изучению нового предмета. Цели урока:
Слайд 12
устно Вычислите: 6 7 10 80 289 72 8 5 8100 170
Слайд 13
Запись, составленная из чисел с помощью арифметических действий (сложение, вычитание, умножение, деление, возведение в степень) называет числовым (арифметическим) выражением . 2 2 0 Значением числового выражения называется число, полученное в результате выполнения указанных в числовом выражении действий. Изучение темы
Слайд 14
Два числовых выражения, соединенные знаком «=», образуют числовое равенство . Если значения левой и правой частей числового равенства совпадают, то равенство называют верным , в противном случае – неверным . верное неверное Изучение темы
Если значения левой и правой частей числового равенства совпадают, то равенство называют верным , в противном случае – неверным . верное неверное Изучение темы
Слайд 15
Если в данном выражении на некотором этапе вычислений требуется делить на нуль, то это выражение не имеет смысла . Изучение темы
Слайд 16
Киоск задач №1 Установите, какие из следующих выражений имеют смысл и какие не имеют. Для имеющих смысл найдите числа, которым они равны. а) б) в) не имеет смысла -3/7 54/95
Слайд 17
Киоск задач №1 (первая, вторая строчки), №3, №4 (д – з), №5, №6 (первая, третья строчки), №7 (а, б), №13
Слайд 18
Домашнее задание П.1 (изучить, определения выучить), №2, №4 (а – г), №6 (б, д, з)
Слайд 19
Итоги урока О каких выражения мы сегодня говорили? Какое выражение называется числовым? Что называют значением числового выражения? Что такое числовое равенство? Какие виды равенств вы знаете? Когда числовое выражение не имеет смысла?
Слайд 20
Спасибо за урок, Дети Творческих успехов Вам В новом учебном году!
Числовые выражения 1 урок Алгебра 7 класс Мерзляк ФГОС
§ 1. ВВЕДЕНИЕ В АЛГЕБРУ
ВВЕДЕНИЕ В АЛГЕБРУ
Технологическая карта урока № 1
Тема урока Введение в алгебру
Тип урока Урок изучения нового материала
Формируемые результаты
Предметные: познакомить учащихся с числовыми выражениями, с выражениями с переменными, алгебраическими выражениями, целыми выражениями, закрепить навыки вычисления значений числовых выражений.
Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.
Планируемые результаты
Учащийся научится вычислять значение числового выражения, находить значение выражения с переменными при заданных значениях переменной.
Основные понятия
Буквенное выражение, числовое выражение, значение числового выражения, переменная, выражение с переменными, значение переменной, значение выражения с переменными, алгебраическое выражение, целое выражение.
1. Организационный момент
Здравствуйте, ребята!
Как Ваше настроение?
Настроены ли Вы на работу?
Все ли принадлежности приготовлены к уроку?
Тогда в добрый путь!
Улыбнемся друг другу!
1.1.
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Дорогие ребята! Мы с Вами уже не первый год занимаемся изучением такой нужной, сложной, и одновременно интересной науки «математики». За это время мы многое узнали, многому научились. Давайте вспомним хотя бы толику тех знаний, которые мы с Вами получили.
Давайте вспомним хотя бы толику тех знаний, которые мы с Вами получили.
Придя в начальную школу, о каких числах вы узнали в первую очередь?
Какие операции над ними Вы научились выполнять?
(Это натуральные числа, числа, применяемые при счете предметов. Мы умеем складывать, вычитать, умножать и делить натуральные числа.)
В курсе математики 5-6 класса мы познакомились с десятичными и обыкновенными дробями, целыми и рациональными числами. И так же научились выполнять над ними арифметические операции.
Можно было бы человеку обойтись без этих чисел? Для чего они нам нужны?
(учащиеся предлагают свои варианты ответов, среди которых могут быть такие: дроби появились в связи с необходимостью что — то делить на равные части, целые числа — это долг и доход, для измерения понижения уровня моря и температуры и т.п.).
И кажется что этого багажа знаний вполне достаточно для повседневной жизни. Однако мы пришли в 7 класс и продолжаем заниматься математикой. Правда теперь наш учебник называется «Алгеброй».
Тема нашего сегодняшнего урока: Числовые выражения
Цели: Выявление уровня вычислительных умений и навыков с рациональными числами. Повторить правила сложения, умножения, деления десятичных и обыкновенных дробей, правила действий с отрицательными и положительными числами. Углубление и систематизация сведений о числовых выражениях. Формирование умения находить значение числового выражения.
3. Изучение нового материала
(Методические комментарии к этапу
В курсе математики 5 класса учащиеся познакомились с буквенными выражениями и в дальнейшем многократно встречались с этим понятием.
Следует подчеркнуть, что обозначение чисел буквами, конструирование буквенных выражений и их преобразование, работа с формулами были первыми шагами в науку «Алгебра». Хотя этот параграф и насыщен терминами, но многие из них знакомы учащимся: числовое выражение, значение числового выражения, буквенное выражение, переменная, значение переменной, значение выражения при заданном значении переменной.
Следует заметить, что в 5 и 6 классах понятие «переменной» не вводилось, вместо него использовался термин «буква» в буквенном выражении. Поэтому, возможно, следует обратить внимание учащихся на то, что термин «выражение с переменными» означает то же, что и «буквенное выражение».
Также можно провести аналогию между буквами (переменными) в алгебраических выражениях и переменными в записи алгоритмов, с которыми учащиеся могли ознакомиться в ходе изучения курса информатики.
В параграфе не рассматривается формальное определение буквенного выражения. Однако из текста ясно, как конструируется буквенное выражение.
Схема, изображённая на с. 5 учебника, помогает лучше усвоить понятие алгебраического выражения. Разделяя алгебраические выражения на две группы — целые и дробные — мы таким образом выделяем объект, который будет изучаться в курсе алгебры 7 класса.
Отметим, что поскольку дробные выражения в этом курсе не рассматриваются, то соответствующий термин здесь не вводится.)
Теоретический материал § 1
Числовое выражение – это такое выражение, которое составлено из чисел, знаков математических действий и скобок.
Например:
3+5⋅(7−4) — числовое выражение;
3+:−5 — не числовое выражение, а бессмысленный набор символов.
Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.
Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.
Например:
a2−3b — алгебраическое выражение.
Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.
Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.
При упрощении вычислений часто используются законы сложения и умножения.
— переместительный закон.
— сочетательный закон.
— распределительный закон.
В результате упрощений числового выражения получается число, которое называют значением числового выражения.
Выполнив указанные действия в первом примере, получим
3+5⋅(7−4)=18 .
Число 18 в ответе есть значение данного числового выражения.
О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.
Например, алгебраическое выражение a2−3b при a=−16 и b=−14 имеет значение 298 , т. к.
a2−3b=(−16)2−3⋅(−14)=256+42=298 ,
а вот алгебраическое выражение a2−3/a+2 при a=−4 имеет значение −6,5 ,
т. к. (−4)2−3/−4+2=16−3/−2=13/−2=−6,5 .
И это же алгебраическое выражение a2−3/a+2 при a=−2 не имеет смысла, т. к. a+2=−2+2=0 , т. е. будет деление на ноль.
Обрати внимание!
А на ноль делить нельзя!
Вывод:
если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;
если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.
Так, в примере a2−3/a+2 значение a=−4 — допустимое, а
значение a=−2 — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!
4. Первичное закрепление нового материала.
Учебник № 1, 2, 4 (1–3), 6, 8
Дидактический материал № 1 (1–3), 2 (1–3), 3 (1–3)
Рабочая тетрадь №3,4
4.1. Найди значение выражения −8,9−8,1
Найди значение выражения −9,2−(−7,2).
4.2. Прочитай выражение и найди его значение.
В данном числовом выражении 2+(−4,3) записана
Прочитай выражение и найди его значение.
В данном числовом выражении 4,3÷(−2) записано
4.3. Какие свойства действий позволяют, не выполняя вычислений, утверждать, что верно равенство: 473+(37+25)=(473+37)+25 ?
Какие свойства действий позволяют, не выполняя вычислений, утверждать, что верно равенство: 471+35=35+471 ?
4.4. Найди значение выражения (ответ округлите до тысячных):
83,542−52,8=
4.5. Выполни действия: 379,78⋅51−23,746:3,83=
4.6. Найди значение выражения: (14,35−1,75):1,4+4,7=
4.7. Выполни действия: (дробь не сокращай) 12−8=
4.8. Выполни действие: −2,8−12=
4.9. Определи значение выражения:
4.10. Найди значение выражения наиболее рациональным способом:
42,9⋅ −2,9⋅ =
4.11. Вычисли значение алгебраического выражения ,
если a= 10,8, b= 0,6.
4.12. При каких значениях переменной имеет смысл выражение
4.13. Имеет ли смысл данная дробь? Если имеет смысл то найти ее значение. =
4.14. В выражении 8⋅12+18:3−2 расставь скобки так, чтобы его значение было наибольшим.
5. Повторение
Учебник № 23
6. Итоги урока
Вопросы 1–3
1. Как иначе называют буквенные выражения?
2. Какие выражения называют алгебраическими?
3. Какие алгебраические выражения называют целыми?
7. Информация о домашнем задании
Учебник § 1, вопросы 1–3, № 5 (1, 2), 7, 9
Рабочая тетрадь №1, 2
ВАРИАНТ № 1 1.Запишите а)произведение б)частное в)сумму г)произведение 2.Найдите ; б) ; в)
г) | ВАРИАНТ № 3 1.Запишите а)произведение б)частное в)сумму г)произведение 2.Найдите ; б) ; в)
г)
| ВАРИАНТ № 2 1.Запишите а)произведение б)сумму в)разность г)частное 2.Найдите ; б) ; в) г) | ВАРИАНТ № 4 1.Запишите а)произведение б)сумму в)разность г)частное 2.Найдите а) в) 0,25 + : г)
|
Числовые выражения — формулы, примеры и алгоритм решения в 7 классе
Основой математики являются числовые выражения. В 7 классе они изучаются подробнее, поскольку к ним применяются специальные методики, позволяющие выполнять операции упрощения. Последние используются для оптимизации вычислений при решении задач по различным дисциплинам с физико-математическим уклоном. Однако специалисты рекомендуют изучить теорию, которая поможет избежать множества ошибок при расчетах величин.
Общие сведения
Многие начинающие математики часто путают два понятия: числовые и алгебраические выражения. Между ними существует разница, которая заключается в определениях. Числовое выражение — вид математического тождества, состоящего только из чисел, скобок и знаков арифметических операций. Например, тождество «5+8/3−4*2» является числовым выражением. Оно означает последовательность математических знаков, объединенных в одну логическую цепочку.
Алгебраическим называется совокупность переменных и числовых выражений, имеющих логическое завершение. Объяснение смысла логики выражения имеет такой вид: совокупность чисел и переменных, связанных между собой арифметическими операциями умножения, деления, сложения и вычитания. Например, выражение «5t-2/3» — алгебраическое, поскольку в нем присутствует переменная «t».
Математическим выражением не является набор символов, не имеющий логического завершения. Например, 234±4678++* — обыкновенный ряд, который можно составить из цифр и знаков арифметических операций. Последние имеют следующие обозначения:
Произведение — вид арифметической операции, позволяющей умножить одну величину на другую. Она состоит из трех основных элементов. К ним относятся: I множитель, II множитель и произведение (результат). Математики утверждают, что для сокращения сложения применяется умножение, то есть 3+3+3+3+3+3=3*6=18. Если рассчитать оба выражения, то они будут равными между собой.
Деление — арифметическая операция, используемая для поиска сомножителей искомого числа. Она состоит из следующих обязательных компонентов: делимого, делителя и частного. Первый элемент — составное значение, второй — один из множителей первого, а частное — результат операции деления.
Сложение — простейшая арифметическая операция, составление которой осуществляется минимум из трех элементов и позволяющая увеличивать искомую величину на определенное значение. Компоненты имеют следующие названия: два слагаемых и результат, который называется суммой.
Вычитание — операция, необходимая для уменьшения искомого числа на заданную величину. Она состоит из трех компонентов: уменьшаемого, вычитаемого и разности. Первое — числовое значение, от которого отнимается вычитаемое.
Однако у каждой операции есть определенный приоритет.
Приоритет операций
При вычислении математических выражений существует определенный приоритет арифметических операций. Сначала выполняются умножение и деление. Они обладают максимальной величиной приоритета. Иногда для оптимизации вычислений можно выполнять действие над числами или переменными в любой последовательности, то есть пример «2*26/13» можно решить двумя способами:
В первом случае операция займет больше ресурсов: сначала требуется 2 умножить на 26, высчитать результат, а затем его поделить на 13. Это не слишком удобно. Однако для оптимизации вычислений рекомендуется применять второй способ, поскольку особого труда не составляет 26 разделить на 13, а затем результат перемножить с двойкой.
Сложение и вычитание имеют также одинаковый уровень приоритета. Можно сначала для удобства выполнить сложение, а затем вычитание или наоборот. Специалисты рекомендуют руководствоваться важным принципом: вычисления должны быть максимально упрощены. Чтобы задать приоритет какому-либо математическому действию, необходимо взять часть выражения в скобки (сгруппировать). В результате этого первой будет выполняться операция, находящаяся в скобках.
Для примера нужно найти значение выражения: 2*2−2 (3−2)*7/14−25/5. Решать его правильно по такой методике с учетом приоритета:
Если не учитывать приоритет выполнения операций, то найти значение числового выражения можно по такой схеме:
Если сравнить два результата, то они не совпадают. На основании этого можно сделать вывод, что приоритет имеет значение при выполнении вычислений и нарушать его нельзя, поскольку исчезнет логика выражения. Однако не только скобки позволяют установить очередность операций. Существуют некоторые исключения.
Частные случаи или исключения
В алгебре, как и во всех дисциплинах с физико-математическим уклоном, учитывается скорость вычислений. Это существенно влияет на время выполнения какого-либо задания. В некоторых случаях выражение можно упростить, используя формулы сокращенного умножения и выполняя математические преобразования с элементами тождества. Для этих целей рекомендуется пользоваться соответствующими правилами:
Следует отметить, что в первом случае обязательно требуется проверить равенство знаменателя нулевому значению. Для этого следует указать величину переменной, которая не должна превращать знаменатель в 0.
Методика вычисления
Математики разработали специальную методику нахождения значения выражения. Она сводится к разбиению числового выражения на части. Этот подход впервые использовал Пифагор. Суть его состоит в следующем:
Для демонстрации алгоритма необходимо решить пример: 9*7−21 (74/(43+31))/7−64-(27−3*9). Практическая реализация методики имеет следующий вид:
Следует отметить, что этот алгоритм позволяет реализовать принцип «дробления» задания на несколько компонентов. Разбивать тождество можно в произвольном порядке.
Таким образом, для расчета значения числового выражения нужно воспользоваться специальным алгоритмом, который позволит существенно оптимизировать вычисления.
Предыдущая
АлгебраАлгебра как наука — история появления, классификация раздела и понятия
бесплатных рабочих листов для вычисления выражений с переменными; 6-8 классы, предалгебра и алгебра 1
Вы здесь: Главная → Рабочие листы → Вычислить выражения
С помощью этого генератора рабочих листов вы можете создавать рабочие листы для печати для оценки простых выражений переменных, когда задано значение переменной (ей). Есть три уровня, первый уровень включает только одну операцию. Например, ученик может найти значение выражения 2 ( t — 5), когда t имеет значение -6.
Эти рабочие листы подходят для лучших классов 6, 7 и 8, включая курсы предварительной алгебры и алгебры 1.
Чтобы настроить рабочие листы, вы можете контролировать количество задач, уровень сложности, диапазон используемых чисел (вы можете включать отрицательные числа и десятичные дроби), рабочую область под проблемами, границу вокруг проблем и дополнительные инструкции.
Основные инструкции к рабочим листам
Каждый рабочий лист генерируется случайным образом и поэтому уникален. Ключ ответа генерируется автоматически и помещается на вторую страницу файла.
Вы можете использовать генератор для создания рабочих листов либо в формате html, либо в формате PDF — и то, и другое легко распечатать. Рабочий лист html имеет то преимущество, что вы можете сохранить его прямо из браузера (выберите «Файл» → «Сохранить»), а затем, , отредактируйте его в Word или другом текстовом редакторе.
Вот несколько быстрых ссылок на готовые рабочие листы. Обновите страницу рабочего листа, чтобы получить еще одну такую же, пока вы не будете удовлетворены проблемами и макетом.
Рабочие листы готовые
Ключ к учебным пособиям по алгебре
Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй.Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 расширяют охват действительной системы счисления.
=> Узнать больше
Понимание алгебраических выражений Факты и рабочие листы для детей
Не готовы приобрести подписку? Щелкните, чтобы загрузить бесплатную версию образца Загрузить образец
Загрузить этот образец
Этот образец предназначен исключительно для участников KidsKonnect!
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь на эту страницу, чтобы начать загрузку!
Зарегистрируйтесь
Уже зарегистрировались? Авторизуйтесь, чтобы скачать.
В этом уроке мы попытаемся применить и расширить ваше предыдущее понимание арифметики на алгебраические выражения . Кроме того, мы будем писать и оценивать числовые выражения, включающие целые показатели степени, в то же время записывая, читая и оценивая выражения, в которых буквы обозначают числа.
См. Файл фактов ниже для получения дополнительной информации о понимании алгебраических выражений или, в качестве альтернативы, вы можете загрузить нашу 31-страничную рабочую таблицу «Понимание алгебраических выражений» для использования в классе или дома.
Основные факты и информация
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
- Напомним, числовое выражение представляет собой математическую комбинацию чисел, операций и группирующих символов. Это математическая фраза, представляющая одно значение. Эти операции включают сложение, вычитание, умножение и деление.
- Алгебраическое выражение — это выражение, включающее переменные и константы, а также алгебраические операции: сложение, вычитание, умножение и деление.Пример алгебраического выражения:
- Эти выражения представлены с использованием неизвестных переменных, констант и коэффициентов. Комбинация этих трех элементов называется терминами выражений.
- В отличие от алгебраического уравнения, алгебраическое выражение не имеет сторон или знака равенства.
ЧАСТИ АЛГЕБРАИЧЕСКОГО ВЫРАЖЕНИЯ
- Переменная
- Переменная — это буква или символ, представляющий неизвестное значение.
- Коэффициент
- Коэффициент — это число, умноженное на переменную в алгебраическом выражении.
- Термин (-а)
- Термин — это имя, данное числу, переменной или числу и переменной, объединенным путем умножения или деления.
- Константа
- Константа — это число, значение которого не может быть изменено.
- Известно, что все выражение (т. Е. 5x — 3) является биномиальным членом, поскольку в нем есть два маловероятных члена.
ВИДЫ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
- Существует три основных типа алгебраических выражений, а именно мономиальные, биномиальные и полиномиальные выражения.
- Мономиальное выражение
Алгебраическое выражение, содержащее только один член
Примеры мономиальных выражений: 8xy, 7x, 9y, 12z⁴ и т. Д. - Биномиальное выражение
Алгебраическое выражение, содержащее два маловероятных члена
Примеры биномиальных выражений являются: 8xy + 7x, 9y + 12z⁴ и т. д. - Полиномиальное выражение
Алгебраическое выражение с более чем одним членом с неотрицательными целыми показателями переменной
Примеры полиномиальных выражений: 8xy + 7 + 9y + 12z⁴ и т. Д.
ЗАПИСЬ ЧИСЛОВЫХ ВЫРАЖЕНИЙ
- При работе с алгебраическими выражениями из словесных утверждений вам необходимо ознакомиться с ключевыми терминами, представляющими четыре операции: сложение, вычитание, умножение, деление.
- Используйте круглые скобки () или квадратные скобки, чтобы сгруппировать вычисления, чтобы быть уверенным, что некоторые вычисления выполняются в особом порядке.
- Когда вы используете круглые скобки, вы говорите «сначала сделайте это».
- Напишите числовое выражение, используя приведенную ниже словесную фразу:
- Сумма восьми и числа, умноженного на пять
- Глядя на пример, вы должны понимать, что вам нужно получить сумму восьми и числа, а затем умножьте полученный ответ на пять.
- Это должно быть сделано в первую очередь — сумма восьми и числа
- Затем, какой бы ответ ни был, умножьте его на пять.
- Операция, которая должна быть выполнена первой, должна быть заключена в круглые скобки.
- Итак, алгебраическое выражение, которое мы можем получить:
- Напишите числовое выражение, используя приведенную ниже словесную фразу:
- Сумма восьми и произведение числа и пяти
- Сравнивая с первым примером, оба включают те же числа и те же операции. Более того, в обоих примерах используются числа восемь и пять, переменная, а также операции сложения и умножения. Но означают ли они одно и то же? №
- В примере 2 операция, которая должна быть выполнена в первую очередь, — это умножить число на пять, а затем прибавить восемь к полученному результату.
- Это нужно сделать в первую очередь — произведение числа и пяти
- Затем, каким бы ни был ответ, прибавьте к восьми
- Итак, получаем алгебраическое выражение:
- Давайте сравним две словесные фразы.
- Сумма восьми и числа, умноженного на пять.
- Сумма восьми и произведение числа и пяти.
- Мы можем сказать, что оба словесных утверждения могут иметь в точности одинаковые числа и могут включать одни и те же операции. Однако они имеют разное значение.При оценке они дадут разные ответы.
- Обратите внимание на данную фразу и сгруппируйте числа с операциями, которые необходимо выполнить в первую очередь.
ПОРЯДОК ОПЕРАЦИЙ
- В выражении с несколькими операциями используйте правила, называемые Порядком операций.
- Некоторые выражения выглядят сложно, потому что они содержат круглые и квадратные скобки. Вы можете думать о скобках как о «внешних» скобках. Сначала вы выполняете оценку в круглых скобках.
- ПОРЯДОК ДЕЙСТВИЙ
- Сначала выполните все операции, указанные в скобках.
- Все операции умножения и деления выполняются слева направо.
- Все операции сложения и вычитания выполняются слева направо.
- Помимо круглых скобок (), скобки [] и фигурные скобки {} — это другие виды символов группировки, которые используются в выражениях. Чтобы оценить выражение с разными символами группировки, сначала выполните операцию в самом внутреннем наборе символов группировки, а затем оцените выражение изнутри.
- 2 x [(9 x 4) — (17 — 6)]
- Сначала выполните операции, указанные в скобках ().Умножайте, вычитайте и переписывайте. Проделайте операции в скобках []. Вычтите и перепишите. Умножьте 2 и 25, чтобы получить 50.
- 2 x {5 + [(10 — 2) + (4 — 1)]}
- Сначала выполните операции, указанные в скобках. Вычтите, а затем перепишите. Далее проделываем операции в скобках []. Добавить и переписать. Затем выполните операции в фигурных скобках {}.
- Добавляем и перепишем. Умножьте 2 и 6, чтобы получить 32.
ОЦЕНКА АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
- Чтобы оценить алгебраическое выражение, замените переменные их значениями.Затем найдите значение числового выражения, используя порядок операций.
- a² — (b³ — 4x), если a = 7, b = 3 и x = 1
- Заменить a на 7, b на 3 и x на 1.
- Вычислить 7² и 3³, затем умножить 4 и 1
- вычтите
ОЦЕНКА ПОДОБНО УСЛОВИЯМ
- Если у вас есть 3 пакета с одинаковым количеством x книг в каждом, у вас всего 3x книги. Если есть еще 2 мешка с x книгами в каждом, теперь у вас есть 3x + 2x = 5x книг.
- Это можно сделать, поскольку количество книг в каждой сумке одинаково. Термины 3x и 2x называются подобными терминами.
- Рассмотрим другой пример. Если у Овна есть подносы, на каждом из которых по b пирожных, то у него a x b пирожных.
- Если у Джейн вдвое больше пирожных, чем у Овна, у нее 2 x ab = 2ab пирожных.
- Вместе у них получается 2ab + ab = 3ab пирожных.
- Подобные термины
- Два термина называются одинаковыми терминами, если они включают в себя одну и ту же переменную и каждая переменная имеет один и тот же индекс.
- Свойство распределения объясняет сложение и вычитание похожих терминов. Скажем, например:
- 2ab + ab = 2 x ab + 1 x ab = (2 + 1) ab = 3ab
- Термины 2a и 3b не похожи на термины, потому что переменные разные. Термины 3a и 3a² также не похожи на термины, потому что индексы разные.
- Для суммы 8x + 3y + 7x слагаемые 8x и 7x подобны слагаемым и могут складываться. Подобных членов для 3y нет, поэтому, используя свойство коммутативности для сложения, сумма составляет:
- 8x + 3y + 7x = 8x + 7x + 3y = 15x + 3y.
- Для добавления похожих терминов используется принцип произвольного сложения.
- Из-за коммутативности и ассоциативности умножения (принцип произвольного порядка умножения) порядок множителей в каждом члене не имеет значения.
- Следовательно, 5a x 3b = 15ab. Это то же самое, что и 15ba. То же самое с 12ab x 2b²a = 24a²b³ = 24b³a².
Рабочие листы по пониманию алгебраических выражений
Это фантастический комплект, который включает все, что вам нужно знать о понимании алгебраических выражений на 31 странице с углубленным изучением.Это готовых к использованию рабочих листов «Понимание алгебраических выражений», которые идеально подходят для обучения студентов пониманию арифметики и алгебраических выражений. Кроме того, мы будем писать и оценивать числовые выражения, включающие целые показатели степени, в то же время записывая, читая и оценивая выражения, в которых буквы обозначают числа.
Полный список включенных рабочих листов
- План урока
- Понимание алгебраических выражений
- Два выражения
- Поместите в банку
- Произнесите алгебраическое выражение
- Поместите в слова
- Время сопоставления
- Что такое какое?
- Что приходит первым?
- Порядок действий
- Объединение одинаковых терминов
- Проверьте себя!
Ссылка / цитирование этой страницы
Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник.
Понимание алгебраических выражений. Факты и рабочие листы: https://kidskonnect.com — KidsKonnect, 1 июля 2020 г.
Ссылка будет отображаться как «Понимание алгебраических выражений, факты и рабочие листы»: https://kidskonnect.com — KidsKonnect, 1 июля 2020 г.
Использование с любой учебной программой
Эти рабочие листы были специально разработаны для использования с любой международной учебной программой.Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы.
Частей выражения
Алгебраические выражения — это комбинации
переменные
, числа и хотя бы одну арифметическую операцию.
Например,
2
Икс
+
4
y
—
9
является алгебраическим выражением.
Срок:
Каждое выражение состоит из терминов.
Термин может быть числом со знаком, переменной или константой, умноженной на переменную или переменные.
Фактор:
То, что умножается на другое. Фактор может быть числом, переменной, термином или более длинным выражением. Например, выражение
7
Икс
(
y
+
3
)
имеет три фактора:
7
,
Икс
, а также
(
y
+
3
)
.
Коэффициент:
Числовой коэффициент выражения умножения, содержащего переменную. Рассмотрим выражение на рисунке выше,
2
Икс
+
4
y
—
9
. В первом семестре
2
Икс
, коэффициент равен
2
: во втором семестре,
4
y
, коэффициент равен
4
.
Постоянный:
Число, значение которого не может быть изменено.В выражении
2
Икс
+
4
y
—
9
, термин
9
является константой.
Как условия:
Термины, содержащие одинаковые переменные, такие как
2
м
,
6
м
или же
3
Икс
y
а также
7
Икс
y
. Если в выражении есть несколько постоянных членов, они также похожи на термины.
|
|
|
|
|
|
|
|
|
|
Пример:
Определите термины, такие как термины, коэффициенты и константы в выражении.
9
м
—
5
п
+
2
+
м
—
7
Во-первых, мы можем переписать вычитания как добавления.
9
м
—
5
п
+
2
+
м
—
7
знак равно
9
м
+
(
—
5
п
)
+
2
+
м
+
(
—
7
)
Итак
термины
находятся
9
м
,
(
—
5
п
)
,
м
,
2
, а также
(
—
7
)
.
Как условия
— это термины, содержащие одинаковые переменные.
9
м
а также
9
м
пара
как условия
. Постоянные условия
2
а также
—
7
также похожи на термины.
Коэффициенты
— числовые части термина, содержащего переменную.
Итак, вот
коэффициенты
находятся
9
,
(
—
5
)
, а также
1
. (
1
коэффициент при члене
м
.)
В
постоянный
термины — это термины без переменных, в данном случае
2
а также
—
7
.
Алгебраические выражения должны быть написаны и интерпретированы осторожно.Алгебраическое выражение
5
(
Икс
+
9
)
является
нет
эквивалентно алгебраическому выражению,
5
Икс
+
9
.
Посмотрите разницу между двумя выражениями в таблице ниже.
| Словесные фразы | Алгебраическое выражение |
| В пять раз больше числа и девяти | 5 ( Икс + 9 ) |
| Девять больше, чем в пять раз больше | 5 Икс + 9 |
При написании выражений для неизвестных величин мы часто используем стандартные формулы.Например, алгебраическое выражение «расстояние, если скорость
50
миль в час, а время
Т
часов «это
D
знак равно
50
Т
(по формуле
D
знак равно
р
Т
).
Выражение вроде
Икс
п
называется властью. Здесь
Икс
это база, а
п
— показатель степени. Показатель степени — это количество раз, когда основание используется в качестве фактора.Словосочетание для этого выражения: »
Икс
к
п
th
мощность.»
Вот несколько примеров использования экспонент.
| Словесные фразы | Алгебраическое выражение |
| Семь раз м в четвертой степени | 7 м 4 |
| Сумма Икс в квадрате и 12 времена y | Икс 2 + 12 y |
Икс раз в кубе y в шестой степени | Икс 3 ⋅ y 6 |
Написание и интерпретация числовых выражений
«В математике нам часто приходится переписывать слова и фразы, используя числа и символы.Сегодня мы попрактикуемся в написании и интерпретации математических фраз, которые чаще называются математическими выражениями ».
Представьте следующие ситуации:
- «У Лии четыре двоюродных брата. У Амелии троих двоюродных сестер в пять раз больше, чем у Лии. Сколько кузенов у Амелии?
- У Ганса шесть карандашей, у Рассела — двенадцать карандашей. Учитель купил в три раза больше карандашей, чем у Ганса и Рассела вместе взятых. Сколько карандашей купил учитель? »
Теперь помогите студентам научиться писать выражения для представления этих ситуаций.Многие студенты, вероятно, захотят найти ответы, и это нормально. Однако важно помочь им написать числовое выражение, представляющее ситуацию. Способность ученика переводить слова в математические символы и цифры очень важна при решении задач.
Спросите студентов, есть ли у них идеи, как написать выражение для числа двоюродных братьев Амелии. Если идей несколько, запишите их на доске. Работайте в классе, чтобы определить, какое из выражений правильное.Это потребует от учащихся использовать свои практические знания о порядке операций из предыдущего урока. (И 4 × 5 — 3, и 5 × 4 — 3 являются правильными выражениями.)
Спросите студентов, «Какие подсказки вы нашли в ситуации, чтобы помочь написать выражение? Какие конкретные слова были для вас подсказками? » Студенты, скорее всего, скажут «раз больше» при указанном умножении. Студенты также, вероятно, скажут «меньше» указанного вычитания.
Математические выражения похожи на фразы в классе английского языка — в них нет «знаков препинания» (напр.г., знак равенства в математике). Математические уравнения похожи на предложения в классе английского языка — они имеют «пунктуацию» (например, знак равенства в математике). Итак, 4 × 5 — это выражение, а 4 × 5 = 20 — это уравнение.
Опять же, спросите, как написать выражение для количества карандашей, купленных учителем во второй ситуации. Работайте в классе, чтобы определить, какие из выражений, придуманных учащимися, верны. (И 3 × (6 + 12), и (6 + 12) × 3 — правильные выражения.) Важно, чтобы учащиеся использовали круглые скобки в этой ситуации, чтобы указать, что сначала нужно найти сумму 6 и 12, а затем эту сумму следует умножить на 3. По этой причине понимание учащимися порядка операций очень важно для этот урок.
Спросите студентов, «Какие подсказки вы нашли в ситуации, чтобы помочь написать выражение? Какие конкретные слова были для вас подсказками? » Учащиеся, скорее всего, скажут «раз больше» при указании умножения и «вместе» при указании сложения.
Помогите студентам ознакомиться с некоторыми ключевыми терминами, прежде чем продолжить. «Есть четыре основных операции: сложение, вычитание, умножение и деление. Результат каждой операции имеет свой срок. Результатом сложения двух чисел является сумма. Результат вычитания — разница. Результатом умножения двух чисел является произведение. Результатом деления двух чисел является частное ». Напишите на доске следующую таблицу и предложите учащимся записать ее в своих математических тетрадях.Последний столбец таблицы будет заполнен после того, как студенты закончат практический рабочий лист «Написание числовых выражений».
Эксплуатация | Результат | Другие ключевые слова или фразы |
Дополнение | Сумма | |
Вычитание | Разница | |
Умножение | Товар | |
Отдел | Частное |
Теперь раздайте практический рабочий лист по написанию числовых выражений (M-5-6-3_Практический рабочий лист по написанию числовых выражений и КЛЮЧ.docx). Попросите учащихся работать в парах, чтобы написать выражения для каждой из шести ситуаций. Следите за успеваемостью учеников во время их работы.
Обеспечьте необходимое вмешательство и поддержку по мере необходимости. Изучающим английский язык и другим учащимся, испытывающим трудности с обучением грамоте, может потребоваться дополнительная поддержка для перевода между словами и символами. Сосредоточьтесь на ключевых словах и фразах, приведенных в таблице выше. Вы также можете повесить эти слова и фразы на стене в своем классе.
Попросите шесть студентов добровольно написать на доске выражения для каждой ситуации.Попросите других учеников убедиться, что у них такие же выражения. Если у них другое выражение лица, попросите их также написать это на доске. Обратите внимание, что для каждой ситуации можно написать два или три выражения (KEY также предоставляется в M-5-6-3_Writing Numerical Expressions Practice Worksheet и KEY.docx). Попросите класс использовать порядок операций, чтобы убедиться, что разные выражения, написанные учащимися для конкретной ситуации, имеют одинаковое значение.
После того, как учащиеся заполнили Рабочий лист по написанию числовых выражений, попросите их назвать любые другие «ключевые слова» или фразы для заполнения последнего столбца таблицы. «Просмотрите ситуации. Опознали ли вы какие-либо другие ключевые слова или фразы в этих ситуациях, указывающие на конкретную операцию? » Учащиеся, скорее всего, узнают некоторые слова и фразы, перечисленные ниже в третьем столбце. Если нет, предложите их и помогите им определить ситуацию из рабочего листа по написанию числовых выражений, в которой использовалось это слово или фраза.
Эксплуатация | Результат | Другие ключевые слова или фразы |
Дополнение | Сумма | Итого, всего более |
Вычитание | Разница | Менее |
Умножение | Товар | раз больше, раз больше |
Отдел | Частное | Разделено на |
Чтобы попрактиковаться в интерпретации числовых выражений, представьте Игры на сопоставление выражений 1, 2 и 3 (M-5-6-3_Игры на сопоставление выражений 1, 2 и 3.docx).
Каждой паре учеников потребуется копия каждой из трех версий игры. Важно подготовить их заранее, так как 10 карт в каждом игровом наборе необходимо вырезать перед игрой. Если возможно, скопируйте каждый игровой набор на бумагу разного цвета. Это поможет отделить разные версии игры друг от друга.
Попросите учащихся работать в парах. Раздайте игру «Соответствие выражений» 1 и представьте Игру 1 следующим образом. «Теперь мы будем использовать игру на совпадение, чтобы попрактиковаться в интерпретации числовых выражений.Игра на совпадение состоит из 10 карт. На пяти карточках есть словосочетание, а на пяти — математическая фраза или выражение. Цель состоит в том, чтобы сопоставить каждую словосочетание с соответствующим математическим выражением. Для начала положите на стол все 10 карточек с надписью. Работайте вместе, чтобы найти все подходящие наборы карточек ».
Когда все группы закончат игру на сопоставление выражений 1, спросите учащихся, какие выражения были наиболее сложными для сопоставления их фраз.Если учащиеся не считают это трудным, обязательно обсудите фразу «на четыре меньше, чем сумма 7 и 3», поскольку она часто является наиболее сложной для учащихся. Студенты часто думают, что это следует записать как 4 — (7 + 3). Напомните учащимся, что порядок задачи на вычитание важен. Например, нахождение «на четыре меньше» 20 фактически означает, что вы вычитаете 4 из 20, что записывается как 20-4.
Теперь раздайте игры на совпадение выражений 2 и 3 каждой паре учащихся. Для игры 2 вы можете предложить учащимся положить 10 карточек так, чтобы надписи не были видны.Затем студенты могут по очереди переворачивать две карточки. Если две обнаруженные карты совпадают, они сохраняют эту пару карт. Победителем считается учащийся с наибольшим количеством матчей по окончании игры. Также предоставляется третья игра на соответствие выражений. Сложность немного увеличивается от игры 2 к игре 3.
За 5–8 минут до конца урока раздайте каждому учащемуся учетную карточку. Представьте выражение 7 + 8 × 3 и попросите учащихся написать словосочетание, описывающее это выражение.Также представьте словосочетание «на 4 меньше, чем произведение 9 и 2». Попросите студентов написать математическое выражение, представляющее эту фразу.
Соберите все эти «выходные листы» до того, как ученики выйдут из класса. Просмотрите выходные листы перед следующим уроком, чтобы определить типичные ошибки, которые делают учащиеся, и конкретных учащихся, нуждающихся в дополнительной поддержке. (7 + 8 × 3 можно описать как на 7 больше, чем произведение 8 и 3. Выражение 9 × 2 — 4 или (9 × 2) — 4 может представлять «на 4 меньше, чем произведение 9 и 2» .)
Добавочный номер:
Используйте следующие стратегии и упражнения, чтобы удовлетворить потребности ваших учеников во время урока и в течение года.
Блок 2 | Математический класс миссис Арнольд
Прямая инструкция
Решите, проходите ли вы сегодня прямое обучение.
Dreambox (2 дня в неделю)
Перейдите на Clever.com и войдите в Dreambox. Вы работаете над своей целью — 5 уроков по 60 минут в неделю.
Практика
Заполните свой пакет для раздела, в котором вам сегодня нужна помощь. Вы также можете войти на MobyMax.com, чтобы пройти назначенные уроки.
Независимое исследование
Щелкните любой из ресурсов ниже, чтобы делать заметки и практиковаться.
Стандарты
EE.1 Применяйте свойства операций как стратегии для сложения, вычитания, разложения и расширения линейных выражений с рациональными коэффициентами.
- Объясните, как упростить выражения
- Упростить выражения (объединить похожие термины)
- Решение многоступенчатых уравнений
Видео:
- Понятия «Нравится» — Math is Fun
- Как комбинировать термины «Нравится»?
- Свойства операций
Коммутативная собственность
Ассоциативное свойство
Обратное свойство
Понятия «Нравится»
Распределительная собственность
Решение уравнений
Двухшаговые уравнения
Практика:
MGSE7.EE.2 Поймите, что переписывание выражения в различных формах в контексте проблемы может прояснить проблему и то, как соотносятся количества в ней.
Практика:
MGSE7EE.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в форме (целые числа, дроби и десятичные дроби), применяя свойства операций как стратегии для вычислений с числами, преобразовывая формы как уместно, и оценка разумности ответов с помощью мысленных вычислений и стратегий оценки.
- Решение многоступенчатых задач со словами
Видео:
Практика:
EE.4 Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах.
- Знайте, что означают решения уравнений и решения неравенств
- Решить неравенства
- Графические неравенства
- Перевести уравнения / выражения
- Напишите неравенство из задачи со словами
- Решите алгебраические уравнения из задачи о словах
- Решение алгебраических выражений
- Решить проблему неравенства слов
Видео:
Практика:
Игры и другие ресурсы:
Словарь y
Алгебраическое выражение — математическое выражение, состоящее из переменных, чисел и операций.Следует упростить.
Коэффициент — число, которое используется для умножения переменной.
Константа — собственный номер
Equation- математическое утверждение, в котором говорится, что две вещи равны. У него будет знак равенства. Решаемо
Term- одиночное число или переменная
Числовое выражение — представление единственного значения. Он может состоять из одного или нескольких чисел и операций.
Переменная — символ неизвестного числа
Рациональное число — число, которое можно получить путем деления двух целых чисел
Linear Equation- уравнение, которое при построении графика образует прямую линию
Распределительное свойство — свойство, указывающее, что умножение суммы на число аналогично умножению каждого слагаемого на число с последующим сложением произведений.
Коммутативное свойство — свойство , в котором указано, что вы можете изменить порядок чисел и по-прежнему получать тот же ответ при сложении или умножении
.
Ассоциативное свойство — свойство , которое указывает, что группировка чисел для вычисления в первую очередь приведет к одинаковым ответам, когда мы складываем или умножаем
.
Количество — указывает, сколько есть чего-то
Термины «Нравится» — Термины, переменные и показатель степени которых совпадают.
Translate — изменение написанных слов на числа и операции и наоборот
EE.1 Сложение и вычитание линейных выражений
EE.3 Двухшаговые уравнения
Выражения, эквивалентные 8-му классу
Домашний комплект для звонка в дверь
Снятие рулевого колеса Pontiac sunfire
8-й класс. 9 класс. 10-й класс . 11 класс. 12 класс. Посмотреть меньше; Предмет. … Творческое мышление и самовыражение Здоровье, благополучие и физическое развитие…
Weighmax w ct20
RS4 — 8.EE.1 — Копия студента (поиск эквивалентных числовых выражений, используя свойства целочисленных показателей) RS5 — 8.EE.2 (решение нелинейных уравнений с использованием квадратных корней и кубических корней) RS5 — 8.EE.2 — Копия для учителя (решение нелинейных уравнений с использованием квадратных корней и кубических корней)
Гессиан логарифмической вероятности
Отображение 8 лучших рабочих листов, найденных для — Эквивалентные выражения для 8-го класса с использованием экспонент. Вот некоторые из рабочих листов для этой концепции: упрощение алгебраических выражений для 9-го класса, единица обучения для 8-го уровня, pdf-формат урока для 8-го уровня, пакет алгебраических выражений, набор показателей 1, обучение математике нового поколения в штате Нью-Йорк, упрощение радикальных выражений для 9-го класса, пример работы из.
Округ Уоррен, штат Огайо, жесткость воды
Выражения и уравнения Выражения и уравнения Узнать больше 8.EE.C.8.A Помните, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно. EngageNY математика 8-й класс 8 Эврика, рабочие листы, системы счисления, выражения и уравнения, функции, геометрия, статистика и вероятность, примеры и пошаговые решения, видео, рабочие листы, игры и упражнения, которые подходят для 8-го класса Common Core Math, по оценкам , по доменам
Project 64 сохранить ярлык состояния
1 августа 2018 · Введение в стандарты уровня обучения гласит: «Несмотря на важность использования всех типов технологий, упор на навыки подготовки к алгебре требует внедрения графической технологии. .«До этого раздела В 4 классе ученики определяли, эквивалентны ли две заданные дроби, используя различные методы. 5. Сад Сэма представляет собой идеальный квадрат. Каждая сторона имеет размер 8 футов. Каков периметр его сада? 6. Лесли рисовал треугольник на доске. Каждая сторона имеет размер 30 см. Каков периметр треугольника? 7. Каков периметр шестиугольника, все стороны которого равны 4 ярду? 8. Если две стороны прямоугольного поля имеют ширину 2 км. , и два
Infoweb siemens
Ресурсы для 6-го класса!… Урок 6.04 «Вычисление алгебраических выражений» … Урок 6.07 «Эквивалентные выражения» 6.07 Справочное видео Глава 26. Алгебра 6-8 классов: упрощение и решение рациональных выражений {{cp.topicAssetIdToProgress [46772] .percentComplete}}% пройденный курс Progress Best Score
Цены на комплекты горелки для пайки
Шестой класс Задания по математике. Мы начинаем замечать, что математические навыки на уровне средней школы проявляются в этом возрасте. Эти рабочие листы разработаны и приведены в соответствие с основными стандартами обучения математике.Выпущено 3-8 контрольных вопросов по английскому языку и математике за 2019 год. … 8 класс Искусство английского языка. 9 класс по английскому языку. 10 класс по английскому языку.
Низкая громкость Bluetooth в машине
Что такое «Письмо в 8-м классе»? В 8-м классе учащиеся совершенствуют и развивают ранее полученные знания и навыки во все более сложных сочинениях. Ожидается, что ученики 8-х классов будут регулярно писать связные и целенаправленные сочинения, состоящие из нескольких абзацев, без ошибок и с разнообразной структурой предложений.Учащиеся восьмых классов могут …
Охлаждающая подставка для ноутбука с кондиционером
Наш пакет премиальных рабочих листов содержит 10 заданий, которые помогут вашим ученикам понять каждую тему, требуемую на уровне 6-го класса по математике. Просмотрите рабочие листы для 6-го класса. Рабочие листы по математике и другие ресурсы ниже перечислены по темам.
Фотографии тюрьмы округа Белл 2020
19 сентября 2016 · Эквивалентные дроби … При этом мы сможем комбинировать похожие термины для упрощения выражений.8-й класс … 8-й класс 8-й класс будет изучать … 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 … Решите пропорции, используя эквивалентные дроби. … Подставить в алгебраические выражения.
Ez дренаж в глинистой почве
B. 8 сантиметров C. 9 сантиметров D. 10 сантиметров ID: 300987 A Common 2 Что из следующего эквивалентно выражению ниже? () 34 мм22 () 85 м A. 11 мм2 54 B. 71 мм2 34 C. 11 мм2 D. 73 мм2 ID: 303389 CCF37_nutrition.eps B Общий 3 Диаграмма рассеяния ниже показывает соотношение между граммами жира и граммами белка в
Под броней рядом со мной
2 дня назад · Адвентус и Салазар объявляют о результатах бурения на месторождении Эль-Домо, отмеченном 45 баллами.00% меди в эквиваленте более 4,22 метра сорт 19,11% меди, 24,36 г / т золота, 10,93% цинка, 309,5 г / т серебра …
S10 4.3 turbo build
В математике седьмого класса упор делается на: (1) соотношения и пропорции, (2) рациональные числа и числа со знаком, (3) линейные уравнения, (4) масштабные чертежи, площадь, площадь поверхности и объем и (6) статистическое мышление. Программа Math Galaxy Seventh Grade Math охватывает все стандартные математические стандарты Common Core для седьмого класса, перечисленные ниже. Шестиклассники собрали на 150 банок больше, чем седьмые.Вместе ученики обоих классов собрали в общей сложности 530 банок. Сколько банок собрали шестиклассники? Сколько банок собрали семиклассники? Шаг 1. Подумайте о том, что вы знаете. • Вас попросят найти количество банок, собранных по каждому сорту.
Just aircraft superstol build
Released 2019 3-8 ELA and Mathematics State Test Questions. … 8 класс Искусство английского языка. 9 класс по английскому языку. 10 класс по английскому языку. Общее ядро для 8-го класса Общее ядро для математики Дополнительные уроки математики для 8-го класса Видео, примеры, решения и уроки, которые помогут учащимся 8-го класса знать и применять свойства целочисленных показателей для создания эквивалентных числовых выражений.Например, 3 2 × 3-5 = 3-3 = 1/3 3 = 1/27. Общее ядро: 8.EE.1 Предлагаемые учебные цели
Слово-шаблон листа для ответов в виде пузыря
Начните изучать 8-й класс доалгебры, блок 3: уравнения с одной переменной, неравенства и их приложения.
