Содержание
Виды углов: острый, прямой, тупой, развёрнутый, выпуклый и полный
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
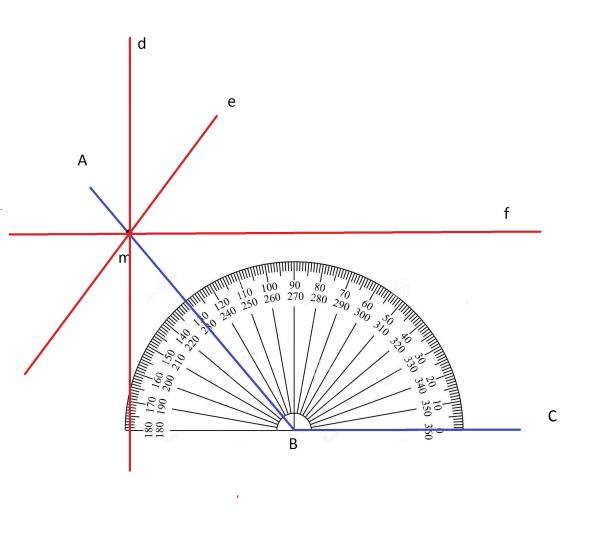
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.
Как проверить прямой угол без угольника
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные
конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или
разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или
проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах
и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна
квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5,
Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ.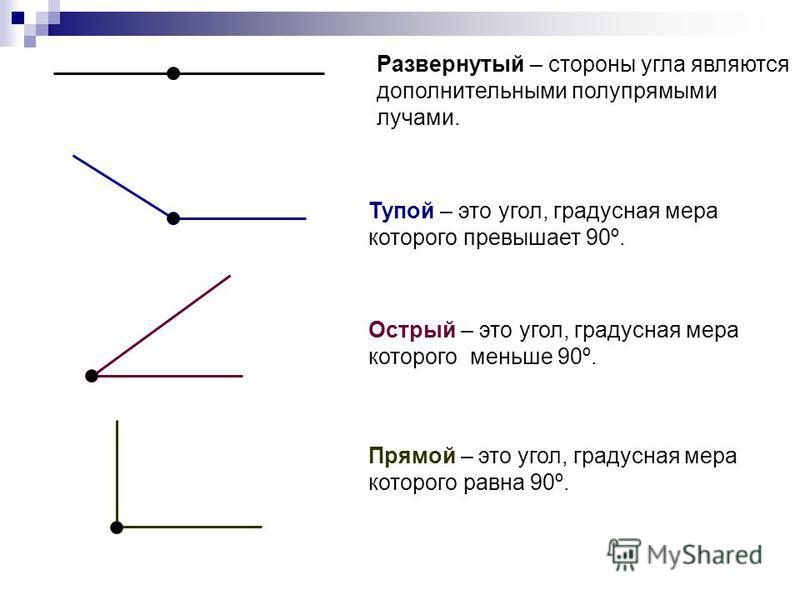 Например, мы отметили 2,5 метра (или 250
Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако
это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или
линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°.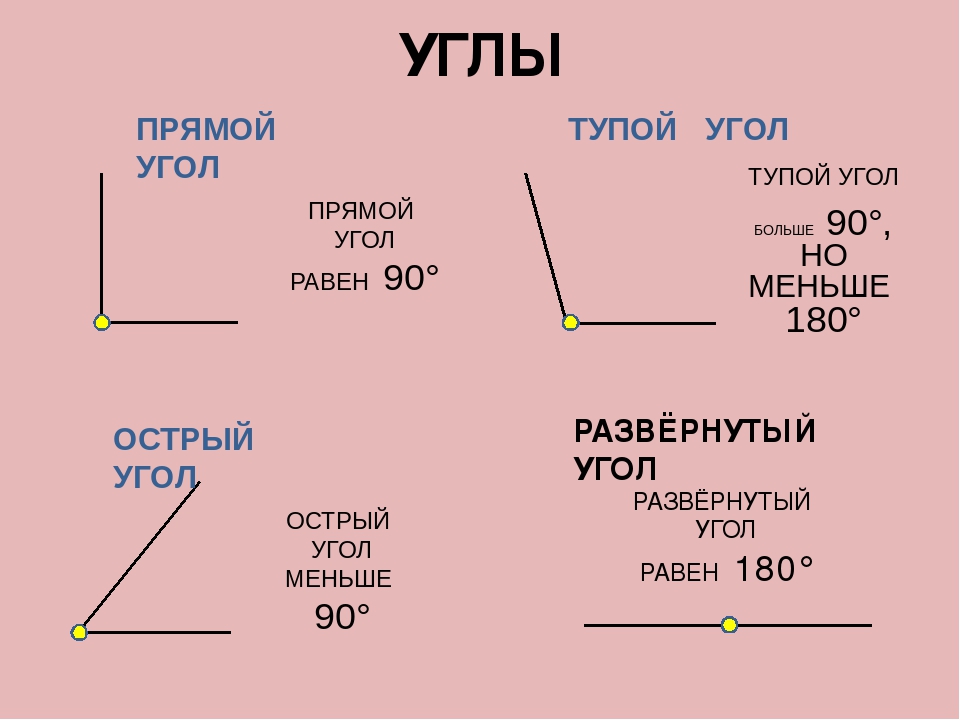 Для формирования подобных
Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет
вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.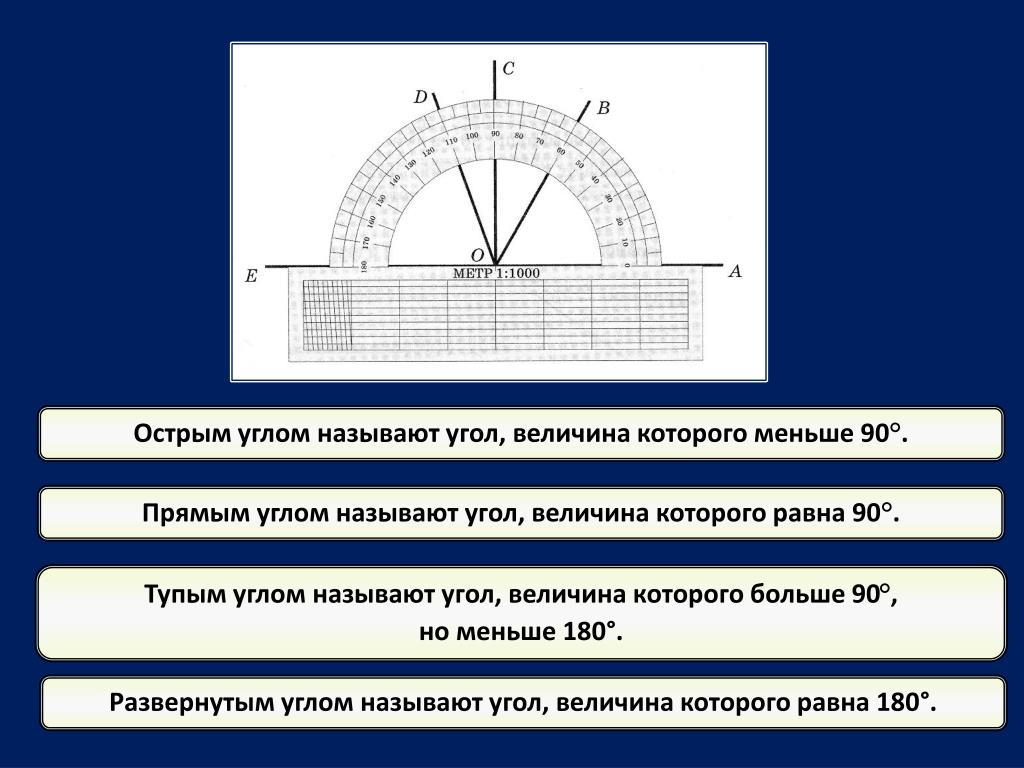
Оцените публикацию:
Оценка: 4.3 (104 голосов)
Смотрите также другие статьи
Какой угол больше 90 градусов — MOREREMONTA
Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о , иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера тупого угла всегда больше 90 о , но меньше 180 о . Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о . Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о , а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о , 90 о , 180 о , 270 о .
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о .
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о .
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о .
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о .
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов.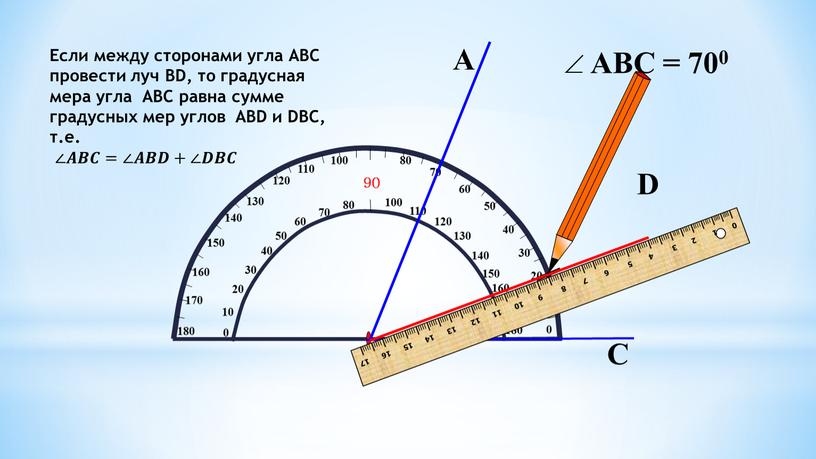 Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом.
Градус — это угол, который равен части развернутого угла,обозначается знаком
часть градуса называется минутой , обозначается знаком
часть минуты называется секундой , обозначается знаком
Пример: (двадцать градусов пятнадцать минут сорок семь секунд)
Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.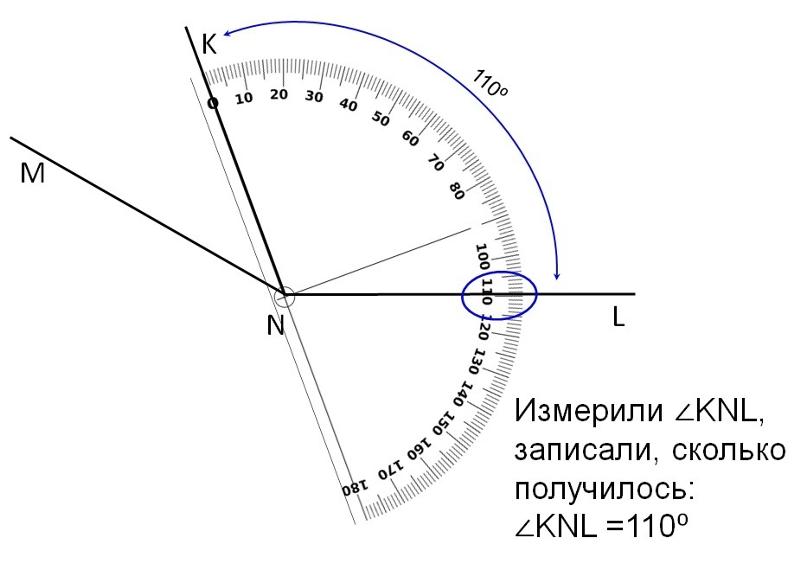
Пример:
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеетменьшую градусную меру.
- Развернутый угол равен.
- Неразвернутый угол меньше.
- Если лучделит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Основные типы углов:
- Острый угол — угол, градусная мера которого меньше 90 ° .
- Прямой угол — угол, градусная мера которого равна 90 ° .
- Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .

- Развернутый угол — угол, градусная мера которого равна 180 °.
Поделись с друзьями в социальных сетях:
Прямо́й у́гол (др.-греч. ὀρθὴ γωνία ) — угол в π / 2 <displaystyle pi /2> радиан или 90°, половина развёрнутого угла. Угол, стороны которого перпендикулярны друг другу. При пересечении перпендикулярных прямых образуются прямые углы.
Величина прямого угла в разных единицах:
- 90°
- π / 2 <displaystyle pi /2>радиан
- 100 град
- 1/4 оборота или полного угла
- 5400 угловых минут
- 324000 угловых секунд
Некоторые геометрические фигуры, у которых один или несколько углов являются прямыми, имеют собственные названия:
- Прямоугольный треугольник — треугольник, у которого один угол прямой.
- Прямоугольник — параллелограмм, у которого все углы прямые.
- Квадрат — равносторонний прямоугольник, ромб с прямыми углами.

- Прямоугольная трапеция — трапеция, хотя бы один из углов которой — прямой.
Как высчитать угол 90 градусов рулеткой
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см.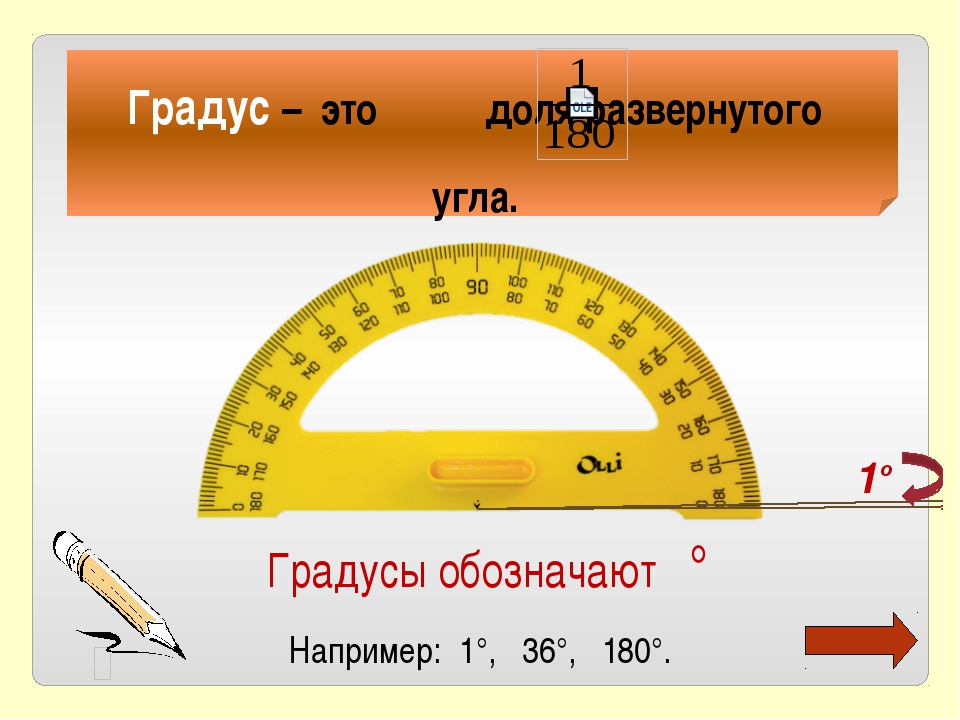 То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Теорема Пифагора
Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.
А теперь вернемся к нашим замерам и применим теорему на практике.
Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Египетский треугольник
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?
a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.
Как проверить угол с помощью египетского треугольника?
Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.
Как отмерить угол, используя рулетку
Можно самостоятельно смастерить угольник для замера углов:
- Соединяем две рейки одна перпендикулярно другой.
- Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
- Прибиваем третью рейку к одной отметке.
- Измеряем гипотенузу, прибиваем рейку ко второй метке.
- Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
- Обрезаем лишние концы.
Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.
Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.
Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.
У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.
Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.
Один и тот же размер при измерении разными рулетками может не совпадать.
Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.
Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.
Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:
- от предмета
Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.
Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.
Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.
Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.
Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.
На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.
Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.
Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.
При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.
Проделав два измерения нужно сложить результаты и получите точный размер.
На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.
Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.
В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.
Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.
Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.
Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.
А при использовании шурупа легко рисуются окружности нужного диаметра.
Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.
После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.
Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.
Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.
Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.
Писать конечно нужно карандашом, после чего все это легко стирается резинкой.
С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.
Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.
Ровно в месте перегиба и будет требуемый результат — 58см.
Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.
Вытягиваете ленту на 2м 11см и складываете ее пополам.
Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.
Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.
Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.
Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.
Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.
В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.
Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.
Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.
Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.
Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.
Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.
Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.
Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.
Угол, виды углов и их измерение
Определение. Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.
Если плоскость круга разделить на 360 равных частей радиусами, то часть круга — это угловой градус, который обозначается знаком « ° » (читается — «градус»).
Следовательно, 1° = часть круга.
Круг составит * 360 = 1° * 360 = 360°.
Угол, равный плоскости круга, составляет 360° и называется полным углом.
Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит угол в 360′: 2 = 180°.
Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом.
Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в 360° : 4 = 90°.
Угол, равный четвертой части круга, составляет 90° и называется прямым углом.
Отвлекаясь от плоскости, в которой расположен круг, изобразим углы таким образом:
Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.
Например, прямой угол (рис. 1) мы трижды развернули вокруг вершины угла, при этом на двух рисунках (рис. 2 и 4) мы передвинули вершину угла по плоскости листа.
Инструментом для измерения углов служит транспортир.
Для измерения угла следует совместить вершину угла и штрих с цифрой 0 на шкале транспортира. Одна сторона угла должна совпадать с прямой линией транспортира, на которой стоит 0, а вторая сторона угла пересекать шкалу транспортира (полуокружность с разметкой в угловых градусах).
На пересечении стороны угла и шкалы транспортира считывается градусная мера данного угла.
Мы рассмотрели полный, развернутый и прямой углы. Существует еще два типа углов: острые и тупые. Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.
Например. острые углы:
Углы, градусная мера которых больше 90°, но меньше 180°*, называются тупыми углами.
Тупые углы (штриховой линией обозначен прямой угол в составе тупого угла) приведены на рис. 5, 6,7.
Чтобы построить заданный в градусной мере угол, необходимо иметь транспортир, линейку и карандаш.
19. Какой угол называется острым, какой – прямым, а какой – тупым?
Острый
угол это угол градусная мера которого
до 90 градусов.
Прямой
угол это угол градусная мера которого
90 градусов
Тупой
угол это угол градусная мера которого
больше 90 градусов.
Острый
угол — это угол меньше 90°. Тупой угол —
это угол больше 90°, но меньше 180°. Прямой
угол — это угол = 90°.
20. Какие углы называются смежными? Чему равна их сумма?
Смежные
углы
— два угла с общей вершиной, одна из
сторон которых — общая, а оставшиеся
стороны лежат на одной прямой (не
совпадая) . Сумма смежных углов равна
180°. Или
Два
угла называются смежными,
если у них одна сторона общая, а другие
стороны являются дополнительными
лучами. сумма смежных углов равна 180°.
Каждый из этих углов дополняет другой
до развернутого угла.
21. Какие углы называются вертикальными? Каким свойством они обладают?
Вертикальные
углы —
два угла, у которых стороны одного
являются продолжениями сторон другого.
Вертикальные углы равны. (Вертикальными
называются углы,
образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).
22.
Какие прямые называются перпендикулярными?
Две
пересекающиеся прямые называются
перпендикулярными
(или взаимно перпендикулярными), если
они образуют четыре прямых угла. Или
Перпендикулярные
прямые это
прямые пересекающиеся под углом 90
градусов. Или Две прямые, образующие
при пересечении прямые углы, называют
перпендикулярными.
23.
Объясните,
какой отрезок называется перпендикуляром,
проведенным из данной точки к данной
прямой. Что такое основание перпендикуляра?
Перпендикуляром
к данной прямой
называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Этот конец
отрезка называется основанием
перпендикуляра.
Перпендикуляром
к данной прямой
называется отрезок прямой, перпендикулярной
к данной, который имеет одним из своих
концов их точку пересечения. Конец
отрезка, лежащий на данной прямой,
называется основанием перпендикуляра.
24.
Что такое теорема и доказательство
теоремы?
В
математике утверждение, справедливость
которого устанавливается путем
рассуждений, называется теоремой,
а само рассуждение – доказательством
теоремы.
Теоре́ма
— утверждение, для которого в
рассматриваемой теории существует
доказательство (иначе говоря, вывод) .
В отличие от теорем, аксиомами
называются
утверждения, которые, в рамках конкретной
теории, принимаются истинными без всяких
доказательств или обоснований.
Доказательство
—
это утверждение, объясняющее теорему.
Теорема
— такая
гипотеза, которую требуется доказать;
Гипотеза
всегда требует доказательства.
Доказательство
— доводы,
подтверждающие действенность, правильность
теоремы.
определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Определение 6
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение:
1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» .
Определение 11
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Острый, тупой, прямой и правый
Угол измеряет величину поворота
Названия углов
По мере увеличения угла название меняется:
Попробуйте сами:
В одной схемеЭта диаграмма может помочь вам запомнить: Также: Acute, Obtuse и Reflex расположены в алфавитном порядке. |
Также: буква «А» имеет острый угол.
Будьте осторожны при измерении
| Меньший угол — тупой угол , , но больший угол — угол отражения |
Поэтому при именовании углов убедитесь, что
что вы знаете , какой угол
просил !
Положительные и отрицательные углы
При измерении от линии:
- положительный угол идет против часовой стрелки (направление, противоположное движению часов)
- отрицательный угол идет по часовой стрелке
Пример: −67 °
Части угла
Угловая точка угла называется вершиной
И две прямые стороны называются руками
Угол равен повороту между каждым плечом.
Как маркировать углы
Есть два основных способа маркировать углы:
1. Назовите угол, обычно строчной буквой, например a или b , или иногда греческой буквой, например α (альфа) или θ (тета)
2. или тремя буквами на форме, которые определяют угол, при этом средняя буква указывает на то, где на самом деле угол (его вершина).
Пример угла « a » равен « BAC », а угол « θ » равен « BCD »
.
Дополнительные уголки
Два угла являются дополнительными, если в сумме
дают 90 градусов (Прямой угол).
Эти два угла (40 ° и 50 °) равны дополнительных углов , потому что в сумме они дают 90 °:
Обратите внимание, что вместе они составляют прямой угол.
Но углы не обязательно должны быть вместе.
Эти два дополняют друг друга, потому что 27 ° + 63 ° = 90 °
Играй с этим …
(Перетащите точки)
Прямоугольный треугольник
В прямоугольном треугольнике два непрямых угла дополняют друг друга, потому что в треугольнике три угла складываются в 180 °, а 90 ° уже взят из прямого угла.
| Когда два угла складываются в 90 °, мы говорим, что они «дополняют» друг друга. Дополнительный происходит от латинского completum , что означает «завершенный» … , потому что прямой угол считается полным углом. | |
| Орфография: будьте осторожны, это , а не «Дополнительный угол» (с буквой «i»)… вот такой угол вы получите бесплатно! |
Дополнительный и дополнительный
Связанная идея — Дополнительные углы — в сумме они равны 180 °
Как вспомнить, что есть что? Ну по алфавиту это:
- Дополнение к 90 °
- Дополнение к 180 °
Вы также можете подумать:
- « C » из C , дополнительный для « C orner» (Прямой угол) и
- « S » из S дополнительный для « S traight» (180 ° — прямая линия)
Или вы можете подумать:
- когда вы правы вы получите комплимент (звучит как комплимент e )
- «добавка» (например, витаминная добавка) — это что-то дополнительное, поэтому больше
типов углов — Бесплатная математическая справка
Типы углов
Вы, конечно, использовали слово «угол» в повседневной жизни, но оно также имеет важное значение в математике.Одна из тем, с которой вы захотите познакомиться, — это различные типы или классификации углов, определяемые величиной угла. Эта страница представляет собой простое и понятное руководство для начинающих по различным типам углов.
Три основных типа углов
Острый — любой угол менее 90 градусов. Эти углы кажутся «острыми», как лезвие ножа.
Пример: угол ABC составляет 40 градусов. Угол ABC острый.
Правый — любой угол, равный 90 градусам. Это как края деревянного бруска.
Пример: Угол CAT составляет 90 градусов. Угол КПП — это прямой угол.
Тупой — любой угол, который составляет более 90 градусов, но менее 180 градусов. Это «толстые» углы, очень широкие.
Пример: угол DEF составляет 125 градусов. Тогда угол DEF тупой.
Особый случай
Прямой — любой угол, равный 180 градусам.Это даже не совсем угол … это просто прямая линия!
Пример: Точки ABC лежат на линии L, образуя ПРЯМОЙ ЛИНИЙ. Тогда линия L прямая.
Взаимосвязь между несколькими углами
Вертикальные углы — Два угла, образованные пересекающимися линиями. Они не могут быть смежными, но всегда равны по размеру. Они находятся напротив друг друга в углах буквы «X», образованной линиями.
На рисунке выше углы 1 и 3 и углы 2 и 4 вертикальны, потому что они расположены напротив друг друга.Теперь углы 1 и 2 и углы 3 и 4 НЕ являются вертикальными углами.
Дополнительные уголки — Два угла, сумма которых составляет 90 градусов.
Пример: угол A = 30 градусов и угол B = 60 градусов.
Тогда угол A + угол B = 90 градусов. Можно сказать, что углы A и B дополняют друг друга.
Дополнительные углы — Два угла, сумма которых составляет 180 градусов. Дополнительные углы можно разместить так, чтобы они образовывали прямую линию.
Пример: угол A = 80 градусов и угол B = 100 градусов. Тогда угол A + угол B = 180 градусов. Можно сказать, что углы A и B дополнительные.
углов и градусов. Объяснение 1. 7. по 9. класс.
Геометрия — углы и градусы. Объяснение 1. 7. по 9. класс.
Июль 2003 г. Rasmus ehf.
Геометрия
— Углы
и степени
Урок 1.
Углы измеряются в градусах. А
круг (полный оборот) составляет 360 градусов.
Посмотрите на 1/4 круга.
Некоторые общие углы
А | |
Угол между | |
Угол, который |
Подробнее об углах, градусах
и аналогичные цифры
Половина | |
Дополнительный |
Пример:
Сколько градусов составляет угол X?
Вычислить: |
Аналогичные цифры
Фигурки
с точно такой же формой находятся аналогичные фигурки .Соответствующие углы в
одинаковые треугольники равны по размеру. Это правило относится ко всем
полигоны.
Похожие цифры | ||
Похожие цифры | ||
Похожие цифры | ||
не похоже | ||
не похоже |
Суммы углов
Попрактикуйтесь в этих методах и попробуйте Тест 1 по геометрии.Не забудьте использовать Контрольный список, чтобы отслеживать свою работу.
Что такое угол 45 градусов? — Определение, факты и пример
Угол 45 градусов
Когда два луча пересекаются в одной конечной точке, они образуют угол. Общая конечная точка называется вершиной, а лучи — плечами угла.
Угол измеряется в ° или радианах. Если два плеча угла проходят в противоположных направлениях, это прямой угол.Прямой угол составляет 180 °. Угол можно измерить с помощью транспортира, а угол измерения 90 градусов называется прямым углом. Под прямым углом две руки перпендикулярны друг другу.
Если прямой угол разделен на две равные части, каждый угол составляет 45 °.
Построение угла с помощью транспортира
Шаг 1 : Нарисуйте луч и назовите его AB.
Шаг 2 : Держите центральную точку транспортира в точке A.Поскольку угол открывается вправо, выберите 45 ° в списке, который начинается справа и перемещается против часовой стрелки. Отметьте точку C.
Шаг 3 : Соедините A и C. Здесь меры.
Углы 45 градусов в реальной жизни:
Дополнительные знания:
Построение угла с помощью циркуля
Шаг 1 : Нарисуйте отрезок прямой и серединный перпендикуляр, пересекая дуги с радиусом больше половины длины MN.Пусть серединный перпендикуляр пересекает отрезок прямой в точке О.
Шаг 2 : Нарисуйте дугу с центром в точке O и радиусом OM, разрезая серединный перпендикуляр в точке P.
Шаг 3 : Соедините M и P прямой линией. меры .
Угол измерения в градусах можно также построить, построив биссектрису прямого угла.
Интересные факты
|
Геометрия: Угол
Угол — это объединение двух лучей, имеющих общую конечную точку. Два луча представляют собой стороны угла, а общая конечная точка называется вершиной . Углы пригодятся в строительстве зданий и мостов. В телекоммуникациях для хорошего распределения сигнала важны углы.На рисунке 1 показан угол.
Запоминание терминов
| Преобразовать | — поменять. |
| степень | — угловая мера, эквивалентная 1/360 полного оборота. |
| Радиан | — угловая мера, эквивалентная 1 / полного оборота. |
| Вращение | — круговое движение объекта вокруг центра. |
| Союз | — состояние присоединения. |
Присвоение имени углу
Угол обозначается символом «\ angle».Ставится перед этикеткой уголка.
Угол может быть назван тремя разными способами:
1. Использование метки вершины — заглавной буквы.
2. Использование строчной буквы или цифры внутри угла.
3. Использование трех заглавных букв, в которых средняя буква — вершина, а две другие — метки точек двух лучей, образующих угол.
Пример 1:
4
Пояснение:
Используя вершину, угол может быть назван как `\ angle`B.
Используя число внутри угла, его также можно назвать `\ angle`1.
Используя три заглавные буквы угла, его также можно назвать `\ angle`ABC или` \ angle`CBA.
Следовательно, угол можно назвать 4 способами.
Пример 2:
`\ angle`E,` \ angle`FEG или `\ angle`GEF
Пояснение:
Rays и разделяет общую конечную точку, которая является E.E также является вершиной, поэтому угол можно назвать `\ angle`E.
Используя три заглавные буквы, в которых средняя буква — вершина, а две другие — точки двух лучей, угол также можно назвать `\ angle`FEG или` \ angle`GEF.
Пример 3:
Пояснение:
Средняя буква имени — вершина угла.Следовательно, K — вершина угла, а две другие буквы — точки двух сторон угла.
Пример 4:
3
Пояснение:
Углы:
`\ angle`MON или` \ angle`NOM
`\ angle`NOP или` \ angle`PON
`\ angle`MOP или` \ angle`POM
Измерение угла
Размер угла определяет, насколько широко открывается угол.circ` или 2`pi` радиан.
Градусы также могут быть преобразованы в радианы и наоборот. Чтобы преобразовать градусы в радианы, умножьте градус на / 180. Умножьте радиан на 180 /, чтобы преобразовать радианы в градусы.
Пример 5:
Пример 6:
Она вегетарианка
Пояснение:
Пример 7:
Угол B
Пояснение:
Преобразование радианов в градусы;
/4 * 180 / = 135
Угол B больше в градусах.
Классификация углов
Углы классифицируются в соответствии с их размерами. Они подразделяются на острые, правые, тупые, прямые и рефлекторные углы. На рисунке 2 показаны классификации углов.
Острый угол — это угол, размер которого больше 0 градусов, но меньше 90 градусов.
Прямой угол — угол, размер которого равен точно 90 градусам.
Тупой угол — это угол, размер которого больше 90 градусов, но меньше 180 градусов.
Прямой угол — это угол, размер которого составляет точно 180 градусов.
Угол отражения — это угол, размер которого больше 180 градусов, но меньше 360 градусов.
Пример 8:
Тупой угол
Пояснение:
«100 ^ circ» находится под тупым углом, так как она больше «90 ^ circ», но меньше «180 ^ circ». circ».
Преобразование градусов в радианы;
90 * / 180 = / 2
Как называется угол в 90 градусов?
Прямой угол — это особый вид угла.Все прямые углы одинаковы, независимо от длины их сторон. Их обычно можно найти вокруг дома, школы, магазина и района. После этого урока вы повсюду будете видеть прямые углы!
Перпендикулярные линии: определение и примеры
Перпендикулярные линии имеют форму буквы «Т» и обладают особыми свойствами, которых нет у неперпендикулярных линий.В этом уроке мы рассмотрим способы определить, являются ли две прямые перпендикулярными.
Урок восьмиугольника для детей: определение и факты
Вы видите восьмиугольники каждый день, но можете ли вы идентифицировать один, когда видите его? В этом уроке вы узнаете о восьмиугольниках, включая определение, особенности и некоторые интересные факты.
Что такое тупой угол? — Определение и примеры
В этом уроке вы узнаете, что такое углы, прямые и тупые углы; вы увидите несколько примеров разных тупых углов.После завершения урока проверьте свои знания с помощью краткой викторины.
Что общего у квадратов, прямоугольников и прямоугольных треугольников? Все они содержат хотя бы один прямой угол! В этом уроке мы расскажем, что такое прямой угол, и обсудим формы, которые их содержат.
Что такое Пи? — Количество и использование
Узнайте, откуда взялось число пи, как его оценивают математики, а также о том, как это число используется в мире науки и математики.В конце концов, вы можете проверить свои знания с помощью викторины.
Что такое тупой треугольник? — Определение и формула площади
В этом уроке вы узнаете, что такое тупой угол, и узнаете, как он делает тупые треугольники уникальными.Вы также откроете для себя формулу площади тупого треугольника. Затем вы можете проверить свои знания с помощью небольшой викторины.
Угол отражения: определение и примеры
Углы отражения используются реже, чем другие углы, но их легко определить в повседневной жизни.Этот урок определяет углы рефлекса, объясняет, как их измерять, и исследует взаимосвязь между рефлекторным, острым и тупым углами.
Сходства и различия четырехугольников
Посмотрите этот видеоурок, чтобы узнать, как найти сходства и различия между двумя четырехугольниками.Узнайте, на каких аспектах четырехугольников вам нужно сосредоточиться, чтобы найти сходства и различия.
Свойства прямоугольных треугольников: теоремы и доказательства
В этом уроке вы узнаете о свойствах и теоремах, связанных с прямоугольными треугольниками, которые имеют широкий спектр приложений в математике и естественных науках.В частности, мы обсудим и докажем теорему Пифагора и теорему о высоте прямоугольного треугольника. Давайте начнем.
Числовая линия — это визуальное представление всех действительных чисел. В этом уроке мы узнаем, как определять точки на числовой прямой.Мы также попрактикуемся в сложении и вычитании, позволяя числовой прямой делать всю тяжелую работу.
Углы 90, 180, 270 и 360 градусов
Углы составляют физические структуры повсюду вокруг нас, от углов улиц и дорожных знаков до зданий и кресла, на котором вы сейчас сидите.
